Non-linear finite element analysis of a Ti6Al4V/Inconel 625 joint

doi:10.3723/ut.38.013 Underwater Technology, Vol. 38, No. 1, pp. 13–16, 2021 www.sut.org

Non-linear finite element analysis of a Ti6Al4V/Inconel 625 joint obtained by explosion welding for sub-sea applications

Pasqualino Corigliano* Department of Engineering, University of Messina, Contrada di Dio - 98166, Messina, Italy

Received 13 August 2020; Accepted 11 January 2021

Abstract

Industries have shown interest in the use of dissimilar metals to make corrosion-resistant materials combined with good mechanical properties in marine environments. Explosive welding can be considered a good method for joining dissimilar materials to prevent galvanic corrosion. The aim of the present study was to simulate the non-linear behaviour of a Ti6Al4V/Inconel 625 welded joint obtained by explosion welding from the values of the tensile ultimate strength and yielding strength of the parent materials. The present study compared the stress-strain curve from tensile loading obtained by the non-linear finite element analysis with the experimental stress-strain curve of a bimetallic joint. The applied method provides useful information for the development of models and the prediction of the structural behaviour of Ti6Al4V/Inconel 625 explosive welded joints.

Keywords: explosive welded joints, non-linear finite element analysis, marine structures

1. Introduction

The task of joining different materials represents an important challenge, and in recent decades the explosion welding technique has become popular. Developments in explosive welding have been reviewed by Findik (2011), and bimetallic welded joints for marine application have been investigated by Young and Banker (2004). The predominant explosive welded joint used in the marine industry is the Al/Steel type joint for shipbuilding applications, and several experimental investigations have been reported (Corigliano et al., 2018a; 2018b; Kaya, 2018; Han et al., 2003; Li et al., 2015; Findik, 2011; McKenney and Banker, 1971; Acarer and Demir, 2008; Chao et al., 1997). In addition to the Al-steel joint, other dissimilar materials can be used in marine environments, such as stainless steel and Inconel 625 joints (Milititsky et al., 2010).

Industries have shown interest in deeper-depth drilling, creating the need for new materials that can fulfil more requirements such as protection from corrosion, reduction of self-weight and higher strength (Alemán et al., 1995). Within this context, stainless steel alloys could be replaced by titanium alloys, which have a good combination of strength, creep resistance and resistance to corrosion. Since titanium has a higher potential than most other metals commonly used in seawater piping systems, it is the other metal, and not titanium, that becomes corroded. If another metal with equal galvanic potential is used (i.e. Alloy 625) throughout the system, galvanic corrosion will not occur (Francis et al., 2020). It has been shown that Ti – Inconel (Nickel alloy 625) coupling can be used for marine applications, as they belong to the same group (Francis et al., 2020). However, if traditional welding techniques are used, these materials would be difficult to join, and corrosion would not be avoided. Explosion welding for bimetallic materials has been developed to overcome such difficulties, using material of high strength metallurgically bonded to a thin corrosionresistant clad alloy.

The aim of the present study was to simulate the non-linear behaviour of a Ti6Al4V/Inconel 625 joint produced by explosion welding starting from the values of the tensile ultimate strength and yielding strength of the parent metals, and to observe differences in experimental tests. In recent work, Topolski et al. (2016) investigated the microstructure and properties of a bimetallic Ti6Al4V/Inconel 625; this investigation served as reference for the comparison of the non-linear finite element analysis of the present study.

The present author has previously applied procedures, based on finite element analysis (FEA) and validated by means of experimental data, for the analysis of Al-Steel explosive welded joints under static and fatigue loadings (Corigliano et al., 2018a; 2018b),

and structural steel under static and fatigue loading (Corigliano et al., 2015).

2. True stress–strain curves determination from static tensile strengths

For a bimaterial specimen subjected to tension, in the elastic phase the stress (σ) will vary for each material, but the strain (ε) will remain uniform. Therefore, multiplying the strain by each Young’s modulus (E), the following is assumed:

σ ε 1 1 =E ; σ ε 2 2 =E , (1)

where subscripts 1 and 2 refer to Ti6Al4V alloy layer and Inconel 625 layer, respectively. Multiplying the stress by each area (width w and height h), the total force P is expressed as:

σ σ 1 1 2 2hw + h w= P (2)

Therefore:

Eh w+ E h w=1 1 2 2ε ε P , (3)

and the axial strain is:

ε = P wE h+ Eh1 1 2 2 ( ) , (4)

which allows the evaluation of the axial stresses as:

σ1 1 =E P 1 1 2 2wE h+ Eh ( ) (5)

σ2 2 =E P 1 1 2 2wE h+ Eh ( ) (6)

Equations 5 and 6 show that in layer two, as E2 is nearly two times as large as E1, layer 2 is subjected to a stress (σ) that is almost double that of layer 1. The non-linear FEA requires the true stress and true strain curve of the two considered materials as input.

Various methods to obtain the true strain curve have been described elsewhere that generally require multiple parameters. A method using just the values of the ultimate and yielding stresses was recently developed by Kamaya (2016). The method is based on the Ramberg-Osgood equation as follows:

E

σ ε

σ = + y y σ α       y σ σ m       (7) Assuming the plastic strain at yielding εpy = 0.002, a is calculated as:

α

Eεpy σ y (8)

The relationship between m and the ultimate and yielding stresses was found equal to:

= m l      . 393 n       u y σ σ

.0 754

(9)

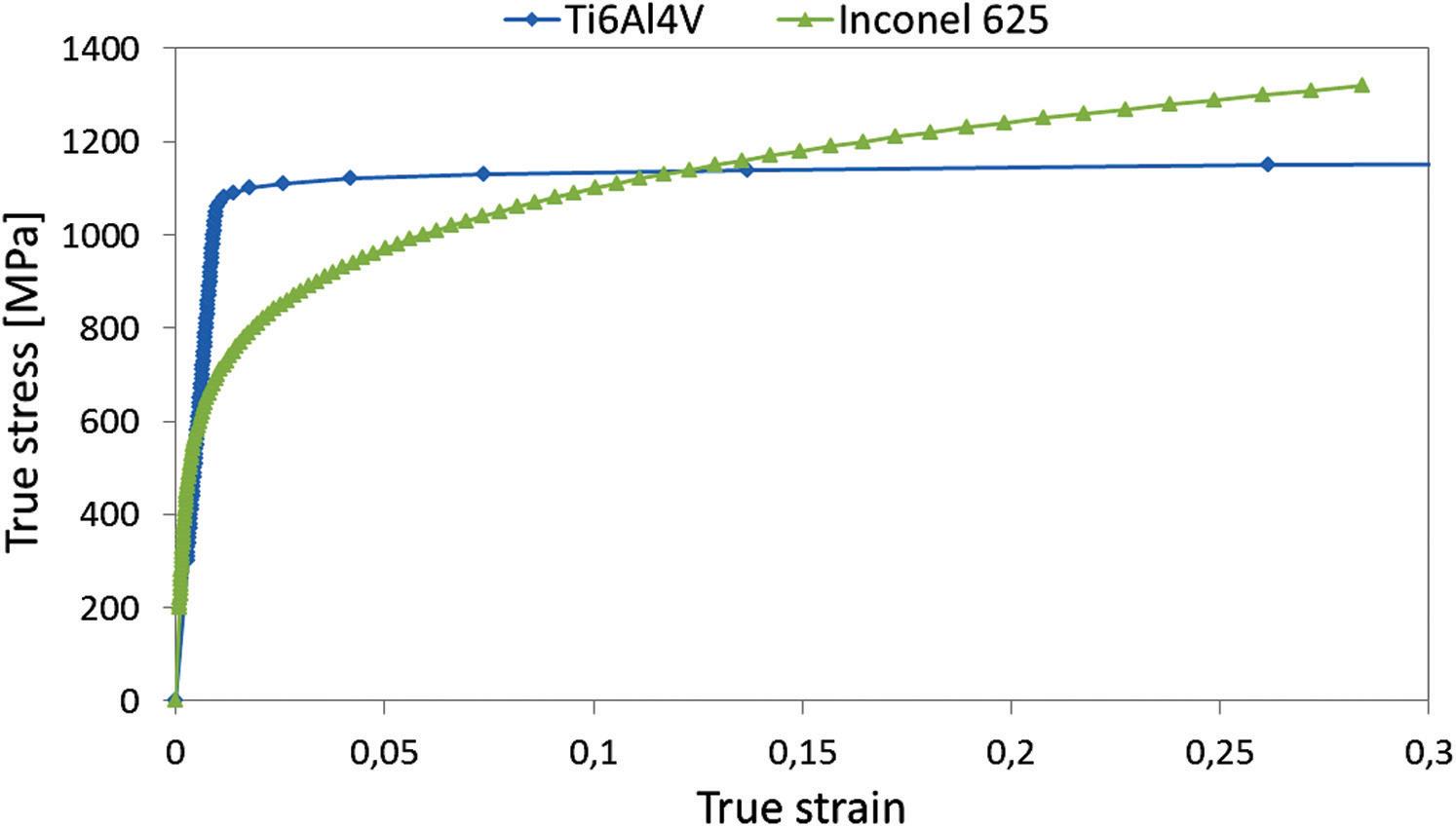
The used values of the ultimate and yielding strength were determined on the parent metals (Topolski et al., 2016); these are shown in Table 1. The obtained true stress–strain curves for the two different metals are shown in Fig 1.

Table 1: Ultimate and yielding strengths determined on the parent metals in (Topolski et al., 2016)

Ti6Al4V Inconel 625

σy [MPa] 1054 σy [MPa] 570 σu [MPa] 1079 σu [MPa] 1025

Fig 1: True stress-true strain curves of TI6Al4V and Inconel 625

3. Non-linear finite element analysis

A non-linear analysis using the Ansys software was performed with a Ti6Al4V and Inconel 625 joint. The parameters of the analysed specimen were 15 mm for the width, and 2 mm height for the Ti6Al4V layer and 3.7 mm height for the Inconel 625 layer, as shown in Fig 2. These parameters were chosen to enable a comparison with the experimental results reported in Topolski et al. (2016), in which the same type of joint obtained by explosion welding was analysed.

The used Young moduli for the FEA are equal to 200 GPa for Inconel 625 and 110 GPa for the

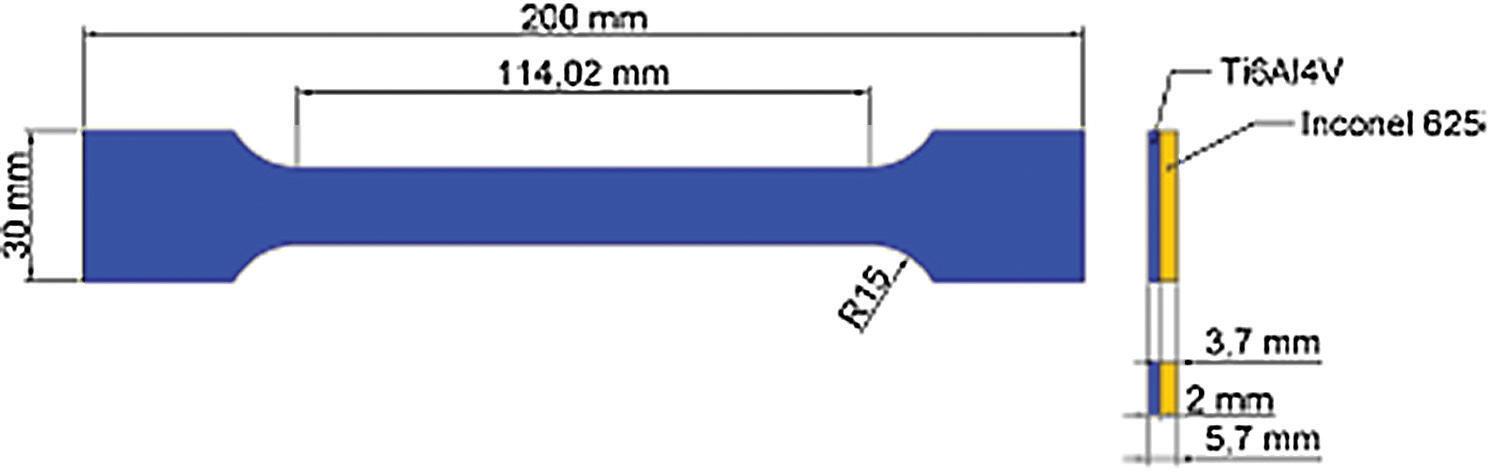
Fig 2: Specimen geometry, Ti6Al4V-Inconel 625

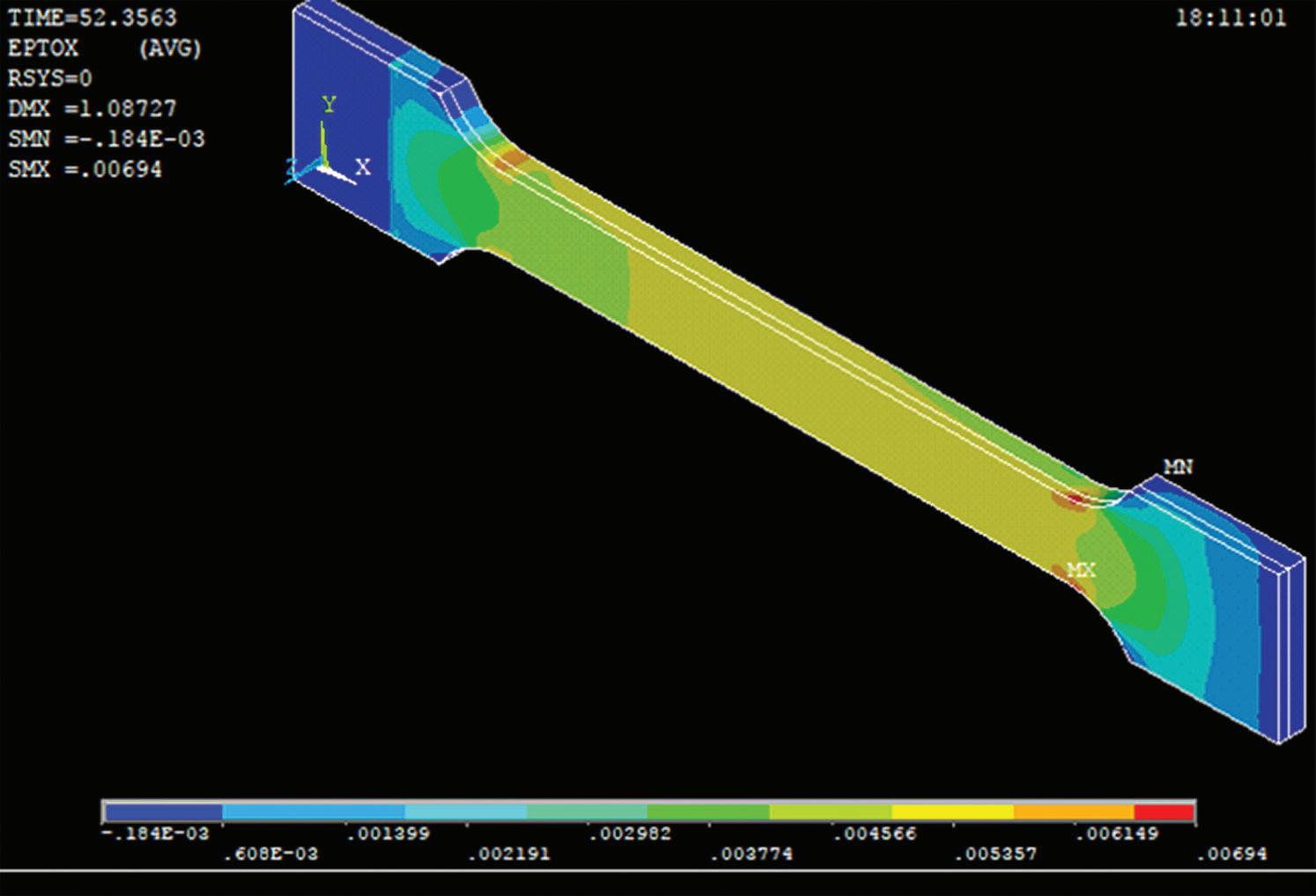
Fig 3: FE model of the bimetallic joint in Ansys Fig 4: Longitudinal strain at 550 MPa

Fig 5: Longitudinal strain at 1000 MPa

Fig 6: Results of the non-linear finite element analysis and comparison with the experimental results of Topolski et al. (2016)

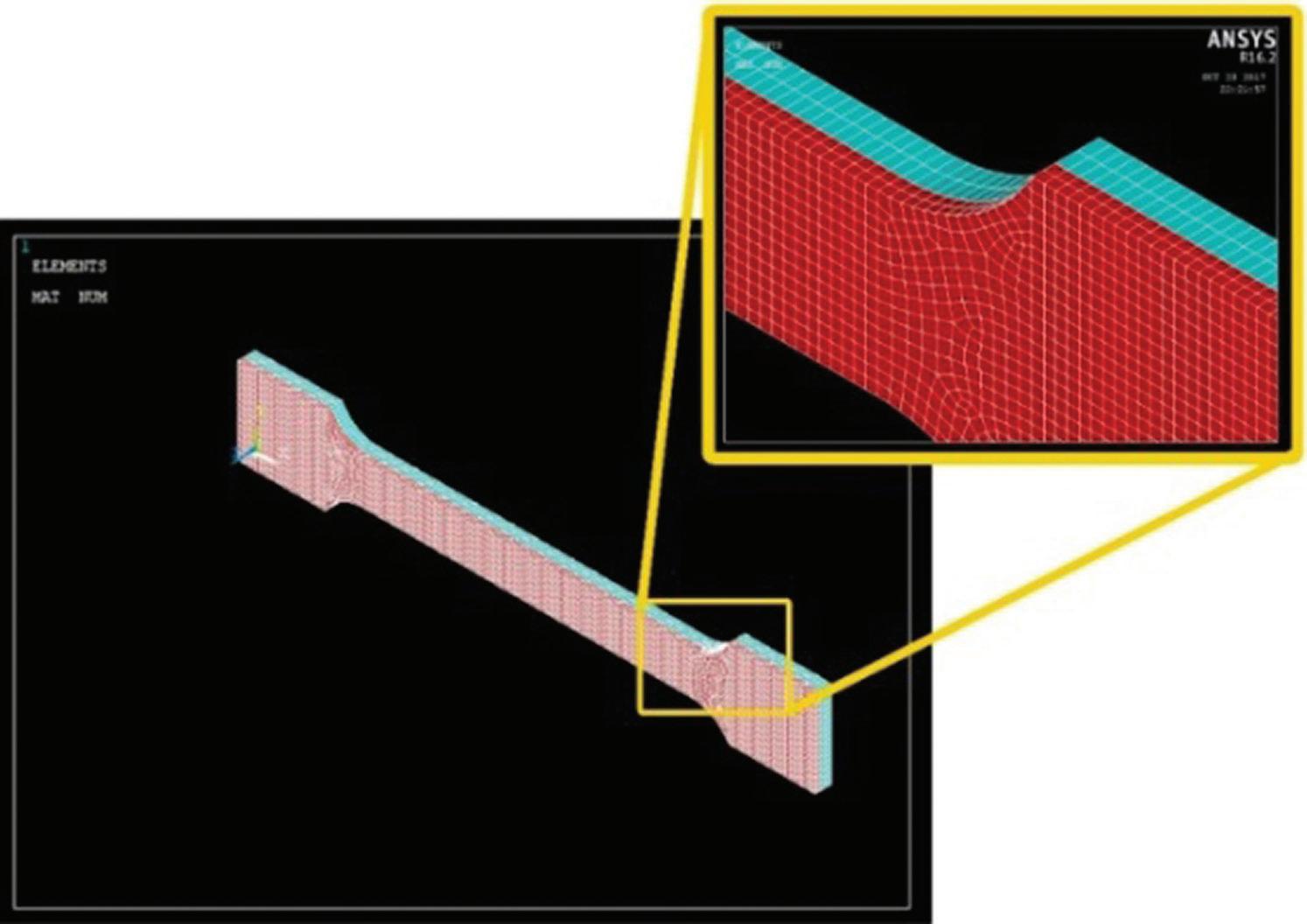
Ti6Al4V layer. The SOLID186 was chosen for the used element – this consists of 20 nodes, each with three degrees of freedom: translation along the x, y and z directions. It is able to support plasticity, hyperplasticity, creep and large deflections, as well as simulate deformations of nearly incompressible elastoplastic materials and completely incompressible hyperelastic materials.

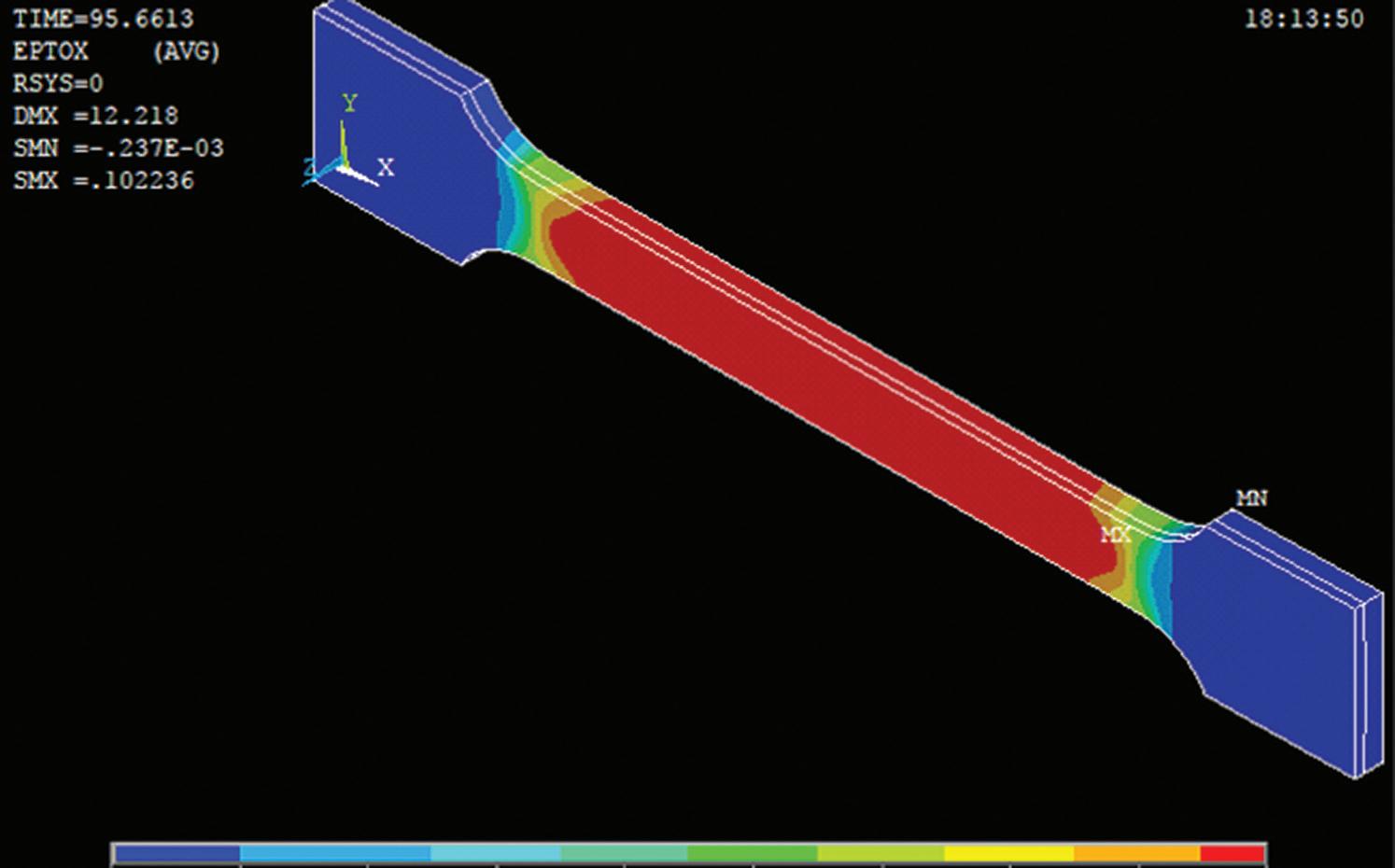
The multilinear kinematic hardening (TB, KINH) model was chosen for the procedure, and the true stress–strain curves of Fig 1 were used as input. The FE model is shown in Fig 3. The results of the longitudinal strain for two values of the applied tensile stress σ = F/A) equalled 550 MPa and 1000 MPa are reported in Figs. 4 and 5 respectively.

Fig 6 compares the engineering stress–strain curve obtained by the non-linear finite element analysis with the experimental ones: the ‘as received’ bimetal junction (without having undergone heat treatments after the explosion welding process) and the bimetal junction with heat treatment obtained in Topolski et al. (2016). Fig 6 also shows the stress–strain curves of the two ‘as received’ base materials.

The stress–strain curve obtained from the nonlinear FEA for applied stresses lower than 500 MPa is similar to the experimental curve obtained for the Inconel 625. For higher stresses there is a change in slope owing to the yielding of the Inconel 625, and the slope becomes similar to that of the Ti6Al4V alloy. As E2 is nearly two times as large as E1, layer 2 is subjected to a stress that is almost double that of layer 1. Therefore, for a nominal stress of 550 MPa, layer 1 (titanium) is subjected to a stress of 360 MPa, and layer 2 (Inconel alloy) is subjected to a stress of 653 MPa, which is higher than its yield strength.

The FEA results show differences in bimetallic ‘as received’ specimens at low stress values, and higher differences for stress values above 500 MPa. These differences may be caused by the presence of residual stresses and hardening (which cannot be considered in the FEA model), resulting from

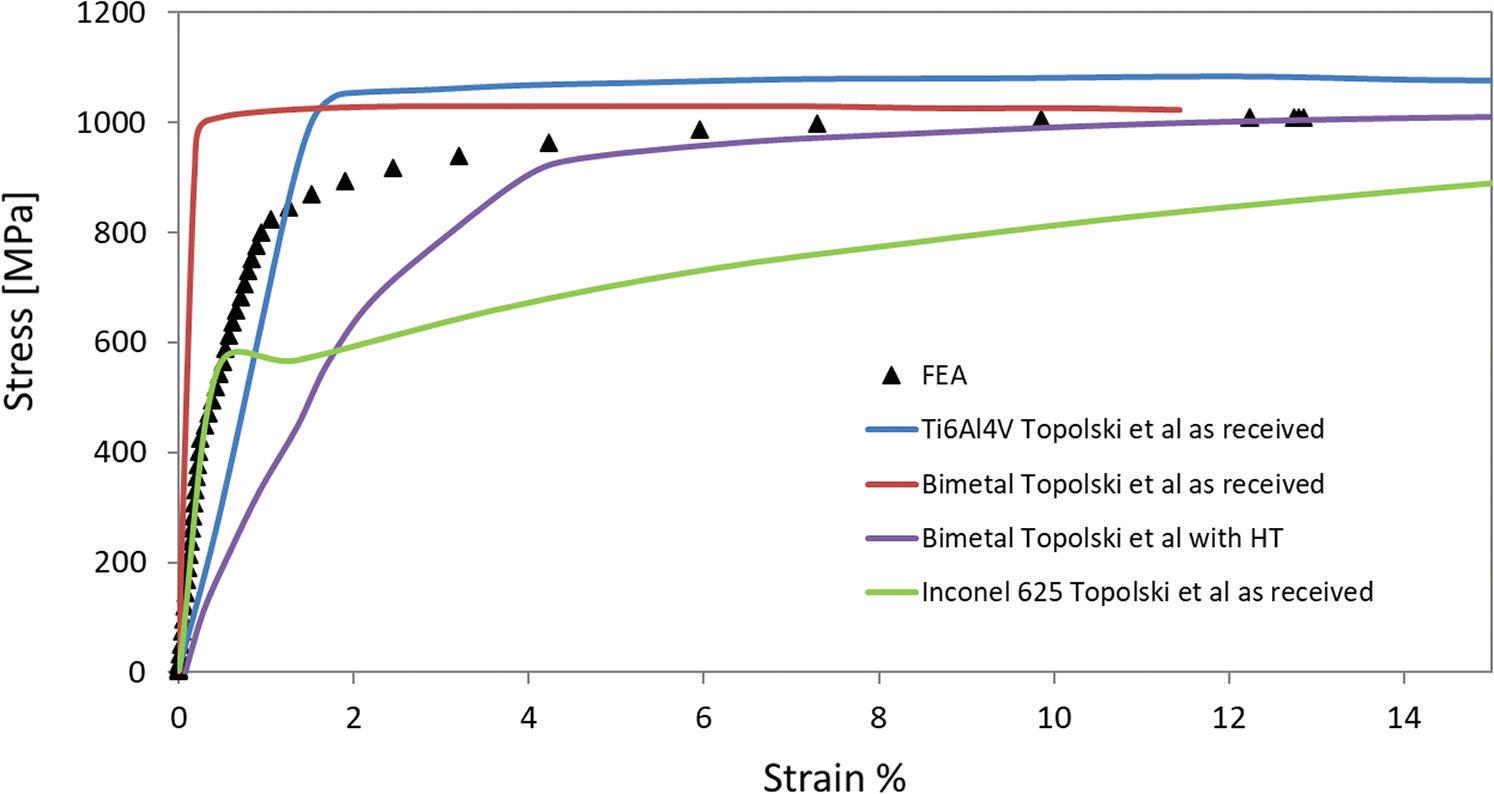
the explosion welding process, as experimentally detected by means of hardness measurements in Topolski et al. (2016). Moreover, the experimental results in Topolski et al. (2016) showed that the bimetal joint is stiffer than the Inconel 625 parent metal, revealing that the Inconel layer had hardened as a result of the explosion welding process. For very high stress values higher than 900 MPa, the curve obtained by FEA is similar to the experimental curve reported in Topolski et al. (2016).

4. Conclusion

A non-linear finite element analysis of a Ti6Al4V/ Inconel 625 explosive welded joint was performed. A method to construct the non-linear stress–strain curves of the parent metals was applied for the static ultimate tensile stress and tensile strength. The results of the finite element analysis showed that, for applied stresses lower than 500 MPa, the slope is similar to the experimental slope of the Inconel 625 alloy. For higher stresses there is a change in slope caused by the yielding of the Inconel 625, and the slope becomes similar to that of the Ti6Al4V alloy. Some differences in bimetallic ‘as received’ specimens were observed for low stress values, with higher differences for stress values above 500 MPa. These differences may be owing to the presence of residual stresses and hardening (which cannot be considered in the FEA model) resulting from the explosion welding process. For high stress values higher than 900 MPa, the curve obtained by FEA is similar to the experimental curve reported in Topolski et al. (2016). The applied method provides useful information for the development of models and the prediction of behavior of Ti6Al4V/Inconel 625 explosive welded joints.

Acknowledgement

The present study is part of the research activities of the Research Project PRIN (Announcement 2015) ‘CLEBJOINT’, project funded by the Italian Ministry of Scientific and Technological Research.

References

Acarer M and Demir B. (2008). An investigation of mechanical and metallurgical properties of explosive welded aluminium–dual phase steel. Materials Letters 62: 4158–4160. Alemán B, Gutiérrez I and Urcola JJ. (1995). Interface microstructures in the diffusion bonding of a titanium alloy Ti 6242 to an INCONEL 625. Metallurgical and Materials Transactions A 26: 437–446. Chao RM, Yang JM and Lay SR. (1997). Interfacial toughness for the shipboard aluminum/steel structural transition joint. Marine Structures 10: 353–362. Corigliano P, Crupi V, Fricke W, Friedrich N and Guglielmino E. (2015). Experimental and numerical analysis of fillet-welded joints under low-cycle fatigue loading by means of full-field techniques. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 229: 1327–1338. Corigliano P, Crupi V, Guglielmino E and Sili AM. (2018a).

Full-field analysis of AL/FE explosive welded joints for shipbuilding applications. Marine Structures 57: 207–218. Corigliano P, Crupi V and Guglielmino E. (2018b). Non linear finite element simulation of explosive welded joints of dissimilar metals for shipbuilding applications. Ocean

Engineering 160: 346–353. Findik F. (2011). Recent developments in explosive welding. Materials & Design 32: 1081–1093. Francis R, Turnbull A and Hinds G. (2020). Bimetallic corrosion (Guides for good practice in corrosion control

No. 5). National Physical Laboratory Report. Available at http://eprintspublications.npl.co.uk/id/eprint/8617, last accessed <1 February 2021>. Han JH, Ahn JP and Shin MC. (2003). Effect of interlayer thickness on shear deformation behaviour of AA5083 aluminium alloy/SS41 steel plates manufactured by explosive welding. Journal of Materials Science 38: 13–18. Kaya Y. (2018). Microstructural, mechanical and corrosion investigations of ship steel-aluminum bimetal composites produced by explosive welding. Metals 8: 544. Li X, Ma H and Shen Z. (2015). Research on explosive welding of aluminum alloy to steel with dovetail grooves.

Materials & Design 87: 815–824. McKenney CR and Banker J. (1971). Explosion-bonded metals for marine structural applications. Marine Technology Society Journal 8: 285–292. Milititsky M, Gittos MF, Smith SE and Marques V. (2010).

Assessment of dissimilar metal interfaces for sub-sea application under cathodic protection. In: Proceedings of

Materials Science & Technology 2010, 17–21 October,

Houston, USA. Topolski K, Szulc Z and Garbacz H. (2016). Microstructure and properties of the Ti6Al4V/Inconel 625 bimetal obtained by explosive joining. Journal of Materials Engineering and Performance 25: 3231–3237. Kamaya M. (2016) Ramberg–Osgood type stress–strain curve estimation using yield and ultimate strengths for failure assessments. Int. J. Press. Vessel. Pip. 137: 1–12. Young GA and Banker JG. (2004). Explosion welded, bimetallic solutions to dissimilar metal joining. In Proceedings of the Society of Naval Architects and Marine Engineers 13th Offshore Symposium, 24 February, Houston,

USA.