MATHEMATICS
MATHEMATICS
Master Mathematical Thinking
Grade 2
Acknowledgements
Academic Authors: Muskan Panjwani, Animesh Mittal, Anjana AR, Anuj Gupta, Gitanjali Lal, Simran Singh
Creative Directors: Bhavna Tripathi, Mangal Singh Rana, Satish
Book Production: Sanjay Kumar Goel, Vishesh Agarwal
Project Lead: Neena Aul
VP, Learning: Abhishek Bhatnagar
All products and brand names used in this book are trademarks, registered trademarks or trade names of their respective owners.
© Uolo EdTech Private Limited
First impression 2024
Second impression 2025
This book is sold subject to the condition that it shall not by way of trade or otherwise, be lent, resold, hired out, or otherwise circulated without the publisher’s prior written consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser and without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of both the copyright owner and the above-mentioned publisher of this book.
Book Title: Imagine Mathematics 2
ISBN: 978-81-979482-6-8
Published by Uolo EdTech Private Limited
Corporate Office Address: 85, Sector 44, Gurugram, Haryana 122003
CIN: U74999DL2017PTC322986
Illustrations and images: www.shutterstock.com, www.stock.adobe.com and www.freepik.com
All suggested use of the internet should be under adult supervision.
Preface
Mathematics is an essential tool for understanding the world around us. It is not just another subject, but an integral part of our lives. It shapes the very foundation of our understanding, personality and interaction with the world around us. Studies from across the globe have shown that proficiency in mathematics significantly influences career prospects and lifelong learning.
According to the NEP 2020, mathematics and mathematical thinking are crucial for empowering individuals in their everyday interactions and affairs. It focuses on competencies-based education, which essentially means actively and effectively applying mathematical concepts in real life. It also encourages innovative approaches for teaching maths, including regular use of puzzles, games and relatable real-world examples to make the subject engaging and enjoyable.
It is in this spirit that Uolo has introduced the Imagine Mathematics product for elementary grades (1 to 8). This product’s key objective is to eliminate the fear of mathematics by making math exciting, relatable and meaningful for children.
Imagine Mathematics positions itself on the curricular and pedagogical approach of the Gradual Release of Responsibility (GRR), which has been highly recommended by the NEP 2020, the NCF 2023 and other literature in learning educational pedagogies. Subsequent pages elaborate further on this approach and its actualisation in this book.
This book incorporates highly acclaimed, learner-friendly teaching strategies. Each chapter introduces concepts through real-life situations and storytelling, connecting to children’s experiences and transitioning smoothly from concrete to abstract. Clear explanations and simple steps are provided for problem-solving. Engaging facts, error alerts and fun activities are integrated throughout to keep learning interesting and holistic. Importantly, concepts are interconnected across topics and grades, providing a scaffolding that ensures comprehensive and meaningful learning.
This book supports learners at all levels, providing opportunities to build critical thinking skills through questions and activities aligned with Bloom’s Taxonomy. For those seeking a greater challenge, the book includes thought-provoking questions that push learners to apply, analyse and evaluate. Additionally, the problems are rooted in real-world contexts, making the learning experience both relatable and meaningful.
In addition, the book is technologically empowered and works in sync with a parallel digital world, which contains immersive gamified experiences, video solutions and practice worksheets, among other things. Interactive exercises on the digital platform make learning experiential and help in concrete visualisation of abstract mathematical concepts. We invite educators, parents and students to embrace Imagine and join us in nurturing the next generation of thinkers, innovators and problem-solvers. Embark on this exciting journey with us and let Imagine be a valuable resource in your educational adventure.
Product Package at a Glance
Welcome to our comprehensive learning package designed to enhance educational experiences through three key components: print materials, digital resources and assessment tools. Our print materials provide in-depth and accessible information in a pedagogically suitable way, our digital resources offer interactive and engaging learning experiences, while our assessment tools ensure thorough understanding and progress tracking.
Engaging Textbooks
Teacher Manuals
ASSESSMENT
Competency-based Model Assessments
Question Paper Generator
Student and Teacher Apps
Video Solutions
Interactive Tasks & Exercises
Byte Size Lesson Modules
Key NEP Recommendations
The National Education Policy (NEP) 2020, introduced by the Government of India, represents a transformative shift in the country’s education system. It aims to create a more holistic, dynamic and multidisciplinary approach to education. NEP 2020 focuses on fostering conceptual understanding, skills and values that align with the demands of the 21st century, while also preserving India’s rich cultural heritage. UOLO is fully committed to actualising the vision of NEP 2020 by meticulously adhering to its outlined recommendations.
1. Focus on conceptual understanding
2. 21st century skills, values and dispositions
3. Critical thinking and problem-solving
4. Application in real life
5. Holistic and integrated learning
6. Experiential learning
7. Enjoyable and engaging
8. Computational and mathematical thinking
9. Technology-based solutions
10. Factoids on India
Competency-based Education
NEP Pages 12, 17, and 22
Teaching and Learning Pedagogy
NEP Pages 3, 11, 12, 18, and 27
National Pride
NEP Pages 15, 16, and 43
11. Assessment of core concepts and application skills Assessments
NEP Pages 12, 18, and 22
Our Key Features: Aligning with the NEP
The GRR Approach
Pedagogical approach that empowers students to learn by the teacher progressively transitioning the responsibility to the students.
Competency-based Assessments
Test papers designed to evaluate understanding of core concepts and application of skills.
3 8 11
Contextual Learning
Introducing concepts through real-life situations and connecting them to students’ experiences.
Classroom Activity
A hands-on classroom activity to investigate and understand mathematical concepts in an engaging and concrete way.
Recall and Revisit
Introductory page with a quick recall of concepts done in previous grades.
Translating Words into Action!
Critical Thinking Questions
Intellectually stimulating questions designed to enhance problem-solving and analytical-thinking skills, promote deeper understanding and foster independent thinking.
Real-Life Math Problems
Scenario-based questions designed to help in applying theoretical knowledge to real-world scenarios, reasoning skills and improves reading comprehension & analytical abilities.
Common Misconceptions
Concise snippets of information designed to caution against potential errors and misconceptions
Think, Analyse and Answer
A quick, mathematical-thinking question
Fun Facts
Facts related to the concepts, or bite-sized information about the contribution of Indian scholars to mathematics
Gradual Release of Responsibility
The Gradual Release of Responsibility (GRR) is a highly effective pedagogical approach that empowers students to learn progressively by transitioning the responsibility from the teacher to the students. This method involves comprehensive scaffolding—including modelling, guided practice, and ultimately fostering independent application of concepts.
GRR, endorsed and promoted by both the NEP 2020 and NCF, plays a pivotal role in equipping teachers to facilitate age-appropriate learning outcomes and enabling learners to thrive.
The GRR methodology forms the foundation of the Imagine Mathematics product. Within each chapter, every unit follows a consistent framework:
1. I Do (entirely teacher-led)
2. We Do (guided practice for learners supported by the teacher)
3. You Do (independent practice for learners)
GRR StepsUnit Component Source
Understanding Large Numbers
Dhruv was reading a newspaper. He came across news about different states in India that participated in the COVID vaccination drive and the number of vaccinations given until August 2023. Given below is the data of four states.
Real Life Connect
Theoretical Explanation
I do
Examples
Delhi Haryana Sikkim Goa 3740916145546836 1360477 2874477
All About 7-Digit and 8-Digit Numbers
While reading the news, Dhruv got confused and could not read the numbers given in the data. The numbers of vaccinations given were either 7-digit numbers or 8-digit numbers.
Did You Know?
Sikkim Goa Delhi Haryana 1360477 2874477 3740916145546836
Did You Know?
7-digit Numbers 8-digit Numbers
Place Value, Face Value and Expanded Form Reading and Writing 7-Digit and 8-Digit Numbers
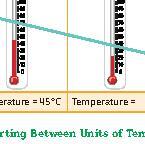
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?
Let us help Dhruv understand 7-digit and 8-digit numbers!
Normal body temperature = 37°C.
Example 8: Example 9:
Aliya’s body temperature = 37°C + 2.3°C = 39.3°C
We know that the greatest 6-digit number is 999999. Now, if we add 1 to this number, we get 1000000. 999999 + 1 = 1000000
So, Aliya’s body temperature was 39.3°C.
Example 9:
1000000 is the smallest 7-digit number and is read as “Ten Lakhs”. We saw in the news article that the number of vaccinations administered in Sikkim was 1360477. Let us try to place this 7-digit number in the place value chart.
The temperature difference is 16.3°C. Write the readings of the given thermometers.
2
GRR StepsUnit Component
Do It Yourself Challenge
Do It Yourself 14B
Source
1 Identify the shape for which the net is drawn. a b c d
2 Look at the net and identify the object it belongs to.
3 Draw the net of the given shapes.
The Kumbh Mela is a major pilgrimage where Hindu pilgrims take the holy bath in the Ganges. The number of people who visited the Kumbh Mela in 1980 were 20,356,817 and those who visited in 1989 were 29,304,871. In which year did less than 25 crore people visit to the Kumbh Mela?
a 1980 b 1989 c Both years d None of the year
4 Rishi and Megha made the net of a square-based pyramid. Who made the net correctly? Explain your answer with reasons.
a Rishi’s drawing
You do
Chapter Checkup
Challenge
Case Study
b Megha’s drawing
Guess the best units of length (m or cm) and weight (kg or g) for the given objects.
5 Draw the net of a hexagonal prism.
and Ordering Numbers
Challenge
Numbers
a The digit in the hundreds and ones place is 6.
a The digit in the hundreds and ones place is 6.
b The digit in the lakhs place is 4 less than the digit in the ones place.
6 Show using nets how a rectangular prism is different from a rectangular pyramid.
Critical Thinking
Critical Thinking
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
b The digit in the lakhs place is 4 less than the digit in the ones place.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
d The face value of the digit in the thousands place is 5.
d The face value of the digit in the thousands place is 5.
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
Case Study
Case Study
Population of Countries
Population of Countries
Cross Curricular
Cross Curricular
The population of different countries is shown using a table. Read the data carefully and answer the questions.
The population of different countries is shown using a table. Read the data carefully and answer the questions.
Country
Population
Country Population
Germany
Germany
France
France
United
Poland
Italy
83,294,633
83,294,633
64,756,584
67,736,802
64,756,584 United
41,026,067
58,870,762
1 Which country has the least population?
1 Which country has the least population?
a Italy b Germany c Poland d United Kingdom
a Italy b Germany c Poland d United Kingdom
2 Which country has the greatest population?
2 Which country has the greatest population?
a Poland b United Kingdom c Italy d Germany
a Poland b United Kingdom c Italy d Germany
Pearson, P. D., & Gallagher, G. (1983). Contemporary Educational Psychology. Fisher, D., & Frey, N. (2021). Better learning through structured teaching: A framework for the gradual release of responsibility. Fisher, D., & Frey, N. (2014). Checking for understanding: Formative assessment techniques for your classroom.
3 Which country has approximately double the population than that of Poland?
3 Which country has approximately double the population than that of Poland?
4 Arrange the countries in ascending order as per their population.
4 Arrange the countries in ascending order as per their population.
5 If all the digits in the population of each country is rearranged to form the greatest number, then which country will have the greatest population?
5 If all the digits in the population of each country is rearranged to form the greatest number, then which country will have the greatest population?
The NEP Tags
The National Education Policy (NEP), 2020, outlines essential skills, values, dispositions and learning approaches necessary for students to thrive in the 21st century. This textbook identifies and incorporates these elements throughout its content, activities and exercises. Referred to as “NEP Tags,” they are defined as follows:
Art Integration
Bringing creativity and fun into learning by combining art with maths. Students construct and demonstrate understanding through an art form.
Collaboration
Working effectively with others. Includes clear communication, teamwork, active listening and valuing diverse approaches.
Cross Curricular
Integrating mathematical concepts with other subjects to see the real-life applications of maths.
Experiential Learning
Gaining knowledge and skills through direct, hands-on experiences rather than a traditional classroom setting.
Communication
Explaining mathematical ideas, processes and solutions to others, whether through verbal explanations, written work or visual representations.
Value Development
Promoting ethics, and human & constitutional values, like empathy, respect for others, cleanliness, courtesy, democratic spirit, spirit of service, respect for public property, responsibility and equality.
Creativity
Using imagination and original thinking to solve problems and explore mathematical concepts in innovative ways. Also includes finding unique solutions, and designing original problem-solving strategies.
Education Standards as per the NCF 2023
The National Curriculum Framework for School Education (NCF), released in 2023, is based on the vision of the National Education Policy (NEP), 2020, and enables its implementation. The NCF provides guidelines for designing school syllabi and textbooks in India. It aims to improve the quality of education by making it more relevant, engaging, inclusive and learner-centric. To achieve this, the NCF has articulated precise Learning Standards through well-defined Curricular Goals and Competencies. These statements serve to harmonise the syllabus, content, pedagogical practices and assessment culture, ensuring a cohesive and comprehensive educational experience.
Curricular Goals: Statements that give direction to curriculum development and implementation in order to achieve the Curricular Aims. They are also specific to a School Stage (e.g., the Foundational Stage) and a Curricular Area (e.g., Mathematics).
Competencies: Learning achievements that are observable and can be assessed systematically. These Competencies are derived from the Curricular Goals and are expected to be attained by the end of a Stage.
Curricular Goals
CG-8
Develops mathematical understanding and abilities to recognize the world through quantities, shapes, and measures
Competencies
C-8.1 Sorts objects into groups and sub-groups based on more than one property
C-8.2 Identifies and extends simple patterns in their surroundings, shapes, and numbers
C-8.3 Counts up to 99 both forwards and backwards, and in groups of 10s and 20s
C-8.4 Arranges numbers up to 99 in ascending and descending order
C-8.5 Recognises and uses numerals to represent quantities up to 99 with the understanding of decimal place value system
C-8.6 Performs addition and subtraction of 2-digit numbers fluently, using flexible strategies of composition and decomposition of both numerical and word problems
C-8.7 Recognises multiplication as repeated addition and division as equal sharing
C-8.8 Recognises, makes, and classifies basic geometric shapes and their observable properties, and understands and explains the relative relation of objects in space
C-8.9 Selects appropriate tools and units to performs simple measurements of length, weight and volume of objects in their immediate environment
C-8.10 Performs simple measurements of time in minutes, hours, day, weeks, and months
C-8.11 Performs simple transactions using money up to INR 100
C-8.12 Develops adequate and appropriate vocabulary for comprehending and expressing concepts and procedures related to quantities, shapes, space, and measurements
C-8.13 Formulates and solves simple mathematical problems related to quantities, shapes, space, and measurements
The above is an abridged version of the curricular goals and competencies relatioship in Maths for the Foundational Stage (NCF 2023, pages 340–341). The next section shows the coverage of all these competencies across the chapters.
Curricular Goals
CG-8
Develops mathematical understanding and abilities to recognize the world through quantities, shapes, and measures
Mapping with NCF 2023
Competencies
C-8.1 Sorts objects into groups and sub-groups based on more than one property
C-8.2 Identifies and extends simple patterns in their surroundings, shapes, and numbers
C-8.3 Counts up to 99 both forwards and backwards, and in groups of 10s and 20s
C-8.4 Arranges numbers up to 99 in ascending and descending order
C-8.5 Recognises and uses numerals to represent quantities up to 99 with the understanding of decimal place value system
C-8.6 Performs addition and subtraction of 2-digit numbers fluently, using flexible strategies of composition and decomposition of both numerical and word problems
C-8.7 Recognises multiplication as repeated addition and division as equal sharing
C-8.8 Recognises, makes, and classifies basic geometric shapes and their observable properties, and understands and explains the relative relation of objects in space
C-8.9 Selects appropriate tools and units to performs simple measurements of length, weight and volume of objects in their immediate environment
C-8.10 Performs simple measurements of time in minutes, hours, day, weeks, and months
C-8.11 Performs simple transactions using money up to INR 100
C-8.12 Develops adequate and appropriate vocabulary for comprehending and expressing concepts and procedures related to quantities, shapes, space, and measurements
C-8.13 Formulates and solves simple mathematical problems related to quantities, shapes, space, and measurements
Ch 1Ch 2
1
Numbers up to 8 Digits
Let’s Recall
Numbers are used everywhere in our daily lives. These numbers are formed using the digits 0 to 9 and are written using commas after every period, starting from the one’s period.
Chapter at a Glance: Walkthrough of Key Elements
For example, let us say the pin code of your area is 201301. This is a 6-digit number. It can be written using commas by representing it in a place value chart.
1
Numbers up to 8 Digits
NumberLakhs Thousands Ones Lakhs (L)Ten Thousand (TTh)Thousands (Th)Hundreds (H)Tens (T)Ones (O) 2,01,3012 0 1
Each of these digits has a place value and a face value. Let us write the face value, place value, expanded form and number name for 201301. periods place
Let’s Recall
Numbers are used everywhere in our daily lives. These numbers are formed using the digits 0 to 9 and are written using commas after every period, starting from the one’s period.
Let’s Recall: Introductory page with a quick recall of concepts learnt in the previous grade
For example, let us say the pin code of your area is 201301. This is a 6-digit number. It can be written using commas by representing it in a place value chart.
Expanded form: 2,00,000 + 1000 + 300 + 1
NumberLakhs Thousands Ones Lakhs (L)Ten Thousand (TTh)Thousands (Th)Hundreds (H)Tens (T)Ones (O) 2,01,3012 0 1 301
Dhruv was reading a newspaper. He came across news about different states in participated in the COVID vaccination drive and the number of vaccinations given August 2023. Given below is the data of four states.
Each of these digits has a place value and a face value. Let us write the face value, place value, expanded form and number name for 201301.
Number name: Two lakh one thousand three hundred one Letʹs Warm-up Fill in the blanks.
1 The place value of 8 in 8,60,765 is
Let’s Warm-up: Quick 4–5 questions to test the pre-knowledge
2 The number 4,36,536 can be written in words as:
3 The place value of the digit in 4,15,124 and 4,67,890 is the same. 4 8,76,504 has 6 in the place.
Expanded form: 2,00,000
Haryana Sikkim Goa
All About 7-Digit and 8-Digit Numbers
Connect: Concept introduction with a
Letʹs Warm-up Fill in the blanks.
1 The place value of 8 in 8,60,765 is 2 The number 4,36,536 can be written in words as: 3 The place value of the
Above 40
Example 9:
While reading the news, Dhruv got confused and could not read the numbers given data. The numbers of vaccinations given were either 7-digit numbers or 8-digit Sikkim Goa Delhi Haryana 1360477 2874477 3740916145546836 7-digit Numbers 8-digit Numbers
I scored out of 4.
Place Value, Face Value and Expanded Form
Reading and Writing 7-Digit and 8-Digit Numbers
Dhruv was reading a newspaper. He came across news participated in the COVID vaccination drive and the August 2023. Given below is the data of four states.
Delhi Haryana 3740916145546836
Did You Know?
Let us help Dhruv understand 7-digit and 8-digit numbers! We know that the greatest 6-digit number is 999999. Now, if we add 1 to this number, we get 1000000.
Example 8: Example 9: 37.5°C – 21.2°C = 16.3°C The temperature difference is 16.3°C. Write the readings of the given thermometers.
All About 7-Digit and 8-Digit Numbers
999999 + 1 = 1000000
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature? Normal body temperature = 37°C. Aliya’s body temperature
Examples: Solved problems showing the correct method and complete solution
While reading the news, Dhruv got confused and could data. The numbers of vaccinations given were either
1000000 is the smallest 7-digit number and is read as “Ten Lakhs”. We saw in the news article that the number of vaccinations administered in Sikkim 1360477. Let us try to place this 7-digit number in the place value chart.
Do It Together: Guided practice for learners with partially solved questions
Value, Face Value and Expanded Form Reading and Writing 7-Digit and 8-Digit Numbers
Converting Between Units of Temperature
Let us help Dhruv understand 7-digit and 8-digit numbers! We know that the greatest 6-digit number is 999999. Now, if we add 1 to this number, we get 1000000. 999999 + 1 = 1000000 1000000 is the smallest 7-digit number and is read We saw in the news article that the number of vaccinations 1360477. Let us try to place this 7-digit number in
Did You Know: Interesting facts related to the topic
Do It Yourself: Exercise at the end of each topic with practice questions
Error Alert: Caution against misconceptions
1 Identify the shape for which the net is drawn. a b c d
NEP Tags: To show alignment with NEP skills and values
2 Look at the net and identify the object it belongs to. a b c d
3 Draw the net of the given shapes.
4 Rishi and Megha made the net of a square-based pyramid. Who made the net correctly? Explain answer with reasons.
a Rishi’s drawing b Megha’s drawing
Chapter Checkup: Chapter-end practice exercises aligned to different levels of Blooms Taxonomy
5 Draw the net of a hexagonal prism.
6 Show using nets how a rectangular prism is different from a rectangular pyramid.
Picture-based Questions: Questions featuring visual stimuli to foster comprehension and interpretation
Critical Thinking
Challenge: Critical thinking questions to enhance problem-solving and analytical-thinking skills
Case Study: Scenario-based questions designed to help apply theoretical knowledge to real-world situations
Real-life Questions: Questions that help make connections with real life or other subjects
Challenge
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
a The digit in the hundreds and ones place is 6.
Thinking
b The digit in the lakhs place is 4 less than the digit in the ones place.
a The digit in the hundreds and ones place is 6.
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
d The face value of the digit in the thousands place is 5.
What is the secret code?
b The digit in the lakhs place is 4 less than the digit in the ones place.
e The digit in the tens place is the biggest 1-digit number.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
Sanya
d The face value of the digit in the thousands place is 5.
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
a The digit in the hundreds and ones place is 6.
b The digit in the lakhs place is 4 less than the digit in the ones place.
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
Case Study
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
Case Study
d The face value of the digit in the thousands place is 5.
What is the secret code?
e The digit in the tens place is the biggest 1-digit number.
Population of Countries
Population of Countries
Country Population
Cross Curricular
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice. Critical Thinking
The population of different countries is shown using a table. Read the data carefully and answer the questions.
The population of different countries is shown using a table. Read the data carefully and answer the questions.
Case Study
Population of Countries
Country Population
The population of different countries is shown using a table. Read the data carefully and answer the questions.
1 Which country has the least population? a Italy b Germany c Poland d United Kingdom
1 Which country has the least population?
2 Which country has the greatest population?
Italy b Germany c Poland d United Kingdom
a Poland b United Kingdom c Italy d Germany
2 Which country has the greatest population? a Poland b United Kingdom c Italy d Germany
3 Which country has approximately double the population than that of Poland?
4 Arrange the countries in ascending order as per their population.
1 Which country has the least population?
3 Which country has approximately double the population than that of Poland?
5 If all the digits in the population of each country is rearranged to form the greatest
Critical
Cross Curricular
1 Numbers up to 200
Let’s Recall
We know how to make a 10. 1 tens = 10 ones. Let us make a bundle of 10.
sticks or 10 ones = 1
or 1
= 10
A number that has tens and ones is a 2-digit number. For example, numbers like 32, 66 and 78 are all 2-digit numbers. Here are some more numbers:
Let’s Warm-up
Match the sticks and the bundles with the correct number they make.
Understanding Numbers up to 200
Soham’s father bought 10 boxes of sweets for a festival. There are 10 sweets in each box. He asked Soham to count all the sweets.
In the evening, some more boxes with 10 sweets in each were added. Soham could easily count up to 100. This was more than 100!
Introducing 3-digit Numbers
Let us help Soham count numbers greater than 100.
Think and Tell
There are 20 boxes with 10 sweets in each. How many tens and hundreds does it have?
Building Numbers
The table shows numbers 101 to 200.
We can also write numbers by counting forward and backwards.
Counting Forward: 113, 114, 115, 116, 117
Counting Backwards: 140, 139, 138, 137, 136
Let us build some of these numbers with place value blocks.
Remember!
2-digit numbers end with 99. 3-digit numbers start from 100.
Place Value and Expanded Form
Let us learn to read the place value of the digits in a 3-digit number.
Error Alert!
123 =
1 is at the Hundreds place. The place value of 1 is 100.
Proper way of writing number names:
167: one six seven
167: one hundred sixty-seven
3 is at the Ones place. The place value of 3 is 3. 2 is at the Tens place. The place value of 2 is 20.
123 = 1 hundreds + 2 tens + 3 ones = 100 + 20 + 3.
This is known as the expanded form of the number.
Example 1: Write the place value of the digits in 154. Also, write its expanded form.
Expanded form of 154 = 100 + 50 + 4.
Write the place value of the digits in 196. Also, write its expanded form.
Expanded form of 196 = + 90 + .
Do It Yourself 1A
1 Fill in the missing numbers.
a 111, 112, , ,
b 155, , , 158,
c 189, , 191, ,
2 Look at the blocks. Write the numbers shown by the blocks.
a b c
3 Write the numbers for the number names and represent the numbers using blocks.
a one hundred forty-three b one hundred sixty-one c one hundred eleven
4 Write down the place value of the red digits in the numbers.
a 132 b 114 c 123 d 156 e 155 f 198
5 The expanded form of the numbers are given. Write the numbers.
a 100 + 30 + 8 b 100 + 00 + 4 c 100 + 90 + 2
6 There are 206 bones in the human body. Write the number as a number name.
Challenge
1 How many more tens and ones should we add to 132 to get 152? Draw tens and ones to show.
Use for 1 tens, and for 1 ones.
Comparing and Ordering Numbers
Let us compare 80 and 100 to find which is greater. 3-digit numbers are always more than 2-digit numbers. So, 100 is greater than 80: 100 > 80. We can also say that 80 is less than 100: 80 < 100.
Remember!
We use the signs '<' and '>' to show less than and more than. The alligator always opens its mouth towards the greater number.
Greater than or more than Less than or smaller than
Let us compare more numbers. Which number is greater—183 or 187?
1. Compare the hundreds. Both numbers have 1 hundreds each. Since the hundreds are the same, compare the tens.
2. Compare the tens.
Both numbers have 8 tens each.
Since the tens are the same, compare the ones.
3. Compare the ones. In 183, there are 3 ones. In 187, there are 7 ones.
So, 187 is more than or greater than 183. We can write this as 187 > 183.
Number Window
Look at the number chart. Let us place a number window on the number 155.
1 step left or backwards from 155 is 154.
1 row up from 155 is 145.
Increasing and Decreasing Order
1 step right or forward from 155 is 156.
1 row down from 155 is 165.
In increasing order, we write the numbers starting with the smaller number. In decreasing order, we write the numbers starting with the greater number.
Example 2: Look at the window placed on 178. Write the correct numbers.
Number that is 1 less than 178: 177
Number that is 1 more than 178: 179
Number that is 10 less than 178: 168
Number that is 10 more than 178: 188
Write these numbers in increasing and decreasing order—123, 143, 111, 132, 109.
Do It Yourself 1B
Circle the box with the greater number.
2 Which number is greater? Which one is smaller? Are they equal? Use <, > or = signs to show.
3 Which number comes before the given number?
a 123 b 134 c 199
4 Which number comes after the given number?
a 112 b 100 c 179
5 Arrange these numbers in increasing and decreasing order.
a 123, 114, 109, 154, 134 b 112, 110, 119, 117, 118
c 73, 100, 99, 101, 111 d 100, 187, 119, 111, 99
6 The tiger is the national animal of India. In India, the Nagarhole tiger reserve has 141 tigers, Corbett tiger reserve has 160 tigers, Bandipur tiger reserve has 150 and Dudhwa tiger reserve has 135 tigers. Arrange the tiger reserves in ascending order on the basis of the number of tigers.
Challenge Critical Thinking
1 I am 1 more than the number which is 10 less than 95. What number am I?
More Types of Numbers
Four friends are participating in a sack race. Tina is watching them. She is confused. Who is winning this race?
Ordinal Numbers
Let’s help Tina. We need to mark the position of each friend in the race. first (1st) second (2nd) third (3rd) fourth (4th)
The numbers first, second, third and fourth tell us the position of each friend. These numbers are known as ordinal numbers.
The ordinal numbers up to 10
Example 3: Three students are in a lunch line. Circle the first and the third student.
Read the letters. Answer the questions.
Did You Know?
The numbers used for counting—1, 2, 3, and so on are called cardinal numbers.
a The grapes are in the position.
b The is in the 5th position.
c The apple is in the position.
d The sunflower is in the position.
Read the text. Colour the boxes accordingly. The first box is coloured red.
a Colour the 2nd and the 4th box red.
b Colour the 3rd and the 10th box yellow.
c Colour the 6th and the 8th box green.
d Colour the 7th and the 9th box pink.
1 Meena is standing 5th in a line. Soham is the last person in the line. Tina is standing between Meena and Soham. What is Tina’s position in the line?
Odd and Even Numbers
Today, Tina and her friends are practising for the pair race.
Everyone has a partner. They are even in number. Tina also wants to join, but she does not have a partner. She is the odd one out. Let us learn what odd and even numbers are.
Pair 1
Pair 2 6 leaves 7 leaves
Pair 2
Pair 3
Pair 1
Pair 3Not in a pair
6 is an even number. 7 is an odd number.
Example 4: There are 5 candies. Are they odd or even in number?
Think and Tell
One candy is not in a pair. 5 is an odd number. So, these candies are odd in number.
If we add two odd numbers. Do we get an odd number or an even number?
Circle the balls for each number to make a pair. If one is left, cross it ( ). Write if they are odd or even.
Circle the objects in pairs. Write if they are odd or even.
Write True or False.
a Riya has 3 mugs. She has an odd number of mugs.
b Jiya has 8 pens. She has an even number of pens.
c Mohan has 5 apples. He can form 4 pairs.
Draw circles to show an even number. Draw triangles to show an odd number.
1 Rupa has 6 mangoes.
a How many pairs can she make from them?
b How many more pairs of mangoes does she need to make 10 mangoes?
Points to Remember
• 10 tens make one hundreds or 100.
• A 3-digit number is always more than a 2-digit number.
• Ordinal numbers are used to show the positions of objects in a line.
• An even number of objects will always be in pairs.
• In an odd number of objects, one object is always left without a pair.
Math Lab
Setting: Group of 10
What to do?
What’s My Position?
Collaboration & Experiential Learning
Things Needed: Slips with the name of each player
1 In your group, pick two slips to choose the caller and the player.
2 The other students will stand in a line. The caller will stand first and say, “I am first.”
3 The caller will ask the player, “Who is second in the line?”; “Who is fourth in the line?”; “Who is sixth in the line?” and so on.
4 Each time, the player needs to touch the student in the named position and call out his/her name. The team will check and decide if the player is right.
5 If the player is right, he/she can switch positions with the student in line. And the game will continue with the next player.
Chapter Checkup
Soma, Daman, Rajiv and Suhani were planting saplings. Soma planted 159 saplings, Daman planted 148 saplings, Rajiv planted 198 saplings and Suhani planted 184 saplings. Who planted the maximum number of saplings? Do you also plant seeds?
Challenge
1 There are 1 hundreds, 7 tens and 9 ones blocks.
a What number do they make?
b If 2 tens blocks are taken away, what is the remaining number?
2 A building has five floors. Rohan lives on the 5th floor. Juhi lives on the floor above Riya. Riya lives on the 2nd floor. On which floor does Juhi live?
Real-Life Maths
Value Development
Rohan lives in the 1st (purple) house on the street. His friend Raman lives in the 5th house.
1 What is the colour of Raman’s house? a Blue b Orange c Green d Purple
2 What is the position of the yellow house? a 2nd b 4th c 5th d 7th
3 Choose the correct option. Fill in the blank.
a The 3rd house is . (blue/orange).
b The only green house is on the street. (7th/9th)
4 Write True or False.
a The orange houses are in the 3rd and 6th position on the street.
b The purple house, other than Raman’s house, is 4th on the street.
5 How will you help an elderly person find their home if they are lost?
2 A ition of 2-digit Numbers
Let’s Recall
We use numbers to tell how many things there are.
These are 4 apples.
These are 5 bananas.
Now let us put the apples and bananas together and count!
4 apples and 5 bananas together are 9 fruits! This is called addition.
4 + 5 = 9
When items are together, we use addition to find the total.
Let’s Warm-up
Match the following.
I scored out of 5.
Adding 2−digit Numbers
Seema: Hi Meena, I have 15 coloured pencils in my colour box.
Meena: I have 13 crayons in my colour box.
Seema: Let us find out how many things we have in total.
Addition without Regrouping
Let us help Meena and Seema count the things. Show the things using place value blocks. 1 tens5 ones = + 15 coloured pencils
Now, let us add 15 and 13 using the place value blocks.
15 coloured pencils with Seema 13 crayons with Meena
1 tens =1 ones =
When we add numbers, the result is always known as the sum of the numbers. Example: 12 +12 = 24 The sum of 12 and 12 is 24. Add the ones. 5 ones and 3 ones = 8 ones Add the tens. 1 tens and 1 tens = 2 tens 2 tens 8 ones = 28
Vertical Method
We can add numbers by writing them one below the other. Adding 23 and 32. Add the ones.
Example 1: Add 34 and 25.
The sum of 34 and 25 is 59.
Horizontal Method
Let us add 2 numbers by writing them side by side. Add 24 and 35.
Step 1: Add the ones. 24 + 35
Step 2: Add the tens. 24 + 35
So, 24 + 35 = 59.
Example 2: Add 42 and 32 by writing the numbers side by side.
+ 32 = 74
5 9
Mental Addition
Sometimes we need to add numbers quickly. Let us learn how to add 47 and 22 mentally. We know 22 has 2 tens and 2 ones, so we can write it as: 47 + 22 = 47 + 20 + 2 = 67 + 2 (jump by 2 tens or 20) = 69 (then add 2 ones)
Example 3: Add mentally: 53 and 34. We can write it as, 53 + 34 = 53 + 30 + 4 = 83 + 4 = 87
Add mentally: 24 and 43. 24 + 43 = ________________ =
Do It Yourself 2A Add. 34 + 42 = 7____
Remember!
When we add 0 to any number, the sum is the same as the number itself.
Example: 12 + 0 = 12.
Add mentally and circle the sums with the correct answer. a 34 + 12 = 46
34 + 21 = 55
Challenge
33 + 14 = 87
14 + 13 = 21
72 + 22 = 50
56 + 21 = 77
Arjun is trying to add 43 and 14 mentally. He does 43 + 14 = 43 + 14 + 4. Is he correct? What will be the digit in the ones place of the sum? 1
Addition with Regrouping
Seema has 15 coloured pencils.
15 coloured pencils 1 tens 5 ones = +
Her friend gave her 5 more. 5 coloured pencils
How many coloured pencils does Seema have now?
Let us add and find out.
Step 1
Draw the place value blocks.
Step 2 We first add the ones.
Here, we get 5 + 5 = 10 ones. 10 ones make 1 tens. So, we change the 10 ones to 1 tens.
Step 3
Move the 1 tens to the tens place.
Step 4 Now add the tens.
There are 0 ones. So we write 0 in the ones place. We get 2 tens and 0 ones. 2 tens = 20 The sum of 15 and 5 is 20.
So, 15 + 5 = 20.
Addition with Regrouping to 10
Let us understand how to add two 2-digit numbers by regrouping.
Adding 25 and 15
Step 1: Add the ones.
5 ones + 5 ones = 10 ones 10 ones = 1 tens + 0 ones
Step 2: Write 0 in the onesplace. Move 1 tens to the tens place.
So, the sum of 25 and 15 is 40.
Add 48 and 22.
The sum of 48 and 22 is
Step 3: Add the tens. 2 tens + 1 tens + 1 carry over tens = 4 tens. Write 4 in the tens place.
Regrouping When the Sum is More Than 10
Here, we are going to look at sums where we always get more than 10 by adding the digits in the ones place.
Let us add 15 and 26.
Step 1: Add the ones. 5 ones + 6 ones = 11 ones 10 ones = 1 tens + 1 ones
Step 2: Write 1 in the ones place. Move 1 tens to the tens place.
So, the sum of 15 and 26 is 41.
Add 16 and 26.
Step 3: Add the tens. 1 tens + 2 tens + 1 carry over tens = 4 tens. Write 4 in the tens place.
In regrouping we always shift the 10 ones from the ones place to the tens place as 1 tens.
Circle the correct answer.
Draw the tables and add the numbers by writing them one below the other.
21 + 9
59 + 19
Challenge Pot A has 13 flowers and Pot B has 17 flowers. How many tens do you need to add to get the total? 1 Critical Thinking
Adding More Than 2 Numbers
Let us now learn how to add three numbers: 8, 4 and 6.
Step 1
Write the numbers one below the other.
Step 2
Add any two numbers first.
Step 3
Then, add the third number to the sum of the first two numbers.
Let us now find the sum of 8, 4 and 6 using the number line.
1. Start from the first number, 8. Jump forward by 4, to reach 12.
So, 8 + 4 + 6 = 18.
Let us add 12, 15 and 25 using the vertical method.
2. Start from 12 and jump forward by the third number, 6. We will reach 18.
Did You Know?
Shakuntala Devi was an Indian Mathematician, and known as a human computer, because she could do long calculations quickly in her head.
Step 1
Write the numbers one below the other.
Step 2
Add the ones. Regroup if the sum is equal to or more than 10.
Step 3
Add the tens.
So, 12 + 15 + 25 = 52.
Example 4: Find the sum.
We get 12 in the ones place. 12 = 1 tens and 2 ones We write only 2 in the ones place. 1 tens is moved to the tens place.
Think and Tell
What comes in the ones place if we add 34 and 16?
Remember!
The answer can be checked by changing the order of the numbers and adding them again. 15 + 12 + 12 = 39; 12 + 12 + 15 = 39; 12 + 15 + 12 = 39 In all the cases the sum is equal to 39.
Add 2, 8 and 5 using the number line and the vertical method. Check if the answer is the same.
Add the numbers using the number line. Draw jumps to show addition.
Story Sums
We can use the CUBES method to solve story sums. In the CUBES method, we follow the 5 given steps .
C Circle the Numbers U Underline the Question B Box the Key Words
E Evaluate/Draw
Circle the numbers
S Solve and Check!
Rina and Geeta went to buy apples. Rina bought 18 apples. Geeta bought 15 apples. How many apples did they buy in total?
Box the keywords
Underline the question
Apples Rina bought = 18
Apples Geeta bought = 15
Total number of apples = 18 + 15
Rina and Geeta have 33 apples in total. Solve and check!
C: Circle the numbers.
U: Underline the question.
B: Box the key words.
E: Evaluate/draw.
S: Solve and check!
Evaluate
Rohan solved 15 sums on Monday, 23 sums on Tuesday and 17 sums on Wednesday. How many sums did he solve in total? Solve using the CUBES method, given above.
Sums solved by Rohan on Monday = 15
Sums solved by Rohan on Tuesday = Sums solved by Rohan on Wednesday = Total sums solved = Rohan solved sums in total.
Riya bought 24 candies, and her friend Aryan gave her 37 more candies. How many candies does Riya have now?
Arun makes murukkus (a deep-fried snack). He makes 42 murukkus, and his friend makes 26 murukkus. How many murukkus do they make in total?
In a garden, there are 48 red roses, 32 yellow roses and 17 white roses. How many roses are there in the garden?
A balloon seller has 56 red balloons, 21 blue balloons and 12 green balloons. How many balloons are there in total?
Create a real life problem on adding 42 and 39.
Challenge
Sara finds the smallest sum using the given numbers. Which two numbers did she add, and what was the sum?
Points to Remember
•Addition is when we keep numbers together to find the total.
•We use the “+” sign to show that we are adding numbers.
• When we add, we start with the ones place and then move to the tens place.
• If we add 0 to a number, it doesn’t change the number.
• If we change the order of the numbers we are adding, the sum does not change.
Math Lab
Setting: In groups of 4
Things Needed:
Collaboration & Communication
• Printed copies of number grid 1–100 (1 per group) Race to 100!
• Small tokens, coins or stones (1 per player)
• Deck of number cards of 1–10 (1 deck per group)
Let’s play:
1 Each group gets a game board, game markers and a deck of cards.
2 Players take turns to draw two cards from the deck.
3 Add the two numbers together to find the sum.
4 Move your token forward by that many spaces on the game board.
5 If you get the sum wrong, stay in your current position.
6 The first player to reach 100 wins!
Chapter Checkup
1 Using a number line, add the given numbers.
8 + 2
13 + 21
3 Solve using the vertical method.
7 + 5 + 2
2 Add the numbers by drawing place value blocks.
18 + 2
4 Add the numbers horizontally.
5 Find the correct answer.
23 + 42
32 + 45
7 + 3 + 2
18 + 0 + 27
62 + 14
6 Meals are served on banana leaves, mostly in the South Indian states. Rohan brought 23 banana leaves, and Soham brought 46 leaves. What is the total number of leaves?
7 A fruit vendor has 28 apples, 41 oranges and 29 bananas. How many fruits does the vendor have in total?
• Addition of 2-digit Numbers
8 Mohan likes to share things with his brother. Mohan bought 15 comic books, 12 colouring books and 10 notepads and shared them with his brother. How many books did he buy in total? Do you also share things with others?
What number will you get if you add the smallest 2-digit number to a dozen? 1 Challenge
Critical Thinking
The sum of three odd 2-digit numbers is an even number. Write true or false. Explain your answer with an example.
Real-Life Maths
Bird Feeders
Bird feeders are containers placed outside to give food and water for birds. Raha and her friends make bird feeders with coconut shells to be kept at various locations in their society. On Day 1, Raha collected 8 shells and her friends collected 31 shells. On Day 2, they got 5 more shells. Read the questions and answer them.
1 Draw place value blocks to show the total number of shells collected by Raha’s friends on Day 1?
2 How many bird feeders did Raha and her friends make on Day 1?
3 What is the total number of bird feeders that they made?
4 Name 2 reusable waste materials that can be used to make bird feeders. Value Development & Cross Curricular
3 Subtraction of 2-digit Numbers
Let s ecall
Let us say we have 9 candies.
If we give 4 candies to a friend, how many candies do we have left?
We learnt that we use subtraction when items are taken away. So here, we are giving the candies away to a friend. We will use subtraction to find how many candies we have left.
In addition, we jump forward. In subtraction, we jump backwards.
We had 9 candies, so we start from 9. To subtract 4, we will take 4 backward jumps from 9. We will reach 5.
So, we are left with 5 candies!
9 candies – 4 candies = 5 candies
We can also write this as:
Subtracting 2-digit Numbers
Sara loves to read books.
Sara is reading a book on planets. There are 56 pages in the book.
Sara has finished reading 12 pages. How many pages are left?
Subtraction without Regrouping
Let us help Sara find out how many pages are left. Here we see the pages are decreasing in number. So, we have to subtract.
Vertical Method
Let us subtract 12 pages from 56 pages. 1 page = 1 ones = 10 pages = 1 tens =
Steps
Write down the numbers 56 and 12 according to their place value.
Using Place Value
Blocks
Write the bigger number on top and the smaller number below during subtraction.
We are left with 4 ones in the ones place.
Start with the ones place. We have 6 ones in the ones place. We take away 2 ones.
We are left with 4 tens in the tens place.
Subtract the tens place. We have 5 tens in the tens place. We take away 1 tens.
Mental Subtraction
Sometimes we need to subtract numbers quickly.
Let us learn how to subtract 12 from 56.
Mark 56 on a number strip. We know 12 = 10 + 2. Move backwards by 10 steps directly, and then go 2 steps back to reach 44.
Count backwards by 2 ones
Jump backwards by 1 tens
Therefore, 44 pages are left for Sara to read. We can use this strategy to solve it mentally.
Let us subtract: 44 – 23.
1. Keep the bigger number 44 in mind.
2. Count backwards by 2 tens as 34, 24 to reach 24.
3. Count backwards by 3 ones as 23, 22, 21 to reach 21.
4. So, 44 – 23 = 21.
by
Example 2: Find 78 – 34.
Go back by 3 tens from 78 to reach 48. Then move back by 4 ones to reach 44.
So, 78 – 34 = 44.
Subtract 49 from 99.
Go back by _______ tens from 99 to reach . Then move back by ones to reach
So, 99 – 49 = .
Draw jumps on the number grid to solve.
Did You Know?
Operations like addition, subtraction, multiplication and division were first devised by the Indian mathematician Brahmagupta.
Challenge
Meera said you get the same number when you subtract 0 from that number. Sheena said you get the same number when you subtract 1 from that number. Who is correct? Explain your answer with an example.
Subtraction with Regrouping
Sara had 44 pages left to read. She read 3 more pages. She had 44 – 3 = 41 pages left.
The next day, Sara read 13 pages. How many pages are left now?
Subtracting by Regrouping 1s
We have to subtract 13 from 41.
Steps Using Place Value Blocks
Write the numbers according to the place value. Show the bigger number using blocks.
Subtract the ones place. We cannot take away 3 from 1.
We shift 1 tens from the tens place to the ones place as 10 ones.
We are not left with 3 tens..
1 tens = 10 ones
get 11 ones in the ones place. Take away 3 ones from 11 ones.
41 – 13 = 28. So, 28 pages are left.
Example 3: ubtract from .
So, 20 – 8 = 12.
Example 4: ol e .
Finding the Missing Number
Sara was solving a puzzle in her book. She had to find the missing number. We can find the missing numbers in subtraction by using addition.
Let us now learn how to find the missing numbers in a subtraction problem.
Bigger number
Smaller number 10 is the answer.
Steps
Check the ones place.
Check the tens place.
Explanation
We add the digit of the smaller number and the answer in the ones place to find the missing digit of the bigger number. 4 + 0 = 4
We subtract the digit of the answer in the tens place from the digit of the bigger number in the tens place. 2 – 1 = 1
Checking Subtraction Using Addition
If we subtract 8 from 19 we will get 11.
When we add the answer of subtraction to the smaller number, we get the bigger number as the answer.
Checking the answer using addition:
Addition and Subtraction Facts
Let us understand how addition and subtraction are related.
There are 8 apples and 5 mangoes.
So, using 3 different numbers 8, 5 and 13 we can write the addition and subtraction facts as given below:
Example 5: Write down the subtraction and addition facts of and . There are 9 fish and 8 turtles:
Example 6: ind the missing number. Check the ones place. Then check the tens place.
Write down the addition and subtraction facts for the following numbers.
a 9, 6 and 15
There are 9 shells and 6 stones.
b Write down the addition and subtraction facts for 3, 8 and 11.
Draw the place value blocks and subtract with regrouping.
Draw things to show the addition and subtraction facts of 13.
Write 2 subtraction problems using the following digits such that the answer is between 10 and 50.
We can use the CUBES method to solve story sums. In the CUBES method, we follow the 5 given steps.
Circle the numbers
Satish has 18 storybooks. He gives 10 storybooks to Manish. How many books does Satish have left?
Box the keywords
Underline the question
Number of storybooks Satish has = 18
Number of storybooks Satish gives to Manish = 10
C: Circle the numbers.
U: Underline the question.
B: Box the key words.
E: Evaluate/draw.
S: Solve and check!
Solve and Check!
Number of storybooks left with Satish = 18 – 10 TensOnes 18 – 10 8
Satish has 8 storybooks left. To check, we add 10 to 8 to get 18. So, our answer is correct.
Remember!
When we add the small number and the answer, we get the big number. Then our answer is correct. here are to cars. are sold. How man are left?
Number of toy cars = 33
Number of toy cars sold =
Number of toy cars left = TensOnes 33 –
Jiya had 51 flowers. Raju had 31 flowers. How many more flowers than Raju does Jiya have?
Mohan has 45 fruits with him. Minal has 21 fruits with her. How many fewer fruits than Mohan does Minal have?
A thatched house has a roof that is made from straws or reeds. In an Indian village there are 27 houses. Out of these 15 houses are thatched and the remaining are concrete. How many houses are concrete?
28.
Sheetal has 23 bananas and 12 apples in her bag. How many more apples should she buy to have a single apple for lunch every day for two weeks?
Points to Remember
•When we subtract, the number of things becomes less.
• We can add the answer and the small number to see whether the subtraction is correct.
•We can find the missing number in subtraction by adding or subtracting.
•Any three related numbers will have 4 addition and subtraction facts.
• One child from each pair will use any four numbers, such as 5, 3, 6 or 8 to make an addition pyramid.
Addition pyramid; Start from the bottom and add the 2 numbers next to each other and write the answer on top.
Subtraction Pyramid: Start from the top and subtract the one number given below. Write the answer next to it.
• The pair which makes the correct pyramid will win.
Solve
Write down the addition and subtraction facts for the following numbers.
8 and 17
3 and 7
9 and 14
Ghungaroos are anklets that are worn by classical dancers in India. There are 46 bells in Sunita's ghungaroos, and 35 bells in Sarika's ghungaroos. Who has more bells in ghungaroos and how many more?
A 7-year-old child has 22 teeth, whereas an adult usually has 32 teeth. How many more teeth does an adult have than a child?
Meena buys a pencil for �8. She gives the shopkeeper a �50 note. How many notes of �20 and coins of �2 are returned to her?
I am a 2-digit number. I am 10 more the number that is than 40 less than 80. What number am I? 2 Challenge
1
Robin takes away 13 from 54 and then again takes away 10. How many ones are there in the answer?
Real-Life Maths
Father's Birthday
Jay is planning a small party for his father’s birthday. He bought some decorations and snacks. He had �99. The cost of ribbons is �43. Snacks are for �50.
1 How much money did he spend?
2 How much money is left with him after buying ribbons?
3 How much money is left with him after buying both the things?
4 Can Jay buy wrapping paper of �13 with the money left?
5 Do you celebrate birthdays of your family members? If yes, write 5 lines on it.
4 Multiplication
Letʹs Recall
A vegetable market is a place where we can buy vegtables and fruit.
We know how to count vegetables.
These are 3 cabbages. These are 4 cauliflowers.
We also know how to add the vegetables. Addition will help us find the total number of vegetables.
So, the total number of vegetables = Number
Letʹs Warm-up
Match the following.
Understanding Multiplication
Raghu bought 5 bunches of balloons. Each bunch has 3 balloons in it. How many balloons are there altogether?
Bunch 1Bunch 2Bunch 3Bunch 4Bunch 5
3 balloons3 balloons3 balloons3 balloons3 balloons
Using Repeated Addition
To find out how many balloons Raghu had in all, we will add 3 balloons 5 times.
When we add the same number over and over again, it is called repeated addition.
5 bunches of 3 balloons
Group 1
Group 2
Group 3
Group 4
Group 5
3 balloons + 3 balloons + 3 balloons + 3 balloons + 3 balloons = 15 balloons
Raghu bought 15 balloons in total.
Example 1: There are 3 plates with 2 biscuits on each. How many biscuits are there in total?
2 2 2=6 + 3 plates of 2 biscuits on each + There are 6 biscuits in all.
3 bunches of _____ flowers in each
There are 3 bunches of flowers with flowers in each. How many flowers are there in all the bunches together? 5 + + 5
There are flowers altogether.
It Yourself 4A Look at the pictures and answer the questions.
1 How many leaves are there in total?
There are leaves in total.
2 How many cookies are there in all?
3 Fill in the blanks.
4 A cow has 4 legs. How many legs do 2 cows have? Draw a picture to show repeated addition.
1 Riya is adding 6 three times. What is the total that Riya will get? Draw a picture to show the repeated addition.
Making Equal Groups
Think and Tell
Do you remember Raghu, who had 5 bunches of balloons? We can also say he has 5 groups of 3 balloons each. Let us help him find the total number of balloons.
Group 1Group 2Group 3Group 4Group 5
3 balloons3 balloons3 balloons3 balloons3 balloons groups of balloons = balloons
Will it be easy to find the total if there are unequal groups of things? 5 3 15
Example 2: There are 3 groups of mangoes. Each group has 2 mangoes. How many mangoes are there in total?
Adding 2 mangoes 3 times
Group 1 2 mangoes
Group 2 2 mangoes
Group 3 2 mangoes groups of mangoes = mangoes 3 2 6
There are plates. Each plate has 4 guavas. What is the total number of guavas?
groups of guavas = guavas
Tick ( ) the image which shows equal groups.
Circle the following in groups of 3. Write the total.
groups of 3 stars = stars
There are bicycles. Each bicycle has wheels. There are wheels in all.
There are baskets. Each basket has fruits. There are fruits in all.
Match the following. One has been done for you.
There are 3 groups. 8 + 8 + 8 = 24 grapes
1 Sabha shows 3 jars in which she has put sweets in equal groups of 10. Do the jars show equal distribution? Explain your answer.
Writing Multiplication Sentences
Hi, Riya. I got 5 bunches of 3 balloons yesterday.
Yes. How did you calculate so fast? Wow! You got 15 balloons?
I used multiplication. Raghu Riya
Multiplication is a fast way of adding repeatedly. We use the ‘×’ sign for multiplication.
Here are the 5 bunches of balloons which Raghu bought.
5 groups of balloons × 3 balloons in each group = 15 balloons
This can also be written as:
5 × = 3 15
Number of groups
5 groups of 3 balloons
Number of things in each group
Number of things in total
This can be read as any one of the following:
5 groups of 3 are 15.
5 times 3 is 15.
5 threes are 15.
Example 3: There are 3 ladybugs. Each ladybug has 4 spots on it. How many spots are there in total?
4 + 4 + 4 + 4 + 4
5 groups of 4
5 × 4 = 20
There are 20 spots in total.
Did You Know?
Brahmagupta, an Indian mathematician was the first to talk about multiplication.
There are boxes of crayons. Each box has 5 crayons. How many crayons are there in total?
Think and Tell
If there are 6 groups and each group has 5 stars, how many stars are there in total?
+ + + groups of 5
_____ × 5 = 20
There are crayons in all.
Read the problem to fill in the blanks.
Never put a different number of things in groups during multiplication. Error Alert!
+ + + + + = Do It Yourself 4C
a There are 7 vases. Each vase has 3 roses. How many roses are there in total?
2
groups of = times × =
There are roses in total.
b There are 4 cakes. Each cake has 4 candles on it. How many candles are there in total?
groups of = times + + + _______ = × =
There are candles in total.
Match the following.
a 2 times 4
b 5 times 2
c 4 times 2 Complete the following.
d 3 times 3
1 Draw dots on the ladybugs to show 5 × 5 = 25.
Points to Remember
•Adding the same number, again and again, is called repeated addition.
•In multiplication, the number of things in each group remains the same.
•Multiplication is a fast way to do repeated addition.
•For multiplication, we use the ʻ×ʹ sign.
•For multiplication, we do the following:
Number of groups × Number of things in each group = Total number of things
Math Lab
Setting: Group of 10
Creativity & Value Development
Flower Jewellery!
Things Needed: Paper flowers, string
Method:
1 Make 2 earrings using paper flowers, with 6 flowers in each. Make 5 armlets, with 8 flowers in each. Make 2 necklaces with 10 flowers in each.
2 Write a multiplication sentence for each piece of paper jewellery given above.
3 After writing the multiplication sentence, show the jewellery set to your teacher and discuss the answers.
4 You may also gift this beautiful jewellery set to a family member.
Chapter Checkup
Find the number of things in total.
a + + + =
There are mangoes in all. b + =
There are books in all.
Identify the number of groups and things in each group in the pictures.
a groups of pieces of chalk in each group.
b groups of marbles in each group.
a 6 groups of 3
b 2 groups of 3
c 3 groups of 6
a 2 groups of 4
b 3 groups of 2
c 4 groups of 2
Draw pictures for each multiplication sentence. a 3 × 6 = 18 b 2 × 2 = 4 c 3 × 7 = 21
Complete the table.
a 2 + 2 + 2 + 2 = 10 × 2
3 + 3 + 3 + 34 times 34 × 3 = 12
b 4 groups of 10 is 14
c 7 times 5 is 35 d 10 + 10 = 10 × 2
Tuk-tuk is another name for autorickshaws, which are common vehicles in India. A tuk-tuk has 3 wheels. How many wheels will 4 tuk-tuks have?
Kabaddi is a popular traditional sport in India. Each team has 7 players. How many players are playing in two teams?
1 Sana adds 6 to itself 6 times and gets 35. Rohan makes 6 groups of 6 and gets 36. Who is correct? Explain your answer.
2 On Diwali, we light lamps in the house. Rina placed 3 lamps near every pillar in the house. Shina placed 2 lamps near every corner. There are 5 pillars and 6 corners in the house. Who placed more lamps?
Multiplication
Cross Curricular & Value Development
Environment Day
It’s World Environment Day! Jiya and her family are planting trees in the nearby park. Look at the picture to answer the questions.
1 Jiya plants 2 saplings of the neem tree in each row. If there are 5 rows, which of the following does not represent the number of saplings planted by Jiya?
a 5 × 2
c 5 groups of 2
b 2 + 2 + 2 + 2
d 10
2 Rahul has planted 2 rows of mango tree saplings. If each row has 4 saplings each, how many saplings did he plant?
a 4 + 4
c 14
3 Fill in the blanks.
b 4 × 3
d 20
a 4 saplings each in 2 rows = groups of
b 10 saplings each in 3 rows = groups of
4 Write 2 things that you want to do on World Environment Day.
5 Multiplication Tables 2, 5 and 10
Let’s Recall
An apple a day keeps the doctor away! Is each plate a group?
Yes! Each plate has the same number of apples.
There are 5 groups with 2 apples each.
Let us count the total number of apples.
2 + 2 + 2 + 2 + 2 = 10
This is repeated addition, which is the same as multiplication.
We can also write this as 5 groups of 2 or 5 × 2 = 10.
So, 2 + 2 + 2 + 2 + 2 = 5 groups of 2 = 5 × 2 = 10
Let’s Warm-up
Fill in the blanks.
1 pears + pears = pears
2 These are 2 groups of pears each.
3 We can say, 2 × pears = pears.
I scored out of 3.
Multiplication Tables
Meena and Tina go to an apple farm. The farmer puts apples in baskets. The farmer tells them that all baskets have an equal number of apples. Let us help them count the total number of apples.
Multiplication by 2
We learnt that repeated addition is called multiplication. When items are grouped and each group has the same number of items, multiplication can be used to find the total number of items.
For example, if the farmer has 2 baskets, with 1 apple each, we get:
Number of groups
sign of multiplication
Total number of items
Number of items in each group
Each basket is a group, and the number of apples is the number of items in each group.
What if each group had 2 apples?
We would get 2 × 2 = 4.
This way of multiplying by 2 gives us the “Multiplication Table of 2”.
Let us read the multiplication table of 2 together:
2 × 1 = 22 ones are 2
2 × 2 = 42 twos are 4
2 × 3 = 62 threes are 6
2 × 4 = 82 fours are 8
2 × 5 = 102 fives are 10
2 × 6 = 122 sixes are 12
2 × 7 = 142 sevens are 14
2 × 8 = 162 eights are 16
2 × 9 = 182 nines are 18
2 × 10 = 20 2 tens are 20
Let us learn multiplication by counting steps. Imagine you are playing a game where the steps are numbered. The rule is to jump two steps at a time.
This process of counting in 2s is multiplication by 2. +2+2+2+2+2+2+2+2+2+2 01234567891011121314151617181920
Start at step 0. Each jump that you make is of 2 steps. So, you reach 2 on the first jump, then on the second jump you reach 4, on the third you reach 6 and so on.
2468101214161820
Example 1: How many groups of 2 cars are there?
Group 1
There are 3 groups of 2 cars.
Group 2
Complete this table.
GroupsMultiplication fact
1 group of 2 1 × 2 = 2
2 groups of 2 2 × 2 = 4 3 × 2 = 6
4 groups of 2 4 × 2 = 5 × 2 =
It Yourself 5A Fill in the blanks.
2 groups of 2
Write the multiplication fact for the given pictures
Anju loves spending time with her grandparents. She is helping her grandmother serve idlis to the guests. She is counting idlis with the help of the number line. Fill in the blanks.
Draw a picture representing 2 groups with 5 apples in each group. What is the total number of apples in the picture?
Challenge
Use the multiplication table of 2 to complete the puzzle. One has been done for you.
Multiplication by 5
The next day, Tina went to the apple farm alone. She collected 5 apples. Can you help her count the number of apples? Here, we have 5 groups of 1 apple each.
5 × 1 = 5 apples
What if Tina had 5 baskets of 2 apples? She would have 5 × 2 = 10 apples. This is called multiplication by 5.
Let us learn how to read the multiplication table of 5.
5 × 1 = 55 ones are 5 5 × 2 = 105 twos are 10 5 × 3 = 155 threes are 15
5 × 4 = 205 fours are 20
5 × 5 = 255 fives are 25
5 × 6 = 305 sixes are 30
× 7 = 355 sevens are 35
× 8 = 405 eights are 40
× 9 = 455 nines are 45
× 10 = 505 tens are 50
Let us play the game of steps again. Now, the rule is that you jump five steps.
Start at step 0. Each jump that you make is of 5 steps. So, you reach 5 on the first jump, then on the second jump you reach 10, on the third you reach 15 and so on.
Example 2: Tom, the rabbit wants to reach the hole. How many times will he jump to reach the hole?
Tom will jump 6 times to reach the hole.
Ahana is playing a game of skip counting with her friend. She jumps in steps of 5. Draw her jumps.
Draw a picture to show 5 groups with 6 grapes in each group. Write down the total number of grapes in the picture.
The grid has numbers shaded in yellow to show skip counting by 5. Which number is incorrectly marked?
Multiplication by 10
Tina saw that the farmer had 10 small baskets. There was 1 apple in each basket.
Here, we have 10 baskets of 1 apple.
10 × 1 = 10 apples.
What if the farmer had 10 baskets with 2 apples in each?
He would have 10 × 2 = 20 apples.
This is called multiplication by 10.
Let us read the multiplication table of 10.
Remember!
A number, when multiplied by 10 always has a “0” at the end.
Let us play the game of steps once again. Now, the rule is that you jump ten steps.
01234567891011121314151617181920
You start at 0. Each jump that you make is of 10 steps. So, you reach 10 on the first jump, then on the second jump you reach 20, on the third you reach 30, and so on.
Example 3: There are 10 pencil boxes with 3 pencils in each pencil box. How many groups of pencils are there? Also, what is the total number of pencils.
10 groups of 6 crayons equal 60.
10 × 6 = 60
Mitthu wants to reach the red chilli. He jumps 10 steps each time.
0102030405060708090100
5 jumps of 10 steps each. 5 × 10 =
How many times does Mitthu jump?
Write the multiplication fact. × =
Write the multiplication fact.
0102030405060708090100
jumps of 10 each means × =
0102030405060708090100
jumps of 10 each means × =
Draw any object to show 10 groups of 3.
Rohan goes to kirtans with his grandparents. He plays the jhika (an Indian musical instrument) with jingles. If one jhika has 10 jingles, how many jingles will 10 jhikas have?
I have two numbers. Their product is 40. One number is 10. What is the other number? 1
Multiplication Rules
Meena and Tina went to the farm one evening. They collected apples. Let us use multiplication to count them.
Multiplication by 1
They have 2 baskets, with 1 apple in each, so we get: 2 × 1 = 2
When a number is multiplied by 1, the answer is the number itself.
Each basket is a group, and the number of apples is the number of items in each group.
Multiplication by Zero
Meena and Tina also saw two empty baskets on the farm. It had no apples in it.
There are 2 groups of 0 apples.
2 × 0 = 0
When you multiply 0 by any number, the answer is always 0.
Doubles
Add the number twice or multiply by 2 to get the double of any number. Double means two times of a number.
What is the double of 5?
5 + 5 = 10 2 × 5 = 10
Order in Multiplication
Two numbers can be multiplied in any order. The product remains the same. 5 groups of 4 is the same as 4 groups of 5. Both will give the same answer.
5 × 4 = 4 × 5 = 20
Example 4: Fill in the blanks.
a 3 × 1 = 3
c 3 × 4 = 4 × 3 = 12
b 4 × 0 = 4
d Double of 8 = 16
Did You Know?
Triple means adding the number three times.
ohit s father ga e him empt ases. How man flowers are there in the vases?
Look at the pictures to find the total number of eggs.
a If 4 × 5 = 20, 5 × 4 =
Double of 4
9 × 4 = × 9 =
LED lamps save electricity. There are 10 lamp posts on a road. Each lamp post has 1 LED lamp. Total number of lamps = .
Diya wants to buy a chocolate for her house helper’s daughter. She saves 2 rupees every day for 10 days. How much money does Diya save in total?
I am a number between 20 and 30. Double of me is 48. Which number am I? 1
Story Sums on Multiplication
Tina sees a big basket that can hold 8 apples. The farmer tells Tina that he has 10 such baskets. How many apples can 10 baskets hold?
What do we know?
The number of baskets the farmer has = 10.
The number of apples each basket can hold = 8.
What do we want to know?
How many apples can 10 baskets hold?
How do we find the answer?
The total number of apples that 10 baskets can hold = The number of baskets × The number of apples that each basket holds
Solve to find the answer.
10 × 8 = 80 apples
So, 10 baskets can hold 80 apples.
here are ases in the house. ach ase has flowers in it. How man flowers are there in total?
What do we know?
The number of vases in the house = 5
The number of flowers in each vase =
What do we want to know?
The total number of flowers in all the vases
How do we find the answer?
The total number of flowers = The total number of vases × The number of flowers in each vase
Solve to find the answer.
5 × = flowers
So, there are flowers in total.
A bookstore has 10 shelves, and each shelf can hold 6 books. How many books are there in the bookstore?
Mishti Doi is a sweet from West Bengal. It is a yoghurt made from milk and jaggery. If Manan has 9 boxes of Mishti Doi, and each box contains 10 packets of Mishti Doi. How many Mishti Doi packets are there in all?
There are 6 oranges in a fruit basket. If there are 10 such fruit baskets, how many oranges are there in total?
Tom made 4 batches of cupcakes, and each batch had 10 cupcakes. How many cupcakes did Tom make in total?
Create your own story problem showing 2 × 10.
Challenge
Critical Thinking
The teacher asks Seerat to find 8 times 5. However, she does not know the table of 8. How will she find the answer?
Points to Remember
• The multiplication of any number by 1 is always the same number.
• The product of any number by zero is always zero.
• Double means adding the number to itself or multiplying by 2.
Math Lab
Setting: In groups of 4
Multiplication Bingo
Things Needed: Bingo cards on a 5 × 5 grid, with ‘BINGO’ written across the top and answers written to the caller’s problems in the remaining squares with some filler answers, caller list showing a list of multiplication problems, pencils.
Method:
Collaboration & Communication 5 × 2 =2 × 9 =10 × 6 =
1 A caller reads a multiplication problem aloud from the caller list.
2 Other students will solve the problem and cut the answer from the bingo cards.
3 Students who solve the problem and cut the whole line of their bingo card either horizontally, vertically or diagonally are the winners.
Write True or False.
2 × 6 = 12
5 × 1 = 0
7 × 0 = 1
10 × 5 = 50
Show multiplication on a number line. 01234567891011121314151617181920
in the blanks with the correct number. Each blank has the same number.
Say the multiplication table of 2 and colour each number in it red. Say the multiplication table of 5 and colour each number in it green. 12345678910
Dosa is a thin, crispy pancake made with urad dal and rice batter. If 7 dosas can be cooked on a single tawa, then how many can be cooked on 10 such tawas?
Rahul and his 4 friends are going on a trip. Below is the list of items he has decided to take on the trip. Calculate the total number of items he will be taking with him.
Solve the maze from left to right and from top to bottom to help the astronaut reach a space station.
2
I have made a tower of blocks. My tower is of 5 floors. Each floor has 4 blocks. I think I have used 20 blocks in all to make the tower. Am I right or wrong?
Real-Life Maths
Value Development
Birthday Celebration
Raina and Reyansh are twins. They plan to celebrate their birthday with kids in an orphanage. They made a goody bag to be shared with all. They included 2 lollipops, 1 book, 5 cookies, 1 toy and 4 pencils. There were 10 kids in the orphanage. Read the questions and answer them.
1 What things are included in the goody bag? Tick all the correct options.
a toffees
b lollipops
c pencils
d toy
2 How many lollipops do they need in total?
4 If 5 × 10 = 50 then what is 10 × 5?
3 How many toys do they need in total?
5 Have you ever celebrated your birthday differently? Share your ideas.
6 Numbers up to 999
Let’s Recall
Toys are so much fun!
Do you know that the toy at the store has a price tag on it?
Let us say that the price of the teddy bear is �65.
We write 65 as: 6 tens and 5 ones.
The place value of the digit at the tens place is 60.
The place value of the digit at the ones place is 5.
Let us say that the price of the basketball is �195.
We write 195 as: 1 hundreds, 9 tens and 5 ones.
The place value of the hundreds place is 100.
The place value of the digit at the tens place is 90.
The place value of the digit at the ones place is 5.
Let’s Warm-up
Match each number with its expanded form.
Understanding Numbers up to 999
Pooja and Rohit went to buy candies with their father.
Pooja: Father, let us buy candies for my birthday.
Father: Okay, 200 candies for your school friends and 25 candies for your park friends.
Pooja: Wow! 225 candies!
Rohit: How did you count that? Please teach me to count beyond 200.
Writing Numbers up to 999
Let us help Rohit count numbers more than 200. We know how to count and write numbers from 0 to 100.
We can write numbers more than 200 the same way as we write numbers from 1 to 100. Numbers 201 to 300
Counting Forward and Backwards
Read the numbers on the grid again. Read them this way:
Counting FORWARD 271272273274275276277278279280
Counting BACKWARDS
200199198197196195194193192191
ount forward and backwards to ll in the missing numbers. a 276278280282 b 299297 Do It Together
Hundreds, Tens and Ones
We know that a 3-digit number has hundreds, tens and ones. We can show a 3-digit number using place value blocks.
We also know that 10 ones = 1 tens, and 10 tens = 1 hundreds.
Hundreds TensOnes
Let us now see how the 225 candies are shown using place value blocks.
So, 225 candies are shown as 2 hundreds blocks, 2 tens blocks and 5 ones blocks. = 225
Think and Tell
Let us see some numbers that are shown as hundreds. one hundred
of the
Did You Know?
The numbers that we use today, 0 to 9, started in ancient India!
The Burj Khalifa in Dubai is the tallest building in the world. It has 163 floors. Write the number as a number name.
Write the number that has:
a 4 hundreds, 6 tens and 5 ones b 7 hundreds, 7 tens and 7ones c 6 hundreds and 3 ones d 5 hundreds and 5 ones
Show the given numbers using place value blocks. Use for hundreds, for tens and for ones.
I have 2 hundreds. I have no tens and 1 more ones than the number of hundreds.
Place Value and Expanded Form
We saw that Rohit and Pooja’s father bought 225 candies.
Now, let us write the number using a place value and an expanded form.
Did You Know?
Aryabhata, an Indian mathematician worked on the place value system.
Place Value and Face Value
Place value is the value of a digit based on its position in a number. Each digit has a place value, such as ones, tens, hundreds and so on. The face value of a digit is the value of the digit itself.
For example, in 225, there are 2 hundreds, 2 tens and 5 ones. We can write 225 as:
Remember!
The place value of 0 is always 0 no matter what its position in the number is.
So, the place value of the hundreds place is 200. The place value of the digit at tens place is 20. The place value of the digit at ones place is 5. = 5 = 20 = 200
Example 2: Write the place value and face value of the coloured digits. 234 4 ones; 4 953 9 hundreds; 9806 0; 0 662 6 tens; 6
Expanded Form and Number Names
Let us understand the expanded form of numbers up to 999.
Expanded form refers to writing a number as the sum of its place values. We can write the number name of a given number using its expanded form.
Expanded form of 983:
Standard Form – 983
Expanded Form – 900 + 80 + 3
Number Name – nine hundred eighty-three
Write the number name and expanded form for the given numbers. a 453
Expanded Form:
Number Name:
Place Value of 3: Face Value of 4:
Place Value of 3: Face Value of 4:
Do It Yourself 6B
Write the place value of all the digits in the given numbers. Then, write the numbers in their expanded form.
Write the number. Write its number name.
Tick () the numbers in which the place value of: a 7 is
Some temples in India have steps. The Rameshwaram temple has 127 steps. Write the number name and expanded form for the given number.
Solve the riddle. • I am a 3-digit number. • My ones digit is less than 1. • My tens digit is the greatest single digit number. • My hundreds digit is 5.
am I?
Comparing and Forming Numbers
Pankaj and Ria like to play with marbles.
Pankaj had 120 marbles and Ria had 69 marbles.
Pankaj: I have more marbles than you.
Ria: No, I think I have more.
Comparing Numbers
Who has more marbles?
Ria has 69 marbles.
Pankaj has 120 marbles.
It is a 2-digit number.
Remember!
It is a 3-digit number.
A number that has more digits is always greater!
So, Pankaj has more marbles than Ria as 120 > 69 (120 is more than 69).
A 3-digit number is always more than a 2-digit number.
Compare 547 and 328
Both are 3-digit numbers. We first compare the digits in the hundreds place of both the numbers.
5 is greater than 3
So, 547 > 328 (547 is greater than 328).
Now, when the number of digits is the same and the digits in the hundreds place are also the same, then, we compare the digits in the tens place to see which is greater or smaller.
For example, compare 437 and 453.
Same digit in the hundreds place.
4 is equal to 4, 4 = 4
Since the digits in the hundreds place are the same, we compare the digits in the tens place.
3 is less than 5. So, 437 < 453.
Now, when the number of digits is the same and the digits in the hundreds and tens places are also the same, then, we compare the digits in the ones place to see which is greater or smaller.
For example, compare 847 and 849.
Same digits in the hundreds and tens places. Compare the digits in the ones place.
7 is less than 9. So, 847 < 849.
When both the numbers are equal, we use the equal to sign
344 = 344
Example 3: ompare and .
Remember!
Compare the digits in the tens and ones places ONLY if the digits in the hundreds place of the two numbers are the same!
Same digits in the hundreds and tens places. Compare the digits in the ones place.
9 is greater than 1. So, 689 > 681.
Ordering Numbers
We learnt how to compare two numbers. Let us now compare more than 2 numbers.
Let us compare 34, 871 and 679.
We know that 2-digit numbers are always smaller than 3-digit numbers. So, 34 is less than both 871 and 679. Now, let us compare 871 and 679.
8 is greater than 6
So, 871 is greater than 679, or we can also say 679 is less than 871. Numbers, when written from the smallest to the largest, are arranged in increasing or ascending order.
The three numbers in this order would be: 34, 679, 871 or 34 < 679 < 871. Numbers, when written from the largest to the smallest, are arranged in decreasing or descending order.
The three numbers in this order would be: 871, 679, 34 or 871 > 679 > 34.
ompare and arrange the numbers and in increasing and decreasing order.
81 is a 2-digit number while 421 and 612 are 3-digit numbers.
So, 81 is __________________________ both 421 and 612.
We can also see that 421 < 612 because the digit in the hundreds place is smaller in 421.
So, the increasing order (smallest to largest) is , , .
The decreasing order (largest to smallest) is , , .
Forming Numbers
We can form numbers by arranging the digits in ascending or descending order. To form the greatest number, arrange the given digits in descending order. To form the smallest number, arrange the given digits in ascending order. We can form 3-digit numbers by arranging any 3 given digits.
Let us form numbers using the digits 2, 8 and 4.
Smallest Number
Digits arranged in ascending order
Example 4: orm the greatest and smallest number using and .
Greatest number: Arrange the given digits in descending order to get 953.
Smallest number: Arrange the given digits in ascending order to get 359. Use the digits 4, 5 and 1 to form the greatest and smallest 3-digit number. Smallest number
5 Cross Curricular Challenge
Houses are built using bricks. Bricks are used to make walls along with cement. Toni built a wall using 790 bricks. His neighbour, Ramu, also built a wall but he used 689 bricks. Who used more bricks?
The digit at the ones place is 1. 1
Critical Thinking & Value Development
Reyansh planted trees with an NGO but forgot the number. Help him find his number.
The hundreds place has the greatest digit.
The place value and face value of the digit at the tens place is the same.
Points to Remember
• While writing the number name of a 3-digit number, we write the hundreds place first, then the tens and then the ones place together.
• Place value is the value of a digit based on its position in a number. The place value of a digit is not fixed.
• Expanded form refers to writing a number as the sum of its place values.
• In increasing order, we arrange the numbers from smallest to greatest. In decreasing order, we arrange the numbers from greatest to smallest.
Setting: In groups
Things Needed: 1 abacus, 1 pencil
Method:
1 Students are to understand how to show numbers on an abacus. Then, each group should think of two 3-digit numbers.
2 The groups take turns to show one number at a time on the abacus to the other groups, who then write the number and its number name in their notebooks.
Numbers on the Abacus!
3 The group that writes the number and number name correctly, gets a point.
4 The next group then shows their 3-digit number on the abacus and the game continues.
5 The group that gets the maximum points, wins the game.
Write the place value of each digit in the given numbers. Write the numbers in their expanded form. Draw place value blocks for each. Use for hundreds, for tens and for ones.
Compare the numbers using the symbols <, > or =.
Write the numbers in decreasing order.
a 559, 678, 345 b 109, 289, 678 c 345, 696, 873
a 540, 330, 257 b 678, 447, 567 c 600, 120, 499
A colony has many different houses arranged in rows on different streets. The houses in a row are usually numbered. There are four houses on a street with numbers in the order 223, 224, 225 and 226. What will be the number of the next house?
Choose the numbers from the balloons and fill in the boxes.
Form the greatest and smallest 3-digit number using the digits 6, 1 and 4.
Critical Thinking & Art Integration
Colour the boxes by following these instructions.
Colour the box green if the digit in the ones place is greater than 5.
Colour the box yellow if the digit in the tens place is greater than 5.
Colour the box pink if the digit in the hundreds place is greater than 5.
Metro Ride
A metro train is a train that runs just in a city and connects one area to another. Jenny is visiting her cousin’s house during summer break in Delhi. She sees the Metro train for the first time. She sees the pillars and tries to read the number on each pillar. Look at the picture and answer the questions.
1 How many metro pillars are shown in the picture?
2 If the metro is moving towards the right, the pillar numbers are (increasing/decreasing)
3 Write the number name of the smallest pillar number shown in the picture.
4 Use the digits of the greatest pillar number in the picture to form the smallest number.
7 A ition and Subtraction of 3-digit Numbers
Let’s Recall
Imagine we have 25 marbles. We find 13 more marbles. How many marbles do we have?
We will add 13 to 25 to find the total number of marbles.
25 = 2 tens + 5 ones
13 = 1 tens + 3 ones
So, there are 38 marbles in all.
Now, what if we lose 15 marbles, how many marbles will we have?
We will subtract 15 from 38 to find the number of marbles left.
38 = 3 tens + 8 ones
15 = 1 tens + 5 ones
We have 23 marbles left.
Let’s Warm-up
I scored out of 4.
Operations on 3-digit Numbers
Rakesh is a fruit seller.
He bought 115 mangoes on Monday. He bought 123 apples on Tuesday.
To find the total number of fruits, we need to add the number of fruits bought on Monday and Tuesday.
Addition of 3-digit Numbers
Addition without Regrouping
How many fruits are there with Rakesh? There are 115 mangoes and 123 apples.
We know that
Let us add the 2 numbers using place value blocks. = 1 hundreds (H), = 1 tens (T) and = 1 ones (O).
Thus, the sum of 115 and 123 is 238.
Now let us see if we get the same answer by adding vertically.
Step 1
Step 2
Write the numbers vertically. Add the digits in the ones place. 5 + 3 = 8 ones
Step 3
Add the digits in the tens place. 1 + 2 = 3 tens
Step 4
Add the digits in the hundreds place. 1 + 1 = 2 hundreds
We get 2 hundreds, 3 tens and 8 ones.
115 + 123 = 238 fruits
Example 1: Add 143 and 206 by using the place value blocks and writing the numbers vertically.
Use for 1 hundreds (H), for 1 tens (T) and for 1 ones (O).
Add 215 and 652 using the place value blocks and writing numbers vertically.
Use for 1 hundred (H), for 1 ten (T) and for 1 one (O).
Addition with Regrouping
The total number of fruits Rakesh has is 238.
Now, Rakesh has bought 177 bananas.
Let us see how many fruits are there now.
Let us add the 2 numbers using place value blocks.
Remember!
When we add, the number of things becomes greater.
10 ones = 1 tens
Now let us see if we get the same answer by adding vertically. 415
Step 1
Add the ones.
8 ones + 7 ones = 15 ones
10 ones = 1 tens
Write 5 and move 1 tens to the tens place.
Step 2
Add the tens.
3 tens + 7 tens + 1 tens = 11 tens
10 tens = 1 hundreds
Write 1 and move 1 hundreds to the hundreds place.
Step 3
Add the hundreds.
2 hundreds + 1 hundreds + 1 hundreds = 4 hundreds
Write 4 in the hundreds place.
So, we see that we get the same answer on adding 238 and 177 using place value blocks and vertical addition.
Example 2: Add 289 and 32.
Error Alert!
Write the numbers according to their place value.
Add 256 and 34.
Add 239 and 562 by writing numbers vertically.
Do It Yourself 7A
Add the 3-digit numbers without regrouping.
Add the 3-digit numbers without regrouping.
Draw the place value blocks to add.
Use for 1 hundreds (H), for 1 tens (T) and for 1 ones (O).
Add the given 3-digit numbers vertically.
Chapter 7 • Addition and Subtraction of 3-digit Numbers
Rohan is trying to find the number added to 245 to get 356. Yash helped him and said all the digits in the number are the same. Is he right? What is the number?
Subtraction of 3-digit Numbers
Raghu had 475 fruits on Wednesday. He sold 322 fruits. How many fruits are left with him now?
To find the number of fruits left, we need to subtract 322 from 475.
Remember!
Subtraction Using Place Value Blocks
Let us see how we can subtract 2 numbers using place value blocks.
Step 1
Show the bigger number using place value blocks.
475
Step 2
Cross out or take away as many blocks as in the smaller number.
475 – 322
Step 3
Count the number of hundreds, tens and ones left. That will give us the answer.
475 – 322 = 153
Vertical Subtraction
Let us see how we can subtract 2 numbers by writing them vertically.
Subtraction means taking something away from a group. We take away the smaller number from the bigger number. The number of things becomes less in subtraction.
Step 1
Write the numbers vertically as per their place values.
Subtract the ones.
5 ones – 2 ones = 3 ones
Write 3 in the ones place.
Step 2
Subtract the tens.
7 tens – 2 tens = 5 tens
Write 5 in the tens place.
Step 3
Subtract the hundreds.
4 hundreds – 3 hundreds = 1 hundreds
Write 1 in the hundreds place.
Here, we can see that we get the same answer on subtracting 322 from 475 using place value blocks and vertical subtraction.
There are 153 fruits left with Raghu.
We
Remember!
When we subtract the same number from itself, we get 0. 9 – 9 = 0
Example 3: Subtract 23 from 138 by writing the numbers vertically and using the place value blocks and vertical subtraction.
Use for 1 hundreds (H), for 1 tens (T) and for 1 ones (O).
Solve 567 – 123 using the place value blocks and vertical subtraction.
Use for 1 hundreds (H), for 1 tens (T) and for 1 ones (O).
Draw place value block and subtract.
Use for 1 hundreds (H), for 1 tens (T) and for 1 ones (O).
Subtract the numbers vertically.
Medha creates the largest possible number using the digits 4, 3 and 5 and subtracts the smallest 3-digit number from it. Find the digit at the ones place of the difference. 1
Solving Word Problems on Addition and Subtraction
Shreya and her friends went to a library.
Teacher: Could you please help me arrange the books?
Shreya: Yes, ma’am.
There were 135 books on the table. The teacher gave 125 more books.
Shreya and her friends arranged 100 books. How many books are left to be arranged?
Identifying the Right Operation
First, there were 135 books. Then, 125 more books were added. So, Shreya needs to add 135 and 125 to find the total number of books.
Remember!
When we have to find the total number, or how many in all, we add.
There are 260 books in all. Shreya and her friends arranged 100 books. So how many are remaining?
We have to subtract 100 from 260.
Remember!
When we have to find how many are left or remaining, we subtract.
So, we get 160 when we subtract 100 from 260. Thus, 160 books are left to arrange.
Example 3:
There were 235 apples in a basket. 125 apples were sold. How many apples are left?
Add or Subtract? Solve
Addition
Subtraction
We have to find out how many are left. So, we subtract.
Read the situation. Choose whether to add or subtract. Then, solve.
There were 234 students in the hall. 150 more students joined them. How many students are there in the hall now?
Rahul had 262 crayons, but he lost 130 crayons. How many crayons are left?
Word Problems on Addition and Subtraction
The Food Corporation of India stores wheat in bags in large godowns. Wheat is stored to protect it from insects. 350 bags were sold to the shopkeepers directly. 573 bags were transported to other places. What is the total number of wheat bags?
What do we know?
Wheat bags sold to shopkeepers = 350
Wheat bags transported to other places = 573
What do we find?
Total number of wheat bags. How do we find?
The keyword ‘total’ tells us that we need to add. 350 + 573
Solve to find the answer.
So, the total number of wheat bags is 923.
Chikankari kurtas are made in Lucknow. A factory makes 124 kurtas. 120 kurtas were sold. How many kurtas are left? Use the method given below to solve.
What do we know?
What do we find?
How do we find (keyword)?
Solve to find the answer.
Do It Yourself 7C
Identify the correct operation and solve.
a There are 456 books on a table. The teacher keeps 198 more books on the table. How many books are there on the table?
2
b There were 568 toys in a toy store. 232 were sold. How many toys are left?
3
A farm is a place where animals are kept. Read the table, find the correct operation and solve the problems.
a What is the total number of sheep and goats on the farm?
b How many more dogs are there than sheep?
Pappad is a thin wafer or flat bread. It is made up of dried lentils. A shopkeeper had 583 packets of pappad. He sold 272 packets. How many packets are left with the shopkeeper?
4
Tigers are kept safely in the tiger reserves. Corbett has 260 tigers, and Kanha has 105 tigers. How many tigers are there in total at the Corbett and Kanha Tiger reserves?
Challenge
1 Critical Thinking
Vidit writes a 3-digit number with the tens digit as 0, the ones digit as 4 and the hundreds digit as 2. Suhaan writes the number by reversing the same digits. Then they add the numbers. What do they get?
Points to Remember
• We write numbers according to their place value while adding and subtracting them.
• To add or subtract numbers, we start from the ones place and move higher on the place value chart.
• In word problems, words like join, add, added, put together, total and in all tell us that we need to add the numbers.
• In word problems, words like take away, subtract, less than, fewer, left and remaining tell us that we need to subtract the numbers.
Setting: In groups of 4
Materials Required: Number chits, pencil, operation chits, place value blocks
Method:
Make chits for numbers 0 to 9. Make 2 operation chits by writing the addition ‘+’ and subtraction ‘ –’ symbols on them.
Player 1 will pick 3 chits and form a 3-digit number.
Player 2 will again pick 3 chits and form a 3-digit number.
Player 3 will choose the operation chit: addition or subtraction.
Player 4 will solve it using place value blocks.
Repeat the cycle until everyone gets their turn to solve.
Draw place value blocks to solve.
4 a
Fill in the blanks.
456 + 456 = 9 hundreds + tens + 2 ones
5
b c Identify the correct operation and solve.
763 + 234 = hundreds + 9 tens + 7 ones
435 + 546 = 9 hundreds + 8 tens + ones
a Rahul bought 345 books and arranged 115 books on the shelf. How many books are left to be arranged on the shelf?
b Mona had 123 marbles. Her friend Tina had 167 marbles. How many marbles are there in all?
A book fair is a place where many different types of books are sold. There are 568 English books and 345 Hindi books in a book fair. Which books are fewer, and by how much?
6 Cross Curricular Phool jhadu is made up of broom grass. The flower of this plant is used for cleaning. Heera makes 145 jhadus in one month and 206 jhadus in another month. How many jhadus did she make it in all?
7 Cross Curricular Rohit baked a batch of 340 biscuits for an event. He baked 105 more biscuits for the same event. He sold 130 biscuits at the event. How many biscuits does he have now?
9
8 Given below are place value blocks to show a number.
[Hundreds = , Tens = , Ones = ]
a What is the number shown by the place value blocks?
b What will the new number be, if Anaisha adds 145 to this number?
1 Challenge
2
Column 1
Critical Thinking & Creativity
A milkman delivers milk to different houses. Solve the riddles in Column 2 and match them to the correct house numbers in Column 1. Add or subtract to find the answers.
Column 2
a Mr Parikh’s house no. is 299. My number is 100 more than 216.
b Mr Ahmad’s house no. is 300. My number is 25 less than 267.
c Ms Shah’s house no. is 316. My number is the number before 300.
d Mrs Paul’s house no. is 242. My number is 10 less than 310.
Create a word problem on subtracting 456 from 124 and solve it.
Real-Life Maths
Soap Making
Ria makes organic soap using plants, olive oil, coconut oil and water. Ria and her friends plan to put a stall in the school fair and then donate money earned for books for orphanages. They make 237 bars of soap and sell 168. Later, they made 134 more bars.
1 How many bars of soap did they make first?
a 237
c 168
b 134
d 234
2 How many soap bars were left after selling the bars the first time?
3 What is the total number of soap bars they have in the end?
4 Have you ever helped anyone in need? How? Cross Curricular & Value Development
Multiplication Tables
3, 4 and 6
Let's Recall
There are 5 groups of 4 flowers.
To find the total number of flowers, we add 4 five times. So, we are adding the same number again and again. This is known as repeated addition.
Let's Warm-up
Match the following.
Multiplication Tables
Aditya is helping his mother to set the table. Some guests are coming for lunch.
Place 3 plates on the table. Bring 2 bowls for each plate.
How many bowls should I bring?
Multiplying by 3
Multiplying by 3 means counting all the groups of 3 together.
3 groups of 2 = 6 or 3 twos are 6
3 × 2 = 6 bowls
Remember!
Let us count the number of bowls to build the multiplication table of 3. 3 ones are 33 × 1 = 3
Multiplication is repeated addition.
3 eights are 243 × 8 = 24 3 nines are 273 × 9 = 27 3 tens are 303 × 10 = 30
Example 1: Count the number of groups. Count the number of ducks in each group. Write the multiplied answer.
There are 3 groups. There are 5 ducks in each group. The multiplied answer is: 3 × 5 = 15
Draw stars to show the table of 3. 3 × 5
Fill in the missing numbers using the table of 3.
a 3, 6, 9, b 18, 21, , 27 c 12, , 18, 21 d , 24, , 30 e 9, , , f 15, , ,
Use the table of 3 to find the answer mentally. a 3 × 6 b 3 × 9 c 3 × 5 d 3 × 8 e 3 × 10 f 3 × 4
Fill in the blanks. a 3 × = 18 b 3 × = 30 c 3 × = 6 d 3 × = 27
Write the multiplication statement for the following from the table of 3. Draw circles to show it.
I am a number less than 20. I come in the multiplication table of 3. I have 2 in the ones place. What number am I? 1 Critical Thinking
Multiplying by 4
Aditya is helping his mother lay the table for dinner. Aditya is sitting at the table with his parents. Aditya’s sister, Mohi, walks in.
Aditya, place 1 more plate for Mohi. Place 3 cookies on each plate.
Sure Mom!
There were 3 plates. Aditya placed one more plate. There are 4 plates now. He placed 3 cookies on each plate. 3+
4 groups of 3 = 12 4 × 3 = 12 cookies
Let us count the number of cookies to build the table of 4.
4 ones are 44 × 1 = 4
4 twos are 84 × 2 = 8
4 threes are 124 × 3 = 12
4 fours are 164 × 4 = 16
4 fives are 204 × 5 = 20
4 sixes are 244 × 6 = 24
4 sevens are 284 × 7 = 28
4 eights are 324 × 8 = 32
4 nines are 364 × 9 = 36
4 tens are 404 × 10 = 40
Example 2: Count the number of groups. Count the number of marbles in each group. Write the multiplication fact.
There are 4 groups of 6 marbles.
4 × 6 = 24
Write the multiplication fact.
a 4 groups of 3 b 4 groups of 8 c 4 groups of 2
d 4 groups of 6 e 4 groups of 9 f 4 groups of 1
Use the table of 4 to find the answer mentally.
a 4 × 5 b 4 × 3 c 4 × 10
Fill in the blanks.
a 4 are 20 b 4 are 40 c 4 are 36 d 4 are 16
4 are 8 f 4 are 24
Write the multiplication statement for the following using the table of 4. Draw any object to show it.
28 b 36 c 16
1 Critical Thinking
There are 4 boxes with an equal number of books. How many books are there in total, if there are:
a 6 books in each box? b 8 books in each box?
c 3 books in each box?
Multiplying by 6
After lunch, everyone played a game with balloons.
Mohi, we are 6 members. We need 4 balloons for each member!
How many balloons do we need in total?
Multiplying by 6 means counting all the groups of 6 together.
So, 6 members with 4 balloons will have a total of:
Multiplication
3, 4 and 6
6 × 4 = 24 balloons or 6 fours are 24.
Let’s count the number of balloons to build the table of 6.
6 ones are 66 × 1 = 6
6 twos are 126 × 2 = 12
6 threes are 186 × 3 = 18
6 fours are 246 × 4 = 24
6 fives are 306 × 5 = 30
6 sixes are 366 × 6 = 36
6 sevens are 426 × 7 = 42
6 eights are 486 × 8 = 48 6 nines are 546 × 9 = 54 6 tens are 606 × 10 = 60
Example 3: Count the number of groups. Count the number of pens in each group. Write the multiplication fact.
There are 6 groups of 7 pens.
Multiplication fact: 6 × 7 = 42
Write the multiplication statement for the pictures. a Do It Yourself 8C b
Fill in the missing numbers using the table of 6.
Use the table of 6 and answer.
Multiplying 2-digit Numbers
Meghna went to a shop to buy some eggs. In the shop, she saw eggs in trays. There were 4 trays, and each tray had 12 eggs in it. She wondered how many eggs would there be in total.
But I don’t know how to find 4 × 12.
Multiplication without Regrouping
To multiply a 2-digit number with a 1-digit number, we can use the column method.
The shopkeeper has 4 trays with 12 eggs in each tray.
We need to multiply 12 by 4.
Let us multiply 12 by 4 using the multiplication table of the smaller number 4.
Step 1
Write the 2-digit number according to its place value in the table. Write the smaller number below it. TO 12 ×4
Step 2
Multiply the smaller number with the ones of the 2-digit number.
4 × 2 = 8
Write 8 in the ones place.
Step 3
Multiply the smaller number with the tens of the 2-digit number.
4 × 1 = 4
Write 4 in the tens place.
So, 12 × 4 = 48.
So, 23 × 3 = 69. Example 4: Multiply 23 × 3.
Did You Know?
Brahmagupta, an Indian Mathematician was the first one to explain the rules of multiplication.
Chaach is a curd-based drink. It has a cooling, refreshing effect on the body in summer. Each jug has 3 glasses of chaach. 13 such jugs will have 13 × 3 = glasses of chaach.
Rina multiplied 13 by a number to get 52. What is the number? 1
Multiplication with Regrouping
Let us learn how to group ones and tens to make multiplication of larger numbers easier.
Regrouping Ones and Tens
Abdul has 93 marbles in each packet. He has 4 such packets. To see how many marbles Abdul has in total, we need to multiply 93 by 4.
Look at the given steps:
Step 1
Write the 2-digit number according to its place value in the table.
Write the smaller number below it.
Step 2
Multiply the smaller number with the ones digit of the 2-digit number.
4 × 3 = 12. 12 has 1 tens and 2 ones.
Write 2 in the ones place and carry over the 1 to the tens place.
Step 3
Multiply the smaller number with the tens of the 2-digit number.
9 × 4 = 36. We carried over 1 tens.
36 + 1 = 37
Write 3 in the hundreds place and 7 in the tens place.
So, 93 × 4 = 372.
Example 5: Multiply 63 by 8.
So, 63 × 8 = 504
1 84 × 2
Multiply.
Solve.
a 18 × 4 b 45 × 2 c 6 × 61
d 3 × 92 e 5 × 59
28 × 6
Makar Sankranti is celebrated with kite flying to mark the end of winters. There are 13 types of kites available at stalls A and B.
If stall A sells 2 kites of each type, the total number sold is = 13 × 2 = 26 kites.
If stall B sells 6 kites of each type, the total number sold is = 13 × = kites.
Write True or False. By multiplying 41 by 6, we will get 7 ones. Explain your answer by showing multiplication.
How many tens will you get when you multiply 92 by 5?
21 × 3 = and 21 × 30 = . 1
Look at the pattern and fill in the missing numbers. 24 × 2 = 48 and 24 × 20 = 480.
Chapter 8 • Multiplication Tables 3, 4 and 6
Story Problems on Multiplication
Let us explore some story problems on multiplication.
Meghna went to another shop and saw 6 trays, with 30 eggs in each tray. How many eggs were there in total?
What do we know?
Total trays = 6
Eggs in each tray = 30
What do we want to know?
We need to find the total number of eggs.
How do we find the answer?
Total number of eggs = Total trays × Eggs in each tray
Solve to find the answer.
= 30 × 6 = 180 eggs
So, there are 180 eggs in all.
A hall has 86 desks, and 4 people can sit at each desk. How many people can sit in the hall?
What do we know?
Total desks =
People at each desk =
What do we want to know?
We need to find the .
How do we find the answer?
Number of = Total desks × People at each desk
Solve to find the answer.
86 × 4 =
There are 98 packets and 5 candies in each packet. How many candies are there in total? A bus has 46 seats, and there are 4 such buses. How many seats are there in total? There are 6 pins in each pouch. If there are 52 such pouches, how many pins are there in total?
Bamboo is used for making garden fences. It is an eco-friendly choice. 6 bamboo poles are needed to fence a garden. Each pole costs ₹85. What is the total cost of all the bamboo poles?
Challenge
Critical Thinking & Creativity
Create a word problem to multiply 68 × 3. Find the answer. 1
Points to Remember
•We can use the multiplication tables to multiply numbers by 3, 4 and 6.
•To multiply 2-digit numbers with 1 digit, we can use the column method.
• Always multiply the ones digit first and then multiply the tens digit.
•While adding, regroup ones and tens wherever needed.
Setting: Whole class
Learning & Communication
What Is My Position!
Materials Required: 150 ice-cream sticks, 6 transparent glasses
Method:
Take 1 glass and 36 ice-cream sticks.
Make bundles of tens with the ice-cream sticks. Put the single sticks next to them. Put all of these in one glass.
Make 4 such groups of ice-cream sticks in 4 glasses.
This shows 4 groups of 36 or 4 × 36.
Put all the ice cream sticks together and find the total.
Multiply 36 by 4 using the column method.
Match your answer with the total number of ice-cream sticks. Discuss the answer in class.
Try
more multiplication problems using both methods.
Use the table of 3 and write the answer.
Solve mentally by using the table of 4.
Fill in the blanks by using the table of 6.
Multiply.
25 × 4
In cricket, a six is scored when the ball is hit over the boundary without bouncing and touches the ground outside the field of play. In a cricket match, if Rahul scored 6 runs on each of the 7 balls he played, how many runs did Rahul score?
Garba is a folk dance from Gujarat. It is done during the Navratri days. If 28 dancers are there in 4 rows, how many dancers are there in total?
There are 6 plates of dosa, and each plate costs �85. How much do all the dosas cost in total?
Challenge
Solve the multiplication problems and complete the crossword. First, solve across, and then down.
Across Down
1. 6 × 8 2. 9 × 9
3. 8 × 9 4. 4 × 6
5. 3 × 5 6. 6 × 9
7. 8 × 8
8. 4 × 10
Write a word problem to show the multiplication of 42 by 5. 2
Sugarcane Juice
We get sugarcane juice by pressing sugarcane. It refreshes us. Sonesh and his friends decided to distribute free juice during the summer to the people passing by. They have 5 jugs of juice. Each jug has 81 cups of juice. Read the questions and answer.
1 Why should we drink sugarcane juice in summer?
2 How many jugs of juice do they have?
3 How many cups of juice does each jug have?
4 How many cups of juice will they be able to distribute?
5 Which juice do you like? Value Development & Cross Curricular
9 Introduction to Division
Let’s Recall
3 groups with 2 birds in each.
4 groups with 5 balloons in each.
Let’s Warm-up Match the pictures with the correct statement.
Understanding Division
Sam has 6 chocolates.
Sam wants to share the chocolates with his friend, Ravi.
Both of them should have the same number of chocolates.
How many chocolates will Sam share with Ravi?
Division as Equal Sharing
Let us divide the 6 chocolates equally between Sam and Ravi.
First, each boy takes 1 chocolate.
We strike out 2.
4 chocolates are left with Sam.
Then, again they take 1 more chocolate each.
We strike out 2 more chocolates.
Now, 2 chocolates are left with Sam.
Then, they take 1 more chocolate each.
We strike out 2 chocolates. Sam
No more chocolates are left with Sam.
We get 2 groups of 3 chocolates.
Do It Together
Example 1: Share 4 laddoos between Meena and Tina.
Strike out 2 laddoos. Meena and Tina get 1 laddoo each.
Strike out 2 remaining laddoos. Meena and Tina get 2 laddoos each.
Example 2: There are 10 apples. Circle to show 2 apples in each basket.
Remember!
There are 2 apples in each basket. There are 5 groups of 2 apples.
Share 16 strawberries among 4 friends. Draw circles around the strawberries to show equal sharing.
The children will get strawberries each. We get 4 groups of strawberries.
Circle the set of pictures that show equal sharing. One has been done for you.
In division, an equal number of objects is kept in each group.
b c Draw and share the objects equally.
a Share 9 carrots among 3 rabbits.
Each rabbit will get carrots.
b Share 8 biscuits between 2 friends. Each friend will get biscuits.
How many items will each child get?
a 8 bananas shared equally among 4 children.
b 12 cupcakes shared equally among 4 children.
There are 20 mangoes. Draw pictures to divide the mangoes among 5 children. How many mangoes did each child get?
Challenge
Critical Thinking & Art Integration
There are 18 laddoos. Draw plates and laddoos to share the laddoos on any number of plates such that there are an equal number of ladoos on each plate.
Division as Repeated Subtraction
Next day, 8 chocolates were divided between Sam and Ravi. They got 4 chocolates each.
Let us understand this using subtraction.
There were 8 chocolates. Sam Ravi
One chocolate was taken by each.
8 – 2 = 6. 6 chocolates are left.
One more chocolate was taken by each.
6 – 2 = 4. 4 chocolates are left
One more chocolate was taken by each.
4 – 2 = 2. 2 chocolates are left.
Again, one more chocolate was taken by each.
2 – 2 = 0. No chocolates are left.
We see that 2 is subtracted from 8 four times. This means 8 divided by 2 is equal to 4. So, division is also known as repeated subtraction.
Let us see this using a number strip.
The answer is 4 because we are subtracting 2 four times until we get 0. 2 – 2 = 0 4 – 2 = 2
Division Fact
Dividing 8 in equal groups of 2 can be written as 8 ÷ 2 = 4. This is the division fact. ‘÷’ is the symbol used to show division.
We keep subtracting from the total until the answer is 0.
Total number of things.
8 divided into groups of 2 will give 4 equal groups.
Number of things in each group. Number of groups.
Example 3: Divide 12 pencils among a group of students such that each student gets 3 pencils. Use repeated subtraction to find the number of students.
3 is subtracted from 12 four times.
12 ÷ 3 = 4 is the division fact, so 4 students get 3 pencils each.
Example 4: Show the division fact 12 ÷ 4 using a number strip. We start going back from 12 by 4 steps.
The answer is 3 because we are subtracting 4 three times until we get 0. 0123456789101112131415 4 – 4 = 0
Divide 15 apples into groups of 5. Show using repeated subtraction and using a number strip. Write down the division fact.
5 is subtracted times until we get 0.
Division fact is 15 ÷ 5 = .
Do It Yourself 9B
Use repeated subtraction to show the answer. How many children will get these items if:
a 18 chocolates are shared equally in groups of 6?
b 14 pens are shared equally in groups of 2?
c 8 apples are shared equally in groups of 4?
Circle the correct division fact.
a 12 books shared in groups of 3. 3 ÷ 12 12 ÷ 3 12 ÷ 12
2 Show the repeated subtraction by showing jumps on the number strip.
b 15 pencils shared in groups of 5.15 ÷ 5 5 ÷ 15 15 ÷ 15
3 Art Integration 0123456789101112131415 0123456789101112131415
4
a 15 ÷ 3
b 10 ÷ 5
Write True or False.
a 15 objects in 3 equal groups, with 5 objects in each group.
b 12 objects in 4 equal groups, with 2 objects in each group.
c 20 in 4 equal groups can be written as 4 ÷ 20.
Challenge Critical Thinking & Art Integration
1 Ravi has 8 vases. He has to put 24 flowers equally in the vases. How many more flowers does he need to put in the vases given below so that no flower is left with him? Show by drawing the flowers.
Division and Multiplication Facts
Let us see how multiplication and division are related.
Case 1: 8 chocolates are divided between Sam and Ravi. They have 4 chocolates each.
We have 2 groups of 4.
Division fact:8÷ 2 = 4
How do we get this using multiplication?
Say the table of 2 until we get 8.
2 × 4 = 8. (Multiplication fact)
So, 8÷ 2 = 4.
Case 2: 8 chocolates are divided among 4 children. They get 2 chocolates each. We have 4 groups of 2.
Division fact: 8÷ 4 = 2
Say the table of 4 until we get 8.
4 × 2 = 8. (Multiplication fact)
So, 8 ÷ 4 =2.
For 1 multiplication fact, there can be 2 division facts:
Error Alert!
Divide 12 in 3 equal groups is written as:
Example 5: Write the division fact and the multiplication fact for 4 groups of 3 balloons.
We have 4 groups of 3.
Multiplication fact: 4 × 3 = 12
Division facts: 12 ÷ 4 = 3 and 12 ÷ 3 = 4
Write down the division fact from the given multiplication fact.
= 15
Do It Yourself 9C
Think and Tell!
Can you divide 13 mangoes among 4 friends?
How many will each friend get?
Fill in the blanks to write down the division and the multiplication facts.
Draw pictures to show the groups and write the multiplication facts. Then write one division fact for the multiplication fact.
a 4 groups with 2 in each b 6 groups with 3 in each
Anna can think of only one division fact for 6 × 4 = 24. How many division facts does a multiplication fact have? Can you help her?
Shweta has 18 roses with her. She needs to make 6 garlands with an equal number of flowers in each garland. How many roses will each garland have?
We know 18 ÷ 6 = 3 (We say the table of 6 until we get 18, 6 × 3 = 18)
Each garland will have 3 flowers in it.
Let us understand other ways of writing and solving division.
Long Division
We will use the division house to divide two numbers.
18 ÷ 6 = 3 can be written as:
1. Write the bigger number inside the division house.
3. Say the table of 6 until we get 18. 6 × 3 = 18. So, 3 is the answer.
2. Write the smaller number outside the division house.
Example 6: Solve 15 ÷ 5.
We say the table of 5 until we get 15. 5 × 3 = 15. So, 3 is the answer.
Solve 16 ÷ 4. Do It Together
We say the table of until we get 16. × = 16. So, is the answer. 4
Do It Yourself 9D
Solve the given sums to find the answer.
Write down the sums and solve using the long division method. a 18 ÷ 2 b 20 ÷ 5 c 16 ÷ 2
Use the long division method to show 21 chocolates in 7 groups of 3.
Word Problems on Division
We can use the CUBES method to solve story sums. In the CUBES method, we follow the 5 given steps.
18 flowers are kept equally in 3 baskets. How many flowers are there in each basket?
S: Solve and check! Circle the numbers.
C: Circle the numbers.
U: Underline the question.
B: Box the key words.
E: Evaluate/draw.
Underline the question. Box the key words.
Total number of flowers = 18
Number of baskets = 3
Flowers in each basket = 18 ÷ 3
There are 6 flowers in each basket.
Check: 3 × 6 = 18. So, the answer is correct.
Mother bought 30 sweets for a festival. She has to give an equal number of sweets to 6 members of the family. How many sweets will each family member get?
Total number of sweets =
Number of family members =
C: Circle the numbers.
U: Underline the question.
B: Box the key words.
E: Evaluate/draw.
S: Solve and check! 6 30
The number of sweets each family member will get = 30 _____ 6. Each family member will get sweets.
There are 12 pencils. The pencils are kept equally in 4 pencil boxes. How many pencils are there in each box?
There are 20 cherries. The cherries are placed equally on top of the 5 cakes. How many cherries are there on each cake?
Rita has 10 apples. She wants to give an equal number of apples to 5 friends. How many apples will each friend get?
Jalebi is one of the most popular desserts in India. Nidhi has 18 jalebis and she wants to distribute them equally among 6 friends. How many jalebis will each friend get?
Sherry has 35 candies. She wants to share these among 7 children. Merry says, “Multiply 35 and 7 to get the number of candies each child gets”. Is Merry correct? Explain your answer.
Points to Remember
• Division means a set of things shared equally among groups.
• The same number is subtracted unless 0 is left.
• The symbol ÷ is used to show division.
• Division and multiplication are related.
Share Math Lab
Setting: In groups of 4
Materials required: Buttons/rajma beans/beads, A4 size paper with pictures of 5 shirts printed on it. (Make sure the shirts do not have buttons)
Method:
The students will then check the division facts using long division. 1 2 3 4
Each group should get 25 buttons/beans/beads and the A4 sheet with shirts printed on it.
Two members of the group will place buttons on the shirts given, so that each shirt has an equal number of buttons.
The remaining two members will write the division fact, looking at the equal sharing.
Chapter Checkup
Circle to make equal groups.
a Make groups of 4. There are groups of 4.
b Make groups of 2. There are groups of 2.
Divide the objects using repeated subtraction.
a 12 balls in 4 boxes. b 18 pencils in 3 boxes.
c 20 marbles in 5 boxes. d 16 books on 2 shelves.
Write down the division facts for the given multiplication fact. a 2 × 3 = 6
3 × 8 = 24
3 × 3 = 9 Solve.
Solve using long division.
Fill in the blanks.
a 35 ÷ 5 is . b 18 ÷ 3 is . c 28 ÷ 4 is .
Amlas or gooseberries boost appetite. They are rich in vitamins. Julia has 18 amlas. She needs to divide these equally into 6 packets. How many amlas will there be in each packet?
Jack has 20 packets of rice. He wants to give an equal number of packets to 5 families. How many packets of rice will each family get?
If 36 ÷ 6 = 6 is a divison fact, its multiplication fact with the same two numbers is 6 × 6 = 36. Find one more division fact that we get by multiplying two numbers that are the same.
I am a 1-digit number. If I am multiplied by 6, the product is 24. When I divide 36, the answer is 9. Who am I? 1 2 Challenge
Annual Function
Christmas Carols are performed during Christmas. Ruhaan and his class are planning to sing Christmas Carols. Look at the picture and answer the questions.
1 How many children are there? a 10 b 11 c 12 d 9
2 How many groups of 2 can they form?
3 Can they form 4 groups with 3 children in each group?
4 If not, how many more/less children do they need?
5 One of Ruhaan’s friends was feeling nervous about singing. What should Ruhaan do to encourage him?
Introduction to Fractions
Let’s Recall
We all love pizza, and it comes in pieces that are equal in size! It is split into 4, 6 or 8 pieces. But when we cut them ourselves, we might cut them into pieces that are not equal.
This pizza is divided into 2 equal parts.
This pizza is cut into 2 parts that are not equal.
A complete pizza is called one whole. When something is divided into equal parts, we get 2 or more parts that are exactly equal in size.
Equal parts
Let’s Warm-up
Parts that are not equal
Tick () the pictures showing equal parts. 1 2 3 4
Understanding Fractions
Sonu and Neha were having dinner. Only one chapati was left. Both of them wanted to eat it.
What can they do?
Parts
of Whole
Mother gave them an idea to cut the chapati into parts. Let us us see how the chapati can be divided. These show parts of a whole. whole 2 parts2 parts 3 parts
Fraction means part of a whole.
Equal and Unequal Parts
Remember!
Whole of something means a complete thing.
Let us see, if we can divide a chapati in different ways. When something is divided into parts that are not equal, the parts are called unequal parts. Unequal parts do not fractions. When the parts are of the same size, they are equal parts.
Think and Tell
Equal PartsUnequal Parts
Error Alert!
Shape divided into unequal parts
One half
Shape divided into equal parts
One half Can we divide all things in equal parts?
Example 1: Tick () the pictures that show unequal parts.
Here, the 3 parts are unequal parts. Here, the 2 parts are equal parts. Here, the 2 parts are unequal parts. Here, the 3 parts are equal parts.
Example 2: Divide the whole into equal parts. 2 parts 4 parts 3 parts
1 Tick () the box for the image that is divided into equal parts. Write the number of equal parts.
2 Draw a line such that it cuts the shape into 2 equal parts.
Halves, Thirds and Fourths
Let us learn more about fractions. We have a whole circle. Let us divide the circle in equal parts.
3 equal parts3 equal parts
one-third two-thirds
One-half means one out of two equal parts or halves. 1 whole2 equal parts one-half
equal parts4 equal parts
Did You Know?
In ancient India, people knew about fractions. The fraction one-half was called ardha.
Example 3: Colour one-half of the rectangle green.
Shade the shapes to show the given fractions. 1 Three-fourths
1 Challenge
of
Critical Thinking
Rachel cut the squares into 2 equal parts and shaded one part. Which of these DO NOT show the squares that Rachel might have cut out?
Reading and Writing Fractions
Let us understand how we can read and write fractions using numbers.
One-half
One out of two equal parts is shaded.
Top part shows the number of parts shaded.
Bottom part shows the total number of equal parts.
Remember!
The parts shaded in a whole make the fraction.
1 part out of 3 equal parts is shaded.
1 part out of 4 equal parts is shaded.
3 parts out of 4 equal parts are shaded. 2 parts out of 3 equal parts are shaded.
Shade the parts or write the correct fraction.
Write the fraction of the pizza left.
Naisha and Raina order an aloo parantha and divide it into two parts. Naisha is hungry. So Raina gives her the bigger part. Has Raina done the correct thing? Is each piece called a half?
Write the fraction in numbers. Draw any shape to show the fractions.
one-third b one-half c three-fourths d two-thirds
Draw any figure or shape and divide it into equal parts. Shade a part and write its fraction.
1 Priyanka uses old newspapers to wrap gifts. She cuts a sheet of an old newspaper into four equal parts and used one part of it to wrap a birthday gift. What is the fraction of the newspaper which was unused? How else can old newspapers be used?
Points to Remember
• When we divide a shape or thing into equal parts, then each part is a fraction of the whole.
• When an object is cut into parts and the parts are not of the same size, they are called unequal parts.
• When a whole is divided into 2 parts, each part is called one-half.
• When a whole is divided into 4 equal parts, each part is called one-fourth.
• When a whole is divided into 3 equal parts, each part is called one-third.
Setting: In groups of 4
Fun with Paper
Material required: A4 size white paper, colours, pencils
Method:
Take an A4 size paper.
Fold it by bringing the opposite edges together. Unfold the paper.
Then draw a line to show that the paper is split into two equal halves.
Try to divide the sheet into three or four equal parts and show the fractions you have learnt so far.
Shade these paper fractions and use them to make a collage.
Fill in the blanks.
a 1 2 means part out of equal parts.
b 1 4 means part out of equal parts.
c 1 3 means part out of equal parts.
d 3 4 means parts out of equal parts.
e 2 3 means parts out of equal parts.
Look at the shaded part of the shape. Circle the fraction that represents the shaded portion.
Write the fraction of the coloured part in words.
Colour the shapes on each petal of the flower to match the given fraction. Colour the flowers with your own choice of colours. One has been done for you.
Apple pie is a dessert made from apples cooked under or inside the pastry. Write the fraction of one part for the given apple pie. One has been done for you.
Write True or False.
a One-half is written in words as 1 2 .
b Two-thirds can also be written as 2 3 .
c When one out of 4 parts is shaded, the fraction is 1 4 .
d 3 4 can be shown by shading 1 out of 4 parts.
any shape of your choice and show the
1 Neha, Shreya and Garima want to eat pizza. They ordered one pizza and came up with three different ways to cut the pizza, so that each gets an equal share. Who is correct and why?
Neha Shreya Garima
2 Diya wants to shade 3 parts of the given flower pink. She has already shaded 1 part.
a What fraction of the flower has she already shaded?
b What fraction more of the flower does she need to shade?
Real-Life Maths
Value Development
Vegetable Cutting
Jaya is in the kitchen with her parents. She is learning to cut vegetables from her father. Look at the picture and answer the questions.
1 The tomato is cut in half. Write its fraction.
2 What is cut into unequal parts?
a apple b tomato c cucumber d watermelon
3 Which vegetable or fruit is one whole?
a tomato
b watermelon c apple d cucumber
4 Do you think all vegetables can be cut equally? Give an example.
11 Measurement
Let’s Recall
We use a school bag every day! What items do we have in our school bag?
We have our books. We have our pencil box, which has our pencils and erasers in it. We also have our water bottle.
The pencil is long. The crayon is short. The pencil is longer than the crayon.
Is the book heavier or lighter than the pencil?
The book is heavier than the pencil! Try holding them both in your hands.
Look at your water bottle. It holds water.
So, does the bottle hold more water than the glass?
The bottle can hold more water than the glass. So the bottle has more capacity than the glass.
Let’s Warm-up
Circle the correct answer.
Which is the tallest?Which is the heaviest? Which has the most capacity?
Length
Real Life Connect
Sunny and Priya have two ropes.
Sunny says, “I have a long rope.”
Priya says, “I have a short rope.”
Length Using Things Around Us
We measure length to see how long or short something is.
I have a short rope. I have a long rope.
Sunny and Priya can use their hands and arms to find the length of the ropes. But their hands and arms are of different lengths. Is there a better way to measure the ropes?
They can use a pencil to measure the length of each rope.
Sunny’s rope is 4 pencils long.
Priya’s rope is 2 pencils long.
Let us use something else. How about a stick?
Sunny’s rope is 2 sticks long.
Priya’s rope is 1 stick long.
We can use other things too. We may use a book, a crayon, a spoon or blocks to measure length.
Remember!
The thing should be shorter than the thing we are measuring. But it should not be too tiny, like a grain.
Think and Tell
Can we measure a tall door with a small crayon? How about with a roll of newspaper?
Example 1: Find the length.
Bottle = 3 crayons long.
Table = 3 books long.
Viraj wants to know how tall his toys are. He is using some blocks. Fill in the blanks with the help of blocks.
1 The teddy is blocks tall.
2 The toy giraffe is about blocks tall.
3 The paper fan is blocks tall.
4 The teddy is 2 blocks taller than the toy car. The toy giraffe is taller than the paper fan (2 blocks/1 block).
Look at the picture. Tick () the correct answer.
a To measure the length of a tree ( ), we can use: A rope A ball
b To measure how tall a door is ( ), we can use:
Look at the picture. Fill in the blanks.
sharpener A stick Do It Yourself 11A b Mat = crayons long.
Sofa = pencils long.
How many blocks long are these things? Which is the longest?
Rani measured the height of her doll using crayons. How tall is her doll? Draw crayons to show.
The height of Rani’s doll is about crayons.
Challenge
Thinking & Art Integration
Use a sketch pen to draw the longest and the shortest path from A to B. 1
Length by Standard Units
Ridhi measures her bottle using her pencil. The bottle is 2 pencils tall. The next day, she measures her bottle again. The bottle is 3 pencils tall.
Ridhi: How is this possible?
Mother: You must have sharpened your pencil. It has become shorter now. Things we use to measure length can be of different lengths. We need a fixed or standard way to measure things. This helps us to get the correct measurement each time.
Centimetre
We can use a ruler to measure things in fixed units. It measures in centimetres. The short form of centimetre is ‘cm’.
This is 1 centimetre or 1 cm on a ruler.
This is a 15 centimetre or 15 cm long ruler.
We mostly use centimetres to measure short lengths. An eraser, a pair of scissors, a pencil and many other things can be measured with a ruler. Let us see some examples:
These marks on a ruler tell us how many centimetres long a thing is.
When using a ruler, always start from 0 cm. Never measure from the middle or the end of the ruler.
Example 2: Look at the picture. What is the length of this pen?
We can see that the length of the pen is 9 cm.
Metre
Metre is another standard unit of length. The short form for metre is ‘m’.
We use a metre rod or a measuring tape to measure length in metres. We use metres to measure long lengths, like a room or a piece of cloth.
A tailor measures clothes with a measuring tape.
A carpenter measures doors and windows with a measuring tape or rod.
Example 3: Which of these will we measure in metres?
A spoon can be measured in centimetres. A bed is longer than a spoon. So, it needs to be measured in metres.
Fill in the blank with the correct unit of length (m or cm).
A door is measured in ______ . 2 A lamp post is measured in ____ .
A mirror is measured in . 4 A phone is measured in .
3 The car is m shorter.
4
The average length of a small car is 3 m. How much shorter is the given car than the average length?
2 m
The length of the mango tree leaf is 30 cm and the length of the peepal tree leaf is 12 cm. Which leaf is longer and by how much?
Challenge
1
Critical Thinking
The length of a crayon is 10 cm. How many crayons of the same length are needed to measure a plant sapling of length 1 m?
Hint: 1 m = 100 cm.
Weight
Heena and Amir want to check whose bag is heavier. They go to a park and put their bags on each side of a seesaw.
Whose bag is heavier?
Can we find out how heavy Amir’s bag is? Let us see!
Did You Know?
On a seesaw, when one side is heavier, it goes down, and the lighter side goes up!
Heena Amir
Mango leaf
Peepal leaf
Weight Using Things Around Us
We measure weight to see how heavy or light something is.
Look at the weight balance. It is the same as a seesaw.
1 pumpkin is heavier than 1 corn cob.
Let us add more corn cobs to the other side.
The weight of 5 corn cobs is the same as that of 1 pumpkin.
Shall we add more corn cobs?
Now, 8 corn cobs are heavier than a pumpkin.
We can also use blocks to check the weight of things.
Example 4: Find the weight of the carrots, using the blocks.
Look at the weight balances. Fill in the blanks.
Trees have a big trunk of wood and many branches. Shrubs are medium sized plants. Which is lighter—a tree or a shrub?
5 blocks are equal to one brick. How many blocks would be equal to two such bricks?
Weight by Standard Units
A vegetable seller is using a balance to measure the weight of some vegetables.
Look at the weight bars. Shopkeepers and vegetable sellers use weights like these on one side of the balance. On the other side, they put the vegetables that they want to weigh.
Weight bars come in grams and kilograms.
Gram
A gram is a standard unit to measure weight. The short form of gram is ‘g’.
These are gram weights.
We use gram weights to measure light things like fruit, candy and small vegetables.
Example 5: Ramu is buying some fruits. The seller puts the fruits on the balance. How many grams of fruits has Ramu bought?
3 weight bars of 100 grams = 100 g + 100 g + 100 g = 300 g
So, Ramu bought 300 g of fruits.
Read the weight of the weight bars. Write the weight of these things in grams.
Bag of rice A candle
Kilogram
A kilogram is another standard unit to measure weight. The short form of kilogram is ‘kg’.
These are kilogram weights.
We use kilogram weights to measure heavier things. We measure sacks of rice and grains, watermelons and our body weight in kilograms.
Example 6: What is the the weight of the pineapples?
1 kg + 2 kg = 3 kg
Weight of pineapples = 3 kg g
Did You Know?
1 How many weights of 2 kg are put on the balance to weigh 4 kg of potatoes?
kg + 2 kg = kg
So, the seller has put weights of 2 kg to weigh 4 kg of potatoes.
2 How many weights of 1 kg and 2 kg should he put to weigh 5 kg of potatoes? kg + kg + kg = 5 kg Items
Think and Tell
Can you tell another way to measure 5 kg of potatoes with 1 kg and 2 kg weights?
Match the items with the correct units in which they should be measured.
Units of Weight
b A spoon of salt
c A sack of wheat
a A basket of tomatoes kilograms grams
d Candy floss
Circle the correct weight for the given items.
Tom wants to weigh a watermelon of 8 kg. He only has a 10 kg weight and a 2 kg and a 1 kg weight. How will he measure the weight of the watermelon?
Capacity
Ritu has a bucket and a mug. She pours 5 mugs of water into the bucket, but it is not even half filled!
What else should I use to fill this bucket faster? Should I use a glass or a jug?
A glass or a jug—which of them will hold more water? Which of them can fill the bucket faster?
Think and Tell
What holds more water—a tank or a river?
Capacity Using Things Around Us
Capacity is how much liquid a bucket, a mug, a jug or any other vessel can hold. Each of them has it own capacity.
The capacity of a bucket is more than a mug. Similarly, a cup has less capacity than a bucket!
We can use smaller containers to fill a bigger container. This helps to measure capacity.
Example 7: How many spoons of soup can this bowl hold— 40 spoons or 5 spoons?
The soup in the spoon is much less than in the bowl. A bowl can hold about 40 spoons of soup.
Look at the picture. Which pot has less capacity?
The _______ pot has (less/more) capacity. It can be filled with glasses while the red pot takes glasses to fill.
Use the jug to fill the glasses. Colour to show filled glasses. How many glasses are you able to fill?
What is the capacity of the jug in cups?
A pot is half filled with 6 glasses of water. What is the capacity of the pot?
Capacity by Standard Units
So far, we have measured capacity using glasses, mugs, or jugs. We should have a standard way to measure capacity.
Millilitre
Millilitre is a standard unit to measure capacity. The short form of millilitre is ‘mL’.
We measure small amounts of liquids in millilitres, like a cup of tea or a spoon of cough syrup. 5 mL50 mL200 mL
Did You Know?
Earlier, the low cost method of collecting rain water was in stepwells known as Bawaris
Example 8: Which of these are measured in mL? Tick () the correct option.
How much is the capacity of these containers? Choose from the options given below.
30 mL
Litre
The litre is another standard unit for measuring capacity. The short form of litre is ‘L’.
Usually, buckets, water cans, bottles and barrels are measured in litres.
Example 9: A water dispenser bottle holds 20 L of water. In a day, 12 L of water is used from the bottle. How much water is left in the bottle for the next day?
Total water in the can = 20 L
Water used = 12 L
Remaining water: 20 – 12 = 8 L
So, 8 L of water is left in the bottle.
Look at the containers. About how much is the capacity of these containers? Choose from the options given below.
Circle
Kheer is a pudding made of milk, sugar and rice. Father makes kheer in a pot. How much kheer can a pot hold—500 mL or 150 L?
Draw 2 containers with different capacities. Label the containers with ‘More Capacity’ and ‘Less Capacity’.
Challenge
Critical Thinking & Value Development
We should conserve water wherever possible. Leela’s water tank was full with 20 L of water. Leela used half of the water for washing clothes and half of the remaining amount for cooking and drinking. How much water is left in the tank now?
Points to Remember
•We measure length to see how long or short something is.
•Centimetre (cm) and metre (m) are the standard units of length.
•We measure weight to see how heavy or light something is.
•Gram (g) and kilogram (kg) are the standard units of weight.
•We measure capacity to see how much liquid something can hold.
•Millilitre (mL) and litre (L) are the standard units of capacity.
Setting: Whole class
Measure the Water
Materials Required: A glass, a litre bottle, a bucket and water.
Method:
Line up the glass, bucket and bottle on a table.
Fill the glass with water to the brim. Pour the water from the glass into the bottle.
Count the number of glasses it took to fill the bottle. Write on the board. Now, pour the water from the bottle into the bucket.
Count the number of bottles it took to fill the bucket. Write on the board.
the findings with the class.
Tina wants to measure a piece of cloth that is 6 m long. Which of these sticks will she use if she wants to use the least number of sticks?
What is the missing weight that balances the scale? Hint: Ten 100 gram(g) weights = 1 kg
Real-Life Maths
Summer Camp
The students of Class 2 go to a summer camp. They learnt how to stay with each other and share things. Look at the picture and answer the questions.
1 Which tent is the farthest from the campfire? a purple tent b orange tent c blue tent
2 Genie walks to her tent which is 15 m away and Jai walks to his tent which is 21 m away. Who walked more? How much more?
3 Genie walks from her tent to the campfire which is 15 m away and then back to her tent. What distance did she walk?
4 Have you ever been camping? Why is it important to share things with others at the camp?
12
Let’s Recall
Shapes and Pa erns
Have a look around at your surroundings. Think about how some things look different to others.
Some things are big and some are small. Compare the size of a toy with the size of your house. The toy is tiny and the house is really big.
Now let's look at these colourful blocks.
Each block can be put together in different ways. Each block has a different shape and a different size.
Look at this picture of two building blocks. Do A and B look the same?
No. We can see that A is bigger than B.
Let us look at another picture. Is A bigger than C?
We can see in the picture that A is smaller than C.
So, we can say that:
A is bigger than B. A is smaller than C. B is the smallest. C is the biggest.
Let’s Warm-up
All About Lines
Mother and brother are making a rangoli design. Sarita also wants to join them.
Mother: Sarita, draw a straight line and then a curved line on top.
Sarita: I do not know how to draw these lines.
Let us help Sarita understand these types of lines.
There are 3 kinds of straight lines.
Standing line Sleeping line Slanting line
You can use a ruler to draw these lines. They do not bend.
These are curved lines:
Curved lines bend. You cannot draw them with a ruler.
Example 1: Read the word: CORAL
Which letters of the word have straight lines? Which ones have curved lines? Fill in the table.
Trace the lines to help the monkeys reach the bananas. One is done for you. Name the line.
Sleeping Line
Trace the shape using straight and curved lines. a b c d Integration Do It Yourself 12A
3
How many of each type of lines do you see in the picture?
a Sleeping lines b Standing lines
c Slanting lines d Curved lines 2 a b lines. lines.
Look how the butterflies fly to the flowers. Trace and write the kind of lines they make on their way.
c Letter with slanting and standing lines. 4
Read the word: LATIN. Choose and write the letters.
a Letter with only a standing line.
b Letter with sleeping and standing lines.
3 friends were playing. Look at the lines they ran on, to reach the ball. 1
a Who ran on a curved line?
Foxy Montu
Bruno
All About Shapes
b Who ran on slanting lines?
c Who ran straight?
d Who ran the least distance?
Sarita went into her house and saw that her dad had bought some photo frames.
Sarita: These photos look so good!
Dad: Different shapes of the photo frames make these look even better.
Flat Shapes
These frames show different flat shapes. Square, rectangle, circle, triangle and oval are examples of flat shapes.
Features of Flat Shapes
4 sides, 4 corners Square 4 sides, 4 corners
0 sides, 0 corners Circle 0 sides, 0 corners Oval
Now, look at this shape: It is a triangle. 3 sides, 3 corners
Think and Tell
Are there more flat shapes? What about a star and a heart shape? Are they flat shapes too?
Example 2: Look at the picture. Count the number of each flat shape.
Triangle = 1; Rectangle = 2; Circle = 3; Square = 4
Colour the shapes as instructed. One is done for you.
Rectangle: Yellow
Triangle: Red
Drawing Flat Shapes
Square: Blue
Circle: Orange
Let us learn how to make flat shapes. We are using some ice cream sticks.
Triangle
Square
Rectangle
Circles and ovals
Think and Tell
Can we make a circle or an oval with ice cream sticks?
1 sleeping and 2 slanting sticks
2 standing and 2 sleeping sticks
All four sticks need to be of the same length.
2 standing and 4 sleeping sticks
The opposite sticks need to be of the same length.
They have curved lines. We can use a thread to make them.
Did You Know?
A square is also a rectangle! Its opposite sides are of equal length.
We can also draw flat shapes on dot paper. Let us see how shapes can be drawn on dot paper.
Triangle Square Rectangle
Join the dots to draw some flat shapes. Write the features.
Features of flat shapes
Square—Corners = . Sides = .
Triangle—Corners = . Sides = .
Rectangle—Corners = . Sides = .
Complete the shapes by joining the dots. Name the shapes.
Raha has travelled to many countries in the world. She has the following visa stamps on her passport. Name the shape of each stamp.
Look at the pictures. Count the number of squares, rectangles, triangles, circles and ovals.
a b c
Write True or False.
a A square has 3 sides and 3 corners.
b A rectangle has 4 equal sides.
c Both a circle and an oval have 0 sides and 0 corners.
Draw a figure using at least 3 shapes and colour them with different colours.
Challenge
How many triangles are there in this rectangle? 1
Solid Shapes
Harsh goes to the room to play with his brother. These are the toys they are playing with—
Mom: Harsh, do you know the shapes of these toys? What shape do you see in these toys?
Harsh: Hmm! They look like squares, rectangles and triangles. Are they flat shapes too?
Features of Solid Shapes
The toys are solids. We can hold them in our hands. They are not made or drawn on flat surfaces. The shapes of these toys are called solid shapes. Let us learn more about solid shapes and their features.
This block is a cube.
A cube has 6 faces, 8 corners and 12 edges.
This block is a cuboid.
A cuboid has 6 faces, 8 corners and 12 edges.
The drum is a cylinder.
A cylinder has 3 faces, 0 corners and 2 edges.
The stack is a cone.
A cone has 2 faces, 1 corner and 1 edge.
The ball is a sphere.
A sphere has 1 face, 0 corners and 0 edges.
Example 3: Name the solid shapes of these objects.
Coffee mug Birthday cap
This coffee mug is a cylinder. The cap is a cone.
Name the solid shape shown by each object.
Cuboid
Think and Tell!
Two cylinders are put on top of each other. What solid shape will they make?
Cylinder Cone Sphere
Flat Shapes in Solid Shapes
When you draw or trace around a solid shape on a sheet of paper, you get a flat shape. Let us look at the tracing of some solid shapes below and see which flat shapes they create.
Think and Tell!
What other shape do you get on tracing a cone and a cylinder?
Example 4: Which object should we trace to get a square?
Cap Ball Dice
The cap is a cone, and the ball is a sphere. We will get a circle on tracing them.
The dice is a cube. We can get a square by tracing one of its sides.
Example 5: What shape does the shadow of each object make? Rectangle Triangle Circle Square
Match the shape with the shadow it makes. One is done for you.
) the odd one out.
Vinay needs to draw a circle. Which of these blocks from his block set can he use?
Name the flat shapes made by each solid shape. Draw them.
a Cube b Cylinder c Sphere d Cone
Jon made a tower with his blocks. Count and write down the number of solid shapes he used in this tower.
Cube b Cuboid c Cylinder
Make a solid using any two solid shapes put together. Draw its shadow in your notebooks.
10 such bangles are put one over the other. What shape will it make?
Patterns Around Us
Joy’s father is putting a new sheet on the bed.
Joy: Wow! So many squares.
Father: Yes, Joy. These are making a lovely pattern!
Joy: What is a pattern?
Repeating Patterns
The design on this bedsheet is made up of 3 colours. They are repeated one after another in every line.
Light Green Grey Yellow Light Green Grey Yellow
A shape, number or design that repeats itself in a fixed order makes a pattern. Let us see some more patterns.
This pattern repeats a green triangle and a yellow rectangle, one after the other.
Now, let us see a letter pattern. Here, the letters A and B are repeated.
We can also make patterns with turning shapes. This pattern repeats a blue and a green triangle. The blue triangles are the right way up but the green ones are upside down.
Did You Know?
Honeycombs are the best example of patterns in nature.
Example 6: Look at this pattern. What is repeated in this pattern?
In this pattern, 2 crosses are repeated after every 2 right arrows
Growing Patterns
Joy now knows what patterns are. He can make patterns too! One day, he was making a pattern with his happy and sad stickers.
His sister, Riya, sees this. “Let us have more happy faces in the pattern than sad ones,” she says.
“How? Will it still be a pattern?” Joy is not sure.
“Yes, it will be. Let me show you,” says Riya.
Joy’s pattern is made up of happy and sad stickers. But this is a different pattern.
1 happy 1 sad2 happy
This is called a growing pattern.
1 sad 3 happy
Let us look at another growing pattern. Here, we are adding 1 orange square to each next part of the pattern.
Example 7: Is this a growing pattern. How?
Yes, this is a growing pattern. The pink squares are increasing by 1 each time.
Draw the next part of the growing pattern.
Number Patterns
Joy went to the bookstore with his sister, Riya. He saw a diary where designs were made using numbers.
Joy: Look at this diary. Is this also a pattern?
Riya: Yes, Joy. You can use numbers as well to make patterns. Let me show you!
These are some patterns using numbers: 1 1 1 2 2 2 3 3 3 3
Here, 1 and 2 are repeating. Here, 3 is repeated with a turn. 3, 6, 9, 12, 15—Here, 3 is being added each time.
Example 8: What will come next in this number pattern? 2424
This pattern repeats 2 and 4. So, the next two numbers will be 2 and 4. Fill in the next numbers to complete the pattern.
Which of these options show a pattern? Name the type of pattern.
2, 3, 4, 2, 3, 4
Extend the given patterns.
d 1, 4, 7, 10, , , e f 1, 3, 2, 1, 3, 2, , ,
Joy and Riya have some happy and sad face stickers. They pasted them in different ways. Who has created a pattern with the stickers? Riya’s stickers: Joy’s stickers:
Look at the growing pattern. Colour the blank balls.
Look at the growing pattern. Fill in the blank.
In this pattern, we are adding square/s each time.
In this pattern, we are adding 1 (square/circle) each time.
Fill in the blanks to complete the pattern.
In this pattern, we are adding 1 square and triangle each time.
Roy arranged a few number cards in this way:
Is this making a pattern? If not, arrange them to make a number pattern.
Points to Remember
•Lines can be straight ( ) or curved ( ).
•Straight lines can be sleeping, standing or slanting.
•Square, rectangle, circle, triangle and oval are all flat shapes.
•Cube, cuboid, cylinder, cone and sphere are all solid shapes. •Patterns can be repeating, turning, growing or number patterns.
Math Lab
Setting: In groups of 4
Method:
Experiential Learning & Collaboration
Make a Pattern
Collect leaves, erasers, sharpeners, bottle caps or any other such small objects in your group.
Two members will dip these objects in paint and stamp them on paper to make a pattern. You may create a repeating or a growing pattern.
The other two members will cut the shapes formed.
Use this to decorate your class.
Take turns in your groups. Create as many patterns as you can.
the correct name from the box for each line.
Trace to draw the flat shape. Then, write the name of the shape you get.
Write the kinds of lines you see in these letters—standing, sleeping, slanting and curved.
Draw and colour the shapes to complete the next part of the pattern.
Look at the pictures. Count the number of squares, rectangles, triangles, circles and ovals. 6
Draw the next part of the growing pattern.
Look at the solid shapes.
a Which of these solid shapes will give us a square, each time when it is traced?
b Which of these solid shapes can give us a circle, when traced?
c Which of these solid shapes can give us a rectangle, when traced?
Create a growing pattern with colours and numbers on the given strip.
a Draw a pattern of these shapes.
b Draw a growing pattern with these shapes.
Challenge
1
2
Meera makes garlands outside a temple. Jay is helping her make the garlands. Jay made a pattern in the garland. It starts with 1 flower and 1 leaf, and grows by 2 flowers at each step. Draw the pattern that Jay made up to 5 terms.
Sowing seeds is mainly done using seed drills. The seeds are sown in pairs, with 1 pair in the first row, 2 pairs in the second row and so on. Write the number pattern formed for the first 10 rows.
Real-Life Maths
Shadow Storytelling
There was no electricity in the house. Jay and Neha couldn’t sleep, so they started making animal shadows using their fingers. They played with them and narrated a full story to the whole family. Look at the picture and answer the questions.
1 Which animal shadows are there in the picture?
a Rabbit
c Snail
b Dog
d All
2 How many animal shadows are there?
3 What shadow/s will be formed if we shine some light on a cone?
4 Make animal shadows using your hands and write a story using them.
13 Time
Let’s Recall
We know that the sun is a big bright ball in the sky.
We can understand what time it is by observing the sun.
The sun rises early in the morning. We wake up every morning and start our day.
The sun keeps rising slowly and gets brighter and hotter. This is afternoon.
The sun then slowly starts setting in the evening. It gets cooler and pleasant. This is when we come out and play with friends!
Finally it is night! And there is no sun in the sky anymore! This is when we go off to bed.
Let’s Warm-up
Let us match the pictures to the correct time of the day.
Reading Time on a Clock
Mia was getting ready for her drawing class. It starts at 5 o’ clock in the evening.
Mia: Mother, am I on time?
Mother: Yes, it is not yet 5 o’ clock. It is half past 4.
Mia: Mother, what do you mean by half past?
Mother: Let me show you how to read the half past time.
Time on a Clock
We use a clock to read time. A clock has numbers 1 to 12 written on it.
The short hand tells us the hour, and the long hand tells us the minutes.
Minute hand Hour hand
The minute hand is on 12.
The hour hand is on 5.
This is 5 o’ clock or 5:00.
The minute hand is on 12.
The hour hand is on 10.
This is 10 o’ clock or 10:00.
Now, let us see how to read time to the half hour.
Hour hand
Minute hand
The minute hand is on 6.
The hour hand is between 4 and 5.
So, this is 4:30 or half past 4.
The minute hand is on 6.
The hour hand is between 7 and 8.
So, this is 7:30 or half past 7.
The long hand is the minute hand and the short hand is the hour hand.
hand
We should always do our work on time. Draw clocks to show the time for 4 different activities that you do during the day.
Challenge
1
Thinking & Art Integration
Suman and Suraj take turns to play on the swing. Each play for 30 minutes and take turns. If Suman starts at 5:30, what time will Suraj take his turn. Draw a clock to show the time.
Reading the Calendar
Mili was excited about her summer holiday.
Mili: Mom, when will the vacation start?
Mother: It will start in May.
Days and Months
Mili’s birthday is in April.
Mili: Will my birthday come after the holiday?
Mother: No. May comes after your birthday.
Let us help Mili understand the days of the week and the months of the year.
Days of the Week
There are 7 days in a week.
Let us understand yesterday, today and tomorrow using the days of the week.
If today is a Monday, tomorrow will be a Tuesday.
If yesterday was a Sunday, today is a Monday.
The table below shows the sweets available in a shop each day.
Look at the table and fill in the blanks.
1 is available on Friday.
2 Laddoo is available on Wednesday.
3 Cupcakes are available on and Sunday.
4 Gulab Jamun is available on .
Months of the Year
There are 12 months in a year. The year starts in January and ends in December.
Look at the calendar.
A calendar shows the year, months, days and dates.
February has 29 days in leap year.
February has 28 days in non-leap year.
CupcakeIce cream cone
Laddoo Gulab jamun PuddingFruit CakeCupcake
There are 30 days in April, June, September and November.
There are 31 days in January, March, May, July, August, October and December.
There are 30 + 31 = 61 days in November and December.
Did You Know?
• There are 365 days in a year and 366 days in a leap year.
• A leap year comes every 4 years. February has 29 days in a leap year.
Example 1: Read the calendar given above. Answer the questions.
1 Which is the first month of the year? January
2 Which is the last month of the year? December
3 Which month comes after March? April
Example 2: Fill in the blanks.
1 The months with only 30 days are April, June, September and November.
2 There were 29 days in February 2024.
Colour the months given on the side with 30 days in yellow and the months with 31 days in green.
1 How many months are coloured in yellow?
2 How many months are coloured in green?
3 How many days are there in January and February? 4 months
Do It Yourself 13B
Fill in the blanks with the correct answer.
[Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday]
a Thursday comes after .
b comes before Friday.
c lies between Monday and Wednesday.
d If today is Monday, tomorrow will be .
e If today is a Thursday, yesterday was a .
Look at the calendar given in the lesson. Write True or False.
a There are only 30 days in the month of August.
b January and December each have 31 days.
c There are 7 months with 31 days.
The Hindu calendar is based on the cycles of the moon. Twisha’s birthday comes in Magha (month) as per the Hindu calendar. Twisha’s birthday is in the first month of the year. This year, her birthday is before Sunday and after Friday.
a Which month is Twisha’s birthday?
b Which day is Twisha’s birthday?
Saina goes to an orphanage every Saturday. She goes to an old age home every Sunday. Which are the days in the week that Saina does not go to the orphanage or old age home?
I am an even-numbered month between two months that start with the same letter. Which month am I?
Mili was packing her bag for the trip.
Mili: Do I have to take a sweater for the trip?
Mother: No, it is summer. We do not need sweaters.
Mili: Which months are summer?
Let us help Mili with the seasons throughout the year. There are 5 different seasons in India. They are winter, spring, summer, monsoon and autumn.
Mili also wants to know about the different festivals that come in different seasons:
Mahavir JayantiDussehraHoliRaksha BandhanChristmas
Ram NavamiDiwaliBaisakhiJanmasthamiMakar Sankranti
Independence DayVasant Panchami
Republic Day
Did You Know?
A festival like Eid is not seasonal. It does not fall in a particular season. Its timing keeps changing every year.
Think and Tell
Is there any other festival you celebrate at home? Which season does it fall in?
Look at the table on the previous page and answer the questions.
1 Which months are the monsoon season? July and August
2 How many months are there in autumn?
3 Which season comes after winter?
4 Which season comes before summer?
Do It Yourself
Match the correct months with the seasons.
Fill in the blanks.
a Independence Day is celebrated in the season.
b The season comes after spring.
c Autumn comes after the season.
d Christmas is celebrated in the season.
Write True or False.
a Spring comes after summer.
b Dussehra is celebrated in the summer season.
c Winter comes after autumn.
Answer the following questions.
a Are Independence Day and Republic Day celebrated in the same season?
b How many months of winter are there?
c From which month does summer start?
Era spends her summer holidays with her grandparents every year. Which are the months that Era spends with them?
Challenge
Critical Thinking & Value Development
Lily celebrates Holi every year with her grandmother. She visits her before school starts in April. Which month does Lily visit her grandmother?
Story Problems on Time
It is Thursday! Noni is happy. She has art class at school!
Timetables
Let us look at Noni’s school timetable. Below is Noni’s timetable at school. There are 6 periods every day.
DAYS
MondayEnglishScienceEVS MathsCraftSports
TuesdaySportsEnglishScienceComputerMathsMaths
WednesdayMathsArtEnglishMusicEVSScience
ThursdayMathsMathsArt EnglishScienceHindi
FridayDanceScienceMaths EVSEnglishHindi
Saturday HOLIDAY
Sunday HOLIDAY
Noni has to pack her bag for Thursday. She will take her Maths book, Art book, English book, Science book and Hindi book to school that day.
Example 3: Look at Noni’s timetable. Choose the correct answer.
1 On which day of the week does Noni have her Computer class? a Tuesday b Monday c Friday
2 Noni has her dance class on ____________ . a Wednesday b Saturday c Friday Friday
13 • Time
Look at Noni’s timetable and fill in the blanks.
1 On Friday, Noni has her class in Period 3.
2 On Thursday, Noni has her class in Period 6.
3 Noni has her art class on and .
Estimating Time Taken
We take different amounts of time to do different activities. Some activities take hours, some take days and some take months.
Seed to grow into a plant Winter holidays Doing homework Brushing teeth
Write if the given activities take minutes, hours, days or months.
1 Bathing 2 Watching a film 3 Summer holidays Do It Together Minutes
Time Duration
Mia’s mother goes to drop Mia off at school. She starts at 8:00 and reaches the school at 9:00. She then goes to the market and gets there at 9:30.
1 How much time did Mia’s mother take to reach the school? 1 hour
2 At what time did Mia and her mother leave their house? 8:00
3 At what time did Mia’s mother reach the market? 9:30
4 If they started at 9:00, at what time would they reach the school? 10:00
Rashi goes to the market at 5 o’ clock. She comes back at 8 o’ clock. How much time did Rashi spend at the market?
1 Time Rashi goes to the market =
2 Time Rashi comes back from the market =
3 Rashi spent __________ at the market. 8 o’ clock
Do
It Yourself 13D
Read Noni’s timetable given on page 189 and answer the questions.
a How many Maths classes does Noni have on Tuesday?
b How many days in the week does Noni have the Science class?
c How many Sports classes does Noni have in a week?
Jia wakes up at 7 o’ clock in the morning every day. She takes around 2 hours to get ready for school. At what time does Jia go to school every day?
A train timetable is a list of stations a train stops at and its scheduled time. The table below shows the timetable of a train. Look at the table and answer the questions.
Station AStation BStation CStation DStation EStation F 9:0010:3011:0012:302:003:30
a The train reaches Station D at .
b The train reaches Station at 2:00.
c The train reaches Station C at o’ clock.
d The train reaches Station B at half past .
Fill in the blanks with hours, days or months for the given activities.
a Filling a large water tank . b Knitting a sweater .
c Growing a seed into a plant . d Yoga class .
Make your own class timetable. Make it interesting and colourful.
1
Sana has a lot of activities to do tomorrow. Seeren has a wedding to attend on the last day of this month. What should Sana and Seeren choose (calendar or timetable) to manage their activities?
Maps and Directions
Reading Maps
Mother asks Mili to go to the grocery shop to buy rice for dinner.
Mili: Mother I don’t know how to go to the grocery store from our home.
Mother: It’s simple to find your way around through directions. Directions
Let’s look at a map and learn directions on the map. We use a compass. A compass is a tool for finding directions. The red line is the path taken by Reena to reach the school. Reena goes straight, then right, then right, then straight and finally reaches the school.
Words like left, right and straight help us understand the directions to reach a place. A set of directions gives us a particular way to get from one place to another.
Did You Know?
We use different mobile apps for locating directions to a place.
There are four major directions—north, south, east and west. If we stand facing the east, then north will be on our left side, and south will be on our right side.
Reena’s
Example 4: Look at the map given above and answer the questions.
1 What is to the North of the restaurant? Hospital
2 What is to the East of the pet shop? Bakery
3 What is to the East of the hospital? Flower shop
Look at the map above and tick the correct option. Do It Together
1 What is to the South of the flower shop? Police station / Supermarket
2 What is to the West of the school? Airport / Pet shop
3 What is to the South of the airport? School / Hospital
Do It Yourself 13E
Look at the map and use the words east, west, north and south to fill in the blanks. Use the compass for reference.
a The cafe is to the of the pharmacy.
b Where is the museum? It is to the of the school.
c Draw a line to show the route from the cafe to the museum.
Draw the map to show the distance from your classroom to the main gate of your school.
Mia, Sia and Tia are going from place A to place B and have no idea of direction. Mia says to use the map on the phone to reach B. Tia says they should just go straight and see where it goes. Sia says they would never be able to reach B. Who is correct? Mia, Sia or Tia? Explain your answer.
1
Points to Remember
• A clock helps us to read time.
•There are 7 days in a week. Monday is the first day of the week.
•There are 12 months in a year. January is the first month of the year.
• There are 5 seasons in India—winter, spring, summer, monsoon and autumn.
•A calendar shows the year, months, days and date.
Festivals
Setting: In groups of 5
Material required: One sheet of white chart paper
Method:
1 Ask each group to choose 1 festival, like Makar Sankranti, Eid, Christmas, etc.
Collaboration & Art Integration
2 Ask them to go to the library or use the internet at home to search for facts about the respective festivals.
3 The groups will make a collage of various things which are done in the chosen festival.
4 Arrange the festivals in the order of the months they occur in.
5 Each group will present their collage.
Chapter Checkup
Choose the correct time from the box and write the time in words.
4:00 2:00 10:30 11:30 a b c d
Math Lab
Goes for a walk every Monday, Wednesday and Friday. Goes to the market every Sunday. 2
The table below shows Neha’s father’s schedule. Read and follow the instructions. Has breakfast every day at 9 o’ clock. Leaves for the office every weekday at 10:30.
a Show the breakfast time on the clock. b Draw hands to show the time he leaves for the office.
c On which days does Neha’s father not go for a walk?
d Where does Neha's father go every Sunday?
e Neha’s father has a habit of walking, as it helps him remain fit. Does he go for a walk on Thursday?
Read the calendar and answer the questions: 3 Calender
a How many Saturdays are there in this month?
b How many days are there in this month?
c How many Mondays are there in this month?
Look at the picture in the seasons and festival section given above and answer the questions. 4
a The year begins with the season.
b Which season comes after the summer season?
c Which months does the spring season fall in?
d and months are the monsoon season.
Write 2 activities that take hours, days and months.
Jantar Mantar is a place where time is read by looking at the shadows of the arms of the sundials placed. Tanya goes to Jantar Mantar in Jaipur. She sees the shadow of the sundial’s arm and realises it is twelve thirty. Draw the time seen by Tanya on the clock.
Read Sunita’s daily timetable and answer the questions. 7:008:309:301:304:308:3010:00
Wake up Have breakfast Leave for office Come home Have tea Have dinner Go to bed
a At what time does Sunita have her dinner?
b What does Sunita do at 9:30?
c What time does Sunita go to bed?
Look at the map and answer the questions.
a From the Start, go north 3 squares. Where are you now?
b Go east 3 squares from the position you reached in part a. Where are you now?
c Give directions to get from the dentist to the pool. Critical Thinking & Creativity
Which month am I? I am the month, starting with the first letter of the alphabet. I have the same number of days as the month before me. Sanya is walking to her house in the morning. The sun is to her right. She turns right twice and then turns left once. What direction is Sanya facing?
Map—Zoo
Today is Raina’s day out at the zoo. Look at the map to help her find her way in the zoo.
1 You enter the zoo from the zoo gate and go left. What do you see?
a Car parking
c Hippo
b Giraffe
d Elephant
2 Suppose you go and stand facing the camel. In which direction are the birds?
3 What is to the east of the ostrich?
4 Write the directions from the elephant to the cafe.
5 Should we tease animals in the zoo? How should we take care of them?
CAFE
Zebra Lion Monkey
Puma Elephant Hippo
Giraffe
14 Money
Let’s Recall
How do we buy things?
When we go to the market, we take money with us. We give money to the shopkeeper. He gives us what we want to buy.
Money is what we give for buying chocolates, books, crayons, clothes, etc. But do we give the same amount of money for all these items?
No! Some things are expensive and some are cheap. For example, our clothes are more expensive than a chocolate.
Let’s Warm-up
Read the following sentences and write True (T) or False (F).
1 We do not need money to buy things. ________
2 We pay more money to buy a pen than for shoes.
3 All coins and notes have the same value.
4 A shopkeeper takes money to sell things. I scored out of 4.
Indian Currency
Riya goes to a shop with her mother. She wants to buy a storybook.
Riya: I like this book. How much does it cost?
Shopkeeper: 100 rupees.
Riya’s mother pays for the book. Riya is very happy.
Indian Coins and Notes
Indian money comes in notes and coins. They can be rupees or paise. Paise come only in the form of coins. Rupees come both in the form of notes and coins. We use the symbol to show the amount in rupees.
Coins:
Notes:
There are some coins that were used in the olden days. They are no longer in use. Let us see some of those.
1 rupee is equal to 100 paise.
So, 1 rupee is equal to two 50-paise coins.
Did You Know?
Indian notes are made of a special paper. It is called ‘rag paper’. This paper is strong and does not tear easily.
2 rupees is equal to four 50-paise coins.
Example 1: Look at the price and circle the correct note or coin.
Look at the notes and coins. Write the amount using the rupee symbol.
Look at the things. Tick () if the note or the coin shows the correct cost.
Vegetable soup is very good for health. It contains nutrients from all the vegetables. Rama sells the each cup for 20. Tick the coins that show the amount.
Write if true or false.
a There is a 15 coin.
b There is a 300 note.
c There is a 2 coin.
d There is a 10 coin and note.
Read the statement and match it with the correct note.
a Riya bought a box of crayons for 100.
b Raj bought a packet of balloons for 50.
c Tina bought a red pen for 10.
Operations on Money
The next day, Riya goes to another shop. She wants to buy a new lunch box from here.
Riya: I like this lunch box. How much does it cost?
Shopkeeper: This lunch box costs 50.
Riya is confused about how she should pay for it. She does not have a 50-rupee note.
Counting Money to Pay
Let us see the different ways in which Riya can pay for the lunch box:
1 Five 10 notes.
2 Two 20 notes and one 10 note.
3 Three 10 notes and one 20 note.
Example 2: Sam’s mother buys a doll for 75. Write 2 ways in which she can pay.
Fill in the blanks with the correct answers.
a For 20 we can exchange 5 coins.
b For 100 we can exchange 50 notes.
c 10 notes make ₹70.
How will you pay for crayons worth 56, using 10 notes and 2 coins? Draw.
Ruhaan has to buy a crayon worth ₹200. How can he make up the amount using 20 notes or 10 notes?
Sana visited the Red Fort with her mother. Red Fort is a historical fort in Delhi which was the main residence of the Mughal emperors. The ticket cost them ₹70. Write 2 ways in which Sana can pay for the tickets.
Raj has a ₹100 note with him. He wants ₹50 and ₹10 notes. How many of each note can he get if he exchanges ₹100 with his friend?
Adding and Subtracting Money
Do you remember that Riya has to pay ₹50 for the lunch box? Suddenly, Riya remembers that she also needs to buy a water bottle. The water bottle costs ₹90. Riya needs to pay now. Let’s see what she has to pay for both items!
50 for a lunch box 90 for a bottle
Cost of lunch box
Cost of water bottle
Total amount
So, Riya will pay ₹140.
Remember!
Always add the costs of different objects to find the total cost.
Think and Tell
Which notes can Riya use to make the payment of 140 rupees?
The next day, Riya goes to the shop with one ₹20 note. She buys a packet of biscuits for ₹15. She gives the ₹20 note to the shopkeeper. How much money will Riya get back? Let us see.
Money Riya paid the shopkeeper: ₹20
Total cost of the packet of biscuits: ₹15
₹20 is more than ₹15.
So we subtract ₹15 from ₹20 = 20 – 15 = ?
Riya gets back ₹5from the shopkeeper. Here, ₹5 is called the change which Riya gets back from the shopkeeper.
Example 3: Ram buys a new cap for 35 and crayons for 40. How much money will he pay?
Cost of new cap
Cost of crayons
Total amount paid
So, Ram will pay ₹75.
Error Alert!
To find the amount of change, the cost of the item is subtracted from the amount that is paid to the shopkeeper.
a Arun buys 1 ice cream and 1 packet of chips from a shop. How much money will he pay altogether?
b Nisha has 87. She buys a cap. How much money is she left with?
c Tina buys a toy car. She gives 90 to the shopkeeper. How much change will she get back from the shopkeeper?
Riya’s uncle has a farm. On the farm, there are many animals. Read the cost of a meal for each animal. Then, answer the questions.
a What is the cost of the cow’s meal?
b How much will Riya’s uncle pay for 2 goats’ meals?
c How much will the meals of 3 hens cost?
Challenge
Rina has three ₹5 coins and two ₹2 coins. She wants to buy a pencil for ₹7. Can Rina buy the pencil with the coins she has? If she gives all the coins to the shopkeeper, what amount will she get back?
Points to Remember
• We use the symbol for the rupee amount.
•We use notes and coins as money.
•We add the prices of the things bought to find the total amount.
• We always get back change from the shopkeeper if we pay more than the cost of the things.
Math Lab
Setting: In groups of 5
Material required: Pots, plants
Method:
Experiential Learning & Value Development
Selling Plants
Work together to put plants in pots.
Sell the plants in your neighborhood or at a school fair.
Count the money you make and use it to buy books.
Donate the books to an orphanage.
Chapter Checkup
Draw rectangles for the notes and circles for the coins to show the amount.
a Show 10 using 1 coins.
b Show 50 using 10 notes.
It’s time for Kriti to prepare yummy hot upma. She goes to the market and buys different ingredients. Look below and answer the questions.
a What is the price of curry leaves?
b How much will Kriti pay for semolina and curd?
c Kriti purchases the vegetables and gives 80. How much money will she get back?
Fill in the blanks.
a Three notes of 10 will make .
b Tina has five coins of 1 each. She has in all.
c Raj bought a pencil for 10 and an eraser for 7. He paid to the shopkeeper.
d My mother gave me 35 and I purchased a candy for 8. Now, I have left.
Ravi has a habit of saving money in his money bank to buy gifts for his family. Ravi has saved 15. He wants to save 10 more. How much money will Ravi have after saving?
Priya had 74 and her father gave her 50 more. How much money does she have now?
Raj has 30. He buys a toy car for 15 and a ball for 10. How much money has Raj spent in total?
Your brother had 67. Then he gave 35 to you. How much money does he have left now?
Rishabh and his friends wants to donate some sweets to the orphanage. The sweets would cost them 300. If they have 130, how much more money do they need to buy the sweets?
Aanya has 25. She wants to buy a toy that costs 15 and a box of chocolates that costs 8. Aanya’s friend offers her a deal: if she helps with some chores, the friend will give her an extra 5. Should Aanya accept the deal? Why or why not?
Nita says she has three different coins in her bag that add up to 17. Rita says she also has three coins in her bag but they add up to 20. Which coins do Nita and Rita have in their bags?
Real-Life Maths
The Puppet Show
Kathputli is an art of telling stories using string puppets in Rajasthan. Mira and her two friends went for a puppet show. Her mother gave her three 100 notes. She buys tickets for 200. Answer the questions.
1 How much money did Mira’s mother give her?
2 Draw rectangles to show the money that Mira’s mother gave her.
3 How much money is she left with, after buying the tickets? a 100 b 200 c 300 d 50
4 Have you ever visited a puppet show? Draw a picture. Cross Curricular & Creativity
15 Data Handling
Letʹs Recall
We see a lot of flowers in this garden! How many flowers are there?
Let us count together!
There are 13 red flowers in the garden.
There are 15 yellow flowers in the garden.
We now know the number of flowers that are there in the garden. We also know the colours of the flowers. We also know the number of each type of flower.
This type of information, that includes numbers, is called ʻdataʹ.
Letʹs Warm-up
Count the number of shapes. Complete the table and fill in the blanks.
1 How many are there?
2 How many are there?
3 How many are there?
4 Which shape appears the most?
5 Which shape appears the least?
I scored out of 5.
Understanding Data
It is Preeti’s birthday. She went to the market with her father to shop for her birthday party.
Father: Please choose the things that you want to buy.
Preeti: I need party hats, candles, balloons and many other things. Here are the items Preeti buys for the birthday party.
Counting Data
Preeti came home after shopping.
Preeti: Hello mother! I am home.
Mother: Please count all the items you bought and put them away properly. Let us help Preeti count!
We can help Preeti count by drawing a table to show the number of each item.
A table helps us read the data easily.
Example 1: A farm had four different animals. Count and write the number of each animal on the farm.
Count the circles of each colour and fill in the table.
Number of Circles 4
Count and write the number of each type of ice cream. Do It Yourself 15A
Shelly went to the zoo with her father on Sunday. She saw the following animals in it. Count the number of each type of animal she saw.
Pottery is an art where clay is used to make vessels. It helps the mind and body work together. Rina made the given number of pots in her new pottery class. Fill in the blanks.
Rashi loves collecting things from her garden. This is what she has collected on 3 days. a Count and write the number of items collected on each day.
b On Monday, Rashi plucked 4 flowers from the plants. Has she done the right thing? Why or why not?
Challenge
1 Look at the shapes. If 2 more circles are added, how many more circles will there be than rectangles?
Organising Data
Preeti’s mother decided to go and buy some fruits and vegetables. She asked Preeti to quickly make a list of fruits and vegetables she needed to buy.
Here is the list of fruits and vegetables:
ItemsHow much?
Mangoes1 kg
Carrots3 kg
Potatoes7 kg
Apples5 kg
Think and Tell
Preetiʹs mother wants to buy double the quantity of each item for a party. How many of each item would she buy?
The list will help Preeti’s mother to remember all the items she needs to buy from the market.
Example 2: Palak needs to buy 1 packet of sugar, 2 cakes of soap, 10 spoons and 1 packet of salt. Help her to make a list of all the items.
ItemsHow many?
Look at the pictures and help Seema make a list of all the things she needs for her camping trip.
Cap: Umbrella:1
Pants: ______ pair/s
It Yourself 15B
Shoes:1 pair
Nisha and her mother want to bake a cake for her grandmother’s birthday. Look at the pictures and make a list of all the things she has to buy.
Tina needs to buy a few things for her art class. She needs 1 drawing book, 2 bottles of paint, 3 paint brushes and 5 sheets of white paper. Make a list of all the things she needs.
Meena went to the market to buy 1 bottle of shampoo, 1 packet of sugar, 3 plates, 1 packet of chilli powder and 2 packets of biscuits. Make a list of all the things she bought.
Packing your own bag for school is a good habit. Make a list of 5 things that you put in your school bag every day and how many of each there are.
1 Rohit bought 2 bananas on Monday. On Tuesday, he bought 5 more than what he bought on Monday. On Wednesday, he bought 10 more than what he bought on Monday. Make a list to show how many bananas he bought each day.
Reading Data Tables
Remember the list of fruits and vegetables Preetiʹs mother needed?
Let us find some information from the list.
a How much potato did she need? 7 kg
b Which is more: apples or potatoes?Potatoes
c Which vegetable did she need the least of?Mangoes
d Name the fruits needed. Apples and Mangoes
Example 3: The table shows the number of legs of different creepy crawlies. Creepy Crawlies BeetleCentipedeSpider
a How many legs does a spider have? 8 legs
b Which creepy crawly has the most number of legs?Centipede
c Which two creepy crawlies have the same number of legs?Beetle and Ant
The list shows the number of flowers that grew in the garden from January to April.
a Which month had the most flowers?
b Which month had the least flowers?
c March has one less flower than January. True or False? False
Reading books is a good habit. Pooja made a list of the number of pages she read from a book on three days. Read the table and fill in the blanks.
a The most number of pages were read on .
b The number of pages read on Day 1 is .
c The number of pages read on Day 3 is (more/less) than the number of pages read on Day 1.
The table shows the number of chocolates sold on four days. Read the table and write if True or False.
a The most chocolates were sold on Day 2.
b 16 chocolates were sold on Day 4.
c Only 6 chocolates were sold on Day 3.
d More chocolates were sold on Day 1 than on Day 4.
There was a sports event at the school. Here is a list of how many students participated in the different sports. Read the table and answer the questions.
a How many students participated in football?
b Which activity had the most students taking part?
c Was there any activity where only ten students took part? If yes, name the activity.
Raman likes bird-watching from his garden. Read the table showing the number of birds he counted in different seasons.
a In which season does he count the most birds?
b In which season does he count the least birds?
c How many birds does he count altogether in Winter and Summer?
d How many fewer birds does he count in Autumn than in Spring?
1 Read the table and make a list of all the things Rahul bought.
4 tooth brushes
5 Cakes of Soap
1 Bottle of Shampoo
Pictograph
On Preeti’s birthday, they played a game, in which all her friends had to blow up as many balloons as they could.
Name of FriendsNumber of Balloons
Preeti made a table to record the data.
Let us learn how to show the above data using a pictograph. A pictograph shows the data using pictures.
NameNumber of Balloons
1 Make a table and write the headings.
2 Write the names in Column 1.
From the table we see:
3 Draw pictures in Column 2 to show the balloons blown by each child. Draw 1 picture for 1 balloon.
1 Param blew the largest number of balloons.
2 Rahul blew the smallest number of balloons.
3 Sia blew 3 balloons.
A pictograph helps us to see the data clearly.
Example 4: Read the pictograph showing the number of flowers sold in a flower shop. Answer the questions.
FlowerNumber of Flowers Sold
Roses
Daisies
Orchids
Carnations
a Which flowers were sold the least? Daisies
b Which flowers were sold more than carnations? Roses
c How many orchids were sold? 5
Different students played different sports on Sports Day.
Draw a pictograph to show the above data. 1 = 1 student. Read the data given in the table. Sport
Read the pictograph and answer the questions.
Which sport was played by the most students?
Was there any sport that was played by only one student?
Which sport was played by the same number of students as hockey?
The table shows the stationery items bought by students of a class. Draw a pictograph to show the data. [1 = 1 student]
Sahil went to a market to buy vegetables. Read the pictograph and answer the questions.
VegetablesNumber of Vegetables
Tomato
Capsicum
Carrot
Mushroom
a Which vegetable did Sahil buy the most of?
b How many mushrooms did he buy?
c Which did he buy more of—mushrooms or tomatoes? How many more?
The table shows the number of flowers that grew at Sara’s house from January to April.
MonthNumber of Flowers
January
February
March
April
a Which month had the most flowers?
b Which month had the least flowers?
c How many flowers grew in January?
d What was the total number of flowers in the 4 months?
Ask any 5 friends about the number of family members living in their houses. Draw a pictograph to show the data in a table.
Challenge
1 Look at the pictograph in Q2 above and answer.
a A customer buys 5 less carrots than the number of carrots that Sahil bought. How many carrots did he buy?
b Another customer buys 5 mushrooms more than the number of mushrooms bought by Sahil. How many mushrooms did he buy?
Points to Remember
•When counting data, count the same type of objects.
•Count each object only once.
•Making lists helps us to remember the things we need.
•Read the list carefully when looking for information.
•A pictograph shows the data using pictures.
Setting: In pairs
Collaboration & Experiential Learning
Materials: Pencil box of each partner, notebook and pencil.
Method:
1 Each partner will check the otherʹs pencil box.
2 In your notebook, make a list of all the items in their pencil box.
a How many students have crayons?
b How many pencils are there in all?
c Which item do the students have the least of?
d Which item do the students have the most of?
Math Lab
Count them in the image and answer the following questions.
bug snail ant bee
a How many bugs are there?
c Which insect are there the most?
b How many bees are there?
d Which two insects are equal in number?
b Write the total number of things she bought. 4
Mona went to a toy shop. She bought 3 green balls, 4 red balls, 2 dolls and 1 car.
a Make a table to show the things that she bought.
Suveera and Inaaya sell sandwiches in their summer break to collect money to donate to a school for the blind. Read the pictograph and answer the questions.
DayNumber of Sandwiches Sold
Monday
Tuesday
Wednesday
Thursday
Friday
a How many sandwiches were sold on Thursday?
b On which day were more sandwiches sold—Monday or Friday? How many more?
c How many sandwiches were sold in the week?
A survey was done where a few students were asked their favourite colour. The data is given below. Draw a pictograph to show the data. Draw a box to show 1 colour. blue, red, blue, blue, red, green, blue, yellow, blue, green, blue, blue, green, red, yellow, yellow, green, yellow, green, green, green
Challenge
Critical Thinking
1 Aadya loves watching butterflies. Count the different butterflies she saw today. Tick ( ) the INCORRECT options.
a There are 6 blue butterflies.
b There are 5 yellow butterflies.
c The number of red butterflies is 3 less than the number of blue butterflies.
d The number of red and yellow butterflies is the same.
2 Aadya draws a pictograph for the above data. If she draws 1 picture to show 2 butterflies, how many pictures will she draw to show the blue butterflies?
Real-Life Maths
Sona and her friends are cleaning the beach today.
Value Development
1 Look at the picture and draw a pictograph for their activities. 1 child =
Activities
Working with a garbage bag Sweeping with a broom Wearing a cap or hat
Number of Children
2 How many children are carrying a garbage bag?
3 How many children are wearing a hat?
4 Is what Sona and her friends are doing important? Why or why not?
Answers
Chapter 1
Let’s Warm-up
1. 24 2. 55 3. 31 4. 46
Do It Yourself 1A
1. a. 113, 114, 115 b. 156, 157, 159 c. 190, 192, 193
2. a. 111 b. 133 c. 150
3. a. 143 b. 161 c. 111
4. a. 30 b. 4 c. 100 d. 6 e. 50 f. 100
5. a. 138 b. 104 c. 192 6. two hundred six
Challenge 1. 2 tens
Do It Yourself 1B
1. a. 122 b. 166. c. 102
2. a. 123 < 143 b. 133 < 193 c. 129 = 129
3. a. 122 b. 133 c. 198 4. a. 113 b. 101 c. 180
5. a. 109, 114, 123, 134, 154 b. 110, 112, 117, 118, 119 154, 134, 123, 114, 109 119, 118, 117, 112, 110 c. 73, 99, 100, 101, 111 d. 99, 100, 111, 119, 187 111, 101, 100, 99, 73 187, 119, 111, 100, 99
6. Dudhwa tiger reserve, Nagarhole tiger reserve, Bandipur tiger reserve, Corbett tiger reserve
Challenge 1. 86
Do It Yourself 1C
1. 2.
3. a. third b. mango c. second d. fourth
4.
Challenge 1. 6th
Do It Yourself 1D
1. a. Odd b. Even 2.
3. a. True b. True c. False
4. Drawing may vary. Sample drawings. EvenOdd
Challenge 1. a. 3 pairs b. 2 pairs
Chapter Checkup
1. a. 102, 104, 106, 107 b. 163, 164, 167, 168
2. a. 136 b. 161 3. a. 124 b. 197, 199 c. 136
4. a. 142 b. 195 c. 198 d. 176
5. a. 100 + 20 + 2 b. 100 + 30 + 4 c. 100 + 60 + 7 d. 100 + 70 + 6
6.a. 1st b. 2nd c. 3rd d. 4th e. 5th
7. Even- penguins, apples Odd- balloons, sunflowers 8. Rajiv
Challenge 1. a. 179 b. 159 2. 3rd floor
Real Life Maths
1.d. Purple 2.b. 4th 3.a. orange b. 7th
4.a. True b. False 5. Answers may vary.
Chapter 2
Let’s Warm-up 1. 5 2. 4 3. 9 4. 7 5. 8
Do It Yourself 2A
1. a. 7 tens 6 ones = 76 b. 10 tens 1 one = 101
2. a. 33 b. 45 c. 39 d. 74 e. 93 f. 77
3. 4. a, d, f
Challenge 1. No, he is wrong. 7
Do It Yourself 2B
1. a. 40 b. 60 c. 70 2. a. 32 b. 66 c. 54
3. a. 70 b. 42 c. 50 d. 61 4. a. 30 b. 78 c. 40 d. 40 e. 75 f. 83
Challenge 1. 3 tens
Do It Yourself 2C
1. a. 9 b. 12 c. 8 2. a. 6 b. 1 c. 54
3. a. 45 b. 58 c. 99 4. a. 79 b. 63 c. 73
Challenge 1. Answers may vary. Sample answer: 42 + 37 = 79.
Do It Yourself 2D
1. 61 candies 2. 68 murukkus 3. 97 roses
4. 89 balloons 5. Answers may vary. Sample answer In a grocery store, there are 42 mangoes on one shelf and 39 mangoes on another shelf. How many mangoes are there in total?
Challenge 1. 22, 26; 48
Chapter Checkup
1. a. 10 b. 14 c. 12 2. a. 34 b. 20 c. 45
3. a. 29 b. 65 c. 60 4. a. 39 b. 70 c. 95
5. a. 65 b. 77 c. 76 6. 69 leaves
7. 98 fruits 8. 37 books
Challenge 1. 22 2. False. For example: 15 + 11 + 17 = 43
Real-Life Maths
1. 2.c. 39 3. 44
4. Answers may vary. Sample answers. egg cartons and cardboard
Chapter 3
Let’s Warm-up 1.a. 4 b. 4 2. a. 6 b. 0 c. 2
Do It Yourself 3A 1. a. 42 b. 46 c. 48 d. 54 2. a. 11 b. 24 c. 61 d. 56
3.a. 23 b. 31 4. a. 41 b. 31 c. 11 d. 81 5. a. 4 b. 2
Challenge 1. Meera is correct. For example 51 – 0 = 51.
Do It Yourself 3B
1. a. 19 b. 29
2. a. 9 + 6 = 15 b. 3 + 8 = 11 6 + 9 = 158 + 3 = 11
15 – 6 = 911 – 3 = 8 15 – 9 = 611 – 8 = 3
3. a. 18 b. 36 c. 26 4. a. 6, 3 b. 2, 8 c. 8, 2 d. 5, 3
5. Answers may vary
Challenge 1. Answers may vary. Sample answers: 73 – 61 and 61 – 34.
Do It Yourself 3C
1. 20 flowers 2. 24 fruits 3. 12 concrete houses
4. Answers may vary.
Challenge 1. 2 more apples
Chapter Checkup
1. a. 22 b. 19 c. 30 d. 16 2. a. 32 b. 17 c. 10
3. a. 33, 33 + 12 = 45 b. 40, 40 + 30 = 70
4.a. 9 + 8 = 17, 8 + 9 = 17, 17 – 8 = 9, 17 – 9 = 8
b. 4 + 3 = 7, 3 + 4 = 7, 7 – 4 = 4, 7 – 3 = 4
c. 5 + 9 = 14, 9 + 5 = 14, 14 – 5 = 9, 14 – 9 = 5 5. SUNLIGHT
6. a. 5, 3 b. 9, 5 c. 8, 0 d. 7, 2 7. Sunita, 11 ghungaroos
8. 10 teeth 9. Answers may vary. Sample answer.Two 20 rupee notes and one 2-rupee coin
Challenge 1. 1ones 2. 50
Real-Life Maths
1. d 2. �56 3. �6 4. No 5. Answer may vary.
Chapter 4
Let’s Warm-up
1. 7 vegetables 2. 5 vegetables 3. 6 vegetables
4. 9 vegetables 5. 8 vegetables
Do It Yourself 4A
1. 2, 2, 2, 2, 8, 8 2. 1, 1, 1, 1, 1, 5, 5
3. a. 2 + 2 + 2 = 6 b. 4 + 4 = 8
4. Cow 1Cow 2 4 + 4 = 8 legs
Challenge 1. Riya will get- 6 + 6 + 6 = 18
Do It Yourself 4B
1. b 2. 3, 9 3. a. 3, 2, 6 b. 4, 3, 12
4.
5.a. 21, 3 groups of 7 b. 18, 6 groups of 3 c. 15, 3 groups of 5 d. 14, 7 groups of 2
Challenge 1. No, the distribution is not equal since one of the jars have only 9 sweets.
Do It Yourself 4C
1. a. 3, 3, 3, 3, 3, 3, 3, 21; 7, 3, 7, 3; 7, 3, 21; 21
b. 4, 4, 4, 4; 4, 4, 4, 4, 16; 4, 4, 16; 16
2. a. 8 bananas b. 10 flowers c. 8 balloons d. 9 candies
3. a. 8 b. 6 + 6 + 6, 3 groups of 6, 3 × 6 = 18
c. 3 + 3 = 6
Challenge 1.
Chapter Checkup
1. a. 8, 8, 8, 8, 32, 32 b. 5, 5, 10, 10
2. a. 4, 5 b. 3, 10 3. a. c b. c
4. Answers may vary. Sample answer:
3 + 3 + 3 + 3 4 times 3 4 × 3 = 12
b. 3 + 3 2 times 3 2 × 3 = 6
6. a. false b. false c. True d. True 7. 12 wheels
8. 14 players
Challenge 1. Rohan is correct because 6 + 6 + 6 + 6 + 6 + 6 = 36
2. Rina placed more lamps.
Real-life Maths
1. b 2.a. 4 + 4
3. a. 2 groups of 4 b. 3 groups of 10
4. Answers may vary. Sample answers: Plant trees, water the plants
Chapter 5
Let’s Warm-up 1. 3, 3, 6 2. 3 3. 3, 6
Do It Yourself 5A
1. a. 2 groups of 2, 2 × 2 = 4; b. 2 groups of 3; 2 × 3 = 6;
c. 2 groups of 5, 2 × 5 = 10 2. a. 2 × 4 = 8
b. 2 × 6 = 12 3. 6, 6 × 2 = 12
4. 10 apples
Challenge 1.
Do It Yourself 5B
1. 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
2. 5 × 3 = 15, 5 × 1 = 5, 5 × 2 = 10, 5 × 5 = 25
3. 0123456789101112 +5 +5
4. 30 grapes
Challenge 1. Number 34 is incorrectly marked.
Do It Yourself 5C
1. a. 10 × 6 = 60 b. 10 × 4 = 40 c. 5 × 10 = 50
2. a. 5, 5 × 10 = 50 b. 7, 7 × 10 = 70
3. Students will draw any objects showing 10 groups with each group having 3 objects. So a total of 30 objects.
4. 20, 30, 40, 50, 60, 70, 80, 90
Challenge 1. The other number is 4. Do It Yourself 5D
1. a. 0 b. 2 2. a. 20 b. 4; 36
3. a. 8 b. 44 c. 30 d. 40
4. 10 5. 20 rupees
Challenge 1. 24
Do It Yourself 5E
1. 60 books 2. 90 mishti dois 3. 60 oranges
4. 40 cupcakes 5. Answers may vary. Sample answer Lisa collected 2 jars of marbles, and each jar contained 10 marbles. How many marbles did Lisa collect in total?
Challenge 1. Seerat knows the table of 5, so she can find 5 times 8 to get 40 which is equal to 8 times 5.
Chapter Checkup
1. a. True b. False c. False d. True
2. a. 01234567891011121314151617181920
b. 01234567891011121314151617181920
3. a. 5 + 5 = 10 b. 2 + 2 + 2 + 2 + 2 = 10 4. a. 2 × 8 = 16
b. 5 × 8 = 40 c. 10 × 1 = 10 d. 0 × 8 = 0
5. ×102 3306 4408
6.
7. 70 dosas 8. a. 10 hats b. 5 × 6 = 30, 30 T-shirts
c. 5 × 2 = 10, 10 pairs
Challenge
1.
2. Yes, you are right as 5 × 4 = 20
Real-Life Maths
1. b, c, d 2. 20 lollipops 3. 10 toys 4. 50
5. Answers may vary.
Chapter 6
Let’s Warm-up 1. 9 tens, 3 ones
2. 1 hundreds, 2 tens, 1 ones 3. 1 hundred, 4 tens, 8 ones
4. 1 hundreds, 6 tens, 3 ones 5. 1 hundreds, 9 tens, 9 ones
Do It Yourself 6A
1. a. 721, 723, 724, 726, 727, 729, 730
b. 810, 812, 814, 815,817, 819, 820
2.a. 403, 404, 406, 407, 408, 409, 410, 411, 412, 413, 414, 415, 416
3. one hundred sixty-three 4. a. 465 b. 777 c. 603 d. 505
5. a.
b.
c.
d.
Challenge 1. The number is 203
Do It Yourself 6B
1. a. 3 hundreds + 9 tens + 8 ones 398 = 300 + 90 + 8
b. 1 hundreds + 7 tens + 0 ones
170 = 100 + 70 + 0
c. 6 hundreds + 5 tens + 4 ones
654 = 600 + 50 + 4
2. a. 984, nine hundred eighty-four
b. 576, five hundred seventy-six
c. 702, seven hundred two 3. a. 701 b. 567 c. 345
4. Number name of 127 is One hundred twenty-seven expanded form: 100 + 20 + 7
Challenge 1. 590 Do It Yourself 6C
1. a. 879 b. 901 c. 204
2. a. Greatest = 709; Smallest = 97 b. Greatest = 783; Smallest = 446
c. Greatest = 865; Smallest = 175 d. Greatest = 538; Smallest = 159
3. Increasing order: 100, 345, 620, 789 decreasing order: 789, 620, 345, 100
4. Greatest number: 752 Smallest number: 257
5. Toni used more bricks.
Challenge 1. The number formed is 901 Chapter Checkup
1. a. 303, 304, 305, 306, 307, 308, 310 b. 602, 603, 605, 606, 607, 608, 609
2. a. 567
+ 60 + 7 b. 202
3. Before: 78, 179, 966, Between: 246, 434, 255, After: 457, 516, 699,
c. 986
4. a. 345 > 232 b. 999 > 678 c. 945 = 945 d. 34 < 344
e. 123 < 856 f. 899 < 999
5. a. 678, 559, 345 b. 678, 289, 109
c. 873, 696, 345 6. a. 257, 330, 540 b. 447, 567, 678
c. 120, 499, 600 7. The next house number is 227
8. Less than 500: 123, 459, 229, 289
More than 500: 985, 769, 590, 890
9. The greatest number is 641 the smallest number is 146
Challenge 1. HTO 451
2. There are 6, 3-digit odd numbers between 101 and 115.
Hint: Do not count 101 and 115.
Real-Life Maths
1.b. 8 2. increasing
3. five hundred seventy-six 4. 358
Chapter 7
Let’s Warm-up 1. 98 2. 22 3. 13, 65 4. 15
Do It Yourself 7A
1. a. 129 b. 661 c. 182 2. a. 349 b. 699 c. 997
3. a. 666 b. 912 c. 665 4. a. 835 b. 549 c. 978
d. 870 e. 939 f. 693
Challenge 1. Yes,111
Do It Yourself 7B
1. a. 443 b. 131 c. 550
2. a. 524 b. 616 c. 820 3. a. 180
b. 000 c. 670 d. 780 e. 620 f. 234 4. 167
Challenge 1. 543 – 345 = 198. The digit at the ones place is 8.
Do It Yourself 7C
1. a. addition, 654 b. subtraction, 336 2. a. 361 b. 55
3. 311 packets 4. 365 tigers
Challenge 1. 606
Chapter Checkup
1. a. 699 b. 615 c. 996 2. a. 123 b. 333 c. 423
3. a. 549 b. 1077 c. 704 d. 115 e. 350 f. 244
4. a. 1 b. 9 c. 1
5. a. Subtraction, 230 b. Addition, 290
6. Hindi, 223 7. 351 jhadus 8. 315 biscuits
9. a. 256 b. 401
Challenge 1. a. My number is before 300. b. My number is 10 less than 310.
c. My number is 100 more than 216. d. My number is 25 less than 267. 2. Answers may vary. Sample answer. There are 456 coconuts in a farm. 124 coconuts are sold. How many coconuts are left in the farm?
Real-Life Maths
1.a. 237 2. 69 3. 203 4. Answers may vary.
Chapter 8
Let’s Warm-up
1. 2 + 2 + 2 + 2 + 2 + 2 2. 6 + 6 + 6
3. 8 + 8 + 8 + 8 + 8 4. 4 + 4 + 4 5. 6 + 6 + 6 + 6
Do It Yourself 8A
1. a. 3 × 6 = 18 b. 3 × 5 = 15 c. 3 × 3 = 9 d. 3 × 9 = 27
2. a. 12 b. 24 c. 15 d. 21, 27 e. 12, 15, 18 f. 18, 21, 24
3. a. 18 b. 27 c. 15 d. 24 e. 30 f. 12
4. a. 6 b. 10 c. 2 d. 9 e. 8 f. 3
5. a. 3 × 8 = 24
b. 3 × 4 = 12
c. 3 × 10 = 30
Challenge 1. 12
Do It Yourself 8B
1. a. 4 × 3 = 12 b. 4 × 8 = 32 c. 4 × 2 = 8 d. 4 × 6 = 24
e. 4 × 9 = 36 f. 4 × 1 = 4 2. a. 20 b. 12 c. 40
3. a. fives b. tens c. nines d. fours e. twos f. sixes
4. a. 4 × 7 = 28
b. 4 × 9 = 36
c. 4 × 4 = 16
Challenge 1. a. 24 b. 32 c. 12
Do It Yourself 8C
1. a. 6 × 7 = 42 b. 6 × 5 = 30 c. 6 × 4 = 24 2. a. 36
b. 18 c. 30 3. a. 42 b. 24 c. 48 d. 60 e. 18 f. 54 4. a. 5 b. 7 c. 9 d. 2 e. 8 f. 3
1.
Do It Yourself 8D
1. a. 6 b. 2 c. 0 2. a. 48 b. 99 c. 82 3. a. 20 × 4 = 80 b. 34 × 2 = 68 c. 44 × 2 = 88 4. 13 × 3 = 39
Challenge 1. 4
Do It Yourself 8E
1. a. 96 b. 96 c. 156 2. a. 72 b. 90 c. 366 d. 276 e. 295 f. 168 3. 6;78
4. No; on multiplying 41 and 6, we will get 6 at the ones place.
5. 6 tens
Challenge 1. 63 and 630
Do It Yourself 8F
1. 490 candies 2. 184 seats 3. 312 pins 4. ₹510
Challenge 1. Answers may vary. Sample answer
A pond has 68 fish. If a lake has fish three times that of the pond, how many fish are there in the lake?
Chapter Checkup
1. a. 24 b. 15 c. 6 d. 3 e. 9 f. 30
2. a. 36 b. 32 c. 20 d. 24 e. 28 f. 40
3. a. 7 × 6 = 6 × 7 = 42 b. 6 × 10 = 10 × 6 = 60
c. 6 × 5 = 5 × 6 = 30 4. a. 74 b. 90 c. 148 5. a. 100
b. 190 c. 282 d. 168 e. 410 f. 138
6. 42 runs 7. 112 dancers 8. 510
Challenge 1.
2. Answers may vary. Sample answer. A vegetable vendor sells 5 baskets of tomatoes, and each basket contains 42 tomatoes. How many tomatoes does he sell?
Real-Life Maths
1. Answers may vary. Sample answer: To keep ourselves cool in summer. 2. a. 5 3. 81 cups 4. 81 × 5 = 405
5. Answers may vary.
Chapter 9
Let’s Warm-up 1. 4 groups of 6 2. 5 groups of 2
3. 2 groups of 4 4. 3 groups of 2
Do It Yourself 9A
1. a. b.
c. 2. a. 3 b. 4 3. a. 2 bananas b. 3 cupcakes
4. 4 mangoes
Challenge 1. Answer may vary.
Do It Yourself 9B
1. a. 3 children b. 7 children c. 2 children
2. a. 12 ÷ 3 b. 15 ÷ 5
3. a.
3 – 3 = 0 9 – 3 = 6 6 – 3 = 3 12 – 3 = 915 – 3 = 12
01234567891011121314 15
5 – 5 = 0 10 – 5 = 5
b. 01234567891011121314 15
4. a. True b. False c. False
Challenge 1. Students will draw 1 flower in each of the last two vases. So, Ravi needs to draw 2 more flowers.
Do It Yourself 9C
1. 4 × 3 = 12, 12 ÷ 4 = 3 2. a. 20, 20 b. 6 c. 28, 4
3. a. 8 ÷ 4 = 2, 8 ÷ 2 = 4 b. 12 ÷ 3 = 4. 12 ÷ 4 = 3
c. 30 ÷ 5 = 6. 30 ÷ 6 = 5
4. a. 4 × 2 = 8, 8 ÷ 4 = 2
b. 6 × 3 = 18, 18 ÷ 6 = 3
Challenge 1. Each multiplication fact has 2 division facts. Multiplication fact: 6 × 4 = 24
Division facts: 24 ÷ 4 = 6; 24 ÷ 6 = 4
Do It Yourself 9D 1. a. 4 3 12 b. 5 4 20
2. a. 6 b. 7 c. 7 d. 2
3. a. 9 b. 4 c. 8 d. 7 e. 7 4. 21 ÷ 7 = 3
Challenge 1. 12 6 2 2 3 4 3 2 1
Do It Yourself 9E
1. 3 pencils 2. 4 times 3. 2 apples 4. 3 friends
Challenge 1. No, they need to divide 35 by 7 instead of multiplication.
Chapter Checkup
1. a. 3 b. 6 2. a. 3 balls b. 6 pencils c. 4 marbles d. 8 books 3. a. 6 ÷ 3 = 2, 6 ÷ 2 = 3
b. 24 ÷ 3 = 8, 24 ÷ 8 = 3 c. 9 ÷ 3 = 3, 9 ÷ 3 = 3
4. a. 7 b. 8 c. 9 d. 9 5. a. 5 b. 10
c. 10 d. 10 6. a. 7 b. 6 c. 7 7. 3 amlas 8. 4 packets
Challenge 1. 9 ÷ 3 = 3 2. 4
Real-Life Maths
1. a. 10 2. 5 groups 3. No 4. They will need 2 more children 5. Answer may vary.
Chapter 10
Let’s Warm-up 2 and 3
Do It Yourself 10A
1. 2.
3. 4.
(Answer may vary) (Answer may vary)
Challenge 1. a and b
Do It Yourself 10B
1. a. 2 4 b. 1 3 c. 1 2 d. 3 4
2. a. d.
3. Yes Raina has done the correct thing. No, each piece will not be called a half since they are not equal.
4. a. One-third b. One-half c. Three-fourths d. Two-thirds 1 3 1 2 3 4 2 3
4. 4 crayons
5. Answers may vary. Sample answer.
Challenge 1 B A B A
Longest path
Do It Yourself 11B
1. a. metre b. centimetre 2. 9 cm
Shortest path
Challenge 1. The part which was unused is three-fourth. Answers may vary. Sample answer: Old newspapers can also be used to make paper bags.
Chapter Checkup
1.
2. a. 1, 2 b. 1, 4 c. 1, 3 d. 3, 4 e. 2, 3
3. 1 2, 1 4 , 2 3, 1 3
4. 1 2 3 4 1 3 1 4 2 3
5. a. One-half b. Three-fourths c. One-fourth d. One-half e. Two-thirds f. Three-fourths
6.
7. b. One-third c. One-fourth
8. a. True b. True c. True d. False
9. Figures may vary. Sample figures. a. b.
Challenge 1. Garima is correct because it shows three equal parts. 2. a. one-fourth b. two-fourths
Real-Life Maths
1. 1 2 2. c. Cucumber 3. Watermelon
4. Not all vegetables can be cut equally. Vegetables like spring onions cannot be cut equally.
Chapter 11
Let’s Warm-up
Do It Yourself 11A
1. a. A rope b. A stick 2. a. 10 b. 8
3. 14 blocks, 13 blocks, 5 blocks, The bottle is the longest.
3. 1 m 4. Mango leaf, 18 cm
Challenge 1. 10 crayons
Do It Yourself 11C
1. Bananas 2. Oranges 3. a. 10, 1 b. 2, 1
4. Shrub 5. 3
Challenge 1. 10 blocks
Do It Yourself 11D
1. a. kilograms b. grams c. kilograms d. grams
2. a. 200 g b. 15 kg 3. a. 700 g b. 8 kg
4. 2000 g < 3 kg
Challenge 1. Tom will put a 2 kg weight along with the watermelon on one side and the 10 kg weight on the other side to balance the watermelon.
Do It Yourself 11E
1. Bucket 2. a. 15 b. 12 3. 4. 5 glasses
Challenge 1. 6 cups 2. 12 glasses of water
Do It Yourself 11F
1.
2.
3. 500 mL 4. Answers will vary.
Challenge 1. 5 L
Chapter Checkup
1.
2. Red strip = 4 blocks long; Green strip = 8 blocks long Green strip 3. 7 cm 4. a. b.
5. a. 8 kg b. 100 g 6. 300 g 7. Pot A
8. 2 L. Figures may vary.
Challenge 1. Tina will use 3 m, 2 m and 1 m sticks.
2. 500 g of weight needs to be put to balance
Real-Life Maths
1. a. purple tent 2. Jai, 6 m more
3. 30 m
4. Answers will vary.
Chapter 12
Let’s Warm-up 1.a. b.
2. a. b.
Do It Yourself 12A
1. a. b. c. d.
2. a. 4 b. 5 c. 3 d. 0 3. a. , straight lines or slanting lines
b. , curved lines 4.a. I b. L, T c. N
Challenge 1. a. Bruno b. Foxy c. Montu d. Montu
Do It Yourself 12B
1. a. , Square b. , Triangle
2. a. Oval b. Rectangle c. Square d. Triangle
3. a. Squares – 2, Rectangles – 1, Triangles – 2, Circles – 2, Oval – 0; b. Squares – 5, Rectangles – 1, Triangles – 1, Circles – 4, Oval – 0; c. Squares – 1, Rectangles – 4, Triangles – 3, Circles – 0, Oval – 2
4. a. False b. False c. True
5. Figures may vary.
Challenge 1. 8 triangles
Do It Yourself 12C
1. Book 2. c 3. a. square b. rectangle, circle/oval
c. circle d. triangle, circle/oval 4. a. 4 b. 2 c. 1
5. Figures may vary.
Challenge 1. Cylinder
Do It Yourself 12D
1. a. not a pattern b. number pattern c. growing pattern
d. repeating pattern e. repeating pattern
2. a. b. c. d. 13, 16, 19
e. f. 1, 3, 2
3. Joy 4. a. b. c.
5. a. one b. circle c. one
6. a. 20, 24 b. 6, 5 c. 3 5 d. 7 7
Challenge 1. No. Answers may vary. Sample answer: 5, 4, 3, 5, 4, 3
Chapter Checkup
1. a. Sleeping line b. Standing line c. Slanting line
d. Curved line
2. a. Rectangle b. Oval c. Triangle d. Square
3. a. NO b. GROW c. NO
4. a. Standing and sleeping b. Slanting
c. Standing and slanting d. Sleeping and slanting.
5. a. b.
6. a. Squares - 2, Rectangles - 1, Triangles - 5, Circles - 1, Ovals - 0 b. Squares - 1, Rectangles - 0, Triangles - 5, Circles - 0, Ovals - 0
7. a. b.
c.
8. a. Cube b. Cylinder c. Cuboid
9. Answers may vary. Sample answer.
121221222122221
10. Figures may vary. Sample figures:
a.
b.
Challenge 1. FLFFLFFFLFFFFL 2. 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
Real-Life Maths
1.d. all 2. 5 full shadows
3. If we shine a light from the top on a cone, we get a shadow in the form of a circle. If we shine a light from the side, we get a shadow in the form of a triangle.
4. Answers may vary.
Chapter
13
Let’s Warm-up 1. Evening 2. Night 3. Noon
4. Morning
Do It Yourself 13A
1. 2 o’ clock or 2:00, 3 o’ clock or 3:00, Half past 9 or 9:30, Half past 10 or 10:30
2.
3. a. False b. True c. False
4. Answers may vary. Sample answer.
Breakfast Afternoon nap Play time Lunch time
Challenge 1. 6:00
Do It Yourself 13B
1. a. Wednesday b. Thursday c. Tuesday
d. Tuesday e. Wednesday 2. a. False b. True c. True
3. a. January b. Saturday
4. Monday, Tuesday, Wednesday Thursday and Friday Challenge 1. April
Do It Yourself 13C
1. a. December b. May c. August d. October e. March
2. a. monsoon b. Summer c. monsoon d. winter
3. a. False b. False c. True 4. a. No b. 3 months
c. May 5. May and June
Challenge 1. March
Do It Yourself 13D
1. a. 2 Maths Classes b. 5 days c. 2 Sports Classes 2. 9 o’ clock
3. a. 12:30 b. E c. 11 d. 10 4. a. hours b. days
c. months d. hours 5. Answers will vary.
Challenge 1. Sana should choose a timetable. Seeren should choose a calendar.
Do It Yourself 13E
1. a. east b. east
c.
2. Answers may vary.
Challenge 1. Mia; because maps show us direction. Chapter Checkup
1.a. 10:30 or half past 10 b. 11:30 or half past 11
c. 4:00 or four o’ clock d. 2:00 or two o’ clock
2. a. b.
c. Tuesday, Thursday, Saturday, Sunday d. Market e. No
3. a. 5 b. 31 c. 5 4. a. Winter b. Monsoon
c. March and April d. July and August
5. Answers may vary.
6.
7. a. 8:30 b. Leave for office c. 10:00
8. a. postbox b. cafe
c. 2 squares north and then 3 squares east
Challenge 1. August 2. East
Real-Life Maths
1. a. car parking 2. west 3. Ice cream
4. Go straight; take the second left, then right; then left.
5. No. By not disturbing them.
Chapter 14
Let’s Warm-up 1. False 2. False 3. False 4. True
Do It Yourself 14A
1. Candy, Cap 2. 50 paise, ₹10, ₹20, 25 paise
3. a. False b. False c. True d. True 4. a. ₹100 note
b. ₹50 note c. ₹10 note
Challenge 1. 8 coins
Do It Yourself 14B
1. a. four b. two c. Seven
2. Five ₹10 notes and three ₹2 coins
3. Ten ₹20 notes or twenty ₹10 notes
4. Answers may vary. Sample answers.
Method 1: One ₹50 note and one ₹20 notes.
Method 2: Three ₹20 notes and one ₹10 note.
Challenge 1. One ₹50 note and five ₹10 notes
Do It Yourself 14C
1. a. ₹55 b. ₹51 c. ₹18 2. a. ₹75 b. ₹98 c. ₹60
3. Answers may vary. Sample answer: Suresh bought a book for ₹50 and a pencil box for ₹30. How much money did he spend on the two items?
Challenge 1. Yes, ₹12
Chapter Checkup
1. a. Ten ₹1 coins b. Five ₹10 notes
2. a. ₹20 b. ₹25 c. ₹70 d. ₹15
3. a. ₹5 b. ₹92 c. ₹15
4. a. ₹30 b. 5 c. 17 d. 27 5. ₹25 6. ₹124 7. ₹25
8. ₹32 9. ₹170
Challenge 1. Yes, Reason: Aanya will be left with more money and helping is a good deed.
2. Nita has coins of ₹10, ₹5 and ₹2 Rita has coins of ₹10, ₹5 and ₹5
Real-Life Maths
1. ₹300 2. draw 3 rectangles 3. a
4. Answer will vary
Chapter 15
Letʹs Warm-up
1. 4 2. 2 3. 3 4. Triangle
5. Rectangle
Do It Yourself 15A
1. 3, 4, 3, 2 2. 3432 3. 5, 3,
4. a. 7, 7, 8 b. No, she has not done the right thing. We should not pluck flowers from the plants.
Challenge 1. 1
Do It Yourself 15B
1. Items Number of Items
Bowl 1 Whisk 1 Flour1 packet
Milk1 packet Sugar2 packets 2. Items Number of Items Drawing book1 Paint bottles2 Paint brushes3 White paper5
3. Things Meena Needs to BuyNumber of Things Shampoo 1 bottle Sugar 1 packet
3
2 packets
4. ThingsNumber of Things
Pencils 2
Eraser 1
Sharpener 1
Notebooks 3
Books 3
(answer may vary)
Challenge 1. Days Number of Bananas
Monday Tuesday Wednesday 2 bananas 7 bananas 12 bananas
Do It Yourself 15C
1. a. Day 2 b. 10 pages c. less
2. a. True b. True c. True d. False
3. a. 40 b. Football c. Yes, Table Tennis
4 a. Spring b. Rainy c. 25 d. 20
Challenge: 1. Items Number of Items Hand towels 10 Toothbrushes 4 Bottle of Shampoo 1
Do It Yourself 15D
1. Stationery ItemsNumber of Students Pens
Pencils Crayons
2. a. Carrot b. 5 c. Mushrooms, 1
3. a. February b. April c. 6 d. 23
4. Answer may vary. Sample answer: 1 = 1 member
Name of the friendNo. of family members
Rakhi
Sana
Suraj
Mayank
Garvit
Challenge 1. a. 5 b. 10 Chapter Checkup
1. 4, 3, 4, 1 2. a. 13 b. 19 pencils c. Chalk
d. Pencils 3. a. 4 b. 4 c. Bees and bugs
d. Bees = bugs; ants = snails
4. a.
Toys Number of Toys Purchased Green ball 3 Red Ball 4
Doll 2
Car 1 b. Total: 10 things
5. a. 5 b. Friday, 3 c. 27
6. Favourite ColourNumber of Students Blue Red Green Yellow
Challenge 1. c and d 2. 3 pictures to show 6 butterflies
Real Life Maths
1. Activities Number of Children
Working with a garbage bag
Sweeping with a broom
Wearing a cap or hat
2. 4 3. 3 4. Answers may vary.
About the Book
Imagine Mathematics seamlessly bridges the gap between abstract mathematics and real-world relevance, offering engaging narratives, examples and illustrations that inspire young minds to explore the beauty and power of mathematical thinking. Aligned with the NEP 2020, this book is tailored to make mathematics anxiety-free, encouraging learners to envision mathematical concepts rather than memorize them. The ultimate objective is to cultivate in learners a lifelong appreciation for this vital discipline.
Key Features
• Let’s Recall: Introductory page with a quick recall of concepts learnt in previous grades
• Real Life Connect: Introduction to a new concept related to real-life situations
• Examples: Solved problems showing the correct method and complete solution
• Do It Together: Guided practice for learners with clues and hints to help solve problems
• Think and Tell: Probing questions to stimulate Higher Order Thinking Skills (HOTS)
• Remember: Key points for easy recollection
• Math Lab: Fun cross-curricular activities
• Error Alert: A simple tip-off to help avoid misconceptions and common mistakes
• Did You Know? Interesting facts related to the application of concept
• Challenge: Critical thinking questions to enhance problem-solving and analytical thinking skills
• Real-Life Maths: Scenario-based questions to apply theory to real-life situations
• QR Codes: Digital integration through the app to promote self-learning and practice
About Uolo
Uolo partners with K-12 schools to provide technology-enabled learning programs. We believe that pedagogy and technology must come together to deliver scalable learning experiences that generate measurable outcomes. Uolo is trusted by over 15,000+ schools across India, Southeast Asia and the Middle East.
ISBN 978-81-979482-6-8
hello@uolo.com
