Imagine_Maths_CB_Grade3_SS_AY25 by Uolo

Master Mathematical Thinking

MATHEMATICS

Master Mathematical Thinking

Acknowledgements

Academic Authors: Muskan Panjwani, Animesh Mittal, Anjana AR, Anuj Gupta, Gitanjali Lal, Simran Singh

Creative Directors: Bhavna Tripathi, Mangal Singh Rana, Satish

Book Production: Sanjay Kumar Goel, Vishesh Agarwal

Project Lead: Neena Aul

VP, Learning: Abhishek Bhatnagar

All products and brand names used in this book are trademarks, registered trademarks or trade names of their respective owners.

First impression 2024

Second impression 2025

This book is sold subject to the condition that it shall not by way of trade or otherwise, be lent, resold, hired out, or otherwise circulated without the publisher’s prior written consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser and without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of both the copyright owner and the above-mentioned publisher of this book.

Book Title: Imagine Mathematics 3

ISBN: 978-81-979482-4-4

Published by Uolo EdTech Private Limited

Corporate Office Address:

85, Sector 44, Gurugram, Haryana 122003

CIN: U74999DL2017PTC322986

Illustrations and images: www.shutterstock.com, www.stock.adobe.com and www.freepik.com

All suggested use of the internet should be under adult supervision.

Preface

Mathematics is an essential tool for understanding the world around us. It is not just another subject, but an integral part of our lives. It shapes the very foundation of our understanding, personality and interaction with the world around us. Studies from across the globe have shown that proficiency in mathematics significantly influences career prospects and lifelong learning.

According to the NEP 2020, mathematics and mathematical thinking are crucial for empowering individuals in their everyday interactions and affairs. It focuses on competencies-based education, which essentially means actively and effectively applying mathematical concepts in real life. It also encourages innovative approaches for teaching maths, including regular use of puzzles, games and relatable real-world examples to make the subject engaging and enjoyable.

It is in this spirit that Uolo has introduced the Imagine Mathematics product for elementary grades (1 to 8). This product’s key objective is to eliminate the fear of mathematics by making math exciting, relatable and meaningful for children.

Imagine Mathematics positions itself on the curricular and pedagogical approach of the Gradual Release of Responsibility (GRR), which has been highly recommended by the NEP 2020, the NCF 2023 and other literature in learning educational pedagogies. Subsequent pages elaborate further on this approach and its actualisation in this book.

This book incorporates highly acclaimed, learner-friendly teaching strategies. Each chapter introduces concepts through real-life situations and storytelling, connecting to children’s experiences and transitioning smoothly from concrete to abstract. Clear explanations and simple steps are provided for problem-solving. Engaging facts, error alerts and fun activities are integrated throughout to keep learning interesting and holistic. Importantly, concepts are interconnected across topics and grades, providing a scaffolding that ensures comprehensive and meaningful learning.

This book supports learners at all levels, providing opportunities to build critical thinking skills through questions and activities aligned with Bloom’s Taxonomy. For those seeking a greater challenge, the book includes thought-provoking questions that push learners to apply, analyse and evaluate. Additionally, the problems are rooted in real-world contexts, making the learning experience both relatable and meaningful.

In addition, the book is technologically empowered and works in sync with a parallel digital world, which contains immersive gamified experiences, video solutions and practice worksheets, among other things. Interactive exercises on the digital platform make learning experiential and help in concrete visualisation of abstract mathematical concepts. We invite educators, parents and students to embrace Imagine and join us in nurturing the next generation of thinkers, innovators and problem-solvers. Embark on this exciting journey with us and let Imagine be a valuable resource in your educational adventure.

Product Package at a Glance

Welcome to our comprehensive learning package designed to enhance educational experiences through three key components: print materials, digital resources and assessment tools. Our print materials provide in-depth and accessible information in a pedagogically suitable way, our digital resources offer interactive and engaging learning experiences, while our assessment tools ensure thorough understanding and progress tracking.

PRINT

Engaging Textbooks

Teacher Manuals

ASSESSMENT

Competency-based Model Assessments

Question Paper Generator

Student and Teacher Apps

Video Solutions

Interactive Tasks & Exercises

Byte Size Lesson Modules

Key NEP Recommendations

The National Education Policy (NEP) 2020, introduced by the Government of India, represents a transformative shift in the country’s education system. It aims to create a more holistic, dynamic and multidisciplinary approach to education. NEP 2020 focuses on fostering conceptual understanding, skills and values that align with the demands of the 21st century, while also preserving India’s rich cultural heritage. UOLO is fully committed to actualising the vision of NEP 2020 by meticulously adhering to its outlined recommendations.

1. Focus on conceptual understanding

2. 21st century skills, values and dispositions

3. Critical thinking and problem-solving

4. Application in real life

5. Holistic and integrated learning

6. Experiential learning

7. Enjoyable and engaging

8. Computational and mathematical thinking

9. Technology-based solutions

10. Factoids on India

Competency-based Education

NEP Pages 12, 17, and 22

Teaching and Learning Pedagogy

NEP Pages 3, 11, 12, 18, and 27

National Pride

NEP Pages 15, 16, and 43

11. Assessment of core concepts and application skills Assessments

NEP Pages 12, 18, and 22

Our Key Features: Aligning with the NEP

The GRR Approach

Pedagogical approach that empowers students to learn by the teacher progressively transitioning the responsibility to the students.

Competency-based Assessments

Test papers designed to evaluate understanding of core concepts and application of skills.

3 8 11

Contextual Learning

Introducing concepts through real-life situations and connecting them to students’ experiences.

Classroom Activity

A hands-on classroom activity to investigate and understand mathematical concepts in an engaging and concrete way.

Recall and Revisit

Introductory page with a quick recall of concepts done in previous grades.

Translating Words into Action!

Critical Thinking Questions

Intellectually stimulating questions designed to enhance problem-solving and analytical-thinking skills, promote deeper understanding and foster independent thinking.

Real-Life Math Problems

Scenario-based questions designed to help in applying theoretical knowledge to real-world scenarios, reasoning skills and improves reading comprehension & analytical abilities.

Common Misconceptions

Concise snippets of information designed to caution against potential errors and misconceptions

Think, Analyse and Answer

quick, mathematical-thinking question

Fun Facts

Facts related to the concepts, or bite-sized information about the contribution of Indian scholars to mathematics

Gradual Release of Responsibility

The Gradual Release of Responsibility (GRR) is a highly effective pedagogical approach that empowers students to learn progressively by transitioning the responsibility from the teacher to the students. This method involves comprehensive scaffolding—including modelling, guided practice, and ultimately fostering independent application of concepts.

GRR, endorsed and promoted by both the NEP 2020 and NCF, plays a pivotal role in equipping teachers to facilitate age-appropriate learning outcomes and enabling learners to thrive.

The GRR methodology forms the foundation of the Imagine Mathematics product. Within each chapter, every unit follows a consistent framework:

1. I Do (entirely teacher-led)

2. We Do (guided practice for learners supported by the teacher)

3. You Do (independent practice for learners) GRR Steps Unit

Understanding Large Numbers

Dhruv was reading a newspaper. He came across news about different states in India that participated in the COVID vaccination drive and the number of vaccinations given until August 2023. Given below is the data of four states.

Real Life Connect

Theoretical Explanation

I do

Delhi Haryana Sikkim Goa 37409161 45546836 1360477 2874477

The temperature can change with different weather conditions. On a sunny day, the air feels warm, and the thermometer shows a higher temperature. On a cloudy or rainy day, the air feels cooler, and the temperature on the thermometer drops. Weather conditions like rain, wind and sunlight can all affect the temperature of the air.

All About 7-Digit and 8-Digit Numbers

Temperature Range (°C) Weather

While reading the news, Dhruv got confused and could not read the numbers given in the data. The numbers of vaccinations given were either 7-digit numbers or 8-digit numbers.

Temperature Range (°C)

Below 0 Very Cold 0–10 Cold 11–20 Mild 21–30 Warm 31–40 Hot

Examples

Did You Know?

Sikkim Goa Delhi Haryana 1360477 2874477 37409161 45546836

Above 40 Very Hot

Did You Know?

Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.

7-digit Numbers 8-digit Numbers

Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?

Normal body temperature = 37°C.

Place Value, Face Value and Expanded Form Reading and Writing 7-Digit and 8-Digit Numbers

Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.

Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?

Aliya’s body temperature = 37°C + 2.3°C = 39.3°C

Let us help Dhruv understand 7-digit and 8-digit numbers!

Normal body temperature = 37°C.

So, Aliya’s body temperature was 39.3°C.

Aliya’s body temperature = 37°C + 2.3°C = 39.3°C

We know that the greatest 6-digit number is 999999. Now, if we add 1 to this number, we get 1000000. 999999 + 1 = 1000000

Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?

So, Aliya’s body temperature was 39.3°C.

To find the difference, subtract the lowest temperature from the highest temperature.

37.5°C – 21.2°C = 16.3°C

Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?

The temperature difference is 16.3°C. Write the readings of the given thermometers.

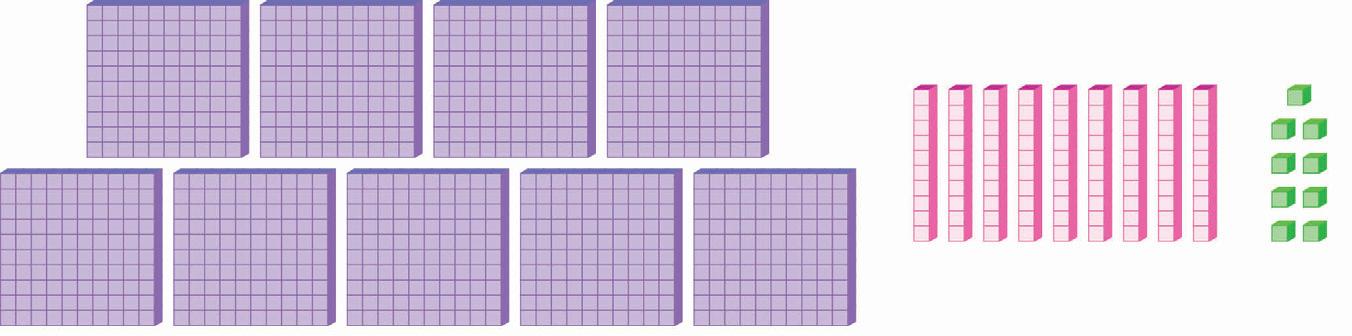
1000000 is the smallest 7-digit number and is read as “Ten Lakhs”. We saw in the news article that the number of vaccinations administered in Sikkim was 1360477. Let us try to place this 7-digit number in the place value chart.

To find the difference, subtract the lowest temperature from the highest temperature. 37.5°C – 21.2°C = 16.3°C

The temperature difference is 16.3°C. Write the readings of the given thermometers.

Temperature = 45°C Temperature = Temperature = Temperature =

Converting Between Units of Temperature

Temperature = 45°C Temperature = Temperature = Temperature =

Celsius (°C) is like the universal language of temperature. Fahrenheit (°F) is another way to talk about temperature. We learnt that water freezes at 0°C and boils at 100°C. In Fahrenheit, water freezes at 32°F and boils at 212°F.

Converting Between Units of Temperature

GRR Steps Unit Component

Do It Yourself

You do

Chapter Checkup Challenge

Case Study

Do It Yourself 14B

1 Identify the shape for which the net is drawn. a b c d

Do as directed.

a Write the greatest 7-digit number that has the smallest odd digit at its hundreds, ten thousands and lakhs place.

b Write the smallest 8-digit number that has the digit 7 at all its odd positions, starting from the ones place.

2 Look at the net and identify the object it belongs to.

3 Draw the net of the given shapes.

Critical Thinking & Cross Curricular

The Kumbh Mela is a major pilgrimage where Hindu pilgrims take the holy bath in the Ganges. The number of people who visited the Kumbh Mela in 1980 were 20,356,817 and those who visited in 1989 were 29,304,871. In which year did less than 25 crore people visit to the Kumbh Mela?

a 1980 b 1989 c Both years d None of the year

4 Rishi and Megha made the net of a square-based pyramid. Who made the net correctly? Explain your answer with reasons.

Comparing, Ordering and Rounding-Off Large Numbers

a Rishi’s drawing

Chapter Checkup

b Megha’s drawing

During COVID, India offered support to 150 affected countries in the form of vaccines, medical equipment and medicines. Given below is the data of the number of vaccine doses supplied by India to four different countries.

Guess the best units of length (m or cm) and weight (kg or g) for the given objects. a b c

5 Draw the net of a hexagonal prism.

6 Show using nets how a rectangular prism is different from a rectangular pyramid.

Comparing and Ordering Numbers

Measure the objects.

Rahul: Which country did India supply the greatest number of vaccine doses to?

Challenge

Bran: We could compare the numbers to find the country to which India supplied the greatest number of vaccine doses.

Comparing Numbers

Critical Thinking

1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.

a The digit in the hundreds and ones place is 6.

What if Rahul wanted to compare the number of vaccines sent to Nepal and Australia? Let us find out.

b The digit in the lakhs place is 4 less than the digit in the ones place.

c The digit in the ten lakhs and ten thousands place is the smallest odd number.

Since 94,99,000 has 7 digits and 3,09,13,200 has 8 digits, 3,09,13,200 > 94,99,000.

d The face value of the digit in the thousands place is 5.

Thus, Australia was donated more vaccine doses.

e The digit in the tens place is the biggest 1-digit number. What is the secret code?

Remember!

e The digit in the tens place is the biggest 1-digit number. What is the secret code?

Now, what if we want to compare two numbers with the same number of digits? Let us consider 4,13,23,456 and 4,13,23,657.

A number with more number of digits is always greater.

2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.

James has some cotton candy which is 3 cm longer than the cotton candy shown below. How long is James’ cotton candy?

2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.

Chapter 1 • Numbers up to 8 Digits

Case Study

200

How much longer is the red straw than the blue straw?

Cross Curricular

Population of Countries

The population of different countries is shown using a table. Read the data carefully and answer the questions.

Country

Convert the lengths.

Germany

Convert the weights.

The population of different countries is shown using a table. Read the data carefully and answer the questions.

United Kingdom 67,736,802

a 5 kg into g b 4 g 64 cg into g c 5487 g into mg d 43 kg 7 dag into kg

United

A baby koala is called a joey. A young joey weighs about 0.38 kg. How much is that in g?

58,870,762

A candle weighs 125 g. How much is it in mg?

1 Which country has the least population?

a Italy b Germany c Poland d United Kingdom

2 Which country has the greatest population?

a Poland b United Kingdom c Italy d Germany

Pearson, P. D., & Gallagher, G. (1983). Contemporary Educational Psychology. Fisher, D., & Frey, N. (2021). Better learning through structured teaching: A framework for the gradual release of responsibility. Fisher, D., & Frey, N. (2014). Checking for understanding: Formative assessment techniques for your classroom.

a Poland b United Kingdom c Italy d Germany

3 Which country has approximately double the population than that of Poland?

4 Arrange the countries in ascending order as per their population.

5 If all the digits in the population of each country is rearranged to form the greatest number, then which country will have the greatest population?

The NEP Tags

The National Education Policy (NEP), 2020, outlines essential skills, values, dispositions and learning approaches necessary for students to thrive in the 21st century. This textbook identifies and incorporates these elements throughout its content, activities and exercises. Referred to as “NEP Tags,” they are defined as follows:

Art Integration

Bringing creativity and fun into learning by combining art with maths. Students construct and demonstrate understanding through an art form.

Collaboration

Working effectively with others. Includes clear communication, teamwork, active listening and valuing diverse approaches.

Cross Curricular

Integrating mathematical concepts with other subjects to see the real-life applications of maths.

Experiential Learning

Gaining knowledge and skills through direct, hands-on experiences rather than a traditional classroom setting.

Communication

Explaining mathematical ideas, processes and solutions to others, whether through verbal explanations, written work or visual representations.

Value Development

Promoting ethics, and human & constitutional values, like empathy, respect for others, cleanliness, courtesy, democratic spirit, spirit of service, respect for public property, responsibility and equality.

Creativity

Using imagination and original thinking to solve problems and explore mathematical concepts in innovative ways. Also includes finding unique solutions, and designing original problem-solving strategies.

Education Standards as per the NCF 2023

The National Curriculum Framework for School Education (NCF), released in 2023, is based on the vision of the National Education Policy (NEP), 2020, and enables its implementation. The NCF provides guidelines for designing school syllabi and textbooks in India. It aims to improve the quality of education by making it more relevant, engaging, inclusive and learner-centric. To achieve this, the NCF has articulated precise Learning Standards through well-defined Curricular Goals and Competencies. These statements serve to harmonise the syllabus, content, pedagogical practices and assessment culture, ensuring a cohesive and comprehensive educational experience.

Curricular Goals: Statements that give direction to curriculum development and implementation in order to achieve the Curricular Aims. They are also specific to a School Stage (e.g., the Foundational Stage) and a Curricular Area (e.g., Mathematics).

Competencies: Learning achievements that are observable and can be assessed systematically. These Competencies are derived from the Curricular Goals and are expected to be attained by the end of a Stage.

Curricular Goals

CG-1

Understands numbers (counting numbers and fractions), represents whole numbers using the Indian place value system, understands and carries out the four basic operations with whole numbers, and discovers and recognises patterns in number sequences

CG-2

Analyses the characteristics and properties of two- and three-dimensional geometric shapes, specifies locations and describes spatial relationships and recognises and creates shapes that have symmetry

Competencies

C-1.1 Represents numbers using the place value structure of the Indian number system, compares whole numbers, and knows and can read the names of very large numbers

C-1.2 Represents and compares commonly used fractions in daily life (such as ½, ¼) as parts of unit wholes, as locations on number lines and as divisions of whole numbers

C-1.3 Understands and visualises arithmetic operations and the relationships among them, knows addition and multiplication tables at least up to 10×10 (pahade) and applies the four basic operations on whole numbers to solve daily life problems

C-1.4 Recognises, describes, and extends simple number patterns such as odd numbers, even numbers, square numbers, cubes, powers of 2, powers of 10, and Virahanka–Fibonacci numbers.

C-2.1 Identifies, compares and analyses attributes of two- and three-dimensional shapes and develops vocabulary to describe their attributes/properties

C-2.2 Describes location and movement using both common language and mathematical vocabulary; understands the notion of map (najri naksha)

C-2.3 Recognises and creates symmetry (reflection, rotation) in familiar 2D and 3D shapes

C-2.4 Discovers, recognises, describes and extends patterns in 2D and 3D shapes

The above is an abridged version of the curricular goals and competencies relatioship in Maths for the Foundational Stage (NCF 2023, pages 340–341). The next section shows the coverage of all these competencies across the chapters.

Mapping with NCF 2023

C-1.1 Represents numbers using the place value structure of the Indian number system, compares whole numbers, and knows and can read the names of very large numbers

CG-1

C-1.2 Represents and compares commonly used fractions in daily life (such as ½, ¼) as parts of unit wholes, as locations on number lines and as divisions of whole numbers

C-1.3 Understands and visualises arithmetic operations and the relationships among them, knows addition and multiplication tables at least up to 10 × 10 (pahade) and applies the four basic operations on whole numbers to solve daily life problems

C-1.4 Recognises, describes and extends simple number patterns such as odd numbers, even numbers, square numbers, cubes, powers of 2, powers of 10, and Virahanka–Fibonacci numbers.

C-2.1 Identifies, compares and analyses attributes of twoand three-dimensional shapes and develops vocabulary to describe their attributes/properties

C-2.2 Describes location and movement using both common language and mathematical vocabulary; understands the notion of map (najri naksha)

C-2.3 Recognises and creates symmetry (reflection, rotation) in familiar 2D and 3D shapes

C-2.4 Discovers, recognises, describes and extends patterns in 2D and 3D shapes

C-3.1 Measures in non-standard and standard units and evaluates the need for standard units

CG-2

Analyses the characteristics and properties of twoand three-dimensional geometric shapes, specifies locations and describes spatial relationships, and recognises and creates shapes that have symmetry

CG-3

Understands measurable attributes of objects and the units, systems and processes of such measurement, including those related to distance, length, weight, area, volume and time using nonstandard and standard units

C-3.2 Uses an appropriate unit and tool for the attribute (like length, perimeter, time, weight, volume) being measured

C-3.3 Carries out simple unit conversions, such as from centimetres to metres, within a system of measurement

C-3.4 Understands the definition and formula for the area of a square or rectangle as length times breadth

C-3.5 Devises strategies for estimating the distance, length, time, perimeter (for regular and irregular shapes), area (for regular and irregular shapes), weight, and volume and verifies the same using standard units

C-3.6 Deduces that shapes having equal areas can have different perimeters and shapes having equal perimeters can have different areas

C-3.7 Evaluates the conservation of attributes like length and volume, and solves daily-life problems related to them

C-4.1 Solves puzzles and daily-life problems involving one or more operations on whole numbers (including word puzzles and puzzles from ‘recreational’ areas, such as the construction of magic squares)

C-4.2 Learns to systematically count and list all possible permutations or combination given a constraint, in simple situations (e.g., how to make a committee of two people from a group of five people)

CG-4 Develops problem-solving skills with procedural fluency to solve mathematical puzzles as well as daily-life problems, and as a step towards developing computational thinking.

C-4.3 Selects appropriate methods and tools for computing with whole numbers, such as mental computation, estimation or paper-pencil calculation, in accordance with the context

C-5.1 Understands the development of zero in India and the Indian place value system for writing numerals, the history of its transmission to the world, and its modern impact on our lives and in all technology

CG-5 Knows and appreciates the development in India of the decimal place value system that is used around the world today

1 Numbers up to 8 Digits

Let’s Recall

Numbers are used everywhere in our daily lives. These numbers are formed using the digits 0 to 9 and are written using commas after every period, starting from the one’s period.

Chapter at a Glance: Walkthrough of Key Elements

For example, let us say the pin code of your area is 201301. This is a 6-digit number. It can be written using commas by representing it in a place value chart.

1 Numbers up to 8 Digits

Number Lakhs Thousands Ones Lakhs (L) Ten Thousand (TTh) Thousands (Th) Hundreds (H) Tens (T) Ones (O) 2,01,301 2 0 1 3 0 1

Each of these digits has a place value and a face value. Let us write the face value, place value, expanded form and number name for 201301. periods place

Let’s Recall

Numbers are used everywhere in our daily lives. These numbers are formed using the digits 0 to 9 and are written using commas after every period, starting from the one’s period.

Let’s Recall: Introductory page with a quick recall of concepts learnt in the previous grade

For example, let us say the pin code of your area is 201301. This is a 6-digit number. It can be written using commas by representing it in a place value chart.

Number name: Two lakh one

Dhruv was reading a newspaper. He came across news about different states in participated in the COVID vaccination drive and the number of vaccinations given August 2023. Given below is the data of four states.

Each of these digits has a place value and a face value. Let us write the face value, place value, expanded form and number name for 201301.

Letʹs Warm-up Fill in the blanks.

1 The place value of 8 in 8,60,765 is 2 The number 4,36,536 can be written in words as:

Expanded form:

Let’s Warm-up: Quick 4–5 questions to test the pre-knowledge

the place.

Large Numbers Concept Explanation: Clear and elaborate explanation of a concept 2

All About 7-Digit and 8-Digit Numbers

I scored out of 4.

While reading the news, Dhruv got confused and could not read the numbers given data. The numbers of vaccinations given were either 7-digit numbers or 8-digit

Did You Know?

Temperature Range (°C) Weather

Below 0 Very Cold

0–10 Cold

7-digit Numbers 8-digit Numbers

I scored out of 4.

Place Value, Face Value and Expanded Form

Dhruv was reading a newspaper. He came across news participated in the COVID vaccination drive and the August 2023. Given below is the data of four states. Delhi Haryana

Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.

Reading and Writing 7-Digit and 8-Digit Numbers

Did You Know?

Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?

11–20 Mild

Normal body temperature = 37°C.

21–30 Warm

31–40 Hot

Let us help Dhruv understand 7-digit and 8-digit numbers! We know that the greatest 6-digit number is 999999. Now, if we add 1 to this number, we get 1000000.

Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.

Aliya’s body temperature = 37°C + 2.3°C = 39.3°C

All About 7-Digit and 8-Digit Numbers

Above 40 Very Hot

999999 + 1 = 1000000

Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?

So, Aliya’s body temperature was 39.3°C.

Normal body temperature = 37°C.

Examples: Solved problems showing the correct method and complete solution

While reading the news, Dhruv got confused and could data. The numbers of vaccinations given were either

Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?

Aliya’s body temperature = 37°C + 2.3°C = 39.3°C

So, Aliya’s body temperature was 39.3°C.

1000000 is the smallest 7-digit number and is read as “Ten Lakhs”. We saw in the news article that the number of vaccinations administered in Sikkim 1360477. Let us try to place this 7-digit number in the place value chart.

To find the difference, subtract the lowest temperature from the highest temperature. 37.5°C – 21.2°C = 16.3°C

Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?

To find the difference, subtract the lowest temperature from the highest temperature.

The temperature difference is 16.3°C. Write the readings of the given thermometers.

37.5°C – 21.2°C = 16.3°C

The temperature difference is 16.3°C.

Do It Together: Guided practice for learners with partially solved questions

Write the readings of the given thermometers. Temperature = 45°C Temperature = Temperature = Temperature =

Let us help Dhruv understand 7-digit and 8-digit numbers!

We know that the greatest 6-digit number is 999999.

Converting Between Units of Temperature

Now, if we add 1 to this number, we get 1000000.

1000000 is the smallest 7-digit number and is read

Chapter 15 • Time and Temperature

We saw in the news article that the number of vaccinations 1360477. Let us try to place this 7-digit number in

What

Let

Fill

Word Problems on Length

Did You Know: Interesting facts related to the topic

Do It Yourself: Exercise at the end of each topic with practice questions

After making a pair of trousers with 2 m of cloth, Sana thought of buying 1 m 55 cm of cloth for making a shirt. Let us see what

of cloth she has together.

Cloth bought by Sana for making a pair of trousers = 2 m Cloth required by Sana for making a shirt = 1 m 55 cm = 1.55 m Total

NEP Tags: To show alignment with NEP skills and values

Error Alert: Caution against misconceptions

1 Identify the shape for which the net is drawn.

2 Look at the net and identify the object it belongs to. a b c d

3 Draw the net of the given shapes.

4 Rishi and Megha made the net of a square-based pyramid. Who made the net correctly? Explain answer with reasons.

a Rishi’s drawing b Megha’s drawing

Chapter Checkup: Chapter-end practice exercises aligned to different levels of Blooms Taxonomy

5 Draw the net of a hexagonal prism.

6 Show using nets how a rectangular prism is different from a rectangular pyramid.

Picture-based Questions: Questions featuring visual stimuli to foster comprehension and interpretation

Challenge

Challenge: Critical thinking questions to enhance problem-solving and analytical-thinking skills

Case Study: Scenario-based questions designed to help apply theoretical knowledge to real-world situations

Real-life Questions: Questions that help make connections with real life or other subjects

Critical Thinking

1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.

Critical Thinking

a The digit in the hundreds and ones place is 6.

1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.

b The digit in the lakhs place is 4 less than the digit in the ones place.

a The digit in the hundreds and ones place is 6.

c The digit in the ten lakhs and ten thousands place is the smallest odd number.

d The face value of the digit in the thousands place is 5.

b The digit in the lakhs place is 4 less than the digit in the ones place.

e The digit in the tens place is the biggest 1-digit number.

What is the secret code?

c The digit in the ten lakhs and ten thousands place is the smallest odd number.

d The face value of the digit in the thousands place is 5.

2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.

Case

e The digit in the tens place is the biggest 1-digit number. What is the secret code?

a The digit in the hundreds and ones place is 6.

b The digit in the lakhs place is 4 less than the digit in the ones place.

2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.

c The digit in the ten lakhs and ten thousands place is the smallest odd number.

Case Study

Study

What is the secret code?

d The face value of the digit in the thousands place is 5.

e The digit in the tens place is the biggest 1-digit number.

2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.

Population of Countries

The population of different countries is shown using a table. Read the data carefully and answer the questions.

Population of Countries

The population of different countries is shown using a table. Read the data carefully and answer the questions.

Country Population

Population of Countries

The population of different countries is shown using a table. Read the data carefully and answer the questions.

1 Which country has the least population?

a Italy b Germany c Poland d United Kingdom

2 Which country has the greatest population?

1 Which country has the least population? a Italy b Germany c Poland d United

a Poland b United Kingdom c Italy d Germany

2 Which country has the greatest population?

3 Which country has approximately double the population than that of Poland?

a Poland b United Kingdom c Italy d Germany

4 Arrange the countries in ascending order as per their population.

1 Which country has the least population?

3 Which country has approximately double the population than that of Poland?

5 If all the digits in the population of each country is rearranged to form the greatest

Cross Curricular

1 Place Value

Let’s Recall

We use numbers in our daily lives.

Imagine you are at a grocery shop. Different items have different prices.

Let us say that the price of a packet of cookies is ₹45.

45 can be understood as 40 + 5.

45 is also the same as 4 tens + 5 ones. So, this 2-digit number has 4 in the tens place and 5 in the ones place.

We can therefore say that the place value of the digit in the ones place is 5.

The place value of the digit in the tens place is 4 tens or 40.

Now, let’s say that the price of a bag of rice is ₹259.

259 has 2 hundreds 5 tens and 9 ones.

So, 259 = 200 + 50 + 9.

The place value of the digit in the ones place is 9 ones or simply 9. The place value of the digit in the tens place is 5 tens or 50. The place value of the digit in the hundreds place is 2 hundreds or 200.

Let’s Warm-up

Write the place value of the underlined digit.

All About 4-digit Numbers

Ajay has been collecting coins in his money bank for the past 2 years.

Ajay: Dad! I have been collecting coins in my money bank. It is very heavy now. I wonder how many coins I have collected.

Ajay starts counting and finds that he has 999 coins.

Dad: Here, take 1 more coin, Ajay!

Ajay: How many coins do I have now, Dad?

Understanding 4-digit Numbers

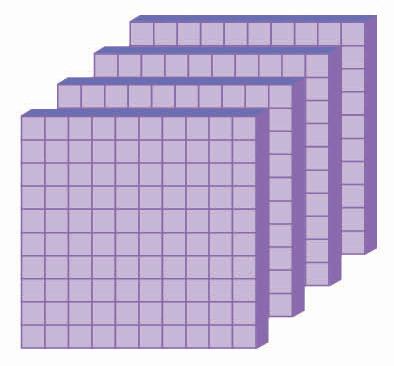
We have already learnt about 3-digit numbers. 999 is a 3-digit number. We can show 999 using place value blocks as:

Place Value and Expanded Form of 4-digit Numbers

When we add 1 to 999, we get:

Place Value and Face Value

Place value is the value that every digit in a number has, based on its position. The face value of a digit is the digit itself.

We already know the places ones, tens and hundreds. The place to the left of the hundreds is called the ‘Thousands’ place.

Thousands Hundreds Tens Ones

Let us understand more about place value and face value using a 4-digit number 1536.

Did You Know?

Numbers like 1001; 1221; and 7337 can be read the same forward and backwards. These are called palindromic 4-digit numbers.

The number can be written using place value as:

6 ones or 6

3 tens or 30

5 hundreds or 500 1 thousand or 1000

Expanded Form

We already know that when we write a number as the sum of the values of its digits, the number is said to be in expanded form. Let us write the expanded form of 4257.

The place value and expanded form of the number 4257 can be written as given below:

7 × 1 = 7 or 7 ones

5 × 10 = 50 or 5 tens

2 × 100 = 200 or 2 hundreds

4 × 1000 = 4000 or 4 thousands

Write the place value of each digit in 4319. Also, write the number in the expanded form.

Let us write the number 4319 using place value.

9 ones or 9 × 1 = 9 tens or 3 hundreds or or 4 × 1000 =

Standard Form Expanded Form

Number Names

Let us learn how to read a 4-digit number and write it as a number name.

2000 + 200 + 30 + 8 two thousand

2 thousands 2 hundreds 3 tens 8 ones two hundred thirty eight

Therefore, the number 2238 can be read as two thousand two hundred thirty-eight.

Example 1: Read and write the number formed by the blocks.

4000 + 100 + 10 + 6 four thousand one hundred sixteen

Note: 10 + 6 will be read as sixteen and not ten six.

The number 4116 can be read as four thousand one hundred sixteen.

Read and write the number formed by the blocks. Do It Together

3000 + 400 + 50 + 7 four hundred seven

The number 3457 can be read as .

Do not use ‘and’ while writing the number names.

seven thousand eight hundred forty-two Error Alert!

seven thousand eight hundred and forty-two

4-digit Numbers on the Abacus

We have seen that blocks are useful when reading and writing numbers. We can also read numbers using an abacus. An abacus can have any number of rods. Here, we will be using an abacus that has 4 rods—ones, tens, hundreds and thousands.

Let us look at the steps to read a number on an abacus.

Step 1: Count the number of beads on each rod.

2 beads at the thousands place

3 beads at the hundreds place

5 beads at the tens place

4 beads at the ones place

Step 2: Write the corresponding number of beads in the place value table.

Th H T O

2 3 5 4

The number 2354 is read as two thousand three hundred fifty-four.

Example 2: Which number is formed by the beads on the abacus?

Count the number of beads on each rod and write in the place value table.

Th H T O

4 0 5 7

The number is 4057 and is read as four thousand fifty-seven.

Count the beads on the abacus to find the number.

The number is read as five thousand ________ hundred ________ one.

Write the numbers by counting the blocks.

Count the beads. Read and write the number.

Show the numbers on the abacus by drawing circles for the beads.

Write the

in words.

Write the place value and face value of the underlined digit.

a 3215 b 5362 c 7314

d 6892 e 8113 f 9686

Write the numerals.

a three thousand two hundred forty-five b five thousand three hundred eighty-six

c seven thousand forty d six thousand eight

Write the numbers in expanded form. a 2148

The longest highway in India is NH44. Its length is 4112 kilometres. Write the length in words.

1 Critical Thinking

Read the hints to find the year.

• The value of the thousands place is 1000.

• The hundreds place has the digit of the largest value.

• The tens place digit is 2 less than the hundreds place digit.

• The sum of all the digits is 20.

Comparing and Ordering Numbers

Ray and Jim are at their school library. Both of them are looking at the books in the library.

Ray: Look Jim! This book has 1235 pages.

Jim: My dad has two books that have 885 pages and 1145 pages.

Ray: Wow! I wonder which book has more pages.

Comparing, Ordering and Forming Numbers

We have learnt in our previous lessons that a number with more digits is greater than the number with fewer digits.

Comparing Numbers

As 1235 and 1145 are 4-digit numbers and 885 is a 3-digit number, 1235 and 1145 are greater than 885.

Let us now compare the 3 numbers 1235, 1145 and 885.

Step 1: Write the numbers in the place value chart.

1235 and 1145 are 4-digit numbers. 885 is a 3-digit number.

So, 1235 and 1145 are greater than 885.

Let us now compare 1235 and 1145.

= 1 2 > 1

Step 2: Compare the digits at each place starting with the thousands place.

Since 2 > 1 at the hundreds place, the number 1235 is greater than 1145.

Example 3: Compare the numbers 3174 and 3147. Both numbers have the same number of digits. Both numbers have the same digits at the thousands and the hundreds place = 3 and 1.

Let us check the digit at the tens place.

3 1 7 4 3 1 4 7

As 7 > 4, 3174 > 3147.

Ordering Numbers

Always compare the digits at each place from left to right.

Let us now arrange the three numbers 1235, 1145 and 885 in ascending and descending order.

Ascending Order

Descending Order

1 = 1 2 > 1

Arrange the numbers from lowest to highest.

Ascending order: 885 < 1145 < 1235

1 = 1 2 > 1

Arrange the numbers from highest to lowest.

Descending order: 1235 > 1145 > 885

Example 4: Arrange the numbers in ascending and descending order. 510, 2168, 1321, 6344

Put the numbers in a place value chart and compare. 510 is the smallest number since it has 3 digits and the others have 4 digits.

2 1 6 8 1 3 2 1 6 3 4 4 1 < 2 < 6

Ascending order: 510 < 1321 < 2168 < 6344

Descending order: 6344 > 2168 > 1321 > 510

Arrange the numbers in ascending order. 1765, 4372, 6145, 4538

Start comparing from the thousands place.

1765 4372 6145 4538 6 > >

Compare the hundreds place for 4372 and 4538.

4372 4538 >

The ascending order is: 1765 < < ___________ < 6145.

Forming 4-digit Numbers

Do you know that we can form the smallest and greatest 4-digit numbers, using all the digits in a given set of 4 digits without repetition? This can be done by arranging the given set of numbers in either ascending or descending order.

Let us use the digits 3, 5, 1, and 7 to form the smallest and the largest number.

1357 is the smallest number.

7531 is the greatest number.

Let us now try forming the smallest number using the digits 4, 8, 0, 7 where one of the digits is 0.

Place the digits in ascending order. 0 is placed in the hundreds place. If we place 0 in the thousands place, we get 0478 which is a 3-digit number.

So, 4078 is the smallest number formed using the digits 4, 8, 0, 7.

Even and Odd Numbers

Numbers that have 0, 2, 4, 6, 8 in their ones place are called even numbers.

24, 36, 78, 592, 5240, 4318 are even numbers.

Numbers that have 1, 3, 5, 7, 9 in their ones place are called odd numbers.

13, 77, 681, 179, 4525, 5297 are odd numbers.

Remember!

An even number of things can be put in pairs (groups of 2).

Odd numbers have one left over when you put the odd number of things in pairs.

Form the smallest and the greatest number using the following digits: 3, 5, 9, 0.

Smallest number place the digits in order.

Th H T O 5

Greatest number place the digits in order.

Th H T O 9

Therefore, is the smallest and is the greatest 4-digit number formed using the digits 3, 5, 9, 0.

Do It Yourself 1B

Group the numbers as even or odd numbers.

Compare the following numbers using the symbols >, <,

Arrange the following numbers in ascending and descending order.

a 1765, 4390, 7430, 7935 b 773, 7880, 9573, 2860

c 4853, 7943, 392, 3067 d 8546, 9404, 157, 6583

Form the smallest and the greatest numbers using the given set of digits.

a 4, 2, 7, 6 b 6, 1, 3, 7 c 5, 0, 2, 1 d 8, 6, 0, 5

e 2, 0, 9, 8 f 1, 5, 0, 7 g 2, 5, 7, 8 h 4, 2, 8, 9

Match the following.

a 9999

b 1000

c 9876

d 1023

Smallest 4-digit number

Greatest 4-digit number

Smallest 4-digit number using different digits

Greatest 4-digit number using different digits

The length of the river Nile is 6650 km, and of the river Amazon is 6575 km. Which river is longer?

The Indian Railways is one of the largest railway networks with 7325 stations. Form the largest number possible using the same digits.

Anahita has written the largest 4-digit number where any number of digits can be the same. Hetal has written the largest 4-digit number where all four digits are different. Who has the largest number? 1

Rounding off 3-digit Numbers

Lina goes to the shop with her mother to buy return gifts for her birthday party.

Mother: Take out the list of guests, Lina.

Lina: I forgot to bring the list!

Mother: No problem, Lina! I remember that there were about 30 names on the list.

When they get home, Lina finds that there were 27 names on the list.

Did you notice the word ‘about’ before the number 30? The number 30 is not the exact number but close to the exact number, 27. The number 30 is the rounded off number.

We use rounding off when we do not know the exact number but come close to the actual number.

Let us see how 27 is rounded off to 30.

Step 1: Draw a number line and write the numbers between 20 and 30.

Step 2: Look for the nearest 10 of the number.

27 is between 20 and 30 but is closer to 30.

Therefore, the number 27 is rounded off to 30.

Example 5: Round off 125 to the nearest 10.

Look for the nearest 10 of the number on the number line.

125 is exactly between 120 and 130. When the digit in the ones place is 5 or more, we round off to the higher 10.

Therefore, 125 is rounded off to 130.

Round off 286 to the nearest 10.

Look for the nearest 10 of the number on the number line.

286 is between __________ and 290 but is closer to __________ .

Therefore, it is rounded off to .

If the number is exactly in between, it is rounded off to the higher ten.

Fill in the blanks.

a There are 38 students in my class. 38 can be rounded off to .

b There are 73 trees in a park. 73 can be rounded off to .

c 44 is between 40 and 50 but is closer to .

d 123 is between 120 and 130 but is closer to .

Round off the numbers to the nearest 10. a

Draw an arrow to match each number to its nearest 10. a 273

b 227

c 370

d 358

A langar is a community kitchen in a gurudwara. Rina and Sia helped in the kitchen and served food to 632 people. To the nearest 10, about how many people did they serve?

The Delhi Metro connects Delhi with its neighbouring cities. It has 268 trains and 256 stations. Round off the number of trains and stations to the nearest 10.

I am a 3-digit number.

If you round me off to the nearest 10, I round down and not up. My tens digit is odd, but I am even. Who am I?

Points to Remember

• A 4-digit number always has 4 places—thousands, hundreds, tens and ones.

• The place value of a digit depends on the position that it occupies in a number.

• To compare numbers, start comparing from the digits on the left.

• If the digit in the ones place is 0, 1, 2, 3 or 4, then round off the number to the smaller tens; otherwise round off to the higher tens.

Math Lab

Experiential Learning & Cross Curricular

Mystery Number Hunt

Setting: In groups of 4

Materials Required:

Prepare a set of clue cards, each with a hint about a specific 4-digit number as mentioned below:

The year India got Independence.

The year in which COVID spread.

Smallest number with the digits 5, 0, 1, 7.

Largest number with the digits 7, 2, 9, 5.

Method:

1 Distribute the clue cards to each team.

2 The teams need to find the 4-digit number for each of the four hints.

3 The team that correctly identifies the mystery numbers wins!

Chapter Checkup

1 Write the numerals.

a one thousand four hundred forty-two b three thousand eight hundred fifty-seven

c four thousand two hundred eight d five thousand three hundred nine

e six thousand forty-five f five thousand twenty-eight

2 Write the numbers in words.

a 2471

d 7308

b 4205

c 5374

e 7564 f 8421

3 Write the place value of the underlined digit.

a 1056

d 8379

b 3814

c 5807

e 7291 f 9092

4 Write the standard form of the numbers.

a 2000 + 100 + 80 + 5

d 5000 + 700 + 20 + 5

b 3000 + 400 + 70 + 1 c 8000 + 80 + 9

e 4000 + 600 + 0 f 6000 + 0 + 70 + 0

5 Write the expanded form of the numbers.

a 1382

d 6484

b 3641 c 5327

e 7500 f 9032

6 Form the smallest and the greatest 4-digit number using the following digits.

a 2, 0, 3, 1

d 4, 1, 0, 7

b 8, 6, 0, 5

e 3, 4, 2, 7

7 Draw abacuses to show the following numbers.

a 860

d 4856

b 4072

e 9030

8 Arrange the numbers in ascending and descending order.

a 565, 2390, 730, 8935 b 773, 880, 7573, 1860

c 5853, 6943, 792, 7081 d 7846, 8704, 657, 5683

e 8753, 2265, 8734, 4867 f 7428, 7354, 8754, 5436

9 Round off the numbers to the nearest ten.

a 64 b 97 c 393 d 421

c 5, 4, 2, 8

f 3, 6, 0, 8

c 3184

f 7465

10 The Great Hornbill is a colourful bird in India. It is called the 'farmer of the forest', There are 62 types of hornbill in the world. About how many types are there in the world?

11 Create your own word problem on comparing two 4-digit numbers.

a The thousands place is equal to the number of legs a spider has. 1 Challenge

Aditya is looking for a 4-digit number. Help him find the number. These clues will help you. Write the number, its number name and expanded form.

b The hundreds place is equal to the number of wheels in a car.

c The tens place is equal to the number of wings a bird has.

d The ones place is equal to the number of faces of a cube.

Fill the numbers 284, 43, 168, 905 in the empty circles such that they meet the conditions.

Real-Life Maths

a K2

c Mount Everest

Mountain Peaks

Disha and her friends are planning to climb mountains as their summer vacation activity. They are reading about mountains and they find out the heights of 5 mountain peaks in the Himalayan range: Mount Everest—8848 m, K2—8611 m, Annapurna—8041 m, Mount Kailash—6638 m and Kedarnath—3583 m.

1 Which is the highest mountain peak from the given list?

b Annapurna

d Kailash

2 Arrange the mountains peaks from smallest to greatest.

3 Name the mountain peak which is the smallest. Write the length in expanded form and in words.

4 Have you ever climbed mountains? Share your experience in words.

Cross Curricular

2 Addition of 3-digit Numbers

Let�s Recall

Mother and father brought fruit from the market! The fruits are so nice and fresh!

They brought a bag of pears. How many pears are there? There are 4 pears.

They brought a bag of oranges. How many oranges are there? There are 5 oranges.

How much fruit is there in total? Let us put them together and count to see!

Adding the pears and oranges, we have a total of 9 fruits.

Putting objects together and counting them is addition!

We can write this as: 4 + 5 = 9 or

Mental Addition

Som and his friend Max enjoyed going to the seashore. They collected seashells!

Som collected 5 blue seashells and 4 red seashells, while Max collected 4 blue seashells and 5 red seashells.

Adding 2-digit Numbers Mentally

Som uses a few tricks to quickly find the number of shells collected. Let us learn how to add numbers mentally using the properties.

Properties of Addition

Total number of seashells with Som = 5 blue seashells + 4 red seashells = 9 seashells

5 blue seashells

4 red seashells

Total number of seashells with Max = 4 blue seashells + 5 red seashells = 9 seashells

5 + 4 = 4 + 5 = 9

Order Property of Addition

Numbers can be added in any order. Their sum always remain the same.

For example: 2 + 3 = 5

3 + 2 = 5

5 red seashells 4 blue seashells

So, both the boys collected the same number of seashells.

Addition by 1

When 1 is added to a number, the sum is the number that comes after it. This next number is called the successor.

For example: 10 is the successor of 9.

Addition with 0

When 0 is added to a number, the sum is the number itself.

For example: 10 + 0 = 10

Remember!

When a number is added to another, the sum is always bigger than both the numbers. The only time this does not happen is when one of the numbers is 0.

For example, 4 + 5 = 9. 9 is greater than both 4 and 5.

However, 4 + 0 remains 4.

Example 1: Fill in the blanks.

a 7 + 11 = 11 + 7

b 14 + 19 = 19 + 14

Find the missing number.

Example 2: Find the sum.

a 45 + 1 = 46

b 17 + 0 = 17

1 6 + 9 = + 6 2 + 1 = 14 3 8 + =

Addition by Expanding Numbers

Expanding Both the Numbers

Som collects 45 marbles and Max collects 34 marbles. How many marbles do they collect in total?

Let us add by expanding the 2 numbers.

Total marbles = 45 marbles + 34 marbles

Add by expanding the numbers.

Step 1: Expand both the numbers.

45 4 tens + 5 ones = 40 + 5

34 3 tens + 4 ones = 30 + 4

Step 3: Add the tens.

40 + 30 = 70

Chapter 2 • Addition of 3-digit Numbers

Step 2: Add the ones.

5 ones + 4 ones = 9 ones

Step 4: Add the tens and ones to get the sum.

70 + 9 = 79

Expanding Only One Number

Let us see how can we solve the same problem by expanding only 1 number.

Total marbles = 45 marbles + 34 marbles

45 can be written as 45.

Expand 34 30 + 4

Step 1: Add the tens in 34 to 45.

45 + 30 = 75

+ 4

+ 4 =

Example 3: Find the sum of the numbers.

1 Add 47 and 12 by expanding both the numbers.

47 40 + 7 (Split 47 into 40 and 7)

12 10 + 2 (Split 12 into 10 and 2)

Thus, 47 + 12 = 59.

2 Add 48 and 31 by expanding only one number.

Expand 31.

31 30 + 1

Thus, 48 + 31 = 79.

Add the given numbers by expanding them.

1 15 + 53 53 50 + 15 10 + 5 1 5 10 + 5 5 3 + +

Thus, 15 + 53 = .

Adding by Counting Forward

Step 2: Add the ones in 34 to the answer.

75 + 4 = 79

Numbers can also be added mentally by counting forward.

Now, let us add 52 and 26 mentally.

Step 2: Skip count by the same number of tens as the tens in the second number 26. 26 has 2 tens.

52 62, 72

Step 1: Keep the bigger number in mind, 52.

Step 3: Count forward by the same number of ones as in the second number 26. 26 has 6 ones.

So, 52 + 26 = 78.

Example 4: Find the sum of 41 and 36 mentally.

Keep the number 41 in mind.

= 77

Think and Tell What is the sum of the smallest 2-digit number and the largest 2-digit number?

Find the sum of 32 and 53 mentally.

Keep the number 32 in mind.

Skip count by tens.

Count forward by . 32 + 53 = .

2 • Addition of 3-digit Numbers

2 Add and complete the crossword.

3 Find the sum by expanding both the numbers.

a 14 + 41 b 46 + 23 c 27 + 11

d 24 + 55 e 64 + 33 f 35 + 33

4 Find the sum by expanding only one number.

a 17 + 32 b 44 + 21 c 71 + 10

d 30 + 59 e 57 + 22 f 63 + 25

5 Use the given grid to add 41 + 37. Fill in the missing numbers. Write the answer.

6 There are 48 species of butterflies in the Butterfly Park in Bannerghatta National Park. 30 more species were added to the park. How many butterfly species are there in total?

1 Rajitha formed the smallest and biggest numbers using the digits 3 and 4 and added the two numbers as shown. Is the problem solved correctly? If not, solve correctly.

Addition of 3-digit Numbers

Som and Max now started collecting pebbles. After collecting different coloured pebbles, they put the pebbles in their buckets.

Som: I collected 234 pebbles.

Max: I collected 313 pebbles.

Adding 3-digit Numbers

We have learnt how to add two-digit numbers quickly. Now, let us learn how to add 3-digit numbers.

Addition without Regrouping

Som: How many pebbles did we collect in total?

Max: We should add the number of pebbles each of us collected.

Now, add 234 and 313.

Step 1: Add the ones.

4 + 3 = 7

Write 7 in the ones column.

Remember!

Always add from right to left—add the ones, then the tens, and finally the hundreds.

Step 2: Add the tens.

3 + 1 = 4

Write 4 in the tens column.

Example 5: Add 417 and 512.

Add the ones: 7 + 2 = 9

Add the tens: 1 + 1 = 2

Add the hundreds: 4 + 5 = 9

2 • Addition of 3-digit Numbers

Step 3: Add the hundreds. 2 + 3 = 5

Write 5 in the hundreds column.

Example 6: What is the sum of 183 and 604? H T O

1 8 3 + 6 0 4

7 8 7

Thus, 183 + 604 = 787.

Addition with Regrouping

Som: I have 786 pebbles.

Max: I have 546 pebbles.

654 + 321 = Do It Together

Add 654 and 321. H T O 6 5 4 + 3 2 1 5

Som: How many pebbles do we have in total?

Max: Let us add 786 pebbles and 546 pebbles.

Step 1: Add the ones.

6 ones + 6 ones = 12 ones

Regroup 12 ones as 1 tens and 2 ones.

H T O 1

7 8 6 + 5 4 6 2

Step 2: Add the tens.

8 + 4 + 1 = 13 tens

Regroup 13 tens as 3 tens and 1 hundred.

7 8 6 + 5 4 6 3 2

Step 3: Add the hundreds.

7 + 5 + 1 = 13 hundreds

Regroup 13 hundreds as 3 hundreds and 1 thousand.

T O 1 1 7 8 6 + 5 4 6 1 3 3 2

So, 786 + 546 = 1332.

Example 7: Add 156 and 325.

Example 8: Add 368 and 489.

So, 156 + 325 = 481.

Remember!

So, 368 + 489 = 857.

When there are more than 9 tens, then regroup 10 tens into 1 hundred.

Addition of 3-digit Numbers

Error Alert!

ALWAYS remember to add the carryover.

Example 9: Add 189, 234 and 608.

Add 189 and 234 Add 423 and 608

So, the sum of 189, 234 and 608 is 1031.

Example 10: In a school, there are 145 students in Grade 1, 211 students in Grade 2 and 242 students in Grade 3. How many students are there in the three grades together?

Students in Grade 1: 145

Students in Grade 2: 211

Students in Grade 3: 242

Total number of students = 145 + 211 + 242

So, there are a total of 598 students in the three grades.

Add 876 and 129.

876 + 129 =

Adding 4-digit Numbers

Som and Max collected more pebbles and put them in their buckets.

Som: Max! I have a total of 1543 pebbles.

Max: I have a total of 2014 pebbles.

Som: How many pebbles did we collect?

Max: Let us add the numbers.

Total pebbles = 1543 pebbles + 2014 pebbles

Did You Know?

Blaise Pascal invented the first mechanical adding machine called Pascaline that can add and subtract numbers, in 1642.

Let us add 1543 and 2014 to find the total number of pebbles.

Step 1: Add the ones.

Step 2: Add the tens.

Step 3: Add the hundreds.

Step 4: Add the thousands.

1543 + 2014 = 3557

So, Max and Som collected 3557 pebbles.

Example 11: Add 1234 and 8765.

Th H T O

1 2 3 4 + 8 7 6 5

9 9 9 9

So, 1234 + 8765 = 9999.

Example 12: Add 1254, 2121 and 2322.

Add 1254 and 2121. Th H T O 1 2 5 4 + 2 1 2 1

3 3 7 5

So, 1254 + 2121 + 2322 = 5697.

Chapter 2 • Addition of 3-digit Numbers

Add 3375 and 2322. Th H T O 3 3 7 5 + 2 3 2 2 5 6 9 7

Find the sum of 1454 and 2323.

Do It Yourself 2B

Find the sum. a 456 + 232 b 741 + 256

2 Write True or False.

147 + 541 d 325 + 473

a The sum of 144 and 215 is 359. b The sum of 121 and 212 is 313.

c The sum of 541 and 145 is 786. d The sum of 614 and 314 is 928.

3 Find the missing numbers.

4 Find the sum. Fill in the blanks.

5 Add.

6 Answer the questions.

a What is 1234 more than 5145? b What is 2174 more than 1211?

7 Jaspal bought a raincoat for his house helper for ₹456. He bought an umbrella for his guard for ₹235. How much money did he spend? Do you spend money to help people in need? How?

8 Draw place value blocks to show and add 209 and 108. Use for 1 hundred (H), for 1 ten (T) and for 1 one (O).

9 A farmer packs 1245 oranges in the first carton, 2311 oranges in the second carton and 1421 oranges in the third carton. How many oranges does he pack in total? Draw as many oranges as in the thousands place.

c Which two numbers have a sum of 525? Challenge

1 Read the numbers and answer the questions.

a Find the pair of numbers that will give a 4-digit sum.

b Which two numbers, when added, will have 0 at the ones place?

Estimating the Sum

Som and Max now collected coloured stones from the seashore. Som collected 37 stones and Max collected 42 stones.

Som: So, we have about 80 stones in total!

Max: How did you find that out so fast? Let us find out!

Step 1: Round off both numbers to the nearest 10.

Step 2: Add the rounded-off numbers.

40 + 40 = 80

Thus, the estimated sum of 37 + 42 is 80.

Check how close the estimated answer is to the actual answer.

37 + 42 = 79

79 is close to 80.

Hence, the estimated answer is close to the actual answer.

Remember!

An estimate is a smart guess about something. Estimation is used to find quick answers that are very close to the actual answer.

While rounding off to the nearest tens, we round up when the digit at the ones place is 5 or more.

Example 13: Estimate the sum of 36 and 53 by rounding off to the nearest 10. Also, check how close the estimated answer is to the actual answer.

36 rounded off to the nearest 10 is 40.

53 rounded off to the nearest 10 is 50.

So, the estimated sum of 36 and 53 is 40 + 50 = 90.

36 + 53 = 89

89 is close to 90.

Thus, the estimated answer is close to the actual answer.

Find the estimated sum of 24 and 78. Compare with the actual sum.

24 rounded off to the nearest 10 is .

78 rounded off to the nearest 10 is .

So, the estimated sum of 24 and 78 is . is close to .

So, the estimated sum is to the actual sum.

Do It Yourself 2C

Find the estimated sum of the numbers by rounding off both numbers to the nearest 10.

a 17 and 34 b 84 and 17 c 15 and 54 d 47 and 41

2 Round off the numbers to the nearest 10 and find the sum. Check whether the answer is close to the actual answer.

a 31 + 36 b 58 + 23

c 12 + 17 d 21 + 47

3 Ria made 43 cookies and 66 puff pastries to give to the old age home. Estimate the food items she made in all? Do you help and respect the elderly in your house?

4 Coral Island in Andaman and Nicobar is famous for sea-life creatures. Nisha found 78 starfish and Rohit found 52 starfish. About how many starfish did they find together?

5 Round off the numbers to the nearest 10 and find the sum. AAlso find the actual sum of the numbers and round it off to the nearest 10. Check if the answer is the same in both cases.

a 48 + 32 b 35 + 57 c 52 + 19 d 11 + 10

Challenge Critical Thinking

1 Jai scored 35 points in round 1, 48 points in round 2 and points in round 3. When he rounded off the scores, the estimated total was 170. What could be his score in round 3?

Word Problems

Som and Max were collecting driftwood to build a sandcastle. Som collected 15 pieces of wood. Max collected 12 pieces of wood. How many pieces of wood did they collect in total?

We can solve a word problem in different ways. Let us use the CUBES method to find the answer.

CUBES

C: Circle the numbers.

U: Underline the question.

B: Box the keywords.

E: Evaluate/draw.

S: Solve and check.

Evaluate:

Circle the numbers.

Som collected 15 pieces of wood. Max collected 12 pieces of wood.

How many pieces of wood did they collect in total ?

Underline the question. Box the keywords.

15 pieces of wood + 12 pieces of wood = 15 + 12

Solve:

So, Som and Max collected 27 pieces of wood in total.

Check the answer using the order property of addition.

12 + 15

Thus, the answer is correct.

Example 14: There are 654 cherry trees and 256 plum trees on Joseph’s farm. How many trees are there in total?

Let us apply the CUBES method to solve the word problem.

There are 654 cherry trees and 256 plum trees on Joseph’s farm. How many trees are there in total ?

Evaluate:

trees + 256 trees Solve:

CUBES

C: Circle the numbers.

U: Underline the question.

B: Box the keywords.

E: Evaluate/draw.

S: Solve and check.

Check the answer using the order property of addition.

Thus, the total number of trees on Joseph’s farm is 910.

There are 480 girls and 435 boys in a school. How many students are there in the school?

Number of girls = 480

Number of boys =

Total number of students = 480 +

Thus, the total number of students in the school is .

Do It Yourself 2D

A toy shop sold 134 toys in the month of January and 217 toys in the month of February. How many toys were sold in these two months together?

2 The cost of a bicycle is ₹4231, and the cost of a music system is ₹4566. What is the total cost of both the items?

3 The government of India has schemes like the Rashtirya Krishi Vikas Yojana to encourage the use of high-yielding seeds. Raju buys seeds for farming. He buys 2 packets of seeds. The first packet contains 28 seeds, and the second packet has 35 seeds. How many seeds are there in total?

4 In a new school, 218 students enrolled in Grade 2, 317 students enrolled in Grade 3 and 165 students enrolled in Grade 4. How many students enrolled for all the grades combined?

5 The length of Sankesula Barrage is 1300 m and the length of Nagarjuna Sagar Dam is 250 m more than Sankesula Barrage. What is the length of Nagarjuna Sagar Dam?

6 Mr Saxena went to the market and purchased a few items. Look at the table and answer the questions that follow.

Quilt

Hair dryer

Perfume

Bag

₹2150

₹3015

₹900

₹220

a How much money in total did Mr Saxena spend on a hair dryer and a quilt?

b How much money in total did Mr Saxena spend on a bottle of perfume and a bag?

c What is the total amount spent by Mr Saxena if he bought all 4 items?

7 Create a word problem on adding two 3-digit numbers.

1 Nisha has 3 green beads, 4 red beads and 3 blue beads. Ria has 5 green beads, 6 red beads and 2 blue beads. What will be the sum of the numbers formed by these beads?

Points to Remember

Hundreds Tens Ones

• When two numbers are added, then each number is called the addend. The result we get is called the sum.

• The order does not matter when two numbers are added.

• When 1 is added to any number, then the sum is the successor of that number.

• When 0 is added to any number, then the sum is the number itself.

• To solve word problems using the CUBES strategy, circle the numbers, underline the question, box the keywords, evaluate the problem and finally solve and check the answer.

Math Lab

Setting: In pairs

Let’s Add

Collaboration & Experiential Learning

Materials Required: Place value stand, beads, three dice, paper and pencil.

Method:

1 Students in each pair take turns to roll the 3 dice together.

2 Form the largest number and the smallest number from the three digits.

3 Show the numbers using beads.

4 Add the beads in the hundreds place, tens place and ones place to find the sum.

5 Find the sum of the two numbers using the column method of addition.

6 Check the answer with the beads in the place value stand.

7 The pair that solves the addition first wins!

Chapter Checkup

1 Find the missing term.

a 45 + 1 =

d 5 + 3 = 3 +

b 14 + 0 =

e 1 + = 84

2 Find the sum by expanding the numbers.

a 35 + 61

d 21 + 48

3 Add without regrouping.

a 814 + 111

d 5164 + 2231

b 19 + 70

e 64 + 25

b 457 + 121

e 6170 + 3128

4 Estimate the sum to the nearest ten.

a 84 + 8

b 34 + 17

c 87 + = 48 + 87

f + 18 = 18

c 56 + 23

f 35 + 42

c 146 + 723

f 4517 + 4021

c 25 + 52

5 Find the sum of the numbers and then round off the result to the nearest 10.

a 56 + 11

6 Find the missing digits. a

b 23 + 49

c 45 + 36

7 Find the value of:

a 78 more than 361. b 145 more than 456. c 847 more than 254.

d 325 more than 481. e 748 more than 369. f 415 more than 871.

8 The National Library of India, located in Kolkata, is India�s largest library. In a library, there are 1025 mathematics books, 987 science books and 689 Hindi books. What is the total number of books in the library?

9 At a carnival, there were 1547 men, 2048 women, 1023 boys and 1988 girls.

a How many boys and girls were there at the carnival?

b How many men and women were there at the carnival?

c What is the total number of people who went to the carnival?

Chapter 2 • Addition of 3-digit Numbers

10 Vishwa has just started collecting tazos. He has 47 tazos. His friend Ishan had 18 more tazos than Vishwa 2 weeks earlier. How many tazos does Ishan have now, if he collected 37 more tazos in the last 2 weeks?

11 Write a word problem on adding two 3-digit numbers with regrouping.

Challenge

1 Complete the magic triangle. Fill in the circles with the numbers 50, 100, 130, 80, 120 and 70 such that the 3 numbers along each side add up to 300.

2 The estimated sum of 2 numbers is 30. One of the numbers is 23 and the other number is a 1-digit number. Write all the numbers that can be the second number.

Real-Life Maths

Endangered Species

Indian leopards are one of the most endangered species in India. They are protected by the Ministry of Environment and Forests. The table shows the number of leopards in different states of India.

1 The estimated total number of leopards in Goa and Bihar is . a 30 b 70 c 100 d 103

2 Find the total number of leopards in Kerala and Andhra Pradesh.

3 Are the number of leopards in Andhra Pradesh and Kerala more than that in Chattisgarh? Say Yes/No.

4 How can you help protect endangered species? Cross Curricular & Value Development

3 Subtraction of 3-digit Numbers

Let�s Recall

We love playing with toys. And we love it even more when we share our toys with our friends.

Now, imagine you have these 8 toys. You give 2 toys to your friend.

How many toys will you have left?

When we take away objects from a group, we use subtraction to count what is left!

Let us subtract by counting backwards. We had 8 toys, so let us mark this on a line as shown. We gave away 2 toys, so we jump 2 places backward.

We reach 6!

We can say, 8 toys − 2 toys = 6 toys.

Mental Subtraction

Hockey is one of the oldest games played in India. There are 22 players on the field in a hockey match.

Subtracting 2-digit Numbers Mentally

Amit and Anand love playing hockey! They organise hockey tournaments each year. This year, Amit sold 38 tickets and Anand sold 64 tickets.

Properties of Subtraction

Subtracting 1

When 1 is subtracted from a number, the difference is the number before it. This �before� number is called the predecessor.

For example, 10 – 1 = 9. 9 is the predecessor of 10.

Subtracting 0

When 0 is subtracted from a number, the difference is the number itself.

For example, 34 – 0 = 34.

Subtracting the Same Number

When a number is subtracted from itself, the difference is 0.

For example, 56 – 56 = 0.

Example 1: 1 19 – 19 = 0

Fill in the blanks.

= 19

By Counting Forward on a Number Line

Remember, Amit sold 38 tickets and Anand sold 64 tickets. Let us see how many more tickets Anand sold than Amit. We can also subtract 2-digit numbers by counting forward on a number line. Subtract 38 from 64 using the number line.

2 + 10 + 10 + 4 = 26

64 – 38 = 26

Thus, Anand sold 26 more tickets than Amit.

Example 2: Subtract 42 from 78 using the number line.

8 + 10 + 10 + 8 = 36.

78 – 42 = 36.

The difference of 78 and 42 is 36.

Fill in the blanks to subtract 12 from 35 using the number line.

8 + 10 + =

35 – 12 =

The difference of 35 and 12 is .

By Expanding the Smaller Number

We can also subtract 2-digit numbers by expanding the smaller number. Let us subtract 38 from 64 using this method.

Step 1

Identify the smaller number.

The smaller number is 38.

Step 3

Subtract the tens in the smaller number from the larger number.

64 – 30 = 34

The difference of 64 and 38 is 26.

Example 3: Subtract 25 from 84.

84 – 20 = 64

64 – 5 = 59

The difference of 84 and 25 is 59.

Step 2

Expand the smaller number into tens and ones.

Step 4

Subtract the ones in the smaller number from the number you got in Step 3. 34 – 8 = 26

Subtract 16 from 45 by expanding the smaller number.

45 – 10 = 35; – 6 =

The difference of 45 and 16 is .

45 – 16 = ?

Write True or False.

a 27 – 0 = 27

b 64 – 64 = 0

c 76 – 0 = 75

d 82 – 1 = 81 e 93 – 93 = 93 f 43 – 0 = 0

2 Subtract by counting forward.

a 21 – 13 = b 45 – 36 =

3 Subtract by expanding the smaller number.

a 41 – 17 = b 63 – 26 =

c 56 – 27 =

c 71 – 24 =

4 Jagadish Chandra Bose Aquarium in Gujarat is the first underwater aquarium in India. There were 43 species of fish in one section. Due to some re-construction, 15 species of fish were shifted to a new home. How many jumps of ten will you take to find the number of species of fish left in the section?

5 Jaya had 61 roses, and she gave 46 roses to her sister. Draw as many roses as the number of tens that remain with Jaya. 1 rose = 1 tens.

6 Danish is subtracting 46 from a number. He takes 2 jumps of 10 and one jump of 3. What is the number that Danish is subtracting 46 from?

1 Solve the puzzle.

a Choose two numbers from the circle. Subtract the smaller number from the greater number.

b Write the difference in the circle between the two numbers.

c Repeat steps 1 and 2 to complete the puzzle.

Subtraction of 3-digit Numbers

We saw how to subtract two 2-digit numbers. Now, let us learn how to find the difference between two 3-digit numbers.

Subtracting 3-digit Numbers

A read-a-thon is a contest of reading books! The Orchid School arranges an annual read-a-thon for primary (1 to 5), middle (6 to 8) and secondary (9 to 12) grade students. The table below shows the number of books read by the students in each category and the total number of books they need to read in all.

Reading Contest

Students are curious to know the least number of books they need to read to reach their goal.

Subtraction without Regrouping

Primary grade students want to find the least number of books they need to read to reach their goal.

They have read 513 books and their goal is to read 925 books. We can subtract to find out how many more books the students need to read to reach their goal.

So, let us subtract 513 from 925.

Step 1: Write the numbers in column.

Step 2: Subtract the ones.

Step 3: Subtract the tens.

Step 4: Subtract the hundreds. Thus, 925 – 513 = 412

Remember!

We always begin subtraction from the ones place.

So, the students in primary grade at Orchid School need to read a minimum of 412 more books to reach their goal.

Example 4: Subtract 325 from 837.

H T O

8 3 7 – 3 2 5

5 1 2

So, 837 – 325 = 512.

Subtract and fill in the boxes. 1 2 Do It Together

Example 5: Subtract 120 from 682. H T O 6 8 2 – 1 2 0 5 6 2

So, 682 – 120 = 562.

Subtraction with Regrouping

Let us subtract 457 from 742.

Step 1

Write the numbers in the columns.

Step 2

Subtract the ones.

7 ones cannot be subtracted from 2 ones.

So, regroup 4 tens and 2 ones as 3 tens and 12 ones.

Write 12 over the 2 in the ones column, and 3 over the 4 in the tens column.

12 – 7 = 5 ones

Write 5 in the ones column.

Step 3

Subtract the tens.

5 tens cannot be subtracted from 3 tens.

So, regroup 7 hundreds and 3 tens as 6 hundreds and 13 tens.

13 – 5 = 8 tens

Write 8 in the tens column.

Step 4

Subtract the hundreds.

6 – 4 = 2 hundreds

Write 2 in the hundreds column.

So, 742 – 457 = 285.

Never forget to change the digits in case of a carryover! Error Alert!

Example 6: Subtract. 1 238 from 894. 2 293 from 548.

Complete the subtraction.

Adding and Subtracting Together

Addition can be used to verify the difference from subtracting two numbers. The sum of the difference and the smaller number should be equal to the larger number.

Let’s solve 679 – 458:

Step 1 Subtract 458 from 679.

Step 2 Add the difference with the smaller number.

The sum will be the same as the larger number.

So, 679 – 458 = 221 and 221 + 458 = 679.

GREATER NUMBER – SMALLER NUMBER

DIFFERENCE

Example 7: Solve 302 – 239 and verify.

DIFFERENCE + SMALLER NUMBER

GREATER NUMBER

Solve 489 – 276 and verify. Do It Together

Do It Yourself 3B

1 Subtract to find the answer. a

2 Arrange the following numbers in columns and subtract them in your notebook.

a 758 − 426 b 689 − 566 c 483 – 150

3 Write in columns and find the difference by regrouping.

a 624 − 276 b 570 − 383 c 600 − 257 d 704 − 239 e 300 − 114 f 801 − 568

4 Yukti collected 469 bottles for recycling. Priya collected 227 fewer bottles than Yukti. How many bottles did Priya collect? Do you recycle plastic bottles and paper?

5 Read the data on the number of tickets for a play sold by 3 friends. Read the table and answer the questions.

a Akhil sold 159 fewer tickets than Joginder and Mohan sold together. How many tickets did Akhil sell?

b How many more tickets would each of them need to sell so that each of them sells 350 tickets?

6 Deer have 327 bones. Cats have 235 bones. How many more bones do deer have than the cat? Verify your answer.

Challenge

Critical Thinking

1 Form the largest number and the smallest number from the digits 5, 8 and 2. Find the difference of the numbers formed.

Subtracting 4-digit Numbers

Let us see how to subtract 1s, 10s, 100s and 1000s from a 4-digit number.

Subtract 6 from 5469

Subtract the digits in the ones place.

9 – 6 = 3

So, 5469 – 6 = 5463

Subtract 40 from 5469

Subtract the digits in the tens place and retain all other digits.

6 – 4 = 2

5469 – 40 = 5429

Subtract 300 from 5469

Subtract the digits in the hundreds place and retain all other digits.

4 – 3 = 1

5469 – 300 = 5169

Subtract 2000 from 5469

Subtract the digits in the thousands place and retain all other digits.

5 – 2 = 3

5469 – 2000 = 3469

Now what if we want to subtract bigger numbers? Let us learn through an example.

Let us subtract 7564 from 9687.

The steps remain the same.

Step 1: Subtract the ones.

Step 2: Subtract the tens.

Step 3: Subtract the hundreds.

Step 4: Subtract the thousands.

So, 9687 – 7564 = 2123.

Example 8: Subtract.

1 4 from 9127 7 – 4 = 3 So, 9127 – 4 = 9123. 2 400 from 8654 6 – 4 = 2 So, 8654 – 400 = 8254.

Example 9: Subtract 1102 from 4325. Th H T O 4 3 2 5 – 1 1 0 2 3 2 2 3

So, 4325 – 1102 = 3223.

Subtract and fill in the table.

3789 – 1569 = .

Subtract.

a 3468 – 5 b 5296 – 40 c 6807 – 600 d 8547 – 7000

2 Write in columns and find the difference.

a 3735 − 2524 b 6398 – 2202 c 7957 − 1542 d 9853 − 1540

3 Find the difference and arrange in ascending order.

a 4561 – 1230 b 8184 – 5173 c 9427 – 1327 d 9936 – 1121

4 The government has set up schools across the states to provide education to millions of children. There are 3872 government schools in Mizoram and 2702 in Nagaland. Find the difference in the number of government schools in the two states.

5 Amit is arranging funds for donating school books to underprivileged children. He needed ₹6987 and was able to arrange ₹5860. How much more money does he need to arrange?

1 If ‘THAT DOWD’ is written as ‘9869 3423’. What will the message be if DOWD is subtracted from THAT?

Estimating the Difference

A play has been organised in a local theatre. Veena, Manisha and Sonia are selling tickets for the play.

About how many more tickets do each of them need to sell to reach 50 tickets?

We can estimate to find out how many more. We can round off 28 to the nearest tens which is 30.

Thus, 50 – 30 = 20 tickets.

So, Veena needs to sell about 20 tickets more to reach the goal of selling 50 tickets.

Similarly, we can round off 17 to the nearest tens which is 20.

Remember!

When we don’t need an exact answer, we can estimate by rounding off numbers.

Thus, 50 – 20 = 30 tickets.

So, Manisha needs to sell about 30 tickets more to reach her goal of selling 50 tickets.

Finally, we can round off 33 to the nearest tens which is 30.

Thus, 50 – 30 = 20 tickets.

So, Sonia needs to sell about 20 tickets more to reach her goal of selling 50 tickets.

Let us look at some more examples.

Remember!

The rules of rounding off remain the same in estimation.

Example 10: Round off 53 and 29 to the nearest tens and then estimate their difference.

53 is rounded off to 50.

29 is rounded off to 30.

Estimated difference = 50 – 30 = 20.

So, the estimated difference is 20.

Estimate the difference of 32 and 16.

Do It Yourself 3D

Use rounding off to estimate the difference.

2 Round off the numbers to the nearest tens. Find the estimated difference.

a 43 − 31 b 57 − 21

53 − 28 d 30 – 14

58 − 36

96 − 15

3 Marari is a beach in Kerala that is famous for its beautiful seashells. Ajay collected 42 seashells at the beach. He gave 23 seashells to Vijay. About how many seashells does Ajay now have?

4 Arun used the rounding off strategy to find 43 – 19. He rounded off 43 to 50 and 19 to 20 and then estimated the difference. Was Arun right? Why or why not?

5 Navin and Darshana are twins who went to an orphanage to celebrate their birthday. They took 96 chocolates with them. Navin distributes 17 chocolates. Darshana distributes some chocolates. About how many chocolates did Darshana distribute if there were 68 chocolates left?

Challenge

Critical Thinking

1 Form the smallest and the greatest 2-digit numbers using any digits from 5, 9, 8, 1. Find the estimated sum and difference of the two numbers. [Note: Do not repeat digits while forming the numbers.]

Word Problems

Vijay was surprised to know that Jacob reads a lot of storybooks. There were a total of 728 books in a bookcase in Jacob’s bedroom until he sold 193 of them. Can you help Vijay count the number of books left in the bookcase?

Here’s a trick to solve such problems. Let us start finding the total number of books left in the bookcase.

Remember!

We subtract when we need—

• to find out how much is left.

• to find out the difference between two numbers.

Let us rewrite the problem.

CUBES

C: Circle the numbers.

U: Underline the question.

B: Box the keywords.

E: Evaluate/draw.

S: Solve and check.

Underline the question. Box the keywords. Circle the numbers.

Vijay was surprised to know that Jacob reads a lot of storybooks. There were a total of 728 books on a bookcase in Jacob’s bedroom, until he sold 193 of them. How many books were left in the bookcase?

Evaluate: 728 – 193 =

Solve Check

Solve to find the answer.

If 728 – 193 = 535, then 193 + 535 should be equal to 728.

728 – 193 = 535 So, the answer is correct. So, 535 books were left in the bookcase.

Example 11: Write a word problem on subtracting two 3-digit numbers. Many such word problems are possible. One such word problem is given.

Ramu collected 801 ceramic dolls. Chandru collected 763 ceramic dolls. Who collected more dolls and by how much?

Manish has 423 seashells. He has 345 more seashells than Babita. How many seashells does Babita have? Use the CUBES method.

Circle the numbers.

Underline the question. Box the keywords.

Evaluate: 423 – = ?

Solve:

Babita has seashells.

Do It Yourself 3E

Ravi has 478 stickers, and his friend, Shashi, has 689. Who has more stickers, and how many more?

2 In a cricket match, Team A scored 435 runs and Team B scored 146 runs less than Team A. How many runs did Team B score?

3 Amisha went on a picnic with her friends. She had ₹700 with her and she spent ₹592 out of it. How much money was left with her?

4 There are 5397 bags of wheat in the warehouse. If 3075 bags are taken out, how many bags will remain in the warehouse?

5 Nikhil bought 5788 pairs of shoes for his newly opened shop in January. On 1st February, he had 1475 pairs left. How many pairs of shoes did he sell in January?

6 Amit collects stamps from all over the world. He has 467 stamps in his stamp collection. His father gives him another 133 stamps. How many more stamps must he collect if he wants to have 800 stamps in his collection? Do you have a hobby of collecting rare things?

7 Narendra has 442 packages to deliver. David has 464 packages to deliver. Narendra delivers 174 packages, and David delivers 188. Who is closer to finishing his deliveries?

8 Laila went on a trip with her family. She spent ₹3142 out of ₹5275. How much money does she have left?

9 Create a word problem on subtracting two 3-digit numbers.

1 Raj has two numbers in his mind. He gives a clue—�You will get a difference of 60 when the numbers are rounded off�. What are the numbers that Raj could have thought of?

Points to Remember

• We always subtract a smaller number from a bigger number. The answer of subtraction is called the difference.

• When we subtract 0 from a number, the difference is the number itself.

• When we subtract any number from itself, the difference we get is always zero.

• The difference of 2-digit numbers can be estimated by rounding off the numbers to the nearest tens.

Math Lab

Setting: In groups of 3.

Collaboration & Experiential Learning

Chit Game for Subtraction!

Method:

Materials Required: Number chits from 0 to 9.

1 Make chits for numbers 0 to 9 using sheets of paper.

2 Shuffle the chits.

3 Player 1 picks 3 different chits and forms a 3-digit number. Everyone must pick chits at random

4 Player 2 picks 3 chits from the remaining ones and forms a 3-digit number. Hint: Try forming the biggest possible numbers!

5 Player 3 finds the difference of these numbers correctly.

6 The team with the smallest difference wins.

Chapter Checkup

1 Fill in the blanks using the subtraction facts.

a − 64 = 0 b 59 – 0 = c − 1 = 92

d 23 – 23 = e 16 − = 16 f 75 – 1 =

2 Subtract by counting forward.

a 52 – 29 = b 61 – 46 = c 64 – 35 =

d 92 – 67 = e 43 – 24 = f 71 – 42 =

3 Subtract by expanding the smaller number.

a 52 – 27 = b 84 – 55 = c 76 – 29 =

d 23 – 14 = e 68 – 49 = f 62 – 21 =

4 Arrange the following numbers in columns and find the difference.

a 456 – 234 b 842 − 587 c 210 − 187

d 734 – 542 e 863 − 185 f 2456 – 1214

5 Round off to the nearest tens and then find the estimated difference.

a 96 − 12 b 82 – 29 c 61 − 44

6 In an office, 678 pages were kept for printing in a month, out of which 259 pages have been printed. How many pages are still left for printing?

7 985 people came to watch a hockey match. 197 people left after one hour and another 668 left before half-time. How many people watched the whole match?

8 A vegetable vendor bought 925 kg of potatoes from the market. 123 kg of potatoes were rotten. He could sell only 678 kg. How many kg of potatoes does he have left?

9 The first crewed landing on the Moon was in 1969. The last crewed moon-landing mission took place in 1972. How many years� gap was there between the 2 landings?

10 An artist collected 915 cardboard rolls for an art exhibition. He used 268 cardboard rolls for his first exhibit, and 380 cardboard rolls for his second exhibit. How many cardboard rolls did he have left?

11 Create a word problem on subtracting two 4-digit numbers.

1 Which two numbers will have the least and the highest difference? 962 473 609

2 Solve the crossword.

Across a 247 – 133 c 9795 – 2735

Down b 9789 – 8432 d 689 – 421

Real-Life Maths

The Indian Post is one of the most widely distributed postal systems in the world. The operation of the office includes banking, communication, transport of goods and many more activities. The table shows the number of post offices in some states.

1 How many tens will you jump to find the difference between the number of post offices in Goa and Nagaland? a 0 b 3 c 7 d 10

2 Write True or False.

a There are 82 fewer post offices in Nagaland than in Mizoram.

b There are 154 more post offices in Goa than in Mizoram.

3 How much more is the number of post offices in Haryana than in Jammu and Kashmir?

4 What is the difference in the number of post offices in Nagaland and Haryana?

5 We can even deposit money in the post office as we do in banks. Do you have a habit of saving money?

Cross Curricular & Value Development

Understanding Multiplication

Raghu, a farmer, wants to plant some saplings on his farm. He plants an equal number of saplings in different rows. He also has to take care of the saplings by watering them.

Multiplication Facts

Let us look at the ways in which Raghu can arrange the saplings.

2 in each group 4 groups Total saplings = 4 + 4 = 8 saplings

Total saplings = 2 + 2 + 2 + 2 = 8 saplings

In both arrangements, the number of saplings in each row is different but the total number of saplings in the field is equal.

We can write this addition sentence using multiplication as:

These are called the Multiplication Facts

Multiplication facts show us the properties of multiplication.

Order Property of Multiplication

We can multiply two numbers in any order, and the product always remains the same.

Example: 4 × 2 = 2 × 4 = 8

Multiplicative Property of One

When multiplying a number by 1, the product is always the number itself.

Example: 4 × 1 = 4

Multiplicative Property of Zero

When multiplying a number by 0, the product is always zero.

Example 1: Fill in the blanks.

4 × 0 = 0

6 × 5 = 5 × 6

1 × 15 = 15

Example 2: Find the product. 5 × 2 = 10 9 × 0 = 0

Example: 4 × 0 = 0 Fill

State True or False.

a When you multiply any number by 1, you get the same number.

b When you multiply a number by 0, you always get 1.

c Order matters when multiplying numbers.

Find the missing numbers. a 9 × 3 = × 9 b 2 × = 0 c × 7 = 7

d 5 × 8 = 8 × e 47 × = 47 × 94 f × 1 = 123

Thrissur Pooram is a grand festival in Kerala. It has customs involving elephants. Two rows of 15 elephants stand face to face. Write the repeated addition and multiplication sentence for two rows of 15 elephants.

Sophie is helping her mom bake cookies. The recipe is for 3 batches of 4 cookies each. Sophie wants to know if the total number of cookies will be the same if she makes 4 batches of 3 cookies each. Can you help Sophie determine the correct order of multiplication? In what ways do you help your parents in the kitchen?

Challenge

1 There are 5 dots in 4 rows each. 4 dots are removed as shown. Rearrange the remaining dots in the same number of rows and write the multiplication sentence.

Critical Thinking

Building Multiplication Tables

Do you remember Raghu who owns a field? Raghu also owns a flower shop. Raghu sells the flowers in batches of 1, 2, 3 and so on. The number of petals in each types of flower also varies. Let us see the number of petals in different batches of flowers.

Table of 6

The first type of flower has 6 petals. The number of petals in different batches can be given as:

1 ﬂower with 1 × 7 = 7

1 flower with 6 petals 1 × 6 = 6

1 ﬂower with 1 × 7 = 7

2 ﬂowers with 7 petals each 2 × 7 = 14

2 flowers with 6 petals each 2 × 6 = 12

2 ﬂowers with 7 petals each 2 × 7 = 14

3 ﬂowers with 7 petals each 3 × 7 = 21

2 ﬂowers with 7 petals each 2 × 7 = 14

3 ﬂowers with 7 petals each 3 × 7 = 21

3 flowers with 6 petals each 3 × 6 = 18

4 ﬂowers with 7 petals each 4 × 7 = 28

3 ﬂowers with 7 petals each 3 × 7 = 21

4 ﬂowers with 7 petals each 4 × 7 = 28

5 ﬂowers with 7 petals each 5 × 7 = 35

4 flowers with 6 petals each 4 × 6 = 24

4 ﬂowers with 7 petals each 4 × 7 = 28

5 ﬂowers with 7 petals each 5 × 7 = 35

6 ﬂowers with 7 petals each 6 × 7 = 42

5 ﬂowers with 7 petals each 5 × 7 = 35

5 flowers with 6 petals each 5 × 6 = 30

6 ﬂowers with 7 petals each 6 × 7 = 42

7 ﬂowers with 7 petals each 7 × 7 = 49

6 ﬂowers with 7 petals each 6 × 7 = 42

7 ﬂowers with 7 petals each 7 × 7 = 49

8 ﬂowers with 7 petals each 8 × 7 = 56

7 ﬂowers with 7 petals each 7 × 7 = 49

8 ﬂowers with

8 ﬂowers with 7 petals each 8 × 7 = 56

Example 3: Multiply.

Complete the 6 times table. 6 18 24

Table of 7

7 petals each

7 petals each 3 × 7 = 21

7 petals each 4 × 7 = 28

4 ﬂowers with 7 petals each 4 × 7 = 28

5 ﬂowers with 7 petals each 5 × 7 = 35

6 ﬂowers with 7 petals each 6 × 7 = 42

6 flowers with 6 petals each 6 × 6 = 36

6 ﬂowers with 7 petals each 6 × 7 = 42

7 ﬂowers with 7 petals each 7 × 7 = 49

7 flowers with 6 petals each 7 × 6 = 42

7 ﬂowers with 7 petals each 7 × 7 = 49

8 ﬂowers with 7 petals each 8 × 7 = 56

8 flowers with 6 petals each 8 × 6 = 48

8 ﬂowers with 7 petals each 8 × 7 = 56

9 ﬂowers with 7 petals each 9 × 7 = 63

10 ﬂowers with 7 petals each 10 × 7 = 70

9 flowers with 6 petals each 9 × 6 = 54

10 ﬂowers with 7 petals each 10 × 7 = 70

10 ﬂowers with 7 petals each 10 × 7 = 70 10 flowers with 6 petals each 10 × 6 = 60

The second type of flower has 7 petals. The number of petals in different batches can be given as:

1 ﬂower with 1 × 7 = 7

2 ﬂowers with 7 petals each 2 × 7 = 14

3 ﬂowers with 7 petals each 3 × 7 = 21

4 ﬂowers with 7 petals each 4 × 7 = 28

5 ﬂowers with 7 petals each 5 × 7 = 35

6 ﬂowers with 7 petals each 6 × 7 = 42

7 ﬂowers with 7 petals each 7 × 7 = 49

8 ﬂowers with 7 petals each 8 × 7 = 56

9 ﬂowers with 7 petals each 9 × 7 = 63

10 ﬂowers with 7 petals each 10 × 7 = 70

Example 4: Find the product. 1 5 × 7 = 35 2 8 × 7 = 56 3 3 × 7 = 21

Complete the 7 times table. 7 14 28 63

Table of 8

The third type of flower has 8 petals. The number of petals in different batches can be given as:

1 ﬂower with 1 × 8 = 8

2 ﬂowers with 2 × 8 = 16

3 ﬂowers with 3 × 8 = 24

4 ﬂowers with 4 × 8 = 32

5 ﬂowers with 5 × 8 = 40

6 ﬂowers with 6 × 8 = 48

7 ﬂowers with 7 × 8 = 56

8 ﬂowers with 8 × 8 = 64

9 ﬂowers with 9 × 8 = 72

10 ﬂowers with 8 petals each 10 × 8 = 80

Example 5: Find the product. 1 4 × 8 = 32 2 9 × 8 = 72 3

8 times

Table of 9

The last type of flower has 9 petals. The number of petals in different batches can be given as:

Example 6: Find the product.

1 6 × 9 = 54 2 9 × 9 = 81

Complete the 9 times table.

Tables of 10, 20, …, 90

Multiplication by 10

A flower has 10 petals. How can we find the numbers of petals in 8 such flowers?

Number of flowers = 8

Total number of petals = 8 × 10 petals = 80 petals

1 ﬂower with 1 × 9 = 9

2 ﬂowers with 9 petals each 2 × 9 = 18

3 ﬂowers with 9 petals each 3 × 9 = 27

4 ﬂowers with 9 petals each 4 × 9 = 36

5 ﬂowers with 9 petals each 5 × 9 = 45

6 ﬂowers with 9 petals each 6 × 9 = 54

7 ﬂowers with 9 petals each 7 × 9 = 63

8 ﬂowers with 9 petals each 8 × 9 = 72

9 ﬂowers with 9 petals each 9 × 9 = 81

10 ﬂowers with 9 petals each 10 × 9 = 90

Did You Know?

Samarth Bhagyesh Patel, a 7-year old boy from India, holds the record for solving 10 random multiplication problems correctly the fastest, with a time of 1 minute 30.6 seconds. Chapter 4 • Multiplication Tables

To multiply any number by 10, write 0 at the ones place and multiply the number by 1. Examples:

5 × 10 = 50 11 × 10 = 110 154 × 10 = 1540

Multiplication by 20, 30, 40, …, 90

To multiply any number by 20, 30, 40, ...,90 write 0 at the ones place and multiply the remaining numbers. Examples:

5 × 20 = 100 3 × 70 = 210

Error Alert!

NEVER place zeroes in the wrong place when multiplying by 10.

15 × 10 = 105 15 × 10 = 150

Example 7: Multiply.

1 9 × 70

Add zero at the end and multiply 9 with 7.

9 × 7 = 63

9 × 70 = 630

2 14 × 10

Add zero at the end and multiply 14 with 1.

14 × 1 = 14

14 × 10 = 140

Fill in the missing numbers.

8 × 90 = 720

Remember!

On multiplication by 10, 20, 30, …, 90, there is always 0 in the ones place.

3 10 × 90

Add 0 at the end and multiply 10 with 9.

10 × 9 = 90

10 × 90 = 900

7 × 800 = 5600 Do It Together 50

1 5 × 10 = 2 60 × = 420 3 80 × 8 = 4 ____ × 40 = 280

Tables of 100, 200, ..., 900

Multiplication by 100

To multiply any number by 100, write 0s at the ones place and the tens place, and then multiply the number by 1.

4 × 100 = 400

44 × 100 = 4400

444 × 100 = 44400

Note: A product of 100 will always have two zeroes at the end.

Multiplication by 200, 300, 400, …, 900.

To multiply any number by 200, 300, …, 900 write zeroes in the ones and tens places. Multiply the remaining numbers.

3 × 200 = 600

9 × 500 = 4500

Example 8: Multiply.

65 × 100

65 × 100 = 6500 1

Add 2 zeroes at the end and multiply 65 by 1.

65 × 1 = 65

Fill in the blanks.

100 × 300

100 × 300 = 30000 2

Add 2 zeroes at the end and multiply 100 by 3.

100 × 3 = 300

800 × 9

800 × 9 = 7200 3

Add two zeroes at the end and multiply 8 with 9.

8 × 9 = 72

Fill in the blanks.

a 9 weeks = days

b 5 days = hours

c 1 hour = minutes

d weeks = 70 days Compare using >, < or =.

Find the product.

8 × 9

80 × 3

Complete the multiplication facts. a 8 × 8 =

× 4

7 × 90 =

× 10

Raj gives 6 candies to each of his 9 friends. How many candies did he distribute altogether? Do you share things with your friends?

A cricket player has scored 5 centuries in one day internationals. How many runs has he scored in centuries? (1 century = 100 runs)

Create a word problem on multiplying two numbers.

1 In the 2011 World Cup match between South Africa and India, Gautam Gambhir hit 7 fours, and Sachin Tendulkar hit 3 sixes. How many runs did they both make in total by hitting fours and sixes?

Points to Remember

• The order does not matter when two numbers are multiplied by each other.

• When a number is multiplied by 1, the product is always the number itself.

• When a number is multiplied by 0, the product is always 0.

• To multiply a number by 10, put a zero to the right of the number.

• To multiply any number by 20, 30, 40, ...,90, write 0 at the ones place and multiply the remaining numbers.

• To multiply a number by 100, put 2 zeroes to the right of the number.

• To multiply any number by 200, 300, …, 900, write zeroes in the ones and tens places. Multiply the remaining numbers.

Math Lab

Setting: In groups of 3.

Dice Game Collaboration & Experiential Learning

Materials Required: Two dice, a number grid as shown below Method: Roll the dice together. Multiply your two numbers. Colour the product on the grid. The first person to colour four numbers in a row wins.

Chapter

Checkup

1 Write (T) for True and (F) for False.

a 45 × 8 = 8 × 45 b 4 × 6 = 24

c 89745 × 0 = 89745 d 5 × 8 = 40

e 9 × 8 = 72 f 6 × 600 = 3600

2 Find different ways to multiply and get make the number in the centre.

3 Look at the pattern. Add or multiply to complete the pattern.

a 8, 16, 24, ______, ______, ______, ______, ______

b 13, 26, 39, , , , ,

c 30, 40, 50, , , , ,

d 18, 27, 36, , , , ,

e 14, 28, 42, , , , ,

f 200, 400, 600, , , , ,

4 Compare using >, <, or =.

× 70

c 44 × 100

e 48975 × 1 0

4 • Multiplication Tables

8 × 700

5 Use multiplication to fill in the spaces.

6 Rajesh has 10 cookie boxes. There are 7 cookies in each box. How many cookies does he have in total? Draw the boxes using rectangles and cookies using circles.

7 Wild roses have 5 petals. There are 6 wild roses in a bouquet. How many petals are there in the bouquet? Do you take care of plants at home?

8 A female German Shepherd gives birth to 8 puppies in a litter. There are 3 German Shepherds in a dog shelter. How many puppies will be born in the shelter?

9 Vivan bought 9 chocolates, each worth ₹6. He paid the shopkeeper ₹100. How much money did he get in return?

Challenge

1 Complete the puzzle

2 There are 9 layers in a fruit desert. Each layer needs 8 fruits for the outer decoration. The even numbered layers will have grapes, and the odd numbered layers will have blueberries. How many grapes and how many blueberries are required?

Wooden Toys!!

Channapatna toys are traditional wooden toys that come from the town of Channapatna in Karnataka. Traditionally, ivory wood is used to make the famous dolls.

1 A wooden stacker toy has 6 rings. There are 2 such toys. The multiplication sentence for the number of rings is .

2 A wooden dog toy needs 4 wheels. How many wheels do 7 wooden dog toys need?

3 The cost of a wooden rattle is ₹90. If there are 4 wooden rattles in a box, what is the total cost?

4 A wooden kitchen set has a pair of plates, a pair of tumblers, a pair of spoons, a pair of pans, a pair of baskets and a pair of pots. What is the total number of pieces in the kitchen set?

5 Create and draw your favourite wooden toy.

5 Multiplication by 2-digit Numbers

Let’s Recall

Let us say we have 5 balloons. We can call them 1 group of 5 balloons.

Now, suppose we have 6 groups of 5 balloons.

How many balloons do we have in total?

5 + 5 + 5 + 5 + 5 + 5 = 6 × 5 = 30

We have 30 balloons.

We learnt in the previous chapter that this is called a multiplication fact.

Let’s Warm-up

Multiplying Numbers

Rahul: Hi, Aisha! Do you have recipes for baking cakes?

Aisha: Hi, Rahul! Yes, I have a recipe that makes 1 cake.

Rahul: But we have an order for 24 cakes. How can we bake 24 cakes?

Aisha: Don’t worry, Rahul! We can multiply all the amounts of the ingredients by 24! So, if for 1 cake we need 1 cup of sugar, for 24 cakes, we will need 24 × 1 = 24 cups of sugar.

Remember!

On multiplying a number by 1, the product is always the number itself.

Multiplying by Expanding the Bigger Number

We saw how Rahul and Aisha found the amount of sugar needed for 24 cakes.

What if each cake required 2 cups of flour? What would they have done then?

They would use multiplication again! In this case it would be, 24 × 2 cups. But how can we calculate that? Let us learn.

Using the Box Method

We can multiply bigger numbers by 1-digit numbers by expanding the bigger number.

Step 1

Expand the bigger number.

24 = 20 + 4

Step 3

Multiply the smaller number with the ones and then the tens.

20 4

2 × 2 × 20 = 40 2 × 4 = 8

Step 2

Write the numbers as done below.

20 4 2 ×

Step 4

Add all the products. 40 + 8 = 48

So, they need 48 cups of flour for the cakes!

Now, what if Rahul and Aisha wanted to make 240 cakes? How would they find the amount of flour needed?

Each cake requires 2 cups of flour. In this case it would be 240 × 2 cups.

Step 1: Expand the bigger number.

240 = 200 + 40 + 0

Step 2: Write the numbers as shown below.

Step 3: Multiply the smaller number with the ones, tens and the hundreds.

Step 4: Add all the products.

400 + 80 + 0 = 480

So, they need 480 cups of flour.

Remember!

The product of any number with zero is always 0.

Let us see more examples of multiplication by expanding the bigger number.

Example 1: Solve by expanding the bigger number.

92 × 2

× 2 ×

= 180 2 × 2 = 4 180 + 4 = 184 So, 92 × 2 = 184.

800 + 80 + 4 = 884 So, 221 × 4 = 884. Find the product of 122 and 3 by expanding the bigger number.

+ 60 + =

122 × 3 = .

Using the Lattice Method

The lattice method of multiplication uses a grid to multiply 2 numbers.

Let us multiply 43 by 7 using the lattice method.

Number of rows is the same as the number of digits in the multiplier

Step 1: Make a grid with 2 columns and 1 row and draw diagonals across each box in the grid. Write the numbers.

Step 2: Multiply 4 and 3 by 7 and write the products.

Number of columns is the same as the number of digits in the multiplicand

Step 3: Extend the diagonal and add the digits along the diagonals to get the result. Regroup 2-digit numbers in any diagonal and carry over to the next left diagonal.

So, 43 × 7 = 301.

Now, let us multiply 6 × 283.

1: Draw the grid and write the numbers.

2: Multiply 2, 8 and 3 by 6 and write the products.

3: Extend the diagonal and add the digits along the diagonals to get the result.

4: Regroup the 2-digit numbers in diagonals and carry over to the next left diagonal if required.

So, 283 × 6 = 1698.

Example 2: Multiply 71 by 9

Example 3: Multiply 421 by 4

So, 71 × 9 = 639.

So, 421 × 4 = 1684.

Find the product of 523 and 5 using the lattice method.

Did You Know?

Vedic Math is like a magical toolbox for solving math problems. It is an ancient system from India that helps you add, subtract and multiply numbers in your head.

So, 523 × 5 = .

Multiply the following using the box method.

a 32 and 3 b 20 and 4 c 21 and 4

d 124 and 2 e 111 and 4 f 223 and 3

Find the product using the lattice multiplication method.

a 16 and 3 b 41 and 6 c 55 and 8

d 185 and 3 e 502 and 7 f 716 and 9

Annie wants to multiply 123 by 3 by expanding the bigger number. How many tens will she multiply by 3?

423 = and 8 = . Draw the symbols to show the digits of the product.

The first ropeway in India the Rajgir ropeway is 333 m long. If the cabin makes 3 trips, how much distance has the cabin travelled? Find out using the lattice method.

1 Samir multiplied 321 by 2 as given below. Mark the error that he made. Solve correctly.

Multiplying by 1-digit Numbers

We have learnt to multiply by expanding the bigger number.

Let us now learn to multiply by the vertical multiplication method.

Multiplying by 1-digit Numbers without Regrouping

Let us multiply 122 by 3 using the vertical multiplication method.

Step 1

Multiply by the digit in the ones place.

3 × 2 ones = 6 ones

We get 122 × 3 = 366.

Step 2

Multiply by the digit in the tens place.

Step 3

Multiply by the digit in the hundreds place.

2 tens = 6 tens

Example 4: Multiply 232 by 2.

3 × 1 hundred = 3 hundreds

Multiply 121 by 4.

232 × 2 = 464

× 4 =

Multiplying by 1-digit Numbers with Regrouping

Now, let us see how to multiply numbers with regrouping.

Multiply 16 by 4.

Step 1

Multiply the number by the digit in the ones place.

6 × 4 = 24

24 = 2 tens and 4 ones. Write 4 in the ones place. Regroup 2 tens in the tens place.

Step 2

Multiply the number by the tens digit. 1 × 4 = 4.

Add the regrouped tens to 4.

4 + 2 = 6.

So, 16 × 4 = 64.

Now, let us try multiplying a 3-digit number with a 1-digit number.

Let us find the product of 116 and 4.

Step 1

Multiply the number by the digit in the ones place.

4 × 6 ones = 24 ones

24 = 2 tens and 4 ones. Write 4 in the ones place.

Regroup the 2 tens in the tens place.

Step 2

Multiply the number by the digit in the tens place, and add the regrouped ones, if any.

4 × 1 ten = 4 tens

4 tens + 2 tens (regrouped) = 6 tens

Step 3

Multiply the number by the digit in the hundreds place, and add the regrouped tens, if any.

4 × 1 hundred = 4 hundreds

So, 116 × 4 = 464.

When multiplying 2 numbers with regrouping, multiply the digit in the tens or hundreds with the 1-digit number. Do not add the carried over tens or hundreds to the digit in the tens or hundreds place, before multiplying.

Example 5: Find the product of 175 and 5.

Find the product of 237 and 6.

Do It Yourself 5B

Find the product of the numbers.

Multiply the numbers with regrouping.

Multiply by writing in columns.

Daniel solved a multiplication problem as given here. Circle the error and solve it correctly.

Banu wants to stitch a 5 layer quilt using 230 pieces of old cloth in each layer. How many pieces of cloth will she need? Do you recycle or donate your old clothes?

1 hour on the planet Venus is equal to 243 Earth hours. How many Earth hours will 7 hours

1 Janu wants to construct a square shaped dog house for her pet. Each wall will require 120 bricks. How many bricks will she require in total?

Multiplying 2-digit Numbers

Rahul: We need 12 chocolate chips for 1 cake. How many chocolate chips will we require for 24 cakes?

Aisha: We will multiply to find the right number of chocolate chips, 12 × 24.

Multiplying by 2-digit Numbers without Regrouping

We need to multiply 24 and 12 to help Rahul and Aisha.

Step 1

Multiply by the ones.

Step 2

Multiply by the tens.

Step 3 Add

NEVER place the numbers in incorrect place value columns for multiplication.

Example 6: Multiply 23 by 21.

Multiply 13 by 12. Do It

23 × 21 = 483.

13 × 12 =

Multiplying by 2-digit Numbers with Regrouping

We learnt how to multiply a 2-digit number with another 2-digit number. But what if the numbers require regrouping? Let us learn!

Multiply 28 × 14.

Step 1

Multiply by the ones.

Step 2

by the tens.

The product of 28 and 14 is 392.

Example 7: Find the product of 34 and 25.

The product of 34 and 25 is 850.

Chapter 5 • Multiplication by 2-digit Numbers

and

the

45 × 31 =

Do It Yourself 5C Find the product.

Multiply by writing in columns.

a 12 × 56 b 15 × 86 c 18 × 95 d 24 × 27

e 48 × 26 f 39 × 26 g 39 × 45 h 58 × 34

Cotton candy was first made in the 19th century. Fill in the blank.

1 cotton candy needs 14 g of sugar. 21 cotton candies need g of sugar.

In a garden, there were 23 rows of trees. Parul planted 5 trees in each row. How many trees were there in the garden? Why is it good to plant trees? Do you help in taking care of the plants and trees in your neighbourhood?

1 What is the product of the greatest 2-digit number and the smallest 2-digit number?

Estimating the Product

Rina’s birthday is in a week. She and her father are planning the party!

Father: Dear, we need to plan your upcoming birthday party. Let us estimate the number of gift packets we will need.

Rina: Of course, Dad! I am excited. We will have 46 guests, and we will give 5 gift packets to each. How many packets will we need?

Father: We will need around 250 packets.

Rina: Great, Dad! How did you find that out so fast?

Estimation

Rina’s father had to find 46 × 5.

He estimated the number of packets by rounding off to the nearest 10. Let us learn more about estimation.

Step 1

Round off the bigger number to the nearest 10.

46 is rounded up to 50.

Step 2

Multiply the numbers.

50 × 5 = 250

The estimated product of 46 and 5 is 250.

Round down

Did You Know?

In 1960, Anatoly Karatsuba developed a method of multiplying numbers quickly by breaking down larger numbers into smaller numbers. It is called the Karatsuba Algorithm

Round off

If the ones digit is less than 5, round down to the same tens.

Round up

If the ones digit is 5 or more than 5, round up to the next tens.

Example 8: Estimate by rounding off the bigger number to the nearest 10 for 63 × 5.

Round off the bigger number to the nearest 10.

63 is rounded down to 60.

Multiply the numbers.

60 × 5 = 300

The estimated product of 63 and 5 is 300.

Estimate the product by rounding off the bigger number to the nearest 10.

1 88 × 8

Round off the bigger number to the nearest 10. is rounded to .

Multiply the numbers.

90 × 8 ≈ _______ .

The estimated product of 88 and 8 is _______ .

2 92 × 5 ≈ × 5 ≈

The estimated product of 92 and 5 is .

Do It Yourself 5D

Round off the following to the nearest ten.

Estimate the product by rounding off the bigger number to the nearest ten.

44 × 5

81 × 2

Find the estimated product. Round off the first number to the nearest 10. Compare the answer with the actual product by finding their difference.

66 × 22

Round off the 2-digit number and estimate the product. Begin at the start and follow the correct answers through the maze until you get to the end.

Jaipur is famous for lac bangles made from the natural resin lac. Riya is packing bangles in boxes. She packs 45 boxes with each box having 24 lac bangles. What is the estimated number of bangles that she packed? (Hint: Round off both the numbers)

�I am a number rounded off to 50. The product of my digits is 15.� What number am I? 1

Word Problems

Sheena is helping her mother in their toy shop. Sheena�s mother has asked her to count all the balls. There are 14 bags containing the same number of balls.

Sheena: I have counted the balls in one bag. There are 34 balls.

Mother: Great! Are you going to count the balls in all the bags one by one?

Sheena: No no, I have learnt the magic of multiplication. I will find the total using multiplication.

Step 1

What do we know?

Balls in 1 bag = 34

Bags = 14

do we need to find?

no. of balls = 34 × 14

Example 9: Sachin's school has organised a charity program for Christmas. He wants to knit 128 scarves for the needy. Each scarf requires 4 balls of yarn. Find the total number of balls of yarn he needs to knit the scarves.

No. of balls of yarn required for 1 scarf = 4

No. of scarves to be made = 128

Total no. of balls of yarn required = 128 × 4

Total no. balls of yarn needed = 512.

Sona used 23 beads to make a necklace. How many beads does she need to make 22 such necklaces?

No. of beads in a necklace = _____ .

No. of necklaces to be made = .

Total no. of beads required = × .

The total number of beads required for 22 necklaces is . 23

A box contains 13 erasers. How many erasers would there be in 12 such boxes?

The cost of a notebook is �100. How much will 12 such notebooks cost?

In an orchard, there are 64 apple trees in a row. How many trees are there in all if there are 7 such rows?

There are 12 Scouts and Guides leaders in school. Each leader has 26 students in their team. How many students are there in total?

There are 45 balloons in a packet. How many balloons will there be in 54 such packets?

Christmas is celebrated on December 25th each year to honour the birth of Jesus Christ. Sally went to Mr Jacob’s store to buy Christmas decoration items. Read the price list and answer the questions.

a What would be the price of 45 candles?

b How much would Sally pay for the stars if she bought 25 stars?

c Sally bought a packet with 45 bells. How much did she pay for the bells?

Critical Thinking

In a day Deepak swims a length of 50 m from the start point to the end and swims back to the start point. If he practises for 6 days, what total length does he swim in 6 days?

Points to Remember

• On multiplying a number by 1, the product is always the number itself.

• On multiplying a number by 0, the product is always 0.

• We use estimation to quickly get a rough idea of the result without performing actual multiplication.

• To round off to the nearest 10, look at the digit in the ones place—if it is 5 or greater, we round up to the next higher 10, and if it is 4 or smaller, we keep the same number of tens.

Math Lab

Let’s Play Bingo!!

Collaboration & Experiential Learning

Setting: In pairs

Material Required: Bingo strip, bingo sheet, paper and pencil.

Method:

Bingo Strip

9 × 12 53 × 13 71 × 7

31 × 11 89 × 61 107 × 3

45 × 12 25 × 27 98 × 15

1 Each pair will take two bingo sheets.

Bingo Sheet 90 500 490

300 5400 300

500 900 2000

2 The teacher will call out the multiplication problem from the strip.

3 The students will estimate the product and cross out on the sheet.

4 The first pair to cross out 5 numbers on the sheet will win the ‘Quick 5’ round.

5 The first pair to cross out all the numbers on the sheet wins the ‘Full House’ round.

Chapter Checkup

1 Write 'T' for True and 'F' for False. a 62 × 0 = 0

1 × 55 = 56 c 1 × 91 = 92

2 Find the product using the box method. a 12 × 4 b 29 × 3

3 Multiply using the lattice method. a 43 × 7

63 × 8

88 × 0 = 0

28 × 6

205 × 7

381 × 7

× 5

4 Multiply. a 221 × 4 b 243 × 2 c 210 × 3 d 231 × 2

5 Find the product. a 27 × 10 b 20 × 63 c 83 × 50 d 378 × 6

6 Find the estimated product by rounding off the bigger number to the nearest 10. a 12 × 6 b 34 × 4 c 34 × 3 d 44 × 2

7 A bus that can seat 76 people makes 16 trips in a day. If the bus is completely full on all 16 trips, how many people travelled in the bus?

8 A crate holds 45 apples. How many apples are there in 12 such crates?

9 A box contains 6 chocolates, and there are 15 boxes. If each box costs ₹9, how much money will Raj need to buy all the chocolates?

10 The Constitution of India has 234 pages. How many pages are there in 6 such books?

11 A sheet of stickers has 56 stickers. How many stickers are there on 56 such sheets?

12 39 buses were arranged to take some children for a picnic. If 25 children could sit in a bus, how many children went for the picnic?

13 36 children paid ₹50 each at the entrance of Arignar Anna Zoological Park, one of the largest zoological parks in India. How much money was paid at the entrance?

14 In a multiplex theatre, there are 4 auditoriums. 425 people can sit in each auditorium. How many people can watch films in the multiplex theatre at one time? And how many at two times?

15 Write a word problem on multiplying two 2-digit numbers.

Challenge

The product of two numbers is 60 and their sum is 17. What are the two numbers? Fill in the blanks with the correct operation. 22 3 4 12 = 276

Real-Life Maths

Toll Plaza Charges

The money paid at the toll plazas on the highway is called toll tax. The money from the toll tax is used for repairing and maintaining the highways. The table below shows different tolls for cars in different toll plazas.

of the toll Plaza Nashri Panchvati Manavasi Debra

1 Which of these is the total toll tax paid for 2 cars at Manavasi?

2 The total toll cost for 3 cars at Debra is ₹ .

3 Find the total cost of the toll at Nashri for 7 cars.

4 What is the total cost of 10 cars passing through Manavasi and Debra?

5 What should we do to keep the toll plazas clean?

Name

6 Division

Let’s Recall

Imagine there are 4 cookies.

Let us share these cookies between two children. Sharing doubles the joy of eating!

How can we share the cookies between two children, so that each child gets the same number of cookies?

Let us give 1 cookie to each child.

Now, the children have 1 cookie each, but we still have 2 cookies left.

Let us give 1 more cookie to each child.

Now, the children have 2 cookies each and no cookies are left.

We distributed 4 cookies between 2 children. Each child got 2 cookies.

This breaking up of a number into equal parts is called division. In the above case, 4 was divided into 2 groups.

The result—the number of cookies with each child was 2.

This can also be written as 4 ÷ 2 = 2.

Let’s Warm-up

Write True or False.

1 The marbles can be distributed equally among 6 friends. ______________

2 The marbles can be distributed equally among 2 friends.

3 The marbles can be distributed equally among 4 friends.

4 The marbles can be distributed equally among 3 friends. ______________

I scored out of 4.

What Division Means

Sera, Mona and Amir have come to Soham’s house to play. Soham’s mother baked cookies for the kids.

Soham, here are 12 cookies. Place an equal number of cookies on 4 plates.

Soham placed the cookies equally on 4 plates. All the kids enjoyed the cookies.

Understanding Division

Soham’s mother asked him to share 12 cookies equally among four plates. Equal sharing is also known as division.

In other words, division helps us share or separate things into equal parts. It is represented by the “÷” sign. Let us see how Soham distributed the cookies across four plates!

Equal Sharing

Soham distributed 12 cookies across 4 plates and, each plate had 3 cookies.

Example 1: Swapna has 24 candies. She gives 8 candies to each of her friends. Among how many friends does Swapna share the candies?

Number of candies Swapna has = 24

Number of candies she shares with each friend = 8

To find the number of friends, we will make groups of 8 candies.

Group 1

Group 2

Group 3

As there are 3 groups of 8 candies, Swapna shares the candies among 3 friends.

Riya has 30 stickers. She can use only 5 stickers on each gift box. On how many gift boxes can the stickers be put?

Let us share 30 stickers in groups with 5 stickers in each group. Group Group ____ Group 20 1

Group 10

Group 3 Group 5

As there are groups of 5 stickers, Riya can put stickers on gift boxes.

Division as Repeated Subtraction

Komal has 20 coins, and she wants to put 5 coins in each pouch. How many pouches does she need? Let us help her divide 20 by 5 using repeated subtraction.

Subtract 5 from 20 until we get 0.

Count the number of times 5 has been subtracted.

We subtracted 5 four times. So, there are four 5s in 20. Hence, Komal requires 4 pouches to keep the coins.

Example 2: How many 7s are there in 21?

Subtract 7 from 21 until we get 0.

Count how many times 7 has been subtracted.

We subtracted seven 3 times. So, there are three 7s in 21.

Find the number of 6s in 24.

Subtract 6 from 24 until we get 0.

Count how many times 6 has been subtracted. We subtracted 6 times.

So, there are 6s in .

Remember!

Always count how many times the number has been subtracted, not the number itself.

Circle the objects to share them equally among the number of people shown. a

4 people b

Colour an equal number of balloons in red, blue and green.

7 people

9 people

Look at the picture. Draw apples to show an equal number of apples in each basket. Fill in the blanks.

Total number of apples =

Number of baskets = Number of apples in each basket =

Divide using the repeated subtraction method.

a How many 1s are there in 9? b How many 11s are there in 22?

c How many 9s are there in 27? d How many 8s are there in 32?

Kartik helps his parents with household chores. Today he helped his mother cook. Kartik made 15 rotis. If there are 5 family members in the house and each gets an equal number of rotis, how many rotis will each member get?

Naina has 36 matchsticks. If she uses 3 matchsticks every day, how many days will it take her to use up all the matchsticks?

63 7 9 9 = 10 Challenge

1 Put the correct mathematical symbol to make the statement correct.

Division and Multiplication

Sudha and Vishal go to the market to sell oranges. Vishal asks, “How many oranges do you have Sudha?”

I have 6 baskets with 4 oranges in each basket. How many oranges do you have?

I have 24 oranges in 6 baskets.

After reaching the market they find that they have an equal number of oranges in each of their baskets.

Writing Divison Sentences

Sudha has 6 baskets with 4 oranges in each basket. 4 + 4 + 4 + 4 + 4 + 4 = 6 × 4 = 24

Vishal has 24 oranges in 6 baskets.

So, 24 divided among 6 groups will have 4 each.

Remember!

Division is all about sharing or distributing things into equal groups. On the other hand, multiplication is like adding equal groups of things together.

This can be written as:

24 (number of oranges) ÷ 6 (number of baskets) = 4 (number of oranges in each basket)

This is called ‘Dividend’.

This is called ‘Divisor’.

The above division can be given as:

Dividend ÷ Divisor = Quotient, where:

Dividend = The number which is being divided.

Divisor = The number which divides a given number.

This is called ‘Quotient’.

Quotient = The number we obtain when we divide one number by another.

50 pencils are divided equally into 5 packets. Write a division sentence to show the number of pencils in each packet.

Dividend = Divisor = Quotient =

Division sentence = ÷ = .

Division and Multiplication Facts

In the above example, we saw that 6 × 4 = 24 and 24 ÷ 6 = 4. This tells us that division and multiplication are closely related.

Using the dividend, divisor and quotient, the division and multiplication facts can be given as:

Division fact = Dividend ÷ Divisor = Quotient or Dividend ÷ Quotient = Divisor

Multiplication fact = Quotient × Divisor = Dividend

Remember!

Multiplication fact

6 × 4 = 24

For most multiplication facts, there are two division facts.

Division fact

24 ÷ 6 = 4

24 ÷ 4 = 6

Error Alert!

A multiplication fact is given as: Quotient × Divisor = Dividend For 10 ÷ 2 = 5. 5 × 2 = 10 2 × 10 = 5

Example 3: Write the multiplication fact for 32 ÷ 8 = 4.

Dividend = 32, Divisor = 8, Quotient = 4

Multiplication fact = Quotient × Divisor = Dividend

Therefore, the multiplication fact for 32 ÷ 8 = 4 is 4 × 8 = 32.

Example 4: Write the division facts for 12 × 3 = 36.

Here the dividend is 36. Both 12 and 3 can be the divisor.

So, the division facts are 36 ÷ 3 = 12 and 36 ÷ 12 = 3.

Find the division and multiplication facts.

Using Multiplication Tables

We can use the multiplication tables to help us with division.

Suppose we want to divide 12 bananas equally among 3 children.

As we need to divide 12 items among 3 children, we will use the multiplication table of 3 and see how many times 3 is 12.

We can see that, 3 times 4 equals 12. Therefore, each child will get 4 bananas.

Example 5: Find 54 ÷ 6 using the multiplication table. We look for the multiplication fact that gives us 54 when multiplied by 6.

In the multiplication table for 6, we find that 6 × 9 = 54.

Therefore, 54 ÷ 6 = 9.

Solve the following using multiplication tables.

42 ÷ 7 7 × 6 = 42

Therefore, 42 ÷ 7 = 6.

72 ÷ 9 9 × 8 = 72

Therefore, 72 ÷ 9 = .

72 ÷ 8 × =

Therefore, ÷ = .

Properties of Division

There are four properties of division.

1 When we divide any number by 1, we get the same number.

For example, 2 ÷ 1 = 2.

From the given repeated subtraction, we can say that there are two 1s in 2.

2 When we divide any number by itself, the answer is always 1.

For example, 8 ÷ 8 = 1.

From the repeated subtraction, we can say that there is one 8 in 8.

3 When we divide 0 by any number, the answer is always 0.

For example, 0 ÷ 6 = 0.

If 0 things are divided among 6 children, each child will get nothing. Therefore, 0 divided by a number always equals 0.

Did You Know?

Brahmagupta was an Indian mathematician who taught us important rules for dividing numbers and even explained what happens when you try to divide by zero.

4 You can’t divide any number by 0. There is no answer.

This can be seen using repeated subtraction as given: We will keep on subtracting 0 from the number but will not get 0 as the answer.

Example 6: Find 26 ÷ 1.

When we divide any number by 1, we get the same number.

Therefore, 26 ÷ 1 = 26.

Example 7: Find 54 ÷ 54.

When we divide any number by itself, the answer is always 1.

Therefore, 54 ÷ 54 = 1.

Solve the division problems.

It Yourself

Answer the following using the properties of division.

Fill in the blanks using multiplication tables.

Write the division facts for the multiplication facts.

a 7 × 4 = 28 b 5 × 9 = 45 c 3 × 6 = 18

d 8 × 2 = 16 e 10 × 3 = 30 f 6 × 7 = 42

Find the divisor.

Dividend Divisor Quotient

a 20 ÷ = 10

b 42 ÷ = 7

c 30 ÷ = 5

d 63 ÷ = 7

There are 18 cream rolls at a party. If each child gets 1 cream roll, how many children are there at the party?

A teacher had 45 notebooks to be distributed among 9 students so that each student gets 5 notebooks. Write the multiplication fact.

A group of students is conducting a project to clean up litter from a beach. They collected 36 pieces of trash in one hour. If they want to divide the trash equally into 4 bags for proper disposal, how many pieces of trash will go into each bag?

Create a word problem involving division of two numbers. Also write the multiplication fact.

Points to Remember

• Division means sharing equally. It is represented by “÷”.

• Dividend ÷ Divisor = Quotient

• Division and multiplication are closely related and are opposite operations.

• When you divide any number by 1, you get the same number.

• When you divide any number by itself, the answer is always 1.

• When you divide 0 by any number, the answer is always 0.

• You cannot divide any number by 0; there is no answer.

Math Lab

Setting: In groups of 5

Let's Stick It!

Collaboration & Experiential Learning

Materials Required: 30 paper sticks for each group, pen and paper Method:

1 Distribute the sticks among the groups.

2 The teams need to use the sticks and make as many equal groups of sticks as possible.

3 The teams will write down the multiplication and division facts for the groups formed in their notebook.

4 The team that makes the most correct groups wins!

Chapter Checkup

1 Circle the objects to share them equally among the number of people shown. a 3 people b 8 people c 6 people

people

2 Divide using the repeated subtraction method.

a 24 ÷ 3

56 ÷

3 Write the multiplication fact for the given division facts. a 36 ÷ 3 = 12 b 88 ÷ 4 = 22

4 Write two division facts for each multiplication fact.

a 9 × 5 = 45 b 4 × 8 = 32

e 4 × 6 = 24 f 9 × 8 = 72

5 Answer the problems using multiplication tables. a 27 ÷ 9

6 Write two examples for each property of division.

a When you divide any number by 1, you get the same number.

b When you divide any number by itself, the answer is always 1.

c When you divide 0 by any number, the answer is always 0.

d You can’t divide any number by 0. There is no answer.

7 There are 20 toy cars to be divided among 20 children. How many toy cars will each child receive?

8 Ruma baked 32 cupcakes. If she distributes them equally among 4 children in an NGO, how many cupcakes will each child get?

9 A group of 36 people were travelling to see the 7 wonders of the world. When they reached Agra to see the Taj Mahal, the travel guide divided them into groups of 6. How many groups did the travel guide form?

Challenge

1 Use any two numbers from the box to complete the division sentence on the caterpillar.

2 Each row and column is a division problem. Write the possible numbers in the empty spaces.

Real-Life Maths

Cross Curricular & Value Development

Aquarium Arrangement

A marine biologist is a scientist who studies sea animals and their homes. Mr. Sharma is a marine biologist. He made an aquarium for a local science museum. The aquarium has 27 different types of fish. He wants to put these fish into 3 tanks, with each tank having the same number of different types of fish.

Answer the following questions:

1 How many types of fish are there in each tank?

a 6 b 7 c 8 d 9

2 Write the division sentence for the number of fish in each tank.

3 If Mr Sharma had 36 different types of fish and still used 3 tanks, how many types of fish would each tank have? a 10 b 11 c 12 d 13

4 If Mr Sharma had 18 types of fish and 3 tanks, each tank would have 6 types of fish. (True/False)

5 What should we do to protect sea creatures?

7 Division by 1-digit Numbers

Let�s Recall

In the previous chapters, we learnt that multiplication and division are closely related.

We use multiplication to find the total number of objects when we know the number of groups and items in each group.

For example, there are 4 groups containing 3 smileys each. How many smileys are there?

There are 4 × 3 = 12 smileys.

We use division when we want to group a set of items into equal groups, so that each group contains the same number of items.

For example, let us say we want to form 4 equal groups of these 12 smileys:

Now, the groups will be formed as before:

This time, we say that 12 ÷ 4 = 3

We formed 4 groups containing 3 smileys each.

So, 4 × 3 = 12 and 12 ÷ 4 = 3.

Let’s Warm-up

Match the following.

Dividing Numbers

Arjun has 62 marbles. He wants to share them equally among his 2 friends, Karan and Rohan.

I will put 1 marble at a time in each of two bags until I finish all the 62 marbles.

But that will take a lot of time. We can use the multiplication table of 2.

Long Division

But we only know the table of 2 up to 20!

Sometimes the numbers are large, and we may not be able to divide them using the multiplication table. That is when we use long division.

In long division, we write the division terms as shown:

A number that divides another number.

Value left after the division.

Quotient

Divisor Dividend

Remainder

Long Division without Remainder

The number we get when we divide one number by another.

The number that is to be divided.

Let us help Arjun divide the marbles among his friends.

The first thing we do is write the dividend and divisor in the division house. 2 6 2

Step 1

Take the first digit of the dividend (62) which is 6. Divide it by 2 and write the answer above 6.

Step 2

Multiply 3 and 2 and put the answer right below 6.

Step 3

Subtract 6 from 6. That is 6 – 6 = 0.

Step 4

Bring down the next digit 2 of the dividend and write it next to 0.

Now we repeat the same steps for the next digit:

Did You Know?

Brahmagupta, an Indian mathematician, introduced the concept of zero, which is very important when we divide numbers, especially when we have remainders.

Therefore, each friend will get 31 marbles. Arjun, Karan and Rohan are also fond of stamps. They have 489 stamps. They divide the stamps equally using the same method.

On dividing 489 by 3, each friend gets 163 stamps.

Example 1: Divide.

Division with Remainder

Is it always possible to share something equally?

Rohan has 5 crayons, and he wants to share them equally between Arjun and Karan.

Left over

When we divide, it is not always possible for things to be shared equally. This can result in having something left over, which will give us a remainder other than zero.

Kavya has a pack of 35 biscuits. She wants to share the biscuits among her classmates so that each of them gets 3 biscuits. Let us see how many classmates will get 3 biscuits. Do you share your things with your friends?

Quotient (Number of classmates who will get 3 biscuits)

Divisor

Remainder (Number of biscuits Kavya has left)

Is there a way to check whether our division is correct?

Yes, we can check division by using the formula: (Quotient × Divisor) + Remainder = Dividend

Can the remainder be greater than the divisor? Think and Tell

Let us check the above division using the formula: Here, Quotient = 11, Divisor = 3, Remainder = 2 and Dividend = 35

(11 × 3) + 2 = 35

33 + 2 = 35

35 = 35

Hence, our division is correct.

Do not forget to add the remainder to the product of the quotient and divisor. The division 67 ÷ 5 = 13, R = 2 can be checked as:

(13 × 5) = 67

(13 × 5) + 2 = 67

Example 2: Divide the numbers. Check your answer.

Checking Division:

(Quotient × Divisor) + Remainder = Dividend

(93 × 5) + 3 = 468

465 + 3 = 468

468 = 468

Hence, our division is correct.

Solve and check the given divisions.

Checking Division:

(Quotient × Divisor) + Remainder = Dividend

(217 × 7) + 4 = 1523

1519 + 4 = 1523 1523 = 1523

Hence, our division is correct.

Checking division:

(Quotient × Divisor) + Remainder = Dividend

(14 × 3) + 2 = 44

42 + 2 = 44

44 = 44

Word Problems

Checking division: Checking division:

Let us explore some word problems on division. A shopkeeper has 2896 pencils. He keeps the pencils in packs of 8. How many packs of pencils does the shopkeeper have?

What do we know?

Total number of pencils = 2896

Number of pencils in each pack = 8

What do we need to find?

Number of packs of pencils that the shopkeeper has.

How to find?

Divide to find the answer.

2896 ÷ 8

Solve to find the answer.

Did You Know?

Yuvraj Panwar from India holds the world record of solving 28 division sums of 4 Digits by 1 Digit in 1 minute.

We can find the number of packs by dividing the total number of pencils by the number of pencils in each pack. Therefore, the shopkeeper has 362 packs of pencils.

Example 3: A library has 486 books. If each shelf holds 6 books, what is the total number of shelves in the library?

Total number of books = 486

Number of books each shelf holds = 6

We need to find the number of shelves. Therefore, there are 81 shelves in the library.

Example 4: Alex has 152 stickers. He divides the stickers equally among 7 of his friends. How many stickers will he have left?

Total number of stickers = 152

Number of friends = 7

We need to find out the number of stickers Alex has left.

Thus, Alex is left with 5 stickers.

of stickers each friend gets.

Remember!

If the question is about what is left after dividing, we find the remainder, not the quotient.

A jug can hold 7 cups of juice. How many jugs are required to hold 819 cups of juice?

Number of cups one jug holds = 7

Total cups of juice to be filled = 819

We need to find the number of required to hold .

Thus, .

Find the quotient using the long division method.

Find the quotient and remainder.

Solve and check your answer.

Match the following.

Rohan took biscuits for hungry puppies to an animal shelter. There are 57 puppies at the shelter. If each doghouse can hold 9 puppies, how many puppies will be left without a doghouse?

You have 3548 flower seeds. How many seeds will you be left with after planting them in rows of 6?

Water is being collected from various localities at regular intervals to check the level of impurities in it. There are 74 cups of water samples collected from various localities. If each tray holds 8 cups for checking impurity levels, how many trays will be needed?

A school has 513 storybooks. If each classroom gets 9 storybooks, how many classrooms will receive them?

A store puts some shirts of different brands on sale. Answer the questions.

Brand A Brand B Brand C

Cost of 3 shirts = ₹360 Cost of 5 shirts = ₹475 Cost of 2 shirts = ₹128

a What is the price of 1 shirt of Brand A?

b Which brand shirt is cheaper—Brand B or Brand C?

Challenge

Critical Thinking

When I divide my number by 7, I get 560. When I divide the same number by 56, what will I get?

Points to Remember

• Long division helps us to divide large numbers.

• In long division, we write the dividend, divisor, quotient and remainder as shown:

• A remainder is a left-over number that we get when we divide numbers.

Math Lab

Setting: In 4 groups

Quotient Divisor Dividend

Remainder

Divide and Learn!

Collaboration & Experiential Learning

Materials Required: 6 paper cups, 40 pebbles or beads for each group

Method:

Each group to take 40 pebbles/beads.

Divide the 40 pebbles/beads equally into 6 cups. Write the number of items in each cup. Write a division statement to show the division. 1 2 3

Solve the same problem using long division.

Connect the pebble/bead activity with the long division method.

Chapter Checkup

1 Find the quotient.

6 9 0

9 4 5

2 Find the remainder.

3 Solve and check the divisions.

4 Fill in the blanks with the help of long division.

a (10 × 4) + = 43 b ( × 2) + 1 = 49

c ( × 6) + 2 = 50 d (7 × 9) + = 64

e ( × 3) + 1 = 352 f (42 × 5) + = 214

5 At a zoo, there are 5245 tickets to be sold. If each booklet contains 5 tickets, how many booklets need to be prepared?

6 A firefighter is a person whose job is to put out fires and help people in emergencies. There are 720 firefighters at the fire station, and they need to form 3 equal teams to go to different parts of the city. How many firefighters will be on each team?

7 Nisha collected 156 packets of pulses to give to families affected by the flood. She distributed 10 packets to each family. How many families got the packets?

What number needs to be added to 156 so that it can be divided by 7 without a remainder?

The diagram shows a staircase with 16 steps having the same length and a total height of 256 cm. Answer the questions.

a What is the height of each of the 16 steps?

b If the length of the staircase is 600 cm, what is the length of each step?

Total length 600 cm

Value Development & Cross Curricular Real-Life Maths

Exploring Ancient Egypt

The ancient Egyptians constructed massive pyramids and temples using large stone blocks. To move these heavy stones, they used teams of workers. Historians estimated that a single, large stone block could weigh up to 56 tons. Answer the following questions:

1 If the Egyptians divided the weight of the stone (56 tons) equally among the 8 workers, how many tons would each worker have to move?

a 2 tons b 5 tons c 7 tons d 50 tons

2 If they had only 4 workers available, how much heavier would each worker�s load be compared to having 8 workers?

a Twice as heavy b Three times as heavy

c Five times as heavy d Ten times as heavy

3 Dividing the weight of the stone by the number of workers makes the stone lighter. (True/False)

4 The fewer workers they have, the less each worker needs to carry. (True/False)

5 The 8 workers are going to move the 56-ton block using levers. What�s one important thing they should remember to do so everyone stays safe and healthy?

8 Shapes and Patterns

Let�s Recall

Drawing shapes is so much fun! Let us draw some shapes that we have already learnt about.

Lines

Standing Line

Flat Shapes

STRAIGHT LINES

Sleeping Line

Slanting Line

These are shapes that can be drawn on paper.

CURVED LINES

Solid Shapes

These shapes are like the objects we see in the real world. Let us look at some examples.

Let’s Warm-up

Dice: Cube Duster: Cuboid Bottle: Cylinder Party cap: Cone Football: Sphere

2-D Shapes

Mohit’s class is playing a ‘shape hunt’ game in the classroom. The teacher asks the students to find objects that have the same shape and raise their hands to answer.

Mohit: I can see rectangles on the noticeboard and in my notebook.

Teacher: Very good, Mohit!

Sujata looks out of the window and says, “I see circles in the sun and the wall clock.”

Teacher: Excellent, Sujata!

The students continue discussing objects with similar shapes.

Features of 2-D Shapes

There are four basic shapes that we can see in objects around us—square, circle, triangle and rectangle.

Basic shapes are also called 2-dimensional or 2-D shapes. They are flat and have no height. So, a 2-D shape has only length and width, or breadth.

There are 2 more features of 2-D shapes—sides and corners.

Sides: The line segments that form the shape are called sides.

Corners: A corner is a point where two sides meet.

Let us check the number of sides and corners in the 4 basic 2-D shapes.

Square

Triangle Rectangle Circle

Corners = 4; Sides = 4 Corners = 4; Sides = 4 Corners = 3; Sides = 3 Corners = 0; Sides = 0

Opposite sides are equal. All sides are equal. Sides may or may not be equal. Round in shape.

Let us learn about another feature of a circle.

The distance between the centre and the edge of the circle is always the same.

This is called the radius of the circle.

We can draw 2-D shapes on dot paper by joining the dots. Let us see how.

Think and Tell

How many sides and corners does this shape have? Are the sides in the shape straight?

Example 1: Look at the picture. Count the shapes and fill in the table.

Example 2: Write True or False.

a A rectangle has 4 sides and 4 corners.

b Only the opposite sides are equal in a square.

c Any circle has a centre.

There are coloured dots on the dot paper. Join the dots to draw the sides of the shape. One is done for you. Write the number of triangles, circles, squares and rectangles.

Yellow dots: Corners of a rectangle

Green dots: Corners of a square

Red dots: Corners of a triangle

Blue dots: Touching the edges of a circle

Triangle: Circle: _______ Square:

Do It Yourself 8A

What is the shape of these objects?

Colour the squares red, circles orange, rectangles pink and triangles brown, in the given picture.

Count and write the number of shapes in the figure.

Square = Rectangle =

Triangle = Circle =

Write True or False.

a A triangle has 3 curved sides.

b The opposite sides of a rectangle are equal in length.

c An oval has 0 sides and 0 corners.

d The 4 sides of a square are straight sides.

Challenge

The square figure is made with smaller squares. Count and write the number of squares.

Symmetry and Maps

Mohit and Sujata enjoyed learning about 2-D shapes in their maths classroom. The art teacher gives them square sheets of paper.

Teacher: Fold the paper in half. Then, open it and draw dotted lines on the fold.

Sujata: Mohit, look! I got two similar rectangles when I drew a line on the fold.

Mohit: But I got two equal triangles! How does this happen?

Let us help Sujata and Mohit understand this!

Symmetry

The two same rectangles or triangles are because of symmetry in a square! A shape is symmetrical if it can be divided in such a way that the two halves are exact copies of each other.

Many figures and shapes around us show symmetry. They are called symmetrical. Look at these examples:

A line that divides the shape into equal halves is called the line of symmetry. It can be a standing, sleeping or slanting line. Let us look at the line of symmetry in 2-D shapes.

Line of Symmetry

Standing lines of symmetry: Sleeping lines of symmetry: Slanting lines of symmetry:

Some shapes can have more than one line of symmetry. For example, a square can be divided into equal halves by standing, sleeping or two slanting lines. It has 4 lines of symmetry.

Similarly, a rectangle has 2 lines of symmetry. It has a standing and a sleeping line of symmetry.

Did You Know?

In a circle, the number of lines of symmetry cannot be counted. It has infinite lines of symmetry.

Example 3: Which of these shapes do not show symmetry along the dotted line?

A leaf

A jug A smiley face A butterfly

The jug does not show symmetry along the dotted line. The leaf, smiley face and butterfly show symmetry. So they are symmetrical.

Draw any one line of symmetry on each shape. Colour the two halves with different colours. One is done for you. 1 2 3 4 5

Mirror Image

Look at the girl standing in front of the mirror. What do you notice?

The girl can see her mirror image. Look at some more examples of mirror images.

1 2

The line between the object and its mirror image is called the mirror line. Example 4: Draw the mirror image of the given grid. A mirror image is reversed and is the same distance away from the mirror line as the object is.

Colour the squares to make a mirror image of the shaded figure.

Simple Maps

Sujata�s family plans to visit her grandparent�s village. They want to find out the places they can visit. Father suggests they use a map of the village.

A map is a drawing that shows an area. It shows large areas on a small sheet of paper. It helps us to locate a place and find the route to go there. For example, from the park the pond is two steps up and 1 step to the left.

Example 5:

1 Use the above map to fill in the blanks with left, right, up and down.

a To reach the fire station from the shop, take two steps left.

b To reach the fair from the school, take two steps up.

2 Write a route from the pond to the shop. Take one step up and 3 steps left to reach the shop from the pond.

1 Use the above map to fill in the number of steps.

a The hospital to the fair is steps.

b The park to the hospital is steps.

2 Write a route from the house to the fair.

Which of these shapes show symmetry along the dotted line?

Draw a line of symmetry on these figures.

Draw the mirror image of these figures along the mirror line.

Colour the other grid such that it is the mirror image of the coloured grid given.

Use the map showing Sujata�s grandparents� village. Answer the questions.

a Go 4 steps up from the house and then 1 step to left then you will reach the .

b Go 2 steps up and 2 steps right from the school and you will reach the .

c Write a way to the park from the fire station such that the hospital doesn't come in between.

Colour the grid in yellow and blue such that one side is the mirror image of the other.

Critical Thinking & Cross Curricular

Muggu is another name for rangoli in Andhra Pradesh. Ratna draws a rangoli design on paper, as shown. She is trying to see two equal halves in the design by drawing lines. What lines are these? Can you draw them?

3-D Shapes

In the evening, Mohit went to the park with his father and sister Tina. They saw an ice-cream cart and asked their father to buy them an ice cream each.

Mohit: I want this triangular one, with three circles on the top.

Tina: I don’t want ice cream. I want a can of juice.

Mohit saw the shape of his sister’s can. He wondered what he should call this shape. Let us help Mohit learn more about shapes!

Look at the shapes of different objects given below. These everyday objects have the following shapes—cube, cuboid, cylinder, cone and sphere. These shapes are called solid shapes or 3-D shapes.

Solid Shapes

Real Life Connect

Features of 3-D Shapes

We can measure the length, width and height of a 3-D shape.

Each 3-D shape has faces, edges and corners.

• The surface of a 3-D shape is its face. The face can be flat or curved.

• Two faces meet at an edge. The edge can also be straight or curved.

• Two or more edges meet at a corner.

plane faces curved edge curved face curved edge

Let us look at the number of sides, corners and edges in each solid shape.

6 plane faces 12 straight edges

8 corners

6 plane faces 12 straight edges

8 corners

Building 3-D Shapes

2 plane faces and 1 curved face

2 curved edges

No corners

1 plane face and 1 curved face

1 curved edge

1 corner or vertex

We can use toothpicks and clay to make a 3-D shape, such that toothpicks become the edges and balls of clay become the corners of it.

Tracing 3-D Shapes

1 curved face

No edges

No corners

We can use everyday objects like cans, matchboxes and cardboard boxes to trace 3-D shapes. Tracing 3-D shapes will give us flat shapes or 2-D shapes.

Example 6: Name the 3-D shape of the given objects. Also, name the 2-D shape you get on tracing them.

3-D Shape Cylinder

2-D Shape Circle Circle Square

Shanaya is building shapes using sticks for the edges and clay balls for the vertices. Write the number of vertices and edges that these two shapes have. Fill in the table.

Match the descriptions with the solid shapes.

a 6 plane rectangular faces

b Only 1 curved face

c 1 plane and 1 curved face

d 6 plane square faces

e 2 plane faces and 1 curved face

Cube

Cone

Cylinder

Cuboid

Sphere

Ramya made 3-D shapes using toothpicks and clay. She used 8 clay balls and 12 toothpicks of the same size. Which 3-D shape did she make? Find out by drawing the shape in your notebooks.

Name 3 solid objects that, when traced, give rectangles. Trace one of them.

Challenge

1 Critical Thinking

Yohaan put together 5 sugar cubes, one on top of the other. Which new 3-D shape did he make? What 2-D shapes will he get on tracing the sides of the new 3-D shape?

3-D Shapes as 2-D Shapes

Views of Objects

Every night, after dinner, Mohit sits down with his sister Tina to draw. Today, they are drawing a cup-and-plate set.

Tina’s drawing looks like this: Mohit’s drawing looks like this:

Why do these drawings of the same thing look different?

Tina looked at the cup-and-plate set from the top. Mohit looked at the cup-and-plate set from the side. This is why their drawings look different.

3-D objects look different when we view them from the top, sides or front. Let us look at some more examples:

The top and side view of an umbrella and the front and side view of a scooter can be given as:

Nets of 3-D Shapes

Now, let us use paper folding to make some 3-D shapes. The 2-D shapes that can be folded to make 3-D shapes are called nets.

Net of a Cylinder Net of a Cone Net of a Cube Net of a Cuboid

Example 7: Ritik is riding a bicycle. Which pictures show him from the sides?

Pictures A, C and E show Ritik from the sides. Picture B shows him from the front. Picture D shows the back view.

Look at the object. Draw the front, side and top view. Also, draw its net.

Which view shows these objects from the side?

Draw the front and side views of these objects.

Look at the pictures. Draw the top view of these objects.

Draw your maths textbook from the top and any one side. What shapes do you get in each drawing? Draw the net of the 3-D shape that the textbook looks like.

Patterns Around Us

A net where all the faces are rectangles belongs to which solid shape? Draw it.

Sujata’s mother got a new saree.

Sujata: Maa, your saree is beautiful! Oh, the border has red and yellow rectangles one after another.

Mother: Yes, Sujata! It is a pattern!

Sujata: A pattern? On a saree border?

Understanding Patterns

The shapes that repeat one after another make patterns. Patterns can be seen everywhere around us. Some examples of patterns in our day-to-day lives are given below.

Patterns in buildings

Patterns on a bedsheet

Patterns of a flower

Patterns follow a rule. Let us look at a few patterns to understand some rules.

Repeating Pattern

Patterns repeat a unit. A repeating unit could be one or many lines, shapes, colours, numbers, letters, or objects.

Here, the shapes that are being repeated are squares and triangles.

Rotating Pattern

Here, the colours of the balls are repeated as yellow, red and green.

The unit changes direction with each next step in a rotating pattern.

In this pattern, the arrow changes direction clockwise as up, right, down, left and up.

Growing Pattern

In this pattern, 1 triangle and 1 star are added to the next unit. repeating unit repeating unit

In this pattern, the rectangle is rotated with each step as up, right, up and right.

One or many lines, shapes, colours, numbers, letters or objects are added to every next unit to grow the pattern. Thus, the pattern increases in number or size.

In this pattern, 1 triangle is added to the next unit.

Number Patterns

These patterns are made of numbers. They also follow the same rule of repeating a unit.

Combination of Patterns

Sometimes, the unit of the pattern has a pattern within itself. The pattern is made of a combination of patterns.

Do not add random parts to the pattern. It can disrupt the overall flow of the pattern. Error Alert!

Secret Message

A secret message is a fun way of writing a message using patterns. Let us try to read a secret message: 5H5O5W 5A5R5E 5Y5O5U5?

Here, the number 5 is repeated after each letter of the alphabet. Highlight the alphabet letters and see the message: 5H5O5W

The message is: HOW ARE YOU?

Tiling Patterns

Have you ever noticed how the tiles are arranged on a footpath?

When a floor or wall is completely covered with tiles that are arranged without any gap in between, it is called tiling. It follows a pattern too!

Let us have a look at these tiling patterns:

Did You Know?

Hawa Mahal in Jaipur has a huge number of patterns in it. The jharokhas (windows) of the palace display a honeycomb-like pattern.

Example 8: What would be the next two units in the pattern? Label the repeating unit.

Repeating Unit

Example 9: Which of these shapes can be used in tiling patterns?

Both the shapes can be used in tiling patterns, as shown here:

Complete the tiling pattern by colouring the white shapes. A part of each pattern is coloured for you.

Underline the repeating units in the pattern.

Colour the units to complete the pattern.

Extend the pattern by drawing the next 3 figures.

Challenge

Braille is a special way of reading and writing for blind people. It uses the dots as shown. If the given image shows the Braille alphabet, code your name using them.

Points to Remember

• A square, rectangle, triangle and circle are some examples of 2-D shapes.

• A cube, cuboid, cone, cylinder and sphere are some examples of 3-D shapes.

• A shape is in symmetry if it can be folded or divided into two equal halves.

• A pattern is a series or sequence of repeating units. It can be formed with a set of lines, shapes, colours, numbers, letters, or objects.

• The pattern made for covering a surface with tiles of the same shape and size is called tiling.

Math Lab

Setting: In pairs

Experiential Learning & Collaboration

Create a Figure with Shapes!

Materials Required: 1 tangram set of shape cutouts. Prepare Material: You may do it at home or in class. Take a white square sheet of paper. Draw the shapes on it, as shown in the picture here. You may colour each shape as shown. Then cut along the lines to get 1 set of shapes.

What to Do?

• In class, with your partner, point to any one figure made with tangram-shaped cutouts.

• Remember the figure and the placement of the shapes. Arrange the shapes to create the figure in 5 minutes. The pair that makes the figures first, wins the round.

• Continue playing the game till you have created all the figures.

Integration

1 a Write the number of shapes in the given figure.

b Colour the squares pink, circles red, triangles green and rectangles blue.

Square = Rectangle = Triangle = Circle =

2 Draw one line of symmetry on each figure.

3 Name the 3-D shape of the given objects.

4 Draw a net of the cardboard boxes used for packing cake.

5 Draw a mirror image of the given picture.

6 Complete the patterns.

7 Complete the number patterns.

a 12, 16, 20, 24, 28, , ,

c 32, 37, 42, 47, , ,

8 Colour to complete the tiling patterns.

b 48, 56, 64, 72, , ,

d 29, 32, 35, 38, , ,

9 Draw and write the shape of a table when seen from the side and the top.

10 a Make a tiling pattern of your own choice by colouring the shapes.

b Draw another tiling pattern using triangles, rectangles and squares. Colour it.

Challenge

Anaya places 3 cubes next to each other in different ways. In how many ways can she do it? What possible shapes will she get by joining 3 cubes?

How many different triangles can be made using the dots on this circle?

Maps

Sara and her friends are planning a swim party at her place after the football match. Sara draws a map to explain the path. Read the map to answer following questions.

1 Which place does the �+� sign show?

2 Circle the picture on the map that shows the football ground.

3 Which place does the (H) sign show? a Hospital b Hotel

c Guesthouse d Sara�s house

4 Find the way from the football ground to Sara�s house.

5 Which view (top/front/side) is given for the parking area?

Lake View Road

Lodhi Street

MG Road

Sara�s House

9 Length, Weight and Capacity

Let’s Recall

We know that we use length to tell how long something is. For example, our foot is longer than our finger.

We can use our body parts to measure length!

Let us use our forearms to measure the length of the table. As shown, this table is about 2 forearms long!

Weight is the measure of how heavy an object is.

When we go to a vegetable market, the vendor uses a seesaw-like object to compare and measure weights. This machine is called a weighing balance. It helps us compare the weights of objects.

The side with 5 apples is heavier. So, that side will go down as shown.

The capacity of an object tells us how much liquid it can hold. Look at the jug, for example. It holds juice!

Now we pour the juice into glasses. Let us say it fills 5 glasses.

We can say that the capacity of the jug is 5 glasses.

Let’s Warm-up

Write True or False.

1 The book is 7 forearms long.

2 The watermelon is heavier than the pen

3 The capacity of each glass is less than that of the jug .

I scored out of 3.

John wanted to buy a string of lights to decorate his house. He went to a light shop for it.

Sure! Here are some strings. I want a string of lights, please.

The shopkeeper showed him different lengths of string. John picked the suitable length of string and went home.

Measuring Length

We saw that the shopkeeper showed different lengths of string lights. Length refers to how long or tall an object is from one end to another. It is also the distance between two places. The length of objects and the distance between places are measured using standard units.

Units of Length

We can use different units based on the type of length to be measured.

Type

Short length Centimetres cm Nail, safety pin

Long length Metres m Cloth, wire

Short distance Metres m Distance from bedroom to kitchen

Long distance Kilometres km Distance from home to hospital

Height Centimetres, Metres cm, m Height of a tower

To identify the correct unit when measuring length, first identify the type of length and then choose the unit to be used. Circle the correct unit for measuring the following things.

1 Length of the school ground cm m km

2 Length of the bus cm m km

3 Distance between two countries cm m km

4 Length of a shoe cm m km

5 Height of a street light pole cm m km

6 Height of a flagpole cm m km

Measuring Length Using a Ruler

A ruler is a tool used to measure the length of small objects.

A ruler with short and long lines on it is shown below. The longer lines that have a number written on them are centimetre lines. The distance between two centimetre lines is 1 centimetre. 1 cm

Short line

Long line

Did You Know?

Burj Khalifa is the tallest building in the world. Its height is 828 m.

To measure an object using a ruler, place the ruler against the object. Make sure that one end of the object is at 0 cm.

Remember!

Another name for a ruler is a ‘scale’.

Let us measure the length of a crayon!

This crayon is 6 cm long.

Ravi is using a ruler to find the length of different things at his house.

1 The length of the photo frame is cm.

2 Ravi measured the length of a pan. Draw an arrow to help him mark the ruler at 14 cm.

Converting Units of Length

We have learnt that metre and centimetre are two units of length. Did you know there is a relationship between centimetres and metres?

1 metre = 100 centimetres

Do you remember John who wanted to buy a string of lights? John asked for a 2 m long string but the shopkeeper is used to measuring the string in centimetres. Let us help the shopkeeper to convert m into cm.

We know that, 1 m = 100 cm.

2 m = 2 × 100 = 200 cm

Therefore, the shopkeeper will give John a string of 200 cm.

What if John wanted a 2 m 50 cm string?

We have already found that 2 m = 200 cm

2 m 50 cm = 200 cm + 50 cm = 250 cm

We can also convert cm to m.

Do not forget to add the length given in cm after converting m to cm. 3 m 45 cm = 3 × 100 cm = 300 cm 3 m 45 cm = 3 × 100 + 45 cm = 300 cm + 45 cm = 345 cm

Error Alert!

Let us convert 300 cm into m.

300 cm = 100 cm + 100 cm + 100 cm = 1 m + 1 m + 1 m (as 1 m = 100 cm) = 3 m

Therefore, 300 cm = 3 m.

Example 1: Convert:

1 8 m to cm

1 m = 100 cm

8 m = 8 × 100 cm = 800 cm

Remember!

The unit ‘metre’ is longer than the unit ‘centimetre’. The unit km is the longest.

2 400 cm to m.

100 cm = 1 m

Then, 400 cm = 100 cm + 100 cm + 100 cm + 100 cm = 1 m + 1 m + 1 m + 1 m = 4 m

Length

Word Problems on Length

The next day, John went to buy two ropes. He wanted one rope of length 38 cm and another of 52 cm. Let us find the total length of rope that John bought.

Length of the first rope = 38 cm

Length of the second rope = 52 cm

As we need to find the total length, we will add the lengths given.

38 cm + 52 cm = 90 cm

Therefore, the total length of the two ropes is 90 cm.

Example 2: Chintu’s height is 125 cm, and Neelu’s height is 132 cm. How much taller is Neelu than Chintu?

Chintu’s height = 125 cm

Neelu’s height = 132 cm

To find out how much taller Neelu is than Chintu, subtract Chintu’s height from Neelu’s height.

132 cm – 125 cm = 7 cm

Therefore, Neelu is 7 cm taller than Chintu.

On Monday, Soumya travelled a distance of 6 km, and on Tuesday, she covered 12 km. What is the total distance she covered over the two days?

Distance travelled on Monday = 6 km

Distance covered on Tuesday =

As we need to find the total distance covered, we will _______ the distances.

6 km = km

The total distance travelled by Soumya is km.

Do It Yourself 9A

1 Write the suitable unit to measure the following.

a The distance between two cities b A pipe

c A phone d The length of hands of a person

2 Measure and write the length of the following objects.

3 Convert the following into cm.

a 6 m b 8 m

c 9 m 9 cm d 4 m 15 cm

e 7 m 26 cm f 2 m 52 cm

4 Convert the following into m.

a 700 cm b 600 cm

c 400 cm d 800 cm

e 500 cm f 900 cm

5 A mobile tower is communication equipment installed to support better phone networks. A mobile tower with a height of 14 m is mounted on top of a building which is 22 m high. What is the total height of the tower from the ground?

6 The length of a monitor lizard is about 2 m, and the length of a python is about 6 m. Which is longer and by how much in cm?

1 Look at the metre tape given below. How many more boxes do you need to colour to show 1 m 30 cm? Shade in the metre tape.

Weight

Naveen went to the doctor's clinic as he wasn't feeling well.

The doctor asked him to step on a weighing scale. Naveen saw the numbers move on the weighing scale. Dr Smith wrote down the measurement.

Measuring Weight

Why do you need to know my weight, Dr Singh?

Weight helps me keep track of how well you are growing!

Weight is the measurement of the heaviness of an object. We saw that Dr Singh used a weighing scale to measure Naveen’s weight. Can a fruit vendor use the same weighing scale to weigh fruit?

No! The weighing scale for measuring human weight is different from the weighing machine used for fruit and vegetables. Different types of weighing machines are shown below.

Did You Know?

The weight of an elephant is around 3500 kg.

machine

Units of Weight

We have learnt that we measure the weight of an object in grams or kilograms.

Grams to measure lighter weights

Kilograms to measure heavier weights

Some of the common weights used with weighing scales are:

Traditional Scale

Tabletop Scale

Hanging Scale Platform Scale

Weighing

to measure body weight

Below are some items found in a bakery.

Tick ( ) the suitable weight measurement unit for each item.

Converting Units of Weight

There are some items which can be measured both in grams and kilograms, like a packet of sugar!

The relationship between grams and kilograms can be given as:

1 kilogram = 1000 grams

Let us find out how many grams are there in 2 kg.

We know that, 1 kg = 1000 g.

Therefore, 2 kg = 2 × 1000 g = 2000 g

g 2 kg

Multiply the kg by 1000 to convert it into g. 5 kg = 5 × 100 g = 500 g 5 kg = 5 × 1000 g = 5000 g

Example 3: Uma has luggage weighing 7 kilograms and 300 grams. How many grams of weight does she have?

Weight of Uma’s luggage = 7 kg and 300 g

We know that, 1 kg = 1000 g.

7 kg = 7 × 1000 g = 7000 g

7 kg 300 gm = 7000 g + 300 g = 7300 g

Therefore, the total weight of Uma’s luggage is 7300 g.

Read the sentences that show things Rama noticed at the market. Fill in the blanks.

1 The shopkeeper has 5 kg of apples. He has 5000 g of apples.

Cupcake

bread

Oven

Error Alert!

2 Riya bought 2 kg and 500 g of carrots. She bought g of carrots.

3 A bag of potatoes weighs 8 kg. The bag weighs g.

4 Meena purchased 3 kg and 450 g of bananas. She purchased ______ g of bananas.

Word Problems on Weight

Do you remember Naveen who went to the doctor? The doctor found his weight to be 25 kg. The doctor saw that Naveen’s weight was 23 kg at the last visit. Let us find the increase in Naveen’s weight.

Naveen’s current weight = 25 kg

Naveen’s previous weight = 23 kg

Increase in weight = current weight – previous weight = 25 kg – 23 kg = 2 kg

Therefore, Naveen’s weight has increased by 2 kg.

Bhanu’s suitcase weighs 15 kg, while Vidya’s suitcase weighs 19 kg. How much heavier is Vidya’s suitcase compared to Bhanu’s suitcase?

Weight of Bhanu’s suitcase = kg

Weight of Vidya’s suitcase = 19 kg

Difference in weight = – = kg

Therefore, Vidya’s suitcase is kg heavier than Bhanu’s suitcase.

1 Write the correct unit to measure the weight of the given objects. a Feather b Car c Pillow

2 Convert kg into g.

a 8 kg

b 9 kg c 1 kg 500 g

d 4 kg 200 g e 3 kg 300 g f 7 kg 750 g

3 Farah has a pet cat which weighs 3 kg and 600 g. How much does the pet weight in grams?

4 A wholesale vegetable market is called a sabzi mandi in Hindi. Shalu went to the sabzi mandi and bought 4 kg of vegetables and 5 kg of fruit. How much more fruit did she buy than vegetables?

5 The weight of a watermelon is 5 kg. Seema cuts it into two pieces. The weight of one of the pieces is 2 kg. What is the weight of the other piece?

6 A scrap dealer is a person who buys scrap (old newspaper, plastics, etc.) materials at a very low cost. Rohit sold 4 kg and 200 g of newspapers and 700 g of magazines to the scrap dealer. Find the total weight of articles sold.

Challenge

1 3 blocks of wood A, B and C have different weights. Without using the weights, and just using the pan balance, can you tell which one is heavier? Write the process.

Capacity

Asha’s family and friends are going on a picnic. Asha is helping her mom to make orange juice.

Asha: How much juice should we take with us, Mom?

Mom: There will be 8 members at the picnic. 2 bottles of juice will be sufficient.

Asha pours the juice into the bottles and puts them inside the basket.

Measuring Capacity

In the case of liquids like water, milk and juice, we need to find the capacity. Capacity is defined as the maximum quantity a container can hold when it is full.

Given below are some containers with different capacities.

Units of Capacity

As different containers have different capacities, we use different standard units to measure the capacity. Millilitre (mL) and litre (L) are the units used for measuring capacity.

Millilitre to measure small capacities

Litre to measure large capacities

Water bottles, cans and jars are usually measured in litres.

Measuring cups, syringes and measuring spoons are measured in mL.

Circle the suitable measurement unit for the following objects.

Converting Units of Capacity

Let us now understand how the units of capacity are related to each other.

1 litre = 1000 mL

Asha’s mom made a 2 L jug of juice for the picnic. Let us find out the capacity of the jug in mL.

We know that, 1 L = 1000 mL.

Then, 2 L = 2 × 1000 mL = 2000 mL

What if they need 4 L 250 mL of juice?

Then, 4 L = 4 × 1000 mL = 4000 mL

Think and Tell Is 2 L of juice sufficient for a group of 30 people?

4 L 250 mL = 4000 mL + 250 mL = 4250 mL

So, the quantity of juice in mL is 4250 mL.

Word Problems on Capacity

Asha had 2 L of orange juice. Her mother made 5 L of mango juice. Let us find out the total amount of juice that Asha was taking to the picnic.

Amount of orange juice = 2 L

Amount of mango juice = 5 L

Total amount of juice = 2 L + 5 L = 7 L

Therefore, the total amount of juice is 7 L.

Example 4: Rima opened a 900 mL bottle of milk. She filled a 250 mL glass with it. How much milk is left in the bottle?

Total amount of milk in the bottle = 900 mL

Amount of milk filled in the glass = 250 mL

Amount of milk left in the bottle = 900 mL – 250 mL = 650 mL

Aman filled a mini truck with 44 L of petrol, a car with 30 L of petrol and a bike with 5 L of petrol. With how much petrol did he fill the three vehicles?

Amount of petrol to fill the truck = 44 L

Amount of petrol to fill the car =

Amount of petrol to fill the bike =

Total amount of petrol used to fill the 3 vehicles = 44 L + + =

Circle the items that are measured in mL.

Items

a Cough syrup

b Syringe c Tub of water d Bucket of water e Hand sanitizer f Barrel of water

2 Convert the following into mL. a 2 L

6 L

3 Lemonade is a drink made with lemon, water and sugar. It is an easy way to get a dose of Vitamin C. Rohan wants to make lemonade for his friends. He needs 3 litres of water for the recipe. How many millilitres of water does he need?

4 Taking care of plants by watering them is a good habit. Mohan filled a 500 mL water bottle three times to water his plants. How much water did he use in total?

5 Raju poured 4 L of water into a jug and then transferred 750 mL of the water into a glass. How much water is left in the jug?

6 Mohit bought a car with a fuel tank of capacity 38 L, while Soham bought a car with a fuel tank of capacity 45 L. What is the total capacity of both tanks?

1 Ramesh the milkman has jars with capacities of 2 L, 4 L and 6 L. The 6 L jar is filled with milk. He needs to give 3 L of milk to a customer. Find a way to measure the 3 L of milk.

Points to Remember

Measurement

Weight 1 m = 100 cm

Measured in cm, m and km Capacity Length

Measured in g and kg

Measured in mL and L

L = 1000 mL 1 kg = 1000 g

Math Lab

Setting: In groups of 5

Let's Jump!

Materials Required: Measuring tape Method:

1 Do this activity on your school playground.

3 He/she will then take three tries to jump.

Collaboration & Experiential Learning

2 One child from the group will guess the length to which he/she can jump.

4 Select the best jump and measure it using measuring tape.

5 Write it down in a notebook.

6 All the members of the group will repeat the same activity.

7 Add the lengths of the jumps of the whole group.

8 Compare it with other groups. The group with the highest total will win.

Chapter Checkup

1 Circle the object whose capacity is measured in litres (L).

Glass of juice 1 km = 1000 m

2 Circle the object which is measured in metres (m).

a The length of a spoon b The height of a tree c The width of a book

d The length of a swimming pool e The height of a house f The length of a room

3 Circle the object which is measured in kilograms (kg).

a An empty box b A banana c A cylinder

d A lollipop e A bag of flour f Two apples

4 Find the length in cm.

5 Convert the lengths into centimetres (cm).

a 5 m

d 8 m 50 cm

2 m

4 m 900 cm

6 Convert the lengths into metres (m).

9 m

6 m 890 cm

a 200 cm b 300 cm c 1000 cm d 1100 cm

1200 cm

7 Convert the weight into grams (g).

a 8 kg

1300 cm

9 kg

7 kg 450 g d 2 kg 999 g

3 kg 760 g

4 kg 640 g Chapter 9 • Length, Weight and Capacity

8 Change litres (L) into millilitres (mL).

2 L

9 A fully growth goliath frog found in central Africa weighs 3 kg 250 g. How much does the frog weigh in grams?

10 When Ahana brushes her teeth, she leaves the tap running. She uses 5 L 500 mL of water. Sameer only turns on the tap when he rinses his mouth after brushing his teeth. He uses 1 L 200 mL of water. How much water does Sameer save?

Challenge

Critical Thinking

1 A ribbon of length 1 metre is cut into 4 equal pieces. How many cuts were made?

2 In Hina�s house there are six trees growing in a line at intervals of 3 metres. Can you tell the distance between the two trees at either end?

Real-Life Maths

Cross Curricular & Value Development

Summer Time Activity

Fruit smoothies are a mixture of fruits, milk and sometime nuts. Yash is free, as his school summer break is going on. He helps his father in the kitchen to make fruit smoothies for his family. He uses 225 mL of milk, 2 bananas and 50 g of sugar for a banana smoothie. He also makes a mango smoothie and uses 225 mL of milk, 1 mango, 20 g of sugar, 10 g of nuts and some ice cubes. Read and answer the questions.

1 What quantity of nuts does he use in a mango smoothie? a 10 g b 10 mg c 10 kg d 10 m

2 How much milk does he use in both smoothies?

3 If he has 1 kg of sugar, how much will be left with him after he makes both the smoothies?

4 Do you help your parents with house chores? How?

Orange Smoothie Orange Banana Avocado

Mango M Almond milk

Pineapple juice

10 Time

Let’s Recall

An early bird catches the worm! So we should always be punctual!

The clock helps us to read time. Take a look at this clock.

Notice that it has numbers from 1 to 12 written on it. It has two “hands”. One is big, and one is small. They point at the numbers at all times and help us to see the time.

The big hand that moves faster is called the minute hand.

The smaller hand moves slower and is called the hour hand.

Let us say that the hour hand is at 8 and the minute hand is at 12 as shown. What is the time?

The time is 8 o’ clock.

Now, let us say the hour hand is between 8 and 9 and the minute hand is at 6. We say it is 8:30 or eight-thirty. We can also say it is half past 8.

Let’s Warm-up

Draw the hour hand and the minute hand for the time given below.

Time on a Clock

Sonu and Tina are playing during lunchtime. The teacher said, ʻʻKids, lunchtime will be over at 1 o’ clock. After that, we will go to the art class. So, hurry up!ˮ

Tina: I want to play some more! But I do not want to miss the art class either.

Sonu: Let me check the time. It is quarter to 1 now. We have 15 minutes more to play.

Tina: Thanks, Sonu! I wish I could read the clock too!

Remember!

The minute hand is always longer than the hour hand.

Reading Time

To read time, we look at the minute hand and the hour hand. The longer hand is the minute hand, and the shorter hand is the hour hand. We see numbers 1 to 12 on the clock. The face of a clock is called the dial.

Did You Know?

hour hand

minute hand

Both the hour and the minute hands always move towards increasing numbers. The direction in which they move is called the clockwise direction.

Reading Time on a Clock

Hour time: The hour hand on the number shows the hour time. When the time is to the hour, the minute hand is on 12, and the hour hand tells us the hour. It is read as o’ clock.

For example, if the hour hand is on 1 and the minute hand is on 12, the time is 1 o’ clock. Notice the change in the hour hand from one clock to the next.

Remember!

It is 0 minutes when the minute hand is on 12. So, the minute hand is always on 12 when it is a full hour.

Minute Time

There are 60 minutes in an hour. When the minute hand moves from one number to another, 5 minutes have passed. We keep adding 5 more minutes as the minute hand keeps moving to the next number. Look at the clocks given.

The term �past� is used when the minute hand is on the right side of the clock face, from 12 up to 6.

The term �to� is used when the minute hand is on the left side of the clock face, from 6 up to 12.

Now look at the time on these 2 clocks. 5:15 five fifteen 8:55 eight fifty-five

How many times does the hour hand point to a number in one day? Think and Tell

The minute hand has moved 3 places, so, the total number of minutes = 5 + 5 + 5 = 15 minutes.

The hour hand is between 5 and 6. So, the hour hand shows 5. Thus, the time is 5:15.

The first clock shows 15 minutes past 5.

Similarly, the time on the second clock is 8:45 or quarter to 9.

Let us read time by the minutes on the clock.

8:00 8 o’ clock 8:15 15 minutes past 8 or quarter past 8 8:30 30 minutes past 8 or half past 8 8:45 15 minutes to 9 or quarter to 9

Draw the hour and minute hands on the clock to tell the time. Write the time in one more way.

4 o’ clock 20 minutes past 5 5 minutes to 3

5:20

Time as a.m. and p.m.

One day has 24 hours. On the clock, we have numbers only from 1 to 12. When the hour hand of the clock goes around once, it completes 12 hours. In a day, the hour hand goes around the clock twice to complete 24 hours.

A new day begins at 12 o’ clock midnight. From 12 o’ clock midnight until 12 o’ clock noon is a.m.

The next 12 hours, from 12 o’ clock noon until 12 o’ clock midnight, are p.m.

Digital Clocks

This type of clock displays the time in a digital format using numbers, rather than traditional clock hands. These clocks are found in mobile phones, cars, etc.

Example 1: Every morning, Tara gets on her school bus at 8 o’ clock. What time is it—8:00 a.m. or 8:00 p.m.?

It is a.m. from midnight 12 o’ clock to noon 12 o’ clock. 8 o’ clock in the morning is before noon. So, Tara gets on the bus at 8:00 a.m.

Look at Jay ’s chart of a day. Tell the time of his activities in a.m. and p.m.

8:30 a.m. Brush teeth 10:00 Have breakfast 4:00 Play outdoors 6:30 Study 8:30 Go to bed

3 Read the time of Sai’s daily activities. Fill in the blanks with a.m. or p.m.

a Sai wakes up at 7 in the morning.

b He reaches school by 9 in the morning.

c Sai comes back from school at 1 after noon.

d He goes to play with his friends at 6 in the evening.

4 Draw the hour hand and the minute hand to show the time on the given clocks.

5 The August Kranti Rajdhani Express runs between Delhi and Mumbai at 5:30 p.m. every day. It reaches Mumbai Central the next day at half past 10 in the morning. Write the times in a.m. and p.m.

Challenge

Critical Thinking

1 Sneha reaches the lunch room 5 minutes before 12 noon. Veena reaches 5 minutes after 12 in the afternoon. Whose time is in a.m.? Write that time.

Units of Time on a Clock

Tina: Thanks, Sonu! Now I can tell time too!

Sonu: You are welcome, Tina!

Just then the bell rings and their teacher comes over.

Teacher: Remember, the art class is 60 minutes long. Be back on time.

Tina: Sonu, why did the teacher say 60 minutes? I thought the art class was for 1 hour.

Sonu: Tina, one hour is the same as 60 minutes. Let us see how.

Here, we can see that the time now on the clock is 1 o’ clock. When the hour hand reaches 2, the time will be 2 o’ clock, thus 1 hour will have passed.

Think and Tell

1 o' clock 2 o' clock

Converting Time

How many hours do you spend at your school every day?

We know that the hour and minute hands move around the clock. When the hour hand moves from one number to another, the minute hand moves around the clock. When the minute hand moves from one number to another, 5 minutes will have passed.

So, 1 hour = 60 minutes.

Example 2: Write the number of minutes that have passed by looking at the movement of the minute and hour hands.

Time Taken: The minute hand moves from 2 to 3. So, the time taken is 5 minutes. The hour hand remains on 8.

Time Taken: The hour hand takes a complete round. So, the time taken is 1 hour = 60 minutes.

Jenny is doing various activities. Look at the clocks to fill in the table.

2 hours and 15 minutes = 60 + +

15 = minutes

Estimating Time

Different activities take different amounts of time. Some activities take less than a minute, such as sneezing, snapping fingers or clapping hands. Some activities take a few minutes and some even take hours to complete. For example:

Brushing teeth Packing the school bag Time in school Stitching a shirt Take minutes Take hours

So, different activities take different times to complete. Guessing which activity will take how much time to complete is called estimating time. By doing this, we can plan our activities and day better.

Example 3: Look at some of Mia’s activities. Which activities will take her minutes, an hour and more than an hour to complete?

Look at the activities. Write ‘M’ if it takes minutes, and write ‘H’ if it takes hours to complete.

Putting on a T-shirt Playing a football match

Putting on shoes Drinking a glass of water Celebrating a birthday

Do It Yourself 10B

Fill in the blanks.

a The minute hand of a clock completes one round in minutes.

b The hour hand of a clock completes one round in hours.

2 How many hours/minutes have passed between the times given?

a 3:00 to 4:00 b 4:00 to 7:00 c 11:45 to 12:00 d 3:30 to 5:45

3 Write whether the activity will take minutes or hours to complete.

a Filling a glass of milk b Watering a plant

c Eating a banana d Washing, ironing and folding some clothes

4 A marathon is 26.2 miles long. Eliud Kipchoge also completed a marathon in around 2 hours at the Berlin Marathon on September 25, 2022. In how many minutes did he complete the marathon?

5 The Shatabdi Express is a day train that runs between Delhi and Meerut. Vibu started at 6:45 a.m. from Delhi and reached Meerut at 8:00 a.m. How many minutes did the train take?

1 If = 1 hour and = 10 minutes, then how will you represent 160 minutes using these symbols?

Calendar

Mia’s school has a new rule. Students can wear dresses of their choice every second Friday of the month.

Mia is getting ready for school this morning.

Mia: Mummy! I don’t want to wear my uniform today! Can I wear my new dress? I know it is 4th August. Is it the second Friday of the month? Does the rule apply today?

Reading a Calendar

A calendar can help Mia with what she wants to know.

A calendar tells us which day of the week, month and year it is today. For example, 4 August 2023 is a Friday. It is the first Friday of the month.

Units of Time on a Calendar

Days of the week, months and a year are the units of time on a calendar.

Days of the Week: A day is the smallest unit of time on a calendar. There are 7 days in a week.

Months and Year: A month is longer than a week. There are 12 months in a year.

Unscramble the names of the months and days.

Interpreting a Calendar

Remember the new dress rule in Mia’s school, starting from the second Friday of August. Mia was not sure if she could wear her new dress on 4 August. Let us read a calendar to help her!

The second Friday will be on 11 August. Mia can wear her dress then, but not today!

AUGUST 2023

Reading a calendar is fun! It helps us know the day and dates for special events and count the number of days left before the event.

Some months have 30 days, while others have 31. February is special, as it has either 28 or 29 days.

A year has 365 days. If February has 29 days, the year is called a leap year. A leap year has one extra day, making it 366 days.

Remember!

A leap year comes after every 4 years.

Did You Know?

The year 2024 was a leap year. It has 29 days in February. In total, there are 366 days in 2024.

We also find dates on a calendar which can be written in different ways. We usually write dates as: date/month/year. For example, in 11/09/2024, 11 is the date, 09 is the month and 2024 is the year. We can also write the date as Date Month Year, which is 11 September 2024.

Example 4: Rehan’s birthday is on 10 July and Muskaan’s birthday is on 15 July. Use the 2024 calendar above to answer.

1 On what days are their birthdays?

Rehan’s birthday is on Wednesday. Muskaan’s birthday is on Monday.

2 How many days will be left to celebrate Muskaan’s birthday after Rehan’s birthday? 5 days

Read the calendar for March 2024. Fill in the blanks.

1 The day of the week on 2 March: Saturday

2 The day of the week on 16 March:

3 The date on the first Monday:

4 The number of Sundays in the month: 5

5 The number of Saturdays in the month: ______________

Match the units of time on a calendar.

a 2024 Day of the week

b January Month

c 26th Year

d Friday Date of the month

2 Write True or False.

a Sunday is a month.

b December is a month.

c May is the first day of the week.

d A leap year has 29 days in February.

3 Read the calendar. Fill in the blanks.

a There are (5/4) Sundays in this month.

b The month starts from (Monday/Tuesday).

c On 25 May, the day is (Tuesday/Thursday).

d 2 May is a Tuesday. The next Tuesday will be on

May.

e In this month, Saturdays are on the dates 6, , and .

4 Anand has been practising for a dance performance for two weeks now. How many days has he practised?

5 Look at the May 2034 calendar in Q3 and create a calendar for the month of June 2034. Use colours to decorate it.

6 26 January—Republic Day is a national holiday in India. The Constitution of India was adopted by the Constituent Assembly on 26 November, 1949 but was implemented on 26 January, 1950. How many months did it take to implement the Constitution?

1 How many leap years are there between the years 2014 and 2058?

Timelines and Ages

On a timeline, the years, months or days of the events are always written in the order in which they come first.

Making a Timeline

A timeline helps us to show the journey over the year, in a year or in a month. We mark special years, months, days and dates on a timeline. We can show the special years of our life events on a timeline. Look at the timeline of special school events in Mia’s life.

We can also show the months and dates of special events and festivals on a year timeline. Look at this timeline showing some celebrations and festivals in a year.

Example 5: Birthdays of 4 friends born in the same year are given in the table. Show them on a timeline.

Anu 21 August

Samira 12 April

Danny 10 November

Raj 7 May 12 April

Remember!

On a timeline, we always mark events in the order in which they come first. So, we will mark birthdays in the order of the months as they come in a year.

Samira’s birthday 7 May Raj’s birthday 21 August Anu’s birthday 10 November Danny’s birthday

The table shows some of the days that Mia wants to celebrate. Show them on the timeline.

14 July 2 April 10 January 23 July 10 September 8 August

Reading a Birth Certificate

A birth certificate gives details of where and when you were born, along with the details about your parents, and it is made after you are born. It also shows if the baby born is a boy or a girl, the place of birth, parents’ names and the registration number.

You write dates every day in your notebook. Dates can be seen on many other papers. Let us take a look at this birth certificate:

Ria was born on 14 July in the year 2016. These dates can help us to know how much time has passed since she was born.

Example 6: Look at Ria’s birth certificate. Answer the questions.

1 What is Ria’s place of birth?

Ria’s place of birth is New Delhi.

2 How old would Ria would have been on 14 July 2020?

There are four years up to 2020. So, Ria would have been 4 years old on 14 July 2020.

3 In what year will Ria be 15 years old?

Add 15 to the year 2016: 2016 + 15 = 2031. So, Ria will be 15 years old in the year 2031.

B I R T H

THIS DOCUMENT ACKNOWLEDGES THAT born on

MOTHER’S NAME Place of Birth

INCH Ria It’s a girl July 14, 2016 Surbhi Jain Aakash Jain New Delhi 8 19 WNDLS-2016

Registration Number Signature FATHER’S NAME

Look at Mayank’s birth certificate. Read the statements to fill his birth certificate.

1 Mayank’s date of birth is: 8 October 2020.

2 His mother ’s name is and his father ’s name is .

3 He was born in St Mary�s Hospital, Goa.

Think and Tell

B I R T H

THIS DOCUMENT ACKNOWLEDGE THAT born on

MOTHER’S NAME Place of Birth

Mayank It’s a boy St. Mary’s Hospital, Goa 7 20 W-GOA-2020

FATHER’S NAME

WEIGHT LBS LENGTH INCH

Registration Number Signature

4 In the year 2030, Mayank will be years old. How many years old were you last year? In which year would you be 10 years old?

There are 5 festivals in the month of October and November. The table shows the festivals in a particular year. Draw them on a timeline.

Navratri Starts Diwali Dusshera Bhai Dooj Guru Nanak Jayanti 3 October 1 November 12 October 3 November 27 November

Sunita Lal Raman Lal

2 The table shows the months in which the school is planning sports events in the year 2024. Draw this sports schedule on a timeline.

Cricket match

Football match Kho-Kho match Tug-of-war match Basketball match

February November December October August

3 Read the timeline. Answer the questions.

Rina was born Rina went to school Rina's baby sister was born Rina won a dance competition Rina went to college Rina got a job

2000 2004 2007 2015 2018 2024

a In which year was Rina born?

b How old was Rina when her sister was born?

c How old was she when she won the dance competition?

d How old will Rina be in 2034?

4 Tinu was born on 31 July 2015. His friend Mitu was born on 31 July 2021. Who is older? By how many years?

Challenge

Critical Thinking

1 Seema is twice as old as her brother. She is also 10 years older than her brother. Guess the ages of Seema and her brother.

Points to Remember

• When the hour hand moves from one number to another, 1 hour has passed.

• When the minute hand moves from one number to another, 5 minutes have passed.

• 1 hour = 60 minutes

• The time from midnight to 12 o’ clock noon is a.m. The time from 12 o’ clock noon to 12 o’ clock midnight is p.m.

• There are 7 days in a week. A year has 12 months.

• A year has 365 days. A leap year has 366 days.

• On a timeline, the events are always written in the order in which they come first.

Math Lab

My Birth Certificate

Setting: In pairs

Preparation at Home: Ask for help from your parents to fill in the birth certificate given on the right side.

Discussion: Exchange your birth certificate with your partner. Look at the birth dates on the certificates. Determine how old your partner is currently or will be this year. This activity will help children to look at dates and understand the concept of a calendar.

Creativity & Experiential Learning

Form Number

Government of ____________ BIRTH CERTIFICATE

This is to certify that this information is taken from the original record of birth which is in the register for the year __________

Name:

Sex:

Date of Birth:

Place of Birth:

Name of Father:

Name of Mother:

Date of Registration:

Registration Number: Date: Signature of issuing authority

Chapter Checkup

1 Look at the minute and hour hands. What time is it?

2 Draw a clock to show the times given.

a 10 minutes past 12

b Half past 1 c Quarter to 7

3 How many hours have passed between the times given?

a 5:20 to 7:20

4 Write the time using a.m. or p.m.

a 7:30 in the morning

b 9:15 to 11:15 c 2:10 to 4:10

b 6:15 in the evening

c 5 minutes to 12 midnight d 5 minutes after 12 midnight

5 Write if the following activities would take less than a minute, some minutes or hours to complete.

a Making tea b Washing a shirt

c Blinking your eyes 5 times d A picnic day

6 Fill in the blanks.

a The date on the last day of the year is always December.

b If today is 30 April 2023, the date tomorrow will be .

c If today is 12 June 2023, yesterday’s date was .

d If today is Monday, 1 June 2023, the date after a week will be .

7 Draw a timeline with the following events in Virat Kohli�s life. U-19 England

July 2006 April 2011 5 November 1988 March 2008 October 2002

8 Draw a calendar for the month of July. The month starts on a Sunday. Then, answer the questions.

a How many Sundays are there in the month?

b What is the date on the 2nd Saturday?

c Write the dates of all Mondays.

9 Rama woke up at 7 o’ clock in the morning and went to bed at 9 o’ clock that night. Write the time she woke up and went to bed, using a.m. and p.m.

10 Aditi turned 7 years old on 28 August 2007. In which year will she be 14 years old?

Challenge

1 Today is Monday, 17 April 2023. Arun’s uncle is coming to stay with them after 5 days. On what day and date will Arun’s uncle come?

2 How many times between 3 p.m. and 6 p.m. do the hour hand and the minute hand coincide? Justify your answer.

Railway Station

Priya is travelling to Indore for her cousin�s wedding. She went to the railway station to board a train. Outside the railway station she saw a clock showing 3:00 p.m. Priya knew that there were still 50 minutes for her train to leave. The train was late and finally arrived 50 minutes after the actual departure time. Read the questions and answer them.

1 The train was delayed by minutes.

2 What was the actual time of Priya’s train?

a 3:50 a.m.

c 3:00 p.m.

3 At what time did the train finally arrive?

4 Was the train delayed by an hour?

b 3:50 p.m.

d 4:05 p.m.

5 A sweeper cleaned the platform for an hour. How many minutes did he clean the platform for? How do you help in keeping the platforms clean?

11 Money

Let�s Recall

Money is important to get things that we need in our daily lives. When we go to the market to buy food, we take money with us. The shopkeeper gives us what we need in exchange for money. These are the commonly used coins and banknotes in India:

Now, let us say we want to buy a chocolate for ₹50. In how many different ways can we pay for it?

We can pay with:

Five ₹10 notes.

Let’s Warm-up

Two ₹20 notes and one ₹10 note. One ₹20 note and three ₹10 notes. One ₹50 note.

Fill in the blanks with the number of notes or coins.

1 We can get ₹10 notes or coins for ₹20.

2 We can get ₹5 coins for ₹30. 3

Understanding Money

Grandfather: Mohit, let us go and buy bread from the shop.

Mohit: Of course, grandfather!

They went to the store. The shopkeeper gave the packet of bread and charged them ₹21.50.

Grandfather made the payment and they both returned home.

Writing Rupees and Paise

We have already learnt about the types of coins, that is rupee coins and paise coins. Let us learn to write the rupees and paise together.

Rupee and Paise Amounts

Grandfather paid ₹21.50 for the packet of bread.

₹21.50

Did You Know?

Each Indian banknote has its value written in the script of 17 languages.

The number on the left of the dot shows rupees.

The dot separates the rupees and paise.

The number on the right of the dot shows paise.

The amount ₹21.50 can be read as “twenty-one rupees fifty paise”.

On the way home, Mohit asked his grandfather to buy a pack of pencils. The shopkeeper said that the pack costs ₹19.05.

Let us see how to read this amount.

₹19.05 paise

The amount ₹19.05 can be read as nineteen rupees five paise.

Remember!

If the paise amount is less than 10, write a 0 after the dot. rupees

Example 1: Write ₹52.50 in words. rupees

₹52.50 paise

₹52.50 = fifty-two rupees fifty paise.

Example 2: Write thirty-eight rupees seven paise in figures.

Thirty-eight rupees = ₹38

Seven paise = 07

Thirty-eight rupees seven paise = ₹38.07

Write the amounts in figures and words.

1 ₹23.25 = twenty-three __________ paise

2 ₹ = thirty-six rupees sixty paise

3 ₹42. = rupees eighty paise

4 ₹ .03 = sixty-one rupees paise

Counting Money

Do you remember Mohit and his grandfather, who went to buy the packet of bread? When the shopkeeper asked him to pay ₹21.50, Mohit helped his grandfather to count the notes and coins shown below.

Is the number of notes and coins counted by Mohit correct? Let us find out.

Step 1

Add the rupee notes and coins.

Two ₹10 notes = ₹10 + ₹10 = ₹20

₹20 and one ₹1 coin = ₹20 + ₹1 = ₹21

Step 2

Think and Tell

Is there any other way to make up the amount of ₹21.50?

Write the paise amount separated by a dot, along with the total rupee amount.

₹21 and one 50 paise coin = ₹21.50.

Two ₹10 notes, one ₹1 coin and one 50 paise coin = ₹21.50. The amount taken out by Mohit is correct.

Count and write the amount in figures.

₹500 + ₹ = ₹600

₹600 + ₹20 = ₹

₹ + ₹2 = ₹

₹622 and paise = ₹

In figures = ₹

Converting Rupees into Paise

We can convert rupees into paise using some simple steps. Let us convert ₹23.25 into paise.

Step 1

Step 2

Remove the dot and ₹ sign. Write paise with the number.

₹23.25 = 2325 Therefore, ₹23.25 = 2325 paise.

Remove the ₹ sign before writing paise with the number.

₹15.36 = ₹1536 paise ₹15.36 = 1536 paise

Example 3: How will you convert ₹93 into paise?

Here, we see only money in rupees.

Step 1

Step 2

Remove the �₹� sign and Write paise with the number. add 2 zeroes after the number. Therefore, ₹93 = 9300 paise.

₹93 = 9300

Convert into paise.

1 ₹125.36 = 2 ₹56 = Therefore, ₹125.36 = paise. Therefore, ₹56 = paise.

Converting Paise into Rupees

We can also convert paise into rupees using some simple steps. Let us convert 5212 paise into rupees.

Step 1

Step 2

Remove the word ‘paise’ and Put the sign of �₹� before the number. put a dot after counting 2 numbers Therefore, 5212 paise = ₹52.12. from the right of the given number.

5212 paise = 52.12

2 places from the right

Example 4: Convert 8400 paise to rupees.

Remove the word ‘paise’ and put a dot after counting 2 numbers from the right of the given number.

8400 paise = 84.00

Put the sign of �₹� before the number.

Therefore, 8400 paise = ₹84.00

₹84.00 can also be written as ₹84.

Convert into rupees.

1 12365 paise = 2 8700 paise = Therefore, 12365 paise = ₹ . Therefore, 8700 paise = ₹ .

Do It Yourself 11A

Write the amount in words.

Write the amount in numerals.

a fifty-six rupees seventy paise b twenty-nine rupees eighty-eight paise

c thirty-five rupees fifty-seven paise d sixty-eight rupees fifty paise

e seventy-three rupees twenty-two paise f fifteen rupees sixty-six paise

Count the money and write the amount in figures. Notes

Fill in the blanks.

a ₹25.36 = paise b 802 paise = ₹

c 2125 paise = ₹ d ₹125.36 = paise

e 36125 paise = ₹ f ₹358.80 = paise

The price of petrol in Mumbai as of July 2024 was ₹103.44. Write the amount in words.

Mahi feels bad that she has more money in her gullak than her younger sister Meher. How much money should she transfer from her gullak to Meher's gullak so that they have the same amount of money?

Mahi�s Gullak: One note of ₹50, one note of ₹20, coins of ₹10, ₹5 and ₹5

Meher�s Gullak: Three notes of ₹20 and one coin of ₹10

Word Problems on Money

The next day, Mohit and his grandfather went to the market. They bought a packet of tea for ₹52.50 and a packet of biscuits for ₹40.00. Let us find out how much money they spent in total.

Step 1

Write the information given in the question.

Remember!

Cost of tea = ₹52.50; Cost of biscuits = ₹40.00.

0 after the dot means 0 paise. Therefore, ₹40.00 = ₹40

Step 2

Choose the correct operation.

We need to find the total amount spent; hence we will add the costs.

Step 3

Add the paise amounts. Then, add the rupee amounts. Both amounts have to be added separately.

Therefore, Mohit and his grandfather spent ₹92.50 in total.

Example 5: Neeraj had ₹175.50 with him. He spent ₹53.00 on buying coloured pencils. How much money does Neeraj have left?

Money Neeraj had = ₹175.50

Money spent on coloured pencils = ₹53.00

We need to find the amount Neeraj has left. Hence, we will subtract the given amounts.

Amount left with Neeraj = ₹122.50.

Anushka had ₹135.00 already. Her mom gave her ₹42.50, and her dad gave her ₹37.00. How much money does Anushka have in total?

Money with Anushka = ₹135.00

Money given by mom =

Money given by dad =

We need to find the total amount Anushka has; hence we will the amounts.

Add rupees and paise vertically, separated by a dot. Hence, Anushka has ₹ in total.

The price of a lunch box is ₹85.50, but Priya only has ₹72. How much more money does she need, to buy the lunch box?

Vaibhav saved his pocket money to buy a football for ₹50.50. He then shared the idea of saving money with Neeraj who saved ₹75.00. How much money did they save together?

The price of a cricket bat is ₹235.50, and a ball costs ₹45.00. What is the total price of the bat and the ball?

Snake plants and money plants can purify the air and are easy to care for. Divya spent ₹238 on the snake plant and ₹125.50 on the money plant. How much did she spend in total?

John and Maria have ₹284.50 and ₹156.00, respectively. Richa has an amount equal to the difference between the amounts John and Maria have. What amount does Richa have?

Challenge

Anand bought a pencil box. He gave ₹100 to the shopkeeper and got ₹28.50 back. What was the cost of the pencil box?

Making Bills

John went to the nearby stationery shop to buy some items. He saw that one pencil costs ₹5.00, one eraser costs ₹6.50, one notebook costs ₹15.00 and one sharpener costs ₹12.00. He bought 3 pencils, 1 eraser, 2 notebooks and 1 sharpener.

The shopkeeper gave him a bill.

A bill shows the details of how much we are paying for each item bought from the shop. It also tells us the total amount we have to pay for the items we bought.

Let us learn how to make a bill.

Step 1

Make a table as shown. Write the names of the items bought and the quantity of each item.

Stationery Shop

Step 2

Find the amount of each item.

Amount = Quantity × Rate per item

Step 3

Find the total by adding the money in the amount column. Remember!

Stationery Shop

If John buys 6 pencils and 1 notebook, will his bill be the same? How? Think and Tell

Quantity = Number of items bought

Vishal purchased the following items from Adarsh Departmental Store: Two loaves of bread for ₹25.00 each. One packet of milk for ₹19.50. One packet of butter for ₹60.00. Three chocolates for ₹14.00 each.

Complete the bill and find the amount paid by Vishal.

Adarsh Departmental Store

The amount paid by Vishal = .

Vipin went to a nearby store to buy the following items. What total amount does he need to pay?

Manya went to buy some items from the nearby store. The shopkeeper gave her the following bill. Is the bill correct? If not, prepare the correct bill for her.

Sam purchased the following items from the nearby supermarket: Two ice creams for ₹20.00 each. Three packets of cookies for ₹15.00 each. One packet of chips for ₹24.50. Two bottles of juice for ₹26.00 each.

Prepare a bill and find the amount paid by Sam.

A supermarket is a self-service shop. It is big and has a variety of products. Ravi, Joe and Tanya went shopping to a supermarket. Look at the items and their prices. Fill in the table.

a 2 bananas for ₹

c 5 toffees for ₹

Challenge

1 banana for ₹ 5 bananas for ₹

b 1 teddy for ₹ 1 teddy for ₹ 1 teddy for ₹

2 toffees for ₹ 4 toffees for ₹

Ravi buys Joe buys Tanya buys

Amount paid = ₹ Amount paid = ₹ Amount paid = ₹

Critical Thinking

Sahil had a ₹200 note with him. He went to buy some fruit from the nearby fruit store. He added 4 apples costing ₹20.00 each, 3 oranges costing ₹8.00 each, 1 papaya costing ₹35.50 and 4 guavas costing ₹12.00 each to his shopping cart. Will he be able to purchase all the fruit he added to his cart?

Points to Remember

• When we write rupees and paise together, they are separated by a dot with rupees on the left and paise on the right.

• To convert rupees into paise, remove the dot and �₹� sign and write paise.

• To convert paise into rupees, remove the word paise and put a dot after counting 2 numbers from the right, and put the �₹� sign with the given number.

• A bill shows the details of how much we are paying for each item bought from the shop.

• Amount = Quantity × Rate per item.

• A bill shows the details of how much we are paying for each item bought from the shop and the total amount we have to pay for the items we bought.

Math Lab

Collaboration & Experiential Learning

Shopping Spree

Setting: In groups of 5.

Materials Required: Price tags with various items and their cost in rupees and paise.

Play money in the form of rupees and paise.

Pen and paper.

Method: Display the items along with their price tags.

1 The teams select the items they want to purchase and write the quantity on the paper.

2 The teams find the total amount they need to pay.

3 The teams use the play money for their purchases.

4 The team with the correct amount and money in hand wins!

Chapter Checkup

1 Write the amount in words.

a ₹52.36 b ₹65.14 c ₹71.05

2 Write the amount as numerals.

a thirty-eight rupees sixty-five paise b twenty-nine rupees fifty-five paise

3 Convert the amount given in rupees to paise.

a ₹25.15 b ₹52.25 c ₹235.48

4 Write the amount in rupees.

a 3256 paise b 15236 paise c 52364 paise

5 Match the amounts in rupees and paise.

In rupees

In paise

a ₹2.35 348 paise

b ₹3.48 3480 paise

c ₹23.56 235 paise

d ₹34.80 2356 paise

6 Look at the bills and correct them if you find a mistake.

7 Divya purchased some items from the nearby store. Prepare a bill and find the amount paid by Divya.

Three packets of rice for ₹45.00 each. Two packets of chips for ₹18.00 each.

One packet of milk for ₹17.50.

8 Baking is a way of cooking by using heat in an oven. Seema is a baker who makes cupcakes. A pack of cupcakes costs her ₹136.50 to make. Each pack uses ₹55 worth of sugar. How much money does she spend on the other ingredients?

9 Reena has to pay school fees of ₹535.50 but she has only ₹425.00 with her. How much more money does she need?

10 Shyam donates some part of his salary to the poor and needy. He donated ₹152.00 at a mall and ₹58.50 to the poor sitting outside a temple. How much money did he donate in all? Have you seen donation boxes in markets or malls?

Raman made a bill for 5 packets of biscuits, each costing ₹12.00, and 2 cans of juice, each costing ₹35.00. The customer gave him a ₹200 note. How much change will Raman return to the customer? Who has more money, and by how much? 1 2 Challenge

Ajay had these coins in his pocket. Rahul had these coins in his pocket.

Ancient Money

Long before the use of metal coins, people in our country used kauris (sea shells) as money. Sheena and her friends were playing with the kauris to buy things. They decided that 1 paisa = 10 kauris and 1 rupee = 100 paisa. Read the questions and answer them.

1 How many kauris will make one rupee?

a 10

b 100

c 500

d 1000

2 If a toy costs 10 paisa, how much will it cost in kauris?

3 Convert 5 rupees into paisa.

4 If you want to choose something for your own currency (like the rupee and paisa in India), what will that thing be and why?

12 Fractions

Let�s Recall

Sharing food and eating together is so much fun! In the picture, the friends are sharing a cake and enjoying it together!

How can they cut the cake so that everybody gets an equal piece?

The cake is a whole. We divide the whole cake into as many pieces as the number of children, so that each of them gets an equal “fraction” of the cake.

We can say that a fraction is a part of a whole and can be used to split a whole object into equal parts.

Let’s Warm-up

Look at the pictures. Can the pictures in columns 1 and 2 be the two equal parts of a whole? Say Yes or No.

Understanding Fractions

Ravi and Manya are feeling hungry. Mother bakes a pizza for them.

Ravi: Wow! The pizza looks yummy. I can’t wait to eat it.

Manya: Yes, Ravi! Let me cut the pizza into equal parts first.

Manya cuts the pizza into equal parts and they both enjoy their meal.

Parts of a Whole

Fraction: Fractions are equal parts of a whole.

Let us learn how to divide a whole object into equal parts!

Whole

A full or complete object or collection of objects is a whole. Whole means 1.

Half

When a whole is divided into two equal parts, then each part is called half of the whole. It is written as 1 2 , half, or one-half.

A whole pizza half or 1 2

One-fourth

When a whole is divided into four equal parts, then each part is called one-fourth of the whole. It is written as 1 4 .

Two-thirds

When a whole is divided into three equal parts, and 2 out of 3 parts are shaded or used, it is called two-thirds or 2 3 . 2 3 1 4

One-third

When a whole is divided into three equal parts, then each part is called onethird of the whole. It is written as 1 3 . 1 3

Three-fourths

Three out of four equal parts is called three fourths. It is written as 3 4 . 3 4

Did You Know?

Brahmagupta (598-668 CE), an Indian mathematician, provided rules for fractions in his book �� Brahmasphutasiddhanta.��

Think and Tell

Can we divide the given pizza into 5 equal parts? What would each piece be called?

Example 1: What fraction of the shape is shaded?

Total number of equal parts = 4

Number of parts shaded = 1

1 out of 4 equal parts is shaded; hence, 1 4 fraction is shaded.

Example 2: Which shape is not divided into equal parts?

Divided into 2 equal parts Divided into 4 equal parts

What fraction of the given shape is

1 shaded? 2 not shaded?

Total number of equal parts = 4

Not divided into equal parts Divided into 3 equal parts

Number of parts shaded = out of 4 parts are shaded; hence, fraction is shaded.

Number of parts not shaded = 1

1 out of parts are not shaded, hence fraction is not shaded.

Do It Yourself 12A

1 Write the fraction for the shaded portion in each figure.

2 Colour each shape to represent the given fraction.

a half or 1 2

b Three-fourths or 3 4 c one-third or 1 3

d one-fourth or 1 4

e two-thirds or 2 3 f Three-fourths or 3 4

3 Match the shaded figures to the fractions they represent.

5 Cross

4 Shade one-third or 1 3 of each shape.

Three-fourths

Evaporation is the process by which water turns into water vapour. 4 cups of water was boiled and 2 cups of water evaporated. What fraction of the water turned into water vapour?

1 Rajiv folded a sheet of paper. First, he folded it in half. Then, he folded it in half again, and one more time. After opening the paper, he coloured each equal part in different colours. What fraction represents each of these equal parts? Challenge

Fractions of a Collection

We already know that fractions are equal parts of a whole. We also know that:

2 means 1 part out of 2 equal parts.

3 means 1 part out of 3 equal parts.

4 means 1 part out of 4 equal parts.

The above facts can be used to shade or find the fractional part of a collection or group of objects.

Half of a collection of objects:

Let us find and shade 1 2 of a collection of 12 bananas.

Divide the number of bananas into two equal groups, as shown below:

Clearly 1 2 of the collection of 12 bananas = 12 ÷ 2 = 6 bananas in each group.

Shading 1 2 of the collection of bananas can be shown as:

The number of shaded bananas is half of all the bananas, and all the bananas are double the number of shaded bananas.

One-third of a collection of objects:

Let us now find and shade 1 3 of a collection of 12 bananas.

Clearly 1 3 of the collection of 12 bananas = 12 ÷ 3 = 4 bananas in each group.

Shading 1 3 of the collection of bananas can be shown as:

One-fourth of a collection of objects:

Let us now find and shade 1 4 of a collection of 12 bananas.

Clearly 1 4 of the collection of 12 bananas = 12 ÷ 4 = 3 bananas in each group.

Shading 1 4 of the collection of bananas can be shown as:

From the above discussion; we can say that:

• To find 1 2 of a collection, we divide the number of objects by 2.

• To find 1 3 of a collection, we divide the number of objects by 3.

• To find 1 4 of a collection, we divide the number of objects by 4.

Example 3: Colour one-third of the collection of crayons.

Total number of crayons = 15

Collection of crayons we want to colour = 1 3

1 3 of a collection of 15 is 5. Hence 5 crayons can be coloured as:

Example 4: Find.

1 1 2 of 20 apples

– Divide 20 apples into 2 equal parts.

– Count the number of apples in 1 part.

2 1 3 of 24 trees

– Divide 24 trees into 3 equal parts.

– Count the number of trees in 1 part.

24 = 8

Colour one-fourth of the collection of balls.

Total number of balls = 8

Collection of balls we want to colour = ____ of 8 balls = ____ balls

balls can be coloured as:

Do It Yourself 12B

Colour to show the given fraction of the collection.

b 1 2 a 1 2 c 1 3

Write True or False.

a 1 4 of 16 apples is 4 apples.

b 1 2 of 10 pears is 2 pears.

c 1 3 of 6 mangoes is 6 mangoes. d 2 3 of 18 grapes is 6 grapes. Find.

a 1 2 of 18 b 1 3 of 9 c 1 3 of 21 d 1 4 of 12

Ramya had 12 plants. She put 1 3 of the plants in her living room. How many plants did she put in her living room? 4

Draw a shape or figure and divide it into parts and shade parts to show any fraction.

Critical Thinking d 1 4

1 There are 12 bears in a zoo. 1 3 of them are brown. The number of black bears is twice the number of brown bears. Are there any other colour of bears in the zoo?

Identifying Fractions

We learnt what fractions as parts of a whole look like. Let us now learn how to write a fraction numerically.

Writing a Fraction

Remember, we divided the pizza into two, three and four equal parts. We also learnt that:

half = 1 2 ; one-third = 1 3 and one-fourth = 1 4

Let us see how a fraction is written.

(Number of parts chosen)

(Total number of equal parts)

0 can never be the denominator. This is because we never divide a number by 0.

Let us now learn how to write other fractions.

Find the fraction of the blue parts in the given figure.

Fraction of the blue parts = Number of parts chosen Total number of parts = 5 8

Error Alert!

Always write the total number of parts in the denominator. For instance, the fraction of 2 slices of cake out of 7 slices will be given as: 7 2 2

Example 5: What fraction of the given figure is coloured pink?

Number of parts coloured pink = 7

Total number of parts = 12

The fraction of pink parts = Number of parts coloured pink Total number of parts = 7 12

Example 6: What fraction of the balls are

a Red? b Green?

a Number of red balls = 8

Total number of balls = 11

Fraction of red balls =

Number of red balls

Total number of balls = 8 11

b Number of green balls = 3

Total number of balls = 11

Fraction of green balls =

Number of green balls

Total number of balls = 3 11

What fraction of the balloons are:

a Yellow? b Green?

a Number of yellow balloons =

Total number of balloons = 7

Fraction of yellow balloons =

b Number of green balloons =

Total number of balloons = 7

Fraction of green balloons =

Number of balloons

Total number of balloons =

Number of balloons

Total number of balloons =

Word Problems

Now, let us learn how to solve word problems on fractions. Manya cut the pizza into 8 equal parts. She ate 3 slices and Ravi ate the remaining 5. What fraction of the pizza was eaten by Manya?

We know that,

Fraction = Number of parts chosen

Total number of parts or Number of objects chosen

Total number of objects

To solve a word problem on fractions:

Step 1: Find the total number of parts / objects chosen.

In the above case, number of parts chosen = number of slices eaten by Manya = 3

Step 2: Find the total number of parts / objects. Here, the total number of slices of pizza = 8

Step 3: Write the given information in the form of fractions.

The fraction of pizza eaten by Manya = Number of slices eaten by Manya Total number of slices = 3 8

Manya ate 3 8 of the pizza.

Example 7: Wasim ordered a pizza. The pizza was divided into 6 slices.

If he ate 1 3 of the pizza then how many slices did he eat?

whole

slices

1 3 of 6 slices = 2

Total number of slices = 6

1 3 of a collection is 1 part out of 3 equal parts.

Each equal part has 2 slices.

Slices eaten by Wasim = 1 3 of 6 = 2 slices.

Wasim ate 2 slices of the pizza.

About 1 3 of the earth’s surface is covered with land.

Example 8: Ranu bought a packet of bread which had 12 slices. She gave 1 2 of the packet to a street dog. How many slices of bread did she give to the dog?

Total number of slices of bread = 12

Fraction of bread given to the dog = 1 2

12 slices split into 2 equal parts gives 6 slices in each part. (12 ÷ 2 = 6)

So, the number of slices given to the dog = 6 slices. Did You Know?

Mohit bought 15 roses to decorate his house. He put 1 3 of the roses in a vase. How many roses did he put in the vase?

Total number of roses = Fraction of roses in the vase =

Number of roses put in the vase =

1 What fraction of the given figures is shaded?

2 Colour to show the given fraction.

3 Write the fractions for the coloured and uncoloured parts of the collections.

4 Kavya places 17 roses in a beautiful vase. It holds 8 red roses and 9 pink roses. What fraction of the roses are red?

5 The students of Class 3 collected 24 waste bottles for a recycling project. One-half of the bottles were plastic. How many bottles were plastic?

6 Vishal has 12 shirts. 1 4 of his shirts are blue. How many shirts are blue?

7 There are 25 building blocks in a bag. Ravi uses 16 blocks to build a house. What fraction of the building blocks remain unused?

8 Rani has 27 books. She donates 1 3 of the books. How many books does Rani have left? Do you donate your old books?

1 4 5 of a certain number of buses is 16. What is the total number of buses?

2 Look at the given figure. What fraction of the figure is left unshaded?

Points to Remember

• A full or complete object is a whole. Whole means 1.

• Fractions are equal parts of a whole or a collection.

• Two halves, three one-thirds, or four one-fourths make a whole.

• To find 1 2 of a collection, we divide the number of objects equally into 2 parts.

• To find 1 3 of a collection, we divide the number of objects equally into 3 parts.

• To find 1 4 of a collection, we divide the number of objects equally into 4 parts.

• In a fraction, the numerator tells us the number of parts chosen and the denominator tells us the total number of parts.

Math Lab

Setting: In groups of 2.

Collaboration & Experiential Learning

Let’s Find the Fraction!

Materials Required: A small bag, 30 marbles of two colours, paper and pen.

Method:

1 Put the marbles into the bag and give it a good shake.

2 Each student in the group takes a handful of marbles.

3 They record the fraction of each colour on the paper.

4 The student who writes the fractions first is the winner!

Chapter Checkup

1 Write the fractions.

a Half = b One-third =

c Three-fourths = d Numerator: 5; Denominator: 8 =

e One-fourth = f Numerator: 7; Denominator: 12 =

2 Write the fraction of the given collections.

Collection of Objects Fraction Green capsicums = Yellow capsicums = Pink stars = Blue stars =

3 Colour as per the fractions given.

4 Solve.

5 Tim has a cake. He wants to share it equally among him and his 4 friends. If the cake is divided into 5 equal parts, what fraction of the cake does each friend get? Do you share things with your friends?

6 Meena bought 9 flowers from the market, of which 1 3 were tulips. How many of the flowers were tulips?

7 Manya planted 6 plants in her garden, of which 2 were rose plants. What fraction of the plants were rose plants?

8 There are 24 apples in a basket. If 1 4 of the apples are rotten, how many apples are still good?

9 Raj wanted to celebrate his housekeeper's birthday. He sent invitations to 18 friends for the birthday party, but 3 of them were unable to attend. What fraction of the friends attended the party?

a 1 2 of 12 b 1 3 of 15 c 1 4 of 4 d 1 2 of 8 Challenge

1 Use the clue to find the correct fraction from the given possibilities of images.

Clue: I am less than 2 and a half wholes. I am more than a whole. You can make me out of 4 halves. What am I?

2 Show and colour halves in 4 different ways in the given figure. Critical Thinking & Art Integration

Balanced Diet

A balanced diet is very important for our body. It includes a variety of food groups, such as fruits, vegetables, grains and proteins. Each food group should make up a certain portion of our daily intake. Riya’s parents give her a balanced meal, this is what her plate looks like.

1 What fraction of a healthy plate is filled with fruits and vegetables?

a 2 8 b 1 8 c 3 8 d 5 8

2 The fraction of proteins in the plate is .

3 Write if True or False.

a Grains cover 2 8 of the plate.

b 3 4 of the plate is proteins.

4 What fraction of the plate is not proteins?

5 Do you eat healthy food?

13 Data Handling

Let�s Recall

Going to the market with our parents is so much fun!

What did we buy today? Let us see our shopping bags!

So many things! Is there a better way to show what we bought?

We can put all this data together in a table. We can also write the quantities of items that we bought. This gives all the information together in a single view!

Data put together in an organised way is called information.

We have presented the data related to our shopping in the table above.

Let’s Warm-up

Read the table that shows the number of balloons a man sold in a week.

Answer the questions.

1 On which day did he sell the most balloons?

2 On which day did he sell the least balloons?

3 On which days did he sell the same number of balloons?

4 On which day did he sell 6 balloons?

Understanding Data

Yash’s school organised a cricket tournament. He helped with scorekeeping in each match. He noted down the number of wickets taken by each player.

Amir took 8 wickets, Vihan took 7, Avyaan took 8, Deepak took 9, Prabhakar took 6, and Shreshth took 7 wickets.

Data Tables

Can Yash put this data together in a better form? Are there any details that he can draw from this data?

To better understand the data, let us try to put it in a table.

Data is a collection of numbers or values that we can sort and use to understand things.

Step 1

Make a table with 2 rows and label them.

Remember!

Arranging data into meaningful chunks that can be easily understood is called data handling.

Step 2

Write the names of the players.

Player Amir Vihan Avyaan Deepak Prabhakar Shreshth

Wickets Taken 8 7 8 9 6 7

Step 3

Write the wickets taken by each player.

Remember!

A list helps organise information about things.

What if Yash wanted to identify the player who took the highest number of wickets? We can see in the table that Deepak took the most wickets, which is 9.

We can re-order the data table in descending order, so that bowlers with a higher number of wickets appear first.

Player Deepak Amir Avyaan Shreshth Vihan Prabhakar

Wickets Taken 9 8 8 7 7 6

So, now we know that Deepak, Amir, and Avyaan were the top 3 bowlers in the tournament.

Example 1: A car seller collects the following data on sales of cars from his shop.

Colour

Number of Cars Sold 15 20 17 12 6

1 Which colour has the most number of cars sold?

2 What is the total number of cars sold?

Total number of cars sold = 15 + 20 + 17 + 12 + 6 = 70

Shruti organised a survey to note the favourite sports of the students in her class. The following data was gathered:

Football, Cricket, Tennis, Badminton, Football, Football, Cricket, Tennis, Football, Badminton, Badminton, Cricket, Cricket, Cricket, Tennis, Tennis, Cricket, Football, Football, Football, Cricket, Badminton, Football, Cricket, Cricket, Football, Tennis, Badminton, Badminton, Cricket, Badminton, Cricket

Complete the data table on the favourite sport of the students.

Do It Yourself 13A

Write True or False.

a Raw data is an organised form of data.

b Writing the numbers in ascending or descending order makes it easier to find the greatest or smallest from the data.

c Collecting data makes it easy to understand.

d The data collected from surveys is called raw data.

Organise the raw data of marks obtained in maths out of 100, from the highest to the lowest.

65, 70, 78, 58, 80, 98, 45, 77, 99, 83, 89.

Fruits are very good for you because they have fiber, which helps your stomach and intestines work well and stay healthy. The choices of fruit of 28 students in a class are given below. Draw a table to show the data.

Apple, Orange, Banana, Mango, Apple, Grapes, Banana, Grapes, Apple, Grapes, Banana, Mango, Apple, Grapes, Mango, Apple, Banana, Grapes, Mango, Banana, Apple, Orange, Mango, Orange, Grapes, Banana, Orange, Mango.

Grains are the harvested seeds of grasses. They are common staple foods. They are also called cereals. Given below is the data showing the grain that some people eat. Read the data and fill in the blanks.

Grains Rice Wheat Maize Barley Ragi

Number of People 25 24 2 3 5

a The number of people who eat barley is .

b The number of people who eat ragi is ___________ (more/less) than those who eat rice.

c The most people eat as their main food.

1 The table shows the sale of cutlets in 2 shops for 4 weeks. Look at the table and answer the questions.

a If Shop A sold half the number of cutlets in Week 5, than it sold in Week 4, how many cutlets did it sell in Week 5?

b If Shop B sold 10 more cutlets in Week 2 and Week 3 each, how many more did it sell in these 2 weeks than Shop A?

Pictograph

Do you remember Yash who noted down the wickets taken by the players in a data table? The table helped us to compare the wickets taken by each player.

Players Amir Vihan Avyaan Deepak Prabhakar Shreshth

What if Yash wanted to represent the data in an interesting way using pictures?

Drawing a Pictograph

When we use pictures or symbols to show data, it is called a pictorial representation or pictograph.

The same data of the players can be represented in a pictograph.

Players Wickets Taken

Amir

Vihan

Avyaan

Deepak

Prabhakar

Shreshth

Key: = 1 wicket

The key tells us the meaning and value of the picture or symbol.

In the above chart, so many symbols have to be entered! This can get very tiresome. Is there a quicker way to represent the data?

What if each was 2 wickets instead of 1?

The chart would then become:

Player Wickets Taken

Amir

Vihan

Avyaan

Deepak

Prabhakar

Shreshth

Key: = 2 wickets

The symbols that are drawn in a pictograph should be of the same size. Error Alert!

Half a symbol can be used to show that it has half of the value of the whole symbol.

In this key, stands for 2 wickets, so stands for 1 wicket.

Think and Tell

Why is it important to select a key in a pictograph?

Example 2: Draw a pictograph for the data shown in the table. Take the key as, = 5 balls bowled.

Key: = 5 balls bowled

Bowlers with the number of balls bowled. (Key: = 5 balls bowled)

Bowlers Balls Bowled

Jasprit

Bhuvneshwar

Shami

Mukesh

Jaidev

A trip was organised for the students of class 3. The data shows how many students from 4 sections went on the trip. Represent the data using a pictograph.

Section Number of Students

One represents 1 student.

Section Number of Students

Section A

Section B

Section C

Section D = 1 student

Reading a Pictograph

Let us look at a weather data pictograph! The pictograph shows the rainfall received by a city in different months.

Month

June

July

August

September

Key: = 5 cm

What if we wanted to know the rainfall in the month of July?

There are 5 symbols in July. As per the key, each symbol equals 5 cm of rain.

Did You Know?

Indian mathematicians, P.C. Mahalanobis and C. R. Rao have played a major role in the field of statistics. Statistics is all about collecting, organising and understanding data.

So, let us find the rainfall in July:

5 10 15 20 25

Total rainfall in the month of July = 25 cm

What if we want to find the month with the least rainfall?

We can see that September has the least number of symbols. There are 2 symbols. So, each symbol = 5 cm.

Therefore, 2 × 5 = 10 cm of rain was received in September.

Think and Tell

Will it be easier or more difficult to make the same pictograph if the key is = 1 cm?

7 friends went shopping to buy chocolates. The pictograph shows the number of chocolates purchased by each of them. Read the pictograph and answer the questions.

Shubh

Mangal

Aahan

Jennifer

Param

Shruthi

Devyani

Name Number of Chocolates

Key: = 2 chocolates

1 How many chocolates did Ahaan purchase?

Number of symbols of chocolates for Ahaan = 2 and .

Key: chocolates

Thus, Ahaan purchased chocolates.

2 Who purchased the most chocolates? How many?

The number of symbols for is the most. The number of chocolates purchased = ________

Write True or False.

a A pictograph represents data using pictures and objects.

b In a pictograph, more pictures mean a bigger number.

c Pictographs help us understand and interpret the data.

Draw the symbols to complete the pictograph for the data. = 2 children

The pictograph shows the number of books borrowed from the library on different days of the week. Read the pictograph and answer the questions. = 2 books

a How many books were borrowed on Wednesday?

b On which day was the highest number of books borrowed and how many?

c What is the difference in the number of books borrowed on Tuesday and Thursday?

Segregating waste makes it easier to recycle materials. The pictograph shows the number of households that segregate different types of waste. Read the graph and answer the following questions.

Type of Waste

Wet Waste

Dry Waste

Sanitary Waste

E-waste

Key: 1 bin = 1 unit

Number of Households

a How many more households segregate wet waste compared to e-waste?

b If 3 more households start segregating wet waste, how many will there be in total?

c Do you or your family practice waste segregation at home? If so, how do you do it? If not, why not?

Create a new question on the pictograph shown in Q5.

Challenge

1 Look at the pictures and answer the questions.

Critical Thinking

a If = 10 animals, pictures will be drawn for 50 animals.

b If 2 = 10 snowflakes, ____ pictures will be drawn for 20 snowflakes.

Bar Graph

We learnt about representing data pictorially. Are there other ways to represent data?

Let us look at Yash’s data table again. The table shows wickets taken by the players in the tournament.

Players Amir Vihan Avyaan Deepak Prabhakar Shreshth

Drawing a Bar Graph

A bar graph is a chart that uses bars to show comparisons between categories of data. It has a horizontal axis (x–axis), and a vertical axis (y–axis). The horizontal axis shows what is being measured and the vertical axis shows the number for the categories being measured. Let us learn how to draw a bar graph. We will use Yash’s data above.

Step 1

Draw the x-axis and y-axis and label them.

Step 4

Write the names of the players on the x-axis, and the number of wickets taken on the y-axis.

Step 2

Write the title of the graph.

Wickets Taken by the Players

Avyaan Amir Shreshth Deepak Vihan

Example 3: Draw a bar graph for the following data.

Step 3 Write the scale.

Step 5

Draw the rectangular bars for the number of wickets taken by each player.

Favourite Fruit

The table shows the number of pencils with 5 students. Complete the bar graph for the data given in the table.

Interpreting a Bar Graph

Now that we have learnt to draw bar graphs, can we read and interpret them? Let us read the given graph and answer some questions.

Marks Scored by the Students

1 Which students scored 8 marks?

Both Alex and Anaisha scored 8 marks.

2 Who got more marks—Ann or Piya? How many more?

Ann scored 7 marks and Piya scored 6 marks.

Ann scored 1 more mark than Piya.

Ashutosh Akram VinayRobin Atif

Example 4: The bar graph shows the number of buckets of water filled by the members of the family in a week. Who filled the most number of buckets and how many?

Tallest bar is for the father = 8 divisions

1 division = 1 bucket

Thus, the father filled the most buckets, which is 8.

The bar graph shows the time spent on homework in different subjects in a month. Read the graph and answer the questions.

1 What is the difference in the number of hours spent on the Maths homework and the English homework?

Number of hours spent on the Maths homework = 9

Number of hours spent on the English homework =

Difference in the hours spent = – = hours

2 Arrange the subjects in ascending order of the time spent on homework.

he data shows the number of people who use different modes of transport. Draw a bar graph to show the data.

The data shows the number of states in 4 countries. Draw a bar graph for the data given in the table.

Country Myanmar Nepal Bangladesh Bhutan Number

Drinking the right amount of water is important because it helps your body work properly. The bar graph shows the number of glasses of water that 5 students drink in a day. Read the bar graph and answer the questions.

a Who drank the most and least number of glasses?

b How many more glasses did Nimisha drink than Rajat?

c How many fewer glasses did Raghav drink than Shoaib?

Read the bar graph showing the favourite TV channels of children in a class. Answer the questions.

a How many children like sports?

b Which channel is the most popular and how many children like it?

c What is the difference of the number of children who like sports and the number of children who like adventure?

d On how many children was the survey conducted?

Challenge

1 The bar graph shows the story books read by students of class 3 in their summer break. Read the questions and answer them.

a If 2 more students read the story, �Red Riding Hood�, then which two books will show the same bars?

b If the scale shows 1 division = 2 books, how many divisions will you colour for, �Beauty and the Beast�?

Points to Remember

• Data is a collection of numbers gathered to give some information.

• Organisation of data means to arrange the collected data in a proper format to make it more meaningful.

• Pictographs represent the data in the form of pictures or objects.

• A bar graph is a graph or chart with rectangular bars of different heights that represent the number value of each item.

Math Lab

Experiential Learning & Art Integration

Objective: To record and represent the data in a bar graph. Material required: Sheet of paper and pencil, colourful origami sheets.

Method:

1 Ask all the students in the class the mode of transport they use to come to school.

2 Note down the information in a table.

Ask the students to take squared paper and draw horizontal and vertical lines on it.

They will mark all the modes of transportation on the horizontal axis and the number of students on the vertical axis.

Finally, they will strips from the origami sheet of appropriate heights and paste on the grid to represent the number of students taking the different modes of transportation. 3 4 5

Chapter Checkup

1 The data given below shows the favourite colour of the students in a class. Organise the data in a table.

Orange, Pink, Blue, Yellow, Black, Black, Black, Orange, Orange, Pink, Blue, Yellow, Yellow, Pink, Pink, Pink, Blue, Blue, Pink, Pink, Orange, Black, Black, Orange, Orange, Pink, Blue, Blue, Blue, Black, Pink, Yellow, Yellow, Pink, Blue, Orange, Orange, Pink, Black, Black, Yellow, Yellow, Pink, Yellow, Blue, Black

2 Favourite hobbies of 40 students of a class were noted. Create a pictograph for the given data. Use = 1 student.

Singing, Dancing, Sports, Watching TV, Reading, Dancing, Singing, Singing, Sports, Sports, Watching TV, Watching TV, Watching TV, Dancing, Sports, Sports, Sports, Watching TV, Dancing, Dancing, Singing, Reading, Reading, Singing, Watching TV, Sports, Dancing, Dancing, Watching TV, Watching TV, Sports, Dancing, Singing, Reading, Reading, Watching TV, Singing, Dancing, Sports, Sports

3 A film is like a story that you can watch on a big screen, like at the cinema or on a TV. Some children were asked about their favourite genre of films—comedy, musical, or action. Study the pictograph and answer the questions that follow.

Films

Number of Children

Key: CINEMA TICKET = 2 students

a How many children like musical films?

b Which type of film is liked by the least number of children?

c How many more children like musical films than action films?

4 The bar graph shows the runs in the first 10 overs of a cricket match. Study the bar graph and answer the questions that follow.

a How many runs were scored in the 5th over?

b In which over were the most runs scored?

c How many runs were scored in all the overs?

5 The table shows the household size in a country. Draw a bar graph to show this data.

Challenge

1 Meher records the number of squirrels that visit her garden each day. She makes a pictograph, with one showing 2 squirrels. She records the squirrels that visited on Sunday as . How many squirrels visited her garden on Sunday?

2 The pictograph shows the number of tomatoes used by 3 cooks for a dish. Read the pictograph and answer the questions.

Name

Ramesh

Suresh

Tarachand

Key: = 2 tomatoes

Number of Tomatoes

a If you remove 2 pictures of tomatoes from Suresh's row, how many tomatoes did he use?

b If the key changes to 1 picture = 4 tomatoes, how many pictures should be drawn for Tarachand?

Rainfall Chart

Rainfall charts are used for showing the amount of rain measured for various months. We measure rainfall to know about the climate and its changes. Look at the bar graph and answer.

1 Which month shows the highest rainfall? a January

2 shows the lowest rainfall.

3 Which month shows the second highest rainfall?

4 Can you think of any other real life usage of a bar graph? Give an example.

Answers

Chapter 1

Let’s Warm-up 1. 90 2. 9 3. 800 4. 00 5. 3

Do It Yourself 1A

1. a. 2356 b. 4111 c. 3344 d. 5431

2. a. 4746 b. 5625 c. 5241

3. a.

H T O b.

H T O c.

4. a. one thousand five hundred thirty-two

b. three thousand one hundred fifty-six

c. four thousand eight hundred eleven

d. six thousand five hundred eighteen

e. seven thousand two hundred ninety-four

f. eight thousand forty-three

5. a. 200, 2 b. 5000, 5 c. 4, 4 d. 90,9 e. 8000,8 f. 9000,9

6. a. 3245 b. 5386 c. 7040 d. 6008

7. a. 2000 + 100 + 40 + 8 b. 4000 + 000 + 30 + 6

c. 6000 + 100 + 00 + 5 d. 7000 + 200 + 00 + 3

e. 8000 + 200 + 00 + 0 f. 6000 + 500 + 60 + 6

8. Four thousand one hundred twelve

Challenge 1. 1973

Do It Yourself 1B

1. Odd: 83, 91, 63, 149 Even: 36, 78, 164, 348

2. a. < b. < c. < d. > e. < f. >

3. Ascending order a. 1765, 4390, 7430, 7935

b. 773, 2860, 7880, 9573 c. 392, 3067, 4853, 7943

d. 157, 6583, 8546, 9404

Descending order a. 7935, 7430, 4390, 1765

b. 9573, 7880, 2860, 773 c. 7943, 4853, 3067, 392

d. 9404, 8546, 6583, 157

4. Smallest: a. 2467 b. 1367 c. 1025 d. 5068 e. 2089 f. 1057 g. 2578 h. 2489

Greatest: a. 7642 b. 7631 c. 5210 d. 8650 e. 9820 f. 7510 g. 8752 h. 9842

5. a. Greatest 4-digit number b. Smallest 4-digit number

c. Greatest 4-digit number using different digits d. Smallest 4-digit number using different digits

6. River Nile 7. Largest formed number is 7533.

Challenge 1. Anahita since she has written the largest number, 9999

Do It Yourself 1C

1. a. 40 b. 70 c. 40 d. 120 2. a. 30 b. 70

c. 80 d. 140 e. 260 f. 320 g. 440 h. 550

3. a. 270 b. 230 c. 370 d. 360 4. about 630 people

5. 270 trains; 260 stations

Challenge 1. Option b. 752

Chapter Checkup

1. a. 1442 b. 3857 c. 4208 d. 5309 e. 6045 f. 5028

2. a. two thousand four hundred seventy one

b. four thousand two hundred five

c. five thousand three hundred seventy four

d. seven thousand three hundred eight

e. seven thousand five hundred sixty four

f. eight thousand four hundred twenty one

3. a. 50 b. 10 c. 800 d. 8000 e. 7000 f. 90

4. a. 2185 b. 3471 c. 8089 d. 5725 e. 4600

f. 6070 5. a. 1000 + 300 + 80 + 2

b. 3000 + 600 + 40 + 1 c. 5000 + 300 + 20 + 7

d. 6000 + 400 + 80 + 4 e. 7000 + 500 + 00 + 0

f. 9000 + 000 + 30 + 2 6. Smallest: a. 1023 b. 5068

c. 2458 d. 1047 e. 2347 f. 3068

Greatest: a. 3210 b. 8650 c. 8542 d. 7410 e. 7432

f. 8630

7. a.

H T O b.

8. Ascending order a. 565, 730, 2390, 8935

b. 773, 880, 1860, 7573 c. 792, 5853, 6943, 7081

d. 657, 5683, 7846, 8704 e. 2265, 4867, 8734, 8753

f. 5436, 7354, 7428, 8754 Descending order

a. 8935, 2390, 730, 565 b. 7573, 1860, 880, 773

c. 7081, 6943, 5853, 792 d. 8704, 7846, 5683, 657

e. 8753, 8734, 4867, 2265 f. 8754, 7428, 7354, 5436

9. a. 60 b. 100 c. 390 d. 420

10. 60 types 11. Answer may vary Sample answer: Anna saved ₹5500 and Divya saved ₹4510. Who saved more money?

Challenge 1. i. 8426 ii. eight thousand four hundred twenty-six iii. 8000 + 400 + 20 + 6

Real-Life Maths

1. c. Mount Everest

2. Kedarnath < Mount Kailash < Annapurna < K2 < Mount Everest

3. Kedarnath; 3000 + 500 + 80 + 3; three thousand five hundred eighty-three

4. Answers may vary.

Chapter 2

Let’s Warm-up 1. 7 2. 17 3. 10 4. 16

Do It Yourself 2A

1. a. > b. < c. = d. <

2. 7 + 5 = 5 + 7 + 0 + 12 = 12 + 0 = 7 + 1 = 8 + 0 + 71 = 71 = 72

3. a. 55 b. 69 c. 38 d. 79 e. 97 f. 68

4. a. 49 b. 65 c. 81 d. 89 e. 79 f. 88

5. 78 6. 78 species

Challenge 1. No, it is not solved correctly. Instead of adding 43 and 34, 43 is added twice. The correct answer is 77.

Do It Yourself 2B

1. a. 688 b. 997 c. 688 d. 798

2. a. True b. False c. False d. True 3. 3, 6, 8

4. a. 800 b. 631 c. 1110 d. 1130

5. a. 3333 b. 3395 c. 9359 d. 9277

6. a. 6379 b. 3385 7. ₹691 8. 317 9. 4977 oranges

Challenge 1. a. 539 and 614 b. 286 and 614 c. 239 and 286

Do It Yourself 2C

1. a. 50 b. 100 c. 70 d. 90

2. a. 70, Yes b. 80, Yes c. 30, Yes d. 70, Yes

3. 110 food items 4. 130 starfish

5. a. 80, 80, Same b. 100, 90, Different c. 70, 70, Same d. 20, 20, Same

Challenge 1. Between 75 and 84

Do It Yourself 2D

1. 351 toys 2. ₹8797 3. 63 seeds 4. 700 students 5. 1550 m

6. a. ₹5165 b. ₹1120 c. ₹6285

7. Answer may vary. Sample answer.

Uma has collected 726 red roses and 492 yellow roses. How many roses has Uma collected in all?

Challenge 1. 905

Chapter Checkup

1. a. 46 b. 14 c. 48 d. 5 e. 83 f. 0

2. a. 96 b. 89 c. 79 d. 69 e. 89 f. 77

3. a. 925 b. 578 c. 869 d. 7395 e. 9298 f. 8538

4. a. 90 b. 50 c. 80 5. a. 70 b. 70 c. 80

6. a. 374, 539 b. 546, 264, 810 c. 543, 617, 1160

7. a. 439 b. 601 c. 1101 d. 806 e. 1117 f. 1286

8. 2701 books 9. a. 3011 boys and girls b. 3595 men and women c. 6606 people

10. 102 tazos

11. Answers may vary. Sample answer: Akil has made 390 candles and Anu has made 528 more candles than Akil. How many candles have they made altogether?

2. The 1-digit numbers can be 5, 6, 7, 8 or 9.

Real-Life Maths

1. 100 2. 815 leopards

3. No. Chattisgarh has more leopards.

4. Answers may vary.

Chapter 3

Let’s Warm-up

1. 8 2. 6 3. 5 4. 3

Do It Yourself 3A

1. a. True b. True c. False d. True e. False f. False

2. a. 8 b. 9 c. 29 3. a. 24 b. 37 c. 47 4. 2 jumps

5. 6. 69

Do It Yourself 3B

1. a. 460 b. 201 c. 245 2. a. 332 b. 123 c. 333

3. a. 348 b. 187 c. 343 d. 465 e. 186 f. 233

4. 242 bottles 5. a. 301 tickets b. Joginder-68; Mohan-172; Prasad-19 6. 92 bones

Challenge 1. 594

Do It Yourself 3C

1. a. 3463 b. 5256 c. 6207 d. 1547

2. a. 1211 b. 4196 c. 6415 d. 8313

3. a. 3331 b. 3011 c. 8100 d. 8815

Ascending order = 3011, 3331, 8100, 8815

4. 1170 schools 5. ₹1127

Challenge 1. The new message will be AOOA = 6446

Do It Yourself 3D

1. a. 50 b. 30 2. a. 10 b. 40 c. 20 d. 20 e. 20 f. 80 3. 20 seashells 4. No, since 43 was rounded off to 50 instead of 40. 5. 10 chocolates

Challenge 1. Estimated sum = 120; Estimated difference = 80

Do It Yourself 3E

1. Shashi, 211 stickers 2. 289 runs 3. ₹108

4. 2322 bags 5. 4313 pairs of shoes 6. 200 stamps

7. Narendra 8. ₹2133 9. Answer may vary.

Challenge 1. Answers may vary. Sample answer: 93 and 32.

Chapter Checkup

1. a. 64 b. 59 c. 93 d. 0 e. 0 f. 74

2. a. 23 b. 15 c. 29 d. 25 e. 19 f. 29

3. a. 25 b. 29 c. 47 d. 9 e. 19 f. 41

4. a. 222 b. 255 c. 23 d. 192 e. 678 f. 1242

5. a. 90 b. 50 c. 20 6. 419 pages

7. 120 people 8. 124 kg

9. 3 years 10. 267 cardboard rolls

11. Answer may vary. Sample answer: There are 8567 books in a library. 1245 books were sent for binding. How many books were left in the library?

Challenge 1. Least Difference = 609 and 473

2. a. 1 b. 1

Highest difference = 962 and 473

7 6 0 8 d. 2 0 3 5 4

Real-Life Maths

1. c 2. a. True b. False 3. 1005 post offices

4. 2359 post offices 5. Answer will vary.

Chapter 4

Let’s Warm-up 1. 3; 12 2. 5; 20 3. 10; 30 4. 24 5. 48

Do It Yourself 4A

1. a. 5 b. 8 c. 4, 2 d. 13, 13, 13, 13, 13, 5

2. a. True b. False c. False 3. b. 9 × 8

4. a. 3 b. 0 c. 1 d. 5 e. 94 f. 123

5. Repeated addition = 15 + 15 = 30

Multiplication sentence = 2 × 15 = 30

6. The order of multiplication doesn’t matter as the product always remains the same.

Challenge 1. New number of dots = 20 – 4 = 16

Multiplication sentence = 4 × 4 = 16

Do It Yourself 4B

1. a. 63 b. 120 c. 60 d. 10 2. a. > b. < c. < d. =

3. a. 72 b. 100 c. 160 d. 240 e. 360 f. 7000

4. a. 64 b. 630 c. 80 d. 900 e. 100 f. 600

5. 54 candies 6. 500 runs 7. Answers may vary Sample

answer: The cost of a book is ₹45. What is the cost of 20 such books?

Challenge 1. Total runs scored by both = 46

Chapter Checkup

1. a. True b. True c. False d. True e. True

f. True 2. a. 6 × 4, 12 × 2, 1 × 24

b. 5 × 6 , 10 × 3, 30 × 1 3. a. 32, 40, 48, 56, 64

b. 52, 65, 78, 91, 104 c. 60, 70, 80, 90, 100 d. 45, 54, 63, 72, 81 e. 56, 70, 84, 98, 112 f. 800, 1000, 1200, 1400, 1600

5. a. b.

3 4 5 6

70 cookies

8. 24 puppies 9. ₹46

Challenge

1. 9 × 4 = 36 × 8 5 × 5 =

7. 30 petals

2. Total number of grapes = 4 × 8 = 32 Total number of blueberries = 5 × 8 = 40

Real-Life Maths

1. 6 × 2 = 12 2. Option b

3. Cost of 4 wooden rattles = ₹360

4. Total number of pieces = 6 × 2 = 12

5. Answers may vary.

Chapter 5

Let’s Warm-up 1. 3 × 9 2. 4 × 8 3. 6 × 3 4. 4 × 5

Do It Yourself 5A

1. a. 96 b. 80 c. 84 d. 248 e. 444 f. 669

2. a. 48 b. 246 c. 440 d. 555 e. 3514 f. 6444

3. 2 tens 4. 5. 999 m

Challenge 1. 300 20 1 2 × 300 × 2 = 600 2 × 20 = 40 2 × 1 = 2

2 × 321 = 600 + 40 + 2 = 642

Do It Yourself 5B

1. a. 633 b. 464 c. 244 2. a. 2890 b. 5551 c. 2288

3. a. 909 b. 888 c. 1152 d. 848 e. 468 f. 1295

4. 2247 5. 1150 cloth pieces 6. 1701 Earth hours

Challenge 1. 480 bricks

Do It Yourself 5C

1. a. 403 b. 1020 c. 440 2. a. 672 b. 1290 c. 1710

d. 648 e. 1248 f. 1014 g. 1755 h. 1972

3. 294 g 4. 115 trees

Challenge 1. 990

Do It Yourself 5D

1. a. 50 b. 40 c. 80 d. 90 e. 50 f. 80 g. 40 h. 30

2. a. 200 b. 180 c. 120 d. 160

3. a. 1540; 88 b. 240; 24 c. 100; 10 d. 690; 69

5. 1000 bangles

Challenge 1. 53

Do It Yourself 5E

1. 156 erasers 2. ₹1200 3. 448 trees

4. 312 students 5. 2430 balloons

6. a. ₹540 b. ₹1250 c. ₹2025

7. Answer may vary. Sample answer: There are 35 students in each section of grade 3. How many students are there in Grade 3, if there are 5 sections?

Challenge 1. 600 m

Chapter Checkup

1. a. T b. F c. F d. T

2. a. 48 b. 87 c. 168 d. 1435

3. a. 301 b. 504 c. 2667 d. 3020

4. a. 884 b. 486 c. 630 d. 462

5. a. 270 b. 1260 c. 4150 d. 2268

6. a. 60 b. 120 c. 90 d. 80

7. 1216 people 8. 540 apples 9. ₹135

10. 1404 pages 11. 3136 stickers

12. 975 children 13. ₹1800

14. 1700 people, 3400 people

15. Answer may vary. Sample answer: The cost of 1 pencil box is ₹315. What is the cost of 5 pencil boxes?

Challenge 1. Numbers are 12 and 5

2. 22 3 4 12 = 276 + × ×

Real-Life Maths

1. option d 2. 240 3. ₹1155 4. ₹1400

5. Answers may vary.

Chapter 6

Let’s Warm-up

1. True 2. True 3. False 4. True

Do It Yourself 6A

1. a. 2 cups b. 3 buttons c. 2 crayons

3. 18, 3, 6 4.

Challenge 1. 63 ÷ 7 ÷ 9 + 9 = 10

Do It Yourself 6B

1. a. 25 b. No answer c. 0 d. 1 e. 0 f. No answer

2. a. 10 b. 9 c. 8 d. 14 e. 9 f. 8

3. a. 28 ÷ 7 = 4 and 28 ÷ 4 = 7 b. 45 ÷ 5 = 9 and 45 ÷ 9 = 5

c. 18 ÷ 3 = 6 and 18 ÷ 6 = 3 d. 16 ÷ 8 = 2 and 16 ÷ 2 = 8

e. 30 ÷ 10 = 3 and 30 ÷ 3 = 10 f. 42 ÷ 6 = 7 and 42 ÷ 7 = 6

4. a. 2 b. 6 c. 6 d. 9 5. 18 children 6. 9 × 5 = 45

7. 9 pieces 8. Answer will vary. Sample answer: Rahul bought 55 roses to put in vases in a party hall. If he put 5 roses in each vase, how many vases did he use?

Multiplication fact: 11 × 5 = 55

Challenge 1.

Chapter Checkup

1. a. 5 things b. 3 dice c. 2 coins d. 7 balls

2. a. 8 b. 6 c. 5 d. 9 e. 8 f. 7 g. 6 h. 10

3. a. 12 × 3 = 36 b. 22 × 4 = 88 c. 12 × 8 = 96

d. 8 × 5 = 40 e. 5 × 5 = 25 f. 10 × 6 = 60 g. 8 × 6 = 48

h. 4 × 9 = 36 4. a. 45 ÷ 9 = 5 and 45 ÷ 5 = 9

b. 32 ÷ 4 = 8 and 32 ÷ 8 = 4 c. 15 ÷ 5 = 3 and 15 ÷ 3 = 5

d. 14 ÷ 7 = 2 and 14 ÷ 2 = 7 e. 24 ÷ 4 = 6 and 24 ÷ 6 = 4

f. 72 ÷ 9 = 8 and 72 ÷ 8 = 9 g. 20 ÷ 2 = 10 and 20 ÷ 10 = 2

h. 21 ÷ 3 = 7 and 21 ÷ 7 = 3 5. a. 3 b. 9 c. 9 d. 7

e. 7 f. 6 g. 9 h. 10 6. Answers may vary.

7. 1 toy car 8. 8 cupcakes 9. 6 groups

Challenge

2. Answers may vary. Sample answer. 24 6 ÷

Real-Life Maths

1. d. 9 2. 27 ÷ 3 =9 3. c. 12 4. True

5. Answers will vary.

Chapter 7

Let’s Warm up 1. 4 2. 15 3. 7 4. 36

Do It Yourself 7A

1. a. 17 b. 12 c. 100 d. 17

2. a. 18, 1 b. 11, 2 c. 58, 3 d. 82, 2

3. a. Quotient = 20; Remainder = 1 b. Quotient = 44; Remainder = 0 c. Quotient = 64; Remainder = 4

d. Quotient = 284; Remainder = 6 4. a. 38 b. 49 c. 59

d. 44 e. 41 5. 3 puppies 6. 2 seeds 7. 10 trays

8. 57 classrooms 9. a. ₹120 b. Brand C

Challenge 1. 70

Chapter Checkup

1. a. 15 b. 13 c. 12 d. 91 e. 189 f. 99 g. 1321 h. 1121 2. a. 3 b. 0 c. 3 d. 0 3. a. Q = 22; R = 3

b. Q = 20; R = 5 c. Q = 80; R = 5 d. Q = 307

4. a. 3 b. 24 c. 8 d. 1 e. 117 f. 4

5. 1049 booklets 6. 240 firefighters 7. 15 families

Challenge 1. 5 2. a. 16 cm b. 32 cm

Real-Life Maths

1. c. 7 tons 2. a. Twice as heavy 3. False 4. False

5. Answer may vary. Sample answer. Everyone needs to know exactly when to push or pull the levers together to move the block safely and avoid accidents.

Chapter 8

Let’s Warm-up

Challenge 1. These are called lines of symmetry. There are 4 lines of symmetry in the rangoli.

Do It Yourself 8C

1. a. Cube b. Cylinder c. Sphere d. Cone

2. a. Cuboid b. Sphere c. Cone d. Cube

e. Cylinder 3. Cube 4. box, book, eraser

Challenge 1. Yohaan makes a cuboid. Rectangle and square

Do It Yourself 8D

1. a. View B b. View B

2. Drawings may vary. a. , b. , c. ,

3. Drawings may vary

a. b.

2. 3. 4.

Do It Yourself 8A

1. a. Square b. Circle c. Rectangle 2.

3. Square = 2, Rectangle = 2, Triangle = 1, Circle = 6

4. a. False b. True c. True d. True

5. Answers may vary.

Challenge 1. 6

Do It Yourself 8B

1. b and d 2. a. b. c. d.

4. Drawings may vary , Rectangle

Challenge 1. Cuboid Left Front Top Base Right Base

Do It Yourself 8E

1. a.

c. d.

2. a. b.

3. a. b.

5. a. park b. hospital c. 5 steps to the right, 1 step up 6.

c. d.

e. 44, 48, 52 f. 55, 45, 35 4. d

5. a. THE CAR IS RED b. I LIKE DOSA

6. Figures may vary. Sample figure.

Challenge 1. Answers may vary.

Chapter Checkup

1. a. Square = 1, Rectangle = 7, Triangle = 2, Circle = 5

2. a. b. c. d.

3. a. cone b. cube c. cylinder d. cuboid

4. Side Side

5. 6. a. b. c.

7. a. 32, 36, 40 b. 80, 88, 96 c. 52, 57, 62 d. 41, 44, 47

8. a. b.

9. Side: Rectangle Top: Circle

10. a. Colouring may vary b. Answers may vary

Challenge 1. She can do it in 4 different ways. She will get only a cuboid.

2. 4 triangles can be made but 8 triangles can be seen.

Real-Life Maths

1. Hospital 2. Circle football ground. 3. b. hotel

4. Step on MG Road, turn to the right and walk straight. The house is on the left. 5. top

Chapter 9

Let’s Warm-up

1. False 2. True 3. True

Do It Yourself 9A

1. a. Kilometres b. Metres c. Centimetres d. Centimetres

2. a. 8 cm b. 11 cm c. 10 cm d. 15 cm

3. a. 600 cm b. 800 cm c. 909 cm d. 415 cm

e. 726 cm f. 252 cm 4. a. 7 m b. 6 m c. 4 m

d. 8 m e. 5 m f. 9 m 5. 36 m

6. The python is longer by 400 cm.

Challenge 1. 24 more boxes

Do It Yourself 9B

1. a. grams b. kilogram c. grams d. kilogram e. grams f. kilogram 2. a. 8000 g b. 9000 g c. 1500 g

d. 4200 g e. 3300 g f. 7750 g 3. 3600 g

4. 1 kg 5. 3 kg 6. 4 kg 900 g

Challenge 1. First weigh blocks A and B. Take the heavier one and then weigh it with C. Whichever is the heavier of the two, will be the heaviest.

Do It Yourself 9C

1. a, b, e 2. a. 2000 mL b. 6000 mL c. 9000 mL

d. 4500 mL e. 9200 mL f. 5850 mL

3. 3000 mL 4. 1 L 500 mL 5. 3 L 250 mL 6. 83 L

Challenge 1. He first uses the 2 L jar to get 2 L of milk and then pours 1 L in the 2 L jar such that it is half filled to make it 3 L of milk in total.

Chapter Checkup

1. a. ; d. ; e. 2. b, d, e, f 3. c. ; e

4. a. 12 cm b. 4 cm c. 7 cm d. 8 cm

5. a. 500 cm b. 200 cm c. 900 cm d. 850 cm

e. 1300 cm f. 1490 cm 6. a. 2 m b. 3 m c. 10 m

d. 11 m e. 12 m f. 13 m 7. a. 8000 g b. 9000 g

c. 7450 g d. 2999 g e. 3760 g f. 4640 g

8. a. 2000 mL b. 7000 mL c. 4000 mL d. 5800 mL

e. 6550 mL f. 8900 mL 9. 3250 g 10. 4 L 300 mL

Challenge 1. 3 cuts 2. 15 m

Real-Life Maths

1. a. 10 g 2. 450 mL 3. 930 g 4. Answers may vary.

Chapter 10

Let’s Warm-up 1. Half past 4 2. 5:00

Do It Yourself 10A

1. A. Hour hand B. Minute hand

2. a. 12:00 or 12 o’ clock b. 10:15 or Quarter past 10

c. 2:30 or Half past 2 d. 12:20 or 20 minutes past 12

3. a. a.m. b. a.m. c. p.m. d. p.m.

4. a. b. c. d.

5. Train starting time: 5:30 p.m., Train End time: 10:30 a.m.

Challenge 1. Sneha, 11:55 a.m.

Do It Yourself 10B

1. a. 60 b. 12

2. a. 1 hour b. 3 hours c. 15 minutes d. 2 hours 15 minutes

3. a. Minutes b. Minutes c. Minutes d. Hours

4. 120 minutes 5. 75 minutes

Challenge 1.

Do It Yourself 10C

1. a. Year b. Month c. Date of the Month d. Day of the week

2. a. False b. True c. False d. True

3. a. 4 b. Monday c. Thursday d. 9 e. 13, 20, 27

4. 14 days

Challenge 1. 11

Do It Yourself 10D

1. Navratri Starts Dusshera Diwali Bhai Dooj Guru Nanak Jayanti

3 October 12 October 1 November 3 November 27 November

2. Cricket match Basketball match Tug-of-war match Football match Kho-Kho match February August October November December

3. a. 2000 b. 7 years c. 15 years d. 34 years

4. Tinu; 6 years

Challenge 1. 20 years and 10 years

Chapter Checkup

1. a. 1:50 or 10 minutes to 2 b. 1:30 or half past 1

c. 10:45 or quarter to 11

2. a. b. c.

3. a. 2 hours b. 2 hours c. 2 hours

4. a. 7:30 a.m. b. 6:15 p.m. c. 11:55 p.m. d. 12:05 a.m.

5. a. Some minutes b. Some minutes c. Less than a minute

d. hours 6. a. 31 b. 1 May, 2023 c. 11 June, 2023

d. Monday, 8 June 2023

7. Born in Delhi Played for Delhi U-15 U-19 England Tour Won U-19 World Cup Won ODI World Cup

5 November 1988 October 2002 July 2006 March 2008 April 2011

8. Sun Mon Tues Wed

a. 5 Sundays b. 14 July c. 2, 9, 16, 23 and 30

9. Woke up at 7 a.m.; Slept at 9 p.m. 10. 2014 Challenge 1. Saturday, 22 April 2023 2. 3 times.

Real-Life Maths

1. 50 minutes 2. b. 3:50 p.m. 3. 4:40 p.m.

4. No 5. 60 minutes, Answers may vary.

Chapter 11

Let’s Warm-up

Do It Yourself 11A

1. a. Twenty-eight rupees fifty paise b. Thirty-six rupees twentyfive paise c. Forty-nine rupees seventy paise d. Fifty-seven rupees thirty-five paise e. Sixty-five rupees thirtyseven paise f. Seventy-one rupees seventy-five paise

g. Eighty-eight rupees sixty-two paise

h. Ninety-two rupees forty-eight paise

2. a. ₹56.70 b. ₹29.88 c. ₹35.57 d. ₹68.50 e. ₹73.22 f. ₹15.66 3. a. ₹32.50 b. ₹45.25 c. ₹160.50 d. ₹252.50

4. a. 2536 paise b. ₹8.02 c. ₹21.25 d. 12536 paise

e. ₹361.25 f. 35880 paise

5. One hundred three rupees forty-four paise.

6. Mahi should transfer 2 coins of ₹5.

Challenge 1. 1 of ₹500, 1 note of ₹100 and 1 note of ₹20; 2 coins of ₹2, 1 coin of ₹10 and 1 coin of ₹5

Do It Yourself 11B

1. ₹13.50 2. ₹125.50 3. ₹280.50

4. ₹363.50 5. ₹128.50

Challenge 1. ₹71.50

Do It Yourself 11C

1. ₹96.50 2. No, the bill is not correct.

New Era Store

Toy car 1 ₹85.00 ₹85.50 Storybook 2 ₹35.00 ₹70.00

Box of crayons 1 ₹30.00 ₹30.00

Notebook 4 ₹12.00 ₹48.00

Total ₹233.50

3. Sam paid ₹233.00

Super Market

Ice cream 2 ₹20.00 ₹40.00

Cookies 3 ₹15.00 ₹45.00

Chips 1 ₹24.50 ₹24.50 Juice 2 ₹26.00 ₹52.00 Total ₹161.50

4. Ravi buys: a. ₹10.00 b. ₹75.50 c. ₹10.00

Amount Paid = ₹95.50

Joe buys: a. ₹5.00 b. ₹75.50 c. ₹4.00

Amount Paid = ₹84.50

Tanya buys: a. ₹25.00 b. ₹75.50 c. ₹8.00

Amount Paid = ₹108.50

Challenge 1. Yes

Chapter Checkup

1. a. Fifty-two rupees thirty-six paise

b. Sixty-five rupees fourteen paise

c. Seventy-one rupees five paise

2. a. ₹38.65 b. ₹29.55 3. a. 2515 paise

b. 5225 paise c. 23548 paise 4. a. ₹32.56

b. ₹152.36 c. ₹523.64 5. a. 235 paise

b. 348 paise c. 2356 paise d. 3480 paise

6. All in one mart

Item Quantity Rate per item Amount

Pen 5 ₹12.00 ₹60.00

Marker 2 ₹55.00 ₹110.00

Ruler 1 ₹11.50 ₹11.50

Pencil box 3 ₹65.00 ₹195.00 Total ₹376.50 All in one mart

Item Quantity Rate per item Amount

Sugar 1 ₹39.50 ₹39.50

Marker 3 ₹45.00 ₹135.00

Oil 2 ₹72.00 ₹144.00

Curd 2 ₹35.00 ₹70.00 Total ₹388.50

7. Store

Item Quantity Rate per item Amount

Rice 3 packets ₹45.00 ₹135.00

Chips 2 packets ₹18.00 ₹36.00

Milk 1 packet ₹17.50 ₹17.50 Total ₹188.50

Divya has to pay ₹188.50.

8. ₹81 .50 9. ₹110.50 10. ₹210.5

Challenge 1. ₹70 2. Rahul has one rupee more than Ajay.

Real-Life Maths

1. d 2. 100 kauris 3. 500 paisa 4. Answers may vary.

Chapter 12

Let’s Warm-up 1. No

Do It Yourself 12A

1. a. 1 2 b. 1 3 c. 1 4

2. Sample answers:

a. b. c.

d. e. f.

3. a. One-fourth b. Three-fourths c. Half

4. Sample answers: a. b. c.

5. 2 4

Challenge 1. 1 8

Do It Yourself 12B

1. a. 8 pumpkins b. 7 bats c. 6 mangoes d. 4 apples

2. a. True b. False c. False d. True

3. a. 9 b. 3 c. 7 d. 3 4. 4 plants

5. Answer may vary. Challenge 1. No.

Do It Yourself 12C

1. a. 4 8 b. 5 9 c. 4 9 d. 7 16

2. Sample answers: a. b. c. 6 trees b. 5 tomatoes

3. a. 4 9, 5 9 b. 3 9, 6 9 c. 6 11, 5 11 d. 6 13 , 7 13

4. 8 17 5. 12 plastic bottles 6. 3 blue shirts

7. 9 25 8. 18 books

Challenge 1. 20 buses 2. 8 10

Chapter Checkup

1 2

2. a. 5 12 , 7 12 b. 9 17, 8 17

3. Sample answers: a. b. c. 9 kites d. 7 balls

4. a. 6 b. 5 c. 1 d. 4 5. 1 5 6. 3 flowers 7. 2 6 8. 18 apples 9. 15 18

Challenge 1. A 2. Answer may vary. Sample answer.

Real-Life Maths

1. c. 3 8 2. 3 8 3. a. True b. False 4. 5 8

5. Answer may vary.

Chapter 13

Let’s Warm-up 1. Tuesday 2. Friday 3. Monday and Wednesday 4. Thursday Do It Yourself 13A

1. a. False b. True c. False d. True 2. 99, 98, 89, 83, 80, 78, 77, 70, 65, 58, 45

3. Fruit Number of Students Apple 6 Banana 6

Grapes 6 Mango 6 Orange 4

4. a. 3 b. less c. rice

Challenge 1. a. 20 cutlets b. 20 cutlets

1. a. True b. True c. True 2. Favourite Swing

3. a. 8 books b. Friday, 11 books c. 1 book

4. Drawings may vary. Sample answer: Flavour Number of Ice Creams Vanilla Strawberry Chocolate Mango

5. a. 1 household b. 8 households c. Answers may vary.

6. Answers may vary.

5 b. 4

Scale: 1 Division = 1 State

3. a. Most = Nimisha; Least = Raghav and Eric b. 1 glass c. 1 glass 4. a. 4 children b. Cartoon, 9 children c. 1 child d. 26 children 5. Answer will vary

Challenge 1. a. Red Riding Hood and Town Mouse and Country Mouse b. 5 divisions Chapter Checkup 1.

Fruit Number of Students

Favourite Hobby Number of Students

Singing

Dancing

Sports

Watching TV

Reading

3. a. 20 children b. Action c. 4 children 4. a. 1 run b. 6th over c. 63 runs

Number of People in a Household Challenge 1. 8 2. a. 7 tomatoes b. 2

Real-Life Maths 1. c. February 2. June 3. April 4. Answer may vary.

About the Book

Imagine Mathematics seamlessly bridges the gap between abstract mathematics and real-world relevance, offering engaging narratives, examples and illustrations that inspire young minds to explore the beauty and power of mathematical thinking. Aligned with the NEP 2020, this book is tailored to make mathematics anxiety-free, encouraging learners to envision mathematical concepts rather than memorize them. The ultimate objective is to cultivate in learners a lifelong appreciation for this vital discipline.

Key Features

• Let’s Recall: Introductory page with a quick recall of concepts learnt in previous grades

• Real Life Connect: Introduction to a new concept related to real-life situations

• Examples: Solved problems showing the correct method and complete solution

• Do It Together: Guided practice for learners with clues and hints to help solve problems

• Think and Tell: Probing questions to stimulate Higher Order Thinking Skills (HOTS)

• Error Alert: A simple tip-off to help avoid misconceptions and common mistakes

• Remember: Key points for easy recollection

• Did You Know? Interesting facts related to the application of concept

• Math Lab: Fun cross-curricular activities

• Challenge: Critical thinking questions to enhance problem-solving and analytical thinking skills

• Real-Life Maths: Scenario-based questions to apply theory to real-life situations

• QR Codes: Digital integration through the app to promote self-learning and practice

About Uolo

Uolo partners with K-12 schools to provide technology-enabled learning programs. We believe that pedagogy and technology must come together to deliver scalable learning experiences that generate measurable outcomes. Uolo is trusted by over 15,000+ schools across India, Southeast Asia and the Middle East.

ISBN 978-81-979482-4-4

hello@uolo.com