Master
Mathematical Thinking
MATHEMATICS
MATHEMATICS
Master Mathematical Thinking
Grade
Acknowledgements
Academic Authors: Animesh Mittal, Muskan Panjwani, Anjana AR, Gitanjali Lal, Anuj Gupta, Simran Singh
Creative Directors: Bhavna Tripathi, Mangal Singh Rana, Satish
Book Production: Sanjay Kumar Goel, Vishesh Agarwal
Project Lead: Neena Aul
VP, Learning: Abhishek Bhatnagar
All products and brand names used in this book are trademarks, registered trademarks or trade names of their respective owners.
© Uolo EdTech Private Limited
First impression 2024
Second impression 2025
This book is sold subject to the condition that it shall not by way of trade or otherwise, be lent, resold, hired out, or otherwise circulated without the publisher’s prior written consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser and without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of both the copyright owner and the above-mentioned publisher of this book.
Book Title: Imagine Mathematics 7
ISBN: 978-81-979482-1-3
Published by Uolo EdTech Private Limited
Corporate Office Address:
85, Sector 44, Gurugram, Haryana 122003
CIN: U74999DL2017PTC322986
Illustrations and images: www.shutterstock.com, www.stock.adobe.com and www.freepik.com
All suggested use of the internet should be under adult supervision.
Preface
Mathematics is an essential tool for understanding the world around us. It is not just another subject, but an integral part of our lives. It shapes the very foundation of our understanding, personality and interaction with the world around us. Studies from across the globe have shown that proficiency in mathematics significantly influences career prospects and lifelong learning.
According to the NEP 2020, mathematics and mathematical thinking are crucial for empowering individuals in their everyday interactions and affairs. It focuses on competencies-based education, which essentially means actively and effectively applying mathematical concepts in real life. It also encourages innovative approaches for teaching maths, including regular use of puzzles, games and relatable real-world examples to make the subject engaging and enjoyable.
It is in this spirit that Uolo has introduced the Imagine Mathematics product for elementary grades (1 to 8). This product’s key objective is to eliminate the fear of mathematics by making math exciting, relatable and meaningful for children.
Imagine Mathematics positions itself on the curricular and pedagogical approach of the Gradual Release of Responsibility (GRR), which has been highly recommended by the NEP 2020, the NCF 2023 and other literature in learning educational pedagogies. Subsequent pages elaborate further on this approach and its actualisation in this book.
This book incorporates highly acclaimed, learner-friendly teaching strategies. Each chapter introduces concepts through real-life situations and storytelling, connecting to children’s experiences and transitioning smoothly from concrete to abstract. Clear explanations and simple steps are provided for problem-solving. Engaging facts, error alerts and fun activities are integrated throughout to keep learning interesting and holistic. Importantly, concepts are interconnected across topics and grades, providing a scaffolding that ensures comprehensive and meaningful learning.
This book supports learners at all levels, providing opportunities to build critical thinking skills through questions and activities aligned with Bloom’s Taxonomy. For those seeking a greater challenge, the book includes thought-provoking questions that push learners to apply, analyse and evaluate. Additionally, the problems are rooted in real-world contexts, making the learning experience both relatable and meaningful.
In addition, the book is technologically empowered and works in sync with a parallel digital world, which contains immersive gamified experiences, video solutions and practice worksheets, among other things. Interactive exercises on the digital platform make learning experiential and help in concrete visualisation of abstract mathematical concepts. We invite educators, parents and students to embrace Imagine and join us in nurturing the next generation of thinkers, innovators and problem-solvers. Embark on this exciting journey with us and let Imagine be a valuable resource in your educational adventure.
Product Package at a Glance
Welcome to our comprehensive learning package designed to enhance educational experiences through three key components: print materials, digital resources and assessment tools. Our print materials provide in-depth and accessible information in a pedagogically suitable way, our digital resources offer interactive and engaging learning experiences, while our assessment tools ensure thorough understanding and progress tracking.
Engaging Textbooks
Teacher Manuals
ASSESSMENT
Competency-based Model Assessments
Question Paper Generator
Student and Teacher Apps
Video Solutions
Interactive Tasks & Exercises
Byte Size Lesson Modules
Key NEP Recommendations
The National Education Policy (NEP) 2020, introduced by the Government of India, represents a transformative shift in the country’s education system. It aims to create a more holistic, dynamic and multidisciplinary approach to education. NEP 2020 focuses on fostering conceptual understanding, skills and values that align with the demands of the 21st century, while also preserving India’s rich cultural heritage. UOLO is fully committed to actualising the vision of NEP 2020 by meticulously adhering to its outlined recommendations.
1. Focus on conceptual understanding
2. 21st century skills, values and dispositions
3. Critical thinking and problem-solving
4. Application in real life
5. Holistic and integrated learning
6. Experiential learning
7. Enjoyable and engaging
8. Computational and mathematical thinking
9. Technology-based solutions
10. Factoids on India
Competency-based Education
NEP Pages 12, 17, and 22
Teaching and Learning Pedagogy
NEP Pages 3, 11, 12, 18, and 27
National Pride
NEP Pages 15, 16, and 43
11. Assessment of core concepts and application skills Assessments
NEP Pages 12, 18, and 22
Our Key Features: Aligning with the NEP
The GRR Approach
Pedagogical approach that empowers students to learn by the teacher progressively transitioning the responsibility to the students.
Competency-based Assessments
Test papers designed to evaluate understanding of core concepts and application of skills.
3 8 11
Contextual Learning
Introducing concepts through real-life situations and connecting them to students’ experiences.
Classroom Activity
A hands-on classroom activity to investigate and understand mathematical concepts in an engaging and concrete way.
Recall and Revisit
Introductory page with a quick recall of concepts done in previous grades.
Translating Words into Action!
Critical Thinking Questions
Intellectually stimulating questions designed to enhance problem-solving and analytical-thinking skills, promote deeper understanding and foster independent thinking.
Real-Life Math Problems
Scenario-based questions designed to help in applying theoretical knowledge to real-world scenarios, reasoning skills and improves reading comprehension & analytical abilities.
Common Misconceptions
Concise snippets of information designed to caution against potential errors and misconceptions
Think, Analyse and Answer
A quick, mathematical-thinking question
Fun Facts
Facts related to the concepts, or bite-sized information about the contribution of Indian scholars to mathematics
Gradual Release of Responsibility
The Gradual Release of Responsibility (GRR) is a highly effective pedagogical approach that empowers students to learn progressively by transitioning the responsibility from the teacher to the students. This method involves comprehensive scaffolding—including modelling, guided practice, and ultimately fostering independent application of concepts.
GRR, endorsed and promoted by both the NEP 2020 and NCF, plays a pivotal role in equipping teachers to facilitate age-appropriate learning outcomes and enabling learners to thrive.
The GRR methodology forms the foundation of the Imagine Mathematics product. Within each chapter, every unit follows a consistent framework:
1. I Do (entirely teacher-led)
2. We Do (guided practice for learners supported by the teacher)
3. You Do (independent practice for learners)
GRR Steps Unit Component
Understanding Large Numbers
Dhruv was reading a newspaper. He came across news about different states in India that participated in the COVID vaccination drive and the number of vaccinations given until August 2023. Given below is the data of four states.
Real Life Connect
Theoretical Explanation
I do
Delhi Haryana Sikkim Goa 37409161 45546836 1360477 2874477
The temperature can change with different weather conditions. On a sunny day, the air feels warm, and the thermometer shows a higher temperature. On a cloudy or rainy day, the air feels cooler, and the temperature on the thermometer drops. Weather conditions like rain, wind and sunlight can all affect the temperature of the air.
All About 7-Digit and 8-Digit Numbers
Temperature Range (°C) Weather
While reading the news, Dhruv got confused and could not read the numbers given in the data. The numbers of vaccinations given were either 7-digit numbers or 8-digit numbers.
The temperature can change with different weather conditions. On a sunny day, the air feels warm, and the thermometer shows a higher temperature. On a cloudy or rainy day, the air feels cooler, and the temperature on the thermometer drops. Weather conditions like rain, wind and sunlight can all affect the temperature of the air.
Temperature Range (°C)
Below 0 Very Cold 0–10 Cold 11–20 Mild 21–30 Warm 31–40 Hot
Examples
Did You Know?
Sikkim Goa Delhi Haryana 1360477 2874477 37409161 45546836
Did You Know?
Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.
Above 40 Very Hot
7-digit Numbers 8-digit Numbers
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?
Normal body temperature = 37°C.
Place Value, Face Value and Expanded Form Reading and Writing 7-Digit and 8-Digit Numbers
Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?
Aliya’s body temperature = 37°C + 2.3°C = 39.3°C
Let us help Dhruv understand 7-digit and 8-digit numbers!
Normal body temperature = 37°C.
So, Aliya’s body temperature was 39.3°C.
Aliya’s body temperature = 37°C + 2.3°C = 39.3°C
We know that the greatest 6-digit number is 999999. Now, if we add 1 to this number, we get 1000000. 999999 + 1 = 1000000
Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?
So, Aliya’s body temperature was 39.3°C.
To find the difference, subtract the lowest temperature from the highest temperature.
37.5°C – 21.2°C = 16.3°C
Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?
The temperature difference is 16.3°C.
1000000 is the smallest 7-digit number and is read as “Ten Lakhs”. We saw in the news article that the number of vaccinations administered in Sikkim was 1360477. Let us try to place this 7-digit number in the place value chart.
To find the difference, subtract the lowest temperature from the highest temperature.
Write the readings of the given thermometers.
37.5°C – 21.2°C = 16.3°C
The temperature difference is 16.3°C. Write the readings of the given thermometers.
2
Temperature = 45°C Temperature = Temperature = Temperature =
Converting Between Units of Temperature
Temperature = 45°C Temperature = Temperature = Temperature =
Celsius (°C) is like the universal language of temperature. Fahrenheit (°F) is another way to talk about temperature. We learnt that water freezes at 0°C and boils at 100°C. In Fahrenheit, water freezes at 32°F and boils at 212°F.
Converting Between Units of Temperature
Celsius (°C) is like the universal language of temperature. Fahrenheit (°F) is another way to talk about temperature. We learnt that water freezes at 0°C and boils at 100°C. In Fahrenheit, water freezes at 32°F and boils at 212°F.
GRR Steps Unit Component
Do It Yourself Challenge
You do
Chapter Checkup Challenge Case Study
Do It Yourself 14B
1 Identify the shape for which the net is drawn. a b c d
Do as directed.
a Write the greatest 7-digit number that has the smallest odd digit at its hundreds, ten thousands and lakhs place.
b Write the smallest 8-digit number that has the digit 7 at all its odd positions, starting from the ones place.
2 Look at the net and identify the object it belongs to.
Challenge Critical Thinking & Cross Curricular
3 Draw the net of the given shapes.
The Kumbh Mela is a major pilgrimage where Hindu pilgrims take the holy bath in the Ganges. The number of people who visited the Kumbh Mela in 1980 were 20,356,817 and those who visited in 1989 were 29,304,871. In which year did less than 25 crore people visit to the Kumbh Mela?
a 1980 b 1989 c Both years d None of the year
4 Rishi and Megha made the net of a square-based pyramid. Who made the net correctly? Explain your answer with reasons.
Comparing, Ordering and Rounding-Off Large Numbers
Chapter Checkup
a Rishi’s drawing b Megha’s drawing
During COVID, India offered support to 150 affected countries in the form of vaccines, medical equipment and medicines. Given below is the data of the number of vaccine doses supplied by India to four different countries.
Guess the best units of length (m or cm) and weight (kg or g) for the given objects. a b c
5 Draw the net of a hexagonal prism.
6 Show using nets how a rectangular prism is different from a rectangular pyramid.
Comparing and Ordering Numbers
Measure the objects.
Rahul: Which country did India supply the greatest number of vaccine doses to?
Challenge
Challenge
Bran: We could compare the numbers to find the country to which India supplied the greatest number of vaccine doses.
Comparing Numbers
Critical Thinking
Critical Thinking
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
a The digit in the hundreds and ones place is 6.
a The digit in the hundreds and ones place is 6.
What if Rahul wanted to compare the number of vaccines sent to Nepal and Australia? Let us find out.
b The digit in the lakhs place is 4 less than the digit in the ones place.
b The digit in the lakhs place is 4 less than the digit in the ones place.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
Since 94,99,000 has 7 digits and 3,09,13,200 has 8 digits, 3,09,13,200 > 94,99,000.
d The face value of the digit in the thousands place is 5.
d The face value of the digit in the thousands place is 5.
Thus, Australia was donated more vaccine doses.
Remember!
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
Now, what if we want to compare two numbers with the same number of digits? Let us consider 4,13,23,456 and 4,13,23,657.
A number with more number of digits is always greater.
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
James has some cotton candy which is 3 cm longer than the cotton candy shown below. How long is James’ cotton candy?
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
Chapter 1 • Numbers up to 8 Digits
Case Study
Case Study
200
How much longer is the red straw than the blue straw?
Cross Curricular
Cross Curricular
Population of Countries
Population of Countries
The population of different countries is shown using a table. Read the data carefully and answer the questions.
Convert the lengths.
The population of different countries is shown using a table. Read the data carefully and answer the questions.
Country Population
Country Population
83,294,633
Germany
Germany
Convert the weights.
83,294,633
a 8 m into km b 4 hm 35 m into hm c 1232 m into mm d 897 m into dam
France 64,756,584
France
64,756,584
United Kingdom
United
Poland
Poland
67,736,802
67,736,802
a 5 kg into g b 4 g 64 cg into g c 5487 g into mg d 43 kg 7 dag into kg
41,026,067
41,026,067
A baby koala is called a joey. A young joey weighs about 0.38 kg. How much is that in g?
Italy
A candle weighs 125 g. How much is it in mg?
Italy 58,870,762
58,870,762
1 Which country has the least population?
1 Which country has the least population?
a Italy b Germany c Poland d United Kingdom
a Italy b Germany c Poland d United Kingdom
2 Which country has the greatest population?
2 Which country has the greatest population?
a Poland b United Kingdom c Italy d Germany
a Poland b United Kingdom c Italy d Germany
Pearson, P. D., & Gallagher, G. (1983). Contemporary Educational Psychology. Fisher, D., & Frey, N. (2021). Better learning through structured teaching: A framework for the gradual release of responsibility. Fisher, D., & Frey, N. (2014). Checking for understanding: Formative assessment techniques for your classroom.
3 Which country has approximately double the population than that of Poland?
3 Which country has approximately double the population than that of Poland?
4 Arrange the countries in ascending order as per their population.
4 Arrange the countries in ascending order as per their population.
5 If all the digits in the population of each country is rearranged to form the greatest number, then which country will have the greatest population?
5 If all the digits in the population of each country is rearranged to form the greatest number, then which country will have the greatest population?
The NEP Tags
The National Education Policy (NEP), 2020, outlines essential skills, values, dispositions and learning approaches necessary for students to thrive in the 21st century. This textbook identifies and incorporates these elements throughout its content, activities and exercises. Referred to as “NEP Tags,” they are defined as follows:
Art Integration
Bringing creativity and fun into learning by combining art with maths. Students construct and demonstrate understanding through an art form.
Collaboration
Working effectively with others. Includes clear communication, teamwork, active listening and valuing diverse approaches.
Cross Curricular
Integrating mathematical concepts with other subjects to see the real-life applications of maths.
Experiential Learning
Gaining knowledge and skills through direct, hands-on experiences rather than a traditional classroom setting.
Communication
Explaining mathematical ideas, processes and solutions to others, whether through verbal explanations, written work or visual representations.
Value Development
Promoting ethics, and human & constitutional values, like empathy, respect for others, cleanliness, courtesy, democratic spirit, spirit of service, respect for public property, responsibility and equality.
Creativity
Using imagination and original thinking to solve problems and explore mathematical concepts in innovative ways. Also includes finding unique solutions, and designing original problem-solving strategies.
Education Standards as per the NCF 2023
The National Curriculum Framework for School Education (NCF), released in 2023, is based on the vision of the National Education Policy (NEP), 2020, and enables its implementation. The NCF provides guidelines for designing school syllabi and textbooks in India. It aims to improve the quality of education by making it more relevant, engaging, inclusive and learner-centric. To achieve this, the NCF has articulated precise Learning Standards through well-defined Curricular Goals and Competencies. These statements serve to harmonise the syllabus, content, pedagogical practices and assessment culture, ensuring a cohesive and comprehensive educational experience.
Curricular Goals: Statements that give direction to curriculum development and implementation in order to achieve the Curricular Aims. They are also specific to a School Stage (e.g., the Foundational Stage) and a Curricular Area (e.g., Mathematics).
Competencies: Learning achievements that are observable and can be assessed systematically. These Competencies are derived from the Curricular Goals and are expected to be attained by the end of a Stage.
NCF Page 218
Curricular Goals
CG-1
Understands numbers and sets of numbers (whole numbers, fractions, integers, rational numbers, and real numbers), looks for patterns, and appreciates relationships between numbers
CG-2
Understands the concepts of variable, constant, coefficient, expression, and (one-variable) equation, and uses these concepts to solve meaningful daily-life problems with procedural fluency
Competencies
C-1.1 Develops a sense for and an ability to manipulate (e.g., read, write, form, compare, estimate, and apply operations) and name (in words) large whole numbers of up to 20 digits, and expresses them in scientific notation using exponents and powers
C-1.2 Discovers, identifies, and explores patterns in numbers and describes rules for their formation (e.g., multiples of 7, powers of 3, prime numbers), and explains relations between different patterns.
C-1.3 Learns about the inclusion of zero and negative quantities as numbers, and the arithmetic operations on them, as given by Brahmagupta
C-1.4 Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line
C-1.5 Explores the idea of percentage and applies it to solve problems
C-1.6 Explores and applies fractions (both as ratios and in decimal form) in daily-life situations
C-2.1 Understands equality between numerical expressions and learns to check arithmetical equations
C-2.2 Extends the representation of a number in the form of a variable or an algebraic expression using a variable
C-2.3 Forms algebraic expressions using variables, coefficients, and constants and manipulates them through basic operations
C-2.4 Poses and solves linear equations to find the value of an unknown, including to solve puzzles and word problems
C-2.5 Develops own methods to solve puzzles and problems using algebraic thinking
The above is an abridged version of the curricular goals and competencies relatioship in Maths for the Foundational Stage (NCF 2023, pages 340–341). The next section shows the coverage of all these competencies across the chapters.
Mapping with NCF 2023
C-1.1 Develops a sense for and an ability to manipulate (e.g., read, write, form, compare, estimate, and apply operations) and name (in words) large whole numbers of up to 20 digits, and expresses them in scientific notation using exponents and powers
C-1.2 Discovers, identifies, and explores patterns in numbers and describes rules for their formation (e.g., multiples of 7, powers of 3, prime numbers), and explains relations between different patterns.
C-1.3 Learns about the inclusion of zero and negative quantities as numbers, and the arithmetic operations on them, as given by Brahmagupta
C-1.4 Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line
C-1.5 Explores the idea of percentage and applies it to solve problems
C-1.6 Explores and applies fractions (both as ratios and in decimal form) in daily-life situations
C-2.1 Understands equality between numerical expressions and learns to check arithmetical equations
C-2.2 Extends the representation of a number in the form of a variable or an algebraic expression using a variable
C-2.3 Forms algebraic expressions using variables, coefficients, and constants and manipulates them through basic operations
C-2.4 Poses and solves linear equations to find the value of an unknown, including to solve puzzles and word problems
C-2.5 Develops own methods to solve puzzles and problems using algebraic thinking
C-3.1 Describes, classifies, and understands relationships among different types of twoand three-dimensional shapes using their defining properties/attributes
C-3.2 Outlines the properties of lines, angles, triangles, quadrilaterals, and polygons and applies them to solve related problems
C-3.3 Identifies attributes of three-dimensional shapes (cubes, parallelepipeds, cylinders, cones), works hands-on with material to construct these shapes, and also uses twodimensional representations of three-dimensional objects to visualise and solve problems
C-3.4 Draws and constructs geometric shapes, such as lines, parallel lines, perpendicular lines, angles, and simple triangles, with specified properties using a compass and straightedge
C-3.5 Understands congruence and similarity as it applies to geometric shapes and identifies similar and congruent triangles
CG-1
Understands numbers and sets of numbers (whole numbers, fractions, integers, rational numbers, and real numbers), looks for patterns, and appreciates relationships between numbers
CG-2
Understands the concepts of variable, constant, coefficient, expression, and (one-variable) equation, and uses these concepts to solve meaningful daily-life problems with procedural fluency
CG-3
Understands, formulates, and applies properties and theorems regarding simple geometric shapes (2D and 3D)
C-4.1 Discovers, understands, and uses formulae to determine the area of a square, triangle, parallelogram, and trapezium and develops strategies to find the areas of composite 2D shapes
C-4.2 Learns the Baudhayana-Pythagoras theorem on the lengths of the sides of a right-angled triangle, and discovers a geometric proof using areas of squares erected on the sides of the triangle, and other related geometric constructions from the Sulba-Sutras
C-4.3 Constructs various designs (using tiling) on a plane surface using different 2D shapes and appreciates their appearances in art in India and around the world
C-4.4 Develops familiarity with the notion of fractal and identifies and appreciates the appearances of fractals in nature and art in India and around the world
C-5.1 Collects, organises, and interprets the data using measures of central tendencies such as average/mean, mode, and median
C-5.2 Selects, creates, and uses appropriate graphical representations (e.g., pictographs, bar graphs, histograms, line graphs, and pie charts) of data to make interpretations
C-6.1 Applies both inductive and deductive logic to formulate definitions and conjectures, evaluate and produce convincing arguments/proofs to turn these definitions and conjectures into theorems or correct statements, particularly in the areas of algebra, elementary number theory, and geometry
C-7.1 Demonstrates creativity in discovering one’s own solutions to puzzles and other problems, and appreciates the work of others in finding their own, possibly different, solutions
C-7.2 Engages in and appreciates the artistry and aesthetics of puzzle-making and puzzle-solving
C-8.1 Approaches problems using programmatic thinking techniques such as iteration, symbolic representation, and logical operations and reformulates problems into series of ordered steps (i.e., algorithmic thinking)
C-8.2 Learns systematic counting and listing, systematic reasoning about counts and iterative patterns, and multiple data representations; learns to devise and follow algorithms, with an eye towards understanding correctness, effectiveness, and efficiency of algorithms
C-9.1 Recognises how concepts (like counting numbers, whole numbers, negative numbers, rational numbers, zero, concepts of algebra, geometry) evolved over a period of time in different civilisations.
C-9.2 Knows and appreciates the contributions of specific Indian mathematicians (such as Baudhayana, Pingala, Aryabhata, Brahmagupta, Virahanka, Bhaskara, and Ramanujan)
CG-4
Develops understanding of perimeter and area for 2D shapes and uses them to solve day-to-day life problems
CG-5
Collects, organises, represents (graphically and in tables), and interprets data/information from daily-life experiences
CG-6
Develops mathematical thinking and the ability to communicate mathematical ideas logically and precisely
CG-7
Engages with puzzles and mathematical problems and develops own creative methods and strategies to solve them
CG-8 Develops basic skills and capacities of computational thinking, namely, decomposition, pattern recognition, data representation, generalisation, abstraction, and algorithms in order to solve problems where such techniques of computational thinking are effective
CG-9 Knows and appreciates the development of mathematical ideas over a period of time and the contributions of past and modern mathematicians from India and across the world
CG-10 Knows about and appreciates the interaction of Mathematics with each of their other school subjects Recognises interaction of Mathematics with multiple subjects across Science, Social Science, Visual Arts, Music, Vocational Education, and Sports
1
Numbers up to 8 Digits
Let’s Recall
Numbers are used everywhere in our daily lives. These numbers are formed using the digits 0 to 9 and are written using commas after every period, starting from the one’s period.
Chapter at a Glance: Walkthrough of Key Elements
For example, let us say the pin code of your area is 201301. This is a 6-digit number. It can be written using commas by representing it in a place value chart.
1 Numbers up to 8 Digits
Number Lakhs Thousands Ones Lakhs (L) Ten Thousand (TTh) Thousands (Th) Hundreds (H) Tens (T) Ones (O) 2,01,301 2 0 1 3 0 1
Each of these digits has a place value and a face value. Let us write the face value, place value, expanded form and number name for 201301. periods place
Let’s Recall
Numbers are used everywhere in our daily lives. These numbers are formed using the digits 0 to 9 and are written using commas after every period, starting from the one’s period.
Let’s Recall: Introductory page with a quick recall of concepts learnt in the previous grade
For example, let us say the pin code of your area is 201301. This is a 6-digit number. It can be written using commas by representing it in a place value chart.
Expanded form:
Number name: Two lakh
Dhruv was reading a newspaper. He came across news about different states in participated in the COVID vaccination drive and the number of vaccinations given August 2023. Given below is the data of four states.
Each of these digits has a place value and a face value. Let us write the face value, place value, expanded form and number name for 201301.
Letʹs Warm-up Fill in the blanks.
1 The place value of 8 in 8,60,765 is 2 The number 4,36,536 can be written in words as:
Let’s Warm-up: Quick 4–5 questions to test the pre-knowledge
3 The place value of the digit in 4,15,124 and 4,67,890 is the same. 4 8,76,504 has 6 in the place.
Expanded form: 2,00,000 + 1000 + 300 + 1 Number
All About 7-Digit and 8-Digit Numbers
I scored out of 4.
The temperature can change with different weather conditions. On a sunny day, the air feels warm, and the thermometer shows a higher temperature. On a cloudy or rainy day, the air feels cooler, and the temperature on the thermometer drops. Weather conditions like rain, wind and sunlight can all affect the temperature of the air.
While reading the news, Dhruv got confused and could not read the numbers given data. The numbers of vaccinations given were either 7-digit numbers or 8-digit
Temperature Range (°C) Weather
3 The place value of the
Explanation: Clear and elaborate explanation of a concept
Temperature Range (°C) Weather
Below 0 Very Cold
0–10 Cold
Dhruv was reading a newspaper. He came across news participated in the COVID vaccination drive and the August 2023. Given below is the data of four states.
The temperature can change with different weather conditions. On a sunny day, the air feels warm, and the thermometer shows a higher temperature. On a cloudy or rainy day, the air feels cooler, and the temperature on the thermometer drops. Weather conditions like rain, wind and sunlight can all affect the temperature of the air.
11–20 Mild
21–30 Warm
31–40 Hot
Place Value, Face Value and Expanded Form
Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.
Reading and Writing 7-Digit and 8-Digit Numbers
Did You Know?
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?
Normal body temperature = 37°C.
Above 40 Very Hot
Let us help Dhruv understand 7-digit and 8-digit numbers! We know that the greatest 6-digit number is 999999. Now, if we add 1 to this number, we get 1000000.
Aliya’s body temperature = 37°C + 2.3°C = 39.3°C
Normal body temperature = 37°C.
Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.
999999 + 1 = 1000000
So, Aliya’s body temperature was 39.3°C.
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?
Aliya’s body temperature = 37°C + 2.3°C = 39.3°C
So, Aliya’s body temperature was 39.3°C.
All About 7-Digit and 8-Digit Numbers
Examples: Solved problems showing the correct method and complete solution
While reading the news, Dhruv got confused and could data. The numbers of vaccinations given were either
Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?
To find the difference, subtract the lowest temperature from the highest temperature. 37.5°C – 21.2°C = 16.3°C
Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?
The temperature difference is 16.3°C. Write the readings of the given thermometers.
37.5°C – 21.2°C = 16.3°C
The temperature difference is 16.3°C.
1000000 is the smallest 7-digit number and is read as “Ten Lakhs”. We saw in the news article that the number of vaccinations administered in Sikkim 1360477. Let us try to place this 7-digit number in the place value chart.
To find the difference, subtract the lowest temperature from the highest temperature.
Do It Together: Guided practice for learners with partially solved questions
Write the readings of the given thermometers.
Converting Between Units of Temperature
Place Value, Face Value and Expanded Form
2 4
Reading and Writing 7-Digit and 8-Digit Numbers
Let us help Dhruv understand 7-digit and 8-digit numbers!
We know that the greatest 6-digit number is 999999.
Converting Between Units of Temperature
Now, if we add 1 to this number, we get 1000000.
Celsius (°C) is like the universal language of temperature. Fahrenheit (°F) is another way to talk about temperature. We learnt that water freezes at 0°C and boils at 100°C. In Fahrenheit, water freezes at 32°F and boils at 212°F.
Celsius (°C) is like the universal language of temperature. Fahrenheit (°F) is another way to talk about temperature. We learnt that water freezes at 0°C and boils at 100°C. In Fahrenheit, water freezes at 32°F and boils at 212°F. Did You Know?
15 • Time and Temperature
1000000 is the smallest 7-digit number and is read
We saw in the news article that the number of vaccinations 1360477. Let us try to place this 7-digit number in
What
Let us see how you would write it in metres.
1 m = 100 cm
1
Did You Know: Interesting facts related to the topic
Example 3: Convert 2356 dm to m.
Fill in the blanks to convert 5 m 230 mm to m. mm = 1 m
1 mm = 1 m 5 m 230 mm = 5 m + 230 × 1 m = 5 m + m = m
Word Problems on Length
After making a pair of trousers with 2 m of cloth, Sana thought of buying 1 m 55 cm of cloth for making a shirt. Let us see what length of cloth she has together.
Cloth bought by Sana for making a pair of trousers = 2 m
Cloth required by Sana for making a shirt = 1 m 55 cm = 1.55 m
Total cloth required by Sana = 2 m + 1.55 m
So, the total cloth required by Sana is 3.55 m.
Do It Yourself: Exercise at the end of each topic with practice questions
NEP Tags: To show alignment with NEP skills and values
It Yourself 14B
Error Alert: Caution against misconceptions
1 Identify the shape for which the net is drawn.
2 Look at the net and identify the object it belongs to.
3 Draw the net of the given shapes.
4 Rishi and Megha made the net of a square-based pyramid. Who made the net correctly? Explain answer with reasons.
a Rishi’s drawing b Megha’s drawing
Chapter Checkup: Chapter-end practice exercises aligned to different levels of Blooms Taxonomy
5 Draw the net of a hexagonal prism.
6 Show using nets how a rectangular prism is different from a rectangular pyramid.
Picture-based Questions: Questions featuring visual stimuli to foster comprehension and interpretation
Challenge
Challenge: Critical thinking questions to enhance problem-solving and analytical-thinking skills
Case Study: Scenario-based questions designed to help apply theoretical knowledge to real-world situations
Critical Thinking
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
a The digit in the hundreds and ones place is 6.
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
Real-life Questions: Questions that help make connections with real life or other subjects 8
b The digit in the lakhs place is 4 less than the digit in the ones place.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
a The digit in the hundreds and ones place is 6.
d The face value of the digit in the thousands place is 5.
b The digit in the lakhs place is 4 less than the digit in the ones place.
e The digit in the tens place is the biggest 1-digit number.
What is the secret code?
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
code.
d The face value of the digit in the thousands place is 5.
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
a The digit in the hundreds and ones place is 6.
b The digit in the lakhs place is 4 less than the digit in the ones place.
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
Case Study
Case Study
Thinking Case Study
d The face value of the digit in the thousands place is 5.
e The digit in the tens place is the biggest 1-digit number.
What is the secret code?
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
Population of Countries
The population of different countries is shown using a table. Read the data carefully and answer the questions.
Population of Countries
Country Population
The population of different countries is shown using a table. Read the data carefully and answer the questions. Country Population
Population of Countries
The population of different countries is shown using a table. Read the data carefully and answer the questions.
1 Which country has the least population?
a Italy b Germany c Poland d United Kingdom
2 Which country has the greatest population?
1 Which country has the least population? a Italy b Germany c Poland d United Kingdom
a Poland b United Kingdom c Italy d Germany
2 Which country has the greatest population? a Poland b United Kingdom c Italy d Germany
3 Which country has approximately double the population than that of Poland?
58,870,762 1 Which country has the least population?
4 Arrange the countries in ascending order as per their population.
3 Which country has approximately double the population than that of Poland?
5 If all the digits in the population of each country is rearranged to form the greatest
Cross Curricular
Cross Curricular
1 Integers
Let’s Recall
Integers are a set of numbers that include whole numbers and their negative counterparts, without any fractional parts. This makes them different from rational numbers.
For example, temperatures above 0° are considered positive temperatures, and temperature below 0° are considered negative temperatures.
We can compare integers using the rules as given below:
Rule 1
Positive integer > Negative integer
Example: 25 > – 45
Rule 2
Positive integer with greater numerical value > Positive integer with smaller numerical value
Example: 45 > 26
Rule 3
Negative integer with smaller numerical value > Negative integer with greater numerical value
Example: –25 > –52
We can also arrange integers in ascending or descending order, using the above comparison rules as:
Smaller to greater
For example,
Ascending order: –5 < –2 < 1 < 5 < 9
Descending order: 9 > 5 > 1 > –2 > –5
Let’s Warm-up
Fill in the blanks with the > or < sign.
Greater to smaller
Addition and Subtraction of Integers
Sara was watching a news report with her parents. The reporter showed the weather forecast, displaying the temperature of different cities across the country, as shown below:
City Temperature
Jaipur 28℃
Bengaluru 18℃
Shimla –2℃
Sonmarg –6℃
Srinagar –10℃
Sara: Dad, what does this minus sign before the temperature of Shimla, Sonmarg and Srinagar mean?
Dad: This means that the temperatures in these cities are below 0℃ and it is very cold there.
Sara wonders how cold is something when it is even below 0℃.
Addition of Integers
We have studied the addition of integers with like and unlike signs in our previous class. Let us recall it.
Rule 1: For the addition of integers with like signs:
Step 1
Add the absolute values of the integers.
Step 2
Place the common sign before the sum.
Remember!
The absolute value (shown by symbol ||) of an integer is the numerical value of the integer regardless of the sign. E.g., The absolute value of 5 is 5 and –4 is 4.
For example: The sum of the temperatures in Bengaluru and Jaipur can be given as: |18℃|+|28℃| = 46℃
Similarly, the sum of the temperatures in Shimla and Sonmarg can be given as: |–2℃|+|–6℃| = 2℃ + 6℃ = 8℃
As both the integers have the (–) sign, (–2℃) + (–6℃) = (–8℃)
Rule 2: For the addition of integers with unlike signs:
Step 1
Subtract the smaller absolute value from the greater absolute value.
Step 2
Place the sign of the integer with the greater absolute value before the difference.
The sum of the temperatures in Bengaluru and Srinagar can be given as: 18℃ + (–10℃) or, |18℃| – |–10℃| = 18℃ – 10℃ = 8℃ (as the integer with the greater absolute value has a positive sign)
Remember!
Temperature above 0℃ is denoted by the (+) sign.
Temperature below 0℃ is denoted by the (–) sign.
Do It Together
Example 1: Add the given integers.
1 −35 and −42
As the integers have like signs; add the integers and place the common sign before them.
(−35) + (−42) = −77
Example 2: Simplify [35 + (−12)] + [−47 + 39].
= [35 −12] + [−8]
= 23 – 8
= 15
2 −27 and 15
As the integers have unlike signs; find the difference and place the sign of the integer with the greater value.
(−27) + 15 = −12
Example 3: Rohan opened a bank account by depositing ` 1500 in his account in June 2021. He deposited ` 750 in July 2021 and withdrew ` 1100 in August 2021. Find his balance.
Amount deposited in June = `1500; Amount deposited in July = `750
Total amount deposited in June and July = `1500 + `750 = `2250
Amount withdrawn = `1100 = –1100 (as an amount withdrawn is denoted by a negative sign)
Balance = 2250 + (–1100) = 2250 – 1100 = ₹1150
The balance is ₹1150.
The temperature of water in a bowl is 85℃. It dropped by 33℃ after 20 minutes. The temperature dropped by a further 13℃ in the next 10 minutes. What is the temperature of the water after 30 minutes?
Temperature of water in the bowl = 85℃
Temperature drop in 20 minutes =
Temperature drop in the next 10 minutes = –13℃
Total temperature drop = (–33) + (–13) =
Temperature after 30 minutes = 85℃ + =
Properties of Addition of Integers
Closure Property
If a and b are two integers, then a + b = c
where c will always be an integer.
For example,
1 5 + 4 = 9 2 −9 + 5 = − 4
Here, the results 9 and −4 are also integers.
Commutative Property
For any two integers a and b, a + b = b + a
For example,
1 (−7) + (2) = (2) + (−7) = (−5)
Here, the sum (−5) remains the same regardless of the order in which the integers are added.
Did You Know?
Indian mathematicians, Aryabhata and Brahmagupta, made significant contributions to the understanding and calculation of integers.
Associative Property
For any three integers a, b and c, (a + b) + c = a + (b + c)
For example,
1 (2 + 5) + (−3) = 2 + (5 + (−3)) = 4
Here, the sum (4) remains the same regardless of the order in which the 3 integers are added.
Existence of Additive Identity
For any integer a,
For example,
1 7 + 0 = 0 + 7 = 7
a + 0 = 0 + a = a
2 −9 + 0 = 0 + −9 = −9
Example 4: Verify if m + n is an integer, if m = 17 and n = −12.
m + n = 17 + (−12) = 5
Here 5 is also an integer, hence verified.
Existence of Additive Inverse
For any integer a, another integer –a exists so that: a + (–a) = 0
For example,
1 5 + (−5) = 0
2 (−6) + 6 = 0
Example 5: What is the additive inverse of 25 and −30?
Additive inverse of 25 = −25.
Additive inverse of −30 = 30.
Fill in the blanks using the properties of integers. Also, name the property used.
1 32 + (−17) = + 32; Property used =
2 −36 + = −36; Property used = Existence of additive identity
3 (12 + 3) + (−5) = + (3 + ( )); Property used =
4 18 + = 0; Property used =
Subtraction of Integers
We have recalled the addition of integers. Let us now recall the subtraction of two integers.
If a and b are two integers, then a – b = a + (–b), i.e., to subtract an integer b from another integer a, add the additive inverse of b to a and keep the sign of the integer with the greater absolute value.
Let us subtract (–12) from (–15).
Here, a = (–15); b = (–12) (–15) – (–12) = (–15) + (additive inverse of (–12)) = (–15) + (12) = (–3)
Example 6: Subtract the given integers.
1 −46 from −67 = −67 – (−46) = −67 + (additive inverse of −46) = −67 + 46 = −21
Example 7: Simplify: [321 – (−125)] – [−145 + (−241)].
321 – (−125) = 321 + 125 = 446
−145 + (−241) = −145 – 241 = −386 446 – (−386) = 446 + 386 = 832
2 123 from −156 = −156 – (123) = −156 + (additive inverse of 123) = −156 + (−123) = −279
Example 8: The record high temperature of Canada is 38℃ and the record low is –63℃. What is the difference in the high and low temperatures?
Record high = 38℃
Record low = –63℃
Difference in temperature = 38 – (–63) = 38 + (63) = 101℃.
The difference in the high and low temperatures is 101℃.
Example 9: The sum of two integers is −36. If one integer is 39, find the other. Let the other integer be x.
Given that x + 39 = −36 ⇒ x = −36 – 39 = −75
Hence, the other integer is −75.
Example 10: The difference of an integer p and (−10) is −3. Find the value of p.
p – (−10) = −3 ⇒ p + 10 = −3
⇒ p = −3 – 10 = −13
Hence, p = −13.
Example 11: The points scored by Raman and Rashi in five rounds of a video game are given. Who won the game and by how many points?
Points scored by Raman in 5 rounds = 8 + (−3) + (−5) + 10 + (−6) = 4
Points scored by Rashi in 5 rounds = 6 + 4 + (−2) + (−7) + 8 = 9
Rashi won the overall game by 9 – 4 = 5 points.
Mt Everest, the highest peak in Asia, is 29,029 feet above sea level. The Assal Lake in Africa is 510 feet below sea level. What is the difference in the depth/height of these two places?
Height of Mt Everest above sea level = 29,029 feet
Depth of Assal Lake below sea level = Difference in depth = 29,029 – =
Properties of Subtraction of Integers
Closure Property
If a and b are two integers, then a − b = c where c will always be an integer.
For example, 1 15 − 4 = 11 2 −15 − 5 = − 20
Here, the results 11 and −20 are also integers.
Commutative Property
For any two integers a and b, a − b ≠ b − a
For example, 1 (−17) − (5) = −23 but, (5) − (−17) = (23)
Here, the difference changes as the position of the integer changes.
Associative Property
For any three integers a, b and c, (a − b) − c ≠ a − (b − c)
For example,
1 (12 − 5) − (9) = 7 – 9 = −2, but 12 − (5 −9) = 12 – (−4) = 12 + 4 = 16
When we subtract 3 or more integers, the order in which the subtractions are performed changes the result.
In general,
Subtraction Property of Zero
where a is an integer.
For example,
1 25 – 0 = 25
2 −36 – 0 = −36
a – 0 = a
When we subtract zero from any integer, the result is the same as the integer.
Example 12: Verify if m – n ≠ n − m, if m = 29 and n = −15.
m − n = 29 − (−15) = 44
n − m = −15 − (29) = −44
As 44 ≠ −44; m – n ≠ n − m is verified.
4 (25 – 12) – 15 ≠ 25 – (12 − ); Property used = Do It Together
Fill in the blanks using the properties of integers. Name the property used.
1 45 − (−27) = ; where is also an integer; Property used = Closure property
2 −100 − = −100; Property used =
3 36 − = 36; Property used =
Do It Yourself 1A
a 5 and –9 b 15 and 14 c –28 and 59 d (–23) and 12 e 32 and –122 f –136 and –25 g –152 and 365 h 158 and –125
Find the additive inverse of the given integers. a 48 b –72 c 98 d –124
Subtract.
a 8 from –9 b –12 from 17 c 25 from –32 d 38 from –20
e –36 from –98 f 54 from 223 g 136 from –182 h –214 from 156
Determine the missing integers in the given equations.
a 12 + = 18 b – (–17) = 10 c 956 – = 422 d 215 – 136 =
e –548 + = –267 f – 192 = 564
Fill in the blanks.
a The sum of –5 and 8 is .
b Subtracting 15 from –20 gives
c The absolute value of –10 is
d If you have `2000 in your bank account and you spend `3000, your account balance becomes ` .
e If I have a gain of `310 and a loss of `125, my net result is .
f Adding the additive inverse of –8 to –8 gives
Subtract 2369 from the sum of –3652 and 5864.
State True or False.
a The commutative property of addition holds true for integers.
b The associative property of subtraction holds true for integers.
c The commutative property of subtraction holds true for integers.
d The associative property of addition holds true for integers.
Fill in the blanks using the properties. Also, name the property used.
a (21) + (13) = + (21); Property used =
b + 0 = –3; Property used =
c (–35 + 13) + = –35 + ( + (–16)); Property used =
d (–23) – = –23; Property used =
Verify the following if p = 32, q = 29 and r = −17.
a p – (−q) = p + q
The sum of two integers is 142. If one integer is −89, find the other.
Simplify.
a [128 + (−78)] + [−145 − (−92)] b [−214 − (124)] + [−136 + (45)]
c [262 − (−132)] − [165 − (−87)] d [−324 + (121)] − [−145 − (213)]
The altitude of Mount Mitchell in North Carolina, USA, is 2037 metres. A hiker climbs to an altitude of 1200 m and then descends to an altitude of 500 m. How much lower is the hiker than the altitude of Mount Mitchell?
A basketball team scores 80 points in the first quarter, loses 25 points in the second quarter, and then scores 15 points in the third quarter. In the final quarter, they scored 10 more points than they lost in the second quarter. What is the team’s total score?
The hottest temperature recorded in India is 51℃ which was recorded in 2016 in the state of Rajasthan while the coldest temperature was recorded in 1995 in Ladakh which was −45℃. What is the difference in the hottest and coldest temperature so recorded?
Create
Challenge
Tina and Asha were asked to solve their puzzles. They need to shade the integers in a way where the sum of the integers comes up to be –3. Tina has shaded her puzzle. Help Asha shade the integers in her puzzle by shading a total 5 integers.
Multiplication and Division of Integers
Rahul and Megha are watching a submarine show on TV. They listen to an announcement that the submarine has descended 14 km in 20 minutes.
Rahul: Wow! The speed of the submarine is really fast. I wish I could travel in such a submarine some day.
Megha: That’s true, Rahul! Although I’m not really fond of underwater adventures, I’m wondering how deep this submarine will travel in the 40 minutes.
Multiplication of Integers
Multiplying Integers
Multiplying integers with unlike signs:
The submarine descends 14 kilometres in 20 minutes. As the sea level is 0, the distance above the sea is in a positive direction. Similarly, the distance below the surface can be taken as negative.
We can say that the submarine travels –14 kilometres in 20 minutes. Therefore, it travels –28 kilometres in 40 minutes as shown.
Starting from 0, we always move to the negative side (in this case, we will move in the downward direction) when multiplying integers of unlike signs.
So, (2) × (–14) = –28
Multiplying integers with like signs:
Case 1: When both the integers are positive:
Let us take an example of a door. The pushing of the door represents the positive sign, and pulling represents the negative sign.
Now, imagine that there are two people standing on the same side of the door. When both people push the door from the same side, the door moves in the pushed direction. This signifies that the product of two positive integers is always positive!
So, (4) × ( 5) = +20
Case 2: When both the integers are negative:
Let us think of the same example again. This time, let us assume that they pull the door from the same side. The door moves in the pulled direction.
This signifies that the product of two negative integers is always positive!
So, (–4) × ( –5) = +20
The above discussion leads us to the following two rules of multiplication of integers.
Rule 1: The product of two integers with unlike signs is always negative. Rule 2: The product of two integers with like signs is always positive.
Multiplication of more than two negative integers:
Let us now multiply three integers, –5, –12 and –7, and see the result.
Here, we first multiply the initial two numbers, i.e., –5 and –12.
(–5) × (–12) = 60 (Negative × Negative = Positive)
Now, multiply the result with the third number, i.e., 60 × (–7).
60 × (–7) = –420 (Positive × Negative = Negative)
The final result has a negative sign when we multiply 3 negative integers.
Let us now multiply the above result (– 420) with another negative integer (–2).
(–420) × (–2) = 840
Here, the final result is positive when we multiply 4 negative integers.
The above discussion leads us to the conclusion that:
If the number of negative integers multiplied is even, then the product is positive.
If the number of negative integers multiplied is odd, then the product is negative
Example 13: Multiply the given integers.
1 −12 and 15
As the signs are unlike, the result will be negative. Hence, (−12) × 15 = −180.
Think and Tell
What will be the sign of the final product when 99 negative integers are multiplied?
2 −25 and −22
As the signs are like, the result will be positive. Hence, −25 × −22 = 550
Example 14: What will you get on multiplying –5, –6, –2 and –4?
We will first multiply the initial two numbers, i.e., –5 and –6.
(–5) × (–6) = 30 (Negative × Negative = Positive)
Multiply the result with the third number, i.e., 30 × –2.
30 × (–2) = –60 (Positive × Negative = Negative)
Now, multiply the result with the fourth number i.e. (–60) × (–4).
(–60) × (–4) = 240 (Negative × Negative = Positive)
Error Alert!
Do not forget to place the correct sign (+ or –) before the resultant product.
Example 15: What will be the sign of the final product if 10 negative and 9 positive integers are multiplied?
We know that if the number of negative integers multiplied is even, the final product is even. As 10 is an even number, the sign of the final product of 10 negative and 9 positive integers will be positive.
Example 16: Simplify: [125 × (−32)] + [−36 × (−120)].
[125 × (−32)] + [−36 × (−120)]
= [−4000] + [4320] = 320
Example 17: Aakash sells apples at a loss of ₹25 per kg, and mangoes at a profit of ₹37 per kg. If he sells 28 kg of apples and 39 kg of mangoes in a day, what is his net profit or loss?
Loss per kg on apples = ₹25; Weight of apples sold = 28 kg;
Total loss = ₹25 × 28 = ₹700 = −₹700
Profit per kg on mangoes = ₹37; Weight of mangoes sold = 39 kg;
Total profit = ₹37 × 39 = ₹1443
As the Total profit > Total loss, there will be a net profit.
Net profit of the day = ₹1443 + (−₹700)
= ₹1443 − ₹700 = ₹743.
A store loses ₹125 a day for six days. How much money has been lost in total over these six days?
Money lost by the store every day = Money lost in 6 days = (–125) × =
So, the store loses ₹ in 6 days.
Properties of Multiplication of Integers
Closure Property
If a and b are two integers, then a × b = c
where c will always be an integer.
For example,
1 13 × (–3) = –39
2 (–25) × (–9) = +225
Here –39 and +225 are both integers.
Commutative Property
For any two integers a and b, a × b = b × a.
Here, the order of the 2 integers does not change the product.
For example,
1 (15) × (–3) = (–3) × (15) = –45
Associative Property
For any three integers a, b, and c, (a × b) × c = a × (b × c)
Here, the way the 3 integers are grouped does not change the final product.
For example,
1 (–2 × 3) × (–4) = –2 × (3 × (–4)) = 24
Distributive property of multiplication of integers over addition Existence of multiplicative identity
For any three integers a, b and c, a × (b + c) = (a × b) + (a × c)
Here, on multiplying an integer with the sum of 2 integers gives the same result as multiplying the first integer with each addend and then adding the products.
For example,
1 –4 × (3 + 2) = –4 × 5 = –20 and (–4 × 3) + (–4 × 2) = (–12) + (–8) = –20
For any integer a, a × 1 = a
Here any integer multiplied by 1 will result in the same integer.
For example,
1 –4 × 1 = –4
2 17 × 1 = 17
Existence of multiplicative inverse Multiplication property of zero Multiplication of an integer by –1
For any integer a, a × 1 a = 1 a × a = 1 or (–a) × – 1 a = – 1 a × (–a) = 1
Here, the product of any non-zero integer and its reciprocal is 1.
For example,
1 Multiplicative inverse of (–12) is – 1 12
For any integer a, a × 0 = 0
For any integer a, a × (–1) = –a
For example,
1 –10 × 0 = 0
2 5 × 0 = 0
Example 18: What is the multiplicative inverse of −14 ?
Multiplicative inverse of –14 = 1 –14
Example 19: What should be multiplied with 10 to get its additive inverse?
–1 should be multiplied with 10 to get its additive inverse.
10 × –1 = (–10) = additive inverse of 10
For example,
1 12 × (–1) = –12
2 –25 × (–1) = 25
Think and Tell
Why does the concept of the multiplicative inverse not apply to zero?
Do It Together
Example 20: Verify if (m × n) × o = m × (n × o), if m = 12, n = −8 and o = 5.
(m × n) × o = (12 × −8) × 5 = −96 × 5 = −480
m × (n × o) = 12 × (−8 × 5) = 12 × −40 = −480
As, the products of both statements are equal, (m × n) × o = m × (n × o) is verified.
Fill in the blanks using the correct property of multiplication of integers. Also name the property used.
1 (–25) × (–8) = ( ) × ( )
Property used:
2 52 × = 52
Property used:
3 23 × (13 + ) = (23 × ) + ( × 14)
Property used: Distributive property of multiplication of integers over addition
4 (17 × 5) × = × (5 × (–9))
Property used: Associative property
a 12 × 15
d –14 × (–6)
b –11 × 6
e 25 × 0
What will be the sign of the product if we multiply the integers?
a 5 negative integers and 5 positive integers
b 12 negative integers and 20 positive integers
c 25 negative integers and 35 positive integers
Write the multiplicative inverse of the given integers.
a 21 b −32
Solve.
a –11 × 5 × (–2)
d 25 × (–12) × 3
b 56 × (–12) × 0
c –21 × 13
f 56 × (–1)
c −54
c 12 × (–1) × (–8)
e –23 × 15 × (–2) × 5 f –6 × (–12) × (–3) × (–10)
Fill in the blanks using the correct property of multiplication.
a 36 × 0 =
c (–12) × (56) = × (–12)
b (–123) × = –123
d 56 × (–12 + 23) = × (–12) + 56 ×
e × (–1) = 2198 f (123 × 143) × (–36) = × (143 × (–36))
Verify the following, if m = 8; n = −3 and o = −5
a m × n = n × m b (m × n) × o = m × (n × o)
Simplify.
A submarine descends 55 feet per minute from sea level. Where will the submarine be in relation to the sea level 8 minutes after it starts descending? Write your answer as an integer.
A shooter gets 10 points every time he hits the target and loses 6 points for missing the target. What is his overall score if he hits the target 20 times and misses 25 times?
Ocean trenches are the deepest places on the ocean floor. The lowest point of the Hawaiin Trench is 5500 m deep. The lowest point of the Puerto Rico Trench, in the Atlantic Ocean is around 1.5 times lower than the Hawaiin Trench. Write the approximate depth of the Puerto Rico Trench as an integer.
Create a word problem to multiply 2 integers 24 and −12.
Challenge
A test has 25 questions. The test awards 5 points if the answer is correct, and takes away 2 points if the answer is incorrect. A student answered 7 questions incorrectly. How many points did the student score if he answered all the questions? 1
Division of Integers
Do you remember the submarine which travelled 14 km in 20 minutes? What if we need to find the distance travelled by the submarine in 10 minutes? This can be done with the help of division.
Dividing Integers
Division of two integers with unlike signs
We already know that division facts come from multiplication facts. So, if the submarine travels –14 kilometres in 20 minutes, we need to find how far it would have travelled in half the time.
The above calculation can be represented as (–14) 2 = –7. This implies that the submarine travelled 7 km below sea level in 10 minutes.
Division of two integers with like signs
Dividing a positive integer by another positive integer results in a positive quotient. For example, 250 5 = +50
Dividing a negative integer by another negative integer again results in a positive quotient.
For example, –250 –5 = +50
Rules for division of integers can be given as:
Rule 1: The quotient of two integers with unlike signs is always negative
Rule 2: The quotient of two integers with like signs is always positive
Example 21: Divide (–625) by 25.
–625 25 = –25 (as Negative ÷ Positive = Negative)
Example 22: Simplify: 125 −25 ÷ 5 + 35 × 10.
The above expression can be solved using the DMAS rule.
125 − 25 ÷ 5 + 35 × 10
= 125 – 5 + 350 = 470
Example 23: The product of two integers is −336. If one integer if 28. What is the value of the other integer?
Let the other integer be x.
Given that x × 28 = −336
⇒ x = −336 ÷ 28 = −12
Hence, the other integer is −12.
Example 24: Ravi participated in an online test where each incorrect answer deducts 3 points. If Ravi’s total negative score is –450, how many questions did he answer incorrectly?
Score of each incorrect answer: (–3)
Total negative score: (–450)
Number of questions answered incorrectly: (–450) ÷ (–3) = 150
Hence, 150 questions were answered incorrectly.
In a basketball match, Team A and Team B played four quarters. If Team A’s total score for the match was –48 points, what was their average score per quarter?
Number of quarters played = 4
Team A’s total score for the match =
Average score per quarter = (–48) ÷ 4 =
Properties of Division of Integers
Closure Property
If a and b are two integers, then a ÷ b = c
where c may or may not be an integer.
For example, 1 –25 ÷ 5 = –5 = integer
2 –(–18) ÷ (5) = 3.6 = non-integer
Commutative Property
For any two integers a and b, a ÷ b ≠ b ÷ a
This means that while dividing two integers, a change in the order of the integers can change the answer.
For example,
1 (22) ÷ 11 = 2 but, 11 ÷ (22) = 0.5
Division of an integer by itself
While dividing a non-zero integer by itself, the result is always 1.
For any non-zero integer a, a ÷ a = 1
Division of an integer by –1
When dividing an integer by –1, the result is the additive inverse of the integer.
For any integer a, a ÷ (–1) = (–a)
Example 25: Check whether the quotient of 482 ÷ 3 is an integer.
482 ÷ 3 = 160.66 which is not an integer.
Associative Property
For any three integers a, b, and c, (a ÷ b) ÷ c ≠ a ÷ (b ÷ c)
This means that when dividing three or more integers, the order in which the divisions are performed changes the final result.
For example, 1 (625 ÷ 25) ÷ 5 = 25 ÷ 5 = 5 but, 625 ÷ (25 ÷ 5) = 625 ÷ 5 = 125
Division of an integer by 1
When dividing an integer by 1, the result is always the integer itself.
For any integer a, a ÷ 1 = a
Division of zero by an integer
When dividing zero by an integer, the result is always zero.
For any integer a, 0 ÷ (a) = 0
Think and Tell
Can you think of special cases where the commutative property may hold true for division?
Example 26: Prove that the integers 256 and 16 are not commutative under division.
256 ÷ 16 = 16 but 16 ÷ 256 = 1 16
As 16 ≠ 1 16, integers are not commutative under division.
Fill in the blanks.
Remember!
Dividing any non-zero integer by zero is undefined in mathematics and does not yield a valid result.
Do It Yourself 1C
Find the quotient.
a 72 ÷ (–4) b (–56) ÷ 7 c –176 ÷ (–11) d 192 ÷ (–12)
e 344 ÷ 43 f (–984) ÷ 12 g (–676) ÷ (–26) h –585 ÷ (–13)
Solve.
a (–88 ÷ 4) ÷ (–1) b 125 ÷ (125 ÷ 5) c (192 ÷ (–16)) ÷ 4 d 324 ÷ (–18 ÷ 2)
e (900 ÷ (18)) ÷ 6 f (–3060 ÷ (–36)) ÷ 5 g 0 ÷ (–1508 ÷ 29) h (1000 ÷ (20)) ÷ 100
Find the number which when divided by (–1) gives 145.
Write True or False.
a (–250) ÷ 1 = –250 b 0 ÷ (–378) = –378 c (–39) ÷ (–39) = 1 d (–90) ÷ 3 = 30
The product of two numbers is 800. If one of the integers is −25, what is the value of the other integer?
Verify the following for the values of m = 12, n = 3 and o = 2.
a m ÷ n ≠ n ÷ m b (m ÷ n) ÷ o ≠ m ÷ (n ÷ o)
Give two pairs of integers such that a ÷ b = –15.
A 25 storey building has its car parks on 3 levels in the basement with each floor height as 5 metres. The lift in the building descends at the rate of 2 m/sec. If Era starts from the 20th floor, how long will it take her to reach the second basement?
A parachute is a cloth canopy which fills with air and allows a person or heavy object attached to it to descend slowly when dropped from an aircraft. A parachute descends at the rate of 20 m/min. At a certain moment, it was at a height of 1800 m above ground level. How long will it take to reach the height of 300 m above ground level?
In the first level of a video game, 2 points are deducted for each time a character falls. In the second level, each fall deducts 4 points. Rahul lost 10 points in the first level and 16 points in the second level. In which level did Rahulʹs character fall more often?
The temperatures recorded in Leh in the last week of March 2023 were −6℃, −4℃, −5℃, −6℃, −3℃, −2℃, −2℃.
What is the average temperature of Leh for the week?
Hint: Average = Total temperature across 7 days No. of days
Critical Thinking
The temperature recorded at 12 noon was 18℃ above zero. If it falls at the rate of 3℃ per hour until midnight, at what time will the temperature be 6℃ below zero? What will be the temperature at midnight?
Points to Remember
• Integers are positive numbers, negative numbers and zero.
• To add integers with like signs, add the absolute values and place the common sign.
• To add integers with unlike signs, find the difference of the absolute values and use the sign of the integer with the greater absolute value.
• To subtract an integer b from another integer a, add the additive inverse of b to a.
• The product of two integers with like signs is positive.
• The product of two integers with unlike signs is negative.
• The quotient of two integers with like signs is positive.
• The quotient of two integers with unlike signs is negative.
Math Lab
Setting: In groups of 5
Collaboration & Experiential Learning
Integer Operations Relay
Materials Required: Index cards with different integer expressions written on them, stopwatch or timer Method:
– 52 = ?
Place the index cards face down on a table. Start the stopwatch or timer and begin the relay.
� (–4) = ?
The first team member will pick up an index card, read the expression aloud, solve it and return it to their team to tap the next person, who will then run to pick up the next index card.
The relay continues until all the index cards have been used or until a designated time limit is reached.
The team with the highest number of correct solutions wins the game!
Chapter Checkup
Add or subtract the given integers.
Solve and write the additive and multiplicative inverse.
Find the product.
a 25 × (–89)
d (245) × (–57)
Divide.
a 363 by (–11)
d (–5472) by 36
b (–125) × (–26)
e (1245) × (–142)
b (−384) by 12
e 2852 by 23
Fill in the blanks using the appropriate property of integers.
a (–156) + 389 = 389 +
b 524 + = 523
c (–36) × 48
f (–2365) × (123)
c 450 by (–25)
f (–9594) by (–41)
c 1885 × = (–1885)
d × (–17) = ( ) × 23 e –45 × (33 + 2) = (–45 × ) + ( × 2) f 64 ÷ (–1) = ______
Simplify.
a 42 ÷ (–6 + 5)
b –64 ÷ 4 × (2 – 6)
c (9 ÷ 3) + 7 × (4 ÷ 2)
d 4(–12 + 6) ÷ 3 e 7 × (5 + 3) ÷ 4 × (9 – 2) f (6 + 2) – 15 ÷ (5 × 2)
Add the sum of (135) and (–325) to the difference of 253 and (–528).
What should be multiplied with (–165) to get a product of 9240?
Add the product of 25 and (–36) to the quotient of 2380 divided by (–68).
What should be divided from 23,072 to get (–412)?
Anish and Ravi took part in a quiz. Anish scored 55, –80 and 65 points in 3 successive rounds. Ravi’s score is double of Anish’s score. What were their scores?
The balance in Suhani’s bank account is −₹2000 due to some penalty charges. Her mother told her that she should always maintain a balance of ₹10,000 as savings so that she can use it in case of any emergency. How much money should she deposit in her account to maintain her savings?
What value do you learn from Suhani’s mother?
An aeroplane is flying at 12,000 feet. The plane climbs 15,000 feet to approach the cruising altitude. After a few minutes at this new altitude, the plane hits turbulence and descends 23,945 feet. Express each increase and decrease in altitude as an integer operation and determine the new altitude of the plane.
Mercury conducts heat well, allowing it to respond quickly to temperature changes. A mercury thermometer records a temperature of 6°F at 11 a.m. If the temperature drops by 3°F every hour, what will be the temperature by 4 p.m. of the same day?
1 Kajal gets into the elevator on the fourth floor of a shopping mall. She goes up 10 floors to reach the food court. After an hour, she goes down 5 floors to buy books. On which floor is she now?
2 Read the statements and choose the correct option.
Assertion (A): The value of 12 × –16 × –20 –24 × 8 is −20.
Reason (R): As there are 2 negative numbers in the numerator and 1 in the denominator, the answer will be negative.
a Both A and R are correct, and R is the correct explanation for A. b Both A and R are correct, and R is not the correct explanation for A. c A is true, but R is false. d A is false, but R is true.
Case Study
Cross Curricular
Temperature Transition of Elements
The melting point is the temperature at which a solid turns into a liquid or gas, while the boiling point is the temperature at which a liquid changes into vapour. Given below is a list of temperatures of different elements in degrees Celsius (℃). Read the data table and answer the questions.
1 When magnesium is heated from its melting point to its boiling point, by how many degrees celsius would the temperature increase? a 1740℃ b 440℃ c 1640℃ d 540℃
2 Which element has the highest boiling point? How much higher is it compared to the boiling point of chlorine?
3 Calculate the temperature range (difference of the melting and boiling points) for each element. Which element has the narrowest range?
4 Imagine a situation where the temperature is increased from −250℃ to 0℃. Which of the elements would have changed their state from liquid to gas?
What is the melting point of nitrogen in ℉?
5 The formula for converting the unit of temperature from ℃ to ℉ is ℉ = 9 5 × ℃ + 32.
2 Fractions and Decimals
Let’s Recall
A fraction represents a part of a whole. It has two parts: a numerator and a denominator.
Let us say Raghav has a chocolate bar, and he divides it into 5 equal parts. So, here, a chocolate bar is considered a whole and each part is considered a part of a whole.
If Raghav eats 2 parts, 3 out of 5 parts are left.
So, the chocolate left can be represented as 3 5 .
Here, 3 is the numerator and 5 is the denominator.
Types of Fractions
Proper Fraction
Numerator < Denominator
For example, 1 2 , 3 4 , 5 9
Improper Fraction
Numerator ≥ Denominator
For example, 2 2 , 7 4 , 15 9
How can we write the fraction of chocolate left with Raghav as a decimal?
Mixed Fraction
Whole number + Proper fraction
For example, 23 4 , 51 2 , 6 5 11
Multiply the denominator and numerator with a number such that we get 10, 100 or 1000 in the denominator. Here we can multiply the numerator and denominator with 20.
3
5 = (3 × 20) (5 × 20) = 60 100 = 0.6
Hence, 0.6 of the chocolate is left with Raghav.
Types of Decimals
Like Decimals:
Same number of digits after the decimal point.
For example: 2.35, 3.54, 1.45
Let’s Warm-up
Fill in the blanks.
Unlike Decimals:
Different number of digits after the decimal point. For example: 2.35, 2.3, 2.351
1 The numerator is always than the denominator for proper fractions. (smaller/greater)
2 A mixed fraction has a part and a fractional part. (integer/whole number)
3 is the denominator in 5 8 .
4 Unlike decimals have number of digits after the decimal point. (same/different)
5 The fraction 25 50 can be written as in its decimal form.
I scored out of 5.
Real Life Connect
Mean, Median and Mode Operations on Fractions
Riya is a computer science engineer. She got a job at a big company. After completing a month with the company, Riya is happy to get her first salary. She spends 2 5 of her salary on the house rent, 1 4 on food and saves the remaining salary.
Addition and Subtraction of Fractions
Riya wanted to check what fraction of her salary she spent. How could she do that?
Let us find out!
Adding and Subtracting Fractions
To find the fraction of salary spent, we will add the individual parts of the salary spent.
Addition of Fractions
Fraction of salary spent by Riya on house rent = 2 5
Fraction of salary spent by Riya on food = 1 4
Fraction of total salary spent by Riya = 2 5 + 1 4
Take the LCM of 5 and 4.
LCM of 5 and 4 is 20.
2 5 = 2 5 ×
Thus, Riya spends 13 20 of her salary.
Addition of mixed numbers
Remember!
Sum of like fractions = Sum of numerators Common denominator
Did You Know?
Musicians use fractions to understand and create rhythms.
Let us now see how to add mixed fractions. For example: Add 4 1 5 + 2 1 3
Add the whole number parts → 4 + 2 = 6
Add the fractional parts → 1 5 + 1 3
Add the final whole and fractional parts, 6 + 8 15 = 6
Thus, 4 1 5 + 2 1 3 = 6 8 15
Subtraction of Fractions
We know that Riya spent 13 20 of her salary. What fraction of Riya’s salary is left with her?
Remember!
Difference of like fractions = Difference of numerators Common denominator
Fraction of salary left = Total salary – Fraction of salary spent = 1 − 13 20 = 20 20 − 13 20 = 7 20
Subtraction of Mixed Numbers
Let us now see how to subtract mixed fractions. For example, Subtract: 9 4 5 – 3 1 6 We can do so by converting the mixed fractions to improper fractions.
9 4
5 = 49 5 3 1 6 = 19 6
Find the LCM of 5 and 6.
LCM of 5 and 6 = 30
49 5 = 294 30 19 6 = 95 30
9 4
5 – 3 1 6 = 294 30 − 95 30 = 199 30 = 6 19 30
Thus, 9 4 5 – 3 1 6 = 6 19 30
Example 1: Add.
1 8 9 + 5 6
8 9 = 8 × 2 9 × 2 = 16 18 5 6 = 5 × 3 6 × 3 = 15 18 16 18 + 15 18 = 31 18 31 18 = (1 × 18) + 13 18 = 18 18 + 13 18 = 113 18
Thus, 8 9 + 5 6 = 1 13 18
Example 2: Subtract.
1 3 8 from 3 4
3 4 –3 8
LCM of 4 and 8 = 8 3 4 –3 8 = 6 – 3 8 = 3 8
Thus, 3 4 –3 8 = 3 8
= 10 18 + 9 18 = 19 18 = 3 + 19 18 = 3 + 1 1 18 = 4 1 18
Thus, 2 5 9 + 1 1 2 = 4 1 18
LCM of 5 and 7 = 35 182 – 85 35 = 97 35 = 2 27 35
Thus, 5 1 5 – 2 3 7 = 2 27 35
Example 3: Parth jogged 3 1 3 km and Priya jogged 7 8 km. Who jogged the longer distance? How much more was it?
Parth jogged more since 3 1 3 is greater than 7 8
To find how much more Parth jogged, subtract 7 8 km from 3 1 3 km. = 3 1 3 − 7 8 = 10 3 − 7 8
LCM of 3 and 8 = 24;
Thus, Parth jogged 2 11 24 km more than Priya. 2 2 3 7 from 5 1 5 51 5 – 23 7 = 26 5 –17 7
Multi-step Problems on Adding and Subtracting Fractions
Do you remember when Riya got her first salary? When she gets her next salary, she spends 1 3 of her salary on the house rent, 1 12 of her salary on transportation and 1 4 of her salary on food.
Let us see what fraction of salary is left with her.
Thus, the next month Riya saves 1 3 of her salary.
Example 4: Simplify.
32 5 +1 7 10 – 3 8 15 + 24 5 17 5 + 17 10 –53 15 + 14 5
(Converting the mixed fraction to an improper fraction)
102 + 51 – 106 + 84 30 (LCM of 5, 10 and 15 = 30) 131 30 = 411 30
Example 5: Mary is baking a cake and needs 3 4 cups of flour. She accidentally adds 2 5 cups extra, but then realises her mistake and removes 1 8 cup. How much flour does she have now?
The initial amount of flour Mary needed = 3 4 cups
Extra flour added = 2 5 cups
Total flour = 3 4 + 2 5 = 15 + 8 20 = 23 20 cups
Flour removed = 1 8 cups
Flour left = 23 20 − 1 8 = 46 − 5 40 = 41 40 = 1 1 40 cups
Thus, Mary has 1 1 40 cups of flour.
Example 6: Sarah baked a pie and shared 3 8 with her neighbours and 1 6 with her colleagues. Later, she ate 1 4 of the pie. What fraction of the pie was left?
The baked pie can be considered as a whole.
Pie shared with neighbours = 3 8; pie shared with colleagues = 1 6
Pie eaten by Sarah later = 1 4
Total pie eaten or shared = 3 8 + 1 6 + 1 4 = 9 + 4 + 6 24 = 19 24
Pie left = 1 − 19 24 = 24 − 19 24 = 5 24
Thus, 5 24 of the pie was left.
Pihu brought 17 cups of juice. She used 4 3 4 cups to make fruit punch, 6 1 3 cups to make flavoured jelly and drank the remaining amount. How much juice did she drink?
Total juice with Pihu = 17 cups
Juice used to make fruit punch = 4 3 4 cups
Juice used to make flavoured jelly = 6 1 3 cups
Total juice used to make fruit punch and flavoured jelly = + =
Juice left for drinking = − =
Do It Yourself 2A
Subtract.
Compare using appropriate symbols. (>, < or =) a 2 2 3
Simplify.
Answer the given questions.
a By how much is 5 2 3 less than 7 7 8 ?
b What must be added to 2 2 5 to get 4 1 4 ?
c What is the perimeter of a triangle with sides of 1 4 cm, 1 8 9 cm and 4 5 cm?
d Find the perimeter of a rectangle which is 7 11 cm long and 2 9 cm wide.
e Subtract the difference of 7 1 4 and 9 2 5 from the sum of 2 3 4 and 4 5 6
Aisha painted 3 5 of the wall and her sister painted 1 6 of the wall. What portion of the wall did they paint together?
Ram drank 3 4 of a bottle of mango juice, and Lila drank 2 9 of a bottle of orange juice. How much juice did they consume in all?
A rectangular piece of cloth is 3 8 m long and 2 5 m wide. Find the amount of lace needed for the cloth.
Shikha studies for 5 2 3 hours daily. She devotes 2 4 5 hours of this time to science and maths. How much time does she devote to other subjects? Why is it important to be disciplined in studies? How much time do you spend studying?
A gallon is a unit of measurement used to measure liquids. It is commonly used in the United States to measure larger quantities of liquid. A jug has 2 1 4 gallons of water. If Nishant drinks 4 7 gallons of water each day from the jug, then what quantity of water will be left in the jug after 3 days?
Carlton has 30 yards of string. He uses 11 2 5 yards of string to tie a parcel and 6 1 4 yards of string to tie a box. How much length of string is left with Carlton?
Multiplication of Fractions
Riya found out the fraction of her salary she spent and saved during the first month.
If she earns ₹60,000 in a month, then let us see how much money she spent and how much she saved. To find the amount of money spent or saved by Riya, we need to multiply the total amount earned by the fraction of the amount spent or saved.
Multiplication of a Fraction by a Whole Number
The fraction of money spent by Riya = 13 20 of her total salary
Total salary = ₹60,000
Amount spent = 13 20 1 × 60,000 = ₹39,000
Thus, she spent ₹39,000.
The fraction of money saved by Riya = 7 20 of her total salary
Total salary of Riya = ₹60,000
Amount saved = 7 20 × 60,000 = 7 × 60,000 20 = ₹21,000
Thus, Riya saved ₹21,000. 3000
Example 7: Solve: 4 × 7 2 = 4 × 7 2 = 28 2 = 14
Remember!
When the fraction is used with the word “of”, it acts as an operator. “of” means multiplication.
Example 8: Solve: 30 × 2 4 5 = 30 × 14
Example 9: Rohan had ₹10,000 in his bank account. He used 2 5 of the money in paying his monthly bills. How much money was spent by Rohan?
Total amount of money with Rohan = ₹10,000
Fraction of money spent = 2 5
Total amount spent = 2 5 × 10,000 = ₹4000
Thus, Rohan spent ₹4000 in paying bills.
Rajeev went shopping and carried ₹5000 with him. He spent 3 8 of the total amount. How much money did he spend?
Total amount of money with Rajeev = ₹5000
Fraction of money spent = 3 8
Total amount spent = ₹5000 × 3 8 = = ₹
Thus, Rajeev spent .
Multiplication of a Fraction by a Fraction
Riya keeps half of her saved salary in her bank account and gives half of her savings to her father for investment. How much money does she give to her father?
Fraction of savings given to her father = 1 2 of 7 20
= 1 2 × 7 20 = 7 40
Amount given to her father = 7 40 of ₹60,000 = 7 40 × ₹60,000 = ₹10,500
Thus, Riya gives ₹10,500 to her father for investment. 2000
Example 10: Multiply.
1 3 5 × 2 5
Multiply the numerator with the numerator and the denominator with the denominator.
3 × 2 5 × 5 = 6 25
Remember!
Multiplication of numerators
Multiplication of denominators
into an improper fraction first, then multiply.
Example 11: Jack and Jill had 5 litres of glucose water. Jack consumed 1 5 of it, and Jill consumed the remaining amount. Find out how much glucose water Jack and Jill consumed individually.
Total quantity of glucose water = 5 litres
Fraction of glucose water consumed by Jack = 1 5
Glucose water consumed by Jack = 1 5 × 5 = 1 litre
Glucose water consumed by Jill = 5 litres – 1 litre = 4 litres
(Converting the mixed fraction to an improper fraction)
(Solving the values inside the brackets)
Simplify.
Perform the given calculations.
a 2 2 5 ×
Answer the given questions.
a 1 5 of 1000 grams
c What is 3 4 of 2 hours?
e What is 7 8 of 5 dozen?
b 5 6 of a metre
d How many days are 2 7 of 7 weeks?
f How many days are 2 3 of a leap year?
Human bones make up about 1 7 of the total body weight. If a person weighs 63 kg, what would be his bone weight?
Ram has 2 1 5 litres of milk. He uses only 1 3 of it and gives the remaining amount to his friend.
a How much milk did he use?
Simran and her friends ate
b How much milk did his friend get?
pizzas. The total weight of a pizza was 800 g. What weight of pizza did Simran and her friends eat?
Pihu helped her mother cook 30 small cookies. She shared two-thirds of the cookies with her sister, and one-fifth of the cookies with her neighbours. How many cookies did she distribute? Do you help your parents in the kitchen?
The ratio of the science books, novels and English books in a library is 2:3:5. If the total number of books is 1500, what is the difference in the number of science books and English books?
Read the statements and decide which of the given options is correct.
Assertion (A): When you multiply two fractions, the product is always less than each of the individual fractions.
Reasoning (R): Multiplying fractions involves multiplying the numerators together and the denominators together.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
e Both A and R are false.
Dividing Fractions
Riya divided her savings in half, giving one part to her father and keeping the other part in her bank account. Let us see what fraction of money she kept in her bank account.
Division of a Fraction by a Whole Number
Riya saved 7 20 of her salary and kept half of the savings in her bank account. So, we will divide 7 20 by 2 to find the fraction of the amount kept in the bank account.
Let us find 7 20 ÷ 2.
Write the whole number as a fraction.
Reverse the '÷' symbol to '×'.
Let us look at the Keep, Change and Flip method.
Write the reciprocal of the fraction formed.
Multiply the fractions to get the answer.
Keep Change Flip Answer
Thus, Riya kept 7 40 of the savings in her bank account.
Example 13: Divide 4 5 by 2.
Error Alert!
Always multiply by the reciprocal while dividing a fraction.
Division of a Whole Number by a Fraction
What if we want to divide 2 by half? How many halves do we get?
Let us divide 2 by half, 2 ÷ 1 2
Write the whole number as a fraction.
Replace the '÷' symbol with '×'.
Example 15: Divide 12 by 3 4 .
Write the reciprocal of the fraction divisor. Multiply the fractions to get the answer.
Division of a Fraction by Another Fraction
Now, let us learn to divide a fraction by another fraction. Divide 1 3 by 1 9 Flip Change Keep
Example 17: Divide 1 4 by 1 3 . 1 4 ÷ 1 3 = 1 4 × 3 1 = 1 × 3 4 × 1 = 3 4
18:
Example 19: The product of two numbers is 9 10 . If one of the numbers is 15 22 , what is the other number?
Let the other number = x
Given that, 15 22 × x = 9 10
x = 9 10 ÷ 15 22 (Transposing 15 22 from the LHS to the RHS)
x = 9 10 × 22 15 = (3 × 11) (5 × 5) = 33 25
Hence, 33 25 is the other number.
5 2 3 by 5 7 .
Multi-step Problems on Operations on Fractions
Riya saved 1 3 of her salary in the next month. She gave 5 11 of the savings to her father for investment and kept the remaining savings in her bank account. During that month, she earned ₹66,000.
Let us find out what amount of money she kept in her bank account.
Total amount saved = 1 3 × ₹66,000 = ₹22,000
Savings given to father for investment = 5 11 of the savings = 5 11 × ₹22,000 = ₹10,000
Savings deposited in the bank account = Total savings – Savings given to father = ₹22,000 − ₹10,000 = ₹12,000
Thus, Riya kept ₹12,000 in her bank account.
Example 20: In a fruit market, 3 5 of the fruits are mangoes. The total number of mangoes is 48, and 5 8 of the remaining fruits are apples. How many apples are there in the market, and what fraction of the total fruits are apples?
Fraction of fruits that are mangoes = 3 5; Total number of mangoes = 48 3 5 of the total fruit = mangoes = 48
So, the total number of fruits = 48 × 5 3 = 80
Remaining fruits = 80 – 48 = 32
Do It Together
Fraction of the remaining fruits that are apples = 5 8
Total number of apples = 5 8 × 32 = 20
Fraction of fruits that are apples = 20 80 = 1 4
Example 21: A man sells orange juice. A medium glass contains 350 mL, whereas the large glass is 4 5 more than the medium and the small glass is 1 3 of the large glass. If three people drink 1 small, 1 medium and 2 9 of a large glass respectively, then find the total quantity of juice drunk by three of them.
Quantity of a medium glass of juice = 350 mL
Quantity of a large glass of juice = 350 mL + 4 5 of 350 mL
= 350 mL + 4 5 × 350 mL = 350 mL + 280 mL = 630 mL
Quantity of a small glass of juice = 1 3 of a large glass of juice
= 1 3 × 630 mL = 210 mL
Let us find 2 9 of a large glass = 2 9 × 630 mL = 140 mL
Total juice consumed by three people = 1 small glass + 1 medium glass + 2 9 of large glass = 210 mL + 350 mL + 140 mL = 700 mL
Thus, the total quantity of juice that three people drank was 700 mL.
Preeti baked a cake and shared 6 16 with her neighbours and 5 12 with her friends. Later, she gave 2 5 of what was left to her sister. What fraction of the cake was left with Preeti at the end?
Cake shared with neighbours = 6 16
Cake shared with friends = 5 12
Total cake shared = + =
Fraction of cake remaining after sharing = 1 – =
Fraction of cake given to her sister = 2 5 × =
Fraction of cake remaining after sharing with the sister = – = 4
Do It Yourself 2C
Find the reciprocal of the given numbers.
and simplify.
Answer the given questions.
a The perimeter of an equilateral triangle is 3 7 m. What is the length of each side?
b The product of two numbers is 4 5 . If one of the numbers is 2 3, find the other.
c What is 96 divided by the sum of 12 8 and 8 12 ?
Akshay has a piece of cloth that is 12 cm long. He cuts it into small pieces of length 2 3 cm each. How many pieces of cloth will he have?
The area of a rectangular field is 43 3 4 cm2. If its breadth is 12 1 2 cm, find its length.
Orange juice is an excellent source of vitamin C. The natural sugars in orange juice provide a quick source of energy, making it a great pick-me-up beverage. A large can of orange juice contains 18 1 3 litres of juice. If the entire quantity of juice has to be poured into small containers, each of capacity 1 5 6 litres, then find the number of containers required.
Seema bought 5 9 kg of fruits. She packed them equally into 15 packets.
a Find the weight of 1 packet of fruit in kg.
b She sold 5 packets of fruit. How many kg of fruits did she sell?
3 7 of the people at a restaurant are males. If the number of females is 28 more than males, then how many females are there at the restaurant?
1 3 of all the shirts at a shop are printed, 1 4 of the remaining shirts are striped and the rest of the shirts are plain shirts. If there are 96 plain shirts, then how many shirts are there in total?
3 8 Value Development of all the players at an event are football players. If there are 72 players in all then how many players at the event are non-football players? Do you participate in any sports events? What are the benefits of playing sports?
Rakul spends 1 5 of her money on house rent, 1 4 of the money on food and 2 5 of the money on other expenses. She is left with ₹3000. How much money did she have initially?
A cistern has two holes. One leaks at the rate of 1 4 gallons per half an hour, whereas the other leaks at the rate of 1 5 gallons every quarter of an hour. In how many hours will the cistern be empty if it contains 500 gallons of water?
Operations on Decimals
Riya and her mother visited the market to buy fruit and vegetables. The shopkeeper weighed the purchases using a digital scale. They purchased 5.755 kg of vegetables and 7.35 kg of fruits.
Addition and Subtraction of Decimals
Let us see the total weight of the items purchased by Riya and her mother.
To find the total weight, we need to add. Here, the weights are unlike decimals.
Like decimals are decimals with the same number of decimal places after the decimal point. For example, 25.36 and 52.65 are like decimals.
Unlike decimals are decimals with a different number of decimal places after the decimal point. For example, 52.45 and 65.124 are unlike decimals.
Adding and Subtracting Decimals
Let us learn how to add the decimals 5.755 and 7.35.
Step 1: Convert the decimals into like decimals.
Here, 5.755 and 7.35 as 7.350.
Step 3: Add as whole numbers are added.
We can use the same method to subtract decimals.
Step 2: Write the digits in the column method aligning the decimal points and the digits.
Step 4: In the sum, put the decimal point directly below the other decimal points.
O . t h th 1 1
. 7 5 5
3 1 0 5
Let us now find the difference of the weights of the fruits (5.755 kg) and vegetables (7.35 kg) purchased.
Step 1: Convert the decimals into like decimals. Here, 5.755 and 7.35 as 7.350.
Step 2: Write the digits in the column method aligning the decimal points and the digits.
Step 3: Subtract as whole numbers are subtracted.
Step 4: In the difference, put the decimal point directly below the other decimal points.
t h th
. 3 5 0
7 5 5
5 9 5
Example 22: What is the sum of 125.23, 213.523, 148.58 and 326.125?
Example 23: Subtract 235.28 from 365.
Example 24: By how much should 365.14 be decreased to get 245.85?
Let 365.14 be decreased by x to get 245.85.
365.14 – x = 245.85 x = 365.14 – 245.85 = 119.29
Error Alert!
The misalignment of decimal points leads to an incorrect answer.
Example 25: The length of a rope is 102 m 80 cm. If a piece measuring 59.35 metres is cut from it, what is the length of the remaining rope?
Length of rope = 102 m 80 cm
As the measure is not in decimal form, we can write it as a decimal by converting it to the higher unit as 102.8 m.
Length of the rope cut = 59.35 m
Length of the remaining rope = 102.80 – 59.35 = 43.45 m
Add the sum of 367.25, 125.2 and 512 to the difference of 563.24 and 321. Do It Together
Sum = 367.25 + 125.2 + 512 = ....(1)
= 563.24 − 321 =
Adding (1) and (2) gives + =
Multi-step Problems on Adding and Subtracting Decimals
Riya and her mother spent ₹596.75 on purchasing vegetables and ₹895.45 on purchasing fruit. They also made miscellaneous purchases of ₹1236. If they gave ₹3000 to the shopkeeper, how much change did they receive?
Amount spent on vegetables = ₹596.75
Amount spent on fruit = ₹895.45
Amount spent on miscellaneous purchases = ₹1236
Did You Know?
The great Indian mathematician Aryabhatta formulated the first ten decimal places.
Total amount spent = 596.75 + 895.45 + 1236 = ₹2728.2
Change received from the shopkeeper = 3000 – 2728.2 = ₹271.80
Example 26: Simplify 125.12 + 214.35 – 321.69 – 154.25 + 148.6
Add the decimal numbers with like signs separately, 125.12 + 214 .35 + 148.6 = 488.07 …………. (1)
−321.69 – 154.25 = −(321.69 + 154.25) = −475.94…… (2)
From 1 and 2 we get, 488.07 – 475.94 = 12.13
Example 27: A drum has 59.55 kg of rice in it. A pack of 25.5 kg of rice is emptied into the drum. After this, 312 5 kg of rice is used. What is the weight of the rice left in the drum?
Quantity of rice in the drum = 59.55 kg
Quantity of rice in the packet = 25.5 kg
Total quantity of rice after emptying the packet = 59.55 + 25.5 = 85.05 kg
Quantity of rice used = 312 5 = 157 5 = 31.4 kg
Quantity of rice left in the drum = 85.05 – 31.4 = 53.65 kg
Example 28: Mayra took 7 4 hours to finish her maths homework, 1.2 hours to complete her science homework and spent 7 10 hours less time on her social studies homework compared to the time she spent on the maths homework. What was the total amount of time she spent completing her homework that day?
Time to finish maths homework 7 4 hours = 1.75 hours
Time to finish science homework = 1.2 hours
Time to finish social studies homework = 7 10 = 0.7 hours less than maths homework = 1.75 – 0.7 = 1.05 hours
Total time to finish the homework = 1.75 + 1.2 + 1.05 = 4 hours
Sushant had 182 5 cups of sugar. He used 2.25 cups to make milkshake, 63 4 cups for making a dessert and 1.45 cups for baking a cake. How many cups of sugar were left?
Total cups of sugar = 182 5 = 18.4 cups
Sugar used = 2.25 + 63 4 + 1.45 = 2.25 + + 1.45 = cups.
Sugar left = 18.4 − = cups.
a 223.25 and 12.9
d 332, 127.456 and 122.26
Subtract.
a 322.36 from 438.2
d 438.236 from 752.23
Fill in the blanks.
b 315.36 and 218.234
c 128.2 and 236.54
e 136.23, 556.14 and 25.125 f 152.214, 235.3 and 365.28
b 132.89 from 325.566
c 118.5 from 732.55
e 856.18 from 998.856 f 1065.235 from 1189.15
a 236.45 + = 568.2 b 514.7 − = 241.23 c + 321 = 512.47
d − 475 = 251.487 e 785.5 + 324.21 = f 987 – 562.26 =
What should be added to 389.265 to get 625.56?
By how much should 235.125 be decreased to get 126.24?
Subtract the difference of 469.251 and 829.23 from the sum of 356.21 and 585.236.
Simplify: 126.256 + 325.46 – 195.264 + 326.152 – 256.369
A recipe requires 3.75 cups of flour, 2.5 cups of sugar, and 1.25 cups of butter. How much of these ingredients are needed in total for the recipe?
Ravi goes to buy a big box of sweets. He purchases 10.5 kg of sweets, and the weight of the empty box is 1 kg 350 g. What is the total weight of the sweets and of the box?
Ronita pays ₹635.80 every month for cable and internet. She came to know about a new plan by another company that offered ₹452.75 for internet plus an additional ₹126.55 for cable. If Ronita switches to the plan, how much will she save every month?
A kilobyte (KB or Kbyte) is a unit of measurement for computer memory or data storage. Sumit downloaded three applications on his mobile that were 986.48 KB in total. If one of the apps was 256.36 KB and the other was 485.84 KB, how big was the third application?
Sam ordered a coffee and a waffle. Find the change he will receive if he paid $10.
Rhea donated 35.65 kg of sugar, 78 kg 540 g of flour, 17 kg 320 g of rice and some pulses to an NGO. If the total weight of the items donated was 142.63 kg, what was the weight of the pulses donated?
Sam saved ₹3652.45 in June and ₹4578.58 in July. He then purchased a bicycle worth ₹2468.75 and a helmet worth ₹689.48. How much money was he left with at the end of July?
Coffee: $1.46
Garlic bread: $3.95
Ice tea: $2.89 Waffle: $0.85
The amounts deposited and withdrawn by Manish in the initial four months of the year are shown below. What is the difference in the total amounts deposited and withdrawn in the four months?
The distance travelled (in km) by Mohit in a week was recorded on a bar graph. What is the ratio of the distance travelled in the last 3 days to the initial 4 days of the week?
The average temperature in Amsterdam for 5 months is given in the line graph. Is it correct to say that the increase in temperature from February to March is one-fourth of the increase from February to June? Give a reason for your answer.
Multiplication and Division of Decimals
Riya's younger brother, Naman and their father are going to the market to purchase a new computer system for Riya. On the way to the market, they stop at the petrol pump. Naman notices the displayed prices of various fuels on the board.
Naman: Dad, how much fuel are we putting in the car today?
Father: We are going to fill our car with 35 litres of diesel.
Naman's curiosity is sparked as he begins to calculate the amount they will need to pay at the pump.
Multiplying and Dividing Decimals
Let us find the amount paid by Naman’s father.
To find the amount paid by Naman’s father, we need to multiply. To multiply two decimal numbers follow the given steps.
Step 1: Multiply the decimal numbers ignoring the decimal points, just like whole numbers.
Step 2: Count the total number of decimal places and place the decimal point in the product accordingly.
87.89 × 35 = ₹3076.15
Hence, Naman's father paid ₹3076.15 for the fuel.
Remember!
The product should have the same number of decimal places as the sum of the number of decimal places in both the multiplicand and the multiplier.
Naman saw that one of the autorickshaw drivers paid ₹1018.75 for filling CNG. He started wondering how much CNG this driver must have put into his autorickshaw tank. Let us find out!
Step 1: Make the divisor a natural number by multiplying the divisor and the dividend by a power of 10 81.5 × 10 815 1018.75 × 10 10187.5
Step 2: Place the decimal point directly above the decimal point in the dividend.
Step 3: Divide the whole number part and then the tenth part.
Hence, the auto-rickshaw driver filled the tank with 12.5 kg of CNG.
Example 29: Multiply.
1
and 132
× 132 = 60350.4
Example 30: Divide.
1 3259.36 by 26 125.36 26 3259.36
Think and Tell
Do we get a natural number on dividing 2 decimal numbers?
Example 31: The product of two decimal numbers is 191.52. If one of the decimal numbers is 12.6, find the other decimal.
Let the other decimal be x.
Given that, 12.6 × x = 191.52
x = 191.52 ÷ 12.6 = 15.2.
Hence, the product of 12.6 and 15.2 gives 191.52.
Example 32: Find the cost of 11.5 litres of milk at the rate of ₹54.5 per litre.
Cost of 1 litre of milk = ₹54.5
Cost of 11.5 litres of milk = ₹54. 5 × 11.5 = ₹626.75
Example 33: A ribbon 30 m 80 cm long is to be divided into 11 equal pieces. Find the length of each piece.
Length of the ribbon = 30 m 80 cm = 30.8 m
Length of each piece if divided into 11 equal pieces = 30.8 11 = 2.8 m.
Find the missing dimension of the given rectangle with area 143.75 cm2 .
Area of rectangle = 143.75 cm2; Breadth of rectangle = 11.5 cm
Length = Area Breadth = =
Hence, the length of the rectangle is cm.
cm
Multi-step Problems on Operations on Decimals
Naman and his father reached the market. Naman’s father purchased a computer system for ₹60,225 with an additional tax of ₹10,840.5. He made a payment of ₹12,000 and paid the rest of the amount in six equal installments. What is the amount paid by Naman’s father for each installment.
Total cost of the computer system = 60,225 + 10,840.5 = ₹71,065.5
Balance amount after paying ₹12,000 = ₹71,065.5 − ₹12,000 = ₹59,065.5
The amount paid in each installment = 59065.5 6 = ₹9844.25
Hence, Naman’s father paid ₹9844.25 in each installment.
Example 34: A fruit vendor is selling oranges at ₹35.60 per kg and apples at ₹86 per kg. If Meera buys 21 4 kg of oranges and 1.75 kg of apples, what will be the total cost she needs to pay?
21 4 kg oranges = 2 kg + 0.25 kg = 2.25 kg
Cost of 2.25 kg oranges at ₹35.60 per kg = 2.25 × 35.6 = ₹80.1
Cost of 1.75 kg apples at ₹86 per kg = 1.75 × 86 = ₹150.5
Total amount paid = 80.1 + 150.5 = ₹230.6
Did You Know?
The decimal system of currency in India was introduced on April 1, 1957.
Example 35: Fifteen individuals visited a restaurant. Each one of them ordered the items shown in the table. While paying the total bill, they found that ten members of the group forgot to bring money. To cover the bill, how much additional money did each of the remaining individuals need to contribute?
Number of individuals = 15
Cost of meal per person = 25.45 + 34.95 + 70.25 + 15 = ₹145.65
Total bill = 15 × 145.65 = ₹2184.75
As 10 people forgot to bring money, the amount would now be paid by 5 people.
Amount paid by each individual = 2184.75 ÷ 5 = ₹436.95
Additional amount to be paid by each of the remaining individuals = ₹436.95 – ₹145.65 = ₹291.30
During a visit to a history museum, a group comprising 12 adults and 5 children purchased tickets. With each adult ticket priced at ₹125.5 and each child's ticket priced at ₹75.5, what is the overall difference in the total cost of the tickets for the adults and children combined?
Price of 12 adult tickets at ₹125.5 per ticket = 12 × 125.5 = Price of 5 child tickets at ₹75.5 per ticket = 5 × 75.5 = Difference in the cost = − = ₹
If 365 × 124 = 45,260, then find the following without actual multiplication.
a 36.5 × 124 b 3.65 × 12.4
Find the quotient.
a 0.165 ÷ 1.5
d 23.85 ÷ 1.8
Fill in the blanks.
b 42.7 ÷ 14
c 36.5 × 1.24
c 49.08 ÷ 0.02
e 487.36 ÷ 3.2 f 1117.5 ÷ 12.5
a 68.527 × = 23.63 b × 1.6 = 52 c 2177.35 ÷ = 62.21
d 74.2 × 12.3 = e 984.576 ÷ = 25.6 f 616.54 ÷ 14.5 =
The product of two decimals is 3538.29. If one of them is 41.5, find the other.
Find the area and perimeter of the given square.
A cloth of length 2.35 m is needed to make a shirt. How many metres of cloth are needed to make 48 such shirts?
In July 2024, the value of 1 euro = ₹90.61 and the value of 1 dollar = ₹83.73. How much money in Indian rupees does Mrunal have if she has 8 euros and 15 dollars with her?
A car moving at a constant speed covers a distance of 452.8 km in 8 hours. Find the distance covered by the car in 2 4 5 hours.
Suhani bought 7 kg 650 g of sugar at ₹38 per kg, 2 kg 485 g of rice at ₹62 per kg and 5 kg 725 g of flour at ₹46 per kg for making a donation at a blind school. What is the total amount paid by Suhani for the donation items? Have you ever donated to needy people?
Rahul has a can with 25.5 litres of milk. He fills 8 bottles equally with the milk, with 1 1 2 litres of milk left. Find the volume of milk in each bottle.
Kunal has a rectangular garden measuring 5.8 m by 7.25 m. What is the cost of fencing the garden if the cost of fencing is ₹58.5 per m?
Sunish bought a music system for ₹25,526.75. He made a down payment of ₹10,250 and paid the rest in 15 equal installments. What is the amount paid in each installment?
Mayra bought 2 pairs of shoes for ₹525.75 a pair, three T-shirts for ₹263.50 each, five pairs of socks for ₹50.25 a pair and one bag for ₹755. What was the total cost of the items purchased?
Sam used some cloth to make 8 banners and 3 tablecloths. He used 2 m 75 cm of cloth for each banner and 1.55 m of cloth for each tablecloth. Find the total length of cloth used. Also, find the cost of the cloth used if the cost of 1 m of cloth is ₹75.5.
Sharvil has 25 red ribbons each measuring 45.65 m, 3 blue ribbons each measuring 520.75 m and 2 green ribbons each measuring 368.15 m. If she used the ribbons for her project and is left with 560.2 m of the ribbons, how much ribbon was used for the project?
Saumya is making a report on the computer. She wants to place a figure which is 12.75 cm wide so that it appears centred on the page. The width of the page is 22.63 cm. How much margin should she leave at both ends so that the figure is centred?
Points to Remember
• The numbers of the form a b , where a and b are whole numbers and b ≠ 0 are called fractions.
• To add/subtract unlike fractions, find the LCM of the denominators, convert them into like fractions and then perform addition/subtraction.
• To multiply one fraction with another, multiply the numerators, multiply the denominators, and then write the answer in the lowest form.
• A reciprocal of a fraction can be obtained by interchanging the numerator and the denominator.
• To divide two or more fractions, multiply the first fraction with the reciprocal of the other fraction.
• Decimals can be added or subtracted by converting them to like decimals and aligning the decimal points in the column method.
• To multiply decimal numbers multiply as whole numbers are multiplied count the total number of decimal places place the decimal point at the same number of decimal places in the product.
• To divide decimal numbers convert the divisor to a whole number place the decimal point just above the decimal point in the dividend divide as whole numbers are divided.
Math Lab
Fraction Collage Addition
Aim: Adding unlike fractions using hands-on visual representation.
Materials Required: Coloured construction paper, pen, paper, scissors, glue stick
Setting: In pairs
Method:
1 Each pair to take 3 paper plates, divide 2 paper plates into different number of equal parts, write the fraction for each part and then cutout the parts.
2 Students need to then take all the parts and give them to the teacher.
3 The teacher then gives out any 2 fractions to each pair.
4 Students will then place the 2 fractional parts on a new plate, and find the sum of the two fractions.
5 Repeat with more fractions.
Add or subtract the given decimals.
a 122.56 + 36.2 b 321.4 + 12.63 c 536.3 + 311.236 d 756.59 + 413.5 + 623.12
e 336.8 – 285.123 f 586.4 – 387.25 g 658.412 –
Multiply or divide the given decimals.
a 212.5 × 35 b 110.52 × 21.5 c 156.52 × 12.29 d 315.13 × 81.2
e 498.8 ÷ 4 f 304.8 ÷ 12 g 90.15 ÷ 1.5 h 23.94 ÷ 6.3
Answer the given questions.
a Which is more: The product of 3 1 5 and 2 1 4 or the quotient of 2 1 3 and 4 1 6 ?
b Which is less: The product of 25 and 4 75 or the sum of 3 1 4 and 5 4 5 ?
c What is the difference in the quotient of 4 and 2 7 and the product of 2 5 and 15?
d What is the sum of the product of 9 and 1 1 2 and the sum of 9 1 2 and 7 1 3 ?
Simplify.
a 1 2 3 +
Solve to find the answer.
a A train covers a distance of 48 3 4 miles in 1 1 4 hours. How far does it go in 2 hours?
b Find the value of x, if 2 13 of x = 26.
c Find the value of x, if 22 2 9 × x = 1800
d The product of two numbers is 3 5 . If one of the numbers is 2 3, find the other.
e 6 7 of a number is 180. Find the number.
f The product of two numbers is 21 3 5 . If one number is 7 47 55 , find the other.
Miya has 3 5 of a cake. She ate 2 3 of it.
a Find out what fraction of the cake she ate. b What fraction of the cake is left with her?
Aarav scored 452.65 out of 600 in the final examination. How many marks did he lose?
There is 0.625 kg of powdered milk in each tin. If a carton contains 12 tins, find the total mass of powdered milk in the carton.
The average growth rate of a hair strand is 1 cm 8 mm per month. What would be the total length of a strand of hair after 3 years of growth?
A tank is 4 5 full. When 65 litres of water are drawn from it, it is 7 12 full. Find out how much water is left in the tank.
Piyush walks at a speed of 4 1 5 km per hour for 5 hours, and then at the speed of 3 1 4 km per hour for the next 3 hours. Find the distance travelled by Piyush in 8 hours.
Sack A contains 125.35 kg of rice, sack B contains 25.65 kg more rice than sack A, and sack C contains 13.49 kg less rice than sack B. What is the total weight of the rice in all three sacks?
Abhinav and his family prefer eating healthy food even when they go out. At a restaurant, the family ordered 3 vegetable bowls, 2 apple pies and 4 milkshakes. How does choosing healthy food over junk food affect our health?
a How much did the family spend at the restaurant?
b How much change will they receive if they paid an amount of ₹1000?
A planet completes 1 3 5 turns about its axis each day.
a How many turns will it complete in a week?
b How many turns will it complete in one fortnight?
Himani travels 1 3 of a distance by train, 2 5 by bus and walks for the remaining distance. If she walks for 16 km, then find:
a the distance travelled by bus. b the distance travelled by train.
c the total distance.
Ravi bought 8.6 kg of sugar. He poured the sugar equally into 5 bottles. There was 0.35 kg of sugar left. What was the mass of sugar in 1 bottle?
Mohit's family went on a road trip. They reached point A on the first day and point B on the second day. How many more kilometres do they need to drive to reach their destination? If their car travels 11.5 km per litre, how many litres of fuel will they need for the trip?
1 The graph shows the amount saved by Monika during 5 weeks.
a If the amount saved in Week 6 is 2.25 times what was saved in Week 2, how much was saved in Week 6?
b If Monika wants to save a total of ₹12,000 by the end of the seventh week, how much should she save in the seventh week?
2 Read the statements and decide which of the statements are necessary to answer the given question. Julia baked a batch of cookies and divided them equally into boxes. Each box contains the same number of cookies. What is the total number of cookies?
Statement 1: Julia divided the total number of cookies into 8 boxes.
Statement 2: Each box contains 5 cookies.
a Statement 1 alone is sufficient, but Statement 2 alone is not sufficient.
b Statement 2 alone is sufficient, but Statement 1 alone is not sufficient.
c Both statements together are sufficient, but neither statement alone is sufficient.
d Each statement alone is sufficient.
e Statements 1 and 2 together are not sufficient.
Case Study
A Charitable Cause
A group of students decided to organise a charity event to raise funds for their local animal shelter. They planned to sell custom-made bracelets and donate a fraction of the proceeds to the shelter. Here is how their plan unfolds : They created 3 different types of bracelets: A, B and C.
• For every 5 bracelets of type A sold, they would donate 2 5 of the proceeds to the shelter.
• For every 3 bracelets of type B sold, they would donate 3 7 of the proceeds to the shelter.
• For every 5 bracelets of type C sold, they would donate 5 8 of the proceeds to the shelter.
During the event:
ο They sold 35 bracelets of type A for ₹75.5 each.
ο They sold 21 bracelets of type B for ₹90.5 each.
ο They sold 28 bracelets of type C for ₹120.5 each.
1 How much money did they get by selling type A bracelets? a ₹2625 b
2 How much money did they donate on selling type B bracelets? a ₹1900.5 b ₹814.5
c ₹2108.75 d ₹1057
3 Which type of bracelet let them donate the highest amount?
4 What is the total amount donated to the animal shelter from the proceeds of each type of bracelet sale?
5 If you need to donate or to run a charity event in your colony or community, how will you do it?
3 Data Handling
Let’s Recall
Tanay’s school organised an interschool sports competition. The given table shows the number of medals won by the top 5 schools in an interschool competition.
The process of gathering data and recording information is called data collection.
The data collected can be represented using a tally marks table, as shown below.
Let us answer a few questions related to the data.
1 What is the number of medals won by School B?
The number of medals won by School B is 26.
2 Which school won the least number of medals?
The minimum number of medals is 11 which is won by School A.
Let’s Warm-up
Study the table given above and answer the questions.
1 Which school won the maximum number of medals?
2 What is the total number of medals won by all schools?
3 What is the difference in the number of medals won by School D to the number of medals won by School E?
4 What is the ratio of the number of medals won by School C and the number of medals won by the rest of the schools?
I scored out of 4.
Mean, Median and Mode Mean, Median and Mode
Ria’s parents are planning to go on a vacation to Jaipur for the first time.
Ria: Papa! What is the weather in Jaipur like?
Ria’s father checks the online weather forecast for Jaipur for the next 15 days and finds the following:
Ria: Papa! The temperature is so different every day. What clothes should we pack?
Arithmetic Mean or Mean
One possibility is that Ria and her father want to make a decision based on a single value that represents the entire data. But what will that value be and how is it calculated?
The arithmetic mean, mean or average of data is a value that can represent all of the data. It is defined as the sum of all the observations of data divided by the total number of observations.
Mean = Sum of all observations
Number of observations
= 570 15 °C = 38°C
So, the average or mean temperature is 38 °C.
Remember!
The mean of the data may not always be an observation from the data.
We can also organise the above data in tabular form and find the mean. Let us look at the steps for the same.
Step 1
Create a grouped data table. The observation column is denoted by x, while the frequency is denoted by f
We know that, mean = Sum of all observations No. of observations
Step 2
Find the sum of all observations.
First, multiply each observation by its frequency and list the products in a column as shown, and then find the sum.
Sum of all observations = 570
We can represent the sum of all observations as ∑( f × x). The symbol S (called sigma) is a Greek letter that represents summation
Step 3
Find the total number of observations as the sum of all the frequencies.
We see from the table that the total number of observations is 15.
In general, the total observations can be denoted as ∑f.
Step 4
Calculate the mean.
Mean = Sum of all observations No. of observations = ∑( f × x) ∑f = 570 15 = 38°C
The mean is 38°C.
To find the total number of observations, never add all the observations. We always add their frequencies. Error Alert!
Therefore, if Ria and her father want to make a decision based on a single temperature that reflects the overall duration of their stay, they should pack their clothes based on the mean temperature of 38 °C.
Example 1: Find the mean of the first 5 natural numbers.
First five natural numbers — 1, 2, 3, 4 and 5
Mean = Sum of all observations No. of observations
= 1 + 2 + 3 + 4 + 5 5 = 15 5 = 3
So, the mean of the first five natural numbers is 3.
Think and Tell
Could the mean be more than the highest value of the data?
Example 2: Data on the number of books read by students in a class is represented in the frequency distribution table below:
Remember!
Find the mean of the data.
We know that, mean = Sum of all observations No. of observations = ∑( f × x) ∑f
Let us find ∑f and ∑( f × x).
The summation sign is especially helpful in the case of large data. There is no need to write each observation separately.
Thus, the mean = S( f × x) Sf = 44 18 = 2.44 books
Do It Together
Example 3: The mean of seven numbers 8, 6, 10, 7, 9, 8 and m is 8. What is the value of m?
Mean = Sum of all observations No. of observations
8 = 8 + 6 + 10 + 7 + 9 + 8 + m 7
56 = 48 + m m = 8
Example 4: The mean of x, x + 1, x + 3, x + 5, x + 7 is 228.2. What is the value of x?
Mean = Sum of all observations Total number of observations
228.2 = x + (x + 1) + (x + 3) + (x + 5) + (x + 7) 5
228.2 × 5 = 5x + 16
5x + 16 = 1141 or 5x = 1141 − 16
5x = 1125 x = 225
Example 5: The mean of five numbers is 13. One of the observations which was 15, was removed. Find the new mean.
Mean = Sum of all observations No. of observations = 13 = Sum of all observations 5
Sum of all observations = 13 × 5 = 65
It is given that 15 was removed, the new sum of 4 observations will be = 65 – 15 = 50.
New mean = 50 4 = 12.5
Example 6: The mean of 6 numbers is 30. If we remove one number, the mean increases by 1. Find the removed number.
Given that the mean of 6 numbers is 30, so the sum of the numbers will be:
Mean = Sum of all observations No. of observations = 30 = Sum of 6 numbers 6
Sum of 6 numbers = 30 × 6 = 180
Given that when a number is removed, the new mean increases by 1 = 30 + 1 = 31
Sum of remaining 5 numbers = 31 × 5 = 155
The value of removed number = Sum of 6 numbers − Sum of remaining 5 numbers = 180 – 155 = 25. Hence, the removed number is 25.
Find the arithmetic mean or the average of the marks (out of 10) in a class test.
Step 1
Let us find ∑f and ∑( f × x).
Step 2
Find the mean.
Mean = ∑( f × x) Σf = 30 =
Thus, the arithmetic mean or the average marks of the students is
Mode
We learnt that the average can represent the whole set of data. But what if Ria’s father wants to take a decision based on the temperature that occurs most frequently?
In this case, Ria and her father must choose what is called the mode of the data.
A value in the data that occurs most frequently is called the mode.
Let us once again consider the data gathered by Ria’s father when they were planning to go on a vacation.
Step 1
Arrange the temperatures (in °C) in ascending order.
30, 32, 32, 32, 34, 36, 37, 40, 41, 42, 42, 42, 42, 44, 44
Step 2
Find the observation that occurs most frequently.
The observation with the highest frequency is the mode and not the frequency.
5
3
Remember!
Mode will always be an observation from the given data.
30 °C, 32 °C, 32 °C, 32 °C, 34 °C, 36 °C, 37 °C, 40 °C, 41 °C, 42 °C, 42 °C, 42 °C, 42 °C, 44 °C, 44 °C
Occurs thrice
Occurs 4 times Occurs twice
We see that the observation 42 °C occurs the most, i.e., 4 times. Thus, it is the mode of the data.
So, Ria and her father can pack their clothes for the most frequent temperature, or the mode of the data, 42 °C.
Case 1: More than one mode
It is possible that in a set of data, there are several observations with the same highest frequency (more than 1). In such a case, all such observations are modes.
For the given data:
2, 2, 3, 4, 4, 5, 6, 6, 7, 7
The modes are → 2, 4, 6 and 7
Case 2: No defined modes
If all the values in a set of data occur exactly once, there is no value that can be considered the mode. In this case, the data is said to have no mode.
For the given data:
1, 2, 3, 4, 6, 7
The mode does not exist because each observation occurs exactly once.
Example 7: The marks scored (out of 20) by Vikas in various class tests during a term are 18, 15, 17, 13, 17, 19, 17, 16 and 14. Find the mode.
Step 1
Arrange the marks in ascending order.
13, 14, 15, 16, 17, 17, 17, 18, 19
Step 2
Find the observation that occurs most frequently. 13, 14, 15, 16, 17, 17, 17, 18, 19
Occurs thrice
The observation 17 occurs the most, i.e., 3 times. Thus, it is the mode of the data.
Vivaan wrote a few numbers on a piece of paper. The most frequent number (i.e., mode) was 8. One number got wiped out. Can you find out what that number was?
4, 6, 6, 7, 8, 3, 8, 6, 5, 8
Let us start by arranging the data in ascending order
3, 4, 5, 6, 6, 6, 7, 8, 8, 8
Can the missing number be 3? No, because then the modes will be 8 and 6.
Can the missing number be 4? No, because then the modes will be 8 and 6.
Can the missing number be 5? , because then the mode(s) will be .
Can the missing number be 6? , because then the mode(s) will be .
Can the missing number be 7? , because then the mode(s) will be
Can the missing number be 8? , because then the mode will be .
Median
What if Ria and her father decided to make a balanced decision by selecting a temperature value that falls exactly in the middle of the temperature extremes? So, they would predict exactly as many hotter days as there were cooler days.
The median is the middle value in a set of data when arranged in ascending or descending order.
Let us find the median of the data collected by Ria’s father.
We arrange the data in ascending order.
30, 32, 32, 32, 34, 36, 37, 40, 41, 42, 42, 42, 42, 44, 44
Values less than 40 Median Values more than 40
Let us learn more about median calculation.
Case I: When the total number of observations is an odd number,
Error Alert!
By using
n 2 + 1
, you find the median place and NOT the median itself. The observation in that place is the median.
When the total number of observations is odd, the median would be the observation in the middle, i.e.,
n + 1 2
th observation in the arranged data. Let us consider the following data.
20 15 4 10 17 8 1
Arrange the data in ascending order.
1 4 8 10 15 17 20
Find the total number of observations.
Total number of observations is 7.
The
n + 1 2
Here, the
th observation in the arranged data is the median.
7 + 1 2
th observation, which is the 4th observation is the median.
Remember!
When arranged in ascending or descending order, the median has half of the observations lying to its left and the other half to its right.
Find the median.
1 4 8 10 15 17 20
Less than median Median More than median
Thus, the median value is 10. Exactly three values are more than 10 and three values are less than 10.
Case II: When the total number of observations is even
Let us consider the same data as above, but just add another observation to it. So, the new data is:
20 15 4 10 17 8 1 22
New observation
Arrange the data in ascending order.
1 4 8 10 15 17 20 22
Find the two middle observations since the total number of observations is 8, which is even.
1 4 8 10 15 17 20 22
Two middle observations
The median is the average of the middle two observations.
Median is (10 + 15) 2 = 12.5
Here, the two observations are 10 and 15.
Example 8: Find the median of the given data:
10, 8, 14, 16, 10, 6, 18, 14, 16
Here, n = 9, which is an odd number.
By arranging the data in ascending order, we get:
6, 8, 10, 10, 14, 14, 16, 16, 18
Middle value
Thus, the median is 14.
We can also use the formula to find the median.
Median =
n + 1 2
The 5th observation is 14. Thus, the median is 14.
Think and Tell
Is it necessary that the median will always be present in the data?
observation = 5th observation
Example 9: The median of the given data is 50. What is the value of a? 15, 20, 25, a, 80, 120
Total observations = 6 (Even number)
Median = 3rd term + 4th term 2 50 = 25 + a 2
25 + a = 50 × 2
a = 100 − 25 = 75
The heights of 7 girls of a class are given in the following table: Do It Together
Name Radha Avni Rita Jaya Shikha Shilpi Rinki
Find the median height.
Arrange the heights (in cm) in ascending order. 148, , , , , , 171
The total number of observation = 7, which is an (even/odd) number. The middle observation is The median height is cm.
Range
Do you remember Ria and her father who checked the online weather forecast report? The temperature of Jaipur for the next 15 days are as follows:
Ria’s father wanted to find the range of the temperature.
The difference between the largest and the smallest observation in a set of data is called the range of the data. Here, the highest temperature is 44 °C, and the lowest temperature is 30 °C. Hence, Range = 44 °C − 30 °C = 14 °C.
Choosing the Right Measure of Central Tendency
From the previous sections, we learnt about the different ways in which Ria and her father could have made the decision about their packing. The mean, median and mode helped them decide. These are called the measures of central tendency.
But which measure of central tendency do we choose, and why?
We can choose the appropriate measure of central tendency according to the purpose of our exercise. The following table highlights when each measure of central tendency should be used.
Mean
When to Use
• To find one value that represents the whole data.
Example Sachin Tendulkar’s average score in the One-Day International Cricket matches are 44.8 runs. He played 463 matches. This means that if we replace all his scores in individual matches with this average, it would represent his performance throughout his career.
Median Mode
• To find a “middle” value in data that has a sizeable number of observations.
• To see which observation divides the entire set of data into two equal halves or parts.
In an exam, if the median score was 75%, this implies that exactly half the number of students who participated scored below 75%, and the other half scored above 75%
• To recognise the most commonly occurring observation.
A shopkeeper sells T-shirts in 5 sizes: extra small, small, medium, large and extra large. The most frequently sold T-shirt size represents the modal size, and is the most important for his business.
Example 10: A researcher wants to study the duration of the commute of some people in a city. The researcher randomly selects 15 people and records the duration of their commute in minutes. The dataset consists of the following durations of commute: 25, 30, 33, 40, 42, 50, 53, 60, 62, 70, 74, 78, 85, 90, 93. Which measure of central tendency should the researcher use to describe the average duration of their commute? What is the range of the given data?
Using Mean:
As the researcher wants to describe the average duration of their commute, the mean can be given as:
Mean = (25 + 30 + 33 + …….. + 93) 15 = 885 15 = 59 minutes
Using Median:
Remember!
One or more measures could possibly be good measures.
Another way of describing the average duration of their commute is by using the median. It can be given as:
Median = As the data has an odd number of observations, the median will be the
th = 8th observation.
th observation =
Hence, the median for (25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95) is 60 minutes. Middle value
Using Mode:
We know that the mode is the most commonly occurring observation, but in the above case, none of the data values are repeating. Therefore, the mode cannot be used to describe the average duration of their commute for the above data.
Range of the given data = Highest value − Lowest value = 93 − 25 = 68
Which measure of central tendency should the retailer use to plan his purchase for the upcoming week, considering the sales record of shirts in five sizes during the first week of the month? Also, find the range of the given data.
Using Mean and Median:
As the retailer is dealing with (categorical/numerical) data, he (can/canʼt) use the mean or median to plan his purchase for the upcoming week.
Using Mode:
As the mode is used to recognise the (most/least) commonly occurring observation, the retailer can use the mode to plan his upcoming purchase.
The mode for the given data is Therefore, only the can be used to plan the purchase for the upcoming week.
Range = − =
Find the mean of the first 10 odd numbers.
Find the mode of the given years of experience of teachers in a school: 12, 5, 7, 10, 3, 2, 1 ,7, 6, 7, 5, 10, 7, 4, 2, 1, 4, 4
The given table shows the number of pages having a certain number of illustrations.
No. of Illustrations (per page) 2
Find the mean number of illustrations per page.
A genre is a category or type of art, like books, movies, or music, that has a particular style, form, or content. The librarian at a school keeps track of the types of books that children choose from the library. She notices that the last 10 books belonged to the following genres: Fiction, Poetry, Drama, Drama, Fiction, Fantasy, Poetry, Drama, Drama and Fantasy, at a school. Find the modal genre.
The mean of x, x + 2, x + 3, x + 5 and x + 7 is 92. What is the value of x?
The enrolment in a school during six consecutive years is given below. Find the median of the data.
Year 2018 2019 2020 2021 2022 2023
Enrolments 1555 1670 1850 1780 1400 2540
An ecologist studies ecosystems, including forests, and analyses tree heights as part of understanding forests structure and health. The heights of the trees collected by an ecologist are as follows (in metres): 5, 7, 10, 12, 15, 18, 22, 30. What is the range of the given data?
The mean of 5 numbers is 26. One of the observations, which was 6, was removed. Find the new mean. Is the new mean greater or less than the original mean?
The mean of 5 numbers is 38. If we add one more number, the mean reduces by 2. Find the added number.
The numbers 2, 4, 6, 6 , 2x + 1, 9, 9, 10, 11 are written in ascending order. If the median of the given data is 7, find the value of x
A group of soldiers went on a journey. They had to take a road trip through India passing through many rivers along the way. The rivers are listed, and the lengths of the rivers (in kilometres) are given.
Find the mean length of the rivers visited by the troop.
The scores of the team members of a golf team are shown below. 72, 73, 72, 76, 72, 74, 73, 75, 76, 74, 72
Which measure of central tendency would be the most appropriate to find the average score of the team members? Also find the range of the given data.
The mean attendance of a class from Monday to Saturday was 33. If the mean attendance from Monday to Thursday was 32 and that from Thursday to Saturday was 34, then find the attendance on Thursday.
A data set has 50 different values. 47 values are between 1 and 5, whereas 3 values are more than 50. Which measure of central tendency will better represent the typical value of the data set?
Organisation and Representation of Data
Annie owned a warehouse. She kept a stock of multiple products in her warehouse. She collected the details of all the products, including the stock available and the sale of the products.
Making Bar Graphs
Remember!
Numerical information or facts collected are known as data.
Annie recorded the data of the stock available at her warehouse for different categories of products in a table.
Annie wondered how to represent the data using a bar graph. Let us find out.
Step 1
Draw the x-axis and the y-axis.
Step 2
Label both the axes.
Draw the bars.
Double Bar Graphs
Ria made a list of pizza toppings, according to the choices of boys and girls.
Favourite pizza toppings Girls Boys
Remember!
The double bar graph is drawn to compare two data sets.
Here, two sets of data are given. So, if we want to represent how many boys and how many girls chose the same type of topping, we need to draw two bars of different colours side by side for boys and girls separately to compare two sets of data simultaneously. This is known as a double bar graph.
Let us learn how to draw a double bar graph for the two data sets given above:
Step 1
Draw two perpendicular axes—horizontal and vertical and label both axes.
Step 2
Take the scale as 1 division = 5 children.
Step 3
Draw bars of equal width with equal spacing between types of pizza toppings and heights corresponding to the number of children.
Step 4
Draw two bars for each type of topping, first for the girls and second for the boys. Place them next to each other on the graph.
Example 11: The runs scored by a cricketer in the first six overs are given:
You Know?
The first bar graph appears in a book by William Playfair in 1786.
Draw a bar graph for the data.
The runs a cricketer scored in the first six overs are shown in the bar graph below.
Example 12: A survey was conducted in a residential colony to understand about people's interest in sports.
Sport
Consider this data and draw a double bar graph by choosing an appropriate scale. This bar graph represents the number of people who love watching or participating in their favourite sports.
60 students from a certain locality use different modes of travel to school, as given below:
Draw the bar graph representing the above data.
Fill in the blanks.
A bar graph consists of rectangular bars of equal . b The spaces between two consecutive bars are
Basketball Cricket Swimming Hockey
Scooter Car Bus Rickshaw Bicycle
c In a bar graph, the bars can be represented either or d The of a bar represents the frequency of the corresponding data.
The table shows the number of points scored by Rahul in 10 rounds of a game. Represent the data using a bar graph.
of the Game
The table shows the favourite sport of 300 students of a school. Represent the data using a bar graph.
Calorie refers to the amount of energy that food provides when consumed. The table below displays the average intake of various nutrients (in calories) by rural and urban groups for a particular day. Using a suitable scale, draw a double bar graph to compare the data.
The performance of a student in the 1st term and 2nd term exam is given. Draw a double bar graph by choosing an appropriate scale.
The data on the production of paper (in lakh tonnes) by two different companies X and Y over the years is given. Read the data and represent the data in the form of a double bar graph. on a chart paper. Use origami sheets to make the bars.
The given data shows the number of toys manufactured by various manufacturing units of a company in five days of a week. Is it possible to draw two different bar graphs using the same data? If yes, then draw.
Interpreting Bar Graphs
Annie stored the data for the total revenue generated in the last year for the products in the form of a bar graph.
Annie wanted to check which category generated the most revenue. Let us see.
The rectangular bar for fruit and vegetables is the highest.
The amount of revenue generated for fruit and vegetables is ₹4,00,000.
Horizontal bar graph
Unlike vertical bar graphs or column graphs, there is another type of bar graph known as a horizontal bar graph.
A horizontal bar graph is drawn with rectangular bars of lengths proportional to the values that they represent, the same as a vertical bar graph.
The only difference is that in a horizontal bar graph, the vertical axis shows the data categories that are being compared and the horizontal axis represents the values corresponding to each datacategory.
Let us study an example to understand.
The bar graph represents the data collected on the popularity of the types of music liked by students. After observing the bar graph, answer the given questions:
1 Is this a vertical or horizontal bar graph?
Here, the vertical axis displays the music category, while the horizontal axis represents the corresponding value of each music category. So, this is a horizontal bar graph.
2 Which type of music is the most popular?
Jazz is the most popular type of music among the students.
3 How many students were asked about their favourite music?
Total number of students = 12 + 8 + 7 + 14 = 41
So, 41 students were asked about their favourite music.
Example 13: The bar graph depicts the pass percentage of five different students in a class examination. Observing the bar graph, answer the questions:
1 Name the student whose pass percentage is more than 90%. Prem is the student whose pass percentage is 100%, which is more than 90%.
Scale: 1 division = 2 students
Remember!
Do not forget to label the axes and write the
Hip hop
Classical Rock Jazz Type of Music
Number
2 Name the student who has the lowest pass percentage.
Suman has the lowest pass percentage, which is 50%.
3 Find the number of students whose pass percentage is less than 80%.
Suman and Raman are the two students whose pass percentage is less than 80%.
4 Find the number of students whose pass percentage is more than 70%.
Raman, Prem, Ankita and Rosy are the students whose pass percentage is more than 70%.
Thus, 4 students pass with more than 70%.
Think and Tell
Does the width of the bar in a bar graph have any significance?
Example 14: The double bar graph shows the favourite sports of boys and girls in a school. Study the graph carefully and answer the questions.
1 In which sport have the most boys shown interest? The most boys have shown interest in cricket.
2 Who has more interest in basketball? More girls have shown interest in basketball.
3 How many students in total like football? There are a total of 19 students who like football.
4 Which sports do 12 girls like? Basketball is liked by 12 girls.
5 How many girls like cricket? Cricket is liked by 5 girls.
The double bar graph represents the data collected on the popularity of Indoor Games and Outdoor Games as participant sports for students in Grades 5 to 8.
1 Is there any grade in which more students prefer indoor games?
2 What percentage of students prefer indoor games in Grade 6?
3 What percentage of students prefer outdoor games in Grade 7?
4 70% of students of which grade prefer outdoor games?
Raman Suman Prem Ankita Rosy
Favourite Sport in a School
Popularity Survey: Indoor Games vs Outdoor Games
Do It Yourself 3C
1 cm on a scale of a bar graph represents 5 ft. Find the actual height of the building if this is represented by a bar of 5 cm height in the bar graph.
The double bar graph shows the performance of a student in the 1st and 2nd terms.
a In which subject is the performance of the student in the 2nd term poorer than in the 1st term?
b In which subjects did the student perform the best in 1st term? How many marks did he score?
c What was the total of the marks scored in 1st term?
d What is the difference of the total marks scored in 1st and 2nd term?
The table shows the cost price and profits earned by a merchant for 4 different types of merchandise P, Q, R and S.
a Choose an appropriate scale and draw a double bar graph for the given data.
b Which merchandise gives the most profit on selling?
The bar graph shows the monthly expenditure of a family on fuel (in ₹) in a year. Read the bar graph and answer the questions.
a What was the family’s expenditure on fuel in March?
b In which month did the family spend the most on fuel? How much did they spend?
c What was the total expenditure of the family on fuel in the full year?
d What is the ratio of the expenditure in the first six months and the expenditure in the last 6 months on fuel?
Expenditure on Fuel (in ₹)
The data shows the rainfall on different days of the week. Study the data and answer the questions.
a Draw a bar graph of the data. b On which day was the rainfall the highest?
c What is the ratio of the rainfall on the first two days and the last two days?
The bar graph shows the number of people with their shirt sizes. Read the bar graph and answer the questions.
a How many people wear medium-sized shirts?
b How many people wear extra-large sized shirts?
c What is the ratio of the people who wear large-sized shirts to those who wear small-sized shirts?
d How many people are there in total?
The bar graph shows the number of cars sold by two showrooms in seven months.
a How many cars in total were sold by Showroom A in the first three months?
b How many cars in total were sold by Showroom B in the last three months?
c Which showroom sold more cars in the first 4 months?
d What is the ratio of the total number of cars sold by Showroom A and Showroom B?
Challenge
The double bar graph shows the percentage of profits earned by two companies, A and B, over the years. Read the graph and answer the questions.
a If the income of Company A in 2011 was ₹1,42,500, what was its expenditure in that year?
b The income of company A in 2010 was equal to its expenditure in 2011, what was the total income (in lakhs) of company A in 2010 and 2011 together? Hint: Consider income as the selling price and expenditure as the cost price.
Points to Remember
• Mean:
Mean = Sum of all observations No. of Observations
• Mode:
Observation that occurs the greatest number of times in the data.
Will always be an observation from the given data.
• Median:
The middle value of a set of data when the data is arranged in ascending or descending order.
For odd number of observations, the median is given by the
n + 1 2
th observation.
For even number of observations, the median is given by the average of the two observations in the middle, i.e.,
n 2
th and
n 2 + 1
th observations.
• A bar graph is another way of representing numerical data using bars of uniform width drawn vertically or horizontally with equal spacing between them.
Math Lab
Revealing Academic Trends
Collaboration & Creativity
Objective: To compare the marks obtained in all the subjects by a student in the first and second unit tests in class VII by drawing a double bar graph, using paper cutting and pasting.
Setting: In pairs
Method:
Materials Required: Graph paper, origami sheets, pencil, eraser, sketch pens/glitter pens, glue and scissors.
1 Collect your marks for all the subjects in each term and tabulate the data.
2 Draw two perpendicular axes on the graph paper and label them to show what they represent.
3 Choose an appropriate scale and cut the strips of origami sheets of different lengths (or heights) according to the marks obtained in different subjects in each term, representing one term with one colour, say blue, and the other term with another colour, say green.
4 Paste these strips of paper adjacent to each other, representing a double bar graph.
5 Create 4 questions based on the created double bar graph.
6 Exchange the bar graph with your pair and answer the created questions.
7 Have a discussion around what other question could have been created on the same bar graph.
For each set of data, find the mean, median and mode. a 8, 12, 16, 13, 9, 10, 15, 12 b 12, −15, −32, −11, −15, 14, −30, −18
Find the mean and median of:
a the first 10 natural numbers. b the first 8 prime numbers. c the factors of 36.
The given bar graph shows the production of food grains in an Indian state for five consecutive years. Read the bar graph and answer the given questions.
a In which year was the production highest? What was the production in that year?
b What was the production in 2016?
c What is the ratio of the production in 2015 to the total production?
The runs scored by 11 players in a cricket match are given below: 6, 15, 120, 50, 100, 80, 20, 15, 8, 10, 15,
Prepare a frequency distribution table and find the mode and range of the given data.
The recorded rainfall values (in mm) for each of the last 10 days in Meghalaya during the month of June 2023 was:
Which measure of central tendency would be most suitable to represent the rainfall and why? What were the range of the given data?
The data shows the total population of India based on the census conducted from 1971 to 2021, after every 10 years. Draw a bar graph for the given data.
The marks obtained (out of 10) by the students in a class test are given below:
4, 6, 7, 5, 3, 5, 4, 5, 2, 6, 2, 5, 1, 9, 6, 5, 8, 4, 6, 7
Find the mean and median of the data using a frequency distribution table.
The bar graph represents the number of people who use various electronic appliances. Study the graph and answer the given questions.
a How many people use TV compared to telephones?
b How many more people use computers than iPods?
c Find the total number of people who participated in this survey.
d Give the graph a suitable title.
The number of electric bulbs sold in a store over a week is depicted in the given bar graph.
a On which day was the highest number of bulbs sold and how many?
b How many bulbs were sold in the entire week?
c What fraction of the total bulbs were sold on Tuesday?
d What is the average number of bulbs sold over the week?
Look at the bar graph which shows the approximate length of some national highways in India. Read the bar graph and answer the questions.
a Which national highway is the shortest?
b What is the length of the National Highway 9?
c The length of which National Highway is about three times the length of the National Highway 10?
The marks obtained by Kunal in his annual examination are shown below.
90 85 80
Draw a bar graph to represent the given data. Create 3 questions based on the given bar graph.
The sizes of 10 shirts are as follows: 80, 85, 90, 80, 80, 85, 85, 90, 80, 95
Find the modal size. If the size of one shirt is misread as 80 instead of 85, find the correct modal size.
The teacher of class 7 found the mean weight of a class consisting of 20 students as 45 kg. Later, two more students Ankit and Suhani weighing 55 kg and 52 kg, respectively, join the class. What is the mean weight of the class now?
Mohan secured 75, 82, 79 and 76 marks in four tests. What is the lowest number of marks he can secure in his next test, if he needs to maintain a mean score of 80 marks in five tests?
The weights (in kg) of 15 students are as follows: 27, 30, 42, 43, 36, 34, 35, 37, 28, 29, 31, 44, 41, 32, 33.
If 30 kg is replaced by 25 kg and 41 kg by 45 kg, then find the new median.
1 In the bar graph, the salaries of 5 employees are shown. Spot the error and explain why this bar graph is misleading. Represent the data in tabular form and redraw the correct graph.
₹1000
2 The bar graph given below shows the sales of books (in thousands) from six branches of a publishing company during two consecutive years, 2010 and 2011.
Read the given statements and choose the correct option.
Assertion (A): The ratio of the total sales of Branch B2 for both years to the total sales of branch B4 for both years is 210:170.
Reason (R): Ratio is the relation between two numbers which shows how much bigger one quantity is than another.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Raj Sahil Nivira Yuvan Kabir
Cross Curricular
The Geomorphology Project
Soumya, a Grade 7 student, dreams of becoming a geomorphologist. She wants to learn about the processes that shape the Earth's surface, like how mountains form and erode. Soumya has recorded the heights of various mountain peaks and put the data on a bar graph. Look at the bar graph and answer the questions.
1 The mountain peaks arranged in the decreasing order of their heights is -
a Mt Everest > Kanchenjunga > Annapurna > Nanga Parbat > Nanda Devi > Aconcagua
b Mt Everest > Kanchenjunga > Nanda Devi > Annapurna > Nanga Parbat > Aconcagua
c Mt Everest > Kanchenjunga > Nanga Parbat > Annapurna > Nanda Devi > Aconcagua
d Aconcagua > Nanda Devi > Annapurna > Nanga Parbat > Kanchenjunga > Mt Everest
2 What is the ratio of the heights of the highest and lowest peaks?
3 By how much is Mount Everest taller than the average height of the other mountains recorded by Soumya?
4 What is the median height of the mountains recorded by Soumya? If a mountain with height 8600 m is added to the list, will it affect the overall median? Justify your answer.
5 Compare the heights of these mountains with those in other parts of the world, such as the Rockies or the Alps. What differences or similarities do you notice?
4 Introduction to Probability
Let’s Recall
In a classroom of 14 students, there are 6 boys and 8 girls. We can find the ratio of the number of boys and girls and write it in the simplest form.
1 Ratio of girls to boys = Girls in the classroom Boys in the classroom = 8 6
2
3 Ratio of girls in the classroom to the total number of students = Girls in the classroom Total number of students in the classroom
Let’s Warm-up
Match the ratios to their simplest forms.
Understanding Probability
The twins, Ajay and Rocky, get a bag of marbles for their birthday. They are distributing these marbles among themselves.
Ajay: Rocky, how do we distribute these marbles? I want all of the red marbles.
Rocky: Ajay! Let us put our hands inside the bag and pick one marble at a time. I am sure you will get red every time you pick a marble.
Ajay: I think it is impossible to pick a red marble each time, Rocky. I see very few red marbles in the bag.
We can infer from the above conversation that Ajay and Rocky are trying to predict whether Ajay will be able to pick all of the red marbles from the bag.
In various life situations, we can often not accurately predict the outcome, whether the event is sure to happen or impossible. In such cases, we use words like sure, impossible, likely, unlikely or equally likely.
These terms convey the uncertainty about the happening of an event. To measure this uncertainty, we use the concept of probability.
Chance
Understanding Probability
Chance is the likelihood of some event happening. It can be expressed using words, such as sure, impossible, unlikely, even chance, likely and certain
Let us see some examples.
Impossible Event: A crow flying underwater
Sure Event: The sun rising in the East
When events have more, less or even a chance of happening, they can be called likely, unlikely or equally likely, respectively.
Likely Event: Carrying an umbrella during the monsoon
Unlikely Event: Child going to school on a Sunday
Equally likely Event: Tossing a coin and getting heads
The chance that an event will happen is called the probability of that event. Look at the spinner. Let us look at the chances of the wheel stopping at different colours.
Wheel stopping at blue:
Equally likely, as 6 out of 12, which is half of the parts, are shaded in blue (light blue and dark blue).
Wheel stopping at green:
Impossible, as the colour is not on the wheel.
Wheel stopping at red:
Unlikely, as 3 out of 12 parts are shaded in red.
Wheel stopping at blue, red or
Sure, as wherever the wheel stops, it will stop on one of these colours.
Example 1: What are the chances of the given events when you roll the dice?
1 Getting a 3, 4 or 5. Equally likely
2 Getting a 6. Unlikely
3 Getting a number from 1 to 6. Sure
4 Getting the number 0. Impossible
Example 2: Name one event for each.
1 Sure: Birds flying in the air
2 Impossible: A man flying in the air
3 Equally likely: Getting either an odd number or an even number on rolling a dice
Example 3: Suman spins a spinner. What is the chance of the following events?
1 Getting the letter A.
Equally likely as 3 out of 6 parts have the letter A.
2 Getting the letter B.
Unlikely, as 1 out of 6 parts have the letter B.
3 Getting the letter D.
Impossible as the letter D is not there on the spinner.
Example 4: Keshav draws a card from a set of cards numbered from 51 to 100. Write the chance of drawing these number cards, in words.
1 A multiple of 10.
Multiples of 10 between 51 and 100 are 60, 70, 80, 90 and 100. 5 out of 50 cards are multiples of 10. So, the event is unlikely.
2 Odd numbered card.
Number of odd numbers between 51 to 100 = 25. 25 out of 50 cards are odd numbered cards. So, the event is equally likely.
Write the chance of the given events happening, using words like sure, impossible, likely, unlikely and equally likely.
a Getting a number greater than 5 on rolling a dice.
b Getting heads on tossing a coin.
c A lion flying in the sky.
d A child going to school on Monday.
e Picking a pencil from a box of pencils.
Ramesh spins the spinner as shown. What is the chance of the following events?
a Getting an even number.
b Getting a number from 1 to 10.
c Getting the number 5 or 6.
d Getting the number 20.
Ajay spins the spinner. What is the chance of the spinner stopping at:
a yellow?
b red?
c green?
In football, a goal is scored when the ball completely crosses the goal line between the two goalposts and beneath the crossbar. What is the likelihood of securing a goal in the 11th attempt if a team secures 5 goals out of 10 attempts?
Era draws a card from a set of cards numbered from 1 to 40. Write the chance of drawing these number cards, in words.
a Factor of 40 b Even-number card Draw a spinner with
1 to 5 where the number 3 has an ‘equally likely’ probability.
Name one event for each.
You are playing a game using the spinners shown. Answer the questions.
a You want to move down. On which spinner are you more likely to spin “Down”? Explain.
b You want to move forward. Which spinner would you spin? Explain.
Theoretical Probability
Ajay and Rocky want to know the probability of picking a red marble from the bag of marbles.
Let us help Ajay and Rocky understand how to find the probability of getting a red marble.
The probability of an event is the number that measures the chance or likelihood that an event will occur. Probabilities are between 0 and 1, including 0 and 1. We can sometimes measure probability using fractions.
Let Us Understand Some Terms
Outcomes and Events
Experiment: An action that produces clearly defined results is called an experiment. Flipping a coin and rolling dice are examples of an experiment.
Outcome: Each possible result of an experiment is called its outcome. For example, getting tails when a coin is tossed is an outcome.
Event: A collection of one or more outcomes is an event.
Favourable Outcome: The outcome that is the same as what we guessed is called a favourable outcome.
Finding the Probability of an Event
When all possible outcomes are equally likely, the probability of an event is the ratio of the number of favourable outcomes to the number of possible outcomes. The probability of an event is written as P(event).
P(event) = number of favourable outcomes number of possible outcomes
This is also known as the theoretical probability.
Let us now find the probability of getting a red marble from the bag of 20 marbles. Given below are the marbles that were in the bag.
The bag has a total of 20 marbles. There are only 4 red marbles in the bag.
The chance of selecting a red marble is 4 out of 20. We can write the probability of the event as: 4 20
Number of favourable outcomes
Number of possible outcomes = 1 5
Example 5: Ajay spins the colour spinner. Answer the questions.
1 How many possible outcomes are there?
On the spinner, there are 3 reds, 1 blue, 1 green and 1 purple. So, the number of possible outcomes = 6.
2 How many times can the arrow land on red?
Since there are 3 reds, the arrow can land on red 3 times.
Probability of an event
3 How many times can the arrow land on all the colours but not purple?
Since there are 5 other coloured sections on the spinner except purple, the arrow can land on other colours 5 times.
Example 6: What is the probability of guessing the correct answer to a true-false question?
In a true-false question, either the answer is true or false. So, total number of outcomes = 2
Favourable outcomes = 1
Probability of getting a correct answer = 1 2
Example 7: Ramesh rolls the dice. What is the probability of rolling an odd number?
There are 6 numbers on a dice. 3 of them are odd numbers 1, 3 and 5.
P(event) = number of favourable outcomes number of possible outcomes
P(odd) = 3 6
On simplifying the fraction, we get, P(odd) = 1 2
Therefore, the probability of rolling an odd number is 3 6 or 1 2
Did You Know?
S.R. Srinivasa Varadhan is an Indian mathematician awarded the 2007 Abel Prize by the Norwegian Academy of Sciences and Letters for his fundamental contributions to probability theory.
Example 8: Use the spinner to find the theoretical probability of the event for the given events.
1 Spinning blue.
Total number of outcomes = 6
Number of blues = 2
Probability of getting blues = 2 6 = 1 3
2 Spinning a factor of 6.
Factors of 6 = 4 factors (1, 2, 3, 6)
Probability of getting a factor of 6 = 4 6 = 2 3
2 3 5 4 6 1
Example 9: Rakesh randomly chooses one of the letters in the word EXPLORE. What is the theoretical probability of choosing a vowel?
P(event) = number of favourable outcomes number of possible outcomes
There are 3 vowels in the word EXPLORE (e, o and e).
There are a total of 7 letters.
Therefore, the probability of choosing a vowel is 3 7
Example 10: A box contains 5 blue marbles, 4 red marbles, 6 black marbles, 4 white marbles and 5 green marbles. One marble is drawn at random. Write each probability as a fraction.
1 P(green)
Number of green marbles = 5; total number of marbles = 5 + 4 + 6 + 4 + 5 = 24
P(green) = 5 24
2 P(not blue)
Number of marbles not blue = 4 + 6 + 4 + 5 = 19; total number of marbles = 5 + 4 + 6 + 4 + 5 = 24
P(not blue) = 19 24
3 P(red or black)
Number of red or black marbles = 4 + 6 = 10; total number of marbles = 5 + 4 + 6 + 4 + 5 = 24
P(red or black) = 10 24 = 5 12
There are 10 cards in a box which are marked with distinct numbers from 1 to 10. If a card is drawn without looking, what is the probability of drawing a prime number card?
Cards in the box are 1, 2,
The number of cards that have prime numbers is
Total number of cards =
Therefore, the probability of drawing a prime number card = .
Sameer spins the number spinner shown. Answer the questions.
a How many possible outcomes are there?
b What are the favourable outcomes of spinning a number greater than 3?
c How many times can the arrow land on an even number?
d How many times can the arrow land on a prime number?
What is the probability of guessing the correct answer to a multiple-choice question if there are 5 choices?
Apples and peaches are good sources of vitamin C, which supports immune function and skin health. There are 12 pieces of fruit in a bowl. Seven of the pieces are apples, and two are peaches. What is the probability that a randomly selected piece of fruit will not be an apple or a peach?
Each letter of the alphabet is printed on an index card. What is the theoretical probability of randomly choosing any letter except Z?
Anand plays a word board game. He places 98 lettered tiles and 2 blank tiles in a bag. Players will draw tiles from the bag one at a time without looking. What is the probability that the first tile drawn will be?
a A blank tile
b Labelled with a letter
Use the spinner to find the theoretical probability of the event for the given events.
a Spinning red
c Spinning an odd number
e Spinning a number less than 7
b Spinning a 1
d Spinning a multiple of 2
f Spinning a 9
A dodecahedron has 12 faces numbered 1 through 12. Find the probability and describe the likelihood of each event.
a Rolling a 1
c Rolling a multiple of 3
b Rolling a number less than 9
d Rolling a number greater than 6
A box contains 6 black crayons, 4 blue crayons, 5 red crayons, 3 yellow crayons and 2 white crayons. One crayon is chosen at random. Write each probability as a fraction.
A letter is picked at random from the word EFFERVESCENCE. Which of the given statement(s) is TRUE about the letter picked?
a The probability of picking the letter E is 5 12
b The probability of picking the letter F is the same as that of the letter C.
c The probability of picking the letter V is the least.
d The probability of picking the letter R is 1 13 .
Numbers from 1 to 25 are written on slips of paper and one is selected at random. Write the theoretical probability of each event.
a P(odd number)
c P(not 4)
b P(three-digit number)
d P(positive number)
Write 2 events based on the situation given in Q10. Write their theoretical probability.
Challenge
Amit calculates the probability of getting a number less than 3 when randomly choosing an integer from 1 to 10.
Favourable outcomes
Total outcomes = 3 10
Describe Amit’s error and give the correct probability.
Experimental Probability
Ajay and Rocky think of checking how many red marbles Ajay gets when he picks marbles at random from the bag. They start picking marbles one by one from the bag and listing the frequencies in a table.
They are surprised to note that they picked red marbles as many as 7 times in 20 trials.
Probability that is based on such observations or repeated trials of an experiment is called experimental probability.
The experimental probability of a red marble being picked is 7 20
Think and Tell
P(event) = Number of times the event occurs
Total number of trials
How does the experimental probability compare with the theoretical probability of picking a red marble?
Example 11: The table shows the results of spinning a coin 25 times. What is the experimental probability of getting heads?
Heads turned up 6 times in a total of 6 + 19 = 25 spins.
P(event) = number of times the event occurs total number of trials
P(heads) = 6 25
Therefore, the experimental probability is 6 25.
Example 12: The table shows the results of rolling a dice 50 times. What is the experimental probability of rolling an odd number?
The table shows 10 ones, 8 threes and 11 fives.
So, an odd number was rolled 10 + 8 + 11 = 29 times in a total of 50 rolls.
P(event) = number of times the event occurs total number of trials
P(odd) = 29 50
Therefore, the experimental probability is 29 50.
Example 13: The bar graph shows the results of spinning the spinner 100 times.
Write the theoretical and experimental probabilities of the events.
1 Spinning a number greater than 4.
Numbers on the spinner greater than 4 = 2 (5, 6)
Theoretical probability of spinning a number greater than 4 = 2 6 = 1 3
Number of times a number greater than 4 is spun = 13 + 16 = 29
Experimental probability of spinning a number greater than 4 = 29 100
2 Spinning a multiple of 2.
Multiples of 2 = 2, 4, 6
Theoretical probability of spinning multiples of 2 = 3 6 = 1 2
Number of times multiples of 2 are spun = 22 + 19 + 16 = 57
Experimental probability of spinning multiples of 2 = 57 100
The spinner shows 3 different colours and 3 numbers, one on each section. The spinner is spun 15 times, and the outcome is recorded in the table below. Find the probability of the spinner stopping at the numbers 6 and 7.
P(event) = number of times the event occurs total number of trials
P(6) =
P(7) =
The probability of the spinner stopping at 6 = . Probability of the spinner stopping at 7 = .
Do It Yourself 4C
A spinner has four sections marked A, B, C and D. The table shows the results of several spins. Find the experimental probability of spinning each letter as a fraction in its simplest form.
Malati has a bag of marbles. She removes one marble at random, records the colour and then places it back in the bag. She repeats this process several times and records her results in the table. Find the experimental probability of drawing each colour.
Mala tossed a coin many times. She got 40 heads and 60 tails. She said the experimental probability of getting heads was 40 60. Explain and correct her error.
A quality control inspector is responsible for ensuring that products meet specified standards of quality and safety before they reach the consumer. A company produces electronic devices, and it is known that 5 out of 100 of the devices are defective. The quality control inspector randomly selects a device from a batch of 100. What is the probability of selecting a device which is not defective?
Use the bar graph to find the experimental probability of the event.
a Spinning a 6
b Spinning an even number
c Spinning an odd number
d Spinning a number less than 3
e Spinning a 7
Not spinning a 1
a Spinner
One hundred and twenty randomly selected students at a school are asked to name their favourite sport. The results are shown in the table.
Find the experimental probability that a student selected at random has the response given. a P(cricket) b P(hockey) c P(baseball) d P(football)
The bar graph shows the results of spinning the spinner 200 times.
Compare the theoretical and experimental probabilities of the events.
a Spinning a 4 b Spinning a 3 c Spinning a number greater than 4 d Spinning an odd number
Create a question such that an event has the same theoretical and experimental probability.
Challenge Critical Thinking
1
There are 700 students at a high school. You survey 75 randomly selected students and find that 60 plan to go to college after completing high school. How many students are likely to go to college after completing high school?
Points to Remember
• Probability measures the chance of an event happening.
• An impossible event has no chance of happening.
• An event with even chances has the same likelihood of happening or not happening.
• A good chance event is more likely to happen than not to happen.
• A certain event has a sure chance of happening.
• An experiment is an investigation or a procedure that has varying results.
• The possible results of an experiment are called outcomes.
• A collection of one or more outcomes is an event.
• The outcomes of a specific event are called favourable outcomes.
• The probability of an event is a number that represents the likelihood that the event will occur.
• Probability that is based on repeated trials of an experiment is called experimental probability.
Rolling Dice!
Setting: In groups of 3
Materials Required: One six-sided dice, paper and pencil Method:
1 Write all the possible outcomes of rolling a dice.
2 Roll the dice and note the outcome on paper.
3 Repeat this experiment 36 times.
4 Draw a table and list the frequency of outcomes in it.
Chapter Checkup
Write the chance of the given events happening, using words like sure or impossible.
a January coming before February is a/an event.
b The sun setting in the East is a/an event.
c A child going to school on a Wednesday is a/an event.
Use the labels on the right to describe the chance that a dice when rolled will show:
a Kitten with wings b Child wearing woollens in winter
5 Choose an expression from those in the list below that best describes the probability of each outcome.
We know that all numbers on a fair dice are equally probable. Has your dice turned out to be fair?
What is the chance of the events happening? Fill in the blanks with words like sure, impossible, likely, unlikely or equally likely.
Fiction books have stories that come from the author’s imagination, whereas non-fiction books are based on real facts and true events. A library has 3000 fiction books, and 4000 non-fiction books. What is the probability that a book selected at random is fiction?
A dice is rolled once. List the outcomes in each of these events.
a A number less than 3 is rolled.
c An even number is rolled.
e A 5 is not rolled.
b A number less than 3 is not rolled.
d An even number is not rolled.
f A 7 is not rolled.
You spin the spinner. Find the favourable outcomes of the event and the number of ways the event can occur.
a Spinning a 1
c Spinning an odd number
e Spinning a number greater than 0
b Spinning a 3
d Spinning an even number
f Spinning a number less than 3
Use the spinner to find the theoretical probability of the events.
a Spinning blue
c Spinning an even number
b Spinning a 1
d Spinning a 4
10 coloured discs are placed in a hat. 5 are red, 3 are yellow and 2 are black. If one disc is drawn from the hat, what is the probability that the disc will be:
a Red? b Black?
c Red or black?
d Not black? e Blue? f Red, yellow or black?
The 26 letters of the alphabet are written on cards and placed in a box. If one card is picked at random from the box, what is the chance that the letter on the card is:
a X?
c M or N?
b A vowel?
d A letter in the word MATHEMATICS?
Each student in a class planted a tree on different days of the week. The number of students who planted a tree on a particular day is shown using the circle graph. What is the probability that a randomly picked student planted a tree on Wednesday?
The numbers from 1 to 25 are written on cards. If one card is chosen at random, what is the probability that the number on the card will be:
6 Other, 6 Number of Students Planting Trees
10
8
a An odd number? b A multiple of 5? c A factor of 24? d A number that contains the digit 2?
The bar graph shows the results of picking a numbered tile from a bag 100 times. Use the bar graph to find the experimental probability of the given events.
a Picking a 2
b Picking an even number
c Not picking a 5
d Picking a number less than 3
If the probability of an event is 1 5, how many times, on average, would you expect it to occur in 20 trials?
Challenge
Read the statements and choose the correct option.
Assertion (A): If a dice is thrown, the probability of getting a number greater than 4 and less than 5 is zero.
Reason (R): Probability of an impossible event is zero.
a Both A and R are true, and R is the correct explanation of the A.
b Both A and R are true, and R is not the correct explanation of the A.
c A is true, but R is false.
d A is false, but R is true.
In a class of 30 students, each student is given a coloured card randomly. The cards are either red, blue or green. What is the probability that a randomly selected student has a blue card? Choose the correct option.
Statement 1: There are 8 red cards.
Statement 2: The probability that a randomly selected student has a green card is 2 5 .
a Statement 1 alone is sufficient to answer the question.
b Statement 2 alone is sufficient to answer the question.
c Statements 1 and 2 together are sufficient to answer the question.
d Statements 1 and 2 together are not sufficient to answer the question.
Case Study
Cross Curricular
Suhani’s Creative Challenge
The beads jewellery market in Jaipur is a thriving segment of the city’s renowned jewellery industry, known for its rich tradition, skilled craftsmanship, and diverse range of products. Suhani creates handcrafted necklaces using colourful beads in Jaipur. She keeps all her beads in a small cloth bag. She usually makes 25 necklaces a day. When she started making her last necklace of the day, she saw that she had run out of blue beads. She counted the remaining beads in the bag. She found 5 black beads, 7 green beads, 8 red beads and 7 yellow beads. Suhani decided that these beads were enough to make a bracelet. So, she put them back in the bag and started picking beads at random to make the bracelet.
1 What is the probability that the first drawn bead is red?
a 7 27 b 8 28
c 8 27 d 8 25
2 Which of the following is an impossible event?
a The bead drawn is not red.
c The bead drawn is blue.
b The bead drawn is either green or yellow.
d The bead drawn is neither red nor black.
3 What is the probability that the bead is either red or black?
4 What is the probability that the drawn bead is neither green nor black?
5 Simple Equations
Let’s Recall
We already know how to frame algebraic expressions.
Let us look at these pictures and try to guess the algebraic expressions formed by each of them.
We don’t know the amount of money in the bag. So, let the amount be ₹x.
Let’s Warm-up
We also have a 10-rupee coin with us.
So, the total amount we have is ₹(x + 10). Here, x is the variable, and 10 is a constant.
Now, we have two bags with the same amount of money in each. Let the amount of money in each bag be ₹x.
So, the sum of money in the two bags would be ₹2x We also have a 10-rupee coin.
So, the total amount of money we have is ₹(2x + 10).
Match each statement with its expression.
Mean, Median and Mode Linear Equations in One Variable
Bhakti is a college student planning a summer holiday. To earn enough money for the trip, she has taken a part-time job at the local bank that pays ₹75 per hour. She opened a savings account with an initial deposit of ₹500 on January 1. If the summer holiday begins on April 1 and the trip will cost approximately ₹11,000, how many hours will she have to work to earn enough to pay for her holiday?
Forming Linear Equations
Let the number of hours worked by Bhakti be x
She will be earning ₹75 per hour. So, the money earned by her would be ₹75x. She already has ₹500 in her savings account. So, the total money saved by Bhakti = 75x + 500. We know that the cost of the trip = ₹11,000. So, 75x + 500 = 11,000
This is an equation in x. You can get the minimum number of hours worked by Bhakti to save ₹11,000 by solving this equation. We will solve this equation later in this chapter using different methods.
Let us form a few more equations of this type. Consider this statement: ‘Seven added to a number equals 12’. We can write the statement in an equation as: x + 7 = 12.
In the expression (x + 7), the exponent of x is 1, so it is a linear expression.
Also, (x + 7) has only one variable. Hence, we can call x + 7 = 12 a linear equation in one variable.
The word linear means forming a line. The graph of a one variable equation with the highest power of one is a straight line. That is why such equations are called linear. the variable equality equation
x + 7 = 12
x + 7 = LHS; 12 = RHS
Remember!
In an equation, the left-hand side (LHS) is equal to the right-hand side (RHS).
Let us see what value of x will make the LHS and RHS equal in the above equation.
Let us put the value of x = 2
LHS = 2 + 7 = 9 ≠ RHS = 12
Let us now put the value of x = 5
LHS = 5 + 7 = 12 = RHS
Hence, we can say that x = 5 is the solution of the given equation.
Equations can have one or more variables, and each of those variables can have a power of one or more.
An equation which involves only one variable with the highest exponent as 1 is called a linear equation in one variable
A linear equation in one variable is an equation that can be written in the form ax + b = 0, where a and b are constants and a ≠ 0.
For example: 2x + 3 = 7, x + 2 = 9, and a + 3 = 5.
What about x2 + 4 = 13? Is it a linear equation?
No, because the variable x has the exponent 2.
x + 3y = 5 is a linear equation in two variables.
2x + 3y + z = 25 is a linear equation in three variables.
Example 1: Write the given mathematical statements as linear equations.
1 The sum of x and 8 gives 12.
The sum of x and 8 is x + 8.
The equation is x + 8 = 12.
2 Three more than 2 times of x gives 17.
Two times x is 2x. Three more than two times x is 2x + 3.
The equation is 2x + 3 = 17.
Example 2: Convert the given equations into statements.
1 x + 3 = 8
The sum of x and 3 gives 8.
2 3x + 5 = 26
Five more than three times x gives 26.
Example 3: Check whether the value given in the brackets is the solution of the given equations.
1 x + 3 = 9 (x = 5)
Substituting x = 5 in the equation, we get
LHS = 5 + 3 = 8
RHS = 9
8 ≠ 9 ⇒ LHS ≠ RHS
Hence, x = 5 is not the solution of the given equation.
2 2x – 8 = 12 (x = 10)
Substituting x = 10 in the equation, we get
LHS = 2 × 10 − 8 = 20 – 8 = 12
RHS = 12
12 = 12 ⇒ LHS = RHS
Hence, x = 10 is the solution of the given equation.
Example 4: Akash scored 15 out of 41 points for the home team in a basketball game. His teammates scored x points in total. Write an equation to represent the given situation.
Points scored by Aakash + points scored by his teammates = 41
15 + x = 41; Thus, 15 + x = 41 represents the given situation.
Sahil scored twice as many runs as Aakash in a cricket match. Together, their runs fell four short of a century. Form an equation to represent the situation.
Let the runs scored by Aakash be x
Sahil scored twice as many runs as Aakash = Together, their runs fell four short of 100 = 100 − 4 = 96
This situation can be represented in the form of an equation as: x + = .
On simplifying the equation, we get, =
Which of the following are equations?
a 5x + 5 = 35 b 3a – 7 + 24 c 5x 2 + 3 2 = 18 5
Tick () the linear equations in one variable and cross () the others.
a x + 9 = 14 b x + 12 = 4
d 7x + 3 = 10 e x2 + 7 = 29
Draw balls to balance the given equation.
x + 2 = 5
Form equations for each of the given statements.
a A number added to half of itself is 9. b The sum of thrice a number and 5 is 17.
c Half of a number is 15. d Half of the sum of 32 times of a number and 5 is 27.
e Two more than the number of frogs is 8. f The number of students increased by 10 is 38.
Match each statement with its equation.
Statement
Equation
a One-tenth of a number gives 7. 10 – x = 7
b 10 subtracted from a number gives 7. x + 27 = 77
c A number subtracted from 10 gives 7. 1 10 x = 7
d The sum of a number and 27 is 77. x – 10 = 7
Write an equation for the given situations.
a I have m candies. Lina has 3 fewer candies than I have. We both have a total of 18 candies.
b Tina is c years old. Her 12-year-old sister is 3 years older than Tina.
c Rajat is twice as old as his brother Rakesh. The sum of their ages is 18 years.
d The length of a rectangle with a perimeter of 18 cm is 3 cm more than its breadth.
Check whether the value given in the brackets is the solution of the given equations.
Write the given equations in statement form.
a y – 9 = 81 b 4q – 5 = 15 c 30z = 1650
Challenge
1
Two different car rental companies charge different rates. Company A charges a $50 flat fee plus $2 per mile. Company B charges a $30 flat fee plus $3 per mile. If Neha wants to travel a distance of 10 miles, which company's car will cost her less?
Solving Equations: Same Operation on Both Sides
Earlier in this chapter we learnt how to set up an equation for the given situation. Now, we will learn how to solve the equation formed.
To maintain the equality between the LHS and RHS of the equation we perform the same operation on both sides of the equation. Look at the table below showing the equations and the operations performed to maintain the equality.
Addition
If x − 5 = 10 then
x − 5 + 5 = 10 + 5 (Adding 5 to both LHS and RHS)
x = 15
If x 3 = 9 then
x
Multiplication
If x + 2 = 5 then
Subtraction
x + 2 − 2 = 5 – 2 (Subtracting 2 from both LHS and RHS)
x = 3
3 × 3 = 9 × 3 (Multiplying both LHS and RHS by 3)
x = 27
Division
If 7x = 21 then ÷ 7 = 21 ÷ 7 (Dividing both LHS and RHS by 7)
= 3
In Bhakti’s situation, we wanted to know the number of hours she would work to save for her trip.
We had set up an equation as: 75x + 500 = 11,000 where x is the minimum number of hours.
Let us solve this equation to get the value of the variable x. First, subtract 500 from both sides of the equation.
75x + 500 – 500 = 11,000 – 500
On simplifying both sides, we get,
75x = 10,500
Remember!
Divide both sides by 75. This will give us just x on the LHS.
75x 75 = 10,500 75 ; So, x = 140
While solving a two-step equation like this, we always add or subtract the same number from both sides of the equation, then we perform multiplication or division on both sides of the equation.
Therefore, Bhakti would need to work for a minimum of 140 hours to save enough money for her trip. Let us check our result by putting the value of x = 140 in the original equation (75x + 500 = 11,000).
LHS = 75 × 140 + 500 = 10,500 + 500 = 11,000 = RHS
As LHS = RHS, our solution is correct.
Do It Together
Example 5: Solve x + 8 = −5 and verify the result. Example 6: Solve 13a – 7 = 19 and verify the result.
We shall subtract 8 from both sides of the equation.
x + 8 – 8 = −5 – 8
On simplifying both sides, we get,
x = −13
Verification: Substituting x = −13 in the given equation
x + 8 = −5, we get
−13 + 8 = −5
−5 = −5
Hence, the solution is verified as correct.
Example 7: Solve 5x 2 = 25
5x 2 × 2 5 = 25 × 2 5 [Multiplying both sides by 2 5 ]
⇒ 5 2 × 2 5 × x = 25 × 2 5
We shall add 7 to both sides.
13a – 7 + 7 = 19 + 7
On simplifying both sides, we get, 13a = 26
We will now divide both sides by 13.
13a 13 = 26 13 ; So, a = 2.
Verification: Substituting a = 2 in the given equation
13a – 7 = 19 we get
13 × 2 −7 = 21
21 = 21
Hence, the solution is verified as correct.
Example 8: Solve 5m 4 + 13 = 23
x = 10 5m 4 + 13 – 13 = 23 – 13 [Subtracting 13 from both sides] 5m 4 = 10 5m 4 × 4 5 = 10 × 4 5 ⇒ 5 4 × 4 5 × m = 10 × 4 5 [Multiplying both sides by 4 5 ] m = 8
1 Solve 13c 12 = 9.
We shall multiply both sides of the equation with 13c 12 × = 9 × ⇒ 13 12 × × c = 9 ×
On simplifying both sides, we get, c =
2 Solve 3b + 20 = 32 and verify the result.
We shall subtract from both sides of the equation.
3b + 20 – = 32 –
On simplifying both sides, we get,
3b =
We should now divide both sides of the equation by .
3b = ⇒ b =
Verification: Substituting b = in the given equation, we get
3 × + 20 = + = = RHS
Hence, the solution is verified as correct.
Write the first step you will use to separate the variable and then solve the equation.
Solve the given equations and verify the answer.
Aakash solved the equation 12 + x = 20 and got 32. Is the answer correct? If not, find the correct answer.
Describe a real-world situation for each of the given equations and solve.
Challenge
What would you do to make equation 1 and equation 2 equivalent?
Solving Equations: Transposition
We know the equation, 75x + 500 = 11,000 where x is the minimum number of hours. Instead of subtracting 500 from both sides of the equation, we can move 500 from the LHS to the RHS by reversing the operation from addition to subtraction.
75x = 11,000 – 500
On simplifying the equation, we get,
75x = 10,500
Instead of dividing both sides by 75, we can simply move 75 from the LHS to the RHS by reversing the operation from multiplication to division.
x = 10,500
On further simplification, we get, x = 140
Thus, Bhakti would have to work for a minimum of 140 hours to save enough money for the trip.
We got the same value for the variable despite using different methods.
Did You Know?
The idea of using letters to represent variables was first suggested by French mathematician François Viète (1540–1603) in his work.
The method used above for solving the equation is called the transposition method. In this method, we move terms from one side of the equation to the other with the purpose of separating the variable on one side, and the constants on the other side. However, while moving the terms from one side of the equation to the other, we should change the operator sign as:
Remember!
Transpose means to change the position or order of two things. Using the transposition method, we shift a term from one side to the other.
Example 9: Solve x + 15 = 32 and verify the result.
x = 32 – 15 [Transposing 15 from LHS to RHS]
x = 17
So, x = 17
Example 11: Solve x + 8 3 = 13.
x + 8 = 13 × 3 [Transposing 3 from LHS to RHS]
x + 8 = 39
x = 39 – 8 [Transposing 8 from LHS to RHS]
So, x = 31
Example 13: (x + 2) 5 = (2x 8) 6
(x + 2) 5 = (2x 8) 6 [Cross multiply]
6(x + 2) = 5(2x 8)
6x + 12 = 10x − 40
12 + 40 = 10x − 6x ⇒ 52 = 4x or 4x = 52
x = 52 4 = 13
Simple Equations
Example 10: Solve 5x – 7 = 13.
5x = 13 + 7 [Transposing 7 from LHS to RHS]
5x = 20
x = 20 5 [Transposing 5 from LHS to RHS]
So, x = 4.
Example 12: 5x + 9 = 7x – 1
9 = 7x – 5x– 1 [Transposing 5x from LHS to RHS]
⇒ 9 = 2x −1
9 + 1 = 2x ⇒ 2x = 10 [Transposing –1 from RHS to LHS]
x = 10 2 = 5 [Transposing 2 from LHS to RHS]
Example 14: 2 5 (x – 3) + 1 2 (x + 5) = 4
Multiply both the sides with LCM of 5 and 2 = 10
10 × 2 5 (x − 3) + 10 × 1 2 (x + 5) = 10 × 4
4(x − 3) + 5(x + 5) = 40
4x −12 + 5x + 25 = 40
9x + 13 = 40
9x = 40 – 13 = 27 ⇒ x = 27 9 = 3
1 Solve 13c 12 = 26 and verify the result.
13c = 26 × 12 [Transposing ______ from LHS to RHS]
13c =
c = [Transposing from LHS to RHS]
So, c =
Verification: Substituting c = in the given equation we get
13 × 12 = 12 = = RHS
Hence, the solution is verified as correct.
3 Solve 0.8(2x − 3) – 0.5x = 6.
2 Solve 3b + 20 = 32 and verify the result.
3b = 32 – 20 [Transposing from LHS to RHS]
3b =
b = [Transposing from LHS to RHS]
So, b =
Verification: Substituting b = in the given equation we get
3 × + 20 = + = = RHS
Hence, the solution is verified as correct.
1.6x – 2.4 – 0.5x = 6 [Opening the brackets of LHS]
1.6x – 0.5x = 6 + 2.4
On simplifying the RHS, we get, x =
Error Alert!
The number lying exactly outside the brackets should not be moved to the other side before opening the brackets.
Do It Yourself 5C
Solve each equation by the transposition method.
a x + 4 = 10 b a + 9 = 13 c x + 2 7 = 5 7
d n + 2.6 = 4 e x – 9 = 3 f x – 5.4 = 12.8
g −14 + a = 27 h p –5 9 = 7 9 i x – 6.5 = 15
Solve each of the equations.
2x 4.5 = 30 2
a 4y = 20 b 90 = 15y c −9a = 108 d −7m = −21
j 8 = 6 f x 3 = −11 g w 9 = −5
g 3.2 = 20
Solve the given equations.
a 6x + 14 = 16 b 7 + 5x – 3x = 21 c 1.2x + 4.8x = 18
d 6(5x − 2) + 2 = 30 e 7(x − 4) + 13 = 6
g 5(3x − 2) + 5 = 5x +15 h (x – 10) 3 = (5 – 3x) 4
5x + 12 = 0.2(10x −15)
j 3(x − 6) + 4(x + 4) = 5(x − 2) k 1 2 (3x + 1) –2 3 (2x + 5) = 3 2 l 1
Give three linear equations in which x = –3 satisfies the equation.
Challenge
What is the number?
a I’m thinking of a number. If 60 is subtracted from it, the result is 4.
b The sum of 13 and an unknown number is 46.
c A certain number decreased by 21 is 81.
d The product of 7 and a number is 56.
e A number when divided by 7 gives the quotient 5.
f If 10 is subtracted from thrice a number, the answer is 35.
g A number is multiplied by 3 and then 5 is added to it to get the answer as 20.
Applications of Simple Equations
In general, we come across many real-life problems, which can be solved using the concept of linear equations in one variable.
Let us solve a real-life problem using some steps.
Kajal takes 10 rounds in a square garden. Find the side of the square if the total distance covered by her is 2560 m.
Step 1: Note down what is given and what is required.
Given: The garden is square.
Required: Measure of each side of a square garden.
Step 2: Denote the unknown by some variable. Let the measure of each side of this square garden be x.
Step 3: Translate the statements into algebraic expressions.
Taking 1 round of the square garden = Perimeter of the garden = 4x
Step 5: Solve the equation to find the value of the variable.
4x = 2560 10 ; x = 64 m
So, each side of the square garden measures 64 m.
Step 4: Form an equation as per the condition given in the problem. 10 × 4x = 2560
Example 15: Fifteen subtracted from five times a number gives 5. What is the number?
Let the number be x
Given that fifteen subtracted from five times a number gives 5.
Equations
So, the equation can be written as: 5x – 15 = 5.
Add 15 to both sides of the equation,
5x – 15 + 15 = 5 + 15 ⇒ 5x = 20
Divide both sides of the equation by 5.
5x 5 = 20 5 ⇒ x = 4
Hence, the required number is 4.
Example 16: The sum of two numbers is 25. If one of the numbers exceeds the other by 7, then find the numbers.
Let the first number be x; The second number will be x + 7.
As per the given condition, x + x + 7 = 25
On simplifying, we get, 2x + 7 = 25
x = 18 2 ; x = 9
So, one of the numbers is 9. The other number = x + 7 = 9 + 7 = 16.
So, the required numbers are 9 and 16.
Example 17: The sum of two consecutive numbers is 13. Find the numbers.
Let one number be x; Its consecutive number will be (x + 1).
As per the given condition, x + (x + 1) = 13
On simplifying, we get, 2x + 1 = 13
x = 12 2 ; x = 6
So, one of the numbers is 6. The other number is 6 + 1 = 7.
Example 18: The cost of three pens and four pencils is ₹248. If one pen costs ₹15 more than one pencil, then find the cost of each pen and each pencil.
A pen costs ₹15 more than a pencil. So, the cost of the pen is dependent on the cost of the pencil.
Hence, let us assume the cost of one pencil to be x.
Then the cost of a pen = 15 + x
The cost of 4 pencils = 4x and the cost of 3 pens = 3(15 + x)
Total cost of 3 pens and 4 pencils = ₹248
3(15 + x) + 4x = 248
On opening the brackets, we get,
45 + 3x + 4x = 248
On simplifying, we get,
45 + 7x = 248
x = 203 7 ; x = 29
Thus, the cost of a pencil is ₹29. And the cost of a pen = 15 + x = 15 + 29 = ₹44.
The cost of each pen is ₹44, and the cost of each pencil is ₹29.
Example 19: There are 50 paise and 20 paise coins in a purse. The number of 20 paise coins is 4 times that of 50 paise coins. If the total value of the money is ₹26, find the number of coins of each denomination.
Let the number of 50 paise coins be x.
Then, the number of 20 paise coins will be 4x.
Therefore, the value of x coins of 50 paise = 50x paise
Also, the value of 4x coins of 20 paise = 20 × 4x paise = 80x paise
The total value of the money = ₹26 or 2600 paise
As per the given condition, we have,
50x + 80x = 2600
On simplifying, we get,
x = 2600
130 ; x = 20
Since, x = 20, 4x = 4 × 20 = 80
Hence, there are 20 coins of 50 paise and 80 coins of 20 paise.
Example 20: Suhani is four times as old as Rahul. Five years ago, the sum of their ages was 50. What are their present ages?
Let the present age of Rahul be x
Present age of Suhani = 4 times the age of Rahul = 4x
Rahul’s age 5 years ago = x − 5
Suhani’ age 5 years ago = 4x – 5
Given that the sum of Suhani and Rahul’s age 5 years ago was 50, we get,
(x – 5) + (4x – 5) = 50
x – 5 + 4x – 5 = 50
5x –10 = 50 ⇒ 5x = 50 + 10
⇒ 5x = 60 ⇒ x = 12
Hence, Rahul’s present age = 12 years and Suhani’s present age = 4 × 12 = 48 years.
The length of a rectangular plot exceeds its breadth by 5 metres. If the perimeter of the plot is 142 metres, find the dimensions of the plot.
Let the breadth of the plot be x metres.
So, the length will be (x + 5) metres.
We know that perimeter of a rectangle = 2(Length + Breadth)
As per the given condition, 2(x + 5 + x) = 142 metres
On simplifying the LHS, we get,
2(2x + 5) = 142 ⇒ _____ + 10 = _____
On transposing 10 from the LHS to the RHS, the operation changes from addition to subtraction.
4x = 142 − 10
On simplifying, we get,
x = 132
4 ; x =
Breadth of the rectangular plot is metres.
Length of the rectangular plot is metres.
Twice the number decreased by 22 is 48. Find the number.
A number when added to its half gives 72. Find the number.
The sum of two numbers is 95. If one exceeds the other by 3, find the numbers.
Divide 20 into two parts so that one part is 8 more than the other. What are the two parts?
Find three consecutive numbers so that the sum of the second and the third exceeds the first by 24.
The angles of a triangle are x°, (x + 40)° and (x − 10)°. Find the angles.
Three sides of a triangle measure (2x + 3) units, (2x + 5) units and 3x units. Find the measure of the sides if its perimeter is 148 units.
The age of Olivia’s mother is 5 years more than three times Olivia’s age. Find Olivia’s age if her mother is 44 years old.
There are 320 books and magazines in total in a bookshop. There are three times as many books as magazines. How many books are there?
The cost of five books and three pens is ₹730. If a book costs ₹50 more than a pen, then find the cost of the book and the pen.
Sameer has 20 stamps more than three times the number of stamps Rakesh has. If both together have 140 stamps, how many stamps does Rakesh have?
A vegetable seller has 31 kg of onions. He divides the onions in two bags so that one bag weighs 5 kg more than the other. Find the weight of the bags.
Five years from now, Satish will be 11 2 times his present age. How old is he now?
A bat and a ball together cost ₹1200. The cost of the ball is 1 5 of the cost of the bat. Find the costs of the bat and the ball.
Heena’s mother is 4 times as old as she is. After 20 years, her age will be twice that of Heena’s. Find their present ages.
Two small jugs and one large jug can hold 8 cups of water. One large jug can hold 2 cups more than the small jug. Find out how many cups of water each jug can hold.
Nisha saves money in her money bank. She has ₹10 and ₹20 notes in her money bank. The number of ₹10 notes is 3 times that of ₹20 notes. If the total amount is ₹250, find the number of notes of each denomination. Why is saving money important?
Points to Remember
• An equation is a statement of equality which has one or more than one variable.
• An equation in one variable is called a linear equation if the highest power of the variable is one.
• The value of the variable in an equation is called the solution of the equation.
• To solve an equation, we can:
a Add the same number on both sides.
b Subtract the same number from both sides.
• The process of shifting a number from one side of an equation to the other by changing the sign is called transposition. Savita is Tina’s older sister. The sum of the ages of Savita and Tina is 18 years, and the difference of their ages is 4 years. Find the ages of Savita and Tina.
c Multiply both sides by the same non-zero number.
d Divide both sides by the same non-zero number.
Math Lab
Setting: In groups of 3.
Collaboration & Experiential Learning
Modelling Simple Equations!
Materials Required: Rectangular paper strips in blue and square paper strips in yellow and pink. Method:
1 Make rectangular paper strips coloured blue and square paper strips coloured yellow and pink from the chart paper.
2 A blue rectangular strip represents a variable. A yellow square strip represents a positive constant, and a pink square strip represents a negative constant.
3 A yellow and a pink strip collectively represent zero.
4 Think of a linear equation, say 3x + 4 = 2x – 5.
5 Represent the linear equation by using rectangular and square strips.
6 Subtract or remove strips to solve the equation.
7 Repeat the same process to find the solution for other linear equations.
Chapter Checkup
Frame equations for the given situations.
a One and a half times a number is 150.
b I am thinking of a number. Five times that number is 65.
c 3 subtracted from 5 times of p gives 22.
d Double of a number added to 36 gives 48.
e 31 is 9 more than 4 times the number p.
Find the value of the unknown by performing the same operation on both sides.
a x – 3 = −20
x – 3 = 7 d x + 5 19 = 3 19
Solve the equations.
a 9x = 18
d −18 = −6x
g y + 7 = 4
4a = 12
x + 10 = −10
−3y = −27
x – 17 = −20
Find the solution of each of the equations.
12
d −13 2 x = 26
=
f 9(x + 14) = 27 g 3 − x 5 = 6
The Sroda Treasure is the world's greatest treasure discovered in Poland in the 1980s. Nikita found an old treasure map that leads to a hidden treasure. The map contains a series of clues that involve solving equations to reveal the final code to open the treasure. The clues can be given as: a 5m + 3 = 28
Help Nikita find the final code if it can be denoted by the word “moon”.
Nine added to thrice a whole number gives 45. Find the number.
Two-thirds of a number is greater than one-third of the number by 3. Find the number.
Divide 38 into two parts so that one part is 18 more than the other.
The length of a rectangle is 5 m greater than its breadth, and its perimeter is 250 m. Find the length and breadth of the rectangle.
Rohan went to the market with some money. He spent one-third of the money on buying medicines. He saw a donation box outside the medical store and donated ₹50. How much money did Rohan initially have if he was left with ₹350? Where have you seen such donation boxes? Discuss with your friends and family about these donation drives.
When you divide a certain number by 13, the quotient is −18 and the remainder is 7. Find the number.
Find three consecutive even numbers whose sum is 96.
Find three consecutive numbers so that the sum of the second and the third number exceeds the first by 14.
If one side of a square is represented by 4x – 7 and the adjacent side is represented by 3x + 5, find the value of x
Each of the two equal sides of an isosceles triangle is three times as large as the third side. If the perimeter of the triangle is 28 cm, find each side of the triangle.
There are three packets of goods, p, q and r. The weight of packet p is 1 1 2 kg more than that of packet q, and the weight of packet r is 2 1 2 kg more than that of packet q. If their total weight is 32 kg, find the weight of the packets.
The price of 2 notebooks and 3 textbooks is ₹120, but a notebook costs ₹10 more than the textbook. Find the cost of both the notebook and the textbook.
Ramesh has a certain number of toffees. His sister has double the number of toffees compared to Ramesh. If together they have 54 toffees, then how many toffees does Ramesh have?
Challenge
d Both statements together are not sufficient. 1 2
Read the statements and decide which of the given options is correct.
Assertion (A): The solution of the equation (4x − 7) = (2x − 5) is −1.
Reason (R): Adding or subtracting the same number from both sides of an equation keeps the equation balanced.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Sushant gave an exam in which 5 marks are given for every right answer, and 2 marks are deducted for every wrong answer. How many right answers did Sushant gave?
Statement 1: Sushant scored a total of 120 marks.
Statement 2: Sushant attempted 45 questions out of the given 50 questions.
a Statement 1 alone is sufficient, but Statement 2 alone is not sufficient.
b Statement 2 alone is sufficient, but Statement 1 alone is not sufficient.
c Both statements together are sufficient.
Cross Curricular
Atomic Charge Equations
The overall charge of an atom is determined by adding the charges of its electrons and protons. Negatively charged ions are referred to as anions, while positively charged ions are known as cations. For example the overall charge of the sodium cation is −10 + a. Read the table and answer the questions.
cation
1 Which of the given expressions shows the overall charge of the chlorate anion?
a b + 17 b −b + 17
c b − 17 d −b – 17
2 Which of the following equations shows the charge from the proton in the carbonate anion if the overall charge of the atom is −2.
a f – 2 = −32
b f = −32 −2
c f + 32 = −2 d f = −2 + 32
3 What is the charge from a proton in a sodium cation if the overall charge of the atom is +1?
a 9 b 10
c 11 d −11
4 What is the charge from the electron in the magnesium anion if the overall charge of the atom is +2?
5 The overall charge of the atom in the barium cation is +2. The charge from the proton in the cation is 110 more than the charge from an electron. What is the charge from the electron and proton in the cation?
6 Angle Pairs and Parallel Lines
Let’s Recall
To help understand how much a line segment, line or ray is inclined on another, we have the geometrical idea of angles.
Steps to measure an angle using a protractor
1 Place the centre of the protractor over the vertex (the point where the two arms of the angle meet).
2 Make sure that the baseline of the protractor (the straight line at the bottom) is aligned with one of the angleʼs arms.
3 Look at where the other arm of the angle crosses the markings on the protractor. The number where the arm crosses is the measure of the angle in degrees.
Measure of the angle in degrees
Let’s Warm-up
Measure the angles. Fill in the blanks.
Angle Pairs
The teacher asked the students to find examples for different types of angles that they see around them.
Mukesh: I found an angle in the partially opened door. I found an angle when I open the book and hold the other end.
Teacher: Now, try to find the measure of these angles and find the sum.
Mukesh: They are adding up to 180°.
Teacher: These are related to a special geometrical concept. We will learn more about them today.
Pairs of Angles
Angle pairs are pairs of angles that can be classified on the basis of their properties. They can be complementary, supplementary, adjacent or linear pairs of angles.
Complementary and Supplementary Angles
Complementary Angles
Angles pairs that add up to 90°.
One angle is a complement of the other.
Did You Know?
Eratosthenes was an ancient Greek scholar who calculated the size of the Earth by using the angles of the sunʼ s rays at noon at two different locations, Alexandria and Syrene.
Supplementary Angles
Angles pairs that add up to 180°.
One angle is a supplement of the other.
Example 1: Check whether the angles are complementary or supplementary.
1 24°, 66°
24° and 66° are complementary angles because their sum is 90°.
2 168°, 12°
168° and 12° are supplementary angles because their sum is 180°.
Remember!
3 29°, 61°
29° and 61° are complementary angles because their sum is 90°.
Supplementary and complementary angles may or may not have a common arm.
Example 2: Find the complement and supplement of the given angles.
1 17°
Complement of 17° = 90° – 17° = 73°; Supplement of 17° = 180° – 17° = 163°
2 83°
Complement of 83° = 90° – 83° = 7°; Supplement of 83° = 180° – 83° = 97°
Think and Tell
Are angles AOC and COB supplementary?
Measure the angles and label them as complementary or supplementary angles. Do It Together
Adjacent Angles
Two angles are classified as adjacent when they share a common arm, a common vertex, and their non-common sides extend to the opposite sides of the common arm. For example: ∠XOY and ∠YOZ are adjacent angles with a common vertex O and a common arm OY.
Example 3: Name the adjacent angles of the angles given below.
1 ∠POQ
1 Adjacent angles of ∠POQ are ∠POT and ∠QOR.
2 Adjacent angles of ∠TOS are ∠ROS and ∠POT.
3 Adjacent angles of ∠ROS are ∠TOS and ∠QOR.
4 Adjacent angles of ∠POT are ∠POQ and ∠TOS.
Fill in the blanks with the names of adjacent angles.
Think and Tell
Is there any adjacent pair of angles on line XY?
1 Adjacent angles of ∠FCE are ∠DCE and ∠FCA.
2 Adjacent angles of ∠ACB are and .
3 Adjacent angles of ∠ECD are and .
4 Adjacent angles of ∠FCD are and
Linear Pair of Angles
A linear pair of angles comprises two adjacent angles whose sum is 180°. These angles share a common vertex and a common side, while their non-shared sides together create a straight line.
For example, in the adjoining figure, ∠KOL and ∠MOL are a linear pair of angles.
Let us now measure the angles in the given figure to find the linear pair of angles.
∠ACG = 60°, ∠ACD = 100°, ∠GCB = 120°, ∠DCB = 80°, ∠ACF = 135°, ∠FCB = 45°.
Here, the linear pairs of angles are:
∠ACG and ∠GCB
∠ACD and ∠DCB
∠ACF and ∠FCB
Example 4: Check whether the given adjacent angles are linear pair of angles.
56°, 56°
Sum of angles = 56° + 56° = 112°
(Since the angles do not add up to 180° they are not a linear pair of angles.)
Example 5: Solve for x. (4x + 10)° (x – 20)° 4x + 10° + x – 20° = 180° (Linear pair of angles)
x – 10° = 180°
= 190° ⇒ x = 38°
Find the value of x in each case:
Vertically Opposite Angles
Vertically opposite angles are pairs of angles that are formed by the intersection of two lines, and they share the same vertex while being opposite to each other. These angles are always equal in measure.
For example, ∠KON and ∠LOM are a pair of vertically opposite angles. Similarly, ∠KOL and ∠NOM are also a pair of vertically opposite angles.
Let us see some important rules.
The sum of all angles about a point is equal to 360°.
For example: ∠1 +
360°
Example 6: Look at the figure and answer the questions.
The sum of all the angles lying on one side of a line at a specific point equals 180°
1 Are the following pairs of angles vertically opposite angles?
∠AXT, ∠YXC: Yes ∠PCQ, ∠BCQ: No
∠YBC, ∠YBS: No ∠AYU, ∠XYB: Yes
2 Find the vertically opposite angle to:
∠PCQ—∠XCB is vertically opposite to ∠PCQ.
∠YBC—∠SBR is vertically opposite to ∠YBC.
Example 7: The supplement of an angle is one-third its measure. Find the angle and its supplement. Let the measure of the required angle be x.
Supplement of x = 180°– x
Supplement of x = 1 3 x
180° – x = 1 3 x
3(180° – x) = x
540° – 3x = x
540° = 4x
x = 135°
Supplement of the angle = 180° – 135° = 45°
So, the angle is 135° and supplement of the angle is 45°.
Find the value of x in each case.
75°
(3x – 15)°
We know that vertically opposite angles are equal. Hence, 3x – 15° =
3x = 75° + 15° =
3x = 90° ⇒ x =
Check whether the given angles are complementary, supplementary or neither.
a 80°, 100° b 45°, 135° c 60°, 120° d 35°, 125°
e 27°, 63° f 40°, 53° g 37°, 37° h 78°, 33°
Find the complement and supplement of the given angles.
a 33° b 72° c 41° d 89°
Measure the given angles. Identify whether the pairs of angles are complementary, supplementary or neither. a b c
Draw a rectangle ABCD and identify all pairs of supplementary angles.
Find the value of x.
(4X − 45)° (3x � 50)°
+ 15)°
(2x + 25)°
If the angles (3x + 10)° and (7x – 20)° are complementary angles, find the value of x
If the angles (4y + 13)° and (3y – 8)° are supplementary angles, find the measures of these angles.
Find the value of the unknown variables.
An angle exceeds its complement by 30°. Find the measure of the angle.
The traffic sign means ‘no stopping’. If one angle of intersection is 30°, what will be the measure of angle a? Give a reason for your answer.
The supplement of an angle is half its measure. Find the angle and its supplement.
Two complementary angles are in the ratio 5:4. Find the measures of the angles.
Two supplementary angles are in the ratio 13:5. Find the measures of the angles.
If one angle measures 46° less than its supplement and another angle measures 20° more than its complement, find the measures of both angles.
Challenge
Critical Thinking
The ratio between a complementary and supplementary angle of an angle is 4:9. Find the angle. 1
Parallel Lines
While having lunch, some school kids talked about their weekend experiences.
Rajni: This weekend, I explored the deep forest near our village.
Friend: Wow, that sounds thrilling! What happened next?
Rajni: I noticed something interesting about the trees. Some trees had trunks that were equally spaced from one another, whereas others leaned on or crossed over each other.
Parallel Lines and Transversals
The trees Rajni spotted in the forest area whose trunks were equidistant from each other are related to the geometry of parallel lines. Let us understand parallel lines and the associated geometry in detail.
Two or more lines are called parallel if they are in the same plane and don't cross even if you keep extending them in both directions. The distance between parallel lines is the same everywhere. We denote two lines p and q to be parallel as p ‖ q.
Parallel lines are found all around us in our daily lives. Some examples from our daily life include window blinds, zebra crossings, lines on notebook paper and railroad tracks.
When two or more lines are intersected by another line at distinct points, this line is called their transversal. The lines may or may not be parallel.
Transversal intersecting non-parallel lines
Angles Made by a Transversal
Exterior angles: ∠2, ∠3, ∠5, ∠8
Pairs of alternate exterior angles:
∠3 and ∠5, ∠2 and ∠8
Pairs of interior angles on the same side of the transversal:
∠1 and ∠6, ∠4 and ∠7
When two parallel lines are cut by a transversal:
• Corresponding angles are equal. ∠AMX = ∠CLM
Transversal intersecting parallel lines
Interior angles: ∠1, ∠4, ∠6, ∠7
Pairs of alternate interior angles: ∠4 and ∠6, ∠1 and ∠7
Pairs of corresponding angles: ∠2 and ∠6, ∠3 and ∠7
∠4 and ∠8, ∠1 and ∠5
• Alternate interior and exterior angles are equal. ∠BML = ∠MLC and ∠XMA = ∠DLY
• The sum of interior angles on the same side of a transversal is 180°.
∠AML + ∠MLC = 180°.
Conversely, if two lines intersected by a transversal have equal corresponding angles, equal alternate interior/exterior angles, and same-side interior angles adding up to 180°, then the lines are parallel.
Think and Tell
If line a is parallel to line b and line b is parallel to line c, is line a parallel to line c?
Example 8: Check whether any of the pairs of lines are parallel or not based on the information given.
Since corresponding angles are equal, the lines m and n are parallel. 1 115° 105° r p q
For 2 lines to be parallel, the alternate exterior angles should be equal. In this figure, the alternate exterior angles are 105° and 115°.
So, line p is not parallel to line q.
Let the two angles that form the linear pair be x. Therefore,
x + 65° = 180° (Linear pair)
x = 180° – 65° = 115°
Example 9: In the figure, SP ꠱ RQ and QP has been extended to T. Given ∠TPS = 95°, find the value of x°, y° and z°.
From the figure, 95° + x° = 180° (Linear pair)
x° = 180° − 95°
x° = 85°
y° = 95° (corresponding angles)
x° + z° = 180° (interior angles on the same side of the transversal)
85°+ z° = 180°
z° = 180° – 85°
z° = 95°
In the figure, it is given that PQ ꠱ XR, ∠QPR = 65°and ∠XRY = 60°. Find 1 ∠PQR 2 ∠PRQ
In the figure, ∠PQR = ∠XRY = 60° ( angles)
As the name suggests, the alternate interior angles are pairs of interior angles on either side of the transversal.
Constructing Parallel Lines
Constructing a line parallel to a given line l passing through an external point P.
Step 1: Mark point Q on line l
Step 2: Draw a line segment PQ by connecting points P and Q.
Step 3: From the point Q, draw an arc with a chosen radius to intersect line l and line segment PQ at points B and A, respectively.
A
Step 4: Draw another arc from point P, using the same radius as before, to intersect line segment PQ at point C.
Step 5: Draw an arc from point C with radius equal to AB, cutting the previously drawn arc at point D.
Step 6: Connect points PD and extend the line on both sides to obtain the desired line m, which is parallel to the given line l
Constructing a line parallel to a given line at a fixed distance.
Step 1: Choose any two points A and B on line XY.
Step 2: Construct right angles ∠CAY and ∠DBY at points A and B, respectively.
Step 3: Draw arcs with centres at A and B, each with a radius, let us say 4 cm, intersecting CA at point E and DB at point F.
Step 4: Connect points EF and extend this line on both sides to achieve the desired parallel line relative to XY, maintaining a distance of 4 cm from it.
Checking for Parallel Lines
Let us say you have been given two lines, p and q. To check whether these two lines are parallel or not, we can follow the steps given below:
1 Draw another transversal line that cuts across both lines p and q.
2 Now, where the transversal crosses lines p and q, you'll see some corresponding and alternate angles.
3 Using a protractor, measure the size of the corresponding angles (or alternate angles).
4 Compare the measurements of the corresponding angles (or alternate angles). If they have the same measurement, that's awesome! It means the lines p and q are parallel. If the measurements are not the same, the lines are not parallel.
Example 10: Draw any ΔABC. Construct a line h, parallel to BA, and position it 2 cm away from it so that it doesn’t intersect at any part of the triangle.
1 Draw ΔABC with sides of suitable length.
2 Choose any two points P and Q on the line segment AB.
3 Construct the right angles ∠XPA and ∠YQA at points P and Q, respectively.
4 Draw arcs with centres at P and Q, each with a 2 cm radius, intersecting XP at point E and YQ at point F.
5 Join EF and extend this line on both sides to achieve the desired parallel line h at a distance of 2 cm from AB.
This is a right-angled triangle ΔPQR. Construct a line t, parallel to RQ and position it 2.5 cm away from RQ so that it intersects the triangle.
Do It Yourself 6B
Check whether the following sets of lines are parallel or not by drawing a transversal and measuring alternate or corresponding angles.
Identify all the pairs of corresponding angles and pairs of alternate angles in the figure.
Check whether the lines are parallel in each case, based on the known angles.
Construct a line AB and select a point C that lies outside it. Use a ruler and compass to draw a line through C that is parallel to AB.
Draw a line parallel to a line p at a distance of 5.9 cm.
In the given figure, l ꠱ m. Also, p and q are transversals.
Note that p is not parallel to q, find the values of a° and b°.
A line (DE) parallel to the side BC of ΔABC passes through A. The angles are ∠DAB = 90° and ∠EAC = 60°. Find the measure of all the angles of the triangle.
Draw a line labelled n and construct a perpendicular line from any point on n. Select a point Q located at a distance of 5.5 cm from n along the perpendicular line. Finally, draw another line labelled m through point Q so that it is parallel to line n.
Construct ∠XYZ = 45°, ensuring that XY measures 4.2 cm and YZ measures 5.6 cm. Construct a line through Z that is parallel to YX, and another line through X that is parallel to YZ, intersecting at point D. Determine the measurements of XD, YD and ZD.
In a trapezium PQRS, it is known that PQ ꠱ RS. Also, ∠PQR = 150° and ∠QPS = 120°. Find the value of the other two angles.
Find the value of the indicated unknown angles.
Due to the effect of the wind, rain sometimes falls to the ground at an angle. If the rain makes an angle of 60° with the clouds, at what angle would this rain hit the ground? Assume that rain drops travel in a straight line. Illustrate with a rough diagram.
Find the measures of the unknown angles.
Anna wants to draw a birthday card for her grandmother. The dimensions of the card will be 10 cm × 8 cm. She wants to draw a little box in the centre to write a birthday quote for her grandmother. All of the sides of this box are 2 cm inside the respective edges of the greeting card. Suggest the construction steps to neatly draw this box on the greeting card. Do you draw cards for your family members?
[Hint: Construct a line that runs parallel to the edges of the greeting card, maintaining a distance of 2 cm from the edges.]
Points to Remember
• The sum of supplementary angles is 180°.
• The sum of complementary angles is 90°.
• Adjacent angles have a common vertex and a common arm.
• A linear pair of angles shares a common vertex and a common side, while their non-shared sides together create a straight line.
• Vertically opposite angles are angles that are opposite to each other when two lines intersect.
• Parallel lines are two or more lines that are always the same distance apart and never meet, no matter how far they are extended.
• A transversal intersects two or more lines at distinct points.
Setting: In pairs.
Methods:
Parallel Line Art
Materials Required: Drawing paper, a ruler, pencils, coloured pencils or markers
1 Begin by drawing two parallel lines horizontally across the paper, leaving some space between them.
2 Choose a point near the top of the paper and draw a diagonal line (the transversal) that intersects the parallel lines.
3 Label the points where the transversal crosses the parallel lines as A, B, C, D and so on.
4 Number the corresponding angles, alternate interior angles and alternate exterior angles, and colour them using different colours.
5 Cut out one of the corresponding angles and superimpose on the other corresponding angle.
6 Now, cut out one of the alternate interior angles and superimpose on the other alternate interior angle.
7 Measure the interior angles on the same side of the transversal.
8 As you work on this activity, take the time to understand each angle type and discuss with your partner how they relate to parallel lines and the transversal.
Chapter Checkup
Check whether the given angles are supplementary, complementary or neither.
Find the supplement of the given angles.
Find the complement of the given angles.
Find the value
Find the values of ∠ABC, ∠ACB and ∠CAB.
5 Angled parking lets the driver park easily with minimal steering. The yellow lines in a parking space are parallel. What is the measure of ∠m?
Identify the figures in which the lines are parallel. 7
8
Find the measure of the unknown angles, as indicated in each figure.
In the figure given below, c || d || e. Lines a and b are the transversals. Find the value of g°, m°, y° and h°.
10 Find the values of w°, x°, y° and z° in the figure shown below.
PQRS is a parallelogram. Given ∠QPS = 115°, find the value of the other angles of the parallelogram.
ABCD is a trapezium. The diagonals of the trapezium intersect at Q. Given, ∠QBA = 63° and ∠BAQ = 47°. Find the values of ∠QDC and ∠DCQ.
Draw a line parallel to the line l at a distance of 4.5 cm from the line.
Challenge
1 Read the statements and choose the correct option.
Assertion (A): If a transversal intersects two parallel lines, then the interior angles on the same side of the transversal are supplementary angles.
Reason (R): The sum of the measures of two supplementary angles is 180°.
a Both A and R are correct, and R is the correct explanation for the A.
b Both A and R are correct, and R is not the correct explanation for the A.
c The A is true, but R is false.
d Both A and R are false.
2 Jacob builds a shape using the magnets as shown in the figure in which A || B, C || E and F || D. Find:
Case Study
Cross Curricular
Exploring Angles
The image shows the aerial view of the buildings in a tech park. Mary and her friends decide to cover the buildings in the aerial view during a walk on a weekend. Look at the image and answer the questions that follow.
1 Find the value of x
2 What is the angle between block A and block B?
3 What is the measure of ∠C?
4 The angle between the training centre and headquarters is 18% of 1662 3 ° . Is the training centre parallel to block B? (Used the answer that you got in Q2)
a Yes
c Can’t say
b No
d None of these
7 Triangles and Their Properties
Let’s Recall
Look at the given triangles. What do you observe about their sides and angles?
Triangles can be classified on the basis of their sides and angles.
On the basis of sides
Equilateral triangle Isosceles triangle
Scalene triangle
All sides are equal. All angles are equal.
Acute-angled triangle
All three angles are less than 90°.
Let’s Warm-up
Two sides are equal. Two angles (base angles) are equal.
On the basis of angles
Obtuse-angled triangle
No equal sides. No equal angles.
Right-angled triangle
One angle is more than 90°, and the rest are less than 90°.
Match the measures with the correct type of triangle.
1 60°, 70°, 50°
2 90°, 45°, 45°
3 AB = BC = CA
4 100°, 30°, 50°
5 AB = BC
Isosceles triangle
Obtuse-angled triangle
Acute-angled triangle
Equilateral triangle
Isosceles-right triangle
One angle is equal to 90°, and the rest are less than 90°.
I scored out of 5.
Mean, Median and Mode Understanding Triangles and Their Properties
Raj and Riya are travelling on a train. Suddenly, the train passes by a bridge on the other track. The children watch the bridge as it passes by.
Raj: Riya, do you notice something in this triangle-based design? Just look at how accurate and precise the triangles are!
Riya: The end of the straight beam is exactly at the centre of the adjoining ends!
Raj: Not only that, the straight beam is also exactly perpendicular to the base!
Medians and Altitudes
This straight beam here is the median and also the altitude. Let us learn more about medians and altitudes.
Median of a Triangle
A median is a line segment that connects a vertex of the triangle to the midpoint of the opposite side.
Each triangle has three medians, one from each vertex.
The point where the medians intersect is called the centroid of the triangle. The centroid is often denoted by the letter ‘G’. It is also called the centre of gravity of the triangle.
G is the centroid of DABC. Let us look at centroids in different types of triangles.
Think and Tell
How will you show the median in an equilateral, isosceles and scalene triangle?
Acute-angled Triangle
Properties of a median and a centroid
• A median always lies inside the triangle.
• All three medians of a triangle are concurrent, i.e., they all intersect at a common point, that is, the centroid.
• The centroid of a triangle divides each median in the ratio 2:1. For example, in DABC, AD and CE are the medians of sides BC and AB, respectively. The two medians meet at point G. AG:GD = CG:GE = 2:1
• A centroid always lies inside the triangle, irrespective of the type of triangle.
• The part of the median that is closer to the vertex is always greater than the one closer to the midpoint of the opposite side.
Altitude of a Triangle
In the bridge, the straight beam that is exactly perpendicular to the base of a triangle is the altitude
An altitude is a line segment perpendicular to one side of a triangle, and it extends from a vertex to the opposite side.
Each triangle has three altitudes, one from each vertex.
The point where the altitudes intersect is called the orthocentre of the triangle. The orthocentre is often denoted by the letter ‘O’.
Properties of an altitude and orthocentre
• An altitude may or may not lie inside the triangle.
Orthocentre
• All three altitudes of a triangle are concurrent, that is, they intersect at a common point called the orthocentre.
• The orthocentre is not always located inside the triangle. It can be inside, on the triangle, or outside the triangle, depending on the type of triangle.
• The orthocentre lies:
i inside in an acute-angled triangle.
ii on the vertex of a right-angled triangle.
iii outside in an obtuse-angled triangle.
Acute-angled triangle
Remember!
Right-angled triangle
Obtuse-angled triangle
A median ‘bisects’ a side into two equal halves. The altitude is ‘perpendicular’ to the side it is drawn on from a vertex.
Example 1: In triangle ABC, AD and CE are medians on sides BC and AB, respectively. The medians intersect at point G. AG = 2.4 cm, DC = 3 cm. Find AD and BC.
AD is the median on the opposite side BC.
Therefore, BD = DC = 3 cm.
BC = BD + DC = 3 + 3 = 6 cm
G is the centroid where AD and CE intersect. Therefore, AG:GD = 2:1 (property of a centroid)
Since AG = 2.4 cm, GD = 2.4 ÷ 2 = 1.2 cm
AD = 2.4 + 1.2 = 3.6, so AD = 3.6 cm.
Example 2: Choose the correct option.
1 How many altitudes can a triangle have? a 1 b 2 c 3
2 The point at which the three altitudes of a triangle intersect is called the a centroid b centre c orthocentre d incentre
In DPSQ, PR and QT are medians on the sides SQ and PS, respectively. The medians intersect at point G. If PG = 8 cm and QR = 7 cm, then find SQ and PR.
SR = QR (Since PR is the median to side and R is the of SQ.)
SQ = SR + . So, SQ =
PG:GR = 2: (Property of a centroid)
PR = PG + (G lies between P and R)
So, PR =
Fill in the blanks.
a is a line segment that connects a vertex of the triangle to the midpoint of the opposite side.
b is a line segment perpendicular to a side of the triangle.
c The point where the altitudes intersect is called the of the triangle.
d An may or may not lie inside the triangle.
Draw a triangle and the medians to its 3 sides.
In a DABC, BD is the median on the opposite side AC. AD = 5 cm. Find the length of AC.
The centre of mass of an object is the point where the total mass of the object can be considered to be concentrated. Which of the following can be considered as the centre of mass in a triangle?
a centroid b altitude c orthocentre d median
In a DABC, AD and CE are two medians on the opposite sides BC and AB, respectively. The two medians intersect at point G. If AG = 2 cm and BD = 4 cm, find AD and BC.
CF, EB and AD are the medians of a DACE. Use the given figure to answer the following questions.
a If BG = 5 cm, find GE and BE.
b If CG = 16 cm, find GF and CF.
c If AD = 30 cm, find AG and GD.
d If GF = x, find GC and CF.
e If AG = 9x and GD = 5x – 1, find x and AD.
If PS is a median of DPQR, then find the value of ∠PSR.
1
If the orthocentre and the centroid of the triangle are the same, then what kind of a triangle is it? Give a reason for your answer.
Properties of Angles of a Triangle
Notice that the triangles used to design the triangular structure in the bridge look exactly of the same size and shape. The lengths of the sides and the measures of the angles look the same, such that when each of these are joined together, they give the bridge a symmetrical design.
But how would the engineers be sure of building triangles of a certain measure such that the bridge also looks symmetrical? This is only possible by verifying the measures using some properties of triangles. Let us learn about them.
Angle Sum Property of a Triangle
The sum of all the angles of a triangle is 180°, but how do we know for sure?
Method 1
Let us take a triangular piece of paper and cut out its 3 angles.
(∠A, ∠B and ∠C)
Place them together such that the vertices lie on the same point.
We see that the 3 angles form a straight line or a straight angle.
So, we can say that the sum of the 3 angles of a triangle is equal to 180°.
Here, ∠A + ∠B + ∠C = 180°.
Method 2
Let ABC be any triangle. Through A, draw a line XAY parallel to BC and mark the angles, as shown in the figure.
XY is parallel to BC, and the transversal AB cuts them. So, ∠1 = ∠4 (Alternate interior angles)
XY is parallel to BC, and the transversal AC cuts them. So, ∠2 = ∠5 (Alternate interior angles)
Adding both sides, we get ∠1 + ∠2 = ∠4 + ∠5.
Adding ∠3 to both sides we get,
∠1 + ∠2 + ∠3 = ∠3 + ∠4 + ∠5
∠3 + ∠4 + ∠5 = ∠XAY = 180° (∠XAY is a straight angle)
Therefore, ∠1 + ∠2 + ∠3 = 180°.
Hence, the sum of all the angles of a triangle is 180°.
Example 3: What is the measure of the third angle in a triangle where 2 angles measure 45° and 87°?
The sum of the angles in a triangle is 180°.
Let the missing angle be x.
45° + 87° + x = 180°
x = 180° cc 132° = 48°
So, the measure of the third angle is 48°.
Example 4: The angles of a triangle are in ratio 9:11:16. Find the measures of all the angles.
Let the angles of the triangle be 9x, 11x and 16x.
We know that the sum of the angles in a triangle is 180°.
So, 9x + 11x + 16x = 180°
36x = 180°
x = 5°
So, the measures of the angles are 9x = 45°, 11x = 55° and 16x = 80°.
Thus, the measures of the angles of the triangle are 45°, 55° and 80°.
Example 5: In ∠ADC, AB = AC. What is the value of ∠DAC?
According to the question, AB = AC
∠ABC = ∠ACB = 55°
∠ACB = ∠ACD = 55°
In DDAC,
∠ACD + ∠CDA + ∠DAC = 180° (Sum of interior angles inside a triangle is 180°)
55° + 35° + ∠DAC = 180°
90° + ∠DAC = 180°
∠DAC = 180° – 90°
∠DAC = 90°
The angles of a triangle are (x + 5)°, (x + 10)° and (2x + 5)°. Find the measures of all the angles of the triangle.
Using the angle sum property of a triangle.
∠BAC + ∠ABC + ∠ACB =
(x + 5)° + (x + 10)° + (2x + 5)° = 180° + 20° = 180°
So, x =
Using the value of x,
(x + 5)° = ; (x + 10)° = ; (2x + 5)° =
The measures of the angles are 45°, and .
Exterior Angle Sum Property of a Triangle
Let us learn about the exterior angle sum property of a triangle.
Consider a triangle as shown below with angles a, b and c. Extend one of the sides to form ∠e.
The two opposite interior angles a
exterior angle
Notice that the interior opposite angles of the triangle when rearranged and joined together overlap ∠e exactly. So, ∠a + ∠b = ∠e
Statement: If the side of a triangle is extended, then the exterior angle formed is equal to the sum of the two interior opposite angles.
Proof: Let the side BC be extended to D, forming the exterior ∠ACD, i.e., ∠4.
In the DABC, we have ∠CAB + ∠ABC + ∠BCA = 180°
(Sum of the angles of a triangle is 180°.)
Step 1: ∠1 + ∠2 + ∠3 = 180°
Step 2: ∠3 + ∠4 = 180° (Linear pair)
∠3 + ∠4 = ∠1 + ∠2 + ∠3 (From steps 1 and 2)
∠4 = ∠1 + ∠2
Hence, ∠ACD = ∠CAB + ∠ABC
Remember!
The exterior angle of a triangle is greater than each one of the interior opposite angles. Here, ∠ACD > ∠CAB and ∠ABC.
Example 6: The interior angles of the triangle given on the side AB are in the ratio 2:3.
Determine the angles of the triangle, where BC is extended to D and ∠ACD = 100°.
Let the given interior angles be 2x and 3x.
Step 1
Using the exterior angle property of a triangle,
∠CAB + ∠ABC = ∠ACD
Putting the values of the respective angles
2x + 3x = 100°
5x = 100° or x = 20°.
The exterior angle property applies to the exterior angle and the two opposite interior angles. Never apply it to a wrong set of angles.
Step 2
∠CAB = 2x = 2 × 20° = 40°
∠ABC = 3x = 3 × 20° = 60°
∠ACB + ∠ACD = 180° (Linear pair)
∠ACB + 100° = 180°
∠ACB = 180° – 100° = 80°
Hence, the angles of the triangle ABC are 40°, 60° and 80°.
Example 7: In the adjoining figure, if the line segments PQ and RS intersect at point T so that ∠PRT = 75°, ∠RPT = 60° and ∠TSQ = 75°, find ∠PTS.
The side RT of a DPRT is extended to S, the exterior angle = sum of the interior angles.
∠PTS = ∠TPR + ∠PRT
Putting the values, ∠PTS = 60° + 75° = 135°
The angles of the triangle PQR are . Do It Together
In a DPQR, QR is extended to S such that ∠PRS = 140°. Find the measure of ∠PQR and ∠PRQ, if ∠QPR = 80°.
Step 1
∠PQR + ∠QPR = ∠ (Using the exterior angle sum property)
Putting the values of the respective angles,
∠PQR + 80° = So, ∠PQR =
Step 2
∠PQR + ∠QPR + ∠PRQ = (Angle sum property)
Putting the values of the respective angles, 60° + + ∠PRQ = 180°
∠PRQ =
Find the values of x and y in the figures.
The angles of a triangle are in the ratio 5:6:7. Find the measures of the angles.
One of the exterior angles of a triangle is 130°, and the interior opposite angles are in the ratio 2:3. Find the angles of the triangle.
Astronomers often use the positions of three celestial bodies to form a triangular pattern for triangulation. Three celestial bodies form a triangle with interior angles a, b and c. If a = 45°, b = 60° then what is the value of c?
In a DABC, ∠A is 50° more than ∠B and 20° less than ∠C. What are the angles of the triangle?
In a DABC, ∠A – ∠B = 15°, ∠B – ∠C = 30°. Find the measure of each angle of the triangle.
In the adjoining figure, the side BC of a DABC is extended to form a ray BD. CE is drawn parallel to BA. Without using the angle sum property of a triangle:
a Show that ∠ACD = ∠A + ∠B; and
b ∠A + ∠B + ∠C = 180°.
Shown here is a picture of the Incheon Bridge in South Korea. The bridge was built using cables. There is a vertical pole, QT, standing on the road SU such that the angles (marked in green) between the cables and the pole are equal. If the sum of the angles (marked in white) made by the same cables with respect to the road is 80°, then find the measure of ∠PQT.
In which triangle is the measure of each exterior angle twice the measure of its interior angle? Explain your answer with a figure.
Properties of the Sides of a Triangle
Any three points that do not fall in a straight line can be joined to form a triangle, as seen in the triangular structure used to build the bridge. But can we draw a triangle with sides of any given length? Let us find out.
Triangle Inequality Property
Triangles are bound by something called “the triangle inequality property”. Let us learn about it.
Statement: The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
Consider DABC, as shown in the adjoining figure.
Let the sides opposite to the vertices, A, B and C be denoted by a, b and c, respectively.
Side BC = a, side AC = b, side AB = c
So, as per the property:
a + b > c a + c > b b + c > a
Let us test this for a triangle that has the following dimensions:
a = 2, b = 3, c = 4
Did You Know?
The Bermuda Triangle, also known as the “Devil’s Triangle”, is a region in the western part of the North Atlantic Ocean where several aircraft and ships have disappeared under mysterious circumstances. The three vertices of the Bermuda Triangle on the map are Miami, Bermuda and Puerto Rico.
Therefore, this triangle satisfies the triangle inequality property.
Now, let us look at this property in another way. We know that a + b > c, a + c > b and b + c > a.
So, |a – c| < b. Similarly, |a – b| < c and |b – c| < a.
Each of the left-hand sides of the inequalities represents the difference between the two sides and the right-hand side, which is the third side.
So, the inequality property of triangles can also be rephrased as: The difference of the lengths of any two sides of a triangle is less than the length of the third side.
Example 8: Is it possible to draw a triangle with the sides 4 cm, 5 cm and 1 cm?
Using the triangle inequality property, we see that the sum of lengths of two smaller sides (1 cm + 4 cm) is not greater than the length of the third side (5 cm).
Thus, it will not be possible to draw a triangle with the given lengths.
Example 9: The lengths of the two sides of a triangle are 9 cm and 13 cm. What could be the possible values of the third side of the triangle?
We know that Side 1 + Side 2 > Side 3. (The triangle inequality property.)
Finding the sum of the two sides, Side 1 + Side 2 = 13 + 9 = 22 cm
We know that Side 1 – Side 2 < Side 3. (The triangle inequality property.)
Finding the difference of the two sides, Side 1 – Side 2 = 13 – 9 = 4 cm
Therefore, the length of the third side of the triangle has to be more than 4 cm but less than 22 cm.
The lengths of the two sides of a triangle are 4 cm and 12 cm. What could be the possible values of the third side of the triangle?
We know that Side 1 + Side 2 > . (The triangle inequality property.)
Finding the sum of the two sides, Side 1 + Side 2 = + = .
We know that Side 1 – Side 2 < . (The triangle inequality property.)
Finding the difference of the two sides, Side 1 – Side 2 = – = .
Therefore, the length of the third side of the triangle has to be than but less than .
State which of the following sets of lengths will form a triangle.
S is any point on the side QR of triangle PQR. Fill in the blanks with the >, < or = signs. a PS PR + SR b PS PQ – QS
If the following are the lengths of the two sides of a triangle, what are the possible values of the third side? a 3 cm and 6 cm b 14 cm and 9 cm
34 cm and 7 cm In
your answer.
triangle cannot be formed if any of the three sides is longer than the sum of the other two sides. For example, in DABC,
Delhi, Mumbai and Chennai are metropolitan cities in India. The distance from Delhi to Mumbai is around 1450 km, from Mumbai to Chennai is around 1350 km and from Chennai to Delhi, it is 2200 km. Will these three places form a triangle on the map?
Challenge
Critical Thinking
O is any point in a DABC. If AB = 5 cm, BC = 6 cm and AC = 7 cm. Prove that AO + BO + CO > 9 cm.
Mean, Median and Mode Right-angled Triangles
Riya: It is so much fun learning about the properties of triangles.
Raj: Yes. But, I still have a question. Remember the railway bridge we saw? One of the angles was 90°. It looked special! What kind of triangles are these?
Riya: Such special triangles are called right-angled triangles!
Let us see right-angled triangles in things around us.
A right-angled triangle is formed when one of the angles in the triangle is a right angle, or 90°.
It has two shorter sides that are called the legs of the triangle. The side opposite to the right angle is called the hypotenuse, which is the longest side of a right-angled triangle.
Here, ∠C is a right angle; AB is the hypotenuse; and sides AC and CB are the legs. Here, AC will be called the perpendicular, and BC will be called the base of the DABC.
The Pythagoras Theorem
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In DACB, ∠C is the right angle, AB is the hypotenuse and AC and BC are the legs.
Here, AB2 = BC2 + AC2
If side AB = c, side AC = a, Side BC = b
Then, c2 = a 2 + b2
Let us now look at some properties that the Pythagoras Theorem produces.
Did You Know?
Bhaskara II, also known as Bhaskaracharya (12th century), presented an elegant visual proof for the Pythagorean theorem using a square and four congruent right triangles.
Property 1: The hypotenuse is the longest side of a right-angled triangle.
Proof: We know that, c 2 = a 2 + b2 (Pythagoras property)
Therefore, c 2 > a 2 and c 2 > b2
c > a and c > b
Hence, in a right-angled triangle, the longest side is the hypotenuse.
Property 2: Of all the line segments that can be drawn to a given line from a point outside it, the perpendicular line segment is the shortest.
Proof: Let l be the given line and P a point outside it. Draw PQ perpendicular to line l.
Let R be a point other than Q on line l. Join PR.
Now DPQR is a right-angled triangle, ∠Q = 90°. PR is the hypotenuse, and PQ is one of the legs of the right-angled triangle PQR.
In a right-angled triangle, the hypotenuse is the longest side.
Therefore, PQ < PR.
This is true for all the points other than Q on line l
Hence, PQ is the shortest of all the line segments that can be drawn from P to line l.
Converse of the Pythagoras Property
Statement: If the square of one of the sides of a triangle is equal to the sum of the squares of the other two sides, then it is a right-angled triangle with the angle opposite to the longest side being the right angle.
Thus, if in DABC, AB2 = AC2 + BC2, then DACB is a right-angled triangle, right-angled at C.
Pythagorean Triplets
Three positive numbers a, b and c are said to form a Pythagorean triplet if they satisfy the Pythagoras property i.e., the square of one of the sides of a triangle is equal to the sum of the squares of the other two sides.
c 2 = a 2 + b2
Some Pythagorean triplets are (3, 4, 5); (5, 12, 13); (8, 15, 17); (7, 24, 25); (12, 35, 37).
Forming a Pythagorean Triplet
Consider any two natural numbers, a and b, where a > b.
Then, (a 2 – b2), (2ab), (a 2 + b2) form a Pythagorean triplet.
Think and Tell
Example 10: In the given figure, find the value of H if DABC is a right-angled triangle.
Step 1
Using the Pythagoras theorem, AC2 = AB2 + BC2
Putting the values, H2 = 52 + 122
H2 = 25 + 144
Step 2
In a right-angled triangle ABC, if AB2 = AC2 + BC2, then the right angle is— a Angle ABC b Angle BAC c Angle ACB d Angle CAB A
Adding the values, H2 = 169 = 13 × 13 So, H = 13 cm
Two poles of heights 8 m and 16 m, respectively are placed at the same level, 6 m apart from each other. What is the distance between their tops?
Draw the figure and label the vertices to show the right-angled triangle.
AB = 8 m, CD = 16 m and BD = 6 m
Draw AE || BD meeting CD at E. Then, ABDE is a rectangle.
Using the properties of a rectangle, ED = and AE =
In a right-angled triangle AEC, we have, AC2 =
Putting the values, AC2 = , AC =
The distance between the tops of the two poles is
Do It Yourself 7D
Which of the following sets of lengths of a triangle belong to right-angled triangles?
a 2 cm, 3 cm and 6 cm b 6 m, 8 m and 10 m c 15 cm, 20 cm and 25 cm
Find the missing lengths of each of the triangles.
If (k, 24, 25) is a Pythagorean triplet, find the value of k
The sides of a rectangle are 12 cm and 16 cm. Find the length of its diagonal.
The hypotenuse of a right-angled triangle is 26 cm. The length of the base is 10 cm. What is the length of the altitude of the triangle?
Find the values of x and y in the given figure.
The 45° rule is a principle used to maximise the range of a projectile. According to this rule, when launching an object (like a ball), the angle of projection that achieves the maximum horizontal distance is 45 degrees. A person throws a ball at a 45° angle, it reaches the maximum height of 12 m after the ball travelled 20 m. What is the horizontal distance between the ball on the ground and the person?
Create a word problem on the first property of the Pythagoras theorem.
A right-angled triangle has a hypotenuse of length 10 units. If the difference between the lengths of the legs is 2 units, find the lengths of the legs of the triangle.
Congruence
In a class, the teacher showed different things to the students.
Teacher: Did you notice something special about these things?
Rashi: Yes, the notebook has all the pages of the same size.
Teacher: Yes, Rashi. Did you notice something about the ₹500 notes?
Rashi: Yes, all the notes are similar.
Teacher: Very good Rashi. Such shapes are called congruent shapes.
Rashi: What does congruent mean?
When one figure is placed on the top of another and they match exactly in shape and size, then the figures are said to be congruent. This method of comparing shapes is called the method of superposition.
Let us understand congruency in detail.
Congruence in Shapes and Figures
Congruence of Line Segments, angles and shapes
Let us see congruence in line segments, angles and shapes.
Line Segments
Example 11: Show that rectangle ABCD is congruent to rectangle MNOP.
In the given figure, we can see that:
AD = MN (corresponding sides) and AB = MP (corresponding sides)
Therefore, rectangle ABCD = rectangle MPON under the correspondence ABCD MPON.
Example 12: In the given figure, lines a and b are parallel to each other. Which angle is congruent to 6 and 7 if 1 ~ = 3 and 4 ~ = 2?
We can see that: 1 and 3; 4 and 2 are opposite angles.
Similarly, 7 and 5; 6 and 8 are also opposite angles.
Therefore, 7 = 5 and 6 = 8.
Square ABCD is congruent to square PQRS under the correspondence ABCD PQRS.
Fill in the blanks.
We know that ABCD PQRS.
The correspondence is ABCD PQRS. 1 A 2 S 3 BC 4 PQR
The corresponding sides are: .
Did You Know?
The mirror image of an object is congruent to the actual object.
Do It Yourself 7E
A line segment AB = 10 cm. If AB ~ = CD, then CD = ?
Draw any two congruent shapes.
In the given figure, if a = b = c, name the angle which is congruent to AOC. 2 Art
What is the measurement of x in the following pairs of geometrically congruent figures?
An archer noticed that two circular targets have the same radius. Are the two circular targets congruent? Why or why not?
Two species of butterflies, Monarch and Viceroy, have similar wing patterns due to evolution. If Monarch butterflies have a wing pattern with 5 distinct spots, how many distinct spots will there be in the wing pattern of Viceroy butterflies?
Read the two statements and decide which of the following options is correct.
Assertion (A): If two angles are congruent, their corresponding sides are also congruent.
Reason (R): Two angles are congruent if they have the same measure.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Rectangle PQRS contains three small congruent rectangles. If the breadth of one of the small rectangles is 5 cm, what is the area of rectangle PQRS in square cm?
Congruence in Triangles
Jeena’s mother made some biscuits at home. Jeena noticed that the biscuits were in the same shape as a triangle.
Mother: Jeena, can you find how many triangular biscuits are congruent to each other?
Jeena: How can I find that out?
To help Jeena figure out the triangles that would be congruent to each other, let us first learn about some congruence rules.
SSS Congruence Criteria
SSS stands for Side-Side-Side.
Did You Know?
The Great Pyramid of Giza’s sides are nearly perfectly congruent.
When all the three sides of one triangle are equal to the corresponding three sides of another triangle, then the two triangles are said to be congruent by SSS congruence criteria.
In DABC and DPQR,
AB = PQ (Side)
BC = QR (Side)
AC = PR (Side)
Therefore, using SSS congruence criteria, DABC = DPQR.
Example 13: In the given figure, AD = BC and AC = BD. Show that DABD ˜ = DBAC.
In DABD and DBAC,
AD = BC (given)
AC = BD (given)
AB = BA (common side)
Therefore, by SSS congruence criteria, DABD ~ = DBAC.
Remember!
The corresponding parts must always be equal for two figures to be congruent.
The triangles in the given figure are congruent by SSS congruence criteria. Write the congruence in symbolic form.
In DABC and DDEC,
AB = DE (side)
BC = ( ) = ( )
Therefore, by congruence criteria D _________ = D
SAS Congruence Criteria
SAS stands for Side-Angle-Side.
If any two sides and the angle included between the two sides in a triangle are equal to the two sides and the angle included between them in another triangle, then the two triangles are said to be congruent by SAS congruence criteria.
In DABC and DPQR,
AC = PR (side)
CAB = RPQ (angle)
AB = PQ (side)
Therefore, DABC = DPQR.
Remember!
If even one pair of corresponding sides and angles are unequal then the triangles are not congruent.
Example 14: AB = AC and AD is the bisector of BAC. Show that DABD = DACD.
In DABD and DACD, AB = AC (given) (side)
BAD = CAD (AD is the bisector of BAC) (angle)
AD = AD (common side)
Therefore, by SAS congruence criteria, DABD ~ = DACD.
Find the measurements of the unknown sides or angles in the following pair of congruent triangles. We know that DPQR ~ = DXYZ.
So,
PQ = XY = z
QR =
PR = = x and
ASA Congruence Criteria
ASA stands for Angle-Side-Angle.
If any two angles and the side that is between the two angles in a triangle are equal to the corresponding two angles and the side between the two angles, then the two triangles are said to be congruent by ASA congruence criteria.
In DABC and DPQR,
ABC = PQR (Angle)
BC = QR (Side)
ACB = PRQ (Angle)
Therefore, DABC ~ = DPQR.
Example 15: Prove that the diagonal of a parallelogram divides it into two congruent triangles.
In DACD and DDBA,
CAD = BDA (alternate interior angles of a parallelogram)
AD = DA (common)
CDA = BAD (alternate interior angles of a parallelogram)
Therefore, by ASA congruence criteria,
DACD ~ = DDBA.
Error Alert!
In ASA, do not include any side but only the side between the angles.
Prove that DAOC and DDOB are congruent.
In DAOC and DDOB,
CAO = (given)
AO = (given)
AOC = (vertically opposite angles)
Therefore, by congruence criteria,
D ~ = D .
RHS Congruence Criteria
RHS stands for Right angle-Hypotenuse-Side.
If in a given right-angled triangle, the hypotenuse and a side are equal to the hypotenuse and side of another right-angled triangle, then the two triangles are said to be congruent by the RHS congruence criteria.
In DABC and DPQR,
ABC = PQR = 90° (right angle)
AC = PR (hypotenuse)
BC = QR (side)
Therefore, DABC = DPQR.
Example 16: Show that the bisector PS divides DPQR into two congruent triangles.
In DPQS and DPRS,
PSQ = PSR (= 90°)
PQ = PR = 3 cm
QS = SR (PS is a bisector)
Therefore, by RHS congruence criteria, DPQS = DPRS.
In the given figure, prove that DABD ~ = DACD.
In DABD and DACD,
ABD = = (common side) = = cm
Therefore, by congruence criteria DABD = DACD.
Do It Yourself 7F
In the given figure, PR = SQ and RS = QP.
a Write all the pairs of equal parts in DPRS and DSQP.
b Is DPRS ~ = DSQP? Why or why not?
In the given figure, show that DPRS = DPRQ
8.5 cm 8.5 cm 30º 30º
In the given figure, AB = BC and BD is the median. Is DABD ~ = DCBD?
In the given figure, AD is the bisector of BAC, and CPD = BPD. Prove that DCAP ~ = DBAP. C
In the given figure, AS = BR and PR = QS. Is DAPS congruent to DBQR?
In the figure, check whether the pair of triangles ADB and BCA are congruent or not. 45º 45º 30º 30º A B D C
If ABCDE is a regular pentagon, then show that DABC ~ = DAED.
In the given figure, AB = BC, ADB = CDB = 90°.
Prove that:
a ΔABD = ΔCBD
b A = C
c AD = CD
In the given figure, AC = BC, A = B and DCA = ECB.
Prove that:
a DDBC ~ = DEAC
b DC = EC
BX is the bisector of ABC. If P is any point on BX, then prove that the perpendiculars drawn from P to AB and BC are equal.
In the given figure, if BA || RP, QP || BC and AQ = CR, then prove that DABC ~ = DPRQ.
The iconic triangular windows of the Louvre Pyramid in Paris have dimensions that form triangles with angles of 60°, 60°, and 60°. Is it true that all the windows will be congruent? Give a reason for your answer.
Line segments AB and CD bisect each other at O. AC and BD are joined, forming triangles AOC and BOD. Are the two triangles congruent? If yes, state the three equality relations between the parts of the two triangles that are given or otherwise known.
Points to Remember
• The median is a line segment that connects the vertex of a triangle to the midpoint of the opposite side.
• The point where the medians intersect is called the centroid of the triangle.
• An altitude is perpendicular to a side of the triangle, and it extends from a vertex to the opposite side.
• The point where the altitudes intersect is called the orthocentre of the triangle.
• The sum of the interior angles of a triangle is 180°.
• The exterior angle formed is equal to the sum of the two interior opposite angles.
• The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
• The difference of the lengths of any two sides of a triangle is less than the length of the third side.
• In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
• Two planes are said to be congruent when they are superposed such that they cover each other exactly.
• Triangles congruency can be proved using the SSS, SAS, ASA or RHS congruency rule.
Math Lab
Finding Pythagoras’ Triplets with Squares
Objective: To find out if the group of given natural numbers is a Pythagorean triplet.
Setting: In groups of 5.
Materials Required: Squares on squared paper with different areas like 3 sq. units, 4 sq. units, 5 sq.units etc, chart paper, pencil, ruler.
Method:
1 In groups, take a set of squares.
2 Arrange 3 squares from the given set of squares to form a triangle.
3 Place the triangles on the chart paper and trace out the triangle formed.
4 Count the number of small squares on each square that make up the side of the triangle. Write the length on the sides of the triangle traced.
5 Measure all the angles of the triangle.
6 Is this triangle a right-angled triangle?
7 Repeat the activity by finding more squares that can form the sides of the triangle.
8 Write the proof of the Pythagoras Theorem for each of these triangles.
Chapter Checkup
Write True or False.
a There can be only two acute angles in a triangle.
b The sum of the lengths of any two sides of a triangle is greater than the third side.
c Two angles are congruent if the sum of their measures is 180°.
d Two lines are congruent if they are parallel.
Which of the following sets of angles will form a triangle?
a 30°, 40° and 110°
b 34°, 29° and 120°
c 50°, 120° and 10°
Which of the following sets of lengths of a triangle will form a right-angled triangle?
a 6 m, 8 m and 9 m
b 9 cm, 12 cm and 15 cm
Find the missing angles for the following figures.
a
c 26 cm, 24 cm and 10 cm
DABC is an isosceles triangle with AC = BC. Will DABC be a right-angled triangle, if AB2 = 2AC2? Give reasons for your answer.
In a 52-inch plasma television set, the length of the screen’s diagonal is 52 inches. If the screen’s width is 48 inches, find the height of the screen.
Vanshika has two right triangles. The first has legs of length 6 cm and 8 cm, and the second has legs of length 10 cm and 6 cm. Determine if these right triangles are congruent.
Sam had a rectangular sheet of paper of dimensions 50 cm × 30 cm. He cut four congruent isosceles triangles from the rectangle, as shown in the figure. The two sides of each triangle = 10 cm. Find the area of the remaining portion.
A ladder 13 m long reaches a window which is 5 m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 12 m high. Find the width of the street.
In the given figure, altitudes PS, QT and RU of DPQR are equal. Show that the measure of each angle in DPQR is 60°.
In the given figure, BD = CD, ED = FD, DE AB and DF AC. If B = 50°, find C.
The Eiffel Tower has triangular lattice structures that are congruent in design. If one section of the lattice measures 50 metres on each side, and another section is congruent but scaled up by a factor of 2, what are the new dimensions of the scaled-up section?
In DABC, ∠A = 60°, ∠B = 80° and the bisectors of ∠B and ∠C meet at O. Find ∠C and ∠BOC.
1 Consider the image shown. Choose which of the given options is correct.
Assertion (A): (AC)2 = (AD)2 + 2(BD)2 + (CD)2
Reason (R): According to the Pythagoras theorem, (Hypotenuse)2 = (Perpendicular)2 + (Base)2
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, and R is not the correct explanation of A.
c A is true, but R is not true.
d R is true, but A is not true.
2 Read the two statements and decide whether these statements are sufficient to find ΔABC ≅ ΔDEF.
Statement 1: ∠A = ∠D, ∠B = ∠E and AB = DE
Statement 2: BC = EF.
a Statement 1 alone is sufficient, but Statement 2 is not sufficient.
b Statement 2 alone is sufficient, but Statement 1 is not sufficient.
c Both statements together are sufficient, but neither alone is sufficient.
d Statements 1 and 2 together are not sufficient.
Triangular Triumph
The 2028 Summer Olympics are to be held in Los Angeles. Countries from all over the world will be competing against each other in 35 different sports. The flags of a few countries are to be made by the volunteers for the games. Flags are typically used to represent countries, states, organisations, or groups and can convey messages of identity and solidarity.
Look at the flags given below and answer the related questions.
1 A volunteer has to make the flag of Nepal. He cuts the cloth for the triangular shape on the top with ∠ACB measuring 30°. If ∠B = 90°, what will be the measure of ∠CAB?
a 30° b 45°
c 60°
90°
2 The flag of the Bahamas consists of a black triangle situated at the hoist with three horizontal bands (aquamarine-gold-aquamarine). The width to length ratio is 1:2.
To make the triangle block, cloth is cut into triangles where the length of AB = 24 cm, AC = 20 cm. What is the length of CD?
a 12 cm b 15 cm c 16 cm d 24 cm
3 Look at the flag of the Czech Republic. It has two equal horizontal bands of white (top) and red with a blue isosceles triangle based on the hoist side. If ∠ACB = 70° then what is the value of x° + y°?
4 The flag of the Seychelles is shown. It consists of 5 different coloured sections starting from one end and diverging towards the other end. What are the values of ∠AFC and ∠EAF?
8 Ratio and Proportion
Let’s Recall
Sam has a big farmhouse. He has various kinds of animals on the farm. The farm has horses, sheep, buffaloes, cows, dogs, swans, hens, chickens and many more. There is a total of 100 animals at the farm.
There are 3 horses, 10 sheep, 5 buffaloes, 8 cows, 6 dogs, 6 swans, 4 hens and 7 chicks on the farm.
We know that a ratio is the number or amount of one thing compared to another thing.
For example, the ratio of hens to chicks can be given as:
4 hens to 7 chicks or 4:7 or 4 7 .
Similarly, the ratio of horses to sheep 3:10
Buffaloes to cows 5:8
Horses to swans 3:6 = 1:2
Let’s Warm-up
Read the graph and fill in the blanks.
1 The ratio of Pooja's income to Arushiʼs income is .
2 The ratio of the highest income to the lowest income is .
3 The ratio of the difference of the incomes of Rachna and Amit to that of Rohan and Divya is .
4 The ratio of the sum of the incomes of Pooja and Divya to that of Arushi and Rachna is .
Pooja Divya Arushi Name Rohan Rachna
Ratio and Proportion
Aman and Nisha jog every day in a nearby park. Aman jogs 5 km every day, whereas Nisha jogs 7 km every day.
Equivalent Ratios
We know that ratios are the comparison of two quantities of the same unit. The ratio of the distance jogged by Aman to that by Nisha can be given as:
Aman jogged 35 km in a week, whereas Nisha jogged 49 km in a week. The ratio of distances covered by them in a week can now be given as 35:49.
If the HCF of both terms of a ratio is 1, then the ratio is said to be in its simplest form.
HCF of 35 and 49
To reduce a ratio to its simplest form, divide the terms by their HCF. 35 ÷ 7 49 ÷ 7 = 5 7
We saw that the ratio of distances jogged by Aman and Nisha in a day was 5:7, and the ratio of distances jogged in a week was 35:49, which when simplified, gave 5:7.
The ratios 5:7 and 35:49 are called equivalent ratios as they can be simplified to the same value.
We can find the equivalent ratio of a given ratio by multiplying or dividing the numerator and denominator by the same natural number.
For example, 5 7 = 5 × 2 7 × 2 = 10 14 = 5 × 3 7 × 3 = 15 21 = 5 × 4 7 × 4 = 20 28
Comparing Ratios: Let us compare 3:5 and 4:12 using the steps.
Step 1
Write the ratios in their simplest form.
3:5 = 3 5 ; 4:12 = 4 12 = 1 3
Step 2
Convert into like fractions.
LCM of 5 and 3 = 15 3 5 = 9 15 ; 1 3 = 5 15
Think and Tell
How many equivalent ratios does 2:3 have?
Step 3
Compare the numerators of the like fractions.
As 9 > 5; 9 15 > 5 15 ; hence 3:5 > 4:12
Using the steps of comparison, we can arrange the ratios in ascending or descending order.
Let us now learn to divide a certain quantity into two or more ratios.
The ratio of apples to oranges to guavas on a farm is 2:3:4. If there are 927 fruits in total, find the quantity of apples. 5 7 5:7 =
Step 1
Find the total number of parts by adding the ratios.
2 + 3 + 4 = 9
Hence, there are 206 apples.
Step 2
Find the number of parts given to the asked quantity as a fraction.
Apples = 2 9
Step 3
Multiply the number of parts given to the quantity with the total quantity.
2 9 × 927 = 206
Example 1: If the ratio of red balls to blue balls in a bag is 4:3, find an equivalent ratio when there are 24 red balls.
Ratio of red balls blue balls = 4 3
Ratio with 24 red balls = 4 × 6 3 × 6 = 24 18
So, the equivalent ratio of 4:3 with 24 red balls is 24:18.
Example 2: Show the given ratios in their simplest form.
1 100 cm to 5 m
5 m = 5 × 100 cm = 500 cm
100 cm : 5 m = 100 cm : 500 cm
100
500 = 1 × 100 5 × 100 = 1 5 = 1:5
2 4 L to 120 mL
Did You Know?
The ratio of the sizes of the moon and sun is 1: 400.
4 L = 4 × 1000 mL = 4000 mL
4000 mL : 120 mL
4000 120 = 100 × 40 3 × 40 = 100 3 = 100:3
Example 3: Compare the ratios and fill in the boxes with the correct sign (>, < or =).
1:8 3:32
LCM of 8 and 32 = 32
So, 1 8 = 4 32
As 4 > 3, 4 32 > 3 32
Hence, 1:8 > 3:32
Example 4: Find the ratios.
1 If A:B = 4:9 and B:C = 2:5, find A:C
A:B = 4:9 = 4 9; B:C = 2:5 = 2 5
A:C = A C = A B × B C = 4 9 × 2 5 = 8 45
Hence, A:C = 8:45
2 If A:B = 1:2 and B:C = 6:7, find A:B:C
To find A:B:C; the value of B must be the same in both ratios.
Value of B in the 1st ratio = 2; Value of B in the 2nd ratio = 6
LCM of 2 and 6 = 6
A:B = 1:2 = 1 × 3 2 × 3 = 3 6; B:C = 6 7
Hence, A:B:C = 3:6:7
Example 5: A piece of string that is 84 inches long is cut into three parts so that the lengths of the parts of the string are in the ratio 6:10:5. Find the length of each part.
Total number of parts = 6 + 10 + 5 = 21
Length of the 1st part = 6 21 × 84 = 24 inches;
Length of the 2nd part = 10 21 × 84 = 40 inches;
Length of the 3rd part = 5 21 × 84 = 20 inches.
Do It Together
Example 6: The ratio of two numbers is 2:3. If each number is increased by 7, the ratio so formed is 3:4. Find the numbers.
Let the numbers be 2x and 3x
Given, (2x + 7):(3x + 7) = 3:4
2x + 7
3x + 7 = 3 4
8x + 28 = 9x + 21 (Using cross multiplication)
9x – 8x = 28 – 21 = 7
x = 7
2x = 7 × 2 = 14
3x = 7 × 3 = 21
Hence the numbers are 14 and 21.
Example 7: Sunita purchased two colours of ribbons from the market. The red ribbon was 2 3 4 m long, and the blue one was 1 5 8 m long. What is the ratio of the length of the red ribbon to that of the blue ribbon?
Ratio of the length of the red ribbon to the length of the blue ribbon = 2 3 4 :1 5 8 = 11 4 : 13 8
To write the ratios in their simplest form, multiply both sides with the LCM of the denominator.
LCM of 4 and 8 = 8; Hence, 11 4 × 8 = 22; 13 8 × 8 = 13
The required ratio is 22:13.
Arrange the ratios 1:3, 5:7, 4:15 and 2:5 in descending order.
1:3 = 1 3; 5:7 = 5 7 ; 4:15 = 4 15 and 2:5 = 2 5
LCM of 3, 7, 15 and 5 = 1 3 = ; 5 7 = ; 4 15 = ; 2 5 =
Hence, the descending order is > > >
Do It Yourself 8A
A bouquet of 45 roses has 32 red roses and the rest are white. What is the ratio of red to white roses?
Show the given ratios in their simplest form.
a 120 cm to 3 m b 6 L to 240 mL c 5 km to 800 m d 240 sec to 1 hour
Fill in the blanks to make the given ratios equivalent.
a 6:1 = 30: b ____ :25 = 8:5 c 5: = 20:16 d 55:60 = ____ :12
Compare the ratios and fill in the boxes with the correct sign (>, <, =).
a 1:7 5:21 b 10:5 14:9 c 7:15 6:13 d 8:15 9:20
Arrange the ratios 2:5, 7:12, 3:7, 9:2 and 11:14 in ascending order.
If A:B = 5:11 and B:C = 7:13, then find A:C and A:B:C.
Draw a rectangle and a square such that the ratio of their perimeters is 10:9.
A recipe requires 1 2 3 cups of sugar and 2 1 6 cups of flour. What is the ratio of cups of sugar to cups of flour?
The angles of a triangle are in the ratio 2:3:4. What is the sum of the largest and smallest angles of the triangle?
The ratio of the lengths of three pieces of ribbon is 3:4:6. If the shortest piece is 12 inches long, find the total length of the ribbon.
Three friends, Rehan, Bobby and Heera, share a sum of money in the ratio of 2:3:5. If they receive a total of ₹3700, how much does each friend receive?
Simran and Shiva are conducting an experiment to test the growth of two different types of plants, tomato (Solanum lycopersicum) and pepper (Capsicum annuum). Initially, the ratio of the height of the tomato plant to the pepper plant is 7:5. After a week of applying a nitrogen based fertiliser, each plant's height increases by 9 cm.
The new ratio of the heights of the tomato plant to the pepper plant becomes 5:4. Find the initial heights of the tomato and pepper plants before the fertiliser was applied.
Challenge
1 Read the statements and choose the correct option.
Critical Thinking
Assertion (A): If the ages of Priya and Surbhi are in the ratio 7:8, and after six years the ratio of their ages will be 10:11, their present ages are 14 years and 16 years respectively.
Reason (R): Priya is younger than Surbhi.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Proportional Terms
Do you remember Aman and Nisha, who jog in the park for distances in the ratio 5:7? We also saw that the ratio of the distances covered by them in a week was 35:49, which is equivalent to 5:7. The two ratios can also be said to be in proportion as they are equal.
Second term (b) Means Extremes
First term (a)
35:49 5:7 :: Equivalent Ratios
Sign of proportionality
Third term (c)
Fourth term (d)
Proportionality Condition
Two ratios are said to be in proportion if the increase or decrease in one ratio leads to an increase or decrease in the other ratio.
If a:b :: c:d then,
Product of Means = Product of Extremes
b × c = a × d
Example 8: Find out whether the numbers are in proportion or not.
1 2, 3, 14, 21
2 × 21 = 3 × 14
42 = 42 = Proportional
Example 9: Find the value of x in the proportion 25:15 :: x:42.
Product of Means = Product of Extremes ⇒ 15 × x = 25 × 42
⇒ x = 25 × 42 15 = 70 Example 10: Find the value of x in the proportion
Example 11: A worker earns ₹3000 in 5 days. In how many days will he earn ₹5000?
Days required to earn ₹3000 = 5 days
Let the days required to earn ₹5000 = x days
₹3000:5 days:: ₹5000:x
3000x = 5000 × 5
x = (5000 × 5)
3000 = 25 3 days
Example 12: Each bag of marbles sold by Seema contains 9 blue marbles and 5 red marbles. If she sells 117 blue marbles in a day, how many red marbles has she sold?
Using the method of proportion, 9:5 :: 117:x
⇒ 9 × x = 5 × 117 ⇒ x = 5 × 117 9 ⇒ x = 65
Hence, Seema has sold 65 red marbles.
Example 13: What number must be added to each of the numbers 8, 21, 13 and 31 so that they are in proportion?
Let the number to be added be x
Then, (8 + x):(21 + x) :: (13 + x):(31 + x)
8 + x 21 + x = 13 + x 31 + x
Let us subtract 1 from both the sides to remove x from the numerator,
8
Error Alert!
The sign of the operator changes during transposition from LHS to RHS and vice versa.
= –378 – 18x ⇒ 5x = 25 ⇒ x = 5
Hence, 5 must be added to 8, 21, 13 and 31 to make them proportional.
Hence, the fourth term is . Do It Together
The first three terms of a proportion are 4.2, 1.2 and 0.7. Find the fourth term.
Let the fourth term be x; 4.2: :: :x
4.2 × x = × ⇒ x = ___ × ___ 4.2 =
Continued Proportion
Any three quantities a, b and c are said to be in continued proportion if,
Using the proportionality condition;
Example 14: What is the value of the first proportional if 10 and 4 are in continued proportion?
The proportion can be given as: x:10 :: 10:4. ⇒ 4x = 10 × 10 ⇒ x = 100 4 = 25
Hence, the value of the first proportional is 25.
Find the third proportional to 1 3 and 2 9 if the terms are in continued proportion.
Let the third term = x.
Do It Yourself 8B
Find whether the numbers are in proportion or not. a 5, 6, 15, 18
Find the value of x in each of the proportions.
Find the third proportional for each set of continued proportions.
Gasoline is a liquid fuel that is made from oil. It is used to power cars, motorcycles and other vehicles. A car can travel 126 miles on 18 gallons of gasoline. How much gasoline will it need to go 175 miles?
A charity organisation wants to donate TV sets to a local school. If 4 TV sets cost ₹1,12,000, how much will 23 such TV sets cost? Have you ever participated in a charity event?
If 270 kg of grass would feed 42 cows for 21 days, for how many days would 360 kg of grass feed the same number of cows?
What number should be subtracted from each of the numbers 23, 30, 57 and 78 to make them in proportion?
Challenge
Critical Thinking
1 Rohan, Kunal, and Vicky are classmates in Grade 8. They noticed that their ages form a continued proportion. Kunal is twice the age of Rohan (in years). Based on the information provided, which of these can never be Vicky's age? (Note: All ages are in whole numbers.)
a 15 years b 16 years c 32 years d 36 years
Unitary Method
Rahul, a friend of Aman and Nisha, also jogs in the same park. He covers a distance of 42 km in 12 days. How much distance does he cover in a week? Let us find out!
The distance covered by Rahul can be found using the unitary method. In this method, we first find the value of 1 unit and then the number of units asked.
Step 1
Value of many
Value of one ÷
Distance covered in 1 day = 42 ÷ 12 = 3.5 km
Step 2
Value of one
Value of many ×
Distance covered in a week = 3.5 × 7 = 24.5 km
Example 15: Komal reads 518 pages of a book in two weeks. In how many days will she read a book containing 1221 pages?
Number of pages read in 2 weeks or 14 days = 518
Number of pages read in 1 day = 518 14 = 37; Number of days for to read 35 pages = 1 day
Number of days for 1 page = 1 37 ; Number of days for 1221 pages = 1 37 × 1221 = 33 days
Example 16: 30 women can finish a piece of work in 18 days. How many women can finish the same work in 20 days?
In 18 days, the number of women who can do a piece of work = 30
∴ In 1 day, the number of women who can do a piece of work = 30 × 18 (fewer days, more women)
∴ In 20 days, the number of women who can do the piece of work = 30 × 18 20 = 27 (more days, fewer women)
Hence, 27 women can finish the same work in 20 days.
Example 17: An electric car travels 200 miles on a single charge. How far can a different electric car, equipped with the same battery technology, travel on a single charge if its battery capacity is 1.5 times that of the first car's?
Distance travelled by the first car on a single charge = 200 miles
Battery capacity of the second car = 1.5 times the first car
Distance travelled by the second car on 1.5 times the charge = 200 × 1.5 = 300 miles
A machine produces 208 toys in a day if it runs for 6.5 hours. How many toys will it produce in a day if the machine runs for 20 hours?
Number of toys produced in 6.5 hours = 208
Number of toys produced in 1 hour = 208 ÷
Number of toys produced in 20 hours = × =
Do It Yourself 8C
2 kg of potatoes cost ₹16. How many potatoes (in kg) can be bought for ₹120?
A car travels 150 km in 3 hours. How far does it travel in 9 hours?
If the cost of 15 pens is ₹300, find the cost of 5 such pens.
A healthy human heart beats about 375 times in 5 minutes. How many times does it beat in an hour?
If 12 men can do a piece of work in 18 days, in how many days will 8 men complete it?
A 20-cm-long candle burns for 50 minutes. How long will another candle of the same thickness and material, but 10 cm longer than the previous one burn?
19 bags of wheat of equal weight weigh 332.5 kg. How much will 35 such bags weigh?
33 m of cloth is required to make 15 shirts. How many shirts can be made with 110 m of cloth?
8 similar books stacked, one on top of the other weigh 1840 grams. How many such books will weigh 4.37 kg?
If 12 workers can build a wall in 5 days, how many workers will be required to build the same wall in 3 days?
d Neither Conclusion I nor Conclusion II follows. Challenge
1 Read the given statement followed by the conclusions. Choose the correct option.
Statement: One box can hold 35 sweets, and 11 teaspoons of flour are needed to make 5 such sweets.
Conclusion I: More than 300 teaspoons of flour are required to make enough sweets to fill 5 such boxes.
Conclusion II: There will be 170 sweets in 5 boxes.
a Only Conclusion I follows.
b Only Conclusion II follows.
c Both Conclusion I and Conclusion II follow.
Speed, Distance and Time
Do you remember Rahul who jogs in the nearby park? If he takes 35 minutes to cover a distance of 3.5 km, then what is his speed? Let us find out!
The distance an object travels per unit of time. S = D ÷ T
Speed
Distance
Length of the path between two points. D = S � T
Speed of Rahul = Distance Time = 3.5 km 35 = 0.1 km per minute.
Remember!
Time
Duration of an event. T = D ÷ S
The unit of speed depends on the unit of distance and the time taken.
Example 18: Find the speed of a train (in m/s) if it travels 1200 m in 20 seconds.
Distance = 1200 m, Time = 20 seconds
Speed = Distance Time = 1200 m 20 sec =60 m/s
Example 19: A rocket travels at a constant speed of 25 metres per second for 3 minutes. Calculate the distance travelled by the rocket.
Speed = 25 m/s, Time = 3 minutes = 60 seconds × 3 = 180 seconds
Distance travelled = Speed × Time = 25 m/s × 180 s = 4500 m
Example 20: Richa lives in Town A. If Richa pedals her bicycle at a speed of 18 km/hr, how long will it take her to reach Town B?
Speed = 18 km/hr; Distance = 45 km
Time = Distance Speed = 45 18 = 2.5 hours
Kunal covers a distance of 4.5 km at the rate of 1.5 km/hr, whereas Soham covers a distance of 8 km at the rate of 2 km/hr. What is the ratio of the time taken by both of them?
Distance covered by Kunal = 4.5 km; Kunal’s speed = Time taken by Kunal = Distance ÷ Speed =
Distance covered by Soham = ; Soham’s speed = 2 km/hr; Time taken by Soham = Distance ÷ Speed = Ratio of the time taken by both of them = :
Do It Yourself 8D
Find the speed of a car if it travels 400 m in 25 seconds.
Kavita walks 500 m in 6 min. Find her speed in m/s to two decimal points.
A whale swims at a constant speed of 8.5 m/s for 1 minute. Calculate the distance travelled by the whale.
A train travels at a speed of 20 m/s and travels a distance of 3.2 km. Calculate the time taken by the train to complete this journey in minutes.
The distance between Delhi and Uttarakhand is 372 km. If John travels by car at a speed of 48 km/hr, how many minutes will he take to reach Uttarakhand?
The earth takes one year to go around the sun. The distance travelled is 940 million km if there are 365 days in a year.
a Calculate the speed the earth travels at in km per day.
b Calculate the speed of the earth in km per hour.
Kirti travelled 36,000 m at a speed of 8 km/hr. Mihir travelled 45 km at a speed of 10 km/hr.
a Whose journey took the shortest time?
b What is the time difference in minutes?
Rahul writes down his jogging times for each day.
Mon—17 min; Tue—12 min; Wed—15 min; Thu—8 min; Fri—No jogging.
a State on which day he jogs the farthest. How is jogging beneficial?
b He jogs at a constant speed of 5.5 km/hr. Calculate the distance he jogs each day.
1 The towns P, Q and R are on a straight line. Town R is between Q and P. How far is P from R?
Which of the given statements is sufficient to answer this question?
Statement 1: The distance from P to Q is 300 km.
Statement 2: The distance from P to R is half of the distance from R to Q.
a Statement 1 alone is sufficient, but Statement 2 alone is not sufficient.
b Statement 2 alone is sufficient, but Statement 1 alone is not sufficient.
c Both statements 1 and 2 together are sufficient.
d Both statements 1 and 2 alone are not sufficient.
Points to Remember
• Ratios are the comparison of two quantities of the same unit.
• If the HCF of both terms of a ratio is 1, then the ratio is said to be in its simplest form.
• Equivalent ratios are the ratios that are the same when we reduce them to the simplest form.
• Two ratios are said to be in proportion if the increase or decrease in one ratio leads to the same increase or decrease in the other ratio.
• If a:b :: c:d, then a × d = b × c.
• In the unitary method, we first find the value of 1 unit and then the number of units asked.
• We can find the speed, distance or time taken by using the formula Distance = Speed × Time.
Math Lab
Artistic Ratios
Art Integration & Experiential Learning
Setting: In groups of 4
Materials Required: Coloured pencils or any markers, large sheets of paper or canvas for each student or group, rulers, pencils and erasers, designs on square grids
Method:
• Distribute figures drawn on square grids to different groups.
• The groups draw a grid on their large sheets of paper or canvas. The size and number of squares in the grid will depend on the image used as a reference. Emphasise the importance of maintaining the proportions when drawing on the grid.
• Explain that each square in their grid represents a corresponding square on the reference image. This process introduces the concept of proportion.
• After the image is scaled and grid lines are drawn, groups start colouring each square based on the colours they see in the reference image. Ensure the colours and ratios in the grid are the same as in the original image.
Chapter Checkup
• The groups showcase their artwork and discuss the ratios and proportions they used in the designs.
If 51:85 and x:5 are equivalent, then find the value of x.
The ratio of two numbers is 7:8. If each number is reduced by 24; the ratio is 5:6. Find the numbers.
A machine can produce 32 widgets in 5 minutes. How many widgets can it produce in an hour?
A plane travels 2,90,000 metres in 9000 seconds. What is the speed of the plane?
Suman cycles for 5 1 2 minutes at a speed of 4 m/s. Find the distance she travels.
If 25 men can construct a building in 150 days, in how many days will 30 men do the same work?
A mouse runs a distance of 5.5 metres in 30 seconds. Calculate the speed of the mouse to two decimal points.
A pancake recipe requires 1 2 tablespoon of baking powder; 1 3 4 tablespoons of sugar and 2 5 8 tablespoons of flour. What is the ratio of baking powder to sugar to flour required?
A beetle travels at a speed of 0.2 m/s. It travels a distance of 1.09 m before it is caught in a jar. Find the time taken by the beetle to fly before getting caught.
A stick 4 feet long is held perpendicular to the ground, casting a shadow 3 feet long. At the same time, an electrical pole casts a shadow 90 feet long. What is the height of the electrical pole?
Vivek, a dedicated runner who maintains a steady pace of 8.0 mph, is training for the Boston Marathon, which covers a distance of around 28 miles. Based on this pace, calculate the time it will take him to complete the race.
The ratio of the ages of Suresh and his son Kartik is 11:5. If the ratio of their ages 5 years ago was 5:2, find their present ages.
The ratio of Sunil’s expenditure to his saving is 4:1. If his total income is ₹18,000, how much does he save and spend? Do you save money?
What number should be added to each of the numbers 10, 18, 22 and 38 to make them in proportion?
Challenge
Critical Thinking
A certain amount was divided among Kirti, Vikas and Avinash in the ratio 1 3 : 1 4 : 1 5 . If the amount received by Avinash is ₹28,800, find the total amount distributed.
Given that fifteen marbles cost ₹1.50:
Which of the following statements are true for the given data?
Statement 1: The number of marbles that can be bought for ₹30 is 300.
Statement 2: The cost of 45 marbles will be ₹3.50.
Statement 3: The unitary method is a technique for solving a problem by first finding the value of a single unit, and then finding the necessary value by multiplying the single unit value.
a Statements 1 and 2 are correct, and Statement 3 is incorrect.
b Statements 1 and 3 are correct, and Statement 2 is incorrect.
c Statements 2 and 3 are correct, and Statement 1 is incorrect.
d Only statement 2 is correct.
Balancing Nutrients in Soil
In a school science project, a group of Grade 8 students decided to investigate the nutrient levels in soil to understand how it affects plant growth. They chose three different areas in their school garden for their experiment. Each area had different soil compositions due to varying levels of fertiliser usage over the years.
Area A had soil that was regularly fertilised with nitrogen-rich fertiliser. Area B had soil that received sporadic fertilisation with phosphorus-based fertiliser. Area C had soil that was left unfertilised for several years.
The students collected soil samples from each area and tested them for nitrogen, phosphorus, and potassium levels, which are crucial for plant growth.
Results:
• Area A: Nitrogen content = 0.08%, Phosphorus content = 0.03%, Potassium content = 0.05%
• Area B: Nitrogen content = 0.05%, Phosphorus content = 0.07%, Potassium content = 0.04%
• Area C: Nitrogen content = 0.02%, Phosphorus content = 0.01%, Potassium content = 0.03%
1 Which area has the highest ratio of nitrogen to phosphorus content?
a Area A
c Area C
b Area B
d Insufficient information
2 The ratio of nitrogen to phosphorus in Area A is
3 The ratio of potassium to nitrogen in Area B is .
4 True or False: Area C has the lowest nitrogen content among all areas.
5 True or False: Area A has the highest phosphorus content among all areas.
9 Percentage, Profit and Loss, Simple Interest
Let’s Recall
The employees in Maya's office come to the office either by train, bus, bicycle or car. The pie chart shows the fraction of employees who opt for different types of transportation.
What fraction of the employees come to the office by bicycle? 3 10
Which transportation is opted for by the highest number of employees? Car
Let’s Warm-up
Percentage and Its Applications
In 2011, the total population of Kota was about 19,50,000. There are 10,20,000 females, and the rest are males.
Percentages, Decimals, Fractions and Ratios
Rakesh wants to find the percentage of females in the city. How can he do that? Let us see!
Percentages, Decimals and Fractions
The term per cent has been derived from the Latin word ‘per centum’, which means ‘out of one hundred’
Percent is denoted as ‘%’.
37 parts shaded out of 100
As a fraction, 37 100
To convert a fraction to a percentage, multiply the fraction by 100 and put a percentage symbol (%).
For example,
Fraction of females in the city = 6,75,000 15,00,000
Percentage of females in the city = 6,75,000 15,00,000 × 100 = 45%
a = (a × 100)%
To convert a decimal to a percentage, multiply the decimal number by 100 and put the percentage symbol (%).
For example,
0.25 = (0.25 × 100) % = 25%
As a decimal, 0.37
As a percentage, 37%
a % = a 100
To convert a percentage to a fraction, remove the percentage symbol (%) and write 100 in the denominator.
For example, convert 48% into a fraction.
48% = 48 100 = 12 25
a% = a ÷ 100
To convert a percentage to a decimal, remove the percentage symbol (%) and divide the number by 100.
For example,
81% = (81 ÷ 100) = 0.81
Example 1: Convert the given fractions into percentages.
Example 2: Convert the given percentages into fractions and decimals
As a fraction: 23% = 23 100
Example 3: Convert the decimals into percentages.
56% = 56 100 = 14 25 56% = 56 ÷ 100 = Do It Together
Convert the percentages into fractions and decimals.
1 56%
= 120 ÷ =
Percentage and Ratios
Do you remember the survey conducted by Rakesh? He found the ratio of the number of males to females to be 11:9.
He wanted to find the percentage of males in the city. Let us see!
Convert ratios into percentages
To convert a ratio to a percentage, we write the ratio as a fraction and then convert it into a percentage.
If there are 11x males, then there are 9x females in the city.
Total number of people in the city = 20x
The ratio of males to the total number of people = 11:20
Percentage of males in the city =
11 20 × 100
% = 55%
Thus, the male population is 55% of the total.
Convert percentages into ratios
Did You Know?
Only 0.006% of the earth’s water is available for human use.
65% of the people in a meeting were male. Let us find the ratio of males to females in the meeting.
The percentage of males in the meeting = 65%
The percentage of females in the meeting = 100% – 65% = 35%
The ratio of males to females = 65%:35% = 65 100 : 35 100 = 65:35 = 13:7
Thus, the ratio of males to females in the meeting is 13:7.
Example 4: In a class, 25% of the students are enrolled in the science club. What is the ratio of science club members to the total number of students?
The percentage of students enrolled in the science club = 25%
The ratio of the science club members to the total number of students = 25%:100% = 25 100 : 100 100 = 25:100 = 1:4
Thus, the ratio of science club members to the total number of students is 1:4.
Example 5: At a bookstore, 30% of the books are fiction. If there are 300 books in total, what is the ratio of fiction to non-fiction books?
The percentage of fiction books at the bookstore = 30%
The percentage of non-fiction books at the bookstore = 100% – 30% = 70%
The ratio of fiction to non-fiction books = 30%:70% = 30 100 : 70 100 = 30:70 = 3:7
Thus, the ratio of fiction books to non-fiction books is 3:7.
Error Alert!
Ratio of fiction books to total books
Fiction:Non-fiction Fiction:(Fiction + Non-fiction) 3:7 3:(3 + 7) 3:10
Example 6: In a collection of coins, the ratio of quarters to dimes is 3:17. What percentage of the total coins are dimes?
The ratio of quarters to dimes = 3:17
The ratio of dimes to total coins = 17:(3 + 17) = 17:20
The percentage of dimes = 17 20 × 100% = 85%
Thus, 85% of the total coins are dimes.
At a zoo, the ratio of monkeys to elephants is 3:5. If there are 64 monkeys and elephants in the zoo, what percentage are monkeys?
The ratio of monkeys to elephants = 3:5
The ratio of monkeys to total animals =
The percentage of monkeys at the zoo =
Think and Tell
What percentage of the animals are elephants if there are 400 animals in the zoo?
Do It Yourself 9A
Find out what fraction of the figure is coloured, and also write the percentage of the coloured part.
Express the percentages as decimals.
Express the given decimals as percentages.
If 29% of Earth's surface is covered with land, represent the percentage of Earth's surface covered with water as a decimal.
In a class of 30 students, 20% are enrolled in the art club. What is the ratio of art club members to the total number of students?
In a jar of candies, 25% are blue and the rest are red. What is the ratio of blue to red candies?
At a party, 30% of the attendees are children. If there are 50 people in total, what is the ratio of children to adults?
In a garden, the ratio of roses to tulips is 3:2. If there are 50 flowers in total, what percentage are roses?
In a group of 80 people, 75% prefer apple pie over donuts. What is the ratio of apple pie lovers to donut lovers?
An alloy is a mixture of two or more metals. 22-karat gold is an alloy that contains 22 parts pure gold out of 24 parts, and the rest is some other metal. Express the ratio of pure gold in 22-karat gold to the other metal.
Sudha, a kind-hearted woman, shares a special bond with Rita, the daughter of her housekeeper. As Rita's birthday approaches, Sudha decides to bake her a homemade cake. The recipe requires 2 cups of flour and 3 cups of sugar. What percentage of the dry ingredients is sugar? How can celebrating birthdays across social divides help to challenge societal prejudices?
In a company, every 1 out of 10 employees is a manager. Based on this information, read the assertion and the reason given and choose the correct option.
Assertion (A): 11.11% of the total people are managers.
Reason (R): The ratio of managers to employees is 1:9.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Percentage and Percent Change in Real Life
After a year, 10% of the total number of people migrated to the city. Rakesh wants to know how many people were there after a year. Let us see!
Finding Percent and Percent Change
Finding the Percentage of a Given Quantity
Total number of people in the city = 15,00,000. Percentage of people migrated = 10%
Let us find 10% of 15,00,000.
To find a% of b, we multiply a 100 by b. a% of b = a 100 × b
10% of 15,00,000 = 10 100 × 15,00,000 = 1,50,000
Thus, 1,50,000 people migrated to the city that year.
Total number of people after a year = 15,00,000 + 1,50,000 = 16,50,000
Finding a Number as a Percentage of Another
The following year, 1,65,000 people migrated to another city. What percentage of the people were left the city? Let us see!
The total number of people = 16,50,000
Number of people who migrated = 1,65,000
Let us find out what percent of 16,50,000 is 1,65,000.
Let a% of 16,50,000 = 1,65,000
a% = Number of parts
Total number of parts × 100
=
1,65,000 16,50,000 × 100
% = 10%
Thus, 10% of the people migrated to another city.
Finding a Whole Number Using the Percentage
Find a number of which 5% is 48.
Assume the number to be a.
5% of a = 48
5 × 1
100 × a = 48 ⇒ 1 20 × a = 48
⇒ a = 48 × 20 = 960
Thus, the number is 960.
Percent Change (Increase or Decrease)
Find the percent change when 80 is increased to 88. Percent change =
Amount of increase or decrease Original amount × 100
Example 7: Find:
Example 8: What percent of:
1 200 is 40?
Let
Example 9: Find the number of which:
1 5% is 23
Let the number be a. 5% of a = 23
5 × 1 100 × a = 23
Example 10: Find the percent change when:
Word Problems on Percentage
After 5 years, the population of Kota city becomes 18,00,000. What is the total percentage increase in the population?
We know that the initial population of Kota city was = 15,00,000
Population of the city after 5 years = 18,00,000
Population increase = 18,00,000 – 15,00,000 = 3,00,000
Percentage increase in the population
Thus, the population increased by 20%.
Example 11: A school bus stops at a distance of 22 km from the school while travelling to a picnic spot which is 55 km away. What percentage of the distance is remaining for the bus to reach the picnic spot?
Fraction of the distance remaining for the bus to reach the picnic spot 552233 == 5555
Percentage of remaining distance 33 3 ===×100%×100%60% 55 5
Thus, 60% of the distance remains for the bus to reach the picnic spot.
Example 12: After discarding 15% of his oranges, a farmer has 3400 oranges left. How many oranges did the farmer have initially?
Percentage of oranges discarded = 15%
Percentage of oranges left = 100% – 15% = 85%
Let the total number of oranges be x
85% of x = 3400; 85 100 × x = 3400 ⇒ x = 3400 × 100 85 = 4000
Thus, the farmer initially had 4000 oranges.
Example 13: There are 5000 students in a school. 3600 students participated in the annual function. What percentage of students did not participate in the annual function?
Number of students that did not participate in the function = 5000 – 3600 = 1400
Percentage of students who did not participate 1400 7 =×100%=×100%=28% 5000 25
Thus, 28% of the total students did not participate in the annual function.
Example 14: A person’s salary was first increased by 20% and then reduced by 10%. What is the percentage change in the salary of the person?
Increase in salary initially = 20%
Decrease in salary afterwards = 10%
Let the initial salary be 100.
Salary after first increment = 100 + 20 100 � 100 = 100 + 20 = 120
Salary after decrement = 120 − 10 100 � 120 = 120 − 12 = 108
So, the salary becomes 108 after an increment of 20% and then a decrement of 10%.
Percentage change in salary = 108 − 100 100 � 100% = 8 100 � 100% = 8%
Thus, there is an 8% increase in the salary.
Example 15: In an election, Candidate A received 12% of the total potential votes. The total population who could have voted was 1,53,600. If 54% of the people did not cast any votes, how many votes did Candidate B get?
Percentage of total votes that Candidate A gets = 12%
Percentage of people who did not cast any vote = 54%
Total number of people who voted = 1,53,600
Percentage of total votes that Candidate B gets = 100% − 12% −54% = 34%
Number of total votes that Candidate B gets = 34 100 � 1,53,600 = 52,224
Thus, Candidate B got 52,224 votes.
Example 16: In a sales competition, Team B sold 30% more products than Team A, and Team A sold 15% fewer products than Team C. Team D sold 25% more products than Team C. By what percentage is the number of products sold by Team D more than that sold by Team A?
Products sold by Team B = 30% more than Team A
Products sold by Team A = 15% less than Team C
Products sold by Team D = 25% more than Team C
Let the products sold by C be 100.
Products sold by A = 15% less than 100 = 100 − 15 100 � 100 = 85
Products sold by D = 25% more than 100 = 100 + 25 100 � 100 = 125
Percentage by which products sold by D is more than those sold by A = 125 − 85 85 � 100% = 40 85 � 100 = 47.05%.
Thus, D sold 47.05% more products than A.
On Sunday, 845 people went to an exhibition. On Monday, only 169 people went. What is the percentage decrease in the number of people visiting the exhibition on Monday?
Number of people who went to the exhibition on Sunday = 845
Number of people who went to the exhibition on Monday = 169
Change in the number of people = − =
Decrease in percent = × 100% = × 100% = %
Thus, there was a % decrease in the number of people visiting the exhibition on Monday.
a 25% of 250
c 125% of 45
Express.
a 5 cm as a percentage of 4 m 25 cm
b 30% of 750
d 14% of 4800
b 450 mL as a percentage of 3 L
c 75 seconds as a percentage of 2 minutes 30 seconds. d 800 grams as a percentage of 5 kilograms.
Find the number of which:
a 12% is 48.
c 125% is 5 hours 20 minutes.
Find the percent change.
a 320 is decreased to 272
c 150 is increased to 195
b 2 66 3 % is 567.
d 20% is 3 m 40 cm.
b 110 is increased to 165
d 400 is decreased to 360
The concentration of acetic acid in a vinegar solution is 40%. After some dilution, the concentration increases to 50% acetic acid. What is the percent change in the concentration of acetic acid?
Yash scored 360 marks out of 500, and Jaya scored 450 marks out of 600. Who has the better percentage?
At a community gathering focused on promoting environmentally friendly practices, such as using bicycles instead of smoke-emitting vehicles, there are 1440 people in total. If 40% of the people at the gathering are women, how many women are attending the event? How does using bicycles help the environment?
There are 450 women employees in a factory. How many employees are there in total in the factory if the factory has 55% male employees?
If ₹500 is to be divided among Ravi, Raju and Roy so that Ravi gets two parts, Raju three parts and Roy five parts, how much money will each get? What will this be in percentages?
Muntz metal (also known as yellow metal) is an alloy of copper and zinc known for its durability and resistance to corrosion, making it suitable for marine and architectural applications. A variation of this alloy contains 26% copper, and the rest is zinc. What quantity of alloy is required to get 1480 g of zinc?
The population of a city decreases by 8% every year. If the current population of the city is 1,69,280, what was the population of the city 2 years ago?
In an examination, B scored 20% more than A, and A scored 10% less than C. D obtained 20% more marks than C. By what percentage are the marks obtained by D more than those obtained by A?
The cost of a car goes down every year by 20% of its previous value. Find its original cost if the cost of it after 2 years is ₹5,65,000.
The marks scored by Rahul in various subjects (out of 100) are shown using a bar graph. What is the average percentage of the marks scored by him?
Is the percentage increase from 80 to 100 the same as the percentage decrease from 100 to 80? Why or why not?
With an increase in excise duty, the price of petrol goes up by 4%. Before the hike, the price of petrol was ₹95 per litre. A man travels 3456 km every month and his car gives a mileage of 16 km per litre. What is the increase in the monthly expenditure of the man (in the nearest ₹) on travelling due to the hike in petrol prices?
Profit and Loss
Raju is a fish seller. He has a shop and purchases fish from multiple fishermen and sells it further.
Profit and Loss Percentages
Raju purchases the fish for ₹50,000 and sells it all for ₹60,000. How much money does he earn? Let us see!
Price at which Raju purchases the fish = ₹50,000 Price at which Raju sells the fish = ₹60,000 Money earned by Raju = ₹60,000 – ₹50,000 = ₹10,000
Cost Price
The price at which goods are purchased.
Selling Price
The price at which goods are sold.
When Selling Price > Cost Price
Profit% = Profit CP × 100 %
Finding SP when CP and profit/loss % are given:
SP = 100 + Profit % 100 × CP OR 100 – Loss% 100 × CP
Example 17: Find the profit or loss percentage.
1 CP = ₹1500 and SP = ₹1800 SP > CP
Profit% 18001500 300 = ×100%=×100% 1500 1500 =20% Profit
Example 18: Find.
Loss
When Cost Price > Selling Price
Loss% =
Loss CP × 100
%
1 CP when profit% = 20% and SP = ₹1800
CP 100 100 = SP= 1800 ×× 100 +Profit%100+20
1005 =1800=1800= ×× 1206 ₹1500
Calculate:
Profit and loss are always calculated on the cost price.
Finding CP when SP and profit/loss % are given: CP = 100 100 + Profit % × SP OR 100 100 – Loss% × SP
2 CP = ₹2000 and SP = ₹1500
CP > SP
Loss% 20001500 500 = ×100%=×100% 2000 2000 =25%
2 SP when profit% = 15% and CP = ₹3000 SP 100+Profit%100+15 = CP= 3000 ×× 100 100 115 =3000= × 100 ₹3450
Discount = 15% of 500 = 15 500 × 100 = ₹75 Do
1 CP when SP = ₹1600 and loss% = 20%
CP 100 SP × == 100Loss% =
Marked Price and Discount
2 SP when CP = ₹2500 and profit% = 12% SP 100+Profit% = CP= × 100 =
Raju labelled the prices on the fish counters. He labelled a particular type of fish with a price of ₹500.
Marked Price: The price on the label of an item is called its marked price. The marked price can be different from the selling price. The marked price is denoted by MP.
Discount: When a shopkeeper reduces a certain amount from the marked price of an article and sells it to the customers, the reduction is called a discount. The discount amount is given as a certain percentage of the marked price.
If a discount is given then Marked Price > Selling Price and Discount = Marked Price – Selling Price
Discount % = %
Find the discount if Marked Price = ₹500 and discount % = 15%.
Example 19: Find the discount if discount % = 35% and Marked Price = ₹8000.
Discount = 35% of 8000 = 35 100 × 8000 = ₹2800
Thus, the discount is ₹2800.
Example 20: Calculate the discount % if the discount is ₹1700 and the Marked Price = ₹8500.
Discount% =
Example 21: Find the discount percentage if the Marked Price (MP) = ₹2000; Selling Price (SP) = ₹1600.
Discount Amount = Marked Price − Selling Price
Discount Amount = ₹2000 − ₹1600 = ₹400
Discount Percentage = Discount Amount MP � 100
Discount Percentage = 400 2000 � 100 = 20%
What is the discount % if the Marked Price = ₹1600 and discount = ₹80? Discount% =
Word Problems on Profit and Loss
Do you remember Raju the fish seller? He buys some more fish for ₹1,00,000. He sells the fish for ₹1,05,000.
How much profit does Raju earn?
CP of fish = ₹1,00,000; SP of fish = ₹1,05,000
Profit = SP – CP = ₹1,05,000 – ₹1,00,000 = ₹5000
Thus, Raju earns ₹5000 on selling the fish.
Example 22: Utkarsh sold a plot of land for ₹5,00,000, gaining 25%. For how much did he purchase the plot?
SP = ₹5,00,000 and Profit = 25%
CP = 100 SP × 100+Profit% = 100 100+25 × ₹5,00,000 = 4 5 × ₹5,00,000 = ₹4,00,000
Thus, Utkarsh purchased the plot for ₹4,00,000.
Example 23: Samuel buys a laptop at ₹90,000. After three years, he sells it at ₹75,000. Calculate the loss %.
CP = ₹90,000 and SP = ₹75,000
Loss % = Loss 100% × CP = ₹90,000 – ₹75,000 ₹90,000 × 100% = 2 16% 3
Thus, Samuel sells the laptop at a loss of 2 16% 3 .
Example 24: Jessica sold an air conditioner for ₹32,500 at a loss of 20%. Find the cost price of the air conditioner. At what price should she have sold it to gain 20%?
SP = ₹32,500 and loss = 20%
CP = 100 SP × 100 Loss% = 100 10020 × ₹32,500 = 100 80 × ₹32,500 = ₹40,625
Thus, the cost price of the air conditioner was ₹40,625.
If the gain was 20%,
SP = 100 +Profit% CP × 100 = 100+20 100 × ₹40,625 = 120 100 × ₹40,625 = ₹48,750
Thus, Jessica should have sold the air conditioner at ₹48,750 to gain 20%.
Example 25: A farmer sold 2 bullocks for ₹48,000 each. On one bullock, he gained 25%; and on the other, he lost 20%. Find the percentage of his total profit or loss.
SP of each bullock = ₹48,000
of the first bullock
Total cost price = ₹38,400 + ₹60,000 = ₹98,400; Total selling price = ₹48,000 + ₹48,000 = ₹96,000
CP > SP, so a loss was incurred. Loss = CP − SP = ₹98,400 − ₹96,000 = ₹2,400
Thus, the farmer incurred a total loss of 2.44%.
Example 26: During the annual Rajasthan International Folk Festival held at the Mehrangarh Fort in Jodhpur, a shop sells traditional Indian pottery. The festival is known for showcasing rich Indian heritage and crafts. At one of the stalls, a beautiful clay pot is marked with a price (MP) of ₹1,200. During the festival, the shop offers a special price (SP) of ₹960 for the pot. What is the discount percentage offered on the clay pot?
Discount Amount = MP − SP
Discount Amount = ₹1,200 − ₹960 = ₹240
Discount Percentage = Discount Amount Marked Price × 100
Discount Percentage = ₹240 ₹1,200 × 100 = 20%
So, the discount percentage offered on the clay pot is 20%.
Example 27: Anjali bought a pair of jeans for ₹950 and sold it for ₹1000, whereas Rahul bought another pair of jeans for ₹1050 and sold it for ₹1070. The shipping cost for Anjali was ₹50, while for Rahul it was ₹30. Who incurred the greater loss?
For Anjali: For Rahul:
Cost price of a pair of jeans = ₹950
Selling price of a pair of jeans = ₹1000
Shipping cost = ₹50
Total cost for Anjali = ₹950 + ₹50 = ₹1000
Total revenue for Anjali = Selling price = ₹1000
Since CP = SP, there is neither profit nor loss.
Cost price of a pair of jeans = ₹1050
Selling price of a pair of jeans = ₹1070
Shipping cost = ₹30
Total cost for Rahul = ₹1050 + ₹30 = ₹1080
Total revenue for Rahul = Selling price = ₹1070
Since CP > SP, there will be loss.
So, Anjali made neither a profit nor a loss, while Rahul incurred a loss of ₹10. Therefore, Rahul incurred the greater loss.
Example 28: The profit% earned by selling an article for ₹240 is equal to the loss% incurred by selling the same article for ₹160. At what price should the article be sold to make a 25% profit?
Selling price of the article when there is profit = ₹240
Selling price of the article when there is loss = ₹160
Cost price (CP) is the same in both the cases. Take the cost price as x.
If the profit% and the loss% is the same, then the profit and the loss on the same article will be the same.
so, 240 − x x � 100 = x − 150 x � 100
240 − x x � 100 = x − 150 x � 100
240 − x = x − 150
2x = 240 – 150 = 80
x = 40
CP = ₹240 − ₹40 = ₹200
Given: There must be a profit of 25%
SP = 100 + 25 100 � 200 = 250
Thus, the article should be sold at ₹250 to make a profit of 25%.
Example 29: On selling 25 shirts for ₹5000, there is a loss equal to the cost price of 10 shirts. What is the cost price of each shirt?
Selling price of 25 shirts = ₹5000
According to question,
Loss incurred after selling 25 shirts = Cost price of 10 shirts
CP of 25 shirts – SP of 25 shirts = CP of 10 shirts
CP of 15 shirts = SP of 25 shirts
CP of 15 shirts = ₹5000
CP of 1 shirt = ₹333.33
Thus, the cost of each shirt is ₹333.33.
Example 30: A baker mixes 15 kg of flour at ₹10 per kg with 20 kg of flour of another variety at ₹15 per kg and sells the mixture at ₹18 per kg. What is the baker’s profit?
Total cost price of 35 kg of flour = 15 × ₹10 + 20 × ₹15 = ₹150 + ₹300 = ₹450
Total selling price of 35 kg of flour = 35 × ₹18 = ₹630
Profit = ₹630 – ₹450 = ₹180
Thus, the baker’s profit is ₹180.
Jennifer buys an old scooter for ₹47,000 and spends ₹8000 on repairs. If she sells the scooter for ₹58,000, what is her profit %?
Total CP of scooter = ₹47,000 + ₹8000 = ₹
SP of scooter = ₹
Profit% =
Find the gain or loss.
a CP = ₹620 and SP = ₹745 b CP = ₹5230 and SP = ₹6000 c CP = ₹50,000 and SP = ₹49,812
Select the correct answer.
a CP = ₹405 and SP = ₹510 then gain = ?
i ₹100
b CP = ₹10,235 and SP = ₹9400 then loss = ? i ₹800
₹835
c CP = ₹2000 and SP = ₹2500 then profit% = ?
i 25%
40%
d CP = ₹2000 and SP = ₹1800 then loss% = ?
Find the missing term.
a SP = ₹500, CP = ₹450 then profit = ?
c SP = ₹450, MP ₹585 then discount% = ?
b CP = ₹2364, loss = ₹364 then SP = ?
d MP = ₹3060, SP = ₹2550 then discount% = ?
The marked price of a toy car is ₹540. If the discount given by the shopkeeper is 20%, what is the selling price of this toy?
Mia sold a ring which she had bought from an exhibition for ₹9000, to her friend for ₹7600. What is the cost price of the ring for Mia’s friend?
Alex’s father bought a scooter for ₹49,000. He spent ₹6000 on transportation and ₹5000 on repairs. If he sells the scooter for ₹58,000, what is the total profit/loss?
In a community drive to increase awareness about how water coolers are beneficial for respiratory health, by maintaining humidity levels, the members of the drive are promoting buying water coolers. The marked price of a water cooler is ₹8350. The shopkeeper offers a discount of 18% on it. Find its selling price.
A man sold two watches at the same price, one at a 10% profit and the other at a 10% loss. Find his overall percentage of gain or loss.
A dealer incurs a loss of 5% if he sells an article for ₹1805. What price must he sell the article for to gain 5% on that article?
A shop sells eco-friendly products like solar lamps and recycled paper at a subsidised price, to promote sustainable living. The shopkeeper marks his products at 35% above the cost price and allows a discount of 20% on the marked price. Find his gain or loss percent. How do you recycle old newspapers?
On selling 17 balls at ₹720, there is a loss equal to the cost price of 5 balls. What is the cost price of the ball?
The percentage profit earned by selling an article for ₹1920 is equal to the percentage loss incurred by selling the same article for ₹1280. At what price should the article be sold to make a 25% profit?
A trader mixes 26 kg of rice at ₹20 per kg with 30 kg of rice of another variety at ₹36 per kg and sells the mixture at ₹30 per kg. What is the trader’s profit?
A shopkeeper purchased 200 bulbs for ₹10 each. However, 5 bulbs were fused and had to be thrown away. The remaining were sold at ₹12 each. Find the percentage of gain or loss.
Real Life Connect
Read the statements and choose the correct option.
Assertion (A): The vendor buys oranges at ₹26 per dozen and sells them at 5 for ₹13. The vendor’s gain percent is 20%.
Reason (R): Gain percent = Gain Cost Price × 100%
Which of the following options is correct?
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Simple Interest
Emma had saved ₹5000. She deposited the money in her bank. The manager told her that they would add a certain percentage to her total savings every month. Emma was really happy to hear that.
Using the Formula
The manager said that they would give her an extra 2% every month. He said she could get an extra ₹100 the next month. Emma was confused. Let us see how she gets the extra money.
SI = P × R × T 100 Principal Money borrowed or deposited
Simple Interest
The extra amount paid by the borrower.
Money deposited in the bank = ₹5000; Rate of interest = 2% per month; Time = 1 month
SI = PRT 100 ×× = ×× 500021 100 ₹ = ₹100
Amount = P + SI = ₹5000 + ₹100 = ₹5100 Thus, Emma gets ₹5100 after a month.
Rate
Rate of interest given on the principal amount.
Time
The period of time for which money is borrowed or deposited.
Did You Know?
In the 12th century, Bhaskara II, an Indian mathematician developed formulas for simple interest calculations, providing the most essential tool for commerce and finance.
Do It Together
Example 31: SI = ₹54, R = 9% per annum, T = 1 year. P = ?
SI = ₹54, R = 9% per annum, T = 1 year
SI = PRT 100 ×× ⇒ 54 = 91 100 P ×× ; P = 5400 9 = ₹600
Example 32: Find the missing values.
1 P = ₹1000, R = 10% per annum and T = 3 years; A= ?
SI = P � R � T 100 = 1000 � 10 � 3 100 = ₹300
A = ₹1000 + ₹300 = ₹1300
2 P = ₹4000, R = 5% per annum and SI = 1 2 of P; T = ?
T = SI � 100 P � R = 1 2 � 4000 � 100 4000 � 5 = 10 years
3 P = ₹9000, T = 5 years and SI = ₹4500, R =?
R = SI � 100 P � T = 4500 � 100 9000 � 5 = 10%
4 R = 5% per annum, T = 5 years and SI = ₹3000; P = ?
P = SI � 100 T � R = 3000 � 100 5 � 5 = ₹12,000
Find P if SI = ₹1000, R = 10% and T = 5 years.
SI = ₹1000, R = 10% and T = 5 years
SI = PRT 100 ×× ⇒ P = SI100 × = RT × = =
Word Problems on Simple Interest
Do you remember Emma, who deposited ₹5000 in the bank? How much money does Emma get after a year?
Principal = ₹5000, R = 2% per month and T = 1 year = 12 months
SI = P × R × T 100 = ₹5000 × 2 × 12 100 = ₹1200; A = P + SI = ₹5000 + ₹1200 = ₹6200
Thus, Emma gets ₹6200 after a year.
Example 33: Shilpa lends a sum at 5% per annum to a friend who promises to return the sum with the interest after 5 years. What amount will she get if the interest she gets is ₹1250?
SI = ₹1250, R = 5% and T = 5 years
P = SI × 100 R × T = ₹1250 × 100 5 × 5 = ₹5000; A = P + SI = ₹5000 + ₹1250 = ₹6250
Thus, Shilpa gets ₹6250 back from her friend.
Example 34: Raghav has a certain sum deposited in a bank at 5% per annum. Anshul also has the same sum deposited in the same bank at 9% per annum. The difference in the annual interest received by each of them is ₹440. Find the total sum of money deposited by them.
Let the money deposited by Raghav and Anshul be ₹x
Interest received by Raghav after a year = x × 5 × 1
100 = ₹ 5 100 x
Interest received by Anshul after a year = x × 9 × 1
100 = ₹ 9 100 x
Difference in the annual interest = ₹440
So, ₹ 9 100 x – ₹ 5 100 x = ₹440 ⇒ ₹ 4 100 x = ₹440 ⇒ x = ₹11,000
So, Raghav and Anshul each deposited ₹11,000.
Total sum of money deposited by Raghav and Anshul = ₹11,000 + ₹11,000 = ₹22,000
Example 35: Vishesh invested an amount of ₹10,000 divided into two different schemes, A and B, at the simple interest rate of 10% p.a. and 15% p.a., respectively. If the total amount of simple interest earned in 2 years is ₹2450, what was the difference of the amounts invested in each of the schemes?
Let the amount invested in scheme A be x; Amount invested in scheme B = 10,000 – x
SI from scheme A + SI from scheme B = Total SI
××102(10,000)152 ×× + 100 100 xx = 2450; = 30(10,000) 20 + 2450 100100 x x
+=⇒+= 2030(10,000–)2,45,000203,00,000–302,45,000 xxxx
⇒= 30 –203,00,000 –2,45,000 xx ⇒=⇒= 1055,000 5500 xx
10,000 – x = 10,000 − 5500 = ₹4500
Difference of the amounts invested in the two schemes = 5500 – 4500 = ₹1000
Example 36: Find the total amount a person gets when he deposits ₹40,000 at a rate of 1 5 2 % per annum for 3 4 4 years in a bank.
P = ₹40,000, R = 1 5 2 % per annum = 11 2 % per annum and T = 3 4 4 years = 19 4 years
SI = ₹40,000 × 11 2 × 19 4 100 = ₹40,000 × 11 × 19 100 × 2 × 4 = ₹10,450; A = P + SI = ₹40,000 + ₹10,450 = ₹50,450
Thus, the person gets ₹50,450 from the bank after 3 4 4 years.
Mr Wilson took out a loan of ₹1500 with simple interest for as many years as the rate of interest. If he paid ₹375 as interest at the end of the loan period, what was the rate of interest?
P = ₹1500, R = T = R, SI = ₹375
SI = P × R × T 100 = P × R × R
100 = × R × R
100 ; R2 = × 100 =
Find the simple interest and amount.
a P = ₹5000, R = 5% per annum and T = 3 years
c P = ₹2000, R = 10% per annum and T = 3 years
Find the time taken.
a P = ₹7500, R = 3% per annum and SI = ₹2250
c P = ₹3375, R = 15% per annum and SI = ₹1518.75
Find the principal amount.
a R = 6% per annum, T = 8 years and SI = ₹23,520
b P = ₹6000, R = 12% per annum and T = 5 years
d P = ₹2250, R = 2% per annum and T = 4 years
b P = ₹2000, R = 4% per annum and SI = 1 4 of P
d P = ₹12,000, R = 1 4 2 % per annum and SI = ₹3510
b R = 5% per annum, T = 1 9 3 years and SI = ₹2800
c R = 1 5 2 % per annum, T = 3 1 2 years and SI = ₹23,100 d R = 3 12 5 % per annum, T = 1 1 4 years and SI = ₹31,500
Find the rate of interest.
a P = ₹9500, T = 7 years and SI = ₹1995
c P = ₹12,500, T = 1 4 5 years and SI = ₹3412.5
b P = ₹20,000, T = 12 years and SI = ₹18,000
d P = ₹3,60,000, T = 1 9 2 years and SI = ₹1111.5
A principal of ₹40,000 is deposited in a bank which offers simple interest at a rate of 10% per annum. What is the total amount at the end of 2 years?
Akila needed some urgent funds, and her friend decided to help her. She borrowed a sum of money from her friend and paid an interest of ₹450 after a year at an interest rate of 4.5% per annum. How much money did Akila borrow? Do you help a friend in need?
Preeti, a small-scale entrepreneur, took out a loan of ₹2,50,000 from a bank under the Prime Minister's Employment Generation Programme (PMEGP), a scheme by the Government of India to promote entrepreneurship and create self-employment opportunities. The loan was offered at an interest rate of 8% per annum. Calculate the simple interest she has to pay after 4 years.
A man earns an interest of ₹720 on a sum he lent at 18% per annum for two years. Had he earned 12% more interest on the same amount at the same time, what would have been the rate of interest?
Bela borrowed a certain sum of money at the rate of 5% per annum for the first three years, 8% per annum for the next four years, and 12% per annum for the period beyond 7 years. If she pays a total amount of interest of ₹17,845 at the end of 10 years, find the amount she borrowed.
A certain sum of money lent out at a certain rate of interest per annum triples itself in 15 years. In how many years will it quadruple itself?
Points to Remember
• Percent means out of 100.
• To convert fractions to percentages,
• To convert percentages to fractions, = % 100 a a
• To convert decimals to percentages, multiply the decimal by 100 and put the percentage symbol (%).
• To convert percentages to decimals, remove the percentage symbol (%) and divide by 100.
• To convert a ratio to a percentage,
• To find the percent change, Percent change =
• Profit/Loss % =
• When there is a profit,
• When there is a loss, SP = 100Loss% CP 100 × and CP = 100 SP 100Loss% ×
• Simple interest SI = PR T 100 ××
Math Lab
Communication & Collaboration
Discount Shopping
Aim: To practise calculating discounts and final prices, using percentages.
Setting: In pairs
Materials Required: Paper or pen, list of items with original prices (Example, ₹500, ₹1000, ₹1200, etc.) With a discount percentage given on each items. Assign a discount percentage to each item. (Example, 10%, 15%, 20%, etc.).
Method:
1 Each team to take the list of items with their discounts.
2 Each group to calculate the sale price of each item after the discount.
3 Discuss the answers within the group.
4 After this, give the students a budget (example, ₹5000) and ask them to choose the items from the list within the budget.
5 Each team to showcase their work to the rest of the class.
Chapter Checkup
Express:
a 4 5 as a percentage b 18.75% as a fraction c 1 2 5 % as a fraction d 2 11 5 as a percentage
e 0.48 as a percentage f 1 4 2 % as a decimal g 5.64 as a percentage h 1 8 8 % as a decimal
Evaluate.
a 25% of ₹460 b 1 12 2 % of 20 L c 1 50 2 % of 1000 d 5% of 3 kg 200 g
Find the profit or loss for the given cases. Fill in the blank.
a CP = ₹150, SP = ₹200, Profit = b CP = ₹1580, SP = ₹1235, Loss = c CP = ₹5100, SP = ₹5235, Profit = d CP = ₹458, SP = ₹369, Loss =
What percent of:
a 6 L is 20 mL? b 20 km is 1000 m? c ₹15 is ₹2 and 10 p? d 4.5 kg is 0.9 kg?
Find the percentage when: a 12 is increased to 18 b 15 is increased by 15 c 200 is decreased to 180
Find the profit% or loss%.
a CP = ₹50, SP = ₹65 b CP = ₹150, SP = ₹125 c CP = ₹1000, SP = ₹896
Find the discount%.
a Discount = ₹80, MP = ₹640 b Discount = ₹289, MP = ₹1156 c Discount = ₹155, MP = ₹775
Find the missing terms in the questions.
a P = ₹500, R = 2% p.a., T = 3 years, A = ? b P = ₹5500, R = 14 1 2 % p.a., T = 1 6 2 years, A = ?
A person buys a pen for ₹100 and sells it for ₹125. What is the gain or loss? What is the gain % or loss %?
A cobbler spends ₹80 on leather, ₹10 on strings and adhesives and ₹10 on polishing to make a pair of shoes. He sells each pair for ₹180. How much profit % or loss % does he make?
Green energy, such as solar and wind power, is crucial for reducing carbon emissions and combating climate change. Following the announcement of new increased subsidies, the price of an energy company's stock increases from ₹54 per share to ₹72 per share in a week. By what percentage has the stock's price increased?
In a school of 480 students, the ratio of boys to girls is 7:8.
a What percentage of the total students are boys?
b What percentage of the total students are girls?
Dharmendra thinks of three numbers. The first two numbers are 20% and 50% more than the third number respectively. What is the ratio of the first two numbers?
Kapil’s expenditure is 20% of his total income. His salary increases by 20%, but his savings remain the same. What is the percentage increase in Kapil’s expenditure? How does saving help us when in need?
A person allowed a discount of 12% and sold an item at ₹880. What is the marked price on the item?
Sonu sells a watch at a 5% discount. If he sold the watch at a 6% discount, then he would have earned ₹27 less. What is the marked price of the watch?
Sunita borrows ₹5000 for 2 years at the rate of 4 p.a. and lends it to Arya at the rate of 1 6 4 % p.a. for 2 years. What is the gain earned by Sunita?
Seats for Mathematics, Physics and Biology in a school are in the ratio 6:8:12. There is a proposal to increase these numbers by 40%, 50% and 75% respectively. What will be the ratio of the increased seats?
Read the statements and choose the correct option.
Assertion (A): A sum of ₹1000 was lent to two people, equally one at the rate of 5% and the other at the rate of 8%. The simple interest earned after one year is ₹65.
Reason (R): SI = PRT 100
Options:
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Case Study
The Greenhouse Project
A school decided to build a greenhouse to educate students about sustainable farming. They planned to grow organic vegetables and fruits, which they would sell to the local community. The project was also part of a larger initiative to raise awareness about climate change and sustainable living practices.
The school invested ₹50,000 in building the greenhouse. This included the cost of materials, labour, and initial seeds. In the first year, the greenhouse generated ₹70,000 in revenue from selling produce. The yearly maintenance costs, including water, fertilisers, and electricity, were ₹20,000. To cover the initial costs, the school took out a loan of ₹30,000 at an annual simple interest rate of 8%. The loan is to be repaid in 3 years.
To attract more customers, the school decided to mark the price of their products higher and then offer a discount. The total marked price of the products was ₹80,000, and they offered a 10% discount on the marked price.
Answer the following questions:
1 What was the total profit made by the greenhouse in the first year? a ₹0 b ₹20,000 c ₹30,000 d ₹50,000
2 What was the selling price of the products after the discount? a ₹68,000 b ₹70,000 c ₹80,000 d ₹72,000
3 The percentage profit made by the greenhouse in the first year was %.
4 The total amount of the loan repaid after 3 years, including interest, was ₹36,000. (True/False)
5 How does sustainable living help the environment?
Cross Curricular & Value Development
3
10 Rational Numbers
Let’s Recall
We know that a fraction is a part of the whole. It is a way of expressing a number that is the ratio of two natural numbers.
If the numerator is less than the denominator, then the fraction is a proper fraction.
For example: 7 10
If the numerator is greater than or equal to the denominator, then the fraction is an improper fraction.
For example: 11 10
When the numerator and the denominator have no common factor other than 1, the fraction is said to be in standard form.
For example: 16 20 can be reduced to 4 5, where 4 and 5 are prime numbers.
Equivalent fractions always represent the same part of the whole.
For example: 2 3 and 6 9 are equivalent fractions.
Let’s Warm-up
Fill in the blanks.
1 Fractions with the same denominator are called .
2 A fraction with the denominator greater than the numerator is called a .
3 A fraction with the numerator greater than the denominator is called an .
4 147 8 is a fraction.
5 17 2 is a/an fraction.
Introducing Rational Numbers
Rahul and Saumya learnt about the conversion of units in the classroom. They are now trying to convert different units in real life.
Rahul: Saumya, can you convert 1236 m above sea level into km? What type of number will you get?
Saumya: Yes, Rahul! 1236 m above sea level = +1236 m or + 1236 1000 km.
Rahul: That’s right! What about 1236 m below sea level in km?
Saumya got confused as to how to convert this data in km and what these numbers are called. Let’s find out!
Rational Numbers: Representing, Standard Form, Equivalent
Representing Rational Numbers
Saumya needs to convert 1236 m below sea level into km.
We know that:
1236 m below sea level = –1236 m
It can be converted to km as: = – 1236 1000 km
Denominator p q
Think and Tell
Are all fractions rational numbers?
Numerator
Any number that can be written in the form p q where p and q are both integers and q ≠ 0 is called a rational number. Rational numbers are numbers that can be written as fractions, where one integer is divided by another. This includes whole numbers, fractions, and decimals.
For example, both + 1236 1000 and – 1236 1000 are rational numbers where both numerator and denominator = integer and denominator ≠ 0.
Rational numbers include natural numbers, whole numbers, integers, fractions and decimals.
Did You Know?
Integers ,–8,–3,–2,–1, 1,2,3,4,… ,8,…
Baudhayana, an ancient Indian mathematician, introduced the concept of rational numbers in his "Baudhayana Sulba Sutra," offering the earliest known evidence of rational thinking in ancient Indian mathematics. –8
Do It Together
There are two types of rational numbers. Let us learn more about them!
Positive Rational Numbers
In a rational number p q , if p and q are both positive or negative integers, then p q is called a positive rational number.
For example, 3 5 and –4 –7 are both positive rational numbers.
Negative Rational Numbers
In a rational number p q , if either p or q is a negative integer, then p q is called a negative rational number
For example, –3 5 and –4 7 and 4 –7 are all negative rational numbers.
Now, let us learn how to represent the rational number 3 5 on a number line.
Step 1: Since it is positive, the fraction will be shown on the number line between 0 and 1. Divide the space between 0 and 1 into 5 subunits since the denominator is 5.
Step 2: Identify the numbers between which the given rational number lies. Here, 3 5
Step 3: Check the value of the denominator. Divide each unit by the value equal to that of the denominator. Here, we will divide each unit into 5 subunits.
Step 4: Mark 3 5 on the number line.
Let us now represent – 4 7 on a number line.
Follow the steps to mark the given rational number. Since it is negative, the fraction will be shown between 0 and –1 on the number line. Divide the space between 0 and –1 into 7 subunits since the denominator is 7.
Example 1: Identify positive and negative rational numbers.
Example 2: Write a rational number whose numerator is (2 × (–1)) and denominator is (6 × (– 2)).
Numerator = (2 × (–1)) = –2; Denominator = (6 × (– 2)) = –12
Fraction = –2 –12 = Numerator Denominator .
The required rational number is –2 –12
Example 3: Represent 2 3 and –1 3 on a number line.
Represent 5 6 , –0.5 and – 5 6 on a number line.
Convert –0.5 into a fraction with denominator 6.
–0.3 =
Rational Numbers in Standard Form
A rational number p q , is said to be in standard form if q is a positive integer and the only common factor between p and q is 1. We can reduce any rational number to its standard form by dividing the numerator and denominator by their HCF.
If the denominator is negative, multiply or divide the rational number by –1.
Let us reduce 63 45 and 63 – 45 to the standard form. The HCF of 63 and 45 is 9.
63
45 has a positive denominator; hence, dividing both the numerator and denominator by 9,
63 ÷ 9
45 ÷ 9 = 7 5 is the standard form of 63 45.
Example 4:
1 Reduce –15 75 to the standard form.
The HCF of 75 and 15 is 15.
63
– 45 has a negative denominator; hence, make the denominator positive by multiplying both the numerator and denominator with −1. 63 × (–1) – 45 × (–1) = – 63 45
Now, divide both the numerator and denominator by 9, – 63 ÷ 9 45 ÷ 9 = – 7 5 is the standard form of 63 – 45
So, we will divide the numerator and denominator by 15.
–15 75 = –15 ÷ 15 75 ÷ 15 = –1 5
Hence, the standard form of –15 75 is –1 5
2 Reduce –3 –15 to the standard form.
The denominator cannot be negative; so, –3 –15 = –3 × (–1) –15 × (–1) = 3 15
Divide the numerator and denominator by the HCF of 3 and 15, that is, 3.
3 15 = 3 ÷ 3 15 ÷ 3 = 1 5
Hence, the standard form of –3 –15 is 1 5 .
Example 5: Express 0.9 in the form of p q .
0.9 = 9 10
Reduce 12 –18 to the standard from.
Hence, the standard form of 12 –18 is . Do It Together
The denominator cannot be negative; so, 12 –18 = × × =
The HCF of and is
Equivalent Rational Numbers
Are the rational numbers – 18 20 and – 27 30 the same?
If two or more rational numbers have equal simplest forms, then these rational numbers are called equivalent rational numbers.
Let us start by simplifying –18 20 and –27 30 to their standard form:
Thus, –18 20 = –27 30 = –9 10 .
Therefore, –18 20 = –27 30 are equivalent.
–18 20 = –18 ÷ 2 20 ÷ 2 = –9 10 –27 30 = –27 ÷ 3 30 ÷ 3 = –9 10 a b = c d
Product of the numerator of the first rational number with the denominator of the other rational number
Product of the denominator of the first rational number with the numerator of the second rational number
i.e., –18 20 = –27 30 (–18) × (30) = (20) × (–27) = 540 = equivalent rational numbers
Example 6: Express –3 5 as a rational number with denominator 20.
We know that, 20 ÷ 5 = 4
Hence, –3 5 × 4 4 = –12 20 .
Example 7: Find four rational numbers that are equivalent to 4 7 .
4 7 = 4 × 2 7 × 2 = 4 × 3 7 × 3 = 4 × 4 7 × 4 = 4 × 5 7 × 5
4 7 = 8 14 = 12 21 = 16 28 = 20 35
Therefore, the rational numbers that are equivalent to 4 7 are 8 14, 12 21, 16 28 and 20 35 .
Example 8: Check whether 6 –18 and –9 27 are equivalent.
Expressing 6 –18 and –9 27 in standard form:
6 –18 = 6 × (–1) –18 × (–1) = –6 ÷ 3 18 ÷ 3 = –1 3 –9 27 = –9 ÷ 3 27 ÷ 3 = –1 3
Since the standard forms of both rational numbers are the same, 6 –18 and –9 27 are equivalent rational numbers.
Example 9: Esha drank 1 2 of a bottle of orange juice. Shahid drank 0.5 of the same bottle. Did they consume the same amount of orange juice?
Fraction of juice Esha drank = 1 2
Fraction of juice Shahid drank = 0.5 = 1 2
Since 1 2 = 1 2
They drank the same amount of juice.
Express the shaded portion as a rational number. a b c d
Express the following rational numbers in the form of p q
Which of these are negative rational numbers?
Find a rational number whose numerator is (3 × (–2)) and denominator is (7 × (– 4)).
Represent these on a number line.
Reduce the given rational numbers to their standard forms.
Find the value of x if:
Write three equivalent fractions for the given rational numbers.
Rayan shared his pudding with a friend. He ate 1 3 of the cup and his friend ate 0.5 of the cup. Did they eat the same amount of pudding? Do you share things with your friends?
Statement: Maya, Riya and Sia shared a pizza. The pizza was cut into equal parts. They each ate one part. No pizza was left.
Which of the following conclusions do not follow for the given statement?
Conclusion 1: The pizza was cut into 3 equal parts.
Conclusion 2: Maya got more pizza than Riya.
Conclusion 3: If Tia joins them, each of them will get 1 5 th of pizza.
Comparison and Properties of Rational Numbers
Comparing and Ordering Rational Numbers
When we look at two integers, say –2 and 2, we can easily say that 2 is greater than –2.
But can we do the same for rational numbers? Let us compare the rational numbers 1 6 and 4 9
Step 1: Both the rational numbers must be expressed with a positive denominator.
Think and Tell
What makes fractions different from rational numbers?
LCM of 6 and 9 = 18
Step 2: Calculate the LCM of the two denominators. 1 6 and 4 9
Step 3: Express both the rational numbers with the same denominator.
Now, let us arrange the rational numbers 1
The LCM of 5, 6, 8 and 9 is 360; so,
, –1
Step 4: Compare the numerators of the rational numbers obtained.
Since, 8 > 3, 8 18 > 3 18 . Therefore, 4 9 > 1 6 .
and –3 8 in ascending and descending order.
Example 10: Which of the two rational numbers is greater, –4 3 or –8 7 ?
The two rational numbers are: –4 3 and –8 7
The LCM of 3 and 7 is 21. –4 3 = –4 × 7 3 ×
= –28
We know that –24 > –28; Therefore, –24
Remember!
A positive rational number is always greater than a negative rational number.
Example 11: Arrange the given rational numbers in descending order.
–3 5 , –7 10, 3 10 –11 15 , –13 20
The LCM of 5, 10, 15 and 20 is 60.
We know that, 18 > –36 > –39 > –42 > –44
So, 18 60 > –36 60 > –39 60 > –42
Therefore, 3
Arrange the given rational numbers in ascending order.
The LCM of 3, 9 and 27 is
Ascending order:
Rational Numbers Between Two Rational Numbers
We know that the number of whole numbers or integers between two given numbers is limited. But the number of rational numbers between any two numbers is infinite.
Let us find rational numbers between 1 –2 and 2 3 using the following steps:
Step 1: Both the rational numbers must be expressed with a positive denominator. Step 2: Calculate the LCM of the two denominators.
Step 3: Express both the rational numbers with the same denominator.
Step 4: Write the rational numbers in between the two rational numbers having the same denominator, in increasing order. –1 2 = –1 × 3 2 × 3 = –3 6 , 2 3 = 2 × 2 3 × 2 = 4 6 –3 6 <
We can find more rational numbers between the same numbers. We know that: –3 6 = –30 60 and, 4 6 = 40 60
So, the rational numbers: – 29 60 , – 28 60 , – 27 60 … , 37 60, 38 60, 39 60 lie between – 30 60 and 40 60 or – 1 2 and 2 3 .
If we proceed in a similar way, we can find infinite rational numbers between any two given rational numbers!
Example 12: List five rational numbers between – 1 2 and 1 2 .
Let us multiply and divide the numerator and denominator of – 1 2 and 1 2 by 3 to expand the range.
–1 × 3 2 × 3 = –3 6 1 × 3 2 × 3 = 3 6
Therefore, the rational numbers between –3 6 and 3 6 are: –2 6 , –1 6 , 0, 1 6 , 2 6 .
Example 13: Write six rational numbers between 1 3 and 4 5 .
To expand the range, multiply the numbers 1 3 by 5 and 4 5 by 3.
1 3 = 1 × 5 3 × 5 = 5 15 4 5 = 4 × 3 5 × 3 = 12 15
Remember!
0 is also a rational number because it has a non-zero denominator.
Therefore, the rational numbers between 1 3 and 4 5 are 6 15 , 7 15 , 8 15 , 9 15 , 10 15 and 11 15 .
Example 14: The points P, Q, R, S, T, U, V and W on a number line are such that:
VT = TU = UW and PR = RS = SQ. Name the rational numbers represented by R, S, T and U. W
R = 7 3 , S = 8 3 , T = –13 3 , U = –14 3
1 × 4 4 = 3 × 4 4 = Do It Together
List four rational numbers between 1 and 3.
Let us multiply and divide 1 and 3 by 4 to expand the range.
We know that, > . So, the rational numbers between 1 and 3 are:
Properties of Rational Numbers
If we multiply the numerator and denominator of a rational number p q with the same non-zero integer (say, m ≠ 0), the rational number remains unchanged.
If we divide both the numerator and denominator of a rational number p q by the same non-zero integer m (where m ≠ 0), the value of the rational number remains unchanged. p q = p × m q
For example, if 2 3 is a rational number and –5 is an
integer then, 2 3 = 2 × –5 3 × –5 = –10 –15
Example 15: Express –3 7 with denominator 49.
We will multiply the numerator and denominator by 7.
–3 7 = –3 × 7 7 × 7 = –21 49
For example, if 7 77 is a rational number and 7 is an integer then, 7 77 = 7 ÷ 7 77 ÷ 7 = 1 11
35 63 = 35 ÷ 63 ÷ = 5 Do It Together
Express 35 63 with numerator 5.
We will divide the numerator and denominator by .
Example 16: Radha and Kashish needed sheets for an art project. Radha bought a packet that has sheets of paper that are 1 7 of an inch thick. Kashish bought a packet that has 2 7 inches thick sheets. Which girl bought the thicker paper?
Thickness of Radha’s packet = 1 7
Thickness of Kashish’s packet = 2 7
LCM of 3 and 7 is 21.
1 × 7 3 × 7 = 7 21 and 2 × 3 7 × 3 = 6 21
Since, 7 > 6
1 3 > 2 7
So, Radha bought the thicker paper.
Compare the given rational numbers. a 4 7 and 5 9 b 2 3 and 7 3
and 9 –4
The points P, Q, R, S, T, U, V and W on a number line are such that:
VT = TU = UW and PR = RS = SQ. Name the rational numbers represented by R, S, T and U.
List 5 rational numbers between the following.
Which of the given rational numbers is the greatest?
Arrange the given rational numbers in ascending order.
Arrange the temperatures (given in °C) in order from warmest to coldest.
Raman and Farhan were talking about whose bottle can hold more water. They poured the water from their bottles into glasses. Raman filled 11 5 glasses, while Farhan filled 13 7 glasses. Whose bottle can hold more water? How do you use water responsibly in times of need?
In 2020, Punjab produced approximately 16.1 million tonnes of wheat, while Uttar Pradesh produced about 32.4 million tonnes. Express these figures as rational numbers and compare the wheat production in these two states. Identify a possible value for wheat production (in million tonnes) that another state might have, falling between these two figures.
Which rational number is greater?
a The rational number whose numerator is the largest two-digit number and denominator is the smallest three-digit number.
b The rational number whose numerator is the smallest three-digit number and denominator is the largest three-digit number.
Operations on Rational Numbers
Missy and her sister run a grocery store. At the store, there is a drum full of wheat flour that weighs 65 2 kg. Missy added 39 2 kg more flour to the drum.
How much does the drum of wheat flour weigh now?
Addition and Subtraction of Rational Numbers
We have already learnt how to add and subtract integers and fractions. Applying the operations of addition and subtraction to rational numbers is similar to that.
Addition of Rational Numbers
When we add two rational numbers, we have to make sure that the denominators are always positive. If not, then we multiply the numerator as well as the denominator with (–1) to make it positive.
Case 1: Addition of rational numbers that have the same denominator.
For two rational numbers a b and c b , the sum is:
Let us now help Missy figure out the total weight of the wheat drum after she added more flour to it.
We will add 65 2 and 39 2 , using the given steps:
Step 1: Add the rational numbers.
Step 2: Reduce the obtained rational number to the standard form. 65 2 + 39 2 = 65 + 39 2
104 2
The LCM of 104 and 2 is 2. 104 2 = 104 ÷ 2 2 ÷ 2 = 52
∴ 65 2 + 39 2 = 52 kg. The total weight of the wheat drum is 52 kg.
Case 2: Addition of rational numbers that have different denominators. Let us add 2 5 and 1 –15
Step 1: Check the LCM of the denominators. Step 2: Add the rational numbers.
The LCM of 5 and 15 is 15.
2 5 = 2 × 3 5 × 3 = 6 15; 1 –15 = 1 × (–1) –15 × (–1) = –1 15 6 15 + –1 15 = 6 + (–1) 15 = 6 – 1 15 = 5 15
Step 3: Reduce the obtained rational number to the standard form.
5 15 = 5 ÷ 5 15 ÷ 5 = 1 3
2 5 + –1 15 = 1 3
Example 17: Add the rational numbers: 13 15 and –8 15
13 15 + –8 15 = 13 + (–8) 15 = 13 – 8 15 = 5 15 (We can see the denominators are the same.) 5 15 = 5 ÷ 5 15 ÷ 5 = 1 3
13 15 + –8 15 = 1 3
Example 18: Add the rational numbers: –8 7 and 1.2
Let us change 1.2 to p q form. 1.2 = 6 5
The LCM of the denominators 7 and 5 is 35. So, let us rewrite the rational numbers:
–8 7 = –8 × 5 7 × 5 = –40 35 ; 6 5 = 6 × 7 5 × 7 = 42 35
So, –8 7 + 6 5 = –40 35 + 42 35 = –40 + 42 35 = 2 35 –8 7 + 6 5 = 2 35
Example 19: A shopkeeper sold 2 1 2 kg of sugar and 3 3 5 kg of rice to a customer. How much in total did he sell?
Weight of sugar = 2 1 2 kg = 5 2 kg
Weight of rice = 3 3 5 kg = 18 5 kg
Total weight = 5 2 + 18 5
The LCM of 2 and 5 is 10.
5 2 = 25 10 18 5 = 36 10
So, 25 10 + 36 10 = 61 10 = 6 1 10
Therefore, the total is 6 1 10 kg.
Simplify 2 5 + 0.75 + 5 12 .
0.75 = 75 100 = 3 4
The LCM of the denominators 5, 4 and 12 is Rewriting the rational numbers:
2 5 = 2 × 12 5 × 12 = 24 0.75 = 3 4 = 3 × 4 × = 45 5 12 = 5 × 12 × =
So, 2 5 + 0.75 + 5 12 = + + =
Additive Inverse
We have already learnt that if adding one integer to another gives the sum as zero, then the integers are said to be the additive inverses of each other.
Similarly, if the sum of two rational numbers is zero, then they are said to be the additive inverses of each other.
i.e., p q + – p q = 0. So, p q and – p q are additive inverses of each other.
The additive inverse of 5 7 = – 5 7
Example 20: What is the additive inverse of –6 7 ?
Write the additive inverse of the following.
1 5 14 = 2 19 –21 = 3 –12 –17 = Do It Together
Subtraction of Rational Numbers
At the end of the month, when the drum was emptied out, Missy measured the weight of the empty drum.
Missy: See! This empty drum itself weighs 35 3 kg.
Sister: Wait, so how much wheat flour did we have when the drum weighed 65 2 kg?
Let us say, a b and c d are two rational numbers. On subtracting c d from a b, we will get:
The additive inverse of –6 7 is 6 7 . or
This means adding the additive inverse or the negative of c d
Now, to find the actual weight of the wheat flour, subtract the weight of the empty drum from the weight of the drum when it was filled with wheat flour.
Total weight of the drum filled with wheat flour = 65 2 kg
Weight of the empty drum = 35 3 kg
Actual weight of the wheat flour = 65 2 –35 3 kg
Therefore, the actual weight of the wheat flour is 20 5 6 kg.
Example 21: Subtract the rational numbers –8 9 and –3 5 . The LCM of 9 and 5 is 45. –8 9 = –8 × 5 9 × 5 = –40 45 –3 5 = –3 × 9 5 × 9 = –27 45
–27 45 –(–40) 45 = (–27) 45 + 40 45 = –27 + 40 45 = 13 45
Therefore, (–3) 5 –(–8) 9 = 13 45
We can write this as:
Example 22: The sum of two rational numbers is –1 2 . If one of the numbers is 5 6 , find the other.
Let the number be x. Then, 5 6 + x = –1 2 ⇒ x = –1 2 –5 6 LCM of 2 and 6 = 6. Hence, x = –3 6 –5 6 ⇒ x = –3 – 5
Therefore, the other number is –4 3 .
Example 23: Kanak was boiling 2 1 2 L of milk. She accidentally forgot to turn off the gas stove on time and 0.25 L of milk evaporated. How much milk was left?
Amount of milk Kanak was boiling = 2 1 2 = 5 2 L
Amount of milk evaporated = 0.25 L = 1 4 L
Amount of milk left = 5 2 –1 4 = 10 4 –1 4 = 9 4
Example 24: From a rope of 12.2 metres, two pieces of lengths 10 3 and 33 9 metres are cut off. What is the remaining length of the rope?
Length of the rope = 12.2 m = 61 5 m
Total length of pieces cut = 10 3 + 33 9 = 30 9 + 33 9 = 63 9 = 7 m
Remaining length of the rope = 61 5 – 7 =
What number should be added to –3 8 to get 6 7 ?
Let the required number be x
Then, –3 8 + x = 6 7 ⇒ x = 6 7 –(–3) 8 = 6 7 + 3 8
LCM of 8 and 7 = . Hence, x = + ⇒ x =
x =
Do It Yourself 10C
Add the given rational numbers. a 12 3 and 14 5
0.8 + 2 5
e 8 3 and –8 5 f – 15 7 and 17 3
Find the additive inverse of the given rational numbers. a 5 7 b 11 8
Subtract the first rational number from the second rational number.
a 3 6 and 1 2
Evaluate.
Express each of the given rational numbers as the sum of an integer and a rational number. a 54 17 b – 0.6
The sum of two rational numbers is –2. If one of the numbers is –14 5 , find the other number.
What number should be added to –5 7 to get –1?
A carpenter bought a piece of wood 17 4 metres long. He then cut off 3.4 metres of the wood. How long is the piece of wood now?
The distance from Ghaziabad to Delhi is 57 2 kilometres, and the distance from Delhi to Gurgaon is 32.7 kilometres. What is the total distance from Ghaziabad to Gurgaon via Delhi?
(Write your answer as a fraction.)
Create a word problem on adding two rational numbers.
How much did the taxi driver save if he earned ₹800?
Statement 1: He spent ₹ 630 9 on tea and snacks, ₹ 508 2 on food, ₹44 on repairs of the taxi and saved the rest.
Statement 2: The taxi driver spent 46% of his earnings.
Which of the statements are sufficient to answer the question?
i Statement 1 alone is sufficient.
ii Statement 2 alone is sufficient.
iii Both Statement 1 and Statement 2 together are sufficient.
iv Either Statement 1 and Statement 2 alone are sufficient.
Multiplication and Division of Rational Numbers
Missy and her sister donate flour to a local charity event. They distribute 11 4 kg of flour each to 23 people.
How much flour is donated in total? How will they find out?
Multiplication of Rational Numbers
If a b and c d are two rational numbers, then: i.e.,
Product of two rational numbers = Product of the numerators Product of the denominators
Total number of people = 23 Total
Therefore, the total amount of flour donated is 63 4 kg.
Example 25: Multiply 11 12 and 3 11 .
11 12 × 3 11 = 11 × 3 12 × 11 = 33 132 = 1 4
Therefore, the product is 1 4 .
Example 26: Find the area of a square plot of land where each side measures 14 3 metres.
Measure of each side = 14 3 m
We know that the area of a square = Side × Side
= 14 3 × 14 3 = 14 × 14 3 × 3 = 196 9 m2
Therefore, the area of the square plot is 196 9 = 21 7 9 m2
Do It Together p q × q p = 1 = q p × p q
Each sheet of metal is 5 7 inches thick. If Megha stacks 2 sheets one on top of the other, how thick will the stack be?
Thickness of each sheet =
Thickness of two sheets = ×
Therefore, the thickness of the stack of two metal sheets will be .
Reciprocal or Multiplicative Inverse of a Non-zero Rational Number
We now know that p q is a rational number, where p and q are integers and q ≠ 0.
If p ≠ 0, then the rational number q p is called the reciprocal or the multiplicative inverse of p q such that:
The rational numbers p q and q p are called the reciprocals or the multiplicative inverses of each other.
For example, the multiplicative inverse of 11 4 is 4 11
Example 27: Find the product of 3 7 and its reciprocal.
As 3 7 × 7 3 = 1, so the reciprocal of 3 7 is 7 3 .
Example 28: Find the reciprocal of 15 and justify your answer.
The reciprocal of a number is 1 divided by the given number.
So, the reciprocal of 15 is 1 15
If p = 2m × r and q = n × 2r, then find the reciprocal of p q . Do It Together
The given rational number is: p q = 2m × r
Division of Rational Numbers
Verification: The product of the given number with its reciprocal must be 1.
15 × 1 15 = 1
Hence, verified.
So, the reciprocal of p q is:
Missy sold 108 5 kg of flour to some people in 4 hours. How much flour did she sell in an hour? To find out, we will have to divide 108 5 by 4 1, i.e.,
Division is the inverse of multiplication.
When we divide one rational number by another rational number, we can write it as:
5 × 1 4
We can see that 1 4 is the reciprocal or the multiplicative inverse of 4 1 .
So, to divide, we can multiply a given rational number with the reciprocal of the other rational number.
Therefore, the quantity of flour Missy sold in an hour is 27 5 kg.
Hence, we can say that if a b and c d are two rational numbers, then:
Example 29: Divide –0.75 by 4 3 . –0.75 = –75 100 = –3 4 –3 4 ÷ 4 3 = –3 4 × 3 4 = –3 × 3 4 × 4 = –9 16
Example 30: Find (m + n) ÷ (m – n) if m = 4 7 and n = –2 7 m + n = 4 7 + –2 7 = 2 7 m – n = 4 7 ––2 7 = 4 7 + 2 7 = 6 7 . (
Example 31: By what number should we multiply – 6 5 to get the product as 12?
Required number = 12 ÷ –6 5 = 12 × –5 6 = –10
Example 32: The area of a room is 261 4 m2. If its breadth is 87 16 metres, what is its length?
We know that the area of a rectangle = length × breadth
261 4 = length × 87 16; length = 261 4 ÷ 87 16 = 261 4 × 16 87 = 1044 87 = 12
Thus, the length of the room is 12 metres.
Example 33: If the cost of 2.5 kg of fruit is ₹120, find the cost of 1 kg of fruit.
Cost of 2.5 kg = ₹120
Cost of 1 kg = ₹120 2.5 = ₹120 5 2 = ₹120 × 2 5 = ₹48.
Hence, the cost of 1 kg of fruit is ₹48.
Write the reciprocal of the given rational numbers.
Find the product.
Divide the given rational numbers.
Simplify.
Divide the reciprocal of 2 5 by –4 5 .
Find the multiplicative inverse of
The product of two rational numbers is – 4 30 . If one number is 8 9 , then find the other.
Multiply the sum of 6 7 and 5 9 by the product of 4 –9 and 15. Find (m + n) ÷ (m – n) if:
A sunflower grows around 5 2 cm in a day under ideal conditions. How much will the sunflower grow after 2.5 days?
Sambhav is training for a race. He ran 11 1 4 km in total in 5 days. How far did he run each day? Write one benefit of physical exercise.
Rima has a piece of ribbon of length is 153 60 m, She would need 20 such pieces for an art work she is making. What is the length of ribbon required?
Rama builds a garden in her backyard that is 41 3 metres in length and 1.75 metres in width. Which of the following statements is true?
Statement 1: The area of the garden is more than 7 m2.
Statement 2: The perimeter of the garden is 12.16 m.
Points to Remember
• A number in the form p q , where p and q are integers and q ≠ 0, is called a rational number.
• If in a rational number p q , q is always a positive integer and the only common factor between p and q is 1, it is in standard form.
• Two rational numbers are equivalent if their standard forms after reduction are equal.
• There are infinite rational numbers between any two rational numbers.
• To add or subtract rational numbers, their denominators must be the same.
• If the sum of two rational numbers is zero, they are additive inverses.
Math Lab
Setting: In groups of 10.
Collaboration & Experiential Learning
Learn Fun!
Materials Required: Cards with rational numbers from – 9 10 to 9 10 written on them in a box.
Method:
Each group will stand in a straight line.
One student will be given a rational number, and he/she will pick up another card and add the two rational numbers together.
Depending on the answer, the student will switch places forward or backwards with another student in the line.
The student already at the position would pick up a card and do the same.
Repeat this 10 times, and the group that finishes first wins.
Chapter Checkup
Find the rational number whose numerator is (65 – 32) and denominator is (3 × 9).
Represent 3 2 and –3 4 on a number line.
Reduce the rational numbers to the standard form. a 8 72
– 12 60
Find the additive inverse of the following.
a 4 5 + 6 7 b 4 7 + 13 14
Find three rational numbers equivalent to the following.
Find the value of x
List five rational numbers between the following.
a 3 5 and 4 5 b 2 9 and 3 9 c – 1 2 and – 3 2 d – 1 and 1
Evaluate.
Find the multiplicative inverse of (–5 × 12 15) – (–3 × 2 9 ).
Do – 4 9 and – 16 36 represent the same number? Why or why not?
Divide the sum of 65 12 and 8 3 by their difference.
What
A library has a collection of 18,000 books, each belonging to a specific genre, which is a category of literature characterised by similarities in form, style or subject matter. If 1 6 of the books are mystery novels, 2 6 are science fiction and the rest are historical fiction, how many historical fiction books are there?
As of 2024, the fastest car in the world is the SSC Tuatara. It's top speed is 212 25 km in 1 minute. How much distance can it cover in 3.75 minutes at this speed?
Sakshi was playing in a park. She noticed an insect that crawled 31 6 inches in one minute. The next minute, the insect crawled 2.75 inches. How far did the insect crawl in total? Write one way by which we can be kind towards smaller organisms such as insects.
Tanmay is buying a computer on sale. The original price was ₹12,000. If the sale price is 5 6 of the original price, how much did he pay for the computer?
A worker at a shop is filling the new fish aquarium. The aquarium has a capacity of 40 gallons. If he fills 20 25 of the aquarium, how many more gallons of water will he need to fill it to the brim?
Challenge
Critical Thinking
I simplified a rational number to − 1 7 by removing the common factor 7. What was the original rational number?
d A is false, but R is true. 1 2
Read the statements and choose the correct option.
Assertion (A): The price marked on an Air conditioner is ₹30,000. If its sale price is 5 6 of the marked price then it is bought for ₹25,000.
Reason (R): There was a sale of ₹5000 on the AC.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
Carbon Emissions
Carbon emissions contribute significantly to global warming, and various sectors of the economy contribute differently to total emissions. The total global carbon emissions in a given year are estimated to be around 40 billion metric tonnes. Below is the distribution of these emissions across different sectors:
Energy Production: 7 20 of total emissions.
Transportation: 30% of total emissions.
Industry: 0.25 of total emissions.
Agriculture: 6.8 billion metric tonnes.
Residential: 8:100 of total emissions.
Answer the following questions:.
1 What is the combined fraction of total carbon emissions from the energy production and industry sectors?
2 How many metric tonnes of carbon emissions are produced by the transportation sector?
a 10 billion metric tonnes
c 8 billion metric tonnes
b 12 billion metric tonnes
d 6 billion metric tonnes
3 The industry sector contributes 25% of the total emissions. Express this percentage as a decimal and a fraction.
4 What decimal of the total emissions do the agriculture emissions represent?
5 Discuss the importance of reducing emissions across all sectors to slow down climate change. Cross Curricular & Value Development
311 Construction of Triangles
Let’s Recall
It is important to know how to construct angles of different measures and their angle bisectors before learning to construct triangles. Let us recall some constructions.
Constructing an angle of 90°
Let us look at the steps for constructing an angle of 90° or a perpendicular to a line segment.
1 Draw a line segment BC.
2 Starting from point B, use any convenient radius to draw an arc that intersects BC at point P.
3 From point P, using the same radius as in step 2, draw another arc intersecting the previously drawn arc at point Q.
4 Starting from point Q, with the same radius as before, draw another arc that intersects the arc drawn in step 2 at point R.
5 Using points R and Q as centres and a radius greater than half of QR, draw arcs above the line, cutting each other. Mark the point as S.
6 Connect points B and S with a line segment, extending it to form a ray BA. SB⊥BC.
Constructing an Angle Bisector
Let us look at the steps for constructing an angle bisector to an angle of any given measure.
An angle bisector is a line that divides an angle into two equal parts.
1 To bisect, ∠PQR, place the compass point on point Q and draw an arc that intersects both sides of the angle. Label the points of intersection as A and B.
2 With the same compass width, draw arcs from points A and B cutting each other. Label the point of intersection as C.
3 Draw a straight line from Q to C. This line is the angle bisector of ∠PQR.
Let’s Warm-up
State whether the statements are True or False.
1 You construct an angle of 90° by bisecting a 120° angle.
2 An angle bisector bisects the angle into 3 equal parts.
3 When an angle bisector of a 60° angle is constructed, we get two angles of 30° each.
4 While bisecting an angle, the compass width can be less than half of the width of the arc.
5 You can construct an angle of 15° by bisecting an angle of 45°.
Constructing Triangles
Once upon a time in a quiet neighbourhood, there lived a curious young boy named Max. He loved to explore and learn about the world around him. His favourite moments were when his engineer uncle, Uncle Charlie, came to visit. Uncle Charlie always carried a mysterious geometry box, filled with special tools like compasses and rulers.
Max: Uncle Charlie, what’s inside your geometry box?
Uncle Charlie: Well, Max, it is filled with special tools like compasses and rulers that we can use to draw triangles. Would you like to learn how?
Max: Absolutely, Uncle!
A triangle has 3 angles and 3 sides. To construct a unique triangle, we need a minimum of three measurements (at least one being a side).
You can construct a triangle with the following criteria:
1 Side-Side-Side (SSS) Criterion: Three sides
2 Side-Angle-Side (SAS) Criterion: Two sides and one included angle
3 Angle-Side-Angle (ASA) Criterion: Two angles and one included side
4 Right Angle-Hypotenuse-Side (RHS) Criterion: Hypotenuse and one other side
Let us discuss constructing triangles in each of the cases listed above, one by one.
Constructing Triangles: SSS Criterion
A triangle can be constructed with the lengths of its 3 sides given.
Construct a PQR with sides of length 5.3 cm, 4.5 cm and 6 cm.
First draw a rough outline of PQR with the measures marked.
Given below are the steps of construction.
1 Draw a line segment PQ measuring 5.3 cm in length.
Did You Know?
Ancient civilisations such as the Babylonians and the Egyptians used concepts associated with triangles for surveying, and to create perfectly square corners for their buildings.
2 Draw an arc with the centre at point P and a radius of 4.5 cm.
3 Draw a second arc with the centre at point Q and a radius of 6 cm, intersecting the previous arc at point R.
4 Join PR and QR. PQR is the required triangle.
Try constructing a PQR with sides of length 3 cm, 3 cm and 7 cm.
We know that the sum of the lengths of any two sides of a triangle is greater than the length of the third side. Clearly, 3 cm + 3 cm = 6 cm < 7 cm. Hence, no triangle with side lengths of 3 cm, 3 cm and 7 cm is possible.
When we try constructing a triangle with the given measures, we see that the two arcs of radius 3 cm do not meet.
Therefore, a triangle cannot be constructed with the lengths given.
Example 1: Construct an equilateral triangle of side 5.8 cm.
An equilateral triangle can be constructed when the length of only one of its sides is given. Since the lengths of all 3 sides of an equilateral triangle are equal, we can construct the triangle given the length of 1 side.
1 Draw a line segment AB of length 5.8 cm.
2 Draw an arc with the centre at point A and a radius of 5.8 cm.
3 Without changing the extension of the compass, draw a second arc with the centre at point B and a radius of 5.8 cm, intersecting the previous arc at point C.
4 Join AC and BC. ABC is the required equilateral triangle.
Construct triangles of the measures given. Write the type of triangle.
1 ABC with AB = 3.8 cm, BC = 3.2 cm and CA = 4.3 cm
Think
Do It Yourself 11A
Fill in the blanks.
a A triangle can be constructed with the length of sides given.
b A triangle cannot be constructed if the sum of the lengths of any two sides is than the length of the third side.
c We need the length of side to construct an equilateral triangle.
Construct triangles with the length of 3 sides given.
a 4 cm, 5 cm, 3.5 cm b 6 cm, 4.5 cm, 5.1 cm c 5.2 cm, 4.8 cm, 3.8 cm
The lengths of the three sides of a triangle are given as 6 cm, 8 cm and 10 cm. Construct the triangle and determine its type (e.g., scalene, isosceles or equilateral).
Can a triangle be constructed if the sides measure 5 cm, 12 cm and 13 cm? Explain your answer.
The picture shows the traffic sign board which says ΄School Children Traffic΄. Construct the outline of the sign board with side 4.5 cm. Write the type of triangle.
Using a compass and a ruler, construct RST with side lengths of 5 cm, 6 cm and 7 cm.
In ABC, AB = 4.3 cm, BC = 7.4 cm, and CA = 6.1 cm. Construct the triangle and find its angles using a protractor.
1 The perimeter of a triangle is 18 cm. The lengths of its sides are in the ratio 2:3:4. Construct the triangle using a compass.
Constructing Triangles: SAS Criterion
A triangle can be constructed if the lengths of any 2 sides and an included angle are given.
Construct a PQR with QR = 7.3 cm, PQ = 4.5 cm, and PQR = 60° using a ruler and a compass.
Draw a rough outline of PQR as illustrated in the diagram.
1 Draw a line segment QR with a length of 7.3 cm.
2 From point Q, form an ZQR measuring 60°.
3 Using Q as the centre and a radius of 4.5 cm, draw an arc that intersects QZ at point P
4 Connect points P and R. PQR is the required triangle.
Error Alert!
In the construction of PQR with side QR = 6.8 cm, PQ = 4.3 cm and PQR = 55°, the arc with a radius of 4.3 cm should be drawn from Q and not R.
Example 2: Construct ∆FGH with side FG = 4.8 cm, FH = 3.3 cm and HFG = 50°. Find the measure of the unknown side.
1 Draw a line segment FG with a length of 4.8 cm.
2 From point F, form ZFG measuring 50° using a protractor.
3 Using F as the centre and a radius of 3.3 cm, draw an arc that intersects FZ at a point named H.
4 Join HG. Length of GH = 3.7 cm
Construct a DEF with side DE = 5.8 cm, EF = 4.2 cm, and DEF = 30° using a ruler and a compass. Find the difference of the measures of the two unknown angles.
Do It Yourself 11B
Which of these measures will help you construct triangles using the SAS criterion?
a ABC with A = 60°, AB = 5 cm, BC = 6 cm
b XYZ with YX = 6 cm, X = 45°, XZ = 5 cm
c PQR with PQ = 3 cm, QR = 4 cm, Q = 30°. d LMN with LM = 7 cm, L = 50°, M = 65°
Construct triangles with the given measures.
a XYZ with XY = 5.7 cm, Y = 60°, YZ = 4.8 cm
b ABC with AB = 6.2 cm, BC = 8.7 cm, CBA = 60°
You have information about two sides of a triangle, one with a length of 3.9 cm and the other with a length of 5.9 cm, and the included angle measures 80°. Construct the triangle and label the vertices.
In XYZ, side XY = 5.4 cm, side XZ = 7.8 cm and YXZ = 45°. Construct XYZ and find the measures of XYZ and YZX. Also, classify XYZ based on its angles and sides.
PQR has sides PQ = 6.3 cm, QR = 7.1 cm and PQR = 30°. Construct PQR and identify the type of triangle it is based on its angles and sides. Name the longest side of the triangle.
Two sides of a triangle measuring 4.1 cm and 6.5 cm are given, and the included angle is 120°. Construct the triangle and find the measures of the other 2 angles.
Anita is building a cardboard signpost for a hiking trail. She wants to create a triangular sign, and she knows that two sides of the triangle are 12 cm and 8 cm long, with an included angle of 45°. Using a ruler and a compass, help Anita construct the triangular-shaped sign.
Critical Thinking
Raj wants to make a bird’s nest in the shape of an isosceles triangle of length 25 cm in his garden. The angle between them is 65°. Raj wants to make a sample before constructing the actual one, with sides 1 5 th of the original length. Help Raj construct the sample bird’s nest. What is the length of the third side?
Constructing Triangles: ASA Criterion
A triangle can be constructed with the given measures of two angles and length of the included side.
Construct a XYZ with side XY = 5.7 cm, ZXY = 45° and ZYX = 75° using a compass.
Draw a rough outline of XYZ as illustrated in the diagram given below.
Error Alert!
While constructing XYZ using the ASA criteria, construct the angles ZXY and ZYX of the given line segment XY and not angles XZY and ZXY.
1 Draw a line segment XY with a length of 5.7 cm.
2 At point X, form an PXY measuring 45°.
3 At point Y, draw an QYX measuring 75°. Identify the point of intersection between XP and YQ as Z.
X Y 5.7 cm
Example 3: Construct a ∆RST with side ST = 6.8 cm, RST = 47° and RTS = 76°. Find the length of the unknown sides. Identify the type of triangle based on its sides.
1 Draw a line segment ST with a length of 6.8 cm.
2 From point S, draw ZST measuring 47° using a protractor.
3 From point T, draw YTS measuring 76° using a protractor.
4 Identify point R as the intersection of SZ and TY.
RST is the required triangle.
RST is a scalene triangle as all its sides have unequal lengths.
Remember!
In a triangle, the sides opposite larger angles are always longer than the sides opposite smaller angles.
Do It Together
Construct a MNO with side ON = 4.4 cm, MNO = 49° and MON = 79°. Find the difference in the length of the unknown sides.
Art Integration
A = 45°, B = 60°, and side AB = 7.5 cm. Construct ABC with the measures given.
Given that X = 30°, Y = 75°, and side XY = 6.2 cm in XYZ, construct XYZ and find the lengths of sides XZ and YZ.
PQR has P = 40°, Q = 70°, and side PQ = 5.4 cm. Perform the construction of PQR and find the measure of R.
In DEF, D = 50°, E = 70°, and side DE = 5.8 cm. Construct DEF and determine the lengths of sides DF and EF.
LMN has L = 60°, M = 45°, and side LM = 9.7 cm. Draw LMN and calculate the lengths of sides LN and MN.
Determine the kind of triangle based on its sides and angles.
Challenge
Critical Thinking & Art Integration
1 Tom is designing a roof for a small playhouse. He knows that the two angles at the base of the triangular roof are 45° and 60°, and the length of the base of the roof is 6 cm. Using a ruler and a compass, help Tom construct the triangular pattern for the roof on paper. What steps should he follow to accurately create the roof for his playhouse?
2 Construct a DEF in which D = 50°, ED = 7 cm and E = 60°. Also, construct the angular bisectors of any of its two angles and name its intersection point as P.
Constructing Triangles: RHS Criterion
A right-angled triangle can be constructed when the lengths of its hypotenuse and one of the other sides are given. One of the angles measures 90°, so this helps us construct a triangle under the RHS criterion.
Construct a LMN right-angled at M, whose hypotenuse is 9 cm and one of the shorter sides is 7.5 cm.
Draw a rough outline of LMN as illustrated in the diagram.
1 Draw a line segment MN, making it 7.5 cm long. M N 7.5 cm
3 Use point N as the centre and a radius of 9 cm to draw an arc that intersects the line XM at a point named L.
Did You Know?
Nagara style of architecture involved the construction of triangles in the design of shikaras.
2 From point M, construct a 90° angle labelled as XMN.
4 Join L and N by drawing the line segment LN. LMN is the required triangle.
Example 4: Construct a right-angled triangle whose sides measure 6.3 cm, x cm and 4.3 cm. It is also known that ’x’ is less than 6.3 cm.
From the information given, it is clear that the hypotenuse of the triangle measures 6.3 cm, since the hypotenuse is the longest side in a right-angled triangle.
1 Draw a line segment AB, making it 4.3 cm long.
2 From point A, construct a 90° angle labelled XAB.
3 Use point B as the centre and a radius of 6.3 cm to draw an arc that intersects XA at point C.
4 Join points C and B. ABC is the required triangle.
Construct a right-angled triangle whose sides measure 7.3 cm, x cm and 5.9 cm. It is also known that ’x’ is the smallest side of the triangle.
Given that one leg of a right-angled triangle is 4.5 cm and the hypotenuse is 6.3 cm, construct the right triangle and determine the length of the unknown side.
In a right triangle, if you know that one leg measures 4.2 cm and the hypotenuse measures 8.2 cm, construct the right triangle and calculate the length of the remaining side.
ABC is a right triangle with hypotenuse AC measuring 9.5 cm and one leg AB measuring 6.6 cm. Construct ABC and find the length of side BC. Also, measure the value of the two unknown angles.
Given that a right triangle has a hypotenuse of 7.1 cm and one leg measuring 3.8 cm, construct the right triangle and determine the measure of the unknown angles.
In a right triangle XYZ, the hypotenuse XY is 9.4 cm long, and one leg XZ measures 5.7 cm. Construct XYZ and calculate the measure of the angle opposite to YZ.
Solar panels generate energy from sunlight which is a source of renewable energy. The picture shows the panel inclined at 90°. Take the length of the largest side as 5.1 cm and length of one of the legs as 4.3 cm to construct the triangle.
1 Sarah has a right-angled, triangular flower garden in her backyard. The largest side of this garden measures 15 m and the smallest side measures 6 m. If 1 cm on paper is equal to 3 m on the ground, construct a right-angled triangle representing Sarah’s garden on paper. What is the approximate length of the unknown side of Sarah’s garden?
Points to Remember
• A triangle can be constructed with the SSS, SAS, ASA and RHS criteria.
• The sum of the lengths of any two sides of the triangle is greater than the length of the remaining side.
• Measure and mark lengths accurately using a ruler and a compass. Small errors in measurement can lead to significant differences in the constructed triangle.
• If angles are known, use a protractor to construct them accurately. Ensure that the angles match the measurements given as closely as possible.
Math Lab
Communication & Experiential Learning
Triangle Challenge
Aim: Learn how different triangles can be constructed using different measures.
Material Needed: A ruler, compass, protractor, cardboard, chart paper.
Settings: In pairs
Instructions for the students:
1 Work in pairs.
2 Each pair will select any one criterion to construct the triangle.
3 The pair will pick the lengths and measure of angles according to the criteria they choose.
4 Follow the steps to construct the triangle on the chart paper and cut out the triangle.
5 Construct the same triangle on the cardboard.
6 Make a wall painting by pasting the triangle from the chart paper on the cardboard.
7 Discuss with your teacher and friends how each triangle formed is different from each other and which among them can be used in the construction of buildings/bridge.
Chapter Checkup
What triangle construction criterion will be used for constructing triangles with the given measures?
a Length of 3 sides
b Length of 2 sides and included angle
c Length of the hypotenuse of a right-angled triangle and one of its sides
d Measures of 2 angles and included side
Construct a triangle with sides measuring 5 cm, 7 cm and 8 cm, and identify its type based on its angles.
Perform the construction of a triangle named PQR with side lengths of 4.5 cm, 6.3 cm and 9.0 cm. Determine the classification of PQR based on its sides and angles.
Construct a triangle, DEF with side lengths DE = 7.1 cm and EF = 4.8 cm and an included angle E of 30°. Identify the criterion used to construct the triangle.
Given ABC, where A is 40°, B is 70° and side AB is 6.0 cm. Construct ABC and calculate the lengths of sides AC and BC.
Draw XYZ with known angles X = 60°, Y = 45° and an included side XY measuring 5.2 cm. Find the length of sides XZ and YZ through geometric construction.
Construct a triangle using two side lengths of 5.0 cm and 6.0 cm, and an included angle of 45°. Determine the measures of the remaining two angles in the triangle.
Draw a right triangle with a known leg length of 3.5 cm and a hypotenuse of 5.0 cm. Calculate the length of the other leg using geometric construction.
Given that the hypotenuse AC measures 7.8 cm and one leg AB is 6.0 cm long, construct ABC and find the length of the remaining leg.
Given UVW, where U is 50°, V is 70°, and side UV is 5.5 cm, construct UVW and determine the sum of the lengths of sides UW and VW.
John is planning to build a model bridge for his science project. The actual bridge has a right-angled triangular shape, with the largest side measuring 45 cm and one leg measuring 30 cm. If John wants to represent the model bridge on paper using a scale of 10 cm on the model equal to 1 cm on paper, construct a scaled right-angled triangle on paper to represent John’s model bridge. What is the approximate length of the unknown side of the model bridge?
Challenge
Critical Thinking
d Both A and R are true and R is not the correct explanation for A. 1 2
Mohan constructed a triangle by using the following measurements: AB = 7 cm, BC = 3 cm and A = 40°.
Is it possible to construct this triangle uniquely? What other data do you need to construct this unique triangle? Which rule will you apply for constructing it?
Read the statements and choose the correct option.
Assertion(A): A triangle can be constructed with the base measuring 6 cm and the base angles measuring 50° and 95°.
Reason(R): We can construct a triangle using the ASA construction rule when the measures of two angles and the length of the included side are given.
a A is true and R is false.
b A is false and R is true.
c Both A and R are true and R is the correct explanation for A.
Triangles Around Us
Triangles play a very important role in the field of construction. Construction of roofs, sun shades and bridges involve the construction of a triangular structure. Triangles bring stability to the structure and enable it to support heavy weights such as vehicles.
1 What type of triangle is used in the bridge shown above?
a isosceles
c Scalene
b equilateral
d none of these
2 To construct the above type of triangle, what data would be required?
a Measure of base length and one angle
c Length of one side
b Measure of two angles
d Length of all 3 sides
3 Draw the triangle shown in the image above by taking the length of the side of the triangle as 6.1 cm. Construct the triangle for the bridge using a pencil and a compass.
4 Draw the triangle ADC with DC as 4.5 cm.
12 Perimeter and Area
Let’s Recall
What do you notice about these two shapes?
All sides and angles are equal. All angles are equal, but not all sides are equal.
One of the shapes has sides of equal length, while the other shape has sides that are not all equal in length.
The shapes that have equal sides and angles are regular shapes, whereas shapes with either unequal sides, angles or both are irregular shapes.
Let us say that Raghu has a small, L-shaped kitchen garden. This garden is made by joining a rectangle and a square. He wants to grow vegetables in the rectangular part and fruit in the square part of the garden, as shown here.
He also wants to fence it all around. Let us see how we can find the length of the fence required for his garden and the area of the garden on which he can grow fruit and vegetables.
Perimeter of the garden
= Sum of lengths of all sides of the garden
= 10 m + 4 m + 2 m + 2 m + 8 m + 2 m
= 28 m
Area of the garden
= Area of the vegetable garden + Area of the fruit garden
= Area of rectangle + Area of square
= (10 m × 2 m) + (2 m × 2 m)
= 20 sq. m + 4 sq. m
= 24 sq. m
So, the length of the fence required for Raghu’s garden is 28 m and the area of the garden on which he can grow fruit and vegetables is 24 sq. m.
Let’s Warm-up
Fill in the blanks.
Mean, Median and Mode Squares, Rectangles, Triangles and Parallelograms
Richa and Rahul go to the park daily at 6:00 a.m.
Richa: I run around a rectangular park of length 120 m and breadth 60 m.
Rahul: I run around a square park of length 40 m.
Let us see who covers the greater distance.
Perimeter and Area of Squares and Rectangles
Let us find the distance covered by Richa and Rahul around the park.
Since Richa runs around the rectangular park, we need to find the perimeter of a rectangle.
Perimeter of the rectangular park = Perimeter of rectangle
= 2 (l + b)
= 2 (120 + 60)
= 2 × 180 = 360 m
Since Rahul runs around the square park, we need to find the perimeter of a square.
Perimeter of the square park = Perimeter of square = 4s = 4 × 40 = 160 m
Here, 360 > 160. So, Richa covers the greater distance.
Both parks must be completely covered in grass. How can we determine the amount of grass needed for each park?
To find the amount of grass needed for each park, we need to find the area of the parks.
For a rectangular park, area = l × b
Area of the park = 120 × 60 = 7200 sq. m
So, in this case, 7200 sq. m of the rectangular park needs to be covered with grass.
For a square park, area = s × s
Area of the park = 40 × 40 = 1600 sq. m
So, in this case, 1600 sq. m of the square park needs to be covered with grass.
Remember!
Perimeter of a rectangle = 2 (l + b), where l = length, b = breadth
Area of a rectangle = l × b
Perimeter of a square = 4s, where s = side
Area of a square = s × s
Example 1: The breadth of a rectangular field is double its length. If the area of the field is 338 sq. m, find the cost of fencing it at ₹20 per m.
Given: Area = 338 sq. m; Length = L; Breadth = 2L
Area = Length × Breadth
338 = L × 2L
L × 2L = 338 sq. m
2 × L × L = 338 sq. m
L × L = 169 sq. m = 13 m × 13 m
L = 13 m
So, B = 2 × 13 = 26 m.
Perimeter of the field = 2 (L + B) = 2 (13 + 26) = 2 × 39 = 78 m
Cost of fencing 1 m = ₹20
Cost of fencing 78 m = ₹20 × 78 = ₹1560
So, the cost of fencing the field is ₹1560.
Example 2: The length and breadth of a rectangular field are in the ratio 3:2. If the perimeter of the field is 320 m, find the cost of reaping the field at ₹25 per 50 sq. m.
Let the length of the rectangular field be 3x, and the breadth of the rectangular field be 2x
Perimeter of the rectangular field = 2 (l + b) = 2 (3x + 2x)
= 2 × 5x = 10x
Given, perimeter of the rectangular field = 320 m
So, 10x = 320 m
x = 320 ÷ 10 = 32 m
Therefore, L = 3 × 32 = 96 m, B = 2 × 32 = 64 m
Area = L × B = 96 × 64 = 6144 sq. m
Cost of reaping the field per 50 sq. m = ₹25
Cost of reaping the field per sq. m = ₹ 0.50
Total cost of reaping the field is = 0.50 × 6144 = ₹3,072
Example 3: A wire is in the shape of a rectangle. Its length is 42 cm and breadth is 28 cm. If the same wire is bent in the shape of a square, what will be the measure of each side? Also, find out which shape encloses more area?
Since the shape of the wire is changed from rectangle to square:
Perimeter of the square = Perimeter of the rectangle
4 × side = 2(l + b)
4 × side = 2(42 cm + 28 cm)
4 × side = 2 × 70
Side = 2 × 70 4 = 35 cm
Area of square = side × side = 35 cm × 35 cm = 1,225 sq. cm
Are of rectangle = l × b = 42 cm × 28 cm = 1,176 sq. cm
1,225 sq. cm > 1,176 sq. cm
So, the side of the square is 35 cm and it encloses more area.
Perimeter and Area
Did You Know?
Baudhayana, an Indian mathematician was able to construct a circle almost equal in area to a square and vice versa.
Example 4: Find the area of a square, the measures of the perimeter and area of which are in the ratio 3:4. Let the perimeter of the square be P. Let the area of the square be A.
We are given that, P:A = 3:4
This means, 4P = 3A.
Now, A = s × s and P = 4s.
So, 4P = 3A 4 × 4s = 3 × s × s
16s = 3 × s × s
3s = 16
s = 16 3 = 5.3 (approx.)
So, the area of the square = 5.3 × 5.3 = 28.09 sq. units (approx.)
How many tiles of size 12.5 cm by 10 cm can be cut out of a tile of size 125 cm by 65 cm?
Size of 1 tile to be cut = 12.5 cm × 10 cm
Area of 1 tile to be cut =
Size of the tile to be used for cutting = 125 cm × 65 cm
Area of tile to be used for cutting =
Number of tiles =
So, tiles can be cut from the tile of size 125 cm × 65 cm.
Do It Yourself 12A
Find the perimeter and area of the given figures.
Find the area of the square if its perimeter is given below. a 16 cm
Find the area of a rectangle if its perimeter and length are given below, respectively. a 10 cm, 2 cm b 18 cm, 5 cm c 48 cm, 21 cm d 94 m, 38 m
The perimeter of a rectangle is equal to the perimeter of a square with a side length of 15 m. If the rectangle is 18 m long, what is its breadth?
The cost of fencing a square field at ₹12 per metre is ₹24,000. Find the area of the field.
The breadth of a rectangular field is thrice its length. If the area of the field is 1083 sq. m, find the cost of fencing it at ₹25 per m.
How many rectangles of 20 cm by 6 cm can be cut out of a sheet that is 105 cm by 45 cm?
What are the measures of the rectangle if the length and the breadth are in the ratio of 2:3, and the ratio of its perimeter to area is 5 : 3? Also, find its perimeter and area.
The size of the Indian 10 rupee note is 123 mm × 63 mm. Find the area and perimeter of the note.
Create a word problem to find the area of a rectangle.
1 If the length of a rectangle is made 3 times the original length, and its breadth is made one-sixth of the original, then find the ratio of the area of the new rectangle so formed to the area of the original rectangle.
2 A rectangle and a square both have the same area of 49 sq. cm each. If both the figures are of integral dimensions and the length is of the maximum possible measure, then which of the two, the square or rectangle has a greater perimeter than the other?
Area of Parallelograms
We know that Richa runs around the rectangular park of length 120 m and breadth 60 m.
What if the shape of the park is a parallelogram with the same measures? How would you find its area?
Let us say we have to find the amount of grass in the park. For this, we need to find the area of the park. The park is in the shape of a parallelogram. So, if we know the area of a parallelogram, we can find the area of the park too.
So, let us draw a parallelogram ABCD of any length (base = BC) and breadth (AB) on squared paper, as shown below. Draw a perpendicular AP (height) on BC to obtain a triangle ABP.
Think and Tell
Can you find the area of the parallelogram by counting squares?
Cut off the triangle ABP and paste it on the other side of the parallelogram to obtain a rectangle, as shown below. What do you see?
From the above picture, we can make these observations.
• the length of the rectangle is the same as the base of the parallelogram.
• the breadth of the rectangle is the same as the height of the parallelogram.
So, the area of a parallelogram = area of a rectangle
= l × b
= AD × AP
= BC × AP (AD = BC, these are opposite sides of a rectangle.)
= b × h
Now, the area of the park = b × h = 120 × 60 = 7200 sq. m
Therefore, 7200 sq. m of grass is grown in the park.
Example 5: The base of a parallelogram is triple its height. If its area is 363 sq.cm, find the base and the height of the parallelogram.
Let the base of the parallelogram be b, and the height of the parallelogram be h
We are given that, b = 3h
Area of the parallelogram = 363 sq. cm
b × h = 363 sq. cm
3h × h = 363 sq. cm
3 × h × h = 363 sq. cm
h × h = 363 ÷ 3 = 121 = 11 × 11
h = 11 cm
So, b = 3h = 3 × 11 = 33 cm
Example 6: PQRS is a parallelogram of area 1470 sq. cm. SO and QT are the heights on the sides PQ and SP, respectively. PQ = 30 cm, PS = 25 cm. Find the length of SO and QT.
According to the diagram, SO is a height on PQ.
Area of the parallelogram = 1470 sq. cm
b × h = 1470 sq. cm
PQ × SO = 1470 sq. cm
30 × SO = 1470 sq. cm
SO = 1470 ÷ 30 = 49 cm
Similarly, QT is a height on PS.
So, PS × QT = 1470 sq. cm
25 × QT = 1470 sq. cm
QT = 1470 ÷ 25 = 58.8 cm
So, SO = 49 cm, QT = 58.8 cm.
DEFG is a parallelogram. GH is the height from G to DE, and GI is the height from G to EF. If DE = 18 cm and GH = 9 cm.
1 Find the area of the parallelogram.
Area of the parallelogram = b × h = × = =
2 Find GI, if EF = 12 cm.
Area of the parallelogram = EF ×
Find the area of the parallelograms.
Find the missing measure.
a b = 11 cm, h = ?, A= 88 sq. cm
c b = ?, h = 16 cm, A = 252.8 sq. cm
b b = 9.2 cm, h = ?, A = 152.4 sq. cm
d b = ?, h = 7.6 cm, A = 70.68 sq. cm
Parallelogram-shaped tiles are preferred in the footpaths to decrease the gaps and have a seamless finish. The base of a parallelogram is twice its height. If its area is 648 sq. cm, find the base and the height of the parallelogram.
The difference in the lengths of two adjacent sides of a parallelogram is 8 cm. The perimeter of the parallelogram is 64 cm. If the perpendicular on the longer side of the parallelogram is the same as the difference in the lengths of the adjacent sides, what is its area?
The adjacent sides of a parallelogram are in the ratio 4 : 3. If the longer side is 8.5 cm, find the perimeter of the parallelogram.
In a parallelogram PQRS, PQ = 25 cm, QR = 15 cm, PL SR and PM QR. If PL = 10 cm, then find PM.
Rashmi is celebrating her mother's birthday. She makes parallelogram-shaped buntings for decoration. The height of each bunting is 5 cm and the base length is 12 cm. What is the area of each bunting? Do you also help in putting up decorations at home?
LMNO is a parallelogram, where NE LM and MF LO.
a If LM = 21 cm, LO = 15 cm and NE = 10 cm, then find MF.
b If LM = 30 cm, NE = 12 cm and MF = 20 cm, then find LO.
Challenge
1 The length of one side of a parallelogram is three-fourths of the other side. 2 perpendiculars are dropped from adjacent corners. The length of the perpendicular on the larger side is 18 m. What is the length of the perpendicular on the smaller side?
Area of Triangles
We know that Richa runs around the rectangular park of length 120 m and breadth 60 m.
What if the residents of a colony decide to construct a shortcut between two parallel roads outside the park?
For this, they build a diagonal path that divides the park into two triangular halves.
Let us see how we can find the area of each triangular region.
So, let us draw a rectangle ABCD and cut it along the diagonal BD to obtain two triangles ABD and BDC.
Superimpose one triangle over another so that the vertices A, B, and D of Δ ABD fall on vertices C, D, and B of ΔCDB, respectively. What do you see?
Think and Tell
When two triangles of the same size look the same and on superimposition, they cover each other exactly, then what are such triangles called?
From the above picture, we can see that the two triangles cover each other exactly.
So, ΔABD ΔCDB Area of ΔABD = Area of ΔCDB
So, the area of the rectangle ABCD = area of ΔABD + area of ΔCDB = area of ΔABD + area of ΔABD (As the area of ΔABD = the area of ΔCDB)
= 2 × area of ΔABD
So, the area of ΔABD = area of ΔCDB = 1 2 × b × h
Area of a triangle = 1 2 × b × h, where b is the base and h is the height.
Now, we will find the area of each half of the park (triangle) to get the area of the park.
The area of one triangular region of the park = 1 2 × b × h = 1 2 × 60120 × 60 = 3600 sq. m
Area of the park = 2 × 3600 sq. m = 7200 sq. m
Triangles as Part of Parallelograms
Look at the given parallelogram. Two triangles ABC and PBC are joined together to form a parallelogram, where the base and height of the triangle ABC are the same as the base and height of the parallelogram ABPC.
So, area of ΔABC = 1 2 × (area of parallelogram)
= 1 2 × (base × height)
= 1 2 × (c × h), where c = base of the parallelogram, h = height of the parallelogram
Example 7: Find the area of triangle ABC in each of the given figures.
1 Base of the triangle = 10 cm, height = 5 cm
Area of the triangle ABC = 1 2 × (base × height) = 1 2 × (10 × 5) = 1 2 × 50 = 25 sq. cm
Example 8: Find the area of the shaded region.
2 Base of the parallelogram = 12 cm, height = 6 cm
Area of ΔABC = 1 2 × (area of parallelogram) = 1 2 × (base × height) = 1 2 × (12 × 6) = 1 2 × 72 = 36 sq. cm
Area of the shaded region = Area of square ABCD – area of ΔADE – area of ΔEFB – area of ΔDFC = (DC × DA) –
= (24 cm × 24 cm)
216 sq. cm
Therefore, the area of the triangle = 1 2 × = sq. m Do It Together
The area of a triangle is half of the area of the square. If the side of the square is 12 m, find the area of the triangle.
Area of the triangle = 1 2 × area of square
Side of the square = 12 m
So, the area of the square = = sq. m
Do It Yourself 12C
Find the area of the triangle in the given figures.
Find the missing measure in the triangle where b is the base, h is the height and A is the area. a b = 11 cm, h = 8 cm, A = ? b b = 15.8 cm, h = ?, A = 49.77 sq. cm c b = ?, h = 7.6 cm, A = 39.90 sq. cm
ΔSTU is a right-angled triangle with S = 90°, ST = 6 cm, TU = 10 cm, and SU = 8 cm. OS is perpendicular to TU. Find OS.
ΔSTU is a right-angled triangle with S = 90°, ST = 6 cm, TU = 10 cm, and SU = 8 cm. OS is perpendicular to TU. Find OS.
In ΔABC (see figure), AB = 15 cm, BC= 8 cm and AD = 7.5 cm. Find: a area of ΔABC b altitude CE
In ΔABC (see figure), AB = 15 cm, BC= 8 cm and AD = 7.5 cm. Find: a area of ΔABC b altitude CE
The base and height of a triangle are in the ratio 3 : 4. If the area of the triangle is 96 sq. cm, find its base and height.
The base and height of a triangle are in the ratio 3 : 4. If the area of the triangle is 96 sq. cm, find its base and height.
ABCD is a rectangle with dimensions 30 m by 25 m. AOB is a triangle so that O is the point of intersection of the diagonals. Find the area of the shaded region.
ABCD is a rectangle with dimensions 30 m by 25 m. AOB is a triangle so that O is the point of intersection of the diagonals. Find the area of the shaded region.
Find the area of the shaded region.
Find the area of the shaded region.
EFGH is a rectangle in which EF = 28 cm and EH = 22 cm. P, Q, R, and S are midpoints of the sides of the rectangle EFGH. Find the area of the shaded region.
The Great Pyramid of Giza is one of the Seven Wonders of the Ancient World. It has 4 triangular faces. The current height of each face is around 147 metres and the base length is around 230 metres. What is the area of each face of the Great Pyramid of Giza?
Challenge
1 The figure shows a square ABCD of side 14 cm, and a triangle CEF. The ratio of lengths DF to FC is 1: 4 and DF = BG = BE. Find the difference between the 2 shaded areas.
Mean, Median and Mode Circles
Behind a building, there is a circular field of radius 7 m. The field is full of grass, but for the G20 summit, a fountain inside a circular fence of a radius of 2 m is to be built exactly in the centre of the field for aesthetic reasons. Let us find the length of the fence required for the fountain.
Circumference of Circles
We know that a circle is a curved path of points equidistant from a fixed point called the centre. The distance of these fixed points from the centre is called the radius, and the curved path forming the boundary of the circle is called the circumference.
Circumference RadiusDiameter
Remember!
• All the radii of a circle are equal.
• The distance between two points on the circle through the centre of the circle is the diameter of the circle. The diameter is always double the radius.
Now, we know that a fountain inside a circular fence is to be built exactly in the centre of the field. For this, we need to find the length of the fence.
Since finding the length of the fence is the same as finding the circumference of the circular fence, it is sufficient to find the circumference of the circle.
If we know the circumference of a circle, we can find the length of the circular fence too.
Circumference
Diameter = 3.14, this ratio is called a constant and denoted by π (pi). Its approximate value is 22 7 or 3.14.
Therefore, C D = π, where C = circumference, D = diameter
C = Dπ
C = π × 2r = 2πr
Thus, circumference = 2πr
(Note: Take the value of π as 22 7 unless stated otherwise.)
Now, let us find the length of the fence required for the fountain. Look at the given picture.
Radius of the circular fence = 2 m
Circumference = 2πr = 2 × 22 7 × 2 = 12.57 m
Did You Know?
March 14th (3/14) every year is celebrated as Pi Day in honour of the mathematical constant 'π'.
So, the length of the circular fence required to build the fountain is 12.57 m approximately.
Example 9: The difference of the circumference and the diameter of a circle is 60 cm. Find the radius of the circle.
Given: C – D = 60 cm
2πr – 2r = 60
2r (π – 1) = 60
2 ×
22 – 7 7
15 7 r = 30
r = 230 × 7
= 60
= 30
151 = 14 cm
A piece of wire is bent in the shape of a square of side 66 cm. If the same wire is bent in the form of a circle, what will the radius of the circle be? Also, find the cost of the wire if 1 cm of wire costs ₹4.
(Take π = 3.14)
Side of the square (made using wire) = 66 cm
So, the perimeter of the square = 4s = 4 × = cm
Circumference of the circle = cm
r = cm
Cost of 1 cm of wire = ₹4
Cost of cm of wire = ₹4 × = ₹
Do It Yourself 12D
Find the circumference of the circle for the radii. (Take π = 22 7 ) a 14 cm b 28 cm c 42.7 cm
Find the diameter of the circle for the given circumference. a 75.42 cm b 352 cm c 502.85 cm
The circumference of a circular playground is 286 m. Find its diameter.
The circumference of a circle exceeds the diameter by 90 cm. Find its radius.
Find the perimeter of a semicircle in which the diameter is 50 cm. (Take π = 3.14)
Find the ratio of the circumferences of two circles whose radii are in the ratio 5:6.
The radius of the passenger car tyre is around 40 cm. Find the distance covered by a car tyre in 140 revolutions.
To fence a circular garden, the total cost is ₹36,500 at the rate of ₹40 per metre. Find the radius of the garden.
The diameter of the wheel of a truck is 57.15 cm, How many revolutions will it make to cover 1 km 30 m?
The largest Ferris wheel in the world is the "Ain Dubai," also known as the "Dubai Eye". The radius of Ain Dubai is 125 metres. It has 48 cabins. What is the approximate distance between two adjacent cabins?
A wire is bent into the shape of a square of side 88 cm. If the same wire is looped in the form of a circle, what will the radius of the circle be?
1 The diameter of a circular field is 96 metres. An adult man starts walking around the field at a speed of 8 metres per minute. However, after completing one round, he decides to take a 5-minute break. After the break, he resumes walking, but his speed decreases by 20% due to fatigue. Moreover, instead of walking directly along the circumference for the second round, he decides to take a path that deviates slightly inward, reducing the total distance by 10%. What is the total time taken by the man to walk around the field twice, including the break? (Take π = 3.14)
Area of Circles, Semicircles and Quadrants
We know that a fountain inside a circular fence is to be built exactly in the centre of the circular field.
Now, what if we have to find the area of the field used for building the fountain?
To find the area of this region, we need to find the area of the circle.
Let us understand the relationship between a rectangle, a circle and its area.
So, take a circle of radius r and shade one-half of the circle. Cut the circle into eight sectors and join them together to form a parallelogram. This is not even nearly a rectangle.
The greater the number of sectors, the more appropriate the rectangle.
We keep repeating this step until the lines of the sectors are indistinguishable and we get a perfect rectangle.
In each case given here, what do you observe?
• breadth of the rectangle = radius of the circle = r
• length of the rectangle = length of half the total number of sectors = half of the circumference
So, area of the circle = area of the rectangle
= l × b
= half of the circumference of the circle × radius of the circle = 1 2 × 2πr × r = πr2
Now, using this formula, let us find the area of the field used for building the fountain.
Area of the circle = πr2
= 22 7 × 2 × 2 = 12.57 sq. m
So, the area of the field used for building the fountain is 12.57 sq. m approximately.
Error Alert!
Example 10: Find the area of the shaded region in the figures.
Area of the circle = πr2
Area of the semicircle = 1 2 πr2
= 22 7 × 28 × 428 = 1 2 × 22 7 × 14 × 14
= 2,464 sq. cm = 308 sq. cm
Example 11: The ratio of the areas of circle S and circle T is 2:3. If the radius of circle T is 21 cm, what is the area of circle S?
Radius of circle T = 21 cm; The ratio of areas of circle S to circle T = 2:3
Let the area of any circle be x sq. cm.
So, the area of circle S = 2x, and the area of circle T = 3x
Now, the area of circle T = 3x
3x = πr2
3x = 22 7 × 21 × 21
x = 22 × 21 × 213 1 7 × 3 = 462 sq. cm
Therefore, the area of circle S = 2x = 2 × 462 sq. cm = 924 sq. cm
Area of a quarter of a circle (quadrant) = 1 4 πr2
Example 12: Find the distance covered by a bus tyre of radius 20 cm in 70 revolutions.
Radius of the tyre = 20 cm
Length of 1 revolution of the tyre = 2πr
= 2 × 22 7 × 20 = 880 7 cm
Length of 70 revolutions of the tyre = 880 7 × 70 = 8,800 cm
So, the distance covered by the bus tyre is 8,800 cm.
Example 13: A horse is tied with a rope affixed to one corner of a square farm of side 24 m. If the length of the rope is 6 m, find the area of the farm on which the horse can graze. Also, find the remaining area of the farm. (Take π = 3.14)
Side of the square farm = 24 m, length of the rope = 6 m = radius
The area in which the horse can graze is in the shape of a quadrant.
So, the area of the quadrant = 1 4 × πr2 = 1 4 × 3.14 × 6 × 6 = 1 4 × 113.04 = 28.26 sq. m
Therefore, the horse can graze in an area of 28.26 sq. m.
Now, the remaining area of the farm = Area of the square farm – Area in which the horse grazes = (24 × 24) – 28.26 = 547.74 sq. m
A piece of wire in the shape of a square of side 15 cm is reshaped in the form of a circle. Find the radius and the area of the circle.
Side of the square = 15 cm
Perimeter of the square = 4s
So, the perimeter of the square = 4 × 15 cm =
Perimeter of the circle =
Find the area of the circle for the radii. (Take π = 22 7 )
Find the diameter of the circle for the areas.
154 sq. cm
616 sq. cm
Find the area of the figures. (Take π = 22 7 )
sq. cm
sq. cm
Find the ratio of the areas of two circles whose radii are in the ratio 4:7.
The ratio of the areas of circle P and circle Q is 25:36. If the radius of circle Q is 36 cm, what is the area of circle P?
Metal washers are circular discs with a hole in the centre through which a fastener like a screw fits. They are used to evenly distribute the load of the fastener across the material it connects to. A small metallic washer of radius 8 mm has a hole of 2.5 mm radius. What is the area of the washer?
Copper is used in electric wiring as it is a good conductor of electricity. It is usually coiled in the form of a circle in electrical appliances. A copper wire in the form of a circle encloses an area of 1386 sq. cm. If the same wire is bent to form a square which is to be used in an induction cooktop, find its area.
1 Sonal was making a party hat using a sheet of golden paper as shown in the figure. Find the area of the sheet of paper used to make 20 party hats.
Combined Shapes
We know that a fountain inside a circular fence is to be built exactly in the centre of the circular field, and the rest of the field is covered with grass.
Now, what if we have to find the area of the field covered with grass?
To find the area of this region, we need to find the area between two circles.
Radius of outer circle = R
Radius of inner circle = r
Then, the area between the two circles, = Area of outer circle − Area of inner circle
Now, the area of the field with grass = Area of the total field − Area of the field used for building the fountain
Radius (R) of the outer circle = 7 m; Radius (r) of inner circle = 2 m
Area of the field without grass = Area of the field – Area of the fountain = π (72 − 22) = π (49 − 4) = 22 7 × 45 = 141.43 sq. m
Think and Tell
These circles have the same centre, but different radii. What are such circles called? Where else do you find such circles in real life?
Example 14: Shreya has cut out two semi-circular pieces from a rectangular sheet of paper of size 12 cm × 8 cm. Find the area and perimeter of the figure obtained. (Take π = 3.14)
We are given that the length of the rectangle = 12 cm, breadth of the rectangle = 8 cm = the diameter of the semicircle. So, the radius of the circle = 4 cm.
Now, the perimeter of the green part of the figure = Lengths of the rectangle + Perimeter of 2 semicircles (Perimeter of a circle) = (2 × 12) + 2πr
= 24 + 2 × 3.14 × 4
= 24 + 25.12 = 49.12 cm
Area of the green part of the circle = Area of the rectangle – 2 × Area of a semicircle
= 12 × 8 – 2 × 1 2 × πr2
= 96 – 3.14 × 4 × 4
= 96 – 50.24 = 45.76 sq. cm
From a circular sheet of paper of radius 24 cm, two full circles and a quarter circle of radius 1.6 cm each and a square of side 6 cm are cut out. Find the area of the remaining sheet of paper. (Take π = 3.14)
We are given that, the radius of the circular sheet = R = 24 cm
The radii of two full circles = r1 = 1.6 cm each and the radius of a quarter circle = r2 = 1.6 cm
Side of the square = 6 cm
The area of the remaining sheet of paper = Area of the sheet − (Area of 2 full circles + Area of a quarter circle + Area of the square)
Find the area of the figures. (Take π = 22 7 )
Find the area of the shaded region.
14
From a circular sheet of metal of radius 8 cm, a quarter circle of radius 5 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Three circular sheets of radius 25 cm are cut out of a rectangular metal sheet of length and breadth 1.50 m and 90 cm, respectively. What area of the metal sheet is left? (Take π = 3.14)
Sanchita has a piece of paper which is in the shape of a square of side 32 cm. She makes some special types of notepads in a circular shape out of the paper. The notepad is made such that it has the biggest possible diameter so that she can use the maximum amount of paper. Find the area of the remaining portion of the square paper. (Take π = 22 7 .). Why is saving paper important?
A rectangular sheet of paper is 50 cm long and 38 cm broad. 27 buttons, each with a radius of 2.5 cm, have been cut out from it. Find the area of the remaining sheet. (Take π = 22 7 )
While making a mask, Ranita removed two circles of radius 6 cm each, and a rectangle of length 5 cm and breadth 2 cm from a circular card of radius 44 cm. Find the area of the remaining mask. Create a similar mask and find the area of the mask that you have created. (Take π = 22 7 )
Perimeter and Area
1 Two circles are drawn inside a big circle of diameter 28 cm. The diameters of the two circles are 1 4 and 3 4 of the diameter of the big circle as shown in the given figure. Find the ratio of the areas of the unshaded part and the shaded part of the circle.
Mean, Median and Mode Word Problems on Perimeter and Area
A housing society is built on a plot of land of length 200 m and breadth 180 m. It has two kinds of pavement areas given below.
1 A path 2 m wide runs inside along the sides of the plot.
2 Crossroads 3 m wide, run at right angles through the centre of the plot and parallel to its sides.
Let us find the area of the crossroads.
Think and Tell
How would you calculate the area of the plot without the pathways, crossroads, and fountains?
To find the area of the crossroads, we must first find the area of the two roads and the area of the intersecting square, and then find their difference.
Length of the road that is parallel to the length of the plot = 196 m
Breadth of this road = 3 m
Area of this road = 196 × 3 = 588 sq. m
Length of the road that is parallel to the breadth of the plot = 176 m
Breadth of this road = 3 m
Area of this road = 176 × 3 = 528 sq. m
The intersection of the crossroads is a square where two squares overlap each other. So, to find the area of the crossroads, we need to subtract the area of 1 square from the area of the two roads.
Therefore, the area of 1 square = 3 × 3 = 9 sq. m
Thus, the area of the crossroads = 588 + 528 – 9 = 1107 sq. m
Example 15: The four semicircular grass plots shaded around a square shaped building are to covered in turf at ₹24 per sq. m. If the side of the square is 15 m, then calculate the cost of laying the turf.
(Take π = 3.14)
Area of 4 shaded regions = 4 × 1 2 × πr2 = 4 × 0.5 × 3.14 × 7.5 × 7.5 = 353.25 sq. m
Cost of laying turf per sq. m = ₹24
Cost of covering 353.25 sq. m = 353.25 sq. m × ₹24 = ₹8,478
Example 16: A path 3.5 m wide runs inside a rectangular piece of land of length 20 m and breadth 15 m. Find the area of the path. Also, find the cost of levelling the path at the rate of ₹100 per 10 sq. m.
Length of the rectangle = 20 m, breadth of the rectangle = 15 m.
Width of the path = 3.5 m
Length of the inner rectangle = 20 – 3.5 – 3.5 = 13 m
Breadth of the inner rectangle = 15 – 3.5 – 3.5 = 8 m
So, area of the path = Area of the outer rectangle – Area of the inner rectangle = 20 × 15 – (13 × 8) = 300 – 104 = 196 sq. m
Cost of levelling 1 sq. m = ₹100 per 10 sq. m
Cost of levelling 196 sq. m = 196 10 × 100 = ₹1960
So, the cost of levelling 196 sq. m of the path is ₹1960.
Cost of constructing sq. m = ₹520 × = ₹ Do It Together
A square plot of land of side 150 m has two roads of width 2 m passing through its centre and parallel to its sides. Find the cost of constructing the roads at the rate of ₹520 per sq. m.
Side of the square = 150 m, width of the road = 2 m.
Length of road 1 (parallel to the length of the square land) = 150 m
Width of road 1 = 2 m
Area of road 1 = 150 × 2 = sq. m
Area of the roads = Area of road 1 + Area of road 2 – Area of the common square
Cost of constructing 1 sq. m of road = ₹520
Perimeter and Area
Do It Yourself 12G
The Lincoln Memorial is a monument dedicated to Abraham Lincoln, featuring a large rectangular structure with a colonnade of Doric columns. Its floor has a length of 57.8 metres and a width of 36.1 metres. What is its floor area?
In a circular garden of diameter 160 m, a pond is constructed in the centre in the form of a circle of radius 28 m. Find the area of the remaining garden. (Take π = 3.14)
A rectangular field of dimensions 100 m × 50 m has crossroads running parallel to the two sides and cutting at right angles through the centre of the field. If both roads are 2 m wide, find:
a the area covered by the roads.
b the cost of grassing the remaining area at the rate of ₹110 per 10 sq. m.
A room has four walls, each measuring 18.4 m × 10.2 m. It has two doors with a height of 1 m and a width of 2 m. It also has three windows of size 1 m × 0.6 m. Find the cost of whitewashing the walls at the rate of ₹80 per sq. m.
A circular track has to be covered with grass. The inner circumference of the circular track is 176 m. The track is 8 m wide. Calculate the total area of the track that will be covered with grass.
A swimming pool of length 12 m and breadth 5 m is to be built with a coping 1.5 m wide all around it. Find the area of the coping. Also, find the cost of the coping if the rate is ₹50 per sq. m.
Carpets are used to provide insulation from cold. In most cold countries, wall to wall carpets are also used. The cost of carpeting a hallway of 15 m width at ₹150 per square metre is ₹45,000. Find the length of the hallway.
A rectangular sheet of metal measuring 60 cm by 45 cm is used to create an open-top box. Small squares, each with a side length of 10 cm, are cut out from each corner of the sheet. The remaining portion is then folded to form the box. Calculate the total surface area of the inside of the box that needs to be painted.
Seema is cycling at a speed of 12 km/hr. How long will she take to complete a round of a circular field of radius 80 m? (Take π = 3.14)
A circular parking lot has an area of 628 square metres. A security camera is installed at the centre of the parking lot and can monitor an area with a radius of 15 metres. Will the security camera cover the entire parking lot? (Take π = 3.14)
A cow is tied with a rope affixed to one corner of a rectangular lawn of length 30 m and breadth 20 m. If the length of the rope is 8 m, find the area of the lawn on which the cow can graze. Also, find the remaining area of the lawn. Write
1 A dining tent is being set up in a camping area. The radius of the tent is 25.5 m. Holes are being dug to fix wooden sticks. These wooden sticks will be used to tie the ropes that will hold the tent in place. The sticks are to be placed at a distance of 3.5 m from the edge of the tent.
a How many wooden sticks are needed, if they are to be placed 7 m apart along the curved path?
b The circular stage at the centre where the food will be placed is 8.5 m in radius. Find the area left for the people to sit in.
Points to Remember
• Perimeter of a rectangle = 2 (l + b), where l = length, b = breadth
• Area of a rectangle = l × b
• Perimeter of a square = 4s, where s = side
• Area of a square = s × s
• Area of a parallelogram = area of a rectangle = b × h
• Area of a triangle = 1 2 × b × h
• Circumference of a circle = 2πr
• Area of a circle = πr2
• Area between two circles = π (R2 − r2)
Math Lab
Setting: In groups of 5
Circle Art Gallery
Art Integration & Collaboration
Materials Required: Large sheets of paper, rulers, circular objects of various sizes, coloured pencils, markers or paints, a pair of scissors
Method:
1 Each group must collect a large sheet of paper from their teacher. Look at and read the circumference written on the board.
2 Each group shall use a circular object to trace a circle onto the paper of the circumference given and find its area.
3 Each group shall then make another circle of area equal to one-third of the previous circle.
4 Repeat step 3 until the area is equal to less than 0. Stop when you get a negative number.
5 Now, use the circles you created so far to overlap and position them creatively to form a beautiful circular design to display in a circular art gallery. One such design is shown.
Chapter Checkup
Find the area of the figures given below.
and Area
The area of a square is 81 sq. cm. Find the area of the square formed by joining the midpoints of the square.
If the length of a rectangle is doubled and its breadth is one-third of the original, then find the ratio of the area of the new rectangle to the area of the original rectangle.
A man wants to acquire a rectangular plot 160 m long and of the same area as that of a square plot of side 108 m. Find the width of the rectangular plot.
A floor 6.68 m long and 8.2 m wide is covered with rectangular tiles of size 64 cm by 32 cm. Find the total cost of the tiles at the rate of 20.50 per tile.
A park is in the shape of a quadrilateral PQSR, where QR is the diagonal, SO is perpendicular to QR, and RX is perpendicular to PQ. If PQ = 25 cm, QR= 24 cm, RX = 6 cm, and SO = 5 cm, find the area of the park.
ABCD is a parallelogram of area 1520 sq. m. DP and BQ are the heights on the sides AB and DA, respectively. AB = 28 cm, AD = 32 cm. Find the length of DP and BQ.
Support structures in 3D printing are designed as scalene right angled triangles to make the structure strong and easy to remove after the print. Find the area of a scalene right-angled triangle whose base is 15 cm and altitude is 8 cm.
The sum of the circumference and the radius of a circle is 153 cm. Find the diameter and the circumference of the circle. Also, find the area of the circle.
Find the area of the shaded region.
A hedge row needs to be planted around a rectangular lawn 22 m long and 15 m wide. If 5 shrubs can be planted to form a metre of the hedge, how many shrubs will be needed in total?
The Wankhede Stadium is located in Mumbai, India, and is one of the most famous cricket venues in the world. It is roughly circular. The radius of the ground is around 70 metres. The ground is to be levelled, and new grass is to be planted in it. If the cost of levelling and planting is ₹120 per sq. m, then what is the total cost of levelling and planting grass? (Use π = 3.14)
The Shalimar Bagh in Srinagar has an approximate length of 587 metres and width of 251 metres. What is the area of the Bagh?
Ravi was cutting out shapes from a circular sheet of paper of radius 27 cm. He cuts four circles of radius 1.6 cm, a rectangle of length 5 cm and breadth 3 cm and a square of side 4 cm from it. Find the area of the remaining sheet.
The inner and outer circumferences of a circular track are 308 m and 352 m, respectively. Find the width of the track.
The ratio of two adjacent sides of a parallelogram is 7:3. Its perimeter is 120 cm. Find its area if the altitude corresponding to the larger side is 14 cm.
The inner circumference of the Monaco Grand Prix Circuit is 3.337 km while the inner circumference of the Indianapolis Motor Speedway is around 4.023 km. Estimate the difference between the areas.
Inside a rectangular garden 25 m long and 15 m wide, a 1.5 m margin is left for planting lilies. If 4 lily stems can be planted in 1 sq. m, and each lily stem costs ₹35, find the total expenditure incurred.
Tara is helping her mother to put lace on the edge of a circular cushion of diameter 18 cm. Find the length of the lace required, and also find its cost if one metre of lace costs ₹22. Do you help your parents with daily chores?
2
e Both A and R are incorrect. 1
The perimeter of a rectangle is 80 m. What is the maximum area this figure can have if the sides are natural numbers in metres?
Read the statements and choose the correct option.
Assertion (A): If the radius of a circle is 14 m then the area of the circle is 88 sq. cm and its circumference is 616 m.
Reason (R): The area of a circle is given by the formula A = πr2, while the circumference is given by C = 2πr, where r is the radius.
a Both A and R are correct, and the R is the correct explanation for the Assertion.
b Both A and R are correct, but the R is not the correct explanation for the Assertion.
c The A is correct, but the R is incorrect.
d The A is incorrect, but the R is correct.
Case Study
Designing a Living Space
Before the construction of any building, first a plan is made to understand the area and the appearance of the space inside a building. Tia makes a plan for a 1 BHK home with the little knowledge she has about the area and perimeter. Look at the plan and answer the questions.
1 The length and breath of the garden area is: a 12 m × 26 m b 4 m × 24 m
5 m × 22 m d 8 m × 5 m
2 The area of the bathroom is:
3 The perimeter of the living area is
4 What is the perimeter of the kitchen and dining area together?
5 Tiles have to be fitted in the bathroom. The area of one tile is 4 sq. m. How many tiles will this area require?
Cross Curricular
13 Algebraic Expressions
Let’s Recall
A number pattern is a pattern or sequence of numbers that follows a certain rule or order.
For example, in the table of 3, its multiples 3, 6, 9, 12, 15... form a number pattern, where the next number is obtained by adding 3 to the preceding one.
Let us find the rule and next number for the number pattern 35, 34, 32, 29, 25, 20, 14,….
On observing the numbers, we can see that the numbers are decreasing by (1, 2, 3, 4 and so on...).
The next number in the pattern will be 14 − 7 = 7.
Let us see another pattern. Here the numbers are multiplied by 4 each time.
The next number in the pattern will be 256 × 4 = 1024.
Let’s Warm-up
Find the pattern and fill in the blanks to find the next number.
1 105, 100, 95, 90,
2 9, 19, 29, 39, 49,
3 15, 28, 41, 54, 67,
4 90, 75, 60, 45, 30,
5 2, 4, 8, 16, 32, 64,
Mean, Median and Mode Generating Rules in Formulas and Patterns
Priya and Rahul are architects. They need to find the perimeter and area of different shapes to make their drawings.
Priya: Rahul, the measures of different shapes are always different. It takes me a lot of time to find the perimeter and area of the shapes.
Rahul: You are right, Priya! Earlier, I also used to struggle with this issue. But now, I’ve started using some formulas and rules to find the area and perimeter.
Let us see what rules and formulas Rahul is using.
Finding Formulas
We know that the perimeter of a shape is defined as the total length of its boundary. Let us look at the perimeter of some regular shapes.
Perimeter = 3a
where a = length of the side.
Perimeter = 4a where a = length of the side.
The formula for area of some shapes can be given as:
Perimeter = 5a where a = length of the side.
Perimeter = 6a where a = length of the side.
Area = a2 where a is the length of the side.
Area = a × b
where a is the length of the rectangle, and b is the width of the rectangle.
Example 1: Find the perimeter and area of a square of side 10.5 cm.
Perimeter of a square = 4a; here a = 10.5 cm
Perimeter = 4 × 10.5 = 42 cm
Area of a square = a2 = 10.52 = 110.25 cm2
Area = 1 2 × b × h where b is the length of the base of the triangle and h is its height.
Think and Tell
Find the measure of each side of a square for which the perimeter of a square is equal to its area.
Example 2: Sambit is making a triangular-shaped structure for his bird house. If the structure has a base of 10 cm and a height of 25 cm, what is the area?
The length of the base of the triangular-shaped structure = 10 cm
The length of the height of the triangular-shaped structure = 25 cm
Area of the triangular structure = 1 2 × base × height = 1 2 × 10 × 25 10 × 25 = 125 cm2
Example 3: Find the difference in the areas of the given rectangles.
Length of rectangle, l = 10 cm
Breadth of rectangle, b = 6 cm
Area of rectangle = l × b = 10 × 6 = 60 sq. cm
Length of rectangle, l = 12 cm
Breadth of rectangle, b = 4 cm
Area of rectangle = l × b = 12 × 4 = 48 sq. cm
Difference in area = 60 sq. cm 48 sq. cm = 12 sq. cm
Example 4: A wire is in the shape of a regular pentagon with a side length of 8 cm. If the same wire is bent in the form of a square, what would be the area of the square?
The side of the regular pentagon = 8 cm
Length of the wire = Perimeter of pentagon = 5 × length of the side of pentagon = 5 × 8 = 40 cm
Length of the side of the square = 40 4 = 10 cm
Area of the square = side × side = 10 × 10 = 100 square cm
Example 5: The area of a square is equal to the area of a rectangle. If the side of the square is 10 cm, find the breadth of the rectangle if the length of the rectangle is 25 cm.
The length of the side of the square = 10 cm; and the length of the rectangle = 25 cm
Area of square = side2 = 102 = 100 cm2
Given, that the area of a square = area of rectangle
Area of the rectangle = length × breadth = 100 cm2
25 × breadth = 100 cm2
The breadth of the rectangle = 100 25 = 4 cm
Find the perimeter of the given figures. Which figure has the greatest perimeter?
The length of the side of the given triangle a = 15.7 cm
Perimeter of triangle = 3a =
3 × ____ = cm
The length of the side of the given pentagon a =
Perimeter of pentagon = 5a = 5 × ____ = cm
On comparing, the perimeter of the is the greatest.
The length of the side of the given hexagon a = 6.5 cm
Perimeter of hexagon = 6a = 6 × 6.5 = cm
Number Patterns
Let us see some rules for number patterns. If n is a natural number, then,
Rule
(n + 1) is its successor
2n is an even number
Example
If n = 25, then n + 1 = 25 + 1 = 26 is the successor of 25
If n = 7, then 2n = 2 × 7 = 14, which is even
(2n + 1) is an odd number If n = 9, then 2n + 1 = 2 × 9 + 1 = 18 + 1 = 19, which is odd
Sum of n natural numbers = n(n + 1) 2 If n = 11, then n(n + 1) 2 = 11(11 + 1) 2 = 11 × 12 2 = 66 is the sum of the first 11 natural numbers
Let us see some more number pattern rules:
Number
3, 5, 7, 9…
Each term of the pattern can be given by (2n + 1), where n is a natural number
9, 19, 29, 39, 49… Each term of the pattern can be given by (10n − 1), where n is a natural number
Example 6: Find the sum of the first 20 natural numbers.
We know that the sum of n natural numbers = n(n + 1) 2
Putting n = 20 in the given formula, we get 20(20 + 1) 2 = 20 × 21 2 = 210
Example 7: Find the rule for the number pattern. Also, find its 21st term.
1, 4, 7, 10, 13…. First term = 1
Successor term = Predecessor term + 3
If the rule = 3n, for n = 1 the first term must be 3, but here the first term is 1
Hence, the rule for the given number pattern = 3n − 2
The 21st term of the pattern = 3 × 21 − 2 = 63 − 2 = 61
Example
When n = 12, 12th term = (2 × 12 + 1) = 25
When n = 6 6th term = (10 × 6 − 1) = 59
Remember!
The pattern must be true for all the natural numbers.
Find the difference of the sum of the first 15 natural numbers and the sum of the first 10 natural numbers.
We know that the sum of n natural numbers = n(n + 1) 2
The sum of the first 15 natural numbers = The sum of the first 10 natural numbers = Difference =
Do It Yourself 13A
If 89 is the successor of a natural number n, then what is the value of n?
If an even number is denoted by n; the next even number can be given as
The height of a triangle is 20 cm. If its area is 175 cm2, find the length of its base.
The perimeter of a square is 62 cm. Find its area.
Find the sum of the first 12 natural numbers and the sum of the first 18 natural numbers.
Find the rule for the given pattern: 1, 3, 5, 7, 9,…. Also, find the 100th term of the pattern.
Sudha donated triangular-shaped mirrors at a local orphanage on her birthday. Each mirror has a base of 8 feet and a height of 5 feet. What is the area of the each mirror?
A wire is in the shape of a regular pentagon of perimeter 30 cm. If the same wire is bent in the form of a regular hexagon, what would be the length of each side of the hexagon?
The areas of a square and a rectangle are equal. If the side of the square is 35 cm and the length of the rectangle is 50 cm, find the breadth of the rectangle.
During cell division, certain bacteria can double their population every hour under optimal conditions. Starting with a single bacterium, the number of bacteria doubles each hour. If the initial bacterial population starts at 1, how many bacteria will there be after 5 hours?
Challenge
Critical Thinking
Kunal has a square plot of an area double that of Nikhil’s rectangular plot. If the length of Nikhil’s plot is 25 m and its perimeter is 75 m, find the perimeter of Kunal’s plot.
Algebraic Expressions and Terms
Kushal went to school after 10 days, as he had been ill. He saw some maths problems in the homework and got confused. He saw various letters of the alphabet, along with numbers. Let us help him out.
Parts of an Expression
An algebraic expression is an expression made up of variables and constants and joined using mathematical operators (like addition, subtraction, multiplication, or division)
A variable in an algebraic expression is the letter used to represent a certain quantity.
A constant in an algebraic expression is the number of which the value is fixed.
The parts of an algebraic expression are called the terms
We saw that 3x2 − 4y consists of two terms 3x2 and − 4y. The term 3x2 is a product of 3, x and x; we can say that 3, x and x are the factors of the term 3x2. Hence, a term is a product of its factors. The term 4y is a product of the factors 4 and y.
One of the ways to show algebraic expressions is by using algebraic tiles. Let us represent 3x2 + 3x − 4 on the algebraic tiles.
An expression can be shown with the help of a factor tree as:
Error Alert!
Terms
The minus sign ‘−’ is included in a term. For the expression 5y − 3x the terms are 5y and 3x 5y and −3x
x y −6 y y
In a term of an algebraic expression, any of the factors with the sign of the term is called the coefficient of the product of the other factors in that term. A coefficient can be a numerical factor, an algebraic factor or the product of two or more factors.
For example, in the term −5xy, −5 is the coefficient of xy or −5x is the coefficient of y, or −5y is the coefficient of x.
Example 8: List the coefficients of a and b in the expressions.
Think and Tell
What is the coefficient of xy in the term xy?
Example 9: Express the expression 8x 4x2 + 3y using a factor tree.
Factors Expression
Terms
Factors
x − 4x2 + 3y 8x −4x2 3y 8 x −4 x x 3 y
Did You Know?
Brahmagupta, an Indian mathematician, introduced the concept of zero and negative numbers in algebraic equations, laying the foundation for modern algebraic notation. Chapter 13 • Algebraic Expressions
Do It Together
Example 10: Using constants, variables and mathematical operations, form algebraic expressions for the given statements.
1 Sum of thrice a and twice b
Sum of thrice a and twice b = 3 × a + 2 × b = 3a + 2b
2 Three-fourth y added to one-third z
Three-fourth y added to one-third z = 3 4 y + 1 3 z
Draw the factor tree for 15ab − 5a2b + 5a and write the factors of the term 5a2b.
The factor tree for the expression can be given as:
Expression 15ab − 5a2b + 5a Terms
15
The factors of the term −5a2b are −5, , , and .
Like and Unlike Terms
The terms are called like terms when they have the same algebraic factors. If the algebraic factors of two terms are different, they are called unlike terms.
For example, in the expression 15xy + 28x2 − 8xy + y2, the algebraic factors of the terms 15xy and −8xy are the same i.e., xy, hence 15xy and −8xy are like terms. The algebraic factors of 28x2 are x and x and the algebraic factors of y2 are y and y, hence 28x2 and y2 are unlike terms.
Example 11: List the like terms in the expression 5x2y + 4xy xy 9yx2 .
The like terms are 5x2y and −9yx2 since both have the same algebraic factors, i.e., x2y.
4xy and −xy are also like terms since they have the same algebraic factors, i.e., xy.
Example 12: Group the like terms from the terms given. xy2 , −y2x2, 5y2x, −10x2y2 and 3xy2
Like terms = xy2, 5y2x, 3xy2 y2x2, −10x2y2
Do It Together
Write the like terms for the given expressions.
1
2 2x2y + 5x − 3x − 7y2x
3 12b − 5ab + 7ba2 + 9a2b
Types of Algebraic Expressions
Based upon the number of terms, algebraic expressions are classified as:
Monomial: An algebraic expression that contains only one term is called a monomial.
For example, 3y, 4a2b, −8 are monomials.
Binomial: An algebraic expression that contains two terms is called a binomial.
For example, 2xy − 2x, a2 + 5ab, 7pq − 8 are binomials.
Trinomial: An algebraic expression that contains three terms is called a trinomial.
For example, 4ab + 5b − 3c, 4xy2 + 2xy − 3 are trinomials.
Quadrinomial: An algebraic expression that contains four terms is called a quadrinomial.
For example, 5pq + 7qr − p2 + 8pr, 8x2y − 3xy + 7zx − 8yz are quadrinomials.
An expression with more than one term is called a polynomial.
Example 13: Which among the following is a binomial expression?
A binomial has two terms, hence the expressions ab + c and xy − zx are binomials. Thus, 2 and 4 are binomial expressions.
Example 14: Find the odd one out.
1 x + y + 8 2 2z + y − z 3 x2 − y2 4 2ab + a + 3y
All the given expressions are trinomials except x2 − y2 which is a binomial. Thus, 3 is the odd one out.
4 3x Do It Together
Identify the terms in the expressions and classify them as monomial, binomial, trinomial or quadrinomial.
1 9xvy + 7 − 9xy + 3xv
2 2x2 + 5 2x2, 5 Binomial
3 −7a + 5 + 6b
Do It Yourself 13B
Using constants, variables and mathematical operations, form algebraic expressions for the given statements.
a Addition of x and y
b One-fourth of a number a added to thrice the number b.
c 3 less than z added to the product of x and y
d The product of m and n subtracted from twice the product of p and q.
List the coefficients of a and b in the expressions.
a 6a2b + 12bc b 3ac − 10ba c 15ba2 + 12ac + 7b2c
Identify the terms in the following expressions.
Find the odd one out. a 8mn, 6mn2, 5nm,
Group the like and unlike terms.
Draw a factor tree for the given expressions.
Maria has made twice as many paintings as John. If John has made x paintings, write an algebraic expression for the total number of paintings they have made together.
A rectangle has a length that is 5 cm longer than its width. If the width is w cm, write an algebraic expression for the perimeter of the rectangle.
Create
Which of the following statements are true?
i 6mn + 2mn2 + 3 is a binomial.
ii 3 × m is a monomial.
iii 9pq + 2qr + 5s has 9, 2, 5 as constant terms.
iv 4a2 + 5ab + 3c + 8 is a trinomial with no constant term.
Critical Thinking
a Statements i, ii, iii are true. b Only statements i, ii are true.
c Statements i, iii, iv are true. d Only statement ii is true.
Kushal learnt about the basic terms in algebraic expressions. The next day, when he went to school, the teacher introduced the class to the addition and subtraction of algebraic expressions.
Addition of Algebraic Expressions
We know that we can add or subtract two quantities only if they have the same unit. The same rule applies to algebraic expressions. While adding two algebraic expressions, we add only the like terms.
Let us add the expressions 3x + 2 and 4x − 2y + 1 using algebraic tiles.
We can also add polynomials using the horizontal or column method. Let us add 6p2 + 9pq + 5q2 and 4p2 + 5pq + q2 using both methods.
Horizontal Method
Step 1: Write the expressions to be added with a ‘+’ sign between them.
(6p2 + 9pq + 5q2) + (4p2 + 5pq + q2)
Step 2: Write the like terms together.
6p2 + 4p2 + 5pq + 9pq + q2 + 5q2
Step 3: Add the numerical coefficients of all the terms and keep the algebraic factor the same.
(6 + 4)p2 + (5 + 9)pq + (1 + 5)q2 10p2 + 14pq + 6q2
Hence, (6p2 + 9pq + 5q2) + (4p2 + 5pq + q2) = 10p2 + 14pq + 6q2
Column Method
Write the like terms one below the other and then add. The above expression can be added as:
6p2 + 9pq + 5q2 + 4p2 + 5pq + q2 (6 + 4)p2 + (9 + 5)pq + (5 + 1)q2
= 10p2 + 14pq + 6q2
Example 15: Add 5xy 3y + 2z and 3xy 8z + 2y by both the column and horizontal methods.
Horizontal Method
5xy − 3y + 2z + 3xy − 8z + 2y
= 5xy + 3xy − 3y + 2y + 2z − 8z
= (5 + 3)xy + (−3 + 2)y + (2 − 8)z
Column Method
= 8xy − y − 6z 5xy − 3y + 2z + 3xy + 2y − 8z
(5 + 3)xy + (−3 + 2)y + (2 − 8)z
= 8xy − y − 6z
Example 16: Add the expressions.
4ab + 3b; 5ac − 5b; 12ab − 3ac and ab − 4ac + 12b
Writing all the expressions with a ‘+’ sign between them, we get
(4ab + 3b) + (5ac − 5b) + (12ab − 3ac) + (ab − 4ac + 12b)
4ab + 12ab + ab + 3b − 5b + 12b + 5ac − 3ac − 4ac
= (4 + 12 + 1)ab + (3 − 5 + 12)b + (5 − 3 − 4)ac
= 17ab + 10b −2ac
Remember!
Add the numerical coefficients along with their signs.
Example 17: Add 4x2 5xy2 + 14xy 3yz to the sum of 2x2 + 7xy2 3xy and 5xy 8yz 2xy2 .
We first find the sum of 2x2 + 7xy2 − 3xy and 5xy − 8yz − 2xy2
2x2 + 7xy2 − 3xy + 5xy − 8yz − 2xy2
= 7xy2 − 2xy2 − 3xy + 5xy − 8yz + 2x2 (Writing the like terms together)
= (7 − 2)xy2 + (−3 + 5)xy − 8yz + 2x2
= 5xy2 + 2xy − 8yz + 2x2
Adding the above sum to the expression 4x2 − 5xy2 + 14xy − 3yz, we get,
(5xy2 + 2xy − 8yz + 2x2) + (4x2 − 5xy2 + 14xy − 3yz)
5xy2 − 5xy2 + 2xy + 14xy − 8yz − 3yz + 2x2 + 4x2
= (5 − 5)xy2 + (2 + 14)xy + (−8 − 3)yz + (2 + 4)x2
= 16xy − 11yz + 6x2
Do not leave out the unlike terms after adding the like terms.
Example 18: Suhani has `(6y2 + 5y + 2) and Dev has `(8y2 − 3y − 8). If y = 5; find the total amount of money they have.
Money Sohani has = `(6y2 + 5y + 2); Money Dev has `(8y2 − 3y − 8)
Total amount = 6y2 + 5y + 2 +
Putting y = 5 in 14y2 + 2y − 6 we get, 14 × 52 + 2 × 5 − 6 = 14 ×
Hence, they have `354 altogether.
Add the expressions using the column method.
4pqr + 9pr2 − 3pr and 10pr2 − 12pqr
4pqr + − 3pr + ____________________ +
2 3
Do It Yourself 13C
Add the monomials. xy and x b 3
Add the expressions using the column method. a 2x + 3y and x + y
Add the expressions using the horizontal method.
Match the expressions with their answers.
Add 4ab2 7a2b + 12bc to the sum of:
Show addition of 4x 3y + 4 and 3x 2 using algebraic tiles.
Kunal wants to help his friend who is going through a tough time. He bought a shirt for his friend for ₹(3x2 + 2xy + 9y2) and spent on a meal worth ₹(5x2 − xy + 3y2). How much money did he spend in total to show his support and friendship?
Read the statements and choose the correct option.
Assertion (A): The perimeter of the given triangle is 6a + 3.
Reason (R): The area of a triangle is 1 2 × base × height.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Subtraction of Algebraic Expressions
Like addition, while subtracting two algebraic expressions, we subtract only the like terms.
Subtracting a term is the same as adding its inverse. In subtraction, we change the sign of the expression to be subtracted and add it to the expression from which the subtraction is to be done.
Let us subtract the expression −
As there is a minus sign in between, we need to flip the sign of the subtrahend, and the above algebraic tiles can be solved as:
So, 2x2 + 3x 2 ( x2 x + 2) = 3x2 + 4x 4
We can also subtract polynomials using the horizontal or column method. Let us subtract 5ab2 − 7ab + 6a2 from 14ab2 + 10ab + 10a2 using both methods.
Horizontal Method
Step 1: Write the expressions to be subtracted in brackets with a ‘−’ sign between them.
(14ab2 + 10ab + 10a2) (5ab2 − 7ab + 6a2)
Step 2: Change the sign of the subtrahend expression.
14ab2 + 10ab + 10a2 5ab2 + 7ab − 6a2
Step 3: Write the like terms together.
14ab2 5ab2 + 10ab + 7ab + 10a2 − 6a2
Step 4: Subtract the numerical coefficients of all the terms and keep the algebraic factor the same.
(14 5)ab2 + (10 + 7)ab + (10 − 6)a2
= 9ab2 + 17ab + 4a2
Remember!
Column Method
Write the like terms one below the other. Change the sign of the subtrahend and then add.
14ab2 + 10ab + 10a2 5ab2 − 7ab + 6a2
+ (14 5)ab2 + (10 + 7)ab + (10 − 6)a2 = 9ab2 + 17ab + 4a2
We indicate the change of the sign of each term in the expression to be subtracted below the original sign of each term.
Example 19: Subtract 8xy + 3yz − 16xz from 9yz + 22xz by both the column and horizontal methods.
Horizontal Method
(9yz + 22xz) − (8xy + 3yz − 16xz)
= 9yz + 22xz − 8xy − 3yz + 16xz
= 9yz − 3yz + 22xz + 16xz − 8xy
= (9 − 3)yz + (22 + 16)xz + (−8)xy
= 6yz + 38xz − 8xy
Column Method
9yz + 22xz
3yz − 16xz + 8xy − + −
(9 − 3)yz + (22 + 16)xz + (−8)xy
= 6yz + 38xz − 8xy
Example 20: What should be subtracted from 5mn2 + 6nm 8n2 to get 12mn2 3mn + 5?
Let X denote the required algebraic expression,
Then, (5mn2 + 6nm 8n2) X = (12mn2 3mn + 5)
X = (5mn2 + 6nm 8n2) (12mn2 3mn + 5)
X = 5mn2 + 6nm 8n2 12mn2 + 3mn 5
X = 5mn2 12mn2 + 6nm + 3mn 8n2 5
X = (5 12)mn2 + (6 + 3)mn 8n2 5
X = 7mn2 + 9mn 8n2 5
Hence, 7mn2 + 9mn 8n2 5 must be subtracted from 5mn2 + 6nm 8n2 to get 12mn2 3mn + 5.
Subtract 14x2z + 12xz 13yz from 24x2z 13xz + 3yz using both the horizontal and column method. Horizontal Method
(24x2z 13xz + 3yz) − ( ) = 24x2z 13xz + 3yz −
+ 3yz
Subtract using the column method.
a (3ab − 5) from (ab − 9)
12xy − 3y2 from 9y2 − 5xy
c (9y − 2y2 − 4) from (4y2 + 5y − 7) d (−b2 + 7ab) from (5b2 − 3ab + 8)
Subtract using the horizontal method.
a (10x2 − 7x) from (−10x + 8x2) b (mn2 + 2mn − 8n2) from (5mn − 6
Subtract the
Mohan has a ribbon of length (3m + 3) metres. He used (3m − 5) metres of ribbon from it. How much ribbon does he have left with him?
Show the subtraction of
Read the statement and the conclusions. Choose the correct option.
Statement: P = 6a2 + 12ab + 3ab2; Q = 5ab – 8ab2; R = 15ab – 4a2 + 9
Conclusion I: 3Q = 15ab – 24ab2
Conclusion II : The value of P – R + 3Q = 10a2 + 12ab – 21ab2 – 9
a Only Conclusion I follows. b Only Conclusion II follows.
c Both conclusions follow. d Neither conclusion follows.
Simplifying Algebraic Expressions
Simplifying an algebraic expression means to write the expression in simpler form with a fewer number of terms. For this we need to group all the like terms and then solve. We come across different types of brackets while simplifying an algebraic expression. These brackets are removed in a certain order.
Let us simplify the expression: 2x2 − [3x − {4x2 − (3y − 2x − 2y)}]
Step 1: Solve the expression inside the small brackets ( ) and then remove it.
2x2 − [3x − {4x2 − (3y − 2x − 2y)}]
= 2x2 − [3x − {4x2 − (y − 2x)}]
= 2x2 − [3x − {4x2 − y + 2x}]
Step 2: Solve the expression inside the curly brackets { } and then remove it.
2x2 − [3x − {4x2 − y + 2x}] = 2x2 − [3x − 4x2 + y − 2x]
Remember!
If there is a negative sign before the brackets, the sign of every term within the brackets will be changed when removing the brackets.
Step 3: Solve the expression inside the square brackets [ ] and then remove it.
2x2 − [3x − 4x2 + y − 2x] = 2x2 − [x − 4x2 + y] = 2x2 − x + 4x2 − y
Step 4: Solve the rest of the expression.
2x2 − x + 4x2 − y = 6x2 − x − y
Example 21: Simplify the expression.
2a − [3a − {5ab + (ab − 5a − 3ab)}]
Solving and removing the small brackets in the expression, we get
2a − [3a − {5ab + (−5a − 2ab)}] = 2a − [3a − {5ab − 5a − 2ab}]
Solving and removing the curly brackets in the expression, we get
2a − [3a − {3ab − 5a}] = 2a − [3a − 3ab + 5a]
Solving and removing the square brackets in the expression, we get
2a − [3a − 3ab + 5a] = 2a − [8a − 3ab] = 2a − 8a + 3ab
Solving the rest of the expression, we get
2a − 8a + 3ab = −6a + 3ab
Finding the Value of an Expression
An algebraic expression is formed by using one or more variables. The expression changes with the change in the value of the variables. To find the value of an expression, we need to substitute a specific value of each variable in the expression, and then perform the arithmetic operations.
Let us substitute the value of x = 5 in the expression x2 − 2x + 3 and find the value.
Putting x = 5, we get (5)2 − 2(5) + 3 = 25 − 10 + 3 = 18.
Example 22: Find the value of the expression
5a3 + 2a2 − 12a + 3 for a = 7.
Putting a = −7, we get
5 × (−7)3 + 2 × (−7)2 − 12 (−7) + 3
= 5 × (−343) + 2 × 49 + 84 + 3
= −1715 + 98 + 87 = −1530
Example 23: Add the expressions 3mn2 + 5m2n + 4 and
Error Alert!
Use the correct signs when performing the arithmetic operations.
3 × (−5) = 15 3 × (−5) = −15
4mn2 + 7m2n + 3mn. Find the value of the expression for m = 2 and n = 1.
Adding 3mn2 + 5m2n + 4 and − 4mn2 + 7m2n + 3mn, we get (3mn2 + 5m2n + 4) + (−4mn2 + 7m2n + 3mn) = (3 − 4)mn2 + (5 + 7)m2n + 4 + 3mn = −mn2 + 12m
Putting m = 2 and n = 1, we get
= (2) × (1)2 + 12(2)2 × 1 + 4 + (3 × 2 × 1)
= −2 + 48 + 4 + 6 = 56
Example 24: An ice-cream seller sold (x2 + 3x 5) ice creams on Saturday and (5x + 3x2 + 2) ice creams on Sunday. What is the difference in the number of ice creams sold on Sunday and on Saturday, if x = 10?
Number of ice creams sold on Saturday = (x2 + 3x − 5); Number of ice creams sold on Sunday = (5x + 3x2 + 2)
Difference in the number of ice creams sold on Saturday and on Sunday = (5x + 3x2 + 2) − (x2 + 3x − 5)
= (5x + 3x2 + 2) − x2 − 3x + 5 = 2x2 + 2x + 7.
Putting x = 10 in the above expression, we get,
2x2 + 2x + 7 = 2 (10)2 + 2 (10) + 7 = 227.
Subtract the expression 5xy + 7x2 from 9x2 − 3xy + 5. Find the value of the expression for x = 1 and y = −1.
Subtracting 5xy + 7x2 from 9x2 − 3xy + 5, we get
(9x2 − 3xy + 5) − ( ) = 9x2 − 3xy + 5 − − = (9 − )x2 + (−3 − )xy + 5 = x2 − xy + 5
Putting x = 1 and y = −1, we get = =
Do It Yourself 13E
= 5, find:
a (a + 6) b (2a − 3)
Simplify the expressions.
a 5x − (y − 2x + 8y)
c 3a − [5ab −(2a − 3ab)]
Simplify and find the value for m = −2.
a (5m − 3m2 − 6m) − 2m2
c {2m − (5m2 + 5m) + 3m2}
Find the value of the expressions, when x = 1, y = −1.
a x2 + y2 b 5x2 + 2y2 − 1
Simplify.
a 5x + [7x2 + 2 − (2x2 + y2) + (4x − 3y)]
c 2pq + [4pq2 − {3
c (a2 − 3a + 5) d 3a 5
b (10m − 3mn + 4m) + 5mn
d {4x2 − (3x2 + 2x + 5) + 6x}
b 2(m2 − m) + 3(m2 + m)
d [6m2 − {2m + 5 −(2m2 − 8)} + 3]
c 3x2 − 4xy + 8 d 2x3y + 3x2 − 5x
b [2m2 + {5mn − (8n + 2nm) + 6m} − 5m2]
Add the expressions and find their value for x = −2 and y = 1.
a 4x 3y and 5y + 2x b x2y + 2xy and 3xy 4
Find the value of A − 2B + C, if A =
The amount of water in a water tank can be given by the expression (250a2 + 100a) litres. If Pooja used (50a) litres of water, find the amount of water left in the tank when a = 3.
Rohan’s age can be given by the expression 2x + [3x − {4x + (4 − x)}]. If x = 5, find Rohan’s age.
The internet became widely available to the public in the year 1990. In a week, Rahul spends x minutes on the internet, Vivek spends twice the amount of time spent by Rahul, and Ankit spends 10 more minutes than Vivek. Write the total time spent by them in the form of algebraic expressions. Also find the amount of time spent by each one of them if x = 22.
Read the given statement and the conclusions. Choose the correct option.
Statement: Manisha has a triangular plot with sides (3x2 + 3y + 15) m, (2x2 – y + 30) m and (7x2 + 2x – 10) m.
Conclusion I: The perimeter of her plot is (12x2 + 2y + 2x + 35) m
Conclusion II: If x = 2 and y = 1, the perimeter of her plot is between 90 m and 100 m.
a Only Conclusion I follows. b Only Conclusion II follows.
c Both conclusions follow. d Neither conclusion follows.
Points to Remember
• An algebraic expression is formed by applying mathematical operations on variables and constants.
• Expressions are a combination of terms connected by positive and negative signs.
• A term is a product of the factors.
• The terms are called like terms when they have the same algebraic factors. If the algebraic factors of two terms are different, they are called unlike terms.
• Based upon the number of terms, algebraic expressions are classified as monomial, binomial, trinomial, or quadrinomial.
• To add or subtract an algebraic expression, combine the like terms and then perform the operation.
• To find the value of an expression, replace the variable by the given value.
• To simplify algebraic expressions, we start simplifying the brackets from inside to outside.
Math Lab
Collaboration & Experiential Learning
Algebraic Expression Scavenger Hunt
Aim: Simplify algebraic expressions and solve them for given values of variables.
Setting: In groups of 3
Materials Required: Markers, index cards, envelopes for index cards, a list of algebraic expressions
Method:
Instruct each group to choose one expression from their envelope and work together to:
• Identify the key variables and constants in the expression.
• Simplify the expression if possible.
The group that solves all the expressions first wins.
Classify the expressions as monomial, binomial, trinomial and quadrinomial.
ab + 4a − 5ac, 3yx2 + 5xy − 3yx − 8, m × n, 2x2 + y
State whether the pair of terms is like or unlike.
a 5m2n, 6n2m b 2ab, −3ba
c x2y, −5yx
d 2p2q2, 8q2p2 e 3mn, −5m f 6ab2, −2ab2
Draw a factor tree for the expressions.
a x2y + yx b 2cb2 + 6ab + 8c c pq − 5pq2 + 9
Find the rule for the pattern: 14, 27, 40, 53…. Also, find the 15th term of the pattern.
The length of the base of a triangle is 32 cm. If its area is 184 cm2, find its height.
Add the following.
a 5a2b, −3ab2, −7ab2 and 14a2b b (10x + 12y – 12xy – 12), (18 – 5x – 10y + 5xy) and 9xy
Find the perimeter of the rectangle. The dimensions are given in metres.
3a + 2
6a – 7
What will be the formula for the perimeter of an isosceles triangle if the length of the two equal sides is a, and the length of the unequal side is b?
What will be the value of y3 + 4y2 – 7y – 2 if y = –3?
Find the value of the expression 4x3 – 5y2 + 7 if x = 2, y = 3.
What should be added to x2 + 2xy + y2 to obtain 5x2 + 7xy?
What should be subtracted from 5x + 8y + 12 to get –3x + 9y + 17?
Find the value of the expression m3 3 + 5m – 3 – 5n if m = –5, n = 3.
Simplify and find the value for m = −1, n = −1.
Sunita, a passionate reader of mystery novels, had ₹(15a2 + 3ab + 3b2). After saving up for months, she spent ₹(10a2 − ab + b2) on a collection of thrilling mystery books by her favourite authors. How much money does she have left to continue her reading adventure? How is reading books beneficial?
Sunil has a rope which is (5x − 2y + 2) metres long and is attached to another rope of length (3x − xy + 5) metres. Find the total length of the rope, if x = 5 and y = 2.
Kunal has an equilateral triangular-shaped wooden frame with a perimeter of 96 cm. He wants a square frame with the length of each side equal to that of the triangular frame. What will be the perimeter of the square frame?
Challenge
1 What value of a and b will make the statement true? (3x2 + 14xy – ay2) – (bx2 – 12xy + 3y2) = 8x2 + 26xy –12y2
2 Is 3x – 2y = 0?
Statement 1: x = 2 3 y
Statement 2: y = 6
a Statement 1 alone is sufficient, but statement 2 alone is not sufficient.
b Statement 2 alone is sufficient, but statement 1 alone is not sufficient.
c Both statements together are sufficient, but neither statement alone is sufficient.
d Each statement alone is sufficient.
e Statements 1 and 2 together are not sufficient.
Case Study
Planning a Beautiful Garden
An architect is a person who designs buildings and other structures. They plan how buildings will look and how they will be built, considering things like safety, functionality, and aesthetics. Samira and her family have recently purchased a plot of land for their new home. The plot has a total area of (4x2 + 3x − 2) m2. They are very excited to build their dream house on it and plan to utilise the remaining space for a beautiful garden.
After consulting with an architect, they decided to construct a house that occupies an area of (x2 + 2x + 1) m2 on the plot, and the rest was reserved for constructing the garden.
Answer the following questions:
1 What is the expression for the area of the garden?
2 If x = 2, what is the area of the garden?
3 For x =2, if the cost of landscaping the garden is ₹500/m2. How much did the family spend on landscaping?
4 If Samira’s neighbour’s garden is (x2 + 4) m2 in area, what is the total garden area altogether? Cross Curricular
14 Exponents and Powers
Let’s Recall
We have learnt about large numbers. Large numbers are those that are significantly larger than the numbers we commonly come across in our daily lives. They are used to represent quantities and values on a much larger scale. Large numbers are crucial in various fields, such as mathematics, physics, astronomy, computer science, and finance, where extremely large quantities or measurements are involved.
We often encounter lakhs and crores in our daily conversations. Let us look at some examples.
A ‘lakh’ is equal to 10 ten thousands. We often talk about car prices in lakhs.
A ‘crore’ is equal to 100 lakhs. When it comes to houses, we usually mention prices in crores.
Let’s Warm-up
Match the following correctly. 1 100 hundreds
(Ten Crore)
(Ten Lakh)
(One Crore)
Price: ₹10,00,000 (Rupees Ten Lakh Only)
Price: ₹1,00,00,000 (Rupees One Crore Only)
Mean, Median and Mode Exponents
A celebrity hired a marketing team that promised to double her social media followers every week.
In the first week, she only had 2 followers.
In the second week, the team helps her to increase the followers to a total of 4.
In the third week, the number of followers reached 8.
Each week, the number of followers increased in a pattern.
Exponential Form
The celebrity wants to understand the pattern.
First week: 2 followers
Second week: 2 × 2 followers = 4 followers
Third week: 2 × 2 × 2 followers = 8 followers
This means 2 is multiplied by itself 3 times.
Week 1 2
4 Week 2
Week 3 8
This can be written as 23 and read as 2 raised to the power of 3.
2 is called the base and 3 is the power or index or exponent
Fourth week: 2 × 2 × 2 × 2 followers = 24 = 16 followers
Fifth week: 2 × 2 × 2 × 2 × 2 followers = 25 = 32 followers
The number of followers she had in the 5th week is 32.
This way of writing a number that is multiplied by itself a number of times is called the exponential form or power notation.
Let us generalise for the number a. When a is multiplied n times by itself, it is written as
This is read as a raised to the power of n.
A number raised to the power 1 gives the number itself.
21 = 2
31 = 3
101 = 10 and so on. 23 Power or Exponent Base
10 × 10 102
10 squared or 10 raised to the power of 2
Base = 10, Exponent = 2
Base = 10, Exponent = 3
Think and Tell
10 × 10 × 10 103 10 cubed or 10 raised to the power of 3
What will be the exponent value of n for 7n = 7? Product
10 × 10 × 10 × 10 × 10 105 10 raised to the power of 5
Base = 10, Exponent = 5
A number raised to the power of 2 is called the square of that number, a2. For example, the square of 5 = 52 = 5 × 5 = 25.
A number raised to the power of 3 is called the cube of that number, a3. For example, the cube of 5 = 53 = 5 × 5 × 5 = 125.
Power of Positive Integers
• A positive integer raised to any number is always positive.
22 = 2 × 2 = 4
23 = 2 × 2 × 2 = 8 Positive
34 = 3 × 3 × 3 × 3 = 81
Power of Negative Integers
• A negative integer raised to an odd positive power is negative. (–1)odd positive integer = –1
(–1)1 = –1
(–1)3 = (–1) × (–1) × (–1) = –1
(–2)5 = (–2) × (–2) × (–2) × (–2) × (–2) = –32
Negative
• A negative integer raised to an even positive power is positive.
(–1)even positive integer = 1
(–1)2 = (–1) × (–1) = 1
(–1)4 = (–1) × (–1) × (–1) × (–1) = 1
(–3)6 = (–3) × (–3) × (–3) × (–3) × (–3) × (–3) = 729
Exponents and Prime Factors
Positive
We already learnt that a prime factor is a natural number whose factors are 1 and itself. We find the prime factors of any given number with the help of the prime factorisation method.
For example, the prime factors of 216 are:
Hence, 216 can be written as the product of prime factors in exponential form as 23 × 33. 2 × 2 × 2 × 3 × 3 × 3
Number 2 is multiplied 3 times, hence 2 × 2 × 2 = 23
Number 3 is multiplied 3 times, hence 3 × 3 × 3 = 33
Example 1: Write the base and power of:
1 58
Base = 5 and Power = 8
Example 2: Write the exponential form for:
1 8 × 8 × 8 × 8 × 8 × 8 = 86
= (–a)12
2 (–24)15
Base = –24 and Power = 15
Example 3: Express the numbers as the product of prime factors in exponential form.
1 525
Prime factorisation of 525 = 3 × 5 × 5 × 7 = 3 × 52 × 7
2 −216
Prime factorisation of –216 = –1 × 2 × 2 × 2 × 3 × 3 × 3 = −(23 × 33)
3 –1500
Prime factorisation of –1500 = –1 × 2 × 2 × 3 × 5 × 5 × 5 = −( 22 × 3 × 53)
Example 4: What is the square and cube of 25?
Square of 25 = 252 = 625
Cube of 25 = 253 = 15,625
Example 6: Evaluate. 1 94 – 33
= (9 × 9 × 9 × 9) − (3 × 3 × 3) = 6561 – 27 = 6534
Example 7: Find the value of x.
Example 5: Simplify. 43 × (−5)2 43 × (−5)2
1 10x = 1000 2 6x = 1296
10x = 1000 = 10 × 10 × 10 = 103
10x = 103 x = 3 6x = 1296 = 6 × 6 × 6 × 6 = 64 6x = 64 So, x = 4
Find the prime factors of 768. Express the prime factors using exponents.
Prime factors of 768 =
factors in exponential form =
Comparing Numbers in Exponential Form
The numbers in exponential form can be compared by comparing their expanded forms.
Let us compare 153 and 56.
153 = 15 × 15 × 15 = 3375 and 56 = 15,625
As 15,625 > 3375; hence 56 > 153
But what if the bases are the same while comparing two numbers.
To compare 32 and 34, we do not need to expand the numbers. We can compare the exponent. The number with the greater exponent is greater. So, 34 > 32.
On expanding, we get
32 = 3 × 3 = 9 and 34 = 3 × 3 × 3 × 3 = 81
As 81 > 9; hence 34 > 32.
Example 8: Which of the given numbers is smaller: 75 or 57?
75 = 7 × 7 × 7 × 7 × 7 = 16,807 and 57 = 5 × 5 × 5 × 5 × 5 × 5 × 5 = 78,125
As 16,807 < 78,125; hence 75 < 57
Example 9: Which is greater 12.7 × 1014 or 11.9 × 107?
12.7 × 1014 = 127 × 1013
11.9 × 107 = 119 × 106
Number of digits in 127 × 1013 will be greater than the number of digits in 119 × 106.
Hence, 12.7 × 1014 > 11.9 × 107
Compare and fill in the blanks with the correct sign or value.
Powers of Rational Numbers
Rational numbers can also be written in the exponential form. If a rational number p q , is multiplied n times by itself, it is written as:
Example 10: Write the following in exponential form.
1 7 5 × 7 5 × 7 5 × 7 5 =
7 5
4
Example 11: Write the following in exponential form. 1 1 2187
On finding the prime factors of 2187, we get
2187 = 3 × 3 × 3 × 3 × 3 × 3 × 3
So, we can write 1 2187 in exponential form as: 1 2187 = 1 3 × 1 3 × 1 3 × 1 3 × 1 3 × 1 3 × 1 3 =
Example 12: Simplify and find the value of
Example 13: Find the value of a, when 1 3a = 27
3a = 3 × 3 × 3 = 33 3a = 33
So, a = 3.
Example 14: Find the value of t, when
On finding the prime factors of the numerator and denominator we get, −32 = −2 × −2 × −2 × −2 × −2 243 = 3 × 3 × 3 × 3 × 3
So, we can write −32 243 in exponential form as:
t = 4.
Simplify
Reciprocal of a Rational Number
The reciprocal of a number is the multiplicative inverse of that number. If p q is a non-zero rational number, then its reciprocal will be q p
The reciprocal of
So, the reciprocal of
Example 15: Find the reciprocal of
We know the reciprocal of
The reciprocal of
Example 16: Find the reciprocal of (–12)8.
The reciprocal of –12 will be
The reciprocal of (–12)8 is
Do It Yourself 14A
Write the base and power of the following:
Write the following in the exponential form.
Find the square and cube of the numbers.
Evaluate:
Express the numbers as products of powers of prime factors.
Find the reciprocal of each of the following.
Which is greater?
Simplify.
Find the value of x.
Kalpabta a large baniyan tree in Jagannath Temple in Puri is 500 years old. Express the year as the power of prime factors.
Mexico is the largest country for producing glass marbles. Vivek sells marble balls of different colours. He sold 78,125 marble balls in the month of July. Express this number as a power of 5.
Challenge
Critical Thinking
Ramu scored 3125 points in a game. Ramu expressed his points as 5x+1. What is the value of x? 1
Laws of Exponents
Do you remember the celebrity who has a team that helps her to increase her followers? The celebrity fell ill in the 5th week and was not able to track the increase in her followers for the next 3 weeks. Now, she wants to know the number of followers she has in total.
Multiplying Powers
Multiplying powers with the same base
We know that there were 32 followers in the fifth week: 25
If the same pattern follows, the number of followers in the next three weeks = 25 × 23 = 256
We can also find the number of followers in 8 weeks as 28 = 256
(1)
(2)
From (1) and (2), it can be concluded that, 2 = 2(5 + 3) = 28
Hence, if a is a non-zero number and m and n are whole numbers then, am × an = a(m + n)
Remember!
The base value a should be the same in this case to add the exponents.
Multiplying powers with the same exponents
Let us multiply 24 by 34 and find the result.
24 = 16; 34 = 81
So, 24 × 34 = 1296
Also, 64 = 1296.
Error Alert!
Never use this law for addition of two expressions. 32
Hence, if a and b are non-zero numbers and m is a whole number then, am × bm = (a × b)m
Example 17: Find the value of –54 × –55
Using the law of exponents, −54 × –55 = –5(4 + 5) = –59 = –19,53,125
Example 18: Simplify
Do It Together
Simplify and express the result in exponential form.
Dividing Powers
Dividing powers with the same base
Let us divide 46 by 42 and find the result, 46 ÷ 42 = 4 × 4 × 4 × 4 × 4 × 4 4 × 4 = 4 × 4 × 4 × 4 = 44
46 ÷ 42 = 46 − 2= 44
Hence, if a is a non-zero number and m and n are whole numbers than, am ÷ an = a(m − n)
Dividing powers with the same exponents
Let us divide 54 by 64 and find the result.
Hence, if a and b are non-zero numbers and m is a whole number then,
What if the value of both bases and exponents are equal? Let us find out!
Let us divide 46 by 46
Using the above laws 46 ÷ 46 = 4(6 − 6) = 40
Also, 46 46 = 4 × 4 × 4 × 4 × 4 × 4 4 × 4 × 4 × 4 × 4 × 4 = 1
(1)
(2)
From 1 and 2, we can conclude that if a is a non-zero number, then a0 = 1
These are called zero exponent numbers.
Example 19: Simplify and find the value of
Example 20: Simplify and find the value of (−3)3
Simplify and find the value of: Do It
Power of a Power
Let us simplify (53)2 and find the result.
53 = 5 × 5 × 5 = 125
(53)2 = 1252 = 15,625
Also, 56 = 15,625
Hence, if a is a non-zero number and m and n are whole numbers, then (am)n = amn
Example 21: Simplify (32)3.
Here, 32 is raised to the power of 3. = 32 × 32 × 32 = 3(2 + 2 + 2) = 36
Example 23: Find the value of n, when
Example 22: Simplify [(k)4]2 = (k)(4 × 2) = (k)8
Simplify and find the value of
So, n = 5.
Simplifying Exponential Expressions
We have learnt about the laws of exponents. Let us now learn to simplify expressions using the same laws. Factorise the numbers and write them in exponent form, to simplify wherever required.
Let us simplify ((62)3 × 69) 65
By using the law of multiplication: ((62)3 × 69) 65 = (66 × 69) 65 = 615 65
Using the law of division: 615 65 = 6(15 − 5) = 610
Example 24: Simplify: 38 × t7 92 × t3
38 × t7
92 × t3 = 38 × t7 (32)2 × t3 = 38 × t7 34 × t3 (Using the law: (am)n = amn)
38 × t7 34 × t3 = 38 − 4 × t7 − 3 = 34 × t4 (Using the law: am ÷ an = am n )
34 × t4 = (3t)4 = 81t4 (Using the law: am × bm = (a × b)m )
Example 25: Simplify: 53 × 104 × 12 600 × 8
53 × 104 × 12
600 × 8 = 53 × (5 × 2)4 × 4 × 3 3 × 2 × 100 × 8 = 53 × 54 × 24 × 22 × 3 3 × 2 × 52 × 22 × 23
= 57 × 26 × 3
3 × 52 × 26 (Since am × an = am + n) = 57 − 2 × 26 − 6 × 31 − 1 (Since am an = am − n)
= 55 × 20 × 30
= 55 × 1 × 1 = 55 (Since a0 = 1)
36 = 6 × 6 = 62 and 216 = 6 × 6 × 6 = 63
36 × 64 × a 7 × b 216 × a 4 × b2 =
Using the law: xa × x b = xa + b
Simplify using the laws of multiplication of exponents and express the answer in exponential form.
× (–1)3
Solve using the laws of division of exponents and fill in the blanks.
Simplify and express in exponential form.
Evaluate:
Find the value of (20 + 30) × (60 + 71).
Solve and match with the solution. a 24 × 23
c (−5)4 × (−4)4
d 50 × (−17)1
Find the value of p for which 6p × 63 = 362
Simplify and express the answer in exponential form: a 212 × m8 (2m)6 b 62 × 243 44 × 35
Find the value of n in each of the following.
a 9 × 3n + 2 = 243
The force on a surface is the product of pressure on the surface and the area of the surface. The pressure on the surface is 43 pascal and the area of the surface is 45 m2. Find the force on the surface.
The weight of an adult dolphin is 23 × 5 × 11 kg and weight of an adult shark is 24 × 53 kg. Find the product of the weights.
Critical Thinking
1 Read the statements and choose the correct option.
Assertion (A): 46 × 56 = 206
Reason (R): am × bm = (ab)m
a A is true but R is false.
b A is false but R is true.
c Both A and R are true and R is the correct explanation for A.
d Both A and R are true but R is not the correct explanation for A.
Expressing Large Numbers in the Standard Form
With the help of the social marketing team, the celebrity is able to increase her followers in the same pattern. The number of followers she will have in 10 weeks is 1024.
We can write 1024 as 1.024 × 1000 = 1.024 × 103.
Similarly, we can write 10,48,000 as 1.048 × 10,00,000 = 1.048 × 106
A number in standard form will be K × 10n, where K is a number between 1 and 10 and n is an integer.
Example 26: Express 8980000000 in the standard form.
8980000000 = 8.98 × 1000000000 = 8.98 × 109
Example 27: Write 7.05 × 106 in the usual form.
7.05 × 106 = 7.05 × 1000000 = 7050000
604000000 = × = × 10 Do It Together
Express 604000000 in the standard form.
Express the number in standard form.
Write the number in the usual form.
3 × 104
Sumit read that the earth is around 4.54 × 109 years old. Express the number in the usual form.
If 8.3279 × 10n = 8,32,79,000, what is the value of n?
Find the number from the following expanded form. Write it in exponential form. 7 × 106 + 5 × 105 + 4 × 103 + 6 × 102 + 8 × 101 + 2 × 100
Express the numbers in the statements in the standard form.
a The distance between India and the United States is 13568000 m.
b The population of India was around 1410000000 in 2021.
c The distance between Venus and Uranus is around 2760000000 km.
d The diameter of Jupiter is around 140000000 m.
1 Raj was solving a problem as shown below.
5–4 × 7–3
35–5 = 5–4 × 7–3
5–5 × 7–5 = 5 49
Identify the error and rectify it.
Points to Remember
• A number multiplied by itself a number of times is called the exponential form or power notation an, a raised to the power of n.
• If a is a non-zero number and m and n are whole numbers, then am × an = a(m + n)
• If a and b are non-zero numbers and m is a whole number, then am × bm = (ab)m
• If a is a non-zero number, m and n are whole numbers and m > n then am ÷ an = a(m – n)
• If a and b are non-zero numbers and m is a whole number, then am ÷ bm = am bm =
• If a is a non-zero number, and m and n are whole numbers, then (am)n = amn
• If a is a non-zero number, a raised to the power 0 is 1: a0 = 1.
• A number in the standard form will be K × 10 , where K is a number between 1 and 10 and n is an integer.
Math Lab
Setting: In groups of 5
Materials Needed:
• Exponent cards (23, 52, 100)
Experiential Learning & Collaboration
Exponent Bingo!
• Bingo cards with answers to the exponent cards written
• Markers
Method:
• Create exponent cards and bingo cards.
• Distribute the bingo cards and markers among the students.
• Draw the exponent cards one by one and call out the expression.
• Students will find the answer to the exponent and cross out the corresponding answer given on the bingo card.
• The first group to complete a row or column shouts “Bingo!” and is the winner.
Write the following in exponential form.
a 8 × 8 × 8 × 8 × 8 × 8
b (–15) × (–15) × (–15) × (–15) × (–15) × (–15) × (–15) × (–15)
Consider: p = 3 & q = 4 and find:
Write the value of the following:
Express the numbers as the product of prime factors in exponential form.
Simplify:
Compare and write the correct sign.
7.2 × 102 3.8 × 103
Match the numbers with their other forms.
a 9.1 × 106 9.1 × 107
b 90100 91100000000
c 9.11 × 1010 9100000
d 91000000 9.01 × 104
Find the value of n
The weight of the blue whale is 202193.335 kg. Express the weight in scientific notation.
Find the distance in centimetres for the aircraft moving at the speed of 690 km/hr and covering the distance in 3 hours 20 minutes.
According to the census, the male population of a country in 2011 was 623700000. Express this in standard form. The distance between Earth and Venus currently is 188200000 km. Express the distance in the standard form.
Challenge
There are 1000 bacteria in a colony. The colony of bacteria increases exponentially by 4 times each hour.
Statement 1: The population of bacteria between hour 2 and hour 3 can be around 4.80 × 105.
Statement 2: The population of bacteria between hour 4 and hour 5 can be around 7.68 × 105.
a Only Statement 1 is true.
b Only Statement 2 is true.
c Both statement 1 and statement 2 are false.
d Both statement 1 and statement 2 are true.
What is the value of b in (−48)−1 ÷ b? Which of the given statements is sufficient to answer the given question?
Statement 1: (−48)−1 when divided by an even number leaves an even remainder.
Statement 2: (−48 )−1 when divided by b results in (−6)−1.
a Only Statement 1 is sufficient, but Statement 2 is not sufficient.
b Only Statement 2 is sufficient, but Statement 1 is not sufficient.
c Both Statements are sufficient.
d Both Statements are not sufficient.
Case Study
Cross Curricular
Exponents in Computers
Computers and storage devices are widely used today. Bytes are the units used to measure the capacity of storage devices. An electronic store sells storage devices like hard disks, CDs, DVDs, flash drives and RAM for computers. 1 GB = 1000 MB
1 The capacity of a CD is 700 MB. The capacity of a CD in exponential form is
a 21 × 51 × 72 MB
c 22 × 52 × 71 MB
b 23 × 55 × 71 MB
d 22 × 5 × 72 MB
2 The capacity of a hard disk is 512GB. The capacity of a hard disk in MB is
a 5.12 × 102 MB
c 51.2 × 105 MB
b 5.12 × 105 MB
d 5.12 × 103 MB
3 The maximum capacity of the hard disk that the store sells is a 32TB hard disk. What is the capacity of the hard disk in MB? Write the answer in the standard form.
(Hint: 1 TB = 1000 GB)
4 Radha bought 2 flash drives, each with a capacity of 64MB and 8GB respectively. Write the difference in capacity in exponential form in MB.
3
15 Symmetry
Let’s Recall
Look at the given pictures. What do you observe? Do they have anything in common in relation to symmetry?
All of these objects exhibit symmetry. Let us understand when a shape exhibits symmetry. When a shape or design cut from a sheet of paper is folded once in such a way that one half of the shape completely overlaps the other, the shape is said to exhibit symmetry and is symmetrical. All parts of the symmetrical figures, objects and shapes are the same in shape and size. The line along which you fold a figure to obtain two equal parts is called the line (axis) of symmetry. The line of symmetry can be vertical, horizontal or diagonal. One shape can have more than one line of symmetry.
line of symmetry
Let’s Warm-up
Match the following.
Horizontal line of symmetry
horizontal and vertical lines of symmetry
1 Butterfly Two lines of symmetry
2 Letter H One line of symmetry
3 Plus sign Infinite lines of symmetry
4 Sun Four lines of symmetry
lines of symmetry
Mean, Median and Mode
Understanding Symmetry
Sakshi went to a summer carnival. There were many games, swings, rides and a circus show. She bought a ticket from the ticket counter and entered the carnival. She then went to her favourite rides—the merry-go-round and the big wheel. She concluded her day with the circus show.
Reflection Symmetry
Let us look at the ticket counter closely. Is it symmetrical in any way? How can you say?
When we draw a line, one half of the ticket counter is exactly the same as the other half. These halves are nothing but flipped images of one another.
So, we can say that these flipped images have reflection symmetry, and the figure or object is reflectively symmetrical about the given line. The line which divides the figure into two symmetrical parts is called the line of symmetry
Think and Tell
What other structures in the carnival have a line of symmetry? Draw their lines of symmetry.
Remember!
Reflection symmetry exists if there is at least one line which divides a figure into halves such that one half is the mirror image of the other half.
We also observe reflection symmetry through mirror reflections. If a plain mirror is placed along or in the centre of the object, the reflection of the object is visible in the mirror. The image looks identical to the object. Therefore, the mirror acts as the line of symmetry between the image and the object. The image looks flipped in its reflection. Let us see the reflection of some letters and numbers.
A A R R E E 3 3 7 7
Let us also see this through a real-life example. Look at the given picture of Mount Taranaki in New Zealand. What do you see?
Chapter 15 • Symmetry
Did You Know?
The Ranakpur Jain temple constructed by Dharna Shah in the 15th century is symmetrical in structure featuring 1444 carved pillars, despite which the idol can be seen unobstructed from all directions.
The reflection of the mountain in the still water looks exactly the same in size and shape as the mountain itself. The surface of the water is the line of symmetry in the picture.
One Line of Symmetry
There are three types of lines of symmetry: horizontal line of symmetry, vertical line of symmetry and diagonal line of symmetry. Let us look at some examples with different types of lines of symmetry.
Vertical line of symmetry
Horizontal line of symmetry
Diagonal line of symmetry
Many figures or objects do not have any lines of symmetry. Such figures/objects are said to be asymmetrical. Look at some of the examples given below.
Example 1: Look at the given figures. Answer the given questions.
1 Which figure is symmetrical?
2 Draw the line of symmetry on the symmetrical figure.
3 What type of line of symmetry does it have? a b
Figure (a) is not symmetrical, but Figure (b) is symmetrical about the diagonal line of symmetry.
Diagonal line of symmetry a b
No line of symmetry
Example 2: Complete the given patterns using the dotted line as the mirror line.
Look at the given figures. Answer the following questions.
1 Are the given figures symmetrical?
2 Draw lines of symmetry if they are symmetrical.
3 What type of line of symmetry do they have?
Figure (a) is symmetrical about the vertical line of symmetry, but Figure (b) is about the line of symmetry.
More than One Line of Symmetry
Some objects, shapes, letters and numbers have more than one line of symmetry. They may have two, three, four or more lines of symmetry. Some examples are:
Two Lines of Symmetry
Four Lines of Symmetry
Three Lines of Symmetry
More than Four Lines of Symmetry
Example 3: Look at the given figures. Answer the given questions.
1 Are the given figures symmetrical?
2 How many lines of symmetry do they have?
3 Draw lines of symmetry on each of the given figures.
1 Both figures are symmetrical.
2 Figure (a) is symmetrical about the midpoints of the opposite sides, and Figure (b) is symmetrical about the opposite vertices of the star. The lines of symmetry are shown here for each of the figures.
3
2 lines of symmetry 6 lines of symmetry
Example 4: Shade as many squares as required such that the given figure is symmetrical about the given lines of symmetry.
1 2
Look at the given figures. Answer the questions. Do It Together
a Are the given figures symmetrical? ___________________________________________ .
b How many lines of symmetry do they have? ___________________________________________
c Draw the lines of symmetry in each of the given figures.
1 2 lines of symmetry lines of symmetry
Error Alert!
While finding the diagonal line of symmetry, do NOT change the direction of the shape. Keep the shape static, and then mark the diagonal line of symmetry.
On rotation, this shape has a diagonal line of symmetry. Originally, this shape had a vertical line of symmetry. Figure 1 Figure 2
) the figures that show reflection symmetry.
Is the given dotted line in the figures a line of symmetry? If not, then draw the figure with the correct line of symmetry.
b c d e f g h
Identify and draw the lines of symmetry in the given figures.
e f g h
The word ‘DICTIONARY’ was invented by John of Garland in 1220. Which letters of the word ‘DICTIONARY’ have no line of symmetry?
Complete the given figures such that they are symmetrical about the given mirror line of symmetry.
Draw two ways in which the squares can be shaded along the diagonal line so that the grid has symmetry about the given line.
a two squares b three squares
How would you shade the squares away from the diagonal line?
Shade the squares such that the given figures are symmetrical about the given dotted line of symmetry. a b c d
On the given grid, draw a quadrilateral with an area of 13 square units which has exactly one line of symmetry.
Challenge
b Is the figure symmetrical? If so, draw the lines of symmetry. 1
Critical Thinking
In a park, there is a flowerbed in the shape of a regular hexagon. There is a semi-circular flowerbed on the outside of each edge of the hexagon.
a Draw a rough sketch of the flowerbed.
Rotational Symmetry
Do you remember Sakshi, who enjoyed going on the big wheel at the carnival? Let us look at it closely.
The big wheel has passenger cabins in four different colours: red, yellow, blue and green. These cabins are placed opposite to each other and have the same colour. For example, the two red cabins shown in the picture here are placed opposite each other.
When the wheel rotates about its centre in a particular direction (clockwise or anticlockwise), such that the cabins of the same colours appear to be opposite to each other, and the big wheel looks exactly the same as before. This happens after every half turn, that is, 180°. This is rotational symmetry.
Half turn (180°)
So, we can say that rotational symmetry is a type of symmetry exhibited by an object when it can be rotated around a central point by a certain angle in a direction and still appear unchanged at specific intervals during a full rotation.
The central point around which the object rotates is called the centre of rotation. For example, look at the given ceiling fan. When it is turned on, the blades OA, OB, and OC of the fan start rotating in the clockwise direction, at an angle of 120°. The rotation takes place around the point O. So, O is the centre of rotation.
Order and Angle of Rotational Symmetry
Every figure or object that has rotational symmetry looks exactly the same at some point during the 360° rotation. The number of times the figure looks the same as the original during the rotation of 360° is called the order of rotational symmetry, and the minimum measure of the angle through which a figure or an object has to be rotated to get the original figure is called the angle of rotation.
Let us look at some figures.
We can find their order of rotation and angle of rotation in the given way. Rotation through 90° Rotation through 180° Rotation through 270° Rotation through 360°
The letter B fits onto itself only once when rotated through 360°. It has a symmetry of order 1 with an angle of rotation of 360° (360° ÷ 1). Such figures do not show rotational symmetry since rotational symmetry of order 1 does not exist.
Rotation through 90° Rotation through 180° Rotation through 270° Rotation through 360°
The letter H fits onto itself only twice when rotated through 360°. So, it has a rotational symmetry of order 2 with an angle of rotation of 180° (360° ÷ 2).
through 120° Rotation through 240° Rotation through 360°
Here, the equilateral triangle is a regular polygon. The order of rotational symmetry of a regular polygon is always the same as its number of sides. As the equilateral triangle is rotated by 120° three times the order of rotational symmetry of the equilateral triangle is the same as its number of sides, that is, 3, and the angle of rotation is 120° (360° ÷ 3).
Here, the windmill is rotated by 90° four times. Here, the order of rotational symmetry is 4, and the angle of rotation is 90° (360° ÷ 4).
Rotation through 90° Rotation through 180° Rotation through 270° Rotation through 360°
Therefore, we can say that if we know any one of the following, we can calculate the other on its basis.
• Order of rotational symmetry
• Angle of rotational symmetry
For example, we know the order of rotational symmetry of the equilateral triangle is 3. So, we can calculate the angle of rotational symmetry of the equilateral triangle as 360° order of rotational symmetry . This means, the angle of rotational symmetry of the equilateral triangle is 360° ÷ 3 = 120°.
Remember!
Angle of rotational symmetry = 360° order of rotational symmetry OR
Order of rotational symmetry = 360° angle of rotational symmetry
Think and Tell
What is the order and angle of rotational symmetry of the big wheel?
Example 5: Write the order of rotational symmetry for each of the given figures.
Angle of rotational symmetry of the image = 180°.
So, the order of rotational symmetry = 360° 180° = 2
Thus, the shape will fit onto itself two times in a complete rotation.
600
Angle of rotational symmetry of the image = 60°.
So, the order of rotational symmetry = 360° 60° = 6
Thus, the shape will fit onto itself six times in a complete rotation.
Example 6: Write the order and angle of rotational symmetry of the given figure.
Rotation through 90° Rotation through 180° Rotation through 270° Rotation through 360°
This figure fits onto itself four times in a complete rotation. So, the order of rotational symmetry is 4.
Now, the angle of rotational symmetry = 360° order of rotational symmetry = 360° 4 = 90°.
Write the order and angle of rotation of the given figures.
Rotation through Rotation through Rotation through This figure fits onto itself times in a complete revolution. So, the order of rotational symmetry is .
Now, the angle of rotational symmetry = 360° order of rotational symmetry = 360° = .
Both Reflection and Rotational Symmetry
Some figures have both rotational symmetry as well as reflection symmetry. The table given below shows some examples of such figures.
Infinite lines of symmetry
Rotational symmetry of infinite order
Here, notice that the square, equilateral triangle, and pentagon have the same order of rotational symmetry and lines of symmetry as the number of sides in the shapes. This is because they are regular polygons.
Remember!
In every regular polygon, the order of rotational symmetry and the number of lines of symmetry are the same as the number of sides in the shape.
Fractals
A fractal is a never-ending pattern. They are created by repeating a simple process over and over in a loop.
Fractal patterns are extremely familiar since nature is full of fractals, like clouds, mountains, trees, coastlines and so on.
The Indian rangoli is an example of a fractal pattern.
Do It Together
Example 7: Write the number of lines of symmetry and the order of rotational symmetry of the given figure. Also, draw the lines of symmetry in the given figure.
The given figure shows reflective symmetry about the diagonals and the central point. So, the number of lines of symmetry = 4
The given figure is rotationally symmetrical after every quarter turn (90°). So, the order of rotational symmetry = 4
Example 8: What is the minimum number of squares that can be shaded to get a shape with four lines of symmetry and rotational symmetry of order 4? Draw and show your answer.
The minimum number of squares that can be shaded to get a shape with four lines of symmetry and a rotational symmetry of order 4 is 8, as shown.
Write the number of lines of symmetry and the order of rotational symmetry of the given figure. Also, draw the lines of symmetry in the given figure.
This is a regular octagon.
Number of lines of symmetry =
Order of rotational symmetry = number of lines of symmetry =
Classify the given figures as rotationally symmetrical with order more than 1 or not showing rotational symmetry.
Given the angle of rotation, find the order of rotational symmetry.
What letters of the English alphabet have:
a both lines of symmetry and rotational symmetry?
b rotational symmetry but no reflection symmetry?
c reflection symmetry but no rotational symmetry?
d neither reflection symmetry nor rotational symmetry?
Explain your answer by drawing lines of symmetry and rotational symmetry for at least 1 of the letters.
Look at the given figures. Answer the questions.
a
i Mark the centre of rotation in each of the given figures.
ii If each figure is turned up to 360° about the centre point, then how many times will the figure match the original?
iii Find the angle of rotation of the given figures.
Esha rotated the given shape as shown.
a Did she rotate it clockwise or anticlockwise?
b What degree of rotation did she make?
c Did the figures look identical after rotation? If yes, find the angle of rotation.
d What is the order of rotation of the shape?
Look at the given grids. Some squares are shaded in each of the grids. Answer the given questions.
1
centre of rotation
2
a Write the order of rotational symmetry and angle of rotation for the given figures.
b Do these figures show reflection symmetry? If yes, draw the lines of symmetry. If no, shade the squares of the grid to make them symmetrical.
Anu wants to make rangoli on Diwali. She doesn’t know how to make them, but she knows about rotational symmetry. She uses her knowledge and the help of her friends to draw the following rangoli designs. Look at these designs and answer the following questions.
a Find the lines of symmetry in each of the given designs.
b Write the order of rotational symmetry for each of these designs. Use it to find the angle of rotation as well.
c Make a card for your neighbour with Diwali wishes using a design with 4 lines of symmetry.
Figure
Figure
The Taj Mahal is a magnificent mausoleum built by the Mughal Emperor Shah Jahan in memory of his favourite wife, Mumtaz Mahal. It is located in Agra, India. It exhibits a vertical line of symmetry. Name three more historical monuments that show lines of symmetry.
Draw a shape with:
a Rotational symmetry and reflective symmetry.
b Rotational symmetry but no reflective symmetry.
c Reflective symmetry but no rotational symmetry.
d Rotational symmetry of order 2 but no reflective symmetry.
Challenge
Critical Thinking & Art Integration
a Order: 2 b Order: 3 c Order: 4 1
Colour the parts of the given figure in such a way that the figure has the given order of rotational symmetry.
Points to Remember
• An object has reflection symmetry if there is at least one line which splits it in half so that the portions on either side of the line are identical to each other. This line is called the line of symmetry, or axis of symmetry.
• If an object rotates around a fixed point at a certain angle and it looks exactly the same after rotation, then the object is said to have rotational symmetry. This fixed point is called the centre of rotation.
• The number of times the figure coincides with itself during the rotation of 360° is called the order of rotation.
Math Lab
Experiential Learning
Let’s Play with Windmills
Aim: To make a paper windmill to showcase rotational symmetry.
Settings: In pairs
Materials Required: A pencil, a ruler, an eraser, a pair of scissors, pushpins, a stick and coloured paper
Method:
1 Cut out a bigger square from the coloured paper. Fold the paper along two diagonals of the square.
2 Cut the lines to about 2 3 of the line. Do not cut far into the middle.
3 Take the right corner of every triangle and pin the ends together at the centre.
4 Now fix the pinned ends to the end of a stick using a pushpin.
5 Try rotating the windmill.
6 Extend this to make a windmill with different number of blades. Notice how changing the number of blades changes the order of rotation, angle of rotation and rotational symmetry.
Chapter Checkup
Is the given dotted line in the given figures a line of symmetry? Draw the correct line of symmetry, wherever required. a b c d f
Identify and draw lines of symmetry in the given figures.
b c d e f
Satya has drawn an incorrect mirror image of the object. Identify the error and correct it.
Look at each letter of the English alphabet. Some letters have one line of symmetry, and some letters have more than one line of symmetry.
Find:
a at least 5 letters that have a horizontal line of symmetry.
b at least 5 letters that have a vertical line of symmetry.
c at least 2 letters that have both a vertical and a horizontal line of symmetry.
Complete the given table. Use the table to find the order of rotation and angle of rotation for each of the given figures.
S. No. Figure
Number of times a shape looks the same
Complete the given figures such that they are symmetrical about the given lines of symmetry (mirror line).
Name and draw.
a A triangle that has no rotational symmetry.
b A quadrilateral that has no reflection symmetry.
c A triangle that has only 2 lines of symmetry.
d A polygon that has both reflection symmetry and rotational symmetry of order 9.
e A quadrilateral with reflection symmetry but no rotational symmetry.
Which digits of the mobile number ‘8432657910’ have both reflective and rotational symmetry?
This clock has been reflected in a mirror. What time is it?
Which of the given faces of the dice has fewer than three lines of symmetry?
If the given shape is turned 270° clockwise and then 45° anticlockwise, find the new position of point C.
Shade the squares such that the given figures are symmetrical about the lines of symmetry and are also rotationally symmetrical. a b
Shade the squares such that the given figures have rotational symmetry of the order stated below. a
Order 2 b
Order 4
What section of these circular grids should be shaded such that the overall shape in the first grid has one line of symmetry, and the second grid has a rotational symmetry of order two? Make sure you mark your line of symmetry.
Reflective symmetry
Rotational symmetry of order 2
What is the minimum number of squares that can be added to the given shape such that the final shape has a rotational symmetry of order 4?
Seema made a pattern by joining regular hexagons as her art and craft activity. She drew lines passing through the centre of the regular hexagons. A part of the pattern with some shapes shaded is given below.
a Which shape is a vertical reflection of shape P?
b How many lines of symmetry does each shape have?
c What is the order of rotational symmetry for each shape?
b How many lines of symmetry does the London Eye have? 1 Critical Thinking & Cross Curricular
The figure shows the London Eye in London. Mounted on the wheel are 32 ovoid capsules that carry about 25 passengers each. The wheel moves very slowly, two revolutions per hour.
a What is the order of rotational symmetry of this wheel?
2
Read the statements and choose the correct option.
Assertion (A): The number of lines of symmetry for two regular figures of different sizes but the same number of sides is the same.
Reason (R): For two regular figures, if the number of lines of symmetry is the same, the figures need not be identical.
a Both A and R are correct, but the R is not the correct explanation for the A.
b A is correct, but the R is false.
c Both A and R are correct, and the R is the correct explanation for the A.
d Both A and R are false.
Case Study
The instrument that measures wind speed is called an anemometer. Look at the figure given alongside.
In an anemometer, three or four cups are mounted symmetrically at right angles to a vertical axis. As the wind blows, the cup rotates, making the rod spin. The stronger the wind blows, the faster the rod spins.
1 The order of rotation in a 4-cup anemometer is
2 Write True or False.
a The angle of rotation in a 3-cup anemometer is 180°.
b The angle of rotation in a 4-cup anemometer is 90°.
3 The figure shows the aerial view of the cups along with the rod. Draw the 3 cups of the anemometer, when it is rotated anticlockwise by 270°.
4 The 3-cup anemometer rotates 90° when the wind speed is 1.2 mph. What will be the degree of rotation, when the wind speed is 4.8 mph? (Given: The cups rotate at a uniform interval)
Cross Curricular & Art Integration
16 Visualising Solid Shapes
Let’s Recall
We see shapes all around us. Shapes can be 2-D or 3-D. A 2-D shape has only two dimensions, and a 3-D shape has three dimensions. The basic unit of any shape or figure is a point. In this picture, we can see shapes, lines and curves.
We also know that we can see lines, curves or 2-D shapes in 3-D shapes.
For example, a triangular prism has 2 triangular faces and 3 rectangular faces. The edges of the shapes are straight lines. There are no curves in a triangular prism.
Let us now recall some solid shapes that we have learnt about.
Let’s Warm-up
A packaging company has boxes in different shapes. Name the shapes of these boxes. 1 2
Cube
Cuboid
Cylinder
Cone Sphere Square
3-D Shapes and 2-D Shapes
Yashvi: Priya, have you noticed the shapes of these blocks we are playing with?
Priya: Yes! Some blocks are square, and some are triangular in shape.
Yashvi: Well, these are not exactly squares and triangles. These are called three-dimensional shapes. They have different features.
Priya: What are these features?
Yashvi: Let us find out!
Features of 3-D Shapes
Yashvi and her sister Priya were playing with building blocks. Yashvi noticed how the shape of one block was different from another.
Shapes or figures can be categorised as one-dimensional, two-dimensional and three-dimensional shapes depending on their dimensions and properties.
But what are one-dimensional, two-dimensional and three-dimensional shapes or figures?
Remember!
Some figures have no dimensions and are called 0-D figures. For example, a point is a 0-D shape. Here A, B, C are points.
One-dimensional figures are shapes that exist only in one dimension, which is typically length.
Examples of 1-D figures include lines, line segments, and curves that have no width or height but only length.
Two-dimensional figures are shapes that exist in two dimensions, which are length and breadth. These shapes have a flat surface, like a plane, and do not have depth. For example, squares, rectangles or circles.
Three-dimensional figures are shapes or objects that exist in three dimensions, which are length, breadth and height.
Unlike 2-D figures, 3-D figures have volume and occupy space in three dimensions.
In a 3-D shape, every individual flat or curved surface is called a face.
The line segment where two faces meet is called an edge.
The point where two or more edges meet is called a vertex
Examples of 3-D figures include cubes, cuboids, cones, spheres, cylinders, pyramids and prisms.
Vertex Edge
Face
Remember!
Solid shapes with straight edges and flat sides are called polyhedrons.
We already know the features of a cube, cuboid, cone, sphere and cylinder. Let us differentiate between prisms and pyramids.
Now, a prism and a pyramid are both three-dimensional shapes, but they differ in a few key ways.
Prism Pyramid
Apex
A prism is a 3-D solid that has two bases that are polygonal in shape and rectangular sides perpendicular to the base. There are two bases in a prism that are joined by the edges.
A glass prism is an example of triangular prism of triangular prism that is used in science experiments, like splitting a ray of white light.
A pyramid is a 3-D solid that has one polygonal base and triangular faces. There is only one base in a pyramid.
The sides are triangular, and they meet at a point at the top called an apex.
The pyramids in Egypt, such as the Great Pyramid of Giza, are iconic examples of pyramid-shaped structures.
Prisms and Pyramids are named as per the shape of their bases like square prism, square pyramid.
Remember!
A tetrahedron is a type of pyramid. In the word, tetra means four and hedra means face. So, it is a pyramid with 4 triangular faces.
Think and Tell
Can we say a cylinder is a circular prism and cone is a pyramid?
Example 1: Write the number of faces, edges and vertices in a square pyramid. Write the type of faces. A square pyramid has 5 faces, 8 edges and 5 vertices. It has 1 square face and 4 triangular faces.
Name the given 3-D shapes. How are these two shapes different?
2
1 is a hexagonal prism, and 2 is a hexagonal pyramid. The lateral faces of a hexagonal prism are rectangular, and the lateral faces of a hexagonal pyramid are triangular.
How many dimensions does a solid have?
Fill in the blanks.
a The solid that has only one vertex is a .
b If three cubes are joined side by side, the shape obtained is a .
c The number of edges in a football is .
d A square prism is also called a .
e The polygon region of a solid shape is called a .
The pillar of the Ashoka Pillar has one curved surface and two flat faces. Name the 3-D shape.
Identify the prisms or pyramids.
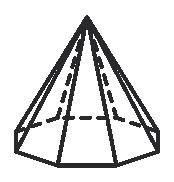
Write down the number of edges and vertices in the 3-D shapes.
Sphere b Cone c Tetrahedron d Triangular prism
If a certain number of ₹2 coins are placed one on top of another, what shape will be obtained?
Name two 3-D shapes in which the number of faces, vertices and edges of one shape is equal to the number of faces, vertices and edges of the other. Draw one face of both the 3-D shapes.
How is an octagonal prism different from an octagonal pyramid? How are the shapes similar?
Shreya formed a 3-D shape with 4 congruent triangles joining at a point. What 3-D shape did she form?
The figure shows a glass greenhouse. Look at the figure and choose the correct answer.
a The figure is made only of triangular prisms.
b The figure is made of a rectangular prism and square pyramid.
c The figure is made of a rectangular prism and triangular prism.
d The figure is made of 2 rectangular pyramids.
Nets of 3-D Shapes
Yashvi and Priya got a gift from their mother in the evening.
Yashvi: Look Priya, how lovely the gift wrapping is!
Priya: Yes, Yashvi! We can easily make these wrappings that open like a box! Let us open it and see!
The shape of the gift box is a triangular pyramid. When the box is opened, 4 triangles can be seen. This is called the net of the shape.
The faces of a solid shape tell us the number of flat or 2-D shapes in their net.
The net of a shape is a term used to describe what a 3-D shape would look like if it is opened out and laid flat.
Nets look like paper cutouts or frameworks of shapes, and when we fold them, they become 3-D objects. A solid shape can have more than one net.
Let us see the nets of some prisms. A prism has 2 opposite, identical and parallel bases that are polygonal. Its net has 2 polygonal bases and the same number of rectangular faces as the edges of the polygonal bases. The exception is the cube where all 6 faces are square.
Remember!
The opposite faces of a prism are identical. So, in a net the opposite faces will also be identical.
Given below are the nets of some pyramids. A pyramid has one polygonal base and the same number of triangular faces as the sides of the polygonal base.
Let us also see the nets of shapes that have curved faces.
Cylinder
A cone has a circular base and one curved surface pointed towards the top, called the apex.
The net of a cone is a full circle for the base, and a part of another circle for the curved surface of the cone.
Example 3: Is the given figure a net of a cube? Why?
A cylinder has a curved surface that is rectangular in shape and two parallel circular faces.
The net of a cylinder is formed of two circles, with each attached to one of the opposite sides of the rectangle.
A cube is a 3-D solid object with six square faces and all the sides of a cube are of the same length.
The figure has 6 squares, and on folding, it will form a cube.
Example 4: Which of these is a net for a square pyramid?
1 2
Option 1 can’t be folded into a square pyramid as it will result in a pyramid that is open on one side.
Option 2 can be folded to form a square pyramid. Therefore, option b is the correct answer.
Did You Know?
Madhava, the founder of the Kerala School of Mathematics and Astronomy worked on Pell’s equation which aids in 3D modelling and animation.
Example 5: Draw the nets of an octagonal prism and a triangular pyramid.
Octagonal Prism
Triangular Pyramid
List the faces of a heptagonal prism. Draw the net of the shape.
Number of faces =
2 faces rectangular faces
Net of a heptagonal prism
Cone
List the number of faces and the type of faces for each of these 3-D shapes.
a Octagonal prism b Nonagonal pyramid c Rectangular prism d Cone
The Louvre Pyramid, a large glass-and-metal triangular prism is located in Paris. Name the shapes needed to draw the net of a triangular prism.
Do a cube and a square prism always have the same nets?
Match the solids with their correct nets.
Look at the nets. Name the 3-D shape for each net.
Draw the nets of a cone and a triangular pyramid to show how they are different.
Draw the nets of the shapes.
a Pentagonal prism b Hexagonal pyramid
A cylinder has a diameter of 14 cm and length of 15 cm.
Which of the following is the correct net for the cylinder?
Draw the net of a cube that has a side of 4 cm and label all the dimensions.
This is the net of a triangular prism. Label the base.
Draw the net of a triangular pyramid where the dimensions of a triangle’s edges are 5 cm × 5 cm × 5 cm.
Seema has two bangles and a sheet of paper. If she rolls the paper and attaches the bangles to each end edge-to-edge, what shape will she get?
Dice are cubes with dots on each face. Opposite faces of a dice always have a total of seven dots on them.
Here are two nets to make dice (cubes); the dots are drawn on some of the faces. Complete the net by drawing the dots in each.
Oblique and Isometric Sketches
Yashvi and Priya are working on their project where they need to draw different 3-D shapes on paper.
Yashvi: Priya, can we draw a cuboid-shaped box on a sheet of paper?
Priya: I wonder too! A cuboid is a 3-D shape, while we can only draw 2-D shapes on paper.
Let us help them.
Oblique Sketches
An oblique sketch is a simple 2-D drawing of a 3-D shape where the front face is shown as if it’s full size, while the other faces are drawn at a smaller scale and at an angle to give a basic 3-D impression.
Let us draw an oblique sketch of a cube of dimensions 4 units × 4 units × 4 units.
Step 1: Draw a square of dimensions 4 units × 4 units.
Step 2: Draw another square of the same dimensions leaving two square units from each corner as shown.
Step 3: Join the corresponding corners using dotted lines.
This oblique sketch represents a cube of dimensions 4 units × 4 units × 4 units.
We can also draw oblique sketches of 2 or more cubes put together.
The oblique sketch shows three cubes, each with 2 cm edges, placed side by side to form a cuboid.
Isometric Sketches
An isometric sketch is the image of the object which is drawn in such a manner that the original dimensions of the object remain intact irrespective of its position. Isometric sketches are drawn on isometric sheets.
Now, let us draw an isometric sketch of a cuboid of dimensions 7 units × 2 units × 2 units.
Step 1: Draw a line of 7 units to show the length and 2 units to show the breadth.
Step 2: From the vertices of the rectangle drawn, draw 4 parallel line segments of 2 units each as shown.
This isometric sketch represents a cube of dimensions 7 units × 2 units × 2 units.
Example 6: Draw an oblique sketch of a cuboid with dimensions 5 units × 4 units × 1 unit.
Step 3: Join all 4 vertices of the line segments to form another rectangle.
While drawing isometric sketches make sure the lines are always parallel and right through the dots.
Example 7: Draw an isometric sketch for a cuboid with dimensions 4 units × 1 unit × 4 units.
Example 8: The dimensions of a cuboid are 5 units, 2 units and 3 units. Draw three different isometric sketches of this cuboid.
Draw an oblique sketch and isometric sketch of a cuboid with dimensions 4 units, 3 units and 4 units.
Error Alert!
Make an oblique sketch of the isometric sketch.
Make an isometric sketch of the oblique sketch. 2
Draw an oblique sketch of a cube that has a side of 5 units.
Draw an oblique sketch and an isometric sketch of a cube with the dimensions given. a 3 units b 6 units
Write the dimensions of the given oblique sketches. a
Write the dimensions of the isometric sketches.
Reema placed three cubes of dimensions 3 cm × 3 cm × 3 cm end to end. What shape did it form? What are the dimensions of the shape formed? Draw its oblique and isometric sketches.
Draw the oblique and isometric sketches of the given shapes.
Visualising Solid Shapes
We now know that any shape that has length, breadth and height is called a solid shape or a 3-D shape. The gift boxes that Yashvi and Priya received were lying on the table. From the side, when Priya looked at them, the shapes appeared to be square. She went over and looked at the box from the top, and she realised it looked rectangular in shape.
A solid shape, when viewed from different angles, looks different.
Cross Section and Shadows
Let us say we slice a sphere in half. Then, the cross section of the sphere will be a circle.
A cross section is the shape that we get when a solid shape is intersected by a plane.
Let us look at the cross section of a cuboid.
Cuboid
Vertical Cross Section
Horizontal Cross Section
We see squares.
We see rectangles.
Example 9: Draw horizontal and vertical cross sections of a triangular prism.
Triangular Prism Horizontal Cross Section
Example 10: Draw a horizontal cross section of a square pyramid.
So, the horizontal cross section of a square pyramid is a square.
Shadows
Another way to visualise 3-D shapes is by their shadows. Let us place a ball on a surface. If we bring a source of light in front of the solid, we can see that a somewhat circular shadow is formed on the wall/ screen. Similarly, if we place a cone, the shadow obtained will be triangular in shape.
Thus, we can conclude that, if the light of a torch is projected at a 3-D object, the shadow of that object on the plane will be in the form of a 2-D shape.
Example 11: Let us see what the shadow of a cylinder will look like when light falls on it from the side. The shadow of the cylindrical object obtained is rectangular in shape.
In the figure, we can see all three views. Do It Together Front View Chapter 16 • Visualising Solid Shapes
1 Here are the shadows of some objects when seen under the light of a torch. Name the possible solid that might match each shadow.
ball
party hat
2 Name the shape of the cross section in each of the given solids. What will the shadow of the cylinder and cone look like when light is shown from the top and side? Draw the shadows.
Shadow of the cylinder
Shadow of the Cone Top Side Top Side
Views of 3-D Shapes
When we see an object from a different angle, it does not look the same. We have different views when we see them from different sides. Each object has a top view, front view and side view. Side View Front View Top View
We can also draw the 3 views of a structure made with small cubes.
Rectangle
Do It Together
Example 12: Draw the front, top and side views of the object.
Object
Draw the shapes of the three views of the given objects.
Do It Yourself 16D
What shapes do you get when you give a vertical and a horizontal cross section to the following? a A party hat b A dice c A brick d A ball
Match the shapes with their horizontal cross sections. a b c d e 2
Draw the shadow of the objects.
b c d e
Draw the front, top and side views of the following cube structures. a b c d
Draw the front, side and top views of each object. a b c
Can a cube cast a shadow in the shape of a rectangle? Give a reason for your answer.
Name the 3-D shape that could have possibly caused these shadows.
b c d
Kush has a 3-metre-long cylindrical pipe that has a radius of 7 cm. If he slices the pipe along the base horizontally, what will its cross-sectional area be?
Points to Remember
• One-dimensional figures are shapes or objects that exist only in one dimension and have only a length, like lines and curves.
• Two-dimensional figures are shapes or objects that exist in two dimensions, which are length and breadth.
• Three-dimensional figures are shapes or objects that exist in three dimensions, which include length, breadth, and height.
• A cross section is the shape obtained when a solid shape is intersected by a plane.
• If a torchlight is projected at a 3-D object, the shadow of that object on the plane will be in the form of a 2-D shape.
• Each object has a top view, a front view and a side view.
Game of Shadows
Aim: To visualize shadow and cross-sections of solids.
Setting: In groups
Material Required: A packet of clay, a plastic knife, a notebook, a torch, and a white sheet of paper
Method:
1 Work in groups to make any 2 solid shapes using clay.
2 Ensure that each group is making 2 different solid shapes.
3 Shine torch light on the shape from the top and side to see the shadow that gets formed.
4 Cut a horizontal cross-section of the solid shape.
5 Discuss among your groups, and make a chart to display the solid shape, write its features, draw its cross section and shadow.
6 Display the chart before the class.
Name the 3-D shapes.
Name the 3-D shapes of the objects.
Draw (i) an oblique sketch and (ii) an isometric sketch for a cuboid of dimensions 5 cm, 1 cm and 1 cm.
What shadow will be formed by the objects when light falls on them from the front?
a b c
What will the horizontal and vertical cross sections of the objects in question 8 be?
The Florence flask is a glassware used in the lab to hold and heat liquids. Draw the top and front view.
Name the different plane shapes needed to draw the net of a heptagonal prism and heptagonal pyramid.
Make an oblique sketch of the given isometric shapes.
A dice has A, B, C, D written in a clockwise order on the adjacent faces, and E and F on the top and bottom faces respectively. When C is on the top, what letter will be on the bottom?
Challenge
Critical Thinking & Cross Curricular
1 Vansh cuts a cuboid cake of dimensions 20 cm × 10 cm × 4 cm exactly in half. What two possible cross sections does he get, and what is the cross-sectional area of both sections?
2 Ram placed 5 cubes of 2 cm each, edge to edge. He then placed 4 cubes of the same measurement on top of them and then three, two and one. How many cubes did he place in total? Draw the front, top and side views of the structure formed.
3 Platonic solids are a set of five 3-D shapes in which all the faces are regular polygons of the same type. They are named after the Greek philosopher Plato. Plato associated the octahedron and dodecahedron with Air and Ether.
a How many vertices does a regular octahedron have?
b Which of the following is the net of a dodecahedron ? i ii iii iv None of these
4 Read the statements and choose which option is correct.
Assertion (A): The side view of a square pyramid appears to be a triangle.
Reason (R): A square pyramid is a 3-D geometric shape with 1 square base and 4 triangular faces.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Case Study
Cross Curricular & Communication
3-D Shapes in Space
Our solar system comprises of many planets, stars, natural and artificial satellites, asteroids and many more. All these appear in 3-D shapes.
Sanjay decides to make a 3-D model of an artificial satellite and an asteroid as shown below.
Artificial Satellite
Asteroid
1 The figure shown is the artificial satellite that Sanjay wants to make. The 3-D shape he will use to make it is a
2 Look at the octahedron asteroid shown and answer.
Number of vertices =
Number of faces =
Number of edges =
3 The vertical and horizontal cross sections of the octahedron are a:
a hexagon and hexagon
c hexagon and circle
b Quadrilateral and hexagon
d square and triangle
4 Draw the possible net of the artificial satellite shown.
5 Draw any 2 views of the artificial satellite.
Answers
Chapter 1
Let’s Warm-up 1. < 2. < 3. < 4. > 5. >
Do It Yourself 1A
1. a. −4 b. 29 c. 31 d. −11 e. −90 f. −161 g. 213
h. 33 2. a. −48 b. 72 c. −98 d.
124 3. a. −17 b. 29
c. −57 d. −58 e. −62 f. 169 g. −318 h. 370 4. a. 6
b. −7 c. 534 d. 79 e. 281 f. 756 g. 497 h. 940
5. a. 3 b. −35 c. 10 d. −₹1000 e. ₹185 f. 0 6. −157
7. a. True b. False c. False d. True 8. a. 13, Commutative property b. −3, Existence of additive identity c. −16, 13, Associative property d. 0, Subtraction property of zero 9. Students will verify by placing the values.
10. 231 11. a. −3 b. −429 c. 142 d. 155
12. 1537 m 13. 105 points 14. 96℃
15. Answer will vary. Sample answer: The temperature was –5℃ at night and rose by 10℃ by morning. What was the temperature in the morning?
Challenge 1. Answers may vary. Sample answer: Students can shade: –11, 5, –5, 2
Do It Yourself 1B
1. a. 180 b. −66 c. −273 d. 84 e. 0 f. −56
2. a. negative sign b. positive sign c. negative sign
3. a. 1 21 b. − 1 32 c. − 1 54
4. a. 110 b. 0 c. 96 d. −900 e. 3450 f. 2160
5. a. 0 b. 1 c. 56 d. 56, 23 e. −2198 f. 123
6. Students will verify by placing the values.
7. a. 345 b. −1190 c. 6200
8. 440 feet below sea level, –440. 9. 50 points
10. 8250 m below sea level or –8250.
11. Answer may vary. Sample answer:
The temperature of a deep freezer decreases by −12℃ every hour. What will be the temperature after 1 day?
Challenge 1. 76 points
Do It Yourself 1C
1. a. −18 b. −8 c. 16 d. −16 e. 8 f. −82 g. 26 h. 45
2. a. 22 b. 5 c. –3 d. −36 e. 8.33 f. 17 g. 0 h. 0.5
3. −145 4. a. True b. False c. True d. False
5. −32 6. Students will verify by placing the values.
7. Answers may vary. Sample answers: First pair: a = −270, b = 18
Second pair: a = 30, b = –2 8. 55 seconds 9. 75 minutes
10. First level 11. −4℃
Challenge 1. 8 p.m., –18℃
Chapter Checkup
1. a. 106 b. 523 c. −2011 d. 340 e. 617 f. −1462
2. a. −38; 38; 1 −38 b. −78; 78; 1 −78 c. −305; 305; 1 −305
3. a. −2225 b. 3250 c. −1728 d. −13,965
e. −1,76,790 f. −2,90,895
4. a. −33 b. –32 c. –18 d. −152 e. 124 f. 234
5. a. –156 b. –1 c. –1 d. 23, –17 e. 33, –45 f. –64
6. a. −42 b. 64 c. 17 d. −8 e. 98 f. 6.5
7. 591 8. −56 9. −935 10. −56 11. 40, 80
12. ₹12,000. The value that we learn from Suhani’s mother is managing personal finances.
13. +12,000 feet; +15,000 feet; −23,945 feet; New altitude = +3055 feet
14. –9℉
Challange 1. 9th floor 2. Option a
Case Study
1. b. 440 ℃ 2. Magnesium, 1124 ℃ 3. Nitrogen 4. oxygen, chlorine and nitrogen 5. −346 ℉
Chapter 2
Let’s Warm-up 1. smaller 2. whole number 3. 8 4. different 5. 0.5
Do It Yourself 2A
1. a. 11 9 b. 13 22 c. 109 120 d. 4 1 18
b. 21
b. 117 20 c. 2169 180 cm d. 171 99 cm e. 513 30 6. 23 30 of the wall 7. 35 36 of a bottle 8. 111 20 m 9. 213 15 hours
10.
Challenge 1. 1 6 , 1 4, 1 12 , 3 8, 1 8
Do It Yourself 2B 1. a. 104 5 b. 10 c. 115 d. 2 e. 5 f. 19 27 g. 5 5 21 h. 44 7 2. a. 3 10 b. 13 c. 11 3 d. 41
11 6 c. 48 9 d. 10 5 18 4. a. 200 grams b. 831 3 cm c. 11 2 hours
d. 14 days e. 521 2 or 43 8 dozens f. 244 days 5. 9 kg 6. a. 11 15 litres b. 1 7
1. Option
It Yourself
45 players 11. ₹20,000
Challenge 1. 384 8 13 hours
Do It Yourself 2D
1. a. 236.15 b. 533.594 c. 364.74 d. 581.716 e. 717.495
f. 752.794 2. a. 115.84 b. 192.676 c. 614.05 d. 313.994 e. 142.676 f. 123.915 3. a. 331.75 b. 273.47 c. 191.47 d. 726.487 e. 1109.71 f. 424.74 4. 236.295 5. 108.885
6. 581.467 7. 326.235 8. 7.5 cups 9. 11.85 kg
10. ₹56.50 11. 244.28 KB 12. $7.69 13. 11.12 kg 14. ₹5072.8 15. ₹18,698.61
Challenge 1. 1204:1615 2. No, the increase in temperature from Feb to March is 3.7 times and not exactly 4 times.
Do It Yourself 2E
1. a. 1.8 b. 729.3 c. 42.693 d. 125.35 e. 273.2675
f. 638.5376 2. a. 4526 b. 45.26 c. 45.26 3. a. 0.11
b. 3.05 c. 2454 d. 13.25 e. 152.3 f. 89.4
4. a. 0.345 b. 32.5 c. 35 d. 912.66 e. 38.46 f. 42.52
5. 85.26 6. 15,562.5625 cm2; 499 cm 7. 112.8 m
8. ₹1980.83 9. 158.48 km 10. ₹708.12 11. 3 litres 12. ₹1526.85 13. ₹1018.45 14. ₹2848.25
15. 26.65m, ₹2012.075 16. ₹2879.6 m
Challenge 1. 4.94 cm
Chapter Checkup
1. a. 17 39 b. 17 18 c. 8 7 12 d. 62 7 e. 17 9 f. 1 g. 5 7 15
h. 651 56 2. a. 131 3 b. 16 c. 1898 d. 75 3. a. 158.76
b. 334.03 c. 847.536 d. 1793.21 e. 51.677 f. 199.15 g. 410.932 h. 346.665 4. a. 7437.5 b. 2376.18
c. 1923.6308 d. 25,588.556 e. 124.7 f. 25.4 g. 60.1
h. 3.8 5. a. Product of 31 5 and 21 4 b. Product of 25 and 4 75
c. 8 d. 301 3 6. a. 929 30 b. 314 17 c. 100 147 d. 207 280
7. a. 78 miles b. 169 c. 81 d. 9 10 e. 210 f. 23 4 8. a. 2 5
b. 1 5 9. 147.35 marks 10. 7.5 kg 11. 64.8 cm
12. 175 litres 13. 303 4 km 14. 413.86 kg 15. a. ₹948.48
b. ₹51.52 16. a. 111 5 turns b. 222 5 turns 17. a. 24 km
b. 20 km c. 60 km 18. 1.65 kg 19. 125 km, 39.2 litres
Challenge 1. a. ₹2821.5 b. ₹2910.07 2. Option c
Case Study
1. c 2. b 3. Type C 4. ₹3980.25 5. Answer may vary.
Chapter 3
Let’s Warm-up 1. School B 2. 92 medals 3. 6 medals 4. 19 : 73
Do It Yourself 3A
1. 10 2. 7 3. 4.25 4. Drama 5. 88.6 6. 1725 7. Range = 25 metres 8. 31, greater 9. 26 10. 3 11. 1356.25 km 12. Mean; Range = 4
Challenge 1. 32 2. Mode
Do It Yourself 3B
1. a. width b. equal c. horizontally, vertically d. height
Number of points scored in different rounds of the game
Challenge 1. Yes, it is possible to draw two different bar graphs. We can do so by taking different scales. Answer may vary. One can be drawn using 1 division = 5000 toys and other can be drawn using 1 division = 10,000 toys as shown below.
Do It Yourself 3C
1. 25 ft. 2. a. English b. Maths and Science; 80 marks c. 360 marks d. 26 marks 3. a.
b. Merchandise S
4. a. ₹2200 b. January and August, ₹2400 in each
c. ₹24,200 d. 60:61
5. a.
Rainfall on different days of the week
y x Scale:
b. Friday c. 19:30 6. a. 400 people b. 300 people
c. 35:36 d. 1550 people 7. a. 210 cars b. 210 cars
c. Showroom A d. 17:16
8. Answer will vary. Sample answers.
a. How many cars in total were sold by Showroom B in the first three months?
b. What is the ratio of the number of cars sold by both the showrooms in the last 3 months?
Challenge 1. a. ₹1,05,555.56 b. ₹2,48,055.56
Chapter Checkup
1. a. 11.875; 12; 12 b. −11.875; −15; −15
2. a. 5.5; 5.5 b. 9.625; 9 c. 10.11; 6
3. a. 2018, 90 million tonnes b. 70 million tonnes c. 60:350
4. 15; 114
5. Median, as the given data has a sizable number of observations; 124 mm.
6.
7. 5; 5 8. a. 2 lakhs b. 1 lakh more c. 45 lakhs d. Number of Users of Different Electronic Applianes
9. a. Friday, 225 bulbs b. 875 bulbs c. 8 35 d. 175 bulbs
10. a. NH 10 b. 811 km c. NH 3
11.
Marks obtained by Kunal in his annual examination
Questions may vary. Sample questions.
1. What is the total of the marks obtained by Kunal in all the subjects?
2. In which Subject did Kunal score the highest marks?
3. What are the average marks obtained by Kunal?
12. 80; 85 13. 45.77 kg 14. 88 marks 15. 34 kg
Challenge 1. The graph is misleading; the numbers on the y-axis start at 19. It should always start at 0. The tabular form and correct graph would be:
Name
of employees
Raj Sahil Nivira Yuvan Kabir
Salaries (in thousands) 26 24 25 22 27
2. Option a Case Study
1. Option c 2. 88:69 3. 880 m
4. 8150 m; yes the median height will change to 8300 m.
5. Answer may vary
Chapter 4
Let’s Warm-up 1. 1:2 2. 1:5 3. 1:3 4. 4:5
Do It Yourself 4A
1. a. Unlikely b. Equally likely c. Impossible d. Likely e. Sure 2. a. Equally likely b. Sure c. Unlikely d. Impossible 3. a. Impossible b. Equally likely c. Unlikely 4. Equally likely 5. a. Unlikely b. Equally likely 6.
Challenge 1. Answers may vary. Sample answers: a. Wearing a mask due to increasing pollution b. Travelling to the moon c. Christmas falls in the month of January. d. Sun sets in the west. 2. a. Spinner B, as it has two sections out of six that represent ʻʻDownʼʼ b. Any of the two spinners as each of them has 2 sections out of six that represent ʻʻForwardʼʼ.
Do It Yourself 4B
1. a. 8 b. 4, 5, 6, 7, 8 c. 4 d. 4 2. 1 5 3. 1 4
4. 25 26 5. a. 1 50 b. 49 50 6. a. 1 3 b. 1 6 c. 1 2 d. 1 2 e. 1 f. 0 7. a. 1 12 b. 2 3 c. 1 3 d. 1 2
8. a. 3 10 b. 1 5 c. 9 10 d. 0 e. 1 2 f. 3 5 9. b and d
10. a. 13 25 b. 0 c. 24 25 d. 1
11. Answers may vary. Sample answer: a. P(prime number).
Theoretical Probability = 9 25
b. P(number greater than 19). Theoretical probability = 6 25
Challenge 1. Error: He included the number 3 also whereas the numbers are 1 and 2 only; 1 5
Do It Yourself 4C
1. 7 20, 7 40, 11 40, 1 5 2. 6 25, 1 5, 3 10, 13 50 3. Mala has found the probability of getting heads over the number of times she gets a tail; 2 5 4. 19 20 5. a. 7 50 b. 12 25 c. 13 25 d. 7 25 e. 0
f. 21 25 6. a. 1 4 b. 1 6 c. 11 60 d. 17 60
7. a. Theoretical probability > Experimental probability
b. Theoretical probability > Experimental probability
c. Theoretical probability = Experimental probability
d. Theoretical probability = Experimental probability
8. Answer may vary. Sample answer:
A coin was tossed 20 times. Heads turned up 10 times on the coin. What is the theoretical and experimental probability of the coin turning up heads?
Challenge 1. 560 students
Chapter Checkup
1. a. Impossible b. Sure 2. a. Sure b. Impossible
c. Likely 3. a. Equally likely b. Unlikely c. Impossible
d. Impossible e. Sure
4. 3 7 5. a. 1 3 b. 2 3 c. 1 2 d. 1 2 e. 5 6 f. 1
6. a. 1,1; 2 b. 3, 3, 3; 3 c. 1, 1, 3, 3, 3; 5 d. 2, 2, 2; 3 e. 1, 1, 2, 2, 2, 3, 3, 3; 8 f. 1, 1, 2, 2, 2; 5 7. a. 1 4 b. 3 8 c. 5 8 d. 1 8 8. a. 1 2 b. 1 5 c. 7 10 d. 4 5 e. 0 f. 1 9. a. 1 26 b. 5 26 c. 1 13 d. 4 13 10. 6 30 or 1 5 11. a. 13 25 b. 1 5 c. 8 25 d. 8 25 12. a. 9 50 b. 39 100 c. 81 100 d. 19 50 13. 4 times
Challenge 1. a 2. c
Case Study
1. c 2. c 3. 13 27 4. 5 9
Chapter 5
Let’s Warm-up 1. 2n + 3 2. 5n – 2 3. 3p + 2 4. 2n – 5 5. 3m – 5
Do It Yourself 5A
1. a, c 2. a. b. c. d. e. f.
3. Students will draw 3 balls on RHS of the balance.
4. a. x + x 2 = 9 b. 3x + 5 = 17 c. x 2 = 15 d. 32x + 5 2 = 27
e. x + 2 = 8 f. x + 10 = 38 5. a. 1 10 x = 7 b. x – 10 = 7
c. 10 – x = 7 d. x + 27 = 77 6. a. m + m – 3 = 18 OR 2m – 3 = 18
b. c + 3 = 12 c. x + 2x = 18 OR 3x = 18 d. 2(2x + 3) = 18
7. a. No b. No c. Yes d. No e. Yes f. No
8. Statements may vary. Sample statements a. 9 subtracted from y gives 81. b. 5 subtracted from 4 times q gives 15. c. 30 times z equals 1650. d. The sum of 9 times x and 5 gives 50. e. 12 added to 4 times x is 28. f. 2 added to one-fourth of y equals 8. Challenge 1. Company B
Do It Yourself 5B
1. a. Add 7 to both sides; x = 7 b. Subtract 9 from both sides; x = −9 c. Add 2 to both sides; x = 8
d. Subtract 5 from both sides; x = −2 e. Add 8 to both sides; y = 4
f. Divide by 4 from both sides; a = 15 g. Multiply by 3 in both sides; b = 27 h. Multiply by 7 in both sides z = 42 5 or 8 2 5
2. a. x = –7 b. x = 26 c. z = 9 4 d. p = 14 e. x = 2 f. x = 10
g. y = 4 h. a = 8 3. Incorrect; 8
4. Answers may vary. Sample answers: a. Veena had saved some money in her money bank. She spent ₹75 on buying stationery items. If she is now left with ₹150, how much money did she have to begin with? ₹225 b. Ankur has 249 postcards. He added new postcards to his collection. If he has 350 postcards in all, how many new postcards did he add to his collection? 101 postcards c. The age of Rima’s grandmother is 9 times Rima’s age. If the age of Rima’s grandmother is 72, what is the age of Rima? 8 years
Challenge 1. We shall either multiply both sides of equation 1 by 6 or divide both sides of equation 2 by 6.
Do It Yourself 5C
1. a. x = 6 b. a = 4 c. x = 3 7 d. n = 1.4 e. x = 12 f. x = 18.2
g. a = 41 h. p = 4 3 i. x = 21.5 2. a. y = 5 b. y = 6 c. a = –12 d. m = 3 e. j = 48 f. x = –33 g. w = 45 h. g = 64
i. x = 67.5 3. a. x = 1 3 b. x = 7 c. x = 3 d. x = 4 3 OR x = 11 3
e. x = 3 f. y = 2 g. x = 2 h. x = 55 13 i. x = –5 j. x = –4
k. x = 26 l. x = –9
4. Answer may vary. Sample answer.
x + 6 = 9; x −2 = −5; 2x = −6
Challenge 1. a. 64 b. 33 c. 102 d. 8 e. 35 f. 15 g. 5
Do It Yourself 5D
1. 35 2. 48 3. 46 and 49 4. 6; 14 5. 21, 22, and 23
6. 50°, 90°, and 40° 7. 43 units, 45 units, and 60 units
8. 13 years 9. 240 books 10. Book = ₹110; Pen = ₹60
11. 30 stamps 12. 13 kg and 18 kg 13. 10 years
14. Bat = ₹1000; ball = ₹200 15. 10 years; 40 years
16. Small jug = 2 cups; large jug = 4 cups
17. ₹10 = 15 notes, ₹20 = 5 notes
18. Answers may vary. Sample answer.
A bicycle rental shop charges a flat fee of ₹100 to rent a bike plus ₹30 per hour for the duration of the rental. Write a linear equation for the total cost of renting a bike for x hours. Find the total cost given by a person to rent the bicycle for 4 hours.
Challenge 1. 11 years; 7 years
Chapter Checkup 1. a. 11 2 x = 150 b. 5x = 65 c. 5p − 3 = 22
d. 2x + 36 = 48 e. 4p + 9 = 31 2. a. −17 b. 3 c. 10 d. –2 19 e. 1 f. 1 3. a. x = 2 b. a = 3 c. y = 9 d. x = 3
e. x = −20 f. x = −3 g. y = −3 h. q = 42 i. x = −58
4. a. y = −3 b. x = 5 c. x = 12 d. x = –4 e. x = 33 f. x = –11
g. x = –27 h. x = 5 i. m = 15 j. l = 10 k. a = 14 l. y = 5
5. 5668 6. 12 7. 9 8. 10; 28 9. Length = 65 m; breadth = 60 m. 10. ₹600 11. –227 12. 30, 32, and 34 13. 11, 12, and 13 14. 12 15. 4 cm; 12 cm; 12cm 16. 105 6 kg, 91 3 kg, 115 6 kg 17. ₹30; ₹20 18. 18 toffees
19. 3 years; 33 years
Challenge 1. Option d 2. Option c
Case Study
1. Option a 2. Option d 3. Option c 4. −10
5. Charge from the electron = −54; Change from the proton = 56
Chapter 6
Let’s Warm-up 1. 27° 2. 142° 3. 180° 4. 213°
Do It Yourself 6A
1. a. Supplementary b. Supplementary c. Supplementary d. Neither e. Complementary f. Neither g. Neither h. Neither 2. a. Complement = 57°; Supplement = 147° b. Complement = 18°; Supplement = 108° c. Complement = 49°; Supplement = 139° d. Complement = 1°; Supplement = 91°
3. a. Neither b. Complementary c. Supplementary
4. a.
A D C B ∠A and ∠B, ∠B and ∠C, ∠C and ∠D, ∠A and ∠D
5. a. 25° b. 216° c. 50° 6. 10° 7. 113°, 67°
8. a. 45° b. m = 120°, n = 60° c. 30°
9. 60° 10. 30°. The angles in vertically opposite sides are equal 11. 120°, 60° 12. 50°, 40°
13. 130°, 50° 14. x = 67°, y = 55°
Challenge 1. 18
Do It Yourself 6B
1. a. Not parallel b. Not parallel c. Not parallel d. Parallel 2. Pairs of corresponding angles: 2 and 6, 2 and 10, 6 and 10, 1 and 5, 1 and 9, 5 and 9, 3 and 7, 7 and 11, 3 and 11, 4 and 8, 8 and 12, 12 and 4. Pairs of alternate angles: 2 and 8, 1 and 7, 3 and 5, 4 and 6, 1 and 11, 2 and 12, 3 and 9, 4 and 10, 6 and 12, 5 and 11, 7 and 9, 8 and 10.
3. a. Not parallel b. Not parallel c. Not parallel d. Parallel
4. D A B P Q R C S l 5. P q B A 5.9 cm 5.9 cm E F
6. a° = 118°, b° = 108°
7. ∠ACB = 60°, ∠ABC = 90°, ∠BAC = 30°
8. Q n m 5.5 cm 9. XD = 5.6 cm; YD = 9 cm; ZD = 4.2 cm
10. ∠PSR = 60°, ∠QRS = 30°
11. a. x° = 80°, y° = 32° b. m° = n° = 70° c. p° = 60°, q° = 105°
d. h° = 45°, g° = 72°
12. 60°
60°
13. a. y° = 35°, x° = 50° b. 108°
14. Steps: i. Draw a rectangle ABCD of length 10 cm × 8 cm.
ii. Mark any two points A and B on any edge of the outer rectangle.
iii. Construct right angles at points A and B, respectively.
iv. Draw arcs with centres at A and B, each with a 2 cm radius, intersecting the perpendiculars at A and B at points E and F.
v. Connect points EF and extend this line on both sides to achieve the desired parallel line. vi. Repeat the process for the other three sides. vii. Connect the corresponding points on these lines to form the inner rectangle.
Challenge 1. d. = 126°
Chapter Checkup
1. a.Neither b. Neither c. Complementary d. Supplementary e. Neither f. Neither g. Complementary h. Complementary 2. a. 146° b. 61° c. 54° d. 14° 3. a. 64° b. 50° c. 43°
d. 4° 4. a. 20° b. 29° c. 28° d. 22.5° 5. ∠ABC = 75°, ∠ACB =67°, ∠CAB = 38° 6. 115° 7. a. Not parallel b. Parallel c. Not parallel 8. a. 115° b. 130° c. 95° 9. m° = 137°, g° = 137°, y° = 67°, h° = 67° 10. x° = 105°, y° = 120°, w° = 105°, z° = 60° 11. ∠PQR = 65°, ∠RSP = 65°, ∠QRS = 115° 12. ∠QDC = 63°, ∠DCQ = 47°
13. P Q B 4.5 cm 4.5 cm A m P
Challenge 1. Option b 2. a 40° b. 96° c. 84° d. 84°
Case Study
1. 33.3° 2. 23.34° 3. Option d 4. Option b
Chapter 7
Let’s Warm-up 1. Acute-angled triangle
2. Isosceles-right triangle 3. Equilateral triangle
4. Obtuse-angled triangle 5. Isosceles triangle
Do It Yourself 7A
1. a. Median b. Altitude c. orthocentre d. altitude
2. A C B 3. 10 cm
4. Option a 5. AD = 3 cm, BC = 8 cm
6. a. GE = 10 cm, BE = 15 cm b. GF = 8 cm, CF = 24 cm
c. AG = 20 cm, GD = 10 cm d. GC = 2x, CF = 3x
e. x = 2, AD = 27 7. 72°
Challenge 1. Equilateral triangle since in an equilateral triangle, the median is the the same as the altitude.
Do It Yourself 7B
1. a. 105° b. 165° 6 or 27.5° c. x = 70°, y = 55° d. x = 30°, y = 30°
2. 50°, 60°and 70° 3. 52°, 78°, 50° 4. 75°
5. 70°, 20° and 90° 6. 80°, 65°, and 35°
7. Prove using the linear pair of angles and the exterior angle property.
8. 50°
Challenge 1. Equilateral triangle
60°
Do It Yourself 7C
1. a, c 2. a. < b. > 3. a. 3 cm < x < 9 cm
b. 5 cm < x < 23 cm c. 27 cm < x < 41 cm
4. Yes. As we have shown, the triangle inequality property holds true for this statement, hence, PQ + QR + PR > 2 PS.
5. Yes
Challenge 1. Solve using the Triangle Inequality Theorem.
Do It Yourself 7D
1. b, c 2. a. 16 m b. 24 cm c. 18 m 3. 7 4. 20 cm
5. 24 cm 6. x = 5 cm; y = 12 cm 7. 16 m 8. Answers may vary. Sample answer: A ladder 13 m long is placed on the ground in such a way that it touches the top of a vertical wall 12 m high. Find the distance of the foot of the ladder from the bottom of the wall.
Challenge 1. 8 m and 6 m
Do It Yourself 7E
1. 10 cm 2. Figures may vary. Sample figures. 3 cm 3 cm
3. a. 4.2 cm b. 55° c. 4 cm d. 7.2 cm
4. The circular targets are congruent, since if the radius of one circle is equal to the radius of the other circle, then, the circles are congruent. 5. 5 spots 6. ∠DOB or ∠BOD
Challenge 1. Option D 2. 150 cm2
Do It Yourself 7F
1. a. PR = SQ RS = QP PS = PS b. Yes; By SSS congruence ΔPRS ≅ ΔSQP. 2. Prove using the SAS congruence criteria.
3. Prove using the ASA congruence criteria.
4. Yes 5. Yes, ΔADB ≅ ΔBCA 6. Yes
7. Prove using the SSS congruence criteria.
8. a. Prove using RHS congruence criteria.
b. Prove using the corresponding parts of congruent triangles
c. Prove using the corresponding parts of congruent triangles
9. Prove using the ASA congruence criteria.
10. a. Prove using the ASA congruence criteria.
b Prove using the corresponding parts of congruent triangles.
11. Prove using the alternate interior angle property. 12. No
Challenge 1. Yes, OC = OD; ∠AOC = ∠BOD and OA = OB
Chapter Checkup
1. a. False b. True c. False d. False 2. a, c 3. b and c
4. a. ∠P = 16; ∠Q = 94° b. ∠x = 50° c. ∠y = 63°
5. Prove using the Pythagoras Theorem. 6. 20 inches
7. Not congruent; Use the SSS congruence criteria.
8. 1300 cm2 9. 17 m
10. Show using the RHS congruence criteria and angle sum property of triangle.
11. 50° 12. 100 metres
13. ∠C = 40°; ∠BOC = 120°
14. Answers may vary. Sample answer: The heights of two buildings are 34 m and 29 m, respectively. If the distance between the two buildings is 12 m, what is the distance between the tops of the buildings?
Challenge 1. Option A 2. Option A
Case Study
1. Option C 2. Option C 3. 180°
4. ∠AFC = 145° and ∠EAF = 35°
Chapter 8
Let’s Warm-up 1. 44:53 2. 123:74 3. 5:7 4. 162:229
Do It Yourself 8A
1. 32:13 2. a. 2:5 b. 25:1 c. 25:4 d. 1:15
3. a. 5 b. 40 c. 4 d. 11 4. a. < b. > c. > d. >
5. 2:5 < 3:7 < 7:12 < 11:14 < 9:2
6. A:C = 35:143; A:B:C = 35:77:143
7. Answer may vary. Sample answer: 12 cm 8 cm 9 cm 9 cm
8. 10:13 9. 120° 10. 52 inches
11. ₹740, ₹1110 and ₹1850 12. 21 cm; 15 cm
Challenge 1. Option b
Do It Yourself 8B
1. a. Yes b. No c. No d. No 2. a. 12 b. 42 c. 6 7 d. 8 15 3. a. 9 b. 1 2 c. 28 125 d. 29.4
4. 25 gallons 5. ₹6,44,000 6. 28 days 7. 6
Challenge 1. a. 15 years
Do It Yourself 8C
1. 15 kg 2. 450 km 3. ₹100 4. 4500 times
5. 27 days 6. 75 minutes 7. 612.5 kg 8. 50 shirts
9. 19 books 10. 20 workers
11. Answer will vary. Sample answer: A car travels 240 kilometers using 16 litres of petrol. How much petrol will be needed to travel 450 kilometers?
Challenge 1. Option a
Do It Yourself 8D
1. 16 m/s 2. 1.39 m/s 3. 510 m 4. 2.67 minutes (approx.) 5. 465 minutes 6. a. 25,75,342.47 km/day
b. 1,07,305.94 km/hour 7. a. Both took same time
b. Zero minutes 8. a. Monday b. Monday: 1.558 km, Tuesday: 1.1 km, Wednesday: 1.375km, Thursday: 0.733 km, Friday: 0 km
Challenge 1. Option c
Chapter Checkup
1. 3 2. 84; 96 3. 384 widgets 4. 32.22 m/s 5. 1320 metres 6. 125 days 7. 0.18 m/s 8. 4:14:21 9. 5.45 seconds 10. 120 feet 11. 3.5 hours 12. Suresh = 55 years; Kartik = 25 years 13. ₹3,600; ₹14,400 14. 2
Challenge 1. ₹1,12,800 2. Statements 1 and 3 are correct but statement 2 is incorrect.
Case Study 1. Option a 2. 8:3 3. 4:5 4. True 5. False
Chapter 9
Let’s Warm-up 1. coffee 2. juice 3. 38 100
4. 10 100 5. 5 100
Do It Yourself 9A
1. a. 11 20 b. 9 2500 c. 9 400 d. 141 250 e. 33 200
2. a. 62 100 ; 62% b. 1 2; 50% c. 5 8; 62.5%
3. a. 0.48 b. 0.0125 c. 0.00005 d. 0.112 e. 0.124
4. a. 20% b. 120% c. 234% d. 1210% e. 0.48%
5. 0.71 6. 1:5 7. 1:3 8. 3:7 9. 60% 10. 3:1 11. 11:1 12. 60%
Challenge 1. Option d
Do It Yourself 9B
1. a. 62.5 b. 225 c. 56.25 d. 672 2. a. 1 3 17 % b. 15%
c. 50% d. 16% 3. a. 400 b. 850.5 c. 4 hours 16 minutes
d. 17 m 4. a. 15% decrease b. 50% increase
c. 30% increase d. 10% decrease 5. 25% increase
6. Jaya 7. 576 women 8. 1000 employees
9. ₹100, ₹150, ₹250; 20%, 30%, 50% 10. 2000 g
11. 2,00,000 12. 331 3 % 13. ₹8,82,812.5 14. 84%
Challenge 1. No, because the base values for the calculations are different. The percentage increase is calculated relative to the smaller number (80), and the percentage decrease is calculated relative to the larger number (100). 2. ₹820.8
Do It Yourself 9C
1. a. Gain of ₹125 b. Gain of ₹770 c. Loss of ₹188 2. a. (ii) b. (ii) c. (i) d. (i) 3. a. ₹50 b. ₹2000 c. 23 9 117 % d. 162 3 % 4. ₹432 5. ₹7600 6. Loss = ₹2000 7. ₹6847 8. 1% loss 9. ₹1995 10. 8% gain 11. ₹60 12. ₹2000 13. ₹80 14. Gain = 17%
Challenge 1. Option a
Do It Yourself 9D
1. a. ₹750; ₹5750 b. ₹3600; ₹9600 c. ₹600; ₹2600 d. ₹180; ₹2430 2. a. 10 years b. 6.25 years c. 3 years
d. 6.5 years 3. a. ₹49,000 b. ₹6000 c. ₹1,20,000
d. ₹2,00,000 4. a. 3% b. 7.5% c. 6.5% d. 0.0325%
5. ₹48,000 6. ₹10,000 7. ₹80,000 8. 20.16%
9. ₹21,500
Challenge 1. 22.5 years
Chapter Checkup
1. a. 80% b. 3 16 c. 11 500 d. 1140% e. 48%
f 0.045 g. 564% h. 0.08125 2. a. ₹115 b. 2.5 L c. 505 d. 160 g 3. a. ₹50 b. ₹345 c. ₹135 d. ₹89 4. a. 1 3 %
b. 5% c. 14% d. 20% 5. a. 50% b. 100% c. 10%
6. a. 30% profit b. 162 3 % loss c. 10.4% loss 7. a. 12.5%
b. 25% c. 20% 8. a. ₹530 b. ₹10,683.75
9. Gain = ₹25, 25% 10. Profit% = 80% 11. 331 3 %
12. a. 462 3 % b. 531 3 % 13. 4:5 14. 100%
15. ₹1000 16. ₹2700 17. ₹225
Challenge 1. 14:20:35 2. Option a
Case Study
1. a. ₹0 2. Option d 3. 0% 4. False 5. Answer may vary.
Chapter 10
Let's Warm-up 1. like fractions 2. proper fraction
3. improper fraction 4. mixed 5. improper
Do It Yourself 10A
1. a. 1 4 b. 3 8 c. 2 4 d. 4 8
2. Answers may vary. Sample answers: a. –7 1 b. 7 5 c. Denominator can vary. 0 5 d. –1 2
3. None. 4. –6 –28
5. a.
6 b. 1
6. a. –8 5 b. –1 3 c. 3 5 d. –5 7 7. a. –12 b. –44 c. 21 d. 19
8. Answers may vary. Sample answers: a. 14 26; 21 39; 28 52 b. 60 100; 84 140; 3 5
9. No
Challenge 1. Conclusion 2 and conclusion 3 do not follow. Do It Yourself 10B
1. a. 4 7 > 5 9 b. 2 3 < 7 3 c. –1 2 > –3 5 d. 13 –24 > 9 –4
2. R = 4 3; S = 5 3; T = –7 3 ; U = –8 3 3. Answers may vary. Sample answers:
a. –1 6 , –2 6 , –3 6 , –4 6 , –5 6 , b. –31 45 , –32 45 , –33 45 , –34 45 , –35 45 ,
c. 7 36, 8 36, 9 36, 10 36, 11 36 d. –55 90 , –56 90 , –57 90 , –58 90 , –59 90
4. a. 8 3 b. 9 10 c. 4 11 d. 3 9 5. a. –10 9 < 2 9 < 7 18 < 5 12
b. –14 20 < 4 –6 < 10 –16 < –1 3 c. –3 5 < 4 –7 < –3 6 < –1 3 d. –4 5 < –2 3 < 3 5 < 5 6
6. a. 9 3 > 44 15 > –3 8 > –14 7 b. 9 10 > 7 8 > 3 4 > –3 4
c. 32.8 > 4.4 > –3.9 > –5.0 d. 8 7 > –3 9 > –4 8 > –1
7. Raman 8. Sample answer. 24 Challenge 1. a Do It Yourself 10C
1. a. 34 5 b. 6 5 c. 27 5 d. –7 5 e. 16 15 f. 74 21
2. a. –5 7 b. –11 8 c. –1 2 d. 9 11 3. a.
5. Answer may vary. Sample answers:
9. 306 5 km 10. Answers may vary. Sample answer. Raj bought 14 9 m of cloth. He again bought 13 8 m of cloth. How much cloth does he have in total?
Challenge 1. (iv) Either Statement 1 and Statement 2 alone are sufficient.
Do It Yourself 10D
b. –17 8 10. 25 4 cm 11. 9 4 km 12. 153 3 m
Challenge 1. Both statements are true.
Chapter Checkup
5. Answers may vary. Sample answers: a. 2 12; 3 18; 4 24 b. – 18 24; – 27 36 ; – 36 48 c. 8 14; 12 21; 16 28 d. –2 22; –3 33; –4 44
6. a. 56 b. 80 c. 4 d. –20
7. Answer may vary. Sample answer: a. 19 30, 20 30, 21 30, 22 30, 23 30
b. 13 54, 14 54, 15 54, 16 54, 17 54 c. –4 6 , –5 6 , –6 6 , –7 6 , –8 6 d. –2 3 , –1 3 , 0, 1 3, 2 3
8. a. 13 10 b. –1 10 c. 3 10 d. 40 49 e. 1 f. 9 10 g. 25 8 h. –13
9. – 3 10 10. Yes, as both are equivalent rational numbers.
11. 97 33 12. 1 4 13. 9000 books 14. 159 5 km
15. 71 12 inches 16. ₹10,000 17. 8 gallons
18. Answers may vary. Sample answer.
A gardener has 7 8 litres of liquid fertilizer. He needs to divide it equally among 1 2 litres of water to dilute it properly for his plants. How many litres of water can he mix with the fertilizer?
Challenge 1. –7 49
2. b
Case study
1. Option b 2. Option b 3. 0.25; 1 4
4. 0.17 5. Answers may vary.
Chapter 11
Let’s Warm-up 1. False 2. False 3. True 4. False
5. False
Do It Yourself 11A
1. a. three b. less c. one 2. a.
A
3. Scalene Triangle since none of the sides are equal. 5. Equilateral Triangle
4. Yes. In a triangle, the sum of the lengths of 2 smaller sides is greater than the length of the largest side.
Scalene triangle; Acuteangled triangle; QR
Scalene triangle; Obtuseangled triangle
Scalene triangle; Acute angled triangle
Do It Yourself 11B
Do It Yourself 11D
1. 4.4 cm 2. 7 cm
3. BC = 6.8 cm; BAC = 46°, 4. 32°, 58° BCA = 44°
5. ZXY = 54° 6.
Challenge 1. 13.8 m
Chapter Checkup
1. a. SSS b. SAS c. RHS d. ASA
2. Acute-angled triangle 3. Scalene triangle; Obtuseangled triangle (111°, 40°, 28°)
10. Sum of length of sides UW and VW = 6 cm + 4.9 cm = 10.9 cm
34
4. SAS criterion. 5. AC = 6 cm; BC = 4.1 cm
Challenge 1. No, it is not possible to construct the unique triangle, since we cannot determine the position of point C uniquely. We need the length of the other side or measure of another angle to construct the triangle uniquely. We will use the SSS rule or SAS rule to construct this triangle.
2. Option c
Case study
1. Option b
Equilateral triangle.
2. Option c
We need the length of one side of the equilateral triangle as three sides of the triangle are equal.
3. 4.
6. XZ = 3.8 cm; YZ = 4.7 cm 7. 55° and 80°.
Chapter 12
Let’s Warm-up 1. 96 cm, 92 sq. cm
2. 1254 sq. cm, 52,625 sq. cm
Do It Yourself 12A
1. a. P = 21 cm, A = 25.16 sq. cm b. P = 18 cm, A = 20.25 sq. cm 2. a. 16 sq. cm b. 64 sq. cm
c. 169 sq. m d. 729 sq. m
3. a. 6 sq. cm b. 20 sq. cm c. 63 sq. cm d. 342 sq. m
4. 12 m 5. 2,50,000 sq. m 6. ₹3800
7. 39 8. Length = 2 units; Breadth = 3 units; Perimeter = 10 units; Area = 6 sq. units
9. Perimeter = 372 mm; Area = 7,749 sq. mm
10. Answers may vary. Sample answer.
Sana is planning to tile her kitchen floor. The kitchen is rectangular in shape, with a length of 8 meters and a width of 6 meters. How much area does she need to cover with tiles?
Challenge 1. 1:2
2. Perimeter of the rectangle is greater than the square
Do It Yourself 12B
1. a. 63 sq. cm b. 48 sq. cm c. 21 sq. cm
2. a. 8 cm b. 16.56 cm c. 15.8 cm d. 9.3 cm
3. Height = 18 cm, base = 36 cm 4. 160 sq. cm
5. 29.75 cm 6. 16.7 cm (approx.) 7. 60 sq. cm
8. a. 14 cm b. 18 cm
Challenge 1. 24 m
Do It Yourself 12C
1. a. 104 sq. cm b. 40 sq. in c. 22.5 sq. cm
2. a. 44 sq. cm b. 6.3 cm c. 10.5 cm 3. 4.8 cm
4. a. 30 sq. cm b. 4 cm 5. Base = 12 cm, height = 16 cm 6. 562.5 sq. cm 7. a. 875 sq. cm b. 615 sq. cm
8. 16,905 sq. m
Challenge 1. 117.6 sq. cm
Do It Yourself 12D
1. a. 88 cm b. 176 cm c. 268.4 cm
2. a. 24 cm b. 112 cm c. 160 cm
3. 91 m 4. 21 cm 5. 128.5 cm
6. 5:6 7. 35,200 cm 8. 145.17 m
9. 574 revolutions 10. 16.36 m 11. 56 cm
Challenge 1. 85.07 minutes
Do It Yourself 12E
1. a. 154 sq. cm b. 1386 sq. cm c. 38.5 sq. cm
d. 346.5 sq. cm 2. a. 14 cm b. 28 cm c. 7 cm d. 21 cm
3. a. 77 sq. cm b. 346.5 sq. mm c. 346.5 sq. mm
d. 18.865 sq. cm 4. 16:49 5. 2828.57 sq. cm
6. 181.5 sq. mm 7. 1089 sq. cm
Challenge 1. 27,154.2 sq. cm
Do It Yourself 12F
1. a. 1148 sq. cm b. 33.6 sq. cm c. 329 sq. cm
2. a. 42 sq. cm b. 11.43 sq. cm c. 420 sq. cm
3. 181.335 sq. cm 4. 7612.50 sq. cm 5. 219.43 sq. cm
6. 1369.64 sq. cm 7. 5848.28 sq. cm
Challenge 1. 3:5
Do It Yourself 12G
1. 2086.58 sq. m 2. 17,634.24 sq. m
3. a. 296 sq. cm b. ₹51,744 4. ₹59,593.60
5. 1609.15 sq. m 6. 42 sq. m, ₹2100 7. 20 m
8. 2300 sq. m 9. 150.72 s 10. yes
11. 50.29 sq. cm, 549.71 sq. cm 12. Answer may vary. Sample answer
The length of the side of a square picnic mat is 62 cm. Find the area and the perimeter of the square picnic mat.
Challenge 1. a. 26 sticks b. 1814.92 sq. m
Chapter Checkup
1. a. 18 sq. cm b. 24 sq. cm c. 462 sq. cm 2. 40.5 sq. cm
3. 2:3 4. 72.9 m 5. ₹5483 (approx) 6. 135 sq. cm
7. DP = 54.29 m, BQ = 47.5 m 8. 60 sq. cm
9. 42 cm, 132 cm, 1386 sq. cm 10. 96.43 sq. cm
11. 370 shrubs 12. ₹1,846,320
13. 147,337 sq. m 14. 2227.96 sq. cm 15. 7 m
16. 588 sq. cm 17. 0.4016 sq. km 18. ₹15,540
19. 56,57 cm, ₹1244.57
Challenge 1. For length = 20 m and breadth = 20 m, the area is the maximum. 2. Option D
Case Study
1. Option c 2. Option d 3. Option c 4. 72 m
5. 12 tiles
Chapter 13
Let’s Warm-up 1. 85 2. 59 3. 80 4. 15 5. 128
Do It Yourself 13A
1. 88 2. n + 2 3. 17.5 cm 4. 240.25 cm2 5. 249
6. (2n − 1), 199 7. 20 feet2 8. 5 cm 9. 24.5 cm
10. 32 bacteria
Challenge 1. 100 m
Do It Yourself 13B
1. a. x + y b. a 4 + 3b c. z – 3 + xy d. 2pq − mn
2. a. 6ab; 6a2, 12c b. 3c, –10b; –10a c. 15ba, 12c; 15a2, 7bc
d. 5ac, 3b, –6c; 3a 3. a. 5m2 , mn b. 6ab, 8a2bc, –2bc2 , –ca
c. 0.5xy, 1.2x2y, –3.3y d. 2 5 yz, 5 6 x2y, 0.6xy
4. a. 6mn2 b. 5p2q c. 0.5zx d. ab2
5. Like terms Unlike terms
a. (m2n, 5m2n, 8nm2), (3mn, 6nm) 5m, 7n
b. (2a2c, 3ca2), (3ac2 , c2a) 5b2a, 8b2c
c. (pqr, 9qrp, 6rpq), (8rp, 5pr) pq2
d. (5mln, 5lmn), (6lk2m, k2lm) 2klm
6 a. Expression 5xy + 8yz 5xy 8yz
5 x y 8 y z Terms Factors b. Expression 3pq2 – 5pr + 2 3pq2 – 5
2 3 p q q –5 p r 2 Terms Factors
c. Expression 1.2x2y – 3xyz
1.2x2y –3xyz
1.2 x x y –3 x y z Terms Factors
d. Expression m + mn2 – 6l + 8nl m mn2 – 6l 8nl m m n n – 6 l 8 n l Terms Factors
7. 3x 8. (4w + 10) cm 9. Answer may vary
Challenge 1. Option d
Do It Yourself 13C
1. a. 5xy + x b. 8p2 c. ab d. 17x2y
2. a. 3x + 4y b. 4x + 4y c. –2a + 7b + 2 d. a + 15b – 15c
3. a. x + 3y b. 3p2 + 5q2 + 3r2 c. 6a2 + 3b2 + 16ab2
d. 31a + 16b – c 4. a. 11xy – 3x b. 3x2 + 4x
c. 7ab2 – 4b + 6ac d. 7pq + 4pr e. –2pq + 10pr
f. 4a2b – 9ab + 3c 5. a. 19ab2 + 2a + 17bc – 4a2b
b. 5ab2 – 20a2b + 27bc
6. 1 1 1 1 4x − 3y + 4 x x x y −1 −1 y y + 3x − 2 = x x x x 1 1 y y y 7x − 3y + 2 x x x x x x x
7. 1 10 mn2 –7 15 mn + 1 9 77 n2 8. ₹(8x2 + xy + 12y2)
Challenge 1. Option b
Do It Yourself 13D
1. a. –2ab – 4 b. 12y 2 – 17xy c. 6y2 – 4y – 3
d. 6b2 – 10ab + 8 2. a. –3x – 2x2 b. 3mn – 7mn2 + 10n2
c. –2p2q + 3q2 – 13 d. 6ab + 7ac + 3bc + 3
3. 5a2 – 27a + 6b – 8 4. 5xz2 – 5xy – 19yz + 4x2z – 3
5. 9xy2 + 6xy – 15x2y + 5y2 6. 8 metres
7.
x2 x2 +
8. Answer will vary. Sample answer.
An orchard grows two types of apple trees. The yield from the first type of apple tree can be represented by the expression 5x2 + 4x + 3 kilograms of apples, while the yield from the second type of tree is represented by 3x2 + 2x – 5 kilograms. What is the total apple yield from both types of trees?
Challenge 1. Option c
Do It Yourself 13E
1. a. 11 b. 7 c. 15 d. 3 2. a. 7x – 9y b. 14m + 2mn
c. 5a – 8ab d. x2 + 4x – 5 3. a. –18 b. 18 c. –2 d. 26
4. a. 2 b. 6 c. 15 d. − 4 5. a. 5x2 + 9x – y2 – 3y + 2
b. –3m2 + 3mn – 8n + 6m c. 6pq2 – 4pq – 6p
d. a + 2ab – 3a2 – 3 6. a. −10 b. −10 7. 14
8. 2400 litres 9. 6 years
10. 5x + 10, Rahul = 22 minutes; Vivek = 44 minutes; Ankit= 54 minutes
Challenge 1. Option a
Chapter Checkup
1. Trinomial, quadrinomial, monomial, binomial
2. a. Unlike b. Like c. Unlike d. Like e. Unlike f. Like
3. a. Expression x2y + yx x2y yz x x y y z
Terms
c. Expression pq – 5pq2 + 9 pq –5pq2 9 p q –5 p q q 9
Terms Factors
6 a b 8 c Terms Factors
4. (13n + 1); 196 5. 11.5 cm 6. a. 19a2b – 10ab2 b. 5x + 2y + 2xy + 6 7. (18a – 10) metres 8. 2a + b 9. 28 10. –6 11. 4x2 + 5xy – y2 12. 8x – y – 5 13. −84.67
14. a. −2 b. −18 15. ₹(5a2 + 4ab + 2b2) 16. 33 metres 17. 128 cm
Challenge 1. a = 9; b = –5 2. Option a Case Study
1. Option c 2. Option c 3. ₹5500 4. (4x2 + x + 1) m2
Chapter 14
Let’s Warm-up 1. 10,000 (Ten Thousand) 2. 1,00,000 (One Lakh) 3. 10,00,000 (Ten Lakh) 4. 1,00,00,000 (One Crore) 5. 10,00,00,000 (Ten Crore)
Do It Yourself 14A
1. a. 9; 11 b. −17; 9 c. n; 10 d. 3 8; 5 e. –7 11; 8 2. a. 54 b. (–9)7 c. 73 × 85 d. n
3. a. 64; 512 b. 121; 1331 c. 324; 5832 d. 441; 9261
e. 900; 27,000 4. a. 4913 b. –3125 c. 5184 d. 8 729
e. 121 144 f. 16 1029 5. a. 26 b. 3 × 5 × 7 c. 25 × 31 ×
d. 2 × 3 × 173 e. 27 × 31 × 51 6. a.
4 d. (−2)5 7. a. 34 b. Both are
a. 94 b. (−12)3 c.
9 4. a. 1 b. 1 c. 1 d. 1 5. 16 6. a. 128 b. −27 c. 1,60,000 d. −17 7. 1 8. a. 26 × m2 b. 23
c. 56 × 711 × 112 d. ab 9. a. 1 b. 7
10. 65,536 N 11. 8,80,000
Challenge 1. option c
Do It Yourself 14C
1. a. 8.64 × 105 b. 5.5 × 106 c. 4.152 × 109 d. 6.14 × 1011
2. a. 30000 b. 455000 c. 71100000 d. 9800000000
3. 4540000000 years 4. 7 5. 7504682; 7.504682 × 106
6. a. 1.3568 × 107 b. 1.41 × 109 c. 2.76 × 109 d. 1.4 × 108
Challenge 1. The powers of the numbers in the numerator and denominator is negative. So, the final answer will be 245.
Chapter Checkup
1. a. 86 b. (−15)8 c. 3 7 9 d. –2 11
6 ×
4 15 7 2. a. 2401
b. 1 c. 8 d. 25 3. a. 38,416 b. −1 c. 10,00,000 d. 1 4. a. 28 b. 2 × 3 × 97 c. 2 × 5 × 109 d. 2 × 52 × 41 5. a. 2700 b. – n3 102 c. 0 d. 16 6. a. < b. < c. < 7.
Case Study
Chapter 15
Let’s Warm-up 1. One line of symmetry 2. Two lines of symmetry 3. Four lines of symmetry 4. Infinite lines of symmetry
Do It Yourself 15A
8. Answers may vary. Sample answers: Red Fort, Golden Temple, Qutub Minar
1. c. d. 2. a. Yes b. No, c. Yes d. Yes
e. No, f. No, Line of symmetry not possible g. Yes
h. No, Line of symmetry not possible
9. Shapes may vary. Sample shapes.
a. x x x x x
3. a. b. c. d.
e. f. g. h.
5. a. b. c.
6. Answers may vary. Sample answers: a. b.
4. N, R
b. c. d.
Challenge 1. Colours may vary. Sample figures.
a. b. c.
Chapter Checkup
1. a. Yes b. Yes c. No, d. Yes e. No,
We would shade the squares along the diagonal line at an equal distance on both sides.
7. a. b.
c. d.
Challenge 1. a. b. Yes, It has 6 lines of symmetry
Do It Yourself 15B
1 a. more than 1 b. No rotational symmetry c. more than 1
d. No rotational symmetry e. more than 1 f. more than 1
g. No rotational symmetry h. No rotational symmetry
2. a. 5 b. 3 c. 4 d. 2 3. a. Letter H, I, O, X b. Letter N, S, Z
c. Letter A, B, C, D, E, K, M, T, U, V, W, Y d. Letter F, G, J, L, P, Q, R
f. No, Lines of symmetry may vary. Sample answer:
2. a. 1, b. 0, c. 4, d. 2, e. 1, f. 4,
3. Error: The marked portion of the mirror image should be flipped on the opposite side.
Object Mirror image Correct image:
Object Mirror image
4. a. B, C, D, E, K b. A, T, U, V, W c. X, O
5. S. No. Figure Rotation
4. i. a. ii. a. 4 b. 4 c. 4 d. 6
iii. a. 90° b. 90° c. 90° d. 60°
5. a. Anticlockwise b. 90° c. No d. 1
6. a. Figure 1: Order of rotational symmetry = 4, angle of rotation = 90°; Figure 2: Order of rotational symmetry = 2, angle of rotation = 180°
b. Figure 1: No Figure 2: Yes
7. a. 4 lines of symmetry in each figure.
b. For both the figures, order = 4, angle of rotation = 90°
c. Answer may vary. Sample answer:
Happy Diwali
7. a. Scalene triangle b. Parallelogram c. None
1
d. Nonagon, 140° 40° e. Trapezium 1
8. 0 and 8 9. 7:15 10. Each of the given faces have 2 lines of symmetry.
11. The new position of C will replace H in the original
Challenge 1. Triangular pyramid 2. Option c
Do It Yourself 16B
1. a. 10; 2 octagonal identical faces and 8 rectangular faces
b. 10; 1 nonagonal base and 9 triangular lateral faces
c. 6; all rectangular or both square/rectangular faces
12. Answer may vary. Sample answers: a. b.
13. Answer may vary. Sample answers: a. b.
14. Figure may vary. Sample figures:
15. Minimum of 6 squares should be added to get a rotational symmetry of order 4.
d. 2; 1 circular base and 1 curved lateral face
2. Triangle and square/rectangle 3. No
4. a. b. c. b.
5. a. Triangular prism b. Rectangular prism/cuboid
c. Cone d. Square pyramid e. Cylinder
f. Pentagonal pyramid
6. 7.
16. a. Shape Q b. P – 1, Q – 1, R – 1, S – 1, T – 1, U – 0 c. Rotational symmetry of order 1 Challenge 1. a. 32 b. 32 2. Option c
Case Study
1. Option a 2. a. false b. true
3.
4. Angle of rotation when the wind is 1.2 mph = 90°
Angle of rotation when the wind speed is 4.8 mph = 90° × 4.8 mph 1.2 mph = 360°
Chapter 16
Let’s Warm-up 1. Pentagonal prism 2. Cone 3. Triangular prism 4. Cylinder
Do It Yourself 16A 1. 3 dimensions 2. a. cone b. cuboid c. 0 d. cuboid/ cube e. face 3. Cylinder 4. a. Pentagonal pyramid b. Square prism or cuboid c. Rectangular pyramid d. Hexagonal prism e. Octagonal pyramid
5. a. E = 0; V = 0 b. E = 1; V = 1 c. E = 6; V = 4 d. E = 9; V = 6
6. Cylinder 7. Cube and cuboid
8. Difference: Octagonal prism: 2 octagonal bases and 8 rectangular lateral faces. Octagonal pyramid: 1 octagonal base and 8 triangular lateral faces. Both are 3-D shapes with octagonal bases.
Challenge 1. Cylinder 2.
Do It Yourself 16C
10. The triangles are the bases.
5. a. 5 units × 4 units × 1 unit b. 3 units × 5 units × 2 units
c. 6 units × 3 units × 3 units 6. a. 4 units × 4 units × 4 units
b. 3 units × 5 units × 2 units c. 5 units × 2 units × 2 units
7. Cuboid, 9 cm × 3 cm × 3 cm
Challenge 1. a. b.
Do It Yourself 16D
1. a. Vertical: triangle, Horizontal: circle b. Horizontal: square, Vertical: square c. Horizontal: rectangle, Vertical: rectangle
d. Horizontal: circle, Vertical: circle 2. a. b. c. d. e.
3. Figures may vary. Sample figures: a. b. c. d. e.
4. a. Front , Top , Side
b. Front , Top , Side
c. Front , Top , Side
d. Front , Top , Side
Top view Front view
11. 2 heptagons and 7 rectangles; 1 heptagon and 7 triangles
12. a. b. 13. Answer may vary. Sample answer:
5. a. Front , Side , Top
b. Front , Side , Top
Challenge 1. Two possible cross section areas can be 40 cm2 and 200 cm2.
c. Front , Side , Top
6. Yes, if the light source creating the shadow falls at an angle on the cube. 7. Answers may vary. Sample answer:
a. Sphere b. Cone c. Cube/cuboid d. Cuboid
Challenge 1. 4200 cm2
Chapter Checkup
1. a. Cone b. Cube c. Cylinder d. Triangular prism
2. a. Cuboid b. Square pyramid c. Cube d. Cylinder
3. a. Octahedron b. Hexagonal prism c. Square/rectangular pyramid d. Cylinder 4. a. Cylinder b. Square pyramid c. Cube d. Triangular pyramid
5. a. b. c. d.
2. Figures may vary. Sample figures: 15; Front Top Side
3. a. 6 b. iii
4. Option a Case Study 1. cuboid
2. 6, 8, 12
3. b 4.
6. Figures may vary. Sample figure: 7. i.
5. Top view
8. a. Rectangle b. Rectangle c. Rectangle
9. a. Horizontal: Vertical:
b. Horizontal: Vertical:
c. Horizontal: Vertical:
Front view
About the Book
Imagine Mathematics seamlessly bridges the gap between abstract mathematics and real-world relevance, offering engaging narratives, examples and illustrations that inspire young minds to explore the beauty and power of mathematical thinking. Aligned with the NEP 2020, this book is tailored to make mathematics anxiety-free, encouraging learners to envision mathematical concepts rather than memorize them. The ultimate objective is to cultivate in learners a lifelong appreciation for this vital discipline.
Key Features
• Let’s Recall: Introductory page with a quick recall of concepts learnt in previous grades
• Real Life Connect: Introduction to a new concept related to real-life situations
• Examples: Solved problems showing the correct method and complete solution
• Do It Together: Guided practice for learners with clues and hints to help solve problems
• Think and Tell: Probing questions to stimulate Higher Order Thinking Skills (HOTS)
• Error Alert: A simple tip-off to help avoid misconceptions and common mistakes
• Remember: Key points for easy recollection
• Did You Know? Interesting facts related to the application of concept
• Math Lab: Fun cross-curricular activities
• Challenge: Critical thinking questions to enhance problem-solving and analytical thinking skills
• Case Study: Scenario-based questions to apply theory to real-life situations
• QR Codes: Digital integration through the app to promote self-learning and practice
About Uolo
Uolo partners with K-12 schools to provide technology-enabled learning programs. We believe that pedagogy and technology must come together to deliver scalable learning experiences that generate measurable outcomes. Uolo is trusted by over 15,000+ schools across India, Southeast Asia and the Middle East.
ISBN 978-81-979482-1-3
