Master
Mathematical Thinking
MATHEMATICS
8
MATHEMATICS
Master Mathematical Thinking
Acknowledgements
Academic Authors: Animesh Mittal, Anjana AR, Gitanjali Lal, Anuj Gupta, Simran Singh
Creative Directors: Bhavna Tripathi, Mangal Singh Rana, Satish
Book Production: Sanjay Kumar Goel, Vishesh Agarwal
Project Lead: Neena Aul
VP, Learning: Abhishek Bhatnagar
All products and brand names used in this book are trademarks, registered trademarks or trade names of their respective owners.
© Uolo EdTech Private Limited
First impression 2024
Second impression 2025
This book is sold subject to the condition that it shall not by way of trade or otherwise, be lent, resold, hired out, or otherwise circulated without the publisher’s prior written consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser and without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of both the copyright owner and the above-mentioned publisher of this book.
Book Title: Imagine Mathematics 8
ISBN: 978-81-979482-0-6
Published by Uolo EdTech Private Limited
Corporate Office Address:
85, Sector 44, Gurugram, Haryana 122003
CIN: U74999DL2017PTC322986
Illustrations and images: www.shutterstock.com, www.stock.adobe.com and www.freepik.com
All suggested use of the internet should be under adult supervision.
Preface
Mathematics is an essential tool for understanding the world around us. It is not just another subject, but an integral part of our lives. It shapes the very foundation of our understanding, personality and interaction with the world around us. Studies from across the globe have shown that proficiency in mathematics significantly influences career prospects and lifelong learning.
According to the NEP 2020, mathematics and mathematical thinking are crucial for empowering individuals in their everyday interactions and affairs. It focuses on competencies-based education, which essentially means actively and effectively applying mathematical concepts in real life. It also encourages innovative approaches for teaching maths, including regular use of puzzles, games and relatable real-world examples to make the subject engaging and enjoyable.
It is in this spirit that Uolo has introduced the Imagine Mathematics product for elementary grades (1 to 8). This product’s key objective is to eliminate the fear of mathematics by making math exciting, relatable and meaningful for children.
Imagine Mathematics positions itself on the curricular and pedagogical approach of the Gradual Release of Responsibility (GRR), which has been highly recommended by the NEP 2020, the NCF 2023 and other literature in learning educational pedagogies. Subsequent pages elaborate further on this approach and its actualisation in this book.
This book incorporates highly acclaimed, learner-friendly teaching strategies. Each chapter introduces concepts through real-life situations and storytelling, connecting to children’s experiences and transitioning smoothly from concrete to abstract. Clear explanations and simple steps are provided for problem-solving. Engaging facts, error alerts and fun activities are integrated throughout to keep learning interesting and holistic. Importantly, concepts are interconnected across topics and grades, providing a scaffolding that ensures comprehensive and meaningful learning.
This book supports learners at all levels, providing opportunities to build critical thinking skills through questions and activities aligned with Bloom’s Taxonomy. For those seeking a greater challenge, the book includes thought-provoking questions that push learners to apply, analyse and evaluate. Additionally, the problems are rooted in real-world contexts, making the learning experience both relatable and meaningful.
In addition, the book is technologically empowered and works in sync with a parallel digital world, which contains immersive gamified experiences, video solutions and practice worksheets, among other things. Interactive exercises on the digital platform make learning experiential and help in concrete visualisation of abstract mathematical concepts. We invite educators, parents and students to embrace Imagine and join us in nurturing the next generation of thinkers, innovators and problem-solvers. Embark on this exciting journey with us and let Imagine be a valuable resource in your educational adventure.
Product Package at a Glance
Welcome to our comprehensive learning package designed to enhance educational experiences through three key components: print materials, digital resources and assessment tools. Our print materials provide in-depth and accessible information in a pedagogically suitable way, our digital resources offer interactive and engaging learning experiences, while our assessment tools ensure thorough understanding and progress tracking.
Engaging Textbooks
Teacher Manuals
ASSESSMENT
Competency-based Model Assessments
Question Paper Generator
Student and Teacher Apps
Video Solutions
Interactive Tasks & Exercises
Byte Size Lesson Modules
Key NEP Recommendations
The National Education Policy (NEP) 2020, introduced by the Government of India, represents a transformative shift in the country’s education system. It aims to create a more holistic, dynamic and multidisciplinary approach to education. NEP 2020 focuses on fostering conceptual understanding, skills and values that align with the demands of the 21st century, while also preserving India’s rich cultural heritage. UOLO is fully committed to actualising the vision of NEP 2020 by meticulously adhering to its outlined recommendations.
1. Focus on conceptual understanding
2. 21st century skills, values and dispositions
3. Critical thinking and problem-solving
4. Application in real life
5. Holistic and integrated learning
6. Experiential learning
7. Enjoyable and engaging
8. Computational and mathematical thinking
9. Technology-based solutions
10. Factoids on India
Competency-based Education
NEP Pages 12, 17, and 22
Teaching and Learning Pedagogy
NEP Pages 3, 11, 12, 18, and 27
National Pride
NEP Pages 15, 16, and 43
11. Assessment of core concepts and application skills Assessments
NEP Pages 12, 18, and 22
Our Key Features: Aligning with the NEP
The GRR Approach
Pedagogical approach that empowers students to learn by the teacher progressively transitioning the responsibility to the students.
Competency-based Assessments
Test papers designed to evaluate understanding of core concepts and application of skills.
3 8 11
Contextual Learning
Introducing concepts through real-life situations and connecting them to students’ experiences.
Classroom Activity
A hands-on classroom activity to investigate and understand mathematical concepts in an engaging and concrete way.
Recall and Revisit
Introductory page with a quick recall of concepts done in previous grades.
Translating Words into Action!
Critical Thinking Questions
Intellectually stimulating questions designed to enhance problem-solving and analytical-thinking skills, promote deeper understanding and foster independent thinking.
Real-Life Math Problems
Scenario-based questions designed to help in applying theoretical knowledge to real-world scenarios, reasoning skills and improves reading comprehension & analytical abilities.
Common Misconceptions
Concise snippets of information designed to caution against potential errors and misconceptions
Think, Analyse and Answer
A quick, mathematical-thinking question
Fun Facts
Facts related to the concepts, or bite-sized information about the contribution of Indian scholars to mathematics
Gradual Release of Responsibility
The Gradual Release of Responsibility (GRR) is a highly effective pedagogical approach that empowers students to learn progressively by transitioning the responsibility from the teacher to the students. This method involves comprehensive scaffolding—including modelling, guided practice, and ultimately fostering independent application of concepts.
GRR, endorsed and promoted by both the NEP 2020 and NCF, plays a pivotal role in equipping teachers to facilitate age-appropriate learning outcomes and enabling learners to thrive.
The GRR methodology forms the foundation of the Imagine Mathematics product. Within each chapter, every unit follows a consistent framework:
1. I Do (entirely teacher-led)
2. We Do (guided practice for learners supported by the teacher)
3. You Do (independent practice for learners)
GRR Steps Unit Component
Understanding Large Numbers
Dhruv was reading a newspaper. He came across news about different states in India that participated in the COVID vaccination drive and the number of vaccinations given until August 2023. Given below is the data of four states.
Real Life Connect
Theoretical Explanation
I do
Delhi Haryana Sikkim Goa 37409161 45546836 1360477 2874477
The temperature can change with different weather conditions. On a sunny day, the air feels warm, and the thermometer shows a higher temperature. On a cloudy or rainy day, the air feels cooler, and the temperature on the thermometer drops. Weather conditions like rain, wind and sunlight can all affect the temperature of the air.
All About 7-Digit and 8-Digit Numbers
Temperature Range (°C) Weather
While reading the news, Dhruv got confused and could not read the numbers given in the data. The numbers of vaccinations given were either 7-digit numbers or 8-digit numbers.
The temperature can change with different weather conditions. On a sunny day, the air feels warm, and the thermometer shows a higher temperature. On a cloudy or rainy day, the air feels cooler, and the temperature on the thermometer drops. Weather conditions like rain, wind and sunlight can all affect the temperature of the air.
Temperature Range (°C)
Below 0 Very Cold 0–10 Cold 11–20 Mild 21–30 Warm 31–40 Hot
Examples
Did You Know?
Sikkim Goa Delhi Haryana 1360477 2874477 37409161 45546836
Did You Know?
Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.
Above 40 Very Hot
7-digit Numbers 8-digit Numbers
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?
Normal body temperature = 37°C.
Place Value, Face Value and Expanded Form Reading and Writing 7-Digit and 8-Digit Numbers
Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?
Aliya’s body temperature = 37°C + 2.3°C = 39.3°C
Let us help Dhruv understand 7-digit and 8-digit numbers!
Normal body temperature = 37°C.
So, Aliya’s body temperature was 39.3°C.
Aliya’s body temperature = 37°C + 2.3°C = 39.3°C
We know that the greatest 6-digit number is 999999. Now, if we add 1 to this number, we get 1000000. 999999 + 1 = 1000000
Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?
So, Aliya’s body temperature was 39.3°C.
To find the difference, subtract the lowest temperature from the highest temperature.
37.5°C – 21.2°C = 16.3°C
Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?
The temperature difference is 16.3°C.
1000000 is the smallest 7-digit number and is read as “Ten Lakhs”. We saw in the news article that the number of vaccinations administered in Sikkim was 1360477. Let us try to place this 7-digit number in the place value chart.
To find the difference, subtract the lowest temperature from the highest temperature.
Write the readings of the given thermometers.
37.5°C – 21.2°C = 16.3°C
The temperature difference is 16.3°C. Write the readings of the given thermometers.
2
Temperature = 45°C Temperature = Temperature = Temperature =
Converting Between Units of Temperature
Temperature = 45°C Temperature = Temperature = Temperature =
Celsius (°C) is like the universal language of temperature. Fahrenheit (°F) is another way to talk about temperature. We learnt that water freezes at 0°C and boils at 100°C. In Fahrenheit, water freezes at 32°F and boils at 212°F.
Converting Between Units of Temperature
Celsius (°C) is like the universal language of temperature. Fahrenheit (°F) is another way to talk about temperature. We learnt that water freezes at 0°C and boils at 100°C. In Fahrenheit, water freezes at 32°F and boils at 212°F.
GRR Steps Unit Component
Do It Yourself Challenge
You do
Chapter Checkup Challenge
Case Study
Do It Yourself 14B
1 Identify the shape for which the net is drawn.
Do as directed.
a Write the greatest 7-digit number that has the smallest odd digit at its hundreds, ten thousands and lakhs place.
b Write the smallest 8-digit number that has the digit 7 at all its odd positions, starting from the ones place.
2 Look at the net and identify the object it belongs to.
3 Draw the net of the given shapes.
The Kumbh Mela is a major pilgrimage where Hindu pilgrims take the holy bath in the Ganges. The number of people who visited the Kumbh Mela in 1980 were 20,356,817 and those who visited in 1989 were 29,304,871. In which year did less than 25 crore people visit to the Kumbh Mela?
a 1980 b 1989 c Both years d None of the year
4 Rishi and Megha made the net of a square-based pyramid. Who made the net correctly? Explain your answer with reasons.
Comparing, Ordering and Rounding-Off Large Numbers
a Rishi’s drawing
Chapter Checkup
b Megha’s drawing
During COVID, India offered support to 150 affected countries in the form of vaccines, medical equipment and medicines. Given below is the data of the number of vaccine doses supplied by India to four different countries.
Guess the best units of length (m or cm) and weight (kg or g) for the given objects. a b c
5 Draw the net of a hexagonal prism.
6 Show using nets how a rectangular prism is different from a rectangular pyramid.
Comparing and Ordering Numbers
Measure the objects.
Rahul: Which country did India supply the greatest number of vaccine doses to?
Challenge
Challenge
Bran: We could compare the numbers to find the country to which India supplied the greatest number of vaccine doses.
Comparing Numbers
Critical Thinking
Critical Thinking
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
a The digit in the hundreds and ones place is 6.
a The digit in the hundreds and ones place is 6.
What if Rahul wanted to compare the number of vaccines sent to Nepal and Australia? Let us find out.
b The digit in the lakhs place is 4 less than the digit in the ones place.
b The digit in the lakhs place is 4 less than the digit in the ones place.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
Since 94,99,000 has 7 digits and 3,09,13,200 has 8 digits, 3,09,13,200 > 94,99,000.
d The face value of the digit in the thousands place is 5.
d The face value of the digit in the thousands place is 5.
Thus, Australia was donated more vaccine doses.
Remember!
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
Now, what if we want to compare two numbers with the same number of digits? Let us consider 4,13,23,456 and 4,13,23,657.
A number with more number of digits is always greater.
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
James has some cotton candy which is 3 cm longer than the cotton candy shown below. How long is James’ cotton candy?
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
Chapter 1 • Numbers up to 8 Digits
Case Study
Case Study
How much longer is the red straw than the blue straw?
Cross Curricular
Cross Curricular
Population of Countries
Population of Countries
The population of different countries is shown using a table. Read the data carefully and answer the questions.
Country
Convert the lengths.
Convert the weights.
The population of different countries is shown using a table. Read the data carefully and answer the questions.
United
United
a 5 kg into g b 4 g 64 cg into g c 5487 g into mg d 43 kg 7 dag into kg
A baby koala is called a joey. A young joey weighs about 0.38 kg. How much is that in g?
58,870,762
A candle weighs 125 g. How much is it in mg?
1 Which country has the least population?
1 Which country has the least population?
a Italy b Germany c Poland d United Kingdom
a Italy b Germany c Poland d United Kingdom
2 Which country has the greatest population?
2 Which country has the greatest population?
a Poland b United Kingdom c Italy d Germany
Pearson, P. D., & Gallagher, G. (1983). Contemporary Educational Psychology. Fisher, D., & Frey, N. (2021). Better learning through structured teaching: A framework for the gradual release of responsibility. Fisher, D., & Frey, N. (2014). Checking for understanding: Formative assessment techniques for your classroom. 200
a Poland b United Kingdom c Italy d Germany
3 Which country has approximately double the population than that of Poland?
3 Which country has approximately double the population than that of Poland?
4 Arrange the countries in ascending order as per their population.
4 Arrange the countries in ascending order as per their population.
5 If all the digits in the population of each country is rearranged to form the greatest number, then which country will have the greatest population?
5 If all the digits in the population of each country is rearranged to form the greatest number, then which country will have the greatest population?
The NEP Tags
The National Education Policy (NEP), 2020, outlines essential skills, values, dispositions and learning approaches necessary for students to thrive in the 21st century. This textbook identifies and incorporates these elements throughout its content, activities and exercises. Referred to as “NEP Tags,” they are defined as follows:
Art Integration
Bringing creativity and fun into learning by combining art with maths. Students construct and demonstrate understanding through an art form.
Collaboration
Working effectively with others. Includes clear communication, teamwork, active listening and valuing diverse approaches.
Cross Curricular
Integrating mathematical concepts with other subjects to see the real-life applications of maths.
Experiential Learning
Gaining knowledge and skills through direct, hands-on experiences rather than a traditional classroom setting.
Communication
Explaining mathematical ideas, processes and solutions to others, whether through verbal explanations, written work or visual representations.
Value Development
Promoting ethics, and human & constitutional values, like empathy, respect for others, cleanliness, courtesy, democratic spirit, spirit of service, respect for public property, responsibility and equality.
Creativity
Using imagination and original thinking to solve problems and explore mathematical concepts in innovative ways. Also includes finding unique solutions, and designing original problem-solving strategies.
Education Standards as per the NCF 2023
The National Curriculum Framework for School Education (NCF), released in 2023, is based on the vision of the National Education Policy (NEP), 2020, and enables its implementation. The NCF provides guidelines for designing school syllabi and textbooks in India. It aims to improve the quality of education by making it more relevant, engaging, inclusive and learner-centric. To achieve this, the NCF has articulated precise Learning Standards through well-defined Curricular Goals and Competencies. These statements serve to harmonise the syllabus, content, pedagogical practices and assessment culture, ensuring a cohesive and comprehensive educational experience.
Curricular Goals: Statements that give direction to curriculum development and implementation in order to achieve the Curricular Aims. They are also specific to a School Stage (e.g., the Foundational Stage) and a Curricular Area (e.g., Mathematics).
Competencies: Learning achievements that are observable and can be assessed systematically. These Competencies are derived from the Curricular Goals and are expected to be attained by the end of a Stage.
NCF Page 218
Curricular Goals
CG-1
Understands numbers and sets of numbers (whole numbers, fractions, integers, rational numbers, and real numbers), looks for patterns, and appreciates relationships between numbers
CG-2
Understands the concepts of variable, constant, coefficient, expression, and (one-variable) equation, and uses these concepts to solve meaningful daily-life problems with procedural fluency
Competencies
C-1.1 Develops a sense for and an ability to manipulate (e.g., read, write, form, compare, estimate, and apply operations) and name (in words) large whole numbers of up to 20 digits, and expresses them in scientific notation using exponents and powers
C-1.2 Discovers, identifies, and explores patterns in numbers and describes rules for their formation (e.g., multiples of 7, powers of 3, prime numbers), and explains relations between different patterns.
C-1.3 Learns about the inclusion of zero and negative quantities as numbers, and the arithmetic operations on them, as given by Brahmagupta
C-1.4 Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line
C-1.5 Explores the idea of percentage and applies it to solve problems
C-1.6 Explores and applies fractions (both as ratios and in decimal form) in daily-life situations
C-2.1 Understands equality between numerical expressions and learns to check arithmetical equations
C-2.2 Extends the representation of a number in the form of a variable or an algebraic expression using a variable
C-2.3 Forms algebraic expressions using variables, coefficients, and constants and manipulates them through basic operations
C-2.4 Poses and solves linear equations to find the value of an unknown, including to solve puzzles and word problems
C-2.5 Develops own methods to solve puzzles and problems using algebraic thinking
The above is an abridged version of the curricular goals and competencies relatioship in Maths for the Foundational Stage (NCF 2023, pages 340–341). The next section shows the coverage of all these competencies across the chapters.
Mapping with NCF 2023
C-1.1 Develops a sense for and an ability to manipulate (e.g., read, write, form, compare, estimate, and apply operations) and name (in words) large whole numbers of up to 20 digits, and expresses them in scientific notation using exponents and powers
C-1.2 Discovers, identifies, and explores patterns in numbers and describes rules for their formation (e.g., multiples of 7, powers of 3, prime numbers), and explains relations between different patterns.
C-1.3 Learns about the inclusion of zero and negative quantities as numbers, and the arithmetic operations on them, as given by Brahmagupta
C-1.4 Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line
C-1.5 Explores the idea of percentage and applies it to solve problems
C-1.6 Explores and applies fractions (both as ratios and in decimal form) in daily-life situations
C-2.1 Understands equality between numerical expressions and learns to check arithmetical equations
C-2.2 Extends the representation of a number in the form of a variable or an algebraic expression using a variable
C-2.3 Forms algebraic expressions using variables, coefficients, and constants and manipulates them through basic operations
C-2.4 Poses and solves linear equations to find the value of an unknown, including to solve puzzles and word problems
C-2.5 Develops own methods to solve puzzles and problems using algebraic thinking
C-3.1 Describes, classifies, and understands relationships among different types of two—and three-dimensional shapes using their defining properties/attributes
C-3.2 Outlines the properties of lines, angles, triangles, quadrilaterals, and polygons and applies them to solve related problems
C-3.3 Identifies attributes of three-dimensional shapes (cubes, parallelepipeds, cylinders, cones), works hands-on with material to construct these shapes, and also uses twodimensional representations of three-dimensional objects to visualise and solve problems
C-3.4 Draws and constructs geometric shapes, such as lines, parallel lines, perpendicular lines, angles, and simple triangles, with specified properties using a compass and straightedge
C-3.5 Understands congruence and similarity as it applies to geometric shapes and identifies similar and congruent triangles
CG-1
Understands numbers and sets of numbers (whole numbers, fractions, integers, rational numbers, and real numbers), looks for patterns, and appreciates relationships between numbers
CG-2
Understands the concepts of variable, constant, coefficient, expression, and (one-variable) equation, and uses these concepts to solve meaningful daily-life problems with procedural fluency
CG-3
UUnderstands, formulates, and applies properties and theorems regarding simple geometric shapes (2D and 3D)
C-4.1 Discovers, understands, and uses formulae to determine the area of a square, triangle, parallelogram, and trapezium and develops strategies to find the areas of composite 2D shapes
C-4.2 Learns the Baudhayana-Pythagoras theorem on the lengths of the sides of a right-angled triangle, and discovers a geometric proof using areas of squares erected on the sides of the triangle, and other related geometric constructions from the Sulba-Sutras
C-4.3 Constructs various designs (using tiling) on a plane surface using different 2D shapes and appreciates their appearances in art in India and around the world
C-4.4 Develops familiarity with the notion of fractal and identifies and appreciates the appearances of fractals in nature and art in India and around the world
C-5.1 Collects, organises, and interprets the data using measures of central tendencies such as average/mean, mode, and median
C-5.2 Selects, creates, and uses appropriate graphical representations (e.g., pictographs, bar graphs, histograms, line graphs, and pie charts) of data to make interpretations
C-6.1 Applies both inductive and deductive logic to formulate definitions and conjectures, evaluate and produce convincing arguments/ proofs to turn these definitions and conjectures into theorems or correct statements, particularly in the areas of algebra, elementary number theory, and geometry
C-7.1 Demonstrates creativity in discovering one’s own solutions to puzzles and other problems, and appreciates the work of others in finding their own, possibly different, solutions
C-7.2 Engages in and appreciates the artistry and aesthetics of puzzle-making and puzzle-solving
C-8.1 Approaches problems using programmatic thinking techniques such as iteration, symbolic representation, and logical operations and reformulates problems into series of ordered steps (i.e., algorithmic thinking)
C-8.2 Learns systematic counting and listing, systematic reasoning about counts and iterative patterns, and multiple data representations; learns to devise and follow algorithms, with an eye towards understanding correctness, effectiveness, and efficiency of algorithms
C-9.1 Recognises how concepts (like counting numbers, whole numbers, negative numbers, rational numbers, zero, concepts of algebra, geometry) evolved over a period of time in different civilisations.
C-9.2 Knows and appreciates the contributions of specific Indian mathematicians (such as Baudhayana, Pingala, Aryabhata, Brahmagupta, Virahanka, Bhaskara, and Ramanujan)
CG-4
Develops understanding of perimeter and area for 2D shapes and uses them to solve day-to-day life problems
CG-5
Collects, organises, represents (graphically and in tables), and interprets data/information from daily-life experiences
CG-6 Develops mathematical thinking and the ability to communicate mathematical ideas logically and precisely
CG-7 Develops mathematical thinking and the ability to communicate mathematical ideas logically and precisely
CG-8 Develops basic skills and capacities of computational thinking, namely, decomposition, pattern recognition, data representation, generalisation, abstraction, and algorithms in order to solve problems where such techniques of computational thinking are effective
CG-9 Knows and appreciates the development of mathematical ideas over a period of time and the contributions of past and modern mathematicians from India and across the world
CG-10 Knows about and appreciates the interaction of Mathematics with each of their other school subjects Recognises interaction of Mathematics with multiple subjects across Science, Social Science, Visual Arts, Music, Vocational Education, and Sports
1
Numbers up to 8 Digits
Let’s Recall
Numbers are used everywhere in our daily lives. These numbers are formed using the digits 0 to 9 and are written using commas after every period, starting from the one’s period.
Chapter at a Glance: Walkthrough of Key Elements
For example, let us say the pin code of your area is 201301. This is a 6-digit number. It can be written using commas by representing it in a place value chart.
1 Numbers up to 8 Digits
Number Lakhs Thousands Ones Lakhs (L) Ten Thousand (TTh) Thousands (Th) Hundreds (H) Tens (T) Ones (O) 2,01,301 2 0 1 3 0 1
Each of these digits has a place value and a face value. Let us write the face value, place value, expanded form and number name for 201301. periods place
Let’s Recall
Numbers are used everywhere in our daily lives. These numbers are formed using the digits 0 to 9 and are written using commas after every period, starting from the one’s period.
Let’s Recall: Introductory page with a quick recall of concepts learnt in the previous grade
For example, let us say the pin code of your area is 201301. This is a 6-digit number. It can be written using commas by representing it in a place value chart.
Expanded form:
Number name: Two lakh
Dhruv was reading a newspaper. He came across news about different states in participated in the COVID vaccination drive and the number of vaccinations given August 2023. Given below is the data of four states.
Each of these digits has a place value and a face value. Let us write the face value, place value, expanded form and number name for 201301.
Letʹs Warm-up Fill in the blanks.
1 The place value of 8 in 8,60,765 is 2 The number 4,36,536 can be written in words as:
Let’s Warm-up: Quick 4–5 questions to test the pre-knowledge
3 The place value of the digit in 4,15,124 and 4,67,890 is the same. 4 8,76,504 has 6 in the place.
Expanded form: 2,00,000 + 1000 + 300 + 1 Number
1
All About 7-Digit and 8-Digit Numbers
I scored out of 4.
The temperature can change with different weather conditions. On a sunny day, the air feels warm, and the thermometer shows a higher temperature. On a cloudy or rainy day, the air feels cooler, and the temperature on the thermometer drops. Weather conditions like rain, wind and sunlight can all affect the temperature of the air.
While reading the news, Dhruv got confused and could not read the numbers given data. The numbers of vaccinations given were either 7-digit numbers or 8-digit
Temperature Range (°C) Weather
3 The place value of the
Explanation:
Dhruv was reading a newspaper. He came across news participated in the COVID vaccination drive and the August 2023. Given below is the data of four states.
The temperature can change with different weather conditions. On a sunny day, the air feels warm, and the thermometer shows a higher temperature. On a cloudy or rainy day, the air feels cooler, and the temperature on the thermometer drops. Weather conditions like rain, wind and sunlight can all affect the temperature of the air.
Temperature Range (°C) Weather
Below 0 Very Cold
0–10 Cold
11–20 Mild
21–30 Warm
31–40 Hot
Numbers 8-digit Numbers
Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.
Place Value, Face Value and Expanded Form
Reading and Writing 7-Digit and 8-Digit Numbers
Did You Know?
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?
Normal body temperature = 37°C.
Above 40 Very Hot
Let us help Dhruv understand 7-digit and 8-digit numbers! We know that the greatest 6-digit number is 999999. Now, if we add 1 to this number, we get 1000000.
Aliya’s body temperature = 37°C + 2.3°C = 39.3°C
Normal body temperature = 37°C.
Drass in Jammu and Kashmir is the second coldest inhabited region on Earth.
999999 + 1 = 1000000
So, Aliya’s body temperature was 39.3°C.
Example 8: Aliya’s body temperature was 2.3°C higher than normal. What was Aliya’s body temperature?
Aliya’s body temperature = 37°C + 2.3°C = 39.3°C
So, Aliya’s body temperature was 39.3°C.
All About 7-Digit and 8-Digit Numbers
Examples: Solved problems showing the correct method and complete solution
While reading the news, Dhruv got confused and could data. The numbers of vaccinations given were either
Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?
To find the difference, subtract the lowest temperature from the highest temperature. 37.5°C – 21.2°C = 16.3°C
Example 9: In a city, the highest temperature was 37.5°C, and the lowest was 21.2°C. What is the difference between these two temperatures?
37.5°C – 21.2°C = 16.3°C
The temperature difference is 16.3°C.
1000000 is the smallest 7-digit number and is read as “Ten Lakhs”. We saw in the news article that the number of vaccinations administered in Sikkim 1360477. Let us try to place this 7-digit number in the place value chart.
To find the difference, subtract the lowest temperature from the highest temperature.
Write the readings of the given thermometers.
The temperature difference is 16.3°C. Write the readings of the given thermometers. Temperature = 45°C
Do It Together: Guided practice for learners with partially solved questions
Converting Between Units of Temperature
Place Value, Face Value and Expanded Form
2 4
Reading and Writing 7-Digit and 8-Digit Numbers
Let us help Dhruv understand 7-digit and 8-digit numbers!
We know that the greatest 6-digit number is 999999.
Converting Between Units of Temperature
Now, if we add 1 to this number, we get 1000000.
Celsius (°C) is like the universal language of temperature. Fahrenheit (°F) is another way to talk about temperature. We learnt that water freezes at 0°C and boils at 100°C. In Fahrenheit, water freezes at 32°F and boils at 212°F.
Celsius (°C) is like the universal language of temperature. Fahrenheit (°F) is another way to talk about temperature. We learnt that water freezes at 0°C and boils at 100°C. In Fahrenheit, water freezes at 32°F and boils at 212°F. Did You Know?
1000000 is the smallest 7-digit number and is read
15 • Time and Temperature
We saw in the news article that the number of vaccinations 1360477. Let us try to place this 7-digit number in
Let
1
1
Fill
Word Problems on Length
Did You Know: Interesting facts related to the topic
Do It Yourself: Exercise at the end of each topic with practice questions
After making a pair of trousers with 2 m of cloth, Sana thought of buying 1 m 55 cm of cloth for making a shirt. Let us see what length of cloth she has together.
Cloth bought by Sana for making a pair of trousers = 2 m
Cloth required by Sana for making a shirt = 1 m 55 cm = 1.55 m
Total cloth required by Sana =
NEP Tags: To show alignment with NEP skills and values
Do It Yourself 14B
Error Alert: Caution against misconceptions
1 Identify the shape for which the net is drawn. a b c d
2 Look at the net and identify the object it belongs to. a b c d
3 Draw the net of the given shapes.
4 Rishi and Megha made the net of a square-based pyramid. Who made the net correctly? Explain answer with reasons.
a Rishi’s drawing b Megha’s drawing
Chapter Checkup: Chapter-end practice exercises aligned to different levels of Blooms Taxonomy
5 Draw the net of a hexagonal prism.
6 Show using nets how a rectangular prism is different from a rectangular pyramid.
Picture-based Questions: Questions featuring visual stimuli to foster comprehension and interpretation
Challenge
Challenge
Challenge: Critical thinking questions to enhance problem-solving and analytical-thinking skills
Case Study: Scenario-based questions designed to help apply theoretical knowledge to real-world situations
Real-life Questions: Questions that help make connections with real life or other subjects
Critical Thinking
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
a The digit in the hundreds and ones place is 6.
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya solve the secret code.
b The digit in the lakhs place is 4 less than the digit in the ones place.
a The digit in the hundreds and ones place is 6.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
d The face value of the digit in the thousands place is 5.
b The digit in the lakhs place is 4 less than the digit in the ones place.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
d The face value of the digit in the thousands place is 5.
1 Sanya wants to solve a 7-digit secret code in a safe. Use the given clues to help Sanya
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice. Critical Thinking
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
a The digit in the hundreds and ones place is 6.
b The digit in the lakhs place is 4 less than the digit in the ones place.
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
c The digit in the ten lakhs and ten thousands place is the smallest odd number.
Case Study
Case Study
Thinking Case Study
d The face value of the digit in the thousands place is 5.
e The digit in the tens place is the biggest 1-digit number. What is the secret code?
Population of Countries
2 Write the greatest 8-digit odd number using only 5 digits. Do not repeat any digit more than twice.
Cross Curricular
The population of different countries is shown using a table. Read the data carefully and answer the questions.
Population of Countries
The population of different countries is shown using a table. Read the data carefully and answer the questions.
Curricular
Country Population
Population of Countries
The population of different countries is shown using a table. Read the data carefully and answer the questions.
1 Which country has the least population? a Italy b Germany c Poland d United Kingdom
1 Which country has the least population?
2 Which country has the greatest population?
a Poland b United Kingdom c Italy d Germany
2 Which country has the greatest population?
3 Which country has approximately double the population than that of Poland?
4 Arrange the countries in ascending order as per their population.
1 Which country has the least population?
3 Which country has approximately double the population than that of Poland?
5 If all the digits in the population of each country is rearranged to form the greatest
Cross Curricular
1 Rational Numbers
Let’s Recall
A rational number is a number that is expressed as p q , where p and q are integers, and the denominator should never be equal to zero.
For example, 12.5, −15, 25, 67 and - 8 9 are all rational numbers.
Let us recap how to represent, order and compare rational numbers.
Identifying and Representing Rational Numbers
Comparing and Ordering Rational Numbers
Let us compare −2.5 and −7 3 using some steps.
Step 1
Write all the rational numbers in the same form.
−2.5 = −25 10 = −5 2 −7 3 remains the same.
Letʼs Warm-up
Step 2
Find the LCM of the denominators in case they are different.
LCM of 2 and 3 = 6
Fill in the blanks with the correct sign. (<, > or =)
Step 3
Find an equivalent rational numbers with the LCM as the denominator.
Any number that can be
Step 4
Compare the numerators.
< −14,
−2.5 < 7 3
Operations on Rational Numbers
Shubhi and Rishabh recorded the temperature in their city over the past 5 days. They record the data in the form of rational numbers.
Both of them performed various operations on the rational numbers and found different data. Let us see how!
Addition and Subtraction of Rational Numbers
Addition of Rational Numbers
The addition of rational numbers is similar to the addition of fractions. However, we first have to convert all the rational numbers to be added into rational numbers with positive denominators.
Let us use the data collected by Rishabh and Shubhi and look at the cases and steps of addition of rational numbers.
1 16 5 + 9 5 = (16 + 9) 5
= 25 5
= 5
−3 2 + 9 5
The LCM of 2 and 5 is 10.
Write the equivalent rational numbers with the denominator as the LCM. −3 × 5 2 × 5 = −15
Adding Rational Numbers with Negative Denominators
Let us add 16 5 and 3 4
Converting 3 4 into a rational number with a positive denominator, we get 3 4 × 1 1 = 3 4
LCM of 5 and 4 = 20
Write the rational numbers with denominators as 20: 16 × 4 5 × 4 = 64 20 and 3 × 5 4 × 5 = 15 20
So, 16 5 + ( 3) 4 = 64 20 + ( 15) 20 = 64 15 20 = 49 20.
Example 1: Add 18 4 , −19 8 and 2.5.
2.5 can also be written as 25 10.
Think and Tell Is
pi a rational number?
Did You Know?
The Indian mathematician Aryabhatta introduced zero. After him, another Indian mathematician Brahmagupta described rules for zero in the 7th century.
The LCM of 4, 8 and 10 is 40.
Write the rational numbers with the denominator as 40:
18 × 10 4 × 10 = 180 40 , −19 × 5 8 × 5 = −95 40 and 25 × 4 10 × 4 = 100 40
Hence, 18 4 + (−19) 8 + 25 10
180 40 + (−95) 40 + 100 40 = 180 − 95 + 100 40 = 185 40 = 37 8
Example 2: A shopkeeper sold 2 1 4 kg, 5 3 8 kg, 1.5 kg and 4
kg of rice to four customers. Find the total amount of rice sold by the shopkeeper. The weights can be expressed as rational numbers as:
2 1 4 = 9 4 , 5 3 8 = 43 8 , 1.5 = 15 10 = 3 2 and 4 2 3 = 14 3
Total weight of rice sold = 9 4 + 43 8 + 3 2 + 14 3
LCM of 4, 8, 2 and 3 = 24
Hence, the total rice sold = 54 24 + 129 24 + 36 24 + 112 24
= 54 + 129 + 36 + 112 24 = 331 24 kg = 1319 24 kg
1 Add 15 4 , 23 5 and 3.6. 3.6 can also be written as
Hence, + + = = = Do It Together
The LCM of 4, 5 and is .
Write the rational numbers with the denominator as = ; ; Hence, + + = = =
2 Add 5 3, 6 ‒13 and ‒2.8.
Converting 6 ‒13 into a rational number with a positive denominator, we get 6 ‒13 × ‒1 ‒1 = ‒2.8 can also be written as =
The LCM of 3, 13 and is .
Write the rational numbers with the denominator as ____. = ; ;
Subtraction of Rational Numbers
We know that subtraction is the opposite or inverse of addition. To subtract two rational numbers, we simply add the additive inverse of the rational number to be subtracted to the first rational number. Also, the rational numbers should have a positive denominator.
For example, 17 37 2 = 17 3 + (-7) 2 = 34 + (-21) 6 = 34 - 21 6 =
What if the rational numbers are in different forms?
We will first convert the numbers into the same form.
Let us subtract 23 5 from 7.85.
Method 1
Convert 23 5 to a decimal.
23 5 = 4.6
7.85 - 4.6 = 3.25
Method 2
Convert 7.85 to a fraction. 7.85 = 785 100
4
What if we have more than two rational numbers with different signs between them? Let us find out!
Simplify: 2 3 + 5 91 6 + 4 3
To simplify the above statement, we will find the LCM of all the denominators and convert them to like rational numbers.
LCM of 3, 9, 6 = 18
Hence, 2 3 + 5 9 + (-1) 6 + 4 3 = 12 + 10 -3 + 24 18 = 43 18
Example 3: Simplify: 7 6 + 8 9-3 12 + -9 15
7 6 + 8 9-3 12 + -9 15 = 7 6 + 8 9 + additive inverse of -3 12 + -9 15
⇒ 7 6 + 8 9 + 3 12 + -9 15 (The LCM of 6, 9, 12 and 15 is 180.)
⇒ 210 180 + 160 180 + 45 180 + -108 180
⇒ 210 + 160 + 45 - 108 180 = 307 180
Example 4: A drum full of sugar weighs 521 12 kg. Suppose the empty drum weighs 12.5 kg. What is the weight of the sugar in the drum?
Weight of the drum with sugar = 521 12 kg
Weight of the empty drum = 12.5 kg = 125 10 = 25 2 kg
Weight of sugar = 521 12 - 25 2 = 521 12 + (-25) 2 = 521 12 + (-150) 12 (The LCM of 12 and 2 is 12.)
= 521 - 150 12 = 371 12 kg
Example 5: Avinash bought 18 kg of flour. He used 3.5 kg in the first week, 4.25 kg in the second week, 4 7 8 kg in the third week and the rest in the last week. How much flour did he use in the last week?
Total flour bought = 18 kg
Let us first convert all the rational numbers to the same form.
3.5 kg = 3 1 2 kg; 4.25 kg = 4 1 4 kg; and 4 7 8 remains the same.
Total flour used in the first three weeks = 3 1 2 + 4 1 4 + 4 7 8 kg
= 7 2 + 17 4 + 39 8 kg = 28 + 34 + 39 8 = 101 8 kg = 12 5 8 kg
Flour used in the last week = 18 − 12 5 8 = 18 − 101 8 = 144 - 101 8 = 43 8 = 5 3 8 kg
Example 6: What decimal number should be subtracted from 19 4 to get -7 5 ?
Let the decimal number subtracted be x.
19 4 - x = - 7 5 ⇒ x = 19 4 + 7 5 = 95 + 28 20 = 123 20 123 20 can be converted to a decimal as: 6.15
Hence, on subtracting 6.15 from 19 4 we get - 7 5 .
1 Subtract 12 5 from 6.25.
Convert both rational numbers to the same form.
Converting 12 5 to decimal form we get 12 5 = 6.25 − = = in fraction form.
2 Subtract 5 ‒2 from 31 2 .
Convert 5 -2 to a positive denominator.
5 -2 × ‒1 ‒1 = 31 2 = − =
Properties of Addition and Subtraction of Rational Numbers
Closure Property
If a b and c d are rational numbers, then a b + c d and a bc d are also rational numbers.
For example: -5 7 + 3 14 = -7 14 or -1 2 (Rational number) For example: - 4.51 2 = -5 (Rational number)
Commutative Property For Addition For Subtraction
If a b and c d are rational numbers, then a b + c
For example: 5 7 + 3 14 = 13 14 and 3 14 + 5 7 = 13 14
So, 5 7 + 3 14 = 3 14 + 5 7
If a b and c d are rational numbers, then
For example: 8 97 9 = 1 9 but 7 98 9 = -1 9 So, 8 97 9 ≠ 7 98 9
Associative Property For Addition For Subtraction
If
, c
and e f are rational numbers,
If a b is a rational number, then a b + 0 = 0 + a b = a b . If
Example 7: Verify if m – n is a rational number if m = –9 11 and n = 6 22. m - n = - 9 116 22 = - 18 - 6 22 = - 24 22 = - 12 11 = rational number
Example 8: Verify that 3 4 + 5 8 = 5 8 + 3 4
Solving the LHS, LCM of 4 and 8 is 8.
3 4 + 5 8 = 6 + 5 8 = 11 8
Solving the RHS, LCM of 4 and 8 is 8.
5 8 + 3 4 = 5 + 6 8 = 11 8
As LHS = RHS, 3 4 + 5 8 = 5 8 + 3 4
Example 9: If 5 4, 3 8 and 7 12 are three rational numbers, then prove that they are not associative under subtraction.
The associative property for subtraction states that
So, 5 43
7 24 ≠ 35 24; hence, rational numbers are not associative under subtraction.
Fill in the blanks using the properties of rational numbers. Also name the property used.
1 5 2 - = 5 2
Property Used = Property Used = Property Used = Additive Inverse Do It
1 Solve.
Do It Yourself 1A
2 Find the additive inverse of the rational numbers.
4 Name the property illustrated through each of the operations.
5 Fill in the blanks using the properties of rational numbers. Also name the property used.
6 Verify the following.
7 What rational number in its decimal form should be added to 21 5 to get - 27 6 ?
8 What rational number in its fraction form should be subtracted from 8.5 to get - 12.25?
9 Simplify: 5 6 + (- 3) 86 12 + (- 3) 242 88 (- 16)
10 In the 2024-25 Union Budget of India, around 1 5 of the total budget was allocated to urban development while around 11 200 of the total budget was allocated to rural development. What was the fraction of the total budget allocated to both urban and rural development?
11 A carpenter bought a piece of wood 12 2 3 feet long. He then cut off 5 8 feet from both ends. How long is the piece of wood now?
12 Suhani purchased 15 4 kg of apples, 2.6 kg of bananas and some oranges from the market. Altogether, she purchased 9 kg of fruit to distribute to the needy. What is the weight of the oranges she purchased? Do you distribute fruits and vegetables to the needy?
1 Find the rational number that must be added and subtracted to take the sum of 8 9 + 5 37 6 to the nearest whole number
2 A school prepared 25.5 litres of juice for its players. The players drank 8 2 5 litres in the first half. In the second half, the players drank 2 3 8 litres more than in the first half. What was the volume of the juice left at the end?
Multiplication and Division of Rational Numbers
Multiplication of Rational Numbers
The multiplication of rational numbers is similar to that of fractions.
Product of two rational numbers = Product of numerators Product of denominators
For example, 12 13 × 5 7 = 60 91 and 7 9 × - 3 8 = 72 = - 7 24
Remember!
What if the rational numbers are in different forms?
Let us see another example and multiply - 4 13 and 0.56.
We will first convert them into the same form as 0.56 = 56 100 = 14 25 (- 4) 13 × 14 25 = (- 56) 325
Example 10: Find the product of 27 18 and 3 6 . 27 18 can be written as 3 2 , and 3 6 can be written as in simplified form.
The product of two rational numbers with similar signs is positive and with opposite signs is negative.
Therefore, 27 18 × 3 6 = 3 2 × 1 2 = 3 4 .
Example 11: Find the product of 13 25 and –8.5.
Write the numbers in the form p q ; hence, - 8.5 = - 85 10 .
13 25 × - 85 10 = - 221 50 17
5
So, the product of 13 25 and - 8.5 = -221 50
Error Alert!
Convert the numbers into the same form before multiplying to avoid errors.
Example 12: The length and width of a rectangular park are 145 3 m and 231 9 m.
What is the perimeter of the park?
Perimeter of the rectangle = 2 × (L + B) = 2 145 3 + 231 9
2 × 435 + 231 9 = 2 1 × 666 9 74 1 = 148 m
Hence, the perimeter of the rectangular park is 148 m.
1 Multiply: 5 9 and 8 -10
The size of Earth is 1 11 times the size of Jupiter. Do It Together
Converting 8 -10 into a positive denominator, we get, 8 -10 × -1 -1 = 5 9 × =
2 Multiply: 2.5 and - 20 35
Converting 2.5 to the same form as the other number we get, 2.5 = × -20 35 =
Division of Rational Numbers
Did You Know?
We know that division is the opposite of multiplication. To divide a rational number by another rational number, we multiply the dividend by the multiplicative inverse of the divisor.
That is a b ÷ c d = a b × d c
Dividend Divisor
For example: 15 4 ÷ 3 6 = 15 4 × 6 3 = 90 12 = 15 2
To divide rational numbers given in different forms, we first convert them to the same form and then divide.
For example: 13 5 ÷ 2 =
1 • Rational Numbers
Did You Know?
The multiplicative inverse of a number is the reciprocal of the number. E.g. the multiplicative inverse of 2 5 is 5 2 .
Example 13: Divide 22 35 by 11 7
22 35 ÷ 11 7 = 22 35 × 7 11
= 22 × 7 35 × 11 2 1 1 5 = 2 5
Example 14: Divide 28 27 by 14 28 27 ÷ 14 = 28 27 × 1 14 = 28 × 1 27 × 14 2 = 2 27
Example 15: Meeta bought 8 3 m of cloth for ₹238. What is the cost of the cloth per metre?
Cost of 8 3 m of cloth = ₹238
Cost of 1 m of cloth = 238 ÷ 8 3 = 238 1 × 3 8 119 4
= ₹ 357 4 = ₹89.25
Example 16: What rational number should be multiplied with 1.2 to get –9 2 as the product?
Let the rational number to be multiplied be x
1.2 × x = -9 2 12 10 × x = -9 2 x = -9 2 � 12 10 = -9 2 × 10 12 = -15 4 3 5 1 4
Hence, -15 4 should be multiplied with 1.2 to get -9 2 as the product.
Example 17: Simplify: 12 5 × 13 18 ÷ 39 9 × 3 5 ÷ 9 8
Solve the numbers inside the brackets first:
12 5 × 13 18 ÷ 39 9 × 3 5 ÷ 9 8 = 12 5 × 13 18 × 9 39 × 3 5 × 8 9 2 1 1 1 3 3 2 1 = 12 5 × 1 6 × 8 15 = 16 75
Example 18: A film ticket costs ₹275. If someone buys more than 4 tickets, the ticket per person costs 8 11 of the usual price. How much will a family of 6 people pay for the tickets?
Actual cost of one ticket = ₹275
Cost per ticket if someone buys more than 4 tickets = 8 11 of 275 = 8 11 × 275 1 = ₹200 25 1
Cost of 6 tickets = ₹200 × 6 = ₹1200.
1 Divide: - 15 8 by 21 5 -15 8 � 21 5 = × = =
2 Divide: 3.5 by (- 19) 25 3.5 can also be written as � (-19) 25 = × = =
Properties of Multiplication and Division of Rational Numbers
Closure Property
For Multiplication For Division
If a b and c d are rational numbers, then a b × c d will also be a rational number.
For example: 2 5 ×= (−3) 2 −6 10 (rational number)
If a b and c d are rational numbers, then a b ÷ c d is not necessarily a rational number.
For example: 6 11 ÷ 0 = not defined (not a rational number)
Commutative Property
For Multiplication For Division
If a b and c d are rational numbers, then ×= a b c d × c d a b If a b and c d are rational numbers, then
Associative Property
For Multiplication For Division
If a b c d , and e f are rational numbers, then
If a b c d , and e f are rational numbers, then
For example:
For example:
Distributive Property
Multiplication over addition and subtraction
If a b c d , and e f are rational numbers, then
For example:
If
Division over addition and subtraction
For example:
If
Division by 1 and 1
If
Division by itself and its additive inverse
Do It Together
Example 20: Solve � 6 5 8 11 7 128 11 � using the distributive property of division over subtraction.
The distributive property of division over subtraction states that
Example 21: If m = 5 6 , n = 18 25 and o = 35 24, then verify (m × n) × o = m × (n × o)
Placing the values of m, n and o in (m × n) × o = m × (n × o), we get
5 6 × 18 25 × 35 24 = 5 6 × 18 25 × 35 24
Solving LHS, we get,
Solving RHS, we get,
As LHS = RHS, 5 6 × 18 25 × 35 24 = 5 6 × 18 25 × 35 24
Fill in the blanks using the properties of rational numbers.
Property Used: Multiplicative Identity
a 2 5 and 18 7
and 5 d 13 15 and −2.5
and 4.2
23 5 and −3.2
2 Divide. a 14 5 by 5 3
−28 15 by 7 (−30) d 31 14 by −7
3 Fill in the blanks.
÷=
4 If a = 5 4 , b = 3 8 and c = 7 12 then verify
5 Fill in the blanks using the properties of rational numbers. Also name the property used.
5 9 × = 5 9
6 Use the distributive property of multiplication over addition/subtraction and solve the following.
7 Simplify and find the multiplicative inverse of the answer.
8 If the product of two rational numbers is 28 3 and one of them is −17 6 , find the other. Also find the multiplicative inverse of the result.
9 The Independence Hall is a historic civic building in Philadelphia, where both the Declaration of Independence and the Constitution of the United States were debated and adopted. Its base is square in shape. Each side of the hall is around 163 5 m in length. What is the area of the base of the Independence Hall?
10 A ribbon of length 357 8 m has been cut into 24 equal pieces. What is the length of each piece?
11 By what decimal number should 3 5 be multiplied to get 3 2 as the product?
12 By what fraction should 4.2 be divided to get 3 as the quotient?
13 During the summer holidays, Mansi read a book. After reading 5 8 of the book, 120 pages were left. How many pages are there in the book? Do you like reading books?
14 A zoo ticket usually costs ₹62.50 for adults. For kids, they are priced at 2 5 of the usual cost. How much will it cost to buy 5 kids’ tickets?
Challenge
Critical Thinking
1 The quotient that you get on dividing the reciprocal of the product of –2 5 and 15 18 by the product is the multiplicative identity. Is the above statement true? Solve to show your answer.
Points to Remember
• A rational number is a number that is expressed as p q , where p and q are integers, and the denominator should never be equal to zero. A negative rational number is always less than a positive rational number.
• To compare two or more rational numbers, make their denominators the same and compare the numerators.
• There is an infinite number of rational numbers between two rational numbers.
• The operations on rational numbers are similar to fractions. The signs need to be kept in mind, like with integers.
Math Lab
Setting: In pairs
Operations Insight!
Collaboration & Communication
Materials Required: Cards with all four operations problems based on their properties written. (Each card will have one property such that all properties get covered)
For Example:
Method:
1 Distribute one card among each pair.
2 Ask the pairs to solve the problem written and identify the property used.
3 Once all the pairs identify the property used in their cards, give them a chance to come and explain the property.
Chapter Checkup
1 Fill in the blanks.
a The sum of a rational number and its additive inverse is
b The reciprocal of a negative rational number is
c The rational number does not have any reciprocal.
d Adding to a rational number gives the rational number itself.
2 Solve and find the multiplicative inverse of the answer.
3 Find the area of a triangle with a base of 156 5 m and a height of 191 2 m.
4 If m = −3 6 , n = 1 5 and o = 8 10 then verify: a m ÷ (n ÷ o) ≠
5 The sum of two rational numbers is − 8 5 . If one of the numbers is 9 17 , find the other.
6 Which rational number should be subtracted from 12 7 to get −15 4 ?
7 Find (m + n) ÷ (m − n), where
8 Simplify.
9 One roll of ribbon is 15 2 3 m long. What is the length of 5 full and one-fourth of such rolls?
10 Nikita distributed 52 1 4 kg of rice equally among 11 families. How much rice did each family get?
11 Rohit practised cricket for 12 5 6 hours last week. He practised 2 1 8 hours this week. For how many hours did Rohit practise cricket in two weeks?
12 Gross domestic product (GDP) is the total monetary or market value of all the finished goods and services produced within a country's borders in a specific time period. Japan's GDP was around 21 5 trillion dollars while India’s GDP was around 677 200 trillion dollars in 2022. Which country had a greater GDP and by how much?
13 Richa ate 1 3 4 pizza, Alex ate 5 6 more pizza than Richa and Prince ate 1 1 2 times what Richa ate. How much pizza did they eat together?
14 Shilpa had ₹750. She spent 2 5 of the money on purchasing a book and 4 9 of the remaining amount on stationery. How much money was left with her?
15 Create a word problem on division of rational numbers.
Challenge
1 Instead of multiplying a number by 3 5 , Ronita divided it by 3 5 . If the difference of the wrong and the correct answer is 80, then find the number.
2 Read the statements and choose the correct option.
Assertion (A): The sum of –3 5 and –4 7 will be positive.
Reason (R): The product of two negative rational numbers is positive.
a A is true, but R is false.
b A is false, but R is true.
c Both A and R are true, and R is the correct explanation of A.
d Both A and R are true, but R is not the correct explanation of A.
Case Study
Mr Sharma's Grocery Initiative
Mr Sharma is opening a new grocery store. Before opening the store, he did some market research and found that the people in his locality use rice more than wheat. He also came to know that people in the locality use corn as well. He went to the wholesaler and ordered 24 bags of rice, 10 bags of wheat and 4 bags of corn. When he weighed the bags, the weight of each bag came out as shown below.
1 What is the total weight of wheat bought by Mr Sharma?
2 How much more rice (in kg) has he bought than wheat? a 47 kg
3 If all the four bags of corn were sold out in 10 days as each family in the locality purchased 1 2 kg of corn, how many families purchased corn? a 37 families b 74 families c 111 families d 148 families
4 Corn was sold at ₹135 per kg and the cost price of one bag was ₹1850. What was the profit earned by Mr Sharma on selling all the four bags?
5 For every kg of rice that Mr Sharma sells, he donates 100 g of rice to the orphanage in his locality. How much rice did he donate, if he sold 15 bags of rice?
2 Solving Equations in One Variable
Letʹs Recall
A linear equation in one variable is an equation that has linear expressions with only one variable.
Let us understand some important terms related to linear equations:
An expression is a combination of terms (variables or numbers or both) that are connected using mathematical operations.
An equation is a mathematical statement with an equal symbol between two expressions.
Letʼs Warm-up
Write ‟Trueʺ if the given equation is a linear equation in one variable, else write ‟Falseʺ.
Mean, Median and Mode
Solving Linear Equations
Vimala, Jaya and Lata are raising money by selling tickets for a hockey tournament. Both Vimala and Jaya have sold the same number of tickets. Jaya has sold thirty-six tickets more than Lata. Vimala has sold three times as many as Lata has. So, how many tickets has Lata sold?
Transposing Method
Let us denote the number of tickets sold by Lata as x. So, the number of tickets sold by Jaya is 36 + x
The number of tickets sold by Vimala is 3x.
Now, according to the situation, Vimala and Jaya sold the same number of tickets.
3x = 36 + x
Let us now solve this equation using different methods.
Balancing Method
In this method, we represent the expressions on two sides of a simple balance.
For the balancing method, we perform the same mathematical operations on both sides of the equation, so that the balance is not disturbed.
The equation is 3x = x + 36
Subtract x from both sides,
3x − x = x + 36 − x ⇒ 2x = 36
Divide both sides by 2, = 236 22 x ⇒ x = 18
Thus, Lata sold 18 tickets.
The method of finding the value of the variable so that it satisfies the equation is called solving a linear equation. The value of the variable obtained from the method is called the solution of the linear equation.
Transposition Method
Transposition is the process of shifting a term of an equation to the other side simply by changing its sign or by applying an opposite operation.
Steps for the transposition method:
Step 1: Identify the variable and constants.
Step 2: Remove the brackets to simplify the LHS and RHS.
Step 3: Move all variable terms to one side and all the constant terms to the other side. The sign will change for those variables and constants.
Step 4: Simplify the LHS and RHS to solve for the variable.
3x = x + 36
Variable = x
Constant = 36 No brackets here 3x – x = 36 2x = 36 x = 18
Hence, both the methods gave the same value of x as 18.
Remember!
While transposing, keep the variable terms on one side of the equation and the constants on the other side.
Example 1: Solve using the balancing method.
5x + 15 = 3x + 33
5x + 15 −15 = 3x + 33 − 15
5x = 3x + 18 ⇒ 5x − 3x = 3x + 18 − 3x
2x = 18 ⇒= 218 22 x x = 9
Example 2: Solve using the transposition method.
8x – 14 = 3x + 11
8x – 3x = 11 + 14
5x = 25 x = 5
Remember!
Error Alert!
x + 3 = 7
On solving the equation: x = 7 + 3 x = 10 x = 7 – 3 x = 4
The mathematical operation is reversed when we move terms from one side to the other side of the equal symbol.
Example 3: One number is twice another number. If 30 is subtracted from both numbers, then the bigger number becomes four times the smaller number. Find the numbers.
Let the smaller number be x and the larger number be 2x.
Given: If 30 is subtracted from both numbers, we get x – 30 and 2x − 30.
According to the question:
2x − 30 = 4(x − 30) ⇒ 2x − 30 = 4x − 120
2x = 90 ⇒ x = 45
Therefore, the smaller number is 45, and the larger number is 2 × 45 = 90.
Example 4: The length of a rectangular field is 10 more than thrice its breadth. The perimeter of the rectangle is 228 m. Find the area of the field.
Let the breadth of the rectangular field be (x). The length is (3x + 10).
The perimeter of the rectangle is given by: 2[(3x + 10) + x] = 228
= 2(3x + 10) + 2x = 228 ⇒ 6x + 20 + 2x = 228
= 8x = 208 ⇒ x = 26
Therefore, the breadth is 26 m, and the length is 3 × 26 + 10 = 88 m.
The area is 26 × 88 = 2288 m2
Find the value of x. 1
2 3x + 4(x – 1) = 10
3x + = 10
Find the value of x using the balancing method.
Draw a rough diagram of a weighing scale to show the equation 3x + 5 = 9.
Find the value of x using the transposition method. a 3x – 5 = 2x + 97 b 5(x – 7) – 2x = 13 – x c 15x – 2(18 + x) = 29 d x + 2(3 + x) = 5(x – 6) e 4x + 7 = 1.5(x + 12) f 1.3(x – 3) + 2.6 = x
Find two consecutive even integers so that two-fifths of the smaller number exceeds two-elevenths of the larger number by 4.
One number is 3 times the other number. If 15 were to be added to both the numbers, then one of the new numbers becomes twice the other new number. Find the numbers.
Chapter 2 • Solving Equations in One Variable
The length of a rectangular field is 7 less than twice its breadth. The perimeter of the rectangle is 196 m. Find the area of the field.
Solve for the value of x.
The rectangles are identical. What is the combined area of the rectangles in square units?
Write 3 equations that have x = 5 as the solution.
1 A two-digit number is greater than 20 but less than 30. The sum of the digits is the same as their product. What is the number?
Simplifying Equations to Linear Form
Do you remember Lata, Jaya and Vimala, who sold hockey tickets? They sold the tickets online as well as offline. The cost of the online ticket was ₹200 more than that of the offline ticket. Five-eighths of the online ticket’s cost is the same as three-fourths of the offline ticket’s cost.
Let us find the cost of each type of ticket. Let the cost of the offline ticket be ‘y ’.
Thus, the cost of the offline ticket is ₹1000 and the cost of the online ticket is ₹1200.
Let us now solve an equation using cross multiplication.
Step 1: Multiply the numerator of one side with the denominator of the other side.
Step 2: Simplify both sides of the equation.
Step 3: Apply the transposition method to find the value of x
Example 5: Solve for x: 2+75+4 = 35 xx
5(2x + 7) = 3(5x + 4)
10x + 35 = 15x + 12
35 – 12 = 15x – 10x 23 = 5x 23 5 x =
Example 6: Solve: (213)39=+1 5115 xxx
Did You Know?
In Chemistry, a chemical equation is considered balanced when both sides of the equation have the same number and type of atoms.
Did You Know?
The great Indian mathematician Aryabhata invented algorithms for solving algebraic equations.
Example 7: Solve: 5x + 3 3 + 2x – 1 4 = 61 12 and find the value of y if x 5 + 6 y = 1.
Taking the LCM at LHS and solving, we get:
4(5x + 3) + 3(2x – 1) 12 =
Chapter 2 • Solving Equations in One Variable
26x + 9 12 = 61
⇒ 26x = 52 ⇒ x = 2
Given that x 5 + 6 y = 1
Substituting the value of x = 2, we get:
2 5 + 6 y = 1 ⇒ 2y + 30 5y = 1
⇒ 2y + 30 = 5y ⇒ 3y = 30 ⇒ y = 10
Example 8: The numerator of a fraction is less than its denominator by 8. If both the numerator and the denominator are increased by 17 then the fraction obtained is 5 6 in its simplest form. Find the original fraction.
Let the denominator be x, then the original fraction will be = X – 8 x
If both numerator and denominator are increased by 17, the new fraction is (x – 8) + 17 x + 17 = 5 6
Simplifying the equation: x + 9 x + 17 = 5 6
Cross multiplying: 6(x + 9) = 5(x + 17).
Solving for x: 6x + 54 = 5x + 85 x = 31
The original fraction is x – 8 x = 31 – 8 31 = 23 31
Solve for x: 3x + 5 2x + 1 = 1 3
3(3x + 5) = 1(2x + 1) Do It Together
Do It Yourself 2B
Write YES if the correct solutions are given for the linear equations, else write NO. a x = 2 for = 5 3 21 x x b x = 6 for
Find the value of x using the cross-multiplication method.
a = 38 6 5 x x b = + 57 2 xx c ++ = 0.452.54 815 xx
d 5(2 – x) – 4(1 + x) 2 – x = 5 8 e 6 3x + 1 9 5x + 3 = f (41)(21)(37) 6 325 xxx +−− +−=
Do as directed.
a Solve: −+ += 3146 43 236 xx and find the value of y if += 23 2 xy .
b Solve: −+ = 4535 1110 xx and find the value of y if += 2 11 3 x y .
The numerator of a fraction is 3 less than the denominator. If the numerator and the denominator both are decreased by 2 then the simplest form of the fraction becomes 3 4 . What is the fraction?
The denominator of a fraction is less than its numerator by 6. If both the numerator and the denominator are decreased by 3 then the fraction obtained is 5 3 in its simplest form. Find the original fraction.
An orange has 10 less calories than a pear and 17 more calories than a watermelon. If 3 oranges have 6 less calories than 1 pear and 3 watermelons, how many calories does an orange have?
Challenge
1 Solve the values of the variables to decode the postal code: 2abc5d.
Critical Thinking
Which of the statements is/are true about the postal code in the above question?
Statement 1: The third digit of the postal code is one more than the second digit.
Statement 2: All the digits of the postal code are prime numbers.
Statement 3: The last digit of the postal code is twice the first digit.
Statement 4: The difference of the fourth and sixth digit is the fifth digit of the postal code.
Application of Linear Equations
Remember Lata and her friends who sold hockey tickets? Jaya sold 54 tickets in total. If she earned a total of ₹58,800 and sold two types of tickets, one for ₹1000 and the other for ₹1200, then how many tickets of each type did she sell?
Linear equations help us in solving real-world problems. We need to set up an equation according to the condition given and solve it to find the value of the unknown.
This method consists of two steps:
1 Translating the word problem into symbolic language
2 Solving the equation
Let us solve a few real-life problems.
Let the number of tickets sold for ₹1000 be x. Then, the number of tickets sold for ₹1200 will be 54 – x
According to the question,
1000x + 1200(54 − x) = 58800 ⇒ 1000x + 64800 − 1200x = 58800
200x = 64800 − 58800 ⇒ 200x = 6000
x = 30 ⇒ 54 − x = 54 − 30 = 24
Thus, Jaya sold 30 tickets for ₹1000 and 24 tickets for ₹1200.
Example 9: Three consecutive even numbers add up to 696. What are the numbers?
Let the three consecutive even numbers be 2x, 2x + 2 and 2x + 4.
Given: The sum of these numbers is 696.
2x + (2x + 2) + (2x + 4) = 696.
6x + 6 = 696 ⇒ 6x = 690
x = 115
The three consecutive even numbers are 230, 232 and 234.
Example 10: The sides of a rectangle are in the ratio 5:4. If the perimeter of the rectangle is 54 cm, what is the measure of each side considering the length to be greater than the breadth?
Given that the sides are in the ratio 5 : 4 and length is greater than the breadth.
Let the length = 5x and breadth = 4x
Perimeter = 2(length + breadth) = 2(5x + 4x) = 2 × 9x = 54
⇒ 18x = 54 ⇒ x = 54 18 = 3
Hence, length = 5 × 3 = 15 cm and breadth = 4 × 3 = 12 cm.
Example 11: If the sum of three consecutive multiples of 9 is 108, then find the second multiple.
Let us assume the smallest multiple of 9 to be 9x
Next multiple = 9(x + 1); Last multiple = 9(x + 2)
So, 9x + 9(x + 1) + 9(x + 2) = 108
27x + 27 = 108 ⇒ 27x = 81 ⇒ x = 81 ÷ 27 ⇒ x = 3
So, we can find that 9x = 9 × 3 = 27, 9(x + 1) = 9 × 4 = 36, 9(x + 2) = 9 × 5 = 45
Thus, the three consecutive multiples of 9 which add up to 108 are 27, 36 and 45.
Example 12: A positive number is 5 times another number. If 21 is added to both the numbers, then the bigger new number becomes twice the smaller new number. What are the numbers?
Let us assume the first number to be x; second number = 5x
According to question,
5x + 21 = 2(x + 21)
5x + 21 = 2x + 42 ⇒ 5x − 2x = 42 − 21
3x = 21 ⇒ x = 7 ⇒ 5x = 35
Thus, the numbers are 7 and 35.
Example 13: Suman’s present age is equal to one-fifth of her mother’s age. Twenty-five years later, Suman’s age will be 4 years less than half the age of her mother. Find their present ages.
Let us assume the mother’s present age to be y years; Suman’s present age = 5 y
According to the condition, + +=− 25 254 52 yy
Multiply both sides of the equation by 10.
2y + 250 = 5(y + 25) − 40 ⇒ 2y + 250 = 5y + 125 − 40
5y − 2y = 250 − 85 ⇒ 3y = 165 ⇒ y = 55
Suman’s present age = 5 y = 55 5 = 11 years
Thus, Suman’s present age is 11 years and her mother's age is 55 years.
Example 14: Tanya takes a test in which there are 60 questions. For each correct answer, x marks will be awarded, and for each incorrect answer, one-fourth of a correct answerʼs marks will be deducted, and 0 marks will be awarded for questions not attempted. Tanya attempts 45 questions out of which 29 are correct. What is the value of x if Tanya is awarded 200 marks?
Marks awarded for each correct answer = x
Marks deducted for each incorrect answer = 4 x
Total number of questions attempted = 45
Total number of correct answers = 29
Total number of incorrect answers = 45 – 29 = 16
Total marks scored = 200
So,
(29)16200 4 x x
29x − 4x = 200 ⇒ 25x = 200 = 200
25 x ⇒ x = 8
Thus, the value of x is 8 marks.
Did You Know?
Knowledge of algebraic expressions can help us plan and schedule our days, as we are often estimating and solving for unknown variables.
Example 15: Two numbers are in the ratio 4:9 and the difference of the numbers is 250. What is the sum of the numbers?
Let the numbers be 4x and 9x (where x is a common factor).
The difference between them is 9x − 4x = 5x, and given difference is 250.
So, 5x = 250 ⇒ x = 50
The two numbers are 4x = 4 × 50 = 200 and 9x = 9 × 50 = 450.
The sum of these numbers is 200 + 450 = 650.
Example 16: Divide 1000 in two parts such that 20% of one number is equal to 30% of the other number.
Let one part be x, and the other part be 1000 − x.
The equation is: 0.2x = 0.3(1000 − x) ⇒ 0.2x = 300 − 0.3x
0.5x = 300 ⇒ x = 600
So, one part is 600, and the other part is 1000 − 600 = 400.
Example 17: A number is increased by 30% and the new number obtained is then decreased by 20% so that the result is 52. Find the numbers.
Let the number be x
The new number, after a 30% increase, is 1.3x, and when decreased by 20%, it becomes 0.8 times 1.3x.
Given that 0.8 × 1.3x = 52
1.04x = 52 ⇒ x = 52 1.04 = 5200 104 = 50
So, the original number is 50.
Example 18: The present ages of Abhijeet and Sahil are in the ratio 2:1. Four years ago, the ratio of their ages was 5:2. Find the present ages of Abhijeet and Sahil.
Let the present age of Abhijeet be 2x and the present age of Sahil be x, where x is a positive integer.
According to the question,
Four years ago, Abhijeet’s age was 2x − 4 and Sahil’s age was x − 4.
The ratio of their ages at that time was given as 5:2.
Hence 2x – 4 x – 4 = 5 2
By cross multiplication:
= 2(2x − 4) = 5(x − 4) ⇒ 4x − 8 = 5x – 20 ⇒ x = 12
Therefore, Abhijeet’s present age = 2x = 2 × 12 = 24 years
Sahil’s present age = x = 12 years
Example 19: Ravi deposited ₹25,000 in his bank account. He deposited currency notes of ₹50, ₹100 and ₹500 in the ratio of 6:2:1. Find the number of notes of each denomination.
Given that ratio of ₹50 notes to ₹100 notes to ₹500 notes = 6:2:1
Let the number of ₹50 notes be 6x, ₹100 notes be 2x, and ₹500 notes be x.
The total value of the notes is [50(6x) + 100(2x) + 500x], which is equal to ₹25,000.
According to the question:
300x + 200x + 500x = 25,000
1000x = 25,000 ⇒ x = 25
Therefore, the number of ₹50 notes is 6 × 25 = 150, the number of ₹100 notes is 2 × 25 = 50, and the number of ₹500 notes is 25.
Example 20: A boat travels downstream between two ports in 4 hours, and upstream in 5 hours, covering the same distance each way. Given that the streamʹs speed is 2 km/hr, determine the boatʹs speed in still water.
Given: The speed of the flow of the stream is 2 km per hour,
Let the speed of the boat in still water be B. We know that the speed of the water is 2 km/hr.
Let the distance be x km.
The speed upstream is B − 2, and the speed downstream is B + 2.
Time taken for travelling downstream is 4 hours and time taken for travelling upstream is 5 hours.
Since distance = speed × time
x = (B − 2) × 5 ............................. (1)
x = (B + 2) × 4 ............................. (2)
Equating (1) and (2) and substituting the values:
(B − 2) × 5 = (B + 2) × 4
5B − 10 = 4B + 8
B = 18
B = 18 km/h
Hence, the speed of the boat in still water is 18 km/h.
A car rental company charges ₹500 per day plus ₹12 per km. If the bill is ₹3320 for a day, then how many kilometres were driven?
Let the distance travelled be x km.
Fixed charges for a day =
Rate of the car for each km =
Total bill amount =
Distance driven =
Form the equation for the cases given.
a Thrice x added to 5 is equal to the difference of half of x and 13.
b The sum of four times y and 11 is equal to the sum of two times y and 56.
c The sum of three consecutive even numbers is 144.
d A train travels from point A to point B, a distance of 240 miles. On the return trip, the train’s speed is increased by 20 mph and takes 2 hours less.
The sum of four consecutive odd numbers is 352. What are the numbers?
The sum of three consecutive multiples of 11 is 429. What are the numbers?
The angles of a triangle are in the ratio 3:4:5. What is the difference between the largest angle and the smallest angle?
Puneet’s age is three times the age of his daughter. If the sum of their ages is 52 years, find the difference of their ages.
Virat scores 20 more runs than twice the number of runs scored by Rohit. Together, their total is four runs short of a triple century. What are the individual scores of Virat and Rohit, respectively?
Animesh left one-half of his property to his daughter, one-third of his property to his son and donated the rest of his property. If the donation was worth ₹5,00,000 then how much did he give to his daughter and son?
A number is decreased by 10% and the new number obtained is then increased by 25%, so that the result is 81. Find the number.
Divide 6000 into two parts so that 15% of one number is equal to 35% of the other number.
Two angles are in the ratio 1:2. When 15 is added to the smaller angle and 15 is subtracted from the bigger angle, the new ratio of the angles becomes 1:1. Find the angles.
The ratio of Naveen’s age to his father’s age is 2:5. After 10 years, the ratio of their ages will be 1:2. What was Naveen’s father’s age at the time of Naveen’s birth?
The Prelims of IBPS PO exam has 100 marks. For each correct answer, x marks are awarded and for each incorrect answer, one-fourth of a correct answer’s marks will be deducted and 0 marks are awarded for questions not attempted. Rashmi attempted 78 questions out of which 56 are correct. What is the value of x if Rashmi scored 50.5 marks?
The ones digit of a two digit number is 0.4 times the tens digit. If you interchange the digits of this two-digit number and add the resulting number to the original number, you get 77. What is the original number?
The speed of the flow of a river is 3 km per hour. A boat goes upstream between two points in 5 hours while it covers the same distance going downstream in 3 hours. What is the speed of the boat in still water?
1 A sum of ₹870 is made up of denominations of ₹5 and ₹10. If the total number of notes is 92 then find the number of notes of each denomination.
2 Two cars simultaneously start from A and B in opposite directions and the distance between them after 4 hours is 60 km. What is the speed of each car?
+ 10) km per h
Points to Remember
• An equation is a mathematical statement with an equal symbol between two expressions.
• Any operation done on one side of an equation must be done on the other side of the equation so that the equation remains balanced.
• We use the transposition method to collect similar terms on one side. Change the signs of terms while using the transposition method and moving terms from one side to the other side.
• While solving the word problems, identify the unknown terms, form an equation and solve for the value of the unknown term.
• The following rules can be applied while solving linear equations:
• The same number can be added or subtracted from both sides of the equation.
• The same number can be used to multiply or divide on both sides of the equation.
• A term can be transposed to the other side of the equation with its sign changed.
Math Lab
Solve and Run Relay
Aim: Solve linear equations in one variable
Materials Required: Chalk, stopwatch and equation cards
Setting: In groups of 4
Method:
Collaboration & Communication
1 Prepare equation cards (unsolved equations on cards should have linear equations).
2 Mark the starting line and finishing line in the classroom or in an open area. There could be different laps.
3 Each team lines up behind the starting line and the first person of each team is given an equation card.
4 The student solves the equation and runs towards the finishing line with the correct solution.
5 Once they reach the finishing line, they hand the card to the next teammate. The next person solves the next equation and continues the relay.
6 Use a stopwatch to calculate the total time taken by each team to complete the race.
7 The team which has the fastest completion time wins the relay race.
Find the value of x.
Draw a rough diagram of a weighing balance to show the equation 2x + 5 = 11.
Solve using the transposition method.
Find the value of x using the cross-multiplication method.
Do as directed.
Place the correct mathematical operations (+, –, ×, ÷) so that the equations are true.
a 2x 3 = 7 for x = 2 b 3(x 1) 4x = 46 for x = 7
c 2x 3(x __ 1) 15x __ 2(2x __ 4) = 18 25 for x = 3 d 3x 4(x __ 3)
If you subtract 1 2 from a number and multiply the result by 1 3 then you get 1 15 . What is the number?
The present age of Shagun is one-fifth of her mother’s age. After twenty-five years, her age will be 4 less than half of her mother’s age. Find the difference of their present ages.
The perimeter of a rectangular swimming pool is 170 m. If the length of the pool is 4 m more than the breadth of the pool, what is the area of the pool?
There is a rectangular plot for a school. The length and breadth of the plot are in the ratio of 15:7. At the rate of ₹150 per metre, it will cost ₹1,32,000 to fence the plot. What are the dimensions of the plot?
The ages of Kushagra and Kush are in the ratio 5:6. Five years later the sum of their ages will be 43 years. What is the age difference between the present ages of Kushagra and Kush?
The angles of a quadrilateral are in the ratio 7:17:19:29. What is the measure of the angles?
Vikram took goats to the field. Half of the goats were grazing. Three-fourths of the remaining goats were playing nearby. The remaining 15 were drinking water from the pond. How many goats were there in total?
₹x is to be divided among three friends A, B, and C. The share of A is two-fifths of the total amount, the share of B is two-thirds of the remaining amount and C’s share is ₹600. What is the value of x?
The ratio of the speed of a boat to the stream is 7:2. The boat takes 6 hours more travelling upstream than downstream. What is the time taken by the boat for the entire journey?
Challenge
Critical Thinking
1 A book has 400 pages. Raj finishes writing 100 pages in x minutes. Raju takes twice the time taken by Raj to write the next 150 pages. Vivek takes 2 hours more than half the time taken by Raju to write the remaining pages. The total time taken to write the book was 33 hours and 20 minutes. How much time is taken by Vivek to write the remaining pages (in hours)?
2 Read the statements and choose the correct option.
Assertion (A) – The difference of two numbers is 25. The larger number is x. The smaller number is x – 25.
Reason (R) – Numbers which follow each other in order, without gaps, from smallest to largest like 12, 13, 14 and 15 are consecutive numbers.
a Both A and R are true and R is the correct explanation of A
b Both A and R are true but R is not the correct explanation of A
c A is true but R is false
d A is false but R is true
Urban Transport Tariffs
A company that provides transportation services charges different prices in different cities based on how many people live there. They also add a fixed fee for every ride, which stays the same no matter which city you are in. The table below shows how much they charge per kilometre and the fixed fee in City A and City B.
1 The amount (x) paid by a customer travelling a distance of 12 km by cab in city A can be given as: a 10 + d = 12x b 10 × d + 12 = x c 10 × 12 + d = x d 10 × x + 12 = d
2 What is the fixed charge for cab services if Neha paid ₹150 for travelling a distance of 11 km in city A? a ₹30 b ₹40 c ₹50 d ₹60
3 What is the per km charge for bikes in city A if Suhani paid ₹45 for travelling a distance of 5 km? a ₹4/km b ₹5/km c ₹6/km d ₹9/km
4 Rahul and Megha wanted to reach the museum in city B. They both live 6 km far from the museum. Rahul took a bike service and paid ₹57 while Megha took an auto and paid ₹76. What is the difference in the per km charge of auto and bike services in city B?
5 Is the given statement true or false? Give your answer with reasons. (Hint: Use the fixed charges as calculated in Q2.)
Shalini will pay ₹127 if she travels 7 km via cab in city B.
6 What safety measures should you take while travelling in cabs?
Polygons and Quadrilaterals
Let’s Recall
Shapes can be made with lines, curves or both lines and curves. A curve is a line that is not straight. It can be bent and twisted in any direction. Curves can be open, closed, simple or non-simple.
Shapes made with only line segments are called polygons. Let us see some polygons and non-polygons:
Polygons: Closed
Non-polygons: Open
The region inside a closed shape is called the interior. The region outside the closed shape is called the exterior.
Exterior Interior
Letʼs Warm-up
Name the shapes as open curves, closed curves, polygons or non-simple curves. 1 2 3 4
Understanding Polygons and Quadrilaterals
Mr Singh owns a tile shop. He sells tiles in a lot of different shapes, like triangles, rectangles, hexagons, etc.
We know that these are called 2-D shapes. Some two-dimensional shapes are made up of straight lines and connected at their endpoints. These are called polygons.
Now, imagine if all of these shapes were made of curves. Could we tile them?
Classifying Polygons
A polygon is a simple closed curve made up of 3 or more straight sides, with no overlapping or selfintersecting parts.
Remember!
In a polygon, the number of sides is always equal to the number of vertices.
Did You Know?
The term “polygon” comes from the Greek words “poly,” meaning many, and “gonia,” meaning angles.
Think and Tell
Which polygons do you see most often in your everyday life?
In the given polygon ABCDE, AB, BC, CD, DE and EA are the sides. A, B, C, D and E are the vertices. ∠A, ∠B, ∠C, ∠D and ∠E are the angles. Let us see and learn some more terms.
Interior of a Polygon is the region enclosed by the sides of the polygon.
Diagonals are line segments joining opposite vertices of a polygon. E.g. AC, AD
Adjacent Sides are sides that share a common vertex (corner). They are next to each other in the sequence of sides. E.g. (AB-BC, BC-CD, CD-DE, DE-EA)
Exterior of a Polygon is the region outside the sides of the polygon.
Polygons can be convex or concave
Polygons can be regular or irregular
Adjacent Angles are angles that share a common side (arm). They are next to each other in the sequence of angles. E.g. (∠A-∠B, ∠B-
Convex Polygon: In these polygons, the measure of each angle is less than 180º. The diagonals lie inside the polygon.
Concave Polygons: In these polygons, the measure of one of the angles is more than 180º. At least one diagonal lies outside the polygon.
Regular Polygon: In these polygons, the lengths of all the sides and measure of angles are equal.
Irregular Polygon: In these polygons, the lengths of all the sides are not equal.
Polygons can be classified on the basis of their number of sides and vertices.
Bees build their honeycomb cells using hexagons, which maximise storage space while minimising the amount of wax needed. This naturally efficient design inspired scientists and engineers to develop lightweight yet strong structures in aerospace and architecture.
A polygon has to have at least 3 sides.
We know that a diagonal of a polygon is a line segment that joins two vertices of the polygon, which are not already joined by the adjacent sides of the polygon.
Let us draw the diagonals in some polygons.
If a polygon has n sides, then the number of diagonals are n (n − 3) 2 .
In a convex polygon, all the diagonals lie inside the polygon, whereas in a concave polygon, at least one diagonal lies outside the polygon.
Diagonals in a concave polygon
Diagonals in a convex polygon
Example 1: Identify the given polygons as concave or convex.
Convex Polygon
Example 2: Find the number of diagonals in a nonagon.
Number of sides in a nonagon (n) = 9
Number of diagonals in a nonagon
Therefore, a nonagon has 27 diagonals.
Concave Polygon
Think and Tell
Is it possible to have a concave polygon with three sides?
Draw the diagonals in the given polygons. Find the number of diagonals using the formula. Identify the polygon as convex or concave.
Polygon
Number of sides (n) 5
Polygon
Do It Yourself 3A
1 Fill in the blanks.
a A polygon with 7 sides is called a .
b The number of diagonals in a hexagon are
c A polygon with all sides and angles equal is called a
2 Write True or False.
a A triangle is a convex polygon.
b The number of diagonals in an octagon is 7.
c A circle is an example of a 2-D geometrical shape that is not a polygon.
3 Classify the following as convex or concave polygons based on the angles of the polygons.
a 65º, 115º, 111º, 70º, 179º
4 Classify the polygons as concave or convex.
b 176º, 105º, 110º, 66º, 195º, 165º, 83º
a b c d
5 A polygon has 6 sides, and all the angles in the polygon measure 120°. Is this a convex or concave polygon?
6 Draw a hexagon and draw all the diagonals in the polygon.
7 Use the formula to find the number of diagonals in polygons with the number of sides given. Name the polygon. a 4 sides b 8 sides c 9 sides d 10 sides
8 In a regular octagon, how many diagonals can be drawn from one vertex?
9 How many non-overlapping triangles can we make in a polygon with 5 sides by joining the vertices?
10 Draw a figure made up of 4 polygons with 2 being convex and 2 being concave polygons.
Challenge
1 3 squares are joined to form an L shaped figure. Will the new polygons formed be concave or convex? How many diagonals will the new polygon have?
Classifying Quadrilaterals
There are different kinds of quadrilaterals depending on their properties, like the yellow and blue-coloured square-shaped tiles sold by Mr Singh. Let us explore some more information about quadrilaterals.
Properties of Quadrilaterals
In this section, we will see some properties of quadrilaterals and understand regions in and around quadrilaterals.
Exterior of a quadrilateral
Interior of a Quadrilateral
The interior of a quadrilateral refers to the region enclosed by the four sides of the quadrilateral.
Quadrilaterals can be convex or concave
Interior of a quadrilateral
Exterior of a quadrilateral
Convex Quadrilaterals
Exterior of a Quadrilateral
The exterior of a quadrilateral refers to the region outside the four sides of the quadrilateral.
In these quadrilaterals, the measure of each angle is less than 180° .
Concave Quadrilaterals
In these quadrilaterals, the measure of one of the angles is more than 180° Here, ∠R is greater than 180° .
Let us say we have 2 quadrilaterals with the given interior angle measures. Identify the type of each quadrilateral.
1 Quadrilateral ABCD with ∠A = 45° , ∠B = 105° , ∠C = 95° , ∠D = 115°
Since none of the angles measure more than 180°, ABCD is a convex quadrilateral.
2 Quadrilateral PQRS with ∠P = 34° , ∠Q = 201° , ∠R = 71° , ∠S = 54° .
∠Q = 201° which is greater than 180°. So, PQRS is a concave quadrilateral.
Example 3: Place the points J, K, L, M, N and O given below in the quadrilaterals so that:
Only points J, L and M are in the interior.
Only points L, M and N are in the interior.
Only points K, L and O are in the interior.
Example 4: Among the following angles, which one cannot be an interior angle in a convex quadrilateral?
1 73° 2 85° 3 173° 4 211°
In a convex quadrilateral, no angle can exceed 180°.
Therefore, the 211° angle cannot be one of the angles in a convex quadrilateral.
Example 5: Which of the following angles can be one of the interior angles in a concave quadrilateral?
1 33° 2 119° 3 183° 4 Any of the 3 angles given in a, b and c
In a concave quadrilateral, one of the angles can be more than 180°.
Therefore, the correct option is (4) since any of the 3 angles can be interior angles in a concave quadrilateral.
Classify the following as convex or concave quadrilaterals based on the angles of the quadrilaterals.
Angles 150o, 100o, 40o, 70o 75o, 105o, 101o, 79o 216o, 36o, 40o, 68o
Type of Quadrilateral
Trapezium and Kite
Trapezium: A quadrilateral with at least one pair of opposite sides parallel is a trapezium. Let us see trapezium shapes in real life.
Did You Know?
The word “trapezium” comes from the Greek word “trapezion,” meaning “a little table.” It was originally used to describe a quadrilateral with no parallel sides.
Properties of a Trapezium
• One pair of opposite sides is parallel, and the other pair of opposite sides is non-parallel. Here, AB ǁ DC.
• When the non-parallel sides of a trapezium are equal, it is known as an isosceles trapezium. PS = QR.
• The diagonals in an isosceles trapezium are equal. PR = QS.
Supplementary angles in trapezium ABCD are:
A + ∠D = 180°
B + ∠C = 180°
Convex
A kite is a quadrilateral with two pairs of consecutive sides of equal length.
Properties of a Kite
• AC ⊥ BD
• Diagonal BD bisects the angles ∠B and ∠D.
•∠A = ∠C.
Think and Tell
How many pairs of opposite angles in a kite are equal?
• Only diagonal BD bisects diagonal AC and not vice versa.
• Diagonal BD divides the kite into two congruent halves.
Example 6: PQRS is a trapezium where PQ ǁ SR. Find the values of x and y.
From the figure,
∠P + ∠S = 180° (Supplementary angles)
(2y + 3)° 126° 107° (4x − 2)°
2y + 3° + 107° = 180°
2y = 180° 110° = 70°
y = 70 2 = 35°
Example 7: Look at the kite. Find ∠CAD, ∠ADC and ∠ABC.
In ΔABC, ∠BAC = ∠BCA = 50° (Angles opposite to equal sides)
∠BAC + ∠BCA + ∠ABC = 180° (Angle sum property of the triangle)
50° + 50° + ∠ABC = 180°
∠ABC = 180° 100° = 80°
Also, ∠ADB = ∠CDB = 27° (BD bisects ∠D)
Hence, ∠ADC = ∠ADB + ∠CDB = 27° + 27° = 54°
In Δ ADC, ∠ACD = ∠CAD (Angles opposite to equal sides)
∠ACD +∠CAD +∠ADC = 180° (Angle sum property of the triangle)
2∠CAD + 54° = 180°
2∠CAD = 180° 54° = 126°.
So, ∠CAD = 63°
Similarly,
∠Q + ∠R = 180° (Supplementary angles)
4x 2° + 126° = 180°
4x = 180° 124° = 56°
x = 56 4 = 14°
Find the measure of ∠A and ∠C in the given figure.
∠DAC + ∠ACD + ∠CDA = 180° (Angle sum property)
We know that, ∠DAC = ∠ACD ( )
∠DAC + ∠ACD + =
So, ∠DAC + ∠ACD =
∠DAC = ∠ACD =
∠ABC = ∠BCA = ∠CAB (angles of equilateral triangle)
So, ∠ABC = ∠BCA = ∠CAB =
∠A = ∠BAC+ ∠DAC
+ =
Parallelograms
C = ∠BCA+ ∠ACD
+ =
A parallelogram is a quadrilateral with opposite sides that are both parallel and equal in length. We see parallelograms in roofs, solar panels and many other places. Can you think of 2 other places where you see parallelograms?
Properties of a Parallelogram
• The opposite angles of a parallelogram are equal. Here, ∠P = ∠R; ∠S = ∠Q.
• The opposite sides of a parallelogram are parallel and equal. Here, PQ = SR, PS = QR; PQ ǁ SR, PS ǁ QR.
• The diagonals of a parallelogram bisect each other. Here, the diagonals PR and SQ bisect each other at point O.
Let us explore the proofs of parallelograms.
1 If a pair of opposite sides of a quadrilateral are equal and parallel, then the quadrilateral is a parallelogram.
Let PQRS be a quadrilateral such that PQ = SR and PQ ǁ SR.
Consider ΔPQR and ΔRSP, then
PQ = SR (Given)
PR = RP (Common side)
∠QPR = ∠SRP (Alternate angles as PQ ǁ RS)
Hence, ΔPQR ≅ΔRSP (SAS Congruency rule)
Therefore, ∠PRQ = ∠RPS (Corresponding parts of congruent triangles)
Since ∠PRQ and ∠RPS are alternate angles, PS ǁ QR.
As the opposite sides have been shown to be parallel, we can conclude that PQRS is a parallelogram.
2 Any two adjacent angles of a parallelogram are supplementary.
Let PQRS be a parallelogram.
Consider PS ǁ QR and PQ as their transversals. Then, ∠SPQ and ∠RQP are supplementary as they are the interior angles on the same side of the transversal PQ.
Similarly, consider PS ǁ QR and SR as their transversals. ∠PSR and ∠QRS are supplementary, as they are the interior angles on the same side of the transversal SR.
Extending the same reasoning, it can be shown that ∠QPS & ∠RSP and ∠SRQ & ∠PQR are also supplementary, considering PQ ǁ RS along with PS and QR as the transversals, respectively.
3 Diagonals of a parallelogram bisect each other.
Let PQRS be a parallelogram whose diagonals QS and PR intersect at T.
Consider ΔPTQ and ΔRTS, then
PQ = SR (Opposite sides of a parallelogram)
∠TQP = ∠TSR (Alternate angles as PQ ǁ RS)
∠TPQ = ∠TSR (Alternate angles as PQ ǁ RS)
Hence, ΔPTQ ≅ΔRTS (ASA criteria of congruency)
Therefore, PT = TR and QT = ST (Corresponding parts of congruent triangles)
4 Opposite sides and angles of the parallelogram are equal.
Let PQRS be a parallelogram with diagonal PR shown.
Consider ΔPQR and ΔRSP, then
a PR = RP (common side)
b ∠QPR = ∠SRP (Alternate angles as PQ ǁ RS)
c ∠QRP = ∠SPR (Alternate angles as PS ǁ QR)
Hence, ΔPQR ≅ΔRSP (ASA criteria of congruency)
Therefore, ∠Q = ∠S, QR = PS and PQ = SR (Corresponding parts of congruent triangles)
From (b) and (c), ∠QPR + ∠SPR = ∠SRP + ∠QRP ⇒∠P = ∠Q.
Therefore, all the opposite sides and angles have been proven to be equal.
Example 8: ABCD is a parallelogram. Find the values of x and y.
We know that opposite sides in a parallelogram are equal. Hence,
2x + 3 = 35 cm
2x = 35 3 = 32
x = 32 2 = 16 cm
4y + 7 = 23 cm
4 y = 23 – 7 = 16 y = 16 4 = 4 cm
Example 9: If one of the sides of a parallelogram is 15 mm and its perimeter is 80 mm, find the lengths of the other sides.
Since the opposite sides in a parallelogram are equal, let the sides be 15 mm, x, 15 mm and x
15 mm + x + 15 mm + x = 80 mm (Given)
2x + 30 mm = 80 mm
2x = 80 mm – 30 mm
2x = 50 mm or x = 25 mm
Hence, the lengths of the sides in the parallelogram are 15 mm, 25 mm, 15 mm and 25 mm.
Example 10: Find the values of a and b if PQRS is a parallelogram. We know that diagonals in a parallelogram bisect each other. Therefore,
a 3 = 5 ⇒ a = 3 + 5 = 8
a + 2b = 18
⇒ 8 + 2b = 18
⇒ 2b = 18 8 = 10 ⇒ b = 10 2 = 5
Hence, the values of a and b are 8 and 5, respectively.
ABCD is a parallelogram. Find the value of each unknown angle. Consider ΔABC.
⇒ x° + 6x° + 3x° =
⇒ 10x° =
⇒ x° =
Rectangle, Square and Rhombus
Rectangle
A rectangle is a quadrilateral with four right angles and opposite sides of equal length.
Did You Know?
Properties of a Rectangle
• All the angles in a rectangle are right angles and equal. Here, ∠A = ∠B = ∠C = ∠D = 90° .
• The opposite sides of a rectangle are parallel and equal. Here, AB ǁ DC; AD ǁ BC and AB = DC; AD = BC.
• The diagonals are equal and bisect each other.
Indian mathematician, Brahmagupta (598–668 CE) made one of the most prominent contributions in his treatise Brahmasphutasiddhanta, where he introduced Brahmagupta’s formula to calculate the area of a cyclic quadrilateral when all the lengths of all four sides of a quadrilateral are known.
Square
A square is a quadrilateral with equal sides and four right angles.
Properties of a Square
• All the sides of a square are equal. Here, AB = BC = CD = DA.
• All the angles in a square are right angles. ∠A = ∠B = ∠C = ∠D = 90°.
• The opposite sides are parallel. Here, AB ǁ DC; AD ǁ BC.
• The diagonals are equal and bisect each other at right angles.
AO = CO; OD = OB.
Rhombus
A rhombus is a four-sided geometric shape with all sides of equal length and opposite angles of equal measure, but the angles are not necessarily right angles.
Properties of a Rhombus
• All the sides of a rhombus are equal. Here, PQ = QR = RS = SP.
• The opposite sides of a rhombus are parallel. Here, PQ ǁ SR; PS ǁ QR.
• The diagonals bisect each other at right angles. Here, PO = RO and OQ = OS.
• The opposite angles of a rhombus are equal. Here, ∠P = ∠R; ∠S = ∠Q.
Example 11: If the diagonals of a rhombus measure 10 cm and 24 cm, determine the length of one of its sides.
Let PQRS be a rhombus where diagonals PR = 24 cm and QS = 10 cm.
Since, the diagonals of a rhombus bisect each other at right angles, OQ = 5 cm and OP = 12 cm.
In ΔPOQ, we have
OQ2 + OP2 = PQ2 (Pythagoras’ Theorem)
52 + 122 = PQ2
25 + 144 = PQ2
PQ2 = 169. So, PQ = 13 cm
Example 12: The diagonals of rectangle PQRS intersect at T. If ∠QTR = 44°, find ∠TPS
∠QTR = ∠PTS = 44° (Vertically opposite angles)
Since the diagonals of a rectangle are equal and they bisect each other, PT = ST
⇒∠TPS = ∠TSP (Angles opposite to equal sides)
∠TPS + ∠TSP + ∠PTS = 180° (Angle sum property of triangles)
2∠TPS + 44° = 180°
2∠TPS = 136°
∠TPS = 136° 2 = 68°
Example 13: JKLM is a rhombus. Find the values of x and z.
In ΔJKM, JM = JK (Sides of a rhombus)
Therefore, ∠JMK = ∠JKM = x
Also, 120° = ∠JMK + ∠JKM (Exterior angle is the sum of 2 interior angles)
x = 120° or 2x° = 120° ⇒ x = 60°
Also, x = y = 60° (Alternate angles)
In ΔTLM, y + z + ∠LTM = 180° (Angle sum property of triangles)
Substituting the values, 60° + z + 90° = 180°
z + 150° = 180° ⇒ z = 180° 150° = 30°
PQRS is a square. Find the value of x° in the given figure.
PR bisects ∠P, so, ∠RPS = =
110° + 110° + ∠PUT + ∠RUQ = (Sum of angles around a point is )
∠PUT =
Consider ΔPUT:
∠PUT + x + = + x + =
raw quadrilaterals for each of the given conditions such that:
a Only points A, B and C are in the interior.
b Only points B, C and D are in the interior.
c Only points B, F and E are in the interior.
2 Classify the following as convex or concave quadrilaterals based on the angles of the quadrilateral.
a 190o, 60o, 30o, 80o b 65o, 115o, 111o, 69o c 26o, 226o, 30o, 78o
3 Find the value of x and y in the figure shown below.
S Q R 119° 133° (2y + 7)° (5x − 2)°
4 The length of a parallelogram is 15 cm longer than its breadth. If the perimeter of the parallelogram is 130 cm, find the length and breadth of the parallelogram.
5 WXYZ is a parallelogram where two adjacent angles have a ratio of 2:4. Calculate the measures of all the angles in the parallelogram.
6 What value of 'a' and ‘b’ would make the given quadrilateral a parallelogram? (2a+11) (3b–6) (5a–1) (1+2b )
7 JKLM is a rectangle. Find the value of ∠MJL and ∠TJK.
8 Use the properties of a kite to find the value of ∠QPT and ∠TRS.
50° 61°
1 PQRS is a rhombus whose diagonals intersect at Z. Draw a rough diagram and answer the questions given below.
a Name any four pairs of line segments that are equal in length.
b Name any four pairs of angles that are equal in measure.
c Identify three pairs of congruent triangles in this rhombus.
d Is ∠QRZ = ∠ZRS?
e Is ΔQPZ ≅ΔSPZ?
Angle Sum Property
We know that an angle is formed when two straight lines meet at a common vertex.
• Any angle that is formed in the polygon is called an interior angle.
• The angle between a side of a polygon and an extended adjacent side that is formed outside the polygon is called an exterior angle.
The sum of all the interior angles of a triangle is 180°. What about polygons with four or more sides?
Interior Angle Sum Property
Let us find the sum of the angles of any polygon.
Step 1: Mark one of the vertices in the polygon.
Step 2: Draw diagonals from that vertex to form triangles. Count the number of triangles.
Step 3: Since the sum of the angles in a triangle is 180°, multiply 180° by the number of triangles formed inside each polygon.
From this, we can deduce that the sum of the interior angles of a polygon is the product of 2 less than the number of sides of a polygon and 180°. This can be written as:
Sum of interior angles of a polygon = (n – 2) × 180°, where n is the number of sides of the polygon.
The angle sum property does not depend on whether the polygon is a concave polygon or a convex polygon.
Let us find the measure of the missing interior angle in the polygon.
The shape has 6 sides and is therefore a hexagon.
Sum of angles in a hexagon = (6 2) × 180° = 720°
Let the missing angle be x.
720° = 126° + 126° + 106° + 129° + 147° + x
720° = 634° + x
So, x = 720° 634° = 86°
Example 14: Find the sum of the interior angles in a nonagon.
Number of sides in a nonagon = 9
Let us draw a nonagon and draw non-overlapping triangles inside it.
Number of non-overlapping triangles inside a nonagon = 7
The total sum of interior angles inside a nonagon = 7 × 180° = 1260°
Example 15: Find the value of x° in the diagram.
Using the interior angle sum property of the quadrilateral,
x° + 85° + 79° + 114° = 360°
x° + 278° = 360°
x° = 360° – 278° = 82°
Example 16: If one of the angles in a parallelogram is 65°, find the measure of the other angles. Since opposite angles in a parallelogram are equal, let the angles be 65°, x°, 65° and x°.
65° + 65° + x° + x° = 360° (Angle sum property of quadrilaterals)
130° + 2x° = 360°
2x° = 360° – 130° = 230° ⇒ x° = 230° ÷ 2 = 115°.
Hence, the angles of the parallelogram are 65°, 115°, 65° and 115°.
Find the sum of the angles in the figure. Find the measure of the missing angle.
The shape has 7 sides so it is a .
Sum of angles of the =
Measure of the missing angle is .
Exterior Angle Sum Property
The angle between a side of a polygon and an extended adjacent side that is formed outside the polygon is called an exterior angle.
The sum of the exterior angles in any polygon is always a constant, i.e., 360°.
Interior angle + Exterior angle = 180°.
∴ Exterior angle = 180° Interior angle
Let us calculate the measure of the exterior angles to see what the total is.
We see that the sum of the exterior angles in any polygon is 360°.
?
Sum of exterior angles of the hexagon
+
+
+
+
=
Remember!
The angle formed on a straight line is always 180°.
Sum of exterior angles of the pentagon
Similarly, if a polygon has n equal sides, then the measure of each exterior angle of a regular polygon = 360º n .
Example 17: The exterior angle sum of a 30-sided regular polygon is 360°. Find the measure of each angle.
Number of sides = n = 30
∴ The measure of each exterior angle of a regular polygon = 360º n 360º 30 = 12º =
Example 18: Find the value of y in the diagram.
Using the exterior angle sum property of the quadrilateral,
y° + y° + 71° + 109° = 360°
2y° + 180° = 360°
2y° = 360° 180° = 180°
y = 180° 2 = 90°
Example 19: Find the measure of each exterior angle in the figure.
We know that the exterior angle sum = 360°
⇒∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 360°
⇒ (2x
⇒ 30x + 0 = 360°. So, x = 12°
∠A = (2x 1)° = 23°; ∠B = (3x 5)° = 31°;
∠C = (8x + 3)° = 99°; ∠D = (7x 2)° = 82°;
∠E = (4x + 1)° = 49°; ∠F = (6x + 4)° = 76°
Find the measure of the missing angles a, b, c and d. Solve these in your notebook and write the answers below.
The sum of an interior angle and the adjacent exterior angle in a straight line, can never be greater than 180°.
∠a + 122° = 180°.
So, ∠a = 180° 122° = 58°
∠a = 58°
∠b = ,
∠c = ,
∠d =
Do It Yourself 3C
1 Fill in the blanks.
a The sum of the interior angles in a quadrilateral is .
b Each interior angle of a regular hexagon is .
c The polygon in which the sum of all exterior angles is equal to the sum of interior angles is called a .
d The measure of each exterior angle of a regular polygon of 18 sides is .
2 Write True or False.
a The sum of all exterior angles of a polygon is always 360°.
b The number of triangles that can be formed within a polygon with n sides is n.
c The sum of the interior angles of a triangle is 270°.
d It is possible to have a regular polygon where each exterior angle is the right angle.
3 Find the measure of each exterior angle of a regular polygon with: a 3 sides b 8 sides c 12 sides
4 Find the interior angle sum of the given polygons. a b c
5 Find the value of the unknown angle in each of the following.
6 What could be the value of the unknown exterior angle in each case?
7 Find the number of sides of a regular polygon if each of its exterior angles measures: a 40° b 45° c 60°
8 In a parallelogram, one angle measures 60° less than its adjacent angle. Determine the measures of all four angles in the parallelogram.
9 The measures of the exterior angles of a hexagon are (3x – 4)°, (x + 4)°, (7x – 3)°, (8x – 1)°, (2x + 3)° and (9x + 1)°. Find the measure of each angle.
10 The Vijaya Stambha, built by Rana Kumbha in the 15th century to commemorate his victory over the Malwa and Gujarat armies, is a stunning example of Rajput architecture and stands as a symbol of triumph. The base is a regular decagon. What would be the measure of one of the angles of the base of the building?
Challenge
Critical Thinking
1 Rahul pins four nails to a soft wooden board. He then proceeds to tie threads between these nails so that they form a quadrilateral. The total length of thread used is 12 cm. The angles of this quadrilateral are in the ratio 1:2:3:4. Is the quadrilateral formed by the threads convex or concave? Find the measure of the largest angle?
Points to Remember
• Polygons can be classified into different types on the basis of their number of sides and vertices. A polygon with 4 sides and angles is a quadrilateral.
• In a convex polygon, all the diagonals lie inside the polygon, whereas in a concave polygon, at least one diagonal lies outside the polygon.
• The number of diagonals in a polygon with n number of sides = n(n – 3) 2 .
• If a polygon has n number of sides, then the sum of all the interior angles is (n – 2) × 180°.
• The sum of the exterior angles in any polygon is always a constant, i.e., 360°.
Math Lab
Setting: In groups of 3-4
Polygon Sorting Challenge!
Collaboration & Communication
Materials Required: Polygon cards (pre-made or printed), large poster paper or whiteboard, markers, scissors and tape
Method:
1 Discuss the concept of polygons like triangles, quadrilaterals, pentagons, hexagons, etc.
2 Create cards with polygon names and key properties.
3 Draw a table with four columns on poster paper and label it with polygon names.
4 Divide the class into groups and provide cards and the poster paper table.
5 Instruct groups to sort cards into the correct columns based on properties, encouraging discussions.
6 Gather the class to discuss choices and have groups explain their reasoning.
Chapter Checkup
1 Fill in the blanks.
a A polygon with unequal sides and unequal angles is called an .
b The sum of the interior angles of a hexagon is
c The number of diagonals in a pentagon is .
d The sum of the exterior angles of any polygon is always
2 State whether the following statements are true or false.
a The diagonals of a kite bisect each other at right angles.
b The diagonals of an isosceles trapezium are equal.
c The diagonals of a rectangle are perpendicular to each other.
d All quadrilaterals are parallelograms.
3 Which of the interior angles given below would not belong to a convex quadrilateral?
a 100° b 178° c 222° d 2°
4 Identify the polygons as concave or convex.
a b c d
5 How many diagonals will each of these polygons have?
a Convex quadrilateral b Nonagon
c Polygon with 17 sides
6 Which of the sets of angles given below is a set of interior angles of a quadrilateral? a 47°, 58°, 98°, 156°
54°, 59°, 72°, 108°
83°, 68°, 82°, 127°
7 Find each exterior angle of the regular polygons with the given number of sides.
a 4 b 15 c 20
8 Find the number of sides of a regular polygon whose exterior angle measures:
a 18° b 36° c 90°
9 Write the set of exterior angles corresponding to the set of interior angles given below.
a 70°, 90°, 110°, 90°
45°, 60°, 100°, 155° c 80°, 85°, 95°, 100°
10 Find the value of the unknown exterior angle in each case.
a
11 Find the value of the unknown interior angle in each case.
12 In a parallelogram, the adjacent angles are (2z 25)º and (3z + 10)º. Determine the measures of all four angles in the parallelogram.
13 The angles of a pentagon measure x°, (x 5)°, (x + 15)°, (3x 44)° and (x 70)°. Find x
14 In a rhombus, one of the diagonals is of the same length as one of its sides. Determine the measures of the angles in the rhombus.
15 The angles of a hexagon are in the ratio 1:2:3:4:6:8. Find the measure of the smallest and the biggest angles.
16 Find the values of wº, xº, yº and zº.
17 Sohan is designing a logo for his company which is in the shape of a regular 12-sided polygon. How many diagonals connect the interior angles of the polygon? How many triangles can be formed by connecting these interior angles?
18 In a city with several towns connected by bridges, there are 10 towns. If each town is connected to its adjacent town by a direct bridge, how many bridges are needed in total? How many diagonals does this network of bridges have?
Chapter 3 • Polygons and Quadrilaterals
Challenge
1 Read the statements and choose the correct option.
Assertion (A): The sum of the interior angles of any polygon is given by the formula (n – 2) × 180°, where n is the number of sides.
Reason (R): A polygon can be divided into n – 2 triangles.
a Both (A) and (R) are true, and (R) is the correct explanation of (A).
b Both (A) and (R) are true, but (R) is not the correct explanation of (A).
c (A) is true, but (R) is false.
d (A) is false, but (R) is true.
2 Consider a quadrilateral PQRS. If PQ is parallel to RS and PS is parallel to QR, which of the following statements alone is sufficient to prove that quadrilateral PQRS is a square?
Statement 1: ∠PQR = ∠SPQ = 90°
Statement 2: PQ = QR
a Statement 1 alone is sufficient, but Statement 2 alone is not sufficient.
b Statement 2 alone is sufficient, but Statement 1 alone is not sufficient.
c Either statement alone is sufficient.
d Both statements together are sufficient, but neither statement alone is sufficient.
Case Study
Cross Curricular & Value Development
Park Renovation Project
Mr Dhawan got a contract to renovate the park in his society. On analysis, he found that he had to tile the paths, build some climbing structures for the children’s play area, add some more sprinklers in the park and also build a small swimming pool at the centre of the park. Answer the questions.
1 The contractor told Mr Dhawan that each interior angle in the tile was 120°. What was the shape of the tile?
a Square b Pentagon c Hexagon d Octagon
2 The park is rectangular in shape and its length and breadth are 160 m and 120 m, respectively. Mr Dhawan planted the sprinklers across the diagonals of the park. If he planted each sprinkler at a distance of 5 m then how many sprinklers did he plant across each diagonal?
3 The climbing structure was made of 4 bars forming a quadrilateral shape. The angles at the corners are measured and found to be in the ratio 2:3:4:5. Determine whether the climbing structure is a parallelogram.
4 The swimming pool that was built at the centre of the park had opposite sides parallel and equal in length. What was the shape of the swimming pool?
5 What more do you think Mr Dhawan can do to make the park useful and clean? How do you keep the park in your neighbourhood clean?
4 Bar Graphs and Histograms
Letʹs Recall
We have learnt that data is collected and organised in tables, making it easier to understand.
The given table shows the major crop-producing states in India.
This collection of information is called data
From the data set, we can conclude that:
3 states produce rice.
2 states produce wheat.
2 states produce pulses.
So, we can say that rice is the most produced crop.
Letʼs Warm-up
State Crop Produced
West Bengal Rice
Haryana Wheat
Uttar Pradesh Wheat
Odisha Rice
Rajasthan Pulses
Madhya Pradesh Pulses
Tamil Nadu Rice
The given table shows the temperatures (°C) in a month every day for 30 days.
Mean, Median and Mode Frequency Distribution of Grouped and Ungrouped Data
Ahan loves reading books. Every time he finishes reading a book, he writes down its title, author’s name and how much he likes it on a scale of 10.
He writes them in his diary as:
We now know that the details that Ahan collects in his reading log are data.
Data is a collection of numerical figures that represent a specific kind of detail called an observation.
The above data is recorded in a table in an unorganised form. When numerical data is collected in its original form, and in an unorganised form, the data is called ungrouped data or raw data.
We use data to remember information about all sorts of things in our everyday lives, like keeping track of grades in school, the number of goals scored in sports, or even the weather forecast throughout the day. This study of numerical data is called statistics
Think and Tell
Where do you need to organise data in your day-to-day life?
When we organise raw data by arranging it in rows or columns, it is called an array. The data can be arranged either in ascending order or descending order.
An array is like a bookshelf in Ahan’s room where he keeps his books neatly arranged, with each book representing a piece of data. So, in Ahan’s reading log, an array would be a list that holds all the data about the books.
Frequency Distribution of Ungrouped Data
Organising data is like arranging your books neatly on a bookshelf or putting them in specific categories. In the reading log table, Ahan has organised data about five books he has read. This format makes it easy for Ahan to track the books read and find specific information about each book.
By organising data, you can quickly access the information you need and then discover trends or patterns.
Did You Know?
Ungrouped data is also called discrete data.
We saw how Ahan tracks book genres like mystery, horror and science fiction in his reading log.
This helps to know how many times each genre appears, which genres Ahan reads most frequently, and which are less common.
The number of times a number or an observation occurs in a given set of data is called frequency.
Let us create a frequency distribution table and record the number of pages in each book he has read.
Book Title Summer’s Child Sanctuary The Diabolic Last Star Burning Rabbit and Robot Number of Pages 416 320 416 400 448
Step 1: List all the unique values (the different numbers of pages) from Ahan’s reading log as 416, 320, 416, 400 and 448.
Step 2: Count how many times each unique value appears in the data. This gives us the frequency.
416: 2 books; 320: 1 book; 400: 1 book; 448: 1 book
Step 3: Create a table that displays the unique values and their corresponding frequencies.
The range is the difference in the number of pages between the thinnest and thickest books.
Here, the range of the number of pages in the books = 448 - 320 = 128
The range refers to the difference of the smallest and largest values in the data
Example 1: Studies suggest that, on average, students should spend about 5–10 hours per week on extra-curricular activities. Given below are the number of hours spent by 30 students on extra-curricular activities per week.
5, 6, 7, 3, 5, 4, 7, 6, 5, 3, 7, 6, 4, 5, 6, 5, 6, 7, 3, 5, 4, 7, 6, 5, 3, 7, 6, 4, 5, 6.
Arrange the data in a frequency table and find the range of the given data.
Arrange the data in ascending order: 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7
Count the frequency and create the Frequency Distribution Table.
Range = Highest value in the data set – Smallest value in the data set = 7 – 3 = 4
Suppose we have data representing the number of siblings that 30 individuals have. The data set is as follows:
2, 3, 4, 2, 1, 3, 0, 2, 4, 3, 2, 1, 1, 0, 0, 0, 1, 3, 4, 2, 2, 2, 1, 1, 3, 1, 1, 0, 2, 0.
Arrange the data and form a frequency table. Also, find the range of the given data.
Range = Highest value in the data set – Smallest value in the data set
Therefore, the range of the given data = _____ _____ = _____
Do It Yourself 4A
1 In a class, there are 50 students. Each student was asked what their favourite sport was. 40% of the students said cricket, 24% said badminton, 10% said tennis, and the rest did not have any favourite sport. Prepare a frequency distribution table for the number of students who like a sport. Which sport is liked by the minimum number of students?
2 Suppose you have data representing the number of holidays taken in a year by 30 individuals. The holiday data is as follows:
2, 3, 2, 5, 3, 4, 1, 3, 5, 2, 3, 4, 2, 1, 3, 4, 2, 5, 1, 2, 3, 4, 1, 4, 5, 1, 2, 4, 1, 5.
Arrange the data and form a frequency table. Also, find the range of the given data.
3 This table is the frequency distribution that shows the monthly income levels of middle-class families in India.
a How many individuals have the highest monthly income?
b How many individuals have the lowest monthly income? Why is saving money important?
c What is the range?
4 The given data represents the scores (out of 100) of 30 students on a maths test. The data set is as follows: 85, 92, 78, 90, 88, 76, 95, 82, 79, 88, 94, 87, 89, 91, 75, 83, 80, 92, 84, 86, 77, 81, 93, 79, 88, 90, 86, 85, 94, 87.
Arrange the data and form a frequency table. Also, find the range of the given data.
5 The value of π up to 39 decimal places is 3.141592653589793238462643383279502884197. Make a frequency distribution table for the digits 0 to 9 before and after the decimal point.
6 Collect a data set from the students in your class and create a frequency table for the data.
1 Rohan noted down the ages of 20 people in his neighbourhood as: 25, 30, 35, 40, 25, 28, 35, 42, 30, 32, 28, 22, 25, 28, 40, 45, 35, 30, 32, 28. He found out later that he mistakenly noted two entries wrong. He wrote 45 and 25 instead of 43 and 23. Will this affect the range of the data? Justify your answer.
Frequency Distribution of Grouped Data
COVID-19, initially detected in India in early 2020, has significantly affected the nation’s healthcare system, economy, and daily life. This impact led to extensive vaccination campaigns and the implementation of public health measures.
The given table shows the number of COVID-19 cases in various countries worldwide.
While creating a frequency distribution for this data, we track the number of COVID cases for each country separately. This approach is useful when analysing large data sets.
However, sometimes it is beneficial to group data for a broader overview.
One common way to group data is by using ranges or intervals.
For instance, we can group the number of COVID cases to ranges, like 0–2 crores and 3–5 crores. Grouping data can make it easier when we need to deal with large data sets.
When individual observations are arranged into groups, creating a frequency distribution table, it is referred to as grouped data
Let us group the number of COVID cases into the ranges 0–2, 3–5, 6–8 and 9–11.
These ranges are called class intervals.
When the whole range of variable values is classified in some groups in the form of intervals, then each such interval is known as a class interval.
The range of a class interval is called the class limit
The smaller value of a class interval is called the lower class limit, and the greater value is called the upper class limit. For example, in the class interval 3–5, 3 is the lower class limit and 5 is the upper class limit.
The difference between the upper limit and the lower limit of a class interval is called the class size. For the class interval of 3–5, the class size is 2.
The class mark is the midpoint of each class interval. For the class interval 3-5, the class mark is 3 + 5 = 4 2 . Remember! class mark = upper limit + lower limit 2
The class size of any of the class intervals must not differ.
Based on the above information, we can form a frequency distribution table as follows:
Did You Know?
Sir Ronald Fisher introduced the concept of data handling or statistics. Indian mathematicians P. C. Mahalanobis and C. R. Rao have also played a major role in the field of statistics.
Example 2: The marks of 30 students in a science test are given below.
Answer the following questions.
1 What is the size of each class? 5
2 Which class interval has the highest frequency? (10 - 15)
3 Which class interval has the lowest frequency? (0 - 5)
4 What is the class mark of the second class interval? 5 + 10 = 7.5 2 15 2 =
Do It Together 5 72.5
The data below shows the annual income (in thousands) (in ₹) of 40 families in a town.
Prepare a frequency distribution table for the data using the class interval of 5, in your notebooks. Answer the following questions.
1 What is the lower limit of the first class interval?
2 What is the upper limit of the last class interval?
3 What is the size of each class?
4 Which class interval has the highest frequency?
5 Which class interval has the lowest frequency?
6 What is the class mark of the fifth class interval?
The following is the distribution of weights (in kg) of 46 people:
i What is the lower limit of classes 50–60?
ii Find the class marks of the classes 40–50 and 50–60.
iii What is the class size?
2 The observations given below show the ages of people who watch a particular TV channel. Prepare a grouped frequency table for the data: 20, 39, 42, 5, 12, 19, 47, 27, 7, 13, 40, 38, 24, 34, 15, 40, 10, 9, 3, 29, 17, 34, 23, 18, 19.
3 The electricity bill amounts (in ₹) for each of the 24 houses in a village are given below. Construct a frequency table.
215, 203, 120, 350, 800, 600, 350, 400, 120, 340, 150, 562, 452, 125, 658, 235, 645, 450, 207, 489, 263, 500, 153, 450.
4 The average temperatures in Delhi in 2023 are given.
January—14 °C, February—16 °C, March—22 °C, April—28 °C, May—34 °C, June—36 °C, July—33 °C, August—32 °C, September—30 °C, October—26 °C, November—20 °C, December—16 °C
Create a grouped frequency table for the given data with a class limit of 5 °C.
5 The given table shows the marks obtained (out of 20) by students in a class test. Read the table and answer the following questions.
a How many students scored less than 15?
b How many students scored more than or equal to 15 marks?
c What is the class mark of the class interval with a frequency of 6?
d How many students wrote the test?
e What percentage of the students scored less than 15 marks?
6 Create a question on the table given in Q5.
1 Read the statements and identify which of the following statements are required to identify the original list of the 100 individual heights?
Statement 1: The frequency distribution table summarising the height of 100 adults is known.
Statement 2: The height of the shortest person and the tallest person is known.
a Statement 1 alone is sufficient, while Statement 2 alone is not sufficient.
b Statement 2 alone is sufficient, while Statement 1 alone is not sufficient.
c Both statements together are sufficient, but neither statement alone is sufficient.
d Each statement alone is sufficient.
e Both statements together are not sufficient.
Mean, Median and Mode Graphical Representation of Ungrouped Data
India, often celebrated as an agricultural powerhouse, has made significant progress in the global wheat market over the past few decades. Thanks to its diverse agro-climatic zones, extensive cultivation practices and technological advancements, India has emerged as a prominent wheat exporter on the world stage.
Single Bar Graphs
India exports wheat to multiple countries. Let us see approximately how many tonnes of wheat India exported to different countries in the year 2021–22.
Drawing and Reading Bar Graphs
Let us plot the data on a bar graph.
• A bar graph is a pictorial representation of ungrouped data.
• All the bars are of uniform width and the space between all the bars is consistent.
• Bars are drawn over one axis, and the values of the variables are shown across the other axis. The height of a bar represents the value of the variable.
What is the average of the wheat exported to the 5 countries?
Total wheat exported to these 5 countries = 94,000 + 86,000 + 56,000 + 55,000 + 63,000 = 3,54,000 tonnes of wheat
Average = 354000 5 = 70,800 tonnes of wheat
What percentage of the total wheat is exported to Qatar?
Wheat exported to Qatar = 63,000 tonnes
Total wheat exported = 94,000 + 86,000 + 56,000 + 55,000 + 63,000 = 354,000 tonnes
Percentage = 63000 354000 × 100% = 17.8%
Example 3: The number of mathematics books sold by a publishing house on 6 different days is shown using a bar graph. Read the bar graph and answer the questions.
1 How many books were sold on Wednesday?
Number of books sold on Wednesday = 870
2 What percentage of the total books were sold on Thursday?
Number of books sold on Thursday = 970
Total number of books sold = 800 + 700 + 870 + 970 + 670 + 1090 = 5100
Percentage of the total books that were sold on Thursday = 970 5100 × 100% = 19 1 51 %
3 What is the average number of books sold per day over the 6 days?
Total number of books sold = 800 + 700 + 870 + 970 + 670 + 1090 = 5100
Average number of books sold per day over the week = 5100 ÷ 6 = 850
Example 4: The data shows the foreign exchange reserves of a country. Draw a bar graph to represent the data and answer the questions.
1 The foreign exchange reserve in 2013 was how many times that in 2011?
Foreign exchange reserve in 2011 = $2500 million
Foreign exchange reserve in 2013 = $3500 million
3500 ÷ 2500 = 1.4 times
2 By what percentage did the foreign exchange reserve change in 2010 from the previous year?
Foreign exchange reserve in 2010 = $2800 million
Foreign exchange reserve in 2009 = $2600 million
Change in the foreign exchange reserve = $2800 million – $2600 million = $200 million
Percentage change = 200 2600 × 100% ꞊ 7 9 13%
3 What is the ratio of the number of years in which the foreign exchange reserve was above the average reserve to those in which the reserve was below the average reserve?
Total foreign exchange reserve in the past 5 years = 2600 + 2800 + 2500 + 3100 + 3500 = $14,500 million
Average foreign exchange reserve for the 5 years = 14,500 ÷ 5 = $2900 million
Years in which the reserve was above the average reserve, that is, in 2012 and 2013 = 2
Years in which the reserve was below the average reserve = 2009, 2010 and 2011 = 3
Hence, the required ratio is 2:3.
The length (in km) of some major rivers in India are given below. Draw a bar graph for the data and answer the questions.
1 Which is the longest river?
2 Which is the shortest river?
3 What is the ratio of the length of river Mahanadi to that of river Kaveri?
GangaBrahmaputra Kaveri Mahanadi
Length of river Mahanadi = 900 km
Length of river Kaveri =
Ratio of the length of river Mahanadi to that of river Kaveri = : = :
4 What is the difference in the lengths of river Ganga and Narmada?
Length of river Ganga =
Length of river Narmada =
Difference in length = − =
Do It Yourself 4C
1 Refer to the bar graph on the wheat exported by India to different countries and answer the questions.
a What percentage of the total exports was exported to Sri Lanka?
b What percentage of the total exports was exported to Afghanistan?
c What was the ratio of the wheat exported to Qatar to that exported to the Yemen Republic?
d What is the average quantity of wheat exported to these 5 nations?
2 Refer to the bar graph used in Example 3 and answer the questions.
a What percentage of the total books were sold on Friday?
b What percentage of the total books were sold on Saturday?
c What is the ratio of the number of books sold on Thursday to the number of books sold on Friday?
d What is the ratio of the number of books that is less than the average number of books sold and the number of books that is more than the average number of books sold?
3 Refer to the bar graph used in Example 4 and answer the questions.
a What is the foreign exchange reserve for 2013?
b What is the difference in the reserves for 2011 and 2012?
c What is the percentage increase in the reserve for 2013 from that for the previous year?
d What is the ratio of the reserves of 2010 and 2011 together to the reserves of 2012 and 2013 together?
4 The data shows the export of pears in different years. Draw a bar graph for the given data and answer the questions.
a What was the total value of exports in all the years?
b What was the average export value of pears for the given period of time?
c What was the percentage increase in 2018 from 2015?
d Which two years have an average export value of ₹17.1 crores?
5 The bar graph shows the number of students who passed an examination. The total number of students in the school was 450 every year. Read the bar graph and answer the questions.
a How many students passed in 2021?
b What percentage of the students passed in 2018?
c What percentage of the students passed in 2020?
d What was the percentage increase in the number of students passing in 2022 from those passing in 2019?
e Create a question not covered here based on the same bar graph.
Cross Curricular
6 The bar graph shows the approximate populations of different cities in the world. Read the bar graph and answer the questions.
a What is the total population of Delhi and Mumbai?
b What is the difference in the populations of Shanghai and Cairo?
c What is the average population of the six cities?
d What is the difference in the populations of Moscow and New York?
Challenge
1 The teacher asked the students to collect information on the life spans of various animals. The students found the following information:
Animal Crocodile Tortoise Blue Whale Shark Dolphin
Life-Span 50–60 years 80–150 years 50–90 years 20–30 years 40–90 years
One student wants to show the results using a bar graph.
Give one reason why a bar graph is not a good choice for showing this information. If we calculate the average ages of the lifespans of the animals, can we plot a bar graph? If yes, construct a bar graph for the new data.
Double Bar Graphs
India exports fruit, cereals, dairy products, and many other products. Let us see the products that India exported in April–September 2021 and April–September 2022.
Drawing Double Bar Graphs
Let us represent the data on a double bar graph to see the increase or decrease in the exports of various products.
A double bar graph shows two sets of data simultaneously. It helps us compare two sets of data.
Write the scale of the graph.
Label both the axes.
Draw two rectangular bars representing the data.
Example 5: Consider the data shown below for the sales of different brands of laptops by a company during 2020 and 2021. Draw a bar graph to represent the data.
Consider the data shown for the production of cars during the years 2012–14 from different manufacturers. Complete the bar graph.
Reading Double Bar Graphs
Consider the bar graph shown below for the export of various products by India in the years 2021 and 2022. Read the bar graph and answer the questions.
1 What was the percentage increase in the exports of non-basmati rice?
Amount of non-basmati rice exported in 2021 = $2969 million
Amount of non-basmati rice exported in 2022 = $3207 million
Percentage increase in exports = 3207 – 2969 2969 × 100% ≈ 8%
2 Which product category had the greatest increase in exports?
The product category with the greatest increase in exports is other products.
3 What is the average of the percentage increase in the export of each product category?
Percentage increase in exports of fruit = 313 – 301 301 × 100% = 3.98%
Percentage increase in exports of cereal preparations & miscellaneous processed items = 2111 – 1632 1632 × 100% = 29.35%
Think and Tell
Which product has the highest percentage increase from the previous year?
Percentage increase in exports of meat, dairy & poultry products = 2099 – 1903 1903 × 100% = 10.29%
Percentage increase in exports of basmati rice = 2280 – 1660 1660 × 100% = 37.34%
Percentage increase in exports of non-basmati rice = 3207 – 2969 2969 × 100% = 8.01%
Percentage increase in exports of other products = 3761 – 2591 2591 × 100% = 45.16% Average percentage increase = 3.98% + 29.35% + 10.29% + 37.34% + 8.01% + 45.16%
Example 6: The bar graph shows the production of tea by different companies in different years. Read the bar graph and answer the questions.
1 What is the total production of tea by different companies in the year 2016?
Production of tea by company A in 2016 = 60 tonnes
Production of tea by company B in 2016 = 70 tonnes
Production of tea by company C in 2016 = 70 tonnes
Production of tea by company D in 2016 = 40 tonnes
Total tea production in 2016 = 60 + 70 + 70 + 40 = 240 tonnes
2 The total production of the four companies in 2015 is what percentage of the production by Company B and D together in 2017?
Total production of the four companies in 2015 = 50 + 70 + 60 + 50 = 230 tonnes
Total production by company B and D in 2017 = 90 + 50 = 140 tonnes
Required percentage = 230 140 × 100% = 164.28%
3 What is the ratio of the production by Company B in the three years to the production by Company C in the three years?
Production by company B in the three years = 70 + 70 + 90 = 230 tonnes
Production by company C in the three years = 60 + 70 + 80 = 210 tonnes
The required ratio = 230:210 = 23:21
The bar graph shows the number of people who visited four different places in two different years. Read the bar graph and answer the questions. Note: The data is not accurate.
1 Number of people who visited Qutab Minar in 2018 = 700
2 Number of people who visited India Gate in 2019 =
3 What was the percentage increase in the number of people visiting the Taj Mahal in 2019 from 2018?
Number of people who visited Taj Mahal in 2018 = 900
Number of people who visited Taj Mahal in 2019 =
Percentage increase =
4 What is the difference in the average number of visitors in 2018 and 2019?
Average number of visitors in 2018 =
Average number of visitors in 2019 = Difference = − =
Do It Yourself 4D
1 Refer to the double bar graph shown on page 70 for the export of various products in the years 2021 and 2022 and answer the given questions.
a What was the percentage increase in the exports of basmati rice?
b Which product has the least exports?
c What were the total exports for the year 2021?
d What were the total exports for the year 2022?
Qutab Minar
Taj Mahal India Gate Lotus Temple Place
x
2 Refer to the bar graph in Example 6 and answer the questions.
a What is the total production of tea by Company C in three years?
b What is the ratio of the tea produced by Company B in 2015 and 2016 to the total tea production by company D in three years?
c What was the percentage increase in tea production by Company D from 2016 to 2017?
d What was the percentage increase in tea production by Company B from 2015 to 2017?
3 The table below shows the test scores of two students, Ayesha and Ravi, over five subjects. Draw a double bar graph to compare their scores.
Draw a double bar graph to represent the data.
4 The double bar graph shows the different types of fruit sold by two vendors. Read the bar graph and answer the given questions.
a What is the total number of fruits sold by Vendor A?
b What is the total number of fruits sold by Vendor B?
c What is the ratio of the oranges and apples sold to the other three types of fruit sold by Vendor A?
d Which was the highest-selling fruit out of the 5 types of fruit sold by the two vendors together?
e Create a question based on the given double bar graph.
5 The double bar graph shows the runs scored by Virat Kohli and Rohit Sharma in different years. Read the bar graph and answer the questions.
a How many runs were scored in total by Virat Kohli in the given years?
b How many runs were scored in total by Rohit Sharma in the given years?
c What is the difference in the average number of runs scored by Virat Kohli and Rohit Sharma?
d What is the ratio of the runs scored by Virat Kohli before 2017 to the runs scored by Rohit Sharma after 2015?
1 The double bar graph shows the number of film tickets sold by two different cinema halls for different genres of films. Which of the given statements is correct?
Statement 1: The ratio of sci-fi genre tickets sold by Cinema Hall 1 to Cinema Hall 2 is 8:9.
Statement 2: Cinema Hall 2 sold 25% more horror film tickets than Cinema Hall 1.
Statement 3: Cinema Hall 2 sold 60% less drama film tickets than Cinema Hall 1.
a Only Statement 2 is correct.
b Statements 1 and 3 are correct.
c Statements 2 and 3 are correct.
d All statements are correct.
Graphical Representation of Grouped Data
In the city of Metropolis, a team of public health organisations organised a survey to monitor people�s health. They collected data on the number of people and the daily exercise duration in minutes.
Histograms
The data collected for the number of people who exercise for different numbers of minutes is shown below.
Did You Know?
The histogram was first introduced by Karl Pearson.
A histogram is a special type of bar graph. It is a graphical representation of grouped data.
Drawing Histograms
Let us draw a histogram for the above data.
Take the frequency on the y-axis.
Draw bars of equal width.
Take class intervals on the x-axis.
The width of the bars in a histogram must be consistent.
Example 7: The data shows the daily wages of workers in a factory. Draw a histogram for the data given.
The data shows the marks scored by students in an examination of 100 marks. Draw a histogram for the given data.
Reading Histograms
The histogram shows the number of minutes of exercise done.
How many people exercised for more than 1 hour?
1 hour = 60 minutes
So, the number of people who exercised for more than 60 minutes = 75 + 60 + 50 + 40 = 225 people.
What percentage of the total number of people exercised for less than 90 minutes?
Total number of people = 50 + 90 + 75 + 60 + 50 + 40 = 365
Number of people who exercised for less than 90 minutes = 50 + 90 + 75 = 215
Percentage of all the people who exercised for less than 90 minutes = 215 365 × 100% = 58.9%
Example 8: The marks obtained by students in a test are given below. Draw a histogram to represent the data and answer the questions.
48, 41, 35, 85, 99, 57, 69, 87, 76, 41, 23, 35, 22, 48, 47, 86, 97, 65, 53, 52, 84, 97, 74, 73, 34, 46, 98, 99, 56, 57, 36, 74, 98, 46, 65, 66, 97, 89, 85, 84, 86, 47, 74, 73, 71, 66, 61, 67, 34, 23, 24, 24, 43, 54.
Number of Students 5 5 9 6
1 How many students scored more than 30?
Number of students who scored more than 30 = 5 + 9 + 6 + 7 + 7 + 8 + 7 = 49
2 If the pass mark is 40, how many students did not pass the test?
Number of students who did not pass the test = 5 + 5 = 10
3 How many students appeared for the test?
Total number of students who appeared for the test = 5 + 5 + 9 + 6 + 7 + 7 + 8 +
The histogram shows the ages of employees in an office. Observe the graph and answer the questions.
1 How many employees are older than 30 years?
Number of employees older than 30 years = 40 + 30 + 20 + 20 + 5 + 5 = 120
2 What percentage of the total number of employees is older than 40 years?
Number of employees older than 40 years =
Total number of employees =
Percentage of total employees who are older than 40 years =
3 What is the ratio of employees older than 35 years to those younger than 35 years?
Number of employees older than 35 years =
Number of employees younger than 35 years =
Required ratio = :
4 What percentage of the total number of employees is younger than 40 years?
Number of employees who are younger than 40 years =
Total number of employees =
Percentage of total number of employees who are younger than 40 years =
Do It Yourself 4E
1 The data shows the monthly rainfall for a city over different years. Draw a histogram to represent the data and answer the questions.
a What was the total rainfall over the years?
b During which year did the highest rainfall occur?
c What was the percentage increase/decrease in the rainfall during 2014–15 in comparison with the previous year?
d Which two years had the highest percentage difference in rainfall over the previous year?
2 The data shows the ages of US presidents at the time of their inauguration. Draw a histogram to represent the data and answer the questions. (Consider only the ages in years when drawing the histogram.)
Number of Presidents 6 11 17 8 3 1
a How many presidents were more than 66 years old at the time of their inauguration?
b How many presidents were more than 60 years old at the time of their inauguration?
c How many presidents were more than 54 years old?
3 Refer to the histogram on page 75 for the number of minutes people exercised and answer the questions.
a What is the total number of people on whom the survey was conducted?
b What percentage of the total number of people exercised for more than 30 minutes?
c What percentage of the total number of people exercised for less than 120 minutes?
d What is the ratio of the number of people who exercised less than 90 minutes and the number of people who exercised for more than 120 minutes?
4 Refer to the histogram in Example 7 and answer the questions.
a How many workers earn more than ₹300?
b How many workers earn less than ₹500?
c What percentage of the total number of workers earn less than ₹600?
d What is the ratio of the number of workers who earn less than ₹400 to the number of workers who earn more than ₹400?
e How many workers make between ₹400 and ₹600?
5 Refer to the histogram in Example 8 and answer the questions.
a What percentage of the total number of students scored more than 40 marks?
b What percentage of the total number of students scored less than 30 marks?
c What is the ratio of students who scored more than 50 marks to students who scored less than 50 marks?
d What is the difference of the number of students who scored more than 40 marks and the number of students who scored less than 40 marks?
6 Refer to the histogram in Do It Together above and answer the questions.
a How many employees are older than 50 years?
b What is the ratio of the number of employees who are younger than 35 years to those who are older than 35 years?
c What percentage of the total number of employees is older than 25 years?
d Create a question based on the histogram. Creativity
Challenge
Critical Thinking
1 The data shows the ages of the first five Indian presidents at their inauguration, along with their tenure. President
Dr Rajendra Prasad
Dr Sarvepalli Radha Krishnan
Dr Zakir Hussain
V.V. Giri
65 years 1950–1962
73 years 1962–1967
70 years 1967–1969
74 years 1969–1974
Fakhruddin Ali Ahmed 69 years 1974–1977
Can we construct a histogram for this data? Suggest an alternative graphical representation that would be appropriate for this data. Also, draw the graphical representation.
Points to Remember
• A collection of numerical figures that represent a similar kind of information is called data.
• A table is called a frequency distribution table when it shows how many times each specific number or figure appears in a data set.
• In grouped data, individual observations are arranged in groups such that a frequency distribution table of these groups helps provide a convenient way of presenting or analysing the data.
• The number of times a particular observation occurs in the data is called its frequency.
• Ungrouped data can be represented using a bar graph.
• Histograms are special types of bar graphs which are used to represent grouped data. In histograms, the class intervals are shown on the horizontal axis and the heights of the rectangular bars show the frequency of the class interval. There is no gap between the class intervals.
Math Lab
Experiential Learning & Collaboration
The Shoe Size Survey!
Aim: To introduce students to the concept of histograms and help them create one based on real data.
Settings: Whole class
Method:
Materials Required: Chart paper, markers, sticky notes, measuring tape or ruler
1 Discuss with the class that they will conduct a shoe size survey in the class, and then draw a histogram to show the data.
2 The students then use the measuring tapes to measure their shoe sizes and collect the data on a paper.
3 The students will represent the data using histograms on the chart paper and will note down 2 questions related to the created histogram.
4 Each student will then exchange the created histograms and questions with the student next to them.
5 Each student will read the histograms created by the other student and will answer the given questions.
6 They can then display their charts to the whole class at the end.
Chapter Checkup
1 Represent the following data in the form of a frequency distribution.
1, 2, 6, 5, 1, 5, 1, 3, 2, 6, 2, 3, 4, 2, 0, 0, 4, 4, 3, 2, 2, 0, 0, 1, 2, 2, 4, 3, 2, 1, 0, 5, 1, 2, 4, 3, 4, 1, 6, 2, 2.
2 A survey was conducted among students, and the observations below show that the students are preparing for the entrance examinations when they are 12–18 years old. Prepare a frequency table based on the following ages: 13, 14, 13, 12, 14, 13, 14, 15, 13, 14, 13, 14, 16, 12, 14, 13, 14, 15, 16, 13, 14, 13, 12, 17, 13, 12, 13, 13, 13, 14.
3 The given table shows the number of donors of each blood group in a hospital’s blood donation campaign. Blood
a Which blood group has the most donors?
b How many people participated in the blood donation campaign?
4 The populations (approximate) of some Indian states are given in the table below.
State Meghalaya Maharashtra Bihar Andhra Pradesh West Bengal Nagaland Uttarakhand Population (in crores) 3 11 10 8 9 2 11
a What is the population of Meghalaya and Nagaland together?
b Which is the most populated state?
c Which is the least populated state?
5 Dr Radha recorded the pulse rate (per minute) of 29 persons: 61, 75, 71, 72, 70, 65, 77, 72, 67, 80, 77, 62, 71, 74, 79, 67, 80, 77, 62, 71, 74, 61, 70, 80, 72, 59, 78, 71, 72. She wants to construct a frequency table in the inclusive form, taking the class interval 61–65 of equal width. Now, if she needs to convert this data again into the exclusive form in a separate table, how can she do that?
6 The graph shows the percentage break up of sales of units of different products in 2020. Read the bar graph and answer the questions. The total number of units sold by the company was 5,20,000.
a How many units of Product A were sold?
b How many units of Product C were sold?
c What is the difference in the number of units of Product B and units of Product D sold?
d What is the ratio of the units of Product A and units of product C sold?
7 The bar graph shows the number of students who passed out of different colleges in 2022. Read the bar graph and answer the questions.
a How many students passed out of College B?
b The pass percentage of College A is the same as the pass percentage of College E. By what percent is the total strength of College E more than the total strength of College A?
c If 90% of students passed in College B, how many students failed in that college?
d The ratio of the total students who passed out of all the colleges to the total students who failed in all the colleges is 43:9. How many students failed in total from all the colleges?
8 The data shows the number of students of two different schools who participated in different activities at a function. Draw a bar graph to represent the given information.
Number of students from school A 45 30 35 35 30 Number of students from school B 50 25 30 25 25
9 The bar graph shows the cars sold by two different dealers. Read the bar graph and answer the questions.
a How many cars were sold by Dealer A in total?
b How many cars were sold by Dealer B in total?
c What is the ratio of the cars sold in 2019 to those sold in 2022?
d What percent of the total number of cars sold by Dealer A were sold in 2018?
10 The bar graph shows the number of candidates appearing for an entrance exam from various cities. Read the bar graph and answer the questions.
a How many candidates appeared in total in the year 2021?
b How many candidates appeared in total in the year 2022?
c What is the ratio of the number of candidates appearing for the entrance exam from Mumbai and Bangalore in the year 2021?
d What is the average number of candidates appearing for the entrance exam for the year 2021?
e Create two questions on the given bar graph.
11 Draw the histogram for the given data.
12 The histogram shows the heights of students in a school. Study the histogram and answer the questions.
a How many students are taller than 140 cm?
b How many students are shorter than 165 cm?
c How many students are taller than 155 cm?
d What is the ratio of the students who are shorter than 150 cm to those taller than 150 cm?
13 Consider the data given for the number of goals scored by Lionel Messi and Cristiano Ronaldo in various years for their respective clubs. Draw a double bar graph for the data and answer the questions.
a How many goals were scored in total by Messi and Ronaldo individually over the years?
b Who scored more goals over the years?
c What is the ratio of the number of goals scored by Lionel Messi before 2010, and the number of goals scored by Cristiano Ronaldo after 2007?
Challenge
Critical Thinking
1 The histogram shows the frequency distribution of average runs scored by players in a cricket tournament.
Assertion: 70.72% players scored more than 25 runs.
Reason: 127 out of 222 players scored more than 30 runs.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true but R is false.
d A is false but R is true.
2 A bar graph shows the monthly sales figures (in dollars) for a retail store for the first six months of the year. The total sales of the store over 6 months is $27 million. What is the store’s sale in the 4th month?
Statement 1: The average sales in the initial 4 months is $3.5 million.
Statement 2: The average sales in the last 3 months is $6 million.
Graphs and Histograms
a Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer.
b Statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer.
c Both statements 1 and 2 together are sufficient to answer.
d Both statements 1 and 2 together are not sufficient to answer.
Case Study
Decoding Postal Charges in India
The postal charges in India depend on the weight of the parcel as well as the distance that needs to be covered. The given table shows the postal charges in India as per the weight up to 2000 grams and distance covered up to 1000 km. Read the table and answer the questions.
Parcel 1: 150 grams, Locally
Parcel 2: 800 grams, 180 km
Parcel 3: 1600 grams, 500 km
1 Rohan wants to send three parcels to different locations. What is the total amount that he needs to pay for the parcels with the following weights and distances:
2 Compare the cost of sending a 350-gram parcel locally versus sending the same parcel up to 200 kilometres. What is the percentage increase in cost when the parcel is sent up to 200 kilometres instead of locally?
3 If a company needs to send 10 parcels, each weighing 250 grams, all to different destinations within 200 kilometres, calculate the total postal charges. How does the total change if the destinations are between 201 and 1000 kilometres?
4 Mayra wants to send two items locally to one of her relatives, weighing 40 grams and 130 grams each. According to the postal charges in India, decide whether it is cheaper to send the two items as one parcel or as two separate parcels. Show your calculations for each case.
Cross Curricular
5 Pie Charts
Let’s Recall
We have learnt that a pie chart is a type of graph that represents data in a circular graph. The circle represents all the available data, such as favourite fruits or school subjects. Each slice of the pie represents a different category.
Let us read the pie chart showing the number of books read by 4 friends.
Shalini, Priya, Aman and Kuldeep together read 40 books in six months. They represent the data using a pie chart. The pie chart shows the fraction of the total number of books read by each person. Let us find the number of books read by each person.
• Aman read 1 2 of the books = 1 2 × 40 = 20 books
• Shalini read 1 4 of the books = 1 4 × 40 = 10 books
• Priya and Kuldeep read 1 8 of the books = 1 8 × 40 = 5 books
Letʼs Warm-up
The given pie chart shows the favourite colour of some students of class 8. Read the pie chart and answer the questions.
Colour
15
35
25 Pink, 15 Lavender, 10
1 The fraction of students who like yellow is .
2 The most liked colour is
3 The fraction of students who do not like red is .
4 The least liked colour is
5 The difference of the fraction of students who like pink and the fraction of students who like blue is .
I scored out of 5.
Favourite
Yellow,
Blue,
Red,
Priya Shalini Aman Kuldeep
Drawing and Reading Pie Charts
Real Life Connect Suman earns ₹20,000 per month. She is planning her monthly budget. She noted all her expenditures and savings in the form of a table.
Drawing Pie Charts
We know that a pie chart uses a circle to represent the data and hence is also called a circle graph. The whole circle represents all the data we have. The circle is divided into sectors, with each sector proportional to the size of the represented observation. Let us use the above data and learn to draw a pie chart.
Sectors and Central Angles
We know that a complete circle represents 360°. The figure below shows how to find the central angle to draw the sectors.
Central angle
Value of the component × 360°
Sum of all components
Sector
A sector displays the size of some related piece of information.
Using the above formula, the central angles for Suman’s data can be given as:
Remember!
The angle made at the centre of a circle is always 360°.
Example 1: Find the value of the central angle corresponding to 30 comic books out of 150 books.
Central angle = Value of the components Sum of all components × 360° = 30 150 × 360° = 72°
Example 2: Find the central angles for the given activities.
The sum of the measures of the central angles is equal to 360°.
Find the central angles for the given modes of transport.
Drawing a Pie Chart
Let us draw a pie chart using the central angles calculated in the previous section.
× 360° = 72°
× 360° = 126°
× 360° = 54°
× 360° = 45°
× 360° = 63°
Step 1: Draw a circle of any radius. Draw the first angle, keeping the horizontal radius as the base. Write the angle and the value of the data.
Monthly Budget
House Rent, ₹4000
Step 2: Draw the rest of the angles, keeping the previous angle as the base. Colour the sectors in different colours. Label each sector.
Monthly Budget
Savings, ₹3500
Others, ₹2500
House Rent, ₹4000
This is the pie chart of the data given above.
Example 3: Draw a pie chart for the data showing the number of students participating in different school activities.
The pie chart for the table can be drawn as:
Example 4: Draw a pie chart for the table showing the number of books sold by 5 shopkeepers.
The pie chart for the table can be drawn as:
Draw a pie chart showing the
Mark, 40 Arun, 300
Amit, 200
Vinay, 180 Keshav, 80
Do It Yourself 5A
1 There are 1200 residents in a society, of which 375 people know more than three languages. What would be the central angle representing people who know more than three languages?
2 If 45% of the total number of people like biryani, what would be the central angle representing this data?
3 Ruchika scored the given marks in her annual examination. Draw a pie chart for the marks obtained by Ruchika. Subject
4 Draw a pie chart for the data of workers from various states working at a garment factory.
5 The table shows the import of various products by a country. Construct a pie chart to represent the given information.
6 Construct a pie chart to display the percentages of purchasers for different clothing brands. Clothing
7 The table shows the approximate number of lions in 5 countries. Create a pie chart to show the data.
8 Look up the Internet to find the data that shows the number of tigers in 5 national parks in India. Show the data using a pie chart.
1 A sports fest was to be organised in a school. The sports organisation was allotted a budget. The spendings on 5 different sports by the school are represented using ratios.
Football : Cricket = 2 : 3
Cricket : Badminton = 3 : 1
Football : Volleyball = 4 : 5
Volleyball : Basketball = 5 : 3
Represent the given data in a pie chart using degrees.
Reading Pie Charts
Suman saw the annual budget of her state in the local newspaper in the form of a pie chart. Below are two pie charts representing the same data. The first pie chart shows the data in degrees, while the second pie chart shows the data in percentages.
Let us learn how to read and interpret these pie charts.
Let us find the amounts spent on different sectors using the above pie chart if the annual budget of the state government is ₹3,12,000 crore.
Error Alert!
Never divide the central angle by 100 to find the value of a component.
Did You Know?
A Scottish engineer, William Playfair, invented the concept of pie charts in 1801 in his book ‘The Statistical Breviary’, where it was used to visualize the proportion of the Turkish Empire located in Asia, Europe, and Africa. Amount spent on agriculture = 79.2°
° × 3,12,000 or 3,12,000 × 22 100 = ₹68,640 crore Amount spent on healthcare = 136.8° 360° × 3,12,000 or 3,12,000 × 38 100
= ₹1,18,560 crore
Did You Know?
Pie charts can also be used to show surveys, election results, business reports, etc.
Amount spent on infrastructure = 43.2° 360° × 3,12,000 or 3,12,000 × 12 100
= ₹37,440 crore
Think and Tell
Can the sum of the values of all components be less than the total value?
Amount spent on education = 100.8° 360° × 3,12,000 or 3,12,000 × 28 100 = ₹87,360 crore
Example 5: Read the pie chart showing the different items sold by a bakery on a day and answer the given questions if the total sales in one day amounted to ₹24,000.
1 Which was the most sold product of the day?
Rolls and Buns
2 What was the sales value of cupcakes?
24,000 × 20 100 = ₹4800
3 What was the difference of the sales values of cookies and doughnuts?
Cookies = ₹24,000 × 14 100 = ₹3360
Doughnuts = ₹24,000 × 10 100 = ₹2400
Difference = ₹3360 − ₹2400 = ₹960
44%
Example 6: The pie chart represents the expenditure on different items for constructing a flat in Delhi. If the expenditure incurred on cement is ₹1,12,500, find the total cost of constructing the flat.
Expenditure on cement = ₹1,12,500
Let the total cost of constructing the flat = ₹x
We know that,
Value of component = Central angle 360° × Total value
⇒ 1,12,500 = 75° 360° × x
⇒ x = 1,12,500 × 360° 75° = 5,40,000
Hence, the total cost of constructing the flat is ₹5,40,000.
Read the pie chart showing the annual agricultural production of an Indian state and answer the given questions if the production of wheat is 27,000 tonnes.
1 What is the total production?
The central angle of wheat = 120°
Total production = 27,000 × =
2 What is the difference in the production of sugar and rice?
Production of sugar = 100° 360° × =
Production of rice =
Difference =
Do It Yourself 5B
1 The pie chart shows the number of students admitted to different college faculties. If the total number of students is 5 lakhs, find the number of students admitted to each faculty.
Faculties
2 The pie chart shows data related to a survey on office-going people in a city.
a What is the second most popular mode of transport?
b What fraction of the people prefer the bus?
c Which mode of transport is preferred by a quarter of the people?
3 Read the pie chart on the cars sold by a showroom in a year and answer the given questions if the number of type C cars sold was 500.
a What was the total number of cars sold?
b What was the number of type D cars sold?
c How many Type A and Type B cars were sold altogether?
4 2500 students from a certain school were asked about their favourite juice. Read the pie chart and answer the given questions.
a How many students chose orange juice as their favourite?
b Which juice is the favourite of the least number of students? How many students like it?
c What fraction of the students do not have apple juice as their favourite?
5 Read the pie chart showing the number of animals in a zoo and answer the questions if there are 77 elephants in the zoo.
a What is the total number of animals in the zoo?
b Which animal has the lowest number, and how much?
c What is the difference of the numbers of deer and reptiles?
6 Manya surveyed some teenagers in her city about their favourite music. 255 teenagers like classical music. Read the chart and answer the questions.
a How many teenagers were surveyed?
b What is the ratio of teenagers who like rock music to those who like hip-hop?
7 Read the pie chart showing the types of flowers planted by a farmer in his field and answer the given questions if the total number of flowers planted is 1200.
a How many more sunflowers are planted than tulips?
b What is the fraction of roses planted?
c What is the ratio of marigolds to jasmines planted?
8 Cross Curricular The pie chart shows the approximate percentage consumption of different energy forms in India. Read the pie chart and answer the given questions.
a Which is the most consumed form of energy?
b What is the ratio of consumption of Nuclear to the consumption of Renewable energy?
c What is the fraction of the energy consumed by Hydropower and Natural gas?
9 Create two questions on the pie chart given in Q8.
1 A company collects 60,000 tonnes of recyclable material every month. The pie charts shown below give the details of the kinds of materials collected in June and July.
a What is the difference of the central angles for glass in the two months?
b How many tonnes of paper were collected in both months together?
c In which month was more plastic collected, and by how much?
d What is the percentage change in the cardboard collection in the two months?
Points to Remember
• A pie chart is a type of graph that represents data in a circular graph.
• Central angle = Value of the component Sum of all components × 360°
• To draw a pie chart, we make a circle with its radius marked. The first angle is drawn, keeping the radius as the base. The rest of the angles are drawn, keeping the previous angle as the base.
• Value of component = Central angle 360° × Total value = Total value × Percentage value 100
Math Lab
Setting: In groups of 5
What’s Your Favourite?
Collaboration & Communication
Materials Required: Paper, pen, protractor, compass, ruler, pencil and eraser.
Method:
1 Collect different sets of data within the classroom, like favourite colour, fruit, vegetable and subject of the students.
2 Ask the students to tabulate the data.
3 Distribute the different data sets collected among groups.
4 The groups show the collected data with the help of a pie chart showing the values in both degrees and percentages.
5 The group that creates the pie chart first wins!
Chapter Checkup
1 If 23% of the people in a locality prefer fresh juice, what would be the central angle representing this data?
2 Mark the central angles in the pie charts shown below.
Items Sold
Others, 36 Rice, 158
Pulses, 67 Spices, 45 Bread, 54
Items Sold
Sandwiches, 80 Burgers, 72
French fries, 54
Ice creams, 64 Shakes, 90
3 Draw a pie chart for the given data showing the types of pets owned by the families in a locality.
4 Draw a pie chart for the given data showing the favourite subject of students at a school.
5 Draw a pie chart for the given data showing the types of books read by people in a town.
6 The pie chart shows the sales at a stationery shop in a month.
a Which is the most popular item in the store?
b What is the fraction of the notebooks sold in the month?
c What is the percentage of the party supplies sold at the shop?
7 The pie chart shows the percentages of ice creams sold by a vendor in 5 days. If the vendor sold 198 ice creams on Wednesday, then find the total number of ice creams sold in 5 days.
8 The pie chart shows the approximate breakdown of food production by different sectors in India. Read the pie chart and answer the given questions.
a Which sector is the highest food producing sector in India?
b What will be the central angle for livestock?
c What is the ratio of the food produced by the dairy sector and the food produced by fisheries?
9 Read the pie chart showing the sale of various products at a supermarket and answer the questions if the total sales add up to ₹1,00,000.
a What was the percentage of the sales of household items?
b What was the sales value of the most popular product?
c What was the total percentage of the sales for the two least popular products?
10 The pie chart shows the types of workouts preferred by the people in a society.
a If 150 people prefer aerobics, then what percentage of the people prefer running?
b What is the ratio of people who prefer cycling to those who do not prefer going to the gym?
c What percentage of the people do not prefer yoga and meditation?
11 Create two questions on the data given in the above question.
Challenge
1 Read these statements:
Statement 1: The students of a class have 5 favourite sports.
Statement 2: 25% of the students like cricket, 25% like football, 20% like basketball, 15% like tennis, 15% like badminton.
Which of the above statements is/are necessary to make a pie chart?
a Statement 1 alone is sufficient and not statement 2.
b Statement 2 alone is sufficient and not statement 1.
c Together, both the statements are sufficient.
d Both the statements are not sufficient.
2 Read the statements and choose the correct option.
Assertion (A): The given pie chart shows the spending of a country on various sports during a particular year. If the total amount spent on sports during the year is ₹3,60,00,000, the amount spent on Basketball exceeds the amount spent on Tennis by ₹5,00,000.
Reason (R): The amount spent on each sport is given as Central angle of sector 360° × Total amount spent
a Both A and R are true and R is the correct explanation of A.
b Both A and R are true and R is not the correct explanation of A.
c A is true but R is not true.
d A is not true but R is true.
COVID-19: Health Metrics and Pandemic Response
You are a health analyst reviewing data from a health department about the COVID-19 pandemic. The data shown in the pie chart represents the age distribution aspect and case severity aspect of the pandemic in India. The case severity of the patients was proportionate for all ages.
Under 18 years
18 years – 40 years
40 years – 60 years
60+ years
Answer the following questions based on the data. (The data is collected for 2,00,000 people)
1 How many patients were aged between 18 years and 60 years? a 80,000 b 60,000 c 1,40,000 d 1,80,000
2 How many patients above 60 years had moderate symptoms?
3 Find the number of patients who had severe symptoms and were aged less than 18 years.
4 Calculate the number of COVID-19 patients between 18 years and 60 years with mid symptoms?
6 Probability
Let’s Recall
Sanvi and Aditya are playing a game with their father. Their father rolls the dice. What are the possible numbers that can come up? Is it possible that he gets the number 7?
A dice has only 6 numbers, so it is not possible to get the number 7 on rolling the dice.
Probability is a way of guessing how likely something is to happen. It helps us figure out if something is sure, impossible, likely, unlikely or equally likely to happen compared to other events.
Let us look at the chance of the numbers coming up on a dice when rolled.
Getting a number from 1 to 6:
Sure, since there are only 6 numbers on a dice.
Let’s Warm-up
Getting an even number:
Equally likely, since 3 out of 6 numbers are even on a dice.
Getting the number 7:
Impossible, since the number does not appear on a dice.
Write the chance of the given events happening using words like sure, impossible, likely, unlikely and equally likely.
1 A dog flying.
2 The cycle of day and night.
3 Getting heads when a coin is tossed.
4 Drawing a blue marble from a bag containing 6 blue and 2 green marbles.
5 Drawing a green marble from a bag containing 10 yellow and 3 green marbles.
I scored out of 5.
Mean, Median and Mode
Understanding Probability
Naina and her brother Sam are visiting the local village fair. They go to the Wheel of Fortune stall. They are excited to play the game since they will get a prize each time the wheel stops at an even number. The wheel has numbers from 1 to 10. Naina says 8 and spins the wheel. The wheel stops at 8.
Sam: Wow! You guessed right! Now, it’s my turn. I want the number 12.
Naina laughs upon hearing this and says, ‘No chance! You lose a point.’
In other words, we can say that probability helps us make smart guesses, similar to predicting outcomes when playing games, spinning wheels, flipping coins or rolling dice.
For example, the chance of the wheel stopping at a number greater than 10 is an impossible event. The chance of the wheel stopping at numbers from 1 to 10 is a sure event. Let us recall some terms.
The chance of an event happening is its probability.
An outcome is the result of some activity.
Event: The collection of some or all possible outcomes of an activity is called an Event.
Total Outcomes: The total number of possible outcomes is called total outcomes. E.g., in a wheel showing 5 colours, the total outcomes are 5.
Favourable Outcomes: The number of favourable outcomes help us predict the chances of an event happening.
The chance of the occurrence of an event can be measured mathematically, and it is called the probability of the event. Events which have no chance of occurring have a probability of 0.
In general, the probability of a sure event is 1 and the probability of an event that has no chance of occurring or is impossible is 0. For any other event, probability varies between 0 to 1.
Total numbers on the wheel = Total Outcomes = Possible Outcomes = 10
Sure: The wheel stopping at a number from 1 to 10.
Favourable outcomes = 10 (Same as possible outcomes)
Likely: The wheel stopping at a number greater than 4.
Favourable outcomes = 6
(Numbers 5, 6, 7, 8, 9 and 10)
Favourable outcomes > 5 (More than half of the possible outcomes)
Impossible: The wheel stopping at the number 12.
Favourable outcomes = 0
Unlikely: The wheel stopping at a number less than 3.
Favourable outcomes = 2
(Numbers 1 and 2)
Favourable outcomes < 5 (Less than half of the possible outcomes)
Equally Likely: The wheel stopping at a number from 1 to 5.
Favourable outcomes = 5 (Numbers 1, 2, 3, 4 and 5)
Favourable outcomes = Same as half the possible outcomes
Theoretical Probability
Since the wheel shows numbers from 1 to 10, anytime the wheel is spun, it will stop at a number from 1 to 10. In other words, the possible outcomes of the event are the wheel stopping at the numbers 1 to 10.
The total outcomes will be 10. Let us see how.
Probability of the Occurrence of an Event
The term ‘chance’ when used in real life is measured mathematically and is called the probability of the event.
Let E be an event. Then the probability of an event E is the ratio of the number of outcomes favourable to the event E to the number of all possible outcomes of the experiment.
P(E) =
Number of outcomes favourable to the event E Number of all possible outcomes of the experiment
Where, P(E) = probability of an event E and P(E) lies between 0 and 1.
In the above case, the probability of the wheel stopping at an even number can be calculated using the formula.
Here, E = the event of the wheel stopping at an even number.
Total outcomes = 10 (total numbers on the wheel)
Favourable outcomes = 5
Applying the formula,
P(E) = Number of outcomes favourable to the event E
Number of all possible outcomes of the experiment
P(E) = Total number of even numbers
Total numbers on the wheel
P(E) = 5 10 = 1 2
So, the theoretical probability of the wheel stopping at an even number is 5 10 or 1 2
Theoretical probability gives exact probabilities based on mathematical principles in ideal conditions.
For example, if we roll a fair six-sided dice, we know each number has a 1 in 6 chance of showing up because there are 6 sides.
Example 1: Rahul tosses a coin before a cricket match. What is the probability that he gets:
1 heads?
2 tails?
Think and Tell
Is the probability of the wheel stopping at an odd number, the same as the probability of the wheel stopping at an even number? Even number Even number Even number Even number Even number
The possible outcomes when a coin is tossed are heads or tails.
Total possible outcomes of the experiment = 2 (either heads or tails).
1 He gets heads.
E = Event of getting a head
P(E) = Numbers of heads
Total number of outcomes = 1 2
Therefore, the possibility of getting a head is 1 2 .
2 He gets tails.
E = Event of getting a tail
P(E) = Number of tails
Total number of outcomes = 1 2
Therefore, the possibility of getting a tail is 1 2 .
Did You Know?
Anil Kumar Gain, an Indian mathematician, studied stochastic processes and queueing theory, which are ways of understanding and predicting random events and waiting times.
Example 2: A fruit box contains 4 oranges and 8 apples. If a fruit is taken out randomly, what is the probability of it being an apple?
E = Event of getting an apple
P(E) = Number of apples
Total number of fruits = 8 12 = 2 3
Therefore, the possibility of getting an apple is 2 3 .
Example 3: Even numbers between 1 and 25 are written on identical slips, put in a box and mixed up. If a slip is drawn at random, what is the probability of getting:
1 a one-digit number? 2 a prime number?
3 an odd number? 4 a number greater than 1?
There are 12 even numbers between 1 and 25. They are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 and 24.
So, the total number of possible outcomes is 12.
1 There are 4 one-digit numbers - 2, 4, 6 and 8.
So, the number of favourable outcomes = 4
P(E) = Number of 1-digit even numbers Total number of favourable outcomes
P(one-digit number) = 4 12 or 1 3 .
2 2 is the only even prime number.
So, the number of favourable outcomes = 1
P(prime number) = P(E) = 1 12
3 There are no odd numbers.
So, the number of favourable outcomes = 0
P(odd number) = P(E) = 0 12 or 0.
4 All the 12 even numbers are greater than 1 - 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 and 24.
So, the number of favourable outcomes is 12.
P(number greater than 1) = P(E) = 12 12 = 1
Example 4: At a village fair, you have a choice of spinning Spinner A or Spinner B. You win a prize if the spinner lands on a section with a star. Which spinner should you choose if you want a better chance of winning? Give a reason for your answer.
Spinner A Spinner B
The ratio for Spinner A is greater than the ratio for Spinner B. Hence, I should choose Spinner A for a better chance of winning.
Example 5: In a game, the probability of correctly guessing which box contains a tennis ball is 1 5 . How many winners would be expected if 60 contestants played the game?
Probability of correctly guessing a box that contains a tennis ball = 1 5
Number of contestants who played the game = 60
Number of contestants expected to win the game (N) = 60 × 1 5 = 12
So, about 12 contestants are expected to win the game.
Example 6: On a game show, a contestant randomly draws a chip from a bag and replaces it. Each chip denotes either a win or a loss.
The theoretical probability of drawing a winning chip is 3 10. The bag contains 9 winning chips.
1 How many chips are in the bag?
The theoretical probability of drawing a winning chip is 3 10.
This also means that the ratio of the number of winning chips to the total number of chips in the bag is 3:10. If the bag contains 9 winning chips, then the total number of chips in the bag = 9 × 10 3 = 30.
2 Out of 20 contestants, how many do you expect to draw a winning chip?
Number of contestants in the game show = 20
Number of contestants expected to draw a winning chip = 3 10 × 20 = 6.
Theoretical probability is used for simple, well-defined situations like rolling dice and tossing coins. When we find the set of all possible outcomes of more than one event, it is called the sample space. You can use tables and tree diagrams to find the sample space of two or more events.
Spinner A
Spinner B
For example, you randomly choose a crust and style of pizza.
Select Crust
Select Style
Use a tree diagram to find the sample space.
There are 8 different outcomes in the sample space. The 8 different pizzas possible are:
CM, CH, CP, CV, SM, SH, SP, SV
Example 7: A black dice and a blue dice are rolled. If all numbers are equally likely, what is the probability that the sum of the numbers that appear on their faces is equal to 5?
The table shows the sample space for rolling a particular sum on two dice.
There are 36 possible outcomes.
The event of rolling a sum of 5 on two dice has four favourable outcomes.
P(rolling a sum of 5 on two dice) = 4 36 or 1 9 .
A well-shuffled deck of animal picture cards is placed face down on a table. Animals
What is the probability that an animal card drawn at random:
a shows a picture of a bird?
E = Event of getting a card that shows a picture of a bird
= Number of cards that show a bird picture
= Therefore, the possibility of getting a card that shows a picture of a bird is .
b does not show a picture of a bird?
E = Event of getting a card that does not show a picture of a bird
Therefore, the possibility of getting a card that does not show a picture of a bird is .
Mexican Hawaiian Pepperoni Vegetarian
Crispy Thin
Soft Pan
Crispy Thin Soft Pan
c The animal cards and the bird cards are placed side by side. How many different combinations can be made if one of each card type is picked?
28 different combinations are possible. They are:
CD, CT, CG, CR
GD, GT, GG, GR
Do It Yourself 6A
1 Fill in the blanks.
a The probability of an event having no chance of occurring is (0/1).
b The probability of a sure event is (0/1).
c The possible outcomes when you toss a coin are and
d On rolling a dice, the event of getting a prime number has possible outcomes.
2 A glass jar contains 40 marbles in different colours such as black, green, blue and yellow. The probability of drawing a single green marble is 1 5 . What does this mean?
a There are 5 green marbles in the glass jar.
b There are 8 green marbles in the glass jar.
c There are 10 green marbles in the glass jar.
d There is only one green marble in the glass jar.
3 Each letter of the alphabet is printed on an index card. What is the theoretical probability of randomly choosing any letter except Z?
4 Neeta is playing a game using a fair coin. Contestants win the game if the coin lands tails up.
a What is the theoretical probability that the coin will land tails up?
b If 250 contestants play the game, about how many of them are expected to win?
5 Amit rolls a six-sided dice labelled 1 to 6.
a Find the probability of rolling a 4.
b Find the probability of rolling an odd number.
c If Amit rolls the dice 12 times, how many times should he expect a number greater than 4 to be rolled?
6 A game board has a spinner with 10 equal-sized sections, of which 4 are green, 3 are blue, 2 are yellow and 1 is black. What is the sum of the probabilities of the pointer landing in the green, blue, yellow and black sections?
7 A 12-sided solid has equal-sized faces numbered 1 to 12.
a Find the probability of getting a number greater than 10.
b Find the probability of getting a number less than 5.
c If the 12-sided solid is rolled 200 times, how many times would you expect either a 4, 6 or 9 to be rolled?
8 Write 2 events based on the situation given in Q7. Write their theoretical probability.
9 A black dice and a blue dice are rolled. If all numbers are equally likely, what is the probability that the sum of the numbers that appear on their faces is equal to:
a 6?
b 10?
10 Draw a spinner having numbers 1 to 7 where the number 4 has a theoretical probability of 1 4
11 At a school fair, you have the choice of randomly picking a ball from Basket A or Basket B. Basket A has 5 green balls, 3 black balls and 8 yellow balls. Basket B has 7 green balls, 4 black balls and 9 yellow balls. You can win a prize if you pick a black ball. Which basket should you choose if you want a better chance of winning?
Challenge
Critical Thinking
1 Navin is getting dressed. He considers two different shirts, three pairs of pants and three pairs of shoes. He chooses one of each of the articles at random.
Shirts Pants Shoes
Collared shirt
T-shirt
Khakis
Jeans
Sneakers
Flip-flops
Capris Sandals
a How many different outfits are possible?
b What is the probability that he will wear his jeans but not his sneakers?
Experimental Probability
The wheel of fortune that Naina and Sam spin records the number of times the wheel lands on an even number. The picture shows a digital scorecard to record the number of people who have won a prize.
Sam is excited to know that 60 people out of a total of 100 people who have spun the wheel got lucky! The wheel has 10 sections, numbered 1 to 10. Five sections are odd, and the remaining five are even.
Even though the theoretical probability of spinning an even number is equal to that of an odd number, the actual results of the experiment have turned out to be different.
Thus, the experimental probability of spinning an even number in this case is 60 100 or 60%. This is more than the theoretical probability of spinning an even number which is 50%.
Such an experiment where we cannot predict the exact result is called a random experiment.
A Random Experiment is one whose outcome cannot be predicted exactly in advance. That is, a random experiment is an experiment, which, when repeated under identical conditions, does not produce the same outcome every time.
Experimental probability gives the probability based on observed data. We can find the experimental probability by physically doing tests or experiments. The accuracy of experimental probability depends on the number of trials conducted. That is, as the number of trials increases, we get more accurate results.
The experimental probability of an event E can be calculated using the formula,
P(event) ꞊
Number of times the event occurs
Total number of trials
For example, if we toss a coin 100 times and it comes up heads 47 times, the experimental probability of getting heads is 47 out of 100.
Experimental probability is used when theoretical probability is difficult to calculate.
Think and Tell
What will be the approximate experimental probability of getting heads if we toss a coin 1000 times?
Example 8: A coin is tossed 50 times to see how often tails shows up. If tails appears 20 times, what is the experimental probability of getting tails? Write this as a fraction, decimal and percentage.
E = Event of getting tails
Experimental Probability, P(E) = Number of times tails appears
Total number of trials = 20 50 = 2 5
Therefore, the experimental probability of getting tails is 2 5, 0.40, or 40%.
Heads Tails 30 times 20 times
Example 9: Amit randomly pulls a coloured block from a bag. He records the colour and then puts the block back into the bag. The table shows the results of his experiment. If he does the experiment 50 times, predict the number of times he will pull a black block from the bag.
The total number of trials in Amit’s experiment = 2 + 4 + 6 + 8 = 20
P(black) = Number of black blocks
Total number of trials = 4 20
In 20 trials, Amit pulled out a black block 4 times.
In 50 trials, Amit would pull out a black block, 50 × 4 20 ꞊ 10 times
So, Amit will pull out a black block about 10 times.
Example 10: Which of the following is an example of a random experiment?
1 Taking a marble out of a bag containing coloured marbles. Taking a marble out of a bag containing coloured marbles is an example of a random experiment.
2 Measuring the length of a table.
Measuring the length of a table is not an example of a random experiment.
Example 11: In a tennis match, Govind serves an ace – a ball that can’t be returned, 4 aces out of 10 times.
1 What is the experimental probability that Govind will serve an ace in the next game?
P(E) = Number of aces
Total number of serves = 4 10 = 2 5
Therefore, the experimental probability of Govind serving an ace in the next game is 2 5 or 0.40 or 40%.
2 Make a prediction about how many aces Govind will have for the next 40 serves.
In 10 serves, Govind serves an ace 4 times.
In 40 serves, Govind would serve an ace, 40 × 4 10 = 16 times.
So, Govind will serve an ace about 16 times.
Example 12: A bag contains 50 marbles. You randomly draw a marble from the bag, record its colour and then replace it. The table shows the results after 30 draws.
Blue Green Red Yellow Frequency 3 12 9 6
1 Find the experimental probability of drawing a red marble.
The total number of trials in the experiment = 30
P(red) = P(E) = 9 30 or 3 10
2 Predict the total number of red marbles in the bag.
In 30 trials, a red marble was drawn 9 times.
In 50 trials, a red marble would be drawn about, 50 × 9 30 = 15 times
Example 13: We held a survey of all the students in our school to find out how many of them like to dance. The results are shown in the given table.
If we choose a student at random, what is the probability that the student:
1 likes to dance?
55 students like to dance.
Probability that a student likes to dance = 55 110 = 1 2
2 does not like to dance?
55 students do not like to dance.
Probability that a student does not like to dance = 55 110 = 1 2
3 is a boy who likes to dance?
There are 25 boys who like to dance.
Probability that a student is a boy who likes to dance = 25 110 or 5 22
4 is a girl who does not like to dance?
There are 20 girls who do not like to dance.
Probability that a student is a girl who does not like to dance = 20 110 or 2 11
The bar graph shows the results of rolling a dice 300 times. How does the experimental probability of rolling an odd number compare with the theoretical probability?
We first find the experimental probability of rolling an odd number.
The bar graph shows ones, threes and fives.
So, an odd number was rolled + + = times in a total of 300 rolls.
P(odd) = Number of times an odd number was rolled
Total number of rolls = �
Next, we find the theoretical probability of rolling an odd number.
P(odd) = Number of favourable outcomes
Number of possible outcomes = �
The experimental probability of rolling an odd number is %, which is close to the theoretical probability of %.
Do It Yourself 6B
1 Which of the following are examples of a random experiment?
a Tossing a coin
c Throwing a ball
b Drawing a black card from a deck of playing cards
d Rolling two dice together
2 To play a game, you spin the spinner shown. You win if the arrow lands in one of the areas marked ‘WIN’. Leena played this game many times and recorded her results. She won 8 times and lost 40 times. Use Leena’s data to find the experimental probability of winning this game.
3 During a 24-hour period, the ratio of pop songs to rap songs played on a radio station is 60:75.
a What is the experimental probability that the next song played will be a rap song?
b Out of the next 90 songs, how many would you expect to be pop songs?
4 A board game uses a bag of 105 lettered tiles. You randomly choose a tile and then return it to the bag. The table shows the number of vowels and the number of consonants after 50 draws.Predict the number of vowels in the bag.
5 The Venn diagram shows two sports played by 90 Grade 8 students. What is the probability that a randomly chosen student plays:
a both tennis and squash?
c tennis?
b neither tennis nor squash?
d tennis or squash, but not both?
6 We held a survey of all the students in our school to find out how many own a mobile phone. The results are shown in the two-way table.
If we choose a student at random, what is the probability that the student:
a owns a mobile phone?
c is a boy who owns a mobile phone?
b does not own a mobile phone?
d is a girl who does not own a mobile phone?
7 You randomly select 200 pairs of jeans and find 5 defective pairs. About how many pairs of jeans do you expect to be defective in a shipment of 5000?
Challenge
1 The table shows the result of flipping two coins. Read the statements and choose the correct option.
Assertion (A): The experimental probability of getting two tails is 11 50
Reason (R): Experimental probability of an event = Number of times the event occurs Total number of trials
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, and R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Points to Remember
• Probability is the concept which numerically measures the degree of certainty of the occurrence of an event.
• An operation which can produce some well-defined outcomes is called an experiment.
• An experiment in which all possible outcomes are known and the exact outcome cannot be predicted in advance is called a random experiment.
• The collection of all or some of the possible outcomes is called an event.
• Probability of an event P(E) = Favourable outcomes
Total number of outcomes
• The probability of an event always lies between 0 and 1.
• The probability of a sure event is 1 and that of an impossible event is 0.
• Probability cannot be negative.
• The sum of the probabilities of all possible outcomes of an event is 1.
Math Lab
Tossing Coins
Aim: To find the experimental probability of an event.
Collaboration & Experiential Learning
Materials Required: A coin of ₹1, paper and pencil
Setting: In groups of 3
Method:
1 Toss the coin 10 times consecutively and record the result in a table.
2 Count the number of times heads appears and the number of times tails appears.
3 Calculate the probability of getting heads by dividing the number of times heads appeared by the total number of tosses. Similarly, calculate the probability of getting tails.
4 Increase the number of tosses to 20 and take the combined result of the previous tosses. Again, calculate the probabilities.
5 As the number of tosses increases, the probabilities tend to get closer to 1 2.
Chapter Checkup
1 Fill in the blanks.
a The probability of an event that is sure to happen is .
b If an event cannot occur, then its probability is
c The probability of selecting P from the word ‘SPECIAL’ is .
d The probability of an event can’t be more than .
e If a dice is rolled once, the probability of getting an even prime number is
2 Write all the possible outcomes of the following events.
a Flipping a fair coin
b Rolling a standard six-sided dice
c Selecting a single letter at random from the English alphabet
d Flipping two fair coins simultaneously
e Rolling two standard six-sided dice simultaneously
3 Sneha draws a card at random from the cards given. What is the probability of drawing a card that shows a shape with:
a only three sides?
b only four sides?
c more than four sides?
d no sides?
4 Find the probability of getting an A on a random selection of a letter from the word ‘APPRECIATION’.
5 A box contains 100 bolts, two-fifths of which are rusted. One bolt is drawn at random from the box. Find the probability that it is:
a a rusted bolt.
b not a rusted bolt.
6 200 apples are packed in a carton out of which 30 apples are rotten. If one apple is taken out from the carton at random, find the probability of getting a:
a good apple.
b rotten apple.
7 A college student has to select a stream with the given subject combinations:
a Physics, Chemistry, Mathematics
c Accountancy, Mathematics, Economics
b Physics, Chemistry, Biology
d English, Hindi, Social Sciences
Find the probability of getting mathematics as a subject on a random selection of the stream.
8 The bar graph shows the result of spinning a wheel 150 times.
Compare the theoretical and experimental probabilities of the events.
a Wheel stopping at green
b Wheel stopping at red
c Wheel stopping at blue or purple
d Wheel stopping at any colour
9 Prime numbers between 1 and 25 are written on identical slips, put in a box and mixed up. If a slip is drawn randomly, what is the probability of getting:
a a one-digit number?
c an odd number?
b an even number?
d a number greater than 11?
10 The keypad of a mobile phone has digits from 0 to 9 on it. If a person enters a digit at random, what is the probability of typing:
a an even number?
b a multiple of 5? c a factor of 9?
11 In a store, 50 pairs of bangles are on display. The probability that a customer will choose a pair of pearl bangles is 6 25 . How many pearl bangles are on display?
1 Amita has a ₹1 coin, a ₹2 coin, a ₹5 coin and a ₹10 coin in her purse. She needs to pay for a pencil that costs ₹4. Namita says the probability of her using the ₹5 coin is 25%, while Ranita insists that it is 50%. Who is correct - Namita or Ranita?
2 Statement: 300 marbles are placed in a jar, of which 50 are blue. One marble is drawn from the jar at random.
Conclusion I: The probability of drawing a blue marble is one-sixth.
Conclusion II: The probability of drawing a non-blue marble is 80%.
Which of the following conclusions follow?
a Only conclusion I follows
c Either I or II follows
Case Study
b Only conclusion II follows
d Neither I nor II follows
Cross Curricular & Value Development
Observing the Biodiversity!
A biodiversity park is a special area of wild nature where groups of native plants, animals and birds live together. Rashmi was visiting the biodiversity park with her classmates. The children decided to observe the types of birds present there. Over a week, they observed 100 birds, of which 40 were sparrows, 30 were pigeons, 20 were crows and 10 were some other species. Answer the following questions.
1 What is the probability of randomly spotting a sparrow in the park?
2 If Rashmi sees a bird, what is the probability that it is either a pigeon or a crow?
3 The probability of not seeing a sparrow is .
4 If Rashmi sees a bird in the park, it is more likely to be a pigeon than a crow. True or False?
5 Have you ever been to a biodiversity park? What did you see there? What should you keep in mind while visiting the park?
7 Squares and Square Roots
Letʹs Recall
Any number except 0 and 1 can be expressed as the product of its factors. This is called factorisation of the number. A number that has only two factors, the number 1 and itself, is called a prime number, whereas a number that has more than two factors is called a composite number. For example, look at the factors of 6 and 7 given below.
factors of 7 2 factors
Prime Number
factors of 6 4 factors
Composite Number
Every composite number can be expressed as a product of prime factors, no matter what the order is. This is called prime factorisation of the number.
Using factor trees
Using the division method
Choose the smallest prime factor.
Choose any factor pair of 36. Circle the prime factor.
Continue to factorise every number that is not prime.
36 = 3 × 3 × 2 × 2
Letʼs Warm-up
Write True or False.
Keep choosing prime factors and dividing until you get a quotient of 1. Stop factorising when you get 1.
36 = 2 × 2 × 3 × 3
1 Among 3, 7, 8, 9, 11 and 12, the numbers 8, 11 and 12 are the only composite numbers.
2 The only prime factors of 48 are 2 and 3.
3 The prime factorisation of 120 is 2 × 2 × 2 × 2 × 3 × 3 × 5.
4 The prime factorisation of 132 is 2 × 2 × 3 × 11.
5 Prime factorising a number using the factor tree method gives a different result than using the division method of prime factorisation.
I scored out of 5.
Real Life Connect
Square of a Number
Shobhit wants to buy a square table for his home. He requires a table that occupies an area of less than 5 sq. m due to the lack of space. What size table should he purchase?
Square Numbers and Their Patterns
Look at the figures. Each number has been arranged using squares of the same size. Some form complete squares and some do not.
Square of a Number
A number that forms a complete square is a square number or a perfect square. For example, in the above picture, the numbers 1 and 4 form a complete square. These numbers can also be written as the product of two like factors.
For example, 1 can be written as 1 × 1 = 12, and 4 can be written as 2 × 2 = 22.
So, the square of 1 is 1, and the square of 2 is 4.
So, if we multiply a number by itself, we get a square of that number.
Squares of some of the numbers are listed below.
If a number has 4 or 6 in its ones place, then its square ends in 6.
Squares of even numbers are always even.
ʻsquareʹ.
In square numbers, the digits always end in 0, 1, 4, 5, 6 or 9 and not 2, 3, 7 or 8.
Think and Tell
If a number, when divided by 3, leaves a remainder of 2, is it a perfect square?
Let us look at the squares of numbers from 11 to 20. Numbers 11 to 20
If a number has 1 or 9 in its ones place, then its square ends in 1.
If a number has 3 or 7 in its ones place, then its square ends in 9.
If a number has 2 or 8 in its ones place, then its square ends in 4.
Squares of odd numbers are always odd.
If a number has 0 in its ones place, then its square ends in 0. Also, there is an even number of zeroes at the end of a perfect square.
Think and Tell
If a number, when divided by 4, leaves a remainder of 2 or 3, is it a perfect square?
Remember!
The area of a square can be calculated as s × s = s2
Now, let us help Shobhit find the amount of space a square table occupies. To find the amount of space that the table occupies, we must find the area of the table. Since the table is in the shape of a square, it is sufficient to find the square of one side of the table. That is, one side of the table = 1 m.
The square of this side of the table = 1 × 1 = 1 sq. m
So, Shobhit can buy this table since the space it will occupy will be less than 5 sq. m.
Square of Rational Numbers
Think and Tell
Can Shobhit buy a table with different dimensions which will fits inside his room?
We can find the square of rational numbers by dividing the square of their numerator by the square of their denominator. For example, to find the square of a positive rational number 3 4 , we write it as:
Similarly, to find the square of a negative rational number −4 5 , we write it as: −4 5 2 = −4 5 × −4 5 = (−4) × (−4) 5 × 5 = 16 25
Square of Large Numbers
It is easy to find the square of numbers up to 20. But to find squares of numbers beyond 20 is quite difficult. To find the square of numbers beyond 20, we use the distributive property. For example, to find the square of 24, we write it as:
We know that, 24 = 20 + 4 or 30 – 6.
242 = (20 + 4)2
= (20 + 4) (20 + 4)
= 20 (20 + 4) + 4 (20 + 4)
= 202 + 20 × 4 + 4 × 20 + 42
= 400 + 80 + 80 + 16 = 576
Example 1: Find the value of: 1 6 7 2
242 = (30 − 6)2 = (30 − 6) (30 − 6) = 30 (30 − 6) − 6 (30 − 6) = 302 + 30 × (− 6) + (− 6) × 30 + (− 6)2 = 900 − 180 − 180 + 36 = 576
Think and Tell
How many digits will there be in a square of a number?
Example 2: Find the squares of the given numbers.
1 432 2 1172
432 = (40 + 3)2
= (40 + 3) (40 + 3)
= 40 (40 + 3) + 3 (40 + 3)
= 402 + 40 × 3 + 3 × 40 + 32 = 1600 + 120 + 120 + 9 = 1849
Find the square of 136.
1362 = (100 + )2
= (100 + ) (100 + ) = = =
Patterns of Square Numbers
1172 = (100 + 17)2 = (100 + 17) (100 + 17) = 100 (100 + 17) + 17 (100 + 17) = 1002 + 100 × 17 + 17 × 100 + 172 = 10000 + 1700 + 1700 + 289 = 13,689
We know that the side of Shobhit’s square table is 1 m. What if the side of the square table was 2 m?
Let us find out the differences in their areas.
If the side of the table is 1 m, then its area is 12, which is, 1 sq. m.
If the side of the table is 2 m, then its area is 22, which is, 4 sq. m. The difference in their areas is 4 – 1 = 3.
We can also solve this by using a shortcut method:
1 is an odd number, and 2 is an even number, but both are consecutive numbers. For such consecutive numbers, the difference of their squares is equal to either the sum of the numbers or twice the smaller number plus one.
That is, if (n) is any number, then (n + 1)2 – n2 = n + n + 1 = 2n + 1
So, here, 22 – 12 = 2 + 1 = 3 = (2 × 1) + 1
Some more patterns of square numbers are given below.
1 = 1 = 12
1 + 3 = 4 = 22
1 + 3 + 5 = 9 = 32 1 + 3 + 5 + 7 = 16 = 42
Did You Know?
Bhaskaracharya (Bhaskara II, 1114–1185 CE), an Indian mathematician, wrote Siddhanta Shiromani. The first part, called the Lilavati, includes rules for dealing with squares and square roots, among other arithmetic operations.
Think and Tell
How many non-perfect square numbers are there between the squares of two consecutive numbers?
Rule: The sum of the first n odd numbers is n2 Rule: If n is an odd number, then
Think and Tell
If a number cannot be expressed as a sum of successive odd numbers, is the number then a perfect square?
Rule: If n is an odd or even number, then n (n + 2) + 1 = (n + 1)2
Rule: The sum of two consecutive triangular numbers is always a square number.
152 = 225 = 200 + 25 = 2 × 100 + 25 = [1 (1 + 1)] × 100 + 25
252 = 625 = 600 + 25 = 6 × 100 + 25 = [2 (2 + 1)] × 100 + 25
352 = 1225 = 1200 + 25 = 12 × 100 + 25 = [3 (3 + 1)] × 100 + 25
452 = 2025 = 2000 + 25 = 20 × 100 + 25 = [4 (4 + 1)] × 100 + 25
Rule: If a is the tens digit and 5 is the units digit, then (a 5)2 = [a (a + 1)] × 100 + 25
1 × 3 = (2 – 1) (2 + 1) = 22 – 12 = 4 – 1 = 3
11 × 13 = (12 – 1) (12 + 1) = 122 – 12 = 144 – 1 = 143
2 × 4 = (3 – 1) (3 + 1) = 32 – 12 = 9 – 1 = 8
10 × 12 = (11 – 1) (11 + 1) = 112 – 12 = 121 – 1 = 120
Rule: If (a + b) and (a – b) are two numbers, then (a + b) (a − b) = a2 – b2
Pythagorean Triplets 32 + 42 = 9 + 16 = 25 = 52
+ 82 = 36 + 64 = 100 = 102
Rule: If m is any non-zero number and m > 1, then we have (2m)2 + (m2 – 1)2 = (m2 + 1)2
Example 3: Express 225 as the sum of 15 odd numbers.
We know that the sum of the first n odd numbers is n2 .
So, 225 = 152
= Sum of the first 15 odd numbers
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29
Example 4: Express 772 as the sum of two consecutive numbers.
We know that if n is an odd number, then n2 = (n2 – 1) 2 + (n2 + 1) 2 .
So, 772 = (772 – 1) 2 + (772 + 1) 2 = (5929 – 1) 2 + (5929 + 1) 2 = 5928 2 + 5930 2 = 2964 + 2965
Example 5: Express the following numbers as the sum of odd numbers. Identify the number whose square the given number is.
1 64
64 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15
8 numbers are added to get 64.
Thus, 64 = 82. 2 121
121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21
11 numbers are added to get 121.
Thus, 121 = 112
Example 6: Find the squares of the given numbers.
1 35
We know that, (a5)2 = [a(a + 1)] × 100 + 25
352 = [3(3 + 1)] × 100 + 25 = [3 × 4] × 100 + 25 = 12 × 100 + 25 = 1200 + 25 = 1225
Example 7: Evaluate:
1 1542 – 1532
a2 – b2 = (a + b)(a – b) 1542 – 1532 = (154 + 153)(154 – 153)
= 307 × 1 = 307
2 75
752 = [7(7 + 1)] × 100 + 25 = [7 × 8] × 100 + 25 = 56 × 100 + 25 = 5600 + 25 = 5625
2 (17 – 8)(17 + 8)
(a + b)(a – b) = a2 – b2 (17 – 8)(17 + 8) = 172 – 82 = 289 – 64 = 225
Example 8: How many non-square numbers are there between the squares of the given numbers?
1 17 and 18
2 24 and 25
We know that there are 2 n non-perfect square numbers between the squares of two consecutive numbers.
1 Here, n = 17 and n + 1 = 18
The number of non-perfect squares = 2 × 17 = 34
Thus, there are 34 non-perfect square numbers between 17 and 18.
2 Here, n = 24 and n + 1 = 25
The number of non-perfect squares = 2 × 24 = 48
Thus, there are 48 non-perfect square numbers between 24 and 25.
Example 9: Find a Pythagorean triplet if its smallest member is 20.
We know that if 2m, m2 – 1 and m2 + 1 are said to form a Pythagorean triplet, where m is any non-zero number and m > 1, then (2m)2 + (m2 – 1)2 = (m2 + 1)2.
If 2m = 20, then m = 10. So, m2 – 1 = 102 – 1 = 100 – 1 = 99
m2 + 1 = 102 + 1 = 100 + 1 = 101
Thus, the Pythagorean triplet in this case is (20, 99, 101).
If m2 – 1 = 20, then m2 = 21 ⇒ m is not an integer.
If m2 + 1 = 20, then m2 = 19 ⇒ m is not an integer.
In either case, values of m are not possible.
So, the only Pythagorean triplet here is (20, 99, 101) with 20 as its smallest member.
Each of the numbers ends in 5. We know that if a = tens digit and 5 is the units digit, then (a5)2 = [a (a + 1)] × 100 + 25.
1 452 = [4 (4 + 1)] × 100 + 25 = ( × ) × 100 + 25 = × 100 + 25 = + 25 =
2 1152 = [ ( + 1)] × + = ( × ) × + = × + =
Do It Yourself 7A
1 Look at the digits in the units place of each of the given numbers. Answer the given questions. a 961 b 4624 c 5329 d 7688 e 19,753 i What will be the units digits of the squares of the numbers?
ii Which of the numbers will have odd or even squares?
2 Show the square of the numbers 5 and 7 using a square grid.
3 Find the square of the numbers.
4 Find the squares of the given numbers using the distributive property. a 49 b 59 c 98
5 Express the numbers as the sum of odd numbers. a 676 b 729
6 List all the triangular numbers between 20 and 50. Express them as square numbers.
7 Find the difference of the squares of the consecutive numbers. How many non-perfect squares are there between the squares? a 12, 13 b 20, 21 c 17, 18 d 25, 26 e 31, 32
8 Express the squares of the given odd numbers as the sum of two consecutive numbers.
a 57 b 63 c 77 d 39 e 85
9 Evaluate.
a 752 b 512 – 502 c 952 d 782 – 772 e 1052
10 Find using the (a + b) (a − b) rule.
a 75 × 77 b 64 × 68 c 50 × 52 d 91 × 95 e 36 × 40
11 Find a Pythagorean triplet whose smallest member is given below. a 12 b 16 c 28 d 32 e 36
12 Observe the pattern. Write the missing numbers.
42 = 16
342 = 1156
3342 = 111556
33342 = 1 5 6
333342 = 2 = 111111555556
14 Without adding, find the sum.
13 Observe the pattern.
Fill in the missing digits.
92 = 81
992 = 9801
9992 = 998001
99992 = 99980001
999992 = 9 _ _ _ 8 _ _ _ _ 1
9999992 =
15 Shreya made the pattern using stickers of circles. Look at the pattern and answer the questions.
22 22 + (2 + 2 + 1)
a How would you express each square pattern as a square of a number? Write the rule.
b Find the rule of the pattern up to the 6th term.
c Use the rule to find the value of 562
16 Kinetic energy is the energy possessed by a body due to its motion. It is given as 1 2 mv2 where m is the mass of the body and v is the velocity with which the body is travelling. If a truck has a velocity of 12 m per second and a mass of 8000 kg, then compute its kinetic energy. The unit for kinetic energy is kgm2s2.
1 Create a list of four different Pythagorean triplets.
Square Roots
Rakesh, a farmer, owns a mango orchard. To increase his sales in the summer season, he plans to plant 9025 mango trees, arranging them in rows with the same number of trees in each row. Let us see how can we find the number of rows of mango trees he wishes to plant.
Finding Square Roots Using Prime Factorisation
The square root of a number is the value that can be multiplied by itself to get the original number. It is the inverse of a square number. It is denoted using the symbol ‘ ’, which is called the radical symbol.
For example, the square of 4 is 16, but the square root of 16 is 4. We write it as: 16 = 4 × 4 = 4.
Given below is a list of square roots of different numbers.
We can find square roots using different methods: 1 Using successive subtraction 2 Using prime factorisation 3 Using long division
Let us understand how we can find the square root of a number using successive subtraction
We know that the sum of the first n odd numbers is n2 .
⇒ Every square number can be expressed as a sum of successive odd numbers, starting from 1.
For example, for the square number 64, we successively subtract the odd numbers from 64, starting from 1.
64 – 1 = 63 (1 time)
63 – 3 = 60 (2 times)
60 – 5 = 55 (3 times)
55 – 7 = 48 (4 times)
48 – 9 = 39 (5 times)
39 – 11 = 28 (6 times)
28 – 13 = 15 (7 times)
15 – 15 = 0 (8 times)
Error Alert!
Taking the square root of a number NEVER halves its value.
As soon as we get 0, we stop here. Here, odd numbers are subtracted 8 times. So, 64 = 8.
To find the square root using prime factorisation, we follow the steps given below.
Step 1
Express the number as a product of its prime factor.
Step 2
Group the same prime factors together to form pairs.
Step 3
Select one prime factor from each pair and find the product. The product is the square root of the number given.
For example, let us find the number of rows of mango trees the farmer wishes to plant. We know that each row contains as many trees as the number of rows.
⇒ The number of rows is equal to the number of plants in each row. Let the number of plants be x So, the number of rows is also x. So, the total number of plants = number of plants × number of rows
⇒ 9025 = x × x ⇒ 9025 = x2 ⇒ 9025 = x
By prime factorisation, we get
⇒ x = 5 × 5 × 19 × 19
⇒ x = (5 × 5) × (19 × 19)
⇒ x = 5 × 19 = 95
So, the number of rows and the number of plants in each row will be 95.
Square Root of a Rational Number
1805
361 19 19 1
We can find the square root of rational numbers by dividing the square root of their numerator by the square root of their denominator. For example, to find the square root of a positive rational number 16 25, we write it as:
16 25 = 16 25 = 2 × 2 × 2 × 2 5 × 5 = 2 × 2 5 = 4 5
How do we check if a number is a perfect square?
To check if a number is a perfect square, we use prime factorisation. If upon prime factorising the number we get pairs of equal prime factors and no factors are left over, then the given number is a perfect square. For example, let us check whether 784 and 3400 are perfect squares or not.
784
Find the prime factorisation of 784.
784 = 2 × 2 × 2 × 2 × 7 × 7
Group the prime factors into pairs of equal factors until no factor is left over.
784 = 2 × 2 × 2 × 2 × 7 × 7
Since there are pairs of prime factors and no factor is left over, 784 is a perfect square.
3400
Find the prime factorisation of 3400.
3400 = 2 × 2 × 2 × 5 × 5 × 17
Group the prime factors into pairs of equal factors until no factor is left over.
3400 = 2 × 2 × 2 × 5 × 5 × 17
Since all the prime factors do not form pairs, 3400 is not a perfect square. 5 9025
Example 10: Find the square root of 49, using successive subtraction
For a square number 49, we subtract the odd numbers successively from 49.
49 – 1 = 48 (1 time)
48 – 3 = 45 (2 times)
45 – 5 = 40 (3 times)
40 – 7 = 33 (4 times)
33 – 9 = 24 (5 times)
24 – 11 = 13 (6 times)
13 – 13 = 0 (7 times)
As soon as we get 0, we stop there.
Here, 7 odd numbers are subtracted to get 0. So, 49 = 7.
Example 11: Find the square root, using prime factorisation.
1 1764
1764 = 2 × 2 × 3 × 3 × 7 × 7
So, 1764 = (2 × 2) × (3 × 3) × (7 × 7) = 2 × 3 × 7 = 42
Example 12: Show that 4500 is not a perfect square.
Finding the prime factorisation of 4500.
4500 = 2 × 2 × 3 × 3 × 5 × 5 × 5
Clearly, on grouping the prime factors of 4500 into pairs of their equal factors, we are left with a factor of 5, which cannot be paired.
Thus, 4500 is not a perfect square.
Example 13: Show that 3600 is a perfect square. Also, find the number whose square is 3600.
3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
Since there are pairs of equal prime factors and no factor is left over, 3600 is a perfect square.
Now, 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 22 × 22 × 32 × 52 ⇒ (2 × 2 × 3 × 5)2 = 602
So, 3600 is a perfect square of 60.
Example 14: Find the least number by which 7220 should be multiplied to get a perfect square number.
7220 = 2 × 2 × 5 × 19 × 19
Clearly, we do not have pairs of all prime factors, and we are left with a factor 5 which cannot be paired.
So, 5 is the least number, which 7220 should be multiplied by to get a perfect square.
Example 15: Find the smallest square number which is divisible by each of the numbers 8, 10, 12 and 16.
2 8, 10, 12, 16
2 4, 5, 6, 8
2 2, 5, 3, 4
2 1, 5, 3, 2
3 1, 5, 3, 1
5 1, 5, 1, 1 1, 1, 1, 1
The least number divisible by each of the given numbers is their LCM.
LCM of 8, 10, 12, 16 = 2 × 2 × 2 × 2 × 3 × 5 = 240
The smallest square number divisible by 240 must have all even powers in its prime factorization.
Smallest square number = 240 × 3 × 5 = 3600
Thus, the smallest square number which is divisible by each of the numbers 8, 10, 12 and 16 is 3600.
Example 16: The area of a square field is 1225 sq. m. What is the length of the side of the square?
Area of the square field = 1225 sq. m
Area of a square = side × side
Side of the square = Area of square
Side of the square field = 1225 = 5 × 5 × 7 × 7 = 5 × 7 = 35 m
Thus, the side of the square field is 35 m.
Example 17: The product of two numbers is 1872 and their ratio is 13 : 9. Find the numbers.
Let one number be x.
Second number = 1872 x .
The quotient of the numbers = 13 9
According to the question,
x 1872 x = 13 9 ⇒ x2 1872 = 13 9
x2 = 1872 × 13 9 = 208 × 13 = 2704
x2 = 2 × 2 × 2 × 2 ×13 × 13
x = 52
Second number = 1872 52 = 36
Thus, the two numbers are 52 and 36.
Find the smallest number by which 14,580 should be divided to get a perfect square.
14,580 = 2 × 2 × × 3 × × × × ×
Clearly, we do not have pairs of all prime factors, and we are left with a factor which cannot be paired.
So, is the least number by which 14,580 should be divided to get a perfect square.
Do It Yourself 7B
What could be the units digit of the square root of the numbers?
1369
3136
Draw a square with an area of 16 square units. What is the length of each side?
Find the square root of the numbers using successive subtraction. a 144
Check if the given numbers are perfect squares using prime factorisation. Also, find the number whose square is the number given.
Find the square root of the numbers using prime factorisation.
6561
For each of the numbers, find the smallest number by which it should be multiplied to get a perfect square. Also, find the square root of the square number.
Find the smallest number by which the numbers should be divided to get a perfect square. Also, find the square root of the square number.
Find the smallest square number that is divisible by 6, 9, 12, 16 and 18.
The students of a class collected ₹1296 for a COVID relief fund. Each student contributed an amount equal to the number of students in that class. How many students were in the class?
If there is a piece of cloth with an area of 721 sq. cm, can we make a square tablecloth from it, where the length of each side is 27 cm?
1 Five friends—Sheetal, Shyna, Hitesh, Rohit and Hetal, play a number game. Sheetal thinks of a positive integer, which Shyna then doubles. Hitesh triples Shyna’s number, and finally, Hetal multiplies Hitesh’s number by 6. Rohit notices that the sum of these four numbers is a perfect square. What is the smallest number that Sheetal could have thought of?
Finding Square Roots Using Long Division
We know that Rakesh planted 9025 mango trees in his mango orchard. He also has another orchard in which he wishes to plant 1089 orange trees in rows, with the number of rows equal to the number of trees. To find the number of rows, we can use the long-division method. Let us learn how the long-division method works.
For very large numbers, such as 15,625 and 58,081, the prime factorisation method to find their square roots can be time–consuming. In such cases, we use the long-division method. For example, let us find the square root of 58,081.
Step 1
58081 has an odd number of digits. Starting from the ones place, make pairs of digits by placing a bar over them. If the number of digits is odd, even the single digit will have a bar over it.
Step 2
Find the largest number whose square is less than or equal to the first pair (from the left). Take this number as the divisor and also as the quotient. Now, find its product and subtract the result from the first paired number to get the remainder.
Step 3
Bring down the number under the next bar to the right of the remainder.
Step 4
Double the quotient and write it with a blank on its right side.
Step 5
Guess the largest possible number to fill in the blank that will also become the new digit in the quotient.
Here, the new divisor is multiplied by the new quotient to get a product less than or equal to the dividend. This means that 43 × 3 = 129 and 44 × 4 = 176, we choose the new digit as 4. Now, divide in the same way and find the remainder.
Step 6
Repeat steps 3 to 5, as many times as required.
Step 7
As the remainder is 0 and no digits are left in the number, 58081 = 241.
Think and Tell
Can you now find the square root of 5,53,536 using the long-division method?
Now, we can also find the number of rows required to plant orange trees using the long-division method.
1089 has an even number of digits (4). So, there will be 2 (4 ÷ 2) digits in the square root. Therefore, if n is the number of digits, then there will be n 2 digits in the square root of an even number and (n + 1) 2 digits in the square root of an odd number.
So, 33 rows of orange trees will be planted by Rakesh.
Square Root of Decimal Numbers
Find the square root of 31.5844.
We can find the square root of decimal numbers in the same way as the square root of whole numbers.
We need to put the decimal point at it’s correct place.
So, the square root of 31.5844 = 31.5844 = 5.62
Approximate Square Root by the Long–Division Method
If the square root of the number is to be corrected to n decimal places, find the square root by long division up to (n + 1) decimal places first, and then, round off the square root up to n decimal places. For example, let us find the square root of 5 correct to three decimal places.
So, 5 = 2.2360 (up to 4 decimal places)
= 2.236 (up to 3 decimal places)
Thus, 5 = 2.236.
Example 18: Find the square root of 7,12,336.
So, 712336 = 844.
Example 19: Find the estimated square root of 0.12 correct to three decimal places.
So, 0.12 = 0.3464 (up to 4 decimal places) = 0.346 (up to 3 decimal places)
Thus, 0.12 = 0.346.
Example 20: Find the square root of 784 841 and (40 × 160).
For 784 841 , we find the square root of 784 and 841 first.
Now, 784 = 28, 841 = 29
So, 784 841 = 784 841 = 28 29
For (40 × 160), we find the square root of each number first.
That is, (40 × 160) = 40 ×
= 80
Example 21: What lowest number must be subtracted from 5,31,606 to get a perfect square?
7292 is less than 5,31,606 by 165.
So, the lowest number to be subtracted from 5,31,606 to get a perfect square is 165.
The required perfect square number is 5,31,606 – 165 = 5,31,441.
Example 22: What is the greatest 5-digit square number?
Greatest 5-digit number = 99,999
Let us find the square root of 99,999 Clearly, 3162 is less than 99,999 by 143.
So, the least number that has to be subtracted from 99,999 to get a perfect square is 143.
99,999 – 143 = 99,856
Thus, 99,856 is the greatest 5-digit square number.
Example 23: A ladder is placed with its foot 8 m away from the bottom of a wall 15 m high. The top of the ladder reaches the top of the wall. Find the length of the ladder. The ladder forms a right-angled triangle with the wall.
Height of the wall (perpendicular) = 15 m
Width of the ground from the wall to the ladder (base) = 8 m
Length of the ladder (hypotenuse) squared = 152 + 82 = 225 + 64 = 289 = 172
Therefore, the height of the ladder is 17 m.
Example 24: There are (3116 + x) chocolates in a carton, such that the number of chocolates in each row is equal to the total number of rows. What is the least value of x?
Total number of chocolates = 3116
In order to determine the value of x, we need to find the least value of the number of chocolates to be added to 3116 to make it a perfect square number such that the number of rows is equal to the number of columns.
So, 552 < 3116 < 562
Minimum number of chocolates required = 562 – 3116 = 3136 – 3116 = 20
Thus, the least value of x is 20.
Example 25: Find the value of 15376 , and hence evaluate 1.5376 + 153.76 .
So, 15376 = 124
Do It Yourself 7C
How many digits would be there in the square roots of the numbers (without any calculation)?
Find the square root using the long-division method.
Find the least number which must be subtracted from each of the numbers to get a perfect square. Also, find the square roots of the perfect squares so obtained.
Find the lowest number which must be added to each of the numbers to get a perfect square. Also, find the square roots of the perfect squares so obtained.
Find the square roots of the decimal numbers.
Find the square root of the numbers correct to three decimal places.
Simplify.
Find the longest side of a right angled triangular field with the other two sides of 15 m and 20 m.
Beginning from her house, Nancy walks 150 m north and then 360 m west to reach a friend’s house. On her way back, she walks diagonally until she reaches her own house. What distance did she walk while coming back? Why is walking good for us?
Find the greatest number with four digits, which is a perfect square. Also, find the square root of the number obtained.
Create a figure on the given square grid ensuring that the number of squares used should have the square root as an odd number.
Challenge
1 There are (2217 – x) students in a school. During the assembly meeting, the number of students in each row is equal to the total number of rows. What is the least value of x?
Points to Remember
• If a number has 4 or 6 in its ones place, then its square ends in 6.
• In square numbers, the digits always end in 0, 1, 4, 5, 6 or 9 and not 2, 3, 7 or 8.
• Squares of even numbers are always even, and those of odd numbers are always odd.
• To check if a number is a perfect square, we use prime factorisation. If on prime factorising the number, we get pairs of equal prime factors, and no factor is left over, then the number is a perfect square.
• The sum of the first n odd numbers is n2 .
• If m is any non-zero number and m > 1, then we have (2m)2 + (m2 – 1)2 = (m2 + 1)2. So, 2m, m2 – 1, m2 + 1 are said to form a Pythagorean triplet.
• The square root of a number is the value that can be multiplied by itself to get the original number. It is the inverse of a square number. It is denoted using the symbol ‘ ’, called the radical symbol.
Math Lab
Setting: In groups of 4
Method:
Building Square Roots
Materials Required: Graph paper, coloured markers, ruler
Collaboration
1 Start by drawing squares of different sizes (1 × 1, 2 × 2, 3 × 3, etc.) on graph paper.
2 Find the area of the squares drawn.
3 Use a new sheet of graph paper and shade small squares to make bigger squares of any size (for example, shade 4, 9, 16 or 25 small squares).
4 Find the length of the side of the square, and deduce that the length of the side of the square is the square root of the number.
5 Discuss in your groups and compare the area of the squares and the side lengths.
Chapter Checkup
Find the squares of the given numbers.
a 38 b – 47 c 3 7 d – 9 13
Find the value of:
a 452 – 162 b 65 × 67 c 1042 d 120 × 124
Express 324 as the sum of odd numbers.
Find the Pythagorean triplets whose smallest members are 96 and 24.
Which of the numbers are perfect squares? Find their square roots. Verify your answer.
a 265 b 2116 c 8839 d 3136
Find the square roots correct to two decimal places.
a 7.8961 b 33.64 × 67.24 c 3.7589 d 6512.8007
Find the lowest number, which must be added to 6,57,700 to get a perfect square. Also, find the square root of the perfect square so obtained.
Find the greatest square number divisible by each of the numbers 8, 9 and 10.
The length and breadth of a rectangular room are 26 m and 18 m, respectively. What is the length of the longest straight line that can be drawn on the floor of the room?
The floor area of two square rooms is 256 square feet each. If one room's side length is doubled, what is the area of this room compared to the combined area of both original rooms?
Is the square root of a number always smaller than the original number? Provide examples to justify your answer.
Pendulums are used to regulate the movement of clocks because the interval of time for each complete oscillation, is called the period. It is given as T = 2π L g where L is the length of the pendulum and g is the acceleration due to gravity.
If the length of a pendulum is 9.8 m and the acceleration due to gravity is 9.8 m/s2 then what is the value of T?
Take π = 3.14.
The people in a society collected ₹7396 for charity. Each resident contributed the same amount as the number of residents. How many residents were there in the society?
Challenge
1 Is the square root of x greater than 10?
Select the statements which are sufficient to answer the question.
Statement 1: x is greater than 100.
Statement 2: x is smaller than 150.
a Statement 1 alone is sufficient, but Statement 2 alone is not sufficient.
b Statement 2 alone is sufficient, but Statement 1 alone is not sufficient.
c Both statements together are sufficient, but either statement alone is not sufficient.
d Both statements together are not sufficient to answer the question.
2 Read the assertion and the reason to decide which of the following options is correct.
Assertion (A): The square of any positive integer is always greater than the integer itself.
Reason (R): When a number greater than 1 is multiplied by itself, the product is always greater than the original number.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Case Study
Value Development
Let’s Renovate the Park
A committee decided to renovate the rectangular park in their society. The area of the rectangular park is 9600 sq. m. The length of the park is 160 m. A square recreational zone that will include a children's playground, seating areas, and exercise stations is to be constructed inside the park. The square recreational zone is approximately one-fourth of the total area of the park. The park should have space for a garden that is at least 1200 sq. m.
1 What is the side length of the square recreational zone?
2 A path is built inside the park across the diagonals. What will be the length of the path from one corner to the other?
3 How much approximate area is left inside the rectangular park after making the square recreational zone?
4 A circular fountain is to be built at the centre of the park. The radius of the fountain is 5.6 m. The fountain is to be tiled from inside. The cost of tiling is ₹9856 per sq. m. What is the total cost of tiling?
5 Do you visit your city parks? What do you do to keep them clean?
Cubes and Cube Roots
Letʹs Recall
The volume of a solid is the amount of space it occupies. For example, take this solid made of unit cubes. Each side of the solid has a different number of unit cubes. Its volume can be found in two ways:
1 Counting unit cubes layer by layer
To find the volume of this solid by counting cubes layer by layer, we have
Layer 1
Layer 2
Number of unit cubes in layer 1 = 12
Number of unit cubes in layer 2 = 12
Total number of unit cubes = 12 + 12 = 24
To find the volume of this solid by counting cubes along the sides, we have
The volume of the given solid is 24 cu. units. length 4 unit cubes 2 unit cubes 3unitcubes height breadth
Volume of the given solid = 4 × 3 × 2 = 24 cu. units
Letʼs Warm-up
Fill in the blanks.
1 There is an apple and a pineapple on a table. Between both the fruits, occupies more space.
2 If a solid with 2 layers has 5 unit cubes along its length and 3 unit cubes along its breadth, its volume is cu. units.
3 If a solid has 3 layers with 16 sq. unit cubes in each layer, then its volume is ________________ cu. units.
4 If a container is 3 cm long, 2 cm wide, and 2 cm high, then cm cubes will be in the container.
5 A carton is filled with fourteen 2 cm cubes. The volume of the carton is cu. cm.
2 Counting unit cubes along the sides length height breadth I scored out of 5.
Cube of a Number
Jiya received a Rubik’s cube as a gift on her birthday. Upon examining the cube, she noticed it was composed of 27 smaller cubes. She counted the number of small cubes along the length, width and height of the cube and determined that there were 3 small cubes along each dimension. She noticed a relation between the number of small cubes along the length, width and height of the Rubik’s cube, and the total number of small cubes. Can you think what it was?
Perfect Cube
Look at the figures. Each number has been represented using unit cubes. Like squares, some form complete cubes and some do not.
So, when we make a cube using 1 unit cube or 8 unit cubes, we get a complete cube. 1 and 8 are called cube numbers or perfect cubes.
We see that each perfect cube has the same length, breadth and height. So, to find the number of unit cubes in a perfect cube, we multiply the number of unit cubes on one side three times. The product so obtained is called the cube of a number.
For example, we can write the cube of 1 as 1 × 1 × 1 = 13.
Similarly, the cube of 2 is written as 2 × 2 × 2 = 23
Thus, the cube of 1 is 1 and the cube of 2 is 8.
Some more cube numbers are listed in the table.
means ‘cube’.
Cubes of even numbers are always even.
The
digit of the cube of some numbers is the same as the units digit of the number.
Cubes of Negative Integers
Look at the cube numbers.
=
Cubes of odd numbers are always odd.
Think and Tell
What can you say about the units digit of other cube numbers? Also, if a cube of a number is a multiple of 3, is it also a multiple of 27?
(−10)3 = −10 × −10 × −10 = −1000
In each case, the cube of a negative number is negative. So, we can say that the cube of a negative integer is always negative.
Cubes of Rational Numbers
Like squares of rational numbers, we can also find the cubes of rational numbers in the same way. To find the cube of a rational number, we multiply it thrice. For example, to find the cube of a rational number 5 7 , we write it as:
5 7 3 = 5 7 × 5 7 × 5 7 = 5 × 5 × 5 7 × 7 × 7 = 125 343
Similarly, to find the cube of a negative rational number, 8 11 we write it as: 8 11 3 = 8 11 × 8 11 × 8 11 = 11 × 11 × 11 ( 8) × ( 8) × ( 8) = 512 1331
To Check If a Number Is a Perfect Cube or Not
Like perfect squares, we use prime factorisation to check if a number is a perfect cube or not. If, on prime factorising the number, we get a triplet of the same prime factors, leaving behind no other factor, then the number is a perfect cube. For example, let us check if 728 and 3375 are perfect cubes.
8 • Cubes and Cube Roots
Step 1: Find the prime factorisation of 728.
Step 1: Find the prime factorisation of 3375.
728 = 2 × 2 × 2 × 7 × 13
Step 2: Group the prime factors into triplets of the same factors until no factor is left over.
728 = 2 × 2 × 2 × 7 × 13
Since all the prime factors do not form a triplet, 728 is not a perfect cube.
Example 1: Find the perfect cube of:
1 (−18)3 = −18 × −18 × −18 = −5832
3375 = 5 × 5 × 5 × 3 × 3 × 3
Step 2: Group the prime factors into triplets of the same factors until no factor is left over.
3375 = 5 × 5 × 5 × 3 × 3 × 3
Since all the prime factors form a triplet and no factor is left over, 3375 is a perfect cube.
Every cube number is written as a product of three like factors.
Example 2: What will be the digit in the ones place of the cube of the number 1331?
Cube of 1 = 1, digit at the ones place of its cube = 1.
Example 3: What is the smallest number by which 3456 may be multiplied so that the product is a perfect cube?
3456 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
Clearly, not all the prime factors form a triplet, and we are left with a factor of 2 which cannot form a triplet. We require two more 2s to form a triplet of 2.
So, (2 × 2 = 4) is the smallest number with which 3456 is multiplied to get a perfect cube.
Example 4: How many soap bars of dimensions 6 cm × 8 cm × 2 cm can be placed in a cubical carton of length 24 cm?
Volume of a soap bar = 6 × 8 × 2 = 96 cu. cm,
Volume of the cubical carton = 24 × 24 × 24 = 13,824 cu. cm
Number of soap bars that can be placed = 13824 96 = 144
Hence, 144 soap bars of dimensions 6 cm × 8 cm × 2 cm can be placed in a cubical carton of length 24 cm.
Find the least number by which 6561 may be divided so that the product is a perfect cube.
6561 = 3 × 3 ×
Clearly, not all prime factors form a triplet and we are left with a factor which cannot form a triplet.
So, is the lowest number by which 6561 should be divided to get a perfect cube.
Patterns in Cubes
Like perfect squares, we can also create certain patterns for perfect cubes.
Pattern 1
• 1 = 1 = 13
• 3 + 5 = 8 = 23
• 7 + 9 + 11 = 27 = 33
• 13 + 15 + 17 + 19 = 64 = 43
Pattern 2
• 13 + 23 = 1 + 8 = 9 and (1 + 2)2 = 32 = 9 • 13 + 23 + 33 = 1 + 8 + 27 = 36 and (1 + 2 + 3)2 = 62 = 36 • 13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100 and (1 + 2 + 3 + 4)2 = 102 = 100
Rule: If n3 = sum of n odd numbers, then the first odd number = 2 × (n – 1)th triangular number + 1, where (n – 1)th triangular number = sum of (n – 1) consecutive numbers. Rule: 13 + 23 + 33 + 43 + … + n3 = (1 + 2 + 3 +
Pattern 3
• 23 – 13 = (3 × 1)(1 + 1) + 1 • 33 – 23 = (3 × 2)(2 + 1) + 1
Rule: If n and n + 1 are two consecutive numbers, then (n + 1)3 – n3 = 3n(n + 1) + 1.
Example 5: Use the first pattern above to find the value of 83.
1
We know that n3 = the sum of n odd numbers where the first odd number = 2 × (n – 1)th triangular number + 1.
Also, (n – 1)th triangular number = sum of (n – 1) consecutive numbers 83 = sum of 8 odd numbers, where the first odd number = 2 × (8 – 1)th triangular number + 1 = 2 × 7th triangular number + 1
where the 7th triangular number = sum of 7 consecutive numbers = 2 × (1 + 2 + 3 + 4 + 5 + 6 + 7) + 1 = 2 × 28 + 1 = 56 + 1 = 57
So, 83 = 57 + 59 + 61 + 63 + 65 + 67 + 69 + 71 = 512
Example 6: Use the second pattern given above and find the value of 13 + 23 + 33 + 43 + 53 + 63 + 73.
We know that 13 + 23 + 33 + 43 + … + n3 = (1 + 2 + 3 + 4 + … + n)2
So, 13 + 23 + 33 + 43 + 53 + 63 + 73 = (1 + 2 + 3 + 4 + 5 + 6 + 7)2 = 282 = 784
8 • Cubes and Cube Roots
Use the third pattern given above, to find the value of 873 – 863.
We know that if n and n + 1 are two consecutive numbers, then (n + 1)3 – n3 = So, 873 – 863 = 3 ×
The Hardy–Ramanujan number, 1729, is the smallest number expressed as the sum of two cubes in two different ways: 13 + 123 and 93 + 103. Did You Know?
Do It Yourself 8A
Which of these show the cube of the number 4 and 3? Colour the cubes.
Find the cubes of the numbers.
Look at the digits in the units place of each of the numbers. Answer the questions.
1331
i What will be the digit in the ones place of the cube of each number?
ii Which of the numbers will have odd or even cubes?
iii Which of the numbers are not perfect cubes?
Find the cube of the rational numbers.
Find the cube of the decimal numbers.
Check if the numbers are perfect cubes using prime factorisation. Also, find the number whose cube is the number.
Find the smallest number by which the number should be multiplied to get the perfect cube. In each case, find the number whose cube is the new number.
432
What is the least number by which the number should be divided to get the perfect cube? In each case, find the number whose cube is the new number.
Use pattern 1 to find the values of 113 and 203.
Use pattern 2 to evaluate the given expressions.
a 13 + 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 b 13 + 23 + 33 + 43 + 53 +
Use pattern 3 to find the difference of:
a 413 and 403 b 1003 and 993
Savita wants to distribute energy bars to children at an orphanage. How many packs of energy bars of dimensions 8 cm × 10 cm × 2 cm can she place in a cubical carton of length 20 cm?
Challenge
+
1 Mitali forms a solid, as shown. It is made up of 2 cm cubes. What is the volume of this solid? Can we rearrange the cubes to form a perfect cube? If not, how many more 2 cm cubes will be needed to form a perfect cube?
Cube Root of a Number
Snigdha bought a cubical aquarium of volume 1,95,112 cu. cm. She wanted to put it on a square table so that it would fit the table exactly. For this, she needed the measurements of the aquarium.
Cube Root through Prime Factorisation Method
The cube root of a number is the value that can be multiplied by itself to get the original number. It is the inverse of a cube number. It is denoted using the symbol ‘ 3
For any number n, 3 n is called the radical, where 3 is called the index and n is called the radicand.
For example, the cube of 4 is 64 but the cube root of 64 is 4.
We write it as: 3 64 = 3 4 × 4 × 4 = 4.
Given below is a list of cube roots of different numbers.
=
=
=
=
We can find the cube roots using the prime factorisation method. Let us find the cube root of 10,648 and look at the steps involved.
Error Alert!
The cube root of a number is NEVER one-third of its value. Cube root of 1331 = 3 1331 = 1331 3 = 443.67
root of 1331 = 3 1331 = 11
Step 2: Group the same prime factors together in the form of a triplet.
Step 1: Find all the prime factors of the number.
Now, let us find the measure of the aquarium.
3 10648 = 2 × 2 × 2 × 11 × 11 × 11 = 2 × 11 = 22 3
Step 3: Select one prime factor from each group and find the product. The product is the cube root of the number.
We know that the volume of the aquarium is 1,95,112 cu. cm.
⇒ One side of the aquarium is the same as the cube root of its volume.
So, by prime factorisation, we get 1,95,112 = 2 × 2 × 2 × 29 × 29 × 29
So, 3 195112 = 3 2 × 2 × 2 × 29 × 29 × 29 = 2 × 29 = 58
Therefore, one side of the fish aquarium would be 58 cm.
195112
97556
48778
24389
841
29 1
Cube root of a negative perfect cube
To find the cube root of a negative perfect cube, we find the cube root of its absolute value and multiply it by 1. For example, to find the cube root of −343, we write it as:
3 343 = 3 7 × 7 ×−7 = 7 because 3 343 = 3 7 × 7 × 7 = 7
Cube root of a rational number
We can find the cube root of a rational number by dividing the cube root of its numerator by the cube root of its denominator. For example, to find the cube root of a rational number 2197 2744, we write it as:
3 2197 2744 = 3 2197 3 2744 = 3 13 × 13 × 13 3 2 × 2 × 2 × 7 × 7 × 7 = 13 2 × 7 = 13 14
For a negative rational number, we write it as:
3 5832 6859 = 3 5832 3 6859 = 3 –2 ×
Cube root of the product of the integers
To find the cube root of the product of integers, we multiply the cube root of one integer by the cube root of the other integer. For example, to find the cube root of 27 × (−64), we write it as:
3 27 × (–64) = 3 27 × 3 –64 = 3 3 ×
= 3 × − 4 = – 12
Cube root of a perfect cube using a pattern
We know that 03 = 0, 13 = 1, 23 = 8, 33 = 27, 43 = 64, 53 = 125, … and so on.
So, from the above, we get 13 – 03 = 1 – 0 = 1 = 1 + 0 × 6 = 1 + 0(0
–
– 23 = 27 – 8 =
and so on. Rule: (n + 1)3 – n3 = 1 + n(n + 1) × 3
Any cube number can be written as the sum of 1, 7, 19, 37, 61, …, 271 and each of these odd numbers can be obtained using (n + 1)3 – n3 = 1 + n(n + 1) × 3
So, to find the cube root of any number, we successively subtract these odd numbers until we get 0, or a number from which further subtraction is not possible. As soon as we get 0, we count the number of times the subtraction is carried out. This number is the cube root of the given number.
For example, for the cube number 64, we subtract the odd numbers successively from 64. 64 – 1 = 63 (1 time)
63 – 7 = 56 (2 times)
56 – 19 = 37 (3 times)
37 – 37 = 0 (4 times)
As soon as we get 0 or a number from which further subtraction is not possible, we stop there. Here, odd numbers are subtracted 4 times. So, 3 64 = 4.
Example 7: Find the cube root of 4913, using prime factorisation.
4913 = 17 × 17 × 17
So, 3 4913 = 3 17 × 17 × 17 = 17
Example 8: Find the value of
3 64 × (–512)
64 × (–512) = 3 64 × 3 –512 = 3 4 × 4 × 4 × 3 –8 × 8 × 8 = 4 × (–8) = –32
Did You Know?
The famous Rubik’s cube is a popular puzzle invented by Ernő Rubik in 1974. Also, the largest Rubik’s cube in the world is 2.022 m × 2.022 m × 2.022 m.
Example 9: Find the cube root of 729, using successive subtraction
For a cube number 729, we subtract the odd numbers successively from 729.
– 127 = 386 (7
As soon as we get 0, we stop there. Here, odd numbers are subtracted 9 times. So, 3 729 = 9.
Example 10: Find the smallest number that must be subtracted from 624 to make it a perfect cube. Also, find the cube root of the perfect cube obtained.
To find the smallest number, we subtract the odd numbers successively from 624. 624 – 1 = 623 (1 time) 623 – 7 = 616 (2 times) 616 – 19 = 597 (3 times)
– 61 = 499 (5 times) 499 – 91 = 408 (6 times)
– 37 = 560 (4 times)
The next number to be subtracted from 112 is 217. But 217 > 112, so 112 must be subtracted from 624 to get a perfect cube.
So, 112 is the smallest number that must be subtracted from 624 to get a perfect cube.
Now, 624 – 112 = 512
So, 3 512 = 3 (2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2) = 2 × 2 × 2 = 8. 17 4913 17 289 17 17 1
Example 11: Find the smallest number to be added to 400 to make it a perfect cube. Also, find the cube root of the perfect cube obtained.
To find the smallest number, we subtract the odd numbers successively from 400.
400 − 1 = 399 (1 time)
399 − 7 = 392 (2 times)
336 − 61 = 275 (5 times) 275 − 91 = 184 (6 times)
392 − 19 = 373 (3 times) 373 − 37 = 336 (4 times)
− 127 = 57 (7 times)
The next number to be subtracted from 57 is 169. But 169 > 57, so 169 − 57 = 112 must be added to 400 to get a perfect cube.
So, 112 is the smallest number that must be added to 400 to get a perfect cube. Now, 400 + 112 = 512.
Cube root of 512 = 3 (2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2) = 2 × 2 × 2 = 8.
Example 12: What is the least number by which 5000 should be multiplied to get a perfect cube? Find the number of which the new number is the cube.
5000 = 2 × 2 × 2 × 5 × 5 × 5 × 5
We require two more 5’s to form a triplet of 5.
So, (5 × 5 = 25) is the smallest number with which when 5000 is multiplied, we get a perfect cube.
Therefore, 5000 × 25 = 2 × 2 × 2 × 5 × 5 × 5 × 5 × 5 × 5
1,25,000 = 23 × 53 × 53 = (2 × 5 × 5)3 = 503
Example 13: Look at the solid. The shaded portion of the solid has an area of 81 sq. cm. What is its volume?
Area = 81 sq. cm
9 × area of one square = 81 sq. cm
Area of one square = 81 9 = 9 sq. cm = (3)2
Side of square = 3 cm = side of the cube
Volume of 1 cube = 3 × 3 × 3 = 27 cu. cm
Number of cubes = 27
Volume of 27 cubes = 27 × 27 = 729 cu. cm
Example 14: Three numbers are in the ratio 1:2:3. If the sum of their cubes is 15,43,500, then find the numbers.
Let the numbers be x, 2x and 3x.
Then, x3 + (2x)3 + (3x)3 = 15,43,500
⇒ x3 + 8x3 + 27x3 = 15,43,500
⇒ 36x3 = 15,43,500
⇒ x3 = 15,43,500 36 = 42,875
⇒ x = 3 42875
⇒ 42,875 = 5 × 5 × 5 × 7 × 7 × 7
So, 3 42875 = 3 5 × 5 × 5 × 7 × 7 × 7 = 5 × 7 = 35
So, x = 35
⇒ 2x = 2 × 35 = 70, 3x = 3 × 35 = 105
Therefore, the numbers are 35, 70 and 105.
Find the value of
1 3 –1728 2744
3 –1728 2744 = –3 1728 3 2744 = = 2 3 8 × ( 125)
3 8 × ( 125) = 3 8 × 3 125 = = = Do It Together
Do It Yourself 8B
1 Shade the side to show the cube root of 216.
2 Find the cube root using prime factorisation. a 8000
3 Find the cube root of the numbers using successive subtraction.
4 Find the value of:
5 Find the length of each edge of each given cube if its volume is:
a 5,92,704 cu. cm b 85,184 cu. cm
6 Find the smallest number that must be subtracted from each number to make it a perfect cube. Also, find the cube root of the perfect cube obtained. a 408 b 2215
7 Find the smallest number that must be added to each number to make it a perfect cube. Also, find the cube root of the perfect cube obtained.
a 720 b 2700
8 Three numbers are in the ratio 1:3:6. If the sum of their cubes is 15,616, then find the numbers.
9 Inspired by the Orca statue made from cubes at Canada Place, a sculptor decided to create a structure using cubes for his next project. If the structure has a volume of 74,088 cu. cm, then what is the length of each side?
Challenge
Critical Thinking
1 1*28 is a 4-digit number. If the number is a perfect cube, find the missing digit and the cube root of the number.
Points to Remember
• A number that forms a complete cube is a perfect cube.
• Cubes of even numbers are always even, and those of odd numbers are always odd.
• The cube of a negative integer is always negative.
• Prime factorisation confirms if a number is a perfect cube by yielding a triplet of the same prime factors.
• The sum of number cubes equals the square of their sum.
• The difference between consecutive number cubes is three times their product plus 1.
• The cube root, denoted by ʻ3 ʹ, is the inverse of a cube number and can be found via prime factorisation and estimation.
• To find the cube root of a negative perfect cube, find the cube root of its absolute value, and multiply it by 1.
Math Lab
Setting: In groups of 5.
Collaboration & Experiential Learning
Operations Insight!
Materials Required: Building blocks or cubes of different colours
Method:
1 Split into groups and get a bunch of building blocks.
2 Use the blocks to make cubes of different sizes.
3 Count how many blocks you used for each cube.
4 Figure out the volume of each cube by multiplying its side lengths.
5 Talk about how the size of a cube relates to its volume.
Chapter Checkup
1 Find the cube of each of the numbers.
2 Shade the figure that shows the cube of a number. Write the number.
3 Which of the following are perfect cubes? Find the number whose cube is the given number.
4 Using patterns, find the value of:
5 Evaluate:
6 Find the length of the edge of the cube if its volume is 2,26,981 cu. m.
7 Mary is helping her mother in preparing chocolate bars in the shape of a cube with a side length of 5 cm. What is the volume of 25 such bars?
8 Find the smallest number that must be subtracted from 2789 to make it a perfect cube. Also, find the cube root of the perfect cube obtained.
9 Find the smallest number that must be added to 4900 to make it a perfect cube. Also, find the cube root of the perfect cube obtained.
10 What is the least number by which 24,500 should be multiplied to get a perfect cube? Find the number of which the new number is the cube.
11 Find the smallest number by which 53,45,344 should be divided to get the perfect cube. Find the number of which the cube is the new number.
12 Look at the solid. The shaded portion of the solid has an area of 147 sq. cm. What is its volume?
1 In a competition, a school decides to award prizes for three values: punctuality, respect and discipline. The numbers of students getting prizes are in the ratio of 2:3:5. If the product of the numbers is 2,05,770, find the number of students getting the prize for each value.
2 A city wants to construct a large water tank in the shape of a cube to store rainwater during drought periods. If they estimate the tank needs to hold 8000 cubic metres of water,
a What should be the dimensions of the cube?
b If they want to install eight such tanks adjacent to each other, what should be the length of the side of the shape thus formed?
Case Study
Cubes in Urban Planning
In the city, urban planners are faced with the challenge of designing efficient and aesthetically pleasing public spaces. There's a plan to make a new gathering spot downtown. They want it to be a place where people can gather, sit, and enjoy some greenery.
The design team proposes using concrete to make large cubes. These cubes will serve multiple functions, including seating, planters, and artistic displays. Each cube will have a different edge length.
Answer these questions.
1 How many cubic metres of concrete are needed to construct a cube with an edge length of 1.5 metres?
a 1.875 cubic metres
c 3 cubic metres
b 2.25 cubic metres
d 3.375 cubic metres
2 If a cube proposed as a planter has a volume of 64 cubic metres, what is its edge length?
a 4 metres
c 8 metres
b 6 metres
d 16 metres
3 The volume of a cube with an edge length of 2.5 metres, designed for artistic purposes is cubic metres.
4 A cubical design can accommodate 4 smaller cubes of length 1.8 m each with a volume of cubic metres.
Cross Curricular
9 Percentage and Its Applications
Letʹs Recall
Mr Martin’s company has 5 different departments. The graph below shows the distribution of employees across the various departments.
1 What percentage of the people work in the finance department? 11%
2 In which two departments is the number of employees the same?
Admin and Marketing
3 Which department has the highest number of people working in it?
Sales Department
Letʼs Warm-up
Read the graph below which depicts the survey results for favourite colours, and fill in the blanks.
1 The least preferred colour is
The most preferred colour is
3 The percentage of people who prefer yellow is
4 The percentage of people who like green is .
5 The number of people who prefer blue over red is .
Percentage and Percentage Change
In the Indian parliament, there are 542 members, of which 78 are females and the rest are males. What is the ratio of females to the total number of members in the parliament? A ratio means comparing two quantities, and this comparison can be done using fractions or percentages.
Ratio of females to total members = 78:542 or 39:271. What percentage of the total members are female?
Ratio and Percentages
A percentage is a fraction with its denominator as 100. Thus, percentage means per 100, and is denoted by ‘%’. In other words, percent means how many hundredths.
39 271 × 100� = 14106 271 � or 14.39%
So, 14.39% of the parliament is female.
Think and Tell
What is 100% of any number?
Example 1: 1 Convert 0.25 into
Remember!
A fraction can be converted into a percentage by multiplying it by 100.
Error Alert!
We always shift the decimal point two places to the right when we multiply by 100, and two places to the left when we divide by 100.
Example 2: 1 If 40% of a number is 120, find the number.
Let the required number be x.
Then, 40� of x = 120
40 100 × x = 120
Remember!
To convert a percentage value into a fraction or a decimal, divide by 100, remove the percentage symbol and then simplify if required.
x = 100 40 × 120
x = 300
2 Arya has spent 45% of her salary and she has ₹5500 remaining. Find her salary. Let Arya’s salary be x.
Arya spent 45% of x = 45 100 × x = 9 20 x
Money Arya has left = x − 9 20 x = 11 20 x
Money Arya has left = ₹5500
Therefore, 11 20 x = ₹5500
x = 5500 × 20 11 = ₹10,000
Thus, Arya’s salary is ₹10,000.
Example 3: Answer the following.
1 What percent of 5 kg is 1 kg 250 g?
1 kg 250 g = 1000 g + 250 g = 1250 g
5 kg = 5000 g
Required percentage = 1250 5000 × 100% = 25%
2 What percent of 12 km is 3 km 250 m?
3 km 250 m = 3000 m + 250 m = 3250 m
12 km = 12,000 m
Required percentage = 3250 12000 × 100% = 27 1 12 %
Example 4: Smoothies can be an excellent source of protein and fiber, which can help promote feeling full and reduce cravings for unhealthy snacks and processed foods. Sarah drinks a 500 mL smoothie every day. If the smoothie is made of 80% fruit and 20% yogurt, how many millilitres of yogurt are in her daily smoothie?
Total amount of smoothie that Sarah drinks = 500 mL
Percentage of yogurt in the smoothie = 20%
Amount of yogurt in the smoothie = 20% of 500 mL = 20 100 × 500 mL = 100 mL
Example 5: In a competitive exam, a student scored 150 marks. The passing percentage was 35% but the student failed by 25 marks. What were the highest marks for the examination?
Passing percentage for the examination = 35%
Marks scored by the student = 150 marks
Marks by which the students failed the examination = 25 marks
Passing marks required = 150 marks + 25 marks = 175 marks
So, 35% of the highest marks = 175 marks
Highest marks for the examination = 175 35 × 100 = 500 marks
In a school, 35% of the students like playing football, and the remaining students like basketball. If 1300 students like basketball, find the number of students in the school.
Let the total number of students be x.
Percentage of students who like football = 35%
Percentage of students who like basketball = (100% − 35�) = 65%
Number of students who like basketball =
Total number of students =
Percentage Change
Remember that there were 78 women in the Indian parliament. If there were 117 women in the next parliament session, what would be the percentage increase in the number of women?
Percentage change = Amount of increase/decrease Original amount × 100�
Percentage increase = 117 − 78 78 × 100� = 39 78 × 100� = 50�
Thus, the number of females in the next parliament session would increase by 50%.
Error Alert!
Think and Tell
If you score 60 out of 80 in your maths test, what percentage of marks did you score?
Always ensure that you use the original value in the denominator when calculating the percentage change. � change = 39 117 × 100� � change = 39 78 × 100�
Example 6: The price of an article is increased by 20%. Find the original price of the article, if the increased price is ₹3000.
Let the original price of the article be ₹x
Increase in the price = 20% of ₹x = ₹ 20 100 × x = ₹ x 5
Increased price = ₹x + ₹ x 5 = ₹6x 5
Increased price = ₹3000
Since ₹6x 5 = 3000x = ₹2500.
Think and Tell
What will happen in the above question if the price goes down by 10%?
Example 7: The value of piece of a land appreciates every year by 10%. Find the value of the piece of land after two years if the present value is ₹35,00,000.
Present value of the land = ₹35,00,000
Increase in the value of the land after 1 year = 10% of ₹35,00,000 = 10 100 × ₹35,00,000 = ₹3,50,000
Increased value of the land after 1 year = ₹35,00,000 + ₹3,50,000 = ₹38,50,000
Increase in the value of the land after 2 years = 10% of ₹38,50,000 = 10 100 × ₹38,50,000
= ₹3,85,000
Increased value of the land after 2 years = ₹38,50,000 + ₹3,85,000 = ₹42,35,000
Thus, the value of the piece of land after two years will be ₹42,35,000.
Example 8: The price of sugar goes up by 10%. By what percentage must Vijay reduce his consumption of sugar so that his expenditure on sugar remains the same?
Let the consumption of sugar originally be x kg, and let its cost be ₹100.
New cost of x kg of sugar = ₹110
Now, ₹110 can buy x kg of sugar.
₹100 can buy x 110 × 100 kg of sugar = 10x 11 kg of sugar
Reduction in consumption = (x − 10x 11 ) = x 11 kg of sugar
Reduction in percentage of consumption
= Reduction in consumption Original consumption × 100% = x 11 x × 100� = 9 1 11 �
Hence, Vijay must reduce his consumption by 9 1 11 �.
The length of a piece of rope is reduced from 150 cm to 125 cm. Find the percentage decrease.
Original length of the rope = cm
Final length after reduction = cm
Reduction in length = cm
Reduction percentage = Reduction in length Original length × 100� = �
Do It Yourself 9A
1 Convert the decimals into percentages and the percentages into decimals.
2 Express each of the percentages as a fraction.
3 Express each of the percentages as a ratio.
4 Answer the questions.
a What percentage of 30 is 60?
c What percentage of 3 is 9 5 ?
b What percentage of 3 L is 900 mL?
d What percentage of 5 kg is 1500 grams?
5 Find the percentage increase or decrease.
a ₹50 ₹90
b ₹45 ₹20
c ₹98 ₹88
d ₹200 ₹180
6 Solve the given questions.
a Increase ₹190 by 20%
c Decrease 1000 L by 12.5%
b Decrease 150 kg by 30%
d Increase 750 grams by 0.5%
7 The price of olive oil has increased by 10%. If the original price was ₹250 per litre, find the new price.
8 A number is increased by 30% and then reduced by 20%. Find the net increase or decrease in the number.
9 Rajat scored 400 marks out of 500 in the half-yearly exams. He scored 430 marks out of 500 in his final exams. What was the percentage increase in the marks scored by Rajat?
10 Voting gives people an opportunity to choose leaders who make decisions that shape their community and future. In a town with a population of 50,000, the number of registered voters is 35% of the total population. Of the registered voters, 60% voted in the recent election. Of those who voted, 40% were aged between 18 and 30 years old and the rest were older. Calculate:
a The total number of registered voters.
b The number of people who voted in the recent election.
c The number of voters between 18 and 30 years old.
11 The value of a car depreciates every year by 10%. Find its value after 2 years, if its present value is ₹3,50,000.
12 In an examination, a student has to score 30% marks to pass. A student gets 45 marks and fails by 15 marks. Find the highest number of marks that a student can score in the examination.
13 Mr Sharma has a habit of saving money for his family. In a month he gave 20% of his saved money to his mother, 30% to his sister, 25% to his wife and the remaining ₹4500 to his brother. How much money had he saved that month?
1 A company manufactures smartphones. During quality testing, it is found that 15% of the smartphones are defective. Out of the defective phones, 40% can be repaired and sold at a lower price, whereas the remaining 60% are beyond repair and are scrapped. The company manufactures 10,000 smartphones. Answer the questions.
a How many smartphones are defective?
b How many defective smartphones can be repaired?
c How many defective smartphones cannot be repaired and are scrapped?
Application of Percentages
Satya went to purchase a new television for his home at the nearby electronics shop. He asked for a 32-inch television. The purchase price of the television was ₹95,000. The shopkeeper usually sells the television for ₹1,05,000, but due to the festive season, he wanted to clear his stock, so he sold the television for ₹94,000.
Profit and Loss
Let us first discuss the terms cost price and selling price. Cost Price is the price at which an article is purchased by the shopkeeper. Selling price is the price at which an article is sold by the shopkeeper.
We know that when the cost price > the selling price, a loss is incurred, and when the selling price > the cost price, a profit is made.
Let us find the profit or loss incurred for the television sold at the usual price and the festive price.
Usual Selling Price
Selling Price Cost Price
₹1,05,000 − ₹95,000 = ₹10,000
If SP > CP; Profit = SP − CP
Festive Selling Price
Cost Price Selling Price ₹95,000 − ₹94,000 = ₹1000
If CP > SP; Loss = CP − SP
Hence, the shopkeeper would have earned a profit of ₹10,000 if he sold the television at ₹1,05,000, but he incurred a loss of ₹1000 by selling the television at ₹94,000.
Finding Profit or Loss Percentage
The percentage of profit or loss is the amount of profit or loss represented as a percentage of the total. The percentage of profit and loss for the electronics shopkeeper can be given as:
Profit percentage = Profit CP × 100% = 10,000 95,000 × 100 = 10.5% Loss percentage = Loss CP × 100% = 1000 95,000 × 100 = 1.05%
Example 9: Ramesh purchases a TV for ₹5000 and pays ₹250 for its transportation. If he sells the TV for ₹5075, find his percentage profit or loss.
Price at which the TV is bought = ₹5000
Overheads in the form of transportation = ₹250
Therefore, the total cost price of the TV = (5000 + 250) = ₹5250
Selling price of the TV = ₹5075
Since SP < CP, there is a loss.
Loss = CP – SP = 5250 – 5075 = ₹175
Therefore, percentage loss = Loss CP × 100% = 175 5250 × 100% = 10 3 % = 3.33%
Therefore, Ramesh incurred a loss of 3.33%.
Example 10: By selling 240 pens, Kumar lost an amount equal to the CP of 30 pens. Find his loss percentage.
Let us assume that the cost price of each pen is ₹1.
CP of 240 pens = ₹240
Loss = CP of 30 pens = 30 × 1 = ₹30
Loss percentage = Loss CP × 100% = 30 240 × 100% = 12.5%
Therefore, Kumar’s loss percentage is 12.5%.
If the cost price of 10 greeting cards is equal to the selling price of 8 greeting cards, find the gain or loss percent.
Let the cost price of each card be ₹x.
Then, CP of 8 cards = ₹8x
SP of 8 cards = CP of 10 cards = ₹10x
Thus, CP = ₹8x and SP = ₹10x
Since SP > CP there is a profit.
Profit = ₹(10x − 8x) =
Profit% = Profit CP × 100% = =
Therefore, the percent profit is .
Finding Selling Price or Cost Price
We have already studied the meaning of the terms selling price and cost price. We will now look at some of the formulas associated with these two terms.
When CP and Profit/Loss % are given
SP = 100 + Profit� 100 × CP or
SP = 100 - Loss� 100 × CP
When SP and Profit/Loss % are given
CP = 100 100 + Profit� × SP or
CP = 100 100 − Loss� × SP
Example 11: A shopkeeper purchased an old washing machine for ₹2500 and spent ₹500 on transportation and repairs. He then sold the same machine at a profit of 25%. Find the selling price of the machine.
Price at which washing machine was bought = ₹2500
Overheads in the form of transportation and repairs = ₹500
Therefore, the total cost price of the washing machine = (2500 + 500) = ₹3000
Profit percentage = 25%
Selling Price = 100 + Profit� 100 × CP = 100 + 25 100 × 3000 = 125 100 × 3000 = 3750
Hence, the selling price of the washing machine is ₹3750.
Example 12: A shopkeeper sold two watches for ₹6000 each. On one watch he lost 20%, and on the other he made a profit of 20%. What is the total profit or loss on the two watches?
SP of the first watch = ₹6000, Loss% = 20%
CP of the first watch = 100 100 − Loss% × SP = 100 100 – 20 × 6000 = 100 80 × 6000 = ₹7500
SP of the second watch = ₹6000, Profit% = 20%
CP of the second watch = 100 100 + Profit% × SP = 100 100 + 20 × 6000 = ₹5000
Total cost price of the two watches = ₹7500 + ₹5000 = ₹12,500
Total selling price of the two watches = 2 × ₹6000 = ₹12,000 Loss = ₹12,500 – ₹12,000 = 500
So, the shopkeeper suffered a total loss of ₹500.
Example 13: A potter bought pots worth ₹3000 and sold 1 5 of the pots at a loss of 10%. At what gain percent should he sell the remaining goods so as to gain 30% on the whole transaction?
CP of the pots = ₹3000, Gain = 30%
SP of the pots = 100 + Profit� 100 × CP = 100 + 30 100 × 3000 = 130 100 × 3000 = ₹3900
CP of 1 5 of the pots = 1 5 × 3000 = ₹600
SP of 1 5 of the pots at a loss of 10% = 100 − Loss� 100 × CP = 100 – 10 100 × 600 = 90 100 × 600 = ₹540
Therefore, SP of the remaining pots = SP of all the pots – SP of 1 5 of the pots = ₹3900 – ₹540 = ₹3360
CP of the remaining pots = CP of all the pots – CP of 1 5 of the pots = ₹3000 – ₹600 = ₹2400
Profit = SP – CP = ₹3360 – ₹2400 = ₹960
Profit% = Profit Amount CP × 100 = 960 2400 × 100 = 40%
Thus, the potter should be selling the remaining goods at a profit of 40%.
Example 14: An art dealer sold a rare painting at a profit of 25%. Had he sold it for ₹500 more he would have made a profit of 30%. What is the cost price of the painting?
Let the CP of the painting be ₹x; Profit = 25%
SP of the painting with a 25% profit = 100 + Profit� 100 × CP
= 100 + 25 100 × x = 125x 100
SP of the painting with a 30% profit = 100 + Profit� 100 × CP =
5x
100 = 500; So, x = 500 × 100 5 = ₹10,000.
So, the CP of the painting was ₹10,000.
Example 15: Tina sold a bag to Anna at a profit of 10% and Anna sold the same bag at a loss of 5% to Dia. Dia paid ₹4180 for the bag. How much did Tina pay for the bag?
Suppose Tina bought the bag for ₹x.
So, Tina’s CP = x; Profit = 10%
Tina’s SP of the bag = 100 + 10 100 × x = 110 100 × x = 11x 10
Tina’s SP = Anna’s CP = 11x 10
So, Anna’s CP = 11x 10 ; Loss = 5%
Anna’s SP = 100 – 5 100 × 11x 10 = 95 100 × 11x 10 = 209x 200
Anna’s SP = Dia’s CP = 209x 200
So, Dia’s CP = 209x 200 = ₹4180 209x = 4180 × 200 x = 4180 × 200 209 = ₹4000
So, Tina bought the bag for ₹4000.
By selling a T-shirt for ₹648, a shopkeeper loses 4%. For how much should he sell it to gain 4%?
SP of the T-shirt = ₹648; Loss% = 4%
CP of the T-shirt = 100 100 − Loss� × SP = = =
Now, CP = , desired profit% = 4%
Desired SP = 100 + Profit� 100 × CP = = =
Hence, the shopkeeper should sell the T-shirt at ₹ to gain 4%.
Do It Yourself 9B
1 The cost price is ₹39,500. What is the profit or loss if the selling price is: a ₹35,000 b ₹42,000 c
2 Fill in the blanks.
a CP = ₹500; SP = ₹572; Profit/Loss% = b CP = ₹7500; SP = ₹5550; Profit/Loss% = _____ c CP = ₹6724; SP = ; Loss% = 12.5% d CP = ; SP = ₹35,100; Profit% = 8%
3 Akash buys a car for ₹4,47,200 and sells it for ₹5,09,808. What is his profit or loss%?
4 Rahul purchased a bluetooth speaker from an online website for ₹14,500 and sold it to his friend for ₹14,000. Find his profit or loss percentage.
5 A shopkeeper purchased an article for ₹5,000. He spent ₹500 on cartage and sold it for ₹6600. Find his profit percentage.
6 A retailer bought a mixer from a wholesale dealer for ₹4500 and sold it at a loss of 7%. How much did he sell the mixer for?
7 By selling a toy car for ₹819, Vinit loses 9%. At what price should he sell it to make a profit of 5%?
8 David helps his mother in their bakery business. Both David and mother prepared cookies worth ₹10,000 and sold 1 4 of the cookies at a loss of 20%. He wants to gain a profit of 40% on the cookies. At what profit percent should he sell the remaining cookies?
9 Ramu sold a piece of land to Shyam at a profit of 20%. Shyam sold the same piece of land at a loss of 10% to Raj. How much did Ramu pay for the piece of land if Raj paid ₹1,08,000?
10 A bookshop owner purchased 100 notebooks for ₹15 each. However, 5 notebooks had to be thrown away as a few pages had been torn from them. The remaining notebooks were sold at ₹18 each. Find the gain or loss percent.
11 Rakesh sells two watches for ₹1200 each. On one watch, he gains 20% and on the other he loses 20%. What is the cost price of each watch, and what is his total profit or loss percentage?
12 Create a word problem on finding the profit or loss percent of an item.
1 Madhuri sold her gold necklace at a profit of 7%. If she had sold it for ₹2940 more, she would have got a 10% profit. Find the cost price.
Discount
It is the festive season of Diwali and hence the owner of the electronics shop is offering a 10% discount on other appliances as well. The price printed on a music system was ₹40,000. Satya thought of purchasing the music system as well. He wonders how much the music system will cost him. Let us find out.
Finding Discount
Reduction in the usual price of something. The price at which the article is sold.
Discount = Marked Price – Selling Price
Discount = Marked Price × Discount� 100 or
Price on the label of an article. The discount amount expressed as a percentage of the original price.
The discount received by Satya on the music system can be given as: ₹40,000 × 10 100 = ₹4000
The cost of the music system for Satya = Price of the article after discount = ₹40,000 − ₹4000 = ₹36,000
If the shopkeeper had made a profit of ₹1250 after offering the discount, then what was the cost price of the music system? Let us find out!
If the marked price, profit/ loss and discount are given, then the cost price of the article can be found as:
CP = MP – Discount − Profit
CP = MP – Discount + Loss
Hence, the cost price of the music system = ₹40,000 − ₹4000 − ₹1250 = ₹34,750
Example 16: A book with a marked price of ₹600 is available at a discount of 18%. Find the discount offered and the price at which the book is available for sale.
Marked price of the book = ₹600; Discount given = 18%
Discount = MP × Discount Percentage 100 = 600 × 18 100 = ₹108
Therefore, the discount given on the book = ₹108
We know that, SP = MP – Discount
SP = ₹ (600 − 108) = ₹492
Therefore, the book is available for ₹492.
Example 17: The marked price of a radio is ₹12,000. Find the discount percentage allowed on the radio if it is sold for ₹10,500.
Marked price of the radio = ₹12,000; Selling price of the radio = ₹10,500
Discount = MP – SP = ₹ (12,000 – 10,500) = ₹1500
Therefore, discount percentage = Discount MP × 100� = 1500 12,000 × 100� = 12.5�
Example 18: A shopkeeper sold an article for ₹1326 after allowing a discount of 15% on its marked price. Find the marked price of the article.
Let the marked price of the article be ₹x.
Discount allowed = 15%; Selling price of the article = ₹1326
We know that SP = MP × 100 − Discount Percentage 100
1326 = x × 100 − 15 100 ⇒ 1326 = x × 85 100
x = 1326 × 100 85 = ₹1560
Therefore, the marked price of the article was ₹1560.
Remember!
An 18% discount is the same as paying 82% of the original price.
Example 19: A pair of Bluetooth speakers are marked at 40% more than the cost price. What is the profit percent if a discount of 20% is given on the speakers?
Let the cost price of the speakers be ₹100.
Marked price = 40% more than the CP = ₹140
Discount = 20% of MP = 20% of ₹140 = 20 100 × 140 = 28
Selling Price = MP – Discount = ₹140 – ₹28 = ₹112
Profit% = (112 – 100)% = 12%
Example 20: What percent above the cost price should Rhea mark her sarees so that after allowing a discount of 20% on the marked price, she makes a profit of 24%?
Let the cost price be ₹100.
Profit required = 24%
Therefore, SP = ₹124 ............................................................. (1)
Let the marked price be ₹x.
Given that the discount = 20% of ₹x
So, discount = 20 100 × x = ₹ x 5
SP = MP – Discount
= x –x 5 = ₹4x 5 ........................................................................... (2)
From (1) and (2), we get 4x 5 = 124
x = 124 × 5 4 = ₹155.
Hence, the marked price should be 55% above the cost price.
Example 21: A laptop is marked at ₹25,000. After giving a discount of 10% to the customer, a profit of 25% is made. What is the cost price of the laptop?
Marked Price = ₹25,000; Discount = 10%
Discount = 10 100 × 25000= ₹2500
Selling Price = MP – Discount
= ₹25,000 – ₹2500 = ₹22,500
Cost Price = 100 100 + Profit� × SP
= 100 100 + 25 × 22,500 = 100 125 × 22,500 = ₹18,000
So, the cost price of the laptop is ₹18,000.
As part of a Diwali offer, a jeweller allows a discount of 15%. Even after giving the discount, he makes a profit of 6.25%. Amit buys a gold chain which was marked at ₹50,000. Find the cost price of this chain for the jeweller.
Marked price of the chain = ₹50,000; Discount allowed = 15%
SP = MP × 100 − Discount Percentage 100
SP = 50,000 × 100 − 15 100 =
Therefore, the selling price of the chain = ₹ .
Also, given that, the jeweller makes a profit of 6.25%.
CP = SP × 100 100 + Profit Percentage
CP = ₹
Therefore, the cost price of the chain = ₹ .
Finding Successive Discounts
When two discounts are given one after the other, such discounts are called successive discounts. Here the first discount is given on the marked price and the second discount is given on the reduced price.
For example, a shopkeeper offers a 10% discount on T-shirts and a further discount of 7% to increase the sales. Here, 10% and 7% are successive discounts. If the marked price of a T-shirt is ₹2400, the selling price can be found as given below.
Marked price of the T-shirt = ₹2400
First discount = 10� on MP = 10� of 2400 = 2400 × 10 100 = ₹240
Selling price after the first discount = 2400 – 240 = ₹2160
Second discount = 7% of reduced price = 7% of ₹2160 = 7 100 × 2160 = ₹151.2
Selling price after the second discount = 2160 – 151.2 = ₹2008.8
Therefore, the selling price of the T-shirt after deducting two successive discounts is ₹2008.8.
Example 22: A shopkeeper was selling all his items at a 20% discount. During the festive season, he offered a 25% discount over and above the existing discount. If Ramesh bought a shirt which was marked ₹1200, how much did he pay for it?
Marked price of the shirt = ₹1200
First discount = 20% on MP = 20% of 1200 = 1200 × 20 100 = ₹240
Selling price after the first discount = 1200 – 240 = ₹960
Second discount = 25% of reduced price = 25% of ₹960 = 25 100 × 960 = ₹240
Selling price after the second discount = 960 – 240 = ₹720
Therefore, Ramesh paid ₹720 for the shirt.
Example 23: Find the single discount percentage equivalent to two successive discounts of 20% and 10%.
Let the marked price of an article be ₹100.
Then, first discount on it = 20% of ₹100 = 100 × 20 100 = ₹20
Selling price after the first discount = ₹ (100 − 20) = ₹80
Second discount on the reduced price = 10% of ₹80 = 80 × 10 100 = ₹8
Selling price after the second discount = ₹80 − ₹8 = ₹72; Net selling price = ₹72
Therefore, the single discount percentage equivalent to given successive discounts = (100 − 72)% = 28%
Example 24: A shopkeeper offers a discount of 10% on television sets. He offers a further discount of 20% to customers that will pay in cash. What is the marked price of a television set if it was sold for ₹57,600 in cash?
Let the marked price of the television set be ₹100.
First discount = 10% of MP = 10% of 100 = ₹10
So, selling price after the first discount = ₹100 − ₹10 = ₹90
Second discount = 20% of reduced price = 20% of ₹90 = 90 × 20 100 = ₹18
Selling price after the second discount = 90 – 18 = ₹72
For the selling price to be ₹72, the MP must be ₹100.
For the selling price to be ₹57,600, the MP must be = 57,600 × 100 72 = ₹80,000.
Therefore, the marked price of the television set was ₹80,000.
Which is a better offer: two successive discounts of 10% and 8% or a single discount of 18%?
Let the marked price be ₹100.
First discount = 10% of ₹100 = ₹10
Selling price after the first discount = ₹100 − ₹10 = ₹90
Second discount = 8% of ₹90 = 90 × 8 100 = ₹7.2
Selling price after the second discount =
Total discount allowed =
Therefore, a single discount equivalent to two successive discounts of 10% and 8% is %. Therefore, is a better offer.
Do It Yourself 9C
1 The marked price of a radio is ₹4000. Find the discount and the selling price if the rate of discount is given. a 25% b 20% c 12 1 2 % d 10%
2 If ₹175 is the discount offered on an article whose marked price is ₹900, then find its selling price.
3 The marked price of a washing machine is ₹14,500 and its selling price is ₹13,775. Find the discount allowed and the discount percentage.
4 The selling price of a dining table is ₹16,000. Find the marked price if a 20% discount is allowed.
5 A pair of trousers was sold for ₹7500 after a discount of ₹500 was offered on it. What was the percentage of the discount?
6 Two successive discounts of 25% and 12% on an article are equivalent to a single discount of x %. What is x?
7 A shopkeeper allows a discount of 15% on all the goods purchased from his shop. To finish his stock that is close to its expiry date, he further gives a discount of 10% on the older goods. What is the overall rate of discount given to the customer who purchases a good close to its expiry date? Do you check the expiry date of products before your purchase?
8 The marked price of an article is ₹702. The shopkeeper offers a discount of 15%. He gives an additional discount of 10% to the customers who pay in cash. Find the selling price of the article.
9 The cost price of a dining table is ₹15,000, and its marked price is ₹18,000. If a shopkeeper sells it at a loss of 8%, then what is the rate of discount offered by him?
10 The marked price of a sewing machine is 32% above its cost price. What is the rate of discount a shop owner can offer so that he gains 10%?
11 A profit of 12% can be earned by selling a fan after offering a discount of ₹200. If the cost price of the fan is ₹850, then find its marked price.
12 A camera is marked at ₹9000. After giving a discount of 20%, it is sold at a profit of 20%. Find the cost price of the camera.
13 Create a word problem on finding the marked price of an item.
1 The tickets for a circus are sold at half their regular price. Amit, being an early bird, gets an additional discount of 10% on the reduced price. What is the total discount percentage that Amit gets on the regular price?
Satya purchases a TV for ₹94,000 and a music system for ₹36,000 from an electronics store. He asks the owner for the bill. The owner hands over a bill as shown.
Bill No. 1254
Satya has some questions in his mind as he looks at the bill.
1 Do we need to pay tax on the purchase of electronic items?
2 Is tax charged on the marked price or the selling price of the items?
Let us look at the answers to these questions:
1 Yes, we need to pay tax on the purchase of electronic items.
2 Tax is always applied on the selling price of the items. If the selling price and the marked price of an item are the same then tax can be applied on the marked price too.
Date: 07/10/2023
Discount is always calculated on the marked price whereas tax is always calculated on the selling price.
Tax is the money which is collected by the government from the citizens of the country to provide them with the best facilities and infrastructure.
The prevailing tax structure in India before the introduction of the Goods and Services Tax on July 1, 2017, was as shown below.
Let us understand what Sales Tax and Value Added Tax were in the old tax structure.
A sales tax was charged by the government on the sale of different commodities. It was collected by the seller from the customer and given to the government. Therefore, this tax was always calculated on the selling price of an article and then added to the value of the bill.
Value Added Tax
We always add the percentage value of tax. Selling Price = ₹1000, Tax = 5%
= ₹1050
Value Added Tax, or VAT, was the tax that was charged on goods and services at each stage of a supply chain. In the case of sales tax, a hefty amount of tax was paid by the customer alone, whereas, in the case of VAT, everyone in the supply chain (manufacturer, wholesaler, dealer, retailer or customer) paid a small amount of tax, adding up to the same big amount.
Let us understand the new tax structure called the GST (Goods and Services Tax) that was introduced on July 1, 2017.
Goods and Services Tax (GST)
Goods and Services Tax (GST) is an indirect tax, which has replaced many indirect taxes like VAT, Central Excise duty, Sales Tax, Service Tax, etc. It is described as one tax for one nation. Current Tax Structure in India
Tax (GST)
Electronic items are taxable in India as per the latest tax laws. Also, tax is always calculated on the selling price of an article and is added to the value of the bill. Thus, the electronic store that Sam visited correctly included the tax amount in the bill.
Example 25: Amit bought a bluetooth speaker marked at ₹9600. He paid tax of 5% for it. What is the tax and the bill amount to be paid?
Value of the bluetooth speaker = ₹9600
Tax rate = 5%
Tax = 5% of ₹9600 = 9600 × 5 100 = ₹480
Bill amount = ₹9600 + ₹480 = ₹10,080
Example 26: Lakhan bought a suitcase for ₹2520 including tax. The tax on this item is 5%. What was the price of the suitcase before the tax was added? Also state how much the tax is.
The cost price paid by Lakhan = ₹2520
If the original value was ₹100, Lakhan spent ₹105.
For every ₹105 that Lakhan spent, the original cost = ₹100
So, for ₹2520 which Lakhan spent, the original cost = 100 × 2520 105 = ₹2400
Tax = ₹2520 − ₹2400 = ₹120
Example 27: A suitcase is sold for ₹7080 inclusive of tax. What is the tax percentage if the original price is ₹6000?
Let the tax percentage be x%.
₹6000 + x% of ₹6000 = 7080
x 100 × 6000 = 7080 – 6000
60x = 1080
x = 18%
So, the tax on the suitcase is 18%.
Example 28: Mr Sharma bought a shirt for ₹3360 including 12% tax, and a mixer grinder for ₹8496 including 18% tax. Find the total marked price (without tax) of the shirt and the mixer grinder.
Let the marked price of the shirt be ₹x
Price of the shirt including tax = ₹3360
x + 12x 100 = 3360
x = 3360 × 100 112 = ₹3000
Let the marked price of the mixer grinder be ₹y
Price of the mixer grinder including tax = ₹8496
y + 18y 100 = 8496
y = 8496 × 100 118 = ₹7200
Did You Know?
France was the first country to implement the GST in 1954; since then, an estimated 140 countries have adopted this tax system in some form or another.
So, the marked price of the shirt and the mixer grinder = ₹3000 + ₹7200 = ₹10,200.
Renuka buys a cooker marked at ₹6500. She gets a discount of 8%. If the sales tax is 8%, find the amount she pays for the cooker.
Marked price = ₹6500
Discount = 8% of marked price = =
Selling price = Marked Price – Discount = ₹(6500 – ) = ₹
Tax = 8% of Selling price = Therefore, Renuka pays ₹_____________________________
anohar wants to buy a vacuum cleaner to clean his house that costs ₹8000. What amount should he give to the shopkeeper if the GST on the vacuum cleaner is 18%? Do you help your parents in keeping the house clean? How?
2 Akash bought a computer for ₹38,000 and a printer for ₹8000. If the rate of tax is 7% for these items, find the price he must pay to buy these two items.
3 Renu bought a mobile phone for ₹16,240 that included GST of 12%. Find the price of the mobile phone before the GST was added.
4 The tax charged on a refrigerator is 9%. If the tax amount is ₹1170, find the actual selling price.
5 Ajay sells a harmonium for ₹17,280 including the tax. What is the selling price he will get after depositing the tax to the government at the rate of 8%?
6 Amit got a discount of 10% on the suit he bought. The marked price was ₹5000 for the suit. If he had to pay a tax of 10% on the price at which he bought it, how much did he pay?
7 Soap is made through a chemical process called saponification, where fats or oils react with a strong alkali. A soap manufacturer can sell soap at ₹6.36 per piece after adding the GST at the rate of 6%. Still, he will make a profit of 20% from the sale. What is his manufacturing cost per soap?
8 The marked price of a book is ₹750. The shopkeeper gives a discount of 10%. How much will the customer have to pay for it if a tax of 5% is charged?
Challenge
1 During the festive season, a store puts all the shirts at a discount of 20%. Daniel was offered an additional 5% discount on a shirt that had a marked price of ₹2500. He paid a total of ₹2128 including the tax. Find the tax percentage.
Points to Remember
• Percentage means per hundred or out of hundred. The symbol ʻ%ʹ stands for percent, i.e., 1 100.
• Percentage increase/decrease in quantity = Change in Quantity Original Quality × 100%.
• The percentage increase/decrease is the same as a percentage change.
• The percentage of profit or loss is always calculated on the cost price.
• The price printed on an article or written on a label attached to it is called its marked price.
• The deduction allowed from the marked price of an article is called a discount. A discount is always calculated on the marked price.
• If two or more discounts are allowed one after the other, then such discounts are known as successive discounts.
• GST stands for Goods and Services Tax and is a type of indirect tax.
Setting: In groups of 3
Comparing Discounts!
Materials Required: Pen, notebook, item cards with price tags
Method:
1 Set up 3 stores, each with the same items and different price tags.
2 Call out the names of the items available for sale across three different stores: Store 1, Store 2 and Store 3.
3 Instruct the students that Store 1, 2 and 3 are offering discounts of 30%, 40% and 50% respectively.
4 Let the students work in groups to perform their calculations and choose their best buy.
Which one is the best buy?
A pair of sneakers Regular price: ₹4500 Regular price: ₹4900 Regular price: ₹3900
Watch Regular price: ₹5000 Regular price: ₹5500 Regular price: ₹4500
Sunglasses Regular price: ₹6000 Regular price: ₹6500 Regular price: ₹5500
Chapter Checkup
1 Convert into percentages.
2 Convert as directed.
46% into ratio
3 Find the value.
4 Find the percentage change.
5 Find the missing terms.
a
b
c
d ₹6400 ₹192
6 Find the unknown in each case.
a MP = ₹625, SP = ₹500, % Discount =?
b MP = ₹1780, % Discount = 15%, SP =?
7 Last year the average weight of tigers in a forest was 75 kg. Due to diseases like parasites and malnutrition, the average weight decreased to 60 kg. What is the percentage change in the average weight of the tigers?
8 If 65% of the students in a school are boys and the number of girls is 700, find the total number of students in the school.
9 Find the bill amount of a refrigerator which costs ₹27,500 and the GST is charged at 18%.
10 Ajay bought a second-hand car for ₹5,20,350. He polished the car for ₹2500, replaced old parts for ₹15,000 and then resold the car. He managed to make a profit of 14%. How much did he sell the car for?
11 Tulsi got her first salary. She bought a watch for her mother for ₹1980 including tax at 10%. Find the original price of the watch.
12 The cost price of 15 pencils is the selling price of 10 pencils. What is the profit percentage?
13 600 children are having lunch at a school picnic. Out of these, 280 choose to have a vegan meal, 120 choose to have a non-vegetarian meal and the remaining children prefer a vegetarian meal.
a What percentage of the children choose a vegetarian meal?
b What fraction of the children prefer a vegan meal?
c What percentage of the children choose a non-vegetarian meal?
14 A man spends 20% of his salary on house rent. After spending 40% of the remainder, he is left with ₹9600. Find his monthly salary.
15 The price of diesel increases by 60%. By what percentage should Mithun reduce his consumption so that there is no change in his expenditure?
16 A man bought notebooks at ₹72 per dozen and sold them at ₹25 for a packet of 5 books. What was his profit or loss per notebook?
17 Rohit buys a book at a discount of 20%. He manages to get an additional 10% discount on the book since it was slightly torn. What is the marked price of the book if it was sold for ₹1008?
18 Amit buys a television set whose marked price was ₹45,000. He then gets a discount of 15% and pays a tax of 12%. How much does he pay for the television set?
19 A businessman buys 200 litres of vegetable oil at ₹60 per litre. He spends ₹2000 on packaging and ₹6000 on transport. He then sells 1 litre packets for ₹120 each. Does he make a profit? What is the percentage of profit or loss?
20 A reduction of 25% in the price of apples enables a person to buy 2 kg more apples for ₹300. Find:
a The original price per kg of apples.
b The reduced price per kg of apples
Challenge
1 Nidhi sold two books each for ₹120. One book was sold at a profit of 25% and the other at a loss of 25%.
Read the statements and choose the correct option.
Statement I: She neither gained nor lost.
Statement II: She lost ₹16.
Statement III: Her loss is 6.25%.
a Statement I is incorrect, and Statement II and III are correct.
b Statement II and III incorrect, and Statement I is correct.
c Only Statement III is correct.
d Statements I and III are incorrect, and Statement 2 is correct.
2 In a school election, there are two candidates running for the position of student body president: Sarah and Alex. What percentage of the total number of students voted for Alex if there are 600 students in the school who are eligible to vote.
Statement 1: 70% of the eligible students cast their votes.
Statement 2: 60% of the eligible votes were received by Sarah
a Statement 1 alone is sufficient to answer.
b Statement 2 alone is sufficient to answer.
c Statement 1 and 2 together are sufficient to answer.
d Statement 1 and 2 together are not sufficient to answer.
Vaccination Rates and Public Health Impact during the COVID-19 Pandemic
COVID-19 had a great impact on our lives. The COVID-19 pandemic, caused by the SARS-CoV-2 virus, led to a global health crisis starting in late 2019. Vaccination emerged as a key strategy to control the spread of the virus and mitigate its impact on public health. The total COVID cases reported until 20 June, 2024 were 800,000,000.
Read the questions and answer them. (The data is taken from the WHO website and has approximate values)
1 The number of people who had COVID in China was 100 million. What percentage of all the people in the world who were affected by COVID were Chinese?
a 10%
b 12.5%
c 15% d 20%
2 25% of the people who were diagnosed with COVID were American. How many Americans were diagnosed with COVID?
a 150,000,000
c 200,000,000
b 175,000,000
d 250,000,000
3 45 million Covid cases were reported in India. The total cases in the South-East Asia region were 60,000,000. What percentage of the people in the South-East Asia region who had COVID were Indians?
4 There are 1,40,00,00,000 people in India. 70% of the total population was vaccinated with a complete primary series of the COVID-19 vaccine. 25% of the people who took the vaccination were also vaccinated with at least one booster dose. How many people took booster doses?
5 The pandemic made people prioritise personal and public health through practices like handwashing and wearing masks. What else do you think people learnt during the pandemic?
10 Compound Interest
Letʹs Recall
Interest is the money we have to pay when we borrow money, or the money we earn when we lend money. The money that is borrowed or lent is called the Principal. When we add the interest and the principal together, we get the Amount. The Rate of Interest is the percentage used to calculate how much interest is charged on the principal.
Ajay wants to invest ₹10,000 for 10 years. Which bank should he choose?
Community Bank
Open a Savings Account Today!
5% interest per year
Society Bank
Open a Savings Account Today!
6% interest per year
Ajay saw the advertisements for Community Bank and Society Bank. He chose Society Bank as it offers a greater rate of interest on deposits.
Ajay wants to purchase a bike using a loan. Which bank should he choose?
Community Bank
Apply for a loan!
9% interest per year
Society Bank
Apply for a loan!
10% interest per year
Ajay saw the advertisements for Community Bank and Society Bank. He chose Community Bank as it charges a lower rate of interest on loans.
Letʼs Warm-up
Match the interest rate with the amount of interest.
Mean, Median and Mode Simple Interest and Compound Interest
Narendra wants to invest ₹8000 for three years.
• Plan A earns 4% simple interest per year.
• Plan B earns 4% interest compounded annually.
Narendra wonders which plan he should choose.
Finding Simple Interest
Simple interest
Compound interest
Amount 0 Year
Look at the table below that shows the account balances for 3 years under Plan A.
On analysing the table carefully, Narendra understands that the interest in Plan A will always be calculated on the principal deposited by him. This type of interest is called Simple Interest (SI or I)
Principal (P)
Money borrowed or deposited.
Simple Interest (SI or I)
The extra amount paid/earned by the borrower/depositor.
SI = P × R × T 100
The amount at the end of the year can be calculated as:
Amount (A) = P + SI
Rate (R)
Rate of interest on which the principal amount is given.
Time (T)
Time period for which money is borrowed or deposited.
Example 1: A man borrowed ₹15,000 from a cooperative bank at a rate of 8% per annum for 4 years. Find the simple interest and the amount he has to pay back.
Principal (P) = ₹15,000; Rate of interest (R) = 8% per annum; Time (T ) = 4 years
Simple interest = P × R × T 100 = 15,000 × 8 × 4 100 = ₹4800
Amount = Principal + Simple Interest = ₹(15,000 + 4800) = ₹19,800
Example 2: Ankur borrowed a sum of ₹2000 from a bank and returned ₹2480 after 3 years. Find the simple interest and the rate of interest per annum.
Amount = Principal + Interest
₹2480 = ₹2000 + Interest
Remember!
Simple interest is interest that is calculated only on the initial sum (the principal) borrowed or deposited.
₹2480 − ₹2000 = Interest
₹480 = Interest
So, the simple interest is ₹480.
Simple interest = P × R × T 100
₹480 = 2000 × R × 3 100
480 × 100 2000 × 3 = R R = 8%
Thus, the rate of interest is 8%.
Example 3: Sonali deposits a certain amount of money in a bank. If the interest rate decreases from 3 4 3 % to 1 2 3 % per annum, she receives ₹100 less in 2 years. Find the sum of money she deposited.
Rate of interest earlier = 3 4 3 %
Rate of interest later = 1 2 3 %
Difference in the rate of interest = 3 4 3 % – 1 2 3 % = 1 4 %
Simple interest = P × R × T 100
100 = 1 4 P × 100 2 × P = 100 × 100 ×2 P = ₹20,000
Hence, Sonali deposited ₹20,000.
Error Alert!
Time is always considered in years while calculating interest amounts.
Finding the simple interest earned on ₹500 at 6% per annum for 18 months:
The graph shows an amount of ₹4000 deposited into a savings account for 10 years with simple interest.
1 How much interest has been earned, in total, over the last 10 years?
The amount of interest earned will be the difference in the final value (the value after 10 years) and the initial amount invested.
Interest = ₹
2 What is the rate of interest?
The formula for simple interest is SI = P × R × T 100 .
We have just calculated that SI = and we know that P = and T = .
Substituting these values into the formula, we get = 4000 × R × 10 100
Rearranging and solving this, we get, R =
Therefore, the interest rate is, R = %
Do It Yourself 10A
Find the missing figures in the table.
2 You are considering opening a high-yield savings account at Ally Bank. As of July 2024, Ally Bank offers a simple interest rate of 4.25% per annum. You plan to deposit $20,000. Calculate the interest earned and the total amount after 3 years.
3 A certain amount of money amounts to ₹4400 in two years and ₹4600 in three years. Find the principal and rate of interest.
4 Find the interest on a deposit of ₹3650 from January 3, 2016 at the rate of 10% p.a. up to March 17, 2016.
5 Create a word problem on finding simple interest.
1 A person deposited ₹600 for 3 years, ₹900 for 2 years and ₹1500 for 4 years. He received the total simple interest of ₹360. Find the rate of simple interest per annum.
Finding Compound Interest
Do you remember how Narendra planned to invest his money? Let us look at another table that shows the account balances for 3 years under Plan B.
On analysing the table carefully, Narendra understands that any interest earned by him is added back to the principal amount deposited by him. This amount, in turn, is used to calculate the interest for the subsequent year. He likes Plan B and renames it as the ‘Interest on Interest Plan’. This type of interest is called Compound Interest (CI).
The money earned by Plan A = ₹8960
The money earned by Plan B = ₹8998.91
Narendra is delighted to know that with plan B, he will earn ₹8998.91 − ₹8960 = ₹38.91 more than Plan A after three years. So, he chooses Plan B.
Let us find the compound interest on P = ₹1000, R = 5% p.a. for 2 years.
Interest after 1 year:
₹1000 × 0.05 × 1 = ₹50
Interest after next year: ₹1050 × 0.05 × 1 = ₹52.50
Total amount after two years = ₹1000 + ₹50 + ₹52.50 = ₹1102.50
To find the CI, we subtract the principal from the amount compounded annually.
So, CI = A – P = ₹1102.50 – ₹1000 = ₹102.50
Note that simple interest would produce a total amount of only ₹1000 [1 + 0.05 × 2] = ₹1100. Here, SI = ₹100.
The additional ₹2.50 is the interest on ₹50 at 5% for 1 year.
Think and Tell
Narendra wants to invest ₹8000 for 3 years.
• Plan A earns 22% simple interest per year.
• Plan B earns 20% interest compounded annually. Which plan should he choose?
To find a formula for compound interest, consider depositing ₹1000 in a savings account with an annual interest rate of 6%, compounded annually.
Balance at the end of year 1 = Principal + Annual Interest = ₹1000 + ₹1000 × 0.06
Extending the pattern in the table, we can find the balance after 20 years.
Balance at the end of year 20 = ₹1000(1.06)20
Using the pattern in the table, we can write a general formula for the balance in an account that earns interest compounded annually after t years. A = P (1 + r)t
where P = Principal (initial deposit)
r = Annual interest rate (in decimal form)
t = Time (in years)
A = Amount after t years
Compound Interest: Annually
The formula deduced above can be rewritten as:
where P = Principal (initial deposit)
R = Annual interest rate (in %)
n = Time (in years)
A = Amount after n years
= P 1 + R 100 n
Example 4: Find the compound interest on ₹10,000 at 4% per annum for 3 years compounded annually.
P = ₹10,000, R = 4% per annum and n = 3 years
A = P 1 + R 100 n A = ₹10,000
Did You Know?
The interest rate in India averaged 6.37 percent from 2000 until 2023, reaching an all-time high of 14.50 percent in August of 2000 and a record low of 4.00 percent in May of 2020.
A = ₹10,000 ×
A = ₹1 × 104 × 104 × 1.04
A = ₹11,248.64
Compound Interest = Amount – Principal Therefore, Compound Interest = ₹11,248.64 – ₹10,000 = ₹1248.64
Example 5: Find the time required for ₹15,625 to become ₹19,683 at 8% per annum compounded annually.
We know that A = P 1 + R 100 n
We have A = ₹19,683, P = ₹15,625 and R = 8%
Therefore, 19,683 = 15,625 1 + 8 100 n
19,683 15,625 = 108 100 n
On simplifying the RHS, we get,
19,683 15,625 = 27 25 n
27 × 27 × 27
25 × 25 × 25 = 27 25 n
27 25 3 = 27 25 n
On comparing the LHS with the RHS, we get, n = 3
Therefore, the time required is 3 years.
Example 6: If a sum of ₹1200 amounts to ₹1452 at a certain rate of interest compounded annually for 2 years, find the rate of interest.
We know that A = P 1 + R 100 n . Here, A = ₹1452, P = ₹1200 and n = 2. Therefore, 1452 = 1200 1 + R 100 2 1452 1200 = 1 + R 100 2
On simplifying the LHS, we get 121 100 = 1 + R 100 2
R = 100 10 = 10
Therefore, the rate of interest is 10%.
Example 7: Find the simple interest on ₹10,000 for 2 years at 8% per annum. If the compound interest, compounded annually is paid on the same amount, what is the difference in the interest earned in both cases?
P = ₹10,000, T = 2 years, R = 8% p.a.
SI = P × T × R 100 = 10,000 × 8 × 2 100 = ₹1600 A
A = ₹10,000 × ( 1.08 )²
A = ₹11,664
CI = A − P = ₹11,664 − ₹10,000 = ₹1664
Difference = CI − SI = ₹1664 − ₹1600 = ₹64
Hence, the difference in the interest earned in both cases is ₹64.
Example 8: How much will ₹30,000 amount to in two years at compound interest compounded annually, if the rate of successive years is 8% per annum and 10% per annum?
P = ₹30,000; R = 8%; n = 1 year
A = P 1 + R 100 n
= 30,000 1 + 8 100 1
= 30,000 108 100 1
= 300 × 108 = ₹32,400
Now the amount earned in the first year will become the principal for the second year.
The principal, amount and rate for the second year will be:
P = ₹32,400; R = 10%; n = 1 year
A = P 1 + R 100 n = 32,400 1 + 10 100 1
= 32,400 110 100 1
= 324 × 110 = ₹35,640
Hence, ₹30,000 will amount to ₹35,640.
Example 9: The simple interest on a sum of money for 2 years at 5% per annum is ₹1000. What will be the compound interest on the same sum at the same rate for the same period, compounded annually?
SI = ₹1000, T = 2 years, R = 5% p.a.
SI = P × T × R 100
1000 = P × 2 × 5 100
P = ₹10,000
For finding compound interest, we have the formula as:
CI = P 1 + R 100 n − P
CI = 10,000 1 + 5 100 2 − 10,000
CI = 10,000 × ( 1.05 )² − 10,000
CI = 11,025 − 10,000 = ₹1025
Amit receives ₹6050 after investing some money for 2 years at 10% per annum compounded annually. Find the actual amount invested by Amit.
We know that A = P 1 + R 100 n
We have A = ₹ , R = % and n =
Therefore, 6050 = P 1 + 10 100 2
On simplifying the RHS, we get
6050 = P 100 + 10 100 2
6050 = P 11 10 2
P =
Hence, P = ₹
Therefore, Amit had invested a sum of ₹ .
Compound Interest: Half Yearly
When the interest is added to the principal after every half year, the interest is said to be compounded half yearly. As interest is calculated twice in one year, we will divide the rate of annual interest by 2, and double the time.
So, the formula for the amount is modified to:
A = P 1 + R 2 100 2n OR A = P 1 + R 200 2n
Think and Tell
What if the interest is compounded quarterly?
Example 10: What will be the compound interest on ₹40,000 at 16% per annum for 1.5 years, if the interest is compounded half yearly?
The interest is compounded half yearly. So, the amount received after 1.5 years will be calculated using the formula
A = P 1 + R 200 2n
We have P = ₹40,000, R = 16% and n = 1.5 years
Therefore, A = ₹40,000 1 + 16 200 2 × 1.5 A = ₹40,000 1 +
On simplifying the RHS, we get
A = ₹40,000 108 100 3 = ₹40,000 27 25 3
A = ₹40,000 × 27 25 × 27 25 × 27 25
A = ₹64 × 27 × 27 × 1.08 = ₹50,388.48
Compound Interest = Amount – Principal
Therefore, CI = ₹50,388.48 − ₹40,000 = ₹10,388.48
Example 11: What sum will become ₹21,632 at 8% per annum compounded half yearly after one year?
We have A = ₹21,632; R = 8% per annum = 8 2 = 4% per half year; n = 1 year = 1 × 2 = 2 half years
We know that A = P 1 + R 2 100 2n
Putting the values in the above formula, we get
21,632 = P 1 + 8 200 2 21,632 = P 26 25 2
P = 21,632 × 25 × 25 26 × 26 = ₹20,000
₹18,000 is deposited in a bank at 16% per annum for 2 years. Find the amount received if the interest is compounded semi-annually.
The interest is compounded semi annually. So, the amount paid after 2 years will be calculated using the formula:
A = P 1 + R 200 2n
We have P = ₹18,000, R = 16% and n = 2 years
Therefore, A = ₹18,000 1 + 16 200 2 × 2
On simplifying the RHS, we get
A = ₹18,000 1 + 16 200 4
A =
A =
So, the amount received is ₹ .
Do It Yourself 10B
1 Find the amount and the compound interest on ₹1600 for 5 years at 6% per annum, compounded annually.
2 What sum of money will amount to ₹4410 in 2 years at 5% per annum, compounded annually?
3 In how much time will ₹60,000 amount to ₹69,457.50 at 5% per annum compounded yearly?
4 Suhani invested ₹50,000 at 12% p.a. compounded annually. Find the amount she will get: a at the end of the second year. b at the end of the third year.
5 Find the compound interest on ₹2,00,000 for 18 months at 8% per annum, compounded half yearly.
6 Find the simple interest on ₹2500 for 2 years at 10% per annum. If the bank pays compound interest, compounded annually, what is the difference in the interest earned in both cases?
7 Alison is considering investing in a certificate of deposit (CD) at Bank of America. As of July 2024, Bank of America offers a CD with an annual interest rate of 4.75%, compounded annually. Alison plans to invest $30,000. Calculate the amount of money Alison will have in the account after 2 years.
8 The simple interest on a sum of money for 2 years at 6% per annum is ₹9000. Find the compound interest on that sum at the same rate, compounded yearly, and for the same period.
9 Which will earn more interest, and how much?
a ₹15,000 lent at 10% per annum compounded annually for 1 year
b ₹15,000 lent at 10% per annum compounded semi-annually for 1 year
10 What sum will become ₹27,783 at 10% per annum compounded half yearly after 1 1 2 years?
11 Create a question to find the difference in simple interest and compound interest after 3 years.
Challenge Critical Thinking
1 A sum compounded annually becomes 216 125 times of itself in 3 years. Find the rate of interest per annum.
2 If the difference in the compound interest, compounded annually and simple interest on a certain sum for 2 years at 10% per annum is ₹50, find the borrowed sum.
Word Problems
Narendra buys a plot of land near a city to invest his money. The present cost of land per square metre is ₹16,000. Over the past two years, the land’s price has increased at the rate of 20% per annum. Narendra expects that the price will continue to increase at the same rate for the coming two years. Let us help him calculate the expected price of the land after two years.
The price of land appreciates, i.e., every year the price of the land goes on increasing. If the rate of appreciation is constant (rate of R% p.a.), we can find the expected cost of the land after a certain number of years (t years) by using the same formula that we used for calculating compound interest, where P is the original price.
A = P 1 + R 100 n
Present cost of land per square metre = ₹16,000
The rate of appreciation = 20%
Appreciated cost after 2 years = A = P 1 + R 100 n
A = 16,000 1 + 20 100 2
Remember!
Appreciation means an increase in the value of an asset over time, and depreciation means a decrease in the value of an asset over time.
= 16,000 100 + 20 100 2
= 16,000 120 100 2
A = 16,000 × 120 × 120 100 × 100 = 160 × 12 × 12 = ₹23,040
So, the price of the land after two years would be ₹23,040 per square metre.
If, by chance, the cost decreases, then we say that the value has depreciated. If the depreciation is at a constant rate, then we can calculate the depreciated value using the formula:
A = P 1 R 100 n
The formula for compound interest can be applied in various other situations. Wherever there is a constant rate of increase or decrease in the population, this formula can be used.
Example 12: Sonali borrowed ₹10,000 from her friend and returned an amount of ₹11,500 with interest after 2 years. What is the rate of interest per annum paid by Sonali?
Amount = ₹11,500, Principal = ₹10,000, Time = 2 years
SI = Amount – Principal = ₹11,500 – ₹10,000 = ₹1500
Rate = SI × 100 P × T = 1500 × 100 10,000 × 2 = 1,50,000 20,000 = 7.5%
Hence, the rate of interest is 7.5% per annum.
Example 13: Sheetal gave Mohit ₹14,000 at the rate of 11% per annum and received ₹2310 as interest. For how long was Sheetal’s money kept with Mohit?
Principal = ₹14,000, Rate = 11%, Interest = ₹2310
Time = SI × 100 P × R = 2310 × 100 14,000 × 11 = 1.5 years
Example 14: The present population of a town is 3,20,000. If it increases at the rate of 5% p.a., what will be the population after two years?
Present population (P) = 3,20,000
Rate of increase (R) = 5%, Time (n) = 2 years
Population after two years = 3,20,000 1 + 5 100 2
It Together
= 3,20,000
= 3,20,000
= 3,20,000 × 105 100 × 105 100 = 3,52,800
After two years, the population will be 3,52,800.
Example 15: The cost of a new television set is ₹22,000. Its value depreciates every year at the rate of 20%. What will the depreciated price be after two years?
The cost of the television set = ₹22,000
Rate of depreciation = 20%
Time = 2 years
= 22,000 ×
= ₹14,080
So, the depreciated price of the television set after two years is ₹14,080.
Bacteria are growing at the rate of 2.5% per hour. If the bacterial count at 1 a.m. is 16,500, find the bacterial count at 5 a.m.
Population at 1 a.m. =
Number of hours between 1 a.m. and 5 a.m. =
Rate of growth (R) =
Population after 4 hours = 16,500 1 + 2.5 100 4 = 16,500 100 + 2.5 100 4 = = 16,500(1.025)4 = 16,500 × =
So, the bacterial count at 5 a.m. is .
Do It Yourself 10C
deposited ₹8000 in a bank at a rate of 12% per annum. She withdrew the money after 9 months. What is the interest she received? What was the amount she collected from the bank?
2 Kanchan borrowed a sum of money from Sonali at 8% interest per annum. After 4 years, Kanchan had to give Sonali ₹9900 to clear the debt. What was the amount Kanchan borrowed originally?
3 Narendra lent a sum of ₹3200 to Suresh at a rate of 6% interest per annum. Suresh paid Narendra ₹3680 to clear the debt. How long did Suresh use Narendra’s money?
4 Aditya paid ₹6720 to clear a debt of ₹6000 to the bank after 1 year and 6 months. What is the rate of interest charged by the bank?
5 Rahul took out a loan of ₹25,000 from the bank to renovate his house. If the rate of interest is 8.5% per annum compounded annually, what amount will he have to pay to the bank after 3 years to discharge his debt?
6 Yogesh borrowed ₹30,000 from his friend Navin at 12% per annum simple interest. He further lent it to his friend, Akash at the same rate but compounded annually. Find his gain after 4 years.
7 Mr Kumar took out a loan of ₹1,80,000 from a finance company to purchase machinery for his factory. If the company charges compound interest at 8 1 2 % per annum during the first year, 7 1 2 % per annum during the second year and 7% per annum during the third year, how much will he have to pay after 3 years?
8 Lalit paid ₹79,860 after 3 years for a loan from the bank. If the bank charges interest at 10% per annum, compounded annually, find the sum of money borrowed by him.
9 Kamal deposited a sum of ₹6400 in a post office for 3 years, compounded half yearly at 7 1 2 % per annum. What amount will he get on maturity?
10 Mehul tracked the population of a city over the past few years and found that the population is increasing every year at the rate of 10%. If the population of the city at present is 12,50,000, what will be the population after 4 years?
11 Tanya purchased a plot in her nearby locality. She found that the price of a plot is increasing at a constant rate of 5% every year. Find the expected price of the plot after 3 years, if she purchased the plot for ₹2,00,000.
12 Priya purchased a new computer for ₹60,000 in the year 2020. At what cost would she have sold the computer in the year 2022, if the rate of depreciation was 40% every year?
13 RBI, the central bank of India, gives loans to other commercial banks. As of 2024, the rate at which the RBI lends money was 6.5% per annum. What will be the total interest received by RBI if it gives ₹50,00,000 to a bank for 2 years compounded annually?
14 Create your own word problem on compound interest involving finding time when principal, amount and rate of interest are given.
1 Choose the correct option.
Assertion (A): Raj borrows ₹80,000 for 4 years at 10% per annum, compounded annually. Then she has to pay ₹1,17,128 after 4 years.
Reason (R): Interest is the ratio of amount to principal.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Points to Remember
Simple Interest Compound Interest
Simple interest is always calculated on the initial principal amount.
The principal is the same every year.
Simple interest is the same every year.
The total of the initial principal and accumulated interest is used to calculate compound interest.
The amount at the end of the first year is the principal for the next year.
Compound interest is different every year.
Simple interest is less than compound interest. Compound interest is greater than simple interest.
Simple interest = P × R × T 100
Compound Interest = A − P = P 1 + R 100 n – P
The growth has remained uniform over the years. The growth has been rapid over the years.
Math Lab
Setting: In pairs
Simple Interest vs Compound Interest
Materials Required: Paper and a pen
Method:
1 Divide the class into pairs.
2 Provide each pair with a value of the principal, a time period and a rate of interest. Try giving different data to each pair.
3 Ask one student in the pair to find the simple interest and the other student to find the compound interest.
4 Ask them to compare their results.
5 Encourage each pair to share their findings with the other students in the class.
Chapter Checkup
1 Find the missing values in the table.
2 Find the amount and compound interest if the interest is compounded annually.
3 Find the principal if it amounted to ₹16,335 compounded annually at the rate of 10% p.a. in two years.
4 In how many years will ₹8800 amount to ₹10,648 at 10% p.a., compounded annually?
5 At what rate % of compound interest will ₹4000 amount to ₹5324 in three years if compounded yearly?
6 Calculate the compound interest on ₹20,000 for 1 1 2 years at the rate of 10% per annum compounded semi-annually.
7 In how much time will a sum of money double itself if invested at 8% simple interest per annum?
8 A sum of money amounts to ₹780 in two years and ₹1230 in seven years. Find the principal and rate of simple interest.
9 A local government organises blood donations every year in the city. In the initial year, 10,000 people donated blood. Each year, there was an increase of 15% in the number of people who donated blood. How many people donated blood after 2 years?
10 A sum of ₹25,000 invested at 8% p.a. compounded semi-annually amounts to ₹28,121.60. Find the time.
11 The simple interest on a sum of money for 3 years at 10% per annum is ₹4500. What will be the compound interest on the same sum at the same rate for the same period, compounded annually?
12 Kishan borrowed ₹5000 at 8% p.a. for 3 years. Find the difference between compound interest and simple interest, assuming that interest is compounded annually.
13 Aakash deposited ₹12,000 in a bank for 2 years. It is compounded annually at 9% p.a. What amount will he receive on maturity (at the end of 2 years)?
14 The population of a town increases by 4% annually. If the present population is 54,080, what was the population two years ago?
15 The value of a car depreciates at a rate of 10% per year. A car which was bought three years ago is now worth ₹4,73,850. What was its original price?
16 Create a word problem on finding the compound interest when the rate of interest is compounded semi-annually.
Challenge
Critical Thinking
1 The difference between simple interest and compound interest at the rate of 10% for two years is ₹1. What is the principal if the interest is compounded annually?
2 What is the rate of compound interest?
Statement I: A sum of ₹20,000 amounts to ₹24,200 at the rate of compound interest.
Statement II: The amount was invested for a period of 2 years under compound interest.
Option 1: Statement I alone is sufficient to answer.
Option 2: Statement II alone is sufficient to answer.
Option 3: Statements I and II together are sufficient to answer.
Option 4: Statements I and II together are not sufficient to answer.
Analysing Investor Choices
A bank in the city accepts investments from individuals. These investors have the option to put their money into either simple interest or compound interest investments, depending on their preference. The bar graph illustrates the amount invested by four different investors. Analyse the graph and answer the questions.
Scale: 1 division = ₹5000 20000 22000
1 What is the rate of interest provided by the bank if Investor B earns ₹6480 as interest by investing for 3 years at simple interest?
a 10%
c 12%
b 11%
d 13%
2 How long did Investor C invest his money if he received ₹3660.8 as interest by investing at an 8% annual compound interest rate?
a 1 year
c 2 years
b 1.5 years
d 3 years
3 At the start of 2022, Investor A put her money into a simple interest account at a 10% rate. In 2023, she reinvested the amount she received at a 12% rate compounded semi-annually. What was the amount she received in 2024?
a ₹14,400 b ₹14,784
c ₹15,052.8 d ₹14,831.52
4 The interest received by D after 2 years at some rate of interest compounded annually is ₹4642. If the rate of interest is 2% higher, what amount would D receive for the same period?
11 Algebraic Expressions
Letʹs Recall
Look at the number sentences.
+ = 15
− = 4
× ? = 18
In each case, the left-hand side of the sentence has symbols, shapes or objects to represent unknown numbers. We can also represent unknowns using letters of the English alphabet. Such sentences where letters are used are called either expressions or equations.
There are two types of expressions: numeric expressions and algebraic expressions.
Expressions that involve only numbers with different arithmetic operations (+, −, ×, ÷) are called numeric expressions
For example, 8 + 2, 9 – 6, 2 × 3, 14 7 , etc.
Expressions that involve both numbers and letters of the English alphabet with different arithmetic operations (+, −, ×, ÷) are called algebraic expressions.
Each number is a constant, and each letter is a variable.
For example, x + 5, 3 – y, 4s, p 7 , etc.
Like numbers, operations can also be performed on variables. For example, we can add and subtract terms: 2x and 3x.
Letʼs Warm-up
Match the following.
Real Life Connect
Mean, Median and Mode Addition and Subtraction of Algebraic Expressions
After school, Srishti had some free time and was getting bored. To keep herself busy, she started playing with toothpicks. She made a beautiful pattern of triangles and parallelograms using toothpicks, as shown below.
Step 1 3 sides
Step 2 8 sides
Step 3 13 sides
Adding and Subtracting Expressions
After the initial 3 steps, she thought of getting more toothpicks to create a pattern of up to 10 steps.
Let us help Srishti identify the number of toothpicks required to continue the pattern up to 10 steps.
Terms and Factors of an Algebraic Expression
Let us learn about algebraic expressions and its parts.
Variable Constants
Term 1
3 + 5x
Algebraic Expression
Term 2
An algebraic expression has some terms and factors. Given below is a factor tree to identify the terms and factors in an expression. Expression Numerical
Coefficient
The factors in a term are made up of coefficients. These coefficents can be either numerical or literal. The literal factor is the coefficient of the product of the rest of the factors in the term. The case for the constant coefficient is similar.
Numerical Coefficient
Remember!
A factor of the term is always the coefficient of the product of the rest of the factors in the term.
In 3x2, 3 is the coefficient of x2, and x2 is the coefficient of 3. In 5y4, 5 is the coefficient of y4 .
Types of Algebraic Expressions
An algebraic expression can have one or more than one term. Based on the number of terms, we categorise algebraic expressions as:
A polynomial is an algebraic expression consisting of one or more terms. Monomials, binomials, trinomials and quadrinomials are all polynomials.
Remember!
A polynomial with degree 1 is called a linear polynomial. E.g. x + 3
Did You Know?
Polynomials are used in coding theory to create error-correcting codes, which are vital for reliable data transmission and storage.
Example 1: Sort the expressions as monomials, binomials, trinomials and quadrinomials.
Example 2: Look at the algebraic tiles. Use these tiles to form algebraic expressions.
Complete the table.
Addition of Algebraic Expressions
In the evening, Srishti went to play with marbles with her friends Harsh and Damini.
Srishti has some marbles. Harsh has 12 more. Damini has three times the marbles that Srishti and Harsh have together. How many marbles are there in total? Let us see!
To find the total number of marbles the three friends have, we need to first find the number of marbles each of them have, then add all of them to arrive at the answer. But first, we need to understand how to add expressions.
To add two or more algebraic expressions, the like terms are put together and added. For example, consider the two expressions: 3x2 – 7x + 8 and 2x2 + 3x – 5.
Let us add the expressions 3x2 – 7x + 8 and 2x2 + 3x – 5 using the algebra tiles.
1 Show the two expressions using the algebra tiles.
2 Place all the tiles together. Cross out each pair of one negative and one positive tile of the same factor.
3 The remaining tiles show the final answer.
Now, let us add the two expressions using the horizontal method
(3x2 – 7x + 8) + (2x2 + 3x – 5)
= 3x2 + 2x2 – 7x + 3x + 8 – 5 (Place the like terms together)
= 5x2 – 4x + 3
We can also add the two expressions vertically, as shown below.
This is called the vertical method of adding two or more expressions.
Now, to find the total number of marbles the three friends, Srishti, Harsh, and Damini have, we need to add the three expressions. Let us first write the 3 expressions.
Let the number of marbles with Srishti be x.
Number of marbles with Harsh = x + 12
Number of marbles with Damini = 3(x + x + 12) = 3(2x + 12) = 6x + 36
Total number of marbles = (x) + (x + 12) + (6x + 36)
= x + x + 12 + 6x + 36 = 8x + 48
Error Alert!
Unlike terms are never added together.
Example 3: Add the expressions.
1 5p + q – 6 and 8p − 1 2 q + 3 2 2 5 x2y2 6xy + 3 4 and 2y2x2 + 3xy 1 4
5p + q – 6 + 8p − 1 2 q + 3 2 5 x2y2 6xy + 3 4 + 2y2x2 + 3xy 1 4 = 5p + 8p + q − 1 2 q – 6 + 3 = 2 5 x2y2 + 2y2x2 6xy + 3xy + 3 4 1 4 = 13p + 1 2 q – 3 = 8 5 x2y2 – 3xy + 1 2
Example 4: Add using the vertical method.
1 5x2 + 11xy – 9y2, –3x2 + 2y2 – 13xy and 7x2 + 5xy + 8y2
5x2 + 11xy – 9y2 –3x2 – 13xy + 2y2
7 x 2 + 5 xy + 8 y 2
9x2 + 3xy + y2 + 2 8a2 + 5 8 ab + 6a2b, 2 3 a2 –7 8 ab + 4 5 a2b and – 7 3 a2 + 17 8 ab –9 5 a2b 8a2 + 5 8 ab + 6a2b 2 3 a2 –7 8 ab + 4 5 a2b –7 3 a2 + 17 8 ab –9 5 a2b 19 3 a2 + 15 8 ab + 5a2b +
Example 5: Srikanth walked (2x + y + 5) km to the north, then (5x – 1) km to the east and then (5 6 y + 2) km to the south-east. How far did he walk?
The total distance travelled by Srikanth = (2x + y + 5) + (5x – 1) + (5 6 y + 2) = 2x + 5x + y + 5 6 y + 5 – 1 + 2 = 7x + (6 + 5 6 ) y + 6 = 7x + 11 6 y + 6 = 7x + 1 5 6 y + 6
So, Srikanth travelled (7x + 1 5 6 y + 6) km.
The sides of a rectangle are (3a2 + 2ab − 1
) cm and (− 1 6 a
7ab + 3 4) cm. What is its perimeter?
Side 1 of the rectangle = (3a2 + 2ab − 1 2) cm; Side 2 of the rectangle = (− 1 6 a2 – 7ab + 3 4) cm
Perimeter of the rectangle = 2(l + b) = 2((3
So, the perimeter of the rectangle is cm.
Subtraction of Algebraic Expressions
Like addition, we can also subtract two or more algebraic expressions in the same way. But in subtraction, before putting like terms together, we evaluate the minus sign first. For example, consider the two expressions: 5x2 – 2x + 1 and 4x2 + x – 3. Let us first represent them using the algebra tiles.
1 Show the minuend, 5x2 – 2x + 1 using the algebra tiles.
2 To subtract, cancel out as many tiles as given in the subtrahend, 4x2 + x – 3.
a To subtract 4x2, cancel out four x2 tiles.
b To subtract +x, we need at least one +x tile. Since there are not enough +x tiles, we bring in 0 (a pair of +1x and –1x tiles). Then, cancel out one +x tile.
c To subtract –3, we need three –1 tiles. Since there are not enough –1 tiles, we bring in 0 (3 pairs of +1 and –1 tiles)
d The remaining tiles show the final answer.
Now, let us understand how to subtract the two expressions without the algebra tiles. Let us first evaluate the minus sign and then put the like terms together.
So, (5x2 – 2x + 1) − (4x2 + x – 3) = 5x2 – 2x + 1 − 4x2 − x + 3 = 5x2 − 4x2 – 2x – x + 1 + 3 = x2 – 3x + 4
Think and Tell
What happens if we do not evaluate the minus sign?
This method of subtracting two or more expressions is called the horizontal method We can also subtract the two expressions vertically, as shown below.
This is called the vertical method of subtracting two or more expressions.
Example 6: Subtract the expressions.
Example 7: Subtract using the vertical method.
–x2 + 18x2y2 – 9y2 + 20xy from 5x2 + 12x2y2 – 15xy + 7y2
5x2 + 12x2y2 – 15xy + 7y2
–x2 + 18x2y2 + 20xy – 9y2 + – – +
6x2 – 6x2y2 – 35xy + 16y2
Example 8: Vicky bought a shirt for ₹(9x + 15) and a pair of trousers for ₹(11x – 10). If he paid ₹7000, then how much change did he get?
Cost of a shirt = ₹(9x + 15)
Cost of a pair of trousers = ₹(11x – 10)
The amount of money Vicky gave to the shopkeeper = ₹7000
The amount of change he got back = 7000 – (9x + 15 + 11x – 10) = 7000 – ((9x + 11x) + (15 – 10)) = 7000 – (20x + 5) = 7000 − 5 – 20x = 6995 – 20x
So, Vicky gets back ₹(6995 −20x).
= 2x – 5x + 7x + 5 + 1 + 2 = 2x + 7x – 5x + 8 = 4x + 8 Do It Together
What should be added to −5pq + 8q – 6 to get −7pq + 11q – 7?
Let the expression to be added be X.
So, according to the question, we get
−5pq + 8q – 6 + X = −7pq + 11q – 7 X = −7pq + 11q – 7 – (−5pq + 8q – 6) = −7pq + 11q – 7 5pq 8q 6 = −7pq + + 11q – – 7 + =
So, will be added to −5pq + 8q – 6 to get −7pq + 11q – 7.
Simplifying Algebraic Expressions
Let us understand how to simplify two or more expressions. For example, consider the expression:
2x + 5 – (5x – 1) + (7x + 2)
We can write it as:
2x + 5 – (5x – 1) + (7x + 2)
= 2x + 5 – 5x + 1 + 7x + 2
Example 9: Simplify: (4xy2 – 3y + 1) + (9y – 1) – (2y2x + 5y – 3)
(4xy2 – 3y + 1) + (9y – 1) – (2y2x + 5y – 3)
= 4xy2 – 3y + 1 + 9y – 1 – 2y2x − 5y + 3
= 4xy2 −2y2x – 3y + 9y − 5y + 1 – 1 + 3
= 2xy2 + y + 3
Example 10: Subtract p2q3 – pq + 5 from the sum of 8p2q3 + 2pq + 1 and –1 2 pq + 6.
According to the question, let us first add and then subtract.
8p2q3 + 2pq + 1 + ( –1 2 pq + 6) = 8p2q3 + 2pq –1 2 pq + 1 + 6 = 8p2q3 + 1 1 2 pq + 7
Now, 8p2q3 + 1 1 2 pq + 7 – (p2q3 – pq + 5)
= 8p2q3 + 1 1 2 pq + 7 – p2q3 + pq − 5
= 8p2q3 − p2q3 + 1 1 2 pq + pq + 7 – 5
= 7p2q3 + 2 1 2 pq + 2
Perimeter of a triangle = 9a – 5b + 7 + (−5a + 2b – 3) + X Do It Together
The perimeter of a triangle is (4a + 10b – 6) cm. If two of its sides are (9a – 5b + 7) cm and (−5a + 2b – 3) cm, find the third side.
Side 1 = (9a – 5b + 7) cm Side 2 = (−5a + 2b – 3) cm Side 3 = ?
Perimeter of the triangle = (4a + 10b – 6) cm
Let the third side be X.
Do It Yourself 11A
ok at the given algebraic tiles. Write algebraic expressions for the tiles. Also, identify the terms containing
2 Use a factor tree and write the terms, factors and coefficient of ‘a’ in the expressions.
a – 3 4 a2bc b 6a + 5
c 8a2 – 5a + 1 3 d 7 12 a3 + 5abc –4 9a2 – 10
3 Circle the pairs of like terms and cross out the pairs of unlike terms.
a 5a, − 2 3 a b 6xy, 8x2y
c −2a2b2c, 9ab2c2 d − 11 7 abc, −8cba
4 Form algebraic expressions for the statements. Also, write the literal factors and literal coefficients of the numerical coefficient in the expressions.
a The sum of x and y, divided by 8.
b The difference of twice of x and one-sixth of y.
c The product of a and b subtracted from the difference of a and b.
5 Simha bought a few blue straws of length x cm each and a few green straws of length y cm each. Use the pictures to write the algebraic expressions.
A
B
6 Draw algebra tiles to show the expressions. Solve the expressions.
a (2x2 + 4x + 4) + (x2 + x + 2) b (4x2 – 2x + 1) – (x2 + 3x – 2)
7 Add the expressions horizontally. Verify your answer by solving them vertically.
a 3x + y + 1 and 2x – 5y – 4
c −5p2 − 4 5 p + 2 and 3p2 + 5p − 3 4
b 3xy2 + 5xy – 6 and 7y2x – 2xy + 3
d 7 8 pq + 6 7 p – 1 and 5 8 pq + 2 7 p + 8
8 Find the difference of the expressions horizontally. Verify your answer by solving them vertically.
a 5x2 – 3x – 1 and 3x2 – 4x + 7 b 8mn + n3 − 4 5 and 2mn –1 2 n3 + 1 5
c 2y + 3y2 + 8 and y2 + 2y – 4 d 7 – 13pq – 11q and 2pq + 8 – 4q
9 Simplify the expressions.
a 3(5x – 4) – 2(7x + 3) + 4(8x – 2) b 1 2 (2m3 + 4m2) − 3 4 (5m3 – 2m2)
c (−3x2 + 6x3 – 4 – x) + (2x + 1) – (8x2 – 5x + 1)
10 Find the missing expression.
a (6a4 – 4 + 8a) + = (a4 + 5 + 8a + 8a3)
b − (6x2 + 6x + 11) = (10x2 + 4x – 1)
d (x – 2) – (x2 – x + 3) + (4x – 5)
c (−19n2 – 6n + 6) + (−8n2 – 4n – 9) – = (−15n2 + 8n + 7)
11 Subtract (40 – 13p2) from the sum of (−18p2 + p – 32) and (13p + 20p2 – 12).
12 What should be subtracted from (7h – 3ht + 7h3) to get (−6h + 3ht – 9h3)?
13 Harsh has a rope of length (m2 + 13m – 18) metres, and Rohan has a rope of length (8m + 30m2 – 4) metres. What is the difference of the lengths of their ropes?
14 A field is in the shape of a quadrilateral whose sides are (9s2 + 17) metres, (34
+
– 18s
metres, (9s + 2s2) metres and (17s2 – 25) metres. If it needs fencing on all sides, find the length of fencing required for the field.
15 Write a word problem for adding two expressions.
Challenge
1 Find the errors. Also, find the correct solution.
Critical Thinking
Multiplication of Algebraic Expressions
A newly built party hall has an underground parking lot. The owners of the hall have put up a guide map of the parking lot at different places within it.
The owners have decided to allot the cleaning of the parking lot to a third-party vendor. To determine the pricing of cleaning the parking lot, the vendor wants to know its area. Additionally, the owners wants to compare the price quotes from different vendors.
Let us look at the layout of the parking lot and understand how we can find its area.
For this, let us assume that one side of the blue part of the parking lot is x units, and one side of the green part is 1 unit, as shown below.
Then, the area of the parking lot = area of the big rectangle
= length × breadth
= (x + 3) × (x + 4)
= x × (x + 4) + 3 × (x + 4)
= x2 + 4x + 3x + 12
= x2 + 7x + 12
Here, (x + 3) and (x + 4) are binomials. All binomials are polynomials.
Therefore, the area of the parking lot is (x2 + 7x + 12) sq. units.
Multiplying a Monomial by a Monomial
To multiply two monomials, we simply find the product of their numerical coefficients and the variables. For example, let us multiply the two monomials: 4xy and 2y.
4xy × 2y = (4 × 2) × x × (y × y) = 8xy2 .
Constants and variables are put together.
Example 11: Find the product of 5x2yz, ( 2xy), 9xy2z
5x2yz × (−2xy) × 9xy2z
= (5 × (−2) × 9) × (x2 × x × x) × (y × y × y2) × (z × z) = −90x4y4z2
Remember!
All monomials, binomials, trinomials and quadrinomials are polynomials.
Example 12: Find the area of a rectangle whose length is 5x2y, and breadth is 7 5 xy2z.
Length of the rectangle = 5x2y
Breadth of the rectangle = 7 5 xy2z
Area of the rectangle = Length × Breadth
= 5x2y × 7 5 xy2z
= (5 × 7 5 ) × (x2 × x) ×(y × y2) × z
= 7 × x3 × y3 × z = 7x3y3z
Thus, the area of the given rectangle is 7x3y3z
Example 13: Find the volume of a box of length (3a2b) m, breadth (2ab) m and height (5ab2) m.
Length = (3a2b) m, Breadth = (2ab) m, Height = (5ab2) m
Volume = length × breadth × height = 3a2b × 2ab × 5ab2
= (3 × 2 × 5) × (a2 × a × a) × (b × b × b2) = 30a4b4
Example 14: Multiply (12a2b) by (−5abc3). Verify your answer if a = 1, b = −1, c = 2.
(12a2b) by (−5abc3) = (12a2b) × (−5abc3)
= (12 × (−5)) × (a2 × a) × (b × b) × c3
= −60a3b2c3
Verification: (12a2b) × (−5abc3) = (12 × (1)2 × (−1)) × (−5 × (1) × (−1) × (2)3) = −12 × (5 × 8) = −12 × 40 = −480
−60a3b2c3 = −60 × (1)3 × (−1)2 × (2)3
= −60 × 1 × 1 × 8 = −480
Therefore, (12a2b) × (−5abc3) = −60a3b2c3.
Remember!
In expressions with exponents, when bases are the same, powers are added.
Find the product of 2a2b3c, −a2bc2 and 5a3b3c.
2a2b3c × (−a2bc2) × 5a3b3c
= (2 × (−1) × 5) × (a2 × a2 × a3) × ( × × ) × ( × × ) = −
Multiplying a Monomial by a Polynomial
We multiply each term of the polynomial by the monomial using the distributive property. Let us see how we can multiply a binomial and a trinomial by a monomial.
Multiplying a Monomial by a Binomial
Let us consider the binomial (3y + 1) and multiply each of its terms by the monomial (3x).
Step 1: Represent each of the polynomials using the algebraic tiles.
3x (3y + 1)
1 x x x y y y
Step 2: Multiply the two polynomials in the same way as it is done in the multiplication chart. Then, cancel the unlike tiles (or zero pairs of tiles), if any.
Step 3: Calculate the total area of the rectangle so formed.
On multiplying, we count the number of tiles of each term to find the area.
Number of xy’s = 9
Number of x’s = 3
So, the area = 9xy + 3x
Mathematically, 3x (3y + 1) = (3x × 3y) + (3x × 1) = 9xy + 3x
Multiplying a Monomial by a Trinomial
Let us consider the trinomial (2x2 – x + 1) and multiply each of its terms by the monomial (3y). This can be shown using the box multiplication method, as given below.
6x2y –3xy 3y 2x2 3y –x 1
So, 3y(2x2 – x + 1) = 6x2y + (–3xy) + 3y = 6x2y – 3xy + 3y
We can also multiply a monomial by a trinomial horizontally, as shown.
3y (2x2 – x + 1) = (3y × 2x2) – (3y × x) + (3y × 1)
= 6x2y − 3xy + 3y
Remember!
In the box method of multiplication, we expand each factor, multiply using the grid, and then add all the products to get the final product.
Example 15: Find the product of:
1 7a2bc3 (6a2b – 11)
= (7a2bc3 × 6a2b) – (7a2bc3 × 11)
= 42a4b2 c3 – 77a2bc3
2 5a2b3c5 (3a2b + 2abc3 – 5ab4c)
= (5a2b3c5 × 3a2b) + (5a2b3c5 × 2abc3) – (5a2b3c5 × 5ab4c)
= 15a4b4c5 + 10a3b4c8 – 25a3b7c6
Example 16: Simply the given expression and evaluate it for x = –2.
6x(x2 + 3) – 5x2(6x + 5x2) + 7x4(3 – 2x)
6x(x2 + 3) – 5x2(6x + 5x2) + 7x4(3 – 2x)
= (6x × x2 + 6x × 3) – (5x2 × 6x + 5x2 × 5x2) + (7x4 × 3 – 7x4 × 2x)
= (6x3 + 18x) – (30x3 + 25x4) + (21x4 – 14x5)
= 6x3 + 18x – 30x3 – 25x4 + 21x4 – 14x5
= –24x3 + 18x – 4x4 – 14x5
Let us substitute the value of x = –2
= –24(–2)3 + 18(–2) – 4(–2)4 – 14(–2)5
= 192 – 36 – 64 + 448
= 540
Example 17: Multiply (7p3q3r) by (6 – 11p2q2r2). Verify your answer if p = 1, q = −1, r = −2.
(7p3q3r) × (6 – 11p2q2r2)
= (7p3q3r × 6) − (7p3q3r × 11p2q2r2)
= 42 p3q3r – 77p5q5r3
Verification: (7p3q3r) × (6 – 11p2q2r2)
= (7 × (1)3 × (−1)3 × (−2)) × (6 − 11 × (1)2 × (−1)2 × (−2)2)
= (7 × 1 × (−1) × (−2)) × (6 − 11 × 1 × 1 × 4)
= (7 × 2) × (6 – 44) = 14 × (−38) = −532
42p3q3r – 77p5q5r3
= 42 × (1)3 × (−1)3 × (−2) – 77 × (1)5 × (−1)5 × (−2)3
= 42 × 1 × (−1) × (−2) – 77 × 1 × (−1) × (−8)
= 42 × 2 – 77 × 8 = 84 – 616 = −532
Therefore, (7p3q3r) × (6 – 11p2q2r2) = 42p3q3r – 77p5q5r3 = –532.
What is the product of 4x2y and (9x2y2z + 7)?
4x2y (9x2y2z + 7) = (4x2y × ) + (4x2y × ) = +
Multiplying a Polynomial by a Polynomial
For two or more terms in a polynomial, we multiply each term of one polynomial by each term of the other polynomial and then solve the products by putting like terms together to get the final product. Let us see how can we multiply two binomials, a binomial and a trinomial, two trinomials and so on.
Multiplying a Binomial by a Binomial
Multiply (x + 5) and (x + 7)
To multiply a binomial by a binomial, we follow the given steps.
Step 1: Represent each of the polynomials using algebraic tiles.
(x + 5)(x + 7)
Step 2: Multiply the two polynomials in the same way as in the multiplication chart. Then, cancel the unlike tiles (or zero pairs of tiles), if any.
(x + 5)(x + 7)
Step 3: Calculate the total area of the rectangle so formed. On multiplying, we count the number of tiles in each term to find the area.
Number of x2’s = 1
Number of x’s = 12
Number of 1’s = 35
So, the area = x2 + 12x + 35
Mathematically, we use the FOIL method.
The FOIL method is described in this way.
F: Multiply the First terms (x × x) of each binomial.
O: Multiply the Outer terms (x × 7) of each binomial.
I: Multiply the Inner terms (5 × x) of each binomial.
L: Multiply the Last terms (5 × 7) of each binomial.
(x + 5) (x + 7) = (x × x) + (x × 7) + (5 × x) + (5 × 7) = x2 + 7x + 5x + 35 = x2 + 12x + 35
Multiplying a Binomial by a Trinomial
(x + 5) (x + 7)
Think and Tell
Is this FOIL method similar to the BOX method of multiplication? How?
Let us consider the trinomial (5x2 – 2x + 3) and multiply it with the binomial (2x − 1). This can also be shown using the BOX method of multiplication, as given below.
Using the Box Method
Using the Distributive Property 10x3 –4x2 6x –5x2 2x –3 5x2 2x –2x 3 –1
10x3 – 4x2 + 6x – 5x2 + 2x − 3
= 10x3 – 4x2 – 5x2 + 2x + 6x – 3
= 10x3 – 9x2 + 8x – 3 (2x – 1) (5x2 – 2x + 3) = 2x (5x2 – 2x + 3) – 1 (5x2 – 2x + 3)
(2x × 5x2) – (2x × 2x) + (2x × 3) − (1 × 5x2) + (1 × 2x) − (1 × 3) = 10x3 – 4x2 + 6x – 5x2 + 2x − 3 = 10x3 – 4x2 – 5x2 + 2x + 6x – 3 = 10x3 – 9x2 + 8x – 3
Multiplying a Trinomial by a Trinomial
Let us consider the trinomial (x2 – 5x + 6) and multiply it by the trinomial (x2 + 2x − 1). This can also be shown using the BOX method of multiplication.
Using the Box Method
x4 − 5x3 + 6x2 + 2x3 – 10x2 + 12x – x2 + 5x − 6
= x4 − 5x3 + 2x3 + 6x2 – 10x2 – x2 + 12x + 5x − 6
= x4 − 3x3 – 5x2 + 17x – 6
We can also multiply the trinomials using the distributive property of multiplication.
Using the Distributive Property
(x2 + 2x − 1) (x2 – 5x + 6)
= x2 (x2 – 5x + 6) + 2x (x2 – 5x + 6) – 1 (x2 – 5x + 6)
= x4 − 5x3 + 6x2 + 2x3 – 10x2 + 12x – x2 + 5x − 6
= x4 − 5x3 + 2x3 + 6x2 – 10x2 – x2 + 12x + 5x − 6
= x4 − 3x3 – 5x2 + 17x – 6
Multiplying a Quadrinomial by a Trinomial
Let us consider the quadrinomial (x4 + 2x2 – x + 5) and multiply each of its terms by each of the terms of the trinomial (x2 − 2x − 1). This can also be shown using the BOX method of multiplication.
Using the Box Method
= x6 + 2x4 − x3 + 5x2 – 2x5 – 4x3 + 2x2 – 10x – x4 − 2x2 + x − 5
= x6 – 2x5 + 2x4 – x4 − x3 – 4x3 + 2x2 + 5x2 − 2x2 – 10x + x – 5
= x6 – 2x5 + x4 − 5x3 + 5x2 – 9x – 5
x –1
Using the Distributive Property
(x2 − 2x − 1) (x4 + 2x2 – x + 5)
= x2 (x4 + 2x2 – x + 5) − 2x (x4 + 2x2 – x + 5) – 1 (x4 + 2x2 – x + 5)
= x6 + 2x4 − x3 + 5x2 – 2x5 – 4x3 + 2x2 – 10x – x4 − 2x2 + x − 5
= x6 – 2x5 + 2x4 – x4 − x3 – 4x3 + 2x2 + 5x2 − 2x2 – 10x + x – 5
= x6 – 2x5 + x4 − 5x3 + 5x2 – 9x – 5
Example 18: Find the product.
1 (4x + 3y2) and (5x2 – 8y2)
(4x + 3y2) (5x2 – 8y2)
= 4x (5x2 – 8y2) + 3y2 (5x2 – 8y2)
= (4x × 5x2) – (4x × 8y2) + (3y2 × 5x2) – (3y2 × 8y2)
= 20x3 – 32xy2 + 15x2y2 – 24y4
Example 19: Multiply and verify, when a = 1 and b = –1.
(5a – 3b2) and (6ab + 5a)
(5a – 3b2) (6ab + 5a) = 5a(6ab + 5a) – 3b2(6ab + 5a)
= 30a2b + 25a2 – 18ab3 – 15ab2
Verification:
(5a – 3b2) (6ab + 5a) = (5(1) – 3(–1)2) (6(1) (–1) + 5(1))
= (5 – 3) (–6 + 5)
= 2 × (–1)
= –2
2 (3x – 4y + 3) and (3y – 7x + 9)
(3x – 4y + 3) (3y – 7x + 9) = 3x (3y – 7x + 9) – 4y (3y – 7x + 9) + 3 (3y – 7x + 9) = 9xy – 21x2 + 27x – 12y2 + 28xy – 36y + 9y – 21x + 27 = –21x2 + 37xy + 6x – 12y2 – 27y + 27
30a2b + 25a2 – 18ab3 – 15ab2 = 30(1)2 (–1) + 25(1)2 – 18(1)(–1)3 – 15(1)(–1)2
= –30 + 25 + 18 – 15
= –45 + 43
= –2
Therefore, (5a – 3b2) × (6ab + 5a) = 30a2b + 25a2 – 18ab3 – 15ab2
Example 20: If a train travels at (35a2 + 17a – 11) km/hour for (5a – 4) hours, how far has the train travelled?
Speed of the train = (35a2 + 17a – 11) km/hour; Time = (5a – 4) hours
Distance covered = Speed × Time
= (35a2 + 17a – 11) × (5a – 4)
= 35a2 (5a – 4) + 17a (5a – 4) – 11 (5a – 4)
= (35a2 × 5a) – (35a2 × 4) + (17a × 5a) − (17a × 4) − (11 × 5a) + (11 × 4)
= 175a3 – 140a2 + 85a2 – 68a – 55a + 44
= 175a3 – 55a2 – 123a + 44
So, the train travelled (175a3 – 55a2 – 123a + 44) km.
Simplify: (3x2 – 5x + 1) (x – 1) – 2x (2x + 3)
(3x2 – 5x + 1) (x – 1) – 2x (2x + 3)
= 3x2 (x – 1) – 5x (x – 1) + 1 (x – 1) – (2x × 2x) – (2x × 3)
= (3x2 × ) – (3x2 × ) – (5x × ) + (5x × ) + x – 1 – 4x2 –
Do It Yourself 11B
1 Look at the algebraic tiles. Identify the expressions. Draw and complete the multiplication chart of expressions. Write the product you get. a x x 1 1 1 1
Art Integration Chapter 11 • Algebraic Expressions
2 Draw algebraic tiles to find the product of the given polynomials.
a −5x × 4y b (2y – 3)(3x + 4)
3 Find the products.
a −5x2y2z3, 12x2yz, 3yz b ab (−6abc + 5c – 7)
c (3x – 1) (8y + 5)
e (2a2 − 3a + 7) (4a2 + 6a + 11)
d (7y + 9) (3z2 + 6z – 5)
(8p5 − p3 + 7p2 + 10p – 5) (3p2 + 9p + 11)
4 Multiply and verify the result for the values of the variables.
a (5h + 9) (3h – 7), for h = 1 b (9q – 1) (6q2 – q + 5), for q = −4
c (7a2 − 4a − 2) (5a2 − 2a + 9), for a = 0 d (2t3 + 3t2 + 5t − 4) (3t2 − 5t + 11), for t = −2
5 Simplify.
a –2 3 a (3a + 4b – 5c) − 4 5 a (2a – 5b + 7c)
b −a2b (a3 – 3b + a + 2) – ab (b4 −2b2 − 3b) – c (a3 + b2 + 1)
c (a – 5) (a4 – 2b3 + 3c – 4) + 3 7 bc (7a2 − 11)
Find the value of each of the results for a = −1, b = 2, c = 10.
6 Find the area of the rectangles using the lengths and breadths.
a 6x2y, −5x3y2z b 8x –11 5 , 7 5 x + 9
c 9 11 abc, 6 7 a2bc3 + 5 6 ab2c d (3z – 1), (2z2 + 7z – 10)
7 Find the volume of the cuboids using the lengths, breadths and heights (all measures are in centimetres).
a 6pqr, 3p2qr2, 4q2r b 7 2 p2q3r4 , 1 2 pqr, 2p (q + r)
c (p + q), (p – q + 12), 8r d –1 2 pq (r + 1), 7pq, 11qr
8 Find the volume of the cubes using the edges (all measures are in centimetres).
a 3s (stu + 1) b −3s2t3u5
c (−6ab + 2a2 + 3)
4p3q4 (9r + 2q – 5)
9 Find the coefficient of the x4 term in the product of (5x3 − 4x2 + 2x − 1) and (x2 − 3x + 5).
10 Draw a rectangle and write statements to form expressions for the sides of the rectangle. Find the area of the rectangles for given values.
11 Sara wants to build a rectangular garden of length (3x + 2)m and breadth (4x – 1) m. What is the cost of planting the grass in the garden if the cost of planting the grass is �(2x – 3) per sq. m?
Challenge
1 Read the statements and choose the correct option.
Assertion (A): The product of (2x + 3)(x – 1) is 2x2 + x – 3.
Critical Thinking
Reason (R): The distributive property states that a(b + c) = ab + ac, which applies to polynomial multiplication.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Points to Remember
• Each of the constants and variables in an expression is called a factor.
• A factor of the term is always the coefficient of the product of the rest of the factors in the term.
• Two or more terms with the same variables are called like terms, whereas two or more terms with different variables are called unlike terms.
• Expressions with 1, 2, 3 or 4 terms are called monomials, binomials, trinomials and quadrinomials respectively. These are all called polynomials.
• To add or subtract two or more algebraic expressions, the like terms are put together and added or subtracted. In subtraction, before putting like terms together, we evaluate the minus sign first.
• To multiply two polynomials, we multiply each term of one polynomial by each term of the other polynomial and then simplify the products by putting like terms together to get the final product.
Setting: In groups of 3
Collaboration, Communication & Creativity
Algebraic Expressions Storytelling
Materials Required: A4-sized paper for each group, markers or coloured pens, a list of algebraic expressions
Method: All 3 members of each group must follow these steps.
1 Each group collects a story prompt related to algebraic expressions from the teacher. For example, in a magical forest, there were 3x trees, and each tree had 2y birds living in it. Write a story about what happens in the forest. (Each story must have the expressions including their solutions).
2 Complete the story within the time limit set by the teacher.
3 After completing the story, present it to the class one by one within the time limit set by the teacher. (This time limit should be less than the time limit for writing the story.)
4 The group that completes the story and narrates it as well in the least time, wins the storytelling competition.
Chapter Checkup
1 Look at the factor trees. Label the variables, terms, factors and numerical coefficients in each of the expressions.
2 Match the following.
a 4x + y, 2x – 1 quadrinomial
b 8a2b, 9pq, −6x trinomial
c 3xy + x – 1, 8z2 − 3z + 5 monomial
d −6x2y + 2xy – 6x + 4, p2 – 7pq + 4q – 1 binomial
3 Circle the like terms and cross out the unlike terms.
a 2a, − 3 5 a b 6pq, −4x2y
c −7a2b3c, 8ab2c3 d − 5 6 abc, − 1 2 cba
4 Draw algebra tiles to solve.
a (3x2 + 2x – 6) + (–x2 – 2x + 1) b (–x2 + 4x + 2) – (3x2 – 2x – 3)
5 Add the expressions.
a −3m2 + m – 2 and 4m2 + 6m + 7 b 7z3 + 4z2 + z – 1 and 2z3 – 6z2 – 2z + 2
c q2 –5 7 q3 – 7, 3q2 + 4 – 1 7 q3, and 9q2 – 6q – 2
6 Subtract the expressions.
a 8z5 – 9z2 + 1 2 z + z6 + 17z3 from 11z3 + 10z6 – 26z + 1 2 z5
b 2x2 – 3x + 6x4 from 8x4 − 5x2 c −
7 Simplify the expressions.
a (7s2 – 4s4 + 3s) + (5s2 + 6s4) − (9s2 – 8s3 + 2s4) b (8t4 – 3t2 + 2t) – (4t2 – 5t) + (7t – 9t2 + 6t4)
8 Add (3x2 − 2x + 1) to the difference of (−2x3 + x) and (7x – 3 + 7x3).
9 Find the products.
a 6xy2z4, −11x2yz2, 3y3z
c (−2p3 + 8p2 + 10p − 5)(p2 + 3p + 9)
b (4y + 7)(2z2 + 5z – 6)
d st(−5stu + 3u – 9)
e (7a2 − 2a + 8)(3a2 + 5a + 12) f (6p5 − 4p3 + 2p2 + 13p − 1) (4p2 + 7p + 12)
10 Multiply and verify the result for the values of the variables.
a (9h + 4)(2h – 11), for h = 2
b (2a2 − 5a − 8)(4a2 − a + 3), for a = −5
c (7q – 8)(3q2 – 4q + 7), for q = 0 d (2t3 + 5t2 + 7t − 10)(3t2 − 10t + 15), for t = −2
11 Simplify. Find the value of each of the results for a = −1, b = 2, c = 10.
a –1 5 a(8a + 5b – 11c) − 5 6 a(3a – 5b + 12c)
b −2a2b(5a3 – 7b + a + 11) – ab(9b4 −3b2 − 4b) – c(2a3 + 2b2 + 1)
c (a – 7)(a4 – 6b3 + 4c – 5) + 3 7 bc (9a2 − 14)
12 Find the area of the rectangles using the lengths and breadths.
a 7x2y, 8x3y2z b 2x –10 7 , 9 4 x + 11
c 9 13 abc, 4 7 a2bc3 + 1 6 ab2c
d (5z – 3), (2z2 + 9z – 11)
13 Find the volume of the cuboids using the lengths, breadths and heights (all measures are in cm).
a 7 11 p2q3r4 , 2 7 pqr, 2p (q + r)
c − 1 2 pq (r + 5), 9pq, 10qr
b (p + q), (2p – 3q + 14), 7r
14 Find the volume of the cubes using the edges (all measures are in cm).
5s (stu + 2)
2t3u5 c (−7ab + 11a2 + 2)
15 This is a rectangular field. The shaded region is the footpath all around it. Find the difference in the perimeter of the field with and without the footpath. (All measures are in cm.)
16 A construction company is working on a project. They need to find the total cost of materials for building a rectangular structure with a length of (5x + 3) m and a width of (2x − 1) m. If each square metre of material costs ₹100, what is the total cost?
17 Hetal’s mother went to the market to buy some fruit. She bought bananas for ₹(15x + 6), grapes for ₹(13x2 – 9x + 2) and apples for ₹(−8x2 + 4x – 18) less than the cost of the grapes. Find the total amount she spent to buy the fruit.
18 A scientist is studying the growth of a population of rabbits over time. The population of rabbits at the start is represented by the polynomial (2x3 − 3x2 + 5x) and the population growth rate per year is represented by the polynomial (x + 1). Find the population after two years.
19 Create a word problem to multiply a trinomial by a trinomial.
Challenge
1 Ananya has a sheet of chart paper whose sides are (4x + 5) metres and (3x2 – 5 + 6x) metres. If she cuts squares from all the corners of the chart paper of side x metres, find the perimeter of the remaining chart paper.
2 Read the question and identify which statement(s) are sufficient to answer the given question. What is the area of the rectangle?
Statement 1: The length of the rectangle is (x + 2).
Statement 2: The breadth of the rectangle is (3x – 4) and the value of x is 7 cm.
a Statement 1 alone is sufficient, but statement 2 alone is not sufficient.
b Statement 2 alone is sufficient, but statement 1 alone is not sufficient.
c Both statements together are sufficient, but neither statement alone is sufficient.
d Each statement alone is sufficient.
e Statements 1 and 2 together are not sufficient.
Shopping Complex Blueprint
Mr Aneja gets a contract to design a shopping complex as given in the figure. He created a basic layout plan for the shopping complex. The layout is a regular hexagon. It has a circular fountain at the centre. The radius of the circular fountain is 7(x – 13) m.
Answer the following questions.
1 Mr Aneja wanted to calculate the complete area of the shopping complex. What is the area of the shopping complex?
a 6(3x2 + 13x – 56) m2
c 18(x2 + 4x – 20) m2
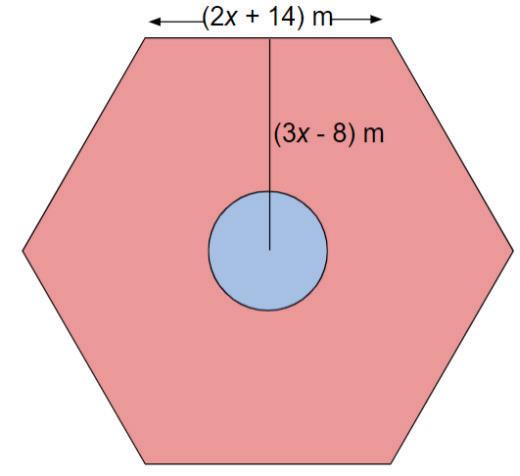
b (18x2 + 65x – 300) m2
d (6x2 + 26x – 112) m2
2 The water sprinklers are to be purchased by Mr Aneja. He wanted to find out how much area the fountain covers. What is the area of the circular fountain?
a (154x2 – 4000x + 26000) m2
c (49x2 – 182x + 828) m2
b 154(x2 – 26x + 169) m2
d 49(x2 – 91x + 441) m2
3 The tiling of the shopping complex is to be done. What will be the area of the floor that has to be tiled if the area of the fountain is not to be tiled? What will be the total cost of tiling the shopping complex if the cost of tiling is ₹80 per sq. m? The fountain region is not to be tiled.
4 If 4 rectangular shops, each with a length of (x – 3) m and a breadth of (x – 9) m are made on the layout, then what is the remaining area on the hexagonal layout?
5 Suggest some ways in which Mr Aneja can make the shopping complex more environmentally friendly.
12 Area of Polygons
Let’s Recall
There are three types of triangles based on the sides: equilateral, isosceles and scalene. Every triangular object has an area and a perimeter. The perimeter depends on the type of triangle. For example, look at the given formulas.
Equilateral Triangle
Perimeter = 3 × side
Isosceles Triangle
Perimeter = (2 × side) + third side
Scalene Triangle
Perimeter = sum of lengths of all sides
However, the area of every triangle can be calculated on the basis of a formula: 1 2 × base × height
Let us say that a farmer has a triangular field of sides 9 m, 12 m and 15 m, as shown below.
He wants to protect cows and cattle from entering his field by fencing it all around. He also wants to grow two types of crops in equal areas of the field. How do you think he would do that? Let us see.
To fence it all around, we need to calculate the perimeter of the field. To grow crops in the field, we need to calculate its area.
Perimeter of the field
Area of the field
= Sum of lengths of all sides of the field = Area of the triangle
= 9 m + 12 m + 15 m = 36 m
1 2 × b (base) × h (height)
1 2 × 9 × 126 = 54 sq. m
To grow two types of crops equally in the field, we split the area of the field into two by dividing it by 2.
So, the area of the field to grow one type of crop = 1 2 × 5427 sq. m = 27 sq. m.
Letʼs Warm-up
Match the following.
1
4 Area of a right triangle of lengths 6 m, 8 m and 10 m
5 Perimeter of a triangle with sides 20 cm, 10 cm and 10 cm
Area of Figures Made with Polygons
In a construction project allotted to a third-party vendor, an office building is to be built in the shape of a parallelogram with a triangle on the side. A reception area is to be added in the shape of a semicircle, as shown below. The vendor wants to know the area of the land that the building will occupy so that he can calculate the cost of its construction.
Area of Figures Made with Parallelograms, Triangles and Circles
Let us find the area of land that the office building will occupy.
Let us find the area of the parallelogram and the triangle with the measures that are given to find the area occupied by the office building.
Base of the parallelogram = 25 m
Height of the parallelogram = 16 m
Area of the parallelogram = base × height
= 25 m × 16 m
= 400 sq. m
Base of the triangle = 10 m
Height of the triangle = 16 m
Area of the triangle = 1 2 × b × h = 1 2 × 10 m × 16 m = 80 sq. m
Total area of land occupied by the building = Area of the parallelogram + Area of the triangle = 400 sq. m + 80 sq. m = 480 sq. m
Area of a triangle = 1 2 × b × h Area of a parallelogram = b × h
Area of a circle = r2 Circumference of a circle = 2 r Remember!
Example 1: A rectangular piece of land is 40 m long and 25 m wide. From its four corners, quadrants of radii 7 m are cut off. What is the area of the remaining plot?
Length of the rectangular piece of land = 40 m
Breadth of the rectangular piece of land = 25 m
Area of the rectangular piece of land = length × breadth
= 40 m × 25 m
= 1000 m²
Radius of each quadrant = 7 m
Area of each quadrant = πr2
= 1 4 × 22 7 × 7 × 7
= 38.5 m²
Area of all 4 quadrants = 4 × Area of each quadrant
= 4 × 38.5 m²
= 154 m²
Area of the remaining plot = Area of the rectangle – Area of 4 quadrants
= 1000 m² – 154 m²
= 846 m²
Thus, the area of the remaining plot is 846 m2.
Example 2: There is a rectangular park around which a path is built as shown. The path is covered with tiles. What is the total cost of tiling at the rate of ₹80/m²?
Length of the outer boundary = 50 m
Breadth of the outer boundary = 30 m
Length of the inner boundary = 40 m
Breadth of the inner boundary = 20 m
Area of the outer rectangle = 50 m × 30 m = 1500 m²
Area of the inner rectangle = 40 m × 20 m = 800 m²
Area of the path = Area of the outer rectangle – Area of the inner rectangle = 1500 m² – 800 m²
= 700 m²
Rate of tiling = ₹80 per m2
Total cost of tiling = 700 × 80 = ₹56,000
Thus, the total cost of tiling the path is ₹56,000.
Example 3: The area of a parallelogram is six times the area of a triangle with base 4 cm and height 6 cm. If the height of the parallelogram is 3 cm, then what is the measure of the base of the parallelogram?
Base of the triangle = 4 cm; Height of the triangle = 6 cm
Area of the triangle = 1 2 × b × h = 1 2 × 42 × 6 = 12 sq. cm
Area of the parallelogram = 6 × area of the triangle = 6 × 12 = 72 sq. cm
Height of the parallelogram = 3 cm
h × b = 72 sq. cm 3 × b = 72 sq. cm
b = 72 3 cm = 24 cm
Base of the parallelogram = 24 cm
Example 4: A rectangle of length 42 cm and breadth 28 cm is covered with non-overlapping circles of the same radius. If the radius of each circle is 7 cm, then find the area of the shaded portion.
Length of the rectangle = 42 cm
Breadth of the rectangle = 28 cm
Area of the rectangle = length × breadth = 42 × 28 = 1176 sq. cm
Radius of the circle = 7 cm
There are 2 full circles, 4 quarter circles and 6 semicircles. We know that 4 quarters make 1 whole and 2 halves make 1 whole. So, there are 6 circles in total.
So, the area of 6 circles = r2 × 6 = 22 7 × 7 × 7 × 6 = 22 × 7 × 6 = 924 sq. cm
Therefore, the area of the shaded region = Area of rectangle – Area of 6 circles = 1176 sq. cm – 924 sq. cm = 252 sq. cm
The figure is made up of a rectangle, a square and a triangle.
1 What is the value of x, if the perimeter of the shape is 86 cm?
Perimeter = 86 cm
9 + 15 + x + 12 + 12 + 12 + 15 = 86 cm + x = 86
x = cm
2 What fraction of the total area is triangular?
Length of the rectangle = 15 cm; Breadth of the rectangle = 9 cm
Area of the rectangle = length × breadth = × = sq. cm
Side of the square = 12 cm
Area of the square = side × side = × = sq. cm
Base of the triangle = 12 cm; Height of the triangle = 9 cm
Area of the triangle = 1 2 × base × height = 1 2 × × ________ = sq. cm
Total area of the figure = Area of the rectangle + Area of the square + Area of the triangle
= + + = sq. cm
Fraction of the area of the triangle of the total area =
Do It Yourself 12A
1 The Place Charles de Gaulle in Paris is a circular plaza with the Arc de Triomphe at its centre. If the radius of this circular track is approximately 120 metres, what is the area of the circular plaza? (Use π = 3.14)
2 A rectangle of length 14 cm has an area of 84 sq. cm. The perimeter of a square is the same as the perimeter of the rectangle. What is the length of side of the square?
3 Find the number of square-shaped tiles of side 100 cm required to tile a 1.5 m wide path around a rectangular park of length 40 m by 32 m.
4 The figure comprises a right-angled triangle and a quarter circle. Find the area of the quarter circle.
5 Every circle in the given figures has a diameter of 28 cm. Find the area of the shaded regions in these squares.
6 John and David are calculating the area of the parallelogram. John multiplies the length of the side CD by the length of line Y. David multiplies the length of side BC by the length of line Z. Who is correct: John, David or both of them? Explain your answer.
7 A park near Aana’s home is in the shape of a rectangle. The park is 8 m long. If Aana walks diagonally across the park, it is a 10 m walk. How much farther would Aana walk if she walked along the length and breadth of the park instead of diagonally across it? Do you go for regular walks? How does it improve your health?
8 The ratio of the two sides of a parallelogram is 4:3. If its perimeter is 56 cm, and the height of the parallelogram is one-eighth of the longer side which is also the base of the parallelogram, then find its area.
9 A puzzle is composed of identical right-angled triangles with side lengths 6 cm, 8 cm and 10 cm. These must be arranged into a rectangular wooden frame of length 162 cm and breadth 36 cm.
a What is the area of each triangle?
b How many triangles fit perfectly into the wooden frame?
c What is the total perimeter of all the triangles used?
10 Fertiliser is a substance added to soil or plants to provide essential nutrients that help them grow better. Raghav wants to spread fertiliser in his entire lawn as shown in the figure. At the market, the fertiliser is sold only in 10 kg bags, costing ₹16 each. If he spreads the fertiliser at a rate of 20 g per sq. m, then find the cost of the fertiliser which he uses for his lawn.
11 Four identical rectangles are arranged in such a way that they form a square, as shown. Each rectangle has a perimeter of 48 cm. The area of the square is 5 times the area of each rectangle. What is the area of each rectangle?
12 The Planet Eden Play Park sign is made up of two identical parallelograms and a triangle. The whole sign has an area of 17 sq. m. What is the area of the triangular part of the sign?
13 The floor of a large room of dimensions 40 m × 12 m is to be paved with square tiles of three different colours: brown tiles on all sides and pink tiles that are twice the number of white tiles. If the side of each square tile is 0.5 m and they are to be arranged as shown in the figure, then find the number of brown, pink, and white tiles.
1 Suppose you have a sheet of paper in the shape of a parallelogram. You fold the paper from the top right-hand corner, as shown in the figure. The shaded area you get is three-eighths of the original area. If you fold the bottom left-hand corner of the sheet, what is the fraction of the shaded area left compared to the original parallelogram?
Area of Quadrilaterals
We have calculated the area of the office building comprising of the parallelogram and the triangle is 480 sq. m. We know that the parallelogram is a type of a quadrilateral. Here both the parallelogram and the triangular parts of the building together form a trapezium, which is also a quadrilateral.
So, area of the building = area of the trapezium = 480 sq. m.
Area of a Trapezium and Rhombus
If the building were not split into a parallelogram and triangle, it would be a trapezoidal-shaped building with a semicircle mounted on top.
To find the area of the office building, we need to find the area of the trapezium.
So, let us draw a trapezium PQRS with PQ ǁ SR. Draw perpendiculars PM and QN from P and Q, respectively, so that PM = QN = h
Then, the area of the trapezium PQRS = Area of PMS + Area of rectangle PQNM + Area of QNR
= 1 2 × SM × PM + MN × QN + 1 2 × NR × QN
= 1 2 × SM × h + MN × h + 1 2 × NR × h
= h 1 2 × SM + MN + 1 2 × NR
= h 1 2 × (SM + NR + 2MN)
Think and Tell
How can we find the area of a trapezium using the area of the triangle only?
= h × 1 2 [(SM + MN + NR) + MN] = h × 1 2 × (SR + PQ) (Since MN = PQ, which are opposite sides of rectangle PQNM)
Hence, Area of a trapezium = 1 2 × (sum of parallel sides) × height
Area of the trapezoidal building = 1 2 × (25 + 10 + 25) × 16 = 1 2 × 60 × 168 = 480 sq. m.
Therefore, the part of the land that the building occupies is 480 sq. m.
Now, what if the shape of the building is a rhombus?
If we know the area of a rhombus, we can find the area of land occupied by the building too.
So, let us draw a rhombus PQRS with PR and QS as its diagonals intersecting each other at O at right angles.
Then, area of rhombus = 4 × area of POQ
= 4 × 1 2 × PO × OQ
= 4 × 1 2 × 1 2 PR × 1 2 QS = 4 × 1 2 × 1 2 PR × 1 2 QS 1 2
= 1 2 × PR × QS = 1 2 × product of its diagonals
So, if all sides of the parallelogram in the building are the same and the measures of the diagonals are 18 m and 25 m, then the area of the rhombus = 1 2 × 189 × 25 = 225 sq. m
Example 5: Look at the figure. Is it a trapezium? If yes, find its area.
We are given that S = P = 90°.
Sum of these angles = 180°
So, PQ and RS are parallel, and PQRS is a trapezium.
Area of trapezium = 1 2 (a + b) × h = 1 2 (22 + 32) × 15 = 1 2 × 5427 × 15 = 405 sq. cm
• Area
Polygons
Remember!
The diagonals of a rhombus divide it into four congruent right triangles.
Think and Tell
How can we find the measure of the sides of a rhombus using the diagonals of a rhombus?
Example 6: Find the area of a rhombus of which each side is 17 cm and one of the diagonals is 16 cm.
Let ABCD be a rhombus with side 17 cm and AC and BD intersect each other at O, with BD = 16 cm. As the diagonals of a rhombus bisect each other at right angles, AOB is a right angle. So, BO = OD = 8 cm.
In AOB, using the Pythagoras theorem,
AO2 + OB2 = AB2 AO2 + 82 = 172 AO2 + 64 = 289
AO2 = 289 – 64 AO2 = 225
AO = 225 = 15 cm
AO + OC = 15 + 15 = 30 cm = AC
Area of rhombus ABCD = 1 2 × AC × BD = 1 2 × 3015 × 16 = 240 sq. cm
Example 7: Find the area of a rhombus where one diagonal is 50 m and second is 20% more than the first diagonal.
Length of the first diagonal = 50 m
Length of the second diagonal = 20% more than 50 m = 50 m + 20% of 50 m
= 50 m + 10 m = 60 m
Area of the rhombus = 1 2 × Product of the diagonals
= 1 2 × 50 m × 60 m
= 1500 m²
Thus, the area of the rhombus is 1500 m².
Example 8: The area of a trapezium is 700 m². The ratio of the parallel sides of the trapezium is 1:3. The distance between the parallel sides is 3500 cm. What is the difference of the lengths of the parallel sides?
Area of the trapezium = 700 m²
Ratio of the parallel sides = 1:3
Let the parallel sides be x and 3x.
Distance between the parallel sides = 3500 cm = 3500 ÷ 100 m = 35 m
Area of a trapezium = 1 2 × (Sum of the parallel sides) × (Distance between the parallel sides)
700 = 1 2 × (x + 3x) × 35
700 = 1 2 × 4x × 35
700 = 70x
x = 10 m
3x = 30 m
Difference of the parallel sides = 3x – x = 30 m – 10 m = 20 m
Example 9: The length of the side of the rhombus is 20 cm. If one of the diagonals of the rhombus is 20% longer than its side, then what is the area of the rhombus?
Length of the side of the rhombus = 20 cm
Length of one of the diagonals = 20% more than 20 cm = 20 cm + 20% of 20 cm = 20 cm + 4 cm = 24 cm
We know that,
The diagonals of a rhombus bisect at 90°.
Let us assume the length of the second diagonal be 2x.
Let us apply the Pythagoras theorem to find the value of x
12² + x² = 20²
144 + x² = 400
x² = 400 – 144 = 256
x = 16 cm
Length of the second diagonal = 2x = 2 × 16 cm = 32 cm
Area of the rhombus = 1 2 × Product of the diagonals
= 1 2 × 24 × 32
= 384 cm²
Thus, the area of the rhombus is 384 cm².
Example 10: Rani attends a school in which the playground is in the shape of a trapezium of height 700 cm. Due to a plantation drive at the school, Rani plants seedlings along each of the parallel sides of the playground. If the area of the playground is 91 sq. m and one of its parallel sides is longer than the other by 8 m, find the length of the parallel sides.
Let the length of the shorter parallel side be a m and the longer parallel side be b m.
Area of the playground = 91 sq. m; Height of the playground = 700 cm = 7 m
Area of the playground = 1 2 × sum of the parallel sides × h
91 = 1 2 × (a + b) × 7
a + b = 9113 × 2 7 = 26 m
Given that, b – a = 8 b = 8 + a
So, a + b = 26 a + b = a + 8 + a = 26
2a + 8 = 26 2a = 26 – 8 = 18 a = 18 2 = 9 m
So, b = 8 + a = 8 + 9 = 17 m
Error alert!
Convert the dimensions into the same unit before any operation.
700 cm = 700 m
Thus, the lengths of the parallel sides of the playground are 9 m and 17 m.
cm = 700 ÷
= 7 m
Example 11: In an isosceles trapezium, the ratio of the parallel sides is 1:2. The lengths of the equal sides are 17 cm. The difference of the lengths of the parallel sides is 16 cm. Find the area of the trapezium. Ratio of the parallel sides = 1:2
Let the parallel sides of the trapezium be x and 2x.
Length of the equal side = 17 cm
Polygons
Difference of the lengths of parallel sides = 16 cm
2x – x = 16 cm
x = 16 cm
Lengths of the parallel sides = 16 cm and 32 cm.
Let us apply the Pythagoras theorem to find the distance between the parallel sides.
17² = h² + 8²
289 = h² + 64
h² = 289 – 64 = 225
h = 15 cm
Area of a trapezium = 1 2 × (Sum of the parallel sides)
× (Distance between the parallel sides)
= 1 2 × (32 + 16) × 15
= 1 2 × 48 × 15
= 24 × 15
= 360 cm²
Thus, the area of the trapezium is 360 cm².
Did You Know?
In 499, Aryabhata, a great mathematician and astronomer from the classical age of Indian mathematics and Indian astronomy, expressed the area of a triangle as one-half the base times the height in the Aryabhatiya.
The area of a rhombus is 336 sq. cm. If one of its diagonals is 14 cm, then find its perimeter.
Area of the rhombus = 336 sq. cm
1
2 × d1 × d2 = 336 sq. cm d1 × d2 = 336 × 2 = 672 sq. cm
One diagonal = 14 cm
So, × d2 = 672 d2 = 672 = ________ cm
To find the perimeter of the rhombus, we need to find the side of the rhombus.
of the rhombus =
Perimeter = 4 × side = 4 × = ________ cm
Area of General Quadrilaterals
What if during the course of the construction, the design of the building is improved and the shape of the parallelogram changes to the shape of a general quadrilateral whose sides are unknown but the measure of the diagonal is 10 m, and the measures of the perpendiculars from its opposite vertices to the diagonal are 5 m and 7 m.
To find the area of the new building, we need to find the area of the quadrilateral and add it to the area of the triangle.
So, let us draw a quadrilateral PQRS with PR as one of its diagonals and QM and SN as perpendiculars drawn from the vertices Q and S, respectively, on diagonal PR.
Area of quadrilateral PQRS = Area of ∆PQR + Area of ∆PRS
= 1 2 × PR × QM + 1 2 × PR × SN = 1 2 × PR × (QM + SN)
= 1 2 × diagonal × sum of lengths of perpendiculars on the diagonal from the opposite vertices
= 1 2 × 10 × (5 + 7)
= 1 2 × 120 = 60 square metres.
So, the area of the new building is 120 square metres.
Example 12: Find the area of a quadrilateral where one diagonal measures 20 cm and the lengths of the perpendiculars drawn from the opposite vertices on the diagonal are 16 cm and 15 cm.
Diagonal = 20 cm; Lengths of perpendiculars from the opposite vertices = 16 cm and 15 cm
Area of the quadrilateral = 1 2 × diagonal × sum of lengths of perpendiculars on the diagonal from the opposite vertices
= 1 2 × 20 × (16 + 15) = 1 2 × 2010 × 31 = 310 sq. cm
Example 13: Shreya wants to place a long rod from one corner of the room to the other across a quadrilateral-shaped floor. If the area of the floor is 2475 sq. m and the perpendicular distances from the opposite corners of the room to the rod are 50 m and 60 m, find the length of the rod.
Lengths of perpendiculars = 50 m and 60 m; Area of quadrilateral-shaped floor = 2475 sq. m
Area of quadrilateral-shaped floor = 1 2 × length of the rod × sum of lengths of perpendiculars on the rod from the opposite corners
2475 = 1 2 × length of the rod × (50 + 60) 2475 = 1 2 × length of the rod × 11055
Length of the rod = 2475 55 = 45 m
Find the area of a quadrilateral and the lengths of the perpendiculars drawn from opposite vertices, where the diagonal is 25 cm and the sum of the lengths of the perpendiculars drawn from the opposite vertices to the diagonal is 12 cm and they are in the ratio 1:2.
Diagonal = 25 cm, Sum of lengths of perpendiculars from the opposite vertices = 12 cm
Area of quadrilateral = 1 2 × diagonal × sum of lengths of perpendiculars on the diagonal from the opposite vertices
= 1 2 × × = sq. cm
Lengths of perpendiculars from opposite vertices are cm and cm.
Do It Yourself 12B
1 Find the area of the figures.
2 A rope of length 80 cm is cut into two pieces. One piece is used to form a rectangle of length 14 cm and width 8 cm. The other piece is bent into a rhombus. Draw the rhombus so formed and label the length of its each side.
3 The Louvre Pyramid in Paris was designed by architect I. M. Pei. It is made up of 673 glass segments, arranged in a pattern that includes triangular and rhombus shapes. If each diagonal in the rhombus shaped glass is around 2.69 metres then what is the area of each glass panel?
4 The diagonal of a quadrilateral is 32 cm, and the perpendiculars dropped on it from the opposite vertices are 12 cm and 15 cm. Find the area of the quadrilateral.
5 A quadrilateral whose area is 170 sq. cm and diagonal measures 17 cm has a perpendicular on the diagonal of length 15 cm. What is the length of the other perpendicular?
6 Two parallel sides of a trapezium are in the ratio 4:6 and the distance between them is 15 cm. If the area of the trapezium is 450 sq. cm, find the lengths of its parallel sides.
7 The area of a rhombus is 672 sq. cm. If the perimeter is 200 cm and the length of one diagonal is 96 cm, find the length of each side of the rhombus as well as the length of the other diagonal.
8 The area of an isosceles trapezium is 185 sq. m. If the lengths of the parallel sides are 32 m and 25 m, then find the lengths of the non-parallel sides.
9 The perimeter of a trapezium is 78 cm. If the ratio of the sides of the trapezium is 6:13:9:11, find the area of the trapezium taking the two largest sides as the parallel sides and the height as 10 cm.
1 Read the statements and choose the correct option.
Assertion (A): The area of a trapezium is equal to the area of a rectangle if the non-parallel sides are equal.
Reason (R): The height of the trapezium is the perpendicular distance between the parallel sides.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Area of Combined Shapes
We know that the shape of the building comprises a parallelogram, a triangle and a semicircle. This is called a combined shape. We also know that the area of the office building that occupies the land is 480 sq. m. What if we have to calculate the construction cost? We then have to find the area of the whole building including the reception area.
For this, we need to calculate the area of all three shapes. Since we already know the total area of the parallelogram and the triangle, it is sufficient to calculate the area of the semicircle only and then add it to the remaining area.
So, diameter of the semicircle = base of the parallelogram = 25 m
Radius of the semicircle = 12.5 m
Area of the semicircle = 1 2 × r2 = 1 2 × 22 7 11 × 12.5 × 12.5 = 245.54 sq. m
So, the total area of the building = 480 + 245.54 = 725.54 sq. m
Area of a Polygon
In our daily lives, we see that not all buildings are square, rectangular, triangular, circular, or quadrilateral shaped. They are also found in the pentagon, hexagonal, heptagonal shapes. For example, the famous Pentagon building in the United States, is a regular pentagon with each side equal to 281 m and a height of 23 m.
To find the area of a regular polygon, we split it into triangles of equal size and find the area of each triangle. These areas are then added together to get the area of the polygon. For example, let us consider a regular pentagon of side 5 cm and length of line joining the center of the polygon to its midpoint of its side is 3 cm.
5cm
This pentagon is split into equal-sized isosceles triangles. How can we find the area of this polygon? Let us see!
To find the area of this polygon, we find the area of each triangle and then add them to find the total.
Area of each triangle = 1 2 × b × h = 1 2 × 5 × 3 = 15 2 = 7.5 sq. cm
There are 5 triangles in the pentagon, so the total area of 5 triangles = 7.5 × 5 = 37.5 sq. cm
Therefore, the area of the pentagon = area of 5 triangles = 37.5 sq. cm
What if the polygons are irregular?
To find the area of irregular polygons, we split it into different geometrical shapes, such as triangles, squares, rectangles, trapeziums, parallelograms, etc. We then find the area of each shape and add them to get the area of the polygon. For example, let us consider the given irregular pentagon.
This pentagon comprises two triangles, one trapezium, and one rectangle.
So, area of the pentagon = area of LMT + area of trapezium MOHT + area of rectangle IGON + area of triangle LIN = 1 2 × LM × MT + 1 2 × (MT + OH) × MO + GO × ON + 1 2 × IN × NL
Remember!
2 × (36 + 80 + 50) + 20 = 1 2 × 166 + 20 = 83 + 20 = 103 sq. cm
The number of triangles formed inside a regular polygon is the same as the number of sides.
Example 14: Find the area of the given figure. (All measures are given in metres.)
Area of the figure = area of ∆ ABI + area of trapezium IBCJ + area of trapezium JCDK + area of trapezium FLJG + area of trapezium GJMH + area of triangle HMA = 1 2 × AI × IB + 1 2 × (IB + JC) × IJ + 1 2 × (DK + JC) × JK + 1 2 × (GJ + FL) × JL + 1 2 × (HM + GJ) × MJ + 1 2 × AM × MH = 1 2 × 35 × 4020 + 1 2 × (40 + 10) × 35 + 1 2 × (35 + 10) × 40 + 1 2 × (50 + 25) × 50 + 1 2 × (50 + 35) × 45 + 1 2 × 2512.5 × 35 = 700 + 1 2 × 5025 × 35 + 1 2 × 4020 × 45 + 1 2 × 75 × 5025 + 1 2 × 85 × 4522.5 + 437.5 = 700 + 875 + 900 + 1875 + 1912.5 + 437.5 = 6700 sq. m
Did You Know?
Many natural objects, such as crystals, snowflakes, and certain minerals, exhibit polygonal shapes due to their atomic or molecular arrangements.
Example 15: In a regular octagon-shaped park with sides of 12 m each, Yamini walks from the centre to the midpoint of a side. If Yamini walks for about 5 m, find the area of the park.
Number of sides in an octagon-shaped park = 8; Measure of each side of the octagon = 12 m
Distance travelled by Yamini from the centre to the midpoint of a side = 5 m
Area of the park = 1 2 × b × h × number of triangles = 1 2 × 126 × 5 × 8 = 240 sq. m
Find the area of the polygon. (All measures in cm.)
Draw a line segment VO so that it touches PW at O, forming a parallelogram QVOP. Draw the height of 9 cm from V on OW.
Now, area of the polygon = area of rectangle STUR + area of parallelogram RUVQ + area of parallelogram QVOP + area of ∆ VOW
Area of the polygon = 22 × 6 + 22 × + 22 × +
Do It Yourself 12C
1 Find the area of the figures.
2 Find the area of the polygons.
a
3 Find the area of the shaded regions.
4 The Parthenon, located on the Acropolis of Athens, is a quintessential example of classical Greek architecture. The layout of the Parthenon is shown. The length of the Parthenon is around 69.5 m and the width is around 30.9 m. What is the total area of the Parthenon?
5 Find the area of a regular hexagon of side 15 cm each. Is there more than one way of finding its area? Draw the figure and find out.
6 Two tiles are fitted together as shown. If the length of one tile is 10 cm, then find the area of the tiling pattern obtained by fitting five such tiles together.
7 A chimney works by allowing smoke and hot gases from a fireplace, stove, or furnace to escape safely out of a building. The measurements of a chimney are given. Find its area.
12 • Area of Polygons
8 An agricultural field is in the shape of a polygon. Find its area, if XR = 9 m, TR = 15 m and TY = 10 m.
9 A floor is in the shape of a polygon. If the floor is tiled with rectangular tiles of dimensions 25 cm × 20 cm, then find the number of tiles that would be required to cover the floor.
10 Create a combined shape of 3 different shapes, give the measurements and find the area of the shape.
1 Gaurav has some right-angled triangular tiles whose sides are 13 cm, 12 cm and 5 cm. He makes the shape using four of these tiles and some square tiles. Find the area of the shape.
Points to Remember
• Area of a square = (side)2; Perimeter of a square = 4 × side.
• Area of a rectangle = length × breadth; Perimeter of a rectangle = 2 (length + breadth)
• Area of a triangle = 1 2 × b × h
• Area of a parallelogram = b × h
• Area of a circle = πr2; Circumference = 2πr
• Area of a trapezium = 1 2 × (sum of parallel sides) × height
• Area of a rhombus = 1 2 × product of its diagonals or base × altitude
• Area of a general quadrilateral = 1 2 × diagonal × sum of perpendiculars on the diagonal from the opposite vertices
• To find the area of a regular polygon, we split it into triangles of equal size and find the area of each triangle. These areas are then added to get the area of the polygon.
Setting: In groups of 3
Polygon Art Gallery
Materials Required: Cut-outs of polygons of different shapes and sizes from coloured sheets of paper, cardboard, rulers, coloured pencils, markers or crayons, a pair of scissors, glue, large cardboard sheets as a canvas for an art gallery, and measuring tape.
Method:
1 Each group must collect a set of coloured sheets of paper and prepare a set of cut-outs of polygons of different shapes and sizes. (This step should preferably be done prior to the class.)
2 Arrange these polygons in such a way that a beautiful and aesthetically pleasing design of a scene is created. For example, a mountain landscape in which mountains can be designed using triangles and trapeziums. Lakes can be created using different irregular polygons such as irregular pentagons, etc., and trees can be created using rectangles and triangles.
3 Measure the sides of each polygon used to create the scene and find their area.
4 In the end, find the total area of the sheet of paper used to create the scene. The group that creates a scene with the least number of polygons wins the game.
Chapter Checkup
1 Find the area of the shaded rhombus if the length of the rectangle is 9.2 cm and the breadth is 6.4 cm.
2 In a rhombus, one diagonal is five times the other. If the area of the rhombus is 1000 sq. cm, find the length of the diagonals.
3 One of the parallel sides of a trapezium is thrice the other. If the area of the trapezium is 350 sq. cm and the height is 14 cm, then find the lengths of the parallel sides.
4 Nishant says, “If the length and breadth of a rectangle are the same as the base and height of a parallelogram, then both the shapes have the same area.” Explain whether Nishant’s statement is always, sometimes, or never true.
5 Find the area of the polygons.
6 Look at the figure. Find the difference between the areas of the regions A and C. (PQRS is a square)
7 Find the area of the figures.
8 The parallel sides of a trapezium are 25 cm and 15 cm. Its non-parallel sides are 13 cm each. Find the area of the trapezium.
9 Mr Chopra arranges 15 parallelogram-shaped tiles on his bathroom floor to make a parallelogram-shaped pattern, as given in the image. What area of the floor is not covered by the tiles?
10 A floor is in the shape of a trapezium whose parallel sides are of length 12 m and 15 m, and the distance between them is 8 m. David wants to paint the floor using a 5 L tin of paint costing ₹2899 in such a way that 1 L of paint covers an area of 10 sq. m. If he has ₹5400 to spend on paint, has David got enough money to buy all he paint the needs?
11 A farmer has a field in the shape of a trapezium where the lengths of its parallel sides are 160 m and 240 m. If the distance between the parallel sides is 150 m, and the field produces 6500 kg of wheat per hectare, then find the amount of wheat in kg the field produces. (Hint: 1 hectare = 10,000 sq. m)
12 Shikhar transformed his square shaped plot of length 40 m into a farm to give shelter to cows. The farm is designed as shown:
a 4 congruent triangular regions are carved from all corners of the square. Each triangle has 2 equal sides of length 5 m.
b There is a circular swimming pool of radius 3 m at the centre of the plot.
c The remaining area of the plot is covered with grass to feed the cows. If the grass is planted at a rate of ₹15 per sq. m, what is the cost of planting the grass? Do you feed animals?
13 Create a word problem to find the area of a combined shape.
1 PQRS is a square with a side 4 cm. The length of ST is 4 cm. PT is equal to RT. What is the area of PST?
2 Decide whether the statements are sufficient to find the area of quadrilateral ABCD.
Statement 1: The sum of the perpendiculars on the diagonal BD from the opposite vertices is 30 cm.
Statement 2: The length of BD is one-third the perimeter of the quadrilateral ABCD. (Perimeter of ABCD = 96 cm)
a Statement 1 alone is sufficient while Statement 2 alone is not sufficient.
b Statement 2 alone is sufficient while Statement 1 alone is not sufficient.
c Both statements together are sufficient.
d Both statements together are not sufficient.
Case Study
Harvesting Success
John, a farmer, has two fields. One is shaped like a trapezium, and the other is shaped like a rhombus. He grew corn in the first field and wheat in the other. The trapezium field has bases of 70 metres and 50 metres and a height of 40 metres while the rhombus has diagonals of 80 metres and 100 metres. He plans to divide these fields for different types of crops.
Answer the questions based on the given information.
1 What is the area of the trapezium-shaped field? a 1600 m² b 2000 m² c 2400 m² d 2800 m²
2 What is the area of the rhombus-shaped field? a 2000 m² b 2500 m²
3 The farmer wants to divide both fields into two equally sized subplots. How large will each subplot be?
4 John build a square-shaped stable inside both of his fields to give shelter to horses. The side of each stable is 3 m. What is the total area of the remaining fields?
13 Surface Area and Volume of Solids
Let�s Recall
We have learnt about two-dimensional shapes. Let us see some basic shapes and revise their perimeter and area.
Perimeter = 2(l + b)
Let’s Warm-up
Perimeter =
Surface Area
An architect has to design a warehouse for storage purposes. First, he prepares a 3-D warehouse model.
Surface Area of Cuboids, Cubes and Cylinders
The architect prepares a cuboid-shaped structure made of cardboard to represent a room. The architect plans the dimensions of the model to be 15 cm × 12 cm × 10 cm.
Surface Area of Cuboids
He wants to paste coloured paper cut-outs on the faces of the cuboid.
Let us see how the area of the coloured paper required by him is calculated.
Let us assume the length to be l, the breadth to be b and the height to be h.
Total surface area
Total surface area = lh + lb + lh + lb + bh + bh = 2 × (lb + lh + bh)
Total area of paper required = 2 × ((15 × 12) + (15 × 10) + (12 × 10)) = 2 × (180 + 150 + 120) = 2 × 450 sq. cm = 900 sq. cm
Hence, the architect requires 900 sq. cm of coloured paper.
Lateral surface area
What if the architect has to paste coloured paper cut-outs on only the walls of the cuboid? We can find the area of the paper required by finding the lateral surface area. The area of the lateral faces is called the lateral surface area.
Lateral surface area = lh + bh + lh + bh = 2h(l + b)
Total area of the walls = 2 × 10 × (15 + 12) = 20 × 27 units = 540 sq. cm
Total surface area = Lateral surface area + (2 × Area of base)
Example 1: Find the lateral surface area and the total surface area of a cuboid with a length of 25 cm, a breadth of 20 cm and a height of 18 cm.
Lateral surface area = 2h (l + b)
= 2 × 18 (25 + 20)
= 36 × 45 = 1620 cm2
Total surface area = 2 × (lb + lh + bh)
= 2 × ((25 × 20) + (25 × 18) + (20 × 18))
= 2 × (500 + 450 + 360) = 2 × 1310 = 2620 cm2
Example 2: The ratio of the length, breadth and height of a cuboid is 5:4:2. What is the total surface area of the cuboid if the length of the cuboid is 60 cm?
Length of the cuboid = 60 cm; Ratio of length, breadth and height = 5:4:2
Breadth of the cuboid = 60 5 × 4 = 48 cm; Height of the cuboid = 60 5 × 2 = 24 cm
Total surface area of the cuboid = 2 × (lb + lh + bh) = 2 × ((60 × 48) + (60 × 24) + (48 × 24)) = 2 × (2880 + 1440 + 1152) = 2 × 5472 cm2 = 10,944 cm2
Example 3: A box which measures 40 cm × 20 cm × 60 cm is to be completely wrapped with decorative paper. How many metres of decorative paper with a width of 1 metre would be required to wrap 75 such boxes?
Let the length, breadth and height of the box be l, b and h, respectively. Then, l = 40 cm, b = 20 cm and h = 60 cm.
Error Alert!
Lateral surface area is the area of the lateral faces (walls) only.
Area of decorative paper needed to cover 75 boxes = 75 × Total surface area of the box
= 75 × [2(lb + bh + hl)]
= {75 × [2(40 × 20 + 20 × 60 + 60 × 40)]} cm²
= {75 × [2(800 + 1200 + 2400)]} cm²
= {75 × [2(4400)]} cm²
= {75 × 8800} cm²
= 6,60,000 cm²
Width of decorative paper = 1 m = 100 cm
∴ Length of decorative paper needed = 660000 100 cm = 6600 cm = 66 m
Hence, the length of decorative paper required to cover 75 boxes is 66 m.
Example 4: Three cubes, each of side 5 cm, are joined end to end. Find the surface area of the cuboid formed.
The dimensions of the cuboid, so formed are
length = l = (5 + 5 + 5) cm = 15 cm
breadth = b = 5 cm
height = h = 5 cm
Surface area of the resulting cuboid = 2(lb + bh + hl)
= [2(15 × 5 + 5 × 5 + 5 × 15)] cm²
5 cm 5cm
5 cm 5 cm 5 cm
= [2(75 + 25 + 75)] cm²
= (2 × 175) cm²
= 350 cm²
Hence, the surface area of the cuboid formed is 350 cm².
Do It Together Remember!
Find the length of a cuboid if the breadth, height and total surface area of the cuboid are 5 m, 3 m and 190 m2, respectively.
Let length = l
Breadth = 5 m
Total surface area = 190 m2
Height = 3 m
Total surface area = 2 × (lb + lh + bh)
190 = 2 × (l × 5 + l × 3 + 5 × 3)
Surface Area of Cubes
A cube is a three-dimensional shape with six square faces.
Let us find the area of a cube. Total surface area Lateral surface area
Lateral surface area
Total surface area = Lateral surface area + (2 × Area of the base)
Example 5: What is the lateral surface area and total surface area of a cube with sides of 80 cm?
Side = 80 cm
Lateral surface area = 4 × Side2 = 4 × 80 cm × 80 cm = 25,600 cm2
Total surface area = 6 × Side2 = 6 × 80 cm × 80 cm = 38,400 cm2
Example 6: If the lateral surface area of a cube is 10,000 m2, what is the length of the side of the cube?
Lateral surface area = 10,000 m2; Let the side of the cube = ɑ
Lateral surface area = 4a2 10,000 = 4a2 a2 = 2500
ɑ = 50 m
A cube is made up of 6 similar faces.
If the length of the side of a cube is increased by 50%, what is the percentage increase in the total surface area of the cube?
Let the length of the side of a cube be ɑ.
Total surface area of a cube = 6ɑ2
New length of the side of the cube = ɑ + 50% of ɑ = ɑ
Total surface area of the new cube =
Increase in the total surface area of the cube =
Percentage increase in the total surface area of the cube =
Surface Area of Cylinders
A cylinder is a solid shape that has circular faces at the top and bottom, and these are joined by a circular cross section.
Lateral surface area = 2πrh
Hollow cylinder
Let the outer radius be R, the inner radius be r and the height of the cylinder be h.
Thickness of the cylinder = R – r
External lateral surface area = 2πRh
Internal lateral surface area = 2πrh
Area of the cross section = π(R2 – r2)
Lateral surface area
External surface area + Internal surface area
= 2πRh + 2πrh
= 2πh (R + r)
Total surface area
External surface area + Internal surface area + Area of 2 base rings = 2πRh + 2πrh + (2 × π (R2 – r2)) = 2π (Rh + rh + (R2 – r2))
Example 7: Find the lateral surface area and total surface area of a cylinder if the radius and height of the cylinder are 7 cm and 10 cm, respectively. (Take π = 22 7 )
Lateral surface area = 2πrh = 2 × 22 7 × 7 × 10 = 440 cm2
Total surface area = 2πr (r + h) = 2 × 22 7 × 7(7 + 10) = 44 × 17 = 748 cm2
Example 8: What is the lateral and total surface area of a hollow cylinder whose internal radius, external radius and height are 7 cm, 14 cm and 20 cm, respectively?
Internal radius (r) = 7 cm External radius (R) = 14 cm Height = 20 cm
Lateral surface area = 2πh (R + r) = 2 × 22 7 × 20(14 + 7) = 2 × 22 7 × 20 × 21 = 2640 cm2
Total surface area = 2π (Rh + rh + (R2 – r2)) = 2 × 22 7 × ((14 × 20) + (7 × 20) + (142 – 72))
= 2 × 22 7 × (280 + 140 + 147) = 2 × 22 7 × 567 = 3564 cm2
Example 9: A lawn mower takes 800 complete revolutions to mow the lawn. Find the area of the lawn if the diameter of the lawn mower is 56 cm and the length is 2 metres.
Let r be the radius and h the height of the lawn mower.
Then, r = 56 2 cm = 28 cm = 28 100 m and h = 2 m
Area of the lawn = Area covered by the lawn mower in 800 revolutions
= 800 × 2πr h = (800 × 2 × 22 7 × 28 100 × 2) m² = 2816 m²
Hence, the area of the lawn is 2816 m²
Example 10: A metal pipe is 84 cm long. The inner diameter of the cross-section is 6 cm, the outer diameter is 6.6 cm. Find the following:
a Its inner curved surface area
b Its outer curved surface area
c Its total surface area
Let r be the internal radius, R the external radius and h the height (length) of the metal pipe.
Then, r = 6 2 = 3 cm,
R = 6.6 2 = 3.3 cm and h = 84 cm
a Inner curved surface area = 2πrh = 2 × 22 7 × 3 × 84 cm² = 1584 cm²
Hence, the inner curved surface area is 1584 cm².
b Outer curved surface area = 2πRh = 2 × 22 7 × 3.3 × 84 cm² = 1742.4 cm²
Hence, the outer curved surface area is 1742.4 cm².
R r h
c Total surface area = [Inner curved surface area] + [Outer curved surface area] + [Area of two bases]
= 2πrh + 2πRh + 2π (R² – r²)
= {1584 + 1742.4 + 2 × 22 7 [(3.3)² – 3²]} cm²
= {1584 + 1742.4 + 44 7 × 1.89} cm²
= 3338.28 cm²
Hence, the total surface area is 3338.28 cm².
Chapter 13 • Surface Area and Volume of Solids
What is the radius of a cylinder whose lateral surface area and height are 330 m2 and 15 m, respectively?
Let the radius of the cylinder be r
Height = 15 m
Lateral surface area = 330 m2
Lateral surface area = 2πrh
330 = 2 × 22 7 × r × 15
r = m
Do It Yourself 13A
1 Find the lateral surface area and total surface area of the cube for the side given.
a ɑ = 17 mm
ɑ = 21 m
ɑ = 28 m
2 Find the lateral surface area and total surface area of a cuboid of the given length, breadth and height.
a l = 12 cm, b = 8 cm and h = 15 cm b l = 60 cm, b = 7 cm and h = 18 cm
c l = 55.5 m, b = 11.5 m and h = 9.25 m
3 Find the lateral surface area and total surface area of the cylinder for the given height and radius.
a r = 12 cm and h = 14 cm
r = 7 2 m and h = 22 m
and
4 Find the lateral surface area and total surface area of a hollow cylinder with the given dimensions. (Use π = 22 7 )
a R = 14 cm, r = 8 cm and h = 1 m b R = 11 dm, r = 1 m and h = 40 cm
c R = 10 dm, r = 80 cm and h = 1.2 m
5 Identify and find the missing dimensions of the solid shapes.
?
6 The perimeter of each face of a cube is 32 cm. What is the total surface area of the cube?
7 The curved surface area of a cylinder is 1200 sq. cm. If the radius of the base of the cylinder is 10 cm, what is its height?
8 A hollow cylindrical tube is open at both ends and is made of iron of 2 cm thickness. The external diameter of the tube is 50 cm and the length of the tube is 140 cm. What is the lateral surface area of the tube?
9 Three similar cubes are placed adjacent to each other. What will be the ratio of the total surface area of the new shape to the sum of the surface areas of the cubes?
10 A cube-shaped kids swimming pool with side length of 3.5 m is to be painted on the inside. What is the cost of painting it at ₹25 per m2?
11 45 circular plates, each of radius 21 cm and thickness 2 cm, are placed one on top of the other to form a cylinder. What is the total surface area of the cylinder?
12 A cuboid-shaped room measures 15 m × 12 m × 6 m. If the cost of whitewashing is ₹19 per m2, then what is the total cost of whitewashing the walls of the room? If the ceiling also has to be whitewashed, what will be the total cost of whitewashing?
13 The area of the base of a cuboidal tank is 12,800 cm2 and the lateral surface area of the tank is 1,08,000 cm2. If the length of the base is eight times the breadth, what is the depth of the tank?
14 Corrosion is a process where metals slowly get damaged and weakened by reacting with their environment. There is a cylindrical iron boiler at Raj’s factory. The boiler is open at the top. It is 6.3 m high and its diameter is 2.8 m. If the boiler gets corroded at a rate of 1.25 m2 per day, then in how many days will the boiler be completely corroded?
15 Create a word problem on finding the lateral surface area of a cuboid.
1 Read the statements and choose the correct option.
Assertion (A): The total surface area of the cylinder with a radius of the base 14 cm and height of 30 cm is 3872 cm².
Reason (R): If r is the radius and h is the height of the cylinder, then the total surface area = (2πrh + 2πr²)
a Both A and R are true and R is the correct explanation of A.
b Both A and R are true but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Volume
Remember the architect who made the warehouse model? He now wants to check the storage capacity of the warehouse. How can he do that? Let us see.
Volume of Cuboids, Cubes and Cylinders
The architect has to calculate the volume to calculate the storage capacity of the warehouse. Volume is the amount of space occupied by a solid shape.
Volume of Cuboids
Let us find the volume of the cuboid.
Volume of the cuboid = Area of the base × Height of the cuboid = (Length × Breadth) × Height = lbh
Length of the diagonal of the cuboid = l2 + b2 + h2
The dimensions of the warehouse are,
Length = 15 metres, Breadth = 12 metres and Height = 10 metres
Volume of the warehouse = 15 metres × 12 metres × 10 metres = 1800 m3
Thus, the volume of the warehouse is 1800 m3.
Units of Volume
Length is one-dimensional, and its standard unit is metre, area is two-dimensional, and its standard unit is metre2, while volume is three-dimensional, and its standard unit is metre3
The other units for volume are cm3, dm3, mm3, km3, etc.
Conversion of volume units
1 m3 = 1 m × 1 m × 1 m
= 100 cm × 100 cm × 100 cm
= 10,00,000 cm3
= 10 dm × 10 dm × 10 dm
= 1000 dm3 = 1000 litres
1 dm3 = 1 dm × 1 dm × 1 dm
= 0.1 m × 0.1 m × 0.1 m = 0.001 m3
= 10 cm × 10 cm × 10 cm = 1000 cm3 = 1 litre since 1 L = 1000 cm3.
Think and Tell
l
What is the difference between volume and capacity?
1 cm3 = 1 cm × 1 cm × 1 cm = 10 mm × 10 mm × 10 mm = 1000 mm3 = 1 mL
Example 11: Find the volume of a cuboid of length, breadth and height 16 cm, 12 cm and 15 cm respectively. Also, find the length of the diagonal.
Length = 16 cm
Breadth = 12 cm
Volume of cuboid = lbh = 16 cm × 12 cm × 15 cm = 2880 cm3
Height = 15 cm
Length of the diagonal = l2 + b2 + h2 = 162 + 122 + 152 = 256 + 144 + 225 = 625 = 25 cm
Example 12: What is the capacity of a container (in litres) of length 60 m, with a breadth that is one-third the length and height that is twice the breadth?
Length = 60 m Breadth = 1 3 × 60 = 20 m Height = 2 × 20 m = 40 m
Volume of a cuboid = lbh = 60 m × 20 m × 40 m = 48,000 m3
We know that, 1 m3 = 1000 L
48,000 m3 = 48,000 × 1000 L = 4,80,00,000 L
Example 13: How many bricks will be required for a wall which is 8 m long, 6 m high and 22.5 cm thick if each brick measures 25 cm × 11.25 cm × 6 cm?
Length of the wall = (8 × 100) cm = 800 cm
Breadth of the wall = 22.5 cm
Height of the wall = (6 × 100) cm = 600 cm
Volume of the wall = (800 × 22.5 × 600) cm³
Volume of 1 brick = (25 × 11.25 × 6) cm³
Number of bricks required = Volume of the wall
Volume of 1 brick = 800 × 22.5 × 600
25 × 11.25 × 6 = 6400 bricks
Example 14: The volume of a reservoir is 108 m³. Water is poured into it at the rate of 60 litres per minute. How many hours will it take to fill the reservoir? [1 m³ = 1000 L]
Volume of the reservoir = 108 m³
= (108 × 1000) litres [since 1 m³ = 1000 L]
Rate of flow of water = 60 litres per minute
Time taken to fill the reservoir = Volume of the reservoir in litres
Rate of flow in litres per minute
= 108 × 1000 60 minutes = 108 × 1000 60 × 60 hours = 30 hours
Find the height of a tank whose capacity is 4,80,000 L if the length and breadth of the tank are 12 m and 800 cm, respectively.
Length = 12 m Breadth = 800 cm = m
Capacity of the tank = 4,80,000 L
1000 L = m3
4,80,000 L = m3
Volume = lbh = h × 12 × h = m
Volume of Cubes
Let us find the volume of a cube.
Volume of a cube = Side × Side × Side
= a × a × a
= a3
Diagonal of a cube = 3 a
Unit cube: A cube with all sides of 1 unit is called a unit cube.
Volume of a unit cube
Volume = Side × Side × Side = 1 unit × 1 unit × 1 unit = 1 unit3
Example 15: Find the volume of a cube of side 15 cm. Side of the cube = 15 cm
Volume of the cube = Side3 = (15 cm)3 = 3375 cm3
Example 16: The volume of a cube is 8000 cm3. If the side of the cube is increased by 20%, then what is the new volume of the cube?
Let the original side of the cube be a
Volume of the cube = 8000 cm3; Volume = Side3
8000 cm3 = Side3 Side = 20 cm
Now, the side is increased by 20%.
New length of the side = 20 cm + 20% of 20 cm = 20 cm + 4 cm = 24 cm
New volume of the cube = 24 cm × 24 cm × 24 cm = 13,824 cm3
Example 17: Find the volume of a cube whose total surface area is 486 cm².
Let the length of each edge of the cube be a cm.
Then, its total surface area = (6a²) cm²
But, the total surface area of the cube = 486 cm²
∴ 6a² = 486
a² = 81
a = 81 = 9
Thus, the length of each side of the cube = 9 cm
Hence, volume of the cube = a³ cubic units
= (9 × 9 × 9) cm³ = 729 cm³
Did You Know?
Shridhara, an Indian mathematician from the 9th century, provided rules for finding the volume of a sphere and the surface area of a sphere.
The side of a cube is 12 cm. What is the capacity of the cube (in mL)?
Side of the cube = 12 cm
Volume = Side3 = cm3
We know that, 1 cm3 = 1 mL
Total capacity of the cube = mL
Volume of a Cylinder
Let us find the volume of a cylinder.
Let the radius of the cylinder be r and the height of the cylinder be h
Volume of the cylinder = Area of the base × Height of the cylinder = πr2 × h = πr2 h
Hollow Cylinder
Volume = Area of the base × Height of the cylinder
= π(R2 − r2) × h
= π(R2 − r2)h
Example 18: What is the volume of a cylinder whose radius and height are 10 cm and 14 cm, respectively?
Radius = 10 cm; Height = 14 cm
Volume of the cylinder = πr2 h = 22 7 × 10 × 10 × 14 = 4400 cm3
Example 19: The difference of the external radius and internal radius of a hollow cylinder is 3 cm. What is the volume of the hollow cylinder if the internal radius is 12 cm and height is 28 cm?
Internal radius (r) = 12 cm; R – r = 3 cm; Height (h) = 28 cm
R – r = 3 R = 3 + 12 = 15 cm
Volume = π(R2 r2)h = 22 7 × (152 − 122) × 28 = 88 × (225 – 144) = 88 × 81 = 7128 cm3
Do It Together
Example 20: Water flows out through a circular pipe whose internal diameter is 2 cm at a rate of 6 metres per second into a cylindrical tank with a base radius of 60 cm. Find the rise in the level of water in 30 minutes.
Volume of water that flows for 1 sec = 22 7 × 1 100 × 1 100 × 6 m³
Volume of water that flows for 30 minutes = 22 7 × 1 100 × 1 100 × 6 × 30 × 60 m³
Volume of water collected in the tank after 30 minutes = 22 7 × 60 100 × 60 100 × h m³
We know that, Volume of water collected in the tank after 30 minutes = Volume of water that flows through the pipe for 30 minutes
22 7 × 60 100 × 60 100 × h = 22 7 × 1 100 × 1 100 × 6 × 30 × 60
h = 3 m
Therefore, the rise in the level of water after 30 minutes is 3 metres.
What is the radius of a cylinder whose volume is 79.2 m3 and height is 70 m?
Height = 70 m Volume = 79.2 m3
Volume = πr2h
79.2 = 22 7 × r2 × 70
r2 = m
Did You Know?
The volume of a human brain varies between approximately 1,053 cm3 and 1,499 cm3 in men and between 975 cm3 and 1,398 cm3 in women.
Do It Yourself 13B
1 Find the volume of the given solids.
a Cube: i a = 16 cm ii a = 24 mm
b Cuboid: i l = 15 cm, b = 10 cm and h = 8 cm ii l = 75 cm, b = 5 cm and h = 60 cm
c Cylinder: i r = 3.5 cm and h = 10 cm ii r = 4.2 m and h = 12 m
2 Find the volume of a hollow cylinder with the dimensions given.
a R = 15 m, r = 8 m and h = 3.5 m b R = 18 cm, r = 7 cm and h = 21 5 cm
c R = 7 mm, r = 2 mm and h = 14 9 mm
3 Identify and find the missing dimension for the given volume of the solid shapes.
=5cm
h = ? l = 17 cm
= 5.5 mm
h = ?
4 The area of the base of a rectangular tank is 1300 cm2. The volume of the tank is 5.2 m3. What is the depth of the tank?
5 A perch is a place where birds rest or sit. It can be a branch, a rod, or any other raised surface. Find the length of the longest perch that can be placed in a hall which is 25 m long, 16 m wide and 6 m high.
6 The diagonal of a cube is 8 3 cm. What is the volume of the cube?
7 A warehouse measures 50 m × 35 m × 20 m. How many cubical wooden crates of length 50 cm can fit inside the warehouse?
8 A container can hold 60 L of water. How many 10 cm ice cubes can be formed from the water in the container?
9 If each edge of a cube is increased by 50%, what is the percentage increase in the volume of the cube?
10 If the volumes of two cubes are in the ratio 1:64 then what is the ratio of their total surface areas?
11 A rectangular block measures 15 cm × 12 cm × 18 cm. What is the volume of the largest cube that can be cut from this cuboid?
12 A cylinder is put inside a cube. The diameter of the cylinder is equal to the side of the cube and its height is the same as the length of the side of the cube. What volume of empty space is left in the cube after placing the cylinder? (Assume the edges of the cube to be a unit.)
13 How many aluminum rods of length 3.5 m and diameter 4 cm each can be made from 1.76 m3 of aluminum?
14 The length of a cuboid is increased by 25%, its breadth is reduced by 50% and its height is increased by 40%. What is the ratio of the volumes of the original cuboid and the newly formed cuboid?
15 Water flows out through a circular pipe of internal diameter 4 cm, at the rate of 3 metres per second into a cylindrical tank with a base radius of 90 cm. By how much will the level of water rise in 45 minutes?
16 If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that
17 Create a word problem on finding the volume of a cylindrical shape.
Challenge
1 Read the statements and choose the correct option.
Assertion (A): The surface area of a cylinder is always greater than its volume.
Critical Thinking
Reason (R): The surface area of a cylinder depends on both the radius and height, while the volume depends only on the height.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Points to Remember
• Total surface area = area of all the faces of a solid shape.
Cuboid – 2(lb + lh + bh); Cube – 6a2; Cylinder – 2πr (r + h); Hollow cylinder – 2π (Rh + rh + (R2– r2))
• Lateral surface area = area of only lateral or curved faces of a solid shape.
Cuboid – 2h (l + b); Cube – 4a2; Cylinder – 2πrh; Hollow cylinder – 2π (R + r)h
• Volume = the amount of space occupied by an object.
Cuboid – lbh; Cube – a3; Cylinder – πr2h; Hollow cylinder – πh (R2 – r2)
• 1 m3 = 1000 L
Volume of Solids
Collaboration & Experiential Learning
Setting: In groups of 3
Materials Required: Cardboard, a pair of scissors, glue, and a pencil
Method:
1 In groups take the cardboard sheets.
2 Two groups to pick one solid out of a cube, cuboid or cylinder. They will be making the solid that they chose.
3 The solid shapes will be made by stacking 2-D shapes, assuming that the cardboard sheet is 1 cm thick.
4 Cut out 2-D shapes like squares, rectangles or circles from the cardboard sheet, that can be stacked to form your solid shape. E.g. Circles will stack up to make a cylinder.
5 Stack 2-D shapes of each type one over the other.
6 Write its measures in your notebooks and find the volume of the solid. Compare your results with the other groups.
Chapter Checkup
1 Identify how many unit cubes can fit inside the cube or cuboid of the dimensions given.
a l = 12 m, b = 10 m, h = 5 m
c l = 10 m, b = 5 m, h = 8 m
b a = 3 m
d a = 6 m
2 Find the capacity (in litres) of the containers of the dimensions given.
a Cube (a = 150 cm)
c Cylinder (r = 8 m, h = 3 m)
b Cuboid (l = 2 m, b = 15 dm, h = 50 cm)
d Hollow cylinder (R = 3 m, r = 120 cm, h = 1.4 dm)
3 What is the height of a cylinder of radius 5 m and a total surface area of 660 m2? Draw the cylinder and mark the dimensions.
4 The radius of the base of the cylinder is 7 mm, and its total surface area is 2640 mm². What is the height of the cylinder?
5 Find the missing dimensions of the solid shapes.
= 9126 m2
= 88 m2
l = 6 dm b = 3 m h = ? l = 5 m
= 1728 cm3
r = 2.6 mm h = ? V = 63 m3 V = 475.904 mm3
6 What is the percentage increase in the total surface area of a cube when each side of the cube is doubled?
7 What is the change in the curved surface area of a cylinder when the radius is doubled and the height is halved?
8 Square holes of dimensions 1 m × 1 m are cut from all the faces of a cube with edges measuring 4 m. What is the total surface area of the faces of the cube now?
9 Three cubes of sides 1 cm, 6 cm and 8 cm are melted to form a new cube. What is the total surface area of the new cube?
10 The outer curved surface area of a hollow cylinder is 31,680 cm2 and it can hold 2,49,480 cm3 of air in it. What is the thickness of the cylinder if the height of the cylinder is 180 cm?
11 What is the ratio of the volume of a cylinder of radius X and height Y to the volume of a cylinder of radius Y and height X?
12 Look at the image shown below. What is the volume of the cylinder formed from the given net? 22 cm 4 cm
13 A square sheet of paper of side 30 cm is folded to form a cylinder. What is the lateral surface area of the cylinder formed?
14 The length and breadth of a wooden box are 50 cm and 30 cm, respectively. The total cost of packaging the box is ₹26,250 at the rate of ₹0.25 per cm2. What is the height of the box?
15 Jimmy created a handmade gift for his mother using a cuboidal wooden box. He wants to wrap the box in coloured paper. The measurements of the wooden box are 60 cm × 40 cm × 30 cm. How many square sheets of coloured paper does he need to buy if the length of each side of a square sheet is 50 cm?
16 A brick measures 15 cm × 5 cm × 5 cm. How many bricks will be required for a wall of dimensions 5 m × 1.5 m × 1.5 m?
17 Water flows into a tank with base measurements of 250 m × 100 m through a square pipe measuring 1.5 m × 1.5 m at the rate of 25 km per hour. In how much time (in minutes) will the water level rise to 3 m?
18 A wooden pipe is in the shape of a hollow cylinder. The internal diameter of the pipe is 28 cm, and its external diameter is 35 cm. The length of the pipe is 48 cm. Find the weight of the pipe if each cm3 of wood weighs 0.8 g.
19 Create a word problem on finding the volume of a cylinder.
A rectangular sheet of paper of dimensions 44 cm by 14 cm is rolled about its longer side. Find the volume of the cylinder thus formed.
Read the statements and answer the questions.
Assertion (A): The volume of two cuboids with the same length and breadth will always be the same, regardless of their heights.
Reason (R): The volume of a cuboid is calculated by multiplying the length, breadth, and height.
Which of the following statements holds true?
a A is true, and R; R is the correct explanation of A.
b A is true, but R; R is not the correct explanation of A.
c A is false, but R is true.
d A is true, but R is false.
Case Study
Theatre Thrills
Mahi’s school organised an annual event, ‘Theatre Thrills’, for the drama and theatre festival. A stage has to be constructed for the event. The stage has a cuboidal shape with dimensions of 5 m by 4 m by 80 cm. Read the questions below and answer.
1 The stage is to be painted. All the faces except the bottom face are to be painted. What is the total area that is to be painted?
2 The cubic-shaped stools are to be placed in the auditorium for the students. The volume of each stool is 2,16,000 cm³. What is the total surface area of the stool? a 21,000 cm²
cm²
3 Many cylindrical dustbins are to be kept at different places. The children are taught to throw away the trash in the dustbins only and not litter at other places to keep the auditorium clean. Mahi is asked to cover the dustbin with coloured paper. How much coloured paper is required by Mahi to cover 8 such dustbins?
30 cm
14 cm
4 An aquarium has to be put outside the gate of the auditorium so that the students learn about different fishes. The aquarium is a cuboid with a length, breadth and height of 120 cm, 50 cm and 1 m, respectively. How much water can the aquarium store (in L) if 1 cm³ = 1 mL?
5 Gift boxes are to be distributed to the winners. Design a gift box for the winner of any one solid shape and find the volume of the gift box.
14 Exponents and Powers
Let’s Recall
We have learnt about numbers that are perfect squares. A number that can be arranged in the form of a square using unit squares is called a perfect square. We have also learnt about perfect cubes. A number that can be arranged in the form of a cube using unit cubes is called a perfect cube. For example, look at the set of unit squares and unit cubes in 64.
The unit squares are arranged in such a way that they form a bigger square. So, 64 is a perfect square.
The unit cubes are arranged in such a way that they form a bigger cube. So, 64 is a perfect cube. 82 = 8 × 8 = 64
We can find the last digit of the square and the cube of any number by looking at the digit in that number's ones place. For example, look at the square numbers and the cube numbers.
Both squares end in 6
142 = 196 and 162 = 256
Letʼs Warm-up
Fill in the blanks.
1 The square of 11 is and its cube is .
This cube ends in 8 This cube ends in 2
123 = 1728 and 183 = 5832
If a number has 2 in its ones place, its cube ends in 8 and vice versa.
2 If the units digit of a number is 3, then the units digit of its square is and that of its cube is
3 The prime factorisation of 48 is .
a Is it a perfect square? (Yes/No)
b The smallest number that 48 should be divided by to get a perfect square is .
4 Reeti says, “125 is a perfect square” whereas Meeti says, “125 is a perfect cube”. Who is correct?
If a number has 4 or 6 in its ones place, the number's square ends in 6. I scored out of 4.
Exponents
Bacteria are very small microorganisms that reproduce very quickly. Under favourable environmental conditions, the bacterial growth shows an increase in the number of bacteria in a population. During binary fission, with each generation, the bacteria split into identical copies every time.
The table given below shows how quickly bacteria grows. Based on the table, let us see how can we find the population of bacteria in its 10th generation.
Exponents of a Rational Number
We saw that for generation 5, the population of bacteria was 32. This was expressed as: 32 = 2 × 2 × 2 × 2 × 2 = 25
It is read as 2 raised to the power 5 or the 5th power of 2.
So, we can say that for generation n, the population of bacteria will be 2n .
Therefore, for generation 10, the population of bacteria will be 210, that is: 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024.
Here, 2 is a rational number. What if the numbers are other types of rational numbers, such as fractions or decimals? Let us see how can we write 0.7 multiplied 10 times or 4 7 multiplied 5 times.
To write such numbers, we use exponents. This helps us read such numbers easily and in less time.
The Indian mathematician, Aryabhata, in the 5th century CE, used the concept of powers with base 10 to express large numbers. He developed a place value system where powers of 10 were implied by position, which is fundamental in our understanding of exponents today. 4 7 × 4 7 × 4 7 × 4 7 × 4 7 = 4 7 5
Did You Know?
A number that can be expressed in exponential form can be either a positive or a negative rational number.
For example, a positive rational number 6 7 when multiplied by itself 6 times is written as:
6 7 6 = 6 7 × 6 7 × 6 7 × 6 7 × 6 7 × 6 7 = 46,656 1,17,649 .
It is read as 6 7 raised to the power 6 or the 6th power of 6 7.
Similarly, a negative rational number, say −7 when multiplied by itself 7 times is written as: (−7)7 = (−7) × (−7) × (−7) × (−7) × (−7) × (−7) × (−7) = −8,23,543
It is read as −7 raised to the power 7 or the 7th power of −7.
Therefore, if any rational number, say a, is multiplied by itself n times, then a × a × a × a … n times = an
It is read as a raised to the power n or the nth power of a.
Positive Integral Exponent of a Rational Number
A positive or negative rational number can be expressed in exponential form. For example, a positive rational number 5 6 when multiplied by itself 6 times is written as:
5 6 6 = 5 6 × 5 6 × 5 6 × 5 6 × 5 6 × 5 6 = 56 66 .
Similarly, a negative rational number, say 6 7 when multiplied by itself 7 times is written as:
We know that positive and negative integers, fractions and decimal numbers all together constitute rational numbers. So, if any rational number, say a b is multiplied n times, then a b n = a b × a b × a b n times = an bn , where a b is the base and n is the exponent.
Example 1: Find the value of:
Example 2: Evaluate:
Negative Integral Exponent of a Rational Number
We have already learnt about how to solve numbers with positive exponents. Now, let us understand how to solve numbers with negative exponents.
Look at the given pattern.
23 = 2 × 2 × 2 = 8 = 16 × 1 2
22 = 2 × 2 = 4 = 8 × 1 2
21 = 2 = 4 × 1 2
20 = 1 = 2 × 1 2
Think and Tell
As the exponent decreases by 1, what do you think about the rule of this pattern? Can we extend this pattern further?
We know that the set of integers is represented by {…, −3, −2, −1, 0, 1, 2, 3, …}. So, if using integers, continuing this pattern with negative exponents, this is what we get as their values.
2 1 = 1 × 1 2 = 1 2
2 2 = 1 2 × 1 2 = 1 4 = 1 22
2 3 = 1 22 × 1 2 = 1 4 × 1 2 = 1 8 = 1 23 and so on.
On observing the pattern, we can say that in each case, exponential numbers are reciprocals of each other.
Remember!
The reciprocal (multiplicative inverse) of a number is 1 divided by that number. For example, the reciprocal of 3 is 1 3
So, if a is any number and n is any positive integer, then its reciprocal is written as a n. It is read as a raised to the power −n.
a n = 1 aⁿ
If a b is any rational number and n is a positive integer, then a b n = 1 a b n = 1
Thus,
Example 3: Express the numbers as negative exponents. 1 (−8) × (−8) × (−8)
Example 4: Evaluate the numbers.
1 (−4)−4
3 (1.2)−2
(1.2)−2 =
Example 5: By what number should 1 6
Let the required number be a. Then,
Think and Tell Is 2 3 -2 = 3 2 2 ? Why?
be multiplied so that the product is 1 14 15 ?
Remember!
When a number has a negative exponent, it represents repeated division. Negative exponents tell us the number of times a number is divided by itself.
So, the required number is 45 49
Example 6: Write the expanded form of 345.28 as negative exponents. 345.28 = 300 + 40 + 5 + 0.2 + 0.08 = 300 + 40 + 5 + 2 10 + 8 100 = (3 × 100) + (4 × 10) + (5 × 1) + 1 10 2 × + 1 10 8 × = 3 × 10² + 4 × 10¹ + 5 × 100 + 2 × 10 ¹ + 8 × 10 ²
Write the expanded form of 23.456 as negative exponents. 23.456 = 20 + 3 + 0.4 + 0.05 + 0.006 = 20 + 3 + 4 10 + + = 2 × 10 + 3 × 1 + 4 × 1 10 + × 1 + × 1 = 2 × 101 + 3 × 100 + 4 × 10−1 + × 10 + × 10
Powers
Do It Yourself 14A
1 Expand and find the value of the numbers.
2 Express the numbers as exponents. a 16 81
3 Express the numbers with negative exponents.
4 Write the expanded form of the numbers using exponents.
5 Which one is larger?
a 2⁵ or 5² b 2⁷ or 7²
6 Solve and express your answer with negative exponents.
7 By what number should 3 3 8 be completely divided so that the quotient is 16?
8 By what number should 3 5 6 be multiplied so that the product is (0.8)4?
9 An insect weighs only 5–3 g. But each day, it can eat 26 times its body weight. How much food can the insect eat on the first day?
1 Vivan’s school had two branches. After the school’s annual day function, the videos for the events were uploaded on the social media channels of both the branches. Since the time it was uploaded, the online traffic has been monitored. The table shows the number of views the video got each week.
The pattern for the number of views for both the branches continued for few weeks.
a What is the ratio of the growth rates of the number of views for both the branches?
b What is the percentage increase in the number of views for the first branch every week?
c What will be the ratio of the number of views for the second branch in week 2 and week 6?
Application of Exponents and Laws of Exponents
We know that the table given below shows how quickly bacteria grow. Each generation increases its population to 2 times.
Exponential Value
What will the bacteria population be after 4 more generations?
We already know that each generation increases its population to 2 times.
Population after 4 more generations = Population after 6 generations × 2⁴ = 2⁶ × 2⁴
We know that, am × an = a(m + n)
Population after 4 more generations = 2(6 + 4) = 1024
What if the powers are negative? Let us see!
We know that, 2(
So, am × an = am + n holds true for any negative integers m and n and rational number a also.
Apart from this, we have some other laws of exponents.
Applying Laws of Exponents
We can apply the laws of exponents in various forms.
For example, let us find the value of
Here, like the laws for positive exponents, we have to find the quotient of two rational numbers when the bases are the same but the powers are different. So, in this case, we apply the law:
Similarly, we can apply other laws as well.
Example 7: Find the value of x for which 7x ÷ 7 5 = 78.
7x ÷ 7−5 = 78 ⇒ 7x−(−5) = 78 ⇒ 7x + 5 = 78
⇒ x + 5 = 8 ⇒ x = 8 – 5 ⇒ x = 3
Example 8: Evaluate:
Example 9: Find the value of:
Example 10: Simplify: 64 × 5−3 × 34 243 × 22 × 10
64 × 5−3 × 34
243 × 22 × 10 = 43 × 5−3 × 34 35 × 22 × 2 × 5 = 43 × 5−3 − 1 × 34 − 5 22 + 1 = (22)3 × 5−4 × 3−1 23 = 26 × 5−4 × 3−1 23 = 26 − 3 × 5−4 × 3−1 = 23 × 5−4 × 3−1 = 23 × 1
Use of Exponents
In our daily lives, we come across numbers like 2 cm, 766 km, 3,59,000 km, 18,76,53,00,000 m, 0.000000045 mm, etc. in the fields of science and engineering. Among these, numbers like 3,59,000 km and 18,76,53,00,000 m are very large and a number like 0.000000045 mm is very small.
Reading these numbers in the usual form is very difficult and time-consuming. So, to read and write these numbers easily in less time, we express them in exponential form using the standard form or scientific notation.
Scientific notation is a way of expressing very large or very small numbers as a product of a decimal number (ranging from 1.0 to 10) and an exponent of 10, where the exponent tells us the number of places the decimal point is moved. For example, 2.9 × 102, 3.6587 × 10−3, etc. 2 4
Therefore, a number can be expressed in the standard form (or using scientific notation) as: k × 10n, where 0 < k < 10 and n is an integer
Now, let us see how we can express 3,59,000 km and 0.000000045 mm using scientific notation.
359000 km
The decimal is moved 5 places to the left.
359000. = 359 × 1000
= 3.59 × 100 × 103 = 3.59 × 102 × 103 = 3.59 × 102 + 3 = 3.59 × 105 km
Example 11: Write the numbers in standard form.
0.000000045 mm
The decimal is moved 8 places to the right.
0.000000045 = 4.5 100000000 = 4.5 108 = 4.5 × 10−8 mm
1 548900000 = 5489 × 100000 = 5.489 × 103 × 105 = 5.489 × 108
2 0.0000000003465 = 3465 10000000000000 = 3465 1013 = 3.465 × 103 1013 = 3.465 × 103 – 13 = 3.465 × 10−10
Example 12: Write the numbers in the usual form.
1 5.67 × 105 = 567 100 × 105 = 567 102 × 105 = 567 × 105 – 2 = 567 × 103 = 5,67,000
2 8.912 × 10−8 = 8912 1000 × 1 108 = 8912 103 × 1 108 = 8912 103 + 8 = 8912 1011 = 8912 100000000000 = 0.00000008912
Example 13: Which is greater, 7.42 × 104 or 5.6 × 107?
7.42 × 104 = 742 100 × 104 = 742 × 104 – 2 = 742 × 102 = 742 × 100 = 74,200
5.6 × 107 = 56 10 × 107 = 56 × 107 – 1 = 56 × 106 = 56 × 10,00,000 = 5,60,00,000
Here, 5,60,00,000 > 74,200.
So, 5.6 × 107 > 7.42 × 104.
Example 14: Find the value of m if 5² × m = 125.
5² × m = 5³
m = 5³ 5²
m = 5³ ²
m = 5
Did You Know?
The distance from the Earth to Proxima Centauri (the star nearest to us after the Sun) is about 4.0 × 1013 km.
Example 15: Find the value of a if 2−5 × 4a + 1 8² × 2−1 = 4²
2−5 × 4a + 1 8² × 2−1 = 2−5 × (22)a + 1 (23)2 × 2−1 = (22)2
2−5 × 22a + 2 26 × 2−1 = 24
2−5 + 2a + 2 26−1 = 24
22a − 3 25 = 24 22a − 3 − 5 = 24 22a − 8 = 24 On comparing, 2a − 8 = 4 2a = 12 a = 6
Example 16: The mass of the Earth is 5.97 × 1024 kg and that of the moon is 7.34 × 1022 kg. What is the combined mass of the two? Express your answer using scientific notation.
Total mass = 5.97 × 1024 + 7.34 × 1022 kg = 5.97 × 1022 × 102 + 7.34 × 1022 kg = (5.97 × 102 + 7.34) × 1022 kg = (597 + 7.34) × 1022 kg = 604.34 × 1022 kg = 6.0434 × 1024 kg
Example 17: The distance from the Sun to the Canis Major Dwarf Galaxy is around 1.47 × 1017 miles. Light travels at a speed of 5.88 × 1012 miles per year. How long does it take (in years) for light to travel from the Sun to the Canis Major Dwarf Galaxy?
Distance from the Sun to the Canis Major Dwarf Galaxy = 1.47 × 1017 miles
Speed of light = 5.88 × 1012 miles per year
The time light takes to travel from the Sun to the galaxy = 1.47 × 1017 5.88 × 1012 =
= 1.47 × 105 5.88
= 1.47 5.88 × 105 = 0.25 × 105
= 2.5 × 10−1 × 105
= 2.5 × 10−1 + 5 = 2.5 × 104 years
Which is smaller, 5.09 × 10 6 or 2.13 × 10 8 and by how much?
5.09 × 10−6 = 509 100 × 1 106
= 509 10 × 1 106 = ____________
2.13 × 10−8 = 213 × 1 10
= 213 × 1 108 = 213 10 =
In scientific notation, ‘× 10’ NEVER means multiplication. It represents the exponent, that is, the number of times we need to move the decimal point towards the left or right to obtain the actual value.
2.5 × 104 = 2.5 × 10 = 25 2.5 × 104 = 2.5 × 10,000 = 25,000
Error Alert!
Do It Yourself 14B
1 Write the numbers in standard form.
a 10980000 b 2300000000000000
c 10.446678 d 453.98785
2 Evaluate:
a 4 9 4 × 4 9 –2 b 7 13 4 ÷ 7 13 2
c 2 3 2 2 d 1 2 × 4 7 2
e 5 6 ÷ 2 3 2 f (3–2+ 8–3+ (–2)–4)0
3 Write the numbers in the usual form.
a 4.21 × 10⁸ b 1.03 × 10⁸ c 40.857 × 10–2 d 3.467 × 10–5
4 Compare the numbers.
a 2.11 × 10², 1.67 × 10–2 b 7.3 × 10–5, 0.7 × 10–8
5 Solve as directed. Give your answers in standard form.
a 6.757869 × 10⁵ + 980.436 × 10³ b 3.87 × 10–7 + 1.02 × 10–7
c 3.6548 × 10⁸ + 154.142 × 10⁶ d 46157.22 × 10² – 23.1572 × 10⁵
6 Find the value of: a (5−9 × 5³) × 15⁵
2 5 –4 × 3 8 –4 × 3 5 4
c 3 4 –5 ÷ 3 4 –2 d ((−2) 2 × (1.6) 3) × (0.8)³ e 2 5 –3 × (2.4)3 × (0.5)0
7 Simplify using laws of exponents.
a 72 × 3−6 × 4²
81 × 16 × 27−2 b 20 × 3−3 × 40 36 × 5 5 × 45
c 9 × t −3 18 × 3 5 × t 5 d 16 × 2m + 1 ÷ (4 × 2m) 16 × 2m + 1 ÷ (2 × 2m + 2)
8 Write the missing number in the equation: –1 5 2 × –1 –2 × 511 = 55
9 Find the value of x.
a 1 2 = 1 8 b 2x = 32 –1 x
10 An ant carries a small amount of food that is 2.78 × 10–3 inches long. Another ant carries an amount of food that is 4.56 × 10−5 inches long. How long are the pieces of food carried by the ants altogether?
11 In the population of a country, 7.7 × 103 people spoke French as their first language and 3.2 × 104 people spoke German. Which language had more speakers and by how much?
12 A swarm of mosquitoes contains as many as 80 million mosquitos per square mile on a 1500 square mile area of land. How many mosquitoes should the swarm have to cover the entire area of land?
13 Scientists discovered that the size of the Antarctic Ocean is 20,330,000 sq. km. How big is the Arctic Ocean, if it is 3 4 th of the size of the Antarctic Ocean? Express your answer in standard form.
Challenge
1 What is the value of 2x + y?
Critical Thinking
Read the statements and choose the option that correctly answers the question above.
Statement 1: 2x = 8
Statement 2: 2y = 16
a Statement 1 alone is sufficient to answer while statement 2 alone is not sufficient.
b Statement 2 alone is sufficient to answer while statement 1 alone is not sufficient.
c Both statements together are sufficient to answer.
d Both statements together are not sufficient to answer.
e Either of the statements alone is sufficient to answer.
Points to Remember
• This representation of numbers with a base and exponent is the exponential form of numbers.
• If any integer, say a, is multiplied by itself n times, then a × a × a × a n times = an It is read as: a raised to the power n or the nth power of a.
• If any rational number, say a b is multiplied by itself n times, then a b n = a b × a b × a b … n times = a × a × a...× n times b × b × b...× n times = an bn , where a b is the base and n is the exponent.
• If a is any number and n is any positive integer, then its reciprocal is written as a n. It is read as: a raised to the power −n
• Some laws of exponents are:
a
=
where m is a positive integer
a
• A number can be expressed in the standard form or scientific notation as k × 10n, where 0 < k < 10 and n is an integer.
Math Lab
Settings: In groups of 4
Communication & Collaboration
Counting Exponentially!
Materials Required: Chart paper; Small rectangular pieces of paper; Counters or rajma beans
Method: All 5 members of each group must follow these steps.
1 Take a chart paper. Place a rectangular piece of paper and paste two counters on the piece of paper. This represents 21 which is equal to 2.
2 Each rectangular piece is to be followed by two more rectangular pieces and each piece of paper has 2 counters.
3 Repeat this process multiple times.
4 The number of counters on each piece of paper shows the base and rectangular pieces of paper placed in a row show the exponent. The total number of counters shows the answer.
5 How many counters will be there in the fourth step? How many counters will be there in the sixth step?
6 Repeat the same activity by keeping 3 counters on each rectangular piece of paper.
Chapter Checkup
1 Write the expanded form of the given numbers using exponents.
2 Identify if the statements are written in standard form or usual form. If the numbers are in standard form, express them in usual form and vice versa.
a The size of a plant cell is 1.275 × 10−5 m.
b The total volume of water on Earth is 1.386 × 109 cu. km.
c The weight of an electron is 0.0000000000000000000000000000911 kg.
3 Which of the following is in usual form? Explain your answer.
a 8.09 × 105 b 0.000000654879 c 9.21 × 10−21
4 Express the given numbers as directed.
a 256 as a power of 2
b 59,049 as a power of 3 c 78,125 as a power of 5
5 Write the reciprocal of the given expressions using exponents.
a 7 9 × 7 9 × 7 9 × 7 9
6 Solve.
d [(2)5 × (−1.5)2] × 1 4 3
7 What power of 49 is equal to 710?
8 Arrange the numbers in ascending and descending orders.
a 210, 323, 642, 128−2, 83 b 310, 273, 7292, 18−2, 93
9 A teacher asked her students to find the multiplicative inverse of x−2. Tanya said the answer is –x2, whereas Sayani said the answer is x−3. Who do you think is right? Explain your answer.
10 Find the value of:
+ 5−3 +
11 Simplify using laws of exponents.
128 × 36 × 4−2
× 36 × 27−1
12 Find the value of x in:
210 ÷ 26 = 2−4 × 23x
13 Simplify: x p + l × x q + p x l + q (x p × x q × x l)2
14 A farm that has 6 × 105 m² of land produces 2.4 × 106 kg of cotton each year. How much cotton is produced per meter square?
15 At a warehouse, each crate weighs 2.2 × 103 kg. If there are 4 × 102 crates, what is their combined weight?
16 The diameters of the planets Jupiter and Saturn are 13.9822 × 104 km and 1.165 × 105 km, respectively. Compare the diameters of these two planets.
17 The size of a plant cell is 0.00002155 m and that of a red blood cell is 0.0000000015 m. Is the plant cell double the size of a red blood cell?
18 The area of the Pacific Ocean is 1.55 × 108 sq. km. The area of the Atlantic Ocean is 1.0646 × 108 sq. km. How many times greater is the area of the Pacific Ocean than the Atlantic Ocean? Express your answer in scientific notation.
Critical Thinking
Read the statement and choose the correct option.
Assertion (A): (a³ × b³) + 2000 = –1000, where a = 5 and b = –2.
Reason (R): (a³ × b³) = (ab)³ and a0 = 1.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Find the value of y if y m + 3 × (y²)m – 1 y³m−9 = 1024
Case Study
Cross Curricular
Elemental Atomic Masses: A Comparative Table
The table shows the mass of an atom for some elements (in kg). Read the data carefully and answer the questions given below.
1 Which of the following is the lightest element?
a Hydrogen
c Gold
b Oxygen
d Iron
2 Which of the following is correct?
a Carbon is the heaviest element.
b Oxygen is 0.6 times heavier than carbon.
c The mass of all the elements is written in standard form.
d The mass of gold is lighter than iron.
3 Which element is approximately 5 times heavier than carbon?
1.6735 × 10–27 kg
1.994 × 10–26 kg
2.656 × 10–26 kg
× 10–26 kg
× 10–26 kg
3.27 × 10–25 kg
4 What is the ratio of the weights (approx) of the heaviest element and the lightest element?
15 Direct and Inverse Proportions
Letʹs Recall
A ratio is defined as the comparison between two quantities of the same unit that indicates how much of one quantity is present in the other quantity.
The ratio of quantities a and b can be given as:
:b = a b
Antecedent Consequent
Ratios are said to be in their simplest form when there are no common factors between the antecedent and consequent except 1.
For example, 12 5 is in its simplest form as the only common factor between 12 and 5 is 1.
We can find the simplest form of a rational number by dividing both the antecedent and consequent by their HCF.
For example, 81 6 = 81 ÷ 3 6 ÷ 3 = 27 2
We can also find the equivalent ratio of a ratio by multiplying or dividing the antecedent and consequent by the same natural number. Equivalent ratios represent the same value when reduced to their simplest form.
For example: Equivalent ratio of 2
Hence, 2 5 = 4 10 = 6 15 = 8 20
Let’s Warm-up
State True or False.
1 There are 45 boys and 39 girls in a hall. The ratio of boys to girls can be given as 39 45
2 The simplest form of the ratio 27:6 = 9:2.
3 11 2 is the simplest form of 88 12 .
4 A ratio can have infinite equivalent ratios.
5 One of the equivalent ratios of 81:30 is 27:10
Proportion
Aakash’s birthday is approaching. His parents are busy preparing for the party.
Father: I talked to the caterer. He is charging ₹250 per guest.
Mother: I have prepared the list, there are 20 guests that are coming to the party.
Father: Great! I also have a list of 5 people who might join the party.
Direct Proportion
We saw that the ratio of number of guests to the amount to be paid is 1:250.
Let us make a table and see how much Aakash's parents need to pay the caterer if the number of guests changes.
Increase in the number of guests
Increase in the amount to be paid
10 ₹2500 10:2500 = 1:250
20 ₹5000 20:5000 = 1:250
25 ₹6250 25:6250 = 1:250
Direct Proportion
If the values of two quantities depend on each other, so that a change in one leads to a change in the other, they are said to be in variation.
Two quantities a and b are said to be in direct proportion if the increase or decrease in the value of a leads to a corresponding increase or decrease in the value of b so that their ratio remains constant.
Thus, a and b are in direct proportion, here a b = c where c is a constant.
Further, if a1 and a2 are the number of guests and b1 and b2 are the corresponding amounts, then
Let us now find the amount to be paid if there are 30 guests at the party.
We know that the amount to be paid for 20 guests = ₹5000
Let the amount to be paid for 30 guests = x
Using the above formula, 20 5000 = 30 x or 20x = 1,50,000
x = 1,50,000 20 = 7500
Hence, the couple needs to pay ₹7500 if 30 guests join the party.
Did You Know?
C.R. Rao, an Indian statistician, contributed to the field of statistics with his methods for estimating proportions and testing hypotheses.
Example 1: Which of the given quantities vary directly with each other? Write Yes/No.
1 The number of pencils and the total cost of the pencils. Yes
2 The number of vehicles on the road and the space on the road. No
Example 2: Observe the tables to find out whether a and b are directly proportional. Also, give the constant of variation in the case of direct proportion. 1
Constant of variation = 13 20; yes.
Example 3: Find the values of a, b, and c if x and y vary in direct proportion.
x 10 a 5 13 y 40 32 b c
Given, x and y are directly proportional.
Therefore, 10 40 = a 32 = 5 b = 13 c Now, 10 40 = a 32 ; = 1 4 = a 32 ; a = 32 4 = 8 and, 10 40 = 5 b ; = 1 4 = 5 b ; b = 5 × 4 = 20 similarly, 10 40 = 13 c ; 1 4 = 13 c ; c = 13 × 4 = 52
Example 4: A bus travels 126 km on 9 litres of petrol. How far would it travel on 5 litres?
Let the distance travelled be x
Travelled (in km) 126 x
Needed (in litres) 9
126 9 = x 5 9x = 630 x = 70
Hence, the bus can travel 70 km on 5 litres of petrol.
The units of ratios in proportion are the same.
Example 5: If the weight of 25 sheets of paper is 60 grams, how many sheets of the same paper will weight 3 kilograms?
Let the number of sheets be x 1 kg = 1000 g
So, 3 kg = 3000 g
25 60 = x 3000 60x = 75,000
x = 1250
Hence 1250 sheets of the same paper will weigh 3 kg.
Example 6: A worker saved ₹148.20 when he worked for 3 days. How much could he save if he worked for 20 days?
Amount saved in 3 days = ₹148.20
Amount saved in 20 days = ₹x
3
20 = 148.20 x ; x = 20 3 × ₹148.20
x = ₹988
Example 7: A human being takes in 1100 litres of oxygen in 2 days. What would be the oxygen intake in a week?
Oxygen intake in 2 days = 1100 litres
Oxygen intake in 7 days = x litres
2 1100 = 7 x ; x = 1100 2 × 7
x = 3850 litres
Example 8: A recipe requires 15 tablespoons of sugar to make 22 cookies.
a How much sugar is required to make 66 cookies?
Let x tablespoons of sugar be required for 66 cookies.
15
22 = x 66
x = 15 × 3 = 45 tablespoons
b If 1 tablespoon weighs 12.5 grams, how many cookies can be made with 375 grams of sugar?
12.5 grams = 1 tablespoon
375 grams = 1 12.5 × 375 = 30 tablespoons
Let, y cookies be made with 30 tablespoons of sugar.
15 22 = 30 y ; y = 22 × 2 = 44 cookies
Example 9: If 10 men or 7 women can earn ₹2100 per day, how much would 20 men and 14 women earn per day?
Earning of 10 men per day = ₹2100
Earning of 1 man per day = ₹210
Earning of 20 men per day 20 × 210 = ₹4200
Earning of 7 women per day = ₹2100
Earning of 7 women per day = ₹300
Earning of 14 women per day =14 × 300 = ₹4200
Total earning of 20 men and 14 women ₹4200 + ₹4200 = ₹8400.
The cost of 12 m of cloth is ₹900. Complete the table using this data. Length of Cloth
of Cloth ₹150
Do It Yourself 15A
1 Which of the given quantities vary directly from each other? Write Yes/No.
a The speed of a car and the time taken by the car to cover a particular distance.
b The number of men required to construct a wall and the time taken by the men.
2 Observe the tables to find out whether a and b are directly proportional. Also, give the constant of variation in the case of direct proportion.
3 Complete the table if x and y vary in direct proportion.
4 Find the cost of 52 kg of rice if 9 kg of rice costs ₹585.
5 A machine in a chocolate factory makes 450 chocolates in 6 hours. How many chocolates will it make in 4 hours?
6 Kamal can type 1020 words in 15 minutes. How many words will he type in 11 2 hours?
7 15 workers can dig a 6 m long stretch in one day, how many workers will be able to dig a 42 m long stretch of the same type in a day?
8 Walking helps burn calories, which can assist in maintaining a healthy weight. Shalini takes 25 minutes to walk a distance of 1.5 km. How much distance will she cover in 40 minutes?
9 A bottling machine manufactures 75 bottles in 40 minutes. How many bottles can it manufacture if it works continuously for a day?
Chapter 15 • Direct and Inverse Proportions
10 A manufacturing company packs the product in cardboard boxes. If five cardboard boxes can be put in 1500 cubic centimetres of space, how much space can 150 such boxes occupy?
11 A cab driver charges a fare of ₹204 for a distance of 8 km. How much will Ravi pay if he travelled from point A to point B which are 22 km apart?
12 72 boxes of certain goods require a shelf of length 17.6 m. How many boxes of the same goods would occupy a shelf of length 19.8 m?
13 Simran donated 5 bags of wheat flour that weigh 90 kg to a flood relief fund. Looking at her initiative, her friends also donated similar bags weighing 576 kg. How many bags of flour have her friends donated?
14 If 20 men or 6 women can earn ₹2400 per day, how much would 40 men and 12 women earn per day?
1 In 14 days, the earth picks up 2.8 × 1010 kg of dust from the atmosphere. Rani says it will pick up 5600 × 109 g of dust in approx. 2.8 days, while Dhani says it will need at least 2800 days. Who is correct, Rani or Dhani?
Inverse Proportion
For Aakash’s birthday party, his parents also ordered 180 laddoos and thought of packing the same number of laddoos in each box as a sweet gesture for each guest.
Problems on Inverse Proportion
Decrease in the number of laddoos in each box
Inverse Proportion
Two quantities a and b are said to be in inverse proportion if the increase or decrease in the value of a leads to a corresponding decrease or increase in the value of b such that their product remains constant.
Thus, a and b are in inverse proportion, if ab = c where c is a constant.
2 = c or Increase in the number of guests
Further, if a1 and a2 are the number of guests and b1 and b2 are the corresponding laddoos to be packed, then
×
Let us now find out the number of laddoos to be packed if there are 30 guests at the party.
We know that for 20 guests, the number of laddoos to be packed = 9
Let the number of laddoos to be packed for 30 guests = x
Using the above formula, 20 × 9 = 30 × x x = 180 30 = 6
Hence, the couple needs to pack 6 laddoos in each box if 30 guests join the party.
Example 10: Which of the quantities vary inversely with each other? Write Yes/No.
1 Number of books and total cost of the books. No
2 Distance travelled by a bus and petrol consumed by it. No
Example 11: If x and y vary inversely, then find the value of a. x 20 a y 5 1
20 × 5 = a × 1
a = 20 × 5 1 = 100
Example 12: A train takes 23 hours to complete a journey if it travels at a speed of 100 km/hr. What should the speed of the train be to cover the same journey in 20 hours?
Let the speed of the train be x.
As the speed increases, the time taken to cover the distance decreases.
Number of Hours 23 20 Speed 100 x
Using the inverse proportion formula, 23 × 100 = 20 × x x = 23 × 100 20 = 115 km/hr
Hence, the train should travel at a speed of 115 km/hr to cover the distance in 20 hrs.
Example 13: 40 labourers are required to construct a building in 1 year. How many labourers are required to construct the same building in 200 days?
Let the number of labourers required be x.
Number of Labourers 40 x Time 365 200
As the time decreases, the number of labourers required increases.
Using the inverse proportion formula, 40 × 365 = x × 200 x = 40 × 365 200 = 73
Hence, 73 labourers are required to finish the work in 200 days.
Example 14: A person has money to buy 10 books worth ₹300 each. How many fewer books will he be able to buy if each book costs ₹200 more?
Number of books bought for ₹300 each = 10
Cost per new book = ₹300 + ₹200 = ₹500
Number of books bought for ₹500 each = ₹300 ₹500 × 10 = 6
Decrease in number of books = 10 − 6 = 4
Example 15: A car can finish a certain journey in 6 hours at a speed of 80 km/hr. By how much should its speed be decreased so that it will take 8 hours to cover the same distance?
The speed of the car to cover the distance in 6 hours = 80 km/hr
The speed of the car to cover the distance in 8 hours = 6 8 × 80 = 60 km/hr
Decrease in the speed of the car = 80 km/hr − 60 km/hr = 20 km/hr
A farmer has enough food to feed 45 cows for 60 days. The farmer buys a few more cows and the food lasts for 54 days. How many cows has he bought?
Let the total number of cows after he buys some cows be x
More cows will consume more food, and hence it will last for fewer days.
Using the inverse proportion formula, 45 × = x × x =
Hence, the farmer bought − 45 = more cows.
Time and Work
Time is the period in which any activity or work happens, while work is a task or series of actions to achieve a certain result. The problems of time and work can be solved using the unitary method or proportions.
We can find the work done in a certain period of time or the time required to complete the work using certain rules:
1
If a person requires x days to complete a task, then the amount of work done in 1 day = 1 x
2
If a person does 1 x of work in one day, then the amount of time required to complete the whole task = x days.
For example, A can do a piece of work in 12 days, and B can do the same work in 18 days. How many days will it take them to complete the work if they work together?
Time taken by A to complete the work = 12 days
∴ Work done by A in 1 day = 1 12 ….(1)
Time taken by B to complete the work = 18 days
∴ Work done by B in 1 day = 1 18 ….(2)
Did You Know?
22,000 workers worked to build the Taj Mahal in 20 years.
Work done by A and B in one day = 1 12 + 1 18 = 3 + 2 36 = 5 36 [Using (1) and (2)]
Time taken by A and B to do the piece of work = 1 5 36 = 36 5 = 7 1 5 days.
Example 16: Suman can do a piece of work in 24 days and Disha in 20 days. If they work on it together for 6 days, what is the fraction of work left?
Time taken by Suman to complete the work = 24 days
∴ Work done by Suman in 1 day = 1 24 ….(1)
Time taken by Disha to complete the work = 20 days
∴ Work done by Disha in 1 day = 1 20 ….(2)
Work done by Suman and Disha in one day = 1 24 + 1 20 = 5 + 6 120 = 11 120 [Using (1) and (2)]
Work done in 6 days = 6 × 11 120 = 11 20
Fraction of work left = 1 – 11 20 = 9 20
So, 9 20 of the work is left.
Example 17: Karim can lay a railway track between two stations in 16 days and Vishal can do the same job in 12 days. With the help of Mukesh, they did the job in 4 days. In how much time can Mukesh alone do the job?
(Karim, Vishal and Mukesh)’s 1 day work = 1 4 (as they complete the work in 4 days)
Karim’s 1 day work = 1 16 ; Vishal’s 1 day work = 1 12
∴ Mukesh’s 1 day work = 1
So, Mukesh can do the work alone in
=
Example 18: A can do a piece of work in 5 days; B and C together can do it in 10 days, while A and C together can do it in 4 days. How long will B alone take to do it?
Portion of work done by A and C together in one day = 1 4
Portion of work done by A in one day = 1 5
Portion of work done by C in one day = Portion of work done by A and C together in one day − Portion of work done by A in one day = 1 4 − 1 5 = 1 20
Portion of work done by B and C together in one day = 1 10
Portion of work done by B in one day= Portion of work done by B and C together in one day − Portion of work done by C in one day = 1 10 − 1 20 = 1 20
Time taken by B to finish the work alone = 20 days
Working together, A and B can finish a piece of work in 30 days. They worked together for 10 days and then B left. After another 40 days, A finished the remaining work. In how many days can A finish the work alone?
Time taken by A and B to finish the work if they worked together = 30 days
(A + B)’s 1 day of work =
(A + B)’s 10 days of work =
Remaining work = (1 – ) =
Now work is done by A in 40 days.
Therefore, the whole piece of work will be done by A in (40 × ) = days
Pipes and Cistern Problems
The problems on pipes and cisterns are similar to time and work.
Portion of a tank filled or emptied Amount of work done
Time taken to fill or empty a tank Time taken to do a piece of work
Inlet pipes
Work done is positive
Cistern
Work done is negative
Outlet pipes
For example, Tap A fills a tank in 4 hours, while Tap B empties it in 6 hours. In how much time will the tank be filled if both the taps are opened together?
Time taken by Tap A to fill the tank = 4 hours
∴ Work done by Tap A in 1 hour = 1 4
Time taken by Tap B to empty the tank = 6 hours
∴ Work done by Tap B in 1 hour = –1 6
Work done by A and B together in 1 hour = 1 4 –1 6 = 3 – 2 12 = 1 12 1 12 of the tank gets filled in 1 hour when both the taps are open
Time taken by taps A and B to fill the tank together = 1 1 12 = 12 hours.
Think and Tell
Is it possible to fill a tank if both the inlet and outlet pipes are opened together and the outlet pipe takes less time compared to the inlet pipe?
Example 19: Pipes A and B can fill a cistern in 10 and 15 hours, respectively. In how much time will the cistern be filled if both the pipes are opened together?
Time taken by Pipe A to fill the cistern = 10 hours; ∴ Work done by Pipe A in 1 hour = 1 10
Time taken by Pipe B to fill the cistern = 15 hours; ∴ Work done by Pipe B in 1 hour = 1 15
Work done by A and B together in 1 hour = 1 10 + 1 15 = 3 + 2 30 = 5 30
Time taken by A and B to fill the cistern together 1 5 30 = 30 5 = 6 hours.
Example 20: Pipes A and B can fill a reservoir in 10 hours and 12 hours, respectively, while a third pipe C empties the full tank in 20 hours. If all three pipes are opened together, how much time will it take to fill the tank completely?
Time taken by Pipe A to fill the reservoir = 10 hours;
∴ Work done by Pipe A in 1 hour = 1 10
Time taken by Pipe B to fill the reservoir = 12 hours;
∴ Work done by Pipe B in 1 hour = 1 12
Time taken by Pipe C to empty the reservoir = 20 hours;
∴ Work done by Pipe C in 1 hour = – 1 20
Work done by A and B and C together in 1 hour = 1 10 + 1
Time taken by A, B and C to fill the reservoir = 1
A pump can fill a tank with water in 2 hours, but due to a leak in the tank, it takes 2 1 3 hours to fill the tank. In how much time can the leakage empty the tank?
Time taken by the pump to fill the tank without leakage = 2 hours
Work done by the pump in 1 hour without leakage =
Time taken by the pump to fill the tank with leakage = 2 1 3 =
Work done by the pump in 1 hour with leakage =
Leakage per hour = 1 2 – =
Time taken due to leakage to empty the tank = hours.
Do It Yourself 15B
1 Which of the quantities vary inversely with each other? Write Yes/No.
a Distance travelled by a car and time taken by the car.
b Number of men required to paint a house and time taken by the men.
2 If x and y vary inversely, then find the value of a.
3 Mohit can finish some work in 6 days. How much work can he do in 1 day?
4 42 women can do a piece of work in 15 days. In how many days can 18 women do the same amount of work?
5 If a box of chocolates is divided among 28 children, they get 6 chocolates each. How many more chocolates would each get, if the number of the children was reduced by 7?
6 A can finish a piece of work in 14 days while B can finish the same work in 21 days. In how much time will they complete the work if they both work together?
7 Three people could fit new doors in a house in 2 days. One of the people fell ill before the work started. How long would the job take now?
8 A group of 4 friends, staying together, consume 42 kg of wheat in 30 days. As there was heavy rain in the city, they gave shelter to a few people and found that the same amount of wheat now lasts for 20 days. How many people came to the group in search of shelter?
9 A car can finish a certain journey in 12 hours at the speed of 60 km/hr. By how much should its speed be increased so that it will take only 9 hours to cover the same distance?
10 A tap P can empty a full tank in 25 hours and another tap Q can empty the same tank in 30 hours. How much time would both taps take to empty the tank if opened together?
11 Manish can finish a piece of work in 40 minutes. He works at it for 8 minutes and then Priya finishes it in 16 minutes. How long will they take together to complete the work?
12 Pipe A can fill a tank in 36 hours. Pipe B can fill it in 18 hours. Pipe C can empty the full tank in 133 hours. If all the pipes are opened together, how much time will be needed to fill the tank?
13 A can do a piece of work in 4 days; B and C together can do it in 3 days, while A and C together can do it in 2 days. How long will B alone take to do it?
14 1800 members of the merchant navy on a ship had enough food for 27 days. Some of them were transferred to a boat, so the food lasted 13 more days. How many of them were transferred to the boat?
15 Recycling is the process of collecting and processing materials that would otherwise be thrown away as trash and turning them into new products. A machine X can recycle 500 plastic bottles in 8 hours. Machine Y can recycle the same number of bottles in 10 hours while machine Z can recycle them in 12 hours. All the machines are started at 11 a.m., machine Z is closed at 1 p.m. and the remaining two machines complete the process. At approximately what time will the work (to recycle 500 plastic bottles) be finished?
1 Read the question and statements to decide which of the following options is correct.
Kavya and Pulkit together can complete the project in 24 days. How many more days will Suman need to complete the rest of the project after Kavya and Pulkit leave after working for 10 days?
Statement 1. Suman and Kavya, together, can complete the project in 30 days.
Statement 2. Pulkit and Suman, together, can complete the project in 20 days.
a Statement 1 alone is sufficient, but Statement 2 alone is not sufficient.
b Statement 2 alone is sufficient, but Statement 1 alone is not sufficient.
c Both statements together are not sufficient.
d Both statements together are sufficient.
Points to Remember
• If the values of two quantities depend on each other, so that a change in one leads to a change in the other, they are said to be in variation.
• Two quantities a and b are said to be in direct proportion, if the increase or decrease in the value of a leads to a corresponding increase or decrease in the value of b so that their ratio remains constant.
• Two quantities a and b are said to be in inverse proportion, if the increase or decrease in the value of a leads to a corresponding decrease or increase in the value of b so that their product remains constant.
• If a person requires x days to complete a job, then the amount of work done in 1 day = 1 x
• Work done by an inlet pipe is always positive, and work done by an outlet pipe is always negative.
Setting: In groups of 4
Collaboration & Experiential Learning
Experiment Using Inverse Proportion
Materials Required: Small containers or cups, water, measuring spoons of different sizes, stopwatch or timer, graph paper
Method:
1 Each group will have a small container and measuring spoons of different sizes.
2 Instruct each group to pour water from the measuring spoon into the container while timing how long it takes to fill the container to a certain level (e.g., halfway).
3 Have each group perform this experiment with different spoons and record the time taken for each.
4 Ask the students to show their results with the help of a graph.
5 Discuss the results as a class and note that as the spoon size increases (greater flow rate), the time taken decreases (inverse proportion).
Math Lab
Chapter Checkup
1 Identify whether the values are in direct or inverse proportion and find the missing values.
2 A recipe requires 880 g of rice flour for 5 persons. How much rice flour is required if the same recipe is made for 12 persons?
3 A labourer is paid ₹4950 for working for 11 days. How much money will he earn if he works for 30 days?
4 Rohan can do a piece of work in a month. What fraction of work can he do in 6 days?
5 Priya has enough money to buy 35 boxes of chocolates worth ₹120 each. How many more boxes of chocolates can she buy if she gets a discount of ₹20 on each box?
6 If 12 men can plough a field in 7 days, how many men can plough the same field in two days?
7 A societyʹs water tank is filled in 4 hours by 8 tankers. How many tankers are required to fill the tank in 2 2 3 hours?
8 20 cows can graze in a field for 32 days. How many cows can graze in the same field for 128 days?
9 A lift can carry 90 people in 6 trips. How many people can it carry in 35 trips?
10 Neha bought tiles for flooring her room. A pile of 15 identical tiles weighs 127.5 kg. What is the weight of 50 such tiles?
11 A and B can do a job in 8 hours, while B and C can do the same work in 12 hours. A, B and C together can finish the job in 6 hours. In how much time can A and C finish the job together?
12 Two pipes P and Q can fill a tank in 25 hours and 35 hours, respectively. How much time will it take to fill the tank if both the pipes are opened simultaneously?
13 Krishvi cycles to her school at a speed of 12 km/hr and reaches the school in 20 minutes. One day her speed was reduced by 2 km/hr due to some traffic on her way. If she left her home at 8:00 a.m., at what time did she reach the school?
14 An NGO collected ₹18,900 to distribute equally among 36 children in an orphanage. If 6 more children are admitted to the orphanage, how much money will each child get?
15 A tap can fill a tub in 24 minutes. Due to a leakage at the bottom of the tub, the tap fills the tub in 36 minutes. How much time will the leakage take to empty the tub if the tub is full?
16 3 kg of wheat contains 1.5 × 105 grains. How many grains are there in 5.5 kg of wheat?
17 Pipe M alone can fill a tank in 50 hours while Pipe N alone can fill the same tank in 40 hours. Pipe O alone empties the tank in 80 hours. If all three pipes are opened together, how much time will it take to fill the tank completely?
18 Sonu can plough a field in 16 days while Kamal can plough the same field in 12 days. If they work together for 3 days, what is the fraction of work left?
19 Bacteria are tiny, single-celled organisms that are found everywhere on earth. In a photograph of a bacteria which is enlarged 2,00,000 times, the length it attains is 2 cm. If the photograph is reduced by 50,000 times, what would be the bacteria’s enlarged length?
20 Darsh, Yash and Pooja can complete a project in 24, 6 and 12 days, respectively. In how much time will they complete the work if they work together?
1 Statement I: X and Y together can complete the work in 30 hours.
Statement II: X works for 16 hours and Y finishes the remaining work alone in 44 hours.
What is the relationship between the efficiency of X and Y?
2 Read the statements and choose the correct option.
Assertion (A): If 6 men can complete a job in 15 days, then adding 4 more men will reduce the time required to 8 days.
Reason(R): Time taken to complete a task is inversely proportional to the number of men working on it.
a A is true, but R is false.
b A is false, but R is true.
c Both A and R are true, and R is the correct explanation of A.
d Both A and R are true, and R is not the correct explanation of A.
Case Study
Cross Curricular & Value Development
Water Conservation and Agriculture
Water is a precious resource, especially for agriculture. Farmers use two types of irrigation systems: traditional flooding and modern drip irrigation. Traditional flooding irrigation wastes a lot of water, while drip irrigation conserves water by delivering it directly to the roots of plants.
A group of farmers decided to switch from traditional flooding to drip irrigation to save water. They found that with traditional flooding, they needed 50 litres of water to irrigate one square metre of land for a day. With drip irrigation, they only needed 20 litres of water for the same area.
1 If a farmer has 100 square metres of land, how much water will he save per day by switching from traditional flooding to drip irrigation?
a 1000 litres b 1500 litres c 3000 litres d 2500 litres
2 If the village has 10 farmers each with 50 square metres of land, how much water in total will they save per day by switching to drip irrigation?
a 10,000 litres b 15,000 litres c 20,000 litres d 25,000 litres
3 If the villageʹs water supply is limited to 50,000 litres per day, how many more square metres of land can be irrigated using drip irrigation compared to traditional flooding?
4 What are some ways you can conserve water at home? Can you think of small changes in your daily routine that could save water?
16 Factorisation and Division of Algebraic Expressions
Let’s Recall
Algebraic expressions are mathematical expressions that contain variables, constants and operations like addition, subtraction, multiplication and division. These expressions can be categorised into various types based on their characteristics and structure.
Monomials
An algebraic expression with only one term.
Example: 7, 3x, 2y2
Binomials
An algebraic expression with two unlike terms separated by addition or subtraction.
Example: 2x + 5, 2y2 z
Let us see how to add or subtract expressions.
Addition of Algebraic Expressions
While adding algebraic expressions, we collect the like terms and add them. The sum of several like terms is the like term whose coefficient is the sum of the coefficients of those terms.
Trinomials
An algebraic expression with three unlike terms separated by addition or subtraction.
Example: x + y + 2, 3x2 + 2x + 1
Subtraction of Algebraic Expressions
To subtract algebraic expressions, change the sign of each term in the second expression and then combine like terms with the first expression, following the rules of addition and subtraction.
Letʼs Warm-up
Solve to find the answer.
Factorisation of Algebraic Expressions
Neha is an architect. She got a new project where she has to design a rectangular garden. The client gave her the desired area in the form of an algebraic expression as 6x2 + 24x + 24.
As Neha knew that, the area of a rectangle is nothing but multiplication of length and breadth, and in this case, multiplication of two algebraic expressions, she used the method of factorisation of algebraic expressions to find the length and breadth of the desired garden and got the length and breadth as: (2x + 4) and (3x + 6).
Let us also learn different methods to factorise an algebraic expression.
Factorising Algebraic Expressions
Similar to natural numbers, algebraic expressions can also be represented as products of factors. These factors can include numbers, algebraic variables or other expressions.
Factorisation is the process of finding expressions that, when multipied, create a given algebric expression. It involves identifying the factors that make up the algebraic expression. The expression 6x2 + 24x + 24 can be factorised as shown below:
Using Common Factors
By identifying a common monomial
When factorising a polynomial expression, we look for the largest monomial that divides all the terms in the expression exactly. This common monomial is then factored out, simplifying the overall expression. For example, let us factorise 6x2y + 12xy2 18xyz using a factor tree.
Expressions:
Terms:
Let us factorise: 7mn2 − 14m2n − 21m2n2 without using the factor tree.
Factors of 7mn2 = 1 × 7 × m × n × n
Factors of − 14m2n = 1 × 2 × 7 × m × m × n
Factors of − 21m2n2 = 1 × 3 × 7 × m × m × n × n
Common factors = 1 × 7 × m × n = − 7mn
Think and Tell
Does the number of terms in a polynomial increase if we multiply it by a monomial?
So, on factorising, 7mn2 − 14m2n − 21m2n2, we get 7mn (n + 2m + 3mn).
By identifying a common binomial:
When factorising a polynomial expression, we look for the largest binomial that evenly divides all the terms in the expression. This common binomial is then factored out, simplifying the expression.
For example, to factorise 4x (x + 2) − 3y (x + 2), the common binomial is (x + 2).
So, 4x (x + 2) − 3y (x + 2) = (x + 2) (4x 3y).
Example 1: Factorise the expression using a factor tree: 15a2b + 18ab2 24ab
Expression:
Terms: 15a2b + 18ab2 24ab 15a2b 18ab
So, 15a2b + 18ab2 − 24ab = 3ab(5a + 6b – 8). 3 × 5 × a × a × b
Example 2: Factorise: 6(2x + 3y) 17(2x + 3y)2 6 (2x + 3y)
Factorise the expressions.
(3
)3 = a × (a − 3) + 7xy (a − 3)3
Using Grouping and Regrouping Terms
In certain algebraic expressions, not every term can be divided by the same monomial or binomial. However, by organising the terms into groups where each group shares a common factor, factorisation can be simplified and made more straightforward.
It Together
Let us see this through an example by factorising the expression: m2 mp + mn np
Step 1: Group the terms in the expression so that each pair of terms shares a common factor.
Step 3: Factor out the common factor and write the factored expression.
Example 3: Factorise: a2b ac2 ab + c2
a2b ac2 ab + c2 = a2b − ab − ac2 + c2
= ab (a − 1) − c2 (a − 1) = (a − 1) (ab c2)
Example 4: Factorise: ap2 + bq2 + bp2 + aq2 . ap2 + bq2 + bp2 + aq2 = ap2 + bp2 + bq2 + aq2 = p2 (a + b) + q2 (b + a) = (p2 + q2) (a + b)
m2 np + mn mp
= m2 + mn mp np
= m (m + n) p (m + n)
= (m p) (m + n)
Step 2: Factorise each group.
Did You Know?
The Indian mathematician Brahmagupta made important contributions to mathematics. In his book Brahmasphuta Siddhanta, he developed rules for working with negative numbers and zero. The book also included many algebraic problems.
Example 5: Create a word problem on factorising the expressions by regrouping the terms.
There can be many different word problems. Example word problem: Lena and Tom are planning a garden. They have a rectangular plot of land where Lena will plant flowers and Tom will plant shrubs. The extent of soil cover required is expressed by the expression 4xy + 12y + 3x + 8. What is the length and breadth of the garden?
Factorise the given expressions.
3m ( + ) + (n + q)
(3m + ) (n + )
( ) (x a)
Do It Yourself 16A
1 Factorise the expressions by identifying the common monomial using a factor tree.
2 Solve to factorise the expressions by identifying the common monomial.
3 Factorise the expressions by identifying the common binomial. a (3y + 2) (y 1) 2 (3y + 2)
(3x + 2) (2x 1) (3x + 2)
(5y 1) (3y + 2) 4 (3y + 2) d (2a + 5) (a 3) (2a + 5)
+ 7)2 (a + 2) (4a + 7)
4 Factorise the expressions by regrouping the terms. a (2x3 3x2 + 4xy 6y)
(x2 7x 2xy + 14y) d (2ab + 5ac 4bd 10cd)
(x2 3x 2x + 6) f (3x2 2xy 15x + 10y) g (6xy 3x2 10y + 5x) h (4x2 12xy + 2x 6y
5 Create an algebraic expression that can be factorised by regrouping terms.
Challenge Critical Thinking
1 A farmer spent ₹(4x2 + 8xy + x + 2y) on buying plants. If he bought (x + 2y) plants, what is the cost of each plant?
Factorisation Using Identities
In the previous section, we were factorising the expressions by spotting a common monomial/binomial term or regrouping the terms. However, not all expressions can be factorised this way. In this section, we will use algebraic identities to factorise the expressions.
Factorisation When the Expression is a Perfect Square
To factorise an expression that is a perfect square, we can use either of the identities:
Identity 1: a2 + 2ab + b2 = (a +
Let us factorise the expression (4m2 + 20mn + 25n2).
2: a2 2
)2
Step 1: Recognise that the expression can be written as the square of a binomial.
Step 2: Determine what squares make up the expression. Here, a = 2m and b = 5n
Step 3: Write the expression by substituting a and b for the corresponding terms.
Example 6: Factorise: 4x2 + 12x + 9
4x2 + 12x + 9 = (2x)2 + 2 × 2x × 3 + (3)2 = (2x + 3)2
Example 7: Factorise: 1 6x2 + 9x4 1 − 6x2 + 9x4 = 1 − 2 × 3x2 + (3x2)2 = (1 3x2)2 (4m2 + 20mn + 25n2) = (2m)2 + 2 × 2m × 5n + (5n)2 = (2m + 5n)2
Do It Together
1 b2 6ab + 9a2
= b2 2 × × b + ( )2
= (b )2
2 Factorise: 9x4 + 24x2 + 16
9x4 + 24x2 + 16 = ( )2 + 2 ×× + ( )2
= ( + )2
Factorisation When the Expression is a Difference of Two Squares
To factorise an expression that is a difference of two squares, we will use the given identity
Identity 3: a2 b2 = (a + b) (a b)
Step 1: Recognise the expression that fits the difference of the squares form.
Step 2: Identify a and b as squared terms separated by subtraction in a2 – b2 .
Step 3: Write the expression as (a + b) (a – b) with the corresponding terms.
Example 8: Factorise: 64 9x2
64 − 9x2 = 82 − (3x)2 = (8 + 3x) (8 − 3x)
Example 10: Factorise: m2 + 2mn + n2 – 1
Factorise the expressions using suitable identities. Do It Together Chapter 16 • Factorisation and Division of Algebraic Expressions
Example 9: Factorise: 5 20b2 5 20 b2 = 5 (1 − 4b2) = 5 (1 − (2b)2) = 5 (1 + 2b) (1 − 2b)
= (m2 + 2mn + n2) – 1 = (m + n)2 – 12 using (a2 + 2ab + b2) = (a + b)2
= [(m + n) + 1] [(m + n) – 1] using (a2 – b2) = (a + b) (a – b)
Factorise the expressions using suitable identities.
m4 − n4
= (m2)2 ( )2
= (m2 n2) ( + )
= (m n) ( + ) (m2 + n2) (16x2 81y2) = (4x)2 − (9y)2 = (4x + 9y) (4x 9y)
Do It Yourself 16B
1 Factorise the expressions using the square of a binomial identity. a a2 + 8a + 16 b x2 + 10x + 25 c b2 + 4b + 4
2 Factorise the expressions using the difference of squares identity.
81 + 18a + a2
3 Factorise the expressions using a suitable algebraic identity.
4 Find the missing term so that the expression can be easily factorised using the square of a binomial identity.
5 What constant must be added to the expressions to create a perfect square?
6 Factorise.
7 Create a question on factorising an expression using identities.
Critical Thinking
1 Oliver wants to install bookshelves in his room. He has a rectangular wall space available with an area represented by the expression (9y2 4x2) sq. cm. Factorise the expression of area and separate the factors as the length and breadth. Determine the length and breadth, if x = 2 and y = 3 and the length of the rectangle is more than its breadth.
Factorisation of Quadratic Trinomials
A quadratic trinomial is a polynomial of the second degree, which means it is a polynomial of the form: (ax2 + bx + c = 0) where x is the variable and a, b and c are not zero.
To factorise a quadratic trinomial, follow the steps given below:
Step 1: Begin with the quadratic equation, (ax2 + bx + c = 0)
Step 2: Find the pair of numbers whose product equals ac and whose sum equals b
Step 3: Break down the middle term of the expression using these two numbers, ax2 + (Number 1)x + (Number 2)x + c = 0. Here, Number 1 = 3 and Number 2 = 4
Step 4: Extract common factors. Write the common factors.
Example 11: Factorise: x2 + x 72.
x2 + x − 72 = x2 + 9x − 8x − 72
= x (x + 9) 8 (x + 9) = (x 8) (x + 9)
Example 12: Factorise: x2 + 3x – 70
x2 + 3x – 70 = x2 + 10x – 7x – 70
= x(x + 10) – 7(x + 10) = (x + 10) (x – 7)
Example 13: Factorise: 8x2 26x + 15
8x2 − 26x + 15 = 8x2 − 20x − 6x + 15
= 4x (2x − 5) − 3 (2x − 5) = (2x − 5) (4x − 3)
Factorise the quadratic trinomials given below.
Example 14: Factorise: 12x2 + 25x + 12
12x2 + 25x + 12 = 12x2 + 9x + 16x + 12
= 3x (4x + 3) + 4(4x + 3) = (4x + 3) (3x + 4)
1 2x2 + x 6 = 2x2 = = (______ x ) (x + 2) 2 x2 2x 15 = x2 − = ____________ + ______ (x 5) = ( ) (x 5)
Creativity
Do It Yourself 16C
How should the middle term of the expressions given below be split to factorise the expressions?
x2 5x + 4
2x2 − 9x + 4
2 Which of the expressions has (x + 1) as one of its factors?
3 Factorise the trinomials.
6x2 − 11x + 4
4 If the area of a rectangle is given by the trinomials, what could the length and breadth of each of these rectangles be?
5 Create a word problem on factorising trinomials.
Challenge
Critical Thinking
1 Can the trinomials be factorised without taking any monomial term common before splitting the middle term?
a b2c3 + 8bc4 + 12c5 b 3c5 18c4 48c3
2 A small business owner models the profit of her store on the quadratic trinomial (3x2 12x 15). If each product sold brings equal profit, and (x − 5) products are sold, what is the algebraic expression for her profit?
Division of Algebraic Expressions
Teacher: Today’s challenge—Tom has 10x candles to share equally between Mini and Mike. How many candles will each get?
Jim: Is it 20x candles?
Teacher: No, we have to divide the candles, so it’s 5x each. We divide 10x by 2.
Jane: Got it! Tom gives 5x candles to each friend.
Teacher: Exactly! Division helps us share things equally, just like equally distributing candles among friends.
This is a simple example of algebraic division. Let us get deeper into algorithms for the division of polynomials.
Dividing Algebraic Expressions
To divide 10x candles between two kids, the teacher divides 10x by 2. Both 2 and 10x are monomials. Division is possible between all kind of polynomials and monomials. Let us learn how to perform these divisions one by one.
Dividing a Monomial by a Monomial
To divide one monomial by another monomial, you can follow these steps: Suppose we want to divide the monomial 12a2b3c4 by 3ab2c2. This can be expressed as follows:
Step 2: Factorise the monomials.
Step 1: Express the monomials to be divided in numerator by denominator form.
So, 12a2b3c4 ÷ 3ab2c2 = 4abc2 .
Example 15: Divide 15x3y5z4 by 5xy3z3 .
Step 4: Simplify the expression.
Step 3: Cancel out matching exponents in the numerator and denominator.
16: Divide 14a
Simplify.
21k9e4y7 6e2m2k3y2
21 × k9 × e4 × y7 6 × k3 × e2 × y2 × m2 =
Do It Together
Dividing a Polynomial by a Monomial
To divide a polynomial by a monomial, you divide each term within the polynomial by the monomial.
Step 2: Divide each term separately by the monomial.
Step 1: Express the polynomial and monomial to be divided in numerator by denominator form.
Example 17: Divide
Step 3: Simplify the expression.
Example 18: Divide
Simplify the expressions.
10j3k4l7 − 18j5k9l2 + 25j 4k3l5 5jk2l =
Dividing a Polynomial by a Polynomial
To divide one polynomial by another polynomial, the first step is to factorise both polynomials, and then eliminate any common factors.
Let’s try to divide x3 4x2 + 3x by x2 x using factorisation.
x3 − 4x2 + 3x x2 x � x(x2 − 4x + 3) x(x −1)
� x(x2 − 3x x + 3) x(x −1) (Factorising by splitting the middle term)
� x(x(x − 3) 1(x − 3)) x(x −1)
16 • Factorisation and Division of Algebraic Expressions
Remember!
The degree of the remainder is always less than the degree of the divisor.
� x(x − 1)(x − 3) x(x 1) � x 3 (By cancelling the common factors)
One other way of dividing polynomials by polynomials is by using long division. To divide one polynomial by another using the long division method, you should follow the steps.
1 Rearrange the terms in the division house.
2 Begin by determining the first term of the quotient, by dividing the first term of the dividend by the first term of the divisor.
3 Multiply all the terms within the divisor by the first term of the quotient, and then subtract this product from the dividend to get the remainder.
4 If the remainder is not zero, treat it as the new dividend and repeat the same process from step 2 onwards until we get the remainder as zero or a polynomial with a degree lower than that of the divisor.
Example 19: Divide 2y2
Example 20: Divide 16x3 − 46x2 + 39x − 9 by 8x − 3 using long division.
16x3 − 46x2 + 39x − 9 2x2 – 5x + 3
Example 21: Divide 10x4 + 17x3 − 62x2 + 30x − 3 by 2x2 + 7x − 1 using long division.
16x3 − 6x2 −40x2 + 15x 24x − 9 24x − 9
8x − 3 −40x2 + 39x + + + 0
Divide the polynomial using long division.
x2 + 21x − 3 2x2 + 7x − 1
Error Alert!
Always check the degree of the quotient after division. It should be less than or equal to the dividend.
Do It Yourself 16D
1 Divide the algebraic expressions.
a 15x3 by 3x
c 24y4z3 by 6yz
b 15a2b4 by 5ab2
d 18x5y 2z by 9xyz2
e 36p4q3r2 by 12p2qr2 f 84j5k7r9 by 7jk3r2
2 Divide polynomials by monomials.
a (2x3 + 4x2 − 6x) by (2x)
c (4a5 − 12a4 + 8a3) by (4a)
b (3y4 − 9y3 + 6y2) by (3y)
d (6m3 − 18m2 + 12m) by (6m)
e (5x6 + 10x5 − 15x4) by (5x2) f (5a3x − 15a2y2 + 3az3) by (3a)
3 Solve the expressions.
a 225abc (4a − 8) (5b − 15) ÷ 125 (a − 2) (b − 3)
b 144ab (a + 5) (b − 4) ÷ 36a (b − 4)
c 28 (a + 3) (a2 + 3a + 70) ÷ 7 (a + 3) d 117abc (a + b) (b + c) (c + a) ÷ 78ab (b + c) (c + a)
4 Divide the polynomials by the binomials using long division.
a (4x3 − 6x2 + 3x − 9) by (x2 − 4) b (3y4 − 9y3 + 6y2 − 12y) by (y2 − 4)
c (x5 + 5x4 + 4x3 + 20x2 + 16x) by (x2 + 4) d (6a4 − 3a3 + 9a2 − 6a) by (a + 2)
e (9b6 + 12b5 − 3b4 − 4b3) by (b2 + 2) f (2c5 − 8c4 + 6c3 − 12c) by (c + 2)
5 Divide the polynomials by the trinomials using long division.
a (3x3 − 5x2 + 2x − 1) by (x2 − 4x + 4) b (4y4 + 6y3 − 2y2 + 8y − 12) by (2y2 − 3y − 6)
c (6a4 − 2a3 + 9a2 − 5a + 3) by (2a2 − a + 1) d (x5 − 3x4 + 5
e (7x3 + 2x2 − 9x − 5) by (x2 − 3x − 2)
6 What must be multiplied by x − 7 to obtain x3−12x2 + 38x − 21?
by (
7 The total amount of water in a bucket kept in sunlight is (x2 + 5x + 6) litres The bucket dries up in (x + 3) days due to evaporation. What is the rate of evaporation per day?
8 Rahul wants to distribute (x3 + 6x2 + 12 + 13x) chocolates among his classmates on his birthday. If there are (x + 3) kids in his class, how many chocolates will each kid get?
1 What must be added to 3x3 − 8x to make it perfectly divisible by x − 1?
2 What must be subtracted from (a4 + 2a3 − 2a2 + a − 1) so that the resulting polynomial is exactly divisible by (a2 + 2a − 3)?
Points to Remember
• When an expression is the product of two or more expressions, then each of these expressions is called a factor of the expression.
• The greatest common factor of two or more monomials is the product of the greatest common factors of the numerical coefficients and the common letters with the smallest powers.
• When a binomial is a common factor, we factorise by writing the expression as the product of this binomial and the quotient of the expression divided by the binomial.
• Difference of Squares Identity:
• Perfect Square Identity:
Math Lab
Materials Required:
Factorisation Bingo
• Bingo cards (pre-made or created by the teacher)
Collaboration & Communication
• Algebraic expressions (to be called out as clues)
• Markers or chips for each student
Steps:
1 Prepare bingo cards with algebraic expressions in grid format.
2 Explain the rules of bingo, where players aim to mark a row, column, or diagonal of squares on their card by matching the expressions called out.
3 Instruct the students to work in pairs. Distribute the bingo cards among the pairs.
4 Call out the algebraic expressions one by one, providing context or stories related to each expression.
5 After calling out an expression, ask the pairs to factorise it and check if it matches any expression on their bingo card. If it matches, they can cover that square.
6 The first pair to complete a row, column or diagonal shouts “Bingo!” and wins the round.
7 Discuss the factorisation process and ask the students to explain how they factorised the expressions and share any patterns they noticed.
8 Play multiple rounds with different expressions and factorisations to reinforce the concept.
Chapter Checkup
1 Factorise the expressions by identifying the common monomial using a factor tree.
2 Factorise the expressions by taking the binomial term common.
a (x + y) (x + y)(2x 11)
b x (x 2z) + y (x 2z) + (2z x)
c (n − 10)2 + (10 − n) d (3a − 1)2 6a +2
e 5x + 10y − 7 (x + 2y)2 f (5x + y) (5x + y)3
3 Factorise the expressions by grouping/regrouping the terms.
a 4a2b 6ab2 2ab + 3b2
b 5x2 10xy + 3xy 6y2
c 3x2 2xy + 6x 4y d 9x2 6x 12xy + 8y
e 4x3 2x2 6xy + 3y f 6x2 + 7xy 18x 21y
4 Factorise the expressions into perfect squares.
a (a2 + 6ab + 9b2) b (x2 10xy + 25y2)
c (4x2 + 4xy + y2)
d (25x2 + 40xy + 16y2)
e (x2 − 14xy + 49y2) f (16a2 − 32ab + 16b2)
5 Factorise the expressions by using the difference of two squares identity.
a (p2 9q2)
b (4x2 − 49y2)
c (a2 − 16b2) d (9m2 25n2)
e (x2 − 36y2) f (25u2 − 4v2)
6 Factorise the quadratic trinomials.
a 6x2 + 11x 2 b x2 5x + 6
c 3x2 + 12x 15 d 3x2 10x + 7
e x2 + 14x + 48
7 Divide the polynomials by the monomials.
a (6x3 + 9x2 − 12x) by 3x
c (12a3b2 − 6a2b3 + 18ab4) by 6ab2
f 2x2 3x 5
b (4a2b3c2 − 8ab2c2d) by 2abc
d (9x5 − 3x4 + 6x3) by 3x2
e (7a4b3c2 − 14a3b2c3 + 21a2b1c4) by 7a2bc2 f (15x6 − 10x5 + 5x4) by 5x3
8 Divide the polynomials by the binomials using long division.
a (2x3 + 4x2 6x) by (x − 2)
c (4x3 + 12x2 − 3x) by (2x − 1)
e (6x4 − 12x2 + 6) by (2x − 3)
9 Divide the polynomials by the trinomials using long division.
a (3x3 + 4x2 2x + 1) by (x2 − 3x + 2)
c (6x3 − 8x2 + 2x − 4) by (2x2 − 3x − 2)
e (x4 + 3x2 − 4) by (x2 + 4x + 4)
b (3x4 − 9x2 + 6x) by (x + 1)
d (5x4 − 13x3 + 9x2) by (5x + 2)
f (7x3 − 7x2 + 14x) by (7x − 4)
b (2x4 − 5x2 + 3) by (x2 − x − 2)
d (5x3 − 6x2 + 3x 2) by (x2 + 2x 1)
f (8x3 − 12x2 − 6x + 9) by (4x2 − 6x − 3)
10 Lucas wishes to plant flowers in a rectangular garden. He wants the area of his garden to be (64x3 − 25xy2).
What are the possible length and breadth combinations of his garden?
Challenge
1 What should be subtracted from x4 + 7x3 + 15x2 + 7x – 5 so that the resulting polynomial is exactly divisible by x2 + 4x – 2?
2 Read the statements and choose the correct option.
Assertion (A): The factorisation of x2 + xy + 2x + 2y is (x + 2) (x – y)
Reason (R): Factorisation is defined as breaking or decomposing an expression into a product of two or more expressions which when multiplied together, give the original expression.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, but R is false.
d A is false, but R is true.
Case Study
Urban Art Space
Suhani, who has a passion for art, decided to build an art gallery in the city. She wanted artists from various places to display their work there. The gallery is designed to have two entrances and exit doors. It is also planned that the gallery will have 8 square shaped windows, and the floor will be covered with square tiles. The architect designed the layout and gave all the measurements. Read the questions related to the gallery and answer them.
1 The area occupied by one door can be given as (2ab + 5b2 + 6ac + 15bc) square units. What are the possible length and breadth of each door?
a (2ab + 5b2) units and (6ac + 15bc) units
c (b – 3c) units and (2a + 5b) units
b (ab + 5b2) units and (3ac + 15bc) units
d (b + 3c) units and (2a + 5b) units
2 The perimeter of one square window can be given as (12a + 20b) units. How much area will each window occupy?
a (4a + 5b)2 square units
c (a + 5b)2 square units
b (3a + 5b)2 square units
d (12a + 20b)2 square units
3 Suhani planned to cover one of the rectangular walls of the gallery with her creations. If the area and the breadth of the wall is (x3 – x2 – 21x –54) square units and (x – 6) units, respectively, then what is the length of this wall?
4 What will be the cost of fitting one square tile if the area of the floor is (6x4 + 11x3 – 3x2 + 27x – 5) square units, and the total cost of fitting is �(3x2 – 2x + 5)?
5 Create a word problem on dividing a polynomial by polynomial. Creativity
17 Linear Graphs
Letʹs Recall
Suppose we conduct a survey in our class, where we ask the students what their favourite sport is. The data set obtained is given below.
The above data can be represented in the form of different graphs.
A bar graph is a pictorial representation of data using bars that can either be horizontal or vertical.
A pie chart is a circular graphical representation used to display data distribution. It divides a circle into sectors, where each sector represents a proportionate part of the whole dataset, making it easy to visualise percentages or proportions of different categories within the data.
Warm-up
Line Graphs and Linear Graphs
A company sells two brands of laptops, A and B. The sales head wants to visualise their daily sales data over a week.
Line Graphs
He makes graphs to show the sales of both brands.
We can say that a line graph displays data that changes continuously over a certain period of time.
How many units of Laptop A were sold in total?
In total, 1000 + 1400 + 1800 + 1600 + 1600 + 2200 + 2400 = 12,000 units of Laptop A were sold.
How many units of Laptop B were sold in total?
In total, 1600 + 1000 + 1800 + 1800 + 2000 + 2400 + 2000 = 12,600 units of Laptop B were sold.
Reading Double Line Graphs
What if the data is represented by one graph?
A graph with two lines on the same graph is called a double-line graph. It is an extension of a regular line graph.
In a double-line graph, we can compare and analyse two related data series simultaneously, on the same graph, for better insight and comparison. This graph outlines the daily sales data of the company over a particular week.
On which day was the highest sale of Laptop A?
The graph shows that the highest number of Laptop A units sold was 2400 on Day 7.
On which day was the lowest sale of Laptop B?
According to the graph, the lowest number of Laptop B units sold occurred on Day 2, with a total of 1000 units.
Example 1: The graph shows the annual percentage of profit earned by the company during the years 2017 to 2022. Read the graph carefully and answer the questions.
1 Find the year where the percentage profit is the lowest.
In the line graph the lowest point is 40, so the lowest profit percentage is in the year 2020.
2 What is the average profit earned during the years 2017 to 2022?
The average profit earned during the years 2017 to 2022
= Total profit percentage
Total number of years
= 60 + 90 + 80 + 40 + 60 + 90 6 = 420 6 = 70%
Example 2: The graph represents the average snowfall in two different cities, A and B, for 10 consecutive days. Read the graph carefully and answer the following questions.
1 What is represented on the x-axis and y-axis respectively?
The x-axis represents ‘Day’, and the y-axis represents ‘Snowfall (in inches)’.
2 On which day did it snow the most and least in City A?
In City A, it snowed the most on day 10 and the least on day 3.
3 On which day did it snow the most and the least in City B?
In City B, it snowed the most on day 9 and 10, and the least on day 2.
4 On which day did both cities have equal levels of snowfall?
Both cities had equal levels of snowfall on days 4 and 10.
The given graph shows the profit gained by two companies over a period of years. Read the graph carefully and answer the following questions.
1 The profit gained in the year 2012 in total was 17,000 units
2 The difference in the highest profit gained by Company A and the lowest profit gained by Company B is
3 The percentage decrease in the profit of company A from 2011 to 2014 is
4 The percentage increase in the profit of company B from 2011 to 2014 is
5 The company that earned more profit overall is .
Drawing Double Line Graphs
We now know how to read a double-line graph. But, how is the graph created?
Let us look at the sales of Laptop C and Laptop D over the week and draw a double line graph.
3 Mark the points.
2 Draw and label the axis.
Remember!
Draw the line graph to represent the above information. Laptop
Scale: 1 division = 500 laptops
1 Select a suitable scale.
Scale: 1 division = 200 units
Laptop A Laptop B
4 Draw line segments to join the points.
A single-line graph represents data from one set of information, while a double-line graph represents data from two different sets of information on the same graph.
Example 3: The table represents the average percentage scored by the students in a class in each subject.
Average Percentage Scored
Example 4: A patient’s body temperature was recorded every hour for two days and is given in the table.
Draw a double line graph for the above information.
The population (in thousands) of men and women in a town in different years is given below.
Draw a double line graph for the above information.
Do It Yourself 17A
1 State True or False.
a A line graph is used to study how data changes over time.
b When interpreting a double-line graph, if one line is consistently higher than the other, it means that the data represented by that line is always greater.
c Line graphs can also be called histograms.
d In a double-line graph, the two lines must always intersect at some point on the graph.
2 The graph shows the number of shirts sold by a shopkeeper in a week.
Answer the following questions.
a On which day were the most shirts sold?
b On which day were the fewest shirts sold?
c What was the percentage increase in the number of shirts sold from Wednesday to Thursday?
d What is the ratio of the number of shirts sold on Tuesday to the average number of shirts sold on all 5 days?
3 Draw a double-line graph for the data on the savings of a sister and brother for four consecutive years.
4 During an intense summer, two cities in the United States, Arizona and Dallas, experienced temperature variations from June to October. To understand the temperature trends, the city planners and residents recorded the temperature in Fahrenheit, as shown in the table below. Represent it as a double line graph.
5 Create a data set to form a double line graph.
1 The graph shows the population of two cities from 2000 to 2004. Read both the statements given below and choose the correct option.
Assertion: City A was most populated in 2004 and least populated in 2001.
Reason: In 2001, the population of City A was 60% of the population of City B.
a Both A and R are true, and R is the correct explanation of A.
b Both A and R are true, but R is not the correct explanation of A.
c A is true, R is false.
d A is false, R is true.
Linear Graph
Raman and his father took their dog Bruno for a training session where they saw a chart displaying the cost of training dogs.
Let us plot a linear graph for the above data.
Think and Tell
How is this graph different from the line graph?
The graph is a straight line. So, it is called a linear graph. What is the difference between a line graph and a linear graph?
A line graph has line segments joined one after the other, but a linear graph is a straight line.
Cartesian Coordinate of a Point
A plane that has an x-axis and a y-axis is called a cartesian plane
The point where the x-axis and the y-axis intersect is called the origin. It is represented by O.
The ordinate is the line parallel to the y-axis. The abscissa is the line parallel to the x-axis.
Remember!
Every point is in the form of coordinates (x, y).
O x y x P(x, y)
Y(Ordinate) (Abscissa)
Did You Know?
Srinivasa Ramanujan, an Indian mathematician, indirectly influenced graph theory through his ground breaking work in number theory. Although he didn't directly study graphs, his insights into partitions of numbers and modular forms laid the foundation for understanding patterns and symmetries, which are fundamental to graph theory.
When we put a point on paper, we can measure the x-coordinate and y-coordinate to find the position of the point. The point is given as P(x, y).
The coordinate axes (x-axis and y-axis) divide a plane into 4 regions, called quadrants.
Region Quadrant
Signs of Coordinates
XOY I (+, +)
YOX’ II (–, +)
X’OY’ III (–, –)
Y’OX IV (+, –)
Here, x is the positive x-axis, and x’ is the negative x-axis.
Similarly, y is the positive y-axis, and y’ is the negative y-axis.
The coordinates of O are (0, 0). Every point on the x-axis has its y-coordinate zero, and therefore, it is of the form (x, 0) and vice versa.
Quadrant 2 (–, +)
x x’ y y’
Quadrant 3 (–, –)
Quad rant 1 (+, +)
Quadrant 4 (+, –)
A point whose x-coordinate is zero and y-coordinate is non-zero will lie on the y-axis.
Example 5: In which quadrant do the following points lie? 1 (4, 3) - First quadrant 2 (–4, 3) - Second quadrant 3 (4, –3) - Fourth quadrant 4 (–4, –3) - Third quadrant
Example 6: Write the abscissa and the ordinate of the point:
1 (3, 4) 2 (4, 3)
We know that abscissa means the x-coordinate, and ordinate is the y-coordinate. Therefore,
1 In (3, 4): The abscissa is 3 and the ordinate is 4.
2 In (4, 3): The abscissa is 4 and the ordinate is 3.
Example 7: What is the perpendicular distance of the point (–2, –3) from the:
1 x-axis? 2 y-axis?
The perpendicular distance of the point (–2, –3) from the: x-axis = 3 units; y-axis = 2 units
Distance can never be negative.
Example 8: Draw the line passing through (2, 3) and (3, 2). Find the coordinates of the points at which this line meets the x-axis and the y-axis.
The line meets the x-axis at (5, 0) and it meets the y-axis at (0, 5)
Plot the given points on a graph.
7)
10)
9)
14)
Drawing a Linear Graph
We know what a linear graph is. But, how do we draw a linear graph? Let us look at the steps below to draw the graph for converting kilograms to grams.
1 Based on the data, choose a suitable scale and draw the x-axis and y-axis.
3 Draw a line to connect all the points.
Now we know how to make a linear graph!
Let us see some examples based on linear graphs.
Scale: x-axis: 1 division = 2 kg y-axis: 1 division =
2 Then, from the data, we mark their respective coordinates on the graph.
Example 9: The table shows the relationship between simple interest and the period of time.
Draw a graph for the above information.
Taking the scale,
1 division = ₹200:
We plot the number of years on the x-axis, and the simple interest on the y-axis.
We then plot the points and connect them.
Error Alert!
The
should always be the same throughout one axis.
Example 10: In the table, we are given the side lengths of a square and its perimeter.
Draw a graph for it. Also, check if the graph obtained is linear or not.
Scale: x-axis: 1 division = 1 cm y-axis: 1 division = 4 cm
Remember!
A straight-line graph is called a linear graph.
The graph obtained is a linear graph.
Example 11: The table shows the area of squares with respect to their sides.
of side
Draw a graph for it. Also, check if the graph obtained is linear or not.
Scale:
x-axis: 1 division = 1 cm
y-axis: 1 division = 5 cm2
The graph obtained is not a linear graph.
Example 12: Draw a graph representing three multiples of 3.
Scale:
x-axis: 1 division = 1 unit
y-axis: 1 division = 1 unit
Sohan was riding his bicycle to school from his home.
Complete the graph for the above data.
Scale:
x-axis: 1 division = 2 units
y-axis: 1 division = 5 units
Reading Linear Graphs
We learnt about the relationship between the number of training hours for dogs and the cost by plotting the points on the graph. But what exactly can we interpret from this?
On the x-axis, we have represented the time taken to train the dogs, with the scale taken as 2 divisions = 1 hour.
On the y-axis, we have represented the cost of training dogs, with the scale taken as 1 division = ₹100.
The cost of training a dog for 1 hour is ₹100.
The cost of training a dog for 2 hours is ₹200.
Similarly, the cost of training a dog for 5 hours is ₹500.
Example 13: From the following graph, find the perimeter of the square that has the given length of the side:
Example 14: Look at the graph and answer the questions.
1 What is represented on the x-axis and the y-axis?
The x-axis represents simple interest, and the y-axis represents deposits.
2 Find the interest on the deposit of ₹2500 for a year.
Interest on the deposit of ₹2500 is ₹200 for a year.
3 To get interest of ₹280 per year, how much money should be deposited?
₹3500 should be deposited every year to get interest of ₹280.
Monica was driving her car. The following graph represents the distance (in km) covered in a particular time (in minutes).
1 The x-axis represents the .
2 The y-axis represents the
3 The distance covered in 4 minutes is .
4 The distance of 5 km was covered in .
Do It Yourself 17B
1 State True or False.
a Every point on the y-axis is of the form (x, 0).
b The graph of every linear equation in two variables need not be a line.
c A point whose y-coordinate is zero and x-coordinate is 5 will lie on the y-axis.
d The coordinates of the origin are (0, 0).
e A point whose x-coordinate is zero and y-coordinate is non-zero will lie on the y-axis.
2 Write the abscissa and the ordinate of each of the following points.
a (9, 4) b (4, –5) c (0, 4) d (–2, –8) e (0, –7)
Chapter 17 • Linear Graphs
3 On which axis do the following points lie?
a (0, 1) b (–8, 0) c (9, 0) d (0, –5) e (0, 0)
4 In what quadrants do the following points lie?
a (–8, 8) b (–9, –2) c (1, –8) d (8, 5) e (–5, 0)
5 Plot the given points on a graph sheet and verify if they lie in a straight line.
6 Draw a line passing through (4, 4) and (–4, –4). Find the coordinates of the points at which the line meets the x-axis and y-axis.
7 The cost of a notebook is ₹50. Draw a graph after making a table showing the cost of 2, 3, 4, … and so on up to 10 notebooks. Use it to find:
a the cost of 7 notebooks.
b the number of notebooks purchased with ₹550.
8 The Rajdhani Express travels from Mumbai Central (MMCT) to New Delhi (NDLS), covering a total distance of around 1400 km. Below is the dataset with the approximated distance covered at various times during the journey. Plot a graph showing the distance covered by the train over the given time.
9 Create a dataset and check whether it forms a linear graph or not.
Critical Thinking
1 Simran is visiting a new city and decides to use a taxi to explore different places. The taxi service in this city charges a fixed initial fee plus a variable rate per kilometre travelled. Simran keeps track of her taxi rides to understand how the fare is calculated. The taxi service charges an initial fee of ₹50 per ride. Here is the fare information she noted for her rides:
For a 5 km ride, the fare was ₹150.
For a 10 km ride, the fare was ₹250.
a Use the information to form an equation for the given scenario.
b List and plot 5 data points on a graph representing the distance and the fare.
Points to Remember
• A line graph displays data that changes continuously over a period of time.
• A plane that has an x-axis and y-axis is called a cartesian plane.
• Every point is in the form of coordinates (x, y).
• A quadrant is a region defined by the two axes (x-axis and y-axis) of the coordinate system.
• A straight-line graph is called a linear graph.
• A line graph has line segments that are joined consecutively, but a linear graph is a straight line.
Math Lab
Collaboration & Experiential Learning
Are All Line Graphs Linear?
Aim: Determine whether a line graph is always a linear graph.
Setting: In groups of 5 members
Method:
Material: A pen, a piece of paper and a sheet of graph paper
1 In groups, look up the Internet to find the average temperature in your city for 5 days.
2 Make a table for the data.
3 Draw a line graph to show the average temperatures.
4 Now on another graph paper, draw a graph to show any one average temperature reading for each of the 5 days.
5 Discuss the results and check how are the 2 graphs different from each other.
Chapter Checkup
1 Write the abscissa, ordinate and the quadrants of the points:
a (5, 4) b (–8, –2) c (–9, –18) d (–5, –10)
2 Draw the points (5, 4) and (4, 5). Do they represent the same point?
3 Plot the following on a graph sheet. Verify if they lie on a line.
a A (4, 6), B (4, 2.5), C (4, 2), D (4, 0) b A (5, 3), B (2, 3), C (2, 5), D (5, 5)
4 Draw a line passing through (1, 3) and (0, 4). Write the coordinates of the point at which this line meets the x-axis and y-axis.
5 The number of electrical appliances manufactured by a factory during five consecutive years is given below.
Years 2000 2001 2002 2003 2004
Number of appliances (in thousands) 10 15 8 12 16
Draw a line graph representing the above data.
6 Look at the figure and complete the following table:
7 Draw a linear graph representing five multiples of 2.
8 Raman and Ansh were walking on a road. The data was collected for the distance they walked in a particular time.
Draw a double-line graph for the data.
9 The following data represents the interest on deposits Farhan made for a year.
Draw a graph for the above data. Does the graph pass through the origin?
Challenge
1 Mr Gupta owns a company. The graph represents the sales data from 2015 to 2022. The sales in 2022 and 2023 were thrice and twice of that in 2017 and 2016, respectively. The sales in 2024 were at an all time high. Is it possible to draw the graph for the sales from 2015 to 2024?
2 The question consists of a question and two statements, labelled (1) and (2), which contain certain data. You need to decide whether the data given in the statements is sufficient for answering the question.
Question: What is the area of the triangle ΔPQR?
Statement 1: The coordinates of point P are (7,8).
Statement 2: The coordinates of points Q and R are (7,0) and (3,0).
a Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
b Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
c Both statements together are sufficient to answer the question, but neither statement alone is sufficient.
d Each statement alone is sufficient to answer the question.
Case Study
Let's Drive with Mariam!
Mariam, a life skills trainer, goes to various cities by car. She often find herself struggling with the travelling time. To manage her schedule efficiently, she tracks the distance travelled by her car in 5 hours. Refer to the given graph and help Mariam by answering the given questions.
1 What is the speed of the car in which Mariam is driving?
a 20 m/hr
c 30 km/hr
b 20 km/hr
d 1km/20hr
2 How many kilometres would Mariam drive in 8 hours, if the same trend follows?
Scale: x-axis: 1 division = 1 hour
y-axis: 1 division = 10 km
3 How much distance will be travelled by Mariam in 2.5 hours?
a 60 km
c 40 km
b 55 km
d 50 km
4 If Mariam increases her speed by 10 km/hr, how much less time will she take to cover 60 km?
5 Give one tip to ensure safety while driving.
Answers Answers
Chapter 1
Let’s Warm-up
1. < 2. < 3. < 4. = 5. = Do It Yourself 1A
1. a. 0.5
2. a. 12 7 b. 13 2 c. 5 9
3. a. 10 11 b. 11
4. a. Closure property b. Associative property
c. Subtraction property of zero
5. a. 0; Additive Identity b. 9 16; 5 8; Associative Property
c. 3 5; Subtraction Property of Zero
6. Students will verify using the properties.
7. 8.7
Do It Yourself 1B
1.
2.
36 35
3. a. 7 48 b. 20 33 c. 9 14 d. 14 5 or − 24 5 e. 40 3 or 1 13
4. a. Students will solve using the associative property of multiplication.
b. Students will solve using the associative property of division over subtraction.
c. Students will solve using the commutative property of multiplication.
5. a. 1; Multiplicative Identity b. 11 6 ; Multiplicative Inverse c. 1; Division by 1
6. a. 7 2 b. 19 15 c. 13 5 7. a. 11 4 , 4 11 b. 1, 1 8. 56 17 ; 17 56
9. A = 26,569 25 sq.m or 1062 19 25 10. 55 1m 64 11. 2.5
12. 7 5 13. 320 pages 14. �125
Challenge 1. The statement is false, 9
Chapter Checkup
1. a. zero b. negative c. 0 d. Zero
6
–39
2.
f. 1 9 g. 3 4 h. 125 338 3. 1489.8sq. m
4. Students will prove using the given values for m, n and o. 5. − 181 85 or 2 11 85 6. 153 28 7. − 1 31 8. a. –1 3 b. 7 4
9. 1 82m 4 10. 4 3 4 kg or 4.75 kg 11. 23 14 hours 24
12. Japan; 163 200 trillion dollars 13. 23 6 24 pizza 14. ₹250
15. Answers may vary. Sample answer.
Nitin is filling small containers with water. He has 7 8 of a gallon of water and wants to fill each container with 1 4 of a gallon. How many containers can Nitin fill?
Challenge 1. 75 2. Option b
Case Study
1. b 2. c 3. d 4. ₹2590 5. 19 kg
Chapter 2
Let’s Warm-up
1. False 2. True 3. False 4. True 5. False
Do It Yourself 2A
1. a. 3 b. 1 c. 3 2. 3. a. 102 b. 12 c. 5 d. 18 e. 4.4 f. 13 3 or 4.33
4. 20, 22 5. 15, 45 6. 2205 square metres.
7. a. 9 cm b. 5 cm c. 23 8 cm or 2.875 cm. 8. 266 square units
9. Answer may vary: Sample answer.
a. x + 2 = 7 b. 2x + 3 = x + 8 c. 3x 5 = x + 5 9. 22
Challenge 1. 22
Do It Yourself 2B
1. a. No b. Yes c. No
2. a. 8 27 b. 5 c. 43 14 d. 38 67 e. 3 f. 143 52
3. a. y = 3 b. y = 1 3 4. 11 14 5. 18 12 6. 47 calories
Challenge 1. Statements 1, 3 and 4
Do It Yourself 2C
1. a. 3x + 5 = 1 2 x 13 b. 4y + 11 = 2y + 56
c. n + (n + 2) + (n + 4) = 144 d. st = 240; (s + 20)(t – 2) = 240
2. 85, 87, 89, and 91 3. 132, 143, and 154 4. 30°
5. 26 years 6. Rohit - 92 runs, Virat - 204 runs
7. Daughter - ₹15,00,000; Son - ₹10,00,000 8. 72
9. 4200, 1800 10. 30, 60 11. 30 years 12. 1
13. 52 14. 12 km/h
Challenge 1. 10 notes of ₹5, 82 notes of ₹10 2. 25 km/h, 35 km/h.
Chapter Checkup
1. a. 2 b. 4 c. 3 2.
3. a. 78 b. 18.5 c. 4 d. 10 e. 7 f. 0
4. a. 3 b. 4 c. 7 d. 8 e. 109 30 f. 5
5. a. 40 b. 8 c. 35 22
6. a. + b. −,+ c. +, +; −, + d. +, +; +, −
7. 7 10 8. 44 years 9. 1802.25 sq. m
10. 300 metres by 140 metres 11. 3 years
12. 35°, 85°, 95°, and 145° 13. 120 goats 14. ₹3000
15. 21 hours
16. Answers may vary. Sample answer.
Sides of triangle: 2x, x, x + 4
Side of square: x + 1
Challenge 1. 9 5 6 hours 2. b
Case Study
1. Option c 2. Option b 3. Option c
4. ₹1.5 per km 5. False 6. Answers may vary.
Chapter 3
Let’s Warm-up 1. Open curve 2. Closed curve
3. Polygon 4. Non-simple curve
Do It Yourself 3A
1. a. heptagon b. 9 c. regular polygon
2. a. True b. False c. True
3. a. Convex polygon. b. Concave polygon.
4. a. Convex polygon. b. Convex polygon.
c. Concave polygon. d. Concave polygon.
5. Convex polygon 6.
7. a. 2, Quadrilateral b. 20, Octagon c. 27, Nonagon d. 35, Decagon
8. 5 9. 3 10. Figures may vary. Sample figure.
Challenge 1. Concave polygon. Number of diagonals = 12
Do It Yourself 3B
1. Figures may vary. Sample figures.
b.
a.
c.
2. a. Concave Quadrilateral b. Convex Quadrilateral
c. Concave Quadrilateral
3. x = 9.8°, y = 27° 4. 40 cm, 25 cm
5. 60°, 120°, 60° and 120°. 6. a = 4, b = 7
7. ∠ MJL = 70°; ∠ TJK = 20° 8. ∠QPT = 40°, ∠TRS = 29°
Challenge 1. Answer may vary. Sample answers:
a. PZ & ZR, ZQ & ZS, PQ & PS, RS & QR
b. ∠ QPS & ∠ QRS, ∠ PQR & ∠ PSR, ∠ QSR & ∠ PSQ, ∠ PQS & ∠ RQS
c. ∆ QPR ≅∆ SPR, ∆ QRS ≅∆ QPS, ∆ QZR ≅∆ SZP
d. Yes e. Yes
Do It Yourself 3C
1. a. 360° b. 120° c. quadrilateral d. 20°
2. a. True b. False c. False d. True
3. a. 120° b. 45° c. 30°
4. a. 360° b. 900° c. 1800°
5. a. 261° b. 96° c. 20°
6. a. 123° b. 70° c. 60°
7. a. 9 b. 8 c. 6
8. 120°, 60°, 120° and 60°
9. 32°, 16°, 81°, 95°, 27° and 109° 10. 144°
Challenge 1. Convex quadrilateral, 144°
Chapter Checkup
1. a. irregular polygon b. 720° c. 5 d. 360°
2. a. True b. True c. False d.False
3. Option C 4. a. Concave polygon b. Convex polygon
c. Concave polygon d. Convex polygon
5. a. 2 b. 27 c. 119 6. Option c
7. a. 90° b. 24° c. 18° d. 10°
8. a. 20 sides b. 10 sides c. 4 sides
9. a. 110°, 90°, 70°, 90° b. 135°, 120°, 80°, 25° c.100°, 95°, 85°, 80°
10. a. 103° b. 127° c. 110°
11. a. 240° b. 150° c. 123° d. 111° e. 196° f. 148°
12. 53°, 127°, 53°, 127° 13. 92°
14. 60°, 120°, 60°, 120° 15. 30°, 240°
16. a. w° = 50°, x° = 125°, y° = 10°, z° = 45°
b. x° = 15°, y° = 11° c. x° = 101°, y° = 19°
17. 54 diagonals, 10 non-overlapping triangles
18. 10 bridges, 35 diagonals
Challenge 1. Option a 2. Option d
Case Study
1. Option c 2. Option b 3. No 4. Parallelogram
5. Answers may vary
Chapter 4
Letʹs Warm-up
Challenge 1. Yes, the range will get affected as the highest value of the incorrect data set has been replaced with some other value. Do It Yourself 4B 1. a. 50 b. 45; 55 c. 10 2.
Tennis
2. Number
3. Class intervals (Electricity bill in ₹) Frequency
3. a. 14 b. 14 c. 60,000
5.
5. a. 20 students b. 8 students c. 7.5 d. 28 e. 71.43%
6. Answers may vary Sample answer. What percentage of students scored more than 10 marks?
Challenge 1. e Do It Yourself 4C
1. a. 26.55% b. 15.5% c. 63:86 d. 70,800 tonnes
2. a. 13.14% b. 21.37% c. 97:67 d. 217:293
3. a. $3500 million b. $600 million c. 12.9% d. 53:66
6. Answers
a. 103.3 crores b. 17.217 crores c. 8.97% d. 2016 and 2019
5. a. 400 students b. 66.67% c. 77.78% d. 14.28%
e. Answer may vary. Sample answer. What is the ratio of students who passed in 2018 to those who passed in 2020?
6 a. 48 million b. 5 million c. 20.5 million d. 6 million
Challenge 1. One reason a bar graph is not suitable for displaying this data is that a bar graph is good for showing single values for each category, but the life spans are given as ranges, not single values. A bar graph can't show the full range from the lowest to the highest number for each animal. Yes, we can plot the graph as:
a. 4 presidents b. 12 presidents c. 29 presidents
3. a. 365 people b. 86.30% c. 75.34% d. 43:18
4. a. 550 workers b. 380 workers c. 82.35% d. 23:45 e. 330
5. a. 81.48% b. 9.25% c. 35:19 d. 34
6. a. 10 employees b. 23:16 c. 84.6% d. Answers may vary. Sample answer. What is the ratio of the number of employees who are younger than 40 years to those who are older than 40 years?
Challenge 1. The data set only contains five ages (65, 73, 70, 74 and 69). Histograms are more effective and meaningful when used with larger data sets where the distribution of data can be more clearly seen. Also, the ages provided are relatively close to each other, and with such a small range, a histogram won't show a clear pattern or trend.
A bar graph will be an appropriate graphical representation for the given data set and can be given as:
Do It Yourself 4D
1. a.
2.
4. a. 300 fruits b. 340 fruits c. 7:8 d. Banana e. Answer may vary. Sample answer. What is the ratio of bananas sold by both the vendors?
5. a. 8040 runs b. 6940 runs c. 157.14 d. 188:223 Challenge 1. a Do It Yourself 4E
Chapter Checkup 1.
3. a. AB b. 48 4. a. 5 crores b. Maharashtra and Uttarakhand c. Nagaland
6. a. 1,04,000 units b. 83,200 units c. 83,200 units d. 5:4
7. a.
9. a. 3400 cars b. 3600 cars c. 11:14 d. 17.65%
10. a. 1,62,000 b. 1,83,000 c. 15:13 d. 27,000
e. Answers may vary. Sample answers.
a. What is the average number of candidates appearing for the entrance exam for the year 2022?
b. What is the ratio of the number of candidates appearing for the entrance exam from Delhi and Bhopal in the year 2022?
Chapter 5
Let’s Warm-up 1. 3 20 2. blue 3.
12. a. 105 students b.
Study
1. b 2. c 3. ₹590, ₹120
4. Mayra should send both items as one parcel.
Ruchika’s Score EVS, 125 Science, 100
Start.
English, 115 Hindi, 120 Maths, 140 4. No. of workers from various states working in a garment factory Tamil Nadu, 620 Kerala, 300 Others, 100 Andhra Pradesh, 340
Karnataka, 440 5. Import Items
Plastics, ₹180
Furniture, ₹150 Gems, `150
Fuels and oil, ₹240
% of Buyers
Chemicals, ₹180
Others, 10 Brand 0, 20 Brand M, 25 Brand P, 30 Brand N, 15 7. Number of Lions Mozambique 1500 Kenya 2500 Botswana 3000 Angola 1000 Malawi
8. Answer may vary.
Do It Yourself 5B
1. Education = 40,000, Arts = 1,00,000, Law = 70,000, Commerce = 1,65,000, Science = 1,25,000
2. a. Shared cab b. 1 8 c. Shared cab
3. a. 2000 cars b. 360 cars c. 1140 cars
4. a. 600 students b. Apple juice; 250 students c. 9 10
5. a. 700 animals b. Tigers; 35 c. 21
6. a. 1500 teenagers b. 15:17
7. a. 75 plants b. 5 16 c. 9:5
8. a. Coal b. 1:11 c. 19 1 0 0
9. Answers may vary. Sample answer.
a. What is the ratio of consumption of Renewable source of energy to the consumption of coal?
b. Which is the least consumed form of energy?
Challenge 1. a. 21.6° b. 28,800 tonnes c. June, 1800 tonnes d. 25%
Chapter Checkup
1. 82.8°
2. a. Items Sold 67° 54° 45° 36° 158° Pulses, 67 Spices, 45 Others, 36 Rice, 158 Bread, 54
b.
Sandwiches, 80 Shakes, 90 Burgers, 72 Ice creams, 64 Items Sold Frenchfries, 54
3. No. of Families Owning Pets Others, 16 Rabbit, 12 Dog, 26 Cat, 20 Birds, 6 54° 27° 72° 90° 117°
4. No. of Students 84° 45° 77° 35° 119° Others, 175 French, 225 English, 420 Maths, 595 Science, 385
5. Adventure, 600 Comedy, 760 Books Read
Biography, 440 Fantasy, 280 Novels, 320 114° 42° 90° 66° 48°
6. a. Notebooks b. 1 4 c. 15.08% 7. 900 ice creams
8. a. Agriculture b. 90° c. 2:1
9. a. 20% b. ₹30,000 c. ₹25% 10. a. 18% b. 1:7 c. 68%
11. Answer may vary.
Challenge 1. b 2. a Case Study
1. iii 2. 10,000 3. 3000 4. 84,000
Chapter 6
Let’s Warm-up 1. Impossible 2. Sure 3. Equally likely 4. Likely 5. Unlikely
Do It Yourself 6A
1. a. 0 b. 1 c. heads; tails d. 3 2. b 3. 25 26
4. a. 1 2 b. 125 contestants 5. a. 1 6 b. 1 2 c. 4
6. 1 7. a. 1 6 b. 1 3 c. 50 times
8. Answers may vary. Sample answers.
a. What is the probability of getting a prime number?
b. What is the probability of getting a number less than 7?
9. a. 5 36 b. 1 12 10. 1 2 3 4 5 4 7 6
11. Basket B, 4 20 or 20%.
Challenge 1. a. 18 outfits b. 2 9
Do It Yourself 6B
1. a, b, d 2. 1 6 or 0.16 or 16.67%
3. a. 5 9 or 0.55 or 55.55% b. 40 times 4. 63
5. a. 10 90 or 11.11% b. 53 90 or 58.88% c. 35 90 or 38.88%
d. 27 90 or 30% 6. a. 61 125 or 48.8% b. 64 125 or 51.2%
c. 29 125 or 23.2% d. 25 125 or 20% 7. 125 pairs of jeans
Challenge 1. a Chapter Checkup
1. a. 1 b. 0 c. 1 7 d. 1 e. 1 6 2. a. Heads, Tails
b. 1, 2, 3, 4, 5, 6
c. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y and z
d. (Heads, Heads), (Heads, Tails), (Tails, Heads), (Tails, Tails)
e. (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
3. a. 1 8 or 0.125 or 12.5% b. 3 8 or 0.375 or 37.5%
c. 3 8 or 0.375 or 37.5% d. 1 8 or 0.125 or 12.5%.
4. 21 126 = 5. a. 2 5 b. 3 5 6. a. 17 20 b. 3 20 7. 1 2
8. a. Theoretical Probability is greater.
b. Experimental probability is greater.
c. Experimental probability is greater.
d. Both are equal to 1.
9. a. 4 9 = or 44.44% b. 1 9 = or 11.11% c. 8 9 = or 88.88%
d. 4 ) 9 = or 44.44% 10. a. 51 ) 102 == or 50% b. 1 10 = or 10%
c. 3 10 = or 30% 11. 12 pearl bangles
Challenge 1. Ranita 2. a Case Study
1. Option b 2. Option a 3. 0.6 4. True 5. Answers may vary
Chapter 7
Letʹs Warm-up
1. False 2. True 3. False 4. True 5. False Do It Yourself 7A
1. a. i. 1 ii. Odd square b. i. 6 ii. Even square c. i. 1 ii. Odd square d. i. 4 ii. Even square
e. i. 9 ii. Odd square
4. a. 2401
+ 57 + 59 + 61 + 63 + 65 + 67 + 69
6. 21, 28, 36, 45; 21 + 28 = 49 = 72, 28 + 36 = 64 = 82, 36 + 45 = 81 = 92
7. a. 25, 24 b. 41, 40 c. 35, 34 d. 51, 50 e. 63, 62
8. a. 1624 + 1625 b. 1984 + 1985 c. 2964 + 2965 d. 760 + 761 e. 3612 + 3613
9. a. 5625 b. 101 c. 9025 d. 155 e. 11,025
10. a. 5775 b. 4352 c. 2600 d. 8645 e. 1440
11. a. (12, 35, 37) b. (16, 63, 65) c. (28, 195, 197) d. (32, 255, 257) e. (36, 323, 325) 12. 11115556, 1111155556, 333334
13. 9999800001, 999998000001 14. a. 64 b. 289 c. 441
15. a. 22, 32, 42, …, n2 + (2n + 1) = (n + 1)2
b. 22, 32, 42, 52, 62, 72 c. 3136 16. 5,76,000 kgm2s2
Challenge 1. Answers may vary. Sample answer.
(3, 4, 5); (5, 12, 13); (8, 15, 17); (7, 24, 25)
Do It Yourself 7B
1. a. 3 or 7 b. 4 or 6 c. 2 or 8 d. 1 or 9 e. 2 or 8
2. Length of each side = 4 units
3. a. 12 b. 6 c. 21 d. 30 e. 13
4. a. Not a perfect square b. Not a perfect square
c. A perfect square, 86 d. Not a perfect square
e. A perfect square, 163
5. a. 81 b. 94 c. 142 d. 157 e. 25 34
6. a. 3; 162 b. 2; 102 c. 31; 310 d. 39; 780 e. 10; 200
7. a. 2, 68 b. 3, 42 c. 5, 54 d. 17, 42 e. 13, 66
8. 144 9. 36 students 10. No
Challenge 1. 5
Do It Yourself 7C
1. a. 1 digit b. 2 digits c. 2 digits d. 2 digits e. 3 digits
2. a. 256 b. 278 c. 324 d. 356 e. 381
3. a. 12, 38 b. 59, 72 c. 76, 94 d. 248, 166 e. 479, 358
4. a. 17, 75 b. 4, 68 c. 24, 418 d. 41, 279 e. 24, 532
5. a. 2.65 b. 6.52 c. 8.88 d. 90.01 e. 32.14
6. a. 0.894 b. 9.219 c. 2.645 d. 3.464 e. 3.098
7. a. 304 b. 17 16 c. 16 d. 10.56 8. 25 m 9. 390 m
10. 9801, 99 11. Answers may vary. Challenge 1. 8
Chapter Checkup
1. a. 1444 b. 2209 c. 9 49 d. 81 169
2. a. 1769 b. 4355 c. 10,816 d. 14,880
3. 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + 31 + 33 + 35
4. (96, 2303, 2305); (24, 143, 145)
5. a. Not a perfect square b. Perfect square, 46 c. Not a perfect square d. Perfect square, 56
6. a. 2.81 b. 47.56 c. 1.93 d. 80.70
7. 21; 811 8. 3600 9. 31.62 m
10. Twice the combined area of the original rooms
11. No. The square root of 1 is 1. 12. 6.28 13. 86
Challenge 1. Option A 2. Option D
Case Study
1. Option B 2. Option B 3. 7200 sq. m 4. ₹9,71,407.36
5. Answer will vary.
Chapter 8
Letʹs Warm-up
1. Pineapple 2. 30 3. 48 4. 12 5. 112
Do It Yourself 8A
1.
2. a. 3375 b. 17,576 c. 59,319 d. 17,71,561
3. i. a. 1 b. 0 c. 3 d. 0
ii. Odd cubes: a, c; even cubes: b, d iii. b, c
4. a. 64 343 b. 512 729 c. 125 4913 d. 5832 35,937
5. a. 21.952 b. 1.728 c. 28.094464 d. 0.000512
6. a. Not a perfect cube. b. Perfect cube; 24 c. Perfect cube; 47 d. Perfect cube; 49
7. a. 4; 12 b. 4; 8 c. 2; 18 d. 4; 24
8. a. 9; 4 b. 15; 7 c. 21; 12 d. 6; 21
9. 1331, 8000 10. a. 2025 b. 6084
11. a. 4921 b. 29,701 12. 50 packs
Challenge 1. No, 12 cubes
Do It Yourself 8B
1.
2. a. 20 b. 25 c. 28 d. 36
3. a. 3 b. 6 c. 12 d. 10
4. a. 32 46 b. 28 51 c. –70 d. 228
5. a. 84 cm b. 44 cm 6. a. 65; 7 b. 18; 13
7. a. 9; 9 b. 44; 14 8. 4, 12, 24 9. 42 cm
Challenge 1. 7; 12
Chapter Checkup
1. a. 68,921 b. 2197 343 c. 8 729 d. 46.656
2. The shaded cube shows the cube of number 3.
3. a. Perfect cube; 94 b. Not a perfect cube c. Not a perfect cube d. Perfect cube; 51
4. a. 2197 b. 4356
5. a. 8 10 or 0.8 b. 14 20 c. 1600 d. 2.2
6. 61 m 7. 3125 cu. cm 8. 45; 14 9. 13; 17
10. 14; 70 11. 17; 68 12. 2058 cu. cm
Challenge 1. 38; 57; 95 2. a. 20 metres b. 160 metres
Case Study
1. d 2. a 3. 15.625 cubic metres 4. 23.328 cubic metres
Chapter 9
Letʹs Warm-up
1. Red 2. Blue 3. 17% 4. 31% 5. 68
Do It Yourself 9A
1. a. 20% b. 56% c. 0.45 d. 0.135 e. 1.205
2. a. 1 250 b. 1 800 c. 5 8 d. 23 200 e. 6 5
3. a. 21:10 b. 11:2000 c. 131:200 d. 11:500 e. 77:500
4. a. 200% b. 30% c. 60% d. 30%
5. a. 80%, increase b. 55.55%, decrease c. 10.2%, decrease d. 10%, decrease
6. a. ₹228 b. 105 kg c. 875 L d. 753.75 grams
7. ₹275 8. 4% increase 9. 7.5%
10. a. 17,500 b. 10,500 c. 4200
11. ₹2,83,500 12. 200 marks 13. ₹18,000
Challenge 1. a. 1500 smartphones b. 600 smartphones
c. 900 smartphones
Do It Yourself 9B
1. a. ₹4500, loss b. ₹2500, profit c. ₹1500, loss d. ₹5500, profit
2. a. Profit%, 14.4% b. Loss%, 26% c. ₹5883.5 d. ₹32,500
3. Profit% = 14% 4. 3.45%, Loss 5. 20% profit 6. ₹4185
7. ₹945 8. 60% 9. ₹1,00,000 10. Gain, 14%
11. ₹1000 and ₹1500; Loss, 4%
12. Answers may vary. Sample answer.
Maya bought a set of 5 books for ₹2200. She sold each book for ₹600. Calculate the total profit% or loss% incurred by Maya.
Challenge 1. ₹98,000
Do It Yourself 9C
1. a. ₹1000; ₹3000 b. ₹800; ₹3200 c. ₹500; ₹3500 d. ₹400; ₹3600
2. ₹725 3. ₹725, 5% 4. ₹20,000 5. 6.25% 6. 34%
7. 23.5% 8. ₹537.03 9. 23.33% 10. 16.66% 11. ₹1152
12. ₹6000 13. Answer may vary. Sample answer.
Maya bought a laptop at a store that was having a sale. The store offered a 15% discount on the marked price of the laptop. After applying the discount, Maya paid ₹34,000 for the laptop. If the store sold the laptop at its marked price, the shopkeeper would have made a profit of 20% on the cost price.
Challenge 1. 55%
Do It Yourself 9D
1. ₹9440 2. ₹49,220 3. ₹14,500 4. ₹13,000
5. ₹16,000 6. ₹4950 7. ₹5 8. ₹708.75 Challenge 1. 12%
Chapter Checkup
1. a. 250% b. 12.5% c. 64% d. 16% e. 380% f. 8.54% g. 0.3% h. 278.9%
2. a. 23:50 b. 1 1250 c. 0.058 d. 1:6 e. 0.014 f. 101 300
3. a. ₹62.5 b. 2 L c. 312.5 cm d. 48.05 kg
4. a. 30%, increase b. 80%, increase c. 16 2 3%, decrease d. 25%, decrease
5. a. CP = 7200 Profit%, 12% b. Loss = ₹23 Loss%, 5% c. SP = ₹7276 Profit%, 7% d. SP = ₹6208 Loss%, 3%
6. a. 20% b. ₹1513
7. 20% 8. 2000 students 9. ₹32,450 10. ₹6,13,149
11. ₹1800 12. 50% 13. a. 33.33% b. 7 15 c. 20%
14. ₹20,000 15. 37 1 2 % 16. Loss, ₹1 17. ₹1400
18. ₹42,840 19. Profit, 20% 20. a. ₹50 b. ₹37.5
Challenge 1. Option A 2. Option C Case Study
1. Option b 2. Option c 3. 75% 4. 245,000,000
5. Answer will vary.
Chapter 10
Let’s Warm-up
1. ₹100 2. ₹200 3. ₹140 4. ₹240 5. ₹360
Do It Yourself 10A
1. a. ₹112; ₹912 b. ₹2582.86; ₹3486.84 c. 2.5 years; ₹5700 d. ₹192; ₹9792 e. 4.5%; ₹1800 2. $2550, $22550
3. P = ₹4000, R = 5% p.a. 4. ₹74.79
5. Answers may vary. Sample answer.
Ravi deposits ₹12,000 in a savings account at a local bank. The bank offers a simple interest rate of 6% per annum. Ravi plans to keep his money in the account for 4 years. How much interest will Ravi earn after 4 years, and what will be the total amount in his account at the end of 4 years?
Challenge 1. 3.75%
Do It Yourself 10B
1. A = ₹2141.16, CI = ₹541.16 2. P = ₹4000 3. 3 years
4. a. ₹62,720 b. ₹70,246.40 5. ₹24,972.8 6. SI = ₹500, Difference = ₹25 7. $32,917.6875 8. CI = ₹9270
9. a. ₹1500 b. ₹1537.5; option b will earn more interest by ₹37.5. 10. ₹24,000
11. Answers may vary Sample answer.
Anita deposits ₹10,000 in a bank that offers a 7% interest rate per annum. Calculate the difference between the simple interest and the compound interest after 3 years, if the compound interest is compounded annually.
Challenge 1. 20% 2. ₹5000
Do It Yourself 10C
1. ₹720, ₹8720 2. ₹7500 3. 2.5 years 4. 8% p.a.
5. ₹31,932.23 6. ₹2805.58 7. ₹2,24,643.825
8. ₹60,000 9. ₹7981.94 10. 18,30,125
11. ₹2,31,525 12. ₹21,600 13. ₹6,71,125
14. Answer may vary. Sample answer.
Sunita borrowed a sum of ₹10,000 from the bank at the interest rate of 10% per annum, compounded annually, and paid back an amount of ₹12,100. For how much time did she borrow the sum?
Challenge 1. Option C
Chapter Checkup
1. a. ₹525; ₹4025 b. ₹3200; ₹3592 c. ₹97.2; ₹2797.2 d. 9%, ₹1800 2. a. ₹5940.5, ₹940.5 b. ₹85,753.152, ₹13,753.152
3. ₹13,500 4. 2 years 5. 10% per year 6. ₹3152.5 7. 12.5 years 8. ₹600, 15% 9. 13,225 people 10. 1.5 years 11. ₹4965 12. ₹98.56 13. ₹14,257.2 14. 50,000 15. ₹6,50,000 16. Answers may vary.
Challenge 1. ₹100 2. Option 3
Case Study
1. c 2. c 3. d 4. ₹25,538
Chapter 11
Let’s Warm-up
1. 5p 2. 15 3. 7p 4. 5b 5. −5b
Do It Yourself 11A
1. a. –x2 + 2x + 3; –x2, –2x b. –x2 + 5x + 6; –x2, 5x
c. –x2 + 4x + 2; –x2, 4x d. 2x + 7; 2x
2. a. Term is 2 3 4 abc . Factors are 3 ,,,, 4 aabc. The coefficient of ‘a’ is 3 4 abc
b. Terms are 6a and 5. Factors are 6, a; 5. The coefficient of ‘a’ is 6.
c. Terms are 8a2, –5a and 1 3 . Factors are 8, a, a; −5, a; 1 3 .
The coefficients of ‘a’ are 8a and −5.
d. Terms are 3 7 12 a , 5abc, 2 4 9 a and –10. Factors are 7 ,,,; 12 aaa 4 5,,,;,,; 9 abcaa –10. The coefficients of ‘a’ are
2 7 12 a , 5bc and 4 9 a.
3. Circle a and d; cross out b and c
4. a. 8 xy + ; x, y; x, y b. 1 2 6 xy ; x, y; x, y
c. (a – b) – ab; a, b, a, b; a, b, ab
5. Figure A: 2 xy + Figure B: 2 yx +
6. a. 2 356 xx++ b. 2 353 xx−+
7. a. 543 xy b. 2 1033 xyxy+−
c. 2 215 2 54pp −++ d. 128 7 87pqp++
8. a. 2 28 xx+− b. 3 3 61 2 mnn+−
c. 2 212 y + d. 1157pqq
9. a. 3326 x b. 11732 42 mm−+ c. 32 61164 xxx−+−
d. 2 610xx −+− 10. a. 59843 aa−++ b. 2 161010 xx++
c. 2 121810 nn 11. 2 151484 pp+−
12. 3 13616hhth −+
13. 2 (29514) mm−+ metres 14. 2 (10431) ss+− metres
15. Answers may vary. Sample answer: Rohit has (5x + 7) fiction books and (x + 3) non-fiction books in his library. How many books does he have in all?
Challenge 1. 2 3 p2 1 4 –1 4 –2 5 – pq2 p2 pq2 ; 1122 35ppq +
Do It Yourself 11B
1. a. ×
Expression: (−3x + 2y) (2x + 4) Product: −6x2 – 12x + 4xy + 8y
Expression: (3 – 2x
Product: 22x – 15 − 8x2 2. a. product = −20xy b. product = 6
2 + 42yz – 35y + 27z2 + 54z – 45
f 24p7 + 72p6 + 85p5 + 12p4 + 82p3 + 152p2 + 65p – 55
4. a. −56 b. −3885 c. −18 d. −594
5. a. 82 5 b. −24 c. − 702 7 6. a. −30x5y3z sq. units
b. 56 5 x2 + 1723 25 x − 99 5 sq. units
c. 54 77 a3b2c4 + 45 66 a2b3c 992 5 sq. units
d. (6z3 + 19z2 – 37z + 10) sq. units
7. a. 72p3q4r4 cubic cm. b. 7 2
c. (−6ab + 2a2 + 3)3 cu. cm d. 64p9q12 (9r + 2q – 5)3 cu. cm
9. −19
10. Answers may vary. Sample answer:
Length = (2x + 5) units; Breadth = (x – 3) units
Area = (2x2 – x – 15) square units.
11. ₹(24x3 – 26x2 – 19x + 6)
Challenge 1. Option a
Chapter Checkup
1. a. Terms: 2 6 pq and 2 8 pq. Factors of 2 6 pq are 6,,,pqq ,, pqq are variables. 6 is the numerical coefficient of 2pq . Factors of 2 8 pq are 8,,,ppq . ,, ppq are variables. 8 is the numerical coefficient of 2 pq
b. Terms: –mn, 2n2 and –3m2. Factors of –mn are m and n m and n are variables. –1 is the numerical coefficient of mn. Factors of 2n2 are 2, n, n n and n are variables. 2 is the numerical coefficient of n2. Factors of –3m2 are –3, m, m m and m are variables. –3 is the numerical coefficient of m2 .
2. a. Binomial b. Monomial c. Trinomial d. Quadrinomial
3. Circle a and d; cross out b and c
4 a. 2 25 x b. 2 465 xx −++ 5. a. 2 75mm++
b. 32 921 zzz−−+ c. 23 6 1365 7 qqq
6. a. 6532 15 53 969 22 zzzzz −−+−
b. 42 273 xxx −+ c. 42 5 11 13 4 yy −++
7. a. 33823 sss ++ b. 42 141614 ttt −+
8. 32 9342 xxx++−
9. a. −198x3y6z7 b. 8yz2 + 20yz − 24y + 14z2 + 35z – 42
c. −2p5 + 2p4 + 16p3 + 97p2 + 75p – 45
d. −5s2t2u + 3stu – 9st e. 21a4 + 29a3 + 98a2 + 16a + 96
f. 24p7 + 42p6 + 56p5 – 20p4 + 18p3 + 111p2 + 149p – 12
10. a. −154 b. 7236 c. −56 d. −940
11. a. 2027 30 b. 214 c. 372 7
12. a. 56x5y3z sq. units b. 9 2 x2 + 263 14 x − 110 7
sq. units
e. 8a4 + 32a2 + 9a + 77
c. 36 91 a3b2c4 + 3 26
a2b3c2 3 26
sq. units
d. (10z3 + 39z2 − 82z + 33) sq. units
13. a. 4 11 p4q5r5 + 4 11 p4q4r 996 5 cu. cm
b. (14p2r – 7pqr + 98pr – 21q2r + 98qr) cu. cm
c. (−45p2q3r2 – 225p2q3r) cu. cm
14. a. 125s3 (stu + 2)3 cu. cm b. 64s6t9u15 cu. cm
c. (−7ab + 11a2 + 2)3 cu. cm d. 27p9q12 (2r + 5q – 6)3 cu. cm
15. 2 (102630) xx+− cm
16. ₹100 (10x2 + x – 3) 17. ₹(34x2 − 7x + 28)
18. 2x5 + x4 + x3 + 7x2 + 5x
19. Answers may vary. Sample answer:
Sana has (x2 + 2x + 3) pencils and the cost of each pencil is ₹(x3 + 4x – 1) What is the price of all the pencils?
Challenge 1. 2 () 620xx + metres 2 Option c
Case Study
1. Option a 2. Option b
3. (–136x2 + 4082x – 26392), �80(– 136x2 + 4082x – 26392)
4. (– 140x2 + 4130x – 26470) m2 5. Answers may vary.
Chapter 12
Letʹs Warm-up
1. 15 cm 2. 16 sq. m 3. 12 cm 4. 24 sq. m 5. 40 cm
Do It Yourself 12A
1. 45,216 sq. m 2. 10 cm 3. 225 tiles 4. 192.5 sq. m
5. a. 471 sq. cm b. 168 sq. cm c. 280 sq. cm
6. Both John and David 7. 4 m 8. 32 sq. cm
9. a. 24 sq. cm b. 243 triangles c. 5832 cm
10. ₹54.656 11. 115.2 sq. cm 12. 2 sq. m
13. 204 brown tiles, 1144 pink tiles and 572 white tiles.
Challenge 1. 3 8 × 3 8 = 9 64 of the original area.
Do It Yourself 12B
1. a. 477 sq. cm b. 485 sq. cm c. 87 sq. units 2. 9 cm
3. 3.62 sq. m 4. 432 sq. cm 5. 5 cm
6. 24 cm and 36 cm 7. 50 cm; 14 cm 8. 7.38 m
9. 240 sq. cm
Challenge 1. Option C
Do It Yourself 12C
1. a. 501 sq. cm b. 9064.28 sq. cm c. 56.57 sq. cm
2. a. 269 sq. cm b. 1913 sq. m c. 519 sq. cm
3. a. 9 sq. cm b. 10.2 sq. cm 4. 2147.55 sq. m
5. 585 sq. cm; Yes 6. 450 sq. cm 7. 26.2 sq. cm
8. 58 sq. m 9. 830 tiles
10. Answers may vary Sample answer:
Area = 310 sq. cm
10 cm
8 cm
20 cm
Challenge 1. 314 sq. cm
Chapter Checkup
1. 29.44 sq. cm 2. 20 cm and 100 cm
3. 12.5 cm and 37.5 cm. 4. Always true.
5. a. 1866 sq. m b. 34,997.5 sq. cm 6. 44 sq. cm
7. a. 313.71 sq. cm b. 4882.5 sq. cm 8. 240 sq. cm
9. 15 sq. m 10. No 11. 19,500 kg 12. ₹22,825.65
13. Answers may vary Sample Answer.
A community park is designed in the shape of a rectangle with a semicircle attached to one of its shorter sides. The rectangular part of the park is 40 meters long and 20 meters wide. Find the total area of the park.
Challenge 1. 4 ² 2 cm 2. Option C
Case Study
1. Option C 2. Option D 3. 1200 m², 2000 m²
4. 6382 m2
Chapter 13
Let’s Warm-up 1. Perimeter = 64 cm
2. Area = 154 cm2 3. Area = 100 cm2
4. Area = 90 cm2 5. Perimeter = 45 cm
Do It Yourself 13A
1. a. 1156 mm2; 1734 mm2 b. 1764 m2; 2646 m2
c. 3136 m2; 4704 m2 2. a. 600 cm2; 792 cm2
b. 2412 cm2; 3252 cm2 c. 1239.5 m2; 2516 m2
3. a. 1056 cm2; 1961.14 cm2 b. 484 m2; 561 m2
c. 4.4 m2; 23.65 m2 4. a. 13,828.57 cm2; 14,658.29 cm2
b. 52,800 cm2; 66,000 cm2 c. 1,35,771.43 cm2; 1,58,400 cm2
5. a. 7.5 cm b. 10 m c. 12 dm
6. 384 cm2 7. 19.09 cm 8. 42,240 cm2
9. 7:9 10. ₹1531.25 11. 14,652 cm2
12. ₹6156, ₹9576 13. 150 cm 14. 49.28 days
15. Answer may vary. Sample answer.
Lena is designing a cuboid shaped storage box for her craft supplies with dimensions of 4 feet in length, 3 feet in width, and 2 feet in height. She plans to paint only the sides of the box, to give it a fresh look. What is the area of the box she will paint?
Challenge 1. Option A Do It Yourself 13B
1. a. i. 4096 cm3 ii. 13,824 mm3
b. i. 1200 cm3 ii. 22,500 cm3
c. i. 385 cm3 ii. 665.28 m3
2. a. 1771 m3 b. 3630 cm3 c. 220 mm3
3. a. 36 cm b. 42 mm c. 0.35 m d. 11 dm
4. 4000 cm 5. 30.28 m 6. 512cm3 7. 2,80,000
8. 60 9. 1 237 % 2 10. 1:16 11. 1728 cm3
12. 1 – π 4 a³ 13. 400 14. 8:7 15. 400 cm
16. Students will prove using the formulas.
17. Answer may vary. Sample answer.
A cylindrical water tank has a diameter of 2 meters and a height of 3 meters. The tank is to be filled with water. How much water (in cubic meters) can the tank hold when it is full?
Challenge 1. Option d
Chapter Checkup
1. a. 600 b. 27 c. 400 d. 216 2. a. 3375 litre b. 1500 litre c. 6,03,428.6 litre d. 3326.4 litre 3. 16 m
4. 53 mm 5. a. 39 m b. 30 cm c. 2.55 m d. 12 cm e. 4.2 m f. 22.40 mm
6. 300% 7. 0 8. 90 m2 9. 486 cm2 10. 7 cm
11. X:Y 12. 154 cm3 13. 900 cm2 14. 637.5 cm 15. 5 approx. 16. 30,000 bricks 17. 80 minutes
18. 13,305.6 g
19. Answer will vary Sample answer.
Maria has a cylindrical flower pot with a height of 80 cm and a base that has a diameter of 40 cm. What is the volume of soil she needs to fill the pot completely?
Challenge 1. 2156 cm3 2. Option C
Case Study
1. Option B 2. Option C 3. 10,560 cm² 4. 600 L
5. Answers may vary.
Chapter 14
Let’s Warm-up 1. 121; 1331 2. 9; 7
3. 24 × 3 a. No b. 3 4. Meeti
Do It Yourself 14A
1. a. 4096 b. 1 343 c. 64 125 d. 81 16
2. a. 2 3 4 b. 3 1 c. 5 4 3 d. 7 6 3
3. a. 9 4 8 b. 1 5 4 c. 11 7 5 d. 10 9 6
4. a. 4 × 101 + 5 × 100 + 1 × 10−1 + 2 × 10−2 + 3 × 10−3
b. 5 × 102 + 4 × 101 + 1 × 100 + 0 × 10−1 + 5 × 10−2 + 6 × 10−3
c. 1 × 102 + 0 × 101 + 7 × 100 + 0 × 10−1 + 2 × 10−2 + 3 × 10−3 + 5 × 10−4 + 6 × 10−5
d. 5 × 103 + 3 × 100 + 6 × 10−1 + 7 × 10−2 + 1 × 10−3
5. a. 2⁵ b. 2⁷ 6. a. 3 4 6 b. 10 9 1 c. (43)–1 d. (2)−1
7. 32 27 8. − 32 135 9. 0.512 g
Challenge 1. a. 5 : 4 b. 400% c. 1 : 256
Do It Yourself 14B
1. a. 1.098 × 10⁷ b. 2.3 × 1015 c. 1.0446678 × 10¹
d. 4.5398785 × 10²
2. a. 16 81 b. 49 169 c. 16 81 d. 4 49 e. 25 16 f. 1
3. a. 421000000 b. 103000000 c. 0.40857 d. 0.00003467
4. a. 2.11 × 10² > 1.67 × 10−2 b. 7.3 × 10−5 > 0.7 × 10−8
5. a. 1.6562229 × 10⁶ b. 4.89 × 10−7 c. 5.19622 × 10⁸
d. 2.300002 × 10⁶
6. a. 243 5 b. 256 c. 27 64 d. 1 32 e. −216 f. 125 128
7. a. 8 9 b. 3125 2187 c. 243t2 2 d. 2
8. 5−2
9. a. x = 3 b. x = 5 10. 0.0028256 inches
11. German, 2.43 × 104 12. 120000 million
13. 1.5247500 × 107 sq. km
Challenge 1. c
Chapter Checkup
1. a. 6 × 101 + 5 × 100 + 8 × 10−1 + 7 × 10−2 + 9 × 10−3
b. 9 × 102 + 7 × 101 + 8 × 100 + 9 × 10−1 + 6 × 10−2 + 7 × 10−3 + 5 × 10−4
c. 4 × 103 + 8 × 102 + 7 × 101 + 6 × 100 + 9 × 10−1 + 0 × 10−2 + 2 × 10−3 + 3 × 10−4
2. a. Standard form, 0.00001275 b. Standard form, 1386000000
c. Usual form, 9.11 × 10−29 kg
3. b since it has not been expressed as k × 10n 4. a. 2⁸ b. 310 c. 57
5. a. 9 7 4 b. 8 3 8 c. 5 2 6
6. a. 1 b. 960 c. 25 9 d. 9 8 e. 1 4 f. 243 2 7. 495
8. a. Ascending order: 128−2, 83, 210, 642, 323; Descending order: 323, 642, 210, 83, 128−2
b. Ascending order: 18−2, 93, 273, 310, 7292
Descending order: 7292, 310, 273, 93, 18−2
9. Neither is correct. The multiplicative inverse of a number a is 1 a So, the multiplicative inverse of x–2, is 1 x–2 = x2
10. a. 1 b. 1 c. 7 4 11. a. 18 b. 1250 c. 1
12. a. x = 3 b. x = 13 8 c. x = 3 13. 1 14. 0.25 kg
15. 8,80,000 kg 16. The diameter of Jupiter is more than the diameter of Saturn. 17. No 18. 1.46 (approx.) times
Challenge 1. Option d 2. y = 2
Case Study
1. a 2. c 3. iron 4. 200 : 1
Chapter 15
Letʹs Warm-up
1. False 2. True 3. False 4. True 5. True
Do It Yourself 15A
1. a. No b. No 2. a. NO b. YES; 7 12
3. 88, 228, 304, 209 4. ₹3380 5. 300 chocolates
6. 6120 words 7. 105 workers 8. 2.4 km
9. 2700 bottles 10. 45000 cc 11. ₹561
12. 81 boxes 13. 32 bags 14. ₹9600
Challenge 1. Rani is correct.
Do It Yourself 15B
1. a. No b. Yes 2. 2 3. 1 6 of the work 4. 35 days
5. 2 chocolates 6. 2 8 5 days 7. 3 days 8. 2 members
9. 20 km/h 10. 7 13 11 hours 11. 1 13 3 minutes
12. 23 13 121 hours 13. 12 days 14. 585 members
15. 2:43 p.m.
Challenge 1. Option d
Chapter Checkup
1. a. Direct Proportion; 65 b. Inverse Proportion; 40
2. 2112 g 3. ₹13,500 4. 1 5 of the work 5. 7 boxes
6. 42 men 7. 12 tankers 8. 5 cows 9. 525 people
10. 425 kg 11. 8 hours 12. 14 7 12 hours
13. 8:24 a.m. 14. ₹450 15. 72 minutes
16. 2.75 × 105 grains 17. 30 10 13 hours 18. 9 16 of work
19. 0.5 cm 20. 3 3 7 hours
Challenge 1. X is equally efficient to Y 2. Option b Case Study
1. Option c 2. Option b
3. 1500 sq. m 4. Answer will vary.
Chapter 16
Letʹs Warm-up
1. 17y + 9x 2. 17xy + 6x 3. –6z + 5y2 4. 4x – 17y
Do It Yourself 16A
1. a. 3(3) xx + b. 2 22 ( 1) yy c. 5ab(a + 2b) d. 2 6(3) xyxy
e. 22 423) ( cc f. 22 3 (32) pqpq
2. a. 7(3) xxy b. 2 5(23) abba c. 3 4(43) pqpq
d. 23 6(31) mnmn e. 42 5(5) xyxy f. 23 10(31) abab
g. 2 11(2) xx + h. 3 7(21) yy i. 2 17(2) abab
3. a. (32)(3) yy+− b. 2(1)(32) xx−+ c. 5(32)(1) yy+−
d. (25)(4) aa+− e. (3y – 6)(2y – 6) f. 2(3) x +
g. (47)((47)(2)1) aaa+++− h. 2 ) (43)(25(43) xxx −+−−
i. 2 } (4){(2)3(4) xxx +−−+
4. a. 2 (2)(23) xyx+− b. (32)(2) adbc −+ c. (2)(7) xyx
d. (2)(25) adbc −+ e. (3)(2) xx f. (5)(32) xxy
g. (35)(2) xyx h. (42)(3) xxy +− i. (32)(23) xyx
5. Answers may vary. Sample answer: (4pq + 12qr − 2ps − 6rs)
Challenge 1 ₹(41) x +
Do It Yourself 16B
1. a. (4)2 a + b. (5)2 x + c. (2)2 b + d. (9)2 a +
2. a. (2)(2) aa+− b. (5)(5) xx+− c. (34)(34) bb+−
d. (74)(74) pp+− e. ()() abab +− f. (ax + y)(ax – y)
g. (109)(109) bb+− h. (2)(2) xyxy+−
3. a. (41)2 ax b. 3(9)(9) xyxyxy +− c. 22 ()()() ababab ++−
d. 2 (9)(9)(9) bbb+−+ e. (118)2 x f. (127222 ) yx
g. (74)2 y h. (8)2 y 4. a. 49 b. 6x c. c2 d. 12r
5. a. 1 4 b. 16 c. 1 d. 25 4 e. 16 f. 144 g. 49 h. 64
6. a. 22 (4(2)(2) ) mnmnmn +−+ b. (1)(1) abab−−++
c. (2)(2) abcabc −+−− d. 2 xy yx +
7. Answers may vary. Sample answer. Given the expression 9x2 − 24x + 16, factorise it using the appropriate algebraic identity.
Challenge 1. 13 cm, 5 cm
Do It Yourself 16C
1. a. −4x − x b. –8x − x c. –8x − 3x d. –16x − x 2. c
3. a. (31)(23) xx b. (23)(2) xx c. (21)(2) xx
d. (32)(2) xx e. (31)(32) xx f. (96)(1) xx
g. (35)(2) xx h. (31)(52) xx
4. a. (32); (7)xx b. (52); (7)xx
c. (414); (1)xx d. (21) x ; (23) x
5. Answers may vary. Sample answer. The area of a rectangular field can be given by the expression x2 + 7x + 10. What is the length and width of the garden?
Challenge 1. a. Yes b. Yes 2. 3(1) x +
Do It Yourself 16D
1. a. 2 5 x b. 2 3ab c. 32 4 yz d. 4 2 xy z e. 22 3 pq f. 447 12 jkr
2. a. 2 23xx+− b. 3232 yyy −+ c. 432 32 aaa −+
d. 2 32mm−+ e. 432 23 xxx +− f. 223 5 5 3 axayz −+
3. a. 36abc b. 4(5) ba + c. 2 4(370) aa++ d. 3 () 2 cab +
4. a. Q = 4x – 6 b. Q = 3y2 – 9y + 18
R = 19x – 33 R = –48y + 72
c. Q = x3 + 5x2 d. Q = 6a3 – 15a2 + 39a – 84
R = 16x R = 168
e. Q = 9b4 + 12b3 – 21b2 – 28b + 42
R = 56b – 84
f. Q = 2c4 – 12c3 + 30c2 – 60c + 108
R = –216
5. a. Q = 3x + 7 b. Q = 2y2 + 6y + 14
R = 18x – 29 R = 86y + 72
c. Q = 3a2 + a 2 + 13 4 d. Q = x2 – x + 4
R = –9a 4 – 1 4 R = 3x2 + 2x
e. Q = 7x + 23 f. Q = 3y2 + 8y + 20
R = 74x + 41 R = 108y2 + 21y – 126
6. 2 53xx−+ 7. (x +2) litres per/day.
8. 2 (34) xx++ chocolates
Challenge 1. 5 2. 2 a −+
Chapter Checkup
1. a. 2(3) xx + b. 3a(b − 3) c. 4y2(y + 2) d. 7x(y − 2)
2. a. (x + y)(12 – 2x) b. (x − 2z)(x + y −1) c. (10 − n)(11 − n)
d. 3(3a − 1)(a −1) e. (x + 2y)(5 − 7x − 14y) f. (5x + y) (1 – (5x + y)2)
3. a. b(2a − 1)(2a − 3b) b. (5x + 3y)(x − 2y) c. (x + 2)(3x − 2y)
d. (3x − 4y)(3x − 2) e. (2x2 − 3y)(2x −1) f. (x − 3)(6x + 7y)
4. a. (a + 3b)2 b. (x − 5y)2 c. (2x + y)2 d. (5x + 4y)2
e. (x − 7y)2 f. 16(a − b)2
5. a. (p + 3q)(p − 3q) b. (2x + 7y)(2x − 7y) c. (a + 4b)(a − 4b)
d. (3m + 5n)(3m − 5n) e. (x + 6y)(x − 6y) f. (5u − 2v)(5u + 2v)
6. a. (6x − 1)(x + 2) b. (x − 2)(x − 3) c. 3(x −1)(x + 5)
d. (x −1)(3x − 7) e. (x + 6)(x + 8) f. (x + 1)(2x − 5)
7. a. 2 234 xx+− b. 2 24abcbcd c. 2322 aabb −+
d. 32 32xxx −+ e. 22 2 23 ababcc −+ f. 3232xxx −+
8. a. Q = 2x2 + 8x + 10 b. Q = 3x3 – 3x2 – 6x + 12 R = 20 R = – 12
c. Q = 2x2 + 7x + 2 d. Q = x3 – 3x2 + 3x 6 5 –R = 2 R = 12 5
e. Q = 3x3 + 9x2 2 + 3x 4 + 9 8 f. Q = x2 –3x 7 + 86 49 R = 75 8 R = 344 49
9. a. Q = 3x + 13 b. Q = 2x2 + 2x + 1 R = 31x – 25 R = 5x + 5
c. Q = 3x + 1 2 d. Q = 5x – 16 R = 19x 2 – 3 R = 40x – 18
e. Q = x2 – 4x + 15 f. Q = 2x R = – 44x – 64 R = 9
10. Length Breadth
x (8x + 5y)(8x − 5y)
(8x + 5y) x(8x − 5y)
(8x − 5y) x(8x + 5y)
x(8x + 5y) (8x − 5y)
x(8x − 5y) (8x + 5y)
(8x + 5y)(8x − 5y) x
Challenge 1. (5 – 7x) 2. option d Case Study
1. d 2. b 3. (x2 + 5x + 9) units. 4. ₹(2x2 + 5x − 1)
5. Answers may vary.
Chapter 17
Letʹs Warm-up
1. Badminton 2. Chess 3. Badminton 4. Chess
Do It Yourself 17A
1. a. True b. True c. False d. False 2. a. Thursday b. Wednesday c. 125% d. 20:17
5. Answers may vary. Sample answer. The number of books read by two students Ronak and Priya in 6 months is given below. Draw a double line graph representing the given data.
Ronak 5 7 8 6 9 10 Priya 3 4 6 7 8 9
Challenge 1. Option b Do It Yourself 17B
1. a. False b. False c. False d. True e. True
2. a. Abscissa = 9, Ordinate = 4 b. Abscissa = 4, Ordinate = –5
c. Abscissa = 0, Ordinate = 4 d. Abscissa = –2, Ordinate = –8
e. Abscissa = 0, Ordinate = –7
3. a. y-axis b. x-axis c. x-axis d. y-axis e. Origin
4. a. Second b. Third c. Fourth d. First e. Second
5. Scale: x-axis = 1 division = 1 unit y-axis = 1 division = 20 units
x-axis: 1 division = 200 km y-axis: 1 division = 2 hours
The points do not lie in a straight line.
6. Scale: x-axis = 1 division = 1 unit y-axis = 1 division = 1 unit
9. Answer may vary. Sample answer. The dataset represents the number of hours studied and the corresponding scores on a test.
of hours studied 1 2 3 4 5
Scale: x-axis = 2 divisions = 1 hour y-axis = 1 division = 10 marks
(0, 0)
7. Scale: x-axis = 1 division = 1 unit y-axis = 1 division = 50 units
The graph is not linear.
Challenge 1. a. F = 50 + 20d
b. Graph:
Scale: x-axis: 1 division = 5 km y-axis: 1 division = ₹100
Distance – Fare Graph
Chapter Checkup
1. a. Abscissa = 5, Ordinate = 4; first quadrant.
b. Abscissa = −8, Ordinate = –2; third quadrant.
c. Abscissa = −9, Ordinate = −8; third quadrant.
d. Abscissa = –5, Ordinate = –10; third quadrant.
2. Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1
C(4, 0) and B(0, 4)
5 Scale: x-axis: 1 division = 1 year
8. Scale: x-axis: 1 division = 5 minutes Y-axis: 1 division = 5 m
Ansh Raman
3. a.
b. The points lie on a line.
Scale: x-axis: 1 division = 1 unit
6. a. –2; 1.5; (–2, 1.5)
b. 3; 1; (3, 1)
c. 1; –3; (1, –3)
d. –3; –2; (–3, –2)
7. Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit
9. Scale: x-axis: 1 division = ₹100 Y-axis: 1 division = ₹500
Deposit
x y Simple Interest
Yes.
Challenge 1. No 2. Option c
Case Study
1. b. 20 km/hr 2. 160 km 3. d. 50 km 4. 1 hour 5. Answer may vary.
About the Book
Imagine Mathematics seamlessly bridges the gap between abstract mathematics and real-world relevance, offering engaging narratives, examples and illustrations that inspire young minds to explore the beauty and power of mathematical thinking. Aligned with the NEP 2020, this book is tailored to make mathematics anxiety-free, encouraging learners to envision mathematical concepts rather than memorize them. The ultimate objective is to cultivate in learners a lifelong appreciation for this vital discipline.
Key Features
• Let’s Recall: Introductory page with a quick recall of concepts learnt in previous grades
• Real Life Connect: Introduction to a new concept related to real-life situations
• Examples: Solved problems showing the correct method and complete solution
• Do It Together: Guided practice for learners with clues and hints to help solve problems
• Think and Tell: Probing questions to stimulate Higher Order Thinking Skills (HOTS)
• Error Alert: A simple tip-off to help avoid misconceptions and common mistakes
• Remember: Key points for easy recollection
• Did You Know? Interesting facts related to the application of concept
• Math Lab: Fun cross-curricular activities
• Challenge: Critical thinking questions to enhance problem-solving and analytical thinking skills
• Case Study: Scenario-based questions to apply theory to real-life situations
• QR Codes: Digital integration through the app to promote self-learning and practice
About Uolo
Uolo partners with K-12 schools to provide technology-enabled learning programs. We believe that pedagogy and technology must come together to deliver scalable learning experiences that generate measurable outcomes. Uolo is trusted by over 15,000+ schools across India, Southeast Asia and the Middle East.
ISBN 978-81-979482-0-6
