Imagine_Maths_TM_Grade8

MATHEMATICS

Teacher Manual

MATHEMATICS

Master Mathematical Thinking

Grade 8

Foreword

Mathematics is not just another subject. It is an integral part of our lives. It shapes the very foundation of our understanding, personality and interaction with the world around us.

However, due to the subject’s abstract nature, the stress of achieving high academic scores and complex teaching methods, most children develop a fear of mathematics from an early age. This fear not only hinders their mathematical thinking, logical reasoning and general problem solving abilities, but also negatively impacts their performance in other academic subjects. This creates a learning gap which widens over the years.

The NEP 2020 has distinctly recognised the value of mathematical thinking among young learners and the significance of fostering love for this subject by making its learning engaging and entertaining. Approaching maths with patience and relatable real-world examples can help nurture an inspiring relationship with the subject. It is in this spirit that Uolo has introduced the ImagineMathematics product for elementary grades (1 to 8). This product’s key objective is to eliminate the fear of mathematics by making learning exciting, relatable and meaningful for children. This is achieved by making a clear connection between mathematical concepts and examples from daily life. This opens avenues for children to connect with and explore maths in pleasant, relatable, creative and fun ways.

This product, as recommended by the NEP 2020 and the recent NCF draft, gives paramount importance to the development of computational and mathematical thinking, logical reasoning, problem solving and mathematical communication, with the help of carefully curated content and learning activities.

ImagineMathematics strongly positions itself on the curricular and pedagogical approach of the Gradual Release of Responsibility (GRR), which has been highly recommended by the NEP 2020, the latest NCF Draft and other international educational policies. In this approach, while learning any new mathematical concept, learners first receive sufficient modelling, and then are supported to solve problems in a guided manner before eventually taking complete control of the learning and application of the concept on their own. In addition, the book is technologically empowered and works in sync with a parallel digital world which contains immersive gamified experiences, video solutions and practice exercises among other things. Interactive exercises on the digital platform make learning experiential and help in concrete visualisation of abstract mathematical concepts.

In ImagineMathematics, we are striving to make high quality maths learning available for all children across the country. The product maximises the opportunities for self-learning while minimising the need for paid external interventions, like after-school or private tutorial classes.

The book adapts some of the most-acclaimed, learner-friendly pedagogical strategies. Each concept in every chapter is introduced with the help of real-life situations and integrated with children’s experiences, making learning flow seamlessly from abstract to concrete. Clear explanations and simple steps are provided to solve problems in each concept. Interesting facts, error alerts and enjoyable activities are smartly sprinkled throughout the content to break the monotony and make learning holistic. Most importantly, concepts are not presented in a disconnected fashion, but are interlinked and interwoven in a sophisticated manner across strands and grades to make learning scaffolded, comprehensive and meaningful.

As we know, no single content book can resolve all learning challenges, and human intervention and support tools are required to ensure its success. Thus, ImagineMathematics not only offers the content books, but also comes with teacher manuals that guide the pedagogical transactions that happen in the classroom; and a vast parallel digital world with lots of exciting materials for learning, practice and assessment. In a nutshell, ImagineMathematics is a comprehensive and unique learning experience for children.

On this note, we welcome you to the wonderful world of ImagineMathematics. In the pages that follow, we will embark on a thrilling journey to discover wonderful secrets of mathematics—numbers, operations, geometry and measurements, data and probability, patterns and symmetry, algebra and so on and so forth. Wishing all the learners, teachers and parents lots of fun-filled learning as you embark upon this exciting journey with Uolo.

Rational Numbers 1

Rational Numbers 1

Clear and concise lessons that can be implemented through the academic year with each perfectly aligned to the topics covered in the Imagine Mathematics learners’ content book.

Rational Numbers 1

Rational Numbers 1

Learning Outcomes

Learning Outcomes as recommended by the NEP 2020 and the latest National Curricular Framework (NCF).

Alignment to NCF

Learning Outcomes

C-1.4: Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line

Let’s Recall

Recap to check if students know how to add and subtract integers, decimals and fractions. Ask students to solve the questions given in the Let’sWarm-up section.

the properties of rational numbers for addition and subtraction.

and divide rational numbers given in different forms.

Vocabulary rational number: a number expressed as P q , where p and q are integers, and the denominator ≠ 0

Alignment to NCF

Teaching Aids

Vocabulary to help know the important terms that are introduced, defined or emphasized in the chapter.

C-1.4: Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line

Let’s Recall

Sheet of paper; Flash cards; Clothes pegs; pieces of thread; Number line drawn on a sheet of paper; Bingo cards; Problem Cards; Question cards with different addition and subtraction problems based on their properties; Turkey cards; Crayons; Table cards

Recap to check if students know how to add and subtract integers, decimals and fractions. Ask students to solve the questions given in the Let’sWarm-up section.

A concise and organized lesson plan that outlines the activities and extension ideas that are to be used to facilitate learning.

QR Code: Access to digital solutions and other interactive resources.

Rational Numbers 1

Clear, specific and measurable learning outcomes that show what students should know, understand, or do by the end of the lesson.

Rational Numbers 1

Learning Outcomes

Recap exercises to check the understanding of prerequisite concepts before starting a topic.

rational numbers for multiplication and division.

Alignment to NCF

C-1.4: Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line

Students

Let’s Recall

find rational numbers between two rational numbers.

order them.

Recap to check if students know how to add and subtract integers, decimals and fractions. Ask students to solve the questions given in the Let’sWarm-up section.

add and subtract rational numbers given in different forms. identify and apply the properties of rational numbers for addition and subtraction. multiply and divide rational numbers given in different forms. identify and apply the properties of rational numbers for multiplication and division.

Vocabulary rational number: a number expressed as P q , where p and q are integers, and the denominator ≠ 0

Alignment to NCF

Teaching Aids

C-1.4: Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line

Let’s Recall

Sheet of paper; Flash cards; Clothes pegs; pieces of thread; Number line drawn on a sheet of paper; Bingo cards; Problem Cards; Question cards with different addition and subtraction problems based on their properties; Turkey cards; Crayons; Table cards

Aids and resources that the teachers may use to significantly improve the teaching and learning process for the students.

Recap to check if students know how to add and subtract integers, decimals and fractions. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

rational number: a number expressed as P q , where p and q are integers, and the denominator ≠ 0

Teaching Aids

Sheet of paper; Flash cards; Clothes pegs; pieces of thread; Number line drawn on a sheet of paper; Bingo cards; Problem Cards; Question cards with different addition and subtraction problems based on their properties; Turkey cards; Crayons; Table cards 1

Answers, provided at the end of each chapter, for the questions given in Do It Together and Think and Tell sections of the Imagine Mathematics book.

Period Plan

The teacher manuals corresponding to ImagineMathematics books for Grades 1 to 8 align with the recently updated syllabus outlined by the National Curriculum Framework for School Education, 2023. These manuals have been carefully designed to support teachers in various ways. They provide recommendations for hands-on and interactive activities, games, and quizzes that aim to effectively teach diverse concepts, fostering an enriched learning experience for students. Additionally, these resources aim to reinforce critical thinking and problem-solving skills while ensuring that the learning process remains enjoyable.

In a typical school setting, there are approximately 180 school days encompassing teaching sessions, exams, tests, events, and more. Consequently, there is an average of around 120 teaching periods throughout the academic year.

The breakdown of topics and the suggested period plan for each chapter is detailed below.

Rational

Addition of

Between Two Rational Numbers

Numbers; Subtraction of Rational Numbers

Properties of Addition and Subtraction of Rational Numbers

Multiplication of Rational Numbers; Division of Rational Numbers

Properties of Multiplication and Division of Rational Numbers

Trapezium

Rhombus,

Reading

Area of Figures Made With Parallelograms, Triangles and Circles

Area of a Trapezium and Rhombus

Area of General Quadrilaterals

Area

Surface Area of Cuboids

Surface Area of Cubes

Surface Area of Cylinders Volume of

Direct

Using Common Factors

Using Grouping and Regrouping Terms

Factorisation Using Identities

Factorisation of Quadratic Trinomials

Dividing a Monomial by a Monomial

Dividing a Polynomial by a Monomial

Dividing a Polynomial by a Polynomial

Revision

Reading Double Line Graphs

Drawing Double Line Graphs

Cartesian Coordinate of a Point

Drawing a Linear Graph

Reading Linear Graphs

Numbers in General Form; Reversing Digits

Letters for Digits; Number Puzzles and Patterns

Test of Divisibility

Rational Numbers 1

Learning Outcomes

Students will be able to: represent rational numbers on a number line and compare and order them. find rational numbers between two rational numbers. add and subtract rational numbers given in different forms. identify and apply the properties of rational numbers for addition and subtraction. multiply and divide rational numbers given in different forms. identify and apply the properties of rational numbers for multiplication and division.

Alignment to NCF

C-1.4: Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line

Let’s Recall

Recap to check if students know how to add and subtract integers, decimals and fractions. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

rational number: a number expressed as P q , where p and q are integers, and the denominator ≠ 0

Teaching Aids

Sheet of paper; Flash cards; Clothes pegs; Pieces of thread; Number line drawn on a sheet of paper; Bingo cards; Problem cards; Question cards with different addition and subtraction problems based on their properties; Turkey cards; Crayons; Table cards 1

Chapter: Rational Numbers

Identifying and Representing Rational Numbers; Imagine

Maths Page 2

Comparing and Ordering Rational Numbers

Learning Outcomes

Students will be able to represent rational numbers on a number line and compare and order them.

Teaching Aids

Sheet of paper; Flash cards; Clothes pegs; Pieces of thread

Activity

Remind the students what rational numbers are and show them a few examples.

Ask the students to work in groups. Distribute a sheet of paper, the set of 5 flash cards with rational numbers written on them, the clothes pegs, and the pieces of thread to each group.

Instruct them to draw a number line on the sheet of paper and represent the rational numbers written on the flash cards on the number line. Then, ask them to note the order of the numbers on the number line and arrange them in ascending/descending order to create buntings using flash cards, clothes pegs and threads. Announce that the fastest group to get the arrangement correct wins! Discuss their approach in the class.

After the activity, give the students some practice questions and encourage them to solve the problems using the LCM in their notebooks.

Extension Idea

Ask: Which is greater: 4 5 6 or 4 11 12 ?

Say: 4 5

Rational Numbers Between Two Rational Numbers

Learning Outcomes

Students will be able to find rational numbers between two rational numbers.

Teaching Aids

Number line drawn on a sheet of paper

Activity

Ask the students to work in groups.

Imagine Maths Page 5

Distribute a sheet of paper with a number line drawn on it to each group. Give them two rational numbers, say 2 3 and 4 5 , and ask them to mark the numbers on the number line. Ask questions like: How can you place two rational numbers with different denominators on number line?

Discuss their responses and help them deduce that to place two numbers on the number line, the denominators need to be the same.

Instruct them to make the denominators the same by finding their LCM. Then, instruct them to mark the numbers on the number line and find the rational numbers between them.

Encourage the students to share their number lines and explain the rational numbers they represented between the given end points. Encourage them to write their learnings in their notebooks and give them more questions for practice.

Addition of Rational Numbers;

Subtraction of Rational Numbers

Learning Outcomes

Students will be able to add and subtract rational numbers given in different forms.

Teaching Aids

Bingo cards; Problem cards

Activity

Imagine Maths Page 7

Briefly talk about adding and subtracting rational numbers. Make problem cards (Example, 2 5 +

8 , –1 3 + 7 6 , 0.625 – 5 –3 , etc.) and bingo cards (showing answers to the corresponding problem cards).

2291

1000

Bingo cards

Divide the class into groups. Distribute a bingo card to each group.

Problem cards

Shuffle the problem cards and put them into a box. Pick a card and read out the problem. Instruct the students to solve it (encourage them to use the LCM method) and check whether the answer lies on their bingo card. If it does, they should cross out that number. The first group to cross out a row and a column on their bingo card wins!

Ask the students to write the answers in their notebooks.

Extension Idea

Ask: Which decimal number should be subtracted from 12 5 to get – 3 8 ?

Say: 12 5 – x =

; 12

96 + 15 40 = 111 40 = 2.775.

Rational Numbers

Learning Outcomes

Students will be able to identify and apply the properties of rational numbers for addition and subtraction.

Teaching Aids

Question cards with different addition and subtraction problems based on their properties

Activity

Briefly talk about adding and subtracting rational numbers.

Ask the students to work in pairs. Give each pair question cards with different addition and subtraction problems based on the properties, such as 2 5 + 3 4 and 3 4 + 2 5 .

Instruct each student in the pair to solve one question and then compare their answers to see if they got the same result. Help them deduce that if their answers match, it shows that rational numbers follow the commutative property of addition.

Repeat the activity for other properties of addition and subtraction by giving them a variety of questions. Ask questions like: What should you add to/subtract from – 3 2 to get – 3 2 ? Discuss student responses. Instruct the students to note down their observations and learnings in their notebooks.

Extension Idea

Ask: What is the additive inverse of 3 5 + 75 –103 ?

Say:

5103530305303030

. The additive inverse of –11 30 is 11 30 . Multiplication of Rational Numbers; Imagine Maths Page 12

Division of Rational Numbers

Learning Outcomes

Students will be able to multiply and divide rational numbers given in different forms.

Teaching Aids

Turkey cards; Crayons

Activity

Briefly revisit the concepts of multiplying and dividing rational numbers.

Prepare turkey cards with questions written on the body (centre) and blank feathers for students to fill in the answers.

Ask the students to work in groups. Distribute one turkey card and crayons to each group.

Instruct them to solve the questions on the cards in their notebooks and write the corresponding answers on the feathers. Ask them to shade the feathers as they get the answer to each question. After the activity, encourage the groups to exchange cards to verify their solutions. The group with all the correct answers gets to showcase their turkey card on the teacher’s table for the rest of the day.

Extension Idea

Properties of Multiplication and Division of Imagine Maths

Page 13

Rational Numbers

Learning Outcomes

Students will be able to identify and apply the properties of rational numbers for multiplication and division.

Teaching Aids

Table cards

Activity

Ask the students to work in groups. Distribute a card with a table drawn on it to each group. Write one problem for each property of rational numbers for multiplication and division on the board. Instruct students to solve the problems in their notebooks, deduce the concepts and fill in the table with their learnings. Once they are done, discuss their findings. Have them check whether their result is the same as other groups. Discuss their challenges and help them bridge the gaps, if any.

Ask questions like: What should be multiplied by – 1 7 to get 0?

PropertyMultiplicationDivision ClosureFollowsDoesn’t follow Associative Distributive Commutative

Answers

1. Identifying and Representing Rational Numbers

Do It Together

2. Comparing and Ordering Rational Numbers

Think and Tell

No, pi (π) is not a rational number; pi (π) approximately equals 3.14159265359 ... and is a non-terminating nonrepeating number. Hence ‘pi’ is not a rational number.

Think and Tell

Both –4 5 and 4 –5 are equivalent and represent −0.8.

Do It Together

Therefore, the rational numbers can be written as: –3

, 8 3 , 17 10

The LCM of 1, 6, 3 and 10 is 30

The equivalent rational numbers are: –

Compare the numerators: 80 > 65 > 51 > −90

Descending order = 8 3 > 13 6 > 1.7 > –3

3. Rational Numbers Between Two Rational Numbers

Do It Together

LCM of 9 and 12 = 36; hence,

Five rational numbers between – 4

and 7 12

–6 36 , –

36 ,

36 , 13 36 , 14 36

4. Addition of Rational Numbers

Do It Together

1. 152336759272239 451020202020 ++=++=

2. 56–28650–180–1092 ++=++= 3–1310390390390 622311

390165

5. Subtraction of Rational Numbers

Do It Together

1. 625126252403857717 –=–===3 10051001001002020

2. 757512 –=+==6 2–2222

6. Properties of Addition and Subtraction of Rational Numbers

Do It Together

1. 0 2. 5 2 3. –12 25

7. Multiplication of Rational Numbers

Do It Together

1. 5 9 × 16 –7 = 80 –63

25 10 × –19 3 = – 475 30 = –95 6

8. Division of Rational Numbers

Do It Together

× 25 –19 = 875 –190 = 175 –38

9. Properties of Multiplication and Division of Rational Numbers

Solving Equations in One Variable 2

Learning Outcomes

Students will be able to:

solve linear equations using the transposing method. simplify equations to the linear form and solve them. apply linear equations in solving real-life problems.

Alignment to NCF

C-2.2: Extends the representation of a number in the form of a variable or an algebraic expression using a variable

C-2.4: Poses and solves linear equations to find the value of an unknown, including to solve puzzles and word problems

C-2.5: Develops own methods to solve puzzles and problems using algebraic thinking

Let’s Recall

Recap to check if students know about the balancing and transposing methods to solve linear equations. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

variable: something that can change or that has no fixed value equation: a statement that uses an equal sign to show the equality of two expressions

Teaching Aids

Puzzle cutouts with linear equations and solutions written; Interlocking puzzles with linear equations and their solutions; Word problem cards

Chapter: Solving Equations in One Variable

Transposing Method

Learning Outcomes

Students will be able to solve linear equations using the transposing method.

Teaching Aids

Puzzle cutouts with linear equations and solutions written

Activity

Discuss the transposing method to solve linear equations.

Ask the students to work in groups. Distribute puzzle cutouts with linear equations and solutions to each group.

Instruct the groups to arrange the cutouts in such a way that the solution of the linear equation is placed next to it. Ask them to solve the equations in their notebooks to complete the puzzle. Record the time taken by each group to complete the puzzle. Check the puzzles created and announce the fastest/winning group.

Extension Idea

Imagine Maths Page 20

Ask: Sarah is three years older than twice her brother’s age. If Sarah is 13 years old, what is her brother’s age?

Say: Let Sarah’s brother’s age be x years. Then, 2x + 3 = 13 ⇒ x = 5. So, her brother is 5 years old.

Simplifying Equations to Linear Form

Learning Outcomes

Students will be able to simplify equations to the linear form and solve them.

Teaching Aids

Interlocking puzzles with linear equations and their solutions

Activity

Show the students some equations and simplify them to form linear equations. Ask the students to work in groups. Distribute puzzle interlocking cards with linear equations and their solutions to each group.

Imagine Maths Page 23

Instruct the groups to simplify and solve the linear equations in their notebooks and join them to the interlocking pieces with their solutions. Record the time taken by each group to complete all the puzzles. Check the puzzles created and announce the fastest/winning group.

Learning Outcomes

Students will be able to apply linear equations in solving real-life problems.

Teaching Aids

Word problem cards

Activity

Ask the students to work in groups. Distribute cards to each group containing different word problems, such as:

(1) Thelengthofarectangleis5.5metresmorethan2.5timesitswidth.Iftheperimeteroftherectangleis40metres, finditslengthandwidth.

(2) Simranthoughtoftwoconsecutiveoddnumbersthathaveasumof44.Whatarethetwonumbersshethoughtof?

(3) Acabcharges₹650perdayplus₹8perkm.IfRohitpaid₹1750foraday,howmanykilometresdidhetravel?

Instruct the students to pick one card each, create a linear equation based on the problem on their card and solve it in their notebooks. Once they have solved the problem, ask them to pass on their cards to the other members of their group to solve the problems. Then, ask them to discuss their answers within their group. Discuss the answers with the whole class.

Extension Idea

Instruct: Create your own word problem that involves a variable.

Say: There can be many such problems. One could be: Tomhas$20morethantwicetheamountofmoneyJanehas inherwallet.IfTomhas$50,howmuchmoneydoesJanehave?

1. Transposing Method

2. Simplifying Equations to Linear Form

3. Application of Linear Equations

Polygons 3

Learning Outcomes

Students will be able to:

classify polygons based on their properties. deduce the interior angle sum property of polygons and apply it. deduce the exterior angle sum property of polygons and apply it.

Alignment to NCF

C-3.2: Outlines the properties of lines, angles, triangles, quadrilaterals, and polygons and applies them to solve related problems

Let’s Recall

Recap to check if students know how to identify open curves, closed curves, polygons and non-polygons. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

polygon: a 2-D shape made up of 3 or more line segments

convex polygon: a polygon in which the measure of each angle is less than 180°

concave polygon: a polygon in which the measure of one of the angles is more than 180°

Teaching Aids

Polygon convex and concave cututs of a pentagon, hexagon, heptagon, octagon, nonagon and decagon; Sheet of paper with 4 polygon shapes drawn on it; Pair of scissors

Imagine Maths Page 34

Learning Outcomes

Students will be able to classify polygons based on their properties.

Teaching Aids

Polygon concave and convex cutouts of a pentagon, hexagon, heptagon, octagon, nonagon and decagon

Activity

Show the students some cutouts of polygons and non-polygons. Discuss and bring out the fact that polygons are simple closed shapes made up of 3 or more straight sides.

Ask the students to work in groups of 5. Distribute the five shape cutouts to each group.

Draw the table on the board and ask the students to copy it into their notebooks.

PolygonNumber of sides (n)DiagonalsConvex/Concave

Instruct each student in the group to outline one polygon in their notebook and then draw its diagonals. Ask them to complete the table and then discuss in groups to deduce the formula for finding the number of diagonals in a polygon with n sides.

Ask questions like: How can you find the number of diagonals in a polygon with n sides? What do you notice about the diagonals of a concave polygon?

Ask the students to trace the other polygons in their notebooks, and draw their diagonals. They can then check the number of diagonals that they get against what they have written in the table. Angle

Imagine Maths Page 37

Learning Outcomes

Students will be able to deduce the interior angle sum property of polygons and apply it.

Teaching Aids

Polygon cutouts (heptagon, octagon, nonagon, decagon)

Activity

Begin with a discussion on how the sum of the angles in a triangle is 180°.

Ask the students to work in groups of 4. Distribute 4 polygon cutouts to each group and ask each student in a group to take one polygon.

Draw the table on the board and ask the students to copy it into their notebooks.

PolygonNumber of TrianglesSum of Interior Angles

Instruct the students to mark one of the vertices in the polygon, draw diagonals from that vertex to form triangles, count the number of triangles and multiply it by 180°. Ask them to complete the table and then discuss within their groups how to deduce the formula to find the angle sum of a polygon with n sides.

Ask questions like: How can you find the missing interior angle of a polygon?

Give the students some problems where they need to find the missing angle in a given polygon.

Extension Idea

Ask: If the interior angle sum of a regular polygon is 900°, what is the measure of each angle and the total number of sides in the polygon?

Say: We know that the interior angle sum of a polygon can be found using the formula (n – 2) × 180°. Here, the interior angle sum is given as 900°. So, (n – 2) × 180° = 900° or n = 7. A polygon with 7 sides is a heptagon.

For a regular heptagon, we can find the measure of each angle as 900 7 = 128.6°.

Exterior Angle Sum Property of Polygons

Learning Outcomes

Students will be able to deduce the exterior angle sum property of polygons and apply it.

Teaching Aids

Sheet of paper with 4 irregular convex polygons drawn on it; Pair of scissors

Activity

Begin the class with a discussion on how the measure of a complete angle is 360°.

Instruct the students to work in groups of 4. Distribute the sheet with shapes drawn on it to each group.

Instruct each student to pick any one shape and extend all the arms of its angles to show the exterior angles. Then, they should cut out the exterior angles and turn them around to make an angle. Ask them to discuss within their groups and deduce the exterior angle sum property of a polygon.

Explain that the sum of the exterior angles in a polygon is 360°.

Imagine Maths Page 39

Give the students some problems where they need to find the missing angle in a polygon using the exterior angle sum property.

Extension Idea

Ask: What is the measure of each exterior angle of a regular polygon with 9 sides?

Say: Number of sides of a regular polygon = 9. So, exterior angle = 360 ÷ 9 = 40°.

Answers

1. Classifying Polygons

Think and Tell

Triangles are polygons that are most commonly seen in our everyday life.

No, it is not possible to have a concave polygon with three sides. A concave polygon has at least four sides.

Do It Together

Polygon

Number of side (n) 5 67

Diagonals 5 914

Convex/Concave ConcaveConvexConvex

2. Angle Sum Property of Polygons

Do It Together

The shape has 7 sides so it is a heptagon.

Sum of angles of the heptagon = (n – 2) × 180°

Measure of the missing angle is 900° – (67° + 138° + 143° + 152° + 108° + 134°) = 900° – 742° = 158°.

3. Exterior Angle Sum Property of Polygons

Do It Together

a + 122° = 180°. So, a = 180° – 122° = 58°.

a = 58°, b = 99°, c = 109°, d = 82°.

Quadrilaterals 4

Learning Outcomes

Students will be able to:

classify quadrilaterals based on their properties.

identify the properties of a trapezium and a kite and apply them to solve problems. identify the properties of a parallelogram and apply them to solve problems. identify the properties of a rhombus, a square and a rectangle and apply them to solve problems.

and apply it.

of quadrilaterals and apply it.

Alignment to NCF

C-3.2: Outlines the properties of lines, angles, triangles, quadrilaterals, and polygons and applies them to solve related problem

C-3.4: Draws and constructs geometric shapes, such as lines, parallel lines, perpendicular lines, angles, and simple triangles, with specified properties using a compass and straightedge

C-7.3: Proves theorems using Euclid’s axioms and postulates – for angles, triangles, quadrilaterals, circles, area-related theorems for triangles and parallelograms

Let’s Recall

Recap to check if students know the properties of quadrilaterals like diagonals, opposite sides, opposite angles, adjacent sides and adjacent angles.

Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

supplementary angles: a pair of angles whose sum is 180°

bisect: dividing a line, angle or shape into two equal parts

congruent: figures having exactly the same shape and size

transversal: a line that intersects two or more lines at distinct points

Teaching Aids

Cutouts of concave and convex quadrilaterals (parallelogram, rectangle, trapezium, kite, rhombus); Protractor; Ruler; Straws; Glue

Chapter: Quadrilaterals

Learning Outcomes

Students will be able to classify quadrilaterals based on their properties.

Teaching Aids

Cutouts of concave and convex quadrilaterals (parallelogram, rectangle, trapezium, kite, rhombus); Protractor; Ruler

Activity

Begin by the class by showing the students a convex and a concave quadrilateral.

Ask them the similarity and the difference between the two and have a discussion on convex and concave quadrilaterals.

Divide the class into small groups or pairs. Distribute a cutout of a quadrilateral to each group.

Instruct the groups to measure each interior angle of their quadrilateral cutout using the protractors. Ask them to also measure the sides and the perpendicular distance between opposite sides using a ruler to check if they are parallel and equal.

Ask them what additional features they noticed that define the shape.

Draw a table on the board as shown. Ask the students to copy the table into their notebooks and record their results in the table.

Name of Quadrilateral: Additional

Guide them to identify the type of quadrilateral based on the measures recorded.

Extension Idea

Ask: The measures of four angles of a quadrilateral are 30°, 70°, 50° and x. If the sum of these four angles is 360°, identify the type of quadrilateral.

Say: As 30° + 70° + 50° + x = 360°, then x = 360° – 150° = 210°. So, it is a concave quadrilateral.

Trapezium and Kite

Learning Outcomes

Imagine Maths Page 45

Students will be able to identify the properties of a trapezium and a kite and apply them to solve problems.

Teaching Aids

Straws; Pair of scissors; Glue

Activity

Begin the class by showing the students shapes of a trapezium and a kite.

Explain that a quadrilateral with only one set of opposite sides parallel is a trapezium, while a quadrilateral where both pairs of adjacent sides are of equal length is a kite.

Ask the students to work in pairs. Distribute a set of straws to each pair. Instruct them to cut the straws and paste them in their notebooks to create both a trapezium and a kite using the properties of each shape.

Following this, present two problems (one for each shape) involving missing angles to be solved by applying the respective properties. For example:

1. Giventhattwoadjacentanglesofatrapeziummeasure70°and110°,determinethemeasuresoftheothertwoangles.

2. Iftheanglebetweentwounequalsidesofakiteis110°,andtheanglebetweenthetwolongersidesis50°,calculate themeasuresoftheremainingtwoangles.

Ask the students to work individually on these problems and then engage in group discussions to compare and analyse their solutions.

Parallelograms

Learning Outcomes

Imagine Maths Page 47

Students will be able to identify the properties of a parallelogram and apply them to solve problems.

Teaching Aids

Straws; Pair of scissors; Glue

Activity

Begin the class by showing the students the shape of a parallelogram.

Explain that a quadrilateral in which both pairs of opposite sides are equal and parallel is called a parallelogram and discuss its properties.

Ask the students to work in pairs. Distribute a set of straws to each pair. Ask them to cut the straws and paste it in their notebooks to create a parallelogram using the properties of the shape.

Following this, present a problem involving missing angles to be solved by applying the properties of a parallelogram. For example:

Giventhattwoadjacentanglesofaparallelogrammeasure60°and120°,determinethemeasuresoftheremaining twoangles.

Ask the students to work individually on these problems and then engage in group discussions to compare and analyse their solutions.

Extension Idea

Ask: If the opposite sides of a parallelogram measure 15 cm and 20 cm, are the two triangles formed by the longer diagonal congruent?

Say: Yes, the triangles are congruent using the SAS congruence criterion, as the opposite sides and opposite angles are equal. Additionally, the SSS congruence criterion applies since the diagonal serves as the common side.

Learning Outcomes

Students will be able to identify the properties of a rhombus, a square and a rectangle and apply them to solve problems.

Teaching Aids

Straws; Pair of scissors; Glue

Activity

Begin the class by showing the students the shapes of a rhombus, a square and a rectangle.

Explain that a rectangle is a parallelogram with only right angles and that it shares its properties with a square, which has all sides equal. Explain that a square which has equal sides and angles, differs from a rhombus where all the sides are equal but only the opposite angles match and one diagonal is longer than the other. Discuss all the properties of these shapes.

Ask the students to work in pairs. Distribute a set of straws to each pair. Ask them to cut the straws to create a rhombus, a square and a rectangle using the properties of each shape, in their notebooks.

Following this, present a problem (one for each shape) to be solved by applying the respective properties. For example:

1. Thelengthandthebreadthofarectangleare6cmand8cm,findthelengthofitsdiagonal.

2. Findthelengthofthediagonalofasquareifitsareais100sq.cm.

3. Thelengthsofthediagonalsofarhombusare16cmand12cm.Determinetheperimeteroftherhombus.

Ask the students to work individually on these problems and then engage in group discussions to compare and analyse their solutions.

Ask the students to compare the shapes based on their properties. Also ask them what common properties these shapes share.

Imagine Maths Page 52

Learning Outcomes

Students will be able to deduce the interior angle sum property of quadrilaterals and apply it.

Teaching Aids

Cutouts of quadrilaterals; Protractor

Activity

Ask the students to work in pairs. Distribute 5 cutouts of quadrilaterals to each pair.

1 4 2 3

Quadrilateral 1

Quadrilateral 2

Quadrilateral 3

Quadrilateral 4

Quadrilateral 5

Then ask the students to cut the angles of a quadrilateral and then turn them around to form a complete angle to deduce that the sum of all the interior angles of a quadrilateral is 360°. Ask questions like: Is the sum of all four angles the same for each quadrilateral? Discuss the interior angle sum property of quadrilaterals.

Give the students some problems based on finding missing angles to solve.

Extension Idea

Instruct: Determine the measures of all the angles given that one angle of a parallelogram measures 100°. Say: As the opposite angles of a parallelogram are equal and using the interior angle sum property, the sum of the other two angles will be 360° – 200° = 160°. So, the angles measure 100°, 100°, 80° and 80°.

Exterior Angle Sum Property of Quadrilaterals

Learning Outcomes

Imagine Maths Page 52

Students will be able to deduce the exterior angle sum property of quadrilaterals and apply it.

Teaching Aids

Cutouts of quadrilaterals (parallelogram, rectangle, trapezium, kite, rhombus); Protractor

Activity

Ask the students to work in pairs. Distribute 5 cutouts of quadrilaterals to each pair. Instruct them to outline a quadrilateral on a sheet of paper, extend the angles, cut off the exterior angles and turn them around to form a complete angle. Help them deduce that the sum of all the exterior angles of a quadrilateral is 360°.

Then, ask them to measure each exterior angle of a quadrilateral using a protractor. Ask them to add the measures of all four exterior angles. Guide them to record their observations in a table as shown.

Ask questions like: Is the sum of all four exterior angles the same for each quadrilateral? Discuss the exterior angle sum property of quadrilaterals. Give the students some problems based on finding missing angles to solve.

Extension Idea

Ask: In a quadrilateral, the exterior angles are in the ratio 1:2:3:4. What is the measure of each exterior angle of the quadrilateral?

Say: As the sum of the exterior angles is 360°, +2+3+4=360°10= 360=360xxxxxx . So, the measures of the exterior angles are 36, 72,108 and 144 .

Answers

1. Properties of Quadrilaterals

Do It Together Angles 150 , 100 , 40 , 70 75 , 105 , 101 , 79

2. Trapezium and Kite

Think and Tell

Only one pair of opposite angles are equal in a kite.

Do It Together

B

A C

54

D

DAC + ACD + CDA = 180 (angle sum property)

DAC = ACD( AD = CD )

DAC + ACD + 54 =180

DAC = ACD = 63

ABC + BCA = CAB (angles of equilateral triangle)

So, ABC = BCA = CAB = 60

A = DAC + CAB = 63 +60 =123

C = ACD + BCA = 63 +60 123

3. Rhombus, Square and Rectangle

Do It Together

Since, in : ABC: 63180xxx ⇒ 10180 x ⇒

⇒ 18; 354; 6108xxx And,

⇒ 18 ax

⇒ 354bx

⇒ 6108cx

PR bisects P, so, RPS= 90 =45 2

110 + 110 + PUT + RUQ = 360 PUT = 70

Since, in PUT

⇒ 4570180 x 65 x ⇒

4. Angle Sum Property of Quadrilaterals

Do It Together

Interior Angles of a QuadrilateralMissing Angle

1. 55°, 75°, , 145° 80°

2. 35°, , 110°, 140° 85°

3. 60°, 100°, 120°, 40°

4. , 90°, 70°, 160°

Construction of Quadrilaterals 5

Learning Outcomes

Students will be able to:

construct a quadrilateral with 4 sides and 1 diagonal given. construct a quadrilateral with 3 sides and 2 diagonals given.

construct a quadrilateral with 2 adjacent sides and 3 angles given. construct a quadrilateral with 3 sides and 2 included angles given. construct a quadrilateral with 4 sides and 1 angle given. construct special quadrilaterals.

Alignment to NCF

C-3.2: Outlines the properties of lines, angles, triangles, quadrilaterals, and polygons and applies them to solve related problems

C-3.4: Draws and constructs geometric shapes, such as lines, parallel lines, perpendicular lines, angles, and simple triangles, with specified properties using a compass and straightedge

C-3.5: Understands congruence and similarity as it applies to geometric shapes and identifies similar and congruent triangles

Let’s Recall

Recap to check if students know how to identify different quadrilaterals using their properties. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

quadrilateral: four-sided polygon

Teaching Aids

Protractor; Ruler; Compass; Paper strips; 2 sets of straws of 5 different lengths

Chapter: Construction of Quadrilaterals

Construction with 4 Sides and 1 Diagonal

Learning Outcomes

Students will be able to construct a quadrilateral with 4 sides and 1 diagonal given.

Teaching Aids

2 sets of straws of 5 different lengths; Ruler; Compass

Activity

Imagine Maths Page 59

Begin the class by discussing how to construct a triangle and the measures of sides and angles needed to construct it. Ask the students to work in pairs. Distribute 1 set of 5 straws of different lengths (e.g., 4.3 cm, 3.6 cm, 5.6 cm, 4.7 cm and diagonal = 6 cm), a ruler and a compass to each student. Instruct them to form a quadrilateral by connecting the straws.

Ask questions like: Were you able to make a unique quadrilateral? How many triangles does the shape have? Could you make the quadrilateral if one of the lengths was not given? Help them understand the uniqueness of the quadrilateral made using the lengths of 4 sides and 1 diagonal. Encourage the students to explore different combinations of straw lengths for making quadrilaterals.

Instruct them to construct a quadrilateral ABCD in their notebooks using a compass and with the given lengths (AB = 4.3 cm, BC = 3.6 cm, CD = 5.6 cm, DA = 4.7 cm and AC = 6 cm). When they are done, ask them to compare the quadrilaterals constructed with their partners to see that both are exactly the same.

Extension Idea

Ask: Can you think of a set of measures of 4 sides and 1 diagonal which can be used to make a quadrilateral?

Say: There could be many such sets. One could be: AB = 3 cm, BC = 4 cm, CD = 5 cm, DA = 6 cm and AC = 7 cm for quadrilateral ABCD.

Construction with 3 Sides and 2 Diagonals

Learning Outcomes

Students will be able to construct a quadrilateral with 3 sides and 2 diagonals given.

Teaching Aids

2 sets of straws of 5 different lengths; Ruler; Compass

Activity

Imagine Maths Page 60

Ask the students to work in pairs. Distribute 1 set of 5 straws of different lengths (e.g., sides: 4.2 cm, 3.8 cm, 5.5 cm and diagonals: 7.6 cm, 6.7 cm).

Instruct them to form quadrilateral KLMN by connecting the straws, where 2 straws are used as diagonals of the quadrilaterals.

Ask questions like: Were you able to make the quadrilateral uniquely? How many triangles does your shape have? Could you make the quadrilateral if one of the side lengths were not given? Help them understand the uniqueness of the quadrilateral made using 3 sides and 2 diagonals.

Encourage the students to explore different combinations of straw lengths for making quadrilaterals.

Instruct them to construct a quadrilateral in their notebooks using a compass and with the given lengths. When they are done, ask them to compare the quadrilaterals constructed with their partners to see that both are exactly the same.

Construction with 3 Angles and 2 Included Sides

Learning Outcomes

Imagine Maths Page 61

Students will be able to construct a quadrilateral with 2 adjacent sides and 3 angles given.

Teaching Aids

Paper strips; Protractor; Ruler; Compass

Activity

Ask the students to work in groups. Provide them with paper strips. Instruct them to cut 4 lengths, two of them being PQ = 5 cm and RQ = 6 cm. Give them three angles as 60°, 90°, 75°.

Instruct the students to use the two strips for PQ and RQ and arrange them at a 90° angle using a protractor. Ask them to arrange the other strips at given angles to form a quadrilateral.

Ask them whether the given sides in their quadrilateral are included between the three angles and how they can make them included. Help them deduce that if the sides aren’t included between the angles, they won’t all get the same quadrilateral.

Instruct them to use a compass, protractor and ruler to construct a quadrilateral with the specified measures of 3 angles and 2 included sides in their notebooks.

Extension Idea

Ask: Can a unique quadrilateral be drawn if the measures of 2 opposite sides are given along with 3 angles?

Say: No quadrilateral can be drawn for the given criteria because there are multiple quadrilaterals with different side lengths and angles that can satisfy the given information.

Construction with 3 Sides and 2 Included Angles

Learning Outcomes

Imagine Maths Page 63

Students will be able to construct a quadrilateral with 3 sides and 2 included angles given.

Teaching Aids

Paper strips; Protractor; Ruler; Compass

Activity

Ask the students to work in groups. Provide them with paper strips. Instruct them to cut 4 lengths, three of them being AB = 5 cm, CD = 3 cm and BC = 6 cm. Give them two angles as 60°, 30°.

Instruct the students to use the strips for AB and BC and arrange them at a 60° angle using a protractor. Ask them to arrange the other two sides at a 30° angle.

Ask them whether the given angles in their quadrilateral are included between the three sides and how they can make them included. Help them deduce that if the angles aren’t included between the sides, they won’t all get the same quadrilateral.

Instruct them to use a compass, protractor and ruler to construct a quadrilateral with the given measures. Discuss their approach to the construction.

Extension Idea

Ask: If you double the measures of the sides to form a quadrilateral, do the angles also need to be doubled?

Say: No, we don’t double the angles because doing so will make the sum of the interior angles of the quadrilateral more than 360°.

Construction with 4 Sides and 1 Angle

Learning Outcomes

Students will be able to construct a quadrilateral with 4 sides and 1 angle given.

Teaching Aids

Paper strips; Protractor; Ruler; Compass

Activity

Imagine Maths Page 64

Ask the students to form groups of 4 and distribute the teaching aids. Provide 1 set of 4 paper strips of different lengths (e.g., KL = 4.2, ML = 3.8, MN = 5.5, KN = 7.6) and tell them that angle L measures 75°.

Instruct each group member to form quadrilateral KLMN by connecting the strips taking a different base. Ask questions like: Were you able to make the quadrilateral uniquely? How is your quadrilateral different and similar to that of your partner? Help them understand the uniqueness of the quadrilateral made using the measures of 4 sides and 1 angle. Encourage the students to explore different combinations of strip lengths for making quadrilaterals. Instruct them to construct a quadrilateral in their notebooks using a compass with the given lengths and taking the same base.

When they are done, ask them to compare the quadrilaterals constructed with their partners to see that both are exactly the same.

Constructing Special Quadrilaterals

Learning Outcomes

Students will be able to construct special quadrilaterals.

Teaching Aids

Protractor; Ruler; Compass

Activity

Imagine Maths Page 66

Discuss the features/properties of special quadrilaterals like a square, rectangle, kite, parallelogram and rhombus. Ask the students to work in groups and prompt one student from each group to pick one special quadrilateral.

Instruct the students to try constructing the quadrilateral with a minimum number of known measures using a protractor, ruler and compass. Discuss how we do not need 5 measures to construct these quadrilaterals and the number of measures actually needed to construct each.

Then, encourage the groups to explain the construction of their quadrilaterals by showcasing their work to the class. Discuss the various approaches the students came up with and address their doubts, if any. Encourage them to pick another quadrilateral within their groups and construct it in their notebooks.

Extension Idea

Instruct: Suggest a set of measures of elements to construct a kite.

Say: One set of measures for kite ABCD could be: BC = CD = 8 cm, AB = DA = 6 cm and AC = 10 cm.

Answers

1. Construction with 4 Sides and 1 Diagonal

Do It Together

2. Construction with 3 Sides and 2 Diagonals

Do It Together

4. Construction with 3 Sides and 2 Included Angles Do It Together

Rough Figure

5. Construction with 4 Sides and 1 Angle Do It Together

3. Construction with 3 Angles and 2 Included Sides

Do It Together

6. Constructing Special Quadrilaterals

Think and Tell

Yes, the length of one side of a square can be helpful. Do It Together

Cla ification and Tabulation of Data 6

Learning Outcomes

Students will be able to:

organise data in frequency distribution tables for ungrouped data. organise data in frequency distribution tables for grouped data. read and interpret frequency distribution tables of grouped data.

Alignment to NCF

C-5.2: Selects, creates, and uses appropriate graphical representations (e.g., pictographs, bar graphs, histograms, line graphs, and pie charts) of data to make interpretations

Let’s Recall

Recap to check if students know how to read and interpret data in a table. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

grouped data: data arranged in categories or ranges for easier analysis ungrouped data: individual data points without categorisation or grouping frequency distribution: a tabular representation showing the number of occurrences of each value or range in a dataset

Teaching Aids

Chart paper; Sticky notes; Matchsticks; Glue; Strips of paper

Chapter: Classification and Tabulation of Data

Learning Outcomes

Students will be able to organise data in frequency distribution tables for ungrouped data.

Teaching Aids

Chart paper; Sticky notes

Activity

Begin by explaining the objective of the day’s activity: to determine the most common shoe size among the students in the class. Distribute a sticky note to each student and instruct them to write down their shoe size.

Create a blank frequency distribution table on chart paper with columns labelled ShoeSize and TallyMarks.

Ask the students to work in groups. Provide each group with the frequency distribution table drawn on chart paper. Collect the sticky notes containing the shoe sizes. Review the collected data by calling the shoe sizes from the sticky notes one by one and have each group draw tally marks corresponding to each size on their chart paper. Once all the data is tallied, count the tally marks for each shoe size to determine its frequency, representing the number of students wearing shoes of that size.

Instruct the students to identify the shoe size with the highest frequency to determine the most common shoe size among the Grade 8 students.

Extension Idea

Ask: What is the range of a data set which has 10 observations and all the observations are 10?

Say: Range = 10 – 10 = 0 Drawing

Learning Outcomes

Students will be able to organise data in frequency distribution tables for grouped data.

Teaching Aids

Chart paper; Matchsticks; Glue

Activity

Begin by introducing the concept of grouping data. Ask the students the number of hours they study in a week and record the data in a table on the board. Discuss how to group the number of hours into ranges like 0–2, 3–5, 6–8, 9–11, and so on.

Ask the students to form groups. Distribute chart paper to each group.

Instruct the students to convert the discrete data into grouped data, form the frequency distribution table on chart paper using the matchsticks as tally marks and writing the frequency for each group. Encourage them to showcase their work in the class.

Using their tables, define related concepts such as class intervals, class limits, class marks, class size, etc. Discuss how grouping the data reduces the task of managing large sizes of ungrouped data. Help the students compare and observe the difference and similarities between the two tables. Discuss their responses. Encourage them to write their learnings in their notebooks.

Extension Idea

Ask: If you group the data into intervals of 0–5 instead of 0–2 and 3–5, what differences will arise in their frequencies?

Say: The interval 0–5 will include a wider range of values compared to the separate intervals of 0–2 and 3–5. Therefore, you may observe a higher frequency in the 0–5 interval compared to the frequencies observed in the 0–2 and 3–5 intervals.

Reading a Frequency Distribution Table of Grouped Data Imagine Maths Page 79

Learning Outcomes

Students will be able to read and interpret frequency distribution tables of grouped data.

Teaching Aids

Chart paper (with a grouped frequency distribution table); Strips of paper

Activity

Introduce the concept of population density and its distribution across different states in India. Display a grouped frequency distribution table (drawn on chart paper) showing the population density ranges and the number of states falling within each range.

Ask the students to work in groups.

Instruct the groups to carefully examine the table and interpret the data. Ask them to discuss the following questions: Whichrangehasthehighestnumberofstates?Whichrangehasthelowest?

WhatpercentageofIndianstateshaveapopulationdensitybetween101and500peoplepersquarekilometre?

Provide each group with 2 strips of paper. Instruct each group to create 2 questions related to the table. Have each group pass their question strips to another group. Instruct each group to answer the questions they received.

Answers

1. Frequency Distribution of Grouped and Ungrouped Data

Think and Tell

In daily life, you need to organise data in activities like making to-do lists, managing schedules, and tracking expenses.

2. Frequency Distribution of Ungrouped Data

3.

7

Bar Graphs and Histograms

Learning Outcomes

Students will be able to:

draw and read single bar graphs. draw double bar graphs for given data. read double bar graphs. draw histograms for given data. read and interpret histograms.

Alignment to NCF

C-5.2: Selects, creates, and uses appropriate graphical representations (e.g., pictographs, bar graphs, histograms, line graphs, and pie charts) of data to make interpretations

Let’s Recall

Recap to check if students know how to read and interpret a bar graph. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

data: facts, figures, or other pieces of information that can be used to learn about something frequency: number of times a particular observation occurs in the data histogram: bar graphs which are used to represent grouped data

Teaching Aids

Graph paper; Coloured paper; Glue stick; Slips of paper; Pair of scissors; Chart paper with a double bar graph; Chart paper with a histogram

Chapter: Bar Graphs and Histograms

Drawing and Reading Bar Graphs

Learning Outcomes

Students will be able to draw and read single bar graphs.

Teaching Aids

Graph paper; Coloured paper; Glue stick; Slips of paper; Pair of scissors

Activity

Begin the lesson by briefly revisiting the concept of a bar graph. Explain that the students will be creating a visual representation of the average number of hours spent on extra-curricular activities per week by the students of a school.

Draw a table on the board listing the activities and the number of hours spent.

Divide the class into groups and give each group graph paper, coloured paper, and a glue stick.

Instruct them to draw two axes on graph paper, with the x-axis representing the activities and the y-axis representing the hours. Ask them to label the x-axis with the names of the activities and the y-axis with the appropriate intervals to accommodate the weekly hours. Instruct them to use the data in the table to make bars for each activity. They can cut and paste coloured paper strips of appropriate lengths to create the bars. Remind them to make the strips of the same width.

Ask questions like: How many hours a week are spent on volunteer work? What is the average number of hours per week spent on all these activities? On which activity is the greatest number of hours spent?

Encourage everyone to answer the questions.

Discuss their understanding and ask them to write the answers in their notebooks. Give each group 2 slips of paper. Ask them to discuss and create 2 questions based on the data, write them on the slips, pass the slips to another group, and answer the questions they receive in their notebooks.

Extension Idea

Ask: What changes are required if you want to make a horizontal bar graph?

Say: To make a horizontal bar graph, the x-axis and y-axis would switch roles, with the activities labelled on the y-axis and the hours on the x-axis. The bars would then extend horizontally from the y-axis, representing the number of hours spent on each activity.

Learning Outcomes

Students will be able to draw double bar graphs for given data.

Teaching Aids

Graph paper; Coloured paper; Glue stick; Pair of scissors

Activity

Begin the lesson by explaining the importance of sports in physical and mental development. Explain that the purpose of the day’s activity is to create a visual representation of the favourite sports of 130 students.

Divide the class into groups. Distribute graph paper, coloured paper and glue to each group.

Draw a table on the board as shown.

Instruct the students to draw two axes on their graph paper, with the x-axis representing the sports and the y-axis representing the number of students. Ask them to label the x-axis with the name of each sport and the y-axis with appropriate intervals to accommodate the data. Using the data in the table, ask the students to plot 2 bars in two different colours for each sport – one representing the number of girls and the other representing the number of boys – by cutting and pasting rectangular strips of coloured paper of appropriate lengths. Remind them that the widths of the strips should be the same.

Encourage the students to scale their axes to represent the data accurately. Explain that each square on the graph paper can represent a certain number of students. Ensure that they give the bar graph an appropriate title. Encourage a discussion on the bar graph formed by each group.

Extension Idea

Instruct: Create questions to ask other students about the bar graph.

Say: You can ask a lot of questions about the bar graph. One such question could be: Whichsportwaschosenas thefavouritebythemoststudents?

Reading Double Bar Graphs

Learning Outcomes

Students will be able to read double bar graphs.

Teaching Aids

Chart paper with a double bar graph; Slips of paper; Pair of scissors

Activity

Begin the lesson by talking about the values of compassion and social responsibility. Explain how even the smallest contributions make big impacts on the lives of people in need.

Imagine Maths Page 92

Create a double bar graph on chart paper where the monetary contributions of a donation drive in a school are shown across 4 weeks in July and in August.

Ask the students to work in groups. Distribute the chart paper with the double bar graph to each group. Instruct them to examine the graph closely and note down any patterns or differences they observe in the contributions.

Ask questions like: Whichweekhadthehighestcollectioninbothmonths?Whichweekhadthelowestcollection?What istherangeofthecollectionsforJuly?Whatarethetotalandaverageweeklycollectionsinbothmonths?

Provide each group with 2 slips of paper. Instruct each group to create 2 questions related to the bar graph. Have each group pass their slips to another group. Instruct each group to answer the questions they received.

Drawing Histograms

Learning Outcomes

Students will be able to draw histograms for given data.

Teaching Aids

Graph paper; Coloured paper; Glue stick; Pair of scissors

Activity

Imagine Maths Page 96

Introduce the concept of using histograms to represent grouped data. Explain that the students will be creating a histogram on temperature ranges throughout a year for a city.

Draw a table on the board as shown.

Divide the class into groups. Distribute graph paper, coloured paper, and a glue stick to each group.

Instruct them to draw two axes on the graph paper, as they would do for a bar graph. Emphasise marking the class intervals on the x-axis. Instruct them to use the data in the table to make bars of equal width for each temperature range. They can cut and paste coloured paper strips to create the bars. Ask them to make sure there are no gaps between the bars.

Ask the students to check whether the graph accurately shows the temperature ranges for the months by adjusting the height of the bars. Each coloured paper strip can stand for a certain number of months. Ask each group to give their graph an appropriate title.

Ask questions like: What are the similarities and differences between a bar graph and a histogram? Encourage everyone to share their learnings.

Extension Idea

Ask: How will the height of the bar change if I reduce the scale to half?

Say: The height of each bar will increase. For example, if 1 division on the scale initially represented 2 months, reducing the scale to 1 month means the bar’s height must be increased from 2 divisions to 4 divisions to accurately represent 4 months.

Learning Outcomes

Students will be able to read and interpret histograms.

Teaching Aids

Chart paper with a histogram

Activity

Prepare a histogram on chart paper showing the heights (in cm) of 25 students of Grade 8. Ask the students to work in groups. Distribute sheets of chart paper with the histogram to each group.

Ask the students to examine the histogram closely and answer the questions.

Ask questions like: How many students have a height between 140 cm and 160 cm? How many students are more than 150 cm tall? How many students are less than 145 cm tall? What is the average height of the students?

Instruct the students to answer these questions. Discuss their responses and encourage them to write the answers in their notebooks.

Extension Idea

Ask: What percentage of the students are taller than 150 cm?

Say: 12 25 × 100% = 48%. So, 48% of the students are taller than 150 cm.

1. Drawing and Reading Bar Graphs

Do It Together

1. 1 division = 500 km

2. Longest river = Brahmaputra

3. Shortest river = Kaveri

4. Length of river Mahanadi = 900 km

Length of river Kaveri = 800 km

Ratio of the length of river Mahanadi to that of river Kaveri = 900:800 = 9:8

5. Length of river Ganga = 2500 km

Length of river Narmada = 1300 km Difference in length = 2500 – 1300 = 1200 km

2. Drawing Double Bar Graphs

Do It Together

4. Drawing Histograms

Do It Together

3. Reading Double Bar Graphs

Think and Tell

Other products have the highest percentage increase from the previous year since the gap between the exports of 2021 and 2022 is the highest.

Do It Together

2. Number of people who visited India Gate in 2019 = 700

3. Number of people who visited Taj Mahal in 2018 = 900

Number of people who visited Taj Mahal in 2019 = 1000

Percentage increase = 100 900 × 100% = 11.11%

4. Average number of visitors in 2018 = 700 + 900 + 600

+500 = 2700

4 = 675

Average number of visitors in 2019 = 760 + 1000 + 700

+500 = 2960

4 = 740

Difference = 740 − 675 = 65

5. Reading Histograms

Do It Together

2. Number of employees older than 40 years = 20 + 20 + 5 + 5 = 50

Total number of employees = 30 + 45 + 40 + 30 + 20 + 20 + 5 + 5 = 195

Percentage of total employees who are older than 40 years = 50 195 × 100% = 25.64%

3. Number of employees older than 35 years = 30 + 20 + 20 + 5 + 5 = 80

Number of employees younger than 35 years = 30 + 45 + 40 = 115

Required ratio = 80:115 = 16:23

4. Number of employees who are younger than 40 years = 30 + 45 + 40 + 30 = 145

Total number of employees = 195

Percentage of total number of employees who are younger than 40 years = 145 195 × 100% = 74.36%

Pie Charts 8

Learning Outcomes

Students will be able to:

find the measure of the angle for each given sector (fraction) in a circle. draw a pie chart for the given data. read and interpret a pie chart.

Alignment to NCF

C-5.2: Selects, creates, and uses appropriate graphical representations (e.g., pictographs, bar graphs, histograms, line graphs, and pie charts) of data to make interpretations

Let’s Recall

Recap to check if students know how to read and interpret pie charts where the sectors are divided into halves, fourths or eighths.

Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

sectors: divisions of a circle displaying the size of some related piece of information central angle: angle formed at the centre of a circle

Teaching Aids

Sheet with a table showing 4 genres and columns for the number of students and measures of the central angle; Sector cutouts with different central angles; Glue stick; Chart paper; Pie chart drawn on a sheet of paper; Question cards

Chapter: Pie Charts

Sectors and Central Angles

Learning Outcomes

Students will be able to find the measure of the angle for each given sector (fraction) in a circle.

Teaching Aids

Sheet with a table showing 4 genres and columns for the number of students and measures of the central angle

Activity

Begin by reminding students about pie chart representation of data. Discuss how the whole circle represents data in the form of sectors with each sector having a central angle. Discuss the central angles formed by different sectors inside the circle like one-fourth forms a 90° angle and one-eighth forms a 45° angle.

Give them categories, such as, book genres (fiction, thriller, documentary, mystery) and ask them to pick their favourite by raising their hands when you call out each genre one by one. Note down the data in a table on the board:

Genre Number of Students Measure of the Central Angle

Fiction

Thriller

Documentary

Mystery

Ask questions like: If 10 out of 40 students in the class like fiction, how many students out of 360 would like fiction?

Bring out the formula for finding the central angle for this category on the board. Write the measure of the central angle for fiction on the board.

Ask the students to work in groups and copy the table drawn on the board, in their notebooks.

Instruct them to find the central angle for each category using the formula. Ask them to compare their angle measures with the other group members to check if their answers are correct.

Ask questions like: How do you know that the measures of the angles are correct?

Give the students some more data and ask them to find the central angle.

Extension Idea

Ask: What should be the percentage for the data category that has a central angle of 90°?

Say: 90 360 = 1 4; 1 4 × 100% = 25%.

Learning Outcomes

Students will be able to draw a pie chart for the given data.

Teaching Aids

Sector cutouts with different central angles; Glue stick; Chart paper

Activity

Begin the class with a discussion on how to find the central angles for given data. Draw a table with data showing favourite activity of 100 students, on the board.

Ask the students to work in groups. Distribute the chart paper, glue stick and sector cutouts with different central angles (e.g., 10°, 20°, 30°, 45°, etc.) to each group. Make sure that the cutouts with central angles needed for each category are also included. Instruct the students to read the data and calculate the central angle for each category in their notebooks. They can then discuss within their groups if all the members got the same answer.

Ask them to draw a circle on the chart paper with the same radius as in the sector cutouts. Guide the students to use the cutouts to find the angles for their respective categories and paste them onto their circles. Guide them in starting with the first sector cutout, using the horizontal radius as the base, and recording both the angle and its value. Instruct them to continue pasting the remaining sector cutouts, using the previous one as the base. Encourage students to label the sectors in their circles with the angles and corresponding values.

Invite the groups to showcase their work. Initiate a class discussion to review what the students have learned. Encourage them to recreate the same pie chart in their notebooks using protractors and rulers.

Extension Idea

Ask: What change should the number of sectors undergo if you remove one category of data from the pie chart?

Say: The number of sectors will decrease by 1 with the decrease in the number of categories. The measures of all the angles will also change thereby changing the size of each remaining sector.

Reading Pie Charts Imagine Maths Page 111

Learning Outcomes

Students will be able to read and interpret a pie chart.

Teaching Aids

Pie chart drawn on a sheet of paper; Question cards

Activity

Begin the class by discussing real-life examples where pie charts are used.

Present this scenario to the class:

Rohitrecordeddataonthedifferentfruitssoldbyafruitsellerinaday.Hesawthatthetotalsalesforthatday amountedto₹12,000.

Prepare the pie chart (as shown) on a sheet of paper and some question cards.

Whichwasthemostsoldproductoftheday?

Whatwasthesalesvalueofbananas?

Whatwasthedifferenceofthesalesofapplesandkiwis?

Ask the students to work in groups. Distribute the teaching aids to the students.

Ask the students to read the pie chart and answer the questions given on the question cards in their notebooks.

Discuss the responses with the whole class and encourage the students to write the answers in their notebooks.

Extension Idea

Ask: Can the total percentage in the pie chart be more than 100?

Say: No, a pie chart represents 100% of a whole, and each sector or slice corresponds to a portion of that whole. Therefore, the sum of all the percentages in a pie chart should always equal 100%.

1. Sectors and Central Angles

Do It Together

2. Drawing a Pie Chart

Do It Together

3. Reading Pie Charts

Think and Tell

No, the sum of all the values of all the components cannot be less than the total value.

Do It Together

1. 27,000 × 120 360 = 9000 tonnes

2. Production of sugar = 100 360 × 27,000= 7500 tonnes

Production of rice = 60 360 × 27,000= 4500 tonnes

Difference = 7500 − 4500 = 3000 tonnes.

Probability 9

Learning Outcomes

Students will be able to:

the theoretical probability of an event.

the experimental probability of an event.

Alignment to NCF

C-6.2: Applies concepts from probability to solve problems on the likelihood of everyday events

Let’s Recall

Recap to check if students know how to find the chance of the given event happening. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

probability: chances that an event will happen event: a possible outcome or a set of possible outcomes of an activity or test experiment: an activity or test that is repeated and in which all possible outcomes are known outcome: a possible result of an activity or test

Teaching Aids

Coin; Small bags with 3 red, 4 blue, 5 yellow and 8 green marbles; Spinner 1 with numbers 1, 3, 5, 7, 9; Spinner 2 with numbers 2, 4, 6, 8, 10

Chapter: Probability

Learning Outcomes

Students will be able to find the theoretical probability of an event.

Teaching Aids

Coin; Small bags with 3 red, 4 blue, 5 yellow and 8 green marbles; Spinner 1 with numbers 1, 3, 5, 7, 9; Spinner 2 with numbers 2, 4, 6, 8, 10

Activity

Show the students a coin and ask them what we will get if we flip a coin. Discuss the total possible outcomes and the favourable outcomes of flipping a coin and how to write the probability of the event.

Ask the students to work in groups. Distribute a bag of marbles to each group. Ask them to count the marbles and find the theoretical probability of picking a marble of each colour at random from the bag. Discuss one example and guide them if necessary. For example: The total number of marbles (20) represents the total outcomes, and the number of red marbles (3) represents the favourable outcomes. So, the theoretical probability of picking a red marble is 3 . 10

Ask questions like: What is the theoretical probability of getting a black marble? A green marble?

Extension Idea

Ask: Show the students the two spinners.

Ask: Spinner 1 has even numbers less than 11 and Spinner 2 has odd numbers less than 10. What is the theoretical probability of getting a number less than 5 when both spinners are spun together?

Say: Total outcomes = 10, Favourable outcomes = 4. So, theoretical probability = 4 . 10

Experimental Probability

Learning Outcomes

Students will be able to find the experimental probability of an event.

Teaching Aids

Small bags with 3 red, 4 blue, 5 yellow and 8 green marbles

Activity

Imagine Maths Page 125

Discuss the concept of experimental probability using the example of a coin. Explain that if we toss a coin 50 times, we can count how often we get heads to find the experimental probability. Discuss how if heads appears 20 times out of 50 coin tosses, the experimental probability of getting heads is 20 50 or 2 5 .

Ask the students to work in groups. Distribute a bag of marbles to each group. Draw a table on the board as shown. Instruct the students to copy the table into their notebooks.

Colour Red Blue Yellow Green

Number of Times Picked

Instruct the students to pick a marble from the bag and record the colour they get in the table using tally marks. Then, they should put the marble back into the bag and repeat the activity. Ask them to do this a total of 25 times. Once the table is filled, instruct them to write the answers to these questions in their notebooks: What istheexperimentalprobabilityofpickingaredmarble?Whatistheexperimentalprobabilityofpickingablueorgreen marble?

Extension Idea

Ask: On flipping a coin 20 times, we get heads 12 times and tails 8 times. What is the experimental probability of getting tails as a percentage?

Say: Total outcomes = 20, Favourable outcomes = 8. So, experimental probability = 40%.

Answers

1. Theoretical Probability

Think and Tell

Yes, the probability of the wheel stopping at an odd number is the same as the probability of the wheel stopping at an even number.

Do It Together

1. P(E) = 4 11

Therefore, the possibility of getting an animal card that shows a bird picture is 4 11

2. P(E) = 7 11

Therefore, the possibility of getting an animal card that does not show a bird picture is 7 11 .

2. Experimental Probability

Think and Tell

The approximate experimental probability of getting heads if we toss a coin 1000 times is 50%.

Do It Together

The bar graph shows 48 ones, 50 threes, and 49 fives.

So, an odd number was rolled 48 + 50 + 49 = 147 times in a total of 300 rolls.

P(odd) =

Number of times an odd number was rolled147 = Total number of rolls 300 = 49%.

Next, we find the theoretical probabiliity of rolling an odd number.

P(odd) = Number of favourable outcomes31 = = Number of possible outcomes62 = 50%.

The experimental probability of rolling an odd number is 49%, which is close to the theoretical probability of 50%.

Squares and Square R ts 10

Learning Outcomes

Students will be able to:

find the square of a number.

identify patterns in square numbers to help find the square of a number.

find the square root of a number using prime factorisation.

find the square root of a number using long division.

Alignment to NCF

C-1.4: Recognises, describes, and extends simple number patterns such as odd numbers, even numbers, square numbers, cubes, powers of 2, powers of 10, and Virahanka–Fibonacci numbers

Let’s Recall

Recap to check if students know how to express a number as a product of prime factors. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

square root: a value that, when multiplied by itself, gives the original number perfect square: a number obtained by multiplying an integer by itself

Teaching Aids

Connecting cubes; Problem cards; Rule cards; Puzzle cards

Chapter: Squares and Square Roots

Square Numbers

Learning Outcomes

Students will be able to find the square of a number.

Teaching Aids

Connecting cubes

Activity

Imagine Maths Page 132

Introduce the concept of perfect squares. Show an example of a perfect square using connecting cubes. For instance, build a 2 × 2 square with 4 connecting squares.

Ask the students to work in groups. Distribute building blocks or connecting cubes to each group.

Instruct them to join the connecting cubes to form a square structure. Ask them to note the number of cubes forming one side of the square and the total number of cubes used to form the square. Explain that the total number of cubes tells us the square of the number (side).

Ask questions like: How can you tell if a model is a perfect square or not just by looking at it? Can you tell for bigger numbers like 2025?

For larger numbers like 2025, introduce the prime factorisation method. Provide students with examples of large numbers and guide them through finding the prime factors and determining if they form a perfect square. Give the students some practice questions on using the prime factorisation method to identify whether given numbers are perfect squares.

Instruct them to find the squares of different numbers and provide them with more practice questions.

Extension Idea

Ask: What is the smallest number by which 288 must be multiplied so that we get a perfect square?

Say: 288 = 2 × 2 × 2 × 2 × 2 × 3 × 3. There is one 2 that is not in a pair. So, if the number is multiplied by 2, we get a perfect square.

Patterns of Square Numbers

Learning Outcomes

Imagine Maths Page 137

Students will be able to identify patterns in square numbers to help find the square of a number.

Teaching Aids

Problem cards; Rule cards

Activity

Begin by discussing various patterns of square numbers using examples for each rule, referring to page 137 of the content book.

Prepare problem cards and respective rule cards. (Make sure problems related to all types of rules are covered.)

Ask the students to work in groups. Distribute the problem cards to each group and place the rule cards on the table. Instruct the groups to read the problem and pick the rule card that will be used to solve the problem from the table. Ask them to solve the problem using the rule in their notebooks. Then, have each group showcase their pattern to the group sitting next to them and ask them to verify it. Rotate the problem cards among the groups for more practice.

Finding Square Roots Using Prime Factorisation

Learning Outcomes

Students will be able to find the square root of a number using prime factorisation.

Teaching Aids

Puzzle cards

Activity

Begin the class by introducing the method of prime factorisation to find the square root of a number. Provide examples and guide the students through a few practice problems.

Ask the students to work in groups. Distribute the puzzle cards to each group.

Ask them to match the edges of their cards until all the edges match with equivalent expressions. The final solution will be a 3 × 3 grid as shown.

Ask questions like: With which card did you begin matching the cards? Which letter card did you place in the middle of the square? Top right corner? Bottom left corner?

Extension Idea

Ask: If there is a garden of area 242 sq. m, can all its sides be 22 m each?

Imagine Maths Page 140

Say: 242 = 2 × 11 × 11. As 242 isn’t the square of 22, the sides of the garden can’t be 22 m each.

Finding Square Roots Using Long Division

Learning Outcomes

Students will be able to find the square root of a number using long division.

Teaching Aids

Puzzle cards

Activity

Begin the class by explaining the methods of finding the square root of large numbers by the long division method. Prepare the puzzle cards with square numbers and their square root.

Imagine Maths Page 143

Ask the students to form groups. Distribute cards with square numbers and corresponding square root cards to each group.

Instruct the groups to find the square root of the given numbers by the long division method and join them with the corresponding square root cards. The first group to join all the puzzle cards correctly wins!

Extension Idea

Ask: If the area of a square photo frame is 2079.36 sq. cm, what is the length of each side?

Say: Area = side × side = side2; Length of each side = 2079.36 = 45.6 cm.

1. Square Numbers

Think and Tell

No, such a number won’t be a perfect square.

Think and Tell

No, such a number won’t be a perfect square.

Think and Tell

The square of an n-digit number will either have (n × n) − 1 or n × n digits.

Do It Together

a. 61 is a 2-digit number. So, it will have either (2 × 2) – 1 or 2 × 2 digits, that is, either 3 digits or 4 digits.

224, 253 and 917 are 3-digit numbers. So, it will have either (3 × 3) – 1 or 3 × 3 digits, that is, 8 digits or 9 digits.

b. The numbers that end in 2, 3, 7 or 8 are never perfect squares. So, the numbers 253 and 917cannot be perfect squares.

2. Patterns of Square Numbers

Think and Tell

There are 2n non-perfect square numbers between the squares of n and (n+ 1).

Think and Tell

No, if a number cannot be expressed as a sum of successive odd numbers, then it is not a perfect square.

3. Finding Square Roots Using Prime

4. Finding Square Roots Using Long Division

Think and Tell

Yes, we can find the square root of 5,53,536 using the long division method.

Think and Tell

If n is the number of digits, then there will be n 2 digits in the square root of an even number and n+ 1 2 digits in the square root of an odd number.

Cubes and Cube R ts 11

Learning Outcomes

Students will be able to:

find the cube of a number and identify perfect cubes.

find the cube root of a number using prime factorisation.

find the cube root of a number using estimation.

Alignment to NCF

C-1.4: Recognises, describes, and extends simple number patterns such as odd numbers, even numbers, square numbers, cubes, powers of 2, powers of 10, and Virahanka-Fibonacci numbers

Let’s Recall

Recap to check if students know how to find the volume of a solid by counting unit cubes. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

prime factorisation: a way of expressing a number as a product of its prime factors estimation: the process of guessing an answer that is close to the actual answer cube root: any number multiplied by itself three times to get a cube perfect cube: a number obtained by multiplying an integer by itself three times

Teaching Aids

Connecting cubes; Puzzle cards; Jigsaw puzzle pieces

Chapter: Cubes and Cube Roots

Perfect Cube

Learning Outcomes

Students will be able to find the cube of a number and identify perfect cubes.

Teaching Aids

Connecting cubes

Activity

Introduce the concept of perfect cubes. Explain that a perfect cube is a number that can be formed by multiplying an integer by itself three times.

Show an example of a perfect cube using connecting cubes. For instance, build a 2 × 2 × 2 cube with 8 connecting cubes.

Divide the class into groups. Distribute building blocks or connecting cubes to each group.

Instruct the students to join connecting cubes to form a cubic structure. Ask them to note the number of connecting cubes forming one side and the total number of connecting cubes used to form the cubic structure.

Imagine Maths Page 150

Discuss how the total number of connecting cubes gives us the cube of the number. Ask questions like: How can you tell if a model represents a perfect cube or not just by looking at it?

For larger numbers, like 2744, introduce the prime factorisation method for determining if the number is a perfect cube. Instruct the students to find the cubes of different numbers and give them more practice questions.

Extension Idea

Ask: What is the smallest number by which 3087 must be multiplied so that we get a perfect cube?

Say: 3087 = 7 × 7 × 7 × 3 × 3. If the number is multiplied by 3, we get a perfect cube.

Cube Root Through Prime Factorisation Method

Learning Outcomes

Students will be able to find the cube root of a number using prime factorisation.

Teaching Aids

Puzzle cards

Activity

Begin the class by introducing the method of prime factorisation to find the cube root of a number. Provide examples and guide the students through a few practice problems.

Divide the class into groups. Distribute the puzzle cards to each group.

Imagine Maths Page 155

Instruct them to match the edges of their cards until all the edges match with equivalent expressions. The final solution will be a 3 × 3 grid as shown.

Ask questions like: Which letter card did you place in the middle of the square? Top right corner? Bottom left corner? Bottom right corner?

Extension Idea

Instruct: 2*97 is a 4-digit number. If the number is a perfect cube, find the missing digit and the cube root of the number.

Say: Using the trial and error method, we can check whether 2197 is a perfect cube. The prime factorisation of 2197 is:

So, 2197 is a perfect cube and the missing digit is 1. The cube root of 2197 is 13.

Cube Root Through Estimation

Learning Outcomes

Students will be able to find the cube root of a number using estimation.

Teaching Aids

Jigsaw puzzle pieces

Activity

132197

13169

1313 1

Imagine Maths Page 159

Explain that the purpose of the day’s activity is to calculate cube roots quickly. Demonstrate the steps to estimate the cube root of a large number, such as 42,875, using grouping and estimation techniques as shown below.

42875

Group 2Group 1

42 lies between 27 and 64.

(33 = 27 and 43 = 64)

3 < 4

Units digit = 5, its cube = 125

So, the units digit of the cube root of the number = 5.

the tens digit of the cube root of the given number = the smaller number = 3

42875

3 = 35.

Divide the class into groups.

Distribute the jigsaw puzzle pieces to each group.

Instruct them to search for the relevant pieces of the jigsaw puzzle and join the pieces to get the estimated cube root. Finally, ask them to find the cube roots of different numbers by giving them more practice questions. Discuss the answers and let them write the answers in their notebooks.

Extension Idea

3

Ask: The volume of a cubical box is 32,768 cubic cm. What is its total surface area?

Say: The sides of the cubical box measure 32768 3 = 32 cm. So, its total surface area is 6 × (side)2 = 6 × (32)2 = 6144 square cm.

Answers

1. To Check If a Number Is a Perfect Cube or Not

Think and Tell

The units digit of the cubes of even numbers are always even. The units digit of the cube of some numbers is the same as the units digit of the number. The units digit of the cubes of odd numbers are always odd.

Yes, if the cube of a number is a multiple of 3, it is also a multiple of 27.

Do It Together

59,049 = 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3

Clearly, not all prime factors form a triplet, and we are left with a factor 3 which cannot form a triplet.

So, 3 is the lowest number by which 59,049 should be divided to get a perfect cube.

2. Patterns in Cubes

Do

It Together

We know that if n and n + 1 are two consecutive numbers, then (n + 1)3 − n3 = 3n (n + 1) + 1.

So, 873 – 863 = 3 × 86 × 87 + 1 = 22,446 + 1 = 22,447

3. Cube Root Through Prime Factorisation Method

Do It Together

1. 3 3 3 –17281728126 =–=–=–2744 147 2744

2. 33 3 8×(125)=8×125= 2 × (−5) = −10

4. Cube Root Through Estimation

Think and Tell

The number of digits in the cube root of a number depends on the number itself. In general, if you have a number n, then the number of digits in its cube root, denoted as 3 n can vary depending on the value of n.

Do It Together

592 lies between 512 and 729.

83 = 512 and 93 = 729

So, the tens digit of the cube root of the given number = the smaller number = 8

Units digit = 4, its cube = 64

So, the units digit of the cube root of the number = 4. Thus, 592704 3 = 84.

Percentages 12

Learning Outcomes

Students will be able to: solve word problems on ratios and percentages. solve word problems on percentage change.

Alignment to NCF

C-1.5: Explores the idea of percentage and applies it to solve problems

Let’s Recall

Recap to check if students know the basics of percentages. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

percentage: part of a whole represented as a fraction of 100 ratio: a relation or comparison between numbers or things based on amount or degree

Teaching Aids

Situation cards; Question cards

Chapter: Percentages

Ratio and Percentages

Learning Outcomes

Students will be able to solve word problems on ratios and percentages.

Teaching Aids

Situation cards; Question cards

Activity

Ask the students to work in groups. Distribute cards to each group with this situation:

Imagine Maths Page 164

Inasportseventorganisedatschool,atotalof400studentsparticipated.20%studentsparticipatedinAthletics,15% participatedinBasketball,30%participatedinFootballand35%participatedinCricket.

Make some question cards (as many as possible) and distribute to each group.

Whatistheratioofthenumberofstudentswhoparticipatedinathleticstothosewhoparticipatedinbasketball?

Howmanymorestudentsparticipatedincricketthaninfootball?

Instruct each student in the group to pick one question card, solve the problem in their notebook and write the answer. The group who solves the maximum number of problems correctly wins.

If time permits, shuffle the question cards among the groups. Discuss the answers with the whole class.

Extension Idea

Ask: If 60% of the football participants were male, then how many female football participants were there?

Say: Number of football participants = 30% of 400 = 120 participants. 60% of 120 = 72 participants were male. So, number of female football participants = 120 – 72 = 48 participants.

Percentage Change

Learning Outcomes

Students will be able to solve word problems on percentage change.

Teaching Aids

Situation cards; Question cards

Activity

Ask the students to work in groups.

Distribute cards to each group with this situation:

Aaronhasabakery.Readtheratecardthatisdisplayedinhisshop.

Imagine Maths Page 166

Afteraweek,thereweresomechangesinthepricesoftheproducts.

Make some question cards (as many as possible) and distribute to each group. Ifthereisanincreaseof10%inthepriceofbread,whatisthenewprice?

Whatisthepercentagechangeinthepriceofpizza,ifthenewpriceis₹480?

Instruct each student in the group to pick one question card, solve the problem in their notebook and write the answer. The group who solves the maximum number of problems correctly wins.

If time permits, shuffle the question cards among the groups. Discuss the answers with the whole class.

Extension Idea

Ask: What is the new price of cookies if it was first increased by 20% and then decreased by 10%?

Say: Initial increased price = ₹120 + 20% of ₹120 = ₹120 + ₹24 = ₹144. Final price of the cookies = ₹144 – 10% of ₹144 = ₹144 – ₹14.4 = ₹129.6.

Answers

1. Ratio and Percentages

Think and Tell

100% of any number is the number itself.

Think and Tell

Percentage of marks scored = 60 80 × 100% = 75%

Do It Together

Number of students who like basketball = 1300

Total number of students = 1300 65 × 100 = 2000

2. Percentage Change

Think and Tell

Increase in consumption = 10x 9 − x = 1 9 x kg of sugar Reduction in percentage of consumption

= x 9 x 100% = 11 1 9 %

Vijay has to increase his consumption by 11 1 9 %.

Do It Together

Original length of the rope = 150 cm

Final length after reduction = 125 cm

Reduction in length = 25 cm

Reduction percentage = Reduction in length

Original length × 100% = 25 150 × 100% = 16 2 3 %.

Profit/Lo , Discount and Tax 13

Learning Outcomes

Students will be able to:

solve problems on finding the profit/loss percentage, cost price or selling price if any two are given. solve word problems on finding the discount amount. solve word problems on finding the tax amount.

Alignment to NCF

C-1.5: Explores the idea of percentage and applies it to solve problems

Let’s Recall

Recap to check if students know how to find the cost price, selling price, profit and loss. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

profit: the money that you make when you sell something at a price higher than its cost price loss: the money that you lose when you sell something at a price lower than its cost price tax: money collected by the government of a country for public use

Teaching Aids

Bags of small items (like candies, pencils or buttons) having tags inside with statements (like CP = ₹150, sell at a profit of ₹15); Blank tags; Items with price tags showing the marked price and % discount offered; Play money; Situation cards; Question cards

Chapter: Profit/Loss, Discount and Tax

Learning Outcomes

Students will be able to solve problems on finding the profit/loss percentage, cost price or selling price if any two are given.

Teaching Aids

Bags of small items (like candies, pencils or buttons) having tags inside with statements (like CP = ₹150; sell at a profit of ₹15); Blank tags

Activity

Revisit the concepts of cost price (CP), selling price (SP), profit, and loss. Discuss the formulas for finding the profit/loss percentage, cost price or selling price if any two are given. Prepare bags of small items (like candies, pencils, or buttons) having tags with statements inside. (Make sure that the statement tags inside each bag are different.)

CP = ₹150; sell at a profit of ₹15 CP = ₹125; sell at a profit of ₹25

Ask the students to work in groups of 3. Distribute 2 blank tags and 2 bags of items (one with a profit tag and one with a loss tag) to each group.

Instruct the students to open the bags and look at the tags inside. Ask them to find the selling price (SP) and profit/loss percentage for each bag. They will then use the blank tags to prepare price tags showing the selling price (SP) and profit or loss%.

SP = ₹165; Profit percentage = 10% SP = ₹100; Loss percentage = 20%

Once they are done, instruct the groups to pass their bags to the group sitting next to them. Make sure these do not contain the price tags provided by the teacher. Each group will then look at the new tags and find the cost price of each item. Ask them to also find the total CP of the items, the total SP and the profit/loss percentage.

Extension Idea

Ask: Raj bought a vintage watch and sold it at a profit of 12%. If he had sold it for $180 more, he would have made a profit of 15%. What was the cost price of the watch?

Say: When Raj sold the watch at a 12% profit, SP was 112% of CP: SP1= CP + 0.12 × CP = 1.12CP. If he had sold it for $180 more at a 15% profit, SP would have been 115% of CP: SP2 = CP + 0.15 × CP = 1.15CP. As the difference of the selling prices is $180, we can write the equation: SP2 − SP1 = 180 ⇒ 1.15CP − 1.12CP = 180 ⇒ CP = $6000.

Finding Discount

Learning Outcomes

Students will be able to solve word problems on finding the discount amount.

Teaching Aids

Items with price tags showing the marked price and % discount offered; Play money

Imagine Maths Page 176

Activity

Introduce the concept of discount. Discuss the important formulas related to discount. Convert the classroom into a shop by putting some items on the table with price tags showing the marked price and % discount offered.

Ask the students to work in groups. Distribute play money to each group. Distribute the price tags for the items on the table to each group.

Instruct the students to discuss in their groups and calculate the amount that they need to pay for each item after deducting the discount amount. Ask the students to choose 2 items (with the least cost) that they want to buy and then use the play money to pay the teacher for those items. Once the students have a thorough understanding of the concept, introduce the concept of successive discounts.

Ask questions like: Does the order in which successive discounts are applied affect the final price of an item?

Give them various word problems based on discount for practice.

Extension Idea

Ask: A supermarket offers a 15% discount on the value of purchases above $50. If a customer’s total bill amount comes to $70, how much will the final bill amount be with the discount?

Say: The discount is applicable only on the amount exceeding $50.

Amount eligible for discount = Total bill amount − Threshold amount = $70 − $50 = $20; Discount = 15% of $20 = 15 100 × $20 = $3. Therefore, the customer will pay $70 − $3 = $67 after the discount.

Tax Imagine Maths Page 180

Learning Outcomes

Students will be able to solve word problems on finding the tax amount.

Teaching Aids

Situation cards; Question cards

Activity

Instruct the students to refer to page 180 and 181 of the ImagineMathematics book to understand the types of taxes applied in India.

Ask the students to work in groups. Distribute cards (with various situations) to each group.

Amitawenttopurchasesomeitemsforhernewhouse.Shepurchasedafanfor₹3500,andlightsandfittingsfor ₹25,350fromonestore;andkitchenappliancesfor₹1,28,600fromanotherstore.

Make question cards and distribute them among the groups.

Whatamountdidshepayforthefanandlightsandfittingsif18%GSTwasappliedonthefinalbill?

WhatistheSPofthekitchenappliancesiftheamountgivenisinclusiveof18%GST?

Instruct each student in the group to pick one question card and solve the problem in his/her notebook.

Instruct the groups to exchange the situation and question cards with other groups to solve a variety of problems. Discuss the answers with the whole class.

Answers

1. Finding Profit or Loss Percentage

Do It Together

Profit = ₹(10x − 8x) = 2x

Profit% ꞊ Profit CP × 100% = 2 ×100% 8 x x = 25%

Therefore, the percent profit is 25%.

2. Finding Selling Price or Cost Price

Do It Together

100 100 = ×648=×648=675 100–4%96 æö ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø

Now, CP = 675, desired profit% = 4%

Desired SP = 100+Profit% ×= 100 æö ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø CP

100 100 æö ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø

100+4%104×675=×675=702

Hence, the shopkeeper should sell the T-shirt for ₹702 to gain 4%.

3. Finding Discount

Do It Together

SP = 50,000 × 100 – 15 100 æö ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø

Therefore, the selling price of the chain = ₹42,500. Also, given that, the jeweller makes a profit of 6.25%.

CP ꞊ SP × 100 100+Profit% æö ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø = 42,500 × 100 100+6.25% æö ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø

CP ꞊ ₹40,000

Therefore, the cost price of the chain = ₹40,000.

4. Finding Successive Discounts

Do It Together

Selling price after the second discount = 90 – 7.2 = 82.8

Total discount allowed = 10 + 7.2 = 17.2

Therefore, a single discount equivalent to two successive discounts of 10% and 8% is 17.2%.

Therefore, 18% is a better offer.

5. Tax

Do It Together

Marked price = ₹6500

Discount = 8% of marked price = 6500 8 ×= 100 ₹520

Selling price = Marked Price – Discount = ₹(6500 – 520) = ₹5980

Sales tax = 8% of Selling price = 5980 8 ×= 100 ₹478.4

Therefore, Renuka pays ₹5980 + ₹478.4 = ₹6458.4

Compound Interest 14

Learning Outcomes

Students will be able to:

find the simple interest, if the principal, rate of interest and time period are given. deduce the formula for compound interest and apply it. solve word problems on simple and compound interest.

Alignment to NCF

C-1.5: Explores the idea of percentage and applies it to solve problems

Let’s Recall

Recap to check if students know how to find simple interest. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

principal: the initial amount invested or borrowed interest rate: the price you pay to borrow money

Teaching Aids

Cards with questions related to simple interest; Cards with questions related to compound interest; Situation cards; Question cards

Chapter: Compound Interest

Finding Simple Interest

Learning Outcomes

Imagine Maths Page 186

Students will be able to find the simple interest, if the principal, rate of interest and time period are given.

Teaching Aids

Cards with questions related to simple interest

Activity

Begin with revising the terms associated with simple interest like principal, time, rate etc. Discuss real-life scenarios where students may come across the terms. Discuss the simple interest formula. Ask the students to note down the formula in their notebooks.

Prepare cards with questions on simple interest.

Principal = `80,000

Time = 5 years

Simple interest = `50,000

Rate = ?

Ask the students to work in pairs. Distribute question cards among the pairs. Ask them to solve the problem in their notebooks. Then, have them exchange cards with other groups and solve as many problems as possible.

Discuss the answers with the whole class.

Extension Idea

Ask: Sam invested a certain amount of money in a fixed deposit account. In 2 years, the total amount in the account grew to ₹5500, and in 3 years, it grew to ₹6000. What was the principal amount he invested and the annual interest rate?

Say: We know: Amount in 2 years = ₹5500; Amount in 3 years = ₹6000; Interest earned in 1 year = ₹6000 − ₹5500 = ₹500. So, interest earned in 2 years = ₹500 × 2 = ₹1000. Principal = Amount – Interest = ₹5500 − ₹1000 = ₹4500.

Simple Interest = 1000 = 4500 × × 2 R11.11% 100 R ⇒

Hence, the principal is ₹4500, and the rate of interest is 11.11% p.a.

Finding Compound Interest

Learning Outcomes

Students will be able to deduce the formula of compound interest and apply it.

Teaching Aids

Cards with questions related to compound interest

Activity

Prepare cards with questions related to compound interest.

Imagine Maths Page 191

Ask the students to work in pairs. Instruct them to open page 191 of their ImagineMathematicsbooks, go through the page and note down their observations. Have a discussion around what they understand. Bring out what compound interest is and how it is different from simple interest.

Once the students understand the application of compound interest, distribute the question cards among the pairs.

Saradepositedacertainamountofmoneyintoafixeddepositaccountwhereinterestiscompoundedannually.After2 years,shereceived₹8500asthematurityamountatanannualinterestrateof8%.Whatwastheinitialamountsheinvested?

Ask the pairs to read the problem and solve it in their notebooks.

Once the students have thoroughly understood the concept, introduce compounding half-yearly and quarterly. Ask the pairs to solve the same problem by taking the rate of interest as compounded half-yearly and then quarterly. Ask them to observe and note down the impact on the rate of interest when compounded yearly, half-yearly and quarterly in their notebooks.

Extension Idea

Ask: Suman invested ₹10,000 for 2 years in two plans. Plan A earns 15% interest compounded annually. Plan B earns 14% interest compounded half-yearly. What is the total interest amount received from both plans?

Say: Amount on ₹10,000 at 15% compounded annually:

A = 10,000 2 15 ×1=10,000×1.15×1.15=13,225 100 `

Amount on ₹10,000 at 14% compounded half yearly:

A = 10,000

4 14 2 ×1=10,000×1.07×1.07×1.07×1.07=13,107.96 100 `

Thus, the total interest received = ₹(13,225 – 10,000) + ₹(13,107.96 – 10,000) = ₹6,332.96.

Word Problems

Learning Outcomes

Students will be able to solve word problems on simple and compound interest.

Teaching Aids

Situation cards; Question cards

Activity

Ask the students to work in groups. Distribute different situation cards to the groups. Sunishborrowedanamountof₹1,00,000fromafriendattherateof10%for3years.

Make question cards and distribute these to the groups.

WhatamountwillSunishpayifhisfriendchargedhimsimpleinterest?

Howmuchinterestwillhepayiftheinterestiscompoundedannually?

Imagine Maths Page 196

Instruct each student in the group to pick a question card and solve the problem in their notebooks.

Ask the groups to exchange their situation and question cards with other groups to solve a variety of problems. Discuss the answers with the whole class.

Answers

1. Finding Simple Interest

Do It Together

1. Interest = ₹4500 − ₹4000 = ₹500

2. We have just calculated that SI = ₹500 and we know that P = ₹4000 and T = 10 years.

Substituting these values into the formula, we get 500

= 4000××10 100 R

Rearranging and solving this, we get, R = 50,000 40,000

The interest rate is therefore, R = 1.25 %.

2. Compound Interest: Annually

Think and Tell

Simple interest on ₹8000 at 22% per year for 3 years

= 8000×22×3 =5280 100 `

Amount after 3 years = ₹8000 + ₹5280 = ₹13,280

Amount on ₹8000 at 20% compounded annually

A = 8000 3 20 ×1=8000×1.2×1.2×1.2=13,824 100 `

As the amount received in Plan B is more, he must choose Plan B.

Do It Together

We have A = ₹6050, R = 10% and n = 2

Therefore, 6050 = P 2 10 ×1+ 100

On simplifying the RHS, we get

6050 = P 2 100+10 × 100

6050 = P 2 110 × 100

6050 = P 2 11 × 10

6050 = P 121 × 100

P = 605000 =5000 121

Hence, P = ₹5000

Therefore, Amit had invested a sum of ₹5000.

3. Compound Interest: Half-yearly and Quarterly Do It Together

On simplifying the RHS, we get

A = ₹18,000 3 4 ×1+ 100

A = ₹18,000 3 100+4 × 100

A = ₹18,000 3 104 × 100

A = ₹18,000 × 1.04 ×1.04×1.04

A = ₹20,247.552

So, the amount received by Ajay is ₹20,247.55.

4. Word Problems

Do It Together

Population at 1 a.m. = 16,500

Number of hours between 1 a.m. and 5 a.m. = 4

of growth (R) = 2.5% per hour

after 4 hours = 16,500 4 2.5 ×1+ 100

16,500 4 102.5 × 100

16,500 4 ×1.025

= 16,500 × 1.025 × 1.025 × 1.025 × 1.025

= 18,213

So, the bacteria count at 5 a.m. is 18,213.

Algebraic Expre ions: A ition and Subtraction 15

Learning Outcomes

Students will be able to: draw a factor tree for an expression and list the terms and factors. add and subtract algebraic expressions using the horizontal and vertical method.

Alignment to NCF

C-2.2: Extends the representation of a number in the form of a variable or an algebraic expression using a variable

C-2.3: Forms algebraic expressions using variables, coefficients, and constants and manipulates them through basic operations

Let’s Recall

Recap to check if students know how to add and subtract two terms. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

variable: something that can change or that has no fixed value factor: any one of two or more numbers that are multiplied together to give a product coefficient: the constant part of an algebraic term involving multiplication

Teaching Aids

Cards (each with a unique algebraic expression); Chart paper; Coloured pencils; Algebra tiles made using blue, green, red and yellow paper cutouts

Chapter: Algebraic Expressions: Addition and Subtraction

Terms and Factors of an Algebraic Expression Imagine Maths Page 202

Learning Outcomes

Students will be able to draw a factor tree for an expression and list the terms and factors.

Teaching Aids

Cards (each with a unique algebraic expression); Chart paper; Coloured pencils

Activity

Start by introducing the concept of algebraic expressions. Explain how factor trees help in finding the terms and factors of a given algebraic expression.

Ask the students to work in groups.

Distribute two cards each containing an algebraic expression (like 2t3 + 9t2 + t – 12), chart paper and coloured pencils to each group.

Instruct the students to draw a three-layered tree diagram on the chart paper for each expression on the cards. Ask them to put the expression in the first layer, the different terms of the expression in the second layer, and the factors of each term in the third layer.

Guide the students through the process of factorising the terms. Demonstrate how to factorise the first term step by step. Encourage students to collaborate within their groups to factorise the remaining terms. Instruct them to use different colours to represent the different layers for the expression, terms, and factors, and label each layer clearly to indicate what it represents.

Give the students more practice questions on drawing factor trees for given expressions and listing the terms and factors.

Extension Idea

Instruct: Createanexpression that has 5x3, 7x2, 3x and 2 as its terms.

Say: We can create many expressions using the given terms. One such expression could be: 5x3 – 7x2 – 3x + 2.

Learning Outcomes

Students will be able to add and subtract algebraic expressions using the horizontal and vertical method.

Teaching Aids

Algebra tiles made using blue, green, red and yellow paper cutouts

Activity

Introduce algebra tiles to the students. Explain the values of the various cutouts and that these will be called algebra tiles.

+1 =–1 = x = –x = x2 = –x2 =

Bring out the fact that a pair of negative and positive tiles together represent 0.

Ask the students to work in pairs. Distribute algebra tiles among the pairs.

Instruct the students to add (2x2 + 3x +5) and (x2 – 2x –3) using the algebra tiles. Ask them to arrange algebra tiles to represent (2x2 + 3x +5). Then, ask them to place algebra tiles representing (x2 – 2x –3) below the previous set. Instruct them to remove any pair of algebra tiles that make zero. Explain that the remaining number of algebra tiles (3x2 + x +2) would show the answer.

Answer: 3x2 + x + 2

Instruct the students to write the expressions one below the other and the answer below them. Ask them to observe the expressions and the answer and try to understand the rules for adding expressions using the vertical method.

Have a discussion on the rules of addition.

Then, ask the students to add the expressions (4x2 – 6x +3) and (–6x2 + 2x –7) using the vertical method in their notebooks.

Discuss the answers.

Give the students more practice questions on adding and subtracting algebraic expressions using the horizontal and vertical methods.

Extension Idea

Instruct: Subtract 31722 –+–564 nmmnn from 22 . 245 +–732 mnmnn

Say: On subtracting the expressions, we get 529322 +–42154 mnmnn

Answers

1. Terms and Factors of an Algebraic Expression

Think and Tell

In algebra, like terms are terms that have the same variables raised to the same powers. In the expressions 4zy2 and 7yz2, although both involve the variables z and y, the powers of these variables are different.

Do It Together

ExpressionsTermsFactorsCoefficient of x

–5xyz –5xyz –5, x, y, z –5 yz 9x + 1 9x, 19, x; 1 9

2 7–+2–17 68xyxyz

2. Addition of Algebraic Expressions

Do It Together

22 1 23–+2–7–+13 6 24 aaabab æö ÷ ç ÷ ç = ÷ ç ÷ ÷ ç èø

2 2–5+171 64 aab æö ÷ ç ÷ ç = ÷ ç ÷ ÷ ç èø

2 17 1 =2×–2×5+2× 64 aab

2 17 1 =–10+ 32 æö ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø aab cm

So, the perimeter of the rectangle is

2 17 1 –10+ 32 æö ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø aab cm.

3. Subtraction of Algebraic Expressions

Think and Tell

If you do not evaluate the minus sign between two algebraic expressions, it means you are not performing the operation of subtraction. Instead, you are performing the operation of addition.

Do It Together

=–7+11–7+5–8+6 pqqpqq

=–7+5+11–8–7+6 pqpqqq =–2+3–1 pqq

So, –2+3–1 pqq will be added to –5+8–6 pqq to get –7+11–7. pqq

4. Simplifying Algebraic Expressions

Do It Together

(4+10–6)=9–5+7+(–5+2–3)+ abababX

=4+10–6–(9–5–7)–(–5+2–3) Xababab

=4+10–6–9+5–7+5–2+3 Xababab

=4–9+5+10+5–2–6–7+3 Xaaabbb

=13–10Xb

So, the third side of the triangle is (13b – 10) cm.

Multiplication of Algebraic Expre ions 16

Learning Outcomes

Students will be able to:

multiply a monomial by a monomial.

multiply a monomial by a polynomial.

multiply a polynomial by a polynomial. multiply polynomials using identities.

Alignment to NCF

C-2.2: Extends the representation of a number in the form of a variable or an algebraic expression using a variable

C-2.3: Forms algebraic expressions using variables, coefficients, and manipulates them through basic operations

Let’s Recall

Recap to check if students know how to represent a multiplication statement as arrays. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

algebraic expression: mathematical phrase with numbers and variables

polynomial: an algebraic expression with multiple terms

monomial: an algebraic expression with one term

trinomial: an algebraic expression with three terms

Teaching Aids

Sheet of paper; Paper cutouts for representing the algebraic terms x,y, 1,x2,xy,(a+b),a,b,ab,a2,b2; Glue

Chapter: Multiplication of Algebraic Expressions

Multiplying a Monomial by a Monomial

Learning Outcomes

Students will be able to multiply a monomial by a monomial.

Teaching Aids

Paper cutouts for representing the algebraic terms 1, x, y and xy

Activity

Start the class by discussing the box method of multiplying two numbers. Ask the students to work in groups. Distribute the cutouts to each group.

Instruct them to use the box method to multiply two monomials, 2x and 2y, by representing the monomials using the paper cutouts. Ask them to place the two x cutouts along a row and the two y cutouts along a column, multiply them one by one and place the xy cutouts to show the products. Next, ask them to add the products to get the final answer (4xy).

Imagine Maths Page 216

Once they are done, ask them to write the answers in their notebooks and then discuss the answers within their groups. Discuss their results.

Discuss the rule of multiplying monomials.

Repeat the activity by giving the students two more multiplication problems to solve using the cutouts as well as the rule.

Extension Idea

Ask: What is the value of xy multiplied by the product of 6y and –4?

Say: 6y × (–4) = –24y. On multiplying this by x y, we get 24xy2 .

Multiplying a Monomial by a Polynomial

Learning Outcomes

Students will be able to multiply a monomial by a polynomial.

Teaching Aids

Paper cutouts for representing the algebraic terms x, 1, and x2

Activity

Start the class by briefly revisiting the box method of multiplying two numbers. Ask the students to work in groups. Distribute the cutouts to each group.

Imagine Maths Page 217

Instruct them to use the box method to multiply a monomial x and a polynomial (x + 1) by representing them using the paper cutouts. Ask them to place one x cutout along a row and one x and one 1 cutout along a column, multiply them one by one and place the x2 and x cutouts to show the respective products. Next, ask them to add the products to get the final answer (x2 + x).

Once they are done, ask them to write the answers in their notebooks. Discuss their results. Discuss the rule of multiplying a monomial by a polynomial. Ask questions like: How would you multiply a trinomial by a monomial?

Repeat the activity by giving the students two more multiplication problems to solve using the cutouts as well as the rule.

Extension Idea

Ask: Verify the product of 5x2(x + 5) for x = 1.

Say: 5x2(x + 5) = 5x3 + 25x2. For x = 1, LHS = 5(1)2 (1 + 5) = 30, RHS = 5(1)3 + 25(1)2 = 5 + 25 = 30. Hence, LHS = RHS = 30.

Multiplying a Polynomial by a Polynomial

Learning Outcomes

Students will be able to multiply a polynomial by a polynomial.

Teaching Aids

Paper cutouts for representing the algebraic terms x, y, 1, and xy; Sheet of paper; Glue

Activity

Imagine Maths Page 218

Ask the students to work in groups. Distribute cutouts to represent a polynomial multiplication, such as (x + 2)(y + 2) = 2x + xy + 2y + 4, a sheet of paper and glue to each group.

Instruct them to arrange and paste the terms of the two polynomials in the corresponding rows and columns. Ask questions like: How would you find the product?

Instruct them to find the product and paste the respective cutout at each intersection of a row and column. Then, ask them to add the individual products and simplify to find the answer in their notebooks.

Repeat the activity with a trinomial and binomial multiplication. Demonstrate how to solve such multiplication problems on the board.

Give the students some practice questions to solve in their notebooks. Give them some problems on going from products to factors, this will enhance their learning by enabling a strong grasp of the concept.

Applying Identities to Multiply

Learning Outcomes

Students will be able to multiply polynomials using identities.

Teaching Aids

Imagine Maths Page 222

Sheet of paper; Paper cutouts for representing the algebraic terms (a+b),a,b,ab,a2,b2;Glue

Activity

Ask the students to work in groups. Distribute a big square of side (a+b), a square of side b, 2 rectangles of sides a and b, and 2 squares of side a to each group.

Instruct them to paste the big square on a sheet of paper and then arrange the smaller squares and rectangles onto the big square. Ask them to find the areas of the small squares and rectangles and add them to get the area of the big square. Help them derive the identity (a+b)2 = a2 + 2ab+b2, explaining that as the small squares and rectangles completely overlap the big square, their areas are equal. Encourage them to write the derivation in their notebooks. Help them derive the other identities similarly.

Give the students practice questions on using algebraic identities to solve an expression, like (60)2, 982, and (x2 – 52), and ask them to solve these in their notebooks individually.

Discuss the answers with the whole class.

Extension Idea

Ask: What will be the side length of a square whose area is x2 + 8x + 16?

Say: Area = x2 + 8x + 16 = x2 + 2 × 4x + 42 = (x + 4)2. So, the side length of the square is (x + 4).

Answers

1. Multiplying a Monomial by a Monomial

Do It Together

223332 (2×(1)×5)×(××)×(××)×(××) aaabbbccc =–

774

10abc =–

2. Multiplying a Monomial by a Polynomial

Do It Together

2222 (4×9)(4×7) xyxyzxy=+

3628432 xyzxy=+

3. Multiplying a Polynomial by a Polynomial Think and Tell

Yes. While the FOIL method is a specific way to perform multiplication for binomials, the BOX method is a more general approach that can be extended to larger algebraic expressions by creating a grid for each term.

Do It Together

22

2 (3)(31)(5)(51)146 xxxxxxxxx

322 2 3355146 xxxxxxx =––++–––

32 3121 xx =––

4. Applying Identities to Multiply

Think and Tell

Yes, the distributive property can be used to derive algebraic identities. In each of the identities we can distribute a and b from one pair of brackets to those of the second pair of brackets and simplify further to derive the result.

5. Using Identities

Do It Together

222 So, (4)+2×4×6+(6)=(4+6) yyxxyy

For x = 1, y = 2,

2 222 (4+6)=(4×2+6×1)=(8+6)=14=196 yx

Therefore, the value of 22 16+48+36=196 yxyx

6. Simplifying Expressions

Do It Together

2222 2 2

–––

ppppp pppp ppp p

=(×)(×2)+(×2) +(2×)(2×2) +(2×2)+(2×) (2×2)+(2×2)

432322 4 2+2+24+4+24+4 4 =pppppppp =p +

Visualising Solid Shapes

Learning Outcomes

Students will be able to: draw views of 3-D shapes. draw and interpret a map (with a scale). classify polyhedrons based on their properties. deduce and apply Euler’s formula.

Alignment to NCF

C-3.3: Identifies attributes of three-dimensional shapes (cubes, parallelepipeds, cylinders, cones), works hands-on with material to construct these shapes, and also uses two-dimensional representations of three-dimensional objects to visualise and solve problems

Let’s Recall

Recap to check if students know how to identify the properties of a prism and a pyramid. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

map: a symbolic representation that emphasises connections between objects or places polyhedrons: 3-D shapes with flat polygonal faces, straight edges and vertices

Teaching Aids

Board duster; Wooden 3-D shapes like a cube and a cone; Colourful unit cubes; Crayons; Chart paper; Toothpicks (around 100); Clay; Cube; Prism; Pyramid; Sphere; Solid cylinder

Chapter: Visualising Solid Shapes

Views of 3-D Shapes

Learning Outcomes

Students will be able to draw views of 3-D shapes.

Teaching Aids

Board duster; Wooden 3-D shapes like a cube and a cone; Colourful unit cubes; Crayons

Activity

Show the students the board duster and highlight how 3-D shapes look different when we look at them from different sides. Show them a cone placed on top of a cube and discuss the top, front and side views that the students can see. Discuss how the shape of the top view of the cone-cube structure is the same as the top view of a cube. Ask the students to work in groups. Distribute the colourful unit cubes and crayons. Instruct the groups to form a cube structure using the unit cubes up to a height of 4 cubes. Once done, ask the students to draw the front, side and top views of the cube structure in their notebooks and colour them as per the colours of the cubes. Ask them to compare their drawings within their groups, making sure that the colours also match.

Discuss the different views of the cube structure with the whole class.

Ask questions like: Why do we get different views from 3-D shapes?

Extension Idea

Ask: Based on the given three views of the cube structure, can you draw the 3-D shape?

Say: This is the 3-D shape for these views.

Mapping Space Around Us

Learning Outcomes

Students will be able to draw and interpret a map (with a scale).

Teaching Aids

Chart paper; Crayons

Activity

Top FrontRight

Imagine Maths Page 235

Begin the class by discussing the usage of maps, for example, where students might use a map. Ask the students to work in groups. Distribute chart paper and crayons. Draw symbols on the board that the students can use to show different places in the school like the playground, main building, office building, library etc. Instruct the groups to draw a map of their school by using symbols to show different places. Ask them to use a scale of 1 cm = 500 m. Allow the groups to come up and show their maps to the rest of the class. Run a discussion around the maps drawn.

Give the students some questions on reading the map like: What is the actual distance between the gate and the school building? What is the distance between the school library and the playground on the map?

Learning Outcomes

Students will be able to classify polyhedrons based on their properties.

Teaching Aids

Toothpicks (around 100); Clay; Cube; Prism; Pyramid; Sphere

Activity

Show the students a cube, prism, sphere and pyramid. Highlight that the 3-D shapes with flat polygonal faces, straight edges and vertices are called polyhedrons (like the cube, prism and pyramid) but that when a 3-D shape has at least one curved face, it is a non-polyhedron (like the sphere).

Divide the students into groups of 4. Distribute toothpicks and clay to each group.

Instruct them to use their understanding of the properties of 3-D shapes to form them using toothpicks for the edges and clay balls for the vertices. Each student of a group should create one of these polyhedrons: square prism, square pyramid, hexagonal prism, hexagonal pyramid. They should then write the properties of these shapes in their notebooks.

Start a discussion on the properties of each shape by having one group display one shape and talk about its properties.

Ask questions like: How many clay balls did you use for the square prism? For the hexagonal pyramid? How many faces does a square pyramid have? How many does a hexagonal prism have?

Extension Idea

Ask: What is the similarity and difference between these two polyhedrons?

Say: They are both prisms. However, one is a regular prism and the other is an irregular prism.

Euler’s Formula

Learning Outcomes

Students will be able to deduce and apply Euler’s formula.

Teaching Aids

Cube; Solid cylinder

Activity

Imagine Maths Page 241

Show the students a polyhedron and non-polyhedron. Bring out how it is easy to see and find out whether a given 3-D shape is a polyhedron or not.

Ask the students to work in groups. Draw a table on the board as shown.

3-D Shapes Faces (F)Vertices (V)Edges (E)F + VE + 2

Prism Cube Cuboid Pyramid Cylinder

Cone

Instruct the students to copy the table into their notebooks, fill it in with the number of faces, edges and vertices for each given shape and then put the values in the given formulas.

Ask questions like: Are the values of F + V equal to E + 2 for all the shapes? What is this formula called?

Give the students some questions on finding the third value where two of the values of faces, edges and vertices are given. Also ask them to identify the shape.

Extension Idea

Ask: Raina was making a polyhedron using cardboard and sticking tape. She decided to make a polyhedron with 20 faces, 32 edges and 12 vertices. Verify if such a polyhedron can be made using Euler’s formula.

Say: We know that Euler’s formula is: F + V – E = 2. Putting the values in the formula, we get 20 + 12 – 32 = 0 ≠ 2. So, it is not a polyhedron.

Answers

1. Views of 3-D Shapes

Do It Together

SolidFront ViewSide ViewTop View

2. Mapping Space Around Us

Think and Tell

No, it will not be useful to have the same scale for a route map and a city/country map.

Think and Tell

A map is a symbolic representation that emphasises connections between objects or places whereas a picture is a photo of an object or place.

Do It Together

1. School to Café

On the map, the distance from the school to the café = 1.6 + 2.3 = 3.9

Scale = 1 cm = 5 km

Actual distance = 3.9× 5 = 19.5 km

2. Children’s Park to the School via the Supermarket and Hospital.

On the map, the distance from the children’s park to the school = 1.2 + 1.5 + 4 + 1 + 1.2 = 8.9

Actual distance = 8.9 × 5 = 44.5 km

3. Polyhedrons

Think and Tell

Yes, a regular polygon is always a convex polygon.

Think and Tell

A polyhedron with 7 edges is not possible.

Think and Tell

All prisms have rectangular lateral faces.

Think and Tell

An 8-edge prism is a cube

A 9-edge prism is a triangular prism. There are no prisms with 7 or 10 edges.

Do It Together

The polyhedron is an octagonal prism.

Faces = 10 Vertices = 16 Edges = 24

4. Euler’s Formula

Do It Together

FacesVerticesEdgesName of the Polyhedron

144 6 Tetrahedron

2 122030 Dodecahedron

Area of Polygons

Learning Outcomes

Students will be able to:

find the area of figures made with parallelograms, triangles and circles. find the area of a trapezium and a rhombus.

find the area of general quadrilaterals.

find the area of combined shapes.

Alignment to NCF

C-4.1: Discovers, understands, and uses formulae to determine the area of a square, triangle, parallelogram, and trapezium and develops strategies to find the areas of composite 2D shapes

Let’s Recall

Recap to check if students know how to find the perimeter and area of a triangle. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

parallelogram: a flat closed 2-D figure with opposite sides that are equal and parallel trapezium: a quadrilateral in which one pair of opposite sides is parallel rhombus: a flat, closed figure in which all four sides are equal in length, and both pairs of opposite sides are parallel

Teaching Aids

Cutouts of a parallelogram, a triangle, and two semi-circles; Chart paper; Glue stick; Cutouts of a trapezium and rhombus; Cutouts of general quadrilaterals; Cutouts of a rhombus, trapezium, parallelogram and general quadrilateral; Ruler

Chapter: Area of Polygons

Triangles and Circles

Learning Outcomes

Students will be able to find the area of figures made with parallelograms, triangles and circles.

Teaching Aids

Cutouts of parallelogram, triangle, two semi-circles; Chart paper; Glue stick

Activity

Revisit the formulas for finding the area of a parallelogram, triangle and circle. Ask the students to note the formulas in their notebooks.

Ask the students to work in small groups. Distribute the teaching aids to each group. Make sure that all the groups get cutouts of the same size.

Instruct the groups to measure and label the lengths of the sides of the cutouts and stick them on the chart paper using glue to create a new shape. Ask them to be careful not to overlap any of the smaller shapes. Instruct them to find the area of the new shape created, in their notebooks.

Ask questions like: How did you find the area of the shape formed? What other shape can you form using the same cutouts?

Discuss how the answer for all the groups was the same even though the shapes were arranged differently by different groups to make the combined shapes.

Give them more problems to solve if time permits.

Extension Idea

Ask: A circular swimming pool of diameter 2.8 m was made (inscribed) within a square piece of land. What is the area of the remaining piece of land?

Say: The total area of the square piece of land = 2.8 × 2.8 = 7.84 sq. m. and the area of the circular pool = 22 7 × 1.4 × 1.4 = 6.16 sq. m. The area of the remaining piece of land = 7.84 – 6.16 = 1.68 sq. m. Area of a Trapezium and Rhombus

Imagine Maths Page 250

Learning Outcomes

Students will be able to find the area of a trapezium and a rhombus.

Teaching Aids

Cutouts of a trapezium and rhombus; Chart paper; Glue stick

Activity

Begin the class by showing the students cutouts of a trapezium and a rhombus and discussing the properties of these two shapes.

Ask the students to work in pairs. Distribute cutouts of a trapezium and rhombus to each pair.

Instruct the pairs to stick the shapes on the chart paper and label the vertices. Ask them to derive the formula for finding the area of the given shapes by dividing them into smaller shapes. Let the students try to derive the formula. Give them hints like: Thetrapeziumcanbedividedinto2trianglesandonerectangletoderivetheformula. Theoppositeverticesoftherhombuscanbejoinedtoderivetheformula.

When they are done, let the students share their findings with the rest of the class. Ask them to open page 250 of their ImagineMathematics books and check whether they have derived the formula correctly or not.

Once all the students understand the formula, give them practice problems on finding the area and other measures of a trapezium and rhombus.

Extension Idea

Ask: Is it possible for a rhombus and a trapezium to have the same area? Give one example. Say: Yes, it is possible for a rhombus and a trapezium to have the same area. For example, consider a rhombus with diagonals of length 40 cm and 10 cm and a trapezium with parallel sides of lengths 8 cm and 12 cm and a height of 20 cm. Both figures would have an area of 200 cm2.

Area of General Quadrilaterals

Learning Outcomes

Students will be able to find the area of general quadrilaterals.

Teaching Aids

Cutouts of general quadrilaterals; Chart paper; Glue stick

Activity

Imagine Maths Page 252

Begin by discussing the features of a quadrilateral. Discuss various types of quadrilaterals. Ask the students to work in pairs. Distribute a cutout of a general quadrilateral and chart paper to each pair.

Instruct the pairs to stick the shape on the chart paper and label the vertices. Ask them to derive the formula for finding the area of the shape. Let the students try to derive the formula. Give them hints like: Join one vertex to the opposite vertex to form a diagonal and divide the quadrilateral into 2 triangles.

Once they are done, let the students share their findings with the rest of the class. Ask them to open page 252 of their ImagineMathematics books and check whether they have derived the formula correctly or not.

Once all students understand the formula, give them practice problems on finding the area of general quadrilaterals.

Extension Idea

Ask: Rhea has a wall shaped liked a quadrilateral where h1 = 5 feet, h2 = 6 feet and BD = 21 feet. What is the area of the wall?

B

Learning Outcomes

Students will be able to find the area of combined shapes.

Teaching Aids

Cutouts of a rhombus, trapezium, parallelogram and general quadrilateral; Glue stick; Ruler; Sheets of paper

Activity

Recap the area formulas for a rhombus, trapezium and general quadrilateral.

Ask the students whether we can derive a formula for all shapes in real life. Give real-life examples of shapes or buildings that are a combination of various shapes like ThePentagoninUSA.

Ask the students to work in groups. Distribute the shape cutouts, a sheet of paper and a glue stick to each group.

Instruct the groups to paste the shapes on the sheet of paper in any way they like without overlapping to make a combined shape like the given example.

Ask them to measure the lengths needed to find the area of each shape and label the figure. Each student of the group should find the area of one of the shapes and then the group should add the areas to get the area of the complete figure.

Discuss the answers.

Ask questions like: Will the area of the combined shape be the same if the quadrilaterals are arranged differently?

Give the students more questions for practice.

Answers

1. Area of Figures Made With Parallelograms, Triangles and Circles

Do It Together

1. Perimeter = 86 cm

9 + 15 + x + 12 + 12 + 12 + 15 = 86 cm

75 + x = 86

x = 11 cm

2. Length of the rectangle = 15 cm; Breadth of the rectangle = 9 cm

Area of the rectangle = length × breadth = 15 × 9 = 135 sq. cm

Side of the square = 12 cm

Area of the square = side × side = 12 × 12 = 144sq. cm

Base of the triangle = 12 cm; Height of the triangle = 9 cm

Area of the triangle = 1 2 × base × height = 1 2 × 12 × 9 = 54 sq. cm

Total area of the figure = Area of the rectangle + Area of the square + Area of the triangle = 135 + 144 + 54 = 333 sq. cm

Fraction of the area of the triangle of the total area = 54 333 = 6 37

2. Area of a Trapezium and Rhombus

Think and Tell

To find the area of a trapezium (trapezoid) using the area of only a triangle, we need to divide the trapezium into two triangles and use the formula for the area of a triangle. We can do so by drawing a diagonal from one vertex to the opposite vertex, splitting the trapezium into two triangles.

Think and Tell

Since the diagonals bisect each other at right angles, they split up the rhombus into four congruent right triangles. We can use the Pythagorean theorem to find the length of onehalf of a side of the rhombus.

If d1and d2 are the diagonals of the rhombus, the side of the rhombus can be given as: 22 12 + 22 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ ÷÷ çç÷÷ èøèø

dd

Do It Together

One diagonal = 14 cm

So, 14 × d2 = 672 ⇒ d2 = 672 14 = 48 cm

To find the perimeter of the rhombus, we need to find the side of the rhombus.

dd

1448 + =+ 2222

æöæö æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ ÷÷ ÷÷ çç çç ÷÷ ÷÷ çç ÷÷ ÷÷ çç çç÷÷ èøèø èøèø

Side of the rhombus = 22 22 12 22

=7+24 =625 =25 cm

Perimeter = 4 × side = 4 × 25 = 100 cm

3. Area of General Quadrilaterals

Do It Together

Area of quadrilateral = 1 2 × diagonal × sum of length of perpendiculars on the diagonal from the opposite vertices

= 1 2 × 25 × 12 = 150 sq. cm

Lengths of perpendiculars from opposite vertices are 4 cm and 8 cm.

4. Area of Combined Shapes

Do It Together

Area of the polygon = 22 × 6 + 22 × 9 + 22 × 9 + 1 2 20 9

= 22 × (6 + 9 + 9) + 90

= 22 × 24 + 90 = 528 + 90 = 618 sq. cm

Surface Area and Volume of Solids 19

Learning Outcomes

Students will be able to:

deduce and apply the formula for the surface area of a cuboid. deduce and apply the formula for the surface area of a cube. deduce and apply the formula for the surface area of a cylinder. deduce and apply the formula for the volume of a cuboid. deduce and apply the formula for the volume of a cube. deduce and apply the formula for the volume of a cylinder.

Alignment to NCF

C-5.2: Visualises and uses mathematical thinking to discover formulae to calculate surface areas and volumes of solid objects (cubes, cuboids, spheres, hemispheres, right circular cylinders/cones, and their combinations)

Let’s Recall

Recap to check if students know about perimeter and area of 2-D shapes. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

surface area: the measurement of the total area of the outer surface of a three-dimensional object volume: the measurement of the space occupied by the entire three-dimensional object

Teaching Aids

Sheets of paper; Ruler; Pair of scissors; Cuboidal box; Unit cube boxes; Cubical box; Cardboard circular discs; Cylindrical jar

Chapter: Surface Area and Volume of Solids

Surface Area of Cuboids

Learning Outcomes

Imagine Maths Page 262

Students will be able to deduce and apply the formula for the surface area of a cuboid.

Teaching Aids

Sheets of paper; Ruler; Pair of scissors

Activity

Discuss how to find the area of rectangles using the formula by giving the measures of length and width. Discuss the nets of a cuboid and the number of rectangles that can be seen in the net of a cuboid.

Ask the students to form equal groups. Distribute the teaching aids to each group.

Instruct the groups to draw the nets of 2 cuboids of different dimensions on the sheet. Ask them to cut out the nets, measure the lengths of the sides and write the measures inside each rectangle. Instruct them to find the area of each rectangle and add the areas. Ask them what this area represents. Discuss the total surface area of a cuboid.

Ask the students to establish a relationship between the area of a rectangle and the surface area of a cuboid. Discuss the formula for the surface area of a cuboid.

Give the students questions on finding the surface area of a cuboid given the lengths of the edges or on finding the missing length, width, or height of a cuboid when two of these dimensions and the surface area are given.

Surface Area of Cubes

Learning Outcomes

Students will be able to deduce and apply the formula for the surface area of a cube.

Teaching Aids

Sheets of paper; Ruler; Pair of scissors

Activity

Imagine Maths Page 263

Discuss how to find the area of a square using the formula by giving the measure of its side. Discuss the nets of a cube and the number of squares that can be seen in the net of a cube.

Ask the students to form equal groups. Distribute the teaching aids to each group.

Instruct the groups to draw the nets of 2 cubes of different dimensions on the sheet. Ask them to cut out the nets, measure the lengths of the sides and write the measures inside each square. Instruct them to find the area of each square and add the areas. Ask them what this area represents. Discuss the total surface area of a cube.

Ask the students to establish a relationship between the area of a square and the surface area of a cube. Discuss the formula for the surface area of a cube.

Give the students questions on finding the surface area of a cube given the lengths of the edges or on finding the missing side length of a cube when its surface area is given.

Extension Idea

Ask: A painted box of dimensions 8 cm × 5 cm × 3 cm has a 72 sq. cm painted surface including all its faces. What is the length (as a whole number) of the side of the largest cube that uses the same amount of paint as the box? What is the surface area of such a cube? Explain.

Say: The painted area is 72 sq. cm. The maximum area of the cube can be 72 sq. cm. So, area of cube < 72 sq. cm ⇒⇒22 6<72<12 aa . So, the maximum value of a can be 3 cm. Hence, the largest possible cube that can be painted has a side of length 3 cm. Surface area of a cube with side length 3 cm = 6 × 3 cm × 3 cm = 54 sq. cm.

Surface Area of Cylinders

Learning Outcomes

Imagine Maths Page 264

Students will be able to deduce and apply the formula for the surface area of a cylinder.

Teaching Aids

Sheets of paper; Ruler; Pair of scissors

Activity

Discuss how to find the area of a rectangle and circle using the respective formulas by giving the measures of the sides and radius. Discuss the nets of a cylinder and the number of circles and rectangles that can be seen in the net of a cylinder.

Ask the students to form equal groups. Distribute the teaching aids to each group.

Instruct the groups to draw the nets of 2 cylinders of different dimensions on the sheet. Ask them to cut out the nets, measure the lengths of the sides and radii and write the measures inside the rectangle and each circle. Ask them to find the area of the rectangle and circles and add the areas. Ask them what this area represents. Discuss the total surface area of a cylinder.

Ask the students to establish a relationship between the area of rectangles, circles and the surface area of a cylinder. Discuss the formula for the surface area of a cylinder.

Give the students questions on finding the surface area of a cylinder given the height and radius or on finding the missing height or radius of a cylinder when one of the two dimensions and the surface area are given.

Extension Idea

Ask: A cylindrical block has a diameter of 2 metres and a height of 10 metres. If both the height and diameter are doubled, how does this affect the surface area?

Say: Original total surface area = 2π + 20π = 22π sq. m, New total surface area = 8π+80π = 88π sq. m. So, the new surface area is 4 times the original surface area.

Volume of Cuboids

Learning Outcomes

Students will be able to deduce and apply the formula for the volume of a cuboid.

Teaching Aids

Cuboidal box; Unit cubes

Imagine Maths Page 267

Activity

Discuss the concept of volume and how it applies to cuboids. Emphasise that it represents the amount of space inside the cuboid.

Ask the students to form equal groups. Distribute a cuboidal box and some unit cubes to each group.

Instruct them to find the number of unit cubes that fit inside the cuboidal box. Then, ask them to count the number of unit cubes along the length, breadth and height of the cuboidal box. Using this, ask them to establish a relationship between the total number of cubes and the number of cubes along the edges of the cuboidal box to deduce the formula for the volume of a cuboid.

Ask questions like: How is the total number of cubes inside the box related to the product of the number of cubes along the length, breadth and height?

Give the students some questions on finding the volume of a cuboid given the lengths of its edges or on finding a missing dimension given the other two dimensions and the volume of the cuboid.

Volume of Cubes

Learning Outcomes

Students will be able to deduce and apply the formula for the volume of a cube.

Teaching Aids

Cubical box; Unit cubes

Activity

Imagine Maths Page 268

Discuss the concept of volume and how it applies to cubes. Emphasise that it represents the amount of space inside the cube.

Ask the students to form equal groups. Distribute a cubical box and some unit cubes to each group.

Instruct them to find the number of unit cubes that fit inside the cubical box. Then, ask them to count the number of unit cubes along each side of the cubical box. Using this, ask them to establish a relationship between the total number of cubes and the number of cubes along each side of the cubical box to deduce the formula for the volume of a cube.

Ask questions like: How is the total number of cubes inside the box related to the product of the number of cubes along each side?

Give the students some questions on finding the volume of a cube given the length of one side or on finding the missing length given the volume of the cube.

Extension Idea

Ask: A large cubical block made of solid wood has a side length of 2 metres. You are given 64 smaller solid wooden cubes, each with a side length of 5 centimetres. If you have to carve out these cubes from the large cubical block, what is the volume of the large cubical box left, if these small cubes are carved out of the box?

Say: Volume of large cube = 2 m × 2 m × 2 m = 8 cu. m = 80,00,000 cu. cm. Volume of each tiny cube = 5 cm × 5 cm × 5 cm = 125 cu. cm. Volume of tiny cubes = 64 × 125 = 8,000 cu. cm. Volume left = 80,00,000 – 8000 = 79,92,000 cu. cm.

Volume of a Cylinder

Learning Outcomes

Students will be able to deduce and apply the formula for the volume of a cylinder.

Teaching Aids

Cardboard circular discs; Cylindrical jar

Activity

Discuss the concept of volume and how it relates to cylinders. Emphasise that it represents the amount of space inside the cylinder.

Ask the students to form equal groups. Distribute a cylindrical jar and some thin circular discs made of cardboard to each group.

Instruct them to find the number of discs that fit inside the cylindrical jar. Then, ask them to find the radius of each discs. Using this, ask them to establish a relationship between the total number of discs and the radius of the discs to deduce the formula for the volume of a cylinder.

Ask questions like: How is the total number of discs inside the jar related to the radius of the discs?

Give the students some questions on finding the volume of a cylinder given the height and radius or on finding the missing height or radius given one of the two dimensions and the volume of the cylinder.

Extension Idea

Ask: You want to bake a cylindrical birthday cake with a fixed height of 20 cm. You have enough batter to make a cake with a total volume of 8000 cu. cm. What is the maximum diameter you can create for the cake while using all the batter?

Say: Volume = π  2 ××20 2 D = 5π D2. So, 5π D2 = 8000 ⇒ D2 = 8000 5ð5π = 1600 π ⇒ D = π 1600 = 15.92 cm. Therefore, the maximum diameter of the cake you can create with the available batter is approximately 15.92 cm.

Answers

1. Surface Area of Cuboids

Do It Together

Total surface area = 2 × + + lblhbh

190=2×5+3+15 =10+6+30llll

⇒⇒ 160= 16= 10 m ll .

2. Surface Area of Cubes

Do It Together

New length of the side of the cube = ɑ + 50% of ɑ = ɑ + 1 2 a

= 3 2 a

Total surface area of the new cube = 6 × 3 2 a × 3 2 a = 27 2 a2

a2

3. Surface Area of Cylinders

Do It Together

r = 330×7 2×22×15 m = 7 2 m

4. Volume of Cuboids

Think and Tell

Capacity is the maximum amount of a substance that an object can hold whereas volume is the total amount of space occupied by an object.

Do It Together

Breadth = 800 cm = 8 m

Capacity of the tank = 4,80,000 L

1000 L = 1 m3

4,80,000 L = 480 m3

Volume = lbh = 12 × 8 × h

h = 480 128 m = 5 m

5. Volume of Cubes

Do It Together

Side of the cube = 12 cm

Volume = Side3 = 12 × 12 × 12 cm3 = 1728 cm3

We know that, 1 cm3 = 1 mL

Total capacity of the cube = 1728mL

6. Volume of Cylinders

Do It Together

r2 = 79.2×7 22×70 m2 =0.36 m2

r = 0.6 m

Exponents and Powers

Learning Outcomes

Students will be able to:

simplify expressions involving positive exponents of a rational number. simplify expressions involving negative exponents of a rational number. apply laws of exponents to simplify exponential expressions. solve word problems on expressing large numbers in the standard form.

Alignment to NCF

C-2.1: Extends the understanding of powers (radical powers) and exponents

Let’s Recall

Recap to check if students know the concepts of squares and cubes. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

binary fission: a process in which a single bacterial cell splits into two cells to multiply exponent: the number of times a number is multiplied by itself

Teaching Aids

Cards (each with rational number written on it); Cards (with exponents); Cards (+, –, ×, ÷); Word problem cards

Chapter: Exponents and Powers

Positive Integral Exponent of a Rational Number

Learning Outcomes

Imagine Maths Page 276

Students will be able to simplify expressions involving positive exponents of a rational number.

Teaching Aids

Cards (each with a rational number written on it)

Activity

Begin the class by explaining that if any number, say 2, is raised to the power n, i.e., 2n it means 2 is being multiplied by itself n times.

Divide the class into groups of 10. Distribute a card containing a base number, such as –2 3 , to each group. Assign a unique number (from 1 to 10) to each student within the group.

In their notebooks, instruct the first student to raise the base number to the power of 1, i.e., 1 –2–2 = 33 ; the second student to raise it to the power of 2, i.e., 2 –2–2–24 =×= 3339 ; and so on up to the tenth student.

Ask how they can speed up calculations while staying accurate. Discuss how they are not required to calculate their result from scratch; instead, they can use the result obtained by the preceding student.

Extension Idea

Ask: If 5125 = 7343 m , what is the value of m?

Say: 3 5×5×5=5=125 and 3 7×7×7=7=343; so,

Negative Integral Exponent of a Rational Number

Learning Outcomes

Imagine Maths Page 277

Students will be able to simplify expressions involving negative exponents of a rational number.

Teaching Aids

Cards (each a with rational number written on it)

Activity

Begin the class by explaining that if any number, say 2, is raised to the power –n, i.e., 2–n, it means the result will be the reciprocal of the exponential power, i.e., 1 . 2n

Divide the class into groups of 10. Distribute a card containing a base number, such as 1 2 , to each group. Assign a unique integer (from –1 to –10) to each student within the group.

In their notebooks, instruct the first student to raise the base number to the power of –1, i.e., –1 –1 11==2 2 2 ; the second student to raise it to the power of –2, i.e., –2 2 –2 11==2=2×2=4 2 2 ; and so on up to the tenth student.

Ask how they can speed up calculations while staying accurate. Discuss how they are not required to calculate their result from scratch; instead, they can use the result obtained by the preceding student.

Extension Idea

Ask: How do we express this in decimals: 5×10–5 ?

Say: We can write it as: –5 5 5×10=5×=5×1115=5×==0.00005. 10×10×10×10×10100000100000 10

Applying Laws of Exponents

Learning Outcomes

Students will be able to apply laws of exponents to simplify exponential expressions.

Teaching Aids

Cards (with exponents); Cards (+, –, ×, ÷)

Activity

Imagine Maths Page 280

Begin the class by discussing the basic concepts of exponents and their properties. Briefly discuss the importance of simplifying exponential expressions.

Prepare cards showing rational numbers raised to some exponential power, for instance, –3 8 11 and 55 . Also prepare cards showing mathematical operators (+, –, ×, ÷).

Ask the students to work in pairs. Distribute one exponent card to each student and one operator card to each pair.

Instruct the pairs to combine the two exponents using the operator on their card to form a mathematical expression.

For example: –38 11 × 55 .

Ask them to solve the resultant expression and write the answers in their notebooks. Instruct the students to exchange cards with other pairs and solve the expressions.

Extension Idea

Ask: 2 5×125=25. xx What is the value of x?

Say: +3 334 5×125=5×(5)=5×5=5=5 xxxxxxxxx and 2224 25(5)5 . So, 44 5=54=4=1. xxx

Use of Exponents

Learning Outcomes

Imagine Maths Page 281

Students will be able to solve word problems on expressing large numbers in the standard form.

Teaching Aids

Word problem cards

Activity

Begin the class by explaining what standard form is and its importance in dealing with large numbers. Give some examples of large numbers written in standard form.

Chapter

Distribute a word problem card to each student.

Thevalueofanantiqueiteminthemarket50yearsagowas₹4.Howmuchwoulditcostnowifeveryfiveyearsitsvalue increasedtothepreviousvalueraisedtothepowerof2?

Instruct the students to follow the CUBES strategy to solve the problem. Circulate around the classroom to provide assistance and guidance as needed.

Instruct the students to exchange cards and solve another word problem.

Once they have completed the word problems, review the answers together as a class.

1. Positive Integral Exponent of a Rational

3.

7296472911390625531441

2. Negative Integral Exponent of a Rational Number

Think

At each step, the value is decreased to half the previous value. We can extend this pattern further as:

4. Use of Exponents

Direct and Inverse Proportions 21

Learning Outcomes

Students will be able to:

solve problems on direct proportion. solve problems on inverse proportion. solve problems on time and work. solve problems on pipes and cisterns.

Alignment to NCF

C-1.6: Explores and applies fractions (both as ratios and in decimal form) in daily-life situations

Let’s Recall

Recap to check if students know how to find the simplest form and equivalent ratios of given ratios. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

variation: a change or difference in something direct proportion: when two quantities increase or decrease at the same rate inverse proportion: when one quantity increases while the other decreases and vice versa

Teaching Aids

Counters; Chocolates or candies; Water; Building blocks; Stopwatch; Bowls; Bottles of water; 2 funnels of different widths

Chapter: Direct and Inverse Proportions

Direct Proportion

Learning Outcomes

Students will be able to solve problems on direct proportion.

Teaching Aids

Counters

Activity

Ask the students to form groups. Distribute counters to each group.

Imagine Maths Page 289

Instruct the students to imagine that they are organising a party and the counters are cookies. Ask them to group 4 cookies (counters) per plate and then find the number of cookies that can be put on 2, 3 or 10 plates.

Ask questions like: What is the ratio of the number of plates to the number of cookies?

Instruct the students to write the ratio of plates to cookies in the simplest form in their notebooks. Discuss their answers and let them deduce the concept of direct proportion.

Draw a table as shown on the board and ask the students to copy it into their notebooks.

Help them notice the variation in quantities. Encourage them to write their learnings in their notebooks. Give the students some practice questions based on direct proportion.

Extension Idea

Ask: If the ratio of friends to cookies is 1:5, for how many friends should 45 cookies be made?

Say: If the ratio of friends to cookies is 1:5, it means that for every group of 1 friend, there are 5 cookies. Therefore, 45 cookies should be made for 9 friends.

Problems on Inverse Proportion

Learning Outcomes

Students will be able to solve problems on inverse proportion.

Teaching Aids

Chocolates or candies; Water

Imagine Maths Page 292

Activity

Ask the students to form groups and give each group a set number (say 12) of chocolates or candies. Guide them to divide the items first into groups of 2, then 3, and finally 6. Let them deduce by observation that as the number of groups increases, the number of items in each group decreases.

Ask questions like: How does the ratio of chocolates or candies to groups affect the number of chocolates or candies in each group? Encourage the students to discuss their observations within their groups and write their learnings in their notebooks.

Ask the students to repeat the activity using 18 chocolates or candies.

Extension Idea

Ask: If it takes 5 students 4 hours to clean a classroom, how many hours will it take for 10 students to clean the same classroom, assuming they work at the same rate?

Say: As the number of students is inversely proportional to the time taken, it will take 10 students 2 hours to clean the same classroom.

Time and Work

Learning Outcomes

Students will be able to solve problems on time and work.

Teaching Aids

Building blocks; Stopwatch

Activity

Imagine Maths Page 293

Ask the students to work in pairs. Provide each student with an identical set of building blocks. Explain that their challenge is to individually construct a tower of 40 building blocks within a specified time frame. Start the timer as soon as they begin building. Once they are done, ask questions like: What did you notice about the amount of work you could complete within the given time? Record the time each of them took to complete the construction.

Then, ask them to pair up to construct the tower and note how it takes less time to complete a task when a greater number of people work together.

Demonstrate how a problem on time and work is solved. Then, give the students some practice questions on time and work. Discuss their responses and encourage them to write their learnings in their notebooks.

Pipes and Cisterns Problems

Learning Outcomes

Students will be able to solve problems on pipes and cisterns.

Teaching Aids

Bowls; Bottles of water; 2 funnels of different widths; Stopwatch; Water

Imagine Maths Page 295

Activity

Take the students to an open ground. Divide the students into groups.

Distribute the teaching aids to each group.

Ask the students to pour water from the bottle into the bowl using the first funnel and record the time taken to fill the bowl completely.

Ask the students to empty the bowl, use the second funnel to fill the bowl completely and note the time taken.

Ask the students to empty the bowl again, use both funnels simultaneously to fill the bowl completely and note the time taken.

Encourage a discussion around what the students noticed about the time taken to fill the bowl in all three cases. Give them some practice problems based on pipes and cisterns.

Extension Idea

Ask: What will happen if there is one outflow pipe in the bowl? Does it affect the flow of water?

Say: Yes, the outflow pipe affects the flow of water, and the time taken to fill the bucket increases.

Answers

1. Direct Proportion

Do It Together

Length of Cloth 2 m5 m8 m15 m20 m

Cost of Cloth `150 `375 `600 `1125 `1500

2. Problems on Inverse Proportion

Do It Together

Using the inverse proportion formula, 45 × 60 = x × 54

⇒ x = 45×60

54 = 50

Hence, the farmer bought 50 − 45 = 5 more cows.

3. Time and Work

Do It Together

Time taken by A and B to finish the work if they worked together = 30 days

(A+B)’s 1 day of work = 1 30

(A+B)’s 10 days of work = 10 30

Remaining work = 1 – 10 30 = 20 30

Now 20 30 work is done by A in 40 days.

Therefore, the whole piece of work will be done by A in 40 × 30 20 = 60 days

4. Pipes and Cisterns Problems

Think and Tell

No, it is not possible.

Do It Together

Time taken by the pump to fill the tank without leakage = 2 hours

Work done by the pump in 1 hour without leakage = 1 2

Time taken by the pump to fill the tank with leakage = 1 2 3 = 7 3 hours

Work done by the pump in 1 hour with leakage = 3 7

Leakage per hour = 137–61 –== 271414

Time taken by leakage to empty the tank = 14 hours.

Factorisation and Division of Algebraic Expre ions 22

Learning Outcomes

Students will be able to:

factorise algebraic expressions using common factors. factorise algebraic expressions by grouping and regrouping terms.

factorise an expression using identities when the expression is a perfect square or difference of two squares.

factorise quadratic trinomials.

divide a monomial by a monomial.

divide a polynomial by a monomial.

divide a polynomial by a polynomial.

Alignment to NCF

C-2.3: Forms algebraic expressions using variables, coefficients, and constants and manipulates them through basic operations

Let’s Recall

Recap to check if students know how to add or subtract algebraic expressions. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

factorisation: process of finding expressions that when multiplied, create a given expression

Teaching Aids

Chart paper; Pair of expression cards with polynomials having common factors; Glue stick; Paper cutouts of a rectangle and circle; Puzzle cards; Problem cards; Factor cards; Expression cards (e.g. 10p2qr, 5pq); Factor cards for each expression on the expression cards and extra cards (2, 5, p, q, q, r, r, 5, p, q)

Chapter: Factorisation and Division of Algebraic Expressions

Using Common Factors

Learning Outcomes

Students will be able to factorise algebraic expressions using common factors.

Teaching Aids

Imagine Maths Page 302

Chart paper; Pair of expression cards with polynomials having common factors; Glue stick; Paper cutouts of a rectangle and circle

Activity

Revise the concept of identifying factors of natural numbers. Relate it to identifying factors of monomials. Create expressions cards (e.g., 6+12+4–24222324 xyxyxyxy ) with one expression on each card. Make sure to cover all types of expressions.

Divide the class into groups of 3.

Distribute 2 expression cards and the other teaching aids to each group.

Terms:

Factors:

Instruct the groups to paste the expression cards on the chart paper and write the type of expression (monomial, binomial, etc.) on the left. Ask the group members to work together to form factor trees for the two expressions by pasting rectangle cutouts to show the terms and circle cutouts to show the factors. Ask them to also label the expression, terms and the factors by writing on the side. Ask questions like: Do you see some common factors? How can you factor them out?

Discuss their responses to bring out that the expression can be factorised as 2x2y (3x2 + 6y + 2y2 – y3). Discuss how the expression can be factorised without drawing a factor tree. Give the students more practice questions and ask them to write the factors and common factors in their notebooks.

Extension Idea

Ask: Can the expression 7xy + 15z be factorised?

Say: The common factor is 1, hence the expression cannot be factorised further.

Using Grouping and Regrouping Terms

Learning Outcomes

Imagine Maths Page 303

Students will be able to factorise algebraic expressions by grouping and regrouping terms.

Teaching Aids

Problem cards with terms of an algebraic expression written on them

Activity

Show the students four numbers 3, 7, 9 and 21 and ask them to identify the pairs of numbers that have common factors. Discuss how to factorise algebraic expressions by grouping and regrouping terms by identifying the

common factors. Demonstrate 1 or 2 examples on the board. Explain that this process makes factorisation simpler. Prepare sets of 4 cards each having one term of an expression, such as 3a2b – 2ac2 – 6ab + 4c2

Ask the students to work in groups and distribute a set of 4 cards to each group. Instruct them to arrange the cards to group the terms to be able to find the maximum number of common factors. Ask them to write the arranged expression in their notebooks and factor out the common factors to write the factored expression.

Ask questions like: Was regrouping needed for all the expressions? How did you identify the terms to be regrouped? Discuss their approach and rotate the problem cards among the groups for more practice.

Extension Idea

Ask: If the area of a rectangular plot is 25x4y3 – 5x2

15

2 – 3x2, how will you find the length and breadth?

Say: The length and breadth can be found by factorising the expression by regrouping terms. 25x4y3 – 5x2y + 15x4y2

2)(5y

Factorisation Using Identities

Learning Outcomes

3); L = (5x4y2 – x2), B = (5y + 3).

Imagine Maths Page 305

Students will be able to factorise an expression using identities when the expression is a perfect square or difference of two squares.

Teaching Aids

Puzzle cards with 3 expressions

Activity

Prepare puzzle cards with algebraic expressions (some perfect squares, and some in the form a2 – b2), where one card has the expression and the other has the factorised answer.

Ask the students to work in groups. Distribute the puzzle cards.

Instruct the students to factorise the expressions and match the cards.

Ask questions like: Are you able to factorise the expressions using common factors or regrouping? How are these expressions different from those you have dealt with previously? Help them deduce that not all expressions can be factorised using common factors or regrouping.

On the board, draw shapes like a square with side length (a + b) and a rectangle with length (a + b) and breadth (a – b). Ask them to multiply the dimensions to find the area. Ask questions like: How can you use this learning to factorise? Discuss their answers and demonstrate how identities can be used to factorise expressions.

Instruct the students to look at their expressions again to identify which of the three identities will be used for factorisation. Let them solve to write the factors and common factors in their notebooks.

Factorisation of Quadratic Trinomials

Learning Outcomes

Students will be able to factorise quadratic trinomials.

Teaching Aids

Problem cards; Factor cards; Glue stick

Imagine Maths Page 307

Activity

Define what a quadratic trinomial is and explain the steps to factorise a quadratic polynomial. Demonstrate a few examples on the board.

Prepare problem cards with quadratic trinomials written on them, and factor cards, some with correct factors and some with random factors written on them.

Divide the class into groups and distribute 1 problem card and 4 factor cards (2 correct and 2 random) to each group. Instruct the students to find the factors of the trinomial in their notebooks. Then, ask them to identify the correct factor cards as its solution and paste them with the problem card to complete the circle. Ask them to check with other groups whether they got the same factors.

Discuss the answers and let the groups exchange cards and solve.

Extension Idea

Ask: If you paid x2 + 5x + 6 rupees at a vegetable shop and bought x + 3 lemons, what is the price of each lemon?

Say: When we factorise the given polynomial, we get (x + 3) and (x + 2) as factors. So, if (x + 3) is the number of lemons, (x + 2) is the price of each lemon.

Dividing a Monomial by a Monomial

Learning Outcomes

Students will be able to divide a monomial by a monomial.

Teaching Aids

Imagine Maths Page 309

Expression cards (e.g., 10p2qr, 5pq); Factor cards for each expression on the expression cards and extra cards (2, 5, p, q, q, r, r, 5,p,q)

Activity

Begin by briefly revising division of an expression by numbers. Prepare expression cards (e.g. 10p2qr) and factor cards for each expression on the cards and some extra cards (2, 5, p, q, q, r).

Ask the students to work in groups. Distribute the expression and factor cards to each group.

Give the students a division problem, such as 10p2qr by 5pq. Instruct them to represent the numerator and denominator as a product of prime factors by placing factor cards in the numerator and denominator. Ask them to remove the common factor cards from the numerator and denominator and group the rest. Tell them that the expression formed by the remaining cards is the answer.

Give the students more practice questions and ask them to solve the problems first by using the factor cards and then in their notebooks.

Discuss the answers and ask them to share their learnings with the whole class.

Extension Idea

Instruct: Form a monomial division problem with the variables a,b,c where the quotient is a2 .

Say: There can be many such problems. One of them could be a3bc ÷ abc.

Dividing a Polynomial by a Monomial

Learning Outcomes

Students will be able to divide a polynomial by a monomial.

Teaching Aids

Puzzle cards

Activity

Briefly explain how each term of the polynomial is divided by the monomial in polynomial by monomial division. Prepare puzzle cards where one has the dividend (e.g. (5x3 + 10x2 – 15x)), another has the divisor (5x) and the third has the answer (x2 + 2x – 3) written on them.

Ask the students to work in groups, Distribute 2 sets of puzzle cards to each group. Instruct them to solve the division problem in each set to match the puzzle cards for the dividend and divisor with the card showing the correct solution. Once they are done, ask them to discuss their results in their groups and write the solution in their notebooks as well.

Give the students more division problems for practice.

Dividing a Polynomial by a Polynomial

Learning Outcomes

Students will be able to divide a polynomial by a polynomial.

Teaching Aids

Puzzle cards

Activity

Imagine Maths Page 309

Imagine Maths Page 310

Begin the class by explaining the methods of dividing a polynomial by a polynomial: by factorising and eliminating common factors and by long division. Prepare puzzle cards with polynomial division problems and their solutions.

Ask the students to work in pairs. Distribute a division problem card and some solution cards to each pair.

Tell each pair to solve the problems individually such that one partner solves by factorising and cancelling the common factors, and the other solves by the long division method. When they are done, ask them to compare to check whether they got the same answer by both methods. Finally, ask them to match the problem card with the correct solution card and showcase their completed puzzle to the class.

Discuss their approaches and encourage them to write their answers in their notebooks.

Answers

1. Using Common Factors

Think and Tell

No, multiplying a polynomial by a monomial does not change the number of terms in the original polynomial. When you multiply a polynomial by a monomial, you distribute the monomial to each term in the polynomial, but you don’t add or remove any terms.

Do It Together

1. 4a3 – 9a2b2

–9a2b2 4a3

4 × a × a × a –1 ×9× a × a × b × b

= a2(4a – 9b2)

2. (a – 3)(a + 7xy(a – 3)2)

= (a – 3)(a + 7xy(a2 – 6a + 9))

= (a – 3)(a + 7xya2 – 42axy + 63xy)

2. Using Grouping and Regrouping Terms

Do It Together

1. = 3mn + 3mq + 2pn + 2pq

= 3m(n+q) + 2p(n + q)

= (3m + 2p)(n + q)

2. x(x – a) – b(x–a)

= (x–b)(x – a)

3. Factorisation When Expression is a Perfect Square

Do It Together

= b2 + 2 × (–3a) × b + (–3a)2

= (b – 3a)2

4. Factorisation When the Expression is

a Difference of Two Squares

Do It Together

= (m2)2 – (n2)2

= (m2 – n2)(m2 + n2)

= (m – n)(m+n)(m2 + n2)

5. Factorisation of Quadratic Trinomials

Do It Together

1. 2x2 + x – 6

= 2x2 + 4x – 3x – 6

= 2x(x + 2) – 3(x + 2)

= (2x – 3)(x + 2)

2. x2 – 2x – 15

= x2 – 5x + 3x – 15

= x(x – 5) + 3(x – 5)

= (x + 3)(x – 5)

6. Dividing a Monomial by a Monomial

Do It Together

1. 779–34–27–2–2625–2 = 22 keymkeym

2. 9–27–26–3 16 3 zdc = 753 16 3 zdc

7. Dividing a Polynomial by a Monomial

Do It Together

1. 47 226 34 18 2–+5 5 jkljkljkl

2. 547233446 323323323 12266 444 abcabcabc bacbacbac ++

= 34233–+133 22 abcabc

8. Dividing a Polynomial by a Polynomial

Do It Together

Linear Graphs 23

Learning Outcomes

Students will be able to:

read and interpret a double line graph. draw a double line graph using the given data. identify, plot and label points and axes on a coordinate plane. draw a linear graph using the given data. read and interpret a linear graph.

Alignment to NCF

C-5.2: Selects, creates, and uses appropriate graphical representations (e.g., pictographs, bar graphs, histograms, line graphs, and pie charts) of data to make interpretations

Let’s Recall

Recap to check if students know how to read and draw bar graphs and histograms. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

axis: a fixed line on a graph used for marking measurements coordinate: a unit that locates a specific point on a graph quadrant: a region that is defined by two axes

Teaching Aids

Sheet with a double line graph; Graph paper; Cards showing the population of 2 cities in 5 different years; Coloured pencils; Cards showing 4 pairs of coordinates; Sheet with a linear graph

Chapter: Linear Graphs

Reading Double Line Graphs

Learning Outcomes

Students will be able to read and interpret a double line graph.

Teaching Aids

Sheet with a double line graph

Activity

Recall what a line graph is and what its purpose is. Ask the students to open page 316 in their content books and discuss the difference between a line graph and a double line graph.

Ask the students to work in pairs. Distribute a sheet with a double line graph to each pair. Ensure the graph has clear labels, titles and axes. For example, it could be a double line graph representing a comparison of the week’s sales of Company A and Company B.

Ask questions like: On which day did Company A have the highest sales? By how much did the sales of Company B exceed that of Company A on Wednesday?

Instruct the students to analyse the graph and write the answers in their notebooks. Discuss the answers with the whole class.

Give the students more questions for practice.

Extension Idea

Ask: The graph represents the time two friends spent gardening. Who spent more time gardening? Find the percentage difference in the number of hours spent.

Say: Friend A spent 28 hours gardening in total whereas Friend B spent 16.5 hours. Friend A spent more time gardening. So, the percentage difference is: 28 − 16.5 28 × 100 = 11.5 28 × 100 = 41.07%.

Drawing Double Line Graphs

Learning Outcomes

Students will be able to draw a double line graph using the given data.

Teaching Aids

Imagine Maths Page 316

Imagine Maths Page 318

Graph paper; Cards showing the population of 2 cities in 5 different years; Colour pencils

Activity

Recall how to read and interpret a double line graph.

Ask the students to work in pairs. Distribute graph paper and a card showing the population of 2 cities in different years to each pair.

Instruct the students to use this data to draw a double line graph on the graph paper. Provide guidance on labelling the axes and choosing an appropriate scale. Ask the students to use different colours to represent the two different data sets on the graph.

Ask them to point out the similarities and differences between single line graphs and double line graphs. If time permits, provide real-world examples of situations where double line graphs are used to compare two related sets of data for further analysis.

Extension Idea

Instruct: If the population of City C is given for different years, draw a line graph to represent the data on the same graph paper.

Say: This data can be represented on the same graph using a pencil in a third colour.

Cartesian Coordinate of a Point

Learning Outcomes

Students will be able to identify, plot and label points and axes on a coordinate plane.

Teaching Aids

Graph paper; Cards showing 4 pairs of coordinates

Activity

Imagine Maths Page 321

Discuss what a cartesian plane is and how it works. Show the students some examples. Ask them to look at the second graph on page 321 and the first graph on page 322. Review the concepts of x-axis, y-axis, quadrants, and coordinates and demonstrate how to plot points on the coordinate plane.

−3,

Divide the class into groups of 4. Distribute graph paper and a card containing 4 pairs of coordinates to each group. For example:

Instruct the students to plot each coordinate on the graph paper, labelling the points as A, B, C and D.

Ask questions like: What quadrants do your coordinates lie in? If you join all the coordinates, does this form any shape?

Extension Idea

Ask: A point lies equidistant from both the x-axis and y-axis in the third quadrant. What are the coordinates of the point if the area of the region is 4 sq. units?

Say: If the area is 4 sq. units and the point is equidistant from the x-axis and y-axis, then the point is at a distance of 2 units from each axis. As it falls within the third quadrant, its coordinates are (−2, −2)

Drawing a Linear Graph

Learning Outcomes

Students will be able to draw a linear graph using the given data.

Teaching Aids

Graph paper

Activity

Discuss the concept of linear graphs. Ask the students to look at the graph on page 323 of their content books. Explain how to draw a linear graph using given data points. Discuss the importance of labelling the axes with appropriate units and the significance of connecting the plotted points with a straight line.

Ask the students to work in pairs. Distribute graph paper to each pair. Provide different sets of data representing linear relationships, for example, distance vs. time for a vehicle.

Instruct each student to plot the coordinates on the graph paper. Provide guidance on labelling the axes and selecting appropriate scales for the graph. Guide them to connect the plotted points with a straight line to represent the linear relationship.

Ask the students in each pair to review each other’s work.

Ask questions like: How can we use the graph to guess what might happen next or understand the relationship better?

Extension Idea

Ask: How is a graph showing simple interest earned over time different from a graph showing compound interest?

Say: Compound interest curves are non-linear due to exponential growth, showing increasing rates over time. Simple interest graphs are linear as they maintain a constant growth rate, resulting in straight lines. Reading Linear Graphs Imagine Maths Page 325

Learning Outcomes

Students will be able to read and interpret a linear graph.

Teaching Aids

Sheet with a linear graph

Activity

Begin by revising what linear graphs are and how they represent relationships between 2 variables. Divide the class into groups. Distribute a sheet with a linear graph on it to each group. Ensure that the graph has clear labels, titles and axes. For example, it could be a linear graph representing the perimeter and side length of squares.

Ask questions like: What is the perimeter of a square with a side length of 4 units? What is the length of the side of a square with a perimeter of 18 units?

Instruct the students to analyse the linear graphs and answer the questions in their notebooks.

Discuss the students’ interpretations of the graphs. Summarise the key learnings from the activity and emphasise the importance of being able to read and interpret linear graphs.

Answers

1. Reading Double Line Graphs

Do It Together

1. The profit gained in the year 2012 in total was 17,000.

2. The difference between the highest profit gained by Company A and the lowest profit gained by Company B is 9000.

3. The percentage decrease in the profit of Company A from 2011 to 2014 is 83.33%.

4. The percentage increase in the profit of Company B from 2011 to 2014 is 0%.

5. The company that earned more profit overall is Company B

2. Drawing Double Line Graphs

4. Cartesian Coordinate of a Point

Do It Together

5. Drawing a Linear Graph

Do It Together

6. Reading Linear Graphs

Do It Together

1. The x-axis represents time (in minutes).

2. The y-axis represents distance (in km).

3. The distance covered in 4 minutes is 2.5 km.

4. The distance of 5 km was covered in 8 minutes.

3. Linear Graph

Think and Tell

In this graph, all the points are collinear, i.e., lie on a line, so it is called a linear graph.

Playing with Numbers 24

Learning Outcomes

Students will be able to:

deduce and apply the general form of numbers. solve number puzzles and patterns.

deduce the divisibility rules of 2, 3, 5, 9 and 10, and apply them.

Alignment to NCF

C-1.2: Discovers, identifies, and explores patterns in numbers and describes rules for their formation (e.g., multiples of 7, powers of 3, prime numbers), and explains relations between different patterns C-7.2: Engages in and appreciates the artistry and aesthetics of puzzle-making and puzzle-solving C-8.2: Learns systematic counting and listing, systematic reasoning about counts and iterative patterns, and multiple data representations; learns to devise and follow algorithms, with an eye towards understanding correctness, effectiveness, and efficiency of algorithms

Let’s Recall

Recap to check if students know how to write numbers in their expanded form. Ask students to solve the questions given in the Let’sWarm-up section.

Vocabulary

divisibility rule: rule determining whether a given number is divisible by the divisor leaving no remainder pattern: an arrangement of shapes, lines, letters, numbers, or colours that keep repeating

Teaching Aids

Number cards (containing 2-digit and 3-digit numbers); Blank slips of paper; Circular cutouts; Chart paper; Glue; Number cards showing numbers up to 5 digits

Chapter: Playing with Numbers

Numbers in General Form; Reversing Digits

Learning Outcomes

Students will be able to deduce and apply the general form of numbers.

Teaching Aids

Number cards (containing 2-digit and 3-digit numbers); Blank slips of paper

Activity

Begin the class by demonstrating a 3-digit number and how it can be expressed in its general form. Also, demonstrate the division properties of the number by reversing the digits.

Divide the class into groups of 4 and distribute the number cards (2-digit and 3-digit numbers) and blank slips. Each group gets one 2-digit number card and one 3-digit number card.

For the 2-digit number, ask the students to form a new number on the blank slips by reversing the order of the digits. Instruct them to add the two 2-digit numbers and check the numbers by which the sum is divisible; then, do the same thing after subtracting the numbers.

For the 3-digit number, ask the students to form two new numbers on the blank slips by reversing the order of the digits in cyclic order. Ask them to find the sum of the numbers and check by which numbers the sum is divisible. Instruct the students to solve and write the answers in their notebooks.

Letters for Digits; Number Puzzles and Patterns

Learning Outcomes

Students will be able to solve number puzzles and patterns.

Teaching Aids

Circular cutouts; Chart paper; Glue

Activity

Imagine Maths Page 333

Start the class by showing the students some patterns and ask them to identify the rule of the pattern.

Divide the class into groups of 4. Distribute circular cutouts, chart paper and glue to each group.

Instruct the students to form different patterns (such as triangular numbers, square numbers, geometric sequence, arithmetic sequence) by pasting the circular cutouts on chart paper. Ask the students to write the rule of the pattern in their notebooks.

Instruct the groups to exchange patterns with other groups and ask them to identify the pattern rule. Ask them to write the rule in their notebooks.

Encourage a discussion on the different patterns formed by the groups. If time allows, give the students a few more patterns and ask them to identify the rule.

Extension Idea

Ask: What is the missing number in the pattern: 3, 7, 16, 32, ?, 93?

Say: 3 + 22 = 7, 7 + 32 = 16, 16 + 42 = 32, 32 + 52 = 57, 57 + 62 = 93. So, the missing number is 57.

Learning Outcomes

Students will be able to deduce the divisibility rules of 2, 3, 5, 9 and 10, and apply them.

Teaching Aids

Number cards showing numbers up to 5 digits

Activity

Form 2 groups of students. Assign different numbers to each group such as 2, 5 and 10 to Group 1; and 3 and 9 to Group 2.

Take the students out to the playground. Scatter the number cards on the playground facing down. Ask the students of each group to go one by one and pick a number card and check whether the number is divisible by any of their assigned numbers (Group 1: 2, 5, 10; Group 2: 3, 9) or not. If it is, they should bring the card back to their group. The group that brings back the maximum number of cards wins. If time allows, reshuffle the cards and make the students play in groups where each group is assigned one number for which they need to check divisibility by.

Extension Idea

Ask: What values of x and y will make the number 54x 345y divisible by 2, 3, 5, 9 and 10?

Say: x = 6 and y = 0, so the number is 5463450.

Answers

1. Numbers in General Form

Do It Together

1. 59

2. 872

2. Reversing Digits

Do It Together

18 = 3 (1 + 2 + 3), hence the quotient = 37.

3. Letters for Digits

Think and Tell

A is not –4 since we are adding whole numbers and –4 is not a whole number.

Do It Together

There are two unknowns A and B.

We know that: B + A = 8 and 2 + B = A

Substituting the value of A in the first equation, we get B + (2 + B) = 8

2B + 2 = 8

2B = 6 or B = 3

2 + B = A ⇒ 2 + 3 = A

⇒ A = 5

Thus, A = 5 and B = 3.

Think and Tell

No, the value of A and B cannot be 9 as the digit is represented by a single letter.

4. Number Puzzles and Patterns

Do It Together

In the sequence, each successive term is obtained by multiplying the preceding term by 3.

Hence, 4th term = 18 × 3 = 54; 5th term = 54 × 3 = 162

6th term = 162 × 3 = 486; 7th term = 486 × 3 = 1458

5. Test of Divisibility

Do It Together

Divisibility by 2 = The number ends with 0, hence it is divisible by 2.

Divisibility by 3 = The sum of the digits of the number is 21, hence it is divisible by 3.

Divisibility by 5 = The number ends with 0, hence it is divisible by 5.

Divisibility by 9 = The sum of the digits of the number is 21, hence it is not divisible by 9.

Divisibility by 10 = The number ends with 0, hence it is divisible by 10.

Answers Solutions

Chapter 1

Let's Warm-up

1. 15+8 52 23 +== 431212

2. 52.31 + 61.2 = 113.51  3. −23 + 69 = 46

4. 7–10 753 –== –8488 5. 89 − 47.25 = 41.75

Do It Yourself 1A

1. a. 4 5 is > 0 but < 1. Divide the space between 0 and 1 in 5 equal intervals.

b. 2 –4 lies between 0 and −1, divide the space between 0 and −1 in 4 equal intervals.

c. 7 4 lies between 1 and 2, divide the space between 0 and 2 in 8 equal intervals.

d. –6 5 lies between −1 and −2, divide the space between 0 and −2 in 10 equal intervals.

2. The space between 0 and −1 is divided into 4 equal parts, each part represents −1 4 . The points can be marked as:

Q

Point Q represents –7 4

3.a. 331 ÷= 933

b. 221 ÷= 1628 ––

c. 8 –28 × 184 =÷ –1284 = –2 7

d. –16 –42 × –116 = –142 ÷ 28 221

4. Answersmayvary.Sampleanswers:

a. 521053155420 ×=; ×=; ×= 821683248432

b. –93–3–92–18–93–27 ÷= ; ×= ; ×= 12341222412336

c. 62126236318 ×=; ÷=; ×= 82168248324

d.

–45 –153–5–152–30–153 ÷ =; ×=; ×= 21372124221363

5.a. 13 and 45

LCM of 4 and 5 = 20 15312512 = and=; <; 4205202020 Hence 13 < 45

b. –57 and 812

Since 5 –57 –is a negative number, < 8 812

c. –3 –0.4 and 14

–3 =–0.214; –0.4< –0.214; 14 Hence 3 –0.4<–14

d. 216 and 972

LCM of 9 and 72 is 72

216 = 972 ; 1616 =; 7272 hence, 216 = 972

e. –6–5 and 1112

LCM of 11 and 12 = 132

–55 –6–72–5 = and= 1113212132

–72–55 < 132132 , hence –6–5 < 1112

f. 14 and 2.8 5

14 14 =2.8;2.8=2.8; Hence, =2.8 55

g. 18 5 and −3.2

Since −3.2 is a negative number, 18 5 > −3.2

h. 19 2 and 53 7

LCM of 7 and 2 = 14

1913353106133106 = and =;> 2147141414 ; Hence, 1953 > 27

6.a. −3.5, 9185 , 2,, 5472 = 35 –10 , 9985 ,,, 5472

LCM of 10, 7, 5, 4, 2 is 140.

3514490 –×=–1014140 ; 928252 ×= 528140 ;

935315820160570350 ×=;×=;×= 435140720140270140

Since 490160252315350 –<< << 140140140140140

Therefore, –3.5<<<2<8915 7542

b. 5 17 , –0.75, 1.25, 1,=0.56, –0.75, 1.25, 1.17, 0.7 9 610 –0.75<0.56<0.7<1.17<1.25; 571 therefore, –0.75<<<1<1.25 9106

c. 8 213 , –2, 1.25, 1,=0.88, –2, 1.25, 1.5, 3.25 9 44 –2<0.88<1.25<1.5<3.25; therefore,–2<<1.25<1<8213 944

d. 3 273127 –, 1.5, 4.2, 2,= –, 1.5, 4.2,, 2 55255 = –1.5, 1.5, 4.2, 2.4, 1.4 –1.5<1.4<1.5<2.4<4.2; 372 therefore, –<<1.5<2<4.2 255

e. 161 18 , 3, –2.5, 3, –345 = 16132518 ,, –, 3, –34105

LCM of 3, 4, 10, 5, is 60

163201319525150180–18–216 =,=, –=–,3=, = 360460106060560

–216150180195320 < –<<< 6060606060 ; therefore, –18 116 <–2.5<3<3<. 5 43

f. 3–253617 , 2.1, ,, 5252 = 321–253617 ,, ,, 510252

LCM of 2, 5, 10 = 10

3621–25–12536721785 =,, =,=,= 51010210510210

–1256217285

<<<< 1010101010 ; therefore, –2533617 <<2.1<< 2552

7.a. – 13 5 = 3 –2 5 b. –16 –2 8 c. –211 –3 62

d. –18–91 ==–2 844

a. −13 5 b. −16 8 c. −21 6 d.  −18 8

8. Answersmayvary.Sampleanswers: 1426

––912 and LCM of 9 and 12 = 36 –=–14562678 and–=–9361236 ; 5678 –>–3636

Four rational numbers between 567857 – and– are– , 363636 585960 –, –, –. 363636

Word Problem

1. Simran’s red cloth = 15 4 m = 3.75 m; Raj’s green cloth = 4.6 m; Since 3.75 < 4.6, Raj bought the larger piece of cloth.

1B

1.a. 4+6 4610 +== 7777

b. 5–7 + 911

LCM of 9, 11 is 99. 555763 =; –= –9991199

55–63 8 = –9999

c. (–12)(–13) + 215

LCM of 2, 15 is 30 –12)–180)–13)–26) = and= 2301530 (((( –180–26–206 += 3030 30 = 103 –15

d. −2 + 4 + 2.5 = 4.5

e. 8 + (−24) + 14.5 = −1.5

f. 17 + 18.44 + (−12) = 23.44

2.a. 8+2 8–210 –== 11111111

b. 27–38 938 –11 –== 13393939

c. 57252853 ––=––= –1215606060

d. = (( –13)–6) –815 –195–147 48 += 120120120

e. 92811413950819131 ––1.3=+–=–= 7–9636310630630630

f. 8–1478821023167 ––=+–= 15115165165165165

g. 13926045168473 ––2.1=––= ––416–80808080

h. –16 17235756030887 ––=+–= 537105105105105

3. 2127 += –56 x

2721–135126261 = ––=–= –= –8.7 65303030 x

4. 8.5 − x = −12.25 8.5 + 12.25 = x

x = 20.75 = 207583 = 1004 or 3 20 4

5. Length of first rope = 5=338 77 mm

Length of second rope = 3851143579 –=–= 73212121

Total length = 3879114791934 +=+==9 m 72121212121 m

6. Amount earned = ₹480

Amount spent = ₹ 153253 + 22 = 406 =203 2 `

Amount saved = ₹480 − ₹203 = ₹277

7. a. Closure property  b. Associative property

c. Subtraction property of zero

8.a. 1212 –+=0 77

b. 1313–=0 22 c. 55+=0 –99 d. 2121–=0 1414

9. 5–36–328536328 +–+––=––––+ 687145–1568714515

= ( 5 –12–3)–6+8 20–9 ++ 24141 = 11152 –+ 241415

385900112

=–+ 840840840 = 403 –840

10. 32+60–42 857 5025 +–=== 936363618 7 =1 18

7 18 should be subtracted to make 1 7 18 equal to the nearest whole number, such that − 77 1–=1 1818

11 18 should be added to make 1 7 18 equal to the nearest whole number, such that − 711 1+=2 1818

11. a. 25.5 + 12 2 =25.5+12.67=38.17 kg

3

Era has 38.17 kg of wheat and rice.

b. 25.5 kg − 37 kg=25.5kg-18.5kg=7kg

2

The difference between the weight of wheat and corn is 7 kg.

Word Problems

1. Length of the wood = 2 12feet 3 = 38 feet 3

Length of the wood cut from both ends = 510 2 ×=feet 88

Length of the wood left = 381030430274137 –=–== 3824242412

5 =11 feet. 12

2. Total flour bought = 18 kg

Total flour used in the first three weeks = 3+4+4127 538 kg

= 161439 ++ 538 kg = 384+560+585 1529 = kg 120120 = 12 89 kg 120

Flour used in the last week = 18 − 12 8963131 ==5 120120120 kg

3. Apples = 15 kg; 4 Bananas = 2.6 kg

Total fruits purchased = 9 kg

Oranges purchased = 9 − 15 –2.6

4

9 − 3.75 − 2.6 = 2.65 kg

Oranges purchased = 2.65 kg

4. Total juice prepared = 25.5 litres

Juice consumed = 8+8+2223 558 litres = 424219 ++ 558

= 672+95 8419 += 5840 = 767 =19.175 litres 40

Juice remaining = 25.5 − 19.175 = 6.325 L

1C

1.a. 21836 ×= 5735 b. –5525 ×= –818

c. –1242–504–36 ×= = 710705

d. 13–25–325–13 ×== 15101506

e. 163860832 ×== –197–133–7 f. 23–32–736–368 ×== 5105025

g. 11–27–297–27 ×== 194483676 h. –51–281428 ×= 515

2.a. 14514342 ÷= ×= 535525

b. –1336–1310–130–65 ÷=×== 610636 216108

c. 12–41225300 ÷=×== –15 5255–4–20

d. 31–731131–1–31 ÷=×=×= 14114–7–98–198

e. –287–28–30840÷=×==8 15–30157105

f. 345134196463817 ÷=×=== 1 7197513572121

g. –3648–3610–360–3 ÷=×== 101010484804

h. 486548–14–672 ÷=×= 17–1417651105

3. –1728 ×= 63 x 28616856 =×== 3–17–51–17 x = –56 17

Multiplicative inverse of –5617is. 17–56

4.a. 31–7–21–7 ××== 28914448

b. 54–4574–1260–144 –4.5 ÷ ×=× ×== =–2 79105945055

c. –8–714–8–7528020 ×÷=××== 1135113 1446233

d. –9–6–13–9–62108 × ÷=××= –752–75–13455

e. 2516152516104000401 ×÷=××===13 4510451530033

f. –4 –4–408–17 348343 ÷×=××== 1039108972030

5.a. LHS = 53752110535 ××=×== 4812496384128

RHS = 53715710535 ××=×== 48123212384128

Hence, LHS = RHS

b. 537 LHS= –÷= 4812 103771284 –÷=×= 88128756

5737 RHS= ÷– ÷ 412812 = 5123126036 ×–×=–47872856

1203684 =–= 565656

Hence, LHS = RHS

c. LHS = 57 ×= 412 35 48

RHS = 75 × 124 = 35 48

Hence, LHS = RHS

d. LHS = 537103777 ––=––=–=0 48888888

RHS = 5375410414 ––=––=+= 48848888

Hence, LHS ≠ RHS

6. Length of the plot = 185 3 m

A = 18518534,2252 ×==3802 3399 sq. m

P = 1857402 4×==246 333 m

7. Length of each piece = 357 ÷24 8

=×==357135711955m=1m 8241926464

8. Cost for adults = ₹ 250 4

Cost for one kid = 52501250 ×= 8432 ``

Cost for five kids = 12505625010 ×==195 3213232 ```

9. A = 389 sq.m 4 ; L = 247 m 3

389247 =× 43 B

38931167179 =×==1 m 4247988988 B

10. 5793117711 × ×+–×× 82131521348

315311309 +–208155712 = 3153111 +–2081548

LCM of 208, 15, 48 = 3120

4725+6448–715 3120 = 10458 3120 = 1743 520

The multiplicative inverse of 1743 520 is 520 1743

11. Let the total pages be x

Fraction read = 5 8

Fraction left = 3 8

According to question, 3 8 ofx = 120

Total pages in the book = x = 120 × 8 3 = 320

Word Problems

1. Number of paper towels = 8

Total length of 8 towels = 88 1 8 m= 705 8 m

Length of 5 towels = 705 8 ÷ 8 × 5 = 705 8 × 1 8 × 5 = 3525 64 m= 55 5 64 m

2. Kapil’s earning = ₹18,000

Expenditure on rent = 2 9 × ₹18,000 = ₹4000

Expenditure on food = 3 7 × (₹18,000 − ₹4000) = 3 7 × ₹14,000 = ₹6000

Expenditure on shopping = 1 4 × (₹14,000 − ₹6000) = 1 4 × ₹8000 = ₹2000

Total expense = ₹4000 + ₹6000 + ₹2000 = ₹12,000

Savings in a year = (₹18,000 − ₹12,000) × 12 = ₹72,000

Chapter Checkup

1. The space between 0 and –1 is divided into 4 equal parts, each part represents –1 4 . The points can be marked as:   0

P −1 −2 1 2 3 –4 2 –4 –1 4

Point P represents − 1 4 .

2. –93–27 ×= 29387

3.a. 54 –< 78

b. LHS = 31 = 93 ; hence, 31 = 93

c. –12–3–15–3 =;= 82102

Hence, –12–15 = 810

d. 21 =1.105; 19

Since, 1.105 < 1.75; hence, 21 <1.75 19

e. –1612 = –2;= –2 8 –6

Hence,=–1612

8 –6

f. 32 32 = 6.4;hence,<7.2 55 h

g. 963 = 535 ; 1365 = 735

Since, 6365 < 3535 ; hence, 913 < 57

h. 295858512951 =;since,>;hence,> 366636

4.a. 125–3–753675–45–3525 ,,,,=,, ,, 1022663030303030

753625–35–45 >>>> 3030303030 ;

Hence, 55–71 >1.2>> > –1 2662

b. 8175851317 ,, –,–, 3100100123

= 16001050510–6503400 ,,–,, 600600600600600

340016001050510650 >>>–> –600600600600600

Hence, 178 1 > > 1.75> –0.85>–1 33 12

c. 183251521 , –5,,, 510065 ; = 108015009757501260 ,–,,, 300300300300300

Since, 126010809757501500 >>>>–

300300300300300

Hence, 21183>>3.25>2> –5 556

5.a. 12 7 = −1.714 b. − 8 3 = −2.66

c. 10 8 = −1.25 d. − 15 8 = −1.875

a. −12 7 b. –8 3 c. –10 8 d. –15 8

6. Answermayvary.Sampleanswer:

LCM of 5 and 4 is 20. 12481890 = and= 520420

Hence, four rational numbers between the given numbers can be − 10 20 , −  20 20, 10 20, 20 20 .

7.a. L÷318 –HS= ÷ 6510

= 3110313 ÷×= ÷=×4= 2 –658 –66 4

RHS=÷÷318 65 –10 = 11051025 ×5×= ×= 28288

Hence, LHS ≠ RHS

b. LHS = 318 ×+ 6510 – = 114151 ×+= ×= 255252

RHS = 3138312151 ×+ ×=+== 656103 –030 –302

Hence, LHS = RHS

c. 5 –31 LH 6 – S= = 15621 = 303030

RHS==+=+=131361521 5656303030

Hence, LHS ≠ RHS

d. LHS=++318 65 –10

= 1568924151 ++= +== 3030103030302

318328 RHS=++=++ 651061010

151015301 =+= += 301030302

Hence, LHS = RHS …

8.a. The sum of a rational number and its additive inverse is zero.

b. The reciprocal of a negative rational number is negative.

c. The rational number 0 does not have any reciprocal.

d. Adding zero to a rational number gives the rational number itself.

9. 98 += 75 –1 x 8913645181 = = = 517858585 x = –11 2 85

10. 1215 = 4 7 x 1215 += 74 x 48105153 =+= 282828 x

11. A = 115619114898 ××==1489.8 sq. m 25210

12.a. 27123523 += +=; 563030 –30 – the multiplicative inverse is 30 23

b. 3515 ×= 7856 ; the multiplicative inverse is 56 15

c. 98271643 =+= 2366 ––6 ; the multiplicative inverse is 6 43 .

d. 1221252×==9 7428 ; the multiplicative inverse is 1 9 .

e. 13251326338 ÷= ×= 526525125 – ; the multiplicative inverse is 125 –338

f. 191457 1 –1443 +== 175155 – 115 ; the multiplicative inverse is 51 43

g. 172417591003 ÷=×= 659624144 ; the multiplicative inverse is 144 1003

h. 2429696 ×= 1339507 ; the multiplicative inverse is 507 696 .

13. Length of one roll = 2 15m 3 = 47 m 3

Length of 5rolls=5114721473291 ×= ×= m=82m 4434344

–

4. Pizza eaten by Richa = 1=37 44

Pizza eaten by Alex = 75211031 +=+= 46121212

Pizza eaten by Prince = 3721 ×= 248

Total pizza eaten = 7312142626316723 ++=++==6 41282424242424

5. Let the number be x

According to question, 53–=80 35 xx

25–9 =80 15 xx

16 80; 15 x x = 75

The number is 75.

6. Total money Shilpa had = ₹750

–18 131118

14. 585815161516 +÷=÷+ 6969181818 1

= –÷= ×= 3 18 –181831

15. Average time taken (in secs) = 100.26+90.75+91.63+98.55 =95.2975 seconds 4 =

1 minute 35.2975 seconds

16. 125271585 ×++÷× 7985191516

2011331 =+++

––4756

21

= 2000+525+3724+350 2599 = 2100 2100 –

Word Problems

1. Cricket practiced in last week = 12 5 hours 6

Cricket practiced this week = 2 1 hours 8

Total hours =12+2=+517717 6868

3085135923 =+==14 hours 24242424

2. Total rice = 1209 52kg=kg 44

Number of families = 15

Each family gets = 209209120929 ÷15=×= =3 kg 44156060

3. Vivek’s rectangular plot:

L = 256175256175 m;=m; =×=2986.66 sq. m 5353 BA

Shwets’s square plot: 18918918935721 =m;=×==8930.25 sq m 2224 SA

Shweta’s plot has more area. Difference = 8930.25 − 2986.66 = 5943.59 sq.m

Money spent on book = 2 ×750= 300 5 `

Money spent on stationary = 44×750–300=×450=200 99 `

Money left = ₹750 − (₹300 +₹200) = ₹250

Chapter 2

Let's Warm-up Linear Equation

17 = 7x − 32

17 + 32 = 7x − 32 + 32

49 = 7x

49

7 = 7 7 x

7 = x

e. 11x + 1 = 3 11+1–1=3–1 x 11x = 2

11 11 x = 2 11

x = 2 11

f. 5x − 11 = 2x + 7

5–11+11=2+7+11 xx

5=2+18 xx

5x − 2x = 2x − 2x + 18

3x = 18

3 3 x = 18 3 ⇒ x = 6

3. a. 3x − 5 = 2x + 97

3x − 2x − 5 = 97

x − 5 = 97 ⇒ x = 97 + 5

x = 102

b. 5(x − 7) − 2x = 13 − x

5x − 35 − 2x = 13 − x

3x − 35 = 13 − x

3x + x − 35 = 13

4x − 35 = 13

4x = 13 + 35 ⇒ 4x = 48 ⇒ x = 12

c. 15x − 2(18 + x) = 29

15x − 36 − 2x = 29

13x − 36 = 29

13x = 29 + 36 ⇒ 13x = 65 ⇒ x = 5

d. x + 2(3 + x) = 5(x − 6)

x + 6 + 2x = 5x − 30

3x + 6 = 5x − 30

6 = 2x − 30 ⇒ 6 + 30 = 2x

36 = 2x ⇒ 18 = x

e. 9x + 3 = 13(2x + 8)

9x + 3 = 26x + 104

3 = 17x + 104

3 − 104 = 17x

− 101 = 17x 101

–17 = x

f. 5(x − 17) = 7(x − 19)

5x − 85 = 7x − 133

5x = 7x − 133 + 85

5x = 7x − 48

5x − 7x = − 48

−2x = − 48

x = 24

4. a. 3x + 4(x − 2) = 41

3x + 4x − 8 = 41

7x − 8 = 41 ⇒ 7x = 49 ⇒ x = 7

b. x − 1.5(x − 3) = 2(x − 3)

x − 1.5x + 4.5 = 2x − 6

−0.5x + 4.5 = 2x − 6

2.5x = 10.5 ⇒ x = 4.2

c. 3(1.5x + 1) = 16.5

4.5x + 3 = 16.5 ⇒ 4.5x = 13.5 ⇒ x = 3

d. 2.4x + 4.8 = 1.2x + 6

2.4x − 1.2x = 6 − 4.8

1.2x = 1.2 ⇒ x = 1

e. 4x + 7 = 1.5(x + 12)

4x + 7 = 1.5x + 18

2.5x = 11 ⇒ x = 4.4

f. 1.3(x − 3) + 2.6 = x 1.3x − 3.9 + 2.6 = x

1.3x − 1.3 = x ⇒ 1.3–=1.3 xx

⇒ 0.3x = 1.3 ⇒ x = 13 3 (or approximately 4.33)

5. Let the smaller number be x and the larger number be 2x.

Given: If 30 is subtracted from both numbers, we get x − 30 and 2x − 30.

According to the question:

2x − 30 = 4(x − 30) ⇒ 2x − 30 = 4x − 120

2x = 90 ⇒ x = 45

Therefore, the smaller number is 45, and the larger number is 2 × 45 = 90.

6. Let the smaller even integer be x, and the larger even integer be x + 2.

According to the question:

22–( + 2) = 4 511 xx

22–10(+2) =4 55 xx

(22–10(+2)) =220 xx

22– 10–20=220xx

12–20=220 x 12x = 240 240 = 12 x

x = 20 x + 2 = 22

So, the smaller even integer is x = 20, and the consecutive even integer is x + 2 = 22.

7. Let the smaller number be x and the larger number be 3x. Given: If 15 is added to both numbers, we get x + 15 and 3x + 15.

According to the question:

3x + 15 = 2(x + 15) ⇒ 3x + 15 = 2x + 30

⇒ x = 15

Therefore, the smaller number is 15, and the larger number is 3 × 15 = 45.

8. a. 18 cm 15 cm

Perimeter = 54 cm12 cm x

x + 18 + 12 + 15 = 54

x + 45 = 54

x = 9 cm

b.

x 4 cm

x + 3 3x x − 1

Perimeter = 56 cm

3x + 5

x + 3 + x + 4 + 3x + x − 1 + 3x + 5 = 56 cm

9x + 11 = 56 cm

9x = 45 cm

x = 5 cm

c. 2x + 3

2(x + 1) x + 4 x + 3

Perimeter = 35 cm x

x

2x + 3 + x + x + 4 + x + 3 + x + 2(x + 1) = 35 cm

2x + 3 + x + x + 4 + x + 3 + x + 2x + 2 = 35 cm

8x + 12 = 35 cm

8x = 23 cm

x = 23 8 cm

Word Problems

1. Let Monty’s present age be x. After 30 years, his age will be (x + 30). According to the question:

x + 30 = 3x + 6

2x = 24 x = 12

Therefore, Monty’s present age is 12 years.

2. Let Harsh’s present age be x. Harsh’s mother is (30 + x) years old.

Given: In 12 years, Harsh’s age will be (x + 12), and his mother’s age will be (30 + x + 12).

According to the question:

30 + x + 12 = 3(x + 12)

42 + x = 3x + 36 ⇒ 2x = 6

⇒ x = 3

Therefore, Harsh’s present age is 3 years, and his mother’s age is 30 + 3 = 33 years.

3. Let the breadth of the rectangular field be (x). The length is (2x − 7).

The perimeter of the rectangle is given by: 2[(2x − 7) + x] = 196

= 2(2x − 7) + 2x = 196

= 4x − 14 + 2x = 196

= 6x = 210

= x = 35

The breadth is 35 m, and the length is 2 × 35 − 7 = 63 m. The area is 35 × 63 = 2205 square meters.

4. Ratio of ₹50 notes to ₹100 notes to ₹500 notes = 6:2:1

Let the number of ₹50 notes be 6x, ₹100 notes be 2x, and ₹500 notes be x

The total value of the notes is [50(6x) + 100(2x) + 500x], which is equal to ₹25,000.

According to the question:

300x + 200x + 500x = 25,000

1000x = 25,000 x = 25

Therefore, the number of ₹50 notes is 6 × 25 = 150, the number of ₹100 notes is 2 × 25 = 50, and the number of ₹500 notes is 25.

5. Let Naveen’s age be 2x and his father’s age be 5x

After 10 years, their ages will be (2x + 10) and (5x + 10).

2B

2 + 101 =

5 + 102 x x

4x + 20 = 5x + 10

x = 10

Father’s present age = 5 × 10 = 50 years, Naveen’s present age = 2 ×10 = 20 years.

Father’s age at the time of Naveen’s birth = (50 −20) years = 30 years.

1.a. 5 =3 2–1 x x for x = 2: ≠ 5(2)10=3

2(2)–13

No, the solution given is not correct.

b. 75 = +1–1xx

For x = 6: 75 =

6 +16–1

1 = 1

Yes, the solution given is correct.

c. 7+15+6 = 34 xx

For x = 3;

22

3 21 4 ≠

No, the solution given is not correct.

2.a. 5–4 7 x = 8 9

9 (5x − 4) = 7 ×8

45x − 36 = 56

45x = 92

x = 92 45

b. +5+1 –69 zz = 3 4 z

9(z+5)– 6(z+1) 54 = +3 4 z

4(9z + 45 − 6z − 6) = 54 (z + 3)

4(3z + 39) = 54z + 162

12z + 156 = 54z + 162

−6 = 42z

z = − 1

7

c. –(4–3) 2–3–yy yy = ⇒ –4 +3 1 42–3+ yy yy = ⇒ 4–4 1 43–3 y y = 1 4

4(4y − 4) = (3y − 3)

16y − 16 = 3y − 3

13y = 13

y =1

d. 69 = 3 + 1)+ ( 53nn

6(5n + 3) = 9(3n + 1)

30n + 18 = 27n + 9

3n = −9

n = −3

e. 4+12–13–7 +–=6 325 xxx

3 =1

y

y = 3

b. 4–53+5 = 1110 xx

10(4x − 5) = 11(3x + 5)

40x − 50 = 33x + 55

7x = 105

x = 15

10(4 + 1)+15(2–1)–6(3–7) =6

30 xxx

40x + 10 + 30x − 15 − 18x + 42 = 180

70x − 18x + 37 = 180

52x = 143

x = 143 52

3.a. ⇒ 3–8 =63–8=30 5 x xx x

−8 = 27x ⇒ x = 8 –27

b. 57 = +2 xx

5(x + 2) = 7x ⇒ 5x + 10 = 7x

10 = 2x ⇒ x = 5

c. 0.4+5 8 x = 2.5+4 15 x

15(0.4x +5) = 8(2.5x + 4)

6x + 75 = 20x + 32

75 − 32 = 20x − 6x

43 = 14x ⇒ x = 43 14

d. 5(2–)–4(1+) 2–xx x = 5 8

10–5–4–4 2–xx x = ⇒ 6–9 5 82–x x = 5 8

8 (6 − 9x) = 5 (2 − x)

48 − 72x = 10 − 5x

38 = 67x ⇒ x = 38 67

e. 69 = 3+15+3 xx

6(5x + 3) = 9(3x + 1)

30x + 18 = 27x + 9

3x = −9

x = −3

4. a. 3–14+6 + 23 xx = 43 6

3(3–1)+2(4+6) 43 = 66 xx

9x − 3 + 8x + 12 = 43

17x + 9 = 43

17x = 34

x = 2

Putting x =2; 23 + 2 y = 2

3 1 + y = 2

Putting x = 15; 152+=11 3 y

5 + 2 =11 y

2 =6 y

y = 1 3

5. Let the denominator of the fraction be x. Then, the numerator is x − 3.

The fraction is –3 x

x

Given: When both the numerator and denominator are decreased by 2, the new fraction becomes –5 . –2 x x

According to the question, the simplest form of this new fraction is 3

4 The equation becomes:

–5 –2 x x = 3 4

Solving for x:

4(x − 5) = 3(x − 2)

4x − 20 = 3x − 6

x = 14

So, the fraction is –3 x x . = 14–3 14 = 11 . 14

6. Let the smaller angle be x and the bigger angle be 2x.

Given: When 15 is added to the smaller angle and 15 is subtracted from the bigger angle, the new ratio becomes 1:1.

According to the question:

+15

2–15 x x = 1 1

x + 15 = 2x − 15

x = 30

So, the smaller angle is 30°, and the bigger angle is 2 × 30 = 60°.

7. a. –1 1 = 7–273 a a

3(a − 1) = 7a − 27

3a − 3 = 7a − 27 24 = 4a

a = 6

b. 2+67–34 = 43 bb

3(2b + 6) = 4(7b − 34)

6b + 18 = 28b − 136

154 = 22b

b = 7

c. 11–443+17 = 54 cc

4(11c − 44) = 5(3c + 17)

44c − 176 = 15c + 85

29c = 261

c = 9

d. 9–7 29 = 7+3)1 (3 d d

31(9d − 7) = 29(7d + 3)

279d − 217 = 203d + 87

76d = 304

d = 4

Given postal code is 2abc5d. Substituting values of a, b, c, d, we get, the postal code as 267954.

Word Problem

1. Let the present age of Abhijeet be 2x and the present age of Sahil be x, where x is a positive integer.

According to the question,

Four years ago, Abhijeet’s age was 2x − 4 and Sahil’s age was x − 4. The ratio of their ages at that time was given as 5:2.

Hence 2–4 –4 x x = 5 2

By Cross multiplication:

2(2x − 4) 5(x − 4)

4x − 8 5x − 20

x 12

Therefore, Abhijeet’s present age 2x 2 12 24 years

Sahil’s present age x 12 years

2C

1.

a. 3x + 5 = 1 2 x − 13

b. 4y + 11 = 2y + 56

c. Let the three consecutive even numbers be n, n + 2, and n + 4.

Equation: n + (n + 2) + (n + 4) = 144

d. Let the original speed of the train be s and the time taken for the initial trip be t.

Equation for the first trip: st = 240

On the return trip, the speed is increased to s + 20 and the time taken is t − 2.

Equation for the return trip: (s + 20)(t − 2) = 240

2. Let the four consecutive odd numbers be x, x + 2, x + 4, and x + 6.

x + (x + 2) + (x + 4) + (x + 6) = 352

4x + 12 = 352

4x = 340

x = 85

So, the four consecutive odd numbers are 85, 87, 89, and 91.

3. Let the three consecutive multiples of 11 be 11x, 11x + 11, and 11x + 22.

11x + (11x + 11) + (11x + 22) = 429

33x + 33 = 429

33x = 396

x = 12

So, the three consecutive multiples of 11 are 132, 143, and 154.

4. Let the original number be x

The new number, after a 10% decrease, is 0.9x, and when increased by 25%, it becomes 1.25 times 0.9x. 1.25 × 0.9x = 81

1.125x = 81

x = 81

1.125

x = 72

So, the original number is 72.

5. Let the angles be 3x, 4x, and 5x

The sum of angles in a triangle is 180°

3x + 4x + 5x = 180°

12x = 180°

x = 15°

Smallest angle = 3x = 3 times 15 = 45°

Largest angle = 5x = 5 times 15 = 75°

The difference between the largest and smallest angles is 75° − 45° = 30°.

6. Let one part be x, and the other part be 6000 − x

The equation is:

0.15x = 0.35(6000 − x)

0.15x = 2100 − 0.35x

0.5x = 2100

x = 4200

So, one part is 4200, and the other part is 6000 − 4200 = 1800.

7. Let the daughter’s age be x. Puneet’s age is then 3x

The sum of their ages is given by:

x + 3x = 52

4x = 52

x = 13

Puneet’s age is 3 times 13 = 39 years. The difference in their ages is 39 − 13 = 26 years.

8. The ratio of the numbers = 2:1

So, let the numbers be 2x and x. The sum is given by:

2x + x = 45

3x = 45

x = 15

So, the two numbers are 2 times 15 = 30 and 15.

9. Let the cost of the chair be x. The cost of the table is then (x + 550). The total cost is given by:

x + (x + 550) = 15,550

2x + 550 = 15,550

2x = 15,000

x = 7,500

So, the cost of the chair is ₹7,500, and the cost of the table is ₹7,500 + ₹550 = ₹8,050.

10. Let the runs scored by Rohit be x. Virat’s runs are then (2x + 20). The total runs are given by:

x + (2x + 20) = 300 − 4

3x + 20 = 296

3x = 276

x = 92

So, Rohit’s score is 92, and Virat’s score is 2 ×92 + 20 = 204.

11. Let the initial number of pencils be x. The total cost is given

by:

4x + 4(2x + 10) = 280

4x + 8x + 40 = 280

12x + 40 = 280

12x = 240

x = 20

So, Amit initially had 20 pencils.

12. Let x be the total estate. Animesh left:

Daughter: 1 2 x

Son: 1 3 x

Donation: x − 1 2 1 2 x + 1 3 x 1 2 = 1 6 x

Given − the donation was ₹5,00,000:

1 6 x = ₹5,00,000

x = ₹30,00,000

Daughter’s share = 1 2 x = 1 2 × ₹30,00,000 = ₹15,00,000

Son’s share = 1 3 x = 1 3 × ₹30,00,000 = ₹10,00,000

So, Animesh gave ₹15,00,000 to his daughter and ₹10,00,000 to his son.

13. Let the two digits be x and y, where x is the digit in the tens place, and y is the digit in the one’s place.

The number is 10x + y.

According to the question, one’s digit is 0.4 times the ten’s digit:

y = 0.4x

Also,

(10y + x) + (10x + y) = 77

11x +11y = 77

x + y = 7 …. (1)

Substituting the value of y in (1)

x + 0.4x = 7

1.4x = 7

x = 5

And, y = 0.4×5 = 2

So, the original number is 10x + y = 10(5) + 2 = 52.

14. Let the speed of the boat in still water be B and the speed of the current be C

Let the distance be x km.

The speed upstream is BC, and the speed downstream is B + C.

Given − the speed of the flow of the river is 3 km per hour, Time downstream is 5h and time upstream is 3h.

Since Distance = Speed × time

x = (B − C) × 3 ……. (1)

x = (B + C) × 5 ……... (2)

Equating (1) and (2) and substituting the values:

(B − 3) × 3 = (B + 3) × 5

3B − 9 = 5B + 15

2B = 24

B = 12 km/h

Hence the speed of the boat in still water is 12 km/h.

15. Let x be the number of ₹5 notes and y be the number of ₹10 notes.

According to question, 5x + 10y = 870 …………(1)

And x + y = 92

x = 92 − y ……….. (2)

Now, substituting this expression for x into the first equation: 5(92 − y) + 10y = 870

460 − 5y + 10y = 870

5y = 410

y = 82

So, x = 92 − 82 = 10

16. Given − Distance between two places A and B is 300 km.

Two cars start simultaneously from A and B in opposite directions.

The distance between them after 4 hours is 60 km

Distance travelled by both of them = 300 − 60 = 240 km/h.

The speed of one car = s km/h

Speed of the second car = (s + 10) km/h

We know, Distance = Speed × time

According to the question,

Distance travelled by car A in 4 hours = 4s km/h

Distance travelled by car B in 4 hours = 4(s + 10) km/h

Distance travelled by both of them = 4s + 4(s + 10) = 240

= 4s + 4s + 40 = 240

8s = 200

s = 25 km/h

and s + 10 = 25 + 10 = 35 km/h

The speed of one car is 25km/h and that of the second car is 35 km/h.

Chapter Checkup

1. a. 2x + 1 = 5 ⇒ 2x = 4 ⇒ x = 2

b. 2x + 2 = x + 6 ⇒ x = 4

c. 3x + 4 = x + 10 ⇒ 2x = 6 ⇒ x = 3

2.a. 4x + 14 = 56

4x + 14 − 14 = 56 − 14

4x = 42 4 4 x ⇒ = 42 4

x = 10.5

b. 3x + 4 = x + 18

3x + 4 − x = x + 18 − x

2x + 4 = 18 ⇒ 2x + 4 − 4 = 18 − 4

2x = 14 2 2 x ⇒ = 14 2 ⇒ x = 7

c. 5x − 7 = 2x + 11

5x − 2x − 7 = 2x − 2x + 11

3x − 7 = 11

3x − 7 + 7 = 11 + 7 ⇒ 3x = 18

3 3 x = 18 3 ⇒ x = 6

d. 3x − 4 =1 − 2x

3x − 4 + 2x = 1 − 2x + 2x

5x − 4 = 1

5x − 4 + 4 = 1 + 4

5x = 5 5 5 x ⇒ = 5 5 ⇒ x = 1

e. 5x + 48 = 3(4x − 5)

5x + 48 = 12x − 15

5x + 48 − 5x = 12x − 15 − 5x

48 = 7x − 15

48 + 15 = 7x − 15 + 15

63 = 7x 63 7 ⇒ = 7 7 x ⇒ x = 9

f. 11(x + 1) = 12(x − 1)

11x + 11 = 12x − 12

11x + 11 − 11x = 12x − 12 − 11x

11 = x − 12

11 + 12 = x − 12 + 12 ⇒ 23 = x

3.a. 5(x + 3) = 3(1.5x + 18)

5x + 15 = 4.5x + 54

0.5x + 15 = 54

0.5x = 39 ⇒ x = 78

b. 6(2x + 11) = 8(2x − 1)

12x + 66 = 16x − 8

66 = 4x − 8

74 = 4x ⇒ x = 18.5

c. 8x − 7 − 3x = 6x − 2x − 3

5x − 7 = 4x − 3 x − 7 = − 3 ⇒ x = 4

4.

d. 10x − 5 − 7x = 5x + 15

3x − 5 = 5x + 15

−2x − 5 = 15

−2x = 20 ⇒ x = −10

e. 5(x − 1) = 2(x + 8)

5x − 5 = 2x + 16

3x − 5 = 16

3x = 21 ⇒ x = 7

f. 4x − 3 = (3x + 1) + (5x − 4)

4x − 3 = 3x + 1 + 5x − 4

4x − 3 = 8x − 3

−3 = 4x − 3 ⇒ x = 0

a. 5x + 7 = 35 for x = 7:

If we substitute x = 7, we get, 5(7) + 7 = 35 + 7 = 42, which is not equal to the right side, 35. Therefore, option x = 7 is not the correct solution.

b. 3(x − 2) = 4(x + 3) for x = 18:

If we substitute x = 18, we get,

LHS = 3(18 − 2) = 3(16) = 48

RHS= 4(18 + 3) = 4(21) = 84.

The left side is 48, and the right side is 84, so x = 18 is not the correct solution.

c. 4x + 3 − 2(x + 1) = 8x for x = 1 6 :

If we substitute x = 1 6 , we get

LHS = 4 1 6 + 3 − 2 1 2 1 6 + 1 1 2

LHS = 2 3 + 3 − 1 3 − 2

= 1 +1 3 = 4 3

RHS = 8 1 2 1 6 1 2 = 4 3 = LHS

Therefore, x = 1 6 is the solution of the given equation.

d. 4(x + 1) − 3(2x − 18) = 2x − 2 for x = 15:

If we substitute x = 15, we get

LHS = 4(15 + 1) − 3(2(15) − 18)

= 4(16) − 3(30 − 18)

= 64 − 36 = 28, RHS = 2(15) − 2

= 30 − 2 = 28 = LHS

Therefore, x = 15 is the correct solution.

e. 5(x + 9) − 2x = 90 for x = 15:

If we substitute x = 15, we get

LHS = 5(15 + 9) − 2(15)

LHS = 5(24) − 30

LHS = 120 − 30 = 90 = RHS

Therefore, x = 15 is the correct solution.

5.a. 39 = 2(+2)10 x x

30x = 18x + 36

12x = 36 ⇒ x = 3

b. 4(+2)+3 27 = 2+3(–1)17 x xx ⇒ 4+11 4 + 8 + 327 27 == (2+3–3)175–317 xx xxx

17 (4x + 11) = 27 (5x − 3)

68x + 187 = 135x − 81

268 = 67x ⇒ x = 4

c. 5+11)4(+6) = 2326 ( xx

26 (5x + 11) = 92 (x + 6)

130x + 286 = 92x + 552

38 x = 266 ⇒ x = 7

d. 3+1 5 x = 4( + 3)–4 8 x

8 (3x + 1) = 5 (4(x + 3) − 4)

24x + 8 = 20x + 60 − 20

4x = 32 ⇒ x = 8

e. 7(x − 3) + 2 = 11(8–)–3 7 x

7x − 21 + 2 = 88–11–3 7 x

7x − 19 = 85–11

7 x

49x − 133 = 85 − 11x

60x = 85 + 133

60x = 218

x = 218 60 ⇒ x = 109 30

f. 11(2+1) 11 x = 6x − 4 − 3x

22+11 11 x = 3x − 4

22+11=11(3–4) xx

22x + 11 = 33x − 44

11 + 44 = 11 x

55 = 11x ⇒ x = 5

6.a. 2–1 17 = +312 y y

12(2y − 1) = 17 (y + 3)

24y − 12 = 17y + 51

7y = 63

y = 9

b. 3+2 3 = 9+45 m m

5(3m + 2) = 3(9m + 4)

15m + 10 = 27m + 12

−12 m = 2

m = − 1 6

c. 5+14 =3 2 z z

5+14=6zz

14 = z

d. 251 –= 5315 aa 6–25 1 = 1515 a 191 –= 1515 a = – a 19

e. 5w + 73=–14 22 w

10+73–28 = 22 ww

10w + 7 = 3w − 28

7w = −35

w = −5

f.

3 +7 5 4 = 24 –4

b b

5

4 3 + 7 4 b = 5 2 –4 5 b

3b + 28 = 2b − 20

b = −48

7.a. F = 9 +32 5 C

When F = − 40

−40 = 9 + 32 5 C

−40 − 32 = 9 5 C ⇒ −72 = 9 5 C

⇒ 5 –72×= 9 C −40 = C

b. 9+44(2–1) = 107 xx

7(9x + 4) = 10 × 4(2x − 1)

63x + 28 = 80x − 40

68 = 17x x = 4

Then + 3 = 8 xy xy

Putting x = 4

4+ 3 = 48 y y 8(4 + y) = 12y

⇒

32 + 8y = 12y ⇒ 32 = 4y ⇒ y = 8

c. 2+1–23+2 –= 10615 xxx

3(2+1)–5(–2)3+2 = 3015 xxx

6+3–5+103+2 = 3015 xxx

+133+2 = 3015 xx

15 (x + 13) = 30 (3 + 2x)

15x + 195 = 90 + 60x

105 = 45x ⇒ x = 105 45 ⇒⇒ x = 7 3

Then, 25+=4 xm

2 7 3 + 5 m = 4 ⇒ 6 7 + 5 m = 4

5 m = 4 − 6 7 ⇒ 5 m = 22 7 ⇒ m = 35 22

8.a. 9(a + 1) − 4(a + 2) = 6

9a + 9 − 4a − 8 = 6

5a + 1 = 6

5a = 5 a =1

b. 11(b − 2) = 2(b + 1) + 3

11b − 22 = 2b + 2 + 3

11b − 22 = 2b + 5

9b = 27

b = 3

c. 2(–2) 1 = 3(3–5)3 c c

6(c − 2) = 3(3c − 5)

6c − 12 = 9c − 15

3 = 3c ⇒ c = 1

d. 2+7 1 = 3(7–8)4 d d

4(2d + 7) = 21d − 24

8d + 28 = 21d − 24

52 = 13d d = 4

e. 11–3(2+5)7–21 = 34 eee

11–6–157–21 34 eee

5– 157–21 = 34 ee

4(5e − 15) = 3(7e − 21)

20e − 60 = 21e − 63

e = The number is 8130011423.

9.a. 2(2) +3 =7

b. 3(7−1)+4(7) = 46

c. 2(3)+3(3+1) 18 = 15(3)–2(2(3)+4)25

d. 3(4)+4(4+3)4+2(3(4)–7) + 20 7 = 2

10. Let the numbers be 4x and 9x (where x is a common factor). The difference between them is 9x − 4x = 5x, and given difference is 250.

So, 5x = 250

x = 50

The two numbers are 4x = 200 and 9x = 450.

The sum of these numbers is 200 + 450 = 650.

11. Let the number be represented byx. The expression can be written as 1 2x − 1 2 1 2 × 1 3 = 1 15

Multiplying both sides by 3 to clear the fraction: x − 1 2 = 1 5. Adding 1 2 to both sides: x = 1 5 + 1 2 = 7 10

12. Let the three consecutive even numbers be 2x, 2x + 2, and 2x + 4.

Given: The sum of these numbers is 696. 2x + (2x + 2) + (2x + 4) = 696.

6x + 6 = 696 ⇒ 6x = 690

x = 115

The three consecutive even numbers are 230, 232, and 234.

13. Let the original fraction be –8 x x

If both numerator and denominator are increased by 17, the new fraction is –8+17 +17 x x = 5 6

Simplifying the equation: +9 +17 x x = 5 6

Cross − multiplying: 6(x + 9) = 5(x + 17). Solving for x: 6x + 54 = 5x + 85 x = 31

The original fraction is –8 x x = 31–8 31 = 23 31.

Word Problems

1. Let the present ages of Kushagra and Kush be 5x and 6x, respectively

Given: After five years, their ages will be (5x + 5) and (6x + 5) years respectively, and the sum = 43 years.

Hence, (5x + 5) + (6x + 5) = 43

Combining like terms, 11x + 10 = 43 hence, x = 3.

Present age of Kushagra = 5x = 5 × 3 = 15 years.

Present age of Kush = 6x = 6 × 3 = 18 years.

The difference between their ages is 18 − 15 = 3 years.

2. Let Shagun’s present age be x.

Her mother’s age = 5x.

After twenty − five years,

Shagun’s age will be x + 25 and her mother’s age will be 5x + 25.

According to question −

x + 25 = 1 2 (5x + 25) − 4.

x + 25 + 4 = 1 2 (5x + 25)

x + 29 = 1 2 (5x + 25)

2x + 58 = 5x + 25

3x = 33

x = 11.

Shagun’s present age is 11 years, and her mother’s present age is 5 ×11 = 55 years.

The difference in their present ages is 55 − 11 = 44 years.

3. Let the breadth of the pool be x. So, the length is x + 4.

The perimeter of the rectangle is given by 2 (length + breadth)

Given: Perimeter = 170 m.

So, 2 × (x + (x + 4)) = 170.

Therefore, 4x + 8 = 170

4x = 162

x = 40.5.

The length of the pool is x + 4 = 40.5 + 4 = 44.5 m, and the breadth is x = 40.5 m.

Area = 44.5 × 40.5 = 1802.25 sq m

4. Let the common ratio be m. So, the number of ₹50 notes is 12m, ₹100 notes is 8m, and ₹500 notes is 7m

The total amount of money is the sum of the product of the number of notes and their denominations.

Hence, according to the question,

50 ×12m + 100 ×8m + 500 ×7m = 24,500.

600m + 800m + 3500m = 24,500.

4900m = 24,500.

m = 5.

The number of ₹50 notes is 12 × 5 = 60, ₹100 notes is 8 × 5 = 40, and ₹500 notes is 7 × 5 = 35.

5. Let the length of the plot be 15x and the breadth be 7x.

Given: The cost of fencing is ₹150 per meter.

The perimeter of the rectangle is 2 × (length + breadth)

So, 2 × (15x + 7x) ×150 = 1,32,000.

44x ×150 = 1,32,000

44x = 880

x = 20.

Length = 15 × 20 = 300 meters, breadth = 7 × 20 = 140 meters. Therefore, the dimensions of the plot are 300 meters by 140 meters.

6. Let G be the total number of goats. Given −

Grazing goats: 1 2 × G

Playing goats: 3 4 × 1 2 × G

Drinking goats: 15

G − 1 2 × G − 3 4 × 1 2 × G = 15

G − 1 2 × G − 3 8 × G = 15

G − 4 8 × G − 3 8 × G = 15

G − 7 8 × G = 15

1 8 G =15

G = 120

Therefore, there were 120 goats in total.

7. Let the speed of the boat be 7x and the speed of the stream be 2x

Hence, speed downstream = 7x + 2x = 9x speed upstream = 7x − 2x = 5x

Given: The boat takes 6 hours more traveling upstream than downstream.

Let t hours be the time taken downstream.

Since, Distance = speed × time

Hence, Distance downstream = 9x × (t) …… (1)

Distance upstream = 5x × (t + 6) …… (2)

Equating (1) and (2):

9x × (t) = 5x × (t + 6)

9t = 5t + 30

4t = 30

t = 7.5 h

The total time for the entire journey is t + t + 6 = 7.5 + 7.5 + 6 = 21 hours

8. Let the angles be 7x, 17x, 19x, and 29x in degrees.

The sum of angles in a quadrilateral is 360°.

7x + 17x + 19x + 29x = 360°

72x = 360°

x = 5

Therefore, the angles are 35°, 85°, 95°, and 145°.

9. Let x be the time taken by Raj to write 100 pages. Raju takes twice the time taken by Raj to write the next pages, so 2x

Vivek takes 2 hours more than half the time taken by Raju,

so (1 2 × 2x) + 2.

The total time taken to write the book is x + 2x + (1 2 × 2x) + 2 =33 hours and 20 minutes. = 33 1 3 h

x + 2x + x + 2 = 33 1 3

4x + 2 = 33 1 2 = 100 3

4x = 94 3

x = 47 6 = 7 5 6 hours

10. Let x be the total money.

The share of A is 2 5 of the total money, so 2 5 × x

The share of B is 2 3 of the remaining money, so 2 3 × 3 5 x

C’s share is given as ₹600.

2

5 × x + 2 3 × 3 5 x + 600 = x

2 5 x + 2 5 x + 600 = x

4 5 x + 600 = x

1 5 x = 600

x = 3000

Therefore, the total amount of moneyx is ₹3000.

11. Let the son’s present age be S, then the father’s present age is S + 20.

Twelve years ago, the age of the father was six times that of his son.

S + 20 − 12 = 6 × (S − 12)

S + 8 = 6S − 72

5S = 80

S = 16

The son’s present age is 16 years, and the father’s present age is 16 + 20 = 36 years.

12. Let the son’s present age be S, then the father’s present age is 3S

After five years, the age of the father will be 3S + 5, and the age of the son will be S + 5.

3S + 5 = 5 2 × (S + 5)

6S + 10 = 5S + 25

S = 15

The son’s present age is 15 years, and the father’s present age is 3 × 15 = 45 years.

Chapter 3

Let's Warm-up

1. Open curve   2. Closed curve

3. Polygon   4. Non-simple curve

Do It Yourself

3A

1.a. A polygon with 7 sides is called a heptagon.

b. 6(6–3) =9

2

The number of diagonals in a hexagon is 9.

c. A polygon with all sides and angles equal is called a regular polygon.

d. A polygon with 10 sides is called a decagon.

e. A regular polygon is a 2D shape where the sides are all straight-line segments of equal length.

2.a. A triangle is a convex polygon. TRUE

b. The number of diagonals in an octagon are 7. FALSE

c. A circle is an example of a 2-D geometrical shape that is not a polygon. TRUE

d. A rectangle is a regular polygon. FALSE

3.a. Since all the angles (65°, 115°, 111°, 70°, and 179°) in the polygon are less than 180°, it is a convex polygon.

b. Since one angle (195°) in the polygon is more than 180°, it is a concave polygon.

4.a. Since all the angles in the given polygon are less than 180°, it is a convex polygon.

b. Since all the angles in the given polygon are less than 180°, it is a convex polygon.

c. Since not all the angles in the given polygon are less than 180°, it is a concave polygon.

d. Since not all the angles in the given polygon are less than 180°, it is a concave polygon.

e. Since not all the angles in the given polygon are less than 180°, it is a concave polygon.

5. Since all the angles in the 6-sided polygon are 120°, which is less than 180°, it is a convex polygon.

6.

7. Number of diagonals in a polygon = (–3) 2 nn

a. 4(4–3) =2 2 diagonals; Square

b. 8(8–3) =20 2 diagonals; Octagon

c. 10(10–3) =35 2 diagonals; Decagon

8.

9.

In a regular octagon, 5 diagonals can be drawn from one vertex.

So, 3 non-overlapping triangles can be made in a pentagon by joining the vertices.

Word Problem

1. A polygon with 7 sides is called a heptagon.

3B

Number of diagonals in a heptagon = 7(7–3)7×4 28 ===14

222

Since, one angle in the heptagon is more than 180°, it is a concave polygon.

1.a. The sum of the interior angles of a quadrilateral is 360°.

b. Sum of interior angles = (–2)×180° n Multiplying by

⇒ 22 (–2)×180°=2×(2)×2×90°=(24)×90°. 22 nnn

The sum of the interior angles of a polygon of n sides is (2n −4) right angles.

c. Each interior angle of a regular hexagon is 120°

d. ⇒⇒ 1800 (–2)×180°=1800°–2==10 180 =10+2=12 nnn

If the number of sides of a regular polygon is 12, then the interior angle sum is 1800°.

2.a. The sum of the interior angles of a triangle is 270°. FALSE

b. The number of triangles that can be formed within a polygon with n sides is n. FALSE

c. The maximum measure of the interior angle of a regular polygon is 180°. FALSE

d. It is possible to have a polygon whose sum of interior angles is 540°. TRUE

e. If each interior angle of a regular polygon measures 168°, the polygon has 30 sides. TRUE

3. Interior angle sum = (–2)×180° n

a. (7–2)×180°=900°

b. (13–2)×180°=1980°

c. (17–2)×180°=2700°

d. (20–2)×180°=3240°

e. (22–2)×180°=3600°

4. 20 right angles = 20×90°=1800°

⇒ (–2)×180°=1800° n

⇒ 1800 –2==10 180 n

⇒ =10+2=12 n

Yes, it is possible to construct a polygon, the sum of whose interior angles is 20 right angles. Such polygon will have 12 sides.

5. Interior angle sum = 2520°

Since, (–2)×180°=2520° n

Then, 2520° –2==14 180° n

⇒ =14+2 n

⇒ =16 n

Measure of each interior angle = 2520° =157.5° 16

Word Problem

1. Number of sides in an octagonal tile = 8

Sum of the interior angles = (n − 2) × 180° = (8 − 2) × 180° = 6 × 180° = 1080°

Measure of each interior angle = 1080° =135° 8

So, the measure of each interior angle if the tile is a regular octagon is 135°.

b. The measure of each exterior angle of a regular polygon is 360° n .

c. 360° =20° 18

The measure of each exterior angle of a regular polygon of 18 sides is 20°.

d. Measure of each exterior angle = 360° =45° 8

Interior angle = 180° − Exterior angle = 180° − 45° = 135° In case of a regular polygon that has 8 sides, each interior angle is 135° and each exterior angle is 45°

2.a. The sum of all exterior angles of a polygon is always 360°. TRUE

b. It is possible to have a polygon whose exterior angle is 175°. FALSE

c. It is possible to have a regular polygon whose each exterior angle is 1 8 th of a right angle. TRUE

d. Each exterior angle = 180° (–2)× n n . FALSE

3. Each exterior angle in a regular polygon = 360 n , where n is the number of sides.

a. 360° =120° 3

b. 360° =72° 5

c. 360° =45° 8

d. 360° =30° 12

e. 360° =15° 24

4. Measure of each exterior angle of a regular polygon = 360 n

⇒ 360° = Measure of each exterior angle of a regular polygon n

a. 360° ==9 40° n

b. 360° ==8 45° n

c. 360° ==6 60° n

d. 360° ==5 72° n

e. 360° ==4 90° n

3C

1.a. Sum of exterior angles of any polygon = 360°. If sum of interior angles = 360°

So, the polygon is a quadrilateral. The polygon in which the sum of all exterior angles is equal to the sum of interior angles is called a quadrilateral.

5. (3 –4)°+(+4)°+(7–3)°+(8–1)°+(2 +3)° +(9+1)°=360° xxxxx x

(3–4++4+7–3+8–1+2+3+9+1)°=360° xxxxxx (3++7+8+2+9)+(–4+4–3–1+3+1)°=360° xxxxxx

⇒ 360°

30+0°=360°==12° 30 xx

So, =12° x    Then, (3–4)°=(3×12–4)°=32° x (+4)°=(12+4)°=16° x (7 – 3)°=(7×12–3)°=81° x (8–1)°=(8×12–1)°=95° x (2+3)°=(2×12+3)°=27° x (9+1)°=(9×12+1)°=109° x

Word Problem

1. Number of sides in a heptagon = 7

Measure of each exterior angle of a regular polygon = 360°360°==51.43°

7 n

Chapter Checkup

1.a. A polygon with unequal sides and unequal angles equal is called an irregular polygon

b. (6 − 2) ×180°=720°

The sum of the interior angles of a hexagon is 720°.

c. A polygon that has at least one interior angle more than 180° is called a concavepolygon

d. 5(5–3)10==5

22

The number of diagonals in a pentagon is 5

e. The sum of the exterior angles of any polygon is always 360°

2. The number of diagonals in any polygon is given as (–3) 3 nn , where n is the number of sides.

a. A convex quadrilateral has 4 sides. 4(4–3) 4 2 22

b. A triangle has 3 sides. 3(3–3) 0 ==0 22

c. ⇒ 17(17–3) 238 n=17 ==119 22

3.a. Since all the angles in the given polygon are not less than 180°, it is a concave polygon.

b. Since all the angles in the given polygon are less than 180°, it is a convex polygon.

c. Since all the angles in the given polygon are not less than 180°, it is a concave polygon.

d. Since all the angles in the given polygon are less than 180°, it is a convex polygon.

4. The sum of interior angles in a polygon is given as (n − 2) × 180°, where n is the total number of sides in a polygon.

a. Sum of interior angles = (9 −2) ×180°=1260°

b. Sum of interior angles = (13 −2) ×180°=1980°

c. Sum of interior angles = (16 −2) ×180°=2520°

d. Sum of interior angles = (21 −2) ×180°=3420°

e. Sum of interior angles = (33 −2) ×180°=5580°

5. Sum of interior angles = (–2)×180° n

⇒ Sum of interior angles = +2 180° n

a. ⇒ 1800° =+2=12 180° n sides

b. ⇒ 2700° =+2=17 180° n sides

c. ⇒ 3240° =+2=20 180° n sides

d. ⇒ 3780° =+2=23 180° n sides

e. ⇒ 4500° =+2=27 180° n sides

6. Measure of each exterior angle of a regular polygon = 360° n

a. 360° =40° 9

b. 360° =24° 15

c. 360° =18° 20

d. 360° =10° 36

e. 360° =8° 45

7. 360° = Measure of each exterior angle of a regular polygon n

a. 360° ==9 40° n

b. 360° ==8 45° n

c. 360° ==5 72° n

d. 360° ==4 90° n

e. 360° ==3 120° n

8. Adjacent angles of a parallelogram = (5–5) x ° and (10+35)° x Sum of adjacent angles of a parallelogram are supplementary.

(5x − 5)° +(10x + 35)° = 180°

5x − 5° + 10x + 35° = 180°

15x + 30° = 180°

15x = 180° − 30°

15x = 150° 150°

= 15 x

x = 10°

Now, 5x − 5 = 5(10°) −5° =50° − 5° = 45°

And, 10x + 35° = 10(10°) + 35° = 100° + 35° = 135° Required ratio = 45° : 135° = 1 : 3

9. Interior angle sum of a pentagon = (5 − 2) ×180° = 540°

x° + (x − 5)° +(x + 15)° +(3x − 44)° + (x −70)° =540°

7x −104° = 540°

x = 92°

10. Given the ratio of angles of quadrilateral = 1:2:3:4

Let the angles of a quadrilateral be x, 2x, 3x and 4x respectively.

Interior angle sum property = x + 2x + 3x + 4x = 360°

⇒ 360° 10==36° 10 x =36° x

2=2×36=72° x 3=3×36=108° x 4=4×36=144° x

So, 4–=144°–36°=108° xx

11.Given the ratio of angles of hexagon = 1:2:3:4:6:8

Let the angles of a quadrilateral be , 2, 3, 4,6 xxxxx and 8x respectively.

Interior angle sum = (6–2)×180°=720° +2+3+4+6+8=720° xxxxxx

⇒ 24=720° x

⇒ 720° ==30° 24 x =30° x

8=8×30°=240° x

So, the smallest angle = 30°and the greatest angle = 240°.

12.Sum of interior angles = (7–2)×180°=900°

Since three angles = 120°

So, the sum of these three angles = 120°+120°+120°=360°

The sum of remaining four angles = 900°–360=540°

So, the measure of each of these four angles = 540° =135° 4

13.Each exterior angle of a n sided polygon = 50°

So, 360°1 , ==7 505 n

It is not possible to have 1 7 5 sides as it is not a whole number.

14.If the exterior angle = x, the interior angle = 5 × x

The interior and exterior angles of a regular polygon are supplementary.

x + 5x = 6x = 180°

x = 30°

⇒ ==360°360° = 12 30 n n

The polygon has 12 sides.

15.Sum of interior angles 1800(–2) 180 n

⇒ (1800°) =10°=( – 2) 180° n

⇒ n = 12

Diagonals of polygon (–3)12(12–3) 12 × 9 ====54 222 nn

So, total number of diagonals of a polygon is 54.

16 Sum of the interior angles of polygon = (n − 2) ×180° = 4 × 360° = 1440°

⇒ 1440° –2== 180° n 8

⇒ =8+2=10 n

Number of sides in the polygon = 10

So, each interior angle = 1440° =144° 10

And each exterior angle = 180° –144°=36°

17 The least number of sides in a regular polygon = 3; which is an equilateral triangle.

Let each angle of the triangle be x

Sum of all the angles of a triangle = 180°

So, ⇒⇒ 180° + + = 180°3 = 180° = 3 xxxxx

⇒ = 60° x

Thus, the minimum interior angle possible for a regular polygon = 60°

Now, exterior angle = 180° − 60° = 120°

So, the maximum exterior angle possible for a regular polygon is 120°

18 a. Ratio between the exterior angle and the interior angle = 1:2

Let the exterior angle be x and the interior angle will be 2x.

Interior angle + Exterior angle = 180°

2x + x = 180°

3x = 180° ⇒ x = 60°

b. x= 60°

2 = 120° x

c. Sum of interior angles = (n −2) × 180° = n × 120°

n × 180° − 2 × 180° = n ×120°

180°n − 360° = 120°n

180°n −120°n = 360°

60°n = 360°

360° = 60° n

n = 6

So, the number of sides in the polygon = 6 Word Problems

1. Number of diagonals in a regular polygon

= (–3) 2 nn , where n is the number of sides.

If the spider builds its web in the shape of a regular hexagon: 6(6–3) =9 2

There will be 9 diagonals.

If it builds a web with an octagon: 8(8–3) =20 2 There will be 20 diagonals.

2. If all the sides of a polygon as well as all the angles are equal, then the polygon is a regular polygon.

So, Sarika drew a regular polygon.

3. Number of sides of the logo = n = 12

So, the number of diagonals = 12(12–3) =54 2

10 non-overlapping triangles can be formed by connecting these interior angles.

4. A regular football has all its faces as pentagon. Sum of interior angles in a regular pentagon = (5 2) × 180° = 540°

Each interior angle of a regular pentagon = 540° =108° 5

So, the measure of each interior angle of the regular pentagons on the footballs is 108°

5. Let the first angle be x

So, second angle = 2x Third angle = 40°

x + 2x + 40° = 180°

3x + 40° = 180°

3x = 140°

140° = 3 x =46.67° x 2=2×46.67°=93.33° x

So, the three angles are 46.67, 93.33 and 40.

6. Let each of the 10 vertices of the decagon represent 10 towns. As each town is connected to its nearest neighbour, the sides of the decagon represent the bridges. So, there are 10 bridges in total.

Since, each angle in a rectangle is right angle, TJK + MJL = 90°

20°+ MJL = 90°

MJL = 90° − 20° = 70°

Hence, MJL =70° and TJK = 20°.

4. (2y +7)° + 119° = 180° (Interior angles on the same side of the transversal)

2y°+ 126° = 180°

2y° = 180° − 126° = 54°

y = 54°

2 = 27°

(5x −2)° + 133° = 180° (Interior angles on the same side of the transversal)

5x° + 131° = 180°

5x° = 180° − 131°

x = 49° 5 = 9.8°

And, the number of diagonals = 10(10–3) 10(7)70 ===35 222

Chapter 4

Let's Warm Up

Column A

1. Vertices

2. Sides

3. Adjacent Sides

4. Opposite sides

5. Opposite Angles

Do It Yourself

4A

1. Figures may vary. Sample figures.

a.

b.

Column B

PS, QR Q,S

P, Q, R, S PS, SR PS, SR, QR, PQ

P 50°

61°

5. In QPS, Q T R S

SQP = PSQ = 50° (Angles opposite to equal sides)

SQP + PSQ + SPQ = 180° (Angle sum property of the triangle)

50° + 50° + SPQ = 180°

SPQ = 180° − 100° = 80°

QPT = SPQ 2 = 80° 2 = 40° (Longer diagonal bisects the angles)

Hence, QPT = 40°.

In QRS,

SQR = QSR = 61° (Angles opposite to equal sides)

SQR + QSR + SRQ = 180° (Angle sum property of the triangle)

61° + 61° + SRQ = 180°

SRQ = 180° − 122° = 58°

TRS = SRQ 2 = 58° 2 = 29° (Longer diagonal bisects the angles)

Hence, QPT = 40° and TRS = 29°

6. Diagonals of a parallelogram bisect each other. Therefore,

2.a. Concave Quadrilateral

b. Convex Quadrilateral

c. Concave Quadrilateral

3. JTK = MTL = 140° (Vertically opposite angles)

We know that diagonals in a rectangle are equal and bisect each other. Therefore,

TJ = TK

In Δ TJK, TJK = TKJ (Angles opposite to equal sides) Also, TJK + TKJ + JTK = 180° (Angle sum property of the triangle)

TJK + TJK + 140° = 180°

2 TJK = 180° − 140° = 40°

TJK = 40° 2 = 20°

7. Opposite angles in a parallelogram are equal and adjacent angles are supplementary. Therefore, the angles of the parallelogram are 80°, 100°, 80° and 100°.

8. We know that the opposite sides in a parallelogram are equal. Let the breadth of the parallelogram be x. Therefore, the length will be x + 15 cm.

Perimeter = x + (x + 15) + x + (x + 15) = 130 cm

4x + 30 cm = 130 cm

4x = 130 cm − 30 cm = 100 cm

x = 100 4 cm = 25 cm

Breadth = 25 cm, Length = 25 + 15 cm = 40 cm

9. Let the adjacent angles be 2x and 4x. Since, the adjacent angles in a parallelogram are supplementary,

2x + 4x = 180°

6x = 180°

x = 180° 6 = 30°

Therefore,

2x = 2 × 30° = 60°

4x = 4 × 30° = 120°

Therefore, the angles in the parallelogram are 60°, 120°, 60° and 120°.

10. Answermayvary.Sampleanswer.

P Q R

S

Z

a. Four pair of equal line segments are:

PZ & ZR, ZQ & ZS, PQ & PS, RS & QR

b. Four pair of equal angles are:

QPS & QRS, PQR & PSR, QSR & PSQ, PQS & RQS

c. Congruent triangles: QPR SPR, QRS QPS, QZR SZP

d. Yes. Diagonals of a rhombus bisect the angles though which they pass.

e. In QPZ and SPZ,

SZ = ZQ (Diagonals bisect each other)

SP = PQ (Sides of the rhombus)

PZ = PZ (Common arm)

Therefore, QPZ SPZ.

Word Problem

1. Shortest distance through from one corner to the other corner is through the diagonal of the square. Let the length of the diagonal be l.

Using the Pythagoras theorem, l2 = a2 + a2 = 2002 + 2002 = 2× 2002

l = 200 2 m

4B

1. Sum of the interior angles of a quadrilateral is 360°.

a. 47° + 58°+ 98° + 157° = 360°

b. 54°+ 59° + 72° + 108° = 293°

c. 63° + 107° + 74° + 116° = 360°

d. 83° + 68° + 82° + 127°= 360°

Hence, option b is not a set of interior angles of a quadrilateral.

2. Sum of the exterior angles of a quadrilateral is 360°.

a. 57° + 82°+ 98°+ 123° = 360°

b. 58° + 52°+ 77°+ 125° = 312°

c. 65° + 85°+ 85°+ 125° = 360°

d. 49° + 78°+ 103°+ 130° = 360°

Hence, option b is not a set of exterior angles of a quadrilateral.

3. Sum of the interior angles of a quadrilateral is 360°.

a. a° + 71° + 75°+ 100° = 360°

a° + 246° = 360°⇒ a° = 360° − 246° = 114°

b. b° + 20° + 23°+ 93° = 360°

b° + 136° = 360° ⇒ b° = 360° − 136° = 224°

c. c° + 68° + 79°+ 81° = 360°

c° + 228° = 360° ⇒ c° = 360° − 228° = 132°

d. e° + 110° + 22°+ 28° = 360°

e° + 160° = 360° ⇒ e° = 360° − 160° = 200°

e. d° + 54° + 58°+ 138° = 360°

d° +250° = 360° ⇒ d° = 360° − 250° = 110°

f. f ° + 47° + 15°+ 51° = 360°

f ° +113° = 360°⇒ f ° = 360° − 113° = 247°

4. Sum of the exterior angles of a quadrilateral is 360°.

a. x° + 131° + 76° + 46° = 360°

x° + 253° = 360° ⇒ x° = 360° − 253° = 107°

b. y° + 103° + 78° + 103° = 360°

y° + 284° = 360° ⇒ y° = 360° − 284° = 76°

c. z° + 46° + 80° + 111° = 360°

z°+ 237° = 360° ⇒ z° = 360° − 237° = 123°

d. t ° + 51° + 86° + 100° = 360°

t ° + 237° = 360° ⇒ t° = 360° − 237° = 123°

e. u° + 126° + 51° + 53° = 360°

u° + 230° = 360° ⇒ u° = 360° − 230° = 130°

f. u° + 53° + 90° + 111° = 360°

u° + 254° = 360° ⇒ u° = 360° − 254° = 106°

5. a. z° = 94° (corresponding angles)

x° + 83° = 180° (Interior angles on the same side of the transversal)

x° = 180°− 83° = 97°

y° + 68° + 94° = 180° ( Angle sum property of Triangle)

y° = 180°− 162° = 18°

b. 4y° + (3y −30)° = 180° (Interior angles on the same side of the transversal)

7y° −30° = 180°⇒ 7y° = 180°+ 30° = 210°

y° = 210°

7 = 30°

4y° = (2x+10)° (opposite angles are equal in a parallelogram)

4 × 30° = (2x+10)° ⇒ 120° = 2x° + 10°

2x° = 120° − 10°⇒ x° = 110° 2 = 55°

c. z° = 37° (alternate angles)

y° = 27° (alternate angles)

x° + y° + z° = 180° (Angle sum property of triangle)

x° + 27°+ 37° = 180°⇒ x° = 180° − 64° = 116°

6. Since, the adjacent angles in a parallelogram are supplementary,

(3y − 10)° + (2y + 15)° = 180°

5y° + 5° = 180° ⇒ 5y° = 180° − 5° = 175°

y° = 175° 5 = 35°

Angles are

(3y − 10)° = (3 × 35 − 10)° = 95°

(2y + 15)° = (2 × 35 + 15)° = 85°

As the opposite angles in a parallelogram are equal, the angles of the parallelogram are 95°, 85°, 95° and 85°

7. Let the angles in a parallelogram be x and x − 60°. Since, the adjacent angles in a parallelogram are supplementary,

x + x − 60° = 180°

2x − 60° = 180°

2x = 180° + 60° = 240°

x = 240°

2 = 120°

other adjacent angle = x − 60° = 120° − 60° = 60°

As the opposite angles in a parallelogram are equal, the angles of the parallelogram are 120°, 60°, 120° and 60°.

8. Let the angle be x. Since opposite angles are equal,

x + x = 2x = 150°

x = 150°

2 = 75°

Adjacent angle = 180° − 75° = 105°

The angles of the parallelogram are 105°, 75°, 105° and 75°.

9. (7x − 3)° + (3x + 4)° + (2x + 10)° + (5x + 9)° = 360° (Angle sum property of quadrilaterals)

17x° + 20° = 360°

17x° = 360° − 20° = 340°

x = 340°

17 = 20°

Therefore, the angles of the quadrilateral are

(7x − 3)° = (7 × 20 − 3)° = 137°

(3x + 4)° = (3 × 20 + 4)° = 64°

(2x + 10)° = (2 × 20 + 10)° = 50°

(5x + 9)° = (5 × 20 + 9)° = 109°

10. Since, the adjacent angles are supplementary,

z° + 73° = 180°

z

° = 180° − 73° = 107°

BCD = z° = 107°

BCD + y° + 45° = 180° (Angle sum property of triangle)

107° + y° + 45° = 180°

° = 180° − 152° = 28°

y

x° = 45° (Alternate angles)

Word Problem

1. Let the angles of the quadrilateral be x, 2x, 3x, and 4x.

x + 2x + 3x + 4x = 360°

10x = 360°

x = 360°

10 = 36°

2x = 2 × 36° = 72°

3x = 3 × 36° = 108°

4x = 4 × 36° = 144°

Therefore, the angles of the quadrilateral are 36°, 72°, 108° and 144°.

Since, all the angles are less than 180°, it’s a convex quadrilateral.

Chapter Checkup

1.a. The diagonals of a kite bisect each other at right angles. True

b. The diagonals of an isosceles trapezium are equal. True

c. The opposite angles of a trapezium may be equal. False

d. The diagonals of a rectangle are perpendicular to each other. False

e. All the quadrilaterals are parallelograms. False

2. Interior angles in a convex quadrilateral are less than 180°. Hence, 222° can’t be an interior angle in a convex quadrilateral.

3. Interior points: P, Q, R; Exterior points: S, T, U

4. Sum of the interior angles of a quadrilateral is 360°.

a. 47°+ 58°+ 98° + 156° = 359°

b. 54°+ 59°+ 72°+ 108°= 293°

c. 63°+ 100°+ 74°+ 116° = 353°

d. 83°+ 68°+ 82°+ 127° = 360°

Hence, option d is a set of interior angle of a quadrilateral.

5. Sum of the exterior angles of a quadrilateral is 360°.

a. 57°+ 82°+ 98°+ 120° = 357°

b. 53° + 69° + 77° + 111° = 310°

c. 65° + 85° + 85° + 125° = 360°

d. 49° + 75° + 103° + 130° = 357°

Hence, option c is correct.

6. Each interior angle has a corresponding exterior angle and both of them are supplementary.

a. Supplement of 70° = 180° − 70° = 110°

Supplement of 90° = 180° − 90° = 90°

Supplement of 110°= 180° − 110° = 70°

Supplement of 90° = 180° − 90° = 90°

b. Supplement of 45° = 180° − 45° = 135°

Supplement of 60° = 180° − 60° = 120°

Supplement of 100°= 180° − 100° = 80°

Supplement of 155° = 180° − 155° = 25°

c. Supplement of 80° = 180° − 80° = 100°

Supplement of 85° = 180° − 85° = 95°

Supplement of 95° = 180° − 95° = 85°

Supplement of 100° = 180° − 100° = 80°

7. Sum of the interior angles of a quadrilateral is 360°.

a. l° + 58° + 21° + 41° = 360°

l° + 120° = 360° ⇒ l° = 360° − 120° = 240°

b. m° + 88°+ 64°+ 58° = 360°

m° + 210° = 360° ⇒ m° = 360° − 210° = 150°

c. n° + 97° + 66°+ 74° = 360°

n° + 237° = 360° ⇒ n° = 360° − 237° = 123°

8. Sum of the exterior angles of a quadrilateral is 360°.

a. p° + 48° + 92°+ 117° = 360°

p° + 257° = 360°⇒ p° = 360° − 257° = 103°

b. q° + 89°+ 93° + 51° = 360°

q° + 233° = 360°⇒ q° = 360° − 233° = 127°

c. r° + 90°+ 67° + 93° = 360°

r° + 250° = 360° ⇒ r° = 360° − 250° = 110°

9. Since, the adjacent angles of a parallelogram are supplementary,

(2z − 25)° + (3z + 10)° = 180°

5z° −15° = 180°

5z° = 180° + 15° = 195°

z = 195°

5 = 39°

Therefore, the adjacent angles are

(2z − 25)° = (2 × 39 − 25)° = 53°

(3z + 10)° = (3 × 39 + 10)° = 127°

Hence, the angles of the parallelogram are 53°, 127°, 53° and 127°.

10. We know that opposite sides in a parallelogram are equal. Let the breadth of the parallelogram be x. Therefore, the length will be x + 20 cm.

Perimeter = x + (x + 20) + x + (x + 20) = 140 cm

4x + 40 cm = 140 cm

4x = 140 cm − 40 cm = 100 cm

x = 100 4 cm = 25 cm

Breadth = 25 cm,

Length = 25 + 20 cm = 45 cm

11. Opposite angles in a parallelogram are equal and adjacent angles are supplementary. Therefore, the angles of the parallelogram are 140°, 40°, 140° and 40°.

12. Let the adjacent angles be 2x and 3x. Since adjacent angles in a parallelogram are supplementary, 2x + 3x = 180°

5x = 180°

x = 180°

5 = 36°

Therefore,

2x = 2 × 36° = 72°

3x = 3 × 36°= 108°

Hence, the angles in the parallelogram are 72°, 108°, 72° and 108°.

13. Q P R S 60°

60° 60° 60° 60°

60°

Consider the rhombus PQRS, where the diagonal PR is equal to the sides of the rhombus.

PSR and PQR are equilateral triangles.

Thus, all the angles in these two triangles are equal to 60°.

Therefore, the angles of the rhombus are 60°, 120°, 60° and 120°.

14. a. x° = 125° (Vertically opposite angles)

w° = 50° (alternate angles)

z° + 135° = 180° (Linear pair)

z° = 180° − 135° = 45°

x° + y ° + z° = 180° (Angle sum property of triangle)

125° + y° + 45° = 180°

y

° = 180° − (125° + 45°) = 10°

b. 3x° + 135° = 180° (interior angles on the same side of the transversal)

3x° = 180° − 135° = 45°

x° = 45° 3 = 15°

5y° + 125° = 180° (interior angles on the same side of the transversal)

5y° = 180° − 125° = 55°

y° = 55° 5 = 11°

c. x° + 79° = 180° (interior angles on the same side of the transversal)

x° = 180°− 79° = 101°

6y + 4° + 3y + 5° = 180° (interior angles on the same side of the transversal)

9y + 9° = 180°

9y = 171°

y = 171° 9 = 19°

15. Q P R S

Consider rhombus PQRS with diagonals PR and QS. In PSR and PQR, PS = PQ (sides of rhombus)

RS = RQ (sides of rhombus)

PR = PR (common arm)

PSR PQR (SSS criterion)

Hence, SPR = QPR (c.p.c.t) & QRP = QRS (c.p.c.t)

Similarly, in PQS and RQS, RQS = PQS & RSQ = PSQ

Hence, the diagonals of a rhombus bisect its angles.

16. Since, the diagonals bisect the angles in rhombus, RSQ = PSQ= 52°

PSR = 2 PSQ= 2 × 52° = 104°

PSR = PQR = 104° (opposite angles are equal in parallelogram)

PSR + QPS = 180°

104° + QPS = 180° (Adjacent angles are supplementary)

QPS = 180° − 104° = 76°

QPS = QRS = 76°

Word Problems

1. Let the angles be 2x, 3x, 4x and 5x

2x + 3x + 4x + 5x = 360°

14x = 360°

x = 360° 14 = 25.71°

Angles are

2x = 2 × 25.71° = 51.42°

3x = 3 × 25.71° = 77.13°

4x = 4 × 25.71° = 102.84°

5x = 5 × 25.71° = 128.55°

Since, all the angles are different, we can conclude that climbing structure is not a parallelogram.

2. In a parallelogram, opposite sides are equal so the length of opposite side is 24 m.

In a parallelogram, the opposite angles are equal and the adjacent angles are supplementary, so the angles are 120°, 60°, 120° and 60°.

Chapter 5

Let's Warm-up

1. Exactly two pairs of adjacent sides are equal. Kite

2. Exactly one pair of opposite sides are parallel. Trapezium

3. All angles in a quadrilateral are right angles, but only the opposite sides are equal. Rectangle

4. All sides are equal, but all angles may not necessarily be equal. Rhombus

Do It Yourself

5A

3. a. DB = 7.1 cm, AC = 8.5 cm  b. ZX = 9.7 cm, WY = 9.6 cm

4. a. 4.9 cm D

Word Problem

1. 4 cm 4 cm 4 cm 4 cm A

B D

C 104° 112°

Word Problem C Chapter Checkup 1.a. 4.5cm 5.1 cm 7.2 cm 3.9 cm

6.8 cm

X U V

V U S T c. 5.8 cm 7.4cm 3.5 cm 6.1 cm

4.2 cm

W

b. 6.2 cm 7.3 cm 8.9cm 5.7 cm 4.5 cm

M N K L 2.a. EP = 2.8 cm        b. NI = 3.7 cm 5.5 cm 4.7cm 7.6cm 6.9 cm

3.2cm N I P

E 6.8cm 4.7cm 3.2cm 5 cm 7.4 cm

E N 3. a. GE = 4.3 cm, FH = 5.4 cm  b. KI = 8.4 cm, JL = 7 cm 45° 60° 120° 6 cm

E P I N  c. NE = 6.7 cm 8.3cm 3.9 cm 6.5 cm

4.2 cm 7.1cm I P

5 cm H E F

115°

G I J

K L 7 cm 4.9 cm 70° 90°

cm 6 cm

10. We can construct only one trapezium with the given measures.

Word Problem

1. Diagonals of a rhombus bisect each other. We can use this property to construct the rhombus using ruler and compass.

Chapter 6

Let's Warm-up

Ascending order:

20, 20, 20, 20, 20, 20, 20, 25, 25, 25, 25, 25, 25, 25, 25, 25, 30, 30, 30, 30, 30, 30, 30, 30, 30, 35, 35, 35, 35, 35

Do It Yourself

6A

1.

of students = 50

who like cricket

of50=×50=20

Tennis is liked by the minimum number of students.

2.a. Highest monthly income is ₹85 thousands. 14 individuals have the highest monthly income.

b. Lowest monthly income is ₹25 thousands. 14 individuals have the lowest monthly income.

c. Range = Maximum value of the data − Minimum value of the data = 85,000 − 25,000 = 60,000

3. Ascending order:

5. Ascending order:

4.

1. a. The smaller value of a class interval is called the lowerclass limit. So, the lower-class limit of 50-60 is 50.

b. The class mark is the midpoint of each class interval.

40+50 90 ==45 22 and 50+60 110 ==55 22

c. The difference between the upper limit and the lower limit of a class interval is called the class size.

30 − 4040 − 30 = 10

40 − 5050 − 40 = 10

50 − 6060 − 50 = 10

60 − 7070 − 60 = 10

70 − 8080 − 70 = 10

So, class size = 10

2.a. 37, 39, 44, 48, 48, 50, 52, 53, 55, 56, 58, 58, 59, 60, 60, 60, 61, 62, 64, 67, 68, 70, 75, 77, 78, 84, 88, 90, 98, 100

4. a. Number of individuals that have 2 or 3 siblings = 10

b. Total number of individuals with 4 or 5 siblings = 6

c. Percentage of individuals with 0-1 siblings = 10/26 × 100 = 38.46%

d. Range = 9 − 0 = 9

5. a. Number of students that scored marks less than or equal to 15 = 7+6+7=20

b. Number of students that scored more than or equal to 15 marks = 8

c. Class mark of the class interval with frequency 6 = 5+10 15 ==7.5 22

d. Number of students who wrote the test = 7+6+7+8=28

e. Percentage of students that scored less than 15 marks

Number of students that scored less than 15 marks

= Total number of students 7+6+7 20 =×100=×100=71.41% 7+6+7+828

Word Problems

1. Ascending order:

0, 1, 2, 3, 5, 6, 7, 7, 8, 9, 10, 10, 12, 13, 13, 13, 15, 16, 18, 20, 21, 21, 23, 23, 23, 24, 24

Frequency (Number

students)

b. The highest observation is 100.

c. The lowest observation is 37.

d. Range = 109 − 30 = 79

e. 8 observations are 75 and more.

f. 5 observations are less than 50.

3. Ascending order:

3, 5, 7, 9, 10, 12, 13, 15, 17, 18, 19, 19, 20, 23, 24, 27, 29, 34, 34, 38, 39, 40, 40, 42, 47

(Weight in kg)

− 18 = 2

Frequency (Number of students) Tally

iii. 8 + 0 + 8 = 16 students.

iv. 27 + 29 2 = 28

3.

ObservationsFrequencyTally Marks

4. Ascending order:

12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 15, 15, 16, 16, 17

AgesFrequencyTally Marks

12 4

13 12

14 9

15 2

16 2

17 1

5.a. Blood group AB has the highest frequency of 15. So, AB has the most donors.

b. Number of people that participated in the blood donation campaign = 14 + 10 + 15 + 9 = 48

6. Class interval Class limit

Word Problems

1.a. 3 crores + 2 crores = 5 crores

b. Maharashtra and Uttarakhand are the most populated states.

c. Nagaland is the least populated state.

2. Ascending order:

0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 4

The

by a household is 4.

3. Ascending order:

Converting this data again into the exclusive form.

c. Number of books sold on Thursday: Number of books sold on Friday = 970:670 = 97:67

d. Average of books sold per day = 5100 850 6

Required Ratio = (800 + 700 + 670) : (870 + 970 + 1090) = 2170:2930 = 217:293

3.a. Foreign exchange reserve in 2013 = $3500 million

b. Foreign exchange reserve in 2011 = $2500 million

Foreign exchange reserve in 2012 = $3100 million

Difference in the foreign exchange reserve for 2011 and 2012

= $3100 million − $2500 million = $600 million

c. Foreign exchange reserve in 2013 = $3500 million

Foreign exchange reserve in 2012 = $3100 million

Increase in foreign reserve = $3500 million − $3100 million = $400 million

Percentage increase = $400 million $3100 million × 100% = 12.9%

d. Sum of foreign exchange reserves in 2010 and 2011

= $2800 million + $2500 million = $5300 million

Sum of foreign exchange reserves in 2012 and 2013

=$3100 million + $3500 million = $6600 million

Required ratio = $5300 million: $6600 million = 53:66 4.

Chapter 7

Let's Warm-up

1. Investor A made an investment of ₹4000.

2. The investment made by D is ₹6000.

3. The highest investment is made by C.

4. The difference between the investments of B and C is ₹2000.

5. The total investment made by all the investors is ₹24,000.

Do It Yourself

7A

1. Total wheat exported = 96,000 + 87,000 + 56,000 + 55,000 + 63,000 = 357,000 tonnes

a. Wheat exported to Sri Lanka = 96,000 tonnes

Percentage of wheat exported to Sri Lanka = 96,000 3,57,000 × 100% = 26.89%

b. Wheat exported to Afghanistan = 55,000 tonnes

Percentage of wheat exported to Afghanistan = 55,000 3,57,000 × 100% = 15.4%

c. Wheat exported to Qatar = 63,000 tonnes

Wheat exported to the Yemen Republic = 87,000 tonnes

Wheat exported to Qatar: Wheat exported to the Yemen Republic = 63,000 tonnes: 87,000 tonnes = 63:87

d. Average wheat exported = Total wheatexported No. of nations 357000 5 = 71,400 tonnes of wheat

2. Total number of books sold = 800 + 700 + 870 + 970 + 670 + 1090 = 5100

a. Number of books sold on Friday = 670

Required percentage = 670 5100 × 100% = 13.14%

b. Number of books sold on Saturday = 1090

Required percentage = 1090 5100 × 100% = 21.37%

a. Total export in all years = 15.6 + 14.8 + 16.7 + 17.0 + 19.4 + 19.8 = 103.3 crores

b. Average export in all years = 103.3 17.217 6 crores

c. Export of pears in 2015 = 15.6 crores

Export of pears in 2018 = 17.0 crores

Increase in export = 17.0 − 15.6 crores = 1.4 crores

Percentage increase = 1.4 15.6 × 100% = 8.97%

d. Exports in 2016 = 14.8 crores

Exports in 2019 = 19.4 crores

Average exports in 2016 and 2019 = 14.8+19.4 2 crores = 17.1 crores

So, 2016 and 2019 had an average export of 17.1 crores.

5. Total number of students in School = 450

a. Total number of students who passed in 2021 = 400

b. Total number of students who passed in 2018 = 300

Percentage of students who passed in 2018

= 300 ×100%=66.67% 450

c. Total number of students who passed in 2020 = 350

Percentage of students who passed in 2020

= 350 ×100%=77.78% 450

d. Total number of students who passed in 2019 = 350

Total number of students who passed in 2022 = 400

Increase in number of students = 400 − 350 = 50

%percentage increase = 50 ×100%=14.28% 350

Word Problem

1.a. Total population of Delhi and Mumbai = 28 + 20 million = 48 million

b. Difference between the population of Shanghai and Cairo = 25 million − 20 million = 5 million

c. Total population of all the cities = 28 + 25 + 18 + 20 +20 +12 = 123 million

Average population = 123 6 million = 20.5 million

d. Difference between the population of Moscow and New York = 18 − 12 = 6 million

7B

1. a. Basmati export in 2021 = $1660 million

Basmati export in 2022 = $2280 million

Percentage increase in exports = 2280–1660 ×100%=37.34% 1660

b. Fruit have the least exports

c. Total exports for the year 2021 (in million $) = 301 + 1632 + 1903 + 1660 + 2969 + 2591 = $11,056 million

d. Total exports for the year 2022 = 313 + 2111 + 2099 + 2280 + 3207 + 3761 = $13,771 million

2. a. Total tea production by Company C in three years = 80 +70 + 60 = 210 tonnes

b. Total tea production by Company B in 2015 and 2016 = 70 + 70 = 140 tonnes

Total tea production by Company D in three years = 50 + 40 + 50 = 140 tonnes

Required ratio = 140 tonnes : 140 tonnes = 1:1

c. Production by Company D in 2016 = 50 tonnes

Production by Company D in 2017 = 40 tonnes

Percentage increase in production by Company D from 2016 to 2017

= 50–40 ×100%=25% 40

d. Production by Company B in 2015 = 70 tonnes

Production by Company B in 2017 = 90 tonnes

Percentage increase in production by Company B from 2015 to 2017

= 90–70 ×100%=28.57% 70

a. People visiting Qutub Minar in 2018 = 700 People visiting Qutub Minar in 2019 = 760

Percentage increase = 760–700 ×100%=8.57% 700

b. Total number of people who visited India Gate in both years = 600 +700 = 1300

c. Total number of people who visited Lotus Temple in both years

= 500 + 500 = 1000

Total number of people who visited Taj Mahal in both years = 900 +1000 = 1900

Required ratio = 1000:1900 = 10:19

d. Percentage increase in visitors at Qutub Minar

= 760–700 ×100%=8.57%

700

Percentage increase in visitors at Taj Mahal

= 1000–900 ×100%=11.11%

900

Percentage increase in visitors at India Gate

= 700–600 ×100%=16.67%

600

Percentage increase in visitors at Lotus Temple

= 500–500 ×100%=0%

500

India Gate has the highest percentage increase in the number of visitors.

4. a. Total number of fruit sold by vendor A = 60 + 80 + 100 + 40 +20 = 300

b. Total number of fruit sold by vendor B = 80 + 70 + 90 + 60 + 40 = 340

c. Oranges and apples sold by vendor A = 60 + 80 = 140

Banana, pear and melon sold by vendor A = 100 + 40 + 20 = 160

Required ratio = 140:160 = 7:8

d. Banana was the most sold fruit out of all fruit by the two vendors.

5. a. Number of movie tickets sold for a comedy genre by both theatres

= 180 + 200 = 380

b. Total tickets sold by Cinema Hall 1

= 80 + 180 + 160 + 180 + 160 = 760

c. Total tickets sold by Cinema Hall 2 = 100 + 160 + 160 + 200 + 100 = 720

d. Sci-fi tickets sold by Cinema Hall 1 = 180 Sci-fi tickets sold by Cinema Hall 2 = 160

Required percentage = 160 ×100%=88.89% 180

Word Problem

1.a. Total runs scored by Virat Kohli = 1320 + 1000 + 680 + 760 + 1520 + 1400 + 1360 = 8040

b. Total runs scored by Rohit Sharma = 1200 + 480 + 800 + 500 +1280 + 1140 + 1540 = 6940

c. Average runs scored by Virat = 8040 7 = 1148.57

Average runs scored by Rohit Sharma = 6940 7 = 991.43

Difference of average runs scored = 157. 14

Taj mahal Indian Gate Lotus

d. Runs scored by Virat Kohli before 2017 = 1320 + 1000 + 680 + 760 = 3760

Runs scored by Rohit Sharma after 2015 = 500 +1280 + 1140 + 1540 = 4460

Required ratio = 3760:4460 = 188:223

7C

1.

a. Total number of people surveyed = 50 + 90 + 75 + 60 + 50 + 40 = 365

b. Number of people who exercised for more than 30 mins = 90 + 75 + 60 + 50 + 40 = 315

Required percentage = 315 ×100%=86.30% 365

c. Number of people who exercised for less than 120 mins = 50 + 90 + 75 + 60 = 275

Required percentage = 275 ×100%=75.34% 365

d. Number of people who exercised for less than 90 mins = 50 + 90 + 75 = 215

Number of people who exercised for more than 120 mins = 50 + 40 = 90

Required ratio = 215:90 = 43:18

2.

a. Number of workers earning more than ₹300 = 100 + 150 + 180 +120 = 550

b. Number of workers earning less than ₹500 = 50 + 80 + 100 + 150 = 380

c. Total number of workers = 50 + 80 + 100 + 150 + 180 + 120 = 680

Number of workers earning less than ₹600 = 50 + 80 + 100 + 150 + 180 = 560

Required percentage = 560 ×100%=82.35% 680

d. Number of workers earning less than ₹400 = 50 + 80 + 100 = 230

Number of workers earning more than ₹400 = 150 + 180 +120 =450

Required Ratio = 230:450 = 23:45

e. Number of workers making between ₹400 − ₹600 = 150 + 180 = 330

3.a. Number of students who scored more than 40 marks = 9 + 6 + 7 + 7 + 8 + 7 = 44

Total number of students = 5 + 5 + 9 + 6 + 7 + 7 + 8 + 7 = 54

Required percentage = 44 ×100%=81.48% 54

b. Number of students who scored less than 30 marks = 5

Required percentage = 5 ×100%= 54 = 9.25%

c. Number of students who scored more than 50 marks = 6 + 7 + 7 + 8 + 7 = 35

Number of students who scored less than 50 marks = 5 + 5 + 9 = 19

Required Ratio = 35:19

d. Number of students who scored more than 40 marks = 9 + 6 + 7 + 7 + 8 + 7 = 44

Number of students who scored less than 40 marks = 5 + 5 = 10

Required Difference = 44 − 10 = 34

4. a. Number of employees older than 50 years = 5 + 5 = 10

b. Number of employees younger than 35 years = 30 + 45 + 40 = 115

Number of employees older than 35 years = 30 + 20 + 20 + 5 + 5 = 80

Required Ratio = 115:80 = 23:16

c. Number of employees older than 25 years = 45 + 40 + 30

+ 20 + 20 + 5 + 5 = 165

Total number of employees = 30 + 45 + 40 + 30 + 20 + 20 +

5 + 5 = 195

Required percentage = 165 ×100%=84.6% 195

d. Total number of employees = 30 + 45 + 40 + 30 + 20 + 20 + 5 + 5 = 195

Scale: 1 division = 100 mm

a. Total rainfall over the years = 700 + 600 + 550 + 650 + 800 = 3300 mm

b. Highest rainfall occurred in 2016-2017.

c. Rainfall during 2014-2015 = 550 mm

Rainfall during 2013-2014 = 600 mm

Percentage decrease in rainfall = 600 mm–550 mm ×100%=8.33% 600 mm

d. On observing the graph, the highest difference in rain can be seen in the years 2015-2016 and 2016-2017. Hence the highest percentage difference in rainfall over previous year will be in the year 2015-2016 and 2016-2017.

Word Problem 1.

a. Number of presidents aged more than 66 at the time of inauguration = 3 + 1 = 4

b. Number of presidents aged more than 60 at the time of inauguration = 8 + 3 + 1 = 12

c. Number of presidents aged more than 54 at the time of inauguration = 17 + 8 + 3 + 1 = 29

Chapter Checkup

1.a. Units of Product A sold = 20% of 5,20,000 = 20 ×5,20,000=1,04,000 100

b. Units of Product C sold = 16 % of 5,20,000 = 16 ×5,20,000=83,200 100

c. Units of Product B sold = 12% of 5,20,000 = 16 ×5,20,000=62,400 100

Units of Product D sold

= 28% of 5,20,000 = 28 ×5,20,000=1,45,600 100

Units of Product D − Units of Product B

= 1,45,600 − 62,400 = 83,200

d. Units of Product A : Units of Product C

= 104000 : 83200 = 5:4

2.a. Number of students passing from college B = 360

b. If the pass percentage of college A is the same as the pass percentage of college E, then the ratio of the pass percentage of college A and the pass percentage of college E to the total number of students in college A and the total number of students in college E is the same. Percentage of the total strength of E that is greater than the total strength of A

= 400–320 80 ×100%=×100%=25% 320 320

c. Let the number of students in college B be x 90% of x = 360

x = 360 ×100=400 90

Total number of students who failed

= 400 − 360 = 40

d. Total number of students who passed from all the colleges

= 320 + 360 + 280 + 360 + 400 = 1720

Let the number of students who failed be x 1720 : x = 43 : 9

x = 1720 ×9 =360 43

3.a. Total students who attended the workshop = 160 + 140 + 160 + 120 + 180 = 760

b. Number of students who attended the workshop on Monday = 160

Percentage = 160 ×100%=21.05% 760

c. Number of students who attended the workshop on Monday = 160

Number of students who attended the workshop on Wednesday = 160

Required ratio = 160 : 160 = 1:1

d. Number of students who attended the workshop on Tuesday = 140

Number of students who attended the workshop on Friday = 180

Percentage = 140 ×100%=77.78% 180

5.a. Cars sold by Dealer A = 600 + 500 + 800 + 800+ 700 = 3400

b. Cars sold by Dealer B = 700 + 600 + 700 + 900 + 700 = 3600

c. Number of cars sold in 2019 = 500 + 600 = 1100

Number of cars sold in 2022 = 700 +700 = 1400

Required Ratio = 1100:1400 = 11:14

d. Cars sold by Dealer A in 2018 = 600

Total cars sold by Dealer A = 600 + 500 + 800 + 800 + 700 = 3400

Percentage = 600 ×100%=17.65% 3400

6.a. Total sale of C2 for both years = 100,000 + 80,000 = 180,000 biscuits

Total sale of C4 for both years = 90,000 + 80,000 = 170,000 biscuits

Required percentage = 170,000 ×100%=94.44 % 180,000

b. Total sales of all companies in 2019 = 90,000 + 80,000 + 70,000 + 90,000 + 80,000 = 410,000

Average sale of all companies in 2019

= 410,000 82,000 5 packets of biscuits

c. Average sales of C1, C2, and C3 in 2019

= 90,00080,00070,000 80,000 3 biscuits

Average sales of C3, C4, and C5 in 2020

= 80,00080,00070,000 76,666.67 3 biscuits

Required percentage = 76666.67 ×100%= 95.83% 80000

d. Total sales of all companies in 2020 = 100,000 + 100,000 + 70,000 + 80,000 + 80,000 = 430,000

Average sale of all companies in 2020

= 430,000 =86,000 5 packet of biscuits

7.a. Total candidates appearing in 2021 = 30 + 25 + 25 + 26 + 31 + 25 = 1,62,000

b. Total candidates appearing in 2022 = 31 + 30 + 29 + 30 + 34 + 29 = 1,83,000

c. Number of candidates appearing for test in Mumbai in 2021 = 30,000

Number of candidates appearing for test in Bangalore in 2021 = 26,000

Required ratio = 30,000:26,000 = 15:13

d. Average number of candidates appearing in each city in 2021

= 1,62,000 =27,000 6

e. Number of candidates appearing for the test in Delhi in 2021 = 25,000

Number of candidates appearing for the test in Bhopal in 2021 = 25,000

Required percentage = 25,000 ×100%=100% 25,000

9.a. Number of students taller than 140 cm

= 20 + 25 + 21 + 15 + 15 + 10 = 106 students

b. Number of students shorter than 165 cm

= 30 + 25 + 30 + 35 + 20 + 25+ 21 + 15 + 15 = 216 students

c. Number of students shorter than 150 cm

= 30 + 25 + 30 + 35 + 20 + 25 = 165 students

Number of students taller than 150 cm

= 21 + 15 + 15 + 10 = 61 students

Required ratio = 165:61

d. Number of students taller than 155 cm = 15 + 15 + 10 = 40 students

10.a. Total cars = 40 + 58 + 117 + 120 + 100 + 80 = 515

b. Cars on the road after 9 a.m. = 120 + 100 + 80 = 300

c. Cars on the road before 11 a.m. = 40 + 58 + 117 + 120 + 100 = 435

d. Cars on the road between 6 a.m. - 9 a.m. = 40 + 58 + 117 = 215

Cars on the road after 10 a.m. = 100 + 80 = 180

Required ratio = 215:180 = 43:36

Word Problems

1.a. Number of players with an average of less than 30 = 20 + 15 +30 + 30 = 95

b. Number of players with an average of more than 20 = 30 + 30 + 45+ 27 + 40 + 15 = 187

c. Total number of players = 20 + 15 +30 + 30 + 45+ 27 + 40 + 15 = 222

Number of players with an average of less than 40 = 20 + 15 +30 + 30 + 45+ 27 = 167

Required percentage = 167 ×100%=75.22% 222

d. Total number of players = 222

e. Number of players with an average of more than 25 = 30 + 45+ 27 + 40 + 15 = 157

Required percentage = 157 ×100%=70.72% 222

f. Number of players with an average of more than 25 = 157

Number of players with an average of less than 25 = 20 + 15 + 30 = 65

Required ratio = 157:65

2.

a. Total number of goals scored by Messi = 8 + 17 + 16 + 38 + 47 + 53 + 73 + 60 + 41 = 353

Total number of goals scored by Ronaldo = 12 + 23 + 42 + 26 + 33 + 53 + 60 + 55 + 51 = 355

b. Ronaldo scored more goals over the years

c. Number of goals scored by Messi before 2010 = 8 + 17 + 16 +38 + 47 = 126

Number of goals scored by Ronaldo after 2007 = 42 + 26 + 33 + 53+ 60 + 55+51 = 320

Required Ratio = 126:320 = 63:160

Chapter 8

Let's Warm-up

1. The fraction of students who like yellow colour is 3 20

2. The most liked colour is blue.

3. The fraction of students who do not like red colour is 3 4

4. The least liked colour is lavender.

5. The difference in the fraction of students who like pink colour to the ones who like blue colour is 1 5 .

Do It Yourself

8A

1. Central angle

= People who know more than three languages

Total no.of people × 360°

= 375 1200 × 360° = 112.5°

2. Central angle = 45 100 × 360° = 162°

The central angle representing 45% of people liking biryani is 162°.

3. The pie chart for the table can be given as:

StatesNo. of workersCentral angle

Karnataka440 440 1800 × 360° = 88°

Tamil Nadu620 620 1800 × 360° = 124°

Andhra Pradesh 340 340 1800 × 360° = 68°

Kerala 300 300 1800 × 360° = 60°

Others 100 100 1800 × 360° = 20°

No. of workers from various states working in a garment factory

Andhra Pradesh, 340 124°

Tamil Nadu, 620

Kerala, 300

Others, 100

68° 60° 20° 88° Karnataka, 440

4. The pie chart for the table can be given as:

Item Import (in billions) Central angle Fuels

× 360° = 96°

Plastics,

Import Items

Furniture,

Fuels

5. The pie chart for the table can be given as:

Smartphones brand Sales in numberCentral angle Brand

Word Problem

1. The pie chart for the table can be given as:

6. The pie chart for the table can be given as:

1. Students admitted to Education = 8 ×5,00,000= 100 40,000

Students admitted to Arts = 20 ×5,00,000= 100 1,00,000

Students admitted to Law = 14 ×5,00,000= 100 70,000

Students admitted to Commerce

= 33 ×5,00,000= 100 1,65,000

Students admitted to Science = 25 ×5,00,000= 100 1,25,000

2.a. Shared Cab

b. Central angle associated with bus = 45°

Fraction of people preferring the bus = 45 1251 0.125

360 10008

c. Since a quarter of 360° is 90°, shared cab is preferred by a quarter of the people.

3.a. Given that, the number of type C cars sold were 500, that is 25%.

Therefore, the total number of cars sold = 500 ×100 25 = 2000.

b. Percentage of type D cars = 18

Number of type D cars = 18 ×2000=360. 100

c. Percentage of Type A and Type B cars together = 35 + 22 = 57

Number of type A and type B cars together = 57 ×2000=1140

100

4. Total students = 2500

a. Central angle associated with orange juice = 86.4°

Number of students who like orange juice = 86.4° ×2500=600 360°

b. Apple juice is the least popular juice.

Number of students who like it = 36° ×2500=250 360°

c. Central angle for students not liking apple juice = (360° − 36°) = 324°

Fraction = 324°9 =0.9= 360°10

5.a. Given that, the number of elephants = 11% = 77

Total number of animals in the zoo = 77×100 =700 11

b. Tigers are the lowest in number.

Number of tigers = 5 ×700=35 100

c. The difference in the percent of deer and reptiles = (28% − 25%) = 3%

Difference in number = 3 ×700=21 100

6.Total plants = 1200

a. Number of sunflower plants = 82.5° ×1200=275 360°

Number of tulip plants = 60° ×1200=200 360°

Difference between number of sunflower plants and tulip plants = 75.

b. Central angle for rose plants sown = 112.5°

Faction = 112.5° =0.3125==31255

360° 10,00016

c. Number of marigold plants = 67.5° ×1200=225 360°

Number of jasmine plants = 37.5° ×1200=125 360°

Ratio of marigold to jasmine = 225:125 = 9:5

7. Given that, the number of girls who like basketball = 648. Let the total number of girls = x

According to question, 360° x=648×=1800 129.6°

a. Number of girls interested in volleyball = 45° ×1800=225

360°

Percentage of girls interested in volleyball = 225 ×100%=12.5%

1800

b. Number of girls who like swimming = 59.4° ×1800=297

360°

Number of girls who like cricket = 72° ×1800= 360 360°

Ratio of the girls who like swimming to cricket = 297:360 = 33:40

c. Number of girls liking tennis = 54° ×1800=270 360°

Number of girls liking basketball = 648

Fraction of girls like tennis and basketball = 270 + 64891851 == 18001800100

Word Problem

1. Given that, teenagers who like classical music = 17% = 255

a. Number of teenagers surveyed = 100 255×=1500 17

b. Number of teenagers who like rock music = 30 30%= 100

Number of teenagers who like hip hop = 34 34%= 100

Ratio of teenagers liking rock music to hip hop

= 3034:=30:34= 100100 15:17

Chapter Checkup

1. Given that, percentage of people preferring fresh juice = 23 Let the total number of people = 100

Number of people preferring fresh juice = 23 ×100=23 100

Let the central angle be x; 23=×100 360° x 23×360 100 x x = 82.8°

2.a. Total items sold = 80

The table for the pie chart can be given as:

ItemsNo. of Items soldCentral angle

Rice 35 35 ×360°=157.5° 80

Pulses 15 15 ×360°= 80 67.5°

Bread 12 12 ×360°=54° 80

Spices 10 10 ×360°= 80 45°

Others 8 36° 8 ×360°= 80

Items Sold

Spices, 10

Others, 8 Rice, 35

Bread, 12

Pulses, 15

b. Total items sold = 300

The table for the pie chart can be given as:

ItemsNo. of Items soldCentral angle

Shakes 75 75 ×360°=90° 300

Sandwiches66 66 ×360°=79.2° 300

Burgers 60

60 ×360°=72° 300

French fries45 45 ×360°=54° 300

Ice creams54

54 ×360°=64.8° 300

3. Total number of families = 80

The pie chart for the table can be given as:

PetNo. of familiesCentral angle

4. Total number of students = 1800

The pie chart for the table can be given as: SubjectNo. of StudentsCentral angle

5. Total number of people in the town = 2400

The pie chart for the table can be given as:

Novels 320

Comedy760

Books Read

2400

320 ×360°=48° 2400

114° 760 ×360°= 2400

Novels, 320 144° 42° 90° 66° 48°

Comedy, 760

Biography, 440 Fantasy, 280

Adventure, 600

6.a. Notebooks

b. Central angle for notebooks = 90°

Fraction = 90°1 = 360°4

c. Central angle for party supplies = 54.3°

Percentage of party supplies sold

= 54.3° ×100%=15.08% 360°

7. Let the number of ice creams sold in 5 days = x Ice creams sold on Wednesday = 22% = 198 According to the question, 22% of x =198

198 =×100=900 22 x

The total number of ice creams sold in 5 days = 900

8.a. Percentage of sales of household items

= 72° ×100%=20% 360°

b. The most popular product is produce. Sale = 108° ×1,00,000=30,000 360° `

c. The two least popular products are dairy and beverages. Total central angle = 36° + 54° = 90°

Percentage sales = 90° ×100=25% 360°

9.a. Given that, the number of people who prefer aerobics = 150

Let the total number of people be x; according to question, 36 of=150 360 x

Therefore, =1500 x

Given, central angle for running = 64.8°

Number of people who prefer running

= 64.8° ×1500=270 360°

Percentage = 270 ×100%=18% 1500

b. Number of people who prefer cycling

= 43.2° ×1500=180

360°

Number of people who do not prefer to gym

= 360°–57.6° ×1500=1260 360°

Ratio = 180:1260 = 1:7

c. Central angle of people who do not prefer yoga and meditation = (360° − 115.2°) = 244.8°

Percentage = 244.8° ×100%=68% 360°

10.a. Central angle for glass used in July = 26 ×360°=93.6° 100

The difference in the value of the central angle made by the glass in both months = 93.6° − 72° = 21.6°

b. Paper collected in June = 93.6° ×60,000=15,600tonnes 360°

Paper collected in July = 22 ×60,000=13,200tonnes 100

Total paper collected = 15,600 + 13,200 = 28,800 tonnes

c. Plastic collected in June = 126° ×60,000=21,000 360° tonnes

Plastic collected in July = 32 ×60,000=19,200 100 tonnes

In June 21,000 − 19,200 = 1800 tonnes of more plastic was collected.

d. Percentage of cardboard collection in June = 43.2° ×100%=12%

360°

Given, percentage of cardboard collection in July = 15%

Percentage change (increase) = 15–12 ×100%=25% 12

Word Problems

1.a. Total amount paid for electricity bill = ₹7200

Amount of bill paid for electronics category = 32 ×7200= 2304 100 ``

b. Given, percentage of consumption for kitchen appliances = 24%

Central angle = 24 ×360°=86.4° 100

c. Bathroom appliance consumed the least electricity.

2. The total number of students = 200

The pie chart for the table can be given as:

3.

4.

for Spinner A is greater, than the ratio for Spinner B. Hence, I should choose Spinner A for a better chance of winning.

Ice cream flavourNo. of studentsCentral angle Vanilla

×360°=

90° 50 ×360°= 200

Favourite Ice Cream Flavour

Chapter 9

Mango, 55

Guava, 50 Vanilla, 35 Chocolate, 60

Let's Warm-up

1. A dog flying. Impossible

2. The cycle of day and night. Sure

3. Getting heads when a coin is tossed. Equally likely

4. Drawing a blue marble from a bag containing 6 blue and 2 green marbles. Likely

5. Drawing a green marble from a bag containing 10 yellow and 3 green marbles. Unlikely

Do It Yourself

9A

1.a. Selecting a vowel from the letters a, e, i, o, u. - Sure

b. If today is Saturday, tomorrow will be Friday. - Impossible

c. Drawing a white ball from a bag containing 8 white and 4 red balls. - Likely

d. Getting a number 2, when a dice is rolled. - Unlikely

e. Getting a tail when a coin is tossed. - Equally likely

2.a. The probability of an event having no chance of occurrence is 0.

b. The probability of a sure event is 1.

c. The possible outcomes when you toss a coin are heads and tails.

d. When rolling a dice, the event of getting a prime number has 3 possible outcomes.

P (picking a black ball from Basket B) > P (picking a black ball from Basket A)

Hence, I should choose Basket B for a better chance of winning.

5. P (pointer landing in the green section) = 4 10

P (pointer landing in the blue section) = 3 10

P (pointer landing in the yellow section) = 2 10

P (pointer landing in the black section) = 1 10

Sum of P(pointer landing in the green, blue, yellow, and black sections) = 4+3+2+1 4321 10 +++===1 101010101010

6. There are 26 letters in the English alphabet.

Total number of possible outcomes = 26

Number of favourable outcomes for the event of choosing any letter except Z = 25

Therefore, the theoretical probability of randomly choosing any letter except Z 25 = 26

7. Total number of marbles in the glass jar = 40

P (drawing a single green marble) = 1 5

So, the number of green marbles in the glass jar = 1 ×40=8

5 Hence, option b is correct.

8. Probability of correctly guessing a box that contains a tennis ball = 1

5

Number of contestants who played the game = 60

Number of contestants expected to win the game

N = 1 60×=12

5

So, about 12 contestants are expected to win the game.

9.a. The possible outcomes when a coin is tossed are Heads and Tails.

Total possible outcomes of the experiment = 2 (either heads or tails)

Number of tails1

PE

()= =

Total number of outcomes2

Therefore, the theoretical probability of getting a tail is 1 2

b. Number of contestants who play the game = 250

Number of contestants expected to win = probability of getting tails × number of contestants who play the game

= 1 ×250=125

2

So, about 125 contestants are expected to win.

10. Possible outcomes on rolling a six-sided dice are 1, 2, 3, 4, 5, and 6.

So, the total number of possible outcomes = 6

a. The event of rolling a 4 has only one favourable outcome.

P(rolling a 4) = 1 6

b. The event of rolling an odd number has 3 favourable outcomes (1, 3, and 5).

P(rolling an odd number) = 31 = 62

c. The event of rolling a number greater than 4 has 2 favourable outcomes (5 and 6).

P(rolling a number greater than 4) = 21 = 63

Number of times the dice is rolled by Amit = 12

Number of times, Amit would expect a number greater than 4 to be rolled = 1 12×=4 3

11. Possible outcomes = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12.

So, the total number of possible outcomes = 12

a. The event of rolling a number greater than 10 has two favourable outcomes (11 and 12).

P(rolling a number greater than 10) = 21 = 126

b. The event of rolling a number less than 5 has four favourable outcomes (1, 2, 3, and 4).

P(rolling a number less than 5) = 41 = 123

c. The event of rolling either a 4, 6, or 9 has three favourable outcomes.

P(rolling either a 4, 6, or 9) = 31 = 124

If the 12-sided solid is rolled 200 times, the number of times a 4, 6, or 9 can be expected = 1 ×200=50

4

So, we can expect either a 4, 6, or 9 to be rolled about 50 times in 200 trials.

12. The table below shows the sample space for rolling a particular sum on two dice.

+ 123456

1 234567

2 345678

3 456789

4 5678910

5 67891011

6 789101112

There are 36 possible outcomes.

a. The event of rolling a sum of 5 on two dice has four favourable outcomes.

P(rolling a sum of 5 on two dice) = 41 = 369

b. The event of rolling a sum of 6 on two dice has five favourable outcomes.

P(rolling a sum of 6 on two dice) = 5 36

c. The event of rolling a sum of 10 on two dice has three favourable outcomes.

P(rolling a sum of 10 on two dice) = 31 = 3612

13. The table below shows the sample space for the experiment of tossing a coin and rolling a dice together.

123456

H H1H2H3H4H5H6

T T1T2T3T4T5T6

a. The possible outcomes are: H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6

b. There are 12 possible outcomes in all.

c.i. The event of tossing a head and rolling a 6 has only one favourable outcome (H6).

P(tossing a head and rolling a 6) = 1 12

ii. The event of tossing a head has 6 favourable outcomes (H1, H2, H3, H4, H5, H6).

P(tossing a head) = 61 = 122

iii. The event of tossing a tail and rolling a number less than 3 has two favourable outcomes (T1, T2)

P(tossing a tail and rolling a number less than 3)

= 21 = 126

iv. The event of rolling a 5 or a 6 has four favourable outcomes (H5, H6, T5, T6).

P(rolling a 5 or a 6) = 41 = 123

v. The event of tossing a head and not rolling a 6 has five favourable outcomes (H1, H2, H3, H4, H5).

P(tossing a head and not rolling a 6) = 5 12

vi. The event of not rolling a 6 has ten favourable outcomes (H1, H2, H3, H4, H5, T1, T2, T3, T4, T5).

P(not rolling a 6) = 105 = 126

14. The table below shows the sample space for rolling a particular sum on two dice.

+ 123456

1 234567

2 345678

3 456789

4 5678910

5 67891011

6 789101112

There are 36 possible outcomes.

The event of rolling a sum of 7 on two dice has six favourable outcomes.

Hence, the probability of rolling a sum of 7 on two dice = 61 = 366

This also means that the probability of winning the game is 1

6

Number of contestants who played Ajay’s game = 500

Number of people expected to win the game = 1 ×500=83 6 (Approximately)

Hence, about 83 people out of 500 are expected to win Ajay’s game.

Word Problems

1.a. The theoretical probability of drawing a winning chip is 3 10 This also means that the ratio of the number of winning chips to the total number of chips in the bag is 3:10.

If the bag contains 9 winning chips, then the total number of chips in the bag = 10 9×=30 3 .

b. Number of contestants in the game show = 20

Number of contestants expected to draw a winning chip = 3 ×20=6 10

2.a. We can make an organized list to find the sample space. collared shirt − khakis − sneakers; collared shirt − khakis − flip-flops

collared shirt − khakis − sandals; collared shirt − jeans − sneakers

collared shirt − jeans − flip-flops; collared shirt − jeans − sandals

collared shirt − capris − sneakers; collared shirt − capris − flip-flops

collared shirt − capris − sandals; T-shirt − khakis − sneakers

T-shirt − khakis − flip-flops; T-shirt − khakis − sandals

T-shirt − jeans − sneakers; T-shirt − jeans − flip-flops

T-shirt − jeans − sandals; T-shirt − capris − sneakers

T-shirt − capris − flip-flops; T-shirt − capris − sandals

So, 18 different outfits are possible.

b. The event of Navin wearing his jeans but not his sneakers has four favourable outcomes (collared shirt − jeans − flipflops, collared shirt − jeans − sandals, T-shirt − jeans − flipflops, T-shirt − jeans − sandals).

Hence, the probability that Navin will wear his jeans but not his sneakers = 42 = 189

9B

1.a. Tossing a coin is an example of a random experiment.

b. Drawing a black card from a deck of playing cards is an example of a random experiment.

c. Throwing a ball is not an example of a random experiment.

d. Taking a marble out of a bag containing coloured marbles is an example of a random experiment.

e. Rolling two dice together is an example of a random experiment.

f. Measuring the length of a table is not an example of a random experiment.

PE

2. Experimental probability, Number of times Leena wins ()= Total number of trials 81 == 486

Therefore, the experimental probability of winning this game is 1 6 or 0.16 or 16.67%.

3.a. Number of aces42 ()= == Total number of serves105 PE

Therefore, the experimental probability of Govind serving an ace in the first match of the next game is 2 5 or 0.40 or 40%.

b. In 10 serves, Govind serves an ace 4 times. In 40 serves, Govind would serve an ace, 4 40×=16 10 times So, Govind will serve an ace about 16 times.

4.a. The total number of songs played in a 24-hour period = 60 + 75 = 135

Number of times a rap song is played755 ()= == Total number of songs played1359 PE or 0.55 or 55.55%.

b. In 135 trials, a pop song was played 60 times.

In the next 90 trials, a pop song is expected to be played, 60 90×=40 135 times

5.a. The total number of trials in the experiment = 30 ()==93 3010 Pred

b. In 30 trials, a red marble was drawn 9 times. In 50 trials, a red marble would be drawn, 9 50×=15 30 times

6. The total number of trials in the experiment = 50 ()==303 505 Pvowel

The number of vowels in the bag full of 105 lettered tiles is expected to be = 3 105× 5 = 63

7.a. This is the part where the circles overlap. 10 students play both tennis and squash.

10

( )= 90 Pbothtennisandsquash or 11.11 %

b. This is the part outside of both circles.

53 students play neither tennis nor squash.

53 ( )= 90 Pneithertennisnorsquash or 58.88%

c. These are both parts of the tennis circle.

25 + 10 = 35

35 students play tennis.

35 ()= 90 Ptennis or 38.88%

d. This is the part inside either circle but not in both.

25 + 2 = 27

27 students play tennis or squash but not both.

27 ( )= 90 Ptennisorsquashbutnotboth or 30%

8.a. 61 students own a mobile phone.

Probability that a student owns a mobile phone = 61 125 or 48.8%

b. 64 students do not own a mobile phone. Probability that a student does not own a mobile phone = 64 125 or 51.2%

c. There are 29 male students who own a mobile phone. Probability that a student is a male, who owns a mobile phone = 29 125 or 23.2%

d. There are 39 male students who do not own a mobile phone.

Probability that a student is a male, who does not own a mobile phone = 39 125 or 31.2%

e. There are 25 female students who do not own a mobile phone.

Probability that a student is a female who does not own a mobile phone = 25 125 or 20%

9.a. Number of times two tails appears1 ()= =

Total number of trials12 PE

Therefore, the experimental probability of getting two tails is 1 12 or 0.083 or 8.33%

In 12 trials, two tails appeared 1 time. In 600 trials, two tails is expected to appear,

1 600×=50

12 times

b. Number of times two tails appears2211 ()

Total number of trials10050 PE

Therefore, the experimental probability of getting two tails is 11 50 or 0.22 or 22%

In 100 trials, two tails appeared 22 times. In 600 trials, two tails is expected to appear, 22 600×=132

100 times

c. As the number of trials increases, the prediction of results tend to be more accurate. Hence, it is important to conduct a large number of trials when using experimental probability to predict results.

Word Problem

1. Experimental probability, Number of defective pairs51 ()= ==

Total number of pairs of jeans20040 PE

In 5000 trials, the number of jeans expected to be defective would be, 1 5000× 40 = 125

So, 125 jeans are expected to be defective in a shipment of 5000.

Chapter Checkup

1. a. The probability of a sure event is 1.

b. If an event cannot occur, then its probability is 0.

c. The probability of selecting P from the word SPECIAL is 1 7

d. The probability of an event can’t be more than 1.

e. If a dice is rolled once, the probability of getting an even prime number is 1 6 .

2.a. The possible outcomes of flipping a fair coin are heads and tails.

b. The possible outcomes of rolling a standard six-sided dice are 1, 2, 3, 4, 5, and 6.

c. The possible outcomes of selecting a single letter at random from the English alphabet are a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, and z.

d. The possible outcomes of flipping two fair coins simultaneously are (Heads, Heads), (Heads, Tails), (Tails, Heads), (Tails, Tails).

e. The possible outcomes of rolling two standard six-sided dice simultaneously are:

(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6) (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6) (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6) (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)

3.a. Number of cards that shows a triangle1 ()= = Total number of outcomes8 PE

Therefore, the probability of getting a card that shows a triangle is 1 8 or 0.125 or 12.5%.

b. The cards that show a shape with four sides include a square, rectangle and rhombus.

Number of cards that shows a quadrilateral3 ()= = Total number of outcomes8 PE

Therefore, the probability of getting a card that shows a quadrilateral is 3 8 or 0.375 or 37.5%.

c. The cards that show a shape with more than four sides include a pentagon, an octagon, and a hexagon.

Number of cards that show a shape with more than four sides 3 ()= =

Total number of outcomes8 PE

Therefore, the probability of getting a card that shows a shape with more than four sides is 3 8 or 0.375 or 37.5%.

d. The card that shows a shape with no sides is that of a circle.

Number of cards that shows a circle1 ()= =

Total number of outcomes8 PE

Therefore, the probability of getting a card that shows a circle is 1 8 or 0.125 or 12.5%.

4. Number of letters in the given word = 12

Number of A’s in the given word = 2

P (getting an A) = 2 12 = 1 6

5. Number of favourable outcomes for the event = 2

Total number of streams = 4

P (Mathematics as a subject)

= Number of favourable outcomes21 ==

Total number of outcomes42

6.a. Theoretical number of favourable outcomes1 (green)= = number of possible outcomes5 P

Experimental

P

number of times a green colour was spun (green)=

total number of spins

151 == 15010

1 5 > 1 10, theoretical probability is greater in this case.

b. Theoretical number of favourable outcomes1 (red)= = number of possible outcomes5 P

Experimental

number of times a red colour was spun357 (red)= == total number of spins 15030 P 7 30 > 1 5, experimental probability is greater in this case.

c. Theoretical number of favourable outcomes2 (blue or purple)= = number of possible outcomes5 P

Experimental

number of times a blue or purple colour was spun (blue or purple)= total number of spins

25+42 67 == 150150

P 67 150 > 2 5, experimental probability is greater in this case.

d. Since, all the five sections of the spinner are coloured, the theoretical and experimental probability of the wheel stopping at a coloured section is the same that is 1.

7. There are 9 prime numbers between 1 and 25. They are 2, 3, 5, 7, 11, 13, 17, 19 and 23.

So, the total number of possible outcomes is 9.

a. Favourable outcomes for the event of getting a one-digit number are 2, 3, 5, and 7.

So, the number of favourable outcomes = 4

P (one-digit number) 4 9 or 44.44%

b. 2 is the only even prime number.

So, the number of favourable outcomes = 1

P (even number) = 1 9 or 11.11%

c. All prime numbers between 1 and 25 are odd except 2 which is an even prime number.

So, the number of favourable outcomes = 8

P (odd number) = 8 9 or 88.88%

d. Prime numbers between 1 and 25,that are greater than 11 are 13, 17, 19, and 23.

So, the number of favourable outcomes is 4.

P (number greater than 11) = 4 9 or 44.44%

8. Possible outcomes of randomly typing a digit in the keypad of a mobile phone are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

So, the total number of possible outcomes are 10.

a. There are five even numbers from 0 to 9. They are 0, 2, 4, 6, and 8.

So, the number of favourable outcomes is 5.

P (typing an even number) = 5 10 = 1 2 or 50%

b. There is only 1 multiple of 5 from 0 to 9, that is 5.

So, the number of favourable outcomes is 1.

P (typing a multiple of 5) = 1 10 or 10%

c. Factors of 9 are 1, 3, and 9.

So, the number of favourable outcomes is 3.

P (typing a factor of 9) = 3 10 or 30%

d. There are nine natural numbers from 0 to 9. They are 1, 2, 3, 4, 5, 6, 7, 8, and 9.

So, the number of favourable outcomes is 9.

P (typing a natural number) = 9 10 or 90%

e. There are four prime numbers from 0 to 9. They are 2, 3, 5, and 7.

So, the number of favourable outcomes is 4.

P (typing a prime number) = 4 10 = 2 5 or 40%

f. There are four composite number from 0 to 9. They are 4, 6, 8, and 9.

So, the number of favourable outcomes is 4.

P (typing a composite number) = 4 10 = 2 5 or 40%

9. Number of pearl bangles on display =50 × 6 25 = 12

10. Amita can pay the cost of the pencil using either ₹5 coin or ₹10 coin.

P(using a ₹5 coin) = 1 2 = 50%.

11. Possible outcomes when two coins are tossed together are HH, HT, TH, TT.

So, the total number of possible outcomes is 4.

a. There is only one favourable outcome for getting two tails (TT).

P (2 tails) = 1 4 = or 25%

b. There are three favourable outcomes for getting at least 1 head (HT, TH, HH).

P(at least 1 head) = 3 4 or 75%

12. The sample space for the event of rolling two dice together is listed below.

(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6) (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6) (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)

So, the total number of possible outcomes is 36.

a. The favourable outcomes for the event of getting a pair of same numbers are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6).

So, the number of favourable outcomes is 6. Probability of getting a pair of same numbers, ()==61 366 PE or 16.66%

b. The favourable outcomes for the event of getting even numbers on both the dice are listed below.

(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)

So, the number of favourable outcomes is 9. Probability of getting even numbers on both the dice, 91 ()== 364 PE or 25%

Word Problems

1.

a. P(rusted bolt) = 2 5

b. P(not rusted bolt) = 1−P(rusted bolt) = 1–=23

55

2.a. Number of apples packed in a carton = 200; Number of rotten apples = 30

Number of good apples = 200 − 30 = 170; P(Good apple) = 17017 = 20020 or 85%

b. P(rotten apple) = 303 = 20020 or 15%

Chapter 10

Let's Warm-up

1. Among 3, 7, 8, 9, 11 and 12, the numbers 8, 11 and 12 are the only composite numbers. False

2. The prime factors of 48 are 2 and 3 only. True

3. The prime factorisation of 120 is 2 × 2 × 2 × 2 × 3 × 3 × 5. False

4. The prime factorisation of 132 is 2 × 2 × 3 × 11. True

5. Prime factorising a number using the factor tree method gives a different result than using the division method of prime factorisation. False

Do It Yourself 10A

1.a. 5329–

i. 1 because the unit digit of the number is 9.

ii. odd square because the number is odd.

iii. 5329 =73 × 73, so it is a perfect square.

b. 961–

i. 1 because the unit digit of the number is 1.

ii. odd square because the number is odd.

iii. 961 =31 × 31, so it is a perfect square.

c. 4624–

i. 6 because the unit digit of the number is 4.

ii. even square because the number is even.

iii. 4624 =2 × 2×2 × 2×17 × 17, so it is a perfect square.

d. 7688–

i. 4 because the unit digit of the number is 8.

ii. even square because the number is even.

iii. 7688 =2 × 2× 2 ×31 × 31, so it is not a perfect square.

e. 19,753–

i. 9 because the unit digit of the number is 3.

ii. odd square because the number is odd.

iii. 19753 is a prime number, so it is not a perfect square.

f. 83,245–

i. 5 because the units digit of the number is 5.

ii. odd square because the number is odd.

iii. 83,245 = 5 × 16,649, so it is not a perfect square.

2.a. (55)2 = 55 × 55 = 3025

b. 2 7 8 = 7 8 × 7 8 = 49 64

c. 2 12 –13 = –12 13 × –12 13 = 144 169

d. (925)2 = 925 × 925 = 8,55,625

e. 2 4 5 = 4 5 × 4 5 = 16 25

f. (208)2 = 208 × 208 = 43,264

3.a. 56545

71309

11187 1717 1

b. 29054 34527

31509 503503 1

c. 27396 23698

431849

6545 = 5 × 7 × 11 × 17, not a perfect square

9054 = 2 ×3 × 3× 503, not a perfect square

7396 =2 × 2× 43 × 43, a perfect square = (2 × 43)2 = (86)2

d. 25786

112893 263263 1

5786 = 2 × 11 × 263, not a perfect square

e. 16326569

163163

4.a. 25780 22890

51445 17289 1717 1

b. 29072

26,569 = 163 × 163, a perfect square = (163)2

5780 =2 × 2 × 5 ×17 × 17

5 is the smallest number with which when 5780 is multiplied, we get a perfect square.

Therefore, 5780 × 5 = 2 × 2 × 5 × 5 × 17 × 17

28,900 = 22 × 52 × 172 = (2 × 5 × 17)2 = 1702

9072 =2 × 2×2 × 2×3 × 3×3 × 3 × 7

7 is the smallest number with which when 9072 is multiplied, we get a perfect square.

Therefore, 9072 × 7 =2 × 2×2 × 2×

3 × 3×3 × 3×7 × 7

63,504 = 22 × 22 × 32 × 32 × 72 = (2 × 2 × 3 × 3 × 7)2 = 2522

c.

d. 26272 23136

3267 =3 × 3× 3 ×11 × 11

3 is the smallest number with which when 3267 is multiplied, we get a perfect square.

Therefore, 3267 × 3 = 3 × 3 × 3 × 3 × 11 × 11

9801 = 32 × 32 × 112 = (3 × 3 × 11)2 = 992

2 is the smallest number with which when 6272 is multiplied, we get a perfect square.

=

e.

18,432 =2 × 2×2 × 2×2 × 2×2 × 2

×2 × 2× 2 ×3 × 3

2 is the smallest number with which when 18,432 is multiplied, we get a perfect square.

Therefore, 18,432 × 2 =2 × 2×2 × 2×2 × 2×2 × 2×2 × 2×2 × 2

×3 × 3

36,864 = 22 × 22 × 22 × 22 × 22 × 22 × 32

= (2 × 2 × 2 × 2 × 2 × 2 × 3)2 = 1922

f. 243740 221870 310935 33645 31215 3405 3135 345 315 55 1

5.a. 23456 21728 2864 2432 2216 2108 254 327 39 33

1

b. 58575

43,740 =2 × 2×3 × 3×3 × 3×3 × 3

× 3 × 5

(3 × 5 =) 15 is the smallest number with which when 43,740 is multiplied, we get a perfect square.

Therefore, 43,740 × 15 =2 × 2×3 × 3

×3 × 3×3 × 3×3 × 3×5 × 5

6,56,100 = 22 × 32 × 32 × 32 × 32 × 52 = (2 × 3 × 3 × 3 × 3 × 5)2 = 8102

3456 =2 × 2×2 × 2×2 × 2× 2 ×3 ×

3× 3

(2 × 3 =) 6 is the smallest number by which when 3456 is divided, we get a perfect square.

Therefore, 3456 6 =2 × 2

×2 × 2×2 × 2×3 × 3

576 = 22 × 22 × 22 × 32= (2 × 2 × 2 × 3)2 = 242

8575 =5 × 5×7 × 7× 7

7 is the smallest number by which when 8575 is divided, we get a perfect square.

Therefore, 8575 ÷ 7 =5 × 5×7 × 7

1225 = 52 × 72 = (5 × 7)2 = 352

c. 25808

22904

21452 2726 3363 11121

d.

235972

217986

178993

23529

2323

5808 =2 × 2 ×2 × 2× 3 ×11 × 11

3 is the smallest number by which when 5808 is divided, we get a perfect square.

Therefore, 5808 ÷ 3 =2 × 2×2 × 2× 3 ×11 × 11

1936 = 22 × 22 × 112 = (2 × 2 × 11)2 = 442

35,972 =2 × 2× 17 ×23 × 23

17 is the smallest number by which when 35972 is divided, we get a perfect square.

Therefore, 35972 ÷ 17 =2 × 2× 23 × 23

2116 = 22 × 232 = (2 × 23)2 = 462

e.

295400

247700

223850

311925

33975

51325

5265 5353

1

f. 267392

233696

216848

28424 24212

22106

31053

3351

3117

339

1313

1

95,400 =2 × 2× 2 ×3 × 3×5 × 5× 53

2 × 53 = 106 is the smallest number by which when 95,400 is divided, we get a perfect square.

Therefore, 95400 ÷ 106 =2 × 2×3 ×

3×5 × 5

900 = 22 × 32 × 52 = (2 × 3 × 5)2 = 302

67392 =2 × 2×2 × 2×2 × 2×3 × 3×

3 × 3× 13

13 is the smallest number by which when 67392 is divided, we get a perfect square.

Therefore, 67392 ÷ 13 =2 × 2×2 × 2

×2 × 2×3 × 3×3 × 3

5184 = 22 × 22 × 22 × 32 × 32 = (2 × 2 ×

2 × 3 × 3)2 = 722

10B

1.a. 676 = 262 = sum of first 26 odd numbers = 1 + 3 + 5 + 7 + 9

b. 729 = 272 = sum of first 27 odd numbers = 1 + 3 + 5 + 7 + 9

35 + 37 + 39 + 41 + 43 + 45 + 47 + 49 + 51 + 53

c. 289 = 172 = sum of first 17 odd numbers = 1 + 3 + 5 + 7 + 9

+ 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + 31 + 33

d. 900 = 302 = sum of first 30 odd numbers = 1 + 3 + 5 + 7 + 9

+ 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + 31 + 33

+ 35 + 37 + 39 + 41 + 43 + 45 + 47 + 49 + 51 + 53 + 55 + 57 +

59

e. 1225 = 352 = sum of first 35 odd numbers = 1 + 3 + 5 + 7 +

9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + 31 +

33 + 35 + 37 + 39 + 41 + 43 + 45 + 47 + 49 + 51 + 53 + 55 +

57 + 59 + 61 + 63 + 65 + 67 + 69

f. 1024 = 322 = sum of first 32 odd numbers = 1 + 3 + 5 + 7

+ 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + 31 +

33 + 35 + 37 + 39 + 41 + 43 + 45 + 47 + 49 + 51 + 53 + 55 +

57 + 59 + 61 + 63

2. Triangular numbers from 20 to 50 = 21, 28, 36, 45

Sum of two consecutive triangular numbers is a square number such as 21 + 28 = 49 = 72, 28 + 36 = 64 = 82, 36 + 45 =

81 = 92

3.a. 132 − 122 = 2 × 12 + 1 = 25, so there are 2 × 12 = 24 nonperfect squares.

b. 212 − 202 = 2 × 20 + 1 = 41, so there are 2 × 20 = 40 nonperfect squares.

c. 182 − 172 = 2 × 17 + 1 = 35, so there are 2 × 17 = 34 nonperfect squares.

6. 216, 18, 24, 28, 30 28, 9, 12, 14, 15

LCM of 16, 18, 24, 28, 30 =2 × 2×2 × 2×3 × 3× 5 × 7 = 5040

To make the number a perfect square, multiply 5040 by 35, then 5040 × 35 = 1,76,400 is the required number.

So, the least number which is a perfect square and is divisible by 16, 18, 24, 28 and 30 is 1,76,400.

9, 6, 7, 15 22, 9, 3, 7, 15 31, 9, 3, 7, 15 31, 3, 1, 7, 5

51, 1, 1, 7, 5

71, 1, 1, 1, 1

7. Let the number Sheetal could have thought of be x.

So, according to the question,

x + 2 × x + 3 × 2x + 6 × 3 × 2x = perfect square

x + 2x + 6x + 36x = perfect square

45x = perfect square

5 × 3 × 3 × x = perfect square

For the number to be a perfect square, it should be multiplied by 5.

So, the number that is a perfect square is 5 × 5 × 3 × 3 = 225.

Therefore, the number that Sheetal could think of is 5. Word Problems

1. Total number of plants in the garden = area of the square garden = (45)2 = 45 × 45 = 2025

2. Total number of students in the school = number of students in a row × total number of rows = 63 × 63 = 3969

d. 262 − 252 = 2 × 25 + 1 = 51, so there are 2 × 25 = 50 nonperfect squares.

e. 322 − 312 = 2 × 31 + 1 = 63, so there are 2 × 31 = 62 nonperfect squares.

f. 492 − 482 = 2 × 48 + 1 = 97, so there are 2 × 48 = 96 nonperfect squares.

4.a. 572

b. 632 = (632 – 1)

3968

3970

c. 772 = (772 – 1)

d.

(632 + 1)

f. 172 = (172 – 1)

+ (172 + 1)

= 289 – 1

+ 289 + 1

= 288

+ 290 2 = 144 + 145

5.a. 752 = [7 (7 + 1)] × 100 + 25 = 7 × 8 × 100 + 25 = 5625

b. 512 − 502 = (51 + 50) (51 − 50) = 101 × 1 = 101

c. 952 = [9 (9 + 1)] × 100 + 25 = 9 × 10 × 100 + 25 = 9025

d. 782 − 772 = (78 + 77) (78 − 77) = 155 × 1 = 155

e. 1052 = [10 (10 + 1)] × 100 + 25 = 10 × 11 × 100 + 25 = 11,025

f. 992 − 982 = (99 + 98) (99 − 98) = 197 × 1 = 197

6.a. 75 × 77 = (76 − 1) (76 + 1) = 762 − 12 = 5776 − 1 = 5775

b. 64 × 68 = (66 − 2) (66 + 2) = 662 − 22 = 4356 − 4 = 4352

c. 50 × 52 = (51 − 1) (51 + 1) = 512 − 12 = 2601 − 1 = 2600

d. 91 × 95 = (93 − 2) (93 + 2) = 932 − 22 = 8649 − 4 = 8645

e. 36 × 40 = (38 − 2) (38 + 2) = 382 − 22 = 1444 − 4 = 1440

7. The members of a Pythagorean triplet are given by 2m, m2 − 1 and m2 + 1.

a. If 2m = 12, then m = 6. So, m2 − 1 = 62 − 1 = 36 − 1 = 35 and m2 + 1 = 62 + 1 = 36 + 1 = 37

Thus, the Pythagorean triplet in this case is given by (12, 35, 37)

If m2 − 1 = 12, then m2 = 13 ⇒ m is not an integer.

If m2 + 1 = 12, then m2 = 11 ⇒ m is not an integer.

In either case, values of m are not possible.

So, the only Pythagorean triplet here is (12, 35, 37) with 12 as its smallest member.

b. If 2m = 16, then m = 8. So, m2 − 1 = 82 − 1 = 64 − 1 = 63 and m2 + 1 = 82 + 1 = 64 + 1 = 65

Thus, the Pythagorean triplet in this case is given by (16, 63, 65)

If m2 − 1 = 16, then m2 = 17 ⇒ m is not an integer.

If m2 + 1 = 16, then m2 = 15 ⇒ m is not an integer.

In either case, values of m are not possible.

So, the only Pythagorean triplet here is (16, 63, 65) with 16 as its smallest member.

c. If 2m = 28, then m = 14. So, m2 − 1 = 142 − 1 = 196 − 1 = 195 and m2 + 1 = 142 + 1 = 196 + 1 = 197

Thus, the Pythagorean triplet in this case is given by (28, 195, 197)

If m2 − 1 = 28, then m2 = 29 ⇒ m is not an integer.

If m2 + 1 = 28, then m2 = 27 ⇒ m is not an integer. In either case, values of m are not possible.

So, the only Pythagorean triplet here is (28, 195, 197) with 28 as its smallest member.

d. If 2m = 32, then m = 16. So, m2 − 1 = 162 − 1 = 256 − 1 = 255 and m2 + 1 = 162 + 1 = 256 + 1 = 257

Thus, the Pythagorean triplet in this case is given by (16, 255, 257)

If m2 − 1 = 32, then m2 = 33 ⇒ m is not an integer.

If m2 + 1 = 32, then m2 = 31 ⇒ m is not an integer. In either case, values of m are not possible.

So, the only Pythagorean triplet here is (32, 255, 257) with 32 as its smallest member.

e. If 2m = 36, then m = 18. So, m2 − 1 = 182 − 1 = 324 − 1 = 323 and m2 + 1 = 182 + 1 = 324 + 1 = 325

Thus, the Pythagorean triplet in this case is given by (36, 323, 325)

If m2 − 1 = 36, then m2 = 37 ⇒ m is not an integer. If m2 + 1 = 36, then m2 = 35 ⇒ m is not an integer.

In either case, values of m are not possible.

So, the only Pythagorean triplet here is (36, 323, 325) with 36 as its smallest member.

f. If 2m = 48, then m = 24. So, m2 − 1 = 242 − 1 = 576 − 1 = 575 and m2 + 1 = 242 + 1 = 576 + 1 = 577

Thus, the Pythagorean triplet in this case is given by (48, 575, 577)

If m2 − 1 = 48, then m2 = 49 ⇒ m is not an integer.

If m2 + 1 = 48, then m2 = 47 ⇒ m is not an integer. In either case, values of m are not possible.

So, the only Pythagorean triplet here is (48, 575, 577) with 48 as its smallest member.

8. 42 = 16

342 = 1156

3342 = 111556

33342 = 11115556

333342 =1111155556

3333342 = 111111555556

9. 92 = 81

992 = 9801

9992 = 998001

99992 = 99980001

999992 = 9999800001

9999992 =999998000001

10.a. 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = sum of first 8 odd numbers = 82 = 64

b. 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27

+ 29 + 31 + 33 = sum of first 17 odd numbers = 172 = 289

c. 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 +

27 + 29 + 31 + 33 + 35 + 37 + 39 + 41 + 43 = sum of first 22 odd numbers = 222 = 484

Word Problem

1.a. Pattern 1 = 22 = 4

Pattern 2 = 22 + (2 + 2 + 1) = 4 + 5 = 9 = 32

Pattern 3 = 32 + (3 + 3 + 1) = 9 + 7 = 16 = 42

… Pattern n = n2 + (n + n + 1) = (n + 1)2

So, the rule is n2 + (2n + 1) = (n + 1)2

b. Pattern 1 = 22 = 4

Pattern 2 = 22 + (2 + 2 + 1) = 4 + 5 = 9 = 32

Pattern 3 = 32 + (3 + 3 + 1) = 9 + 7 = 16 = 42

Pattern 4 = 42 + (4 + 4 + 1) = 16 + 9 = 25 = 52

Pattern 5 = 52 + (5 + 5 + 1) = 25 + 11 = 36 = 62

Pattern 6 = 62 + (6 + 6 + 1) = 36 + 13 = 49 = 72

c. 562 = (55 + 1)2 = 552 + (2 × 55 + 1) = 3025 + (110 + 1) = 3025 + 111 = 3136

10C

1.a. 1369 has 9 in its units place, so its square root will have 3 or 7 in its units place.

b. 3136 has 6 in its units place, so its square root will have 4 or 6 in its units place.

c. 5184 has 4 in its units place, so its square root will have 2 or 8 in its units place.

d. 8281 has 1 in its units place, so its square root will have 1 or 9 in its units place.

e. 9604 has 4 in its units place, so its square root will have 2 or 8 in its units place.

f. 2916 has 6 in its units place, so its square root will have 4 or 6 in its units place.

2.a. 144 − 1 = 143 (1 time), 143 − 3 = 140 (2 times), 140 − 5 = 135 (3 times)

135 − 7 = 128 (4 times), 128 − 9 = 119 (5 times), 119 − 11 = 108 (6 times)

108 − 13 = 95 (7 times), 95 − 15 = 80 (8 times), 80 − 17 = 63 (9 times)

63 − 19 = 44 (10 times), 44 − 21 = 23 (11 times), 23 − 23 = 0 (12 times)

So, 144 = 12.

b. 36 − 1 = 35 (1 time), 35 − 3 = 32 (2 times), 32 − 5 = 27 (3 times), 27 − 7 = 20 (4 times), 20 − 9 = 11 (5 times)

11 − 11 = 0 (6 times)

So, 36 = 6.

c. 441 − 1 = 440 (1 time), 440 − 3 = 437 (2 times), 437 − 5 = 432 (3 times), 432 − 7 = 425 (4 times)

425 − 9 = 416 (5 times), 416 − 11 = 405 (6 times),

405 − 13 = 392 (7 times), 392 − 15 = 377 (8 times)

377 − 17 = 360 (9 times), 360 − 19 = 341 (10 times), 341 − 21 = 320 (11 times)

320 − 23 = 297 (12 times), 297 − 25 = 272 (13 times), 272 − 27 = 245 (14 times)

245 − 29 = 216 (15 times), 216 − 31 = 185 (16 times), 185 − 33 = 152 (17 times)

152 − 35 = 117 (18 times), 117 − 37 = 80 (19 times), 80 − 39 = 41 (20 times)

41 − 41 = 0 (21 times)

So, 441 = 21.

d. 900 − 1 = 899 (1 time), 899 − 3 = 896 (2 times), 896 − 5 = 891 (3 times)

891 − 7 = 884 (4 times), 884 − 9 = 875 (5 times), 875 − 11 = 864 (6 times)

864 − 13 = 851 (7 times), 851 − 15 = 836 (8 times), 836 − 17 = 819 (9 times)

819 − 19 = 800 (10 times), 800 − 21 = 779 (11 times), 779 − 23 = 756 (12 times)

756 − 25 = 731 (13 times), 731 − 27 = 704 (14 times), 704 − 29 = 675 (15 times)

675 − 31 = 644 (16 times), 644 − 33 = 611 (17 times), 611 − 35 = 576 (18 times)

576 − 37 = 539 (19 times), 539 − 39 = 500 (20 times), 500 − 41 = 459 (21 times)

459 − 43 = 416 (22 times), 416 − 45 = 371 (23 times), 371 − 47 = 324 (24 times)

324 − 49 = 275 (25 times), 275 − 51 = 224 (26 times), 224 − 53 = 171 (27 times)

171 − 55 = 116 (28 times), 116 − 57 = 59 (29 times), 59 − 59 = 0 (30 times)

So, 900 = 30.

e. 169 − 1 = 168 (1 time), 168 − 3 = 165 (2 times), 165 − 5 = 160 (3 times)

160 − 7 = 153 (4 times), 153 − 9 = 144 (5 times), 144 − 11 = 133 (6 times)

133 − 13 = 120 (7 times), 120 − 15 = 105 (8 times), 105 − 17 = 88 (9 times)

88 − 19 = 69 (10 times), 69 − 21 = 48 (11 times), 48 − 23 = 25 (12 times)

25 − 25 = 0 (13 times)

So, 169 = 13.

f. 100 − 1 = 99 (1 time), 99 − 3 = 96 (2 times), 96 − 5 = 91 (3 times)

91 − 7 = 84 (4 times), 84 − 9 = 75 (5 times), 75 − 11 = 64 (6 times)

64 − 13 = 51 (7 times), 51 − 15 = 36 (8 times), 36 − 17 = 19 (9 times)

19 − 19 = 0 (10 times)

So, 100 = 10.

3.a. 36561

32187

3729 3243 381 327 39 33 1

b. 28836 24418 472209 4747

1

c. 220164 210082 715041 7171

1

d. 15724649 157157 1

e. 17329929 173173 1

4.a. 2401

6561 =3 × 3×3 × 3×3 × 3×3 × 3

So, 6561

= (3 × 3)×(3 × 3)×(3 × 3)×(3 × 3) = 3 × 3 × 3 × 3 = 81

8836 =2 × 2×47 × 47

So, 8836 = (2 × 2)×(47 × 47) = 2 × 47 = 94

20164 =2 × 2×71 × 71

So, 20164 = (2 × 2)×(71 × 71)

= 2 × 71 = 142

24649 =157 × 157

So, 24649 = 157 × 157) ( = 157

29929 =173 × 173

So, 29929 = 173 × 173) ( = 173

a. 2500 = 7×7×7×7 5×5×2×2×5×5 = 77 525 = 49 50

b. 3364 3600 = 2×2×29×29 2×2×2×2×3×3×5×5

= 2×29 2×2×3×5 = 58 60

c. 4761 5625 = 3×3×23×23 3×3×5×5×5×5 = 3×23 3×5×5 = 69 75

d. 625 1156 = 5×5×5×5 2×2×17×17 = 5×5 2×17 = 25 34

e. 4096 6241 = 2×2×2×2×2×2×2×2×2×2×2×2

2×2×2×2×2×2

79 = 64 79

5.a. 28748

24374

32187

3729 3243

381

327

39

33 1

b. 25202

32601

3867

17289

1717

1

c. 23100

21550

5775

5155

3131

1

d. 215600

27800

23900

21950

3975

5325

565

1313

1

e. 24000

22000

21000

2500

2250

5125

525

55

79×79 =

8748 =2 × 2×3 × 3×3 × 3×3 × 3× 3

3 is the least number with which when 8748 is multiplied, we get a perfect square.

8748 × 3 =2 × 2×3 × 3×3 × 3×3 × 3×

3 × 3

26,244 = (2 × 3 × 3 × 3 × 3)2 = 1622

5202 = 2 ×3×3×17× 17

2 is the least number with which when 5202 is multiplied, we get a perfect square.

5202 × 2 =2×2×3×3×17×17

10,404 = (2 × 3 × 17)2 = 1022

3100 =2×2×5×5× 31

31 is the least number with which when 3100 is multiplied, we get a perfect square.

3100 × 31 =2×2×5×5×31×31

96,100 = (2 × 5 × 31)2 = 3102

15,600 =2×2×2×2× 3 ×5×5× 13 (3 × 13 =) 39 is the least number with which when 15600 is multiplied, we get a perfect square.

15,600 × 39 =2×2×2×2×3×3×5×5 ×13×13

6,08,400 = (2 × 2 × 3 × 5 × 13)2 = 7802

f. 275712

237856

218928

29464

24732

22366

71183

13169 1313 1

6.a. 29248

24624

22312

21156

2578

17289

1717 1

b. 25292 22646 31323 3441 3147

75,712 =2×2×2×2×2×2× 7 × 13×13

7 is the least number with which when 75712 is multiplied, we get a perfect square.

75,712 × 7 =2×2×2×2×2 × 2×7×7× 13×13

5,29,984 = (2 × 2 × 2 × 7 × 13)2 = 7282

9248 =2×2×2×2× 2 ×17×17

2 is the least number by which when 9248 is divided, we get a perfect square.

9248 ÷ 2 =2× 2×2×2×17×17

4624 = (2 × 2 × 17)2 = 682

5292 =2×2×3×3× 3 ×7×7

3 is the least number by which when 5292 is divided, we get a perfect square.

5292 ÷ 3 =2×2×3×3×7×7

1764 = (2 × 3 × 7)2 = 422

c. 214580 27290

33645

14,580 =2×2×3×3×3×3×3× 3× 5

5 is the least number by which when 14,580 is divided, we get a perfect square.

14,580 ÷ 5 =2×2×3×3×3×3× 3×3

2916 = (2 × 3 × 3 × 3)2 = 542

d. 229988

4000 =2×2×2×2× 2 ×5×5× 5

(2 × 5 =) 10 is the least number with which when 4000 is multiplied, we get a perfect square.

4000 × 10 =2×2×2×2×2×2×5×5× 5×5

40,000 = (2 × 2 × 2 × 5 × 5)2 = 2002

29,988 =2×2×3×3×7×7× 17

17 is the least number by which when 29,988 is divided, we get a perfect square.

29,988 ÷ 17 =2×2×3×3×7×7

1764 = (2 × 3 × 7)2 = 422

e. 256628

228314

314157

34719

111573

11143

1313 1

f. 2408980

2204490

5102245

1120449

111859

13169

1313 1

56,628 =2×2×3×3×11×11× 13

13 is the least number by which when 56,628 is divided, we get a perfect square.

56,628 ÷ 13 =2×2×3×3×11×11

4356 = (2 × 3 × 11)2 = 662

4,08,980 =2×2× 5 ×11×11×13×13

5 is the least number by which when 4,08,980 is divided, we get a perfect square.

4,08,980 ÷ 5 =2×2×11×11×13×13

81,796 = (2 × 11 × 13)2 = 2862

7. LCM of 6, 9, 12, 16, 18 = 2 × 2 × 2 × 2 × 3 × 3 = 16 × 9 = 144

So, the smallest square number which is divisible by 6, 9, 12, 16 and 18 is 144.

Word Problems

26, 9, 12, 16, 18

23, 9, 6, 8, 9

23, 9, 3, 4, 9

23, 9, 3, 2, 9

33, 9, 3, 1, 9

31, 3, 1, 1, 3 1, 1, 1, 1, 1

1. Amount collected for relief fund = ₹1296

Number of students in the class = contribution of each student in the class

= 1296 = 2×2×2×2×3×3×3×3 = 2 × 2 × 3 × 3 = 36

2. Length of square table cloth = (27)2 = 27 × 27 = 729 sq. cm

Since the piece of cloth has an area of 721 sq. cm, so we can say that this piece of cloth is not sufficient.

10D

1.a. 81 is a 2-digit number (even), so 2 n = 2 2 = 1, the square root will have 1 digit.

b. 289 is a 3-digit number (odd), so 1 2 n = 31 2 = 4 2 = 2, the square root will have 2 digits.

c. 8464 is a 4-digit number (even), so 2 n = 4 2 = 2, the square root will have 2 digits.

d. 2304 is a 4-digit even number (even), so 2 n = 4 2 = 2, the square root will have 2 digits.

e. 18,496 is a 5-digit even number (odd), so 1 2 n = 51 2 = 6 2 = 3, the square root will have 3 digits.

f. 14,641 is a 5-digit odd number (odd), so 1 2 n = 51 2

= 6 2 = 3, the square root will have 3 digits.

2.a.

c.

= 324

d.

= 356

382 is less than 1456 by 12.

So, the least number to be subtracted from 1456 to get a perfect square is 12.

Thus, the required perfect square number is 1456 − 12 = 1444. 1444 = 38

b. 722 is less than 5243 by 59.

So, the least number to be subtracted from 5243 to get a perfect square is 59.

Thus, the required perfect square number is 5243 − 59 = 5184. 5184 = 72

942 is less than 8912 by 76.

So, the least number to be subtracted from 8912 to get a perfect square is 76.

Thus, the required perfect square number is 8912 − 76 = 8836. 8836 = 94

d.

e. 358

3

f.

1662 is less than 27,804 by 248.

So, the least number to be subtracted from 27,804 to get a perfect square is 248.

Thus, the required perfect square number is 27,804 − 248 = 27,556.

27556 = 166

3582 is less than 1,28,643 by 479.

So, the least number to be subtracted from 1,28,643 to get a perfect square is 479.

Thus, the required perfect square number is 1,28,643 − 479 = 1,28,164.

128164 = 358

5602 is less than 3,13,684 by 84.

So, the least number to be subtracted from 3,13,684 to get a perfect square is 84.

Thus, the required perfect square number is 3,13,684 − 84 = 3,13,600. 313600 = 560

4.a. 5608 is greater than 742 by 132.

The next perfect square is 752 = 5625

So, the least number to be added to 5608 to get a perfect square is 5625

− 5608 = 17.

Thus, the required perfect square number is 5625 and 5625 = 75.

4620 is greater than 672 by 131.

b.

The next perfect square is 682 = 4624

So, the least number to be added to 4620 to get a perfect square is 4624

− 4620 = 4.

Thus, the required perfect square number is 4624 and 4624 = 68.

c. 1,74,700 is greater than 4172 by 811.

The next perfect square is 4182 = 1,74,724

So, the least number to be added to 1,74,700 to get a perfect square is 1,74,724 − 1,74,700 = 24.

Thus, the required perfect square number is 1,74,724 and 174724 = 418.

d.

e.

f.

77,800 is greater than 2782 by 516. The next perfect square is 2792 = 77,841

So, the least number to be added to 77,800 to get a perfect square is 77,841 − 77,800 = 41.

Thus, the required perfect square number is 77,841 and 77841 = 279.

2,83,000 is greater than 5312 by 1039.

The next perfect square is 5322 = 2,83,024

So, the least number to be added to 2,83,000 to get a perfect square is 2,83,024 − 2,83,000 = 24.

Thus, the required perfect square number is 2,83,024 and 283024 = 532.

5,43,291 is greater than 7372 by 122.

The next perfect square is 7382 = 5,44,644

So, the least number to be added to 5,43,291 to get a perfect square is 5,44,644 − 5,43,291 = 1353.

Thus, the required perfect square number is 5,44,644 and 544644 = 738.

e. 92169216

92.16+0.9216=+= 10010000

2×2×2×2×2×2×2×2×2×2×3×3 + 10×10

2×2×2×2×2×2×2×2×2×2×3×3 10×10×10×10

2×2×2×2×2×32×2×2×2×2×3 9696 = + =+ 10

=9.6+0.96=10.56

8. Greatest 4-digit number = 9999

99

9 99 99

81

1891899

1701

198

Since remainder ≠ 0, 9999 is not a perfect square.

So, 992 is less than 9999 by 198.

So, the least number to be subtracted from 9999 to get a perfect square is 198.

Thus, the required perfect square number is 9999 − 198 = 9801.

99

9 98 01

81

1891701

9. Smallest 5-digit number = 10,000

100

1 1 00 00 1

200

2000

Since remainder = 0, 10,000 is the smallest perfect square of 5 digits.

So, 10000=100.

Word Problems

1. Longest side = 15+2022 = 225+400 = 625 = 5×5×5×5 = 5 ×

2. 360 m 150 m

Distance she walks diagonally = 150+36022

Chapter

b.

9 –

2

2.a. 452 − 162 = (45 + 16) (45 − 16) = 61 × 29 = 1769

b. 65 × 67 = (66 − 1) (66 + 1) = 662 − 12 = 4356 − 1 = 4355

c. 852 = [8 (8 + 1)] × 100 + 25 = 8 × 9 × 100 + 25 = 7225

d. 120 × 124 = (122 − 2) (122 + 2) = 1222 − 22 = 14,884 − 4 = 14,880

3. 324 = 182 = sum of 18 odd numbers = 1 + 3 + 5 + 7 + 9 + 11 +

13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + 31 + 33 + 35

4. If 2m = 96, then m = 48. So, m2 − 1 = 482 − 1 = 2304 − 1 = 2303 and m2 + 1 = 482 + 1 = 2304 + 1 = 2305

Thus, the Pythagorean triplet in this case is given by (96, 2303, 2305)

If m2 − 1 = 96, then m2 = 97 ⇒ m is not an integer.

If m2 + 1 = 96, then m2 = 95 ⇒ m is not an integer.

In either case, values of m are not possible.

So, the only Pythagorean triplet here is (96, 2303, 2305) with 96 as its smallest member.

If 2m = 24, then m = 12. So, m2 − 1 = 122 − 1 = 144 − 1 = 143 and m2 + 1 = 122 + 1 = 144 + 1 = 145

Thus, the Pythagorean triplet in this case is given by (12, 143, 145)

If m2 − 1 = 24, then m2 = 25 ⇒ m = 5 but the smallest member will be 2m = 10 in this case.

If m2 + 1 = 24, then m2 = 23 ⇒ m is not an integer.

In either case, values of m are not possible.

So, the only Pythagorean triplet here is (24, 143, 145) with 24 as its smallest member.

5.a. 16

1 2 65

1 26165

156

9

Since remainder ≠ 0, 9999 is not a perfect square.

b. 46

4 21 16

16 86516

516 0

Since remainder = 0, 2116 is a perfect square. So, 2116 = 462.

Verification:

2116 =2 × 2×23 × 23

2116 = 2×2×23×23 = 2 × 23 = 46

c. 94 9 88 39

Since remainder ≠ 0, 8839 is not a perfect square.

d. 56

5 31 36 25

636

Since remainder = 0, 3136 is a perfect square. So, 3136 = 562

Verification: 23136 21568

Since remainder = 0, 72,361 is a perfect square. So, 72,361 = 2692

Verification: 26972361 269269 1

72,361 =269 × 269 72361=269×269=269

f. 326 3 10 69 28

Since remainder ≠ 0, 1,06,928 is not a perfect square.

6.a. 2.81

7 .89 61

8.

9.

c.

=

=

6,57,700 is greater than 8102 by 1600.

The next perfect square is 8112 = 6,57,721.

So, the least number to be added to 6,57,700 to get a perfect square is 6,57,721 − 6,57,700 = 21.

Thus, the required perfect square number is 657721and 657721811.

10. 28, 9, 10 24, 9, 5 22, 9, 5 31, 9, 5 31, 3, 5

51, 1, 5 1, 1, 1

LCM of 8, 9, 10 = 2 × 2 × 2 × 3 × 3 × 5 = 8 × 9 × 5 = 360

To make the number a perfect square, multiply 360 by 10, then 3600 × 10 = 3600 is the required number.

So, the least number which is a perfect square and is divisible by 8, 9 and 10 is 3600.

Word Problem

1. The longest straight line that can be drawn on the floor of the room is the diagonal of the rectangular room.

So, length of the diagonal = 261822 = 676324

= 1000 = 1010 = 31.62 m

Chapter 11

Let's Warm-up

1. The size of a pineapple is bigger than an apple. So, pineapple occupies more space. There are an apple and a pineapple on a table. Between both fruits, pineapple occupies more space.

2. Length = 5 unit cubes, Breadth = 3 unit cubes, Height =

Number of layers = 2

Volume of the solid = 5 × 3 × 2 = 30 cu. units

If a solid with 2 layers has 5 unit cubes along its length, and 3 unit cubes along its breadth, its volume is 30 cu. units.

3. Number of unit cubes in one layer = 16, Number of layers = 3

Volume of the solid = 16 × 3 = 48 cu. units

If a solid has 3 layers with 16 unit cubes in each layer, then its volume is 48 cu. units.

4. Length = 3 cm, Breadth = 2 cm, Height = 2 cm

Volume = 3 × 2 × 2 = 12 cu. cm.

So, 12 unit cubes will be in the container.

If a container is 3 cm long, 2 cm wide, and 2 cm high, then 12 units cubes will be in the container.

5. Side of each cube = 2 cm, Volume of a cube = 2 × 2 × 2 =

8 cu. cm

Number of 2-cm cubes = 14, Volume = 14 × 8 = 112 cu. cm

A carton is filled with fourteen 2 cm cubes. The volume of the carton is 112 cu. units.

Do It Yourself

11A

1.a. Cube of 15 = 15 × 15 × 15 = 3375

b. Cube of 26 = 26 × 26 × 26 = 17,576

c. Cube of 39 = 39 × 39 × 39 = 59,319

d. Cube of 47 = 47 × 47 × 47 = 1,03,823

e. Cube of 74 = 74 × 74 × 74 = 4,05,224

f. Cube of 88 = 88 × 88 × 88 = 6,81,472

g. Cube of 53 = 53 × 53 × 53 = 1,48,877

h. Cube of 92 = 92 × 92 × 92 = 7,78,688

i. Cube of 121 = 121 × 121 × 121 = 17,71,561

2.i.a. Cube of 8 =8 × 8 × 8 = 512; digit at unit’s place = 2

b. Cube of 7 = 343, digit at unit’s place of its cube = 3

c. Cube of 3 = 27, digit at unit’s place of its cube = 7

d. Cube of 6 = 216, digit at unit’s place of its cube = 6

e. Cube of 1 = 1, digit at unit’s place of its cube = 1

f. Cube of 0 = 0, digit at unit’s place of its cube = 0

g. Cube of 7 = 343, digit at unit’s place of its cube = 3

h. Cube of 0 = 0, digit at unit’s place of its cube = 0

ii. Odd cubes − 27, 63, 1331, 24,387; even cubes − 8, 216, 5800, 1,25,000

iii. The numbers 63,5800, and 24,387 are not a perfect cube because, 63 = 7 × 3 × 3; 5800 = 2 × 2 × 2 × 5 × 5 × 29; 24,387 = 3 × 11 × 739

3.a. 3 4 7 = 4 7 × 4 7 × 4 7 = 4×4×4 7×7×7 = 64 343

b. 3 8 –9 = –8 9 × –8 9 × –8 9 = –8×–8×–8 9×9×9 = –512 729

4.a. (2.8)3 = 2.8 × 2.8 × 2.8 = 21.952

b. (1.2)3 = 1.2 × 1.2 × 1.2 = 1.728

c. (0.56)3 = 0.56 × 0.56 × 0.56 = 0.175616

d. (0.08)3 = 0.08 × 0.08 × 0.08 = 0.000512

e. (4.7)3 = 4.7 × 4.7 × 4.7 = 103.823

f. (5.89)3 = 5.89 × 5.89 × 5.89 = 204.336469

g. (3.04)3 = 3.04 × 3.04 × 3.04 = 28.094464

h. (9.1)3 = 9.1 × 9.1 × 9.1 = 753.571

5.a. 52195

439439 1 2195 = 5 × 439, not a perfect cube.

b. 213824

= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3, a perfect cube

23

= 243

So, 13,824 is a perfect cube of 24.

c. 47103823

472209

4747 1

d. 7117649

716807

72401 7343 749

77 1

1,03,823 =47 × 47 × 47, a perfect cube = 473

So, 1,03,823 is a cube of 47.

1,17,649 = 7 × 7 × 7 × 7 × 7 × 7, a perfect cube = 73 × 73 = (7 × 7)3 = 493

So, 1,17,649 is a perfect cube of 49.

e. 2389010 31,94,505 564,835 12,96712,967 1

f.

5857375 5171475 534295 196859

19361

1919

6.a. 2432

3,89,010 = 2 × 3 × 5 × 12,967, not a perfect cube.

8,57,375 = 5 × 5 × 5 × 19 × 19 × 19, a perfect cube = 53 × 193 = (5 × 19)3 = 953

So, 8,57,375 is a perfect cube of 95.

b. 2128

432 =2 × 2 × 2× 2 ×3 × 3 × 3

We require two more 2s to form a triplet of 2.

So, (2 × 2 =) 4 is the smallest number with which when 432 is multiplied, we get a perfect cube.

Therefore, 432 × 4 =2 × 2 × 2×2 × 2 ×2 ×3 × 3 × 3

1728 = 23 × 23 × 33 = (2 × 2 × 3)3 = 123

128 =2 × 2 × 2×2 × 2 × 2× 2

We require two more 2s to form a triplet of 2.

So, (2 × 2 =) 4 is the smallest number with which when 128 is multiplied, we get a perfect cube.

Therefore, 128 × 4 =2 × 2 × 2×2 × 2 × 2 ×2 × 2 × 2

512 = 23 × 23 × 23 = (2 × 2 × 2)3 = 83

c.

2916 = 2 × 2 ×3 × 3 × 3×3 × 3 × 3

We require one more 2 to form a triplet of 2.

So, 2 is the smallest number with which when 2916 is multiplied, we get a perfect cube.

Therefore, 2916 × 2 = 2 × 2 × 2 × 3 × 3 × 3

× 3 × 3 × 3

5832 = 23 × 33 × 33 = (2 × 3 × 3)3 = 183

d.

3456 =2 × 2 × 2×2 × 2 × 2× 2 ×3 × 3 × 3

We require two more 2s to form a triplet of 2.

So, (2 × 2 =) 4 is the smallest number with which when 3456 is multiplied, we get a perfect cube.

Therefore, 3456 × 4 =2 × 2 × 2×2 × 2 × 2

×2 × 2 × 2×3 × 3 × 3

13,824 = 23 × 23 × 23 × 33 = (2 × 2 × 2 × 3)3 = 243

e.

310125

31125 3375 5125 525 55

248672

224336

212168

26084

23042

31521

3507

13169

1

10,125 = 3 ×3 × 3 × 3×5 × 5 × 5

We require two more 3s to form a triplet of 3.

So, (3 × 3 =) 9 is the smallest number with which when 10125 is multiplied, we get a perfect cube.

Therefore, 10,125 × 9 =3 × 3 × 3

×3 × 3 × 3×5 × 5 × 5

48,672 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 13 × 13

We require one more 2, 3, and 13 to form a triplet of 2, 3, and 13.

So, (2 × 3 × 13 =) 78 is the smallest number with which when 48,672 is multiplied, we get a perfect cube.

Therefore, 48,672 × 78 = 2 × 2 × 2 × 2 × 2

× 2 × 3 × 3 × 3 × 13 × 13 × 13

37,96,416 = 23 × 23 × 33 × 133 = (2 × 2 × 3 × 13)3

= 1563

g.

2121500

260750

330375

310125

33375

31125

3375

5125

525 55 1 7.a.

2576

2288

2144

272 236 218

39 33

1

b. 35145

51715

7343

749 77 1

1,21,500 = 2 × 2 ×3 × 3 × 3× 3 × 3 ×5

× 5 × 5

We require one more 2 and 3 to form a triplet of 2 and 3.

So, (2 × 3 =) 6 is the smallest number with which when 1,21,500 is multiplied, we get a perfect cube.

Therefore, 1,21,500 × 6 =2 × 2 × 2×3 ×

3 × 3×3 × 3 × 3×5 × 5 × 5

7,29,000 = 23 × 33 × 33 × 53 = (2 × 3 × 3 × 5)3 = 903

(3 × 3 =) 9 is the smallest number by which when 576 is divided, we get a perfect cube.

Therefore, 576 ÷ 9 =2 × 2 × 2×2 × 2 × 2

64 = 23 × 23 = (2 × 2)3 = 43

(3 × 5 =) 15 is the smallest number by which when 5145 is divided, we get a perfect cube.

Therefore, 5145 ÷ 15 =7 × 7 × 7

343 = 73 c.

236288

218144

29072

24536

22268

21134 3567

3189

77 1

36,288 =2 × 2 × 2×2 × 2 × 2 ×3 × 3 × 3 × 3 × 7

(3 × 7 =) 21 is the smallest number by which when 36,288 is divided, we get a perfect cube.

Therefore, 36,288 ÷ 21 =2 × 2 × 2×2 × 2 × 2×3 × 3 × 3

1728 = 23 × 23 × 33 = (2 × 2 × 3)3 = 123

e.

255566

327783

39261

33087

31029

7343

749

77

1

2158760

279380

239690

319845

36615

32205

3735

5245

749

77 1

55,566 = 2 × 3 ×3 × 3 × 3×7 × 7 × 7

(2 × 3 =) 6 is the smallest number by which when 55,566 is divided, we get a perfect cube.

Therefore, 55,566 ÷ 6 =3 × 3 × 3×7 × 7 × 7

9261 = 33 × 73 = (3 × 7)3 = 213

1,58,760 =2 × 2 × 2× 3 ×3 × 3 × 3× 5

× 7 × 7

(3 × 5 × 7 × 7 =) 735 is the smallest number by which when 1,58,760 is divided, we get a perfect cube.

Therefore, 1,58,760 ÷ 735 =2 × 2 × 2×

3 × 3 × 3

216 = 23 × 33 = (2 × 3)3 = 63

= 2 × (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14

+ 15 + 16 + 17) + 1

= 2 × 153 + 1 = 307

183 = 307 + 309 + 311 + 313 + 315 + 317 + 319 + 321 + 323 +

325 + 327 + 329 + 331 + 333 + 335 + 337 + 339 + 341 = 5832

203 = sum of 20 odd numbers, where the first odd number = 2 × (20 − 1)th triangular number + 1 = 2 × 19th triangular number + 1

Also, 19th triangular number = sum of 19 consecutive numbers

= 2 × (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14

+ 15 + 16 + 17 + 18 + 19) + 1

= 2 × 190 + 1 = 381

203 = 381 + 383 + 385 + 387 + 389 + 391 + 393 + 395 + 397 +

399 + 401 + 403 + 405 + 407 + 409 + 411 + 413 + 415 + 417 +

419 = 8000

9. a. 13 + 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 = (1 + 2 + 3 + 4 + 5 +

6 + 7 + 8 + 9)2 = 452 = 2025

b. 13 + 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 + 103 + 113 + 123

= (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12)2 = 782 = 6084

c. 13 + 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 + 103 + 113 + 123 +

133 + 143 + 153

= (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14

+ 15)2 = 1202 = 14,400

10. a.413 − 403 = 3 × 40 × (40 + 1) + 1 = 3 × 40 × 41 + 1 = 4921

b. 563 − 553 = 3 × 55 × (55 + 1) + 1 = 3 × 55 × 56 + 1 = 9241

c. 893 − 883 = 3 × 88 × (88 + 1) + 1 = 3 × 88 × 89 + 1 = 23,497

d. 1003 − 993 = 3 × 99 × (99 + 1) + 1 = 3 × 99 × 100 + 1 =

f. 3,97,535 = 5 ×43 × 43 × 43

5397535

4379,507

431849

4343 1

5 is the smallest number by which when 3,97,535 is divided, we get a perfect cube.

Therefore, 3,97,535 ÷ 5 =43 × 43 × 43

79,507 = 433

8. 113 = sum of 11 odd numbers, where the first odd number = 2 × (11 − 1)th triangular number + 1 = 2 × 10th triangular number + 1

Also, 10th triangular number = sum of 10 consecutive numbers

= 2 × (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) + 1

= 2 × 55 + 1 = 111

113 = 111 + 113 + 115 + 117 + 119 + 121 + 123 + 125 +127 + 129 + 131 = 1331

153 = sum of 15 odd numbers, where the first odd number = 2 × (15 − 1)th triangular number + 1 = 2 × 14th triangular number + 1

Also, 14th triangular number = sum of 14 consecutive numbers

= 2 × (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14)

+ 1

= 2 × 105 + 1 = 211

153 = 211 + 213 + 215 + 217 + 219 + 221 + 223 + 225 +227 + 229 + 231 + 233 + 235 + 237 + 239 = 3375

183 = sum of 18 odd numbers, where the first odd number

= 2 × (18 − 1)th triangular number + 1 = 2 × 17th triangular number + 1

Also, 17th triangular number = sum of 17 consecutive numbers

29,701

Word Problems

1. Volume of chocolates = 8 × 10 × 2 = 160 cu. cm, volume of cubical carton = 20 × 20 × 20 = 8000 cu. cm

2.

Number of packs of chocolates = 8000 160 = 50

There are 15 cubes. Side of each cube = 2 cm

Volume of the solid = 2 × 2 × 2 × 15 = 120 cu. cm

No, on rearrangement also, the solid will not be a perfect cube. For this, we need a total of 27 cubes. So, 27 − 15 = 12 more cubes are needed to form a perfect cube. 11B

1.a.

3 8000 = 3 2×2×2×2×2×2×5×5×5

c. 221952

e. 2110592

2.a. 3 32768 97336

= 3 2×2×2×2×2×2×2×2×2×2×2×2×2×2×2 2×2×2×23×23×23

= 32 23×2 = 32 46

b. 3 –21952 132651 = 3 –2×–2×–2×–2×–2×–2×–7×–7×–7 3×3×3×17×17×17

= –28

51

c. 3 125×–2744

= 3 3 –343000=–5×–5×–5×–2×–2×–2×–7×–7×–7 =−70

d. 3 –1728×–6859 = 3 11852352

3 2×2×2×2×2×2×3×3×3×19×19×19 = 228

3.a. 27

27 − 1 = 26 (1 time); 26 − 7 = 19 (2 times); 19 − 19 = 0 (3 times)

So, 3 27 = 3.

b. 216

216 − 1 = 215 (1 time); 215 − 7 = 208 (2 times); 208 − 19 = 189 (3 times)

189 − 37 = 152 (4 times); 152 − 61 = 91 (5 times); 91 − 91 = 0 (6 times)

So, 3 216 = 6.

c. 512

512 − 1 = 511 (1 time); 511 − 7 = 504 (2 times); 504 − 19 = 485 (3 times)

485 − 37 = 448 (4 times); 448 − 61 = 387 (5 times); 387 − 91 = 296 (6 times)

296 − 127 = 169 (7 times); 169 − 169 = 0 (8 times)

So, 3 512 = 8.

d. 1728

1728 − 1 = 1727 (1 time); 1727 − 7 = 1720 (2 times); 1720 − 19 = 1701 (3 times)

1701 − 37 = 1664 (4 times); 1664 − 61 = 1603 (5 times); 1603 − 91 = 1512 (6 times)

1512 − 127 = 1385 (7 times); 1385 − 169 = 1216 (8 times); 1216 − 217 = 999 (9 times)

999 − 271 = 728 (10 times); 728 − 331 = 397 (11 times);

397 − 397 = 0 (12 times)

So, 3 1728 = 12.

e. 1000

1000 − 1 = 999 (1 time); 999 − 7 = 992 (2 times); 992 − 19 = 973 (3 times)

973 − 37 = 936 (4 times); 936 − 61 = 875 (5 times); 875 − 91 = 784 (6 times)

784 − 127 = 657 (7 times); 657 − 169 = 488 (8 times); 488 − 217 = 271 (9 times)

271 − 271 = 0 (10 times)

So, 3 1000 = 10.

f. 1331

1331 − 1 = 1330 (1 time); 1330 − 7 = 1323 (2 times);

1323 − 19 = 1304 (3 times)

1304 − 37 = 1267 (4 times); 1267 − 61 = 1206 (5 times); 1206

− 91 = 1115 (6 times)

1115 − 127 = 988 (7 times); 988 − 169 = 819 (8 times); 819 − 217 = 602 (9 times)

602 − 271 = 331 (10 times); 331 − 331 = 0 (11 times)

So, 3 1331 = 11.

4.a. Volume = 5,92,704 cu. cm

Edge of the cube = 3 volume = 3 592704

= 3 2×2×2×2×2×2×3×3×3×7×7×7

= 2 × 2 × 3 × 7 = 84 cm

b. Volume = 85,184 cu. cm

Edge of the cube = 3 volume = 3 85184

= 3 2×2×2×2×2×2×11×11×11

= 2 × 2 × 11 = 44 cm

c. Volume = 2,38,328 cu. cm

Edge of the cube = 3 volume = 3 238328

= 3 2×2×2×31×31×31 = 2 × 31 = 62 cm

5.a. To find the smallest number, we subtract the odd numbers successively from 408.

408 − 1 = 407 (1 time); 407 − 7 = 400 (2 times); 400 − 19 = 381 (3 times)

381 − 37 = 344 (4 times); 344 − 61 = 283 (5 times); 283 − 91 = 192 (6 times)

192 − 127 = 65 (7 times)

The next number to be subtracted from 65 is 169. But 169 > 65, so 65 must be subtracted from 408 to get a perfect cube. So, 65 is the smallest number that must be subtracted from 408 to get a perfect cube. Now, 408 − 65 = 343.

3 343 = 3 777 = 7

b. To find the smallest number, we subtract the odd numbers successively from 2215.

2215 − 1 = 2214 (1 time); 2214 − 7 = 2207 (2 times); 2207 − 19 = 2188 (3 times)

2188 − 37 = 2151 (4 times); 2151 − 61 = 2090 (5 times); 2090 − 91 = 1999 (6 times)

1999 − 127 = 1872 (7 times); 1872 − 169 = 1703 (8 times); 1703 − 217 = 1486 (9 times)

1486 − 271 = 1215 (10 times); 1215 − 331 = 884 (11 times); 884 − 397 = 487 (12 times)

487 − 469 = 18 (13 times)

The next number to be subtracted from 18 is 547. But 547 > 18, so 18 must be subtracted from 2215 to get a perfect cube.

So, 18 is the smallest number that must be subtracted from 2215 to get a perfect cube.

Now, 2215 − 18 = 2197.

3 2197 = 3 13×13×13 = 13

c. To find the smallest number, we subtract the odd numbers successively from 4150.

4150 − 1 = 4149 (1 time); 4149 − 7 = 4142 (2 times); 4142 − 19 = 4123 (3 times)

4123 − 37 = 4086 (4 times); 4086 − 61 = 4025 (5 times);

4025 − 91 = 3934 (6 times)

3934 − 127 = 3807 (7 times); 3807 − 169 = 3638 (8 times);

3638 − 217 = 3421 (9 times)

3421 − 271 = 3150 (10 times); 3150 − 331 = 2819 (11 times);

2819 − 397 = 2422 (12 times)

2422 − 469 = 1953 (13 times); 1953 − 547 = 1406 (14 times);

1406 − 631 = 775 (15 times)

775 − 721 = 54 (16 times)

The next number to be subtracted from 54 is 817. But 817 > 54, so 54 must be subtracted from 4150 to get a perfect cube.

So, 54 is the smallest number that must be subtracted from 4150 to get a perfect cube.

Now, 4150 − 54 = 4096.

3 4096 = 3 2×2×2×2×2×2×2×2×2×2×2×2

= 2 × 2 × 2 × 2 = 16

d. To find the smallest number, we subtract the odd numbers successively from 1392.

1392 − 1 = 1391 (1 time); 1391 − 7 = 1384 (2 times); 1384 − 19 = 1365 (3 times)

1365 − 37 = 1328 (4 times); 1328 − 61 = 1267 (5 times);

1267 − 91 = 1176 (6 times)

1176 − 127 = 1049 (7 times); 1049 − 169 = 880 (8 times);

880 − 217 = 663 (9 times)

663 − 271 = 392 (10 times); 392 − 331 = 61 (11 times)

The next number to be subtracted from 61 is 397. But 397 > 61, so 61 must be subtracted from 1392 to get a perfect cube.

So, 61 is the smallest number that must be subtracted from 1392 to get a perfect cube.

Now, 1392 − 61 = 1331.

3 1331 = 3 11×11×11 = 11

e. To find the smallest number, we subtract the odd numbers successively from 6893.

6893 − 1 = 6892 (1 time); 6892 − 7 = 6885 (2 times); 6885 − 19 = 6866 (3 times)

6866 − 37 = 6829 (4 times); 6829 − 61 = 6768 (5 times); 6768 − 91 = 6677 (6 times)

6677 − 127 = 6550 (7 times); 6550 − 169 = 6381 (8 times);

6381 − 217 = 6164 (9 times)

6164 − 271 = 5893 (10 times); 5893 − 331 = 5562 (11 times);

5562 − 397 = 5165 (12 times)

5165 − 469 = 4696 (13 times); 4696 − 547 = 4149 (14 times);

4149 − 631 = 3518 (15 times)

3518 − 721 = 2797 (16 times); 2797 − 817 = 1980 (17 times); 1980 − 919 = 1061 (18 times)

1061 − 1027 = 34 (19 times)

The next number to be subtracted from 34 is 1141 But 1141 > 34, so 34 must be subtracted from 6893 to get a perfect cube.

So, 34 is the smallest number that must be subtracted from 6893 to get a perfect cube.

Now, 6893 − 34 = 6859.

3 6859 = 3 19×19×19 = 19

6.a. 720 − 1 = 719 (1 time); 719 − 7 = 712 (2 times); 712 − 19 = 693 (3 times)

693 − 37 = 656 (4 times); 656 − 61 = 595 (5 times); 595 − 91 = 504 (6 times)

504 − 127 = 377 (7 times); 377 − 169 = 208 (8 times)

The next number to be subtracted from 208 is 217. But 217 > 208, so 217 − 208 = 9 must be added to 720 to get a perfect cube.

So, 9 is the smallest number that must be added to 720 to get a perfect cube.

Now, 720 + 9 = 729.

3 729 = 3 9×9×9 = 9

b. 2700 − 1 = 2699 (1 time); 2699 − 7 = 2692 (2 times); 2692 − 19 = 2673 (3 times)

2673 − 37 = 2636 (4 times); 2636 − 61 = 2575 (5 times); 2575 − 91 = 2484 (6 times)

2484 − 127 = 2357 (7 times); 2357 − 169 = 2188 (8 times); 2188 − 217 = 1971 (9 times)

1971 − 271 = 1700 (10 times); 1700 − 331 = 1369 (11 times); 1369 − 397 = 972 (12 times)

972 − 469 = 503 (13 times)

The next number to be subtracted from 503 is 547. But 547 > 503, so 547 − 503 = 44 must be added to 2744 to get a perfect cube.

So, 44 is the smallest number that must be added to 2700 to get a perfect cube.

Now, 2700 + 44 = 2744.

3 2744 = 3 2×2×2×7×7×7 = 14

c. 4021 − 1 = 4020 (1 time); 4020 − 7 = 4013 (2 times); 4013 − 19 = 3994 (3 times)

3994 − 37 = 3957 (4 times); 3957 − 61 = 3896 (5 times); 3896 − 91 = 3805 (6 times)

3805 − 127 = 3678 (7 times); 3678 − 169 = 3509 (8 times); 3509 − 217 = 3292 (9 times)

3292 − 271 = 3021 (10 times); 3021 − 331 = 2690 (11 times); 2690 − 397 = 2293 (12 times)

2293 − 469 = 1824 (13 times); 1824 − 547 = 1277 (14 times); 1277 − 631 = 646 (15 times)

The next number to be subtracted from 646 is 721. But 721 > 646, so 721 − 646 = 75 must be added to 4021 to get a perfect cube.

So, 75 is the smallest number that must be added to 4021 to get a perfect cube.

Now, 4021 + 75 = 4096.

3 4096 = 3 2×2×2×2×2×2×2×2×2×2×2×2

= 2 × 2 × 2 × 2 = 16

d. 9201 − 1 = 9200 (1 time); 9200 − 7 = 9193 (2 times); 9193 − 19 = 9174 (3 times)

9174 − 37 = 9137 (4 times); 9137 − 61 = 9076 (5 times); 9076 − 91 = 8985 (6 times)

8985 − 127 = 8858 (7 times); 8858 − 169 = 8689 (8 times); 8689 − 217 = 8472 (9 times)

8472 − 271 = 8201 (10 times); 8201 − 331 = 7870 (11 times); 7870 − 397 = 7473 (12 times)

7473 − 469 = 7004 (13 times); 7004 − 547 = 6457 (14 times); 6457 − 631 = 5826 (15 times)

5826 − 721 = 5105 (16 times); 5105 − 817 = 4288 (17 times);

4288 − 919 = 3369 (18 times)

3369 − 1027 = 2342 (19 times); 2342 − 1141 = 1201 (20 times)

The next number to be subtracted from 1201 is 1261.

But 1261 > 1201, so 1261 − 1201 = 60 must be added to 9201 to get a perfect cube.

So, 60 is the smallest number that must be added to 9201 to get a perfect cube.

Now, 9201 + 60 = 9261.

3 9261 = 3 3×3×3×7×7×7 = 3 × 7 = 21

e. 5811 − 1 = 5810 (1 time); 5810 − 7 = 5803 (2 times); 5803 − 19 = 5784 (3 times)

5784 − 37 = 5747 (4 times); 5747 − 61 = 5686 (5 times);

5686 − 91 = 5595 (6 times)

5595 − 127 = 5468 (7 times); 5468 − 169 = 5299 (8 times);

5299 − 217 = 5082 (9 times)

5082 − 271 = 4811 (10 times); 4811 − 331 = 4480 (11 times);

4480 − 397 = 4083 (12 times)

4083 − 469 = 3614 (13 times); 3614 − 547 = 3067 (14 times); 3067 − 631 = 2436 (15 times)

2436 − 721 = 1715 (16 times); 1715 − 817 = 898 (17 times)

The next number to be subtracted from 898 is 919.

But 919 > 898, so 919 − 898 = 21 must be added to 5811 to get a perfect cube.

So, 21 is the smallest number that must be added to 5811 to get a perfect cube.

Now, 5811 + 21 = 5832.

3 5832 = 3 2×2×2×3×3×3×3×3×3 = 2 × 3 × 3 = 18

7. Let the three numbers be x, 3x, and 6x.

Sum of their cubes = x3 + (3x)3 + (6x)3 = 15,616

x3 + 27x3 + 216x3 = 15,616

244x3 = 15,616

x3 = 15616 244 = 64

x = 3 64 = 3 4×4×4 = 4

3x = 3 × 4 = 12

6x = 6 × 4 = 24

So, the numbers are 4, 12, and 24.

8. 1*28 is a perfect cube and a 4-digit number.

Using hit and trial method, putting digits 0 to 9 in reverse order in place of ‘*’ and checking if it is a perfect cube.

So, for * = 7, we get 1728 as the 4-digit number.

2 × 3

3

3, a perfect cube = 23 × 23

33 = (2 × 2 × 3)3 = 123

So, the missing digit is 7 and the cube root of 1728 = 12.

Word Problem

1. Volume = 74,088 cu. cm

Length of each side of the cube = 3 volume = 3 74088

= 3 2×2×2×3×3×3×7×7×7

= 2 × 3 × 7 = 42 cm

11C

1.a.

1000

13 = 1      Unit’s digit = 0, its cube = 0    So, the units digit of the cube root of the number = 0

So, tens digit of the cube root of the number = 1

So, 3 1000 = 10.

b.

c.

6859

6 lies between 1 and 8.  Unit’s digit = 9, its cube = 729 (13 = 1, 23 = 8, 1 < 2)    So, the units digit of the cube root of the number = 9

So, tens digit of the cube root of the number = the smaller number = 1

So, 3 6859 = 19.

17576

17 lies between 8 and 27.  Unit’s digit = 6, its cube = 216 (23 = 8, 33 = 27, 2 < 3)     So, the units digit of the cube root of the number = 6

So, tens digit of the cube root of the number = the smaller number = 2

So, 3 17,576 = 26.

d.

35937

35 lies between 27 and 64.  Unit’s digit = 7, its cube = 343

(33 = 27, 43 = 64, 3 < 4)     So, the units digit of the cube root of the number = 3

So, tens digit of the cube root of the number = the smaller number = 3

So, 3 35937 = 33.

e.

79507

79 lies between 64 and 125.  Unit’s digit = 7, its cube = 343 (43 = 64, 53 = 125, 4 < 5)    So, the units digit of the cube root of the number = 3

So, tens digit of the cube root of the number = the smaller number = 4

So, 3 79507 = 43.

2.a.

135651

132 lies between 125 and 216.   Unit’s digit = 1, its cube = 1

(53 = 125, 63 = 216, 5 < 6)      So, the units digit of the cube root of the number = 1

So, tens digit of the cube root of the number = the smaller number = 5

So, 3 132651 = 51

b.

Check: 51 × 51 × 51 = 1,32,651.

140608

140 lies between 125 and 216.   Unit’s digit = 8, its cube = 512

(53 = 125, 63 = 216, 5 < 6)       So, the units digit of the cube root of the number = 2

So, tens digit of the cube root of the number = the smaller number = 5

So, 3 140608 = 52

Check: 52 × 52 × 52 = 1,40,608.

300763

c.

300 lies between 216 and 343.   Unit’s digit = 3, its cube = 27

(63 = 216, 73 = 343, 6 < 7)       So, the units digit of the cube root of the number = 7

So, tens digit of the cube root of the number = the smaller number = 6

So, 3 300763 = 67

d.

Check: 67 × 67 × 67 = 3,00,763.

474552

474 lies between 343 and 512.   Unit’s digit = 2, its cube = 8

(73 = 343, 83 = 512, 7 < 8)       So, the units digit of the cube root of the number = 8

So, tens digit of the cube root of the number = the smaller number = 7

So, 3 474552 = 78

Check: 78 × 78 × 78 = 4,74,552.

3. Volume = 7,78,688 cu. cm

Length of each side of the cube = 3 volume = 3 778688

778688

778 lies between 729 and 1000.   Unit’s digit = 8, its cube = 512

(93 = 729, 103 = 1000, 9 < 10)     So, the units digit of the cube root of the number = 2

So, tens digit of the cube root of the number = the smaller number = 9

So, 3 778688 = 92. Therefore, each side of the cube = 92 cm.

4. 3 15125× X = 55

15125 × X = 553 = 166375

X = 166375 15125 = 11

5. a3 − 41 = 117608

a3 = 117608 + 41 = 117649

a = 3 117649

117649

117 lies between 64 and 125.   Unit’s digit = 9, its cube = 729

(43 = 64, 53 = 125, 4 < 5)      So, the units digit of the cube root of the number = 9

So, tens digit of the cube root of the number = the smaller number = 4

So, 3 117649 = 49. Therefore, a = 49.

Word Problem

1. Volume = 29.791 cu. cm

Length of each side of the cubical box = 3 volume = 3 29.791

= 3 29791 1000 = 3 3 29791 1000 = 3 29791 10

29791

29 lies between 27 and 64.    Unit’s digit = 1, its cube = 1

(33 = 27, 43 = 64, 3 < 4)      So, the units digit of the cube root of the number = 1

So, tens digit of the cube root of the number = the smaller number = 3

So, 3 29791 = 31. Therefore, 3 29791 10 = 31 10 = 3.1

Thus, side of the box = 3.1 cm.

Surface area = 6 × side × side = 6 × 3.1 × 3.1 = 57.66 sq. cm

Chapter Checkup

1.a. (41)3 = 41 × 41 × 41 = 68,921

b. 33 613 1 77 = 13×13×13 7×7×7 = 2197 343

c. 3 2 –9 = –2×–2×–2 9×9×9 = –8 729

d. (84)3 = 84 × 84 × 84 = 5,92,704

e. (9.8)3 = 9.8 × 9.8 × 9.8 = 941.192

f. (3.6)3 = 3.6 × 3.6 × 3.6 = 46.656

2.a. 2830584 2415292 2207646 47103823

1

a perfect cube

= 23 × 473 = (2 × 47)3 = 943

So, 8,30,584 is a cube of 94.

b.

2210000 2105000 252500 226250 313125 54375 5875 5175 535 77 1

c. 2328500 2164250 382125 327375 59125 51825 5365 7373

1

d.

3132651

3. 224500

2,10,000 =2 × 2 × 2× 2 × 3 ×5 × 5 × 5× 5 × 7, not a perfect cube.

3,28,500 = 2 × 2 × 3 × 3 ×5 × 5 × 5 × 73, not a perfect cube.

1,32,651 = 3 × 3 × 3 × 17 × 17 × 17, a perfect cube

= 33 × 173 = (3 × 17)3 = 513

So, 1, 32, 651 is a cube of 51.

24,500 = 2 × 2 ×5 × 5 × 5× 7 × 7 We require one more 2 and 7 to form a triplet of 2 and 7. So, (2 × 7 =) 14 is the smallest number with which when 24500 is multiplied, we get a perfect cube. Therefore, 24,500 × 14 =2 × 2 × 2 ×5 × 5 × 5×7 × 7 × 7

3,43,000 = 23 × 53 × 73 = (2 × 5 × 7)3 = 703 4.

53,45,344 =2 × 2 × 2×2 × 2 × 2×

17 × 17 × 17× 17

17 is the smallest number by which when 53,45,344 is divided, we get a perfect cube.

Therefore, 5345344 ÷ 17 = 2 × 2 × 2

× 2 × 2 × 2 × 17 × 17 × 17

3,14,432 = 23 × 23 × 173 = (2 × 2 × 17)3 = 683

5.a. 133 = sum of 13 odd numbers, where the first odd number = 2 × (13 − 1)th triangular number + 1

= 2 × 12th triangular number + 1

Also, 12th triangular number = sum of 12 consecutive numbers

= 2 × (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12) + 1

= 2 × 78 + 1 = 157

133 = 157 + 159 + 161 + 163 + 165 + 167 + 169 + 171 +173

+ 175 + 177 + 179 + 181 = 2197

b. 13 + 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 + 103 + 113

6.a.

= (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11)2 = 662 = 4356

250 047

250 lies between 216 and 343.   Unit’s digit = 7, its cube = 343

(63 = 216, 73 = 343, 6 < 7)     So, the units digit of the cube root of the number = 3

So, tens digit of the cube root of the number = the smaller number = 6

So, 3 250047 = 63

3250047

383349

327783

39261

33087

31029

7343

749

77

1

b.

729 000

250047 =3 × 3 × 3×3 × 3 × 3

×7 × 7 × 7

3 250047

= 3 3×3×3×3×3×3×7×7×7

729 = 93       Unit’s digit = 0, its cube = 0

So, tens digit of the  So, the units digit of the cube root of the number = 0 cube root of the number = 9

So, 3 729000 = 90

2729000

2364500

2182250

391125

330375

310125

33375

31125

3375

5125

525

55 1

729000

3 729000

=

884 736

c.

884 lies between 729 and 1000.   Unit’s digit = 6, its cube = 216

(93 = 729, 103 = 1000, 9 < 10)     So, the units digit of the cube root of the number = 6

So, tens digit of the cube root of the number = the smaller number = 9

So, 3 884736 = 96

2884736

2442368

2221184

2110592

255296

227648

213824

26912

23456

21728 2864 2432 2216 2108 254 327 39 33 1

884736 =2 × 2 × 2×2 × 2 × 2×2 × 2

× 2×2 × 2 × 2×2 × 2 × 2×3 × 3 × 3

3 884736

= 3 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3

= 2 × 2 × 2 × 2 × 2 × 3 = 96

7.

d.

103 823

103 lies between 64 and 125.   Unit’s digit = 3, its cube = 27

(43 = 64, 53 = 125, 4 < 5)      So, the units digit of the cube root of the number = 7

So, tens digit of the cube root of the number = the smaller number = 4

So, 3 103823 = 47

b. 3 –2744

=

c. 3 40961000000

=

= 3 2×2×2×2×2×2×2×2×2×2×2×2

=

d. 3 10.648 = 3 10648 1000 = 3 3 10648 1000

= 3 3 2×2×2×11×11×11

9. To find the smallest number, we subtract the odd numbers successively from 2789.

2789 − 1 = 2788 (1 time); 2788 − 7 = 2781 (2 times);

2781 − 19 = 2762 (3 times)

2762 − 37 = 2725 (4 times); 2725 − 61 = 2664 (5 times); 2664 − 91 = 2573 (6 times)

2573 − 127 = 2446 (7 times); 2446 − 169 = 2277 (8 times); 2277 − 217 = 2060 (9 times)

2060 − 271 = 1789 (10 times); 1789 − 331 = 1458 (11 times); 1458 − 397 = 1061 (12 times)

1061 − 469 = 592 (13 times); 592 − 547 = 45 (14 times)

The next number to be subtracted from 45 is 631. But 631 > 45, so 45 must be subtracted from 2789 to get a perfect cube. So, 45 is the smallest number that must be subtracted from 2789 to get a perfect cube.

Now, 2789 − 45 = 2744.

3 2744 = 3 2×2×2×7×7×7 = 2 × 7 = 14

10. To find the smallest number, we subtract the odd numbers successively from 4900.

4900 − 1 = 4899 (1 time); 4899 − 7 = 4892 (2 times);

4892 − 19 = 4873 (3 times)

4873 − 37 = 4836 (4 times); 4836 − 61 = 4775 (5 times);

4775 − 91 = 4684 (6 times)

4684 − 127 = 4557 (7 times); 4557 − 169 = 4388 (8 times); 4388 − 217 = 4171 (9 times)

4171 − 271 = 3900 (10 times); 3900 − 331 = 3569 (11 times); 3569 − 397 = 3172 (12 times)

3172 − 469 = 2703 (13 times); 2703 − 547 = 2156 (14 times); 2156 − 631 = 1525 (15 times)

1525 − 721 = 804 (16 times)

The next number to be subtracted from 804 is 817. But 817 > 804, so 817 − 804 = 13 must be added to 4900 to get a perfect cube.

So, 13 is the smallest number that must be added to 4900 to get a perfect cube.

Now, 4900 + 13 = 4913. 3 4913 = 3 17×17×17 = 17

11. Number of cubes in solid 1 = 27 unit cubes, Volume of solid 1 = 27 cu. units

Number of unit cubes in solid 2 = 32 unit cubes, Volume of

solid 2 = 32 cu. units

Difference in the volume = 32 − 27 = 5 cu. units

12. Area = 147 sq. cm

3 × area of square = 147 sq. cm

Area of square = 147 3 = 49 sq. cm = (7)2

Side of square = 7 cm = side of the cube

Volume of 1 cube = 7 × 7 × 7 = 343 cu. cm

Number of cubes = 6

Volume of 6 cubes = 343 × 6 = 2058 cu. cm

Word Problems

1. Side of the cube = 5 cm

Volume of 1 cubical bar= 5 × 5 × 5 = 125 cu. cm

Volume of 25 cubical bars = 125 × 25 = 3125 cu. cm

2. Let the number of students getting prizes be 2x, 3x, 5x.

Product = 2x × 3x × 5x = 30x3 = 2,05,770

x3 = 205770 30 = 6859

x = 3 6859 = 3 19×19×19 = 19

Number of students getting the prize for punctuality = 19 × 2 = 38

Number of students getting the prize for respect = 19 × 3 = 57

Number of students getting the prize for discipline = 19 × 5 = 95

Chapter 12

Let's Warm-up

1. The least preferred colour is red.

2. The most favoured colour is blue

3. The percentage of people who prefer yellow is 17%

4. The percentage of people who like green is 31%

5. The number of people who prefer blue over red are 68

Do It Yourself

12A

1.a. 5656 0.56= ×100%=56% 100100 ⇒

b. 22 0.2= ×100%=20%

c. 1414 0.14= ×100%=14% 100100 ⇒

d. 55 0.5= ×100%=50% 1010

e. 4242 0.42= ×100%=42% 100100

2.a. 13.5 13.5%==0.135 100

b. 45 45%==0.45

c. 120.5 120.5%==1.205

d. 675 675%==6.75

e. 0.5 0.5%==0.005

3.a. 0.4%===0.441

1001000250

b. 0.125%===0.1251251

100100000800

c. 62.56255 62.5% === 10010008

d. 11.5%===11.511523

1001000200

e. 120%==1206 1005

4.a. 210 210% ==21:10 100

b. 2×5+1 1 111 2%=×==11:500 55100500

c. 65.5655131 65.5%====131:200

1001000200

d. 15×5+2 2 177 15%=×==77:500 55100500

e. 0.555511 0.55%====11:2000 10010,0002000

5.a. 60 ×100%=2×100%=200%

30

b. 1 L = 1000 mL

So, 3L = 3000 mL

900 ×100=30%

3000

c. 991÷3×100=××100=60% 553

d. 1 kg = 1000 g

So, 5 kg = 5000 g

1500 ×100=30%

5000

Word Problems

1. Percentage of boys = 35%

Percentage of girls = 100 − 35% = 65%

Number of girls = 650

Let the total number of students be x.

So, 65 650=65% of=× 100 xx

65x

650= 100

65,000 =1000=

65 x

So, there are 1000 students in the school.

2. Marks scored by Samaira out of 500 = 460

Percentage = 460 ×100=92% 500

Marks scored by Mysha out of 450 = 370

Percentage = 370 ×100=82.22% 450

Since, 92%>82.22%

So, Samaira scored better.

3. Let the number be x.

45% of x = 135

45 ×=135

100 x

45x = 13,500 13,500 = 45 x

x = 300

So, the number is 300.

4. Millilitres of yogurt = 20 20% of 500 mL=×500=100 mL 100

There are 100 millilitres of yogurt in her daily smoothie.

5. Number of students who passed the test

= 65 65% of 40=×40=26 100

So, 26 students passed the test.

6. Population = 50,000

Percentage of registered voters = 35%

a. Number of registered voters = 35 ×50,000=17,500 100

b. Number of people who voted in the recent election = 60% of 17,500 = 60 ×17,500=10,500 100

c. The number of voters between 18 and 30 years old = 40 % of 10,500 = 40 ×10,500=4200 100

7. Let the total marks be x

So, 30303 30% ofmarks=×== 10010010 xx x

Passing marks = 45 + 15 = 60

We can write, 3 =60 10 x

3x = 600 600

= 3 x

x = 200

So, the highest number of marks that a student can score in the examination is 200.

8. Let the amount of money he had be x

Percentage of money he left for his: Mother = 20% of x

Sister = 30% of x Wife = 25% of x

Brother = 100-20+30+25%=100–75%=25%of x

25 ×=4500

100 x `

x = ₹18,000

So, the man left ₹18,000.

9. Total number of smartphones = 10,000

a. 15 15% of10,000=×10,000=1500 100 So, 1500 smartphones are defective.

b. 40 40%of1500=×1500=600 100

So, 600 smartphones can be repaired.

c. 60 60%of1500=×1500=900 100

So, 900 smartphones cannot be repaired and are scrapped.

12B

1. Percentage change

= Amount of increase or decrease Original amount × 100%

a. 24–20 4 ×100%=×100%= 20% 20 20

b. 40–3010×100%=×100%=33.33% 30 30

c. 90–5040×100%=×100%=80% 50 50

d. 110–10010×100%=×100%=10%

e. 15–5 10 ×100%=×100%=200% 55

2.a. 30–1515×100%=×100%=50% 30 30

b. 45–2025×100%=×100%=55.55%

45 45

c. 98–88 10 ×100%=×100%=10.20% 98 98

d. 150–10050×100%=×100%=33.33% 150

e. 200–180 20 ×100%=×100%=10%

3.a. 5 80+5% of 80=80+×80=80+4=84

b. 45 180+45% of 180=180+×180=180+81=261

c. 34 34034%of340=340×340=340115.6=224.4 –

d. 25 19025%of190=190×190=19047.5=142.5 –

e. 9 1689%of168=168× 8 168=16815 – .12=152.8

f. 20 80+20% of 80= 80+×80=80+16=96

4.a. 20 190+20% of 190=190+×190 100 =190+38=228 ````

b. 30 150 kg–30%of150 kg=150 kg– 100 ×150 kg=150kg–45kg=105 kg

c. 60 1500+60% of1500=1500+ 100 ×1500=1500+900=2400 ``` ````

d. 12.5 1000 L–12.5%=1000 L–×1000 L 100 =1000 L–125 L= 875 L

e. 0.5 750 grams+0.5%=750 grams+×750 grams 100 =750 grams+3.75 grams=753.75 grams

5. Let the number be x.

Increased by 30%:

10+3 303 13 +×=+== 100101010 xx xx xxx

Then reduced by 20%:

13×10 132013 –×= 101001010×10

xxx xxxx

2×13 13026104 -=–= 10×10100100100

Percentage change = 104 –100 × 100%

104–100 = ×100% 100

41 =×100%=×100%=4% 100 25

x x x xx x x x

6. Original price = ₹250 per litre

New price = 10 250+×250=250+25=275 100 `````

Word Problems

1. Rajat’s score out of 500

In half yearly = 400 In final exams = 430

Percentage increase = 430–400 30 ×100%=×100% 400 400 =7.5%

2. Number of female workers in 2021 = 1200

Number of female workers in 2022

= 12 14400 1200+×1200=1200+=1200+144=1344 100 100

The total number of female workers in 2022 is 1344.

3. Current population = 1,28,000

Population after 1 year

= 5 1,28,000+×1,28,000=1,28,000+6400=1,34,400 100

Population after 2 years

= 5 1,34,400+×1,34,400=1,34,400+6720=1,41,120 100

Population after 3 years

= 5 1,41,120+×1,41,120=1,41,120+7056=1,48,176 100

So, the population of the city after 3 years will be 1,48,176.

4. Present value of the car = ₹3,50,000

Value of the car after one year

= 10 3,50,000–×3,50,000 100

=3,50,000–35,000=3,15,000 `` ```

Value of the car after one year 10 =3,15,000–×3,15,000=3,15,000–31,500 100

=2,83,500 ```` `

So, the value of the car is ₹2,83,500 after two years.

Chapter Checkup

1.a. 5 5:2=×100%=250% 2

b. 3 3:9=×100%=33.33% 9

c. 15 15:120=×100%=12.5% 120

d. 11 11:70=×100%=15.71% 70

e. 80 80:125=×100%=64% 125

2.a. 4 ×100%=16% 25

b. 3×5+4 4 19 3×100%=×100%=×100%=380% 555

c. 3×2+2 28 2×100%=×100%=×100%=266.67% 333

d. 3 ×100%=60%

5

e. 14 ×100%=8.54% 164

3.a. 3 ×100%=0.3% 1000

b. 135 ×100%=135% 100

c. 2789 ×100%=278.9% 1000

d. 166 ×100%=1660% 10

e. 567 ×100%=56.7% 1000

4.a. 123 46%=46×==23:50 10050

b. 16×3+2 2 505011 16%= %=%=×==1:6 33331006

c. 3×5+1 1 16161 3%= %=%=× 5555100 164 ===4:125 500125

d. 17 140%=140×==7:5 1005

e. 119 950%=950×==19:2 1002

5.a. 18181 0.008 ×=×== 10010001001,00,00012,500

b. 2.46×=×==12461246123 100100100100005000

c. 652×==1652163 10010025

d. 33×3+2 2 33%=%=×=1011101 333100300

e. 15×3+2 2 15%==×=47147 333100300

6.a. 1.8 = 0.018 100

b. 0.06 =0.0006 100

c. 5.8 =0.058 100

d. 1×5+2 2 71 1%=%=×=0.014 555100

e. 4×3+1 1 131 4%=%=×=0.04 333100

7.a. 54 ×100%=90% 60

b. 25 ×100%=20% 125

c. 8.5 ×100%=12.14% 70

d. 51.25=1.25×100%=20.83% 46 ⇒

8.a. 551 % of500=××500=6.25 4 4100 ```

b. 1 11 % of 1600 L=××1600 L=2 L 8 8100

c. 25 25% of 120 cm=×120 cm= 30 cm 100

d. 1551 15.5% of 310 kg=××310 kg=48.05 kg 10100

e. 90 90% of 1 L=×1 L= 0.9 L 100

9.a. 215-210 5 ×100%=×100%=2.32% 215 215

b. 86-45 41 ×100%=×100%=91.11% 45 45

c. 530–450 80 ×100%=×100%=17.77% 450 450

d. 250–110 140 ×100%=×100%=127.27% 110 110

10. Total number of children = 600

Number of children who chose vegan meal = 280

Number of children who chose non-vegetarian meal = 120

Number of children who chose vegetarian meal = 600 − (280 + 120) = 600 − 400 = 200

a. Percentage of children who chose vegetarian meal = 200 ×100%=33.33% 600

b. Fraction of children who preferred a vegan meal = 2807 60015

c. Percentage of children who chose non-vegetarian meal = 120 ×100%=20% 600

Word Problems

1. Weight of Ms. Sheela last year = 75 kg

Weight of Ms. Sheela this year = 60 kg

Percentage change = 75–60 ×100%=20% 75

So, the percentage decrease in her weight is 20%.

2. Number of balls in the bag = 450

Number of green balls = 16 16% of450=×450=72 100

Number of blue balls = 24 24% of450=×450=108 100

Number of white balls = 10 10% of450=×450=45 100

Number of red balls = 8 8% of450=×450=36 100

Number of yellow balls = 450–(72+108+45+36) =450–261=189

So, there are 72 green balls, 108 blue balls, 45 white balls, 36 red balls, and 189 yellow balls.

3. Let the total number of students be x

Percentage of boys = 65%

Number of boys = 6513 ×= 10020 x x

Number of girls = 700

13 =+700 20 x x 13+14,000

= 20 x x

20=13+14,000 xx

20–13=14,000 xx

7x = 14,000

x = 2000

So, there are 2000 students.

4. Present value ₹9,00,000.

Value after 1 year = 30 9,00,000–×9,00,000 100

=9,00,000–2,70,000=6,30,000 `` ```

Value after 2 years = 30 6,30,000–×6,30,000 100

=6,30,000–1,89,000=4,41,000 `` ```

So, the value of the car after two years is ₹4,41,000.

5. Passing percentage = 35%

Passing marks = 70 + 35 = 105

Let the total marks be x

Then, 35 ×=105

100 x

35x = 10,500 10500 = 35 x

x = 300

So, the maximum marks are 300.

6. Percentage of sand = 3 30% 4

Percentage of gravel = 1 45% 4

Weight of the sand = 8.7 kg

Let the weight of the mixture be x kg

3 30%of8.7 4 x kg

30×4+3 123 %of=%of =8.7 44 xx

123 ×=8.7

400 x

x = 28.29 kg

Let the weight of the mixture be y kg

Weight of the cement = 3.5 kg

Percentage of cement = 31 100–30+45% 44

=100–(30+45)++31 44 =100–76%=24%

So, 24% of y = 3.5 24 ×=3.5 100 y

y = 14.58 kg

7. Let the price of diesel be ₹x and its consumption be y. Then, expenditure = Price × Consumption

⇒ Expenditure = ₹xy

`` `

x xxx x x

Since, the price of the diesel increases by 60%, Then, increased price = 60 +60% of =+ 100 160 ==1.6 100

Expenditure remains the same = ₹xy

` `

xyy yy

Reduced consumption = Expenditure == Price1.6x1.6 105 == 168

yy y y

Reduction in consumption = 5 –3 8 ×100%=×100% 8 1 =37% 2

8. Number of students in the school who are eligible to vote = 600

Percentage of students who casted their vote = 70%

a. Number of votes = 70 ×600=420 100

b. Number of the total students who voted for Alex 40 =×420 = 168 100

Percentage of the total students who voted for Alex 168 =×100=28% 600

c. Number of votes Sarah got = 60 60%of420=×420 100 =252

9. Percentage reduction in price = 25%

New price = 300 =150 2 ` ` per kg

a. Let the original price be ₹x

Percentage change = Old price–new price =25% oldprice –150 25 = 100 x x 100–15,000=25 xx

75x = 15,000 15000 ==200 75 x `

b. Reduced price = old price − new price =₹200 − ₹150 = ₹50

10. Let the man’s monthly salary be x.

Salary spent on the house rent = 20 20% of =× 100 20 == 1005

xx xx

Remaining salary = 5– 4 –== 555 xx xx x

40% of the remainder 44048 =40% of =×= 5100525 xxx

Salary left = ₹9600.

So,

48=+9600 525 xx

2.a. CP = SP − P ⇒ ₹572 − ₹72 = ₹500

b. SP = CP + P = ₹7282 + ₹208 = ₹7490

c. SP = CP − L = ₹9684 − ₹684 = ₹9000

d. CP = SP − P = ₹1973 − ₹273 = ₹1700

e. SP = CP − L = ₹6,76,000 − ₹18,500 = ₹6,57,500

f. CP = SP + L = ₹7894 + ₹306 = ₹8200

3. CP for the retailer = ₹4500

SP = ₹6000; since SP > CP; profit is earned.

P = SP − CP = ₹6000 − ₹4500 = ₹1500

P% = 1500 ×100%=33.33% 4500

4. CP = ₹1,25,000, P = ₹5000

P% = 5000 ×100%=4% 125000

5. CP of 100 books = ₹1500

Books discarded = 5

SP of 95 books = ₹1710

Since SP > CP, profit is earned.

P = ₹1710 − ₹1500 = ₹210

P% = 210 ×100%=14% 1500

6. SP= ₹56,320; L% = 12%

CP = 100100×=×56,320=64,000 100–% 100–12 SP L ``

7. CP of 5 oranges = ₹40 ⇒ CP of one orange = ₹8

SP of one orange = ₹9; P = ₹9 − ₹8 = ₹1

P% = 1 ×100%=12.5%

8 Word Problems

1. CP of the car = ₹4,46,000; SP = ₹5,20,000

Since, SP > CP; profit = ₹5,20,000 − ₹4,46,000 = ₹74,000

2. SP of the saree = ₹1700, CP = ₹2000; L = ₹2000 − ₹1700 = ₹300

3. CP of the bluetooth speaker = ₹14,500; SP = ₹14,000

Since CP > SP, loss is made; L = ₹14,500 − ₹14,000 = ₹500

48–=9600

525 xx

L% = 500 ×100%=×100%=3.45% 14,500 Loss CP

4. SP of the bicycle = ₹819; L = 9%

12 =9600

25 x

x= ₹20,000

So, the man’s monthly salary is ₹20,000.

Chapter 13

Let's Warm-up

1. The cost price of the bed is ₹25,000.

2. The selling price of the bed is ₹27,000.

3. The selling price of the mattress is ₹9000.

4. The profit earned on the sale of the bed is ₹2000.

5. The loss incurred on the sale of the mattress is ₹1000.

Do It Yourself 13A

1. CP = ₹40,000

a. SP = ₹35,000; since CP>SP, loss is incurred. Loss = ₹40,000 − ₹35,000 = ₹5000

b. SP = ₹42,000; since SP > CP, profit is earned

Profit = ₹42,000 − ₹40,000 = ₹2000

c. SP = ₹38,000; since CP > SP, loss is incurred.

Loss = ₹40,000 − ₹38,000 = ₹2000

d. SP = ₹45,000; since SP>CP, profit is earned

Profit = ₹45,000 − ₹40,000 = ₹5000

CP = 100 100–9 ×₹819 = ₹900

SP for a profit of 5% = 100+5 ×900=945 100 `

5. Watch 1: SP = ₹1200; P% = 20

Watch 1: CP = 100 ×1200=1000 100+20 `

Watch 2: SP = ₹1200; L% = 20

Watch 2: CP = 100 ×1200=1500 100–20 `

Total CP = 1000+1500=2500 ```

Total SP = ₹1200 + ₹1200 = ₹2400

Since CP > SP, loss is incurred; L = ₹2500 − ₹2400 = ₹100

L% = 100 ×100%=×100%=4% 2500 Loss CP

6. Let the CP of the necklace be x. Profit earned by Madhuri = 7%

Profit percent earned had she sold the jewelry for ₹2940 more = 10%

⇒ Difference in profit percent = 10% − 7% = 3%

Since profit is earned on the CP, 3% of x = ₹2940

100 =2940×=98,000 3 x ``

7. Profit = 5% = 0.05CP; SP = CP + 0.05CP =1.05CP

Loss if the coat was sold for ₹1650 less = 5%

Hence, SP = CP − 0.05CP = 0.95CP

According to question, 1.05CP − 0.95CP = 0.10 of CP = ₹1650

0.10 CP = ₹1650

CP = 100 1650×=16,500 10 ``

13B

1. Given, MP = ₹4000

a. Discount = 25%; discount = 25 4000×= 100 ₹1000

Selling Price = Marked Price − Discount = 4000 − 1000 = ₹3000

b. Discount = 20%; discount = 20 4000×= 100 ₹800

SP = MP − Discount = 4000 − 800 = ₹3200

c. Discount = 12 1 2 % = 25 % 2 ; discount = 25 4000×=500 2×100 `

SP = MP − Discount = 4000 − 500 = ₹3500

d. Discount = 10%; Discount = 10 4000×=400 100 `

SP = MP − Discount = 4000 − 400 = ₹3600

2. MP of the washing machine = ₹14,500; SP = ₹13,775

Discount = ₹14,500 − ₹13,775 = ₹725

Percentage discount = 725 ×100%=5% 14,500 ` `

3. SP of the dining table = ₹16,000; discount = 20%

MP = 100 16,000×= 100-20 ` ₹20,000

4. MP = ₹900, Discount = ₹175

SP = ₹900 − ₹175 = ₹725

5. SP of the trousers = ₹7500; discount offered = ₹500

MP = ₹7500 + ₹500 = ₹8000

Percentage discount = 500 ×100%= 8000 ` ` 6.25%

6 Total discount offered = ₹78 + ₹24 = ₹102; MP = ₹702

SP = ₹702 − ₹102 = ₹600

7. Let the MP of the article = 100; first Discount = 25% of ₹100 = ₹25;

SP after the first successive discount = ₹100 − ₹25 = ₹75

Second discount = 12% of reduced price = 12% of ₹75= ₹9

SP after the second successive discount = ₹75 − ₹9 = ₹66

Total Discount (x) = ₹100 − ₹66 = ₹34

Discount % = 34 ×100%=34% 100

8. SP = ₹51,000; discount offered = 15%

Discount % = 51,000 ×100%=60,000 100–15 `

9. Let the marked price of the coat be ₹100.

First discount = 12% of MP = 12% of 100 = ₹12

SP after the first discount = ₹100 − ₹12 = ₹88

Second discount = 10% of ₹88 = ₹8.8

SP after the second discount = ₹88 − ₹8.8 = ₹79.2

For the selling price to be ₹79.2, the MP must be ₹100. For the selling price to be ₹7920, the MP must be = 7920 ×100=10,000 79.2 `

10. CP of the article = ₹850; P = 12% = 12 ×850=102 100 `

SP = ₹850 + ₹102 = ₹952

Discount offered = ₹200; MP = ₹952 + ₹200 = ₹1152

11. MP of the article = ₹9000; discount offered = 20%

= 20 ×9000=1800 100 `

SP = ₹9000 − ₹1800 = ₹7200

Profit earned = 20%

CP = 100 ×7200=6000 100 +20 `

Word Problems

1. MP of the article = ₹17,800

Discount offered = 25% = 25 ×17,800=4450 100 `

SP = ₹17,800 − 445013,350``

2. Given, CP of the dining table = ₹15,000; MP = ₹18,000

Loss incurred = 8% = 8 ×15,000=1200 100 `

SP = CP − Loss = ₹15,000 − ₹1200 = ₹13,800

Discount = ₹18,000 − ₹13,800 = ₹4200

% Discount = 4200 ×100=23.33% 18,000

3. Let the CP be ₹100.

MP = 32% of ₹100 = ₹32

Profit to be gained = 10% of ₹100 = ₹10

SP = ₹100 + ₹10 = ₹110

Discount = ₹132 − ₹110 = ₹22

% discount = 22 ×100%=16.66% 132

4. Let the MP of the goods be ₹100

First discount = 15% of ₹100 = 15 ×100=15 100 ``

SP after the first discount = ₹100 − ₹15 = ₹85

Second discount = 10% of reduced price = 10 ×85=8.5 100 ``

SP after the second discount = ₹85 − ₹8.5 = ₹76.5

Total discount = ₹100 − ₹76.5 = ₹23.5

% discount = 23.5 ×100%=23.5% 100

13C

1. SP of computer ₹38,000; SP of printer ₹8,000

Total SP = ₹38,000 + ₹8,000 = ₹46,000

Rate of sales tax = 7%

Sales tax = 7 ×46,000=3220 100 `

Total amount paid = ₹46,000 + ₹3220 = ₹49,220

2. Price of the harmonium including VAT = ₹17,280

Rate of VAT = 8% of SP

Let the SP be ₹100, VAT = 8 ×100=8 100 `

SP including VAT = ₹100 + ₹8 = ₹108

SP of the harmonium = 17,280 ×100= 108 ` ₹16,000

3. Let the SP of the refrigerator be x.

According to the question, 9 ×=1170 100 x

x = ₹13,000

4. MP = ₹5000; Discount = 10% of ₹5000 = ₹500

SP = ₹5000 − ₹500 = ₹4500

Tax applied = 10% of SP = 10 ×4500=450 100 `

Amount paid = ₹4500 + ₹450 = ₹4950

5. SP including VAT = ₹19,610

VAT = 6% of SP

Let the SP be ₹100, then SP including VAT = ₹106

Actual SP (original price) = 19,610 ×100=18,500 106 ` `

6. SP of the soap including VAT = ₹6.36; VAT = 6% of SP

Let the SP be ₹100, VAT = 6 ×100=6 100 ``

SP including VAT = ₹106

Actual SP (original price) = 6.36 ×100=6 106 ` `

Profit earned = 20% of CP

CP = 100 ×6=5 100+20 `

7. SP of the vacuum cleaner = ₹8000

GST = 18%

Amount Manohar should give to the shopkeeper

= 100+18 8000×=9440 100 `

Word Problem

1. Bill amount for Renu ₹16,240

GST 12%

SP before GST 100 16,240×=14,500 100+12 `

Chapter Checkup

1.a. Given, SP = ₹8064, P = ₹864

CP = SP − P = ₹8064 − ₹864 = ₹7200

P% = 864 ×100%=12% 7200

b. Given, CP = ₹6800, P = ₹476

SP = CP + P = ₹6800 + ₹476 = ₹7276

P% = 476 ×100%=7% 6800

c. Given, SP = ₹8250, P = ₹750

CP = SP − P = ₹8250 − ₹750 = ₹7500

P% = 750 ×100%=10% 7500

2.a. Given, CP = ₹460, SP = ₹437

L = CP−SP = ₹460 − ₹437 = ₹23

L% = 23 ×100%=5% 460

b. Given, SP = ₹468, L = ₹52

CP = SP+L = ₹468 + ₹52 = ₹520

L% = 52 ×100%=10% 520

c. Given, CP = ₹6400, L = ₹192

SP = CP −L = ₹6400 − ₹192 = ₹6208

L% = 192 ×100%=3% 6400

3.a. Given, MP = ₹625; SP = ₹525

Discount = MP − SP = ₹625 − ₹525 = ₹100

b. Given, MP = ₹1780, discount = 15% = 15 ×1780=267 100 `

SP = MP − Discount = ₹1780 − ₹267 = ₹1513

4. Let the CP of 1 pencil be ₹x

CP of 10 pencils = ₹10x

Given, SP of 10 pencils = CP of 15 pencils = ₹15x

Profit = ₹15x − ₹10x = ₹5x

Profit % = 5 ×100%=50% 10 x x

5. Let the CP be ₹100. Then, MP = ₹125

MP of the television = ₹12,000

CP = 100 12,000×=9600 125 `

Given, discount offered = 10% on MP = 10 ×12,000=1200 100 `

SP = MP − Discount = ₹12,000 − ₹1200 = ₹10,800

Profit = ₹10,800 − ₹9600 = ₹1200

Profit percent = 1200 ×100%=12.5% 9600

6. Let the MP be ₹100

First discount = 20% of ₹100 = 20 ×100=20 100 ``

SP after first discount = ₹100 − ₹20 = ₹80

Second discount = 5% of reduced price = 5 ×80=4 100 ``

SP after second discount = ₹80 − ₹4 = ₹76

Total discount = ₹100 − ₹76 = ₹24

% discount = 19 ×100%=24% 100

7. Given, SP of the refrigerator = ₹27,500; GST = 18%

GST = 18 ×27,500=4950 100 ``

Bill amount = SP + GST = ₹27,500 + ₹4950 = ₹32,450

8. Given, CP of notebooks per dozen = ₹72

CP of one notebook = ₹6

SP of a packet of 5 notebooks = ₹25

SP of one notebook = ₹5

Since, CP>SP; loss is incurred.

Loss per notebook = ₹6−₹5 = ₹1

9. CP of 200 litres of oil = ₹12,000

Amount spent on packaging and transport = ₹2000 + ₹6000 = ₹8000

Total cost to the businessman = ₹12,000 + ₹8000 = ₹20,000

SP of 1 litre oil = ₹120

SP for 200 litres = ₹24,000

Since SP >CP, profit is earned.

Profit = ₹24,000 − ₹20,000 = ₹4000

Profit % = 4000 ×100%=20% 20,000

10. MP of the TV set = ₹45,000; discount offered = 15% of MP

Discount = 15 ×45,000=6750 100 `

SP = ₹45,000 − ₹6750 = ₹38,250

Sales tax applied = 12% on SP = 12 ×38,250=4590 100 `

Total bill amount = ₹38,250 + ₹4590 = ₹42,840

Word Problems

1. SP of the sofa = ₹3210; Profit = 7% on CP.

Let the CP be ₹100, then P = ₹107

CP of the sofa = 3210 ×100=3000 107 `

If SP = ₹3360, P = ₹3360 − ₹3000 = ₹360

360 %=×100%= 3000 P 12%

2. Purchase price of the car for Ajay = ₹5,20,350

Overhead expenses on car = ₹2500 + ₹15,000 = ₹17,500

Total cost to Ajay = ₹5,20,350 + ₹17,500 = ₹5,37,850

Profit made = 14% on CP = 14 ×5,37,850=75,299 100 `

SP of the car = ₹5,37,850 + 75,299=` ₹6,13,149

3. MP of a pair of gloves, a jacket, and a sweater = ₹186 + ₹839 + ₹345 = ₹1370

Discount offered = 20% on MP = 20 ×1370=274 100 `

Bill amount = ₹1370 − 274=1096``

4. Price of the watch including VAT = ₹1980

VAT = 10%

Let the SP be ₹100, then SP including VAT will be ₹110

SP of the watch (original price) = 100 1980×=1800 110 `

Chapter 14

Let's Warm-up

1.

2.

3.

4.

5. 12% of ₹3000 ₹200

Do It Yourself 14A

1.a. Amount = Principal + Interest

₹6240 = ₹5780 + Interest

Interest = ₹6240 − ₹5780 = ₹460

b. Amount = Principal + Interest

Amount = ₹3520 + ₹250 = ₹3770

c. Amount = Principal + Interest

₹972 = ₹850 + Interest

₹972 − ₹850 = Interest

₹122 = Interest.

d. Amount = Principal + Interest

Amount = ₹9450 + ₹550 = ₹10,000

e. Amount = Principal + Interest

₹672 = Principal + ₹72

₹672 − ₹72 = Principal

₹600 = Principal

f. Amount = Principal + Interest

₹7288 = Principal + ₹1233

₹7288 − ₹1233 = Principal

₹6055 = Principal

2.a. P = ₹800; R = 3.5% p.a.; T = 4 years

SI = ××800×3.5×4 100100 PRT = = ₹112

A = P + SI = ₹800 + ₹112 = ₹912

b. P = ₹4750; R = 1 12 2 % p.a.; T = 2 years

SI = 1 4750×12×2 ×× 2 100 100 PRT = = ₹1187.5

A = P + SI = ₹4750 + ₹1187.5 = ₹5937.5

c. P = ₹160; R = 10% p.a.; T = 1 2 years

SI = 1 160×10× ×× 2 100100 PRT = = ₹8

A = P + SI = ₹160 + ₹8 = ₹168

d. P = ₹8500; R = 8.5% p.a.; T = 1 year

SI = ××8500×8.5×1 100100 PRT = = ₹722.5

A = P + SI = ₹8500 + ₹722.5 = ₹9222.5

e. P = ₹9600; R = 8% p.a.; T = 3 months

SI = 3 9600×8× ×× 12 100100 PRT = = ₹192

A = P + SI = ₹9600 + ₹192 = ₹9792

3.a. R = 4% p.a.; T = 73 days = 73 365 years

SI = ₹60 = ×× 100 PRT 73 ×4× 365 60 100 P = , 60×100×365 =7500 4×73 P = `

b. R = 5% p.a.; T = 3 years; SI = ₹57

SI = ×× ×5×3 57 100 100 PRTP =

= 57×100 5×3 P = P = ₹380

c. R = 7% p.a.; T = 5 years; SI = ₹904

SI = ×× ×7×5 904 100 100 PRTP = 904×100 7×5 P =

P = ₹2582.85

4.a. A = P + SI

₹8325 = ₹7500 + SI

₹8325 − ₹7500 = SI ₹825 = SI

So, the simple interest is ₹825.

SI = ×× 100 PRT

7500××2 825= 100 R

825×100

× 7500×2 R

R = 5.5% Thus, the rate of interest is 5.5% p.a.

b. A = P + SI

₹21,800 = ₹20,000 + SI

₹21,800 − ₹20,000 = SI

₹1800 = SI

So, the simple interest is ₹1800.

SI = ×× 100 PRT

20,000××2 1800× 100 R

1800×100 = 20,000×2 R

R = 4.5% Thus, the rate of interest is 4.5% p.a.

c. A = P + SI

₹641.25 = ₹625 + SI

₹641.25 − ₹625 = SI

₹16.25 = SI

So, the simple interest is ₹16.25.

SI = ×× 100 PRT

16.25= 100 R

146

625×× 365

16.25×100×365 = 625×146 R

R = 6.5%

Thus, the rate of interest is 6.5% p.a.

5.a. SI = ×× 100 PRT

4800×7.5×

900= 100 T ⇒ 900×100 = 4800×7.5 T

T = 2.5 years. So, the time is 2.5 years.

b. SI = ×× 100 PRT

3500×5×

700= 100 T ⇒ 700×100 = 3500×5 T

T = 4 years. So, the time is 4 years.

c. SI = ×× 100 PRT

500×12.5× 31.25= 100 T ⇒ 31.25×100 = 500×12.5 T

T = 0.5 years or 6 months. So, the time is 0.5 years.

d. SI = ×× 100 PRT

600×3.5× 12.60= 100 T ⇒ 12.60×100 = 600×3.5 T

T = 0.6 years. So, the time is 0.6 years.

6.a. P = ₹450; R = 7% p.a.; T = 5 years

A = 1+ 100 RT P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 4501+=4507×5135 100100 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø = ₹607.5

b. P = ₹5000; R = 10% p.a.; T = 3 years

A = 1+ 100 RT P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 10×3 50001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 130 5000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹6500

c. P = ₹3200; R = 7.5% p.a.; T = 2 years

A = 1+ 100 RT P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 3200 7.5×2 1+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 115 3200 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹3680

d. P = ₹720; R = 8.5% p.a.; T = 3 years

A = 1+ 100 RT P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 720 8.5×3 1+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ èø = 125.5 720× 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹903.6

7.a. P = ₹4000, A = ₹5400, T = 5 years, R = ?

SI = A − P = ₹5400 − ₹4000 = ₹1400

SI = ×× 100 PRT

4000××5 1400= 100 R

1400×100 = 4000×5 R

R = 7% p.a. So, the rate of interest is 7% p.a. When P = ₹5600, T = 3 years, R = 7% p.a., A = ?

SI = ××5600×7×3 = 100100 PRT = ₹1176

A = ₹5600 + ₹1176 = ₹6776

8. P = ₹3650, R = 10% p.a., T = 3 Jan 2016 to 17 Mar 2016 = 29 days of January + 29 days of February (since 2016 is a leap year) + 17 days of March = 75 days

SI = ××3650×10×75 = 100100×366 PRT = ₹74.79

9. We know that amount in 2 years = ₹4400

Amount in 3 years = ₹4600

Interest earned in 1 year = ₹4600 − ₹4400 = ₹200

So, interest earned in 2 years will be = ₹200 × 2 = ₹400

Since Principal = Amount − Interest = ₹4400 − ₹400

= ₹4000

Since Simpe Interest = ×× 100 PRT

4000××1 200= 100 R

200×100 = 4000 R

R = 5%

Hence, principal is ₹4000, and the rate of interest is 5% p.a. 10.

a. Yes, if we extend the line backwars, it will pass through the origin (0, 0).

b. Interest on ₹2500 for a year is ₹200.

c. To get interest of ₹280, we should deposit ₹3500 for a year.

Word Problems

1. P = ₹8000, R = 12% p.a., T = 9 12 years

SI = ××8000×12×9 = 100100×12 PRT = ₹720

So, the interest received by Savita is ₹720.

A = P + SI = ₹8000 + ₹720 = ₹8720

So, Savita collected ₹8720 from the bank.

2. R = 8% p.a., T = 4 years, A = ₹9900, P = ?

A = P + SI, =+ 100 PRT AP , =1+ 100 RT AP æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

84

9900=1+ 100 × P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø ; 100+32 9900= 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

9900×100 = 132 P

Principal = ₹7500.

So, the amount borrowed by Kanchan originally was ₹7500.

3. P = ₹3200, R = 6% p.a., A = ₹3680, T = ?

SI = A − P = ₹3680 − ₹3200 = ₹480

SI = 100 PRT

3200×6×

480= 100 T

480100

32006 T =

T = 2.5 years. So, Suresh used Narendra’s money for 2.5 years.

4. A = ₹6720, P = ₹6000, T = 1 year and 6 months = 1.5 years, R = ?

SI = A − P = ₹6720 − ₹6000 = ₹720

SI = 100 PRT

720= 100 R

6000××1.5

720×100 = 6000×1.5 R

R = 8% p.a.

So, the rate of interest charged by the bank is 8% p.a.

5. Principal invested by A = ₹12,000, T = 4 years, Interest = ₹3840, Rate of interest =?

SI = 100 PRT

12000××4 3840= 100 R

3840×100 = 12000×4 R

R = 8% p.a.

New rate of interest = 8 + 2 = 10%

Amount = Principal + Simple Interest = 12000 + 12000×10×4 100 = 12,000 + 4800 = ₹16,800

So, the amount A would receive after the increase in the rate of interest is ₹16,800.

14B

1. P = ₹2500, T = 2 years, R = 10% p.a.

SI = 2500×10×2 = 100100 PRT = ₹500

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 10 25001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 2 110 2500 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹3025

CI = A − P = ₹3025 − ₹2500 = ₹525

Difference = CI − SI = ₹525 − ₹500 = ₹25

2. P = ₹1600, T = 5 years, R = 6% p.a.

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 5 6 16001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 5 106 1600 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹2,141.16

CI = A − P = ₹2,141.16 − ₹1600 = ₹541.16

3. SI = ₹9000, T = 2 years, R = 6% p.a., CI = ?

SI = 100 PRT

9000= 100 P

×6×2

P = ₹75,000

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 6 75,0001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹84,270

CI = A − P = ₹84,270 − ₹75,000 = ₹9270

4. A = ₹4410, T = 2 years, R = 5% p.a., Principal = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

₹4410 = 2 5 1+ 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

₹4410 = 2 105 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

P =₹4000

5. P = ₹8000, A = ₹8820, T = 6 months = 61 = 122 year, R = ?

Since, the interest is compounded quarterly, we will use the formula, amount = 4 1+ 400 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

₹8820 = 1 4× 2 80001+ 400 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø 2 8820 =1+ 8000400 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø 2 441 =1+ 400400 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

Taking square roots on both the sides, we get, 21 =1+ 20400 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

21 –1= 20400 R

1 = 20400 R

R = 400 =20% 20 p.a.

6. P= ₹60,000, A = ₹69,457.50, R = 5% p.a., T =?

=1+ 100 n R AP æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

5 69,457.50=60,0001+ 100 næö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

69,457.50105 = 60,000100 næö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

1.157625 = 1.05 n 3 1.05=1.05 n

Therefore, n = 3 years

Word Problems

1. P = ₹25,000, R = 8.5% p.a., T = 3 years, A =?

=1+ 100 n R AP æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

3 8.5 =25,0001+ 100 A æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

3 108.5 =25,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

=₹31,932.23

2. Principal borrowed by Yogesh = ₹30,000, R = 12% p.a., T = 4 years

Amount to be paid by Yogesh to Navin after 4 years

= 1+ 100 RT P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 12×4 30,0001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 148 30,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹44,400

Amount to be received by Yogesh from Akash after 4 years

= 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 4 12 30,0001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 4 112 30,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹47,205.58

Amount gained by Yogesh = ₹47,205.58 − ₹44,400 = ₹2805.58

3. P = ₹6400, T = 3 years, R = 1 7% 2 p.a. compounded half yearly, A = ?

A = 2 1+ 200 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2×3 7.5 64001+ 200 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 6 207.5 6400 200 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹7981.94

4. P = ₹18,000, R = 16% p.a. compounded quarterly, T = 1 1 4 years = 5 4 years, A =?

A = 4 1+ 400 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 5 4 4 16 18,0001 400 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 5 416 18,000 400 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 5 104 18,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 5 18,0001.04 = ₹21,899.75

5. P = 1,80,000, R for the first year = 8.5%, R for the second year = 7.5%, R for the third year = 7%, T = 3 years, amount after three years =?

Amount after the first year = 1 8.5 1,80,0001 1,95,300 100 æö ÷ ç ÷ ç = ÷ ç ÷ ç ÷ ç èø ` = `1,95,300

Amount after the second year

= 1 7.5 1,95,3001 2,09,947.5 100 æö ÷ ç ÷ ç = ÷ ç ÷ ç ÷ ç èø `

Amount after the third year

= 1 7 2,09,947.51 2,24,643.825 100 æö ÷ ç ÷ ç = ÷ ç ÷ ç ÷ ç èø `

Amount to be paid after three years = ₹2,24,643.825

6. A = ₹79,860, T = 3 years, R = 10% p.a. compounded annually, P = ?

1 100 n R AP æö ÷ ç ÷ ç = ÷ ç ÷ ç ÷ ç èø

3 10 79,8601 100 P æö ÷ ç ÷ ç = ÷ ç ÷ ç ÷ ç èø

3 110 79,860 100 P æö ÷ ç ÷ ç = ÷ ç ÷ ç ÷ ç èø

P = ₹60,000

14C

1. Present population (P) = 12,50,000, rate of increase (R) = 10%, time (t) = 4 years

Population after four years = 4 10 12500001 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 4 110 1250000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 18,30,125

2. P = 90,000, R = 7%, t = 2 years

Population after two years = 2 7 900001 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 107 90000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 1,03,041

3. Present price of the plot = ₹2,00,000, rate of appreciation = 5%, t = 3 years

Expected price after 3 years = 3 5 2,00,0001 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 3 105 2,00,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹2,31,525

4. Cost of the car = ₹2,50,000, rate of depreciation = 10%, t = 3 years

Worth of the car after three years = 3 10 2,50,0001 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 3 90 2,50,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹1,82,250

5. Cost of the computer = ₹60,000, rate of depreciation = 40%, t = 2 years

Price of the computer after two years

= 2 60 60,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹21,600

6. Production in 2017 = 15,625 units, rate of increase in production = 4% per year, t = 3 years

Production in 2020 = 3 4 15,6251+ 100 æö

= 3 104 15,625 100 æö

ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 17,576 units

7. Purchase price of a refrigerator = ₹45,000, rate of depreciation = 3% p.a., t = 3 years

Value of the refrigerator after three years

= 3 97 45,000 100 æö

= ₹41,070.285

8. Cost of an antique vase = ₹2500, rate of appreciation = 6% per year, t = 3 years

Price of the antique vase after three years =

106 2500

ç èø = ₹2977.54

9. Current cost of a mobile phone = ₹20,000, rate of depreciation = 6% per year, t = 4 years

Price of the mobile phone after 4 years =

= 4 94 20,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹15,614.97

6 20,0001–100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

10. Current fare for a certain route of a bus = ₹5, rate of increase in fare = 10%, t = 2 years

Fare after 2 years = 2 10 51+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 110 5 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹6.05

11. Cost of a residential flat = ₹10,00,000, rate of appreciation = 10% per year, t = 4 years

Value of the flat after 4 years = 4 10 10,00,0001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 4 110 10,00,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹14,64,100

12. Current population of bacteria = 4,50,000, Rate of growth = 3% per hour, t = 2 hours

Population of bacteria at the end of two hours

= 2 3 4,50,0001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 103 4,50,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 4,77,405

13.  Value of a constructed house two years ago = ₹1,60,000, value of a constructed house after two years = ₹2,30,400, t = 2 years, rate of appreciation =?

2,30,400 = 2 1,60,0001+ 100 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2,30,400 =1+ 1,60,000100 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø 2

2

1.44=1+ 100 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø Taking square roots on both sides, we get,

1.2=1+ 100 R

1.2–1= 100 R

0.2= 100 R

=20% R per year

14. Present value of Ajay’s car = ₹3,88,800, rate of depreciation = 10% p.a., t = 2 years, purchase price of the car two years ago (P) =?

3,88,800=1–100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2 10

2 90 3,88,800= 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ èø 388800×100×100 90×90 P = = ₹4,80,000

Chapter Checkup

1.a. P = ₹10,000, R = 12% p.a., T = 3.25 years

SI = ×× 100 PRT = 10000×12×3.25 100 = ₹3900

A = P + SI = ₹10,000 + ₹3900 = ₹13,900

b. P = ₹560, R = 4% p.a., T = 73 days = 73 365 years

SI = ×× 100 PRT = 560×4×73 100×365 = ₹4.48

A = P + SI = ₹560 + ₹4.48 = ₹564.48

c. P = ₹2700, R = 9% p.a., T = 146 days = 146 365 years

SI = ×× 100 PRT = 2700×9×146 100×365 = ₹97.2

A = P + SI = ₹2700 + ₹97.2 = ₹2797.2

2.a. SI = ₹4.50, T = 5 months = 5 12 years, R = 4.5% p.a., P = ?

SI = ×× 100 PRT

4.50 = ×4.5×5 100×12 P

4.50×100×12 = 4.5×5 P

P = ₹240

b. SI = ₹392, T = 3.5 years, R = 3.5% p.a., P = ?

SI = ×× 100 PRT

392= 100 P

×3.5×3.5

392×100 = 3.5×3.5 P

P = ₹3200

3. SI = A − P = ₹11,800 − ₹10,000 = ₹1800

SI = ×× 100 PRT

10,000××2 1800= 100 R

1800×100 = 10,000×2 R

=9% R

4. Amount after two years = ₹780, amount after seven years = ₹1230, P = ?, rate of simple interest = ?

SI for five years = ₹1230 − ₹780 = ₹450

SI for one year = 450 =90 5 `

SI for two years = 2 × ₹90 = ₹180

Now, P = ₹780 − ₹180 = ₹600

SI = ×× 100 PRT

600××2 180= 100 R

R = 15%

5. Let principal (P) = ₹a, R = 8% p.a. simple interest, amount (A) = ₹2a, T = ?

Using formula, A = P + SI, we get, 2a = a + SI

2a − a = SI

SI = a

We know that SI = ×× 100 PRT

×8× = 100 aT a

×100=×8× aaT

100 = 8 T =12.5 T years

6. P = ₹7000, R = 10% p.a. compounded annually, time (n) = 4 years, CI = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

=

CI = A − P = ₹10,248.7 − ₹7000 = ₹3248.7

7. P = ₹30,000, R = 12% p.a., n = 2 years, CI = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 12 30,0001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 2 112 30,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹37,632

CI = A − P = ₹37,632 − ₹30,000 = ₹7632

8. P =₹5000, R = 12% p.a. compounded annually, n = 2 years, CI = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 12 50001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 2 112 5000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹6272

CI = A − P = ₹6272 − ₹5000 = ₹1272

9.a. P = ₹5000, R = 9% p.a., n = 2 years, A = ?, CI = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 9 50001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ èø = 2 109 5000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹5940.5

CI = A − P = ₹5940.5 − ₹5000 = ₹940.5

b. P = ₹72,000, R = 6% p.a., n = 3 years, A = ?, CI = ?

A = 3 6 72,0001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 3 106 72,000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹85,753.152

CI = A − P = ₹85,753.152 − ₹72,000 = ₹13,753.152

10. A =₹16,335, R = 10% p.a. compounded annually, n = 2 years, P = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2 10 16,335=1+ 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø 2 110 16,335= 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

16,335×100×100 = 110×110 P

P = `13,500

11. P =₹8800, A = ₹10,648, R = 10% p.a. compounded annually, n = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

10,648=88001+ 100 næö ÷ ç ÷ ç ÷ ç ÷ ç ÷ èø

10

10,648110 = 8800100 næö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

1.21=1.1 n 2 1.1=1.1 n Hence, n = 2 years

12. P = ₹4000, A = ₹5324, n = 3 years, R = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ èø

5324=40001+ 100 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø 3 1.331=1+ 100 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø 3 3 1.1=1+ 100 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

3

Taking cube roots on both the sides, we get, 1.1=1+ 100 R æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

1.1–1= 100 R

0.1= 100 R

R = 10% per year

13. P = ₹7000, R = 8% p.a. compounded annually, n = 2 years, CI = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 8 70001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 2 108 7000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹8,164.8

CI = A − P = ₹8,164.8 − ₹7000 = ₹1164.8

14. P = ₹20,000, R = 10% p.a. compounded semi-annually, n = 1 1 2 years

2 =1+ 200 n R AP æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

3 2× 2 10 = 20,000×1+ 200 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

3 210 =20,000× 200 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 2,31,52.5 `

CI = A − P = ₹23,152.5 − ₹20,000 = ₹3152.5

15. P = ₹1,60,000, R = 10% p.a. compounded semi-annually, n = 2 years

2 =1+ 200 n R AP æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2×2 10 =1,60,0001+ 200 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ èø

4 210 =1,60,000 200 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø =1,94,481 `

CI = A − P = ₹1,94,481 − ₹1,60,000 = ₹34,481

16. P = ₹25,000, R = 8% p.a. compounded semi-annually, A = ₹28,121.60, n = ?

2 =1+ 200 n R AP æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2 8 28,121.60=25,0001+ 200 n æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2 28,121.60208 = 25,000200 n æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

1.124864 = 2 1.04 n

Since, 1.124864 = 3 1.04

Therefore, 2=3 n

3 ==1.5 2 n years

17. R = 10% p.a., Time = 2 years, CI − SI = ₹1, P = ?

As per the given condition, CI − SI = ₹1

1+––=1 100100 n RPRT PP æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2 10 ×10×2 1+–– =1 100 100 P PP æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2 11 ––=1 105 P PP æö

÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

121pp–P–=1 1005

121–100–20 =1 100 PPP =1 100 P

P = ₹100

Word Problems

1. P = ₹5000, R = 8% p.a., Time = 3 years, CI − SI = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 3 8 50001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 3 108 5000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹6298.56

CI = A − P = ₹6298.56 − ₹5000 = ₹1298.56

SI = 5000×8×3 = =1200 100100 PRT ` =₹1200

So, CI − SI = ₹1298.56 − ₹1200 = ₹98.56

2. P = ₹12,000, n = 2 years, R = 9% p.a. compounded annually, A = ?

A = 1+ 100 n R P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 2 9 120001+ 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 2 109 12000 100 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ₹14,257.2

3. Present population (A) = 54,080, rate of increase (R) = 4% annually, time (t) = 2 years, population two years ago (P) = ?

2 4 54,080=1+ 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2 104 54,080= 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

54,080×100×100 = =50,000 104×104 P

4. Present cost of a mobile phone (A) = ₹15,000, rate of depreciation (R) = 5%, time (t) = 2 years, ccost of the mobile phone two years ago (P) = ?

2 5 15,000=1–100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

2 95 15,000=× 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø 15,000×100×100 = =16,620.49 95×95 P `

5. Present value of a car (A) = ₹4,73,850, rate of depreciation (R) = 10%, time (t) = 3 years, price of the car three years ago (P) = ?

3 10 4,73,850=1–100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

3 90 4,73,850= 100 P æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

4,73,850×100×100100 = =6,50,000 90×90×90 P `

Chapter 15

Let's Warm-up

Match the following.

1. 8p − 3p −5b

2. 7 + 8 5b

3. 2p + 5p 5p

4. 9b − 4b 15

5. −9b + 4b 7p

Do It Yourself

15A

1.a. 2 –+2+3 xx

The terms containing variables are: − x2, 2x

b. 2 –+5+6 xx

The terms containing variables are: −x2, 5x

c. 2 –+4+2 xx

The terms containing variables are: x2 , 4x

d. 2x + 7

The term containing a variable is 2x. 2.a.

3 4 a2bc

d.

Factors = 8, a, a; −5, a; 1 3

The coefficient of ‘a’ in 8a2 is 8a; The coefficient of ‘a’ in −5a is −5.

9ab 2 7 a  1

9ab

b.

3 4 aabc

The expression 2 3 –4 abc has only one term that is 2 3 –4 abc

Factors = 3 –,,,, 4 aabc .

The coefficient of ‘a’ is 3 –4 abc

6a +5

6a 5

6 a

The expression 6a + 5 has two terms 6a and 5.

Factors = 6, a; 5.

The coefficient of ‘a’ is 6. c.

8a2 −5a + 1 3

8a2 −5a

8 a −5

1 3 aa

The expression 8a2 − 5a+ 1 3 has three terms 8a2, −5a and 1 3 .

9 ab

−1 2 7 a 2 7 a

The expression 2 9––1 7 aba has three terms 9ab, 2 –7 a and −1.

factors = 9, a, b; 2 7 , a; −1.

The coefficient of ‘a’ in 9ab is 9b. The coefficient of ‘a’ in 2 –7 a is 2 –7 . e.

7 12 a3 +5abc

7 12 a3

7 12

4 9 a2 −10

4 9 a2

5abc −10

4 9 aaa 5 abcaa

The expression 7432+5––10

12 9 aabca has four terms

3 7 12 a , 5abc, 2 4 –9 a and −10.

The factors of 7432+5––10

12 9 aabca are 74,,,;5,,,;–,,;–10 12 9 aaaabcaa

The coefficient of ‘a’ in 3 7 12 a is 2 7 12 a ; The coefficient of

‘a’ in 5abc is 5bc; The coefficient of ‘a’ in 2 4 –9 a is 4 –9 a

3. MonomialsBinomialsTrinomialsQuadrinomials −3y,

5 –3 ab , 5 6 stu

2x + 5, 51 –23 p

22 1 45 2 xa , 113 –2+ 64 ghi , 11+–2271 84pq ,

2 5 9–+2+ 6 xypqqp , 11–+2–135 68pqryzp

4.a. 5a, − 2 3 a b. 6xy, 8x2y c. 2a2 b2 c, 9ab2c2

d. 11 7 abc, 8cba e. 3x2, 4x2

5.a. The numerical factor of the expression 2 3 –4 ab is 3 –4 .

b. The numerical factors of the expression 6+5 a are 6 and 5.

c. The numerical factors of the expression 2 1 8–5+ 3 aa are 8, −5 and 1 3 .

d. The numerical factors of the expression 2 9––1 7 aba are 9, 2 –7 and −1.

e. The numerical factors of the expression 7432+5––10 12 9 aabca are 7 12 , 5, 4 –9 and −10.

6. In 2x + 5, the numerical coefficient of x is 2. In −3y, the numerical coefficient of y is −3.

In 22 1 –4++5 2 xa , the numerical coefficient of x2 is −4 and the numerical coefficient of a2 is 1 2

In 5 –3 ab , the numerical coefficient of ab is 5 –3 .

In 113 –2+ 64 ghi , the numerical coefficient of g is 11 6 , the numerical coefficient of h is −2, and the numerical coefficient of i is 3 4

In 11+–2271 84pq , the numerical coefficient of p2 is 11, and the numerical coefficient of q2 is 7 . 8

In 2 5 9–+2+ 6 xypqqp , the numerical coefficient of xy is 9, the numerical coefficient of pq is 5 6 , the numerical coefficient of q is 2 and the numerical coefficient of p2 is 1.

In 51 –23 p , the numerical coefficient of p is 5 2

In 5 6 stu, the numerical coefficient of stu is 5 6

In 11–+2–135

68pqryzp , the numerical coefficient of pqr is 11, the numerical coefficient of yz is 13 –6 , and the numerical coefficient of p is 2.

7.a. + 8 xy , literal factors of the expression + 8 xy are x and y.

In 8 x the literal coefficient of 1 8 is x. In 8 y the literal coefficient of 1 8 is y.

b. 1 2–6 xy , literal factors of the expression 1 2–6 xy are x and y. In 2x the literal coefficient of 2 is x and the literal coefficient of 1 –6 is y

c. (ab) − ab, literal factors of the expression (ab) − ab are a,b,a,b. In ab; the literal coefficient of 1 is a and literal coefficient of −1 is b; in −ab, the literal coefficient of −1 is ab.

d. (4a + b), literal factors of the expression are a,b. In 4a the literal coefficient of 4 is a. In b the literal coefficient of 1 is b.

8.a. y + 5 is a polynomial because it is an algebraic expression with two terms.

b. −3 is a polynomial because it can be expressed as −3x0

c. 2 3 –5++5 2 xy a is not a polynomial because the power of the variable in the second term is −1 which is not a whole number.

d. 7 –11 ab is a polynomial because it is an algebraic expression with one term.

e. 113 –2+ 64 h pk is a not a polynomial because the power of the variable in the first and third term is −1 which is not a whole number.

f. 9+–2211 84 s kpkq is a polynomial because it is an algebraic expression with three terms.

g. 9 is a polynomial because it can be expressed as 9x0 .

h. 2 52 –+2+–65 bcbc a is not a polynomial because the power of the variable in the fourth term is −1 which is not a whole number.

Word Problem

1. Algebraic expression for Figure A is 2x + y and the algebraic expression for Figure B is 2y + x.

15B

1.a. Show the 2 expressions using algebra tiles.

Place all the tiles together.

Show the final answer in the form of an algebraic expression.

2 3+5+6 xx

b. Show the minuend, 2 4–2+1 xx using algebra tiles.

To subtract, cancel out as many tiles as given in the subtrahend, 2 +3–2xx .

To subtract 2 x , cancel out one 2 x tile.

To subtract + 3x, we need at least three + x tiles. Since there are not enough + x tiles, we bring in 0 (3 pairs of + 1x and − 1x tiles). Then cancel out the three + x tiles.

To subtract −2, we need two −1 tiles. Since there are not enough −1 tiles, we bring in 0 (2 pairs of +1 and −1 tiles).

d. 76+–1 87pqp and 52++8 87pqp

7652128+–1+++8=++7 878787 pqppqppqp

Verification:

7 8 pq + 6 7 p −1

+ 5 8 pq + 2 7 p +8

12 8 pq+ 8 7 p +7

3.a. 2 5–3–1 xx and 2 3–4+7 xx

The remaining tiles show the final answer.

x2 x2 x2 xxxxx

1 1 1

So, the resulting algebraic expression is 3x2 − 5x + 3.

2. a. 3x + y + 1 and 2x − 5y − 4 3++1+2–5–4 3+2+–5+1–4=5–4–3 xyxy xxyyxy =

Verification:

3x + y +1

+2x −5y −4

5x −4y −3

b. 3xy2 + 5xy − 6 and 7y2x − 2xy + 3

3xy2 + 5xy − 6 + 7y2x − 2xy + 3

= 3xy2 + 7y2x + 5xy − 2xy − 6 + 3

= 10xy2 + 3xy − 3

Verification:

2 3 xy + 5 xy 6

+ 2 7 yx 2 xy + 3

2 10 xy + 3 xy −3

c. 2 4 –5–+2 5 pp and 2 3 3+5–4 pp

22

22

= =

43 –5–+2+3+5–54 –5+3–+5+2–43 54 –2++215 54

2

pppp pppp pp

Verifcation:

–2 5 p –4 5 p +2

+ 2 3 p + 5 p 3 4

2 2 p + 21 5 p + 5 4 –

22 22 22

5–3–1–(3–4+7) 5–3–1–3+47 5–3–3+4–1–72+–8

xxxx xxxx xxxxxx = ==

2

Verification:

2 5 x 3 x −1

2 3 x 4x +7 −+−

2 2 x + x −8

b. 3 4 8+–5 mnn and 3 2–+11 25 mnn

8+––2–+411 525

æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

mnnmnn mnnmnnmnn

33 333

4113 =8+––2+–=6+–1 5252

Verification:

8mn + 3n 4 5

2mn 3 1 2 n + 1 5 −+−

6mn + 3 3 2 n −1

c. 2 2+3+8 yy and 2 +2–4yy 22 222 2+3+8–(+2–4) =2+3+8––2+4=2+12 yyyy yyyyy

Verification:

2 y + 2 3 y +8

2 y + 2 y −4 −−+

0+ 2 2 y +12

d. 7–13–11pqq and 284pqq

7–13–11–(2+8–4) =7–13–11–2–8+4=–1–15–7 pqqpqq pqqpqqpqq

Verification:

7 13 pq 11q

8 + 2 pq 4q −−+ −1− 15 pq 7q

4.a. 3(5–4)–2(7+3)+4(8–2) xxx

= 15–12–14–6+32–8 xxx

= –18+32–8xx

= 33–26 x

b. 3232 ) 13 (2+4–( ) 5–2 24 mmmm

= 3232 +2–+153 42 mmmm

= –+11732 42 mm

c. 23 2 (–3+6–4–)+(2+1)–(8–5+1) xxxxxx

23 2 = –3+6–4–+2+1–8+5–1 xxxxxx

223 = –3–8+6–4+1–1–+2+5 xxxxxx

23 =–11+6–4+6 xxx = 32 6–11+6–4 xxx

d. 2 (–2)–(–+3)+(4–5) xxxx

= 2 –2–+–3+4–5 xxxx

= 2 6–10–xx = 2 –+6–10 xx

5.a. Let the missing expression be x 443 ) (6–4+8)+=(+5+8+8 aaxaaa

434 =+5+8+8–6+4–8 xaaaaa =–5+9+843 xaa

b. Let the missing expression be a

22 –(6+6+11)=(10+4–1) axxxx

22 =10+4–1+6+6+11 axxxx

2 =16+10+10axx

c. Let the missing expression be x

222 (–19–6+6)+(–8–4–9)–=–15+8+7 nnnnxnn

222 –19–6+6–8–4–9+15–8–7= nnnnnnx

222 –19–8+15–6–4–8+6–9–7= nnnnnnx

2 –12–18–10=nnx

d. Let the missing expression be x

2 2442 –(4–5)+(7–9+6=(8–3+2) ) xqqqqqqqq

22442 –4+5+7–9+6=8–3+2 xqqqqqqqq

2442 –13+12+6=8–3+2 xqqqqqq

4224 =8–3+2+13–12–6 xqqqqqq

42 =2+10–10 xqqq

6. We will first find the sum of 2 (–18+–32) pp and 2 (132012) pp and then subtract 2 ) 40–1 (3 p from it. Sum of 2 (–18+–32) pp and 2 (13+20–12) pp

= 22 (–18+–32)+(13+20–12) pppp

= 2 2+14–44 pp

Subtracting 2 ) 40–1 (3 p from 2 (2+14–44) pp , we get, 22 ) (2+14–44)–(40–13 ppp

=2+14–44–40+1322 ppp

2 =15+14–84 pp

7. Let the algebraic expression to be subtracted from

3 () 7–3+7hhth to get 3 () –6+3–9hhth be x

33 ) (7–3+7–=(–6+ ) 3–9 hhthxhhth

(7–3+7–(–333 ) 6+– ) 9= hhthhhthx

33 7–3+7+6–3+9= hhthhhthx

3 =13–6+16 xhhth

8. To find how much is 5 (6–2) y greater than 52 ) (9+5+3yy , we need to subtract 52 ) (9+5+3yy from 5 (6–2) y 552

55252 (6–2)–(9+5+3

=6–2–9–5–3=–3–7–3 ) yyy yyyyy

9. The wrong coefficients in the first step are circled in the solution below.

æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

22222222 21122112 –––=––+ 35353445 ppqppqppqppq

The correct solution is:

æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

22222222 21122112 –––=––+ 35353535 ppqppqppqppq

= 21122222 ––+ 3355 pppqpq

= 1122 + 35ppq

Word Problems

1. Difference in the lengths of the ropes of Rohan and Harsh

= 22 (8+30–4)–(13–18) + mmmm

= 8m + 30m2 − 4 − m2 − 13m + 18

22 =30–+8–13–4+18 mmmm

2 =(29–5+14) mm metres

2. Length of the fence required for the field 22 22 (9+17) +(34+7–18 +(9+2 +–) 2 ) (175) smetersss metersssmeterssmeters

=

= 2 222 9+17+34+7–18+9+2+17–25 ssssss

= 2222 9–18+2+17+34+9+17+7–25 ssssss

= 2 (10+43–1) ss metres

Chapter Checkup

1.a.

Expression

Terms Factors

6pq2 8p2q +

6pq2

6 8 qqpqpp

8p2q

Factors inside the rectangular box are the variables. Factors inside the circle are the numerical coefficients.

Expression

Terms Factors

Factors inside the rectangular box are the variables.

Factors inside the circle are the numerical coefficients.

2. a. 4x + y, 2x − 1 quadrinomial

b. 8a2b, 9pq, −6x trinomial

c. 3xy + x − 1, 8z2 − 3z + 5 monomial

d. −6x2y + 2xy

6x + 4, p2 − 7pq + 4q − 1 binomial

3.a. −5 is a polynomial.

b. 3 –+7 x is not a polynomial.

c. 2 7 –2++5 2 ab a is not a polynomial.

d. 2 52 –+2+–65 pqqp a is not a polynomial.

4. a.  2a, − 3 5 a b.  6pq, −4x2y

c. −7a2b3c, 8ab2c3 d.  − 5 6 abc, − 1 2 cba

5.a. 22 (3+2–6)+(––2+1) xxxx

Show the two expressions using algebra tiles.

Place all the tiles together. Cross out each pair of one negative and one positive tile of the same factor.

The remaining tiles show the final answer.

The resulting expression is 2 2–5 x .

b. 22 (–+4+2)–(3–2–3) xxxx

Show the minuend, 2 (–+4+2) xx using algebra tiles. x

To subtract, cancel out as many tiles as given in the subtrahend, 3x2 − 2x − 3.

To subtract 3x2, we need three x2 tiles. Since there are not enough x2 tiles, we bring in 0 (3 pairs of x2 and −x2 tiles).

To subtract −2x, we need at least two −x tiles. Since there are not enough −x tiles, we bring in 0 (2 pairs of x and −x tiles).

To subtract −3, we need three −1 tiles. Since there are not enough −1 tiles, we bring in 0 (3 pairs of 1 and −1 tiles).

The remaining tiles show the final answer.

The resulting expression is 2 –4+6+5 xx .

6.a. 2 –3+–2 mm and 2 4+6+7 mm 22 –3+–2+4+6+7 mmmm

= 22 –3+4++6–2+7 mmmm

= 2 +7+5mm

b. 32 7+4+–1 zzz and 32 2–6–2+2 zzz

3232 7+4+–1+2–6–2+2 zzzzzz

= 3322 7+2+4–6+–2–1+2 zzzzzz

= 32 9–2–+1 zzz

c. 23232 51 ––7+3+4–+9–6–2 77 qqqqqq

= 22233 51 +3+9–––6–7+4–2 77 qqqqqq

= 23 6 13––6–5 7 qqq

7.a 3655263 11 11+10–26+–8–9+++17 22 zzzzzzzzz æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 3655263 11 11+10–26+–8+9–––17 22 zzzzzzzzz

= 3366 552 11 11–17+10––26–+–8+9 22 zzzzzzzzz

= 3652

5315 –6+9––+9 22

zzzzz zzzzz

6532

15 53 = 9––6+9–22

b. 4224 8–5–(2–3+6) xxxxx

= 8–5–2+3–64224 xxxxx

= 42 2–7+3 xxx

c. 312424–6+8––+5–5 42yyyy æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 312424–6+8+–5+5 42yyyy

= 322244+–6–5+8+5 44yyyy

= 42 5 –11++13 4 yy

8.a. 2424234 7–4+3+5+6–9+8–2 ssssssss

2224443 =7+5–9–4+6–2+3+8 ssssssss =3+3+823 sss

b. 42224 (8–3+2)–(4–5)+(7–9+6) tttttttt

42224 =8–3+2–4+5+7–9+6 tttttttt

44222 =8+6–3–4–9+2+5+7 tttttttt

42 =14–16+14 ttt

c. 234432 (7+5–4)–(8+6)–(9+3) kkkkkk

234432 =7+5–4–8–6–9–3 kkkkkk

223344 =7–3+5–9–4–8–6 kkkkkk

234 =4–4–12–6 kkk

9. Difference of 3 (–2+) xx and 3 (7–3+7) xx

= 33 (7–3+7)–(–2+) xxxx

= 33 7–3+7+2–xxxx

= 33 7+2+7––3 xxxx

= 3 9+6–3 xx

Adding 2 (3–2+1) xx to 3 (9+6–3) xx , we get, 3232 (9+6–3)+(3–2+1)=9+6–3+3–2+1 xxxxxxxx

= 32 9+3+4–2 xxx

10. Let the algebraic expression to be added to (6k5 + 1) to get (10k5 + 9k) be x. 55 (6+1)+=(10+9) kxkk

55 =10+9–6–1xkkk 5 =4+9–1xkk

11. 4444 (2–8)–(4+6–5)=2–8–4–6+5 pppppppp

= 4 –2–14+5 pp

12. Let the algebraic expression to be taken away from 4 (6–4–3) cc to get 42 (–3+–3+8) cc be x

4 42 (6–4–3)–=(–6++8) ccxcc

=6–4–3+6––8442 xcccc

=6–5+3–842 xccc

Word Problems

1. Perimeter of the field =2(l + b)

2 =2(9+7–4+3) xxx

2 =2(9+10–4) xx

2 =(18+20–8 xx ) cm

Perimeter of the footpath. = 2(+) lb

= 2 2(4–3+7+4) xx

= 2 2(4–3+11) xx

= ( 2 8–6+22 xx ) cm

Difference between the perimeter of the field and the footpath = 22 (18+20–8)–(8–6+22) xxxx

= 22 18+20–8–8+6–22 xxxx

= 2 m ( c 10+26–30) xx

2. Price of bananas = ₹ (15x + 6)

Price of grapes = ₹ (13x2 − 9x + 2)

Price of apples = 22 (13–9+2)–(–8+4–18) xxxx

= 22 13–9+2+8–4+18 xxxx

= 2 (21–13+20) xx `

Total amount spent to buy fruits

= 22 (15+6)+(13–9+2)+(21–13+20) xxxxx

= 22 13+21+15–9–13+6+2+20 xxxxx

= 2 (34–7+28) xx `

3. Length of the chart paper = (3x2 − 5 + 6x) metres

Breadth of the chart paper = (4x + 5) metres

Cutting squares from the corners of the chart paper does not change the perimeter of the chart paper.

Hence, the perimeter of the chart paper = 2(l + b)

= 2(3x2 − 5 + 6x + 4x + 5)

= 2(3x2 + 10x)

= (6x2 + 20x) metres

Chapter 16

Do It Yourself 16A

c. x x x 1111

y xy xy xy y y y y

y

y

x x

x x

1. a. 1111

x2 x2 x2 x2 x2 x2

x yyyy yyyy xyxy xyxy

x x x x

x x x x x x x x

Expression: (−3x + 2y) (2x + 4)

Product: −6x2 − 12x + 4xy + 8y

b. 1 1 1 xxxx xxxx xxxx xxxx

Expression: (3 − 2x) (4x − 5)

Product: 22x − 15 − 8x2

2.a. y y y y

x xy xy xy xy

x xy xy xy xy

x xy xy xy xy

x xy xy xy xy

x xy xy xy xy

product = −20xy

b. x x 1111111

x x2 x2 xxxxxxx

x x2 x2 xxxxxxx

x x2 x2 xxxxxxx

x x2 x2 xxxxxxx

x x2 x2 xxxxxxx

product = −10x2 + 35x

y xy xy xy y y y y 1 x x x 1 1 1 1

1 x x x 1 1 1 1

1 x x x 1 1 1 1

product = 6xy + 8y − 9x − 12

3.a. (−5x2y2z3) (12x2yz)(3yz) = (−5 × 12 × 3) (x2y2z3 × x2yz × yz) = −180 × x2+2 × y2+1+1 × z3= −180 × x4 × y4 × z5 = −180 x4y4z5

b. ab (−6abc + 5c − 7) = −6a2b2c + 5abc − 7ab

c. (3x − 1) (8y + 5) = 3x (8y + 5) − 1 (8y + 5) = 24xy + 15x − 8y − 5

d. (7y + 9) (3z2 + 6z − 5) = 7y (3z2 + 6z − 5) + 9 (3z2 + 6z − 5) = 21yz2 + 42yz − 35y + 27z2 + 54z − 45

e. (2a2 − 3a + 7) (4a2 + 6a + 11)

= 2a2 (4a2 + 6a + 11) − 3a (4a2 + 6a + 11) + 7 (4a2 + 6a + 11)

= 8a4 + 12a3 + 22a2 − 12a3 − 18a2 − 33a + 28a2 + 42a + 77

= 8a4 + 32a2 + 9a + 77

f. 9z (2z − 5) = 18z2 − 45z

g. (p3 + 5p2 + 11p − 6) (2p2 + 5p + 10)

= p3 (2p2 + 5p + 10) + 5p2 (2p2 + 5p + 10) + 11p (2p2 + 5p +

10) − 6 (2p2 + 5p + 10)

= 2p5 + 5p4 + 10p3 + 10p4 + 25p3 + 50p2 + 22p3 + 55p2 +

110p − 12p2 − 30p − 60

= 2p5 + 15p4 + 57p3 + 93p2 + 80p − 60

h. (8p5 − p3 + 7p2 + 10p − 5) (3p2 + 9p + 11)

= 8p5 (3p2 + 9p + 11) − p3 (3p2 + 9p + 11) + 7p2 (3p2 + 9p +

11) + 10p (3p2 + 9p + 11) − 5 (3p2 + 9p + 11)

= 24p7 + 72p6 + 88p5 − 3p5 − 9p4 − 11p3 + 21p4 + 63p3 +

77p2 + 30p3 + 90p2 + 110p −15p2 − 45p − 55

= 24p7 + 72p6 + 85p5 + 12p4 + 82p3 +152p2 + 65p − 55

4.a. (5h + 9) (3h − 7) = 5h (3h − 7) + 9 (3h − 7)

= 15h2 − 35h + 27h − 63 = 15h2 − 8h − 63

For h = 1, 15h2 − 8h − 63 = 15 (1)2 − 8 × 1 − 63 = −56

b. (9q − 1) (6q2 − q + 5) = 9q (6q2 − q + 5) − 1 (6q2 − q + 5)

= 54q3 − 9q2 + 45q − 6q2 + q − 5 = 54q3 − 15q2 + 46q − 5

For q = −4, 54(-4)3 − 15(−4)2 + 46(−4) − 5 = 54 × (−64) − 15 ×

16 + 46 × (−4) − 5= −3456 − 240 − 184 − 5 = −3885

c. 7a2 − 4a − 2) (5a2 − 2a + 9)

= 7a2 (5a2 − 2a + 9) − 4a (5a2 − 2a + 9) − 2 (5a2 − 2a + 9)

= 35a4 − 14a3 + 63a2 − 20a3 + 8a2 −36a − 10a2 + 4a − 18 =

35a4 − 34a3 + 61a2 − 32a − 18

For a = 0, 35a4 − 34a3 + 61a2 − 32a − 18 = 35(0)4 − 34(0)3 + 61(0)2 − 32 × 0 − 18 = −18

d. (2t3 + 3t2 + 5t − 4) (3t2 − 5t + 11)

= 2t3 (3t2 − 5t + 11) + 3t2 (3t2 − 5t + 11) + 5t (3t2 − 5t + 11) − 4 (3t2 − 5t + 11)

= 6t5 − 10t4 + 22t3 + 9t4 − 15t3 + 33t2 + 15t3 − 25t2 + 55t − 12t2 + 20t − 44

= 6t5 − t4 + 22t3 − 4t2 + 75t − 44

For t = −2, 6(−2)5 − (−2)4 + 22(−2)3 − 4(−2)2 + 75(−2) − 44 = −192 − 16 − 176 − 16 − 150 − 44 = −594

5.a. 2 3 a (3a + 4b − 5c) − 4 5 a (2a − 5b + 7c) = −2a2 − 8 3 ab +

10

3 ac − 8 5 a2 + 4ab − 28 5 ac

= 22 –30–40+50–24+60–84 15 aabacaabac

= 2 –54+20–34 15 aabac

For a = −1, b = 2, c = 10, 2 –54+20–34 15 aabac

= 2 –54(–1)+20 (–1)(2)–34(–1)(10)

15

= –54–40+34024682 == 15155

b. a2b (a3 − 3b + a + 2) − ab (b4 − 2b2 − 3b) − c (a3 + b2 + 1)

= −a5b + 3a2b2 − a3b − 2a2b − ab5 + 2ab3 + 3ab2 − a3c − b2c −

c For a = −1, b = 2, c = 10, −(−1)5 (2) + 3 × (−1)2 (2)2 − (−1)3(2) − 2(−1)2(2) −(−1) (2)5 + 2(−1)(2)3 + 3(−1) (2)2 − (−1)3(10) − (2)2(10) − 10

= 1 × 2 + 3 × 1 × 4 + 1 × 2 − 2 × 1 × 2 + 1 × 32 − 2 × 8 − 3 × 4

+ 1 × 10 − 4 × 10 − 10

= 2 + 12 + 2 − 4 + 32 − 16 − 12 + 10 − 40 − 10 = −24

c. (a − 5) (a4 −2b3 + 3c − 4) + 3 7 bc (7a2 − 11)

= a (a4 −2b3 + 3c − 4) − 5 (a4 −2b3 + 3c − 4) + 3 7 bc (7a2 − 11)

= a5 − 2ab3 + 3ac − 4a − 5a4 + 10b3 − 15c + 20 + 3a2bc − 33 7 bc

For a = −1, b = 2, c = 10;

(−1)5 − 2 (−1) (2)3 + 3(−1)(10) − 4(−1) − 5(−1)4 + 10(2)3 − 15(10)

+ 20 + 3(−1)2(2)(10) − 33 7 (2) (10)

= −1 + 2 × 8 − 3 × 10 + 4 − 5 + 10 × 8 − 150 + 20 + 3 × 2 × 10

− 33 7 (2) (10)

= −1 + 16 − 30 + 4 − 5 + 80 − 150 + 20 + 60 660 –7

= −6 − 660 7 = –42–660 7 = 702 7

6.a. Area of rectangle = 6x2y × −5x3y2z = −30x2+3 y1+2 z = −30x5y3z sq. units

b. Area of rectangle = 117 8–+9 55 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø xx

− 11 5 7 +9

= 2 2

1800–77 56 99 +–5255

xx xx

56172399 =+–sq.units 5255

c. Area of rectangle = 232 96554 += 117677 abcabcabc a1+2 b1+1 c1+3 + 45 66 a1+1 b1+2 c1+1

= 5445324232 + sq.units 7766 abcabc

d. Area of rectangle = (3z − 1) (2z2 + 7z − 10) = 3z (2z2 + 7z − 10)

− 1 (2z2 + 7z − 10)

= 6z3 + 21z2 − 30z − 2z2 − 7z + 10

=(6z3 + 19z2 − 37z + 10) sq. units

7. We know that, Volume of cuboid = l × b × h cubic units

a. Volume of cuboids = 7 2 p2q3r4 × 1 2 pqr × 2p (q + r)

= 7 2 p2+1+1 q3+1+1 r4+1 + 7 2 p2+1+1 q3+1 r4+1+1

= 77455446 + cu.cm

22pqrpqr

b. Volume of cuboids = (p + q) × (p − q + 12) × 8r

= 8r (p + q) (p − q) + 96r (p + q) = 8r (p2 − q2) + 96rp + 96rq

=(8rp2 − 8rq2 + 96rp + 96rq) cu. cm

c. Volume of cuboids = − 1 2 pq(r + 1) × 7pq × 11qr

= − 77 2 p1+1 q1+1+1 r (r + 1)

= 23 232 7777 – –cu.cm 22 pqr pqr

8.a. Volume of cube = 3s (stu + 1) × 3s (stu + 1) × 3s (stu + 1)

= 27s3 (stu + 1)3 cu. cm

b. Volume of cube = −3s2t3u5 × (−3s2t3u5) × (−3s2t3u5)

= −27s2+2+2 t3+3+3 u5+5+5 = −27s6t9u15 cu. cm

c. Volume of cube = (−6ab + 2a2 + 3) × (−6ab + 2a2 + 3)

× (−6ab + 2a2 + 3)

= (−6ab + 2a2 + 3)3 cu. cm

d Volume of cube = 4p3q4 (9r + 2q − 5) × 4p3q4 (9r + 2q − 5) ×

4p3q4 (9r + 2q − 5)

= 64p3+3+3 q4+4+4 (9r + 2q − 5)3 = 64p9q12 (9r + 2q − 5)3 cu. cm

9. (5x3 − 4x2 + 2x − 1) (x2 − 3x + 5)

= 5x3 (x2 − 3x + 5) − 4x2 (x2 − 3x + 5) + 2x (x2 − 3x + 5) − 1 (x2 −

3x + 5)

= 5x3+2 − 15x3+1 + 25x3 − 4x2+2 + 12x2+1 − 20x2 + 2x1+2

− 6x1+1 + 10x − x2 + 3x − 5

= 5x5 − 15x4 + 25x3 − 4x4 + 12x3 − 20x2 + 2x3 − 6x2 + 10x − x2 +

3x − 5

= 5x5 − 19x4 + 39x3 − 27x2 + 13x − 5

So, the coefficient of x4 in the product is −19.

Word Problem

1. Length of the rectangular garden = (3x + 2) m, breadth of the garden = (4x − 1) m

Area = (3x + 2) (4x − 1) = 3x (4x − 1) + 2 (4x − 1) = 12x2 − 3x + 8x − 2

= (12x2 + 5x − 2) sq. m

16B

1.a. (6a + 7b) (6a + 7b) = (6a + 7b)2

Using the identity: (a + b)2 = a2 + 2ab + b2, we get (6a + 7b)2 = (6a)2 + 2 × 6a × 7b + (7b)2 = 36a2 + 84ab + 49b2

b. (9a − 5b) (9a − 5b) = (9a − 5b)2

Using the identity: (a − b)2 = a2 − 2ab + b2, we get (9a − 5b)2 = (9a)2 − 2 × 9a × 5b + (5b)2 = 81a2 − 90ab + 25b2

c. (4.7x + 3.4y) (4.7x + 3.4y) = (4.7x + 3.4y)2

Using the identity: (a + b)2 = a2 + 2ab + b2, we get (4.7x + 3.4y)2 = (4.7x)2 + 2 × 4.7x × 3.4y + (3.4y)2 = 22.09x2 + 31.96xy + 11.56y2

d. 2 222222 373737 ++=+ 565656 æöæöæö ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ èøèøèø ababab

e.

Using the identity: (a + b)2 = a2 + 2ab + b2, we get

22 2

222222 373377 +=+2××+ 565566 æöæö æö ÷÷ ÷ ççç ÷÷ ÷ ççç ÷÷ ÷ ççç ÷÷ ÷ ççç ÷÷ ÷ ççç èøèø èø abaabb

= 9 25 a4 + 7 5 a2b2 + 49 36 b4

444 444 111 ++=+xxx xxx

Using the identity: (a + b)2 = a2 + 2ab + b2, we get 22

4 424 8 4 448 1 +=()+2××+=+2+111 xxxx xxxx

f. 2 3–3–=3–222 111111ppp

Using the identity: (a − b)2 = a2 − 2ab + b2, we get 22

22 2 22 12 3–=(3)–2×3×+=9–11 1111 11 pppp

p + 4 121

g. 2 222222 111111 ––=–565656 pqpqpq

Using the identity: (a − b)2 = a2 − 2ab + b2, we get

22 2 222222 111111 –=–2××+ 565566 pqppqq

= 1 25 p4 − 1 15 p2q2 + 1 36 q4

h.

888 888 111 ––=–ppp ppp

Using the identity: (a − b)2 = a2 − 2ab + b2, we get

8 828

i. 2 212121 ––=–353535 xyxyxy

Using the identity: (a − b)2 = a2 − 2ab + b2, we get

2 2122114 –=–2××+=–3533559 xyxxyyx

4 15 xy + 1 25 y2

2. a. (85)2 = (80 + 5)2 = (80)2 + 2 × 80 × 5 + (5)2 = 6400 + 800 + 25 = 7225

b. (192)2 = (200 − 8)2 = (200)2 − 2 × 200 × 8 + (8)2 = 40,000 − 3200 + 64 = 36,864

c. (108)2 = (100 + 8)2 = (100)2 + 2 × 100 × 8 + (8)2 = 10,000 + 1600 + 64 = 11,664

d. 88 × 114 = (100 − 12) (100 + 14) = (100 + (−12)) (100 + 14) = (100)2 + 100 (−12 + 14) + (−12 × 14)

=10,000 + 100 × 2 − 168 = 10,000 + 200 − 168 = 10,032

e. (4.5x + 1.7y)2 = (4.5x)2 + 2 × 4.5x × 1.7y + (1.7y)2 = 20.25x2 + 15.3xy + 2.89y2

f. 5.2 × 6.8 = (6.0 − 0.8) (6.0 + 0.8) = (6.0)2 − (0.8)2 = 36 − 0.64 = 35.36

g. 22 2 151155 +=+2××+ 262266 abaabb

= 1 4 a2 + 5 6 ab + 25 36 b2

h. 2 2 74 –85xy = 2 2 7 8 x − 2 × 7 8 x2 × 4 5 y + 2 4 5 y

= 49 64 x4 − 7 5 x2y + 16 25 y2

i. 2 6 5–11 p = (5p)2 − 2 × 5p × 6 11 + 2 6 11

= 25p2 − 60 11 p + 36 121

3. a. 9x2 + 42xy + 49y2 = 2 5 9 6 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 42 × 5 6 × 4 –5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 49 2 4 –5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 9 × 25 36 − 28 + 49 × 16 25 = 25 4 − 28 + 784 25 = 625+3136 100 − 28 = 625+3136–2800 100 = 961 100

b. 9x2 + 30xy + 25y2 = 2 5 9 6 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 30 × 5 6 × 4 –5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 25 2 4 –5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 9 × 25 36 − 20 + 16 = 25 4 − 20 + 16 = 25–80+64 4 = 9 4

c. 36x2 + 60xy + 75y2 = 2 5 36 6 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 60 × 5 6 × 4 –5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 75 2 4 –5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 36 × 25 36 − 40 + 75 × 16 25 = 25 − 40 + 48 = 33

d. x2 + 4xy + y2 = 2 5 6 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 4 × 5 6 × 4 –5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

+ 2 4 –5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 25 36 − 8 3 + 16 25 = 625–2400+576 900 = − 1199 900

4.a. (5a − 4b)2 − (7a + 2b)2 + 4a2 − 6ab = (5a)2 − 2 × 5a × 4b + (4b)2 − (7a)2 + 2 × 7a × 2b + (2b)2 + 4a2 − 6ab

= 25a2 − 40ab + 16b2 − (49a2 + 28ab + 4b2) + 4a2 − 6ab

= −20a2 − 74ab +12b2

b. 2 3522 + 46 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø ab + 2 3522 –78 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø ab − 3a2b2

= 2 2 3 4 a æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 2 × 3 4 a2 × 5 6 b2 + 2 2 5 6 b æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 4 441+144 784 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø a + 35–15–84 28 a2b2 + 4 400+225 576 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø b =

585 784 a4 − 64 28 a2b2 + 625 576 b4 = 585 784 a4 − 16 7 a2b2 + 625 576 b4

c. (p2 + q2) (p2 − q2) + (q2 + r2) (q2 − r2) + (r2 + p2) (r2 − p2) = (p2)2 − (q2)2 + (q2)2 − (r2)2 + (r2)2 − (p2)2

= p4 − q4 + q4 − r4 + r4 − p4 = 0

d. (a + b) (a − b) (a2 + b2) = (a2 − b2) (a2 + b2) = a4 − b4

5.a. 2224 3399981 +–+=–+=–44161616256 æöæöæöæöæöæö çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ èøèøèøèøèøèø xxxxxx

b. (x + 7) (x − 7) (x2 + 49) = (x2 − 49) (x2 + 49) = (x4 − 2401)

6.a. x + 1 x = 7

Squaring both sides, we get

2 2 1 +=(7) æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø x x

x2 + 2 1 x + 2 × x × 1 x = 49

x2 + 2 1 x + 2 = 49

x2 + 2 1 x = 49 − 2 = 47

b. From the previous part, x2 + 2 1 x = 47

Squaring both sides, we get

2 22 2 1 +=(47) æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø x x

x4 + 4 1 x + 2 × x2 × 2 1 x = 2209

x4 + 4 1 x + 2 = 2209

x4 + 4 1 x = 2209 − 2 = 2207

c. 2 2 11 ++ æöæö ÷ ÷ç ç ÷ ÷ç ç ÷ ÷ç ç ÷ ÷ç ç ÷ ÷ ç ÷ èøçèø xx xx = 7 × 47 = 329 (from parts a and b)

7.a. x 1 x = 11

Squaring both sides, we get

2 2 1 –=11 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø x x

x2 + 2 1 x − 2 × x × 1 x = 11

x2 + 2 1 x − 2 = 11

x2 + 2 1 x = 11 + 2 = 13

b. From the previous part, x2 + 2 1 x = 13

Squaring both sides, we get

2 22 2 1 +=(13) æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø x x

x4 + 4 1 x + 2 × x2 × 2 1 x = 169

x4 + 4 1 x + 2 = 169

x4 + 4 1 x = 169 − 2 = 167

c. From the previous part, x4 + 4 1 x = 167

Squaring both sides, we get

2 42 4 1 +=(167) æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø x x

x8 + 8 1 x + 2 × x4 × 4 1 x = 27,889

x8 + 8 1 x + 2 = 27,889

x8 + 8 1 x = 27,889 − 2 = 27,887

8.a. (x + y)2 = x2 + y2 + 2xy = 15 + 2 × 5 = 15 + 10 = 25; x + y = 25 = 5

b. (x − y)2 = x2 + y2 − 2xy = 15 − 2 × 5 = 15 − 10 = 5; x − y = 5

c. x4 − y4 = (x2)2 − (y2)2 = (x2 + y2) (x2 − y2) = 15 (x + y) (x − y)

=15 × 5 × 5 = 75 5 (values taken from part a and b)

d. 1 2 xy (9x − 5y)2 − 1 2 xy (9x + 5y)2 = 1 2 xy (81x2 + 25y2

− 90xy) − 1 2 xy (81x2 + 25y2 + 90xy)

= 81 2 x3y + 25 2 xy3 − 45x2y2 − 81 2 x3y − 25 2 xy3 − 45x2y2

= −90x2y2 = −90 (xy)2 = −90 × (5)2 = −90 × 25 = −2250

e. x8 − y8 = (x4)2 − (y4)2 = (x4 + y4) (x4 − y4) = (x4 + y4) (x2)2 − (y2)2

= (x4 + y4) (x2 + y2) (x2 − y2)

= (x4 + y4) (x2 + y2) (x + y) (x − y)

= (x4 + y4) 15 × 5 × 5 …(1)

Given,x2 + y2 = 15

squaring both sides, we get (x2 + y2)2 = (15)2

x4 + y4 + 2x2y2 = 225

x4 + y4 + 2 × (5)2 = 225

x4 + y4 = 225 − 2 × 25 = 225 − 50 = 175

So, (1) implies x8 − y8 = 175 × 75 5 = 13,125 5

f. (x − y)2 (x + y)2 = ( 5 )2 × 52 = 5 × 25 = 125 (values from a and b)

9.a. (3p + 8)2 − 96p = (3p − 8)2

LHS: (3p + 8)2 − 96p = (3p)2 + 2 × 3p × 8 + (8)2 − 96p = 9p2 + 48p + 64 − 96p = 9p2 − 48p + 64 = (3p − 8)2 = RHS

Hence verified.

b. (5ab + 7b)2 − (5ab − 7b)2 = 140ab2

LHS: (5ab)2 + 2 × 5ab × 7b + (7b)2 − [(5ab)2 − 2 × 5ab × 7b + (7b)2]

= 140ab2 = RHS

Hence verified.

c. (2x + 5y)2 − (2x − 5y)2 − 40xy = 0

LHS: 4x2 + 25y2 + 20xy − (4x2 + 25y2 − 20xy) − 40xy = 4x2 + 25y2 + 20xy − 4x2 − 25y2 + 20xy − 40xy = 40xy − 40xy = 0 = RHS

Hence verified.

10. 4x = 982 − 382

4x = (98 − 38) (98 + 38) = 60 × 136 = 8160

x = 8160

4 = 2040

11.a. 22 (34.12)–(22.90)

21.56–10.34 = (34.12+22.90)(34.12–22.90)

11.22

= 57.02×11.22

11.22 = 57.02

b. (4.57+7.81)2

32.58–20.20 = (4.57)+22(7.81)+2×4.57×7.81

12.38

= 20.8849+60.9961+71.3834

12.38 = 153.2644

12.38 = (12.38)2

12.38 = 12.38

c. p + a = 12

squaring both sides, we get (p + a)2 = (12)2

p2 + a2 + 2pa = 144

p2 + a2 + 2 × (−2) = 144

p2 + a2 − 4 = 144

p2 + a2 = 144 + 4 = 148.

Word Problem

1. Let the price of the first book be ₹x Price of another book = ₹(4x − 12)

Given that the number of second books he purchased = price of first book = x

Total cost of the second book = ₹x (4x − 12)

Total price that Jacky has to pay = ₹x (4x − 12) + ₹x = ₹(4x2 − 12x + x) = ₹(4x2 − 11x)

Chapter Checkup

1.a. 6xy2z4 × (−11x2yz2) × 3y3z = −198x1+2 y2+1+3 z4+2+1 = −198x3y6z7

b. (4y + 7) (2z2 + 5z − 6) = 4y (2z2 + 5z − 6) + 7 (2z2 + 5z − 6) = 8yz2 + 20yz − 24y + 14z2 + 35z − 42

c. (−2p3 + 8p2 + 10p − 5) (p2 + 3p + 9) = −2p3 (p2 + 3p + 9) + 8p2 (p2 + 3p + 9) + 10p (p2 + 3p + 9) − 5 (p2 + 3p + 9)

= −2p5 − 6p4 − 18p3 + 8p4 + 24p3 + 72p2 + 10p3 + 30p2 + 90p − 5p2 − 15p − 45

= −2p5 + 2p4 + 16p3 + 97p2 + 75p − 45

d. st(−5stu + 3u − 9) = −5s2t2u + 3stu − 9st

e. (7a2 − 2a + 8) (3a2 + 5a + 12) = 7a2 (3a2 + 5a + 12) − 2a (3a2

+ 5a + 12) + 8 (3a2 + 5a + 12)

=21a4 + 35a3 + 84a2 − 6a3 − 10a2 − 24a + 24a2 + 40a + 96

= 21a4 + 29a3 + 98a2 + 16a + 96

f. (6p5 − 4p3 + 2p2 + 13p − 1) (4p2 + 7p + 12) = 6p5 (4p2 + 7p + 12) − 4p3 (4p2 + 7p + 12) + 2p2 (4p2 + 7p + 12) + 13p (4p2

+ 7p + 12) − 1 (4p2 + 7p + 12)

=24p7 + 42p6 + 72p5 − 16p5 − 28p4 − 48p3 + 8p4 + 14p3 + 24p2 + 52p3 + 91p2 + 156p − 4p2 − 7p − 12

= 24p7 + 42p6 + 56p5 − 20p4 + 18p3 + 111p2 + 149p − 12

2.a. (9h + 4) (2h − 11) = 9h (2h − 11) + 4 (2h − 11) = 18h2 − 99h + 8h − 44 = 18h2 − 91h − 44

For h = 2, 18h2 − 91h − 44 = 18 (2)2 − 91 × 2 − 44 = 72 − 182

− 44 = −154

b. (2a2 − 5a − 8) (4a2 − a + 3) = 2a2 (4a2 − a + 3) − 5a (4a2 − a

+ 3) − 8 (4a2 − a + 3) = 8a4 − 2a3 + 6a2 − 20a3 + 5a2 − 15a

− 32a2 + 8a − 24 = 8a4 − 22a3 − 21a2 − 7a − 24

For a = −5, 8(−5)4 − 22(−5)3 − 21(−5)2 − 7(−5) − 24 = 8 × 625

− 22 × (−125) − 21 × 25 + 35 − 24 = 5000 + 2750 − 525 + 35

− 24 = 7236

c. (7q − 8) (3q2 − 4q + 7) = 7q (3q2 − 4q + 7) − 8 (3q2 − 4q + 7) = 21q3 − 28q2 + 49q − 24q2 + 32q − 56 = 21q3 − 52q2 + 81q

− 56

For q = 0, 21(0)3 − 52(0)2 + 81(0) − 56 = − 56

d. (2t3 + 5t2 + 7t − 10) (3t2 − 10t + 15)

= 2t3 (3t2 − 10t + 15) + 5t2 (3t2 − 10t + 15) + 7t (3t2 − 10t + 15) − 10 (3t2 − 10t + 15)

= 6t5 − 20t4 + 30t3 + 15t4 −50t3 + 75t2 + 21t3 − 70t2 + 105t

− 30t2 + 100t − 150

= 6t5 − 5t4 + t3 − 25t2 + 205t − 150

For t = −2, 6(−2)5 − 5(−2)4 + (−2)3 − 25 (−2)2 + 205 (−2) − 150 = 6 × (−32) − 5 × 16 − 8 − 25 × 4 + 205 × (−2) − 150

= −192 − 80 − 8 − 100 − 410 − 150 = −940

3.a. 1 5 a (8a + 5b − 11c) − 5 6 a (3a − 5b + 12c)

= − 8 5 a2 − ab + 11 5 ac − 15 6 a2 + 25 6 ab − 10ac

= 8 5 − 15 6 a2 + 25 6 − 1 ab + 11 5 − 10 ac

= –48–75 30 a2 + 25–6 6 ab + 11–50 5 ac

= − 41 10 a2 + 19 6 ab − 39 5 ac

For a = −1, b = 2, c = 10, 41 10 (−1)2 + 19 6 (−1) (2) − 39 5 (−1) (10) = 41 –10 19 –3 + 390 5 = –123–190+2340

30

= 2027 30

b. −2a2b(5a3 − 7b + a + 11) − ab(9b4 −3b2 − 4b) − c(2a3 + 2b2 + 1)

= −10a5b + 14a2b2 −2a3b −22a2b − 9ab5 + 3ab3 + 4ab2 − 2a3c − 2cb2 − c

= −10a5b − 9ab5 + 14a2b2 −2a3b −22a2b + 3ab3 + 4ab2 − 2a3c − 2cb2 − c

For a = −1, b = 2, c = 10, −10 (−1)5 (2) − 9 (−1) (2)5 + 14 (−1)2 (2)2 −2 (−1)3 (2) − 22 (−1)2 (2) + 3 (−1) (2)3 + 4 (−1) (2)2 − 2 (−1)3 (10) −2 (10) (2)2 − 10

= 20 + 288 + 56 + 4 − 44 − 24 − 16 + 20 − 80 − 10 = 214

c. (a − 7) (a4 − 6b3 + 4c − 5) + 3 7 bc (9a2 − 14)

= a (a4 − 6b3 + 4c − 5) − 7 (a4 − 6b3 + 4c − 5) + 3 7 bc (9a2 − 14)

= a5 − 6ab3 + 4ac − 5a − 7a4 + 42b3 − 28c + 35 + 27 7 a2bc

− 6bc

For a = −1, b = 2, c = 10, (−1)5 − 6 (−1) (2)3 + 4 (−1) (10)

− 5(−1) − 7 (−1)4 + 42 (2)3 − 28 (10) + 35 + 27 7 (−1)2 (2) (10)

− 6 (2) (10)

= −1 + 48 − 40 + 5 − 7 + 336 − 280 + 35 + 540 7 − 120

= 540 7 − 24 = 540–168 7 = 372 7

4.a. Area = 7x2y × 8x3y2z = 56x5y3z sq. units

b. Area = 109 9109

c. 31312222 5656 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø pqpq = 22 313222 –= 565 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø pqp

− 2 × 3 5 p2 × 1 6 q2 + 2 2 1 6 q æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 9 25 p4 − 1 5 p2q2 + 1 36 q4

d. 2–2–77 1111 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

pp = 2 7 2–11 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

p = (2p)2 − 2 × 2p × 7 11

+ 2 7 11 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

æöæöæöæö çççç÷÷÷÷ çççç÷÷÷÷ çççç÷÷÷÷ çççç÷÷÷÷ çççç÷÷÷÷ èøèøèøèø xxxxx

2–+11=2+11–+11 74 474

= 9 2 x2 + 22x − 45 14 x − 110 7 =

2 308–45 9 110 +–2147 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø xx

= 4p2 − 28 11 p + 49 121

e. 44 44 11 +–æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ ÷÷ çç÷÷ èøèø xx xx = (x4)2 − 2 4 1 x æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø = x8 − 8 1 x

2 308–45 9 110 +–2147 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø xx 9 2 x2 + 263 14 x 110 7

2 308–45 9 110 +–2147 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø xx sq. unit

c. Area = 9 13 abc

f. 88 88 11 –+ æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ ÷÷ çç÷÷ èøèø pp pp = (p8)2 −

2 8 1 p

æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø = p16 − 16 1 p

g. 1414 3535 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø xyxy = 22 141 –= 353 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø xyx

232324232 41363 +=+ 769126

æ öæ ö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ è øè ø abcabcabcabc sq. units

d. Area = (5z − 3) × (2z2 + 9z − 11) = 5z (2z2 + 9z − 11) − 3 (2z2 + 9z − 11)

= (10z3 + 45z2 − 55z − 6z2 − 27z + 33 = 10z3 + 39z2 − 82z + 33) sq. units

5.a. Volume = 7 11 p2q3r4 × 2 7 pqr × 2p (q + r) = 4 11 p4q4r5 (q + r)

− 2 × 1 3 x × 4 5 y

+

2 4 5 y æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 1 9 x2 − 8 15 xy + 16 25 y2

h. (11a − 7b) (11a − 7b) = (11a − 7b)2 = (11a)2 − 2 × 11a × 7b + (7b)2 = 121a2 − 154ab + 49b2

i. (3.5x + 7.4y) (3.5x + 7.4y) = (3.5x + 7.4y)2 = (3.5x)2 + 2 × 3.5x × 7.4y + (7.4y)2 = 12.25x2 + 51.8xy + 54.76y2

44455446 =pqr+pqrcu.cm 1111

æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

b. Volume = (p + q) × (2p − 3q + 14) × 7r

= [p (2p − 3q + 14) + q (2p − 3q + 14)] × 7r

= (2p2 − 3pq + 14p + 2pq − 3q2 + 14q)7r

= 14p2r − 21pqr + 98pr + 14pqr − 21q2r + 98qr

= (14p2r − 7pqr + 98pr − 21q2r + 98qr) cu. cm

c. Volume = − 1 2 pq (r + 5) × 9pq × 10qr = (−pqr −5pq) 45pq2r =(−45p2q3r2 − 225p2q3r) cu. cm

6.a. Volume = 5s (stu + 2) × 5s (stu + 2) × 5s (stu + 2) = 125s3 (stu + 2)3 cu. cm

b. Volume = 4s2t3u5 × 4s2t3u5 × 4s2t3u5 = 64s6t9u15 cu. cm

c. Volume = (−7ab + 11a2 + 2) × (−7ab + 11a2 + 2) × (−7ab + 11a2 + 2) = (−7ab + 11a2 + 2)3 cu. cm

d. Volume = 3p3q4 (2r + 5q − 6) × 3p3q4 (2r + 5q − 6) × 3p3q4 (2r + 5q − 6) = 27p9q12 (2r + 5q − 6)3 cu. cm

7.a. (8a + 11b) (8a + 11b) = (8a + 121b)2 = (8a)2 + 2 × 8a × 11b + (11b)2 = 64a2 + 176ab + 121b2

b. 27272222 ++ 5656 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø abab = 22 272222 += 565 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø aba + 2 × 2 5 a2 × 7 6 b2 + 2 2 7 6 b æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 4 25 a4 + 14 15 a2b2 + 49 36 b4

8.a. (88)2 = (90 − 2)2 = (90)2 − 2 × 90 × 2 + (2)2 = 8100 − 360 + 4

= 7744

b. (212)2 = (200 + 12)2 = (200)2 + 2 × 200 × 12 + (12)2 = 40000

+ 4800 + 144 = 44,944

c. (53)2 = (50 + 3)2 = (50)2 + 2 × 50 × 3 + (3)2 = 2500 + 300 + 9

= 2809

d. 45 × 124 = (100 − 55) (100 + 24) = (100 + (−55)) (100 + 24)

= (100)2 + 100 (−55 + 24) + (−55 × 24) = 10,000 − 100 × 31 − 1320 = 10,000 − 3100 − 1320 = 5580

e. (2.2x + 3.3y)2 = (2.2x)2 + 2 × 2.2x × 3.3y + (3.3y)2 = 4.84x2

+ 14.52xy + 10.89y2

f. 6.4 × 5.8 = (6.0 + 0.4) (6.0 − 0.2) = (6.0 + 0.4) (6.0 + (−0.2))

= (6.0)2 + 6.0 (0.4 − 0.2) + (0.4 × (−0.2))

= 36 + 1.2 − 0.08 = 37.12

g. (197)2 = (200 − 3)2 = (200)2 − 2 × 200 × 3 + (3)2 = 40,000

− 1200 + 9 = 38,809

h. 22 181 += 2112 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø aba + 2 × 1 2 a × 8 11 b + 2 8 11 b æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 1 4 a2

+ 8 11 ab + 64 121 b2

i. 22 35322 –= 8118 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø xyx − 2 × 3 8 x2 × 5 11 y + 2 5 11 y æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 9 64 x4 − 15 44 x2y + 25 121 y2

j. 2 5 3–11 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø p = (3p)2 − 2 × 3p × 5 11 + 5 11 2

= 9p2 − 30 11 p + 25 121

9.a. 16x2 + 64xy + 64y2 = 16

2 4 –9 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 64 42 –93 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø + 64

2 2 3 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 256 81 − 512 27 + 256 9 = 256–1536+2304 81 = 1024 81

b. 4x2 + 20xy + 25y2 = 2 4 4–9 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 20 42 –93 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø + 25 2 2 3 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 64 81

− 160 27 + 100 9 = 64–480+900 81 = 484 81

c. 49x2 + 84xy + 36y2 = 2 4 49–9 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 42 84–93 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø + 2 2 36 3 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 784 81 − 672 27 + 144 9 = 784–2016+1296 81 = 64 81

10.a. (2a − 3b)2 − (5a + 6b)2 + 6a2 − 11ab

= 4a2 − 12ab + 9b2 − (25a2 + 60ab + 36b2) + 6a2 − 11ab

= 4a2 − 12ab + 9b2 − 25a2 − 60ab − 36b2 + 6a2 − 11ab

= −15a2 − 83ab − 27b2

b. 22 11232222 ++–4678 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø abab − 5a2b2 = 1 16 a4 + 1 12 a2b2

+ 1 36 b4 + 4 49 a4 − 3 14 a2b2 + 9 64 b4 − 5a2b2

= 113 784 a4 + 97 576 b4 − 431 84 a2b2

11.a.

2224 44161616256 +–+=–+=–55252525625 æöæöæöæöæöæö çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ èøèøèøèøèøèø xxxxxx

b. (x + 8) (x − 8) (x2 + 64) = (x2 − 64) (x2 + 64) = (x4 − 4096)

12.a. x + 1 x = −5

Squaring both sides, we get 2 2 1 +=(–5) æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø x x

x2 + 2 1 x + 2 × x × 1 x = 25

x2 + 2 1 x + 2 = 25

x2 + 2 1 x = 25 − 2 = 23

b. From the previous part, x2 + 2 1 x = 23

Squaring both sides, we get 2 22 2 1 +=(23) æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø x x

x4 + 4 1 x + 2 × x2 × 2 1 x = 529

x4 + 4 1 x + 2 = 529

x4 + 4 1 x = 529 − 2 = 527

13.a. x 1 x = 15

Squaring both sides, we get

x − 1 x 2 = ( 15 )2

x2 + 2 1 x − 2 × x × 1 x = 15

x2 + 2 1 x − 2 = 15

x2 + 2 1 x = 15 + 2 = 17

b. From the previous part, x2 + 2 1 x = 17

Squaring both sides, we get 2 22 2 1 +=(17) æö

÷ ç ÷ ç ÷ ç ÷ ç ÷ ÷ ç èø x x

x4 + 4 1 x + 2 × x2 × 2 1 x = 289

x4 + 4 1 x + 2 = 289

x4 + 4 1 x = 289 − 2 = 287

14.a. (x + y)2 = x2 + y2 + 2xy = 17 + 2 × (−4) = 17 − 8 = 9; x + y

= 9 = 3

b. (x − y)2 = x2 + y2 − 2xy = 17 − 2 × (−4) = 17 + 8 = 25; x − y

= 25 = 5

c. x4 − y4 = (x2)2 − (y2)2 = (x2 + y2) (x2 − y2) = 17 (x + y) (x − y)

= 17 × 3 × 5 = 255

d. 1 2 xy (7x − 8y)2 − 1 2 xy (7x + 8y)2 = 1 2 xy (49x2 + 64y2

− 112xy) − 1 2 xy (49x2 + 64y2 + 112xy)

= 49 2 x3y + 32xy3 − 56x2y2 − 49 2 x3y − 32xy3 − 56x2y2 = −112

x2y2 = −112 (xy)2

= −112 (−4)2 = −1792

e. x8 − y8 = (x4)2 − (y4)2 = (x4 + y4) (x4 − y4) = (x4 + y4) (x2)2 − (y2)2

= (x4 + y4) (x4 − y4) =(x4 + y4) × 255 (from c.)

x2 + y2 = 17

squaring both sides, we get (x2 + y2)2 = (17)2

x4 + y4 + 2x2y2 = 289

x4 + y4 + 2 × (−4)2 = 289

x4 + y4 = 289 − 2 × 16 = 289 − 32 = 257

So, (1) implies x8 − y8 = 257 × 255 = 65,535.

Word Problems

1. Area of the rectangular structure = (5x + 3) × (2x − 1) = 5x (2x −

1) + 3 (2x − 1) = 10x2 − 5x + 6x − 3 = (10x2 + x − 3) sq. m

Cost of a sq. m of material = ₹100

Total cost of the structure = ₹100 (10x2 + x − 3)

2. Population after two years = (2x3 − 3x2 + 5x) (x + 1)2 = (2x3 − 3x

Chapter 17

Let's Warm-up

1. I have a triangular base, with 3 triangular faces meeting at a vertex: triangular pyramid.

2. I have two parallel and congruent square faces: square prism.

3. I have a square base with 4 flat triangular faces: square pyramid.

4. I have two triangular bases and 3 rectangular faces: triangular prism.

Do It Yourself

17A

1. a.

It is made with a cone, a cylinder and a hemisphere.

c. It is made with a cylinder and 2 hemispheres.

2.a. Front view

b. Side view

b. It is made with a cylinder surmounted by a cone.

d. It is made with a sphere surmounted by a cone.

3. a. Front View: Side View: Top View:

b. Front View: Side View: Top View:

c. Front View: Side View: Top View:

d. Front View: Side View: Top View:

4. a. Front View: Side View: Top View:

b. Front View: Side View: Top View:

c. Front View: Side View: Top View:

d. Front View: Side View: Top View:

5. a. Front View: Side View: Top View:

b. Front View: Side View: Top View:

c. Front View: Side View:

Top View:

Word Problem

1. If two or more blocks are arranged in the same pattern: Front View: Side View:

Top View:

17B

1.a. The garden is the farthest from the main building, as the distance on the map = 1.3 cm + 0.6 cm + 16 cm + 2 cm = 19.9 cm

b. The reception is the nearest to the main building.

c. Distance on map from main building to Library = 1.3 cm + 0.6 cm + 16 cm = 17.9 cm

Garden = 1.3 cm + 0.6 cm + 16 cm + 2 cm = 19.9 cm

So, the library is nearer.

d. Distance on map from main building to Library = 1.3 cm + 0.6 cm + 16 cm = 17.9 cm

Sports ground = 1 cm + 2.5 cm + 14 cm + 1 cm = 18.5 cm

So, the library is nearer.

2.a. Distance on map = 1.3 cm + 0.6 cm + 16 cm + 2 cm = 19.9 cm

Actual distance = 19.9 × 10 m = 199 m

b. Distance on map = 3.6 cm

Actual distance = 3.6 × 10 m = 36 m

c. Distance on map = 2 cm + 16 cm + 2 cm = 20 cm

Actual distance = 20 × 10 m = 200 m

d. Distance on map = 5 cm + 1 cm + 2 cm + 1 cm + 2.5 cm + 14 cm + 1 cm = 26.5 cm

Actual distance = 26.5 × 10 m = 265 m

3.a. 12.5 × 5.5 km = 68.75 km

b. 4.7 × 5.5 km = 25.85 km

c. 7.3 × 5.5 km = 40.15 km

4. 1 mm = 6 m

So, 1 m = 1 6 mm

⇒ 72 m = 1 6 × 72 mm = 12 mm

Thus, the distance on the map for an actual distance of 72 m is 12 mm.

5. Answersmayvary.Sampleanswer:

a.

6. 1

So,

⇒

Since,

Word Problem

17C

1.a. If all the faces of a polyhedron are regular, then it is a regular polyhedron.

b. A rectangular prism is also called a cuboid

c. The polygonal regions forming a polyhedron are called faces

d. A triangular pyramid is also called a tetrahedron

2.a. No, since a polyhedron must have at least 4 faces.

b. Yes, for example, a tetrahedron.

1. Answersmayvary.Sampleanswer: WA

c. Yes, a square pyramid has a square face and 4 triangular faces.

3.a. A prism has a minimum of 5 faces, and the maximum number of faces a prism can have is infinite.

b. A pyramid has a minimum of 4 faces, and the maximum number of faces a prism can have is infinite.

4. To make a pyramid, we would need a square base along with the given 4 congruent equilateral triangular faces.

C I B A

E

Edges: AB, BC, CD, DE, EF, FA, GH, HI, IJ, JK, KL, LG, AL, BK, CJ, DI, EH, FG

Vertices: A, B, C, D, E, F, G, H, I, J, K, L

6. Answermayvary,sampleanswer: ABCDEFGH is heptagonal pyramid.

H FG A B C D E

Faces: ABCDEFG, ABH, BCH, CDH, DEH, EFH, FGH, GAH

Edges: AB, BC, CD, DE, EF, FG, GA, AH, BH, CH, DH, EH, FH, GH

Vertices: A, B, C, D, E, F, G, H

⇒

7. No, a cylinder is not a polyhedron since it has curved faces. The 3-D shapes with flat polygonal faces, straight edges and vertices are called polyhedrons.

Word Problem

1.

The figure built by Sam is a decagonal pyramid. A decagonal pyramid has 11 faces, 20 edges and 11 vertices.

17D

1.a. Prisms have two parallel bases with rectangular faces connecting corresponding vertices, while pyramids have a single base with triangular faces connecting to a common apex.

2.a. F = 5; V = 6; E = 9

Since, F + V − E = 2

LHS = 5 + 6 − 9 = 11 − 9 = 2 = RHS

b. F = 10; V = 10; E = 18

Since, F + V − E = 2

LHS = 10 + 10 − 18 = 2 = RHS

c. F = 8; V = 6; E = 12

Since, F + V − E = 2

LHS = 8 + 6 − 12 = 2 = RHS

3.a. F = 5; E = 9

Since, F + V − E = 2

5 + V − 9 = 2

V = 6

b. F = 8; V = 12

Since, F + V − E = 2

8 + 12 − E = 2

E = 18

c. F = 9; E = 16

Since, F + V − E = 2

9 + V − 16 = 2

V = 9

d. F = 20; V = 12

Since, F + V − E = 2

20 + 12 − E = 2

E = 30

4. Number of sides of the polygonal base = n, so the number of vertices of the polygon = n

So, the number of faces of the pyramid = 2 + n

And, the number of vertices of the pyramid = n + n =2n

Since, F + V − E = 2

2 + n + 2n −E=

2 + 3n −E = 2

2 + 3n −2 = E

E = 3n

5.a. F = 8; V = 12; E = 18

Since, F + V − E = 2

LHS = 8 + 12 − 18 = 2 = RHS

b. F = 9; V = 9; E = 16

Since, F + V − E = 2

LHS = 9 + 9 − 16 = 2 = RHS

c. F = 7; V = 10; E = 15

Since, F + V − E = 2

LHS = 7 + 10 − 15 = 2 = RHS

Word Problem

1. F = 10; V = 15; E = 20

Since, F + V − E = 2

LHS = 10 + 15 − 20 = 5 ≠ RHS

Since, the Euler’s formula is not verified, such polygon can’t be made.

Chapter Checkup

1. a. Top View: Side View: Front View:

b. Top View: Side View: Front View:

c. Top View: Side View: Front View:

2. a. Front View: Side View: Top View:

b. Front View: Side View: Top View:

c. Front View: Side View: Top View:

3. a. Front View: ⇒ 6

b. Front View: ⇒ 5

c. Front View: ⇒ 20

Top View: ⇒ 25

Side View: ⇒ 3

Side View: ⇒ 4

Top View: ⇒ 6

Top View: ⇒ 5

Side View: ⇒ 30

4. Answers may vary. Sample answer:

WASHROOM

BED ROOM

WASHROOM

BAL CO NY

LIVING ROOM

DINING ROOM

BAL CO NY

BED ROOM KITCHEN

5.a. The distance between the dairy and the railway station on the map = 4 cm + 7.5 cm = 11.5 cm

b. Sam lives nearest to the park.

c. The distance between the park and the railway station on the map = 7.5 cm + 4 cm + 8 cm = 19.5 cm.

Actual distance= 19.5 × 4.5 = 87.75 km

d. Distance on map = 8 cm

Actual distance = 8 × 4.5 km = 36 km.

e. Distance on map = 7.5 cm + 4 cm = 11.5 cm

Actual distance = 11.5 × 4.5 km = 51.75 km.

6. 1 mm = 300 m

1m 1 300 mm

Distance on map for an actual distance of 15 km = ?

15 km = 15 × 1000 m = 15 × 1000 × 1 300 mm = 50 mm

So, distance on the map for an actual distance of 15 km is 50 mm.

7. The minimum number of faces that a polyhedron can have is 4.

8.a. Tetrahedron

b. Pyramid

9.a. F = 5; V = 6

Since, F + V − E = 2

5 + 6 − E = 2

E = 9

Triangular prism

b. F = 5; V = 5

Since, F + V − E = 2

5 + 5 − E = 2

E = 8

Rectangular pyramid

c. F = 8; E = 12

Since, F + V − E = 2

8 + V − 12 = 2

V = 6

Octahedron

d. F = 7; E = 15

Since, F + V − E = 2

7 + V − 15 = 2

V = 10

Pentagonal prism

e. V = 8; E = 12

Since, F + V − E = 2

F + 8 − 12 = 2

F − 4 = 2

F = 6

Cube

f. V = 12; E = 18

Since, F + V − E = 2

F + 12 − 18 = 2

F = 8

Hexagonal prism

10.a. F = F = 8; V = 6; E = 14

Since, F + V − E = 2

LHS = 8 + 6 − 14 = 0 ≠ RHS

Since, the Euler’s formula is not verified, the polyhedron does not exist.

b. F = 9; V = 9; E = 16

Since, F + V − E = 2

LHS = 9 + 9 − 16 = 2 = RHS

Since, the Euler’s formula is verified, the polyhedron exists.

Word Problems

1.

On arranging the three cubes next to each other, Sudha got a cuboid.

Front view:

Side view:

Top view:

2. Scale: 1 cm = 0.5 km

The greatest distance on the map between the dairy and the post office = 4 cm + 6 cm + 2.5 cm = 12.5 cm

Actual distance = 12.5 × 0.5 km = 6.25 km

The smallest distance on the map between the dairy and the post office = 5 cm + 3 cm + 3 cm = 11 cm

Actual distance = 11 × 0.5 km = 5.5 km

3. Given that the solid having only triangles as faces and 6 vertices:

If the solid contain exactly 8 triangles, then number of faces = number of triangles = 8

Since, F + V − E = 2

8 + 6 − E = 2 ⇒ E = 12

As the shape having 6 vertices, 8 faces and 12 edges is an octahedron, the solid contains only 8 triangles.

Chapter 18

Let's Warm-up

1. Perimeter of an equilateral triangle of length 5 cm

2. Area of a triangle of length 4 m and height 8 m

3. Perimeter of a triangle of sides 3 cm, 4 cm, and 5 cm

4. Area of a right triangle of lengths 6 m, 8 m, and 10 m

5. Perimeter of a triangle of sides 20 cm, 10 cm, and 10 cm

Do It Yourself 18A

1. Length of the rectangle = 14 cm

Area = 84 sq. cm

Since, Area = Length × Breadth

84 = 14 × Breadth

Breadth = 84 6 14 cm

40 cm

24 sq. m

16 sq. m

15 cm

12 cm

So, Perimeter of the rectangle = 2 × (Length + Breadth)

= 2×(14+6)=2×20=40 cm

Given that, Perimeter of the square = Perimeter of the rectangle

Perimeter of the square = 40 cm

4 ×Side = 40 cm

Side = 40 10

4 cm

So, the side of the square is 10 cm.

2. Area of a tile = 100 cm × 100 cm = 10,000 sq. cm = 1 sq. m

m

m 43 m

Length = 40 m + 1.5 m + 1.5 m = 43 m

Breadth = 32 m + 1.5 m + 1.5 m = 35 m

Area of the entire region = 43 ×35 1505 . mmsqm

Area of the park = 40 ×32 =1280 . mmsqm

Area of the path = area of the entire region − area of the park

= 1505–1280=225 . sqm

Number of the tiles required

= Area of the path225==225

Area of one tile1

So, 225 square-shaped tiles are required.

3. 9 m

A B

C D 6 m

Radius of the circle = BC ABC is a right-angled triangle.

So, AC2 = AB2 + BC2

9=6+222 BC

2 81–36==45 BC = 45=35 BC m

Area of a quarter circle = 1 × 4 Area of a circle

= 112222 ×=××(35)=35.35 sq. m 447 r

So, the area of the quarter circle is 35.35 sq. m.

4. Diameter = 32 cm

So, radius = 32 cm=16 cm 2

a.

16 cm

16 cm

25 cm

Area of the square = 25 cm × 25 cm = 625 sq. cm

Area of a quarter circle = 1 × 4 Area of a circle

= 22 11221408 ×=××(16)= sq. cm 4477 r

Area of the shaded region

= 625–=1408625×7–1408 =423.85 77 sq. cm

b. 32 cm

16 cm

16 cm

Side of the square = 16 cm + 16 cm = 32 cm

Area of the square = 32 cm ×32 cm=1024 sq. cm

Area of 4 quarter circles = 1 4×× 4 Area of a circle

= 2 1 4×× 4 r

2 =1××(16)=225632 sq. cm 77

Area of the shaded region = 5632 1024–=219.43 sq. cm 7

c. B

8. Area of the sign = 17 sq. m

Area of the 2 parallelograms = 2×(7.5×1)=15 sq. m

Area of the triangle = 1715=2 sq. m –

9. Area of the room = 39 m × 15 m=585 sq. m

Area of one tile = 3 m × 3 m=9 sq. m

Total number of tiles = 585 =65 9

P R D

16 cm

32 cm

Side of the square = 16 cm+ 16 cm = 32 cm

Area of the square = 32 cm ×32 cm=1024 sq. cm

Area of 2 quarter circles = 2 1 ×× 4 Area of a circle = 2

2 1 ×× 4 r

2 122281616sq. cm 277

Area of two right triangles = 1 2××16×16=256sq. cm 2

Area of the shaded region

= 2816 1024256=365.71 sq. cm 7

5. Area of a parallelogram = base×height

A

B Z C D Y

Y and Z are the horizontal and vertical heights of the given parallelogram, respectively.

Considering Y, area = AB × Y or CD × Y

Considering Z, area = AD × Z or BC × Z

John’s answer = CD × Y

David’s answer = BC × Z

So, both John and David are correct.

6. Since, the two sides of the parallelogram are in the ratio = 4:3

Let the two sides be 4x and 3x

Then the perimeter = 4+3+4+3=56 cm=14 xxxxx

56 ==4

14 x

Therefore, the sides of the parallelogram are 4×4=16 cm and 3×4=12 cm.

Height = 1 ×16=2 8 cm

Area = 16×2=32 sq. cm.

7. Area of the wooden frame = 162 cm ×36 cm=5832 sq. cm

a. Area of each triangle = 1 ×6×8=24 sq. cm 2

b. Number of triangles = 5832 =243 24

c. Total perimeter of all the triangles used = Number of triangles × Perimeter of each triangle = 243×(6+8+10)=5832 cm.

There are 39 =13 3 brown tiles along the length, and 15 =5 3 brown tiles along with the breadth.

So, number of brown tiles = (13 + 5 + 13 + 5−4) = 32

Let the number of white tiles = x

So, number of pink tiles = twice of number of white tiles = 2x

Then, 32++2=65 xx

32+3=65 x 3=33 x =11

x

2=22 x

So, there are 32 brown tiles, 22 pink tiles and 11 white tiles.

10. A B C D

Let the length of a rectangle = l and breadth = b

Perimeter of each rectangle = 2×(+)=48 cm=(+)=24 cm lblb

AB = BC = CD = DA = +=24 cm lb

Area of the square = 24 cm × 24 cm ×= 576 sq. cm

Area of the square = 5 × area of each rectangle

Then the area of each rectangle = 576 =115.2 sq.cm 5

Word Problems

1. Let’s say Aana walked from point A to C.

Distance she moved along the length and breadth = distance from A to C = AB + BC

8 m

A B C D

Let BC = x

x 10 m

In right triangle ABC, using the Pythagoras rule:

AB2 + BC2 = AC2

82 + x2 = 102

64 + x2 = 100

x2 = 36

x = 6

BC = 6

Distance from A to C if walked along the length and breadth = 8 m + 6 m = 14 m.

Therefore, she must have walked = 14 m − 10 m = 4 m

So, the required distance = 4 m.

2. Area of the lawn = area of the square + 3 × area of the semi-circle = 2 1 (32×32)+3××=(1024)+3× 2

r

122××16×16=2230.85sq.m 27

Fertilizer for 1 sq. m = 20 g

Fertilizer for 2230.85 sq. m = 20 × 2230.85 g = 44617 g = 44.617 kg

Cost of 10 kg fertilizer = ₹16

Cost of 44.617 kg fertilizer = ₹16 10 × 44.617 = ₹71.39

3. A A A

A 12 cm 32 cm 15 cm

B F E

B B C C C (B) E E

D (D)

Let the area of the parallelogram ABCD be A.

Fraction of the shaded region = 3 8

Fraction of the newly obtained shaded region = 3 8 × 3 8 = 9 64

So, the fraction of the shaded area we obtained in the end compared to the original parallelogram is 9 64 . 18B

1.a.

6 cm B

7 cm

G

2. D C

Area = 1 2 × 32 × (12 + 15) = 1 2 × 32 × 27 = 432 sq. cm

3. Since, the parallel sides are in the ratio 4:6

Let the sides be 4x and 6x

Height = 15 cm

Area = 1 2 × (4x + 6x) × 15 = 450 sq. cm

75x = 450

32 cm

25 cm 16 cm

F E H I

A C D

IE = IH + HE

32 cm = IH + 25 cm

IH = 7 cm

And GC = FD = 16 cm

Area of the trapezium ABCG = 1 2 × (6 + 16) × 7 = 77 sq. cm

Area of the rectangle CDFG = 25 × 16 = 400 sq. cm

Total area = 400 + 77 = 477 sq. cm

b. 27 cm

B A E F

18 cm

12 cm 10 cm D C

25 cm

Area of the trapezium ABCD = 1 2 × (27 + 18) × 12

= 270 sq. cm

Area of the trapezium CDEF = 1 2 × (18 + 25) × 10

= 215 sq. cm

Total area = 270+ 245 = 485 sq cm

E

DA B C

c. 16

2 5 F

Height = 16 − 5 = 11 units

12

Area of the rectangle ABCD = 2 × 5 sq. units

Area of the trapezium CDEF = 1 2 × (2 + 12) × 11 = 77 sq. units

Total area = 10 + 77 = 87 sq. units

x = 450 75 = 6

So, the sides are: 4x = 4 × 6 = 24 cm and 6x = 6 × 6 = 36 cm.

4. Perimeter = 200 cm

Length of each side = 200 4 = 50 cm

Area = 672 sq. cm = 1 2 × d1 × d2

672 = 1 2 × (96) × d2

d2 = 14 cm

5. Area = 204 sq. cm = 1 2 × d1 × d2 = 1 2 × 12 × d2

204 × 2 = 12 × d2

408 12 × d2

d2 = 34 cm

6. B A

D E F C

Area = 1 ×(32+25)×=185 2 AE =6.5 m AE

= = DEFCandABEF =++ DCDEEFFC

32 =2+25mDE =3.5 DEm

ADAEDE =7.38 ADm

2222 ( = +=6.5)+(3.5)

So, lengths of the non-parallel sides is 7.38 m.

7. Area = 170 sq. cm

Length of Diagonal = 18 cm

Length of Perpendicular1 = 15 cm

Let length of Perpendicular2 = x cm

Area = 1 ×17×(15+) 2 x

17 170=×(15+) 2 x

x =5 cm

So, the length of the other perpendicular is 5 cm.

8. Length of the rope = 80 cm

l of the rectangle = 14 cm

b of the rectangle = 8 cm

P of the rectangle = 2 × (14 + 8) = 44 cm

Remaining length of the rope = 80 − 44 cm = 36 cm

P of the rhombus = 36 cm

Each side of the rhombus = 36 =9cm 4

9. Area of one tile 1 =×(24+20)×8=176 sq. cm 2 =0.0176sq. m

Area of the floor = 2992 sq. m

Number of tiles 2992 ==1,70,000 0.0176

Cost of 1 sq. m = ₹7.50

Cost of 2992 sq. m = ₹7.50 × 2992 = ₹22,440

10. As every rhombus is a parallelogram, and the area of a parallelogram = base × height

Area of the given rhombus = 64×36=2304 sq. m

Perimeter of the rhombus = 4×64=256 m

Area of the square = 2304 sq. m

Side of the square = 2304=48 m

Perimeter of the square = 4×48=192 m

Difference between the perimeters = 256192=64m –11. If the ratio of the sides of a trapezium is 6:13:9:11 and P = 78 cm

Then, let the sides be 6x, 13x, 9x, 11x 6+13+9+11=78=39 xxxxx

78 ==2

36 x 6=6×2=12 x 13=13×2=26 x 9=9×2=18 x 11=11×2=22 x

Area = 1 ×(22+26)×10=240 sq. cm

Word Problem

2

1.a. Width of the road = One and quarter times the height of the wall 1×4+1 1==15 444

Width of the road = 5525 of 5=×5==6.25 m 444

b. Area of the wall = 12 sq. m, length of base = 12 5 = 2.4 m

So, length of the side of the rhombus = 2.4 m

Area of the rhombus = 2.4×6.25 =15 sq. m

18C

1.a. 22 cm

B

C A

D E

16 cm 15 cm

9 cm

24 cm

F

Area of trapezium BCDE = 1 (1622)9171 2 sq. cm

Area of rectangle ABEF = 15×22=330 sq. cm

b.

Total area = 171 + 330 = 501 sq. cm

100 cm

60 cm

30 cm

60 cm

130 m 55 cm

1.3 m = 1.3 × 100 cm = 130 cm

Area of the triangle = 1 ×60×55=1650 sq. cm

Area of the rectangle

2

= 60 130×60=100×60=6000 sq. cm 2 –

Area of the semicircle = 2 12260××=1414.28 272 sq. cm

Total area = 1650+6000+1414.28=9064.28 sq. cm

c. Area of the semicircle = 2 1229××=31.82 272 sq. cm

Area of the triangle

= 191×9×10=×9×5.5=4.5×5.5=24.75 sq. cm 222 –

Total area = 31.82 + 24.75 = 56.57 sq. cm

2.a. Area of ABCH = 1 ×(9+16)×5=62.5 2 sq. cm

Area of CDHG = 16×9=144 sq. cm

Area of EFGD = 1 ×(9+16)×5=62.5 sq. cm 2

Total area = 62.5 + 144 + 62.5 = 269 sq. cm

b. H

J 8 m 8 m 35 m 18 m

E G

I D A

22 m 50 m

C F

60 m

B

Area of EDJF = 8×35=280 sq. m

Area of BCDJ = 1 ×(22+60)×8=328 2 sq. m

Area of ABFG = 1 ×(60+35)+50×18=1305 2 sq. m

Total area = 280 + 328 + 1305 = 1913 sq. m

A B C

G H

I 14 cm 5 cm 35 cm

4 cm 4 cm 2 cm

F

c. D

Area of ABC = 1 ×14×5=35 sq. cm 2

E

Area of ACHG = 14×(354)=14×31=434 sq. cm –

Area of DFIH = 4×(144)=4×10=40 sq. cm –

Area of DEF = 1 ×2×10=10 sq. cm

2

Total area = 35+434+40+10=519 sq. cm

3.a. 5.5 cm

F

8 cm 5 cm A

12 cm

b.

F

E 3 cm

D H

C G

Since, GH = HB GH = HB = 6 cm

B

So, area of AHB = 1 ×3 cm×6 cm=9 sq. cm 2

D 2 cm

1.2 cm 4.2 cm 2.4 cm 6 cm

G

1 cm C A B E F I H

Area of DEFG = 1 ×(6+4.2)×2=10.2 sq. cm 2

E

4. A x 60° B

D 15 cm

C O

F Each triangle in the hexagon has all angles of 60°, so all 6 triangles are equilateral triangles.

So, in triangle AOX, 222 =+ AOOXAX

2 22 15 15=+ 2 OX

2 22556.25= OX –

2 168.75= OX = 168.75=12.9913 OX ≈ cm

Area of triangle AOB = 1 ×15×13=97.5 2 sq. cm

So, the area of all 6 triangles = area of the hexagon = 97.5 × 6 = 585 sq. cm

Other way, From the above figure, Diagonal = 15 + 15 cm = 30 cm (all triangles are equilateral) Distance between the diagonal and the base = altitude of the triangle = 13 cm

So, A

D E

30 cm 13 cm 15 cm B

x 15 cm

C

Area of one trapezium = 1 ×(15+30)×13=292.5 2 sq. cm

Area of the hexagon = area of 2 trapeziums = 2 × 292.5 sq. cm = 585 sq. cm

5. 6 cm 10 cm 2 cm 2 cm 18 cm 18 cm 9 cm

Area = 22 12261226 (45×10)××+×× 272272 –= 450sq. cm

6. A B C

2 cm 3.4 cm

F D E 8 cm 8 cm

Area of ABEF = 2×(83.4)=2×4.69.2 sq. cm –

Area of BCDE = 1 ×(2+8)×3.4=17 sq.cm 2

Total area = 9.2 + 17 = 26.2 sq. cm

7. XR = 9 m, TR = 15 m and TY = 10 m

4.4 m

T XY 2 m 3.6 m

P Q R S

Since, TR = TX + XR 15 =+9 mTXm =159 TX –=6 TX m

And, TX + XY = TY

6 +=10 mXYm

XY = 4 m

XR = XY + RY

9 m = 4 m + RY

RY = 5 m

Area of PXT = 1 ×6×4.4=13.2 sq. m 2

Area of PQYX = 1 ×(4.4+2)×4=12.8 2 sq. m

Area of QRY = 1 ×5×2=5 2 sq. m

Area of RST = 1 ×15×3.6=27 2 sq. m

Total area = 13.2 + 12.8 + 5 + 27 = 58 sq. m

8. Area of a tile = 25×20=500 . sqcm A F

Area of PES = 1 ×6×8=24 2 sq. cm

Area of PQRS = 8 × 8 = 64 sq. cm

Area of A = Area of DEFG − Area of PES = 108 sq. cm − 24 sq. cm

= 84 sq. cm

Area of C = Area of PQRS − Area of PES = 64 sq. cm − 24 sq. cm

= 40 sq. cm

So, Difference between A and C = 84 − 40 = 44 sq. cm

2 m2 m 2 m 2 m 3 m

B C D 2.5 m

2.5 m 4 m 1 m

P Q R S E

Area of ABS = 1 ×2.5×2=2.5 . 2 sqm

Area of BCQS = 1 ×(2.5+4)×(2+3)=16.25 . 2 sqm

Area of CQD = 1 ×4×(2+2)=8 . 2 sqm

Area of PED = 1 ×2×1=1 . 2 sqm

Area of EFRP = 1 ×(2.5+1)×(3+2)=8.75 . 2 sqm

Area of FAR = 1 ×(2+2)×2.5=5 . 2 sqm

Total area = 2.5+16.25+8+1+8.75+5=41.5 . 41.5 ×10,000 . =4,15,000 . sqm sqcmsqcm

Number of tiles = 4,15,000 =830 500

So, 830 tiles are required.

Word Problem

1. Area of the triangular tiles = 1 ×5×12=30 sq. cm 2

Area of bigger square tile = 12×12=144sq. cm

Area of smaller square tile = 5×5=25 sq. cm

Total area of the shape = 4×30+144×2×25=120+144+50 =314sq. cm

Chapter Checkup

1.

In triangle PES, 222 =+ ESPEPS

22 =6+8=36+64=100 ES =10 ES cm

So, EF = 10 cm + 2 cm = 12 cm

Area of DEFG = 9 × 12 = 108 sq. cm

2. y

x x

y x x y

Since, the area of rectangle = × lengthbreadth

But the area of parallelogram = baseheight

If the length and breadth of a rectangle are the same as the base and height of the parallelogram, then both the shapes will always have the same area.

So, Nishant’s statement is always true.

3.a.

A B 6 cm 6 cm

C

D

Area of 2 quarter circles = 2 122 2×××(6)=56.57 sq. cm 47

Area of square = (6+6)×(6+6)=12×12=144 sq. cm

Area of 2 circles = 2 22 2××(6)=226.28 7 sq. cm

Area of the shape = 226.28 + 144 − 56.57 = 313.71 sq. cm

24 cm

b. 95 cm

63 cm

Area of trapezium = 1 ×24+(9563)×63=1764 sq. cm 2 –

Area of quarter circle = 2 122××(63)=3118.5 sq. cm 47

Total area = 1764+3118.5=4882.5 sq. cm

4. 9.2 cm 9.2 cm 6.4 cm 6.4 cm

Area of the rhombus

= 12 11××=×9.2×6.4=29.44sq. cm 22 dd

Area of shaded region = 29.44 sq. cm

13 cm

5. 25 cm

Z B

A D 15 cm 5 cm

C Y

BC = BZ + ZY + YC

25 = 2BZ + 15 (Since, BZ = YC and AD = ZY)

BZ = 5 cm

In triangle ABZ, 222 =+ ABAZBZ 2222 13=+5=144 AZAZ

AZ = 12 cm

Area = 1 ×(15+25)×12=240 sq. cm

2

6. Let the diagonals be d and 5d

Area = 12 1 ×× 2 dd

1 1000 . =××5 2 sqcmdd

2 2000=5d

2 400= d =20 cm d and 5=5×20=100 cm d

So, the diagonals are 20 cm and 100 cm.

7. Let the parallel sides be 3 xandx

So, 1 350=×(+3)×14

2 xx

700 =50=4

14 x =12.5 cm x And 3=3×12.5=37.5 cm x

So, the lengths of the parallel sides are 12.5 cm and 37.5 cm.

H

Area of AEP = 1 ×95×90=4275 sq. cm 2

Area of EDRP = 1 ×(90+115)×(95+30)=12,812.5 sq. cm 2

Area of CDR = 1 ×100×115=5750 sq. cm 2

Area of ABC = 1 ×(95+95+30+100)×76=12,160 sq. cm 2

Total area = 4275+12812.5+5750+12,160 = 34,997.5 sq. cm

9. 160 m

150 m

240 m

Area = 1 ×(160+240)×150=30,000 sq. cm

2

Amount of wheat in 1 hectare = 6500 kg

Amount of wheat in 10,000 sq. m = 6500 kg

Amount of wheat in 30,000 sq. m = 6500 ×30,000 10,000 = 19,500 kg

So, the field produces 19,500 kg of wheat.

10. Area of one triangle = 1 ×5×5=12.5 2 sq. m

Area of 4 triangles = 4 × 12.5 sq. m = 50 sq. m

Area of the swimming pool = 22 ×3×3=28.29 7 sq. m

Area of square region = 40 m × 40 m = 1600 sq. m

Area of the grass region = 1600 sq. m − 50 sq. m − 28.29 sq. m

= 1521.71 sq. m

Cost of planting per sq. m of the grass = ₹15

Cost of planting 1521.71 sq. m of grass = ₹15 × 1521.72 = ₹22.825.65

Word Problems

15 m

8.a. A B C

G22 m

F

E D

15 m 58 m 12 m 8 m

Area of GFEH = 1 ×(22+58)×15=600 sq. cm 2

Area of ADEH = 15×58=870 sq. cm

Area of ABCD = 1 ×(8+58)×12=396 sq. cm 2

Total area = 600 + 870 + 396 = 1866 sq. cm

b. A B

1. Area of 1 tile = 1×0.5=0.5 sq. m

Area of 15 tiles = 15×0.5=7.5 sq. m

Area of the entire floor = 9×(0.5×5)=9×2.5=22.5 sq. m

Area of the uncovered floor = 22.57.5=15 sq. m –

2. 12 m

8 m

15 m

Area of the floor = 1 ×(12+15)×8=108 sq. m 2

30 cm 100 cm 90 cm 115 cm

E D P Q R 95 cm 95 cm 76cm

C

Paint required for 10 sq. m = 1L

Paint required for 108 sq. m = 1 ×108=10.8 10 L

Cost of 5L paint = 2899 `

Cost of 10.8 L paint = 2899 ×10.8=6261.84 5 ` `

Amount of money David has = ₹5400

Since, ₹5400 < ₹6261.84

So, David does not have enough money to buy all the paint he needs.

Chapter 19

Let's Warm-Up

20 cm

1.

12 cm

Area = 100 cm2

= 2 × 2 22 ×12×26cm

7 = 1961.14 cm2

b. Lateral Surface Area = 2 rh

= 2 × 2227××22m 72 = 484 m2

Total Surface Area = 2 r(h + r)

= 2 × 22277××+22m 722

= 2 ×= 561 m2

c. Lateral Surface Area = 2 rh

2. 4.

7cm

3.

5.

10 cm

15 cm

12 cm

15 cm

Do It Yourself 19A

1.

a. Lateral Surface area = 2(l + b)h = 2 × (12+8) × 15 cm2 = 600 cm2

Total Surface area = 2(lb + lh + bh)

Perimeter = 45 cm

Perimeter = 64 cm

Area = 154 cm2

Area = 90 cm2

= 2(12×8+12×15+8×15) cm2 = 792 cm2

b. Lateral Surface area = 2(l + b)h = 2 × (60 + 7) × 18 cm2 = 2412 cm2

Total Surface area = 2(lb + lh + bh)

= 2(60×7+ 60×18+7×18) cm2 = 3252 cm2

c. Lateral Surface area = 2(l + b)h = 2 × (55.5 + 11.5) × 9.25 m2 =1239.5 m2

Total Surface area = 2(lb + lh + bh)

= 2(55.5×11.5+55.5×9.25+11.5×9.25) m2 = 2516 m2

2.a. Lateral Surface Area = 4a2 = 4 × 21 × 21 m2 = 1764 m2

Total Surface Area = 6a2 = 6 × 21 × 21 m2 = 2646 m2

b. Lateral Surface Area = 4a2 = 4 × 17 × 17 mm2 = 1156 mm2

Total Surface Area = 6a2 = 6 × 17 × 17 mm2 = 1734 mm2

c. Lateral Surface Area = 4a2 = 4 × 28 × 28 m2 = 3136 m2

Total Surface Area = 6a2 = 6 × 28 × 28 m2 = 4704 m2

d. Lateral Surface Area = 4a2 = 4 × 35 × 35 dm2 = 4900 dm2

Total Surface Area = 6a2 = 6 × 35 × 35 dm2 = 7350 dm2

e. Lateral Surface Area = 4a2 = 4 × 80.5 × 80.5 cm2 = 25,921 cm2

Total Surface Area = 6a2 = 6 × 80.5 × 80.5 cm2 = 38,881.5 cm2

3.a. Lateral Surface Area = 2 rh = 2 × 2 22 ×12×14cm 7 = 1056 cm2

Total Surface Area = 2 r(h + r)

= 2 × 2 22 ×12×(14+12)cm

7

= 2 × 2227××0.40m 74

= 4.4 m2

Total Surface Area = 2 r(h + r)

= 2 × 22277××+0.40m 744

= 2 × 2227××2.15m 74 = 23.65 m2

4.a. Lateral Surface Area =2(+) hRr

= 2 × 2 22 ×100×(14+8)cm

7 =13,828.57 cm2

Total Surface Area = 2 (Rh + rh + (R2–r2))

= 2 × 222 22 ×100×14+8×100+(148)cm

= 2 ×

7 –

2 22 ×(1400+800+132)cm

7 = 14,658.29 cm2

b. Lateral Surface Area = 2(+) hRr

= 2 × 2 22 ×120×(100+80)cm

7

= 2 1,35,771.43 cm

Total Surface Area

= 22 2 + + ( ) hRrhRr æö ÷ ç ÷ ç ÷ ç èø –

= 2 × 222 22 ×120×100+80×120×(10080)cm 7 –

= 2 × 2 22 ×(12000+9600+3600)=1,58,400 7 cm

c. Lateral Surface Area = 2() hRr

= 2 × 2 22 ×40× (110+100)cm 7 52,800 cm2

Total Surface Area

= 22 2 ) ++( hRrhRr –

= 2 × 222 22 × 40×110+100×40+(110100) cm

7 –

= 2 × 22 22 ×( 4400+4000+2100)cm= 66,000 cm

7

5.a. Total Surface area of Cuboid = 2(++) lblhbh

2(30×15+30 +15)hh ⇒ m2 = 1800 m2

900 + 90h = 1800 ⇒ =10 h m

b. Lateral surface area of Cube = 4a2 = 225 cm2

2 =56.25 a ⇒ a = 7.5 cm

c. Total Surface Area = 2 r(h + r)

⇒ 2 221111 2×××+ dm 722 h = 605 dm2

1331242 + 77 h ⇒ =605 ⇒ h = 12 dm

d. Lateral Surface Area = 2(+) hRr

⇒ 2 × 2 2219××(2+)m= 72 R 627 m2

2+=10.5 R ⇒ R = 8.5 m

6. Perimeter of the face of the cube = 4a = 32 cm =8 acm ⇒ cm

Total surface area of the cube = 6=6×8=384222 acmcm2

7. Given R = 50 2 cm = 25 cm, r = 25 − 2 cm = 23 cm, h = 140 cm

Lateral surface area of the cylindrical tube

= 2(+) hRr = 2 × 2 22 ×140×(25+23)cm= 7 42,240 cm2

8. Curved surface area of cylinder = 2 =1200 . rhsqcm 22 2× ×10×=1200=19.09 cm 7 hh ⇒

9.

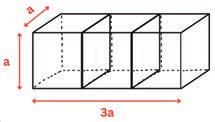
Let the length of edges of each cube be ‘a’ units

Sum of the surface area of three cubes = 3 × 6 a2 = 18 a2

New shape is a cuboid where l = 3a, b = a, h = a

Total surface area of new shape = 2(++ )lblhbh

= 2(3×+3×+×)= aaaaaa 14 a2

Required Ratio = 14 a2 : 18 a2 = 7 : 9

10. Surface area of cubical box = 6 a2 = 6 × 202 cm2 = 2400 cm2

Surface area of cuboidal box = 2(++) lblhbh

= 2 (25×20+25×16+20×16) = 2440 cm2

Difference in the surface area = 2440 cm2 − 2400 cm2

= 40 cm2

Surface area of cuboidal box is more than cubical box by 40 cm2

Word Problems

1. Area of four walls = 2(+)lbh = 2(15+12)×6 = 324 m2

Cost of whitewashing = ₹19 ×3224= ₹6156

Surface area to be whitewashed including ceiling

= Area of four walls + Area of Ceiling

= 2(+)+ =2(15+12)×6+15×12= lbhlb 504 m2

Total cost of whitewashing = ₹19 ×504 = ₹9576

2. Let the breadth of the tank be ‘b’ cm.

Therefore, the length of the tank will be ‘8b’ cm

Area of the base of the tank = 8b × b = 12,800 cm2

8=12,80022cm=40 cm. bb ⇒

Length of the base = 8b = 8 × 40cm = 320 cm

Let the depth of the tank be ‘h’ cm

Lateral Surface Area = 2(+)lbh = 1,08,000 cm2

2(320+40)h = 1,08,000 =150 hcm ⇒ cm

3. Radius of the base of the cylinder = 21 cm, Height of the cylinder = 45 × thickness of each plate = 45 ×2 =90 cmcm

Total surface area of the cylinder = 2 r(h + r) = 2 × 2 22 ×21×(90+21)cm= 7 14,652 cm2

4. Wet surface area = Area of four walls of the tank + Area of base

=2(+)+=2(12+4.5)×2.25+12×4.5=128.25m2 lbhlb

5. Inner radius = 5.6 =2.8 2 mm; height of tank = 11m

Area of tank to be plastered

= Lateral Surface Area + Area of the base of the tank

= 2 rh + 2 r = 2 ×

222 22 22 ×2.8×11+×(2.8) m=218.24m 77

Cost of plastering the tank = ₹45 ×218.24 = ₹9820.8

6. Radius of boiler = 2.8 =1.4 2 mm; height of boiler = 6.3 m

Area of Boiler = Lateral Surface Area + Area of base of the boiler = 2 rh + 2 r = 2 × 222 22 22 ×1.4×6.3+ ×(1.4) m= 61.6 m 77

No. of days taken by boiler to get completely corroded

61.6 = = =49.28

Areaofboilerdays

Areaofboilercorrodingperday

7. Area of each face of the cube = a2

1.25

Since, the container is open at the top, only five faces have to be painted area of cubical container to be painted 2222 = 5×a=5×(3.5) m=61.25 m

Cost of painting the container = ₹25 × 61.25 = ₹1531.25 19B

1.a. Volume of cuboid = lbh = 15 × 10 × 8 cm3 = 1200 cm3

Length of diagonal

=++=22222215+10+8=19.72 cm lbh

b. Volume of cuboid = lbh = 75 × 5 × 60 cm3 = 22,500 cm3

Length of diagonal

=++=22222275+5+60=96.18 cm lbh

c. Volume of cuboid = lbh = 45.5 × 8.5 × 6.5 cm3 = 2513.875 m3

Length of diagonal

222222 = ++= 45.5+8.5+6.5=46.74 m lbh

2.a. Volume of cube = 333 = 16=4096 cm a ,

Length of diagonal = 3=163acm cm

b. Volume of cube = 333 = 24=13,824 amm

Length of diagonal = 3=243 cm a

c. Volume of cube = 333 = 30=27,000 m a

Length of diagonal = 3=303 m a

d. Volume of cube = 33 3 = 50.5=1,28,787.625dm a

Length of diagonal = 3=50.53 dm a

e. Volume of cube = 33 3=130.5=22,22,447.63cm a

Length of diagonal = 3=130.53 cm a

3. a. Volume of cylinder = 2 rh = 23 22 ×3.5×10 cm 7 = 385 cm3

b. Volume of cylinder = 2 rh = 23 22 ×4.2×12 m 7 = 665.28 m3

c. Volume of cylinder = 2 rh = 23 22 ×0.8×35 dm 7 = 70.4 dm3

4. a. Volume of cylinder = 22 () Rrh –

= 223 22 ×(158×3.5 m= ) 7 – 1771 m3

b. Volume of cylinder = 22 () Rrh –= 223 2 7) 2 21 ×(18×cm 75 – = 3630 cm3

c. Volume of cylinder = 22 () Rrh – = 22 22 14 ×(72 ) × 79 –mm3 = 220 mm3

5. Let the edges of the cubes be x and y , respectively.

Ratio of volumes of cubes = 33:=1:64xy ⇒ Ratio of sides =:=1:4 xy

Ratio of surface area of cubes = 6:6=222222 := 1:4 =1 :16 xyxy

6. Let the edges of cube be ‘a’ cm.

Diagonal of cube = a 3 = 8 3 cm ⇒ a = 8 cm

Volume of cube = 3333 =8 cm=512 cm a

7. Let the edges of the cube be ‘a’ units.

Volume of cube = 3a

Given, Diameter of base of cylinder = a ⇒ Radius of base of cylinder = 2 a

Height of cylinder = a

Volume of cylinder = 2 rh = 2 3 ××= 44 a aa

Empty space left in the cube = Volume of cube − Volume of cylinder 333 = =1 44 aaa

8. Let the edges of the cube be ‘a’ units. Original volume of the cube = 3a

Increased edges of the cube = 1+=503 1002 aa

New volume = 3 3 327 = 28 aa

% Increase in the volume of the cube

= New volumeoriginal volume

Originalvolume –

= 33 3

–

27 1 8 ×100%=237% 2 aa a

9. The largest cube that can be cut has the edge of length of smallest dimension of the cuboid. Hence, the length of the edges of the cube will measure 12 cm.

Volume of this cube = 3333 =12 cm=1728 cm a

10. a. Volume of cuboid = lbh = 3 17×5 ×=3060 cm=36 cm hh ⇒

b. Volume of cylinder = 2 rh = 23 22 ×5.5×hmm 7 = 3993 m 3 m=42 h ⇒ mm

c. Volume of cylinder = 22 () Rrh –

223 22 = ×(2111×=352 7 ) hm –3 mh ⇒ = 0.35 m

d. Volume of cube = 3a = 1331 dm3 ⇒ a = 11 cm

11. Let the length, breadth and height of the cuboid be l, b, and h respectively.

Volume of the cuboid = lbh

Increased volume of cuboid = 255040

1+ ×1×1+ 100100100 lbh –5177 =××lbh=lbh 4258

Ratio of volumes of original cuboid and new cuboid

= 7 : =8 :7 8 lbhlbh

Word Problems

1. 1 litre = 1000 cm3; 60 L = 60,000 cm3

Volume of the ice cubes = a3 = 103 cm3 =1000 cm3

No. of ice cubes that can be formed from the water in the container 3 3 60,000 cm = =60 1000 cm

2. Volume of the tank = 5.2 m3 = 5.2 × 106 cm3

Also, volume of the tank = Area of the base of tank × Depth of tank

Depth of tank

= 63 2 5.2 × 10 cm volume of the tank = =4000 cm Areaof the base of tank 1300 cm

3. Length of aluminum rod: h = 3.5 m, radius of each rod: r

= 4cm =2 cm=0.02m 2

Volume of each aluminum rod = 2 rh

= 23 22 ×0.02×3.5 m= 7 0.0044 m3

Volume of aluminum = 1.76 m3

Number of rods that can be made

= volume of aluminium1.76== 400 volumeofeachaluminiumrod0.0044

4. Longest perch that can be placed in the hall would be equal to the diagonal of the hall.

Diagonal of the hall = 222222 ++= 25+16+6=30.28m lbh

5. Volume of the cubical crates

= 333 33 =50 cm=1,25,000 cm= 0.125m

a

Volume of the warehouse = lbh

= 50m×35m×20m=35,000m3

No. of crates that can fit in the warehouse

= 3 3 35000m

Volume of the warehouse = =2,80,000 Volume of the cubicalcrates .125m

6. Internal radius of pipe = 4cm = =2cm=0.02m 2 r

Volume of water flowing out of pipe per second

= 2 rh = 233 22 ×0.02×3 m= 0.00377 m

7

Volume of water of water flowing out of pipe in 45 minutes

= Volume of water flowing out of pipe per second 3 ×45×60 m

= 0.00377×45×60=10.179m3

Given, the radius of base of the cylindrical tank = 90 cm= 0.9 m

Let the level to which the water rises in the cylindrical tank be h

Volume of water of water flowing out of pipe in 45 minutes

= Volume of water stored in cylindrical tank

= 2 rh = 233 22 ×0.9× m= 10.179 m 7 h

=3.998 400 cm hm ⇒≈

Chapter Checkup

1.

a. Lateral Surface area = 2(l + b)h = 2 × (150 + 120) × 90 cm2 = 48,600 cm2

Total Surface area = 2(lb + lh + bh) = 2(150×120+150×90+120×90) cm2 = 84,600 cm2

b. Lateral Surface area = 2(l + b)h = 2 × (12 + 0.5) × 11 m2 = 275 m2

Total Surface area = 2(lb + lh + bh) = 2(12×0.5+12×11+0.5×11) m2 = 287 m2

c. Lateral Surface area = 2(l + b)h = 2 × (80 + 50) × 110 cm2 = 28,600 cm2

Total Surface area = 2(lb + lh + bh) = 2( 80×50+80×110+50×110) cm2 = 36,600 cm2

d. Lateral Surface area = 2(l + b)h = 2 × (2000 + 150) × 900 cm2 = 2 38,70,000 cmcm2

Total Surface area = 2(lb + lh + bh) = 2( 2000×150 + 2000×900 +150× 900) cm2 = 44,70,000 cm2

2.a. Lateral Surface Area = 4a2 = 4 × 15 × 15 cm2 = 900 cm2

Total Surface Area = 6a2 = 6 × 15 × 15 cm2 = 1350 cm2

b. Lateral Surface Area = 4a2 = 4 × 3.75 × 3.75 dm2 = 56.25 dm2

Total Surface Area = 6a2 = 6 × 3.75 × 3.75 dm2 = 84.375 dm2

c. Lateral Surface Area = 4a2 = 4 × 5.5 × 5.5 m2 = 121 m2

Total Surface Area = 6a2 = 6 × 5.5 × 5.5 m2 = 181.5m2

d. Lateral Surface Area = 4a2 = 4 × 6.5 × 6.5 m2 = 169 m2

Total Surface Area = 6a2 = 6 × 6.5 × 6.5 m2 = 253.5 m2

3.a. Lateral Surface Area = 2 rh = 2 × 2 22 ×2.25×16 cm 7 = 226.29 cm2

Total Surface Area = 2 r(h + r) = 2 × 2 22 ×2.25×(2.25+16)cm 7 = 2 258.11 cmcm2

b. Lateral Surface Area = 2 × rh = 2 × 2 22 ×17.5×12 cm 7 =1320 cm2

Total Surface Area = 2 r(h + r)

= 2 × 2 22 ×17.5×(17.5+12)cm 7 = 3245 cm2

c. Lateral Surface Area = 2 rh = 2 × 2 22 ×21 ×16 m 7 = 2112 m2

Total Surface Area = 2 r(h + r) = 2 × 2 22 ×21×(21+16)m 7 = 4884 m2

d. Lateral Surface Area = 2 = 2 × 2 22 ×161×180 cm 7 = 1,82,160 cm2

Total Surface Area = 2 r(h + r) = 2 × 2 22 ×161×(161+180)cm 7 = 3,45,092 cm2

4.a. Lateral Surface Area = 2() hRr = 2 ×

22 22 ×30×(50+20)mm=13,200mm

7

Total Surface Area = 22 2= ) ++( hRrhRr – 2 ×

22 ×( 30×50+20×30+5020 mm=26,400mm

2222

7 ) –

b. Lateral Surface Area = 2(+) hRr

= 2 × 2 22 ×250×(50+12)mm= 97,428.57

7 mm2

Total Surface Area = 22 2= ) ++( hRrhRr –

2 ×

22 ×( 250×50+12×250+5012 mm

222

–

7 =1,12,231 ) 7.7 mm

2

c. Lateral Surface Area = 2(+) hRr = 2 × 22 22 ×1.25× (4+1.5)m= 43.214 m

7

Total Surface Area = 22 2 ) + +( hRrhRr –

22 2××(1.25×4 +1.5×1.25+41.5 m=129.64 m

2222

7 ) –

d. r = 11 mm, R = 2.5 cm and h = 0.15 m

Lateral Surface Area = 2(+) hRr = 2 ×

22 ×150×(25+11)mm= 33,942.86 mm

22

7

Total Surface Area = 22 2 ) ++( hRrhRr –222

22 2××(150×25+11×150+25011 mm

–

7 =4,26,4 ) 039.3 mm

2

5.a. Volume of cube = a=1.23333 m=1.728 m

Length of diagonal = a 3 = 1.23 =1.23 mm

b. Volume of cuboid = lbh = 12 33 ×10×18 mm=2160 mm

Length of diagonal

= 222222 ++= 12+10+18=23.83 m lbh

c. Volume of cuboid

= lbh = 250 × 150 × 600 cm3 = 2,25,00,000 cm3

Length of diagonal

= 222222 ++= 250+150+600=667.08 lbh cm

d. Volume of cuboid

= lbh = 20 × 10 × 40 cm3 = 8000 cm3

Length of diagonal

= 222222 ++= 20+10+40=45.82 lbh cm

e. Volume of cube = 33 =2.6 a mm3 = 17.576 mm3

Length of diagonal = a 3 = 2 .63 mm= 2.63 mm

f. Volume of cuboid

= lbh = 15 × 8 × 1.8 m3 = 216 m3

Length of diagonal

= 222222 ++= 15+8+1.8=17.09 lbh m

6.a. Volume of cuboid = lbh = 12 × 10 × 5 m3 = 600 m3

No. of unit cubes that can fit = 600

b. Volume of cube = = a3 = 33 m3 = 27 m3

No. of unit cubes that can fit = 27

c. Volume of cuboid = lbh = 10 × 5 × 8 m3 = 400 m3

No. of unit cubes that can fit = 400

7.a. Volume of cylinder = 2 rh = 2 22 ×1.05×2 7 cm3 = 6.93 cm3

b. Volume of hollow cylinder = (–22 ) Rrh

= 223 22 ×(15–11.2×12.6 mm= 7 ) 3942.576 mm3

c. Volume of cylinder = 2 rh = 23 22 ×50×133 cm 7 = 10,45,000 cm3

d. Volume of hollow cylinder = (–22 ) Rrh

= 223 22 ×(20–12×21mm=16,896 7 ) mm3

e. Volume of hollow cylinder = (–22 ) Rrh

= 223 22 ×(16.1–14×45 ) m= 7 3 8939.7 m m3

8. 1 litre = 1000 cm3

a. Volume of cube

= 333 3 a=150 cm=3375000 cm=3375 litre

b. Volume of cuboid = lbh = 200 33 ×150×50 = 1500000 cmcm = 1500 litre

c. Volume of cylinder = 2 rh = 2 22 ×800×300 7 cm3 =603428571 cm3 = 6,03,428.6 litre

d. Volume of hollow cylinder = (–22 ) Rrh

= 223 22 ×(300–120×14 ) cm= 7 cm3 = 33,26,400 cm3 = 3326.4 litre

9. Let the edges of the original cube be ‘a’ units. Original surface area = 6a2

New surface area after doubling the edges= 6(2)=2422 aa

Increase in the surface area = 24 222 –6=18 aaa

% increase in the surface area = Increase in surface area ×100% Original surface area = 2 2 18 ×100%=300% 6 a a

10. Let the radius of base of cylinder be ‘r’ and its height be ‘h’. Original curved surface area =2 rh

New curved surface area after radius is doubled and height is halved

New curved surface area =2 (2) =2 2 h rrh

Change in surface area = 2– 2 rh =0 rh

11. Let the height of the cylinder be h

Total surface area of cylinder = 2(+) rhr = 660m2

22 2××5(5+)=660

7 h

5 + h = 21 ⇒ h = 16m

12. Let the radius of the cylinder be ‘r’ and height of the cylinder be ‘h’.

Total surface area of cylinder = 2(+) rhr = 2640m2

22 2× ×7×(7+)=2640

7 h

So, h = 53 mm

13. Total surface area of the cube = 6=6×42222 m=96m a Area of each square hole = 1 × 1 m2 = 1 m2

Total area of the square holes = No. of faces of cube × Area of each square hole = 6 × 1 m2 = 6 m2

Total area of the faces of the cube after removing square holes = 96 − 6 m2 = 90 m2

14. Volume of the cube = a3

Total volume of the cubes = 13 + 63 + 83 cm3 = 729 cm3

Let the edges of the new cube be ‘a’ units.

Volume of the new cube = Volume of cubes melted together a3 = 729 cm3 ⇒ 3 =729= 9 cm a

Total surface area of the new cube = 22 6=6(9)= 486 a cm2

15. Let the outer radius and inner radius of the hollow cylinder be R and r respectively.

Height of hollow cylinder = 180 cm

Outer curved surface area = 2 Rh = 31,680 cm2

22 2×××180 7 R = 31680 ⇒ R = 28 cm

Inner volume of cylinder = Amount of air held 2 rh = 249480 cm3 ⇒ 2 22 ××180 7 r = 249480

⇒ r2 = 441 ⇒ r = 21 cm

Thickness of the cylinder = 28 cm − 21 cm = 7 cm

16. We know that Volume of cylinder = 2 rh

Let the volumes of cylinders be V1 and V2 ,respectively. V1 = 2 XY , V2 = 2 YX

2

2 2 == VXYX VY YX = X:Y

17. Let the radius of the base be r and its height be h h = 4 cm

Perimeter of the Base = 22 2=2××=22cm 7 rr 3.5 cm r ⇒

Volume of the cylinder = 223 22 = ×3.5×4=154cm 7 rh

18. Internal radius: r = 28 =14cm 2 , External radius:

R = 35 =17.5cm 2 , Length of the pipe: h = 48 cm

Volume of the pipe = 22 ( ) –Rrh

= 22 3 22 ×(17.5–14×48 =16632 cm 7 )

Weight of pipe = Volume of the pipe × weight of wood per cm3

= 16632 ×0.8g=13305.6g

19.a. Total Surface area = 6=912622 amm2

⇒ a = 39 m

b. Lateral Surface area = 2(+) = lbh 8100 cm2

2(60+)×45 = b 8100

60+ b = 90 ⇒ b = 30 cm

c. Lateral Surface Area = 2=88 rh m2

2211

2× ××=88 72 r ⇒ r = 2.55 m

d. Total Surface Area = 222 ) 3520 2 ++(–=m 7 rhrhRr

222 22 3520 2× ×8+3×8+(–7 ) 3m 7 RR=

8R + 24 + R2 − 9 = 80

R2 + 8R = 65

R2 + 13R 5R − 65 = 0

R(R + 13) 5(R + 13) = 0

R = 5, 13

R = 13 is not possible, thus, R = 5 m

20. a. Volume of cube = 3 =1728 a cm3

⇒ a 3 =1728=12 cm

b. Volume of cuboid = lbh = 63 m3 = 5 ×3×=63 h ⇒ h = 63 =4.2 15 m

c. Volume of cylinder = 2 rh = 475.904 mm2

2 22 ×2.6× 7 h = 475.904 ⇒ h = 22.40 mm

d. Volume of hollow cylinder = (–22 ) Rrh = 1056 cm3

= 22 22 ×(14–×3.5=1056 7 ) r

196 −r2 = 96 ⇒ r = 10 cm

Word Problems

1. Lateral Surface area of the cylinder = Area of square sheet = 30 × 30 cm2 = 900 cm2

2. Surface area of the box =

3 Cost of packaging the box26250=105000 cm

Rate of packaging the box0.25 =

Given, length of the wooden box = 50 cm; Breadth of the wooden box = 30 cm

Using, Surface area of the box = 2(++) lblhbh = 2 105000 cmcm3

2(50×30+50×+30×) hh = 105000

1500 + 80h + 52500

⇒ h = 637.5cm

3. Total surface area of cuboidal box = 2(++) lblhbh

22 =2(60×40+60×30+30×40)cm=10800 cm

Area of one colored square sheet = 50 × 50 = 2500 cm2

No. colored square sheet required =

2

Total surface area of cuboidal box10800 cm = =4.32

2

Area of one colored square sheet 2500 cm = 5 (approx)

4. Volume of Brick = lbh = 15 cm × 5 cm × 5 cm = 375 cm3

Volume of Wall = lbh = 5 m × 1.5 m × 1.5 m = 11.25 m3

= 11250000cm3

No. of bricks required

=

Volume of Brick 375 cm

3 3 Volume of Wall 11250000 cm = =30,000

5. Volume of water flowing out of pipe per hour

= Area of cross-section of pipe × Speed of water

= 1.5 × 1.5 × 25000 = 56,250 m3

Volume of water to be filled in the field

= Area of the field × Level of water

= 250 × 100 × 3 m3= 75000m3

Time required = Volume of water to be filled in the field

Volume of water flowing out of pipe

= 75000 56,250 = 1 1 3 hour = 80 minutes

Chapter 20

Let's Warm-up

1. The square of 11 is 121 and its cube is 1331.

2. If the units digit of a number is 3, then the units digit of its square is 9 and that of its cube is 7.

3. The prime factorisation of 48 is 24 × 3.

a. Is it a perfect square? No

b. The smallest number that should the given number be divided by to get a perfect square is 3.

4. Reeti says, “125 is a perfect square”, whereas Meeti says, “125 is a perfect cube.” Meeti is correct.

Do It Yourself 20A

1. a.46 = 4 × 4 × 4 × 4 × 4 × 4 = 4096

b. (−7)−3 = 111 –×–×–777 æöæöæö ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ èøèøèø = 1 –343

c. 7 4 5 = 4444444 ×××××× 5555555 = 16384 78125

d. –4 2 –3 = 3333 –×–×–×–2222 æöæöæöæö çççç÷÷÷÷ çççç÷÷÷÷ çççç÷÷÷÷ çççç÷÷÷÷ çççç÷÷÷÷ èøèøèøèø = 81 16

e. (0.02)5 = 0.02 × 0.02 × 0.02 × 0.02 × 0.02 = 0.0000000032

f. (6.1)−2 = 2 1 6.1 = 10 61 × 10 61 = 100 3721

2.a. 45.123 = 4 × 10 + 5 × 1 + 1 × 111 +2× + 3× 101001000

= 4 × 101 + 5 × 100 + 1 × 10−1 + 2 × 10−2 + 3 × 10−3

b. 541.056 = 5 × 100 + 4 × 10 + 1 × 1 + 0 ×

111 +5×+6× 101001000

= 5 × 102 + 4 × 101 + 1 × 100 + 0 × 10−1 + 5 × 10−2 + 6 × 10−3

c. 107.02356 = 1 × 100 + 0 × 10 + 7 × 1 + 0 ×

11111 +2×+3×+5×+6×

10100100010000100000

= 1 × 102 +0 × 101 + 7 × 100 + 0 × 10−1 + 2 × 10−2 + 3 × 10−3

+ 5 × 10−4 + 6 × 10−5

d. 28.54687 = 2 × 10 + 8 × 1 + 5 × 11111 +4×+6×+8×+7×

10100100010000100000

= 2 × 101 + 8 × 100 + 5 × 10−1 + 4 × 10−2 + 6 × 10−3 + 8 × 10−4 + 7 × 10−5

e. 5003.671 = 5 × 1000 + 3 × 1 + 6 × 111 +7×+1× 101001000

= 5 × 103 + 3 × 100 + 6 × 10−1 + 7 × 10−2 + 1 × 10−3

3.a. 5−10 = 10 1 5

Reciprocal of 10 1 5 = 510

b. 3 2 3 = 3 3 2 3

Reciprocal of 3 3 2 3 = 3 3 3 2 = 3 3 2

c. 5 –4 7 = 5 7 –4 æö

Reciprocal of 5 7 –4 æö

d. (−20)−2 = 2 1 (–20)

Reciprocal of 2 1 (–20) = (−20)2

e. –6 3 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 6 5 3

Reciprocal

f. (1.1)−8

4.a.

Reciprocal

777777 ××××= 111111111111

=

=

5.a. 3 2 3 + 333 32486472 =+=+= 433272727 æöæöæö ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ èøèøèø 1–1 7283 == 2738 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

× æöæöæöæöæö ÷÷÷÷÷ ççççç ÷÷÷÷÷ ççççç ÷÷÷÷÷ ççççç ÷÷÷÷÷ ççççç ÷÷÷÷÷ ççççç èøèøèøèøèø æö æö ÷ ÷ ç ç ÷ ÷ ç ç ÷ ÷ ç ç ÷ ÷ ç ç ÷ ÷ ç ÷ ç èø èø = 45 22 85 ×(3)××52 2 2) 5 ( =2 ×2 × 3 × 3 × 5 2 ×

5 2 × 5

æö

= 319 125 = –1 125 319 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

æöæöæöæö çççç÷÷÷÷ çççç÷÷÷÷ çççç÷÷÷÷ çççç÷÷÷÷ çççç÷÷÷÷ èøèøèøèø æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

11×11×113×3 = × 6×6×6121×121

3 1111 = =×× 2×2×2×3×11311 2 = 2−3 × 33−1

4

1000 5 .

1 0–

= –5

3–5 6 (–1)×1005 5 ×× æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = =(–1)×100×63–5

= (−1) × 3 100 6 × 6−2 = (−1) × 6−2 × –3 6 100

6. Let the number be x.

According to question, –3 3 ÷=16 8 x æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

33 8181×=16;×= 3 316 x x æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

5121 ×=; 2716 x 32 = 27 x

The number is 32 . 27

7. –3 4 4 –5 4 ×(0.8) 65 x= æö æö çç÷÷ çç÷÷ = çç÷÷ çç÷÷ çç÷÷ èø èø

34 64 –55 ×x= æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

43 835 4333 =×–45(–1)×2×5(–1)2 = 56 5×2×35×3 × x= æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø = –32 135

The number is –32 . 135

8. Let the number be x. –8 5

32 += 23 x æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

58

22 = –33 x æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø = 864–256 6561 = 608 6561

The number is 608 . 6561

9. Let the number be x.

76

55 –= 66 x æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

76

55 =–66 x æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø = 6 5 6

= –15625

279936

The number is –15625 279936

10. (0.4)2 × (0.01)2 × 3 1 2 (6)−1 =

= 0.02 × 0.0001 × 6 = 0.000012

So, Shreya’s answer is incorrect. Word Problems

1. Weight of a frog larva = 5−3 g

Food it eats on the first day = 26 × 5−3 g = (22)3 × 5−3 g

= (4 × 5−1)3 g = 3 4 5 g

= (0.8)3 g = 0.512 g

2. a. Each week, the views are increasing by 5 times.

b. If the number of the week is n, where n = 0,1,2,3.., then the rule of the pattern is 5n+1

20B

c. Number of views in the 4th week = 5n+1 = 54+1 = 55

1.a.

= –1 3 4 3 = –3 4 3 = 3 3 4 = 27 64

b.

æö

ç

ç ÷ ç ÷ ç ÷ ç èø

–4–44 –233 ×× 85 5 æöæöæö ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ èøèøèø = 444 5 83 ×× –235 æöæöæö ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ èøèøèø = (−1)4

× 4 4 5 2 × 34 4 (2) 3 × 4 3 5 = 1 × 4 4 5 2 × 12 4 2 3 × 4 3 5

= 212− 4 = 28 = 256

c. (5− 9 × 5− 3) × 155 = 5− 9 − 3 × (3 × 5)5 = 5− 12 × 35 × 55

= 5−12+5 ×35 = 5− 7 × 35 = 5 7 3 5 = 243 78125

d. –5–2 –1–1 ÷ 28 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø ÷ –32 225 ÷ 54 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

= (–2)÷(–8)52 ÷ 34 5 ÷ 5 22 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

= (–2)÷(–2)56 ÷ 3–4

5 2 = 5–6 –2 ÷ –1 5 2

= (−2)−1 ÷ 2 5 = 1 –2 × 5 2 = 5 –4

e. 3 –2 –5 6 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = –6 –5 6 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 6 –6 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 46656 15625

2.a. (3−2 + 8−3 + (−2)−4)0 = 1

b. 3 –30 –2 ÷(2.4)×(0.5) 5

æö ÷ çæö ÷ ç ÷ ÷ çç ÷ ÷ çç ÷ ÷ çç ÷ ÷ ç ÷ çç ÷ èø ÷ ç ÷ ç èø

= 33 –524××1 210 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

= 33 –510÷×1 224

æö ÷ çæöæö ÷ ç ÷÷ ÷ ççç÷÷ ÷ ççç÷÷ ÷ ççç÷÷ ÷ çç÷÷ ççç ÷ èøèø ÷ ç ÷ ç èø

= –5 2 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × –5 2 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × –5 2 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × 24 10 × 24 10 × 24 10

= (− 1) × 3 × 3 × 24 = − 216

c. –4–5 37 × 79 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø = 45 79 × 37 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø =

= 310–4 7 = 36 7 = 729 7

d. 2–5–1 –4–4–4 ×× 999 æöæöæö ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ èøèøèø = 2–5–1 –4 9 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = –4 –4 9 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 4 –9 4 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 6561 256

e. ((−2)−2 + (1.6)−3) × (0.8)3 = 3 15 + 48 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × (0.8)3

= 1125 + 4512 × 3 8 10 = 128+125 512 × 512 1000 = 253 1000 = 0.253

–2 4 625×(–5)

5 = 4–2 4 5×(–5)

5 = (−5)−2 = 2 1 (–5) = 1 25

b. 8×2×334 3×64 = 334 6 2×2×3 3×2 = 64 6 2×3 3×2 = 33 = 27 is same

as 5(–2)

4 × –3 –2 3 = 2 –3 –2) 4×3 ( = 23 2 (–2)3 (–2) = 33 = 27

c. 11 56 6 6×6 = 11 11 6 6 = 1 is same as 20 × 30 × 70 = 1

5.a. 7687000000 = 7687 × 1000000 = 7.687 × 103 × 106 = 7.687 × 109

b. 2300000000000000 = 23 × 100000000000000 = 2.3 × 101 × 1014 = 2.3 × 1015

c. 10.446678 = 1.0446678 × 101

d. 65.9084 = 6.59084 × 101

e. 98.0000324 = 9.80000324 × 101

f. 453.98785 = 4.5398785 × 102

f. 3 –1 –1 ( 1 –7)+ 7

æö ÷ ç æö ÷ ç ÷ ÷ ç ç ÷ ÷ ç ç ÷ ÷ ç ç ÷ ÷ ç ÷ ç ç ÷ èø ÷ ç ÷ ç èø

= 1,10,592 343

3.a. –62 –2 72×3×4 81×16×27 =

= 3 –1 +7 7 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 3 –1+49 7 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 3 48 7

× 1 9 = 3125 2187

c. –3 –5–8 9× 18×3× t t = –3 –5–8 9× 9×2×3× t t = 2–3 2–5–8 3× 2×3×3× t t

= 5 5 555 –5 =×3=(3)=243 3 t ttt

d. +1 +1+2 16×2–4×2 16×2–2×2 mm mm = 52 53 2×2–2×2 2×2–2×2 mm mm

= 52 53 ) () 2 (2–2 22–2 m m = 3 2 2 2 = 23 −2 = 2

a. (−5)3 ×(−5)−5

b. 8×23 ×34 3×64

g. 4320000000 = 432 × 10000000 = 4.32 × 102 × 107 = 4.32 × 109

h. 10980000 = 1098 × 10000 = 1.098 × 103 × 104 = 1.098 × 107

6.a. 1.03 × 108 = 103 100 × 108 = 103 × 108 − 2 = 103 × 106 =

103000000

b. 3.467 × 10−5 = 3467 1000 × 10−5 = 3467 × 10−5 − 3 = 3467 × 10−8

= 3467 × 8 1 10 = 3467 100000000 = 0.00003467

c. 6.0945× 10−3 = 60945 10000 × 10−3 = 60945 × 10−3−4

= 60945 × 10−7 = 60945 × 7 1 10 = 60945 10000000 = 0.0060945

d. 4.21 × 104 = 421 100 × 104 = 421 × 104−2 = 421 × 102 = 42,100

e. 8.7 × 1011 = 87 10 × 1011 = 87 × 1011−1 = 87 × 1010 =

870000000000

f. 1.768 × 104 = 1768 1000 × 104 = 1768 × 104−3 = 1768 × 10 = 17680

g. 54.1 × 106 = 541103 100 × 106 = 541 × 106−1 = 541 × 105 = 54100000

h. 40.857 × 10−2 = 40857 1000 × 2 1 10 = 40857 100000 = 0.40857

× −2 −3 (−2)5 34

20 × 30 ×70

4. 625 × (−5)−2 54

c. 611 65 ×66

a. (−5)3 × (−5)−5 = (−5)−2 = 2 1 (–5) = 1 25 is same as

7.a. 3.4 × 103 = 34 10 × 103 = 34 × 103−1 = 34 × 102 = 3400, 8.05 × 106 = 805 100 × 106 = 805 × 106−2 = 805 × 104 = 8050000; 8050000 > 3400 So, 8.05 × 106 is greater.

b. 2.11 × 102 = 211 100 × 102 = 211 × 102−2 = 211 × 100 = 211 × 1 = 211, 1.67 × 10−2 = 167 100 × 2 1 10 = 167 10000 = 0.0167; 211 > 0.0167, so 2.11 × 102 is greater.

c. 7.3 × 10−5 = 73 10 × 5 1 10 = 73 1000000 = 0.000073, 0.7 × 10−8

= 7 10 × 8 1 10 = 7 1000000000 = 0.000000007; 0.000073 > 0.000000007, so 7.3 × 10−5 is greater.

8.a. 675.7869 × 105 + 980.436 × 103 = 103 × [675.7869 × 102 + 980.436] = 103 × [67578.69 + 980.436] = 68,559.126 × 103 = 6,85,59,126 = 6.8559126 × 107

b. (3.87 × 10−7) × (1.02 × 10−3) =

278 100000 + 456 10000000 = 27800456 10000000 = 28256 10000000 = 0.0028256 inches

2. Number of people spoke French = 7.7 × 103

Number of people spoke German = 3.2 × 104

7.7 × 103 = 77 10 × 103 = 77 × 103−1 = 77 × 102 = 7700, 3.2 × 104

= 32 10 × 104 = 32 × 104−1 = 32 × 103 = 32000; 32000 > 7700, so

German language had more speakers by 32000 − 7700 = 24300

6 9 10

× 6 9 10 102 100 × 3 1 10

= 387 1000000000 × 102 10000 = 39474 100000000000000 = 39474 × 10−14 = 3.9474 × 104 × 10−14 = 3.9474 × 10−10

c. 0.000000000043 − 0.000000000892 = 43 1000000000000 − 892 1000000000000 = 43 1012 − 12 892 10 = 12 43–892 10

= 12 849 10 = −849 × 10−12 = −8.49 × 102 × 10−12

= −8.49 × 10−10

d. 0.0000000071192 ÷ 0.0000000006472

= 71192 1000000000000 ÷ 6472 10000000000000 = 71192 × 10−12 ÷ 6472 × 10−13 =

= 711920 6472 = 110 = 1.1 × 102

9. Let the missing number be x. 2 1 –5 × –1 x × 511 = 55, 2 1 5 – × –1 x æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 55−11

= 5−6, (−5)−2 × –1 x æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 5−6, –1 x æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = ––

6 2 5 5 = 2–6 5 = 5−4, –1 x æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 5−4 ⇒ x2 = 5−4 ⇒ = (52)−2 = (5−2)2 ⇒ x = 5−2

10. m+32m–3 3m–9 ()yy y = 1024, m+32m–2 3m–9 × yy y = 1024, m+3+2m–2 3m–9 y y = 1024, 3m+1 3m–9 y y = 1024, y3m+1−3m+9 = 1024, y10 = 1024, y10 = (2)10, y = 2.

Word Problems

1. Amount of food carried by one ant = 2.78 × 10−3 in

Amount of food carried by another ant = 4.56 × 10−5 in

Total amount of food carried by the ant altogether = 2.78 × 10−3 + 4.56 × 10−5 = 278 100 × 1 1000 + 456 100 × 1 100000 =

= 2.43 × 104

3. Total area of the land = 1500 sq. mile

Number of mosquitoes in per square mile of land = 80 million

Number of mosquitoes in 1500 sq. mile of land = 80 million × 1500 sq. miles = 120000 million sq. miles

4. Mass of a dust particle = 7.32 × 10−10 mg

Mass of 6 million dust particles = 7.32 × 10−10 × 6,000,000 =

7.32 × 6 × 10−10 × 106 = 43.92 × 10−4 = 4.392 × 101 × 10−4 =

4.392 × 10−3 mg

5. Size of an Antarctic Ocean = 20,330,000 sq. km

Size of an artic ocean = 3 4 × 20,330,000 sq. km = 3 × 5082500

sq. km = 15247500 sq. km = 1.5247500 × 107 sq. km

Chapter Checkup

1.a.

342.4567 = 3 × 100 + 4 × 10 + 2 × 1 + 4

× 111 +5× + 6× 101001000 + 7 × 1 10000 = 3 × 102 + 4

× 101 + 2 × 100 + 4 × 10−1 + 5 × 10−2 + 6 × 10−3 + 7 × 10−4

d. 21.4879 = 2 × 10 + 1 × 1 + 4 × 111 +8× + 7× 101001000

+ 9 × 1 10000 = 2 × 101 + 1 × 100 + 4 × 10−1 + 8 × 10−2 + 7 ×

10−3 + 9 × 10−4

e. 4876.9023 = 4 × 1000 + 8 × 100 + 7 × 10 + 6 × 1 + 9

× 111 +0× + 2× 101001000 + 3 × 1 10000 = 4 × 103 + 8 × 102 + 7 × 101 + 6 × 100 + 9 × 10−1 + 0 × 10−2 + 2 × 10−3 + 3 × 10−4

2.a. –2 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × –2 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × 2 5 – × 2 5 – × 2 5 – × 2 5 – = 6 2 5 –Reciprocal of 6–6 25 is . ––52 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

×

Reciprocal of 8 3 8 is 8 3

c. 7 9 × 7 9 × 7 9 × 7 9 = 4 7 9

Reciprocal of 4 7 9 is –4 9 7 .

d. 5 555555 ×××× 11111111111 –1 –æöæöæöæöæöæö çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ = çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ çççççç÷÷÷÷÷÷ èøèøèøèøèøèø

Reciprocal of 5 –5 11 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø is –11 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

e. 1 10 × 1 10 × 1 10 × 1 10 × 1 10 × 1 10 = 6 1 10 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

Reciprocal of 6 1 10 is (10) −6 .

3.a. 2 6 7 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø − –2 636491296–2401–1105 =–== 7493617641764 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

b. 5 12 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø ÷ 2 3 25 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 32 123 ÷ 525 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

= 12 5 × 12 5 × 12 5 × 25 3 × 25 3 = 960

c. 4 9 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × 4 5 9 × 2 2 5 = 9

= 25 729

d. [(6)5 × (−1.5)2] × 3 1 4 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 6 × 6 × 6 × 6 × 6 × 2 –3 2 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

× 3 1 4 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

= 6 × 6 × 6 × 6 × 6 × –3 2 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × –3 2 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × 1 4 × 1 4 × 1 4 = 3 × 3 ×

3 × 3 × 3 × 1 8 × (−3) × (−3) = 2187 8

e. 2 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 1 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 4 25 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø + 1 25 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 25 4 + 25

= 25 + 100 4 = 125 4

f. [(−0.2)4 ÷ (0.03)3] × –1 6 æö

÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = –1 6 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø ÷ 3 3 100 × 65

= 5 43 110 × –× 0 5 6 3 æöæö çç÷÷ çç÷÷ çç÷÷ çç÷÷ çç÷÷ èøèø

= –1 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × –1 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × –1 5 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × –1 5 æö ÷ ç ÷

4.

× 49 ×

= 495

6.a. 210, 323 = (25)3 = 215, 642 = (26)2 = 212, 128−2 = (27)−2 = 2−14, 83 = (23)3 = 29

Ascending order: 2−14, 29, 210, 212, 215 ⇒ 128−2, 83, 210, 642, 323

Descending order: 215, 212, 210, 29, 2−14 ⇒ 323, 642, 210, 83, 128−2

b. 310, 273 = (33)3 = 39, 7292 = (36)2 = 312, 18−2 = (2 × 32)−2 = 2−2 × 3−4, 93 = (32)3 = 36

Ascending order: 2−2 × 3−4, 36, 39, 312, 310 ⇒ 18−2, 93, 273, 310, 7292

Descending order: 310, 312, 39, 36, 2−2 × 3−4 ⇒ 7292, 310, 273, 93, 18−2

7. x−2 = 2 1 x , Multiplicative inverse = x2

Neither Tanya nor Sayani is correct because Tanya’s answer is negative x2, and Sayani’s answer has power as 2 less than −1, and the product of each of the two gives x−2 × (−x)−2 = x−4 and x−2 × x−3 = x−5, which are incorrect.

8. Kamya is right because the fraction is the reciprocal of the number with the negative exponent.

9.a. (8−2 + 5−3 + (−3) −4)0 = 1 as the power is 0.

b. –2 3 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø ÷ (1.7)−3 × (0.2)0 = 3 –3 2 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø ÷ 17 10 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × 1 = 3 –3 2 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

10 17 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 3 –3 2 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × 3 17 10 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø =

3 –317 × 210 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 3 –51 20 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

c. 4 2 7 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × –5 4 7 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 4 2 7 × 5 7 4 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = 7 64

d. 32 –4–4–4 +–111111 æöæöæö ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ ççç÷÷÷ èøèøèø = 3 64+176+484 11 –= 596 1331

e. ((−1)−2 + (1.01)3) × (0.1)−3 = 3 101 1+ 100 æö ÷ ç

10.a. 2 ––128×3×462 243×36×27 = 7622 –5232 –2×3×(2 3×(2×3)(3 )× )

= 764 5 –223 –2 2×3×2 3×23(3 ) ×× = 116 723 ––2 2×3 3×2( ) ×3

= 117 2 2×3–2 = 29 × 3−7

b. 40×3×4–30 81×45×5 = 330 425 ––2×5×3×4 3×5×3×5 = 3 5–6 –3 2×3×1

3−9 ×55 = 35 9 2×5 3 = 8×3125 19683 = 25000 19683

c. 8–5 ––

3 24××49 21×3× p p = 8–5–2–3 3×8××7 3×7×3× p p = 5 –4 3×8××7 3 p = 168 × 34 × p5 = 13608p5

d. +1 +2 +1 15×5 +20×5×5 3×5 + 20 ×5 mm mm = +1 +1 +2 +1 5×3×5+ 20×5 3×5+ 20 ×5 mm mm = +2 +1 +2 +1 3×5+ 20×5 3×5+ 20 ×5 mm mm = +1 +1 515+20) 515+20) ( ( m m = 1

11.a. 210 ÷ 26 = 2−4 × 23x − 1 ⇒ 24 = 2−4 + 3x −1 ⇒ 24 = 23x −5 ⇒

4 = 3x − 5 ⇒ 9 = 3x ⇒ x = 3

b. 3 5 8 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø × –8 5 8 x æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = –10 5 8 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø ⇒

–38 5 8 x æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø = –10 5 8 æö ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç èø

⇒ 3 − 8x =−10 ⇒ 13 = 8x ⇒ x = 13 8

c. 72x+1 ÷ 343 = 2401 ⇒ 72x+1 ÷ 73 = 2401 ⇒ 72x+1 − 3 = 74 ⇒

2x − 2 = 4 ⇒ 2x = 6 ⇒ x = 3

12.a. 1.275 × 10−5 m is in standard form. 1.275 × 10−5 m = 1275 1000

× 10−5 = 1275 100000000 = 0.00001275

b. 0.005 cm to 0.01 cm is in usual form. 0.005 = 5 1000 = 5 × 10−3, 0.01 = 1 100 = 1.0 × 10−2

c. 3.84 × 108 m is in standard form. 3.84 × 108 = 384 100 × 108 = 384 × 106 = 384000000

d. 1.386 × 109 cu. km is in standard form. 1.386 × 109 = 1386 1000 × 109 = 1386 × 106 = 1386000000

e. 0.0000000000000000000000000000911 kg is in usual form.

0.0000000000000000000000000000911 = 911

10000000000000000000000000000000

= 9.11 × 102 ×10−31 = 9.11 × 10−29 kg

13. 0.000000654879 and 0.000122434 are in usual form because they have not been expressed as k × 10n

14. 5 2 (1296) = 5 ( 1296) = (36)5 = 6,04,66,176. Yes, Srishti is correct.

15. + + + 2 × × (× ) × plqplq pql xxx xxx = + ++++ ()++2 plqplq pql x x = 2 + 2+2 2(++) plq pql x x =

2( + + ) 2(++) pql pql x x = 1

Word Problems

1. Total area of the land = 6 × 105 m; Quantity of cotton roduced = 2.4 × 106 kg

Quantity of cotton planted per metre = 5 6 6 ×10 2.4 ×10

= 6 × 105 − 6 2.4 = 6 ×10 2.4 = 6 2.4×10 = 6 24 = 1 4 = 0.25 kg

2. Weight of 1 crate = 2.2 × 103 kg; Number of crates = 4 × 102 = 400

Weight of 400 crates = 2.2 × 103 × 400 = 2200 × 400 = 8,80,000 kg

3. Area of a Pacific Ocean = 1.55 × 108 sq. km, Area of Atlantic Ocean = 1.0646 × 108 sq. km

Area of Pacific Ocean is greater by 8 8 1.55 ×10 1.0646×10 = 1.46 (approx.) times

4. Size of a plant cell = 0.00002155 m, Size of a red blood cell = 0.0000000015 m

According to the question, Size of a plant cell = 2 × size of red blood cell = 2 × 0.0000000015 m = 0.000000003 m ≠ 0.00002155 m

No, the size of a plant cell is not a double.

5. Diameter of Jupiter = 13.9822 × 104 km = 1,39,822 km

Diameter of Saturn = 1.165 × 105 km = 1165 1000 × 105 km = 1,16,500 km

1,39,822 km > 1,16,500 km, so diameter of Jupiter is greater than the diameter of Saturn.

Chapter 21

Let's Warm−up

1. 1.If there are 45 boys and 39 girls in a hall. The ratio of boys to girls can be given as 39 45 False

2. The simplest form of ratio 27:6 = 9:2. True

3. 11 2 is the simplest form of 88 12 False

4. A ratio can have infinite equivalent ratios. True

5. One of the equivalent ratios of 81:30 is 27:10. True

Do It Yourself

21A

1.a. The speed of a car and the time taken by the car to cover a particular distance. No

b. The number of men required to construct a wall and the time taken by the men. No

c. The number of pencils and the total cost of the pencils. Yes

d. The number of vehicles on the road and space on the road. No

2.a. No

a 5152535

b 36108190282

Ratio 5:365:365:3835:282

b. Yes

a 7284256

b 12487296

Ratio 7:127:127:127:12

Constant of proportion = 7 12

c. Yes

a 117653913

b 1801006020

Ratio 13:2013:2013:2013:20

Constant of proportion = 13 20

3. X Y 11 19 11 ×152 19 = 88 152

132 19 ×132 11 = 228

176 19 ×176 11 = 304

19 ×361 19 = 209 361

4. Cost of 9 kg of rice = ₹585

Cost of 52 kg of rice = ₹x

⇒ 9585 == 52 x x 585 ×52= 9 ₹3380

5. No. of chocolates made in 6 hours = 450

No. of chocolates made in 4 hours = x

⇒ 6450450==×4= 300 46 x x chocolates

6. 11 2 hours 60 +30minutes =90minutes

No. of words Kamal can type in 15 minutes = 1020

No. of words Kamal can type in 90 minutes = x 15 90 = 1020 x ⇒ x = 1020 15 ×90=6120 words

7. Amount saved in 3 days = ₹148.20

Amount saved in 20 days = ₹x ⇒ 3148.2020 = = × 20 3 x x ₹148.20 = ₹988

8. Distance covered by Shalini in 25 minutes = 1.5 km

Distance covered by Shalini in 40 minutes = x km 251.540==×1.5 40 25 x x km = 2.4 km

9. Number of minutes in a day = 24 × 60 min = 1440 min

Number of bottles manufactured in 40 min = 75

Number of bottles manufactured in 1440 min = x

⇒ 4075==×75

1 144 40 0 4 40 x x = 2700 bottles

10. Space required for 5 boxes = 1500 cc

Space required for 150 boxes = x cc

⇒ 51500150 == ×1500=45,000 150 5 x x cc

11. Number of workers required for digging 6 m in a day = 15

Number of workers required for digging 42 m in a day = x

61542==×15

42 6 x x = 105 workers

12. Cab charges for 8 km = ₹204 Cab charges for 22 km = ₹x

⇒ 820422==×204=561

22 8 x x ``

13. No. of boxes in the shelf length of 17.6 m = 72

No. of boxes in the shelf length of 19.8 m = x 17.67219.8 == × 19.8 17.6 x x 72 = 81 boxes

14. Amount paid for 8 days of work = ₹2000

Amount paid for 12 days of work = ₹x 8200012 = = × 12 8 x x ₹2000 = ₹3000

15. No. of tablespoons of sugar required to make 22 cookies = 15

No. of tablespoons of sugar required to make 154 cookies

= 154 ×15=105 22

Amount of sugar in 1 tablespoon = 12.5 g

Amount of sugar in 105 tablespoons = 105 × 12.5 g = 1312.5 g

16. Amount of plain flour required to make 20 brownies = 75 g

Amount of plain flour required to make 35 brownies

= 35 20 ×75g = 131.25 g

Amount of sugar required to make 20 brownies = 325 g

Amount of sugar required to make 35 brownies

= 35 ×325 20 g = 568.75 g

Rohit has enough flour but an insufficient amount of sugar to make 35 brownies.

17. Length of the shadow of 480 cm pole = 120 cm

Length of the shadow of 1260 cm pole = 1260 ×120 480 cm = 315 cm = 3 m 15 cm

18. Number of days required to pick up 2.8 × 1010 kg dust = 14 days

Number of days required to pick up 5600 ×109 g dust

= 9 10 5600×10 2.8 × 10 ×1000 × 14 = 2.8 days

Word Problems

1. Weight of 5 bags of sugar = 90 kg

No. of x bags of sugar = 576 kg = x

590576 == 57690 x x × 5 = 32 bags

2. 4 hours = 4 × 60 minutes = 240 minutes

Distance travelled by Karishma in 112 minutes = 7 miles

Distance travelled by Karishma in 240 minutes = x

1127240==×7 240 112 x x miles = 14.999 miles ≈ 15 miles

21B

1.a. Distance travelled by the car and time taken by the car. No

b. Number of men required to paint a house and time taken by the men. Yes

c. Number of books and total cost of the books. No

d. Distance travelled by a bus and petrol consumed by it. No

2. 18 × 4 = 36 × a

18×4 ==2 36 a

3. No. of days taken by 42 women to complete work = 15

No. of days required for 18 women to complete the work

= 42 ×15

18 = 35

4. No. of chocolates received by each of the 28 students = 6

Since the number of students is reduced by 7,

No. of chocolates received by each of the 21 students

= 28 ×6

21 = 8

Increase in number of chocolates = 8 − 6 = 2

5. No. of pair of shoes bought for ₹450 each = 15

Increased cost per pair =₹450 + ₹300 = ₹750

No. of pair of shoes bought for ₹750 = 450 ×15 750 = 9

Decrease in number of shoes = 15 − 9 = 6

6. Time taken by three people to fit the door = 2 days

Time taken by 2 people to fit the door = 2× 3 2 days = 3 days

7. No. of days wheat lasts for 4 friends = 30 days

No. of people for which wheat would last 20 days = 30 × 4 20 = 6

Increase in number of people = 6 −4 = 2

8. Speed to car to cover the distance in 12 hours = 60 km/h

Speed of car to cover the distance in 9 hours = 12 9 × 60 =80 km/h

Increase in the speed of car = 80 km/h − 60 km/h = 20 km/h

9. Amount of time required by Mohit to finish the task = 6 days

Amount of work done by him in one day = 1 6

10. Amount of time required by Suhani to revise the entire course = 30 days

Fraction of course revised in 20 days = 20 30 = 2 3

11. Amount of time taken A to complete the work = 14 days

Work done by A in one day = 1 14

Amount of time taken by B to complete the work = 21 days

Work done by B in one day = 1 21

Work done in one day by both A and B = 1 14 + 1 21 = 3

Number of days required by A and B to finish the work = 42 5 days = 2 8 5 days

12. Amount of time taken by Manish to finish the piece of work = 40 minutes

Amount of work done by Manish per minute = 1 40

Portion of work completed by Manish in 8 minutes = 8 40 = 1 5

Portion of work left = 1 − 1 5 = 4 5

Priya finishes 4 5 work in 16 minutes.

Time required by Priya to finish the whole work alone = 5 4 × 16 minutes = 20 minutes

Amount of work done by Priya per minute = 1 20

Work done in one minute by both Manish and Priya

= 1 20 + 1 40 = 2 +1 40 = 3 40

Number of minutes required by Manish and Priya to finish the work = 40 3 = 13 1 3 minutes

13. Time required by X to complete the work = 20 hours

Amount of work done by X in 1 hour = 1 20

Time required by Y to complete the work = 12 hours

Work done by Y in 1 hour = 1 12

Amount of work completed by X by working alone for first 4 hours = 4 20 = 1 5

Amount of work left now = 1–14 = 55

Work done by X and Y in one hour = 1 20 + 1 12 = 3 +5 60 = 8 60 = 2 15

Amount of time required to complete the remaining work by

X and Y together = 4 5 =6 2 15 hours

Total time required to finish the work = 4 + 6 = 10 hours

14. Portion of the tank filled by the taps in one hour = 11115+10+6 31 ++== 2353030

Time required to fill the tank = 30 31 hour

15. Portion of the tank emptied by P in one hour = 1 25

Portion of the tank emptied by Q in one hour = 1 30

Portion of the tank emptied by P and Q in one hour

= 11 + 2530 = 6+511 = 150150

Time required to empty the full tank = 150 11 hour = 13  7 11 hours

16. Portion of the repaired tank filled per hour = 1 3.5

Portion of the tank with leakage filled per hour = 1 4

Let the time taken by the leakage to empty the tank be x hours.

Portion of the tank emptied by the leakage in one hour = 1 x

1 4 = 1 3.5 –1 x 11121871 = === 3.547428 –28 x

x = 28 hours

17. Portion of the tank filled each hour by Pipe A = 1 36

Portion of the tank filled each hour by Pipe B = 1 18

Portion of the tank emptied each hour by Pipe C = 1 133

Portion of the tank filled each hour = 111 + 3618 –133 121 = +–3636133

31399–36363

= –= = 3613347884788

Time required to fill the tank = 4788 363 = 13 23 121 hours

18. Portion of work done by A and C together in one day = 1 2

Portion of work done by A in one day = 1 4

Portion of work done by C in one day

= Portion of work done by A and C together in one day

− Portion of work done by A in one day

= 1 2 − 1 4 = 2 − 1 4 = 1 4

Portion of work done by B and C together in one day = 1 3

Portion of work done by B in one day

= Portion of work done by B and C together in one day −

Portion of work done by C in one day 4–3 111

=–== 341212

Time taken by B to finish the work alone = 12 days

19. No of days food will last for 1800 sailors = 27

No. of sailors on the ship for the food to last for 13 more days or (13 + 27) = 40 days = 27 × 1800 40 = 1215

No. of sailors transferred to the boat = 1800 − 1215 = 585

20. Portion of recycling done by X in one hour = 1 8

Portion of recycling done by Y in one hour = 1 10

Portion of recycling done by Z in one hour = 1 12

Portion of recycling done in one hour by all three machines 111 =++ 81012

15+12+1037

= = 120120

Portion of recycling done between 11 a.m. and 1 p.m. =2×=3737 12060

Portion of recycling remaining = 3723 1 –= 6060

Portion of recycling done by X and Y in one hour

= 10+8 11 189 +=== 810808040

Time required to finish the remaining portion of work

= 23 60 9 40 = 234046 ×= 60927 hours = 46 ×60 27 minutes

= 102.22 minutes

Time of finishing recycling 500 bottles = 1 p.m. + 102. 22 minutes ≈ 2:43 p.m.

Word Problems

1. Portion of work done by Anshi in one day = 1 18

Portion of work done by Vinita in one day = 1 15

Portion of work finished by Vinita in 10 days = 10 × 1 15 = 2 3

Portion of work remaining = 21 1–= 33

Time required by Anshi to finish the remaining work = 1 3 1 18

= 18 3 = 6 days

2. Portion of work done by Julie in one hour = 1 15

Portion of work done by Nimish in one hour = 1 10

Portion of work done in hour by Julie and Nimish combined

= 1 15 + 1 10 = 2+351 == 30306

Amount of work finished by Julie and Nimish in 2 hours = 1 2 × 6

= 1 3

Amount of work remaining = 1 1 –3 = 2 3

= 10 hours

Time taken by Julie to complete the rest of the work = 2 3 1 15

Total time taken to complete the whole task = 10 + 2 = 12 hours

3. Work done by Suman (S) and Kavya (K) in one day = 1 30 …. (1)

Work done by Kavya (K) and Pulkit (P) in one day = 1 24 ….. (2)

Work done by Pulkit (P) and Suman (S) in one day = 1 20 ….. (3)

Adding 1, 2 and 3

2 (S + K + P) = 4+5+6 111151 ++=== 3024201201208

⇒ (S + K + P) = 1 16

Work done by Suman, Kavya and Pulkit in 10 days = 10 × 1 16

Work remaining = 1–=53 88

Word done by Suman in one day = Work done by Suman, Kavya and Pulkit − Work done by Kavya and Pulkit

= 1 16 − 1 24 = 1 48

Time taken by Suman to complete the rest of the work

= 3 348 8 =×= 181 48 18 days

Chapter Checkup

1.a. Direct Proportion

m = 13 ×15065 30 = 104

150 140

13:3013:30

b. Inverse Proportion; 15 × 32 = 10 × 48 = 480

12 10

n 15×32 40 12 = 48

c.

2. Cost of 18 markers = ₹576

Cost of 28 markers = ₹x

1857628 = =×576=896

28 18 x x ``

3. Rice flour required for 5 persons = 880 g

Rice flour required for 12 persons = xg

588012 = =×880g=2112g

12 5 x x

4. 30 minutes = 0.5 hour (1 hour = 60 minutes)

Distance travelled in 0.5 hour = 6 km

Distance travelled in 5 hours = xkm

0.565==×6km=60km

5 0.5 x x

5. Amount paid for 11 days of work = ₹4950

Amount paid for 30 days of work = ₹x

11495030 = = × 30 11 x x ₹4950 = ₹13,500

6. No. of days in a month = 30

No. of days Rohan works = 6

Fraction of work Rohan can do in 6 days = 6 30 = 1 5

7. No. of tablets Tablets bought for ₹25,000 = 20

No. of tables that can be bought for ₹10,000 = x

25,0002010,000==×20=8

10,000 25,000 x x

8. Cost of each of the 35 boxes = ₹120

Cost of each box after discount of ₹20 = ₹120 − ₹20 = ₹100

No. of boxes that can be bought at ₹100 each = 35×120 = 100 42

No. of more boxes that can be bought = 42 − 35 = 7

9. No. of men required to plough the field in 7 days = 12

No. of men required to plough the field in 2 days = 12 ×7 2 = 42

10. 25 km = 2 m on map.

600 km = xm

252600 == ×2m=48m.

600 25 x x

11. No. of tankers required to fill the society tank in 4 hours = 8

No. of tankers required to fill the society tank in 2 2 3 hours = 4×8 8 3 = 12 tankers

12. No. of cows grazing the field for 32 days = 20

No. of cows grazing the field for 128 days = 3220 128 × = 5

13. Quantity of apples bought for ₹1750 = 5 kg

Quantity of apples that can be bought for ₹2500 = x

175052500 == ×5kg=7.14kg

2500 1750 x x

14. Let the amount of work done per hour by A, B, and C be 111 , . and ABC

111 + = BC12 ……….(i)

111 + = BC12 ……….(ii)

1111 + += 6 ABC ………(iii)

Putting values from (i) in (iii)

1 8 + 1 C = 1 6

8–6 11121 =–=== 68484824 C

Putting values from (ii) in (iii)

111 + = 126

A

1 A = 1 6 − 1 12 = 2 1 12 = 1 12

11112+131 += + = == 122424248 AC

Time required for A and C to finish the job together = 8 hours

15. No. of people carried in 6 trips = 90

No. of people carried in 35 trips = x

69035==90=525

35 6 x x ×

16. Weight of 15 identical tiles = 127.5 kg

Weight of 50 identical tiles = xkg

15127.550 = =×127.5Kg=425kg

50 15 x x

17. Fraction of the tank filled by P in one hour = 1 25

Fraction of the tank filled by Q in one hour = 1 35

Fraction of the tank filled in one hour if both pipes operate simultaneously

= 117+512 + == 2535175175

Time taken by pipes to fill the tank = 175 12 = 14 7 12 hours

18. Daily consumption of water by 40 students = 13,000 litres

Daily consumption of water by 60 students = xlitres

4013,00060 = =×13,000 60 40 x x litres = 19,500 litres = 1.95 × 104 litres

19. Total amount distributed to 36 children = ₹18,900

Increased number of children = 36 + 6 = 42

Amount received by each child = ₹18,900 42 = ₹ 450

20. Let the time taken by the leak to empty the tub be x minutes.

Fraction of the tub emptied in one minute = 1 x

Therefore, 111 =–

3624 x 1113–21

= –= = 24367272 x minutes x =72minutes

21. No. of grains in 3 kg = 1.5 × 105 grains

No. of grains in 5.5 kg = x 5 5 31.5 × 105.5 = = ×1.5 ×10

5.5 3 x x grains = 2.75 × 105 grains

22. Fraction of the tank filled by Pipe M in one hour = 1 50

Fraction of the tank filled by Pipe N in one hour = 1 40

Fraction of the tank emptied by Pipe O in one hour = 1 80

Fraction of the tank filled in every hour

= 111 +–504080 = 8 +10 –5 400 = 13 400

Time taken by the tank to be filled completely = 400 13 hours = 30 10 13 hours

23. Fraction of the farm ploughed by Sonu in one day = 1 16

Fraction of the farm ploughed by Kamal in one day = 1 12

Fraction of the farm ploughed by Sonu and Kamal together in one day

= 1 16 + 1 12 = 3 4 48 = 7 48

Amount of work left after three days = 1–3×=1–77 4816

= 9 16

24. Time taken to reach school at the speed of 12 km/hr = 20 minutes

Reduced speed = 12 km/hr − 2 km/hr = 10 km/hr

Time taken to reach school at reduced speed = 12 ×20 10 minutes = 24 minutes

Time at which Krishvi will reach school = 8:00 a.m. + 24 minutes = 8:24 a.m.

25. Fraction of the tank filled by P in one hour = 1 8

Fraction of the tank filled by Q in one hour = 1 12

Fraction of the tank filled in one hour by P and Q combined

= 1 8 + 1= 3 2 24 = 5 24

Fraction of the tank filled after 3 hours = 3×=55 248

Fraction of the tank yet to be filled = 5 1–8 = 3 8

Time taken by P to fill the rest of the tank = 3 8 1 8 = 3 hours

26. Bacteria’s enlarged length when enlarged 2,00,000 times = 2 cm

Bacteria’s enlarged length when enlarged 2,00,000 − 50,000 = 1,50,000 times = x cm

⇒ 2,00,00021,50,000==×2cm=1.5cm

1,50,000 2,00,000 x x

Word Problems

1. Fraction of work completed by Darsh, Yash and Pooja together each day

= 1114+2+17

+ + = = 246122424

Time taken by Darsh, Yash and Pooja to finish the work = 24 7 hours = 3 3 7 hours

2. No. of 45 minutes batches taken by Manisha = 10

Increased duration of each batch = 45 + 30 minutes = 75 minutes

No. of 75 minutes batches that Manisha can take = 45×10 75 = 6

3. Fraction of work done by Mohan in one day = 1 24

Fraction of work done by Subhash in one day = 1 9

Fraction of work done by Vipul in one day = 1 12

Fraction of work done Subhash and Vipul together in one day

= 1 9 + 1 12 = 4+37 = 3636

Fraction of work remaining after three days = 7 1–3× 36

= 5 12

Time taken by Mohan to complete the remaining work =

5 12 1 24 = 10 days

4. Let the fraction of work done by X and Y in one hour be 1 x and 1 y respectively.

Fraction of work finished by X and Y together in one hour

= 1 x + 1 y = 1 30

Hence, 1 y = 1 30 − 1 x

Amount of work finished by X in 16 hours = 16 x

Amount of work left for Y to finish = 1 − 16 x

Time taken by Y to finish the remaining work = 16 1–1 x y

= 16 1–11 –30

x y = 44 hours

Solving for X, 1–=–164444 30 xx

28 x = 14 30

x = 60 hours

1111 =–= 306060 y or y = 60 hours

Hence, time required for Y to finish the work alone is 60 hours.

Chapter 22

Let's Warm−up

1. (6+5)+(12+3)=17+9 xyyxyx

2. (8+5)+(12–2)=17+6 xyxxyxxyx

3. 22 (6 + 5)– 12=–6+5 zyzzy

4. (7–5)–(12+3)=4–17 xyyxxy

Do It Yourself

22A

1.a. 2 3+9xx

2 3 x 9 x

3××xx 3×3× x

2 3+9=3(+3) xxxx

b. 4y–2y32

3 4 y 2 2y

2×2×××yyy 2××yy

322 4y – 2y=2(2–1) yy

c. 5ab22 +10ab

2 5ab 10ab2

5×××aab 2×5×××abb

22 5ab+10ab=5(+2) abab

d. 6–1832 xyxy

3 6 xy 2 18 xy

2×3××××xxxy 2×3×3×××xyy

322 6–18=6(–3) xyxyxyxy

8–42 12 cc

e. 4 8c 12c2

2×2×2××××cccc 2×2×3××cc 8–422212=4(2–3) cccc

f. 9pq323 – 6pq

9pq32 6pq3

3×3××××ppqq 23 pqqq

32322 9pq–6pq=3(3–2) pqpq

g. 4322 12 – 20 mnmn

43 12mn 22 20mn

22 2×2×3××××× mmnnn

2 2×2×5×××mnn

4322222 12–20=4(3–5) mnmnmnmn

h. 3223 15xy–25xy

15xy32 25xy23

3×5×××22 xxy 22 5×5×××xyy

322322 15xy–25xy=5(3–5) xyxy

i. 20a–30ab532

20a5 30ab32

2×2×5××32 aa

3 2×3×5×××abb

532322 20a30ab10(23) aab

2.a. 2 7–217(–3) xxyxxy

b. 3222 10–15=5(2–3) abababba

c. 4323 16–12=4(4–3) pqpqpqpq

d. 342323 18–6=6(3–1) mnmnmnmn

e. 524342 25–5=5(5–) xyxyxyxy

f. 342323 30–10=10(3–1) abababab

g. 322 11+22=11(+2) xxxx

h. 433 14–7=7(2–1) yyyy

i. 2322 17–34=17(–2) abababab

j. 5332 19–38=19(–2) cccc

k. 42222 23–46=23(–2) pqpqpqpq

l. 32322 27–18=9(3–2) mnmnmnmn

m. 433433 29–58=29(–2) xyxyxyxy

n. 322322 33–22=11(3–2) abababab

o. 2 37–74=37(–2) xxyxxy

3.a. 32 } (–2)(+4)–3(+4)=(+4){(–2)–3(+4) xxxxxx

b. (3 + 2) (2 –1)–(3 + 2) xxx

= (3+2)(2–1–1)=(3+2)(2–2)=2(–1)(3+2) xxxxxx

c. (5–1)(3+2)–4(3+2) yyy

= (3+2)(5–1–4)=(3+2)(5–5) yyyy = 5(32)(1) yy

d. (2+5)(–3)–(2 + 5) aaa = (2+5)(–3–1)=(2+5)(–4) aaaa

e. 2 ( + 3)( + 5)–( + 3) xxx

=(+3)(+5–(+3))=(+3)(+5––3)=2(+3) xxxxxxx

f. (2 – 4)(3–6)–2 (3–6)yyy

=(3 – 6)(2–4–2)=(3 – 6)(2–6)yyyy

g. 2 (4 + 7) ( + 2)–(4 + 7)=(4+7)((4+7)(+2)–1)aaaaaa

h. 32 (4 – 3)( + 2)–5(4 – 3)=(4–3)(+2–5(4–3))xxxxxx

i. (3 + 2)( –1) –2(3 + 2) yyy =(3+2)(–1–2)=(3+2)(–3) yyyy

4. a. 32 2 2 2–3+4–6= (2–3) +2(2–3)=(+2)(2–3) xxxyyxx yxxyx

b. 3+6–4–2=3(+2) –2(+2)=(3–2)(+2) abaccdbdabc dbcadbc

c. 2 –7–2+14=(–7) –2(–7)=(–2)(–7) xxxyyxx yxxyx

d. 2+5–4–10=(2+5) –2(2+5)=(–2)(2+5) abacbdcdabc dbcadbc

e. 2 – 3 – 2 + 6=(–3)–2(–3)=(–3)(–2)xxxxxxxx

f. 2 3–2–15+10=(3–2) –5(3–2)=(–5)(3–2) xxyxyxxy xyxxy

g. 2 6–3–10+5=3(2–) –5(2–)=(3–5)(2–) xyxyxxyx yxxyx

h. 2 4–12+2–6=4(–3) +2(–3)=(4+2)(–3) xxyxyxxy xyxxy

i. 6xy −9x2 − 4y + 6x = 3x (2y − 3x) − 2(2y − 3x) = (3x − 2) (2y − 3x)

5. a. 4233 40–60=20(2–3) abababba

b. 32322 43–86=43(–2) pqpqpqpq

c. 4322222 4 ) 7–94=4 –2 (7 mnmnmnmn

d. 524342 ) 50–25= ( 252–xyxyxyxy

e. 532322 ) 53–106=532 (–aabaab

f. 2 57–114=57(–2) xxyxxy

g. 2 (2–1)(+3)–3(2–1)=(2–1)((+3)–3(2–1)) =(2–1)(+3–6+3)=(2–1)(–5+6) aaaaaa aaaaa

h. 2 3+6+2+4=3(+2)+2(+2)=(3+2)(+2) xxxxxxxx

i. 32 2 2 2–+4–2=(2–1) +2(2–1)=(+2)(2–1) aaabbaa baaba

6. a. 322 2 3+2–3–2=(3+2) –(3+2)=(3+2)(–) aaabbaa baaab

b. 322 2–19–7=(2–19–7) aaaaaa

c. 233422222 15–20+35=5(3–4+7) yzyzyzyzzyz Word Problem

1. 2 4+8 + + 2=4(+2)+1(+2)=(4+1)(+2) xxyxyxxyxyxxy

No. of plants bought = x + 2y

Cost of each plant = ₹(4x + 1)

22B

1.a. 222 –4– 2(+2)(–2)aaaa

b. 25–=2225–=(5+)(5–) xxxx

c. 222 9–16=(3)–4=(3+4)(3–4) bbbb

d. 222 49–16=(7)–4=(7+4)(7–4) pppp

e. 22–=(+)(–) ababab

f. 22222–=()–=(+)(–) axyaxyaxyaxy

g. 222 100–81=(10)–9=(10+9)(10–9) bbbb

h. 2222–4=()–2=(+2)(–2) xyxyxyxy

i. 222 1–=1–=(1+)(1–) dddd

j. 422222 –100=()–10=(+10)(–10) bbbb

k. 2222 25–=5–()=(5+)(5–) axaxaxax

l. 144–=12–()623233 =(12+ )(12–)aaaa

2.a. 2222 +8+16=+2×4×+4=(+4) aaaaa

b. 2222 +10+25=+2×5 ×+5=(+5)xxxxx

c. 2222 +4+4 =+22 +2=(+2)bbbbb

d. 222 22 81+18+=9+2 ×9×+=(+9)aaaaa

3.a. Using, (–)=–2+222 abaabb

22 –14+ ?=–2×7×+?bbbb

Missing term = 72 = 49

b. Using, (–)=–2+222 abaabb

222 –?+9=–? +3 xx

Missing term = 2× ×3 6 xx

c. Using, (–)=–2+222 abaabb ?–2+=?–2××22 + cddcdd

Missing term = c2

d. Using, (–)=–2+222 abaabb 36–?+=6–?+222 rr

Missing term = 2 ×6×=12rr

4.a. 22 1 +=+2×× 2 aaaa

Constant term = 2 11 = 24

b. –8+=–2×4×+22 yyyy

Constant term = 2 4=16

c. 2 2 9–6=3–2 ×3×1dddd

Constant term = 12 = 1

d. 22 5 +5=+2 × × 2 xxxx

Constant term = 2 525 = 24

e. 22 –40+ 25=(5)–2×4×5 bbbb

Constant term = (4)2 = 16

f. 24+=2×12×+22 xxxx

Constant term = 122 = 144

g. 22–14=–2×7× xxxx

Constant term = 72 = 49

h. 22–16=–2×8× xxxx

Constant term = 82 = 64

5.a. 22 22 1–8+16=1–2×4×1+(4)=(4–1) axaxaxaxax

b. 3322 22 3–243=3 (–81) =3(–(9))=3(+9)(–9) xyxyxyxy xyxyxyxyxy

c. 4422222222 22 –=()–()=(+)(–) =(+)(+)(–) abababab ababab

d. 42222 22 –81=()–(9)=(+9) (–9)=(+9) (–9)(+9) bbb bbbb

e. 22 22 64–176+121=8–2×11×8+(11)=(11–8) xxxxx

f. 42242222

22222 49–168+144=(7)–2×7×12+ (12)=(12–7) xxyyxxy yyx

g. 2222 49–56+16=(7)–2×7×4+4(7–4) yyyyy

h. 64 − 16y + y2 = 82 − 2 × 8 × y + y2 = (y − 8)2

c. 222222 +4––4+4–4–abcabababc

= a2 − 2 × a × 2b + (2b)2 c2

= (a − 2b)2 c2

= (a − 2b + c)(a − 2bc)

d. 2 22 22 22 +2+=+2 × ×+=+ xyxxyyxy yxyyxxyx æöæöæöæöæö ÷÷÷÷÷ ççççç ÷÷÷÷÷ ççççç ÷÷÷÷÷ ççççç ÷÷÷÷÷ ççççç ÷÷÷÷÷ ççççç èøèøèøèøèø

Word Problem

1. (9–4).2222 =(3)–(2) =(3+2)(3–2). yxsqcmyx yxyxsqcm

Putting the values X = 2 and Y = 2

Length = 3y + 2x = 3 × 3 + 2 × 2 = 13 cm

Breadth = 3y – 2x = 3 × 3 − 2 × 2 = 5 cm

22C

1.a. Middle term = − 5x = − 4x − x

b. Middle term = − 9x = − 8x − x

c. Middle term = − 11x = − 8x − 3x

d. Middle term = − 17x = − 16x − x

2. x2 − 13x + 42 = x2 − 6x − 7x + 42 = x(x − 6) − 7(x − 6) = (x − 6) (x − 7)

x2 − 12x + 35 = x2 − 7x − 5x + 35 = x(x − 7) − 5(x − 7) = (x − 5) (x − 7)

x2 + 11x + 10 = x2 + 10x + x + 10 = x(x + 10) +1(x + 10)

= (x + 1) (x + 10)

x2 − 9x + 14 = x2 − 7x − 2x + 14 = x(x − 7) − 2(x − 7)

= (x − 2) (x − 7)

Hence, option c is the correct answer.

3.a. 3x2 − 23x + 14 = 3x2 − 21x − 2x + 14 = 3x (x − 7) − 2(x − 7) = (3x − 2) (x − 7)

Lengths and breadths could be (3x − 2) and (x − 7).

b. 5x2 − 37x + 14 = 5x2 − 35x − 2x + 14 = 5x (x − 7) −

2 (x − 7) = (5x − 2) (x − 7)

Lengths and breadths could be (5x − 2) and (x − 7).

c. 4x2 − 18x + 14 = 4x2 − 4x − 14x + 14 = 4x (x − 1) − 14 (x − 1) = (4x − 14) (x − 1)

Lengths and breadths could be (4x − 14) and (x − 1).

d. 4x2 − 8x + 3 = 4x2 − 6x − 2x + 3 = 2x (2x − 3) − 1 (2x − 3) = (2x − 1) (2x − 3)

Lengths and breadths could be (2x − 1) and (2x − 3).

4.a. 6x2 − 11x + 3 = 6x2 − 9x − 2x + 3 = 3x (2x − 3) − 1 (2x − 3) = (3x − 1) (2x − 3)

b. 2x2 − 7x + 6 = 2x2 − 4x − 3x + 6 = 2x (x − 2) − 3 (x − 2) = (2x − 3) (x − 2)

c. 2x2 − 5x + 2 = 2x2 − 4x − x + 2 = 2x (x − 2) − 1 (x − 2) = (2x − 1) (x − 2)

d. 3x2 − 8x + 4 = 3x2 − 6x − 2x + 4 = 3x (x − 2) − 2 (x − 2) = (3x − 2) (x − 2)

e. 9x2 − 9x + 2 = 9x2 − 6x − 3x + 2 = 3x (3x − 2) − 1 (3x − 2) = (3x − 1) (3x − 2)

f. 9x2 − 15x + 6 = 9x2 − 9x − 6x + 6 = 9x (x − 1) − 6 (x − 1) = (9x − 6) (x − 1)

g. 3x2 − 11x + 10 = 3x2 − 6x − 5x + 10 = 3x (x − 2) − 5 (x − 2) = (3x − 5) (x − 2)

6.a. 44222222

222222

mnmnmn mnmnmn mnmnmn

22

–16=()–(4)=(+4) (–4)=(+4) (–(2)) =(+4)(–2)(+2)

b. 2222 22 ––2–1=–(+2+1)=–(+1) abbabbab =(–(+1))(+(+1)) abab =(––1)(++1) abab

h. 15x2 − 11x + 2 = 15x2 − 6x − 5x + 2 = 3x (5x − 2) − 1 (5x − 2) = (3x − 1) (5x − 2)

5.a. Yes

b2 c3 + 8bc4 + 12c5 = b2c3 + 6bc4 + 2bc4 + 12c5 = bc3 (b + 6c) + 2c4 (b + 6c) = (b + 6c) (bc3 + 2c4) = c3 (b + 6c) (b + 2c)

b. Yes

3c5 − 18c4 − 48c3 = 3c5 − 24c4 + 6c4 − 48c3 = 3c4 (c − 8) + 6c3 (c − 8) = (c − 8) (3c4 + 6c3 ) = 3c3 (c + 2) (c − 8)

Word Problem

1. Total profit = No. of products sold × Profit per product sold

3x2 − 12x − 15 = 3 (x2 − 4x − 5) = 3 (x2 − 5x + x − 5) = 3 (x (x − 5) + 1 (x − 5)) = 3 (x + 1) (x − 5)

Since (x − 5) is the number of products sold, therefore the profit per product is 3(x + 1).

22D

1.a. 15x3 3x = 5x3 − 1 = 5x2

b. 15a3b4 5ab2 = 3a2 − 1 b4 − 2 = 3ab2

c. 24y4z3 6yz = 4y4 − 1 z3 − 1 = 4y3z2

d. 18x5y2z 9xyz2 = 25 −1y2 −1 z2 −1 = 2x4y z

e. 36p4q3r2 12p2qr2 = 3p4−2 q3−1r2−2 = 3p2q2

f. 84j5k7r9 7jk3r2 = 12j5−1k7−3r9−2 = 12j4k4r7

2.a. 2x3 + 4x2 −6x 2x = 2x3 2x 4x2 2x 6x 2x + = x2 +2x −3

b. 3y4 − 9y3 +6y2 3y = 3y4 3y 9y3 3y 6y2 3y + = y3 3y2 2y

c. = a4 −3a3 +2a2 4a5 − 12a4 +8a3 4a = 4a5 4a 12a4 4a 8a3 4a + +

d. 3232 2 6–18+1261812=–+=–3+2 6666 mmmmmm mm mmmm

e. 654654 432 2222 5+10–1551015=+–=+2–3 5 55 5 xxxxxx xxx xxxx

f. 5a3x −

3.a. 225abc (4a− 8) (5b− 15) (125 (a− 2) (b− 3)

225 × 4 × 5 × abc (a− 2) (b− 3)

= 125 (a− 2) (b− 3) 36abc

b. 144ab (a + 5) (b − 4)

36a (b − 4) = 4b (a + 5)

c. 28 (a + 3) (a2 + 3a + 70)

7(a + 3) = 4(a2 + 3a + 70)

d. 117abc (a + b) (b + c) (c + a)

78ab (b + c) (c + a) c(a + b) 3 2 =

4.a. 4x −6

x2 − 4 4x3 −6x2 + 3x −9

4x3 +0x2 −16x −6x2 + 19x −9

−6x2 + 0x +24

19x −33

b. 3y2 −9y + 18

y2 − 4 3y2 −9y3 +6y2 −12y +0

3y4 +0y3 −12y2 −9y3 +18y2 −12y +0

−9y3 +0y2 +36y

18y2 −48y +0

18y2 +0y +72 −48y +72

c. x3 +5x2

x2 + 4 x3 −5x4 +4x3 +20x2 +16x +0

x5 +0x4 +4x3 5x4 +0x3 +20x2 +16x +0

5x4 +0x3 +20x3 0 16x +0

d. 6a3 15a2 +39a −84

a + 2 6a4 −3a3 +9a2 −6a +0

6a4 +12a3 15a3 +9a2 −6a +0

−15a3 +30a2

39a2 −6a +0

39a2 +78a −84a 0 −84a −168

168

e. 9b4 +12b3 21b2 −28b +42

b2 + 2 9b6 +12b5 −3b4 −4b3 +0b2 +0b +0

9b6 +0b5 −18b4 12b5 −21b4 −4b3 +0b2 +0b +0

12b5 +0b4 +24b3 −21b4 −28b3 +0b2 +0b +0 −28b3 +42b2 +0b +0

−21b4 +0b3 −42b2 −28b3 +0b2 −56b

42b2 +56b +0

42b2 +0b +84

56b –84

f. 2c4 −12c3 +30c2 −60c +108

c + 2 2c5 –8c4 +6c3 –0c2 –12c +0

2c5 +4c4 −12c4 +6c3 +0c2 –12c +0

d. x2 x +4

–

x5 –2x4 –x3 +2x2

–x4 +6x3 –4x2 –4x +8

–––

–12c4 –24c3

30c3 +0c2 –12c +0

30c3 +60c2

−60c2 –12c +0

–60c2 –120c

108c +216 ––216

5.a. 3x +7

x2 + 4x + 4 3x3 –5x2 +2x –1

–

3x3 –12x2 +12x

7x2 –10x –1

–

7x2 –28x +28

18x −29

2y2 – 3y – 6 4y4 +6y3 –2y2 +8y –12

4y4 –6y3 –12y2

12y3 +10y2 +8y –12

12y3 +18y2 –36y

28y2 +44y –12

––

–x4 +2x3 +x2 –2x 4x3 –5x2 –2x +8

4x3 –8x2 –4x +8

3x2 +2x +0

e. 7x +23

x2 – 3x –2 7x3 +2x2 –9x –5

–

7x3 –21x2 –14x 23x2 +5x –5

–

23x2 –69x –46

74x +41

f. 3y2 +8y 20

3y3 – 6y2 –3y +6 9y5 +6y4 +3y3 –18y2 +9y –6

–

9y5 –18y4 –9y3 +18y2

24x4 +12y3 –36y2 –9y –6

––

24y4 –48y3 –24y2 +48y

60y3 –12y2 –39y –6

60y3 –120y2 –60y +120

108y2 +21y −126

6. x3 −5x 3

x – 7x3 – 12x2 + 38x –21

–

x3 –7x2 −5x2 +38x –21

28y2 –42y –84

86y +72 –

c. 3a2 + a 2 +13 4

2a2 – a + 1 6a4 –2a3 +9a2 –5a +3

––

–5x2 +35x 3x –21

3x –21 0

Hence, x – 7 must be multiplied by x2 – 5x + 3.

6a4 –3a3 +3a2 a3 +6a2 –5a +3

––

a3 –a2 2 + a 2

13a2

2 –11a 2 +3

13a2

− 9a 4 1 4 –

2 –13a 4 + 13 4

7. a3 +1

a2 + 2a – 3 a4 +2a3 –2a2 +a –1 a4 +2a3 –3a3 a2 +a –1 a2 +2a –3 a +2

–

–

Hence, −a + 2 must be subtracted from a4 + 2a3 − 2a2 + a − 1 to make it exactly divisible by a2 + 2a − 3.

8. 3x2 +3x +5

x −1 3x3 +0x2 −8x +0

3x3 −3x2

3x2 −8x +0

3x2 −3x +5x +0

−5x +5 −5

Hence, 5 must be added to 3x3 8x to make it exactly divisible by x 1.

Word Problem

1. x2 +3x +4

x +3 x3 +6x2 +13x +12

x3 +3x2

3x2 +13x +12

3x2 +9x 4x +12

4x +12 0

Each kid will get (x2 + 3x + 4) chocolates.

Chapter Checkup

1. a. 2x2 + 6x = 2x (x + 3)

b. 3ab − 9a = 3a (b − 3)

c. 4y3 + 8y2 = 4y2 (y + 2)

d. 5x2 − 15x + 10 = 5 (x2 − 3x + 2)

e. 6m2 n + 12mn2 = 6mn (m + 2n)

f. 7xy − 14x = 7x (y − 2)

2. a. (x + y) − (x + y) (2x − 11) = (x + y) (1 − 2x − 11) = − 2 (x + y) (x + 5)

b. x (x − 2z) + y (x − 2z) + (2z − x) = (x − 2z) (x + y − 1)

c. (n − 10)2 + (10 − n) = (10 − n) (10 − n + 1) = (10 − n) (11 − n)

d. (3a − 1)2 − 6a + 2 = (3a − 1)2 − 2 (3a − 1) = (3a − 1) (3a − 1 − 2)

= 3 (3a − 1) (a − 1)

e. 5x + 10y − 7 (x + 2y)2 = 5 (x + 2y) − 7 (x + 2y)2 = (x + 2y)

(5 − 7x − 14y)

f. (5x + y) − (5x + y)3 = (5x + y) (1 − (5x + y)2)

3. a. 4a2 b − 6ab2 − 2ab + 3b2 = 2ab(2a − 3b) − b(2a − 3b) = (2ab − b)

(2a − 3b) = b(2a − 1) (2a − 3b)

b. 5x2 − 10xy + 3xy − 6y2 = 5x (x − 2y) +3y (x − 2y) = (5x + 3y) (x − 2y)

c. 3x2 − 2xy + 6x − 4y = x (3x − 2y) + 2(3x − 2y) = (x + 2) (3x − 2y)

d. 9x2 − 6x − 12xy + 8y = 3x (3x − 2) − 4y(3x − 2) = (3x − 4y) (3x − 2)

e. 4x3 − 2x2 − 6xy + 3y = 2x2(2x − 1) − 3y (2x − 1) = (2x2 − 3y)(2x − 1)

f. 6x2 + 7xy − 18x − 21y = x (6x + 7y) − 3 (6x + 7y) = (x − 3) (6x + 7y)

4. a. a2 + 6ab + 9b2 = a2 + 2 × a × 3b + (3b)2 = (a + 3b)2

b. x2 − 10xy + 25y2 = x2 − 2 × x × 5y + (5y)2 = (x − 5y)2

c. 4x2 + 4xy + y2 = (2x)2 + 2 × 2x × y + y2 = (2x + y)2

d. 25x2 + 40xy + 16y2 = (5x)2 + 2 × 5x × 4y + (4y)2 = (5x + 4y)2

e. x2 − 14xy + 49y2 = x2 − 2 × x × 7y + (7y)2 = (x − 7y)2

f. 16a2 − 32ab + 16b2 = 16 (a2 − 2ab + b2) = 16 (a − b)2.

5. a. p2 − 9q2 = p2 − (3q)2 = (p + 3q) (p − 3q)

b. 4x2 − 49y2 = (2x)2 − (7y)2 = (2x + 7y) (2x − 7y)

c. a2 − 16b2 = a2 − (4b)2 = (a + 4b) (a − 4b)

d. 9m2 − 25n2 = (3m)2 − (5n)2 = (3m + 5n) (3m − 5n)

e. x2 − 36y2 = x2 − (6y)2 = (x + 6y) (x − 6y)

f. 25u2 − 4v2 = (5u)2 − (2v)2 = (5u − 2v) (5u + 2v)

6. a. 6x2 + 11x − 2 = 6x2 + 12x − x − 2 = 6x (x + 2) −1 (x + 2)

= (6x − 1) (x + 2)

b. x2 − 5x + 6 = x2 − 3x − 2x + 6 = x (x − 3) − 2 (x − 3)

= (x − 2) (x−3)

c. 3x2 + 12x − 15 = 3x2 + 15x − 3x − 15 = 3x (x + 5) − 3(x + 5)

= 3(x − 1) (x + 5)

d. 3x2 − 10x + 7 = 3x2 − 7x − 3x + 7 = x (3x − 7) − 1 (3x − 7) = (x − 1) (3x − 7)

e. x2 + 14x + 48 = x2 + 8x + 6x + 42 = x (x + 8) + 6 (x + 8)

= (x + 6) (x + 8)

f. 2x2 − 3x − 5 = 2x2 − 5x + 2x − 5 = x (2x − 5) + 1(2x − 5) = (x + 1) (2x − 5)

7. a. 6x3 + 9x2 − 12x 6x3 3x 3x 3x 3x = + 9x3 12x = 2x2 + 3x − 4

b. 4a2 b3 c2 − 8ab2 c2 d 4a2 b3 c2 8ab2 c2 d 2abc 2abc 2abc = = 2ab2 c − 4bcd

12a3 b2 − 6a2 b3 + 18ab4 12a3 b2

c. +

6a2 b3 18ab4 6ab2 6ab2

6ab2 6ab2

= = 2a2 − ab + 3b2

d. 9x5 + 3x4 + 6x3 9x5 3x2 3x2 3x2 3x2 = 3x4 6x3 = 3x3 + x2 + 2x

7a4 b3 c2 − 14a3 b2 c3 + 21a2 bc4 7a4 b3 c2

e. +

14a3 b2 c3 21a2 bc4 7a2bc2 7a2bc2

= = a2b2 − 2abc + 3c2

7a2bc2 7a2bc2

f. 15x6 − 10x5 + 5x4 15x6

5x3 5x3 5x3 5x3 = + 10x5 5x4 = 3x3 + 2x2 + x

8. a. 2x2 +8x +10 x − 2 2x3 +4x2 −6x +0

2x3 −4x2 8x2 −6x +0

8x2 −16x 10x +0

10x –20 20

b. 3x3 −3x2 −6x +12 x + 1 3x4 +0x3 −9x2 +6x +0

3x4 +3x3 −3x3 −9x2 +6x +0

−3x3 +3x2

−6x2 +6x +0

−6x2 −6x

12x +0

12x +12

−12

c. 2x2 +7x +2

2x − 1 4x3 +12x2 −3x +0

4x3 −2x2

14x2 −3x +0

14x2 7x 4x +0

4x −2 2

d. x3 −3x2 +3x 6 5

5x + 2 5x4 −13x3 +9x2 +0x +0

5x4 +2x3

−15x3 +9x2 +0x +0

−15x3 −6x2

15x2 +0x +0

15x2 +6x −6x +0

−6x 12 5 12 5

e. 3x3 +9x2 2 +3x 4 + 9 8

2x − 3 6x4 +0x3 −12x2 +0x +6

6x4 −9x3

9x3 −12x2 +0x +6

9a3 − 27x2 2

3x2 2 +0x +6

3x2 2 − 9x 4 9x 4 − 27 8

9x 8 +6 75 8

f. x2 − 3x 7 + 86 49

7x − 4 7x3 −7x2 +14x +0

7x3 −4x2 −3x2 +14x +0

3x3 + 12x 7 86x 7 +0

86x 7 − 344 49 344 49

9. a. 3x +13

x2 − 3x +2 3x3 +4x2 −2x +1

3x3 −9x2 +6x

13x2 −8x +1

13x2 −39x +26

31x −25

b. 2x2 +2x +1

x2 − x −2 2x4 +0x3 −5x2 +0x +3

2x4 −2x3 −4x2

2x3 −x2 +0x +3

2x3 −2x2 −4x

x2 +4x +3

x2 x −2 5x +5

c. 3x + 1 2 2x2 − 3x −2 6x3 −8x2 +2x −4

6x3 −9x2 −6x

x2 +8x −4

x2 − 3x 2 −1

19x 2 −3

d. 5x –16

x2 + 2x –1 5x3 –6x2 +3x –2

–

5x3 +10x2 –5x −16x2 +8x –2

–

–16x2 –32x +16

40x −18

e. x2 −4x +15

x2 + 4x +4 x4 +0x3 +3x2 +0x –4

x4 +4x3 +4x2

––4x3 –16x2 –16x

−4x3 –x2 +0x –4

––

15x2 +16x –4

15x2 –60x +60

−44x −64

Word Problem

1. Area of the garden = 64x3 − 25xy2 = x(64x

= x ((8x)2 − (5y)2 ) = x (8x + 5y) (8x − 5y)

(8

Chapter 23

Let's Warm-up

1. The most favourite sport among the students is badminton

2. The least favourite sport among the students is chess

3. Students like badminton more than hockey.

4. Students like chess less than cricket.

Do It Yourself 23A

1. a. A line graph can be a whole, unbroken line. TRUE

b. A line graph is used to study how data changes over time. TRUE

c. When interpreting a double-line graph, if one line is consistently higher than the other, it means that the data represented by that line is always greater. TRUE

d. Line graphs can also be called histograms. FALSE

e. In a double-line graph, the two lines must always intersect at some point on the graph. FALSE

f. The horizontal axis in a line graph represents categories of the given data, while the vertical axis represents values or quantities. TRUE

2.a. The most number of shirts was sold on Thursday.

b. The least number of shirts was sold on Wednesday.

c. 45 − 20 20 25 20 500 4 5 4 × 100% = × 100% = × 100% = % = 125%

d. Average number of shirts sold on 5 days = 170 5 30 + 40 + 20 + 45 + 35 5 == 34

Ratio = 40 : 34 = 20 : 17

3.a. City A was most populated in 2004 and least populated in 2001.

b. × 100% = 60% 10,000 6000

So, there were 60% of people in City A in comparison to city B in the year 2001.

c. 100% = 40% 10,000 14,000 10,000

4. Scale: 1 division = 500 units

5.

23B

1.a. Every point on the y-axis is of the form (x, 0). FALSE

b. The graph of every linear equation in two variables need not be a line. FALSE

c. A point whose y-coordinate is zero and x-coordinate is 5 will lie on the y-axis. FALSE

d. The coordinates of origin are (0, 0). TRUE

e. A point whose x-coordinate is zero and y-coordinate is non-zero will lie on the y-axis. TRUE

2. a. Abscissa = 9, Ordinate = 4

b. Abscissa = 4, Ordinate = −5

c. Abscissa = 0, Ordinate = 4

d. Abscissa = −2, Ordinate = −8

e. Abscissa = 0, Ordinate = −7

3.a. Since, the x-coordinate is 0, then the point lies on the y-axis.

b. Since, the y-coordinate is 0, then the point lies on the x-axis.

c. Since, the y-coordinate is 0, then the point lies on the x-axis.

d. Since, the x-coordinate is 0, then the point lies on the y-axis.

e. Since, the x-coordinate and the y-coordinate are both 0, then the point lies on the origin.

4.a. (−8, 8) lies in the second quadrant.

b. (−9, −2) lies in the third quadrant.

c. (1, −8) lies in the fourth quadrant.

d. (8, 5) lies in the first quadrant.

e. (−5, 0) lies in the second quadrant.

5.

The points do not lie in a straight line.

6. Scale:

x-axis = 1 division = 1 unit

y-axis = 1 division = 1 unit

The line passing through (4, 4) and (−4, −4) meets the x-axis and y-axis at the origin, whose coordinates are (0, 0).

7. y = x2

x 12345

y 12 = 122 = 432 = 942 = 1652 = 25

Scale:

x-axis = 1 division = 1 unit

y-axis = 1 division = 5 units

12345

The points do not lie in a line. So, y = x2 is not a linear graph.

Word Problem

1.Cost of a notebook = ₹50 =

x y

11 × ₹50 = ₹50

22 ×₹50 = ₹100

33 × ₹50 = ₹150

44 × ₹50 = ₹200

55 × ₹50 = ₹250

66 × ₹50 = ₹300

77 × ₹50 = ₹350

88 × ₹50 = ₹400

99 × ₹50 = ₹450

1010 × ₹50 = ₹500

Scale:

x-axis = 1 division = 1 unit

y-axis = 1 division = 50 units

a. The cost of 7 books is ₹350.

b. The number of books purchased with ₹50 = 1

The number of books purchased with ₹550 = 1 50 550 11

Chapter Checkup

1. a. Abscissa = 5, Ordinate = 4; first quadrant.

b. Abscissa = − 8, Ordinate = − 2; third quadrant.

c. Abscissa = − 9, Ordinate = − 8; third quadrant.

d. Abscissa = − 5, Ordinate = − 10; third quadrant.

e. Abscissa = 14, Ordinate = − 21; fourth quadrant.

2. a. The points lie on a line.

Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit

b. The points do not lie on the line.

Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit

c. The points lie on a line.

Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit

3. Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit

No, from the graph we can see that A (5, 4) and B (4, 5) do not represent the same point.

4. Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit

When we extend the line joining the points A (2, 3) and B (3, 2), it meets the x-axis at P (0,5) and y-axis at Q (5,0).

5. Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit

When we extend the line joining the points A (1, 3) and B (0, 4), it meets the x-axis at C (4,0) and y-axis at B (0, 4).

6. The line joining the points that have the same x-coordinates will be parallel to the y-axis.

7. The line joining the points having y-coordinate constant will be parallel to the x-axis.

8. a. Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit

The figure formed on joining X (0, 0), Y (3, 0) and Z (0, 3) along with x-axis is a triangle.

b. Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit

The figure formed by joining the points A (6, 6), B (4, 4), C (3, 3), D (5, 5) is a straight line.

9. x 12345

y

Scale: x-axis: 1 division = 1 unit y-axis: 1 division = 1 unit

PointAbscissaOrdinateCoordinates

A −21.5(−2, 1.5)

B 3 1 (3, 1)

C 1−3(1, −3)

D −3−2(−3, −2)

11. a. A = (−6, −2); B = (−2, −2); C = (2, 2); D = (−2, 2); P = (7, 4); Q = (7, 0); R = (3, 0); S = (2, −1); T = (4, −1); U = (4, −3); V = (2, −3)

b. The opposite sides of the quadrilateral ABCD are parallel and equal, so it is a parallelogram. STUV is a rectangle

c. ΔPQR is a right triangle, so

PRPQ2 QR2 = 42 42 32 4 2 units.

d. Area of ΔPQR 1 2 4 4 8 square units.

Word Problems

1. Scale: x-axis: 1 division = 1 year

Y axis: 1 division = 2 units

2. a. i.5 crores. ii.10 crores. iii.15 crores.

iv. 6 crores.

b. 10 crores − 5 crores = 5 crores

So, the difference between the sales between 2017 and 2021 is 5 crores.

c. In 2017 and 2018 = 10 crores − 5 crores = 5 crores

In 2021 and 2022 = 15 crores − 10 crores = 5 crores

3. Scale:

x-axis: 1 division = 5 minutes

y-axis: 1 division = 5 m

4. Scale:

x-axis: 1 division = ₹100

y-axis: 1 division = ₹500

Ansh Raman

Yes, the graph passes through the origin.

Chapter 24

Let's Warm-Up

1. 235 =(2×100)+(3×10)+(5×1)

2. 362 =(3×100)+(6×10)+(2×1)

3. 894 =(8×100)+(9×10)+(4×1)

4. 1265 =(1×1000)+(2 × 100)+(6×10)+(5× 1)

5. 3657 =(3×1000)+(6×100)+(5×10)+(7× 1)

Do It Yourself

24A

1. a. 75 = 7 × 10 + 5

b. 98 = 9 × 10 + 8

c. 235 = 2 × 100 + 3 × 10 + 5

d. 954 = 9 × 100 + 5 × 10 + 4

2.a. 3 × 10 + 4 = 34

b. m × 10 + n = 10m + n

c. 6 × 100 + 0 × 10 + 2 = 602

d. 9 × 100 + 5 × 10 + 0 = 950

3. Reverse of 25 = 52

The sum of any two-digit number and its reverse is completely divisible by 11, therefore the quotient is (2 + 5) = 7.

4. 582, 258 and 825

The sum of any three-digit number and two other numbers formed by interchanging the order of digits in cyclic order is completely divisible by 37, therefore the quotient is 3(5 + 8+ 2) = 45.

5.a. A + 3 = 5 ⇒ A = 5 − 3 ⇒ A = 2

or 4 + A = 6 ⇒ A = 6 − 4 ⇒ A = 2

b. A × A = 4

The numbers that can satisfy the above condition is 2 × 2 = 4 or 8 × 8 = 64

As 8 does not satisfy the condition, and placing A = 2 gives, 32 × 2 = 64; A = 2 is the correct answer.

c. B + 2 = 7 ⇒ B = 7 − 2 ⇒ B = 5

⇒ A + B = 7 ⇒ A + 5 = 7 ⇒ A = 7 − 5 ⇒ A = 2

d. Since, A × B = B

The values of A and B that can satisfy the above condition can be 1,5; 6, 2; 6, 8 or 3, 5

On trial and error, we find that 62 × 6 =372

Hence, A = 6 and B = 2 is the correct answer.

e. 6A × B = A1B

The values of A and B that can satisfy the above condition can be 1,5; 6, 2; 6, 8 or 3, 5;

On trial and error, we find that, 63 × 5 = 315

Hence, A = 3 and B = 5 is the correct answer.

f. 2 + 3 = B ⇒ B can be 5

B + 3 = C ⇒ 5 + 3 = C ⇒ C can be 8

A + B = C ⇒ A + 5 = 8 ⇒ A = 8 − 5 ⇒ A can be 3 Placing all the values in the sum, we get 325 + 533 = 858 (satisfy the sum).

Hence, A = 3; B = 5 and C = 8

6. 1623 A

B 11 C 8

D 7 E 12

4 FG 1

16 + 2 + 3 + A = 34 ⇒ A = 13

A + C + 7 + 4 = 34 ⇒ 13 + C + 7 + 4 = 34 ⇒ C = 10

B + 11 + C + 8 = 34 ⇒ B + 11 + 10 + 8 = 34 ⇒ B = 5

16 + B + D + 4 = 34 ⇒ 16 + 5 + D + 4= 34 ⇒ D = 9

16 + 11 + E + 1 = 34 ⇒ E = 6

3 + C + E + G = 34 ⇒ 3 + 10 + 6 + G = 34 ⇒ G = 15

2 + 11 + 7 + F = 34 ⇒ F = 14 1623 13

5 11 10 8

9 7 6 12

4 1415 1

7.a. 21 = 1 + 2 + 3 + 4 + 5 + 6

So, 21 is a triangular number.

b. 45 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9

So, 45 is a triangular number.

c. 90 ≠ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13

So, 90 is not a triangular number.

d. 105 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14

So, 105 is a triangular number.

e. 153 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17

So, 153 is a triangular number.

8.a. 32

Since, 2 × 2 = 4

So, the unit digit of the square of 32 will be 4.

b. 55

Since, 5 × 5 = 25

So, the unit digit of the square of 55 will be 5.

c. 69

Since, 9 × 9 = 81

So, the unit digit of the square of 69 will be 1.

d. 108

Since, 8 × 8 = 64

So, the unit digit of the square of 108 will be 4.

e. 236

Since, 6 × 6 = 36

So, the unit digit of the square of 236 will be 6.

9. 21, 34, 55, _____, 144

Since, the next digit is the sum of the two previous numbers

Then,

213455A = 89144

+ 21 + 34 + 55

So, 34 + 21 = 55

55 + 34 = 89

89 + 55 = 144

So, the missing number is 89.

10. 9375, 1875, 375, _____, _____, _____.

Each term in the pattern is being divided by 5, such that:

1875 = 9375 ÷ 5; 375 = 1875 ÷ 5; A = 375 ÷ 5 = 75

B = 75 ÷ 5 = 15; C = 15 ÷ 5 =3

So, the next three terms are 75, 15 and 3.

11. A 9643260

92

BCDE

16 F 52 G 88

HI 768412

4472 JK 36

A

The statement given by Suhani is incorrect.

correct magic square can be given

24B

1. A number is divisible by 2 if the last digit of the number ends with 0, 2, 4, 6 or 8. Hence, 36,126, 65,254, 72,362 and 81,658 are divisible by 2.

2. A number is divisible by 3, if the sum of the digits of the number is divisible by 3.

a. 1 + 3 + 6 + 5 + 3 = 18 is divisible by 3. b. 2 + 5 + 3 + 4 + 1 = 15 is divisible by 3.

c. 3 + 5

9

2

4 = 23 is not divisible by 3.

d. 4 + 7 + 3 + 2 + 2 = 18 is divisible by 3.

e. 6 + 5 + 2 + 4 + 6 = 23 is not divisible by 3.

3. A number is divisible by 5, if the last digit is 0 or 5 and divisible by 10 if the last digit is 0.

a. Since, the last digit is 5, 25,365 is divisible by 5 but not divisible by 10.

b. Since, the last digit is 2, 36,152 is not divisible by 5 and 10.

c. Since, the last digit is 0, 48,630 is divisible by 5 and 10.

d. Since, the last digit is 5, 7,02,365 is divisible by 5 but not divisible by 10.

e. Since, the last digit is 0, 9,43,270 is divisible by 5 and 10.

4. A number is divisible by 9 if the sum of the digits of the number is divisible by 9.

a. 3 + 8 + 8 + 5 + 5 = 29 is not divisible by 9.

b. 4 + 9 + 3 + 6 + 5 = 27 is divisible by 9.

c. 5 + 7 + 7 + 8 + 0 = 27 is divisible by 9.

d. 6 + 4 + 8 + 2 + 2 = 22 is not divisible by 9.

e. 8 + 2 + 6 + 7 + 4 = 27 is divisible by 9.

5.a. Since, the last digit is not 0, it is not divisible by 10.

b. 5 + 4 + 3 + 9 + 5 + 3 = 29 is not divisible by 3.

c. 5 + 9 + 4 + 9 + 0 = 27 is divisible by 9.

d. 6 + 0 + 5 + 8 + 9 = 28 is not divisible by 3.

6. a. 1250 2, 3, 9

b. 3646 3, 5, 9

c. 5214 2, 3

d. 9558 2, 5, 10

7. If 35x27 is divisible by 3, then, 3 + 5 + x + 2 + 7 = 35 + x should be divisible by 3.

35 + 1 = 36 is divisible by 3.

35 + 4 = 39 is divisible by 3.

35 + 7 = 42 is divisible by 3.

So, the possible value x =1, 4, 7

8. If 4z41 is divisible by 9, then,

4 + z + 4 + 1 = 9 + z should be divisible by 9. 9 + 0 = 9 is divisible by 9.

9 + 9 = 18 is divisible by 9.

The smallest and largest value of z will be 0 and 9, respectively.

9. 492x35y is divisible by 2, 3, 5, 9 and 10.

• If 492x 35y is divisible by 2, then it must end with an even number. So, x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and y = 0, 2, 4, 6, 8.

• If 492x 35y is divisible by 3, then 4 + 9 + 2 + × + 3 + 5 + y = 23 + × + y should be divisible by 3.

So, x = 1, 2, 4, 5, 7, 8 and y = 0, 2, 4, 6, 8.

•If 492x 35y is divisible by 5 if y = 0 or 5

So, x = 1, 2, 4, 5, 7, 8 and y = 0 or 5

• If 492x 35y is divisible by 9, then 4 + 9 + 2 + x + 3 + 5 + y = 23 + x + y should be divisible by 9.

So, x = 4 and y = 0 or 5

•If 492x 35y is divisible by 10 if y = 0

So, x = 4 and y = 0

Hence, if 492x 35y is divisible by 2, 3, 5, 9 and 10, then, x = 4 and y = 0.

Word Problem

1. Rajat’s number < 56,829 < Seema’s number

Both the numbers are divisible by 9.

5 + 6+ 8 + 2 + 9 = 30

Since, 27 and 36 are the nearest numbers to 30 which are both divisible by 9.

Since, 30 − 3 = 27, So, Rajat’s number = 56,829 − 3 = 56,826

Since, 30 + 6 = 6, So Seema’s number = 56,829 + 6 = 56,835

Chapter Checkup

1.a. 51 = 5 × 10 + 1

b. 36 =3×10+6

c. pq = p ×10 + q

d. 230 =2×100+3×10+0

e. 354 = 3 × 100 + 5 × 10 + 4

f. 709 =7×100+0×10+9

2. 84 and 48.

Since, 8 + 4 = 12

And, the sum of any two-digit number and its reverse is completely divisible by 11.

So, the quotient = 11

3. 631, 163 and 316 is divided by 30.

3 (6 + 3 + 1) = 30

So, the quotient = 37.

4.a. 1 + A = 6 ⇒ A = 6 − 1 = 5

B + 3 = A

⇒ B + 3 = 5

⇒ B = 5 − 3

⇒ B = 2

b. 1AB × B = 6AB

As B × B = B

5.

OR A + B = 7

⇒ 5 + B = 7

⇒ B = 7 − 5

⇒ B = 2

The value of B can be 1, 5, or 6

The values of A can be any between 0 − 9.

On trial and error, we find that 125 × 5 = 625

Hence; A = 2 and B = 5

c. 3A × B = 2BB

As A × B = B

The values of A and B that can satisfy the above condition can be 1,5; 6, 2; 6, 8 or 3, 5

On trial and error, we find that 36 × 8 = 288

Hence A = 6 and B = 8

3 A 92215

BC

3 16 92215 208

6.

a. 21 < 27 < 28

(1 + 2 + 3 + 4 + 5 + 6) < 27 < (1 + 2 + 3 + 4 + 5 + 6 + 7)

So, 21 is not a triangular number.

b. 55 < 65 < 66

(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) < 65 < (1 + 2 + 3 + 4 +

5 + 6 + 7 + 8 + 9 + 10 + 11)

So, 65 is not a triangular number.

c. 91 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13

So, 91 is a triangular number.

d. 171 < 180 < 190

(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 +

15 + 16 + 17 + 18) < 180 < (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +

10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19)

So, 180 is not a triangular number.

e. 595 < 600 < 630

(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 +

15 + 16 + 17 + 18 + 19 + 20 + 21 + 22 + 23 + 24 + 25 + 26 +

27 + 28 + 29 + 30 + 31 + 32 + 33 + 34)

< 600 <

(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 +

15 + 16 + 17 + 18 + 19 + 20 + 21 + 22 + 23 + 24 + 25 + 26 +

27 + 28 + 29 + 30 + 31 + 32 + 33 + 34 + 35)

So, 600 is not a triangular number.

10.

divisible by 3.

So, when z = 1, 4, 7; 57, 3 z 5 is divisible by 3. Thus, when z = 2, 3, 5, 6, 8, 9 the number 57,3z5 not divisible by 3.

11.

2

The smallest value of x to make the number 47

7. a. Since, 1 × 1 × 1 1, then the unit digit of the cube of 51 is 1.

b. Since, 2 × 2 × 2 8, then the unit digit of the cube of 72 is 8.

c. Since, 5 × 5 × 5 125, then the unit digit of the cube of 85 is 5.

d. Since, 9 × 9 × 9 729, then the unit digit of the cube of 119 is 9.

e. Since, 7 × 7 × 7 343, then the unit digit of the cube of 387 is 3.

8. 7, 56, 448, _____, _____

The given sequence is being formed by multiplying each term by 8:

7 × 8 56

56 × 8 448

448 × 8 3584 3584 × 8 28,672

Therefore, the next two terms in the sequence are 3584 and 28,672.

The

The last digit is zero.

The

The

The last digit is not zero. No

The last digit is not zero.

Word Problem

1. Total number of students = 917

Number of rows = 9

To arrange 917 students in 9 rows, 917 must be divisible by 9. 9+1+7=17 is not divisible by 9. So, Sarah will not be able to arrange them in rows of 9.

About the Book

Imagine Mathematics seamlessly bridges the gap between abstract mathematics and real-world relevance, offering engaging narratives, examples and illustrations that inspire young minds to explore the beauty and power of mathematical thinking. Aligned with the NEP 2020, this book is tailored to make mathematics anxiety-free, encouraging learners to envision mathematical concepts rather than memorize them. The ultimate objective is to cultivate in learners a lifelong appreciation for this vital discipline.

Key Features

• Let’s Recall: Helps to revisit students’ prior knowledge to facilitate learning the new chapter

• Real Life Connect: Introduces a new concept by relating it to day-to-day life

• Examples: Provides the complete solution in a step-by-step manner

• Do It Together: Guides learners to solve a problem by giving clues and hints

• Think and Tell: Probing questions to stimulate Higher Order Thinking Skills (HOTS)

• Error Alert: A simple tip off to help avoid misconceptions and common mistakes

• Remember: Key points for easy recollection

• Did You Know? Interesting facts related to the application of concept

• Math Lab: Fun cross-curricular activities

• QR Codes: Digital integration through the app to promote self-learning and practice

About Uolo

Uolo partners with K-12 schools to provide technology-based learning programs. We believe pedagogy and technology must come together to deliver scalable learning experiences that generate measurable outcomes. Uolo is trusted by over 10,000 schools across India, South East Asia, and the Middle East.

hello@uolo.com