Engineering Quarterly Summer 2021

EngineeringQuarterly

TheEngineeringQuarterlyisanewsletter publishedfourtimes eachyearbytheUniversityofMarySchool ofEngineering.In eachissue,wetryto includearticlesfromeachofthefiveengineeringmajorsthatwecurrentlyofferoncampus: ElectricalEngineering,MechanicalEngineering,CivilEngineering,ComputerScience, andConstructionManagement.Theintended audienceoftheEngineeringQuarterlyisengineers,engineeringstudents,engineering alumni,futureengineeringstudents,andpeopleworkinginfieldsrelatedtoengineering suchasscience,computing,andmathematics.

Inthisissuewedescribeoursummer activities.Wearebuildinganewbuilding, teachingsummercourses,performingserviceactivities,andpreparingforthefall.As usual,wealsoincludesomeproblemsfrom ourcoursesthatyoumightliketotry.Enjoy!

Dr.TerryPilling DeanofEngineering

THE JOURNEYOFAN ORDAINED ENGINEER

studentswouldfinishtheirmiddleandhigh schooleducation,andlaterwouldbeledinto seminary,wheretheywouldfinishtheirtheologicalstudies,andeventuallybecomepriests. Thepriestencouragedallinterestedstudents toreturntotheirparentsthatdayanddiscuss thisproposalwiththem.Khalidwasfascinatedandgotveryexcited.Hecouldnotwait toreturnhomeanddiscussthiswithhisparents.Thiswasthefirsttopicthatheopened withhismomduringlunch.

“NO”,wastheanswerfromhismother, whothreatenedtotellhisfather,whowasall againstanytypeofstudiesthatdoesnotput foodonthetable.Hisfatherhadhighhopes forKhalid,whowasatthetopofhisclass,he wantedhimtobecomeeitheradoctororan engineer,asmostparentsdreamedthattheir childrenbecomeintheMiddleEastregionof theworld.

“Butwhy?”askedKhalidwithatone ofdisappointmentmixedwiththetearsthat weremoisteninghischeeks.“Weneedyouto besuccessful”quippedhismother,“Andwe wantyoutogetmarriedandhavechildren,I wanttobeagrandmaoneday”...Khalidwas utterlysaddened.Hetriedtoconversewith themforthenextfewdays,butitwasalost cause.

Thiswasthefirstbig“NO”inKhalid’s self-planforhislife.Forsure,itwasnotthe last.

KhalidhadnochoicebuttofinishhismiddleschoolatDeLaSalle.Hishighschoolwas completedatoneofthehighschoolsthatwere newlyestablishedbytheQueenofJordanfor giftedstudents.DuringHighSchool,there weresomeAmericanteachers,andmanystudentstherewerefortunateandwelltodo. TheywouldvisittheUSinthesummerand returntotelltheirfriendsunlimitedstories aboutthebeauty,technology,andadvancementoftheUS.Itmadesensetoanyhigh achieverthattheUSisthelandofsuccess.So wasthecaseforKhalid.

Insenioryear,hegotascholarshiptofinishhisundergraduatestudiesatTexasTech University,hisparents,aswasthenormthen, werenotcomfortablesendingtheir17-yearoldtoacountrysofarthattheyknownothing about,andknownorelativeorfriendinthat statetohelphimifheneededwhilehewas there.Theanswerwasanother“NO”.This meantonething,thathehadtofacetheTExam.

ing,andsoon.Khalidwasabletosecurea gradethatwouldallowhimtogetintotheengineeringschoolattheUniversityofJordan, wherehestudiedElectricalEngineeringfor fiveyearsuntilhefinishedin2002.

Hereceivedamaster’sdegreeinComputerEngineeringfromtheUniversityof Massachusetts-Lowellin2004,andaPhD ininElectrical/BiomedicalEngineeringfrom TheGeorgeWashingtonUniversityin2011.

WhilethatwouldlookimpressiveonaresuméorLinked-Inprofile,therewasmoreto theactualstorythatwaslessglamorous.They saythatthedevilisinthedetails.Inreality, itwasGodwhowasgoverningallthedetails. Duringhisstudies,Godwasalwaysinthepicture.TheeffectofGod’spresencewasnot onlygrowing,butopposingmanyofthepaths andplansthatKhalidhadforhimself.

Asanygraduatestudentwhostudiesinthe US,Khalidwasalwayslookingforascholarshiptofinishhisstudies.Unfortunately,both Universitieswherehedidhisgraduatestudiesdidnotofferscholarshipsforinternational studentsattheSchoolofEngineering.Furthermore,internationalstudentswerenotable toworkfulltimeintheUS.Khalidwasunabletosupporthimselfbecausethelawrequiredhimtobeafull-timestudent.His part-timeworkoncampuswouldonlypayhis phoneandelectricbills.Thiswasanother huge“NO”thatlefthimfinanciallydependent onhisparentsuntilhefinishedschoolatthe ageof30.Alongwithachangeofhisthesisprojectbyhisadvisorthatcausedhimto losetwoyearsofworkandstartfromscratch, Khalidwentintomedicaldepression.Itlasted forayear.

However,GodWhoisallLove,andWho isbeyondLove,doesnotleavehischildren strandedinlifewithoutsupportandwithoutHisGrace.ThroughallthedisappointmentsinKhalid’seducation,Godarrangedfor KhalidtomeethisfuturewifeSara,anative JordanianandthedaughterofaGreekOrthodoxPriest,throughamiraculousmutualconnectioninJordan,whiletheywerebothstudyingintheStates.Themutualconnectionwas amanwhosenameliterallymeant“Grace”.

In1991,aCatholicpriestfromtheLatinPatriarchateofJerusalemrodehiscaranddrove forthreehoursintheHolyLandtovisitaclass of7thgradersatCollegeDeLaSalle(Fréres), aCatholicFrenchSchoolintheheartofAmman,thecapitalofJordan.Amongthese7th graderswasKhalid,whowasallearsforwhat thepriesthadtosay.TheCatholicFather cametopromoteaboardingschoolinBeit Jala,asmallcityintheHolyLand.There,the

TheT-Exam(Tawjihi)isthedreadedNationalHighSchoolExamthatwasarequirementforallhighschoolstudentsinJordan, thegradeofwhichwasthebasisfortheextremelycompetitiveuniversityadmission.It wasthenightmarethatallfamilieshadtoface atonepointintheirchildren’slives.Atthat time,therewereonlyfivepublicuniversities inJordan.Schooladmissionwasnotbased onthestudents’choice,butratherontheirTgrade.Topstudentswenttothelimitedseats ofMedicalSchool,thentheseatsofDentistryopened,thenPharmacy,thenEngineer-

Khalidwashopingthatupongraduation, hewouldworkinabigcompanythatwould makethehugeamountofinvestmentthat Khalid’sfamilyputlovinglyfromtheirheart andtheirownpocketallworthwhile.HeappliedtohundredsofpostsinDC.Mostof themrequiredsecurityclearance,whichwas impossibletogetasaninternationalstudent. Healsoappliedtomanypostsacrossthe country,buttheUSwasstillsufferingfrom recession.HisworkintheEngineeringfield wasnothappeningintheUS.Ashewascloser tograduation,andbeinginthenation’scapital,hewasabletogetconnectedtotwoindividualswhowereatthehighestrankofthe WorldBankGroup,thatpromisedtohelphim getemployedthere.Thisalsowastonoavail. Hisdreamsandhisowndefinitionofsuccess wereslowlyfadingaway...Godhadatotally

differentdefinition.Theoutcomeofthoseinvestmentswouldnotbefinancial,butrather spiritual.

Thelightoftheendofthetunnelbecamea littleapparent,Khalidwasabletoworkasan academicadvisorattheUAEembassyinDC, whilehiswifewasworkingattheJordanian Embassy.Lessthanayearlater,thecouple movedwiththeirtwochildrentotheirhome countryofJordan.Theywerehopingtohave abetterchancetoservethechurchasworking professionalswhilebeingclosetotheirfamilies.Khalidwasappointedasanassistant professoratthefirstCatholicUniversityin Jordan,TheAmericanUniversityofMadaba, whichwasownedbytheLatinPatriarchateof Jerusalem.Thepastroadthatwasfilledwith “NO”signs,startedtoslowlyevolvetoshowingthe“YES”sign,andbothsignsweredirectingtothesamedestination.

In2013,Khalidandafriendconnected withthedirectorsoftheOrthodoxEducationalSocietywhichisthemainumbrellafor severalOrthodoxSchoolsinJordan.They foundeda“FocusGroup”andstartedplanningmanyactivitieswiththesolepurpose ofbringingtheOrthodoxChristiansinJordanclosertotheChurchandtoeachother. Theywereabletoplanmanyactivities,among whichvisitstodifferentchurchesacrossJordan,tourismtripstoreligiousandbiblical sites,soccertournamentforallthefellowships acrossthecountry,andlecturesandQandA sessionsinparishioners’homesbypriests.

KhalidalsoreceivedtheblessingfromSts. ConstantineandHelenparishpriestinAmmantoestablishafellowshipministryforcollegeandworkingprofessionals.Hewasresponsibleofgivingthemtheweeklylectures anddevotionalsaswellasorganizingactivitieswiththem.HewasalsoacommittedparticipantintheDivineLiturgyandchurchservicesasamemberofthechoir.Khalidhas alsocompletedthreeyearsofstudyingByzantinemusicnotationandchanting.

ItbecameclearthatKhalid’scareerwas notdestinedsolelyforacademiaorengineering.ThecallingtoservetheChurchwasclear asthesun.Khalidtooktheblessingfrom hisspiritualfathertopursueordinationtothe priesthood.Hisspiritualfatherwashappy tohearthenews,gavehimtheblessing,but urgedhimtostudyTheologyfirst.In2016, heenrolledintheAntiochianHouseofStudy, atheologyschoolinNewJerseyandCaliforniathatofferedaprogrambycorrespondence withcertainresidencyrequirements.HereceivedhisMasterofTheologydegreein2020.

KhalidwasinvitedtoserveastheofficedirectorforthenewlyelectedOrthodox BishopofJordan,tohelpwiththereorganizationoftheArchdiocese.Whilehewasserving there,afacultypositionopenedattheUniversityofMary,Khalidtookthechanceandapplied.Hewashiredandstartedworkingin Fall2019.

InHiswords,Khalidwouldsay:“Iknew thattheUniversityofMarywouldbegreat, butwhenIcamehere,itwasbeyondmyfarthestimagination.Thisisaplacelikeno other!”Headds:“Here,yourwholelifecan beformedtobecomeavocation,notjusta career.Here,bothstudentsandfacultyare formedtofulfilltheircallingbyGod,andthe

reasonoftheirlifeonearth,nomatterwhat theydoinlife”

KhalidandwasordainedintheAntiochian OrthodoxChurchinApril2021asDeacon Damian.ThepresidentoftheUniversity, MonsignorJamesP.Shea,thevicepresident, DianeFladelandandherhusband,aswellas severalofhisEngineeringcolleagueswere presentathisordination.

Thesepresentationsarebeingdevelopedtogetherwithhandsonexercisesforpossible deploymentasworkforcedevelopmentopportunitiesandcoverthesamecontentthatwill bepresentedinEME298,ourcourseonmanufacturingtechnology.Thetopicscovered includedshopsafety,metrology,machining, andwelding.WeintheEngineeringSchool areexcitedtohaveLelandjoiningusthisfall!

RECORD ENROLLMENT

WeattheUniversityofMarySchoolofEngineeringareblessedtohaveDamianasour friendandcolleagueandwefullysupporthis plantobecomeapriestandstartanOrthodox churchintheBismarck/Mandanareawhile hecontinuestodesignandteachcoursesand guidestudentsasaprofessorinourdepartmentofElectricalEngineering.

TheUniversityofMaryhasarecordnumberofnewfreshmenstudentscominginthe fallandthatrecordincludesarecordnumber ofnewEngineeringstudentswithit.Wehave 64newfreshmenjoiningusinthefallwhich isdividedintodisciplinesasfollows

LelandVetter,anexperiencedmachinist withmanyyearsofbothteachingandindustryexperience,isjoiningusthisfallasour newShopCzar.Lelandwillteachsafetyand theuseofthemachineshopequipmentas wellasoverseeingandguidingtheactivities ofourstudentsusingourmachineshop.LelandjoinedusinJulyandpresentedaseriesof topicsonmachineshopsafetyandfundamentalstoourMechanicalEngineeringfaculty.

Wehavesplitseveralofourfreshmancourses intomultiplesectionstoaccommodatethese newstudentssincewehaveapolicyofmaintainingsmallclasssizes.Itisfundamental toourprogramthatwehavenomorethan 20studentsinthemajorityofourcourses. Webelievethatitismucheasierforstudents tolearnwhentheclasssizesaresmallsince thisenablesmoreone-on-oneinteractionbetweentheprofessorandthestudent,encouragesactiveparticipationinclass,studentpresentations,andallowsustocombinesome ofourtheorycourseswiththeircorrespondinglaboratorycourses.Combiningtheoreticalstudyandlaboratoryexperienceenables thestudenttoimmediatelyapplytheirtechnicalknowledgetopracticalapplication,experimentation,andtesting.Thisiscrucialto solidifyingtheunderstandingoftheabstract mathematicsandtechnicalmaterialbyputting itinapracticalcontext.Asourenrollment continuestoincreasewewillcontinuetocalve offmultiplesectionsofcoursesuntilwereach ouroverallenrollmentcapof250students. Wehavedesignedourbuildingsothatthe classroomsandlaboratoriesareoptimizedfor 250studentsandourultimategoalistohave thatnumberasasteadystate.

NEW MACHINIST JOINSOUR TEAM ByJAMESCARRICO

NEW CONSTRUCTION MATERIALS LABORATORY

Thissummerwebeganconstructionofour newadditionforourConstructionManagementandCivilEngineeringprograms.

buildingwhichisscheduledforfallof2022. Upuntilthispointwehavebeenluckytohave localcompaniesallowingustousetheirlaboratoryandtestingfacilitiestoteachourstudents.Havingourownfacilitiesattachedto ourengineeringschoolwillmakethelogistics mucheasierforthestudentsanditwillalso allowustousethefacilitiesandequipmentat ourdiscretionwhichisnecessaryifwewant studentstobeabletoworkonprojectsaround theclockaswedowithourotherlaboratories intheEngineeringbuilding.

N

Wehavecompletedthedesignofournew ConstructionManagementdegreewhichhas beenindevelopmentsincespringof2019. ProfessorsMatthewScerbakandRichard Garmanhaveusedtheirindustryexperience aswellasthemissionandvaluesoftheUniversityofMarytodesignanoutstandingprogramwhichisuniqueinthenation.

CommonCoreRequirements (takenbyallmajors)

FYE122FirstYearExperienceSeminar (withPresident’sSeminar)

ENG121CompositionII

COM110OralCommunication

ART:SELECTONEOFTHEFOLLOWING

ART108IntroductiontoPhotography

ART116IntroductiontoFilm

ART121ArtofRomeandParis(Romecampus)

ART127IntroductiontoDrawing

ART210TopicsinTextileArts

COM200VisualCommunication

ENG140IntroductiontoNarrative

THR105ActingTechniqueI

MUS196IntroductiontoMusic

MUS211ConcertBand(3semesters)

MUS212ConcertChoir(3semesters)

GLOBALSTEWARDSHIP:

POL101ResponsibleCitizenship

andoneofthefollowing:

ANT171CulturalAnthropology

SOC107GeneralSociology

HIS103/104WesternCivilizationand

WorldHistoryIorII

ECN101EconomicsofSocialIssues

CTH/HIS330Catholicism&TheModernWorld

CLA/HIS311GrandeurofRome(Romecampus)

Language(any300levelorabove)

THEOLOGY:

THE120SearchforGod

THE/CTH234Benedict-yesterday&today

PHILOSOPHY:

PHI108SearchforTruth

andoneofthefollowing:

PHI208/308PhilosophicalEthics

PHI/CTH210SearchforHappiness: FaithandReasoninLife.

SENIORASSESSMENT:

HUM499seniorassessment

ConstructionManagement

DegreeRequirements

ART127IntroductiontoDrawing

BUS215PrinciplesofManagement

BUS454ProjectManagement

CHE111GeneralInorganicChemistryI

CHE111LGeneralInorganicChemistryLab

CMT257CMFundamentals

CMT321ConstructionMaterialsandMethodsI

CMT322ConstructionDetailingandAnalysisI

CMT343ConstructionCostEstimatingI

CMT345BldgMechandElecSystems

CMT360InternationalBuildingCode

CMT421ConstrMatandMethodsII

CMT422ConstrDetailingandAnalysisII

CMT430ConstructionSafety

CMT443ConstructionConceptualEstimating

CMT466CAPMCertificationSeminar

CMT470ConstrSchedulingandControl

CMT481SeniorCapstoneI

CMT482SeniorCapstoneII

COM414BusinessCommunication

ECI313GeneralSurveyingwithLab

ECI313LGeneralSurveyingLab

ECI444Contracts&Specifications

ENR101IntroductiontoEngineering

ENR200ComputingforMath&Engineering

ENR201EngineeringMechanicsI

ENR203EngineeringMechanicsII

ENR203LEngineeringMechanicsIILab

ENR460EngineeringEconomy

GLG203EarthDynamics&Geophysics

MAT209CalculuswithAnalyticGeometryI

PHY203IntroductiontoPhysics

PHY203LIntroductiontoPhysicsLab

HUM499SeniorCompetencyTesting

ChooseTwoConcentrationOptions:

BusinessLeadership

BUS326Management/LeadershipConcepts

BUS328OrganizationalBehavior

BusinessManagement

ACC101PrinciplesofAccountingI

BUS401OperationsManagement

EngineeringSystems

ENR210ComputerAidedMeasurement

ENR419EngineeringDataAnalysis

SoilMechanics

ECI412SoilMechanicswithLab

ECI414FoundationEngineering

StructuralMechanics

ECI351StructuralMechanicswithLab

ECI451SteelDesign

ENR445ReinforcedConcrete

AdditionalRequiredCourses:

ENR470iswaivedforstudentswhoselect theStructuralMechanicsconcentration.

CMT411InterdisciplinaryFluency

ENR470EngineeringEthics

Total:135-137SemesterCredits

Programlength:4academicyears/128weeks

CONFERENCE

TheWillistonBasinPetroleumConferencewashostedintheBismarckEventCenterfromMay11toMay13,2021.Wehada

booththerefortheUniversityofMaryandthe SchoolofEngineering.

Ourmainpurposeinbeingatthisconference istoraiseawarenessamongthecompanies aboutourengineeringprogramandourstudents.Hopefullythecontactsthatwehave madewillbeasourceofinternshipsandpossiblycareersforourstudentsandgraduates.

OnJune21-23,theUniversityofMary hostedthe2021RisingLeadershipNorth Dakotaforhighschoolstudentsenteringtheir freshmanthroughsenioryear.

Studentswhotakepartdiscover:

• Keynotetopicsofleadership,motivation,andattitude.

• Toursofvariousbusinessesinthe Bismarck-Mandancommunity.

• Acareerfairandnetworkingopportunities

Theeventincludedvisitstothedifferent academicschoolsoncampusandvisitstoarea businesses.

TheConstructionMaterialsLaboratorywas sponsoredbyMillerInsulationandwillcontainourwetlabsforconcreteandasphalt workaswellasacraneandtestingequipment.

OurCivilEngineeringandConstructionManagementdepartmentsarelookingforwardto thecompletionofthisnewadditiontoour

WILLISTON BASIN PETROLEUM

RISING LEADERS ACADEMY VISITS CAMPUS ByRODRIGODACOSTAAPARECIDO

WhenthestudentsvisitedtheEngineering Schoolwefirsttoldthemabitaboutourengineeringprogramandthetypesofcareers someonecangetwithanengineeringdegree. Thenwegaveeachofthemelectronicsbreadboards,wires,batteries,andLED’sandwe challengedthemtowireseveralcircuitsto lightuptheLED’s.

TheGoBabyGoprojecthereattheUniversity ofMarywasinitiatedfiveyearsagoasapartnershipbetweenPhysicalTherapyandEngineeringwhereEngineeringfacultyandstudentsworkside-by-sidewithPhysicalTherapydoctoralstudentstoadaptride-ontoys thathelpwiththeinclusionanddevelopment ofchildrenwithspecialneeds.

gineeringMechanicsII(Deformablematerials)+Lab,aswellastheUniversity’salgebrabasedphysicscourse PHY203-Introduction toPhysics

Theintentwastoshowthemhowelectricity worksandalsohowyoucanwirecircuitswith breadboards.

Theeventwentwellandthestudents seemedtoenjoythechallengeofbuilding electriccircuits.Ashowofhandsrevealed severalofthemplantogotocollegeforengineeringaftertheygraduate.

ThePTstudentswoulddecidehowtobest accommodatetheneedsofthechildandthe engineeringstudentswoulddesigntheframe andelectronicstomeetthoseneeds.

Allofthesecourses wereaccelerated7weekcourses.This wasthefirstsummer thattheentireEngineeringMechanics coursesequencewas offeredinonesummerandthateither coursewasoffered ina7-weekformat. Justlikeinthenormalacademicyear, studentsweretasked todohands-onassignmentsinaddition tothetraditionaltextbookcoursematerial.StudentsinENR201 (in-personandonline)successfullydesigned andbuiltcatapultsthatlaunchedaracquetballtohittheirprofessorintheface(ortheir target)10metersaway.

In2006,ColeGallowaystartedaninclusionmovementforchildrenwithmotorimpairments,called GoBabyGo,attheUniversityofDelaware’sDepartmentofPhysicalTherapy.Thisprogramincludesmodifyinganelectrictoycarinanywaynecessary forachildwithmotorordevelopmentaldelaystoaccesstheirenvironmentandinteract withtheirpeers.

Thestudentsworkedoverseveralweeks todesignthemodificationsthatwouldbenefit thechildrenandtheirfamilies.

Theyaddedelectronicfeaturesand modificationstothe frame,alongwith specialcompartmentstoholdbackpacksandfeeding equipmentwhennecessary,andaftera fewweeksofdesign andbuildthestudents hadthegreatpleasureofgivingthe carstothechildren andwatchingthemlearntousethecontrolsto moveontheirown.Itwasabeautifulexperience.

StudentsinENR203Lsuccessfullydesigned andbuiltapapertrussbridgeand3Dprinted cablebridgetomeetcertainweightanddeflectionrequirements.Thepapertrusspicturedspanneda2footgap,weighedlessthan threepounds,andcarried67.5lbsbeforefailing!

SUMMER COURSES ByERICGARCIA

Theengineeringbuildinghousedthree coursesthissummer.Thesewerethesophomorelevelengineeringmechanicscourseseries: ENR201-EngineeringMechanics(ParticlesandRigidBodies) and ENR203+L-En-

InadditiontotheEngineeringMechanics courses,Physics203wasofferedthissummerintheEngineeringfacilitiesandmight havebeenthefirstclassofstudentstobe hostedintheengineeringbuildingthatwas allwomen.Boththelectureandlabsections wereheldintheEngineeringfacilities.StudentsinPhysics203evenusedsomeofthe catapultsdesignedbystudentsinENR201in pastschoolyearstoanalyzeprojectilesand performcalculationstodeterminewheretheir

GO BABY GO! ByRODRIGODACOSTAAPARECIDO

professorshouldstandtohithimintheface. Thepicturedteamsucceeded.Itwasnota goodsummerforDr.E.Garcia’sface.

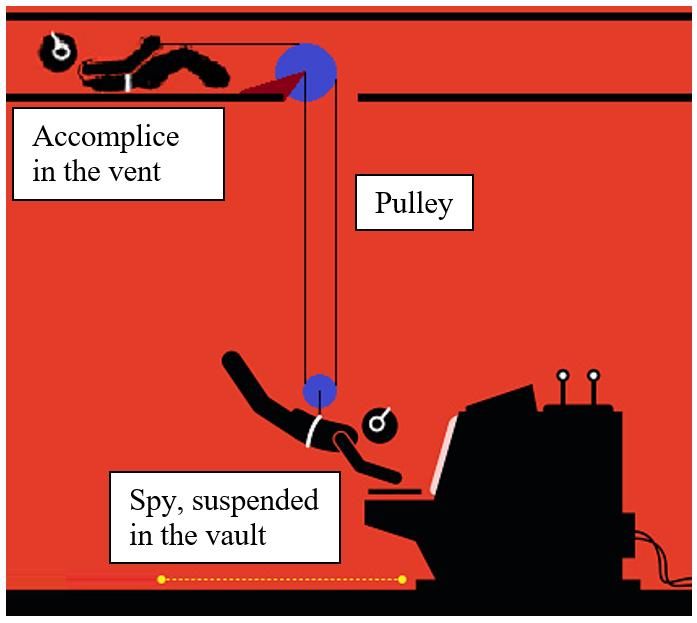
Inordertostealacomputerfilefroma securedvault,aspyandanaccomplicemust dropdownthroughanairventintheceilingtoaccessthecomputerwhilethevault islocked.Thespyislowereddowntothe computerusingaharnessandpulleysystem,whichisanchoredtotheventandby theaccomplice(asshowninthepicture).

Mytwo-year-olddaughtergotaheadstart. Shewasrunningataconstantvelocityof 1.5m/sandwas2maheadwhenmynephew begantorun.Mynephewstartedatrestand acceleratedataconstantrateuntilhecaught uptomydaughter6secondsafterhestarted running.

(a) Howfardidmynephewrunwhenhe caughtuptomydaughter?

(b) Whatwasmynephew’sacceleration?

(c) Howfastwasmynephewrunningwhen hecaughtuptomydaughter?

ENR203PROBLEM ByERICGARCIA

Therigidbeamshownispinnedto thetopofthethreesquare 1 5ft × 1 5ft columnsmadeofconcretethat hasacompressivestrengthof3500psi.

ΣFx =0 T fs =0

348N µs(84kg)(9 81m/s2)=0

µs =0 42

• PHY203Problem:

(a) 11m (b) 0 61m/s2 (c) 3 67m/s

• ENR203Problem:

FA =628 63kips

FB =586 67kips

FC =544 70kips

Oncethespyhasaccessedanddownloaded thenecessaryfiles,theaccomplicepullson theropeandraisesthespybacktothevent. Assumethemassoftheropeandharnessis negligible,thereisnofrictioninthepulley, andtheropeisalwayscompletelytaught.

(a) Determinethetensionforceintherope ifthespyhasamassof67kgandis loweredataconstantaccelerationof 0 4m/s2

(b) Determinethepullingforcetheaccomplicemustexerttoraisethespybackto theceilingventat 0 6m/s2

(c) Iftheaccomplicehasamassof84kg, whatistherequiredcoefficientofstatic frictionbetweentheaccomplicesclothingandtheventtonotslipwhentrying topullthespyupwiththeforcefound inpart(c)?

Determinetheforcesupportedbyeachcolumniftherigidbeamissubjectedtothe distributedloadshown.Assumethecalculatedforcesanddeformationsarelocatedat thecenterofeachsquarecolumn.

OnedayduringthesummerIandseveral oftheotherfacultywereintheofficeworking onourABETaccreditationrubricsandour lecturenotesforourfallcourseswhenIstumbledacrossaninterestingproblemfromthe internet.Imentionedittotheothersandwe endedupspendingacoupleofhourschatting aboutitandworkingoutthesolution.Supposeyoustartselectingrandomnumbersbetween0and1andaddingthemtogether.On average,howmanyselectionswillyouhave tomakebeforethesumexceeds1?Forexample,supposemyfirstpickis0.2andthenmy secondpickis0.9.Thesumis 0 2+0 9=1 1 andsinceitisalreadybiggerthan1Istopafter makingonlytwoselections.IfIdiditagain Imayget 0 13+0 54+0 21+0 89=1 77 whereIonlyexceeded1afterthefourthpick.

NoticethatinthefirstcaseIonlywentto onedecimalplaceandinthesecondIwentto twodecimalplaces.Weareassuminganinfinitenumberofdecimalplacesinourchoices sothatineachoftheaboveexamplesweare assuminganinfinitestringofzerosafterthe digitsIhaveshown.

SoinmytwoexampletrialsIfirstexceeded1afteronlytwoselectionsandthen Iexceeded1after4selections.Ifwestopat onlytwotrialsthentheaveragenumberofselectionsittakestoexceed1wouldbe:

Avg = 2+4 2 =3

Inotherwordsformysimpleexperimentwith twotrialsittakes,onaverage,threeselections ofnumbersbetween0and1beforetheirsum exceeds1.

Mytwo-year-olddaughterandthree-yearoldnephewdecidedtohaveafootracedown alongdriveway.

Nowthatyougettheidealet’sseewhat happensifweincreasethenumberoftrials.In ordertodoalargenumberoftrialstheeasiest methodistojustwriteacomputerprogramto doit.HereisaprogramwritteninCwhere theuserentersthenumberoftrialstoperform andthenthecomputerwilldothemand,when itisfinished,itwilloutputtheresultingaveragenumberofselectionstoexceed1among allthetrials.Hereistheprogram:

ENR201PROBLEM ByERICGARCIA

PHY203PROBLEM ByERICGARCIA

CALCULATING e ByTERRYPILLING

e.c

#include <stdio.h>

#include <stdlib.h>

#include <math.h>

#include <time.h>

#define NUM20 int main( int argc, char ** argv){ if (argc!=2){ fprintf(stderr,"Usage%sTRIALS\n", argv[0]); fprintf(stderr,"TRIALS=numberof trialstoaverage\n"); fprintf(stderr,"Thecomputerpicks randomnumbers\n"); fprintf(stderr,"between0and1 untilthesumisgreaterthan 1.\n"); return 1; } double S,sum=0; int TRIALS=atoi(argv[1]); int iteration; int histogram[NUM]; long MAX=pow(2,31); for ( int j=0;j<NUM;j++)histogram[ j]=0; srand(time(0)); for ( int i=0;i<TRIALS;i++){

S=0;

iteration=0; while (S<=1){

iteration++; S=S+rand()/(1.0 *MAX); } if (iteration<NUM)histogram[ iteration]++;

} for ( int j=0;j<NUM;j++)sum=sum+j * histogram[j]; printf("%d%lf\n",TRIALS,sum/TRIALS) ; return 0; }

IfIcompilethecodeusing gcce.c and thenruntheprogramfor1000trialsusing ./a.out1000,hereistheoutputfromthe program:

10002.686000

whichmeansthatin1000trialstheaverage numberofselectionsthecomputerhadto makesothatthesumwasbiggerthan1was 2.686selections.

NowwhatifIincreasethenumberoftrialsfurther?Howabout5000trials?Hereis whatIget:

50002.713200

andfor10,000trialsIget:

100002.713100

Thisisveryinteresting.Itseemslike,asIincreasethenumberoftrials,theresultisgettingcloserandcloserto2.71andthisisavery interestingnumber.Thereisamathematical constantwhichisveryfamiliartoallcalculus studentscalledEuler’sNumber,or e,whichis thebaseofthenaturallogarithmandisalmost asfamousas π.Like π, e isirrationalandsoit hasinfinitelymanydecimalplaces.Thefirst 20digitsare:

e=2.7182818284590452353

Now,theresultofourlittlerandomnumber experimentisanumberthatlookslikeitcould be e.Thiscouldjustbeacoincidenceandso whatcanwedototestthepossibility?Tobe absolutelycertainoneshoulddevisea mathematicalproof toshowthattheresultofourexperimentwillapproach e asthenumberoftrialsgoestoinfinity.However,beforewespend abunchoftimeandeffortfindingamathematicalproofweshouldfirsttrytogiveourselves abitmoreconfidencethatitreallyistrue.

Let’swritea Bash shellscriptwhichwill startatasmallnumberoftrials(128inthe casebelow)anditwillrunthesimulationand outputtheresult.Thenitwilldoublethenumberoftrialsandrunthesimulationagain.It willcontinuetodoublethenumberoftrials overandoveruntilitreachesahugenumber oftrials(229 inthecasebelow)outputting theresulteachtime.Thenwewillgraphthe resultingnumberversusthenumberoftrials andseeif,asthenumberoftrialsgetslarger andlarger,theresultseemstoconvergeon e Hereisour Bash script:

e.sh

#!/bin/bash i=128; MAX=$( echo "2^29"|bc l) if [ ee.dat]; then rm fe.dat fi while [$i le$MAX]; do let i=i * 2; ./a.out$i>>e.dat done gnuplot pe.gnuplot&

NoticethatthatitusesourCprogramtodo eachsimulationanditoutputsalloftheresults toafilecalled e.dat forlatergraphingand whenitisfinisheditgraphstheresultusing Gnuplot.Hereisa Gnuplot scriptwhich willgraphtheresults.

e.gnuplot

set termx11 settitle "Iterationstoe" setxlabel "Trials" setlogscale x2 setformat x"%.1tx10^{%T}" setformat y"%.3f" plot "e.dat"u1:2 with lines, 2.7182818wl

YoumightwanttotypeintheCprogram,the Bash script,andthe Gnuplot scriptonyour Linuxcommandterminalandplaywiththem. WhenIrunthe Bash scripthereisthegraph thatpopsup:

atruthistrue,and why afactisafact,is whatscienceandmathematicsareallabout. Inmaththereasonwhysomethingistrueis calleda mathematicalproof andinsciencethe reasonwhysomethingisafactiscalleda scientifictheory

DERANGED CARDS ByTERRYPILLING

Ican’thelpbutshow youanothercoolfind. Asmostengineeringstudentsknow, LeonardEuler(pronounced“oiler”the sameastheEdmontonOilershockey team)wasamathematicianwhodida hugeamountofmathematicalworkthatis usedthroughoutengineering.Infact,Euler wasbornin1707,oneyearafterBenjamin Franklin,andlivedfor76years.Hisparents wantedhimtobeapriest,butafterregisteringinTheologyattheUniversityofBasel, Switzerlandattheageof14hequicklydiscoveredaloveformathematicsanddecidedto switchmajors.Hewouldvisitmathematician JohannBernoulliintheeveningsandwork oninterestingmathematicsproblemsandhe quicklybecameoneofthegreatestmathematiciansofalltime.Heeventuallytooka professorshipinRussia,gotmarried,had13 children,andproducedsomanypapersand booksthathis OperaOmnia,orcollected works,isstillbeingcompiledover300years laterwhere,atpresent,itconsistsof73volumeswithmanymoreyettoappear.Tosay hewasprolificisanunderstatementsincehe wasthemostprolificmathematicianofall time.Hewascalled“AnalysisIncarnate”by mathematicalbiographerEricTempleBell1

, NoticethatIhaveindicatedtheexactvalueof e asahorizontallineonthegraph.Indeed, itlooksfromthegraphthatasIincreasethe numberofiterationstheresultingvalueapproaches e!

Soitseemsthatifyouselectrandomnumbersbetween0and1itwilltakeyou,onaverage, e picksbeforethesumexceeds1.Whyis that?Theremustbesomereason!Well,that iswhatmathematicsisfor!Nowthatyouhave confidencethatitistrue,youshouldgoabout findingout why itistrue.Thisisexactlywhat findinga mathematicalproof means.Truths andFactsarefuntoknow,butthereason why

ThestoryIwanttorelateinthisarticlebeginswithacardgamethatwasplayedbackin the1600’scalled‘coincidence’whereaplayer betsthatasthecardsaredealtfromashuffled deckacoincidencewilloccurwhereacard willcomeoutintheexactsamespotthatit wasoriginallyintheunshuffleddeck.Inother words,thedealertakes13cardsfromAceto King,shufflesthem,andthendealsthemout oneatatime.Asthecardsaredealttheplayerscount“one”,“two”,etc.andif,forexample,theycount“eight”atthesametimethe8 isdealtthenitisacoincidenceandthedealer losesandplayerwins.Ifall13cardsaredealt withnocoincidenceoccurringthedealerwins andtakestheplayersmoney.

Obviously,wheneverthereismoneyinvolvedinanygame,theplayer,andespecially thedealer,wanttofigureouttheoddsofwinning.Sointheearly1700’sitwasabitofa challengeinthemathematicalcommunityto figureouttheprobabilityofacoincidenceoccurring.ThisiswhenEulerheardaboutit.He thenproceededtosolveitandtheresulthegot wasabitsurprising.Letmeshowyouhowhe didit.

Thefirstthinghedidisisolatewhathe waslookingfor.Hethoughtaboutwhathad

1See TheMenofMathematics byEricTempleBell.

tohappeninorderforacoincidenceto not occur.Fornocoincidencetooccur,eachofthe shuffledcardshastoresideinadifferentpositionfromitsoriginalone.Eulerknewthat ifyoutook13objectsandyoupickedthemat random,thereare13!(i.e.13factorial)differentwaystodoit.Thisisbecausethereare13 choicesforyourfirstpick,then12remaining foryoursecondpick,etc.Thetotalnumberof differentarrangementsistherefore 13!=13× 12×11 ···×2×1=6227020800.Thatisalot ofdifferentorderings!WhatEulerwantedto findoutwashowmanyofthesehadnocards thatareinthesamespottheystartedinbeforethedeckwasshuffled.Inotherwordshe wantedtoknowhowmanyofthedifferentarrangementswere“derangements”–meaning nocardsremained“arranged”.Heinvented thesymbol Π(n) todenotethenumberofderangementsof n objects.Togetafeelforthis let’slookatacoupleofexamples.Suppose youhadonly1object.Thenobviouslyitwill bethefirstoneyoupicksinceitistheonlyone youpick.Thusitwillbeinthesameposition itstartedinandhenceitisnotaderangement.

Hencetherearenoderangementsof1object and Π(1)=0.Whatabouttwoobjects, a and b.Theoriginalorderis ab andifyouchoose themoneatatimethereareonlytwopossible ordersyoucanget.Either ab againorelse ba Thesecondcasehasneither a or b inthesame spotitstartedinandsoitisaderangement.

Hence Π(2)=1.Whataboutthreeobjects withoriginalorder abc?Herearethe 3!=6 possiblewaystopickthem:

abc bcacab

cbaacbbac

ofthese,onlythetwoinboldfacearederangementsandso Π(3)=2.Eulerwenton tocomputeafewmoreandfound Π(4)=9, Π(5)=44, Π(6)=265,andsoon.However,ifyoutrytodothisyourselfyouwill finditexcruciatinglytediousandprettymuch impossibletodoforthe13cardsweareafter.Thenumberofpermutations, 13!,isjust toomanytowritedownandthentrytosift outtheonesthatarederangements.SoEuler neededtofigureoutaformulainstead.Here iswhathedid:

Startwith n objectsinorder: a1a2 ...an andlookatwaystoderangethem.First,in anyderangement, a1 cannotappearinthefirst spotoritwouldn’tbeaderangement.Sothere aretwopossibilities.Either a1 endsupin thesecondspot,oritendsupsomewhereelse downtheline.

Case1: If a1 isinthesecondspotthenone oftheother n 1 objectsmustbein thefirstspot.Let’sjustassumethat a2 istherefornowbutmultiplyby n 1 attheendtoaccountforthesamething withanyoftheothersinthatspot.Our sequencethusstartsout a2a1 andthen followedbyaderangementof a3 ...an However,thenumberofderangements of a3 an is Π(n 2).Andsointhe casewhere a1 endsupinthesecond spotwehave (n 1)Π(n 2) possible derangements.

Case2: Inthiscase a1 doesnotendupin thefirstorsecondspot.Inthiscase oneoftheother (n 1) objectsarein thefirstspot(againwewilljustassume

it’s a2 andthenmultiplyby (n 1) attheendtoaccountforalltheother choices.Sincewealsodon’twant a1 in thesecondspoteither,weneedtheremainingobjectstobeaderangementof a1a3a4 ...an andthereare Π(n 1) of those.

Hencethetotalnumberofderangementsof n objectsisgivenbyaddingupthenumberswe foundinthetwocasesabove

Π(n)=(n 1)[Π(n 1)+Π(n 2)] Eulerfoundthisrecursionrelation.Sincewe knowthat Π(1)=0 and Π(2)=1 wecanuse theformulatogenerate Π(3)

Π(3)=(3 1)[Π(3 1)+Π(3 2)] =2[Π(2)+Π(1)]=2[1+0]=2 Wecannowhappilywriteacomputerprogramusingthisrecursionrelationandfindout what Π(13) is.However,itwouldbemore convenienttohaveaformulaintermsof n ratherthanarecursionrelationsowedon’t havetocomputeallthepreviousonesinordertogetthenextone.Youcandothisby workingoutafewofthemfromtherecursion andtryingtodetectthepattern.Eulerdidthis andfoundthat

Pi(13)=2290792932

Probability=0.367879

Sotheprobabilitythatthedealerwillwinis justoverathird.Soitlookslikeaprettygood betfortheplayerthatoneofthecardswill comeoutinitscorrectspot!

Thisisnottheendofthestoryhowever.If youtaketheinverseoftheprobabilityabove youwillfindaveryinterestingnumberappears.Tryit!Euleraskedhimselfthefollowingquestion:“whathappensif n becomes reallylarge?”Dothingsgetbetterorworse forthedealerandbyhowmuch.Wellitis easytofigurethisout.Juststartwithhisformulaandtakethelimitas n →∞.Let’sdo it.Theequationfortheprobabilityis

probability(n)= Π(n) n! = n k=0

andtakingthelimitgives

probability(∞)= ∞ k=0

( 1)k k!

( 1)k k!

Nowrecallthepowerseriesrepresentationthe exponentialfunction

Π(n)= n! n k=0

( 1)k k! Youcanprovethisformulabyinductionby knowingitistruefor n =1 and n 2 Π(1)= 1

Π(2)=2 2 k=0

1)k k! =1 1=0

( 1)k k! =2(1 1+1/2)=1

andshowing,usingourrecursionrelation,that beingtruefor Π(n 2) and Π(n 1) implies itistruefor Π(n)

Inanycase,nowwehaveaformulasuch that,given n,wecaneasilyfindthenumberof derangements Π(n).WecanwriteasimpleC programwitha for looptofindthat

Π(13)=2290792932

Nowwecometotheprobability.The probabilitythatyouwillgetaderangement outofarandomlyshuffled13cards–i.e.the probabilitythatthedealerwillwin(sinceno cardisinitsoriginalspot)isgivenbythetotal numberofderangementsdividedbythetotal numberofpossiblearrangementsincluding thederangements.WewillincludethiscomputationinourCprogramasfollows

derange.c

#include <stdio.h> #include <stdlib.h> int main( int argc, char ** argv){ if (argc!=2){printf("usage:%sN\n", argv[0]); return 1;} int N=atoi(argv[1]); int a=1; double k=1; double n=1; for ( int i=1;i<=N;i++){

a= 1*a;

n=n * i;

k=k+a/n; }

printf("Pi(%d)=%.0lf,Probability= %lf\n",N,n *k,k); return 0; }

Runningthiswith n =13 givesthefollowing output

ex = ∞ k=0

xk k!

Weseethatourprobabilityequationisnothingbutthisseriesevaluatedat x = 1.Hence

probability(∞)= e 1 = 1 e

andinsertingthedecimalvalueofEuler’sfamousnumber e =2 71828 wefindthat forlarge n theprobabilitythatanarbitrarysequenceofcardswillbeaderangementis

probability(∞)=0 367879 whichisexactlywhatwegottosixdecimal placesalreadywith n =13.Soclearlytheseriesconvergesveryquickly.Itisremarkable thatacombinatoricsproblemaboutthenumberofderangementsindealingcardsresults in 1/e.Itonceagainshowshowthesestrange irrationalnumberslike e and π tendtopopup inthemostunexpectedplaces.

ReadEuler,readEuler.Heisthe masterofusall.

–Laplace

ChallengefortheReader

Writeagamewhichdealsout13cards andcheckswhetherornotitisaderangement.Thenhavethecomputer playagainstitselfafewhundredthousandtimesandseeifyougetthepredictedprobabilityascalculatedhere.

ContactInformation

Formoreinformationaboutourengineeringprogramemail:Engineering@umary.edu

Nextissue:November,2021