Guía docente - Matemática 3

GUÍA

3

3

MATEMÁTICA

Silvia Vasconcellos

Introducción

Presentación

Estructura del libro didáctico

Secciones

Conéctate

Actualiza tu información

La esencia de la matemática

Actividades

Desafíos

¡Eres el profesor!

Glosario

Autoevaluaciones

Recortables

Íconos

Abordaje pedagógico

Objetivos

Contenido

Competencias

Modelo pedagógico

Capítulo 01: NÚMEROS REALES

Actividades previas y complementarias

La esencia de la matemática

Actividades

Desafíos

Capítulo 02: POLINOMIOS

Actividades previas y complementarias

Actividades

Desafíos

Capítulo 03: ÁLGEBRA

Actividades previas y complementarias

La esencia de la matemática

Actividades

Desafíos

Capítulo 04: SISTEMAS DE ECUACIONES E INECUACIONES

Actividades previas

Actividades complementarias

La esencia de la matemática

Actividades

Desafíos

Capítulo 05: FUNCIONES DE SEGUNDO GRADOS

Conéctate

Actualiza tu información

La esencia de la matemática

Actividades

Desafíos

Material extra

Capítulo 06: TEOREMA DE THALES

Actividades previas

Actividades complementarias

La esencia de la matemática

Actividades

Desafíos

Capítulo 07: PITÁGORAS Y TRIGONOMETRÍA

Disparador

La esencia de la matemática

Actividades

Desafíos

Actividades extra

Capítulo 08: ESTADÍSTICA

Disparador

Actualiza tu información

La esencia de la matemática

Actividades

Desafíos

Tutorial de cómo realizar gráficos estadísticos

Histogramas con geogebra

Capítulo 09: PROBABILIDAD

Disparador

Actualiza tu información

La esencia de la matemática

Actividades

Desafíos

Plan de las autoevaluaciones

Anexos

INTRODUCCIÓN

El libro Matemática 3 pertenece a la serie Matemática, destinada a los estudiantes de los primeros años del Nivel Medio o Secundario (12 a 15 años). A partir de conocimientos ya adquiridos, estimula el aprendizaje mediante el uso de diferentes disparadores cognitivos.

La presentación del contenido favorece el pensamiento crítico y el desarrollo de otras capacidades intelectuales. Dentro del marco de los requerimientos curriculares actuales, promueve el aprendizaje de la matemática en consonancia con la cosmovisión bíblico–cristiana, de tal forma que los conceptos matemáticos se relacionan como una parte del todo. La matemática y la religión no son dos elementos separados porque las personas integran ambos conocimientos en la vida.

Como recurso didáctico complementario, la serie ofrece de forma gratuita objetos digitales de aprendizaje (ODA), de acceso fácil y directo.

PRESENTACIÓN

El libro para el estudiante constituye una unidad coherente de contenidos matemáticos que han sido creados y regulados por Dios haciendo posible la abstracción y la lógica.

El objetivo de este libro y de toda la serie es ser una herramienta que acompañe la labor docente y el proceso de aprendizaje de los estudiantes. Ni el libro ni esta guía docente pretenden ser una limitante para el quehacer pedagógico. Por el contrario, su propósito es facilitar el aprendizaje y ser un instrumento de apoyo.

Esta guía docente complementa las actividades propuestas en el libro para el estudiante y amplía las ideas. Recuerde que siempre debe adaptar las propuestas a la realidad de su grupo.

El libro para el estudiante sigue una secuencia didáctica determinada, pero usted puede modificarla adecuándola mejor a sus estudiantes. Puede acomodar el orden de los contenidos, según su planificación.

Antes de iniciar el estudio y las actividades, se sugiere que puedan comprender el propósito que cumple cada una de las secciones y el simbolismo de los íconos, para que en el transcurso de la lectura puedan avanzar con fluidez. Lea las pp. 6 y 7 del libro para el estudiante.

Algunos detalles a tener en cuenta:

• Este libro fue diseñado teniendo en cuenta el contenido programático de varios países. Estos son: Argentina, Uruguay, Paraguay, Chile, Perú, Ecuador y Bolivia.

• Por esta razón, se trabajó con asesores representantes de los mismos que analizaron cada capítulo y brindaron sugerencias, para garantizar que el presente material pueda ser utilizado en sus países.

• Es pertinente destacar que puede haber contenidos dentro del libro, que en algún país se trabajen en cursos posteriores. En ese caso, se sugiere saltearlos, y argumentar que es el docente quien lidera y dirige esa clase, y escoge qué temas se darán y cuáles no.

• Si faltara contenido se le puede adicionar todo lo que el docente considere pertinente.

• No están resueltas todas las actividades del libro. Sí todas las actividades de las secciones Actividades y Desafíos, pero no las del desarrollo del capítulo. Solamente aquellas que se consideró pertinente resolver. Las más sencillas quedan a cargo del alumno y del docente. También hay indicaciones al respecto.

ESTRUCTURA DEL LIBRO DIDÁCTICO

Matemática 3 está compuesto de secciones que buscan acercar a los estudiantes al aprendizaje práctico. El principal aporte, tanto a los docentes como a los alumnos, es la gran cantidad de actividades que tiene el mismo.

SECCIONES

El libro presenta actividades para recordar (traer nuevamente a la mente conceptos ya conocidos), de comprensión, de aplicación, de análisis, de evaluación y de creación. Actividades introductorias, que reafirman el nuevo conocimiento aprendido, actividades para practicar y entrenar, y también desafíos para ampliar el espectro de razonamiento del alumno. A continuación, se describen brevemente cada una de las secciones.

CONÉCTATE

Las dos primeras páginas de los capítulos tienen como objetivo disparar el tema que se va a desarrollar en el capítulo.

Esta sección consta de un versículo, que tiene relación con algún concepto trabajado a lo largo del capítulo, o con la sección “La esencia de la matemática”, sobre el final del capítulo. Pero siempre tiene relación. No está elegido al azar.

También contiene un organizador, para que sea claro el contenido a trabajar. Otra vez, será el docente quien elegirá, de acuerdo con su planificación o su programa, o con el grupo que le ha tocado, el orden y los temas a trabajar.

Y, finalmente, contiene un “disparador”. El mismo es una página de actividades, que el alumno podrá realizar con los conocimientos previos que posee, pero que puede generarle determinadas dudas que irá solucionando con el transcurso de las clases.

Tiene justamente ese fin: que el alumno traiga a su memoria, conocimientos que poseía, pero quizás olvida con el correr de los años, los ponga en práctica, y finalmente le genere curiosidad para así dar un nuevo tema, o uno ya conocido en mayor profundidad (actividades de “recordar”, según la revisión de la taxonomía de Bloom, por Anderson & Krathwohl, 2001 y “motivación”, según la pedagogía adventista).

ACTUALIZA TU INFORMACIÓN

En esta sección se encuentra el desarrollo de los temas del capítulo. Generalmente se trabaja de la siguiente manera: bajo el título del tema a dar, hay una actividad disparadora, que nuevamente tiene el fin de provocar curiosidad, a pesar de que la podrán realizar con los conocimientos que ya poseen. Luego el desarrollo teórico, donde se formalizan nuevos conceptos, y finalmente una nueva sección de actividades, donde pondrán en práctica los nuevos conceptos adquiridos (proceso de motivación, exploración y aplicación).

LA ESENCIA DE LA MATEMÁTICA

Esta sección está enfocada a relacionar un tema del capítulo con una enseñanza. Esta puede ser presentada de cuatro formas diferentes:

• una porción de la Biblia aplicada

• algún conocimiento matemático relacionado con la naturaleza, el segundo “libro” de Dios

• una situación relacionada con las vicisitudes de la vida

• algo relacionado con algún trabajo útil

Se sugiere, que frente a la disponibilidad de tiempo que tenga el docente con el transcurrir del año, se realice de igual forma esta actividad. Pues es lo que hace a nuestra razón de ser (se sigue proceso de creación, sobre todo; actividades creativas).

ACTIVIDADES

En esta sección se realizaron múltiples actividades y ejercicios, no con el fin de que las hagan todas, sino con el fin de que el profesor elija la cantidad, y especifique cuáles son las adecuadas para su grupo, su nivel, y sus temas a dar.

En estas actividades se intenta alcanzar los primeros niveles de pensamiento del alumno, por lo cual es conveniente que el profesor las elija de forma adecuada, para, en al menos un momento de cada unidad, se alcancen todos los niveles: recordar, comprender, aplicar y analizar.

DESAFÍOS

Esta sección es interesante. Aquí el docente elegirá cuáles realizar en clases, cuáles enviar de tarea, o cuáles darles a unos alumnos y a otros, de acuerdo con el nivel, al grupo y a diversos factores que él o ella considere.

Tienen un nivel de complejidad un poco mayor, y en general son problemas, cuyo fin es que el alumno no tenga que aplicar un conocimiento de forma directa, sino que tenga que pensar y buscar estrategias diferentes para resolverlo. Se sugiere trabajo en grupos (para esto se recomienda leer a Pere Pujolàs Maset: El aprendizaje cooperativo: algunas ideas prácticas, Universidad de Vic, noviembre de 2003).

Esta sección intenta alcanzar los niveles más elevados de pensamiento del alumno, de forma conjunta con la sección “La esencia de la matemática”: aplicar, analizar, evaluar y crear.

Se recuerdan brevemente los postulados de cada uno de los niveles de pensamiento de La revisión de la taxonomía de Bloom, por Anderson & Krathwohl, 2001; con ejemplos de aplicación en el libro:

Recordar. Reconoce y trae a la memoria información relevante de la memoria de largo plazo (ejemplo: actividad 1 de la página 9, capítulo 1).

Comprender. Habilidad de construir significado a partir de material educativo (pueden ser videos en caso de que se utilice el modelo del Aula invertida), como la lectura (este libro) o las explicaciones del docente (ejemplo: actividad 2 de la página 38, capítulo 2; y actividad 2 de la página 202, capítulo 8).

Aplicar. Aplicación de un proceso aprendido, ya sea en una situación familiar o en una nueva (ejemplo: actividades 1 y 2 de la página 123, capítulo 5).

Analizar. Descomponer el conocimiento en sus partes y pensar en cómo estas se relacionan con su estructura global (ejemplo: actividad 3 de la página 124, capítulo 5).

Evaluar. Comprobación y crítica (ejemplo: actividad 5 de la página 124, capítulo 5).

Crear. Reunir conocimientos y hacer algo nuevo con ellos. Llevar a cabo actividades creadoras, los aprendices generan, planifican y producen (ejemplo: actividad 6 de la página 124, capítulo 5).

¡ERES EL PROFESOR!

En este libro se ha implementado una nueva actividad que atraviesa cada uno de los capítulos. En ella se presenta una consigna y la resolución, que no siempre es correcta. El alumno deberá corregir lo que se ha realizado en el libro, detectando tanto las partes que están correctas como las incorrectas, analizando y creando una forma de evaluar esto y corregirlo.

Parece una simple tarea, pero es muy compleja, de un alto nivel de pensamiento. Al analizar cada una de las partes tendrá que recordar lo que sabe, comprender la consigna y el problema que se plantea, analizar cada una de las partes y descomponerlo para poder pensar en ellas como una estructura global y finalmente evaluarla. Para evaluarla, por ejemplo, deberá escoger el mejor método para resolver el problema matemático presentado.

También se deja a libre criterio del alumno la creación de un método de corrección: se puede plantear que genere una rúbrica, que diseñe un nuevo método con el fin de alentar al “alumno” que realizó este ejercicio, y no desanimarlo, etc.

Un claro ejemplo es la actividad 4 de la página 188, capítulo 7.

GLOSARIO

En esta sección se explican la mayoría de los símbolos utilizados en el libro, para que los tenga en cuenta, tanto el alumno como el docente, a la hora de interpretar lo que dice el libro.

AUTOEVALUACIONES

Las autoevaluaciones no cuentan con las soluciones, dado que pueden ser utilizadas por el docente para evaluar al estudiante.

Constan de cuatro tipos de actividades, englobando los temas dados en la unidad: un falso/verdadero con justificación, consignas de desarrollo, múltiple opción y problemas o desafíos. Se intenta con este método apuntar a distintos métodos de aprendizaje del alumno.

RECORTABLES

En esta sección hay páginas diseñadas para ser recortadas según indicaciones de actividades plasmadas a lo largo del libro, que redirigen a cada página en particular.

ÍCONOS

Acompañan a las secciones. Son los siguientes:

Destaque

Este ícono contiene detalles importantes, aclaraciones o más información que se debe tener en cuenta.

Recuerda

Tiene el fin de traer a colación conceptos, que se supone que ya fueron adquiridos por los alumnos en niveles anteriores, pero que se considera importante destacarlos pues es probable que se confundan, o conceptos ya trabajados en el libro y es necesario tenerlos presentes para el tema que se está desarrollando.

¿De qué se tratará?

Estas son preguntas. Pero no preguntas tan sencillas, sino en la mayoría de los casos tienen un determinado nivel de complejidad, para que el alumno deba pensar más allá de lo obvio, y discutir de forma grupal las respuestas (de los niveles de compresión, análisis y evaluación).

“La calidad de nuestras vidas la determina la calidad de nuestro pensamiento. La calidad de nuestro pensamiento, a su vez, la determina la calidad de nuestras preguntas, ya que las preguntas son la maquinaria, la fuerza que impulsa el pensamiento. Sin las preguntas, no tenemos sobre qué pensar. Sin las preguntas esenciales, muchas veces no logramos enfocar nuestro pensar en lo significativo y sustancial.” El arte de formular preguntas esenciales, Dra. Linda Elder y Dr. Richard Paul. 2002 Foundation for Critical Thinking.

¡Cuidado!

Hay errores que los alumnos suelen cometer más a menudo que otros en esta asignatura. Para eso está este ícono. Para llamar la atención sobre eso y evitar que los cometan.

¡Más ejercitación!

Actividades dentro del teórico del capítulo, que apelan, en general, a los niveles más básicos de pensamiento: comprensión y aplicación.

Contenido digital

Mediante el código QR, para leer con un dispositivo móvil (teléfono celular, tabletas, etc.) y el enlace abreviado para escribirlo en la barra de navegación de la computadora de escritorio o portátil, los alumnos podrán acceder a distintas actividades que servirán de apoyo, y contenidos digitales que desarrollan de forma más amplia los contenidos del capítulo.

ABORDAJE PEDAGÓGICO

OBJETIVOS

Como instituciones adventistas o cristianas en general, nos proponemos:

Nuestra misión

Promover, a través de la educación adventista, el desarrollo integral del educando, para formar ciudadanos autónomos, comprometidos con el bienestar de la comunidad y de la Patria, y también con Dios.

La educación adventista prepara a las personas para ser útiles y felices, vidas plenas que promueven la amistad con Dios, el desarrollo integral de la persona, los valores fundamentados en la Biblia y el servicio altruista, de acuerdo con la misión adventista del séptimo día al mundo.

Nuestra visión

Ser una institución reconocida, como un ambiente seguro para brindar una educación integral fundamentada en valores que capacitarán a sus alumnos para un futuro de éxito.

La Matemática como ciencia (ya de forma más particular) es sin duda, la herramienta principal entre todas las ciencias, porque nos permite adquirir conocimientos precisos, exactos sobre la Creación de Dios. La Matemática es la herencia cultural más grande que se ha transmitido a lo largo de la historia de la humanidad.

Por todas partes la naturaleza presenta evidencias de relaciones matemáticas. Las ideas de número, forma, diseño y simetría se conforman con la realidad natural. Hay leyes naturales que gobiernan la existencia de las cosas y le otorgan armonía. Al estudiar estas leyes, ideas y procesos, las matemáticas pueden revelar al estudiante algunos atributos creativos, y en especial de su constancia.

El principal objetivo para alcanzar en el desarrollo del área de Matemática es articular en forma natural y concreta los contenidos matemáticos, la realidad natural y social y el desarrollo de la fe en un Dios que se presenta como Arquitecto Divino. Y como tal nos muestra su creación, resaltando características de perfección, simetría, equidad, los cuales son conceptos altamente matemáticos. Precisamente en esta articulación está depositada la verdadera riqueza y el valor formativo a nivel físico, social, mental y espiritual del área.

“Las matemáticas constituyen una revelación del pensamiento vivo de Dios, que lo muestra como un Dios de sistema, orden y precisión, en quien se puede confiar. Su lógica es segura. Al pensar en términos matemáticos, por lo tanto, nosotros repensamos los pensamientos de Dios”. (Byrne, A. Christian Approach to Education, Mott Media). “Guía curricular para la enseñanza secundaria adventista”. Instituto de educación cristiana.

Ya en cada tema, es importante también establecer los objetivos en términos de conceptos y competencias. Explicitar los conceptos centrales y secundarios. Deben jerarquizarse y formularse en lenguaje claro. Organizarlos en un mapa conceptual que servirá como hoja de ruta.

Para incorporar los conceptos en la clase, preguntarse: ¿Qué es lo verdaderamente importante de este tema? ¿Cuáles son las ideas que constituyen el corazón de este tema? Responder utilizando un lenguaje claro, sin terminología técnica.

Una vez establecidos los conceptos centrales, construir el mapa conceptual de la unidad y definir preguntas guía.

CONTENIDOS

Capítulo Temas

1 NÚMEROS REALES págs. 8–35

El conjunto de los números reales Características de los diferentes conjuntos numéricos Números irracionales Radicales

• Propiedades de los radicales

• Extracción e introducción de factores en un radical

• Simplificación de un radical

• Racionalización de un radical Operaciones con radicales

• Radicales homogéneos y semejantes

• Adición y sustracción

• Multiplicación

• División

• Potenciación y radicación Intervalos

2 POLINOMIOS págs. 36–59 Polinomios

• Valor numérico de un polinomio

• Grado de monomios y de polinomios

• Polinomios especiales Operaciones con polinomios

• Adición y sustracción

• Multiplicación

• División por monomio

• División por polinomio (métodos)

3 ÁLGEBRA págs. 60–91 Productos notables

• Diferentes casos Factorización

• Por factor común

• Por agrupación de términos

• Aplicación de productos notables Expresiones algebraicas racionales

• Simplificación

• MCD y mcm de expresiones algebraicas racionales

• Operaciones con expresiones algebraicas racionales Cocientes notables

• Cocientes del tipo A2 − B2 A ± B

• Cocientes del tipo A3 − B3 A ± B

4 SISTEMAS DE ECUACIONES E INECUACIONES págs. 92–119

Ecuación de la recta

• Ecuaciones equivalentes Sistemas de ecuaciones

• Método de resolución gráfica

• Clasificación de los sistemas de ecuaciones

• Método de reducción (o método de Gauss)

• Método de sustitución

• Método de igualación

• Resolución de problemas Inecuaciones de primer grado Sistemas de inecuaciones

La esencia de la matemática

El número áureo

Cuando desapruebo...

Las fórmulas en nuestra vida

Monedas en las escrituras

Capítulo Temas

5 FUNCIONES DE SEGUNDO GRADO

págs. 120–147

6 TEOREMA DE THALES

págs. 148–171

7 PITÁGORAS Y TRIGONOMETRÍA págs. 172–199

Introducción

Funciones de la forma f(x) = ax2

Funciones de la forma f(x) = ax2 + c

• Ecuaciones de la forma ax2 + c = 0

Funciones de la forma f(x) = ax2 + bx

• Ecuaciones de la forma ax2 + bx = 0

Funciones de la forma f(x) = ax2 + bx + c

• Ecuaciones de la forma ax2 + bx + c = 0

• Vértice de la función

Problemas con funciones cuadráticas

Razones y proporciones

Semejanza en figuras planas

Homotecia

Teorema de Thales

• Teorema de Thales en un triángulo

• Triángulos semejantes

• Aplicaciones del teorema de Thales

Teorema de Pitágoras

• Introducción

• Aplicaciones del teorema Trigonometría

• Razones trigonométricas en triángulos rectángulos

• Con calculadora

• Razones trigonométricas en triángulos rectángulos notables

• Sin calculadora

• Aplicaciones de la trigonometría

• Más datos

8 ESTADÍSTICA págs. 200–225

Introducción a la estadística Recolección, recuento y organización de datos Variables continuas Presentación de datos

• Diferentes tipos de gráficos Medidas estadísticas: análisis de datos

• Medidas de tendencia central

• Medidas de dispersión

La esencia de la matemática

María Gaetana Agnesi (1718–1799)

9 PROBABILIDAD págs. 226–247

Combinatoria

• Diagrama de árbol

• Combinaciones

• Variaciones

• Permutaciones

• Principio de multiplicación

• Actividades resueltas de combinatoria

Probabilidad

• Generalidades

• Ley de los grandes números Probabilidad y estadística

ANEXOS Glosario pág. 249

Bibliografía pág. 250

Autoevaluaciones págs. 251–260

Recortables págs. 261–272

Thales, el hombre de la sombra

Goniómetro casero

Los cereales integrales

Gedeón y la probabilidad

COMPETENCIAS

La competencia matemática la entendemos como la aptitud de un individuo para identificar y comprender el papel que desempeñan las matemáticas en el mundo, alcanzar razonamientos bien fundados y utilizar y participar en las matemáticas en función de las necesidades de su vida como ciudadano constructivo, comprometido y reflexivo (OCDE, 2004).

Las competencias matemáticas incluyen muchos aspectos tales como pensar matemáticamente, plantear y resolver problemas matemáticos, analizar y diseñar modelos, razonar y representar objetos y situaciones matemáticas, comunicar sobre matemáticas y comunicarse con las matemáticas. A continuación, se presenta un cuadro con las competencias básicas:

Competencias básicas Contribución de la asignatura de Matemáticas

• Todos los bloques de contenido.

Competencia en comunicación lingüística

Competencia matemática

Competencia en el conocimiento y la interacción con el mundo físico

Tratamiento de la información y competencia digital

• Tipos de lenguaje: natural, numérico, gráfico, geométrico y algebraico.

• Expresión oral y escrita en la formulación y expresión de las ideas.

• Procesos de comprensión en la Resolución de Problemas.

• Procesos de argumentación.

• Toda la disciplina.

• Priorización de estilo de enseñanza.

• Formas, relaciones y estructuras geométricas. Visión espacial. Transferencia de formas y representaciones entre el plano y el espacio.

• Modelización.

• La utilización de los lenguajes gráfico y estadístico para la comprensión en medios de comunicación.

• Interacción entre los distintos tipos de lenguaje: natural, numérico, gráfico, geométrico y algebraico como forma de ligar el tratamiento de la información.

• Matemáticas para describir fenómenos sociales.

Competencia social y ciudadana

• Análisis funcional y Estadística.

• Tratamientos de los errores.

• Procesos de Resolución de Problemas.

• La matemática es expresión universal de la cultura.

• Geometría.

Competencia cultural y artística

• Valor de la belleza en las estructuras.

• Valores de sensibilidad y la creatividad, el pensamiento divergente, la autonomía y el apasionamiento estético.

• Técnicas integrales.

Competencia para aprender a aprender

Autonomía e iniciativa personal

• Actitudes de perseverancia, autonomía, sistematización, reflexión crítica, eficacia.

• Resolución de problemas.

• Planificar estrategias, procesos de toma de decisiones.

• Actitudes de perseverancia, autonomía, sistematización, reflexión crítica.

MODELO PEDAGÓGICO

El libro se aborda desde un paradigma constructivista.

“En realidad, nadie puede enseñar matemática. Los profesores eficientes son aquellos que pueden estimular a los estudiantes a aprender matemática. Investigaciones educativas ofrecen contundente evidencia de que los estudiantes aprenden bien matemática solo cuando ellos construyen su propio entendimiento matemático”. MSEB and National Research Council, 1989.

Bajo esta premisa se elabora un texto que promueve fundamentalmente el trabajo del estudiante a partir de actividades que le permiten investigar, formular hipótesis y someterlas a prueba, comunicar sus ideas.

Las aplicaciones a la vida práctica y de creación, le dan un sentido de realidad y humanidad al alumno. Son quizás las actividades más atractivas para el alumnado, y lo que captará realmente la atención de ellos.

Se promueve, tanto el trabajo individual como en pequeños grupos, y motiva la interacción social en la clase, con la certeza de que surgirán valiosas ideas que contribuirán a la construcción del conocimiento.

Si bien la actividad de resolución de problemas es ineludible en la formación matemática de los alumnos, consideramos que debe ser complementada con otras que también generan aprendizajes y que permiten un real afianzamiento y profundización de los conceptos matemáticos. Por eso, como ya se explicó, se plantean diversos tipos de actividades y no solamente se trabaja con problemas.

Se sugiere trabajar con los números reales a lo largo del año, ya que todos los demás temas del curso propician ámbitos de aplicación de los números sin que deba concentrarse su trabajo en una unidad temática específica. Un conjunto adecuado de problemas posibilitaría la aparición de situaciones que requieran operar con números para arribar a la solución. Estos problemas podrían incluir situaciones que involucren el cálculo de probabilidades que estén al alcance de los alumnos.

Espero que sea de bendición para usted como docente y para los alumnos que lo utilicen. Cualquier sugerencia que se tenga, estamos dispuestos a tenerlas en cuenta, respetando obviamente la lectura de la guía docente y los tiempos editoriales.

La autora

Capítulo 01

Fundamentales

• Incorporar el concepto de número real para aplicarlo en la matemática en general.

• Acrecentar el nivel de abstracción de los alumnos.

NÚMEROS REALES

Objetivos

Específicos

• Recordar, conocer y reconocer el conjunto de los números reales.

• Diferenciar las características de los diferentes conjuntos numéricos y generalizar.

• Reconocer los números irracionales y sus características.

• Conocer los radicales y las operaciones a realizarse con ellos.

• Aplicar los números reales en los intervalos.

Contenidos

Generales

• El conjunto de los números reales

• Características de los diferentes conjuntos numéricos

• Números irracionales

• Radicales:

• Propiedades

• Extracción e introducción de factores

• Simplificación

• Racionalización

• Operaciones con radicales:

• Radicales homogéneos y semejantes

• Adición y sustracción

• Multiplicación y división

• Potenciación y radicación

• Intervalos

PRESENTACIÓN DEL CAPÍTULO

Integración fe-enseñanza (IFE)

El número áureo

• Investigar sobre el número de oro, un famoso número irracional, y descubrir en él la belleza matemática, relacionándola con la perfección de la creación de Dios.

Orientaciones metodológicas particulares y estrategias

El tema abordado en este capítulo es bastante abstracto y tiene dos particularidades: es imprescindible que el alumno logre un correcto manejo de estos números para seguir avanzando en conocimientos

matemáticos más profundos, a la vez que necesita de muchos conocimientos previos del alumno para comprenderlo totalmente. Generaliza cuestiones que el alumno ya conocía, pero de forma independiente, para globalizarlas y que ahora se tenga un panorama más amplio y global.

Se sugiere mucho trabajo práctico, trabajo en grupos, preguntas disparadoras, competencias, trabajos orales, etc.

ACTIVIDADES PREVIAS

Página 9

A pesar de que la ecuación presentada en la pizarra debería indicar dos soluciones, +2 y –2, se deja solamente la solución positiva, ya que este tema se desarrollará más adelante y en Pitágoras solamente se utilizan las soluciones positivas por ser estas distancias.

Se intenta que se cumpla con el objetivo de esta página: disparar el tema. Y no confundir al alumno con temas complejos que se desarrollarán luego.

Es importante aclarar que los pitagóricos no conocían los números enteros, pero se lo menciona en los diálogos de forma ilustrativa. Es interesante, quizás como actividad extra, que los estudiantes investiguen acerca de la historia de los pitagóricos.

Actividad 1: Sí hay. Todos los números irracionales.

etc.

Actividad 2: hay diversos enlaces en internet que lo demuestran, y libros de tercer nivel.

ACTIVIDADES COMPLEMENTARIAS

Página 10

Proponemos dos representaciones distintas de los números que aparecen en la tabla del libro del estudiante:

a. Es un número racional.

b. e repite el período 5332 de forma indefinida.

c. 21,5332533253325…

a. Es un número irracional.

b. Se repite el período 28 seguido de un cero, luego dos ceros, luego tres ceros, y así sucesivamente.

c. 6,28028002800028…

a. Es un número racional.

b. Se repite el período 244 de forma indefinida.

c. 45,244244244244…

a. Es un número irracional.

b. En la parte decimal está la sucesión de los números 451, 452, 453, 454, 455…

c. 73,451452453454…

a. Es un número racional.

b. Se repite el período 5810 de forma indefinida, al parecer.

c. 1,5810581058105…

a. Es un número irracional.

b. En la parte decimal aumenta la cantidad de 9 que se le colocan luego del 8.

c. 3,989989998999989…

2. Los números marcados como racionales en la tabla, lo son porque pueden escribirse como fracción o cociente de dos números enteros a y b (siendo b ≠ 0), o bien porque tienen infinitas cifras decimales periódicas.

Es ideal que los alumnos piensen esta respuesta de cada número racional de la tabla en particular, y argumenten su postura. Se puede trabajar de forma oral por grupos en la clase.

La fracción generatriz ha sido presentada y ejemplificada en Matemática 1, p. 97 (ACES).

3. Los números en rojo en las rectas anteriores, son la respuesta correcta. Nota: la √–2 no es una raíz real (perteneciente al conjunto de los números reales); por lo tanto, no se puede graficar en la recta real.

Página 12

1. No. Todos tienen infinita cantidad de elementos. Incluso N, aun cuando tiene primer elemento.

2. Sí, dado que, tomando dos elementos cualesquiera de cada conjunto, se puede establecer si uno es mayor, menor o igual que el otro.

3. Sí. R. Es el que completa la recta numérica.

4. N y Z, pues en cada uno de ellos se comprueba que entre dos elementos puede que no haya otro elemento o si los hay es una cantidad finita o determinada.

5. Son densos los conjuntos Q, I y R. Esto es así pues entre dos números del mismo conjunto existen infinitos números.

6. No. O entre dos números cualesquiera del conjunto siempre hay infinitos números, o puede que no haya ninguno. Son características incompatibles.

7.

Página 13

1. a. La parte decimal está formada por la sucesión de números naturales.

b. 0,1234567891011…

c. 1 2 y 2 9

d. No se puede. Es un número irracional con cifras que no tienen período.

e. Racional, racional, irracional.

A continuación, un texto que amplía el tema de los números irracionales, por la profesora Rossana Genta:

Números reales

Tras distinguir los números componentes de la recta real en tres categorías: (naturales, enteros y racionales), podría parecer que ha terminado la clasificación de los números, pero aún quedan “huecos” por rellenar en la recta de los números reales. Los números irracionales son los elementos de dicha recta que cubren los vacíos que dejan los números racionales.

Los números irracionales, simbolizados con , son los elementos de la recta real que no pueden expresarse mediante el cociente de dos enteros (de ahí su nombre) y se caracterizan por poseer infinitas cifras decimales no periódicas. De este modo, puede definirse al número irracional como un número decimal infinito no periódico.

En general, toda expresión en números decimales es solo una aproximación en números racionales al número irracional referido; por ejemplo, el número racional 1,4142135 es una aproximación de 7 cifras decimales del número irracional raíz cuadrada de 2, el cual posee infinitas cifras decimales no periódicas. Entonces, decimos con toda propiedad que el número raíz cuadrada de dos es aproximadamente igual a 1,4142135 en 7 decimales, o bien es igual a 1,4142135… donde los tres puntos hacen referencia a los infinitos decimales que hacen falta y que jamás terminaríamos de escribir.

Clasificación de los números irracionales

Números irracionales algebraicos. Son la solución de alguna ecuación algebraica. Todas las raíces no exactas de cualquier orden son irracionales algebraicos. Por ejemplo, el número áureo o de oro (φ = (1 + √5)/2 = 1,618...) es una de las raíces de la ecuación algebraica x2 – x –1 = 0, por lo que es un número irracional algebraico.

Otro ejemplo surge de la ecuación x2 = 2 que da origen al irracional algebraico x = √2. Más ejemplos de esta clase son los radicales no enteros: √3 ;5√7; 3√9; etc.

Números irracionales trascendentes. Surgen al escribir números decimales no periódicos al azar o con un patrón que no lleva periodo definido, respectivamente, como los dos siguientes:

0,193650278443757... (las cifras decimales no son periódicas y están elegidas al azar)

0,101001000100001... (las cifras decimales no periódicas tienen un patrón o regularidad)

Estos números no son la solución de ninguna ecuación algebraica.

Los números π (3,14159....) y e = 2,7182... son irracionales trascendentes, puesto que no pueden expresarse mediante radicales.

l d = √2

Lc/D = π

Los números irracionales (algebraicos o trascendentes) se relacionan también con las longitudes de algunas figuras geométricas:

El conjunto formado por todos los números racionales y los irracionales es el de los números reales (R), de modo que todos los números mencionados hasta ahora (naturales, enteros, racionales e irracionales) son reales. Estos números completan la recta numérica punto a punto, por lo que se llama recta real.

Entre los números reales están definidas las mismas operaciones que entre los racionales: suma, resta, multiplicación y división (salvo la división por cero). Pero siguen existiendo algunas radicaciones que no tienen solución en el conjunto de los números reales y darán origen al conjunto de los números Complejos (C). Ejemplos de dichas raíces son: √–2; √–3; 5√–7; 3√–9

Página 14

a. 4

b. –2

c. ∄

d. Número irracional mayor que 6, con los conocimientos que se tienen al alcance. El objetivo de este ejercicio es que vean la dificultad de hallar mentalmente algunas raíces cuadradas, que practiquen la no existencia de algunas raíces, y que comprendan cómo se calcula. O que lo recuerden de años anteriores.

Página 15

2. A cargo del alumno.

3. A cargo del alumno.

4. a. Irracional. Al ser π un factor, el número es irracional.

b. Racional. Se puede escribir como una fracción.

c. Racional. Es periódico, por lo cual también se puede representar con una fracción.

Página 16

Página 17

Página 18

2. A cargo de los alumnos. Actividad que apela a la creatividad y al trabajo participativo.

Página 19

Actividad previa:

1. Se multiplica la fracción por 1, el neutro de la multiplicación. √ 6 √ 6 = 1.

2. Porque al multiplicar denominadores se repite √ 6 , y

3. Potencia de una raíz.

4. En la primera expresión hay radical en el denominador, en la última no. Por definición, se quería simplificar el radical.

5. Se elige el que se quiere eliminar del denominador. En este caso, . Al ser una raíz cuadrada, bastaba con agregar el mismo término para cancelarla.

3. A cargo del alumno.

1.

a. Se escribió el 16 como una potencia.

b. La idea es cancelar el denominador, para lo cual se “completa” cada factor, con la idea de poder simplificarlo.

20

Actividad de creatividad a cargo del alumno. Página 21

Página 22 ?

1. Los radicales que tienen el mismo índice se llaman homogéneos.

Página 23

Respuesta a la pregunta lateral de Luly y Seba.

Página 24

Preguntas previas: Opción 1

Se aplica concepto de potenciación, propiedad distributiva de la multiplicación con respecto a la suma,

Opción 2

Se aplica cuadrado de un binomio: el cuadrado del primer término, más el doble producto del primero por segundo, más el cuadrado del segundo término del binomio. (9 + √ 3 )2 = 81 + 18√ 3 + 3 = 84 + 18√ 3

b. En el primer ejemplo:

• Raíz de una raíz.

• Descomposición de 144 en factores primos.

• Simplificación de un radical.

• Reducción.

En el segundo ejemplo:

• Introducción de factores en un radical.

• Raíz de una raíz y producto de potencias de igual base.

• Reducción.

Página 25 ?

a. ∪ significa “unión” y ∩ significa “intersección”.

b. Dado que pertenecen al conjunto de los números reales, y este es un conjunto denso, todos estos conjuntos son infinitos.

c. A cargo del estudiante. Página 26

ACTIVIDADES DE CIERRE LA ESENCIA DE LA MATEMÁTICA

Página 27

Es una actividad que apela a la creatividad, a la investigación, al trabajo participativo. Se sugiere a cargo del estudiante.

ACTIVIDADES

Página 28

1. A todo número natural le corresponde un punto de la recta, pero a cada punto de la recta no le corresponde un número natural porque lo números naturales, aunque son infinitos, no completan la recta numérica. Entre dos números naturales consecutivos no existe un número natural, pero existen infinitos números racionales e irracionales.

2. Lo mismo que se comentó para los números naturales sucede para los números enteros y racionales. Como los números reales completan la recta numérica entonces en este caso sí podemos afirmar que a cada punto de la recta le corresponde un número real.

3. Se cumple la propiedad de densidad cuando completa la recta numérica un conjunto de números.

4. Respuesta en video del Prof. Adrián Paenza: “¿Dónde hay más puntos?”

En la p. 62 del libro de Adrián Paenza, Matemática... ¿estás ahí?: Sobre números, personajes, problemas y curiosidades, de Editorial Siglo Veintiuno, aparece un buen análisis sobre el número e, relacionado con los depósitos en un banco. La explicación es clara y simple de entender. En la p. 68 de ese mismo libro, el autor comenta acerca de los distintos tipos de infinito, información qu puede ampliar la pregunta 3 sugerida.

5. Se sugiere ver el video “Igualdad de infinitos”

6 y 7. Son preguntas de investigación. Quedan a cargo del estudiante y del docente. Verificar fuentes utilizadas.

8. a. 3 ( 5 2 + 1 4 ) = 3 ( 5 4 + 1 4 )

3 ( 5 2 + 1 4 ) = 3 ( 6 4 ) 3 ( 5 2 + 1 4 ) = 12 4 6 4

Página 29

9. En c. se utilizaron el producto, la adición y la definición de división. En d. se utilizó definición de potencia, cociente de potencias de igual base y definición de potencia.

racionales.

Aclaración: Con las cifras que se ven de cada número, se llega a esas conclusiones al menos.

c. 90 √ 2

d. 8a b 2 y 4 √ 2ab 14.

c. 9 a 2 x 4 √ 3bx

Página 30

Aclaración: Un binomio conjugado de otro binomio es aquel que solo se diferencia por un signo de la operación. Ejemplos: (a + b) y (a – b), (–3m – n) y (–3m + n), (5x – y) y (–5x – y).Aclaración: Un binomio conjugado de otro binomio es aquel que solo se diferencia por un signo de la operación. Ejemplos: (a + b) y

x – y) y (–5x – y).

Página 31

23. El perímetro del triángulo es P = 35 √ 7 u

24. a. 48 3 √ 15 b. 3x 3 √ 2x c. 105

25. En este ejercicio sugerimos que se haga uso de la calculadora. Es bueno que sepan realizar cálculos mentales, a mano, pero también consideramos sumamente útil que sepan hacer uso de los instrumentos que tenemos como este. 1,327

26. a. 75 b. 4x – 4 c.

27. En este ejercicio también se sugiere el uso de calculadora. 0,93 28.

Página 32

32. a. 35 22 Se aplicó simplificación en multiplicación. Regla de signos de multiplicación.

b. 5 Separación en términos y reglas de signos de la división.

c. 1 Potencia de otra potencia, cociente de potencias de igual base.

d. 2–2 = ¼ Potencia de un cociente. Cociente de potencias de igual base.

Esta actividad apela al repaso de temas anteriores. Ver la globalidad de los conjuntos numéricos. El conjunto de los números reales en general.

33. Intervalo [–2;1)

Lenguaje Coloquial

Todos los números reales mayores o iguales que – 2 y menores que 1.

Todos los números reales mayores que – 3 y menores que – 1.

Todos los números reales mayores o iguales que – 1.

La mayor es

que 1 a mayor exponente mayor es la potencia obtenida)

b. A medida que el exponente negativo aumenta en valor absoluto (y la base es un número mayor que 0) menor es la potencia obtenida.

c. En este caso como la base es un número comprendido entre 0 y 1 es mayor

Concluimos que cuando la base es un número comprendido entre 0 y 1 la potencia obtenida será mayor cuanto mayor es el valor absoluto del exponente negativo.

36. A cargo del estudiante.

Página 33

37. Juego de recortables a cargo de grupos de estudiantes. Se sugiere dedicar un día a este juego.

38. Actividad de investigación a cargo del alumno.

Actividad de investigación práctica, a cargo del estudiante. Se sugiere hacer este ejercicio, ya que es una muy buena actividad para ver la importancia de los números reales en la vida práctica.

DESAFÍOS

34

Página 35

6. La diagonal del mantel se divide en 4 partes iguales de 1 m por tanto dicha diagonal es de 4 m (2 m del círculo central y 1 m para rozar el piso en cada punta). Con Pitágoras se averiguan los lados del cuadrado.

Aclaración: si bien Pitágoras no se ha dado en este libro aún, puede que haya alumnos que lo conozcan de años anteriores y está en la sección de desafíos.

7. x= 6 x=5/2 x=5

Las resoluciones de todas las autoevaluaciones estarán juntas, al final. En la sección correspondiente.

Capítulo 02 POLINOMIOS

Objetivos

Fundamentales

• Reincorporar, reafirmar y en algunos casos, apropiarse del concepto de polinomios para aplicarlo en la matemática en general.

• Acrecentar el nivel de abstracción de los alumnos.

Específicos

• Recordar, conocer y reconocer los polinomios, el valor numérico de un polinomio, el grado de monomios y de polinomios, y los polinomios especiales.

• Reconocer diferentes expresiones algebraicas.

• Identificar los polinomios dentro de las expresiones algebraicas en general.

• Realizar operaciones con polinomios como la adición, sustracción y multiplicación.

• Realizar divisiones con polinomios, apreciando las ventajas, e identificando el mejor método para el caso particular que toque resolver, de los diferentes métodos: clásico, Ruffini, Horner, y el Teorema del Resto.

• Resolver situaciones problemáticas aplicando polinomios.

Contenidos

Generales

• Polinomios:

• Valor numérico de un polinomio

• Grado de monomios y de polinomios

• Polinomios especiales

• Operaciones con polinomios:

• Adición y sustracción

• Multiplicación

• División por monomio

• División por polinomio (métodos)

PRESENTACIÓN DEL CAPÍTULO

IFE

Cuando desapruebo…

• Basándonos en una “fórmula matemática”, indagar en el hecho de que las personas exitosas son exitosas mayormente gracias a su esfuerzo, y no tanto a la inteligencia con la cual nacieron, lo que implica que cada persona puede ser tan exitosa como quiera.

Orientaciones metodológicas particulares y estrategias

El tema abordado en este capítulo también es bastante abstracto. No tiene apliación directa más allá de su sabia utilización en otros temas matemáticos que requieren de esta habilidad.

Se sugiere utilizar mucha ejercitación, mucho trabajo práctico, trabajo en grupos, preguntas disparadoras, competencias, trabajos orales, etc.

ACTIVIDADES PREVIAS

Página 37

1. 3.7.13.37 = 10101

Todos los números por los cuales se divide son números primos, descomposición factorial del número 10101. Y cualquier número de dos cifras multiplicado por este número, produce un número de 6 cifras con pares repetidos. Al dividir por todos sus factores primos, menos el original de dos cifras, se obtiene dicho original.

Los ejercicios 2 al 5 son para que el alumno los responda de forma intuitiva. El objetivo es un rastreo de ideas previas acerca del tema Polinomios.

ACTIVIDADES COMPLEMENTARIAS

Página 38

El teórico de Polinomios se da a forma de repaso, porque en la mayoría de los lugares a los cuales llega este libro el alumno ya los estudió. Ya estudió las bases. Y por eso se considera prudente que él mismo busque estos saberes de forma independiente, ayudándolo así a estudiar Matemáticas de forma autónoma. Que recurra a Internet y evalúe, a viejos apuntes, a libros de años anteriores, y así forme la base que le servirá para seguir construyendo los nuevos saberes a adquirir en este nuevo año.

1. Coeficiente de un monomio: es la constante de la expresión (las constantes son los números de la expresión. Esos valores no cambian, son constantes). El número real, distinto de 0, que multiplica a la parte literal.

Parte literal de un monomio: son las variables con sus respectivos exponentes.

Grado de un monomio: es la suma de los exponentes de las variables.

Monomios semejantes: dos monomios son semejantes cuando tienen la misma parte literal.

Monomios opuestos: dos monomios son opuestos cuando, siendo semejantes, sus coeficientes son números opuestos.

Los coeficientes y la parte literal de un polinomio llevan la misma definición anterior, solamente que en plural.

Grado de un polinomio: el término de mayor grado del polinomio determina el grado de este.

Monomio: polinomio de un término solamente.

Binomio: polinomio de dos términos.

Polinomios: en general, un polinomio de cualquier cantidad de términos.

Aclaración: monomio, en este libro, se utiliza como sinónimo de término.

También es importante destacar que en este capítulo, la palabra variable se utiliza como sinónimo de factor literal de polinomios.

2. Monomios semejantes Polinomio completo Monomios opuestos Monomio

Expresión algebraica Monomio Polinomio completo y ordenado Polinomio

Monomio Expresión algebraica Polinomio Expresión algebraica

Binomio Monomio Trinomio o Polinomio Trinomio o Polinomio

Página 39

A cargo del estudiante.

Página 40

A cargo del estudiante.

Página 41

1 y 2 a cargo del estudiante.

3. 2a + b – c = 2.2 + 4 – 3 = 5

4. A cargo del estudiante.

5. m = 3

6 al 8. A cargo del estudiante.

Página 43

1. 2a + 2b

2. Adición de polinomios, monomios semejantes.

3. a. 7x2 + 4y

b. 16ab2c +8a2bc2

4. a. x2 + 3xy – y2

b. –2a – 5b

5. π.r2

6. 113,0973355… cm2

7. Multiplicación

8. ¡Eres el profesor!

Ahora tú serás el profesor, y deberás corregir lo que ha realizado este alumno. Busca alguna estrategia para indicar lo correcto y lo incorrecto. Al finalizar, haz

Página 46

1. A cargo del estudiante.

2. a. No. Es igual a 6a – 4.

b. El resto es de grado 1 y es menor al grado 2 del divisor.

3. A cargo del estudiante. La idea es que explique con palabras una estrategia que le sirva para no cometer errores de signo. Si lo hace, avanzará muchísimo. La explicación oral, y reafirmada con lenguaje escrito, hace maravillas en la matemática. Deben organizar sus ideas, expresarlas claramente, y para eso deben pensar en lo que siempre hacen y corregirlo. Se corrigen a ellos mismos y avanzan.

Página 47

1. A cargo del estudiante.

Aclaración: en este tipo de divisiones también se puede utilizar Ruffini, siempre y cuando se igual el divisor a 0 y así se obtenga su raíz. En el esquema se ubican los coeficientes del polinomio dividendo, y la raíz del polinomio divisor. Cociente

= 6x2 – 10x + 14

= 0

4. A cargo del estudiante.

Página 49

C(x) = 7x

R(x)

C(x) = y – 3

R(x) = 22y2 – 22y + 10

Docentes: estos tipos de ejercicios se pueden resolver fácilmente en GeoGebra.

En el campo de “Entrada”, debajo de la palabra “Divisón”, se escribe el Polinomio dividendo y el Polinomio divisor. Proporciona rápidamente los resultados del Cociente y el Resto.

Resumen del método de Horner*

Con igual signo

Con signo cambiado

En los lugares en que se indica DIVIDENDO, divisor, COCIENTE y resto se colocan solo coeficientes.

En el del divisor la letra ‘d’ simboliza al primer coeficiente del divisor, las demás letras representan a los demás coeficientes, que se colocan con signo cambiado.

La línea punteada que separa el cociente del resto se traza de acuerdo al grado del divisor. Es decir, se cuenta, de derecha a izquierda, tantos lugares como lo indica el grado del divisor.

*Por la Prof. Rossana Genta.

Página 50

1. H(2) = –11; F(1/3) = –48/9

2. Sí, pues 3x – 1 y x – 1/3 son equivalentes.

3. k = 18

Por si quedaran dudas acerca de la definición de raíz de un polinomio, es la siguiente: la raíz de un polinomio P(x), en matemática, es un valor tal que P(α) = 0.

ACTIVIDADES

Página 52

1. Actividad de creatividad a cargo del alumno.

2. 6 – 3 – 2 – 1

3. creciente – a – 4

4. 5xy4z2 – x3y2z2 + 3x2yz + 1

5. 4

6. 5

7. En este libro se trabajan como sinónimos. No hay diferencia.

8. a. 5

b. –131

c. 1

d. 53/32

e. 25/9

9.

a. Sí, están todos los exponentes del 0 al 3.

b. No. Solamente hay exponente 2.

c. Sí, están todos los exponentes del 0 al 3.

d. No. El monomio 1 no tiene grado igual a los demás monomios.

e. El grado absoluto del polinomio es 6.

f. Es posible ordenarlo respecto a las variables a, o c.

g. Se puede ordenar de forma diferente cambiando de variable, u ordenando de forma creciente en vez de decreciente, o viceversa.

11. Actividad de creatividad a cargo del estudiante.

Página 53

12. a. Grado absoluto y relativo del polinomio M respecto de x, es 6.

b. Grado absoluto, 6. Grado relativo del polinomio N respecto a x, 0.

13.

a. O(x) = –3x9 + 5x5 + 9x3 + x

b. P(x, y, z) = 5x4z2 + 3x2yz + 5xy4

14. 48 311

15.

a. A cargo del estudiante.

b. A 6280 l; B 7070 l; 7220 l; 6280 l; 9820 l

c. A 0,94 m2; B 1,18 m2; C 1,37 m2; D 1,57 m2; E 2,36 m2

d. Es la fórmula anterior, multiplicada por 2500, que es el costo del m2. 2500.P(r, h).

Página 54

16. A cargo del estudiante.

17. El polinomio P(x, m) = 3x + 4m no es completo, pero sí es homogéneo.

18. Sugerencia extraída de internet:

19. A cargo del estudiante.

20. a. 8x

b. 71/40 x2y

c. 3z3 – 11y2

21. a. 2b5 + 13b4 – 6b3 + 10b2 + 16b – 21

b. 5b5 + 13b4 – 5b3 + 6b2 + 6b – 11

c. –b5 + b4 – 3b3 – 6b2 – 6b + 10

d. –4b5 + b4 – 4b3 – 2b2 + 4b

22.

a. 2x8 + 3x4 – 9

b. 8x8 – 12x4

c. 4x8 + 12x4

d. 4x8 – 12x4 + 9

23. a. 3x4n3p4

b. 3,5x + 1,5x/y – 1

c. –1,5x2 – 5,5x + 6,5

d. 5a4b4c4 – 3a2b2c2

Página 55

Página 56

31. a. C(x) = 2x3 + 3x2 – 2; R(x) = 0

b. C(x) = 2x2 – 4x + 5; R(x) = –12x + 14

32. a. 80 √ 2

b. –59

c. –4

33. A cargo del estudiante.

34. a= –1; b = –4

35. a = 32; b = c = d = e = 16; f = –16

36.

t x 1 7 1,5 9,86

3 29

5 83 7,5 195,5

10 358

37. A cargo del estudiante.

38. A cargo del estudiante.

Se sugiere un juego para realizar en el salón de clases. Necesitará contar con una computadora lista y proyectar en una pantalla lo que va sucediendo, y cada alumno participará con su teléfono móvil en mano. Cuando tenga lista la sala de espera para jugar, cada jugador deberá leer el código QR, que llevará a una web donde podrá ir respondiendo pregunta a pregunta, por tiempo, y al finalizar, usted mostrará a los resultados.

Ver instructivo paso a paso en el anexo de esta guía.

Página 57

Actividades 39 al 42 – actividades de nivel creativo, reflexivo, crítico, a cargo de los estudiantes.

43. a. A(x) + B(x) = 3x4 + 13x³ – 8x² + x – 10

b. A(x) – B(x) = 3x4 – 3x³ + 4x² + x – 4

c. 3A(x) – B(x) – C(x) = –4x5 + 7x³ +3 x – 23

d. –3B(x) + 4D(x) = – 4x7 – 24x5 – 24x³ + 42x² + 16x + 9

44. Sugerencia para resolver el ejercicio: utilizar el esquema de Ruffini o el Teorema del Resto. Si el resto es 0, el mencionado es un factor; de otra manera, no lo es.

a. No

b. Sí

c. No

d. Sí

DESAFÍOS Página 58

1. a + n + 5

2. a. Q(0) = 2 Q(1) = Q(–1) = 1,6 Q(2) = Q(–2) = 1 Q(3) = Q(–3) = 0,62 Q(4) = Q(–4) = 0,4

b.

c. A cargo del estudiante.

3. a. (12x + 26)cm

b. (8x2 +32x + 30)cm2

c. S/ 15,45

d. S/ 49,14

4. 6 ¡Cuidado! El polinomio P tiene las variables x e y, z no es una variable. Si no lo es, no cuenta para el grado absoluto. Por lo cual, el grado absoluto es 6.

5. a. (10x + 2)(106 + 6)

b. (10x + 2)(106 + 6)(10x + 1)

c. 0,25.0,10.0,10(10x + 2)(106 + 6)(10x + 1)

6. a + 4 + 2a = a – 1 + 3a

a = 5

8. 19

9. M(4) = 16

10. 2a + b – c = 17a

11. 32m2 + 16/3n

64a – 10b

En este juego, tener en cuenta que, en el primer caso, la expresión algebraica dada corresponde a la medida del lado de tres “cuadraditos”, y en el segundo caso, por ejemplo, la expresión (–2b + 7a) corresponde a la medida del lado de 4 cuadraditos, y así sucesivamente. Todos los cuadros blancos que abarca la expresión algebraica, es la medida del lado que proporciona.

12. C(b) = 7b2 – b – 1, R(b) = –4 Por lo tanto m = 7; n = – 1 y p = – 4

Entonces (m.n.p)1/3 =[7.(–1).(–4)]1/3 = 3√ 28

13. m = 4

14. El resto es 18.

15. Al hacer la división de los polinomios dados se obtiene un cociente que representa la cantidad de agua potable por habitante: C(t) = 2t4 – 2t³ + 3t² – 2t + 5/2, R(t) = ½ t – ½

Capítulo 03 ÁLGEBRA

Fundamentales

• Aprender, incorporar, reincorporar, aumentar y/o fortalecer los conocimientos de álgebra.

• Alcanzar un nivel más alto de abstracción en los estudiantes mediante la afirmación del álgebra como herramienta cotidiana.

• Entender el álgebra como una herramienta del día a día, aplicable a diferentes materias, y útil para razonar de forma objetiva.

Objetivos

Específicos

• Identificar los diferentes casos de productos notables. Aplicarlos en la resolución de problemas.

• Utilizar los conocimientos adquiridos de productos notables, en la factorización. Comprender la factorización en sus diferentes casos, y aplicarla en la matemática en general.

• Reconocer las expresiones algebraicas racionales y operar con ellas de diferentes maneras.

• Identificar los cocientes notables, como una herramienta más.

Contenidos

Generales

• Productos notables:

• Diferentes casos

• Factorización:

• Por factor común

• Por agrupación de términos

• Aplicación de productos notables

• Expresiones algebraicas racionales:

• Simplificación

• MCD y mcm

• Operaciones

• Cocientes notables:

• Cocientes de diferentes tipos

PRESENTACIÓN DEL CAPÍTULO

IFE

Las fórmulas en nuestra vida

• En un capítulo que trabaja con productos notables, con fórmulas matemáticas que facilitan tareas, se relaciona con las “fórmulas para la vida” que nos ha dado Dios mediante consejos (por ejemplo, en el libro de Proverbios) que facilitan nuestro pasaje por esta tierra.

Orientaciones metodológicas particulares y estrategias

El tema abordado en este capítulo, como así en los dos anteriores, continúa siendo bastante abstracto. Su aplicación práctica está en relación directa relación con cualquier tema matemático. Pero a esta altura, los alumnos deberían ir logrando una visión global de la relación entre los diferentes temas matemáticos tratados, y como un tema colabora con el siguiente, o sirve de escalón para el mejor manejo de otro.

Se sugiere utilizar mucha ejercitación, trabajo prácitco, trabajo en grupos, preguntas disparadoras, y mucho trabajo oral también para fortalecer la comprensión. No es lo mismo que el alumno desarrolle un producto notable en su cuaderno, a que explique oralmente qué pasos siguió para poder realizarlo. Se requiere pensar y repensar en las estrategias utilizadas, y ordenar el razonamiento seguido para poder expresarlo. Utilizando ese método, se fortalecen los conocimientos y diferentes competencias.

ACTIVIDADES PREVIAS

Página 61

1. (a – b)2 = a2 – 2ab + b2

2. Las tres expresiones comparten 2 rombos, 1 cuadrado y 3 círculos.

3. a. Está bien, pues aplicó la propiedad distributiva de la multiplicación con respecto a la adición, correctamente.

b. Los factores son binomios.

c. Multiplicación o producto de dos binomios.

4. A cargo del estudiante.

Se armó un cuestionario en PDF, que es muy fácil de contestar, utilizando conocimientos previos que pueda tener el alumno, para traer a su mente aquello que conoce, refrescarlo, ponerlo sobre la mesa, cuestionárselo, y entonces que siente las bases para los nuevos conocimientos que se construirán sobre aquellos.

Se sugiere que lo hagan los alumnos en grupos de 3.

Página 63

Definición: El conjugado de un binomio (a + b) es (a – b).

Página 64

1. Corresponde al cuadrado del trinomio (a + b + c).

2. No tiene ningún error.

Se sugiere que ambos videos sean vistos en clase, en pantalla gigante, por todos los alumnos, luego de haber avanzado en este tema. Son muy ilustrativos al respecto de los productos notables.

Se puede dialogar en clase luego, o repasar partes, para terminar de comprender bien lo que allí se dice y poder relacionarlo con las fórmulas que han estudiado.

También lo pueden ver los alumnos, cada uno de forma particular con su celular, y luego discutir las partes que se comprendieron o no, dirigidos por el docente.

Página 67

1.

a. 3a

b. 0,4x

c. a + 1

d. 3b o –3b

e. No tiene

f. 12xy3

2.

a. 3a(b – a)

b. 0,4x(x2 + 2x – 3)

c. (a + 1)(x + y – z)

d. –3b(2 – 3a + 4ab)

f. 12xy

3. A cargo del estudiante.

Página 69

1. z y5 2.5z (z + 5)2

2. (3 + a)2

– 5)2 = (–2m + 5)2

– b)2

+ 1)2

3. En todos los casos, hay dos opciones, por los cambios de signos. Solo se puso un ejemplo. Lo demás queda a cargo del estudiante.

4. a. Podría ser 2x4

b. Efectúo la raíz cuadrado del primer término del trinomio.

Aclaración: Por definición, √ x 2 = |x|

En general, se procede muy rápidamente a cancelar la raíz cuadrada con la potencia 2, pero no siempre es correcto, porque en ese caso estaríamos dejando por fuera algunas soluciones. La incógnita en ese caso, puede ser tanto positiva como negativa, ya que al elevarla a la potencia 2 se transforma en positiva sí o sí (por regla de los signos) y eso permite que la raíz exista siempre. Por lo tanto, no se cancela. La solución es el valor absoluto de la incógnita.

Ejemplo: √ x 2 = 3, entonces x = |3|, es decir, x = 3 o x = –3.

En la actividad anterior se toma solo el valor positivo por cuestiones de simplicidad, pero es algo que se debe tener presente al resolver ecuaciones. Y también en estos casos, en los que hay posibilidades de otras soluciones con cambios de signos, como se explica en el ítem 3.

Página 70

La expresión ordenada es: 64a⁴ + 64a2b2 + 25b⁴

Las raíces cuadradas del primer término y del último son: 8a2 y 5b2

El término central de un trinomio de un cuadrado perfecto debería ser: 80a2b2

Pero es:

64a2b2

La diferencia entre ambos es: 16a2b2

Suma y resta ese término, para mantener la igualdad:

Termina de factorizar (realiza el cálculo en tu cuaderno).

Página 71

(64a2b2 + 64a2b2 + 25b⁴ + 16a2b2) – 16a2b2

(8a2 + 5b2)2 – 16a2b2 = (8a2 + 5b2 + 16a2b2)(8a2 + 5b2 – 16a2b2)

a¹⁰– a4b3 = a4 (a² – b) (a4 + ba² + b2)

x2 – 4 = (x–2)(x+2)

27a³ – 8 = (3a – 2) (9a² + 6a + 4

3. A cargo del estudiante.

4. … las raíces cúbicas de ambos términos del binomio y se multiplica la diferencia de estas raíces por el trinomio obtenido de sumar el cuadrado de ambas raíces más el producto de dichas raíces.

Página 72

1. A cargo del estudiante.

x³ – 27 = (x – 3) (x² + 3x + 9) x³y6 + 27 = (xy2 + 3) (x²y4 – 3xy2+ 9) x³ – 12x² + 48x – 64 = (x –4)3 (x2y3 + z)( x2y3 – z)(x4y⁶ – x2y3z + z2) ( x4y⁶ + x2y3z + z2) –x³ + 6x² – 12x + 8 = –(x – 2)³ x³ – 15x² – 75x – 125 = –(x + 5)³

3. …las raíces cúbicas de cada término… raíz cúbica del primero al cuadrado menos el producto de las raíces cúbicas de cada término del binomio más la raíz cúbica del segundo al cuadrado.

Página 73

1. a. Ordenamos los términos:

6x2 – xy – 2y2 + x + 11y – 15

Se aplica aspa doble

6x2 – xy – 2y2 + x + 11y – 15 = (2x + y – 3)(3x – 2y + 5)

2.

a. (x – 9)(x + 4)

b. (3x – 5y)(2x + 7y + 4)

c. (x – 18)(x + 15)

d. (x + 2)(x + 5)

Aclaración: en el método del aspa simple siempre habrá variantes en los resultados, tomando en cuenta los signos. Tenerlo en cuenta. No hay una solución única prácticamente en ningún caso. Se sugiere hacer hincapié en este importante detalle para que los alumnos visualicen que no existen respuestas únicas ni caminos únicos.

Página 74

1.

2. Significa que, al reemplazar a la variable por un valor numérico, el resultado no sea cero.

3. A cargo del estudiante. El concepto de existencia se utiliza mucho en funciones. Por practicidad, también se utilizó aquí. Pero también se puede decir “las expresiones algebraicas racionales, existen o tienen sentido en matemática, o están definidas”. En este libro, todos esos términos se utilizan como sinónimos.

Página 75

a. x ≠ 6, x ≠ –6

b y c. (x 2)(x + 6) (x 6)(x + 6)

d. x 2 x 6

Página 77 ?

1. Diferencia de cuadrados y factor común.

2. Para poder simplificar.

3. Porque de esta forma se transforma en una multiplicación de la primera expresión de la inversa de la segunda expresión.

Página 78 ?

1. Opinión personal.

2. x2y2z3

Página 79 ?

1. Para hallar el mcm se descompone cada número en factores primos, y luego se multiplican los factores primos y no primos elevados al mayor exponente.

8 = 2.2.2 = 23

15 = 3.5

20 = 22.5

mcm (8, 15, 20) = 23.3.5 = 120

2. Se procede de la misma manera.

x2 = x.x

x3 = x.x.x

mcm (x2, x3) = x3

Aclaración: para buscar fracciones equivalentes se puede hacer la amplificación buscando qué número debe multiplicar numerador y denominador para obtener fracciones equivalentes:

4. Opinión personal.

Página 81

1. a 2 – b 2 a + b = (a + b) (a – b) a + b = a – b

2. x3 + 0x2y + 0xy2 + y3 x + y –x3 –x2y x2 – xy + y2

–x2y + 0xy2 +x2y + xy2 0 xy2 + y3

xy2 – y3

a. a + b2

c. 49x2 - 73√ 5 x + 3√ 5 2

e. x + y + 3z

g. 9x3 - √ 3

4. A cargo del estudiante.

Página 82

b. a2 + 3√ 2a + 3√ 4

d. b2 – 2b + 4

f. 25x4 – 10x2y3 + 4y6

h. –(x – 2)(x2 + 4)

1. Los coeficientes de los polinomios desarrollados coinciden con los números de la fila correspondiente al triángulo de Pascal.

2 y 3. A cargo del estudiante.

LA ESENCIA DE LA MATEMÁTICA

Página 83

Como actividad extra, se sugiere que busquen un compañero y elijan un capítulo de Proverbios. Juntos, léanlo y encuentren al menos una fórmula o consejo de Dios a través de Salomón, y plantéense todas las preguntas mencionadas anteriormente para la fórmula encontrada.

Otra pregunta a las planteadas en la actividad podría ser: ¿qué nos dice de Dios esta fórmula?

Una de las cosas más importantes quizás, es conocer a Dios al leer la Biblia (Juan 17:3). En la medida que nuestra imagen de Dios se haga más clara en nosotros, los cambios o decisiones de lo que haremos serán la transformación natural de mirar a Dios (2da. Corintios 3:18). Por esta razón nos parece necesario buscar la imagen amorosa y tierna de Dios en cada texto. Lo demás, viene por añadidura y a su tiempo.

3.

ACTIVIDADES Página 84

1. xy = 24

2. 60n

a. 16 – 16y + 4y2

c. 9x6 – 6x3y6 + y12

e. 25 – 10m + m2

4. xy + xz + yz = 92

5. 9x2 – 42x + 49

a.

+ (a + b)x + ab

Página 85

9. A cargo del estudiante.

a. –12x2 + 25x – 27

b. 2x3

c. x3 + 3x2 + 15x – 1

11. A cargo del estudiante.

12. (x + y + z)2 = x2 + y2 + z2 + 2(xy + yz + xz)

+ yz + xz) = 3 por datos

(x + y + z)2 = x2 + y2 + z2 + 2 3

b. x4 – 14x2 + 49

d. x2 + 4y2 + 25 + 4xy + 10x + 20y

f. 25x2 – 40xy + 16y2

2 + y2 + z2 = (x + y + z)2 – 6 por trasposición de términos

14.

a. (a + 2b)

c. (1 + m2)

Página 86

15.

cociente está definido para cualquier valor de “b” que no sea 0.

b. (4a – 5z)

d. (1/7 – 3a)

a. –9m(m – 1)(3m + 2)

c. (a + 1)(2x + 3y)

e. (2x – 3y)(x + y – 6z)

g. (x – y)(m3 + m4 + 2m2)

i. 5(3a + 2b – 4x – 5y)

k. (x + 3)(x2 + y2)

16. Errores:

El factor común de los coeficientes no es 2.

17.

b. 10mx(3 – 4mx)

d. (x – 2)(m + 4)

f. (y + 2m)(x – m)

h. (a – 2)(2a – 3b)

j. (7a + 3x)(3a – 5b)

l. 2(2x – 3)(3x + 1)

La división que hace es incorrecta. Olvida el c en el segundo término. Lo demás está bien.

a. (m2 – 1/10)(m2 + 1/10)

b. (5x/6y – 1)(5x/6y + 1)

18. x + 2 (y – 3) o (3 – y) 4m + 1

Página 87

19. A C B

20. En todos se aplicó trinomio de segundo grado o trinomio de la forma x2 + mx + n

(3a – b/3)3 (2xy + 1)3

a. (x + 2)(x2 – 2x + 4)

c. (3x – 2y)(9x2 + 6xy + 4y2)

a. (x – m + a)(x + m – a)

c. [(m + n) – ]2 = (m +n – 1)2

e. (y + 6)2

g. (a – 7)(a + 4)

i. (a + 1)(9a – 1)

24. a. Diferencia de cuadrados.

b. c. Trinomio de cuadrado perfecto.

d. e. i. j. Trinomio de segundo grado (x2 + mx + n)

f. Suma de cubos

g. Diferencia de cuadrados.

h. Diferencia de cubos.

b. (x + ½)(x2 – x/2 + ¼)

d. (4m – n)(16m2 + 4mn + n2)

b. (a + b + 3)[(a + b)2 – 3(a + b) + 9]

d. (x – y – 1)(x + y + 5)

f. –(x – 1)(x2 + 7x + 19)

h. (x – 9)(x – 7)

j. (x – 1)(7x + 6)

a. 3b – 2

b. 18xyz2

c. 11abc3 d. x – 3

e. x – 7

a. 12x2y2

c. (5x + 9y)2(x – 2y)2

e. 30a2b3

f. B

b. (x – 9)(x + 9)

d. 7(x – 3)x4

f. x(5x – 2)(5x + 2)(x + 3) o 9x(25x – 4)(x + 3)

29. Si x a x b x p x q es un cociente notable, se cumple la siguiente proposición: a p = b q = n, siendo n el número de términos.

Por lo cual, en nuestro ejemplo: 2 21 3 = 35 5 = 7, de lo cual se deduce la expresión dada sí es un cociente notable.

Página 89

32. Si el resultado de este cociente notable tiene tres términos significa que es una diferencia de cubos.

Por lo cual a + 1 = 4.3 y por tanto a = 11.

Además b + 5 = 5.3 y se deduce que b = 10.

De modo que a + b = 21.

33. Esto se debe a que unos hacen referencia a los resultados de ciertas multiplicaciones, o sea, a sus productos, y otros a las multiplicaciones propiamente dichas.

La factorización se aplica a los polinomios que se obtuvieron como producto y por tanto son binomios, trinomios, diferencias de monomios, etc.

34. A cargo del estudiante.

35. Respuesta personal.

DESAFÍOS

Página 90

1. x + 3

2. a. 3 x

b. 2 x 2 y 2

c. 2b a + b

3.

a. 5my( 5m 9 + 3y 7 )

c. (a + 1)(a + y + 2)

e. (a + m)(m – z)

b. 13x2y3(13x4y + 2z)

d. (8m – 1)(m – a)

f. (5a + b)(3m – x – 2y)

4. a. Tiene razón ya que el resultado es un cuatrinomio completo de grado 3, por lo tanto, contiene los grados del 0 al 3

b. También pueden escribirse como un trinomio de grado 2 completo y ordenado.

5. a. (5 – t2)3 = 125 + 75x2 + 15x4 + x⁶

b. (2x2 – 3)3 = 8x⁶ – 36x4 + 54x2 – 27

6. “El anterior del cubo de un número” podemos expresarlo como x3 – 1.

“El cubo del anterior de un número” se expresa (x – 1)3 y dichas expresiones no son iguales ya que la primera es un binomio y la segunda la desarrollarla es un cuatrinomio.

Página 91

7. a. –5a5

b. 50a11 w 0 3

c. 10 x 11 3

8.

Al aplicar propiedad distributiva de la multiplicación respecto de la adición obtenemos:

b(b + 1) =

Al sacar factor común en el numerador y común denominador b(b+1) obtenemos:

Al cancelar los opuestos del segundo factor del numerador queda:

9. Como el área de un triángulo se calcula con la expresión Á = b h b h

Entonces la base se calculará con la expresión b = 2Á h

Si reemplazamos en esta última expresión por los binomios dados, obtenemos: b = 2 x + yz

10. a. 2y(y + 2x)

b. x = 7 cm y = 40 cm 2.40(40 + 2.7) = 80(40 + 14) = 4320 cm2

c. A cargo del estudiante.

SISTEMAS DE ECUACIONES E INECUACIONES

Fundamentales

• Partiendo de los conocimientos que los estudiantes ya poseen de la ecuación de la recta (lenguaje coloquial, gráfico, analítico, etc.), generalizar, y construir el conocimiento de los sistemas de dos ecuaciones y dos incógnitas.

• Por otra parte, ver la utilidad de los sistemas de ecuaciones en la vida cotidiana, en resolución de problemas, y resolverlos.

• Relacionar los conocimientos adquiridos de álgebra y polinomios con este tema, viendo cómo unos temas matemáticos más abstractos, facilitan el trabajo en otros temas matemáticos más reales.

Generales

• Ecuación de la recta:

• Ecuaciones equivalentes

• Sistemas de ecuaciones:

• Método de resolución gráfica

• Clasificación

• Método de reducción

• Método de sustitución

• Método de igualación

• Resolución de problemas

Inecuaciones de primer grado

Sistemas de inecuaciones

Objetivos

Específicos

• Conocer y reconocer la ecuación de la recta y sus diferentes presentaciones.

• Comprender el concepto de ecuaciones equivalentes y aplicarlo en diferentes situaciones.

• Comprender el concepto de sistemas de ecuaciones en general, y sistemas de ecuaciones lineales de dos ecuaciones y dos incógnitas en particular. Conocer diferentes métodos de resolución de sistemas de ecuaciones, y saber emplearlos, identificando qué método conviene en qué caso.

• Resolver inecuaciones de primer grado. Aprehender el concepto de inecuación.

• Resolver sistemas de inecuaciones y aplicarlo en resolución de problemas.

Contenidos

IFE

Monedas en las escrituras

• Se analizan dos versículos diferentes del mismo tema, de dos evangelios escritos por distintos autores, llegando a una especie de sistema de dos ecuaciones con dos incógnitas, y relacionar el tema dado en el capítulo con las distintas versiones de la Biblia, diferentes interpretaciones de los autores, y análisis de versículos bíblicos.

PRESENTACIÓN DEL CAPÍTULO

Orientaciones metodológicas particulares y estrategias

Sistemas de ecuaciones e inecuaciones es un tema de fácil comprensión y aplicación en la vida real. Se sugiere comenzar con algún problema práctico justamente, para que el estudiante pueda percibir su aplicabilidad; luego avanzar a lo abstracto como la ecuación de la recta (ecuación analítica, representación gráfica), el concepto de sistemas de ecuaciones y sus diferentes métodos de resolución; y una vez practicado eso, pasar a la resolución de problemas.

Pero es a modo de sugerencia simplemente, quizás para un docente que dé el tema por primera vez, o para un grupo a quien le dificulte el tema. Por lo demás, se puede cambiar el orden cada año y para cada grupo, adaptándolo de la mejor manera.

Sí se sugiere, encarecidamente, utilizar algún programa informático, al menos dos veces a lo largo del tema, para “jugar” con las representaciones gráficas, las interpretaciones, etc. Se puede usar por ejemplo, el programa GeoGebra en clase, mostrando los resultados obtenidos en una pantalla para todos los alumnos, y la aplicación de celular GeoGebra con los alumnos para que ellos puedan construir sus propios sistemas y su resolución de diferentes problemas.

ACTIVIDADES PREVIAS Página 93

1. a = –6

2. A cargo del estudiante.

b.

4. El perro pesa 17 kg, el gato 7 kg, el ratón 3 kg. La última pesa es de 27 kg.

3. a.

ACTIVIDADES COMPLEMENTARIAS

Página 94

Página 95

Página 96 y 97

b. x y 0 2

1 3,333… 3 6

c. f h g

2. a. Pregunta personal.

b. Los cortes con los ejes se calculan de la siguiente manera:

Corte con Ox, y = 0 y se sustituye. 3x – 2.0 = 8, x = 8 3

Corte con Oy, x = 0 y se sustituye. 3.0 – 2y = 8, y = –4

4. a. 2.(–2) + 4 3 = 8 y –2 + 1 3 3 = –1

Verifica ambas ecuaciones, por lo tanto ese par es solución.

b. 4x + 8y = 16 y 3x + y = –3

c. 4.(–2) + 8.3 = 16 y 3.(––2) + 3 = –3

–8 + 24 = 16 y –6 + 3 = –3

d. {4x + 8y = 16 3x + y = 3

7x + 9y = 13

e. 7.(–2) + 9.3 = 13

–14 + 27 = 13 Sí.

c e d b a

Página 98

El sistema de ecuaciones b es el que traduce el enunciado.

La cantidad de habitaciones individuales (x) más la cantidad de habitaciones dobles (y) es 65. Es decir, la primera ecuación.

Cada habitación individual tiene una cama (x), y cada habitación doble tiene dos camas (2y), y cantidad de camas es de 105. Enunciado que se explica en la segunda ecuación.

3.

5.

Página 99

2. Gráfico anterior.

3. Al reemplazar el punto F en el ecuación de la recta se obtiene –3,5 + 7,5 = 4 ≠ 5 por lo que se deduce que el punto no pertenece a la recta. Puede ser que otro alumno haya decidido graficar y ubicar el punto y también puede comprobarse lo mismo.

1.

4.

Página 100

S. = {(8; –2)}

Infinitas soluciones.

1. Las ecuaciones de las rectas son equivalentes.

2. Si están expresadas de la forma y = mx + n, tienen igual pendiente. Si están expresadas de la forma ax + by = c, parecen ser equivalentes, excepto por el c.

3. Opinión personal.

Página 102

1.

Se multiplica la E1 por 2.

Se multiplica la E2 por 3.

Se suman miembro a miembro las ecuaciones equivalentes.

2.

5x + 3y = 14 x 2y = 21

10x + 6y = 28 E3

3x – 6y = 63 E4

10x + 6y = 28

3x – 6y = 63 _______ ___

13x + 0 = 91

Se despeja: x = 91 13 = 7

Lo demás, a cargo del estudiante.

a. { 2x 4y = 8 4x + 4y = 8 Multiplicó por 4 la segunda ecuación.

b. { 2x 4y = 8 6x = 16

Realiza una combinación lineal de dos ecuaciones. Las dos del sistema anterior.

c. { 2x 4y = 8 x = 8 3 Calcula el valor “x”.

3. y = 2 3

No hay una sola forma de hacerlo. Quizás la más sencilla sea sustituir el valor de x hallado en una de las dos ecuaciones originales. Pero también se puede comenzar todo nuevamente y reducir, calculando el valor de “y”. U otras opciones.

4. S. {(–3; 4)} S. = {(–7; 3)}

5. Las ecuaciones lineales son aquellas en las que las incógnitas están elevadas a la potencia 1, y no contienen productos de dichas incógnitas.

Ecuaciones lineales: 5x + 3y = 14; 2x = 5; 1 3 x – y = 0

Ecuaciones no lineales: y = x2 + 3; 5 = xy; 2x = 6 7y

Página 103 Excelente todo.

Página 104

2. El valor de las incógnitas que resuelve el sistema es siempre el mismo, cualquier sea el método de resolución elegido.

Método de igualación: conviene aplicarlo si el sistema planteado tiene la misma incógnita despejada en ambas ecuaciones.

Método de sustitución: conviene aplicarlo si el sistema planteado tiene una incógnita despejada que permita sustituirla en la otra ecuación.

Método de reducción: conviene aplicarlo si el sistema planteado tiene una incógnita con coeficientes opuestos en cada ecuación.

Método gráfico: no suele dar resultados muy exactos, salvo raras excepciones, o que se haga con algún software.

Página 105

1. Datos: primer pedido – 10 kg de A, más 8 kg de B, cuestan U$S 2400. Segundo pedido – 6 kg de A, más 15 kg de B, cuestan U$S 2970.

2. Ecuaciones: 10A + 8B = 2400

6A + 15B = 2970

3. S. = {(120; 150)}

4. 7.120 + 18.150 = 3540 El tercer pedido costará 3540 dólares.

1.

S. {(1; 1)} S. {(7; 2)}

3.

Página 106

1. Tuvo 6 aciertos y 4 fallas en el examen.

2. Se sugiere que en esta actividad se les de libertad de resolución a los alumnos, y luego se haga una puesta en común. Se sugiere debatir si es que hay diferentes caminos, y mostrar la resolución matemática mediante sistemas de ecuaciones como una posibilidad más.

a. x = 7

y = 5 + x y = 5 + 7 = 12

x = 1 + 2z 7 = 1 + 2z z = 3

x + y + z = … 7 + 12 + 3 =22

3. El número es 47.

4. Alejandro cobra $1100 y Thiago $1250 de jornal diario.

5. Aprobaron 20 varones.

6. El número es 263.

Página 107 ?

1.

2.

a. Sí pertenece, como se puede apreciar en el primer gráfico. Porque al representarlo gráficamente está en la zona coloreada, y porque al sustituir en la inecuación, esta se verifica.

b. Respuesta en el gráfico.

c. Sí. El punto (–1; 1), por ejemplo.

del gráfico que la verificarían.

2.

Página 110

1. a. A, E, F, G y H son los puntos

b. B y D.

b.

c.

3. Sí existen. Muchos. Cualquiera que tenga rectas paralelas y direcciones opuestas.

Por ejemplo: { y < 2x + 8 y > 2x 5

4. x > 1 y < 2

5. El c.

LA ESENCIA DE LA MATEMÁTICA Página 111

1. x es el costo en monedas, de cada gorrión.

5x = 2

2x = 1

No se forma un sistema de ecuaciones, ya que no hay dos incógnitas, sino solo una.

2. En la primera ecuación x = 0,4. Cada gorrión cuesta 0,40 moneditas según Lucas. En la segunda ecuación x = 0,5. Cada gorrión cuesta 0,50 moneditas según Mateo.

3. La esencia de la idea de ambos versículos es la misma: si Dios se preocupa por gorriones de poco valor monetario, mucho más se preocupa por nosotros seres humanos que costaron la vida de su Hijo para salvarlos. Por lo tanto, se puede afirmar que ambos textos expresan la misma idea, aunque sean diferentes números.

4. Opinión personal.

5. Se puede destacar: Jesús se ocupa de mostrar un Dios personal que se ocupa de los mínimos detalles de toda su Creación. “La grandeza y majestad de Dios no le impiden que se interese en las preocupaciones de los más débiles de sus criaturas”. EGW. “Jesús asegura la simpatía de Dios por ellos en sus necesidades y debilidades. No se exhala un suspiro, no se siente un dolor, ni ningún agravio atormenta el alma sin que también se estremezca de palpitaciones el corazón del Padre”. EGW, en el DTG 323.

ACTIVIDADES

Página 112

1. Se podría dar otro punto como el de corte con alguno de los ejes, entre otras opciones. No hay una sola posibilidad, sino infinitas.

2. y = 4 3 x + 2

3. Puedo analizar la pendiente y el punto de corte con “y”. Puedo buscar las coordenadas de un punto y verificar a qué ecuación corresponde.

b.

c. Todas las rectas anteriores cortan al eje Oy en el punto (0; 1).

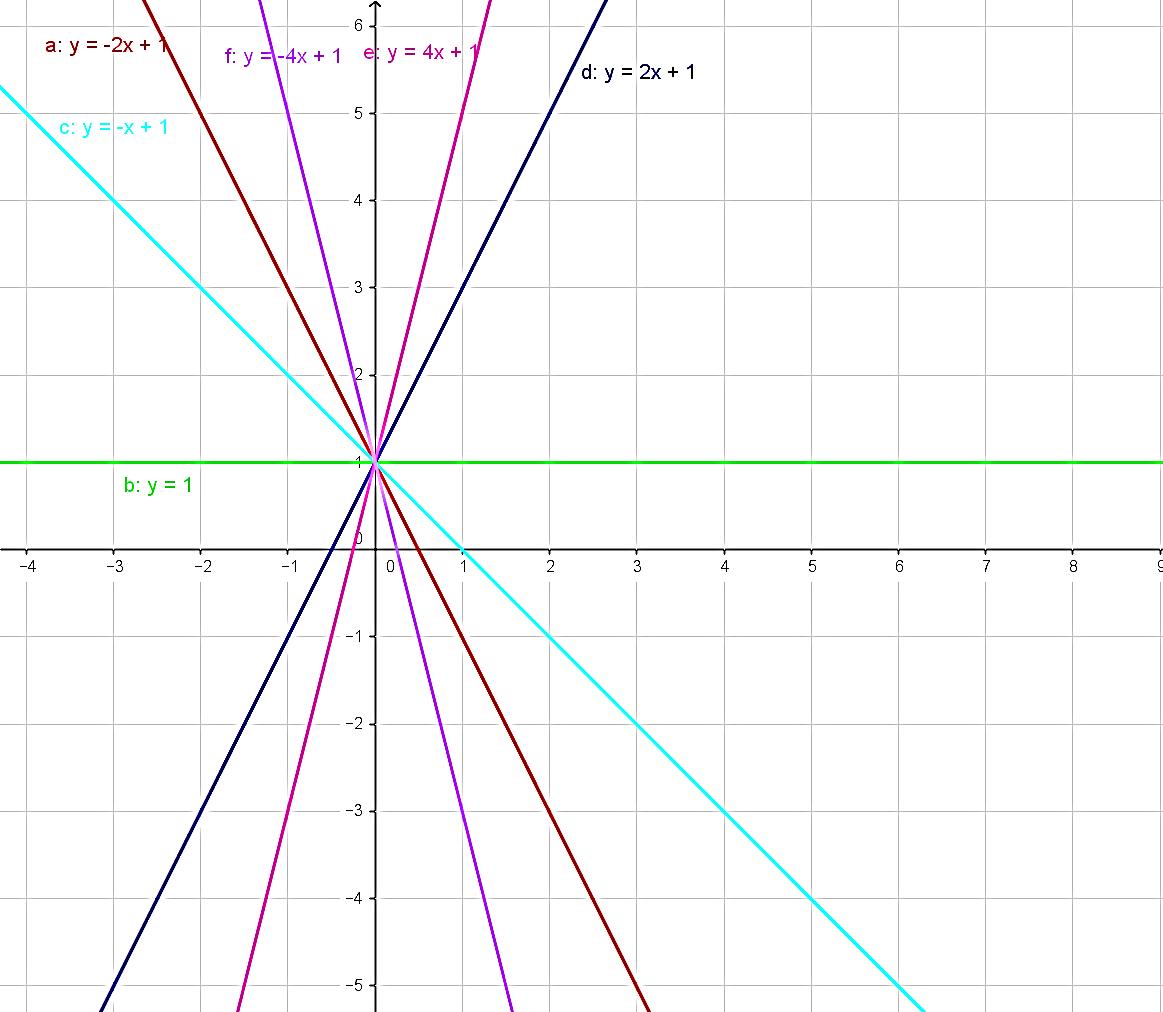
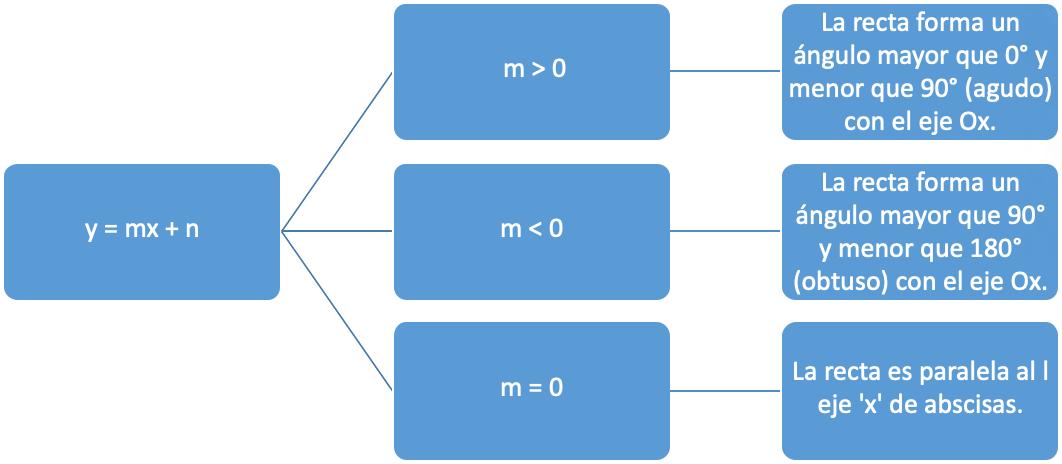
Lo identifico sustituyendo las x y las y. Si se verifica el sistema, si se llega a una igualdad, es la solución.

a. {2x + 6y = 10 x + 3y = 7 Sistema incompatible

b. {5 x + 9y = 18 6 x + 8y = 2 Sistema compatible determinado

c. { x + y = 4 3x + 3y = 12 Sistema compatible indeterminado

a. A simple vista se que ve que ambas ecuaciones, casi que son equivalentes. Los términos en x y en y dan, pero no así el último término. Por lo cual, es un SI.

b. No son ecuaciones equivalentes, por lo cual es un SCD.

c. Son ecuaciones equivalentes, a simple vista. Por lo cual es un SCI.

Existen otros caminos. Por ejemplo, despejar “y” en cada caso y analizar el coeficiente en “x”. Si es el mismo, puede ser SI o SCI. Ahí se observa el término independiente. Si es el mismo, es SCI, y si no, SI. Cualquier otro caso es SCD.

S. {(28; 36)}

11.

a. x – 22,5 = 2,5 – x

b. x = 12,5

12.

S. {(6; –5)}

c. Reemplazando en alguna de las ecuaciones del sistema: y = –10.

a. 2.(83 + y) + y = 178

b. y = (178 – 166):3 y = 4

c. Reemplazando “y” en la segunda ecuación: x = 87

Página 114

14. 15.

;

,

I II III IV

Resuelvo por... Reducción, multiplicando la primera ecuación por ‘–3’.

Solución

16.

Sustitución Reducción. Sustitución luego de multiplicar la primera ecuación por ‘–1’

Clasificación Compatible determinado Compatible determinado Compatible determinado Compatible determinado

Usaría el método gráfico en el caso que ambas ecuaciones estén expresadas con la forma y = mx + n que me facilite hacer la tabla (aunque también podría resolverse por igualación).

a. V

b. V

c. V

d. V

e. F. Ninguno de los enunciados es correcto. Perfectamente se puede resolver por reducción, por ejemplo.

17. Recibió 39 faldas y 88 pantalones.

18. La abuela tiene 60 años y Sofía tiene 10 años.

19. Cada silla cuesta $250 y cada taburete $90.

b.

c.

La zona más oscura es la que representa los puntos del plano que cumplen las condiciones pedidas. Han sido marcados algunos puntos como ejemplo.

d.

e.

21. a.

b.

c.

b.

Página 116

25. Resolver un sistema de ecuaciones por el método gráfico consiste en expresar las ecuaciones de la forma y = mx + n para luego representarlas en un sistema de ejes cartesianos. La solución se encuentra en el punto de intersección de las rectas graficadas.

26. Cuerpo verde: –3,5; cuerpo beige: 0,5; cuerpo rojo: 4,5; cuerpo amarillo: 0,125; cuerpo azul: 98,875.

Cuerpo verde: 2/3; cuerpo amarillo: 4/3; cuerpo rojo: 1/3.

Dado que la primera fila suma 42, y son dos verdes y dos rojos, y la última columna también son dos verdes y dos rojos, los signos de pregunta suman 42. No hace falta sacar más cálculos que esos.

Cuerpo verde: 7; cuerpo rojo: 10; cuerpo azul: 4; cuerpo amarillo 6.

El siguiente es un interactivo muy interesante para que los alumnos trabajen. En muy poquito tiempo, jugando con deslizadores, llegarán a conclusiones que en papel, les costaría mucho más tiempo y esfuerzo llegar. Se sugiere que dedique al menos una clase completa a este juego.

Página 117

27. La pregunta está contestada en el ícono Cuidado, de la página 108.

29.

a. “c” es cualquier valor diferente de ¾. “d”, cualquier valor.

b. Las ecuaciones deben ser equivalentes.

c. c = ¾, y d ≠ 4.

a. Una ecuación es una igualdad entre dos expresiones algebraicas, en cambio un sistema de ecuaciones es un conjunto finito de ecuaciones.

b. Una inecuación es una desigualdad entre dos expresiones algebraicas, en cambio un sistema de inecuaciones es un conjunto finito de inecuaciones.

c. Un sistema de ecuaciones es un conjunto finito de ecuaciones, y uno de inecuaciones, de inecuaciones.

S. {(0,25; –3)}

S. {(2; 5)}

Se deja este “opción múltiple” para que los alumnos refresquen y reafirmen los conceptos adquiridos del tema. Es bastante dinámico y se puede realizar en grupos de 3 alumnos para mayor actividad.

DESAFÍOS Página 118

1. Gato = G

Ratón = R

Perro = P

G + R = 10k

P + R = 20k

P + G = 24k

P + G + R = x

P + G + P + R = 20 + 24 = 44

44 – (G + R) = P + P = 2P = 44 – 10 = 34

P = 17

17 + G = 24, entonces G = 7

17 + R = 20, entonces R = 3

P + G + R = 27 k

2. Existen al menos dos opciones. Que el alumno deduzca la fórmula directamente, o que el alumno realice un gráfico, y luego deduzca la ecuación. Con este problema se puede organizar un debate a resolver en el pizarrón.

y = 3x + b

Si contiene al punto P (1; –3), entonces:

–3 = 3 1 + b

–3 = 3 + b

b = –6

y = 3x – 6

S. {(2; –3)}

S. {(9; 8)}

S. {(7; –11/4)}

3.

Página 119

7. x: cantidad de entradas numeradas y: cantidad de entradas no numeradas

80x + 25y ≥ 15 000

8. a. 1 asarion equivale a 4 cuadrantes.

b. En el tiempo de Jesús, los jornaleros agrícolas solían recibir un denario por un día de trabajo de doce horas (Mateo 20:2).

c. La jornada era de 12 horas diarias.

d. En el siglo I de la era cristiana, dos gorriones costaban un asarion, el salario de cuarenta y cinco minutos (Mateo 10:29).

e. Cuadrante = 1/64 denarios (Mateo 5:26)

Dracma = 1 denario (Mateo 17:24)

Estatero = Mateo 17:27

Denario = 16 asarion (Mateo 20:10)

Asarion = 1/16 denario (Mateo 10:29)

Datos extraídos de https://wol.jw.org/es/wol/d/r4/lp–s/1200003106

9. a. x: peso de una persona, y: pero de otra persona

x + y ≤ 200

b. x: cantidad de pantalones de jean producidos y: cantidad de pantalones deportivos producidos

x + y ≤ 100

c. 200x + 180t ≤ 10 000

Fundamentales

• Apropiarse del concepto de función, nuevamente, y expandirlo.

• Aprender a estudiar, analizar, representar, las funciones de segundo grado, de diversas maneras.

FUNCIONES DE SEGUNDO GRADO

Objetivos

Específicos

• Reconocer el concepto de función y expandirlo.

• Retomar y ampliar el estudio analítico y la representación gráfica de las funciones.

• Partiendo de la función cuadrática más sencilla, construir los diferentes peldaños, con el fin de llegar a analizar de forma analítica y gráfica, cualquier función de segundo grado.

• Resolver ecuaciones de segundo grado.

• Resolver problemas de la vida práctica, utilizando funciones y ecuaciones de segundo grado.

• Diferenciar una ecuación de una función de segundo grado.

Contenidos Generales

• Introducción

• Funciones de la forma f(x) = ax2

• Funciones de la forma f(x) = ax2 + bx

• Ecuaciones de la forma ax2 + bx = 0

• Funciones de la forma f(x) = ax2 + bx + c

• Ecuaciones de la forma ax2 + bx + c = 0

• Vértice de la función

• Problemas con funciones cuadráticas

PRESENTACIÓN DEL CAPÍTULO

IFE

María Gaetana Agnesi

• Se trabaja con la biografía de una mujer matemática muy prominente, que descubre un tipo particular de función. En este análisis se relacionan: el concepto de función, con expresiones algebraicas racionales (dado en un capítulo anterior), con la gran bondad de esta mujer y su inmensa dedicación a la caridad.

Orientaciones metodológicas particulares y estrategias

Este es un tema fundamental. Base para el estudio analítico de las funciones en años posteriores.

Es básico que en este año les quede bien claro a los alumnos el concepto de función, y la aplicación en los diferentes temas matemáticos.

Se presenta un orden para dar los temas, que puede variar grupo a grupo y año a año. Es sumamente adaptable.

Se sugiere que en este capítulo también se trabaje con programas informáticos, y aplicaciones para móviles. Eso acrecentará la comprensión de los alumnos acerca del tema.

Se sugiere también mucho trabajo en grupo y de “ida y vuelta”. Es decir, que partan de la expresión analítica de la función, y lleguen a la representación gráfica. Que partan de la representación gráfica, y lleguen a la expresión analítica. Que trabajen con una función de segundo grado desarrollada, y con una factorizada. Que analicen diferentes estrategias, comparen con sus compañeros, y de esta forma crezcan y se enriquezcan.

CONÉCTATE Página 121

1. h(2) = –2.4 + 6.2 = –8 + 12 = 4 Esto nos lleva a la conclusión de que el arquero saltó hasta unos 4 m de altura para atajar la pelota en el aire. La realidad es que el récord máximo de salto de un ser humano ha sido de 2,45 m (alcanzado por Javier Sotomayor en 1993), por lo cual los egipcios tenían razón.

2. La gráfica correcta ese la c. La altura de la pelota es 0 en el momento inicial y final, por lo cual se descarta la gráfica e.

3. La relación tiempo–altura es una función porque a cada instante de tiempo le corresponde un valor de altura de la pelota que es único. La definición de función puede buscarse en Matemática 2 página 155

4. En el segundo 0 y en el 3. Puede verse en el gráfico c. En la fórmula, al buscar valores de “y” para los cuales les corresponda una altura 0.

ACTUALIZA TU INFORMACIÓN

Página 122

ACTIVIDADES (PP. 140–143)

Para este capítulo se realiza una aclaración importante: en las funciones en las que no se expresa ninguna aclaración acerca del dominio, su dominio, es el conjunto de los números reales.

Otra aclaración importante, antes del desarrollo del capítulo, es que en lo gráficos de funciones de este capítulo se marca, con x, en el eje de las abscisas, y con f(x) en el eje de las ordenadas. Quizás alguno se pregunte por qué f(x) en el eje vertical, y no la y. Y la explicación es la siguiente: estamos trabajando con funciones, no con geometría analítica. En el eje vertical se señalan las imágenes de x.

Sí, es posible. Calculando las imágenes de otros valores del dominio de la función. Por ejemplo, la imagen de 0,1, etc.

Página

3.

4. Ambas tienen una raíz. La raíz es x = 3.

5. La primera premisa está correcta y es la primera imagen. La segunda premisa se corresponde con la segunda imagen, pero no tiene 4 raíces sino solamente 3.

6.

c. Tiene la forma de una parábola.

Página 125

c. Tiene la forma gráfica de una parábola.

9. La diferencia gráfica es que j(x) tiene las ramas de la parábola hacia arriba y k(x) las tiene hacia abajo. La diferencia analítica es que en j(x) el coeficiente es +1 en el término de segundo grado y en k(x) es –1.

b.

A continuación, se presenta un tutorial, desarrollado por la profesora Rossana Genta, de cómo trabajar este tema con solo realizar el gráfico de f(x) y analizar las variaciones del coeficiente del término cuadrático usando deslizadores que al cambiar el valor del coeficiente generan la gráfica correspondiente sin necesidad de graficar las ocho funciones pedidas.

También a continuación, al final de las actividades del capítulo 5, hay un anexo titulado “Expresión polinómica” donde se analizan variaciones de “a” y “c” con GeoGebra. En la primera parte del tutorial analiza las variaciones de “a” (aplicable a este ejercicio) y en la segunda parte analiza las variaciones de “c” aplicables a la propuesta de la página 128.

c. La raíz y el corte con el eje vertical coincide en todas las funciones y el punto (0; 0).

Página 126

en los intervalos de crecimiento y decrecimiento, los paréntesis nunca son rectos porque en el vértice de la parábola (ya sea el punto máximo o mínimo), la función no crece ni decrece, es decir que, ese punto no se incluye en ninguno de los intervalos.

Página 127

1. a es g, b es a y c es h. Por la apertura. Cuanto mayor es el valor del coeficiente cuadrático “a”, más cerrados son los brazos de la parábola. Más se acercan al eje de las ordenadas.

2. Conjunto imagen Intervalo de crecimiento Intervalo de decrecimiento Vértice Concavidad Raíz Corte con oy

[0; +∞) (0; +∞) (–∞; 0) (0

(–∞; 0] (–∞; 0) (0; +∞) (0; 0)

x =0 y = 0

x = 0 y = 0

Página 128

Al término del análisis de este capítulo, hay un anexo titulado “Expresión polinómica” donde se analiza la variación de “a” y de “c”, por la profesora Rossana Genta.

Página 129

La ecuación cuadrática de la forma ax2 + c = 0, se resuelve por trasposición de términos. Vale aclarar que no es el único método de resolución. Se puede factorizar y buscar las raíces, se puede utilizar la fórmula resolvente (de Bhaskara), pero es uno de los métodos. Se puede trabajar con los alumnos las diferentes maneras de resolver, y que ellos elijan la que más cómoda les resulte.

Página 130

b.

3. a. Las gráficas de las funciones de la forma f(x) = a(x – h)2, son idénticas a las del tipo f(x) = ax2 pero con su vértice en el punto (h; 0). Es como que “se mueven” h unidades de veces, hacia la izquierda o la derecha, dependiendo del signo. Si es +, hacia la izquierda, y si es – hacia la derecha.

b. El eje de simetría en estas funciones es x = –h

4. Las gráficas de las funciones de la forma f(x) = a(x – h)2 + k, tienen su vértice en el punto (h, k). Es como que “se mueven” h unidades de veces, igual que en el ítem anterior, y k unidades de veces, dependiendo del signo. Si es + hacia arriba, y si es – hacia abajo.

5. m(0) = (0 – 2)2 – 1 = 4 – 1 = 3 n(0) = (0 + 3)2 – 4 = 9 – 4 = 5 p(0) = –(0 + 3)2 – 4 = –

2. Algunos tips que pueden enriquecer la investigación de los alumnos:

a. Que un grupo busque la biografía de Hankel y prepare un PPT (Power Point) o video para presentar. Luego pueden subirlo a Youtube.

b. Otro grupo puede buscar distintas páginas web y anotar las diferencias entre una página y otra (algunas cosas que una página comenta y otra no).

c. Presentar la biografía como si fuera parte de un noticiero o de un programa de vidas destacadas.

d. Presentar la biografía como si fueran comentarios en Twitter, Instagram, Tik Tok o cualquier otra red social.

e. Armar un pequeño documental de la vida de Hankel al que se le pueden añadir encuestas de cuán conocido es entre los alumnos de otros cursos.

f. Armar una historia de Instagram llamativa o un meme, etc.

Página 132 ?

1. Siempre será así ya que una de las raíces será (0; 0) que es el corte con el eje de las ordenadas también.

2. Sí. En este tipo de funciones las raíces siempre son la solución de f(x) = x(ax + b), por lo cual las raíces serán x = 0; y ax + b = 0, o sea x = –b/a.

Página 133

1. Porque su dominio está acotado.

2. El recorrido “comienza” en el valor y del vértice, hasta el infinito.

3. La concavidad es positiva, y el recorrido se va al infinito positivo.

4. En el intervalo de crecimiento o de decrecimiento, uno de sus valores es la abscisa del vértice.

5. Porque su dominio está acotado.

6. Porque el recorrido incluye el vértice.

1.

Página 134

Aclaración: no está la demostración de la fórmula resolvente, o fórmula resolutiva de segundo grado, o fórmula de Bhaskara, por razones de espacio y porque en la mayoría de los países a los cuales llega este libro no se trabaja. Pero, siempre se puede pedir que busquen en Internet o en otro libro la demostración, y trabajarla en la clase, de forma oral. Es bueno que los alumnos vean demostraciones. Muy positivo para su razonamiento lógico.

3. Se pueden repetir los tips de trabajo de la propuesta de la investigación de Hankel.

Página 136

1. ¡Eres el profesor!

Ahora tú serás el profesor, y deberás corregir lo que ha realizado este alumno. Busca alguna estrategia para indicar lo correcto y lo incorrecto. Al finalizar, haz una evaluación del trabajo. ¡Éxito!

H Completa la tabla, de acuerdo con lo estudiado:

2. Realiza el EA y RG correctos de cada una de las funciones anteriores.

Página 138

1. a. Es de segundo grado.

b. Es el punto más alto al que llega la pelota.

c. Las raíces son 1 y 7. Por lo cual el eje de simetría es x = 1 + 7 2 = 4. Por otro lado f(4) = 9. La máxima altura que alcanza la pelota es de 9 unidades.

d. Significarían que la pelota tocó el piso, ya sea cuando parte, o cuando acaba su recorrido.

e.

b. Al cabo de 20 minutos se alcanza una población máxima de 900 bacterias.

c. Luego de los 20 minutos la población de bacterias comienza a disminuir.

d. A los 10 minutos y a los 30 minutos se alcanza la misma población de 800 bacterias.

e. A los 50 minutos se extingue la población de bacterias.

LA ESENCIA DE LA MATEMÁTICA

Página 139

3. No son funciones de segundo grado. Las de segundo grado deben tener un término de segundo grado, entre otras cuestiones, y este no lo tiene.

4. Opinión personal.

Se deja la siguiente sugerencia, escrita por la profesora Rossana Genta:

“Dejar todo para dedicarse a obras de caridad”.

Para este tema tan delicado sugiero leer el cap. 8 “Martirizarse cuidando a los demás” del libro “Adictos a la infelicidad. Cómo quebrar el ciclo de la insatisfacción” de Carol Cannon, editorial ACES.

Cuidar de manera insalubre implica:

• Procurar resultar indispensable para los demás (para reforzar su autoestima y valor personal).

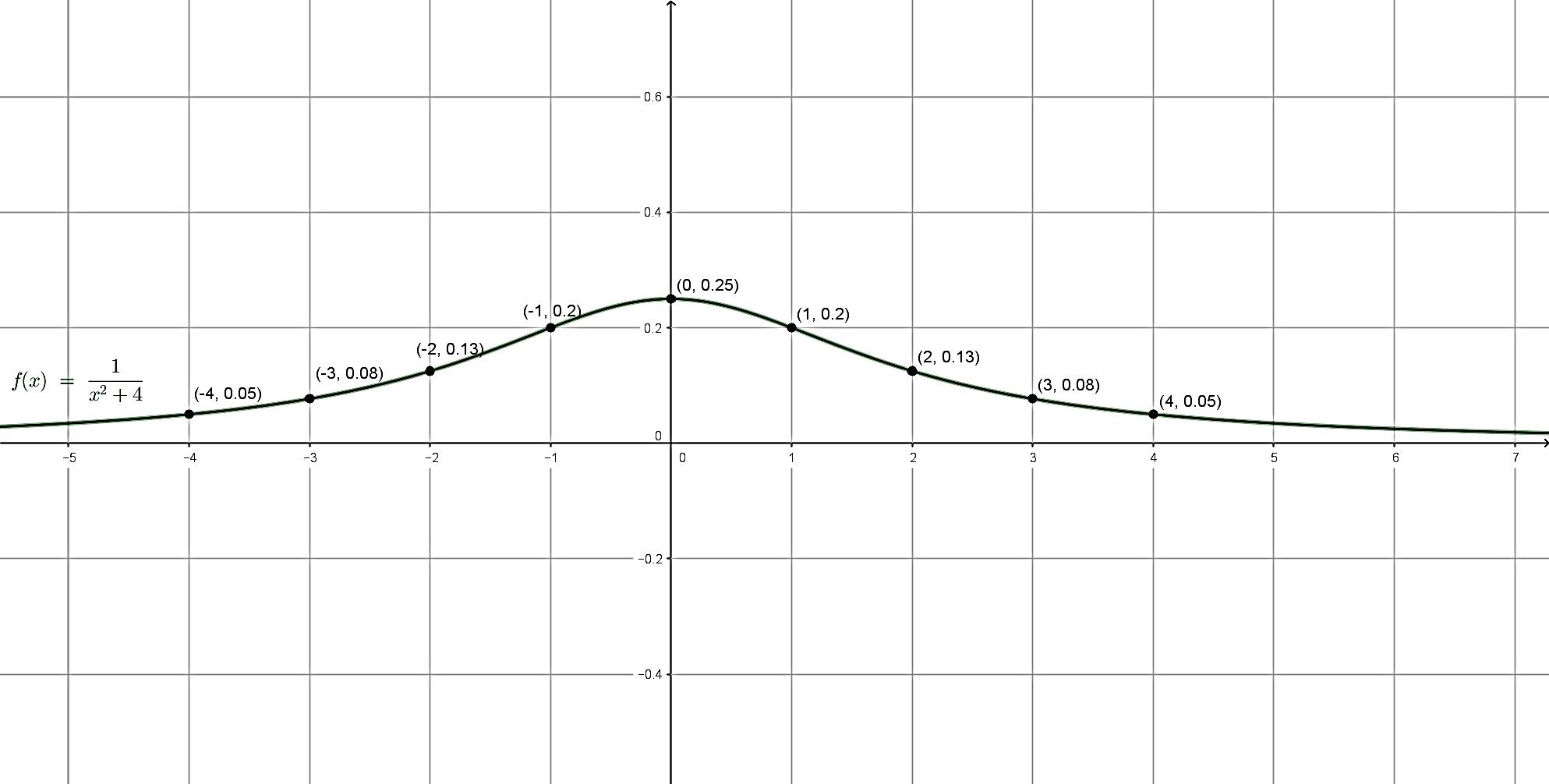
• Anticipar las necesidades de otras personas y satisfacerlas.

• Hacer cosas a otros que deberían hacerse a sí mismos.

• Dar sin el debido respeto, es decir, sin consultar las preferencias del destinatario.

• Dar sin pedir permiso, imponiendo consejos y ausencia no solicitados.

• Dar para recibir aprecio o gratitud y quejarse o sentirse mal si no es valorada su generosidad.

• Dar para conseguir el control por ejemplo “después de todo lo que hice por ti, tengo el derecho de decirte lo que debes hacer”.

• Dar generosamente y luego quejarse, que es una sutil forma de jactancia.

• No poder separarse emocionalmente de cualquiera que esté sufriendo.

• No soportar ver a otras personas experimentando.

El cuidado saludable implica:

• Mostrar una preocupación genuina y respetuosa, sin invadir los límites del otro, dando solo cuando nos pide.

• Ayudar sin esperar recompensa.

• Ayudar sin poner en peligro la propia vida o la de la familia.

• Dejar a los otros responsabilizarse de sí mismo y sus problemas.

• Ayudar sin precipitarse a la hora de ayudar a los demás.

• Ayudar sin sentirse forzado a solucionar la vida de nadie. (“Dios ama al dador alegre”. 2 Corintios 9:7)

• Arreglar cosas, pero no a las personas.

• Dejar a los otros libres con sus problemas, permitiéndoles madurar y que aprendan cómo lidiar con sus propias dificultades y así disfrutar la dignidad que eso produce.

• Decir “No” a amigos y familiares a fin de que se hagan cargo de sus propias necesidades.

Dios pidió al joven rico que done todos sus bienes a los pobres. ¿Le pidió eso a Abraham o a otros ricos de la Biblia? ¿Por qué? Dios nos pide actuar de diferentes formas (acorde a cada uno) para ser compasivos y ayudar al otro.

¿Qué es la compasión? ¿Es asistencialismo? ¿Cuál es más fácil de aplicar y por qué?

Asistencialismo: actitud orientada a resolver problemas sociales a partir de la asistencia externa en lugar de generar soluciones estructurales.

Compasión: es la capacidad de ver la belleza y el potencial en otros o en nosotros mismos en lugar de verlos como objetos llenos de deficiencias. Podría ser sinónimo de comprensión, pero nunca significa lástima.

El significado de la RAE no capta la esencia más profunda de la palabra compasión.

Hay muchas ong destinadas a cortar la dependencia que genera el asistencialismo promoviendo la autonomía y dignidad de las personas.

ACTIVIDADES

Página 140

Dominio: Reales

Dominio: Reales

Conjunto imagen: Reales Conjunto imagen: [0; +∞)

2. D(f) = R

Recorrido: [–5; +∞)

f(3) = 1

f(–2) = –2,333…

Preimágenes de 5= 3,87 y –3,87

Preimágenes de 1: 3 y –3

Dominio: Enteros

Conjunto imagen: Enteros

Página 141

4. a. 0 es la abscisa de los cortes con el eje vertical.

b. 0 es la ordenada de los cortes con el eje horizontal.

c. No todas. Por ejemplo, la función k de la página anterior no corta con el eje de las abscisas.

5. El recorrido siempre es los números reales, salvo que su dominio esté acotado.

6. a. La primera es de primer grado, y la segunda es de segundo grado.

b. Explicado en el ítem anterior.

c. La diferencia de resolución es que la cuadrática se resuelve con una radicación de índice, y tiene dos soluciones.

7. g: R R/g(x) = 7x2

8. f(x) = a(x+4)(x–b)

f(4) = a(4+4)(4–b)=–48

f(–3) = a(–3+4)(–3–b)=–20

Utilizando las dos últimas ecuaciones, con un sistema de ecuaciones se llega a:

a = 2 y b = 7

Por lo tanto, f(x) = 2(x + 4)(x – 7) = (2x + 8)(x – 7)

f(x) = 2x2 – 6x – 56

9. f(x) = x2 – 4

a. Cualquiera del tipo f(x) = ax2 – 4

b. El valor de “a” o las raíces.

Página 142

10. a. f, g, h, j: tienen dos raíces.

b. Propiedad hankeliana directa, en f y g.

Si se factorizan las funciones h, j y k, se puede aplicar en ellas la propiedad Hankeliana. Si no se factorizan, se puede aplicar Baskhara.

En h y l se puede realizar pasaje de térmios.

c. y e.

d. Si el coeficiente cuadrático es positivo el vértice es el mínimo. Y si es negativo, es el máximo.

Página 143

11.

a. La variable independiente es el tiempo que transcurre sin depender de la altura del objeto.

b. La variable dependiente es la altura del objeto.

c. La altura inicial desde la cual se lanza.

d. Investigación a cargo del alumno. Se sugiere consultar y relacionar el tema con los profesores de física.

e. Aclaración: el tiempo, para que tenga sentido la fórmula, está medido en segundos.

14. Una función cuadrática puede tener 0, 1 o 2 raíces. No más. Por lo cual es imposible graficar una función cuadrática de 3 raíces. Pero sí puede obtener una que no lo corte nunca al eje x. Una de 0 raíces.

Ecuación de primer grado.

16. Tiene razón Luly, ya que en la ecuación de f(x) el coeficiente del término cuadrático es +1, y sus brazos están hacia arriba.

No tiene solución en el conjunto de los números reales.

En este caso Luly necesita recordar que si el valor de “c” es negativo (c < 0) la parábola se desplaza hacia abajo.

Dom = (–3;–1)

Página 145

18.

19. a. Es función, ya que a cada valor del dominio existe y es único el valor que le corresponde como imagen.

b. Decrece en (–∞; 0) y e (4; +∞). Crece en (0; 4)

c. Máximo en x = 4 Mínimo en x = 0

d. No tiene raíces reales, ya que no corta al eje de las abscisas.

e. En el punto (0; 1).

f. No es una parábola ya que no tiene eje de simetría vertical, que pase por el vértice de la gráfica. Tampoco posee un único vértice que sea el máximo o mínimo de la gráfica.

20. f(x) = –1(x – 6)2 + 16

a. Tiene otra raíz en x = 10.

b. Se calcula haciendo f(2) = 0. 0 = a.(2 – 6)2 + 16 al despejar se obtiene a = –1.

DESAFÍOS

Página 146

1.

2. Propiedad Hankeliana en ambos casos. Factorización en el primer caso. Pasaje de términos en el segundo caso.

3. Función lineal o función de primer grado Función cuadrática o función de segundo grado Función valor absoluto

Función de tercer grado o parábola cúbica Función de cuarto grado Función racional

4. No es la única. Cualquier función de la forma f(x) = a(x – 4)(x + 3). Es decir que, a puede tomar cualquier valor diferente de cero, y tendremos infinitas funciones que cumplan con esta condición.

5. a es el coeficiente principal de la función. x1 y x2 son las dos raíces de la función. Cuando la expresión no está de esta manera, se escribe de forma desarrollada.

Resumen de las formas de expresar una parábola:

Página 147

Polinómica

Canónica

Factorizada

f(x) = ax2 +bx + c

f(x) = a (x–xv)2 + yv

f(x) = a (x–h)2 + k

f(x) = a (x–x1)(x–x2)

6. La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.

De esto se deduce que la imagen del lateral sí es una parábola.

7. Es una parábola, como lugar geométrico. Pero no es una función, ya que para algunos elementos del dominio hay dos imágenes. Y aunque todas las funciones de segundo grado se representan como parábolas, no todas las parábolas son funciones de segundo grado.

9. a) Se abre hacia arriba ya que el término cuadrático será 4x2 con coeficiente a = +4.

b) Se abre hacia arriba ya que el término cuadrático será 18x2 con coeficiente a = + 18

c) Se abre hacia abajo ya que el término cuadrático será

10. a. La roja tiene una raíz, y la azul y la verde tienen dos raíces.

b. Todas tienen corte con el eje vertical. La roja, en (0; 0); la azul y la verde en (0; 3).

c. Lo único que puede ser considerado un error es que una función tiene como nombre f(x), o cualquier otra letra, pero siempre es una letra que está en “función” de una variable. En este caso, f en función de x. Y en esta imagen están representadas, no como funciones, sino como expresiones de geometría analítica. Por lo demás, está correcta.

MATERIAL EXTRA*

Función cuadrática f(x) = ax2 + c

Análisis de ‘a’ y de ‘c’

(Para trabajar con Geogebra)

Objetivo: Analizar cómo cambia la parábola a medida que varía el valor de ‘a’ (coeficiente del término cuadrático).

1. Para representar una función cuadrática, introducir los siguientes elementos en el campo de Entrada (ver debajo de la zona gráfica o a la izquierda en GeoGebra online clásico):

a = 1 (Intro o Enter);

c = 0 (Enter)

f(x) = ax2 + c (Enter).

Para ingresar x2 puedes hacerlo con ‘Alt+2’..

2. Para modificar el valor del coeficiente cuadrático (que inicialmente es a = 1), posicionarse en ‘a’ de la ventana izquierda de la pantalla, clic derecho Objeto visible. Aparecerá en la zona gráfica un dial deslizador (si no apareció al comienzo). Al mover el deslizador cambia el valor de ‘a’ (si no se mueve usar el modo Elige y mueve del 1er. ícono de la barra).

3. Podrás registrar tus conclusiones en el plano cartesiano o zona gráfica. Para ello acciona el modo Texto de la barra (simbolizado con el ícono ABC). Luego al hacer clic en la zona gráfica aparecerá un cuadro en el cual podrás editar las respuestas o conclusiones a las preguntas.

4. Analizamos el coeficiente del término cuadrático ‘a’

a) ¿Qué sucede con las ramas cuando ‘a’ toma valores positivos? (Para eso mueve el deslizador)

b) ¿Qué sucede con la parábola cuando ‘a’ toma valores negativos?

c) Posicionarse en f(x), clic derecho Rastro o Mostrar Rastro y modificar el deslizador ‘a’ nuevamente para observar y comprobar las conclusiones obtenidas. Sólo observa no registres.

*Realizado por la Prof. Rossana Genta.

d) Para actualizar la pantalla y eliminar el Rastro dejado, pulsar el botón de Deshace que se encuentra en la parte superior derecha de la pantalla.

e) Si te posicionas en el dial deslizador y haces clic derecho Animación podrás observar la variación de ‘a’ automáticamente que se puede pausar con el símbolo que aparece en la parte inferior izquierda de la zona gráfica. Pruébalo.

f) Con clic derecho nuevamente en el deslizador Propiedades/Deslizador puedes colocarlo en forma vertical u horizontal, ampliar el intervalo de variación cambiando el máximo, el mínimo y la variación de deslizamiento, también puedes cambiar la velocidad de animación, la forma en que quieres que se repita su movimiento.

5. Analizamos el término independiente ‘c’ y sus variaciones. Para ello trabajas con el deslizador y registras tus conclusiones.

6. Imprimir y entregar para ser evaluado.

Expresión factorizada (Para trabajar con Geogebra)

Introducir los siguientes comandos, aplicando ‘Introo Enter’ al final de cada ingreso:

a = 2

x1 = –1

x2 = 3

f(x) = a*(x –x1)*(x–x2)

Para determinar las raíces de la función se debe introducir el comando Raíz[<Polinomio>] y entre los corchetes colocar f(x).

Para ver las coordenadas de las raíces en la zona gráfica puedes hacer clic derecho en uno de esos puntos y seleccionas Propiedades/Básico/Etiqueta visible/Valor

Analiza las coordenadas de las raíces y observa qué relación tiene con la fórmula de la función ingresada. Inserta texto con tu conclusión sobre lo observado.

Modificar x1 y x2 con el dial deslizador. Para ingresarlo, clic derecho sobre x1 y luego sobre x2. Observar y registrar qué variaciones se producen en la gráfica cuando:

x1 ≠ x2

x1 = x2

Imprimir o realizar captura de pantalla para entregar y recibir la devolución.

Expresión canónica

(Para trabajar con el programa Geogebra)

Ingresar los siguientes comandos en el campo de entrada:

a = 1 (si estás online aparece un deslizador, que luego necesitarás)

xv = 2 (o ‘h’ Enter)

yv = – 4 (o ‘k’ Enter)

y = a(x–xv)+yv (o la expresión y = a(x–h)2 + k Enter)

El exponente (2) se introduce con con ‘Alt+2’.

Necesitamos marcar el punto correspondiente al vértice de la parábola. Para ello ir al campo de Entrada ingresar: Vértices[<Cónica>] y entre los corchetes colocar la letra correspondiente a la fórmula ‘y’ de la parábola (puede ser ‘c’ o ‘f’).

Es importante que aparezcan las coordenadas del vértice te ayudará a elaborar las conclusiones. Para ello posicionarte en el vértice (puede ser en la ventana izquierda o en el punto de la gráfica) clic derecho, ir a Propiedades/Básico/Etiqueta visible/Valor

Observar las coordenadas del vértice y compararlas con la fórmula de la función cuadrática ingresada. Registra qué notas de especial.

Para analizar las variaciones que se producen en la parábola con ‘xv’, ingresar el dial deslizador (si no apareció al comienzo). Para ello posicionarse en ‘xv’ en la ventana izquierda (vista algebraica), clic derecho y seleccionar Objeto visible.

Desplazar el deslizador de ‘xv’ y registrar qué sucede con la parábola cuando:

xv >0 (toma valores positivos).

xv = 0.

xv < 0 (toma valores negativos).

Posicionarse en la fórmula de la ventana izquierda, clic derecho, Mostrar Rastro, modifica yv con el dial y comprobarás la conclusión antes extraída. Con cel botón Deshace (de la parte superior derecha de la pantalla) vuelves a la gráfica original. ¿Puedes ampliar lo registrado en el punto anterior?

Para analizar las variaciones que se producen en la parábola con ‘yv’, ingresar el dial deslizador (si no apareció al comienzo). Para ello posicionarse en ‘yv’ en la ventana izquierda, clic derecho y seleccionar Objeto visible.

Desplazar el deslizador y analizar qué sucede con la parábola cuando :

yv > 0 (toma valores positivos).

yv = 0.

yv < 0 (toma valores negativos).

Posicionarse en la fórmula de la ventana izquierda, clic derecho, Mostrar Rastro, modifica yv con el dial y comprobarás la conclusión antes extraída. Actualiza la pantalla con cel botón Deshace. ¿Puedes ampliar lo registrado en el punto anterior?

Modificar ‘a’ con el deslizador y analizar para qué valores de ‘a’ el vértice es un máximo y para qué valores es un mínimo. Luego activa Rastro para observar y comprobar.

Imprimir o realizar captura de pantalla para entregar y ser evaluado.

Capítulo 06 TEOREMA DE THALES

Fundamentales

• Trabajar en la resolución de problemas relacionando las razones y proporciones, la semejanza de figuras planas, la homotecia, y el teorema de Thales.

• Relacionar estos temas entre sí, afianzando conceptos matemáticos, y entrenarse en la aplicación de la matemática en la resolución de problemas.

Objetivos

Específicos

• Reflexionar, comprender, analizar y conocer las razones y las proporciones. Aplicarlas en ejemplos de la vida cotidiana.

• Identificar figuras semejantes y matematizarlas.

• Comprender la homotecia, su aplicabilidad, y su relación con los dos temas anteriores.

• Conocer el teorema de Thales, su descubrimiento, algunas de sus aplicaciones. Poder aplicarlos en problemas.

Contenidos

Generales

• Razones y proporciones

• Semejanza en figuras planas

• Homotecia

• Teorema de Thales:

• En un triángulo

• Triángulos semejantes

• Aplicaciones

PRESENTACIÓN DEL CAPÍTULO

IFE

Thales, el hombre de la sombra

• Mediante la biografía de otro gran matemático, indagar en la dificultad que vemos a veces en avanzar o no en un determinado proyecto. Relacionar esto con la Biblia, cuando Dios nos da sabiduría, inteligencia, nos llena del Espíritu de Dios para hacer proyectos, a pesar de nuestras posibles limitaciones.

Orientaciones metodológicas particulares y estrategias

Este es un capítulo con temas sumamente prácticos, y cuyos conocimientos se apoyan mutuamente. Se sugiere realizar introducciones prácticas, luego afianzar las técnicas matemáticas para que logren mayor soltura en los cálculos, y volver a resolver problemas. Se sugiere hacer mucho hincapié en el apoyo de un tema con el otro, y en la construcción de los saberes.

ACTIVIDADES PREVIAS

Página 149

1. a. Cuadrado, triángulos, paralelogramo. Los triángulos rectángulos violeta y verde, ocupan igual superficie. El cuadrado rojo y el paralelogramo, igual. Los triángulos verde y azul, ocupan también igual superficie. El cuadrado, el paralelogramo y el triángulo amarillo, también ocupan igual superficie.

b. El triángulo violeta, es semejante al azul, por ejemplo. Explicación a cargo de cada alumno.

2. a. Los ángulos son iguales, y la longitud de los lados aumenta proporcionalmente. Los llamaría parecidos o semejantes.

b. P1 = 3 cm; P2 = 6 cm; P3 = 9 cm El perímetro de una figura es igual al perímetro de la figura inicial, multiplicada por el número de figura.

Perímetro de figura 3 es igual a P1.3 = 3.3 = 9 cm

c. A1 = x; A2 = 4x; A3 = 9x El área del cuatro triángulo sería A4 = 16, porque

ACTIVIDADES COMPLEMENTARIAS

Página 150 1.

2. a. Hay muchas formas de completar la última proporción.

b. Se hizo así arriba.

Página 151 ?

1. Ambos conceptos implican una división, pero en el caso de la fracción los números que se dividen son enteros (exceptuando el 0 en el denominador), y en la razón se pueden dividir números que no sean enteros.

2. Sí. Es la razón entre la circunferencia de un círculo, y su diámetro.

3.

1. Se necesitarán 6 tazas.

2. No lo es, porque lo cocientes de las divisiones no son iguales.

= 15

= 10

4. De 28/d = 7, d = 4.

= 12

= 7

11

= 1

= 210

= 0,56

Sabiendo que e/f = 7, y e + f = 56, se deducen los valores de f y e. Se iguala a a/b y se deduce que a = 14.

Página 152

Aclaración: La razón de semejanza no es única, depende de qué número se ubique en el dividendo y cuál en el divisor. Pero si hay razón, hay semejanza.

Página 153

En la parte b de la actividad previa que se plantea al comienzo de la página, vale aclarar que esa es una de las razones de semejanza. Si se divide en otro orden, será diferente. Se puede charlar este tema con los alumnos.

También vale aclarar que decir recta MN, o decir MN simplemente, es igual en este libro de texto. En ambos casos, nos estamos refiriendo a una recta.

1. Las circunferencias siempre son semejantes, dado que no tienen ángulos. Solamente un punto y un radio.

2. Los ángulos correspondientes de dos figuras son los que tienen la misma medida. Y los lados correspondientes, los que, siguiendo la secuencia de los demás elementos adyacentes, son semejantes; es decir, si se dividen las medidas de ellos se obtiene el mismo cociente.

3. La escala 1:1 000 significa que a cada unidad del dibujo le corresponden 1 000 de esa misma unidad en el objeto real.

1. En el primer caso son proporcionales, pues los ángulos correspondientes u homólogos son iguales y los lados son proporcionales de constante de proporcionalidad 2 (o 0,5 si se invierte). En el segundo caso es igual, pero la constante de proporcionalidad es 2,5 (o 0,4 si se invierten las razones).

2. Se posiciona el cursor en uno de los vértices del recuadro y arrastrarlo hacia afuera para ampliar o hacia adentro para reducir. Para obtener una imagen no semejante se posiciona el cursor en uno de los puntos medios de los lados del recuadro y se arrastra en cualquier dirección.

3.

Página 155

1. a, b y c:

d. Debería llegar a la conclusión de que, al mover el centro de la homotecia, se mueven todas las imágenes manteniendo la semejanza de las figuras. Al mover un punto del triángulo original, todas las figuras se modifican en su forma, manteniendo la semejanza entre las imágenes con el original.

2. b. de igual tamaño

c. de menor tamaño

e. de mayor tamaño, … inversa

3. Cabe destacar que este ejercicio le permitirá desarrollar, al alumno, habilidades psicomotrices y del uso de elementos de geometría que no utiliza con GeoGebra, o cualquier otro programa informático de geometría. Se le puede pedir al terminar, que explique oralmente el procedimiento realizado.

4. a. paralela

b. es congruente y paralelo a AB

c. proporcionales a los correspondientes de los del ABC y los ángulos son congruentes

d. radio proporcional a r

e. el cuadrado de la constante de proporcionalidad

Página 156

1. EI/KM = FJ/LN

2. GI/IK=HJ/JL

3. EG/GM=FH/HN

4. EM/GI=FN/HJ

5. IK/KM=JL/LN

Extra:

Enlace al teorema de Thales (por Les Luthiers), acompañado de imágenes alusivas realizados por alumnos:

https://youtu.be/d3PdAAOnQFs

https://youtu.be/Q8F538tA–jI

Se presenta el enlace de la famosa canción del “Teorema de Thales” del conjunto Les Luhiers, de Argentina. Cabe destacar que la introducción tiene palabras no tan agradables para alumnos de estas edades, por lo que se sugiere que, si se pasa el video en la clase, se comience a partir del minuto 1:25.

https://youtu.be/OXrYNPJQoTA

Página 157

1. En el segundo caso, porque las rectas cortadas por las transversales no son paralelas.

2. OD = 4,5, AC = 4; BD = 1,5

3. AF = 10,5

4. x = 4 cm

Páginas 158

a. CH = 7,5; GH = 4,5

FK = 3; DE = 8

b. La razón de los lados ABC en relación a GHC es 1,33…, y la de FJK en relación a FDE es 0,5.

Páginas 159

1. Criterios de semejanza de triángulos:

Dos triángulos son semejantes si tienen dos ángulos iguales.

Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo que forman.

Dos triángulos son semejantes si sus lados son proporcionales.

2. Son semejantes porque toda paralela a un lado de un triángulo lo divide en dos triángulos semejantes.

3. A cargo del alumno.

Página 160

2. a. Como los lados opuestos son paralelos y congruentes, JKLM es un paralelogramo.

b. Como J y K son puntos medios de sus lados respectivos, en el MNP se deduce que JK = ML por ser L punto medio de MP.

c. Por lo dicho en (b) se deduce que 2JK = MP.

1.

Página 161

BG = 2GM ya que G es baricentro de ABC.

BF = 2FA ya que FG es paralela media de AMB.

Por tanto, BF = 2FA y BF = 2.6 = 12

Cabe destacar que en la actividad el dibujo no está hecho exactamente a escala, de hecho, se ve mal a propósito, para que los alumnos no se basen en él.

LA ESCENCIA DE LA MATEMÁTICA

Páginas 162 y 163

Las preguntas planteadas al final son solamente una sugerencia. Se pueden plantear muchas preguntas más. Pero sí se apela a trabajar este texto, o leerlo completo en Internet. Es muy rico.

Se dejan aquí sugerencias de otras preguntas para sumar:

• ¿Qué preguntas te planteas en tu vida? ¿Les has encontrado respuesta? Es importante escuchar las preguntas de los alumnos y ayudarlos a buscar respuestas.

• ¿Qué cosas imponentes has visto en tu vida? ¿Qué te impactó de ellas? Todo lo imponente nos habla de Dios.

• ¿Qué actitud te generan las situaciones que están “fuera del alcance” de tu conocimiento o capacidad? ¿Es un desafío? ¿Te genera frustración? ¿Qué te genera?

• ¿Cuáles son tus sombras o vulnerabilidades?

• ¿Qué relación estableces con tus sombras? ¿Las aceptas, las rechazas, buscas cambiarlas?

• Ante algún obstáculo o dificultad, ¿cómo reaccionas? ¿Buscas otro camino? ¿Te desanimas? ¿Por qué?

El hecho de plantear preguntas a partir del texto que les permita contar su experiencia a los alumnos alivia al docente, ya que no necesita tener la respuesta, simplemente abre el diálogo a compartir experiencias y a conocer a los alumnos de otra forma.

Se proporciona a continuación un enlace para realizar un test de dones espirituales. Puede ser útil realizarlo en este contexto.

https://www.vidareal.tv/test/dones–espirituales/

Aparentemente sí son semejantes. Quizás por errores de medidas no da exactamente el mismo número, pero se aproxima mucho.

En este caso cada una de las longitudes de los lados del triángulo original son el doble de las longitudes de los lados de los triángulos semejantes con vértice común en B y en C.

En este caso, cada una de las longitudes de los lados de los triángulos semejantes son el doble de las longitudes de los lados del triángulo original.

3. El primer par de triángulos sí son semejantes por el criterio de semejanza AA (ángulo, ángulo). El segundo par de triángulos: no son semejantes, dado que sus tres lados no son proporcionales.

Página 165

4. y = 8; x = 6 – Cantidad de alambre: 50

w = 4; v = 16,5 – Cantidad de alambre: 57,5

1. Trazamos el segmento AB de 5 cm.

2. En un extremo de AB trazo un segmento AB1 de 7 cm (ya que es pide dividir AB en 7 partes iguales) y lo dividimos en segmentos de 1 cm de longitud.

3. Unimos con una recta punteada los extremos de ambos segmentos (en este caso B y B1).

4. Trazamos las paralelas a BB1 por los puntos marcados en AB1.

5. Las intersecciones de dichas paralelas con AB lo dividen a este en 7 partes iguales.

6. a. ST SP = SR SQ ST SR = SP SQ

b. RS = 4,8

c. Para poder calcular RT necesitamos el valor de PQ, al falta ese dato no se puede determinar la medida de RT.

7. 53,33 m; 40 m; 26,66 m

Página 166

8. x = 3,75 x = 1 x = 2,842 x = –19 x = 3,5

9. a. x = 5

b. x = 12 o x = 4

c. x = 20

d. x = 17/9

5.

10. 27; 40,5 y 22,5. 11. a. y c.

Las figuras 1 a la 6 son trapecios

1 = 2; 3 = 4; trapecios rectángulos

5 = 6 trapecios isósceles

1 y 2 son semejantes a 3 y 4

7=8=9 son triángulos isósceles rectángulo.

b. Los trapecios rectángulos 1 = 2 representan 9/50 cada uno del área del cuadrado.

• Los trapecios rectángulos 3 = 4 representan 7/50 cada uno del área del cuadrado.

• Los trapecios isósceles 5 = 6 representan 6/50 cada uno del área del cuadrado.

• Los triángulos isósceles rectángulos 7 = 8 = 9 representan 2/50 cada uno del área del cuadrado.

Página 167

13. a. x = 30 cm; x = 4 cm

14. a. x = 10; y = 9 b. x = 8, AM = 10; MC = 15; AC = 25 c. y = 12; CN = 6

15. a. x = 50 cm; y = 30 cm b. x = 10 cm; y = 6 cm

El siguiente, es un juego para realizar en grupo.

Se sugiere que el docente proyecte en una pantalla el juego, de tal forma que todos los alumnos lo puedan ver.

Cada alumno, se conectará a su celular, y leerá el código QR proyectado en pantalla. De esta forma, cada alumno será un competidor, y todos competirán por obtener el primer lugar. Es un juego interesante para realizar en grupo.

Se sugiere brindar un tiempo de 3 minutos.

Página 168

16. El poste mide 7,5 m

17.

18. x = 3 cm; y = 2 cm

x = 6

Como la razón de proporcionalidad es 2,5, se observa que:

21 cm = x + 2,5x

21 cm/3,5 = x

6 cm = x

19. En los triángulos equiláteros, las alturas de cada lado coinciden con las medianas, por tanto se divide en dos segmentos tal que uno sea el doble del otro y así: 12 m = x + 2x; por lo que x = 4 m que es la distancia del baricentro al lado AC.

20. a. A cargo del alumno.

b. En la antigüedad no existían los apellidos. Las personas eran conocidas por su nombre, ya que en general las aldeas eran pequeñas. Si era necesario dar un dato más se indicaba el lugar de origen, a su oficio o a características físicas distintitvas (Jesús de Nazaret, Juan el bautista, etc.) De esta forma Thales era identificado por su lugar de origen: Mileto.

21. Opción a.

22. Se plantea la siguiente proporción:

170 cm ____ x

200 cm ____ 150 cm

X = 127,5 m

b. Puede ser para calcular el volumen de agua a la que puede tener acceso. Demás, a cargo del alumno.

c. A cargo del alumno.

23. a. Tomaron las medidas que se indican en la figura. La medida del ángulo señalado en color amarillo, las medidas de los lados del triángulo pequeño, y la base del triángulo grande. Con esas medidas, podrán calcular el largo de cuerda que necesitarán para cruzar, sin haber cruzado, utilizando el teorema de Thales.

b. c. d. y e. A cargo del alumno.

DESAFÍOS

Página 170

1. a. A cargo del alumno.

b. BM = 7,5 cm por paralela media

c. BN = 5,85 cm, por paralela media

d. DF = 3,37 cm aproximadamente, por teorema de Thales.

2.

3. La altura de la palmera es de 16 m = 1600 cm La antena tiene 6000 cm = 60 m de altura

4. a. 1,778 m

b. 3,683 m

c. “Pulgadas de la pantalla x 2,54 cm x 5

d. A cargo del alumno.

5. Si las dimensiones son todas 4 veces menores el volumen será 64 veces menos. 4/64

6. De izquierda a derecha, las medidas de cada triángulo:

7. A cargo de los alumnos.

8. Dos cuadrados siempre son semejantes porque se conservan los ángulos. Dos paralelogramos son semejantes solamente en el caso de que tengan los ángulos congruentes de lo contrario no son semejantes.

Fundamentales

• Conocer el teorema de Pitágoras, o reconocer en algunos casos, y aplicarlo en la resolución de problemas.

• Construir, sobre la base del teorema de Pitágoras y el teorema de Thales, el conocimiento sobre la trigonometría.

PITÁGORAS Y TRIGONOMETRÍA

Objetivos

Específicos

• Comprender el teorema de Pitágoras. Aplicarlo en la resolución de problemas.

• Deducir las fórmulas elementales de la trigonometría, poniendo en juego los temas ya conocidos de Pitágoras y Thales, y todos los cálculos que eso implica.

• Aplicar estos conocimientos en la resolución de problemas.

• Desarrollar habilidades de resolución de problemas y de aplicación de estas fórmulas, y más aún.

• Aprender a utilizar la calculadora científica con la trigonometría.

Contenidos

Generales

• Teorema de Pitágoras:

• Introducción

• Aplicaciones del teorema

• Trigonometría:

• Razones trigonométricas en triángulos rectángulos

• Con calculadora

• Razones trigonométricas en triángulos rectángulos notables

• Sin calculadora

• Aplicaciones de la trigonometría

• Más datos

PRESENTACIÓN

DEL CAPÍTULO

IFE

Goniómetro casero

• Se propone una actividad muy interesante donde habrá que poner en juego: la creatividad de los alumnos, el trabajo en equipo, la puesta en práctica de los conocimientos matemáticos adquiridos en el capítulo, y la relación de todo esto con la buena voluntad que Dios nos pide al hacer un trabajo. Se sugiere tomarse el tiempo para hacerla. Será de mucho provecho para docentes y alumnos.

Orientaciones metodológicas particulares y estrategias

Se continúa trabajando con dos temas muy prácticos: Pitágoras y trigonometría. Se sugiere trabajar en cálculos con calculadora, sin calculadora, en resolución de problemas, trabajo en equipo.

Se sugiere utilizar programas informáticos para visualizar la aplicabilidad de los temas, problemas de la vida real del entorno del alumno.

DISPARADOR

Página 173

1. a. A = b.c/2

b. b. A = a2

c. c. 4bc/2 + a2 = (b+c)2

d. d. 2bc + a2 = (b+c)2

e. e. (b+c)2 = b2 + 2bc + c2

2. a. A cargo del alumno.

b. Esta pregunta tiene el objeto de disparar la curiosidad del alumno. Se propone que no se dé la solución en el momento, sino que lo piensen y hagan algún tipo de justificación. Se contestará más adelante con el desarrollo del tema.

Página 174

La suma de los cuadrados construidos en los catetos, es igual al cuadrado construido sobre la hipotenusa.

Página 175

1. a. Se necesitarán 701 28 cm de listones de madera.

b. Se necesitarán 1320 cm2 de tela amarilla y lo mismo en verde, y 2860 cm2 de tela celeste y lo mismo en rojo.

2. A cargo del alumno.

3. Sí. Son ternas equivalentes. Si la terna (3; 4; 5) se multiplica por 2, se obtiene la primera. Si se la multiplica por 10, se obtiene la segunda. Etc.

4. A cargo del alumno.

5. Se puede alcanzar una altura de 2,92 m.

Página 176

1. Un posible camino para resolver esto es utilizar GeoGebra.

Conclusión a cargo de alumno y los docentes.

Página 177 ?

Le puede haber explicado lo siguiente:

1. Trazas un eje y algunos números en él.

2. Como te piden “raíz de 2”, construyes un triángulo rectángulo cuyos catetos midan 1, sobre el eje.

3. La hipotenusa de ese triángulo, por el teorema de Pitágoras, mide “raíz de 2”.

4. Tomas esa medida con el compás, tomando como centro el 0 del eje, y lo proyectas en el eje. Esa será la ubicación del valor “raíz cuadrada de 2”.

Página 178

1.

2. A cargo de los estudiantes.

3. No. El número pi no se puede representar de esta forma y es irracional.

4. 3,1623 2,6926 10,2956

5. 2,24

6. 40 cm

7. 3,1225 m

8. 42’’

Página 179 ?

La demostración de esto va por el lado de que la raíz cuadrada de todo número primo, es un número irracional. Y 5 es un número primo, por lo cual, su raíz es un número irracional.

https://bit.ly/demoraices

También se sugiere ver en clase, o enviar de tarea, el siguiente video con los alumnos: se considera muy enriquecedor y práctico, con este tema.

https://www.youtube.com/watch?v=jej8qlzlAGw

Página 181 ?

Se responde la pregunta en el mismo texto, abajo. En el párrafo que comienza: “Dado que BE,…”.

Página 182

a. Falso – AC es el cateto opuesto al ángulo de vértice B o adyacente al ángulo de vértice C.

b. Falso – BC es hipotenusa, es el segmento de mayor longitud del triángulo rectángulo.

c. Verdadero.

Página 183

A cargo del alumno.

Página 184

3.

a. El seno y el coseno de un ángulo agudo está comprendido entre 0 y 1.

b. No. Para valores de ángulos agudos entre 0° y 15° la tangente toma valores comprendidos entre 0 y 1. Para ángulos comprendidos entre 45° y 90°, la tangente toma valores mayores que 1.

c. sen α = BC AC = cos β cos α = AB AC = sen β

El seno de un ángulo agudo es igual al coseno del ángulo complementario.

Esto se debe a que en todo triángulo rectángulo los ángulos agudos son complementarios por tanto el

cateto adyacente para uno de ellos es el cateto opuesto para el otro y de esa forma el seno y el coseno de ángulos complementarios coinciden.

4. La tecla Shift, Inv o 2nd se ha colocado en las calculadoras científicas con el objetivo de ampliar la capacidad funcional de la misma. Esto quiere decir que te permitirá acceder a muchas opciones y funciones que sin ella no sería posible.

Esto permite reducir el tamaño del dispositivo de tal forma que la comodidad no limite la funcionalidad. Que sea de dimensiones conservadas para la comodidad del usuario; pero al mismo tiempo tenga la capacidad de realizar muchas funciones.

La calculadora científica tiene funciones principales y secundarias. A las primeras puedes acceder con solo pulsar la tecla correspondiente. Las funciones principales por lo general son las más utilizadas y vienen expresadas sobre la tecla.

Por ejemplo, las teclas que indican los números o algunos signos para realizar operaciones esenciales (suma, resta multiplicación, división y otras); tienen su función expresada sobre la tecla.

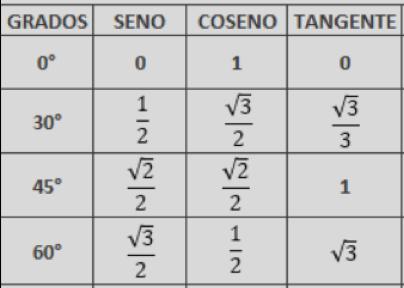
Pero existe un conjunto de funciones, a las que llamaremos secundarias, que están expresadas por encima de las teclas. Comúnmente aparecen en un color diferente que coincide con la tecla Shift, Inv o 2nd.

Aunque se las denomina funciones secundarias, no significa que sean menos importantes, tal vez sean menos utilizadas o poco comunes. A estas funciones solo podrás acceder con la tecla Shift, Inv o 2nd. En trigonometría nos habilita a usar las funciones inversas de seno, coseno y tangente.

Extraído y adaptado de https://bit.ly/calculadoraconshift

5. 90° – (45° + 38°) = 7°

Página 185

La forma incompleja de un ángulo: una medida angular, en el sistema sexagesimal, puede venir expresada en una única unidad (llamada forma incompleja) o en varias (llamada forma compleja). Ejemplo de conversión de forma compleja a incompleja y viceversa: paso de grados decimales a grados sexagesimales.

Forma incompleja: 37,42°

Forma compleja: 37°25’12’’

2.

Página 186

2. Es el mismo valor para ambas razones, pues el seno y el coseno de ángulos complementarios es igual.

1. E = 5/2

2. x = 7/4

3. Si sen A = 2/5 se deduce que CB = 2x y BA = 5x

• Por teorema de Pitágoras; AC = x√21

• D = (cos A + tan B) – sen B; como cos A = sen B

• D = sen B +tan B – sen B

• D = tan B = √21 2

Página 188

1. A cargo del alumno.

2. Libertad para cada alumno.

3. Se puede calcular en primer lugar cualquiera de los dos ángulos agudos.

4. Primera línea: no es cos, sino sin.

• Cuarta línea: olvidó calcular la raíz cuadrada.

• En el área mutliplica cateto por hipotenusa, y debería ser cateto por cateto.

Página 189

1. Los ángulos interiores de cualquier triángulo suman 180°. Como el ángulo del vértice A es de 90°, se deduce que, la suma de los otros dos ángulos es 90°. 2.

3. Si α y β son ángulos complementarios, se tiene que sen α = cos β, cos α = sen β, y tan

4.

sen α = cos(90° – α)

b. cos α = sen(90° – α)

c. tan(90° - α) = 1 tan ∝

d. 1 tan(90° ∝) = tan ∝

e. tan ∝ = sen ∝ cos ∝

Por Teorema de Pitágoras

LA ESENCIA DE LA MATEMÁTICA

Páginas 190 y 191

Como el objetivo de la educación adventista es restaurar la imagen de Dios en el ser humano, es decir, como nuestro concepto de Dios está dañado, es importante restaurarlo. Tal vez sería bueno enfocarnos en la imagen de Dios, que desea habitar en nosotros, y que aparece en la construcción del tabernáculo.

A continuación, se desarrollan sugerencias para trabajar en el aula de algunas preguntas:

b. ¿Cómo demostró Dios la aprobación de la obra realizada en la construcción del tabernáculo? ¿Qué crees que habrán sentido las personas ante la demostración Divina? Ex. 40:34

“Con anhelante interés las multitudes de Israel se agolparon para ver el sagrado edificio. Mientras contemplaban la escena con reverente satisfacción, la columna de nube descendió sobre el santuario, y lo envolvió. “Y la gloria de Jehová llenó el tabernáculo.” Éxodo 40:34. Hubo una revelación de la majestad divina, y por un momento ni siquiera Moisés pudo entrar. Con profunda emoción, el pueblo vio la señal de que la obra de sus manos era aceptada. No hubo demostraciones de regocijo en alta voz. Una solemne reverencia se apoderó de todos. Pero la alegría de sus corazones se manifestó en lágrimas de felicidad, y susurraron fervientes palabras de gratitud porque Dios había condescendido a morar con ellos.” (Patriarcas y profetas pág. 362)

c. ¿Para qué pide Dios la construcción de un santuario o tabernáculo? Éxodo 25:8

“Además, quiero que me construyan un santuario para que yo viva entre ustedes.” Éxodo 25:8

d. ¿Cuál es el mayor deseo de Dios para con nosotros? Juan 1: 14; Romanos 8: 39 y 1° Corintios 3:16

“Todo esto sucedió para que se cumpliera lo que Dios había dicho por medio del profeta Isaías: «¡Presten atención! Una joven virgen quedará embarazada, y tendrá un hijo. Y llamarán a ese niño Emanuel. Este nombre significa «Dios está con nosotros».” Mateo 1: 23

“Aquel que es la Palabra habitó entre nosotros y fue como uno de nosotros.” Juan 1: 14

“¡Nada, absolutamente nada, podrá separarnos del amor que Dios nos ha mostrado por medio de nuestro Señor Jesucristo!” Rom. 8:39

El santuario ilustra todo lo que Dios ha hecho y está haciendo con el fin de volver a unirnos con él. Su mayor deseo no es simplemente vivir entre los seres humanos sino en el corazón de las personas. La belleza del santuario es una representación de cómo nos ve Dios a nosotros: como valiosa morada, su santuario de oro y su lugar preferido para vivir.

“¿Acaso no saben que ustedes son un templo de Dios, y que el Espíritu de Dios vive en ustedes?” 1 Corintios. 3: 16

(Los versículos del inciso (b) y (c) son de la Traducción en Lenguaje actual)

a. Es un triángulo isósceles con AB = BC

b. 18,94 o 10 + 4√ 5

c. 10

3. Longitud del cable: 41,124 m

4. La distancia de A a C es de 6 m.

Página 193

5. La rampa tendrá 12,4 pies de largo.

6. √ 26

7. El trampolín tiene una altura de 5,9 m.

8. AB = 30,5 cm

BC = 17,1 cm

El ángulo en A es de 29° 15’

9. 93,26 m aproximadamente.

10. a. Perím. 1 = 2 =(4 + 2 √ 2 ) cm = 6,83 cm

Perím. 3 = 4 = (6 + 6 √ 2 ) cm = 14, 49 cm

Perím. 5 = (2 + 2 √ 10 + 2 √ 2 ) cm = 11, 15 cm

Perím. 6 = (3√ 2 + √ 10 ) cm = 7,4 cm

Perím. 7 = (2 + √ 2 + √ 10 ) cm = 6,58 cm

Cuadrado armado con las 7 piezas anteriores y con un área de 36 unidades cuadradas.

Página 194

12. P = 27,321 cm; Á = 28,87 cm2

P = 89,134 cm; Á = 240,557 cm2

P = 39,011 cm; Á = 46,977 cm2

P = 22,936 cm; Á = 24,074 cm2

13. a. 2,5 m 0,85 m

b. Está apoyado a 2,351 cm.

c. El ángulo de inclinación que forma con el piso es de 70° 7’ 23’’

b.

14. Hay que alejarse menos de una cuadra: 97,476 m.

15. A cargo del alumno.

Página 195

16. a. 29°

b. 46,53 m

17. El avión debe girar 145°

18. El árbol tiene una altura de 6 m.

Este problema puede ser interesante para acampantes, de modo que puedan calcular a qué distancia colocar la carpa para que, ante cualquier posible caída del árbol no caiga sobre la carpa.

19. El jugador pateó la pelota con un ángulo de elevación de 23°.

20. a. α = 88°

b. α = 50°

c. α = 22°

d. α = 66°

21. 11,325

Página 196

22. a. x + y = 98,626 cm

b. sen α = 0,55275

cos α = 0,833…

tan α 0,6633

c. 25,63 cm

d. 354,5 cm2

23. El avión alcanza una altura de 376,134 m

24. Cada lado del triángulo equilátero es 24 cm:3 = 8 cm

La altura del triángulo es de 6,928 cm o 4.√ 3

25. 40 m. El ángulo agudo es de 45°, por lo cual es un triángulo isósceles. Se pueden evitar cálculos.

26. F – En este caso hipotenusa y cateto adyacente coinciden y su cociente es 1.

F – puedo utilizar la fórmula de seno.

F – La suma de los cuadrados de 1 y de 2 no coincide con el cuadrado de 3.

Página 197

27. La longitud de la cuerda es de 212,132 m

28. El ángulo de elevación de los ojos del jugador es de 16°3’59’’.

29. Cada cateto mide 3 unidades.

30. Los catetos miden 8,66 cm (el que se opone al ángulo de 30°) y 10 cm (el que se opone al ángulo de 60°).

31. Cualquier fracción equivalente a 5/12

32. a. 3 b. √ 2 2 1 2

33. La altura del edificio es de 56,012 m.

34. La antena tiene una altura de 10,392 m

35. La altura de la pirámide es de 36,8787 cm.

DESAFÍOS Página 198

1. Área ABC = 12 cm2, Perímetro: 3 cm + 13 cm + 10 cm = 26 cm

2. El perímetro es de 69,69 cm.

No es un paralelogramo, ya que los ángulos de vértices opuestos, no coinciden.

3. EC = 11,662 cm

4. Por razones trigonométricas se puede resolver ya que todos los ángulos son iguales a 60°:

Aplicando el teorema de Pitágoras:

Con cualquier procedimiento se llega al mismo resultado.

5. La longitud del cable es de 30 m.

6. d = √ 29 cm

Página 199

7. a. 5°19’41’’

b. La Torre de Pisa conocida en italiano como la “Torre Pendente di Pisa”, se encuentra en la ciudad de pisa, exactamente en la Plaza del Duomo de Pisa conocida como “Piazza dei Miracoli”.

8.

9. AD = 10√ 2

10. α = 22°37’12’’

11. Área 1 = 624,8725 m2

Área 2 = 1060,885 m2

Área 3 = 937,685 m2

Área 4 = 742,455 m2

12. A la mitad del valor del ángulo mayor le corresponde una tangente = 12/9 > 1 eso significa que dicha mitad de ángulo es mayor a 45° por tanto el valor del ángulo completo debe ser superior a 90°, en este caso es 106°.

ACTIVIDADES EXTRA*

¿Cómo puede ser tanta coincidencia? (Propuesta I)

Para realizar esta guía es necesario disponer de regla, transportador, goma, lápiz y calculadora.

¿Puede ser que personas que dibujan cosas diferentes coincidan? ¿En qué? Lo veremos con esta actividad.

Les propongo comprobarlo. Para ello trabajaremos en grupos de a 2 alumnos. Cada grupo elige una tarjeta con un número.

(Nota: las tarjetas contienen números del 30 al 70 representan los ángulos agudos de cada triángulo rectángulo que dibujen los alumnos. Se seleccionan valores del 30 al 70 para que resulte sencillo trazarlos. Es importante que se repita dos veces cada valor y cuidar que haya dos parejas, de distintas partes del salón a las que les toque el mismo valor.)

Actividades para cada integrante del grupo

Dibujar un triángulo rectángulo (de diferente tamaño al de sus compañeros) con un ángulo agudo ‘α’del valor de la tarjeta elegida.

Identificar y señalar la hipotenusa (H) el cateto opuesto (CO), y el cateto adyacente (CA) al ángulo agudo del triángulo dibujado.

*Desarrolladas por la Prof. Rossana Genta.

Medir, con la mayor precisión posible, la longitud de cada uno de los lados identificados. Registrar las mediciones.

Valor del ángulo agudo

Con los datos obtenidos por medición directa, calcula los cocientes solicitados en la siguiente tabla. Anotar redondeando los decimales a los centésimos:

Buscar en el aula, el otro grupo que seleccionó la misma tarjeta que ustedes, es decir el otro grupo que dibujó triángulos rectángulos con el mismo ángulo agudo que ustedes.

H Comparar los valores obtenidos en la tabla de registro y analizar con pensamiento crítico:

¿Qué observan? ¿Por qué creen que sucede eso?

¿Comparen su conclusión con otros grupos? ¿Qué notan?

¿De qué dependen los cocientes o razones entre los lados de un triángulo rectángulo?

H Estos tres cocientes obtenidos reciben el nombre de razones trigonométricas. Deducir por qué reciben ese nombre; es decir por qué RAZONES y por qué TRIGONOMËTRICAS.

H Cada razón trigonométrica también tiene una denominación:

sen α = CO/H cos α = CA/H tg α = CO/CA y se leen: “seno de alfa”, “coseno de alfa” y “tangente de alfa” respectivamente.

¿Por qué será esto? (Propuesta II)

Calcular el seno y el coseno de 5 ángulos agudos diferentes cada uno de mayor valor que el anterior. Registra y observa con ojo atento…

¿Qué sucede con el seno y con el coseno a medida que el valor del ángulo aumenta?

¿Entre qué números enteros están comprendidos los valores de seno y coseno de un ángulo agudo?

Calcula la tangente de 5 ángulos agudos diferentes cada uno de mayor valor que el anterior. Anotar. Observar atentamente para responder…

¿Qué notas en relación a lo observado para seno y coseno de un ángulo agudo? Este cuadro puede ayudarte a organizar tus conclusiones.

Análisis de la tangente en relación al seno y coseno de un ángulo agudo cualquiera

Diferencias

Semejanzas

¿Cuál es el resultado de la tg 45°? ¿Por qué crees que se obtiene este resultado?

Trigonometría y uso de la calculadora (Propuesta III)

Para trabajar con las razones trigonométricas no es necesario ya dibujar los triángulos, medir y calcular. La calculadora contiene el programa con todos los datos. Sólo necesitamos aprender a usarla. Así que te invito a completar la siguiente tabla usando tres decimales y redondeando al milésimo.

Debes tener en cuenta que sen, cos y tg en la calculadora figuran como sin, cos y tan.

Para determinar el sen 27° 38’ 16” debes seguir la siguiente secuencia de teclas: sin 27 ° ‘ “ 38 ° ‘ “ 16 ° ‘ “ = 0,463880249

Recuerda que para redondear al milésimo debes mirar la cuarta cifra decimal, si es 5 o más debes sumar uno a la tercera cifra decimal, de lo contrario se mantiene:

Ejemplo: 0,463880249 se redondea como 0,464 pero si fuera 0,4632880249 se redondea 0,463.

Valor de calculadora

Valor redondeado(a los milésimos)

a) sen 38º54’45”

b) cos 15º8’

c) tg 75º49”

d) sen 25º12’50”

e) cos 39º2’8”

f) tg 83º15”

g) sen 72º10’

h) cos 60º

i) tg 18º43’26”

j) cos 50º20”

k) tg 48º50’42”

También se puede determinar el ángulo sabiendo la razón trigonométrica. Por ejemplo:

Se sabe que la tg α = 4,608 en este caso la secuencia a seguir es:

SHIFT tan 4,608 = ° ‘ “

Estas teclas habilitan el uso de la función inversa de la tangente llamada ‘arco tangente’ cuya simbolización es ‘arc tg’ y que en la calculadora aparece como tan– 1.

La calculadora está programada para despejar la incógnita α de la ecuación:

tg α = 4,608

α = arc tg 4,608

α = 77° 45’ 21”

Este mismo procedimiento se utiliza para ‘arc sen’ (sen–1) y ‘arc cos’ (cos–1).

Para probar tus conocimientos y nuevas habilidades adquiridas te propongo completar la siguiente tabla de valores siempre redondeando el resultado al milésimo.

Objetivos

ESTADÍSTICA

Fundamentales

• Acrecentar los conocimientos de estadística e introducirse en la investigación y el análisis de datos.

Específicos

• Apropiarse del origen y el concepto actual de la estadística. Introducirse o reintroducirse en ese campo.

• Desarrollar habilidades para la recolección, el recuento y la organización de datos, con el fin de una investigación. Evaluar la mejor manera de hacerlo de acuerdo a la investigación.

• Diferenciar variables discretas y continuas. Comprender la importancia de las variables continuas y poder trabajar con ellas.

• Conocer las diferentes formas de presentar los datos en una investigación y adquirir la habilidad de evaluar cuál es la mejor presentación, de acuerdo a la investigación realizada.

• Desarrollar los conocimientos de las medidas estadísticas: tanto de medidas de tendencia central, como medidas de dispersión. Diferenciarlas, conocerlas, trabajarlas, y apropiarse de ellas para usarlas en su beneficio en investigaciones.

Contenidos

Generales

• Introducción a la estadística

• Recolección, recuento y organización de datos

• Variables continuas

• Presentación de datos:

• Diferentes tipos de gráficos

• Medidas estadísticas: análisis de datos:

• Medidas de tendencia central

• Medidas de dispersión

PRESENTACIÓN DEL CAPÍTULO

Los cereales integrales

• Se ofrece un gráfico diferente a todos los estudiados en el capítulo, una presentación de datos de una investigación novedosa, con el fin de que los alumnos extraigan conclusiones extrapolando sus conocimientos. Relacionando esto a un tema fundamental: la sana alimentación.

Orientaciones metodológicas particulares y estrategias

Se sugiere que los alumnos trabajen en una investigación. Quizás de forma conjunta con otra asignatura que tengan, en la que deban investigar. Al hacer una investigación completa, tendrán que ir haciendo uso de estos conocimientos, y de esa forma, adquirirán mejor los conceptos.

DISPARADOR

Página 201

1. Es una interesante discusión para que se la plantee a todo el grupo, y se discuta sobre ella. “Según la estadística” el promedio da idea de cuántos perros tendría cada persona si todos tuvieran la misma cantidad. Eso permite saber si hay muchos o pocos perros por persona. Es una frase graciosa, pero que encierra una verdad. La estadística generaliza con el fin de extraer datos.

2. a. ¿Qué cantidad de alumnos hay en 3er año? ¿Qué porcentaje de alumnos están conectados a las redes 4 horas o más al día? ¿Cuál es la cantidad de horas que la mayoría de los alumnos está conectado a las redes? ¿Cuántas horas promedio pasan conectados los alumnos de 3er año? ¿Qué utilidad puede traer estos datos a los directivos?

b. A cargo del alumno. La idea es que funcione como disparador, genere curiosidad, el alumno haga planteos que quizás pueden ser acertados o mejores aún que lo ya hay descubierto. En el teórico del capítulo se responderá.

c. Se está estudiando la manera en que los alumnos utilizan su tiempo libre o el tiempo que están conectados a las redes sociales.

d. A cargo del alumno.

3. La tercera opción es la correcta. Justificación a cargo del alumno.

ACTUALIZA TU INFORMACIÓN

Página 203

Algunos videos de youtube sobre el uso del celular y sus efectos en la salud.

https://youtu.be/KUyiT7TwM9Y (con dibujos animados)

https://youtu.be/1Bxr6604bdI (experimento social, excelente y muy relacionado con la propuesta de esta pág.)

https://youtu.be/n5zTA4n1E14 (en dibujos animados)

Página 205 ?

1. El recuento es el proceso que facilita el cálculo de la frecuencia de cada valor.

2. El corchete incluye dicho valor que se encuentra en el extremo del intervalo, el paréntesis no lo incluye.

Se utiliza 28 ya que es el múltiplo de 7 más cercano al 27, y se pide que se divida en 7 intervalos.

Página 207

1. a. Total de alumnos de un colegio secundario (ya que son adolescentes).

b. 50 alumnos de dicho colegio.

c. Cantantes nacionales favoritos (cualitativa).

2. a.

b. El 30,3% de los alumnos del curso gasta más $50 a la hora de la merienda.

3. Se obtiene el total de datos a.

4. Depende de cada grupo de alumnos.

5. a y b. Es adecuado porque se observa la frecuencia de repetición de valores dentro de cada intervalo.

Página 208

1. a. Se presentan a través de sectores circulares de tamaño proporcional a la frecuencia de cada valor de la variable.

b. Con la siguiente proporción se calcula el ángulo de cada sector circular correspondiente a cada valor. f/total de datos = ángulo del sector circular/360°

c. Toda la población o el total de datos.

2. a. y b. En los dos primeros gráficos las barras son verticales. En el eje horizontal se colocan la variable y el eje vertical la frecuencia.

El primer y el 3er. gráfico representan una única serie o conjunto de datos, mientras que el segundo representa 3 series o conjuntos de datos.

En el tercer gráfico las barras son verticales por lo tanto en el eje horizontal se encuentra la frecuencia y en el eje vertical la variable.

En los 3 gráficos todas las barras son del mismo ancho, no se superponen y su longitud es proporcional a la frecuencia de cada dato.

3.

Página 209

1.

a. La variable se indica en el eje de abscisas (eje horizontal).

b. La frecuencia se indica en el eje de ordenadas (eje vertical).

c. En el punto medio de la parte superior de cada barra.

2.

d.

Página 210

1. a. Sí.

b. Respuesta personal.

c. Se podría estar estudiando el porcentaje de las personas que tienen un trabajo a jornada completa, media o ningún trabajo. El título podría ser, en este caso: % de personas que trabajan.

2. y 3. A cargo del estudiante.

Una sugerencia interesante para estos dos ejercicios es dividir a los alumnos en grupos, de forma que cada grupo tome un tipo de gráfico y busque la variedad y lo presente de forma oral, con evaluación de parte del docente.

4. a. El gráfico indica los tipos de fuentes de energía que se han usado en el mundo (en el escenario de políticas declaradas), a lo largo de los años.

b. Es un tipo de gráfico de barras. Barras apiladas.

c. Es una variable numérica discreta.

d. Hasta 1973 las energías demandadas (y que existían) eran a base de biomasa, carbón y crudo.

A partir de 1974 aparece la energía a base del gas natural o a partir de recursos renovables modernas.

A partir del año 2000 aparece la energía nuclear.

La demanda de energía fue aumentando a medida que transcurren los años, excepto la biomasa que se mantuvo casi igual durante esos mismos años.

Página 211 a y b. A cargo del estudiante.

c. 17,0534%

d. Los nacimientos de ese año han sido 6 438 716.

Página 212

a. Es correcto para los empleados que tiene hasta antes de contratar a Claudio.

b. Se sumó: 9600 + 4000 + 6.1000 + 5.800 + 10.400 = 27600. Y luego se dividió ese número entre la cantidad de personas: 27600 / 23 = 1200

c. No, pues con Claudio serían 11 operarios.

d. Porque pensó que ganaría un sueldo cercano a los $1200, y resulta que no supera los $400.

Página 214 ?

2. Multiplica cada valor por la frecuencia de este modo se evita colocar los 30 valores para luego dividir por 30.

b. 60

c. [205; 266)

d. [205; 266)

e. El intervalo mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas.

f. 4456/20 = 222,8

g.

Página 215 ?

A cargo del estudiante.

Página 216

1. 70 – 70 = 0; 60 – 70 = 10; 85 – 70 = 15; 65 – 70 = 5

2. 7,5

3. Las notas de Luly tienen menos dispersión media, ya que es 7,5. En cambio la de Seba es de 22,5. Esta última, se aleja mucho más.

4. Al comparar las desviaciones medias, concluimos que las notas de Seba presentan mayor alejamiento respecto al promedio. En cambio, las notas de Luly fluctúan cerca del promedio. Si mantiene esa tendencia, superará fácilmente el 60%; en cambio no se puede asegurar lo mismo de Seba.

5. Las calificaciones de Lucía no se alejan del 70%, difícilmente alcanzaría una nota superior al 80%. En este caso, Seba tendría más posibilidades de obtener un 80% o más.

6. Si fuera un cálculo matemático, le daría el premio a Luly. Pero si hay que tomar en cuenta otros factores como circunstancias, esfuerzo, etc. (ver página 51 de este libro), nos deberíamos preguntar: ¿estos cálculos alcanzan para tomar una decisión o tomarías otros factores para hacer tu decisión? ¿En qué casos utilizarías sí o sí estos datos para tomar una decisión? ?

La diferencia en la distribución de los datos es importante y no siempre se refleja en la media, pero sí se refleja en la desviación media que nos permite ver la dispersión o variación de los datos en relación a la media aritmética. La varianza y la desviación estándar son parámetros similares a los de desviación respecto de la media y desviación media, pero se calculan de otra forma. También nos informan de la dispersión de los datos respecto de la media.

LA ESENCIA DE LA MATEMÁTICA

Página 217

1, 2 y 3 a cargo del alumno.

4. a. Variable cualitativa. El impacto en la salud y el medioambiente de distintos alimentos: vegetales, granos integrales, pescado, carne procesada, lácteos.

b. La carne procesada, es lo que impacta de forma más negativa en la salud y el medioambiente de las personas, en general, de estos alimentos que se han estudiado. En lo que menos afecta, es el en uso del agua, pero por lo demás: más mortalidad, más enfermedades coronarias, más cáncer colorrectal, más diabetes, etc.

Lo que impacta en el medioambiente de forma más positiva son los vegetales. Etc.

c. Que en general, impacta de forma positiva en la salud y el medioambiente.

ACTIVIDADES

Página 218

1. a. Pacientes bebés de un determinado pediatra, desde que nacen hasta que caminan.

b. 50 pacientes bebés de ese pediatra.

c. Meses de edad al comenzar a caminar por primera vez los pacientes.

d. No se aclara cómo hizo su elección.

e. No sería útil para una revista científica, pero quizás para su consultorio sí sea posible.

f. Sí: hay investigación, recolección de datos, organización de los mismos en una tabla, y probablemente conclusiones.

g. x = 12,2

Para calcular la desviación media utilizo una media de 12 meses.

2. El conjunto de alumnos del colegio de Puno, Cada alumno del colegio de Puno.

3. Deportes practicados es una variable cualitativa. Índice de ocupación en Somalia (variable cuantitativa discreta).

Página 219

4. a. Cuantitativa discreta.

b. Cualitativa.

c. Cuantitativa continua.

d. Cuantitativa discreta.

e. Cualitativa.

5. Rosana es la que obtuvo mejor tiempo en el promedio de las últimas 5 carreras de 100 metros llanos.

x Marcela = 12,82 seg x Sonia = 12,68 seg x Rosana = 12,48 seg

Karina = 12,56 seg

6. El promedio de los desvíos es 0 (nulo) si no se considera el valor absoluto de los mismos para calcular la desviación media.

Totales

8. Propio de cada alumno.

9.

a. Gráfico de barras.

b. Histograma.

21

c. Gráfico de barras múltiples. No se aplica.

Algunos países tienen en su contenido curricular el tema del “método estadístico”. En beneficio de ellos, se armó este video condensando la mayoría de los conceptos que necesitan, de forma amena y práctica. Se sugiere que cada alumno lo mire de tarea y responda algún tipo de preguntas armadas por el docente, o que lo presente en clase. Quizás un breve resumen.

Página 220

10.

11. Cada alumno responde.

12. Cada alumno responde.

13. a. Media = 1,71

Desviación media = 0,069

b. Media A = 25

Desviación media A = 4

Media B = 30

Desviación media B = 7,2

Página 221

14. Es un gráfico de barras horizontales.

15.

b.

e. y f. Opinión personal.

16. Opiniones a cargo de alumnos y docente.

Página 222

Me = 215

b. Rango = 254 – 185 = 69

c. Tomo un rango de 72, por tanto cada intervalo tendrá 18 de ancho y comienzo por 184, terminando en 256.

e. De los 30 pacientes, 22 tienen más de 200 mg de colesterol por dl de sangre.

18. a. Mo = G 35 600 000

b. Me = G 30 000 000

c.

Página 223

19. Para variables cualitativas como el color preferido, se puede determinar la moda. La media aritmética no se puede calcular ya que no son valores numéricos que se puedan sumar y luego dividir por la cantidad de datos. Solo tiene sentido para números.

La mediana tampoco se puede determinar en variables cualitativas ya que los datos no se pueden ordenar de menor a mayor.

a. La media no se puede determinar por ser variable cualitativa. La mediana tampoco se puede determinar. Solo se puede determinar la moda que es la manzana roja.

b. Al no poder determinar la media, tampoco se pueden calcular las medidas de dispersión.

21. No es posible calcular la media en este caso dado que los datos están agrupados en intervalos de diferente longitud y con un último intervalo abierto.

22. No sería suficiente. Sería muy bueno conocer las desviaciones y variaciones, para saber si son mínimas o muy grandes. Si son muy grandes, habría que pensar mejor qué ropa poner en la maleta.

DESAFÍOS

b. Mo = 38

c. Sin duda es el talle que predomina, pero hay que tener en cuenta que ese día el talle 38 fue pedido por el 30% de los compradores. Por lo cual, se podría hacer un estudio más amplio que incluya todo un mes, y no sugeriría que compren el 50% en ese número, sino un poco menos.

2.

a. Pareja 1: x = 50 Mo = 50 Me = 50 Pareja 2: x = 50 Mo = 50 Me = 50

b. Pareja 1, los desvíos son: 4;

, los desvíos son 40; 32

c. Los desvíos son siempre positivos ya que su fórmula es un valor absoluto, y este, es siempre positivo.

3. 2 11,5

5 9 21 36

7 8 11 2 10,5 13

Página 225

4. La serie C.

5. a. Serie 1: 6, 7, 8, 10, 12 Serie 2: 12, 14, 16, 20, 24

x1 = 8,6 x2 = 17,2

La media de la serie 2 es el doble de la media de la serie 1.

b. Serie 3: 18, 21, 24, 30, 36 Serie 4: 36, 42, 48, 60, 72 (se multiplicó por 3 cada uno de los valores de la serie 1 y 2)

x3 = 25,8 x4 = 51,6

El promedio de la serie 3 es el triple del promedio de la serie 1, y el promedio de la serie 4 es el séxtuple del promedio de la serie 1.

c. Serie 5: 10,11,12,14,16 Serie 6: 12, 13, 14, 16, 18 (se sumó 4 a la primera serie en el primer caso, y 6 a la primera serie en el segundo caso)

x5 = 12,6 x6 = 14,6

Los promedios de estas dos series son el resultado de sumar el mismo número añadido al promedio de la serie 1.

6. El error es que no es un diagrama circular, sino semicircular.

7. a. Temperatura máxima y mínima de cada día de una semana.

b.

c. Promedio máximo = 17° Promedio

= 1°

d. 12,5; 11,5; 8; 9; 7; 8; 7

e. Es posible hacerlo sí, ya que son datos cuantitativos.

h. De los promedios podemos deducir que ha sido una semana de días templados ya que la media de las temperaturas máximas ha sido de 17° pero de noches muy frías con una media de 1°.

La mediana nos informa que la mitad de los días de la semana han sido de temperaturas máximas por debajo de los 18° y la otra mitad con temperaturas por encima de ese valor.

En relación a las temperaturas mínimos, la temperatura de 1° muestra que la mitad de los días hubo temperaturas superiores y la otra mitad inferiores a 1°.

Las temperaturas máximas han tenido más variaciones (unos ± 3°) en relación a la media de 17°. En cambio, las temperaturas mínimas han tenido oscilaciones de unos + 2° en torno a la media de 1°.

ANEXO: TUTORIAL DE CÓMO REALIZAR GRÁFICOS ESTADÍSTICOS*

1. Abrir Excel e ingresar los datos en la cuadrícula (se puede pegar la imagen de la tabla para que se más sencillo copiar los datos en Excel).

2. Seleccionar la tabla de datos ingresada y luego ir a Insertar/Gráficos (se puede elegir cualquiera: de barras, circular, lineal, etc.) En cada paso se pueden ver distintos estilos de gráficas.

*Por Rossana Genta

3. Inmediatamente aparecerá el gráfico correspondiente a la tabla.

4. Al hacer clic en el signo ‘+’ de la derecha del gráfico te permitirá agregar elementos para completar el gráfico con los que puedes probar e interactuar para lograr tu gráfico deseado.

5. El ícono del pincel que se encuentra debajo del signo ‘+’ te permite elegir el Estilo y Color del gráfico.

6. Para calcular la media aritmética de todas las temperaturas máximas puedes posicionar el cursor (con forma de cuz) en un casillero vacío, puede ser el inferior a todas las temperaturas máximas y luego hacer clic en Inicio/Autosuma/Promedio y aparecerá el promedio automáticamente en la celda seleccionada.

7. Para calcular la mediana de todas las temperaturas máximas puedes posicionar el cursor (con forma de cruz) en un casillero vacío, tal vez el que está debajo del promedio calculado y luego hacer clic en Inicio/Autosuma/Más funciones. Aparecerá una ventana y allí seleccionar Buscar una función, anotar Mediana/Ir/Aceptar y aparecerá el valor en el casillero vacío seleccionado.

8. El mismo procedimiento se realiza para calcular la moda (en este caso lo hice para la temperatura mínimas).

HISTOGRAMAS CON GEOGEBRA

1. Abrir GeoGebra online clásico y allí seleccionar Hoja de cálculo.

2. Copiar todos los datos en una sola columna o en una sola fila, se seleccionan todos y luego hacer clic en la pestaña Análisis de una variable (en el ejemplo copié la mayoría de los datos para que se puedan visualizar en la pantalla y no queden cortados)

3. Puede aparecer una gráfica de barras tal vez pero entonces al hacer clic en Histograma y luego en el ícono de ajustes

4. En Ajustes se puede realizar la Definición manual de clases, es decir la división de los datos en intervalos colocando el valor de Inicio y el Ancho del intervalo.

• Además, se puede seleccionar debajo Tabla de frecuencias y Polígono de frecuencias para que se vea en el gráfico.

• Al hacer clic en el símbolo de pantalla podrás Exportar como imagen para pegar luego en el lugar que se desea.

• Al hacer clic en el símbolo de sumatoria ∑x se muestran algunos parámetros de centralización y de dispersión.

Otras aplicaciones de Excel para estadísticas

d) Determinar la moda, mediana y promedio de velocidades y extraer una conclusión.

1) Ingresar los 30 datos en las celdas A1 hasta la A30 de la planilla de cálculo.

2) Para resolver la consigna (a) posicionarse en la celda A31 y luego ir a Modificar/Autosuma/Más funciones/CONTAR.SI allí se abrirá una ventana que te pedirá el rango, o sea de qué valores querés contar entonces anotás A1:A30 (es importante colocar los dos puntos (:) entre A1 y A30. Debajo pedirá el criterio, entonces anotas entre comillas “>100”. Eso significa que le estás p idiendo que cuente cuántos autos entre la celda 1 y la 30 tienen velocidades mayores que 100.

3) Registrar en la planilla de cálculo , en un costado, la respuesta obtenida en forma clara y completa.

4) Para calcular el porcentaje (consigna (b)) posicionarse en la celda B31 y anotar =(A31/30)*100. Esto te permite hacer el cociente entre la frecuencia relativa (calculada en la celda A31) sobre el total de valores y a todo eso multiplicarlo por 100 para calcular el porcentaje.

5) Registrar la respuesta a la consigna (b).

6) Para contestar la consigna (c) te desafío a hacerlo solo utilizando lo indicado en las consignas (2) y (4).

7) Para calcular la moda debes posicionarte en una celda de la columna A que esté vacía y luego ir a Modificar/Autosuma/Más funciones/Moda/Aceptar allí se abrirá un cuadro que nuevamente te pedirá entre qué casillas quieres calcularla (dice Número 1) allí anotas A1:A30 (no olvides colocar entre medio los dos puntos). Aceptar.

8) Para calcular la mediana debes posicionarte en otra celda vacía de la columna A y luego ir a la pestaña Modificar/Autosuma/Más funciones/Mediana/Aceptar. Nuevamente se abrirá otra ventana pidiendo entre qué celdas quieres calcularla así que nuevamente indicas A1:A30. Aceptar.

9) Para determinar el promedio vas a una celda vacía nuevamente y luego sigues los mismos pasos anteriores eligiendo Modificar/Autosuma/Promedio y allí se marcará un recuadro en la planilla de cálculo que deberás lograr que abarque las casillas A1 hasta la A30. Enter y aparecerá el promedio.

10) Anotar la conclusión pedida en la consigna (d) registrándola en la misma planilla de cálculo.

Fundamentales

• Ampliar los conocimientos acerca de la probabilidad, adquiriendo como herramienta la combinatoria.

PROBABILIDAD

Objetivos

Específicos

• Apropiarse de fórmulas de conteo, diagramas, y métodos propios de la combinatoria.

• Recordar conceptos y generalidades de la probabilidad básica.

• Utilizar los conocimientos de la combinatoria, para llegar a cálculos probabilísticos más complejos.

• Resolver problemas utilizando como herramienta la probabilidad.

• Ver un punto de unión entre la probabilidad y la estadística, como una colabora con la otra, y resolver problemas desde esa perspectiva.

Contenidos

Generales

• Combinatoria:

• Diagrama de árbol

• Combinaciones

• Variaciones

• Permutaciones

• Principio de multiplicación

• Actividades resueltas de combinatoria

• Probabilidad:

• Generalidades

• Ley de los grandes números

• Probabilidad y estadística

PRESENTACIÓN DEL CAPÍTULO

IFE

Gedeón y la probabilidad

• Visualizar el hecho de que la probabilidad es una herramienta muy útil para hacer predicciones en la vida cotidiana, pero Dios es mucho más grande que la probabilidad. Si en algún momento tenemos problemas, y nuestra probabilidad de éxito es muy pequeña, con Dios de nuestro lado se transformarán en grandes probabilidades. Él nos indicará la senda por la cual andar, antes que las predicciones de esta ciencia.

Orientaciones metodológicas particulares y estrategias

Se sugiere trabajar en resolución de problemas, en grupos, desarrollando todas las capacidades.

DISPARADOR

Página 227

1. Hay 5 posibilidades que se pueden elegir para la primer cifra del número. El siguiente número debe ser diferente al primero, por tanto quedan 4 opciones para elegir la segunda cifra y, siguiendo el mismo razonamiento, quedan 3 opciones para la tercer cifra del número. De esto se deduce que se pueden formar: 5.4.3 = 60 números con las 3 cifras diferentes usando los datos indicados.

2. Se deja a cargo del alumno y el grupo. Más adelante en el capítulo, se desarrolla el tema.

ACTUALIZA TU INFORMACIÓN

Página 228

Número: es un ente abstracto. Da una idea de cantidad.

Cifra: es cada uno de los caracteres del número.

Dígito: es un símbolo o guarismo utilizado para expresar un numeral o un número. Por ejemplo: 512 es un número. 5, 1 y 2 son las cifras del número. Es un número de 3 dígitos.

1. 24 opciones diferentes.

Página 229 ?

1. El primer cálculo, utiliza la fórmula, solamente que está más simplificado.

2. A cargo del alumno. 210

Página 231 ?

Simplificación. Se divide numerador y denominador por 4.3.2.1

ELECCIONES

Presidente

Angi

Claudio

Marcelo

Eliana

Angie

Carito

Claudio

Marcelo

Eliana Roy

1.

2.

3.

Página 232

1. 10! = 3 628 800

2. 6

3. En el (1) se usa la fórmula de permutaciones. En el (2) se usa el principio de multiplicación.

Página 232

a. C3 1560 = 1560! 3! . 1556! = 631 519 720

b. Para calcular la cantidad de ternas que incluyen a Andy calculamos las combinaciones para 1559 participantes y de la restamos al cálculo par 1560 concursantes.

C3 1559 = 1559! 3! . 1556! = 630 305 259

Al restar este valor a 631519720 obtenemos 1214461 que son las ternas que incluyen a Andy.

c. La respuesta (a) de Marina es correcta pero no la (b).

Página 235

1. a. Para formar una contraseña de 4 letras distintas es necesario tener en cuenta el orden en que se colocan. Por otro lado, tenemos 27 letras para formar grupos de 4. Por lo tanto, usamos la fórmula de variación.

V4 27 = 27! 23! = 421 200

Otra forma de razonarlo es que hay 27 opciones para elegir la primera letra, quedan 26 opciones para la segunda letra, 25 para la tercera y 24 para la última.

b. Como la última letra es A, ahora las variaciones son de 27 elementos en ternas:

V3 27 = 27! 24! = 17 550

2. Todo está correcto.

3. a. 8/20 = 2/5

b. 7/20

c. 5/20 = ¼

Página 237

1. Si ya salió 9 veces cara, es probable que, según la Ley de los grandes números, ahora salga número.

2. Lo más probable que puede suceder, dado que es especialista en lanzar penales, es “convierte el primero”, luego “convierte los tres”, y luego “convierte solo uno”. ¿Por qué? Si es especialista en lanzar penales, es más probable que convierta más de la mitad, es decir dos penales o tres, a que convierta solo uno. Por eso convertir solo una es la última opción. Pero entre que convierta los tres, y que convierta el primero, se cree más probable la segunda opción.

3. Los casos posibles de opciones para sentarse los 5 chicos son 120. Si las 2 chicas se sientan juntas quedan 3 asientos que pueden ser elegidos de 6 formas distintas. Por tanto, la “probabilidad” de que las chicas se sienten juntas es de 1/20.

LA ESENCIA DE LA MATEMÁTICA

Página 239

a. 32000 personas

b. “Van a pensar que la victoria sobre los madianitas será de ellos y no mía”.

Además E. de White en el libro Patriarcas y Profetas pág. 514, 515 explica:

"'Quien tema y se estremezca, que madrugue y regrese a su casa desde el monte de Galaad'. Los que no estaban dispuestos a arrostrar peligros y penurias, o cuyos intereses mundanos desviaban su corazón de la obra de Dios, no fortalecían en modo alguno a los ejércitos de Israel. Su presencia no podía ser sino causa de debilidad... Pero el Señor veía el orgullo y la incredulidad que había en el corazón de su pueblo. Incitado por las conmovedoras exhortaciones de Gedeón, se había alistado de buena gana; pero muchos se llenaron de temor al ver las multitudes de los madianitas. No obstante, si Israel hubiera triunfado, aquellos mismos miedosos se habrían atribuido la gloria en vez de adjudicarle la victoria a Dios."

c. PP 515, 516

"El carácter se prueba a menudo por los medios más sencillos. Los que en un momento de peligro se empeñaban en suplir sus propias necesidades, no eran hombres en quienes se podía confiar en una emergencia. El Señor no tiene en su obra lugar para los indolentes y para los que suelen complacer el apetito. Escogió a los hombres que no permitieron que sus propias necesidades les hicieran demorar el cumplimiento del deber. No solo poseían valor y dominio de sí mismos los trescientos hombres elegidos, sino que eran

también hombres de fe. No los había contaminado la idolatría. Dios podía dirigirlos, y por su medio librar a Israel. El éxito no depende del número. Tanto puede Dios libertar por medio de pocos como de muchos. No le honra tanto el gran número como el carácter de quienes le sirven."

d. Jueces 7:7 quedaron 300 hombres para la batalla.

e. Jueces 8:10 donde dice que quedaban aún 15000 hombres pero ya habían muerto 120000 así que el ejército tenía unos 135000 hombres al menos.

f. Jueces 8:28 “Así fue como Israel venció a los madianitas los cuales nunca más recobraron su poder” (TLA).

g. En Patriarcas y profetas pág. 518 leemos:

"El sistema más completo que los hombres hayan concebido jamás, si está privado del poder y de la sabiduría de Dios, resultará en un fracaso, mientras que tendrán éxito los métodos menos promisorios cuando sean divinamente ordenados, y ejecutados con humildad y fe. La confianza en Dios y la obediencia a su voluntad, son tan esenciales para el cristiano en la guerra espiritual como lo fueron para Gedeón y Josué en sus batallas contra los cananeos. Mediante las repetidas manifestaciones de su poder en favor de Israel, Dios quería guiarlo a tener fe en él, a buscar con confianza su ayuda en toda emergencia. Está igualmente dispuesto a obrar en cooperación con los esfuerzos de su pueblo hoy y a lograr grandes cosas por medio de instrumentos débiles. Todo el cielo espera que pidamos sabiduría y fortaleza. Dios “es poderoso para hacer todas las cosas mucho más abundantemente de lo que pedimos o entendemos”. Efesios 3:20"

Cuando Dios está al control y confiamos en su poder no hay probabilidad ni cálculo que lo pueda predecir, ni hay factores que puedan influir.

?

El Señor abre el entendimiento del investigador honesto. El Espíritu Santo capacita la mente para comprender las realidades de la revelación, y de ese modo la luz divina se comunica con el alma. En esto consiste el abrir los ojos para contemplar el tesoro genuino y así la mente se aferra a las glorias de un mundo mejor. El alma desea ardientemente la excelencia de Jesucristo.—Manuscrito 59, 1906. (Extraído de Exaltad a Jesús, 16/6)

Un punto en el cual muchos han errado ha sido el no ser cuidadosos en seguir las ideas de Dios sino las propias. Cristo mismo declaró: “No puede el Hijo hacer nada por sí mismo, sino lo que ve hacer al Padre”. Juan 5:19. Tan plenamente se despojó de sí mismo, que no hacía de por sí ningún proyecto o plan. Vivía aceptando los planes de Dios para él, y el Padre le revelaba sus planes día tras día. Si Jesús dependió tan plenamente que declaró: “Todo lo que veo hacer al Padre, eso hago”, ¡cuánto más deberían los agentes humanos depender de Dios en cuanto a la instrucción constante para que sus vidas pudieran ser simplemente la realización de los planes de Dios! Oh, si los mortales sujetos a equivocaciones se contentaran de buscar sabiduría de Dios... (Extraído del libro En los lugares celestiales 20/5 pág. 149)

Una relación con la probabilidad es que cuanto más aprendemos lo que Dios ha hecho por nosotros, más probabilidades tenemos de seguir sus caminos y ser más felices en esta vida.

ACTIVIDADES

Página 240

1. a. 5040

b. 120

c. 16

2. 12

3. a. 9999

b. 24

4. 16

5. a. 20

b. 25

6. 495

7. 336

Página 241

8. a. Un experimento determinista es aquel que si se lo repite con las mismas condiciones iniciales se garantiza el mismo resultado.

b. Se llama suceso elemental al formado por un solo resultado posible.

c. Un suceso es imposible si tiene probabilidad 0 de ocurrencia.

d. Un suceso es seguro si tiene probabilidad 1 de ocurrencia. Es decir, hay un 100% de probabilidad de que ocurra.

e. Si todos los sucesos elementales son igualmente probables, se denominan sucesos equiprobables.

9. a. No todas las caras tienen la misma probabilidad de caer, ya que no están en condiciones de igualdad de peso.

b. La cara que en su lado interior tiene un peso adicional (puede ser una bolita de papel), tiene menor probabilidad de salir, ya que por el peso tenderá a caer sobre la superficie y no quedará a la vista. Y la cara contraria a esa, será la que tiene mayor probabilidad de salir.

c. Una estrategia para averiguarlo es tirar el dado 10 veces y registrar las veces que sale cada cara. La cara opuesta a la que más veces salió, es probable que tenga el peso añadido.

10. Espacio muestral: {(b,n); (n,b); (b,r); (r,b); (b,v); (v,b); (b,b); (n,r); (r,n); (n,v,); (v,n); (n,n); (r,v); (v,r); (r,r); (v,v)}

Página 242

11. a. Extraer 2 canicas de una bolsa.

b. Espacio muestral: {(b, b); (b, c); (c, b)}

c. Yoherson extrae una canica blanca y Anlyé, una canica de color.

d. P = 2/3

12. a. E = {(cara, cara); (número, número); (cara, número); (número, cara)}

b. La probabilidad de que salgan 2 caras es 1/4 = 0,25; en cambio, la probabilidad de que salga un número y una cara es 2/4 = 1/2 = 0,5. Por lo cual es más probable que salga un número y una cara.

13. Al lanzar una moneda 4 veces, tengo 2 posibilidades para cada tirada: o sea 2.2.2.2 = 16 opciones.

C(4,2) = 6 son las posibilidades de que salga exactamente 2 veces número, por lo tanto, la probabilidad del total es 6/16 = 3/8 = 0,375

14. a.

E = {(1,c); (1,n); (2,c); (2,n); (3,c); (3,n); (4,c); (4,n)}

b. Hay dos sucesos (2, c) y (4, c). Hay un suceso (3, n)

c. P = 1/8 = 0,125

d. A invención de cada alumno.

15. C3 5 = 5.4.3! 2! . 3! = 10 este sería el espacio muestral. C3 4 = 4.3! 1! . 3! = 4 las opciones de ternas sin Roy.

Por lo tanto, la probabilidad de que Roy esté en el grupo electo es de 6/10 = 3/5 = 0,6

Página 243

16. Sí, porque ambos equipos tienen la misma probabilidad de que los toque iniciar el partico, o elegir cancha. P = ½ = 0,5.

17. La probabilidad de señalar una mujer que haya bebido limonada es de 36/110 = 18/55.

La probabilidad de señalar un varón que haya bebido gaseosa es de 38/110 = 19/55.

18. a. P = 1/10

b. P = 9/10

19. P = 70%. Porque son probabilidades complementarias. La ocurrencia de una, es la no ocurrencia de la otra. Ambas, deben sumar 100%.

20. Hay 9 posibilidades de que la suma sea menor o igual que 6. P = 9/21 = 3/7

Hay 12 posibilidades de que la suma sea mayor que 6. P = 12/21 = 4/7

Allí Carlitos tiene mayor probabilidad de ganar que Belén.

Si se le suma el tema del puntaje:

3.3/7 = 9/7

2.4/7 = 8/7

En ese caso, Belén tiene mayores posibilidades de ganar. No es un juego justo.

Página 244

21. Depende de cada grupo de alumnos.

Se obtuvo cara

No se obtuvo ni cara ni número

probable

Se obtuvo cara o número Muy probable

Se obtuvo cara y número Imposible

Se obtuvo número

b. Se puede deducir que hay 3 caras pintadas de violeta, 2 de rojo, y 1 de turquesa. Porque la frecuencia relativa del color violeta es aproxima a 0,5, es decir, la mitad de las caras del dado, 3. Y dado que la frecuencia relativa del color rojo, prácticamente duplica la del color turquesa, se deduce que hay 2 caras de rojo y 1 turquesa.

c. P = 2/6 = 1/3

24. Depende de la opinión de cada alumno.

Página 245

25. a. 2005: ¼; 2022: 4/5

b. P = ¼; P = 4/5

26. a. Puedo construir 4: 1x24, 2x12, 3x8, 4x6.

b. La diagonal es mayor a 13 cm solo en el rectángulo de 1x 24 pues, por Pitágoras, la diagonal es de 24,02 cm, por tanto la probabilidad es de 1/4 = 0,25.

27. E = {(c,c); (n,c); (c,n); (n,n)}

La probabilidad de que la segunda moneda caiga con la cara hacia arriba es de 2/4 = 1/2 = 0,5.

28. Si se tiene una variación V(m,n), eso significa que hay ‘m’ para la primera posición, ‘m–1’ para la siguiente, ‘m–2’ para la que sigue, hasta llegar a ‘m–n’ posibilidades para la última. El producto de todos estos factores determina la cantidad de variaciones que pueden obtenerse:.V = m.(m–1).(m–2)...(m–n).

29. a. 42/84 = ½

b. 53/84

c. 20/84 = 5/21

d. 27/84 = 9/28

DESAFÍOS

Página 246

1. A cargo del alumno.

2. V(18, 2) = 306

3. a. 177

b. 125/177

c. 12/177

d. 165/177

4. A cargo del docente del grupo y de los alumnos. Ninguna es incorrecta matemáticamente hablando. Una se ajusta a la definición clásica de probabilidad, y la otra a la Ley de los Grandes Números.

5. P(6) = 6! = 720

Página 247

6. a. ¼

b. 3/16

7. a. 2880

b. 6

8. Para formar números de 3 cifras con los 3 dados existen 6.6.6 = 216 opciones de números diferentes, es decir hay 36 posibilidades para cada número inicial.

Si 36 números comienzan con 4 tenemos 36/216 = 1/6 = 0,16666...

9. 1/25

10. a. Como la clave tiene que tener 6 caracteres que incluye 10 números, 10 símbolos y 27 etras mayúsculas y 27 minúsculas, tenemos un total 10+10+27+27 =74 opiones distintas para un único caracter. Para formar entonces una clave de 6 caracteres necesitamos multiplicar 6 veces 74, o sea 746 = 164 206 490 176 y esta es la cantidad de combinaciones posibles en una clave de 6 caracteres.

b. Como usará solo números primos: 1,2,3,5,7, solo las 27 letras minúsculas y los 10 símbolos no convencionales tenemos ahora 5+27+10 = 42 posibilidades diferentes para un único carácter de la clave. Las posibiles combinaciones para una clave de 6 caracteres es ahora de 426 = 5 489 031 74 posibilidades.

11. A cargo del alumno. El objetivo es que razone solamente.

Glosario

Se indican todos los símbolos utilizados en el libro (o al menos la mayoría) y su significado. Algunos pueden variar de la nomenclatura a la que están acostumbrados. Se intentó utilizar los símbolos lo más universales posibles, pero siempre hay variantes de país a país, de región a región, de autor a autor. No afecta al concepto matemáticos, por lo cual se expone allí para no crear confusión.

Bibliografía

Se brindan los principales textos consultados, aunque hay muchos otros, pero se brindan al menos estos para que el docente tenga acceso a más material en caso de necesitarlo.

PLAN DE LAS AUTOEVALUACIONES

El objetivo fundamental de este anexo es servir como apoyo al docente para evaluaciones rápidas, sencillas, de corroborar los conocimientos adquiridos en cada capítulo por el alumno.

Orientaciones metodológicas particulares y estrategias

Cada capítulo tiene una página de autoevaluación donde se tocan todos los temas.

Un ítem de verdadero o falso con justificación, un ítem de desarrollo, un ítem de opciones múltiples con justificación también, y una consigna de resolución de problemas.

Será útil realizar esto en la medida en que se hayan visto todos los contenidos del capítulo. Si no fuera así, se pueden utilizar solamente los ejercicios que tengan conceptos que se hayan visto, y utilizarlos como práctica.

Se puede: trabajar en ellos al final de dar cada tema, previo a la evaluación, como entrenamiento; o trabajarlo como ejercicios aislados; o trabajarlo en grupos. E

La idea de trabajarlo en grupos es: un alumno elige qué ejercicios darle a su compañero, y se distribuyen los ejercicios. Resuelven ayudándose entre todos, y luego intercambian resultados con otros compañeros para enriquecerse. De esa forma se evaluarán, compartirán, desarrollarán muchas habilidades como razonamiento, trabajo en equipo, evaluación, creatividad, abstracción, etc.

CAPÍTULO 1

Página 252

1. F. Al hacer la racionalización el resultado correcto es

F. Es como tener 6 + a + 6 – a = 12

F. Es racional que ya que es periódico (al menos eso parece con las cifras que se ven).

c.

Q = 314/100

Q = 8/2 = 4/1

I No se puede expresar como una fracción

Q = 1414285714/1000000000

I No se puede expresar como una fracción

Q = –2

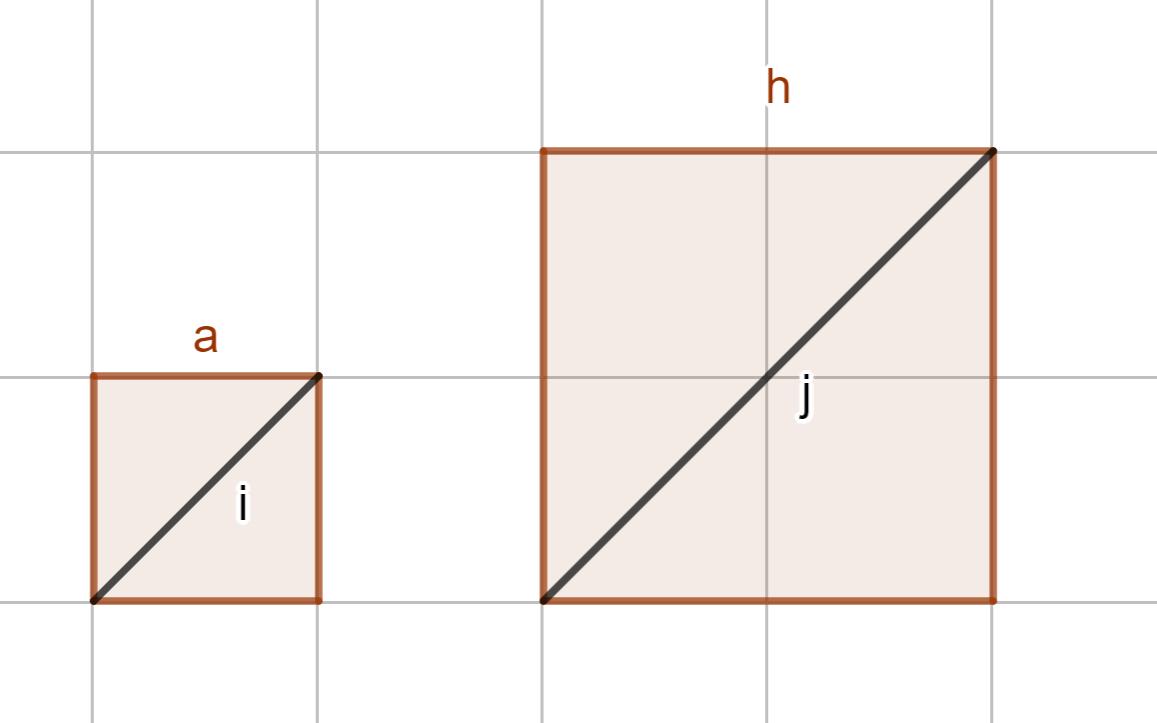
I No se puede expresar como una fracción

Q = 1/10

I No se puede expresar como una fracción

I No se puede expresar como una fracción

3. a. tercera opción

b. primera opción

c. primera opción

4. En el gráfico se ven dos cuadrados donde h = 2a Aplicando el teorema de Pitágoras en ambos tenemos;

Por lo que se demuestra que la diagonal ‘j’ es el doble de ‘i’

En el esquema también se puede comprobar.

CAPÍTULO 2 Página 253

1. V V V

2. a. … se sustituye la parte literal de la expresión por números determinados y se efectúan las operaciones indicadas en ellas.

b. El método de Ruffini se aplica para divisiones en las que el divisor es de la forma ax+b, y el método Horner se utiliza en divisiones en las que el divisor puede ser cualquier polinomio.

c. i. Para calcular el resto de una división cuando el divisor es del tipo ax+b.

ii. Para calcular algún coeficiente del dividendo sabiendo los demás coeficientes, el resto, el divisor del tipo ax+b

3. a. primera y segunda correctas.

b. tercera correcta.

c. primera y tercera correctas.

A + B + C = –4 + 15 + 16 = 27

CAPÍTULO 3 Página 254

1. F. El segundo signo debería ser +.

V.

F. El signo debería ser +.

2. a. A cargo del alumno (secreto: inventa primero un producto de dos polinomios cuyo resultado sea un polinomio de tercer grado, y listo).

b. Secreto: si los coeficientes no tienen divisor en común y todas las letras usadas son diferentes, ¡listo!

4.

c.

3. Segunda opción

CAPÍTULO 4 Página 255

1. F. (6; 0) es la solución.

F. Las ecuaciones del sistema son equivalentes. Sí tiene solución: infinitas soluciones de hecho.

V. Al ser equivalente puede reemplazarse la ecuación en el sistema sin que altere el resultado.

2. a. Secreto: si empiezas con un bosquejo gráfico, es más fácil.

b. Secreto: para que sea incompatible, puedes pensar en dos funciones lineales paralelas (igual coeficiente lineal o pendiente).

c. Secreto: tienes la incógnita “y” despejada en una ecuación. S. {(9; 4)}

3. a. Tercera opción.

b. Segunda opción.

c. Las tres opciones están bien.

4. 23 monedas de Bs 1, y 177 monedas de Bs 2.

CAPÍTULO 5 Página 256

1. V. Es de la forma f(x) = ax2 + bx

V. Si la parábola tiene el vértice en el primer o segundo cuadrante y las ramas o brazos se extienden hacia arriba, no tendrá intersección con el eje ‘x’, por lo tanto, no tiene raíces reales.

F. En este caso el vértice es la única raíz real de la parábola.

2. a. La otra raíz es x = 9 ya que ambas raíces equidistan del eje de simetría.

b. Si se usa la expresión factorizada de la función y se cambia el coeficiente principal se obtienen infinitas funciones de segundo grado con las mismas raíces y el mismo eje de simetría. f(x) = a(x + 1) (x – 9)

c. La fórmula es i(x) = 2(x+1)(x–9) y el vértice es V = (4;–50)

3. a. Primera opción.

b. Todas son incorrectas.

c. Primera y tercera opción.

4. a. 2500 = x2+(x+10)2 = 2x2+20x+100 = 2(x2+10x+50)

Para calcular ‘x’ uso la ecuación 0 = 2x2+20x – 2400 x1 = 30 x2 = –40 (este se descarta) Por lo que se deduce que el lado del cuadrado más pequeño es x = 30 m

b. Perímetro = 3.30 m + 3.40 m+ 10 m = 220 m

CAPÍTULO 6 Página 257

1. V. V.

F. Para que dos polígonos sean semejantes, además de una razón de semejanza, entre las longitudes de los lados, debe tenerse en cuenta que los ángulos correspondientes son congruentes.

2. a. Sí. Al realizar una homotecia, siempre se obtiene una figura semejante.

b. Ambas dos están correctas.

c. Si dos rectas son cortadas por un conjunto de rectas paralelas, la razón entre las medidas de dos segmentos determinados en una de las rectas es igual a la razón entre las medidas de los segmentos correspondientes a estos dos de la otra recta.

3. a. Tercera opción.

b. Primera opción.

c. Tercera opción.

4. x = 6, y = 12

CAPÍTULO 7 Página 258

1. a. F. Si los ángulos crecen de 0° a 90° es cierto que el seno de dichos ángulos aumenta de 0 a 1. Pero para si los ángulos crecen entre 90° y 180° el seno de dichos ángulos disminuye de 1 a 0.

b. F. Si los ángulos crecen de 0° a 90° el coseno de dichos ángulos disminuye de 1 a 0. El coseno de ángulos superiores a 90° y menores que 180°, toman valores comprendidos entre 0 y – 1

c. F. La tangente aumenta siempre desde –∞ a +∞.

2. a. 77°

b. 8,8388 cm

c. A cargo del estudiante.

3. a. Segunda opción.

b. Cuarta opción.

c. Segunda opción.

4. Se encuentra a 26,124 m del árbol.

CAPÍTULO 8 Página 259

1. F. La moda es el valor de mayor frecuencia. Si en esa variable, la mayor frecuencia es la persona más baja, esa será la moda.

F. La media es el cociente entre la suma de los valores de todos los datos registrados y la cantidad de datos (o de registros tomados). En cambio la mediana es el valor que está exactamente en el medio cuando todos los datos están ordenados de forma creciente o decreciente.

V. Seguramente sí. Ambos sirven para representar una variable discreta.

2. a. La suma de todas las frecuencias relativas de una tabla, siempre suman 1 porque representan la centésima parte del 100% de la suma de las frecuencias porcentuales.

b. No siempre. Puede suceder que los datos sean números naturales, pero al calcular la media resulte un número racional.

c. A cargo del estudiante.

3. a. Segunda opción.

b. Tercera opción.

c. Primera opción.

4. a. Si trabaja con intervalos, usaría el histograma.

b. Pictograma, gráfico de barras o gráfico circular.

CAPÍTULO 9 Página 260

1. F. La probabilidad siempre es un valor comprendido entre 0 y 1. Si es 0 trata de un suceso imposible, y si es 1 se trata de un suceso seguro.

V. F. Eso indica que, tomando en cuenta otros momentos del pasado con iguales condiciones a las de este evento, se dio que en 9 de 10 de ellas hubo lluvia. Eso no indica que sea un evento seguro, en este caso la probabilidad debería ser de un 100%.

2. a. Si el número está comprendido entre 100 y 300, entonces solo puede comenzar con 2 en base a los dígitos que pueden usarse. Si comienza con 2 y todas las cifras del número son distintas, entonces quedan 3 posibilidades para el siguiente dígito y 2 posibilidades para el último dígito del número. Por lo tanto, son 3.2 = 6 los números que pueden formarse de 3 cifras con esas condiciones.

b. Con los dígitos 1, 2 y 3 se pueden formar 3.3.3.3.3 = 243 números de 5 cifras. Son pares los que terminan en 2, por lo cual los números pares son un total de 3.3.3.3 = 81 de los 243 originales.

c. Experimento aleatorio es aquel en el que se conocen todos los resultados posibles pero sin tener la certeza de cuál será un resultado particular (lanzar un dado, una moneda, etc.). Experimento Determinista es aquel en el que se sabe con certeza cuál será el resultado.

3. a. Segunda opción.

b. Segunda opción.

c. Segunda opción.

4. El espacio muestral aparece en la tabla. La probabilidad de obtener como resultado de la multiplicación de los valores obtenidos en los dos dados es de 4/36 = 1/9 (con los cuadros sombreados de naranja del espacio muestral)

ANEXO

Ventura es una aplicación desarrollada por el equipo del Portal de Educación Adventista y ACES Educación, basada en el contenido de los libros didácticos, con el objetivo de que el docente pueda utilizarla para evaluar los aprendizajes de sus estudiantes.

Este documento explica paso a paso cómo utilizar Ventura. Si ha utilizado alguna vez aplicaciones similares, como por ejemplo, Kahoot!, le será más fácil aprender a utilizar Ventura.

Requisitos mínimos:

• El docente y los estudiantes jugadores deben encontrarse en la misma habitación

• Computadora del docente con acceso a Internet

• Proyector conectado a la computadora del docente

• Pantalla de proyección

• Teléfonos o dispositivos móviles personales de los estudiantes, conectados a Internet vía Wi-Fi o por medio de la red de telefonía móvil.

Paso a paso:

Ejemplificaremos con un Ventura preparado para la clase de Matemática3

1. Desde la computadora del docente, acceda a http://educacion.editorialaces.com/contenidodigital/matematica-3/

2. Debajo de la descripción del libro didáctico está la sección “Contenido Digital”. Toque en la pestaña “Juegos”.

3. Haga clic en “Polinomios – Matemática 3” o en el botón “Ver”

4. Haga clic en “Jugar”.

5. Después de configurar la sala de espera, haga clic en “Crear Ventura”.

(Los pasos 1 a 5 se resumen en el siguiente video):

6. Una vez creado el Ventura, proyectar la siguiente pantalla y anunciar a los jugadores que ya pueden leer el código QR para ingresar a la sala de espera del Ventura.

7. A medida que los jugadores van leyendo el QR deberán colocar un alias (nombre de jugador) y esperar a que inicie el juego.

Cuenta regresiva

Código QR para escanear

Alias de los jugadores

8. Cuando la cuenta regresiva concluya, aparecerá en pantalla la primera pregunta del juego. Los jugadores deben leer la pregunta en la pantalla de proyección y contestar tocando la pantalla de su dispositivo o teléfono, según el color de la opción que consideren correcta, antes de que se acabe el tiempo para responder.

Proyector (docente)

Teléfono (jugador)

9. Al finalizar el tiempo para cada pregunta, Ventura muestra dos pantallas. La primera es la estadística de las respuestas y la segunda es la tabla de jugadores con el puntaje más alto.

Respuesta correcta

10. Al responder todas las preguntas, se muestra la tabla de jugadores final. El ganador aparece en primer lugar en la tabla. El Ventura ha finalizado.