Guía docente



El libro didáctico es un gran aliado del docente en la presentación de los contenidos en el aula. Por eso, la importancia y necesidad de utilizar libros adventistas se hace cada vez más presente. Desde hace años ACES Educación dedica esfuerzo, estudio, recursos y sobre todo oración en la creación y producción de material didáctico coherente con la filosofía adventista. Este es el desarrollo de un proyecto que pretende colaborar con la tarea de cada docente de matemática para estudiantes de quinto grado.
La epistemología estudia el modo como una persona adquiere el conocimiento. Para la educación adventista, el conocimiento tiene su origen en la fuente de toda sabiduría: Dios.
La Biblia es la base de la comprensión en los diversos campos de estudio, y estos iluminan el estudio de la Biblia. La serie de libros de Matemática promueve un aprendizaje acorde a la filosofía y los valores cristianos, así como de los requerimientos curriculares.
Ver pp. 6 y 7 del libro para el estudiante:

Ver pp. 4 y 5 del libro para el estudiante:

Hay que recordar que ningún libro didáctico contiene todo el conocimiento necesario para el desarrollo del estudiante, pero para muchas personas es la principal fuente de investigación y sistematización.
El uso del libro didáctico permite abrir discusiones relevantes que lleven a los estudiantes a percibir el entorno social con visión crítico-cristiana y construir valores y principios.
En esta propuesta se trata de convertir el aula en un espacio en el que los alumnos aprendan a mirar la realidad matemáticamente, entrar en la lógica del pensamiento y del lenguaje matemático. “Hacer matemática” en la escuela implica generar una actividad de reconstrucción de conocimientos que permita a los alumnos confiar en sus posibilidades y capacidades dadas por Dios para resolver problemas y disponer de saberes matemáticos. Estos van a depender de las experiencias de conocer y utilizar los conocimientos matemáticos. Según el Prof. Adrián Paenza:
“La matemática no está hecha para ser observada, ni para ver lo que hicieron otros (y finalmente frustrarse con eso). No. A la matemática hay que hacerla, transformarla, mejorarla, cambiarla. Y eso solamente se consigue estimulando la creatividad”.
Además, es imprescindible plantear un proyecto de enseñanza que involucre a los alumnos en procesos de producción de conocimientos, mediante situaciones que les permitan pensar, ensayar, explorar, representar, argumentar, discutir, poner en juego lo que saben, comunicar ideas, aceptar las ideas de otros…Y es allí donde resulta esencial la
intervención de los docentes para que los conocimientos que circularon en la clase se reconozcan como saberes matemáticos.
La intención es que el estudiante reconstruya el saber social y científico a través de los desafíos y problemas planteados que le brindan las condiciones que permitan esta reconstrucción desde diferentes perspectivas, lo que permitirá construir conocimientos cada vez más ajustados a los saberes.
Concibiendo que aprender matemática, implica resolver problemas y reflexionar acerca de ellos, es tarea del docente seleccionar propuestas de trabajo, organizar discusiones y analizar diferentes aspectos de la producción. El libro didáctico es un recorte de saberes y estrategias que acompañan la tarea docente, pero no la reemplazan.
En toda situación de enseñanza, la intervención docente estará orientada a organizar espacios de participación de los alumnos, promoviendo que expliciten, justifiquen y validen sus producciones, a la vez que se desarrollan hacia un aprendizaje cada vez más autónomo.
“La evaluación es un proceso esencial para el desarrollo y formación del ser humano. Debe ser un proceso integral que permita valorar no solo el conocimiento y las habilidades sino también la capacidad para aplicar conceptos matemáticos en situaciones prácticas.”
Enfoques a tener en cuenta:
• Evaluación formativa: evaluar de manera continua a través de observaciones diarias, pruebas cortas, ejercicios y actividades grupales.
• Evaluación sumativa: proyectos, trabajos prácticos y exámenes de aplicación de conceptos matemáticos en situaciones reales.
• Autoevaluación y coevaluación: reflexión individual que fomente la responsabilidad sobre su aprendizaje y actividades donde los compañeros brindan retroalimentación constructiva.
• Resolución de problemas: Evaluar la capacidad de los estudiantes para explicar sus razonamientos y procesos.
• Retroalimentación constante: destacar logros y reforzar aspectos que necesiten mejoría.
• Apuntes de clase (Máster en Didáctica de la Matemática Infantil y Primaria).
• La naturaleza y desarrollo del pensamiento lógico matemático. Pensamiento lógico matemático en Educación Primaria.
• Desarrollo del pensamiento lógico-matemático a través de la resolución de problemas. Pensamiento lógico matemático en Educación Primaria.
• El número natural y su didáctica. Aritmética, Algebra y medida. El juego.
• Máster en Didáctica de la Matemática Infantil y Primaria. Enseñanza y aprendizaje de los números racionales. Aritmética, Algebra y medida. El juego.
• Brinnitzer, Evelina y otros. El juego en la enseñanza de la matemática. Novedades Educativas. 2015
• Díaz, Adriana. Aventura Matemática. Aique primaria. 2013
Enlaces:
• Currículo de Educación Primaria (Perú)
Fundamentales
• Leer, escribir, comparar, descomponer números naturales.
Generales
• Sistema de numeración decimal
• Valor posicional
• Lectura de números naturales
Específicos
• Leer, escribir y comparar números teniendo en cuenta el valor posicional y relativo de las cifras.
• Componer y descomponer números de manera multiplicativa y sumativa.
• Escribir los números naturales de forma ascendente y descendente.
• Escribir y descubrir escalas numéricas y uso la recta numérica. Leer, escribir y comparar números romanos.
• Dios cuida de ti
• Composición y descomposición de números naturales
• Valor posicional, relativo y absoluto
• Comparación de números
• Recta numérica
• Redondeo y aproximación
• Escala ascendente y descendente
• Sistema de numeración no posicional: romanos
• Tabla de resta y suma en números romanos
Orientaciones metodológicas particulares
La enseñanza de los números naturales en quinto grado de primaria debe iniciarse con una comprensión sólida del sistema de numeración que los organiza. Es fundamental que los estudiantes se familiaricen con los números, consolidando su manejo y comprensión para que puedan apreciar plenamente su alcance. Este proceso de aprendizaje no solo debe enfocarse en la adquisición de conocimientos abstractos, sino también en su aplicación práctica.
En este sentido, el capítulo aborda distintos usos de los números naturales, como la descomposición y la comparación de números. Estas habilidades son cruciales para que los estudiantes interpreten y utilicen los números en una variedad de contextos. Además,
se subraya la importancia de enseñar los números naturales de manera contextualizada, utilizando ejemplos de la vida cotidiana para que los estudiantes de quinto grado no solo comprendan los conceptos, sino que también valoren su aplicación práctica en su día a día. Este enfoque integral asegura que el aprendizaje sea significativo y relevante para los alumnos, preparándolos para utilizar los números de forma efectiva en múltiples situaciones.

Estrategias sugeridas
Actividades previas
Páginas 8 y 9. Circuito de salud: Rayuela. El juego en la enseñanza de las matemáticas es crucial porque facilita la comprensión de conceptos abstractos a través de la experiencia práctica y el pensamiento lúdico. A través del juego, los estudiantes desarrollan habilidades de resolución de problemas, refuerzan su capacidad de razonamiento lógico y experimentan el aprendizaje de manera activa y divertida. Además, el juego fomenta la colaboración y el pensamiento crítico, convirtiendo el aprendizaje en una actividad atractiva y accesible para todos los alumnos.
Es importante que como maestro, usted prepare el escenario en donde trabajará con sus estudiantes, el enfoque que se hace en estas dos páginas hacen referencia al cuida de la salud, es importante que mediante esta situación de “juego” se aprenda sobre matemáticas pero también sobre el cuidado de la salud.
Página 10: Sistema de numeración decimal. Este sistema permite a los estudiantes comprender la organización y el valor posicional de los números, facilitando operaciones matemáticas como suma, resta, multiplicación y división. Además, es clave para el desarrollo de habilidades matemáticas más avanzadas, asegurando una sólida base en el aprendizaje numérico. Se plantea un juego en donde los estudiantes deben poner a prueba sus conocimientos previos. Existen materiales que puede utilizar o crear según el contexto en donde se encuentre:
• 10 tarjetas con números del 0 al 9 para cada participante (Recortables, p. 197)
• 12 tarjetas con instrucciones (Recortables, p. 197)
Al terminar esta actividad, desafíe a sus estudiantes a crear otros ejercicios que los ayuden a profundizar lo trabajado en clase.
Página 12: Valor posicional. En esta página se plantean datos de cantidad de habitantes de Sudamérica; sin embargo, existen otros países que pueden ser investigados por sus estudiantes y conocer más sobre la cultura de ellos. En esta situación se plantea que los estudiantes puedan realizar la descomposición de los números y también la lectura.
Actividades complementarias
Páginas 12 a 14: Valor posicional. Se sugiere que se tenga un material concreto en el aula, que sea manipulado por el estudiante y lo ayude con la lectura de los números. Puede hacerlo del material más adecuado a su contexto y realizar la lectura usando este modelo:
Otra dinámica que puede utilizar para lectura es la de la construcción de números comenzando con un dígito, luego va aumentando la cantidad. Por ejemplo:
3: tres
32: treinta y dos
324: trescientos veinticuatro
3 245: tres mil doscientos cuarenta y cinco
32 456: treinta y dos mil cuatrocientos cincuenta y seis
324 567: trescientos veinticuatro mil quinientos sesenta y siete
3 245 678: tres millones doscientos cuarenta y cinco mil seiscientos setenta y ocho
Página 17: Juego en el patio. La siguiente imagen ilustra cómo organizar el patio de la escuela, en donde los estudiantes podrían lanzar tapitas, piedritas, etc y, dependiendo el área en donde caigan, obtendrán diferentes puntajes. El docente puede definir el código de color-puntaje; es importante que mencione los colores o formas que puede cada área. Lo importante de esta estrategia es que los estudiantes asimilen los nombres de cada área; es decir, cada figura geométrica, y puedan calcular su propio puntaje, a fin de que desarrollen estrategias para obtener el mayor puntaje posible con la menor cantidad de fichas posible.
Página 22: Sucesión numérica. Ordenación ascendente y descendente. Otra estrategia es preparar tarjetas con números de la misma cantidad de cifras para entregar por grupos. Luego, dar la consigna de ordenarse de manera descendente o ascendente. Esto ayuda a que los estudiantes puedan tener una buena organización, buscar estrategias diversas y divertirse mientras aprenden.
Recursos extra
• Aplicación Number Line.
• Actividades con números romanos.

Página 20: Recta numérica. La aplicación Number Line (ver Recursos extra) ayuda a los estudiantes a visualizar secuencias numéricas e ilustrar estrategias para contar, comparar, sumar, restar, multiplicar y dividir. Puedes elegir líneas numéricas etiquetadas con números naturales, enteros, fracciones. También se puede utilizar una línea numérica personalizada, con o sin marcas de escala, y que cada estudiante establezca su propio intervalo.
Página 24: Números romanos. Trabajar con números romanos refuerza la comprensión de conceptos matemáticos básicos, como la secuencia numérica y la adición. También ayuda a los estudiantes a practicar el reconocimiento y la representación de números en diferentes sistemas numéricos. Compartimos un enlace con actividades adicionales (ver más arriba Recursos extra).

Contenido digital ACES (p. 27)
Repasen los contenidos del capítulo 1 mediante la siguiente actividad interactiva sobre números naturales. Indique a los estudiantes que escaneen el código QR de la p. 27 o visiten el enlace http://aeoda.net/2001
Actividades de cierre

Al final de cada capítulo se presenta la sección Aplico, en donde los estudiantes pondrán en práctica todo lo aprendido, además de realizar una autoevaluación.
Fundamentales
• Resolver problemas a través de la adición, sustracción, multiplicación y división y la aplicación de sus propiedades.
Generales
• Resolución de problemas
• Operaciones y propiedades
Específicos
• Reconocer las propiedades de la suma, resta, multiplicación y división y saber aplicarlas en la resolución de situaciones problemáticas.
• Identificar múltiplos y divisores de un número.
• Identificar y crear series numéricas a través del patrón adecuado.
• Elaborar problemas sencillos con datos proporcionados.
• Resolver ecuaciones e inecuaciones sencillas.
• Calcular los múltiplos y divisores de un número aplicando los criterios de divisibilidad, y realizando factorización de números.
• ¿Acaso hay algo imposible para Dios?
• Propiedades de la adición y la sustracción
• Propiedades de la multiplicación y la división
• Multiplicación y división por la unidad seguida de ceros
• Criterios de divisibilidad
• Múltiplos y divisores
• Múltiplo y divisor común
• Números primos y compuestos
• Factorización
• Operaciones combinadas
• Ecuaciones e inecuaciones
• Patrones y seriaciones
Orientaciones metodológicas particulares
Es recomendable alternar entre métodos concretos, pictóricos y abstractos para consolidar los saberes y el aprendizaje. A continuación se comparten conceptos que sientan las bases de las operaciones y que necesitamos tener presente aun cuando trabajamos con grados avanzados de la escolaridad.
Significado de adición. En la concepción unitaria de la adición hay una cantidad inicial que experimenta un cambio al añadirle una segunda cantidad. El resultado es el incremento de la segunda cantidad sobre la primera.
En la concepción binaria de la adición hay dos cantidades que tienen asignado el mismo pa-
pel. Se realiza una unión o combinación de las dos cantidades que permite llegar al resultado.
Significado de sustracción. En la concepción unitaria de la sustracción hay una cantidad inicial que sufre un cambio al quitarle una segunda cantidad. El resultado es la disminución de la segunda cantidad sobre la primera.
En la concepción binaria de la sustracción hay dos cantidades que tienen asignado el mismo papel. Se valora lo que hay en el todo y en una de las partes, lo cual permite conocer lo que hay en el complemento.
Estrategias aditivas
• Contar todo: Por ejemplo, se colocan 3 objetos. Se añaden 4 objetos, la otra cantidad, y por último se cuentan todos los objetos.
• Partir del primer sumando: Se representa el primer sumando con objetos (3), y se cuenta, a partir de ese número, la otra cantidad (4), evitando contar los tres primeros.
• Partir del sumando mayor: Identifica el sumando mayor y lo representa con objetos (4) y se cuenta a partir de ese número (5, 6 y 7).
Las últimas dos estrategias también sirven para cálculos mentales.
Estrategias sustractivas
• Quitar: Se colocan (7) objetos, se seleccionan (4) que se pierden, se cuentan todos los que quedan. (3).
• Emparejamiento: Se coloca en dos filas paralelas el minuendo y sustraendo y se cuentan los objetos de la fila más grande no emparejados.
Acciones
Hay multitud de acciones que dan sentido a las operaciones aditivas: agregar, acumular, ampliar, añadir, aumentar, dar, disminuir, quitar, recibir, reducir, regalar, retirar, etc.
Estas acciones son muy elementales y los niños entran en contacto con ellas desde una edad muy temprana. Una misma acción puede dar lugar a una adición o una sustracción, por lo que es importante trabajarla con los alumnos en ambos casos.
Enseñanza de la estructura multiplicativa
El aprendizaje de la multiplicación de números naturales requiere de un dominio de la estructura aditiva y de su comprensión.
Los esquemas multiplicativos surgen de la modificación de los esquemas previos de contar y de la ampliación de las relaciones aditivas.
Para el caso de la división, los estudiantes pueden resolver con anterioridad sencillos problemas de división mediante una estrategia de sustracción repetida. La división puede proceder de situaciones simétricas o asimétricas.
La multiplicación
• Multiplicación como suma repetida: la suma es una operación aritmética básica y, a partir de ella, se pueden definir otras operaciones.
• Multiplicación como producto cartesiano: la multiplicación puede definirse como una nueva operación sin acudir a la operación de adición.
La división
La división de números naturales puede ser considerada como una operación en sí misma con características propias que se aplica a la resolución de determinados problemas, entre los cuales están los relativos a repartos equitativos.
Aritmética del número natural. Tech. Apuntes.
Estrategias sugeridas

Actividades previas
Páginas 28 y 29. El capítulo comienza con la adaptación de un desafío planteado por el matemático argentino Adrián Paenza, ya citado en esta guía (ver p. 4).
Pensando en esta premisa es que se propone el desafío “El puente difícil de cruzar” que permite pensar e imaginar posibles soluciones haciendo hincapié en los procesos de pensamiento matemático. Aquí lo importante es la posibilidad de crear estrategias de resolución.
Por experiencia hemos visto en diferentes ocasiones que adultos han necesitado “representar” el problema. El caminar de un lado a otro simulando un puente y haciendo los cálculos en grupo ayuda a la resolución.
Solución: El puente difícil de cruzar (p. 28)
En el primer viaje van los estudiantes 3 y 4 tardan 2 minutos
Vuelve el estudiante 4 tarda 2 minutos
Cruzan los estudiantes 1 y 2 tardan 10 minutos
Vuelve el estudiante 3 tarda 1 minuto
Cruzan los estudiantes 3 y 4 tardan 2 minutos
2 + 2 + 10 + 1 + 2 = 17 minutos
La segunda página acompaña con otro desafío “La carrera” y la importancia de seguir pasos que ayudan a ordenar y resolver situaciones problemáticas.
Solución: La carrera (p. 29)
1. Juana
2. Daiana
3. Melina
4. Yeni
5. Andrea
Actividades complementarias
Página 30. En esta página se invita a la revisión de los datos que aporta una situación problemática.
En ocasiones, los docentes presentamos problemas lo más claros posibles, de modo que el estudiante pueda comprender fácilmente la pregunta planteada. Aquí se espera que los propios estudiantes puedan discernir entre los datos que aporta un problema para su resolución y aquellos que no; o incluso si no aporta datos suficientes.
Una actividad para entender la importancia de ordenar la información que aporta un problema, o analizar los datos es la siguiente:
Separar en frases o partes 2 o 3 situaciones problemáticas diferentes y mezclarlas. Proponer a los estudiantes que “armen” el problema con las piezas adecuadas y lo resuelvan.
Por ejemplo:
Los chicos repartieron invitaciones para una feria de salud.
¿Cuánto pesa cada costal de harina integral?
Amelí repartió 126 tarjetas, David 198 y Andrea 143.
Tenían 550 invitaciones.
Una camioneta cargada de 75 costales de harina integral pesa 4 300 kilos.
¿Cuántas invitaciones quedaron sin repartir?
Sin los costales de harina pesa 2 500 kilos.
Páginas 31 a 34: Operaciones y propiedades. La página 31 propone actividades generales, introduciendo al tema de las operaciones. Se sugiere repasar los términos de cada operación antes de trabajar con los problemas que se presentan en estas páginas, ya que en la página 33 se repasan únicamente los elementos de la resta.
Términos de la suma
125
Sumando + 64
189
Sumando
Suma o total
Términos de la multiplicación 8 Factor x 3
Términos de la resta
185 Minuendo - 40 Sustraendo 24
Diferencia
Términos de la división
Dividendo (cantidad a repartir) 12 6
Resto (cantidad que sobra) 0
2
Divisor (partes a repartir)
Cociente (cantidad que toca a cada parte)
A través de situaciones problemáticas, en estas páginas se presentan las propiedades de las cuatro operaciones básicas. Entenderlas y aplicarlas facilita la resolución de problemas.
Entre las propiedades de la multiplicación encontramos la propiedad anulativa que también es conocida como propiedad de absorción. Recordamos que los términos utilizados en el libro en ocasiones no son específicos de un país.
En el primer problema (p. 32) pueden observarse los cálculos realizados de 3 maneras diferentes, aplicando las propiedades. Éstas se desarrollan luego, al final de la página, pero aquí se solicita poder observar y comparar los resultados como actividad de conflicto cognitivo. Se genera la necesidad de poder entender la diferencia entre los cálculos planteados. Es probable que los estudiantes tengan sus propias hipótesis aun cuando no reconozcan que están infiriendo las propiedades.
Recursos extra
• Números reales y propiedades de las operaciones.

Páginas 36 a 38: Múltiplos y divisores. Como muchos saberes matemáticos, los múltiplos y divisores se van desarrollando de manera espiralada a través de los años de la escuela primaria. En este capítulo se presenta una actividad esperando que los estudiantes puedan resolver recordando estos saberes. Luego se retoma la teoría para reforzar los conceptos.
En primer término se presentan situaciones problemáticas para trabajar el concepto de múltiplos y divisores y luego ejercitación para descubrir múltiplos y divisores comunes.
En este juego deben clasificar los números según sean múltiplos de 3, 7, 8 y 11. Son números de 2 y 3 cifras.
Este es un juego que se puede adaptar para hacerlo en el aula con diferentes “cajas” de múltiplos y diversos números de más cantidad de cifras. Recordemos que el juego es un recurso importante que puede usado en diversos momentos de las clases.
Al finalizar la página 38 se propone un juego en ronda. Es recomendable que primeramente se juegue con consignas más sencillas. Al tener que evitar decir un número, es mejor practicarlo antes con algo más fácil.
Por ejemplo “no decir números que lleven 5”. Se repite la secuencia numérica: 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 17…” pero se saltean los números con 5. Así se puede modificar consignas aumentando la dificultad hasta llegar a las propuestas en el libro.
Este juego se propone para repasar múltiplos y múltiplos comunes. Por cuestiones de espacio se proponen unas pocas consignas de ejemplo, pero la versatilidad del juego permite adaptarlo a cualquier necesidad con respecto a la adquisición de los saberes planteados. El lugar del juego en la presentación del capítulo tiene una intencionalidad de repaso de saberes, pero es de libre uso el momento pedagógico y la intencionalidad que cada docente desea aplicar en función de sus estudiantes.
Contenido digital ACES (p. 36)
Sugiera a los estudiantes la actividad interactiva. Pueden escanear el código QR o bien visitar el enlace corto: http://aeoda.net/2002
Página 39: Números primos y compuestos. Se propone descubrir una frase oculta encontrando los números primos.
Solucionario (p. 39)
La respuesta es: ESPERANZA
4 en línea. Este juego es dinámico y divertido. Es importante aclarar que los broches pueden colocarse ambos en el mismo factor también.
Al mover solo uno de los factores debe ir repasando las tablas para pensar en un producto que aun no se ha marcado que incluya uno de los factores y buscando que pueda dejar en línea 4 fichas propias.
Por ejemplo, en el siguiente tablero se observan marcados los números 2; 6; 8; 10; 16. Para llegar a estos productos podría haberse iniciado con los broches en los números 1 y 2. Luego se corre el broche del 1 al 3 y se obtiene el 6. Si se corre el broche del 3 al 4 se obtiene 8 (ya que el otro broche continúa en el 2). Si el broche se corre del 4 al 5 se marca el 10, y del 5 al 8 se marca el 16.
En el ejemplo la ficha amarilla en el 8 está bloqueando la posibilidad de hacer 4 en línea 2 – 8 – 16 – 27.
Tablero de productos:
Tira de factores:
La recomendación en todos los juegos es que el docente los juegue primero.
Página 42: Criterios de divisibilidad. Los criterios de divisibilidad son pautas que nos permiten saber rápidamente si un número es divisible por otro. Esto permite resolver las divisiones con mayor facilidad, o rapidez, así como saber los divisores de un número. Es importante que recordemos que el 1 tiene un solo divisor, ya que es divisible solamente por sí mismos. El 0 tiene infinitos divisores, ya que se puede dividir por todos los números y siempre se obtiene 0.
Para saber si un número es divisible por 7 o por 8, aplicar el criterio correspondiente es más complejo que con los demás números. Sugerimos presentar muchos ejemplos o realizar varias comprobaciones para recordarlo. Generalmente los criterios de divisibilidad del 2 al 6 son los más recordados. Ejercitar permite afianzar los saberes.

Página 43: Cartas divisoras. En este juego los estudiantes participan utilizando no solo sus conocimientos sino también su cuerpo. Esto lo hace más divertido y favorece el aprendizaje. Es una adaptación del juego de la silla, al moverse de silla los participantes, el estudiante que está sin silla puede conseguir un espacio. En el libro se propone una sola opción, en la que las cartas contienen números menores al 50. Esta puede ser adaptada a diferentes necesidades, comenzando en primer término por números hasta el 10, utilizando números mayores, o buscando divisores comunes. Las cartas pueden ser entregadas por el docente, o escritas por los estudiantes, dando así la posibilidad de pensar números que les permitan conservar su silla.
Página 46: Ecuaciones e inecuaciones. Las ecuaciones y las inecuaciones respetan el mismo procedimiento para su resolución. La diferencia fundamental radica en que las ecuaciones representan una igualdad y las inecuaciones una desigualdad. La desigualdad en estas últimas se cumple por un conjunto de elementos.
Página 48: Patrones y seriaciones. A los fines de resolución de los ejercicios planteados, la diferencia entre patrón y serie no modifica. Pero es importante que como docentes se pueda tener en claro esta situación.
Recursos extra
• Series numéricas: Método de diferencias (PDF)
• Sucesiones, series y patrones
Actividades de cierre
En las páginas 50-51 se propone una secuencia de situaciones problemáticas para resolver aplicando los saberes del capítulo.
Fundamentales
• Resolver problemas con números racionales, porcentajes; además de problemas con proporcionalidad y regla de tres simple.
Generales
• Fracciones
• Representación simbólica y gráfica
• Equivalencia de fracciones
• Fracción de un número
Específicos
• Representar fracciones de forma gráfica y simbólica.
• Leer y escribir números fraccionarios.
• Sumar, restar, multiplicar y dividir fracciones con igual y diferente denominador.
• Resolver operaciones combinadas con fracciones.
• Leer y escribir números decimales.
• Sumar, restar, multiplicar y dividir con números decimales.
• Resolver operaciones combinadas con decimales.
• Relacionar fracciones, decimales y porcentajes.
• Resolver problemas de proporcionalidad directa e inversa.
• Resolver problemas usando regla de tres simple directa.
• Jesús y la ofrenda de la viuda
• Suma y resta de fracciones heterogéneas
• Multiplicación de fracciones
• División de fracciones
• Operaciones combinadas con fracciones
• Fracción y número decimal
• Equivalencia entre fracciones y decimales
• Multiplicación y división con decimales
• Operaciones combinadas con decimales
• Proporcionalidad
• Proporción
• Regla de tres simple directa
Orientaciones metodológicas particulares
El trabajo de los números irracionales, específicamente las fracciones en la primaria es un elemento fundamental para construir una base sólida en el pensamiento matemático de los estudiantes.
El uso de material concreto para el trabajo de fracciones como las tiras fraccionarias,
regletas, o incluso objetos cotidianos como trozos de papel o alimentos, permite a los estudiantes visualizar y manipular las fracciones. Esta manipulación es crucial, ya que, al interactuar físicamente con los materiales, los estudiantes pueden explorar las relaciones entre las partes y el todo, observar equivalencias y desarrollar un sentido intuitivo de cómo funcionan las fracciones en diversas situaciones. Además, el proceso de manipulación fomenta un aprendizaje activo y participativo, donde los estudiantes se convierten en protagonistas de su propio aprendizaje.
Por otro lado, vincular las fracciones con situaciones cotidianas es vital para hacer el aprendizaje relevante y significativo. Cuando los estudiantes ven cómo las fracciones se aplican en la vida diaria, como en la cocina al dividir recetas, o al repartir de manera equitativa entre amigos, se genera un puente entre la matemática y su mundo. Este enfoque contextualizado no solo facilita la comprensión, sino que también motiva a los estudiantes al ver la utilidad y aplicación práctica de lo que están aprendiendo. En el capítulo se plantean situaciones que ayudarán a los estudiantes la mejor comprensión sobre los números fraccionarios.
Estrategias sugeridas
Actividades previas

Páginas 56 y 57: Lectura y escritura de una fracción. ¿Mayor o menor? Se plantea un juego cuya finalidad es recoger los saberes previos de los estudiantes con respecto a comparación, usar las tarjetas que está proporcionadas o se podrían usar tarjetas diseñadas por usted, de acuerdo a la particularidad de sus estudiantes o que desea conocer. Es importante que en esta primera parte pueda realizar las preguntas que se plantean en las páginas ya que son preguntas que ayudan en el pensamiento crítico y uso de la información.
Dobleces. Esta actividad es importante realizarla, dejar a los estudiantes que puedan usar su imaginación para realizar las diferentes representaciones. Ejemplo:
Cada estudiante debe tener una hoja en blanco y representar medios, tercios, cuartos, etc, se debe dar la libertad a los estudiantes de poder realizar sus propias representaciones y compararlas con sus compañeros, el realizar esta actividad con la dirección de usted como maestro ayudará a afianzar en los estudiantes sobre las diversas representaciones que existen y no solo el clásico.
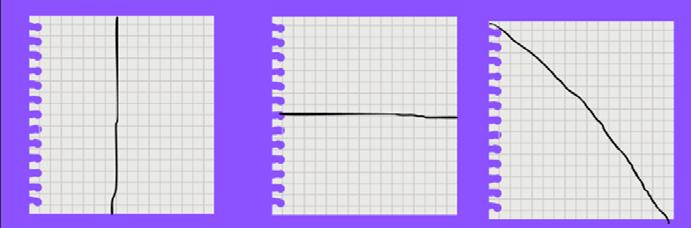
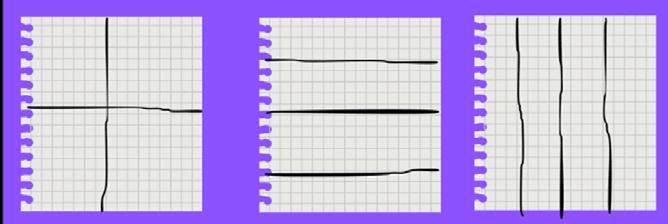
Páginas 58 y 59. Las actividades propuestas para estas páginas están relacionadas con las páginas anteriores. Es importante que los estudiantes reafirmen la teoría sobre fracciones. ¿Qué es una fracción? ¿Es una división? ¿Por qué? ¿De qué? ¿Cómo se representa una fracción?
Representar un entero usando cualquier tipo de figura es importante ya que fomenta la creatividad y se refuerza la definición de fraccionar. Se pueden llevar papeles con diversas formas geométricas y en grupos lograr que ellos puedan crear.

Actividades complementarias
Presentar a los estudiantes retos y realizar preguntas:
• ¿Cuál de las dos imágenes representa una fracción? ¿Por qué?
• Si pintamos uno de los espacios de ambos triángulos, ¿cuál representaría un medio?¿Por qué? ¿Ambos representan ½? Explica tu respuesta. Es importante que los estudiantes argumenten sus respuestas en cada actividad que realicemos.

Páginas 62 y 63. Conocer fracciones equivalentes usando tiras fraccionarias es fundamental, ya que permite a los estudiantes visualizar y comparar diferentes fracciones de manera tangible. Manipular las tiras facilita la comprensión de cómo fracciones distintas pueden representar la misma cantidad. Posteriormente, esta comprensión concreta se transfiere a la simbolización, fortaleciendo el concepto de equivalencia y promoviendo un aprendizaje más profundo y duradero.

Tiras fraccionarias. Se pueden construir tiras fraccionarias para comenzar con las equivalencias de fracciones. Se da a los estudiantes el material concreto y se puede ir manipulando de acuerdo a las indicaciones que usted como docente da. Puede decir, por
ejemplo:
• ¿A cuántos medios es equivalente un entero?
• ¿A cuántos cuartos equivale 3/6?
• ¿Quién es mayor ⅓ o ½? Argumenta.
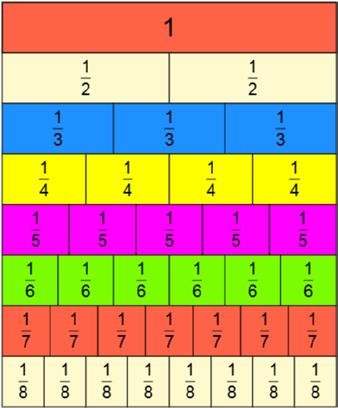

Página 65. Usando las mismas tiras fraccionarias se pueden realizar los cálculos de suma y resta de fracciones homogéneas. Esto va desde la manipulación del material hasta la simbolización. La simbolización en un 50 de primaria es fundamental, ya que los estudiantes manejan información previa; sin embargo, si hubiera estudiantes que tienen dificultades, es importante que se realice todo el proceso para lograr el aprendizaje.
Contenido digital ACES (p. 67)
Repasen el tema de las equivalencias entre fracciones con la actividad interactiva. Sugiera que escaneen el código QR o ingresen a http://aeoda.net/2003
Recursos extra
• Regletas.
• Fracciones.
• Tiras fraccionarias.
Actividades de cierre
En las páginas 76 y 77 se presenta la sección Aplico, en donde los estudiantes pondrán en práctica todo lo aprendido en el capítulo, además de realizar una autoevaluación.
Fundamentales
• Resolver problemas que involucren medidas de longitud, superficie, y tiempo haciendo uso de las equivalencias correspondientes.
Generales
• Concepto de medidas
• Medidas de longitud
• Resolución de problemas
• Equivalencias
• Medidas de superficie
• Resolución de problemas
• Equivalencias
• Área lateral y total
• Medidas de tiempo
• Equivalencias de tiempo
Específicos
• Reconocer las unidades de medida de longitud y realizar equivalencias entre sus múltiplos y submúltiplos.
• Resolver problemas con medida de longitud.
• Resolver problemas que involucren medidas de tiempo y realizar equivalencia.
• Comprender el uso del calendario.
• El creador del tiempo
Orientaciones metodológicas particulares
El estudio de las magnitudes y su medida es importante en el currículo de matemáticas desde el Nivel Inicial hasta secundaria debido a su aplicabilidad y uso extendido en una gran cantidad de actividades de la vida diaria. El estudio de la medición también ofrece oportunidad de aprender y aplicar otros contenidos matemáticos, como operaciones aritméticas, ideas geométricas, conceptos estadísticos y la noción de función. Permite establecer conexiones entre diversas partes de las matemáticas y entre las matemáticas y otras áreas diferentes.
La medida de magnitudes pone en juego un conjunto de destrezas prácticas y un lenguaje cuyo dominio y comprensión no es fácil para los niños de primaria. Es un tema que guarda, además, una estrecha relación con la construcción de los sistemas numéricos y con las formas y figuras geométricas.
Estrategias sugeridas
Actividades previas
Las páginas de inicio traen un recurso versátil y multifacético como es el tangram. Este recurso se puede utilizar para presentar y repasar gran cantidad de saberes.
En el inicio de este capítulo se propone el uso del tangram para armar números, letras
y figuras diversas. El tiempo para realizar estas actividades en una decisión pedagógica que queda a criterio del docente. Pueden realizarse diversas intervenciones o solo las sugeridas en el capítulo.
Se trabajará luego con medida, por lo que este material se usa como disparador de los saberes.
Recursos extra
• Tangram para jugar con las piezas.
• Aprender más sobre geometría con las piezas del tangram.
• Otro tangram.
Actividades complementarias
Páginas 80 y 81: Concepto de medida. Comenzamos jugando. ¿Cuál es el mayor? Propone obtener fichas de los otros participantes según sea el “ganador” de una consigna como tener el pie más largo o saltar más alto.
Las tiras de la sección de recortables utilizadas para realizar algunas mediciones pretenden acompañar el concepto de comparación entre el objeto y el instrumento de medición así como la unidad de medida. Se puede usar para realizar más mediciones y comparaciones o respetar la propuesta de la secuencia. De igual manera con las medidas de la antigüedad (codo, palma, etc) se pueden realizar mediciones de diversos espacios y/u objetos. El medir con las partes del cuerpo deja en evidencia la necesidad de utilizar un sistema de medidas convencional. En esta oportunidad no se proponen muchas actividades al respecto, pero son posibles de realizar antes de la actividad de actualizar las medidas.
Luego de estas actividades lúdicas se presenta el concepto de medir y las unidades de medida de la antigüedad así como también la posibilidad de utilizar unidades de medida no convencionales.
Página 83: Equivalencias. Las equivalencias entre múltiplos y submúltiplos de una unidad de medida se encuentran multiplicando y dividiendo por la unidad seguida de ceros. De ser posible colocar la tabla de equivalencias en un lugar visible del aula para su uso.
Submúltiplos x 10 : 10 : 10 : 10 : 10 x 10 : 10 x 10 : 10
Múltiplos
En ocasiones se usa una tabla en la que se van colocando ceros hacia la derecha o la izquierda para encontrar la equivalencia.
Este procedimiento puede utilizarse, siempre que se explique la razón de esto. Los ceros se colocan porque es el resultado si multiplicamos por 10 o dividimos por 10 respectivamente.
4 dam = ……………. dm (4 x 10 x10 = 400)
2 m= ……………….. km (2:10:10:10 = 0,002)
En el libro no se propone el uso de esta tabla ya que suele completarse sin pensar en la razón de la colocación de los ceros. Se recomienda que se evalúe el utilizarla relacionada a la comprensión de las razones por parte de nuestros estudiantes.
Página 84: Situaciones problemáticas. En esta página se enseña el uso de la regla. Siempre es necesario un repaso para el uso correcto de los instrumentos de medición.
Encontrarán una secuencia de situaciones problemáticas que trabajan con equivalencias de unidades de longitud.
Contenido digital ACES (p. 85)
El juego virtual repasa las equivalencias de medidas de longitud. Escaneen el código QR o bien ingresen a http://aeoda.net/2004
Páginas 86 y 87: Medidas de superficie. Es importante que se trabaje con las fichas de los recortables realizando las comparaciones que se mencionan. Que puedan superponer las fichas reiteradas veces y hacer otras comparaciones además de las propuestas.
Otra sugerencia es realizar fichas de mayor tamaño y usarlas para medir superficies mayores. O utilizar una ficha diferente (crear una) para medir diversos espacios de la institución. El concepto de superficie y de cómo se mide es abstracto, a medida que realizamos más cantidad de experiencias es más factible que lleguemos a la construcción de estos conceptos.
Luego de trabajar con las fichas del tangram y/u otras. Recomendamos trabajar con una ficha cuadrada, como se menciona en el libro, así se llega a la idea de unidades cuadradas (m2, cm2, etc.).
Finalmente están las actividades de estas páginas para realizar con unidades cuadradas (u2). Se puede confeccionar cuadrados de diferentes medidas o dibujarlos en el piso para compararlos. Un cuadrado de 1 cm2; otro de 1 dm2; 1 m2. O en la misma unidad de medida: 1 cm2; 10 cm2; 100 cm2
También pueden realizarse las actividades de la página 87 con fichas cuadradas. Se las ubica representando los dibujos de la página y se realizan las mediciones.
Para los ejercicios 5 y 6 se recomienda dibujar en una hoja cuadriculada para poder recortar y superponer opciones que represente lo solicitado, antes de dibujar en el libro.

Recursos extra
• Medidas de superficie.
Página 88: Áreas lateral y total. En la actividad propuesta en esta página es necesario acompañar a los estudiantes en el análisis de la caja que desarmen para responder. Pueden realizar la actividad de manera individual o en grupos. Dado que las solapas que se usan para unir las distintas cajas confunden y complican a la hora de calcular el área se indica cortarlas.
Página 89: El calendario. Se propone que realicen un calendario mensual individual para organizar sus actividades. Esto puede hacerse para todo el aula. Confeccionar un calendario en tamaño más grande y registrar eventos propios de la escuela y del aula.
Página 92: Medidas de tiempo. Estas actividades propuestas para realizar en un minuto tienen como objetivo introducir el tema. Si bien ya se habla en las páginas anteriores sobre el tiempo, aquí se especifica sobre el sistema sexagesimal. Al realizar actividades durante un minuto se puede “evidenciar” su duración efectivamente.
Se puede agregar actividades diferentes, o usar otro tiempo (mayor o menor) según las propuestas.
En el juego “En un minuto” se proponen actividades relacionadas con algunos saberes. Si bien está dentro de la página, tranquilamente se puede realizar usando otros saberes que sean más significativos o apropiados.
Actividades de cierre
Páginas 96 y 97. Se presentan diversas situaciones problemáticas con medidas de longitud y medidas de tiempo, así como un espacio para dibujar figuras diferentes de igual área.
Fundamentales
• Reconocer las unidades de medida, las equivalencias y las unidades de medida y procesamiento de la información.
Específicos
• Relacionar y diferenciar el volumen y la capacidad.
• Diferenciar el peso y la masa.
• Identificar las unidades menores al litro.
• Determinar las equivalencias entre gramo, kilogramo y tonelada.
• Relacionar las unidades de medidas de temperatura.
• Reconocer las unidades de medida de procesamiento de informática.
Generales
• Unidades de medida: capacidad, noción de volumen, diferencia entre volumen y capacidad, masa y peso, temperatura.
• Equivalencias entre unidades de medidas
• Sistema monetario: en tiempos bíblicos y en la actualidad
• Unidades de medida del procesamiento de la información
Orientaciones metodológicas particulares
• Un desafío gigante
Este capítulo aborda conceptos fundamentales para el aprendizaje de medidas y magnitudes, comenzando con la capacidad y la noción de volumen, y explorando la diferencia entre volumen y capacidad. Se introduce también la masa y peso, junto con la temperatura, para que los estudiantes comprendan estas magnitudes en contextos prácticos. Además, se abordan las equivalencias entre unidades de medida, lo que es esencial para que los estudiantes puedan convertir y comparar diferentes unidades con precisión. El capítulo también explora el sistema monetario, comparando su uso en los tiempos bíblicos con la actualidad, lo que ayuda a los estudiantes a apreciar la “evolución” y la relevancia de las monedas. Finalmente, se introduce el concepto de unidades de medida del procesamiento de la información, resaltando la importancia de que los estudiantes manejen información sobre las unidades de procesamiento actuales, como bytes y bits.
Es crucial que como docentes, contextualicen estos temas con ejemplos de la vida cotidiana para hacerlos más accesibles y significativos para los estudiantes. Este enfoque no solo refuerza la comprensión conceptual, sino que también asegura que los estudiantes puedan aplicar lo aprendido en situaciones prácticas.
Estrategias sugeridas
Actividades previas
Página 102: Cuenta cubos. La propuesta es que se utilicen tarjetas que se han preparado para que los estudiantes usen el conteo de cubos ya que esto les ayudará a tener un previo sobre el volumen de cuerpos geométricos, así también como las diferentes figuras que pueden componer un sólido geométrico.
La idea es que como docente usted pueda llevar diferentes imágenes o cosas de manera concreta, podría comenzar con una actividad previa como el uso del cubo Rubik o llevar cubos pequeños para que los estudiantes armen sus propios cuerpos geométricos.
Como variante, pueden mostrar en cada ron da más de una tarjeta y hacer el conteo total de la cantidad de cubos que tienen entre todas las figuras.
Es importante incidir en las preguntas que se plantean al inicio del capítulo, estas tienen una finalidad pedagógica, en este momento de preguntas, los estudiantes deben responder todo lo que ellos conocen, es importante que usted como maestro escuche y sea un gruía, no existen respuestas incorrectas, sólo se está realizando la construcción de ellas.
Página 103. Se sugiere llevar los instrumentos que se mencionan para que los estudiantes puedan realizar la experiencia.
Contenido digital ACES (p. 103)
Recomendamos ver el video de volumen y capacidad. Escaneen el código QR o ingresen a http:// aeoda.net/2005

Página 107. Es importante tener este cuadro como material manipulable en el aula y poder usarlo cada que sea necesario, esto ayuda a los estudiantes de manera visual y es más práctico al realizar cálculos.
Página 109. Para esta actividad sugerimos llevar o trabajar con materiales concretos, esta experiencia ayudará a los estudiantes tener un aprendizaje más significativo, el plantear actividades de su vida cotidiana en este tema es fundamental.
Página 110. Es importante tener este cuadro como material manipulable en el aula y poder usarlo cada que sea necesario, esto ayuda a los estudiantes de manera visual y es más práctico al realizar cálculos.

Recursos extra
• Cubos.
• Cómo trabajar medidas.
• Medida de magnitudes.
• Billetes de diversos países.
Contenido digital ACES (p. 114)
Averiguen más datos sobre el tema de las medidas de almacenamiento de la información escaneando el código QR o ingresando a http://aeoda.net/2006
Actividades de cierre
En la sección Aplico los estudiantes pondrán en práctica todo lo aprendido en este capítulo, además de realizar una autoevaluación.
Fundamentales
• Comprender las figuras geométricas de dos dimensiones, identificando, describiendo y clasificando diferentes polígonos, basándose en sus ángulos, lados y simetría.
• Aplicar conceptos de medición como perímetro y área.
Específicos
• Reconocer los elementos básicos de la geometría.
• Ubicar puntos en el plano a través de las coordenadas cartesianas.
• Medir ángulos y clasificarlos según sus medidas.
• Identificar los elementos de los polígonos.
• Clasificar triángulos según las medidas de sus lados y ángulos.
• Calcular el perímetro y el área de los triángulos.
CONTENIDOS
Generales
• Ubicación de puntos en el plano
• Plano de coordenadas cartesianas
• Líneas
• Tipos de rectas
• Ángulos y su clasificación
• Polígonos
• Triángulos
• Perímetro y área de triángulos
Orientaciones metodológicas particulares
IFE
• Club de Conquistadores
La geometría es describir, analizar propiedades, clasificar y razonar, y no solo definir. El aprendizaje de la geometría requiere pensar y hacer, y debe ofrecer continuas oportunidades para clasificar de acuerdo a criterios libremente elegidos (construir, dibujar, modelizar, medir), desarrollando la capacidad para visualizar relaciones geométricas.
Todo ello se logra estableciendo relaciones constantes con el resto de los saberes y con otras áreas como el arte o la ciencia, asignando un papel relevante a la parte manipulativa a través del uso de materiales para llegar a los conceptos.
Estrategias sugeridas
Actividades previas
Páginas 118 y 119. El inicio del capítulo trabaja sobre un plano de puntos que los estudiantes utilizarán para dibujar figuras geométricas y describirlas de manera tal que un compañero pueda dibujarlas también. Como introducción a los saberes del capítulo, el plano sobre el que dibujarán puede ser transformado en un plano de coordenadas cartesianas y también el plano sobre el que dibujen diferentes figuras geométricas que serán estudiadas durante las páginas del capítulo.

En el juego de inicio “Dibujo a ciegas” un integrante de la pareja realiza un dibujo simple, utilizando líneas y figuras geométricas y luego lo describe para que lo dibuje el otro integrante que no puede ver el dibujo. Aquí se ponen en juego conocimientos previos de los estudiantes sobre las figuras, el plano cartesiano y la comunicación.
Si bien, el dibujar “sin ver” va a depender mucho de la comunicación acertada y la interpretación, a mayor conocimiento mejor será la descripción que se realice para el compañero.
Previamente a jugar entre dos estudiantes el docente puede hacer el dibujo en un plano como el indicado y ser él quien da la descripción de la figura a sus estudiantes. De esta manera modela la actividad ayudando a ver que expresiones e ideas matemáticas favorecen el dibujo del otro.
En el juego “Somos figuras” se pone el cuerpo en movimiento para representar figuras utilizando distintas partes del cuerpo y un elemento que las una (soga).
Las variaciones que presenta el juego también aumentan la dificultad. En el caso de copiar una figura del pizarrón o de una tarjeta pueden ser más complejas las figuras elegidas, mientras que si se menciona oralmente las figuras deben ser más sencillas. El libro presenta diversas opciones.
Actividades complementarias
Página 120: Encuentra el tesoro. El geoplano es un instrumento en el que se pueden aplicar variados saberes. Es de utilidad para trabajar la geometría de manera manipulativa. Aquí la propuesta es jugar con el geoplano como si fuera un plano de coordenadas cartesianas.
Contenido digital ACES (p. 120)
Observen el video para la construcción del geoplano. También puede comprarse, hay diversos modelos de tamaños y materiales. Escaneen el código QR o visiten http://aeoda.net/2007.
El juego “Encuentra el tesoro” tiene la base de la popular “batalla naval” en la cuál en el plano hay puntos ocupados por “barcos”. En esta oportunidad los puntos son ocupados por letras que forman palabras previamente acordadas con los estudiantes. Los estudiantes deben pensar una manera de indicar los puntos, para marcar las letras del contrincante. Si ya pueden descubrir la relación de la abscisa y ordenada y aplicarlo es un buen momento, en caso de no tener esta información será un desafío inicial para presentar los conceptos.
Actualmente no se definen el punto, la línea y el plano. Son considerados conceptos primitivos. Podemos observar una representación de ellos, pero sin definirlos.
Página 121: Coordenadas cartesianas. En esta página se encuentra teoría y práctica con el plano de coordenadas cartesianas. Se pueden realizar las mismas actividades previamente en el geoplano o actividades similares.
Recursos extra
• Plano cartesiano 1.
• Plano cartesiano 2.
• Plano cartesiano 3.
• Tips para enseñar ángulos de forma creativa.
• Actividades para enseñar ángulos de forma entretenida.
• Ángulos y rectas.
• Ángulos.
Páginas 123 y 124: Tipos de rectas. Uso de regla y escuadra. En primer lugar se trabaja sobre el plano de una ciudad a través de actividades escritas y orales. La situación de describir oralmente la ruta elegida pone de manifiesta la necesidad de ser claro y específico con las indicaciones. El “para allá” o “más allá” no serán suficientes.
Una idea para hacer más dinámica esta propuesta es trabajar de manera grupal. Un estudiante traza la ruta en su mapa y es el encargado de describir oralmente el recorrido. Se proyecta el mapa en el pizarrón y el estudiante asignado debe ir marcando el recorrido con tiza o marcador según corresponda. Los demás estudiantes observan y evalúan. Si consideran que hay errores puede pasar otro estudiante a realizar las correcciones.
En la página 124 se propone un ejemplo para dibujar rectas paralelas, perpendiculares y oblicuas utilizando regla y escuadra. Este es solo un ejemplo, hay otras maneras de dibujarlas y sugerimos que se realicen si se considera necesario. Es un buen momento para recalcar la importancia en la geometría de la prolijidad y exactitud.

También se puede utilizar como un desafío para los estudiantes. En primer término seguir las instrucciones planteadas y luego pensar nuevas instrucciones, diferentes pero con iguales resultados.
Página 126: Ángulos. Aquí encontramos la clasificación de ángulos y se propone el trabajo con el geoplano y otras actividades en el libro. Hay muchas actividades que pueden hacerse en el aula para trabajar con ángulos y sus medidas. Más arriba (ver Recursos extra) dejamos algunas ideas a través de enlaces web.
Página 129: Triángulos. Se propone iniciar con un juego muy divertido que necesita atención y estrategia. Se pueden construir más planos para jugar con otras parejas. Se utiliza un plano de coordenadas cartesianas para trabajar como base de las actividades propuestas. Luego se sugiere trabajar con el geoplano.
Páginas 130 y 131: Clasificación de triángulos. Aquí se repasa la clasificación de triángulos según sus lados y sus ángulos a través de una actividad práctica con tiras de papel.
Como se ha mencionado en otras oportunidades, es importante que la actividad propuesta se realice; es decir, que se preparen las tiras de papel y se formen los triángulos como se indica para comprender la clasificación.

Contenido digital ACES (p. 130)
Proponga a los estudiantes realizar la actividad interactiva para clasificar triángulos escaneando el QR o ingresando a http://aeoda.net/2008
Página 132: Propiedades de los ángulos de los triángulos. Cada propiedad de los ángulos se descubre a través de una actividad manipulativa que está descripta en la página. Se puede realizar siguiendo las instrucciones o con indicaciones del docente previamente y luego en el libro para organizar las ideas.
Página 134: Construcción de triángulos. En esta página se propone un modo específico y bien ordenado para construir un triángulo equilátero solamente con regla y compás. Sugerimos realizar las adaptaciones o modificaciones que consideren necesarias para su grupo de estudiantes. Por ejemplo, se puede colocar el segmento inicial en otro sentido. También se pueden utilizar circunferencias para formar el triángulo equilátero (ver Recursos extra).
Recursos extra
• Triángulos con el geoplano.
• Perímetro y área del triángulo.
• Triángulo equilátero con circunferencias.
Página 137: Área de un triángulo. Se sugiere dibujar los triángulos en hojas cuadriculadas, como se muestra en el libro y recortarlos. Esto permite, al superponerlos, observar claramente la comparación de área.
Actividades de cierre
Páginas 140 y 141. Las actividades propuestas relacionan los triángulos con las coordenadas cartesianas, perímetro y área de los mismos.
Fundamentales
• Identificar los tipos de cuadriláteros y figuras geométricas, calcular áreas y perímetros de estas, reconocer poliedros y cuerpos de revolución y realizar transformaciones isométricas.
Específicos
• Identificar los tipos de cuadriláteros.
• Calcular el perímetro de figuras geométricas.
• Calcular el área de figuras geométricas compuestas.
• Diferenciar los cuerpos geométricos.
• Relacionar y diferenciar el círculo de la circunferencia.
• Reconocer los elementos de un círculo y circunferencia.
• Reconocer ejes y centros de simetría.
• Reconocer los sólidos de revolución y poliedros.
• Realizar las transformaciones isométricas.
CONTENIDOS
Generales
• Cuadriláteros
• Área y perímetro de cuadriláteros
• Figuras compuestas
• Cuerpos geométricos
• Poliedros
• Sólidos de revolución
• Círculo y circunferencia
• Polígonos inscritos y circunscritos en una circunferencia
• Transformaciones isométricas
Orientaciones metodológicas particulares
• La perfección de la creación
En este capítulo se incorporan conceptos claves de la geometría, tales como los cuadriláteros, las áreas y perímetros, y las figuras compuestas. Se abordan también los cuerpos geométricos, incluyendo poliedros y sólidos de revolución, y se exploran las propiedades del círculo, la circunferencia, y los polígonos inscritos y circunscritos en una circunferencia. Además, se introduce el tema de las transformaciones isométricas, que permitirá a los estudiantes experimentar con las figuras a través de simetrías, traslaciones y otras transformaciones.
Es importante que estos temas se trabajen desde lo concreto hasta lo simbólico. El uso de materiales manipulativos y ejemplos tomados de la vida cotidiana permitirá a los estudiantes construir un aprendizaje significativo y duradero. Como docentes, debemos asegurarnos de que los estudiantes no solo memoricen fórmulas, sino que comprendan profundamente cómo estas formas y conceptos se manifiestan en el mundo que los rodea. Este enfoque basado en la manipulación y la observación directa antes de pasar a la
abstracción, es esencial para que los estudiantes puedan aplicar lo aprendido en situaciones reales y, así, desarrollar una comprensión más completa y útil de la geometría.
Estrategias sugeridas
Actividades previas
Página 142. El rey manda. Para jugar, se necesitan 5 paliglobos o palitos de madera por cada integrante del equipo, también podría usarse palitos para brochetas o el material que usted más convenga.
Esta propuesta de inicio es muy importante, ayudará a reconocer el aprendizaje previo de sus estudiantes, la dinámica consiste en que usted pueda dar las primeras indicaciones sobre las construcciones que los estudiantes de manera individual o en grupos puedan realizar, le damos algunos ejemplos:
• “…una figura de tres lados, que tenga un ángulo de noventa grados”.
• “…un cuadrilátero con todos sus lados diferentes”.
• “…una figura con cuatro lados iguales”.
• “…una figura que tenga lados paralelos dos a dos y que tenga cuatro ángulos rectos”.
• “…una figura con cuatro lados iguales y cuatro ángulos iguales”.
• “…un cuerpo geométrico cuyas caras sean seis cuadrados”.

En esta parte usted debe estar muy atenta a los diferentes resultados que da, es importante que observe de manera muy detenida y realice preguntas sobre todo a aquellos estudiantes que necesitan más orientación sobre lo que se está desarrollando.
Es importante que realice las preguntas que se proponen y escuchar las respuestas de sus estudiantes, no olvide que no hay respuesta “mala”, solo necesitan una mayor orientación.
Contenido digital ACES (p. 143)
Recomendamos escanear el código QR y seguir las instrucciones para armar el origami del cubo de papel. O bien, ingresar a http://aeoda.net/2009
Página 145: Propiedad fundamental de los cuadriláteros. Esta actividad se propone para demostrar que la suma de los ángulos internos de un cuadrilátero es igual a 360°, como en cada actividad en primaria, es importante que los estudiantes manipulen material concreto y luego pasar a la simbolización.
Se podría comenzar con un triángulo para demostrar la suma de los ángulos internos igual a 180° y luego tener papeles en forma de cuadrados, rectángulos, etc. y realizar la experimentación con cada una de ellas.
Es importante tener un transportador para corroborar la información.
Únicamente después de haber realizado este proceso podremos abordar ejercicios de cálculo de ángulos.
Página 149: Áreas y perímetro. ¿Qué relación existe entre el área y el perímetro? ¿Qué unidades de medida usamos para el perímetro? ¿Para el área es igual la unidad de medida? ¿Debemos usar las “fórmulas” para el perímetro y el área? ¿Si la figura cambia de forma, cambia el área y perímetro?
Es importante que como maestros en primaria podamos recordar que nuestros estudiantes deben ser guiados para poder aprender, no enseñar “fórmulas”, sino que ellos puedan, mediante la indagación y experimentación, lograr el aprendizaje.

Para enseñar área y perímetro de figuras, es importante que busquemos estrategias adecuadas, es muy importante contextualizar problemas (como la gran mayoría de casos en matemática), sin embargo, también es importante poder guiar al estudiante a que pueda tener estrategias de resolución.
Como estrategia para introducir este tema en específico podemos trabajar con el pupitre de la escuela, cuadernos, las ventanas, etc…todo lo que pueda observar el estudiante.
Estas son algunas preguntas sugerentes:
¿Cuánto medirá de largo? ¿Y de ancho? ¿Cómo medir si no tengo un metro o algún instrumento de medida? (dar siempre opciones para que los estudiantes respondan o guiarlos, pueden usar los pies, palmas, etc…) ¿Cuál es la forma del aula? ¿Cuánto mide el contorno? ¿Y cuánto mide todo el espacio del aula? Si tiene un piso con baldosas o losetas cuadradas podría aprovechar esto para tener la noción de área. Luego de las respuestas de nuestros estudiantes, es muy importante anotar sus ideas para luego consolidar todo ello.
Actividades complementarias

Áreas y perímetros: Uso del geoplano. El geoplano es una herramienta eficaz para enseñar áreas y perímetros, ya que permite a los estudiantes crear y visualizar figuras geométricas de manera concreta. Al estirar bandas elásticas sobre los clavos del geoplano, los alumnos pueden experimentar directamente cómo se forman y miden las figuras, facilitando la comprensión de conceptos como la descomposición de áreas y la medición de perímetros. Esta manipulación activa ayuda a reforzar el aprendizaje y la intuición matemática.
Este mismo recurso nos puede ayudar a trabajar el área, una vez que se tienen las figuras formadas por los estudiantes, podemos preguntar sobre la parte interna (superficie) de la figura, preguntar por ejemplo ¿Cuánto es el área de toda la parte interna de la figura? ¿Cómo hago para dar una medida de toda esa parte interna?, lo ideal es que los estudiantes concluyan en que se están formando figuras cuadradas en la parte interna y contar los “cuadraditos” que contiene cada una de ellas.
Recursos extra
• Cubos de origami sin cortar ni pegar.
Contenido digital ACES (p. 153)
Recomendamos escanear el código QR para utilizar una plantilla de poliedros. O bien, ingresar a http://aeoda.net/2010
También sugerimos escanear el segundo código QR en esta página para acceder a una actividad interactiva de repaso, o bien, ingresar a http://aeoda.net/2011
Actividades de cierre
En la sección Aplico los estudiantes pondrán en práctica todo lo aprendido en este capítulo, además de realizar una autoevaluación.
Fundamentales
• Desarrollar habilidades para recolectar, organizar, representar e interpretar datos de manera efectiva.
• Fomentar el pensamiento crítico y analítico de los estudiantes.
Específicos
• Elaborar encuestas sencillas.
• Registrar la información obtenida en tablas de frecuencia.
• Organizar la información de tablas en diversos tipos de gráficos.
• Interpretar datos e información de diversos gráficos y realizar comparaciones entre ellos.
• Reconocer las medidas de tendencia central (media, moda y mediana).
• Comprender la probabilidad de sucesos como seguros, posibles e imposibles.
Generales
• Estadística
• Recolección de la información – encuesta
• Registro y representación de datos
• Gráfico de barras simple y compuesto
• Gráficos lineales
• Gráficos circulares
• Interpretación y comparación de datos
• Descripción de la información
• Medidas de tendencia central
• Probabilidades
Orientaciones metodológicas particulares
• Daniel y las probabilidades de salir ileso
La estadística es una rama de las matemáticas cuyo objetivo es trabajar sobre métodos que sirvan para recoger, organizar, interpretar y analizar datos, y de esta forma transformarlos en información.
La estadística surge de la necesidad de analizar y organizar la información dada la infinidad de datos que existen, para poder comprenderla y utilizarla. Es un área de las matemáticas pero encuentra su aplicación en muchas otras áreas de conocimiento: medicina, juego, economía, ecología, etc. Por esto puede ser utilizada como una competencia transversal al desarrollo de muchas materias ya que es una herramienta para la interpretación del entorno.
Estrategias sugeridas
Actividades previas
Página 162 ¿Cómo te sientes hoy? Esta actividad puede trabajarse integrada a otras
áreas. Se propone que los estudiantes piensen en las emociones y esto puede ser un trabajo de áreas integradas y que se ocupen varias clases de diversas asignaturas.
Se propone que se dibujen a sí mismos, pero esto es adaptable a los grupos de estudiantes. Pueden dibujar emojis, escribir las palabras, otros. El objetivo es formar una gráfica del estilo de los pictogramas. Esto introduce fácilmente los conceptos que se trabajarán a lo largo de todo el capítulo.
También puede realizarse la actividad planteando otra temática.
La segunda propuesta es “Nuestros nombres”. La actividad es muy sencilla, armar filas de estudiantes organizados por la inicial del nombre. Esta información se pasa a una tabla de frecuencia.
Actividades complementarias

Página 164 Recolección de la información. Se propone una situación a resolver y se presentan los instrumentos posibles para la recolección de información. Se presentan tablas de frecuencia relacionadas con la recolección de información del tema inicial y otra para completar por los estudiantes.
Páginas 165 a 172. En estas páginas se presentan la encuesta, el registro de datos y la representación.
Cada apartado es presentado con una temática diferente para aportar variedad y que puedan ser trabajados en el libro.
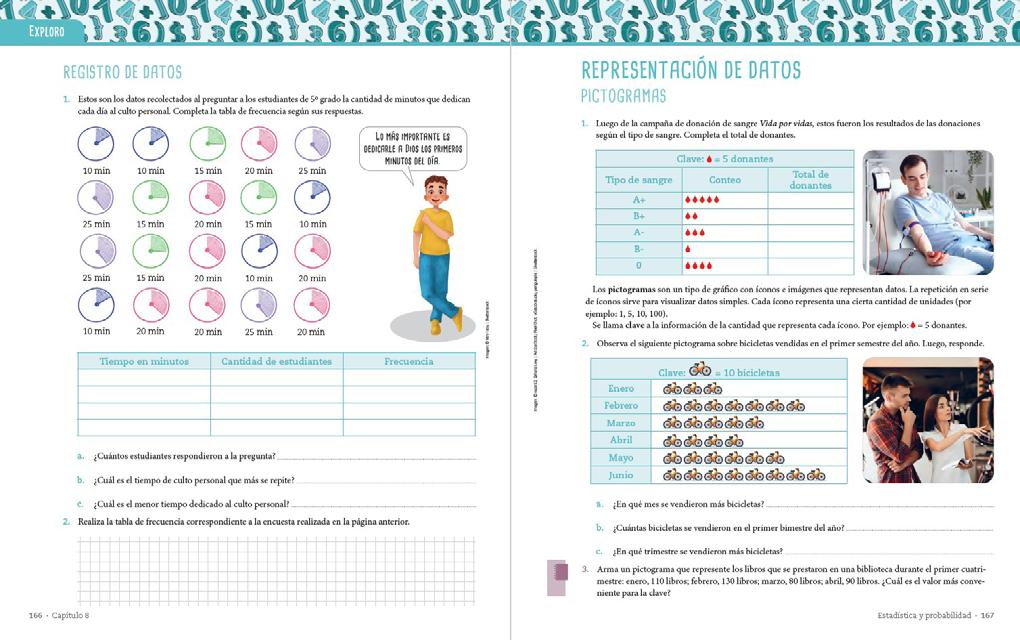
La sugerencia es que se puedan aplicar cada uno de los temas desde la encuesta que realicen. El registro de datos y la representación de los mismos pueden desprenderse directamente de la encuesta realizada aplicando los conocimientos aprendidos en estas páginas. Se observa el ejemplo propuesto en el libro y se adapta a la encuesta que generaron en la página 165.
Se toman varias páginas para presentar los diferentes tipos de gráficos. Dado que se sugiere dar continuidad a la encuesta realizada en grupos, se puede proponer a cada uno de los mismos un gráfico diferente en el cual volcar la información de su encuesta. Luego se usan esos gráficos para explicar la funcionalidad de cada uno.
Como se menciona, cada página presenta un tema y lo desarrolla. Pero es mucho más enriquecedor si se aplica cada tema con el eje planteado por interés de los estudiantes o según el docente considere pertinente.
Páginas 173 y 174 Descripción de la información. Interpretación y comparación de datos. Consideramos que este apartado es tan importante como todos los anteriores. El poder interpretar los datos, realizar un análisis crítico adecuado es una herramienta de gran utilidad.
Se sugiere comenzar escribiendo conclusiones de manera conjunta con el objetivo de ordenar las ideas que puedan surgir de la observación de un gráfico.
Los estudiantes pueden sugerir ideas como:
• “Más chicos eligieron el rojo”
• “Se trata de colores preferidos”
• “El negro es el color que menos les gusta”
Pero es necesario guiarlo con preguntas que atiendan a todos los datos para escribir una conclusión completa: ¿Cuántas personas fueron entrevistadas?; ¿Cómo podemos mejorar la expresión “más chicos eligieron? ¿Qué dato podría ser el inicial de una conclusión?, etc.
Página 175: Medidas de tendencia central. Se presenta una actividad en la que los estudiantes divididos en grupos realizan preguntas cuantitativas a sus compañeros. De esta manera se obtendrán datos cuantitativos que podrán ser utilizados para calcular la media, la moda y la mediana.
Página 177: Probabilidad. Se inicia el tema a través de un juego de dados muy sencillo. En la conclusión las preguntas orientan hacia el concepto de probabilidad. Es un concepto abstracto que a través de juegos puede ser mejor entendido.
Luego se propone jugar con dos dados y se pinta el número de la suma de ambos. Las grillas presentadas en la página 178 ayudan a comprender la probabilidad de resultados.
Página 178: La grilla de David. En este desafío se propone construir una grilla y una tabla para registrar las probabilidades de combinación de dados que ayudan a resolver las preguntas anteriores. Se puede proponer antes del trabajo en esta página que los estudiantes piensen una estrategia para registrar.
Contenido digital ACES (pp. 178 y 182)
La actividad interactiva consiste en seleccionar la respuesta correcta entre tres opciones. Escaneen el código QR o ingresen a http://aeoda.net/2012 Por último, sugerimos descargar y realizar la ejercitación adicional. Escaneen el código QR de la p. 182 o ingresen a http://aeoda.net/2053.
Recursos extras
• Enseñar estadística en primaria.
• Enseñar estadística utilizando el juego.
Actividades de cierre
Páginas 180 y 181. En estas páginas se presenta una secuencia de actividades que relacionan todos los contenidos del capítulo.