AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
MachinelearningsystemsbasedonxgBoost andMLPneuralnetworkappliedinsatellite lithium-ionbatterysetsimpedanceestimation
ThiagoH.R.DonatoandMarcosG.Quiles
DepartmentofAppliedComputation,NationalSpaceResearchInstitute, SaoJosedosCampos,P.0Box12227-010,Brazil InstituteofScienceandTechnology,FederalUniversityofSaoPaulo, SaoJosedosCampos,P.0Box12231-280,Brazil
Abstract. Inthiswork,theinternalimpedanceofthelithium-ionbatterypack(importantmeasureofthedegradationlevelofthebatteries)isestimatedbymeansofmachinelearningsystems basedonsupervisedlearningtechniquesMLP-MultiLayerPerceptron-neuralnetworkandxgBoost-GradientTreeBoosting.Therefore,characteristicsoftheelectricpowersystem,inwhich thebatterypackisinserted,areextractedandusedintheconstructionofsupervisedmodels throughtheapplicationoftwodifferenttechniquesbasedonGradientTreeBoostingandMulti LayerPerceptronneuralnetwork.Finally,withtheapplicationofstatisticalvalidationtechniques, theaccuracyofbothmodelsarecalculatedandusedforthecomparisonbetweenthemandthe feasibilityanalysisregardingtheuseofsuchmodelsinrealsystems.
Keywords: Lithium-ionbattery,Internalimpedance,Stateofcharge,MultiLayerPerceptron, GradientTreeBoosting,xgBoost
1Introduction
Thechoiceforthetechnologytobeappliedintheelectricalpowersystem(EPS)is importanttothesuccessofasatellitemissionsinceitrepresentsaround20to30 percentofasatellitetotalmass.
Forouterspaceapplications,lithium-ionbatterieshavelessthanonehalfofthe massofnickelhydrogenbatteriesforthesamestoredenergy[6]and,forthisreason, canreducethesystemweightofaspacecraft,thusimprovingtheloadefficiencyof satellites.Asaresult,lithium-ionbatteriesarehighlyadoptedinthesatellitesof theUnitedStatesandEuropeanSpaceAgency(ESA)[17].Inaddition,lithium-ion batteriesareexpectedtobecomethethirdgenerationofsatellitepowerstorage batteriesforChinasfuturespaceplatforminsteadofNiMHbatteriesandNiCd batteries.
ThereliabilityofLi-ionbatteriesisanimportantissuesduetothefactthat failuresofLi-ionbatterynotonlyresultinseriousinconvenienceandenormousreplacement/repaircosts,butalsocancauseoverheatingandshortcircuitingwhich DOI:10.5121/acii.2018.51011
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
canleadtocatastrophicconsequences,suchasexplosion.Inordertopreventseverefailuresfromoccurring,andtooptimizeLi-ionbatterymaintenanceschedules, breakthroughsinprognosticsandhealthmonitoringofLi-ionbatteries,withan emphasisonfaultdetection,correctionandremaining-useful-lifeprediction,must beachieved[20].
BatteryPHMhasawidevarietyofmeaning,rangingfromirregularmanual measurementsofvoltageandelectrolytespecificcharacteristicstofullyautomated onlineobservationofvariousmeasuredandestimatedbatteryparameters.AnimportantbatteryPHManalysisconsistsofthemeasurementofitsstateofcharge (SOC).Thestateofcharge(SOC)ofLi-ionbatterysetsisafunctionofitsinternalimpedance.Therefore,thestateofcharge(SOC)canbeestimatedthroughthe methodsdescribedonSection2ordeterminedbythebatteryinternalimpedance measurementorestimationalongtheoperatingcycles,asproposedinthisstudy.
2Li-ionbatterystateofcharge(SOC)estimation
Stateofchargeestimationhasalwaysbeenabigconcernforallbatterydriven devicesbutitsdefinitionpresentsmanydifferentissues[3].Ingeneral,theSOC ofabatteryisdefinedastheratioofitscurrentcapacity(Qt)tothenominal capacity(Qn).Thenominalcapacityisgivenbythemanufacturerandrepresents themaximumamountofchargethatcanbestoredinthebattery.TheSOCcan bedefinedasfollows:
SOCt = Qt Qn (1)
Therefore,oncethenominalcapacityisalreadydefined,themethodsdescribed belowintendtoestimatetheactualbatterycapacityaftercharge/dischargecycles.
Thevariousmathematicalmethodsofestimationareclassifiedaccordingto methodology.TheclassificationoftheseSOCestimationmethodsisdifferentinthe variousliteratures.Oneapproachisaccordingtothefollowingcategories[18]:
2.1Directmeasurements
Directmeasurementmethodsrefertosomephysicalbatterypropertiessuchas theterminalvoltageandimpedance.Manydifferentdirectmethodshavebeen employed:opencircuitvoltagemethod,terminalvoltagemethod,impedancemeasurementmethod,andimpedancespectroscopymethod.
Opencircuitvoltagemethod Thereisapproximatelyalinearrelationshipbetweenthe SOC ofthelead-acidbatteryanditsopencircuitvoltage(OCV )given by:
OCV (t)= a1 ∗ SOC(t)+ a0. (2)
Where SOC(t)istheSOCofthebatteryat t, a0 isthebatteryterminalvoltage when SOC =0,and a1 isobtainedfromknowingthevalueof a0 and OCV (t)at SOC =1.Unlikethelead-acidbattery,theLi-ionbatterydoesnothavealinear relationshipbetweenthe OCV and SOC [4].
Terminalvoltagemethod
Theterminalvoltagemethodisbasedontheterminal voltagedropsbecauseoftheinternalimpedanceswhenthebatteryisdischarging, sotheelectromotiveforce(EMF )ofbatteryisproportionaltotheterminalvoltage. Sincethe EMF ofbatteryisapproximatelylinearproportionaltothe SOC,the terminalvoltageofbatteryisalsoapproximatelylinearproportionaltotheSOC [15].Theterminalvoltagemethodhasbeenemployedatdifferentdischargecurrentsandtemperaturesbut,attheendofbatterydischarge,theestimatederrorof terminalvoltagemethodislarge,becausetheterminalvoltageofbatterysuddenly dropsattheendofdischarge.
OncetheLi-ionbatterydoesnothavealinearrelationshipbetweenthe VOC and SOC,thismethodisnotindicatedduetotheestimationerror.
Impedancespectroscopymethod Theimpedancespectroscopymethodmeasuresbatteryimpedancesoverawiderangeofacfrequenciesatdifferentchargeand dischargecurrents.Thevaluesofthemodelimpedancesarefoundbyleast-squares fittingtomeasuredimpedancevalues. SOC maybeindirectlyinferredbymeasuringpresentbatteryimpedancesandcorrelatingthemwithknownimpedancesat various SOC levels[10].
Coulombcountingmethod TheCoulombcountingmethodmeasuresthedischargingcurrentofabatteryandintegratesthedischargingcurrentovertimein ordertoestimate SOC.Coulombcountingmethodisdonetoestimatethe SOC(t) whichisestimatedfromthedischargingcurrent, I(t)andpreviouslyestimated SOC values, SOC(t 1). SOC iscalculatedbythefollowingequation: SOC(t)= SOC(t 1)+ I(t) Qn ∗ ∆t (3)
2.2Machinelearningsystems
Machinelearningsystemconsistsofanapproachwhichusespatternrecognition andmachinelearningtechniquestodetectchangesinsystemstates[12].Withthis approach,fewinformationregardingtotheanalyzedsystemisnecessaryinorder tobuildprognosticmodelsduetothefactthatonlythemonitoreddataitselfis
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
necessarytoelaboratethem.Forthisreason,machinelearningsystemsareadequateto EPS systemswhicharesufficientlycomplexsuchthatdevelopingan accuratephysicalmodelisprohibitivelyexpensive.Asbatterieshavebeenaffected bymanychemicalfactorsandhavenonlinear SOC,machinelearningsystemsoffer goodsolutionfor SOC estimation.However,thisapproachimpliesinwiderconfidenceintervalsthanotherapproachesandrequiresasubstantialamountofdata fortraining.
Afterthedatapreparation,amachinelearningalgorithmshallbeselectedin ordertobuildthemachinelearningsystem.Theselectionofaproperalgorithm foraspecificapplicationisachallengingfactorinapplyingdatadrivenprognostics methods.Examplesofmachinelearningalgorithmsappliedinmachinelearning systemstoestimateSOC:backpropagationMultiLayerPerceptronneuralnetwork (MLP ),gradientboosting(xgBoost),radialbasisfunction(RBF ),fuzzylogic methods,supportvectormachine(SVM ),fuzzyneuralnetwork,andKalmanfilter [16].
Inthisstudy,twomachinelearningsystemswereapplied:MLPneuralnetwork (Section2.2)andgradientboosting(Section2.3)
MultiLayerPerceptron Inordertobuildanalgorithmcapableofclassifyinga labelattribute,theMultiLayerPerceptron(MLP )neuralnetworkcanbeapplied. The MLP consistsofafeedforwardartificialneuralnetworkmodelthatcanbe usedinclassificationorprognosticissues.
TheMultiLayerPerceptronnetworkcontainsthreeormorelayers(aninputand anoutputlayerwithoneormorehiddenlayers)ofnonlinearly-activatingneurons. Eachneuroncombinetheinputsmultipliedbytheircorrespondentweightsand applyanactivationfunctionwhichoutputisdeliveredasinputofneuronsofthe followinglayer[8,Chapter4].
Inmanypracticalapplicationsofartificialneuralnetworks(ANN),thereexistnaturalconstraintsonthemodelsuchasmonotonicrelationsbetweeninputs andoutputsthatareknowninadvance.Itisadvantageoustoincorporatethese constraintsintotheANNstructure[19].ThemonotonicMultiLayerPerceptron network(MONMLP)isanapproachformulti-dimensionalfunctionapproximation ensuringmonotonicityforselectedinput-outputrelations.Moreover,wedetermine therequirementsforthenetworkstructureregardinguniversalapproximationcapabilities.
2.3GradientTreeBoosting
Gradienttreeboostingistypicallyusedwithdecisiontrees(especiallyCARTtrees) ofafixedsizeasbaselearners.ForthisspecialcaseFriedmanproposesamodificationtogradientboostingmethodwhichimprovesthequalityoffitofeachbase learner.
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
Genericgradientboostingatthe m th stepwouldfitadecisiontree hm(x) topseudo-residuals.Let Jm bethenumberofitsleaves.Thetreepartitionsthe inputspaceinto Jm disjointregions R1m,...,RJmm andpredictsaconstantvalue ineachregion.Usingtheindicatornotation,theoutputof hm(x)forinputxcan bewrittenasthesum:
hm(x)= Jm j=1 bjmI(x ∈ Rjm), (4)
where bjm isthevaluepredictedintheregion Rjm Thenthecoefficients bjm aremultipliedbysomevalue γm,chosenusingline searchsoastominimizethelossfunction,andthemodelisupdatedasfollows:
Fm(x)= Fm 1(x)+ γmhm(x),γm = γargmin n i=1 L(yi,Fm 1(xi)+ γhm(xi))(5)
Friedmanproposestomodifythisalgorithmsothatitchoosesaseparateoptimal value γjm foreachofthetree’sregions,insteadofasingle γm forthewholetree. Hecallsthemodifiedalgorithm”TreeBoost”[7].Thecoefficients bjm fromthetreefittingprocedurecanbethensimplydiscardedandthemodelupdaterulebecomes:
Fm(x)= Fm 1(x)+ Jm j=1 γjmI(x ∈ Rjm),γjm = γargmin xi∈Rjm
L(yi,Fm 1(xi)+γ) (6)
RootMeanSquareError Machinelearningsystemsapplymachinelearning techniquesinasupervisedapproach.Consideringanumericlabelattributeinthe estimativeofthebatterysetimpedance,eachobservedvaluecanbecomparedwith thepredictedone.Thisindividualdeviationiscalledaresidualandtheaggregation ofalltheresidualsisdenominatedtheRootMeanSquareError(RMSE),obtained asfollows[9]:
RMSE = n t=1(ˆ yt yt)2 n (7)
Where:
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
2.4Li-ionbatterystateofcharge(SOC)basedonbatteryinternal impedance
AccordingtothedefinitionoftheSOC,thefunctionwhichprovidesthebattery stateofchargebasedonbatteryinternalimpedanceisobtainedasfollows:
SOCt = SOCt0 + t t0 ( η · I Ct ) dt (8)
Where: – SOCt0:estimatedSOCattime t0,whentheestimationprocessstarts
– SOCt:estimatedSOCattime t – η:currentefficiency
– I:current-assumedtobepositivewhencharging – Cn:capacityofthebatteryattime t
Inthisstudy,thebatteryimpedanceisobtainedthroughthemachinelearning systems(seeSection2.2)whichcanbeappliedinthedeterminationofbatterystate ofcharge(SOC).
Baggingoptimization
Accordingtobaggingoptimizationmethod,atraining set Dofsizen isdividedinto m newtrainingsets Di,eachofsizen,bysampling fromDuniformlyandwithreplacement.Samplingthe m newtrainingsetswith replacement,impliesthatsomeobservationsmayberepeatedineach Di[1].
Thiskindofsampleisalsoknownasbootstrapsample.Inordertoobtainthe resultingensembleofmodels,the m modelsarefittedusingtheabove m bootstrap samples.Finally,allthemodelsareappliedtothescoringsetandthelabelsare combinedbyaveragingtheoutput(forregression)orvoting(forclassification).
3MachinelearningsystemsforLi-ionbatteryimpedance estimation
Thisstudyappliestwomachinelearningsystems(MLPneuralnetwork-Section 2.2andgradientboosting-Section2.3)inordertoestimatethebatteryinternal impedanceandcomparestheobtainedresults.
Toperformthecomparisonbetweenthetwomachinelearningsystems,abattery testingdatabaseprovidedbyNASAAmesResearchCenter[14]wasusedasdata set.ThedatabasecomprisessensormonitoringdataofLi-ionbatteriesmountedin batchesof4andrunningthrough3differentoperationalprofiles(charge,discharge andimpedance)atambienttemperaturesof4,24and44Celsiusdegrees(seeSection 4).
Fromtheanalyzeddataset,featureswereselectedtocharacterizethebattery conditionduringacertainperiodoftime(seeSection5).Afterthedevelopment
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
ofthedataset,machinelearningsystemsaretrained(seeSection6),RootMean SquareError(RMSE)performancemetricisusedtoevaluatetheobtainedmachine learningsystems(seeSection9)and,iftheperformancecriteriaareachieved,they canbeconsideredfeasiblesolutionstoestimatethebatteryinternalimpedancein anonlinebasis.
4DatapreparationforLi-ionbatteryimpedanceestimation
Batteryimpedance,whichdecreasesovertheworkingtimeofabattery,isanimportantanddirectindicatorforestimatingbatterystateofcharge(SOC).Inonline orin-orbitapplications,suchaselectricvehiclesandsatellites,thebatteryinternalimpedancemeasurementormonitoringisdifficult[11].Itcanbeusedcharge transferresistanceandelectrolyteresistanceextractedfromEIStoestimatebattery capacity[14].However,thesefeaturescanonlybeobtainedviaofflinetestsunder theoptimalmeasuringconditionsandbyusingspecializedandexpensiveequipmentforEISmeasurements[5].Theresultsoftheagingexperimentshowedthat increaseinbatterycapacitylossorresistanceinalifetimeisrelatedtooperating conditions,suchasvoltage,current,andtemperature.However,inpracticalapplications,severalcharacteristics,suchascurrentandvoltage,arecontrolledtomeet theloadrequirementsofanassociatedcircuitandthuscannotrepresentbattery aging[13].
4.1Li-ionbatterytestingsetinformation
ThefollowingsectionsapplymachinelearningtechniquesinLi-ionbatteryimpedance estimationusingbatterydataprovidedbyNationalAeronauticsandSpaceAdministration(NASA)AmesPrognosticsCenterofExcellence[14],where134rechargeablelithium-ionbatteriesweretested.
ThelaboratorysetupanddatarecordingwereconductedbyNationalAeronauticsandSpaceAdministration(NASA)AmesPrognosticsCenterofExcellence [14].AccordingtoNASAexperiment,the134rechargeablelithium-ionbatteries areorganizedin34batterysets.Eachbatterysetcontainsthetestdataorganized accordingtoFigure2.
4.2Laboratorysetup
TheexperimentalsetupprimarilyconsistsofasetofLi-ioncells(whichmayreside eitherinsideoroutsideanenvironmentalchamber),chargers,loads,EISequipment forbatteryhealthmonitoring(BHM),asuiteofsensors(voltage,currentandtemperature),somecustomswitchingcircuitry,dataacquisitionsystemandacomputer forcontrolandanalysis.Figure1detailstheassemblyoftheequipment.
Fig.1. Laboratorysetup[14]
Thecellsarecycledthroughchargeanddischargecyclesunderdifferentload andenvironmentalconditionssetbytheelectronicloadandenvironmentalchamber respectively.PeriodicallyEISmeasurementswillbetakentomonitortheinternal conditionofthebatteryusingtheBHMmodule.TheDAQsystemcollectsthe externallyobservableparametersfromthesensors.Theswitchingcircuitryenables thecellstobeinthecharge,dischargeorEIShealthmonitoringstateasdictated bythealgorithmsrunningonthecontrolcomputer[14].

4.3Li-ionbatterytestingsetinformation
TheLi-ionbatteriesareorganizedinbatchesof4arerunthrough3differentoperationalprofiles(charge,dischargeandimpedance)atambienttemperaturesof4, 24and44oC[14]:
1.Chargestep:chargingwascarriedoutinaconstantcurrent(CC)modeat1.5A untilthebatteryvoltagereached4.2Vandthencontinuedinaconstantvoltage (CV)modeuntilthechargecurrentdroppedto20mA
2.Dischargestep:dischargingwasconductedinCCmodeuntilthedischargevoltagereachedapredefinedcutoffvoltage.Fixedandvariableloadcurrentsat1, 2,and4Ampswereusedandthedischargerunswerestoppedat2V,2.2V, 2.5Vor2.7V
3.Impedancemeasurement:measurementwasperformedthroughanelectrochemicalimpedancespectroscopy(EIS)frequencysweepfrom0.1Hzto5kHz
Figure2detailsthebatterydatastructureoftheoperationalprofiles.
4.4Li-ionbatteryimpedancemeasurementrectifier
Inordertoeliminatethenoisegeneratedbytime-varyingcurrentpassingthrough anelectro-chemicalcellorbatteryduetoloadfluctuation,afilteringapproachoran
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
Fig.2. Datastructure[14]
electroniccancellationtechniqueshallbeapplied.Inthelaboratorysetupdescribed above,itwasusedanelectronicdevice.
Time-varyingcurrentflowinginacircuitwhichincludesthecell/batteryis sensedexternallytothecell/batterywithamagnetically-coupledaccurrentprobe therebyproducinganinducedtime-varyingsignal.Thisinducedsignalisamplified totheleveloftheoriginaltime-varyingcurrentandappliedtothecell/battery’s terminalsinphase-oppositiontotheoriginalcurrent.Asaresult,thecomponentof time-varyingcurrentflowinginthecell/battery’sexternalleadsassumesanalternatepatharoundthecell/batteryandiseffectivelycanceledwithinthecell/battery itself[2].
5FeaturesselectionforLi-ionbatteryimpedanceestimation
Inthisstudy,the134rechargeablelithium-ionbatteriesareorganizedin34battery sets.EachbatterysetcontainsthetestdataaccordingtoFigure2.ForeachC-D (chargeanddischarge)cycle,thefollowingfeatureswereextracted[20]:
– F1:duringchargecycle,timeintervalbetweenthenominalvoltageandthe cutoffvoltage
– F2:duringchargecycle,timeintervalbetweenthenominalcurrentandthe cutoffcurrent

– F3:duringdischargecycle,timeintervalbetweentwopredefinedvoltages
– F4:averagetemperatureduringthetimeintervalF1
– F5:averagetemperatureduringthetimeintervalF2
– F6:duringdischargecycle,cutoffvoltage
Thehistoricalsetappliedinthemachinelearningsystemsmodelingincludes thesixfeatures(F1,F2,F3,F4,F5andF6)andthelabelattributewhichcorrespondstotherectifiedbatteryimpedance.Foreachmachinelearningsystem,two
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
regressionmodelsarebuiltinordertoestimatetherealandimaginarycomponents oftherectifiedimpedance.Tables1and2areextractionsofthehistoricalsets correspondingtotherealandimaginarycomponentswhichcontain20records(C-D cycles)foreachoneofthe34batterysets(684records-C-Dcycles,intotal).
Table1. Historicalset-impedancerealcomponent
cycleF1F2F3F4F5F6imp re 2008 4 19966.4076422.609472.31327.007426.30082.45560.06175 2008 4 210226.3756627.891472.12525.674226.53232.63210.05989 2008 4 310635.9686528.063472.34425.675426.33252.50100.05919
Table2. Historicalset-impedanceimaginarycomponent
cycleF1F2F3F4F5F6imp img 2008 4 19966.4076422.609472.31327.007426.30082.4556-0.00096 2008 4 210226.3756627.891472.12525.674226.53232.6321-0.00112 2008 4 310635.9686528.063472.34425.675426.33252.5010-0.00105
6Li-ionbatteryimpedancedatamodeling
Afterthedatapreparation,twomachinelearningtechniques(MLPneuralnetwork -Section2.2andgradientboosting-Section2.3)areappliedinordertoestimate thebatteryinternalimpedance.Foreachappliedtechnique,afewtrainingcycles areexecutedwiththevariationofthetechniquehyperparameters.Therefore,each trainingcyclegeneratesaregressionmodelwhichcanbecomparedwiththeother obtainedregressionmodelsbytheapplicationoftheRMSE(RootMeanSquare Error)validationtechnique,accordingtoSection2.3.
7MLPneuralnetworkwithmonotonicityconstraintsmodeling
Tables1and2areusedtobuildtworegressionmodelsbasedonMLPneural networktechnique(Section2.2).
MultiLayerPerceptronneuralnetworkwithmonotonicityconstraintsimplementsonehidden-layerMultiLayerPerceptronneuralnetwork(MLP)modelsthat enforcesmonotonicrelationsondesignatedinputvariables.Eachtrainingcycleapplies10or20ensemblememberstofitand1,2,3or4hiddennodesinthehidden layer.
Theensemblememberstofitineachtrainingcycleareobtainedaccordingto Section2.4.Eachensemblemembercontainsarandomsubsetof70percentofthe
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
trainingsetand,aftergeneratingthe10or20regressionmodels(dependingon thenumberofensemblememberstofit),theresultcorrespondstothemeanvalue obtainedthroughtheapplicationofallregressionmodels.
ThesetrainingcycleswithdifferentcombinationsresultintodifferentMLPneuralnetworkswithmonotonicityconstraints.Thesedifferentcombinationsofthe hyperparametersaredescribedinTable3.
Table3. MLPneuralnetworkwithmonotonicityconstraintshyperparameters
Hyperparameter Description
Possiblevalues hidden1 numberofhiddennodesinthefirsthiddenlayer 1,2,3,4 n.ensemble numberofensemblememberstofit 10,20 monotone columnindicesofcovariatesforwhichthe monotonicityconstraintshouldhold 1 bag logicalvariableindicatingwhetherornot bootstrapaggregation(bagging)should beused TRUE iter.max maximumnumberofiterationsof theoptimizationalgorithm 500
7.1MLPneuralnetworkmodelingwithmonotonicityconstraintsand 10ensemblememberstofit
Estimativeofrealcomponentofbatterysetimpedance UsingthebackpropagationalgorithmtoupdatetheMLPneuralnetworkweights,monotonicity constraints,10ensemblememberstofitandusingdifferentnumbersofhiddennodes inthehiddenlayer(1,2,3or4),therealcomponentofthebatteryimpedance throughthecyclesisaccordingtheFigure3.
Estimativeofimaginarycomponentofbatterysetimpedance Usingthe backpropagationalgorithmtoupdatetheMLPneuralnetworkweights,monotonicityconstraints,10ensemblememberstofitandusingdifferentnumbersofhidden nodesinthehiddenlayer(1,2,3or4),theimaginarycomponentofthebattery impedancethroughthecyclesisaccordingtheFigure4.
7.2MLPneuralnetworkmodelingwithmonotonicityconstraintsand 20ensemblememberstofit
Estimativeofrealcomponentofbatterysetimpedance UsingthebackpropagationalgorithmtoupdatetheMLPneuralnetworkweights,monotonicity constraints,20ensemblememberstofitandusingdifferentnumbersofhiddennodes inthehiddenlayer(1,2,3or4),therealcomponentofthebatteryimpedance throughthecyclesisaccordingtheFigure5.
Fig.3. EstimatedrealcomponentofbatterysetimpedanceusingMLPneuralnetworkmodeling withmonotonicityconstraintsand10ensemblememberstofit


Fig.4. EstimatedimaginarycomponentofbatterysetimpedanceusingMLPneuralnetwork modelingwithmonotonicityconstraintsand10ensemblememberstofit
Estimativeofimaginarycomponentofbatterysetimpedance Usingthe backpropagationalgorithmtoupdatetheMLPneuralnetworkweights,monotonicityconstraints,20ensemblememberstofitandusingdifferentnumbersofhidden nodesinthehiddenlayer(1,2,3or4),theimaginarycomponentofthebattery impedancethroughthecyclesisaccordingtheFigure6.
ApplyingtheRMSE(RootMeanSquareError)validationtechnique,accordingto Section2.3,eachmodeldevelopedwiththeapplicationofMultiLayerPerceptron
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
Fig.5. EstimatedrealcomponentofbatterysetimpedanceusingMLPneuralnetworkmodeling withmonotonicityconstraintsand20ensemblememberstofit

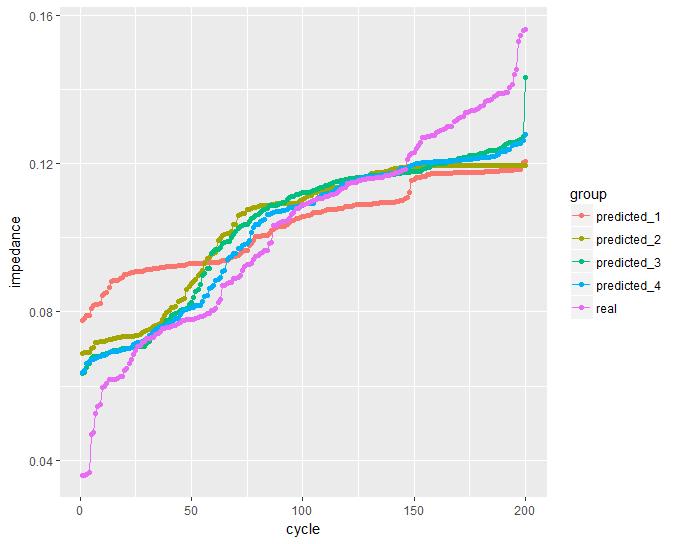
Fig.6. EstimatedimaginarycomponentofbatterysetimpedanceusingMLPneuralnetwork modelingwithmonotonicityconstraintsand20ensemblememberstofit
techniqueintheestimativeofrealandimaginarycomponentsofthebatteryset impedancewasevaluatedandthecorrespondingRMSEvaluesarepresentedin Table4.
Increasingthenumberofensemblememberstofit,therewasnoimpactonthe rootsquaremeanerrorforestimatingtherealcomponentofbatterysetimpedance. However,ahighernumberofensemblememberstofitminimizedtherootsquare meanerrorforestimatingtheimaginarycomponentofbatterysetimpedance.
AccordingtoTable4,ahighernumberofhiddennodesonthehiddenlayer minimizestherootsquaremeanerrorforestimatingtherealandimaginarycomponentsofbatterysetimpedance.
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
Table4. MLPneuralnetworkwithmonotonicityconstraintsmodelvalidation
Batteryimpedance Ensemblememberstofit Hiddennodesonlayer RMSE real 20 1 0.0161220600 real 20 2 0.0124101700 real 20 3 0.0100222800 real 20 4 0.0094165090 imaginary 20 1 0.0011236520 imaginary 20 2 0.0007225610 imaginary 20 3 0.0004410664 imaginary 20 4 0.0003257367
TheMLPmodelswiththelowerrootsquaremeanerrorinestimatingthereal andimaginarycomponentsofbatterysetimpedancehavetheconfigurationof20 ensemblememberstofitand4hiddennodesonthehiddenlayerandanRMSE errorof0.0094165090and0.0003257367,respectively.
8Gradientboostingmodeling
Tables1and2areusedtobuildtworegressionmodelsbasedongradientboosting technique(Section2.3).Thetrainingsetisdividedintotrainingandvalidationsets. Thevalidationsetisusedtoevolvetheregressionmodelsduringeachgradient boostingiteration.Eachtrainingcycleappliesan’eta’equalto0.20or0.60to controlthelearningrateandasubsampleratioofthetraininginstancesof0.80, 0.85,0.90or0.95.
Thesetrainingcycleswithdifferentcombinationsresultintodifferentgradient boostingmodels.Thesedifferentcombinationsofthehyperparametersaredescribed inTable5.
Table5. Gradientboostinghyperparameters
Hyperparameter Description
Possiblevalues objective objectivefunction reg:linear max depth maximumdepthofatree 10 eta controlthelearningrate:scale contributionofeachtreebyafactor of0 <eta <1 0.20,0.60 col sample subsampleratioofcolumns whenconstructingeachtree 0.80
ss sample subsampleratioofthetraininginstance. 0.5meansthatxgboostrandomly collectedhalfofthedatatogrowtrees andthiswillpreventoverfitting 0.80,0.85,0.90,0.95
eval metric evaluationmetricpervalidationcycle rootmeansquareerror nrounds themaxnumberofvalidationcycles 200
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
Thehyperparameter’eta’hasanimportantroleinthegradientboostingmodelingsinceitcontrolsthelearningrate.Thisparameterscalesthecontributionof eachtreebyafactorbetween0and1whenitisaddedtothecurrentapproximation. Itisusedtopreventoverfittingbymakingtheboostingprocessmoreconservative. Lowervaluefor’eta’implieslargervaluefor’nrounds’:low’eta’valuemeansmodel morerobusttooverfittingbutslowertocompute.
8.1Gradientboostingmodelingwitheta=0.20
Estimatingrealcomponentofbatterysetimpedance Buildinganensemble ofdecisiontreesinwhicheachdecisiontreeisbuiltinordertominimizetheerror ofthepreviousone(gradientboostingmethod),settingthemaximumdepthofthe treesto10,applyingtherootmeansquareerrormethodasametrictoevolvethe modelwiththevalidationset,controllingthelearningratethrough’eta’of0.20 andsubsettingthetrainingsetinstanceswithdistinctratios(0.80,0.85,0.90or 0.95),therealcomponentofthebatteryimpedancethroughthecyclesisaccording theFigure7.
Fig.7. Estimatedrealcomponentofbatterysetimpedanceusinggradientboostingmodelingwith eta=0.20
Estimatingimaginarycomponentofbatterysetimpedance Buildingan ensembleofdecisiontreesinwhicheachdecisiontreeisbuiltinordertominimize theerrorofthepreviousone(gradientboostingmethod),settingthemaximum depthofthetreesto10,applyingtherootmeansquareerrormethodasametric toevolvethemodelwiththevalidationset,controllingthelearningratethrough ’eta’of0.20andsubsettingthetrainingsetinstanceswithdistinctratios(0.80,

AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
0.85,0.90or0.95),theimaginarycomponentofthebatteryimpedancethroughthe cyclesisaccordingtheFigure8.
Fig.8. Estimatedimaginarycomponentofbatterysetimpedanceusinggradientboostingmodeling witheta=0.20 8.2Gradientboostingmodelingwitheta=0.60
Estimatingrealcomponentofbatterysetimpedance Buildinganensemble ofdecisiontreesinwhicheachdecisiontreeisbuiltinordertominimizetheerror ofthepreviousone(gradientboostingmethod),settingthemaximumdepthofthe treesto10,applyingtherootmeansquareerrormethodasametrictoevolvethe modelwiththevalidationset,controllingthelearningratethrough’eta’of0.60 andsubsettingthetrainingsetinstanceswithdistinctratios(0.80,0.85,0.90or 0.95),therealcomponentofthebatteryimpedancethroughthecyclesisaccording theFigure9.
Estimatingimaginarycomponentofbatterysetimpedance Buildingan ensembleofdecisiontreesinwhicheachdecisiontreeisbuiltinordertominimize theerrorofthepreviousone(gradientboostingmethod),settingthemaximum depthofthetreesto10,applyingtherootmeansquareerrormethodasametric toevolvethemodelwiththevalidationset,controllingthelearningratethrough ’eta’of0.60andsubsettingthetrainingsetinstanceswithdistinctratios(0.80, 0.85,0.90or0.95),theimaginarycomponentofthebatteryimpedancethroughthe cyclesisaccordingtheFigure10.

AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
Fig.9. Estimatedrealcomponentofbatterysetimpedanceusinggradientboostingmodelingwith eta=0.60


Fig.10. Estimatedimaginarycomponentofbatterysetimpedanceusinggradientboostingmodelingwitheta=0.60
8.3Gradientboostingmodelvalidation
ApplyingtheRMSE(RootMeanSquareError)validationtechnique,accordingto Section2.3,eachmodeldevelopedwiththeapplicationofGradientboostingtechniqueintheestimatingrealandimaginarycomponentsofthebatterysetimpedance wasevaluatedandthecorrespondingRMSEvaluesarepresentedinTable6.
Alower’eta’minimizestherootsquaremeanerrorforestimatingtherealand imaginarycomponentsofbatterysetimpedance.AccordingtoTable6,increasing thenumberofinstancestobeusedinthetrainingprocess,therewasadecrease ontherootsquaremeanerrorforestimatingtherealcomponentofbatteryset impedance.However,ahighernumberofinstancestobeusedinthetrainingprocess
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
Table6. Gradientboostingmodelvalidation
Batteryimpedance ’eta’-Learningrate Subsampleratio RMSE real 0.20 0.80 0.0057317940 real 0.20 0.85 0.0044927730 real 0.20 0.90 0.0034616720 real 0.20 0.95 0.0028836380
imaginary 0.20 0.80 0.0003310718 imaginary 0.20 0.85 0.0006632989 imaginary 0.20 0.90 0.0005046742 imaginary 0.20 0.95 0.0001962272
maximizedtherootsquaremeanerrorforestimatingtheimaginarycomponentof batterysetimpedance.
TheGradientboostingmodelswiththelowerrootsquaremeanerrorinestimatingtherealandimaginarycomponentsofbatterysetimpedancehavethe configurationof’eta’=0.20andasubsampleratioof0.95andanRMSEerrorof 0.0028836380and0.0001962272,respectively.
9Li-ionbatteryimpedancemodelvalidation
AccordingtoRMSEvalidationtechnique(seeSection2.3),theMultiLayerPerceptronmodelwiththehigherperformance(20ensemblememberstofitand4 hiddennodesonthehiddenlayer)andtheGradientTreeBoostingmodelwiththe higherperformance(’eta’=0.20andasubsampleratioof0.95)arecomparedin11 regardingtheestimationoftherealandimaginarycomponentsofthebatteryset impedance.
Fig.11. RMSEStateofcharge(SOC)modelvalidation

AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
10Conclusion
Inthisstudy,twodistinctmachinelearningapproacheswereappliedinorderto estimatethebatteryimpedanceofsatelliteLi-ionbatterysetswhichisusedinthe determinationoftheirstateofcharge(SOC)(seeSection2.4).TheobtainedRMSE (RootMeanSquareError)ofbothapproacheshasdemonstratedthefeasibilityof suchmachinelearningsystemsinestimatingLi-ionbatterysetsbatteryimpedance incaseswhereanerrorbelow0.10isacceptable.
However,oncetheobtainedRMSE(RootMeanSquareError)oftheGradient TreeBoostingmodelislowerinestimatingbothrealandimaginarycomponents ofthebatteryimpedance,thisapproachisrecommendedovertheMultiLayer Perceptronmodel.
Acknowledgements
M.G.QthanksFAPESP(Grant2011/18496-7)andCNPq(Grant310908/2015-9).
References
1.J.A.Aslam,R.A.Popa,andR.L.Rivest.Onestimatingthesizeandconfidenceofa statisticalaudit. ProceedingsoftheElectronicVotingTechnologyWorkshop,7,2007.
2.K.S.Champlin.Methodandapparatusforsuppressingtime-varyingsignalsinbatteries undergoingchargingordischarging,111992.
3.Y.Chang,W.Thestateofchargeestimatingmethodsforbattery:Areview. International ScholarlyResearchNoticesAppliedMathematics,2013:1–7,2013.
4.M.Coleman,C.K.Lee,C.Zhu,andW.G.Hurley.Stateof-chargedeterminationfromemf voltageestimation:usingimpedance,terminalvoltage,andcurrentforlead-acidandlithiumionbatteries. IEEETransactionsonIndustrialElectronics,54:25502557,2007.
5.M.Dalal,J.Ma,andD.He.Lithium-ionbatterylifeprognostichealthmanagementsystem usingparticlefilteringframework. Proc.Inst.Mech.Eng.PartOJ.Risk,225:8190,2011.
6.G.J.Dudley.Lithium-ionbatteriesforspace. ProceedingsoftheFifthEuropeanSpacePower Conference,page17,1998.
7.T.Hastie,R.Tibshirani,andJ.H.Friedman. Theelementsofstatisticallearning:datamining, inference,andprediction,volume02.Springer,USA,2009.
8.S.Haykin. Neuralnetworks-Acomprehensivefoundation,volume02.CambridgeUniversity Press,USA,1999.
9.R.J.HyndmanandA.B.Koehler.Anotherlookatmeasuresofforecastaccuracy. InternationalJournalofForecasting,04:679688,2006.
10.R.Li,J.F.Wu,H.Y.Wang,andG.C.Li.Predictionofstateofchargeoflithium-ion rechargeablebatterywithelectrochemicalimpedancespectroscopytheory. Proceedingsofthe 5thIEEEConferenceonIndustrialElectronicsandApplications,page684688,2010.
11.D.Liu,H.Wang,Y.Peng,W.Xie,andH.Liao.Satellitelithium-ionbatteryremainingcycle lifepredictionwithnovelindirecthealthindicatorextraction. Energies,6:36543668,2013.
12.J.LiuandG.Wang.Amulti-steppredictorwithavariableinputpatternforsystemstate forecasting. MechanicalSystemsandSignalProcessing,23:15861599,2009.
13.M.ParvizandS.Moin.Boostingapproachforscorelevelfusioninmultimodalbiometrics basedonaucmaximization. J.Inf.HidingMultimed.SignalProcess,2:5159,2011.
AdvancedComputationalIntelligence:AnInternationalJournal,Vol.5,No.1,January2018
14.B.SahaandK.Goebel.Batterydataset,2007.NASAAmesResearchCenter,MoffettField, CA.
15.S.SatoandA.Kawamura.Anewestimationmethodofstateofchargeusingterminalvoltage andinternalresistanceforleadacidbattery. ProceedingsofthePowerConversionConference, page565570,2002.
16.M.Schwabacher.Asurveyofdata-drivenprognostics. AIAAMeetingPapers,2005.
17.D.Wang,G.Li,andY.Pan.Thetechnologyoflithium-ionbatteriesforspacecraftapplication. AerospaceShanghai,4:5459,2000.
18.N.Watrin,B.Blunier,andA.Miraoui.Reviewofadaptivesystemsforlithiumbatteriesstateof-chargeandstate-of-healthestimation. ProceedingsofIEEETransportationElectrification ConferenceandExpo,pages1–6,2012.
19.H.ZhangandZ.Zhang.Feedforwardnetworkswithmonotoneconstraints. InternationalJoint ConferenceonNeuralNetworks,03:1820–1823,1999.
20.J.ZhangandJ.Lee.Areviewonprognosticsandhealthmonitoringofli-ionbattery. Journal ofPowerSources,196:60076014,2011.
Authors
ThiagoDonatograduatedatElectricalEngineeringfromFederalUniversityofItajub-UNIFEI(2006)andhasworkedduringfiveyearsinprivatecompanies(EMBRAER-aircraftmanufacturercompany-andTOTVS-softwarecompany)developingsolutionswhichapplymachinelearningtechniquesinthe resolutionofmajorissues.Donatoisenrolledinmaster’sat ComputerSciencefromNationalSpaceResearchInstituteINPE(2018).HasexperienceinMachineLearning,actingon thefollowingsubjects:dataandtextpreparationandmining, neuralnetworkandothermachinelearningclassificationtechniques.
MarcosG.QuilesisanAssociateProfessorattheDepartmentofScienceandTechnology,FederalUniversityofSoPaulo, Brazil.HereceivedtheBSdegree,withhonors,in2003fromthe StateUniversityofLondrina,Brazil,andaPh.D.degreefrom theUniversityofSoPaulo,Brazil,in2009,bothinComputer Science.FromJanuarytoJulyof2008,QuileswasaVisiting ScholarinthePerceptionandNeurodynamicsLabatTheOhio StateUniversity.FromJanuarytoDecemberof2017,Quiles wasanAcademicVisitorattheUniversityofYork,York-UK. HewasawardedaBrazilianresearchproductivityfellowship fromtheBrazilianNationalResearchCouncil(CNPq).Hisresearchinterestsincludenature-inspiredcomputing,machinelearning,complexnetworks,andtheirapplicationsininterdisciplinaryproblems.


