Erik Duchnowski

Summertime Impact of White Roofs on Building Energy Balance and Air Conditioning Flux
Erik Duchnowski 1, Linying Wang 2, and Dan Li 2 1 Boston University Academy, 2 Department of Earth and Environment, Boston University
1. Introduction
Roofs play a vital role in the thermal performance of buildings, influencing indoor comfort, energy consumption, and a building’s overall environmental footprint. Among the range of roofing options, white roofs have garnered substantial attention due to their potential to have a positive impact on many aspects of heat management in buildings and cities. Some ways they do this are well-documented. For instance, they reduce the urban heat island (UHI) effect, a phenomenon where urban areas register higher temperatures than their rural surroundings due to dark surfaces like roads and asphalt roofs absorbing heat. White roofs counteract UHIs by having a high albedo, meaning they reflect more light. This allows them to absorb less heat, which in turn lowers temperature and diminishes energy consumption.
The UHI effect has many causes. One of these causes are urban canyons. These are street configurations in which tall buildings line narrow streets, greeting a canyon-like effect. The canyon shape intensifies UHIs. Tall buildings block wind flow, limiting air circulation and restricting the dissipation of heat. This causes heat to get trapped within and accumulate in the streets. This heat is already high due to materials like concrete and asphalt, which are ubiquitous in urban environments. These materials have high thermal mass and low albedo, meaning they absorb and retain heat effectively while reflecting minimal sunlight. During the day, these surfaces absorb solar radiation, increasing temperature, and at night,
they slowly release stored heat, preventing urban areas from cooling down. This nighttime aspect of the UHI effect can be even more noticeable and pernicious than the daytime aspect. The cumulative effect, however, results in higher temperature within urban canyons compared to surrounding areas.
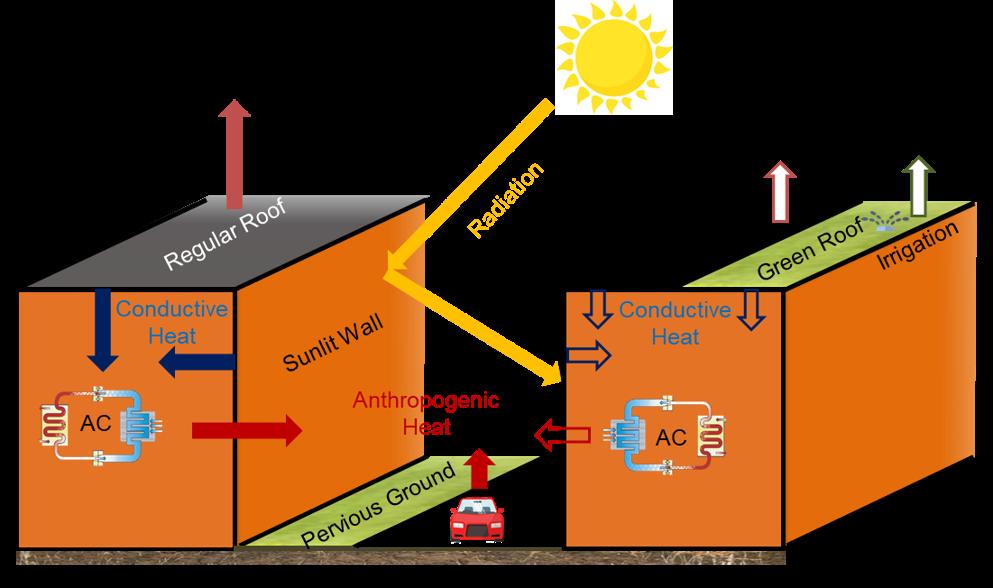
Figure 1. Annotated urban heat canyon from Wang et al. (2020, 2021). A building with a regular dark roof (left) emits more sensible heat and anthropogenic heat through air conditioning than a building with a white or green roof (right).
The adverse effects of UHIs are explained well in a study by Santamouris et. al. (2014). First, UHIs increase peak electricity demand. In Athens, Greece, Santamouris cites, cooling requirements of buildings are doubled, their peak electricity demand is almost tripled, and the Coefficient of Performance (COP) of cooling systems is slashed by up to a quarter due to the UHI effect. In general, for cities in the United States with a population exceeding 100,000, a rise of 1 degree Fahrenheit leads to a 1.5-2% increase in peak electricity demand. This leads to pollution, higher
concentrations of ozone, and larger ecological footprints from our cities. In addition to deteriorating outdoor air quality and thermal comfort, there is increased thermal stress on low-incoming housing as well as intensified public health issues.
Studies have also revealed the effect of white roofs on building energy costs (Rosado et al., 2014). Their implementation can lead to significant reductions in the cost of keeping a building at a desired temperature and are, therefore, economically as well as environmentally beneficial. For instance, Rosado et al. (2014) found that for one California home, $0.886 was saved per square meter of cool roofing, reducing total costs due to heating and cooling by one fifth.
Additionally, according to Li et al. (2014), increasing fractions of cool, white roofs proportionally reduce surface and near-surface UHIs with a nearly linear relationship. The study suggests that for a 1°C reduction in surface UHI in the Baltimore-Washington area, about 30% of roofs need to have an albedo of 0.7. While cool roofs lack the broader benefits of green roofs, like air quality improvement and stormwater runoff reduction, they seem more cost-effective at mitigating UHIs than green roofs.
However, something that remains not well understood is the regional differences in the magnitude of urban air conditioning flux reductions and thus the amount of monetary savings; this is one of the key focuses of this paper. This paper also investigates the controlling factors for the effectiveness of increasing albedo in reducing urban air conditioning flux. Finally, these aspects are examined in future scenarios to examine how these phenomena may change and what the implications are for implementations of white roofs today.
In order to bridge this research gap and to contribute a more comprehensive understanding of the effects of white roofs, this
study uses the Community Land Model Urban (CLMU) (Lawrence et al., 2019), an improved numerical urban climate model that includes parameterizations of urban heat mitigation strategies. Two scenarios are compared for the contiguous United States (CONUS) for a Historical Period (1980 to 2019), a Near-Future Period (2020 to 2059), and a Far-Future Period (2060-2099): one scenario uses regular roofs and the other uses white roofs.
Reductions in air conditioning flux are found to be greatest in the Southeast. Surprisingly, changes in the amount of heat conducted through the outer surface of the roof, the energy that permeates the roof surface into the roof material, prove to be inaccurate predictors of changes in air conditioning use. The white roof effect on AC flux is found to be largely explained by the change in total building conduction. While white roofs markedly reduce roof conduction, they are found to simultaneously amplify wall conduction, suggesting that estimates of energy saving benefit from white roofs need to be adjusted. This result stresses the importance of treating the building as an integrated system rather than an aggregate of independent parts.
2. Methods
The Community Land Model Urban (CLMU) was used. This numerical model provided mean values for all variables in this study for the months June, July, and August of each year. The resolution of the model is 0.125 degrees longitudinally and latitudinally. This translates to plots of land approximately 150 square kilometers in area.
The white roof scenario is one in which all buildings have a white roof with an albedo of 0.7. The regular roof scenario gives different regions of the United States different, lower albedos.
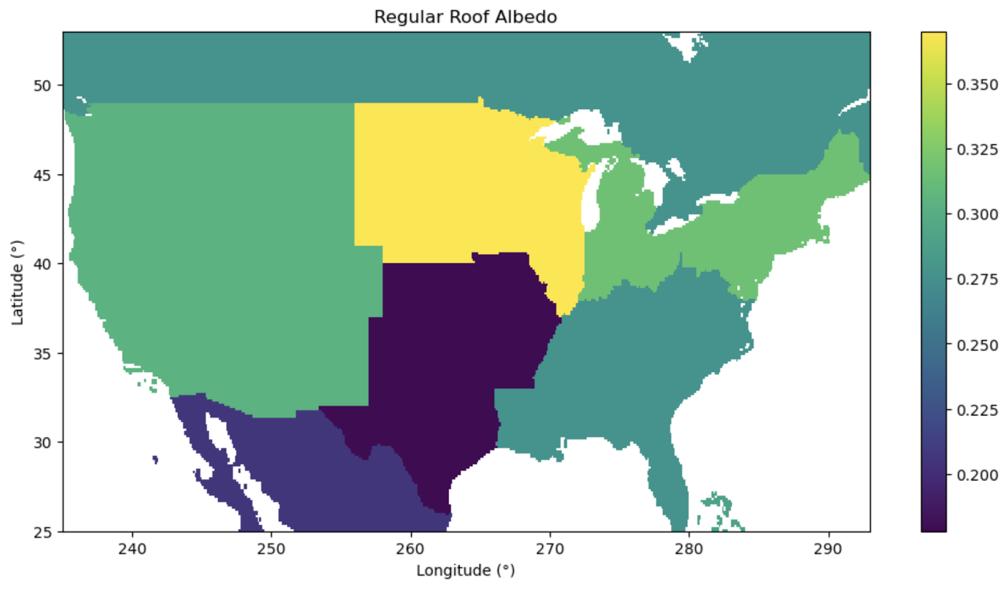
Figure 2. Regular roof albedo for North America used by CLMU.
From Figure 2, we can see how CLMU approximates the regular roof albedo of different regions in the contiguous United States. The region in which buildings already have the highest roof albedo is the North Central United States. In states like Illinois and Minnesota, the model takes regular roofs to have an albedo of 0.375. The region with the lowest regular roof albedo is the South-Central United States. States like Texas and Missouri have roof albedos of just 0.0175. This means that over eighty percent of the solar radiation is absorbed, rather than reflected away. Finally, in the West and in the East of the United States, roofs have albedos of around 0.300.
The building energy budget framework used in this study stems from the framework offered by Oleson and Feddema (2020). Oleson and Feddema provide a complete picture of the heat transfers within buildings, including conductive, convective, and radiative heat.
Conduction refers to the process of heat transfer that occurs when two materials are in direct contact. Heat is transferred when there is
a temperature difference between two adjacent materials or within a material itself. In buildings, conduction commonly occurs through walls, floors, and ceilings. Heat moves from higher temperature areas to lower temperature areas by molecular collisions sound waves within the materials. Different materials can conduct heat better or worse, with insulating materials slowing down the rate of heat transfer and conductive materials facilitating faster heat transfer.
Convection refers to the transfer of heat through the movement of fluids, including both liquids and gasses. Temperature variations that change the fluid’s density cause fluids to circulate and transfer heat. In buildings, convection often occurs within air, where warmer air rises and cooler air sinks, creating natural air currents. Forced convection, on the other hand, involves fans, space heaters, ventilation, and air conditioners driving the movement of air to enhance heat transfer.
Finally, radiation is the transfer of heat through electromagnetic waves without the need for a medium. Unlike conduction and convection, radiation does not require direct contact or a material to travel through. Instead, it can transfer heat across empty space. In buildings, various surfaces, such as walls, windows, and furniture, emit and absorb radiant heat. For example, sunlight entering a room through windows is a form of radiant heat, and objects within the room absorb and emit radiation.
The building energy budget framework that was found to accurately describe the energy dynamics in this study focuses on conduction, and it is summarized by the following equation, where QCD,B is total building conduction, QSH is space heating, QAC is air conditioning, and QV is ventilation. The letter “Q” is used for these variables because it traditionally represents heat or energy in physics and thermodynamics.
0 ≈ QCD,B + QSH - QAC - QV
From this equation, we can see that building conduction and space heating are both inputs, whereas air conditioning and ventilation are outputs. The sum of these building energy budget components is approximately zero because the building’s energy is balanced. If they did not sum to zero, the building would be heating up or cooling down, and this is generally not the case.
Total building conduction can be further divided into four components: the average conduction heat flux through the inner roof (GR,I), through sunlit walls (GW,Sn), through shaded walls (GW,Sh), and through the floor (GF). The letter “G” is used to differentiate between the higher-level sources of conducted heat and components of one of those variables.
CD,B = GR,I+GW,Sn+GW,Sh+GF (2)
In this case, all components contribute positively to the total building conduction. It is worth noting that each of these components must be scaled to the area of the roof, the sunlit walls, the shaded walls, and the floor, respectively, in order to find an accurate value for the total building conduction.
To be clear, building energy balance encompasses more than just the relationship described in Equation 1 and 2, as described by Oleson and Feddema (2020). The energy of every inside surface of the building is also in equilibrium. That is, the sum of the radiation, convection, and conduction is zero for the roof, the sunlit walls, the shaded walls, and the floor. Furthermore, Oleson and Feddema provide an equation for the energy balance of the building’s indoor air based on convection.
The following is a visual representation of the simplified building energy budget framework used in this study:
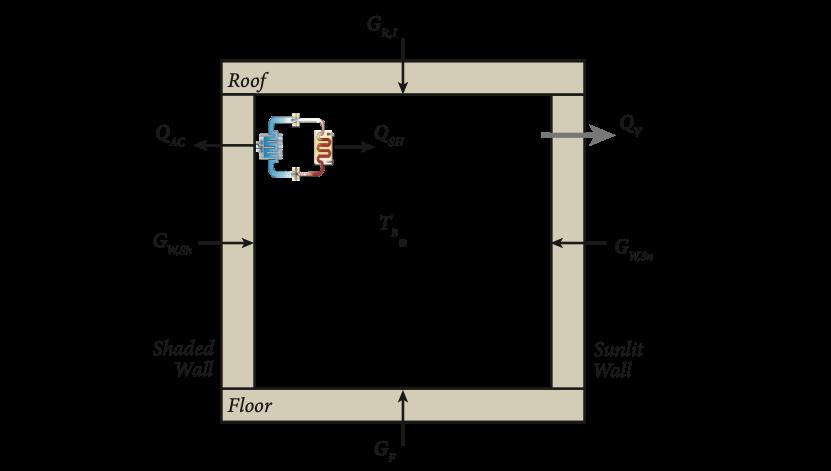
Figure 3. Energy budget framework (adapted from Oleson & Feddema 2020). The components that add heat are illustrated, namely space heating (QSH), conduction through the inner roof (GR,I), through sunlit walls (GW,Sn), through shaded walls (GW,Sh), and through the floor (GF). Two outputs of heat are illustrated, namely air conditioning (QAC) and ventilation (QV). The building’s inner air temperature is TB.
From Figure 3, we can see that GR,I refers to the heat conducted through the inner surface of the roof. This is different from GR,O, the heat conducted through the roof’s outer surface. In particular, GR,I is substantially smaller than GR,O because the roof material absorbs much of the heat.
The same process holds true for the other components of building conduction. Only the heat conducted through the imagined, infinitesimally thin inside surfaces of the building form the variable QCD,B.
3. Results
3.1 The role of total building conduction in air conditioning
In order to find a way to predict the mean air conditioning heat flux of a building, we can use the building energy budget framework already presented. By comparing the plots of each of the major building energy budget components, we find that the total building conduction is quite a good approximation of the mean air conditioning flux.
Figure 4. Energy budget for the whole building with regular roofs for the historical period (1980-2019). Two major inputs of heat are illustrated, namely building conduction (QCD,B), and space heating (QSH). Two outputs of heat are illustrated, namely air conditioning (QAC) and ventilation (QV).
Figure 4 shows that neither space heating nor ventilation contribute very much to the building’s energy balance. It should be noted that while almost all the plotted data is positive (red), that does not mean that each component contributes positively to the building energy budget. The positive values of QAC and QV refer to the positive heat that the building contributes to the urban canyon. Interestingly,
ventilation in the South-Central United States is negative. This indicates that, due to the hotter climate, ventilation heats buildings rather than cooling them, adding extra demand to AC systems. In the North, however, ventilation plays a noticeable role in cooling buildings, taking most of the strain off air conditioning systems.
With the knowledge that total building conduction maps quite closely to the mean air conditioning flux of a building, we can further investigate total building conduction. Breaking it down into its components, we obtain the following plots:
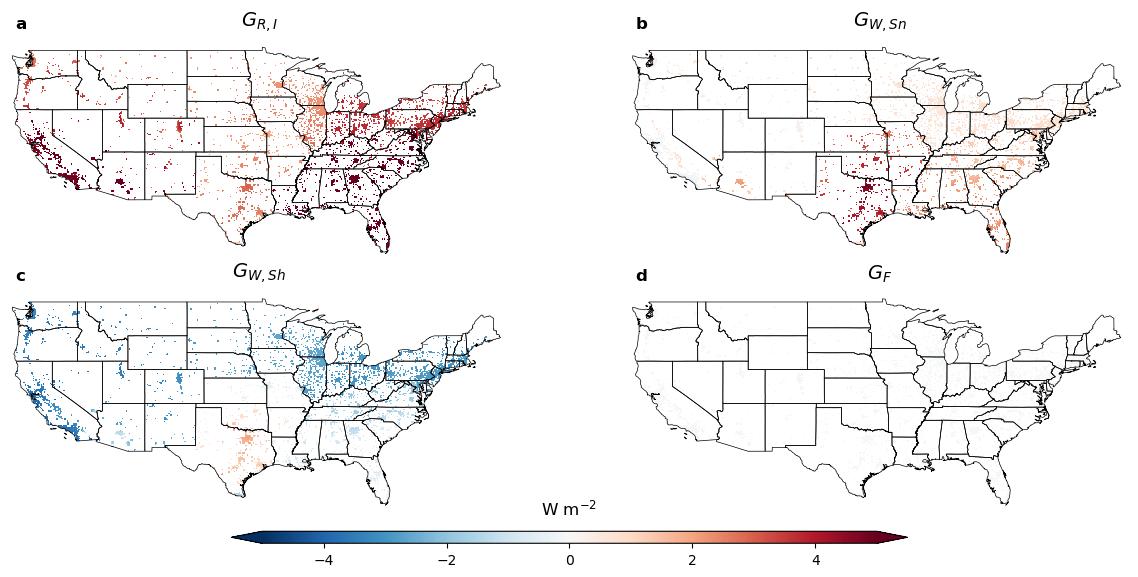
Figure 5. Components of building conduction for the historical period (1980-2019) with regular roofs. The average conduction heat flux through the inner roof (GR,I), sunlit walls (GW,Sn), shaded walls (GW,Sh), and the floor (GF) are shown.
In this case, all components but conduction through the floor play a significant role. The heat conducted through the inner roof and sunlit walls is positive everywhere, whereas conduction through shaded walls is generally negative. Again, however, the South-Central US stands out. Because of the hotter climate, even shaded walls contribute positively to the building’s energy budget.
3.2.1 White roof effects on conduction
It is clear that together, conduction through the inner roof and conduction through the walls do a good job of predicting a building’s air conditioning heat flux. We can now investigate the effect of white roofs on each of these variables.
A higher albedo, however, does not directly affect the conduction through the inner roof. Instead, it has a direct effect on the heat conducted through the outer layer of the roof. It is important, therefore, to investigate how the effect on GR,O of white roofs translates to other changes in the components of total building conduction.
The findings of Liu and colleagues (2022) are similar to this study’s findings that conductive heat flux at the top of the roof is different from the conductive heat flux at the bottom of the roof due to heat storage in the roof, but the findings of Liu and colleagues (2022) are more broadly about the entire building.

Figure 6. White roof effects in the historical period (1980-2019) with regular roofs. All changes are normalized by albedo, with the average change in conduction heat flux through the outer roof (GR,O) and combined sunlit and shaded walls (GW) shown in the bottom row.
The chain effects of white roofs are illustrated for the historical period in Figure 6. Panel (a) illustrates the variable of most direct interest, namely the change in air conditioning heat flux compared to an increase in the albedo of the roof. Panel (b), the change in the total building conduction, looks quite similar to panel (a). However, using the change in total building conduction to predict air conditioning changes slightly overpredicts the magnitude of air conditioning reduction in the North-East. This can be attributed to the larger role ventilation plays in the Northeastern United States, shown in Figure 4.
Of less direct interest is panel (d), the change in the conduction heat flux through the outer roof. This, however, is the most direct effect of white roofs. Changes in outer roof conduction led to changes in inner roof conduction flux, shown in panel (c). The effect of the roof material absorbing heat is substantial, and it cuts the mean energy change value by more than half. To more precisely see the cascading effect of white roofs on the total conduction of heat through the inner surfaces of the building, we can look at the values in Table 1.
Table 1
Mean and Maximum Magnitude Values
The fact that conduction through the outer roof does not cause the same change in conduction through the inner roof is to be expected. What is less obvious, however, is that the change in the conduction flux through the inner roof would not translate one-to-one to the change in total building conduction. Conduction through the inner roof, GR,I, is simply one of the components summed to get QCD,B (see Equation 2). One would expect a change in GR,I to lead to exactly the same change in QCD,B. Because this does not occur, and because floors do not have a significant role in total building conduction, this means that the conduction through the walls must change. Indeed, in panel (e), we see that the heat conducted through the walls is, without exception, positive. We find that the cause of this increase in conduction through the walls is a change in the building’s internal temperature, TB.

Figure 7. White roof effects in the historical period (1980-2019) with regular roofs including change in the building’s temperature normalized by albedo.
Including the change in the building’s internal temperature, TB, in a figure shows that the change in the rate of energy conducted the walls is directly proportional to the change in the building’s internal air temperature. This may come as a surprise as building temperature was expected to remain relatively constant. The reason that it is still possible for the mean internal air temperature to fluctuate is that there is a range of acceptable internal temperatures. The Community Land Model – Urban only turns the air conditioning on when the building’s temperature exceeds a certain limit. Similarly, space heating is only turned on when the building’s temperature falls below a certain level.
The inverse relationship between ΔTB /Δɑ and ΔGW /Δɑ also makes sense. As the temperature inside the building falls, the difference between the building’s temperature and the outside temperature
increases. In accordance with the Second Law of Thermodynamics, this results in more conduction.
3.3 Changes in the effectiveness of white roofs in the future
Up to now, all the data used has been from the historical period (1980-2019). A more useful assessment of the effectiveness of white roofs would also consider future scenarios. The Near-Future Scenario chosen encompasses the years 2020 to 2059, and the FarFuture Scenario chosen spans the years 2060 to 2099. The projected climate for these periods follows the RCP8.5 hotter scenario, one of the most pessimistic projections. In it, our planet’s mean temperature is predicted to increase by 4.3˚C by 2100.
The change in air conditioning flux normalized by albedo for each of these scenarios is shown in the following figure:
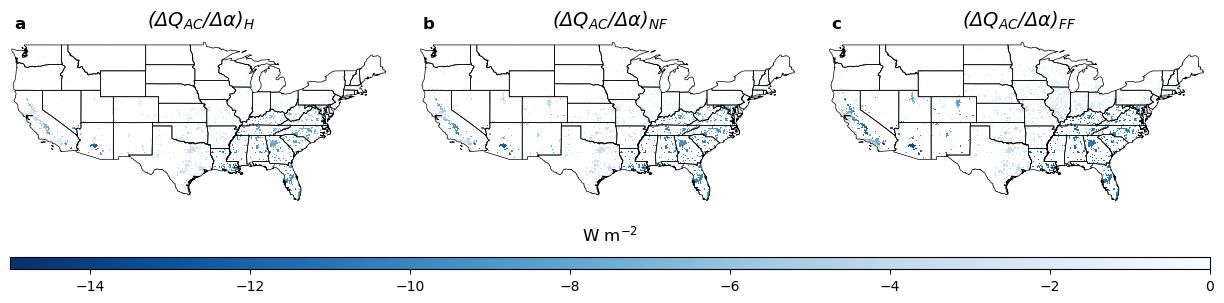
Figure 8. The change in mean urban air conditioning flux normalized by change in albedo in the Historical (H), Near-Future (NF), and Far-Future (FF) Periods.
This shows that, in the future, there will be an increased reduction in air conditioning brought about increases in roof albedo. In Table 2, the mean and maximum magnitude values of each panel above is presented.
Table 2
Mean and Maximum Magnitude
Values
In order to find out why this occurs, it is first necessary to look at changes in all the components of the building energy budget.
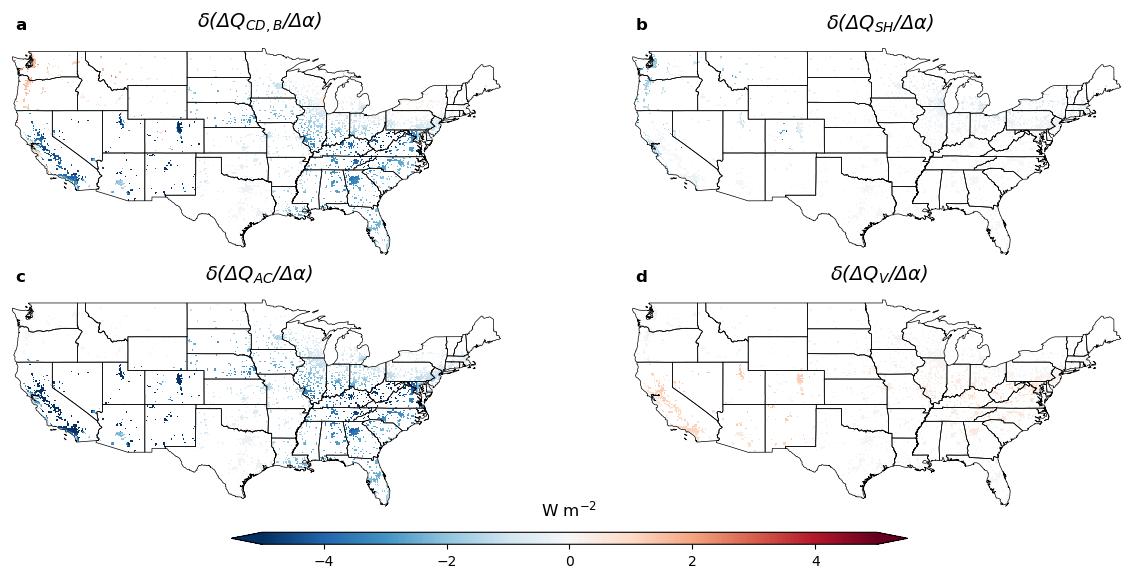
Figure 9. Far-Future changes in the components of the building energy budget. Because the Near-Future scenario involves the same changes as the Far-Future scenario, only less extreme, looking at only the difference between the Historical Period and the Far-Future Period still provides the same insights.
From Figure 9, we can see that changes in space heating and ventilation as a result of increased albedo remain approximately the same, even many decades into the future. The effect of increasing albedo on total building conduction and air conditioning flux, however, becomes even more negative. These changes are also practically identical, meaning that to find out why the effectiveness of white roofs on reducing air conditioning flux increases with time, we can confidently investigate total building conduction to find an answer.
Again, we can break down the building’s total conduction into its four components:
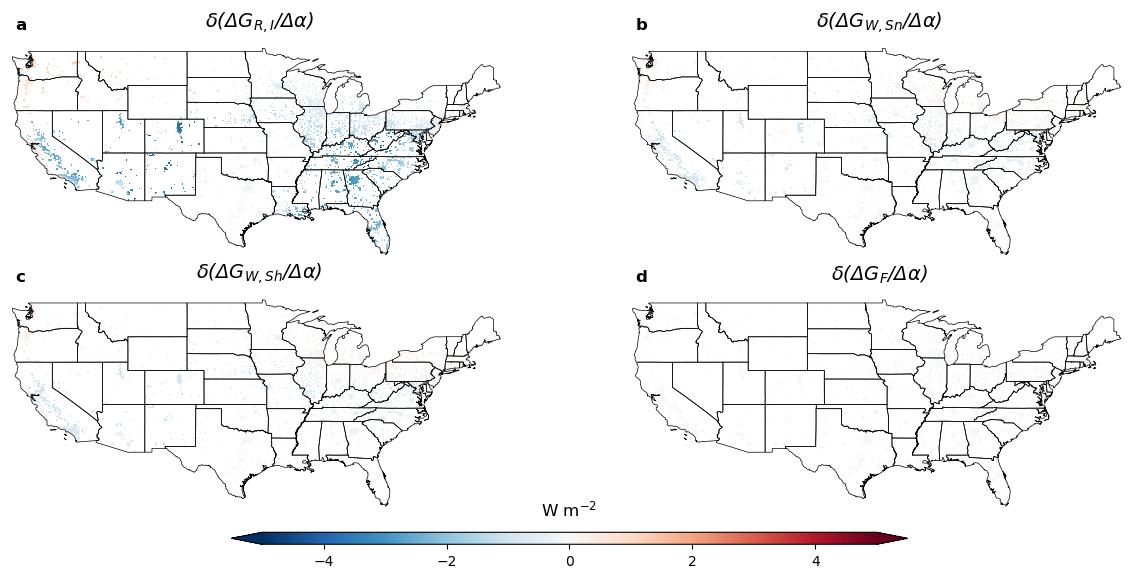
Figure 10. Changes in the components of total building conduction between the Historical Period and the Far-Future Period.
From Figure 10, we see that the floor experiences essentially no change, the walls experience a very slight change, and the inner roof experiences the largest change. As previously mentioned, GR,I depends only on GR,O and the extent to which the roof material decreases GR,O. Because the latter is assumed to stay constant, we can attribute the heightened efficiency of white roofs to a more pronounced decrease in GR,O.
To determine the reason for this, we can turn to the definition of albedo. Albedo is the fraction, or proportion, of reflected radiation to the total amount of incoming radiation that strikes a surface. This proportion stays constant, so as the total radiation hitting the roof’s outer surface increases, the amount reflected by the roof increases at a proportional rate.
4. Discussion
By investigating building energy balance, walls emerge as an increased source of heat conduction when white roofs are implemented. This suggests that white roofs are not as effective at reducing a building’s need for AC as they would be if their effects on buildings came only from the roof. This result stresses that buildings need to be treated as integrated systems rather than aggregates of independent parts. One cannot predict a change to the whole building by only looking at direct effects on the roof, and future studies should keep this in mind. Instead, an accurate way to predict the precise change in AC flux one should expect with a given increase in roof albedo is to calculate the change in the total building conduction.
An implication of this result is that better insulation of walls should be considered to maximize the cooling effects of white roofs. The effects of insulation were investigated, and preliminary results show that a combination of insulated walls and white roofs produce the best effect. However, an investigation of whether white roofs themselves have a larger effect when a building is insulated is beyond the scope of this study. Facades with higher albedos might also be considered. In order for research about such changes to be possible, CLMU would need to include parameters like wall albedo as well as outer-wall conduction.
Despite the counteracting effects of walls, the effectiveness of white roofs is still substantial. It is even found to increase with time. This strengthens the argument for implementing white roofs as only more benefits will be reaped as we move into the future. It is important to recognize, however, the air conditioning demand will still increase as climate change continues to happen. The cost to performance ratio of white roofs can still increase even as the total heat conducted through the inner surfaces of buildings increases.
Real-world measurements should also be made to verify the results of the numerical model. While numerical models offer valuable insights into the potential impacts and efficiency of white roofs in reducing urban heat and building energy consumption, empirical validation is critical to ensure the reliability and applicability of these findings in real-world scenarios. This would involve conducting physical experiments field studies and collecting data from actual buildings with and without white roofs across diverse geographical locations and climates. To specifically verify the results of this study, sensors placed on the outside as well as inside of the roof would be necessary. It would also be important to add sensors to the walls of buildings to confirm the result of increased wall conduction. It would also be advantageous to monitor the building’s energy consumption.
Furthermore, it would be very informative to test whether reducing the range of acceptable building air temperatures would result in a smaller increase in wall conduction. It is possible that this would reduce the temperature difference between the building and the urban canyon, thus decreasing the added conduction through the walls increasing white roofs’ effectiveness and reducing AC flux.
5. References
Lawrence, D. M., R. A. Fisher, C. D. Koven, K. W. Oleson, S. C. Swenson, G. Bonan, et al., (2019): The community land model version 5: Description of new features, benchmarking, and impact of forcing uncertainty. Journal of Advances in Model. Earth Syst., 11.
Li, D., E. Bou-Zeid, and M. Oppenheimer, (2014): The effectiveness of cool and green roofs as urban heat island mitigation strategies. Environ. Res. Lett., 9.
Liu, Y., Z. Luo, and S. Grimmond., (2022): Revising the definition of anthropogenic heat flux from buildings: role of human activities and building storage heat flux. Atmos. Chem. Phys., 22.
Oleson, K. W., and J. Feddema (2020): Parameterization and surface data improvements and new capabilities for the Community Land Model Urban (CLMU). J. Adv. Model. Earth Syst., 12.
Rosado, P., D. Faulkner, D. P. Sullivan, and R. Levinson, (2014): Measured temperature reductions and energy savings from a cool tile roof on a central California home, Energy Build., 80.
Santamouris, M., (2014): Cooling the cities – A review of reflective and green roof mitigation technologies to fight heat island and improve comfort in urban environments. Sol. Energy, 103.
Wang, L., M. Huang, and D. Li, (2020): Where are white roofs more effective in cooling the surface? Geophys. Res. Lett., 47.
Wang, L., M. Huang, and D. Li, (2021): Strong influence of convective heat transfer efficiency on the cooling benefits of green roof irrigation. Environ. Res. Lett., 16.

