sequência positiva, indireta, homopolar, 3i0... como componentes simétricas podem ajudar a compreender um sistema 3Φ?
André Mendes andrephilodeo@gmail.comA abordagem de proteções elétricas e medição de grandezas em sistemas trifásicos implica conhecimento de componentes simétricas. Definitivamente este é um assunto que exige algumas páginas com textos, cálculos, matrizes e gráficos. Apesar da densidade do assunto, que pode assustar à primeira vista, o meu objetivo é introduzir o assunto de forma a auxiliar a interpretação de dados de medições, diagramas de fases (ou fasorial) e, de certa forma, ajudar o leitor a inserir o sensor de corrente da fase A na fase A.
O método de componentes simétricas, ou teorema de Fortescue, é usado na análise de sistemas de potência trifásicos durante condições de desequilíbrio ocasionadas por faltas fase terra, fases abertas, impedâncias desequilibradas, (…) de forma a decompor o sistema 3Φ desequilibrado em outros 3 sis
temas 3Φ balanceados. São eles sequência positiva, sequência negativa e sequência zero (KINDERMAN, 2003 e BLACKBURN, 1997). Por outras palavras, os componentes simé tricas decompõem um sistema trifásico em sequência positiva, negativa e zero (também conhecidas como sequência direta, indireta e homopolar respetivamente).
SEQUÊNCIA POSITIVA (+,1)
Conjunto de 3 fasores balanceados, mesmo módulo e defasados 120º. Sequência ABC.
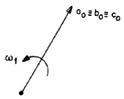
SEQUÊNCIA ZERO (0)
Conjunto de 3 fasores em fase, isto é, mesmo módulo e mesmo ângulo de fase.
O exemplo abaixo mostra as componentes simétricas de sequência positiva, negativa e zero de um sistema trifásico desequilibrado. Somando os vetores de cada componente, obtemos o fasor do sistema em desequilíbrio. A geometria e o diagrama fasorial não são as únicas maneiras de estudar as componentes simétricas. Podemos estudar através das expressões e, mais comummente, de forma matricial.

SEQUÊNCIA NEGATIVA (-,2)

Conjunto de 3 fasores balanceados, mesmo módulo e defasados 120º. Sequência ACB (giro inverso).