IGCSE™ Maths Teacher Guide 4th ed Sample Chapter by Collins

SamplePages

9.1 Standard form 96 Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 Syllabus references Statement Core C1.8/E1.8 Use the standard form A × 10n when n is a positive or negative integer and 1 „ A < 10. Calculate with values in standard form using a calculator Collins references • Student’s Book pages 134–136 Learning objectives • Change a number into standard form. Key words • standard form, index Prior knowledge Students should be able to multiply and divide by 10, 100 and 1000. They should know powers of 10, such as: 105 = 10 × 10 × 10 × 10 × 10 = 100 000, and be shown that: 10–3 = 1 10 × 1 10 × 1 10 = 1 1000 = 0.001 Common mistakes and remediation When inputting numbers on a calculator, students often insert an extra × 10; e.g. to key in 1.3 × 106 they key in , giving an answer that is 10 times larger than required. Point out this error to help students avoid making it Useful tips Suggest that students write these facts into their notes: • When multiplying a number by a positive power of 10, digits move to the left. • When multiplying a number by a negative power of 10, digits move to the right. Starter • Ask these quick fire questions to familiarise students with multiplications by powers of 10: • What are 5 × 10, 5 × 10 × 10, 5 × 10 × 10 × 10? (50, 500, 5000) • What are 10¹, 10², 10³? (10, 100, 1000) • What are 5 × 10¹, 5 × 10², 5 × 10³? (50, 500, 5000) • What are 5 ÷ 10, 5 ÷ 10 ÷ 10, 5 ÷ 10 ÷ 10 ÷ 10? 111 ,, 220200    • What are 10 ¹, 10 ², 10 ³? 111 ,, 101001000    • What are 5 × 10 ¹, 5 × 10 ², 5 × 10 ³? 111 ,, 220200    • Now ask quick fire questions using decimals, e.g. 3.6 instead of 5. Repeat using three digits, e.g. 9.27. SamplePages

Main lesson activity

Arithmetic powers of 10

• Use the notes in the Student’s Book to introduce this topic. Emphasise to students that the power of 10 is called the index. Ask students to draw a place value table as shown below.

thousands hundreds tens units tenths hundredths thousandths 5 5 0

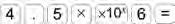
• Then ask students to add the powers of 10 to the column headings, as shown below. thousands hundreds tens units . tenths hundredths thousandths

1000 100 10 1 1 10 1 100 1 1000

• Now ask students to add in the powers of 10 in their index form, as shown below. thousands hundreds tens units . tenths hundredths thousandths

1000 100 10 1 1 10 1 100 1 1000 103 102 101 100 10–1 10–2 10–3

• Students should now be able to see that 5 can be written as 5 × 100, as the 5 is in the 100 column. Similarly, 50 can be written as 5 × 101.

• Explain to students that standard form is of the form a × 10n where 1 „ a < 10 and n is a whole number. Deduce that 52 = 5.2 × 101, and 625 = 6.25 × 102

• Now extend further to consider numbers with digits after the decimal point.

• Conclude that 0.4 = 4 × 10–1, 0.007 = 7 × 10–2, 0.123 = 1.23 × 10–1.

• Refer students to the other examples in the Student’s Book and check their understanding. Students can now do Exercise 9A.

Standard form on a calculator

• Ask students to use their calculators. Input 2 into the display and press the ‘equals’ (=) sign. Now press ‘× 2’ and then repeatedly press the = sign. The answer will double each time, up to 8 589 934 592; the next time they press =, the display will change to standard form (1.717 986 918 × 1010). Discuss what has happened: once the number exceeds a certain size (number of digits) the calculator needs another way to display it.

• Repeat by inputting 2 again, but this time use ‘÷ 2’ and repeatedly press =. Eventually 7.450 580 597 × 10–9 will be displayed. Point out that the same has happened.

• Write 17 179 869 184 on the board. Say that this was the exact answer when 1.717 986 918 × 1010 was displayed. Explain that some rounding has taken place. So 1.717 986 9184 × 1010 = 17 179 869 184 or 1.717 986 918 × 1010 = 17 179 869 180. Say that the calculator is displaying numbers in standard form. Show students the key and input and check the display (4 500 000). Repeat for other numbers.

Plenary

• Allow students to check answers to questions in Exercise 9A by using their calculators.

• More able students can experiment with the ‘scientific notation’ button to convert from ordinary numbers to standard form.

Homework and answers

Homework for this lesson is available in the homework folder. Consolidation and extension exercises are available in the further practice folder. Answers to the exercises can be found in the answers folder.

Lesson 9.1 Standard form Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 97

SamplePages

Calculating with standard form

Syllabus references

Statement Core

C1.8/E1.8 Use the standard form A × 10n when n is a positive or negative integer and 1 ⩽ A < 10. Convert numbers into and out of standard form.

Collins references

• Student’s Book pages 136–139

Learning objectives

• Calculate using numbers in standard form.

Prior knowledge

Students must understand how to write ordinary numbers in standard form and how to convert numbers in standard form to ordinary form.

Common mistakes and remediation

When carrying out calculations with standard form, students may leave answers that are not in standard form, e.g. 23 × 107. Remind students to check that the first number is between 1 and 10.

Useful tips

When multiplying and dividing numbers given in standard form, discourage students from writing the numbers as ordinary numbers and then doing the calculation. Although this is a valid method it can lead to errors with so many digits.

Starter

This starter aims to confirm that students understand the work covered in Lesson 9.1.

• Write the following on the board: a 55 b 16 000 c 23.4 d 0.0008

• Ask students to write these numbers in standard form (5.5 × 101, 16 × 103, 2.34 × 101, 8 × 10–4).

• Now write the following on the board: a 2 × 104 b 3.85 × 105 c 2.62 × 10–5 d 12.4 × 10–1

• Ask students to convert these numbers to ordinary form (20 000, 385 000, 0.000 026 2, 1.24).

9.2

98 Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023

SamplePages

Main lesson activity

• Write 2 × 107 × 6 × 10³ on the board and discuss ways of working it out.

• One possible answer is to deal with the numbers 2 and 6 and then the powers of 10 giving 12 × 1010 and then convert to standard form, 1.2 × 1011.

• A valid method is to first write the numbers as ordinary numbers before doing the calculation. However, this should be discouraged as it can lead to errors with so many digits.

• Repeat for division, e.g. 4 × 10³ ÷ 8 × 105 (5 × 10 ³). Work through Examples 1 and 2.

• Now students can do Exercise 9B.

Plenary

Discuss the answers that students have given for the problem-solving questions in Exercise 9B to confirm their understanding of the work covered in this chapter.

Homework and answers

Lesson 9.2 Calculating with standard form Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 99

SamplePages

Collins references

calculator

Key

Prior knowledge

Common mistakes and

Students

Useful tips

9.3 Standard form without a

86 Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 Syllabus references Statement Extended E1.8 Calculate with values in standard form without using a calculator

• Student’s Book pages 140 142 Learning objectives • Add, subtract, multiply and divide numbers in standard form without using a calculator.

words • No new key words

Students should know how to write large and small numbers in standard form Students should be able to change numbers from standard form to usual notation.

remediation

often have difficulty changing a number from an index notation into standard form. For example, writing 32.5107 × as 3.25108 × . If students are unsure, write the number out in full (in this examples 325 000 000) as an interim step.

Writing numbers out in full is always helpful but it takes more time to do this. The aim is to be able to do it without that step. Starter • Say that throughout this lesson students should not use a calculator. The aim is to be able to work with standard form without a calculator. • Ask students to write out in full: • a 32105 × b 45710 × c 68.7210 × d 40.5810 × e 60.310 × • Check the answers. (a 3 200 000 b 0.0057 c 8 720 000 d 0.000 058 e 300 000) • Ask which numbers were originally written in standard form. (only c) • Ask students to write the other 4 numbers in standard form. (a 63.210 × b 35.710 × d 55.810 × e 3105 × • Ask students if having the number written out in full was helpful. In all cases the index changed by one. The hard part was deciding whether to increase it or decrease it. SamplePages

Main lesson activity

• Write down these four numbers: A = 4.2105 × B = 48.310 × C = 38.510 × D = 26.810 ×

• Ask students to explain how to work out A + B and give the answer in standard form.

• There are three possible methods:

• Write each number out in full: A + B = 420 000 + 83 000 = 503 000 = 5.03105 ×

• Change A so that both indices are 4 and add: A + B = 44445 42108.310(428.3)1050.3105.0310 ×+×=+×=×=×

• Change A so that both indices are 5 and add: A + B = 55 55 4.2100.8310(4.20.83)105.0310 ×+×=+×=×

• Show students all three methods. They can use which ever method they want.

• Point out that it is incorrect to add 4.2 and 8.3 because the indices are different.

• Ask students to use a similar method to work out A – B

• Check that all can get the correct answer of 3.37105 ×

• Now ask students to work out C + D and D – C, giving the answers in standard for.

• Check they get the answers 27.6510 × and 25.9510 ×

• Students can now do Exercise 9C

1 to

• When students have time to finish that move on to multiplication and division. This is easier than addition and subtraction.

• Write down X = 4105 ×

• Say that to multiply X and

To work out X÷Z

810

and 8, and add the indices.

Ask students to work out Y×Z and Y÷Z in a similar way.

If they get the correct

Plenary

410

• Write down these three numbers:

and 1.6107

410

can do the rest of Exercise 9C.

4105

410

• Ask students to find the sum and the product of these numbers. Give the answers in standard form.

• Check they get the correct

• Now ask for the answers

Check they get 4.444107

Homework and answers

447

4.4410

is added to the list.

6.41016

Homework for this lesson is available in the homework folder. Consolidation and extension exercises are

in the further

can be found in the answers folder.

Lesson 9.3 Standard form without a calculator Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 87

Questions

Y = 4

× Z =

510 ×

Y you multiply 4

• 54

XY481032103.21010 + ×=××=×=× •

you divide 4 by 5 and subtract the indices • 53 8 XZ45100.8108107 ÷=÷×=×=× •

•

answers ( 2

× ) they

× 6

answers: 6

× and

•

× and 242.5610 ×

available

practice folder. Answers to the exercises

SamplePages

knowledge

Useful tips

9.4 Surds 86 Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 Syllabus references Statement Core E1.18 Understand and use surds, including simplifying expressions Collins references • Student’s Book pages 142 145 Learning objectives • Simplify simple expressions involving surds Key words • surd Prior

Students should know the meaning and notation of a square root Common mistakes and remediation A common error is to write, for example, () 2 39 = instead of 3. Emphasise the correct answer when this situation occurs.

Answers can be checked with a calculator but students should be able to manipulate expressions without one. Starter • Ask students to complete this inequality with two consecutive integers: ...60... << The answer is 7 and 8 Students should use the facts that 2 749 = and 2 864 = • Ask students to do the same for: 31 (5 and 6); 150 (12 and 13); 210 (14 and 15) SamplePages

Main lesson activity

• Ask students to use a calculator to find 23 × and then 6 . They will see that they are the same.

• Demonstrate why this is the case:

2323232233236

• This is an example of a general result: abab

Hence 236 ×=

• Ask this to check this with other pairs of numbers. For example, does 3721 ×= ?

• Now ask students to find 2 and 8 on their calculators. What do they notice?

• They should see that one is twice the other.

• Write down: 8424222 =×=×=

This works because 4 is a square number.

• Ask learners to simplify in the same way: 18 and 500

They should see that 189232 =×= and 5001005105 =×= . In each case, look for a multiple of a square number.

• Say that expressions that contain a square root are called surds

are 67 or 5311 +

are irrational numbers and cannot be written exactly as decimals.

• Look at this product: ()2832 You can simplify it by multiplying out the bracket:

2832823228232826

() 4223

• Students can check with a calculator that these two expressions have the same value.

Ask students to simplify in the same way: ()5334 +

They should get 15203 + or ()5343 +

Students can now complete Exercise 9D.

Plenary

• 28164 ×== which is an integer.

• Ask students to try to find other example of two different surds whose product is an integer. After a few minutes ask them to share any examples.

• Some possible answers are 3279 ×= ; 3228 ×= ; 2186 ×= ; 20510 ×= The need to look for two numbers that multiply to make a square number.

Homework and answers

Lesson 9.4 Surds Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 87

() 2

×=×××=×××=×= ;

×=

•

Examples

. These

()

−=−×=−×=− or

•

SamplePages

9.5 Rationalising the denominator 86 Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 Syllabus references Statement Core E1.18 Rationalise the denominator Collins references • Student’s Book pages 145 148 Learning objectives • Rationalise the denominator of a fraction containing surds Key words • rationalise Prior knowledge Students should be able to simplify simple expressions involving surds. Common mistakes and remediation Students can have difficulty choosing the correct multiplier for a denominator of the form abc + Emphasise the fact that the only difference is the sign between the terms. Useful tips Students may find it easier at first to write out separately the multiplication for the numerator and the multiplication for the denominator. Starter • Write down 51050 ×= • We could write this as () 5465456203050 +=×+×=+= which gives the same answer. • We could also write ()() 32463(46)2(46)121881250 ++=+++=+++= • Make sure students can see where the four terms come from. • Another way is ()23(19)2(19)3(19)21832750 ++=+++=+++= • Or with a minus sign: ()() 72467(46)2(46)284281250 −+=+−+=+−−= • The answer will always be 50. Ask each student to write one of their own. Ask for some examples and check the result is always 50. SamplePages

and

Lesson 9.5 Rationalising the denominator Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 87 Main lesson activity • Look at this fraction 5 2 . Multiply the numerator and the denominator by 2 : 55252 2222 × == × or 5 2 2 • The denominator (2) is now a rational number. This process is called rationalising the denominator. • Ask students to rationalise the denominators of these: 4 3 ; 10 5 ; 3 6 ; 8 2 Answers: 4 3 3 ; 25 ; 1 6 2 ; 2 • Here is a more complicated example: 10 32 • In this case multiply the numerator and the denominator by 32 + : () () () 103210 32 3232 + = −+ • The denominator is () () () () 32323322329323227 −+=+−+=+−−= • Notice that the difference in signs means that the surds cancel out and the answer is an integer. • So () () () ()1032103210 732 3232 ++ = = −+ or ()10 32 7 + • Ask students to rationalise the denominator of 2 101 + Answer: () () () ()2101 22 101 9101 101101 = =− + +− • Now rationalise the denominator of 15 35 + Answer: () () () () 1535 35355845 25 9543535 ++ ++++ = = = + −+ • Make sure students understand how to simplify the numerator in this case. • More able student may be able to go directly from () ()3535 +− to 9 – 5 but others will prefer to write out the four terms and simplify. • Students can now complete Exercise 9E. Plenary • Ask students to rationalise the denominator of 32 32 + • They should find () () () () 323232 3662 5 26 3232 3232 +++ +++ = = = + −+ • Check that students can multiply each pair of brackets correctly. Homework

answers Homework for this lesson is available in the homework folder. Consolidation and extension exercises are available in the further practice folder. Answers to the exercises can be found in the answers folder. SamplePages

form

Homework

1 Write these standard form numbers out in full:

a 3.5 × 102 b 4.15 × 10 c 5.7 × 10–3 d 1.46 × 10 e 3.89 × 10–2 f 4.6 × 103 g 2.7 × 102 h 8.6 × 10 i 4.6 × 103 j 3.97 × 105 k 3.65 × 10–3 l 7.05 × 102

2 Write these numbers in standard form:

a 780 b 0.435 c 67 800 d 7 400 000 000 e 30 780 000 000 f 0.000 427 8 g 6450 h 0.047 i 0.000 12 j 96.43 k 74.78 l 0.004 157 8

3 Write the appropriate numbers given in each statement in standard form:

a In 1990 there were 24 673 000 vehicles licensed in the UK.

b In 2001 Keith Gordon was one of 15 282 runners to complete the Boston Marathon.

c In 1990 the total number of passenger kilometres on the British roads was 613 000 000 000.

d The Sun is 93 million miles away from Earth. The next nearest star to the Earth is Proxima Centuri, which is about 24 million million miles away.

e A scientist was working with a new particle reported to weigh only 0.000 000 000 000 65 g.

4 How many times smaller is 1.7 × 102 than 1.7 × 105?

5 How many times bigger is 9.6 × 107 than 4.8 × 103?

6 How many times bigger is 1.2 × 105 than 3000?

9.1 Standard

Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023

SamplePages

Calculating with standard form

Homework

1 Find the results of the following, leaving your answers in standard form: a (4 × 106) × (7 × 109) b (7 × 105) × (5 × 107) c (3 × 10–5) × (8 × 108) d (2.1 × 107) × (5 × 10–8)

2 Find the results of the following, leaving your answers in standard form: a (9 × 108) ÷ (3 × 104) b (2.7 × 107) ÷ (9 × 103) c (5.5 × 104) ÷ (1.1 × 10–2) d (4.2 × 10–9) ÷ (3 × 10–8)

3 Find the results of the following, leaving your answers in standard form: a (8 × 109) ÷ (4 × 107) b (12 × 106) ÷ (3 × 104) c (2.8 × 107) ÷ (7 × 10–4)

4 p = 8 × 105 and q = 2 × 107

Find the value of the following, leaving your answer in standard form: a p × q b p ÷ q c p + q d q – p e q ÷ p

5 p = 2 × 10–2 and q = 4 × 10–3

Find the value of the following, leaving your answer in standard form: a p × q b p ÷ q c p + q d q – p e q ÷ p

6 In 2010 the population of Africa was approximately 1 × 109 In 2050 the population of Africa is expected to be 1.8 × 109. By how much is the population of Africa expected to rise? Give your answer in millions.

7 A number, when written in standard form, is greater than 1 million and less than 5 million. Write down a possible value of the number in standard form.

8 Here are four numbers written in standard form: 3.5 × 105 1.2 × 103 7.3 × 102 4.8 × 104 a Work out the largest answer when two of these numbers are multiplied together. b Work out the smallest answer when two of these numbers are added together. Give your answers in standard form.

9.2

Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023

SamplePages

9.3 Standard form without a calculator Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 Homework Do not use a calculator for this worksheet. Write your answers in standard form. 1 Work out: a 55 8.3105.110 ×+× b 54 8.3105.110 ×+× c 8.3105.11054 ×+× 2 Work out: a 65 1.6109.310 ×−× b 86 4.2810310 ×−× c 1.6106.11034 ×−× 3 X = 4410 × and Y = 6510 × Work out a X + Y b X – Y c XY × d 2X 4 A = 8103 × and B = 5210 × a AB × b AB ÷ c BA ÷ d 2B 5 The area of India is 63.2910 × km2 The area of Russia is 1.71107 × km2 Show that the Russia is approximately 5 times larger than India 6 In 2020 the population of Indonesia was 2.68108 × The population of Malaysia was 3.1107 × a Find the total population of the two countries. b Complete this sentence: The population of Indonesia is approximately times the population of Malaysia. 7 6L510 =× ; 3M2.510 =× Find: a LM × b LM ÷ c The reciprocal of L 8 A3105 =× Find 3A 9 38 610M1.210 ××=× Work out M SamplePages

Homework

25 ×

711

a 328

205

2(21)

5203

3(43)

9.4 Surds Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023

Do not use a calculator in this homework. 1 Simplify as much as possible: a

b 67 × c 2.510 × d

× e 312 × f 320.5 × 2 Write as a multiple of 2 or 5 : a

b 50 c 80 d 500 e 72 f 162 3 Show that 83262 += 4 Simplify as much as possible:

b 312 + c 298 + d

e 9040 + f 2002 5 2NA = a Show that if A = 2 then N = 8 b Find N if i

= 3 ii A = 7 iii A = 20 6 Multiply out the bracket and simplify: a

+ b

c ()282 + d ()

e () 6243 + f ()333 + 7 Simplify 3122748 +++ 8 Show that 50982008 +=+ SamplePages

9.5 Rationalising the denominator Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 Homework Do not use a calculator in this exercise 1 Rationalise the denominator. a 6 2 b 6 3 c 1 25 d 3 2 e 5 310 f 4 14 2 Multiply the brackets and simplify a () () 5151 +− b () ()7272 −+ c () ()4848 +− d () ()510510 −+ 3 Multiply and simplify a () ()1323 ++ b () ()4525 −+ 4 Simplify. a () 2 12 + b ()3 12 + 5 Rationalise the denominator a 23 3 + b 42 2 c 42 8 + d 126 3 + 6 True or false? a 10212 += b 1028 −= c 10220 ×= d 1025 ÷= 7 Rationalise the denominator a 1 21 + b 1 52 c 2 35 + d 6 46 8 Rationalise the denominator and simplify. a 58 48 + + b 24 21 + + c 101 103 + + 9 Show that 82 82 + is an integer. SamplePages

form and surds

Consolidation

1 Write down the value of each of the following:

a 3.1 × 0.1 b 3.1 × 0.01

c 3.1 × 0.001 d 3.1 × 0.0001

2 Write down the value of each of the following: a 6.5 × 10–1 b 6.5 × 10–2 c 6.5 × 10–3 d 6.5 × 10–4

3 a What is the largest number you can enter into your calculator? b What is the smallest number you can enter into your calculator?

4 Work out each of the following:

a 3.1 ÷ 0.1 b 3.1 ÷ 0.01 c 3.1 ÷ 0.001 d 3.1 ÷ 0.0001

5 Write down the value of each of the following: a 6.5 ÷ 10–1 b 6.5 ÷ 10–2 c 6.5 ÷ 10–3 d 6.5 ÷ 10–4

6 These numbers are not in standard form. Write them in standard form. a 0.000 03 × 10–2 b 25.6 × 105 c 16 × 102 × 3 × 10–1 d 2 × 104 × 56 × 10–4 e (18 × 102) ÷ (3 × 103) f (56 × 103) ÷ (2 × 10–2)

7 3106A =× and 5105B =× Write in standard form a AB + b AB c 2A d AB ×

8 2104X =× and 4103Y =× Find XY ÷ . Write your answer in standard form.

Ch9 Standard

SamplePages

form and surds

Extension

1 The speed of light is 3.00 × 108 m/s (2.997 924 58 × 108 m/s, to be exact).

It takes about 1.3 seconds for light to travel to the Moon. Use this information to work out the distance to the Moon Give your answer in kilometres.

2 Many people withdraw money from their bank account using a cash machine. In one country, every day there are 8 million withdrawals from 32 000 machines. What is the average number of withdrawals per machine?

3 The mass of Jupiter is 1.899 × 1027 kg.

The mass of the Earth is 6.04 × 1024 kg.

The mass of the Moon is 7.348 × 1022 kg.

a How many times heavier is Jupiter than the Earth? Give your answer in standard form.

b What is the mass of the Moon divided by the mass of the Earth? Give your answer in standard form.

c How many times heavier is Jupiter than the Moon? Give your answer in standard form.

4 Without using a calculator, estimate ()() 35 3.75107.8810 ×÷× Write your answer in standard form.

5 a Write 1000 as a multiple of 10

b Write 2000 as a multiple of 5

6 Simplify 45125245 ++

7 a Show that the reciprocal of 38 + is 38

b Find the reciprocal of 37 +

c Find the reciprocal of 35

Ch9 Standard

SamplePages

form

Answers

Homework

9.1 Standard form

1 a 350 b 41.5 c 0.0057 d 14.6 e 0.0389 f 4600 g 270 h 86 i 4600 j 397 000 k 0.003 65 l 705

2 a 7.8 × 102 b 4.35 × 10–1 c 6.78 × 104 d 7.4 × 109 e 3.078 × 1010 f 4.278 × 10–4 g 6.45 × 103 h 4.7 × 10–2 i 1.2 × 10–4 j 9.643 × 101 k 7.478 × 101 l 4.1578 × 10–3

3 a 2.4673 × 107 b 1.5282 × 104 c 6.13 × 1011 d 9.3 × 107, 2.4 × 1013 e 6.5 × 10 13

1000 5 20 000

9.2 Calculating with standard form

1 a 2.8 × 1016 b 3.5 × 1013 c 2.4 × 104 d 1.05

2 a 3 × 104 b 3 × 103 c 5 × 106 d 1.4 × 10–1

3 a 2 × 102 b 4 × 102 c 4 × 1010

4 a 1.6 × 1013 b 4 × 10–2 c 2.08 × 107 d 1.92 × 107 e 2.5 × 101

5 a 8 × 10–5 b 5 c 2.4 × 10–2 d 1.6 × 10–2 e 2 × 10–1

6 800 million

7 Any value between 1.000 000 01 × 106 and 5 × 106, i.e. any value of the form a × 106 where 1 < a < 5

8 a 1.68 × 1010 b 1.93 × 103

9.3 Standard form without a calculator

1 a 61.3410 × b 8.81105 × c 45.9310 ×

2 a 6.7105 × b 4.25108 × c 49.910 ×

3 a 65.0410 × b 64.9610 × c 21011 × d 1.6109

a 11.610 × b 4108 × c 92.510 ×

10410

76 1.71103.291017.13.295

a 2.99108

b 9 or 10

a 41.2510 × b 2109 × c 7210

2.71016

4210

a 10 b 42 c 5 d 77 e 6 f 4

a 25 b 52 c 45 d 105 e 62 f 92

832224262

a 22 b 33 c 82 d 5 e 510 f 92

a 2242428

i 18

Ch9 Standard

× 4

× 5 ()

×÷×=÷≈ 6

× 8

× 9

× 9.4 Surds 1

+=+= 4

=×=×= b

iii 800 6 a

+ b 123 c 422 + or ()222 + d 1035 e 1236 + or ()436 + f 333 + or () 331 + 7 103 8 50985272122 +=+= and 200810222122 +=+= SamplePages

0.31

0.65

0.065

0.0065

10–7

3.510

2.56

106

10–1

4.8

Ch9 Standard form Cambridge IGCSE® Maths Teacher’s Guide © HarperCollinsPublishers Ltd 2023 9.5 Rationalising the denominator 1 a 32 b 23 c 1 5 10 d 1 6 2 e 1 10 6 f 2 14 7 2 a 4 b 3 c 8 d 15 3 a 533 + b 325 + 4 a 322 + b 752 + 5 a 2 31 3 + b 221 c ()1 81 2 + d 223 + 6 a False b False c True c True 7 a 21 b 52 + c ()1 35 2 d ()1 263 5 + 8 a ()1 128 8 + b 322 c 7210 9 82 82 + () () () () 8282 82162 828282 18 3 6 ++ ++ = = −+ == or 8222232 3 822222 ++ === Consolidation 1 a

b 0.031 c 0.0031 d 0.000 31 2 a

d 0.000 65 3 a 9 999 999 999 × 1099 b 0.000 000 001 × 10 99 (depending on number of digits displayed) 4 a 31 b 310 c 3100 d 31 000 5 a 65 b 650 c 6500 d 65 000 6 a 3 ×

× 102 d 1.12 × 102 e 6 ×

f 2.8 × 106 7 a 6

× b 62.510 × c 91012 × d 1.51012 × 8 6510 × Extension 1 390 000 km 2 250 3 a 3.14 × 102 b 1.22 × 10–2 c 2.58 × 104 4 4107 × 5 a 1010 b 205 6 155 7 a Either () () 3838981 +−=−= or 1 38 = + () () 3838 983838 38 = +− =− b ()1 37 2 c ()1 35 4 + SamplePages