100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC (ĐỀ 41-60) by Dạy Kèm Quy Nhơn Official

ĐỀ THI THỬ TỐT NGHIỆP

THPT MÔN TOÁN

vectorstock com/28062405

Ths Nguyễn Thanh Tú

eBook Collection

100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM

HỌC 2022-2023 - MÔN TOÁN - CÁC

TRƯỜNG TRÊN CẢ NƯỚC - CÓ LỜI GIẢI (ĐỀ 41-60) - 483 TRANG

WORD VERSION | 2023 EDITION

ORDER NOW / CHUYỂN GIAO QUA EMAIL

TAILIEUCHUANTHAMKHAO@GMAIL COM

Tài liệu chuẩn tham khảo

Phát triển kênh bởi

Ths Nguyễn Thanh Tú

Đơn vị tài trợ / phát hành / chia sẻ học thuật :

Nguyen Thanh Tu Group

Hỗ trợ trực tuyến

Fb www.facebook.com/DayKemQuyNhon

Mobi/Zalo 0905779594

SỞGIÁODỤCVÀĐÀOTẠOTHANHHÓA

TRƯỜNGTHPTYÊNĐỊNH

ĐỀTHITHỬTỐTNGHIỆPTHPT–NĂM2022-2023

Câu1. Đồthịhàmsốnàotrongcáchàmsốsauđâycótiệmcậnđứng?

Câu2. Tíchtấtcảcácnghiệmcủaphươngtrình bằng 2 254 24 xx

Câu3. Tậpnghiệmcủaphươngtrình là

A. . B. . C. . D. .  4   2 2 4; 3 

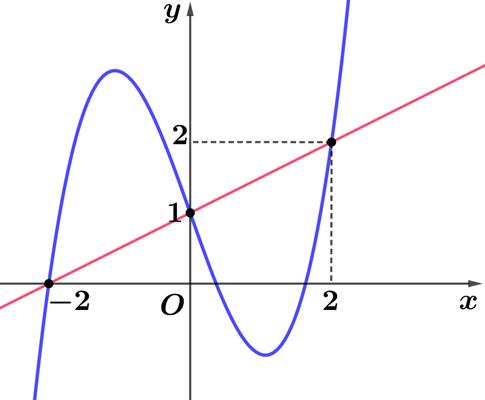
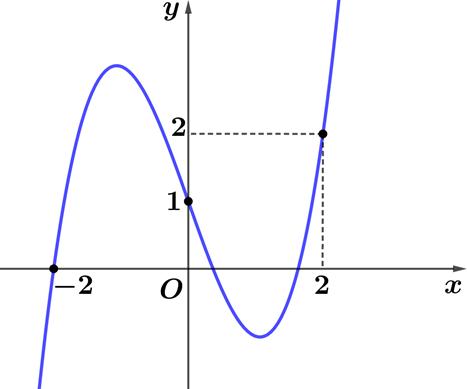
Câu4. Chohàmsố cóđồthị vàđườngthẳng Biết cắt tạiba 3231yxxx

điểmphânbiệtcóhoànhđộlà Tính ? 123,,.xxx123 Txxx 

A. . B. . C. . D. . 3 1 42

Câu5. Tậpxácđịnhcủahàmsố là  2 31yx 

A. B. C. D. 1;

Câu6. Mộthìnhnóncóchiềucaobằng bánkínhđáybằng códiệntíchtoànphầnbằng 43

A. . B. . C. . D. . 9 15 24 12

Câu7. Chohàmsố liêntụctrênmỗikhoảng và vàcóbảngbiếnthiênnhưsau

Tậpnghiệmcủabấtphươngtrình là 20fx

A. B. C. D.  ;1  ;1  1;

Câu8. Chohàmsố cóđạohàmliêntụctrên thoảmãn .Biết yfx 

Câu9. Cóbaonhiêugiátrịnguyêncủathamsố khôngvượtquá10

A. . B. . C. . D. . 2 1 2y xx   2 1 1y x   4 3 1y x   2 y x 





A. B. C. D. 2 2 11

 log1log230



 



 C

:1. dyx 



 

 \1







 0; cot2sin fxfxxxx  .Tính . 2 24f    6f    A. . B. . C. . D. . 2 36  2 80  2 54  2 72 

đểhàmsố đồngbiếntrên m 3 3 x y xm   khoảng ? 2; A. B. C. D. 1110129

Câu10. Thểtích củakhốicầucóbánkính bằng V 3r

A. B. C. D. 3636 9 9

Câu11. Biết làmộtnguyênhàmcủahàmsố trên.Giátrịcủa bằng

A. . B. . C. . D. . 7 9 15 4 23 4

Câu12. Chocáchàm số và với là những số thực dương khác1,có đồ thị như hình vẽ. x ya  xyb  , ab Đường thẳng cắt trục tung, đồ thị hàm số và lần lượt tại Biết rằng 3y x ya  xyb  ,, HMN ,khẳngđịnhnàosauđâyđủng? 23HMMN 

A. . B. . 4223yxx 4223yxx 

C. . D. . 4223yxx  4233yxx 

Câu19. Mộthìnhtrụcóbánkínhđáybằng ,chuvithiếtdiệnquatrụcbằng .Thểtíchcủakhốitrụđã a 10a chobằng

A. B. C. D. 3 a 33a 34a 35a

Câu20. Trongcácmệnhđềsau,mệnhđềnàosai?

A. B.  dln01 xx axaaCa  cosdsinxxxC 

A. . B. . C. . D. . 53ab  23ab  35ab  35ab 

Câu13. Cho khối lăng trụ tamgiác có thể tích. Gọi lần lượt làtrung điểm của các . ABCABC V,, MNP cạnh ; ; .Mặtphẳng chiakhốilăngtrụđãchothành2phần,phầnchứađiểm

C. D. 1 d,1 1 x xxC   

Câu21. Chohàmsố liêntụctrên vàcóbảngbiếnthiênnhưsau

lăngtrụtamgiácđều cócạnhđáybằng Khoảng

Cóbaonhiêugiá trị nguyên của để phương trình có nghiệm trên khoảng m 21 45fm x xx 

A. . B. . C. . D. . 0 1054

Câu22. Chohìnhnón cóchiềucaobằng Cắt bởimộtmặtphẳngquađỉnhvàcáchtâmcủađáy  N 2a N mộtkhoảngbằng tađượcthiếtdiệncódiệntíchbằng Thểtíchkhốinónđãchobằng a 2 411 3 a A. B. C. D.

Câu23. Chohàmsố cóđồthịlàđườngcongtronghìnhvẽdướiđây.Giátrịlớnnhấtcủahàmsốđã yfx  chotrênđoạn bằngbaonhiêu?  1;1

Câu18. Hàmsốnàodướiđâycóđồthịnhưđườngcongtronghìnhdướiđây?



fx   2 1 2dfxx

3Fxx 

có

1V V A. . B. . C. . D. . 25 144 37 144 61 144 49 144 Câu

Chohình

cáchtừ đếnmặtphẳng ABCABC 2a B bằng  ACCA A. B. C. D. 2a 3a 2a 22a Câu15. Nếu thìhàmsố bằng' 32d23 fxxxxC  fx A. B. 431 2 fxxxCx  2 66 fxxxC  C. . D. . 431 2 fxxx  2 66 fxxx  Câu16. Cho .Khiđó bằng  5 2 d10fxx 

 A.

ABBCCC  MNP B

thểtíchlà.Tỉsố bằng 1V

14.

2 5 24dfxx

. B. . C. . D. .42343246

Hỏi

24u 42u 1u A. B. C.

15u 1



Câu17. Chomộtcấpsốcộngcó , .

bằngbaonhiêu?

16u 11u





   d fxxfxC 



yfx  

x fx fx  1 2 3 0 4 3 1



1;3

 ?

1;2

3 a 310 3 a 310a 3 45 9 a

Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?

A. B. C. D. 30 1 2

Câu24. Sốcáchsắpxếp ngườingồivào chiếcghếxếphàngnganglà: 56

A. . B. . C. . D. . 5 6A 6! 5 6C 5!

22 19fxxxxmx

Câu25. Chohàm số có đạo hàm với mọi .Cóbaonhiêu số

A. B. C. D. 6578

Câu26. Chohàmsố biết làmộtnguyênhàm

Câu30. Cóbaonhiêugiátrịnguyêncủathamsố đểhàmsố đồngbiếntrên?

.5476

Câu31. Chohàmsố cóbảngxétdấucủađạohàmnhưsau

2;1

A. .B. . C. . D. .  2;

Câu32. Cóbaonhiêusốnguyêndương đểphươngtrình cóhainghiệm m 2 e1ln12ee1 x xx mmx

phânbiệtkhônglớnhơn 5

A. .B. C. D. .29272826

Câu33. ÔngNamcầnxâydựngmộtbểnướcmưacóthểtích dạnghìnhhộpchữnhậtvớichiềudài  38 Vm  gấp

lầnchiềurộng,đáyvànắpđổbêtông,cốtthép;xungquanhxâybằnggạchvàximăng.Biết 4 3

rằngchiphítrungbìnhlà980.000đ vàởnắpđểhởmộtkhoảnghìnhvuôngcódiệntíchbằng 2/m

diệntíchnắpbể.TínhchiphíthấpnhấtmàôngNamphảichitrả(làmtrònđếnhàngnghìnđồng).

A. đ. B. đ. C. đ. D. đ. 22770000276570002096500023235000 Câu34. Xét ,nếuđặt thì bằng

Câu35. Chohìnhchóp cóđáy làhìnhvuôngcạnh , vuônggócvớiđáyvà . SABCDABCD 2aSA 6SAa  Gócgiữahaimặtphẳng và bằng  SBD ABCD

A. B. C. D. 90 45 60 30

Câu36. Chohìnhchóp cóđáy làtamgiácđều,hìnhchiếuvuônggóccủađỉnh trên SABCABC  ABCDS mặt đáy làtrung điểm của cạnh . Biết và mặt phẳng vuônggóc với mặt HAB 3 2 Sa H  SAC phẳng Thểtíchcủakhốichóp bằng  SBC SABC

Câu37. Với vàlàhaisốnguyêndươngtùyýthỏamãn .Mệnhđềnàodướiđâyđúng? kn kn 

A. B. C. D.  !! ! k n

knk C n   ! !! k n An knk  ! ! k n Cn k   ! ! k n An nk 

Câu38. Chohaisốdương ,thỏamãn .Tính ,,1aba 2 2 loglog2 aa bbloga b

A. B. C. D. 8 5 4 5 24

Câu49. Sốnghiệmnguyêncủabấtphươngtrình là

A. B. C. D. 4213

Câu50. Cho khiđó bằng 35 log5;log7, ab 45 log175

1 2 1 2 3 1 2 1 x y O

yfx  

  

dương đểhàmsố đồngbiến

m 3 gxfx   3;

x nguyên

trênkhoảng ?

củahàmsố và .Khí 2sin1fxxxFx fx01F đó bằng? Fx A. B. 3cos2Fxxxx  3 cos2 3 x Fxxx C. D.  3 cos 3 x Fxxx   3 cos2 3 x Fxx

hàmsố

2 x y x   A. B. C. D. 2x 1 2 x 2y 2x Câu28. Chohìnhchóptứgiáccóđáylàhìnhvuôngcạnhbằng ,chiềucaobằng3.Thểtíchcủakhốichópđã 2 chobằng A. B. C. D. 4126 18 Câu29.

khoảng

nguyênhàmcủahàmsố là  ;2 1 2fx x   A. . B. . C. . D. . 1 2 C x   ln2xC  2 1 2 C x   1 ln2 2 xC 

Câu27. Tiệmcậnđứngcủađồthị

làđườngthẳng 21

Trên

,họ

m

3 fxxmxx  

A. .B. C.



 

 ;2

2 9

0 2(2)d Ixxx   22uxI A. B. C. D. 3 2022 2 2duu 1 2022 0 d uu 3 2022 2 d uu 3 2022 2 1 d 2 uu

22022

3 4 a 33 8 a 3 16 a 3 2 a

A. B. C. D.

1 5 5 x x    

41. Thểtíchcủakhốitứdiệnđềucạnh là a

42. Đồthịhàmsốnàosauđâycóhaiđiểmcựcđạivà điểmcựctiểu?1

43: Chohàmsố cóbảngbiếnthiênnhưsau: yfx 

Câu44: Tìmtấtcảcácgiátrịnguyêncủa trên thỏamãn m 2021;2021

22414323 mm mmm

A.2020. B.2021. C.1. D.0

Câu45. Cho làbasốthựcdươngkhác.Đồthịhàmsố đượccho ;; abc 1;;xxx yaybyc 

ởhìnhvẽdướiđây.Mệnhnàonàosauđâyđúng?

A. B. C. D. abc  cab  bca  acb 

Câu46. Cho làcácsốthựcthayđổithỏamãn và làcácsốthựcdươngthay , ab 2220 log6841 ab ab   , cd

đổi thỏa mãn .Giá trị nhỏ nhất của biểu thức  2 2 2 log7223 c cc dd d  là  221 acbd 

A. B. C. D. 4211255 5 291855 5

Câu47. Chohàmsố , .Khẳngđịnhnàodướiđâyđúng?

C. D. dsin fxxxxC  dsin fxxxxC 

Câu48. Gọi ,, lần lượt là độ dài đường sinh, chiều caovàbánkính của hình trụ Diện tíchtoàn lhR  T phần củahìnhtrụđượcxácđịnhtheocôngthức p S

A. . B. . 2 tp SRlR  222tp SRlR 

C. . D. . 22tp SRlR  2 p SRhR 

Câu

A. B. C. D. 2 ab a    2 aab a   22 2 b a    2 2 ab a  

A. B. C. D. 32 12 a 32 4 a 33 12 a 33 4 a Câu

A. B. C. D. 4223yxx  34 yxx  22 yxx  4223yxx  Câu

Điểmcựcđạicủa

A. . B. . C. . D. 4x 3x 2x 3x

Câu

hàmsốđãcholà



A. . B.



 



1cos fxx x 

dcos fxxxxC

dcos fxxxxC 

hàmlà 42xfx 

B. C

D.  44.2 ln2 x fx    4 4.2.ln2 xfx     42 ln2 x fx    4 2.ln2 xfx   Câu50. Chohàmsố cóđồthịhàmsố nhưhìnhvẽbên 432 fxaxbxcxdxa  yfx   Hàmsố đồngbiếntrênkhoảngnàodướiđây?  122 ygxfxfx  A. B. C. D.  0;2  3; 13 ; 22     ;0

49. Hàmsố cóđạo

BẢNGĐÁPÁN

HƯỚNGDẪNGIẢICHITIẾT

Câu1. Đồthịhàmsốnàotrongcáchàmsốsauđâycótiệmcậnđứng?

ChọnB

Điềukiệnxácđịnh: .101xx

Tậpxácđịnh . 1;D

Câu6. Mộthìnhnóncóchiềucaobằng bánkínhđáybằng códiệntíchtoànphầnbằng 43

A. . B. . C. . D. . 9 15 24 12

Lờigiải

ChọnC

Theogiảthiếttacó . 22 4,35hrlhr 

22.3.5.324 tp Srlr 

Câu7. Chohàmsố liêntụctrênmỗikhoảng và vàcóbảngbiếnthiênnhưsau fx  ;1 1;

Tậpnghiệmcủabấtphươngtrình là 20fx

A. . B. . C. . D. .  ;1  ;1  1; Lờigiải

ChọnD

Tacó: Từbảngbiếnthiênsuyra 202fxfx 21fxx

Tậpnghiệmbấtphươngtrìnhlà . 1;

Câu8. Chohàmsố cóđạohàmliêntụctrên thoảmãn .Biết

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 D D B A B C D D B B B D D B D B A B B A D B A A A 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 A A A B C A C B C C A D B B D A D C B D C C B D B

A. B. C. D. 2 1 2y xx   2 1 1y x   4 3 1y x   2 y x  Lờigiải ChọnD Cáchàmsố , , cóTXĐlà nênđồthịkhôngcótiệmcận 2 1 2y xx  2 1 1y x  4 3 1y x   DR  đứng. Hàmsố có và nênđồthịcótiệmcậnđứng . 2 y x   0;D 0 2 lim xx   0x Câu2.

cácnghiệmcủaphươngtrình bằng 2 254 24 xx  A. B. C. D. 2 2 11 Lờigiải ChọnD Có  2 2 25425422 2 242225422520* xx xx xxxx    có và . *25160 121c xx a  Câu3. Tậpnghiệmcủaphươngtrình là  log1log230

 A. B. C. D.  4   2 2 4; 3    Lờigiải ChọnB Có  log1log230log1log23 xxxx  . 1234 101 xxx x x x           Vậy . S Câu4. Chohàmsố cóđồthị vàđườngthẳng Biết cắt tạiba 3231yxxx C :1 dyx  d C điểmphânbiệtcóhoànhđộlà Tính ? 123,,.xxx123 Txxx  A. . B. . C. . D. . 3 1 42 Lờigiải ChọnA Cóphươngtrìnhhoànhđộgiaođiểm 32 32 311320210 xxxxxxxxxx  Suyra 0123T Câu5. Tậpxácđịnhcủahàmsố là  2 31yx  A. . B. . C. . D. . 

  1;  0; \1

Tíchtấtcả

Lờigiải





 0; .cot2.sin fxfxxxx  .Tính . 2 24f    6f    A. B. C. D. 2 36  2 80  2 54  2 72  Lờigiải ChọnD

yfx 



m m m mm

A. B. C. D. 53ab  23ab  35ab  35ab  Lờigiải ChọnD Tacó , , , .  0;3H log3;3 a M log3;3 bN  log3;0 a HM    log3log3;0 baMN  Theogiảthiết, 23HMMN 23HMMN  2log33log3log3 a ba

5log33log3 ab 33

53 loglogab 

33 5log3logba 53 33 loglogba 53ba

Câu13. Cho khối lăng trụ tamgiác có thể tích. Gọi lần lượt làtrung điểm của các . ABCABC V,, MNP cạnh ; ; .Mặtphẳng chiakhốilăngtrụđãchothành2phần,phầnchứađiểm ABBCCC  MNP B

Dokhôngvượtquá10nên . m 2 10 3 m 

Vìnguyênnên .Vâycó10giátrịnguyêncủathamsố thỏamãn. m  1;2;3;;10m m

Câu10. Thểtích củakhốicầucóbánkính bằng V 3r

A. . B. . C. . D. . 3636 9 9

Lờigiải ChọnB

Tacó . 3344 .336 33 Vr

A. . B. . C. . D. . 25 144 37 144 61 144 49 144 Lờigiải ChọnD

2dfxx

Câu11. Biết làmộtnguyênhàmcủahàmsố trên.Giátrịcủa bằng 3Fxx  fx   2 1



ChọnB Tacó .  

Tacó:

 PCEPCNCECN   

 PCNHBNHBCP 

Tacó: 





x x   2

fx x x      Dođó  

x       2 24f    22 0 44 CC  Hay



x 

f    Câu9. Cóbaonhiêugiátrịnguyêncủathamsố khôngvượtquá10đểhàmsố đồngbiếntrên m 3 3 x y xm   khoảng ? 2; A. . B. . C. . D.

111012

Lờigiải ChọnB Tacó . 2 333 33 xm y xmxm      Hàmsố đồngbiến

khi . 3 3 x y xm 



.cot2.sin fxfxxxx     



cos2sin sin x fxfxxx x 

2 sin-cos 2 sin fxxfxx

sin

2 d2d sinsin

fx xxxxC x

22sin sin

xfxxx

22 sin 636672

trênkhoảng



31302 3223 3



A. . B. . C. . D. . 7 9 15 4 23 4 Lờigiải

22 22 3 11

11 2d2dd29

fxxxfxxxx

cóthểtíchlà.Tỉsố bằng 1V1V V

Câu17. Chomộtcấpsốcộngcó , .Hỏi bằngbaonhiêu?

ChọnA

45 321 uudu uudd

14. Chohìnhlăngtrụtamgiácđều cócạnhđáybằng Khoảngcáchtừ đếnmặtphẳng . ABCABC 2a B

A. . B. .

. D. . 2a 3a 2a 22a Lờigiải ChọnB

A. . B. . 4223yxx 4223yxx  C. D. 4223yxx  4233yxx  Lờigiải

ChọnB

, vàhàmsốcó 4 0a3d

BMACCA

Gọi làtrungđiểmcủa M AC Tacó . BMAC BMAA 

Khiđó . ; 3 BAACA dBMa   Câu15. Nếu thìhàmsố bằng'

bacựctrịsuyra .00abb

A. B. C. D. 3 a 33a 34a 35a

Lờigiải

Chuvithiếtdiệnquatrụclà  2222103 Phrhaaha 

Thểtíchkhốitrụlà .223 33 Vrhaaa  



thức  d01 ln x xa axCa a 

yfx

bảngbiến



ABC  ..1

  

   Xét đồngdạng BGN BME

3 BGBN BMBE  

BG BA  Tacó: . 1HBMEHBGNPCFEVVVV  Lạicó:  113133 332228 HBME VHBBMBE VBBBABC      . 111111 ...... 3326272 HBGN VHBBGBN VBBBABC     111111 3322448 PCFE VPCCECF VCCCBCA     Vậy 131149 87248144 V V   Câu

bằng  ACCA

Xét ,theođịnhlýmenelauytcó: .

AMBECF MBECFA

1 3 CF FA

1 6







C. D.



2 66 fxxx  Lờigiải ChọnD . 322 2366 fxxxCxx   Câu16. Cho .Khiđó bằng  5 2 d10fxx  2 5 24dfxx  A. B. C. D. 42343246 Lờigiải ChọnB

 

32d23 fxxxxC  fx

. 431 2 fxxxCx  2 66 fxxxC 

431 2 fxxx





22 42d4d2d fxxfxxx 

40634

24u 42u 1u A. B. C. D. 15u 11u 16u 11u Lờigiải

Tacó . 21 1 41        

Câu18. Hàmsốnàodướiđâycóđồthịnhưđườngcongtronghìnhdướiđây?

Dựavàođồthịtathấyđườngconglàhàmbậc trùngphươngvớihệsố

Câu19. Mộthìnhtrụcóbánkínhđáybằng ,chuvithiếtdiệnquatrụcbằng Thểtíchcủakhốitrụđã a 10a chobằng

ChọnB

D. 1 d,1 1 x

        d fxxfxC  Lờigiải

Câu20. Trongcácmệnhđềsau,mệnhđềnàosai? A.

 dln01 xx axaaCa 

cosdsinxxxC 

xxC

ChọnA



Theocông



 

Câu21. Chohàmsố liêntụctrên vàcó

thiênnhưsau

1;3

Xéttamgiác có: . SAB

trịlớnnhấtcủa

Yêucầubàitoán .  2138gmgm 

Do . 4;5;6;7

N 2a N mộtkhoảngbằng tađượcthiếtdiệncódiệntíchbằng .Thểtíchkhốinónđãchobằng a

Câu22. Chohìnhnón cóchiềucaobằng Cắt bởimộtmặtphẳngquađỉnhvàcáchtâmcủađáy

ChọnA

Gỉasửtamgiác làthiếtdiệnđiquađỉnhcủahìnhnón . SAB 

tathấy: với nên .

13 fx

Câu24. Sốcáchsắpxếp ngườingồivào chiếcghếxếphàngnganglà: 56

A. B. C. D. 5 6A 6! 5 6C 5! Lờigiải

Sốcáchsắpxếp ngườivào ghếhàngnganglà 56 5 6A

Câu25. Chohàm số có đạo hàm với mọi .Cóbaonhiêu số yfx 

nguyêndương đểhàmsố đồngbiếntrênkhoảng ? m

3 gxfx

A. . B. . C. . D. .6578 Lờigiải

ChọnA

Tacó  22 332339 fxxxxmx

x fx fx  1 2 3 0 4 3 1 Cóbaonhiêugiá trị nguyên của

phương trình có

trên khoảng m 21 45fm x xx   ? 1;2 A. B. C. D. 0 1054 Lờigiải ChọnD Do ,tacó:  24501;2xxx Phươngtrình  2 21 451 45fm x mxxfxgx xx   Xét . 2 14524101;2gxfxxxxfxx   Vì .    10 1;221310 240 fx xxfx x       Bảngxétdấu: x1 2 gx  gx  1g  2g

để

nghiệm





A. B. C. D. 3 45 3 a 310 3 a 310a 3 45 9 a Lờigiải ChọnB S O A B H I

mm

411

N Gọi làtrungđiểmcủa vàkẻ . I ABOHSI    , OHSABdOSABHOa  Xéttamgiácvuông có: . SOI222222 111111 4 OHSOOIaaOI  2 3 Oa I  Lại

. 2

44 4 33 aaSISOIOa

có:

222

2 411 22.233 3 43 3 ABC a S a AB Sa I  33 23 ABa BI 

OBOIIB a Vậythểtíchcủakhốinónlà: . 3 22 1110 ..5.2 333 aVrSOaa   Câu23. Chohàm

cóđồthị

congtronghìnhvẽdướiđây.Giá

hàmsốđã 

 chotrênđoạn bằng



1 2 1 2 3 1 2 1 x y O A.

C. . D.

1 2 Lờigiải





 1;1 3Maxfx

Xéttamgiác có: . OIB

22433

39 aa

số

làđường

yfx

baonhiêu?

1;1

. 30

Theođồthị

1;1x



   x



 



22 19fxxxxmx

    



 

Khiđó

3.gxfx

Câu28. Chohìnhchóptứgiáccóđáylàhìnhvuôngcạnhbằng ,chiềucaobằng3.Thểtíchcủakhốichópđã 2 chobằng

. D. . 4126 18

Lờigiải

Tacódiệntíchđáy nênthểtíchkhốichóplà . 2.24B 11 .4.34 33 VBh

Câu29. Trênkhoảng ,họnguyênhàmcủahàmsố là

ChọnB

Tacó .

Lờigiải

Câu30. Cóbaonhiêugiátrịnguyêncủathamsố đểhàmsố

A. .B. C. D. .5476

ChọnC

TXĐ: D

Tacó . 229fxxmx 

Hàmsốđồngbiếntrên 

0, fxx  2290, xmxx 29033m m

Vì nên . m 3;2;1;0;1;2;3m

Câu31. Chohàmsố cóbảngxétdấucủađạohàmnhưsau fx

Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?

A. .B. . C. . D. .  2;  ;2  2;  2;1 Lờigiải

ChọnA

Từbảngbiếnthiênsuyrahàmsốnghịchbiếntrênkhoảng  2;

Câu32. Cóbaonhiêusốnguyêndương đểphươngtrình cóhainghiệm m 

biệtkhônglớnhơn 5

Hàmsố đồngbiếntrênkhoảng khivàchỉkhi gx  3;    22 0,3;. 30,3; 323390,3; gxx fxx xxxmxx        thì suyra  3;x 2 30,20 xx 2 3390,3:. xmxx .   2 2 3: 39 39 ,3; 3 3 x x m xmMin x x     Tacó  2 3999 323.6 333 x x x x x x    Suyra 6m Vìnguyêndươngsuyra . m  1;2;3;4;5;6m Câu26. Chohàmsố biết làmộtnguyênhàmcủahàmsố và .Khí 2sin1fxxxFx fx01F đó bằng? Fx A. . B. . 3cos2Fxxxx  3 cos2 3 x Fxxx C. D.  3 cos 3 x Fxxx   3 cos2 3 x Fxx Lờigiải ChọnA Tacó .  3 2sin1cos 3 x FxxxdxxxC   Mà .Vậy  30 01cos0012 3 F CC 3cos2Fxxxx Câu27.

hàmsố làđườngthẳng 21 2 x y x   A. B. C. D. 2x 1 2 x 2y 2x Lờigiải ChọnA Tacó nênđồthị

. 2 21 lim 2x x x   2x

Tiệmcậnđứngcủađồthị

hàmsốcótiệmcậnđứnglà

A. . B. .

ChọnA



 ;2 1 2fx x   A. . B. . C. . D. . 1 2 C x   ln2xC  2 1 2 C x   1 ln2 2 xC 



x  

1 ln2 2 fxdxdxxC

đồngbiếntrên? m

fxxmxx  

321 93 3

Lờigiải





2 e1ln12ee1 x xx mmx phân

Lờigiải Chọn

Tacó 2 e1ln12ee1

xx mmx 1 2 e1lnx1e10 x x mm    e1ln1e10 x x mmx        e10 ln1e10 x x mmx      e1 ln1e1 x x mmx      0/ ln1e1 x xtm mmx    Phươngtrình cóhainghiệmphânbiệtkhônglớnhơn Phươngtrình có  1 5  ln1e1 x mmx mộtnghiệmduynhấtkhácvànhỏhơnhoặcbằng 05

.B. C. D. .29272826

Vì nên . 0x ln1e1 x mmx ln11ex mmx 2

Đặt  ln1tmx1ex mx

ChọnC

Tacó:+) ; d2duxx  +) .02;13xuxu 

Tacó . 1e ee 1e xt x

mx mxmt mt     **

Xéthàmsốđặctrưng: trên. e u fumu 

Tacó , và . e0 u fum u m  

Suyra . **e10 x xtmx 

Xéthàmsố ,có ,suyra . e1 x gxmx  e x gxm   0ln gxxm 

*Nếu loại. 1m

*Nếu ,tacó1m Đểthỏamãnbàitoánthì .  5 e1 50 5gm

Kếthợpđiềukiện,suyra . 2;3;;29m

Vậycógiátrịnguyêndương thỏamãn. 28 m

Câu33. ÔngNamcầnxâydựngmộtbểnướcmưacóthểtích dạnghìnhhộpchữnhậtvớichiềudài  38 Vm  gấp lầnchiềurộng,đáyvànắpđổbêtông,cốtthép;xungquanhxâybằnggạchvàximăng.Biết 4 3

rằngchiphítrungbìnhlà980.000đ vàởnắpđểhởmộtkhoảnghìnhvuôngcódiệntíchbằng 2/m 2 9 diệntíchnắpbể.TínhchiphíthấpnhấtmàôngNamphảichitrả(làmtrònđếnhàngnghìnđồng). A. đ B. đ C. đ D. đ22.770.00027.657.00020.965.00023.235.000

Lờigiải ChọnB

Gọichiềurộngcủabểlà .Tacóchiềudàibểlà vàchiềucaocủabể

Câu35. Chohìnhchóp cóđáy làhìnhvuôngcạnh , vuônggócvớiđáyvà . SABCDABCD 2aSA 6SAa 

Gócgiữahaimặtphẳng và bằng  SBD ABCD

A. B. C. D. 90 45 60 30 Lờigiải

ChọnC

Gọi làgiaođiểmcủa và . O ACBD

Từđềbài,tacó:+) ,() BDACBDSABDSACBDSO 

Tacó , SOBDAOBD 

     ;; SBDABCDSOAOSOA  +) .  222tan360 SA ACaAOaSOASOA AO 

Câu36. Chohìnhchóp cóđáy làtamgiácđều,hìnhchiếuvuônggóccủađỉnh trên SABCABC  ABCDS mặt đáy làtrung điểm của cạnh . Biết và mặt phẳng vuônggóc với mặt HAB 3 2 Sa H  SAC

phẳng Thểtíchcủakhốichóp bằng  SBC SABC

là . 3xm 4() xm 2 2 3 m x Khiđótổngdiệntíchbềmặtxâylà:   2 2 2 2 2 2 2228642864327 342234342 3933333 xx Txxxxxx m x x x    Chiphí(tínhtheođồng)xâydựnglà: (đồng). C 327 98000098000027657000 3 CT  Câu34. Xét ,nếuđặt thì bằng 1 22022 0 2(2)d Ixxx   22uxI A. . B. . C. . D. . 3 2022 2 2duu 1 2022 0 d uu 3 2022 2 d uu 3 2022 2 1 d 2 uu Lờigiải



3 2022 2 d Iuu

A D B C S

A. B. C.

3 4 a 33 8 a 3 16 a 3 2 a Lờigiải

 

Câu37. Với vàlàhaisốnguyêndươngtùyýthỏamãn .Mệnhđềnàodướiđâyđúng? kn kn 

A. B. C. D.  !! ! k n

knk C n   ! !! k n An knk  ! ! k n Cn k   ! ! k n An nk 

Lờigiải ChọnD Mệnhđềđúnglà .  ! ! k n An nk 

Câu38. Chohaisốdương ,thỏamãn .Tính ,,1aba 2 2 loglog2 aa bbloga b

A. B. C. D. 8 5 4 5 24

Lờigiải

Tacó . 2 2 l154 oglog2log2log2log2log225 a aa a a a bbbbbb 

Câu39. Sốnghiệmnguyêncủabấtphươngtrình

Câu40. Cho khiđó bằng 35 log5;log7, ab

Câu41. Thểtíchcủakhốitứdiệnđềucạnh là a

Gọitứdiệnđềucạnh là với làtâmcủađáy aSABCO ABC

ChọnB

x H A C B S K ChọnA Giảsử làtamgiácđềucạnh ABC x Kẻ vuônggócvới tại .Tacó (vì ) HK SCK , SCHKSCAB  ABSHC  cùngvuônggócvới Gócgiữa và làgócgiữa và , SCAKBAKBK SCAKBK SAC  SBC  90 22 ABx AKBHK  Mặtkhác,tacó: . 22 222 3 3 2 4 xa CxHSCCHSH   222 111 HKCHSH  222222 33 .23 2 332 44 xa CHSH ax HK CHSHxaxa       Suyra,tacóphươngtrình: . 222 22 3 32 22 xax xxaxa xa   Diệntíchtamgiác là:  ABC2233 2. 42 ABC aSa    Thểtíchcủakhốichóp là: .  . SABC 23133 .. 3224 aaa V

là 23 521 5 5 x x    

. B.

C. . D. .4213 Lờigiải ChọnB Tacó: . 2 2 3 523521 555 5 x xxx       2 2 3523520 xxxx  1 2 3 x  Do nên . x 0;1x Sốnghiệmnguyêncủabấtphươngtrìnhlà2.



A. . B. . C. . D. . 2 ab a    2 aab a   22 2 b a    2 2 ab a   Lờigiải ChọnD Tacó: 2 3333335 45 2 3333 3 llog175log5.72log5log72log5log5log7 og175log45log352log3log521log5       22 22 aab ab aa   

45 log175

A. B. C. D. 32 12 a 32 4 a 33 12 a 33 4 a Lờigiải ChọnA

SOABC

và . 2

ABC aSABACAaa      3 2sin2sin603 BCaa OA A   Tamgiác

6 3 aSOSAOA  

Tacó

113 sinsin60 224

có . SOA 22

Câu42. Đồthịhàmsốnàosauđâycóhaiđiểmcựcđạivà điểmcựctiểu?

44: Tìmtấtcảcácgiátrịnguyêncủa trên thỏamãn m

22414323 mm mmm

A.2020. B.2021. C.1. D.0

Lờigiải ChọnB

Tacó:  22414323 mm mmm

3 10,0 33 fxxx x x xx

fx

Nênhàmsố đồngbiếntrênkhoảng

Xéthàmsố : 21 m fmm 

Tacó: nênhàm đồngbiến 2ln210, mfm m  21 m fmm 

Mặtkhác: 00fmfm

Vậy có2021giátrịnguyênmthỏamãn.  2020;2019;;0m 

Câu45. Cho làbasốthựcdươngkhác.Đồthịhàmsố đượccho ;; abc 1;;xxx yaybyc 

ởhìnhvẽdướiđây.Mệnhnàonàosauđâyđúng?

A. B. C. D. abc  cab  bca  acb  Lờigiải

ChọnD

Dohàmsố nghịchbiếntrên . x ya  1a 

Dohàmsố và đồngbiếntrên . xyb  x yc  ,1bc 

Tacó: . 0;:11 x xxbbxbc bc cc    

Vậy .acb 

Câu46. Cho làcácsốthựcthayđổithỏamãn và làcácsốthựcdươngthay , ab 2220 log6841 ab ab   , cd

đổi thỏa mãn .Giá trị nhỏ nhất của biểu thức  2 2 2 log7223 c cc dd d  là  221 acbd  A. . B. . C. . D. . 4211255 5 291855 5

Lờigiải

 22 22 22 20 log684120684341* ab abababab   Lạicó:   2 2 2 2 2 2 2 log7223log7223 230;,0 c cc dd c cc dd d d dddc       2 2 2 2 121 log722log27** 1;0 1;0 cdcccddd dc dc           

Vậy

VSSO   

1 A. B. C. D. 4223yxx  34 yxx  22 yxx  4223yxx  Lờigiải ChọnD Tacó . 4223yxx  3 44 yxx . 3 0 0440 1 x yxx x   2 124yx  Có làđiểmcựctiểu. 040y 0x  Có làhaiđiểmcựcđại. 180y1x 

yfx  Điểmcựcđạicủahàmsốđãcholà A. . B. . C. . D. 4x 3x 2x 3x Lờigiải ChọnC. Điểmcựcđạicủahàmsốđãcholà 2x Câu

 2021;2021 

23 11362 334312SABCABC aaa

Câu43: Chohàmsố cóbảngbiếnthiênnhưsau:

   2

mmm mmm mm       Xéthàmsố với 23 fxxx 0x

2 2413

432 241432 131232 mm mm mm

    



Tacó:  2 2 2 

Mà  1212210 m mm fmfmm

ChọnC

Tacó: 

 ;;1; MabNcd *M  3;4I 1R

Đặt .Theo tathấy thuộcđườngtròntâm ,bánkính .

Câu50. Chohàmsố cóđồthịhàmsố

 **N 11 21 22xyyx  0,1xy

Từ tathấy thuộcnữađườngthẳng ứngvới .

Khiđó  221 MNacbd 

Suyra . min1291MNNIR

Vậygiátrịnhỏnhấtcủabiểuthức

22 1291acbd



Câu47. Chohàmsố , .Khẳngđịnhnàodướiđâyđúng?

1cos fxx x 

A. B. dcos fxxxxC  dcos fxxxxC 

C. D. dsin fxxxxC  dsin fxxxxC  Lờigiải ChọnC

Tacó: .  1cosdsinxxxxC  

Câu48. Gọi ,, lần lượt là độ dài đường sinh, chiều caovàbánkính của hình trụ Diện tíchtoàn lhR  T

phần củahìnhtrụđượcxácđịnhtheocôngthức p S

A. . B. . 2 tp SRlR 

222tp SRlR 

2 p SRhR 

C. . D. . 22tp SRlR 

Lờigiải ChọnB

Diệntíchtoànphần củahìnhtrụđượcxácđịnhtheocôngthức tpS

Câu49. Hàmsố cóđạohàmlà 

222tp SRlR 

42xfx  A. . B. . C. . D. .  44.2 ln2 x fx    4 42ln2 xfx     42 ln2 x fx    4 2ln2 xfx   Lờigiải ChọnD Tacó:.  4 4 22.ln2 x xfxfx    

hìnhvẽbên 

 yfx  

như

432 fxaxbxcxdxa

đồngbiếntrênkhoảngnàodướiđây?  122 ygxfxfx 

Hàmsố





    ;0 Lờigiải ChọnB Từđồthịhàmsố tathấy: fx  0 0 1 x fx x   Nên ,hay .  411fxaxxx    2 41fxaxx   Suyra: .   2224222111 fxaxaxaaxaxx    Xét có:  122 gxfxfx   2122122 gxfxfxfxfx    Suy ra:  22222 2 2412121132224221 gxaxxaxxaxxaxx        32 3 2 22 32.121364.213 axxxxaxxxx 23 321312322 axxxxxxx     232 32134113 axxxxx     0 1173 0;1 8 01 1173 2;3 8 3 x xa gxx xb x            Vì nêndựavàođồthịhàmsố suyra  2 41fxaxx   fx  0a Nhậnxét:  23 13212441130ga    Nêntacóbảngxétdấu: Dựavàobảngxétdấutacó đồngbiếntrênkhoảng gx  3;

A. B. C. D.  0;2

13 ; 22

SỞGIÁODỤCVÀĐÀOTẠOTHÁIBÌNH

TRƯỜNGTHPTCHUYÊNTHÁIBÌNH

ĐỀTHITHỬTỐTNGHIỆPTHPT–LẦN3–NĂMHỌC2022–2023

Câu1. Trongkhônggian ,cho .Tọađộcủavectơ là: Oxyz23 aijk   a 

A. B. C. D.  2;1;3 3;2;1 2;3;1 1;2;3

Câu2. Chohàmsố cóbảngbiếnthiênnhưhìnhvẽ yfx 

Câu

Khẳngđịnhnàosauđâyđúng?

A.Giátrịcựcđạicủahàmsốlà . B.Giátrịcựcđạicủahàmsốlà . 3CDy 4CDy

C.Giátrịcựctiểucủahàmsốlà . D.Giátrịcựctiểucủahàmsốlà . 3CTy 1CTy

Câu11. Hàmsốnàodướiđâyđồngbiếntrênkhoảng ?

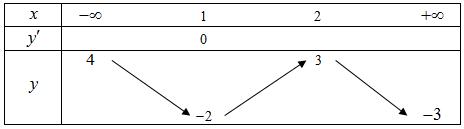
Câu12. Chohàmsố liêntụctrênđoạn vàcóđồthịtrênđoạn nhưhìnhvẽbên. ()yfx

Tổnggiátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố trênđoạn

A.4. B.-1. C.1. D.2.

Câu13. Trongkhônggian ,mộtvectơchỉphươngcủađườngthẳng

14. Trongkhônggian ,chođiểm .

Câu15. Hàmsố với cóđồthịnhưhìnhvẽbên.Mệnhđềnàosauđâylàđúng?

tíchkhốihộpbằng

Câu16. Tínhđạohàmcủahàmsố

Câu8. Sốtổhợpchập3của12phầntửlà

. B. . C. . D. .1728220132036

Câu9. Chohìnhchóp cóđáy làtamgiáccân , cáccạnhbên SABCABC ABACa   120BAC  bằngnhauvàcùngtạovớimặtphẳngđáycácgóc .Thểtíchkhốichóp là 30 SABC A. B. C. D. 33 12 a 3 4 a 33 4 a 3 12 a

Câu10. Trongcáchàmsốsau,hàmsốnàođồngbiếntrên? 

dướiđâycóđồthịnhưđườngcongtronghìnhbêndưới? A. B. C. D. 32 yxx  242 yxx  32 yxx  42 2 yxx  Câu4. Tìmtậpxácđịnh củahàmsố D 25 2yxx  A. . B. . D  0;D C. D.  ;12;D \1;2D Câu5. Tìmhọnguyênhàmcủahàmsố sin3 fxx  A. . B. . C. . D. . cos3xC  1 cos3 3 xC cos3xC  1 cos3 3 xC  Câu6. Cho cấp số nhân có số hạng đầu vàcông bội Số hạng thứ năm của cấp số  n u 13u 2q nhân là  n u A. B. C. D. 596u 532u 548u 524u Câu7. Chokhốihộpchữnhật có , , .Thể

ABCDABCD

 

5

 A.

3. Hàmsốnào

AAa

3 ABa

ACa

12a 34a 315a

A. . B. . C. . D. .  x fe x     1x fx e    1 3 x fx  3xfx

 ;  A. . B. . C. . D. . 33 yxx  1 2 x y x  1 3 x y x    33 yxx 



 1;5



1;5

bằng fx 1;5

là Oxyz 12 112 xyz  

C. . D.  1;1;2u   1;1;2u   1;2;0u   1;2;1u 

làhình

Oxyz 1;2;3M A M trênmặtphẳng

A. B. C. D.  1;2;3A  1;2;0A  1;0;3A  0;2;3A

   0a A.

A. .

Câu

Tọađộđiểm

chiếuvuônggóccủa

là:  Oyz

axb ycxd

B. C. D. 0,0,0bcd 0,0,0bcd0,0,0bcd0,0,0bcd

2 log21yx A. B. C. D.  1 21ln2y x     2 21ln2y x    2 21y x    1 21y x    Câu17. Chohàmsố cóbảngbiếnthiênnhưhìnhvẽ.Tổngsốtiệmcậnngangvàtiệmcậnđứng yfx  củađồthịhàmsốđãcholà A.0. B.2. C.1. D.

Câu18. Vớimọi dươngthỏamãn Khẳngđịnhnàodướiđâyđúng? , ab 3 22 loglog5 ab

A. . B. . C. . D. . 3232ab 2232ab 2332ab 232ab

Câu19. Hàmsố cóđồthịlàhìnhbên.Giátrịcủacơsố bằng  log01 a yxa a

Hàmsố nghịchbiếntrênkhoảngnàodướiđây?

A. . B. . C. . D. . 424 22

Câu20. Tìmtậpnghiệm củabấtphươngtrình . S

A. B. C. D.  5;S  3;S  ;5S  ;3S

Câu21. Tìmtậpnghiệm củabấtphươngtrình . S  2 22 loglogxxx 

A. B. C. D.  2S  0S  0;2S  1;2S

Câu22. Mộtchiếchộpchứa9quảcầugồm4quảmàuxanh,3quảmàuđỏvà2quảmàuvàng(cácquả cầu đôimộtkhácnhau). Lấyngẫunhiên3quảcầutừhộpđó.Xácsuấtđểtrong3quảcầulấy được

Câu23. Chohìnhchóp cóđáy làtamgiácvuôngcântại và .Tamgiác . SABCABC B2 ABa  SAB đềuvànằmtrongmặtphẳngvuônggócvớiđáy.Tínhthểtích củakhốichóp . V . SABC

A. . B. . C. . D. . 33 4 a V 33 3 a V 33 12 a V 3 23 3 a V

Câu24. Chokhốinóncóbánkínhđáybằng ,gócởđỉnhhìnhnónlà .Thểtíchkhốinónbằng 3cm 60

A. . B. . C. . D. . 3 93(cm)  3 33(cm)  3 6(cm) 3 3(cm) 

31. Nếu và thì bằng

Câu32. Tính

Câu33. Trongkhônggianvớihệtrụctọađộ ,cho .Phươngtrìnhmặtphẳng đi Oxyz 1;1;3H  P qua cắtcáctrụctọađộ lầnlượttại (khác)saocholàtrựctâm H Ox,Oy,Oz,,ABCOH

tamgiác là ABC

A. B. C. D. 370xyz 3110xyz 3110xyz 370xyz

Câu34. Trongkhônggianvớihệtrụctọađộ ,mặtphẳng(P)điqua vàchứatrụchoành Oxyz  1;1;3A cóphươngtrìnhlà

A. B. C. D. 340 yz 30 yz 0xy 30xy

Câu35. Chohàmsố liêntụctrênvàcóđồthịnhưhìnhvẽdướiđây.Cóbaonhiêugiátrị yfx  

Câu25.

1 ;3 3   

nguyêncủathamsố đểphươngtrình cónghiệmduynhấttrên ? m  3 3log1fxm  3

A. B. C. D. 2431

Câu36. Chohàmsố cóđạohàmvàliêntụctrênđoạn và Tính fx  1;3,34 f 1 0

21d6fxx giátrịcủa  1f

A. . B. . C. . D. . 18f 12f 116f 110f

Câu37. Chohìnhchóp có đáy làhìnhvuông cạnh , đường thẳng vuônggóc với mặt . SABCD aSA phẳng Khoảngcáchgiữahaiđườngthẳng và bằng ,2ABCDSAa  SBAD

a 3

A. . B. . C. . D. .

5 5 1x

đỏbằng A. B. C. D.

cóítnhất1quảmàu

1 3 19 28 16 21 17 42

Chohìnhtrụcóthiếtdiệnđiquatrụclàmộthìnhvuôngcócạnh .Diệntíchxungquanhcủa 4a hìnhtrụlà A. B. C. D. 28 Sa  224 Sa  216 Sa  24 Sa  Câu26. Tìmnguyênhàm củahàmsố biết Fx 2 21 2fxx x  13F A. . B. .  22ln21Fxxxx   22ln21Fxxxx C. D. 2ln21Fxxxx 22ln21Fxxxx   Câu27. Đườngtiệmcậnđứngcủađồthịhàmsố là 1 2 x y x  A. . B. . C. . D. . 1y 1x 2x 2y Câu28. Giátrịnhỏnhấtcủahàmsố trênđoạn là 335yxx  2;4 A. . B. . C. . D. . 24 min3 y  2;4 min7 y  2;4 min5 y  2;4 min0 y Câu29. Chohàmsố cóbảngbiếnthiênnhưsau yfx 

yfx  A. B. C. D.  ;1  0;1  1;0  1;1

bằng:  2 0 d3Ifxx   2 0 43d Jfxx   A. B.

 2 2 d9fxx  2 1 d2fxx  1 2 d fxx A. B. C.

Câu30. Cho .Khiđó

C. D. 2684 Câu

D. 73117

1 0 1

21 I xx x       

A. B. C. D. 2ln3  4ln3  2ln3  1ln3 

6 3

a 2

a a

Câu38. Trongkhônggianvớihệtrụctọađộ ,cho ; ; .Diệntíchmặt Oxyz 1;2;3A 4;2;3B 4;5;3C cầunhậnđườngtrònngoạitiếptamgiác làmđườngtrònlớnlà ABC

A. B. C. D. 9 36 18 72

Câu39. Chohàmsố xácđịnhtrênvàcóđạohàm .Hàmsốđãcho yfx    2 (1)1fxxxx  nghịchbiếnkhoảngnàodướiđây?

A. . B. . C. . D. .  1;0  ;1  0;1  1;

Câu40. Trongkhônggian với hệ tọa độ Oxyz, mặt cầu cótâm vàcó tiếp diện là mặt  S 1;2;1I phẳng ,cóphươngtrìnhlà

222 1214xyz   222 1211xyz Câu41. Cho ()fx làhàm số liên tục trên tập số thực khôngâmvà thỏa mãn

Tínhtỉsố

46. Chohàm số

ACAAa   trịsincủagócgiữađườngthẳng vàmặtphẳng bằng AC  BCCB

A. B. C. D. 10 4 6 3 3 3 6 4

Câu43. Chohàmsố Gọi làtậphợptấtcảcácgiátrịthựccủathamsố đểgiátrị 221fxxxS m lớnnhấtcủahàmsố trênđoạn bằng .Tínhtổngcácphần  22 gxfxfxm  

1;38

Cóbaonhiêusốnguyêndương saocho

tửcủa S

A. . B. . C. . D. .7205

Câu44. Chohàmsố liêntụctrên.Đồthịhàmsố yfx  

3' yfx 

đượcchotronghìnhbên.Hàmsố cótốiđa 41 8 gxfxxx 

baonhiêuđiểmcựcđại?

A. . B. .23

C. . D. .45

Câu45. Chohìnhchóp cóđáy làhìnhbìnhhành.Gọi làđiểmđốixứngcủa qua SABCDABCD M C vàlàtrungđiểmcủa Mặtphẳng chiakhốichóp thànhhaikhốiđa

BN SC MND SABCD diện,trongđókhốiđadiệnchứađỉnh cóthểtích,khốiđadiệncònlạicóthểtích(tham S1V 2V khảohìnhvẽbên).

2. Câu49. Trongkhônggian với hệ tọa độ Oxyz,cho mặt cầu cótâm

1. C.vôsố.

:2250Pxyz A. B.  222 1214xyz 

 C.



Tính  23120.fxxxx  5 1 d fxx A. 37 6 B. 527 3 C. 61 6 D. 464 3 Câu42. Chohìnhlăngtrụđứng cóđáy vuôngtại , Giá . ABCABCABC,A3ABa

222 1211xyz





1 2 V V

. B. . C. . D. . 1 2 12 7 V V  1 2 5 3 V V  1 2 7 5 V V  1 2 1 5 V V  Câu

với

số thực. Biết rằng nếu  2 3ln3 fxaxaxx  a thì .Khẳngđịnhnàosauđâyđúng? 1;3 max2 fxf   1;3 minfxm   A. . B. . C. . D. .  6;7m  7;8m  8;9m  9;10m Câu47. Chohàm số có đạo hàmtrên đoạn và thỏa mãn ; fx  1;e 10f .Tíchphân bằng 1,1; fxxfxxe      1 d e fxx A. B. C. D. 21 4 e 21 2 e 21 4 e 21 2 e Câu48.

tồntạisốthực

1 ?  2 2321loglogyx xyxyy x    A.3. B.

phẳng  S vàđi

điểm .Bánkínhnhỏnhấtcủamặtcầu ():270 Pxyz  1;2;1,2;5;3AB bằng:  S A. B. C. D. 470 3 546 3 763 3 345 3

để

trình  10;20

m xxx 

HẾT

làtham

lớnhơn thỏamãn x y

thuộc mặt

quahai

Câu50. Trong khoảng cóbaonhiêugiá trị nguyên của tham số m

phương

cóđúng2nghiệmphânbiệt. 2

4log(1)log9(1)

A.23. B.20. C.8. D.15.

Điềukiện . 2 1 20 2 x xx x

Tậpxácđịnh .\1;2D

Câu5. Tìmhọnguyênhàmcủahàmsố sin3 fxx 

A. B.

HƯỚNGDẪNGIẢICHITIẾT

Câu1. Trongkhônggian ,cho .Tọađộcủavectơ là: Oxyz23 aijk

Lờigiải ChọnD Tacó .

231;2;3aijka 

Câu2. Chohàmsố cóbảngbiếnthiênnhưhìnhvẽ yfx 

Khẳngđịnhnàosauđâyđúng?

A.Giátrịcựcđạicủahàmsốlà B.Giátrịcựcđạicủahàmsốlà . 3CDy 4CDy

C.Giátrịcựctiểucủahàmsốlà . D.Giátrịcựctiểucủahàmsốlà . 3CTy 1CTy

Lờigiải

ChọnB

Tacó . 1 sin3cos3 3 xdxxC 

Câu6. Cho cấp số nhân có số hạng đầu vàcông bội Số hạng thứ năm của cấp số

ChọnC

Ápdụng tađược 1 1 n n uuq  44 513248uuq

Câu7. Chokhốihộpchữnhật có , , .Thểtíchkhốihộpbằng . ABCDABCD AAa  3 ABa 5 ACa 

. 312a 34a 315a 35a

ChọnA

Từbảngbiếnthiên,giátrịcựcđạicủahàmsốlà .3CDy

Câu3. Hàmsốnàodướiđâycóđồthịnhưđườngcongtronghìnhbêndưới?

A. . B. . C. . D. . 32 yxx  242 yxx  32 yxx  42 2 yxx  Lờigiải

D Đồthịhàmsốtrênlàđồthịhàmbậcbốntrùngphươngdạng 420yaxbxcxa  42 2 yxx

Câu4. Tìmtậpxácđịnh

Lờigiải

Nhậnthấy  2222534 BCACABaaa   

Dođó,thểtíchhìnhhộpchữnhật là . ABCDABCD  33412 VABBCAAaaaa  

Câu8. Sốtổhợpchập3của12phầntửlà

A. B. C. D. 1728220132036

Lờigiải

ChọnB

Sốtổhợpchập3của12phầntửlà . 3 12220C

Câu9. Chohìnhchóp cóđáy làtamgiáccân , cáccạnhbên . SABCABC ABACa   120BAC  bằngnhauvàcùngtạovớimặtphẳngđáycácgóc .Thểtíchkhốichóp là 30 SABC

A. B. C. D. 33 12 a 3 4 a 33 4 a 3 12 a

Lờigiải

ChọnD

Gọi làhìnhchiếucủa lênmặtphẳng . O S ABC

BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 D A D D B C A B D D D C A D C B D A C B A C D A C 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 D C B C B A A C B D A A C A D C D A B C A C D B A

 a 

. B. . C. . D. .  2;1;3 3;2;1 2;3;1 1;2;3



Chọn

củahàmsố D 25 2yxx  A. . B. . D  0;D C. . D. .  ;12;D \1;2D Lờigiải Chọn



C. D.



cos3xC  1 cos3

xC cos3xC 

cos3



13u 2



 n u A. . B. . C. . D. . 596u 532u 548u 524u Lờigiải

 n u

nhân là

Nhận thấy: , và nênsuyra   , SAABCSAO    , SBABCSBO    , SCABCSCO  haylàtâmđườngtrònngoạitiếptamgiác . OAOBOC O ABC

Tamgiác cântại có ,nên . ABCA  120BAC   30ABCACB 

Khiđó: hay . 2 sin AB OA ACB   22sin30 sin ABa OA a ACB  

Tacó: . 3 tantan30 3 aSOOASAOa    

ChọnA

Câu14. Trongkhônggian ,chođiểm Tọađộđiểm làhìnhchiếuvuônggóccủa Oxyz

1;2;3M A M trênmặtphẳng là:  Oyz

A. B. C. D.  1;2;3A  1;2;0A  1;0;3A  0;2;3A Lờigiải

ChọnD

Câu15. Hàmsố với cóđồthịnhưhìnhvẽbên.Mệnhđềnàosauđâylàđúng? axb ycxd    0a

Thểtíchkhốichóp là . . SABC

1131......sin120 333212SABC ABC a a VSOS aa

Câu10. Trongcáchàmsốsau,hàmsốnàođồngbiếntrên? 

XétđápánDtacó: nênhàmsốđồngbiếntrên. 2 '330 yxx 

Câu12. Chohàmsố liêntụctrênđoạn vàcóđồthịtrênđoạn nhưhìnhvẽbên. ()yfx   1;5  1;5

Tổnggiátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố trênđoạn bằng fx 1;5

A. B. C. D. 0,0,0bcd 0,0,0bcd0,0,0bcd0,0,0bcd Lờigiải

ChọnC

Tiệmcậnngangcủađồthịhàmsốlà (do ) 200a yc c 0a

Tiệmcậnđứngcủađồthịhàmsốlà (do ) 100 d y

hàmsốvớitrục

Câu16. Tínhđạohàmcủahàmsố 2 log21yx

ChọnB

Câu17. Chohàmsố cóbảngbiếnthiênnhưhìnhvẽ.Tổngsốtiệmcậnngangvàtiệmcậnđứng

yfx 

hàmsốđãcholà

A.0. B.2. C.1. D.3.

O C B A S

 

     

A. B.



fe x     1

fx e    1 3 x fx  3xfx Lờigiải ChọnD Hàmsốmũ đồngbiến

ánD. x ya  1a Câu11. Hàm

nàodướiđâyđồngbiếntrênkhoảng ? ;  A. B. C. D. 33 yxx  1 2 x y x  1 3 x y x    33 yxx  Lờigiải Chọn



C. D.

trênkhi dođóchọnđáp

số

B.-1. C.1. D.2. Lờigiải ChọnC Từđồthịtathấy: nên . 151;5 max3;min2 fxfx   11;5 5 maxmin321 fxfx

,mộtvectơchỉphươngcủađườngthẳng là Oxyz 12 112 xyz   A. . B. . C. . D.  1;1;2u   1;1;2u   1;2;0u   1;2;1u  Lờigiải

Câu13. Trongkhônggian



d c 0c

d 0d

Giaođiểmcủađồthị

tungcótungđộâmnên (do ). 00bb

  

x    2 21y x    1 21y x    Lờigiải

A. B. C. D.  1 21ln2y x



21ln2y



củađồthị

Lờigiải

ChọnD

Từbảngbiếnthiêncủahàmsố tacó: yfx 

Đồthịhàmsốđãchonhậnđườngthẳng làtiệmcậnđứng.

Đồthịhàmsốđãchonhậnđườngthẳng làtiệmcậnngang.

Câu18. Vớimọi dươngthỏamãn Khẳngđịnhnàodướiđâyđúng? , ab 3 22 loglog5. ab

Lờigiải ChọnA

3 22 loglog5 ab 32 2 log5 ab 3232ab 

Câu19. Hàmsố cóđồthịlàhìnhbên.Giátrịcủacơsố bằng  log01 a yxa a

Câu22. Mộtchiếchộpchứa9quảcầugồm4quảmàuxanh,3quảmàuđỏvà2quảmàuvàng(cácquả cầu đôimộtkhácnhau). Lấyngẫunhiên3quảcầutừhộpđó.Xácsuấtđểtrong3quảcầulấy đượccóítnhất1quảmàuđỏbằng

A. B. C. D. 1 3 19 28 16 21 17 42

Lờigiải

ChọnC

Gọi làbiếncốtrongbaquảcầulấyđượccóítnhấtmộtquảmàuđỏ.Suyralàbiếncốtrong A A baquảcầulấyđượckhôngcóquảcầunàomàuđỏ.

Khônggianmẫu: 3 984C 

Sốcáchlấyrabaquảcầumàkhôngcóquảcầunàomàuđỏlà .Tacó: 3 620C

PAPAPA 

Câu23. Chohìnhchóp cóđáy làtamgiácvuôngcântại và .Tamgiác . SABCABC B2 ABa  SAB đềuvànằmtrongmặtphẳngvuônggócvớiđáy.Tínhthểtích củakhốichóp . V SABC

A. B. C. D. 424 22 Lờigiải

ChọnD

Diệntích là . ABC 21 222 2 aaa 

Chiềucao củahìnhchóp là SH SABC 3 23 2 aa

Vậy,thểtích củakhốichóp là . V SABC 3 2 123 23 33 a Vaa

Câu24. Chokhốinóncóbánkínhđáybằng ,gócởđỉnhhìnhnónlà .Thểtíchkhốinónbằng 3cm 60

93(cm)

ChọnA

33(cm)

Lờigiải

2 lim x fx   2x

0 lim x fx   0x

 lim0 x fx   0y

B. C. D. 3232ab 2232

 2332ab 232ab

C Tathấyđồthịhàmsốđiquađiểmcótọađộ  4 4;4log444 a a  Mà nên . 01 a  2a Câu20. Tìmtậpnghiệm củabấtphươngtrình . S 45 5 1x A. . B. . C. . D. .  5;S  3;S  ;5S  ;3S Lờigiải ChọnB 4415 1 55413 5 x x xx  Vậytậpnghiệmcủabấtphươngtrìnhlà . 3; Câu21. Tìmtậpnghiệm củabấtphươngtrình . S  2 22 loglogxxx  A. B. C. D.  2S  0S  0;2S  1;2S Lờigiải ChọnA    2 222 22 0 0 loglog : 20 2 0 1 x Ð xx xL xxxxxxxx xN K x         

Chọn

 20516 1 842121

A. B. C. D. 33 4 a V 33 3 a V 33 12 a V 3 23 3 a V Lờigiải

A. B. C. D. 3

 3

3 3(cm) 

6(cm)

ChọnB

Hàmsốliêntụctrênđoạn  2;4

Tacó .Vậy . 335yxx

2 330,2;4yxx

Câu29. Chohàmsố cóbảngbiếnthiênnhưsau yfx 

Hàmsố nghịchbiếntrênkhoảngnàodướiđây?

A. B. C. D.  ;1  0;1  1;0  1;1 Lờigiải

ChọnC

Từbảngbiếnthiêntathấy

Câu30. Cho .Khiđó bằng:

Câu31. Nếu và thì bằng

d9dd9d92d7 fxxfxxfxxfxxfxx 

. 3 33 tan30 h  . 21 .3.3393 3 V Câu25. Chohìnhtrụcóthiếtdiệnđiquatrụclàmộthìnhvuôngcócạnh Diệntíchxungquanhcủa 4a hìnhtrụlà A. . B. . C. . D. . 28 Sa  224 Sa  216 Sa  24 Sa  Lờigiải ChọnC 2 4 2 2 2.2.416 a ra Saaa    Câu26. Tìmnguyênhàm củahàmsố biết . Fx 2 21 2fxx x  13F A. B.  22ln21Fxxxx   22ln21Fxxxx C. D. 2ln21Fxxxx 22ln21Fxxxx   Lờigiải ChọnD  22 d21d2ln2 2 FxfxxxxxxxC x           Mà nên . 13F1C22ln21Fxxxx   Câu27. Đườngtiệmcậnđứngcủađồthịhàmsố là 1 2 x y x  A. . B. . C. . D. . 1y 1x 2x 2y Lờigiải ChọnC nênđườngtiệmcậnđứngcủađồthịhàmsốlà 22 22 11 limlim;limlim 22xx xx x x y y x x     2x Câu28. Giátrịnhỏnhấtcủahàmsố trênđoạn là 335yxx  2;4 A. B. C. D. 24 min3 y  2;4 min7

  2;4 min5 y  2;4 min0 y Lờigiải









24 min27 yy



yfx 

: . 01;01;fxx 

yfx   1;0

Vậyhàmsố nghịchbiếntrênkhoảng

 2 0

Ifxx   2 0 43d Jfxx   A. . B.

Lờigiải ChọnB .  2 22 0 00 43d4d3d1266Jfxxfxxx      

. C. .

.2684

 2 2 d9fxx  2 1 d2fxx  1 2 d fxx A. B. C. D. 73117 Lờigiải ChọnA

  2 12 2 2 2 21 1 1

 

1 0 1 3d 21 I xx x        A. . B. . C. . D. . 2ln3  4ln3  2ln3  1ln3  Lờigiải ChọnA Tacó . 1 1 0 0 111 3dln212ln32 2122 I xxxxx x           2ln3 Câu33. Trongkhônggianvớihệtrụctọađộ ,cho .Phươngtrìnhmặtphẳng đi Oxyz 1;1;3H  P qua cắtcáctrụctọađộ lầnlượttại (khác)saocholàtrựctâm H Ox,Oy,Oz,,ABCOH tamgiác là ABC

Tacó .

Câu32. Tính .

A. B. C. D. 370xyz 3110xyz 3110xyz 370xyz

Lờigiải

ChọnC

Tứdiện có đôimộtvuônggócnênlàtrựctâmtamgiác OABC,, OAOBOC H ABC

OHABC

 ABC H  1;1;3OH 

điquađiểm vàcóvéctơpháptuyếnlà

phươngtrìnhmặtphẳng là .   P3110xyz

Câu34. Trongkhônggianvớihệtrụctọađộ ,mặtphẳng(P)điqua vàchứatrụchoành Oxyz  1;1;3A cóphươngtrìnhlà

A. . B. . C. . D. . 340 yz 30 yz 0xy 30xy Lờigiải

ChọnB

Mặtphẳng(P)điqua vàchứatrụchoành códạng  1;1;3A  P 0bycz

Mà điquađiểm nên  P  1;1;3A303 bcbc 

Chọn phươngtrìnhmặtphẳng là . 13cb  P30 yz

37. Chohìnhchóp có đáy làhìnhvuông cạnh , đường thẳng vuônggóc với mặt . SABCD aSA

,2ABCDSAa  SBAD

Khoảngcáchgiữahaiđườngthẳng và bằng

A. B. C. D. 6 3 a 2 3 a 3 2 a a Lờigiải

ChọnA

Câu35. Chohàmsố liêntụctrênvàcóđồthịnhưhìnhvẽdướiđây.Cóbaonhiêugiátrị

yfx  

nguyêncủathamsố đểphươngtrình cónghiệmduynhấttrên ? m

Tacó .   ,,, dSBADdADSBCdASBC  

Do ,kẻ .Dođó BCSAB AHSBAHBC    , AHSBCdASBCAH  

.Dohàm số làhàm số đồng biến trên  33 1

26 33 SAABaa AH SAAB   

Tacó . 22

Câu38. Trongkhônggianvớihệtrụctọađộ ,cho ; ; .Diệntíchmặt Oxyz 1;2;3A 4;2;3B 4;5;3C

cầunhậnđườngtrònngoạitiếptamgiác làmđườngtrònlớnlà ABC

A. . B. . C. . D. . 9 36 18 72

Lờigiải

ChọnC

Mặtcầunhậnđườngtrònngoạitiếptamgiác làmđườngtrònlớnnêntâmmặtcầulàtâm ABC

đườngtrònngoạitiếptamgiác .ABC

Tacó , .  3;0;0AB  0;3;0BC 

Vì nêntamgiác vuôngtại . .0ABBC  ABCB



;3 3   

Lờigiải

3 3log1fxm 

A. B. C. D. 2431

ChọnD Đặt

3;31;3 lo, 3 g uxu x       33log ux  nênvới phương

.  0; 1;3u 3 1 ;3 3    Do đó yêu cầu bàitoán tương đương với phương trình có nghiệm duy nhất trên 1fum  Từđồthịhàmsốsuyra . 1;3 112 2 41556 m mm m mm           Câu36. Chohàmsố cóđạohàmvàliêntụctrênđoạn và Tính fx  1;3,34 f 1 0 21d6fxx giátrịcủa  1f A. B. C. D. 18f 12f 116f 110f Lờigiải ChọnA Xét ,đặt  1 0 21d Ifxx    212 2 dttxdtdxdx  Với 01;13xtxt  Dođó . 3 1 31 1328 22 dff tIft ffI    

trìnhcónghiệmduynhấttrên

Câu

phẳng

Câu39. Chohàmsố xácđịnhtrênvàcóđạohàm

2 (1)1fxxxx  nghịchbiếnkhoảngnàodướiđây?

ChọnA

Lậpbảngxétdấu fx  Dựavàobảngxétdấu,hàmsố nghịchbiếntrênkhoảng

Câu40. Trongkhônggian với hệ tọa độ Oxyz, mặt cầu cótâm vàcó tiếp diện là mặt

Câu41. Cho ()fx làhàm số liên tục trên tập số thực khôngâmvà thỏa mãn

D Kẻ ,từđó .

AHBCAHBCCB

; ACACH BCCB 

vuôngtại : . ABC A222 1113 2 AHa AHABAC

Xét vuôngtại : . AHC C 6sin 4 AH ACH AC   

Câu43. Chohàmsố .Gọi làtậphợptấtcảcácgiátrịthựccủathamsố đểgiátrị 221fxxxS m lớnnhấtcủahàmsố trênđoạn bằng .Tínhtổngcácphần  22 gxfxfxm   1;38 tửcủa S A. . B. . C. . D. .7205

Lờigiải

ChọnA

Khi .Đặt 1;30;4xfx   0;4fxt

Khiđó,yêucầubàitoán cógiátrịlớnnhấttrênđoạn bằng8 22 htttm

2 232 4418 2 SR      

Suyrabánkínhmặtcầulà . 132 22 RAC Vậydiệntíchmặtcầulà .

.Hàmsốđã

yfx   

A. . B. . C. . D. .  1;0  ;1  0;1  1; Lờigiải

cho



 

yfx

1;0



phẳng

:2250Pxyz A. . B. . 

xyz  222 1211xyz  C. D.  222 1214xyz   222 1211xyz Lờigiải ChọnD Mặtcầu cótâm vàcótiếpdiệnlàmặtphẳng suyra  S 1;2;1I  P  222 225 d, 1 212 III xyzRIP     Phươngtrìnhmặtcầu  222 :1211Sxyz

1;2;1I

,cóphươngtrìnhlà

222 1214

Tính  23120fxxxx  5 1 d fxx A. 37 6 B. 527 3 C. 61 6 D. 464 3 Lờigiải ChọnC Tacó:  1 1 2 0 0 613123d223d 6Ifxxxxxxx    Đặt ,  231d23d txxtxx  Đổicận: 01xt 15xt Suyra .  1 55 2 0 11 6163123d()() fxxxxftdtfxdx    Câu42. Chohình

cóđáy vuôngtại , Giá ABCABCABC,A3ABa ACAAa   trịsincủagócgiữađườngthẳng vàmặtphẳng bằng

  BCCB A. B. C. D. 10 4 6 3 3 3 6 4 Lờigiải



 Xét





lăngtrụđứng

Chọn





Xét vuôngtại : . AAC C 22

ACAAACa 



 

htt tft      

,tacó: 0;4t

  2 2 2 2 0;4 04

Đồngthờitừ suyra

Vậytổngcácphầntửcủa là.   0 7 m m    S7

0;4

00 8,0;4 0;4:8

Vớimọi

2 2 28828ttmttm

2828max28min2870 ttmttttmttm 

yfx  

3' yfx 

Câu44. Chohàm số liên tục trên. Đồ thị hàm số được chotronghìnhbên.

41 8 gxfxxx 

Hàmsố cótốiđabaonhiêuđiểmcựcđại?

diện,trongđókhốiđadiệnchứađỉnh cóthểtích,khốiđadiệncònlạicóthểtích(tham S1V 2V khảohìnhvẽbên). Tínhtỉsố 1 12 7 V V  1 2

A. B. C. D. 2345 Lờigiải ChọnB

Đặt 41 8 hxfxxx 

Tacó: .  30 3 1 1 ''1'1 2 2 hx hxfxxfxx  

Đặt .Khiđóphươngtrìnhtrởthành .

thiên

tx ftttx

0hx 

. SABCDABCD M C

1 5 V V  Lờigiải ChọnC Tacó: . 1 3 BK KMNSB BS  Đặt 2SABCDSBCDSABC V VVVV 1 2 CDMN CDMN CDBS

7 5 V V  1 2

vàlàtrungđiểmcủa Mặtphẳng chiakhốichóp thànhhaikhốiđa BN SC MND SABCD V A. . B. . C. . D. . 1 2

VCDCMCNV V VCDCBCS   . 2 1 1 57 612 2121212 BMKI BMKI CDMNBMKI BCSA

VBMBKBI V VVVV VVVV V VBCBSBA    Vậy 1 2

7 5 V V  Câu46. Chohàm số với làtham số thực. Biết rằng nếu  2 3ln3 fxaxaxx  a thì .Khẳngđịnhnàosauđâyđúng? 1;3 max2 fxf   1;3 minfxm   A. B. C. D.  6;7m  7;8m  8;9m  9;10m Lờigiải ChọnA 2 2 233ln33 3 xfxaxaxxfxaa xx      Vì nên . 1;3 max2 fxf   20f  7 307 10 aaa  2 23 710 3 xfx xx  





 

3 xt

tx        Bảngbiến

củahàmsố

yhx 

3 3 3 

22 1 100 2 22 

Khi

đó,hàmsố cósốđiểmcựcđạinhiềunhất có4nghiệm.

gxhx

Vậyhàmsố cótốiđa3điểmcựcđại.  gxhx 

Câu45. Chohìnhchóp cóđáy làhìnhbìnhhành.Gọi làđiểmđốixứngcủa qua

2 V 5 3 V V  1 2

48. Cóbaonhiêusốnguyêndương saochotồntạisốthực lớnhơn thỏamãn x y

Câu49. Trongkhônggian với hệ tọa độ Oxyz,cho mặt cầu cótâm thuộc

 2 015 7 x fx x      1710ln4;21410ln10;32110ln18f f f    Vậy và . 1;3 max2 fxf   1;3 min16,86mfxf    Câu47. Chohàm số có đạo hàmtrên đoạn và thỏa mãn ; fx  1;e 10f .Tíchphân bằng 1,1; fxxfxxe      1 d e fxx A. . B. . C. . D. . 21 4 e 21 2 e 21 4 e 21 2 e Lờigiải ChọnC  2 111 1 fxxfxfxxfxxfxfx xxx        do ,mà . 111 ln fxfxxC xxx       1; xe 10fln fxxx  2 222 11 11 11 dlndlnd 222444 e e e e xxeeefxxxxxxx       Câu



xyxyy x    A.

Lờigiải ChọnD Điềukiện:

            2

yx xyxyy x     2

xyxyyy

x     2 2

yx xyxyy xy    ,với   loglogloglog0 b aabyaby a b     2 ,0 23 axyab byx     Nếu thì , thì . ab loglog0 a abybab loglog0 a abyb Nên . loglog0 aaab byb223xyyx 2 23 1 y x y    Xéthàmsố với .Tacó . 2 23 1fy y y    1y 2 22 262 0,1 1 fyy y y y      Nên nghịchbiến

. fy  1; Bảngbiếnthiên:

5 01;2 2 xx 

mặt phẳng  S vàđiquahaiđiểm .Bánkínhnhỏnhấtcủamặtcầu ():270 Pxyz  1;2;1,2;5;3AB bằng:  S A. B. C. D. 470 3 546 3 763 3 345 3 Lờigiải ChọnB Gọi làtâmmặtcầu làmặtphẳngtrungtrựccủa I  SIQ  37 ;;2 :22 1;3;2 quaM AB VTPTAB       códạng: 32160xyz Vậy làgiaotuyếncủa2mặtphẳng: Id  32160 270 xyz xyz    +cho vàcho . 2 00;2;11 11 y x Cd z      3 11;3;12 12 y x Dd z     +Đườngthẳng códạng:   0;2;11 : 1;1;1 quaC d VTCPCD       2;2;11 11 xt ytIttt zt        +Bánkính khi .  2 2221382546 14103 393 RIAtttt        13 3 t Vậy . min 54613 33 Rkhit   Câu50. Trong khoảng cóbaonhiêugiá trị nguyên của tham số m để phương trình  10;20 cóđúng2nghiệmphânbiệt. 2 39 4log(1)log9(1)m xxx  A.23. B.20. C.8. D.15. Lờigiải ChọnA

2 2321loglogyx

3. B.1. C.vôsố. D.2.

23023 11 11 yxxy yy xx

2321loglog

23 21log2loglog2log yx

2323loglog

trên

Đểtồntạisốthực lớnhơn thì . y1 

Vớiđiềukiện: thìphươngtrìnhbanđầu 1x  3 3 4log(1)1log1 xxmx 

3 1 log14 x xm 

SỞGIÁODỤCVÀĐÀOTẠOTỈNHPHÚTHỌ

ĐỀTHITHỬTNTHPT-NĂMHỌC:2022-2023–LẦN1–ĐỀGỐC2

Câu1: Từmộtnhómhọcsinhgồm namvà nữ,cóbaonhiêucáchchọrahaihọcsinh? 59

yx y xm

     điểm.

3 log1 1 4

Để phương trìnhcó đúng 2 nghiệm phân biệt thì đồ thị haihàm số có2giao

Câu2: Tậpxácđịnhcủahàmsố là ()22023 1yx=-

A. B. C. D. () 0;+¥  ()() ;11; -¥-È+¥ {}\1;1-

Câu3: Chohàmsố cóđồthịnhưhìnhvẽ. ()yfx =

Từđồthị,điềukiện

có2giaođiểmkhi và . 14 4 m m  10;20m

Sốnghiệmcủaphươngtrình bằng 2()50 fx-=

A. . B. . C. . D. . 0 243

Câu4: Phươngtrìnhđườngtiệmcậnngangcủađồthịhàmsố là 23 1 x y x -+ = + A. B.

Câu5: Nghiệmcủaphươngtrình là 4 5125 x=

Câu6: Đạohàmcủahàmsố là 2023log yx =

A. B. C. D. 1 2023lny x ¢ = 1 ln2023y x ¢ = 1 y x ¢ = ln2023 y x ¢ =

Câu7: Chohàmsố Khẳngđịnhnàodướiđâylàđúng? ()ecos2 x fxx =+

A. B. dsin2 e 2 xx fxxC  dsin2 e 2 xx fxxC 

C. D. desin2 x fxxxC  desin2 x fxxxC 

Câu8: Chocấpsốnhân cósốhạngđầu vàcôngbội .Giátrịcủa bằng () n u 13u= 2q= 4u

A. B. C. D. 5243027

Câu9: Hàmsốnàodướiđâycóbảngbiếnthiênnhưhìnhvẽ?

 .



,m

3;2;....;19m

HẾT

B. C. D.

142 2 14C 2

2 14A

3 2

C. D.

1x=- 3y=

A. B. C. D. 4x= 5x= 7x= 6x=

A. B. C. D. 3232yxx=+23 1 x y x + = + 4231yxx=-+-

Câu10: Nếu và thì bằng

A. . B. . C. . D. . 10 443

Câu11: Biếtphươngtrình cóhainghiệm .Giátrị bằng 2 55 log3log10 xx-+= 12 , xx12xx

A. B. C. D. 2531125

Câu12: Cho .Khẳngđịnhnàodướiđâyđúng? 0,,a>abÎ

A. B. C. D. ()aaaba+b = aaaaba+b += aaaaba+b = a a a

a b-a b =

Câu13: Chohàmsố cóđồthịnhưhìnhvẽ. 42 yaxbxc =++

Điểmcựctiểucủađồthị

hàmsốđãchocótọađộlà

A. B. C. D. () 0;2 () 1;3 () 2;0 () 1;3-

Câu14: Chohàmsốbậcba cóđồthịnhưhìnhvẽ. ()yfx =

Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?

A. B. C. D. () 0;+¥ () 2;0- () 1;1- () ;0-¥

Câu15: Chohàmsốbậcba cóbảngbiếnthiênsau: ()yfx =

Giátrịcựcđạicủahàmsốđãcholà

A. B. C. D. 0 1- 1 3-

Câu16: Cho .Khẳngđịnhnàodướiđâyđúng? ()2 1 d sin xFxC x =+ò

A. . B. . C. .D. . ()4 sin2 cos x Fx x

¢ = ()cot Fxx ¢ =- ()2 1 sin Fx x ¢ =- ()2 1 sin Fx x ¢ =

Câu17: Trongkhônggian ,nếuvectơ thìtọađộcủađiểm là Oxyz 23 OMijk   =-+ M

A. B. C. D. () 2;3;1 - () 2;1;3-- () 2;1;3 - () 3;2;1-

Câu18: Tậpnghiệmcủabấtphươngtrình là ()2 log13 x-<

A. B. C. D. [) 1;9 () 1;9 () 1;+¥ () ;9-¥

Câu19: Chokhốinóncóbánkínhđáy ,thểtích .Chiềucaocủakhốinónđãchobằng 2r= 6V=p

A.3. B. . C.6. D.9. 6

Câu20: Chokhốichópcódiệntíchđáybằng6,chiềucaobằng5.Thểtíchcủakhốichópđãchobằng

A. B. C. D. 3010155

Câu21: Trongkhônggian ,mặtphẳng điquađiểm vànhận làmvectơ Oxyz() P (1;0;1)M (2;1;3)n pháptuyếncóphươngtrìnhlà

A. B. 50xz++= 50xz+-=

C. D. 2350 xyz-+-= 2350 xyz-++=

Câu22: Giátrịlớnnhấtcủahàmsố trênđoạn bằng 42 ()101 fxxx=-+ [3;2] -

A.8. B. . C. . D. . 1 1- 2

Câu23: Trongkhônggian ,cho mặt cầu .Tâm của mặt Oxyz 222 ():426110 Sxyzxyz+++-+-= cầu cótọađộlà () S

A. B. C. D. () 1;2;3 - () 4;2;6 - () 4;2;6- () 2;1;3--

Câu24: Chohàmsố Gọi làgiátrịlớnnhấtcủathamsố đểhàmsốđãchocógiá () 2 4fxm x x

= +0m m trịnhỏnhấttrènđoạn bằng .Khẳngđịnhnàosauđâyđúng? []0;64 -

A. B. C. D. 0(5;7)mÎ 0(1;3)mÎ 0(7;9)mÎ 0(3;5)mÎ

Câu25: Chokhốilăngtrụđứng cóđáylàtamgiácvuôngcântại , (tham . ABCABC¢¢¢ B1ABAA¢ == khảohìnhvẽ).

A. . B. . C. . D. . 1 2 1 6 1 3 1 4

Câu26: Chohàmsố liêntụctrên.Gọi làmộtnguyênhàmcủahàmsố trên thỏa ()fx()Fx ()fx

mãn .Khiđó bằng ()() 317FF-= () 3 1

2dfxxò

21 1 x y x + = +

 5

 2 0 d fxx

5 0 d7fxx

2 d3fxx

C' B' C B

Thểtíchcủakhốilăngtrụđãchobằng

A. . B. . C. . D. . 6 9514

Câu27: Chobấtphươngtrình cótậpnghiệm .Giátrịcủabiểuthức 21 11 215 55 xx æöæö ç÷÷ ç ÷->ç÷ ç÷ç÷ èçøèø () ; Sab = 25ab + bằng

A. B. C. D. 5- 2- 0 3-

Câu28: Cóbaonhiêugiátrịnguyênkhôngâmcủathamsố đểhàmsố m nghịchbiếntrên ()()() 32 2 1 223 3 ymxmxmxm =---+-+ () ; -¥+¥

A. B. C. D. 3412

Câu29: Nếu và thì bằng

A. . B. . C. . D. . 11212728

Câu30: Trongkhođèntrangtrícó7bóngđènloạiIvà8bóngđènloạiII,cácbóngđèntrongkhokhác nhauvềmàusắcvàhìnhdáng.Lấyra7bóngđènbấtkì.Xácsuấtđể7bóngđènlấyracóđủhai loạivàsốbóngđènloạiInhiềuhơnsốbóngđènloạiIIbằng

A. . B. . C. . D. 868 2145 868 2143 521 2145 521 2149

Câu31: Chomặtcầucódiệntíchbằng .Bánkínhcủamặtcầuđãchobằng 20p

A. B. C. D. 525510

Câu32: Chohìnhtrụcóbánkínhđáy ,đườngsinh .Diệntíchtoànphầncủahìnhtrụđãcho 4r= 6l= bằng

A. B. C. D. 80p 96p 56p 64p

Câu33: Chohàm số và .Cóbao ()()42172023fxxmx=---+ ()32520222023gxxxx =-+-+

nhiêugiátrịnguyêncủathamsố đểhàmsố đồngbiếntrênkhoảng m()()()hxgfx = () 2;+¥

A. . B. . C. . D. . 16131514

Câu34: Sốnghiệmnguyêncủabấtphươngtrình . ()222 ln161615 xxxxx +-£+-

A. B. C. D. 2 0 31

Câu35: Chohàmsố thoảmãn và vớimọi .Giátrịcủa ()yfx = ()5 0 4f=-()() 42 fxxfx ¢ = xÎ bằng () 2f

A. . B. . C. . D. 1 43 45 36 - 1-

Câu36: Chohàmsố cóbaonhiêuđiểmcựctrị? () 32 5 log34yxx =-+

A. . B. . C. . D. . 213 0

Câu37: Chohìnhchóptứgiácđều cótấtcảcáccạnhđềubằng (thamkhảohìnhvẽ). SABCD a

Gócgiữađườngthẳng vàmặtphẳng bằng SC () SBD

A. B. C. D. 90° 30° 60° 45°

Câu38: Trongkhônggian , mặt cầu cótâm thuộc trục và đi quahai điểm , Oxyz() S Oy () 2;1;1A cóbánkínhbằng () 0;1;3B-

A. B. C. D. 32393

Câu39: Chohìnhchóp ,cóđáylàtamgiácđềucạnh ,cạnhbên vuônggócvớimặtphẳng . SABC aSA đáy, .Gọi làtrungđiểmcủacanh (thamkhảohìnhvẽ).

3SBa =M AB

Khoảngcáchtừđiểm đếnmặtphẳng bằng M () SBC A.

Câu40: Chohàmsố cóđồthịnhưhìnhdướiđây: ()yfx =

Cótấtcảbaonhiêugiátrịnguyêncủathamsố đểphươngtrình m cónghiệmtrongkhoảng ? ( ) 4420fxxm++--+= () 4;4-

A. B. C. D. 3452

Câu41: Chokhốihộpchữnhật có diệntíchtamgiác bằng ABCDABCD ¢¢¢¢ ,2, ABaADa == CBD ¢ (thamkhảohìnhvẽ) 26a

 4

  4 0

 

   

0 d5fxx

d6gxx

23d fxgxx

B. C. D. 66 33 a 66 22 a 66 11 a 66 44 a

Thểtíchcủakhốihộpchữnhậtđãchobằng

A. B. C. D. 34a 326a 326 3 a 34 3 a

Câu48: Chohìnhtrụcóbánkínhđáybằng .Cắthìnhtrụbởimộtmặtphẳngsongsongvớitrục,cách 2a trụcmộtkhoảngbằng tađượcthiếtdiệnlàmộthìnhchữnhậtcódiệntíchbằng Thể a 283a tíchkhốitrụđãchobằng A.

Câu49: Cho lăng trụ đứng có đáy làtamgiácvuông tại , , . ABCABC¢¢¢ABC B 3 ABBCa ¢ == Lấy hai điểm lần lượt trênhai cạnh và saocho  60ACB= ° , MN AB¢AC ¢ 2,MBAM  ¢ = .Thểtíchkhốiđadiện bằng 3 ACAN  ¢¢ = BMNCC ¢

d fxx ¢ò

Câu42: Chohàm số liên tục trên Biết và thỏa mãn ()fx .()()1,00fxf>= Khiđó bằng () ()2121.fxxxfx ¢+=+ () 22 0

A. . B. . C. . D. . 38 1- 6

Câu43: Chohàm số có đạo hàmtrên thỏa mãn và ()yfx =  ()11f= vớimọi Khiđó bằng ()() 342 4321 fxxfxxx -=++xÎ () 4 1

Câu50: Chohìnhnóncóthiếtdiệnquađỉnhlàtamgiác vuôngtại ,( thuộcđườngtrònđáy). SABS, AB Biết tamgiác cóbánkính đường tròn nội tiếp bằng , đường cao tạo với SAB 2510 - SO mặtphẳng mộtgóc .Diệntíchxungquanhcủahìnhnónđãchobằng () SAB30°

A. B. C. D. 510p 415p 52p 25p

d xfxx ¢ò

A. . B. . C. . D. . 15I= 1I=- 14I= 6I=

Câu44: Cóbaonhiêusốnguyên đểphươngtrình có () 2023;2023aÎ- ()3

11 log871 x xa x +=+ +2 nghiệmphânbiệt?

A. B. C. D. 2028201620272015

Câu45: Trongkhônggian ,chohai điểm , .Xéthai điểm ,thay đổi Oxyz () 1;2;2A-() 3;2;6B MN thuộcmặtphẳng saocho .Giátrịnhỏnhấtcủa bằng. () Oxy 16MN= AMBN +

A. B. C. D. 4134553215

Câu46: Chohàmsố cóđạohàmliêntụctrên.Biết vàđồthị nhưhình ()yfx = ()70f-< ()fx ¢ vẽ.

Hàmsố cótốiđabaonhiêuđiểmcựctrị? ()()4262 627412 gxfxxxx =-+--+

A. B. C. D. 59 7 3

Câu47: Chokhốichóp cóđáylàhìnhvuôngcạnh tamgiác vuôngcântại tamgiác . SABCD ,aSAB ,S

SCD 13 4 Sa CSD==

có .Thểtíchkhốichópđãchobằng

HẾT

A. . B. . C. . D. . 337 16 a 313 24 a 3315 64 a 15 32 a 3

34ap 316ap 3

p 327

B. C. D.

32a

A. B. C. D.

26 27 a 34 9 a

46 27 a

83 27 a

BẢNGĐÁPÁN

HƯỚNGDẪNGIẢI.

Câu1: Từmộtnhómhọcsinhgồm namvà nữ,cóbaonhiêucách

Lờigiải

ChọnC

Tacó . 443 512555437 x x xx -=Û=Û-=Û=

Câu6: Đạohàmcủahàmsố là 2023log yx =

A. . B. . C. . D. . 1 2023lny x ¢ = 1 ln2023y x ¢ = 1 y x ¢ = ln2023 y x ¢ =

Lờigiải

Câu2: Tậpxácđịnhcủahàmsố là ()22023 1yx=A. B. C. D. () 0;+¥  ()() ;11; -¥-È+¥ {}\1;1

Lờigiải ChọnC.

Câu3: Chohàmsố cóđồthịnhưhìnhvẽ. ()yfx =

Sốnghiệmcủaphươngtrình bằng 2()50 fx-=

A. . B. . C. . D. . 0 243

Lờigiải

ChọnD .Dođóphươngtrìnhcóbanghiệmphânbiệt. 5 2()50()2 fxfx-=Û=

Câu4: Phươngtrìnhđườngtiệmcậnngangcủađồthịhàmsố là 23 1 x y x -+ = +

A. B. C. D. 3 2 x= 2y=- 1x=- 3y=

Lờigiải

ChọnB

Câu5: Nghiệmcủaphươngtrình là 4 5125 x= A. B. C. D. 4x= 5x= 7x= 6x=

ChọnB.

Tacó . 2023 1 logln2023yxy x ¢ =Þ=

Câu7: Chohàmsố Khẳngđịnhnàodướiđâylàđúng? ()ecos2 x fxx =+

A. B. dsin2 e 2 xx fxxC  dsin2 e 2 xx fxxC 

C. D. desin2 x fxxxC  desin2 x fxxxC 

Lờigiải

ChọnA ()()sin2decos2de 2 x xxfxxxx C=+=++

Câu8: Chocấpsốnhân cósốhạngđầu vàcôngbội .Giátrịcủa bằng () n u 13u= 2q= 4u

A. B. C. D. 5243027

Lờigiải

ChọnB

Tacó . 33 413224uuq===

Câu9: Hàmsốnàodướiđâycóbảngbiếnthiênnhưhìnhvẽ?

A. B. C. D. 3232yxx=+23 1 x y x + = + 4231yxx=-+21 1 x y x + = +

Lờigiải

ChọnD.

Từbảngbiếnthiêntathấyđồthịhàmsốcótiệmcậnđứng nênloạiA,.C. 1x=-

Hàmsốđồngbiếntrêncáckhoảng và nênchọn. D. () ;1-¥-() 1; -+¥

Câu10: Nếu và thì bằng 5 0 d7fxx 5 2 d3fxx 2 0 d fxx

A. B. C. D. 10 443

Lờigiải

1.C 2.C 3.D 4.B 5.C 6.B 7.A 8.B 9.D 10.C 11.C 12.C 13.A 14.A 15.C 16.D 17.C 18.B 19.D 20.B 21.C 22.B 23.D 24.D 25.A 26.D 27.B 28.A 29.D 30.A 31.A 32.A 33.C 34.B 35.C 36.B 37.D 38.D 39.B 40.B 41.A 42.B 43.A 44.B 45.A 46.C 47.D 48.B 49.C 50.A

rahaihọcsinh?

A. B. C. D. 2 14A 142 2 14C 214 Lờigiải Chọn

chọ



òò

ChọnC

 525255 002002 dddddd734 fxxfxxfxxfxxfxxfxx 

ChọnA

Lờigiải

Hàmsốđãchonghịchbiếntrênkhoảng () 0;+¥

Câu11: Biếtphươngtrình cóhainghiệm .Giátrị bằng

2 55 log3log10 xx-+= 12 , xx12xx

A. B. C. D. 2531125

Lờigiải

ChọnC

:0 log3log10 ÐKx xx > -+=

2 55

Đặt tađượcphươngtrình . 5log tx = ()231050tt-+=D=>

ÁpdụngĐịnhlíViettađược

3 125152512123loglog3log.3.5125ttxxxxxx +=Û+=Û=Û==

Câu12: Cho .Khẳngđịnhnàodướiđâyđúng? 0,,a>abÎ

A. B. C. D. ()aaaba+b = aaaaba+b += aaaaba+b = a a a

Lờigiải

a b-a b =

ChọnC

Câu13: Chohàmsố cóđồthịnhưhìnhvẽ. 42 yaxbxc =++

Điểmcựctiểucủađồthị

hàmsốđãchocótọađộlà

A. B. C. D. () 0;2 () 1;3 () 2;0 () 1;3-

Lờigiải

ChọnA.

Điểmcựctiểucủađồthịhàmsốđãchocótọađộlà .() 0;2

Câu14: Chohàmsốbậcba cóđồthịnhưhìnhvẽ. ()yfx =

Câu15: Chohàmsốbậcba cóbảngbiếnthiênsau: ()yfx =

Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?

A. B. C. D. () 0;+¥ () 2;0- () 1;1- () ;0-¥

Giátrịcựcđạicủahàmsốđãcholà

A. B. C. D. 0 1- 1 3Lờigiải

ChọnC.

Giátrịcựcđạicủahàmsốđãcholà .1y=

Câu16: Cho .Khẳngđịnhnàodướiđâyđúng? ()2 1 d sin xFxC x =+ò

A. B. C. D. ()4 sin2 cos x Fx x

¢ = ()cot Fxx ¢ =- ()2 1 sin Fx x ¢ =- ()2 1 sin Fx x ¢ = Lờigiải

ChọnD.

Có . ()()2 2 1 1 d sin sin xFxCFx x x ¢ =+Þ=ò

Câu17: Trongkhônggian ,nếuvectơ thìtọađộcủađiểm là Oxyz 23 OMijk   =-+ M

A. B. C. D. () 2;3;1 - () 2;1;3-- () 2;1;3 - () 3;2;1Lờigiải

ChọnC ()232;1;3OMijkM   =-+Þ-

Câu18: Tậpnghiệmcủabấtphươngtrình là ()2 log13 x-<

A. B. C. D. [) 1;9 () 1;9 () 1;+¥ () ;9-¥

Lờigiải

ChọnB

Tacó . ()2 3

101 log139 12 xx x xx

ì ì ï->> ï ï ï-<ÛÛ í í ï-ï< <ï î ï î

Vậytậpnghiệmcủabấtphươngtrìnhlà .() 1;9

Câu19: Chokhốinóncóbánkínhđáy ,thểtích .Chiềucaocủakhốinónđãchobằng 2r= 6V=p

A.3. B. . C.6. D.9. 6

Lờigiải





ChọnD

Tacó . () 22 13336 9 3 2 d d

VVVShh Sr p =Þ==== pp

Câu20: Chokhốichópcódiệntíchđáybằng6,chiềucaobằng5.Thểtíchcủakhốichópđãchobằng

A. B. C. D. 3010155

Lờigiải

ChọnB.

Thểtíchcủakhốichópđãcho . 11 ..6.510 33 d VSh===

Câu21: Trongkhônggian ,mặtphẳng điquađiểm vànhận làmvectơ Oxyz() P (1;0;1)M

pháptuyếncóphươngtrìnhlà

A. B. 50xz++= 50xz+-=

C. D. 2350 xyz-+-= 2350 xyz-++=

Lờigiải

ChọnC

Phươngtrìnhmặtphẳng : . () P()()() 21103102350 xyzxyz ---+-=Û-+-=

Câu22: Giátrịlớnnhấtcủahàmsố trênđoạn bằng 42 ()101 fxxx=-+ [3;2] -

A.8. B. C. D. 1 1- 2

Lờigiải

é=Îê ê ¢=-=Û=Îê ê

x fxxxx x

ChọnB. .Hàmsốliêntụctrên ()42101fxxx=-+ [] 3;2. () [] [] [] 3

03;2 420053;2 53;2

ë ; ;.SuyraGTLNcủahàmsố . ()01f=()()5524ff=-=-()223f=- 1

Câu23: Trongkhônggian ,cho mặt cầu

.Tâm của mặt Oxyz 222 ():426110 Sxyzxyz+++-+-=

cầu cótọađộlà () S

A. . B. . C. . D. . () 1;2;3 - () 4;2;6 - () 4;2;6- () 2;1;3--

Lờigiải

ChọnD cótâm . 222 ():426110 Sxyzxyz+++-+-=() 2;1;3--

Câu24: Chohàmsố Gọi làgiátrịlớnnhấtcủathamsố đểhàmsốđãchocógiá () 2 4fxm x x

= +0m m

trịnhỏnhấttrènđoạn bằng Khẳngđịnhnàosauđâyđúng? []0;64 -

Lờigiải

-¢+ =Þ=>" + + [] 0;6

ChọnD .Hàmsốđồngbiếntrên . () ()() 2 2 2 4 0, 44fxmm xfx m x x

Suyra: suyra . [()() 2 2 06 min04164 4 mfxf mm ==-=-Û=Û=± 4m=

Câu25: Chokhốilăngtrụđứng cóđáylàtamgiácvuôngcântại , (tham ABCABC¢¢¢ B1ABAA¢ == khảohìnhvẽ).

C' B'

Thểtíchcủakhốilăngtrụđãchobằng A.

C B

ChọnA

2 11 22ABC ABCABC VAASAAAB ¢¢ ¢¢ ===

Câu26: Chohàmsố liêntụctrên.Gọi làmộtnguyênhàmcủahàmsố trên thỏa ()fx()Fx ()fx

mãn .Khiđó bằng ()() 317FF-= () 3 1

2dfxxò

A. . B. . C. . D. . 6 9514 Lờigiải

ChọnD

Tacó: . ()()()() 3 1

3 2d223114 1 fxxFxFF é ==-= ë ò

Câu27: Chobấtphươngtrình cótậpnghiệm .Giátrịcủabiểuthức 21 11 215 55 xx æöæö ç÷÷ ç ÷->ç÷ ç÷ç÷ èçøèø () ; Sab = 25ab + bằng

A. B. C. D. 5- 2- 0 3Lờigiải

ChọnB.

ĐK: Đặt , . 0x¹ 1 1 5 x t æö ç÷ =÷ ç÷ ç èø 0t>

Bpttrởthành:

(2;1;3)n 

ê=-Î-

0(5;7)

Î 0(7;9)

Î 0(3;5)mÎ

0(1;3)m

. B. . C. . D. . 1 2 1 6 1 3 1 4

Lờigiải

1 2 5111 2150 51010 3KTM5 x t x tt x t xx é> æö + ÷ ê ç -->Û Þ>Û<-Û<Û-<< ç÷ ÷ ê ç èø ë<-

()

Vậytậpnghiệmlà .Dođó () 1;0S=- 252 ab+=-

Câu28: Cóbaonhiêugiátrịnguyênkhôngâmcủathamsố đểhàmsố m

. ()() () n2604868 P n64352145 A A Þ=== w

Câu31: Chomặtcầucódiệntíchbằng .Bánkínhcủamặtcầuđãchobằng 20p

A. . B. . C. . D. 525510

()()() 32 2 1 223 3 ymxmxmxm =---+-+ () ; -¥+¥

nghịchbiếntrên

A. B. C. D. 3412 Lờigiải

ChọnA

Lờigiải

ChọnA

Tacó . 2 22 420455 mc Srrrr =pÛp=pÛ=Û=

Với : luônNBtrên .Dođó thỏamãn.

2m= 4yx=-+ () ; -¥+¥ 2m=

Với :Hàmsốnghịchbiếntrên

2m¹ () ; -¥+¥

()() 2 0,22230, yxmxmxmx  Û¢£"ÎÛ---+-£"Î

ì-< ì ï ï< ï ï Û Û Û< í í ï ï---+£ï----£ï î î

Câu32: Chohìnhtrụcóbánkínhđáy ,đườngsinh .Diệntíchtoànphầncủahìnhtrụđãcho 4r= 6l= bằng

A. . B. . C. . D. 80p 96p 56p 64p

Lờigiải

ChọnA

Tacó . ()() 2244680tp Srrl=p+=p+=p

()()()()() 2

20 2 2 22302230 m m m mmmmmm

Vậy thỏamãnyêucầubàitoán,mànguyênkhôngâm.Dođó có3giá 2m£ m {} 0;1;2

Câu33: Chohàm số và .Cóbao ()()42172023fxxmx=---+ ()32520222023gxxxx =-+-+

nhiêugiátrịnguyêncủathamsố đểhàmsố đồngbiếntrênkhoảng m()()()hxgfx = () 2;+¥

A. . B. . C. . D. . 16131514 Lờigiải

ChọnC

Tacó . ()()()()hxfxgfx ¢¢¢ = ()()()( ) 322 4173102022 xmfxfx=+- -+

()()()()

òò

ChọnA

Lấy7bóngđèntừ15bóngđènthìcósốcáchlà . 7 156435C= ()6435n Þw=

GọibiếncốA:“SốbóngđènloạiInhiềuhơnsốbóngđènloạiII”.

Lấy4bóngđènloạiIvà3bóngđènloạiIIcósốcáchlà . 43 78 CC1960 =

Lấy5bóngđènloạiIvà2bóngđènloạiIIcósốcáchlà . 52 78 C.C588 =

Lấy6bóngđènloạiIvà1bóngđènloạiIIcósốcáchlà . 61 78 CC56 =

. ()1960588562604nA Þ=++=

Đểhàmsố đồngbiếntrênkhoảng cần: ()()()hxgfx = () 2;+¥ vì

()() 02;hxx¢³"Î+¥Þ() 32 4170 xm+-³()()( ) 2 31020220,2 fxfx x -+>">

Suyra .(*) 23417mx£+

Xéthàmsố tacó ()3 417kxx=+ .Suyrahàmsố đồngbiếntrênkhoảng ()2 '120,2 kxxx=>"> ()3 417kxx=+ () 2;+¥

(*) ()()2 2 min4977mkxm +¥ Þ£=Þ-££

Vậycógiátrịcủa 15m

Câu34: Sốnghiệmnguyêncủabấtphươngtrình . ()222 ln161615 xxxxx +-£+-

A. . B. . C. . D. . 2 0 31 Lờigiải

ChọnB.

Điềukiện . ()2221601600 xxxxxxx +->Û+->Û>

ÎÞ trịcủa thỏamãnbàitoán. m Câu29: Nếu và thì bằng  4 0 d5fxx  4 0 d6gxx  4 0 23d fxgxx    A. B. C. D.

Lờigiải ChọnD.

11212728

4 4 4 0 0 0

+ =+= û ò

23d2d3d253628 fxgxxfxxgxx +ù=

A. B. C. D. 868 2145 868 2143 521 2145 521 2149

Lờigiải

Tacó: () ()() 2 2 2

16 ln16lnln16ln16 16 x xxx xxx xx é+ù-= =-++ ê ú ë û++

Bấtphươngtrìnhtươngđương ()() 2 2 ln16ln161616 xxxxxx -++£++(*) ()() 2 2 ln1616ln1616 xxxxxx Û+£+++++

Xéthàmsố trên . ()ln fttt =+() 0;+¥

Tacó: trên .Suyrahàmsố đồngbiếntrên . ()1 10ft t ¢=+>() 0;+¥ ()ln fttt =+ () 0;+¥

Điềukiệnxácđịnh: ()() 2 32 12 340210 2 x xxxx x é-<< ê

Tacó:. () 2 32 36 34ln5 xx y xx

¢ = -+

Cho 0 0 2 x y x

é= ¢ê=Þê= ë

Bảngbiếnthiên:

Từ(*)suyra . 2 2 222111

1616161516225

141414 xxxxxxxx x £++Û+³Û+³Û£Û-££

Sovớiđiềukiệntađược . 1 0 14 x <£

Mà nênsuyrakhôngcógiátrịnguyênnàocủa thoảmãnyêucầubàitoán. xÎ x

Câu35: Chohàmsố thoảmãn và vớimọi .Giátrịcủa ()yfx = ()5 0 4f=-()() 42 fxxfx ¢ = xÎ

bằng () 2f

A. . B. . C. . D. 1 43 45 36 - 1-

Lờigiải

ChọnC.

Từbảngbiếnthiêntathấyhàmsốđãchocó1điểmcựctrị.

Câu37: Chohìnhchóptứgiácđều cótấtcảcáccạnhđềubằng (thamkhảohìnhvẽ). SABCD a

Gócgiữađườngthẳng vàmặtphẳng bằng SC () SBD

A. B. C. D. 90° 30° 60° 45°

Lờigiải

Tacó: . ()() 42 fxxfx ¢ = () () 4 2 fx x fx

¢ Þ=

ChọnD.

Tacóhìnhvẽ:

¢ =Þ-=+òò

Lấynguyênhàm2vế: () () () 5 4 2 1 dd 5 fx x xxx C fx fx

Theogiảthiết suyra . ()5 0 4f=- () ()5 455 2 5436Cfxf x

-=Þ=Þ= +

Câu36: Chohàmsố cóbaonhiêuđiểmcựctrị? () 32 5 log34yxx =-+

A. . B. . C. . D. 213 0

Lờigiải

ChọnB

Gọi (do làhìnhchópđều).

OACBD =Ç ()SOABCDÞ^ SABCD

Tathấy tại ()OCBD OCSBD OCSO ì^ ï ï íÞ^ ï^ ï î O()  () ; SCSBDCSOÞ ==j

-+>Û-+>Ûê> ë

ì ï ï ï= ï í ï ï ï= ï î

. 45 Þj=°

2 sin 2 OC SC Þj==

Tamgiác vuôngtại có . OSCO 2 2 Oa C SCa

Câu38: Trongkhônggian , mặt cầu cótâm thuộc trục và đi quahai điểm , Oxyz() S Oy () 2;1;1A cóbánkínhbằng () 0;1;3B-

A. . B. . C. . D. .32393

Lờigiải

ChọnD

Gọi làtâmcủamặtcầu ,bánkính. I () SR

() 0;;0IOyIb ÎÞ

Mặtcầu điquahaiđiểm , . () S () 2;1;1A() 0;1;3B-AIBIRÛ==

22AIBIÞ=()() 22 41119 bb Û+-+=++440 b Û+=

. ()10;1;0bI Û=-Þ- 3RIB Þ==

Câu39: Chohìnhchóp ,cóđáylàtamgiácđềucạnh ,cạnhbên vuônggócvớimặtphẳng SABC aSA

Gọi làtrungđiểmcủacạnh .Kẻ tại (1). N BCAHSN ^H

Tacó: .(2) ()BCAN BCSAN BCSA ì^ ï ï íÞ^ ï^ ï î BCAHÞ^

Từ(1)và(2),tacó: . ()AHSBC ^ () () ; AHdASBCÞ=

ì ï ï ï= ï í ï ï ï=-= ï î . 2222 11111 6 AHANSAa =+= 66 11 Aa H Þ=

Aa N SASBABa

3 2 2

Trongtamgiácvuông có nêntacó: ASN 22

Nhưvậy () ()() ()1 ;; 2 ddMSBCdASBC = = 166 222 Aa H ==

Câu40: Chohàmsố cóđồthịnhưhìnhdướiđây: ()yfx =

đáy, .Gọi làtrungđiểmcủacanh (thamkhảohìnhvẽ).

3SBa =M AB

Khoảngcáchtừđiểm đếnmặtphẳng bằng M () SBC

ChọnB

Tacóhìnhvẽsau

Do ,mà làtrungđiểmcủacạnh nêntacó: () ABSBCB Ç=M AB . () ()() ()1 ;; 2 ddMSBCdASBC = =

Cótấtcảbaonhiêugiátrịnguyêncủathamsố đểphươngtrình m cónghiệmtrongkhoảng ? ( ) 4420fxxm++--+= () 4;4-

A. B. C. D. 3452

Lờigiải

ChọnB.

Xétphươngtrình trongkhoảng ( )()4420*fxxm++--+= () 4;4()( )

442 *442 441 xxm fxxm xxm

++--= Û++--=-Û ++--=-

é++-=+Ûê ê ê++-=ë

442 441 xxm xxm

Xéthàmsố trongkhoảng ()44 gxxx =++- () 4;4-

Tacó () ()11 ;00 2424 gx gxx xx ¢ ¢ =- =Û= +-

A. B. C. D. 66 33 a 66 22 a 66 11 a 66 44 a Lờigiải

Bảngbiếnthiên

Dựavàobảngbiếnthiên,đểphươngtrìnhđãchocónghiệmthì

Câu42: Chohàm số liên tục trên Biết và thỏa mãn ()fx ()()1,00fxf>=

Khiđó bằng () ()2121fxxxfx ¢+=+ () 22 0

d fxx ¢ò

A. B. C. D. 38 1- 6 Lờigiải

ChọnB

é <+£-<£ Ûê ê <-£+<£ ê ë

22242222

22142215 m m m m

Mà nên . mÎ {}{} 1;24;5mÎÈ

Vậycógiátrịnguyêncủa thỏamãnyêucầubàitoán. 4 m

Câu41: Chokhốihộpchữnhật có diệntíchtamgiác bằng ABCDABCD ¢¢¢¢ ,2, ABaADa == CBD ¢ (thamkhảohìnhvẽ) 26a

Thểtíchcủakhốihộpchữnhậtđãchobằng

ChọnA

Trongmp kẻ thì . (), ABCDCHBD ^ () BDCHCBDHC ¢ ¢^Þ^

Khiđó

vuôngtại có và . CBDD C 225BDBCCDa =+= 22

.2 5 BCCDa CH BCCD = = +

SHCBDHC BD ¢ ¢ ¢¢ =Û==

. 1226 . 2 5 CBD

CBD Sa

Tamgiác vuôngtại có HCC¢C 222 CCHCHCa ¢¢ =-=

Vậythểtíchkhốihôphchữnhậtđãcholà .34ABCD VSCCa ¢ ==

Tacó () ()() () 2 2 121 211 fxxfxxxfx fxx

¢ ¢+=+Û = ++

()2 11 fxxC Þ+=++

Mà nên .Suyra . ()00f=0C= ()2fxx =

Khiđó ()() 22 222 22 00 0

d8fxxfxx ¢ ===ò

Câu43: Chohàm số có đạo hàmtrên thỏa mãn và ()yfx =  ()11f= vớimọi Khiđó bằng ()() 342 4321 fxxfxxx -=++xÎ () 4 1

d xfxx ¢ò

A. B. C. D. 15I= 1I=- 14I= 6I= Lờigiải

Đặt .Đổicận: 44xtdxdt  00 14 xt xt   

44ddd fxxfttfxx 

Đặt Đổicận: 434dd xuxxu  00 11 xu xu  

4dd xfxxfuu





A. B. C. D. 34a 326a 326 3 a 34 3 a

Lờigiải

ChọnA.

   342 342 43214441284* fxxfxxxfxxfxxx    11 1 342 00 0 44d4d1284d12 fxxxfxxxxx 

Tacó:



Nên:  444 000 

0 0



Nên: . 

414 001 ddd12fxxfxxfxx Đặt:  dd dd uxux vfxxvfx               .  4 4 4 1 1 1 .dd44112441124413 xfxxxfxfxxffff      Chọn .  14441244428xfff  

Suyra: .

Vậy  4 1

d281315xfxx  

Câu44: Cóbaonhiêusốnguyên đểphươngtrình có () 2023;2023aÎ- ()3

11 log871 x xa x +=+ +2

nghiệmphânbiệt?

A. . B. . C. . D. .2028201620272015

Lờigiải ChọnB

Điềukiện: .()()() 8 08;77;00; ,7 x D xx ì>ï ï Þ=--È-È+¥ í ï¹¹ï î Xéthàmsố

x x x fx xfx x xx ¢ = +-Þ=- -+- + +-

()() ()()()

11 17ln7 1 log8718ln3.log871

()2 2 3 3

nghịchbiếntrêntừngkhoảngxácđịnh. () ()0 fxxDfxÞ¢<"ÎÞ

Bảngbiếnthiên:

Đểphươngtrình có nghiệmphânbiệtvà thì: () fxa =2 aÎ{} 7;8;9;;2022aÎ

Vậycó giátrị nguyênthỏamãnyêucầubàitoán. 2016a

Câu45: Trongkhônggian ,chohai điểm , .Xéthai điểm ,thay đổi Oxyz () 1;2;2A-() 3;2;6B MN

thuộcmặtphẳng saocho .Giátrịnhỏnhấtcủa bằng. () Oxy 16MN= AMBN +

A. B. C. D. 4134553215

Lờigiải

ChọnA.

Gọi , lầnlượtlàhìnhchiếucủa ,trên ,khiđó: () '1;2;0A-() '3;2;0B AB() Oxy

()() 2 2 2222 '''''' AMBNAAAMBBBNAABBAMBN +=+++³+++

Tacó .'''''''''12 MAABBNMNAMNBMNABAMNB ++³Û+³-Û+³

Nên . ()() 2 222 '''812413AMBNAABBAMBN+³+++=+=

Đẳngthứcxảyra ,,,theothứtựthẳnghàngvà . ÛM'A' BN ' 3 ' AAAM BBBN ==

Câu46: Chohàmsố cóđạohàmliêntụctrên.Biết vàđồthị nhưhình ()yfx = ()70f-< ()fx ¢ vẽ.

Hàmsố cótốiđabaonhiêuđiểmcựctrị?

()()4262 627412 gxfxxxx =-+--+

A. B. C. D. 59 7 3 Lờigiải

ChọnC. Xéthàmsố ()()4262 627412 hxfxxxx =-+--+

()()()3425 644272424 hxxxfxxxx ¢ ¢ Þ=-+-+--+

()()()()() 24222 241272411 hxxxfxxxxx ¢ ¢ Û=---+---+

()()()() 2422 241271hxxxfxxx é ù ¢ ¢ Û=---+-++ ê ú ë û Tacó . ()2422 42 2716276, xxxxxt -+-=---Þ-+-£-"

Với , nên ,khiđó: 6t£-()0ft¢>()() 4222710, fxxxx ¢-+-++>"

()() 2 0 010 1 x hxxx x

Bảngbiếnthiên:

é= ê

Từbảngbiếnthiên và .

()() 0670hf¢ =-<()() 10hh ->

Nênphươngtrình cótốiđa nghiệmnênhàmsố ()()4262 6274120hxfxxxx =-+--+= 4

cótốiđa điểmcựctrị. ()() gxhx = 7

Câu47: Chokhốichóp cóđáylàhìnhvuôngcạnh tamgiác vuôngcântại tamgiác SABCD ,aSAB ,S

SCD 13 4 Sa CSD==

có .Thểtíchkhốichópđãchobằng



Û¢=Û-=Ûê=±

ChọnD

Lờigiải

Gọi lầnlượtlàtrungđiểmcáccạnh .Kẻ tạiH. , EF , ABCDSHFE ^

Khiđótacó: . ()ABSE ABSFESBSH ABFE ^ü ï ï ýÞ^Þ^ ^ï ï þ

Mà tại . SHFE ^ ()SHABCDÞ^ H

Tacó vuôngcântại SABD 11 ; 22 SABaSEABa =Þ==

vuôngở . SDFD 223 4 aFSFSDFD Þ=-=

Xéttamgiác có: SFE 39 ;; 248 SFE SaEFEaSFapa D ===Þ=

Tacó . () ();;2 dOABCDOHaODa ===

22323HDODOHaADa Þ=-=Þ=

Mà . 2 2 2 838323834ABCD SaABADaABaaABa =Þ=Û=Û=

4 OOABaÞ¢==

Thểtíchkhốitrụlà () 222 2.416. Vrhaaa =p=p=p

()()()

SFE aSppSFpSEpFE D Þ=---=

2 315 64

Mà . 2 113151315

SFE a a SSHFESHa SHaSH D==Þ=Þ=

2264232

SABCDABCD aaVSSHa = = =

. 3 2 1131515

333232

Gọi vàcó . IBMCN ¢=Ç // MNBC

A. . B. . C. . D. . 337 16 a 313 24 a 3315 64 a 15 32 a 3

A. B. C. D. 34ap 316ap 332ap 327ap Lờigiải Chọn

()()()()() 15 0 12 3 4 1 01 2 3 2 1 15522d2d24d2d1d 2 224 Ixxxxxxxxé ù ê ú ê ú =+++-++-++-== ê ú ê ú ê ú ë û òòòòò Câu49: Cho lăng

đứng có đáy làtamgiácvuông tại , , . ABCABC¢¢¢ABC B 3 ABBCa ¢ == Lấy hai điểm lần lượt trênhai cạnh và saocho  60ACB= ° , MN AB¢AC ¢ 2,MBAM  ¢ = .Thểtíchkhốiđadiện bằng 3 ACAN  ¢¢ = BMNCC ¢ A. . B. . C. . D. . 326 27 a 34 9 a 346 27 a 383 27 a Lờigiải ChọnC.

trụ

, và .

AB BCa == ° 2 CCa ¢ = 36 2LT Va = + 316 36 LTCBICABCC VVVa ¢ ¢ ===

Tacó:

tan60

+ 32216 ... 33354CMNICIAM AIM VVBCSa == =

Vậy . 346 27CMNICBCNMCBIC VVVa ¢=-=

Câu50: Chohìnhnóncóthiếtdiệnquađỉnhlàtamgiác vuôngtại ,( thuộcđườngtrònđáy). SABS, AB

Biết tamgiác cóbánkính đường tròn nội tiếp bằng , đường cao tạo với SAB 2510 - SO mặtphẳng mộtgóc .Diệntíchxungquanhcủahìnhnónđãchobằng () SAB30°

A. B. C. D. 510p 415p 52p 25p

Lờigiải

ChọnA.

SỞGIÁODỤCVÀĐÀOTẠOVĨNHPHÚC

TRƯỜNGTHPTNGUYỄNVIẾTXUÂN

ĐỀTHITHỬTỐTNGHIỆPTHPT–LẦN3–NĂMHỌC2021–2022

Câu1: Hìnhvẽbênlàđồthịcủahàmsốnào?

A. . B. . C. . D. . 42 4 yxx  34 yxx  42 4 yxx  34 yxx 

Kẻ  30OIABISO^Þ=°

Tacó: .Từđósuyra: ()2 122 251025 22

SAB llSprl l + =Û= -Þ= 210,AB= , và . 10SI= 30 2 SO= 52 2 ROA==

Vậydiệntíchxungquanh: . xq 510Srl=p=p

HẾT

3log,,log,2 x x e yxyyxy π 



A. B. C. D. 3 4 1 2



Câu3: Tổngtấtcảcácnghiệmcủaphươngtrình bằng

C. D. 7 log3 3 1log7  3 log7 3 1log7 

1;4

AI A. B. C. D. 22 2 2 4

Câu7: Tínhbánkính củamặtcầucódiệntíchlà r 16S 3 cm

A. B. C. D. 3 rcm  312.rcm   12.rcm  2 rcm 

Câu8: Cho phương trình . Gọi làhai nghiệm của phương trìnhtrên.Khi đó 1 449280 xx12 , xx tích bằng 12 , xx

A. B. C. D. 2 211

Câu9: Trongkhônggian tíchvôhướngcủahaivectơ bằng ,Oxyz  3;2;1,5;2;4ab 

A. B. C. D. 1571510

Câu10: Chokhốinóncóbánkínhđáylà,chiềucao.Thểtích củakhốinónđólà rhV

Câu2: Chocáchàmsố .Trongcáchàmsốtrêncóbaonhiêu 2 1 2     

hàmsốđồngbiếntrêntậpxácđịnhcủahàmsốđó?

3 log95371 xx x 

A. B.

 A. . B. . C. . D. . 4 1 Vπxdx 4 2 1 Vπxdx 4 1 Vπxdx 4 1 Vxdx 

Câu4: Thểtíchkhốitrònxoaydohìnhphẳnggiớihạnbởicácđường ,trục vàhaiđường yx Ox thẳng khiquayquanhtrụchoànhđượctínhbởicôngthứcnào?

 n u 12u 3q2023u A. . B. . C. . D. . 20222.3 20223.2 20213.2 20232.3

Câu5: Chocấpsốnhân cósốhạngđầu vàcôngbội .Giátrị

Câu6: Trongkhônggian,chotamgiác vuôngcântại gọi làtrungđiểmcủa ABC ,AI ,2BCBC Tính diện tíchxungquanh của hìnhnón nhận được khiquaytamgiác xungquanh trục ABC .

Câu11: Mộtkhốitrụcóthểtíchlà.Nếutăngbánkínhđáylên lầnthìthểtíchcủakhốitrụmớibằng 20 2 baonhiêu?

A. . B. . C. . D. .601208040

Câu12: Trongkhônggian ,mặtphẳngnàosauđâynhận làmvectơpháptuyến? Oxyz 

Câu13: Phươngtrình cótổngtấtcảcácnghiệmbằng 2 254 525 xx 

A. B. C. D. 5 2 5 2 11

Câu14: Kếtquảnàođúngtrongcácphéptínhsau?

A. B. cos2dsin2xxxC  2cos2d2cosxxxC 

C. D. cos2d2sin2xxxC  cos2dsincosxxxxC 

Câu15: Diệntích củahìnhphẳnggiớihạnbởiđồthịhàmsố ,liêntụctrên trụchoành S yfx   ; ab vàhaiđườngthẳng ()chobởicôngthức: , xaxb

A.Vônghiệm. B. C. D. 423

Câu22: Chohàmsố cóbảngbiếnthiênnhưhìnhvẽ yfx 

Câu16: Giátrịnhỏnhấtcủahàmsố trênđoạn là: 335yxx  2;4

y

Câu17: Chokhốilăngtrụcódiệntíchđáy vàchiềucao.Thểtích củakhốilăngtrụđãchođược BhV tínhtheocôngthứcnàodướiđây?

. B. . C. . D. . 6 VBh  VBh  1 3 VBh  4 3 VBh 

Câu18: Chohìnhlậpphương cạnh Gọi làtâmhìnhvông .Tínhthểtích ABCDABCD 3aO ABCD khốichóp . . OABCD 

Chọnkhẳngđịnhđúngtrongcáckhẳngđịnhsau.

A.Hàmsốnghịchbiếntrên . B.Hàmsốđạtcựctiểutại

C.Đồthịhàmsốkhôngcótiệmcận. D.Hàmsốcógiátrịnhỏnhấtlà. 3

sốđãchođồngbiếntrênkhaonrgnàodướiđây?

A. . B. . C. . D. .  ;1  1;1  1;  1;2

Câu21: Chohàmsố cóđồthịnhưhìnhvẽ.Hỏiphươngtrình với cóbao yfx  1mfx2m

nhiêunghiệm?

Câu23: Chobấtphươngtrình .Khiđặt thìbấtphươngtrìnhđãcho

2 22 log24log40 xx 2log tx  trởthànhbấtphươngtrìnhnàosauđây?

Câu24: Tậpxácđịnhcủahàmsố là

Câu25: là1nguyênhàmcủahàmsố và.Tínhgiátrịcủa ()Fx 3 ()41fxx(0)1F

1230

Câu26: Chohàmsố liêntụctrênvàthỏamãn .Tínhtíchphân ()fx 3 0 ()2xfxdx 1 0 (3) xfxdx

A. B. C. D. 2 . 9 6 2 . 3 18

Câu27: Trongkhônggian với hệ tọa độ ,chocác điểm . Phương trìnhnào Oxyz A(4;0;1),(2;2;3) B dướiđâylàphươngtrìnhmặtphẳngtrungtrựccủa AB

A. B. C. . D. 310. xyz30. xyz360. xyz62210. xyz

Câu28: Chohìnhchóp cóđáylàhìnhvuôngcạnh ,hìnhchiếuvuônggóccủa trên SABCD a S() ABCD trùngvớitrungđiểmcủa vàlàtrungđiểmcủa .Cạnhbên hợpvớiđáymộtgóc ADM BCSB Thểtíchkhốichóp theo bằng 060 SADMa

A. B. C. D.

Câu29: Sốmặtphẳngđốixứngcủakhốibátdiệnđềulà

A. . B. . C. . D. . 97 6 8

A. B. C. D. 2 Vrh  21 3 Vrh  21 3 Vrh  2 Vrh 

n  A. . B.

24610 xyz2460 xz 2310xyz2310xyz

1;2;3

A. B. C. D. d b a Sfxx  d b a Sfxx  d b a Sfxx  2d b a Sfxx 

ab 

B. C. D.  2;4 min5 y  24 min0 y  2;4 min3 y  24 min7

A. . B. . C. . D. . 33a 38a 39a 3 3 a Câu19: Phươngtrìnhmặtphẳngđiqua ,songsongvới là  1;1;2A :2210 xyz A. . B. . C. . D. . 2220xyz2250xyz220xyz 2210xyz Câu20: Cho cóbảngxétdấuđạohàmnhưhìnhsau: yfx  Hàm



;1 1x

A. . B. . C. . D. . 2440tt 2430tt 20t 2230tt







 

  1; 

1 51yx

A. B. C. D. 

 (1)F

B. C. D.

12 a 3

Câu30: Tìmtậpnghiệmcủabấtphươngtrình . 3exx 

A. . B. . C. . D. .  ;0 

Câu31: Gieomộtconsúcsắccânđốivàđồngchất,xácsuấtđểmặtcósốchấmchẵnxuấthiện

A. B. C. D. 1 1 3 2 3 1 2

Câu32: Trongkhônggian ,chomặtcầu cótâm vàtiếpxúcvớitrục .Phương Oxyz S 1;2;3A Ox trìnhcủamặtcầu là

Câu39: Cóbaonhiêugiá trị nguyên dương của tham số để bất phương trình m cónghiệm?

A. B. C. D. 9416

Câu40: Tậphợptấtcảcácgiátrịcủathamsố để

222 12313xyz

. B. .

222 12313xyz  C. D.  222 12313xyz  222 12313

trìnhmặtphẳng điquahaiđiểm vàvuônggóc

Câu34: Tínhdiệntíchhìnhphẳng giớihạnbởiđường

Q ,BA

Câu35: Chokhốichóp cóthểtíchbằng vàđáy làhìnhbìnhhành.Biếtdiệntích . SABCD 32aABCD bằng .Tínhkhoảngcáchgiữahaiđườngthẳng và ? SAB 2 a SBCD

A. B. C. D. a 2 2 a 3 2 a 3a

Câu36: Cóbaonhiêugiátrịcủathamsố đểhàmsố đạtgiátrịlớnnhấtbằng m 24 yfxxmx 

A. B. C. D. 3 0 21

Câu37: Khixâynhà,côNgọccầnxâymộtbểđựngnướcmưacóthểtích dạnghìnhhộpchữ 36mV nhậtcóchiềudàigấpbalầnchiềurộng.Biếtrằngđáy,nắpvàcácmặtxungquanhđềuđượcđổ bêtôngcốtthép.Phầnnắpbểđểhởmộtkhoảnghìnhvuôngcódiệntíchbằng diệntíchnắp 2 9 bể.Biếtrằngchiphícho bêtôngcốtthéplà đồng.Tínhchiphíthấpnhấtmàcô

1m1000000

Ngọcphảitrảkhixâybể(làmtrònđếnhàngtrămnghìn)

A. đồng. B. đồng. C. đồng. D. đồng. 21000000219000002090000012600000

Câu42: Trongkhônggianvớihệtrụctọađộ ,chomặtcầu Oxyz222 :24230 Sxyzxyz

:22140PxyzM

Câu43: Gọilàdiệntíchhìnhphẳnggiớihạnbởicácđường .Tìmgiá

Câu44: Chohàmsố cóđạohàmliêntụctrên.Hàmsố cóđồthịnhưhìnhvẽbên yfx 

Sốnghiệmthuộcđoạn củaphươngtrình  2;6  0fxf 

A. B. C. D. 4352

. ABCDABCD  a ,, MNP

Câu38: Chohình lập phương cạnh .Các điểm lần lượt thuộc các cạnh

saocho .Tìmdiệntíchthiếtdiện củahìnhlậpphương

Câu45: Chohàmsố đồthị Gọi làkhoảngcáchtừgiaođiểmhaitiệmcậncủađồthị 2 1



y x

 Cd đếnmộttiếptuyếncủa .Giátrịlớnnhấtcủa cóthểđạtđượclà  C  C d

A. B. C. D. 333222



\0  0;





xyz

tọa độ

Oxyz  2,4,1



Viếtphương



với ? P A. B. :23100

 

 C. D. 

Qyz 





Câu33: Trongkhônggian với hệ

,chohai điểm ; và mặt phẳng

1,1,3B

:3250Pxyz

Qyz

:23110Qyz

:23130

:23120Qyz

và S H 312 yxx  2 yx  A. B. C. D. 937 12 S 343 12 S 397 4 S 793 4 S

cong

 3 aBMCNDP   S khicắtbởimặtphẳng  MNP A. . B. . C. . D. . 253 18 Sa  233 2 Sa  2133 18 Sa  23 2 Sa 

BBCDDA

2 2

xxmxxmxx    

332239233

m 1 4 mx y mx  1 ; 4    là? A. B. C. D.  2;  ;2  2;2 1;2

hàmsố nghịchbiếntrênkhoảng

yfx  1 23 fxfx x     1 ;2 2 x    2 1 2 fxdx x A. B. C. D. 3 2 9 2 9 2 3 2

 và

. 

SN P Độdài

A. . B. . C. . D. . 1 2 213 2

Câu41: Chohàmsố liêntụcvàthỏamãn với .Tính

mặtphẳng .Điểm thayđổitrên ,đểm thayđổitrên

nhỏnhấtcủa bằng MN

22 1

2 myxmxym  của để m3S A. B. C. D. 3m 2m 1 2 m 3 2 m

trị

2,,0

 yfx   dưới:



2 nn uu



A. B. C. D. 233234230231

Câu50: Chohìnhchóp cóđáylà làhìnhchữnhật.Tamgiác nằmtrongmặtphẳng . SABCDABCD SAB vuônggócvới Biếtrằng , và .Tínhdiệntíchkhốicầu  ABCDABa  3ADa   60ASB  ngoạitiếphìnhchóp .SABCD

Câu47: Cho làhàm số liên tục có đạo hàm trên . Biết ()fx ()fx  [0;1],(1)0 f .Khiđó bằng 

121 0 0

A. B. C. D. 1 6 11 48 6 23 0

Câu48: Chođồthịhàmsố nhưhìnhvẽdướiđây: ()yfx 

Gọi làtậptấtcảcácgiátrịnguyêndươngcủathamsố đểhàmsố S m có5điểmcựctrị.Tổngtấtcảcácgiátrịcủacácphầntửcủatập bằng: 21 (2023)3 yfxm  S

A. B. C. D. 7.6.5.9.

Câu49: Chohàmsố liêntụctrên vàcóđồthịlàđườngcongtronghìnhvẽdướiđây



Cóbaonhiêugiá

 2 2 16.328436 fx fx fxfxfxmm    1;9 A. B. C. D. 6 325 31

Câu46: Chodãysố thoảmãn và vớimọi .Giá  n u 12213 2 331  

8 22 l1 og44 4 1

uu uu  



trịnhỏnhấtcủa để bằng n 100 12...5 n n Suuu



11 (),()33fxdxfxdx  

1 2 0() fxdx

yfx   1;9

trị nguyên của tham số để bất phương trình m có nghiệm đúng với mọi giá trị thuộc

A. . B. . C. . D. . 213 2 Sa   213 3 Sa   211 2 Sa   211 3 Sa   HẾT

BẢNGĐÁPÁN

1.C2.C3.C4.A5.A6.B7.D8.B9.C10.B

11.C12.A13.A14.D15.A16.D17.B18.C19.B20.B

21.C22.B23.D24.C25.C26.A27.B28.A29.A30.A

31.D32.D33.B34.A35.D36.C37.A38.C39.C40.D

41.D42.C43.D44.B45.C46.B47.B48.A49.A50.C

HƯỚNGDẪNGIẢICHITIẾT

Câu1: Hìnhvẽbênlàđồthịcủahàmsố

sốđồngbiếntrêntậpxácđịnhcủahàmsốđó?

C đồngbiến →nghịchbiến 2log yx

0x ,1 x ee y ππ

ChọnA

Câu5: Chocấpsốnhân cósốhạngđầu vàcôngbội .Giátrị

ChọnA 12022 12023 .2.3 n n uuqu

Câu6: Trongkhônggian,chotamgiác vuôngcântại gọi làtrungđiểmcủa ABC ,AI ,2BCBC

Tính diện tíchxungquanh của hìnhnón nhận được khiquaytamgiác xungquanh trục ABC .

ChọnB

A. B. C. D. 42 4 yxx  34 yxx  42 4 yxx  34 yxx  Lờigiải ChọnC Hàmsốtrùngphương→LoạiB,D →ChọnC lim x  Câu2: Chocáchàmsố .Trongcáchàmsốtrêncóbaonhiêu 2 1 2 3log,,log,2 x x e yxyyxy π        hàm

Lờigiải



   nghịchbiến →nghịchbiến 1 2 log yx  0x 33 ,1 22 x y     

trình bằng 3 log95371 xx x  A. B. C. D. 7 log3 3 1log7  3 log7 3 1log7  Lờigiải ChọnC TXD: D    3 1 2 2 log95371 95.373 3537330 38370 xx xxx xxx xx x      Đặt 3,0 x tt 12 12 12 123 3 73log7 xx xx tt xx    

Thểtíchkhốitrònxoaydohình

cácđường ,trục vàhaiđường yx Ox thẳng khiquayquanhtrụchoànhđượctínhbởicôngthứcnào? 1;4xx A. . B. . C. . D. . 4 1 Vπxdx 4 2 1 Vπxdx 4 1 Vπxdx 4 1 Vxdx  Lờigiải

nào?

A. B. C. D. 3 4 1 2

Chọn



Câu3: Tổngtấtcảcácnghiệmcủaphương

Câu4:

phẳnggiớihạnbởi

 n u 12u 3q2023u A. . B. . C. . D. . 202223 202232 202132 202323 Lờigiải



AI A. B. C. D. 22 2 2 4 Lờigiải

vuôngcânở làtrungđiểmcủa ABC ,AI ,2

đódiệntíchxungquanhcủahìnhnónlà 122Vrl

Câu7: Tínhbánkính củamặtcầucódiệntíchlà r 16S

Cho phương trình . Gọi làhai nghiệm của phương trìnhtrên.Khi đó

Câu11: Mộtkhốitrụcóthểtíchlà.Nếutăngbánkínhđáylên lầnthìthểtích

củakhốitrụmớibằng 20 2 baonhiêu?

A. . B. . C. . D. .601208040

Lờigiải

ChọnC

Tacó: .  222 ''24480 VrhrhrhV  

Câu12: Trongkhônggian ,mặtphẳngnàosauđâynhận làmvectơpháptuyến? Oxyz  1;2;3n 

A. . B. . 24610 xyz2460 xz

C. . D. . 2310xyz 2310xyz Lờigiải

ChọnA

Mặt phẳng có một vtpt nên mặt phẳng 24610 xyz 

Tổngtấtcảcácnghiệmbằng 5

Câu14: Kếtquảnàođúngtrongcácphéptínhsau?

Câu9: Trongkhônggian tíchvôhướngcủahaivectơ bằng ,Oxyz

3;2;1,5;2;4ab

1510

A. . B. . cos2dsin2xxxC 

C. D. cos2d2sin2xxxC 

cos2dsincosxxxxC 

Câu10: Chokhốinóncóbánkínhđáylà,chiềucao.Thểtích củakhốinónđólà rhV

ChọnD . 1 cos2dsin2sincos 2 xxxCxxC 

Câu15: Diệntích củahìnhphẳnggiớihạnbởiđồthịhàmsố ,liêntụctrên trụchoành S yfx   ; ab vàhaiđườngthẳng ()chobởicôngthức: , xaxb ab 

Tamgiác

 1 1 2 1 2 AIBC BIIC ABAC         Do





cm A. B. C. D. 3 rcm  312.rcm   12.

 2 rcm  Lờigiải ChọnD 2 16 416 2 S r r      Câu8:

tích bằng 12 , xx A. B. C.

Lờigiải ChọnB 1 449280 xx  4.218.280 xx  242 211 2 x x x x      Khiđó 122xx

BCBC

rcm

4.49.280 xx12 , xx

2.1.1.







 



A. B. C. D. 157

Lờigiải ChọnC

352214154415ab

A. B. C. D. 2 .Vrh  21 . 3 Vrh  21 . 3 Vrh  2 .Vrh  Lờigiải ChọnB Thểtích củakhốinónlà V 21 . 3 Vrh 

'2;4;621;2;3n  nhận làmvtpt. 24610 xyz 1;2;3n 

nghiệmbằng 2 254 525 xx  A. B. C. D. 5 2 5 2 11 Lờigiải ChọnA Tacó: . 2 2 25425422 2 5255525421 2 xx xx x xx x      

Câu13: Phươngtrình cótổngtấtcảcác



2cos2d2cosxxxC 



 Lờigiải



A. B. C. D. d

a Sfxx  d

a Sfxx  d b a Sfxx  2d b a Sfxx  Lờigiải

Câu20: Cho cóbảngxétdấuđạohàmnhưhìnhsau:

Câu16: Giátrịnhỏnhấtcủahàmsố trênđoạn là: 335yxx

. 3 2 3533yxxyx

2;4

Câu17: Chokhốilăngtrụcódiệntíchđáy vàchiềucao.Thểtích củakhốilăngtrụđãchođược BhV

Hàmsốđãchođồngbiếntrênkhaonrgnàodướiđây? A. B. C. D.

Câu21: Chohàmsố cóđồthịnhưhìnhvẽ.Hỏiphươngtrình với cóbao

A.Vônghiệm. B. C. D. 423

Câu18: Chohìnhlậpphương cạnh .Gọi làtâmhìnhvông .Tínhthểtích . ABCDABCD 3aO ABCD

chóp . OABCD 

vàođồthị,nhậnthấyđồthịhàmsố cắtcácđườngthẳng tạihaiđiểm

biệtdovậyphươngtrìnhđãchocóhainghiệmphânbiệt.

Câu22: Chohàmsố cóbảngbiếnthiênnhưhìnhvẽ yfx 

Chọnkhẳngđịnhđúngtrongcáckhẳngđịnhsau.

A.Hàmsốnghịchbiếntrên . B.Hàmsốđạtcựctiểutại .  ;1 1x

C.Đồthịhàmsốkhôngcótiệmcận. D.Hàmsốcógiátrịnhỏnhấtlà. 3 Lờigiải

ChọnB

Hàmsốđãchođạtcựctiểutại dođóChọnB 1x

Câu23: Chobấtphươngtrình .Khiđặt thìbấtphươngtrìnhđãcho 2 22 log24log40 xx 2log tx  trởthànhbấtphươngtrìnhnàosauđây?

A. B. C. D. 2440tt 2430tt 20t 2230tt Lờigiải

ChọnD

Tacó: .  2 2 2 22 22 22 log24log40log14log40log2log30 xx xxxx 

Chọn



A. B. C. D.  2;4 min5 y  24 min0 y  2;4 min3 y  24 min7 y Lờigiải Chọn

Tacó

 Giải  

    Tacó

 





2 12;4 0330 12;4 x yx x

24 27;457min27yy yy

tínhtheocông

A. B. C. D. 6 VBh  VBh  1 3 VBh  4 3 VBh  Lờigiải Chọn

Tacó

thứcnàodướiđây?

.VBh 

A. . B.

D. . 33a 38a 39a 3 3 a Lờigiải ChọnC Tacó .  23 1 1 .;..3.39 3 3 OABCD ABCD VdOABCDSaaa      Câu19:

trình

qua ,songsongvới là  1;1;2A :2210 xyz A. . B. . C. . D. . 2220xyz2250xyz220xyz 2210xyz Lờigiải ChọnB Mặtphẳng códạng .  // PP   2201xyzDD Điểm  1;1;21212205AP DD  Phươngtrìnhmặtphẳng . :2250Pxyz

khối

Phương

mặtphẳngđi

yfx 



 

 1;  1;2 Lờigiải Chọn

1;1



1mfx2m nhiêunghiệm?

yfx 

Lờigiải Chọn

Tacó vì nên với . 11mfxfxm  2m1fxm  11m Dựa



phân

fx 1ym 



Dođó,với bấtphươngtrìnhtrởthành: . 2log tx  2230tt

Câu24: Tậpxácđịnhcủahàmsố là  1 51yx 

. B. . C. . D. .

Lờigiải

A. B. C. D. 315 12 a 315 6 a 315 4 a 315 3 a Lờigiải

ChọnC

Hàmsố xácđịnhkhi nêntậpxácđịnhcủanólà .

Câu25: là1nguyênhàmcủahàmsố và.Tínhgiátrịcủa . ()Fx 3 ()41fxx(0)1F (1)F A. B. C. D. 1.2.3.0.

Lờigiải

ChọnC

Tacó: 34()()(41) FxfxdxxdxxxC  

Theogiảthiết nên(0)1F1(1)3CF

Câu26: Chohàmsố liêntụctrênvàthỏamãn .Tínhtíchphân ()fx

ChọnA

Đổicận: 3 3 dtxtdx

00 13 xt xt 

12 (3)()()3399 tdt xfxdxftftdt 

()2xfxdx

A. B. C. . D. 310 xyz30 xyz360 xyz62210 xyz

Lờigiải

Tacó: .Gọi làtrungđiểmcủa (6;2;2)AB  I AB(1;1;2)I

Mặtphẳngtrungtrựccủa điquavànhận làvéctơpháptuyếncóPT: ABI(6;2;2)AB  6(1)2(1)2(2)030 xyzxyz 

Câu28: Chohìnhchóp cóđáylàhìnhvuôngcạnh ,hìnhchiếuvuônggóccủa trên SABCD a S() ABCD

trùngvớitrungđiểmcủa vàlàtrungđiểmcủa .Cạnhbên hợpvớiđáymộtgóc ADM BCSB

060 SADMa

tacó: .  60SBH  015 tan60 2 aSHBH   2 2 2ADMABCDABM aSSS     Dođó 3

115

A. B. C. D. 97 6 8

Lờigiải

ChọnA

Sốmặtphẳngđốixứngcủabátdiệnđềulà. 9

Câu30: Tìmtậpnghiệmcủabấtphươngtrình . 3exx 

A. B. C. D.  ;0  \0  0;

Lờigiải

ChọnA

Có .  3eln3lneln3100 xxxx x x 

Câu31: Gieomộtconsúcsắccânđốivàđồngchất,xácsuấtđểmặtcósốchấmchẵnxuấthiện

A. . B. . C. . D. . 1 1 3 2 3 1 2

Lờigiải

ChọnD

Khônggianmẫukhigieomộtconsúcsắc mặtlà . 66n







 0;  1;





 1;S

1 51yx

101xx

3 0

 1 0 (3) xfxdx A. B. C. D. 2 9 6 2 3 18

Lờigiải

Đặt

 



Vậy 13 3 00 0 

Câu27: Trongkhônggian với hệ tọa độ ,chocác điểm . Phương trìnhnào Oxyz A(4;0;1),(2;2;3) B dướiđâylàphươngtrìnhmặtphẳngtrungtrựccủa AB

ChọnB

Thểtíchkhốichóp theo bằng

ChọnA

312SADM ADM aVSHS  

Gọi làtrungđiểmcủa H AD Từgiảthiết

Câu29: Sốmặtphẳngđốixứngcủakhốibátdiệnđềulà

Câu33: Trongkhônggian với hệ tọa độ ,chohai điểm ; và mặt phẳng Oxyz  2,4,1A 1,1,3B .Viếtphươngtrìnhmặtphẳng điquahaiđiểm vàvuônggóc

:3250Pxyz  Q ,BA

:23100Qyz :23110Qyz

Diệntíchhìnhphẳng giớihạnbởiđườngcong và bằng

Câu35: Chokhốichóp cóthểtíchbằng vàđáy làhìnhbìnhhành.Biếtdiệntích SABCD 32aABCD

bằng .Tínhkhoảngcáchgiữahaiđườngthẳng và ? SAB 2 a SBCD

A. B. C. D. a 2 2 a 3 2 a 3a Lờigiải

ChọnD

Tacó .3 1 2 SABCSABCD VVa 

Do nênkhoảngcáchgiữahaiđườngthẳng và bằngkhoảngcáchtừđiểm

CDSAB  SBCD

đến bằng C mpSABh

3 23 1 1 .... 3 3 3 SABCCSAB SAB VVShaahaha  

Vậykhoảngcáchgiữahaiđườngthẳng và bằngSBCD3a

Câu36: Cóbaonhiêugiátrịcủathamsố đểhàmsố đạtgiátrịlớnnhấtbằng

:23130Qyz

:23120Qyz Lờigiải ChọnB

Tacó ; 3,3,2AB  cóvéctơpháptuyến

1,3,2n  Mặtphẳng điquahaiđiểm vàvuônggócvới nênnhận

:3250Pxyz

P làvéctơpháptuyến,phươngtrìnhmặtphẳng là

Câu34: Tínhdiệntíchhìnhphẳng giớihạnbởiđườngcong và

Vậycó2giátrị cầntìm. m

bể.Biếtrằngchiphícho bêtôngcốtthéplà đồng.Tínhchiphíthấpnhấtmàcô 2 1m1000000 Ngọcphảitrảkhixâybể(làmtrònđếnhàngtrămnghìn) A. đồng. B. đồng. C. đồng. D. đồng.

21000000219000002090000012600000 Lờigiải

ChọnA

Gọichiềurộngcủabểlà .Khiđóchiềudàibểlà vàchiềucaobểlà .  mx 3m x

Sốcáchxuấthiệncủamặtcósốchấmchẵnlà . 3nA Vậy 31 P 62 A Câu32: Trongkhônggian ,chomặtcầu cótâm vàtiếpxúcvớitrục Phương Oxyz S 1;2;3A Ox trìnhcủamặtcầu là  S A. B.  222 12313xyz  222 12313xyz  C. . D. .  222 12313xyz  222 12313xyz Lờigiải ChọnD Tacó .  22 d,2313RAOx Phươngtrìnhmặtcầu cótâm ,bánkính là  S 1;2;3A 13R 

222 :12313Sxyz



với ?

A. B.

C. D. 





    Q . :23110Qyz

S H 312

 2 yx  A. B. C. D. 937 12 S 343 12 S 397 4 S 793 4 S Lờigiải ChọnA Xétphươngtrình . 3 2 0 12 4 3 x xxxx x      



Q ,BA

,0,8,1240,2,3nABn

yxx



 2

 4

 

12 yxx

3 2 3 937 12 12 Sxxxdx

m 24 yfxxmx  .5 A. . B. . C. . D. . 3 0 21 Lờigiải ChọnC Hàmsố đạtgiátrịlớnnhấtbằng5thì , yfx  2 2 4545 xmxxmxx  2 2 45, 45, xmxx xmxx       2 2 45, 45, mxxx mxxx       1 1 m m    Dođógiá

bằng5 . yfx  1 11;1 m m m    

trịlớnnhấtcủahàmsố

2 9

2 62

3xx 

Diệntíchtoànphầncủabểsaukhibỏđimộtkhoảnghìnhvuôngcódiệntíchbằng diệntích 2 9

nắpbểlà . 2 22 2621616 23.3 93 p Sx xx xx x      2 m

Tacó . 23 168816 3..8.8 33p Sx xx  32 1024 3.m 3p S 

DođóchiphínhỏnhấtmàcôNgọccầnphảitrảlà (đồng) 3 1024 3..100000021000000 3 

Câu38: Chohình lập phương cạnh .Các điểm lần lượt thuộc các cạnh ABCDABCD  a ,, MNP saocho .Tìmdiệntíchthiếtdiện củahìnhlậpphương ,, BBCDDA  3 aBMCNDP   S khi

lụcgiác là . MHPKNE

Câu39: Cóbaonhiêugiá trị nguyên dương của tham số để bất phương trình m cónghiệm? 2 2 332239233 xxmxxmxx  

Trongmp dựng , ,khiđó làhìnhthang.  CDDC// NGCCGCD  BMNG

Trongmp gọi .Trongmp gọi BMNGIBGMN   ABCD , HIPABJIPCD 

Trongmp gọi , .  CDDCKNJDDQNJCC

Trongmp gọi  BCCBEMQBC Vậythiếtdiệncủahìnhlậpphươngcắtbởimp làlụcgiác . MNPMHPKNE

Tachứngminhđượchaitứgiác và làcáchìnhthangcân. MKPHMKNE

Tậphợptấtcảcácgiátrịcủathamsố đểhàmsố nghịchbiếntrênkhoảng m 1 4 mx y mx 

+Tacó , ; 2MKBDa

Tacó: .Theoyêucầubàitoánthì:

cắtbởimặtphẳng 

A. B. C. D. 253 18 Sa  233 2 Sa  2133 18 Sa  23 2 Sa  Lờigiải ChọnC

MNP

 22 222222 333 PHAPAHaaa     ; ; 22 22 2 993 aaa MHMBHB  11226 2 2236 OMMKPHaaa            ; 22 22226 9366 aaHOHMOM a    Diệntíchhìnhthang là . MKPH 21122653 2 223618MKPH a SMKPHOHaaa          +Tươngtựtatínhđược 2226 ;; 333 a a NEMEaET  Diệntíchhìnhthang là . MKNE 2112643 2 22339MKNE SMKNEETaaaa      Vậydiệntích

2225343133 18918 Saaa 

 A. B. C. D. 9416 Lờigiải ChọnC Đặt:  230xxmaa Khiđó: 22 222322 2211212 32.333.303333 9279999 aaxxaxax ax ax ax       Nên: 2 2 2 30 030 4422 2322 xxm axxm xmmm axxxmx x              

dương

m

   là? A. B. C. D. 2;.  ;2. 2;2. 1;2. Lờigiải ChọnD



Donguyên

nên m 1.

Câu40:

; 4

 2

mxm yy

  2402222 1112 1 ; 444 4 m m m m m m m                 Vậy: 1;2m

mxmx

Câu42: Trongkhônggianvớihệtrụctọađộ

ChọnB

Dựavàođồthịhàmsố yfx  

Tacó hay  25 02 fxdxfxdx   

Dựavàođồthịtacóbảngbiếnthiênsau

205205 ffffff  

P H I phẳng vàlàgiaođiểmcủađoạn vớimặtcầu PK IH S

vàmặtphẳng khôngcóđiểmchung,gọi làhìnhchiếucủa lênmặt

Câu43: Gọilàdiệntíchhình

Dựabảngbiếnthiênsuyraphươngtrình có3nghiệmphânbiệt.  0fxf 

Câu45: Chohàmsố đồthị Gọi làkhoảngcáchtừgiaođiểmhai

Câu41: Chohàmsố liêntụcvàthỏamãn với .Tính yfx  1 23 fxfx x     1 ;2 2 x    2 1 2 fxdx x A. B. C. D. 3 2 9 2 9 2 3 2 Lờigiải ChọnD Xét .Tacó: 1 ;2 2 x     1 1 2323 ffxxfxfx xxx        Lấytíchphân vếtađược: 2  222 111 222 1 9 23 2 ffxxdxdxxdx xx    Đặt .Đổicận: 2 2 111 tdxdtdxdt xx t  1 2 2 1 2 2 xt xt        Khiđó: 2222 2 1111 1 2222 2 1 93 2223 22 fftfxfxfx xdxdtdxdxdx xtxx x   

,chomặtcầu Oxyz222 :24230 Sxyzxyz vàmặtphẳng Điểm thayđổitrên ,đểm thayđổitrên . :22140PxyzMSN P Độdàinhỏnhấtcủa bằng MN A. B. C. D. 1 2 213 2 Lờigiải ChọnC Mặtcầucótâm ,bánkính và  1;2;1I 3R   222 2.122.114 , 4 212 dIP R     Do

 S 

đómắtcầu

Tacó  ,431MNMKdIPR  

Vây .min1 MN

phẳnggiớihạnbởicácđường .Tìmgiátrị 22 1 2,,0 2 myxmxym  của để m3S A. B. C. D. 3m 2m 1 2 m 3 2 m Lờigiải ChọnD Do nênsuyra . 0m 0,0xy Tọađộgiaođiểmlànghiệmcủahệphươngtrình 2 2 22 220 122 2 myxmyxx xmmxymxy             Tacó hay . 22 0 23 2 m Sxmxdx m    2 43 3 32 m m  Câu44: Chohàmsố cóđạohàmliêntụctrên.Hàmsố cóđồthịnhưhìnhvẽbên yfx   yfx   dưới: Sốnghiệmthuộcđoạn củaphươngtrình  2;6  0fxf  A. B. C. D. 4352 Lờigiải





tiệmcậncủađồthị 2 1 x y x    Cd đếnmộttiếptuyếncủa .Giátrịlớnnhấtcủa cóthểđạtđượclà  C  C d A. B. C. D.

222 Lờigiải ChọnC

333

C 1x 1y

Tacóđồthị cóđườngtiệmcậnđứnglà vàđườngtiệmcậnnganglà .

Suyragiaođiểmcủahaiđườngtiêmcậnlà . 1;1I

Lấy tuỳý. 000 ;,1MxyCx

Suyratiếptuyếncủađồthị tạiđiểm là hay

22 000 :1420 xxyxx

Khoảngcáchtừđiểm đếntiếptuyếncủađồthị

Cho

bằng: 21 (2023)3 yfxm  S

A. B. C. D. 7.6.5.9. Lờigiải

ChọnA Đặt  21 (2023)(2023) 3 hxfxmhx xf 

Tacó 2 2 '. . AA yAAy A 

Sốcựctrịcủa làsốnghiệmđơnhoặcbộilẻcủa 21 (2023)3 yfxm  0hxhx  

020230hfx x  

có3nghiệmđơnphânbiệt.



 C

200 0 1 : 1 yxxy x    .



00 ; Mxy



tạiđiểm là I  C 00 ; Mxy   0 0 4 4 2 2 0 0 20 20 0 0 222122 , 2 1 1 1111121 1 1 xx dI xx x x x x            Dấu“=”xảyrakhivàchỉkhi (thoảmãn). 240 200 0 0 0 1 111 2 1 x xx x x      Câu46: Chodãysố thoảmãn và vớimọi .Giá  n u 12213 2 331 8 22 l1 og44 4 uu uu     12 nn uu   1n trịnhỏnhấtcủa để bằng n 100 12...5 n n Suuu A. . B. . C. . D. .233234230231 Lờigiải ChọnB Tacódãysố thoảmãn vớimọi nêndãysố làcấpsốnhânvớicông  n u 12 nn uu   1n  n u bội 2q suyra .21321 2;24 uuuuu  Dođó  12 11 213 2132 2 2 311 331 8 8 22 22 1 1 log444log44 4 uu uu uu uu           Mà . 1111 21322132 1222228 uuuuVT    Dấu“=”xảyra . 112132 111 1 222132 2 uu uuu  Lạicó . 2 2 2 111 3113 444213log444log31 uuu uu  Suyra .Dấu“=”xảyra .  2 311 8 1 8 log444 VP uu    11 1 210 2 uu Từ suyra .  11 1 2 u Khiđó . 121 11121 ....21 12122 n n n n n qSuuuu q  Suyra .   100 100100 100 2 1 52152251log251233,193 2 n n n S n  Vậygiátrịnhỏnhấtcủa để bằng n 100 125 n n Suuu234 Câu47:

có đạo hàm trên .Biết ()fx ()fx  [0;1],(1)0 f .Khiđó bằng 121 0 0 11 (),()33fxdxfxdx   1 2 0() fxdx A. B. C. D. 1 . 6 11 . 48 6 . 23 0. Lờigiải ChọnB Đặt 1 0 1 (). 3Ifxdx  Đặt  ufxufxdx dvdxvx           1 1 1 0 0 0 11 2 2 03 3Ixfxdxxfxdxxfxdx xfx          1 1 1 1 2 2 2 0 0 0 0 121 ()2()30()0()0 33fxdxxfxdxxdx fxxdxfxx       2 ()2 x fxxfxC   Theobàira  1 22 2 0 11111 (1)02222248 xxfCfx     Câu48: Chođồthịhàmsố nhưhìnhvẽdướiđây: ()yfx  Gọi làtậptấtcảcácgiátrịnguyêndươngcủathamsố đểhàmsố S m có5điểmcựctrị.Tổngtấtcảcácgiátrịcủacácphầntửcủatập

làhàm số liên tục

đểhàmsố có5điểmcựctrịthì m 21 (2023)3 yfxm 

Có2nghiệmphânbiệt.Dựavàođồthịđiềukiện

Donguyêndươngnên m 4,3.mm

Tổngcácgiátrịcácphầntửcủatập làS347. 

Câu49: Chohàmsố liêntụctrên vàcóđồthịlàđườngcongtronghìnhvẽdướiđây

Câu50: Chohìnhchóp cóđáylà làhìnhchữnhật.Tamgiác nằmtrongmặtphẳng SABCDABCD SAB vuônggócvới .Biếtrằng , và .Tínhdiệntíchkhốicầu  ABCDABa  3ADa   60ASB

ngoạitiếphìnhchóp . . SABCD

Cóbaonhiêugiá trị nguyên của tham số để bất phương trình m có nghiệm đúng với mọi giá trị thuộc

B. C. D. 6 325 31

Gọi , lầnlượtlàbánkínhkhốicầungoạitiếphìnhchóp vàbánkínhđường RSABR . SABCD

trònngoạitiếptamgiác ,khiđó SAB  3 22sin603 sinSAB ABaa R ASB 

Do làhìnhchữnhậtnênkhốicầungoạitiếphìnhchóp cũnglàkhốicầu ABCD . SABCD ngoạitiếphìnhchóp . . SABC

Mặtkháchìnhchóp làmộthìnhchópcócạnhbên vuônggócvớimặtđáynên SABC BC

222 2 3339 2326SAB BCaa RR





21 0(2023)3 hxfxm

2 2 2 2 1

3 m m m m         

63918 3





yfx

 1;9

 2

fxfxmm    1;9 A.

Lờigiải ChọnA  2

fx x fxfxfxmm      2 2 1 2 16283 2 3 fx fx fxfxmm             Đặt ,từđồthịtathấyđược tfx   42 fx  4;2t  Để cónghiệmđúngvớimọi khi  2 2 16.328436 fx x fxfxfxmm    1;9x vàchỉkhi cónghiệmđúngvới  2 2 12 31628 23 t t mmtt         4;2t với  2 4;2 3min mmgt    2 12 1628 23 t t gttt        Tacó làhàmnghịchbiếnnên với 1 16 2 t hx   24hxh 4;2t Tacó với nên với 2280tt 4;2t  22 28024 3 t utttuu     . 4;2t Nên . 4;2 42,4;2min24 t gtgt gtg   Khiđó 232414mmgm 

2 16328436 fx fx fx

2 16.328436

A. B. C. D. 213 2 Sa   213 3 Sa   211 2 Sa   211 3 Sa   Lờigiải ChọnC



      213 3 Sa  