100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC (ĐỀ 81-100)

ĐỀ THI THỬ TỐT NGHIỆP

THPT MÔN TOÁN

vectorstock com/28062405

Ths Nguyễn Thanh Tú

eBook Collection

100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM

HỌC 2022-2023 - MÔN TOÁN - CÁC

TRƯỜNG TRÊN CẢ NƯỚC - CÓ LỜI GIẢI (ĐỀ 81-100) - 444 TRANG

WORD VERSION | 2023 EDITION

ORDER NOW / CHUYỂN GIAO QUA EMAIL

TAILIEUCHUANTHAMKHAO@GMAIL COM

Tài liệu chuẩn tham khảo

Phát triển kênh bởi

Ths Nguyễn Thanh Tú

Đơn vị tài trợ / phát hành / chia sẻ học thuật :

Nguyen Thanh Tu Group

Hỗ trợ trực tuyến

Fb www.facebook.com/DayKemQuyNhon

Mobi/Zalo 0905779594

SỞGIÁODỤCVÀĐÀOTẠOQUẢNGNGÃI

TRƯỜNGTHPTCHUYÊNLÊKHIẾT

ĐỀTHITHỬTỐTNGHIỆPTHPT–NĂMHỌC2022–2023–LẦN1

Câu1: Tiệmcậnđứngcủađồthịhàmsố 21 31 x y x   làđườngthẳngcóphươngtrình

Câu2: Trongkhônggian ,Oxyz đườngthẳng 123 : 212 dxyz

Câu3: Đạohàmcủahàmsố cos yx  trên  là

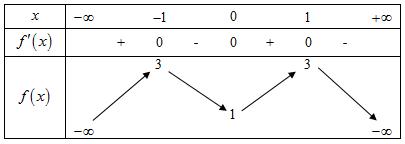
Câu4: Chohàmsốcóbảngbiếnthiênnhưsau

Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây

Câu5: Chokhốilậpphươngcóthểtíchbằng 2.Cạnhcủakhốilậpphươngđãchobằng

A. 2. B. 8. C. 32. D. 1 8 .

Câu6: Trongkhônggian Oxyz,hìnhchiếucủađiểm (1;2;3)M lênmặtphẳng  Oxy làđiểm

A. (1;0;3)P B. (0;2;3)Q C. (1;2;0)N D. (1;2;3)M

Câu7: Chohàmsố 42 yaxbxc  cóđồthịlàđườngcongtronghìnhbêndưới.

Điểmcựctiểucủahàmsốđãcholà

A. 1y B. 1x C. 1x D. 0x

Câu8: Chomặtphẳng  P cắtmặtcầu  ; SOR theomộtđườngtròn.Gọi d làkhoảngcáchtừ O đến  P .Bánkính R củađườngtrònđượctínhtheocôngthứcnàosauđây?

A. RRd  B. RRd   C. 22RRd   D. 22RRd 

Câu9: Hàmsốnàodướiđâycóbảngbiếnthiênnhưhìnhbêndưới?

A. 8 B. 24 C. 6 D. 4

Câu14: Trên ,đạohàmcủahàmsố x y là.

A. 42 11 2 4 yxx  B. 4221yxx 

C. 335yxx  .

Câu10: Chocáchàmsố  , fxgx liêntụctrênđoạn  1;4 .Nếu 

thì  4 1 d fxgxx     bằng:

A.1 B. 6 C. 5 D. 1

Câu11: Chohàmsốbậcba yfx  cóđồthịlàđườngcongtronghìnhbêndưới.

Câu15: Trênmặtphẳngtọađộ,điểmbiểudiễnsốphức 23 zi  cótọađộlà.

A.  2;3 B.  3;2 C.  3;2 D.  2;3

Câu16: Chocấpsốcộng  n u với 132,6uu .Côngsaicủacấpsốcộngnàybằng

A. 4 B. 2 C. 3 D. 2

Câu17: Chohìnhtrụcóđườngkínhđáy 2r vàđộdàiđườngsinh l Diệntíchxungquanhcủahìnhtrụ đãchobằng

A. rl B. 2rl C. 21 3 rl D. 22 3 rl

Câu18: Môđuncủasốphức 23 zi  bằng

A. 13 B.13 C. 5 D. 5

Câu19: Chohàmsốcóđồthịnhưhìnhvẽsau

hàmsốđãcholà.

A.

Câu12: Trongkhônggian Oxyz,chomặtcầu 222 :24610 Sxyzxyz   .Bánkínhcủa  S là.

A. 13R B. 13R C. 14R

Câu13: Chokhốichóp . SABC cóđáylàtamgiácvuôngtại A, 2,4ABAC ; SA vuônggócvớiđáy và 3SA (thamkhảohìnhvẽ).

Sốgiaođiểmcủađồthịhàmsốđãchovớitrụchoànhlà

A. 2 B. 0 C. 3 D.1

Thểtíchkhốichópđãchobằng.

2 z

Câu20: Chosốphức 23 zi  Phầnảocủasốphức bằng

A. 6i B. 6 C. 12i D. 12

Câu21: Trongkhônggian Oxyz,điểmnàodướiđâythuộcmặtphẳng :3210Pxyz ?

A.  1;0;1B . B.  1;0;1D . C.  1;2;0C . D.  0;1;1A .

Câu22: Tậpnghiệmcủaphươngtrình 1 25 x  cóbaonhiêuphầntử?

A. 3. B. 2. C. 0. D.1.

Câu23: Tổngtấtcảcácnghiệmcủaphươngtrình 231 x x bằng

A. 3 B. 4 C. 8 D. 2

Câu24: Trênmặtphẳngtọađộ,biếttậphợpđiểmbiểudiễncácsốphức z thỏamãn 22zi làmột đườngtròntâm I ,bánkính R với

A. 2;1,2IR . B. 2;1,2IR . C. 2;1,2IR . D. 2;1,2IR .

Câu25: Chohàmsố yfx  liêntụctrên vàcóbảngxétdấucủa fx  nhưsau

Câu30: Trong không gian với hệ tọa độ Oxyz,cho hai điểm (1;1;1)M và (5;5;1)N . Mặt phẳng () OMN cóphươngtrìnhlà

A. 2350 xyz B. 2350 xyz

C. 230 xyz D. 250 xyz

Câu31: Tậpnghiệmcủabấtphươngtrình  log20 x là

Sốđiểmcựcđạicủahàmsốđãcholà

A. 2. B. 4. C.1. D. 3.

Câu26: Chohìnhchóp . SABC cóđáylàtamgiácđều,SA vuônggócvớiđáyvà 2 ABSA  (thamkhảo hìnhvẽ).

A. 

Câu32: Diệntíchhìnhphẳnggiớnhạnbởicác

Câu33: Cóbaonhiêusốtựnhiêncónămchữsốphânbiệt,trongđócómặtcảhaichữsố 2và 3? A. 2322 5847 .. AAAA . B. 23 58..3!CC . C. 2322 5847 .. CACA . D. 23 58 . AA .

Câu34: Trongkhônggian Oxyz,chođiểm  1;2;3A Khoảngcáchtừđiểm A đếntrục Ox bằng

A. 4. B. 13. C. 10. D. 5.

Câu35: Cho tập hợp  1;2;3;4;5A . Có bao nhiêu số tự nhiên có 3 chữ số phân biệt và các chữ số thuộc A

Gócgiữahaimặtphẳng  SBC và  ABC bằng

A. 060 B. 030 C. 090 D. 045

Câu27: Chohàmsố 2x fxx  Khẳngđịnhnàodướiđâyđúng

A. 2()d2ln2 x fxxxC  . B. 2()d2x fxxxC  .

C. 22 ()dln22 x fxxxC  D. 2 ()d2ln22 xxfxx C

Câu28: Chohàmsốbậcba yfx  cóđồthịlàđườngcongnhưhìnhbêndưới.

A. 60. B. 20. C.125. D. 30.

4fxdx

thì



A. 2. B. 4. C. 2. D. 8.

Câu37: Nếu 225 xx thìgiátrịcủbiểuthức 443 xxA là

A. 5. B. 25. C. 26. D. 26.

2 22 3 5 41 loglog50 27 xx xx  



?

A. 5. B. 0. C.1. D. 2.

Câu39: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 32228(11)22yxxmxm  cóhaiđiểmcựctrịnằmvềhaiphíacủatrụchoành?

A. 7 B. 5 C. 6 D. 4

Cóbaonhiêugiátrịnguyêncủathamsố mđểphươngtrình 2()fxm  cóbanghiệmthựcphân biệt?

A. 9. B. 5. C. 7. D. 3.

Câu29: Chohàmsố fx cóđạohàmliêntụctrên R Khẳngđịnhnàodướiđâyđúng?

A. ()d'() fxxfx  . B. '()d() fxxfx  .

C. ()d'() fxxfxC  D. '()d() fxxfxC 

3

3

Câu41: . Trong không gian Oxyz, cho hai đường thẳng 1 11 : 112 dxyz   , 2 1 : 121 dxyz 

Đườngthẳng d điquađiểm  5;3;5A cắt 1d , 2d tạihaiđiểm B và C Độdàiđoạnthẳng

BC bằng

A. 32 B. 19 C. 25 D. 23

Câu42: Cho hình chóp . SABC có đáy ABC là tam giác vuông cân tại B với 3ABa BC  , góc  90SABSCB  vàkhoảngcáchtừ A đếnmặtphẳng  SBC bằng 2a .Tínhdiệntíchmặt cầungoạitiếphìnhchóp . SABC.

A.

Câu43: Trêntậphợpsốphức,xétphươngtrình 2210zmz (m làthamsốthực).Cóbaonhiêugiá trịnguyêncủa m đểphươngtrìnhđãchocóhainghiệmphânbiệt 12 , zz thỏamãn 1233zz  ?

A. 3 B. 4 C. 2 D.1

Câu44: Cho Fx làmộtnguyênhàmcủahàmsố 11 fxxx  trên  vàthỏamãn 13F .

Tínhtổng  02FF 

A. 3 B. 2 C. 7 D. 5

Câu45: Chohìnhchóp SABCD cóđáylàhìnhvuôngcạnh a,cạnhbên SA vuônggócvớiđáy,đường thẳng SC tạovớimặtphẳng  SAB mộtgóc 30 Thểtíchcủakhốichóp SABCD

A. 32 3 a B. 32 2 a C. 32a D. 32 4

Câu46: Có bao nhiêu giá trị nguyên của tham số  10;10a

432 3421230 yxaxaxa  nghịchbiếntrênkhoảng ;2?

A.12 B.11 C.10 D.13

hàm số

CMk  thuộckhoảngnàodướidây?

A. (0,2;0,7). B. (1,2;1,7). C. (1,7;2,2). D. (0,7;1,2).

2 xy

xxyy

xfxxfx e  , x  và 02f .Tính  2f .

48: Cho các



bằng

x

3 2 Gọi C là điềm trên tia Ozthòa mãn

Lờigiải

ChọnC

Tacó: 33 32VaaV

Câu6: Trongkhônggian Oxyz,hìnhchiếucủađiểm (1;2;3)M lênmặtphẳng  Oxy làđiểm

A. (1;0;3)P B. (0;2;3)Q C. (1;2;0)N D. (1;2;3)M

Lờigiải

Câu1: Tiệmcậnđứngcủađồthị

Câu2: Trongkhônggian ,Oxyz đườngthẳng 123 : 212 dxyz  cómộtvectơchỉphươnglà

2;1;2u . B.  1;2;3u . C.  1;2;3u . D.  2;1;2u .

Lờigiải

ChọnA

Đườngthẳng 123 : 212 dxyz  cómộtvectơchỉphươnglà:  2;1;2u 

Câu3: Đạohàmcủahàmsố cos yx  trên  là

A. tan yx   . B. sin yx   . C. cot yx   . D. sin yx   .

Lờigiải

ChọnD

Tacó: cos yx  sin yx

Câu4: Chohàmsốcóbảngbiếnthiênnhưsau

Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây

A.  0;2 B.  ;3 C.  2; D.  4;5

Lờigiải

ChọnC

Hìnhchiếucủađiểm (1;2;3)M lênmặtphẳng  Oxy làđiểm (1;2;0)N

Câu7: Chohàmsố 42 yaxbxc  cóđồthịlàđườngcongtronghìnhbêndưới.

Điểmcựctiểucủahàmsốđãcholà A. 1y B. 1x C. 1x D. 0x Lờigiải

ChọnD

Điểmcựctiểucủahàmsốđãcholà 0x

Câu8: Chomặtphẳng  P cắtmặtcầu  ; SOR theomộtđườngtròn.Gọi d làkhoảngcáchtừ O

đến  P .Bánkính R củađườngtrònđượctínhtheocôngthứcnàosauđây?

A. RRd  . B. RRd   . C. 22RRd   . D. 22RRd  . Lờigiải

ChọnC

Tacó 22RRd  

Câu9: Hàmsốnàodướiđâycóbảngbiếnthiênnhưhìnhbêndưới?

ChọnD

Hàmsốđãchođồngbiếntrênkhoảng:  4;5

Câu5: Chokhốilậpphươngcóthểtíchbằng 2 Cạnhcủakhốilậpphươngđãchobằng

A. 42 11 2 4 yxx  . B. 4221yxx  .

C. 335yxx  . D. 3 1 x y x  .

ChọnA

Lờigiải

BảngbiếnthiênlàBBTcủahàmsốbậcbốn 42 yaxbxc  với 0a .Chọnđápán A.

Câu10: Chocáchàmsố  , fxgx liêntụctrênđoạn

Câu11: Chohàmsốbậcba yfx  cóđồthịlàđườngcongtronghìnhbêndưới.

Thểtíchkhốichópđãchobằng.

A. 8 B. 24 C. 6 D. 4 Lờigiải

ChọnD

Thểtíchkhốichóplà 1124 34 332 ABC VSSA  

Câu14: Trên ,đạohàmcủahàmsố x y là.

Điểmcựcđạicủađồthị

hàmsốđãcholà.

hàmsốđãcholà  0;3M

Câu12: Trongkhônggian Oxyz,chomặtcầu 222 :24610 Sxyzxyz   .Bánkínhcủa  S là.

A. 13R . B. 13R . C. 14R . D. 14R .

Lờigiải

ChọnA

Bánkínhcủa  S là 222 123113R

Câu13: Chokhốichóp SABC cóđáylàtamgiácvuôngtại A, 2,4ABAC ; SA vuônggócvớiđáy và 3SA (thamkhảohìnhvẽ).

ChọnA

x y lnx y

Câu15: Trênmặtphẳngtọađộ,điểmbiểudiễnsốphức 23 zi  cótọađộlà.

A.  2;3 . B.  3;2 . C.  3;2 . D.  2;3

Lờigiải

ChọnD

Điểmbiểudiễnsốphức 23 zi  là  2;3

Câu16: Chocấpsốcộng  n u với 132,6uu .Côngsaicủacấpsốcộngnàybằng

A. 4 B. 2 C. 3 D. 2

Lờigiải

ChọnB

Gọi d làcôngsaicủacấpsốcộngđãcho.Khiđó 3122uudd

Câu17: Chohìnhtrụcóđườngkínhđáy 2r vàđộdàiđườngsinh l.Diệntíchxungquanhcủahìnhtrụ đãchobằng

A. rl B. 2rl C. 21 3 rl D. 22 3 rl

Lờigiải

ChọnB

Diệntíchxungquanhcủahìnhtrụđãcholà 2 Srl 

Câu18: Môđuncủasốphức 23 zi  bằng

A. 13. B.13. C. 5. D. 5.

Lờigiải

Lờigiải

ChọnA

Môđuncủasốphức 23 zi  là 4913z .

Câu19: Chohàmsốcóđồthịnhưhìnhvẽsau

Sốgiaođiểmcủađồthịhàmsốđãchovớitrụchoànhlà

A. 2 B. 0 C. 3 D.1

Lờigiải

ChọnC

Đồthịhàmsốđãchocắttrụchoànhtại 3 điểm.

Câu20: Chosốphức 23 zi  .Phầnảocủasốphức bằng

A. 6i B. 6 C. 12i D. 12

Lờigiải

ChọnD

Tacó  222234129512 ziiii  Vậyphầnảocủasốphức bằng 12

Câu21: Trongkhônggian Oxyz,điểmnàodướiđâythuộcmặtphẳng :3210Pxyz ?

A.  1;0;1B .

ChọnA

Tacóđiểmthuộcmặtphẳnglà  1;0;1B

Lờigiải

Câu22: Tậpnghiệmcủaphươngtrình 1 25 x  cóbaonhiêuphầntử?

A. 3. B. 2. C. 0. D.1.

Lờigiải

ChọnD

Tacó 2 11log525 x x 

Vậyphươngtrìnhcónghiệm 2 1log5x .

Câu23: Tổngtấtcảcácnghiệmcủaphươngtrình 231 x x bằng

ChọnB

Tacó 2312310 x x xx 

Xét   2312ln23 x xfxxfx   và 2 2ln20 xfx  với

Khiđó 0fx cótốiđahainghiệm.

Mặtkhác:  130ff

Vậyphươngtrìnhcóhainghiệm 1,3xx ,khiđótổngcácnghiệmbằng 4

Câu24: Trênmặtphẳngtọađộ,biếttậphợpđiểmbiểudiễncácsốphức z thỏamãn 22zi làmột

đườngtròntâm I ,bánkính R với

A. 2;1,2IR . B. 2;1,2IR . C. 2;1,2IR . D. 2;1,2IR . Lờigiải

ChọnD

Gọi  2 ,,1zxyixyi  

Khiđó  22 22212214 zixyixy  . Vậytậphợpđiểmbiểudiễncácsốphức z làmộtđườngtròntâm  2;1I ,bánkính 2R

Câu25: Chohàmsố yfx  liêntụctrên vàcóbảngxétdấucủa fx  nhưsau

Sốđiểmcựcđạicủahàmsốđãcholà A. 2 B. 4 C.1 D. 3 Lờigiải

ChọnC

Nhậnxét fx  đổidấutừdươngsangâmqua 1x .

Vậyhàmsốđãchocómộtđiểmcựcđại.

Câu26: Chohìnhchóp SABC cóđáylàtamgiácđều,SA vuônggócvớiđáyvà 2 ABSA  (thamkhảo hìnhvẽ).

Gócgiữahaimặtphẳng  SBC và  ABC bằng

ChọnB

S

Lờigiải

M C B

Gọi M làtrungđiểm BC

ABC đềunên AMBC  và.

Tacó SAABCHìnhchiếucủa SM trênmặtphẳng  ABC là AM .

Suyra SMBC  (theođịnhlíbađườngvuônggóc).

Có

, ,

và AM ,haylàgóc  SMA

.Dođógócgiữamặtphẳng  SBC và  ABC làgócgiữa SM

Xéttamgiác SAM vuôngtại A có 3 2 AB AM

Câu27: Chohàmsố 2x fxx  .Khẳngđịnhnàodướiđâyđúng

A. 2()d2ln2 x fxxxC 

C. 22 ()dln22 x fxxxC 

ChọnC



B. 2()d2x fxxxC 

. D. 2 ()d2ln22 xxfxx C

x xxxxC

Cóbaonhiêugiátrịnguyêncủathamsố mđểphươngtrình 2()fxm  cóbanghiệmthựcphân biệt?

A. 9 B. 5 C. 7 D. 3

Lờigiải

ChọnC

Xétphươngtrình: 2()()2mfxmfx .

Sốnghiệmcủaphươngtrìnhlàsốgiaođiểmcủađồthịhàmsố ()yfx  vàđườngthẳng 2 m y .

Dựavàođồthịtacóđiềukiệnđểphươngtrìnhcóbanghiệmphânbiệtlà:

3162 2 m m   ;5;4;3;2;1;0;1mm 

Có7giátrịnguyêncủamthỏamãnđiềukiện.

Câu29: Chohàmsố fx cóđạohàmliêntụctrên R.Khẳngđịnhnàodướiđâyđúng?

A. ()d'() fxxfx  B. '()d() fxxfx 

C. ()d'() fxxfxC  D. '()d() fxxfxC  Lờigiải

ChọnD

'()d() fxxfxC 

Câu30: Trong không gian với hệ tọa độ Oxyz,cho hai điểm (1;1;1)M và (5;5;1)N . Mặt phẳng () OMN cóphươngtrìnhlà

A. 2350 xyz B. 2350 xyz C. 230 xyz D. 250 xyz Lờigiải

ChọnA





, (5;5;1)ON

,vectơpháptuyếncủa () OMN : ;(4;6;10)2(2;3;5)nOMON

Câu31: Tậpnghiệmcủabấtphươngtrình  log20 x là

A.  3; B.  12; C.  2;3 D.  ;3

Câu33: Cóbaonhiêusốtựnhiêncónămchữsốphânbiệt,trongđócómặtcảhaichữsố 2và 3?

ChọnA

Gọisốtựnhiêncónămchữsốphânbiệtlà  abcdeabcde  .

+Trườnghợp1: atùyý

Xếphaichữsố 2và 3vào5vịtrí ,,,, abcde có 2 5A cách.

Xếpcácchữsốkhácchữsố 2và 3vào3vịtrícònlạicó 3 8A cách.

+Trườnghợp2: 0a .

Xếphaichữsố 2và 3vào 4 vịtrí ,,, bcde có 2 4A cách.

Xếpcácchữsốkhácchữsố 2; 3 và 0 vào 2 vịtrícònlạicó 2 7A cách.

Vậysốcácsốthỏayêucầuđềbàilà 2322 5847 AAAA số.

Câu34: Trongkhônggian Oxyz,chođiểm  1;2;3A .Khoảngcách

từđiểm A đếntrục Ox bằng

A. 4 B. 13 C. 10 D. 5

Lờigiải

ChọnB

Trục Ox cóVTCP  1;0;0i

 1;2;3OA

,0;3;2OAi  

OAi dAOx i 

  22,32 , 13 1

Câu35: Cho tập hợp  1;2;3;4;5A . Có bao nhiêu số tự nhiên có 3 chữ số phân biệt và các chữ số thuộc A

A. 60 B. 20 C.125 D. 30

Lờigiải

ChọnA

Gọisốtựnhiêncó 3 chữsốphânbiệtlà  abcabc 

Lấy3sốtừtậphợp A có5sốxếpvào3vịtrí ,, abc thìtalậpđược 3 560A sốthỏayêucầu đềbài.

Câu36: Chohàmsố fx liêntụctrên .Nếu  2 0

4fxdx thì  1 0

2 fxdx bằng.

A. 2. B. 4. C. 2. D. 8. Lờigiải

ChọnA

Tacó  1 0

2 Ifxdx  ,đặt 22 2 dttxdtdxdx 

1 2 2 Iftdt

.

Câu37: Nếu 225 xx thìgiátrịcủbiểuthức 443 xxA là

A. 5 B. 25 C. 26 D. 26

Lờigiải

ChọnD

Tacó 2 2244225442344326 xxxx xx xx  .



. Hàm số luôn đồng biến trên  0; .

Mặt khác từ bất phương trình suy ra  2 2 2242001 ftftxxxxx  .

Do  0;1xx  nên có 2 giá trị của x thỏa mãn.

Câu39: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 32228(11)22yxxmxm  cóhaiđiểmcựctrịnằmvềhaiphíacủatrụchoành?

A. 7 B. 5 C. 6 D. 4

Lờigiải

ChọnB

Đểđồthịhàmsốcóhaiđiểmcựctrịnằmvềhaiphíatrụchoànhthìphươngtrình 32228(11)220xxmxm cóbanghiệmphânbiệt.

22 22 3222 2 2610 610 8(11)220 x xxxm xxm xxmxm

Khiđóphươngtrình 22610xxm cóhainghiệmphânbiệtkhác2

  

Câu

Kẻ // HMBCHMAB  mà



Câu41: . Trong không gian Oxyz, cho hai đường thẳng 1 11 : 112 dxyz   , 2 1 : 121 dxyz  .

Đườngthẳng d điquađiểm  5;3;5A cắt 1d , 2d tạihaiđiểm B và C.Độdàiđoạnthẳng

BC bằng

A. 32 B. 19 C. 25 D. 23

Lờigiải

ChọnB

4554

224242

2552551

   1

Lờigiải

ChọnD

Gọi I làtrungđiểm SB

Tacó:+ ISIAIB  ( SAB vuôngtại A)

+ ISICIB  ( SCB vuôngtại C)

ISIBIAICR I làtâmmặtcầungoạitiếphìnhchóp . SABC.

Gọi E làtrungđiểm AC,mà ABC vuôngtại B

Nên IE làtrụcđườngtrònngoạitiếp ABC

xétphươngtrình 2210zmz (m làthamsốthực).Cóbaonhiêugiá trịnguyêncủa m đểphươngtrìnhđãchocóhainghiệmphânbiệt 12 , zz thỏamãn 1233zz  ?

A. 3 B. 4 C. 2 D.1 Lời giải

ChọnC

Xétphươngtrình  1 : 2210zmz

Đểphươngtrình  1 cóhainghiệmphânbiệtthìcó2trườnghợp: TH1:Hainghiệm 12 , zz 2 01011 mmm

263 mm  .Sođiềukiện,nhận 3m .

TH2:Hainghiệm 12,\zz011 m

Khiđó:  2222 12 3 333 zzabab      (luônđúng).

Vì m nguyênnênnhận 0m .

Vậycó2giátrịnguyêncủa m thoảđề.

Câu44: Cho Fx làmộtnguyênhàmcủahàmsố 11 fxxx  trên  vàthỏamãn 13F

Tínhtổng  02FF 

A.

Câu45: Chohìnhchóp . SABCD cóđáylàhìnhvuôngcạnh a,cạnhbên SA vuônggóc

Có      ,,30

BCAB BCSABSCSABSCSBBSC BCSA     

BCa SB a  

Xét SBC vuôngtại B 3 tan303 3

Suyra 222SASBABa   . Vậy

Câu46: Có bao nhiêu giá trị nguyên của tham số  10;10a để hàm số

432 3421230 yxaxaxa  nghịchbiếntrênkhoảng ;2?

12 B.11 C.10 D.13

432 3421230 hxxaxaxa 

32 1212224 hxxaxax

0,;2220

có13 giátrịnguyên a thỏabàitoán.

Câu48: Cho các số phức u, v, w

ChọnD Gọi M , N , P lầnlượtlàđiểmbiểudiễncácsốphức u, v, w trên

Tacó 422ui nên M thuộc  1C có 14;2I , 12R .

Đặt vxyi  ,khiđó  312131312121 vivixyixyi 

 2222 31312121 xyxy 22220xyxy 

Khiđó, N thuộc  2C có 21;1I , 22R

Tacó 2222 wwiwwi  ,khiđó P thuộcđườngtrungtrực d củađoạnthẳng AB với  0;0A ,  2;2B:20dxy 

Do  1C và  2C nằmvềhaiphíacủa d nên SuwvwMPNPMN  .

Đẳngthứcxảyrakhi P làgiaođiểmcủa 12II và d

Tacó  12 15 :15;13 13 xt II Ptt yt    .Thaytọađộđiểm P vào d tacóđược

131315 151320; 222222 tttPwiw 



   

Câu49: Trongkhônggian Oxyz,chođiểm (0;0;3)A vàđiểm B thayđồithuộcmặtphẳng () Oxy sao cho diện tích tam giác OAB bằng 3 2 Gọi C là điềm trên tia Ozthòa mãn

[,][,] dCABdCOBk  . Thể tích của khối tròn xoay tạo bời tập hợp tất cả các điểm M mà CMk  thuộckhoảngnàodướidây?

A. (0,2;0,7). B. (1,2;1,7). C. (1,7;2,2). D. (0,7;1,2).

Lờigiải ChọnD

Tamgiác OABvuôngtại 13 1 22 OOBOAOBB  nằmtrênđườngtròntâm  0;0O , bánkính 1r Tacó  0tan360 OA OBAOBA OB 

Theobàira [,][,] dCABdCOBkCtiaOz  vànằmtrêntiaphângiáctrongcủa  OBAC 

làchânđườngphângiáctrongcủagóc   0 1 30. 23 OBA BOBC OCk 

Tập hợp các điểm M là khối cầu tâm ,C bán kính 1 3 RThể tích khối cầu là 3 3 4414 0.806. 33393 VR 

Câu50: Cóbaonhiêucặpsốnguyêndương (;) xy thỏamãn

SỞGIÁODỤCVÀĐÀOTẠOTỈNHĐẮKNÔNG

ĐỀTHITHỬTNTHPT-NĂMHỌC:2022-2023

Câu1: Chohàmsốbậcba ()yfx = cóđồthịnhưhìnhvẽbên.Sốnghiệmcủaphươngtrình ()2fx=là

Câu10: Đạohàmcủahàmsố ()2x fxx =+ là

A. ()2 1 ln2

x fx ¢=+ B. ()2ln21 xfx ¢=+ C. () 22 ln22

x fx x ¢=+ D. ()21 xfx ¢=+

Câu11: Tậphợpcácđiểmbiểudiễnsốphức zxyi =+ với , xyÎ thỏamãn 4zi-= làđườngtròn cóphươngtrình

A. () 2214xy+-= B. () 22116xy+-=

C. ()22 14xy-+= . D. ()22 116xy-+= .

Câu12: Trong không gian ,Oxyz cho mặt cầu ()()()() 222 :2119Sxyz-+-++= và điểm () 4;2;2M- Mệnhđềnàosauđâylàđúng?

A. 0. B. 2. C. 3. D.1.

Câu2: Điểm M tronghìnhvẽbênlàđiểmbiểudiễncủasốphứcnào?

A.Điểm M làtâmcủamặtcầu () S . B.Điểm M nằmtrênmặtcầu () S .

C.Điểm M nằmtrongmặtcầu () S D.Điểm M lànằmngoàimặtcầu () S

Câu13: Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhvẽsauđây

A. 12 zi =+ B. 2 zi =-+ C. 2 zi =+ D. 12 zi =-

Câu3: Khốinóncóbánkínhđáybằng r,chiềucaobằng h Thểtíchkhốinónbằng

A. 21 3 rhp B. 2 rhp C. 2rhp D. rhp

Câu4: Nếu () 3 1 d2fxx=ò thì () 3 1 2d fxxx éù ë+ûò bằng

A.12 B.18 C.10 D. 20

Câu5: Chocấpsốnhân () n u có 13u=- ,côngbội 2q= .Khẳngđịnhnàosauđâyđúng?

A. 13.2n n u=- B. 13.2n n u= C. 3.2n n u= D. 3.2n n u=-

Câu6: Trong không gian Oxyz, chomặtphẳng ():2320Pxyz+++= . Vectơ nàodưới đâylàmột vectơpháptuyếncủa () P ?

A. ()32;3;2n  = B. ()22;3;1n  = C. ()12;3;0n  = D. ()42;0;3n  =

Câu7: Chohìnhphẳng () H giớihạnbởiđồthịhàmsố 2 21yxx=-- vàtrụchoành.Thểtíchcủavật thểtrònxoaykhiquay () H quanhtrụchoànhbằng

A. 9 8 p . B. 81 80 . C. 9 8 . D. 81 80 p .

Câu8: Chomặtcầu ()222 :24230 Sxyzxyz++-++-= .Tínhbánkính R củamặtcầu () S

A. 9R= B. 3R= C. 3R= D. 33R=

Câu9: Chohìnhchóp SABC cóđáy ABC làtamgiácđềucạnh a và ()SAABC ^ và 3SAa = Thể tíchkhốichóp SABC bằng

A. 33 4 a B. 4 a C. 3 2 a D. 3

A. 331yxx=-++ B. 4231yxx=--+ C. 33 yxx =-+ D. 4231yxx=-++

Câu14: Chohàmsốbậcbốn ()yfx = cóđồthịhàmsố ()yfx ¢ = làđườngcongtronghìnhvẽ,hàm số ()yfx = đãchođồngbiếntrênkhoảngnàodướiđây?

A. () 4;0- B. () ;1-¥- C. () 2;+¥ D. () 0;2

Câu15: Trongkhônggian ,Oxyz mặtphẳngnàodướiđâysongsongvớimặtphẳng () Oxy ?

A. ():10 z a+= B. ():10 x j+= C. ():10 xz b++= D. ():10 y g+=

Câu16: Chophươngtrình 1 4230 xx+ +-= .Khiđặt 2xt= tađượcphươngtrìnhnàosauđây?

A. 2230tt+-= B. 2 230 tt-= C. 230tt+-= D. 430 t-=

Câu17: Mộthộpcó 6 quảbóngđỏđượcđánhsốtừ 1 đến 6.Lấyngẫunhiên 3 quảbóng.Xácsuấtđể tíchcácsốtrên 3 quảbónglấyralàmộtsốchẵnbằng

A. 1 20 . B. 1 10 . C. 19 20 . D. 9 10 .

Câu18: Tiệmcậnngangcủađồthịhàmsố 2 1 x y x

= + là

A. 1x=- B. 2y=- C. 2x= D. 1y=

Câu19: Chohàmsố ()yfx = liêntụctrêntoàn  vàcóđồthịnhưhìnhvẽ.Điểmcựcđạicủađồthị

hàmsốlàđiểmnàosauđây

Câu20: Trongkhônggian Oxyz,đườngthẳng 123 : 212 dxyz--==điquađiểmnàodướiđây?

A. () 1;2;3M--- B. () 2;1;2Q- C. () 2;1;2N-- D. () 1;2;3P

Câu21: Tậpnghiệmcủabấtphươngtrình ()2 log11 x+< là

A. () ;1-¥ . B. () 1;2. C. () 1;1. D. () 1; -+¥ .

Câu22: Trênmặtphẳngtọađộ,cho () 2;3M làđiểmbiểudiễncủasốphức z.Phầnthựccủa z bằng

A. 3. B. 3. C. 2. D. 2.

Câu23: Hàmsố ()fx cómộtnguyênhàmlàhàmsố ()gx trênkhoảng K nếu

A. ()(), fxgxCxK =+"Î . B. ()(), gxfxCxK ¢=+"Î .

C. ()(), gxfxCxK =+"Î D. ()(), fxgxCxK ¢=+"Î

Câu24: Trênkhoảng () 0;+¥ ,đạohàmcủahàmsố 2log yx = là

A. 1 y x ¢ = . B. ln2 y x ¢ = . C. 1 2y x ¢ = . D. 1 ln2y x ¢ = .

Câu25: Thểtíchcủakhốihộpchữnhậtcóđộdàicáccạnhlà ,3,5 aaa bằng

A.15a B. 215a C.15 D. 315a

Câu26: Chohàmsố ()yfx = cóđồthịnhưhìnhvẽsau:

Giátrịcựcđạicủahàmsốbằng

A. 2. B. 1. C. 0. D.1.

Câu27: Tậpnghiệmcủabấtphươngtrình 2 34 x< là

A. () ;2-¥ B. () 2;+¥ C. () 3 ;log2-¥ D. () 3 ;log4-¥

Câu28: TrongHọtấtcảcácnguyênhàmcủahàmsố ()sin4 fxxx =- là

A. 2cos2xxC--+ . B. 2cos2xxC -+ . C. 2 cosxxC--+ . D. 2cos4xxC -+ .

Câu29: Cóbaonhiêusốcó 5 chữsốkhácnhauđượctạothànhtừcácchữsố1,2,3,4,5,6

A. 5P B. 5 6C C. 5 6A D. 6P

Câu30: Chohaisốphức 14 zi =, 212 zi =.Sốphứcliênhợpcủasốphức 1 2

z z là

A. 67 55 i+ B. 67 55 i- C. 43i+ D. 67 1717 i-

Câu31: Cho hàm số bậc ba ()fx có đồ thị như hình vẽ. Số giá trị nguyên của tham số m đề phương trình ()1 fxm += có 3 nghiệmphânbiệtlà

A. 2 B. 3 C. 5

Câu32: Hàmsố ()yfx = liêntụctrên  vàcóđạohàm ()()() 2 11fxxxx ¢ =-- .Hàmsố ()yfx = nghịchbiếntrênkhoảng

A. () 2;1-- B. () 0;1 C. () 1;0- D. () 1;2

Câu33: Cho hình chóp SABC có SA vuông góc với mặt phẳng () ABC , biết 3 2 Sa A= và tam giác ABC đềucạnhbằng a.Góctạobởigiữamặtphẳng () SBC và () ABC bằng

A. 45° B. 90° C. 60° D. 30°

Câu34: Biết 

d4fxx

và 

d1gxx

.Khiđó 

d fxgxx

bằng

A. 5

4

3

3-

Câu35: Chohaisốthực , ab tuỳýkhác 0 thoảmãn 34ab = .Giátrịcủa a b bằng

A. ln0,75. B. 3 log4. C. 4 log3. D. ln12.

Câu36: Xét số phức z thoả mãn 222zi--= . Giá trị nhỏ nhất của biểu thức

152 Pzizi =--+-- bằng

A. 17 B.110 + C. 5 D. 4

Câu37: Trongcácnghiệm () ; xy thỏamãnbấtphươngtrình ()22 2 log21 xyxy++³ .Giátrịlớnnhấtcủa biểuthức 2 Txy =+ bằng

A. 9 B. 9 4 C. 9 8 D. 9 2

Biết ()() 0,1;fxx>"Î+¥ , diện tích S của hình phẳng giới hạn bởi đồ thị (),0, yxfxyxe === và 2 xe = là

A. 5 3 S= B. 1 2 S= C. 2S= D. 3 2 S=

Câu45: Trongkhônggian Oxyz,đườngthẳngđiquahaiđiểm () 1;2;1A- và () 2;1;1B- cóphươngtrình thamsốlà

xt yt zt

-ò bằng

Câu38: Chohàmsố ()fx liêntụctrên .Gọi ()() , FxGx làhainguyênhàmcủa ()fx trên  thỏa mãn ()() 888FG+= và ()() 002FG+=- .Khiđó () 0 2

4d fxx -

A. 5 4 B. 5 C. 5- D. 5 4 -

Câu39: Trong không gian Oxyz cho điểm () 2;1;2A-- và đường thẳng ()111 : 111 dxyz--==Gọi () P làmặtphẳngđiquađiểm A,songsongvớiđườngthẳng () d vàkhoảngcáchtừ () d tới () P làlớnnhất.Khiđómặtphẳng () P vuônggócvớimặtphẳngnàosauđây?

A. 32100xyz+++= B. 320 xz++= C. 2310xyz---= D. 60xy--=

Câu40: Trên tập hợp số phức, xét phương trình 228120zmzm-+-= (m là số thực). Có bao nhiêu giátrịcủa m đểphươngtrìnhđócóhainghiệmphânbiệt 12 , zz thỏamãn 124?zz+=

A.1 B. 4 C. 3 D. 2

Câu41: Chokhốilăngtrụđều ABCABC¢¢¢ cócạnhđáybằng 2a Biếtkhoảngcáchtừđiểm A¢ đếnmặt phẳng () ABC¢¢ bằng a.Thểtíchcủakhốilăngtrụđãcholà

A. 332 6 a B. 332 8 a C. 332 2 a D. 32 2 a

Câu42: Trongkhônggianvớihệtrụctọađộ Oxyz,chobađiểm (2;5;0),(4;7;0)BC và (1;1;3)K Gọi() Q làmặtphẳngđiqua K vàvuônggócvớimặtphẳng () Oxy .Khi 2(;())(;()) dBQdCQ + đạtgiá trịlớnnhất,giaotuyếncủa () Oxy và () Q điquađiểmnàosauđây?

A. (8;4;0)P- B. (15;4;0)N- C. 7 15;;0 2 S æö ç÷ ç÷ ç÷ èø D. (3;2;0)M

Câu43: Chohìnhnón() N cóđỉnh S,chiềucao 3h= Mặtphẳng() P quađỉnh S cắthìnhnón() N theo thiếtdiệnlàtamgiácđều.Khoảngcáchtừtâmđáyhìnhnónđếnmặtphẳng () P bằng 6.Thể tíchkhốinóngiớihạnbởihìnhnón () N bằng

A.12p B. 81p C. 36p D. 27p

Câu44: Cho hàm số ()fx thỏa mãn: ()()()() 22 ln2,1;xfxxfxxfxx ¢ -+="Î+¥ và ()2 1 fe e =

ì ï=+ ï ï ï í=ï ï ï=-+ ï î 23 12

ì ï=+ ï ï ï í=ï ï ï=+ ï î

B. 1 xt yt zt

ì ï=+ ï ï ï í=-+ ï ï ï=ï î

xt yt zt

C. 1 32 2

D. 1 12 xt yt zt

ì ï=+ ï ï ï í=+ ï ï ï=ï î

Câu46: Sốgiátrịnguyêncủathamsố m đểhàmsố () 422 3 ymxmxm =--+ khôngcóđiểmcựcđạilà

B.

2. C.0. D.vôsố

Câu48: Cóbaonhiêugiátrịnguyêncủathamsố () 2022;2022mÎ- đểhàmsố ()3212yxmx =++đồngbiếntrênkhoảng ()1;3?

A. 4034. B. 4032. C. 4030. D. 2022.

Câu49: Trongkhônggianvớihệtọađộ Oxyz,điểmđốixứngcủa () 1;2;3M quatrục Ox cótọađộlà

A. () 1;2;3--. B. () 1;0;0 . C. () 1;2;3 -. D. () 0;2;3 .

Câu50: Chohìnhlăngtrụđứng ABCABC¢¢¢ cóđáy ABC làtamgiácđềucạnh a và 2 AAa ¢ = Gọi M làtrungđiểmcủa AA ¢ Khoảngcáchtừ M đếnmặtphẳng () ABC ¢ bằng

A. 257 19 a . B. 5 5 a . C. 25 5 a . D. 57 19 a . ----------HẾT----------

BẢNGĐÁPÁN

HƯỚNGDẪNGIẢICHITIẾT

Câu1: Chohàmsốbậcba ()yfx = cóđồthịnhưhìnhvẽbên.Sốnghiệmcủaphươngtrình ()2fx=-

Lờigiải

ChọnC () () 3 33 1 11 2dd2d2810fxxxfxxxx éù ë+=+=+=

Câu5: Chocấpsốnhân () n u có 13u=- ,côngbội 2q= Khẳngđịnhnàosauđâyđúng?

A. 132n n u=- B. 132n n u= C. 32n n u= D. 32n n u=-

Lờigiải

A. 0. B. 2. C. 3. D.1.

Lờigiải ChọnD

Câu2: Điểm M tronghìnhvẽbênlàđiểmbiểudiễncủasốphứcnào?

A. 12 zi =+ . B. 2 zi =-+ . C. 2 zi =+ . D. 12 zi =.

Lờigiải

ChọnB

Câu3: Khốinóncóbánkínhđáybằng r,chiềucaobằng h Thểtíchkhốinónbằng

A. 21 3 rhp B. 2 rhp C. 2rhp D. rhp

Lờigiải

ChọnA

Câu6: Trong không gian Oxyz, chomặtphẳng ():2320Pxyz+++= Vectơ nàodưới đâylàmột vectơpháptuyếncủa () P ?

A. ()32;3;2n  = B. ()22;3;1n  = C. ()12;3;0n  = D. ()42;0;3n  = Lờigiải

ChọnB

Câu7: Chohìnhphẳng () H giớihạnbởiđồthịhàmsố 2 21yxx=-- vàtrụchoành.Thểtíchcủavật thểtrònxoaykhiquay () H quanhtrụchoànhbằng

A. 9 8 p B. 81 80 C. 9 8 D. 81 80 p

Lờigiải

ChọnD

ChọnA

Câu4: Nếu () 3 1 d2fxx=ò thì () 3 1 2d fxxx éù

A.12. B.18. C.10. D. 20.

x xx x

é= ê --=Ûêê=ê ë

Phươngtrìnhhoànhđộgiaođiểm 2 1 2101 2

Thểtíchtrònxoaylà () 1 22 1 2

8121d 80 Vxxx -

p =p--= ò .

Câu8: Chomặtcầu ()222 :24230 Sxyzxyz++-++-= .Tínhbánkính R củamặtcầu () S

A. 9R= B. 3R= C. 3R= D. 33R=

Lờigiải

ChọnC

Tacó () ()222 1;2;112133IR--Þ=++--=

Câu9: Chohìnhchóp SABC cóđáy ABC làtamgiácđềucạnh a và ()SAABC ^ và 3SAa = Thể tíchkhốichóp SABC bằng

A. 33 4 a . B. 4 a . C. 3 2 a . D. 3 4 a .

Lờigiải

ChọnD

Thểtíchkhốichóp SABC là 23113 ...3 3344 ABC aaVSSAa == = .

Câu10: Đạohàmcủahàmsố ()2x fxx =+ là

A. ()2 1 ln2

x fx ¢=+ . B. ()2ln21 xfx ¢=+ . C. () 22 ln22

x fx x ¢=+ . D. ()21 xfx ¢=+ .

Lờigiải ChọnB

() () 22ln21 x xfxxfx ¢ =+Þ=+

Câu11: Tậphợpcácđiểmbiểudiễnsốphức zxyi =+ với , xyÎ thỏamãn 4zi-= làđườngtròn cóphươngtrình

A. () 2214xy+-= B. () 22116xy+-=

C. ()22 14xy-+= . D. ()22 116xy-+= .

Lờigiải ChọnB

()() 22 414116zixyixy -=Û+-=Û+-=

Câu12: Trong không gian ,Oxyz cho mặt cầu ()()()() 222 :2119Sxyz-+-++= và điểm

() 4;2;2M.Mệnhđềnàosauđâylàđúng?

A.Điểm M làtâmcủamặtcầu () S B.Điểm M nằmtrênmặtcầu () S

C.Điểm M nằmtrongmặtcầu () S . D.Điểm M lànằmngoàimặtcầu () S .

Lờigiải

ChọnC

()()()()() 222 :21192;1;1,3 SxyzIR -+-++=Þ-= .

Tacó () () 22 2 4;2;22116MIM R-Þ=++-=< .

Vậyđiểm M nằmtrongmặtcầu () S

Câu13: Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhvẽsauđây

Câu14: Chohàmsốbậcbốn ()yfx = cóđồthịhàmsố ()yfx ¢ = làđườngcongtronghìnhvẽ,hàm số ()yfx = đãchođồngbiếntrênkhoảngnàodướiđây?

ChọnA

Lờigiải

Đồthịhàmsốcódạngnhưtrênlàđồthịhàmsốbậc3vàđiquađiểm () 0;1 .Hàmsốcầntìmlà

331yxx=-++

A. () 4;0. B. () ;1-¥- . C. () 2;+¥ . D. () 0;2 . Lờigiải

ChọnB

Dựavàođồthịtacó ()() 0,;1fxx¢>"Î-¥- .Vậyhàmsố ()yfx = đồngbiếntrênkhoảng () ;1-¥-

Câu15: Trongkhônggian ,Oxyz mặtphẳngnàodướiđâysongsongvớimặtphẳng () Oxy ?

A. ():10 z a+= B. ():10 x j+= C. ():10 xz b++= D. ():10 y g+=

Lờigiải

ChọnA

Mặtphẳngsongsongvớimặtphẳng () Oxy là ():10 z a+=

Câu16: Chophươngtrình 1 4230 xx+ +-= .Khiđặt 2xt= tađượcphươngtrìnhnàosauđây?

A. 2230tt+-= B. 2 230 tt-= C. 230tt+-= D. 430 t-=

Lờigiải

ChọnA

Tacó: 1 423042230 xx xx + +-=Û+-= ,khiđóđặt 2xt= tađượcphươngtrình 2230tt+-=

Câu17: Mộthộpcó 6 quảbóngđỏđượcđánhsốtừ 1 đến 6.Lấyngẫunhiên 3 quảbóng.Xácsuấtđể tíchcácsốtrên 3 quảbónglấyralàmộtsốchẵnbằng

A. 1 20 B. 1 10 C. 19 20 D. 9 10 Lờigiải

ChọnC

Sốphầntửcủakhônggianmẫulà ()3 620nCW== .

Gọi A làbiếncố:“tíchcácsốtrên 3 quảbónglấyralàmộtsốchẵn”.

Tacóbiếncốđốicủa A là A:“tíchcácsốtrên 3 quảbónglấyralàmộtsốchẵn”tứclà“lấy được 3 quảbóngmangsốlẻ”.

Từđó ()1nA= .Suyra ()1 20 PA= .

Vậyxácsuấtcủabiếncố A là: ()()

PAPA=-=-= .

Câu18: Tiệmcậnngangcủađồthịhàmsố 2 1 x y x

= + là

A. 1x=- B. 2y=- C. 2x= D. 1y=

Lờigiải

ChọnD

Sốphức zcóđiểmbiểudiễnlà () 2;3M .

23 ziÞ=+

Suyraphầnthựccủa z bằng 2

Câu23: Hàmsố ()fx cómộtnguyênhàmlàhàmsố ()gx trênkhoảng K nếu

x y x®+¥®+¥

Tacó 2 limlim1 1xx

x y x®-¥®-¥

== + .

== + và 2 limlim1 1xx

Vậy 1y= làtiệmcậnngangcủađồthịhàmsố.

Câu19: Chohàmsố ()yfx = liêntụctrêntoàn  vàcóđồthịnhưhìnhvẽ.Điểmcựcđạicủađồthị

hàmsốlàđiểmnàosauđây

A.Điểm N B.Điểm Q C.Điểm P D.Điểm M

Lờigiải

ChọnD

Dựavàohìnhvẽtacó M là

điểmcựcđạicủađồthị

hàmsố

Câu20: Trongkhônggian Oxyz,đườngthẳng 123 : 212 dxyz--==điquađiểmnàodướiđây?

A. () 1;2;3M--- B. () 2;1;2Q. C. () 2;1;2N-. D. () 1;2;3P .

Lờigiải ChọnD

Tacóđườngthẳng d điquađiểm () 1;2;3P

Câu21: Tậpnghiệmcủabấtphươngtrình ()2 log11 x+< là

A. () ;1-¥ B. () 1;2- C. () 1;1- D. () 1; -+¥

A. ()(), fxgxCxK =+"Î . B. ()(), gxfxCxK ¢=+"Î .

C. ()(), gxfxCxK =+"Î D. ()(), fxgxCxK ¢=+"Î

Lờigiải

ChọnB

Hàmsố ()fx cómộtnguyênhàmlàhàmsố ()gx trênkhoảng K nếu ()(), gxfxCxK ¢=+"Î

Câu24: Trênkhoảng () 0;+¥ ,đạohàmcủahàmsố 2log yx = là

A. 1 y x ¢ = B. ln2 y x ¢ = C. 1 2y x ¢ = D. 1 ln2y x ¢ =

Lờigiải

ChọnD () 2 1 logln2yx x ¢¢ == .

Câu25: Thểtíchcủakhốihộpchữnhậtcóđộdàicáccạnhlà ,3,5 aaa bằng

A.15a B. 215a C.15 D. 315a

Lờigiải

ChọnD

Tacó 3.3.515 Vaaaa == .

Câu26: Chohàmsố ()yfx = cóđồthịnhưhìnhvẽsau:

ì+ì ï>>ï ï ï +<ÛÛÛ-<< í í ï+ï ï<< ï î î .

Lờigiải ChọnC ()2 101 log11 11 121 xx x x xx

Câu22: Trênmặtphẳngtọađộ,cho () 2;3M làđiểmbiểudiễncủasốphức z Phầnthựccủa z bằng

A. 3. B. 3. C. 2. D. 2.

Lờigiải

ChọnC

Giátrịcựcđạicủahàmsốbằng

A. 2 B. 1- C. 0 D.1

Lờigiải

ChọnA

Tacógiátrịcựcđạicủahàmsốbằng 2

Câu27: Tậpnghiệmcủabấtphươngtrình 2 34 x< là

A. () ;2-¥ . B. () 2;+¥ . C. () 3 ;log2-¥ . D. () 3 ;log4-¥ .

Lờigiải

ChọnC

Tacó 2 33 342log4log2 x xx <Û<Û<

Vậytậpnghiệmcủabấtphươngtrìnhlà () 3 ;log2-¥

Câu28: TrongHọtấtcảcácnguyênhàmcủahàmsố ()sin4 fxxx =- là

A. 2cos2xxC--+ B. 2cos2xxC -+ C. 2 cosxxC--+ D. 2cos4xxC -+

Lờigiải

Lờigiải

ChọnA

Tacó ()() 2dsin4dcos2 fxxxxxxxC =-=--+

Câu29: Cóbaonhiêusốcó 5 chữsốkhácnhauđượctạothànhtừcácchữsố1,2,3,4,5,6.

A. 5P . B. 5 6C . C. 5 6A . D. 6P .

Lờigiải

ChọnC

Sốcó 5 chữsốkhácnhauđượctạothànhtừcácchữsố1,2,3,4,5,6 là 5 6A .

Câu30: Chohaisốphức 14 zi =, 212 zi =- Sốphứcliênhợpcủasốphức 1 2

z z là

A. 67 55 i+ . B. 67 55 i. C. 43i+ . D. 67 1717 i.

Lờigiải

ChọnA

Tacó 1 2

467 1255 zi i zi==+.

Câu31: Cho hàm số bậc ba ()fx có đồ thị như hình vẽ. Số giá trị nguyên của tham số m đề phương

trình ()1 fxm += có 3 nghiệmphânbiệtlà

A. 2 B. 3 C. 5 D. 4

Lờigiải

ChọnB

Tacó ()()() 11*fxmfxm +=Û=- .Đựavàođồthịphươngtrình () * cóbanghiệmphân biệtkhivàchỉkhi 11304 mm -<-<Û<< ,mà mÎ{} 1;2;3m ÞÎ

Câu32: Hàmsố ()yfx = liêntụctrên  vàcóđạohàm ()()() 2 11fxxxx ¢ =-- .Hàmsố ()yfx = nghịchbiếntrênkhoảng

A. () 2;1-. B. () 0;1 . C. () 1;0. D. () 1;2 .

ChọnC

Tacó ()()() 2 0 110 1 x fxxxx x

é= ê ¢=--=Ûê=± ë .Khiđótacóbảngbiếnthiên

Dựavàobảngbiếnthiênhàmsốnghịchbiếntrênkhoảng () 1;0-

Câu33: Cho hình chóp . SABC có SA vuông góc với mặt phẳng () ABC , biết 3 2 Sa A= và tam giác

ABC đềucạnhbằng a.Góctạobởigiữamặtphẳng () SBC và () ABC bằng

A. 45° B. 90° C. 60° D. 30°

Lờigiải

ChọnA

Gọi I làtrungđiểmcủa BC.Vìtamgiác ABC đềunên AIBC ^ ,lạicó BCSA ^ nên BCSI ^ .Dođógócgiữahaimặtphẳng () SBC và () ABC làgóc  SIA.

Xéttamgiác SAI vuôngtại A có 3 2 Sa A= và 3 2 Aa I=

Dođó  tan145 SA SIASIA AI ==Þ=°

Câu34: Biết () 3 2

d4fxx=ò và () 3 2

d1gxx=ò .Khiđó ()() 3 2

d fxgxxé ë-ù û ò bằng

A. 5. B. 4. C. 3. D. 3.

Lờigiải

ChọnC

3 33

Tacó, ()()()()

ddd413fxgxxfxxgxxé ë-ù=-=-= û ò òò .

2 22

Câu35: Chohaisốthực , ab tuỳýkhác 0 thoảmãn 34ab = .Giátrịcủa a b bằng

A. ln0,75 B. 3 log4 C. 4 log3 D. ln12

Lờigiải

ChọnB

Lấylogaritcơsố3haivếcủađẳngthức 34ab = tađược 3 log4ab = 3 log4a b Þ=

Câu36: Xét số phức z thoả mãn 222zi--= . Giá trị nhỏ nhất của biểu thức

152 Pzizi =--+-- bằng

A. 17. B.110 + . C. 5. D. 4.

Lờigiải

() 999991 max;2; 284222 T Txy æö ç÷ Þ£+=Þ=Û=÷ ç÷ ç èø

-ò bằng

ChọnA

Tậphợpcácđiểmbiểudiễnsốphứczlàđườngtròntâm () 2;2I bánkính 2R= Gọi () 1;1A và () 5;2B lầnlượtlàđiểmbiểudiễnsốphức1i+ và 52i+

Khiđóbiểuthức ()() 22 512117PMAMBAB =+³=-+-= .Dấubằngxảyrakhi M nằmgiữa A và B.(Hìnhvẽtrên)

Câu37: Trongcácnghiệm () ; xy thỏamãnbấtphươngtrình ()22 2 log21 xyxy++³ .Giátrịlớnnhấtcủa

A.

-

Đặt () 0 2

4d.Ifxx -

=ò Đặt 1 4 4 xtdxdt-=Þ=- Đổicận:

Khiđó: ()()() 088 800

111 dt=dt=d 444 Iftftfxx =-òòò

Do ()() , FxGx làhainguyênhàmcủa ()fx trên  nêncó:

()()()()()181 =80804. 404 IGxGGGGI =é-Þ-= ë Tươngtựcũngcó:

()() 804 FFI -= .

Suyra: ()()()()()5 888008210. 4 IFGFG I =+--=--=Þ= .

Câu39: Trong không gian Oxyz cho điểm () 2;1;2A-- và đường thẳng ()111 : 111 dxyz--== -

Gọi () P làmặtphẳngđiquađiểm A,songsongvớiđườngthẳng () d vàkhoảngcáchtừ () d tới () P làlớnnhất.Khiđómặtphẳng () P vuônggócvớimặtphẳngnàosauđây?

A. 32100xyz+++= .B. 320 xz++= . C. 2310xyz---= .D. 60xy--= . Lờigiải

ChọnB

TH1: () ; xy thỏamãn () I ,khiđó: 22 0221. Txyxy <=+£+< TH2: () ; xy thỏamãn () II :

Gọi () 1;1;1 Httt +-+ làhìnhchiếucủa A lênđườngthẳng d.Tacó:

() d có1véctơchỉphương () 1;1;1du  =, ( )1;2;3AHttt  =--+ .Khiđó:

 ^Þ=Û---++=Û=Û=Þ

()()() () .01.11.21.303001;1;1.d d AHuAHutttttH

Gọi K làhìnhchiếucủa Htrên () P .Tacó:

() ()() () ()() max d;d;dPHPHKAHHKAHAHPP ==£Þ=Û^Þ nhận () 1;2;3AH  =-

làmvéctơpháptuyến.

Giảsửmặtphẳng () Q có1véctơpháptuyến Qn  và  QP  .Suyra: Q nAH    phùhợpvới

phươngtrìnhmặtphẳng () Q là 320 xz++= .

Câu40: Trên tập hợp số phức, xét phương trình 228120zmzm-+-= (m là số thực). Có bao nhiêu

giátrịcủa m đểphươngtrìnhđócóhainghiệmphânbiệt 12 , zz thỏamãn 124?zz+=

A.1 B. 4 C. 3 D. 2

Lờigiải

ChọnD

Tacó: 2812mm D¢=-+

TH1: 026 m D¢<Û<< .

Phươngtrìnhcóhainghiệmphức 2 12 812zmimm=±-+-

Tacó 12zz = ,dođó 12142zzz+=Û= 22(812)481242(l)mmmmm Û+-+-=Û-=Û=

TH2: 2 0 6 m m é<D¢ê>Ûê> ë thìphươngtrìnhcóhainghiệmthựcphânbiệt 12 , zz 12 12

Tacó: ()2 12121212 +4+2216 zzzzzzzz=Û-+=

()2 42812281216 mmm Û--+-= 2 2 281241684642 mmmmmm Û-=-+-Û-=-+-

mmm mmm mm Ûïê-=-+

ìé ï-=-+ïê ï

íê ïë ï ï ï-+-³ î 2 2 2

4642 4642 420

ì ì é é ï=± ï= ï ï ê ê ï = ï ï ï ê Ûê Û Û =±í-+=í ê ë ïë ï =- ï ï ï ï ï-+-³-££+ ï î î

m m m mmm m mm m

42 2 8422 80 422 4202222

Vậycó2giátrịthỏamãn.

2 .812 zzm zzm ì+=ï ï í ï=ï î

Gọi M làtrungđiểmcủa BC¢¢

Tacó AABC AMBC

좢¢ ï^ ï í ¢ ï^ î ()BCAAMÞ¢¢¢ ^ ()() ABCAAMÞ¢¢¢ ^

Trongmặtphẳng () AAM ¢ ,kẻ AHAM ¢^ ,suyra ()AHABC ¢¢¢ ^ .

Vậykhoảngcáchtừ A¢ đếnmặtphẳng () ABC¢¢ là AHa ¢ = . 3AMa =

Tacó 222 111 AHAAAM ¢=+¢¢ 2222 1112 3 AAAHAMa Þ=-= ¢¢¢ 6 2 Aa A Þ¢=

Vậythểtíchkhốilăngtrụlà 23 6332 .. 248ABC aaaVAAS¢ ¢ == = .

Câu42: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm (2;5;0),(4;7;0)BC và (1;1;3)K Gọi () Q làmặtphẳngđiqua K vàvuônggócvớimặtphẳng () Oxy .Khi 2(;())(;()) dBQdCQ + đạt giátrịlớnnhất,giaotuyếncủa () Oxy và () Q điquađiểmnàosauđây?

A. (8;4;0)P- B. (15;4;0)N- C. 7 15;;0 2 S æö ç÷ ç÷ ç÷ èø D. (3;2;0)M

Lờigiải

ChọnB

Gọi () ;; nabc  = làpháptuyếncủamặtphẳng () Q

Do () Q vuônggócvới () Oxy nên () ;;0nab  = ,mà () Q điqua K nên ():0Qaxbyab+--=

Trườnghợp1: B, C nằmcùngphíasovới () Q ,khiđó:

A. 332 6 a B. 332 8 a C. 332 2 a D. 32 2 a Lờigiải ChọnB

() ()() ()2222

2436 2,, abab dBQdCQ abab ++ +=+ ++

2222

2836514514 221 abababab abababab +++++=+=£ = +++ +

22222222

Đẳngthứcxảyrakhi ():514190 514 ab Qxy =Þ+-=

Trườnghợp2: B, C nằmkhácphíasovới () Q ,khiđó:

() ()() ()2222

2436 2,, abab dBQdCQ abab ++ +=+ ++

()()2222

22222222

1228362 5 ab ababab abababab -++++-+ =+=£ = +++ + .

Đẳngthứcxảyrakhi ():210 12 ab Qxy =Þ-+-=.

Vậy () Q cóphươngtrìnhlà ():514190Qxy+-=

Điểmquagiaotuyếncủamặtphẳng () Q và () Oxy là (15;4;0)N.

Câu43: Chohìnhnón() N cóđỉnh S,chiềucao 3h= .Mặtphẳng() P quađỉnh S cắthìnhnón() N theo thiếtdiệnlàtamgiácđều.Khoảngcáchtừtâmđáyhìnhnónđếnmặtphẳng () P bằng 6.Thể

tíchkhốinóngiớihạnbởihìnhnón () N bằng

A.12p B. 81p C. 36p D. 27p

Lờigiải ChọnD

Kẻ OMAB ^ và OHSM ^ .Tasuyra ()6OHSABOH^Þ=

Tacó: 22 32 OHOS OM OSOH = =và 2233SMSOOM=+= 6SA Þ= , 33OA=

Vậythểtíchkhốinónlà ()21 33327 3 V=´p´=p.

Câu44: Cho hàm số ()fx thỏa mãn: ()()()() 22 ln2,1;xfxxfxxfxx ¢ -+="Î+¥ và ()2 1 fe e = .

Biết ()() 0,1;fxx>"Î+¥ , diện tích S của hình phẳng giới hạn bởi đồ thị (),0, yxfxyxe === và 2 xe = là

Giảthiết ()() () () 2 1lnln 22xfxfxxx x x fx fx

¢ ¢ - æö ç÷ ÷ Û =Ûç= ç÷ ÷ ç÷ èø() 2lnxxC fx Þ=+ .

+ () ()() 2 2 1lnln 0xxfeCfxxfx e xx =Þ=Þ=Þ= . +Tính () 2 2 2 ln13 dln 22 | e e e e

Sxxx x === ò .

Câu45: Trongkhônggian Oxyz,đườngthẳngđiquahaiđiểm () 1;2;1A- và () 2;1;1B- cóphươngtrình thamsốlà

ì ï=+ xt yt zt

í=ì ï=+ ï ï ï í=ï ï ï=+ ï î

ChọnA

23 12 xt yt zt

Lờigiải

ì ï=+ ï ï ï í=-+ ï ï ï=ï î

C. 1 32 2

D. 1 12 xt yt zt

ì ï=+ ï ï ï í=+ ï ï ï=ï î

Đường thẳng AB đi qua () 1;2;1A- và có 1 vectơ chỉ phương () 1;3;2AB  =- . Do đó phương

Câu46: Sốgiátrịnguyêncủathamsố m đểhàmsố () 422 3 ymxmxm =--+ khôngcóđiểmcựcđạilà

A.4. B.2. C.0. D.vôsố Lờigiải

ChọnA

 Nếu 0m= thì 23 yx = .Hàmsốchỉcóđiểmcựctiểu x =0.Dođó 0m= thỏamãn.

 Nếu 0m¹ thìhàmsốđãcholàhàmbậcbốntrùngphương.

 Nếu ()30mm-< thìhàmsốcó3điểmcựctrị.Khiđóhàmsốcóđiểmcựcđại(không thỏamãnyêucầuđềbài).

 Nếu ()3003mmm-³Û<£ thìhàmsốcó1điểmcựctrịvàđồthịhàmsốcódạngnhư hìnhvẽdướiđây Khiđóhàmsốkhôngcóđiểmcựcđại(thỏamãnyêucầuđềbài).

Vậycó4giátrịnguyên m thỏamãnlà0;1;2;3.

Câu47: Tập nghiệm của bất phương trình ()() 2 2 3 5 log412log53 xx xx -+++-+£ là () ; ab . Khi đótổng 2 ab + bằng

A.1 B. 3 C. 4 D. 2

Lờigiải

ChọnD

Đặt ()240txxt =-+> thìbấtphươngtrìnhtrởthành: ()() 2 35 log12log130 tt +++-£

Xéthàmsố ()()() 2 35 log12log13fttt=+++- trên () 0;+¥ .

()()()() 2 14 0,0;1ln31ln5 t ft t tt Þ¢=+>"Î+¥ ++ nên hàm số đồng biến trên khoảng () 0;+¥

Mà ()() 2 2 02242001. ftftxxxxx <=Þ<Þ-+<Û-<Û<<

Vậy 0,122abab ==Þ+=

Câu48: Cóbaonhiêugiátrịnguyêncủathamsố () 2022;2022mÎ-

trênkhoảng ()

212321 fxxmxfxxm ¢ =++-Þ=++

Xét ()()()() 3

0,1;33210,1;3min

(){}() 2022;20220;1;2;...;20211

Chọn

2022;20222021;2020;;142

Từ ()() 1,2 có 4030 giátrịnguyên m thỏamãnyêucầubàitoán.

Câu49: Trongkhônggianvớihệtọađộ Oxyz,điểmđốixứngcủa () 1;2;3M quatrục Ox cótọađộlà

A. () 1;2;3--- B. () 1;0;0 C. () 1;2;3 -- D. () 0;2;3

Lờigiải

ChọnC

Gọi () ;0;0Hh làhìnhchiếucủa M lêntrục Ox.

Suyra () 1;2;3MHx  =--- và 0MHi  =

Dođó ()11;0;0xH =Þ

Gọi M¢ làđiểmđốixứngcủa M quatrục Ox suyra H làtrungđiểmcủa MM¢ .

Vậy () 1;2;3M¢ -.

Câu50: Chohìnhlăngtrụđứng ABCABC¢¢¢ cóđáy ABC làtamgiácđềucạnh a và 2 AAa ¢ = Gọi

M làtrungđiểmcủa AA ¢ .Khoảngcáchtừ M đếnmặtphẳng () ABC ¢ bằng

Gọi K làtrungđiểm BB¢ suyra () ()() ()() ()1 d,d,d, 2 MABCKABCBABC ¢ ¢ ¢ = = .

Gọi I làtrungđiểm AC suyra 3 2 a BI= .Kẻ BH vuônggócvới BI ¢ tại H.Suyra () ()d,BABCBH ¢ = .

Khiđó 22

¢ × = = +¢

257 19 BIBBa BH BIBB

Vậy () () d57 ,19 aMABC ¢ = . ----------

HẾT----------

SỞGIÁODỤCVÀĐÀOTẠOLÀOCAI

ĐỀTHITHỬTỐTNGHIỆPTHPT

NĂMHỌC2022–2023–LẦN1

Câu1: Thểtíchcủakhốichópcóđáylàtamgiác ABCvuông, ABACa  vàchiềucao 2a là

A. 3 6 a B. 3 3 a C. 32 6 a D. 32 3 a

Câu2: Tínhthểtíchcủakhốitrònxoaykhichohìnhphẳnggiớihạnbởiđồthịhàmsố 2 yx  ,trụchoành vàđườngthẳng 2x ,khiquayxungquanhtrục Ox bằng

A. 32 5  B. 6  C. 5 6  D. 4 . 5 

Câu3: Chobasốdương  ,,1,1 abcab vàcácsốthực  khác0.Đẳngthứcnàosai?

A. 1 loglog a a bb    B. llog ogloga b a

c c b 

C. log(.)loglog a aa bcbc  D. logloglog aab cbc 

Câu4: Cóbaonhiêucáchsắpxếp5họcsinhvàomộtghếdàitừmộtnhómgồm10họcsinh?

A. 105 B. 5 10. C. 5 10.A D. 5 10.C

Câu5: Chohàmsố yfx  cóbảngbiếnthiênnhưsau

Sốđiểmcựctiểucủa

hàmsốđãcho

A. 3 B. 0 C.1 D. 2

Câu6: Họnguyênhàmcủahàmsố 1 54fx x   trên 4 \ 5 

Câu10: Tiệmcậnđứngcủađồthịhàm

Câu11: Trongkhônggian Oxyz,chomặtphẳng

:2230

B.  1;1;3E C.  2;1;3N D.  2;2;1F

Câu12: Tậpnghiệmcủabấtphươngtrình 2 log13 x là

A.  ;8S . B.  1;8S . C.  1;7S . D.  ;7S .

Câu13: Chohàmsố fx liêntụctrên  vàcóđồthịlàđườngcongnhưhìnhvẽbêndưới

Sốnghiệmcủaphươngtrình 20fx trênđoạn  2;3 là

A.1 B. 3 C. 4 D. 2

Câu14: Chocấpsốcộng  n u cósốhạngđầu 15u ,côngsai 2d .Giátrịcủa 4u bằng

A.12. B.11. C. 40. D.13.

Câu15: Họtấtcảnguyênhàmcủahàmsố 2sin fxxx  là

A. 2 2cosxxC  . B. 2 cos xxC  .

C. 2 2cosxxC  D. 2 cos xxC 

d2fxx .Giátrịcủa  2 1 

2d fxxx 

bằng

A.1 B. 3 C. 4 D. 5

Câu17: Chohàmsố    axb ycxd cóđồthịlàđườngcongtronghìnhvẽbên.Tọađộgiaođiểmcủađồthị hàmsốđãchovàtrụchoànhlà

 0;1 B.  1;0 C.  1;0 D.  0;1

Câu18: Phươngtrìnhmặtcầutâm  1;2;3I vàbánkính 3R là

 222 1239  xyz . B. 22224650 xyzxyz .

 222 1239 xyz . D.  222 1233 xyz .

Câu19: Trongkhônggianvớihệtọađộ Oxyz,cho 345  OAijk Tọađộđiểm A là

 3;4;5A B.  3;4;5A C.  3;4;5A D.  3;4;5A

Câu20: Đạohàmcủahàmsố  2 3log  yxx là A.  2 21 ln3   x xx B. 2 ln3  xx

Câu21: Sốphức  24ii bằngsốphứcnàodướiđây?

A. 42i B. 42i C. 42i D. 42i

Câu22: Chohìnhnóncóđộdàiđườngsinhbằng 4,diệntíchxungquanhbằng 8,tínhbánkínhđáy R hìnhtròncủahìnhnónđó:

A. 1R B. 2R C. 4R D. 8R

Câu23: Mộthìnhhộpchữnhậtcóbakíchthước ,2,3 aaa.Thểtíchcủakhốihộpchữnhậtđóbằng

A. 32a B. 36a C. 3 a D. 33a

Câu24: Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a và SAABCD  . Biết 6 3 Sa A .Tínhgócgiữa SC và  ABCD

A. 075 . B. 060 . C. 030 . D. 045 .

Câu25: Trongkhônggian Oxyz,mặtphẳng :270 xyz .Vectơnàodướiđâylàmộtvectơ pháptuyếncủa  

Câu27: Chohàmsố yfx  liêntụctrênđoạn  1;5 vàcóđồthịnhưhìnhvẽ.

Gọi , Mm lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsốtrênđoạn  1;5 .Giátrị Mm bằng

A. 4. B.1. C. 5. D. 2.

Câu28: Hàmsốnàodướiđâycóđồthịnhưhìnhdưới?

Câu

hìnhvẽ.

Khẳngđịnhnàosauđâylàsai?

A.Hàmsốđồngbiếntrên  ;1

1;1;7

A. 12;1;7n  B. 21;2;1n  C. 31;2;7n  D. 

Câu26: Chođườngthẳng  cắtmặtcầu  ; SOR Gọi d làkhoảngcáchtừ O đến  Khẳngđịnhnào dướiđâyđúng?

A. 0d .

B.Hàmsốđồngbiếntrên  1;

C.Hàmsốđồngbiếntrên  ;11;  .

D.Hàmsốnghịchbiếntrên  1;1

Câu30: Chosốphức z thỏamãn 1234 izi Phầnảocủasốphức z bằng

A. 4. B. 4. C. 2. D. 2.

Câu31: Trênmặtphẳngtoạđộ,điểmbiểudiễnchosốphức 32 zi  cótoạđộlà

A.  3;2M B.  2;3P C.  2;3N D.  3;2Q

Câu32: Chohìnhlăngtrụđứng ABCABC cótấtcảcáccạnhbằng a Gọi M làtrungđiểmcủa AA (thamkhảohìnhvẽ).Khoảngcáchtừ M đếnmặtphẳng  ABC  bằng

Câu39: Chosốphức z cóphầnảodươngthoảmãn 1z vàbiểuthức 121 Pzz  đạtgiátrịlớn nhất.Giátrịcủabiểuthức 36 55 Qzi  bằng

A. 0 B. 2 C. 35 5 D. 6 5

Câu40: Cóbaonhiêugiátrịnguyêncủathamsố a thoảmãnhàmsố 1x y xa  nghịchbiếntrênkhoảng

 2; ?

A.1 B. 3 C. 2 D. 0

Câu41: Trongkhônggian Oxyz,chođiểm  1;2;3A ,mặtphẳng :310Pxyz vàmặtphẳng

:330Qxyz .Gọi   làđườngthẳngđiqua A,cắtvàvuônggócvớigiaotuyếncủa

 P và  Q .Sincủagóctạobởiđườngthẳng   vàmặtphẳng  P bằng

A. 2 2 a . B. 21 14 a . C. 2 4 a . D. 21 7 a .

Câu33: Tíchtấtcảcácnghiệmcủaphươngtrình 2 33 log2log70 xx bằng

A. 2 B.1 C. 9 D. 7

Câu34: Trongkhônggian Oxyz,chođiểm  2;1;1A vàđiểm A làđiểmđốixứngvớiđiểm A quatrục Oz.Điểm A nắmtrênmặtphẳngnàotrongcácmặtphẳngdướiđây?

A. 3520 xyz B. 3410 xyz

C. 2410 xyz D. 32510 xyz

Câu35: Gọi S làtậphợpcácsốtựnhiêncó 4 chữsốkhácnhauđượclậptừ  1,2,3,4,5E .Chonngẫu nhiênmộtsốtừtập S.Xácsuấtđểsốđượcchonlàmộtsốchẵnbằng

Câu42: Tìmsốnghiệmnguyêncủabấtphươngtrình  32 3 2log3252logxxx  A. 6 B. 7 C. 8 D. 5

Câu43: Biết Fx và Gx là hai nguyên hàm của hàm số fx trên  và

4 0 4020fxFGmm    . Gọi S là diện tích hình phẳng giới hạn bởi các đường ,,0yFxyGxx  và 4x .Khi 8S thì m bằng:

A. 4 B.1 C. 3 D. 2

Câu36: Chohàmsố yfx  liêntụctrên  vàcóđạohàm  20222023 112. fxxxx  Hàm số yfx  đồngbiếntrênkhoảngnàodướiđây? A.  2; B.  1;2 C.  1;1 D.  ;1

Câu37: Chosốphức z có 12z và  132.wiz Tậphợpcácđiểmbiểudiễnsốphức w là

đườngtròn,tâmvàbánkínhcủađườngtrònđólà

A. 3;3,4IR B. 3;3,4IR C. 3;3,2IR D. 3;3,4IR

Câu38: Trongkhônggian ,Oxyz chobốnđiểm  1;2;1,0;1;3,1;2;3,2;1;2 ABCD Phươngtrình đườngthẳngđiquađiểm A vàvuônggócvớimặtphẳng  BCD là

A. 13 132 xyz  . B. 121 132 xyz   .

C. 235 114 xyz

Câu44: Cho hàm số yfx  có đạo hàm liên tục trên  và thỏa mãn 42 564,.fxxfxxxx  Diệntíchhìnhphẳnggiớihạnbởicácđược yfx  và 1 4 yxfx   bằng

A. 272 15 B. 112 15 C. 32 3 D. 1088 15

      và 12 1 2 4 xxab 

.

Câu47: Trongkhônggian Oxyz,chohaiđiểm  1;2;5A và  3;2;1B .Xétkhốinón  N cóđỉnh I làtrungđiểmcủa AB,đườngtrònđáynằmtrênmặtcầuđườngkính AB.Khi  N cóthểtích lớn nhất thì mặt phẳng chứa đường tròn đáy của  N đi qua điểm  2;3;3C và có phương trìnhdạng 0xbyczd .Tínhgiátrịbiểuthức Tbcd 

A. 53  B. 23  C. 53  D. 23 

Câu48: Trêntậphợpsốphức,xétphươngtrình 2 2 2210zmzm (m làsốthực).Khiphương trìnhcóhainghiệmphânbiệt 1z , 2z saochobiểuthức 2 22 121 10 Tzzzz  đạtgiátrịnhỏ nhấtthìgiátrị m thuộckhoảngnàosauđây?

A. 3 ;3 2    B. 1;2 C.  1;1 D.  2;

Câu49: Có bao nhiêu giá trị thực không âm của tham số m để đồ thị của hàm số

3211 3(1) 2 yxmxmx  cóhaiđiềmcựctrị A và B saocho , AB nằmkhácphíavàcáchđều đườngthẳng 5 : 12dyx ?

A. 0 B. 3 C.1 D. 2

Câu50: Chohìnhnónđỉnh S,đáylàhìnhtròntâm O,bánkính 5R .Mặtphằng ()  qua S,cắthình nóntheothiếtdiệnlàtamgiác SAB códiệntíchbằng 122.Mặtphẳng ()  tạovớiđáyhình nóngóc 45 ;tamgiác OAB nhọn.Thểtích V củakhốinóntạonêntừhìnhnónđãchobằng

ÁN

GIẢICHI

Câu1: Thểtíchcủakhốichópcóđáylàtamgiác ABCvuông, ABACa

Câu2: Tínhthểtíchcủakhốitrònxoaykhichohìnhphẳnggiớihạnbởiđồthị

vàđườngthẳng 2x ,khiquayxungquanhtrục Ox bằng

Câu3: Chobasốdương  ,,1,1 abcab vàcácsốthực  khác0.Đẳngthứcnàosai?

A. 1 loglog a a bb    B. llog ogloga b a

c c b 

C. log()loglog a aa bcbc  D. logloglog aab cbc 

Lờigiải

ChọnA

Câu4: Cóbaonhiêucáchsắpxếp5họcsinhvàomộtghếdàitừmộtnhómgồm10họcsinh?

A. 105 B. 5 10. C. 5 10A D. 5 10C

Lờigiải

ChọnC

Câu5: Chohàmsố yfx  cóbảngbiếnthiênnhưsau

Câu11: Trongkhônggian Oxyz,chomặtphẳng

A.  1;1;3M B.  1;1;3E C.  2;1;3N D.  2;2;1F Lờigiải

ChọnB

Câu12: Tậpnghiệmcủabấtphươngtrình 2 log13 x là

A.  ;8S B.  1;8S C.  1;7S D.  ;7S Lờigiải

ChọnC

101 log13 1;7 17 2 xx x S xx

Câu13: Chohàmsố fx liêntụctrên  vàcóđồthịlàđườngcongnhưhìnhvẽbêndưới

Sốnghiệmcủaphươngtrình 20fx trênđoạn  2;3 là

A.1. B. 3. C. 4. D. 2. Lờigiải

ChọnC

Tacó 202fxfx

A.  0;1 B.  1;0 C.  1;0 D.  0;1

Lờigiải

Dựavàođồthịtathấycó4nghiệm.

Câu14: Chocấpsốcộng  n u cósốhạngđầu 15u ,côngsai 2d .Giátrịcủa 4u bằng

A.12. B.11. C. 40. D.13.

Lờigiải

ChọnB

Tacó 41353211uud

Câu15: Họtấtcảnguyênhàmcủahàmsố 2sin fxxx  là

A. 2 2cosxxC  . B. 2 cos xxC  . C. 2 2cosxxC  . D. 2 cos xxC  .

Lờigiải

ChọnD

Câu16: Biết  2

d2 fxx .Giátrịcủa 

2d fxxx bằng

A.1 B. 3 C. 4 D. 5

Lờigiải

ChọnB

Tacótọađộgiaođiểmcủađồthịhàmsốvàtrụchoànhlà  1;0 .

Câu18: Phươngtrìnhmặtcầutâm  1;2;3I vàbánkính 3R là

A.  222 1239  xyz B. 22224650 xyzxyz

C.  222 1239 xyz D.  222 1233 xyz

Lờigiải

ChọnC

Tacóphươngtrìnhmặtcầutâm  1;2;3I vàbánkính 3R là:  222 1239 xyz .

Câu19: Trongkhônggianvớihệtọađộ Oxyz,cho 345   OAijk Tọađộđiểm A là

A.  3;4;5A B.  3;4;5A C.  3;4;5A D.  3;4;5A

Lờigiải

Câu20: Đạohàmcủahàmsố

ChọnD

Tacó  

2dd2ddd35     fxxxfxxxxfxxxfxx

222 2 22 1

111

Câu17: Chohàmsố    axb ycxd cóđồthịlàđườngcongtronghìnhvẽbên.Tọađộgiaođiểmcủađồthị

hàmsốđãchovàtrụchoànhlà

 xxx yxx xxxx

Câu21: Sốphức  24ii bằngsốphứcnàodướiđây?

A. 42i B. 42i C. 42i D. 42i Lờigiải

ChọnC

Tacó: 2 242442 iiiii

Câu22: Chohìnhnóncóđộdàiđườngsinhbằng 4,diệntíchxungquanhbằng 8,tínhbánkínhđáy

R hìnhtròncủahìnhnónđó:

1R B. 2R C. 4R D. 8R

Lờigiải

ChọnB

Tacó: 8 2 4 xq xq

S SRlR l    

Câu23: Mộthìnhhộpchữnhậtcóbakíchthước ,2,3 aaa Thểtíchcủakhốihộpchữnhậtđóbằng

A. 32a . B. 36a . C. 3 a . D. 33a .

Lờigiải

ChọnB

Tacó 3236 Vaaaa 

Câu24: Cho hình chóp . SABCD có đáy ABCD là hình vuông cạnh a và SAABCD  . Biết 6 3 Sa A .Tínhgócgiữa SC và  ABCD

A. 075 . B. 060 . C. 030 . D. 045 .

Lờigiải ChọnC

Tacó:    ,, SAABCDSAACSCA 

Xéttamgiác SCA vuôngtại A:  063 tan 30 33 2 SAa C SCA ACa 

Câu25: Trongkhônggian Oxyz,mặtphẳng :270 xyz .Vectơnàodướiđâylàmộtvectơ pháptuyếncủa  

A. 12;1;7n  . B. 21;2;1n  . C. 31;2;7n  . D. 41;1;7n  . Lờigiải ChọnB

Câu26: Chođườngthẳng  cắtmặtcầu  ; SOR Gọi d làkhoảngcáchtừ O đến  Khẳngđịnhnào dướiđâyđúng?

A. 0d . B. dR  . C. dR  . D. dR  .

Lờigiải ChọnB

Từhìnhvẽ,trongtamgiác OBH vuôngtại Hdễthấy: dR 

Câu27: Chohàmsố yfx  liêntụctrênđoạn  1;5 vàcóđồthịnhưhìnhvẽ.

Gọi , Mm lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsốtrênđoạn  1;5 .Giátrị Mm

bằng

A. 4 B.1 C. 5 D. 2

Lờigiải

ChọnA

Từđồthịtacó: 4,04MmMm 

Câu28: Hàmsốnàodướiđâycóđồthịnhưhìnhdưới?

A. 331yxx  B. 331yxx C. 4221yxx  D. 4221yxx

Lờigiải

ChọnB

Đâylàđồthịhàmsốbậcba 32 0yaxbxcxda 

Câu29: Chohàmsố yfx  làhàmđathứcbậcbavàcóđồthịnhưhìnhvẽ.

ChọnB

Lờigiải

Khẳngđịnhnàosauđâylàsai?

A.Hàmsốđồngbiếntrên  ;1

B.Hàmsốđồngbiếntrên  1; .

C.Hàmsốđồngbiếntrên  ;11; 

D.Hàmsốnghịchbiếntrên  1;1 .

ChọnC

Lờigiải

ĐápánCviphạmcáchviếtkhoảngđồngbiến,nghịchbiến.

Câu30: Chosốphức z thỏamãn 1234 izi Phầnảocủasốphức z bằng

A. 4. B. 4. C. 2. D. 2.

Lờigiải

ChọnC

Tacó:  34 123412. 12 i izizzi i   Phầnảocủasốphức z bằng 2.

Câu31: Trênmặtphẳngtoạđộ,điểmbiểudiễnchosốphức 32 zi  cótoạđộlà

A.  3;2M . B.  2;3P . C.  2;3N . D.  3;2Q .

Lờigiải

ChọnD

Sốphức 32 zi  cóđiểmbiểudiễnlà  3;2Q

Câu32: Chohìnhlăngtrụđứng ABCABC cótấtcảcáccạnhbằng a Gọi M làtrungđiểmcủa AA (thamkhảohìnhvẽ).Khoảngcáchtừ M đếnmặtphẳng  ABC  bằng

Gọi N làtrungđiểm CC và INBBC  .

Gọi , HK lầnlượtlàhìnhchiếuvuônggóccủa B lên AC và BH 

Ta có  , ACBHACBBACBBHACBK   , khi đó BKABC  hay

11 ,,22 dMABCdBABCBK    

Tacó 222 2

a a a BHBB a BHBK BHBBa a

     Vậy  21 ,14 adMABC  

3 . 3 221 2 37 4

Câu33: Tíchtấtcảcácnghiệmcủaphươngtrình 2 33 log2log70 xx bằng

tíchcácnghiệm 9.

Câu34: Trongkhônggian Oxyz,chođiểm  2;1;1A vàđiểm A làđiểmđốixứngvớiđiểm A quatrục Oz.Điểm A nắmtrênmặtphẳngnàotrongcácmặtphẳngdướiđây?

A. 3520 xyz B. 3410 xyz C. 2410 xyz D. 32510 xyz Lờigiải

ChọnD

Tacó  2;1;1A thuộcmặtphẳng: 32510 xyz .

Câu35: Gọi S làtậphợpcácsốtựnhiêncó 4 chữsốkhácnhauđượclậptừ  1,2,3,4,5E .Chonngẫu

nhiênmộtsốtừtập S.Xácsuấtđểsốđượcchonlàmộtsốchẵnbằng

A. 1 2 . B. 2 5 . C. 3 5 . D. 3 4 .

Lờigiải

ChọnB

Tacósốphầntửcủakhônggianmẫu 4 5nA  .

Gọi A làbiếncố:“sốđượcchonlàmộtsốchẵn”,khiđó 3 42. nAA 

Vậy   3 4 4 5

22 5 nAA PA nA  

Câu36: Chohàmsố yfx  liêntụctrên  vàcóđạohàm  20222023 112. fxxxx  Hàm số yfx  đồngbiếntrênkhoảngnàodướiđây?

A.  2; B.  1;2 C.  1;1 D.  ;1

Lờigiải ChọnB

Tacó: 012012.fxxxx  

Vậyhàmsốđồngbiếntrênkhoảng  1;2

Câu37: Chosốphức z có 12z và  132wiz Tậphợpcácđiểmbiểudiễnsốphức w là

đườngtròn,tâmvàbánkínhcủađườngtrònđólà

A. 3;3,4IR B. 3;3,4IR

C. 3;3,2IR D. 3;3,4IR Lờigiải ChọnD

Tacó:  13213133331314 wizwiziwiiz  

Vậytậphợpbiểudiễnsốphức

w làđườngtròntâm  3;3I bánkính 4R

Câu38: Trongkhônggian ,Oxyz chobốnđiểm  1;2;1,0;1;3,1;2;3,2;1;2 ABCD Phươngtrình đườngthẳngđiquađiểm A vàvuônggócvớimặtphẳng  BCD là

A. 13 132 xyz  B. 121 132 xyz  

C. 235 114 xyz   D. 121 134 xyz   Lờigiải ChọnC

Tacó:  1;1;0,2;2;1,1;1;4BCBD BDBC    làmộtvectơchỉphươngcủamặt phẳng  BCD

Nênđườngthẳngđiqua A vàvuônggócvớimặtphẳng  BCD là 121 : 114 xyz  

Vìđiểm  2;3;5 thuộcđườngthẳng  nên: 235 : 114 xyz  

Câu39: Chosốphức z cóphầnảodươngthoảmãn 1z vàbiểuthức 121 Pzz 

giátrịlớn nhất.Giátrịcủabiểuthức 36 55 Qzi  bằng

A. 0 B. 2 C. 35 5 D. 6 5 Lờigiải ChọnB

Giảsử  ,,,0zabiabb  

Tacó 2222 111zabab  .

Dođó

Câu40: Cóbaonhiêugiátrịnguyêncủathamsố

 ?

A.1 B. 3 C. 2 D. 0 Lờigiải ChọnA Điềukiện xa  .

Xéthàmsố 1x gx xa  có 2 1 , a gxxa xa 

+)Với 1a thìhàmsố 1,1gxx (khôngthoảmãn).

+)Với 1a thìhàmsố gx làhàmbậcnhất/bậcnhấtnênhàm

sốsẽđồngbiếnhoặcnghịch





10 12 2 a a a 

Do a nên 2a .

Câu41: Trongkhônggian Oxyz,chođiểm  1;2;3A ,mặtphẳng :310Pxyz vàmặtphẳng

:330Qxyz Gọi   làđườngthẳngđiqua A,cắtvàvuônggócvớigiaotuyếncủa

 P và  Q .Sincủagóctạobởiđườngthẳng   vàmặtphẳng  P bằng A.

B. 0 C. 355 11 D. 755

ChọnD

Tacómặtphẳng :310Pxyz cóvectơpháptuyến 13;1;1n  vàmặtphẳng

:330Qxyz cóvectơpháptuyến 21;3;1

 ;1;21;1;23dBBtttABttt

làmộtvectơchỉphươngcủađườngthẳng

.

Gọi làgócgiữađườngthẳng  vàmặtphẳng  P ,tacó 1 1 1

7755sincos, 555 5 ABn ABn ABn  

Câu42: Tìmsốnghiệmnguyêncủabấtphươngtrình  32 3 2log3252logxxx 

A. 6 B. 7 C. 8 D. 5 Lờigiải

ChọnB

Điềukiện: 323250 0 0 xx x x   

3 2 32

3ln22ln36ln2ln350ln3 0,0 325ln3ln2 x x x xxx

Suyra 0,0fxx  Tacó:

Từbảngbiếnthiên 0fx khi 08 x  ,vậybấtphươngtrìnhcó7sốnguyên.

Câu43: Biết Fx và Gx là hai nguyên hàm của hàm số fx trên  và

4 0 4020fxFGmm    . Gọi S là diện tích hình phẳng giới hạn bởi các đường

,,0yFxyGxx  và 4x .Khi 8S thì m bằng:

A. 4 B.1 C. 3 D. 2

Lờigiải

ChọnB

Vì Fx và Gx làhainguyênhàmcủahàmsố fx nêngiảsửtrên ,tacó:

 GxFxC  suyra  00 GFC 



Vậy 2 GxFxm  trên 

 , Mà 8S nên 1m .

Tacó 4 44 0 0 0 d2d28 SFxGxxmxmxm   

42 564, fxxfxxxx

 Diệntíchhìnhphẳnggiớihạnbởicácđược yfx  và

.Suyra ft làhàmsốđồngbiếntrênkhoảng

4412 20 xxx x

4412 20 xxx x

12 1 2 4 xxab  với , ab làhaisốnguyêndương,suyra:

Dođó: 12 1 295 4 xx .Suyra:  ;9;5ab .

Câu46: Chokhốilăngtrụđứng . ABCABC cóđáy ABC làtamgiácđềucạnh a,gócgiữamặtphẳng

 ABC  vàmặtđáy  ABC bằng 60 .Thểtíchkhốilăngtrụđãchobằng

A.

Lờigiải

Gọi I làtrungđiểmcủa BC suyra 3 2 Aa I và    ,60ABCABCAIA     .

Xéttamgiác AAI  vuôngtại A có 33 tantan60 22 a a AAAIAIA       Diệntíchtamgiácđều ABC là 23 4ABC Sa 

Vậythểtíchkhốilăngtrụđãchobằng 2 33333 428 ABC aaVSAA a   .

Câu47: Trongkhônggian Oxyz,chohaiđiểm  1;2;5A và  3;2;1B .Xétkhốinón  N cóđỉnh I làtrungđiểmcủa AB,đườngtrònđáynằmtrênmặtcầuđườngkính AB.Khi  N cóthểtích

lớn nhất thì mặt phẳng chứa đường tròn đáy của  N đi qua điểm  2;3;3C và có phương trìnhdạng 0xbyczd .Tínhgiátrịbiểuthức Tbcd 

A. 53  . B. 23  . C. 53  . D. 23  . Lờigiải

ChọnA

Tacó 4;4;443AB AB 

Gọi  C làmặtcầutâm I,đườngkính AB nên  1;0;3 : 23 I C R     

Gọi  P làmặtphẳngchứađáyhìnhnón.

Gọi CD làđườngkínhđườngtròngiaotuyếncủa  P và  C nên 2 CD r

Gọi I làhìnhchiếucủa I trên  P nên hII  và 22212hrR

ÁpdụngbấtđẳngthứcAm–gm:

Câu49: Có bao nhiêu giá trị thực không âm của tham số m để

22,2

1;3;0, ICICdIP

Câu48: Trêntậphợpsốphức,xétphươngtrình 2 2 2210zmzm (m làsốthực).Khiphương trìnhcóhainghiệmphânbiệt 1z , 2z saochobiểuthức 2 22 121 10 Tzzzz  đạtgiátrịnhỏ nhấtthìgiátrị m thuộckhoảngnàosauđây?

A. 3 ;3 2    B. 1;2 C.  1;1 D.  2;

Lờigiải

ChọnA

Xétphươngtrình 2 2 2210zmzm

Tacó 2221mm .

TH1:Phươngtrìnhcóhainghiệmphứccóphầnảobằngkhông

22 210 mm

A. 0. B. 3. C.1. D. 2. Lờigiải ChọnD

 32 2 11 (1) 1 32 yxmxmxyxmxm  

Đểhàmsốcó2điểmcựctrịđiềukiện

42zzm zzm 42zzm zzzzm

nên

trìnhcóhainghiệmcùng

      ,khiđó: 2 22 2 1 2 211 8 10888 3 T mzzzz T z   (loại). Vậygiátrịnhỏnhấtcủa 2 22 121 10 Tzzzz  là 12 khi 2m

là  2 02101 y mmma 1 0 x y xm   Vớiđiềukiện 10my  có2nghiệmKhiđó 32313 1;,;. 66 Ammm Bm      Để , AB nằmkhácphíavàcáchđềuđườngthẳng 5 : 12dyx điềukiệnlà  32 32 32 32 65261250 261256526180 6526125 mmmm mmmmmmm mmmm          32 32 32 32 65261250 261256526180 6526125 0 335 2 335 0 2 mmmm mmmmmmm mmmm m m m                 

Vậycó2giátrịcủa mthỏamãn.

A. 25V B. 75V C. 100V D. 100 3 V  

Lờigiải

ChọnD

SỞGIÁODỤCVÀĐÀOTẠOPHÚTHỌ

ĐỀTHITHỬTỐTNGHIỆPTHPT–NĂMHỌC2022–2023–LẦN2

Câu1: Chotậphợp A gồm12 phầntử.Sốtậpcongồm 3 phầntửcủatậphợp

Câu2: Chocấpsốnhân 

bộicủacấpsố

Câu3: Chohàmsố 42 ;; yaxbxcabc 

Hàmsốđãchođạtcựctiểutại

Câu4: Trongkhônggian Oxyz,mặtcầu (2;4;5)I vàbánkínhbằng 5 cóphươngtrìnhlà

A. 222 (2)(4)(5)25 xyz B. 222 (2)(4)(5)25 xyz 

C. 222 (2)(4)(5)25 xyz  D. 222 (2)(4)(5)5 xyz 

Câu5: Phầnảocủasốphức 52 zi 

A. 2 B. 2i C. 2i D. 2

Câu6: Chosốphức 23 zi  .Sốphứcliênhợpcủa z cóđiểmbiểudiễntrênmặtphẳngtọađộlà

A.  2;3 B.  2;3 C.  2;3 D.  2;3

Câu7: Đạohàmcủahàmsố 5x y là

Câu8: Chobấtphươngtrình 1 9360 xx  Nếuđặt 3(0) x tt thìbấtphươngtrìnhđãchotrởthành bấtphươngtrìnhnàodướiđây?

A. 260tt B. 230tt

Câu9: Trongkhônggian Oxyz,chohaiđiểm  1;2;3A và  3;1;3B .Mặtphẳngtrungtrựccủađoạn thẳng AB cómộtvéctơpháptuyếnlà

Câu10: Chohaisốphức 145 zi  và 223 zi  .Khiđó 12zz

Câu11: Trongkhônggian Oxyz,chovectơ  1;2;2a  .Độdàicủavectơ a  bằng

A. 4. B.1. C. 3. D. 9.

Câu12: Giátrị ln4e bằng

A. 2ln2 B. 3ln2 C. 3ln21  D. 2ln21 

Câu13: Chokhốilăngtrụtamgiác . ABCABC códiệntíchđáybằng 23a ,chiềucaobằng 2a.Thể tíchkhốilăngtrụđãchobằng

A. 36 6 a B. 36 13 a C. 36 3 a D. 36a

Câu14: Chokhốinóncódiệntíchđáybằng 2 vàchiềucaobằng h Thểtíchcủakhốinónđãchobằng

A. 2h B. 4 3 h C. 2 3 h D. 4h

Câu15: Khẳngđịnhnàosauđâylàđúng?

A. 2 1 cot sin dxxC x  . B. 2 1 tan sin dxxC x  .

C. 2 1 tan sin dxxC x  D. 2 1 cot sin dxxC x 

Câu16: Tậpxácđịnh D củahàmsố  2 53yx  là A. ;3D B.  3;D

Câu

Câu20: Cho

ba yfx  cóbảngbiếnthiênnhưhìnhvẽ

Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?

Câu22: Trongkhônggian ,Oxyz đườngthẳngđi

Câu23: Chocácsốthực

,. ababFx  làmộtnguyênhàmcủa fx trênđoạn  ; ab Khẳngđịnh nàosauđâyđúng?

A.  d b a fxxFaFb  . B.  d b a fxxFbFa 

C.  d b a fxxFaFb   . D.  d b a fxxFbFa   .

Câu24: Chohìnhchóp SABCD cóđáy ABCD làhìnhchữnhật, ,2, ABaADaSA  vuônggócvới đáyvà 3SAa  Thểtíchcủakhốichóp SABCD bằng

A. 343 3 a B. 343a C. 323 3 a D. 323a

Câu25: Tậpnghiệmcủabấtphươngtrình 3 log11 x là

A.  4; . B. 1;4 . C.  ;4 . D.  1;4 .

Câu26: Chohìnhchóptứgiácđều SABCD cóđáy ABCD làhìnhvuôngcạnh 2a,cạnhbênbằng 3a Khoảngcáchgiữahaiđườngthẳng BC và SA bằng

A. 3 2 a B. 3a C. 2 2 a D. 2a

Câu27: Lấyngẫunhiên3viênbitừhộpđựng5viênbiđỏvà7viênbixanh.Xácsuấtđểlấyđược3viên bicùngmàubằng

A. 35 44 . B. 9 44 . C. 35 22 . D. 9 22 .

Câu28: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  2;3 để hàm số

3 23 242 2 yxmxm   cócựcđạivàcựctiểuđồngthờihoànhđộđiểmcựctiểunhỏhơn

3?

A. 2. B. 5. C. 3. D. 4.

Câu29: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh 2a, SA vuông góc với đáy và 3SAa  .Gócgiữahaimặtphẳng  SBC và  ABC bằng

A. 045 .

090 .

Câu30: Cho hình phẳng  H giới hạn bởi đồ thị hàm số

60 .

30 .

4 yx  và trục hoành. Thể tích khối tròn xoayđượctạothànhkhiquay  H xungquanhtrụchoànhbằng A. 32 3

Câu31: Chohàmsố yfx  cóđồthịnhưhìnhvẽ.

Sốnghiệmthựcphânbiệtcủaphươngtrình  230 fx là

A. 5. B. 8. C. 6. D. 4.

Câu32: Họtấtcảcácnguyênhàmcủahàmsố 25 2fxxx là

A. 261 2 12 xC  B. 261 2 2 xC  C. 261 2 6 xC  D. 26 2 xC 

Câu33: Biết  1;5M làmộtđiểmcựctrịcủahàmsố 3241yfxaxxbx 

Câu34: Chohàmsố 24 yxx  .Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?

Câu35: Chosốphức z thỏamãn 21(52)(1) ziii  Môđuncủa z bằng

A. 17 B. 13 C. 217 D. 213

Câu36: Cóbaonhiêusốnguyên x thỏamãn

A. 4. B.1. C. 3. D. 2.

Câu39: Chokhốilăngtrụtứgiácđều ABCDABCD  cócạnhđáybằng a Biếtkhoảngcáchtừ C đến mặtphẳng  ABD  bằng 2 a Thểtíchkhốilăngtrụđãchobằng

A. 32a B. 32 6 a C. 32 3 a D. 32 2 a

Câu40: Trongkhônggian Oxyz,chomặtphẳng :430Pxyz vàđiểm  1;1;3A .Mặtphẳng

 QP  vàcắtcáctia , OxOy lầnlượttạicácđiểm B và C saochotamgiác ABC códiện tíchbằng 222 Khoảngcáchtừđiểm  2;2;1M đến  Q bằng

A. 22. B. 86 3 . C. 6 3 . D. 22 3 .

Câu41: Trongkhônggian ,Oxy chohaivecto  1;2;3a  và  1;3;2b  .Giátrị

cos,

xxx

log(329)log(15)12320

A. 24 B. 22 C. 21 D. 23

Câu37: Tổngtấtcảcácgiátrịnguyêncủathamsố m thuộcđoạn  3;3 đểđườngthẳng yxm  cắt đồthịhàmsố 23 1 x y x  tạihaiđiểmphânbiệtcóhoànhđộdươnglà

A. 6. B. 5. C. 6. D. 2.

Câu38: Cho hàm số bậc ba yfx  Biết hàm số  52 yfx   có đồ thị là một Parabol  P như hìnhvẽ.Cóbaonhiêugiátrịnguyêncủathamsố m đểhàmsố  2 22 yfxxm  nghịchbiến trênkhoảng  0;1

Câu42: Mộtkhốinón  N cóbánkínhbằng R vàchiềucaobằng 18,đượclàmbằngchấuliệukhông thấm nước có khối lượng riêng lớn hơn khối lượng riêng của nước. Khối  N được đặt trong mộtcáicốchìnhtrụđườngkínhbằng 6R,saochođáycủa  N tiếpxúcvớiđáycủacốc(tham khảohìnhvẽ).Đổnướcvàocốcđếnkhimứcnướcđạtđộcaobằng 18 thìlấykhối  N ra.Độ caocủanướctrongcốcsaukhiđãlấykhối  N rabằng

Câu43: Chohàmsố

liêntụctrên 1 ;3

Câu44: Cho phương trình 227100zmzm với m là tham số thực. Có bao nhiêu giá trị nguyên của m đểphuongtrìnhcóhainghiệmphứcphânbiệt 12 , zz thỏamãn: 1122 zzzz 

A. 3 B. 2 C.1 D. 4

Câu45: Chophươngtrình 4(3)280 x x m ( m làthamsố).Đểphươngtrìnhđãchocóhainghiệm phânbiệtthỏamãn

12338xx thìgiátrịcủathamsố m thuộckhoảngnàodướiđây?

A.  29;30 . B.  27;28 . C.  30;31 . D.  28;29 .

Câu46: Có bao nhiêu số nguyên dương (2024)aa sao cho tồn tại số thực x thỏa mãn

 3 ln1ln3ln? xx xaeexa     

A. 2022 B. 2019 C. 2023 D. 2018

Câu47: Trong không gian Oxyz, cho đường thẳng 122 : 211 dxyz    và mặt phẳng

:280Pxyz . Tam giác ABC có  1;2;2A và trọng tâm G nằm trên d. Khi các

đỉnh , BC diđộngtrên  P saochokhoảngcáchtừ A tớiđườngthẳng BC đạtgiátrịlớnnhất, mộtvectơchỉphươngcủađườngthẳng

BC là

A.  2;1;1 B.  2;1;1 C.  1;2;0 D.  1;2;0

Câu48: Chosốphức  , zxyixy

làgiátrịlớnnhất,giátrịnhỏnhấtcủabiểuthức 22847Pxyxy  .Khiđó Mm  bằng

A.32. B.36. C.10. D.4.

Câu49: Trongkhônggian Oxyz,chohaiđiểm (1;2;2)M và (2;1;3)S Mặtphẳng () P điqua M và cắtcáctrụctọađộ ,, OxOyOz lầnlượttạicácđiểm ,, ABC saocho M làtrựctâmcủatamgiác ABC Thểtíchcủakhốichóp SABC bằng

A. 7 2 B. 27 8 C. 81 4 D. 27 4

Câu50: Trongmặtphẳng Oxy,gọi () H làtậphợpđiểm (;)Mxy thỏamãn 22(||||)xykxy  với k làsốnguyêndương, S làdiệntíchhìnhphẳnggiớihạnbời () H .Giátrịlớnnhấtcủa k để 250S bằng

A.5. B.4. C.7. D.6.

----------HẾT----------

Câu1: Chotậphợp A gồm12 phầntử.Sốtậpcongồm 3 phầntửcủatậphợp A

ChọnC

Mỗitậpcongồm 3 phầntửcủatậphợp A làmộttổhợpchập3của12.Vậysốtậpcongồm 3 phầntửcủatậphợp A là 3 12C .

Câu2: Chocấpsốnhân  n u có 23u và 36u .Côngbộicủacấpsốnhânđóbằng

A. 1 2 . B. 3. C. 2. D. 1 3 .

Lờigiải

ChọnC

Tacó:côngbộicủacấpsốnhân 3 2 2u q u 

Câu3: Chohàmsố 42 ;; yaxbxcabc  cóđồthịnhưhìnhvẽ.

Hàmsốđãchođạtcựctiểutại

A. 1x B. 1y C. 1y D. 0x

Lờigiải

ChọnD

Từđồthịhàmsốđãchotacóhàmsốđãchođạtcựctiểutại 0.x .

Câu4: Trongkhônggian Oxyz,mặtcầu (2;4;5)I vàbánkínhbằng 5 cóphươngtrìnhlà

A. 222 (2)(4)(5)25 xyz . B. 222 (2)(4)(5)25 xyz  .

C. 222 (2)(4)(5)25 xyz  . D. 222 (2)(4)(5)5 xyz  .

Lờigiải

ChọnB

Phươngtrìnhmặtcầu (2;4;5)I vàbánkínhbằng 5 cóphươngtrìnhlà

222 (2)(4)(5)25 xyz  .

Câu5: Phầnảocủasốphức 52 zi 

A. 2. B. 2i. C. 2i. D. 2.

Lờigiải

ChọnD

Câu6: Chosốphức 23 zi  .Sốphứcliênhợpcủa z cóđiểmbiểudiễntrênmặtphẳngtọađộlà

A.  2;3 . B.  2;3 . C.  2;3 . D.  2;3 .

Lờigiải

ChọnB

Cósốphức 23 zi  nên 23 zi 

Sốphứcliênhợpcủa z cóđiểmbiểudiễntrênmặtphẳngtọađộlà  2;3 .

Câu7: Đạohàmcủahàmsố 5x y là

thìbấtphươngtrìnhđãchotrởthành

Tacó 12452368 zziii  .

Câu11: Trongkhônggian Oxyz,chovectơ  1;2;2a  .Độdàicủavectơ a bằng

A. 4. B.1. C. 3. D. 9.

Lờigiải

ChọnC

Tacó  222 1223a 

Câu12: Giátrị ln4e bằng

A. 2ln2. B. 3ln2. C. 3ln21  . D. 2ln21  .

Lờigiải

ChọnD

Tacó  ln4ln4ln2ln21 ee

Câu13: Chokhốilăngtrụtamgiác . ABCABC códiệntíchđáybằng 23a ,chiềucaobằng 2a.Thể tíchkhốilăngtrụđãchobằng

A. 36 6 a B. 36 13 a C. 36 3 a D. 36a

Lờigiải

ChọnD

Thểtíchkhốilăngtrụđãcholà 36VSha 

Câu14: Chokhốinóncódiệntíchđáybằng 2 vàchiềucaobằng h Thểtíchcủakhốinónđãchobằng

A. 2h B. 4 3 h C. 2 3 h D. 4h

Lờigiải

ChọnB

Thểtíchcủakhốinónđãcholà 2 14 33 Vrhh  .

Câu15: Khẳngđịnhnàosauđâylàđúng?

A. 2 1 cot sin dxxC x  B. 2 1 tan sin dxxC x 

C. 2 1 tan sin dxxC x  D. 2 1 cot sin dxxC x 

Lờigiải

Câu10: Chohaisốphức 145 zi  và 223 zi  .Khiđó 12zz bằng

véctơpháptuyến.

A. 68i B. 22i C. 68i D. 22i

Lờigiải

ChọnD

Tacó 2 1 cot sin dxxC x 

Câu16: Tậpxácđịnh D củahàmsố  2 53yx  là

A.

ChọnA

Câu18: Diệntíchmặtcầucóbánkính 3R bằng A. 36 B.12 C. 36

Câu19: Cho

nhậnvectơ

 1;1;5u  làm

    

2d2d236 fxxfxx

11 00

Câu20: Chohàmsốbậcba yfx  cóbảngbiếnthiênnhưhìnhvẽ

Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?

A.  ;2 B.  0;2 C.  ;0

D.  0; Lờigiải ChọnC

đườngtiệmcậnđứngcủađồthịhàmsố 24

1 x y x   là

13 xt yt zt

.      . C. 1 3 25

Tacóphươngtrìnhthamsốcủađườngthẳnglà

     . D. 1 3 25

xt yt zt

     . Lờigiải ChọnC

zt     

1

d b a fxxFaFb  B.  d b a fxxFbFa 

C.  d b a fxxFaFb   . D.  d b a fxxFbFa   .

Khẳngđịnh

Câu24: Chohìnhchóp SABCD cóđáy ABCD làhìnhchữnhật, ,2, ABaADaSA  vuônggócvới đáyvà 3SAa  Thểtíchcủakhốichóp SABCD bằng

A. 343 3 a B. 343a C. 323 3 a D. 323a

Lờigiải ChọnC

Thểtíchkhốichóp: 3 1123 ...3..2. 333 ABCD aVSASaaa   .

Câu25: Tậpnghiệmcủabấtphươngtrình 3 log11 x là

Lờigiải ChọnA

3 log11134 xxx 

Câu26: Chohìnhchóptứgiácđều SABCD cóđáy ABCD làhìnhvuôngcạnh 2a,cạnhbênbằng 3a . Khoảngcáchgiữahaiđườngthẳng BC và SA bằng

A. 3 2 a . B. 3a. C. 2 2 a . D. 2a .

Lờigiải ChọnD

Tacó     //,,,2,2 BCSADdBCSAdBCSADdBSADdOSADh    

Do chóp SABCD là chóp tứ giác đều nên SOABCD  nên tứ diện OSAD là khối tứ diện vuôngtại 22222222 11111112 222 a O h hSOAOODaaaa 

Tacó 22 2ACaOAOCODa  22 SOSCOCa   .

Vậy ,2dBCSAa  .

Câu27: Lấyngẫunhiên3viênbitừhộpđựng5viênbiđỏvà7viênbixanh.Xácsuấtđểlấyđược3viên bicùngmàubằng

A. 35 44 B. 9 44 C. 35 22 D. 9 22 Lờigiải

ChọnB +)Sốphầntửkhônggianmẫulà 3 12nC  +)GọiAlàbiếncố“lấyđược3viênbicùngmàu”.

.

Vậy 3 12

PA C 

(459 )44

Câu28: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn

3?

độđiểmcựctiểunhỏhơn

2 B. 5 C. 3 D. 4 Lờigiải

ChọnB 2 '3324324 yxmxxxm   0 '0 24 x y xm  

m m mm

Vì m nguyênthuộcđoạn  2;3 nên  2;1;0;1;3m

Câu29: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh 2a, SA vuông góc với đáy và 3SAa  .Gócgiữahaimặtphẳng  SBC và  ABC bằng

A. 045 B. 090 C. 060 D. 030

Lờigiải

ChọnA

Kẻ AHBC  mà SABCSHBC 

Dođógócgiữahaimặtphẳng  SBC và  ABC làgóc  AHS

Tamgiác ABC làtamgiácđềucạnh 2a nên 3AHa  .

Suyratamgiác SAH vuôngcântại  045AAHS

Câu30: Cho hình phẳng  H giới hạn bởi đồ thị hàm số 24 yx  và trục hoành. Thể tích khối tròn

xoayđượctạothànhkhiquay  H xungquanhtrụchoànhbằng

Từđồthị,tathấyhaiđườngthẳng 33 2,2yy cắtđồthịhàmsố

biệt.Vậyphươngtrình

Câu31: Chohàmsố yfx  cóđồthịnhưhìnhvẽ.

Sốnghiệmthựcphânbiệtcủaphươngtrình  230 fx là

32411123fxxxxf

Câu34: Chohàmsố 24 yxx  .Hàmsốđãchonghịchbiếntrênkhoảngnàodướiđây?

ChọnD

Hàmsố 24 yxx  có +)TXĐ:  ;40;D . +) 2

2 4 x y xx    ; 02yx  +)BBT

Hàmsố 24 yxx  nghịchbiếntrênkhoảng  ;4

Câu35: Chosốphức z thỏamãn 21(52)(1) ziii  Môđuncủa z bằng

A. 17. B. 13. C. 217. D. 213.

Lờigiải

trình  1 là:  15;8\2T

Đườngthẳng yxm  cắtđồthịhàmsố 23 1 x y x 

(1) cóhainghiệmphânbiệtdươngkhác1

haiđiểmphânbiệtcóhoànhđộdương

m mm m

Vậycácgiátrịnguyêncủa m trênđoạn  3;3 thỏamãnbàitoánlà: 3;2;1;0

Cách2

Xétphươngtrình: 23 1 x xm x  23 1 x xm x  2

 

Đườngthẳng yxm  cắtđồthịhàmsố 23 1 x y x  tạihaiđiểmphânbiệtcóhoànhđộdương thì (2) có hai nghiệm phân biệt dương khác 1 Khi đó đường thẳng ym  cắt đồ thị hàm số ()yhx  tạihaiđiểmphânbiệttrênkhoảng  0; .DựavàoBBTcủahàmsố ()hx tacó: 1m .

Câu38: Cho hàm số bậc ba yfx  Biết hàm số  52 yfx   có đồ thị là một Parabol  P như hìnhvẽ.Cóbaonhiêugiátrịnguyêncủathamsố m đểhàmsố  2 22 yfxxm  nghịchbiến

trênkhoảng  0;1 .

Vậycó 22 giátrịnguyêncủa x thỏamãn.

Câu37: Tổngtấtcảcácgiátrịnguyêncủathamsố m thuộcđoạn  3;3 đểđườngthẳng yxm  cắt

đồthịhàmsố 23 1 x y x  tạihaiđiểmphânbiệtcóhoànhđộdươnglà

4424 xxttttft

0122122122521222222ft t x x 

trênkhoảng  0;1

 2 2 42220,0;1220,0;1 gxxfxxmxfxxmx    

 420,0;1doxx

2 2 222222,0;122222,0;1 xxmxmxxmx  Đặt    2 222420,0;1hxxxhxxx   .

BBT:

Điềukiệnbàitoán 20122211;0 m m m m m   

Vậycó2giátrịnguyêncủa m thỏamãnbàitoán.

Câu39: Chokhốilăngtrụtứgiácđều ABCDABCD  cócạnhđáybằng a Biếtkhoảngcáchtừ C đến mặtphẳng  ABD  bằng

a Thểtíchkhốilăngtrụđãchobằng

Đặt   ,;. AAbdAABDh     .Gọi OACBD  .

Do . ABCDABCD  làlăngtrụtứgiácđềusuyra O làtrungđiểmcủa AC.Suyra:   ;; dCABDdAABDh 

Tacó: 2222222222222 11114111421212 2 ba hABADAAaaabaabab   3 22 .... 22

ABCDABCD aaVABACAAaa     .

Câu40: Trongkhônggian Oxyz,chomặtphẳng :430Pxyz vàđiểm  1;1;3A Mặtphẳng

 QP  vàcắtcáctia , OxOy lầnlượttạicácđiểm B và C saochotamgiác ABC códiện tíchbằng 222.Khoảngcáchtừđiểm  2;2;1M đến  Q bằng

A. 22 B. 86 3 C. 6 3 D. 22 3 Lờigiải

ChọnA Mặtphẳng  QPQ  códạng: 403xyzdd 

 ;0;0,0;;0 QOxBdQOyCd   . Do B, C lần lượt thuộc các tia , OxOy 0d .





22414 22. 114  





Tacó 1 cos, 14 abab ab   

Câu42: Mộtkhốinón  N cóbánkínhbằng R vàchiềucaobằng 18,đượclàmbằngchấuliệukhông

thấm nước có khối lượng riêng lớn hơn khối lượng riêng của nước. Khối  N được đặt trong

mộtcáicốchìnhtrụđườngkínhbằng 6R,saochođáycủa  N tiếpxúcvớiđáycủacốc(tham

khảohìnhvẽ).Đổnướcvàocốcđếnkhimứcnướcđạtđộcaobằng 18 thìlấykhối  N ra.Độ caocủanướctrongcốcsaukhiđãlấykhối  N rabằng

Câu44: Cho phương trình 227100zmzm với m là tham số thực. Có bao nhiêu giá trị nguyên của m đểphuongtrìnhcóhainghiệmphứcphânbiệt 12 , zz thỏamãn: 1122 zzzz  A. 3 B. 2 C.1 D. 4 Lờigiải

ChọnB

Đểphươngtrìnhcóhainghiệmphức

2 '0710025 mmm 

zz zzzzzz zz

Vậychiềucaocủanướctrongcốc

, TH1: 12zz  ,suyra  3;4m , TH2: 12 zz  1212 10 000() 7 zzzzzmkotm 

Vậy  3;4m

Câu45: Chophươngtrình 4(3)280 x x m ( m làthamsố).Đểphươngtrìnhđãchocóhainghiệm phânbiệtthỏamãn  12338xx thìgiátrịcủathamsố m thuộckhoảngnàodướiđây?

A.  29;30 B.  27;28 C.  30;31 D.  28;29 Lờigiải

ChọnA

Đặt: 2xt

cóhainghiệmdươngphânbiệt 2 12 12 306230 0304423. 23 080 423 mmm ttm mm tt m                     1 11212log xtxt ; 2 2222 2log. xtxt

Suyra  1221222122loglogloglog83.xxtttt 

x t

21 4. 532

 3 3lnln2,473;4;5;.....;2024 3



3 .ln.1ln3ln? xx xaeexa

 

nên 3ln00. xax

e e aeaaeaa  vì (2024)aa nguyên dương.Vậycó2022giátrị.

Câu47: Trong không gian Oxyz, cho đường thẳng 122 : 211 dxyz    và mặt phẳng

:280Pxyz . Tam giác ABC có  1;2;2A và trọng tâm G nằm trên d. Khi các đỉnh , BC diđộngtrên  P saochokhoảngcáchtừ A tớiđườngthẳng BC đạtgiátrịlớnnhất, mộtvectơchỉphươngcủađườngthẳng BC là

A.  2;1;1 B.  2;1;1 C.  1;2;0 D.  1;2;0

Lờigiải

ChọnC

Gọi I làtrungđiểmcủa BC

 21;2;2GdGaaa  .

G làtrọngtâmtamgiác ABC nên 333 3;;4 222 AIAGaaa  





      

2

Khiđó , BCAIBCP  nên BC cóvectơchỉphươnglà  ,12;24;0 PAIn   

trịlớnnhất,giátrịnhỏnhấtcủabiểuthức 22847Pxyxy  .Khiđó Mm  bằng

32. B.36. C.10. D.4.

Vậy

19,9Mm

Câu49: Trongkhônggian Oxyz,chohaiđiểm (1;2;2)M và (2;1;3)S .Mặtphẳng () P điqua M và cắtcáctrụctọađộ ,, OxOyOz lầnlượttạicácđiểm ,, ABC saocho M làtrựctâmcủatamgiác ABC.Thểtíchcủakhốichóp . SABC bằng

A. 7 2 . B. 27 8 . C. 81 4 . D. 27 4 .

Lờigiải

ChọnB

Mặt phẳng () P đi qua M và cắt các trục tọa độ ,, OxOyOz lần lượt tại các điểm (;0;0),(0;;0),(0;0;) AaBbCc

Nênphươngtrìnhmặtphằng () P códạng 1xyz abc  mà 1 12 2 ()MP abc  .

Tacó (1;2;2),(1;2;2)và(0;;),(;0;). AMaBMbBCbcACac    

MàMlàtrựctâm 0 02 AMBCbc ABC acBMAC

Từ(1)và(2)suyra 99 9;;():2290 22 abcPxyz  .

C tạihaiđiểm  1;1,0;6AB .

Miềnnghiệmcủahệ  I làmiềntômàuxanhtrênhìnhvẽ.

Tacó:  22 4213Pxy  22 4213131xyPP 

Trongmặtphẳngtọađộ Oxy,tậphợpcácđiểmcótọađộthỏamãn  1 làđườngtròn  1C tâm

 4;2K , bán kính 113 RP  (đường tròn  1C suy biến thành điểm  4;2K khi 13P ).

Vậytậpcácgiátrịcủa P phảithỏamãn  1C vàmiềnnghiệmcủahệ  I cóđiểmchung.Khi

đótacó:  1 213max;42 KQRPKAKB

919 P 

Tacó (99 9;0;0),(0;;0),(0;0;). 22 ABC

Chiềucaocủakhốichóp SABC là

Diệntíchtamgiác ABC là 243 8 k

Thểtíchkhốichóplà 11243127 .... 33838SABC Vkh

Câu50: Trongmặtphẳng Oxy,gọi () H làtậphợpđiểm (;)Mxy thỏamãn 22(||||)xykxy  với k làsốnguyêndương, S làdiệntíchhìnhphẳnggiớihạnbời () H .Giátrịlớnnhấtcủa k để 250S bằng A.5. B.4. C.7. D.6. Lờigiải

ChọnD

Dotínhđốixứngqua , OxOy của  H nêntachỉcầnxétkhi 0;0xy .Khiđó

22 xykxy  thành  222 22 222 kkkxykxyxy    1H

Do k làsốnguyêndươngnên  1H làđườngtròntâm ; 22 kk I  ,bánkính 2 k R

S

Ở

GIÁODỤCVÀĐÀOTẠOTỈNHPHÚYÊN TRƯỜNGTHPTCHUYÊNLƯƠNGVĂNCHÁNH

ĐỀTHITHỬTNTHPTLẦN1-Nămhọc:2022-2023

Câu1: Trongkhônggian ,chomặtphẳng .Vectơnàodướiđâylàmộtvectơ pháptuyếncủa ?

A. B. C. D.

Câu2: Tậpnghiệmcủabấtphươngtrình là

A. B. C. D.

Câu3: Chohìnhchóp cóđáylàtamgiácđềucạnh . Cạnhbên vuônggócvớimặt phẳng

.Thểtíchkhốichóp

bằng

,

A.

. B.

Câu4: Trênkhoảng

. C.

. D.

.

Câu5: Trongkhônggian

,tọađộhìnhchi

uc

Câu6: Trongkhônggian

,đườngthẳng

Câu7: Trongmặtmặtphẳngtọađộ,điểmbi

Câu8: Chohàmsố

bảngbiếnthiênnhưsau:

Giátrịcựctiểucủahàmsốđãchobằng A.

Câu9: Với

loga a bằng

và

,khiđó

Câu10: Nghiệmcủaphươngtrình