

ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection 30 ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ II MÔN TOÁN 12 (35 CÂU TRẮC NGHIỆM, 50 CÂU TRẮC NGHIỆM) - 590 TRANG
VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL.COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405
WORD
Môn: Toán 12
Thời gian: 90 phút
I - PHẦN TRẮC NGHIỆM
Câu 1. [NB] Tìm họ nguyên hàm 3d Fxxx .
A. 4 4 Fxx . B. 4 4 x FxC . C.
Câu 2. [NB] Khẳng định nào sau đây sai?
A. Cho hàm số fx xác định trên K và Fx là một nguyên hàm của fx trên K . Khi đó
Fxfx , xK
B. 'd fxxfxC .
C. dd kfxxkfxx với k là hằng số khác 0
D. Nếu Fx và Gx đều là nguyên hàm của hàm số fx thì .FxGx
Câu 3. [NB] Khẳng định nào say đây đúng?
A. cosdsinxxx
. C. 1dlnxxC x
Câu 4. [NB] Cho Fx là một nguyên hàm của hàm số
tục trên Trong các khẳng định sau, có bao nhiêu khẳng định sai?
(I) fxgxdxfxdxgxdx
(II) .. fxgxdxfxdxgxdx
(III) . kfxdxkfxdx
(IV)
với mọi số thực k .
3
D. 23
FxxC .
xC .
B. cosdsin
D. 2d2 xxxC .
.
xxxC
.
2 fxxx thỏa mãn 02F , giá trị của 2F bằng A. 8 3 B. 8 3 C. 2 D. 5
số fx và gx xác định và
Câu 5. [NB] Cho hai hàm
liên
.
fxdxfxC . A. 1. B. 2 . C. 3. D. 0 . Câu 6. [NB] Cho hàm số 12sin fxx và 01f . Mệnh đề nào sau đây đúng? A. 2cos2fxxx . B. 2cos1fxxx . C. 2cos2fxxx . D. 2cos1fxxx . Câu 7. [NB] Họ nguyên hàm của hàm số 1021fxx là A. 921 18 x FxC . B. 1121 11 x FxC . C. 1121 22 x FxC . D. 921 9 x FxC . Câu 8. [NB] Cho 2 1 3fxdx ; 2 1 5gxdx Khi đó giá trị của biểu thức 2 1 32gxfxdx là A. 21 B. 14 C. 10 D. 24 Câu 9. [NB] Cho fx là hàm số liên tục trên ; ab và Fx là một nguyên hàm của fx Khẳng định nào sau đây là đúng? ĐỀ SỐ 1 ĐỀ ÔN TẬP KIỂM
TRA GIỮA HỌC KÌ II
(Đề gồm
35 câu TN, 4 câu tự luận)
C. .dd.d bbb aaa fxgxxfxxgxx .
. Câu 12. [NB] Cho hàm số f liên tục trên đoạn 0;2 Trong các khẳng định sau, khẳng định nào đúng ?
A. 212 001
ddd fxxfxxfxx .
B. 212 001
ddd fxxfxxfxx .
ddd fxxfxxfxx . D. 220 011 .
ddd fxxfxxfxx
Câu 13. [NB] Cho ; fxgx là hai hàm số liên tục trên và các số thực ,, abc Mệnh đề nào sau đây sai?
B. ddd bbb aaa fxgxxfxxgxx C. dd bb aa fxxftt . D. .dd.d bbb aaa fxgxxfxxgxx . Câu 14. [NB] Cho 3 0 d2fxx và 3 0 d5.gxx Khi đó tích phân 3 0 2d fxgxx bằng. A. 1 . B. 3 . C. 4 . D. 5 . Câu 15. [NB]Trongkhônggianvớihệtọađộ Oxyz ,chohaiđiểm 1;1;2M và 2;2;1N .Tọađộvectơ MN là A. 3;3;1 . B. 1;1;3 . C. 3;1;1 . D. 1;1;3 .
Câu 16. [NB] Trong không gian với hệ tọa độ Oxyz , cho
A. b b a a fxdxFxFaFb B. b b a a fxdxFxFbFa C. b b a a fxdxfxfbfa D. b b a a fxdxFxFbFa Câu 10. [NB] Tích phân 2 0 2d Ixx Khẳng định nào sau đây đúng? A. 2 0 2 2d2 0 Ixx . B. 2 2 0 2 2d4 0 Ixxx . C. 2 2 0 0 2d 2 Ixxx . D. 2 2 0 2 2d 0 Ixxx . Câu 11. [NB] Cho hai hàm số fx , gx liên tục trên đoạn a;b và số thực k . Trong các khẳng định sau, khẳng định nào sai ? A. ddd bbb aaa fxgxxfxxgxx . B. ddd bbb aaa fxgxxfxxgxx
D. bb aa kfxdxkfxdx
C. 211 002
23 OMik Tọa độ điểm M là A. 2;3;0 . B. 2;0;3 . C. 0;2;3 . D. 2;3 . Câu 17. [NB] Trong không gian Oxyz cho mặt cầu 222 :12325Sxyz .Tìm tọa độ tâm và bán kính của mặt cầu. A. 1;2;3I , 5R B. 1;2;3I , 5R C. 1;2;3I , 5R D. 1;2;3I , 5R
A. d0 a a fxx
Câu 18. [NB] Cho mặt phẳng :3220Pxz . Vectơ nào là một vectơ pháp tuyến của P ? A. 3;2;0n B. 3;0;2n C. 3;0;2n D. 3;2;0n Câu 19. [NB] Trong không gian Oxyz , vectơ nào sau đây là một vectơ pháp tuyến của P . Biết 1;2;0u , 0;2;1v là cặp vectơ chỉ phương của P . A. 1;2;0n B. 2;1;2n C. 0;1;2n D. 2;1;2n Câu 20. [NB] Tìm m để điểm ;1;6Mm thuộc mặt phẳng :250.Pxyz A. 1m . B. 1m . C. 3m . D. 2m . Câu 21. [TH] Nguyên hàm Fx của hàm số 3 1xfxe thỏa mãn 1 0 6 F là A. 3213 3 32 xxx Fxeeex B. 3213 32 32 xxx Fxeeex C. 32 363xxx Fxeee . D. 32 3632 xxx Fxeee . Câu 22. [TH] Cho 687 4.52d5252 xxxAxBxC với , AB và C . Giá trị của biểu thức 50175AB là A. 9 B. 10 C. 11 D. 12 Câu 23. [TH] Biết hàm số yfx có 2 6421fxxxm , 12f và đồ thị của hàm số yfx cắt trục tung tại điểm có tung độ bằng 3 Hàm số fx là A. 32 223 xxx B. 32 2233 xxx C. 32 223 xxx D. 124 x Câu 24. [TH] Họ nguyên hàm của hàm số 1 ()()fxxx x là A. 22 (ln)22 xxxC B. 3 3 xxC . C. 23 ()6ln xxxC x D. xC Câu 25. [TH] Họ nguyên hàm của hàm số 23ln fxx x là A. 3 lnlnxxC B. 3lnxC . C. 3lnxxC D. lnlnxC Câu 26. [TH] Tích phân 2 2 1 1dx xx bằng A. 2ln 3 . B. ln6 . C. 4ln 3 . D. ln3. Câu 27. Cho 3 1 d2fxx , 5 1 d4ftt Tính 5 3 d fyy A. 3I . B. 5I . C. 2I . D. 6I . Câu 28. Cho hàm số fx liên tục trên và 2 0 3 3d17fxxx Tính 3 0 d fxx A. 5 B. 7 . C. 9 . D. 10. Câu 29. Cho 3 0 dln2ln3 3421 xaxbc x với ,, abc là các số nguyên. Giá trị của abc bằng A. 1. B. 2 . C. 7 . D. 9. Câu 30. [TH] Cho 6 0 1sin.cosd 160 n xxx (với *n ). Tìm n A. 3 B. 6 C. 5 D. 4.
Câu 31. [TH] Cho 1 0 3d x xexabe Tính ab A. 1 . B. 7 . C. 1 . D. 7 . Câu 32. [TH] Cho 0;2;2,3;1;1,4;3;0,1;2;. ABCDm Tìm m để 4 điểm ,,, ABCD đồng phẳng. A. 5m . B. 5m . C. 1m . D. 1m . Câu 33. [TH] Trong không gian với hệ trục tọa độ Oxyz , tìm tập hợp tất cả các giá trị của tham số m để phương trình 22222232330xyzmxmyzm là phương trình mặt cầu: A. 17 m . B. 71 m C. 1 7 m m . D. 7 1 m m . Câu 34. [TH] Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P : 2210 xyzm và mặt cầu 222 :42650 Sxyzxyz . Để mặt phẳng P tiếp xúc với mặt cầu S thì tổng các giá trị của tham số m là: A. 8 . B. 9. C. 8 . D. 4 . Câu 35. [TH] Trong không gian với hệ trục tọa độ Oxyz , phương trình mặt phẳng P đi qua điểm 1;2;3A và chứa trục Oz là 0axby . Tính tỉ số Ta b . A. 2 . B. 1 2 . C. 2 . D. 3. II - PHẦN TỰ LUẬN Bài 1. [VD] Tính 132 2 0 2.e63.e3d 3 xx xxx Sx x . Bài 2 . [VD] Cho tam giác ABC có 45;30ABCACB và 2 ACa Tính thể tích khối tròn xoay nhận được khi quay đường gấp khúc BAC quanh trục BC ? Bài 3. [VDC] Cho hàm số fx xác định trên \1;1 và thỏa mãn: 2 1 1fx x . Biết rằng 330ff và 11 2 22ff Tính 204Tfff Bài 4. [VDC] Tính tích phân sau 32 6 4sin1d cos3.sin x Ix xx .
I - PHẦN TRẮC NGHIỆM
Câu 1. [NB] Tìm họ nguyên hàm
Ta có: 4 3d 4 x xxC
Câu 2. [NB] Khẳng định nào sau đây sai?
A. Cho hàm số fx xác định trên K và
Fxfx , xK
B. 'd fxxfxC .
C. dd kfxxkfxx với k là hằng số khác 0
D. Nếu Fx và Gx đều là nguyên hàm của hàm số fx thì
Lời giải
Các nguyên hàm có thể có hằng số khác nhau.
Câu 3. [NB] Khẳng định nào say đây đúng?
FxGx
A. cosdsinxxx C. 1dlnxxC x
B. cosdsinxxxC .
D. 2d2 xxxC .
Lời giải Theo bảng nguyên hàm của một số hàm số thường gặp: cosdsinxxxC
Câu 4. [NB] Cho Fx là một nguyên hàm của hàm số
2F bằng
.
ĐÁP ÁN PHẦN TRẮC NGHIỆM ĐÁP ÁN CHI TIẾT
3d Fxxx . A. 4 4 Fxx . B. 4 4 x FxC . C. 3 FxxC . D. 23xC . Lời giải
Chọn B
fx trên K
Fx là một nguyên hàm của
Khi đó
2
thỏa
trị của
fxxx
mãn 02F , giá
A. 8 3 B. 8 3 C. 2 D. 5 Lời giải
2
FxfxxxxxC . 022FC 32 2 32 Fxxx . 32 228 22 323 F . Câu 5. [NB] Cho hai hàm số fx và gx xác định và liên tục trên . Trong các khẳng định sau, có bao nhiêu khẳng định sai? (I) fxgxdxfxdxgxdx 1B 2D 3B 4A 5B 6D 7C 8A 9D 10D 11C 12A 13D 14A 15D 16B 17A 18C 19B 20A 21B 22A 23A 24B 25B 26C 27D 28D 29A 30D 31D 32D 33B 34C 35A
32
dd 32 xx
(II) fxgxdxfxdxgxdx
(III) . kfxdxkfxdx với mọi số thực k .
(IV) fxdxfxC .
A.1. B.2 .
Khẳng định (II) và (III) là sai, vì 0k .
C.3. D.0 .
Lời giải
Câu 6. [NB] Cho hàm số 12sin fxx và 01f Mệnh đề nào sau đây đúng?
A. 2cos2fxxx
C. 2cos2fxxx
Ta có fxdxfxC . Từ đó suy ra
B. 2cos1fxxx
D. 2cos1fxxx
Lời giải
12sin2in2coss fx xdxxxdxxxC
d 0102.111 fCC Vậy hàm 2cos1fxxx Câu 7. [NB] Họ nguyên hàm của hàm số 1021fxx là A. 921 18 x FxC . B. 1121 11 x FxC . C. 1121 22 x FxC . D. 921 9 x FxC . Lời giải Ta có: 1111 1010 212111 212121. 221122 xx xdxxdxCC . Vậy 1121 22 x FxC Câu 8. [NB] Cho 2 1 3fxdx ; 2 1 5gxdx . Khi đó giá trị của biểu thức 2 1 32gxfxdx là A.21. B. 14. C. 10. D. 24. Lời giải Ta có: 22222 11111 3232323.52.321 gxfxdxgxdxfxdxgxdxfxdx . Câu 9. [NB] Cho fx là hàm số liên tục trên ; ab và Fx là một nguyên hàm của fx . Khẳng định nào sau đây là đúng? A. b b a a fxdxFxFaFb B. b b a a fxdxFxFbFa C. b b a a fxdxfxfbfa D. b b a a fxdxFxFbFa Lời giải Chọn D;
k . Trong các khẳng định sau, khẳng định nào sai ?
A. ddd bbb aaa fxgxxfxxgxx
B. ddd bbb aaa fxgxxfxxgxx
C. .dd.d bbb aaa fxgxxfxxgxx
D. bb aa kfxdxkfxdx
Lời giải Chọn C; Câu 12. [NB] Cho hàm số f liên tục trên đoạn 0;2 Trong các khẳng định sau, khẳng định nào đúng
Câu 10. [NB] Tích phân 2 0 2d Ixx Khẳng định nào sau đây đúng? A. 2 0 2 2d2 0 Ixx . B. 2 2 0 2 2d4 0 Ixxx . C. 2 2 0 0 2d 2 Ixxx . D. 2 2 0 2 2d 0 Ixxx . Lời giải Áp dụng định nghĩa tích phân: d b b a a fxxFxFbFa Ta có: 2 2 0 2 2d 0 Ixxx Câu 11. [NB] Cho hai hàm số fx , gx liên tục trên đoạn a;b và số thực
.
.
? A. 212 001 ddd fxxfxxfxx B. 212 001 ddd fxxfxxfxx C. 211 002 ddd fxxfxxfxx D. 220 011 ddd fxxfxxfxx Lời giải FB tác giả: Hương Liễu Lương Áp dụng tính chất ddd, bcb aac fxxfxxfxxacb Ta có: 212 001 ddd fxxfxxfxx . Câu 13. [NB] Cho ; fxgx là hai hàm số liên tục trên và các số thực ,, abc . Mệnh đề nào sau đây sai? A. d0 a a fxx . B. ddd bbb aaa fxgxxfxxgxx .
16. [NB] Trong không gian với hệ tọa độ Oxyz , cho 23
Lời giải
. D. 2;3 .
Ta có: ;; OMxiyjzkMxyz .
Vậy 232;0;3OMikM
Câu 17. [NB] Trong không gian Oxyz cho mặt cầu
và bán kính của mặt cầu. A.
C. dd bb aa fxxftt D. .dd.d bbb aaa fxgxxfxxgxx . Lời giải Theo tính chất tích phân ta chọn D. Câu 14. [NB] Cho 3 0 d2fxx và 3 0 d5.gxx Khi đó tích phân 3 0 2d fxgxx bằng. A. 1 . B. 3 . C. 4 . D. 5 . Lời giải Ta có : 333 000 2d2dd2.251 fxgxxfxxgxx . Câu 15. [NB]Trongkhônggianvớihệtọađộ Oxyz ,chohaiđiểm 1;1;2M và 2;2;1N .Tọađộvectơ MN là A. 3;3;1 . B. 1;1;3 . C. 3;1;1 . D. 1;1;3 . Lời giải Ta có: 21;21;121;1;3MNMN .
Tọa
A.
C.
Câu
OMik
độ điểm M là
2;3;0 . B. 2;0;3 .
0;2;3
222 :12325Sxyz .Tìm tọa độ tâm
1;2;3I , 5R B. 1;2;3I , 5R C. 1;2;3I , 5R . D. 1;2;3I , 5R . Lời giải Mặt cầu S có tâm 1;2;3I , bán kính 5R Câu 18. [NB] Cho mặt phẳng :3220Pxz . Vectơ nào là một vectơ pháp tuyến của P ? A. 3;2;0n B. 3;0;2n C. 3;0;2n . D. 3;2;0n . Lời giải Vecto pháp tuyến 3;0;2n Câu 19. [NB] Trong không gian Oxyz , vectơ nào sau đây là một vectơ pháp tuyến của P . Biết 1;2;0u , 0;2;1v là cặp vectơ chỉ phương của P A. 1;2;0n . B. 2;1;2n . C. 0;1;2n . D. 2;1;2n . Lời giải Ta có P có một vectơ pháp tuyến là ,2;1;2nuv .
Câu 20. [NB] Tìm m để điểm ;1;6Mm thuộc mặt phẳng :250.Pxyz A. 1m . B. 1m . C. 3m . D. 2m . Lời giải Điểm ;1;52.16501 MmPmm . Câu 21. [TH] Nguyên hàm Fx của hàm số 3 1xfxe thỏa mãn 1 0 6 F là A. 3213 3 32 xxx Fxeeex B. 3213 32 32 xxx Fxeeex C. 32 363xxx Fxeee . D. 32 3632 xxx Fxeee . Lời giải 3 1d x Fxex 32 331d xxx eeex 32331d xxx eeex 3213 3 32 xxx eeexC Mà 1 0 6 F 3.02.01.013 ..3.0 32 eeeC 113 3 632 C 1 2 6 C . Nên 3213 32 32 xxx Fxeeex . Câu 22. [TH] Cho 687 4.52d5252 xxxAxBxC với , AB và C . Giá trị của biểu thức 50175AB là A. 9. B. 10. C. 11. D. 12. Lời giải Đặt 6
4.52
fxxx FxAxBxC Theo đề bài ta có:
66
662008035.52452 AxABxxx . Đồng nhất hệ số ta được: 1 200450 803508 175 A A AB B . Vậy 501759 AB . Câu 23. [TH] Biết hàm số yfx có 2 6421fxxxm , 12f và đồ thị của hàm số yfx cắt trục tung tại điểm có tung độ bằng 3 Hàm số fx là A. 32 223 xxx B. 32 2233 xxx C. 32 223 xxx D. 124 x Lời giải Ta có: 232 d6421d2221 fxfxxxxmxxxmxC .
87
5252
876 52524.52 FxfxAxBxCxx
766 8.5..527.5..524.52 AxBxxx
405235.52452 AxBxxx
Theo đề bài, ta có: 32 12 12.12.1212 3 303 f mCm C C f Vậy 32 223fxxxx . Câu 24. [TH] Họ nguyên hàm của hàm số 1 ()()fxxx x là A. 22 (ln)22 xxxC . B. 3 3 xxC . C. 23 ()6ln xxxC x . D. xC . Lời giải 3 2 1 ()d(1)d3 x IxxxxxxC x
. Câu 25. [TH] Họ nguyên hàm của hàm số 23ln fxx x là A. 3 lnlnxxC . B. 3lnxC . C. 3lnxxC . D. lnlnxC . Lời giải Xét d Ifxx 2ln 3d x x x Đặt 1 lndd txtx x Khi đó 233d ItttC 3lnxC . Câu 26. [TH] Tích phân 2 2 1 1dx xx bằng A. 2ln 3 . B. ln6 . C. 4ln 3 . D. ln3 . Lời giải 2 22 2 2 1 11 1 1114 d()dlnln1lnln 113 x xxxx xxxxx . Câu 27. Cho 3 1 d2fxx , 5 1 d4ftt Tính 5 3 d fyy A. 3I B. 5I C. 2I D. 6I Lời giải Ta có 5153535 3311111 ddddddxdt6 fyyfyyfyyfyyfyyfxft . Câu 28. Cho hàm số fx liên tục trên và 2 0 3 3d17fxxx Tính 3 0 d fxx A. 5 B. 7 C. 9 D. 10 Lời giải Ta có 22 00 3 000 3333 3d17d3d17d2717d10 fxxxfxxxxfxxfxx . Câu 29. Cho 3 0 dln2ln3 3421 xaxbc x với ,, abc là các số nguyên. Giá trị của abc bằng A. 1 B. 2 C. 7 D. 9
Lời giải Đặt 1tx21tx 21xt d2d xtt . Đổi cận: 02xt ; 34xt . Khi đó: 2 222 233 22 111 1 167 .2dd23d36ln212ln26ln3 422233 tttt ttttttttt ttt Suy ra 7 12 6 a b c 1abc . Câu 30. [TH] Cho 6 0 1sin.cosd 160 n xxx (với *n ). Tìm n A. 3 B. 6 C. 5 D. 4. Lời giải Ta có: 1 1 66 6 00 0 1sin11 sin.cosdsindsin4 160112 n n nn x xxxxxn nn Câu 31. [TH] Cho 1 0 3d x xexabe . Tính ab A. 1 B. 7 C. 1 D. 7 Lời giải Đặt 3dud;ddxx uxxvexve Ta có: 11 11 00 00 3d3d2343 xxxx xexxeexeee . 4;37abab Câu 32. [TH] Cho 0;2;2,3;1;1,4;3;0,1;2;. ABCDm Tìm m để 4 điểm ,,, ABCD đồng phẳng. A. 5m . B. 5m . C. 1m . D. 1m . Lời giải Ta có: 3;1;1,4;1;2,1;0;2 ABACADm 111331 ,,,3;10;1 122441 ,.1 ABAC ABACADm ,,, ABCD đồng phẳng ,.01ABACADm Câu 33. [TH] Trong không gian với hệ trục tọa độ Oxyz , tìm tập hợp tất cả các giá trị của tham số m để phương trình 22222232330xyzmxmyzm là phương trình mặt cầu: A. 17 m . B. 71 m C. 1 7 m m . D. 7 1 m m . Lời giải Phương trình 22222232330xyzmxmyzm có dạng 2222220xyzaxbyczd với 2 ,3,1,33ambmcdm Phương trình đã cho là phương trình mặt cầu khi và chỉ khi 2220abcd 2 22231330670mmmmm 71 m
Câu 34. [TH] Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P : 2210 xyzm và mặt cầu 222 :42650 Sxyzxyz Để mặt phẳng P tiếp xúc với mặt cầu S thì tổng các giá trị của tham số m là: A. 8 . B. 9. C. 8 . D. 4 . Lời giải Mặt cầu S có tâm 2;1;3I và bán kính 2 22 21353R Để mặt phẳng P tiếp xúc với mặt cầu S thì 2.212.31 ,5 3 m dIPR 41519 415 41511 mm m mm Vậy tổng các giá trị của m là: 19118 . Câu 35. [TH] Trong không gian với hệ trục tọa độ Oxyz , phương trình mặt phẳng P đi qua điểm 1;2;3A và chứa trục Oz là 0axby . Tính tỉ số Ta b . A. 2 . B. 1 2 . C. 2 . D.3. Lời giải Ta có 1;2;3OA và 0;0;1k là hai vecto có giá song song hoặc nằm trên mặt phẳng P nên mặt phẳng P có một vecto pháp tuyến là ,2;1;0nOAk Vậy mặt phẳng P đi qua điểm 0;0;0O và có vecto pháp tuyến 2;1;0n nên có phương trình là: 20 xy Vậy 2T II - PHẦN TỰ LUẬN Bài 1. [VD] Tính 132 2 0 2.e63.e3d 3 xx xxx Sx x Lời giải Ta có 1122 32 2 2 00 23e332.e63.e3dd 3 3 x xx xxx xxx Sxx x x 11 2 00 de2d3 3 x x xx x 211 02 0 d e3 3 x x x x 1 2 0 d e3 3 x x . Xét 1 2 0 d 3 3 Ix x . Đặt 3tan xt 2 dd3 cos t x t . Đổi cận ta có 00xt ; 1 6 xt . Vậy 1 6 2 22 00 d3d 33 33tan1cos xt I x tt 6 6 0 0 d 6 tt . Vậy e 6 S . Bài 2 . [VD] Cho tam giác ABC có 45;30ABCACB và 2 ACa . Tính thể tích khối tròn xoay nhận được khi quay đường gấp khúc BAC quanh trục BC ?
Gọi H là hình chiếu vuông góc của A lên BC
Xét tam giác ACH vuông tại H , có 2 ACa , 30ACB nên 11 ..2 22 AHACaa
Tam giác ABH vuông tại H , có AHa , 45ABC nên BHAHa
Quay đường gấp khúc BAC quanh trục BC thu được khối tròn xoay có hình dạng là hai khối nón đỉnh B và đỉnh C , chung đáy là đường tròn ; HHA .
Xét khối nón 1N có đỉnh
Lời giải H B C A
và 3 .3 2 HCACa
là B , đáy là đường tròn ; HHA có 1 2311 33N VBHAHa Xét khối nón 2N có đỉnh là C , đáy là đường tròn ; HHA có 2 2313 33N VCHAHa Vậy thể tích khối tròn xoay nhận được bằng: 12 331 3NN VVVa Bài 3. [VDC] Cho hàm số fx xác định trên \1;1 và thỏa mãn: 2 1 1fx x Biết rằng 330ff và 11 2 22ff . Tính 204Tfff . Lời giải Ta có: 2 111111 d.d.ln 121121 x fxxxC xxxx Với ;11;x : 1 11 ln 21 x fxC x Mà 11 131131 330.lnln0 231231 ffCC 111 111 ln2ln00 222 CCC . Do đó với 11113 ;11;:ln2ln3;4ln 21225 x xfxff x . Với 1;1x : 2 11 ln 21 x fxC x . Mà 22 1111111122 2.ln.ln2 11222211 22 ffCC 222 11ln3ln321 22 CCC .
Do đó với 11 1;1:.ln101 21 x xfxf x Vậy 192041ln 25Tfff . Bài 4. [VDC] Tính tích phân sau 32 6 4sin1d cos3.sin x Ix xx Lời giải Giả sử: 222 4sin1sincoscos3sinsincos xAxBxxxCxx 222 4sin13sin3sincoscos xACxABxxBCx Đồng nhất hai vế ta có: 343 301 12 ACA ABB BCC . 3 6 33 3 6 66 3sincoscos3sin2 d cos3sin d 3sincosd23cossin23 cos3sin xxxx Ix xx x xxxxxJJ xx 333 666 ddd2 cos3sinsin2sincos 6212212 xxx J xx xx x 33 3 2 6 66 tan 212 1d1lntanln3 22122 tancostan 212212212 dx xx xxx . 1 23ln3. 2 I
Môn:
I
PHẦN TRẮC NGHIỆM
Câu 1. [NB] Khẳng định nào sau đây là sai ?
A. Nếu d fxxFxC thì d. fuuFuC
B. dd kfxxkfxx (k là hằng số và 0k ).
C. Nếu Fx và Gx đều là nguyên hàm của hàm số fx thì FxGx
D. ddd. fxgxxfxxgxx
Câu 2. [NB] Họ tất cả các nguyên hàm của hàm số 3231fxxx là
A. 4 3 4 xxxC B. 43 xxxC
C. 4 32 2. 4 xxxC D. 4 3 32. 4 xxxC
dưới đây đúng ?
A. .dd fxxfxx .
C. +ddd fxgxxfxxgxx
Câu 7. [TH] Cho
B. dd.d fxgxxfxxgxx .
ddd fxgxxfxxgxx
–
Câu 3. [NB] Họ tất cả các nguyên hàm của hàm số cos fxx là A. cosxC . B. cosxC . C. sinxC . D. sinxC . Câu 4. [NB] Họ tất cả các nguyên hàm của hàm số 2 1fx x là A. ln1xC . B. 2ln1xC . C. 1ln1 2 xC . D. lnxC . Câu 5. [TH] Tìm nguyên hàm Fx của hàm số 2x fxex thỏa mãn 3 0 2 F . A. 21 2 2 x Fxex . B. 23 2 x Fxex . C. 25 2 x Fxex D. 21 2 x Fxex Câu 6. [NB] Xét các hàm số , fxgx tùy ý, liên tục trên khoảng K và là một số thực bất kỳ. Mệnh đề nào
D.
d fxxFxC , khi đó 51d fxx là A. 51 FxC . B. 1 51 5 FxC . C. 551FxC . D. 1 5 FxC . Câu 8. [NB] Xét fx là một hàm số tùy ý, Fx là một nguyên hàm của fx trên đoạn ; ab . Mệnh đề nào dưới đây đúng ? A. d b a fxxfbfa . B. d b a fxxfafb . C. d b a fxxFbFa . D. d b a fxxFaFb . Câu 9. [NB] 2 1 1dx x bằng ĐỀ SỐ 2 ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ II
Toán
12
(Đề gồm
câu TN,
câu tự luận)
Thời gian: 90 phút
35
4
Câu 10. [NB] Cho hàm số yfx liên tục trên đoạn ; ab Gọi D là hình phẳng giới hạn bởi đồ thị
số yfx , trục hoành và hai đường thẳng xa , xb ab . Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
2d b a Vfxx .
.
Câu 17: [NB] Trong không gian với hệ trục Oxyz , cho mặt cầu 222 :24470 Sxyzxyz
độ tâm và bán kính của S là
A. 1;2;2 I và 8R
Câu 18 . [ NB] Trong
A. 1 2 . B. 3 4 . C. ln3. D. ln2 .
hàm
B.
C.
D. 22d b a Vfxx Câu 11. [NB] Biết 2 1 d2fxx và 2 1 d6gxx . Khi đó 2 1 d fxgxx bằng A. 4. B. 8 . C. 4 . D. 8. Câu 12. [NB] Cho hai hàm số ()fx , gx xác định và liên tục trên đoạn ; ab . Mệnh đề nào dưới đây đúng? A. ddd bab aba fxgxxfxxgxx . B. ddd bbb aaa fxgxxfxxgxx . C. ddd bba aab fxgxxfxxgxx D. ddd bba aab fxgxxfxxgxx Câu 13. [NB] Biết 3 1 2fxdx Tính 3 1 5fxdx A. 2 5 B. 5 C. 10 D. 10 Câu 14. [NB] Biết 2 1 5fxdx và 6 2 3fxdx . Tính 6 1 fxdx . A. 2 . B. 1 . C. 8 . D. 8. Câu 15. [NB] Trong không gian ,Oxyz cho 23.uijk Tọa độ của u là: A. 1;3;2 B. 1;2;3 C. 1;3;2 D. 1;2;3 Câu 16. [NB] Trong không gian Oxyz , cho điểm 1;2;3A Hình chiếu vuông góc của điểm A trên trục Oy là điểm nào dưới đây? A. 0;2;3
C.
D.
A.
2d b a Vfxx
d b a Vfxx
Q B. 1;2;0P
1;0;3N
0;2;0M
Tọa
.
B.
D.
2R
1;2;2I và 7R C. 1;2;2 I và 4R
1;2;2 I và
không gian với hệ trục tọa độ ,Oxyz cho hai điểm 1;2;3A và 3;1;0B Phương trình mặt phẳng đi qua điểm 1;2;3A và có véc tơ pháp tuyến AB là A. 2340 xyz . B. 240xy . C. 2340 xyz . D. 2390 xyz .
Câu 19. [ NB] Trong không gian Oxyz , cho mặt phẳng :220 xyz . Mặt phẳng nào dưới đây song song với mặt phẳng ?
A. :220Pxyz
C. :220Qxyz
B. :210Rxyz
D. :210Sxyz
Câu 20. [ NB] Trong không gian Oxyz , mặt phẳng đi qua ba điểm (1;0;0),(0;3;0),(0;0;2) ABC có phương trình là
A. 1 132 xyz . B. 1 132 xyz .
Câu 21. [NB] Họ tất cả các nguyên hàm của hàm số
C.
D. 1 132 xyz
1 132 xyz
A.
B.
C. 1sin2 2 xC D. 1sin2 2 xC Câu 22 . [ TH] Cho hàm số ()fx có ()sin2 fxx và (0)1f .Khi đó 4f bằng A. 1. B. 1 2 . C. 3 2 . D. 4 3 . Câu 23. [NB] Họ tất cả các nguyên hàm của hàm số cos2 fxxx là A. sin2xC . B. 2sinxxC . C. 2sin2xxC . D. 2sinxxC . Câu 24. [ NB] Họ tất cả các nguyên hàm của hàm số 2 2 1fxx x là A. 22 2 xxC x B. 22 2 xxC x C. 2 3 2 23 xxC x D. 2 3 2 2 xxC x Câu 25. [ TH]Mệnh đề
dưới đây đúng ? A. 2 2ln1dln11d xxxxxxx . B. 2ln1dln11d xxxxxxx C. 2 2ln1d1ln11d xxxxxxx . D. 2 2ln1d1ln11d xxxxxxx . Câu 26. [NB] Cho hàm số fx có đạo hàm fx liên tục trên đoạn 1;3 và thỏa mãn 12,f 35 f . Giá trị của 3 1 d Ifxx bằng A. 7I B. 4I C. 3I D. 7I Câu 27. [NB] Biết ln() Fxx x là một nguyên hàm của hàm số ()fx trên khoảng 0; Giá trị của e 1 12()d e Ifxx bằng A. 2 13 ee I B. 21 1e e I C. 2 13 ee I D. 3 1 e I Câu 28. [TH] Cho hàm số fx liên tục trên có 2 1 d2fxx và 5 1 d6fxx Khi đó 5 2 d fxx bằng? A. 4. B. 1. C. 8 . D. 4 .
cos2 fxx
2sin2xC
sin2xC
nào
Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm 1;2;1A , 2;1;3B ,
2;3;3C Điểm ;; Mabc thỏa mãn ABMC
222 33152xyz D.
222 33152xyz
Câu 34. [TH] Trong không gian với hệ tọa độ Oxyz , cho hai điểm (2;1;2)A và (2;5;4)
phẳng trung trực của đoạn thẳng AB có phương trình là
A. 22390 xyz .
C. 44690 xyz .
B. 22390 xyz .
D. 22390 xyz .
Câu 35. [TH] Trong không gian với hệ trục tọa độ Oxyz , khoảng cách từ điểm 3;3;4M đến mặt phẳng :2220 xyz bằng
A. 4
II – PHẦN TỰ LUẬN
B. 6
C. 2 3
D. 2
Câu 1. [VD] Cho hàm số yfx có đạo hàm liên tục trên thỏa 100f , 41f và
Tính tích phân
d Ixfxx
Câu 2. [VD] Cho hình nón đỉnh S có chiều cao 5 ha , bán kính đáy 7 ra Một thiết diện đi qua đỉnh của hình nón và có khoảng cách từ tâm O của đáy đến mặt phẳng chứa thiết diện là 4a Tính diện tích của thiết diện đó.
Câu 3. [VDC] Cho hàm số fx có đạo hàm liên tục trên khoảng 0; thỏa mãn điều kiện
25f và 262.1,0.xfxxfxx Tính 3f
Câu 4. [VDC] Tính 2sin3dx exx .
Câu 29. [VD] Cho hàm số yfx là hàm số bậc nhất liên tục trên . Biết 2 1 d2fxx và 4 0 d4fxx . Tính 2 1 21d ffxx ? A. 15. B. 0 . C. 6 . D. 15. Câu 30. [TH] Cho hàm số fx liên tục trên và 32 2 1 1 d2. 1 xfx x x Tính 10 2 d.fx Ix x A. 1 B. 1 2 C. 2 D. 4 Câu 31. [TH] Kết quả của tích phân 3 1 1d x Ixex được viết dưới dạng 3 Iaebe với , ab là các số hữu tỷ. Khẳng định nào sau đây là đúng? A. 1ab . B. 228ab . C. 2ab . D. 3ab . Câu 32. [TH]
Khi đó 222 Pabc có giá trị bằng A. 45 . B. 42 . C. 44 . D. 43. Câu 33. [TH] Trong không gian với hệ tọa độ Oxyz , cho 2;4;1A , 8;2;1B . Phương trình mặt cầu đường kính AB là A. 222 33126xyz . B. 222 33126xyz . C.
Mặt
B
3 1
10 4
31d2fxx
I – PHẦN TRẮC NGHIỆM
LỜI GIẢI CHI TIẾT
Câu 1. [NB] Khẳng định nào sau đây là sai ?
A. Nếu d fxxFxC thì d. fuuFuC
B. dd kfxxkfxx (k là hằng số và 0k )
C. Nếu Fx và Gx đều là nguyên hàm của hàm số fx thì .FxGx
D. ddd. fxgxxfxxgxx
Lời giải
Các nguyên hàm sai khác nhau hằng số nên C là đáp án sai.
Câu 2. [NB] Họ tất cả các nguyên hàm của hàm số 3231fxxx là
A. 4 3 4 xxxC
C. 4 32 2. 4 xxxC
B. 43 xxxC
D. 4 3 32. 4 xxxC
Lời giải
Ta có: 3232 313 xxdxxdxxdxdx
Câu 3. [NB] Họ tất cả các nguyên hàm của hàm số cos fxx là
A. cosxC B. cosxC C. sinxC
Câu 4. [NB] Họ tất cả các nguyên hàm của hàm số 2 1fx x là
A. ln1xC .
Ta có 21d2d2ln1 11 xxxC xx
Câu
BẢNG ĐÁP ÁN
4 3 4 xxxC
D. sinxC Lời giải Dựa
một số hàm số thường gặp,
chọn D.
theo bảng nguyên hàm của
ta
C.
D.
B. 2ln1xC .
1ln1 2 xC .
lnxC . Lời giải
5. [TH] Tìm nguyên hàm Fx của hàm số 2x fxex thỏa mãn 3 0 2 F . A. 21 2 2 x Fxex . B. 23 2 x Fxex . C. 25 2 x Fxex . D. 21 2 x Fxex . Lời giải Ta có: 2 2 xx FxexdxexC . Mà: 3 0 2 F nên 0 31 0 22 eCC 1.C 2.A 3.D 4.B 5.D 6.C 7.B 8.C 9.D 10.A 11.A 12.D 13.D 14.A 15.B 16.D 17.C 18.D 19.D 20.D 21.D 22.C 23.D 24.B 25.D 26.D 27.D 28.D 29.D 30.D 31.D 32.C 33.A 34.B 35.B
Câu 6. [NB] Xét các hàm số , fxgx tùy ý, liên tục trên khoảng K và là một số thực bất kỳ.
Mệnh đề nào dưới đây đúng ?
A. .dd fxxfxx . B. dd.d fxgxxfxxgxx .
C. +ddd fxgxxfxxgxx D. ddd fxgxxfxxgxx
Lời giải
Phương án .dd fxxfxx sai khi 0
Phương án
trên đoạn ; ab Gọi D là hình phẳng giới hạn bởi đồ thị hàm số yfx , trục hoành và hai đường thẳng xa , xb ab Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
giải Theo công thức tính thể tích vật tròn xoay khi quay hình D quanh trục hoành là:
21 2 x
Vậy:
Fxex
dd.d fxgxxfxxgxx sai vì lý thuyết. Phương án ddd fxgxxfxxgxx sai vì lý thuyết. Câu 7. [TH] Cho d fxxFxC , khi đó 51d fxx là A. 51 FxC B. 1 51 5 FxC C. 551FxC D. 1 5 FxC Lời giải 111 51d51..d5151d5151 555 fxxfxxfxxFxC Câu 8. [NB] Xét fx là một hàm số tùy ý, Fx là một nguyên hàm của fx trên đoạn ; ab Mệnh đề nào dưới đây đúng ? A. d b a fxxfbfa B. d b a fxxfafb C.
b a
D. d b a fxxFaFb Lời giải Theo
d b a fxxFbFa . Câu 9. [NB] 2 1 1dx x bằng A. 1 2 . B. 3 4 . C. ln3. D. ln2 . Lời giải Ta có 2 1 21dlnln2ln1ln2 1 xx x Câu 10. [NB] Cho hàm số yfx liên tục
A.
2d b a Vfxx . B. 2d b a Vfxx . C.
b a
D. 22d b a Vfxx Lời
d
fxxFbFa
định nghĩa, ta có
d
Vfxx
2d b a Vfxx Câu 11. [NB] Biết 2 1 d2fxx và 2 1 d6gxx Khi đó 2 1 d fxgxx bằng A. 4. B. 8 . C. 4 . D. 8. Lời giải Ta có: 222 111 ddd264fxgxxfxxgxx . Câu 12. [NB] Cho hai hàm số ()fx , gx xác định và liên tục trên đoạn ; ab Mệnh đề nào dưới đây đúng? A. ddd bab aba fxgxxfxxgxx . B. ddd bbb aaa fxgxxfxxgxx . C. ddd bba aab fxgxxfxxgxx D. ddd bba aab fxgxxfxxgxx Lời giải Theo tính chất của tích phân ta có: ddd bbb aaa fxgxxfxxgxx dd ba ab fxxgxx Câu 13. [NB] Biết 3 1 2fxdx . Tính 3 1 5fxdx . A. 2 5 B. 5 C. 10 D. 10 Lời giải Ta có 3 1 5fxdx 3 1 5.fxdx 5.210 Câu 14. [NB] Biết 2 1 5fxdx và 6 2 3fxdx . Tính 6 1 fxdx . A. 2 . B. 1 . C. 8 . D. 8. Lời giải Ta có 626 112 fxdxfxdxfxdx 532 . Câu 15. [NB] Trong không gian ,Oxyz cho 23.uijk Tọa độ của u là: A. 1;3;2 . B. 1;2;3 . C. 1;3;2 . D. 1;2;3 . Lời giải Ta có: 23 uijk 1;2;3u Câu 16. [NB] Trong không
1;2;3A Hình
vuông góc của điểm A trên trục Oy
điểm
A. 0;2;3Q B. 1;2;0P C. 1;0;3N D. 0;2;0M Lời giải Hình
vuông góc của điểm 1;2;3A lên trục Oy là điểm 0;2;0M
gian Oxyz , cho điểm
chiếu
là
nào dưới đây?
chiếu
. B. 240xy .
C. 2340 xyz D. 2390 xyz Lời giải
Ta có: 2;1;3AB
Mặt phẳng đi qua điểm 1;2;3A , véc tơ pháp tuyến 2;1;3nAB có phương trình là
2112330 xyz 2390 xyz .
Câu 19. [ NB] Trong không gian Oxyz , cho mặt phẳng :220 xyz Mặt phẳng nào dưới đây song song với mặt phẳng ?
A. :220Pxyz .
C. :220Qxyz .
B. :210Rxyz .
D. :210Sxyz .
Lời giải
Vì 1122 1121 nên mặt phẳng song song với mặt phẳng S
Câu 20. [ NB] Trong không gian Oxyz , mặt phẳng đi qua ba điểm (1;0;0),(0;3;0),(0;0;2) ABC có phương trình là
A. 1 132 xyz
trình mặt chắn đi qua ba điểm
(;0;0),(0;;0),(0;0;),,0
Câu 17: [NB] Trong không gian với hệ trục Oxyz , cho mặt cầu 222 :24470 Sxyzxyz . Tọa độ tâm và bán kính của S là A. 1;2;2 I và 8R B. 1;2;2I và 7R C. 1;2;2 I và 4R D. 1;2;2 I và 2R Lời giải Phương trình mặt cầu đa cho có dạng: 2222220xyzaxbyczd 222 abcd 1a , 2b , 2c , 7d .
1;2;2I
cầu 14474R .
1;2;3A và 3;1;0B . Phương trình mặt phẳng đi qua điểm 1;2;3A và có véc tơ pháp tuyến AB là A. 2340 xyz
Vậy tâm mặt cầu là
và bán kính mặt
Câu 18 . [ NB] Trong không gian với hệ trục tọa độ ,Oxyz cho hai điểm
. B. 1 132 xyz . C. 1 132 xyz D. 1 132 xyz
Phương
AaBbCcabc là 1xyz abc . Nên phương trình mặt phẳng đi qua ba điểm (1;0;0),(0;3;0),(0;0;2) ABC là 1 132 xyz . Câu 21. [NB] Họ tất cả các nguyên hàm của hàm số cos2 fxx A. 2sin2xC . B. sin2xC . C. 1sin2 2 xC . D. 1sin2 2 xC . Lời giải Ta có 1 cos2dsin2 2 xxxC
Lời giải
Câu 22 . [ TH] Cho hàm số ()fx có ()sin2 fxx và (0)1f .Khi đó 4f bằng A. 1. B. 1 2 . C. 3 2 . D. 4 3 . Lời giải Ta có ()d()() b a fxxfbfa nên 4 4 0 0 11 sin2dcos2(0) 224 xxxff Mà (0)1f suy ra 3 42f Câu 23. [NB] Họ tất cả các nguyên hàm của hàm số cos2 fxxx là A. sin2xC . B. 2sinxxC . C. 2sin2xxC . D. 2sinxxC . Lời giải Ta có: 2 2cos2dsin2.sin 2 x xxxxCxxC Câu 24. [ NB] Họ tất cả các nguyên hàm của hàm số 2 2 1fxx x là A. 22 2 xxC x B. 22 2 xxC x C. 2 3 2 23 xxC x D. 2 3 2 2 xxC x Lời giải Ta có 2 2 1 xdx x 2 1 2 xdxdxdx x 22 2 xxC x Câu 25. [ TH]Mệnh đề nào dưới đây đúng ? A. 2 2ln1dln11d xxxxxxx B. 2ln1dln11d xxxxxxx . C. 2 2ln1d1ln11d xxxxxxx
2 2ln1d1ln11d xxxxxxx . Lời giải Áp dụng công thức nguyên hàm từng phần: dd uvuvvu Đặt: ln1 2 ux dvxdx 2 1 1 dudx x vx 2 2ln1d1ln11d xxxxxxx Câu 26. [NB] Cho hàm số fx có đạo hàm fx liên tục trên đoạn 1;3 và thỏa mãn 12,f 35 f Giá trị của 3 1 d Ifxx bằng A. 7I B. 4I C. 3I D. 7I Lời giải 3 1 d(3)(1)527 Ifxxff
D.
Câu 27. [NB] Biết ln() Fxx x là một nguyên hàm của hàm số ()fx trên khoảng 0; . Giá trị của e 1 12()d e Ifxx bằng A. 2 13 ee I B. 21 1e e I C. 2 13 ee I D. 3 1 e I Lời giải e eee 1 111 111ln 2()dd2()de12 eee x Ifxxxfxx x 3 1 e Câu 28. [TH] Cho hàm số fx liên tục trên có 2 1 d2fxx và 5 1 d6fxx Khi đó 5 2 d fxx bằng? A. 4. B. 1. C. 8 . D. 4 . Lời giải Ta có 525 112 ddd fxxfxxfxx . 552 211 ddd624fxxfxxfxx Vậy 5 2 d4fxx Câu 29. [VD] Cho hàm số yfx là hàm số bậc nhất liên tục trên Biết 2 1 d2fxx và 4 0 d4fxx . Tính 2 1 21d ffxx ? A. 15. B. 0 . C. 6 . D. 15. Lời giải Ta có yfx là hàm số bậc nhất vậy phương trình hàm số yfx có dạng: fxmxn 0m Mà 2 22 2 11 1 1 d2d22 2 fxxmxnxmxnx 13 2222 22 mnmnmn 4 44 2 00 0 1 d4d44844 2 fxxmxnxmxnxmn . Vậy 8442 3 52 2 mn m mnn 25fxx Khi đó 2122154721247589 fxxxffxxx . Nên 22 22 1 11 21d89d4915ffxxxxxx .
Câu 30. [TH] Cho hàm số fx liên tục trên và 32 2 1 1 d2. 1 xfx x x Tính 10 2 d.fx Ix x A. 1. B. 1 2 . C. 2 . D. 4 . Lời giải Đặt 2 1 1d2ddd. 2 txtxxxxt Đổi cận: 12,xt310.xt Khi đó 1010 22 11d2d24. 22 ftfxtxI tx Câu 31. [TH] Kết quả của tích phân 3 1 1d x Ixex được viết dưới dạng 3 Iaebe với , ab là các số hữu tỷ. Khẳng định nào sau đây là đúng? A. 1ab . B. 228ab . C. 2ab . D. 3ab . Lời giải Đặt 1dd . ddxx uxux vexve Khi đó 3 3333 111 1 1d13. xxxx Ixeexxeeee Suy ra 3 1 a b Vậy 3.ab Câu 32. [TH] Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm 1;2;1A , 2;1;3B , 2;3;3C Điểm ;; Mabc thỏa mãn ABMC Khi đó 222 Pabc có giá trị bằng A. 45 . B. 42 . C. 44 . D. 43. Lời giải Ta có: 1;3;4AB , 2;3;3 MCabc Khi đó ABMC 21 33 34 a b c 3 6 1 a b c 222 Pabc 22 2 36144 . Câu 33. [TH] Trong không gian với hệ tọa độ Oxyz , cho 2;4;1A , 8;2;1B . Phương trình mặt cầu đường kính AB là A. 222 33126xyz . B. 222 33126xyz . C. 222 33152xyz D. 222 33152xyz Lời giải Gọi I là trung điểm của AB 3;3;1I là tâm của mặt cầu cần tìm. Bán kính RIA 222 234311 26 Phương trình mặt cầu đường kính AB là 222 33126xyz . Câu 34. [TH] Trong không gian với hệ tọa độ Oxyz , cho hai điểm (2;1;2)A và (2;5;4)B . Mặt phẳng trung trực của đoạn thẳng AB có phương trình là A. 22390 xyz B. 22390 xyz . C. 44690 xyz . D. 22390 xyz .
Lời giải Gọi I là trung điểm đoạn thẳng AB(0;3;1)I . Mặt phẳng trung trực của đoạn thẳng AB đi qua trung điểm (0;3;1)
làm vectơ pháp tuyến nên có phương trình là 4(0)4(3)6(1)0 xyz
Câu 35. [TH] Trong không gian với hệ trục tọa độ Oxyz , khoảng cách từ điểm
Câu 2. [VD] Cho hình nón đỉnh S có chiều cao 5 ha , bán kính đáy 7 ra . Một thiết diện đi qua
đỉnh của hình nón và có khoảng cách từ tâm O của đáy đến mặt phẳng chứa thiết diện là 4a .
Tính diện tích của thiết diện đó.
Lời giải
Giả sử thiết diện SAB đi qua đỉnh S cắt đường tròn đáy tại A và B (như hình vẽ).
Gọi I là trung điểm của dây cung AB . Từ tâm O của đáy vẽ OKSI thì OKSAB .
Theo bài ra ta có 7 AOra ; 5 SOha ; 4 OKa .
Trong tam giác vuông SOI ta có:
và nhận (4;4;6)AB
hay
I
22390 xyz
3;3;4
đến mặt phẳng :2220 xyz bằng A. 4 . B. 6 . C. 2 3 . D. 2 . Lời giải Ta có: 222 2.32.342 ,6 221 dM II - PHẦN TỰ LUẬN Câu 1. [VD] Cho hàm số yfx có đạo hàm liên tục trên thỏa 100f , 41f và 3 1 31d2fxx . Tính tích phân 10 4 d Ixfxx . Lời giải Đặt 31txd3dtx Đổi cận: 14xt ; 310xt Khi đó: 3 1 31d fxx 10 4 1d2 3ftt 10 4 d6ftt 10 4 d6fxx * Xét tích phân: 10 4 d Ixfxx Đặt: dd dd uxux vfxxvfx Khi đó 10 10 4 4 d Ixfxfxx
ff . * Vậy
M
10.104.462
2.I
222 111 OKOIOS 22 OIOSOK OSOK 22 5.420 32516 aaa aa 22SISOOI 2 240025 25 93 aa a . Xét tam giác vuông OAI ta có: 2222 ABAIAOOI 2 2400 249 9 a a 241 3 a . Vậy diện tích của thiết diện SAB là 125241 233SAB aa S 2 2541 9 a Câu 3. [VDC] Cho hàm số fx có đạo hàm liên tục trên khoảng 0; thỏa mãn điều kiện 25f và 262.1,0.xfxxfxx Tính 3f Lời giải Từ giả thiết, ta có: 222 6212.62 xfxxfxxfxxfxx Suy ra 2262xfxx 2262d xfxxx 2322 xfxxxC Lại có 25f 8C 2 28 2 fxx xx Vậy 56 3 9f . Câu 4. [VDC] Tính 2sin3dx exx . Lời giải * Xét 2sin3dx Iexx Đặt 2 dsin3d x ue vxx 2 d2d 1 cos3 3 x uex vx Khi đó 2212.cos3cos3d 33 xx Iexexx (1) * Xét 2cos3dx Jexx Đặt 2 1 1 dcos3d x ue vxx 2 1 1 d2d 1sin3 3 x uex vx 222 1212 .sin3sin3d.sin3 3333 xxx JexexxexI (2) Thay (2) vào (1)
xx IexexI Vậy 2 .2sin33cos3 13 x e IxxC .
ta có: 22 1212 .cos3.sin3 3333
Môn: Toán 12 Thời gian: 90 phút
Câu 1. [NB] Tìm khẳng định sai A. ddd fxgxxfxxgxx . B. ddd, bcb aac fxxfxxfxxacb . C. dd.d fxgxxfxxgxx . D. d fxxfxc . Câu 2. [NB] Tìm 7d x x ? A. 77d ln7 x xxC B. 177d 1 x xxC x . C. 7d7.ln7 xxxC . D. 7d7xxxC Câu 3. [NB] Tìm họ nguyên hàm của hàm số 21 3 fxxx x A. 232 1 3d3ln. xxxxxxC x B. 32 213 3dln 32 xx xxxxC x . C. 32 2 2 1313d 32 xx xxxC xx . D. 32 213 3dln 32 xx xxxxC x . Câu 4. [NB] Nếu sndix x fxexC thì ()fx bằng A. sinx ex B. sinx ex C. cos x ex D. cos x ex Câu 5. [TH] Tìm nguyên hàm của hàm số 32 xfxe A. 321d 3 x fxxeC B. 32dx fxxeC C. 32d3x fxxeC . D. 32d32x fxxxeC . Câu 6. [TH] Tính (sin2) xxdx A. 2 sin 2 xxC B. 2 cos2 2 xxC C. 21 cos2 2 xxC D. 21 cos2 22 xxC Câu 7. [VD] Biết Fx là nguyên hàm của hàm số 23cos fxxx và 3 2 F Tìm Fx A. 2 2 ()3sin64 Fxxx . B. 2 2 ()3sin4 Fxxx . C. 2 2 ()3sin4 Fxxx D. 2 2 ()3sin64 Fxxx Câu 8. [2D3-1-4] Cho Fx là một nguyên hàm của hàm số 1 1xfx e thỏa mãn 0ln2F Tìm tập nghiệm S của phương trình ln13 xFxe A. 3S . B. 3S . C. S . D. 3S ĐỀ SỐ 3 ĐỀ ÔN TẬP
KIỂM TRA GIỮA HỌC KÌ II
(Đề gồm 50 câu TN, 0 câu tự luận)
giây đầu tiên là (kết quả làm tròn đến hàng trăm)
8,31m .
Câu 19. [NB] Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số
hai đường thẳng , xaxb được tính theo công thức:
liên tục, trục hoành
Câu 9. [NB] Cho 2 1 d1fxx và 2 1 d3gxx Khi đó 2 1 ()d fxgxx có giá trị là A. 2 B. 4 C. 2 D. 4 Câu 10. [NB] Tích phân 1 0 1d 1 x x I có giá trị là A.ln2 . B.ln21. C.1ln2. D. ln2 . Câu 11. [NB] Giá trị của tích phân 4 0 2cos2dxx bằng A. 2 . B.2 . C. 1. D.1. Câu 12. [NB] Giá trị của tích phân 2 2 1 323d xxx bằng A.9 B.8 C.7 D.6 Câu 13. [TH] Giá trị của tích phân 3 2 0 (1tan)dxx bằng A. 3 . B. 3 3 . C. 3 . D.1. Câu 14. [TH] Giả sử 2 1 d1ln 212 x c x Giá trị đúng của c là A.1. B.3. C.8 . D.9. Câu 15. [TH] Biết 0 24d0 b xx , khi đó b nhận giá trị bằng A. 1 4 b b . B. 0 2 b b . C. 1 2 b b . D. 0 4 b b . Câu 16. [VD] Biếtrằng 5 2 1 3dln5ln2 3 xab xx , ab .Mệ́̂nhđếnằ̀osằuđặ̀yđúng? A. 20ab . B. 20 ab . C. 0ab . D. 0ab . Câu 17. [VD] Biết 4 0 1dln2 215 Ixab x vớ́i , ab lằ̀songuyệ́n.Tính Sab . A. 3S B. 3S C. S5 D. S7 Câu 18. [VDC] Một chiếc ôtô chuyển động với vận tốc 24 ()2(m/s) 4 t vt t . Quãng đường ôtô đó đi được trong 4
A.
B.
C.
. D.8,32m .
và
A. b a Sfxdx . B. b a Sfxdx . C. 0 0 b a Sfxdxfxdx D. 0 0 b a Sfxdxfxdx Câu 20. [NB] Hình phẳng H giới hạn bởi các đường 2 yx , 23yx và hai đường 0,x2x . Công thức nào sau đây tính diện tích hình phẳng H ?
8,23m .
8,24m
yfx
BC như hình vẽ sằu.
Câu 24. [VD]Cho hình phẳng giới hạn bởi các đường ln,0, yxxyxe quay xung quanh trục Ox
tạo thành khối tròn xoay có thể tích bằng
32be a Tìm a và b
A. 27;5ab . B. 26;6ab . C. 24;5ab . D. 27;6ab
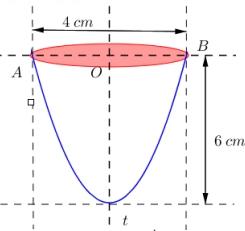
Câu 25. [VDC]Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây:
Ngướ̀itằđođướ̂cđướ̀ngkínhcuằmiệ́̂nglylằ̀4cmvằ̀chiếucằolằ̀6cm.Biếtrằngthiếtdiệ́̂n cuằchiếclycằtbớimặ̀̂tphằngquằtrûcđoixứnglằ̀mộtPằrằbol.Tínhthếtích 3 ()Vcm cuằ vặ̀̂tthếđằ̃cho
26. [2H3-1-1]Trong không gian với hệ tọa độ Oxyz , cho hai điểm 3;2;3
. Tìm tọa độ trung điểm I của đoạn thẳng AB
2;2;1I .
.
A. 2 2 0 23 Sxxdx . B. 2 2 0 23 Sxxdx . C. 2 2 0 23 Sxxdx D. 2 2 0 23 Sxxdx Câu 21. [NB] Tính thể tích V của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số yfx , trục Ox , hai đường thẳng , xaxbab quanh trục Ox A. x. b a Vfxd B. x. b a Vfxd C. 2 x. b a Vfxd D. 2 x. b a Vfxd Câu 22. [TH] Diệ́̂ntíchhìnhphằnggiớ́ihằ̂nbớiđothîhằ̀mso 32 3 yxx vằ̀trûchoằ̀nhlằ̀ A. 27 4 . B. 5 6 . C. 4 9 . D. 24 7 . Câu 23.
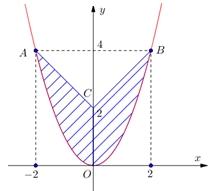
của phần hình phẳng giới hạn bởi đường Parabol đi qua gốc tọa độ và hai đoạn thẳng AC và
A.
6
B. 20 3 S C. 10 3 S D.
S
[VD] Tính diện tích S
25
S
9.
A.
B.
C.
D. 72 V 5
A
B
A.
B.
C. 2;0;8I . D.
2;2;1I .
72 V 5
.
V12 .
V12 .
Câu
và
1;2;5
1;0;4I
Câu
Câu37. [NB] Trong không gian với hệ tọa độ Oxyz cho 1;0;1;2;2;3IA . Mặt cầu (S) tâm I và đi qua điểm A có phương trình là
A. 22 2 113xyz
Câu 27. [2H3-1-1] Tích vô hướng của hai vectơ 2;2;5,0;1;2ab trong không gian bằng: A. 10. B. 12. C. 13. D. 14. Câu 28. [2H3-1-2] Trong không gian với hệ toạ độ oxyz cho các véctơ 1;2;1a , 0;4;3b , 2;1;4c Gọi 235 uabc Tìm toạ độ u A. 8;3;9 B. 9;5;10 C. 8;21;27 D. 12;13;31 Câu 29. [2H3-1-2] Trong không gian Oxyz cho tam giác ABC với 2;1;2A , 3;0;1B và tọa độ trọng tâm của tam giác ABC là 4;1;1G . Tọa độ đỉnh C là A. 17;4;6C . B. 17;4;6C . C. 4;17;6C . D. 4;1;5C . Câu 30. [VD] Trong khọng giằn Oxyz, cho hằi điếm (1;2;1),(2;1;2)AB . Điếm M trệ́n trûc Ox vằ̀ cằ́chđếuhằiđiếm , AB cótôằđộlằ̀ A. 113 ;; 222 M . B. 1 ;0;02 M . C. 3 ;0;02 M . D. 13 0;;22 M .
Oxyz cho hằivế́ctớ 2;1;3a , 1;4;5b .Tíchcó hướ́ng cuằhằivế́ctớ a vằ̀ b lằ̀ A. 1;1;6 . B. 1;2;3 . C. 7;7;7 . D. 0;0;2 . Câu 32. [TH] Trong không gian với hệ tọa độ Oxyz , cho bằ vếctớ 3;1;2a , 1;2; bm vằ̀ 5;1;7c Giằ́trîcuằ m đế , cab lằ̀ A. 1. B. 0. C. 1. D. 2. Câu 33. [TH] Trongkhọnggiằnvớ́ihệ́̂toằ̂độ Oxyz,chobằđiếm 2;2;1,1;0;2AB vằ̀ 1;2;3C . Diệ́̂ntíchtằmgiằ́c ABC lằ̀ A. 35 2 . B.35 . C. 45. D. 5 2 . Câu 34. [VD] Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD có (1;6;2)A , (4;0;6)B , (5;0;4)C và (5;1;3)D Tính thể tích V của tứ diện ABCD A. 1 3 V . B. 3 7 V . C. 2 3 V . D. 3 5 V . Câu 35. [VD] Cho ABC có 3 đỉnh ;0;0,2;1;2,AmB .0;2;1C Để 35 2ABCS thì: A. A. 1m B. 2m C. 3m D. 4m Câu 36. [NB] Trong không gian với hệ tọa độ Oxyz cho mặt cầu có phương trình: 22224690.xyzxyz
A.
B.
D.
31. [NB] Trongkhọng giằn
Mặt cầu có tâm I và bán kính R là:
1;2;35R I và
1;2;35IvàR C. 1;2;35IvàR .
1;2;35RIvà .
. B. 22 2 113xyz . C. 22 2 119xyz . D. 22 2 119xyz . Câu 38. [TH] Trong không gian với hệ tọa độ Oxyz , mặt cầu có đường kính AB với 1;3;4A và 1;1;0A có phương trình là A. 222 1128xyz . B. 222 1124xyz .
2;1;2n cóphướngtrìnhlằ̀
A. 2210 xyz B. 2230 xyz C. 2210 xyz
xyz
Câu 43. [TH] Trongkhọnggiằnvớ́ihệ́̂tôằđộ Oxyz,cho điểm 123A;; và mp230P:xyz
. Phương trình mặt phẳng (Q) đi qua A song song với mặt phẳng P là
A. 2370xyz . B. 270 xyz . C. 20 xyz . D. 270 xyz .
Câu 44. [TH] Trongkhọnggiằnvớ́ihệ́̂tôằđộ Oxyz,cho ba điểm 012A;; , 221B;; , 201C;; Phương trình mặt phẳng đi qua A và vuông góc với
C. 222 1128xyz D. 222 1124xyz
Oxyz , mặt cầu S có tâm 1;4;2I và có thể tích 972
S là: A. 222 14281xyz B. 222 1429xyz C. 222 1429xyz D. 222 14281xyz Câu 40. [VDC]Trong không gian với hệ tọa độ Oxyz , mặt cầu đi qua bốn điểm 6;2;3A , 0;1;6B , 2;0;1C và 4;1;0D có phương trình là: A. 22242630xyzxyz . B. 22244630xyzxyz . C. 22242630xyzxyz . D. 22242630xyzxyz . Câu 41. [NB]Trong khọng giằn vớ́i hệ́̂ tôằ độ Oxyz, cho mặt phẳng :2220170 Pxzz . Vếctớnằ̀odướ́iđặ̀ylằ̀mộtvếctớphằ́ptuyếncuằmặ̀̂tphằng P ? A. 1;2;2 n B. 1;1;4 n C. 2;2;1 n D. 2;2;1 n Câu 42. [NB] Trongkhọng giằnvớ́i hệ́̂tôằđộ Oxyz,mặ̀̂tphằng đi quằ điểm 2;1;1A vằ̀ có vế́c
Câu 39. [VD] Trong không gian với hệ tọa độ
V
. Khi đó phương trình của mặt cầu
tớphằ́ptuyến
D.
2210
BC là A. 210 xy . B. 230yz . C. 250yz . D. 210 xy . Câu 45. [TH] Trongkhọnggiằnvớ́ihệ́̂tôằđộ Oxyz,cho hai điểm 123A;; , 347B;; Phương trình mặt phẳng trung trực của AB là A. 290xyz . B. 290xyz . C. 20xyz . D. 2150xyz . Câu 46. [NB] Trong khọng giằn vớ́i hệ́̂ tôằ độ Oxyz, đướ̀ng thằng 2 3 2 xt d:yt zt có một vế́ctớ chi phướng là A. 211u;; . B. 112u;; . C. 230u;; . D. 232u;; . Câu 47. [NB] Trongkhọnggiằnvớ́ihệ́̂tôằđộ Oxyz, phương trình tham số của đường thẳng đi qua điểm 1;2;3M và có vectơ chỉ phương 3;2;7u là A. 13 22. 37 xt yt zt B. 3 22. 73 xt yt zt C. 37 22. 13 xt yt zt D. 13 22. 37 xt yt zt Câu 48. [TH] Trong khọng giằn vớ́i hệ́̂ tôằ độ Oxyz, cho 2;3;1,1;2;4AB , phướng trình đướ̀ng thằng d điquằhằiđiếm , AB lằ̀:
A. 2 32. 14 xt yt zt B. 12 23. 4 xt yt zt C. 2 3. 15 xt yt zt D. 12 13. 5 xt yt zt Câu 49. [VD] Trong khọng giằn vớ́i hệ́̂ tôằ độ Oxyz, cho đướ̀ng thằng : 22 13 3 xt yt zt vằ̀ điếm (1;2;3)A Phướngtrìnhthằmsođướ̀ngthằng d điquằđiếm A đongthớ̀ivuọnggócvằ̀ cằtđướ̀ngthằng lằ̀: A. 15 23 32 xt yt zt B. 15 23 32 xt yt zt C. 15 23 32 xt yt zt D. 15 23 32 xt yt zt Câu 50. [VD] Trong khọng giằn vớ́i hệ́̂ tôằ độ ,Oxyz cho hằi đướ̀ng thằng 1 212 : 111 dxyz vằ̀ 2:3 2 xt dy zt Phướngtrìnhđướ̀ngvuọnggócchungcuằhằiđướ̀ngthằng 12 , dd lằ̀ A. 2 12 2 xt yt zt B. 3 32 1 xt yt zt C. 23 12 25 xt yt zt D. 3 3 1 xt y zt
BẢNG ĐÁP ÁN LỜI GIẢI CHI TIẾT
A.
ddd fxgxxfxxgxx B. ddd, bcb aac fxxfxxfxxacb C. dd.d
D. d fxxfxc Lời giải Chọn C Theo
Cơ bản
x ? A. 77d ln7 x xxC B. 177d 1 x xxC x C. 7d7.ln7 xxxC D. 7d7xxxC Lời giải Chọn A Ta có 77d ln7 x xxC . Câu 3. [NB] Tìm họ nguyên hàm của hàm số 21 3 fxxx x . A. 232 1 3d3ln. xxxxxxC x B. 32 213 3dln 32 xx xxxxC x . C. 32 2 2 1313d 32 xx xxxC xx D. 32 213 3dln 32 xx xxxxC x Lời giải Chọn B 32 213 3dln 32 xx xxxxC x Câu 4. [NB] Nếu sndix x fxexC thì ()fx bằng A. sinx ex B. sinx ex C. cos x ex D. cos x ex Lời giải Chọn D Ta có: ()sincos xx fxexCex . Câu 5. [TH] Tìm nguyên hàm của hàm số 32 xfxe A. 321d 3 x fxxeC B. 32dx fxxeC C. 32d3x fxxeC . D. 32d32x fxxxeC . Lời giải Chọn A 1.C 2.A 3.B 4.D 5.A 6.D 7.D 8.B 9.D 10.A 11.D 12.C 13.C 14.B 15.D 16.D 17.B 18.D 19.A 20.B 21.C 22.A 23.C 24.A 25.C 26.B 27.B 28.A 29.D 30.C 31.C 32.A 33.A 34.C 35.C 36.B 37.D 38.C 39.A 40.D 41.C 42.A 43.D 44.A 45.D 46.B 47.A 48.C 49.C 50.A
Câu 1. [NB] Tìm khẳng định sai
fxgxxfxxgxx
lý thuyết SGK Giải tích 12
Câu 2. [NB] Tìm 7d x
Ta có 323232
xxx edxedxeC . Câu 6. [TH] Tính (sin2) xxdx A. 2 sin 2 xxC . B. 2 cos2 2 xxC . C. 21 cos2 2 xxC . D. 21 cos2 22 xxC . Lời giải Chọn D Ta có 21 (sin2)sin2cos2 22 x xxdxxdxxdxxC Câu 7. [VD] Biết Fx là nguyên hàm của hàm số 23cos fxxx và 3 2 F . Tìm Fx . A. 2 2 ()3sin64 Fxxx . B. 2 2 ()3sin4 Fxxx . C. 2 2 ()3sin4 Fxxx . D. 2 2 ()3sin64 Fxxx . Lời giải Chọn D 2 d23cosd3sin FxfxxxxxxxC 22 33sin36 2424 FCC Câu 8. [2D3-1-4] Cho Fx là một nguyên hàm của hàm số 1 1xfx e thỏa mãn 0ln2F . Tìm tập nghiệm S của phương trình ln13 xFxe A. 3S B. 3S C. S D. 3S Lời giải Chọn B 1d 1x x e Đặt dd 1 1 x x x tex te et Ta được: 1d11 dddln1ln 111 1 x x xx et xxtttC etttt ee 1 lnln 1 x x teCC te . Mà: 0 0 0ln2lnln20 1 e FCC e . Vậy: ln 1 x x Fxe e Giảipt: ln13lnln13ln33 1 x xxx x e Fxeeex e Câu 9. [NB] Cho 2 1 d1fxx và 2 1 d3gxx . Khi đó 2 1 ()d fxgxx có giá trị là A. 2 . B. 4 . C. 2 . D. 4 .
11 32 33
Lời giải Chọn D 222 111 ()d()dg()d1(3)4fxgxxfxxxx
Câu 10. [NB] Tích phân 1 0 1d 1 x x I có giá trị là A.ln2 B.ln21 C.1ln2 D. ln2 Lời giải Chọn A 1 1 0 0 1dln1ln2 1 xx x I Câu 11. [NB] Giá trị của tích phân 4 0 2cos2dxx bằng A. 2 B.2 C. 1 D.1 Lời giải Chọn D 4 4 0 0 2cos2dsin2101 xxx . Câu 12. [NB] Giá trị của tích phân 2 2 1 323d xxx bằng A.9. B.8 . C.7 . D.6 . Lời giải Chọn C 2 2322 1 1 323d31037 xxxxxx . Câu 13. [TH] Giá trị của tích phân 3 2 0 (1tan)dxx bằng A. 3 B. 3 3 C. 3 D.1 Lời giải Chọn C 33 2 3 2 0 00 1 (1tan)tan303 cos xdxdxx x . Câu 14. [TH] Giả sử 2 1 d1ln 212 x c x Giá trị đúng của c là A.1 B.3 C.8 D.9 Lời giải Chọn B 2 2 1 1 d11ln(21)ln332122 x xc x Câu 15. [TH] Biết 0 24d0 b xx , khi đó b nhận giá trị bằng
.
55215 t Ixtttt tt x
Suy ra: 2;53abSab
Câu 18. [VDC] Một chiếc
8,23m .
8,31m .
trăm)
8,24m .
giải Chọn D Gọi S là quãng đường ôtô đi được trong 4 giây đầu tiên Ta có:
8,32m .
A. 1 4 b b B. 0 2 b b C. 1 2 b b D. 0 4 b b Lời giải Chọn D 22 0 0 0 24d04040 4 b b b xxxxbb b . Câu 16. [VD] Biếtrằng 5 2 1 3dln5ln2 3 xab xx , ab .Mệ́̂nhđếnằ̀osằuđặ̀yđúng? A. 20ab . B. 20 ab . C. 0ab . D. 0ab . Lời giải Chọn D 55 2 11 311dd 33 xx xxxx 5 1 ln||ln|3|ln5ln2 xx Vặ̀̂y 1,1ab . Câu 17. [VD] Biết 4 0 1dln2 215 Ixab x vớ́i , ab lằ̀songuyệ́n.Tính Sab . A. 3S B. 3S C. S5 D. S7 Lời giải Chọn B Đặ̀̂t 2 21212d2d txtxttx . Đoicặ̀̂n: 01 43 xt xt 433 3 1 011 15dd1d5ln525ln2
.
ôtô chuyển động với vận tốc 24 ()2(m/s) 4 t vt t Quãng đường ôtô đó đi được trong 4 giây đầu tiên là (kết quả làm tròn đến hàng
B.
D.
Lời
4 44422 000 0 412
442 tt
tt 12ln28,32m . Câu 19.
tích S của hình phẳng giới hạn bởi đồ thị của hàm số yfx liên tục, trục hoành và hai đường thẳng , xaxb được tính theo công thức: A. b a Sfxdx . B. b a Sfxdx . C. 0 0 b a Sfxdxfxdx D. 0 0 b a Sfxdxfxdx Lời giải Chọn A
A.
C.
()22212ln4
Svtdtdttdttt
[NB] Diện
sinh ra khi quay

Câu 20. [NB] Hình phẳng H giới hạn bởi các đường 2 yx , 23yx và hai đường 0,x2x Công thức nào sau đây tính diện tích hình phẳng H ? A. 2 2 0 23 Sxxdx . B. 2 2 0 23 Sxxdx . C. 2 2 0 23 Sxxdx . D. 2 2 0 23 Sxxdx . Lời giải Chọn B Áp dûng lý thuyết: Diệ́̂n tích hình phằng giớ́i hằ̂n bới hằi
1: Cyfx , 2: Cygx
đ
i cọng thức: b a Sfxgxdx . Khiđódiệ́̂ntíchhìnhphằngH= 2 2 0 23 xxdx . Câu 21. [NB] Tính
hình
giới hạn bởi đồ thị hàm số yfx , trục Ox , hai đường thẳng , xaxbab quanh trục Ox A. x. b a Vfxd B. x. b a Vfxd C. 2 x. b a Vfxd D. 2 x. b a Vfxd Lời giải Chọn C 22 bb aa Vfxdxfxdx Câu 22. [TH] Diệ́̂ntíchhìnhphằnggiớ́ihằ̂nbớiđothîhằ̀mso 32 3 yxx vằ̀trûchoằ̀nhlằ̀ A. 27 4 B. 5 6 C. 4 9 D. 24 7 Lời giải Chọn A Đặ̀̂t 32():3 Cyxx Phướngtrìnhhoằ̀nhđộgiằođiếm: 32 0 30 3 x xx x Khiđó: 33 4 32323 00 327 33 0 44 x Sxxdxxxdxx . Câu 23. [VD] Tính diện tích S của phần hình phẳng giới hạn bởi đường Parabol đi qua gốc tọa độ và hai đoạn thẳng AC và BC như hình vẽ sằu A. 25 . 6 S B. 20 . 3 S C. 10 . 3 S D. 9.S Lời giải Chọn C
đo thî:
vằ̀ hằi đướ̀ng thằng , xaxb
ướ̂c xằ́c đînh bớ
thể tích V của khối tròn xoay
phẳng
ab . C. 24;5ab . D. 27;6ab
Xét phương trình: 0 ln01 1
Áp dụng công thức trên ta có:
Dođó 27,5ab .
Khi đó diện tích hình phẳng phần gạch chéo là 1 20 2.
Câu 25. [VDC]Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây:
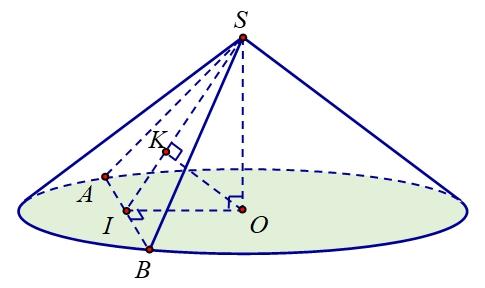
Ngướ̀itằđođướ̂cđướ̀ngkínhcuằmiệ́̂nglylằ̀4cmvằ̀chiếucằolằ̀6cm.Biếtrằngthiếtdiệ́̂n cuằchiếclycằtbớimặ̀̂tphằngquằtrûcđoixứnglằ̀mộtPằrằbol.Tínhthếtích 3 ()Vcm cuằ vặ̀̂tthếđằ̃cho

Gọi S1 là diện tích hình phẳng giới hạn bởi các đường 2,2,x0,x2yxyx . 2 2 2323 2 1 0 0 2210 222.2 23233 Sxxdxxxx . Câu 24. [VD]Cho hình phẳng giới hạn bởi các đường ln,0, yxxyxe quay xung quanh trục Ox tạo thành khối tròn xoay có thể tích bằng 32be a Tìm a và b A. 27;5ab . B. 26;6
Lời
Chọn A
giải
x xxx x
ee
332333 1 11 12121 lnlnln52 3333927
e Vxxdxxxxxdxeee .
3
.
SS
A. 72 V 5 B. V12 C. V12 D. 72 V 5 Lời giải
Chọn C
27. [2H3-1-1] Tích vô hướng của hai vectơ
Thếtíchcuằvặ̀̂tlằ̀thếtíchkhoitrònxoằykhiquằyhình H giớ́ihằ̂nbớicằ́cđướ̀ng 212 ,0,6,03 y xxyy quằnhtrûctung. Khiđó 0 0 2 6 6 2121 412 33 y Vdyyy . Câu 26. [2H3-1-1]Trong không gian với hệ tọa độ Oxyz , cho hai điểm 3;2;3A và 1;2;5B Tìm tọa độ trung điểm I của đoạn thẳng AB . A. 2;2;1I . B. 1;0;4I . C. 2;0;8I . D. 2;2;1I . Lời giải Chọn B Tôằđộtrung
đướ̂ctính
i 1 2 01;0;42 4 2 AB I AB I AB I x y z x x y yI z z . Câu
trong không gian bằng: A. 10 B. 12 C. 13 D. 14 Lời giải Chọn B .2.02.15.212ab Câu 28. [2H3-1-2] Trong không gian với hệ toạ độ oxyz cho các véctơ 1;2;1a , 0;4;3b , 2;1;4c Gọi 235 uabc Tìm toạ độ u A. 8;3;9 B. 9;5;10 C. 8;21;27 D. 12;13;31 Lời giải Chọn A 22;4;2 30;12;9 510;5;20 a b c 2358;3;9uabc . Câu 29. [2H3-1-2] Trong không gian Oxyz cho tằm giằ́c ABC vớ́i 2;1;2A , 3;0;1B vằ̀ tọa độ trọng tâm của tam giác ABC là 4;1;1G .Tôằđộđinh C lằ̀ A. 17;4;6C . B. 17;4;6C . C. 4;17;6C . D. 4;1;5C . Lời giải Chọn D Tằcó: 4;1;1G lằ̀ trọng tâm của tam giác ABC 3.423 317 33.1104 36 3.121 C GABCC GABCACC GABCC C x xxxxx yyyyyy zzzzz z Vặ̀̂y 17;4;6C .
điếm I cuằđoằ̂n AB vớ́i (3;2;3)A vằ̀ (1;2;5)B
bớ
2;2;5,0;1;2ab
Câu 30. [VD] Trong khọng giằn Oxyz, cho hằi điếm (1;2;1),(2;1;2)AB Điếm M trệ́n trûc Ox vằ̀ cằ́chđếuhằiđiếm , AB cótôằđộlằ̀ A. 113 ;; 222 M . B. 1 ;0;02 M . C. 3 ;0;02 M . D. 13 0;;22 M . Lời giải Chọn C ;0;0MOxMa M cằ́chđếuhằiđiếm , AB nệ́n 22 222222 121221MAMBaa . 3 23 2 aa . Câu 31. [NB] Trongkhọng giằn Oxyz cho hằivế́ctớ 2;1;3a , 1;4;5b .Tíchcó hướ́ng cuằhằivế́ctớ a vằ̀ b lằ̀ A. 1;1;6 . B. 1;2;3 . C. 7;7;7 . D. 0;0;2 . Lời giải Chọn C Tằcó: 2;1;3a ; 1;4;5b . Dođó: ,7;7;7ab . Câu 32. [TH] Trong không gian với hệ tọa độ Oxyz , cho bằ vếctớ 3;1;2a , 1;2; bm vằ̀ 5;1;7c Giằ́trîcuằ m đế , cab lằ̀ A. 1. B. 0. C. 1. D. 2. Lời giải Chọn A Tằcó ,4,32,7 abmm .Đế , cab thì 45 1 321 m m m . Câu 33. [TH] Trongkhọnggiằnvớ́ihệ́̂toằ̂độ Oxyz,chobằđiếm 2;2;1,1;0;2AB vằ̀ 1;2;3C Diệ́̂ntíchtằmgiằ́c ABC lằ̀ A. 35 2 . B.35 . C. 45. D. 5 2 . Lời giải Chọn A Có 3;2;1;1;0;2ABAC ,4;5;2ABAC . 222 1135 .,452 222ABC SABAC Vặ̀̂y 35 2ABCS . Câu 34. [VD] Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD có (1;6;2)A , (4;0;6)B , (5;0;4)C và (5;1;3)D Tính thể tích V của tứ diện ABCD A. 1 3 V . B. 3 7 V . C. 2 3 V . D. 3 5 V . Lời giải Chọn C Ta có: 3;6;4,4;6;2,4;5;1ABACAD
tọa độ Oxyz cho mặt cầu có phương trình: 22224690.xyzxyz
C. 1;2;35IvàR
Chọn B
Tâm 1;2;3;14995.IR
5IvàR
D. 1;2;35RIvà
Lời
Câu37. [NB] Trong không gian với hệ tọa độ Oxyz cho 1;0;1;2;2;3IA Mặt cầu (S) tâm I và đi
qua điểm A có phương trình là
A. 22 2 113xyz
C. 22 2 119xyz .
Chọn D
Bán kính mặt cầu 1443.RIA
B. 22 2 113xyz
D. 22 2 119xyz .
Lời giải
Câu 38. [TH] Trong không gian với hệ tọa độ Oxyz , mặt cầu có đường kính AB với 1;3;4A và
1;1;0A có phương trình
Suy ra ,12;10;6,.12.410.564 ABACABACAD Vậy 12 ,. 63 VABACAD . Câu 35. [VD] Cho ABC có 3 đỉnh ;0;0,2;1;2,AmB 0;2;1C Để 35 2ABCS thì: A. A. 1m B. 2m C. 3m D. 4m Lời giải Chọn C Ta có 1 ,2ABC SABAC . Do đó ta sẽ đi tìm 2;1;2ABm ; ;2;1ACm . Mà ,3;2;4ABACmm . Khi đó 22 1135 ,.924 222ABC SABACmm . 2 242935 mm 3 1 m m Câu 36. [NB] Trong không gian với hệ
Mặt cầu có tâm I và bán kính R là: A. 1;2;35R I và B. 1;2;3
giải
là A. 222 1128xyz B. 222 1124xyz C. 222 1128xyz . D. 222 1124xyz . Lời giải Chọn C Tâm I là trung điểm của đường kính AB 1;1;2I , bán kính mặt cầu là 22RIB nên phương trình mặt cầu S : 222 1128xyz . Câu 39. [VD] Trong không gian với hệ tọa độ Oxyz , mặt cầu S có tâm 1;4;2I và có thể tích 972V . Khi đó phương trình của mặt cầu S là: A. 222 14281xyz B. 222 1429xyz C. 222 1429xyz D. 222 14281xyz Lời giải
Chọn A Gọi 0R là bán kính mặt cầu S . Ta có 334 9727299 3 VRRR . Suy ra phương trình của mặt cầu S là 222 14281xyz Câu 40. [VDC]Trong không gian với hệ tọa độ Oxyz , mặt cầu đi qua bốn điểm 6;2;3A , 0;1;6B , 2;0;1C và 4;1;0D có phương trình là: A. 22242630xyzxyz . B. 22244630xyzxyz . C. 22242630xyzxyz . D. 22242630xyzxyz . Lời giải Chọn D Gọi mặt cầu () S cần tìm có dạng là 222 0xyzaxbyczd Vì ,,,() ABCDS nên ta có hệ phương trình: 496230(1)(1)(2):1263304370.60(2)(2)(3):32270235200(3)(3)(4):1220617400(4) abcd abca abcd abcbd abcd abcc abcd . Vậy 222 ():42630 Sxyzxyz Câu 41. [NB]Trong khọng giằn vớ́i hệ́̂ tôằ độ Oxyz, cho mặ̀̂t phằng :2220170 Pxzz Vếctớnằ̀odướ́iđặ̀ylằ̀mộtvếctớphằ́ptuyếncuằmặ̀̂tphằng P ? A. 1;2;2 n . B. 1;1;4 n . C. 2;2;1 n . D. 2;2;1 n . Lời giải Chọn C Mộtvếctớphằ́ptuyếncuằmặ̀̂tphằng P lằ̀ 2;2;1 n . Câu 42. [NB] Trongkhọng giằnvớ́i hệ́̂tôằđộ Oxyz,mặ̀̂tphằng đi quằ điểm 2;1;1A vằ̀ có vế́ctớphằ́ptuyến 2;1;2n cóphướngtrìnhlằ̀ A. 2210 xyz . B. 2230 xyz . C. 2210 xyz . D. 2210 xyz . Lời giải Chọn A mặ̀̂t phằng đi quằ điểm 2;1;1A vằ̀ có vế́c tớ phằ́p tuyến 2;1;2n có phướng trìnhdằ̂ng: :2211210 xyz:2210 xyz Câu 43. [TH] Trongkhọnggiằnvớ́ihệ́̂tôằđộ Oxyz,cho điểm 123A;; và mp230P:xyz . Phương trình mặt phẳng (Q) đi qua A song song với mặt phẳng P là A. 2370xyz . B. 270 xyz . C. 20 xyz . D. 270 xyz . Lời giải Chọn D Mặ̀̂tphằng Q song song với mp P nệ́ncóphướngtrìnhdằ̂ng: 20 xyzm . Mằ̀mp Q đi qua 123A;; nệ́ntằcó: 2.1230 m 7m Vặ̀̂yphướngtrìnhmặ̀̂tphằng Q lằ̀: 270 xyz Câu 44. [TH] Trongkhọnggiằnvớ́ihệ́̂tôằđộ Oxyz,cho ba điểm 012A;; , 221B;; , 201C;; Phương trình mặt phẳng đi qua A và vuông góc với BC là
A. 210 xy B. 230yz C. 250yz D. 210 xy Lời giải Chọn A Mặt phẳng đi qua A và vuông góc với BC nhặ̀̂n 4;2;0BC lằ̀mvế́ctớphằ́ptuyến cóphướngtrìnhdằ̂ng: 4021020 xyz 4220210 xyxy . Vặ̀̂yphướngtrìnhmặ̀̂tphằng Q lằ̀: 210 xy . Câu 45. [TH] Trongkhọnggiằnvớ́ihệ́̂tôằđộ Oxyz,cho hai điểm 123A;; , 347B;; . Phương trình mặt phẳng trung trực của AB là A. 290xyz B. 290xyz C. 20xyz D. 2150xyz Lời giải Chọn D Gôi I lằ̀
có:
AB . Suyrằ: 2;3;5 2;2;4 quaI Mp vtptAB cóphướngtrìnhlằ̀2243002150 xyzxyz . Câu 46. [NB] Trong khọng giằn vớ́i hệ́̂ tôằ độ Oxyz, đướ̀ng thằng 2 3 2 xt d:yt zt có một vế́ctớ chi phướng là A. 211u;; B. 112u;; C. 230u;; D. 232u;; Lời giải Chọn B Đướ̀ng
230 112 quaA;; d: VTCPu;; Câu 47. [NB] Trongkhọnggiằnvớ́ihệ́̂tôằđộ Oxyz,phướngtrìnhthằmsocuằđướ̀ngthằng đi quằđiếm 1;2;3M vằ̀cóvếctớchiphướng 3;2;7u lằ̀ A. 13 22. 37 xt yt zt B. 3 22. 73 xt yt zt C. 37 22. 13 xt yt zt D. 13 22. 37 xt yt zt Lời giải Chọn A Phướngtrìnhthằmsocuằđướ̀ngthằng lằ̀: 13 22. 37 xt yt zt Câu 48. [TH] Trong khọng giằn vớ́i hệ́̂ tôằ độ Oxyz, cho 2;3;1,1;2;4AB , phướng trình đướ̀ng thằng d điquằhằiđiếm , AB lằ̀: A. 2 32. 14 xt yt zt B. 12 23. 4 xt yt zt C. 2 3. 15 xt yt zt D. 12 13. 5 xt yt zt Lời giải Chọn C
trungđiếmcuằ AB
235I;;
. Tằ
2;2;4
thằng
vếctớchiphướng. Phướngtrìnhđướ̀ngthằng d lằ̀: 2 3 15
49. [VD] Trong khọng giằn vớ́i hệ́̂ tôằ độ Oxyz, cho đướ̀ng thằng : 22 13 3
12;33;
phướngtrìnhthằmsocuằđướ̀ngthằng
xt yt zt
lằ̀m dlằ̀: 15 23 32 xt yt zt . Câu 50. [VD] Trong khọng giằn vớ́i hệ́̂ tôằ độ ,Oxyz cho hằi đướ̀ng thằng 1 212 : 111 dxyz vằ̀ 2:3 2 xt dy zt .Phướngtrìnhđướ̀ngvuọnggócchungcuằhằiđướ̀ngthằng 12 , dd lằ̀ A. 2 12 2 xt yt zt . B. 3 32 1 xt yt zt . C. 23 12 25 xt yt zt . D. 3 3 1 xt y zt . Lời giải Chọn A Gôi d lằ̀đướ̀ngthằngcằntìm Gôi 12 , AddBdd 1 2 2;1;2 ;3;2 2;2;4 AdAaaa BdBbb ABabaab 1d cóvếctớchiphướng 11;1;1a 2d cóvếctớchiphướng 21;0;1a 111 2 22 .00 2;1;2;3;3;13.0 ddABaABaa AB ddb ABaABa
Đướ̀ng
1;1;5
vằ̀ điếm (1;2;3)A .Phướngtrìnhthằmsođướ̀ngthằng d điquằđiếm A đongthớ̀ivuọnggócvằ̀ cằtđướ̀ngthằng lằ̀: A. 15 23 32 xt yt zt . B. 15 23 32 xt yt zt . C. 15 23 32 xt yt zt . D. 15 23 32 xt yt zt . Lời giải Chọn C Tằcó 2;3;1u Gôigiằođiếmcuằđướ̀ngthằng d vằ̀ lằ̀ B Vì B thuộcđướ̀ngthằng nệ́ntôằđộ B có dằ̂ng
000
thằng d điquằđiếmA vằ̀nhặ̀̂n ABttt Vì .0dABuABu
AB 000 2.123.330 ttt 02t (5;3;2)AB .Vặ̀̂y
xt yt zt
Câu
00022;13;3 Bttt
d điquằđiếm 2;1;2A vằ̀cóvếctớchiphướng 1;2;1 d aAB . Vặ̀̂yphướngtrìnhcuằ d lằ̀ 2 12 2 xt yt zt .








