PHIẾU BÀI TẬP TOÁN
CHƯƠNG TRÌNH MỚI
vectorstock com/32029674

Ths Nguyễn Thanh Tú
eBook Collection
PHIẾU BÀI TẬP TOÁN 8 CHƯƠNG TRÌNH MỚI
NĂM HỌC 2023 - 2024 (DÙNG CHUNG 3 BỘ
SÁCH KẾT NỐI TRI THỨC, CHÂN TRỜI SÁNG
TẠO, CÁNH DIỀU) (TẬP 1) - 282 TRANG
WORD VERSION | 2024 EDITION
ORDER NOW / CHUYỂN GIAO QUA EMAIL
TAILIEUCHUANTHAMKHAO@GMAIL COM
ĐƠN THỨC NHIỀU BIẾN.
ĐA THỨC NHIỀU BIẾN
A. KIẾN THỨC TRỌNG TÂM
I/ Đơn nhất nhiều biến.
1. Khái niệm.
Đơnthứcnhiềubiếnlàbiểuthức đạisố chỉ gồmmộtsố,hoặcmộtbiếnhoặcmộttíchgiữacácsố và cácbiến.
2. Đơn thức thu gọn.
Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến đã được nâng lên lũythừavớisố mũ nguyêndương.
Trong đơnthứcthugọncóhaiphần:phầnhệ số vàphầnbiến.
Tacũngcoimộtsố làmột đơnthứcthugọnchỉ cóphầnhệ số
Trong đơnthứcthugọn,mỗibiếnchỉđượcviếtmộtlần.
3. Đơn thức đồng dạng.
Hai đơnthức đồngdạnglàhai đơnthứccóhệ số khác0vàcócùngphầnbiến.
Cácsố khác0 đượccoilànhững đơnthức đồngdạng.
4. Cộng trừđơn thức đồng dạng.
Để cộng(trừ)các đơnthức đồngdạng,tacộng(trừ)cáchệ số vớinhauvàgiữ nguyênphầnbiến.
II/ Đa nhất nhiều biến.
1. Định nghĩa.
Đathứcnhiềubiến (hay đathức) làtổngcủanhững đơnthức.Mỗi đơnthức đượccoilàmột đathức.
Mỗi đơnthứctrongtổnggọilàhạngtử của đathức đó.
2. Đa thức thu gọn.
Thugọn đathứcnhiềubiếnlàlàmchotrong đathức đókhôngcònhai đơnthứcnào đồngdạng.
3. Giá trị của đa thức .
Để tínhgiátrị củamột đathứctạinhữnggiátrị chotrướccủacácbiến,tathaynhữnggiátrị chotrước đóvàobiểuthứcxác định đathứcrồithựchiện cácphéptính.
Tài liệu chuẩn tham khảo
Phát triển kênh bởi
Ths Nguyễn Thanh Tú
Đơn vị tài trợ / phát hành / chia sẻ học thuật :
Nguyen Thanh Tu Group
Hỗ trợ trực tuyến
Fb www.facebook.com/DayKemQuyNhon
Mobi/Zalo 0905779594
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Nhận biết các đơn thức nhiều biến, đa thức nhiều biến.
Ví dụ 1. Trongcácbiểuthứcsau,biểuthứcnàolà đơnthức?
a) 2 12xy ; b) 1 ()xy + ; c) 12x ; d) 18; e) 5 2x .
Bàigiải 2 12xy ;18là đơnthức.
Ví dụ 2. Biểuthứcnàodưới đâykhôngphảilà đơnthức?
a) 22 xy ; b) xyxy −+ ; c) 2 2xy ; d) 3 4xy ; e) 1 ()xy + .
Bàigiải
22 xy ; xyxy −+ ; 1 ()xy + ; 3 4xy khôngphảilà đơnthức.
Ví dụ 3. Chobiếtphầnhệ số,phầnbiếncủamỗi đơnthứcsau
a) 2 2xy ; b) 3 1 2 xy
Bàigiải
a) 2 2xy :Hệ số là2,phầnbiếnlàx 2 y.
b) 3 1 2 xy :Hệ số là 1 2,phầnbiếnlà 3 xy
Ví dụ 4. Biểuthứcnàolà đathứctrongcácbiểuthứcsau?
a) 22 23 xyxy −+ ; b) 2 2 x x y ; c) 2018 ; d) ()xxy + .
Bàigiải 22 23 xyxy −+ ; 2018 ; ()xxy + là đathức.
Ví dụ 5. Biểuthứcnàokhôngphảilà đathứctrongcácbiểuthứcsau?
a) 3 2 x x −+ ; b) 2 2 xyx ; c) 2 4 x ; d) 2 1 x xy +
Bàigiải
Dạng 2: Nhận biết các đơn thức đồng dạng
Ví dụ 1. Xếpcác đơnthứcsauthànhtừngnhómcác đơnthức đồngdạng
2231355
73 23466;;;;;;. xyxzxyzxyxyzxzxy
Bàigiải Nhómcác đơnthức đồngdạnglà: Nhóm1: 35 3 26;;. xyxyxy Nhóm2: 3 7 4 ;.xyzxyz Nhóm3: 2215 36 ; xzxz
Ví dụ 2. Trongcác đơnthứcsau, đơnthứcnào đồngdạngvới đơnthức 2 3xyz ?
a) 3xyz ; b) 2 2 3 xyz ; c) 2 3 2 yzx ; d) 2 4xy
Bàigiải 2 2 3 xyz đồngdạngvới đơnthức 2 3xyz
Câub đúng.
Dạng 3: Cộng, trừ các đơn thức đồng dạng
Ví dụ 1. Tínhtổng,hiệucácbiểuthứcsau
a) 22 1 3 3 xyxy + ; b) 22222223xyxyxy ++ ;
c) 222234xyzxyz ; d) 222 21 2 33 xyxyxy ++− .
Bàigiải a) 22 22 1 3 3 110 3 33 =+= + xy yxy xy x b) ( ) 222 2 2 222 22 232316 ++=+= + xy xyxy x y y x
c) ( ) 2 2 2 22 22 2 3 44 3 = −−=− xyzx yzxyz yz x d) 22222 21217 22 33333 ++−=+−= xyxyxyxyxy
Ví dụ 2. Tínhgiátrị biểuthức 2222011122015 Pxyxyxy =+− tại 1 x =− ; 2 y = .
Bàigiải
( ) 222 22201112201520111220158 =+−=+−= Pxyxyxyxyxy
3 2 x x −+ ; 2 1 x xy + khôngphảilà đathức.
Thayx=-1;y=2vào 2 8xy ta được: ()2 2 881281216 =−== xy
Dạng 4: Tìm đơn thức thỏa mãn đẳng thức
Dùng quy tắc chuyển vế giống như đối với với số
Nếu MBA += thì MAB =−
Nếu MBA −= thì MAB =+ .
Nếu BMA −= thì MBA =− .
Ví dụ 1. Xác định đơnthức M để
a) 434323 xyMxy +=− ; b) 333324 xyMxy −= .
Bàigiải
Dạng 6: Thu gọn đa thức
Bước 1: Nhóm các hạng tử đồng dạng với nhau;
Bước 2: Cộng, trừ các đơn thức đồng dạng trong từng nhóm.
Ví dụ 1. Thugọncác đathứcsau
a) 222252 =−−+++ y x y Axyxxy ;
b) 2231 2 22 Bxyxyxyxy =−+++ ;
c) 222222222 Cxyzxyzxyz =+++−+++− ;d) 2222 23 Dxyzxyzxyzxyzxyz =+−−+ .
Bàigiải
=−−+++=−++−++
a) 434323 xyMxy +=− b) 333324 xyMxy −= . ()
3 2 =− =
Mxy x
43 4
= Mxy M
3 3 2 5
4 43 3
x y
Dạng 5: Tính giá trị của đa thức
Ví dụ 1. Tínhgiátrị của đathứcsau:
a) 22 4 + xy xy tại 2 x =− ,
y = ; b) 23 1
a) 22 4 + xy xy tại 2 x =− ,
=−Mxy y M
y () 3 3 33
x Mx xy
Thay giá trị của biến vào đa thức rồi thực hiện phép tính.
3 3
y
33 2 24 4 2 =− =−
+ xy x tại 3 x = , 2 y =− Bàigiải
Thay 2 x =− , 1 2 y = vào 22 4 + xy xy ta được: () () ()
2 2 111 422161413 224 −+−=+−=−=
b) 23 1 2 + xy x tại 3 x = , 2 y =−
Thay 3 x = , 2 y =− vào 23 1 2 + xy x ta được: ()() () 23 117278 323983339 2222 −−+=−−+=+==
=−++−++=++
Axxyxxyxyxyxyxy xyxyxyxy
y
xy
e) 23424232376 =+−+− Exyxxxxy
.
n thức là : 2 4 3 xyz ; 2018
Bài 2. Biểu thức nào là đa thức trong các biểu thức sau?
a) 2 23xyxy ++ ;b) 2 xy + ;c) 2 ()xxy + ;d) 1 2 1 x x +
Bàigiải
Đa thức là 2 ()xxy + ; 2 23xyxy ++
Bài 3. Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng
22222222 125835 337 ;;;;;. xyzxyzxyzxyzxyzxyz
Nhóm các đơn thức đồng dạng là :
Bàigiải
Nhóm 1: 22 1 8 3 ;. xyzxyz Nhóm 2 : 22 2 3 3 ;. xyzxyz Nhóm 3 : 222255 7 ;. xyzxyz
Bài 4. Thu gọn mỗi đơn thức sau:
a) 2223xyxy ;b) 23 4 210 5 xyxyxyz ;c) 232102()() yxyx
d) 223 4 26 3 xyxyx ;e) 222 43 34xyzxyz ;
f) 2223 1 42 4 () axbxyxy với a , b là hằng số Bàigiải
a) ( ) ( ) ( ) 2 3 2223 23236 == ⋅ xyxy xxyyxy
b)
23 2345 44 21021016 55 ⋅⋅== xyxyxyzxxxyyyxy
c) ( ) ( ) ( ) 2332
()()
111 424444 444
()...b...... axbxyxyaxbxyxyaxxxyy abxy
() ()() 2223222223222223
ới a , b là hằng số
Bài 5. Thu gọn các đa thức sau
a) 2231 2 22 =−+++ Axyxyxyxy ;
b) 2222 23 =+−−+ Bxyzxyzxyzxyzxyz
c) 2342423426 =+−+− Cxyxxxxy .
d) 2231 23 42 =−−+ Dxyxyxyxy ;
e) 234234 23423 =−−−++ Exyzxyz ;
f) 222 323 =+−+− Fxyzxyzxyzxyzxyz Bàigiải
a) () 222223131 2 22 2222
Bàigiải
a) 2323678 Axyxyxy =++ ;tại x=2;y= 1 2
Thay x=2;y= 1 2 vào 2323678 Axyxyxy =++ ta được: () 233 2 11135 627282 2224 ++=
b) 33 5 22 2 =+−+− Bxxyxxyxy ;tại x= 1 4 ;y=0.
Thay x= 1 4 ;y=0 vào 623556 2 Bxxyxxyxyx =+−+−− ta được: 23 113 4464 −=
=−+++=++−+=−
Axyxyxyxyxyxyxyxyxyxy ;
b) ( ) 222222222 2323 =+−−+=+−+−=− Bxyzxyzxyzxyzxyzxyzxyzxyzxyzxyzxyzxyz
c) ( ) ( ) 2323442 234242 232 3 4 426462372 =− =+−+++−=− + Cxyxxxyxyxxxxyx xy x x
d) () 2222 2 31311 2323 42424
c) 2626 7434 Cxyxyzx =−++ ;tại x=2;y=1;z=4
Thay x=2;y=1 vào 2626 7434 Cxyxyzx =−++ ta được: 2626 721423144240 −++=
D. BÀI TẬP TỰ LUYỆN.
Bài 1. Trongcácbiểuthứcsau,biểuthứcnàolà đơnthức?
=−−+=−+−+=+
Dxyxyxyxyxyxyxyxyxyxy ;
e) ( ) ( ) ( ) 234234 223344234 234232432322 =−+−++−+ =−−− =−− + + + xx Exyzxyz yyzzxyz
f) ( ) ( ) 222222 2 32332364 =+−+−=+++−−=− Fxyzxyzxyzxyzxyzxyzxyzxyzxyzxyzxyzxyz
Bài 6. Tính giá trị mỗi đa thức sau :
a) 2323678 Axyxyxy =++ ; tại x=2;y= 1 2
b) 623556 2 Bxxyxxyxyx =+−+−− ; tại x=0;y= 1 4
c) 2626 7434 Cxyxyzx =−++ ;tại x=2;y=1
a) 43x ; b) 6 5x ; c) 2xy ; d) 9 5 ; e) 32()xy
Bài 2. Biểuthứcnàodưới đâykhôngphảilà đơnthức?
a) 2 2 3 xy ; b) 1 ()xy ; c) 22 xy + ; d) 3 4xy ; e) xyxy ++
Bài 3. Chobiếtphầnhệ số,phầnbiếncủamỗi đơnthứcsau
a) 3 1 3 xy ; b) 22 3 4 xy .
Bài 4. Thựchiệnphéptính:
a) 2 1 2 xy + 2 2xy ; b) 3 2xy3 1 4 xy
c) 222 2 3 3 xyxyxy ++ ; d) 2222 1 42 5 −++− xx yyy xx y ;
e) 222111 236 xyxyxy ++ ; f) 333191512xyxyxy +−
g) 222 11 3 42 xyxyxy ++− .
Bài 5. Thugọnmỗi đơnthứcsau:
a) 22 11 42 xyx ⋅−⋅ ; b) 2313 32xyxy ;
c) ()2 32 3 4 xy ⋅ ; d) 2 2 1 2 ()xby (b làhằngsố).
Bài 6. Tínhgiátrị của đơnthứcsau
a) 2 2xy tại 1 x =− , 1 4 y = ; b) 32 1 2 xy tại 1 2 x =− , 4 y =− .
Bài 7. a/Xếpcác đơnthứcsauthànhtừngnhómcác đơnthức đồngdạng
22222222 125 835 337 ;;;;;. xyzxyzxyzxyzxyzxyz
b/ Xếpcác đơnthứcsauthànhtừngnhómcác đơnthức đồngdạng
222222222 512 26 425;;;;;;. xyxyxyxyxyxyxy
Bài 10. Xác định đơnthức M để
a) 4444442332 xyMxyxy +=− ; b) 22 23 xMx −= .
c) 2323 3xyMxy +=− ; d) 222273 xyMxy −=
Bài 8. Tínhgiátrị biểuthức
a) 222 2 3 3 xyxyxy ++ tại 3 x = , 1 7 y =− ;
b) 222111 236 xyxyxy ++ tại 3 4 x = , 1 2 y =− ;
c) 33 2xy + 33331020xyxy tại 1 x = , 1 y =− .
d) 2222018162016 +− xyxyxy tại 2 x =− ; 1 3 y =−
Bài 9. Tínhgiátrị củabiểuthức M biếtrằng
a) 24242415106 xyMxyxy −=+ tại 1 2 x =− , 2 y = ;
b) 333 402015 xyMxyxy +=+ tại 2 x =− , 1 5 y = .
CÁC PHÉP TÍNH VỚI ĐA THỨC
NHIỀU BIẾN
A. KIẾN THỨC TRỌNG TÂM
1/ Cộng hai đa thức nhiều biến.
Để cộng hai đa thức theo hàng ngang, ta có thể làm như sau:
• Viết tổng hai đa thức theo hàng ngang ;
• Nhóm các đơn thức đồng dạng với nhau;

• Thực hiện phép tính theo trong từng nhóm , ta được tổng cần tìm.
2/ Trừ hai đa thức nhiều biến.
Để trừđa thức P cho đa thức Q theo hàng ngang, ta có thể làm như sau:
• Viết hiệu P - Q theo hàng ngang, trong đó đa thức Q được đặt trong dấu ngoặc;
• Sau khi bỏ dấu ngoặc và đổi dấu một đơn thức của đa thức Q, nhóm các đơn thức đồng dạng với nhau;
Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
3/ Nhân hai đa thức nhiều biến.
a/ Nhân hai đơn thức:
Tương tự nhưđối với đơn thức một biến, để nhân hai đơn thức nhiều biến ta có thể làm như sau:
• Nhân các hệ số với nhau và nhân các phần biến với nhau;
• Thu gon đơn thức nhận được ở tích .
b/ Nhân đơn thức với đa thức:
Tương tự như trường hợp một biến, ta có quy tắc sau:
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức đó với từng đơn thức của đa thức rồi cộng các kết quả với nhau.
c/ Nhân hai đa thức:
Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các kết quả với nhau.
4/ Nhân hai đa thức nhiều biến.
a/ Phép chia hết một đơn thức cho một đơn thức
Đơn thức A chia hết cho đơn thức B ( 0 B ≠ ) khi mỗi biến của B đều là biến của A với số mũ
không lớn hơn số mũ của nó trong A.
Quy tắc : Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B), ta có thể làm như
sau :
- Chia hệ số của đơn thức A cho hệ số của đơn thức B
- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
- Nhân các kết quả vừa tìm được với nhau.
b/ Phép chia hết một đa thức cho một đơn thức
Đa thức A chia hết cho đơn thức ( 0 B ≠ ) khi mỗi đơn thức của A chia hết cho B.
Quy tắc : Muốn chia đa thức A cho đơn thức B ( trường hợp A chia hết cho B), ta chia mỗi đơn thức của A cho B rồi cộng các kết quả với nhau.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1: Tính tổng (hay hiệu) đa thức nhiều biến.
Ví dụ 1. Tính tổng AB + và hiệu AB của hai đa thức A , B trong các trường hợp sau:
a) 2 Axy =+ và 2 Bxy =−
b) 232 21Axyxxy=−−+ và 3222Bxxy=+− .
c) 22 2 Axyzz =−+ và 22 35 Byzxz =+−
d) 2332315 22 Axyxyxyx =+−+ và 322371 22 Bxyxyxy =−+
Bài giải
a) 2222222 +=++−=++−=++−= ()()()() ABxyxyxyxyxxyyx
2222224 −=+−−=+−+=−++= ()()()() ABxyxyxyxyxxyyy
b)
Bài giải a/
Ví dụ 5. Chocác đathức 22 435 Axyxy =+− ; 2222322 Bxyxy =++ .Tìm đathức C saocho:
a) CAB =+ . b) CAB +=
3232222332 31 +=−+++−−=−++−++−
322223 3
Bài giải a/
222222
323323323323 3322333 −=−++−−−+=−++−++− =−+−++++−=+ ()() ()()() MPxxyxyxxyxyxxyxyxxyxy xxxyxyxyxyxyxy
32323232 3322 2
=+ ()()()()()()MNxxyxyxyxyxyxyxyxyx x b/ ()
c/ 3232 3232 3322 32
−=−+++−−+ =−+++−−+
=++−−+−++=−+
MPxxyxyxxyxy xxyxyxxyxy xxxyxyxyxyxxy
23232323 3236426 3642236959
()() ()()()()
d/ 32232 32232 33222 32
=−+++−−+−−+ =−+++−−+−−+
=++−+−+−−+−+ =−−+
Mxxyxyxyxyxxyxy xxyxyxyxyxxyxy xxxyxyxyxyxyxy xxyxy
32322323 32322323 33222323 624
()()() ()()()()
Dạng 2: Tìm đa thức thỏa mãn đẳng thức cho trước
Ví dụ 4. Tìm đathức A , B biết:
a) 2222232Axyxyxy +−=−+− . b) 22 52221 () Bxxyzxxyz −−=++ .
Bài giải
a/ () 2222 22222222 22222
232 232232 232332
+−=−+− =−+−−−=−+−−− =−+−−+−=−+− () ()()
Axyxyxy Axyxyxyxyxyxy xxyyxyyxy
b/ 22 22 2222 2
−−=++ =+++− =+++−=++−+=+
Bxxyzxxyz Bxxyzxxyz xxyzxxyzxxxyzxyzx
52221 22152
435322 2543322575 =+=+−+++ =−++++=−++
2222222222
()() ()()
CABxyxyxyxy xyxyxxyyxyxyxy
b/ ( ) 222222 222222222222 2222
=−=++−+− =++−−+=++−+− =+−−
322435 322435253423 25
() ()() CBAxyxyxyxy xyxyxyxyxyxyxxyy xyxyxy
Dạng 3: Thực hiện phép tính nhân đơn thức với đa thức
Quytắc: ( ) ABCABAC +=+ (với A, B, C là các đơn thức).
Ví dụ 6. Làmtínhnhân
a/
3232335323 (2).(21)2.2.(2)2.1242 Mxyxyxyxxyyxyxyxyxy =−+=+−+=−+
b/ 3 3 42 1111 (248)2.(4).(8).24 2222 Nxyyxyxyyyyxyxyyxy =−−⋅=+−+−=−−
c/
() ()() ()() 6
Ví dụ 7. Nhân đơnthức A với đathức B biếtrằng 2 2 1 2 Axy =− và 22 443Bxxy=+−
c: ()() ABCDACADBCBD ++=⋅+⋅+⋅+⋅
Ví dụ 8. Thựchiệnphépnhân
a) 2 ()() xyx y x+− ; b) 2 (2)(24) xyxyz +−+ ; c) 22 (2)(24) xyxxyy −++
Bài giải
a/ 2223222()()..()..() xyxxxxyxxyxyyxxyxxyxy y +−=+−++−=−+−
b/ 22 2 322 (2)(24).(2).42.2.()2.4 24228 xyxyzxxxyxzyxyyyz xxyxzxyyyz +−+=+−+++−+ =−++−+
Ví dụ 9. Rútgọnrồitínhgiátrị củabiểuthức a) 11 22 22 Mxyxy
b) 2224 (2)(42) Nxyxxyy =−++ tại 1 2 x = và 2 y
Dạng 5: Thực hiện phép tính chia đơ
Ví dụ 10: Làmphéptínhchia:
a) 53 : xx . b) 7418:6xx .
c) 672478:4xyzxy . d) ( ) 954465:13xyxy
e) 352279 : 155xyzxz
Bài giải:
a) 532 : xxx = . b) 74318:63 xxx = .
c) 67247228:42 xyzxyxz = . d) ( ) 95445 65:135xyxyxy −=− .
e) 35222279 : 155xyzxzxyz =
Dạng 6: Thực hiện phép tính chia đa thức với đa thức
Ví dụ 11: Làmphéptínhchia:
a) ( ) 32125: xxxx +− b) ( ) 4322323915: xyxyxyxy −+ c) 54423322 11 52: 24 xyzxyzxyzxyz
Bài giải:
a) ( ) 322125:125.xxxxxx +−=+−
b) ( ) 4322323 3925:3925 xyxyxyxyxyxy −+=−+
c) 544233224232 11 52:2028 24 xyzxyzxyzxyzxyxzyz +−=+−
Bài 2: Chohai đathức: 2 3351;Mxyzxxy =−+− và 2 553. Nxxyzxyy =+−+−
Tính ;MN NM
Bài giải:
322233 714 xyxyxyxyx =−−+−
b) 32223222333222 (84)(546)(4645) BACxyxyxyxyxyxyxxyxyxyxy +−=−+−+−−−+−−+ 32223222333222 845464645 xyxyxyxyxyxyxxyxyxyxy =−+−+−−−−++− 322233215 xyxyxyxyx =−+−+−
c) 33322232223222 (4645)(546)(84) CABxxyxyxyxyxyxyxyxyxyxy −−=+−−+−−−−−+− 33322232223222 464554684 xxyxyxyxyxyxyxyxyxyxy =+−−+−+++−+ 333222 215 xxyxyxyxy =−+−+
Bài 4: Cho đathức 22 axx Mbycy =++ ( , xy làbiến).Tìm ,, abc biết:
Khi 0,1xy== thì 3 M =− . Khi 2,0xy=−= thì 8. M = Khi 1,1xy==− thì 0. M =
Bài giải:
Khi 0;1;3xyM===− thì: 22 3.0.1.0.13. abcb −=++⇒=−
Khi 2;0;8xyM=−== thì: ( ) ( ) 2 2 8.2.0.2.0482. abcaa =−++−⇔=⇔=
Khi 1;1;0xyM==−= thì: ( ) ( ) ( ) 2 2 02.13.1.1.11 cc =+−−+−→=− .
Vậy 22 23. Mxyxy =−−
Bài 5: Tìm đathứcMbiết:
a) ( ) 22222 6x3x2x; yMxyy−+=+− b) ( ) 222 2x45x7. Myyyxy −−=+−
3351553
MNxyzxxyxxyzxyy
Bài giải:
3351553
xyzxxyxxyzxyy
(3)(35)(55)(13)
xyzxyzxxxyxyy
22 22 22 2
28104
xyzxxyy
−=−−=−−++−=−+−−+ 2 2 ()(28104)28104 NMMNxyzxxyyxyzxxyy
Bài 3: Chocác đathức: 3222546 Axyxyxy =−− ; 322284 Bxyxyxy =−+−
333222 4645 Cxxyxyxyxy =+−−+
Hãy tính:
a) ABC b) BAC +− c) CAB
Bài giải: a)
32223222333222 (546)(84)(4645) ABCxyxyxyxyxyxyxxyxyxyxy −−=−−−−+−−+−−+
32223222333222 546844645 xyxyxyxyxyxyxxyxyxyxy =−−+−+−−++−
a/ ( ) () 22222 2222222222 22222222
6x3x2x (2x)6x3x2x6x3x (6)(23)5
yMxyy Mxyyyxyyy xxyxyxyxyxy
−+=+− =+−−−=+−−+ =−++−+=−++
b/ ( ) 222 222222 22222
−−=+− =+−+−=+−+− =+−−++=−+
2x45x7 (5x7)(2x4)5724 (74)(52)117
Myyyxy Myxyyyxyxyxyy xyyxyxyxyxy
Bài 6: Thựchiệnphéptính
a) 2232235 1 2 2 xyxyxyy
d) ( ) 2 23() xxyxy +−−
b) 3222 1 (36) 3 xyxyxy −−+
e) 23212 21 25xyxxy
c) 222 2423 32 xyyxyxy −++⋅ .
f) 222 ()(21) xyxx −⋅−+
xyxyxyxyxyxyxxyy
Bài giải: a/ 222 3
223 22223 ..()().1( ()( ).( 1) ) xxxyx Axxyxy yxyyx xxyxyxyxxy yxx =+−+−+−− =
=−− −−+=−
b/ 2 2 22
xyyxyxyxyxyxyyxyxy
xyxyxy
Bài 7: Rútgọncácbiểuthứcsau a) 223 ()(1) Axxyxyyxx =−−−−
Bxxyyxyxx xxxyxyxyxyxxx xxyxxyyxyxx xxxyxyxyxxyy
=++−−−++ =+++−+−−+−+−+− =++−+−−− =−+−−+−+=
(31)2(1)(1) ..3.1(2).(2).(1)().().().1 322 ()(32)()22
Bài 8: Rútgọnrồitínhgiátrị biểuthức
a) 22 ()() Pxxyyxy =−+− tại 1 2 x =− và 1 2 y =− ;
b) 23222 ()(1) Qxyxyyxxy =−+−++ tại 10 x =− và 10 y =− .
Bài giải: a/
=−++=+
+=+==
Qxyxyyx xyxyx x
=−+− =−+−++
=−−++
++
y y =
( 1 )(1) xyxxyxyyxyxxy xyxy
x y
12
Bài 9: Chứngtỏ rằnggiátrị củacácbiểuthứcsaukhôngphụ thuộcvàogiátrị củabiến x
a) 23 (32)(3)23Pxxxxxxx =+−++−+ ;
b) 11 (23)61 23 Qxxxx
Bài giải:
a/ 23 23 2323 (32)(3)23.3.2..323
323233 Pxxxxxxxxxxxxxxxx xxxxxx =+−++−+=+−−+−+ =+−−+−+=
Vậygiátrị củacácbiểuthứcsaukhôngphụ thuộcvàogiátrị củabiến x
b/ 22
1111 (23)61.2.(3)6.6. 2323
Qxxxxxxxxxx xxxx
Vậygiátrị củacácbiểuthứcsaukhôngphụ thuộcvàogiátrị củabi
ến
xyxy
(...11.1.1.1)(.11.11.)
Bài giải: 22 22
=−+−−++
Qnnnn nnnnn nnnnn nn =+−−−+−−+ =+−−−−+++ =+∀∈⋮ℤ
Bài 13: Làm tính chia:
a) 88553322 (27):() xyxyxyxy ++− ;
−+ ;
b) 53353332 25: 43 xyxyxyxy
a)
Bài giải: =−−−
b)
++−
533533 533533 422422
32 25: 43 2232 2:5:: 3343 159 3 28
xyxyxyxy xyxyxyxyxyxy xyxyxy
c) 2432432 2432432 3232
(9124): (9:)(12:)(4:) 9124
xyzxyzxyzxyz xyzxyzxyzxyzxyzxyz xyxyzyz =+−+−
Bài 14: Tínhgiátrị biểuthức:
a) ( ) 53324422151020:5 Axyxyxyxy =−+ tại 1;2.xy=−=
b) () () 2 2 24332 236: Bxyxyxyxy =+− tại 2. xy==−
c) ()=−+−223 2 246: 3 Cxyxyxyxy tại 1 ;4. 2 xy==
d) =−
25522212 :2 33 Dxyxyxy tại 3;3.xy=−=
e) ( ) 5432232 20105:5 Exyxyxyxy =+− tại 1;1xy==− .
f) ( ) 54342222 732: Gxyzxyzxyzxyz =−+ tại 1;1;2xyz=−==
Bài giải:
Bxyxyxyxy xyxyxyxy xyxyxyxyxyxy xxyx
436(*)
Thay =−=−2;2xy vào(*)ta được: 22 4.(2)3.(2).(2)6.(2)
4.43.4.(2)121624124 −+−−−−
c) ()=−+− =−++−
=−+−
223 2 3 2
2 246: 3 222 2:4:6: 333 369(*)
Cxyxyxyxy xyxyxyxyxyxy xy
Thay 1 ;4. 2 xy== vào(*)ta được: 2 (3).69.(4)69.1613279 222 −+−=+−=
d)
2552222522522233 121211 :2:2:2(*) 333363 Dxyxyxyxyxyxyxyyx
Thay 3;3.xy=−= vào(*)ta được: 33 11927 .(3).(3)9 6322 −−=+=
e) ( )
=+− =+− =+−
20105:5 20:510:55:5 42(*)
5432232 542322232 332
Exyxyxyxy xyxyxyxyxyxy xyxyy
Thay 1;1xy==− vào(*)ta được: 332 4.(1).(1)2.1.(1)(1) (4)217 −+−−− =−−−=−
f) ( ) 543422225432422222 3322
732:(7:)(3:)(2:) 732(*) Gxyzxyzxyzxyzxyzxyzxyzxyzxyzxyz xyzxzy
=−+=−+ =−+
Thay 1;1;2xyz=−== vào(*)ta được: 3322 7.(1).1.23.(1).22.1(28)6232 −−−+=−−+=−
Bài 15:
Hình ảnhbêndướimôtả cáchcóthể làm để cómộthìnhhộpchữ nhậtcóbakíchthướclàx;y;z. (cm).Cáckíchthướcvàtỉ lệ củahộpphụ thuộcvàocácgiátrị củax;y;z.Tínhdiệntíchcủacác mặtcủahìnhhộpchữ nhật đượcthể hiệnquahình đó.
c/ Họcsinhcóthể trìnhbàyhaicáchnhư sau:
Cách 1:
Diệntíchmãnhvườnhìnhchữ nhậttheox,ylà:
() 2.2122.22.12424 xyxyxxyx +=+=+ (m 2 )
Thayx=4vày=4vào 424xyx + ta được:4.4.4+24.4=160(m 2 )
Vậyvớix=4vày=4thìdiệntíchmảnhvườnhìnhchữ nhật đólà160(m 2 )
Cách 2:
Diệntíchmãnhvườnhìnhchữ nhậttheox,ylà:
(22)(222)424 xyxxyxxyx +++=+ (m 2 )
Thayx=4vày=4vào 424xyx + ta được:4.4.4+24.4=160(m 2 )
Vậyvớix=4vày=4thìdiệntíchmảnhvườnhìnhchữ nhật đólà160(m 2 ).
Bài 17:
KhuvườntrồngmíacủanhàbácMinhban đầucódạngmộthình
vuôngbiếtchuvihìnhvuônglà 20 (m) sau đó đượcmở rộngbên
Lời giải Diệntíchcủacácmặtcủahìnhhộpchữ nhậtlà:
222 xzxzxyxyyzyzxzxyyz +++++=++ (cm 2 )
phảithêm y (m),phíadướithêm 10x (m)nênmảnhvườntrở
thànhmộthìnhchữ nhật (hình vẽ bên)
a/TínhdiệntíchkhuvườnbácMinh saukhi đượcmở rộngtheo x,y.
Bài 16:
Bác Nam có một mảnh vườn hình chữ nhật. Bác chia mảnhvườnnàyralàmhaikhu đấthìnhchữ nhật:Khu thứ nhất dùng để trồng cỏ. Khu thứ hai dùng để trồng hoa. (Với các kích thước có trong hình vẽ).
a/Tínhdiệntíchkhu đấtdùng để trồnghoatheox,y.
b/Tínhdiệntíchkhu đấtdùng để trồngcỏ theox,y.
c/Tínhdiệntíchmảnhvườnhìnhchữ nhậtcủabác Namvớix=4vày=4.
Lời giải
a/ Diệntíchkhu đấtdùng để trồnghoalà:
() 2.122 xyxyx +=+ (m 2 )
b/
Chiềudàikhu đấtdùng để trồngcỏ là:
(212)(1)2121(2)(121)11 yyyyyyy +−+=+−−=−+−=+ (m)
Diệntíchkhu đấtdùng để trồngcỏ là:
() 2.1122.11222 xyxyxxyx +=+=+ (m 2 )
b/TínhdiệntíchkhuvườnbácMinhsaukhi đượcmở rộngkhi
x = 1 ; y = 2

Lời giải a/
Cạnhcủamảnhvườnhìnhvuôngban đầulà20:4=5(m)
Chiềurộngcủakhuvườnsaukhi đượcmở rộnglà:y+5(m)
Chiềudàicủakhuvườnsaukhi đượcmở rộnglà:8x+5(m)
DiệntíchcủakhuvườnbácMinhsaukhi đượcmở rộnglà:
(y+5).(8x+5)=y.8x+y.5+5.8x+5.5=8xy+5y+40x+25(m 2 )
b/Khix=1;y=2thìdiệntíchkhuvườnbácMinhsaukhi đượcmở rộnglà: 8.1.2+5.2+40.1+25=91(m 2 )

Bài 18:
Mộtcửahàngbuổisángbán được xy baogạothìcửahàng đóthu đượcsố tiềnlà 6554 xyxy nghìn đồng.
a/Tínhsố tiềnmỗibaogạomàcủacửahàng đó đãbántheox,y.

b/Tínhsố tiềnmỗibaogạomàcủacửahàng đó đãbánkhix=2;y=2.
Lời giải
a/Số tiềnmỗibaogạomàcủacửahàng đó đãbántheox,ylà:
()() 655465545443 ()::: xyxyxyxyxyxyxyxyxy −=−=− (nghìn đồng).
b/Số tiềnmỗibaogạomàcủacửahàng đó đãbánkhix=2;y=2là:
5443 2.22.2384 −= (nghìn đồng)

Bài 19:
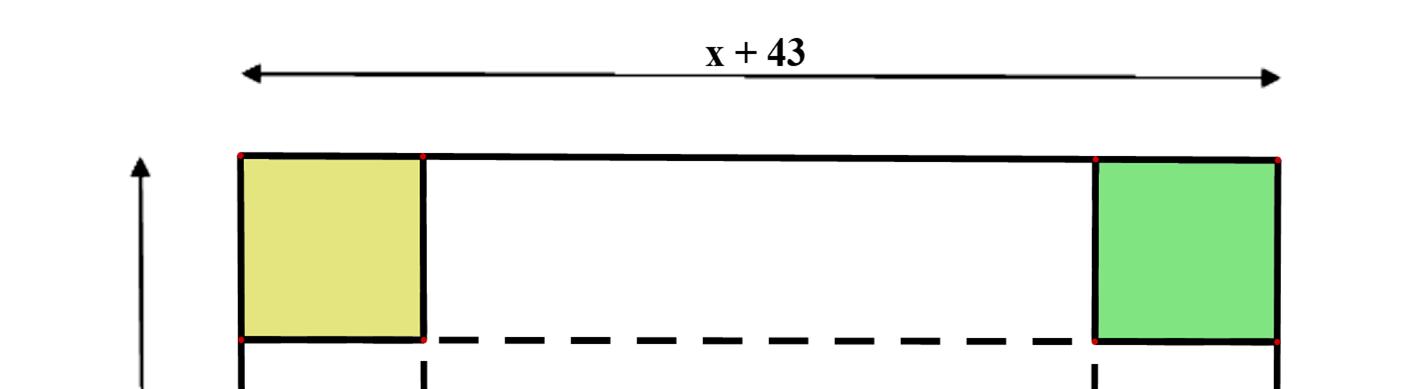
Mộttấmbìacứnghìnhchữ nhậtcóchiềudàilà x + 43 (cm)vàchiềurộnglà x + 30 (cm).Người
tacắt ở mỗigóccủatấmbìamộthìnhvuôngcạnh 2 1 y + (cm) ( phần tô màu) vàxếpphầncònlại
thànhmộtcáihộpkhôngnắp.
a/Tínhdiệntíchxungquanhcủahìnhhộpchữ nhậttrêntheo x; y
b/Tínhdiệntíchxungquanhcủahìnhhộpchữ nhậttrênvới x = 16 ; y = 4
Lời giải
a/Chiềucaocủahìnhhộpchữ nhậtbằngcạnhcủahìnhvuôngcắt đivàbằng 2 1 y + (cm).
Chiềudàicủahìnhhộpchữ nhậtlà: 222 (43)(y1).24322241 xxyxy +−+=+−−=−+ (cm).
Chiềurộngcủahìnhhộpchữ nhậtlà: 222 (30)(y1).23022228 xxyxy +−+=+−−=−+ (cm).
Diệntíchxungquanhcủahìnhhộpchữ nhậttrêntheo x, y là:
−++−++=−++
( ) 22222 2222222 2422
xyxyyxyy yxyyyyxy xyyyxcm
=−++=−++−+ =−+++
2241(228).(1)2(2469).(1) (4x8y138).(1)4.8.13848138 481304138()
b/Diệntíchxungquanhcủahìnhhộpchữ nhậttrênvới x = 16 ; y = 4 là: 242 2 4.16.(4)8.(4)130.(4)4.161381258() cm −+++=
D. BÀI TẬP TỰ LUYỆN.
Bài 1. Tínhtổngcủahai đathức
a) 2223 Axy =+ và 2234 Bxy =−
b) 22235 Axxyy =−+ và 2232 Bxxyy =+−
Bài 2. Tínhtổngvàhiệucủahai đathức M và N với:
a) 22 2 Mxyxy =++ và 22 2 Nxyxy =+−
b) 233210 ,, Mxy=+− và 03225 ,, Nxy=−+−
Bài 3: Tínhtổng AB + vàhiệu AB củahai đathức A , B trongcáctrườnghợpsau:
a) 23 Axy =+ và 2 Bxy =−
b) 232 2 Axyxxy=+−+ và 322 7 Bxxyxy=+−−
c) 22 21Axyzz=−−+ và 22 432Byzxz=++−
d) 23323 311 22 Axyxyxyx =+−+ và 323219 22 Bxyxyxy =−+
Bài 4: Thựchiệnphéptínhsau:
a) 2222 75 ()() Axxyyxxyy =−+−−+−
b) 222222 3253 ()()() Bxyxyxyxyxyxy =−−−−+−
Bài 5: Cho các đa thức 32 221Mxxyxy=−++ ; 2 322Nxyxy=+− và 32 31Pxxyxy=−−+ .
Tính:
a) MN + . b) MP . c) 2 MP . d) MNP ++
Bài 6: Chocác đathức 2 22Mxy=−− ; 2 31Nxy=++ và 2 15 Px =− .Tính
a) MN + . b) MP . c) 2 MP . d) MNP ++
Bài 7: Tìm đathức A , B biết
a) 22222 632 xxyAxyxy −+=+− . b) 2222457 () Bxyyxyxy −−=+−
Bài 8: Tìm đathức M biết:
a) 2223245 () Mxxyxxyy +−=+− . b) 2222 5376() Mxyxxyy −−=−+ .
c) 3232 2132 () Mxxyxxy +−+=−++ . d) 2 690()Mxx−−+= .
Bài 9: Chocác đathức 2221Axyxy=−++ ; 2222 1 Bxyxy=+−− .Tìm đathức C saocho:
CAB =+ .
CAB += .
Bài 10: Tínhgiátrị củacác đathứcsau:
a) 33333 2222 Axxyxyxy =+−++− tại 2 x = , 3 y =−
b) 22446688 Bxyxyxyxyxy =+−+− tại 1 x = , 1 y =−
c) 22331010 Cxyxyxyxy =++++ ⋯ tại 1 x =− , 1 y = .
Bài 11: Thựchiệnphéptính
a) 22 2(132)Mxxx =−+ ; b) 2 1 (234) 2 Nxxx =−+⋅ ;
c) 32 1 (24) 2 Pxyxxyy =−+− . d) 23212 21 25xyxxy
Bài 12: Nhân đathức A với đơnthức B biếtrằng 32311 42 Axyxy =+− và 2(2)Bxy =− .
Bài 13: Rútgọncácbiểuthứcsau
a) 223 3(61)9(2) Axxxxx =+−− ; ĐS: 2 12 Ax =
b) 2 2 1 (2)2()(63) 3 Bxxyxyxyyxy =−+−+− ĐS: 33Bxy =−
Bài 14: Tínhgiátrị củabiểuthức
a) 2232 2(5)(24)(6) Mxxxxxxx =−+−+++ tại 4 x =− ; ĐS: 64 M =−
b) 322 (1)(21)(23) Nxyxyxxxxxyy =+−−+−+− tại 8 x = và 5 y =− ĐS: 80 Q =−
Bài 15: Chobiểuthức 234 (12)2(2)(4)Pxxxxxxx =−+−++− .Chứngtỏ giátrị của P không phụ thuộcvàogiátrị của x
Bài 16: Chứngminhrằnggiátrị củabiểuthứcsaukhôngphụ thuộcvàogiátrị củacácbiến: ( ) ( ) ( ) 273725. Axxxxxx =+−+−+−
Bài 17: Chobiểuthức 105(1,2)2(2,53)Bxxxx =−−+− .Chứngminhrằnggiátrị củabiểuthứcnày luônluônkhông đổi.
Bài 18: Chứngtỏ rằngcácbiểuthứcsaukhôngphụ thuộcvàogiátrị củabiến x :
a) ( ) 22 (53)(1)6103 xxxxxxxx −−−+−−+ ;
b) ( ) 221(1)5xxxxxx ++−+−+
c) ( )( ) ( )( ) 2212312xxxx
Bài 19: Tínhgiátrị củabiểuthức
a) ( ) 222 53(75)7 Pxxxxx =−+−− tại 5 x =− ;
b) ()() Qxxyyxy =−+− tại 1,5 x = và 10 y =
c) 22 (3)(93) Qyxyxyx =+−+ tại 3 x = và 1 3 y =
Bài 20: Chứngminh đẳngthức ( ) 322344 ()xyxxyxyyxy −+++=−
Bài 21: Chứngminh đẳngthức 22 ()()2(1)(1)2 xyxyzxyxy +++−+++=+
Bài 22: Chứngminh đẳngthức 2244()()() xyxyxyxy −++=−
Bài 23: Chứngminh đẳngthức 2233()() xyxxyyxy −++=−
Bài 24: Cho 1 ab = .Chứngminh đẳngthức (1)(1)(1)(1) abbaab +++=++
Bài 25: Làmtínhnhân: a) (27)(31) xx+− ; b) ( ) 2 (52)1 xyxxy−−+ ;
c) (1)(1)(2) xxx−++ ; d) ( )( ) 22 54293 xxxx−+−
Bài 26: Thựchiệnphéptính:
a) (7)(5) xx ; b) 1 1(23) 2 xx
d) 22 ()() xyyxyx −++
Bài 27: Làm tính chia:
a) 5632(357):5 xxxx
b) 67564532 (543):() xyxyxyxy ++−
; c) 11 (41) 22 xxx
c) 5842793 575 5: 893 xyxyxyxy
d) 342424523222 (27): xyzxyzxyzxyz −+
Bài 28: Làm tính chia:
a) 5743(324):6 yyyy +− ;
b) 245672 (235):() xyxyxyxy +−− ;
c) 46244222214 2: 555 xyxyxyxy
d) 32245364732(356): xyzxyzxyzxyz ++ .
274837 3 815 xyxyxy −+
2223 27 xyxzxz −+
S: 24 112 233yyy +−
3456235 xyxyxy−−+
2422151 224 xyyx +−
S: 4335356 yxyzxyz ++
34 37 55 xxx
HÌNH CHÓP TAM GIÁC ĐỀU
A. KIẾN THỨC TRỌNG TÂM
1. Hình chóp tam giác đều.
Hình chóp tam giác đều như hình vẽ bên . Có 4 mặt , 6 cạnh.
Hình chóp tam giác đều S.ABC.
Mặt đáy ABC là một tam giác đều.
Các mặt bên SAB, SBC, SCA là những tam giác cân tại S.
Các cạnh đáy AB, BC, CA bằng nhau
Các cạnh bên SA, SB, SC bằng nhau.
S gọi là đỉnh của hình chóp tam giác đều S.ABC.
2. Diện tích xung quanh hình chóp tam giác đều.
Diện tích xung quanh của hình chóp tam giác đều bằng nữa tích của chu vi đáy với độ dài trung đoạn.
Công thức tổng quát : 1 .. 2 xq SCd = . Với :

+ xq S : Diện tích xung quanh của hình chóp tam giác đều.
+ Chu vi đáy : C = 3.a (a là độ dài cạnh đáy tam giác đều).
+ d: Độ dài trung đoạn của hình chóp tam giác đều.
3. Thể tích hình chóp tam giác đều.
Thể tích của hình chóp tam giác đều bằng một phần ba tích của diện tích đáy với chiều cao
Công thức tổng quát : 1 .S.h 3 V = . Với :
+ V : Thể tích của hình chóp tam giác đều.
+ S : Diện tích đáy.
+ h : Chiều cao của hình chóp tam giác đều.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1: Nhận biết các kiến thức cơ bản của hình chóp tam giác đều.
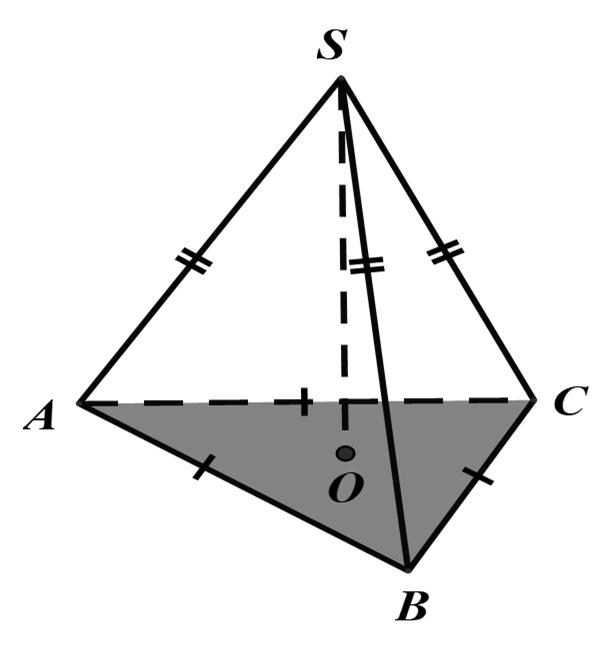
Ví dụ 1. Cho hình chóp đều tam giác đều SABC có đường cao
SO. (Hình vẽ bên).
a) Cho biết các mặt bên của hình chóp có dạng hình gì ? Nêu tên
đỉnh của hình chóp.
b) Kể tên các cạnh bên.
c) Kể tên mặt đáy và các mặt bên của hình chóp.
Lời giải
a) Các mặt bên của hình chóp có dạng hình tam giác cân. Đỉnh của hình chóp là đỉnh S.
b) Các cạnh bên: SA, SB , SC
d) Mặt đáy: ABC . Mặt bên: SAB , SBC , SAC
Ví dụ 2: Hình ảnh bên là khối Rubik có bốn mặt , các mặt bên, mặt đáy là các tam giác đều.

a) Khối Rubik có dạng như hình bên thường được gọi là hình gì ?
b) Cho biết số mặt ,số cạnh ,số đỉnh của hình khối bên ?
c) Hình vẽ bên là hình ảnh một chiếc Robik – 4 mặt , mỗi mặt đều được ghép bởi những tam giác đều nhỏ bằng nhau. Hãy cho biết có bao nhiêu tam giác đều có trên một mặt của chiếc Robic này ?
Lời giải
a) Khối Rubik có dạng như hình bên thường được gọi là hình chóp tam giác đều.


b) Số mặt là 4. Số cạnh là 6, sốđỉnh là 1.
c) Có 13 tam giác đều có trên một mặt của chiếc Robik này.
Dạng 2: Tính diện tích xung quanh của hình chóp tam giác đều.
Sử dụng công thức tổng quát : 1 2 xq SCd =
Ví dụ 3.
Một giỏ hoa gỗ mini có dạng hình chóp tam giác đều (như hình bên) có độ dài cạnh đáy là 10cm và độ dài trung đoạn bằng 20cm. Tính diện tích xung quanh giỏ hoa gỗ mini đó.

Lời giải:
Diện tích xung quanh giỏ hoa gỗ mini là : () 2 11 ...3.10.20300() 22 xq SCdcm ===

Ví dụ 4.
Cho hình chóp tam giác đều S.ABC với kích thước như hình vẽ
a) Tính chu vi tam giác ABC .
b) Cho biết độ dài trung đoạn hình chóp S.ABC.
c)Tính diệntíchxungquanhcủahìnhchóptamgiác đềuS.ABC.
Lời giải:
a) Chu vi tam giác ABC là: C = 3a = 3.6 = 18 (cm).

b) Độ dài trung đoạn hình chóp S.ABC là d = SH = 9 (cm)
c) Diện tích xung quanh của hình chóp tam giác đều S.ABC là :
2 11 22...18.981() xq SCdcm ===
Ví dụ 5.
Cho một hình chóp tam giác đều S.ABC có độ dài cạnh đáy AB
bằng 7cm và đường cao của tam giác cân SAB là SM = 11cm.


Tính diện tích xung quanh của hình chóp tam giác đều S.ABC.
Lời giải:
Diện tích xung quanh của hình chóp tam giác đều S.ABC là : () 2 11 22...7.3.11115,5() xq SCdcm ===
Dạng 3: Tính thể tích của hình chóp tam giác đều.
Sử dụng công thức tổng quát : 1 .S.h 3 V =
Ví dụ 6. Chóp inox đặt trên đỉnh núi Fansipan (Việt Nam) có dạng hình chóp tam giác
đều với diện tích đáy khoảng 1560 cm 2 và chiều cao khoảng 90 cm. Tính thể tích
của chóp inox trên đỉnh núi Fansipan (Việt Nam).
Lời giải Thể tích của chóp inox trên đỉnh núi Fansipan (Việt Nam) là :
2 1 .1560.9046800(cm) 3 V ==
Ví dụ 7. a/ Một khối Rubic có dạng hình chóp tam giác đều. Biết chiều cao khoảng 5,88cm, thể tích của khối Rubic là 44,002 cm 3 . Tính diện tích đáy của khối Rubic.
Lời giải Diện tích đáy của khối Rubic.
1 .S.h 3 V = Suy ra
33.44,002
2
22,45() 5,88 V Scm h ===
b/ Một hình chóp tam giác đều có thể tích là
của hình chóp tam giác đều đó .
Lời giải
Chiều cao của hình chóp tam giác đều đó là :
3 123cm , diện tích đáy là
2 93cm . Tính chiều cao
1 .S.h 3 V = Suy ra 33.123 4() 93 V hcm S ===
C. BÀI TẬP VẬN DỤNG.
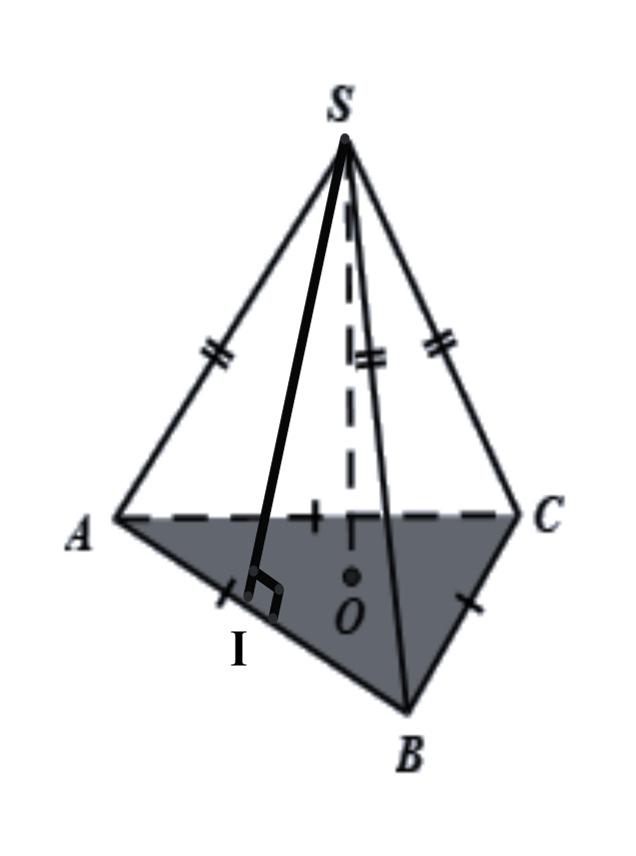
Bài 1 Chohìnhchóptamgiác đều S.ABCnhư hình vẽ. Hãy điền vào
chỗ trống (…) các ý cho đủ nghĩa .
a/ Tên mặt đáy là ………...., đáy là hình…………………
b/ S gọi là ……………của hình chóp tam giác đều.
c/ Tên các mặt bên :……………………………………………….
Các mặt bên là hình……………….bằng nhau.
d/ SA, SB, SC gọi là …………………………..của hình chóp tam giác đều.
Các đoạn SA, SB, SC ………………………………...
e/ Chiều cao của hình chóp tam giác đều là đoạn
…………………….
f/ Trung đoạn của hình chóp tam giác đều là đoạn …………………..
g/ Công thức tổng quát diện tích xung quanh của hình chóp tam giác đều là ……………………………………………………..
h/Côngthứctổngquátthể tíchcủahìnhchóptamgiác đềulà……………………………………..
Lời giải
a/ Tên mặt đáy là ABC, đáy là hình tam giác đều
b/ S gọi là đỉnh của hình chóp tam giác đều.
c/ Tên các mặt bên : SAB; SBC; SAC
Các mặt bên là hình tam giác cân bằng nhau.
d/ SA, SB, SC gọi là cạnh bên của hình chóp tam giác đều.
Các đoạn SA, SB, SC bằng nhau.
e/ Chiều cao của hình chóp tam giác đều là đoạn SO
f/ Trung đoạn của hình chóp tam giác đều là đoạn SI
g/ Công thức tổng quát diện tích xung quanh của hình chóp tam giác đều là
h/ Công thức tổng quát thể tích của hình chóp tam giác đều là 1 .S.h
V =
xq SCd =
Bài 2 Trong các miếng bìa ở hình 1; hình 2; hình 3; hình 4; miếng bìa nào có thể gấp lại (theo các nét đứt) đểđược hình chóp tam giác đều ?
Bài 4
a/ Bộ nam châm xếp hình có dạng hình chóp tam giác đều (như hình
ảnh bên ) có độ dài cạnh đáy khoảng 6 cm và mặt bên có đường cao
khoảng 7 cm. Tính diện tích xung quanh bộ nam châm xếp hình đó.
b/ Một hình chóp tam giác đều và một hình lăng trụđứng tam giác đều như hình vẽ dưới đây (diện tích đáy, chiều cao của các hình khối bằng nhau).
Nếu thể tích lăng trụđứng tam giác đều là V thì thể tích hình chóp tam giác đều là bao nhiêu ? Vì sao ?
Lời giải
Hình 1; hình 4 có thể gấp lại (theo các nét đứt) đểđược hình chóp tam giác đều .
Bài 3
a/ Một chiếc đèn thả trần có dạng hình chóp tam giác đều có tất cả các cạnh đều khoảng 20cm. Độ dài trung đoạn khoảng 17,32 cm. Tính diện tích xung quanh của chiếc đèn thả trần đó.

b/ Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 4cm và chiều cao tam giác đáy là 3,5cm; trung đoạn bằng 5cm. Tính diện tích xung quanh và diện tích toàn phần (tức là tổng diện tích các mặt ) của hình chóp. Lời giải

a/ Diện tích xung quanh của chiếc đèn thả trần đó là : () 2 11 22...3.20.17,32519,6() xq SCdcm ===

b/ Diện tích xung quanh của hình chóp là : () 2 11 22...3.4.530() xq SCdcm === .
c/ Diện tích toàn phần của hình chóp là : 2 1 30.4.3,537() 2 tpxq SSScm =+=+=
Tài liệu dạy học mới 7
Lời giải a/ Diện tích xung quanh bộ nam châm xếp hình đó là : () 2 11 22...3.6.763() xq SCdcm ===
b/ Hình chóp tam giác đều và hình lăng trụđứng tam giác đều có cùng diện tích đáy và chiều cao thì thể thích lăng trụđứng tam giác đều gấp 3 lần thể tích hình chóp tam giác đều. Do đó thể tích lăng trụđứng tam giác đều là V thì thể tích hình chóp tam giác đều là 3 V
Bài 5
Cho hình chóp tam giác đều S.ABC với các kích thước như hình vẽ bên .
a/ Cho biết độ dài trung đoạn của hình chóp S.ABC.
b/ Tính diện tích xung quanh và diện tích toàn phần ( tức là tổng các mặt ) của hình chóp S.ABC.
c/ Tính thể tích của hình chóp tam giác đều S.ABC biết chiều cao của hình chóp khoảng 7,5 cm.
Lời giải
a/ Độ dài trung đoạn của hình chóp S.ABC là SH = 6,93cm.





b/ Diện tích xung quanh của hình chóp S.ABC là () 2 11 ...3.8.6,9383,16() 22 xq SCdcm ===
Diện tích toàn phần của hình chóp S.ABC là
c/ Thể tích của hình chóp tam giác đều S.ABC là
Bài 6
2 83,1627,27110,43() tpxq SSScm =+=+=

3 11 33.S.h.27,27.7,568,175() Vcm ===
Một khối bê tông được làm có dạng hình chóp tam giác đều trong đó cạnh đáy hình chóp là 2m, trung đoạn của hình chóp là 3m. Người ta sơn ba mặt xung quanh của khối bê tông. Cứ mỗi mét vuông sơn cần trả 30 000 đồng (tiền sơn và tiền công). Cần phải trả bao nhiêu tiền khi sơn ba mặt xung quanh ?
Lời giải
Diện tích xung quanh của khối bê tông là () 2 11 22...3.2.39() xq SCdcm ===
Cần phải trả số tiền khi sơn ba mặt xung quanh là 9. 30000 = 270000 (đồng).
Bài 7
Cho tam giác đều lớn . Khi gấp tam giác theo đường có gạch chấm, em có thể tạo thành hình chóp tam giác đều được không?
Lời giải
Khi gấp theo đường gạch chấm ta nhận được một hình chóp tam giác
đều.
HÌNH CHÓP TỨ GIÁC ĐỀU
A. KIẾN THỨC TRỌNG TÂM
1. Hình chóp tứ giác đều.
- Hình chóp tứ giác đều S.ABCD (như hình vẽ bên )
- Hình chóp tứ giác có 5 mặt, 8 cạnh.
- Mặt đáy ABCD là một hình vuông .
- Các mặt bên SAB; SBC; SCD; SDA là những tam giác cân tại S.
- Các cạnh đáy AB; BC; CD; DA bằng nhau.
- Các cạnh bên SA; SB; SC; SD bằng nhau.
- S gọi là đỉnh của hình chóp tứ giác đều S.ABCD.
2. Diện tích xung quanh hình chóp tứ giác đều.
Diện tích xung quanh của hình chóp tứ giác đều bằng nữa tích của chu vi đáy với độ dài trung đoạn.
Công thức tổng quát : 1 2 xq SCd = . Với :
+ xq S : Diện tích xung quanh của hình chóp tứ giác đều.
+ Chu vi đáy : C = 4.a (a là độ dài cạnh đáy hình vuông).
+ d: Độ dài trung đoạn của hình chóp tứ giác đều.
3. Thể tích hình chóp tứ giác đều.

Thể tích của hìnhchóp tứ giác đều bằng một phần ba tíchcủa diện tích đáy với chiều cao
Công thức tổng quát : 1 .S.h 3 V = . Với :
+ V : Thể tích của hình chóp tứ giác đều.
+ S : Diện tích đáy.
+ h : Chiều cao của hình chóp tứ giác đều.
Tài liệu dạy họ
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1: Nhận biết các kiến thức cơ bản của hình chóp tứ giác đều.
Dùng các kiến thức nêu trong phần Kiến thức trọng tâm
Ví dụ 1. Cho hình chóp đều tứ giác đều SABCD có đường cao SO (Hình vẽ bên).
a) Cho biết các mặt bên của hình chóp có dạng hình gì ? Nêu tên đỉnh của hình chóp.
b) Kể tên các cạnh bên.
c) Kể tên mặt đáy và các mặt bên của hình chóp. Lời giải
a) Các mặt bên của hình chóp có dạng hình tam giác cân. Đỉnh của hình chóp là đỉnh S.
b) Các cạnh bên: SA , SB , SC , SD .
d) Mặt đáy: ABCD . Mặt bên: SAB , SBC , SCD , SAD Ví dụ 2: Hình ảnh bên là bảo tàng Louvre bảo tàng nghệ thuật ở Pari có 4
mặt bên là tam giác cân ,1 mặt đáy là hình vuông.
a) Bảo tàng Louvre bảo tàng nghệ thuật ở Pari có dạng như hình bên thường

được gọi là hình gì ?
b) Cho biết số mặt, số cạnh, sốđỉnh của hình khối bên ?
Lời giải
a) Bảo tàng Louvre bảo tàng nghệ thuật ở Pari có dạng như hình bên thường được gọi là hình chóp tứ giác đều.
b) Số mặt là 5. Số cạnh là 8, sốđỉnh là 1.
Ví dụ 3: Trong các hình sau , hình nào có thể gấp được thành hình chóp tứ giác đều ?
Lời giải: Cả 3 hình đều có thể gấp được thành hình chóp tứ giác đều
Dạng 2: Tính diện tích xung quanh của hình chóp tứ giác đều.
Sử dụng công thức tổng quát : 1 .. 2 xq SCd =
Ví dụ 4.
Một túi quà có dạng hình chóp tứ giác đều (như hình bên) có độ dài cạnh
đáy là 12cm và độ dài trung đoạn bằng 8cm. Tính diện tích xung túi quà đó.
Lời giải:
Diện tích xung quanh túi quà hình chóp tứ giác đềulà :
() 2 11 22...4.12.8192() xq SCdcm ===
Ví dụ 5.
Cho hình chóp tứ giác đều S.ABCD với kích thước như hình vẽ.
a) Tính chu vi đáy ABCD.
b) Cho biết độ dài trung đoạn hình chóp S.ABC.
c) Tính diệntíchxung quanh của hình chóp tứ giác đềuS.ABCD.
Lời giải:
a) Chu vi tam giác ABC là: C = 4a = 4.10 = 40 (cm).
b) Độ dài trung đoạn hình chóp S.ABC là d = SI = 12 (cm)
c) Diện tích xung quanh của hình chóp tam giác đều S.ABC là : 2 11 22...40.12240() xq SCdcm ===
Ví dụ 6.
Cho một hình chóp tứ giác đều S.ABCD có diện tích đáy là 400cm 2 , trung đoạnSI = 25cm. Tínhdiện tích xungquanh,diện tích toànphần ( tức là tổng diện tích các mặt ) của hình chóp tứ giác đều S.ABCD.

Lời giải:
a/ Độ dài cạnh đáy của hình chóp tứ giác đều S.ABCD là :
2 Sa = Suy ra 2 400 a = nên a = 20
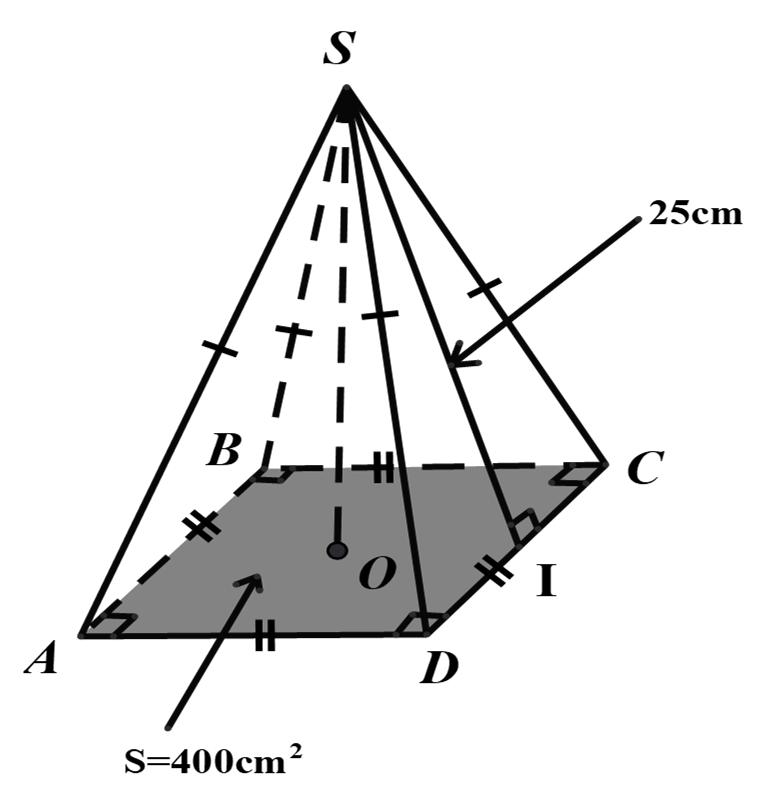


Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là :
() 2 11 22...4.20.251000() xq SCdcm ===
b/ Diện tích toàn phần của hình chóp tứ giác đều S.ABCD là :
tpxq SSScm =+=+=
22 1000201400()
Hình a Hình b Hình c
Tài liệu dạy học mới 3
Dạng 3: Tính thể tích của hình chóp tứ giác đều.
Sử dụng công thức tổng quát : 1 .S.h 3 V =
Ví dụ 7.
a/ Kim tự tháp Kê - ốp ( thế kỉ 25 trước công nguyên) là một hình chóp tứ giác đều, cạnh đáy bằng 233m; chiều cao hình chóp 146,5m. Tính thể tích kim tự tháp Kê - ốp ?
b/ Kim tự tháp Louvre (xây dựng vào năm 1988). Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều có chiều cao 21m, độ dài cạnh đáy là 34m. Tính thể tích của kim tự tháp Louvre ?
Dạng 4: Các bài toán cơ bản về mối quan hệ giữa hình lập phương, hình hộp chữ nhật
với hình chóp tứ giácđều
Vận dụng kiến thức về hình lập phương, hình hộp chữ nhật đã học, các dữ kiện liên quan và tính toán theo yêu cầu bài toán.
Ví dụ 9
Một khối bê tông có dạng như hình vẽ bên.
Phần dưới của khối bê tông có dạng hình hộp chữ nhật , đáy là hình
vuông cạnh 40cm và chiều cao là 25cm. Phần trên của khối bê tông là hình chóp tứ giác đều có cạnh đáy bằng 40cm và chiều cao bằng
100cm. Tính thể tích khối bê tông?
Lời giải
Thể tích phần dưới của khối bê tông có dạng hình hộp chữ nhật là : 40.40.25 = 40000 (cm 3 )
Thể tích phần trên của khối bê tông có dạng hình chóp tứ giác đều là:
2 1 .40.10053333,3 3 ≈ (cm 3 )
Thể tích khối bê tông là : 40000 + 53333,3 = 93333,3 (cm 3 )
Lời giải
a/ Thể tích kim tự tháp Kê - ốp là : ()2 3 1 3.233.146,52651112,8(m) V ==
b/ Thể tích của kim tự tháp Louvre ()2 3 1 3.34.218092(m) V ==


Ví dụ 8.
Cho hình chóp tứ giác đều S.ABCD biết AD = 25mm, SO = 27mm.

Tính thể tích hình chóp tứ giác đều S.ABCD ?
Lời giải
Thể tích hình chóp tứ giác đều S.ABCD là : 23 11 33.S.h.25.275625() Vmm ===

Ví dụ 10
Người ta muốn làm cái nhà kho bằng tôn hình lăng trụ tứ giác đều có
mái che là bốn hình chóp tứ giác đều với kích thước đã cho trên hình .
a/ Tính diện tích tôn cần thiết dùng để lợp mái và che xung quanh,
biết độ dài trung đoạn hình chóp là 8m.
b/ Tính thể tích không khí trong kho sau khi xây dựng xong .
Lời giải
a/Cạnh của hình chóp tứ giác đều là 25 : 2 = 12,5 m

Diện tích xung quanh của 1 hình chóp tứ giác đều là () 2 11 ...4.12,5.8200() 22 xq SCdm ===
Diện tích xung quanh của 4 hình chóp tứ giác đều là :
4.200 = 800 (m 2 )
Diện tích xung quanh của hình hộp chữ nhật là : 4.25.20 = 2000 (m 2 )
Diện tích tôn cần thiết dùng để lợp mái và che xung quanh là 800 + 2000 = 2800 (m 2 )
Tài
b/ Thể tích của một hình chóp tứ giác đều là : 23113125 .S.h.(12,5).5() 3312 Vm ===
Thể tích của bốn hình chóp tứ giác đều là : 3 31253125 4.() 123 m =
Thể tích của hình hộp chữ nhật là :
3 25.25.2012500() m =



Thể tích không khí trong kho sau khi xây dựng xong : 3 3125 1250013541,67() 3 m +≈
C. BÀI TẬP VẬN DỤNG.
Bài 1 Cho hình chóp tứ giác đều S.ABCD như hình vẽ.
Hãy điền vào chỗ trống (…) các ý cho đủ nghĩa .
a/ Tên mặt đáy là ………...., đáy là hình…………………
b/ S gọi là ……………của hình chóp tứ giác đều.
c/ Tên các mặt bên :……………………………………………….
Các mặt bên là hình……………….bằng nhau.
d/ SA, SB, SC, SD gọi là …………………………..của hình chóp tứ giác đều.
Các đoạn SA, SB, SC, SD ………………………………...
e/ Chiều cao của hình chóp tứ giác đều là đoạn …………………….
f/ Công thức tổng quát diện tích xung quanh của hình chóp tứ giác
đều là ……………………………………………………..
g/ Công thức tổng quát thể tích của hình chóp tứ giác đều là
……………………………………..
Lời giải
a/ Tên mặt đáy là ABCD, đáy là hình vuông
b/ S gọi là đỉnh của hình chóp tứ giác đều.
c/ Tên các mặt bên :SAB; SBC; SCD; SAD Các mặt bên là hình tam giác cân bằng nhau.
d/ SA, SB, SC, SD gọi là cạnh bên của hình chóp tứ giác đều.
Các đoạn SA, SB, SC, SD bằng nhau.
e/ Chiều cao của hình chóp tứ giác đều là đoạn SO
f/ Công thức tổng quát diện tích xung quanh của hình chóp tứ giác đều là 1 2 xq SCd =
g/ Công thức tổng quát thể tích của hình chóp tứ giác đều là 1 .S.h 3 V =
Bài 2
a/ Thực hành: Từ tờ giấy cắt ra
một hình vuông rồi thực hiện các
thao tác theo thứ tự từ 1 đến 6 để
có thể ghép được các mặt bên của mộthình chóp tứ giác (hình dưới).
Lời giải: Học sinh thực hành từ
bước 1 đến bước 6 .
b/ Trong các miếng bìa ở hình 1; hình 2; hình 3; hình 4; miếng bìa nào có thể gấp lại (theo các nét đứt) đểđược hình chóp tứ giác đều ?
Bài 3 Tính diện tích xung quanh, diện tích toàn phần ( tổng diện tích các mặt) của các hình chóp tứ giác đều sau đây :
Lời giải Hình 2; hình 3 có thể gấp lại (theo các nét đứt) đểđược hình chóp tứ giác đều .
c/ Trong các miếng bìa ở hình 1; hình 2; hình 3; hình 4; miếng bìa nào không thể gấp được thành hình chóp tứ giác đều ?
Lời giải
Hình 1:
Diện tích xung quanh hình chóp tứ giác đều :
2 1 .4.20.20800() 2 xq Scm ==


Diện tích toàn phần hình chóp tứ giác đều là : 22 800201200(c) m +=
Hình 2:
Diện tích xung quanh hình chóp tứ giác đều : 2 1 .4.7.12168() 2 xq Scm ==
Diện tích toàn phần hình chóp tứ giác đều là : 22 1687217(c) m +=
Hình 3:
Diện tích xung quanh hình chóp tứ giác đều : 2 1 .4.16.15480() 2 xq Scm ==
Lời giải
Hình 1; hình 2; hình 3 không thể gấp được thành hình chóp tứ giác đều .



Tài liệu dạy học mới 8
Diện tích toàn phần hình chóp tứ giác đều là : 22 48016736(c) m +=
Tài liệu dạy học mới 9
Bài 4:
Cho hình chóp tứ giác đều S.ABCD biết SO = 12 cm; CD = 6,5cm.





Tính thể tích hình chóp tứ giác đều S.ABCD ?
Lời giải
Thể tích hình chóp tứ giác đều S.ABCD là : 23 11 .S.h.(6,5).12169() 33 Vcm ===
Bài 5:
Hình bên là một cái lều ở một trại hè của học sinh tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ:
a/ Thể tích không khí bên trong lều là bao nhiêu ?
b/ Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, …) là bao nhiêu ? Biết độ dài trung đoạn của lều trại là 2,24 cm.
Lời giải
a/ Thể tích không khí bên trong lều chính là thể tích hình chóp tứ giác đều :
23118 ...2.22,67() 333 VShm ===≈
b/ Số vải bạt cần thiết để dựng lều chính là diện tích xung quanh hình chóp tứ giác đều.
2 11 22...(2.4).2,248,96() xq SCdm ==≈
Bài 6:
Bộđồ chơi gồm có chim đại bàng và hình chóp để giữ thăng bằng.
Biết hình chóp để giữ thăng bằng là hình chóp tứ giác đều có cạnh
40mm; chiều cao hình chóp tứ giác đều đó là 52mm. Tính thể tích của hình chóp tứ giác đều đó (làm tròn kết quả đến hàng phần mười).
Lời giải
Thể tích của hình chóp tứ giác đều đó là : 3 1 .(40.40).5227733,3()
Vmm ==

Bài 7:
Bác Mai muốn may một cái lều cắm trại bằng vải bạt có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2,5m, chiều cao của cái lều trại là 3m. Tính thể tích khoảng không bên trong lều ?
Lời giải
Thể tích khoảng không bên trong lều là : 3 1 3.(2,5.2,5).36,25() Vm ==

Bài 8:
Vẽ, cắt và gấp mảnh bìa nhưđã chỉ ra ở hình bên dưới đểđược hình chóp tứ giác đều.
a/ Trong hình vẽ bên dưới có bao nhiêu tam giác cân bằng nhau ?
b/ Tính diện tích xung quanh và diện tích toàn phần của hình chóp tứ giác đều này? Biết độ dài trung đoạn của hình chóp tứ giác đều là 9,68 cm.
Lời giải
a/ Trong hình vẽ bên dưới có 4 tam giác cân bằng nhau.
b/ Diện tích xung quanh của hình chóp tứ giác đều là : 2 11 22...(5.4).9,6896,8(c) xq SCdm ===
Diện tích toàn phần của hình chóp tứ giác đều là : 22 96,85121,8() cm +=
Bài 9
Tính thể tích của khối gỗ hình bên, biết rằng khối gỗ gồm một hình
lậpphươngcạnh 20cm vàmộthìnhchóptứ giác đều.Chiềucaokhối
gỗ là 35 cm .
Lời giải
Thể tích phần dưới của khối gỗ có dạng hình hộp chữ nhật là :
320 = 8000 (cm 3 )
Chiều cao của khối gỗ có dạng hình chóp tứ giác đều là
35 – 20 = 15 (cm)


Thể tích phần trên của khối gỗ có dạng hình chóp tứ giác đều là:
2 1 .20.152000 3 = (cm 3 )
Thể tích của khối gỗ là là : 8000 + 2000 = 10000 (cm 3 )
Bài 10
Một tấm bìa hình vuông PQRS cạnh 8cm, tâm O, các trục đối xứng IJ,
KH. Gọi A, B, C, D là các trung điểm các đoạn thẳng OI, OH, OJ, OK.
Cắt bỏ bốn tam giác PAQ, QBR, RCS và SDP (phần tô màu) và gấp
theo các đoạn thẳng AB, BC, CD, DA ta được hình chóp tứ giác đều
S.ABCD. Tính diện tích xung quanh hình chóp có được .
Lời giải
Diện tích xung quanh của hình chóp thì bằng bốn lần diện tích tam giác PAD.
PADPIOKPIAPKDAOD SSSSS =−−−
Lời giải
a/
Thể tích của hình lập phương ABCD.A’B’C’D’ là :
33 1 3027000()Vcm ==
Thể tích hình chóp tứ giác đều S.PQMN là
23 2 1 .(30).9027000() 3 Vcm ==
Vậy thể tích của hình lập phương ABCD.A’B’C’D’ bằng thể tích hình chóp tứ giác đều S.PQMN.
b/
Diện tích xung quanh của hình lập phương là
22 1 4.303600()Scm ==
PIAPKD AOD
=== == ==
SScm Scm Scm
1 .2.44() 2 1 .2.22() 2 416()
Mà : 2 2 22 2
Diện tích xung quanh của hình chóp tứ giác đều là
2 1 2.(4.30).91,245474,4() 2 Scm ==


=−−−=
S164426(cm)
PIOK PAD
Vậy diện tích xung quanh hình chóp có được là : 2 4.4.624()xqPAD SScm ===
Bài 11
Cho hình lập phương ABCD.A’B’C’D’ có cạnh 30cm và hình chóp tứ giác đều S.MNPQ có chiều cao
90cm và cạnh đáy 30cm, độ dài trung đoạn của hình chóp tứ giác đều là 91,24 cm.
a/ So sánh thể tích của hình lập phương và thể tích của hình chóp tứ giác đều.
b/ So sánh diện tích xung quanh của hình lập phương và diện tích xung quanh của hình chóp tứ giác
đều.
Vậy diện tích xung quanh hình lập phương ABCD.A’B’C’D’ bé hơn diện tích xung quanh hình chóp tứ giác đều S.PQMN.
Tài liệu dạy học mới 13
Bài 12
Cho hình chóp tứ giác đều S.MNPQ như hình vẽ bên có chiều cao 15cm và thể tích là 1280 cm 3


a/ Tính độ dài cạnh đáy của hình chóp.
b/ Tính diện tích xung quanh của hình chóp biết, độ dài trung đoạn của hình chóp là 17cm.
Lời giải
a/


Ôn tập chương
HÌNH HỌC TRỰ
A. KIẾN THỨC TRỌNG TÂM.
C QUAN HÌNH CHÓP
Độ dài cạnh đáy của hình chóp là : 2 2
133.1280 ..256() 315 Sa25616()
V VShScm h acm
= === = ==

Vậy độ dài cạnh đáy của hình chóp là 16 (cm).
b/
Diện tích xung quanh của hình chóp tứ giác đều là : 2 11 22...(4.16).17544(c) xq SCdm ===


- Hình chóp tam giác đều có 4 mặt , 6 cạnh.
- Mặt đáy ABC là một tam giác đều.
- Các mặt bên SAB, SBC, SCA là những tam giác cân tại S.
- Các cạnh đáy AB, BC, CA bằng nhau
- Các cạnh bên SA, SB, SC bằng nhau.
- S gọi là đỉnh của hình chóp tam giác đều S.ABC.
= =
Trong đó :
C: Chu vi đáy
1 2 1 . 3
xq sCd VSh
d: Trung đoạn của hình chóp
S: Diện tích đáy
h: Chiều cao của hình chóp.
- Hình chóp tứ giác đều có 5 mặt, 8 cạnh.
- Mặt đáy ABCD là một hình vuông .
- Các mặt bên SAB; SBC; SCD; SDA là những tam giác cân tại S.
- Các cạnh đáy AB; BC; CD; AD bằng nhau.
- Các cạnh bên SA; SB; SC; SD bằng nhau.
- S gọi là đỉnh của hình chóp tứ giác đều S.ABCD.
B. BÀI TẬP ÔN TẬP CHƯƠNG HÌNH HỌC TRỰC QUAN.
Câu 1: Hoàn thành nội dung bảng sau :
Hình
Tên gọi của hình chóp
Tên đỉnh hình chóp
Tên mặt đáy hình chóp
Tên các mặt bên hình chóp
Tên các cạnh bên ; cạnh đáy hình chóp
Tên trung đoạn hình chóp
Tên chiều cao hình chóp
Lờigiải: Hình
Tên gọi của hình chóp
Hìnhchóptamgiác đều Hìnhchóptứ giác đều
Tên đỉnh hình chóp ĐỉnhS ĐỉnhS
Tên mặt đáy hình chóp Mặt đáyABC Mặt đáyABCD
Tên các mặt bên hình chóp
Tên các cạnh bên , cạnh đáy hình chóp
Mặtbên:SAB;SBC;SAC Mặtbên:SAD;SDC;SBC;SAB
Cạnhbên:SA;SB;SC;
Cạnh đáyAB;BC;AC;


Cạnhbên:SA;SB;SC;SD


Cạnh đáyAB;BC;CD;AD.
Tên trung đoạn hình chóp SM SG
Tên chiều cao hình chóp SG SO
Câu 2:
Trong các hình vẽ bên dưới hình nào có thể gấp được hình chóp tam giác đều, hình nào có thể gấp được hình chóp tứ giác đều ?
Lời giải
a/Thể tíchcủahìnhchóptamgiác đềulà: 3 1 .6.48() 3 Vcm == .
b/Thể tíchcủahìnhchóptứ giác đềulà: 3 140 33.10.4()Vcm == .
Lờigiải:
Có thể gấp được hình chóp tam giác đều là hìnhd, hình chóp tứ giác đều là hìnhc.
Câu 3:
a/ Tính thể tích của hình chóp tam giác đều, biết diện tích đáy bằng 6cm 2 và chiều cao bằng 4cm
b/ Tính thể tích của hình chóp tứ giác đều, biết chiều cao bằng 10cm và cạnh đáy bằng 4cm.
c/ Tính độ dài trung đoạn của hình chóp tứ giác đều biết diện tích xung quanh của hình chóp là 60cm 2 , độ dài cạnh đáy 6cm.
d/ Tính diện tích xung quanh và diện tích toàn phần của hình chóp tứ giác đều biết cạnh đáy là 12cm, chiều cao mặt bên là 8cm.
e/ Tính chu vi đáy của hình chóp tứ giác đều biết thể tích của hình chóp là 125cm 3 ,chiều cao của hình chóp là 15cm.
f/ Tính diện tích xung quanh của hình chóp tam giác đều biết độ dài cạnh đáy là 10 cm, trung đoạn của hình chóp là 12cm.
c/Tacó: 2 2 12.60120 24.624.5() xq xq
S SCddcm C = ====
d/Diệntíchxungquanhcủahìnhchóptứ giác đềulà:
2 11 22..(4.12).8192 xq SCdcm === . Diệntíchtoànphầncủahìnhchóptứugiác đềulà:
192+12.12=336cm 2 .

e/Tacó: 1 3 VSh =
2 33.125 25 15 V Scm h === .


Cạnhcủahìnhvuônglà: 255cm =
Chuvi đáycủahìnhchóptứ giác đều: 4.5 = 20 cm.
f/Diệntíchxungquanhcủahìnhchóptamgiác đềulà:
2 11 22..(3.10).12180 xq SCdcm ===
Câu 4:
a/Mộthìnhchóptứ giác đềucócạnh đáy5cm,trung đoạn6,5cm,chiềucaohìnhchóplà 6cm.Tínhdiệntíchxungquanhvàthể tíchcủahìnhchóptứ giác đều?
b/Chohìnhchóptứ giác đềucóchuvimặt đáybằng40cm,trung đoạnbằng13cm,chiều caohìnhchópbằng12cm.Tínhdiệntíchxungquanhvàthể tíchcủahìnhchóptứ giác đều?
c/Mộthìnhchóptứ giác đềucóchiềucaobằng15cm,trung đoạnbằng17cm, độ dàicạnh đáycủahìnhchópbằng16cm.Tínhdiệntíchxungquanh,diệntíchtoànphần ( tổng diện tích các mặt của hình chóp),thể tíchcủahìnhchóptứ giác đều?
d/Chohìnhchóptứ giác đềucócạnh đáy8cm,trung đoạnbằng5cm.Tínhdiệntíchxung quanhvàdiệntíchtoànphần ( tổng diện tích các mặt của hình chóp) củahìnhchóptứ giác đều đó?
e/Tínhdiệntíchxungquanhcủahìnhchóptamgiác đềucó độ dàicạnh đáylà10cm,chiềucaocủamặtbênxuấtpháttừđỉnh củahìnhchóptamgiác đềulà12cm.
d/
Thể tíchcủahìnhchóptứ giác đều:
3 11 ...(16.16).151280() 33 VShcm ===
Diệntíchxungquanhhìnhchóptứ giác đều:
2 11 22...(3.10).12180(cm) xq SCd===
Diệntíchtoànphầncủahìnhchóptứ giác đều:
f/Tínhdiệntíchtoànphầnvàthể tíchcủahìnhchóp tứ giác đềucó độ dàicạnh đáylà72dm,chiềucaolà68,1 dm,chiềucaocủamặtbênxuấtpháttừđỉnhcủahìnhchóp tứ giác đềulà77dm.
Lời giải:
a/Diệntíchxungquanhhìnhchóptứ giác đều:
2 11 22...(4.5).6,565(cm) xq SCd===
Diệntíchtoànphầncủahìnhchóptứ giác đều:
65+5.5=90(cm 2 )

b/Cạnh đáycủahìnhchóptứ giác đềulà:
40:4=10(cm)

Thể tíchcủahìnhchóptứ giác đềulà:
3 11 33...(10.10).12400() VShcm ===
c/
Diệntíchxungquanhhìnhchóptứ giác đều:
2 11 22...(4.16).17544(cm) xq SCd===
Diệntíchtoànphầncủahìnhchóptứ giác đều:
544+16.16=800(cm 2 )
80+8.8=144(cm 2 )
e/Diệntíchxungquanhhìnhchóptamgiác đều:
2 11 ...(4.5).6,565(cm) 22 xq SCd=== .
f/Diệntíchxungquanhhìnhchóptứ giác đều:
2 11 ...(4.72).7711088(dm) 22 xq SCd===
Diệntíchtoànphầncủahìnhchóptứ giác đều:
11088+5184=16272(dm 2 )
Thể tíchcủahìnhchóptứ giác đều:
3 11 33...(72.72).68,1117676,8(d) VShm ===
Câu 5:
Tínhdiệntíchxungquanhvàthể tíchtoànphần (tổng diện tích các mặt); thể tíchcủahình


chóptứ giác đềudưới đây (theo các kích thước cho trên hình vẽ).
Câu 6:
Ngườitathiếtkế chậutrồngcâycódạnghìnhchóp
tamgiác đều (như hình vẽ bên) biết:cạnh đáy khoảng20cm,chiềucaokhoảng35cm, độ dàitrung

đoạnkhoảng21cm.
a/Ngườitamuốnsơncácbề mặtxungquanhchậu.
Hỏidiệntíchbề mặtcầnsơnlàbaonhiêu?
b/Tínhthể tíchcủachậutrồngcây đó (làm tròn kết quả đến hàng phần trăm).Biết đườngcaocủamặt đáyhìnhchóplà17cm.
Lời giải:
a/Diệntíchbề mặtcầnsơnlà:
2 11 22...(3.20).21630(cm) xq SCd===
Lời giải:
Hình 1

Diệntíchxugquanhcủahìnhchóptứ giác đềulà:
2 11 22...(4.6).560(cm) xq SCd===
Diệntíchtoànphầncủahìnhchóptứ giác đều:
60+6.6=96(cm 2 )

Thể tíchcủahìnhchóptứ giác đều:
3 11 ...(6.6).448() 33 VShcm ===
Hình 2
Diệntíchxugquanhcủahìnhchóptứ giác đềulà:
2 11 22...(4.10).13260(cm) xq SCd===
Diệntíchtoànphầncủahìnhchóptứ giác đều:
260+10.10=360(cm 2 )
Thể tíchcủahìnhchóptứ giác đều:
3 11 33...(10.10).12400() VShcm ===
b/Thể tíchcủachậutrồngcây đólà:
3 111 ...(.20.17).351983,33() 332 VShcm ===
Câu 7: Chocáchìnhkhốivàcáckíchthướcnhư hìnhvẽ:
a/Chobiếtcácdạnghìnhkhối ở mỗihìnhvẽ trên?
b/Tínhthể tíchcủamỗihìnhkhối đó.Từđóhãysosánhthể tích hình a và c rồirútra nhậnxét?
Lời giải:
a/ Cácdạnghìnhkhối ở mỗihìnhvẽ :

Hình a:Hìnhhộpchữ nhật.
Hình b:Hìnhlăngtrụđứngtamgiác.
Hình c:Hìnhchóptứ giác đều.
b/ Thể tíchhìnhhộpchữ nhật là: 3 5.5.10250() Vcm == .
Thể tíchcủahìnhlăngtrụđứngtamgiácvuônglà 3 1 2.3.5.1075() Vcm ==
Thể tíchcủahìnhchóptứ giác đềulà 3 1250 33.5.5.10() Vcm ==
Nhận xét :Nếuhìnhchóptứ giác đềuvàhìnhhộpchữ nhậtcócùngdiệntích đáyvàchiều caothìthể tíchcủahìnhhộpchữ nhậtgấp3lầnthể tíchcủahìnhchóptứ giác đều.
Câu 8:
Mộtkimtử thápphalê đencódạnghìnhchóptứ giác đềubiết, độ dàicạnh đáylà8,5cm,chiềucaolà9,5cm.Tínhthể tíchcủakim tử thápphalê đen đó (làm tròn kết quả đến hàng phần mười).
Lời giải:
Thể tíchcủakimtử thápphalê đenlà:
3 1 .8,5.8,5.9,5228,8() 3 Vcm ==
Câu 9: Kimtử thápkínhLouvrelàmộtkimtử tháp đượcxây bằngkínhvàkimloạinằm ở giữasânNepoleoncủabảotàng Louvre,Paris. ĐượcxâytheoyêucầucủaTổngthốngPháp
FrancoisMitterrandvàonăm1983,côngtrìnhlàtácphẩm củakiếntrúcsư nổitiếngngườiMỹ gốcHoaLeohMingPei.
Toànbộ kimtử thápcódạnghìnhchóptứ giác đều đượcxây phủ kínbằngkíncùngcáckhớpnốikimloại,vớitrung đoạn củahìnhchóplà27cm, đáylàhìnhvuôngcạnh35m.Giả sử coicáckhớpnốikhông đángkể,hãytínhdiệntíchkínhtối thiểudùng để phủ kíntoànbộ bể mặtkimtự thápkính
Louvre.

Lời giải

Diệntíchkínhtốithiểudùng để phủ kíntoànbộ bể mặtkimtự thápkínhLouvrechínhlà diệntíchxungquanhcủakimtự tháp.
2 11 22...(35.4).271890(cm) xq SCd===
Câu 10:
Mộtgiá đèncầycódạnghìnhchóptứ giác đều như hìnhbêncó độ dàicạnh đáylà14cm;chiều caocủagiá đèncầylà22cm.Mặtbêncủagiá
đèncầylàcáctamgiáccâncóchiềucaolà 23cm.
Tínhdiệntíchxungquanhvàthể tíchcủagiá
đèncầycódạnghìnhchóptứ giác đềuvớikích thướcnhư trên.
Lời giải:
Diệntíchxungquanhcủagiá đèncầyhìnhchóptứ giác đều:
2 11 22...(4.14).23644(cm) xq SCd===
Thể tíchcủagiá đèncầyhìnhchóptứ giác đều:
3 114312 ...(14.14).22() 333 VShcm ===
Câu 11:
Đèn đá muối Himalaya làmộtloại đèn độc đáocó
bộ phậnchụp đènlàmtừ tinhthể muối.Hìnhbên
làmộtchiếcchụp đèn đámuốicódạnghìnhchóp
tứ giác đều (không tính phần chân để của đèn)
Biếtmặtbêncủachụp đènlàmộttamgiác đềucó
cạnhbằng20cm, đườngcaocủacácmặtbênbằng 22,4cm.Tínhdiệntíchxungquanhcủaphầnchụp đèn.

Lời giải
Diệntíchxungquanhcủaphầnchụp đènlà:
xq SCd===

2 11 22...(4.20).22,4896(cm)
Câu 12:
Hìnhbênlàmộtcáihộpgiấyhìnhchóptamgiác đềudobạn Lantự taylàm đểđựngquàsinhnhậttặngchobạnthân.Biết diệntích đáycủahìnhchópbằng170cm 2 ,chiềucaocủahình chópbằng16cm.

Thể tíchcủachiếchộplàbaonhiêu? (làm tròn kết quả đến hàng phần mười)
Lời giải
Thể tíchcủachiếchộplà 3 11 ...170.16906,7(c) 33 VShm ===


Câu 13:

Tínhthể tíchcủamộtchiếchộpbánhítcódạnghình chóptứ giác đều,có độ dàicạnh đáylà3cmvàchiều caolà3,5cm.
Lời giải :
Thể tíchcủamộtchiếchộpbánhítcódạnghìnhchóptứ giác đềulà: 23 11 33...3.3,510,5() VShcm ===


Câu 14:
Tínhthể tíchcủahìnhchóp ở bêntronghìnhhộpchữ nhậtvớikíchthướcnhư hìnhvẽ
Lời giải:
Chiềucaocủahìnhchóptứ giác đềuchínhlàchiềucaocủahìnhhộpchữ nhật Khi đóthể tíchcủahìnhchóp ở bêntronghìnhhộpchữ nhậtlà:
3 11 33...(5.5).650() VShcm ===
Câu 15: Hãytínhdiệntíchmặtngoàitheocáckíchthướccho ở hìnhdưới đây.Biếtrằng hình1gồmmộthìnhchóptứ giác đềuvà mộthìnhhộpchữ nhật.Hình2gồmhaihình chóptứ giác đều.
Lời giải
Hình 1:
Diệntíchxungquanhcủahìnhchóptứ giác đềulà: () 2 1 .4.5.3,939() 2 cm = .
Diệntíchxungquangcủahìnhhộpchữ nhậtlà: 2 2.(55).240() cm += .
Diệntích đáyhìnhhộpchữ nhậtlà: 5.5 = 25 (cm 2 ).
Diệntíchmặtngoàicủahình1là: 39+40+25= 104 (cm 2 ).
Hình 2:
Diệntíchmặtngoàihình2chínhlàdiệntíchxungquanhcủahaihìnhchóptứ giác đềulà:
2 1 2..(4.6).9,48227,52() 2 cm =

Câu 16:
BạnHàlàmmộtcáilòng đènhìnhquả trám (xem hình bên) là hìnhghéptừ haihìnhchóptứ giác đềucócạnh đáy20cm,cạnh bên32cm,khoảngcáchgiữahai đỉnhcủahaihìnhchóplà 30cm.
a/Tínhthể tíchcủalòng đèn.
b/BạnHàmuốnlàm50cáilòng đènhìnhquả trámnàycần phảichuẩnbị baonhiêumétthanhtre?
(mối nối giữa các que tre có độ dài không đáng kể) ?
Lời giải
a/

Chiềucaocủamỗihìnhchóptứ giác đềulà: 30:2=15(cm).
Thể tíchcủalòng đènquả trámlà:
3 1 2..20.20.154000() 3 Vcm == b/
BạnHàmuốnlàm50cáilòng đènhìnhquả trámnàycầnphảichuẩnbị số métthanhtre là:50.(20x4+32x8)=16800(cm)
Câu 17: Chohìnhkhốibên (với kích thước có trong hình vẽ)
Biếtrằnghìnhkhối đượctạobởi3hìnhchóptam giác đềubiếtchiềucaocủa3hìnhchóptamgiácnày
đềubằngnhauvàdiệntích đáylà 35cm 2
Tínhthể tíchcủahìnhkhốibên.
Lời giải: Chiềucaocủamỗihìnhchóptứ giác đềulà: 30:2=15(cm).
Thể tíchcủahìnhkhốibênlà:
3 1 3..35.1535.15525(). 3 Vcm ===
Câu 18:
Mộtkhốirubikcódạnghìnhchóptamgiác đều ( các mặt khối rubic là các tam giác đều bằng nhau),cóchuvi đáybằng 234 mm, đườngcaocủamặtbênhìnhchóplà 67,5 mm .
a/Tínhdiệntíchxungquanh,diệntíchtoànphần ( tổng diện tích các mặt ) củakhốirubik đó.
b/Biếtchiềucaocủakhốirubiklà 63,7 mm.Tínhthể tíchcủa khốirubik đó.
Lời giải:
a/ Đườngcaomặtbênhìnhchópchínhlàtrung đoạn d = 67,5 mm.
Diệntíchxungquanhcủakhốirubik đólà:
2 11 22...234.67,57897,5(cm) xq SCd=== .
Đáylàtamgiác đềucócạnhlà234:3=78cm;Chiềucaocủatamgiác đáylà67,5cm.

Diệntíchtoànphầncủakhốirubik đólà: 2 1 7897,578.67,510530() 2 tp Scm =+= .
Câu 19:
Tháp đồnghồ cóphầndướicódạnghìnhhộpchữ nhật, đáy làhìnhvuôngcócạnhdài5m,chiềucaocủahìnhhộpchữ

nhậtlà12m.Phầntrêncủathápcódạnghìnhchóptứ giác
đều,cácmặtbênlàcáctamgiáccânchung đỉnh.Chiềucao
củatháp đồnghồ là19,2m.
a)Tínhtheométchiềucao
của phầntrêncủatháp
đồnghồ.
b)Chobiếtthể tíchcủahình
hộpchữ nhật đượctínhtheo
côngthức VSh =⋅ ,trong đó
S làdiệntíchmặt đáy, h là
chiềucaocủahìnhhộpchữ
nhật.Thể tíchcủahìnhchóp đượctínhtheocôngthức 1 3 Sh ,trong đó S làdiệntíchmặt đáy,
h làchiềucaocủahìnhchóp.Tínhthể tíchcủatháp đồnghồ này .
Lời giải
a/Chiềucaocủaphầntrêncủatháp đồnghồ là:19,2–12=7,2(m).


=
b/Thể tíchcủakhốirubik đólà: V = 3 11 ..78.67,5.63,755896,75().
cm
b/Thể tíchcủa phầntrêncủatháplà: 23 1 11 ..5.7,260 33 VShm ===
Thể tíchcủa phầndướicủatháplà: 3 2 .5.5.12300 VShm === .
Thể tíchcủatháp đồnghồđólà: 3 12 60300360 VVVm =+=+=
Câu 20: Kimtự thápKheops–AiCậpcódạnghìnhchóp đều, đáylàhìnhvuông,cácmặtbênlàcáctamgiáccân chung đỉnh (hình vẽ).Chiềucaocủakimtự tháplà139m, cạnh đáycủanódài230m.
a/Tínhthể tíchcủakimtự thápKheops–AiCập (làm tròn đến hàng nghìn).
b/Giả sử ngườitamuốn “làm đẹp” kimtự thápbằngcách dùnggạchmenphẳng đểốpphủ kíntoànbộ bề mặtkimtự tháptrênthìphảidùngtốithiểubaonhiêumétvuônggạch men?Biết độ dàitrung đoạncủakimtự tháplà180m.
Lời giải
a/Thể tíchcủakimtự thápKheops–AiCậplà:
()2 3 11 ...230.1392451000() 33 VShm ==≈
b/ Ngườitamuốn “làm đẹp” kimtự thápbằngcáchdùnggạchmenphẳng đểốpphủ kín toànbộ bề mặtkimtự tháptrênthìphảidùngtốithiểusố métvuônggạchmenlà:
() 2 11 22...4.230.18082800(m) xq SCd===
Câu 21: Đèncắm đấthìnhkimtự tháplàmộtloại đèn đượcthiếtkế bắtmắtgiúpkhông giannhà ở trở nênsangtrọngvànổibậthơn.Phầntrêncủa đèn đượcthiếtkế códạng một hìnhchóptứ giác đềucócạnh đáylà120mm; chiềucaocủa đèncắm đấtlà200mm.Phần dướicủa đèncắm đấtdài130mm (như hình vẽ minh họa bên dưới).
Tínhthể tíchphầntrêncủa đèncắm đấthìnhkimtự tháp đó.
Lời giải :
Chiềucaocủaphầntrêncủa đènlà200–130=70(mm)
Thể tíchphầntrêncủa đèncắm đấthìnhkimtự tháp đólà: ()2 3 11 ...120.70336000() 33 VShmm ===
Câu 22: Đèn để bànhìnhkimtự thápcódạnghìnhchóp tứ giác đềucócạnh đáybằng25cm,chiềucaocủa đèn để bàndài35cm.


a/Tínhthể tíchcủachiếc đèn để bànhìnhkimtự thápnày.
b/BạnKim địnhdáncácmặtbêncủa đènbằngtấmgiấy màu.TínhdiệntíchgiấymàubạnKimcầnsử dụng (coi như mép dán không đáng kể),biết độ dàitrung đoạnchiếc đènhìnhchópnàylà37cm.
c/Nếumỗimétvuônggiấymàulà120000 đồng.HỏibạnKimcầnchuẩnbị ítnhấtbao nhiêutiền để mua đủ giấymàu để dán đượccácmặtbêncủachiếc đèn để bànnày?
Lời giải :
a/Thể tíchcủachiếc đèn để bànhìnhkimtự thápnàylà:
()2 3 11 ...25.357291,7() 33 VShcm === ;
b/DiệntíchgiấymàubạnKimcầnsử dụnglà:
() 22 11 22..d.4.25.371850()0,185m; xq SCcm ====

c/BạnKimcầnchuẩnbị ítnhấtsố tiền để mua đủ giấymàu để dán đượccácmặtbêncủa chiếc đèn để bànnàylà:0,185.120000=22200(đồng).

Câu 23:
BạnMaicầndángiấybóngkínhmàuxungquanhmột chiếclồng đènhìnhchóptamgiác đềuvớikíchthướcnhư hìnhbên.HỏidiệntíchgiấymàMaicầnlàbaonhiêu?
Lời giải :
DiệntíchgiấymàMaicầndùnglàdiệntíchtấtcả cácmặt hìnhtamgiáccủachiếclồng đènhìnhchóptamgiác đều.
Diệntíchmặt đáycủachiếclồng đèn đó là: 2 1 .13,9.16111,2() 2 cm =
Diệntíchmộtmặtbêncủachiếclồng đèn đólà: 2 1 .10.1680() 2 cm =
Diệntíchbamặtbêncủachiếclồng đèn đólà: 3.80 = 240 (cm2).

DiệntíchgiấymàMaicầnlà: 111,2 + 240 = 351,2 (cm2).
Câu 24:
BạnAn đánhrơimộtmôhìnhkimtử thápcódạnglàhìnhchóptứ giác đềuvàomộthộp đựng đầynướcdạnghìnhhộpchữ nhật.Biếthìnhhộpchữ nhậtcókíchthước đáylà
7 x 5cm vàchiềucao 10cm;cònhìnhchóp đềucóchiềucaolà 5cm vàcạnh đáydài 6cm.
Hỏikhivớtmôhìnhra,lượngnướccònlạitronghộplàbaonhiêu?
Lời giải :
Thể tíchcủahìnhhộpchữ nhậtlà:
3 7.5.10350(); cm =
Thể tíchcủahìnhchóptứ giác đềulà:
23 1 3.6.560(cm) = ;
Khivớtmôhìnhra,lượngnướccònlạitronghộplà
3 35060290() cm −= .
Câu 25:
Kimtự thápLouvrelàmộtcôngtrìnhkiếntrúctuyệt đẹpbằngkínhtọalạcngaylốivào củabảotàngLouvre,Pari.Kimtự thápcódạnglàhìnhchóptứ giác đềuvớichiềucao 21mvà độ dàicạnh đáylà34m.Cácmặtbêncủakimtự tháplàcáctamgiác đều (xem hình ảnh minh họa bên).

a/Tínhthể tíchcủakimtự thápLouvre.
b/Tổngdiệntíchthậtsự củasànkimtự tháplà 2 1000m .Hỏinếusử dụngloạigạchhình vuôngcócạnhlà60cm để lótsànthìcầnbaonhiêuviêngạch?
c/MỗimặtcủaKimtự tháp (trừ mặt có cổng ra vào) đượctạothànhtừ 18tấmkínhhình tamgiác đềuvà17hàngkínhhìnhthoixếpchồnglênnhau.Hỏicóbaonhiêutấmkính hìnhthoitrênmỗimặt?
Lời giải :
a/Thể tíchkimtự tháplà: 23 1 .34.218092() 3 Vm ==
b/Diệntíchmộtviêngạchhìnhvuông: ()2 2 0,60,36()Sm ==
Số viêngạchhìnhvuôngcầndùnglà: 1000 2778 0,36 ≈ (viên)
c/Số tấmkínhhìnhthoitrênmỗimặt: ( )17.171 153 2 + = (tấm)
Câu 26:
Hình ảnhbênlà ảnhcủamộtlọ nướchoahìnhkimtự tháp.Khi
đậynắp,lọ códạnghìnhchóptứ giác đều (tính cả thân lọ và
nắp lọ) trong đónắplọ cũnglàhìnhchóptứ giác đềucóchiều
cao5cm,cạnh đáy2,5cm.Chiềucaothânlọ vàcạnh đáylọđều
bằngchiềucaocủanắplọ.Bỏ qua độ dàycủavỏ .Tínhdung
tíchcủalọ nướchoa đóra đơnvị mi – li – lít (làm tròn kết quả
đến hàng đơn vị).Biếtrằng: 3 11cmml = .
Lời giải :
Thể tíchcủalọ nướchoahìnhkimtự tháplà:
A. KIẾN THỨC TRỌNG TÂM.
BÀI TẬP TRẮC NGHIỆM HÌNH HỌC TRỰC QUAN HÌNH CHÓP
23
1 1250 .5.10() 33 Vcm ==
Thể tíchcủanắplọ nướchoalà: 23 2 1125 .(2,5).5() 312 Vcm ==
Dungtíchcủalọ nướchoa đólà
3 250125 73()73ml 312 cm −≈=




Câu 27:
Mộttấmbìa như hìnhbêngấpthànhhìnhchóptamgiác
đềuvớicácmặt đềulàhìnhtamgiác đều.Vớisốđotrên hìnhvẽ,hãytínhdiệntíchxungquanhvàdiệntíchtoàn phầncủahìnhnày.
Lời giải :
Diệntíchxungquanhcủahìnhchóptamgiác đềutrênlà: () 2 1 .3.10.8,7130,5() 2 xq Scm ==

Diệntíchtoànphầncủahìnhchóptamgiác đềutrênlà:
2 1 130,5.8,7.10174() 2 tp Scm =+=
- Hình chóp tam giác đều có 4 mặt , 6 cạnh.
- Mặt đáy ABC là một tam giác đều.
- Các mặt bên SAB, SBC, SCA là những tam giác cân tại S.
- Các cạnh đáy AB, BC, CA bằng nhau
- Các cạnh bên SA, SB, SC bằng nhau.
xq
VSh = =


1 2 1 3 sCd
C: Chu vi đáy
d: Trung đoạn của hình chóp
S: Diện tích đáy
h: Chiều cao của hình chóp.
- Hình chóp tứ giác đều có 5 mặt, 8 cạnh.
- Mặt đáy ABCD là một hình vuông .
- Các mặt bên SAB; SBC; SCD; SDA là những tam giác cân tại S.
- Các cạnh đáy AB; BC; CD; AD bằng nhau.
- Các cạnh bên SA; SB; SC; SD bằng nhau.
- S gọi là đỉnh của hình chóp tứ giác đều S.ABCD.
II/ BÀI TẬP TRẮC NGHIỆM :
Câu 1: Cho hình chóp S.ABCD đều có thể tích bằng 200cm 3 , chiều cao SO bằng 12cm. Độ dài cạnh của hình chóp tứ giác đó là :
A.12 cm . B.13 cm.
C.11 cm. D.16 cm.
Câu 2: Thể tích của hình chóp tứ giác đều có chiều cao là 9cm, cạnh đáy là 5cm là :
A.75 cm 3 B. 225 cm 3
C. 180 cm 3 . D. 60 cm 3 .
Câu 3: Cho hình chóp tứ giác đều S.ABCD có cạnh AB= 8cm, chiều cao SO =10cm.Thể tích của hình chóp tứ giác đều S.ABCD là :
A. 800 3 cm 3 . B. 640 3 cm 3 .
C 800 cm 3 D 640 cm 3
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao
của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là :
A. 6 cm 3 B. 18 cm 3


C. 12 cm 3 D. 9 cm 3
Câu 5: Chohìnhchóptamgiác đềucó độ dàicạnh đáylà5cm, độ dài trung đoạncủa hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là :
A. 40 cm 2 B 36 cm 2


C. 45 cm 2 D. 50 cm 2
Câu 6: Một hình chóp tứ giác đều S.ABCD có độ dài trung đoạn là 12cm và đáy là hình vuông có chu vi là 40cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
A. 10 cm B. 12 cm C. 15 cm D Đáp án khác.
Câu 7: Cho hình chóp tam giác đều S.ABC có thể tích là 100 cm 3 ; chiều cao của hình chóp là 3cm. Độ dài cạnh đáy của hình chóp đó là
A. 1 3 . B. 1 4 . C. 1 5 . D. 1 2 .
Câu 8: Hình chóp tứ giác đều có mặt bên là hình gì ?
A.Tam giác cân . B.Tam giác vuông. C.Tam giác vuông cân . D.Đáp án khác .

Câu 9: Diện tích xung quanh của hình chóp đều bằng
A.Tích nửa chu vi đáy và chiều cao của hình chóp.
B.Tích nửa chu vi đáy và trung đoạn .
C.Tích chu vi đáy và trung đoạn .
D.Tổng chu vi đáy và trung đoạn .
Câu 10: Hình chóp tamgiác đều có chiều cao làh,diệntích đáy là S.Khi đó,thể tíchV của hình chóp đều bằng
A. 3. VSh = . B. . VSh = .
Câu 11: Cho hình chóp tứ giác đều có tất cả các mặt đều là tam giác đều có diện tích xung quanh là 90 cm 2 và chiều cao của hình chóp bằng 7m. Thể tích cảu hình chóp tứ giác đều đó là

A. 210 m 3 . B.630 m 3 .
C.70 m 3 . D. 30 m 3
Câu 12: Trong các hình vẽ bên dưới hình nào có thể gấp theo nét đứt đểđược hình chóp tứ giác đều :
A.Hình b và c . B.Hình c . C.Hình a và c . D.Hình b .
Câu 13: Thể tích của hình chóp tứ giác đều bằng
A.Tích nửa diện tích đáy và chiều cao của hình chóp.
B.Tích một phần ba diện tích đáy và chiều cao của hình chóp .
C.Tích diện tích đáy và trung đoạn .
D.Tích diện tích đáy và chiều cao .
Câu 14: Nhận xét nào sau đây đúng với hình chóp tứ giác đều
A.Thể tích bằng nửa chu vi đáy và chiều cao của hình chóp
B. Hình chóp tứ giác đều có 1 đỉnh, 5 mặt , 8 cạnh
C.Hình chóp tứ giác đều có 4 mặt bên là các tam giác vuông .
D.Diện tích xung quanh bằng tổng chu vi đáy và trung đoạn .
Câu 15: Một mái che giếng trời có dạng hình chóp tứ giác đềuvới độ dài cạnh đáy khoảng 2,2m và độ dài trung đoạn khoảng 2,8m. Cần phải trả số tiền để làm mái che giếng trời đó khi biết giá để làm mỗi mét vuông mái che được tính là 1 800 000 đồng (bao gồm tiền vật liệu và tiền công) là
A. 22176000 đồng B. 23176000 đồng C. 21176000 đồng D Đápánkhác. Câu 16: Một giỏ hoa gỗ mini có dạng hình chóp tam giác đều (như hình bên) có độ dài cạnh đáy khoảng 10cm và độ dài trung đoạn khoảng 20cm. Diện tích xung quanh giỏ hoa gỗ mini đó là :
A. 300 cm 2 . B. 200 cm 2 .
C. 400 cm 2 D . 250 cm 2
A. KIẾN THỨC TRỌNG TÂM.
1. Bình phương một tổng.
Quy tắc: Bìnhphươngcủamộttổnggồmhaisố bằng tổngbìnhphươngmỗi số với2lầntíchhaisốđó.
( )2 22 2 abaabb +=++
Ví dụ: 222 (2)22444 xxxxx +=+⋅⋅+=++ .
2. Bình phương một hiệu.
Quy tắc:Bìnhphươngcủamộthiệugồmhaisố bằnghiệucủatổngbìnhphương mỗisố với2lầntíchhaisốđó.
( )2 22 2 abaabb −=−+ .
Ví dụ: 222 (3)23969 xxxxx −=−⋅⋅+=−+
3. Hiệu hai bình phương.
Quy tắc:Hiệuhaibìnhphươngbằngtíchcủatổngvớihiệucủahaisốđó.
( )( ) ( )( ) 22 ababababab −=+−=−+
Ví dụ: 22242(2)(2)xxxx −=−=−+
4. Lập phương của một tổng.
( )3 3223 33 abaababb +=+++
Ví dụ: 3322332 (1)31311331 xxxxxxx +=+⋅⋅+⋅⋅+=+++
5. Lập phương của một hiệu.
( )3 3223 33 abaababb −=−+− .
Ví dụ: 3322332 (2)323226128 xxxxxxx −=−⋅⋅+⋅⋅−=−+− .
6. Tổng hai lập phương.
Quy tắc:Tổngcủahailậpphươngbằngtíchcủatổnghaisố vớibìnhphươngthiếu củahiệuhaisốđó.
( )( ) 3322 ababaabb +=+−+ .
Chú ý:biểuthức 22 aabb −+ đượcgọilàbìnhphươngthiếucủahiệu.
Ví dụ: ( ) ( ) 33222 2(2)22(2)24 xxxxxxx +=+−+=+−+ .
7. Hiệu hai lập phương.
Quy tắc:Hiệucủahailậpphươngbằngtíchcủahiệuhaisố vớibìnhphươngthiếu
củatổnghaisốđó. ( )( ) 3322 ababaabb −=−++ .
Chú ý:biểuthức 22 aabb ++ đượcgọilàbìnhphươngthiếucủatổng.
Ví dụ: ( ) ( ) 3222 3 3(3)33(3)39 xxxxxxx −=−++=−++ .
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Thực hiện phép tính
Vận dụng linh hoạt các hằng đẳng thức ở phần trọng tâm kiến thức.
Ví dụ 1. Thựchiệnphéptính
a) 2(1) x + ; b) 2(21) x ; c) (3)(3) xx −+ ; d) 22 (2) x +
Ví dụ 2. Khaitriểncácbiểuthứcsau
a) 2(23) xy + ; b) 2(3) xy ;
c) (21)(21) xyxy−+ ; d) 22 1 2(2) 2 xyxy
Ví dụ 3. Khaitriểncácbiểuthứcsau
a) 2() Axyz =++ ; ĐS: 222 222 Axyzxyyzzx =+++++
b) 2() Babc =−− ĐS: 222 222 Babcabacbc =++−−+
Ví dụ 4. Thựchiệnphéptính: a)
Ví dụ 5. Thựchiệnphéptính
a) ( ) 2 (2)24 xxx−++ ; b) ( ) 2 (21)421 xxx+−+ ;
c) 2 11 224 x Pxx
; d) ( ) 22(23)469 Qxyxxyy =+−+
Dạng 2: Viết biểu thức dưới dạng tích
Sử dụng cách viết ngược lại của các hằng đẳng thức đã nêu ở phần trọng tâm kiến thức.
Lưu ý: 2 aaa ⋅= . Như vậy bình phương của một số cũng gọi là dạng tích
của số đó.
Ví dụ 7. Viếtcácbiểuthứcdướidạngbìnhphươngcủamộttổnghoặchiệu
a) 2 69xx++ ; b) 2 961 xx−+ ;
c) 22 1 4 xyxy++ ; d) 2 ()6()9 xyxy−+−+ .
Ví dụ 8. Điềncác đơnthứcvàochỗ “...” để hoànthànhcáchằng đẳngthứcsau
a) 22 6()xxx++…=+… ; b) 22 44(2) xxx−+…=−… ;
c) 22 9(32) xxy −…+…=− ; d) 2 () 39 yy x −……+=…−
Ví dụ 9. Viếtcácbiểuthứcsaudướidạnglậpphươngcủamộttổnghoặchiệu:
a) 32331xxx −+−+ ; b) 32 11 327 xxx+++ ;
c) 64223 33 xxyxyy −+− ; d) 32 ()()()11 327xyxyxy −+−+−+ .
Ví dụ 10. Viếtcácbiểuthứcsaudướidạngtích:
a) 3 27 x + ; b) 3 1 8 x ; c) 33 8xy + ; d) 33827xy
Dạng 3: Tính giá trị của biểu thức
Bước 1: Rút gọn biểu thức (nếu cần).
Bước 2: Thay giá trị của biến vào biểu thức rồi thực hiện phép tính.
Ví dụ 14. Tínhgiátrị biểuthức:
6. Th
chi
nphéptính a) ( ) 2 (3)39Mxxx=+−+ ; b) ( )2 (13)139 Nxxx =−++ ;
a) 326128Axxx=−+−+ tại 28 x =− ; ĐS:27000
b) 32 81261Bxxx=+++ tại 1 2 x = ; ĐS:8
c) 32 (2)6(2)12(2)8Cxyxyxy =+−+++− tại 20 x = , 1 y = ĐS:8000
Ví dụ 15. Tínhbằngcáchhợplí:
a)Tính 3 111; ĐS:1330
b)Tínhgiátrị biểuthức 33 xy biết 6 xy−= và 9 xy⋅= ĐS:378
Ví dụ 16. Tínhgiátrị biểuthức:
a) ( ) ( ) 2 2 (3)39(32)469 Mxxxxxx =+−+−−++ tại 20 x = ; ĐS:72000
b) ( ) 223 (2)2416 Nxyxxyyy =−+++ biết 20xy+= . ĐS:0
Dạng 4: Tính nhanh
Áp dụng các hằng đẳng thức một cách linh hoạt cho các số tự nhiên.
Ví dụ 17. Tínhnhanh
a) 2101 ; b) 22 75507525 −⋅+ ; c) 10397.
Ví dụ 18. Tínhnhanh:
a) 3101 ; ĐS:1030301 b) 32 9869812988 +⋅+⋅+ ; ĐS:1000000
c) 399 ; ĐS:970299 d) 32 13913271327 −⋅+⋅− ĐS:1000
Ví dụ 19. Tínhgiátrị củabiểuthức 2 9124Pxx=−+ trongmỗitrườnghợpsau
a) 34 x = ; ĐS: 10000 P =
b) 2 3 x = ; ĐS: 0 P =
c) 8 3 x =
Dạng 5: Chứng minh đẳng thức. Rút gọn biểu thức
ĐS: 100 P =
Áp dụng các hằng đẳng thức một cách linh hoạt để biến đổi vế này thành vế kia trong một đẳng thức.
Ví dụ 20. Chứngminhcác đẳngthứcsau
a) 22 ()()4 ababab −=+− ; b) 2222 ()()2() xyxyxy ++−=+
Ví dụ 21. Rútgọncácbiểuthứcsau
a) 22 (3)(3) Mxyxy =+−− ; ĐS: 12 Mxy =
b) 2 2()4()(2)4(2) Qxyxyxyxy =−−−+++ ĐS: 2(5)Qxy =−−
Ví dụ 22. Rútgọnbiểuthức:
a) ( ) 332 (2)(2)212Axxxx =++−−+ ;
b) 32 (2)6(2)12(2)8Bxyxyxy =+−+++−
Ví dụ 23. Rútgọncácbiểuthức:
a) ( ) ( ) 23 (3)393Axxxx =−++−+ ;
b) () 2 2 111 (21)4218 224 Bxxxxxx
c) ( ) ( )2222 (2)24(23)469 Cxyxxyyyxyxyx =+−+−−++ .
Dạng 6****: Chứng minh bất đẳng thức; tìm GTLN hoặc GTNN của biểu thức
Bước 1: Đưa các biểu thức về dạng bình phương của một tổng hoặc một hiệu.
Bước 2: Đánh giá dựa vào kết quả 2 0 A và 2 0 A .
Bước 3: Kết luận GTLN hoặc GTNN
M A thì biểu thức A có GTLN là M.
Am thì biểu thức A có GTNN là m .
Ví dụ 24. Chứngminh
a)Biểuthức 2 443 xx−+ luôndươngvớimọi x
b)Biểuthức 2 1 yy luônâmvớimọi y
Ví dụ 25. Tìmgiátrị nhỏ nhấtcủacácbiểuthứcsau
a) 2 45Mxx=−+ ; ĐS: 12 min Mx=⇔=
b) 2 3 Nyy=−− ; ĐS: 131 42 min Ny=⇔=
Bài 9. Khaitriểncácbiểuthứcsau
Bài 2. Viếtcácbiểuthứcdướidạngbìnhphươngcủamộttổnghoặchiệu
a) 2 816xx++ ; b) 2 92416 xx−+ ;
c) 2 9 3 4 xx−+ ; d) 243244xyxyy −+ ;
e) 2 (2)4(2)4 xyxy −−−+ ; f) 2 (3)12 xyxy +− .
Bài 1. Tính:
a) 3(2) x ; b) 3(23) xy ; c) 3 y x x
+ ; d) ( )3 2 23xy + .
Bài 2. Viếtcácbiểuthứcsaudướidạnglậ
Bài 3. Rútgọnbiểuthức:
a) 326128Axxx=−+− ; b) 23 33 1 248 xxx B =−+− ;
c) 3223 (2)6(2)12(2)8 Cxyxyxxyxx =+−+⋅++−
Bài 4. Tínhgiátrị biểuthức:
a) 32 81261Mxxx=−+− tại 25,5 x = ; ĐS:125000
b) 23 1 327 xx Nx=−+− tại 27 x =− ; ĐS:1000
c) 32 32 6128xxx Q y yy =+++ tại 36 x = , 2 y =
Bài 5. Tínhnhanh:
a) 351 ; ĐS:132651
b) 323 89338931218911 +⋅+⋅⋅+ ; ĐS:1000000
c) 32 23923272327 −⋅+⋅−
Bài 1. Đơngiảnbiểuthức:
a) ( ) 2 (3)39 xxx
Bài 3. Tínhnhanh
a) 2103 ; ĐS: 10609 b) 22 968964 +⋅+ ; ĐS: 10000
c) 99101 . ĐS: 9999
Bài 4. Rútgọnbiểuthức
a) 22 (23)(23)Axx=−−+ ; ĐS: 24 Ax =−
b) 2 2 (1)2(21)(1)441Bxxxxx =+−−++−+ ĐS: 2(2)Bx=−+
Bài 1. Tính:
a) 2(47) x + ; b) 2 1 6 3 xy
; c) ( )( ) 23233535 xxyxxy −+
Bài 2. Viếtcác đathứcsaudướidạngbìnhphươngcủamộttổnghoặchiệu.
a) 22 69 xxyy −+ ; b) 2 441 xx++
Bài 5. Tínhgiátrị củabiểuthức
a) 2 1025Nxx=−+ tại 55 x = ;
b) 4 22 4 x Pxyy =−+ tại 1 4; 2 xy== .
Bài 6. Tìmgiátrị nhỏ nhấtcủacácbiểuthứcsau a)
Bài 7. Tìmgiátrị lớnnhấtcủacácbiểuthứcsau a)
b)
Bài 10. Viếtcácbiểuthứcdướidạngbìnhphươngcủamộttổnghoặchiệu
a) 2 44xx++ ;
b) 2 441 xx−+ ;
c) 2 1 4 xx−+ ; d) 2 4()4()1 xyxy+−++
Bài 11. Hoànthiệncáchằng đẳngthứcsau
a) 21025() xx …−+=−… ; b) 2422 4() xxx …−+=…− ;
c) 222 9()xyx−…+=−… ; d) 224(2)()4 xyxy +……−=− .
Bài 12. Chứngminhcác đẳngthứcsau
a) 22222 (1)4(1) aaa−+=+ . b) 22222 ()()2()4 xyxyxyx −+++−=
Bài 13. Rútgọncácbiểuthức
a) 22 (2)(2) Axyxy =+−− ; ĐS: 8 Mxy =
b) 22 (2)4(2)4 Bxyxyyy =−−−+ . ĐS: 22 816 Qxxyy =−+
Bài 14. Khaitriểncácbiểuthứcsau
a) 2()Cxyz =+− ; ĐS: 222 222 Cxyzxyyzzx =+++−−
b) 2(1) Dab =+− . ĐS: 221222 Dabaabb =+++−−
Bài 3. Rútgọncácbiểuthức:
a) 2 (74)(74)(74) xxx +−+− ; b) 2 (2)6(2) xyxyxy +−+ .
Bài 17. Tính: a)
66 xyyx +−
d)
(2) xy + ; e) (3)(3) xyxy −+ ; f) 2(5) x .
Bài 15. Tínhnhanh
a) 2501 ; b) 22 88248812 +⋅+ ; c) 5248 .
Bài 16. Tínhgiátrị củabiểuthức 2 961Qxx=++ trongmỗitrườnghợpsau
a) 33 x = ; ĐS: 10000 Q =
b) 1 3 x = ; ĐS: 0 Q =
c) 11 3 x = ĐS: 100 Q =
Bài 18. Thựchiệnphéptính
a)
(1) x ; b)
(3) y ; c)
Bài 19. Viếtcácbiểuthứcsaudướidạngbìnhphươngcủamộttổnghoặcmộthiệu
a) 2 1025xx−+ ; b)
4914xx++ ; c)
1 4 xx++
Bài 2. Rútgọnbiểuthức:
a) ( ) ( ) 22 (21)421(1)1 Pxxxxxx =−++++−+ ;
b) ( ) ( ) 22223 ()()2 Qxyxxyyxyxxyyy =−++−+−++
Bài 3. Chứngminhgiátrị củacácbiểuthứcsaukhôngphụ thuộcvàogiátrị của x
a) ( ) 23 6(2)2462Axxxx =+−+−− ;
b) ( ) 232(31)93154 Bxxxx =+−+− .
Bài 4. Tínhgiátrị biểuthức:
a) 33() Axyx =++ biết 20 xy+= ;
b) 33 3 Bxyxy =−− biết 1 xy−= .
S:0
S:1
c) 2 11 6363 24 xxx
5525 xyxxyy −++
Bài 8. Tính: a) 3(51) x + ; b) 3(2) xy ;
c) ( ) 2 (45)162025 xxx+−+ ; d) 2 11 6362 39 xxx
Bài 2. Viếtcác đathứcsaudướidạngbìnhphươnghaylậpphươngcủamộttổnghoặc hiệu.
a) 22 1 255 4 xxyy −+ ; b) 32238126 xxyxyy −+− .
Bài 3. Điềncác đơnthứcthíchhợpvàoôtrống
a)
Bài 5. Viếtcácbiểuthứcsaudướidạngtích:
a) 3 1 x + ; b) 3 1 27 x ; c) 33 27 xy ; d) 33278xy +
Bài 6. Rútgọncácbiểuthức:
a) ( ) 23 (2)242Axxxx =+−+−+ ;
b) ( ) ( ) 22 (1)1(1)1Bxxxxxx =−++−+−+ ;
c) ( ) ( )2222 (2)42(3)39 Cxyxxyyyxyxyx =−+++−++ .
Bài 8.
a)Chứngminh 333()3() ABABABAB +=+−+ và 333()3() ABABABAB −=−+−
b)Ápdụng để tính 3 1011. ĐS:1030300
c)Tínhgiátrị biểuthức 33 xy + biết 2 xy+= và 3 xy⋅=− .
Bài 9. Tínhgiátrị biểuthức:
a) ( ) ( ) 23(4)41664 Pxxxx =+−+−− tại 100 x = ;
b) ( ) 223(2)422 Qxyxxyyy =−+++ biết 20 xy+=
S:26
b) 223311111 249827 xxyxy
Bài 4. Rútgọncácbiểuthức: ( ) 2232 (3)93(3)27 xyxxyyxyxy +−+−−−
Bài 20. Rútgọnbiểuthức:
a) 22 ()() xyxy +−− ; b) 22 2()()()() xyxyxyxy −++++−
Bài. Tínhnhanh(khôngdùngMTBT)
a) 298 ; b) 226337 ; c) 2105 ; d) 2 979.
Bài 22. Rútgọnrồitínhgiátrị củabiểuthứcsauvới 19 x =−
22 (32)(27)2(32)(25).Axxxx =++−−++
Bài 23. Rútgọnrồitínhgiátrị củabiểuthứcsauvới 1 5 x = .
22 (31)(7)2(25)(25).Bxxxx =−−+−−+
Bài 4. Cho biểu thức 22 5(3)(3)(23)(6)Axxxx =+−+++− . Rút gọn rồi tính giá trị
củabiểuthức A với 1 5 x =−
Bài 5. Chobiết 15 xy+= và 100 xy =− .Tínhgiátrị củabiểuthức 22Bxy =+
Bài 6. Tínhnhanhgiátrị củabiểuthức
a) 22 39786161 C =+⋅+ ; b) 2 504951 D =−⋅ .
Bài 7. Chứngminh đẳngthức 22 ()()4 xyxyxy +−−= .
Bài 8. Chứngminh đẳngthức ( ) 2222222 3()()()(). xyzxyyzzxxyz ++−−−−−−=++
Bài 17. Chứngtỏ
a) 2 6100xx−+> vớimọi x ; b) 2 450 yy−−< vớimọi y
Bài 18. Tìmgiátrị nhỏ nhấtcủacácbiểuthứcsau
a) 2 611Pxx=−+ ; ĐS: 23 min Px=⇔=
b) 2 Qyy =+ ; ĐS: 11 42 min Qx=⇔=
c) 22 610Kxyxy=+−++ . ĐS:
min
Bài 19. Tìmgiátrị lớnnhấtcủabiểuthức 2 45Bxx=−+ ĐS: 92 max Bx=⇔=
Bài 12. Chứngminhgiátrị củabiểuthức 2 23Pxx=−+ luônluôndươngvớimọi x .
Bài 13. Chứngminhgiátrị củabiểuthức 2 610Qxx=−− luônluônâmvớimọigiátrị của x .
Bài 14. Tìmgiátrị nhỏ nhấtcủabiểuthức 2 1028Pxx=++
Bài 15. Tìmgiátrị nhỏ nhấtcủabiểuthức 2 510 Qxx =− .
Bài 16. Tìmgiátrị lớnnhấtcủabiểuthức 2 1 Pxx=−− .
Bài 24. Chứngminhrằng 22 (23)(21) nn+−− chiahếtcho 8 với n ∈ ℤ .
Bài 25. Tìmgiátrị lớnnhấthoặcgiátrị nhỏ nhấtcủacácbiểuthứcsau:
a) 2 41210Axx=−+ ; b) 2 22Bxx=−− .
Bài. Cho 222 abcabbcca ++=++ .Chứngminhrằng abc ==
Bài 5. Chứngminhgiátrị củabiểuthứcsaukhôngphụ thuộcvàogiátrị củabiến ( ) ( ) 23 (32)964392.Axxxx =+−+−−
Bài 6. Giátrị củabiểuthứcsaucóphụ thuộcvàogiátrị củabiếnkhông? ( ) 32 (1)(1)13(1).Bxxxxxx =+−−++−+
Bài 7. Chứngminh đẳngthức: 332 ()() abababab +=+−+
Bài. Rútgọncácbiểuthứcsau: 333 (2)(2)3(2)(2) xxxxxx ++−+−+− .
Bài. Chứngminh đẳngthức ( ) 3322()()23 xyxyyxy +−−=+ .
Bài. Cho 1 xy−= ,tínhgiátrị củabiểuthức ( ) ( ) 332223 Mxyxy =−−+
PHÂN TÍCH ĐA THỨC THÀNH NHÂN
TỬ BẰNG PHƯƠNG PHÁP DÙNG
HẰNG ĐẲNG THỨC .
A. KIẾN THỨC TRỌNG TÂM.
1. Phân tích đa thức thành nhân tử.
Phân tích đa thức thành nhân tử là viết đa thức dưới dạng tích của những đa thức.
2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức.
Ngoài cách đặt nhân tử chung ta còn sử dụng bảy hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử. Cụ thể :
(1) ()
2 22 2 aabbab ++=+ ; (2) ()2 22 2 aabbab −+=− .
(3) ()() 22 ababab −=+− ; (4) ()3 3223 33 aababbab +++=+ ;
(5) ()3 3223 33 aababbab −+−=− ; (6) ()() 3322 ababaabb +=+−+ ;
(7) ()() 3322 ababaabb −=−++
Ví dụ: Phân tích thành nhân tử các biểu thức
a) 22242(2)(2)xxxx −=−=−+
b) 3232233 612832322(2) xxxxxxx −+−=−⋅+⋅−=− .
c) ()323612961281xxxxxx −+−=−+−−

3 (2)1 x =−−
2 (21)(2)(2)1 xxx =−−−+−+
Ví dụ 2. Phântíchcác đathứcsauthànhnhântử: a)
Ví dụ 3. Phântíchcác đathứcsauthànhnhântử:
a)
Ví dụ 4. Phântíchcác đathứcsauthànhnhântử
b) ( )3 821 x +− .
c) 326128xxx+++ .
d) 32238126 xxyxyy −+−
Dạng 2:Phântích đathức thànhnhân tử bằng phương pháp vận dụng hằng đẳng thức thông qua nhóm số hạng và đặt nhân tử chung.
()
2 (3)33 xxx =−−+
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Phân tích đa thức thành nhân tử bằng phương pháp vận dụng trực tiếp hằng đẳng thức
Bước 1: Biến đổi đa thức đã cho vềđúng dạng hằng đẳng thức cần sử dụng.
Bước 2: Phân tích thành nhân tử.
Ví dụ 1. Phân tích các đa thức sau thành nhân tử:
Nhóm các số hạng xuất hiện hằng đẳng thức thành một nhóm, các số hạng còn lại thành một nhóm

Dùng hằng đẳng thức để viết nhóm các số hạng xuất hiện hằng đẳng thức thành tích
Đặt nhân tử chung ở các nhóm ra ngoài để viết thành tích
Ví dụ 5. Phântíchcác đathứcsauthànhnhântử:
a/ 22 44 xxy −+− ĐS: ( )( ) 22 xyxy
b/ 22 2 xxyyxy ++−− ĐS: ( )( )1 xyxy++−
c/ 2229xxyy−+− ĐS: ( )( )33xyxy−+−−
