70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC (ĐỀ 41-50) by Dạy Kèm Quy Nhơn Official

ĐỀ THI THỬ TỐT NGHIỆP THPT MÔN TOÁN

ễ

Thanh Tú

Collection 70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC - CÓ LỜI GIẢI (ĐỀ 41-50) (251 TRANG)

Ths Nguy

eBook

EDITION

CHUYỂN GIAO QUA EMAIL

COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

WORD VERSION | 2023

ORDER NOW /

TAILIEUCHUANTHAMKHAO@GMAIL

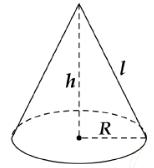
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA TRƯỜNG THPT YÊN ĐỊNH ĐỀ THI THỬ TỐT NGHIỆP THPT – NĂM 2022 - 2023 Câu 1. Đồ thị hàm số nàotrongcáchàm số sau đây có tiệm cận đứng ? A. . B. . C. . D. . 2 1 2 y xx   2 1 1y x   4 3 1y x   2 y x  Câu 2. Tích tất cả các nghiệm của phương trình bằng 2 254 24 xx  A. B. C. D. 2 2 1 1 Câu 3. Tập nghiệm của phương trình là  log1log230 x x A. . B. . C. . D. .  4   2 2 4; 3    Câu 4. Chohàm số có đồ thị và đường thẳng Biết cắt tại ba 3231yxxx    C :1 dyx   d C điểm phân biệt cóhoành độ là Tính ? 123,,.xxx 123 Txxx  A. . B. . C. . D. . 3 1 4 2 Câu 5. Tập xác định của hàm số là  2 31yx  A. B. C. D. 1;  1;  0; \1 Câu 6. Một hìnhnóncó chiều cao bằng bánkính đáy bằng có diện tíchtoàn phần bằng 4 3 A. B. C. D. 9 15 24 12 Câu

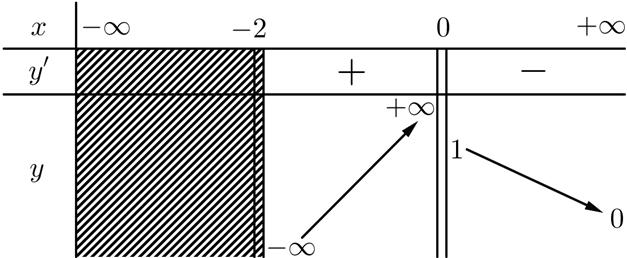
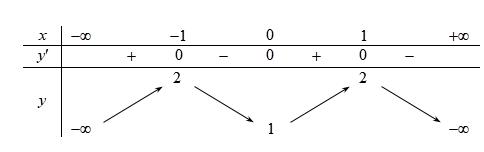
bảng biến thiên như sau fx  ;1 1; Tập nghiệm

là 20fx A. B. C. D.  ;1  ;1  1; Câu 8. Chohàm số có đạo hàmliên tục trên thoả mãn . Biết yfx   0; .cot2.sin fxfxxxx    .Tính . 2 24f    6f    A. . B. . C. . D. . 2 36  2 80  2 54  2 72  Câu 9. Cóbaonhiêugiá trị nguyên của tham số không vượt quá10 để hàm số đồng biến trên m 3 3 x y xm   khoảng ? 2; A. . B. . C. . D. . 11 10 12 9

7. Chohàm số liên tục trên mỗi khoảng và vàcó

của bất phương trình

Câu 10. Thể tích của khối cầu cóbánkính bằng V 3r

Câu 11. Biết là một nguyênhàm của hàm số trên .Giá trị của bằng

Câu 12. Chocáchàm số và với là những số thực dương khác1,có đồ thị như hình vẽ. x ya  xyb  , ab

Đường thẳng cắt trục tung, đồ thị hàm số và lần lượt tại Biết rằng 3y x ya  xyb  ,, HMN , khẳng định nàosau đây đủng? 23HMMN 

A. B. C. D. 53ab  23ab  35ab  35ab 

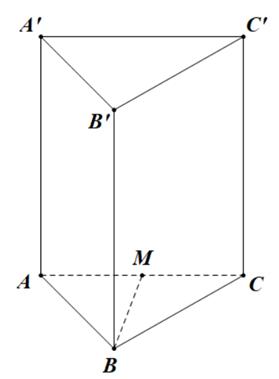
Câu 13. Cho khối lăng trụ



. 36 36 9



fx   2 1 2dfxx A.

C. D.

23 4

3Fxx 

7 9

tamgiác có thể tích . Gọi lần lượt làtrung điểm của các ABCABC V,, MNP cạnh ; ; . Mặt phẳng chia khối lăng trụ đã chothành2 phần, phần chứa điểm ABBCCC  MNP B có thể tíchlà. Tỉ số bằng 1V 1V V A. B. C. D. 25 144 37 144 61 144 49 144 Câu 14. Chohình lăng trụ tamgiác đều có cạnh đáy bằng Khoảng cách từ đến mặt phẳng ABCABC 2a B bằng  ACCA A. . B. . C. . D. . 2a 3a 2a 22a Câu 15. Nếu thìhàm số bằng' 32d23 fxxxxC   fx A. B. 431 2 fxxxCx  2 66 fxxxC  C. D. 431 2 fxxx  2 66 fxxx  Câu 16. Cho .Khi đó bằng  5 2 d10fxx   2 5 24dfxx     A. . B. . C. . D. . 42 34 32 46 Câu 17. Cho một cấp số cộng có , . Hỏi bằng baonhiêu? 24u 42u 1u A. . B. . C. . D. . 15u 11u 16u 11u Câu 18. Hàm số nào dưới đây có đồ thị như đường congtronghình dưới đây?

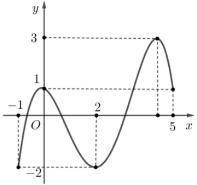
A. . B. . 4223yxx   4223yxx  C. . D. . 4223yxx  4233yxx  Câu 19. Một hình trụ cóbánkính đáy bằng ,chuvi thiết diện qua trục bằng . Thể tích của khối trụ đã a 10a cho bằng A. B. C. D. 3 a 33a 34a 35a Câu 20. Trongcác mệnh đề sau, mệnh đề nào sai? A. . B. .  dln01x x axaaCa  cosdsinxxxC  C. D. 1 d,1 1 x xxC          d fxxfxC   Câu 21. Chohàm số liên tục trên vàcó bảng biến thiên như sau yfx   1;3 x fx fx  1 2 3 0  4 3 1 Cóbaonhiêugiá trị nguyên của để phương trình có nghiệm trên khoảng m 21 45 m fx xx   ? 1;2 A. . B. . C. . D. . 0 10 5 4 Câu 22. Chohìnhnón có chiều cao bằng . Cắt bởi một mặt phẳng qua đỉnh vàcáchtâm của đáy  N 2a N một khoảng bằng ta được thiết diện có diện tích bằng Thể tích khối nón đã cho bằng a 2 411 3 a A. . B. . C. . D. . 3 45 3 a 310 3 a 310a 3 45 9 a Câu 23. Chohàm số có đồ thị là đường congtronghình vẽ dưới đây. Giá trị lớn nhất của hàm số đã yfx  chotrên đoạn bằng baonhiêu?  1;1

1 2 1 2 3 1 2 1 x y O A. B. C. D. 3 0 1 2 Câu 24. Số cách sắp xếp người ngồi vào chiếc ghế xếp hàngnganglà: 5 6 A. . B. . C. . D. . 5 6A 6! 5 6C 5! Câu 25. Chohàm số có đạo hàm với mọi .Cóbaonhiêu số yfx  22 19fxxxxmx    x nguyên dương để hàm số đồng biến trên khoảng ? m  3 gxfx   3; A. . B. . C. . D. . 6 5 7 8 Câu 26. Chohàm số biết là một nguyênhàm của hàm số và .Khí 2sin1fxxx Fx fx01F đó bằng? Fx A. . B. . 3cos2Fxxxx    3 cos2 3 x Fx xx   C. D.  3 cos 3 x Fx xx  3 cos2 3 x Fx x  Câu 27. Tiệm cận đứng của đồ thị hàm số là đường thẳng 21 2 x y x   A. B. C. D. 2x 1 2 x 2y 2x Câu 28. Chohìnhchóp tứ giáccó đáy làhìnhvuông cạnh bằng , chiều cao bằng 3. Thể tích của khối chóp đã 2 cho bằng A. . B. . C. . D. . 4 12 6 18 Câu 29. Trên khoảng , họ nguyênhàm của hàm số là  ;2 1 2fx x   A. . B. . C. . D. . 1 2 C x   ln2xC  2 1 2 C x   1 ln2 2 xC  Câu 30. Cóbaonhiêugiá trị nguyên của tham số để hàm số đồng biến trên ? m 321 93 3 fxxmxx   A. .B. C. D. . 5 4 7 6 Câu 31. Chohàm số có bảng xét dấu của đạo hàm như sau fx

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Câu 32. Cóbaonhiêu số nguyên dương để phương trình

biệt không lớn hơn .5

Câu 33. ÔngNam cần xây dựng một bể nước mưa có thể tích dạng hình hộp chữ nhật với chiều dài

38 Vm 

gấp lần chiều rộng, đáy và nắp đổ bêtông, cốt thép;xungquanhxây bằng gạch vàxi măng. Biết

rằng chiphítrungbìnhlà 980.000đ và ở

35. Chohìnhchóp có đáy làhìnhvuông cạnh , vuônggóc với đáy và . SABCDABCD 2aSA 6SAa  Góc giữa hai mặt phẳng và bằng

của cạnh . Biết và mặt phẳng vuônggóc với mặt H AB 3 2 Sa H

Thể tích của khối chóp bằng

SAC



 2;  2;1

 2 e1ln12ee1 x xx m mx phân

D. .

28 26



.B.

C. . D. . 



;2

cóhai nghiệm m

.B. .

29 27

nắp để hở một khoảng hìnhvuôngcó diện tích bằng 2/m 2 9 diện tích nắp bể. Tínhchiphí thấp nhất màôngNam phải chi trả (làmtròn đến hàngnghìn đồng). A. đ B. đ C. đ D. đ22770000276570002096500023235000 Câu 34. Xét , nếu đặt thì bằng 1 22022 0 2(2)d Ixxx   22uxI A. B. C. D. 3 2022 2 2duu 1 2022 0 d uu 3 2022 2 d uu 3 2022 2 1 d 2 uu



 ABCD A. B. C. D. 90 45 60 30 Câu 36. Chohìnhchóp có đáy làtamgiác đều, hình chiếu vuônggóc của đỉnh trên SABCABC  ABCDS mặt đáy làtrung điểm



3 2 a Câu 37. Với và làhai số nguyên dương tùyý thỏa mãn . Mệnh đề nào dưới đây đúng? kn kn  A. . B. . C. . D. .  !! ! k n knk C n   ! !! k n An knk  ! ! k n Cn k   ! ! k n An nk  Câu 38. Chohai số dương , thỏa mãn .Tính ,,1aba 2 2 loglog2 a a bb loga b A. B. C. D. 8 5 4 5 2 4 Câu 49. Số nghiệm nguyên của bất phương trình là 23 521 5 5 x x     A. B. C. D. 4 2 1 3 Câu 50. Cho khi đó bằng 3 5 log5;log7, ab  45 log175

Câu

SBD



phẳng

SBC SABC

. B. . C. . D. . 3 4 a 33 8 a

16 a

Câu 41. Thể tích của khối tứ diện đều cạnh là a

Câu 42. Đồ thị hàm số nàosau đây cóhai điểm cực đại và điểm cực tiểu?

Câu 43: Chohàm số có bảng biến thiên như sau:

yfx 

Điểm cực đại của hàm số đã cholà

Câu 44: Tìm tất cả cácgiá trị nguyên của trên thỏa mãn m

22414323 m m mmm 

2021;2021

A. 2020. B. 2021. C. 1. D. 0

Câu 45. Cho làba số thực dương khác. Đồ thị hàm số được cho ;; abc 1 ;; x x xyaybyc 

ở hình vẽ dưới đây. Mệnh nàonàosau đây đúng?

A. . B. . C. . D. . abc  cab  bca  acb 

Câu 46. Cho làcác số thực thay đổi thỏa mãn và làcác số thực dương thay , ab 2220 log6841

A. B. C. D. 2 ab a    2 aab a   22 2 b a    2 2 ab a  

A. B. C. D. 32 12 a 32 4 a 33 12 a 33 4 a

1 A. B. C. D. 4223yxx  34 yxx  22 yxx  4223yxx 



A. . B. . C. . D. 4x 3x 2x 3x

 







ab ab   , cd đổi thỏa mãn .Giá trị nhỏ nhất của biểu thức  2 2 2 log7223 c cc dd d    là  2 2 1 acbd  A. . B. . C. . D. . 421 1255 5 291855 5 Câu 47. Chohàm số , . Khẳng định nào dưới đây đúng? 1cos fxx  x  A. . B. . dcos fxxxxC    dcos fxxxxC  

C. . D. . dsin fxxxxC    dsin fxxxxC   Câu 48. Gọi ,, lần lượt là độ dài đường sinh, chiều caovàbánkính của hình trụ . Diện tíchtoàn lhR  T phần của hình trụ được xác định theocông thức tpS A. . B. . 2 tp SRlR  222tp SRlR  C. D. 22 tp SRlR  2 tp SRhR  Câu 49. Hàm số có đạo hàmlà 42xfx   A. B. C. D.  44.2 ln2 x fx    4 4.2.ln2 x fx     42 ln2 x fx    4 2.ln2 xfx    Câu 50. Chohàm số có đồ thị hàm số như hình vẽ bên 432 fxaxbxcxdxa  yfx   Hàm số đồng biến trên khoảng nào dưới đây?  122 ygxfxfx  A. B. C. D.  0;2  3; 13 ; 22     ;0

BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 D D B A B C D D B B B D D B D B A B B A D B A A A 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 A A A B C A C B C C A D B B D A D C B D C C B D B HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. Đồ thị hàm số nàotrongcáchàm số sau đây có tiệm cận đứng ? A. B. C. D. 2 1 2 y xx   2 1 1y x   4 3 1y x   2 y x  Lời giải Chọn D Cáchàm số , , có TXĐ là nên đồ thị khôngcó tiệm cận 2 1 2 y xx   2 1 1y x   4 3 1y x   DR  đứng. Hàm số có và nên đồ thị có tiệm cận đứng . 2 y x   0;D 0 2 lim xx   0x Câu 2. Tích tất cả các nghiệm của phương trình bằng 2 254 24 xx  A. . B. . C. . D. . 2 2 1 1 Lời giải Chọn D Có  2 2 254 25422 2 242225422520* xx xx xx xx    có và . *25160 121c xx a  Câu 3. Tập nghiệm của phương trình là  log1log230 x x A. B. C. D.  4   2 2 4; 3    Lời giải Chọn B Có  log1log230log1log23 x x x x   1234 101 xxx x x x              Vậy . S Câu 4. Chohàm số có đồ thị và đường thẳng Biết cắt tại ba 3231yxxx    C :1. dyx   d C điểm phân biệt cóhoành độ là Tính ? 123 ,, xxx 123 Txxx  A. B. C. D. 3 1 4 2 Lời giải Chọn A Có phương trìnhhoành độ giao điểm 32 32 311320210 xxxxxxxxxx   Suyra 0123.T Câu 5. Tập xác định của hàm số là  2 31yx 

Chọn B Điều kiện xác định: .101xx

Tập xác định . 1;D

Câu 6. Một hìnhnóncó chiều cao bằng bánkính đáy bằng có diện tíchtoàn phần bằng

Theo giả thiết tacó . 22 4,3 5hrlhr

2 35324

Tập nghiệm của

A. B. C. D. 1;  1;  0; \1 Lời giải

B. C. D.

 24 12 Lời giải

9 15

Chọn C



sau fx  ;1 1;



Srlr

Câu 7. Chohàm số liên tục trên mỗi khoảng và vàcó bảng biến thiên như

bất phương trình là 20fx A. B. C. D.  ;1  ;1  1; Lời giải Chọn D Tacó: Từ bảng biến thiênsuyra   202fx fx  21fxx Tập nghiệm bất phương trìnhlà . 1; Câu 8. Chohàm số có đạo hàmliên tục trên thoả mãn . Biết yfx   0; .cot2.sin fxfxxxx    .Tính . 2 24f    6f    A. . B. . C. . D. . 2 36  2 80  2 54  2 72  Lời giải Chọn D

Tacó: cot2sin fxfxxxx    cos2sin sin xfxfx xx x    2 sin-cos 2 sin fxxfxx x x    2 sin fx x x      Do đó .  2 d2d sin sin fx fx xxx xC x x      2 24f    22 0 44 CC  Hay .  2 2.sin sin fxxfxxx x  2 2 sin 636672f     Câu 9. Cóbaonhiêugiá trị nguyên của tham số không vượt quá10 để hàm số đồng biến trên m 3 3 x y xm   khoảng ? 2; A. . B. . C. . D. . 11 10 12 9 Lời giải Chọn B Tacó . 2 333 33 x m y xmxm       Hàm số đồng biến trên khoảng khi . 3 3 x y xm    2; 1330 2 232 3 3 m m m mm        Do không vượt quá10nên . m 2 10 3 m  Vì nguyênnên .Vâycó10giá trị nguyên của tham số thỏa mãn. m  1;2;3;....;10m m Câu 10. Thể tích của khối cầu cóbánkính bằng V 3r A. B. C. D. 36 36 9 9 Lời giải Chọn B Tacó . 3344 .336 33 Vr Câu 11. Biết là một nguyênhàm của hàm số trên .Giá trị của bằng 3Fxx  fx   2 1 2dfxx A. . B. . C. . D. . 7 9 15 4 23 4 Lời giải Chọn B Tacó .    2 22 22 3 11 1 11 2d2dd29 fxxxfxxxx    

Câu 12. Chocáchàm số và với là những số thực dương khác1,có đồ thị như hình vẽ. x ya  xyb  , ab Đường thẳng cắt trục tung, đồ thị hàm số và lần lượt tại . Biết rằng 3y x ya  xyb  ,, HMN , khẳng định nàosau đây đủng? 23HMMN  A. . B. . C. . D. . 53ab  23ab  35ab  35ab  Lời giải Chọn D Tacó , , , .  0;3H log3;3 a M  log3;3 bN  log3;0 a HM    log3log3;0 b a MN  Theo giả thiết, 23HMMN  23HMMN   2log33log3log3 a b a   5log33log3 a b   33 53 loglogab  . 33 5log3logba  53 33 loglogba 53ba Câu 13. Cho khối lăng trụ tamgiác có thể tích . Gọi lần lượt làtrung điểm của các . ABCABC V,, MNP cạnh ; ; . Mặt phẳng chia khối lăng trụ đã chothành2 phần, phần chứa điểm ABBCCC  MNP B có thể tíchlà. Tỉ số bằng 1V 1V V A. . B. . C. . D. . 25 144 37 144 61 144 49 144 Lời giải Chọn D Tacó:  PCEPCNCECN     PCNHBNHBCP 

 Xét ,theo định lýmenelauytcó: . ABC  1 AMBECF MBECFA    1 3 CF FA    Xét đồng dạng BGN BME 1 3 BGBN BMBE   1 6 BG BA  Tacó: . 1HBMEHBGNPCFEVVVV    Lại có:  . 1 13133 ...... 3 32228 HBME VHBBMBE VBBBABC        . 1 11111 ...... 3 326272 HBGN VHBBGBN VBBBABC      1 11111 3 322448 PCFE VPCCECF VCCCBCA       Vậy . 131149 87248144 V V   Câu 14. Chohình lăng trụ tamgiác đều có cạnh đáy bằng Khoảng cách từ đến mặt phẳng ABCABC 2a B bằng  ACCA A. . B. . C. . D. . 2a 3a 2a 22a Lời giải Chọn B Gọi làtrung điểm của M AC Tacó . BMAC BMAA    BMACCA Khi đó   ; 3 BAACAd BMa  Câu 15. Nếu thìhàm số bằng' 32d23 fxxxxC   fx A. . B. . 431 2 fxxxCx  2 66 fxxxC  C. . D. . 431 2 fxxx  2 66 fxxx  Lời giải Chọn D  32 2 2366 fxxxCxx   Câu 16. Cho .Khi đó bằng  5 2 d10fxx   2 5 24dfxx     A. B. C. D. 42 34 32 46 Lời giải Chọn B

Câu 17. Cho một cấp số cộng có

Chọn A

45 321 uudu uudd



A. .

 C. .

33yxx

2222103 Phrhaaha 

trụ là . 22 3..33 Vrhaaa     Câu 20. Trongcác mệnh đề sau, mệnh đề nào sai? A. . B. .  dln01x x axaaCa  cosdsinxxxC  C. D. 1 d,1 1 x xxC          d fxxfxC   Lời giải Chọn A Theocông thức . d01 ln x xa axCa a  Câu 21. Chohàm số liên tục trên vàcó bảng biến thiên như sau yfx   1;3

.   5 5 5 2 2 2 42d4d2d fxxfxxx       40634

, . Hỏi

24u 42u 1u A. . B. . C. . D. . 15u 11u 16u 11u Lời giải

bằng baonhiêu?

Tacó . 21 1 41        

 4223yxx

 Lời giải

Câu 18. Hàm số nào dưới đây có đồ thị như đường congtronghình dưới đây?

4223yxx 

. 4223yxx 

Chọn B

D. . 3 a 33a 34a 35a Lời giải

Dựa vào đồ thị ta thấy đường conglàhàm bậc trùng phương với hệ số , vàhàm số có

a 3d ba cực trị suyra .00abb Câu 19. Một hình trụ cóbánkính đáy bằng ,chuvi thiết diện qua trục bằng . Thể tích của khối trụ đã a 10a cho bằng

Chọn B



Chuvi thiết diện qua trục là

Thể tích khối

x fx fx  1 2 3 0  4 3 1 Cóbaonhiêugiá trị nguyên của để phương trình có nghiệm trên khoảng m 21 45 m fx xx   ? 1;2 A. . B. . C. . D. . 0 10 5 4 Lời giải Chọn D Do ,tacó:  24501;2xxx Phương trình   2 21 451 45 m fx mxxfxgx xx     Xét .  2 14524101;2gxfxxxxfxx    Vì .    10 1;221310 240 fx x x fx x       Bảng xét dấu: x1 2 gx  gx  1g  2g Yêu cầu bàitoán .  2138gmgm  Do . 4;5;6;7mm  Câu 22. Chohìnhnón có chiều cao bằng . Cắt bởi một mặt phẳng qua đỉnh vàcáchtâm của đáy  N 2a N một khoảng bằng ta được thiết diện có diện tích bằng Thể tích khối nón đã cho bằng a 2 411 3 a A. B. C. D. 3 45 3 a 310 3 a 310a 3 45 9 a Lời giải Chọn B S O A B H I Gỉa sử tamgiác là thiết diện đi qua đỉnh của hìnhnón . SAB  N

Gọi làtrung điểm của và kẻ I ABOHSI    , OHSABdOSABHOa  Xéttamgiácvuông có: . SOI 222222 111111 4 OHSOOIaaOI  2 3 Oa I  Lại có: . 2 22244 4 33 aaSISOIOa Xéttamgiác có: . SAB 2 411 22233 3 43 3 ABC a S a AB aSI   33 23 ABa BI  Xéttamgiác có: . OIB 22 22433 5 39 aaOBOIIB a Vậy thể tích của khối nónlà: . 3 2 2 1110 52 333 aVrSOaa      Câu 23. Chohàm số có đồ thị là đường congtronghình vẽ dưới đây. Giá trị lớn nhất của hàm số đã yfx  chotrên đoạn bằng baonhiêu?  1;1 1 2 1 2 3 1 2 1 x y O A. . B. . C. . D. . 3 0 1 2 Lời giải Chọn A Theo đồ thị ta thấy: với nên .  13 fx   1;1x 1;1 3Maxfx Câu 24. Số cách sắp xếp người ngồi vào chiếc ghế xếp hàngnganglà: 5 6 A. . B. . C. . D. . 5 6A 6! 5 6C 5! Lời giải Số cách sắp xếp người vào ghế hàngnganglà 56 5 6A Câu 25. Chohàm số có đạo hàm với mọi .Cóbaonhiêu số yfx  22 19fxxxxmx    x nguyên dương để hàm số đồng biến trên khoảng ? m  3 gxfx   3; A. B. C. D. 6 5 7 8 Lời giải Chọn A Tacó  22 332339. fxxxxmx         Khi đó 3.gxfx   

Hàm số đồng biến trên khoảng khivà chỉ khi gx  3;     22 0,3;. 30,3;. 323390,3;. gxx fxx xxxmx x          thì suyra  3;x 2 30,20 xx     2 3390,3: xmxx       2 2 3: 39 39 ,3; 3 3 x x m x mMin x x     Tacó   2 399 9 3236 3 3 3 x x x x x x    Suyra 6.m Vì nguyên dương suyra . m  1;2;3;4;5;6m Câu 26. Chohàm số biết là một nguyênhàm của hàm số và .Khí 2sin1fxxx Fx fx01F đó bằng? Fx A. . B. . 3cos2Fxxxx    3 cos2 3 x Fx xx   C. . D. .  3 cos 3 x Fx xx  3 cos2 3 x Fx x  Lời giải Chọn A Tacó .  3 2sin1cos 3 xFxxxdx xxC    Mà . Vậy  30 01cos0012 3 F CC   3cos2Fxxxx   Câu 27. Tiệm cận đứng của đồ thị hàm số là đường thẳng 21 2 x y x   A. B. C. D. 2x 1 2 x 2y 2x Lời giải Chọn A Tacó nên đồ thị hàm số có tiệm cận đứng là . 2 21 lim 2 x x x   2x Câu 28. Chohìnhchóp tứ giáccó đáy làhìnhvuông cạnh bằng , chiều cao bằng 3. Thể tích của khối chóp đã 2 cho bằng A. . B. . C. . D. . 4 12 6 18 Lời giải Chọn A Tacó diện tích đáy nên thể tích khối chóplà . 224B 11 .4.34 33 VBh Câu 29. Trên khoảng , họ nguyênhàm của hàm số là  ;2 1 2fx x  

Câu 30. Cóbaonhiêugiá trị nguyên của

 2290, xmxx  29033m m 

Vì nên . m 3;2;1;0;1;2;3

Câu 31. Chohàm số có bảng xét dấu của đạo hàm như sau fx

Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. .B. C. D. .  2;  ;2  2;  2;1

Lời giải Chọn A

Từ bảng biến thiênsuyrahàm số nghịch biến trên khoảng . 2;

Câu 32. Cóbaonhiêu số nguyên dương để phương trình

A. . B. . C. . D. . 1 2 C x   ln2xC  2 1 2 C x   1 ln2 2 xC  Lời giải Chọn B Tacó . 1 ln2 2 fxdxdxxC x   

số để hàm số đồng biến trên ? m 321 93 3 fxxmxx   A. .B. C. D. . 5 4 7 6 Lời giải Chọn C TXĐ: . D Tacó . 229fxxmx  Hàm số đồng

0, fxx 

tham

biến trên

m

cóhai nghiệm m  2 e1ln12ee1 x xx m mx  phân biệt không lớn hơn .5 A. .B. C. D. . 29 27 28 26 Lời giải Chọn C Tacó  2 e1ln12ee1 x xx m mx  1 2 e1lnx1e10 x x m m     e1ln1e10 x x mmx        e10 ln1e10 x x mmx        e1 ln1e1 x x mmx       0/ ln1e1 x xtm mmx     Phương trình cóhai nghiệm phân biệt không lớn hơn Phương trình có  1 5  ln1e1 x mmx một nghiệm duy nhất khác và nhỏ hơn hoặc bằng . 0 5

* Nếu loại. 1m

* Nếu ,tacó1m

e x gxm  

0ln gxxm 

Để thỏa mãnbàitoánthì .  5 e1 50 5 g m 

Kết hợp điều kiện, suyra . 2;3;;29m

Vậy có giá trị nguyên dương thỏa mãn. 28 m

Câu 33. ÔngNam cần xây dựng một bể nước mưa có thể tích dạng hình hộp chữ nhật với chiều dài

38 Vm 

gấp lần chiều rộng, đáy và nắp đổ bêtông, cốt thép;xungquanhxây bằng gạch vàxi măng. Biết 4 3

rằng chiphítrungbìnhlà 980.000đ và ở nắp để hở một khoảng hìnhvuôngcó diện tích bằng 2/m 2 9

diện tích nắp bể. Tínhchiphí thấp nhất màôngNam phải chi trả (làmtròn đến hàngnghìn đồng).

Vì nên . 0x  ln1e1 x mmx ln11ex mmx 2 Đặt .  ln1tmx1ex mx

1e t x t x mx mxmt mt      **

. 

 

. e0



m  

. **e10

 

. 

 

Tacó . 1e ee

Xéthàm số đặc trưng: trên

e u fumu

Tacó

và

u fum

Suyra

x xtmx

Xéthàm số ,có ,suyra

e1 x gxmx



A. đ B. đ C. đ D. đ22770000276570002096500023235000 Lời giải Chọn B Gọi chiều rộng của bể là .Tacó chiều dài bể là và chiều cao của bể là . 3xm 4() xm 2 2 3 m x Khi đó tổng diện tích bề mặt xâylà: .   2 2 2 2 2 2 2228642864327 34.2.2.3.4.3.4 2.. 3933333 x x Txx xxxx m x x x     Chiphí (tínhtheo đồng) xây dựng là: (đồng). C 327 .980000.98000027657000 3 CT    Câu 34. Xét , nếu đặt thì bằng 1 22022 0 2(2)d Ixxx   22uxI A. . B. . C. . D. . 3 2022 2 2duu 1 2022 0 d uu 3 2022 2 d uu 3 2022 2 1 d 2 uu Lời giải

Chọn C

d Iuu

Câu 35. Chohìnhchóp có đáy làhìnhvuông cạnh , vuônggóc với đáy và . . SABCDABCD 2aSA

ABCD A. . B. . C. . D. . 90 45 60 30

6SAa 

Gọi làgiao điểm của và . O ACBD

Từ đề bài,tacó:+) , () BDACBDSABDSACBDSO  



 

 

 ABCDS mặt

trên . SABCABC

Tacó:+) ; d2duxx  +) .02;13xuxu  . 3 2022 2 



 Lời giải O A D B C S

Góc giữa hai mặt phẳng và bằng  SBD

Chọn C





Tacó , SOBDAOBD  

 ; ; SBDABCDSOAOSOA

+) .   222tan360 SA ACaAOaSOA SOA AO 

làtrung

Biết

vuônggóc với mặt H AB 3 2 Sa H  SAC phẳng . Thể tích của khối chóp bằng  SBC SABC A. . B. . C. . D. . 3 4 a 33 8 a 3 16 a 3 2 a Lời giải

Câu 36. Chohìnhchóp có đáy làtamgiác đều, hình chiếu vuônggóc của đỉnh

đáy

điểm của cạnh

và mặt phẳng

x H A C B S K Chọn A Giả sử làtamgiác đều cạnh . ABC x Kẻ vuônggóc với tại .Tacó (vì ) HK SCK , SCHKSCAB   ABSHC  cùngvuônggóc với Góc giữa và làgóc giữa và , SCAKBAKBK SC AKBK  SAC .  SBC  90 22 ABx AKBHK  Mặt khác,tacó: .  22 222 3 3 2 4 xa Cx H SCCHSH   222 111 HKCHSH  222222 33 2.3 2 332 44 xa CHSH ax HK CHSHxaxa       Suyra,tacó phương trình: . 222 22 3 3 2 22 xax xxaxa xa    Diện tíchtamgiác là:  ABC 2233 2. 42 ABC a Sa    Thể tích của khối chóp là: .  SABC 2 3133 3224 aaa V  Câu 37. Với và làhai số nguyên dương tùyý thỏa mãn . Mệnh đề nào dưới đây đúng? kn kn  A. B. C. D.  !! ! k n knk C n   ! !! k n An knk  ! ! k n Cn k   ! ! k n An nk  Lời giải Chọn D Mệnh đề đúng là .  ! ! k n An nk  Câu 38. Chohai số dương , thỏa mãn .Tính ,,1aba 2 2 loglog2 a a bb loga b A. . B. . C. . D. . 8 5 4 5 2 4 Lời giải Chọn B

Tacó . 2 21 5 4 loglog2log2log2log2log 2 2 5 a a a a a a bb bb b b     Câu 39. Số nghiệm nguyên của bất phương trình là 23 521 5 5 x x     A. . B. . C. . D. . 4 2 1 3 Lời giải Chọn B Tacó: . 2 2 3 523521 555 5 x x xx       2 2 3523520 xxxx  1 2 3 x  Do nên . x 0;1x Số nghiệm nguyên của bất phương trìnhlà2. Câu 40. Cho khi đó bằng 3 5 log5;log7, ab  45 log175 A. . B. . C. . D. . 2 ab a    2 aab a   22 2 b a    2 2 ab a   Lời giải Chọn D Tacó: 2 3 3 33 335 45 2 3 3 33 3 llog175log5.72log5log72log5log5log7 og175log45log3.52log3log52.1log5         22 . . 22 aab ab aa       Câu 41. Thể tích của khối tứ diện đều cạnh là a A. B. C. D. 32 12 a 32 4 a 33 12 a 33 4 a Lời giải Chọn A Gọi tứ diện đều cạnh là với làtâm của đáy aSABCO ABCSOABC Tacó và . 2 1 1 3sinsin60 2 2 4 ABC aSABACAaa      3 2sin2sin603 BCaa OA A    Tamgiác có . SOA 226 3 aSOSAOA  

Vậy . 2 3 11362 334312SABC ABC aaaVSSO     Câu 42. Đồ thị hàm số nàosau đây cóhai điểm cực đại và điểm cực tiểu? 1 A. . B. . C. . D. . 4223yxx  34 yxx  22 yxx  4223yxx  Lời giải Chọn D Tacó . 4223yxx  3 44 yxx . 3 0 0440 1 x yxx x   . 2 124yx  Có là điểm cực tiểu. 040y  0x  Có làhai điểm cực đại. 180y 1x  Câu 43: Chohàm số có bảng biến thiên như sau: yfx  Điểm cực đại của hàm số đã cholà A. . B. . C. . D. 4x 3x 2x 3x Lời giải Chọn C. Điểm cực đại của hàm số đã cholà 2x Câu 44: Tìm tất cả cácgiá trị nguyên của trên thỏa mãn m 2021;2021   22414323 m m mmm   A. 2020. B. 2021. C. 1. D. 0 Lời giải Chọn B Tacó:   22414323 m m mmm        2 2 2 2 241.3 3 432 241432 131232 m m m m m m mmm mmm m m         Xéthàm số với 23 fxxx  0x

Nênhàm số đồng biến trên khoảng fx  0;

Mà  1212210 m mm fmf m m 

Xéthàm số : 21 m fmm 

Tacó: nênhàm đồng biến 2ln210, mfm m  21 m fmm 

Mặt khác: 00fmfm

Vậy có2021giá trị nguyênm thỏa mãn.  2020;2019;;0m 

Câu 45. Cho làba số thực dương khác. Đồ thị hàm số được cho ;; abc 1 ;; x x xyaybyc 

ở hình vẽ dưới đây. Mệnh nàonàosau đây đúng?

2 2 2 3 1 0,0 33 fxxx x x x x       

Tacó: 

C. . D. . abc  cab  bca  acb  Lời giải Chọn D Dohàm số nghịch biến trên . x ya  1a  Dohàm

đồng biến trên .

 x yc  ,1bc  Tacó: . 0;: 11 x xxbb x bc bc cc     Vậy . acb  Câu 46. Cho làcác số thực thay đổi thỏa mãn và làcác số thực dương thay , ab 2220 log6841 ab ab   , cd đổi thỏa mãn .Giá trị nhỏ nhất của biểu thức  2 2 2 log7223 c cc dd d    là  2 2 1 acbd  A. . B. . C. . D. . 421 1255 5 291855 5 Lời giải Chọn C Tacó:   22 22 22 20 log684120684341* ab ab ababab     Lại có:   2 2 2 2 2 2 2 log7223log7223 230;,0 c cc dd c cc dd d d dddc             2 2 2 2 121log722log27 ** 1;0 1;0 cdcccddd dc dc             

. B. .

số và

xyb

Đặt .Theo ta thấy thuộc đường tròntâm ,bánkính .  ;;1; MabNcd *M  3;4I 1R

Từ ta thấy thuộc nữa đường thẳng ứng với .  **N 11 21 22xyyx  0,1xy

Khi đó  2 2 1 MNacbd 

Suyra . min1291MNNIR  

Vậy giá trị nhỏ nhất của biểu thức .  2 2 1 291acbd  

Câu 47. Chohàm số , . Khẳng định nào dưới đây đúng? 1cos fxx  x 

A. . B. . dcos fxxxxC  

dcos fxxxxC 

C. D. dsin fxxxxC    dsin fxxxxC 

Lời giải

Chọn C

Tacó: .  1cosdsinxxxxC  

Câu 48. Gọi ,, lần lượt là độ dài đường sinh, chiều caovàbánkính của hình trụ Diện tíchtoàn lhR  T

của hình trụ được xác định theocông thức



tpS A. . B. . 2 tp SRlR  222tp SRlR  C. . D. . 22 tp SRlR  2 tp SRhR  Lời giải Chọn B Diện tíchtoàn phần của hình trụ được xác định theocông thức tpS 222tp SRlR  Câu 49. Hàm số có đạo hàmlà 42xfx   A. . B. . C. . D. .  442 ln2 x fx    4 42ln2 x fx     42 ln2 x fx    4 2ln2 xfx    Lời giải Chọn D Tacó:.  4 4 22ln2 x x fx fx    

phần

Câu 50. Chohàm số có đồ thị hàm số như hình vẽ bên 432 fxaxbxcxdxa  yfx   Hàm số đồng biến trên khoảng nào dưới đây?  122 ygxfxfx  A. B. C. D.  0;2  3; 13 ; 22     ;0 Lời giải Chọn B Từ đồ thị hàm số ta thấy: fx   0 0 1 x fx x   Nên ,hay .  4.11fxaxxx     2 41fxaxx   Suyra: .  2 22 42 2 .2..1.1.1 fxaxaxaaxaxx     Xét có:  122 gxfxfx   2122122 gxfxfxfxfx     Suy ra:  2 22 22 2 2.4121211.3.2.22.42.21 gxaxxaxxaxxaxx             32 3 2 22 32121364213 axxxxaxxxx 23 321312322 axxxxxxx     23 2 32134113 axxxxx     0 1173 0;1 8 01 1173 2;3 8 3 x x a gxx x b x                Vì nên dựa vào đồ thị hàm số suyra  2 41fxaxx   fx  0a Nhận xét:  23 13212441130ga    Nêntacó bảng xét dấu: Dựa vào bảng xét dấu tacó đồng biến trên khoảng . gx  3;

SỞ GIÁO DỤC VÀ ĐÀO TẠO THÁI BÌNH

THÁI BÌNH

Khẳng định nàosau đây đúng?

Trongkhônggian ,cho . Tọa độ của vectơ là: Oxyz 23 aijk   a  A. . B. . C. . D. .  2;1;3  3;2;1  2;3;1  1;2;3 Câu

Chohàm số có bảng biến thiên như hình vẽ yfx 

TRƯỜNG THPT CHUYÊN

ĐỀ THI THỬ TỐT NGHIỆP THPT –LẦN 3 – NĂM HỌC 2022 – 2023 Câu 1.

Giá trị

đại của hàm số là . B. Giá trị cực đại của hàm số là . 3CDy 4CDy C. Giá trị cực tiểu của hàm số là . D. Giá trị cực tiểu của hàm số là . 3CTy 1CTy Câu 3. Hàm số nào dưới đây có đồ thị như đường congtronghìnhbên dưới? A. . B. . C. . D. . 32 yxx  242 yxx  32 yxx  42 2 yxx  Câu 4. Tìm tập xác định của hàm số D 25 2yxx  A. . B. . D  0;D C. D.  ;12;D \1;2D Câu 5. Tìm họ nguyênhàm của hàm số sin3 fxx  A. . B. . C. . D. . cos3xC  1 cos3 3 xC  cos3xC  1 cos3 3 xC  Câu 6. Cho cấp số nhân có số hạng đầu vàcông bội Số hạng thứ năm của cấp số  n u 13u 2q nhân là  n u A. . B. . C. . D. . 596u 532u 548u 524u Câu 7. Cho khối hộp chữ nhật có , , . Thể tích khối hộp bằng . ABCDABCD AAa   3 ABa  5 ACa  A. . B. . C. . D. . 312a 34a 315a 35a Câu 8. Số tổ hợp chập 3 của 12 phần tử là A. . B. . C. . D. . 1728 220 1320 36 Câu 9. Chohìnhchóp có đáy làtamgiáccân , các cạnh bên . SABCABC ABACa   120BAC  bằng nhauvàcùng tạo với mặt phẳng đáy cácgóc . Thể tích khối chóp là 30 SABC A. . B. . C. . D. . 33 12 a 3 4 a 33 4 a 3 12 a Câu 10. Trongcáchàm số sau,hàm số nào đồng biến trên ? 

cực

1;5 Tổng giá trị lớn nhất vàgiá trị nhỏ nhất của hàm số trên đoạn bằng

A. 4. B. -1.

Câu 13. Trongkhônggian , một vectơ

A. B. C. D.  x fe x     1x fx e    1 3 x fx   3xfx Câu 11. Hàm số nào dưới đây đồng biến trên khoảng ? ;  A. B. C. D. 33 yxx  1 2 x y x  1 3 x y x    33 yxx  Câu 12. Chohàm số liên tục trên đoạn vàcó đồ thị trên đoạn như hình vẽ bên. ()yfx   1;5 





1;5

1. D. 2.

chỉ phương của đường thẳng là Oxyz 12 112 xyz   A. . B. . C. . D.  1;1;2u   1;1;2u   1;2;0u   1;2;1u  Câu 14. Trongkhônggian ,cho điểm Tọa độ điểm làhình chiếu vuônggóc của Oxyz  1;2;3M A M trên mặt phẳng là:  Oyz A. B. C. D.  1;2;3A  1;2;0A  1;0;3A  0;2;3A Câu 15. Hàm số với có đồ thị như hình vẽ bên. Mệnh đề nàosau đây là đúng? axb ycxd    0a A. B. C. D. 0,0,0bcd 0,0,0bcd 0,0,0bcd 0,0,0bcd Câu 16. Tính đạo hàm của hàm số 2 log21yx   A. . B. . C. . D. .  1 21ln2y x     2 21ln2y x    2 21y x    1 21y x    Câu 17. Chohàm số có bảng biến thiên như hình vẽ. Tổng số tiệm cận ngangvà tiệm cận đứng yfx  của đồ thị hàm số đã cholà A. 0. B. 2. C. 1. D. 3.

quả cầu từ hộp đó. Xác suất để trong3 quả cầu

Câu 23. Chohìnhchóp có đáy làtamgiácvuôngcân

Câu 18. Với mọi dương thỏa mãn Khẳng định nào dưới đây đúng? , ab 3 2 2 loglog5. ab A. . B. . C. . D. . 3232ab 2232ab 2332ab 232ab Câu 19. Hàm số có đồ thị làhìnhbên.Giá trị của cơ số bằng  log01 a yxa   a A. B. C. D. 42 4 2 2 Câu 20. Tìm tập nghiệm của bất phương trình . S 45 5 1x A. . B. . C. . D. .  5;S  3;S  ;5S  ;3S Câu 21. Tìm tập nghiệm của bất phương trình . S  2 22 loglogxxx  A. . B. . C. . D. .  2S  0S  0;2S  1;2S Câu 22. Một chiếc hộp chứa

cầu gồm

màuxanh,3 quả màu

và2 quả màuvàng(cácquả cầu đôimộ

Lấy

được cóít nhất

quả màu đỏ bằng A. B. C. D. 1 3 19 28 16 21 17 42

tại và .Tamgiác SABCABC B2 ABa  SAB đều và nằm trong mặt phẳng vuônggóc với đáy. Tính thể tích của khối chóp . V . SABC A. B. C. D. 33 4 a V 33 3 a V 33 12 a V 3 23 3 a V Câu 24. Cho khối nóncóbánkính đáy bằng ,góc ở đỉnh hìnhnónlà . Thể tích khối nón bằng 3cm 60 A. B. C. D. 3 93(cm)  3 33(cm)  3 6(cm) 3 3(cm)  Câu 25. Chohình trụ có thiết diện đi qua trục là một hìnhvuôngcó cạnh . Diện tíchxungquanh của 4a hình trụ là A. . B. . C. . D. . 28 Sa  224 Sa  216 Sa  24 Sa  Câu 26. Tìmnguyênhàm của hàm số biết Fx  2 21 2fxx x  13F A. . B. .   22ln21Fxxxx   22ln21Fxxxx   C. D. 2ln21Fxxxx   22ln21Fxxxx   Câu 27. Đường tiệm cận đứng của đồ thị hàm số là 1 2 x y x  A. B. C. D. 1y 1x 2x 2y Câu 28. Giá trị nhỏ nhất của hàm số trên đoạn là 335yxx  2;4 A. B. C. D.  2;4 min3 y  2;4 min7 y  2;4 min5 y  2;4 min0 y Câu 29. Chohàm số có bảng biến thiên như sau yfx 

9 quả

4 quả

đỏ

tkhácnhau).

ngẫu nhiên3

lấy

các trục tọa độ lần lượt tại (khác )saocho là trực

Câu 34. Trongkhônggian với hệ trục tọa độ , mặt phẳng (P) đi qua và chứa trục hoành Oxyz

có phương trìnhlà

. B. . C. . D. . 340 yz 30

Hàm số nghịch biến trên khoảng nào dưới đây? yfx  A. . B. . C. . D. .  ;1  0;1  1;0  1;1 Câu 30. Cho .Khi đó bằng:  2 0 d3Ifxx     2 0 43d Jfxx      A. . B. . C. . D. . 2 6 8 4 Câu 31. Nếu và thì bằng  2 2 d9fxx   2 1 d2fxx   1 2 d fxx A. . B. . C. . D. . 7 3 11 7 Câu 32. Tính . 1 0 1 3d 21 I xx x     A. B. C. D. 2ln3  4ln3  2ln3  1ln3  Câu 33. Trongkhônggian với hệ trục tọa độ ,cho . Phương trình mặt phẳng đi Oxyz 1;1;3H  P qua cắt

H Ox,Oy,Oz,,

H tamgiác là ABC A. B. C. D. 370xyz 3110xyz 3110xyz   370xyz

tâm

ABCO

 1;1;3A

yz 0xy 30xy Câu 35. Chohàm số liên tục trên vàcó đồ thị như hình vẽ dưới đây. Cóbaonhiêugiá trị yfx   nguyên của tham số để phương trình có nghiệm duy nhất trên ? m  3 3log1fxm  3 1 ;3 3    A. B. C. D. 2 4 3 1 Câu 36. Chohàm số có đạo hàmvàliên tục trên đoạn và Tính fx  1;3,34 f  1 0 21d6fxx giá trị của  1f A. . B. . C. . D. . 18f 12f 116f 110f Câu 37. Chohìnhchóp có đáy làhìnhvuông cạnh , đường thẳng vuônggóc với mặt . SABCD a SA phẳng Khoảng cách giữa hai đường thẳng và bằng ,2ABCDSAa  SBAD A. . B. . C. . D. . 6 3 a 2 3 a 3 2 a a

Câu 38. Trongkhônggian với hệ trục tọa độ ,cho ; ; . Diện tích mặt Oxyz 1;2;3A

cầu nhận đường tròn ngoại tiếp tamgiác làm đường tròn lớn là ABC

Câu 39. Chohàm số xác định trên vàcó đạo hàm .Hàm số

nghịch biến khoảng nào dưới đây?

A. . B. . C. .

baonhiêu điểm cực đại?

Câu 45. Chohìnhchóp có đáy làhìnhbìnhhành. Gọi là điểm đối xứng của qua . SABCDABCD M C và làtrung điểm của . Mặt phẳng chia khối chóp thànhhai khối đa BN SC  MND . SABCD

diện, trong đó khối đa diện chứa đỉnh có thể tích, khối đa diện còn lại có thể tích (tham S 1V 2V khảo hình vẽ bên).

 4;2;3B  4;5;3C

C. . D. .

 36 18 72

A. . B. .

đã

yfx    2 (1)1fxxxx   

cho

 1;0  ;1  0;1  1; Câu 40. Trongkhônggian với hệ tọa độ

cótâm vàcó tiếp diện là mặt  S  1;2;1I phẳng ,có phương trìnhlà :2250Pxyz A. . B. .  2 22 1214xyz  2 22 1211xyz   C. D.  2 22 1214xyz    2 22 1211xyz Câu 41. Cho ()fx làhàm số liên tục trên tập số thực khôngâmvà thỏa mãn Tính  23120fxxxx   5 1 d fxx A. 37 6 . B. 527 3 . C. 61 6 . D. 464 3 . Câu 42. Chohình lăng trụ đứng có đáy vuông tại , Giá . ABCABC ABC ,A 3ABa ACAAa   trị sin của góc giữa đường thẳng và mặt phẳng bằng AC  BCCB A. B. C. D. 10 4 6 3 3 3 6 4 Câu 43. Chohàm số . Gọi là tập hợp tất cả cácgiá trị thực của tham số để giá trị 221fxxxS m lớn nhất của hàm số trên đoạn bằng .Tính tổng các phần  22 gxfxfxm   1;38 tử của S A. . B. . C. . D. . 7 2 0 5 Câu 44. Chohàm số liên tục trên . Đồ thị hàm số yfx    3' yfx  được chotronghìnhbên.Hàm số có tối đa 41 8 gxfxxx 

Oxyz, mặt cầu

B. 2 3 C. . D. . 4 5

Tính tỉ số . 1 2 V V A. . B. . C. . D. . 1 2 12 7 V V  1 2 5 3 V V  1 2 7 5 V V  1 2 1 5 V V  Câu 46. Chohàm số với làtham số thực. Biết rằng nếu  2 3ln3 fxaxaxx   a thì . Khẳng định nàosau đây đúng? 1;3 max2 fxf   1;3 minfxm   A. B. C. D.  6;7m  7;8m  8;9m  9;10m Câu 47. Chohàm số có đạo hàmtrên đoạn và thỏa mãn ; fx  1;e 10f .Tíchphân bằng 1,1; fxxfxxe        1 d e fxx A. . B. . C. . D. . 21 4 e 21 2 e 21 4 e 21 2 e Câu 48. Cóbaonhiêu số nguyên dương saocho tồn tại số thực lớn hơn thỏa mãn x y1 ?   2 2321loglogyx xyxyy x    A. 3. B. 1. C. vô số. D. 2. Câu 49. Trongkhônggian với hệ tọa độ Oxyz,cho mặt cầu cótâm thuộc mặt phẳng  S và đi quahai điểm .Bánkính nhỏ nhất của mặt cầu ():270 Pxyz  1;2;1,2;5;3AB bằng:  S A. . B. . C. . D. . 470 3 546 3 763 3 345 3 Câu 50. Trong khoảng cóbaonhiêugiá trị nguyên của tham số m để phương trình  10;20 có đúng 2 nghiệm phân biệt. 2 3 9 4log(1)log9(1)m xx x   A. 23. B. 20. C. 8. D. 15. HẾT

2. Chohàm số có bảng biến thiên như hình vẽ

Khẳng định nàosau đây đúng?

A. Giá trị cực đại của hàm số là

Chọn A

Từ bảng biến thiên,giá trị cực đại của hàm số là

Câu 3. Hàm số nào dưới đây có đồ thị như đường congtronghìnhbên dưới? A. .

BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 D A D D B C A B D D D C A D C B D A C B A C D A C 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 D C B C B A A C B D A A C A D C D A B C A C D B A HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. Trongkhônggian ,cho . Tọa độ của vectơ là: Oxyz 23 aijk   a  A. . B. . C. . D. .  2;1;3  3;2;1  2;3;1  1;2;3 Lời giải Chọn D Tacó . 231;2;3aijka   Câu





yfx

. B. Giá trị cực đại của hàm số là . 3CDy 4CDy C. Giá trị cực

của hàm số là . D. Giá trị cực tiểu của hàm số là . 3CTy 1CTy Lời

tiểu

giải

.3CDy

C. . D.

32 yxx  242 yxx  32 yxx  42 2 yxx  Lời giải Chọn

Đồ thị hàm số trênlà đồ thị hàm bậc





bốn trùng phương dạng .42 0yaxbxcxa 

42 2 yxx

Câu 4. Tìm tập xác định của hàm số D 25 2yxx  A. . B. . D  0;D

. D. .  ;12;D

\1;2D Lời giải Chọn D

Điều kiện 2 1 20 2 x xx x  Tập xác định \1;2D Câu 5. Tìm họ nguyênhàm của hàm số sin3 fxx  A. . B. . C. . D. . cos3xC  1 cos3 3 xC  cos3xC  1 cos3 3 xC  Lời giải Chọn B Tacó . 1 sin3cos3 3 xdx xC    Câu 6. Cho cấp số nhân có số hạng đầu vàcông bội Số hạng thứ năm của cấp số  n u 13u 2q nhân là  n u A. . B. . C. . D. . 596u 532u 548u 524u Lời giải Chọn C Áp dụng ta được 1 1 n n uuq  44 513248uuq Câu 7. Cho khối hộp chữ nhật có , , . Thể tích khối hộp bằng . ABCDABCD AAa   3 ABa  5 ACa  A. B. C. D. 312a 34a 315a 35a Lời giải Chọn A Nhận thấy 

BCACABaaa    Do đó, thể tíchhình hộp chữ nhật là . . ABCDABCD  3..3.4.12 VABBCAAaaaa     Câu

Số tổ hợp chập

của

A. . B. . C. . D. . 1728 220 1320 36 Lời giải Chọn B Số tổ hợp chập 3 của 12 phần tử là . 3 12220C Câu

Chohìnhchóp

, các cạnh bên SABCABC ABACa   120BAC  bằng nhauvàcùng tạo

đáy cácgóc . Thể tích khối chóp là 30 SABC A. . B. . C. . D. . 33 12 a 3 4 a 33 4 a 3 12 a Lời giải

2222534

12 phần tử là

có đáy làtamgiáccân

với mặt phẳng

Chọn D Gọi làhình chiếu của lên mặt phẳng O S  ABC

O C B A S Nhận thấy: , và nênsuyra   , SAABCSAO    , SBABCSBO    , SCABCSCO  hay làtâm đường tròn ngoại tiếp tamgiác . OAOBOC  O ABC Tamgiác cân tại có ,nên . ABCA  120BAC   30ABCACB  Khi đó: hay . 2 sin AB OA ACB   22sin30 sin ABa OA a ACB     Tacó: .  3 .tan.tan30 3 aSOOASAOa     Thể tích khối chóp là . SABC 3 1131sin120 3332 12 SABC ABC a a VSOS aa           Câu 10. Trongcáchàm số sau,hàm số nào đồng biến trên ?  A. B. C. D.  x fe x     1x fx e    1 3 x fx   3xfx Lời giải Chọn D Hàm số mũ đồng biến trên khi do đó chọn đáp án D. x ya  1a Câu 11. Hàm số nào dưới đây đồng biến trên khoảng ? ;  A. . B. . C. . D. . 33 yxx  1 2 x y x  1 3 x y x    33 yxx  Lời giải Chọn D Xét đáp ánDtacó: nênhàm số đồng biến trên . 2 '330 yxx  Câu 12. Chohàm số liên tục trên đoạn vàcó đồ thị trên đoạn như hình vẽ bên. ()yfx   1;5  1;5 Tổng giá trị lớn nhất vàgiá trị nhỏ nhất của hàm số trên đoạn bằng fx  1;5 A. 4. B. -1. C. 1. D. 2. Lời giải Chọn C

Từ đồ thị ta thấy: nên . 1;5 1;5 max3;min2 fx fx  1;5 1;5 maxmin321 fxfx   Câu 13. Trongkhônggian , một vectơ chỉ phương của đường thẳng là Oxyz 12 112 xyz   A. . B. . C. . D.  1;1;2u   1;1;2u   1;2;0u   1;2;1u  Lời giải Chọn A Câu 14. Trongkhônggian ,cho điểm . Tọa độ điểm làhình chiếu vuônggóc của Oxyz  1;2;3M A M trên mặt phẳng là:  Oyz A. . B. . C. . D.  1;2;3A  1;2;0A  1;0;3A  0;2;3A Lời giải Chọn D

15. Hàm số với có đồ thị như hình vẽ bên. Mệnh đề nàosau đây là đúng? axb ycxd    0a A. . B. . C. . D. . 0,0,0bcd 0,0,0bcd 0,0,0bcd 0,0,0bcd Lời giải Chọn C Tiệm cận ngang của đồ thị hàm số là (do ) 200a y c c  0a Tiệm cận đứng của đồ thị hàm số là (do ) 100 d y d c  0c Giao điểm của đồ thị hàm số với trục tungcótung độ âmnên (do ). 00bb d  0d Câu 16. Tính đạo hàm của hàm số 2 log21yx   A. B. C. D.  1 21ln2y x     2 21ln2y x    2 21y x    1 21y x    Lời giải Chọn B Câu 17. Chohàm số có bảng biến thiên như hình vẽ. Tổng số tiệm cận ngangvà tiệm cận đứng yfx  của đồ thị hàm số đã cholà A. 0. B. 2. C. 1. D. 3. Lời giải

Câu

Chọn D Từ bảng biến thiên của hàm số tacó: yfx  Đồ thị hàm số đã cho nhận đường thẳng là tiệm cận đứng. 2 lim x fx   2x Đồ thị hàm số đã cho nhận đường thẳng là tiệm cận đứng. 0 lim x fx   0x Đồ thị hàm số đã cho nhận đường thẳng là tiệm cận ngang.  lim0 x fx   0y Câu 18. Với mọi dương thỏa mãn Khẳng định nào dưới đây đúng? , ab 3 2 2 loglog5 ab A. . B. . C. . D. . 3232ab 2232ab 2332ab 232ab Lời giải Chọn A . 3 2 2 loglog5 ab  32 2 log5 ab  3232ab  Câu 19. Hàm số có đồ thị làhìnhbên.Giá trị của cơ số bằng  log01 a yxa   a A. . B. . C. . D. . 42 4 2 2 Lời giải Chọn C Ta thấy đồ thị hàm số đi qua điểm có tọa độ  4 4;4log444 a a  Mà nên . 01 a  2a Câu 20. Tìm tập nghiệm của bất phương trình . S 45 5 1x A. . B. . C. . D. .  5;S  3;S  ;5S  ;3S Lời giải Chọn B 4 41 5 1 55413 5 x x x x  Vậy tập nghiệm của bất phương trìnhlà . 3; Câu 21. Tìm tập nghiệm của bất phương trình . S  2 22 loglogxxx  A. . B. . C. . D. .  2S  0S  0;2S  1;2S Lời giải Chọn A

Câu 22. Một chiếc hộp chứa 9 quả cầu gồm 4 quả màuxanh,3 quả màu đỏ và2 quả màuvàng(cácquả cầu đôimộtkhácnhau). Lấy ngẫu nhiên3 quả cầu từ hộp đó. Xác suất để trong3 quả cầu lấy

được cóít nhất 1 quả màu đỏ bằng

A. B.

1 3 19 28 16 21 17 42

Lời giải

Chọn C

Gọi là biến cố trongba quả cầu lấy được cóít nhất một quả màu đỏ. Suyra là biến cố trong A A

ba quả cầu lấy được khôngcó quả cầu nàomàu đỏ.

Khônggian mẫu: . 3 984C 

Số cách lấy raba quả cầu màkhôngcó quả cầu nàomàu đỏ là .Tacó: 3 620C

Câu 23. Chohìnhchóp có đáy làtamgiácvuôngcân tại và .Tamgiác . SABCABC B2 ABa  SAB đều và nằm trong mặt phẳng vuônggóc

.    2 2 22 22 0 0 loglog : 20 2 0 1 x Ð xx xL xxxxxxxx xN K x         

  205

8421

PA PAPA 

16 1

với đáy. Tính thể tích của khối chóp . V . SABC A. B. C. D. 33 4 a V 33 3 a V 33 12 a V 3 23 3 a V Lời giải Chọn D Diện tích là . ABC 2 1 222 2 aaa  Chiều cao của hìnhchóp là SH . SABC 3 2.3. 2 aa Vậy, thể tích của khối chóp là . V . SABC 3 2 123 .2.3. 33 a Vaa   Câu 24. Cho khối nóncóbánkính đáy bằng ,góc ở đỉnh hìnhnónlà . Thể tích khối nón bằng 3cm 60 A. . B. . C. . D. . 3 93(cm)  3 33(cm)  3 6(cm) 3 3(cm)  Lời giải Chọn A

3 33 tan30 h   . 21 .3.3393 3 V    Câu 25. Chohình trụ có thiết diện đi qua trục là một hìnhvuôngcó cạnh Diện tíchxungquanh của 4a hình trụ là A. B. C. D. 28 Sa  224 Sa  216 Sa  24 Sa  Lời giải Chọn C 2 4 2 2 22416 a ra Saaa      Câu 26. Tìmnguyênhàm của hàm số biết . Fx  2 21 2fxx x  13F A. . B. .   22ln21Fxxxx   22ln21Fxxxx   C. D. 2ln21Fxxxx   22ln21Fxxxx   Lời giải Chọn D .  2 2 d21d2ln2 2Fxfxxx xxxxC x            Mà nên . 13F 1C22ln21Fxxxx   Câu 27. Đường tiệm cận đứng của đồ thị hàm số là 1 2 x y x  A. . B. . C. . D. . 1y 1x 2x 2y Lời giải Chọn C nên đường tiệm cận đứng của đồ thị hàm số là 22 22 1 1 limlim;limlim 2 2 x x x x x x y y x x          . 2x Câu 28. Giá trị nhỏ nhất của hàm số trên đoạn là 335yxx  2;4 A. . B. . C. . D. .  2;4 min3 y  2;4 min7 y  2;4 min5 y  2;4 min0 y Lời giải

Hàm số liên tục trên đoạn .

số nghịch biến trên khoảng nào dưới

Chọn B

yxx  2

yxx  2;4 min27 yy

sau yfx 

yfx  A. B. C. D.  ;1  0;1  1;0  1;1 Lời giải Chọn C Từ bảng biến

: . 01;01;fxx  Vậy hàm số nghịch biến trên khoảng yfx   1;0 Câu 30. Cho .Khi đó bằng:  2 0 d3Ifxx     2 0 43d Jfxx      A. . B. . C. . D. . 2 6 8 4 Lời giải Chọn B   2 2 2 0 0 0 43d4d3d1266Jfxxfxxx          Câu 31. Nếu và thì bằng  2 2 d9fxx   2 1 d2fxx   1 2 d fxx A. B. C. D. 7 3 11 7 Lời giải Chọn A Tacó .     2 1 2 2 2 2 2 1 1 1 d9dd9d92d7 fxxfxxfxxfxx fxx          Câu 32. Tính . 1 0 1 3d 21 I xx x     A. B. C. D. 2ln3  4ln3  2ln3  1ln3  Lời giải Chọn A Tacó . 1 1 0 0 1 1 1 3dln212ln32 212 2 I xxxxx x               2ln3 Câu 33. Trongkhônggian với hệ trục tọa độ ,cho . Phương trình mặt phẳng đi Oxyz 1;1;3H  P qua cắt các trục tọa độ lần lượt tại (khác )saocho là trực tâm H Ox,Oy,Oz,,ABCO H tamgiác là ABC

 2;4 Tacó

Vậy . 335

330,2;4

Câu 29. Chohàm số có bảng biến thiên như

Hàm

đây?

thiênta thấy

diện có đôi một vuônggócnên là trực tâmtamgiác OABC,, OAOBOC H ABC

có phương trìnhlà

Oxyz  1;1;3A

. B. . C. .

Chọn B

Mặt phẳng (P) đi qua và chứa trục hoành có dạng  1;1;3A 

Mà đi qua điểm nên

P  1;1;3A 303 bcbc 

Chọn phương trình mặt phẳng là . 13cb

P30 yz Câu 35. Chohàm số liên tục trên vàcó đồ thị như hình vẽ dưới đây. Cóbaonhiêugiá

nguyên của tham số để phương

A. . B. . C. . D. . 370xyz 3110xyz 3110xyz   370xyz Lời giải Chọn C

OHABC đi

 ABC H 

OH  phương trình mặt phẳng là .   P 3110xyz   Câu 34.

Tứ

qua điểm vàcóvéc tơ pháp tuyến là

1;1;3

Trongkhônggian với hệ trục tọa độ , mặt phẳng (P) đi qua và chứa trục hoành

 Lời giải

. 340 yz 30 yz 0xy





P 0bycz



trị yfx  

trình có nghiệm duy nhất trên ? m  3 3log1fxm  3 1 ;3 3    A. B. C. D. 2 4 3 1 Lời giải Chọn D Đặt .Dohàm số làhàm số đồng biến trên  33 1 3;31;3 lo, 3 g ux u x        33log ux  nên với phương trìnhcó nghiệm duy nhất trên .  0; 1;3u 3 1 ;3 3    Do đó yêu cầu bàitoán tương đương với phương trình có nghiệm duy nhất trên 1fum  . Từ đồ thị hàm số suyra . 1;3 112 2 41556 m m m m m m             Câu 36. Chohàm số có đạo hàmvàliên tục trên đoạn và Tính fx  1;3,34 f  1 0 21d6fxx giá trị của  1f

Câu

.26 33

cầu nhận đường tròn ngoại tiếp tamgiác làm đường tròn lớn là ABC

Chọn C

Mặt cầu nhận đường tròn ngoại tiếp tamgiác làm đường tròn lớn nêntâm mặt cầu làtâm ABC

đường tròn ngoại tiếp tamgiác . ABC

ABBC

A. B. C. D. 18f 12f 116f 110f Lời giải Chọn A Xét , đặt .  1 0 21d Ifxx    212 2 dttxdtdxdx  Với 01;13xtxt  Do đó 3 1 31 1328 22 dff tIft ffI       Câu 37. Chohìnhchóp có đáy làhìnhvuông cạnh , đường thẳng vuônggóc với mặt SABCD a SA phẳng Khoảng cách giữa hai đường thẳng và bằng ,2ABCDSAa  SBAD A. . B. . C. . D. . 6 3 a 2 3 a 3 2 a a Lời giải Chọn A Tacó .   ,,, dSBADdADSBCdASBC   Do

AHSBAHBC

  , AHSBCdASBCAH   Tacó

, kẻ .Do đó BCSAB  SAABaa AH SAAB   



. 22

38. Trongkhônggian với hệ trục tọa độ ,cho ; ; . Diện tích mặt Oxyz 1;2;3A  4;2;3B  4;5;3C

. B. . C. . D. . 9 36 18 72 Lời giải

 

Tacó , .  3;0;0AB   0;3;0BC  Vì nêntamgiác vuông tại .

ABC B

Suyrabánkính mặt cầu là . 132 22 RAC

. 2 232 44.18 2 SR       Câu

xác định trên vàcó đạo hàm .Hàm số đã cho yfx    2 (1)1fxxxx    nghịch

đây? A. . B. . C. . D. .  1;0  ;1  0;1  1; Lời giải Chọn A Lập bảng

dấu fx  Dựa vào bảng xét dấu, hàm số nghịch biến trên khoảng . yfx   1;0 Câu

tiếp diện là mặt  S  1;2;1I phẳng ,có

trìnhlà :2250Pxyz A. . B. .  2 22 1214xyz  2 22 1211xyz   C. D.  2 22 1214xyz    2 22 1211xyz Lời giải Chọn D Mặt cầu cótâm vàcó tiếp diện là mặt phẳng suyra  S  1;2;1I  P  222 225 d, 1 212 III xyzRIP      Phương trình mặt cầu .  2 22 :1211Sxyz Câu 41. Cho ()fx làhàm số liên tục trên tập số thực khôngâmvà thỏa mãn Tính  23120.fxxxx   5 1 d fxx A. 37 6 . B. 527 3 . C. 61 6 . D. 464 3 . Lời giải Chọn C Tacó:  1 1 2 0 0 613123d223d 6Ifxxxxxxx    Đặt ,  231d23d txxtxx  Đổi cận: 01xt 15xt Suyra .  1 5 5 2 0 1 1 6163123d()() fxxxxftdtfxdx   

Vậy diện tích mặt cầu là

39. Chohàm số

biến khoảng nào dưới

xét

40. Trongkhônggian với hệ tọa độ Oxyz, mặt cầu cótâm vàcó

phương

Câu 42. Chohình lăng trụ đứng có đáy vuông tại , Giá . ABCABC ABC ,A 3ABa ACAAa   trị sin của góc giữa đường thẳng và mặt phẳng bằng AC  BCCB A. . B. . C. . D. . 10 4 6 3 3 3 6 4 Lời giải Chọn D Kẻ , từ đó AHBCAHBCCB   ;AC ACHBCCB   Xét vuông tại : . ABC A222 1113 2 AHa AHABAC  Xét vuông tại : . AAC  C 222ACAAACa   Xét vuông tại : . AHC  C 6 sin 4 AH ACH AC    Câu 43. Chohàm số . Gọi là tập hợp tất cả cácgiá trị thực của tham số để giá trị 221fxxxS m lớn nhất của hàm số trên đoạn bằng .Tính tổng các phần  22 gxfxfxm   1;38 tử của S A. B. C. D. 7 2 0 5 Lời giải Chọn A Khi . Đặt 1;30;4x fx   0;4fxt Khi đó, yêu cầu bàitoán cógiá trị lớn nhất trên đoạn bằng 8 22 htttm  0;4 .   0 0 8,0;4 0;4:8 htt tft       Với mọi ,tacó: 0;4t 2 2 28828ttm ttm    2 2 2 2 0;4 0;4 2828max28min2870ttmtt ttmtt m    Đồng thời từ suyra . Vậy tổng các phần tử của là .   0 7 m m    S7

Câu 44. Chohàm số liên tục trên . Đồ thị hàm số được chotronghìnhbên. yfx    3' yfx  Hàm số có tối đa baonhiêu điểm cực đại? 41 8 gxfxxx  A. B. C. D. 2 3 4 5 Lời giải Chọn B Đặt . 41 8 hxfxxx  Tacó: .   3'0 3 1 1 ''1'1 2 2 hx hxfxx fxx   Đặt .Khi đó phương trình trở thành . 3 xt   3 3 3 22 '1100 2 22 tx ftttx tx           Bảng biến thiên của hàm số :yhx  Khi đó, hàm số có số điểm cực đại nhiều nhất có4 nghiệm.  gxhx  0hx  Vậy hàm số có tối đa 3 điểm cực đại.  gxhx  Câu 45. Chohìnhchóp có đáy làhìnhbìnhhành. Gọi là điểm đối xứng của qua . SABCDABCD M C và làtrung điểm của . Mặt phẳng chia khối chóp thànhhai khối đa BN SC  MND . SABCD

diện, trong đó khối đa diện chứa đỉnh có thể tích, khối đa diện còn lại có thể tích (tham S 1V 2V khảo hình vẽ bên). Tính tỉ số . 1 2 V V A. B. C. D. 1 2 12 7 V V  1 2 5 3 V V  1 2 7 5 V V  1 2 1 5 V V  Lời giải Chọn C Tacó: . 1 3 BK KMNSB BS  Đặt . 2SABCDSBCDSABC V VVVV ..1 2 CDMN CDMN CDBS VCDCMCN V V VCDCBCS   2 1 1 57 .. 612 2121212 BMKI BMKI CDMNBMKI BCSA VBMBKBI V VVVV V VVV V VBCBSBA    Vậy 1 2 7 5 V V  Câu 46. Chohàm số với làtham số thực. Biết rằng nếu  2 3ln3 fxaxaxx   a thì . Khẳng định nàosau đây đúng? 1;3 max2 fxf   1;3 minfxm   A. . B. . C. . D. .  6;7m  7;8m  8;9m  9;10m Lời giải Chọn A  2 2 23 3ln3 3 3 xfxaxaxxfxaa xx      Vì nên . 1;3 max2 fxf   20f  7 307 10 aa a    2 23 710 3 x fx xx  

 2 015 7 x fx x        1710ln4;21410ln10;32110ln18f f f    Vậy và . 1;3 max2 fxf   1;3 min16,86mfxf     Câu 47. Chohàm số có đạo hàmtrên đoạn và thỏa mãn ; fx  1;e 10f .Tíchphân bằng 1,1; fxxfxxe        1 d e fxx A. B. C. D. 21 4 e 21 2 e 21 4 e 21 2 e Lời giải Chọn C   2 111 1 fxxfxfxxfxxfxfx xxx            do ,mà .  111 ln fx fxxC xxx        1; xe  10fln fxxx  2 22 2 1 1 11 11 dlndlnd 222444 e e e e xxeeefxxxxxxx        Câu 48. Cóbaonhiêu số nguyên dương saocho tồn tại số thực lớn hơn thỏa mãn x y1   2 2321loglogyx xyxyy x    A. 3. B. 1. C. vô số. D. 2. Lời giải Chọn D Điều kiện: 23023 11 11 yx xy y y x x                 2 2321loglogyx xyxyy x      2 23 21log2loglog2log yx xyxyyy y x      2 2 2323loglogyx xyxyy xy    , với   loglogloglog0 b a aby aby a b     2 ,0 23 axyab byx     Nếu thì , thì . ab loglog0 a abybab loglog0 a abyb Nên . loglog0aababyb 223xyyx  2 23 1 y x y   

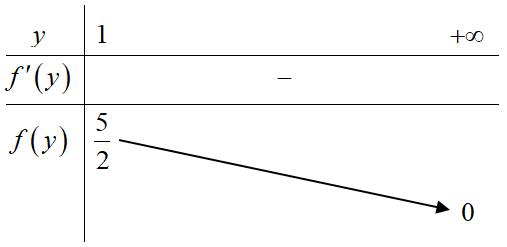
Xéthàm số với .Tacó . 2 23 1fy y y    1y  2 22 262 0,1 1 fyy y y y      Nên nghịch biến trên . fy  1; Bảng biến thiên: Để tồn tại số thực lớn hơn thì . y1 5 01;2 2 xx  Câu 49. Trongkhônggian với hệ tọa độ Oxyz,cho mặt cầu cótâm thuộc mặt phẳng  S và đi quahai điểm .Bánkính nhỏ nhất của mặt cầu ():270 Pxyz  1;2;1,2;5;3AB bằng:  S A. B. C. D. 470 3 546 3 763 3 345 3 Lời giải Chọn B Gọi làtâm mặt cầu là mặt phẳng trung trực của I  SIQ  37 ;;2 :22 1;3;2 quaM AB VTPTAB        có dạng: .32160xyz Vậy làgiao tuyến của 2 mặt phẳng: Id  32160 270 xyz xyz    +cho vàcho . 2 010;2;11 1 y x C d z       3 111;3;12 2 y x D d z       + Đường thẳng có dạng: .   0;2;11 : 1;1;1 quaC d VTCPCD         2;2;11 11 xt ytIttt zt        +Bánkính khi .  2 2 2 2 1382546 14103 393 RIAtttt         13 3 t Vậy . min 54613 33 R khit  Câu 50. Trong khoảng cóbaonhiêugiá trị nguyên của tham số m để phương trình  10;20 có đúng 2 nghiệm phân biệt. 2 3 9 4log(1)log9(1)m xx x   A. 23. B. 20. C. 8. D. 15. Lời giải Chọn A

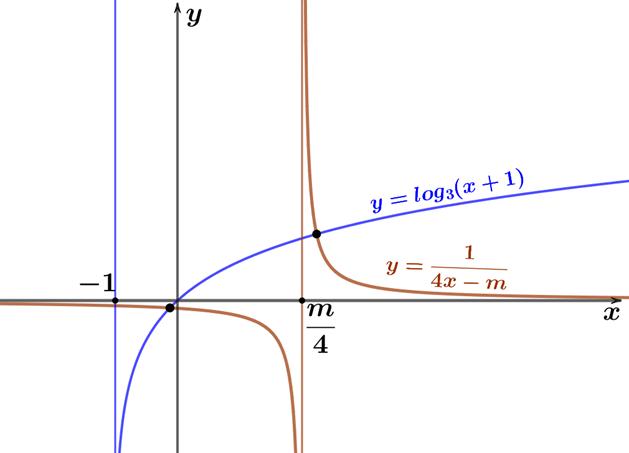
Với điều kiện: thì phương trìnhban đầu 1x  3 3 4log(1)1log1 xxmx   3 1 log14 x xm  Để phương trìnhcó đúng 2 nghiệm phân biệt thì đồ thị haihàm số có2giao 3 log1 1 4 yx y xm      điểm. Từ đồ thị, điều kiện có2giao điểm khi và . 14 4 m m   10;20m ,m .  3;2;....;19m  HẾT

D. desin2 xfxx xC    desin2 xfxx xC 

Câu 8: Cho cấp số nhân có số hạng đầu vàcông bội .Giá trị của bằng () n u 13u= 2q= 4u

A. B. C. D. 5 24 30 27

Câu 9: Hàm số nào dưới đây có bảng biến thiên như hình vẽ?

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH PHÚ THỌ

GỐC 2

gồm namvà nữ, cóbaonhiêucách chọ rahai học sinh? 59 A. . B. . C. . D. . 2 14A 142 2 14C 214 Câu 2: Tập xác định của hàm số là ()22023 1yx=A. . B. . C. . D. . () 0;+¥  ()() ;11; -¥-È+¥ {}\1;1Câu 3: Chohàm số có đồ thị như hình vẽ. ()yfx =

nghiệm của phương

2()50 fx-= A. B. C. D. 0 2 4 3 Câu 4: Phương

tiệm cận ngang của đồ thị hàm số là 23 1 x y x -+ = + A. . B. . C. . D. . 3 2 x= 2y=- 1x=- 3y= Câu 5: Nghiệm của phương trình là 4 5125 x= A. . B. . C. . D. . 4x= 5x= 7x= 6x= Câu 6: Đạo hàm của hàm số là 2023log yx = A. B. C. D. 1 2023lny x ¢ = 1 ln2023y x ¢ = 1 y x ¢ = ln2023 y x ¢ = Câu 7: Chohàm số . Khẳng định nào dưới đây là đúng? ()ecos2 xfx x=+ A. B. dsin2 e 2 x x fxx C  dsin2 e 2 x x fxx C    C.

ĐỀ THI THỬ TNTHPT - NĂM HỌC: 2022-2023 – LẦN 1 – ĐỀ

Câu 1: Từ một nhóm học sinh

Số

trình bằng

trình đường