70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC (ĐỀ 51-60) by Dạy Kèm Quy Nhơn Official

ĐỀ THI THỬ TỐT NGHIỆP THPT MÔN TOÁN

ễ

Thanh Tú

Collection 70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC - CÓ LỜI GIẢI (ĐỀ 51-60) (232 TRANG)

Ths Nguy

eBook

EDITION

CHUYỂN GIAO QUA EMAIL

COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

WORD VERSION | 2023

ORDER NOW /

TAILIEUCHUANTHAMKHAO@GMAIL

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC GIANG

THI THỬ TỐT NGHIỆP THPT– LẦN 1– NĂM HỌC 2022–2023

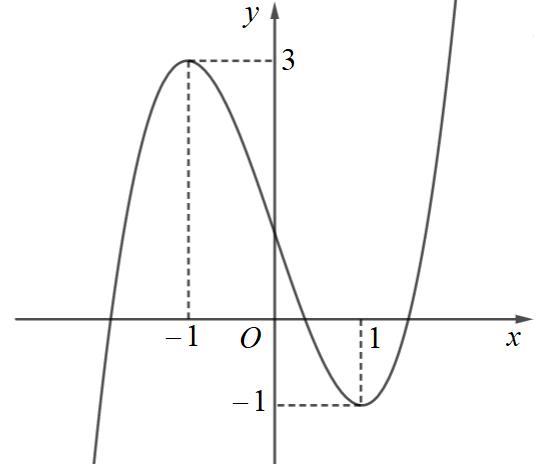
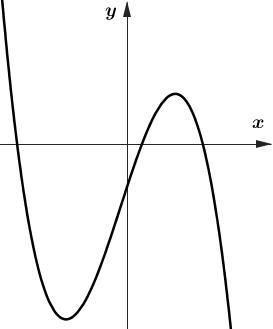
Câu1: Đồ thị của hàm số nào dưới đây có dạng như đường congtronghình vẽ bên dưới ?

Câu2: Cho đa giác đều có đỉnh. Số tất cả cáctamgiác tạo thànhcócác đỉnh đều là đỉnh của đa 20 giác đã cholà

B. C. D. 3 20C 3 20A 3P 20

A. B. C. D. 1 2 x y x   4223yxx  333yxx  4223yxx 

có đồ thị là đường congtronghình vẽ bên dưới yfx  Giá

A. B. C. D. 1 0 4 3 Câu4: Tổng tất cả các nghiệm thực của phương trình bằng 2 43.2320 xx A. B. C. D. 6 5 6 5 Câu5: Nếu thì bằng  1 0 2d6 fxx   1 0 1 2d 3fxxx      A. . B. . C. . D. . 4 7 3 2 Câu6: Chohìnhchóp có đáy làtamgiác đều với và . . SABCABC ,ABa  SAABC  3SAa  Thể tích của khối chóp bằng . SABC A. B. C. D. 3 a 33 4 a 23 4 a 3 4 a Câu7: Cho khối lập phương có cạnh bằng Thể tích của khối lập phương đã cho bằng 3cm A. . B. . C. . D. . 327cm 327 cm 2 39cm 318cm

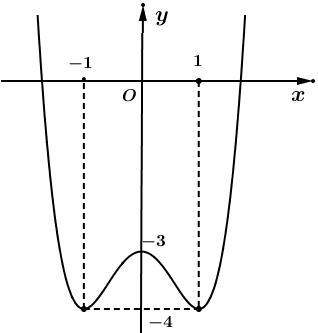
Câu3: Chohàm số trùng phương

trị cực đại của hàm số đã cholà

giống 3 3 nhauvào một giá chứa đồ nằm ngangcó ô trống, mỗi quả cầu được xếp vào một ô.Tính 7 xác suất để ba quả cầu màu đỏ xếp cạnh nhauvà3 quả cầu màuxanh xếp cạnh nhau.

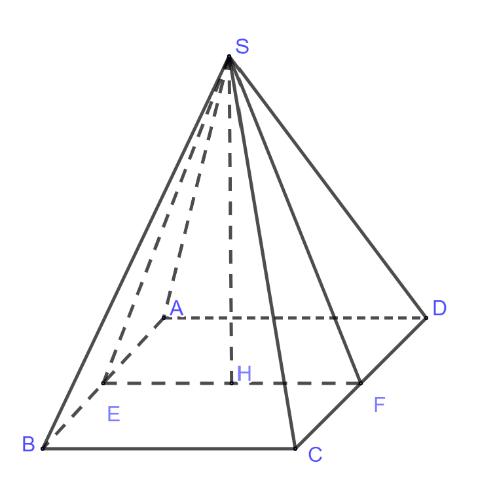
Câu17: Chohìnhchóp có đáy làhình chữ nhật, tamgiác đều và nằm trong mặt SABCDABCD

Chohàm số có đạo hàm

trụ cóbánkính

Câu8: Cho . Khẳng định nào dưới đây đúng? cosxdxFxC  A. B. C. D. sin Fxx   sin Fxx   cos Fxx   cos Fxx   Câu9: Trongkhônggian với hệ tọa độ , mặt phẳng có một vectơ pháp Oxyz :10Pxyz tuyến là A. B. C. D. 41;1;1n  31;1;1n  21;1;1n  11;1;1n  Câu10: Cho số phức thỏa mãn . Biết tập hợp các điểm biểu diễn các số phức z 123zi trong mặt phẳng tọa độ là một đường tròn.Tìmbánkính của đường tròn đó. w1zi R A. . B. . C. . D. . 32R 42R 2R 22R Câu11: Cho số phức , phần thực của số phức bằng 2 zi  2 z A. B. C. D. 4 4 3 3 Câu12: Tập nghiệm của bất phương trình là  ln320 x A. B. C. D. ;1 2 ;1 3    2 ;1 3     1; Câu13: Nếu và thì bằng  5 2 d3fxx   5 2 d2gxx   5 2 d fxgxx     A. . B. . C. . D. 5 6 1 5 Câu14: Cho cấp số nhân , với vàcông bội .Giá trị bằng  n u13u 1 3q 3u A. B. C. D.. 1 4 3 1 9 1 3 Câu15: Tập nghiệm của bất phương trình bằng 1 9 3 x    A. B. C. D. .  ;2 ;2 2;  ;2 Câu16: Xếp ngẫu nhiên quả cầu màu đỏ cókích thước khácnhauvà quả cầu màuxanh

A. . B. . C. . D. . 3 140 3 70 3 160 3 80

phẳng vuônggóc

đáy. Góc giữa hai mặt phẳng và bằng  SBC ABCD A. . B. . C. . D. . 060 090 045 030

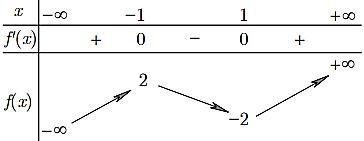
.Hàm số đã chonghich biến ()yfx  22 '()1, fxxxx   trên khoảng nào dưới đây? A. B. C. D.  0;  1;0  ;0  1;

hình trụ đã cho bằng r h A. B. C. D. 2rrh rh 2rh rrh

SAB

với mặt phẳng

Câu18:

Câu19: Chohình

đáy và chiều cao . Diện tíchtoàn phần của

Câu20: Chohàm số có đồ thị là đường congtronghình vẽ bên dưới. Tọa độ giao điểm của axb ycxd    đồ thị hàm số đã chovà trục tunglà A. B. C. D.  0;2  2;0  2;0  0;2 Câu21: Phần ảo của số phức là 43 zi =-+ A. . B. . C. . D. . 4- 4 3i 3 Câu22: Trên mặt phẳng tọa độ , điểm biểu diễn số phức có tọa độ là Oxy 23 zi  A. B. C. D.  3;2  2;3  3;2  2;3 Câu23: Trên khoảng đạo hàm của hàm số là  0; 2log yx  A. . B. . C. . D. . ln2yx   ln2 x y   1 ln2y x   ln2 y x  

yfx  Hàm số

khoảng nào dưới đây? A. . B. . C. . D. .  ;1  3;  4;1  0;3

hạn bởi đồ thị hàm số và trục hoành bằng 22 yxx  A. B. C. D. 4 3  4 3 3 4 3 4 

Câu24: Chohàm số có bảng biến thiên như sau:

đồng biến trên

Câu25: Diện tíchhình phẳng giới

Câu26: Trongkhônggian với hệ tọa độ ,tâm của mặt cầu Oxyz 222 :24610 Sxyzxyz có tọa độ là

B. C. D.

1;2;3

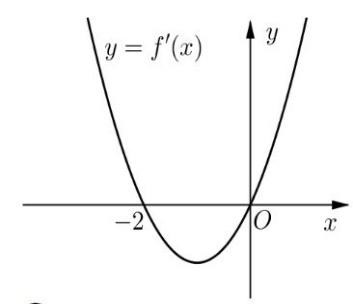
Câu27: Chohàm số bậc ba có đồ thị là đường congtronghìnhbên dưới yfx 

Có tất cả baonhiêugiá trị nguyên dương của tham số để phương trình có đúng ba m 1 fxm  nghiệm thực phân biệt?

. B.

Cho mặt phẳng khôngcó điểm chung với mặt cầu . Gọi là khoảng cách

Khẳng định nào dưới đây đúng?

Câu34: Chohàm số có đồ thị là đường congtronghìnhbên dưới 32 yaxbxcxd 



2;4;6

1;2;3

2;4;6

. C. . D. . 3 4 1 2

Với là số thực dương tùyýkhác .Giá trị của biểu thức bằng a 4 3 4 log64 a a    A. . B. . C. . D. . 1 3 3 1 3 3

Tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình 23 42 x y x    A. . B. . C. . D. . 3 2 x 3 2 x 1 2 x 1 2 x Câu30: Trên khoảng , đạo hàm của hàm số là  0; 2 yx   A. . B. . C. . D. . 21'1 2 yx    21'2 yx    2'2 yx    21' yx   Câu31: Trongkhônggian với hệ tọa độ ,góc giữa hai mặt phẳng và bằng: Oxyz  Oxz Oyz A. B. C. D. 090 060 030 045 Câu32: Chohàm số Khẳng định nào dưới đây đúng? sinx fxex  A. B. cos x fxdxexC   1 cos x fxdxxexC    C. D.  1 cos 1 x fe xdx xC x     cos x fxdxexC   

 P

 P A. B. C. D.



 dR  0d

Câu28:

Câu29:

Câu33:

từ

 ; SORd

đến

Điểm cực đại của đồ thị hàm số đã cholà

B. C. D.  1;3  1;1  1;3  0;1

Câu35: Trongkhônggian ,cho mặt phẳng . Điểm nào dưới đây thuộc Oxyz :2330Pxyz  P

2;1;3M

0;1;0N

. B. . C. . D. .  1;2;0E  1;2;1F

 yfx

Số điểm cực trị của hàm số là  22 yfxx

 fx

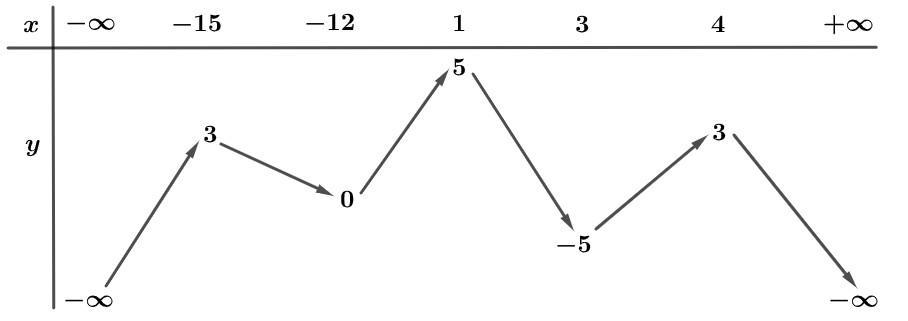
Câu36: Chohàm số , bảng biến thiên của hàm số như sau:

A. 9. B. 5. C. 7. D. 3.

Câu37: Cho khối nóntrònxoay đỉnh , đáy là đường tròntâm ,góc ở đỉnh bằng Mặt phẳng S O 120 thay đổi, đi qua và cắt khối nóntheo thiết diện làtamgiác . Biết rằng giá trị lớn  Q S SAB

nhất diện tíchtamgiác là . Khoảng cách từ đến mặt



phẳng trong trường hợp SAB22a O  Q diện tíchtamgiác đạt giá trị lớn nhất là SAB A. . B. . C. . D. . 2 2 a 3 2 a 2a 6 2 a Câu38: Cho số phức thỏa mãn điều kiện .Giá trị lớn nhất của bằng z 2221 zzzi z A. B. C. D. 221 21 21  2 Câu39: Chohìnhchóp có đáy làhình chữ nhật với . Cạnh bên . SABCD ABCD 2,3ABaBCa  vuônggóc với đáy và đường thẳng SC tạo với một góc .Tính thể tích của SA ()mpSAB 030 V khối chóp theo .SABCDa A. B. C. D. 3 215.Va  3 215 . 3 a V 33 . 3 a V 315 . 3 a V Câu40: Trongkhônggian với hệ tọa độ ,chocác điểm .Tìm tọa độ điểm là điểm Oxyz A(2;3;5) A đối xứng với điểm qua trục AOy A. B. C. D. (2;3;5).A (2;3;5).A (2;3;5)A (2;3;5)A Câu41: Chohìnhchóp có đáy là hìnhchữ nhật , Biết . SABCD ABCD()SAABCD  ,SAABa  . Gọi là trọng tâmtamgiác . Khoảng cách từ đến bằng 2 ADa  G SAD G() SBD

B.  222 :23116Sxyz

D.  222 :2314

Câu44: Trong không gian , cho mặt phẳng

ba điểm Oxyz :220Pxyz , . Gọi là điểm di động trên saochocó một mặt cầu  2;0;2,4;0;4AB  5;2;4C M

đi qua và tiếp xúc với tại .Khi đó, độ dài đoạn cógiá trị nhỏ nhất là

Câu45: Cho là một nguyênhàm của hàm số trên .Tínhtíchphân

Câu46: Có tất cả baonhiêu số nguyên dương saocho ứng với mỗi số đó bất phương trình y y

nghiệm nguyên và số nghiệm nguyên không vượt quá .

A. B. C.D. . 3 a 2 . 9 a 2 . 3 a . 6 a

Trongkhônggian ,chotamgiác có , , . Viết Oxyz ABC 1;3;2A  2;0;5B  0;2;1C phương trình đường thẳng chứa đường trung tuyến kẻ từ đỉnh của tamgiác . d A ABC A. B. 132 : 241 dxyz  132 : 241 dxyz   C. D. 132 : 241 dxyz  241 : 113 dxyz 

điểm và đường thẳng . Gọi Oxyz  1;1;1A :12, 22 xt dytt zt         là mặt phẳng đi qua và chứa Lập phương trình mặt cầu cótâm  P A d  S  2;3;1I saocho tiếp xúc với  S 



 C.



Sxyz

Câu42:

Câu43: Trongkhônggian ,cho

222 :2319Sxyz

Sxyz

222 :2314

và

 P



A. B. C. D. 3

S , AB

PM CM

10 109

2 1 2 Fx x  fx x  0;  2 1 21d fxx  A. . B. .  2 1 2 21d 15fxx  2 1 2 21d 15fxx C. . D. .  2 1 1 21d 15fxx  2 1 1 21d 15fxx

có

3244

x xxx y   x x 6 A. B. C. D. 176903 176930 176910 176923 Câu47: Số nghiệm nguyên của bất phương trình là 23 23loglog1loglog xxxx  A. . B. . C. Vô số. D. . 3 2 1 Câu48: Chohàm số .   5 432 22 12153020304312012023 yxmxxmmxmxm     Có tất cả baonhiêugiá trị nguyên của tham số để hàm số đồng biến trên khoảng ? m  1;3 A. B. C. D. 11 10 2 1

0 3

Câu49: Trong mặt phằng tọa độ ,choParabol vàhai điềm thuộc saocho Oxy

()

Câu50: Trong tập các số phức, cho phương trình ( tham số thực). Hỏi

2(1)620zmzmm có tất cả baonhiêugiá trị ngüyên của để phương trình đã chocóhai nghiệm phân biệt

hạn

và đường

đạt giá trị lớn nhất bằng 2AB () P AB A.. B.. C.. D.. 3 2 3 4 2 3 4 3

():Pyx  , AB

P Diện tíchhình phẳng giới

bời

thẳng

A. B. C.Vô số. D. 0. 1. 2.

m thỏa mãn 12 , zz 12zz 

Câu1: Đồ thị của hàm số nào dưới đây có dạng như đường congtronghình vẽ bên dưới ?

Từ dáng của đồ thị suyra đây là đồ thị của hàm số bậc bốn.

Từ đồ thị suyra ,suyra đồ thị trênlà của hàm số lim

Câu2: Cho đa giác đều có đỉnh. Số tất cả cáctamgiác tạo thànhcócác đỉnh đều là đỉnh của đa 20 giác đã cholà

Chọn A

Số tamgiác tạo thànhcócác đỉnh đều là đỉnh của đa giác đã cholà . 3 20C

Câu3: Chohàm số trùng phương có đồ thị là đường congtronghình vẽ bên dưới yfx 

Giá trị cực đại của hàm số đã cholà

A. . B. . C. . D. . 1 0 4 3

Lời giải

Chọn D

Từ đồ thị suyragiá trị cực đại của hàm số đã cholà .3

BẢNG ĐÁP ÁN 12345678910111213141516171819202122232425 BADBDDADCACBDDBBABADDBCDB 26272829303132333435363738394041424344454647484950 CADCBAACBDBACBDBBCDDBBCDD

A. . B. . C. . D. 1 2 x y x   4223yxx  333yxx  4223yxx  . Lời giải

Chọn

  4223yxx 

Lời

A. . B. .

. 3 20C 3 20A

P 20P

giải

Câu4: Tổng tất cả các nghiệm thực của phương trình bằng 2 432320 xx A. . B. . C. . D. . 6 5 6 5 Lời giải Chọn B Đặt , phương trình đã cho trở thành: 30 x tt   2 8 12320 4 ttm tt ttm    Với 8283 x t x  Với 4242 x t x  Suyra tổng các nghiệm của phương trìnhlà .325  Câu5: Nếu thì bằng  1 0 2d6 fxx   1 0 1 2d 3fxxx      A. B. C. D. 4 7 3 2 Lời giải Chọn D Tacó .    1 1 11 21 0 0 0 00 1 1 1 1 2dd2d2d612 3 3 6 6fxxxfxxxxfxxx           Câu6: Chohìnhchóp có đáy làtamgiác đều với và . SABCABC ,ABa  SAABC  3SAa  Thể tích của khối chóp bằng SABC A. B. C. D. 3 a 33 4 a 23 4 a 3 4 a Lời giải Chọn D Tacó 23 4ABC Sa   Tacó . 23113 ...3. 3344SABC ABC aaVSASa     Câu7: Cho khối lập phương có cạnh bằng . Thể tích của khối lập phương đã cho bằng 3cm A. B. C. D. 327cm 327 cm 2 39cm 318cm Lời giải Chọn A Tacó .33 327cmV Câu8: Cho . Khẳng định nào dưới đây đúng? cosxdxFxC  A. . B. . C. . D. . sin Fxx   sin Fxx   cos Fxx   cos Fxx   Lời giải Chọn D Tacó . cos cos xdxFxCFxx  

w1zi R

số phức z 123zi trong mặt phẳng tọa độ là một đường tròn.Tìmbánkính của đường tròn đó.

A. B. C. D. 32R 42R 2R 22R Lời giải

Chọn A

Tacó  1231331332 ziziiiwi 

Đặt . , wxyixy

Suyra  22 3323132xyii

Câu9: Trongkhônggian với hệ tọa độ , mặt phẳng có một vectơ pháp Oxyz :10Pxyz tuyến là A. B. C. D. 41;1;1n  31;1;1n  21;1;1n  11;1;1n  Lời giải Chọn C Mặt phẳng có một vectơ pháp tuyến là . :10Pxyz 21;1;1n  Câu10: Cho số phức thỏa mãn . Biết tập hợp các điểm biểu diễn các



xy  .  22 3118xy  Suyra điểm biểu diễn các số phức trong mặt phẳng tọa độ là một đường tròncó w1zi bánkính . 32R Câu11: Cho số phức , phần thực của số phức bằng 2 zi  2 z A. B. C. D. 4 4 3 3 Lời giải Chọn C Tacó phần thực của số phức bằng  22234 zii 2 z3 Câu12: Tập nghiệm của bất phương trình là  ln320 x A. . B. . C. . D. ;1 2 ;1 3    2 ;1 3     1; Lời giải Chọn B Tacó 3202 ln320 1 3213 x x x x     Câu13: Nếu và thì bằng  5 2 d3fxx   5 2 d2gxx   5 2 d fxgxx     A. . B. . C. . D. 5 6 1 5 Lời giải Chọn D

ô.Tính 7 xác suất để ba quả cầu màu đỏ xếp cạnh nhauvà3 quả cầu màuxanh xếp cạnh nhau.

+)Alà biến cố “ba quả màu đỏ cạnh nhauvàba quả màuxanh cạnh nhau”.

Xemba quả cầu đỏ lànhómX,ba

Tacó .  5 5 5 2 2 2 ddd325fxgxxfxxgxx          Câu14: Cho cấp số nhân , với vàcông bội .Giá trị bằng  n u13u 1 3q 3u A. B. C. D.. 1 4 3 1 9 1 3 Lời giải Chọn D Tacó . 2 2 31 11 .3. 33uuq     Câu15: Tập nghiệm của bất phương trình bằng 1 9 3 x    A. B. C. D. .  ;2 ;2 2;  ;2 Lời giải Chọn B Tacó . 1 3 1 39log92 x x    ;2x  Câu16: Xếp ngẫu nhiên quả cầu màu đỏ cókích thước khácnhauvà quả cầu màuxanh giống 3 3 nhauvào một giá chứa đồ nằm ngangcó ô trống, mỗi quả cầu được xếp vào một

A. . B. . C. . D. . 3 140 3 70 3 160 3 80 Lời giải

+)Số

Chọn B

phần tử khônggian mẫu . 

74840nAC

quả màuxanhlànhómY. Xếp X,Yvào ôcó cách. 32 36A Hoán vị ba quả cầu đỏ có cách. 3!6  . 2 3.3!36nAA (363

PA Câu17: Chohìnhchóp có đáy làhình chữ nhật, tamgiác đều và nằm trong mặt SABCDABCD SAB phẳng vuônggóc với mặt phẳng đáy. Góc giữa hai mặt phẳng và bằng  SBC ABCD A. B. C. D. 060 090 045 030 Lời giải Chọn A

)84070

Gọi làtrung điểm . H AB

SABABCDSHABCDSHBC  

Câu18: Chohàm số có đạo hàm .Hàm số đã chonghich biến ()yfx 

22 '()1, fxxxx   trên khoảng nào dưới đây?

Lời giải Chọn B .

22 '()1011fxxx x  

Câu19: Chohình trụ cóbánkính đáy và chiều cao . Diện tíchtoàn phần của hình trụ đã cho

Câu20: Chohàm số có đồ thị là đường congtronghình vẽ bên dưới. Tọa độ giao điểm của





 

;mà suyra .

 BCAB 

BCSAB 

 0,(),60SBCABCDSBABSBA  



 



 



B. C. D.

1;0



hàm số nghịch

trên  1;0

Vậy

biến

h A. . B. . C. . D. . 2rrh rh 2rh rrh Lời giải Chọn A

bằng r



hàm

chovà

axb ycxd  

đồ thị

số đã

trục tunglà

 0;2  2;0  2;0  0;2

Lời giải Chọn D

Câu21: Phần ảo của số phức là 43 zi =-+

A. . B. . C. . D. . 4- 4 3i 3

Lời giải

Chọn D

Phần ảo của số phức là. 43 zi =-+3

Câu22: Trên mặt phẳng tọa độ , điểm biểu diễn số phức có tọa độ là Oxy 23 zi 

2;3

Chọn B

2;3

A. . B. . C. . D. .  3;2

Lời giải

Điểm biểu diễn số phức có tọa độ là. 23 zi   2;3

Câu23: Trên khoảng đạo hàm của hàm số là  0; 2log yx 

A. . B. . C. . D. . ln2yx   ln2 x y   1 ln2y x   ln2 y x  

Lời giải

Chọn C

 Tacó: .  2 1 logln2yx x    

Câu24: Chohàm số có bảng biến thiên như sau: yfx 

B. C.



 3;2

số đồng biến trên khoảng nào dưới đây?

Câu25: Diện tíchhình phẳng giới hạn bởi đồ thị hàm số và trục hoành bằng

Xét phương trìnhhoành độ giao điểm: 2 0 20 2 x xx x

Khi đó, diện tíchhình phẳng giởi hạn bởi hai đồ thị trênlà:

Câu26: Trongkhônggian với

A. B. C. D.  ;1  3;  4;1  0;3 Lời giải Chọn D

. 0;3

Hàm

Từ bảng biến thiêntacóhàm số đồng biến trên khoảng

 A. . B. . C. . D. . 4 3  4 3 3 4 3 4  Lời giải Chọn B

2 yxx





0 2 2 4 2d 3 Sxxx 

hệ tọa độ ,tâm của mặt cầu Oxyz 222 :24610 Sxyzxyz có tọa độ là A. . B. . C. . D. .  2;4;6  1;2;3  1;2;3  2;4;6 Lời giải Chọn C Tâm của mặt cầu có tọa độ là . 222 :24610 Sxyzxyz  1;2;3 Câu27: Chohàm số bậc ba có đồ thị là đường congtronghìnhbên dưới yfx 

Có tất cả baonhiêugiá trị nguyên dương của tham số để phương trình có đúng ba m 1 fxm  nghiệm thực phân biệt? A. B. C. D. 3 4 1 2 Lời giải Chọn A Tacó , dựa vào đồ thị hàm số, phương trìnhcó đúng ba  1 1fxmfxm  nghiệm thực phân biệt khivà chỉ khi . 113221,0,1 m m m m     Câu28: Với là số thực dương tùyýkhác .Giá trị của biểu thức bằng a 4 3 4 log64 a a    A. B. C. D. 1 3 3 1 3 3 Lời giải Chọn D Tacó . 3 3 4 4 loglog3 644a a a a    

hàm số là đường thẳng có phương trình 23 42 x y x    A. B. C. D. 3 2 x 3 2 x 1 2 x 1 2 x Lời giải Chọn C Tacó .Do đó tiệm cận đứng của đồ thị hàm số là đường thẳng . 1 2 lim x y    1 2 x Câu30: Trên khoảng , đạo hàm của hàm số là  0; 2 yx   A. . B. . C. . D. . 21'1 2 yx    21'2 yx    2'2 yx    21' yx   Lời giải Chọn B Tacó  1 2 2'2yxx      Câu31: Trongkhônggian với hệ tọa độ ,góc giữa hai mặt phẳng và bằng: Oxyz  Oxz Oyz A. B. C. D. 090 060 030 045 Lời giải Chọn A Dễ thấy, do đôi một vuônggócnên . ;; OxOyOz  Oxz Oyz Vậy góc giữa hai mặt phẳng và bằng  Oxz Oyz 090

Câu29: Tiệm cận đứng của đồ thị

Câu32: Chohàm số . Khẳng định nào dưới đây đúng?

A. . B. .

Chọn A Tacó

sincosx x fxdxexdxexC

Câu33: Cho mặt phẳng khôngcó điểm chung với mặt cầu . Gọi là khoảng cách

đến Khẳng định nào dưới đây đúng?

Chọn C

Vì và mặt cầu khôngcó điểm chungnên

P  ; SOR dR 

Câu34: Chohàm số có đồ thị là đường congtronghìnhbên dưới 32 yaxbxcxd 

Điểm cực đại của đồ thị hàm số đã cholà

A. . B. . C. . D. .  1;3  1;1  1;3  0;1

Lời giải

Chọn B

Điểm cực đại của đồ thị hàm số đã cholà . 1;1

Câu35: Trongkhônggian ,cho mặt phẳng Điểm nào dưới đây thuộc Oxyz :2330Pxyz

Lời giải

thuộc là .  P 0;1;0N

Câu36: Chohàm số , bảng biến thiên của hàm số như sau:





sinx fxex



 1 cos x fxdxxexC   

.  1 cos 1 x fe xdx xC x     cos x fxdxexC    Lời giải

cos x fxdxexC 

C. . D.



  



từ

; SORd O



A. B. C. D.

0d Lời

dR  dR  dR 

giải

. 

 P A. B. C. D. 

E 

F  2;1;3M 

1;2;0

1;2;1

0;1;0

Chọn

Điểm

 yfx  fx

số có5 điểm cực trị.

Câu37: Cho khối nóntrònxoay đỉnh , đáy là đường tròntâm ,góc ở đỉnh bằng . Mặt phẳng S O 120 thay đổi, đi qua và cắt khối nóntheo thiết diện làtamgiác . Biết rằng giá trị lớn

 Q S SAB

nhất diện tíchtamgiác là . Khoảng cách từ đến mặt

Số điểm cực trị của hàm số là  22 yfxx A. 9. B. 5. C. 7. D. 3. Lời giải Chọn B Đặt ;  22 gxfxx 2 212  gxxfxx , 0 gx 2 2 2 1 21 20 21        x xx xx xx 1 0 2 12        x x x x trong đó là nghiệm bội ba,các nghiệm

1x Suyra,hàm



còn lại là nghiệm đơn.

22 yfxx

phẳng trong trường hợp SAB22a O  Q diện tíchtamgiác đạt giá trị lớn nhất là SAB A. . B. . C. . D. . 2 2 a 3 2 a 2a 6 2 a Lời giải Chọn A Gọi đường sinh của hìnhnónlà. l  2 2 1 11 ..sin.sin 2 22 SAB SSASBASBlASBl     . 2 max 1 2 SABS l   Dấu xảy rakhi vuôngcân ở ""    sin190 ASBASBSAB S Do đó 22211 22. 22SAB Slalla  Tamgiác vuôngcân ở SAB .222SABSAa  Góc ở đỉnh của hìnhnónlà .  12060 OSA 

Với : Gọi lần lượt là điểm biểu diễn và .Khi đó: và

2,MI z1i

I .Suyra, quỹ tích điểm là đường tròn cótâm ,bánkính .Do

124

Vậy từ tacó:Giá trị lớn nhất của bằng

3,4 z21

Xét vuông ở : SOA O . cos60 sin603 SOSAa AOSAa            Kẻ ở Kẻ ở . OMAB MOHSM H Tacó: .  ; ABOMABSOABSOMABOH    Mà tại . OHSMOHSAB    ;; HdOQdOSABOH    Tacó 2AMMBa  Xét vuông ở OAM 22 .MOMOAAMa   Xét vuông ở có nên vuôngcân ở SOM OOMSOa  SOM .O Mà là đường cao của tamgiác . OH SOM 2 2 Oa H   2 ; 2 adOQ  Câu38: Cho số phức thỏa mãn điều kiện .Giá trị lớn nhất của bằng z 2221 zzzi z A. B. C. D. 221 21 21  2 Lời giải Chọn C . 2221 zzzi111 zizizi   11 112    zi zi Với ,tacó .  1 23

z



đó,



1;1

21 IM  M

CI 1R

 

MC maxzmaxOMOIR 





 Câu39: Chohìnhchóp có đáy làhình chữ nhật với . Cạnh bên . SABCD ABCD 2,3ABaBCa  vuônggóc với đáy và đường thẳng SC tạo với một góc .Tính thể tích của SA ()mpSAB 030 V khối chóp theo . . SABCDa A. B. C. D. 3 215Va  3 215 3 a V 33 3 a V 315 3 a V Lời giải Chọn B

Tacó: tại B, đường thẳng SC tạo với một góc nên . ()BCSAB  ()mpSAB 030  30CSB 

Do đó: và 33 SBBCa  225.SASBABa  

Thể tích khối chóplà: 3 1215 .... 3 3 aVSAABAD  

Câu40: Trongkhônggian với hệ tọa độ ,chocác điểm .Tìm tọa độ điểm là điểm Oxyz A(2;3;5) A

đối xứng với điểm qua trục AOy A. B. C. D. (2;3;5).A (2;3;5).A (2;3;5)A (2;3;5)A Lời giải

Chọn D

Hình chiếu của lên trục là A(2;3;5)OyH(0;3;0)

Điểm đối xứng với qua nên làtrung điểm của . A AOyH(0;3;0) AA

Do đó (2;3;5).A

Câu41: Chohìnhchóp có đáy là hìnhchữ nhật , Biết . SABCD ABCD()SAABCD  ,SAABa  . Gọi là trọng tâmtamgiác . Khoảng cách từ đến bằng 2 ADa  G SAD G() SBD

A. B. C D. . 3 a 2 . 9 a2 . 3 a . 6 a Lời giải

Chọn B

Chọn hệ trục tọa độ trong đó: ; Oxyz (0;0;0)AO  (a;0;0);D(0;2;0);S(0;0;a)B a

Véc tơ pháp tuyến của mplà () SBD(2;1;2)

Phương trìnhmp: () SBD2220 xyza 

Vậy khoảng cách từ đến là: G() SBD

trình đường thẳng chứa đường trung tuyến kẻ từ đỉnh của tamgiác . d A ABC

A. . B. . 132 : 241 dxyz  132 : 241 dxyz  

C. . D. . 132 : 241 dxyz  241 : 113 dxyz

Lời giải Chọn B

Gọi làtrung điểm M  1;1;3BCM 

Đường trung tuyến cóVTCP vàqua Chọn B AM  2;4;1AM 

1;3;2

Trongkhônggian ,cho điểm và đường thẳng

Khi

tọa độ: G SAD 2 0;; 33 Gaa       ;(;0;);(0;2;)

    222 ,(2;a;2).SBSDaa   

đó trọng tâm của tamgiác có

SBaaSDaa

n 



2 2022 32 3 . 39 aa a a d   

, . Viết Oxyz



A  2;0;5B  0;2;1C phương

Câu42: Trongkhônggian ,chotamgiác có ,

ABC

1;3;2





A 

Gọi Oxyz  1;1;1A :12, 22 xt dytt zt         là mặt

chứa Lập phương trình mặt cầu cótâm  P A d  S  2;3;1I saocho tiếp xúc với .  S  P A. . B. .  222 :23116Sxyz  222 :2319Sxyz C. D.  222 :2314Sxyz  222 :2314Sxyz Lời giải Chọn C qua vàVTCP . d  0;1;2M  1;2;2u  Mặt phẳng cóVTPT .  P  ;2;1;2:2250nAMu Pxyz      Bánkính mặt cầu Chọn C   ; 2 IPRd Câu44: Trong không gian , cho mặt phẳng và ba điểm Oxyz :220Pxyz , . Gọi là điểm di động trên saochocó một mặt cầu  2;0;2,4;0;4AB  5;2;4C M  P đi qua và tiếp xúc với tại .Khi đó, độ dài đoạn cógiá trị nhỏ nhất là  S , AB  PM CM A. . B. . C. . D. . 3 10 109 13

Câu43:

phẳng đi qua và

Lời giải Chọn D Gọi làhình chiếu của lên . H C 4;4;2mpPH  Đường thẳng 2 :0 2 xt ABy zt      ABPO Tacó: và . 2.22.42164OMOAOB OM   6OH . 2 minmin 9 2MCMHMCMHMHOHOM   Vậy min13CM Câu45: Cho là một nguyênhàm của hàm số trên .Tínhtíchphân 2 1 2 Fx x  fx x  0; .  2 1 21d fxx  A. B.  2 1 2 21d 15fxx  2 1 2 21d 15fxx C. D.  2 1 1 21d 15fxx  2 1 1 21d 15fxx Lời giải Chọn D Vì là một nguyênhàm của hàm số nên Fx fx x  Ffx x x    23 11 2 fx xxx      2 1 fx x  Do đó .  2 2 2 1 1 2 111 21dd 21211521 fxx x x x        Câu46: Có tất cả baonhiêu số nguyên dương saocho ứng với mỗi số đó bất phương trình y y có nghiệm nguyên và số nghiệm nguyên không vượt quá . 3244 0 3x xxx y   x x 6 A. B. C. D. 176903 176930 176910 176923 Lời giải Chọn B

+TH1: Nếu thì bất phương trình . 3 log481 yy

314logxy

Để bất ptcó nghiệm nguyên và số nghiệm nguyên không vượt quá x x 6

log11 log5 y y  177147 243177147 243 y y y

Để bất ptcó nghiệm nguyên và số nghiệm nguyên không vượt quá x x 6

      y Vậy

y y y

Số nghiệm nguyên của bất phương trình là 23 23loglog1loglog

xxxx

Điều kiện: .;,0xyy  Từ

  2

x y y   



 

giả thiết. 3244 0 3x xxx y

414 00 3 3 x x xx

(1)

430 x xy



có176904 số nguyên . 3 3      

+TH2: Nếu thì bất phương trình . 3 log481 yy 3 1log4 yx 

 y Câu47:

 A. . B. . C. Vô số. D. . 3 2 1 Lời giải Chọn B Điều kiện 0x Bất phương trình  23 23 2 3 2 3 2 3 loglog1loglog log1log10 log102 log103 23. 2log10 3log10 xxxx xx x x x x x x x x x                               Vậy bất phương trìnhcó nghiệm nguyên. 2 Câu48: Chohàm số   5 432 22 12153020304312012023 yxmxxmmxmxm     Có tất cả baonhiêugiá trị nguyên của tham số để hàm số đồng biến trên khoảng ? m  1;3 A. . B. . C. . D. . 11 10 2 1 Lời giải Chọn C Đặt   5 432 22 12153020304312012023 fxxmxxmmxmxm       4 322 2 606026060431201 fxxmxxmmxm    

có26 số nguyên . 3 3 log3127 log327

tacó số nguyên cần tìm. 17690426176930

():Pyx  , AB() P

Câu49: Trong mặt phằng tọa độ ,choParabol vàhai điềm thuộc saocho Oxy

Diện tíchhình phẳng giới hạn bời và đường thẳng đạt

   32 2 2 0 21101 x fx xmxmxm      Hàm số đồng biến trên suyra đồng biến trên hoặc nghịch yfx   1;3 yfx   1;3 biến trên khoảng  1;3 khônglà cực trị của hàm số 2x fx là nghiệm của phương trình . 2x   1 *Điều kiện cần: là nghiệm của phương trình 2x  1 2 2 1 844210890 9 m mmm mm m     *Điều kiện đủ: Với .Khi đó suyrahàm số 1m   22 60210,1;3 122510 fxxxxx f       yfx  đồng biến trên . 1;3 Vớ .Khi đó suyrahàm số 9m   22 60211410,1;3 183910 fxxxx x f       đồng biến trên . yfx   1;3



Vây nêncó2giá trị nguyên thoả mãn. 1;9mm

giá trị lớn nhất bằng 2AB () P AB A.. B.. C.. D.. 3 2 3 4 2 3 4 3 Lời giải Chọn D Gọi với .Tacó  22 ;,; AaaBbbab  2222 2()4ABbaba    2 2 2 22 : ()()() 1 Axayaxaya B yabxaayabxab baba ba      2 () ()() b b a a Sabxabxdxxabxdx     Đặt txa   23 3 2 0 0 00 () ()()()236 baba ba ba battbaStbatdttbatdt         2222 2 2 2 2 4 Tacó()4()1()4() 4 1() baba baba ba ba       Suyra 33 2()24 663 babaS  Dấu bằng xảy rakhi . 01 (1;1),(1;1)21 abb AB baa       

Câu50: Trong tập các số phức, cho phương trình ( tham số thực). Hỏi 22(1)620zmzmm

có tất cả baonhiêugiá trị ngüyên của để phương trình đã chocóhai nghiệm phân biệt m

thỏa mãn 12 , zz 12zz 

A. B. C.Vô số. D. 0 1 2

Lời giải

Chọn D

Để phương trình đó chocóhai nghiệm phân biệt thỏa mãn thìxét 12 ; zz 12zz 

221620(1)zmzm

Tacó: 243(1)(3)mmmm   

+)TH1: 0   3 (1)(3)0. 1 m mm m 

Thì phương trình(1)cóhai nghiệm thực phân biệt 12 ; zz

Vậy 22 1212 zzzz 

12120zzzz 

Do làhai nghiệm phân biệt nênsuyra 12 ; zz 120zz

TheoVi-ét: (thỏa mãn) 1202101zz m m 

Vậy TH1có1giá trị của m

+)TH 2:0  (1)(3)013. mm m 

Thì phương trình(1)cóhai nghiệm phức phân biệt 2121 12 ; .zzzz z z

Vậy TH2có 2m

Vậy tất cả có2giá trị của thỏa mãn. m

 









Câu1: Hàm số nàosau đây luôn đồng biến trên?

Câu2: Chohàm số có bảng biến thiên như hìnhsau. ()yfx =

Câu3: Tập

tròn đáy bằng . Diện tíchxungquanh h R của hìnhnón đó bằng

chiều caolà vàbánkính của

2Rhp Rhp 22 2RhRp+ 22RhRp+

B. C.

Trongkhônggian , một véctơ pháp tuyến của mặt phẳng có tọa độ là Oxyz () Oxz

B. C. D. ()0;1;1. ()1;0;1. () 0;1;0. () 1;0;0.

Câu6: Tìm khoảng nghịch biến của hàm số , biết . yfx  ()()()()2 325,fxxxx x ¢=-++"Î

B. C. D. () ;5-¥- () 2;3- () 5;2-- () 3;+¥

Câu7: Chohàm số liên tục trên đoạn vàcó bảng biến thiên như hình vẽ dưới. Giá trị

yfx  

TRƯỜNG THPT

NGUYỄN KHYẾN TPHCM THI THỬ TỐT NGHIỆP THPT– LẦN 1– NĂM HỌC 2022-2023

 A. B. C. D. 23fxx 42fxxx  . 3 x fx     log5x fx

Điểm



 A. B. C. D. 2.

= 1y=- 1.x=-

cực đại của hàm số là

yfx

nghiệm của bất phương trình là 250 x-£ A. B. C. D. ( ]2 ;log5. S=-¥ (] 2 0;log5.S= [] 2 0;log5.S= (] 5 0;log2.S=

Một

Câu5:

Câu4:

hìnhnóncó

đường



1;3 lớn nhất của hàm số trên đoạn bằng yfx   1;3 A. B. C. D. 3 5 0 4 Câu8: Hàm số nàosau đây có tập xác định là ?  A. B. C. D. 2 .yx= 53 .yx = 2 .yx p = 1 3 .yx = Câu9: Thể tích khối lăng trụ có diện tích đáy và chiều cao là 220 Bcm  3 hcm  A. .B. .C. .D. . 323 Vcm  320 Vcm  360 Vcm  345 Vcm  Câu10: Trongkhônggian ,cho .Hình chiếu của lên mặt phẳng là Oxyz 23 OAijk   A  Oxz A. .B. .C. .D. .  2;0;3M  0;1;0N  2;0;1P  0;3;0Q



Câu11: Chohàm số liên tục trên vàcó bảng xét dấu đạo hàm như hình vẽ: yfx   Hàm số đã chocóbaonhiêu điểm cực đại? A..B..C..D.. 2 3 4 1 Câu12: Các số theo thứ tự lập thành một cấp số cộng. Khi đó: 5,,9,ab A. .B. .C. .D. 60ab 96ab 72ab 77ab Câu13: Tiệm cận ngang của đồ thị của hàm số có phương trình: 5x y= A. B. C. D. 0x 5y 0y 5x Câu14: Chohàm số .Giá trị của bằng ()24fxx x =- () 2 1 d fxx ¢ò A. B. 5 C. D. 3 7 3 7ln2 3 Câu15: Đồ thị của hàm số cắt trục hoành tại baonhiêu điểm phân biệt? ()()2 242yxx=-+ A. 2 B. 3 C. 4 D. 1 Câu16: Trongkhônggian , mặt cầu có diện tích bằng: Oxyz ()222 : 4630Sxyzxy++-+-= A. B. C. D. 120 40 32 64 Câu17: Trongkhônggian , mặt phẳng đi quaba điểm có Oxyz ()()() 1;0;0,0;2;0,0;0;4A B Cphương trìnhlà A. B. C. D. 0 124 xyz 1 124 xyz 1 124 xyz 1 124 xyz Câu18: Hàm số nàosau đây có đồ thị như hình vẽ ở bên? A. B. . C. D. . 2x y x   21 2 x y x   2 2 x y x   24 22 x y x   Câu19: Khẳng định nàosau đây đúng? A. B. cossinxdxxC  56 1 5 xdxxC  C. . D. . 1 ,1 1 x xe edxCx x     1 ln2023 dxxC x    Câu20: Số nghiệm thực của phương trình: là 2 1ln3ln10 xx  A. B. C. D. 2 1 0 3

Câu21: Gọi làhình phẳng giới hạn bởi các đường ; ; ; . Thể tích của khối  H 0y1x5x x ye  V trònxoay tạo thànhkhiquay quanh trục là.  H Ox A. B. C. D. 5 1 1 x Vedx    2 5 1 x Vedx  5 2 1 x Vedx  5 2 1 x Vedx  Câu22: Chohàm số có đồ thị như hình dưới đây. Số nghiệm thực của phương trình yfx    3 5 1 fx fx   A. 3. B. 5. C. 2. D.4 Câu23: Chohàm số có đồ thị như hình vẽ. Diện tích của hình phẳng gạch chéotronghình yfx  dược tínhtheocông thức nào? A. B.  3 4 0 0 Sfxdxfxdx   0 4 3 0 Sfxdxfxdx    C. D.  0 4 3 0 Sfxdxfxdx   4 3 Sfxdx  Câu24: Trongkhônggian,chohai mặt phẳng và.Giao Oxyz :230Pxyz:10Qxy tuyến của vàcó một vecto chỉ phương là  P Q A. B. C. D.  1;0;1u   1;1;3u   3;0;1u   1;1;3u  Câu25: Chohàm số có đồ thị hàm số như hình vẽ bên 3 yfxaxbxc  Số điểm cực trị của hàm số là 2023yfx A. B. C. D. 2 3 7 5

Câu26: Số tiệm cận đứng của đồ thị hàm số là

a Câu29: Hàm số có đúng ba điểm cực trị khivà chỉ khi

()()

4 2 22023fxmxmx=-++

A. B.

20m m <-Ú> 2m>- 0m< 20 m -<<

Câu30: Nếu đặt thì bất phương trình trở thành:



vàvuônggóc với mặt Oxyz D ()

M-

có

A. B. C. D. 14

x t yt z t ì ï=+ ï ï ï í=ï ï ï=ï î 34 1 13 x t y t zt ì ï=-+ ï ï ï í=-+ ï ï ï=ï î 14 23 xt yt z t ì ï=ï ï ï í= ï ï ï=-ï î 14 0 23 xt y z t ì ï=ï ï ï í= ï ï ï=-+ ï î Câu28: Cho

làtrung điểm các cạnh ABCD 38a , MN , ABAC Thể tích khối

A. B. C. D. 33a 34a 35a 36

22 x y xx  A. B. C. D. 2 1 3 0 Câu27: Trongkhônggian , đường thẳng đi qua điểm

1;0;2

phẳng

phương trìnhtham số là: ():4320230Qxyz+-+=

tứ diện có thể tíchlà . Gọi lần lượt

đa diện bằng BCDNM

C. D.

log tx = 23 log10log10 x x - +³ A. B. C. D. 2 310. t 2 3510. tt 2 9510. tt 2 92010. tt Câu31: Chohàm số xác định vàliên tục trên có đồ thị hàm số như hình vẽ. Hàm số yfx   fx  nghịch biến trên khoảng nàosau đây?  2yfx A. B. C. D. ();4.-¥- ()2;0.- () 4;2.-- () 2;.-+¥ Câu32: Đồ thị của hàm số không cắt đường thẳng khivà chỉ khi () 2 2023x y= ym = A. B. C. D. 2023.m£ 2023.m< 1.m£ 1.m< Câu33: Thực hiện phép biến đổi thìtíchphân .Khi đó: 331tx  7 2 3 3 0 1 1 .d.d 31 x xgtt x     A. B. C. D. ()331.g= ()329.g= ()333.g= ()325.g= Câu34: Trongkhônggian , phương trình mặt cầu cótâm tiếp xúc với trục là: Oxyz () S (1;9;3)I Ox A. . B. . 222 (1)(9)(3)10 xyz   222 (1)(9)(3)45 xyz   C. . D. . 222 (1)(9)(3)82 xyz   222 (1)(9)(3)90 xyz   Câu35: Hìnhchóp có đáy làhìnhvuông,tamgiác đều và . SABCDABCD SAB()() SABABCD  Đường thẳng tạo với mặt một góc thìgiá trị bằng SD () ABCD  tan A. B. C. D. 15 5 5 5 15 3 23 5

Câu36: ÔngA bị nhiễm một loại virusnên phải nhập viện và được điều trị ngay lập tức. Kể từ ngày nhập viện, sau mỗi ngày điều trị thì lượng virustrong cơ thể ôngA giảm đi so với ngày trước đó. 10% Hỏi sauít nhất baonhiêungàythìôngA sẽ được xuất viện, biết rằng ôngA được xuất viện khi lượng virustrong cơ thể khôngquá so với ngày nhập viện 30% ?

A. 11ngày B. 12ngày C. 13ngày D. 14ngày

Câu37: Chohàm số có bảng biến thiên như hìnhbên. Gọi lần lượt làgiá trị lớn nhất ()ygx = , Mm

và nhỏ nhất của hàm số .Khi đó: ( ) 2 18sin2yg x=+ -

Câu38: Một hình trụ được cắt bởi một mặt phẳng songsong với trục vàcách trục một khoảng bằng ,5 thiết diện thu được làhìnhvuôngcó diện tích bằng .Tínhthể tích của khối trụ đó. 16 V

Oxyz'd

A. B. C. D. 2.Mm-= 1.Mm-= 6.Mm-= 4.Mm-=

A. B. C. D. 28.

36.

44.

Vp= 32.Vp=

Vp=

¢ trên

f=+ Câu40: Một hộp gồm quả cầu được đánh số từ đến Lấy ngẫu nhiên quả cầu từ hộp đó. Xác 23 123 2 suất để lấy được quả cầu vàtíchhai số ghitrên quả cầu đó là một số chia hết cho bằng 2 2 6 A. B. C. D. 8 23 95 253 4 11 98 253 Câu41: Trongkhônggian , gọi làhình chiếu vuônggóc của lên mặt

2 12 :32, (2) xat dytt zat         phẳng Lấy các điểm thuộc .Tính tổng tất cả :2360. xz  (0;3;2),(3;1;0)M N   cácgiá trị của tham số để a 'MNd  A. . B. . C. . D. . 4 3 1 2 Câu42: Chohìnhchóp có đáy làhìnhvuông cạnh bằng ,tamgiác đều vàtam . SABCD ABCD a SAB giác vuôngcân tại . Diện tích mặt cầu cótâm và tiếp xúc với mặt phẳng SCD S S () ABCD bằng A. B. C. D. 23 . 4 a p 24 . 3 a p 23 . 2 a p 2 3. ap Câu43: Chohàm số có đạo hàmliên tục trên đoạn vàcó đồ thị như hình vẽ. yfx   0;8 (S2) (S1) (S3) y x O 8 5 3 3 Biết lần lượt là diện tíchhình phẳng giới hạn bởi đồ thị và 12323,3,15SSS yfx  trục .Giá trị của là Ox   6 32 2 5 299310d Ixxxfxxx   

Câu39: Chohàm số có đạo hàmtrên . Biết là một nguyênhàm của ()yfx = () 0;+¥ 23x ()2 xfx

và .Tínhgiá trị () 0;+¥()12f= () ef

. B. C. D. ()e8f= ()e6e2f=- ()e4f= ()e3e2

ượtlàtrungđiểmcủacạnh .Khimặtphẳng tạovớimặtđáycủalăng , MN , AADC ¢ () ANB ¢ trụ mộtgóclà thìkhoảngcáchgiữahai đườngthẳng và bằng o60 DMAN ¢ A. B. C. D. a 3 2 a 2a 6 2 a

Câu47: Chohàm số có đạo hàmtrên vàcó bảng biến thiên như sau: yfx  

Số điểm cực đại của hàm số

A. B. C. D. 15I 65.I 5I 35I Câu44: Chohàm số liên tục trên vàcó đồ thị như hình vẽ bên. yfx   Tổng tất cả cácgiá trị nguyên của tham số để phương trình có đúng m  5 32log6fxm  3 nghiệm thực thuộc nửa đoạn bằng 1 ;25 25    A. B. C. D. 69 57 60 66 Câu45: Có tất cả baonhiêugiá trị nguyên của tham số saochohàm số  23;0m luôn đồng

()() () 4 2 2 8e 92023 x fxx mxmmx =----+

2;5 A. B. C. D. 21 19 14 8 Câu46:

ọi .

biến trên khoảng ?

()

Cholăngtrụ đứng cóchiềucaobằng và làhìnhbìnhhành.G

ABCDABCD¢¢¢¢ 4aABCD lầnl

là   2 2 26813gxfxxx   A. . B. . C. . D. . 8 10 9 7 Câu48: Trongkhônggian , khối đa diện có thể tích với các đỉnh , Oxyz OAMEN 296  0;0;82A ,trong đó làcác số thực dương. Khi thay đổi thì  5;0;0,0;7;0,;;0M N Eab , ab , ab đường thằng tiếp xúc với mặt cầu Mặt cầu cóbánkính nhỏ nhất AE ()2222 : Sxyzc ++= () S bằng

A. B. C. D. 24666 333 8137 74 27222 37 2474 461 Câu49: Xétcác số thực saocho luôn đúng với mọi .Có tối , xy () 3 6 3 18-loga 2 216 27+loga783 x y £ 0a> đa baonhiêugiá trị nguyên dương của ? 2225 Kxyxy =+-+ A. B. C. D. 64. 53. 58. 59. Câu50: Hàm số thỏa: và .Hình fx   21 2 0 ,0 e6 8124 x fx x fxfxxxfx         14f phẳngđượcgiớihạnbởi , vàtrụchoànhcódiệntíchbằng ,trong yfx  1,3xx .e n mp  đó Hệ thức nàosau đây đúng? ,, mnp A. B. C. D. 26 mnp 530 mnp 315 mnp 3219 mnp

Tập nghiệm của bất phương trình là 250 x

Câu4: Một hìnhnóncó chiều caolà vàbánkính của đường tròn đáy bằng . Diện tíchxungquanh h R

của hìnhnón đó bằng

Độ dài đường sinh của hìnhnónlà 22lhR =+

Diện tíchxungquanh của hìnhnón đó bằng

xq SRlRhR pp== +

BẢNG ĐÁP ÁN 1.C 2.D 3.A 4.D 5.C 6.B 7.B 8.B 9.C 10.C 11.A 12.D 13.C 14.B 15.A 16.D 17.C 18.C 19.D 20.A 21.C 22.D 23.C 24.B 25.B 26.A 27.B 28.D 29.A 30.C 31.C 32.D 33.B 34.D 35.A 36.B 37.D 38.C 39.A 40.B 41.B 42.A 43.B 44.D 45.C 46.A 47.A 48.D 49.C 50.B HƯỚNG DẪN GIẢI Câu1: Hàm số nàosau đây luôn đồng biến trên?  A. B. C. D. ()23.fxx=+ ()42 .fxxx =+ ()3 x fxp æö ç÷ =÷ ç÷ ç èø ()()log5. x fx= Lời giải Hàm số đồng biến trên khicó cơ số . x ya =  1a Hàm số có cơ số nênluôn đồng biến trên . ()3 x fxp æö ç÷ =÷ ç÷ ç èø 1 3 a    Câu2: Chohàm số có bảng biến thiên như hìnhsau. ()yfx = Điểm cực đại của hàm số là yfx  A. B. C. D. 2.x= 2y= 1y=- 1.x=Lời giải Từ bảng biến thiêntacó đổi dấu từ dương sangâmkhi đi qua điểm nên ()yfx ¢¢ = 1x=điểm cực đại của hàm số là . yfx  1x=Câu3:

A. B. C. D. ( ]2 ;log5 S=-¥ (] 2 0;log5S= [] 2 0;log5S= (] 5 0;log2S= Lời giải Tacó . 2 25025log5 x x x -£Û£Û£

trình là 250 x-£ ( ]2 ;log5 S=-¥

-£

Tập nghiệm của bất phương

B. C. D.

Lời

2. Rhp .Rhp

2 .RhRp+

.RhRp+

giải

Câu5: Trongkhônggian , một véctơ pháp tuyến của mặt phẳng có tọa độ là Oxyz () Oxz A. B. C. D. () 0;1;1 () 1;0;1 () 0;1;0 () 1;0;0

Lời giải:

Mặt phẳng có phương trìnhlà nên nhận làm véctơ pháp tuyến. () Oxz 0y= () 0;1;0j= 

Câu6: Tìm khoảng nghịch biến của hàm số , biết . yfx  ()()()()2 325,fxxxx x ¢=-++"Î

A. B. C. D. () ;5-¥- () 2;3- () 5;2-- () 3;+¥

Lời giải:

Tacó ()()()()()()() 2 23250320,5 6023 fxxxx xx x

. []()1;3 max5 fx= Câu8: Hàm số nàosau đây có tập xác định là ?

giải:

có điều kiện 2 yx= 0x



xx x ¢=-++<Û-+<¹-Û--<Û-<< Vậy hàm số nghịch biến trên ()2;3.Câu7: Chohàm

liên tục trên đoạn vàcó bảng biến thiên như hình vẽ dưới. Giá trị yfx   1;3 lớn nhất của hàm số trên đoạn bằng yfx   1;3 A. B. C. D. 3. 5. 0. 4. Lời giải: Từ bảng biến thiêntrêntacó

A. B. C. D. 2 .yx= 53 yx = 2 .yx p = 1 3yx = Lời

Hàm

Cáchàm số mũ khôngnguyênnêncó tập xác định là 1 2 3 ; yxyx p == () 0;+¥ Hàm làhàm căn bậc lẻ nên điều kiện là mọi , từ đó có tập xác định 53 yx = x D= Câu9: Thể tích khối lăng trụ có diện tích đáy và chiều cao là 220 Bcm  3 hcm  A. .B. .C. .D. . 323 Vcm  320 Vcm  360 Vcm  345 Vcm  Lời giải Thể tích khối lăng trụ có diện tích đáy và chiều cao là 320 Bcm  3 hcm  320360VBh cm Câu10: Trongkhônggian ,cho .Hình chiếu của lên mặt phẳng là Oxyz 23 OAijk   A  Oxz A. .B. .C. .D. .  2;0;3M  0;1;0N  2;0;1P  0;3;0Q Lời giải

số



Nênhình chiếu của lên mặt phẳng là . A  Oxz 2;0;1P

Câu11: Chohàm số liên tục trên vàcó bảng xét dấu đạo hàm như hình vẽ: yfx  

Hàm số đã chocóbaonhiêu điểm cực đại?

A..B..C..D.. 2 3 4 1

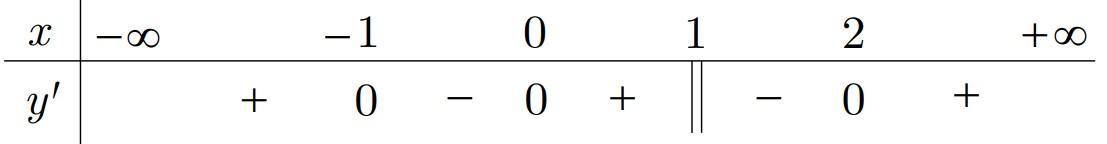
Lời giải

Hàm số liên tục trên vàcó đổi dấu dương sangâmkhiquahai điểm yfx  y  1;1xx

nênhàm số đã chocóhai điểm cực đại.

Câu12: Các số theo thứ tự lập thành một cấp số cộng. Khi đó: 5,,9,ab

A. .B. .C. .D. 60ab 96ab 72ab 77ab Lời giải

Các số theo thứ tự lập thành một cấp số cộng 5,,9,ab

Tacó  232;3;12;3;1OAijkOA A    

27777

bb                      Câu13: Tiệm cận ngang của đồ thị của hàm số có phương trình: 5x y= A. B. C. D. 0x 5y 0y 5x Lời giải Tacó: nênhàm số có1 tiệm cận nganglà đường thẳng l,0 im5lim5 x x x x   5x y= 0.y Câu14: Chohàm số .Giá trị của bằng ()24fxx x =- () 2 1 d fxx ¢ò A. B. 5 C. D. 3 7 3 7ln2. 3 Lời giải Tacó: . ()()() 2 1 d215fxxff ¢ =-= ò Câu15: Đồ thị của hàm số cắt trục hoành tại baonhiêu điểm phân biệt? ()()2 242yxx=-+ A. 2 B. 3 C. 4 D. 1 Lời giải

18711

2 a a a ab ab

Tacó .  2 2 3402 2 2 2 2 x xx xx x        

Trongkhônggian ,mặtcầu códiệntíchbằng: Oxyz ()222 : 4630Sxyzxy++-+-= A. B. C. D. 120 40 32 64 Lời giải Tacó:

Sxyzxy++-+-= ()() 2 226 2 3 1 x y z - + + = Û + Bánkính của là Thể tíchlà .  S4R 2 464 R  Câu17: Trongkhônggian , mặt phẳng đi quaba điểm có Oxyz ()()() 1;0;0,0;2;0,0;0;4A B Cphương trìnhlà A. B. C. D. 0 124 xyz 1 124 xyz 1 124 xyz 1 124 xyz Lời giải Mặt phẳng đi quaba điểm có phương trìnhlà: ()()() 1;0;0,0;2;0,0;0;4A B C.11 124124 xyzxyz    Câu18: Hàm số nàosau đây có đồ thị như hình vẽ ở bên? A. B. .C. D. . 2x y x   21 2 x y x   2 2 x y x   24 22 x y x   Lời giải Từ đồ thị tacó đường tiệm cận đứng là và tiệm cận nganglà .Nên đáp ánlà 2x 1y C. Câu19: Khẳng định nàosau đây đúng? A. . B. . cossinxdxxC  56 1 5 xdxxC  C. D. 1 ,1 1 x xe edxCx x     1 ln2023 dxxC x    Lời giải Tacó: .  202312023 ln2023 20232023 dx dx dx xC x x x     

Câu16:

()222 : 4630.

trình đã cho tương đương với 1

Số nghiệm của phương trìnhlà số giao điểm của đồ thị hàm số với đường thẳng yfx 

. Dựa vào đồ thị ta thấy đường thẳng cắt đồ thị hàm số tại 4 điểm 1 3y 1 3y yfx 

phân biệt nên phương trìnhcó4 nghiệm phân biệt.

Câu23: Chohàm số có đồ thị như hình vẽ. Diện tích của hình phẳng gạch chéotronghình yfx 

dược tínhtheocông thức nào?

Câu20: Số nghiệm thực của phương trình: là 2 1ln3ln10 xx  A. . B. C. . D. . 2 1 0 3 Lời giải ĐK: 303 11 x x x x            Tacó:  2 2 1ln3ln10ln1ln31 xx x x        2 2 2 2 2 ln1ln3132130 216/ 2 216/ 2 xexxexexexe eee x tm eee x tm         Vậy phương trìnhcó2 nghiệm. Câu21: Gọi làhình phẳng giới hạn bởi các đường ; ; ; . Thể tích của khối  H 0y1x5x x ye  V trònxoay tạo thànhkhiquay quanh trục là.  H Ox A. B. C. D. 5 1 1 x Vedx    2 5 1 x Vedx  5 2 1 x Vedx  5 2 1 x Vedx  Lời giải Chọn C. Câu22: Chohàm số có đồ thị như hình dưới đây. Số nghiệm thực của phương trình yfx    3 5 1 fx fx  

D.4 Lời giải Phương



A. 3.

3fx

là một vecto chỉ phương của giao tuyến của vànên chọn B.

Chohàm số có đồ thị hàm số như hình vẽ bên

A. B.  3 4 0 0 Sfxdxfxdx   0 4 3 0 Sfxdxfxdx    C. . D. .  0 4 3 0 Sfxdxfxdx   4 3 Sfxdx  Lời giải     0 4 0 4 3 0 3 0 00 Sfxdxfxdxfxdxfxdx       Câu24: Trongkhônggian,chohai mặt phẳng và.Giao Oxyz :230Pxyz:10Qxy tuyến của vàcó một vecto chỉ phương là  P Q A. B. C. D.  1;0;1u   1;1;3u   3;0;1u   1;1;3u  Lời giải cóvectopháp tuyến ; :230Pxyz  1;2;1Pn  cóvectopháp tuyến :10Qxy  1;1;0Qn  Khi đó giao tuyến

mà  P Q ,1;1;3PQunn   cũng

 1;1;3u   P Q

3 yfxaxbxc  Số điểm



 A. . B.

Lời

Tacó đồ

của vàcó một vecto chỉ phương là

Câu25:

cực trị của hàm số là

2023yfx

. 2 3 7 5

giải

thị hàm: fx

Đường thẳng vuônggóc với mặt phẳng nên đường thẳng D ():4320230Qxyz+-+=

có một vec tơ chỉ phương là D (4;1;3)u  +) Đường thẳng đi qua . D () 1;0;2M-

ï=+

xt yt z t ï ï ï í= ï ï ï=-ï î

A. B. C. D. 33a 34a 35a 36a Lời

giải

Màhàm sốcũng cóhình dạng tương tự. Vậy 2023yfx có cực trị. 2023yfx 3 Câu26: Số tiệm cận đứng của đồ thị hàm số là  22 x y xx  A. . B. . C. . D. . 2 1 3 0 Lời giải TXĐ: (0;)\2D Vì và.  2 2 0 0 1 limlim 2 2 x x x xx xx        2 2 2 2 1 limlim 2 2 x x x xx xx       Nên đường thẳng vàlàhai đường tiệm cận đứng của đồ thị hàm số. 0x 2x Câu27: Trongkhônggian , đường thẳng đi qua điểm vàvuônggóc với mặt Oxyz D () 1;0;2Mphẳng có phương trìnhtham số là: ():4320230Qxyz+-+= A. B. C. D. 14 23 x t yt z t ì ï=+ ï ï ï í=ï ï ï=ï î 34 1 13 x t y t zt ì ï=-+ ï ï ï í=-+ ï ï ï=ï î 14 23 xt yt z t ì ï=ï ï ï í= ï ï ï=-ï î 14 0 23 xt y z t ì ï=ï ï ï í= ï ï ï=-+ ï î Lời

giải

Vậy đường thẳng có phương trìnhtham số là: D 14 23

Câu28: Cho tứ diện có thể tíchlà . Gọi lần lượt làtrung điểm các cạnh . ABCD 38a , MN , ABAC

Thể tích khối đa diện bằng BCDNM

N M B C D A +) 3 3 1 1111 2 8224 AMND AMND AMND ABCD V VAMANAD Va VABACADa   +) 333 526.BCDNMABCDAMND VVVaaa    Câu29: Hàm số có đúng ba điểm cực trị khivà chỉ khi ()() 4 2 22023fxmxmx=-++ A. B. C. D. 20.m m <-Ú> 2.m>- 0.m< 20. m -<< Lời giải 3 2 '()42(2)222 fxmxmxxmxm      2 2 0 0 '()022022 x x fx mxm mxm         Hàm số có đúng ba điểm cực trị khivà chỉ khi ()fx . 0 2 2020 02 2 m m mm m m m       Câu30: Nếu đặt thì bất phương trình trở thành: log tx = 23 log10log10 x x - +³ A. B. C. D. 2 310 t 2 3510 tt 2 9510 tt 2 92010 tt Lời giải Điều kiện: 0x 23 2 log10log109log5log10 x x xx - +³Û -+³ Đặt, ,tacó phương trình: log tx = 2 9510 tt-+³ Câu31: Chohàm số xác định vàliên tục trên có đồ thị hàm số như hình vẽ. Hàm số yfx   fx  nghịch biến trên khoảng nàosau đây?  2yfx

A. B. C. D. ();4.-¥- ()2;0.- () 4;2.-- () 2;.-+¥ Lời giải Tacó bảng xét dấu ; 0;20;fxx  02;0fxx  Tacó:  2''2yfxyfx  Hàm số nghịch biến  2yfx 2022042fx x x  Vậy hàm số nghịch biến trên khoảng  2yfx () 4;2.-Câu32: Đồ thị của hàm số không cắt đường thẳng khivà chỉ khi () 2 2023x y= ym = A. B. C. D. 2023m£ 2023m< 1m£ 1m< Lời giải () () 2 2 2023'2.2023.ln2023 x x y yx = Þ= '00yx=Û= Bảng biến thiên: Từ bảng biến thiênsuyra đồ thị của hàm số không cắt đường thẳng khi () 2 2023x y= ym = và chỉ khi 1.m< Câu33: Thực hiện phép biến đổi thìtíchphân .Khi đó: 331tx  7 2 3 3 0 1 1 dd 31 x xgtt x     A. B. C. D. ()331g= ()329g= ()333g= ()325g= Lời giải Đặt và . Đổi cận: 3 3 3 1 3131 3 t txtxx  2 dxtdt  7 01;2. 3 xtxt  Khi đó  3 7 2 2 2 2 3 4 3 2 2 3 0 1 1 1 1 1 1122 3 33 31 t x t tt dx tdttdt dtgtdt t t x             Suyra .   42 329 3 tt gt g   Câu34: Trongkhônggian , phương trình mặt cầu cótâm tiếp xúc với trục là: Oxyz () S (1;9;3)I Ox A. . B. . 222 (1)(9)(3)10 xyz   222 (1)(9)(3)45 xyz  

222 (1)(9)(3)90 xyz 

Lời giải

FB tác giả: Anh Tu

Gọi là điểm tiếp xúc của mặt cầu với trục .Khi đó làhình chiếu vuônggóc của M () S OxM

lên nên vàbánkính mặt cầu là . IOx(1;0;0)M 90RIM

Suyra phương trình mặt cầu là . 222 (1)(9)(3)90 xyz  

Câu35: Hìnhchóp có đáy làhìnhvuông,tamgiác đều và . . SABCDABCD SAB()() SABABCD 

Đường thẳng tạo với mặt một góc thìgiá trị bằng SD ()

Gọi cạnh hìnhvuông là và làtrung điểm của .Vìtamgiác

Hỏi sauít nhất baonhiêungàythìôngA sẽ được xuất viện, biết rằng ôngA được xuất viện khi lượng virustrong cơ thể khôngquá so với ngày nhập viện 30% ?

A. 11ngày B. 12ngày C. 13ngày D. 14ngày

Lời giải

Gọi Klà lượng virustrong cơ thể ôngAkhi bắt đầu nhập viện.

Sau mỗi ngày điều trị thì lượng virustrong cơ thể ôngA giảm đi so với ngày trước đó, nên 10%

lượng virustrong cơ thể ôngA ở ngày thứ nlà: .(110%)n TK£-

ÔngA được xuất viện khi lượng virustrong cơ thể khôngquá so với ngày nhập viện, nên 30% tacó: (110%) .(110%).30%(110%)30%log30%11.4 n n K K n n

Û-£Û£ Û³



. D. . 222 (1)(9)(3)82 xyz 



 tan A. B. C. D. 15 5 5 5 15 3 23 5 Lời giải A B C D S H

ABCD

ABCDaH AB SAB a nên .Và . Mặt khác,ta cũng có 3 2 SHa  2 22 25 42 a aHDAHADa nêngóc giữa và là .Xéttamgiác ,tacó ()SHABCD  SD() ABCD  SDH SDH  3 2315 tantan 55 5 2 Sa H SDH DH a  

đều cạnh

- -£

Câu37:

Vậy, sauít nhất 12ngàythìôngA sẽ

xuất viện.

Suyra: .4Mm

Gọi là cạnh của thiết diện hìnhvuông.Theo giả thiết tacó .Khi đó, a 2164aa

được

lần lượt làgiá trị lớn nhất ()ygx = , Mm

A. B. C. D. 2Mm-= 1Mm-= 6Mm-= 4Mm-= Lời giải Đặt ,do 2 18sin2t x 2 2 2 0sin1118sin9118sin3 x x x  Khi đó 2 18sin21;1t x  Xéthàm số với , từ đồ thị tasuyragiá trị lớn nhất là khi ,giá trị ygt   1;1t 2M 1t nhỏ nhất

2m 1t

Chohàm số có bảng biến thiên như hìnhbên. Gọi

và nhỏ nhất của hàm số .Khi đó: ( ) 2 18sin2yg x=+

là khi

A. B. C. D. 28Vp= 32Vp= 36Vp= 44Vp= Lời giải

4.ha Do

nêntacó 5  2 2 593 2 a r      Vậy thể tích khối trụ là 29.436.Vrh Câu39: Chohàm số có đạo hàmtrên . Biết là một nguyênhàm của ()yfx = () 0;+¥ 23x ()2 xfx ¢ trên và .Tínhgiá trị () 0;+¥()12f= () ef A. . B. . C. . D. . ()e8f= ()e6e2f=- ()e4f= ()e3e2f=+ Lời giải Theo đề tacó là một nguyênhàm của trên 23x ()2 xfx ¢ () 0;+¥ Do đó thì  0;x () () ()2 2 3xxfxdx ¢ ¢ ¢ =ò ()26xxfx ¢Û= () 6dxfxdx x ¢Û=òò

khoảng cách từ trục của hình trụ đến thiết diện bằng

xCfxÞ+=

Ta lại có: . ()126ln122f CC =Û+=Û= ()6ln2fxx Þ=+()6ln28fee=+=

Câu40: Một hộp gồm quả cầu được đánh số từ đến Lấy

23 123

suất để lấy được quả cầu vàtíchhai số ghitrên quả cầu đó là một

Dotíchhai số ghitrên2 quả cầu là một số chia hết cho6nên

Đặt:  6;12;18A và  3;9;15;21B  2;4;8;10;14;16;20;22C

Khônggian mẫu 2 23nC 

TH1:2 quả cầu có số thuộc A có cách. 2 33C

TH2:1 quả cầu có số thuộc A,1 quả có số không thuộc Acó cách. 11 32060CC

TH3:1 quả cầu có số thuộc B,1 quả cầu có số thuộc Ccó cách. 11 4832CC

Số cách lấy rahai quả cầu màtíchhai số chia hết cho là: cách. 63603295 

9595 253 P C 

Xác suất cần tìmlà: . Chọn B. 2 23

Câu41: Trongkhônggian , gọi làhình chiếu vuônggóc của lên mặt Oxyz'd

nên

(Vì

) () 6.ln

() 0;xÎ+¥lnlnxx =

nhiên quả cầu từ hộp đó. Xác

ngẫu

chia hết cho bằng 2 2 6 A. B. C. D. 8 23 95 253 4 11 98 253

số

Lời giải

2 12 :32, (2) xat dytt zat         phẳng Lấy

thuộc

tổng tất cả :2360 xz  (0;3;2),(3;1;0)M N   cácgiá trị của tham số để a 'MNd  A. B. C. D. 4 3 1 2 Lời giải Theo định líhình chiếu, tacó: ' .0(*) d dMNdMNdMNuMNu   có: 2 (3;2;2);(2;2;2) d MN uaa    (*) 2 2 1 642(2)03404 a aa aa a   

cạnh

SAB giác

Diện tích mặt cầu cótâm và tiếp xúc với mặt phẳng SCD S S

ABCD bằng A. B. C. D. 23 . 4 a p 24 . 3 a p 23 . 2 a p 2 3. ap Lời giải

các điểm

.Tính

Tổng cácgiá trị của là: . a3 Câu42: Chohìnhchóp có đáy làhìnhvuông

bằng ,tamgiác đều vàtam SABCD ABCD a

vuôngcân tại .

()

Gọi lần lượt làtrung điểm của , EF , ABCD Do đều cạnh nên (1)và SAB aSEAB  3 2 Sa E vuôngcân tại nên và SCD SSFCD  1 22 aSFCD Tacó (2) //CDAB ABSF CDSF    Từ (1)và(2) theogiao tuyến  ABSEFABCDSEF  EF Trong kẻ khi đó tại SEFSHEF  SHABCD  H làbánkính mặt cầu cótâm và tiếp xúc với mặt phẳng SH S () ABCD Tacó EFBCa  Xét có vuông tại SEF 22 22 22 3 44 aaSESF aEFSEF S Do đó 222222 11144163 334 Sa H SHSESFaaa  Vậy diện tích mặt cầu cótâm và tiếp xúc với mặt phẳng bằng S () ABCD 2 2 233 44 44 a SR a        Câu43: Chohàm số có đạo hàmliên tục trên đoạn vàcó đồ thị như hình vẽ. yfx   0;8 (S2) (S1) (S3) y x O 8 5 3 3

Biết lần lượt là diện tíchhình phẳng giới hạn bởi đồ thị và 12323,3,15SSS yfx  trục .Giá trị của là Ox   6 32 2 5 299310d Ixxxfxxx    A. B. C. D. 15I 65I 5I 35I Lời giải Tacó . 3 5 8 1 2 3 0 3 5 ()d23,()d3,()d15 SfxxSfxxSfxx        Vậy 8 3 5 8 0 5 3 5 ()d()d()d()d2331535 fxxfxxfxxfxx     Tacó:   6 6 32 2 2 2 5 5 299310d3(23)310d Ixxxfxxxxxxfxxx       Đặt 2310(23)dd xxtxxt   Với ,50xt với .68xt  8 8 8 0 0 0 10d(10)d(())(10)d(()) Itftttftxfx       Tính 8 0 (10)d(())Ixfx   Đặt 8 8 8 0 0 0 10dd (10)d(())(10)()()ddd(())() ux ux xfxxfxfxxvfxvfx                 18(8)10.(0)3518.010.33565. ff   Vậy:   6 32 2 5 299310d65.Ixxxfxxx     Câu44: Chohàm số liên tục trên vàcó đồ thị như hình vẽ bên. yfx  

Tổng tất cả cácgiá trị nguyên của tham số để phương trình có đúng m  5 32log6fxm  3 nghiệm thực thuộc nửa đoạn bằng 1 ;25 25    A. . B. . C. . D. . 69 57 60 66 Lời giải Đặt . 52log tx  Vì nên và mỗi giá trị sẽ có một giá trị 1 ;25 25 x    4;4t 4;4t 1 ;25 25 x    Khi đó bàitoán trở thànhtìm tổng tất cả cácgiátringuyên của tham số để phương trình m có đúng nghiệm thực . 6 3fm t 3 4;4t Phương trình: có đúng nghiệm thực 6 3fm t 3 4;4t 6 11 339 6 212 3 15 6 3 3 m m m m m m              Do nên nên tổng tất cả cácgiá trị nguyên của tham số bằng m  4;5;6;7;8;9;12;15m m . Chọn D. 66 Câu45: Có tất cả baonhiêugiá trị nguyên của tham số saochohàm số  23;0m luôn đồng biến trên khoảng ? ()() () 4 2 2 8e 92023 x fxx mxmmx =----+ () 2;5 A. . B. . C. . D. . 21 19 14 8 Lời giải Tacó: . ()( ) () 4 3 2 482 9 x fxxxemxmm ¢=+---Hàm số đã cho đồng biến trên () 2;5 0,2;5fxx  ( ) () () 4 3 2 482 90,2;5 x xxemxmmx Û+----³"Î Đặt . ()( ) () 4 3 2 482 9 x gxxxemxmm =+---Khi đó ()( )( )( ) 3 2 4 3 4 3 2 412 482 81282 x x x gxxxexxemxxxem ¢=+ ++--=++-Tacó và () () 4 3 2 4 2 3 812812810,2;5xxxxxx x ++-=++->"Î 20,23;0 mm Nên ()( ) () 4 3 2 812820,2;5 x gxxxxemx ¢=++-->"Î Suyrahàm số đồng biến trên , từ đó tacó tập giá trị của hàm số trên gx  2;5 gx 2;5 là .   2;5gg

Vậy hay () ()() 0,2;520gxx g ³"ÎÛ³ 22 4050 emm 2 2525160525160 2 2 e e m     Do nên  23;0m  14;15;;2;1m Vậy có tất cả 14giá trị nguyên của tham số thỏa mãn.  23;0m Câu46: Cholăngtrụ đứng cóchiềucaobằng và làhìnhbìnhhành.Gọi ABCDABCD¢¢¢¢ 4aABCD lầnlượtlàtrungđiểmcủacạnh .Khimặtphẳng tạovớimặtđáycủalăng , MN , AADC ¢ () ANB ¢ trụ mộtgóclà thìkhoảngcáchgiữahai đườngthẳng và bằng o60 DMAN ¢ A. B. . C. . D. . .a 3 2 a 2a 6 2 a Lời giải N E M B' A' C' C A B D D' I K Gọi làtrung điểm cạnh .Suyra E AB MDEANB  Kẻ tại , tại AIDE ^ IAKMI ^ K Tacó .Suyra. ()()( )()()( ) , , 60oANBABCDMDEABCDAIM ¢ = == 0 23 tan603 AMa AI= = Lại có ()() ()() () 1 ,,, .sin2. 2 dANDMdBMDEdAMDEAKAMAMKaa ¢ = = == == Câu47: Chohàm số có đạo hàmtrên vàcó bảng biến thiên như sau: yfx   Số điểm cực đại của hàm số là   2 2 26813gxfxxx   A. . B. . C. . D. . 8 10 9 7

thiên của hàm số :

Dựa vào bảng biến thiên,hàm số có8 điểm cực đại.

gxfu

Câu48: Trongkhônggian , khối đa diện có thể tích với các đỉnh , Oxyz OAMEN 296  0;0;82A ,trong đó làcác số thực dương. Khi thay đổi thì

 5;0;0,0;7;0,;;0

M N Eab , ab , ab

đường thằng tiếp xúc với mặt cầu Mặt cầu cóbánkính nhỏ nhất AE ()2222 : Sxyzc ++= () S

bằng

Lời giải Đặt ,khi đó hàm số khôngcó đạo hàm tại 2 2 ()26813 uxxxx   ()ux 1;4xx    2 2 3621;14; 651;4 xxkhix ux xxkhix            66;14; 261;4 xkhix ux xkhix      Tacó 03uxx  Bảng biến thiên của hàm số :ux Ghép trục để có chiều biến





A. B. C. D. 24666 333 8137 74 27222 37 2474 461 Lời giải

Tacó bốn điểm cùng nằm trên mặt phẳng , ,,, OMNE  Oxy 135 .. 22OMN SOMON   E E E E 11 111 82296 33 2 OAMNEAOMN OMN OMN OMN OMN VVOAS S S S    Do đó nằm ngoàitamgiác E OMN E 117a5111 .5.7 7a51112. 2222OMNOEMOEN b SSSba b    Theo bất đẳng thức Bunhiacôpxkitacó:  2 222222211127a575 333. b abab  Vì tiếp xúc với mặt cầu tâm ,bánkính nên EA  0;0;0O c   22 22 22 2222 22 128. . 3332 ;E 128. 128. . 128 12833312 474 81 46 ab OAOE ab cdOA OAOEab ab             (Dohàm số có đồng biến trên  (),333 128ft t t t    2(128)0,333() 128 ft tft t     ). 333; Vậy mặt cầu cóbánkính nhỏ nhất bằng . () S 2474 461 Câu49: Xétcác số thực saocho luôn đúng với mọi .Có tối , xy () 3 6 3 18-loga 2 216 27+loga783 x y £ 0a> đa baonhiêugiá trị nguyên dương của ? 2225 Kxyxy =+-+ A. B. C. D. 64. 53. 58. 59. Lời giải Tacó   3 618log 2 3 2 216 66 27log()78396loglog2610 xa ya yxaa   