70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC (ĐỀ 71-80) by Dạy Kèm Quy Nhơn Official

Ths

ĐỀ THI THỬ TỐT NGHIỆP THPT MÔN TOÁN

Nguyễ

Thanh Tú

Collection 70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC - CÓ LỜI GIẢI (ĐỀ 71-80) (183 TRANG)

eBook

EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL

COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

WORD VERSION | 2023

TAILIEUCHUANTHAMKHAO@GMAIL

ĐỀ

Câu1: Trongkhônggian,chotamgiác

HỌC 2022-2023

Thể tích của khối chópcó đáy

GIÁO DỤC

ĐÀO TẠO

TRƯỜNG THPT ĐÀO

SỞ

VÀ

TPHCM

SƠN TÂY

THI THỬ TỐT NGHIỆP THPT NĂM

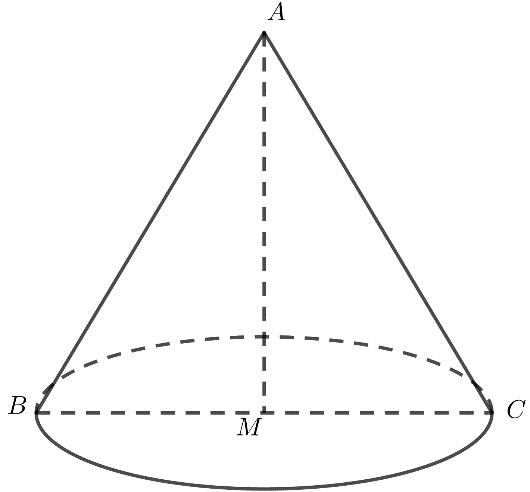
cạnh Gọi làtrung điếm của Khiquaytam ABC2aM BC giác xungquanh trục thì đường gấp khúc tạo thành một hìnhnón.Tính diện tích ABC AM ABC xungquanh của hìnhnón đó A. . B. . C. . D. . 22 xq Sa  24 xq Sa  26 xq Sa  28 xq Sa  Câu2:

làtamgiác đều cạnh và chiều cao bẳng a 4a A. . B. . C. . D. . 33a 34a 33 3 a 34 3 a Câu3: Họ cácnguyênhàm của hàm số là 23 e xfx   A. . B. . 231 de 3 x fxx C   231 de 2 x fxx C   C. . D. . 23dex fxxC    23d2exfxx C   Câu4: Tập xác định của hàm số là  3 42yx A. . B. . C. . D. .  2; 2;   0; Câu5: Trongkhônggian , vectơ là một vectơ pháp tuyến của mặt phẳng nàosau Oxyz  1;1;3n  đây? A. . B. . C. . D. . 330xyz   330xyz 330xyz 330xz Câu6: Hàm số nào dưới đây có đồ thị như đường congtronghìnhbên? A. B. C. D. 21 1 x y x   4221yxx  3221yxx  221yxx  Câu7: Trongkhônggian ,chohaivec tơ và .Tính độ dài . Oxyz  1;1;0u   2;0;1v  2 uv   A. B. C. D. 2 22 30 22 Câu8: Cho khối lăng trụ có diện tích đáy và chiều cao . Thể tích của khối lăng trụ đã cho 5B 6h bằng A. B. C. D. 15 10 180 30 Câu9: Tập nghiệm của bất phương trình là 3 log2 x A. B. C. D.  0;9  0;  9;  ;9 Câu10: Nếu và thì bằng 1 0()d3fxx  3 0()d2fxx  3 1()d fxx

đều

Chọn ngẫu nhiênhai số khácnhau từ 25 số nguyên dương đầu tiên.Xác suất để chọn được hai

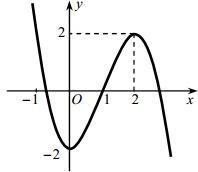
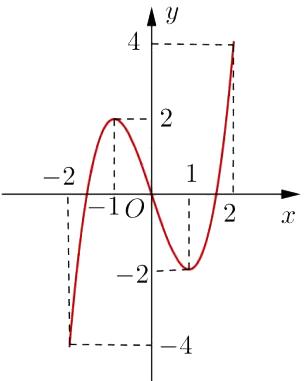
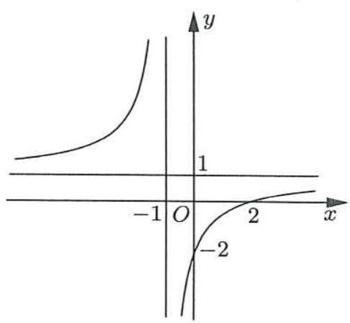
A. B. C. D. 6 5 5 1 Câu11: Với là số nguyên dương bất kỳ, ,công thức nàosau đây đúng? n 3n A. B. C. D. 3! 3!(3)!n An n  3! (3)!n An n  3(3)! ! n An n  33!(3)! ! n An n  Câu12: Phương trình có nghiệm là  log41log25 x x  A. B. C. D. 2x 1x 3x 1x Câu13: Diện tích của mặt cầu bánkính được tínhtheocông thức nào dưới đây? S r A. B. C. D. . 2Sr  24 Sr  22 Sr  24 3 Sr  Câu14: Trongkhônggian cho mặt cầu có phương trình và ,Oxyz () S 22224240xyzxyz đi qua điểm Mặt phẳng nào dưới đây tiếp xúc với mặt cầu tại ? (1;1;0)M SM A. . B. . 330 yz 2350 xyz C. . D. . 320 yz 2350 xyz Câu15: Cho cấp số cộng có số hạng đầu vàcôngsai Giá trị của bằng  n u 12u 5d 4u A. . B. . C. . D. . 17 250 12 22 Câu16: Nếu thì bằng  1 0 ()22fxxdx 1 0() fxdx A. . B. . C. . D. . 4 2 0 1 Câu17: Phần ảo của số phức bằng 34 zi  A. . B. . C. . D. . 4 4 3 4i Câu18: Đường thẳng là đường tiệm cận đứng của đồ thị hàm số nàosau đây? 2x A. B. C. D. 2 x y x  21 1 x y x    2 2 x y x   23 1 x y x    Câu19:

số có tổng là một số chẳn là A. . B. . C. . D. . 313 625 12 25 13 25 1 2 Câu20: Trên đoạn hàm số đạt giá

nàosau đây? 0;2, 42 ()21 fxxx   A. B. C. D. 0x 9x 2x 1x Câu21: Với mọi số thực dương, bằng a 2 2 log4 a A. B. C. D. 2 log2 a  2 2log1 a 2 log1 a 2 2log1 a Câu22: Chohình lăng trụ tamgiác đều có cạnh đáy bằng . Khoảng cách từ điểm đến . ABCABC 2a B mặt phẳng bằng  ACCA A. . B. . C. . D. . 2a 3a 22a 2a Câu23: Cho .Tính theo . 2 log3a 8 log6P a A. B. C. D. 31 Pa  1 1 3 Pa  1 Pa  2 Pa  Câu24: Họ tất cả cácnguyênhàm của hàm số là:  2sin6 fxxx  A. . B. . C. . D. . cos12xxC  3sin2xxC  3cos2xxC  sin12xxC  Câu25: Trongkhônggian , đường thẳng đi qua điểm nào dưới đây? Oxyz 132 : 213 xyz  

trị lớn nhất tại điểm

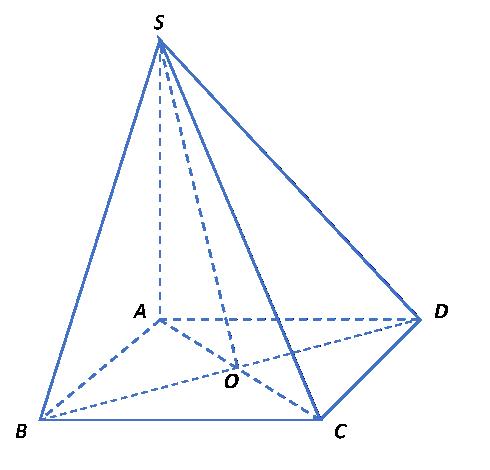
A. Điểm . B. Điểm . C. Điểm . D. Điểm .  1;3;2P  1;3;2N  1;3;2M  1;3;2Q Câu26: Cho số phức thỏa mãn . Tổng phần thực và phần ảo của là z 13170 izi z A. B. C. D. 1 3 3 6 Câu27: Tínhtíchphân bằng cách đặt mệnh đề nào dưới đây đúng? 2 2 1 21d Ixxx  21ux  A. . B. . C. . D. . 2 1 1 d 2 Iuu  2 1 d Iuu  3 0 2d Iuu  3 0 d Iuu  Câu28: Chohai số phức , . Số phức bằng 123 zi  24 zi  12zzz  A. B. C. D. 24i 24i 62i 22i Câu29: Đồ thị hàm số cắt trục tung tại điểm nàosau đây? 3222yxxx  A. . B. . C. . D. .  0;1M  2;0P  0;2Q  1;0N Câu30: Trongkhônggian cho mặt cầu .Tâm mặt cầu có tọa ,Oxyz 222 ():(2)(6)4 Sxyz   () S độ là A. B. C. D.  1;3;0  2;6;0  2;6;0  1;3;0 Câu31: Hàm số nàosau đây đồng biến trên  A. B. C. D. 31yxx 3 2 x y x   31yxx 42 yxx  Câu32: Đạo hàm của hàm số bằng  2 ln21yxx A. . B. . C. . D.   1 1y x   2 1 21y xx   2 1y x  22yx Câu33: Chohàm số có bảng biến thiên như sau: fx Giá trị cực tiểu của hàm số đã cholà CTy A. B. C. D. 1CTy 0CTy 2CTy 3CTy Câu34: Chohìnhchóp có đáy làhìnhvuông cạnh , vuônggóc với đáy và SABCDABCD 2aSA .Góc giữa hai mặt phẳng và bằng 6SAa   SBD ABCD A. . B. . C. . D. . 45 30

theo

 MNP A. B.

432

 43250

 C.

23410

()fx

60 90 Câu35: Trongkhônggian ,cho điểm .Hình chiếu vuônggóc của lêncác trục Oxyz  4;3;2A A

thứ tự là . Phương trình mặt phẳng là ;; OxOyOz ;; MNP

xyz

. 346120 xyz

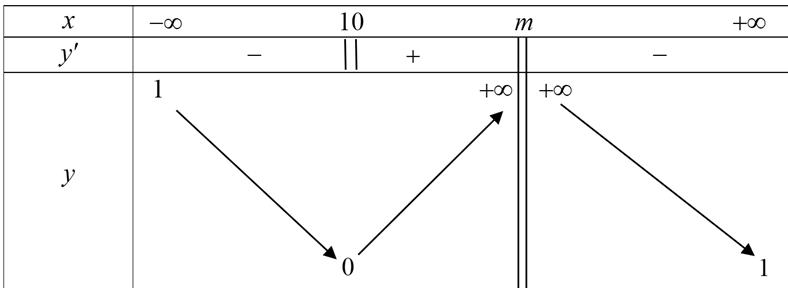
xyz Câu36: Chohàm số có bảng biến thiên như hìnhbên

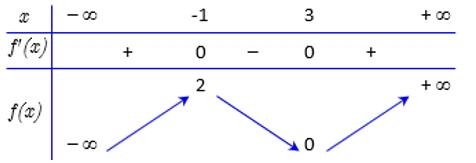
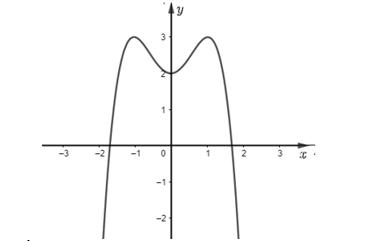
Hàm số đã cho nghịch biến trên khoảng nàotrongcác khoảng dưới đây? A. B. C. D. (1;)  (0;)  (;2)  (1;3) Câu37: Trên mặt phẳng tọa độ, điểm biểu diễn số phức có tọa độ là: 32 zi  A. . B. . C. . D. . (3;2) (2;3) (3;2) (2;3) Câu38: Chohàm số có đồ thị là đường cong như hình vẽ. 42 ,, yaxbxcabc   Giá trị cực tiểu của hàm số đã cholà A. . B. . C. . D. . 1 0 2 1 Câu39: Chohai số phức thỏa mãn và số phức thoả mãn 12 , zz 12 321,22zizzz   w .Giá trị nhỏ nhất của biểu thức bằng: w241 i 2 1 23wPziz   A. . B. C. . D. 26 10 171 4 Câu40: Cóbaonhiêu số nguyên thỏa mãn ? x  2 3 24log2530 xx x      A. B. Vô số. C. . D. . 25 26 24 Câu41: Tìm số giá trị nguyên của tham số thực để tồn tại các số thực thỏa mãn m ; xy . 22 22 22 xymxyxym eexyxyxym     A. B. C. D. 7 9 8 6 Câu42: Trongkhônggian với hệ toạ độ ,chohai mặt phẳng , Oxyz :30Pxyz và mặtcầu . Gọi làđiểmdi động :2250Qxyz   222 :246110 Sxyzxyz  M trên và là điểm di động trên saocho luônvuônggóc với .Giá trị lớn nhất SN PMN  Q của độ dài đoạn thẳng bằng MN A. . B. . C. . D. . 953  14 28 353 

Câu43: Trongkhônggian với hệ tọa độ , từ điểm ta kẻ các tiếp tuyến đến mặt cầu có Oxyz () 1;1;0A () S

tâm ,bánkính . Gọi là một trongcác tiếp điểm ứng với các tiếp tuyến () 1;1;1I- 1R= () ;; Mabc

trên.Tìmgiá trị lớn nhất của biểu thức . 22 Tabc =-+

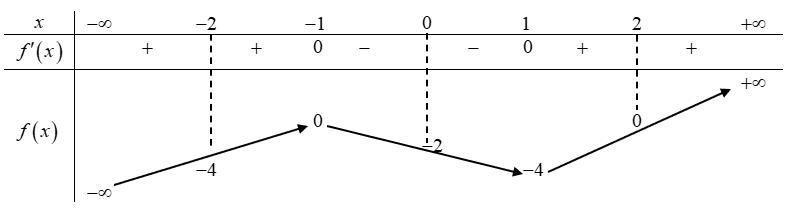
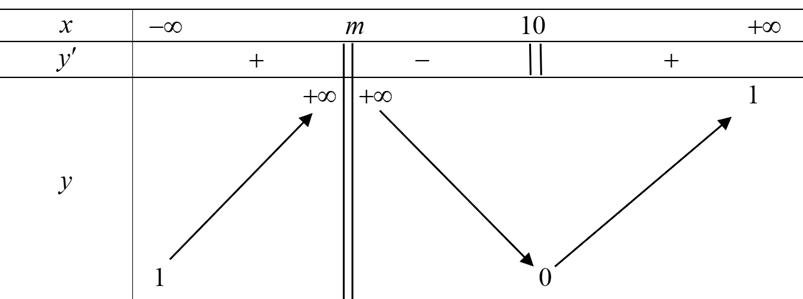
Câu44: Chohàm số liên tục trên vàcó bảng biến thiên như sau

Cóbaonhiêugiá trị nguyên của tham số để phương trình có10 nghiệm

phân biệt thuộc đoạn . 3;3

. 3 1 0 2

Câu45: Chohình

Gọi lần lượt làhai điểm cực trị thỏa mãn và và đồ thị 12 , xx 212xx 1230fxfx

luôn đi qua trong đó làhàm số bậc haicó đồ thị qua điểm   00 ; Mxfx 011;xx  gx 2

cực trị của đồ thị hàm số và điểm Tính tỉ số ( và lần lượt là diện tích yfx  .M

haihình phẳng được tạo bởi đồ thị haihàm như hình vẽ).

, fxgx

A. B. C. D. 341 . 15  341 . 5  3241 . 15  3241 . 5 



 

yfx



ffx m   

. B. .

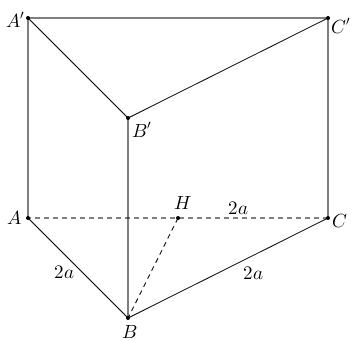
lăngtrụ cóđáy làtamgiácvuôngtại vàgóc . . ABCABCABC ,2 ABCa   60ABC  Biết tứ giác làhìnhthoicó nhọn, mặt phẳng vuônggóc mặt phẳng BCCB  BBC   BCCB ,góc giữa hai mặt phẳng và bằng . Thể tích khối lăng trụ bằng  ABC  ABBA ABC45 A. B. C. D. 3 7 a 3 37 a 33 7 a 36 7 a Câu46:

yfx 

Chohàm số bậc ba có đồ thị là đường cong ở hìnhbên dưới.

S S



A. . B. . C. . D. . 4 29 5 32 7 33 6 35

Câu47: Chohàm số bậc ba có đồ thị như hình vẽ bên dưới.

Số nghiệm thực của phương trình là  4222fxx

A. . B. C. D. 7 9 10 8

Câu48: Trên tập hợp số phức, xét phương trình làtham số thực). Gọi là một giá  260 zzmm  0m

trị nguyêncủa đề phươngtrìnhđócóhai nghiệmphânbiệt thỏamãn .Trong m 12 , zz 12 12 ..zzzz 

khoảng cóbaonhiêugiá trị nguyên ?  0;20 0m

A. B. C. D. 13 10 11 12

Câu49: Trongkhônggian ,chohai điểm , .Xét khối nón ngoại tiếp mặt Oxyz  2;1;3A  6;5;5B  N

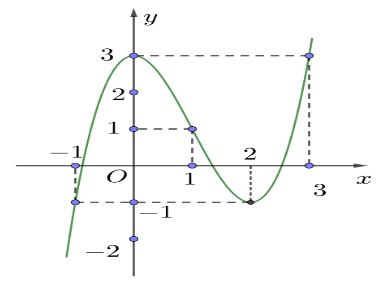
cầu đường kính có làtâm đường tròn đáy khối nón. Gọi là đỉnh của khối nón . ABB S  N

Khi thể tích khối nón nhỏ nhất thì mặt phẳng qua đỉnh vàsongsong với mặt phẳng chứa

yfx 

 N S đường tròn đáy của

trình .Tính .  N 2 0xbyczd Tbcd  A. . B. . C. . D. . 12T 18T 24T 36T Câu50: Chohàm

Biết và ,khi đó fx 51f  1 0 5d1xfxx  bằng  5 2 0 xfxdx  A. B. C. D. 25 23 15 123 5 -------HẾT------

có phương

số có đạo hàmliên tục trên .

BẢNG ĐÁP ÁN 1.A 2.C 3.B 4.A 5.C 6.B 7.C 8.D 9.A 10.B 11.B 12.A 13.B 14.A 15.A 16.D 17.A 18.A 19.B 20.C 21.B 22.B 23.B 24.C 25.B 26.A 27.D 28.A 29.C 30.C 31.C 32.C 33.D 34.C 35.C 36.D 37.A 38.C 39.C 40.C 41.B 42.A 43.D 44.C 45.C 46.B 47.D 48.B 49.A 50.A HƯỚNG DẪN GIẢI CHI TIẾT. Câu1: Trongkhônggian,chotamgiác đều cạnh Gọi làtrung điếm của Khiquaytam ABC2aM BC giác xungquanh trục thì đường gấp khúc tạo thành một hìnhnón.Tính diện tích ABC AM ABC xungquanh của hìnhnón đó A. B. C. D. 22 xq Sa  24 xq Sa  26 xq Sa  28 xq Sa  Lời giải Tacóhìnhnóncóbánkính đường tròn đáy , đường sinh rBMa  2 lABa  Do đó diện tíchxungquanh của hìnhnónlà . Chọn A 22 xq Srla  Câu2: Thể tích của khối chópcó đáy làtamgiác đều cạnh và chiều cao bẳng a 4a A. . B. . C. . D. . 33a 34a 33 3 a 34 3 a Lời giải Tacó: . Chọn C 2 3 1133 4 3343 aaVBh a   Câu3: Họ cácnguyênhàm của hàm số là 23 e xfx   A. . B. . 231 de 3 x fxx C   231 de 2 x fxx C   C. D. 23dex fxxC    23d2exfxx C   Lời giải Áp dụng công thức nguyênhàm mở rộng ,tacó . 1 ede axb axb x C a    2323 1 ede 2 x x x C    Câu4: Tập xác định của hàm số là  3 42yx A. . B. . C. . D. .  2; 2;   0;

Lời giải Điều kiện 202x x  Vậy tập xác định của hàm số là . 2;D Câu5: Trongkhônggian , vectơ là một vectơ pháp tuyến của mặt phẳng nàosau Oxyz  1;1;3n  đây? A. . B. . C. . D. . 330xyz   330xyz 330xyz 330xz Lời giải Mặt phẳng có một vectơ pháp tuyến là: . :330Pxyz  1;1;3n  Câu6: Hàm số nào dưới đây có đồ thị như đường congtronghìnhbên? A. B. C. D. 21 1 x y x   4221yxx  3221yxx  221yxx  Lời giải Nhìnvào đồ thị là đồ thị của hàm số trùng phương bậc bốn. Câu7: Trongkhônggian ,chohaivec tơ và .Tính độ dài . Oxyz  1;1;0u   2;0;1v  2 uv   A. B. C. D. 2 22 30 22 Lời giải Tacó ; . 2;5uv   1210012uv  Suyra . 22 2 24424.24.530uvuuvv   Vậy 230uv  Câu8: Cho khối lăng trụ có diện tích đáy và chiều cao . Thể tích của khối lăng trụ đã cho 5B 6h bằng A. . B. . C. . D. . 15 10 180 30 Lời giải Thế tích khối lăng trụ: ..5.630VBh Câu9: Tập nghiệm của bất phương trình là 3 log2 x A. B. C. D.  0;9  0;  9;  ;9 Lời giải

Tacó: . 3 2 0 log209 3 x x x x    Câu10: Nếu và thì bằng 1 0()d3fxx  3 0()d2fxx  3 1()d fxx A. B. C. D. 6 5 5 1 Lời giải Tacó: . 3 3 1 1 0 0 ()d()d()d5 fxxfxxfxx    Câu11: Với là số nguyên dương bất kỳ, ,công thức nàosau đây đúng? n 3n A. . B. . C. . D. . 3! 3!(3)!n An n  3! (3)!n An n  3(3)! ! n An n  33!(3)! ! n An n  Lời giải Câu12: Phương trình có nghiệm là  log41log25 x x  A. . B. . C. . D. . 2x 1x 3x 1x Lời giải  5250 log41log25 22 41252 x x x x x xx x             Câu13: Diện tích của mặt cầu bánkính được tínhtheocông thức nào dưới đây? S r A. . B. C. . D. . 2Sr  24 Sr  22 Sr  24 3 Sr  Lời giải Diện tích mặt cầu bánkính làr 24 Sr  Câu14: Trongkhônggian cho mặt cầu có phương trình và ,Oxyz () S 22224240xyzxyz đi qua điểm Mặt phẳng nào dưới đây tiếp xúc với mặt cầu tại ? (1;1;0)M SM A. B. 330 yz 2350 xyz C. . D. . 320 yz 2350 xyz Lời giải Mặt cầu cótâm vàbánkính . () S  1;2;1I  2 2 2 121410R  Để mặt phẳng tiếp xúc với mặt cầu tại   SM   ; dIR   Thử đáp ánAtacó .   22 3213 ; 10 31 dI R      Do đó mặt phẳng tiếp xúc với mặt cầu tại 330 yz SM Câu15: Cho cấp số cộng có số hạng đầu vàcôngsai Giá trị của bằng  n u 12u 5d 4u A. . B. . C. . D. . 17 250 12 22

nghĩa số phức, phần ảo của số phức

Câu19: Chọn ngẫu nhiênhai số khácnhau từ 25 số nguyên dương đầu tiên.Xác suất để chọn được hai

Lời giải Tacó 41323517uud Câu16: Nếu thì bằng  1 0 ()22fxxdx 1 0() fxdx A. B. C. D. 4 2 0 1 Lời giải Tacó: .  1 0 ()22 fxxdx   1 1 1 0 0 0 d2d2d12     fxxxxfxx  1 0 d1fxx   Câu17: Phần ảo

bằng 34 zi  A. B. C. D. 4 4 3 4i Lời giải Từ định

là 34 zi  4 Câu18: Đường thẳng là đường tiệm cận đứng của đồ thị hàm số nàosau đây? 2x A. B. C. D. 2 x y x  21 1 x y x    2 2 x y x   23 1 x y x    Lời giải Vì ( hoặc )nên đường thẳng là đường tiệm cận đứng của 2 lim 2  x x x 2 lim 2   x x x 2x đồ

hàm số 2 x y x 

số

số chẳn là A. . B. . C. . D. . 313 625 12 25 13 25 1 2 Lời giải Chọn ngẫu nhiên số khácnhau từ thẻ nên . 2 25 2 25C Gọi là biến cố: “hai số có tổng là một số chẵn”. A -TH1: Chọn số đều lẻ trong tổng số số lẻ: cách chọn 2 132 13C -TH2: Chọn số đều chẵn trong tổng số số chẵn: cách chọn 2 12 2 12C 22 1312ACC Xác suất 22 1312 2 25 12 25 A ACC P C     Câu20: Trên đoạn hàm số đạt giá trị lớn nhất tại điểm nàosau đây? 0;2, 42 ()21 fxxx   A. B. C. D. 0x 9x 2x 1x Lời giải Tacó:

của số phức

thị

có tổng là một

    3 2 3 ()44 0 ()04404101 1 fxxx xTM fxxxxx xTM xKTM           Khi đó:  01;10;29fff   khi 0;2 29Maxfxf 2x Câu21: Với mọi số thực dương, bằng a 2 2 log4 a A. B. C. D. 2 log2 a  2 2log1 a 2 log1 a 2 2log1 a Lời giải  2 2 2222 2 logloglog42log22log1 4 a a a a    Câu22: Chohình lăng trụ tamgiác đều có cạnh đáy bằng . Khoảng cách từ điểm đến . ABCABC 2a B mặt phẳng bằng  ACCA A. . B. . C. . D. . 2a 3a 22a 2a Lời giải Gọi làtrung điểm H AC Tacó .  BHAC BHACCA BHAA      3 , 2.3 2 dBACCABHaa    Câu23: Cho .Tính theo . 2 log3a 8 log6P a A. B. C. D. 31 Pa  1 1 3 Pa  1 Pa  2 Pa  Lời giải   3 8 2 22 2 2 11 11 log6log2.3log2.3log2log31log31 33 33 P a     Câu24: Họ tất cả cácnguyênhàm của hàm số là:  2sin6 fxxx  A. . B. . C. . D. . cos12xxC  3sin2xxC  3cos2xxC  sin12xxC 

Lời giải  2 3sin6dcos2xxxxxC    Câu25: Trongkhônggian , đường thẳng đi qua điểm nào dưới đây? Oxyz 132 : 213 xyz   A. Điểm . B. Điểm . C. Điểm . D. Điểm .  1;3;2P  1;3;2N  1;3;2M  1;3;2Q Lời giải Điểm thuộc đường thẳng vì (thỏa mãn).  1;3;2N 113322 0 213   Câu26: Cho số phức thỏa mãn . Tổng phần thực và phần ảo của là z 13170 izi z A. . B. . C. . D. . 1 3 3 6 Lời giải Tacó:    2 13170 11713 7 137212010 2 1313131910 izi iiiiii i z i iii         Vậy tổng phần thực và phần ảo của là . z 211  Câu27: Tínhtíchphân bằng cách đặt mệnh đề nào dưới đây đúng? 2 2 1 21d Ixxx  21ux  A. B. C. D. 2 1 1 d 2 Iuu  2 1 d Iuu  3 0 2d Iuu  3 0 d Iuu  Lời giải Đặt 21ux  d2duxx Đổi cận 10xu 23xu Khi đó tacó . 1 0 d Iuu  Câu28: Chohai số phức , . Số phức bằng 123 zi  24 zi  12zzz  A. . B. . C. . D. . 24i 24i 62i 22i Lời giải Tacó . 12(23)(4)24 zzziii   Câu29: Đồ thị hàm số cắt trục tung tại điểm nàosau đây? 3222yxxx  A. B. C. D.  0;1M  2;0P  0;2Q  1;0N Lời giải Cho ta được ,suyra đồ thị cắt trục tại điểm . 0x 2y Oy  0;2Q Câu30: Trongkhônggian cho mặt cầu .Tâm mặt cầu có tọa ,Oxyz 222 ():(2)(6)4 Sxyz   () S độ là

A. . B. . C. . D. .  1;3;0  2;6;0  2;6;0  1;3;0 Lời giải Mặt cầu (S)cótâm  2;6;0I Câu31: Hàm số nàosau đây đồng biến trên  A. . B. . C. . D. . 31yxx 3 2 x y x   31yxx 42 yxx  Lời giải Xéthàm số có tập xác định và .Do đó hàm số này 31yxx  2 310, yxx  đồng biến trên  Câu32: Đạo hàm của hàm số bằng  2 ln21yxx A. B. C. D.   1 1y x   2 1 21y xx   2 1y x  22yx Lời giải Điều kiện xác định: 22101xxx Khi đó tacó .         2 2 2 21222 12121 xxx y xxxxx Câu33: Chohàm số có bảng biến thiên như sau: fx Giá trị cực tiểu của hàm số đã cholà CTy A. B. C. D. 1CTy 0CTy 2CTy 3CTy Lời giải Dựa vào bảng biến thiêntacó 3CTy Câu34: Chohìnhchóp có đáy làhìnhvuông cạnh , vuônggóc với đáy và SABCDABCD 2aSA .Góc giữa hai mặt phẳng và bằng 6SAa   SBD ABCD A. B. C. D. 45 30 60 90 Lời giải

Tacó:

SBDABCDBD  

(), OAABCDOABD   (Vì ) (), SOSBDSOBD   ()BDSAC  nênsuyra .   ; SBDABCDAOS   22.6 tan 360 22 SASAa AOS AOS AOACa 

Câu35: Trongkhônggian ,cho điểm .Hình chiếu vuônggóc của lêncác trục Oxyz  4;3;2A A

theo thứ tự là . Phương trình mặt phẳng là ;; OxOyOz ;; MNP  MNP

A. . B. . 10 432 xyz 43250 xyz

C. D. 346120 xyz23410 xyz Lời giải

Tacó tọa độ hình chiếu vuônggóc của lêncác trục là A ;; OxOyOz

 4;0;0;0;3;0;0;0;2MNP

Phương trình mặt phẳng là MNP 1346z120 432 xyz xy 

Câu36: Chohàm số có bảng biến thiên như hìnhbên ()fx

Hàm số đã cho nghịch biến trên khoảng nàotrongcác khoảng dưới đây?

Dựa vào bảng biến thiêntachọn đáp ánD



D. . (1;)  (0;)  (;2)  (1;3) Lời giải

Câu37: Trên mặt phẳng tọa độ, điểm biểu diễn số phức có tọa độ là: 32 zi 

A. B. C. D. (3;2) (2;3) (3;2) (2;3)

Lời giải

Điểm biểu diễn số phức có tọa độ là 32 zi  (3;2)

Câu38: Chohàm số có đồ thị là đường cong như hình vẽ. 42 ,, yaxbxcabc  

Giá trị cực tiểu của hàm số đã cholà A. B. C. D. 1 0 2 1

Giá trị cực tiểu của hàm số đã cholà 2y

Lời giải

Câu39: Chohai số phức thỏa mãn và số phức thoả mãn 12 , zz 12 321,22zizzz   w .Giá trị nhỏ nhất của biểu thức bằng: w241 i

Gọi lần lượt là điểm biểu diễn số phức trên mặt phẳng toa độ. , MN 12 , zz thuộc đường thẳng . 321ziz  , MN 30xy

2222zz MN 

Gọi là điểm biểu diễn số phức K w thuộc đường tròntâm ,bánkính w241 iK

2 1

B. C. . D.

4 Lời

23wPziz  

26 10 171

giải



2 1

2;4I 1R Đặt .Tacó 2;3A

23w PzizNAMK  

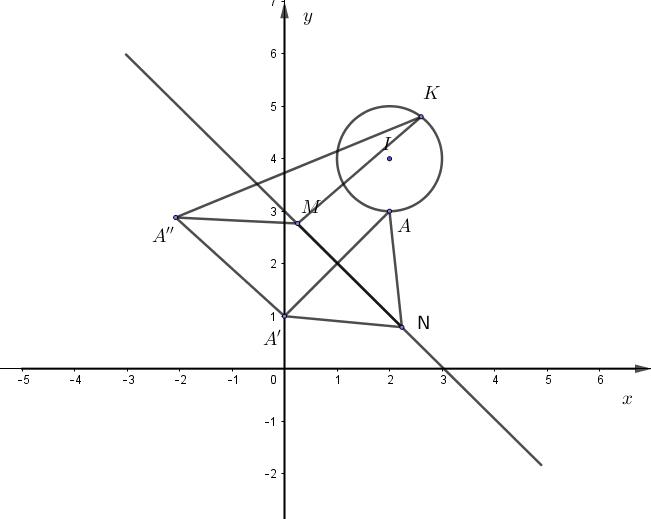
Gọi là điểm đối xứng với qua A Ad 0;1A  Dựng saocho A AANM    2;3A  Tacó PNAMKNAMKMAMKAK    Mà  22 22431171AKAIR     Vậy min171P Câu40: Cóbaonhiêu số nguyên thỏa mãn ? x  2 3 24log2530 xx x      A. B. Vô số. C. . D. . 25 26 24 Lời giải Điều kiện: 25x Tacó: 2 2 0 2402 2 xx x xx x   3 log253025272 x x x  Bảng xét dấu Vậy nêncó26giá trị.  24;23;...;0;2x Câu41: Tìm số giá trị nguyên của tham số thực để tồn tại các số thực thỏa mãn m ; xy 22 22 22 xymxyxym eexyxyxym     A. B. C. D. 7 9 8 6 Lời giải Xéthàm số 1;t ftett  

có9giá trị nguyên của tham số thỏa mãn. m

Câu42: Trongkhônggian với hệ toạ độ ,chohai mặt phẳng , Oxyz

:2250Qxyz  

:30Pxyz

và mặtcầu . Gọi làđiểmdi động

và . 1tfte   00ftt  Ta thấy đổi dấu từ sang khiqua nên . ft  “”“”  0t 00; ftft Do đó .    22 2210,, 10,, xym xyxym exymxy exyxymxy              Dấu xảy rakhivà chỉ khi . “”  22 xym xyxym    Hay   22 22 22 1 22 2 xymxyxym xym eexyxyxym xyxym         Đặt ,tacó: .Vì ;. SxyPxy  2 2 2 30 SPm SSP SPm        240;4SPS Lấy vế theo vế ta được:  122   2233SSm  Xéthàm số ,có .   22;0;4fSSSS  220;0;4fSSS  Yêu cầu bàitoán

.  3  0408fmf m  Vậy

có nghiệm



222 :246110 Sxyzxyz  M trên và là điểm di động trên saocho luônvuônggóc với .Giá trị lớn nhất SN PMN  Q của độ dài đoạn thẳng bằng MN A. . B. . C. . D. . 953  14 28 353  Lời giải Mặt cầu cótâm vàbánkính . Mặt phẳng cóVTPT ,  S  1;2;3I 5R  P  1;1;1Pn  mặt phẳng cóVTPT .  Q  1;2;2Qn  Đường thẳng đi quahai điểm nhận làmVTCP, luôn cắt , gọi  , MN  1;2;2Qn    P làgóc giữa và , làhình chiếu vuônggóc của lên .   PH M P Tacó 1 sincos, 3PQnn   vuông tại MNH Hsin MNMH   3 sin MH MN MH   .     ,,533,MHdMPRdIP MS    3953MNMH  Vậy giá trị lớn nhất của bằng MN953. 





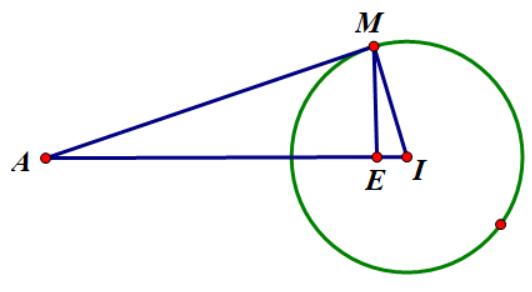
Câu43: Trongkhônggian với hệ tọa độ , từ điểm ta kẻ các tiếp tuyến đến mặt cầu có Oxyz () 1;1;0A () S

tâm ,bánkính . Gọi là một trongcác tiếp điểm ứng với các tiếp tuyến () 1;1;1I- 1R= () ;; Mabc

trên.Tìmgiá trị lớn nhất của biểu thức . 22 Tabc =-+

A. B. C. D. 341 . 15  341 . 5  3241 . 15  3241 . 5  Lời giải

nêntamgiác vuông tại AM SAMIM  IAM M Xét ,có: IAM 5,1IAIM 222MAIAR  thuộc mặt cầu tâm bánkínhlà . M A 2 Khi đó thuộc đường tròngiao tuyến của mặt cầu tâm bánkính và mặt cầu tâm M  C I 1R bánkính . A 2R    2 22 2 22 1111 : :220 114 xyzCP CPxz xyz             Tacó , gọi làtâm đường tròngiao tuyến, khi đó:  12 :1, xt IAyt zt      E .Xét ,có: 34 ;1; 55 EIAPE   IAM .2 5 MAMI rEM IA   thuộc mặt cầu tâm bánkính hay M 34 ;1; 55 E   2 5 R  2 2 2 3 44 1 5 55 abc         Do 22022MPac ca  Khi đó tacó được  2 2 2 3 64 12 5 55 64 aba Tab           

Do là tiếp tuyến của mặt cầu nên

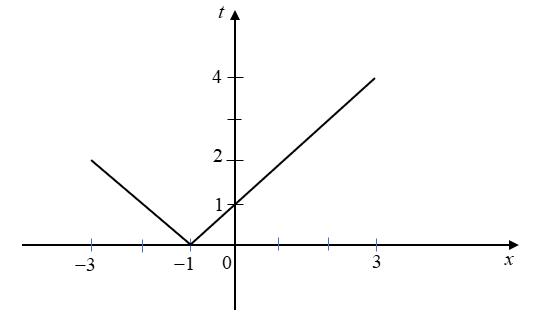
.   2 2 2 2 2 3 643 4 12 5 1 5 5555 aba a b                Tacó .  633 6451 555 ab ab     Áp dụng bất đẳng thức bunhiacopski:    2 2 2 2 63 3 6241 51511 5 55 5 5 ab a b                                 24163241 51 5 555 ab         . 24132413 3241 64 64 55 55 55 ab ab    Câu44: Chohàm số liên tục trên vàcó bảng biến thiên như sau yfx   Cóbaonhiêugiá trị nguyên của tham số để phương trình có10 nghiệm m 12ffx m    phân biệt thuộc đoạn  3;3 A. . B. . C. . D. . 3 1 0 2 Lời giải Đặt .Vì suyra . 1tx  3;3x  0;4t Với mỗi giá trị chota2 nghiệm . 0;2t  3;3x Với mỗi giá trị chota1 nghiệm 02;4t  3;3x

2 fftm  t t 0;2

đa 4 nghiệm . Giả sử cả 4 nghiệm đó đều thuộc thìcho tối đa

8 nghiệm .Theoyêu cầu bàitoánra10 nghiệm nênkhôngcó thỏa yêu cầu. x m

Vậy khôngcógiá trị nào của thỏa mãn. m

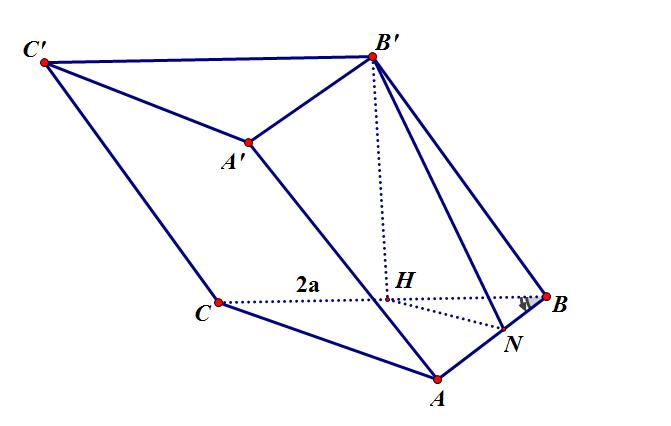
Câu45: Chohìnhlăngtrụ cóđáy làtamgiácvuôngtại vàgóc .

Phương trình trở thành .   2 fftm  Xéthàm trên đoạn .  2gtfft   0;4  2gtftfft   .        1 21 1 11 0 1(L) 0 12 2120 2 3 21 t t t ft t gt fttt ft fft tttft ft                                Vậy hàm số có tối đa

trị

trình 

gtfft   0;4 có tối

 

3 cực

trên đoạn .Suyra phương

ABCABC

,2 ABCa   60ABC

 Biết tứ giác làhìnhthoicó nhọn, mặt phẳng vuônggóc mặt phẳng BCCB  BBC   BCCB ,góc giữa hai mặt phẳng và bằng . Thể tích khối lăng trụ bằng  ABC  ABBA ABC45 A. . B. . C. . D. . 3 7 a 3 37 a 33 7 a 36 7 a Lời giải Tacó:

ABC



thị hàm số và điểm Tính tỉ số ( và lần lượt là diện tích

haihình phẳng được tạo bởi đồ thị haihàm như hình

()()( )( )  ()   0 0 222 2 2 2 2 , ''' ;' '' ,,''45 '''.2 ' .cot60 3 ''' ' 4'.2 3 '23 7 cos 1 3sin 2 2 ' ABC ABCABCABC HNABBNABABBAABCHNBNBNH HNBHBNBH BH HBNBNHN BNNBBBNBN BH aBH a BH ABCABBCABCa aSABBCABC V SB D D ^ ^Þ = == Þ=Þ= DÞ= = DÞ=+ æö ç÷ Û= +÷ ç÷ ç÷ èø Þ= DÞ= = Þ= = = 2 33233 277 aaa H= = Câu46: Chohàm số bậc ba có đồ thị là đường cong ở hìnhbên dưới. yfx  Gọi lần lượt làhai điểm cực trị thỏa mãn và và đồ thị 12 , xx 212xx 1230fxfx luôn đi qua trong đó làhàm số bậc haicó đồ thị qua điểm   00 ; Mxfx 011;xx  gx 2 cực trị của đồ

yfx  .M 1 2 S S1S2S

vẽ).  , fxgx A. . B. . C. . D. . 4 29 5 32 7 33 6 35 Lời giải Khita tịnh tiến đồ thị saocho khi đó diện tíchhình phẳng khôngthay đổi. 00x , đặt 121;3xx    32 2 ; fxaxbxcxdgxmxnxq   2 '32 fxaxbxc  Vìhàm số đạt cực trị tại và nêntacó hệ phương yfx  121;3xx  1330ff trình.

 32 320 6 2760 9 692 80268202 abc ba abc cafxaxxx abcdda                 Màhai đồ thị giaonhau tại 3 điểm nêntacó hệ phương trình:     2 002 112 262 622 gfqda gfmagxaxx nagf              1 3 32 32 1 1 2 2 0 1 5 85 .43.;.43. 12 332 a aS Saxxxdx Saxxxdx S       Câu47: Chohàm số bậc ba có đồ thị như hình vẽ bên dưới. yfx  Số nghiệm thực của phương trình là  4222fxx A. . B. C. D. 7 9 10 8 Lời giải Phương trình         42 42 42 22 22 22 fxx fxx fxx * Phương trình .     42 42 42 42 2,10 222,01 2,23 xxbb fxx xxcc xxdd           * Phương trình .   42 42 222,21fxx xxaa  Bảng biến thiên của hàm số như sau: 42 2 yxx 

Dựa vàoBBTtrêntacó:

- Phương trình khôngcó nghiệm thực. 422,21xxaa

- Phương trình có4 nghiệm thực phân biệt. 422,10xxbb

- Phương trình có2 nghiệm thực phân biệt. 422,01xxcc

- Phương trình có2 nghiệm thực phân biệt. 422,23xxdd

 4222fxx

Vậy phương trình có8 nghiệm thực phân biệt.

260 zzmm

Câu48: Trên tập hợp số phức, xét phương trình làtham số thực). Gọi là một giá

trị nguyêncủa đề phươngtrìnhđócóhai nghiệmphânbiệt thỏamãn .Trong m 12 , zz 12 12zzzz 

khoảng cóbaonhiêugiá trị nguyên ?

Lời giải

Xét phương trình 260zzm

Tacó: . 2 39mm

TH1: Phương trìnhcóhai nghiệm phức phân biệt . 12 9,090zz mm 

Vậy  9;m

Mà . ;0;2010;;19mm m  



zz zz   



TH2: Phương trìnhcóhai nghiệm thực phân biệt 12 9,090zz mm 



zzzzzz zzN z



Vậy có giá trị thỏa mãn. 10



Câu49: Trongkhônggian ,chohai điểm , .Xét khối nón ngoại tiếp mặt Oxyz  2;1;3A  6;5;5B

 N







A. . B. . C. . D. .

10 11 12

0;20 0m

Suyra phương trìnhcóhai nghiệm phức thỏa mãn: . 12 21

Tacó: (luôn đúng) 1121221 2 .... zzzzzz z z

zzL



    



Tacó:

12 121122 12 12z

(vôlý) 120zz



cầu đường kính có làtâm đường tròn đáy khối nón. Gọi là đỉnh của khối nón . ABB S

Khi thể tích khối nón nhỏ nhất thì mặt phẳng qua đỉnh vàsongsong với mặt phẳng chứa

đường tròn đáy của có phương trình .Tính .  N 2 0xbyczd

Mặt cầu đường kính cótâm ,bánkính .

Giả sử thiết diện qua trục hìnhnónlàtamgiác . SMN

Gọi , lần lượt làbánkính đáy và chiều cao của hìnhnón(). rh 6h

S R P 





N S

Tbcd  A.

C. . D. . 12T

 24T 36T

18T

Lời giải



S AB 4;3;4I 3 2 AB R



  1

32 1 2

SMSNMN   22 3 rh rrh    223rrhrh . 29 6 h r h  Thể tích khối nónlà . 2 2 19 . 336 hVrhhfhπ π    2 2 12 3 6 fhh h h  π  0 0 12 h fhh  Bảng

thiên đạt

làtâm đường tròn nội tiếp của tamgiác tacó: I SMN SMN SMN V

MNSB

biến

giá trị nhỏ nhất

12h

Tacó . 32;3;1ISBIS   Phương trình mặt phẳng qua ,có vec-tơ pháp tuyến là  P 2;3;1S 22;2;1AB  2290 xyz Suyra ; ; . Vậy . 2b1c9d 12Tbcd Câu50: Chohàm số có đạo hàmliên tục trên . Biết và ,khi đó fx 51f  1 0 5d1xfxx  bằng  5 2 0 xfxdx  A. B. C. D. 25 23 15 123 5 Lời giải Tacó  1 0 5d1xfxx  Đặt 5d5d uxux  Đổi cận: 00xu .15xu Ta được .  1 0 5d1xfxx    5 5 0 0 d11d1 5525 uu fu ufuu       5 0 d25ufuu   Suyra .  5 0 d25xfxx  Gọi  5 2 0 d Ixfxx   Đặt   2 d2d dd uxx ux vfxvfxx                 5 2 0 5 .2d 0 Ixfxfxxx    5 0 2552d fxfxx 2522525  -------HẾT------

với hệ trục tọa độ ,cho đường thẳng

điểm nàotrongcác điểm sau:

3;4;5D

1;2;3A

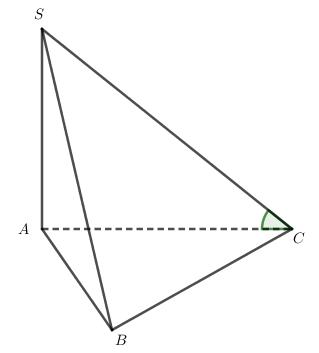
Câu5: Cho khối chóp có đáy làtamgiácvuôngcân tại , vuônggóc với đáy và . SABC ,2AABSA (tham khảo hìnhbên). 3SA

Thể tích khối chóp đã cho bằng

A. 12. B. 2. C. 6. D. 4.

Câu6: Trongkhônggian với hệ tọa độ ,cho mặt cầu .Tính Oxyz 222 :22420 Sxyzxyz  

bánkính của mặt cầu. r

A. . B. . C. . D. . 22r 26r 4r 2r

Câu7: Cho một tổ có15thànhviên. Số cách chọn ra2 người lần lượt làm tổ trưởng và tổ phólà A. B. C. D. 225 30 210 105

Câu8: Trongkhônggian ,cho

SỞ GIÁO DỤC VÀ ĐÀO TẠO THÁIBÌNH TRƯỜNG THPT PHỤ DỰC ĐỀ THI THỬ TỐT NGHIỆP THPT– NĂM HỌC 2022–2023 Câu1: Tập nghiệm của bất phương trình là 1 24 x A. B. C. D. ;1  1; 1;  ;1 Câu2: Tích tất cả các nghiệm của phương trình bằng 2 22 log3log20 xx A. B. C. D. 8 6 16 2 Câu3: Cho . Khẳng định nào dưới đây đúng?  2 1 d ln xFxC xx   A. B. C. D. 1 lnx Fx   1 lnx FxC  2 1 ln Fx xx   2 1 ln Fx x   Câu4: Trongkhônggian

Hỏi

123

  dxyzd qua

C. . D. . 

C 



đi Oxyz

: 345

3;4;5

1;2;3B

điểm Điểm đối xứng với qua mặt phẳng có Oxyz  1;2;3A A  Oyz tọa độ là A. . B. . C. . D. .  1;2;3  1;2;3  1;2;3  1;2;3 Câu9: Trongkhônggian , mặt phẳng có một vectơ pháp tuyến là: Oxyz :230Pxz A. B. C. D. 11;0;2n  41;2;3n  31;2;0n  21;2;3n  Câu10: Đạo hàm của hàm số là: x y

Câu12: Chohàm số có đồ thilà đường congtronghìnhbên.

Toạ độ giao điểm của đồ thị hàm số đã chovà trục tunglà:

 0;2  2;0  2;0  0;2

Câu13: Chohàm số xác định vàliên tục trên đoạn có vàcó đồ thị là đường congtrong yfx   2;2 hình vẽ bên.

Giá trị cực tiểu của hàm số là: yfx 

A. B. C. D. 4 2  1;2 1x

Câu14: Chohàm số bậc ba có đồ thị là đường congtronghìnhbên. yfx 

Cóbaonhiêugiá trị nguyên của tham số để phương trình cóba nghiệm thực phân m  fxm  biệt?

A. B. C. D. lnx y   1x yx  ln x y     1 1 x y x     

và . Đường thẳng có phương Oxyz  1;1;1M  5;5;1N MN trìnhlà: A. B. C. D. 52 53 1 xt yt zt      5 52 13 xt yt zt      32 23 xt yt zt      12 1 13 xt yt zt     

Câu11: Trongkhônggian ,chohai điểm

axb ycxd   

B. C. D.

A. B. C. D. 2 5 3 4 Câu15: Chohàm số liên tục trên đoạn Diện tíchhình phẳng giới hạn bởi đồ thị hàm số yfx   ; ab , trục hoànhvàhai đường thẳng là: yfx  ; xaxbab  A. B. C. D. d a b Sfxx  d b a Sfxx  d b a Sfxx  d a b Sfxx  Câu16: Trên tập , đạo hàm của hàm số là: \0 3log yx  A. . B. . C. . D. . ln3 1 y x   1 ln3y x   ln3 y x   1 ln3y x   Câu17: Cho đồ thị hàm số có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng yfx  yfx  nào dưới đây? A. . B. . C. . D. .  2;2  ;0  0;2  2; Câu18: Đồ thị của hàm số nào dưới đây có dạng như đường congtronghìnhbên? A. . B. . C. . D. . 3 1 x y x   3 1 x y x  241yxx 335yxx  Câu19: Trongkhônggian ,cho mặt cầu .Tâm của có Oxyz 222 :24610 Sxyzxyz   S tọa độ là A. B. C. D.  1;2;3  2;4;6  2;3;4  1;2;3 Câu20: Chohàm số có đồ thị là đường congtronghìnhbên dưới. Điểm cực tiểu của 42 yaxbxc  hàm số đã cholà A. B. C. D. 1cty 0ctx  1;2  0;1 Câu21: Cho cấp số nhân với vàcông bội .Giá trị của bằng  n u12u 1 2q 3u A. . B. . C. . D. 3 1 2 1 4 7 . 2

Câu22: Chohình trụ có đường kính đáy và độ dài đường sinh. Diện tíchxungquanh của hình trụ 2r l

Câu23: Cho khối lập phương có cạnh bằng 4. Thể tích của khối lập phương đã cho bằng

Câu24: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức thỏa mãn là

một đường tròn.Tâm của đường tròn đó có tọa độ là

Câu25: Tiệm cận đứng của đồ thị hàm số

đã

A. B. C. D. 2rl 4rl rl 2 rh

cho bằng

A. . B.

C. . D. .

4 64

16 8

z 22023zi

A. . B. . C. . D. .  0;2  2;0  0;2  2;0

là đường thẳng có phương trình 21 31 x y x   A. . B. . C. . D. . 1 3 x 2 3y 1 3 x 2 3y Câu26: Tập nghiệm của bất phương trình là  log21 x A. B. C. D.  2;12  ;12  ;3  12; Câu27: Giả sử và .Khi đó bằng  9 0 d7fxx   0 9 d1gxx   9 0 23d Ifxgxx    A. B. C. D. 11I 17I 23I 8I Câu28: Nếu và .Khi đó bằng  4 1 d2fxx   4 1 d3gxx   4 1 d fxgxx     A. . B. . C. . D. . 5 6 1 1 Câu29: Trên mặt phẳng tọa độ, điểm biểu diễn số phức có tọa độ là 76 zi  A. B. C. D.  6;7  6;7  7;6  7;6 Câu30: Họ nguyênhàm của hàm số là 2 3sin fxxx  A. . B. . C. . D. . 3 cos xx 6cosxxC  3 cos xxC  6cosxxC  Câu31: Chohàm số có đạo hàm với mọi .Hàm số đã cho đồng yfx   4 (3)2 fxxx   x biến trên khoảng nào dưới đây? A. . B. . C. . D. .  1;2  3;  2;  ;3 Câu32: Trongkhônggian ,góc giữa hai mặt phẳng và bằng Oxyz  Oxy Oyz A. B. C. D. 30 45 60 90 Câu33: Với làcác số thực dương tùyývà , bằng , ab 1a3loga b A. B. C. D. 3loga b 3loga b 1 3loga b 1 3loga b Câu34: Tronghình vẽ bên, điểm biểu diễn số phức Số phức là M z z A. B. C. D. 12i 2i 12i 2i Câu35: Cho số phức , phần ảo của số phức bằng 29 zi  2 z A. B. 36i. C. 18. D. 9. 36

Câu36: Chohìnhchóp có ;tamgiác đều cạnh và .Tìmgóc giữa . SABCSAABC  ABC aSAa  và mặt phẳng . SC  ABC

Câu37: Giải bóng đá Mini cấp trường của một trường THPT,có đội đăng kítham dự trong đó có 16 3 đội 12A1,12A2 và12A3.Ban tổ chức cho bốc thăm ngẫu nhiên để chia đều đội vào4 bảng 16 (mỗi bảng 4 đội) để đá vòng loại. Tínhxác suất để 3 đội của 3 lớp 12A1,12A2 và12A3 nằm ở

A. B. C. D. 060 045 090 030

A. . B. . C. . D. . 3 56 19 28 53 56 16 35 Câu38:

, và SABCDABCD aSAABCD  3 3 Sa A (tham khảo hìnhbên dưới). Khoảng cách từ điểm đến mặt phẳng là A  SCD C A D B S A. . B. . C. . D. . a 2 a 2 2 a 3 2 a Câu39: Số cácgiá trị nguyên của thỏa là x2 3 216log40 x x A. Vô số. B. C. D. 80 17. 78. Câu40: Gọi làhai nghiệm của phương trình và lần lượt làhai điểm biểu diễn 12 , zz 24130zz, AB hai số phức trong mặt phẳng Diện tích của tamgiác bằng 12 , zz Oxy OAB A. B. C. D. 6 12 13. 13 2 Câu41: Cho hàm số có đạo hàm liên tục trên và thỏa mãn yfx   . Diện tíchhình phẳng giới hạn bởi các đường:   3 2 4(34)4, xxfxxfxx       ,hai trục tọa độ và là yfx  2x

3 bảng khácnhau.

Chohìnhchóp ,có đáy làhìnhvuông cạnh

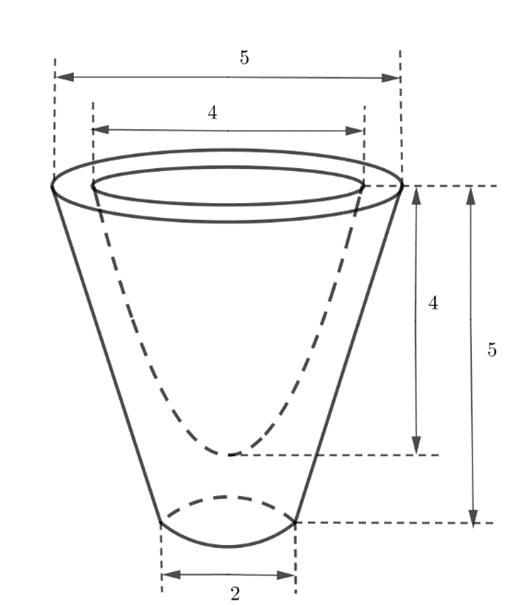
Câu42: Một cáilylàm bằng thủy tinh,cóhình dạng là khối nón cụt vàcáckích thước như hình vẽ. Phần rỗng bêntrongcó thiết diện qua trục làParabol.

Thể tích khối thủy tinh bằng baonhiêu?

Cóbaonhiêugiá trị nguyên của tham số

Cho một cổ vật hình trụ có chiều cao đo được là ,do bị hư hại nênkhi tiến hành đo đạc lại 81cm thu được , với thuộc đường tròn nắp trên như hình 50cm,70cm,80cmABBCCA    ,, ABC vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nàosau đây? A. . B. . 36,56m 30,42m

C. D. 31,03m 30,43m

Câu46: Cho tứ diện có , , , . Biết góc giữa

A. đáp ánkhác. B. C. D. 2  4 3  2. 

A. B. C. D. 43 4  55 4  33 4  65 4  Câu43: Trongkhônggian ,cho điểm và đường thẳng . Gọi Oxyz  0;1;2A 421 : 22 1 dxyz   P là mặt phẳng chứa vàcáchA một khoảng

đến d  5;1;3M  P bằng A. . B. . C. . D. . 2 3 7 3 1 3 1

để hàm

 

m 10



D. .

2018 4

lớn nhất. Khoảng cách từ điểm

Câu44:

số đồng biến

2023;2023

x xm y

trên khoảng  5;5?

2017 2019

Câu45:

ABCD  ABa 5 ACa  90DABCBD   135ABC  hai

và bằng Thể

khối

bằng  ABD BCD30 ABCD A. . B. . C. . D. . 3 2 a 3 32 a 3 23 a 3 6 a

mặt phẳng

tích

tứ diện

Câu47: Trongkhônggian ,chohai điểm và .Xétcác điểm thay đổi sao Oxyz  0;0;10A 19 3;4; 2 B   M chotamgiác không phải làtamgiác nhọn vàcó diện tích bằng 20.Giá trị nhỏ nhất của OAM độ dài đoạn thẳng thuộc khoảng nào dưới đây? MB A. B. . C. . D. .  5;10  3;5 3 ;3 2    3 0; 2    Câu48: Chocác số phức thỏa mãn , là số thuần ảo và ,, zwu 422 zizz  810 610 wi wi .Giá trị nhỏ nhất của thuộc khoảng nàosau đây? 122 uiui  Puzuw  A. B. C. D. 0;5  5;8 8;10 10; Câu49: Cóbaonhiêu số nguyên dương để tồn tại số thực thỏa mãn y 1x  4 2 2log153010 xyx xyxyxyy   A. B. C. D. 16 15 26 27 Câu50: Chohàm số . Biết rằng tập hợp tất cả cácgiá trị  23 202320243273104fxxxxx  thực của tham số để hàm số có số điểm cực tiểu nhiều nhất là m  42 8 hxfxxmx  .Giá trị của biểu thức thuộc khoảng nàosau đây?  ;\ Sabc  22 Taabbabc  A. B. . C. . D. .  1;100  115;130  100;115  130;2023 ---------- HẾT ----------

BẢNG ĐÁP ÁN 1.A 2.A 3.C 4.D 5.B 6.A 7.C 8.D 9.A 10.A 11.C 12.A 13.B 14.C 15.C 16.B 17.C 18.B 19.A 20.B 21.B 22.C 23.D 24.A 25.A 26.A 27.A 28.D 29.D 30.C 31.A 32.D 33.D 34.D 35.A 36.B 37.D 38.B 39.B 40.D 41.B 42.C 43.A 44.D 45.B 46.D 47.D 48.B 49.A 50.B HƯỚNG DẪN GIẢI CHI TIẾT Câu1: Tập nghiệm của bất phương trình là 1 24 x A. B. C. D. ;1  1; 1;  ;1 Lời giải Chọn A 1 24 12 1 x x x     Câu2: Tích tất cả các nghiệm của phương trình bằng 2 22 log3log20 xx A. B. C. D. 8 6 16 2 Lời giải Chọn A 2 22 log3log20 xx 2 2 log12 log24 xx xx           Suyra 12.8xx Câu3: Cho . Khẳng định nào dưới đây đúng?  2 1 d ln xFxC xx   A. B. . 1 lnx Fx   1 lnx FxC  C. D. 2 1 ln Fx xx   2 1 ln Fx x   Lời giải Chọn C Vì .Nên '(x)d FxFxC   2 1 ln Fx xx   Câu4: Trongkhônggian với hệ trục tọa độ ,cho đường thẳng Hỏi đi Oxyz 123 : 345   dxyzd qua điểm nàotrongcác điểm sau: A. . B. . C. . D. .  3;4;5C  3;4;5D  1;2;3B  1;2;3A Lời giải Chọn D Câu5: Cho khối chóp có đáy làtamgiácvuôngcân tại , vuông SABC ,2AABSA

Thể tích khối chóp đã cho bằng

A. 12. B. 2. C. 6. D. 4. Lời giải Chọn B 1111 ACSA2232 3326

Câu6: Trongkhônggian với hệ tọa độ ,cho mặt cầu

của mặt cầu. r

Oxyz 222 :22420 Sxyzxyz  

Bánkính của mặt cầu

r 222 :22420 Sxyzxyz 

222 1122822r

Câu7: Cho một tổ có15thànhviên. Số cách chọn ra2 người lần lượt làm tổ trưởng và tổ phólà

A. . B. . C. . D. . 225 30 210 105

Lời giải

Chọn C

Số cách chọn ra2 người lần lượt làm tổ trưởng và tổ phó từ tổ có15thànhviênlà: 2 15210.A

Câu8: Trongkhônggian ,cho điểm Điểm đối xứng với qua

3SA

góc với đáy và (tham khảo hìnhbên).

VBhAB

 



bánkính

A. B. C. D. 22

 26r 4r 2r Lời giải Chọn

.Tính

 

là

phẳng có Oxyz  1;2;3A A  Oyz tọa độ là A. B. C. D.  1;2;3  1;2;3  1;2;3  1;2;3 Lời giải Chọn D Điểm đối xứng với qua mặt phẳng có tọa độ là . A A  Oyz  1;2;3 Câu9: Trongkhônggian , mặt phẳng có một vectơ pháp tuyến là: Oxyz :230Pxz A. B. C. D. 11;0;2n  41;2;3n  31;2;0n  21;2;3n  Lời giải Chọn A Mặt phẳng có một vectơ pháp tuyến là: . :230Pxz 11;0;2n  Câu10: Đạo hàm của hàm số là: x y A. B. C. D. lnx y   1x yx  ln x y     1 1 x y x      Lời giải Chọn A x y lnx y Câu11: Trongkhônggian ,chohai điểm và . Đường thẳng có phương Oxyz  1;1;1M  5;5;1N MN trìnhlà:

mặt

Câu12: Chohàm số có đồ thilà đường congtronghìnhbên. axb ycxd

Toạ độ giao điểm của đồ thị hàm số đã chovà trục tunglà:

Toạ độ giao điểm của đồ thị hàm số đã chovà trục tunglà  0;2

yfx 

hình vẽ bên.

Giá trị cực tiểu của hàm số là: yfx 

2;2

Câu13: Chohàm số xác định vàliên tục trên đoạn có vàcó đồ thị là đường congtrong

Chọn B

Giá trị cực tiểu của hàm số là tại yfx  21x

A. B. C. D. 52 53 1 xt yt zt      5 52 13 xt yt zt      32 23 xt yt zt      12 1 13 xt yt zt      Lời giải Chọn C  4;6;22;3;1 MN MN u     Phương trình đường thẳng đi qua điểm vàcó vectơ chỉ phương MN  1;1;1M  2;3;1MNu  là:  32

xt ytt zt      

  

A. B. C. D.  0;2  2;0  2;0  0;2 Lời giải

Chọn A





A. B. C. D. 4 2  1;2 1x

giải

Lời

Câu14: Chohàm số bậc ba có đồ thị là đường congtronghìnhbên.

Cóbaonhiêugiá trị nguyên của tham số để phương trình cóba nghiệm thực phân m  fxm 

biệt?

A. B. C. D. 2 5 3 4 Lời giải

Chọn C

Phương trình cóba nghiệm thực phân biệt  fxm 

Đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt  ym  yfx 

 2;2m 

Mà m

Nên . 1;0;1m

Vậy có3giá trị nguyên của tham số để phương trình cóba nghiệm thực phân m  fxm  biệt.

Câu15: Chohàm số liên tục trên đoạn . Diện tíchhình phẳng giới hạn bởi đồ thị hàm số



yfx 

yfx   ; ab ,

là: yfx  ; xaxbab  A. B. C. D. d a b Sfxx  d b a Sfxx  d b a Sfxx  d a b Sfxx  Lời giải Chọn C Diện tíchhình phẳng giới hạn bởi đồ thị hàm số , trục hoànhvàhai đường thẳng yfx  là: ; xaxbab  d b a Sfxx  Câu16: Trên tập , đạo hàm của hàm số là: \0 3log yx  A. B. C. D. ln3 1 y x   1 ln3y x   ln3 y x   1 ln3y x   Lời giải Chọn B Tacó .  3 1 logln3yx x     Câu17: Cho đồ thị hàm số có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng yfx  yfx  nào dưới đây?

trục hoànhvàhai đường thẳng

Câu18: Đồ thị của hàm số nào dưới đây có dạng như đường congtronghìnhbên?

A. . B. . 3 1 x y x   3 1 x y x 

C. . D. . 241yxx 335yxx  Lời giải

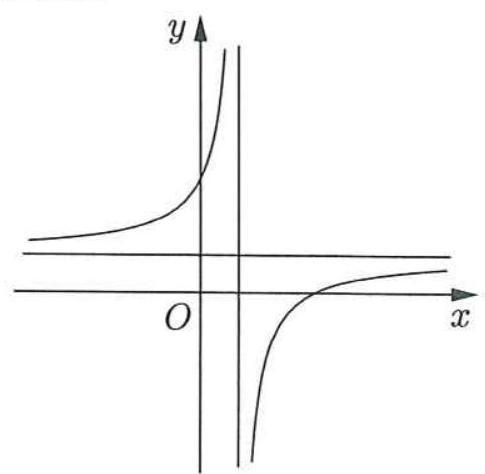
Chọn B

Đồ thị hàm số dạng vàhàm số đồng biến axb ycxd  

định.

Câu19: Trongkhônggian ,cho mặt cầu .Tâm của có Oxyz 222 :24610 Sxyzxyz 

Câu20: Chohàm số có đồ thị là đường congtronghìnhbên dưới. Điểm

A. B. C. D.  2;2  ;0  0;2  2;

Lời giải Chọn C Tacóhàm số đồng biến trên . 0;2



trên tập xác



tọa



 1;2;3

độ là

. B. . C. .

1;2;3

2;4;6

2;3;4

Lời giải Chọn A

 S 

Tâm của có tọa độ là .

1;2;3

cực tiểu của 42 yaxbxc  hàm số đã cholà A. . B. . C. . D. . 1cty 0ctx  1;2  0;1 Lời giải Chọn B Điểm cực tiểu của hàm số đã cholà .0ctx Câu21: Cho cấp số nhân với vàcông bội .Giá trị của bằng  n u12u 1 2q 3u

Lời giải

Chọn B 2

2 31 11 .2. 22uuq   

Câu22: Chohình trụ có đường kính đáy và độ dài đường sinh. Diện tíchxungquanh của hình trụ 2r l đã cho bằng

B. C. D. 2rl 4rl rl 2 rh

Lời giải

Chọn C

Câu23: Cho khối lập phương có cạnh bằng 4. Thể tích của khối lập phương đã cho bằng A. B. C. D. 16 8 4 64

Lời giải

Chọn D 3 464V

Câu24: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức thỏa mãn là z 22023zi

một đường tròn.Tâm của đường tròn đó có tọa độ là A. B. C. D.  0;2  2;0  0;2  2;0

Lời giải

Chọn A

Gọi  , zxyixy

222 220232202322023zi

A. B. C. D. 3 1 2 1 4 7 2





Câu25: Tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình 21 31 x y x   A. B. C. D. 1 3 x 2 3y 1 3 x 2 3y Lời giải Chọn A nên là tiệm cận đứng. 1 3 21 31 lim x x x   1 3 x Câu26: Tập nghiệm của bất phương trình là  log21 x A. . B. . C. . D. .  2;12  ;12  ;3  12; Lời giải Chọn A .  20 log21 212 210 x x x x      Vậy tập nghiệm của bất phương trìnhlà . 2;12S

xyii xy 

Câu29: Trên mặt phẳng tọa độ, điểm biểu diễn số phức có tọa độ là 76 zi 

6;7  6;7  7;6

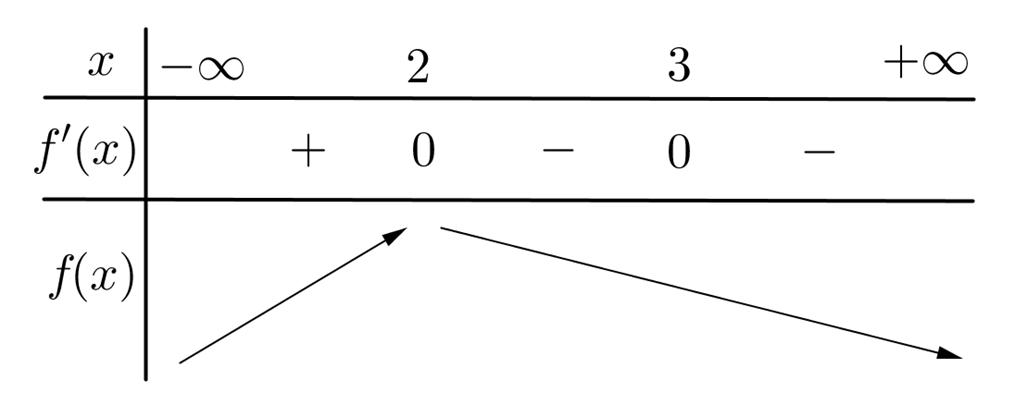
giải

76 zi 

Câu27: Giả sử và .Khi đó bằng  9 0 d7fxx   0 9 d1gxx   9 0 23d Ifxgxx     A. . B. . C. . D. . 11I 17I 23I 8I Lời giải Chọn A .   9 9 0 0 2d3d273111Ifxxgxx     Câu28: Nếu và .Khi đó bằng  4 1 d2fxx   4 1 d3gxx   4 1 d fxgxx     A. B. C. D. 5 6 1 1 Lời giải Chọn D .  4 4 4 1 1 1 ddd231fxgxxfxxgxx        



Lời

Chọn

Điểm

 7;6M Câu30: Họ nguyênhàm của hàm số là 2 3sin fxxx  A. B. C. D. 3 cos xx 6cosxxC  3 cos xxC  6cosxxC  Lời giải Chọn C  2 3 d3sindcos fxxxxxxxC     Câu31: Chohàm số có đạo hàm với mọi .Hàm số đã cho đồng yfx   4 (3)2 fxxx   x biến trên khoảng nào dưới đây? A. B. C. D.  1;2  3;  2;  ;3 Lời giải Chọn A  4 (3)2 fxxx    3 0 2 x fx x   

B. C. D.

7;6

biểu diễn số phức là

hàm số đã cho đồng biến trên . 1;2

Câu32: Trongkhônggian ,góc giữa hai mặt phẳng và bằng Oxyz  Oxy Oyz A. B.

Do mặt phẳng vuônggóc với mặt phẳng nêngóc giữa hai mặt phẳng và

Câu33: Với làcác số thực dương tùyývà , bằng , ab 1a3loga b A. . B. . C. .

. 3loga b 3loga b 1 3loga b 1 3loga b

Lời giải Chọn D . 3

1 l 3 ogloga a bb 

Câu34: Tronghình vẽ bên, điểm biểu diễn số phức Số phức là M z z

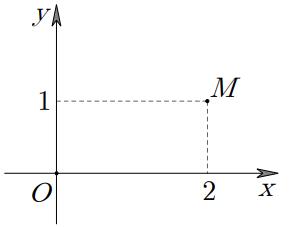
A. B. C. D. 12i 2i 12i 2i

Lời giải

Tacó . 2 297736ziz i Phần ảo của số phức bằng 2 z36

Câu36: Chohìnhchóp có ;tamgiác đều cạnh và .Tìmgóc giữa . SABCSAABC  ABC aSAa 

và mặt phẳng SC  ABC

Vậy

30 45 60 90 Lời giải Chọn D



bằng 

Oxy

Oyz

Oxy

Oyz90

Chọn D Tacó . 2;122 Mzizi 

ảo của số phức bằng

2 z

C. 18. D.

Câu35: Cho số phức , phần

29 zi 

A. . B. 36i.

9. 36 Lời giải Chọn A

của 3 lớp 12A1,12A2 và12A3 nằm ở 3 bảng khácnhau.

Chọn D Chia đều đội vào4 bảng (mỗi bảng 4 đội) có cách. 16 161284 4444 ....nCCCC 

Gọi biến cố :"3 lớp 12A1,12A2 và12A3 nằm ở 3 bảng khácnhau". A

- Sắp xếp 3 lớp 12A1,12A2 và12A3 nằm ở 3 bảng khácnhautrong4 bảng có cách. 3 4A

- Sắp các đội còn lại vàocác4 bảng để được mỗi bảng đủ 4 đội có: cách. 4333 13963 ... CCCC

Suyra cách. 34333 413963 nAACCCC 

Vậy xác suất   16 35 nA PA n  

Câu38: Chohìnhchóp ,có đáy làhìnhvuông cạnh , và SABCDABCD aSAABCD 

(tham khảo hìnhbên dưới). Khoảng cách từ điểm đến mặt phẳng là A  SCD

Sa A

A. B. C. D. 060 045 090 030 Lời giải Chọn B Góc giữa

(do  vuôngcân

cạnh ). SC  ABC  45SCA SAC AA Câu37: Giải bóng đá Mini cấp

của một trường THPT,có đội

đó có 16 3 đội 12A1,12A2 và12A3.Ban tổ chức cho bốc thăm

A. . B. . C. . D. . 3 56 19 28 53 56 16 35 Lời giải

và mặt phẳng là

tại

trường

đăng kítham dự trong

ngẫu nhiên để chia đều đội vào4 bảng 16 (mỗi bảng 4 đội) để đá vòng loại. Tínhxác suất để 3 đội

3 3

C A D B S A. B. C. D. a 2 a 2 2 a 3 2 a Lời giải

nguyênnêncó80giá trị thỏa mãn. x

Câu40: Gọi làhai nghiệm của phương trình và lần lượt làhai điểm biểu diễn 12 , zz

4130zz, AB hai

Chọn B Kẻ tại AHSD  H Dễ thấy ,mà   , CDABCDSACDSAD  AHCD AHSD  AHSCD  Suyra .   ; dASCDAH  Mà . Vậy . 2 2222 111114 2 3 3 Aa H AHADSAaaa        ; 2 adASCDAH Câu39: Số cácgiá trị nguyên của thỏa là x2 3 216log40 x x A. Vô số. B. C. D. 80 17. 78. Lời giải Chọn B  2 2 2 2 4 3 3 2 4 3 2 42160 2 log4003 216log40 0281 81 42160 22 3log40 81 x x x x x x x x x x x x x x x x                                                    

số phức trong mặt phẳng . Diện tích của tamgiác bằng 12 , zz Oxy OAB A. B. C. D. 6 12 13. 13 . 2 Lời giải Chọn D 1212 11113 2222OAB SOAOBzzzz     Câu41: Cho hàm số có đạo hàm liên tục trên và thỏa mãn yfx   Diện tíchhình phẳng giới hạn bởi các đường:   3 2 4(34)4, xxfxxfxx       ,hai trục tọa độ và là yfx  2x A. đáp ánkhác. B. C. D. 2  4 3  2.  Lời giải

Diện tíchhình phẳng giới hạn cần tínhlà

Câu42: Một cáilylàm bằng thủy tinh,cóhình dạng là khối nón cụt vàcáckích thước như hình vẽ. Phần rỗng bêntrongcó thiết diện qua trục làParabol.

Chọn B    3 2 3 2 4(34)44444 xfxxfxxfxxxfxxC x x             Đẳng thức đúng với và 0xC   2 4 . 4fx x  

 2 2 2 0 0 4 dd 42Sfxx x x    





A. B. C. D. 43 4  55 4  33 4  65 4  Lời giải Chọn C Thể tích khối nón cụt là  2 2 22 1 5551 2265 3 34 hRrRr V               Thể tích phần rỗng bêntronglà một chảo parabol 22 2 2.4 8 22 Rh V   Thể tích khối thủy tinh bằng 12 6533 8 44 VV     Câu43: Trongkhônggian ,cho điểm và đường thẳng Gọi Oxyz  0;1;2A 421 : 22 1 dxyz   P là mặt phẳng chứa vàcáchA một khoảng lớn nhất. Khoảng cách từ điểm đến d  5;1;3M  P bằng A. B. C. D. 2 3 7 3 1 3 1 Lời giải

Thể tích khối thủy tinh bằng baonhiêu?

Gọi khoảng cách từ tới mặt phẳng là , khoảng cách từ tới đường thẳng là A

PAH A d không đổi. AK

Nhận xét AHAK 

Dấu xảy ra Khi đó vuônggóc mặt phẳng tại ""  HK AK PK

Mặt phẳng có vectơ pháp tuyến và đi qua

2;1;2dnu

Chọn A



  

. 

 

      22502422212501 xyz ttt t   Suyra . 2;3;3K Mặt phẳng có vectơ pháp tuyến và đi qua  P  2;2;1nAK   2;3;3K :22130Pxyz  Vậy .   222 2.5213132 ; 3221 dMP     Câu44: Cóbaonhiêugiá trị nguyên của tham số để hàm số đồng biến  2023;2023m 10x xm y trên khoảng  5;5? A. B. C. D. 2017 2019 2018 4 Lời giải Chọn D ĐKXĐ: xm  s 2 101 10 10 0 x xxm xm xm xmxm y        TH1: 10m P d A H K

AHK

0;1;2A

:2250AHKxyz

Thế vào 42 2 12 xt yt zt

hàm số đồng biến trên khoảng thì . 10x xm y

TH2: 10m Để hàm số đồng biến trên khoảng thì . 10x xm y

Vậy và nêncó giá trị. 105 m m4

5;5m

Câu45: Cho một cổ vật hình trụ có chiều cao đo được là ,do81cm

bị hư hại nênkhi tiến hành đo đạc lại thu được , với thuộc 50cm,70cm,80cmABBCCA    ,, ABC

đường tròn nắp trên





Để

5;55m



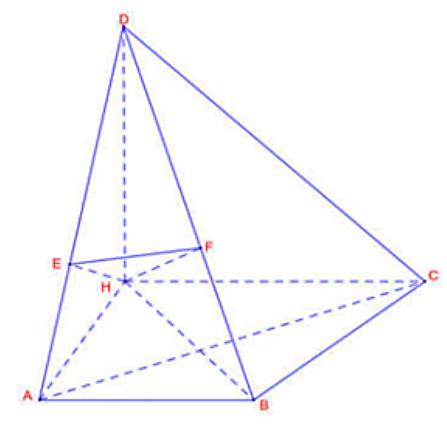
như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nàosau đây? A. . B. . 36,56m 30,42m C. D. 31,03m 30,43m Lời giải Chọn B Đổi: 500,5;700,7;800,8;810,81 cmmcmmcmmcmm     Nửa chuvitamgiácABC: 0,50,70,81 2p m     23 10 ABC Sppapbpcm    Bánkính đường tròn ngoại tiếp tamgiácABC: ..73 430 ABACBC R m S   2 2 3 73 ..0,810,42 30 VRh m       Câu46: Cho tứ diện có , , , . Biết góc giữa ABCD  ABa 5 ACa  90DABCBD   135ABC  hai mặt phẳng và bằng . Thể tích khối tứ diện bằng  ABD BCD30 ABCD A. . B. . C. . D. . 3 2 a 3 32 a 3 23 a 3 6 a Lời giải Chọn D

Dựng .()DHABC  Tacó . Tương tự BADA BAAH BADH   BCDB BCBH BCDH   TamgiácAHBcó vuôngcân tại  ,45 ABaABHHAB    AAHABa  Áp dụng định lýcosin,tacó . 2BCa  Vậy .  2 1 12 sin 2 2 222 ABC a SBABCCBAaa    Dựng và . () HEDA HEDAB HFDB   ()HFDBC  Suyra vàtamgiácHEFvuông tại .  ((),())(,) DBADBCHEHFEHF   E Đặt ,khi đó DHx  22 22 2 , 2 ax xa HE HF ax ax     Suyra .  22 22 32 cos 422 HE xa EHF xa HF xa     Vậy 3 1 36ABCD ABC aVDHS    Câu47: Trongkhônggian ,chohai điểm và .Xétcác điểm thay đổi sao Oxyz  0;0;10A 19 3;4; 2 B   M chotamgiác không phải làtamgiác nhọn vàcó diện tích bằng 20.Giá trị nhỏ nhất của OAM độ dài đoạn thẳng thuộc khoảng nào dưới đây? MB A. B. C. D.  5;10  3;5 3 ;3 2    3 0; 2    Lời giải Chọn D Tacó: 1 .;20;4. 2OAM SOAdMOAdMOA    Suyra: di động trên mặt trụ, bánkính bằng trục là M 4,OA

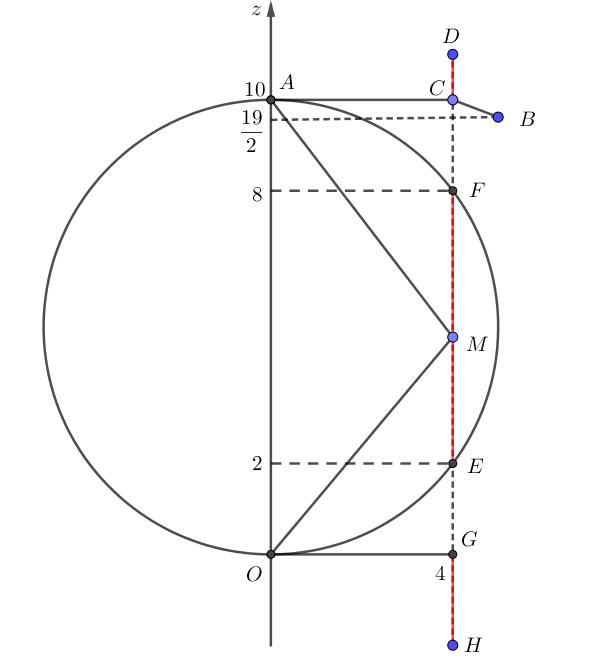
Xét điểm như hình vẽ, D 212 6 . 8 10 HAHAHOHD HO HAHO         +TH1: Nếu tamgiác làtamgiáccógóc thì điểm chạy trên đoạn , OAM  090AMO M EF khi đó cógiá trị nhỏ nhất bằng BM 13 2 BF +TH2: Nếu tamgiác làtamgiáccógóc thì điểm chạy trêntia ,khi OAM  090MAO M CD đó cógiá trị nhỏ nhất bằng BM 5 2 BC +TH3: Nếu tamgiác làtamgiáccógóc thì điểm chạy trêntia ,khi OAM  090MOA M GH đó cógiá trị nhỏ nhất bằng . BM 365 2 BG Sosánhba trường hợp trênta thấy min 5 1,118033989 2 BM Câu48: Chocác số phức thỏa mãn , là số thuần ảo và ,, zwu 422 zizz  810 610 wi wi .Giá trị nhỏ nhất của thuộc khoảng nàosau đây? 122 uiui  Puzuw  A. B. C. D. 0;5  5;8 8;10 10; Lời giải Chọn B

Khi đó tacóhình vẽ như sau:

Từ hình vẽ, ta dễ dàngsuyra: 1 2

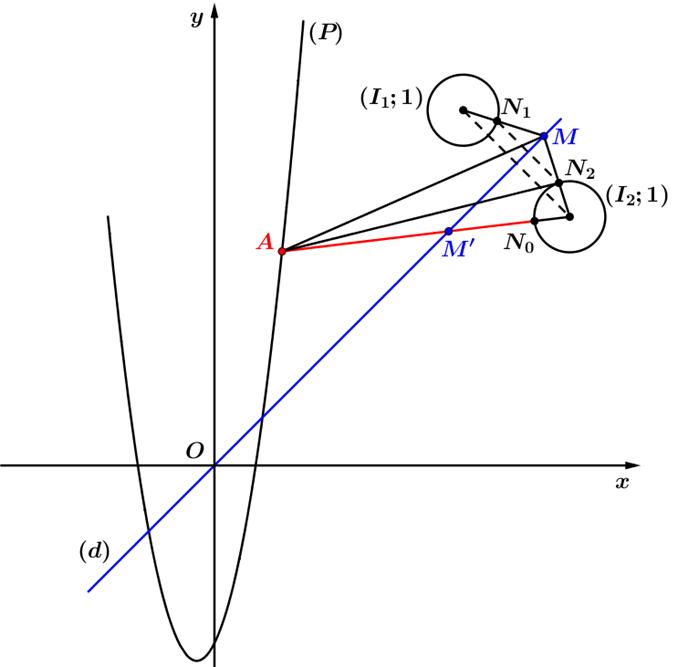
Mặt kháctheo bất đẳng thức đường gấp khúc taluôncó: nên 22MAMNAN

“Cho và ,khi ấy tìmgiá trị nhỏ nhất của đoạn thẳng

Đầu tiênta gọi lần lượt làcác điểm biểu diễn số phức trên mặt phẳng tọa độ 1 ,, ANM ,, zwu Oxy Khi đó tacó:     2 ;:422 :225 : ;:122 AabzizzAPyxx MdyxMcduiui             Đặt ,khi đó  , wxyixy 810 810610 610 wi e kikwiwimim wi      (2) 2 81061061081014820wiwiw iwiwi    Thế vào(2) kết hợp biến đổi đại số, ta được  , wxyixy ,suyra , tức thuộc 2 2 Re14201480 exxyy     2 2 :7101NCxy    1N đường tròntâm ,bánkính . 17;10I 1R Khi đó taluôncó: 1 11PuzuwuzuwMAMNMAMI  Gọi là điểm đối xứng với qua ,khi đó tasuyra tức . 2I 17;10I  d 210;7I 22;1NI 

PMAMIMAMIMAMN 

khi tức

về bàitoán 221PANAI  20NN  minP 2AI



khivà chỉ khi min.Lúcnàytaquy

đơn giản hơn như

2 ;:225AabPyxx  210;7I ”.2AI

Lúcnàytacó: (Cáihàm   2 2 2 2 2 2 21022571046AIa aa a aa     mệt mỏi nha). Chạy TABLEtasuyra . 2638515;8AI  Câu49: Cóbaonhiêu số nguyên dương để tồn tại số thực thỏa mãn y 1x  4 2 2log153010 xyx xyxyxyy   A. B. . C. . D. . 16 15 26 27 Lời giải Chọn A Đầu tiêntacó phương trìnhsau: (*)  4 2 2log153010 xyx xyxyxyy   (1)   4 4 2 2 3010 3010 2log15 2log 15 xy xyy y xyyy xy yy x xx      Giải thích:tacô lập vế phải là một hàmtheo biến luôn đồng biến trên ( y  0; ) 3 4150fyy  0;y  Tiếp theota khảo sáthàm số trên  2 30102log xy y gx xy xx    1; Tacó:. Thế vàotacó  22 130102ln2 ln2 xy y gxy xxx     3y 111 38ln264ln20,1 ln2ln2 x g x x      Suyra thì ,kéotheo đó tacó được: 3y  0gx    2 12log1030 lim y x gxg yy gx         Khi ấy để (*)có nghiệm thì cần có: 1x    2 2 30102log 2log1030 xy yy xy yy xx     (2) Từ (1)và(2)tasuyra (3)   4 4 2 2 2log1030152log25300,3 y yyyyy yyyy    Cho vế trái(3) bằng không giải ra nghiệm (shiftSOLVE) (**),khi đó tacóý tưởng 16,01y sau: Giả sử đảo chiều (3),tacó: (4).   4 4 2 2 2log1030152log25300 y yyyyy yyy    Tới đây ta sẽ chứng minh bất phương trình(4)luôn đúng với mọi .17y