70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC (ĐỀ 81-90) by Dạy Kèm Quy Nhơn Official

ĐỀ THI THỬ TỐT NGHIỆP THPT MÔN TOÁN

ễ

Thanh Tú

Collection 70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC - CÓ LỜI GIẢI (ĐỀ 81-90) (253 TRANG)

Ths Nguy

eBook

EDITION

CHUYỂN GIAO QUA EMAIL

COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

WORD VERSION | 2023

ORDER NOW /

TAILIEUCHUANTHAMKHAO@GMAIL

3: Đạo hàm của hàm số cos yx

Câu 4: Cho hàm số có bảng biến thiên như sau

số đã cho đồng biến trên khoảng nào dưới đây

Câu 5: Cho khối lập phương có thể tích bằng 2 . Cạnh của khối lập phương đã cho bằng

A. 2 . B. 8 . C. 32 .

1 8 .

Câu 6: Trong không gian Oxyz , hình chiếu của điểm (1;2;3)M lên mặt phẳng  Oxy là điểm

A. (1;0;3)P . B. (0;2;3)Q . C. (1;2;0)N . D. (1;2;3)M .

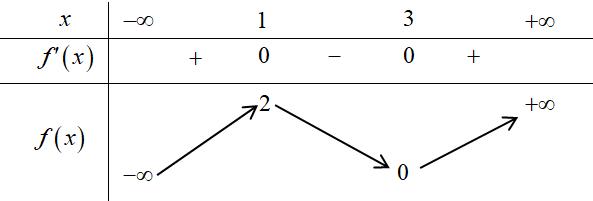
Câu 7: Cho hàm số 42 yaxbxc  có đồ thị là đường

SỞ GIÁO DỤC VÀ ĐÀO TẠO QUẢNG

TRƯỜNG THPT CHUYÊN LÊ KHIẾT ĐỀ THI THỬ TỐT NGHIỆP THPT – NĂM HỌC 2022 – 2023 – LẦN 1 Câu 1: Tiệm cận đứng của đồ thị hàm số 21 31 x y x   là đường thẳng có phương trình A. 2 3 x B. 1 3y C. 2 3y D. 1 3 x Câu 2: Trong không gian ,Oxyz đường thẳng 123 : 212 dxyz  có một vectơ chỉ phương là A.  2;1;2u . B.  1;2;3u . C.  1;2;3u . D.  2;1;2u .

 là A. tan yx   B. sin yx   C. cot yx   D. sin yx  

Hàm

A.  0;2 B.  ;3 C.  2; D.  4;5

NGÃI

Câu

 trên

cong trong hình bên dưới. Điểm cực tiểu của hàm số đã cho là A. 1y B. 1x C. 1x D. 0x Câu 8: Cho mặt phẳng  P cắt mặt cầu  ; SOR theo một đường tròn. Gọi d là khoảng cách từ O đến  P . Bán kính R của đường tròn được tính theo công thức nào sau đây? A. RRd  . B. RRd   . C. 22RRd   . D. 22RRd  .

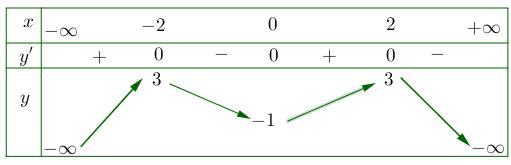
Câu 9: Hàm số nào dưới đây có bảng biến thiên như hình bên dưới?

Câu 11: Cho hàm số bậc ba yfx  có đồ thị là đường cong trong hình bên dưới. Điểm cực đại của đồ thị hàm số đã cho là.

Câu 12: Trong không gian Oxyz , cho mặt cầu 222 :24610 Sxyzxyz   . Bán kính của  S là.

13R .

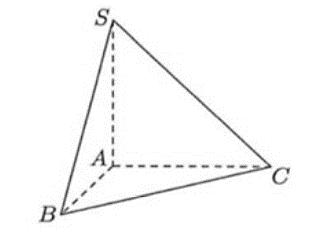
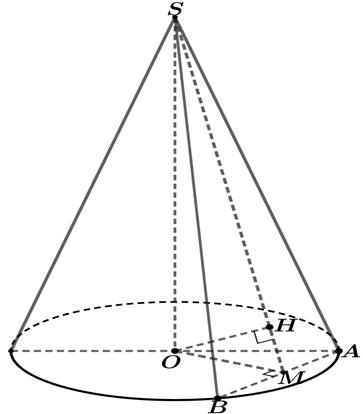
Câu 13: Cho khối chóp SABC có đáy là tam giác vuông tại A, 2,4ABAC ; SA vuông góc với đáy và 3SA (tham khảo hình vẽ).

Thể tích khối chóp đã cho bằng.

x 

 4 1

  và  4 1 d3gxx  thì  4 1

    

A. 1

D. 1

D.  2;1

A. 42 11 2 4 yxx 

4221yxx 

335yxx 

x y

Câu 10: Cho các hàm số  , fxgx liên tục trên đoạn  1;4 Nếu

d2fxx

d fxgxx

bằng:

6 .

 0;3M .

0x .

2x .

N .

14R .

Câu 14: Trên  , đạo hàm của hàm số x y là.

'ln x y

Câu 15: Trên mặt phẳng tọa độ, điểm biểu diễn số phức 23 zi  có tọa độ là.

 2;3 B.  3;2

Câu 16: Cho cấp số cộng  n u với 132,6uu . Công sai của cấp số cộng này bằng

A. 4. B. 2.

Câu 17: Cho hình trụ có đường kính đáy 2r và độ dài đường sinh l. Diện tích xung quanh của hình trụ đã cho bằng

A. rl . B. 2rl .

Câu 18: Mô đun của số phức 23 zi  bằng

A. 13 . B. 13.

Câu 19: Cho hàm số có đồ thị như hình vẽ sau

21 3 rl .

22 3 rl .

5 .

Số giao điểm của đồ thị hàm số đã cho với trục hoành là

Câu 20: Cho số phức 23 zi  Phần ảo của số phức bằng

6i .

12i .

Câu 21: Trong không gian Oxyz , điểm nào dưới đây thuộc mặt phẳng :3210

Câu 22: Tập nghiệm của phương

Câu 24: Trên mặt phẳng tọa độ, biết tập

A. 8 B. 24 C. 6 D. 4

   C. 1' yx   D. 1'x yx

B. ' ln

 3;2

 2;3

12.

Pxyz

1;0;1B

B.  1;0;1D . C.  1;2;0C . D.  0;1;1A .

  ?



trình 1 25 x  có bao nhiêu phần tử? A. 3 B. 2 C. 0 D. 1

 bằng A. 3

C. 8. D. 2.

Câu 23: Tổng tất cả các nghiệm của phương trình 231

điểm biểu diễn các số phức z thỏa mãn 22zi là một

2 z

hợp

đường tròn tâm I , bán kính R với

Số điểm cực đại của hàm số đã cho là

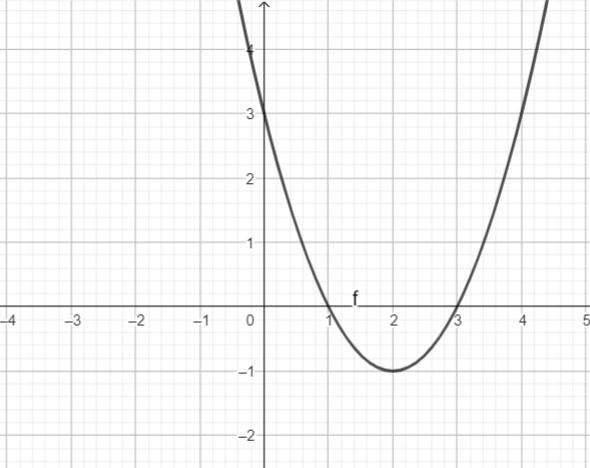
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2()fxm  có ba nghiệm thực phân biệt? A. 9

Câu 29: Cho hàm số fx có đạo hàm liên tục trên R . Khẳng định nào dưới đây đúng?

A. ()d'() fxxfx   . B. '()d() fxxfx   .

C. ()d'() fxxfxC 

D. '()d() fxxfxC  

A. 2;1,2IR . B. 2;1,2IR . C. 2;1,2IR . D. 2;1,2IR .

25: Cho hàm số yfx  liên tục trên  và có bảng xét dấu của fx  như sau

Câu

A. 2 B. 4 C. 1 D. 3

SA vuông

với đáy

Góc giữa hai mặt phẳng  SBC và  ABC bằng A. 060 . B. 030 . C. 090 . D. 045 . Câu 27: Cho hàm số 2x fxx  Khẳng định nào dưới đây đúng A. 2()d2ln2 xfxx xC  B. 2()d2x fxxxC  C. 22

x x

C  . D. 2 ()d2ln22 x x fxx C  Câu

Câu 26: Cho hình chóp . SABC có đáy là tam giác đều,

góc

và 2 ABSA  (tham khảo hình vẽ).

()dln22

fxx

28: Cho hàm số bậc ba yfx  có đồ thị là đường cong như hình bên dưới.

C B A S



Câu 30: Trong không gian với hệ tọa độ Oxyz ,cho hai điểm (1;1;1)M và (5;5;1)N . Mặt phẳng

() OMN có phương trình là

A. 2350 xyz . B. 2350 xyz .

C. 230 xyz . D. 250 xyz .

Câu 31: Tập nghiệm của bất phương trình  log20 x là A.  3; . B.  12; .

Câu 32: Diện tích hình phẳng giớn hạn bởi các đường 243yxx ; 0x và 0y bằng

A. 5 3 . B. 16 9 .

4 3 .

8 3 .

Câu 33: Có bao nhiêu số tự nhiên có năm chữ số phân biệt, trong đó có mặt cả hai chữ số 2 và 3?

A. 2322 5847 AAAA B. 23 583!CC C. 2322 5847 CACA D. 23 58AA

Câu 34: Trong không gian Oxyz , cho điểm  1;2;3A . Khoảng cách từ điểm A đến trục Ox bằng A. 4

Câu 35: Cho tập hợp  1;2;3;4;5A . Có bao nhiêu số tự nhiên có 3 chữ số phân biệt và các chữ số

60.

Câu 36: Cho hàm số fx liên tục trên  Nếu 

Câu 37: Nếu 225 xx thì giá trị củ biểu thức 443 xxA

D. 



C.  2;3 .

thuộc

20 .

125.

30.

2 0 4fxdx  thì  1 0 2 fxdx bằng. A. 2 . B. 4. C. 2. D. 8.

A. 5

C. 26

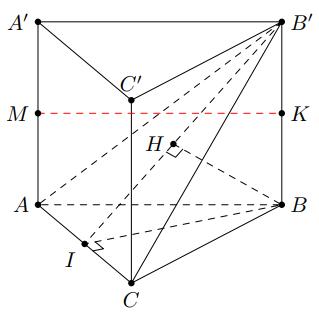
D. 26. Câu 38: Có bao nhiêu số nguyên x là nghiệm của bất phương trình  2 22 3 5 41 log2log50 7 xx xx            ? A. 5. B. 0 . C. 1. D. 2. Câu 39: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 322 2 8(11)22yxxmxm    có hai điểm cực trị nằm về hai phía của trục hoành? A. 7 B. 5 C. 6 D. 4 Câu 40: Cho lăng trụ ''' . ABCABC có đáy là tam giác vuông cân tại B , 3ABa  Hình chiếu vuông góc của ' A lên mặt phẳng () ABC là điểm H thuộc cạnh AC sao cho 2 HCHA  Mặt bên '' () ABBA tạo với đáy một góc 060 Thể tích khối lăng trụ đã cho bằng A. 33 5 a B. 33 2 a C. 3 3 a D. 3 6 a

là

25.

Câu 41: . Trong không gian Oxyz , cho hai đường thẳng 1 11 : 112

Đường thẳng d đi qua điểm

Câu 42: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B với 3ABa BC  , góc

tích mặt cầu ngoại tiếp hình chóp SABC A. 216a B. 22a

28a

212a

Câu 43: Trên tập hợp số phức, xét phương trình 2210zmz (m là tham số thực). Có bao nhiêu giá trịnguyên của m đểphươngtrìnhđãchocóhainghiệmphânbiệt 12 , zz thỏamãn 1233zz 

A. 3. B. 4.

Câu 44: Cho Fx là một nguyên hàm của hàm số 11 fxxx  trên  và thỏa mãn 13F

Tính tổng  02FF 

3 B. 2

Câu 45: Cho hình chóp SABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, đường thẳng SC tạo với mặt phẳng  SAB một góc 30 Thể tích của khối chóp SABCD

. B.

  , 2 1

121 dxyz 

dxyz

, 2d tại

 5;3;5A cắt

hai điểm B và C Độ dài đoạn thẳng

bằng A. 32



SABSCB 

cách từ A đến mặt phẳng  SBC bằng 2a . Tính

và khoảng

diện

a . C. 32a . D. 32 4 a . Câu 46: Có bao nhiêu giá trị nguyên của tham số  10;10a để hàm số 4 32 3421230 yxaxaxa   nghịch biến trên khoảng ;2? A. 12. B. 11. C. 10. D. 13. Câu 47: Cho hàm số yfx  có đạo hàm liên tục trên  thỏa mãn 2 2 x xfxxfx e  , x  và 02f . Tính  2f A. 4 2 2f e  B. 4 2 2f e  C. 22f D. 22 fe  Câu 48: Cho các số phức u , v, w thỏa mãn các điều kiện 422ui , 3121 vivi  và 22 wwi  . Tìm w khi Suwvw  đạt giá trị nhỏ nhất. A. 13 2 w B. 10 2 w C. 17 2 w D. 5 2 w Câu 49: Trong không gian Oxyz , cho điểm (0;0;3)A và điểm B thay đồi thuộc mặt phẳng () Oxy sao cho diện tích tam giác OAB bằng 3 2 . Gọi C là điềm trên tia Ozthòa mãn

32 3 a

2 2

[,][,] dCABdCOBk   Thể tích của khối tròn xoay tạo bời tập hợp tất cả các điểm M mà CMk  thuộc khoảng nào dưới dây? A. (0,2;0,7) . B. (1,2;1,7). C. (1,7;2,2). D. (0,7;1,2). Câu 50: Có bao nhiêu cặp số nguyên dương (;) xy thỏa mãn 222log2(4)(4)?xy xxyy xy     A. 13. B. 18. C. 15. D. 21. ---------- HẾT ----------

thẳng 123 : 212

Câu 3: Đạo hàm của hàm số cos yx  trên  là

giải

Chọn D

Ta có: cos yx  sin yx

Câu 4: Cho hàm số có bảng biến thiên như sau

Hàm số đã cho đồng biến trên khoảng nào dưới đây

A.  0;2 B.  ;3

Chọn D

C.  2; D.  4;5

Lời giải

Hàm số đã cho đồng biến trên khoảng:  4;5

Câu 5: Cho khối lập phương có thể tích bằng 2 Cạnh của khối lập phương đã cho bằng

BẢNG ĐÁP ÁN 1.D 2.A 3.D 4.D 5.C 6.C 7.D 8.C 9.A 10.D 11.A 12.A 13.D 14.A 15.D 16.B 17.B 18.A 19.C 20.D 21.A 22.D 23.B 24.D 25.C 26.B 27.C 28.C 29.D 30.A 31.C 32.D 33.A 34.B 35.A 36.A 37.D 38.D 39.B 40.B 41.B 42.D 43.C 44.C 45.A 46.D 47.A 48.D 49.D 50.C HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Tiệm cận đứng của đồ thị hàm số 21 31 x y x   là đường thẳng có phương trình A. 2 3 x B. 1 3y C. 2 3y D. 1 3 x Lời giải Chọn D Ta có: 1 3 21 lim 31x x x    suy ra tiệm cận đứng là: 1 3 x Câu 2: Trong không gian ,Oxyz đường thẳng 123 : 212 dxyz  có một vectơ chỉ phương là A.  2;1;2u  B.  1;2;3u  C.  1;2;3u  D.  2;1;2u  Lời giải Chọn

  có một vectơ chỉ phương là:  2;1;2u 

A Đường

dxyz

A. tan yx   B. sin yx   C. cot yx   D. sin yx   Lời

Lời giải

Chọn C

Ta có: 3332.VaaV

Câu 6: Trong không gian Oxyz , hình chiếu của điểm (1;2;3)M lên mặt phẳng  Oxy là điểm

A. (1;0;3)P . B. (0;2;3)Q . C. (1;2;0)N . D. (1;2;3)M .

Lời giải

Chọn C

Hình chiếu của điểm (1;2;3)M lên mặt phẳng  Oxy là điểm (1;2;0)N

Câu 7: Cho hàm số 42 yaxbxc  có đồ thị là đường cong trong hình bên dưới.

Điểm cực tiểu của hàm số đã cho là

1y .

Chọn D

Điểm cực tiểu của hàm số đã cho là 0x

Lời giải

Câu 8: Cho mặt phẳng  P cắt mặt cầu  ; SOR theo một đường tròn. Gọi d là khoảng cách từ O

đến  P . Bán kính R của đường tròn được tính theo công thức nào sau đây?

Câu

Hàm

A. 2 . B. 8 . C. 32

D. 1 8

1x .

0x .

A. RRd  B. RRd   C. 22RRd   D. 22RRd  Lời giải



Chọn C Ta có 22RRd 

A. 42 11 2 4 yxx  B. 4221yxx  C. 335yxx  D. 3 1 x y x  Lời giải Chọn A Bảng biến thiên là BBT của hàm số bậc bốn 42 yaxbxc  với 0a . Chọn đáp án A.

số nào dưới đây có bảng biến thiên như hình bên dưới?

Câu 10: Cho các hàm số  , fxgx liên tục trên đoạn  1;4 Nếu  4 1 d2fxx  và  4 1 d3gxx  thì  4 1 d fxgxx     bằng: A. 1. B. 6 . C. 5. D. 1. Lời giải Chọn D Ta có  4 4 4 1 1 1 ddd231fxgxxfxxxx g        . Câu 11: Cho hàm số bậc ba yfx  có đồ thị là đường cong trong hình bên dưới. Điểm cực đại của đồ thị hàm số đã cho là. A.  0;3M . B. 0x . C. 2x . D.  2;1N . Lời giải Chọn A Điểm cực đại của đồ thị hàm số đã cho là  0;3M . Câu 12: Trong không gian Oxyz , cho mặt cầu 222 :24610 Sxyzxyz   . Bán kính của  S là. A. 13R B. 13R C. 14R D. 14R Lời giải Chọn A Bán kính của  S là 222 123113R . Câu 13: Cho khối chóp . SABC có đáy là tam giác vuông tại A, 2,4ABAC ; SA vuông góc với đáy và 3SA (tham khảo hình vẽ).

Câu 15: Trên mặt phẳng tọa độ, điểm biểu diễn số phức 23 zi  có tọa độ là.

Chọn D

biểu diễn số phức 23 zi  là

Câu 16: Cho cấp số cộng  n u với 132,6uu . Công sai của cấp số cộng này bằng

A. 4. B. 2.

Chọn B

giải

Gọi d là công sai của cấp số cộng đã cho. Khi đó 3122uudd .

Câu 17: Cho hình trụ có đường kính đáy 2r và độ dài đường sinh l Diện tích xung quanh của hình trụ đã cho bằng

A. rl .

Chọn B

2rl .

Diện tích xung quanh của hình trụ đã cho là 2 Srl 

Câu 18: Mô đun của số phức 23 zi  bằng

21 3 rl .

giải

rl .

Thể

A. 8 B. 24 C. 6 D. 4 Lời giải Chọn

Thể

112.4 ....34 332 ABC VSSA     . Câu

hàm

x y là. A. 'ln x y . B. ' ln x y    . C. 1' yx   . D. 1'x yx . Lời giải Chọn A x y lnx y

A.  2;3 B.  3;2 C.  3;2 D.  2;3 Lời

tích khối chóp đã cho bằng.

tích khối chóp là

14: Trên  , đạo hàm của

số

giải



Điểm

2;3 .

Lời

D. 22 3

Lời

Chọn A

Mô đun của số phức 23 zi  là

Câu 19: Cho hàm số có đồ thị như hình vẽ sau

Số giao điểm của đồ thị hàm số đã cho với trục hoành là

thị hàm số đã cho cắt trục hoành tại 3 điểm.

Câu 20: Cho số phức 23 zi  . Phần ảo của số phức bằng

6i B. 6

12i

Câu 21: Trong không gian Oxyz , điểm nào dưới đây thuộc mặt phẳng 

A. 13

B. 13. C.

D. 5 .

Lời giải

4913z

Đồ

2. B. 0.

1. Lời giải Chọn C

Lời

Chọn

 Vậy

giải

D Ta có 2

2 234129512ziii i 

phần ảo của số phức bằng 12

:3210Pxyz   ? A.  1;0;1B . B.  1;0;1D . C.  1;2;0C . D.  0;1;1A . Lời giải Chọn A Ta có điểm thuộc mặt phẳng là  1;0;1B . Câu 22: Tập nghiệm của phương trình 1 25 x  có bao nhiêu phần tử? A. 3 B. 2 C. 0 D. 1 Lời giải Chọn D Ta có 2 1 1log525 x x  Vậy phương trình có nghiệm 2 1log5x Câu 23: Tổng tất cả các nghiệm của phương trình 231 x x bằng 2 z 2 z

Lời giải

Chọn B

Ta có 2312310 x x x x  .

Xét   2312ln23 x xfxxfx   và

Khi đó 0fx có tối đa hai nghiệm.

Mặt khác:  130ff

Vậy phương trình có hai nghiệm 1,3xx , khi đó tổng các nghiệm bằng 4.

Câu 24: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức z thỏa mãn 22zi là một

đường tròn tâm I , bán kính R với

A. 2;1,2IR . B. 2;1,2IR . C. 2;1,2IR . D. 2;1,2IR . Lời giải

Chọn D

Gọi  2 ,,1zxyixyi   .

Khi đó  22 22212214 zixyixy 

Vậy tập hợp điểm biểu diễn các số phức z là một đường tròn tâm  2;1I , bán kính 2R

Câu 25: Cho hàm số yfx  liên tục trên  và có bảng xét dấu của fx  như sau

Số điểm cực đại của hàm số đã cho là A. 2. B. 4. C. 1. D. 3.

Lời giải

Chọn C

Nhận xét fx  đổi dấu từ dương sang âm qua 1x

Vậy hàm số đã cho có một điểm cực đại.

Câu 26: Cho hình chóp SABC có đáy là tam giác đều,SA vuông góc với đáy và 2 ABSA  (tham khảo hình vẽ).

Góc giữa hai mặt phẳng

A. 3 B. 4 C. 8 D. 2



  

2 2ln20 xfx

với x 





A. 060 . B. 030 . C. 090 . D. 045 . C B A S

 SBC và

ABC bằng

Gọi M là trung điểm BC .

Lời giải Chọn B

ABC

đều nên AMBC  và.

có SAABCHình



SMBC

Có    , , SBCABCBC AMABCAMBC SMSBCSMBC          . Do đó góc giữa mặt phẳng  SBC và  ABC là góc giữa SM và AM , hay là góc  SMA Xét tam giác SAM vuông tại A có 3 2 AB AM   0 21 tan 30 33 2 AB SA SMA SMA AMAB  . Câu 27: Cho hàm số 2x fxx  Khẳng định nào dưới đây đúng A. 2()d2ln2 xfxx xC  B. 2()d2x fxxxC  C. 22 ()dln22 x xfxx C  . D. 2 ()d2ln22 x x fxx C  Lời giải Chọn C Ta có  221 2d ln22 x x xx xC . Câu 28: Cho hàm số bậc ba yfx  có đồ thị là đường cong như hình bên dưới. M C B A S

chiếu của SM trên mặt phẳng

ABC là AM . Suy ra

 (theo định lí ba đường vuông góc).

Có bao nhiêu giá trị nguyên của tham số m để phương trình 2()fxm  có ba nghiệm thực phân biệt?

A. 9. B. 5. C. 7 . D. 3. Lời giải

Chọn C

Xét phương trình: 2()()2mfxmfx

Số nghiệm của phương trình là số giao điểm của đồ thị hàm số ()yfx  và đường thẳng

Dựa vào đồ thị ta có điều kiện để phương trình có ba nghiệm phân biệt là: 3162 2 m m 

Có 7 giá trị nguyên của m thỏa mãn điều kiện.

Câu 29: Cho hàm số fx có đạo hàm liên tục trên R . Khẳng định nào dưới đây đúng?

A. ()d'() fxxfx   . B. '()d() fxxfx   .

C. ()d'() fxxfxC   D. '()d() fxxfxC   .

Lời giải Chọn D

'()d() fxxfxC  

Câu 30: Trong không gian với hệ tọa độ Oxyz ,cho hai điểm (1;1;1)M và (5;5;1)N Mặt phẳng () OMN có phương trình là

A. 2350 xyz B. 2350 xyz C. 230 xyz



m y



mm 

;5;4;3;2;1;0;1

 D. 250 xyz Lời giải Chọn A Ta có: (1;1;1)OM  , (5;5;1)ON  , vectơ pháp tuyến của () OMN : ;(4;6;10)2(2;3;5)nOMON         Mặt phẳng () OMN đi qua đểm (0;0;0)O là: 2350 xyz Câu 31: Tập nghiệm của bất phương trình  log20 x là A.  3; B.  12; C.  2;3 D.  ;3

+ Trường hợp 1: atùy ý

Xếp hai chữ số 2 và 3vào 5 vị trí ,,,, abcde có 2 5A cách.

Xếp các chữ số khác chữ số 2 và 3vào 3 vị trí còn lại có 3 8A cách.

+ Trường hợp 2: 0a .

Xếp hai chữ số 2 và 3vào 4 vị trí ,,, bcde có 2 4A cách.

Xếp các chữ số khác chữ số 2 ; 3 và 0 vào 2 vị trí còn lại có 2 7A cách.

Vậy số các số thỏa yêu cầu đề bài là 2322 5847 AAAA số.

Lời giải Chọn C  0 202 log20 23 23 10 x x x x x x         

32: Diện tích hình phẳng giớn hạn bởi các đường 243yxx ; 0x và 0y bằng A. 5 3 . B. 16 9 . C. 4 3 . D. 8 3 . Lời giải Chọn D Phương trình hoành độ giao điểm: 2 1 430 3 x xx x    1 2 2 2 0 0 1 3 3 3 2 3 3 1 2 0 1 43d43d43d 2323 3 3 3 8 Sxxxxxxxxx x x xx xx                    . Câu 33: Có bao nhiêu số tự nhiên có năm chữ số phân biệt, trong đó có mặt cả hai chữ số 2 và 3? A. 2322 5847 AAAA B. 23 583!CC C. 2322 5847 CACA D. 23 58AA Lời giải Chọn A Gọi số tự nhiên có năm chữ số phân biệt là  abcdeabcde  .

Câu

Câu 34: Trong không gian Oxyz , cho điểm  1;2;3A . Khoảng cách từ điểm A đến trục Ox

Câu 35: Cho tập hợp  1;2;3;4;5A . Có bao nhiêu số tự nhiên có 3 chữ số phân biệt và các chữ số

Gọi số tự nhiên có 3 chữ số phân biệt là

Lấy 3 số từ tập

abcabc 

. D. 5 . Lời

Chọn B Trục Ox có VTCP  1;0;0i  .  1;2;3OA  ,0;3;2OAi      22,32 , 13 1 OAi dAOx i       

thuộc

Lời giải Chọn A

bằng

4 .

13 .

giải

125



hợp A có 5 số xếp vào 3 vị trí ,, abc thì ta lập được 3 560A số thỏa yêu cầu đề bài. Câu 36: Cho hàm số fx liên tục trên  Nếu  2 0 4fxdx  thì  1 0 2 fxdx bằng. A. 2 B. 4 C. 2 D. 8 Lời giải Chọn A Ta có  1 0 2 Ifxdx  , đặt 22 2 dttxdtdxdx  . Đổi cận: 00;12xtxt   2 0 1 2 2 Iftdt    . Câu 37: Nếu 225 xx thì giá trị củ biểu thức 443 xxA là A. 5 B. 25 C. 26 D. 26 Lời giải Chọn D Ta có 2 2244225442344326 xx xx xx xx 

Câu 38: Có bao nhiêu số nguyên x là nghiệm của bất phương trình  2 22 3 5 41 log2log50 7 xx xx            ? A. 5. B. 0 . C. 1. D. 2 . Lời giải Chọn D Đặt 240txxt   . Khi đó:   2 2 3 5 3 5 log12log130log12log13 t t t t    Xét hàm số  2 3 5 2 14 log12log13' 0,01ln321ln5 t ftt t ft t t t       . Hàm số luôn đồng biến trên  0; . Mặt khác từ bất phương trình suy ra  2 2 2242001ftftxx xx x   . Do  0;1xx  nên có 2 giá trị của x thỏa mãn. Câu 39: Có bao nhiêu

m để đồ thị hàm số 322 2 8(11)22yxxmxm    có hai điểm cực trị nằm về hai phía của trục hoành? A. 7 B. 5 C. 6 D. 4 Lời giải Chọn B Để đồ thị hàm số có hai điểm cực trị nằm về hai phía trục hoành thì phương trình 322 2 8(11)220xxmxm   có ba nghiệm phân biệt.  22 22 322 2 2 2610 610 8(11)220 x xxxm xxm xxmxm       Khi đó phương trình 22610xxm có hai nghiệm phân biệt khác 2 2 2 '1001010 412103 m m m m                . Vì  2;1;0;1;2mm  Câu 40: Cho lăng trụ ''' . ABCABC có đáy là tam giác vuông cân tại B , 3.ABa  Hình chiếu vuông góc của ' A lên mặt phẳng () ABC là điểm H thuộc cạnh AC sao cho 2 HCHA  Mặt bên '' () ABBA tạo với đáy một góc 060 . Thể tích khối lăng trụ đã cho bằng A. 33 5 a B. 33 2 a C. 3 3 a D. 3 6 a Lời giải Chọn B

giá trị nguyên của tham số

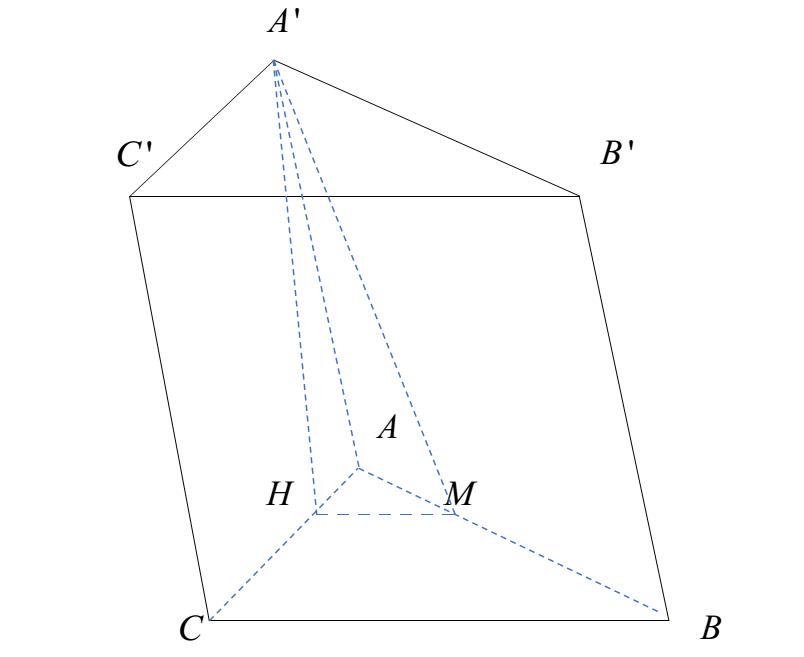
Kẻ // HMBCHMAB  mà    ' 0 ' ' ,'60AHABABAMHABBAABCAMH    0 13 3 '.tan60.3 33 3 a a HMBC AHHM a    . 23'13 ..3 22ABC aVAHSaa    Câu 41: . Trong không gian Oxyz , cho hai đường thẳng 1 11 : 112 dxyz   , 2 1 : 121 dxyz  Đường thẳng d đi qua điểm  5;3;5A cắt 1d , 2d tại hai điểm B và C Độ dài đoạn thẳng BC bằng A. 32 B. 19 C. 25 D. 23 Lời giải Chọn B Gọi   1 21;1;2;;21; BbbbdCcccd      4;2;25;5;24;5 ABbbbACccc    ,, ABC thẳng hàng    1 45 54 1 224242 2 2552551 2 b bkc bkck ABkACbkc bkckkc bkc bkck k                                 12,2,2,1,1,119cBC BC   Câu 42: Cho hình chóp . SABC có đáy ABC là tam giác vuông cân tại B với 3ABa BC  , góc  90SABSCB  và khoảng cách từ A đến mặt phẳng  SBC bằng 2a . Tính diện tích mặt cầu ngoại tiếp hình chóp . SABC. A. 216a B. 22a C. 28a D. 212a

Gọi I là trung điểm SB

Ta có: + ISIAIB  ( SAB vuông tại A)

( SCB vuông tại C )

phânbiệt 12 , zz thỏamãn 1233zz

3. B. 4. C. 2. D. 1.

giải Chọn C

phương trình  1 : 2210zmz

Để phương trình 

Lời giải

Chọn D

ISIBIAICR I là tâm mặt cầu ngoại tiếp hình chóp . SABC. Gọi E là trung điểm

, mà ABC vuông tại B Nên IE là trục đường tròn ngoại tiếp ABC . IEABC tại E . Ta có:      , 1 1 2 , , 2 2 2 , dESBCEC a AESBCC dESBCdASBC ACdASBC                   2 2 a EH  . Ta có: 222 2 2 111 16 112 23 22 a EI EIEHEF aa       26 3. 22 a EBa   6 .23 2 a IB a   Vậy diện tích mặt cầu ngoại tiếp hình chóp . SABC:  22 ; 412IIB SRa  . Câu

2210zmz (m là tham số thực). Có bao nhiêu giá trị

nghiệm

? A.



1 có hai nghiệm phân biệt thì có 2 trường hợp: TH1: Hai nghiệm 12 , zz 2 01011 m mm  Khi đó:   12 12 12 1 2 12 33 336 33 zz zzloai zz zzzz            E A B C S I F H

ISICIB 

43: Trên tập hợp số phức, xét phương trình

nguyên của m đểphươngtrìnhđãchocóhai

 

Lời

Xét

263 mm  . So điều kiện, nhận 3m

Hai nghiệm 12,\zz011 m  Khi đó:  2 22 2 12 3 333zz abab      (luôn đúng).

m nguyên nên nhận 0m Vậy có 2 giá trị nguyên của m thoả đề. Câu 44: Cho Fx là một nguyên hàm của hàm số 11 fxxx  trên  và thỏa mãn 13F . Tính tổng  02FF  A. 3. B. 2. C. 7. D. 5. Lời giải Chọn C Ta có:      11,khi1 2,khi1 11,khi112,khi11 2,khi1 11,khi1 xxx x fxxx xfxx x x xxx                    Ta có:  0 2 02 1 1 11 0121 221FFFFfxdxfxdxxdxdx     .  021211237FF F  Câu 45: Cho hình chóp SABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, đường thẳng SC tạo với mặt phẳng  SAB một góc 30 Thể tích của khối chóp SABCD A. 32 3 a B. 32 2 a C. 32a D. 32 4 a Lời giải Chọn A Có      ,,30 BCAB BCSABSCSABSCSBBSC BCSA       Xét SBC vuông tại B 3 tan303 3 BCa SB a   . Suy ra 222SASBABa   . Vậy 3 2 112 2 333SABCD ABCD aVSASaa    Câu 46: Có bao nhiêu giá trị nguyên của tham số  10;10a để hàm số

TH2:

Vì

4 32 3421230 yxaxaxa   nghịch biến trên khoảng ;2? A. 12. B. 11. C. 10. D. 13. Lời giải Chọn D Xét hàm số  4 32 3421230 hxxaxaxa    3 2 1212224 hxxaxax  Trường hợp 1:     2 0,;2220 112500 20 22 2,24 ,;22 2,24 2,24 2 hx xxaxa a h xxax a axx a a a a                           Trường hợp 2:     2 0,;2220 112500 20 22,;2 2,24 2,24 . 2,24 hx xxaxa a h xxaxaxx a a a a a                                Vậy  2;10a nên có 13 giá trị nguyên a thỏa bài toán. Câu 47: Cho hàm số yfx  có đạo hàm liên tục trên  thỏa mãn 2 2 x xfxxfx e  , x  và 02f . Tính  2f A. 4 2 2f e  B. 4 2 2f e  C. 22f D. 22 fe  Lời giải Chọn A Ta có    2 2 2 2 2 2 2 2 2 2 2 2 2 2 x x x x x x x x x fxxfx efxexfx efx e e e                 2 2 2 2 2 2 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 d 2 2 2 dd 2d x x x x x x x efxxxefx x e ee                        2 2 2 2 4 1 22 0221 22 fef ef f e e e       

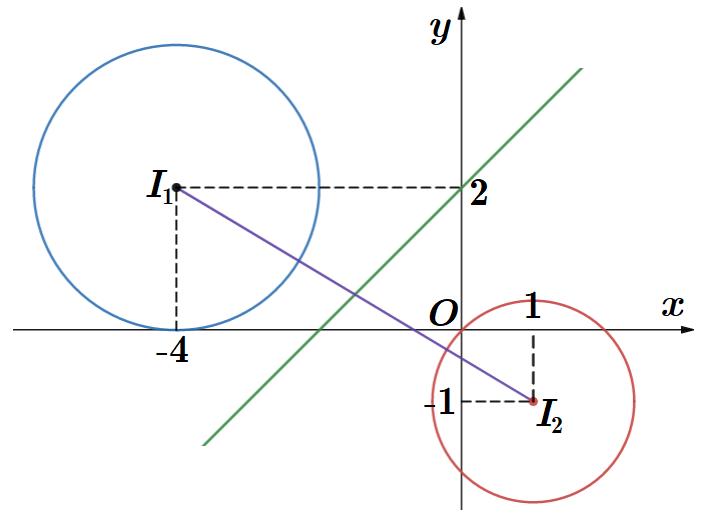
Câu 48: Cho các số phức u , v, w thỏa mãn các điều kiện 422ui , 3121 vivi  và 22 wwi  . Tìm w khi Suwvw  đạt giá trị nhỏ nhất. A. 13 2 w B. 10 2 w C. 17 2 w D. 5 2 w Lời giải Chọn D Gọi M , N , P lần lượt là điểm biểu diễn các số phức u , v, w trên mặt phẳng phức. Ta có 422ui nên M thuộc  1C có 14;2I , 12R . Đặt vxyi  , khi đó  312131312121 vivixyixyi    2 2 2 231312121 xyxy  22220xyxy  Khi đó, N thuộc  2C có 21;1I , 22R Ta có 2222 wwiwwi  , khi đó P thuộc đường trung trực d của đoạn thẳng AB với  0;0A ,  2;2B :20dxy  Do  1C và  2C nằm về hai phía của d nên SuwvwMPNPMN  . Đẳng thức xảy ra khi P là giao điểm của 12II và d Ta có   12 15 :115;13 3 xt II Ptt yt     . Thay tọa độ điểm P vào d ta có được  131315 151320 ; 222222 tt tP wiw     Câu 49: Trong không gian Oxyz , cho điểm (0;0;3)A và điểm B thay đồi thuộc mặt phẳng () Oxy sao cho diện tích tam giác OAB bằng 3 2 . Gọi C là điềm trên tia Ozthòa mãn [,][,] dCABdCOBk   . Thể tích của khối tròn xoay tạo bời tập hợp tất cả các điểm M mà CMk  thuộc khoảng nào dưới dây?

Câu 50: Có bao

A. (0,2;0,7) . B. (1,2;1,7). C. (1,7;2,2). D. (0,7;1,2). Lời giải Chọn D Tam giác OABvuông tại 13 1 22 OOBOAOBB   nằm trên đường tròn tâm  0;0O , bán kính 1.r Ta có   0 tan3.60. OA OBA OBA OB  Theo bàira [,][,] dCABdCOBkCtiaOz   vànằmtrêntiaphângiáctrongcủa  OBAC  là chân đường phân giác trong của góc   0 1 30 . 2 3 OBA BOBC OCk  Tập hợp các điểm M là khối cầu tâm ,C bán kính 1 3 RThể tích khối cầu là 3 3 4414 0806 33393 VR      

nhiêu

nguyên dương (;) xy thỏa mãn 222log2(4)(4)?xy xxyy xy     A. 13. B. 18. C. 15. D. 21. Lời giải Chọn C  2222 2 2 2 22log2(4)(4)loglog24xy xxyy xyxyxyxy xy        2222 2 2 log44log22. xyxyxyxy   Đặt  2 1 log,0l10,0. n2fttttft t t   Ta có     2 2 22 22 0 442226 4 2 ft xyxyxy fxyfxy        

cặp số

  2 2 266226 1,2,3,4266226 1,2,3,4,,,0,0 x x x y y y xyxy xy                      Thay(;) xy thảo điều kiện 1,2,3,4 1,2,3,4 x y    và  2 2 226xy   thì có 15 cặp (;) xy là   (;)1;1,1;2,1;3,1;4,2;1,2;2,2;3,2;4,3;1,3;2,3;3,3;4,4;1,4;2,4;3. xy

Câu

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH ĐẮK NÔNG

ĐỀ THI THỬ TNTHPT - NĂM HỌC: 2022-2023

Câu 8: Cho mặt cầu ()222 :24230 Sxyzxyz++-++-= .

9: Cho hình

tích khối chóp . SABC bằng

nón bằng

Cho

yfx

có đồ thị như hình vẽ bên. Số nghiệm của phương trình ()2fx=là A. 0 . B. 2. C. 3. D. 1. Câu 2: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức nào? A. 12 zi =+ B. 2 zi =-+ C. 2 zi =+ D. 12 zi =Câu 3: Khối nón có bán kính đáy bằng r , chiều cao bằng h . Thể tích khối

B. 2 rhp . C. 2rhp . D. rhp Câu

3 1 d2fxx= ò thì

3 1 2d fxxxé ë+ù û ò bằng A. 12

B. 18. C. 10. D. 20 . Câu

có 13u=- , công bội 2q= . Khẳng định nào sau đây đúng? A. 132n n u=- B. 132n n u= C. 32n n u= D. 32n n u=-

của

P ? A. ()32;3;2n  = B. ()22;3;1n  = C. ()12;3;0n  = D. ()42;0;3n  =

giới hạn bởi đồ thị hàm số 2 21yxx=-- và trục

bằng A. 9 8 p B. 81 80 C. 9 8 D. 81 80 p

hàm số bậc ba ()

21 3 rhp .

4: Nếu ()

()

5: Cho cấp số nhân () n u

Câu 6: Trong không gian Oxyz , cho mặt phẳng ():2320Pxyz+++= . Vectơ nào dưới đây là một vectơ pháp tuyến

()

Câu 7: Cho hình phẳng () H

hoành. Thể tích của vật thể tròn xoay khi quay () H quanh trục hoành

A. 9R= . B. 3R= . C. 3R= . D. 33R= .

cạnh a và ()SAABC

3SAa =

Thể

A. 33 4 a . B. 4 a . C. 3 2 a . D. 3 4 a .

Tính bán kính R của mặt cầu () S

Câu

chóp

SABC có đáy ABC là tam giác đều

^ và

() 4;2;2M. Mệnh đề nào sau đây là đúng?

A. Điểm M là tâm của mặt cầu () S . B. Điểm M nằm trên mặt cầu () S .

C. Điểm M nằm trong mặt cầu () S D. Điểm M là nằm ngoài mặt cầu () S

Câu 13: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ sau đây

A. 331yxx=-++ . B. 4231yxx=--+ . C. 33 yxx =-+ .

D. 4231yxx=-++ .

Câu 14: Cho hàm số bậc bốn ()yfx = có đồ thị hàm số ()yfx ¢ = là đường cong trong hình vẽ, hàm số ()yfx = đã cho đồng biến trên khoảng nào dưới đây?

A. () 4;0- B. () ;1-¥- C. () 2;+¥ D. () 0;2

Câu 15: Trong không gian ,Oxyz mặt phẳng nào dưới đây song song với mặt phẳng () Oxy ?

A. ():10 z a+= B. ():10 x j+= C. ():10 xz b++= D. ():10 y g+=

Câu 16: Cho phương trình 1 4230 xx+ +-= . Khi đặt 2xt= ta được phương trình nào sau đây?

A. 2230tt+-= . B. 2 230 tt-= .

C. 230tt+-= .

D. 430 t-= .

Câu 17: Một hộp có 6 quả bóng đỏ được đánh số từ 1 đến 6 Lấy ngẫu nhiên 3 quả bóng. Xác suất để tích các số trên 3 quả bóng lấy ra là một số chẵn bằng

Câu 10: Đạo hàm của hàm số ()2x fxx =+ là A. ()2 1 ln2 x fx ¢=+ B. ()2ln21 xfx ¢=+ C. () 22 ln22 x x fx ¢=+ D. ()21 xfx ¢=+

Tập hợp các điểm biểu diễn số phức zxyi =+ với , xyÎ thỏa mãn 4zi-= là đường tròn có phương trình

()2 214xy+-= . B. ()2 2116xy+-= . C.

22 14xy-+= D.

22 116xy-+=

cho mặt cầu ()()()() 2 22 :2119Sxyz-+-++= và

Câu 11:

()

Câu 12: Trong không gian ,Oxyz

điểm

Câu 18: Tiệm cận ngang của đồ thị hàm số 2 1 x y x

A. 1x=- B. 2y=-

= + là

C. 2x= D. 1y=

Câu 19: Cho hàm số ()yfx = liên tục trên toàn  và có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số là điểm nào sau đây A. Điểm N .

Câu 20: Trong không gian Oxyz , đường thẳng 123 : 212 dxyz--==đi qua điểm nào dưới đây?

A. ( )1;2;3M--- B. () 2;1;2Q-

C. ( )2;1;2N--

Câu 21: Tập nghiệm của bất phương trình ()2 log11 x+< là

D. () 1;2;3P

A. () ;1-¥ B. () 1;2- C. () 1;1- D. () 1; -+¥

Câu 22: Trên mặt phẳng tọa độ, cho () 2;3M là điểm biểu diễn của số phức z Phần thực của z bằng

A. 3- B. 3

C. 2 D. 2-

Câu 23: Hàm số ()fx có một nguyên hàm là hàm số ()gx trên khoảng K nếu

A. ()(), fxgxCxK =+"Î B. ()(), gxfxCxK ¢=+"Î

C. ()(), gxfxCxK =+"Î . D. ()(), fxgxCxK ¢=+"Î .

Câu 24: Trên khoảng () 0;+¥ , đạo hàm của hàm số 2log yx = là

A. 1 y x ¢ = B. ln2 y x ¢ = C. 1 2y x ¢ =

Câu 25: Thể tích của khối hộp chữ nhật có độ dài các cạnh là ,3,5 aaa bằng

1 ln2y x ¢ =

A. 15a . B. 215a . C. 15. D. 315a .

Câu 26: Cho hàm số ()yfx = có đồ thị như hình vẽ sau:

A. 1 20 B. 1 10 C. 19 20 D. 9 10

Điểm Q.

Điểm P .

Điểm M .

Giá trị cực đại của hàm số bằng

Câu 27: Tập nghiệm của bất phương trình 2 34 x< là

Câu 28: Trong Họ tất cả các nguyên hàm của hàm số ()sin4 fxxx

Câu 30: Cho hai số phức 14 zi

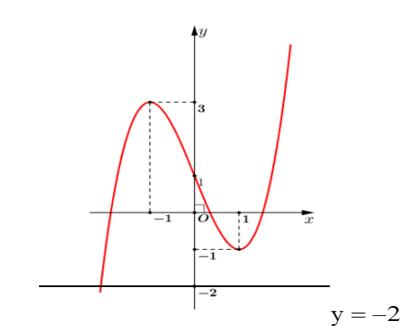
Câu 31: Cho hàm số bậc ba ()fx có đồ thị như hình vẽ. Số giá trị nguyên của tham số m đề phương

()1 fxm += có 3 nghiệm phân biệt là

Câu 32: Hàm số ()yfx = liên tục trên  và có đạo hàm ()()() 2 11fxxxx ¢ =-- . Hàm số ()yfx = nghịch biến trên khoảng A. () 2;1--

() 0;1

() 1;0-

() 1;2

Câu 33: Cho hình chóp . SABC có SA vuông góc với mặt phẳng () ABC , biết 3 2 Sa A= và tam giác

C. 0

D. 1.

A. 2.

2;+¥ C. ( )3 ;log2-¥ D. ( )3 ;log4-¥

() ;2-¥

()

là A. 2

B. 2cos2

C. 2 cosxxC--+ D. 2cos4xxC -+

cos2xxC--+

xxC -+

số khác nhau được

thành

số 1,2,3,4,5,6. A. 5P . B. 5 6C . C. 5 6A . D. 6P .

Câu 29: Có bao nhiêu số có 5 chữ

tạo

từ các chữ

, 2

=. Số

của số phức 1 2 z z là A. 67 55 i+ . B. 67 55 i. C. 43i+ . D. 67 1717 i.

12 zi

phức liên hợp

A. 2 B. 3 C. 5 D. 4

trình

tạo

A. 45° . B. 90° . C. 60° . D. 30° .

 3 2 d4fxx  và  3 2 d1gxx  . Khi đó  3 2 d fxgxx     bằng A. 5. B. 4. C. 3. D. 3.

ABC đều cạnh bằng

. Góc

bởi giữa mặt phẳng () SBC và () ABC bằng

Câu 34: Biết

Câu 35: Cho hai số thực , ab tuỳ ý khác 0 thoả mãn 34ab = . Giá trị của a b bằng

A. ln0,75. B. 3 log4. C. 4 log3. D. ln12.

Câu 36: Xét số phức z thoả mãn 222zi--= . Giá trị nhỏ nhất của biểu thức 152 Pzizi =--+-- bằng

A. 17 B. 110 + C. 5

Câu 37: Trong các nghiệm () ; xy thỏa mãn bất phương trình ()22 2 log21 xyxy + +³ . Giá trị lớn nhất của biểu thức 2 Txy =+ bằng

A. 9 B. 9 4

9 8

9 2

Câu 38: Cho hàm số ()fx liên tục trên  . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên  thỏa mãn ()() 888FG+= và ()() 002FG+=- . Khi đó () 0 2

A. 5 4 . B. 5.

-ò bằng

4d fxx -

5 4.

Câu 39: Trong không gian Oxyz cho điểm () 2;1;2A-- và đường thẳng ()111 : 111 dxyz--==.

Gọi () P là mặt phẳng đi qua điểm A, song song với đường thẳng () d và khoảng cách từ () d tới () P là lớn nhất. Khi đó mặt phẳng () P vuông góc với mặt phẳng nào sau đây?

A. 32100xyz+++= B. 320 xz++= C. 2310xyz---= D. 60xy--=

Câu 40: Trên tập hợp số phức, xét phương trình 228120zmzm-+-= (m là số thực). Có bao nhiêu giá trị của m để phương trình đó có hai nghiệm phân biệt 12 , zz thỏa mãn 124?zz+= A. 1 B. 4 C. 3 D. 2

Câu 41: Cho khối lăng trụ đều . ABCABC¢¢¢ có cạnh đáy bằng 2a . Biết khoảng cách từ điểm A¢ đến mặt phẳng () ABC¢¢ bằng a . Thể tích của khối lăng trụ đã cho là

32 8 a .

32 2 a .

Câu 42: Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm (2;5;0),(4;7;0)BC và (1;1;3)K . Gọi() Q là mặt phẳng đi qua K và vuông góc với mặt phẳng () Oxy . Khi 2(;())(;()) dBQdCQ + đạt giá trị lớn nhất, giao tuyến của () Oxy và () Q đi qua điểm nào sau đây?

A. (8;4;0)P- B. (15;4;0)N- C. 7 15;;0 2 S æö ç÷ ç÷ ç÷ èø D. (3;2;0)M

Câu 43: Chohìnhnón () N cóđỉnh S ,chiềucao 3h= Mặtphẳng () P quađỉnh S cắthìnhnón () N theo thiết diện là tam giác đều. Khoảng cách từ tâm đáy hình nón đến mặt phẳng () P bằng 6 Thể tích khối nón giới hạn bởi hình nón () N bằng

Câu 44: Cho hàm số ()fx thỏa mãn: ()()()()

A. 3

B. 3

D. 32 2

a .

A. 12p

81p

36p

¢ -

"Î+¥

2 1 fe e = .

.ln2,1;xfxxfxxfxx

và ()

Câu 46: Số giá trị nguyên của tham số m để hàm số ()4 223 ymxmxm =--+

có điểm cực đại là

Câu 47: Tập nghiệm của bất phương trình ( )() 2 2 3 5 log412log53 xx xx-+++ -+£ là () ; ab . Khi đó tổng 2 ab + bằng

A. 1 B. 3 C. 4 D. 2

Câu 48: Có bao nhiêu giá trị nguyên của tham số ( )2022;2022mÎ- để hàm số ()3212yxmx =++-

đồng biến trên khoảng ()1;3?

A. 4034 . B. 4032 . C. 4030 . D. 2022 .

Câu 49: Trong không gian với hệ tọa độ Oxyz , điểm đối xứng của () 1;2;3M qua trục Ox có tọa độ là

A. ( )1;2;3--. B. () 1;0;0 . C. () 1;2;3 -. D. () 0;2;3 .

Câu 50: Cho hình lăng trụ đứng . ABCABC¢¢¢ có đáy ABC là tam giác đều cạnh a và 2 AAa ¢ = . Gọi

M là trung điểm của AA ¢ Khoảng cách từ M đến mặt phẳng () ABC ¢ bằng

Biết () ()0,1;fxx>"Î+¥ , diện tích S của hình phẳng giới hạn bởi đồ thị (),0, yxfxyxe = == và 2 xe = là A. 5 3 S= . B. 1 2 S= . C. 2S= . D. 3 2 S= . Câu 45: Trong không gian Oxyz, đường thẳng đi qua hai điểm () 1;2;1A- và () 2;1;1B- có phương trình tham số là A. 1 23 12 xt yt zt ì ï=+ ï ï ï í=ï ï ï=-+ ï î B. 1 23 12 xt yt zt ì ï=+ ï ï ï í=ï ï ï=+ ï î C. 1 32 2 xt yt zt ì ï=+ ï ï ï í=-+ ï ï ï=ï î D. 1 12 xt yt zt ì ï=+ ï ï ï í=+ ï ï ï=ï î

không

C. 0. D.

4. B. 2.

vô số

A. 257 19 a . B. 5 5 a . C. 25 5 a . D. 57 19 a . ---------- HẾT ----------

BẢNG ĐÁP ÁN 1.D 2.B 3.A 4.B.C 5.A 6.B 7.D 8.C 9.D 10.B 11.B 12.C 13.A 14.B 15.A 16.A 17.C 18.D 19.D 20.D 21.C 22.C 23.B 24.D 25.D 26.A 27.C 28.A 29.C 30.A 31.B 32.C 33.A 34.C 35.B 36.A 37.D 38.A 39.B 40.D 41.B 42.B 43.D 44.D 45.A 46.A 47.D 48.C 49.C 50.D HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ bên. Số nghiệm của phương trình ()2fx=là A. 0 . B. 2. C. 3. D. 1. Lời giải Chọn D Câu 2: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức nào? A. 12 zi =+ B. 2 zi =-+ C. 2 zi =+ D. 12 zi =Lời giải Chọn B Câu 3: Khối nón có bán kính đáy bằng r , chiều cao bằng h Thể tích khối nón bằng A. 21 3 rhp . B. 2 rhp . C. 2rhp . D. rhp Lời giải Chọn A Câu 4: Nếu () 3 1 d2fxx= ò thì () 3 1 2d fxxxé ë+ù û ò bằng A. 12. B. 18. C. 10. D. 20 .

5: Cho cấp số nhân ()

Câu 6: Trong không gian Oxyz , cho mặt phẳng ():2320Pxyz+++= Vectơ nào dưới đây là một vectơ pháp tuyến của () P

Câu 8: Cho mặt cầu ()222 :24230 Sxyzxyz++-++-= . Tính bán kính R của mặt cầu () S

A. 9R= . B. 3R= .

Chọn C

3R= .

Lời giải

Ta có () ()222 1;2;112133I R --Þ=++--=

33R= .

Câu 9: Cho hình chóp . SABC có đáy ABC là tam giác đều cạnh a và ()SAABC ^ và 3SAa = . Thể

tích khối chóp SABC bằng

A. 33 4 a .

Chọn D

Lời giải

Lời giải Chọn C () () 3 3 3 1 1 1 2dd2d2810fxxxfxxxxé+ù= + =+= ë û ò ò ò . Câu

n u có 13u=- , công bội 2q= Khẳng định nào sau đây đúng? A. 132n n u=- B. 132n n u= C. 32n n u= D. 32n n u=Lời giải Chọn

? A. ()32;3;2n  = B. ()22;3;1n  = C. ()12;3;0n  = D. ()42;0;3n  = Lời giải Chọn B Câu 7: Cho hình phẳng () H giới hạn bởi đồ thị hàm số 2 21yxx=-- và trục hoành. Thể tích của vật thể tròn xoay khi quay () H quanh trục hoành bằng A. 9 8 p

B. 81 80 . C. 9 8 . D. 81 80 p . Lời giải

2 1 2101 2 x xx x é= ê --=Ûêê=ê ë

() 1 22 1 2 8121d 80 Vxxxp =p--= ò

Chọn D Phương trình hoành độ giao điểm

Thể tích tròn xoay là

C. 3 2 a . D. 3

4 a .

Câu 10: Đạo hàm của hàm số ()2x fxx =+ là

A. ()2 1 ln2

x fx ¢=+ B. ()2ln21 xfx ¢=+

Lời giải

()21 xfx ¢=+

Chọn B () () 2 2ln21 x xfxxfx ¢ =+Þ=+

Câu 11: Tập hợp các điểm biểu diễn số phức zxyi =+ với , xyÎ thỏa mãn 4zi-= là đường tròn

có phương trình

A. ()2 214xy+-= B. ()2 2116xy+-=

C. ()22 14xy-+= D. ()22 116xy-+=

Lời giải

Chọn B () ()2 2 414116zixyixy -=Û+-=Û+-=

Câu 12: Trong không gian ,Oxyz cho mặt cầu ()()()() 2 22 :2119Sxyz-+-++= và điểm () 4;2;2M- Mệnh đề nào sau đây là đúng?

A. Điểm M là tâm của mặt cầu () S . B. Điểm M nằm trên mặt cầu () S .

C. Điểm M nằm trong mặt cầu () S D. Điểm M là nằm ngoài mặt cầu () S Lời giải

Chọn C ()()()() () 2 22 :21192;1;1,3Sxyz IR -+-++=Þ-=

Ta có () ()222 4;2;22116M IM R-Þ=++-=< .

Vậy điểm M nằm trong mặt cầu () S .

Câu 13: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ sau đây

Lời giải

Chọn A

Đồ thị hàm số có dạng như trên là đồ thị hàm số bậc 3 và đi qua điểm () 0;1 . Hàm số cần tìm là 331yxx

Thể tích

SABC là 2 3 113 ...3 3344 ABC a a VSSA a = = = .

khối chóp .

C. () 22 ln22 x x fx ¢=+ D.

=-++ . B. 4231

=--+ . C. 3

A. 331yxx

yxx

3 yxx =-+ .

4231yxx=-++ .

=-++

Câu 14: Cho hàm số bậc bốn ()yfx = có đồ thị hàm số ()yfx ¢ = là đường cong trong hình vẽ, hàm

số ()yfx = đã cho đồng biến trên khoảng nào dưới đây?

A. () 4;0- B. () ;1-¥- C. () 2;+¥ D. () 0;2

Lời giải

Chọn B

Dựa vào đồ thị ta có () () 0,;1fxx¢>"Î-¥- Vậy hàm số ()yfx = đồng biến trên khoảng () ;1-¥- .

Câu 15: Trong không gian ,Oxyz mặt phẳng nào dưới đây song song với mặt phẳng () Oxy ?

A. ():10 z a+= . B. ():10 x j+= . C. ():10 xz b++= . D. ():10 y g+= .

Lời giải

Chọn A

Mặt phẳng song song với mặt phẳng () Oxy là ():10 z a+=

Câu 16: Cho phương trình 1 4230 xx+ +-= . Khi đặt 2xt= ta được phương trình nào sau đây?

A. 2230tt+-= . B. 2 230 tt-= . C. 230tt+-= . D. 430 t-= .

Lời giải

Chọn A

Ta có: 1 423042.230 xx x x + +-=Û+-= , khi đó đặt 2xt= ta được phương trình

2230tt+-=

Câu 17: Một hộp có 6 quả bóng đỏ được đánh số từ 1 đến 6 . Lấy ngẫu nhiên 3 quả bóng. Xác suất để

tích các số trên 3 quả bóng lấy ra là một số chẵn bằng

A. 1 20

Chọn C

B. 1 10

C. 19 20

Lời giải

Số phần tử của không gian mẫu là ()3 620nCW==

Gọi A là biến cố: “tích các số trên 3 quả bóng lấy ra là một số chẵn”.

D. 9 10

Ta có biến cố đối của A là A: “tích các số trên 3 quả bóng lấy ra là một số chẵn” tức là “lấy

được 3 quả bóng mang số lẻ”.

Từ đó ()1nA= . Suy ra ()1 20 PA=

Vậy xác suất của biến cố A là: ()()119 11 2020 PAPA=-=-=

Câu 18: Tiệm cận ngang của đồ thị hàm số

Ta có 2 limlim1

Vậy 1y= là tiệm cận ngang của đồ thị hàm số.

Câu 19: Cho hàm số ()yfx = liên tục trên toàn  và có đồ thị như hình vẽ. Điểm cực đại của đồ thị

hàm số là điểm nào sau đây

A. Điểm N B. Điểm Q C. Điểm P D. Điểm M

Lời giải

Chọn D

Dựa vào hình vẽ ta có M là điểm cực đại của đồ thị hàm số

Câu 20: Trong không gian Oxyz , đường thẳng

x y x= + là

A. 1

=. B. 2y=. C. 2x= . D. 1y= . Lời giải Chọn D

= = +

x x x y x ®+¥ ®+¥= = + và

limlim1

x x x y x ®-¥ ®-¥

--==đi

A. (

1;2;3M

2;1;2Q. C. ( )2;1;2N-. D. () 1;2;3P .

123 : 212 dxyz

qua điểm nào dưới đây?

)

---

()

Chọn

() 1;2;3P

21: Tập nghiệm của bất phương trình ()2 log11 x+< là A. () ;1-¥ . B. () 1;2. C. () 1;1. D. () 1; -+¥ . Lời giải Chọn C ()2 101 log11 11 121 x x x x x x ì ì+> >- ï ï ï ï +<Û Û Û-<< í í ï ï+< < ï ï î î Câu 22: Trên mặt phẳng tọa độ, cho () 2;3M là điểm biểu diễn của số phức z Phần thực của z bằng A. 3- B. 3 C. 2 D. 2Lời giải Chọn C

Lời giải

D Ta có đường thẳng d đi qua điểm

Câu

Số phức z có điểm biểu diễn là () 2;3M .

23 ziÞ=+ .

Suy ra phần thực của z bằng 2.

Câu 23: Hàm số ()fx có một nguyên hàm là hàm số ()gx trên khoảng K nếu

A. ()(), fxgxCxK =+"Î .

C. ()(), gxfxCxK =+"Î

Chọn B

B. ()(), gxfxCxK ¢=+"Î .

D. ()(), fxgxCxK ¢=+"Î

Lời giải

Hàm số ()fx có một nguyên hàm là hàm số ()gx trên khoảng K nếu

()(), gxfxCxK ¢=+"Î

Câu 24: Trên khoảng () 0;+¥ , đạo hàm của hàm số 2log yx = là

A. 1 y x ¢ = B. ln2 y x ¢ = C. 1 2y x ¢ = D. 1 ln2y x ¢ =

Lời giải

Chọn D () 2 1 logln2yx x ¢ ¢ = = .

Câu 25: Thể tích của khối hộp chữ nhật có độ dài các cạnh là ,3,5 aaa bằng

A. 15a B. 215a C. 15 D. 315a

Lời giải

Chọn D

Ta có 3.3.515 Vaaaa = = .

Câu 26: Cho hàm số ()yfx = có đồ thị như hình vẽ sau:

Giá trị cực đại của hàm số bằng

A. 2 B. 1- C. 0 D. 1

Lời giải

Chọn A

Ta có giá trị cực đại của hàm số bằng 2.

Câu 27: Tập nghiệm của bất phương trình 2 34 x< là

A. () ;2-¥ . B. () 2;+¥ . C. ( )3 ;log2-¥ . D. ( )3 ;log4-¥ .

Lời giải

Chọn C

Ta có 2 3

342log4log2 x x x

Vậy tập nghiệm của bất phương trình là ( )3 ;log2-¥ .

Câu 28: Trong Họ tất cả các nguyên hàm của hàm số ()sin4 fxxx =- là

A. 2cos2xxC--+

Chọn A

Ta có ()( ) 2dsin4dcos2 fxxxxxxxC = -=--+

Câu 29: Có bao nhiêu số có 5 chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6. A.

Chọn C

Số có 5 chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6 là 5 6A .

Câu 30: Cho hai số phức 14 zi =, 212 zi =- Số phức liên hợp của số phức 1

67 55 i+ B. 67 55 i-

Chọn A

Ta có 1 2

467 1255 zi i zi==+.

Câu 31: Cho hàm số bậc ba ()fx có đồ thị như hình vẽ. Số giá trị nguyên của tham số m đề phương trình ()1 fxm += có 3 nghiệm phân biệt là

Chọn B

Ta có () ()() 1

fxmfxm +=Û=- .

Câu 32: Hàm số ()yfx = liên tục trên  và có đạo hàm

()

11fxxxx

=-- . Hàm số ()yfx =

<Û<Û<

B. 2

C. 2 cosxxC--+ D. 2

-+ Lời giải

cos2xxC -+

cos4xxC

òò .

B. 5 6C . C. 5 6

D. 6P

Lời

5P .

A .

giải

iLời

z z là A.

43i+

67 1717

giải

Lời

giải

Đựa

biệt

11304

m -<-<Û<< , mà mÎ

1;2;3m ÞÎ

vào đồ thị phương trình

* có ba nghiệm phân

khi và chỉ khi

{}

nghịch

C. () 1;0- D.

1;2

()()()

biến trên khoảng

() 2;1--

() 0;1

()

Lời giải

Chọn C

é= ê ¢

Dựa vào bảng biến thiên hàm số nghịch biến trên khoảng () 1;0-

Câu 33: Cho hình chóp . SABC có SA vuông góc với mặt phẳng () ABC , biết 3 2 Sa A= và tam giác

ABC đều cạnh bằng a . Góc tạo bởi giữa mặt phẳng () SBC và () ABC bằng

A. 45° B. 90° C. 60° D. 30° Lời giải Chọn A

Câu

34:

Gọi I là trung điểm của BC . Vì tam giác ABC đều nên AIBC ^ , lại có BCSA ^ nên

Ta có ()()() 2 0 110 1 x fxxxx x =--=Ûê=±

. Khi đó ta có bảng biến thiên

() 3 2 d4fxx= ò và () 3 2 d1gxx= ò . Khi đó ()() 3 2 d fxgxxé ë-ù û ò bằng A. 5. B. 4. C. 3. D. 3. Lời giải Chọn C Ta có, ()() ()() 3 3 3 2 2 2 ddd413fxgxxfxxgxxé-ù= - =-= ë û ò òò

ý khác 0 thoả mãn 34ab =

Giá trị của a b bằng A. ln0,75. B. 3 log4. C. 4 log3. D. ln12.

BCSI ^ . Do đó góc giữa hai mặt phẳng () SBC và () ABC là góc  SIA Xét tam giác SAI vuông tại A có 3 2 Sa A= và 3 2 Aa I= Do đó   tan145 SA SIA SIA AI ==Þ=°.

Biết

Câu 35: Cho hai số thực , ab tuỳ

Lời giải

Chọn B

Lấy logarit cơ số 3 hai vế của đẳng thức 34ab = ta được 3 .log4ab = 3 log4a b Þ= .

Câu 36: Xét số phức z thoả mãn 222zi--= . Giá trị nhỏ nhất của biểu thức 152 Pzizi =--+-- bằng

A. 17 B. 110 + C. 5 D. 4 Lời giải

Chọn A

Tập hợp các điểm biểu diễn số phức z là đường tròn tâm () 2;2I bán kính 2R= Gọi () 1;1A và () 5;2B lần lượt là điểm biểu diễn số phức 1i+ và 52i+ .

Khi đó biểu thức ()() 22 512117PMAMBAB =+³=-+-= . Dấu bằng xảy ra khi M

giữa A và B . (Hình vẽ trên)

Câu 37: Trong các nghiệm () ; xy thỏa mãn bất phương

nằm

trình ()22 2 log21 xyxy + +³ . Giá trị lớn nhất của biểu thức 2 Txy =+ bằng A. 9 B. 9 4 C. 9 8 D. 9 2 Lời giải Chọn D Ta có: () () () 22 22 22 22 22 021 022 log21 21 22 xy xy I xyxy xy xy II xyxy + éìï<+<êï êí êï<+£+ ï î +³Ûêìêï+> êï êíï+³+êï ëî Xét biểu thức 2 Txy =+ . TH1: () ; xy thỏa mãn () I , khi đó: 22 0221. Txyxy <=+£+< TH2: () ; xy thỏa mãn () II : () 2 2 22 19 2212 28 2 xyxyx y æ ö ÷ ç +³+Û-+-£ ÷ ç ÷ ÷ ç è ø Khi đó: () () 2 2 2 1191 1 221.2 212 42222 22 Txyx y x y é ù æ ö æ ö æöê ú ÷ ÷ ÷ ç ç ç =+=-+ -+£+-+÷ ÷ ÷ ç ç çê ú ÷ ÷ ç÷ ÷ ÷ ç ç èø è ø è ø ê ú ë û

() 999991 max;2; 284222 T Txy æö ç÷ Þ£+=Þ=Û=÷ ç÷ ç èø

Câu 38: Cho hàm số ()fx liên tục trên  Gọi ()() , FxGx là hai nguyên hàm của ()fx trên  thỏa

mãn ()() 888FG+= và ()() 002FG+=- . Khi đó () 0 2

-ò bằng

4d fxx -

A. 5 4 B. 5 C. 5- D. 5 4Lời giải Chọn A

Đặt () 0 2

4d Ifxx -

=ò Đặt 1 4 . 4 xtdxdt-=Þ=- Đổi cận:

Khi đó: () () ()

111 dt=dt=d 444 Iftftfxx =-

Do ()() , FxGx là hai nguyên hàm của ()fx trên  nên có: ()()()()()181 = 80804. 404 IGxGGGGI é ù =ë-Þ-= û Tương tự cũng có:

()() 804 FFI -= . Suy ra: ()()()()() 5 888008210. 4 IFGFG I =+--=--=Þ=

Câu 39: Trong không gian Oxyz cho điểm () 2;1;2A-- và đường thẳng ()111 : 111 dxyz--==.

Gọi () P là mặt phẳng đi qua điểm A, song song với đường thẳng () d và khoảng cách từ () d tới

() P là lớn nhất. Khi đó mặt phẳng () P vuông góc với mặt phẳng nào sau đây?

A. 32100xyz+++= B. 320 xz++= C. 2310xyz---= D. 60xy--= Lời giải

Chọn B

Gọi ( )1;1;1 Httt +-+ là hình chiếu của A lên đường thẳng d . Ta có:

0 8 8 8 0 0

òòò

() d có 1 véc tơ chỉ phương () 1;1;1du  =, ( )1;2;3AHttt  =--+ . Khi đó:

()()() () .01.11.21.303001;1;1. d dAHuAHu t tt ttH

Gọi K là hình chiếu của Htrên () P . Ta có: () ()() () ()() max d;d;dPHPHKAHHKAHAHPP = =£Þ=Û^Þ nhận () 1;2;3AH  =-

làm véc tơ pháp tuyến.

Giả sử mặt phẳng () Q có 1 véc tơ pháp tuyến Qn  và  QP  . Suy ra: Q nAH    phù hợp với

phương trình mặt phẳng () Q là 320 xz++= .

Câu 40: Trên tập hợp số phức, xét phương trình 228120zmzm-+-= (m là số thực). Có bao nhiêu giá trị của m để phương trình đó có hai nghiệm phân biệt 12 , zz thỏa mãn 124?zz+=

A. 1. B. 4. C. 3. D. 2. Lời giải

Chọn D

Ta có: 2812mm D¢=-+

TH1: 026 m D¢<Û<< .

Phương trình có hai nghiệm phức 2 1,2 812zmimm=±-+-

Ta có 12zz = , do đó 12 1 42zzz+=Û= 22(812)481242(l)mmm m m Û+-+-=Û-=Û=

2 812 zzm zzm ì+=-

2 281241684642 m mmmmm Û-=-+-Û-=-+-

4642 4642 420 mmm mmm mm ìé ï-=-+-

 ^Þ =Û---++=Û=Û=Þ

TH2: 2 0 6 m m é<D¢ê>Ûê> ë thì phương trình có hai nghiệm thực phân biệt 12 , zz 12 12 ï ï í ï=ï î

2 2 2

ïê ï Ûïê-=-+ íê ïë ï ï ï-+-³ î 2 2 2 2 4 2 422880 422 4202222 m m m m mm m mm m ì ì é é ï=± ï= ï ï ê ê é ï = ï ï ï ê ê ê Û Û Û =±í-+=í ê ë ë ê ï ï =- ï ï ë ï ï ï-+-³-££+ ï î î Vậy có 2 giá trị thỏa mãn. Câu 41: Cho khối lăng trụ đều . ABCABC¢¢¢ có cạnh đáy bằng 2a . Biết khoảng cách từ điểm A¢ đến mặt phẳng () ABC¢¢ bằng a . Thể tích của khối lăng trụ đã cho là A. 332 6 a B. 332 8 a C. 332 2 a D. 32 2 a Lời giải Chọn B

Ta có: ()2 12 121212 +4+2216 zzzzzzzz =Û -+ = ()

42812281216 mm m Û--+-=

Gọi M là trung điểm của BC¢¢ .

Ta có AABC AMBC

ì¢¢¢ ï^ ï í ï¢¢¢ ï^ î ()BCAAMÞ¢¢¢ ^ ()() ABCAAMÞ¢¢¢ ^

Trong mặt phẳng () AAM ¢ , kẻ AHAM ¢^ , suy ra ()AHABC ¢^¢¢ .

Vậy khoảng cách từ A¢ đến mặt phẳng () ABC¢¢ là AHa ¢ = . 3AMa =

Ta có 222 111 AHAAAM ¢=+¢¢ 2222 1112 3 AAAHAMa Þ=-= ¢¢¢ 6 2 Aa A Þ¢= .

Vậy thể tích khối lăng trụ là 23 6332 .. 248ABC aaaVAAS¢¢¢ ¢ = = = .

Câu 42: Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm (2;5;0),(4;7;0)BC và (1;1;3)K Gọi () Q là mặt phẳng đi qua K và vuông góc với mặt phẳng () Oxy . Khi 2(;())(;()) dBQdCQ + đạt giá trị lớn nhất, giao tuyến của () Oxy và () Q đi qua điểm nào sau đây?

A. (8;4;0)P- B. (15;4;0)N- C. 7 15;;0 2 S æö ç÷ ç÷ ç÷ èø D. (3;2;0)M

Lời giải

Chọn B

Gọi () ;; nabc  = là pháp tuyến của mặt phẳng () Q .

Do () Q vuông góc với () Oxy nên () ;;0nab  = , mà () Q đi qua K nên (): 0Qaxbyab+--= .

Trường hợp 1: B , C nằm cùng phía so với () Q , khi đó:

2436 2,, abab dBQdCQ abab + + + = + + +

2836514514 221 ababab ab ababab ab + + + + + = + = £ = + + + + .

222222

Đẳng thức xảy ra khi ():514190 514 ab Qxy=Þ +-=

Trường hợp 2: B , C nằm khác phía so với () Q , khi đó:

1228362

ab ababab ababab ab -+ + + +-+

222222 22

() ()() ()2222 2222

() ()() ()2222 =

2436 2,, abab dBQdCQ abab + + + = + + + ()()2222

+ = £ = + + + +

Đẳng thức xảy ra khi ():210 12 ab Qxy =Þ-+-= -

Vậy () Q có phương trình là ():514190Qxy+-= .

Điểm qua giao tuyến của mặt phẳng () Q và () Oxy là (15;4;0)N-

Câu 43: Chohìnhnón () N cóđỉnh S ,chiềucao 3h= Mặtphẳng () P quađỉnh S cắthìnhnón () N theo

thiết diện là tam giác đều. Khoảng cách từ tâm đáy hình nón đến mặt phẳng () P bằng 6 Thể

tích khối nón giới hạn bởi hình nón () N bằng

A. 12p B. 81p C. 36p D. 27p

Lời giải Chọn D

Ta có:

32 OHOS OM OSOH = =và 2233SMSOOM=+= 6SA Þ= , 33OA= . Vậy thể tích khối nón là ()2 1 33327 3 V=´p´=p. Câu 44: Cho hàm số ()fx thỏa mãn: ()()()() 22 ln2,1;xfxxfxxfxx ¢ - += "Î+¥ và ()2 1 fe e = . Biết () ()0,1;fxx>"Î+¥ , diện tích S của hình phẳng giới hạn bởi đồ thị (),0, yxfxyxe = == và 2 xe = là A. 5 3 S= . B. 1 2 S= . C. 2S= . D. 3 2 S= . Lời giải Chọn D Giả thiết ()() () () 2 1lnln 22 fxfxx x x x x fx fx ¢ ¢ - æö ç÷ ÷ Û =Ûç= ç÷ ÷ ç÷ èø () 2lnxxC fx Þ=+ + () () () 2 2 1 lnln 0 x x feCfx xfx e x x =Þ=Þ=Þ= + Tính () 2 2 2 ln13 dln 22 | e e e e Sxxx x = = = ò Câu 45: Trong không gian Oxyz, đường thẳng đi qua hai điểm () 1;2;1A- và () 2;1;1B- có phương trình tham số là

Kẻ OMAB ^ và OHSM ^ . Ta suy ra () 6OHSABOH^Þ= .

Lời

Chọn A

Đường thẳng AB đi qua () 1;2;1A- và có 1 vectơ chỉ phương () 1;3;2AB  =- . Do đó phương

ì ï=+ ï ï ï í=ï ï ï=-+ ï î

xt yt zt

trình tham số là 1 23 12

Câu 46: Số giá trị nguyên của tham số m để hàm số ()4 223 ymxmxm =--+ không có điểm cực đại là

A. 4. B. 2. C. 0. D. vô số.

Lời giải

Chọn A

 Nếu 0m= thì 23 yx = . Hàm số chỉ có điểm cực tiểu x = 0. Do đó 0m= thỏa mãn.

 Nếu 0m¹ thì hàm số đã cho là hàm bậc bốn trùng phương.

 Nếu ()30mm-< thì hàm số có 3 điểm cực trị. Khi đó hàm số có điểm cực đại (không thỏa mãn yêu cầu đề bài).

 Nếu ()3003mm m -³Û<£ thì hàm số có 1 điểm cực trị và đồ thị hàm số có dạng như

hình vẽ dưới đây Khi đó hàm số không có điểm cực đại (thỏa mãn yêu cầu đề bài).

Vậy có 4 giá trị nguyên m thỏa mãn là 0; 1; 2; 3.

Câu 47: Tập nghiệm của bất phương trình ( )()

log412log53 xx xx-+++ -+£ là () ; ab . Khi

đó tổng 2 ab + bằng

A. 1. B. 3. C. 4. D. 2. Lời giải Chọn D

Đặt ()240txxt

A. 1 23 12 xt yt zt ì ï=+ ï ï ï í=ï ï ï=-+ ï î B. 1 23 12 xt yt zt ì ï=+ ï ï ï í=ï ï ï=+ ï î

yt zt ì ï=+ ï ï ï í=-+ ï ï ï=ï î D. 1 12 xt yt zt ì ï=+ ï ï ï í=+ ï ï ï=ï î

C. 1 32 2 xt

giải

2 2 3 5

=-+> thì bất phương trình trở thành: ()() 2 3 5 log12log130 t t++ +-£ Xét hàm số ()()() 2 3 5 log12log13ftt t=++ +- trên () 0;+¥ . ()()() () 2 14 0,0;1ln31ln5 t ft t t t Þ¢= + >"Î+¥ + + nên hàm số đồng biến trên khoảng () 0;+¥ Mà ()() 2 2 02242001.ftftxx xx x <=Þ<Þ-+<Û-<Û<< Vậy 0,122abab ==Þ+=

Vì ( ){ }()2022;20222021;2020;...;142

Từ ()() 1,2 có 4030 giá trị nguyên m thỏa mãn yêu cầu bài toán.

Câu 49: Trong không gian với hệ tọa độ Oxyz , điểm đối xứng của () 1;2;3M qua trục Ox có tọa độ là

A. ( )1;2;3--. B. () 1;0;0 . C. () 1;2;3 -. D. () 0;2;3 . Lời giải

Chọn C

Gọi () ;0;0Hh là hình chiếu của M lên trục Ox .

Suy ra ( )1;2;3MHx  =--- và 0MHi  ×= .

Do đó ()11;0;0xH =Þ .

Gọi M¢ là điểm đối xứng của M qua trục Ox suy ra H là trung điểm của MM¢

Vậy () 1;2;3M¢ --

Câu 50: Cho hình lăng trụ đứng ABCABC¢¢¢ có đáy ABC là tam giác đều cạnh a và 2 AAa ¢ = Gọi M là trung điểm của AA ¢ . Khoảng cách từ M đến mặt phẳng () ABC ¢ bằng

Câu 48: Có bao nhiêu giá trị nguyên của tham số ( )2022;2022mÎ- để hàm số ()3212yxmx =++đồng biến trên khoảng ()1;3? A. 4034 B. 4032 C. 4030 D. 2022 Lời giải Chọn C Xét ()() ()() 3 2 212321 fxxmxfxxm ¢ =++-Þ=++ TH1: () () () () ()[] 2 2 1;3 210,1;33210,1;3min 3 10 20 0 m fxx xm x x f m m ì + ï ì ì ï¢³"Î ï ï++³"Î ³- ï ï ï Û Û í í í ï ï ï ³ ³ ï ï ï î î ï³ î Vì ( ){ }()2022;20220;1;2;...;20211m m m ì ïÎï ÞÎ í ïÎ ï î TH2: ()() () ()() [] 2 2 1;3 2101;332101;3max 3 10 20 0 m fxx xmx x f m m ì + ï ì ì ï¢£"Î ï ï++£"Î £- ï ï ï Û Û í í í ï ï ï £ £ ï ï ï î î ï£ î 92114 14 3 0 0 m m m m m ì + ï ì ï £- £- ï ï ï Û Û

í í ï ï£ ï î ï£ ï î

Þ£-

m m m ì

í ïÎ ï î

ïÎï ÞÎ-- -

() ()

A. 257 19 a . B. 5 5 a . C. 25 5 a . D. 57 19 a . Lời giải Chọn D Gọi K là trung điểm BB¢ suy ra () ()() ()() ()1 d,d,d, 2 MABCKABCBABC ¢ ¢ ¢ = = Gọi I là trung điểm AC suy ra 3 2 a BI= Kẻ BH vuông góc với BI ¢ tại H. Suy ra

()d,BABCBH ¢ = Khi đó 22 257 19 BIBB a BH BIBB ¢ × = = +¢ Vậy

19 aMABC ¢ = . ---------- HẾT ----------

()

SỞ GIÁO DỤC VÀ ĐÀO TẠO LÀO CAI

ĐỀ THI THỬ TỐT NGHIỆP THPT

NĂM HỌC 2022 – 2023 – LẦN 1

Câu 1: Thể tích của khối chóp có đáy là tam giác ABC vuông, ABACa  và chiều cao 2a là

Câu 2: Tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số 2 yx  , trục hoành và đường thẳng 2x , khi quay xung quanh trục Ox bằng

. 6

Câu 3: Cho ba số dương  ,,1,1 abcab và các số thực  khác 0. Đẳng thức nào sai?

A. 1 loglog a a b b   B. llog ogloga b a

c c b 

C. log()loglog a a a bcbc  D. logloglog a ab cbc 

Câu 4: Có bao nhiêu cách sắp xếp 5 học sinh vào một ghế dài từ một nhóm gồm 10 học sinh?

A. 105 B. 5 10. C. 5 10A D. 5 10C

Câu 5: Cho hàm số yfx  có bảng biến thiên như sau

Số điểm cực tiểu của hàm số đã cho

A. 3 B. 0

C. 1

Câu 6: Họ nguyên hàm của hàm số 1 54fx x   trên 4 \ 5  

A. 1 ln54. 5 fxdxxC 

C. 1

D. 2

Khẳng định nào sau đây đúng?

ln54. fxdxxC 

A. 3 6 a B. 3 3 a C. 32 6 a D. 32 3 a

C. 5 . 6

32 . 5  B.



 D. 4 5 

 

 B.



ln54. ln5fxdx xC    D.  1 ln54. 5 fxdxxC    Câu 7: Tìm tất cả các nghiệm của bất phương trình 2 32 25 . 52 x x      A. 2 . 1 x x    B. 12 x  C. 21 x  D. 1 . 2 x x    Câu 8: Trên khoảng  0; , đạo hàm của hàm số 1 yx   là A. 11 yx     B. 1 yx   C.  1 yx    D. 1 yx    

12. B. 11.

40 .

Câu 15: Họ tất cả nguyên hàm của hàm số 2sin fxxx  là

2 2cosxxC  .

2 2cosxxC  .

2 cos xxC  .

13.

Câu 9: Nếu  1 0 2fxdx  và  1 0 7gxdx  thì  1 0 23fxgxdx     bằng A. 12. B. 25. C. 17. D. 25. Câu 10: Tiệm cận đứng của đồ thị hàm số 21 1 x y x   là A. 1.x B. 1 2 x C. 1 2 x D. 1.x Câu 11: Trong không gian Oxyz , cho mặt phẳng :2230Pxyz Điểm nào sau đây thuộc mặt phẳng  P ? A.  1;1;3M B.  1;1;3E C.  2;1;3N D.  2;2;1F Câu 12: Tập nghiệm của bất phương trình 2 log13 x là A.  ;8S . B.  1;8S . C.  1;7S . D.  ;7S . Câu 13: Cho hàm số fx liên tục trên  và có đồ thị là đường cong như hình vẽ bên dưới

nghiệm của phương trình 20fx trên đoạn  2;3 là A. 1. B. 3. C. 4 . D. 2 . Câu 14: Cho cấp số cộng  n u có số hạng đầu 15u , công sai 2d . Giá trị của 4u bằng

Số

 2 1 d2fxx  .

của  2 1 2d fxxx    bằng A. 1 B. 3 C. 4 D. 5

   axb

cxd có đồ thị là đường

độ

điểm của đồ thị hàm số đã cho và trục hoành là

2 cos xxC  . Câu 16: Biết

Giá trị

Câu 17: Cho hàm số

cong trong hình vẽ bên. Tọa

giao