39-50)
WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL
TAILIEUCHUANTHAMKHAO@GMAIL COM

Trang 1
Câu 39.(Đề TK BGD 2023) Có bao nhiêu số nguyên x thỏa mãn
22
i giải Chọn D TXĐ: ()() ;44;. D =−∞−∪+∞ Ta có: ()() () ()() () () () () 22 7 37 2 2 7 7 3 2 23 3 7 2 22 373 77 7 7 3 7 7 3 7 1616 l7.1631633 3log7log3 71.l163733log16 log71 log1631log3log16log21 g oglogloglogloglog 34327 logogloglo 16219277927 xx xx xx xx xx ⇔−−<−− ⇔−−<−⇔−< ⇔−<+⇔−< ⇔−<⇔ < < < Kếthợp điềukiệntacó {} 96;95;...;5;5;...;95;96 x ∈−−− .Vậycó184số nguyênxthỏamãn.
BÀI TẬP PHÁT TRIỂN CÂU 39 ĐỀ THAM KHẢO BGD NĂM 2023
Câu 1. Có bao nhiêu số nguyên x thỏa mãn 2 5
2 3 44 loglog 27 125 xx < ?
A. 117 .B. 116 C. 112 D. 56 .
22 2 44 8116 xx
<
A. 68 B. 34 C. 63 D. 33
Câu 3. Có bao nhiêu số nguyên x thoả mãn 22 53 11 loglog6561625 xx ≤

A. 3 . B. 1. C. 5 . D. 0 .
Câu 4. Có bao nhiêu số nguyên x thỏa mãn 2
22 5 20232023 5log>lo812 g xx ?
A. 24 B. 25 C. 26 D. 27
Câu 5. Có bao nhiêu số nguyên x thỏa mãn 4
22 3 169169 9 l> 16 oglogxx ?
A. 8. B. 9. C. 10. D. 11.
Câu 6. Có bao nhiêu số nguyên x thỏa mãn 22 34 44 loglog2716 xx < ?
A. 24. B. 20. C. 21. D. Vô số.
Câu 7. Có bao nhiêu số nguyên âm x thỏa mãn: 22 57 loglog25250 12549 xx <
A. 500. B. 545. C. 444. D. 456
Trang 2
Câu 8. Cóbaonhiêusố nguyên x thỏamãn 5
22 2 5 loglo99 2 g 32 xx < ?
A. 6 B. 3 C. 8 D. 0
Câu 9. Tínhtổngcácsố nguyêndương x thỏamãn 22 23 loglog28312 278 xx ≤ ?
A. 102 B. 0 C. 12 D. 187
Câu 10. Cóbaonhiêusố nguyên x thỏamãn 22 251258 99 loglogxx < ?
A. 63. B. 62. C. 58. D. 56
Câu 11. Cóbaonhiêusố nguyên x thỏamãn: 22 57 44 loglog4925 xx < ?
A. 64. B. 33. C. 66D. 70.
Câu 12. Cho bất phương trình 22 23 3636 loglog24332 xxxx −+−+ < . Gọi S là tập hợp các nghiệm nguyên củabấtphươngtrình đãcho.Tổnggiátrị tấtcả cácphầntử của S bằng
A. 86. B. 89. C. 246. D. 264.
Câu 13. Tìm tổng tất cả các nghiệm nguyên của bất phương trình sau: 33 3 5 loglog2727 2433125 xx ≥ bằng
A. 0 B. 4227 C. 4183 D. 4180
Câu 14. Cóbaonhiêusố nguyên x thỏamãn 22 25 loglo99 258 g 1 xx < ?
A. 56 B. 57 C. 54
Câu 15. Số nghiệmnguyêncủabấtphươngtrình 22 23 2525 loglog94 xx-< là
28
A. 14. B. 5. C. 4. D. 15.
Câu 16. Cóbaonhiêusố nguyên x thỏamãn 22 25 loglog99 62516 xx ≤ ?
A. 192 B. 194 C. 200 D. 201
Câu 17. Cho bất phương trình () ()log2 44 2loglog64 x xx ≥ . Số nghiệm nguyên không vượt quá 2023 củabấtphươngtrình đãcholà
A. 1960. B. 1964. C. 2023. D. 2064.
Câu 18. Biết bất phương trình ()() 2 327 log31.log391 + −−≤ xx có tập nghiệm là đoạn [] ; ab . Tổng =+ Tab bằng A. 3 3log112=+ T B. 3 2log112=−+ T
Câu 19. Bấtphươngtrình () () 2 11 1 2 39log1020 −+ −++≥ xx x cóbaonhiêunghiệmnguyên?
A. Vôsố B. 6 C. 10 D. 9
Câu 22. Bấtphươngtrình 2 2 31 3 log(21)log(21)2320 xxxxx −−+++−−≥ cóbao
nhiêunghiệmnguyênthuộc đoạn [] 2023,2023 ?
A. 2020 . B. 2021. C. 2022 . D. 2023 .
Câu 23. Bấtphươngtrình ( ) ( ) 2 12 2 loglog11 x −≤− cóbaonhiêunghiệmnguyênthuộckhoảng () 10;10 :
A. 16 . B. 14 . C. Vôsố. D. 18 .
Câu 24. Bấtphươngtrình 2 2 2 22
log log 2 1 loglog1
x x xx −≤ có bao nhiêu nghiệm nguyên dương nhỏ hơn 15
A. 13 .B. 15 .C. 16 .D. 14 .
Câu 25. Cho bất phương trình 2 log(41)0 m xxm−++> . Có bao nhiêu giá trị nguyên 2024 m < để bất phương trình nghiệm đúng với mọi x A. 2019. B. 2020 C. 2023 D. 2024
Câu 26. Có bao nhiêu số nguyên thỏa mãn () () 2 2 18820231 2023 88 loglog1loglog1 xxxx ++>+− ?
A. 46 B. 44 C. 43 D. 45
x x
≥
A. Vô số B. 2 C. 3 D. 4
Câu 28. Số các giá trị nguyên của x thỏa ( )() 2 25 3 20231log20 x x −−≤ là
A. Vô số. B. 5 . C. 3 . D. 4 .
Câu 29. Có bao nhiêu số nguyên () 23;23 y ∈− thỏa mãn () ()22 33 2log31log62 xyxxy++≤−+ với mọi x ∈ℝ ?
A. 9 .B. 11 C. 13 D. 15 .
Câu 30. Tập nghiệm của bất phương trình 4 2
1log1 1log2 x x ≤ + là
A. 1 ;2 2 . B. () 2; +∞ .
C. ) 1 0;2; 2 ∪+∞ . D. () 1 ;2; 2 −∞∪+∞ .
Câu 31. Số nghiệm nguyêncủa phương trình 23 log(3)log(2)2 xx−+−= là
A. 0 . B. 1. C. 2 . D. Vô số.
Câu 32. Có bao nhiêu số nguyên x thoả mãn ()() 22 352 log2log32log3 xx −−−< ?
A. 94. B. 92. C. 100. D. 98.
Câu 33. Tập hợp nghiệm của bất phương trình 2323 loglog1log.log xxxx +≥+ có dạng [] ; ab . Tính 3ab + ?
Trang 3
Trang 4
Ôn thi TN THPT năm 2023
A. 9. B. 12. C. 3 D. 4.
Câu 34. Gọi S là tập nghiệm của bất phương trình () 2 422 2loglog.log211 xxx ≥+− . T
hợpcon của tập hợp nào sau đây?
A. [ ) 2; +∞ . B. () ;4−∞ . C. [] 0; +∞ . D. () 1;4 .
−+
11 loglogloglog11 xx xx
A. 17 B. 9 C. 3 D. 16
Câu 36. Có bao nhiêu số nguyên [] 2023;2023 x ∈− thoả mãn ()() 22 20232032 log4log4 xx−≥− ?
A. 4324. B. 1232. C. 1002. D. 4042.
Câu 37. Có bao nhiêu số nguyên x thỏa mãn ( ) () ( ) 2 11 33 log7log2426440 x xx +−+−≤ ?
A. 18 B. 21 C. 19 D. 20
Câu 38. Có bao nhiêu cặpsố nguyên () ; xy thỏa mãn 02020 x ≤≤ và
() 3 log3329? y xxy++=+
A. 2019 . B. 6 . C. 2020 . D. 4 .
Câu 39. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn () () 2 43 loglogxyxy +≥+ ?
A. 115 . B. 59 . C. 58 . D. 116 .
Câu 40. Có bao nhiêu số nguyên x thuộc đoạn [] 2022;2023 thỏa mãn
()() 22 37 log33log4949 xx+>+ ?
A. 4037 B. 4039 C. 4045 D. 4046
Câu 41. Có bao nhiêu số nguyên x thõa mãn: 73 loglog(2) xx<+
A. 48 B. 49 C. 47 D. 50
Câu 42. Có bao nhiêu số nguyên x thỏa mãn ( ) () () 2 22332 2 24log12455420 xxx xxx +++−+++−≤ ?
A. 7B. 6 . C. 19 . D. 20 .
Câu 43.: Nghiệm của bất phương trình 4311 43
11 loglogloglog11 −+ < +− xx xx là (;).xab ∈ Khẳng định nào
sau đây đúng?
A. 2 4. b = B. 2 5. b = C. 2 2. b = D. 2 3. b =
Câu 44. Có bao nhiêu nghiệm nguyên lớn hơn 2023 của bất phương trình () 3 32 3log12logxxx++> .
A. 0. B. 2023. C. 2050. D. 2072.
Câu 45. Có bao nhiêu số nguyên x thỏa mãn 59 0 1 1 1 +logo 1 lg 225 8 1 x x < ?
A. 0 B. 4 C. 5 D. 2
Câu 46. Có bao nhiêu số nguyên () 20;20 y ∈− thoả mãn () ()22 33 2log31log62 xyxxy++≤−+ với mọi x ∈ℝ ? A. 9 . B. 11.
C.
Trang 5
có tất cả bao nhiêu số nguyên?
A. 2 . B. 3 . C. 4 . D. Vô số.
Câu 50. Có bao nhiêu nghiệm nguyên của bất phương trình 3232 log.log2loglog 4 x xxx>− nhỏ hơn 2023 :
A. 2024 B. 2023 C. 2010 D. 2018
Trang 6
Câu 1. Có bao nhiêu số nguyên x thỏa mãn
A. 3 . B. 1.
D. 0
.
2 3 44 loglog 27 125 xx < ?
2 5
A.117 .B.116 C.112 D. 56 .
Lời giải TXĐ: ()() ;22;. D =−∞−∪+∞
L
ời
giải
22 222 535533355 7 11 1 logloglog(1)8log3log(1)4log5log(1)(log)4log3 6561625 3 xx xxx ≤⇔−−≤−−⇔−≤
44 l 125 5.435433 51.l43533 3log5log3 log4 log51 log431log
⇔−< ⇔−<+ ⇔−< ⇔−<
2
⇔ <
xx xx x x x x x x
g 4log15 415 33
3
< −< Kếthợp điềukiệntacó {} 58;57;...;3;3;...;57;58 x ∈−−− .Vậycó 112 số nguyên x
có: ()()
2
2 33 444log34log2xx−<−loglog
()
x x ⇔−−<− log log ()()
4log34log2 log3
4 2 46 x ⇔−< 10131013 x ⇔−<<
ubàitoán. Câu 4. Cóbaonhiêusố nguyên x thỏamãn 2 22 5 20232023 5log>lo812 g xx ? A. 24 B. 25 C. 26 D. 27 Lời giải TXĐ: () 2023;2023. D =− ()() ()() 52 2 2 5 2 522 22 5252 2 8125 202332202335 l2023l20233235 20232023 log>log loglogloglog ogogloglog x xx xx x ⇔−−> ⇔−−>− () () () () () () 2 2552 52 2 5 2 1l5.l2023325 325 l2023 1l5 ogogloglog loglog og og x x ⇔−−>− ⇔−< () () () 2 55 23 55 l202331log2 l2023l og ogog10 x x ⇔−<+ ⇔−< () () 2 2 20231000
1023 ;10231023; x
Kế
x ∈−−−
7
Câu 5. Có bao nhiêu số nguyên x thỏa mãn 4
22 3 169169 9 l> 16 oglogxx ?
A. 8. B. 9. C. 10. D. 11.
Lời giải
Điều kiện: ()() ;55; x ∈−∞−∪+∞
Ta có: 22 57 25250 loglog12549 xx < ()() 22 57 log253log2502 xx ⇔−−<−−
TXĐ: ()13;13. D =−
Ta có: ()()
169169 l 3 g
⇔−>−
⇔−>−
⇔−>
l 2
2 34 3
2423 169 og>loglog169loglog169log
og169log169loglog
1l3. 1 69 o
2 334
2423
oglog169loglog lolog log1 g
xx xx xx x x
343344 3434 4
() () () () ()
2 2 22 2 2 4
243 43 l
⇔−> () () () 2 2 2 3333 24l log1691+logl1 og169og2xx > >⇔ ⇔ 2 2 1442555 169 x xx ⇔>⇔⇔−<−<<
Kết hợp điều kiện ta có {} 4;3;2;1;0;1;2;3;4. x ∈−−−−
Vậy có 9 số nguyên x thỏa mãn.
Câu 6. Có bao nhiêu số nguyên x thỏa mãn 22 34 44 loglog2716 xx < ?
A. 24. B. 20. C. 21. D. Vô số Lời giải
Điều kiện: ()() ;22; x ∈−∞−∪+∞
Ta có: 22 34 44 loglog2716 xx < ()() 2 2 3344 log4log27log4log16 xx ⇔−−<−−
()() 22 34 log43log42 xx ⇔−−<−− ()() 22 344 log4.log4log41 xx ⇔−−−<
() () 2 34 log41.log41 x ⇔−−< () 2 4 3
1 log1 log41 x ⇔−< 3
1 log41 2 14 x ⇔−<
14,14714,147 x ⇔−<< .
Do x ∈ ℤ và ()() ;22; x ∈−∞−∪+∞ nên {} 14,13,...,3,3,4,...14 x ∈−−−
Vậy có 24 số nguyên x thỏa mãn bài toán.
Câu 7. Có bao nhiêu số nguyên âm x thỏa mãn: 22 57 25250 loglog12549 xx <
A. 500. B. 545. C. 444. D. 456
Trang 9
550,983550,983 x ⇔−<< .
1log2 log25 log71 x + ⇔−< 7 5
1log2 log71 2 257 x + ⇔−<
()() 22 57 log25log2251 xx ⇔−−−< ()() 22 5777 log7.log25log2log251 xx ⇔−−−−< () () 2 577 log71.log251log2 x ⇔−−<+ () 2 7 7 5
Do x nguyênâmvà ()() ;55; x ∈−∞−∪+∞ nên {} 550,549,...,6 x ∈−−− .
Vậy có 545 số nguyên âm x thỏa mãn bài toán.
Câu 8. Có bao nhiêu số nguyên x thỏa mãn 5
22 2 5 99 loglo 2 g 32 xx < ?
A. 6 B. 3 C. 8 D. 0 Lời giải
Điều kiện ()() ;33; x ∈−∞−∪+∞
Ta có 5
22 2 5 99 loglo 2 g 32 xx < ()() 22 2255 log9log32log9log25 xx ⇔−−<−−
()() 22 25 log95log92 xx ⇔−−<−− ()() 22 255 log5.log9log93 xx ⇔−−−<
() () 2 25 log51.log93 x ⇔−−< () 2 5 2
3 log9 log51 x ⇔−<
3333 22log51log51log51log51 95959595 xxx ⇔−<⇔<+⇔−+<<+
2 22 2
Lại có x ∈ ℤ và ()() ;33; x ∈−∞−∪+∞ nên {} 6;5;4;4;5;6 x ∈−−− .
Vậy có 6 số nguyên x thỏa mãn bài toán.
Câu 9. Tínhtổng các số nguyên dương x thỏa mãn 22 23 loglog28312 278 xx ≤ ?
A.102 B. 0 C. 12 D. 187 Lời giải
Điều kiện ()() ;22; x ∈−∞−∪+∞
Trang 10
Ta có 22 23 loglog28312 278 xx ≤
()() 2 2 2233 log28log27log312log8 xx ⇔−−≤−−
()() 2 2 2233 1log43log31log43log2 xx ⇔+−−≤+−−
()() 22 23323 log3.log4log43log33log2 xx ⇔−−−≤−
() () 2 2323 log31log43log33log2 x ⇔−−≤−
22 57 44 loglog4925 xx <
()() 2 2 5577 log42log7log42log5 xx ⇔−−<−−
() () () 2 5757 log71log42log7log5 x ⇔−−<−
2log7log5 log4 log71 x ⇔−<
() () 57 2 7 5
3log3log2 log4 log31 x ⇔−≤ () 2 33 log43log6 x ⇔−≤
() () 23 2 3 2
() 2 33 log4log216 x ⇔−≤ 224216220220220xxx ⇔−≤⇔≤⇔−≤≤
Các số nguyên dương của x thỏa mãn yêu cầulà {} 3;4;...;14
Vậy tổng các số thỏa mãn là () 345...146314102 ++++=+= .
Câu 10. Có bao nhiêu số nguyên x thỏa mãn 22 251258 99 loglogxx < ?
A. 63. B. 62. C. 58. D. 56
Lời giải
TXĐ: ()() ;33;. D =−∞−∪+∞
Ta có 22 251258 loglog99 xx < ()() 5 2 2 55 2 logloglo35.93l2 og9gxx <− ⇔ () () ()2525 2 51.952 o loglog3loglg x ⇔<
2 41225 x ⇔−< 2 122912291229xx ⇔<⇔−<<
Kết hợp với điều kiện x nguyên và
2 2 x x > <− ta được: {} 35;34;....;4;3;3;4;...;34;35 x ∈−−−−
Vậy có tất cả 66 số x thỏa mãn.
Câu 12. Cho bất phương trình 22 23 loglog3636 24332 xxxx −+−+ < . Gọi S là tập hợp các nghiệm nguyên
củabất phương trình đã cho. Tổng giá trị tất cả các phần tử của S bằng A. 86. B. 89. C. 246. D. 264. Lời giải
Điều kiện : 2 360 xxx−+>⇔∈ℝ.
Ta có: 22 23 loglog3636 24332 xxxx −+−+ <
()() 2 2 2233 log365log3log365log2 xxxx ⇔−+−<−+−
1 log361log25log3 log3 xx ⇔−+−<−
()() 2 232 2
()() 2 2 2 23 2
log31 log361log25. log3 xx ⇔−+−<
() () 25 5 2 2
52 9 51 3loglog log log x ⇔< () ()55 2 log3lo 912g x ⇔−+ <
()() 3 55 2 9 l10 oglog x < ⇔ 23 910 x ⇔< 10091009 x ⇔−<<
Kết hợp điều kiện ta có {} 31;30;...;4;4;...;30;31 x ∈−−− .
Vậy có 56 số nguyên x thỏa mãn.
Câu 11. Có bao nhiêu số nguyên x thỏa mãn: 22 57 44 loglog4925 xx < ?
Trang 11
() () () 2 2 2 2 23
5log31 log36 log31log2 xx ⇔−+< () () 2 22 log365log31 xx ⇔−+<+
()() 25 22 log36log6 xx ⇔−+< 25 366xx ⇔−+< .
Do x thuộc ℤ nên ta được {} 86;85;...;86;87;88;89 S =−− .
Vậy tổng giá trị tất cả các phần tử của S bằng () 8685...8586878889264 −+−++++++=
Trang 12
Câu 13. Tìm tổng tất cả các nghiệm nguyên của bất phương trình sau: 33 3 5 loglog2727 2433125 xx ≥
bằng
A. 0 B. 4227 C. 4183 D. 4180 . Lời giải
ĐK: () 3 2703*xx−>⇔>
Với ĐK (*) bất phương trình ()() 3 55 3 3 3 log27lo5 g 535 log27logxx ⇔ −≥
15.
x x x > <− −<< 31009 10093 x x << ⇔ −<<− Từ đó
suy ra có 57 số nguyên x th
nghi
củ
ấ
3 3 3 3 log27 logl0 og27loglo 5355g lo 5 g , 5 x x ⇔≥−−−>
() () () 5 33 3
()() ()
3 3 3 55. log27loglog27l5og5 xx ⇔ −≥−
()() () 3 3 3 2 3 3 3 log27loglog27l5.g5 o 55 xx ⇔ −≥
()() ()2 3 33 3 log27log 1555 glo 5 x ⇔−≥−
() () 3 33 3 log270 l 555,1oglg5 o x ⇔−+−<
2 2
1 1log23log2 log log9 2 x ⇔− −<−
Trang 13
22 2 2 232233 2525 logloglog252log3log252log2 94 xx xx
()()
( ) ( ) 2 2 22233 log252log3log25.log22log2 xx Û--<--
() 2 2 2 22
ç÷ç÷ èøèø
( ) ( )( ) 22 2 2 2 22
log31.log31 log31 log25.2.log3log3 x -+Û-<
() () 2 22 log252.log31 x Û-<+
() 2 22 log25log36 x Û-< () 2 253661;61xx Û-<ÛÎ-
Mà ( ) ( ) ;55;; xx ℤÎ-¥-È+¥Î nên {} 7;6;6;7 x Î--
Vậy có bất phương trình đã cho có 4 nghiệm nguyên.
Câu 16. Có bao nhiêu số nguyên x thỏa mãn 22 25 loglog99 62516 xx ≤ ?
A. 192 . B. 194 . C. 200 . D. 201 . Lời giải
Điều kiện: 2 3 90 3 x x x > −>⇔ <− (*).
Ta có: 22 25 99 loglog62516 xx ≤
()() 22 2255 log9log625log9log16 xx ⇔−−≤−−
()() 2 2 22525 log94log5log2.log94log2 xx ⇔−−≤−−
()() 22 25225 log9log2.log94log54log2 xx ⇔−−−≤−
Ôn
thi
TN THPT năm 2023
1 1log2log94log2 log2 x ⇔−−≤−
() () 2 52 5 5
41log2 log9 1log2log2 x ⇔−≤ () () 5 2 2 5
() () () 2 5 2 2 55
log10000 log9 log2 x ⇔−≤ () 2 22 log9log10000 x ⇔−≤
41log2 log9 log2 x + ⇔−≤ () 2 5 2 5
2 910000 x ⇔−≤ 1000910009 x ⇔−≤≤
Kết hợp với điều kiện (*), ta suy ra: 310009 100093 x x
<≤ −≤<−
Vì x ∈ ℤ nên có 194 giá trị nguyên của x thỏa mãn yêu cầu bài toán.
Câu 17. Cho bất phương trình () () log 2 44 2loglog64 x xx ≥ . Số nghiệm nguyên không vượt quá 2023
của bất phương trình đã cho là
A. 1960. B. 1964. C. 2023. D. 2064.
Lời giải
Điều kiện : 0 x > . () () 4 log2 44 2loglog64 x xx ≥ () 2 444 2.log.loglog3 xxx ⇔≥+
444 2.log.log2log3 xxx ⇔≥+ ()2 44 log2log30 xx ⇔−−≥
4 4
≤− <≤
Vì x là số nguyên không vượt quá 2023 nên ta chọn {} 64;65;...;2023 x∈ .
Vậy có 20236411960 −+= nghiệm nguyên không vượt quá 2023 của bất phương trình đã cho.
Câu 18. Biết bất phương trình ()() 2 327 log31.log391 + −−≤ xx có tập nghiệm là đoạn [] ; ab . Tổng =+ Tab bằng
T B. 3 2log112=−+ T C. 2=− T D. 3 3log112=−+ T
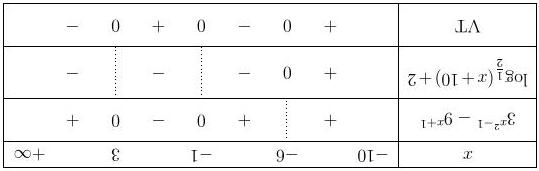
L
+ −−≤
xx xxxx
⇔−−≤⇔−+−≤
Đặt () 3 log31=− x t , bất phương trình trở thành
ttttt x
() () ()
−≤
−≤≤
Vậy ta có 3333 28112 loglog4log3log112 2727 =+=+==−+Tab .
() 1 2 log10201046 ++=⇔+=⇔=− xxx .
Bảng xét dấu
Suy ra ( ][] 10;61;3=−−∪− S .
Vậy bất phương trình có 9 nghiệm nguyên là {} 9;8;7;6;1;0;1;2;3 .
Câu 20. Gọi S là tập hợp gồm tất cả các nghiệm nguyên của bất phương trình 73 loglog(2) xx<+
Tính tổng các phần tử của S
A. 2176 B. 1128 C. 1196 D. 1176 .
Lời giải
Điều kiện 0 x >
Đặt 7log tx = 7 x = và bất phương trình đã cho trở thành:
2 3 log(72) t t <+ 2 71 723()2()1(*) 33 ttt ⇔+>⇔+>
Vì hàm số () 71 ()2() 33 tt ft =+ nghịch biến trên tập (0;) +∞ mà (2)1 f = nên suy ra bất
phương trình (*) trở thành ()(2)ftf > 2 t ⇔<
Ta có 2 t < suy ra 7 log249 xx<⇔< .
Do đó tập nghiệm của bất phương trình đã cho là (0;49) suy ra {} 1,2,3,....,48 S =
Vậy tổng các phần tử của S bằng 123...481176 ++++=
Câu 21. Số nghiệm nguyên của bất phương trình 22 43 log(1)logxx +> là
A.1. B. 2 . C. 3 . D. 4 . Lời giải
Đk: 0 x ≠
Đặt 222 4 log(1)1441 tttxxx =+ += =−
Bất phương trình trở thành
tt ttttt t >−⇔>−⇔+>⇔+>
3 31 log(41)3413141 44
Hàm số 31 ()44 tt ft =+ nghịch biến trên ℝ
Mà (1)1 f = nên ()(1)1 ftft>⇔< 222 4 log(1)114333 xxxx ⇔+<⇔+<⇔<⇔−<<
Đối chiếu với điều kiện và yêu cầu bài toán ta được {} 1,1 x ∈−
Câu 22. Bất phương trình 2 2 31 3 log(21)log(21)2320 xxxxx −−+++−−≥ có bao
nhiêu nghiệm nguyên thuộc đoạn [] 2023,2023 ?
A. 2020 B. 2021 C. 2022 D. 2023
Lời giải
Chọn C
Ôn thi TN THPT năm 2023
Câu 23. Bấtphươngtrình () () 2 12 2 loglog11 x −≤− cóbao nhiêunghiệmnguyênthuộckhoảng () 10;10 : A. 16 B. 14
C. Vôsố. D. 18 . Lời giải
ĐKXĐ: () () () 2 2 2 2
log10 11;22; 10 x xx x
−> ⇔−>⇔∈−∞−∪+∞
−>
Bất phương trình () () 2 12 2 loglog11 x −≤− () 1 2 2 1 log12 2 x ⇔−≥= () 2 14 x ⇔−≥
2 5 x ⇔≥ ( ) ;55; x ⇔∈−∞−∪+∞
Kếthợp điềukiệnta được: ( ) ;55; x ∈−∞−∪+∞
Vậycó14nghiệmnguyênthuộckhoảng () 10;10
log log
2 1 loglog1 x x xx
Lời giải
TXĐ: (1;) +∞ 2 2 31 3 22 3 3
xxxxx xxxxxx
log(21)log(21)2320 log(21)21log(21)21,(1)
−−+++−−≥ ⇔−−+−−≥+++
Xét hàm 3 1 ()log,'()10,0 ln3 yftttftt t ==+=+>∀> , hàm số đồng biến
2 2 (1)(21)(21)2121
⇔−−≥+⇔−−≥+
fxxfxxxx
x x
≥ ⇔ ≤−
2 1 2
Kết hợp với điều kiện xác định, suy ra 2 x ≥ .Vậy có 2022 nghiệm nguyên thuộc đoạn [] 2023,2023 .
Khi
Trang 17
Trang 18
Câu 25. Cho bất phương trình 2 log(41)0 m xxm−++> . Có bao nhiêu giá trị nguyên 2024 m < để bất
ương trình nghiệm đúng với mọi x .
B
1 1(I) 40
2
410(II) 0411 40
>>
⇔⇔> ∆=−<>
Khi ( ) 2 88 0log10 xxx <++⇔>
Khi ( ) 22 88 2 22
xxxx xx x x xxx
++<⇔++< ⇔+<− −> ⇔⇔< +<+−
log11188 188 880 7743 176 17744176
Số nghiệm nguyên của bất phương trình là 43 nghiệm.
≥
Câu 27. Có bao nhiêu số nguyên thỏa mãn 2 421 log22 x
A. Vô số. B. 2 . C. 3 . D. 4 . Lời giải
<< −++> −+<
m xxm xxm
01 410 (1) 40 (2)
2 410xxm−++> với mọi x khi và chỉ khi 1 4103 mm∆=−−< > (loại do 01 m << ).
Với 2 40xxm−+< ta có 2 40 m ∆=−> (do 01 m << ) nên không tồn tại m để bất phương
trình 2 40xxm−+< nghiệm đúng với mọi x .
Vậy {} 420245,6,7...,2023 mm<< = nên có 2019 giá trị m thỏa mãn.
2 2
18820231
46
xx xxxxx
420
1
1313 x ⇔−−≤≤−+ . Kết hợp với điều kiện đang xét ta có 1 31 2 x <<−
TH2: Nếu 12 x << thì 22 4242 422220 22 xx Bptxxxxxxx xx ⇔≥⇔≥⇔−≥−⇔+−≥ () ();1313; x ⇔∈−∞−−∪−++∞ . Kết hợp với điều kiện đang xét ta có () 1;2 x ∈
TH3: Nếu 2 x > thì 22 4242 422620 22 xx Bptxxxxxxx xx ⇔≥⇔≥⇔−≥−⇔−+≤ 37;37 x ⇔∈−+ . Kết hợp với điều kiện đang xét ta có ( 2;37 x ∈+
Vì x là số nguyên nên có 3 giá trị thỏa mãn.
Câu 28. Số các giá trị nguyên của x thỏa ()() 2 25 3 20231log20 x x −−≤ là
A. Vô số. B. 5 . C. 3 . D. 4 .
Trang 20
Điều kiện:
Lời giải
L
i
2 2 25 202310250 00 x x x x −≥ −≥
05 x ⇔<≤
> >
• Trường hợp 1: Xét 5 x = thỏa mãn đề bài.
>
x x x x ⇔ ≠− ≠
>
• Trường hợp 2: Xét 05 x << , ta có 2 25 202310 x −> . Khi đó ()()
2 25 3 20231log20 x x −−≤ 3 log209 xx ⇔−≤⇔≤
Kết hợp với điều kiện ,05xx∈<< ℤ ta có trường hợp này các giá trị x thỏa mãn yêu cầu bài
toán là {} 1;2;3,4 x ∈ .
Vậy {} 1;2;3;4;5 x ∈ nên có 4 giá trị x thỏa mãn yêu cầu bài toán
Câu 29. Có bao nhiêu số nguyên () 23;23 y ∈− thỏa mãn () ()22 33 2log31log62 xyxxy++≤−+ với
mọi x ∈ℝ ?
A. 9 .B. 11 C.13 D. 15 .
Lời giải
Ta có: () () () 22 33 2log31log621 xyxxy++≤−+ với mọi x ∈ℝ .
ĐKXĐ: 2 2
0 32 620, 2 920 y yxxyxy y > −+>∀∈⇔⇔> ′ ∆=−< ℝ .
() () () ()22 33 1log331log62 xyxxy⇔+≤−+
() () 222 3316296230, xyxxyyxxyx ⇔+≤−+⇔−−+−≥∀∈ ℝ () *
TH1: 9 y =
() 55 *6150; 22 xxx
−+≥⇔≤⇔∈−∞ (không thỏa điều kiện bài toán).
TH2: 9 y ≠
() ()() 9 * 99230 y yy >
Kết hợp điều kiện, ta có: {} 10;11;...;21;22 y ∈
ậy có 13 số nguyên y thỏa yêu cầu bài toán. Câu 30.
C. ) 1 0;2;
Trang 21
1
t tt ttt
≤⇔≤⇔−≤ +++ ()
12 0 1 21
Suy ra: 2 2
1 log1 0 2 1 log 2 2 ⇔ ≥ ≥ .
Điều kiện: 30 3 20 x x x −> ⇔> −>
Đặt 22 2 33
log(3)log(3) 32 log(2)2log(2)2 23 ⇔⇔ +−=−=−
2 2 3 132123963690 3 ttttttt t =−⇔=−⇔=−⇔+−= (*)
()369'()3ln36ln60, tttt ftftt =+− =+>∀∈ ℝ
Suy ra ()ft luôn đồng biến nên phương trình ()0ft = có nghiệm duy nhất 1 t =
Với 1 13225 t txx = −==⇔=
Vậy phương trình có nghiệm nguyên duy nhất.
A. 94. B. 92. C. 100. D. 98. Lời giải
⇔<−< {} 2 62,822564,8 50;49;...;2;2;...;49;50
Vậy có 98 giá trị x nguyên thoả mãn.
Câu 33. Tậphợpnghiệmcủabấtphươngtrình 2323 loglog1log.log xxxx +≥+ códạng [] ; ab .Tính 3ab + ?
A. 9. B. 12. C. 3 D. 4. Lời giải 2323 loglog1log.log xxxx +≥+
()()() 23332 log1loglog101loglog10 xxxxx ⇔−+−≥⇔−−≥
34.
ọi S là tập nghiệm của bất phương trình () 2 422 2loglog.log211 xxx ≥+− . Tập hợp S là tập hợp con của tập hợp nào sau đây?
xxxx
Bảng xét dấu: x
)2 222 log.loglog211 xxx −+−
+∞
Dựa vào bảng xét dấu ta thấy tập nghiệm của bất phương trình là [] 1;4 S = . Câu 35. Gọi ; a S b =−∞ làtậpnghiệmcủabấtphươngtrình 4311 43
11 loglogloglog11 xx xx −+ < +− (với ,;0;, abbab ∈> Z nguyên tố cùng nhau). Khi đó 2ab bằng
A. 17 B. 9 C. 3 D. 16 Lời giải
() () 2 2 422222 1 2loglog.log211loglog.log2110 2 xxxxxx ≥+−⇔−+−≥ () () ()2 222 222 log.log2log2110log.loglog2110 xxxxxx ⇔−+−≥⇔−+−≥
Ta có:
2 log01 xx=⇔= . () () ()
2 22 22 22 loglog2110loglog211211 xxxxxx −+−=⇔=+−⇔=+−
1111 loglogloglogloglogloglog1111
43114343 43 433
−+−− <⇔<− +−++ ⇔<⇔<<⇔<< +++ > +< + ⇔⇔⇔<− ++<
>
+
()() 22 20232032 log4log4 xx−≥− ?
A. 4324. B. 1232. C. 1002. D. 4042. Lời giải
()()()() 2222 2023203220232032 log4log4log4log40 xxxx −≥−⇔−−−≥
()() 2 2 202320322023 log4log2023.log40 xx ⇔−−−≥
()() () 2 2 202320322023 log41log20230log40 xx ⇔−−≥⇔−≥
2 5 41. 5 x x x
≥ ⇔−≥⇔ ≤− Mà [] 2023;2023 x ∈− nên {} 2023;...;3;3;...;2023 x ∈−−
Vậy có 4042 giá trị thoả mãn.
Câu 37. Có bao nhiêu số nguyên x thỏa mãn () () () 2 11 33 log7log2426440 x xx +−+−≤ ?
A. 18 B. 21 C. 19 D. 20
L
1 2 2 1
2 2
+≤+ −−≤
⇔⇔ +≤+
x
11 >∈ ℝ
xx xx xx xx x x
24
thi TN THPT n
ă
m
tương đương với bất phương trình () 2 có không quá 728 nghiệm t
+≥+−−≥
xxxx xx xx xx
72422350 log7log242242021 6443118 x
Nhận thấy () 3 log4 fttt =− đồng biến trên [ ) 1; +∞ nên nếu 3 log4 2 7297293367 xx−≥−= thì sẽ
có ít nhất 729 nghiệm nguyên 1 t ≥
Do đó yêu cầu bài toán tương đương với 2 33675758xxx −<⇔−≤≤ (do x nguyên).
Vậy có tất cả 5858116 += số nguyên x thỏa yêu cầu bài toán.
Câu 40. Có bao nhiêu số nguyên x thuộc đoạn [] 2022;2023 thỏa mãn
()() 22 37 log33log4949 xx+>+ ?
Câu 38. Có bao nhiêu cặp số nguyên () ; xy thỏa mãn 02020 x ≤≤ và
() 3 log3329? y xxy++=+
A. 2019 . B. 6 . C. 2020 . D. 4 .
Lời giải
A. 4037 . B. 4039 . C. 4045 . D. 4046 . Lời giải
Ta có: ()() 22 37 log33log4949 xx+>+
()() 22 3377 log3log1log49log1 xx ⇔++>++ ()() 22 37 log1log11 xx ⇔+−+>
ĐK: 1 x >− .
Ta có () 3 log3329 y xxy++=+
() () ()() 3 log33 21
3 3log3333213* x y xy + + ⇔++=++
Xét hàm số () 33t ftt=+ trên R , vì () 33.ln30, t ftt ′ =+>∀ nên hàm số ()ft đồng biến trên R .
Từ đó () * () () () 3 log3321fxfy ⇔+=+ () 3 log3321 xy ⇔+=+ .
Mặt khác ()()() 33 3 02020log331;log6063211;log6063 xxy ≤≤⇔+∈ +∈ () 3 121log606303 y y y ≤+≤ ⇔≤≤ ∈ ℤ . Vậy có 4 cặp () ; xy thỏa mãn.
Câu 39. Cóbaonhiêusố nguyên x saocho ứngvớimỗi x cókhôngquá 728 số nguyên y thỏamãn () () 2 43 loglogxyxy +≥+ ?
A. 115 B. 59 C. 58 D. 116
Lời giải Điều kiện: 0 xy+> và 2 0 xy+> . Khi đó () () () () 3 3 log4 log 2 22 43 loglog4 xy xyxyxyxyxy + +≥+⇔+≥⇔+≥+ ()()
3 log4 2 xxxyxy ⇔−≥+−+ () 1
1 log1 1log3 x ⇔+>
1 1log3 2 13 x ⇔+> 7
7
()() 22 373 log1log3.log11 xx ⇔+−+> () () 2 73 1log3log11 x ⇔−+> () 2 3 7
>− ⇔
x x
7 7
1 1log3 1 1log3
<−−
Vì x nguyên và [] 2022;2023 x ∈− suy ra { }2022;2021;...;4;4;5;...;2022;2023 x ∈−−− .
A. 48 B. 49 C. 47 D. 50 Lời giải Điều kiện: 0 x > .
Đặt 7log tx = 7 x = và bất phương trình đã cho trở thành 2 3 log(72) t <+
t t t
⇔+>⇔+>
2 71 72321(*) 33
Vì hàm số 71 ()2 33
t ft =+ nghịch biến trên tập ℝ mà (2)1 f = nên suy ra bất phương
trình (*) trở thành ()(2)ftf > 2 t ⇔<
Ta có 2 t < suy ra 7 log2049 xx<⇔<< .
Do đó tập nghiệm của bất phương trình đã cho là (0;49) suy ra 1,2,3,....,48 x = .
Vậy có 48 số nguyên
Câu 42. Có bao nhiêu số nguyên x thỏa mãn (
Câu 44. Có bao nhiêu nghiệm nguyên
) () ()
2 22332 2 24log12455420 xxx xxx +++−+++−≤ ?
A.7B. 6 C. 19 D. 20 Lời giải
( ) 3 32 3log12logxxx++> .
A. 0. B. 2023. C. 2050. D. 2072. Lời giải
Đk: 0. x >
xxxxx
+++>⇔++>⇔
Điều kiện của bất phương trình: 32 2 6 1245540(6)(3)0 3
Ta có: 2 2232 24222(3)2 0 xxx xxxx +++−⇔+=+=+⇔=± . ( ) 32 2 log12455420 xxx+++−= 321245544xxx ⇔+++=
Đặt 66,2023.txt=> ,từ giả thiếttacó ()323 32 3log12log ++>ttt
() ()322 32 log1log0 ⇔=++−> ftttt
=− ⇔++=⇔ =−
2 5 (5)(2)0 2 x xx x
Bảng xét dấu của vế trái (VT) bất phương trình đã cho
Từ bảng xét dấu, ta được tập nghiệm của bất phương trình là ()( ]6;33;2 S =−−∪−
Vậy có tất cả 7 số nguyên x thỏa mãn yêu cầu là: 5 ; 4 ; 2 ; 1; 0 ;1; 2 .
Câu 43.: Nghiệm của bất phương trình 4311 43
11 loglogloglog11 −+ < +− xx xx là (;).xab ∈ Khẳng định nào
() ()() () 32 2 32 43 132213ln22ln32ln22ln32ln3 .. ln31ln2 ln2.ln3. −+−− + ′ =−= ++ ++ tt tt ft ttt ttt
Xét ()()() 32 3ln22ln32ln22ln32ln3 =−+−− gttt
Tacó () 2 8484 3..ln()2..ln()3..ln()2.ln() 9999gttttt ′ =+=+
sau đây đúng?
A. 2 4. b = B. 2 5. b = C. 2 2. b = D. 2 3. b = Lời giải

Điều kiện: 3 11 log01(;1). 11 xx x xx >⇔>⇔∈−∞− ++
4311434 43 3 3 3
xxx x xxx x x x x x
−+− <⇔< +−+ +
1111 logloglogloglogloglog 1 111 log1 11 log0.(1) 1 1log1
⇔−< + + Đặt 3 1 log 1 = + x t x ; 0. t > (1) trở thành 2 2 1 01001; t tt t <⇔−<⇔<<
Với 333 2 111 01log1loglog33. 1 111 x xxx t x xxx <− << <⇔<⇔<⇔ >− +++
Đốichiếuvới điềukiệntacó (;2).
Trang 27
=< ′ =⇔ =
()
t gt t
9 2ln 4 0 8 0. 3ln 9 0
Lập bảng biến thiên suy ra hàm số ()gt giảm trên khoảng 6 (2023;) +∞
Mà 6 (2023)0g < () 6 0,(2023;).ftt ′ <∀∈+∞
Suy ra hàm số ()ft luôn giảm trên 6 (2023;) +∞ .
Mà () ()322 32 4log144log40 f =++−=
Suy ra ()()() 6 044404096ftftftxx >⇔>⇔<⇔<⇔<<
Từ yêu cầu bài toán ta có 20234096,. xx <<∈ ℤ
Vậy có 2072 giá trị thỏa mãn.
Câu 45. Có bao nhiêu số nguyên x thỏa mãn
TXĐ: ()1;. D =+∞
Ta
gi
Đặt 5 11 log5 22 t t xx = = thay vào () ∗ ta có
Suyra
9 9 5 5 loglog2424 125125
24 log0 l 0 12 11 og512 5 .5 22 xx x <⇔<⇔<<−<
5 9 5
9 5
2 24 log 125 111,0004 2.5 x
Vậy không có số nguyên x thỏa mãn.
Câu 46. Có bao nhiêu số nguyên () 20;20 y ∈− thoả mãn () ()22
33 2log31log62 xyxxy++≤−+ với mọi x ∈ ℝ ?
A. 9 B. 11 C. 10 D. 8
Lời giải
Giả sử tồn tại số nguyên () 20;20 y ∈− sao cho: () ()22
Cho ()() ()
2 0log4log0 11 x fxx x =⇔−−= ++ ()
333 log3log31log62 xyxxy⇔++≤−+
33 2log31log62, xyxxyx ++≤−+∀∈ ℝ () () () 2 22
() ()22 33 log3.31log62 xyxxy⇔+≤−+ ()2262331yxxyx ⇔−+≥+ ()222963yxxx ⇔+≥++ () 2 2 963 2 xx yfx x ++ ⇔≥= +

() max yfx⇔≥ ℝ () 9,5510201010 yy yyny ∈∈ ⇔≥←→⇔≥→=−= ℤℤ
Câu 47. Trong đoạn [ ]2022;2023 có bao nhiêu số nguyên x thỏa mãn 23 log(21)log(42)2? xx +++≤
A. 2023 . B. 2022 . C. 2021 . D. 2020 . Lời giải
Xét () () 0 22 0221212log21log211 xxx x > >= +> +>= () () 0 33 044142213log42log312 xx x x > >= +>+= +>=
Cộng vế với vế của () 1 và () 2 ta được: 23 log(21)log(42)2 xx +++>
Mà bất phương trình: 23 log(21)log(42)2 xx +++≤ nên 0 x > (loại)
Xét () () 0 22 0221212log21log213 xxx x ≤ ≤= +≤ +≤=
x x ≤ ≤= +≤+= +≤=
() 0 33 044142213log42log314
ộng vế với vế của () 3 và () 4 ta được: 23 log(21)log(42)2 xx +++≤ (thỏa mãn)
Trang 29
2 2 2
−+ ⇔=− −+ ()2 114 xx ⇔−+=−
xx x x
11 4 11
x x ⇔−= ++ () () ()
2214 xxx ⇔+−+=− 138 xx ⇔+=⇔=
Bảng xét dấu
Kết hợp với điều kiện ta được 58 x <<
x nguyên nên {} 6,7 x ∈ . Vậy có 2 giá trị của x thỏa mãn yêu cầu bài toán
Câu 49. Tậpnghiệmcủabấtphươngtrình () () 3 465.2642log30 xx x −+−+≥
cótấtcả baonhiêu số nguyên?
A. 2 B. 3 C. 4 D. Vô số Lời giải
Ta có () () 3 465.2642log30 xx x −+−+≥
t ph
ng trình tương đương với: 3232 log.log2loglog20 xxxx−+−>
()() Ôn thi TN THPT năm 2023
A. 33 2 B. 33 C. 32 D. 16
Câu 7. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa
()()
FF FGFC +=+= ⇔⇔−=
ậy: 24 00
===
BÀI TẬP PHÁT TRIỂN CÂU 40 ĐỀ THAM KHẢO BGD NĂM 2023
Câu 1. Cho hàm số ()fx liên tục trên ℝ . Gọi (),()FxGx là hai nguyên hàm của ()fx trên ℝ thỏa
mãn (7)(7)12FG+= và (1)(1)3FG+= . Khi đó 3 1 (32) Ifxx =− d bằng
A. 3 2 I = . B. 3 I = . C. 3 4 I = . D. 9 I = .
Câu 2. Cho hàm số ()fx liên tục trên ℝ . Gọi ()Fx , ()Gx là hai nguyên hàm của ()fx trên ℝ
mãn ()() 667FG+= và ()() 332FG+= . Khi đó () 2 1 3 fxx d bằng
A. 5 2 B. 5 6 C. 5 D. 15 2
Câu 8. Cho hàm số ()fx liên tục trên ℝ . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên ℝ thỏa mãn ()()888FG−+−= và ()() 111FG+=− . Khi đó, () 3 0 13 Ifxx =− d bằng
A. 9 2 I = . B. 7 6 I = . C. 1 2 I = . D. 3 2 I = .
Câu 9. Cho hàm số ()fx liên tục trên ℝ . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên ℝ thỏa mãn ()() 333FG+= . Cho biết () 3 1 21505Ifxx =+= d , giá trị của ()() 77PFG =+ bằng
A. 2023 P = B. 2020 P = C. 2017 P = D. 1013 P =
Câu 10. Cho hàm số ()fx liên tục trên ℝ . Gọi ()() , xFxGx là hai nguyên hàm của ()fx trên ℝ
thỏa mãn ()() 336FG+= và ()02 G = . Khi đó () 1 0 3 fxdx bằng:
dd
thỏa mãn ()() 27273FG+= và ()() 772FG+= . Tính ()()827 37 45. fxxfxx −+

A. 1 2 B. 5 8 C. 5 8 D. 1 2
Câu 3. Cho hàm số ()fx liên tục trên ℝ . Gọi ()Fx , ()Gx là hai nguyên hàm của ()fx trên ℝ
thỏa mãn ()() 12912911FG+= và ()() 39391FG+= . Tính () () 26 8 511. fxx −+ d .
A. 2022 B. 19 C. 19 D. 2023
Câu 4. Cho hàm số ()fx liên tục trên ℝ . Gọi () Fxx + và ()Gx là hai nguyên hàm của ()fx và thỏa
mãn (6)2(6)12FG+= và (0)2(0)3FG+= . Tính 3 0 (2) Ifxdx =
A. 2. I = B. 3 . 2 I = C. 5 . 2 I = D. 1. I =
Câu 5. Cho ()fx liên tục trên ℝ . Gọi ()() , FxGx là các nguyên hàm của hàm số ()fx trên ℝ . Biết diện tích giới hạn bơi các đường ()(),,0,2yFxyGxxx ==== bằng 6, ()() 407FG−= và ()() 11FG−>− . Khi đó () 2 0 2. fxdx bằng A. 2 B. 8 C. 4 D. 6
Trang 1
A. 3. B. 1. C. 4 3 D. 2 3
Câu 11. Cho hàm số ()fx liên tục trên ℝ . Gọi ()() , FxxGx + là hai nguyên hàm của ()fx trên ℝ thỏa mãn ()() 62612FG+= và ()() 0203FG+= . Khi đó () 2 0 3 fxdx bằng:
A. 5 3 B. 7 C. 4 D. 5
Câu 12. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa
mãn ()() 5 59FG+= và ()() 223FG+=− . Khi đó () 2 1 31 fxx d bằng
A. 3 . B. 5 . C. 2 . D. 3 .
Câu 13. Cho hàm số ()fx liên tục trên ℝ , gọi ()() ; FxGx là hai nguyên hàm của ()fx trên ℝ thoả
B. 3
4
4
Trang 2
C. 5 8 D. 3
Câu 14. Cho hàm số ( )fx liên tục trên ℝ , gọi ( ) ( ) ; FxGx là hai nguyên hàm của ( )fx trên ℝ thoả
mãn ()() 204FG−= và ()() 021FG−= . Tính () 2 3 26 fxdx + ?
Câu 15. Nếu ()Fx là một nguyên hàm của hàm số ()fx trên đoạn [] 0;2 , (2)1F = và () 2 0 5 Fxx = d thì () 2 0 xfxx d bằng
A. 7 .B. 3 .C. 3 .D. 1.
Câu 16. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa mãn ()() 335FG+= và ()() 6610FG+= . Khi đó () 2 1 3 fxx d bằng
A. 3 . B. 5 2 . C. 5 6 . D. 5 .
Câu 17. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa
mãn ()() 2023 20232FG+= và ()() 1 10FG+= . Khi đó () 1012 1 21 fxx d bằng
A. 1 4 B. 4. C. 1. D. 1
Câu 18. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa
mãn ()() 2443 FG−= và ()() 2111 FG−= . Khi đó () 2 1 32 fxx d bằng
A. 2 . 3 B. 3. C. 1.
Câu 19. Cho hàm số ()fx liên tục trên ℝ . Gọi (),() FxGx là hai nguyên hàm của hàm số ()fx trên ℝ
thoả mãn (1)(1)6FG+=− và (4)(4)2FG+= . Khi đó 0 1 (13) fxdx bằng
A. 4. B. 4 3 . C. 4 3 . D. 8 3 .
Câu 20. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa mãn ()() 668FG+= và ()() 000FG+= . Khi đó () 2 0 3 fxx d bằng
A. 1 4 B. 4 C. 3 4 D. 4 3
A. 2 B. 4 C. 6 D. 8
Câu 22. Cho hàm số ()fx liên tục trên R . Gọi ()()() ,, FxGxHx là ba nguyên hàm của ()fx trên
R thỏa mãn ()()() 4 33 3 FGH++= và ()()() 0001FGH++= . Khi đó () 1 0 3 fxx d bằng
A. 1. B. 3 . C. 5 3 . D. 1 3 .
Câu 23. Cho hàm số ()fx liên tục trên R . Gọi ()()() ,, FxGxHx là ba nguyên hàm của ()fx trên
R thỏa mãn ()()() 4 33 3 FGH++= và ()()() 0001FGH++= . Khi đó () 1 0 3 fxx d bằng
A. 1. B. 3 . C. 5 3 . D. 1 3 .
Trang 3
ln 2
e fx x x d
Câu 24. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa mãn ()() 2334 FG−= và ()() 2001 FG−= . Khi đó () 1 0
3 fxx d bằng
A. 1 B. 3 4 C. 3 D. 3 2
Câu 25. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx lần lượt là nguyên hàm của ()fx và ( )gx trên R thỏa mãn ( ) ( ) 23 3 4 2 FG+= và ( ) ( ) 20301 FG+= . Khi đó ()() 11 00 32 fxxgxx + dd bằng
A. 1 B. 1 2 C. 3 D. 3 2
Câu 26. Cho hàm số ()fx liên tục trên R . Gọi ()Fx là một nguyên hàm của ()fx , ()Gx là một nguyên hàm của () fxx + trên R thỏa mãn ()() 224FG+= và ()() 001GF+= . Khi đó () 1 0
2 fxx d bằng
A. 1 B. 1 2 C. 1 4 D. 3 2
Câu 27. Cho hàm số ()fx liên tục trên R . Gọi ()Fx là một nguyên hàm của () fxx , ()Gx là một nguyên hàm của () fxx + trên R thỏa mãn ()() 224FG+= và ()() 001GF+= . Khi đó () 1 0
2 fxx d bằng
A. 1 B. 3 2 C. 3 D. 3 4
Câu 28. Cho hàm số ( )fx liên tục trên ℝ . Gọi ( )Fx , ( )Gx là hai nguyên hàm của ( )fx trên ℝ thỏa mãn ()()552FG−+−= và ()() 1120FG+= . Khi đó () 2 0 13 fxx d bằng
A. 6 . B. 6 . C. 3 . D. 3 .
Trang 4
Câu 29. Cho hàm số ( )fx liên tục trên R . Gọi ( ) ( ) , FxGx là hai nguyên hàm c
()() 119FG+= và ()() 005FG+= .
Câu 36. Cho hàm số ()fx liên tục trên ℝ . Gọi ()Fx là một nguyên hàm của ()fx trên ℝ thỏa mãn
2(2)2(2)3(4)4 FFF+−+= và 4(2)9(2)8(4)5 FFF+−+= . Khi đó 1 1 [6(2)(3)]fxfxx ++ d bằng
A. 9 B. 1 C. 1 D. 7
Câu 37. Cho hàm số ()fx liên tục trên ℝ , gọi ()() , FxGx là hai nguyên hàm của ()fx trên ℝ thỏa
mãn ()() 10105FG+= và ()() 113FG+= . Khi đó 3 0 3(31)d fxx + bằng
π π
sin.cos2sin2 sin xxx Ix fx
+ = d theo a và b
2 3 2 6
()
A. 3 4 ab I ab + = . B. 3 4 ba I ab + = . C. 3 4 ba I ab = . D. 3 4 ab I ab = .
Câu 31. Cho hàm số () 0 fx ≠ , liên tục trên đoạn [] 1;2 và thỏa mãn 1 (1) 3 f = ; () 222 .()12.() xfxxfx ′ =− với [] 1;2 x ∀∈ . Tính tích phân 2 1 () Ifxx = d
A. 1 ln3 4 I = . B. 1 ln3 2 I = . C. 1 ln2 3 I = . D. 1 ln2 2 I = .
Câu 32. Cho hàm số ()fx liên tục trên ℝ . Gọi ()Fx và ()Gx là hai nguyên hàm của ()fx thỏa mãn ()()()() 2339211 FGFG +=+−+− . Khi đó () () 2 2 0 32 xfxdx +− bằng
A. 25 6 . B. 7 6 . C. 43 6 . D. 3 .
Câu 33. Cho hàm số ()fx liên tục trên ℝ . Gọi () Fxx + , ()Gx là hai nguyên hàm của ()fx trên ℝ
thỏa mãn ()() 62612FG+= và ()() 0203FG+= . Khi đó () 2 0 3 fxx d bằng
A. 7. B. 5 3 C. 5. D. 4.
Câu 34. Cho hàm số ( )fx liên tục trên ℝ . Gọi ( )Fx , ( )Gx là hai nguyên hàm của ( )fx trên ℝ
thỏa mãn ()() 2837 FG−= và ()() 8233GF−=− . Khi đó 12 2
1 2 2 fxx + d bằng
A. 4 3 . B. 5 3 . C. 8 3 . D. 1 3 .
Câu 35. Cho hàm số ()fx liên tục trên ℝ . Gọi (),() FxGx là hai nguyên hàm của ()fx trên ℝ thỏa
mãn (5)(5)4FG−+−= và (8)(8)2FG−+−= . Khi đó 3 4 (34) fxx + d bằng
A. 6 B. 1 6 C. 3 D.
A. 3 . B. 1. C. 1 3 . D. 2 .
Câu 38. Cho hàm số ( )fx liên tục trên ℝ . Gọi ( ) ( ) , FxGx là hai nguyên hàm của ( )fx trên ℝ thỏa
mãn ()() 115FG+= và ()() 001FG+= . Khi đó 2023 0 2023 x fx d bằng
A. 2023 B. 2 2023 C. 4 2023 D. 4046
Câu 39. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa mãn ()() 4023 42 FG+= và ()() 001FG+= . Khi đó 2 2 1
ln(ln) e xfx x x d bằng
A. 1011 B. 1011 2 C. 2022 D. 2023 2
Câu 40. Cho hàm số ()fx liên tục trên ℝ . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên ℝ và thỏa mãn ()() 151538FG+= và ()() 3320FG+= . Khi đó () 5 1 3xx d bằng
A. 4 . B. 5 . C. 2 . D. 3 .
Câu 41. Cho 3 0 ()6.fxdx = Tìm giá trị nhỏ nhất của 2 13 01 ()4() Tfxdxfxdx =+ .
A. 40 . B. 30 . C. 20 . D. 10 .
()fx ℝ
Câu 42. Cho làhàmsố liêntụctrên thỏamãn () 2 sin.cos, 2 fxfxxxx π +−=∀∈ ℝ .
Tínhtíchphân () 2 0 Ifxx π = d
A. 1 6 I = B. 3 I π = C. 1 3 I = D. 1 3 I =
Câu 43. Biết 1
e xac x bd xx =− + d với ,,, abcd làcácsố nguyên dương và , ac bd làcácphânsố tốigiản.Tính Sabcd =−+− .
ln 2 1ln
A. 0 B. 3 C. 6 D. 2
Trang 6
Câu 44. Cho 4 0
bằng
d với a , b , c làcácsố nguyên.Giátrị của Iabc =++
2 ln2ln3 3 321 xaxbc x =++ ++

A. 86 I = . B. 24 I = .C. 24 I =− . D. 38 .
Câu 45. Cho hàm số ()fx xác định trên {}\1;3 ℝ thỏa mãn () 2 1 ' 23 fx xx = . Biết
()()573ff−+=− và ()() 028ff+= .Giátrị của ()()() 412Pfff=++− bằng
A. 7 B. 1 C. 1 D. 7
Câu 46. Chohàmsố ()fx có đạo hàmliêntụctrên ℝ thỏamãn ()610 f = , () 6 0 8 fxx = d .Tínhtích
phân () 2 0 .3 Ixfxx ′ = d .
A. 20 I = . B. 12 I = . C. 52 I = . D. 9 I = .
Câu 47. Cho hai hàm số ()fx , ()gx có đạo hàm bằng nhau tại mọi điểm thuộc R và thoả mãn
( ) ( ) ()() 1 335 1 1 fg fg += +=− .Khi đó () 1 0 21 fxx ′ + d bằng
A. 3. B. 3 4 . C. 6. D. 3 2 .
A. 80 9 B. 32 3 C. 36 D. 252
Câu 48. Cho hàm số ()fx xác định trên {} 1;1 R và thỏa mãn () 2 1 1 fx x ′ = ; ()()330ff−+= và 11 2 22ff
.Tínhgiátrị biểuthức ()() 04Pff =+ .
Câu 49. Chohàmsố ()fx liêntụctrên ℝ và ()()
0 216,4ffxx== d .Tính () 1 0 2 Ixfxx ′ = d .
A. 13 B. 12 C. 20 D. 7
Câu 50. Cho hàm số bậc ba ( )yfx = có đồ thị hàm số ( )yfx ′ = như hình vẽ. Tính diện tích hình
phẳngbị giớihạnbởi đồ thị hàmsố ()yfx = vàtrụchoànhbiết ()00 f =
Trang7
Trang8
Ôn thi TN THPT năm 2023
HƯỚNG DẪN LƯỜI GIẢI
Câu 1. Chohàmsố ()fx liêntụctrên ℝ .Gọi (),() FxGx làhainguyênhàmcủa ()fx trên ℝ thỏa
mãn (7)(7)12FG+= và (1)(1)3FG+= .Khi đó 3 1 (32) Ifxx =− d bằng
A. 3 2 I = . B. 3 I = . C. 3 4 I = . D. 9 I = .
Lời giải
Đặt 32 3 dt txdx =− =
Đổicận ()() 1 71 3 IFF =− và ()() 1 71 3 IGG =−
1 27711 3 IFGFG =+−+ () 1 21233 3 I =−= 3 2 I
()()()() ()
t 1 454. 4 txtxxt =− =⇔= dddd
Khi 3 x = thì ()37 t = .
Trang9
()() ()() ()() ()() ()()()() ()()()() ()
dd dd dd dd
272777. 88 fxxfxx fttfxx fxxfxx fxxfxx
Câu 3. Cho hàm số ()fx liên tục trên ℝ . Gọi ()Fx , ()Gx là hai nguyên hàm của ()fx trên ℝ
A. 2022 B. 19 C. 19 D. 2023 Lời giải
dddd
Ta có () () ()()26262626 8888 511.5115118. fxxfxxxfxx −+=−+=−+
Đặt 1 515. 5 txtxxt =− =⇔= dddd
Khi 8 x = thì ()839 t =
26 8 129 39 129 39 129129 3939 51.18 1 18 5 1 18 5 1 18 10 1
10 1
d d
=+−++=
fxx ftt fxx fxxfxx FFGG FGFG −+ =+ =+ =++
10
Trang10 FFGG FGFG −+ =+ =+ =+ =−+− =+−+=
Ta có: 36 00
1 (2).() 2 Ifxdxfxdx == thông qua bước đổi cận tích phân
Ta có
111 .()()(6)(0)6 222 111 22..()2()2(6)2(0) 222
giả thi
IIFFGGFGFG II
+=+−+−=+−++
⇔=−+= =
Ta có [] [] [] [] 1111 2(6)6(0)2(6)2(0)(6)2(6)(0)2(0)3 2222 11155 3.12.33. 2222
Câu 5. Cho ()fx liên tục trên ℝ . Gọi ()() , FxGx là các nguyên hàm của hàm số ()fx trên ℝ . Biết diện tích giới hạn bơi các đường ()(),,0,2yFxyGxxx ==== bằng 6, ()() 407FG−= và
()() 11FG−>− . Khi đó () 2 0 2. fxdx bằng
A. 2 . B. 8 . C. 4 . D. 6 . Lời giải
11 2.240 22 IfxdxFxFF ===−
Do ()() , FxGx là các nguyên hàm của hàm số ()fx trên ℝ . Nên ta có:
()() GxFxC =+
Mà ()()110FGC −>− < . Từ diện tích giới hạn bơi các đường
()(),,0,2yFxyGxxx ==== bằng 6. Ta có:
7. Cho
()() () 2 22 0 00 66.16330 FxGxdxCdxCdxCCC −=⇔=⇔=⇔=⇔=−<
Lúc này, ()() 3 GxFx=− , kết hợp
()()()()()() 4074037404 FGFFFF −= −−=⇔−= .
Vậy: 1 .42 2 I == ,
Câu 6. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của hàm số ()fx trên
1
()
Trang 11
Vậy 26 13
đó, ()
TN THPT năm 2023
Kết hợp với giả thuyết: ()()() 3362.FG+=
Từ () 1 và () 2 , ta được: ()35 G = . Từ đó: () 1 531. 3 I =−=
Câu 11. Cho hàm số ()fx liên tục trên ℝ . Gọi ()() , FxxGx + là hai nguyên hàm của ()fx trên ℝ
thỏa mãn ()() 62612FG+= và ()() 0203FG+= . Khi đó () 2 0 3 fxdx bằng:
IfxxFxFF IfxxGxGG
I
=−=−=−−
11 131381 33 11 131381 33
mãn ()() 333FG+= . Cho biết () 3 1 21505Ifxx =+= d , giá trị của ()() 77PFG =+ bằng
A. 2023 P = . B. 2020 P = . C. 2017 P = . D. 1013 P = . Lời giải
A. 5 3 . B. 7 . C. 4 . D. 5 . Lời giải
Đặt ()()()() GxFxxCFxGxxC =++ =−− .
+=−−+=
() () 01
() ()() () 266 3 3 000 1115 3.60. 3333 ux dudx IfxdxfudufxdxGG = = =→==−=
i ()() ,
d d
22 11
() () ()() () () ()() 3 3 1 1 3 2 1 1 11 212173
Cộng vế theo vế, ta được: ()()()() () 11 2773332.505 22 IFGFGP =+−−=−=
320202023PP ⇔−=⇔=
A. 3.
B. 1. C. 4 3 D. 2 3 Lời giải
111 3.30. 333 ux dudx IfxdxfudufxdxGG = = =→==−
()()()()00.022GxxFxCGFCC =+ =+= = i ( Vì ()02 G = ). ()()()()()()() 2333233321.GxxFxGFFG =+ =+ −=−
Trang 13
?
Ta có () ()() ()() ()() () ()() () 114 000
fxdxFFGGfxdx =−+−= =
1 1 0 0 3
Trang 14
8
Câu 14. Cho hàm số ( )fx liên tục trên ℝ , gọi ( ) ( ) ; FxGx là hai nguyên hàm của ( )fx trên ℝ thoả
mãn ()() 204FG−= và ()() 021FG−= . Tính () 2 3 26 fxdx + ?
A.
Tacó
thì
1111 2626262020 2222 fxdxfxdxftdtFFGG +=++==−=−
4262020326
A.
ục
R . Gọi ( ) ( ) , FxGx là hai nguyên hàm của ( )fx trên R thỏa
Khi đó () 1012 1 21 fxx d bằng
1 4 B. 4. C. 1. D. 1 2 Lời giải
2 2 3 3 3
(2023)(2023)22(2023)2 (2023)(1)1. (1)(1)02(1)0
fxdxFFGGfxdx +=−+−= += .
d
1111 (21)()(2023)(1).1. 2222fxdxfxdxFF−==−==
Câu 18. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa
mãn ()() 2443 FG−= và ()() 2111 FG−= . Khi đó () 2 1 32 fxx d bằng
dd
()() 2.20.052.153 FF ⇔−−=−=−
Câu 16. Cho hàm số ( )fx liên tục trên R . Gọi ( ) ( ) , FxGx là hai nguyên hàm của ( )fx trên R thỏa
5
3
B.
FGFC FF FGFC +=+= ⇔⇔−= +=+=
Vậy: 26 13
ời giải
Trang 15
Ta có: ()() GxFxC =+
FGFFC FF FGFFC −=−−= ⇔⇔−= −=−−=
2(4)(4)32(4)(4)3 (4)(1)2. 2(1)(1)12(1)(1)1
Vậy: [] 24 11
1112 (32)()(4)(1).2. 3333fxdxfxdxFF−==−==
Câu 19. Cho hàm số ()fx liên tục trên ℝ . Gọi (),() FxGx là hai nguyên hàm của hàm số ()fx trên ℝ
A. 4. B. 4 3 C. 4 3 D. 8 3
Vì (),()FxGx là hai nguyên hàm của hàm số ()fx trên ℝ . Giả sử ()() GxFxC =+
Khi đó (1)(1) GFC =+ và (4)(4) GFC =+
1(6)(3)5 (3)(). 336 FF fxdxfxdx=== Ôn thi TN THPT năm 2023
Ta có (1)(1)62(1)6 (4)(1)4 (4)(4)22(4)2
FGFC FF FGFC +=−+=− ⇔⇔−= +=+=
Do đó: 04 11
114 (13)()((4)(1)) 333fxdxfxdxFF −==−=
Chọn B
Câu 20. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa
mãn ()() 668FG+= và ()() 000FG+= . Khi đó () 2 0 3 fxx d bằng
A. 1 4 . B. 4 . C. 3 4 . D. 4 3 .
Lời giải
Ta có: ()() GxFxC =+
()() ()() () () ()() 668268 604. 000200 FGFC FF FGFC +=+= ⇔⇔−= +=+=
1114 (3)()60.4. 3333fxdxfxdxFF==−==
Câu 21. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa mãn ()() 2001 FG−= , ()() 2224FG−= và ()() 111FG−=− . Tính () 2 1
Ôn thi TN THPT năm 2023
fxx ⇔=
3 0 1
L
i có: ()
fxx
1 0 1 3 3
ời giải
1
3
e fx x x d
ln 2
A. 2 . B. 4 . C. 6 . D. 8 . Lời giải
Lạ
0
d () 3 0 1 3 t ft = d () 3 0 1 3 x fx = d .
1 0 3
Ta có: ()() GxFxC =+ ()() ()() ()() 22(2)24(2)6 111
−== ⇔−−=⇔=−
−= −= = = = Do đó ()()() 2 0 208fxFF x =−=− d Vậy () () () ()
FCF FC FG FG F F CC G
Vậy: () 1 0
d
1 3 3 fxx =
Câu 24. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa
22 2 110
lnln1 ln4 222
eefxfxxxfuu x ===−ddd .
Câu 22. Cho hàm số ()fx liên tục trên R . Gọi ()()() ,, FxGxHx là ba nguyên hàm của ()fx trên R thỏa mãn ()()() 4 33 3 FGH++= và ()()() 0001FGH++= . Khi đó () 1
Ta có: ()()()() 2203 330FGFG−−−=
()()()() 203 30 3 FFGG ⇔−−−=
0
C. 5 3 . D. 1 3 . Lời giải
3 fxx
d b
ằng A. 1. B. 3
1 0
Trang 17
1 0
=
3 0 1 3 t
ft
d ()
3 0 1 1 3
d
Câu 25. Chohàmsố ( )fx liêntụctrên R .Gọi ( ) ( ) , FxGx lần lượtlànguyênhàmcủa ( )fx và
()gx trên R thỏamãn ()() 2334 2 FG+= và ()() 20301 FG+= .Khi đó
()() 11 00 32 fxxgxx + dd bằng
A. 1 B. 1 2 C. 3 D. 3 2 Lời giải
Ta có: ()()()() 2320303 32 FGFG+−+=
()()()() 20303 32 FFGG ⇔−+−=
()() 32 00 233 fxxgxx ⇔+= dd
Lại có: ()
3 fxx d ()
3 t ft = d ()
2 gxx d ()
1 3 x fx = d .
Vậy: ()() 11 00 32 31 62 fxxgxx+==
dd .
Câu 26. Cho hàm số ()fx liên tục trên R . Gọi ()Fx là một nguyên hàm của ()fx , ()Gx là một nguyênhàmcủa ( ) fxx + trên R thỏamãn ( ) ( )22 4 FG+= và ( ) ( ) 001GF+= .Khi đó
Ôn thi TN THPT
nguyênhàmcủa () fxx + trên R
fxx d bằng
Ta có: ()()()() 3 200 2 FGGF+−+=
()()()() 2003 2 FFGG ⇔−+−=
Ta có: ()()()() 3 200 2 FGGF+−+=
2003 2 FFGG ⇔−+−=
fxxfxxx ⇔++= dd () 22 00 23 fxxxx ⇔+= dd
00
()
y: ()
111 224 2 fxx ==
Trang 19
() () () () 22
3 fxxxfxxx ⇔−++=
Ta có: ()()
1120 552 FG FG += −+−=
()()()() 1155202FGFG +−−+−=−
()()()() 151518FFGG ⇔−−+−−=
() () 11 55 18 FxGx ⇔+=
()() 11 55 18 fxxfxx ⇔+= dd
() 1 5 9 fxx ⇔= d .
Để tính ()
13 fxx
d , đặt 13 tx =− 3 tx =− dd , đổi cận:. Vậy ()
Câu 29. Cho hàm số ( )fx liên tục trên R . Gọi ( ) ( ) , FxGx là hai nguyên hàm của ( )fx trên R thỏa
mãn ()() 119FG+= và ()() 005FG+= . Khi đó 2 0

1 2 fxx d bằng
A. 2 B. 1 4 C. 8 D. 4 Lời giải
Theo giả thiết ta có: ()() GxFxC =+ , với C ∈ ℝ .
2 3 3 2
FGFFCF FC += = ⇔⇔ −=
+=++=+= +=++
()() ()() ()() ()() () () ()() 1111219 10 9 2 00500505 9 2 C FF FGFFC
1 2 Ifxx = d
t 1 2 2 txxt = = dd
i cận
()
Trang 21
ddd
Khi đó () 2 222 2 2 22 1 111
Câu 32. Cho hàm số ()fx liên tục trên ℝ . Gọi ()Fx và ()Gx là hai nguyên hàm của ()fx thỏa mãn ()()()() 2339211 FGFG +=+−+− . Khi đó () () 2 2 0 32 xfxdx +− bằng A. 25
6
. B. 7 6 . C. 43 6 . D. 3 . Lời giải Ta có () () 222 2 000
Đặt 322 txdtdx =− =−
111 3231 222 fxxfttfxxFF −=−==−−
Khi đó ()() () ()() () 213 031
d dd
2339211231319 FGFGFFGG +=+−+−⇔−−+−−=
()() () ()() 3319313 FFFF ⇔−−=⇔−−=
Suy ra () ()() ()
8818325 3231 332326 IfxxFF =+−=+−−=+= d
2 0
Câu 33. Cho hàm số ()fx liên tục trên ℝ . Gọi () Fxx + , ()Gx là hai nguyên hàm của ()fx trên ℝ
thỏa mãn ()() 62612FG+= và ()() 0203FG+= . Khi đó () 2 0 3 fxx d bằng
A. 7. B. 5 3 C. 5. D. 4. Lời giải Cách 1.
Vì () Fxx + , ()Gx là hai nguyên hàm của ()fx trên ℝ nên ()() GxFxxC =++ .
Ta có ()() ()() ()() ()() () () 626612 626123612212 02033023 02003 FFC FG FC FG FC FFC +++= += ++= += += +++= ()()()() 3603601 FFFF
(5)(5)4
A. 6 . B. 1 6 . C. 3 . D. 1 3 . Lời giải
ddd .
Đặt 343 uxux =+ = dd
Khi đó: 355 488
ddd .
Câu 36. Cho hàm số ()fx liên tục trên ℝ . Gọi ()Fx là một nguyên hàm của ()fx trên ℝ thỏa mãn 2(2)2(2)3(4)4 FFF+−+= và 4(2)9(2)8(4)5 FFF+−+= . Khi đó
1 1 [6(2)(3)]fxfxx ++ d bằng
Cách 2.
Ta có ()() ()() ()() ()() 62612662618 020300203 FGFG FGFG +=++=
() () () () ()() 660026015 FFGG +−++−=
15 2155 33fxxfxxfxxIfxx += = ==
a mãn ()() 2837 FG−= và ()() 8233GF
4 3833483 3 FFFF
Trang 23
A. 9 . B. 1. C. 1. D. 7 . Lời giải
Ta có: 1 11 1 11 [6(2)(3)]6(2)(3) Ifxfxxfxxfxx =++=++
Đặt 22 uxux = = dd , khi đó 12 12 6(2)3() fxxfuu = dd
Đặt 3 vxvx =+ = dd , khi đó 14 12 (3)() fxxfvv += dd
Suy ra, 24 22 3()()3[(2)(2)][(4)(2)]2(2)3(2)(4) IfuufvvFFFFFFF =+=−−+−=−−+ dd 3[2(2)2(2)3(4)][4(2)9(2)8(4)] FFFFFF =+−+−+−+ 3.457=−=
Câu 37. Cho hàm số ()fx liên tục trên ℝ , gọi ()() , FxGx là hai nguyên hàm của ()fx trên ℝ thỏa mãn ()() 10105FG+= và ()() 113FG+= . Khi đó 3 0 3(31)d fxx + bằng
A. 3 . B. 1. C. 1 3 . D. 2 . Lời giải
Vì ()() , FxGx là hai nguyên hàm của ()fx nên ()() GxFxC =+
Ôn thi TN THPT năm 2023
113113213 FGFFCFC FF FGFFCFC +=++=+= ⇔⇔ −= +=++=+=
10105101052105 1011
()() ()() ()() ()() () () ()()
Xét 3 0 3(31)dfxx + Đặt 31d3d txtx =+ =
()()() 310 01 3(31)dd1011 fxxfttFF+==−=
Câu 38. Cho hàm số ()fx liên tục trên ℝ . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên ℝ thỏa mãn ()() 115FG+= và ()() 001FG+= . Khi đó 2023 0 2023 x fx d bằng
A. 2023 B. 2 2023 C. 4 2023 D. 4046 Lời giải
Ta có: ()() GxFxC =+
Theo giả thiết: ()() ()() () () ()() 115215 102 001201 FGFC FF FGFC +=+= ⇔ −= +=+= .
Đặt 1 2023 20232023 x ttxxt = = = dddd + 00xt = = + 20231xt = =
Khi đó ()()()() 202311 000 202320232023104046 2023 x fxfttfxxFF ===−=
ddd
Câu 39. Cho hàm số ()fx liên tục trên R . Gọi ()() , FxGx là hai nguyên hàm của ()fx trên R thỏa mãn ()() 4023 42 FG+= và ()() 001FG+= . Khi đó 2 2 1
ln(ln) e xfx x x d b
A. 1011. B. 1011 2 . C. 2022 .
2023
. Lời giải +Ta có: ()() GxFxC =+
FGFC FF FGFC +=+= ⇔⇔−= +=+=
(4)(4)20232(4)2023 (4)(0)1011. (0)(0)12(0)1
+ Đặt 2 ln ln2 x uxdudx x = =
Trang 25
Do đó, () 2 4 2 10
e xfx xfuduFF x ==−=
ln(ln)111011 ()(4)(0) 222
d
Câu 40. Cho hàm số ( )fx liên tục trên ℝ . Gọi ( ) ( ) , FxGx là hai nguyên hàm của ( )fx trên ℝ và
thỏa mãn ()() 151538FG+= và ()() 3320FG+= . Khi đó () 5 1 3xx d bằng
A. 4 B. 5 C. 2 D. 3 Lời giải
Ta có: ()() GxFxC =+
FGFC FF FGFC +=+= ⇔−= +=+=
()() ()() () () ()() 15153821538 1539 33202320
Vậy () () ()() 515 13
1153 33 33 FF fxxfxx===dd
Câu 41. Cho
()6.fxdx =
Tìm giá trị nhỏ nhất của 2 13 01 ()4() Tfxdxfxdx =+
A. 40 B. 30 C. 20 D.10 Lờ
Trang 26
Câu 43. Biết 1
=−+−+
24 a b c = = =− 38 abc ++=
573ff−+=− và ()() 028ff+= . Giá tr
ℝ thỏamãn () 2 '1 23 fx xx = .Biết ()()
ị c
ln 2 1ln
e xac x bd xx =− + d với ,,, abcd là các số nguyên dương và,ac bd là các phân số
ối giản. Tính Sabcd =−+−
A. 0 . B. 3 . C. 6 . D. 2 .
Lời giải
Đặt 2 1lnln12 x xtxttt x += =− = d d
22 3
e ttt x t xttt t xx ==−=−=−
+
Suy ra 4;3;2;343230 abcdSabcd ==== =−+−=−+−=
Câu 44. Cho 4 0
1
2 ln2ln3 3213 xaxbc x =++ ++
d với a , b , c là các số nguyên. Giá trị của Iabc =++ bằng
A. 86 I = B. 24 I = .C. 24 I =− D. 38
Lời giải
Đặt21 tx=+ 2 21tx =+ 2 21 xt =− xtt = dd .
3 2
tt t t +−+−
Suy ra ()() ()() 6 6 6 0 0 0 ..6686.10852 xfxxxfxfxxf ′ =−=−=−=
Vậy 52 I = .
dd .
A. 13 B. 12 C.
Đặt [][] 22;0;10;2txtxxt = =∈ ∈ dd
Câu 47. Cho hai hàm số ()fx , ()gx có đạo hàm bằng nhau tại mọi điểm thuộc R và thoả mãn
()()
()() 1 335 1 1 fg fg += +=− . Khi đó () 1 0 21 fxx ′ + d bằng
A. 3. B. 3 4 . C. 6. D. 3 2 . Lời giải
Giả thiết suy ra: ()() fxgxC =+
Ta có: ()() ()() 1 335 1 1 fg fg += +=− () () ()() 1 235 33 1 1 2 fC ff fC =+ −= =−+
Do vậy: () () () ()() () 13 3 1 01
1113 2131 2222fxxftdtftff ′′ +===−= d .
Câu 48. Cho hàm số ()fx xác định trên {} 1;1 R và thỏa mãn () 2 1 1 fx x ′ = ; ()()330ff−+= và
11 2 22ff
Trang 29
Khi đó () () 22 00
11 224 t Iftttftt ′′ ==dd
Đặt ()() utut vfttvft == ′ == dd dd .
Ta có () () () () 22 2 0 00
111 3247 444Itftttftftt ′ ==−=−=
dd
Câu 50. Cho hàm số bậc ba ( )yfx = có đồ thị hàm số ( )yfx ′ = như hình vẽ. Tính diện tích hình
ph
ẳng bị giới hạn bởi đồ thị hàm số ()yfx = và trục hoành biết ()00 f = A. 80 9 B. 32 3
252 Lời giải
Giả sử hàm số ()() 2 0 yfxaxbxca ′ ==++≠
Đồ thị hàmsố ()yfx ′ = điquacác điểm ()()() 0;0;4;0;2;4 suyra 00 4241 16404

cc aba abb
== −=−⇔= −==
Vậy () 2 4 fxxx ′ =+ () ()232 1 42 3 fxxxxxxC =+=++ d
Vì ()000fC = =
Suy ra () 32 1 2 3 fxxx =+
Câu 41.(Đề TK BGD 2023) Có bao nhiêu giá trị nguyên của tham số m để hàm số 42 6 yxxmx =−++ cóba điểmcựctrị?
A. 17. B. 15. C. 3. D. 7. Lời giải
Chọn B
Ta có: 3 '412 yxxm =−++ . Xét phương trình () 3 '041201 yxxm =⇔−++= .
Để hàm số có ba điểm cực trị thì phương trình () 1 phải có 3 nghiệm phân biệt.
Ta có: () 3 1412 mxx⇔=−

Xét hàm số () 3 412 gxxx =− có () 2 '1212gxx=− . Cho () 2 '0121201 gxxx=⇔−=⇔=±
Bảng biến thiên của ()gx
Dựa vào bảng biến thiên ta thấy, phương trình () 1 có 3 nghiệm phân biệt khi 88 m −<<
Do {} 7,6,5,...,5,6,7 mm ∈ ∈−−− ℤ
Vậy có 15 giá trị nguyên của tham số m thỏa yêu cầu đề bài.
BÀI TẬP PHÁT TRIỂN CÂU 41 ĐỀ THAM KHẢO BGD NĂM 2023
HÀM SỐ BẬC BA
Câu 1. Có bao nhiêu giá trị nguyên của tham số ( )0;2023 m ∈ để hàm số 32 12 yxxmx =−++ có hai điểm cực trị?
A. 2023 . B. 2022 . C. 2021 . D. 2019 .
Câu 2. Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 32(21)21ymxmxmxm =−−+−− có hai điểm cực trị nằm về hai phía của trục hoành?
A. 4 . B. 2 . C. 1. D. 3. Câu 3. Cho hàm số ( ) ( ) ( ) 322122.fxxmxmx =−−+−+ Tìm tất cả các giá trị thực của tham số m để hàmsố () = yfx có 5 cựctrị
A. 5 2. 4 ≤≤ m B. 5 2. 4 −<< m C. 5 2. 4 << m D. 5 2. 4 << m
Câu 4. Có bao nhiêu giá trị nguyên của tham số m để hàm số 3232yxxm =−+++ có 5 đi
A. 1. B. 3. C. 5. D. 4 .
Câu 5. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ()322332 yxmxmx =−+− đồng biến trên khoảng () 12; +∞ ?
A. 10 . B. 13 . C. 0 . D. 11.
Câu 6. Có bao nhiêu giá trị nguyên của tham số [] 10;10 m ∈− , để hàm số () 323322 ymxmxmxm =−+−+− có 5 điểm cực trị?
A. 9. B. 11. C. 7. D. 10.
Câu 7. Cho hàm số ( ) 3 22.ymxmx =−−− Với giá trị nào của m thì hàm số có cực trị?
A. 02 m << . B. 1 m < . C. 2 0 m m > < . D. 1 m > .
Câu 8. Gọi 12 , xx là hai điểm cực trị của hàm số () 3223 331 yxmxmxmm =−+−−+ . Tìm các giá trị của tham số m để 22 1212 7 xxxx+−=
A. 0 m = . B. 1 2 m =± . C. 9 2 m =± . D. 2 m =± .
Câu 9. Gọi 12 , xx là hai điểm cực trị của hàm số 32 43. yxmxx =+− Tìm các giá trị thực của tham số m để 1240xx+= .
A. 0 m = . B. 1 2 m =± . C. 9 2 m =± . D. 2 m =± .

Câu 10. Tìm tất cả các giá trị của tham số m để đồ thị hàm số 3232yxmx=−+ có hai điểm cực trị ,A B sao cho ,A B và () 1;2 M thẳng hàng.
A. 2 m =− B. 2 m = C. 2 m =± D. 0 m = Câu 11. Cho hàm số ()()()=−−+−+ 322122fxxmxmx . Tìm tất cả các giá trị thực của tham số m để hàm số ()yfx = có 5 cực trị.
A. 5 2. 4 ≤≤ m B. 5 2. 4 << m C. 5 2. 4 << m D. 5 2. 4 −<< m Câu 12. Cho () C là đồ thị hàm số () 32 fxxaxbxc =+++ có điểm cực đại là () 1;3 M và () C cắt trục Oy tại điểm N có tung độ bằng 1. Tính ( )2 f .
A. 1 B. 2 C. 0. D. 1
Câu 13. Cho hàm số 32 1 ()(1) 3 yfxxxmxm ==−+−+ ( với m là tham số), hỏi có bao nhiêu giá trị nguyên của m thuộc khoảng (10;10) để hàm số đã cho đồng biến trên khoảng (1;) +∞
A. 7. B. 10. C. 9. D. 8
Câu 14. Cho hàm số ( ) ( ) 326292.yxmxmx =−+++− Tìm m để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục hoành.
Trang 1
Trang 2
Ôn thi TN THPT năm 2023
HÀM SỐ BẬC BỐN TRÙNG PHƯƠNG
Câu 15. Có bao nhiêu giá trị nguyên của tham số m để hàm số 42 24 yxxmx =−− có ba điểm cực trị?
A. 126. B. 128. C. 127. D. 129.
Câu 16. Tìm tập hợp các giá trị của tham số m để đồ thị hàm số () 42241 yxmxm =+−+− có một
điểm cực trị
A. () 2;2 . B. ()() ;22; −∞−∪+∞ .
C. [] 2;2 . D. ( ][ ) ;22; −∞−∪+∞ .
Câu 17. Biết rằng đồ thị hàm số 42 3 yxxaxb =−++ có điểm cực tiểu là () 2;2 A . Tính tổng Sab =+ .
A. 20 S =− . B. 14 S =− . C. 14 S = . D. 34 S = .
Câu 18. Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 42 2 yxmx =− có ba điểm cực
trị tạo thành một tam giác có diện tích nhỏ hơn.
A. 0 m > . B. 1 m < . C. 01 m << . D. 1 m ≤ .
Câu 19. Có bao nhiêu giá trị nguyên của tham số m để hàm số ()
đúng một cực trị?
2422
20232024ymxmmx =−−− có
A. 2022 B. 2021 C. 2023. D. 2024
Câu 20. Cho hàm số () () 242211ymmxmx =−+−+ . Số giá trị nguyên của tham số m
thuộc đoạn [] 100;100 để hàm số đã cho có 3 điểm cực trị là
A. 103. B. 100. C. 101. D. 102
Câu 21. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 242220231ymxmmx =−−− có đúng một cực trị?
A. 2023 .B. 2022 .C. 2021 .D. 2020 .
Câu 22. Cho hàm số 42 2 yxmxm =−+ . Tìm tất cả các giá trị nguyên của () 2023;2023 m ∈− để hàm số có 3 cực trị
A. 2021 .B. 2022 .C. 2023 .D. 4046 .
Câu 23. Có bao nhiêu giá trị nguyên của tham số m để hàm số 4263 yxxmx =−+ có ba điểm cực trị?
A. 4 . B. 5 . C. 6 . D. 7 .
Câu 24. Có bao nhiêu giá trị nguyên của () 10;10 m ∈− sao cho hàm số () 4224yxmx=+++ có 3 điểm cực trị?
A. 6 . B. 7 . C. 8 . D. 9 .
Câu 25. Hàm số ( ) 42112 ymxmxm =+−+− có một điểm cực trị khi
A. 01 m ≤≤ B. 01mm≤∨≥ C. 0 m = D. 01mm<∨>

Câu 26. Có bao nhiêu giá trị nguyên của tham số ( )0;2023 m∈ để hàm số 42 6 yxxmx =−++ có một điểm cực trị?
A. 2013 B. 2015 C. 2014 D. 2012
HÀM SỐ KHÁC
Câu 27. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 4 3 1 4 x yxxm =−+− có ba điểm cực trị.
A. 4 B. 2 C. 3. D. 5.
Câu 28. Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 432223yxmxmx =−++− có điểm
cực tiểu mà không có điểm cực đại?
A.B..C..D. 6.
Câu 29. Gọi S là tập các giá trị nguyên của tham số m để hàm số 4323412 yxxxm =−−+ có 7 điểm
cực trị. Tổng các phần tử của S là
A. 496 . B. 6 . C. 10 . D. 15 .
Câu 30. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 43441yxxmx =−+−+ có ba điểm cực trị?
A. 17 B. 15 C. 12 D. 8
Câu 31. Có bao nhiêu giá trị nguyên của tham số ()∈ 0;2023 m để hàm số () =−+−− 5280512023yxxmx đồng biến trên khoảng () +∞ 1;?
A. 1971 B. 1973
C. 1990 D. 1991
Câu 32. Tìm tất cả các giá trị của tham số m để hàm số () 432 fxxxmx =+− có 3 điểm cực trị?
A. {} 9 ;\0 2 m ∈−+∞ B. () ;0 m ∈−∞ C. {} 9 ;\0 32 m ∈−+∞ D. () 0; m ∈+∞
Câu 33. Có bao nhiêu giá trị nguyên của tham số m để hàm số 432 418 yxxxmx =−+++ có 3 điểm cực trị ?
A. 127. B. 100. C. 126. D. 115.
Câu 34. Cho hàm số có đồ thị như hình vẽ.
Trang 3
Tìm số điểm cực trị của hàm số
( ) yfx = ( ) ( ) ( ) 42 325Fxfxfx=++
6 3 5 7
A. . B. . C. . D. .
Câu 35. Có bao nhiêu giá trị nguyên của tham số m để hàm số () () 5312 1 53 yfxxxmx ==−++− có bốn điểm cực trị?
Trang 4
A. 1. B. 0 . C. 3. D. 2 .
Câu 36. Có bao nhiêu giá trị nguyên của tham số m để hàm số 4336 yxxmx+5 =−+ có ba điểm cực trị?
A. 17 B. 5 .C. 6. D. 7.
Câu 37. Hình vẽ bên là đồ thị của hàm số ()yfx = . Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số (1) yfxm =++ có 7 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) ( ) 2 ygxfxmfx ==− có đúng 5
điểm cực trị?
A. 10. B. 6. C. 16. D. 13.
Câu 44. Có bao nhiêu giá trị nguyên của tham số m để hàm số 53 1 42023 5 yxxmx =−+++ có bốn điểm
cực trị?
A. 36 B. 34 C. 37 D. 35
Câu 45. Cho hàm số ()yfx = có đồ thị như hình vẽ sau:
A. 6. B. 9. C. 12. D..
Câu 38. Có bao nhiêu giá trị nguyên của m để hàm số ()2 3 31yxxm=−−+ có 5 điểm cực trị
A. 3. B. 2 . C. 1. D. 4 .
Câu 39. Tập hợp các giá trị thực của tham số m để hàm số 43 1 1 4 yxxmx=−−+ có ba điểm cực trị.
A. ( )4;0 . B. ( ) 0; +∞ . C. ( );4−∞− . D. ( ) ( ) ;40; −∞−∪+∞ .




Câu 40. Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 2 22023 3 x yxmx=−−+ có ba điểm
cực trị?
A. 17 B. 15 C. 5 D. 7
Câu 41. Cho hàm số ()yfx = có đạo hàm () 2 6, fxxxx ′ =−∀∈ℝ . Có bao nhiêu giá trị nguyên của tham số m để hàm số () () 32 3 ygxfxxm ==−+ có đúng 6 điểm cực trị?
A. 8. B. 10. C. Vô số D. 6.
Câu 42. Cho hàm số (). yfx = Hàm số ()yfx ′ = có đồ thị như hình vẽ bên dưới.
Tìm tổng các giá trị nguyên của tham số m để hàm số ()()() () 2 20222023 gxfxmfxm =−+ có 5 điểm cực trị.
A. 7 B. 9 C. 14 D. 18
Câu 46. Cho hàm số ()fx biết ()() () 3 22126fxxxxmxm ′ =−−++ . Số giá trị nguyên của tham số m để hàm số đã cho có đúng một điểm cực trị là
A. 7 B. 5 C. 6 D. 4
Câu 47. Tìm số các giá trị nguyên của tham số m để hàm số 4323412 yxxxm =+−+ có 7 điểm cực trị.
A. 6 . B. 5 . C. 4 . D. 26 .
Hàm số () () 42 2 ygxfxx ==− có bao nhiêu điểm cực đại?
A..B..C. 7. D..
Câu 43. Cho hàm số ( )yfx = xác định và liên tục trên ℝ và có bảng biên thiên như hình vẽ
Câu 48. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ ]10;10 để hàm số () 53 3101512 yxxmx+ =−−+ có hai điểm cực trị?
A. 11. B. 12. C. 21. D. 20.
Câu 49. Cho hàm số ()fx có đạo hàm ()() () 3 22526fxxxxmxm ′ =−−−+ . Có tất cả bao nhiêu giá trị nguyên của m để hàm số ( )fx có đúng một điểm cực trị?
A. 6. B. 7. C. 4 . D. 5.
Trang 5
Trang 6
Câu 50. Có bao nhiêu giá trị nguyên của tham số ( ) 12;12 m ∈− để hàm số () 5312 32022 53 m yxxmx + =−−++ có hai điểm cực trị?
A. 8 B. 10 C. 12 D. 14
Câu 51. Có bao nhiêu giá trị nguyên của [] 20;20 m∈− để hàm số 432232023yxxxmxm =+−−++ có một điểm cực trị và là điểm cực tiểu ?
A. 19. B. 17. C. 37. D. 35.
Câu 52. Có bao nhiêu giá trị nguyên của [] 10;10 m ∈− để hàm số () 5432112 212023 20123 yxxxxmx =+−−−+− có hai điểm cực trị ?
A. 20. B. 21 C. 18. D. 17.
Câu 53. Tất cả các giá trị thực của tham số m để hàm số ( ) ( ) 43212fxxxmx =−++− có ba điểm cực trị
A. 11 m −<< B. 01 m << C. 11 m −≤≤ D. 10 m −<≤
Câu 54. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 43215 42 46 fxxxxmx =−−−+ có 3
điểm cực trị, trong đó có đúng 2 điểm cực trị âm.
A.B. 4 C. 6 D. 25.
Câu 55. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 42622yxxmx =−−+ có 3 điểm cực trị.
A. 4 .B. 3 .C. 7 .D. 9.
Câu 56. Có bao nhiêu giá trị nguyên của tham số m để hàm số sau có ba điểm cực trị () () 43222 3426312 yxmxmmxmx =+++−−− ?
A. 1 B. 2 C. 3 D. 4
Câu 57. Cho hàm số ( ) ( ) ( ) ( ) 43221456212fxxmxmxmxm =−++++−+− , với m là tham số. Có
bao nhiêu giá trị nguyên của m thuộc đoạn [] 10; 10 để hàm số ()yfx = có nhiều điểm cực trị nhất?
A. 15. B. 16. C. 13. D. 14 .
HÀM SỐ BẬC BA
Ôn thi TN THPT năm 2023
HƯỚNG DẪN LỜI GIẢI
Câu 1. Có bao nhiêu giá trị nguyên của tham số ( )0;2023 m∈ để hàm số 32 12 yxxmx =−++ có hai
điểm cực trị?
A. 2023 B. 2022 C. 2021 D. 2019
Lời giải
Ta có: 2 '324 yxxm =−++ . Xét phương trình () 2 '032401 yxxm =⇔−++= .
Để hàm số có hai điểm cực trị thì phương trình () 1 phải có hai nghiệm phân biệt.
Ta có: () 2 1324 mxx⇔=−
Xét hàm số () 2 324 gxxx =− có () '624gxx=− . Cho () '062404 gxxx =⇔−=⇔=
Bảng biến thiên của ()gx
Trang 7
Dựa vào bảng biến thiên ta thấy, phương trình () 1 có hai nghiệm phân biệt khi () 48; m∈−+∞ .
Do () 0;2023 m∈ và m∈ℤ {} 1,9,10,...,2022 m ∈
Vậy có 2022 giá trị nguyên của tham số m thỏa yêu cầu đề bài.
Câu 2. Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 32(21)21ymxmxmxm =−−+−− có hai điểm cực trị nằm về hai phía của trục hoành?
A. 4 . B. 2 . C.1. D. 3. Lời giải
Chọn C Đồ thị hàm số có hai điểm cực trị nằm về hai phía đối với trục hoành khi và chỉ khi phương trình 32(21)210 −−+−−=mxmxmxm (1) có 3 nghiệm phân biệt.
⇔−−−++=⇔
=
Ta có (1) 2 2
1 (1)(1)10 (1)10(*) x xmxmxm mxmxm
Phương trình (1) có 3 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt khác 1
Trang 8
Do 1 ∈ =− ℤ mm .

Vậy có 1 giá trị nguyên của tham số thỏa mãn đề bài.
Câu 3. Cho hàm số ()()() 322122.fxxmxmx =−−+−+ Tìm tất cả các giá trị thực của tham số m để
hàm số () = yfx có 5 cực trị.
A. 5 2. 4 ≤≤ m B. 5 2. 4 −<< m C. 5 2. 4 << m D. 5 2. 4 << m
Lời giải
Xét hàm số ( ) ( ) ( ) 322122fxxmxmx =−−+−+ ,
Ta có ()() 2 32212 fxxmxm ′ =−−+−
Hàm số ()yfx = có 5 điểm cực trị () 0 fx ′ ⇔= có hai nghiệm dương phân biệt ( ) ( ) 2 322120 xmxm ⇔−−+−= có hai nghiệm phân biệt dương
Khi đó 606 62 202 mm m mm +>>− ⇔⇔−<<−
Vậy có 3 giá trị nguyên của tham số m để hàm số 3232yxxm =−+++ có 5 điểm cực trị
Câu 5. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ()322332 yxmxmx =−+− đồng biến trên khoảng () 12; +∞ ?
A. 10 B. 13 C. 0 D. 11 Lời giải
Chọn A
Tập xác định: D = ℝ
−−> ⇔−> −>
2 450 20 210
mm m m
m m m m
5 4 1 2 1 2
> <− ⇔< >
5 2 4 m ⇔<< .
Vậy với 5 2 4 m << thỏa mãn yêu cầu bài toán.
Câu 4. Có bao nhiêu giá trị nguyên của tham số m để hàm số 3232yxxm =−+++ có 5 điểm cực trị?
A. 1 B. 3. C. 5. D. 4 Lời giải
Chọn B
Xét hàm số () 3232==−+++ ygxxxm .
Suy ra ()
x ygxxx
BBT
''360
==−+=⇔
Suy ra hàm số () 3232==−+++ ygxxxm có 2 điểm cực trị
Hàm số 3232yxxm =−+++ có 5 điểm cực trị khi 32320−+++= xxm có 3 nghiệm đơn
khác 0 và 2 .
Trang 9
Ta có: ()22 3632yxmxm ′ =−+− ; 0 y ′ = 2 2 xm xm
Đặt 1 2 xm=− ; 2 2 xm=+ , () 12xx <
Ta có bảng biến thiên:
=− ⇔ =+ .
Hàm số đồng biến trên khoảng () 12; +∞ ()0,12;yx ′ ⇔≥∀∈+∞
2 12 x ⇔≤ 212 m ⇔+≤ 122 m ⇔≤− .
Vì m nguyên dương nên {} 1;2;3;4;5;6;7;8;9;10 m ∈
Suy ra có 10 giá trị nguyên dương thỏa mãn bài toán.
Vậy chọn đáp án#A. Câu 6. Có bao nhiêu giá trị nguyên của tham số [] 10;10 m ∈− , để hàm số () 323322 ymxmxmxm =−+−+− có 5 điểm cực trị?
A. 9. B. 11. C. 7. D. 10. Lời giải
TH1: 0 m =
Thay vào hàm số y ta được: 22yx=−+ có 1 điểm cực trị nên 0 m = loại.
TH2: 0 m ≠

Hàm số () 323322 ymxmxmxm =−+−+− có 5 điểm cực trị khi và chỉ khi đồ thị hàm số
()() 323322 fxmxmxmxm =−+−+− cắt trục hoành tại 3 điểm phân biệt
Trang 10
Xét phương trình: ()() 32 033220 fxmxmxmxm =⇔−+−+−=
A. 0 m = .
()() 2 1220xmxmxm ⇔−−+−= () 2 1 220* x mxmxm
= ⇔ −+−=
Để () 0 fx = có 3 nghiệm phân biệt thì () * có 2 nghiệm phân biệt khác 1
≠≠
Đạo hàm: 2 1223.yxmx ′ =+− Có 2 360, mm ′ ∆=+>∀∈ ℝ nên hàm số luôn có hai điểm cực trị 12 , xx .Theo Viet, ta có 12 6 m xx+=− kết hợp với yêu cầu bài toán 1240xx+= . Suy ra
1 2 9,xm =− 2 18 m x = .
′ ⇔∆>⇔>⇔> −+−≠−≠
mm mm mmm
00 0200 22020
Do [] 10;10 m∈− nên ( ]0;10 m∈
Vậy có 10 giá trị m thoả mãn.
Câu 7. Cho hàm số () 3 22.ymxmx =−−− Với giá trị nào của m thì hàm số có cực trị?
A. 02 m << B. 1 m < C. 2 0 m m > < D. 1 m > Lời giải
Tập xác định D = ℝ .
Tính () 2 32 ymxm ′ =−−
()() 2 03201ymxm ′ =⇔−−=
+ TH1: Xét 220 myx ′ = =−<∀ nên hàm số đã cho không có cực trị
+ TH2: Xét 2 m ≠
Hàm số có cực trị khi () 2 020 0 m mm m > ′ ∆>⇔−>⇔ < .
Vậy 2 0 m m > <
Câu 8. Gọi 12 , xx là hai điểm cực trị của hàm số () 3223 331 yxmxmxmm =−+−−+ . Tìm các giá trị
của tham số m để 22 1212 7 xxxx+−= .
A. 0 m = B. 1 2 m =± C. 9 2 m =± D. 2 m =±
Lời giải Đạo hàm: ()22 321.yxmxm ′ =−+− Có 22 110, mmm ′ ∆=−+=>∀∈ ℝ nên hàm số luôn có
hai điểm cực trị 12,.xx Theo định lí Viet, ta có 12 2 12
2 1 xxm xxm += =−
YCBT () () 2 222 121237431742 xxxxmmmm ⇔+−=⇔−−=⇔=⇔=±
Câu 9. Gọi 12 , xx là hai điểm cực trị của hàm số 32 43. yxmxx =+− Tìm các giá trị thực của tham số m để 1240xx+=
Trang 11
Lại có theo Viet: 2 12 121819 4918442 m xxmmm =−⇔−=−⇔=⇔=±
Câu 10. Tìm tất cả các giá trị của tham số m để đồ thị hàm số 3232yxmx=−+ có hai điểm cực trị ,A
B sao cho ,A B và () 1;2 M thẳng hàng.
A. 2 m =− . B. 2 m = . C. 2 m =± . D. 0 m = . Lời giải
Đạo hàm: () 2 0 3632; 0 2 x yxmxxxmy xm = ′′ =−=−=⇔ =
Nên hàm số có hai điểm cực trị 0 y ′ ⇔= có hai nghiệm phân biệt 020 mm ⇔≠⇔≠ .
Tọa độ các điểm cực trị của đồ thị hàm số là: () 0;2 A và () 3 2;24 Bmm .
Suy ra ()1;4, MA =− () 3 21;44 MBmm =−− .
Ba điểm A , B và M thẳng hàng ( ) () 3 0 2144 14 2 mloai mm mthoa = ⇔=⇔ =±
Câu 11. Cho hàm số ()()()=−−+−+ 322122fxxmxmx . Tìm tất cả các giá trị thực của tham số m để hàm số ()yfx = có 5 cực trị
Xét hàm số ()()() 322122fxxmxmx =−−+−+ ,
Ta có ()() 2 32212 fxxmxm ′ =−−+− .
Hàm số ()yfx = có 5 điểm cực trị khi và chỉ khi phương trình () 0 fx ′ = có hai nghiệm dương phân biệt.
Tức phương trình ()() 2 322120 xmxm−−+−= có hai nghiệm phân biệt dương
Trang 12
Ôn thi TN THPT năm 2023
Vậy điều kiện của m là: 5 2 4 m <<
Câu 12. Cho () C là đồ thị hàm số () 32 fxxaxbxc =+++ có điểm cực đại là () 1;3 M và () C cắt trục
Oy tại điểm N có tung độ bằng 1. Tính ( )2 f .
A. 1 B. 2 C. 0. D.1
Lời giải
Ta có
() 32 fxxaxbxc =+++ .
() 2 32 fxxaxb ′ =++ .
() 62 fxxa ′′ =+ .
Theo giả thiết, đồ thị hàm số có điểm cực đại là ( )1;3 M và ( )C cắt trục Oy tại
điểm N có tung độ bằng 1 nên:
( )yfx =
có hai điểm cực trị nằm về hai phía của trục hoành. A. 2 . 6 m m ≥− ≤− B. 2. m ≥− C. 6. m ≤− D. 2 6 3 2 m m m >− <− ≠ Lời giải () () 2 2 '32629. 1 '326290. 29 3 yxmxm x yxmxm m x =−+++ = =−+++=⇔ + = Hàm số có 2 cực trị 2913. 3 m m + ⇔≠⇔≠− () 1 (1)2.ym=+ ()2 29 29 2. 327 m m ym + +
=−−
= +++= =− ′ = ++=

13 13
⇔⇔=
+< ′′ < =−
() () () ()
nguyên của m thuộc khoảng (10;10) để hàm số đã cho đồng biến trên khoảng (1;) +∞
A.7. B.10. C.9. D.8
Lời giải
2 '2(1) yxxm=−+−
Hàm số đồng biến trên khoảng (1;) +∞ khi 2 '2(1)0(1;) yxxmm =−+−≥∀∈+∞
2 21(1;)mxxm ≥−++∀∈+∞
Đặt 2 ()21 gxxx=−++ ta có bảng biến thiên
A. 126. B. 128. C. 127. D. 129. Lời giải
Ta có: 3 '448 yxxm =−− . Xét phương trình () 3 '044801 yxxm =⇔−−= .
Để hàm số có ba điểm cực trị thì phương trình ( )1 phải có 3 nghiệm phân biệt.
Ta có: () 3 1448 mxx⇔=− .
Xét hàm số ( ) 3 448 gxxx =− có ( ) 2 '1248gxx=− . Cho ( ) 2 '0124802 gxxx=⇔−=⇔=± .
Bảng biến thiên của ()gx
Dựa vào bảng biến thiên ta được 2 m ≥ thì thỏa yêu cầu bài toán. {2;3;4;5;6;7;8;9} m ∈
Vậy có 8 giá trị m thỏa yêu cầu bài toán.
Trang 13
Dựa vào bảng biến thiên ta thấy, phương trình () 1 có 3 nghiệm phân biệt khi 6464 m −<< .
Do { }63,62,61,...,63 mm ∈ ∈−−− ℤ
Vậy có 127 giá trị nguyên của tham số m thỏa yêu cầu đề bài.
Câu 16. Tìm tập hợp các giá trị của tham số m để đồ thị hàm số () 42241 yxmxm =+−+− có một
điểm cực trị
A. () 2;2 . B. ()() ;22; −∞−∪+∞ .
C. [] 2;2 . D. ( ][ ) ;22; −∞−∪+∞ . Lời giải
Chọn D
Ta có ()()3222 42424yxmxxxm ′ =+−=+−
Hàm số đã cho là hàm số trùng phương nên có đúng một điểm cực trị khi 0 y ′ = có một nghiệm
Hay () 22 22
0 240 4 x xxm xm
= +−=⇔ =−+ có đúng một nghiệm
2 2 40 2 m m m ≤− ⇔−+≤⇔ ≥
Chú ý:
+ Hàm số 42 yaxbxc =++ có đúng một điểm cực trị khi và chỉ khi 22
0 0 ab ab ≥ +> () 1
Đặc biệt: Hàm số trùng phương () 42 0 yaxbxca =++≠ có đúng một điểm cực trị khi và chỉ khi 0 ab ≥
+ Hàm số 42 yaxbxc =++ có ba điểm cực trị khi và chỉ khi 0. ab < () 2
Câu 17. Biếtrằng đồ thị hàmsố 42 3 yxxaxb =−++ có điểm cựctiểulà ( )2;2 A . Tínhtổng Sab =+ .
A. 20 S =− B. 14 S =− C. 14 S = D. 34 S = Lời giải

Đạo hàm: 3 46 yxxa ′ =−+
Ta thấy hàm số đạt cực tiểu tại 2 x = (thỏa). Vậy 20 14 34 a S b =− = =
Câu 18. Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 42 2 yxmx =− có ba điểm cực
trị tạo thành một tam giác có diện tích nhỏ hơn.
A. 0 m > B. 1 m < C. 01 m << D. 1 m ≤ Lời giải
Tập xác định D = ℝ
Ta có ()32444 yxmxxxm ′ =−=− .
Để hàm số có ba cực trị khi phương trình 0 y ′ = có ba nghiệm phân biệt 0 m ⇔> .
Khi đó phương trình 0 y ′ = có ba nghiệm 0, xxm ==± đồ thị hàm số có ba điểm cực trị () () ()220;0,;,; OAmmBmm
Gọi H là trung điểm của () 2 0; ABHm .
Ta có tam giác OAB cân tại O và có 22 , OHmm =−= 2 ABm = .
Suy ra 22 11 ....2 22 OAB SOHABmmmm ∆ === .
Theo yêu cầu bài toán 2 1101 OAB Smmm ∆ <⇔< << .
Câu 19. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 242220232024ymxmmx =−−− có
đúng một cực trị?
A. 2022 . B. 2021 . C. 2023.D. 2024 . Lời giải
′ = =− ⇔ = =−


Đồ thị có điểm cực tiểu () () () 20 20 2;2 34 22 y a A b y
Thử lại: Với 20, 34 ab=−= ta được 4232034yxxx =−−+ .
Ta có 3 4620;02yxxyx ′′ =−−=⇔=
BBT
Trang 15
Trường hợp 1: 0 = m 2024 y =− nên hàm số không có cực trị. 0
= m (loại).
Trường hợp 2: 2 00 ≠ > mm
Hàm số () 242220232024ymxmmx =−−− có đúng một cực trị
() 222 .202302023002023 mmmmmm ⇔−−≥⇔−≤⇔≤≤ .
Trang 16
Vì 0 ≠ m 02023 m <≤ .
Do ∈ℤ m nên có {} 1;2;....;2023 m ∈
Vậy có tất cả 2023 giá trị m nguyên.
Câu 20. Cho hàm số () () 242211ymmxmx =−+−+ . Số giá trị nguyên của tham số m
thuộc đoạn [] 100;100 để hàm số đã cho có 3 điểm cực trị là
A. 103. B. 100. C. 101. D. 102
Lời giải
Với 2 20mm−= thì hàm số đã cho không thể có 3 điểm cực trị
Với 2 20mm−≠ để hàm số đã cho có 3 điểm cực trị thì () ()() 2 210.abfxmmm==−−<
Lập bảng xét dấu cho ()fm ta được ()()() 0;01;2.fmm<⇔∈−∞∪
Kết hợp [] 100;100 m m ∈ ∈− ℤ có 100 giá trị nguyên của m
Câu 21. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 242220231ymxmmx =−−− có đúng một cực trị?
A. 2023 .B. 2022 .C. 2021 .D. 2020 .
Lời giải
Trường hợp 1: 0 = m 1 =− y nên hàm số không có cực trị.
0 = m (loại).
Trường hợp 2: 2 00 ≠ > mm
Hàm số () 242220231ymxmmx =−−− có đúng một cực trị () 222 .202302023002023 mmmmmm ⇔−−≥⇔−≤⇔≤≤
Vì 0 ≠ m 02023 m <≤ .
Do ∈ ℤ m nên có 2023 giá trị nguyên của tham số m thỏa đề.
Câu 22. Cho hàm số 42 2 yxmxm =−+ . Tìm tất cả các giá trị nguyên của () 2023;2023 m ∈− để hàm số có 3 cực trị
A. 2021 .B. 2022 .C. 2023 .D. 4046 . Lời giải
⇔ phương trình () ∗ có 2 nghiệm phân biệt 0 x ≠ 0 m ⇔> .
Vậy các giá trị nguyên của mthoả mãn yêu cầu bài toán là: 2022 giá trị
Câu 23. Có bao nhiêu giá trị nguyên của tham số m để hàm số 4263 yxxmx =−+ có ba điểm cực trị?
A. 4 . B. 5 . C. 6 . D. 7 . . Lời giải
Ta có 3 4123 yxxm ′ =−+
Xét phương trình () 3 0412301yxxm ′ =⇔−+= .
Để hàm số có ba cực trị thì phương trình () 1 phải có 3 nghiệm phân biệt.
Ta có () 3 13412 mxx⇔=−+
Xét hàm số () 3 412 gxxx =−+
Ta có () 2 1212gxx ′ =−+
() 2 0121201gxxx ′ =⇔−+=⇔=±
Bảng biến thiên của ()gx
Dựa vào bảng biến thiên ta thấy phương trình () 1 có 3 nghiệm phân biệt khi: 88
838 33 mm −<<⇔<<
Do {} 2;1;0;1;2 mm ∈ ∈−− ℤ . Vậy có 5 giá trị nguyên của tham số m thoả mãn yêu cầu đề bài.
Câu 24. Có bao nhiêu giá trị nguyên của () 10;10 m ∈− sao cho hàm số () 4224yxmx=+++ có 3 điểm cực trị?
A. 6 B. 7 C. 8 D. 9 Lời giải
Tập xác định D = ℝ . () () 3 2
0 '4220 4220 x yxmx xm
= =++=⇔ ++=
Hàm số có 3 điểm cực trị ⇔ phương trình () 2 4220 xm++= có hai nghiệm phân biệt khác 0 .
⇔ () 2 4220202 xmmm =−+>⇔+<⇔<−
0 '040 x yxxm xm
= =⇔−=⇔ =∗
2 2
Tập xác định D = ℝ ()32'444 yxmxxxm =−=− () ()
Hàm số có 3 cực trị '0y ⇔= có 3 nghiệm phân biệt
Trang 17
Vì (),10;10mm∈∈− ℤ nên {} 9;8;...;3 m ∈−−− . Vậy có 7 giá trị m thỏa mãn yêu cầu.
Câu 25. Hàm số ( ) 42112 ymxmxm =+−+− có một điểm cực trị khi
A. 01 m ≤≤ . B. 01mm≤∨≥ . C. 0 m = . D. 01mm<∨> .
Trang 18

Lời giải
Trường hợp 1: 0 m = thì hàm số đã cho trở thành 2 1 yx=−+ . Hàm số này có 1 cực trị là cực
đại 0 m = thỏa mãn.
Trường hợp 2: 0 m ≠ thì hàm số đã cho trở thành ( ) 42112 ymxmxm =+−+−
Ta có () ()32 421221 ymxmxxmxm ′ =+−=+−
Câu 27. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 4 3 1 4 x yxxm =−+− có ba điể
trị.
A. 4 . B. 2 . C. 3. D. 5. Lời giải
x x y m x mxm m
= = ′ =⇔⇔ = +−=

0 20 0 1 * 210 2
Ta có: 3231 yxxm ′ =−+−
; () 2 2
YCBT ⇔ y ′ đổi dấu một lần ⇔ Phương trình ( )* vô nghiệm hoặc có nghiệm 0 x =
⇔≤⇔ <
1 1 0 0 2 m m m m ≥
Kết hợp hai trường hợp ta được 01 mm ≤∨≥ .
Giải nhanh: Với a khác 0 thì hàm số đã cho có 1 cực trị () 1 010 0 m abmm m ≥ ⇔≥ −≥⇔ ≤
HÀM SỐ KHÁC
Câu 26. Có bao nhiêu giá trị nguyên của tham số ( )0;2023 m∈ để hàm số 42 6 yxxmx =−++ có một
điểm cực trị?
A. 2013 B. 2015 C. 2014 D. 2012
Lời giải
Ta có: 3 '412 yxxm =−++ . Xét phương trình () 3 '041201 yxxm =⇔−++= .
Để hàm số có một điểm cực trị thì phương trình ( )1 phải có một nghiệm đơn hoặc một nghiệm
đơn và một nghiệm kép.
Ta có: () 3 1412 mxx⇔=−
Xét hàm số () 3 412 gxxx =− có () 2 '1212gxx=− . Cho () 2 '0121201 gxxx=⇔−=⇔=±

Bảng biến thiên của ()gx
Dựa vào bảng biến thiên ta thấy, phương trình ( )1 có một nghiệm đơn hoặc một nghiệm đơn và
một nghiệm kép khi ( ][ ) ;88; m ∈−∞−∪+∞ . Do () 0;2023 m∈ và m ∈ℤ {} 8,9,10,...,2022 m ∈
Vậy có 2015giá trị nguyên của tham số m thỏa yêu cầu đề bài.
Trang 19
Để hàm số có ba điểm cực trị khi phương trình 0 y ′ = có ba nghiệm phân biệt. Ta có: 323231031 xxmxxm −+−=⇔−+= .
Xét hàm số: () 3231fxxx=−+
() 2 36 fxxx ′ =−
() 2 0 0360 2 x fxxx x = ′ =⇔−=⇔ = .
Bảng biến thiên:
Để phương trình có 3 nghiệm phân biệt thì 31 m −<< . Nên có 3 giá trị nguyên.
Câu 28. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 432223yxmxmx =−++− có điểm cực tiểu mà không có điểm cực đại?
A.. B..C..D. 6. Lời giải
Ta có ()()322 46222232 yxmxmxxxmxm ′ =−++=−++ .
= ′ =⇔ −++=
()() 2
0 0 2320* x y xmxm
+) Trường hợp 1: Phương trình (*) có nghiệm 0 x = , khi đó 2 m =− . Thay 2 m =− vào phương trình (*) ta được: 2 0 260. 3 x xx x = −=⇔ =
Ta có xét dấu y ′ như sau:
Ta thấy khi 2 m =− hàm số đã cho có một điểm cực tiểu và không có điểm cực đại.
+) Trường hợp 2: Phương trình (*) có không có nghiệm 0 x = , khi đó 2 m ≠−
Trang 20
Dễ thấy phương trình (*) có 2 nghiệm phân biệt thì phương trình '0 y = có 3 nghiệm đơn phân
biệt, khi đó hàm số đã cho có cả điểm cực đại và điểm cực tiểu.
Khi phương trình (*) vô nghiệm hoặc có nghiệm kép (khác 0) thì phương trình '0 y = có 1
nghiệm đơn hoặc 1 nghiệm đơn và 1 nghiệm kép, lúc này hàm số đã cho có 1 điểm cực tiểu
0 x = .
Như vậy, khi 2 m ≠− , hàm số đã cho có một điểm cực tiểu khi và chỉ khi phương trình (*) vô nghiệm hoặc có nghiệm kép, điều này xảy ra khi và chỉ khi phương trình (*) có 0 ∆≤ () 22 44104410 0982098160. 99 mmmmm
Mà m ∈ℤ , suy ra {} 0;1 m ∈
Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 29. Gọi S là tập các giá trị nguyên của tham số m để hàm số 4323412 yxxxm =−−+ có 7 điểm cực trị. Tổng các phần tử của S là
A. 496 . B. 6 . C.10 . D. 15 .
Lời giải Xét hàm số () 4323412 fxxxxm =−−+
Chọn B
Ta có 32 4124 yxxm ′ =−+− 32 04124yxxm ′ =⇔−=− (1)
Để hàm số có 3 cực trị thì phương trình (1) có 3 nghiệm phân biệt.
Xét () 32412 gxxx =− có () 2 1224 gxxx ′ =−
Ta có () 0 0 2 x gx x = ′ =⇔ =
Để phương trình (1) có 3 nghiệm phân biệt 1640124. mm −<−<⇔−<<
Do {} 11;10;9;...;2;3 mm ∈ ∈−−− ℤ .


Vậy có 15 giá trị nguyên của tham số m thỏa yêu cầu đề bài.
Câu 31. Có bao nhiêu giá trị nguyên của tham số ()∈ 0;2023 m để hàm số
Ta có () 32 121224 fxxxx ′ =−− , () 32
fxxxxx
012122401
′ =⇔−−=⇔=−
Ta có bảng biến thiên
Hàm số ()yfx = có 3 điểm cực trị, để hàm ()yfx = có 7 cực trị thì phương trình () 0 fx = có 4 nghiệm phân biệt khi và chỉ khi 0 05 50 m m m > ⇔<< −< .
Vì m nguyên nên {} 1,2,3,4 m ∈
Tổng các giá trị là 10.
Câu 30. Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 43441yxxmx =−+−+ có ba điểm
cực trị?
A. 17. B. 15. C. 12 D. 8. Lời giải
()
=−+−− 5280512023yxxmx đồng biến trên khoảng () +∞ 1;?
A. 1971 B. 1973
C. 1990 D. 1991 Lời giải
Xét hàm số () =−+−− 5280512023yxxmx
() ′ =−+− 4 516051yxxm
Hàm số đồng biến trên khoảng () +∞ 1; khi () −+−≥ 4 5160510 xxm , ()∀∈+∞ 1; x ()⇔≥−++∀∈+∞ 4 321,1;mxxx .
Xét hàm số () ⇔=−++ 4 321gxxx
() 3 432gxx ′ =−+ ; () 02gxx ′ =⇔=
Ta có BBT:
Trang 22
Ôn thi TN THPT năm 2023
Từ BBT ta có, hàm số đồng biến trên khoảng () +∞ 1; khi 49 m ≥ . Mà ()∈ 0;2023 m và ∈ℤ m nên có 1973 giá trị của m
Câu 32. Tìm tất cả các giá trị của tham số m để hàm số () 432 fxxxmx =+− có 3 điểm cực trị?
A. {} 9 ;\0 2 m ∈−+∞ B. () ;0 m ∈−∞ C. {} 9 ;\0 32 m ∈−+∞ D. () 0; m ∈+∞ Lời giải
Chọn C () ()322 432432 fxxxmxxxxm ′ =+−=+−
Hàm số có 3 điểm cực trị '0 y ⇔= có 3 nghiệm phân biệt và y ′ đổi dấu khi qua 3 điểm nghiệm đó.
Tìm số điểm cực trị của hàm số
( ) ( ) ( ) 42 325Fxfxfx=++
6 3 5 7 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 42 3 325'12'4' FxfxfxFxfxfxfxfx =++ =+
( ) ( ) ( ) ( ) ( ) 2 '4'31 Fxfxfxfx=+
A. . B. . C. . D. . Lời giải Chọn D ( vì với )
∆=+> >

m m m m ⇔⇔ −≠ ≠
cực trị ?
A. 127. B. 100. C. 126. D. 115. Lời giải
Chọn A
Ta có 32 41236 yxxxm ′ =−+++
Xét phương trình 32 4 01236()(1)yxfx xx m ′ ⇔= =−−= .
Để hàm số có ba điểm cực trị thì phương trình (1) có ba nghiệm phân biệt.
Xét hàm số 322 1 ()41236246()12. 3 30 f x fxx x xxx x x =− ′ =−−−⇒=⇔ = =
( ) ( ) ( ) '0'0 Fxfxfx=⇔= ( ) 2 310 fx +> x ∀∈ ℝ () ( ) () 0 '0 '0 fx Fx fx = =⇔ =
Đồ thị hàm số cắt trục hoành tại điểm phân biệt suy ra phương trình có nghiệm phân biệt . (*)
( ) fx 4 ( ) 0 fx = 4 1234 ,,, xxxx
Suy ra {} 107;106;...;1;0;1;...;19 10820 m m −<⇒<∈−−− .Vậy có 127 số nguyên m .
Trang
( ) fx ( ) fx 3 567 ,, xxx
( ) '0fx = 3 567 ,, xxx 1234 ,,, xxxx
Từ đồ thị hàm số suy ra hàm số có điểm cực trị phân biệt suy ra có nghiệm phân biệt lần lượt khác các giá trị . (**)
Từ (*), (**) suy ra phương trình có nghiệm đơn.
Vậy hàm số có điểm cực trị.
( ) '0Fx = 7 ( )Fx 7

Câu 35. Có bao nhiêu giá trị nguyên của tham số m để hàm số () () 5312 1 53 yfxxxmx ==−++− có bốn điểm cực trị?
A. 1 B. 0 C. 3 D. 2 Lời giải
Chọn B
Ta có: () 42 ''21 yfxxxm ==−++− . Xét phương trình () 42 '02101 yxxm=⇔−++−= .
Để hàm số có bốn điểm cực trị thì phương trình () 1 phải có bốn nghiệm phân biệt và ()'' yfx = đổi dấu liên tiếp qua 4 nghiệm đó.
Ta có: () 42112 mxx⇔−=−+ .
Trang 24

Xét hàm số () 42 2 ygxxx ==−+ có () 3 '44 gxxx =−+ . Cho
x gxxxx x
Ôn thi TN THPT năm 2023
Câu 37. Hình vẽ bên là đồ thị của hàm số ()yfx = . Gọi S là tập hợp các giá trị nguyên dương của
() 3 1 '04401 0
= =⇔−+=⇔=− = .
Bảng biến thiên của () 42 2 ygxxx ==−+
Dựa vào bảng biến thiên ta thấy, phương trình () 1 có 4 nghiệm phân biệt khi
0111001 mmm <−<⇔−<−<⇔<< . Với 01 m << ta thấy ()'' yfx = luôn đổi dấu liên
tiếp qua 4 nghiệm đó.
Do mm φ∈⇔∈ ℤ .
Vậy không có giá trị nguyên của tham số m thỏa yêu cầu đề bài.
Câu 36. Có bao nhiêu giá trị nguyên của tham số m để hàm số 4336 yxxmx+5 =−+ có ba điểm cực trị?
A. 17 B. 5 .C. 6. D. 7.
Lời giải
Ta có: 321218 yxxm ′ =−+ . Xét phương trình () 32 0121801yxxm ′ =⇔−+= .
Để hàm số có ba điểm cực trị thì phương trình () 1 phải có 3 nghiệm phân biệt.
Ta có: () 3211218 mxx⇔=−+ .
Xét hàm số () 321218 gxxx =−+ có () 2 3636 gxxx ′ =−+ .
Cho () 2 0 036360 1 x gxxx x = ′ =⇔−+=⇔ =
Bảng biến thiên của ()gx
Dựa vào bảng biến thiên ta thấy, phương trình ( )1 có 3 nghiệm phân biệt khi 06 m <<
Do {} 1,2,3,4,5 mm ∈ ∈ ℤ
Vậy có 5 giá trị nguyên của tham số m thỏa yêu cầu đề bài.
Trang 25
tham số m để hàm số (1) yfxm =++ có 7 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
Lời giải
Xét hàm số ()(1) gxfxm =++
Vì hàm số ()fx có 3 điểm cực trị do đó hàm số ()(1) gxfxm =++ có 3 điểm cực trị
Để hàm số (1) yfxm =++ có 7 điểm cực trị thì phương trình (1) fxm +=− phải có 4 nghiệm
đơn phân biệt hay 3223. mm −<−<⇔−<<
Vì m nguyên dương nên {} 1,2 m∈ .
Câu 38. Có bao nhiêu giá trị nguyên của m để hàm số ()2 3 31yxxm=−−+ có 5 điểm cực trị
A. 3 B. 2 C. 1 D. 4 Lời giải
() ()2 3 31yfxxxm ==−−+
Ta có () ()() 23 23331fxxxxm ′ =−−−+
1 31* x xxm =± ⇔ −+=




() 0 fx ′ = () 3
Để hàm số đã cho có 5 điểm cực trị thì phương trình ( )* phải có ba nghiệm phân biệt khác
1.±
Đặt 3 ()31tgxxx ==−+ là hàm số xác định và liên tục trên ℝ .
() 2 3301gxxx ′ =−=⇔=±
Bảng biến thiên của ()gx
Trang 26
Từ bảng biến thiên ta thấy phương trình ( )* có ba nghiệm phân biệt khác 1± khi và chỉ khi
31 m −<<
Khi đó {} 2;1;0 m∈−− . Có ba giá trị nguyên của .m
Câu 39. Tập hợp các giá trị thực của tham số m để hàm số 43 1 1 4 yxxmx=−−+ có ba điểm cực trị
A. () 4;0 B. () 0; +∞ C. () ;4−∞− D. ()() ;40; −∞−∪+∞



Lời giải
Hàm số 43 1 1 4 yxxmx=−−+ có ba điểm cực trị ⇔ phương trình 0 y ′ = có 3 nghiệm phân biệt
⇔ phương trình 32 3 xxm −= có 3 nghiệm phân biệt.
Xét hàm bậc ba ( ) 323,gxxx =− có
()() 2 00 36;0 24 xy gxxxgx xy = = ′′ =−=⇔ = =− .
Ta có BBT
Dựa vào bảng biến thiên, ta có YCBT 40 m ⇔−<<
Câu 40. Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 2 22023 3 x yxmx=−−+ có ba điểm
cực trị?
A. 17 B. 15 C. 5 D. 7
Lời giải
Tập xác định D = ℝ
Ta có 3 4 4 3 yxxm ′ =−−
Để hàm số có ba điểm cực trị khi phương trình 0 y ′ = phải có 3 nghiệm phân biệt.
Khi đó 3 4 4 3 xxm −=
Xét hàm số ()
3 4 4 3 gxxx =−
Tập xác định g D = ℝ .
( ) 2 44gxx ′ =− ;
Ta có: () 01gxx ′ =⇔=± .
Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy để phương trình 0 y ′ = có 3 nghiệm phân biệt khi
88 33 m −<<
Vì m ∈ ℤ nên {} 2;1;0;1;2 m ∈−−
V
ậy có 5 giá trị nguyên của tham số m thỏa yêu cầu bài toán.
Câu 41. Cho hàm số ()yfx = có đạo hàm () 2 6, fxxxx ′ =−∀∈ℝ . Có bao nhiêu giá trị nguyên của tham số m để hàm số () () 32 3 ygxfxxm ==−+ có đúng 6 điểm cực trị?
A. 8. B. 10. C. Vô số D. 6. Lời giải
Ta có () 0 0 6 x fx x = ′ =⇔ =
()() 232'36'3 gxxxfxxm =−−+
Xét () 32 3 hxxx =− trên ℝ . Ta có ()() 2 0 '36,'0 2 x hxxxhx x = =−=⇔ =
Bảng biến thiên
Yêu cầu bài toán thỏa mãn khi và chỉ khi () '0gx = có đúng 6 nghiệm bội lẻ
TH1: 4004 04 606 mm m mm −<−<<< ⇔⇔<< −+≥≤
TH2: 460610 610 44 mm m mm −<−+<<< ⇔⇔<< −≤−≥
Vậy {} 1;2;3;7;8;9 m∈
Trang 28
Câu 42. Cho hàm số ( )yfx = Hàm số ( )yfx ′ = có đồ thị như hình vẽ bên dưới.
x fx gxfxfxmfxgxx m fx
1 '0 '2'';'02 =− = =−=⇔⇔= = =




ệm bội lẻ 3468 2 m m ⇔−<<⇔−<< .
Hàm số () () 42 2 ygxfxx ==− có bao nhiêu điểm cực đại?
A..B..C. 7. D..
Lời giải
Ta có () ()() 342'44'2 gxxxfxx =−−
Vậy số cực đại cần tìm là. Câu 43. Cho hàm số ()yfx = xác định và liên tục trên ℝ và có bảng biên thiên như hình vẽ
Vậy {} 5;4;3;...;7 m∈−−−
cực trị?
A. 36 B. 34 C. 37 D. 35 Lời giải
Ta có: 42 12 yxxm ′ =−++ . 42 0120yxxm ′ =⇔−++= 4212(1)xxm⇔−=
Hàm số 53 1 42023 5 yxxmx =−+++ có bốn điểm cực trị khi và chỉ khi phương trình (1) có
bốn nghiệm phân biệt.
Xét hàm số: () 42 12 fxxx =− với x ∈ ℝ
Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) ( ) 2 ygxfxmfx ==− có đúng 5 điểm cực trị? A. 10. B. 6. C. 16. D. 13.
ời giải
Trang 29
Ta có: ()() 3 0 4240 6 x fxxxfx x
= ′′ =− =⇔ =±
Bảng biến thiên của hàm số () 42 12 fxxx =− như sau:
Từ bảng biến thiên ta thấy phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi 360 m −<< Do {} 35;34;33;...;1 mm ∈ ∈−−− ℤ
Vậy có tất cả 35 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 45. Cho hàm số ()yfx = có đồ thị như hình vẽ sau:
Trang 30
Câu 46. Cho hàm số ()fx biết ()() () 3 22126fxxxxmxm ′ =−−++ . Số giá trị nguyên của tham số m
để hàm số đã cho có đúng một điểm cực trị là
A. 7 . B. 5 . C. 6 . D. 4 . Lời giải
Cho () 0 fx ′ = 2
Tìm tổng các giá trị nguyên của tham số m để hàm số ()()() () 2 20222023 gxfxmfxm =−+
có 5 điểm cực trị.
A. 7 . B. 9 . C. 14 . D. 18 . Lời giải
Ta có: ()()()() () ()()2022220222 gxfxfxmfxfxfxm ′′′′ =−=− . () () () 0 0 2
′ = ′ =⇔ =



fx gx m fx
Dựa vào đồ thị ta thấy hàm số ()yfx = đạt cực trị tại hai điểm 0, 2 xx==− .
= ′ =⇔ =−
Suy ra () 0 0 2 x fx x
Do đó để hàm số đã cho có 5 điểm cực trị thì phương trình () 2 m fx = có 3 nghiệm phân biệt
khác 0 và 2
Khi đó dựa vào đồ thị ta có: 3162 2 m m −<<⇔−<< .
Do m nhận giá trị nguyên nên {} 5;4;3;2;1;0;1 m ∈−−−−−
Vậy tổng các giá trị nguyên của m là: 14 T =− .
= = −++= .
x x xmxm
0 1 260
Trong đó 0 x = là nghiệm bội chẵn, 1 x = là nghiệm bội lẻ
Để hàm số đã cho có đúng một điểm cực trị thì () 0 fx ′ = chỉ đổi dấu 1 lần.
Trường hợp 1: 2 260xmxm−++≥ , x ∀∈ ℝ
2 6023mmm ⇔−−≤⇔−≤≤ .
Do m ∈ ℤ nên {} 2;1;0;1;2;3 m ∈−−
Trường hợp 2: tam thức 2 26xmxm−++ có hai nghiệm phân biệt trong đó một nghiệm là
1 x =
Khi đó ta có 2 2 602;3 7 7 12.160 mmmm m m mm −−><−> ⇔⇔= = −++=
Vậy {} 2;1;0;1;2;3;7 m ∈−− . Suy ra có 7 giá trị nguyên của m thỏa mãn.
Câu 47. Tìm số các giá trị nguyên của tham số m để hàm số 4323412 yxxxm =+−+ có 7 điểm cực trị.
A. 6 B. 5 C. 4 D. 26 Lời giải
Xét hàm số () 4323412 fxxxxm =+−+
= ′ =⇔+−=⇔=−
=
Trang 32
Dựa vào bảng biến thiên, phương trình () 0 fx = có 4 nghiệm phân biệt khi và chỉ khi
0 05 50 m m m > ⇔<< −<
Vì m nguyên nên {} 1;2;3;4 m∈
Vậy có 4 giá trị nguyên của m Câu 48. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [] 10;10 để hàm số ( ) 53 3101512 yxxmx+ =−−+ có hai điểm cực trị?
A. 11. B. 12. C. 21. D. 20.
Lời giải
Hàm số () 53 3101512 yxxmx+ =−−+ , ta có () 42 '1530151 yxxm =−−+
Phương trình ()()4242 '015301510211 yxxmxxm =⇔−−+=⇔−−=
Xét hàm số () 4221gxxx=−− , có () 3 '44 gxxx =−
Ta có () () 2
x fxx gxxmxm
= ′ = = =−−+=

0 05 260
Trong đó 0 x = là nghiệm bội chẵn và 5 x = là nghiệm bội lẻ
Hàm số đã có một cực trị khi và chỉ khi ( )fx ′ đổi dấu một lần khi và chỉ khi ( ) 0 fx ′ = có một
nghiệm bội lẻ. Ta có 2 trường hợp sau:
+ Trường hợp 1: Phương trình ( ) 0 gx = vô nghiệm hoặc có nghiệm kép khi và chỉ khi 2 06032 mmm ′ ∆≤⇔+−≤⇔−≤≤
+ Trường hợp 2: () 0 gx = có hai nghiệm phân biệt, trong đó có 1 nghiệm 1 5 x =
Với 1 5 x = , ta có: () 31 5251060 11 gmmm =−−+=⇔= (loại vì m không là số nguyên).
Vậy [] 3;2 m ∈− , mà {} 3,2;1;0;1;2 mm ∈ ∈−−− ℤ .

Cho () ()32 0 '0440410 1 x gxxxxx x
= =⇔−=⇔−=⇔ =±
Bảng biến thiên của ()gx
Phương trình ( )1 là phương trình hoành độ giao điểm của đồ thị hàm số ( ) gx và đường thẳng
ym = .
D
ựa vào bảng biến thiên ta thấy để hàm số đã cho có hai điểm cực trị thì phương trình ( )1 phải
có 2 nghiệm đơn phân biệt hoặc có ba nghiệm trong đó có 1 nghiệm kép và hai nghiệm đơn.
Yêu cầu bài toán thỏa mãn khi 1 m ≥− .
Do [] {} 1,0,1,...,5,6,10 10;10 m m m ∈ ∈− ∈− ℤ .
Vậy có 12 giá trị nguyên của tham số m thỏa yêu cầu bài toán.
Câu 49. Cho hàm số ()fx có đạo hàm ()() () 3 22526fxxxxmxm ′ =−−−+ . Có tất cả bao nhiêu giá
trị nguyên của m để hàm số ( )fx có đúng một điểm cực trị?
A. 6. B. 7. C. 4 . D. 5.
Lời giải
Câu 50. Có bao nhiêu giá trị nguyên của tham số () 12;12 m ∈− để hàm số () 5312 32022 53 m yxxmx + =−−++ có hai điểm cực trị?
A. 8 . B. 10. C. 12. D. 14. Lời giải
Ta có () 4223yxmxm ′ =−+−− .
Xét phương trình: () ()()4222 0230130 yxmxmxxm ′ =⇔−+−−=⇔+−−= () 223031xmmx ⇔−−=⇔=−
Xét hàm số () 2 3=−gxx có () 2 gxx ′ = () 0200gxxx ′ =⇔=⇔=
Bảng biến thiên của ()gx
Để hàm số có hai điểm cực trị thì phương trình () 1 phải có 2 nghiệm phân biệt.
Dựa vào bảng biến thiên ta thấy phương trình () 1 có hai nghiệm phân biệt khi 3>−m Do ( ) { },12;122;1;0;...;10;11mmm ∈∈− ∈−− ℤ .
Vậy có 14 giá trị nguyên của tham số m thỏa mãn yêu cầu đề bài.
Câu 51. Có bao nhiêu giá trị nguyên của [ ]20;20 m∈− để hàm số 432232023yxxxmxm =+−−++ có một điểm cực trị và là điểm cực tiểu ?
Trang 34
