10.5.4 Criticism

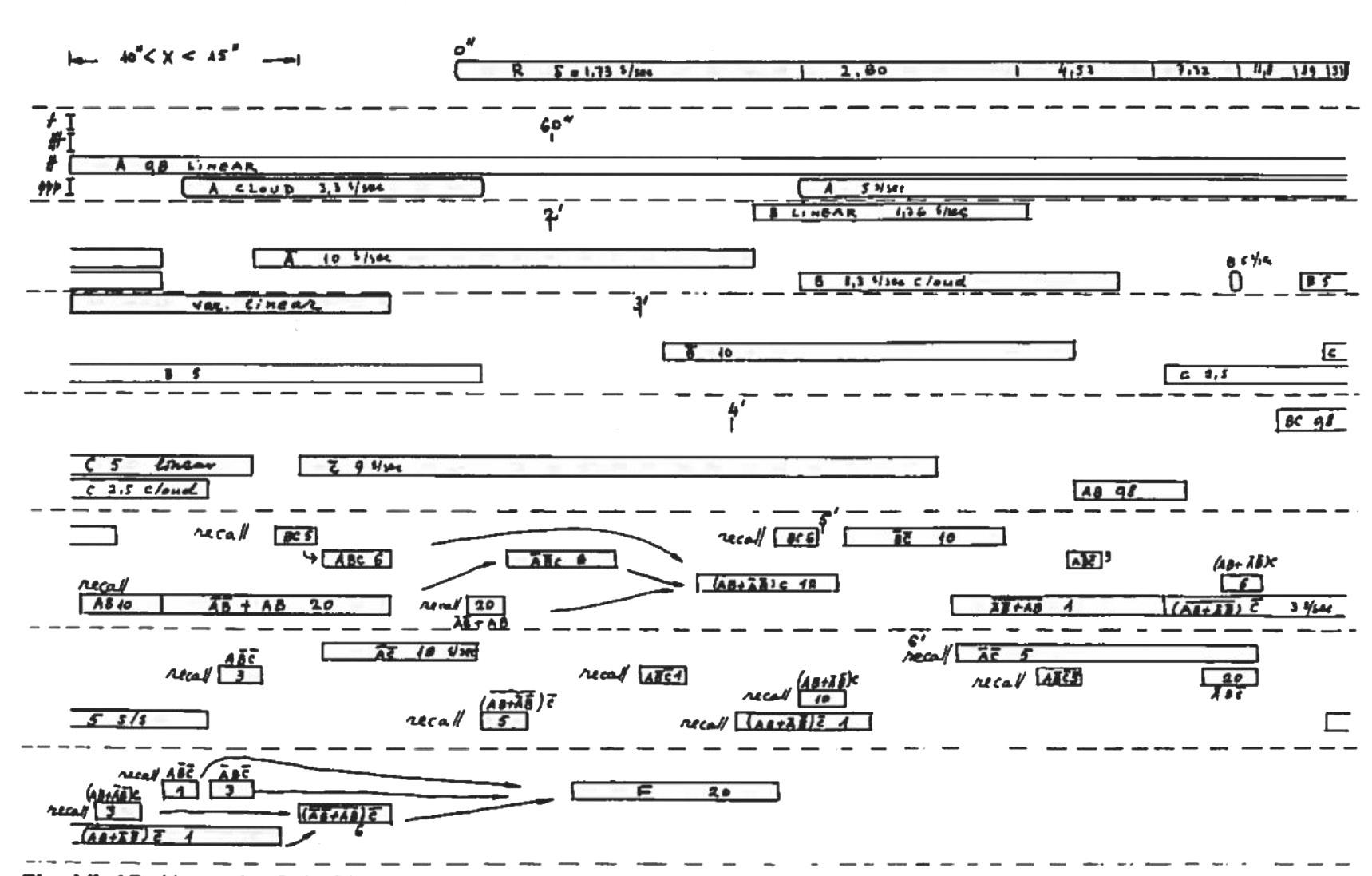
finally F = A.B.C + A.notB.notC + B.notA.notC + C.notA.notB Set[ 8, 5, 13, 9, 12, 2, 1 ] finally F = (A.B + notA.notB).C + not(A.B = notA.notB).notC Set[ 8, 5, 13, 9, 12, 2, 1 ].1 In the score of Herma the analysis of the sets is included. In Musiques formelles Xenakis provides the organisation chart of the piece; the number of notes per second and the dynamics are defined in this.

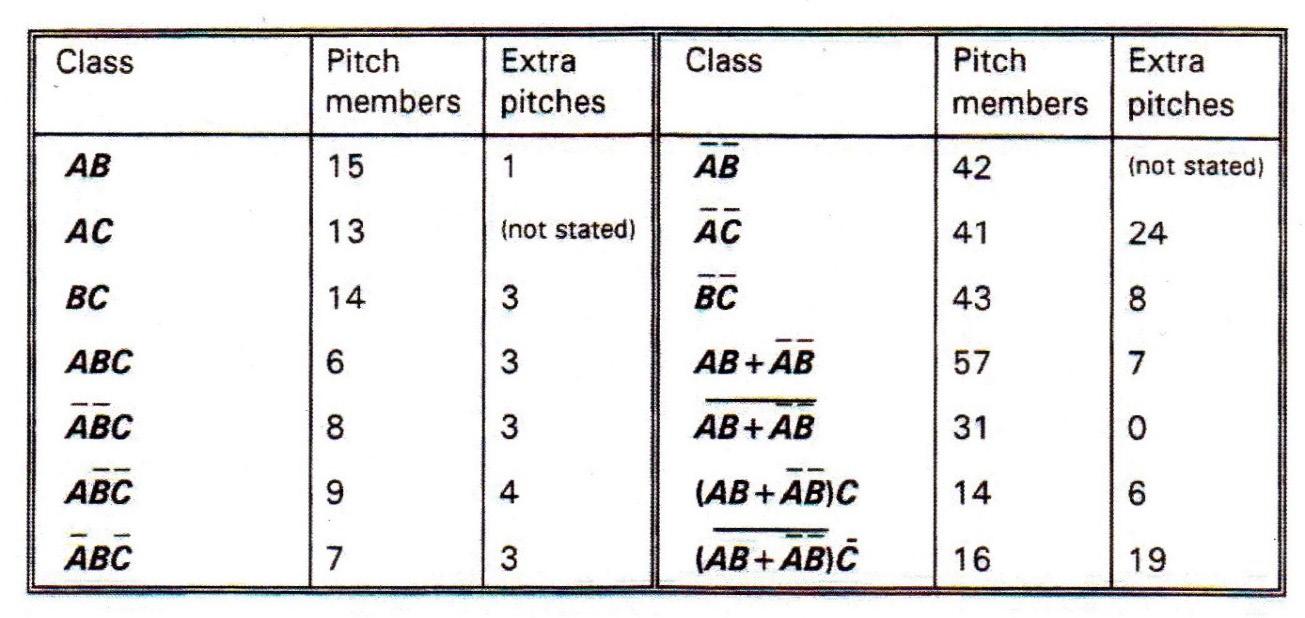
10.5.4 CRITICISM In his article The Limits of Logic: Structure and Aesthetics in Xenakis´s Herma (1995) the author Mathesis Eugene Montague points out inconsistencies in the pitch organisation of Herma. “In terms of the logic, the second part of Herma involved combinations of the sets already sounded-following the functions given above. Study of the score reveals that many of these set-combinations involve pitches that were not stated initially in the (labelled) statements of the sets being combined; they therefore cannot be members of the set-combinations. These pitches, originating outside the logical functions, I have termed ‘additional pitches'.

Eugene Montague says about Musiques formelles: "It is not an easy book to read. Xenakis’ explanations of the mathematics involved are often convoluted and obscure for those unversed in mathematics. Even those who have closely studied and understood the volume have criticised its obstacles; thus, Jan Vriend in his illuminating essay on Xenakis’s cello piece Nomos Alpha condemns the composer’s exposition of the piece in Formalized Music as “absolutely insufficient and misleading".

There are quite a few of these additional pitches in the second part of Herma, as is evident from the table below. Eugene Montague in his publication above mentioned provides the following chart: The dashes above the letters indicate NOT:

This unexpected freedom is all the more peculiar because Xenakis puts the stakes rather high in his ambition to arrive at a synthesis of art and science: “… each one of my works proposes a logical and philosophical thesis. These ‘theses’ are made possible by ‘a new relationship between the arts and sciences ... where the arts would consciously ‘set’ problems which mathematics would then be obliged to solve”.179

In addition to this, there are his statements in interviews that when the pitches that are the result of his processes are not satisfactory to his ear,

179Larry Polansky, ‘A Review of "Arts/Sciences": Alloys-3 by Iannis Xenakis.’

Leonardo, 23(4) (1990).