11.3 Applications

11.3 APPLICATIONS - Modulatory Synthesis Here, the first signal, the carrier (C) is changed by a second signal, the modulator (M). AM (amplitude modulation): term used in radio technology. The modulation concerns the amplitude of C. RM (ring modulation, but basically an AM): frequency mixing, performed by multiplying 2 signals. (Stockhausen’s Mantra (1970) for two pianos is based on this.) FM (frequency modulation): the modulation concerns the frequency of C. - Summation and differential tones When C = 1000 Hz and M = 428 Hz, then we also have 572 Hz (C-M) and 1428 Hz (C+M). When C and M are not singular sinus tones but tones with their own harmonic spectrum, a much larger number of summation and differential tones emerge, all formed from the resonating harmonic. C2+M/C2-M/C3+M/C3-M/C2+M2/C2-M2/C2+M3/, repeat are called shadow tones.

Theoretically, we therefore have a large number of tones. I say theoretically, as in practice by no means all summation and differential tones appear or are even remotely audible. Take the well-known phenomenon of two piccolos both playing high tones. The differential tones are clearly audible here as long as they are not covered by an instrument in the same range as those differential tones. The summation tones are far too high to be heard.

In spectralist theory, another distinction is made, between: harmonic spectra: the ratio between C and M is simple (1:2:3:4:5 and so on) and inharmonic (dissonant) spectra: the ratio between C and M is complex (for example, C = the tone G and M = the tone G . This results in a large number of ‘rough sounds’ (see Helmholz, pag 39).

All these techniques are capable of expanding the total spectrum and choice of frequencies. For this reason, a number of filters can be applied to limit the total of all possibilities. - The index (I) This makes it possible to control the frequency range of sidebands. The sideband is a set of all components of the modulator signal, except C itself. The formula is I = D/M, where I stands for the Index of the modulation, D for the maximum frequency that the spectrum is removed from C, and M is the modulation frequency. If M = 100 Hz and D = 100 Hz, then I = 1. When the index number rises, C becomes less and less prominent; the number of I changes the colour of the sound. When D = 300 Hz and M is still 100 Hz, then I = 3. When C = 1000 Hz and D = 1500 Hz, then the

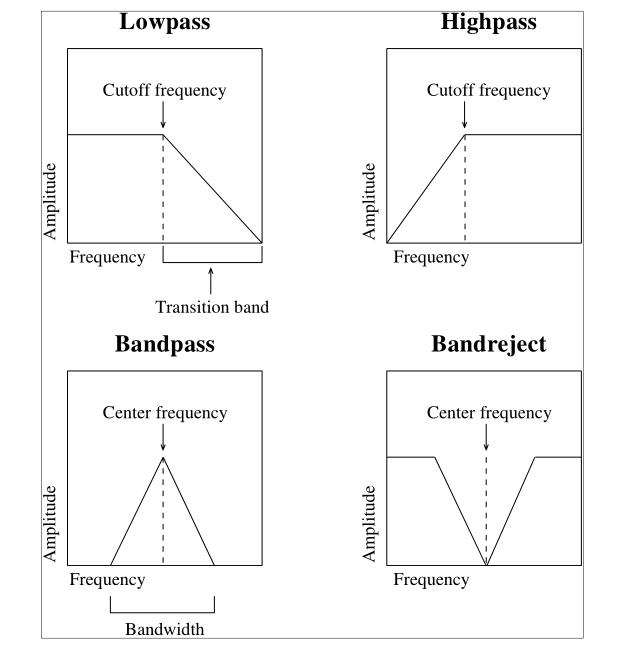
bandwidth of the modulated sound is 1000 + 1500 = 2500 Hz and 1000 – 1500 = -500. This -500 results in a reversal of the phase of the sound and therefore sounds the same as 500 Hz. - Filters Analogous to the electronic studio we distinguish a lowpass and a high pass filter, and a bandpass filter and a band reject filter.

The way in which the one partial is transformed into the other has a big influence on the stability of the timbre chord (colour chord). Techniques for this are: - mutation: one partial gradually transforms into the other by making use of the tones they have in common. - interpolation: one partial transforms into the other through voice leading. Tone 1 (partial 1) goes to tone 2 (partial 2) via a glissando. - spectral distortion: the spectrum changes because the distance between the partials is changed (by a shift of an octave). There are variations on all three techniques, so it is not always clear which one has been used.

Most spectral composers make a selection from tones that can exist by connecting two or more root tones (C and M1 and M2, and so on).