Alle kleuters tellen mee
Nore Wijns
Joke Torbeyns
Hilde Rabaut
Lieven Verscha el

Nore Wijns
Joke Torbeyns
Hilde Rabaut
Lieven Verscha el
1 Wiskunde in de kleuterklas: waarom?
2 Wiskunde in de kleuterklas: hoe? 9
2.1 Een sterke basis 9
2.2 Wiskundige kansen de hele dag door 11
2.3 Een rijk aanbod en kwalitatieve begeleiding 11
2.4 Een leerkracht met kennis van zaken
2.5
1 Het begrip ‘getal’ 24
2 Representaties van getallen 25
2.1 De concrete hoeveelheid 27
2.2 De schematische hoeveelheid 35
2.3 De abstracte representatie: telwoorden 39
2.4 De abstracte representatie: cijfers 45
2.4.1 Spontane aandacht voor cijfers 45
2.4.2 Meercijferige getallen in de kleuterklas 48
2.5 De verschillende representaties koppelen 51
3 Functies van getallen 54
3.1 Het getal als hoeveelheid (kardinaal getal) 54
3.2 Het getal als rangorde (ordinaal getal) 54
3.3 Het getal als code 58
3.4 Het getal als verhouding en maatgetal 60
2 Inhoudstafel
1 De ontwikkelingslijn 64
2 De allereerste vaardigheden voor het bepalen van hoeveelheden 66
2.1 Gevoel voor hoeveelheid 67
2.2 Subiteren 70
3 Spontane aandacht voor hoeveelheden 75
4 Tellen 80
4.1 Akoestisch tellen 82
4.2 Synchroon tellen 85
4.3 Resultatief tellen 87
4.4 Verkort tellen 89
4.5 Inzicht in de overige telprincipes 91
4.5.1 Principe van irrelevante volgorde 92
4.5.2 Principe van abstractie 93
5 De hoeveelheid nul 94 6 Aan de slag 95
7 Een praktijkvoorbeeld 96
Inhoudstafel
1
Hoofdstuk 3
Vergelijken en ordenen van getallen
1
3
3.1
5
5.1
5.2 Vermenigvuldig- en deelstrategieën
6.1
6.2
1 De ontwikkelingslijn 164
2 Patronen rondom ons 165
2.1 Spontane aandacht voor patronen 168
3 Herhalende patronen in de kleuterklas 174
3.1 Wat zijn herhalende patronen? 174
3.2 Patroonvaardigheden: ontwikkeling en stimulering 176
4 Veranderende patronen in de kleuterklas 189
4.1 Wat zijn veranderende patronen? 189
4.2 Patroonvaardigheden: ontwikkeling en stimulering 193
5 Aan de slag 195
6 Een praktijkvoorbeeld 197
204
Inhoudstafel
Laat kleuters kennismaken met de verschillende manieren om concreet materiaal te structureren, want dat biedt heel wat voordelen voor hun verdere wiskundige ontwikkeling.
1. Laat verschillende getalbeelden aan bod komen en vergelijk ze.
2. Toon kleuters hoe je materiaal kan structureren in betekenisvolle situaties.
3. Wijs kleuters expliciet op het voordeel van het structureren van concreet materiaal.
Het is goed om in de kleuterklas verschillende getalbeelden aan bod te laten komen. Bij de jongste kleuters volstaat het om deze getalbeelden te tonen en gebruiken. Zo ga je als leerkracht in interacties met kleuters vaak spontaan gebruik maken van vingerbeelden, zet je hen in de rij per twee, enzovoort. Door kleuters met al deze getalbeelden te laten kennismaken, leren ze dat een bepaalde hoeveelheid op verschillende manieren gerepresenteerd kan worden.






















































Bij de oudere kleuters kan je hier al iets systematischer te werk gaan door bijvoorbeeld verschillende getalbeelden te vergelijken: “Op welke manier kan je nog vijf maken?” maar even goed “Op welke manier kan je nog vijf eieren in de doos leggen?” Wie graag nog een stapje verder gaat, kan samen met de kleuters de voor- en nadelen van de verschillende getalbeelden onderzoeken. Je vertrekt dan van enkele specifieke voorbeelden, stelt gerichte vragen en onderzoekt samen stap voor stap of je algemene




Figuur 5. Visualiseren van de verschillende vervoerswijzen van de kinderen in de klas
Welke materialen komen in jouw klas aan bod bij telactiviteiten?
Zijn dit telkens concrete materialen of gebruik je ook schematische voorstellingen? Bouw je de overgang van concreet naar schematisch bewust op?
Welke getalbeelden komen in jouw klas aan bod? Zit hier veel variatie in?
Met welk getalbeeld wordt er in jouw school gewerkt vanaf het eerste leerjaar?
2.3 De abstracte representatie: telwoorden
Een getal kan tot slot ook op een abstracte manier gerepresenteerd worden, aan de hand van een telwoord of met cijfers (zie deel 2.4). Bij deze representaties kan je de onderliggende hoeveelheid niet meer nagaan door te tellen.
Hoofdstuk 1 Representaties en functies van getallen
Hoeveel heb je gegooid met de dobbelsteen? Liggen er veel of weinig appels in de fruitmand? Hoeveel dagen tot we naar het bos gaan? Er zijn heel wat situaties waarin jonge kinderen hoeveelheden proberen te bepalen. Dat doen ze vaak door de hoeveelheden te tellen. Maar nog voor ze leren tellen, beschikken kinderen al over vaardigheden die hen helpen om hoeveelheden te bepalen.
In dit hoofdstuk geven we eerst een overzicht van de ontwikkelingslijn voor hoeveelheden bepalen (1). Daarna bespreken we achtereenvolgens (2) de allereerste vaardigheden voor het bepalen van hoeveelheden, namelijk gevoel voor hoeveelheid en subiteren, (3) de spontane aandacht van kinderen voor hoeveelheden en (4) tellen. De hoeveelheid nul krijgt ook kort expliciete aandacht (5). We eindigen met enkele tips om rond hoeveelheden bepalen aan de slag te gaan (6) en een praktijkvoorbeeld (7).
leeftijd vaardigheid beschrijving Meer lezen?
0-1 gevoel voor hoeveelheid
subiteren (zonder benoemen van hoeveelheid)
2-3 voorwaarts akoestisch tellen tot 10
3-4 subiteren tot 4
grote aantallen (> 5) benaderend schatten (bv. opmerken wanneer een set van zes blokken plots vermeerderd is met vijf blokken)
kleine aantallen snel en exact bepalen zonder te tellen (bv. het verschil zien tussen twee en drie blokken)
luidop de telwoorden opzeggen in de juiste volgorde (principe van vaste orde van telwoorden)
kleine aantallen tot vier snel en exact bepalen, zonder te tellen, en dit ook zo benoemen (bv. “Dit zijn twee snoepjes.”)
spontane aandacht voor hoeveelheden spontaan hoeveelheden benoemen (bv. “Kijk, drie bomen.”)
p. 67-69
p. 70-74
p. 82-85
p. 70-74
p. 75-79
voorwaarts akoestisch tellen boven 10 p. 82-85
synchroon tellen tot 10 tijdens het tellen van voorwerpen deze één voor één aanwijzen (principe van één-één relatie)
4 resultatief tellen tot 10 tellen van voorwerpen gebruiken om het totale aantal te bepalen (principe van kardinaliteit)
p. 85-86
p. 87-88
subiteren tot 5 p. 70-74
4-5 resultatief tellen boven 10 p. 87-88
5 akoestisch terugtellen van 10 naar 1
6 akoestisch tellen in sprongen van 2, 5 en 10
akoestisch terugtellen vanaf een getal groter dan 10
akoestisch tellen tussen twee getallen
luidop de telwoorden opzeggen in de omgekeerde volgorde
luidop de telwoorden opzeggen in sprongen (bv. “2, 4, 6, 8”)
p. 82-85
p. 82-85
p. 82-85
luidop de telwoorden tussen twee getallen opzeggen in de juiste of de omgekeerde volgorde
verkort tellen tot 10 bepalen hoeveel er van iets zijn door te tellen, zonder elk voorwerp individueel te tellen (bv. een set van acht stoelen per twee tellen)
ongewone eenheden (bv. halve en hele) tellen
tellen van alle soorten objecten (bv. twee paar schoenen) (principe van abstractie)
p. 82-85
p. 89-91
p. 93
Ter info: Het principe van de irrelevante volgorde (zie p. 92) zit vervat in de andere vier telprincipes en wordt daarom niet vermeld in deze ontwikkelingslijn.
Onderzoek naar spontane aandacht voor hoeveelheden
Om die spontane aandacht voor hoeveelheden bij jonge kinderen te onderzoeken, zijn er verschillende taken ontwikkeld. Als kleuterleerkracht kan je die taken, of gelijkaardige situaties en materialen, gebruiken om beter zicht te krijgen op de ontwikkeling van de spontane aandacht voor hoeveelheden van je kleuters.
In een eerste taak worden een speelgoedpapegaai en speelgoedbessen in verschillende kleuren gebruikt (zie Figuur 18). Je vraagt het kind om goed te letten op wat je doet. Dan steek je rustig enkele bessen in de snavel van de speelgoedpapegaai, bijvoorbeeld vier gele bessen. Meteen daarna vraag je het kind om hetzelfde te doen.
Je gebruikt verschillende opdrachten waarbij het aantal bessen en de kleur wisselen. Uiteraard mag je geen enkele tip geven dat het om een numerieke taak gaat, je mag bijvoorbeeld niet de bessen tellen terwijl je ze aan de papegaai geeft, of zeggen: “Goed zo, evenveel bessen.”








Kinderen die spontane aandacht hebben voor hoeveelheden, zullen exact hetzelfde aantal bessen aan de papegaai geven, of opvallend telgedrag vertonen (bv. Het kind zegt: “Eén, twee, drie.” en geeft drie bessen aan de papegaai, ook al had jij er vier gegeven). Andere kinderen letten net heel erg op de precieze handbeweging die je maakte, of doen zelfs je gezichtsuitdrukking na.
Figuur 18. De papegaai en de gekleurde bessen in een taaksituatie waarbij gefocust wordt op de spontane aandacht voor hoeveelheden
Hoofdstuk 2 Bepalen van hoeveelheden
Er zijn vier fases in het leren tellen. In elke fase staat een andere telvaardigheid centraal.
- de fase van het akoestisch tellen: de kleuter zegt de telrij op zonder daar voorwerpen aan te koppelen.
- de fase van het synchroon tellen: de kleuter zegt de telrij op en duidt bij elk telwoord één voorwerp aan.
- de fase van het resultatief tellen: de kleuter kan een aantal voorwerpen tellen en zeggen hoeveel het er samen zijn.
- de fase van het verkort tellen: de kleuter kan een aantal voorwerpen correct tellen zonder ze één voor één te hoeven tellen.
Daarnaast zijn er ook vijf telprincipes die de kleuter stapsgewijs begint te beheersen wanneer hij de verschillende telfases doorloopt. Elke fase gaat gepaard met het beheersen van bepaalde telprincipes. Om akoestisch te kunnen tellen, is bijvoorbeeld enkel het eerste principe van stabiele orde vereist, om synchroon te tellen moet ook het tweede principe van de één-één relatie beheerst zijn.
Er zijn vijf telprincipes bij het leren tellen:
- het principe van de stabiele orde: de kleuter beseft dat je de telrij in een vaste volgorde moet opzeggen (één, twee, drie …).
- het principe van de één-één relatie: de kleuter weet dat elk voorwerp precies één maal geteld moet worden.
- het principe van de kardinaliteit: de kleuter weet dat het laatste telwoord dat je zegt bij het tellen van een aantal voorwerpen, de totale hoeveelheid aangeeft.
- het principe van de irrelevante volgorde: de kleuter weet dat het niet uitmaakt aan welke kant je begint te tellen om de totale hoeveelheid te bepalen.
- het principe van abstractie: de kleuter kan abstractie maken van de aard van de getelde voorwerpen, dit houdt in dat alle soorten objecten verzameld en geteld kunnen worden.
Als een kleuter de verschillende telprincipes kent en correct toepast, dan kunnen we zeggen dat hij conceptueel inzicht heeft in het tellen. De kleuter begrijpt dan het hoe en het waarom van het tellen.
Er zijn verschillende situaties waarin je betekenisvol rond het vergelijken en ordenen van getallen kan werken. We geven hier een uitgewerkt voorbeeld aansluitend bij de voorbereiding van de picknick voor de klasuitstap. Wat nemen we mee in de picknickmand? Waarvan nemen we veel of weinig mee? Wat vinden alle kleuters lekker en moeten we het meest voorzien? En wat is minder geliefd en moeten we het minst voorzien?
wat stimuleren? voorbeeldsituatie vergelijken van getallen
We bereiden met de klas een picknick in het park voor. We zijn met te veel kinderen in de klas om alle spullen in één picknickmand mee te nemen. We verdelen de klas daarom in twee groepen die elk een picknickmand krijgen. De kinderen vullen samen de picknickmanden, onder begeleiding van de leerkracht.
Deze situatie biedt kansen tot het vergelijken: de ene groep kinderen steekt drie pakken met appels in de picknickmand. De andere groep voorziet ook wat koekjes als dessert, en neemt daarom twee pakken appels en één pak koekjes mee. Namen de twee groepen evenveel appels mee? Varieer in de verschillen in aantallen (grote verschillen, kleine verschillen).





begeleiding als leerkracht
Stel gerichte vragen waarbij de kinderen hoeveelheden moeten vergelijken. Denk aan: Wat nemen we mee? Nemen we er veel of weinig van mee? Waarvan nemen we meer mee, waarvan minder?
Benoem de aantallen die vergeleken worden en maak gebruik van de passende begrippen (minder, meer, evenveel). Stimuleer de kinderen om deze woordenschat ook zelf te gebruiken.
Heb aandacht voor de strategie die ze gebruiken om te vergelijken, en verwoord deze strategie. Bied zelf andere mogelijke strategieën aan.
• Wat als we naast elke appel uit jullie mand één appel uit de mand van de andere groep leggen? (één-één relatie)
• Kunnen we de appels ook tellen en zo bepalen wie er meer appels heeft meegenomen? (tellen)
Verloopt dit moeizaam bij jouw kleuters?
• Start met kleine aantallen die kinderen vlot kunnen subiteren, en met aantallen die sterk van elkaar verschillen en op het zicht vergeleken kunnen worden. Bv. De eerste groep neemt negen appels mee, de tweede vier. Welke groep heeft het meest appels mee?
• Ga samen na of het kan helpen om de spullen uit de mand te halen en te structureren. Bv. Kan je de appels of koekjes zo leggen dat je makkelijker kan vergelijken? Denk aan appels per twee, of koekjes per vijf in een zakje en dan het aantal zakjes vergelijken.
Juna heeft nog niet leren optellen en aftrekken, maar beseft dat er iets niet klopt: ze zag dat papa nog een auto in de garage reed, dus moeten er nu méér auto’s zijn. Al in het eerste levensjaar groeit een zeker besef dat er meer blokken zijn wanneer er worden toegevoegd, en, omgekeerd, dat er minder blokken zijn wanneer er worden weggenomen. Deze vroegste stappen noemen we ‘gevoel voor optellen en aftrekken’.
Gevoel voor optellen en aftrekken is aanvoelen dat er meer voorwerpen zijn wanneer er voorwerpen worden toegevoegd, en dat er minder voorwerpen zijn wanneer er voorwerpen worden weggenomen.
Onderzoek naar gevoel voor optellen en aftrekken
Hoe hebben onderzoekers ontdekt dat baby’s al enig gevoel voor optellen en aftrekken hebben? Dit onderzoek lijkt sterk op het onderzoek naar gevoel voor hoeveelheid en subiteren dat in hoofdstuk 2 aan bod kwam. Baby’s zitten in hun kinderstoel en zien een doos met een kleine set van stippen. Die stippen verdwijnen dan achter een scherm. Daarna worden er stippen toegevoegd of weggenomen. Tot slot krijgen de baby’s te zien hoeveel stippen er in de doos zitten. In sommige gevallen klopt het aantal stippen (bv. 2 + 1 => 3), maar in andere gevallen niet (bv. 2 + 1 => 2). Baby’s kijken langer en aandachtiger naar foutieve aantallen. Hieruit leiden onderzoekers af dat baby’s aanvoelen dat er iets niet klopt.

1. Er worden twee stippen geplaatst.

2. Er komt een scherm voor de stippen.

5. Daarna één van beide situaties:
mogelijke of juiste uitkomst


3. Er wordt één stip toegevoegd. 4. De lege hand verdwijnt.

onmogelijke of foute uitkomst
Via de QR-code vind je een filmpje dat toont hoe een baby van tien maanden reageert.
In de kleuterschool leggen kinderen een ontwikkelingstraject af van materieel tellen naar verbaal tellen en in sommige gevallen zelfs al naar mentaal rekenen. Die ontwikkeling kan en mag echter niet geforceerd worden. Elke kleuter legt dit traject op zijn eigen tempo af. Hoe vlot deze ontwikkeling verloopt, hangt af van de leerkansen die een kind thuis en in de klas krijgt.
De ontwikkeling van strategieën verloopt niet in één keer: kinderen zullen niet in elke probleemsituatie op dezelfde strategie terugvallen. Zo zullen ze sommige optellingen al snel uit hun hoofd kunnen oplossen (bv. 1 + 1 = 2), terwijl ze andere optellingen op dat moment nog met een materiële telstrategie oplossen (bv. 2 + 3 = 5).
De strategieën vertellen iets over hoe een kind een probleemsituatie oplost.
1. Heb oog voor de strategieën die je kleuters gebruiken.
2. Ondersteun de ontwikkeling van materiële naar mentale strategieën.
3. Gebruik oplossingsstrategieën die aansluiten bij de betekenis van de opgave.
Heb oog voor de strategieën die jouw kleuters gebruiken bij het aanpakken en oplossen van optel- en aftreksituaties. Inzicht krijgen in de strategie die kleuters gebruiken kan op verschillende manieren:
- Observeer de kleuter: Maakt de kleuter gebruik van het beschikbaar materiaal? Wat doet de kleuter precies met dat materiaal? Hoor je de kleuter tellen? Hoe wordt er geteld? Let op: Niet alle kinderen die een verbale telstrategie gebruiken, tellen ook luidop. Sommigen gaan fluisterend te werk of doen dat zelfs helemaal onhoorbaar. Daardoor is het soms moeilijk om onderscheid te maken tussen een verbale telstrategie en een mentale rekenstrategie.
- Vraag de kleuter om uit te leggen hoe hij te werk gegaan is. Dat is geen eenvoudige opdracht voor kleuters, maar kan wel zinvol zijn voor hun verdere ontwikkeling.
- Verwoord zelf hoe je denkt dat de kleuter een probleemsituatie heeft opgelost en vraag of het klopt. Deze techniek wordt ‘spiegelen’ genoemd.
Eens je zicht hebt op welke strategieën de verschillende kleuters uit jouw klas gebruiken, kan je hen verder op weg helpen om de volgende stap in hun ontwikkeling te zetten. Je ondersteunt hen in de ontwikkeling van materiële en mentale strategieën, door hen stap voor stap te laten kennismaken met nieuwe strategieën.
aftreksituatie rond de bewerking 6 – 2 = ?
veranderingssituatie (afname - resultaat onbekend)
Jan heeft zes knikkers. Hij verliest er twee. Hoeveel heeft hij er nog over?
veranderingssituatie (toename - verandering onbekend)
Jan heeft twee knikkers. Hij krijgt er enkele bij. Nu heeft hij zes knikkers. Hoeveel knikkers heeft hij erbij gekregen?
materiële telstrategie die Marie (5 jaar) gebruikt om de aftreksituatie op te lossen
Marie maakt een groep van zes knikkers.
Daar haalt ze twee knikkers uit weg.
Dan telt ze de overblijvende knikkers: “Eén, twee, drie, vier.” Ze antwoordt: “Vier knikkers.”
Marie maakt een groep van twee knikkers.
Ze voegt knikkers toe tot ze een groep van zes bekomt. Ze telt hoeveel knikkers toegevoegd zijn: “Eén, twee, drie, vier.”
Dat aantal geeft ze als antwoord: “Vier knikkers.”
verbale telstrategie die Pieter (6 jaar) gebruikt om de aftreksituatie op te lossen
Pieter telt twee af van zes en houdt bij hoe vaak hij aftelt: “Zes…, één eraf is vijf, twee eraf is vier.”
Hij antwoordt: “Jan heeft nog vier knikkers over.”
Pieter telt verder van twee tot zes en houdt bij hoeveel er bijkomt: “Twee, …, drie (één erbij), vier (twee erbij), vijf (drie erbij), zes (vier erbij).”
Hij antwoordt: “Jan heeft vier knikkers bijgekregen.”
veranderingssituatie (afname - verandering onbekend)
Jan heeft zes knikkers. Hij verliest er enkele. Nu heeft hij nog twee knikkers. Hoeveel knikkers is hij kwijt?
Marie maakt een groep van zes knikkers.
Daar haalt ze knikkers uit weg tot er nog twee overblijven.
Ze telt hoeveel knikkers ze weggenomen heeft: “Eén, twee, drie, vier.”
Dat aantal geeft ze als antwoord: “Vier knikkers.”
Pieter telt af van zes tot twee en houdt bij hoeveel er af gaan: “Zes, …, vijf (één eraf), vier (twee eraf), drie (drie eraf), twee (vier eraf).”
Hij antwoordt: “Jan heeft vier knikkers verloren.”
vergelijkingssituatie (meer dan - verschil onbekend) Jan heeft zes knikkers. Sara heeft twee knikkers. Hoeveel knikkers heeft Jan meer dan Sara?
Marie maakt een rijtje van zes knikkers.
Daarnaast maakt ze een rijtje van twee knikkers.
Ze telt de knikkers uit de grootste rij die geen overeenkomstige knikker hebben in de kleinste rij: “Eén, twee, drie, vier.”
Ze antwoordt: “Vier knikkers.”
Pieter past één van drie bovenstaande verbale telstrategieën toe.
Tabel 5. Vier aftreksituaties rond de bewerking 6 – 2 = ? met bijhorende materiële en verbale telstrategie
Hoewel patronen vaak talrijk aanwezig zijn in de omgeving van kleuters, zal niet elke kleuter ze spontaan opmerken. Er zijn namelijk grote verschillen in de spontane aandacht voor patronen. Die spontane aandacht kan zich op allerlei manieren uiten. Sommige kinderen zeggen enthousiast: “Kijk juf, jij hebt een patroon op je T-shirt!”, terwijl andere kleuters uit zichzelf patronen maken tijdens vrij spel, bijvoorbeeld een rij met afwisselend één gele en één rode auto, of een veranderend patroon zoals Yin in het voorbeeld hieronder.












Yin (5 jaar) is met de blokken aan het spelen en roept trots: “Kijk juf, ik heb een trap gemaakt!” Juf Karine is onder de indruk: “Wauw, ik zie het. Je maakte een trap met allemaal verschillende kleuren. Hoe heb je dat gedaan?” Yin vertelt hoe ze de verschillende torens steeds hoger maakte. Juf Karine merkt nog op: “Elke toren is precies één blok hoger dan de vorige.”






Tot slot kan je zelf het goede voorbeeld geven. Zet je patroonbril op en ga op zoek naar patronen in je klasomgeving, of voeg er enkele toe. Door deze patronen te benoemen, vestig je de aandacht van je kleuters op patronen. Je kan ook een patroonzoektocht organiseren waarbij je samen met de kleuters (niet spontaan) op zoek gaat naar patronen in de omgeving: in de klas, in de gang, op de speelplaats, of in de buurt van de school. Zo’n zoektocht is een fijne, ongedwongen activiteit, en kan kinderen stimuleren om ook op andere plaatsen (wél spontaan) op zoek te gaan naar patronen. Op die manier wordt aandacht hebben voor patronen een gewoonte.
Wanneer enkele kleuters met concreet materiaal aan de slag zijn, kan je ook meespelen en zelf een (ander) patroon maken om hen te inspireren. Dat kan je dan expliciet benoemen: “Oh, zoveel mooie kleuren. Ik ga er een patroon mee maken.” of “Jij hebt een patroon gemaakt met geel en rood, ik ga er één maken met groen en blauw.” Merk je dat jouw kleuters vooral focussen op patronen met twee verschillende elementen (AB-patronen), maak dan eens een AAB-patroon of ABC-patroon.
Onderzoek naar spontane aandacht voor patronen
Om na te gaan of kleuters spontaan aandacht hebben voor patronen, lieten onderzoekers hen een toren bouwen met blokken in drie verschillende kleuren (zie Figuur 31 voor enkele voorbeelden).







Figuur 31. Drie blokkentorens die met gekleurde blokken gebouwd werden patroon sorteren willekeurig
Een laatste opdracht die je kan doen is een herhalend patroon namaken met andere materialen: je gaat het patroon vertalen. Dit lijkt misschien complex, maar onderzoek toont aan dat heel wat vierjarige kleuters dit eigenlijk helemaal niet zo moeilijk vinden. Sommige kleuters vinden immers een slim trucje om deze taak tot een goed einde te brengen: ze zoeken voor elk element in het patroon een vervanger, en gaan dan één voor één langs elk element in het patroon. Zo zijn er bijvoorbeeld kleuters die zeggen: “Groene vierhoek wordt rood hart. Gele cirkel wordt blauwe driehoek.” Ze lossen deze opdracht dus op zonder gebruik te moeten maken van de onderliggende structuur, waardoor de kracht van deze activiteit verloren gaat.
Het vertalen biedt echter wel een context waarin abstracte labels betekenisvol aan bod kunnen komen. Door gebruik te maken van een bepaalde opbouw kan je kleuters stimuleren om op een meer inzichtelijke manier te vertalen. Zo’n opbouw ziet er als volgt uit:
- de eenheid van het originele patroon identificeren (bv. groen-groen-geel) - de eenheid benoemen met abstracte labels (bv. AAB of biep-biep-boep) - een nieuw patroon maken dat hetzelfde abstracte label of dezelfde ‘naam’ heeft (bv. ster-ster-hart)
Om het vertalen te introduceren, kan je vertellen over een patroonmachine zoals in Figuur 42. Je toont hen de machine en vertelt over de werking: je steekt er een patroon in, kiest nieuwe figuren en dan maakt de machine een patroon met dezelfde eenheid, maar andere figuren. Kunnen de kleuters maken wat er uit de machine zou komen?
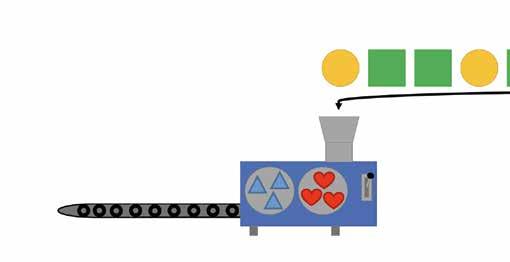

Figuur 42. Een patroonmachine waarin bovenaan een herhalend patroon gestoken wordt. Dat patroon komt er rechts op de lopende band terug uit met andere elementen
Uiteraard kan je net zo goed een zelfgemaakt patroon met kralen tonen en de kleuters vragen om dat patroon na te maken met de kralen die zij mooi vinden. Het vertalen kan bovendien ook over zintuigen heen. Een patroon met rode kraal-gele kraal wordt dan bijvoorbeeld sprong-klap.