Analyse 1 I Reële functies
D-finaliteit basis
Philip Bogaert
Filip Geeurickx
Marc Muylaert
Roger Van Nieuwenhuyze
Erik Willockx
CARTOONS
Dave Vanroye
Hoe gebruik je VBTL ?
Dit boek bevat drie hoofdstukken.
Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting.
Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.
Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt.

1 2
De nummers van de oefeningen hebben een gele kleur. Een sterretje duidt op een extra uitdaging. Achteraan in dit boek vind je de oplossingen
ICT is een ideaal hulpmiddel.
Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets.
Die vind je terug via www.polpo.be.


Wat moet je kennen en kunnen ?
Op het einde van elk hoofdstuk zie je een handig overzicht van wat je moet kennen en kunnen
In dit boek slaan we opnieuw de boeiende weg van de functies in. In het eerste hoofdstuk frissen we je kennis op van de kenmerken van een functie. Vervolgens leer je meer over lineaire en exponentiële groei. Bij lineaire groei zal er per tijdseenheid eenzelfde toename (of afname) zijn. Denk aan een waterkraan waarmee je per minuut één liter water laat stromen. Bij exponentiële groei wordt de hoeveelheid steeds met hetzelfde getal vermenigvuldigd; denk bv. aan de uitbraak van een virus zonder de aanwezigheid van een vaccin. Het laatste hoofdstuk focust op de algemene sinusfunctie. Je maakt kennis met een nieuwe eenheid voor hoeken en zal ondervinden hoe bepaalde constanten hun invloed zullen hebben. Dergelijke sinusfuncties kennen trouwens heel wat toepassingen. Op de foto zie je een stukje skyline van Singapore. Stel : je reist mee in een van de 28 capsules van dit reuzenrad. De hoogte van de capsule, uitgedrukt in functie van de tijd, is een voorbeeld van zo’n sinusfunctie. De auteurs wensen je veel plezier met dit eerste deel analyse.


Analyse 1 I Reële functies
1
2
3 De algemene sinusfunctie
Kenmerken van een functie 1
Hoofdstuktitel 0
De omtrek van een vierkant met zijde z, de oppervlakte van een vierkant met zijde z, het volume van een kubus met zijde z? Je kunt het allemaal voorstellen als een functie. Een functie is een verband tussen twee variabelen, waarbij voor elke x-waarde hoogstens één y-waarde bestaat.
In dit hoofdstuk gaan we dieper in op functies. Welke verschillende representaties zijn er? Wat zijn de kenmerken van zo’n functie? Hoe stellen we ze voor (met en zonder ICT)? En welke Duitse en Zwitserse wiskundigen lagen aan de basis van dit mooie stukje wetenschap?

Kenmerken van een functie
1 Verschillende representaties van een functie
Voorbeeld 1 : omtrek van een vierkant
De omtrek van een vierkant is gelijk aan viermaal de lengte van de zijde van het vierkant.
We kunnen nu volgende tabel opstellen :
De omtrek p hangt af van de grootte van de zijde z.
We noteren : p = 4z Merk op dat met een bepaalde waarde van z (hoogstens) één waarde van p overeenkomt.
We zeggen dat de omtrek p van een vierkant een functie is van de zijde z
We kunnen dit grafisch voorstellen :
We zien dat de grafiek een halfrechte is met de oorsprong als grenspunt. Het voorschrift kunnen we ook noteren als y = 4x of f ( x) = 4x
Algemene notatie : y = f ( x )
↓ ↳ onafhankelijke variabele afhankelijke variabele
Lees : y is een functie van x Met elke x -waarde correspondeert (hoogstens) één y -waarde.
REPRESENTATIE VAN EEN FUNCTIE
VERWOORDING
REPRES E NTATIE
VAN EEN F UNCTIE
REPRESENTATIE VAN EEN FUNCTIE
TABEL VOORSCHRIFT
REPRES E NTATIE
GRAFIEK
VAN EEN F UNCTIE
Voorbeeld 2 : absolute waarde van een reëel getal
We laten met elk reëel getal zijn absolute waarde corresponderen. De absolute waarde van een getal is dat getal zonder toestandsteken.
We kunnen nu volgende tabel opstellen :
Ergeldtook:
Notatie : y = | x |
Grafische voorstelling :
Met elke x -waarde correspondeert juist één y -waarde. Daarom is deze grafiek de grafiek van een functie
REPRESENTATIE VAN EEN FUNCTIE
VERWOORDING
REPRES E NTATIE
TABEL
VAN EEN F UNCTIE
REPRESENTATIE VAN EEN FUNCTIE
VOORSCHRIFT
REPRES E NTATIE
GRAFIEK
VAN EEN F UNCTIE
Voorbeeld 3:
Een reëel getal en zijn kwadraat.
Notatie: y = x 2
Je merkt dat elk reëel getal juist één kwadraat heeft. Voor elke x -waarde is er dus juist één y -waarde. y
Voorbeeld 4 :
Een reëel getal en zijn positieve vierkantswortel.
Notatie: y = √ x
Je merkt dat enkel positieve reële getallen juist één positieve vierkantswortel hebben.
Voorbeeld 5 : het omgekeerde van een reëel getal
We laten met elk reëel getal zijn omgekeerde corresponderen. Het omgekeerde van een (van nul verschillend) getal bekom je door in de breuknotatie teller en noemer van plaats te veranderen.
We kunnen nu volgende tabel opstellen :
Ergeldtook:3,5
Eriséénreëelgetaldatgeenomgekeerdeheeft,namelijk0omdat 1 0 nietgedefinieerdis.
Notatie: y = x 1 = 1 x
Grafische voorstelling :
Deze grafische voorstelling noemen we een hyperbool Merk op: elke rechte evenwijdig met de y-as snijdt de grafiek hoogstens één keer. Met elke x -waarde correspondeert dus hoogstens één y -waarde.
Daarom is deze grafiek de grafiek van een functie.
Tegenvoorbeeld : de baan van een biljartbal

We bekijken het verband tussen de afstand van de bal tot de breedte x en de lengte y van de biljarttafel.
Voor sommige x -waarden (zoals 1,3 en 1,7) zijn er meerdere y -waarden. Dit verband is geen functie.
2 Begrippen functie
Een functie is een verband (een relatie) tussen twee variabelen x en y waarbij voor elke x -waarde hoogstens één y -waarde (functiewaarde) bestaat.
x is de onafhankelijke variabele.
y is de afhankelijke variabele.
Er zijn verschillende representaties van een functie mogelijk: verwoording, letterformule, tabel en grafiek.
Wanneer de twee variabelen reële getallen zijn, dan spreken we van reële functies
Voor reële functies gebruiken we de letters f , g , h , ... of f 1, f 2, f 3, ... De formule die de functie bepaalt, is het functievoorschrift.
Zo spreken we over de functie f met voorschrift f ( x ). De y -waarden noemen we ook de functiewaarden of de beelden
Bekijken we opnieuw voorbeeld 3
hoogstens 1 ‖ nul of één
Het verband tussen een reëel getal en zijn kwadraat is een functie, want elk reëel getal heeft juist één kwadraat. We stellen de functie voor door de letter f. Het functievoorschrift noteren we als f ( x ) = x 2 of y = x 2 .
Wanneer we 5 kwadrateren, krijgen we 25.
Notatie : f ( 5) = 25
Lees : Het beeld (of de functiewaarde of y -waarde) van 5 is 25. Het koppel ( 5, 25) behoort tot de functie.
Dus : ( 5, 25) ∈ f
Elk element van R heeft één beeld. We noemen R het domein van de functie f
Notatie : dom f = R
Lees : Het domein van f is R.
De verzameling van de functiewaarden noemen we het bereik (of beeld) van f . We noteren
Notatie : ber f = R+
Lees : Het bereik van f is R+ .
Bij voorbeeld 4 op blz. 11 wordt het functievoorschrift van de functie g : y = √ x of g ( x )= √ x
g ( 9) = 3 g ( 6) = √6 g ( –4) ∉ R
dom g = R+
ber g = R+
Andere voorbeelden :
1 Elk reëel getal heeft juist één tweevoud, dus dit verband is een functie f 1 met voorschrift f 1( x ) = 2x

2 Beschouw de functie f 2 met f 2( x ) = x 3 – 1

f 1( 3) = 2 · 3 = 6
f 1(– 2) = 2 ( –2) = –4
dom f 1 = R
ber f 1 = R
f 2( –3) = ( –3)3 – 1 = –28
f 2( 0) = 03 – 1 = –1
dom f 2 = R
ber f 2 = R
reële functie
Een reële functie is een functie waarbij de variabelen x en y reële getallen zijn.
domein en bereik
Het domein van een functie f is de verzameling van de x -waarden waarvoor de functiewaarde bestaat.
Notatie : dom f
Het bereik (beeld) van een functie f is de verzameling van de y -waarden waarvoor er een x -waarde bestaat zodat y = f ( x )
Notatie : ber f
Grafisch kunnen we als volgt onderzoeken of een verband tussen twee variabelen een functie is :
Elke rechte evenwijdig met de y -as snijdt de grafiek hoogstens één keer. Dit verband is een functie.
met de y -as die de grafiek meer dan één keer snijden. Dit verband is geen functie.
3 Input-outputmodel van een functie
Voorbeeld 1 :
Lena en Marie willen de rekening van hun jeugdbeweging wat aandikken en gaan daarom taarten bakken. Zij besluiten elke taart die ze bakken te verkopen voor 6 euro per stuk en krijgen alvast 50 euro sponsorgeld van hun ouders.
Het verband tussen het aantal taarten dat ze verkopen en het opgehaalde geld kunnen we schrijven als : f ( x ) = 6x + 50 met x : het aantal taarten f ( x ): het opgehaalde geld
We kunnen nu voor elk aantal verkochte taarten het bedrag berekenen dat wordt opgehaald.

Voorbeeld 2 : We beschouwen het functievoorschrift f ( x ) = –
Op een grafiek geeft dat het volgende : (–3, 9) (–2, 7) y
4 De grafiek van een functie construeren
Om de grafiek van een functie te tekenen, bepalen we een aantal koppels van de functie. We kiezen hiervoor een aantal x -waarden en we zoeken voor elk van die waarden het beeld. Wees niet gierig met het aantal puntenkoppels. Zoek er voldoende !
Voorbeeld 1: grafiek van f met f ( x ) = 2x – 3
–
f (x) = 2x – 3 ( , –2) 1 2 ( , –4) –1 2
(–1, –5)
(–2, –7)
(3, 3)
(2, 1) (1, –1)
(0, –3)
–7
De grafiek van f is een rechte.
Voorbeeld 2 : grafiek van g met g ( x ) = x 2
(–3, 9)
(–2, 4) (–1, 1)
(2, 4)
(1, 1)
(0, 0)
De grafiek van g is een parabool.
5 De grafiek van een functie construeren met ICT
De grafiek van een functie kunnen we eenvoudig tekenen met behulp van ICT. We tekenen met GeoGebra de grafiek van de functies f en g. Om grafieken van functies met een gegeven voorschrift te tekenen met GeoGebra voeren we het voorschrift f ( x) van de functie f in het algebravenster in.
f ( x )= x 4 x 3 2 x 2

f ( x )= x 4 x 3 2 x 2
g ( x )= x 2 x + 3
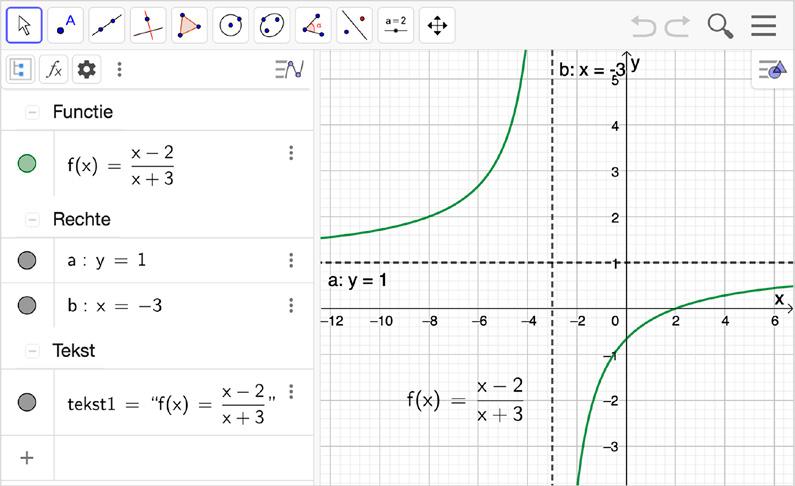
Taak:
Construeer met GeoGebra de grafieken van de functies van vorige bladzijde.
6 Domein, bereik en nulwaarden van een functie bepalen op de grafiek
Beschouwen
we de grafiek van de volgende functie f met voorschrift f ( x )
dom f ber f
Domein
Voor elke x -waarde die behoort tot [ –7, 6] kun je de functiewaarde bepalen. In het voorbeeld hierboven is het domein in het donkerblauw aangeduid.
Notatie : dom f = [ –7, 6]
Lees : Het domein van de functie is [ –7, 6].
Domein bepalen op de grafiek
Het domein van een functie wordt bepaald door de loodrechte projectie van de grafiek op de x -as.
Bereik
Bij deze functie vind je elk reëel getal dat behoort tot [ –4, 2] als functiewaarde. In het voorbeeld hierboven is het beeld in een roze kleur aangeduid. Notatie : ber f = [ –4, 2]
Lees : Het bereik van de functie is [ –4, 2].
Bereik bepalen op de grafiek
Het bereik van een functie wordt bepaald door de loodrechte projectie van de grafiek op de y -as.
Nulwaarde
We merken dat de grafiek de x -as snijdt in het punt met abscis –4 en de x -as raakt in het punt met abscis 4. We noemen –4 en 4 de nulwaarden van de functie f , want : f ( –4) = f ( 4) = 0
nulwaarde van een functie
Een nulwaarde van een functie is een x -waarde waarvoor de functiewaarde nul is.
in symbolen : a is een nulwaarde van f ⟺ f ( a ) = 0
⟺ de grafiek van f snijdt of raakt de x -as in ( a , 0)
Grafische interpretatie
De nulwaarde van een functie is het eerste coördinaatgetal van het snijpunt (of raakpunt) van de grafiek van die functie met de x -as.
Nulwaarden berekenen
Wanneer het voorschrift van de functie gegeven is, kun je de nulwaarden berekenen door het voorschrift gelijk te stellen aan 0.
Voorbeelden
Voorbeeld 1 :
Gegeven:defunctie f met f ( x ) = 2 x 6
dom f = R
ber f = R
f ( x ) = 0
2 x 6 = 0
2 x = 6
x = 3
De nulwaarde van f is 3.
De grafiek van f snijdt de x -as in ( 3, 0)
Controle :
f ( 3) = 2 3 – 6 = 0
Voorbeeld 2 :
Gegeven:defunctie g met g ( x ) = x 2 4
dom g = R
ber g = [ 4, +∞[
g ( x ) = 0
x 2 4 = 0
x 2 = 4
x = 2 of x = 2
De nulwaarden van g zijn –2 en 2.

De grafiek van g snijdt de x -as in ( –2, 0) en ( 2, 0).
Controle :
g ( 2) = 22 – 4 = 0
g ( –2) = ( –2)2 – 4 = 0
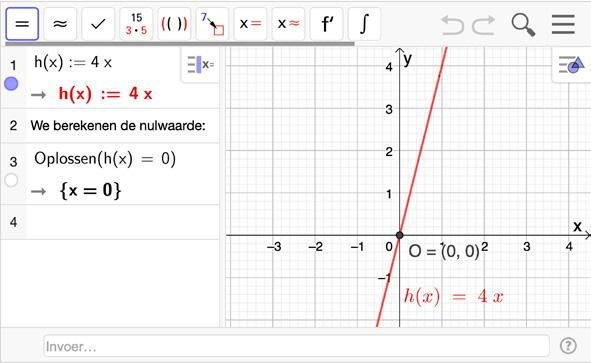
Voorbeeld 3 :
Gegeven:defunctie h met h ( x ) = 4 x
dom h = R ber h = R
h ( x ) = 0
4 x = 0
x = 0
De nulwaarde van h is 0.
De grafiek van h snijdt de x-as in ( 0, 0)
Voorbeeld 4 :
Gegeven:defunctie i met i ( x )= 1 x
dom i = R 0
ber i = R 0
Deze functie heeft geen nulwaarde.
De grafiek van i snijdt de x-as niet.

7 Verloop van reële functies
Wanneer je de stand van je zicht- of spaarrekening regelmatig bijhoudt, dan merk je dat die wijzigt door stortingen of afnamen, met andere woorden de grafiek van de stand van je rekening stijgt of daalt. Ook bij temperatuurmetingen kunnen we merken dat de temperatuur stijgt, daalt of constant blijft aan de hand van de grafiek.
Beschouw de grafiek van de volgende willekeurige functie f
Stijgen en dalen
De bovenstaande grafiek is de grafiek van een functie f . Hierbij is : dom f = ]–∞, 11] en ber f = ]–∞, 3].
Dit is een waardetabel van de functie f
↓ de functiewaarden worden groter als de x -waarden groter worden
↓ de functiewaarden worden kleiner als de x -waarden groter worden
↓ de functiewaarden worden groter als de x -waarden groter worden
Uit de grafiek en de tabel kunnen we het volgende afleiden :
↓ de functiewaarden blijven constant als de x -waarden groter worden
↓ de functiewaarden worden kleiner als de x -waarden groter worden
– In het interval ] –∞, –2[ stijgt de grafiek, de functiewaarden worden groter naarmate de x -waarden groter worden.
– In het interval ] –2, 0[ daalt de grafiek, de functiewaarden worden kleiner naarmate de x -waarden groter worden.
– In het interval ] 0, 4[ stijgt de grafiek, de functiewaarden worden groter naarmate de x -waarden groter worden.
– In het interval ] 4, 7[ stijgt noch daalt de grafiek, de functiewaarden blijven constant (nl. 3) naarmate de x -waarden groter worden.
– In het interval ] 7, 11[ daalt de grafiek, de functiewaarden worden kleiner naarmate de x -waarden groter worden.
stijgend, dalend en constant
Een functie is stijgend in een interval als de functiewaarden in dat interval groter worden bij toenemende x -waarden.
Een functie is dalend in een interval als de functiewaarden in dat interval kleiner worden bij toenemende x -waarden.
Een functie is constant in een interval als de functiewaarden in dat interval gelijk blijven.
Extreme waarden van een functie
Gegeven is de functie f met voorschrift f ( x ) = x 3 – 4x

Die functie stijgt in het interval ]–∞; –1,15[ en gaat bij x = –1,15 over in een dalende functie.
Hierbij is f ( –1,15) = 3,08
We zeggen dat 3,08 een maximum is van de functie voor x = –1,15.
De functie daalt in ]–1,15; 1,15[ en gaat bij x = 1,15 over in een stijgende functie.
Hierbij is f ( 1,15) = –3,08
We zeggen dat –3,08 een minimum is van de functie voor x = 1,15.
We kunnen dit ook in een overzichtelijke tabel plaatsen.
1,15 1,15 +∞
3,08
Maxima en minima noemen we de extreme waarden
Merk op dat een extreme waarde een functiewaarde is en geen x-waarde.
extreme waarden
Als een functie f overgaat van stijgen naar dalen in ( a , f ( a )), dan zeggen we dat de functie een maximum f ( a ) heeft voor x = a .
Als een functie f overgaat van dalen naar stijgen in ( a , f ( a )), dan zeggen we dat de functie een minimum f ( a ) heeft voor x = a
Opmerking :
Een functie kan meerdere maxima en/of minima hebben.

Tekenverloop van een functie
Bij de bovenstaande grafiek merken we het volgende:
– de functie f heeft als nulwaarden –6, 0 en 4, met andere woorden f ( –6) = f ( 0) = f ( 4) = 0;
– als x kleiner is dan –6, dan bevindt de grafiek zich boven de x -as, met andere woorden f ( x ) > 0;
– als x ligt tussen –6 en 0, dan bevindt de grafiek zich onder de x -as, met andere woorden f ( x ) < 0;
– als x ligt tussen 0 en 4, dan bevindt de grafiek zich boven de x -as, met andere woorden f ( x ) > 0;
– als x groter is dan 4, dan bevindt de grafiek zich onder de x -as, met andere woorden f ( x ) < 0.
We kunnen dit in een overzichtelijke tabel plaatsen.
x –∞ –6 0 4 +∞
f ( x ) + 0 – 0 + 0 –
Algemeen :
De grafiek van een functie f bevindt zich onder de x -as ⟺ f ( x ) < 0.
De grafiek van een functie f bevindt zich boven de x -as ⟺ f ( x ) > 0.
f (x) > 0 f
f(x) < 0
De grafiek van een functie f snijdt of raakt de x -as in ( a , 0) ⟺ f ( a ) = 0. f f(x) < 0


8 Een functie bespreken
Het bespreken van een functie betekent dat we volgende kenmerken nagaan : (praktisch) domein, (praktisch) bereik, nulwaarden, snijpunten met de assen, tekenverloop, stijgen/dalen, gedrag op oneindig, extrema (maxima/minima) en symmetrie.
Voorbeeld : bespreek de functie f met voorschrift f ( x ) = x 3 + x 2 – 6x
• Domein : dom f = R
• Bereik : ber f = R
• Nulwaarden : f ( x )= 0
• Snijpunten met de x-as : ( –3, 0), ( 0, 0), ( 2, 0)
• Snijpunt met de y-as : ( 0, 0)
• Tekenverloop :
• Gedrag op oneindig : lim x → +∞ f ( x )=+∞ lim
f iseven
∀ x ∈ dom f : f ( x )= f ( x )
f isoneven
∀ x ∈ dom f : f ( x )= f ( x )
• Symmetrie : f is noch even noch oneven, er is dus geen symmetrie.

9 Toepassingen
Toepassing 1 : een ongelijkheid oplossen
Los volgende ongelijkheid op : 2x 2 – 5x – 3 < 0. Om de ongelijkheid op te lossen gaan we na voor welke waarde van x de functiewaarden van f met voorschrift f ( x ) = 2x 2 – 5x – 3 negatief zijn. We gaan dus met andere woorden na voor welke waarden van x de grafiek van f onder de x -as ligt. We berekenen hiervoor eerst de nulwaarden van f f ( x )= 0 2
Tekenverloop :

Antwoord : V = 1 2 ,3
Toepassing 2 : snijpunten berekenen van twee grafieken
Bereken de snijpunten van de grafieken die bepaald worden door de functies f en g met f ( x ) = –2x + 5 en g ( x ) = 2x 2 – 4x + 1.
Om de snijpunten van de twee grafieken te bepalen, stellen we f ( x ) = g ( x ) en lossen we die vergelijking op. f ( x )= g ( x )
Antwoord : de snijpunten van de grafieken f en g zijn ( –1, 7) en ( 2, 1).

Toepassing 3 : inhoud van een doosje zonder deksel
Aan de vier hoeken van een rechthoekig stuk karton van 90 cm bij 60 cm snij je gelijke vierkanten weg. Van de rest maak je een doos zonder deksel.
Wanneer is de inhoud van de doos maximaal?
Exploreren & analyseren
Als de zijde van het vierkant dat je aan de vier hoeken wegsnijdt gelijk is aan 10 cm, dan is:
– de breedte van het doosje 40 cm;
– de lengte van het doosje 70 cm;
– de hoogte van het doosje 10 cm;
– de inhoud van het doosje 70 ∙ 40 ∙ 10 cm3 = 28 000 cm3
Als de zijde van het vierkant dat je aan de vier hoeken wegsnijdt gelijk is aan 15 cm, dan is:
– de breedte van het doosje 30 cm;
– de lengte van het doosje 60 cm;
– de hoogte van het doosje 15 cm;
– de inhoud van het doosje 60 ∙ 30 ∙ 15 cm3 = 27 000 cm3
Modelleren & mathematiseren
Als de zijde van het vierkant dat je aan de vier hoeken wegsnijdt gelijk is aan x cm, dan is:
– de breedte van het doosje ( 60 – 2x) cm;
– de lengte van het doosje ( 90 – 2x) cm;
– de hoogte van het doosje x cm;
– de inhoud van het doosje ( 90 – 2x) ∙ ( 60 – 2x) ∙ x cm3
Die laatste formule noemen we de inhoudsfunctie van het doosje en het voorschrift noteren we bijvoorbeeld als I( x) met de I van inhoud. We vinden dus:
I( x) = ( 90 – 2x) ∙ ( 60 – 2x) ∙ x
De graad van die functie is 3.
90 cm
1 Exploreren
Wat is er gegeven ? Wat is er gevraagd? Begrijp het probleem. Maak eventueel een bijkomende tekening of schets.
2 Mathematiseren
Welke heuristiek (oplossingsmethode) ga je gebruiken?
3 Berekenen
Welke formule moet je gebruiken ?
Welke bewerkingen zul je uitwerken ?
4 Controleren
Heb je de gegevens gebruikt ? Kan het antwoord kloppen ?
60 cm

5 Geef een antwoord
Dit is demathematiseren. Moet je het antwoord gepast afronden ? Formuleer het antwoord in een zin.
Berekenen
Bij functies met een graad hoger dan twee doen we een beroep op ICT. Plot de grafiek van de functie met wiskundesoftware.

We zien duidelijk dat de grafiek van de functie een maximum bereikt. De top A heeft als coördinaat ( 11,77; 28 520,26)
Demathematiseren
De inhoud van het doosje is maximaal bij:
een hoogte van: 11,77 cm
een breedte van: 36,46 cm
een lengte van: 66,46 cm
De inhoud van het doosje bedraagt dan 28 520,26 cm3 ≈ 28,52 dm3 of 28,52 liter.
Functies
Het woord ‘functie’ werd voor het eerst gebruikt door de Duitse wiskundige Leibniz (1646 –1716), die het begrip koppelde aan gelijk welke grootheid verbonden met een kromme. In 1718 definieerde de Zwitserse wiskundige Johann Bernoulli (1667–1748) een functie als een willekeurige uitdrukking bestaande uit één variabele en verschillende constanten. Zijn landgenoot Euler (1707–1783) voerde de notatie f(x) in. Het is de Duitser Dirichlet (1805 –1859) die de uiteindelijke definitie vastlegde en ook begrippen zoals ‘definitiegebied’ en ‘bereik’ omschreef. Het ‘definitiegebied’ noemen we nu ‘domein’.


Toepassing 4 : mollen in de tuin
Als hij gangen graaft, maakt de mol hoopjes van de overschotten aarde. We vonden een wiskundige molshoop terug die functie f volgt met voorschrift f ( x )= 1 45 x 2 + 4 3 x met x : de horizontale afstand in cm
f ( x ): de hoogte van de molshoop in cm
a Wat is de maximale hoogte van die molshoop ?
b Wat is de maximale breedte van de molshoop ?
c Over welke horizontale afstand is de molshoop minstens 15 cm ?
Oplossing :
a Om de maximale hoogte te weten te komen van de molshoop berekenen we de top van de grafiek f
f

Antwoord: de maximale hoogte van de molshoop is 20 cm.
b Om de maximale breedte te weten te komen van de molshoop bepalen we de nulwaarden van f f ( x )= 0
1 45 x 2 + 4 3 x = 0
x 2 + 60 x = 0
x ( x + 60)= 0
x = 0of x = 60
Antwoord : de molshoop is maximaal 60 cm breed.
c We lossen de ongelijkheid f ( x ) ⩾ 15 op.
f ( x ) 15
1
x 2
x
Antwoord : de molshoop is over een afstand van (45 – 15) cm = 30 cm minstens 15 cm hoog.
10 Differentiequotiënt
a Productiekosten beperken
De totale productiekosten (in duizenden euro’s) van een product hangen af van het aantal productie-eenheden per week volgens het wiskundig model :
k ( q ) = 0,6 ( q – 4)3 + 38,4 met k ( q ): totale productiekost in duizenden euro’s q : aantal productie-eenheden in duizendtallen
a Met hoeveel euro nemen de totale kosten toe als het aantal productie-eenheden toeneemt van 1000 naar 2000 ? En van 2000 naar 3000 ? Maak een tabel van de differentie van k ( q ), nl. ∆k ( q ) = k ( q + 1) – k ( q ) met q = 0, 1, …, 10.
b Bedrijfseconomisch is het van belang om de productiegroei stop te zetten vlak voordat de kosten per extra 1000 eenheden weer snel stijgen. Bij welke toename in duizendtallen is de groei van de totale kosten het kleinst ? Bij welke productie kunnen we het best stoppen ?
Oplossing :

Om de productie op te starten van 0 tot 1000 eenheden bedraagt de kostprijs 22 200 euro. Om de productie te verhogen van 1000 naar 2000 stuks, bedraagt de stijging van de kosten 11 400 euro. Een stijging van 2000 naar 3000 productie-eenheden brengt een meerkost van 4200 euro met zich mee. Het verschil in kosten tussen 3000 en 4000 bedraagt slechts 600 euro enz.
b In de tabel zien we duidelijk dat de supplementaire productiekosten steeds dalen tot een productie van 4000 stuks. Vanaf dan worden de productiekosten per duizend eenheden weer steeds groter. Bedrijfseconomisch gezien is het dan ook interessant om de productie rond de 4000 eenheden te houden.
b Hoe snel reed Sofie ?
Sofie huurt op haar reis een motorscooter. Ze maakt er een testrit mee over een afstand van ongeveer 10 km. Ze doet er een halfuurtje over. Haar rit kun je beschrijven met het volgende functievoorschrift :
d ( t )= 2 t 3 als0 t 15
10125 (30 t )3 als15 < t 30
met d ( t ): afstand in meter, t : tijd in minuten
a Hoeveel kilometer, tot op 1 meter nauwkeurig, reed Sofie effectief ?
Bereken de gemiddelde snelheid in km/h over de hele testrit.
b De gemiddelde snelheid over de hele rit zegt weinig over haar snelheid op een bepaald moment. Hoe verandert die snelheid gedurende de rit ?
Bereken ∆d ( t ) = d ( t + 1) – d ( t ) voor t = 0 tot t = 29.
c Benader de snelheid in m/min op het tijdstip t = 8.
Oplossing :

a Sofie reed effectief d ( 30) = 10 125 m. Gedurende de hele rit reed Sofie aan een gemiddelde snelheid van ( 10,125 2) km/h = 20,25 km/h. Maar dit zegt weinig over haar prestaties gedurende de hele rit.
Daarom berekenen we de afstand (in meter) die Sofie elke minuut gereden heeft.
Uit de tabel blijkt dat Sofie het snelst reed tussen de 14e en 15e minuut. Zij reed toen met een (gemiddelde) snelheid van 1262 m/min of 75,72 km/h.
c Voor een benadering van de snelheid in m/min op het tijdstip t = 8 minuten berekenen we de gemiddelde snelheid over een klein interval, bijvoorbeeld van t = 8 tot t = 8,1 minuten.
d ( 8) = 1024 m
d ( 8,1) = 1062,882 m
∆d ( t ) = d ( 8,1) – d ( 8) = 38,882 m
∆t = 8,1 min – 8 min = 0,1 min
gemiddeldesnelheid = ∆d ( t )
∆ t = 38,882m
0,1min = 388,82m/min
We herhalen nu de berekening op het interval [ 8; 8,01[, [ 8; 8,001[ en [ 8; 8,0001[. [ 8; 8,01[ [ 8; 8,001[ [ 8; 8,0001[
d ( 8,01) = 1027,8448 m
∆d ( t ) = 3,8448 m
∆t = 0,01 min
∆d ( t )
∆ t = 384,48m/min
d ( 8,001) = 1024,384 m
∆d ( t ) = 0,384 m
∆t = 0,001 min
∆d ( t ) ∆ t = 384m/min
d ( 8,0001) = 1024,0384 m
∆d ( t ) = 0,0384 m
∆t = 0,0001 min
∆d ( t )
∆ t = 384m/min
We mogen dus stellen dat Sofie op het tijdstip t = 8 ongeveer met een snelheid van 384 m/min of 23,04 km/h reed. Terminologie differentiequotiënt : We berekenen de toename van de x - en y -waarden over het interval [ x A, x B].
∆ x = x B xA
∆ y = yB yA = f ( x B ) f ( xA )
∆ y
∆ x = ∆ f ( x )
∆ x = f ( x B ) f ( xA ) x B xA
= differentiequotiënt in [ xA , x B ]
= richtingscoëfficiëntvan derechteAB
= gemiddeldesnelheid waarmee y verandert in [ xA , x B ]
Kies het punt B steeds dichter bij het punt A.
De rechte AB valt uiteindelijk samen met de raaklijn t in A. De snelheid waarmee y verandert voor x = x A is dus de richtingscoëfficiënt van de raaklijn in A.
differentiequotiënt
AlsA a , f (a ) enB b , f ( b ) tweepuntenzijnvandegrafiekvaneenfunctie f ,dannoemenwe ∆ y ∆ x = ∆ f ( x ) ∆ x = f ( b ) f (a ) b a het differentiequotiënt ofde gemiddeldeverandering van f over hetinterval [a , b ]
Als ∆ y ∆ x > 0,danstijgtdiefunctieindatinterval;als ∆ y ∆ x < 0,dandaaltdiefunctieindatinterval.
11 Samenvatting
• Je weet dat het verband tussen twee variabelen x en y een functie is als we bij elke x -waarde hoogstens één y -waarde kunnen berekenen. We noemen x de onafhankelijke variabele en y de afhankelijke variabele.
• Je weet wat bedoeld wordt met een functievoorschrift.
De ‘formule’ die de functie bepaalt, noemen we het functievoorschrift. We spreken van de functie f met voorschrift f ( x ). We noemen y de functiewaarde van f in x als f ( x ) = y
Notatie : y = f ( x )
• Je kent de vier representaties van een functie : verwoording, voorschrift, tabel en grafiek.
• Je kent de betekenis van het domein, het bereik en de nulwaarde van een functie.
Het domein van een functie f is de verzameling van de x -waarden waarvoor de functiewaarde bestaat.
Notatie : dom f
Het bereik van een functie f is de verzameling van de y -waarden waarvoor er een x -waarde bestaat
zodat y = f ( x )
Notatie : ber f
Een nulwaarde van een functie is een x -waarde waarvoor de functiewaarde nul is. Een nulwaarde is het eerste coördinaatgetal van het snijpunt of raakpunt van de grafiek van de functie met de x -as.
In symbolen : a is een nulwaarde van f ⟺ f ( a ) = 0
⟺ de grafiek van f snijdt of raakt de x -as in ( a , 0)
• Je kunt een grafiek construeren en je kunt bepalen of de grafiek al dan niet de grafiek van een functie voorstelt.
Een grafiek is de grafiek van een functie als en slechts als elke rechte evenwijdig met de verticale as hoogstens één gemeenschappelijk punt heeft met de grafiek.
• Je kunt op de grafiek van een functie het domein, het bereik, de nulwaarden, het stijgen en dalen en de extrema bepalen.
Een functie is stijgend in een interval als de functiewaarden in dat interval groter worden bij toenemende x -waarden.
Een functie is dalend in een interval als de functiewaarden in dat interval kleiner worden bij toenemende x -waarden.
Een functie is constant in een interval als de functiewaarden in dat interval gelijk blijven.
Als een functie f overgaat van stijgen naar dalen in ( a , f ( a )), dan zeggen we dat de functie een maximum f ( a ) heeft voor x = a
Als een functie f overgaat van dalen naar stijgen in ( a , f ( a )), dan zeggen we dat de functie een minimum f ( a ) heeft voor x = a
• Je kunt een functie bespreken (domein, bereik, nulwaarden, snijpunten met de assen, tekenverloop, stijgen/dalen, gedrag op oneindig, extrema en symmetrie).
• Je weet wat een even en een oneven functie is.
• Je kent de betekenis van het differentiequotiënt.
AlsA a , f (a ) enB b , f ( b ) tweepuntenzijnvandegrafiekvaneenfunctie f ,dannoemenwe ∆ y ∆ x = ∆ f ( x ) ∆ x = f ( b ) f (a ) b a hetdifferentiequotiëntofdegemiddeldeveranderingvan f over hetinterval [a , b ].
Als ∆ y ∆ x > 0,danstijgtdiefunctieindatinterval;als ∆ y ∆ x < 0,dandaaltdiefunctieindatinterval.
12 Oefeningen
Mats wil graag kippen houden. Hij wil voor zijn dieren een rechthoekig loopoppervlak maken van 20 m². De lengte en de breedte kunnen verschillende afmetingen hebben.
a Vul volgende tabel aan.
lengte l (m) 1 2 4 breedte b (m)
b Welke grootheid is de onafhankelijke variabele ? Welke is de afhankelijke variabele ?
c Stel de letterformule op.
d Teken de grafiek.
e Is dit de grafiek van een functie ? Verklaar.
f Welk verband is er tussen de lengte en de breedte van een rechthoek als de oppervlakte constant is ?
Bij de aardappelboer staan de aardappelen geprijsd aan 1,20 euro per kg.
a Geef het verband tussen de te betalen prijs en het aantal kilogram aardappelen.
b Maak de tabel en de grafiek met ICT.
c Is de grafiek de grafische voorstelling van een functie ?
d Hoeveel kilogram aardappelen heb je voor 78 euro ?

Voor het lidmaatschap van voetbalclub FC Gentwerp moet Miel 75 euro per jaar betalen. Voor de wedstrijden op verplaatsing wordt een bijdrage van 1,50 euro per wedstrijd gevraagd.
a Wat kost de hobby per jaar aan Miel als hij 8 keer op verplaatsing gaat spelen ?
b Geef het verband tussen het aantal wedstrijden op verplaatsing en de totale jaarlijkse kost.
c Op het einde van het jaar heeft Miel 93 euro betaald. Hoeveel wedstrijden waren er op verplaatsing ?
Oppervlakte van een cirkel.
a Geef het verband tussen de oppervlakte van een cirkel en de straal.
b Vul de tabel aan. STRAAL OPPERVLAKTE
c Is de volgende zin waar of vals: als je de straal van een cirkel verdubbelt, dan verdubbelt de oppervlakte van de cirkel. Verklaar aan de hand van de tabel.
d Vul aan : als je de straal van een cirkel vijfmaal groter maakt, dan vergroot de oppervlakte …
e Teken de grafiek met behulp van ICT.
f Is het verband lineair, kwadratisch of hyperbolisch ?
g Stelt dit verband een functie voor ?
Gegevenisdefunctie f met f ( x )= x 2 4.
aVerklaarwaarom f eenfunctieis.
bBepaalhetdomein,hetbereikendenulwaarden.
cBereken f ( 2) en f 3 2 .
dBereken x alsjeweetdat f ( x )= 1enals f ( x )= 1 3
eBerekendesnijpuntenmetdeassen.
fConstrueerdegrafiekvan f .
Gegevenisdefunctie f met f ( x )= x 2 3 x .
aVerklaarwaarom f eenfunctieis.
bBepaalhetdomein,hetbereikendenulwaarden.
cBereken f ( 3) en f 2 3
dBereken x alsjeweetdat f ( x )= 2enals f ( x )= 8 9 .
eBerekendesnijpuntenmetdeassen.
fConstrueerdegrafiekvan f
Gegevenisdefunctie f met f ( x )= x 1 x + 2 .
aVerklaarwaarom f eenfunctieis.
bBepaalhetdomein,hetbereikendenulwaarden.
cBereken f (4) en f 1 2
dBereken x alsjeweetdat f ( x )= 5.
eBerekendesnijpuntenmetdeassen.
fConstrueerdegrafiekvan f .
Een superballetje botst een aantal keren na elkaar op de grond.
De baan van het balletje gaat volgens onderstaande grafiek.
a Wat was de maximale hoogte die het balletje heeft bereikt ?
b In welke intervallen stijgt het balletje ?
c In welke intervallen daalt het balletje ? x
Welke grafieken zijn de grafieken van een functie ? Geef telkens het domein, het bereik en de nulwaarden.
Plaats het juiste voorschrift bij de corresponderende grafiek.
f 1 ( x )= 3 x 4
f 2 ( x )= 4 3 x
f 3 ( x )= x 2 3 x + 2
f 4 ( x )= x 2 3 x
f 5 ( x )= 1 x 2
f 6 ( x )= 1 x 2
f 7 ( x )= x 2 3 x f 8 ( x )= x 2 x 3
Ga na of de punten met gegeven coördinaten op de grafiek van de functie met het gegeven voorschrift liggen.
a f ( x )= x 2 3
b f ( x )= x 2 3 x + 2
c f ( x )= x 3 4 x 2 + 3 A 2, 1 2
A( 1,4)
A(2, 5)
d f ( x )= x 4 x + 2
e f ( x )= 4 x 2 + 2
f f ( x )= √2 x + 3
Telkens is er een bepaald functievoorschrift gegeven. Welke uitspraken zijn waar ?
a 1


4 3 is de nulwaarde van f 2 f (x)= x 3 − 4 f is een stijgende functie

b
A 3, 1 3
A √2,1
A( 1, 1)



( 3, 1) is de coördinaat van een punt van de grafiek van f 3 f ( 0) = 12







c 1 4 is een functiewaarde 3 dom f = R\{ 2} 1 4 x = –4 is een verticale asymptoot 2 f (x)= x − 2 x + 4 de grafiek van f is een parabool







Bereken het ontbrekende coördinaatgetal zodat het gegeven punt op de grafiek van f zou liggen.
a f ( x )= x 2 + 1
b f ( x )= x 4 3 x
c f ( x )= x 2 4 x + 5
A(3,...)
B(...,1)
A( 1,...)
B ..., 1 2
A( 2,... )
B(...,5)
Ga na of volgende functies even of oneven zijn.
a f ( x )= x 2 x 4
b f ( x )= x 3 x
c f ( x )= x 2 1 2
15
d f ( x )= x 3 + x 2 + x
e f ( x )= 2 x 2 + x
A( 2,...)
B(...,0)
A 1 2 ,...
B(...,3)
d f ( x )= x 3 x 2 + 3 x 1
e f ( x )= x 4 + 2 x 2 1
f f ( x )= 2 x 3 3 x
Bespreek (domein, bereik, nulwaarden, snijpunten met de assen, tekenverloop, stijgen/dalen, gedrag op oneindig, extrema en symmetrie) de functies waarvan het voorschrift is gegeven. Maak gebruik van ICT.
a f ( x )= x 2 7 x + 6
b f ( x )= x 2 3 + 3 x
c f ( x )= 2 x 3 5 x 2 + x + 2
16 17
d f ( x )= x 4 x 2
e f ( x )= x + 2 x 3
f f ( x )= 1 x 2 1
Bepaal de snijpunten van de grafieken van de functies waarvan het functievoorschrift is gegeven.
a f ( x )= 2 x 4
b f ( x )= x 2 3 x + 2
c f ( x )= x 2 3 + 2 x 1
d f ( x )= 1 x + 3
e f ( x )= 2 x 1 x + 1
f f ( x )= x 2 3 x + 4
g ( x )= x 2
g ( x )= x + 5
g ( x )= x 1
g ( x )= x + 3
g ( x )= 3 x 1
g ( x )= x 2 + 3 x
Los volgende ongelijkheden op. Maak eventueel gebruik van ICT.
a 3 x 2 < 0
b x 2 + 3 0
c 4 x 2 + 8 x 5 < 0
d x 2 + 2 x 3 0
e 4 x 4 x 2 > 0
f 4 x 3 4 x 2 x + 1 < 0
g x 4 2 x 3 + x 2 0
h x 4 3 x 2 4 < 0
Voor welke waarde(n) van x snijdt de grafiek van f de x-as en voor welke waarde(n) ligt de grafiek onder en boven de x-as?
a f ( x )= 3 x + 1 2
b f ( x )= x 2 2 + x
c f ( x )= x 2 6 x + 9
d f ( x )= x 3 + x 2 22 x 10
We maken een vlucht met een luchtballon die beschreven kan worden door de veeltermfunctie h met voorschrift :
h ( t )= 24 2 t + 1 18 t 3 1 216 t 4 met h( t ): hoogte in tientallen meters
t : tijd in uren
t = 0 is het tijdstip waarop we boven de kerktoren vliegen
Gevraagd :
a Schets de grafiek van h (maak gebruik van ICT).
b Hoelang duurt de vlucht ? Werk op 1 minuut nauwkeurig.
c Hoelang zijn we al in de lucht op het ogenblik dat we boven de kerktoren vliegen ? Werk op 1 minuut nauwkeurig.

d Hoe hoog zijn we op het ogenblik dat we boven de kerktoren vliegen ? Werk op 1 meter nauwkeurig.
e Hoelang vliegen we hoger dan 180 meter ? Werk op 1 uur nauwkeurig.
We beschouwen twee even hoge pijlers en de ophangkabel van een hangbrug. Het wegdek valt samen met de x -as en de eerste pijler ligt op de y -as. De stalen kabel voldoet aan de vergelijking h ( x ) = 0,008x 2 – 0,8x + 23 met h ( x ): de hoogte van de kabel boven de brug in m x : de horizontale afstand ten opzichte van de eerste pijler
a Hoeveel meter steken de pijlers boven het wegdek uit ?
b Bereken de afstand tussen de twee pijlers.
c Op hoeveel meter hangt de kabel minimaal boven het wegdek ? Bereken die minimale hoogte.

d Een vrachtwagen rijdt tegen een van de verticale steunkabels (zoals op de foto) van de brug die op 30 m van de uiterst linkse pijler staat. Hoe hoog is die steunkabel ?
Een militair moet via de helikopter gered worden uit vijandig gebied. Om aan de piloot kenbaar te maken waar hij zich precies bevindt, schiet hij een vuurpijl af. De baan van de vuurpijl wordt bepaald door de functie h met h ( t )= 3 8 t 3 21 4 t 2 + 39 2 t + 2 . met t : de tijd in seconden h ( t ): de hoogte boven de grond in meter
a Op welke hoogte wordt de vuurpijl afgeschoten ?
b De vuurpijl ontploft na zes seconden. Wat was de hoogte van de pijl op dat ogenblik ?
c Door de omgeving waarin de militair zich bevindt, moet de vuurpijl minstens 12 meter hoog zijn om gezien te kunnen worden. Hoe lang is de pijl zichtbaar ?
Bepaal het differentiequotiënt van de functies waarvan het voorschrift is gegeven over het gegeven interval.
a f ( x )= x 3 + 2 x 2 4 x + 2interval: [ 1,0]
b f ( x )= x 3 x 2 + 6 x interval: [0,1]
Gegeven : De functie f met f ( x ) = –x 3 – x 2 + 12x
c f ( x )= x 4 + 2 x 3 7 x 2 8 x + 12interval: [2,3]
d f ( x )= x 4 2 5 2 x 2 +2 interval: [ 3, 2]
Gevraagd : Bepaal een interval van R zodanig dat het differentiequotiënt gelijk is aan 0.
Jolien en Gert gaan beiden een halfuurtje joggen. Van beiden kun je de afgelegde weg in meter beschrijven door de functies j en g , met t de tijd in minuten.
j ( t )=
8 t 2 + 40 t als0 t 15
520 t 600 3 als15 < t 30
g ( t )=
140 t als0 t 20
220 t 1600als20 < t 30
a Bereken de gemiddelde snelheid in km/h van Jolien en van Gert over de tijdsintervallen [ 0, 30], [ 0, 10], [ 10, 20] en [ 20, 30]
b Bereken de snelheid in km/h van Jolien en van Gert op het tijdstip t = 10. Controleer je antwoorden met ICT.
Een blok ijs (kubusvormig met ribbe 40 mm) begint langzaam te smelten. Elke minuut worden de ribben 2 mm korter.
a Stel een formule op die het volume geeft in functie van de tijd.
v ( t ) = ?
met v ( t ): in mm3
t : in minuten
b Welke waarden kan t aannemen ?
c Maak een tabel voor ∆v ( t ) = v (t + 1) – v ( t ).
d Hoe snel vermindert het volume op het tijdstip t = 12?
Voor een bepaald product worden de kostenfunctie k en de formule voor de opbrengst o in functie van q gegeven door :
k( q ) = 0,2q 2 + 60 met q : productie-eenheden k( q ) en o( q ) in euro
o( q ) = –0,4q 2 + 24q
a Schets de grafieken van de functies k en o
b Maak tabellen voor ∆k ( q ) en ∆o ( q ) waarbij q loopt van 0 tot 60 en met ∆q = 5.
c Bepaal het voorschrift van de winstfunctie w
d Bij welke productie is er winst ? Bij welke productie is die winst maximaal ?
De groei van een populatie papegaaiduikers laat zich voor een tiental jaren beschrijven door de formule : n ( t ) = 2t 3 + t + 40 met n ( t ): het aantal papegaaiduikers t : het aantal jaren
a Hoeveel papegaaiduikers komen er het eerste jaar bij ?
b En hoeveel het vierde jaar ?
c Wat is de gemiddelde toename per jaar van het aantal papegaaiduikers gedurende de periode [0, 5], [5, 10] en [0, 10] ?
Kenmerken van een functie 1
Exponentiële functies 2
Hoofdstuktitel 0
Penicillium roqueforti is een blauwschimmel die speciaal gekweekt wordt voor het productieproces van kazen als roquefort of stilton. Het Franse merk Papillon houdt er niet van om dat in een labo te doen : ze bakken speciale broden, injecteren die met de blauwschimmel en laten die op het brood gedijen. Da’s maar een van de vele voorbeelden van exponentiële groei. Een bosbrand wint bijvoorbeeld ook razendsnel aan kracht. Dankzij corona weet je hoe snel een virus zich kan verspreiden. Ook de groei van deze zeesterren heeft een exponentieel karakter, dat kom je in dit hoofdstuk te weten.

Hoofdstuktitel 0
De algemene sinusfunctie 3
In Technopolis (Mechelen) kun je de slinger live aan het werk zien. Maar ook in het Panthéon (Parijs, zie foto) en in de universiteiten van Koblenz en Nijmegen zie je de slinger bewegen. Met deze opstelling kon de Franse wiskundige Foucault bewijzen dat de aarde om haar as draait.
Foucault hing in 1851 een gewicht met een massa van 28 kg aan een 67 m lange stalen draad in het Panthéon in Parijs. Hoe langer de draad is, hoe trager de slinger zal bewegen en hoe minder luchtwrijving het geheel zal hebben. Die wrijving zorgt ervoor dat de slinger heen en weer beweegt. Door onder aan de slinger een naaldje te plaatsen dat inwerkt op een grote cirkelvormige krijtmassa, merk je dat de slinger ronddraait. Eigenlijk is het de slinger die mooi blijft hangen en de aarde die eronder beweegt. Een eenvoudig trucje om aan te tonen dat de aarde ronddraait.

