
What does this ancient bell have to do with math?
Turn this book over to find out.


What does this ancient bell have to do with math?
Turn this book over to find out.
Published by Great Minds PBC
Special thanks go to the Gordon A. Cain Center and to the Department of Mathematics at Louisiana State University for their support in the development of Eureka Math.
Great Minds® is the creator of Eureka Math® , Wit & Wisdom® , Alexandria Plan™, and PhD Science® .
Published by Great Minds PBC. greatminds.org
© 2021 Great Minds PBC. All rights reserved. No part of this work may be reproduced or used in any form or by any means—graphic, electronic, or mechanical, including photocopying or information storage and retrieval systems—without written permission from the copyright holder. Where expressly indicated, teachers may copy pages solely for use by students in their classrooms.
Printed in the USA
1 2 3 4 5 6 7 8 9 10 LSC 25 24 23 22 21
ISBN 978-1-68386-911-5
Eureka Math: A Story of Ratios® Contributors
Michael Allwood, Curriculum Writer
Tiah Alphonso, Program Manager—Curriculum Production
Catriona Anderson, Program Manager—Implementation Support
Beau Bailey, Curriculum Writer
Scott Baldridge, Lead Mathematician and Lead Curriculum Writer
Bonnie Bergstresser, Math Auditor
Gail Burrill, Curriculum Writer
Beth Chance, Statistician
Joanne Choi, Curriculum Writer
Jill Diniz, Program Director
Lori Fanning, Curriculum Writer
Ellen Fort, Math Auditor
Kathy Fritz, Curriculum Writer
Glenn Gebhard, Curriculum Writer
Krysta Gibbs, Curriculum Writer
Winnie Gilbert, Lead Writer / Editor, Grade 8
Pam Goodner, Math Auditor
Debby Grawn, Curriculum Writer
Bonnie Hart, Curriculum Writer
Stefanie Hassan, Lead Writer / Editor, Grade 8
Sherri Hernandez, Math Auditor
Bob Hollister, Math Auditor
Patrick Hopfensperger, Curriculum Writer
Sunil Koswatta, Mathematician, Grade 8
Brian Kotz, Curriculum Writer
Henry Kranendonk, Lead Writer / Editor, Statistics
Connie Laughlin, Math Auditor
Jennifer Loftin, Program Manager—Professional Development
Nell McAnelly, Project Director
Ben McCarty, Mathematician
Stacie McClintock, Document Production Manager
Saki Milton, Curriculum Writer
Pia Mohsen, Curriculum Writer
Jerry Moreno, Statistician
Ann Netter, Lead Writer / Editor, Grades 6–7
Sarah Oyler, Document Coordinator
Roxy Peck, Statistician, Lead Writer / Editor, Statistics
Terrie Poehl, Math Auditor
Kristen Riedel, Math Audit Team Lead
Spencer Roby, Math Auditor
Kathleen Scholand, Math Auditor
Erika Silva, Lead Writer / Editor, Grade 6–7
Robyn Sorenson, Math Auditor
Hester Sutton, Advisor / Reviewer Grades 6–7
Shannon Vinson, Lead Writer / Editor, Statistics
Allison Witcraft, Math Auditor
Julie Wortmann, Lead Writer / Editor, Grade 7
David Wright, Mathematician, Lead Writer / Editor, Grades 6–7
Virginia Edition Contributors
Asma Akhras
Leslie Arceneaux, Program Director–Custom Alignments
Christine Bell
Adrienne Bodin, Managing Editor
Jihan Breedlove
Emily Chandrasekhar
Kasey Cole
Heather Curry
Denise Dierolf
Christina Ducoing
Gail Fiddyment
Anne Foster
Peggy Golden, Managing Editor
Amanda Hatch
Amanda Kaplan
Ricky Mikelman
Tricia Miller
Heleena Moon
Jay Powers, Project Manager
Katelin Rowe
Stephanie Saporito
Jada Singleton
Sabrina Tobolski
Kyle Williams
Chris Barbee
Melissa Benner
Erik Brandon
Joseph Phillip Brennan
Beth Brown
Amanda Carter
Nicole Conforti, Project Manager
Kelli Ferko
Winnie Gilbert
Marvin Harrell
Stephen Intlekofer
Laura Khalil
Raena King
Emily Koesters
Sara Lack
Connie Laughlin
Sonia Mabry
Gabrielle Mathiesen
Dave Morris
Lauren Nelson
Trisha Paster
April Picard
Janae Pritchett
Rebecca Ratti
Aly Schooley
Andrew Senkowski
Bridget Soumeillan
Heidi Strate
Mike Street
Cathy Terwilliger
Valerie Weage
Allison Witcraft
Board of Trustees
Lynne Munson, President and Executive Director of Great Minds
Nell McAnelly, Chairman, Co-Director Emeritus of the Gordon A. Cain Center for STEM Literacy at Louisiana State University
William Kelly, Treasurer, Co-Founder and CEO at ReelDx
Jason Griffiths, Secretary, Director of Programs at the National Academy of Advanced Teacher Education
Pascal Forgione, Former Executive Director of the Center on K-12 Assessment and Performance Management at ETS
Lorraine Griffith, Title I Reading Specialist at West Buncombe Elementary School in Asheville, North Carolina
Bill Honig, President of the Consortium on Reading Excellence (CORE)
Richard Kessler, Executive Dean of Mannes College the New School for Music
Chi Kim, Former Superintendent, Ross School District
Karen LeFever, Executive Vice President and Chief Development Officer at ChanceLight Behavioral Health and Education
Maria Neira, Former Vice President, New York State United Teachers



In this module, students build on their understanding of transformations from Grade 7 to explore translations, reflections, rotations, and dilations in the plane (7.7). Exploration of the three rigid motions and dilations is achieved both with and without the structure of the coordinate plane. Exploration also occurs via handson activities by using an overhead projector transparency for rigid motions and a compass and a ruler for dilations.
Students learn how to use transformations to precisely define the concepts of congruence and similarity. Up to this point, congruence has been taken to mean, intuitively, same size and same shape (6.9), and similarity has been taken to mean, intuitively, same shape, different sizes (7.5). An overarching goal of this module is to replace these common ideas with precise definitions.
In Topic A, students sketch the images of geometric figures that have been translated, reflected, and rotated (8.7). They use the coordinate plane and an overhead projector transparency to verify the basic properties of the rigid motions experimentally and, when feasible, deepen their understanding of these properties by using reasoning. Students observe that the basic rigid motions preserve angle measures as well as segment lengths.
In Topic B, students discover that they can sequence various combinations of rigid motions and still maintain the properties of individual rigid motions, setting the stage for a precise definition of congruence. Students also use rigid motions to verify congruent relationships between vertical angles and between corresponding angles formed when parallel lines are intersected by a transversal. Students identify and describe the relationships among pairs of adjacent, supplementary, and complementary angles. They also use the relationships among all angle pairs to solve problems involving unknown angle measures (8.5).
In Topic C, students describe the effect of dilations on two-dimensional figures in general and by using coordinates. They recognize the effect dilation has on a figure when the scale factor is greater than zero but less than one (shrinking of the figure), equal to one (congruence), and greater than one (magnification of the figure). On the coordinate plane, students observe the multiplicative effect that dilation has on the coordinates of an ordered pair. Students then apply this knowledge about points to describe the effect dilation has on figures in terms of their coordinates and to sketch their images (8.7).
Topic D demonstrates that a two-dimensional figure is similar to another if the second two-dimensional figure can be obtained from a dilation followed by a congruence. Knowledge of basic rigid motions is reinforced throughout this topic (8.7), specifically when students describe the sequence that exhibits a similarity between two given figures. Students also apply previous knowledge of proportional relationships to determine whether two figures are similar and, if so, the scale factor of the dilation by which one can be obtained from the other. By looking at the effect of a scale factor on the length of a segment of a given figure, students write proportions to find unknown lengths of segments in similar figures.
8.5 The student will use the relationships among pairs of angles that are vertical angles, adjacent angles, supplementary angles, and complementary angles to determine the measure of unknown angles.
8.7 The student will
a. given a polygon, apply transformations, to include translations, reflections, and dilations, in the coordinate plane; and
b. identify practical applications of transformations.
4.10 The student will
a. identify and describe points, lines, line segments, rays, and angles, including endpoints and vertices; and
b. identify and describe intersecting, parallel, and perpendicular lines.
4.12 The student will classify quadrilaterals as parallelograms, rectangles, squares, rhombi, and/or trapezoids.
5.12 The student will classify and measure right, acute, obtuse, and straight angles.
5.14 The student will
a. recognize and apply transformations, such as translation, reflection, and rotation; and
b. investigate and describe the results of combining and subdividing polygons.
6.9 The student will determine congruence of segments, angles, and polygons.
7.5 The student will solve problems, including practical problems, involving the relationship between corresponding sides and corresponding angles of similar quadrilaterals and triangles.
7.7 The student will apply translations and reflections of right triangles or rectangles in the coordinate plane.
MPS Mathematical Problem Solving. Students will apply mathematical concepts and skills and the relationships among them to solve problem situations of varying complexities. Students also will recognize and create problems from real-world data and situations within and outside mathematics and then apply appropriate strategies to determine acceptable solutions. To accomplish this goal, students will need to develop a repertoire of skills and strategies for solving a variety of problem types. A major goal of the mathematics program is to help students apply mathematics concepts and skills to become mathematical problem solvers.
MCM Mathematical Communication. Students will communicate thinking and reasoning using the language of mathematics, including specialized vocabulary and symbolic notation, to express mathematical ideas with precision. Representing, discussing, justifying, conjecturing, reading, writing, presenting, and listening to mathematics will help students to clarify their thinking and deepen their understanding of the mathematics being studied. Mathematical communication becomes visible where learning involves participation in mathematical discussions.
MRP Mathematical Representations. Students will represent and describe mathematical ideas, generalizations, and relationships using a variety of methods. Students will understand that representations of mathematical ideas are an essential part of learning, doing, and communicating mathematics. Students should make connections among different representations—physical, visual, symbolic, verbal, and contextual—and recognize that representation is both a process and a product.
MCN Mathematical Connections. Students will build upon prior knowledge to relate concepts and procedures from different topics within mathematics and see mathematics as an integrated field of study. Through the practical application of content and process skills, students will make connections among different areas of mathematics and between mathematics and other disciplines, and to real-world contexts. Science and mathematics teachers and curriculum writers are encouraged to develop mathematics and science curricula that support, apply, and reinforce each other.
⬛ Angle Preserving (A transformation is angle preserving if (1) the image of any angle is again an angle, and (2) for any given angle, the angle measure of the image of that angle is equal to the measure of the angle.)
⬛ Basic Rigid Motion (A basic rigid motion is a rotation, reflection, or translation of the plane. Basic rigid motions are the basic examples of transformations that preserve distances and angle measures.)
⬛ Between (A point B is between A and C if (1) A, B, and C are different points on the same line, and (2) AB + BC = AC.)
⬛ Congruence (A congruence is a finite composition of basic rigid motions (rotation, reflections, translations) of the plane.)
⬛ Congruent (Two figures in a plane are congruent if there exists a congruence that maps one figure onto the other figure.)
⬛ Dilation (For a positive number r, a dilation with center O and scale factor r is the transformation of the plane that maps the point O to itself and maps each remaining point P of the plane to its image P' on the ray OP so that OP rOP ′ =⋅ .)
⬛ Directed Line Segment (A directed line segment AB is the line segment AB together with a direction given by connecting an initial point A to a terminal point B.)
⬛ Distance Preserving (A transformation is distance preserving if the distance between the images of two points is always equal to the distance between the original two points.
Since the length of a segment is (by definition) equal to the distance between its endpoints, such a transformation is also said to be length preserving or said to preserve lengths of segments.)
⬛ Midpoint (The midpoint of a segment is the point equidistant from the endpoints.)
⬛ Perpendicular Bisector (A perpendicular bisector of a segment is a line, ray, or segment that passes through the midpoint of the segment and is perpendicular to the segment.)
⬛ Sequence (Composition) of Transformations (A composition of transformations is a transformation that is a sequence of two or more transformations given by applying the first transformation followed by applying the next transformation in the sequence to the image of the first transformation, and so on.
Given transformations G and F, G ° F is called the composition of F and G, and represents first applying the transformation F and then applying G to the image of F.)
⬛ Similar (Two figures in a plane are similar if there exists a similarity transformation taking one figure onto the other figure.
A congruence is a similarity with scale factor 1. It can be shown that a similarity with scale factor 1 is a congruence.)
⬛ Similarity Transformation (A similarity transformation (or a similarity) is a composition of a finite number of dilations or basic rigid motions. The scale factor of a similarity transformation is the product of the scale factors of the dilations in the composition. If there are no dilations in the composition, the scale factor is defined to be 1.)
⬛ Transversal (Given a pair of lines L and M in a plane, a third line T is a transversal if it intersects L at a single point and intersects M at a single but different point.)
⬛ Vector (A (bound) vector is a directed line segment, i.e., an “arrow.” A vector’s initial point is often called its tail and the terminal point is often called its tip The length of a directed line segment (vector) AB is the length of the segment, i.e., AB.)
⬛ Vertical Angles (Two angles are vertical angles if their sides form two pairs of opposite rays.)
⬛ Angles at a point
⬛ Angles on a line
⬛ Area and perimeter
⬛ Parallel and perpendicular lines
⬛ Prime notation (e.g., The image of point P is point P'.)
⬛ Ray, line, line segment, angle
⬛ Supplementary, complementary, and adjacent angles
⬛ Transformation, translation, reflection, rotation
⬛ Triangle, quadrilateral
2These are terms and symbols students have seen previously.
⬛ Compass
⬛ Transparency or patty paper
⬛ Wet or dry erase markers for use with transparency
⬛ Optional: geometry software
⬛ Ruler
⬛ Protractor
⬛ Composition of Rigid Motions3: http://youtu.be/O2XPy3ZLU7Y
3The video was developed by Larry Francis.

Focus Standards: 8.7 The student will
a. given a polygon, apply transformations including translations, reflections, and dilations in the coordinate plane; and
b. identify practical applications of transformations.
Instructional Days: 7
Lesson 1: Applications of Transformations (E)1
Lesson 2: Translations (P)
Lesson 3: Translating Lines (S)
Lesson 4: Reflections (P)
Lesson 5: Sequencing Reflections and Translations (S)
Lesson 6: Rotations (S)
Lesson 7: Rotations of 180 Degrees (P)
The study of rigid motions in this module is not just about how to move geometric figures around the coordinate plane by using reflections, translations, and rotations. Rather, students explore the geometric implications of basic rigid motions in the plane and their effects on figures. In Topic A, lessons on translation, reflection, and rotation show students that lines map to lines, line segments map to line segments, and parallel lines map to parallel lines. In addition to the intuitive notion of figures retaining the same shape under such motions, students confirm their observations from Grade 7 that rigid motions preserve segment length and angle measure.
In Lesson 1, students explore and identify practical applications of transformations, such as in tiling or quilting. Lessons 2 and 3 focus on translation but also set up precise definitions and notation related to transformations that are used throughout the remainder of the module. In Lesson 2, students call on their learning from Grade 7 to translate polygons on the coordinate plane. They extend their understanding to connect vertical and horizontal movement on the coordinate plane to translation along a vector in the plane. As part of that work, students use a transparency to verify
1Lesson Structure Key: P-Problem Set Lesson, M-Modeling Cycle Lesson, E-Exploration Lesson, S-Socratic Lesson


experimentally that translations map lines to lines, segments to segments, rays to rays, and angles to angles. Students also verify experimentally that translations preserve segment length and angle measure. Lesson 3 focuses on the translation of lines, specifically the idea that a translation maps a line either to itself or to a parallel line.
In Lesson 4, students again build on their Grade 7 work to reflect polygons on the coordinate plane and verify experimentally that reflections preserve segment length and angle measure. In Lesson 5, students explore images of figures under a sequence of reflections and translations. They recognize that a reflection followed by a translation does not necessarily place a figure in the same location as a translation followed by a reflection. In Lesson 6, students investigate rotation around a point in a similar manner as the other rigid motions. Students verify experimentally that rotations map lines to lines, etc., and preserve segment length and angle measure. In Lesson 7, students learn that the image of a point ab , () is ab , () under a 180-degree rotation around the origin, and they are provided proof that 180-degree rotations map lines to parallel lines.
Rigid Motions

⬛ Students identify practical applications of transformations and solve problems by using transformations.
Lesson Notes
In this lesson, students use their experience with transformations from Grade 7. They explore reflections and translations through practical applications such as quilting and tiling. This lesson allows students to recall and practice performing transformations. In upcoming lessons, students build a mathematical understanding of translations, reflections, and rotations.
Each student needs a transparency, a dry-erase marker, and a straightedge to use during this lesson and those that follow. As with the use of patty paper in Grade 7, working with a transparency provides a tactile familiarity with transformations, which helps students develop their conceptual understanding of rigid motions. This lesson allows students to experiment with a transparency. Upcoming lessons provide time for teachers to demonstrate how to use a transparency.
Classwork
Opening (4 minutes)
Display the picture of a quilt pattern to activate students’ prior knowledge of rigid motions.
⬛ What do you notice about the pattern?
I notice that the pattern has many repeated shapes.
I wonder how the pattern was created.
⬛ This is a pattern in a quilt. How can we describe the pattern in mathematical terms?
We can describe the shapes and their placements within the pattern.
⬛ In Grade 7, we described preimages, images, and their placements by using translations and reflections, which are transformations. Talk to a partner about how we can describe the pattern by using transformations.
After partners finish their discussions, invite a few students to share their answers. Expect students to say that they can use a reflection to take one figure, such as a large blue arrow, to another. Some students may recognize that they can also use a translation. For example, a translation up and then right takes a green triangle in the bottom left corner to a green triangle in the top right corner.
Additionally, students may recognize that they can use a sequence of reflections and translations or that they can use a rotation. Celebrate all reasonable descriptions and tell students that they will explore transformations and sequences of transformations in this module.
As a class, discuss the pictures in Example 1 and have students describe the transformations they notice.
Example 1
Describe a transformation that takes Figure A to Figure B. Use a transparency, if needed.
Sample student response: A translation right and then down takes Figure A to Figure B.
Sample student response:
A translation up and then left takes Figure A to Figure B. c.
Sample student response:
A reflection over a vertical line takes Figure A to Figure B.
of Transformations
Exercises 1–5 (25 minutes)
Have students work with a partner to complete Exercises 1–5. Once most pairs finish, invite a few pairs to share their answers with the class.
Exercises 1–5
1. Noor wants to design wallpaper for her room that has a pattern of diamonds. Use transformations and a transparency to draw two more repetitions of the pattern.
Sample student response:
Applications of Transformations
3. Doug wants to cover his kitchen floor with tiles shaped like parallelograms. Use transformations and a transparency to create a pattern that Doug can use. Then describe how you made the pattern.
Sample student response:
First, I translated the parallelogram up. Next, I reflected both parallelograms over the vertical line containing the right side of the figures. Finally, I reflected the new pair of parallelograms two more times over the vertical lines containing the right sides of the figure.
4. Choose two cats and label them A and B. Then describe a transformation that takes Figure A to Figure B.
Sample student response:
A translation right and then down takes Figure A to Figure B.
5. Use transformations and a transparency to create a pattern with a figure of your choice. Then trade patterns with a partner and describe the transformations that take one figure to another figure.
Answers will vary. Applications of Transformations
Discussion (4 minutes)
⬛ Display the following picture of a floor tile pattern.
⬛ How does this floor tile pattern remind you of transformations?
The pattern is made up of repeated shapes, which reminds me of translations and reflections.
⬛ What do the vertical and horizontal lines remind you of? How can we use those to describe translations?
The vertical and horizontal lines remind me of the coordinate plane. We can use the grid lines to specifically describe how many units a figure is moved up, down, right, or left.
Closing (3 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We can describe many real-world patterns by using transformations.
⬛ We can create patterns by using transformations.
⬛ Transformations can be seen in areas such as art, quilting, tiling, and wallpaper designs.
Name
Exit Ticket
Date
For the tile pattern shown, Ben thinks that a translation takes Hexagon A to Hexagon B. Sara thinks that a reflection takes Hexagon A to Hexagon B. Who is correct? Justify your answer. A
For the tile pattern shown, Ben thinks that a translation takes Hexagon A to Hexagon B. Sara thinks that a reflection takes Hexagon A to Hexagon B. Who is correct? Justify your answer.
Both Ben and Sara are correct. A translation up takes Hexagon A to Hexagon B. A reflection over a horizontal line also takes Hexagon A to Hexagon B.
1. Describe a transformation that takes Figure A to Figure B. Use a transparency, if needed. a. b.
Sample student response:
Sample student response: A translation left takes Figure A to Figure B A translation left and then up takes Figure A to Figure B
Applications of Transformations
Sample student response:
Sample student response: A reflection over a vertical line takes Figure A to Figure B. A translation down takes Figure A to Figure B.
2. For the tile pattern shown, Jonas thinks that the tiles are being reflected. Eve thinks that the tiles are being translated. Who is correct? Justify your answer. Some of the tiles are labeled to help with your justification.
Both Jonas and Eve are correct. A reflection over a vertical line takes Figure A to Figure C. A translation right and then down takes Figure A to Figure B
Applications of Transformations

Student Outcomes
Students describe a translation that maps a preimage to an image.
Students translate polygons on the coordinate plane and identify the coordinates of the vertices of an image.
Students translate figures in the plane along a given vector.
Lesson Notes
In this lesson and those that follow, students learn about translations, reflections, and rotations by using the structure of the coordinate plane to describe transformations and by moving a transparency on top of a piece of paper. Students confirm their observations from Grade 7 that translations move every point in a preimage the same distance in the same direction and that translations preserve segment lengths and angle measures.
Classwork
Discussion (3 minutes)
⬛ Which transformation takes Rectangle ABCD to Rectangle A'B'C'D', a translation or a reflection? How do you know?
Note to Teacher:
Prime notation is introduced in Grade 7 Module 6. Consider reviewing the meaning of this notation with students.
A translation takes Rectangle ABCD to Rectangle A'B'C'D'. I know because the vertices are still in the same position in Rectangle A'B'C'D' A' is the top left vertex, B' is the top right vertex, C' is the bottom right vertex, and D' is the bottom left vertex.
⬛ Describe the translation that takes Rectangle ABCD to Rectangle A'B'C'D'
Rectangle ABCD is translated up 9 units and then right 10 units.
Rectangle ABCD is translated right 10 units and then up 9 units.
Have students compare Rectangles ABCD and A'B'C'D'. Ask them to describe some of the relationships they see that they learned about in Grade 7 related to a preimage and its image after a translation. Students may notice the following relationships:
Sides AB and A'B' are the same length.
Angle A and angle A' are both right angles, so they have the same measure.
The two rectangles are congruent.
The two rectangles are in different locations in the coordinate plane.
The two rectangles have the same orientation.
⬛ In the next few lessons, we will continue to learn about translations. We will also learn about reflections and rotations. We call translations, reflections, and rotations the basic rigid motions.
⬛ A rigid motion is a transformation that preserves distance. This means that the distance between the images of any two points is the same as the distance between the corresponding preimage points.
Exercises 1–2 (7 minutes)
Have students complete Exercises 1 and 2 independently or in pairs.
Exercises 1. Use Trapezoid EFGH to complete each part.
Scaffolding:
Some students may benefit from drawing the figure with dashed segments after the first translation to the left.
a. Translate Trapezoid EFGH left 2 units and then down 5 units. Label the image E'F'G'H'.
See the graph.
b. Identify the coordinates of the vertices of the image, Trapezoid E'F'G'H' E'(-6, 1), F'(2, 1), G'(0, -2), H'(-4, -2)
2. Use Figure QRSTU to complete each part.
a. Translate Figure QRSTU up 1 unit and then right 11 units. Label the image Q'R'S'T'U'.
See the graph.
b. Identify the coordinates of the vertices of the image, Figure Q'R'S'T'U'. Q'(6, -2), R'(10, -3), S'(9, -8), T'(5, -9), U'(1, -5)
Scaffolding:
For Exercise 1, challenge students with the following question:
⬛ What patterns do you notice in the coordinates of each pair of corresponding points?
The x-coordinates of the vertices of the image are 2 less than those of the corresponding preimage. This pattern relates to translating left 2 units. The y-coordinates of the vertices of the image are 5 units less than those of the corresponding preimage. This pattern relates to translating down 5 units.
For Exercise 2, consider asking a similar question or asking students to predict the coordinates of the vertices of the image before graphing the image.
Have students turn and talk with a partner to discuss how performing translations on the coordinate plane with the figures in Exercises 1 and 2 is similar to and different from the translations they performed with rectangles and right triangles in Grade 7.
Before explaining explicitly what a translation along a vector is, revisit the rectangles from the start of the lesson but without the coordinate plane.
⬛ Describe the translation that takes the preimage to the image.
The preimage is translated to the right and then up.
⬛ Is there more than one image that could be produced by translating the preimage to the right and then up? Explain.
Yes, more than one image could be produced. Since “to the right and then up” is not very specific, you could translate to the right or up a different distance than what is shown in the picture.
⬛ In Grade 7 and during the beginning discussion of this lesson, we described translations in terms of the number of units a preimage is translated horizontally and vertically. How could we precisely describe a translation when the preimage and image are not in the coordinate plane?
We could measure the horizontal and vertical distances between corresponding points on the preimage and image.
⬛ When performing a translation of the plane without the structure of the coordinate plane, we can use a vector to precisely describe the translation.
⬛ A vector is a directed line segment, which is a segment with a direction given by connecting one endpoint (called the initial point or starting point) to the other endpoint (called the terminal point or simply the endpoint). It is often represented as an arrow with a tail and a tip.
– The length of a vector is, by definition, the length of its underlying segment.
Scaffolding:
Post vocabulary words, definitions, and related symbolic notation in a prominent location in the room.
– Visually, we can distinguish a vector from its underlying segment because a vector has an arrow above the name of the segment. Thus, if the underlying segment is segment AB (A and B being its endpoints), then the vector with starting point A and endpoint B is denoted by AB . Likewise, the vector with starting point B and endpoint A is denoted by BA .
– Note that the arrowhead on the endpoint of a vector distinguishes the endpoint from the starting point. Here, vector AB is on the left, and vector BA is on the right.
⬛ We are going to describe how to define a translation T along a vector AB by the use of an overhead projector transparency. Let the plane be represented by a piece of paper on which the vector AB has been drawn. Let P be an arbitrary point in the plane (i.e., the paper), as shown. Note that the line containing the vector AB , to be denoted by LAB, is represented by the dotted line segment. Note, also, that we are using a finite rectangle to represent the plane, which is infinite in all directions, and a finite segment to represent a line, which is infinite in both directions. The rectangle in the picture represents the border of the piece of paper.
⬛ Now trace AB , the line LAB, and the point P exactly on an overhead projector transparency (of exactly the same size as the paper) using a different color, say red. Then P becomes the red dot on the transparency, and AB becomes a red vector on the transparency; we will refer to them as the red dot and red vector, respectively, in this example. Keeping the paper fixed, we slide the transparency along AB so that the red vector on the transparency stays on the line LAB. We move the transparency in the direction from A to B until the starting point of the red vector rests on endpoint B of vector AB , as shown in the picture. In other words, we slide the transparency along the line AB, in the direction from A to B, for a distance equal to the length of vector AB . The picture shows the transparency after it has been slid along AB , and the red rectangle represents the border of the transparency. The point on the plane at the red dot is the image of point P.
⬛ There are different ways to describe and denote the translation of point P
– We can denote the image of P as TranslationP() , or ()TP
– The point ()TP is the image of P by the translation T
– Another way to denote ()TP is simply P'
– In Grade 7, we said that a translation “takes” point P to point P'
– We can also say that a translation maps point P to point P' More formally, T maps P to ()TP
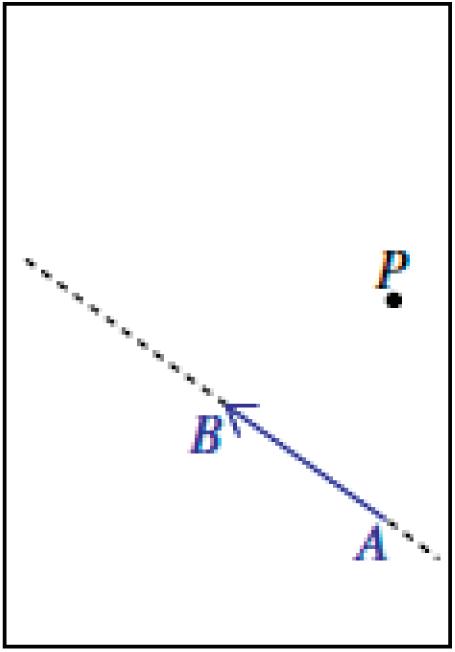

Note to Teacher:
When reading the descriptions about what a translation does, please keep in mind that in the classroom a faceto-face demonstration with transparency and paper is far easier to understand than the verbal descriptions given in this lesson.
Translations
⬛ If we need to be precise, we denote the translation along AB by Translation AB . There is some subtlety in this notation: vector AB has the starting point A and endpoint B, but vector BA has the starting point B and endpoint A. Thus, Translation AB is different from Translation BA . Precisely:
() = TranslationA B AB but () = TranslationB A BA .
⬛ We just covered how a translation T along a vector maps some point P to a point ()TP . Now we examine what T does to the total collection of points in a given figure. Suppose we are given a vertical line L, segment QP, and Figure G The red vertical line is the totality of all the points ()TP where P is a point on the black vertical line. We use ()TL to denote the red line because it is the translation of L. Similarly, if G is a given figure in the plane, then ()TG denotes the collection of all the points ()TP where P is a point in G. We call ()TG the image of G by T, and (as in the case of a point) we also say that T maps G to ()TG .

⬛ The diagram shows a translation of a figure along the vector AB . If G is the black figure, then ()TG is the red figure, as shown.
Scaffolding:
This module utilizes a mix of notations such as Translation (P), T(P), and P' Consider allowing students to use the notation they prefer. The inclusion of formal language and notation in this module provides students with some exposure to content they may encounter in later geometry courses. However, in the classroom it can sometimes be easier to point to a picture and use more familiar language and notation until students are more familiar with the new notations.
Students complete Exercise 3 in pairs to practice translating geometric figures along a vector. Students should describe to their partners what is happening in the translation in order to practice using the vocabulary and notation related to translations. Circulate to check student work. Also, consider calling on students to share their work with the class.
Note: Students are translating a curved figure because figures that consist entirely of line segments can be reproduced elsewhere on the plane by using a ruler and a protractor to measure lengths and measures of angles, without the use of translation. This defeats the purpose of learning to move figures around the plane by translation.
3. Use your transparency to translate the figures along AB . Label the images of the figures appropriately. Solutions are in red.
⬛ In Grade 7, we made some observations about the basic properties of translations in the coordinate plane. Without the structure of the coordinate plane, do you think that translations still move every point in a preimage the same distance in the same direction and that segment lengths and angle measures are preserved?
Have students turn and talk about whether they think the properties of translations still apply without the structure of the coordinate plane. Consider having rulers and protractors available for students to confirm their predictions, though students can also use their transparencies to compare the preimages and images. Then ask the following questions. Encourage students to give examples from Exercise 3 to justify their answers.
⬛ A translation maps lines to lines, segments to segments, and points to points. Do you agree? Explain.
Yes. After the translation, the images are the same figure as their preimages. For example, the image of segment CD is still a segment.
Translations
A translation preserves lengths of segments. Do you agree? Explain.
Yes. Segment C'D' is the same length as its preimage, segment CD.
⬛ Translations map angles to angles. Do you agree? Explain.
Yes. The image of angle EFG is still an angle.
⬛ A translation preserves measures of angles. Do you agree? Explain.
Yes. Angle E'F'G' seems to have the same measure as angle EFG
⬛ How could you be sure the angle measures are the same?
We could use a protractor to measure the angles. If time allows, consider having students use a protractor to measure angle EFG and angle E'F'G'.
⬛ The following are some basic properties of translations:
(Translation 1) A translation maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
(Translation 2) A translation preserves lengths of segments.
(Translation 3) A translation preserves measures of angles.
Students complete Exercise 4 independently or in pairs.
4. Use Quadrilateral ABCD to complete each part.
Challenge students with the following question:
⬛ Suppose M had coordinates , () 29 and N had coordinates , () 10 4 . Would the image of Quadrilateral ABCD be in the same location or a different location than the image in Exercise 4? Why?
The image of Quadrilateral ABCD would be in the same location. The vector would still represent a translation right 8 units and then down 5 units, regardless of where the vector is located.
a. Use your transparency to translate Quadrilateral ABCD along MN . Label the image appropriately. See the graph.
b. Identify the coordinates of the vertices of the image.
A'(1, 0), B'(8, 2), C'(6, -4), D'(3, -4)
c. Describe the translation by using horizontal and vertical units.
A translation down 5 units and then right 8 units.
d. How does MN relate to your description of the translation in part (c)?
The vector represents the description in part (c). The vector represents a translation down 5 units and right 8 units because its endpoint N is 5 units down and 8 units right from its starting point M
Closing (3 minutes)
Summarize or have students summarize the main points of the lesson.
⬛ We can identify the coordinates of the vertices of the image of a figure that has been translated in the coordinate plane.
⬛ We know how to use a vector to translate a figure.
⬛ We know that translations have three basic properties:
– Translations map lines to lines, segments to segments, rays to rays, and angles to angles.
– Lengths of segments are preserved.
– Measures of angles are preserved.
⬛ All translations can be described using a vector. When a translation occurs on the coordinate plane, the horizontal and vertical distances a figure is translated can be represented by a single vector.
Translations
A transformation that preserves distance is known as a rigid motion. After the rigid motion is performed, the distance between any two image points is the same as the distance between the corresponding preimage points.
A translation of a plane along a given vector is a basic rigid motion of a plane.
⬛ A vector is a directed line segment, which is a segment with a direction given by connecting one endpoint (called the initial point or starting point) to the other endpoint (called the terminal point or simply the endpoint). A vector is often represented as an arrow with a tail and a tip.
⬛ The length of a vector is, by definition, the length of its underlying segment.
⬛ Pictorially, vectors distinguish between their starting points and endpoints.

⬛ In the coordinate plane, the horizontal and vertical distances a figure is translated can be represented by a single vector.
The following are the three basic properties of translation:
(Translation 1) A translation maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
(Translation 2) A translation preserves lengths of segments.
(Translation 3) A translation preserves measures of angles.
1. Use Parallelogram QRST to complete each part.
a. Translate Parallelogram QRST up 6 units and then left 5 units. Label the image appropriately.
b. Identify the coordinates of the vertices of the image.
2. Name the vector along which a translation would map point A to its image ()TA

3. Assume there is a translation that maps a segment AB to its image, segment A'B'. If the length of segment AB is 8 units, what is the length of segment A'B'? How do you know?
1. Use Parallelogram QRST to complete each part.
a. Translate Parallelogram QRST up 6 units and then left 5 units. Label the image appropriately.
b. Identify the coordinates of the vertices of the image. Q'(-2, 4), R'(4, 4), S'(2, 1), T'(-4, 1)
2. Name the vector along which a translation would map point A to its image TA()

3. Assume there is a translation that maps a segment AB to its image, segment A'B'. If the length of segment AB is 8 units, what is the length of segment A'B' ? How do you know?
The length of segment A'B' is 8 units because translations preserve lengths of segments. Translations
1. Translate ABC down 4 units. Label and identify the coordinates of the vertices of the image.
y
2. Translate Trapezoid DEFG right 11 units. Label and identify the coordinates of the vertices of the image.
y
3. Translate Quadrilateral STUV right 4 units and then down 6 units. Label and identify the coordinates of the vertices of the image.
4. Use your transparency to translate Figure A along AB . Label the image of Figure A accordingly.
A
5. Use your transparency to translate Figure B along BA . Label the image of Figure B accordingly.
B

Student Outcomes
⬛ Students learn that when lines are translated, they are either parallel to the given line or they coincide.
⬛ Students learn that translations map parallel lines to parallel lines.
Classwork
Discussion (4 minutes)
⬛ Let T be the translation along a given vector AB . If we slide a transparency along the vector AB , it is plausible that C moves to a point C' so that the vector CC' points in the same direction as the vector AB , and the length of the segment CC' is the same length as the segment AB. Let’s accept these conclusions at this point. Here is a pictorial representation of this situation for the case where C does not lie on the line LAB
To clarify, the statement “vector CC' points in the same direction as the vector AB'' means that the point C' is located as shown in the picture to the left below, rather than as shown in the picture to the right.
Still assuming that C is not a point on line LAB, observe from the definition of a translation (in terms of sliding a transparency) that the line LCC′ is parallel to the line LAB. This is because the point C on the transparency is not on the line LAB on the transparency. Therefore, as we slide the line LAB on the transparency along the original LAB, the point C stays away from the original LAB. For this reason, the point C traces out the line LCC′ and has no point in common with the original LAB. In other words, LCC′ ‖ LAB If C is a point on the line LAB, then C′ is also a point on the line LAB, and in this case, LCC′ coincides with the line LAB rather than being parallel to the line LAB.
⬛ Our preliminary findings are summarized as follows: Let T be the translation along AB . Let C be a point in the plane, and let the image T(C) be denoted by C'. Then, the vector CC' points in the same direction as vector AB , and the vectors have the same length. If C lies on line LAB, then so does C′. If C does not lie on LAB, then LCC′ ‖ LAB
Exercise 1 (3 minutes)
Students complete Exercise 1 independently in preparation for the discussion that follows.
Exercises
1. Draw a line passing through point P that is parallel to line L. Draw a second line passing through point P that is parallel to line L and that is distinct (i.e., different) from the first one. What do you notice?

Students should realize that they can only draw one line through point P that is parallel to L.
Discussion (3 minutes)
Bring out a fundamental assumption about the plane (as observed in Exercise 1):
⬛ Given a line L and a point P not lying on L, there is at most one line passing through P and parallel to L
– Based on what we have learned up to now, we cannot prove or explain this, so we have to simply agree that this is one of the starting points in the study of the plane.
– This idea plays a key role in everything we do in the plane. A first consequence is that given a line L and a point P not lying on L, we can now refer to the line (because we agree there is only one) passing through P and parallel to L
Exercises 2–4 (5 minutes)
Students complete Exercises 2–4 independently in preparation for the discussion that follows.
2. Translate line L along the vector AB . What do you notice about L and its image, L′?
L and L′ coincide. L= L′
Scaffolding:
Refer to Exercises 2–4 throughout the discussion and in the summary of findings about translating lines.
3. Line L is parallel to vector AB . Translate line L along vector AB . What do you notice about L and its image, L′?

L and L′ coincide, again. L = L′.
Translating Lines
4. Translate line L along the vector AB . What do you notice about L and its image, L′?

Discussion (15 minutes)
⬛ Now we examine the effect of a translation on a line. Thus, let line L be given. Again, let the translation be along a given AB , and let L′ denote the image of line L. We want to know what L′ is relative to AB and line L
⬛ If L = LAB, or L || LAB, then L′ = L
– If L = LAB, then this conclusion follows directly from the beginning discussion which says if C is on LAB, then so is C′; therefore, L′ = LAB and L = L′ (Exercise 2).
– If L || LAB and C is on L, then it follows from the beginning discussion which says that C′ lies on the line l passing through C and parallel to LAB. However, L is given as a line passing through C and parallel to LAB, so the fundamental assumption that there is just one line passing through a point, parallel to a line (Exercise 1), implies l = L. Therefore, C′ lies on L after all, and the translation maps every point of L to a point of L′. Therefore, L = L′ again (Exercise 3).
– Caution: One must not over-interpret the equality Translation(L) = L (which is the same as L = L′).
– All the equality says is that the two lines L and L′ coincide completely. It is easy (but wrong) to infer from the equality Translation(L) = L that for any point P on L, Translation(P) = P. Suppose the vector AB lying on L is not the zero vector (i.e., assume A ≠ B). Trace the line L on a transparency to obtain a red line L, and now slide the transparency along AB in Exercise 2. Then, the red line, as a line, coincides with the original L, but clearly every point on L has been moved by the slide (the translation). Indeed, as we saw in Example 2 of Lesson 2, Translation(A) = B ≠ A. Therefore, the equality L′ = L only says that for any point C on L, Translation(C) is also a point on L, but as long as AB is not a zero vector, Translation(C) ≠ C.
Strictly speaking, we have not completely proved L = L′ in either case. To explain this, let us define what it means for two geometric figures F and G to be equal, that is, F = G: it means each point of F is also a point of G; conversely, each point of G is also a point of F. We have shown that every point of L′ is also a point of L. To prove L = L′, we would also need to show that every point of L is also a point of L′
However, at this point of students’ education in geometry, it may be prudent not to bring up such a sticky point because they are already challenged with all of the new ideas and definitions. Simply allow the preceding reasoning to stand for now, and consider clarifying later when students are more comfortable with the geometric environment.
⬛ Next, if L is neither LAB nor parallel to LAB, then L′|| L
⬛ If we use a transparency to see this translational image of L by the stated translation, then the pictorial evidence is clear: the line L moves in a parallel manner along AB , and a typical point C of L is translated to a point C′ of L′. The fact that L′|| L is unmistakable, as shown. In the classroom, students should be convinced by the pictorial evidence. If so, leave it at that (Exercise 4).
Here is a simple proof, but to present it in class, begin by asking students how they would prove that two lines are parallel. Ensure students understand that they have no tools in their possession to accomplish this goal. It is only then that they see the need for invoking a proof by contradiction (see discussion above). If there are no obvious ways to do something, then you just have to do the best you can by trying to see what happens if you assume the opposite is true Thus, if L′ is not parallel to L, then they intersect at a point C′. Since C′ lies on L′, it follows from the definition of L′ (as the image of L under the translation T) that there is a point C on L so that Translation(C) = C′ .
It follows from the beginning discussion that LCC′|| LAB . However, both C and C′ lie on L, so LCC′ and L coincide, and we get L || LAB . This contradicts the assumption that L is not parallel to LAB , so L could not possibly intersect L′. Therefore, L′|| L
⬛ Note that a translation maps parallel lines to parallel lines. More precisely, consider a translation T along a vector AB . Then:
If L1 and L2 are parallel lines, so are Translation(L1) and Translation(L2)
⬛ The reasoning is the same as before: Copy L1 and L2 onto a transparency using a red marker, and then translate the transparency along AB . If L1 and L2 do not intersect, then their red replicas on the transparency will not intersect either, no matter what AB is used. So, Translation(L1) and Translation(L2) are parallel.
⬛ These findings are summarized as follows:
Given a translation T along a vector AB , let L be a line, and let L′ denote the image of L by T – If L || LAB or L = LAB , then L′|| L – If L is neither parallel to LAB nor equal to LAB , then L′ || L
Exercises 5–6 (5 minutes)
Students complete Exercises 5 and 6 in pairs or small groups.
5. Line L has been translated along vector AB , resulting in L′. What do you know about lines L and L′?

6. Translate L1 and L2 along vector DE . Label the images of the lines. If lines L1 and L2 are parallel, what do you know about their translated images?

Since L1 || L2, then (L1)′ ‖ (L2)′ .
Translating Lines
Closing (5 minutes)
Summarize, or have students summarize, the lesson.
⬛ We know that there exists just one line, parallel to a given line and through a given point not on the given line.
⬛ We know that translations map parallel lines to parallel lines.
⬛ We know that a line and its image after a translation are either parallel or coincide.
Lesson Summary
⬛ Two lines in the plane are parallel if they do not intersect.
⬛ Translations map parallel lines to parallel lines.
⬛ Given a line L and a point P not lying on L, there is at most one line passing through P and parallel to L.
⬛ A line and its image after a translation are either parallel or coincide.
Exit Ticket (5 minutes)
Name Date
Exit Ticket
Let points A and B be on line L and the vector AC be given, as shown below. Translate line L along vector AC . What do you know about line L and its image, L′? How many other lines can you draw through point C that have the same relationship as L and L′? How do you know?

Let points A and B be on line L and the vector AC be given, as shown below. Translate line L along vector AC . What do you know about line L and its image, L′? How many other lines can you draw through point C that have the same relationship as L and L′? How do you know?

L and L′ are parallel. There is only one line parallel to line L that goes through point C. The fact that there is only one line through a point parallel to a given line guarantees it.
1. Translate ∠XYZ, point A, point B, and rectangle HIJK along vector EF . Sketch the images, and label all points using prime notation.
2. What is the measure of the translated image of ∠XYZ? How do you know? The measure is 38°. Translations preserve angle measure.
3. Connect B to B′. What do you know about the line passing through B and B′ and the line passing through E and F ? BB' ‖ EF
4. Connect A to A′. What do you know about the line passing through A and A′ and the line passing through E and F ? AA' and EF coincide
5. Given that figure HIJK is a rectangle, what do you know about lines that contain segments HI and JK and their images? Explain. Since HIJK is a rectangle, I know that HI ‖ JK . Since translations map parallel lines to parallel lines, then H'I' ‖ J'K' .
Translating Lines

⬛ Students reflect polygons on the coordinate plane across the x- or y-axis and identify the coordinates of the vertices of the images.
⬛ Students reflect figures in the plane across a line and describe a reflection that maps a preimage to an image.
⬛ Students distinguish between translations and reflections.
Lesson Notes
In this lesson, students learn about reflections by using the structure of the coordinate plane to describe the reflection and by using a transparency to represent the plane. Students confirm their observations from Grade 7: Reflections take every point of a figure in the plane to another point in the plane that is the same distance from the line of reflection, and reflections preserve lengths and angle measures.
Classwork
Discussion (3 minutes)
⬛ Which transformation maps ABC to A'B'C', a translation or a reflection? How do you know?
A reflection maps ABC to A'B'C'. I know because the triangles look like mirror images of each other.
Reflections
⬛ Describe the reflection that maps ABC to A'B'C'
ABC is reflected across the y-axis.
⬛ How do you know that the y-axis is the line of reflection?
If you fold the grid along the y-axis, the triangles will line up.
The corresponding points are the same number of units away from the y-axis. Points A and A' are both 4 units from the y-axis, points B and B' are also both 4 units from the y-axis, and points C and C' are both 9 units from the y-axis.
Have students compare the triangles. Ask them to describe some of the relationships they see that they learned about in Grade 7.
⬛ Compare ABC and A'B'C'. Describe a relationship you see between a preimage and its image after a reflection.
Sides AB and A'B' are the same length.
Angle B and angle B' are both right angles, so they have the same measure.
The two triangles are congruent.
The two triangles are in different locations in the coordinate plane.
The two triangles have opposite orientations.
Exercises 1–2 (6 minutes)
Have students complete Exercises 1–2 independently or in pairs.
Exercises
1. Use Parallelogram ABCD to complete the problem.
In Grade 7, students learned that when a figure is reflected, all the corresponding points in the image and preimage are the same distance from the line of reflection. Later in this lesson, students recognize the line of reflection as the perpendicular bisector of the segment connecting a point and its image.
a. Reflect Parallelogram ABCD across the x-axis. Label the image appropriately.
See the graph.
b. Identify the coordinates of the vertices of the image. A'(7, 3), B'(9, 8), C'(5, 8), D'(3, 3)
2. Use Quadrilateral DEFG to complete the problem.
a. Reflect Quadrilateral DEFG across the y-axis. Label the image appropriately.
See the graph.
b. Identify the coordinates of the vertices of the image. D'(0, -5), E'(-5, -6), F'(-9, 4), G'(-5, 2)
Have students turn and talk with a partner to discuss how the reflections on the coordinate plane in Exercises 1 and 2 are similar to and different from the reflections they did with rectangles and right triangles in Grade 7. Then ask the following questions:
⬛ In Exercise 2, what do you notice about point D and its image, point D' ?
Point D and point D' are the same point.
⬛ Why are point D and its image the same point? Explain.
Point D is on the line of reflection. So you cannot reflect point D across the y-axis. The image of point D stays in the same spot.
Revisit the right triangles from the start of the lesson but without the coordinate plane.
⬛ Describe the reflection that maps the preimage to the image.
The preimage is reflected across some vertical line.
⬛ In Grade 7 and during the beginning discussion of this lesson, we described reflections in terms of which axis the preimage is reflected across. How could we precisely describe a reflection when the preimage and image are not on the coordinate plane?
We could measure to determine the point that is exactly halfway between two corresponding points. Then we could draw and label a vertical line through that halfway point.
⬛ When a preimage is reflected on the plane without the structure of the coordinate plane, we need a line to precisely describe the reflection.
The following example describes how to use a transparency for reflection. Be sure to use a transparency that is the same size as the paper.
Let L be a vertical line and let P and A be two points not on L, as shown. Also, let Q be a point on L. The black rectangle indicates the border of the paper.
Trace the line L and the three points onto the transparency exactly, using a red marker.
The line L is the line of reflection. Without moving the paper, flip the transparency across line L, interchanging the left and right sides of the transparency. Keep the traced red line L and point Q aligned with the black line L and point Q on the paper.
The position of the red figures on the transparency now represents the reflection of the original figures. () Reflection P is the point represented by the red dot to the left of L, () Reflection A is the point represented by the red dot to the right of L, and () Reflection Q is point Q itself.
The red rectangle in the diagram represents the border of the transparency. The images of points P and A are labeled with prime notation. The point () Reflection P is point P' and the point () Reflection A is point A'. More importantly, note that line L and point Q have reflected images in exactly the same locations as the original line and point; so, () = Reflection LL and () = Reflection QQ
If we need to be precise, we denote the reflection across line L by ReflectionL

Exercises 3–4 (3 minutes)
Have students complete Exercises 3 and 4 independently.
3. Reflect ABC and Figure D across line L. Label the images.

4. Which figures in Exercise 3 were not moved to a new location after the reflection? Point B and line L were not moved to a new location after the reflection.
Note to Teacher: Sample labels are shown. Students’ labels may vary.
A line of reflection can be any line in the plane. Example 3 has students work with a horizontal line of reflection. The reflected images are shown in red.
⬛ Let L be the horizontal line of reflection, let P be a point on line L, and let T be the figure above the line of reflection.
⬛ Use a red marker to trace line L, point P, and Figure T on the transparency. Reflect point P and Figure T across the horizontal line of reflection.
Exercises 5–7 (5 minutes)
Students complete Exercises 5–7 independently.
5. Reflect the figures across line L. Label the images.

Reflections
6. Use the diagram from Exercise 5 to answer the following questions.
a. Use a protractor to measure the image of ∠ ABC. What do you notice about the measure of the image of ∠ ABC and the measure of ∠ ABC?
The measure of the image of ∠ ABC is the same as the measure of ∠ ABC.
b. Use a ruler to measure the length of segment IJ and its image. What do you notice about the segment lengths?
The length of the image of segment IJ is the same as the length of segment IJ
7. Reflect the figures across line L. Label the images.

Discussion (2 minutes)
⬛ In Grade 7, we made some observations about the basic properties of reflections on the coordinate plane. Without the structure of the coordinate plane, do you think reflections still move every point in a preimage to a point in the image? Do you think that segment lengths and angle measures are preserved for reflections not on the coordinate plane?
Encourage students to use their results from Exercise 6 and their transparencies to justify their reasoning.
⬛ Reflections have the same basic properties as translations. The following are the basic properties of reflections:
(Reflection 1) A reflection maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
(Reflection 2) A reflection preserves lengths of segments.
(Reflection 3) A reflection preserves measures of angles.
Reflections
Have students complete Exercise 8 independently or in pairs.
8. State whether the transformation shown is a translation or a reflection. Then describe the transformation. a.
The transformation is a translation 11 units left.
The transformation is a reflection across the x-axis.
Reflections
The transformation is a reflection across line L.
Discussion (3 minutes)
⬛ Let’s look more closely at an example of a reflection. We can identify a special relationship between the line of reflection and the segment formed by each point and its image.
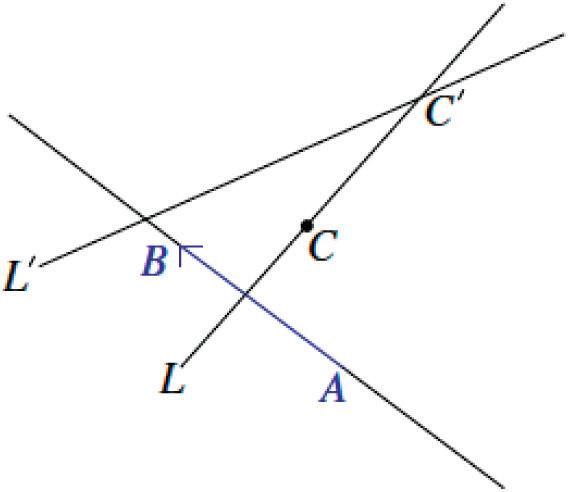
⬛ Let there be a reflection across line L, let P be a point not on line L, and let P' represent () Reflection P . Let the line PP' intersect L at point O and let A be a point on L distinct from point O, as shown.

⬛ What can we say about segments PO and OP'?
A point and its image must be the same distance from the line of reflection, so segments PO and P'O have the same length.
⬛ In other words, we know point O is the midpoint of segment PP' because it is equidistant from both endpoints.
⬛ In general, the line passing through the midpoint of a segment is said to bisect the segment.
⬛ In the diagram, what does the symbol in angle AOP mean?
The symbol means that angle AOP is a right angle.
⬛ So we can say that the line of reflection L is the perpendicular bisector of segment PP'
Discussion (3 minutes)
⬛ A closer look at reflections allows us to find another property that reflections share with translations.
⬛ As with translations, reflections map parallel lines to parallel lines. For example, if L1 || L2and there is a reflection across a line, then () () Reflection LReflectionL 12
⬛ Let there be a reflection across line m. Given L1 || L2, then () () Reflection LReflectionL 12 . We know that any point A on line L1 will be reflected across m to a point A' on () Reflection L1 . Similarly, any point B on line L2 will be reflected across m to a point B' on () Reflection L2 . Because L1 || L2, no point A on line L1 will ever be on L2 and no point B on L2 will ever be on L1. The same can be said for the reflections of points A and B. Since () Reflection L1 shares no points with () Reflection L2 , () () Reflection LReflectionL 12

Closing (3 minutes)
Summarize, or have students summarize, the main points from the lesson.
⬛ We can identify the coordinates of the points of a figure that has been reflected across the x- or y-axis on the coordinate plane.
⬛ We know that reflections have the same three basic properties as translations:
Reflections map lines to lines, segments to segments, rays to rays, and angles to angles.
Lengths of segments are preserved.
Measures of angles are preserved.
⬛ We can distinguish between a translation and a reflection and describe the transformation.
⬛ The line of reflection is the perpendicular bisector of the segment that joins a point not on the line of reflection to its image. Reflections
A reflection across a line is a type of basic rigid motion of a plane.
The following are the three basic properties of reflections:
(Reflection 1) A reflection maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
(Reflection 2) A reflection preserves lengths of segments.
(Reflection 3) A reflection preserves measures of angles.
On the coordinate plane, if a figure is reflected across the x-axis, a point and its image are the same number of vertical units from the x-axis. If a figure is reflected across the y-axis, a point and its image are the same number of horizontal units from the y-axis.
1. Use Trapezoid ABCD to complete the problem.
a. Reflect Trapezoid ABCD across the x-axis. Label the image.
b. Identify the coordinates of the vertices of the image.
2. Reflect CDE across line LAB. Label the image.

3. What is the measure of () ∠ Reflection CDE in Problem 2? Explain.
4. What is the length of () Reflection CE in Problem 2? Explain. Reflections
1. Use Trapezoid ABCD to complete the problem.
a. Reflect Trapezoid ABCD across the x-axis. Label the image.
See the graph.
b. Identify the coordinates of the vertices of the image. A'(-6, -5), B'(-7, -8), C'(0, -8), D'(-1, -5)
2. Reflect CDE across line LAB. Label the image.

3. What is the measure of () ∠ Reflection CDE in Problem 2? Explain.
The measure of () ∠ Reflection CDE is 90° because reflections preserve angle measures.
4. What is the length of () Reflection CE in Problem 2? Explain.
The length of () Reflection CE is 10 cm because reflections preserve segment lengths.
1. Use the quadrilaterals in the coordinate plane to complete the problem.
a. Which quadrilateral is a reflection of Quadrilateral ABCD? Describe the reflection.
Quadrilateral KLMN. Quadrilateral ABCD is reflected across the x-axis.
b. Which quadrilateral is a translation of Quadrilateral ABCD? Describe the translation.
Quadrilateral PQRS. Quadrilateral ABCD is translated left 7 units.
2. Reflect Figure HIJKL across the y-axis. Label and identify the coordinates of the vertices of the image.
3. In the diagram below, = = ∠°mDEF 56 , = ∠°mACB 114 , = AB .12 6units, = JK units 532 , point E is on line L, and point I is not on line L. Let there be a reflection across line L. Reflect and label each of the figures.
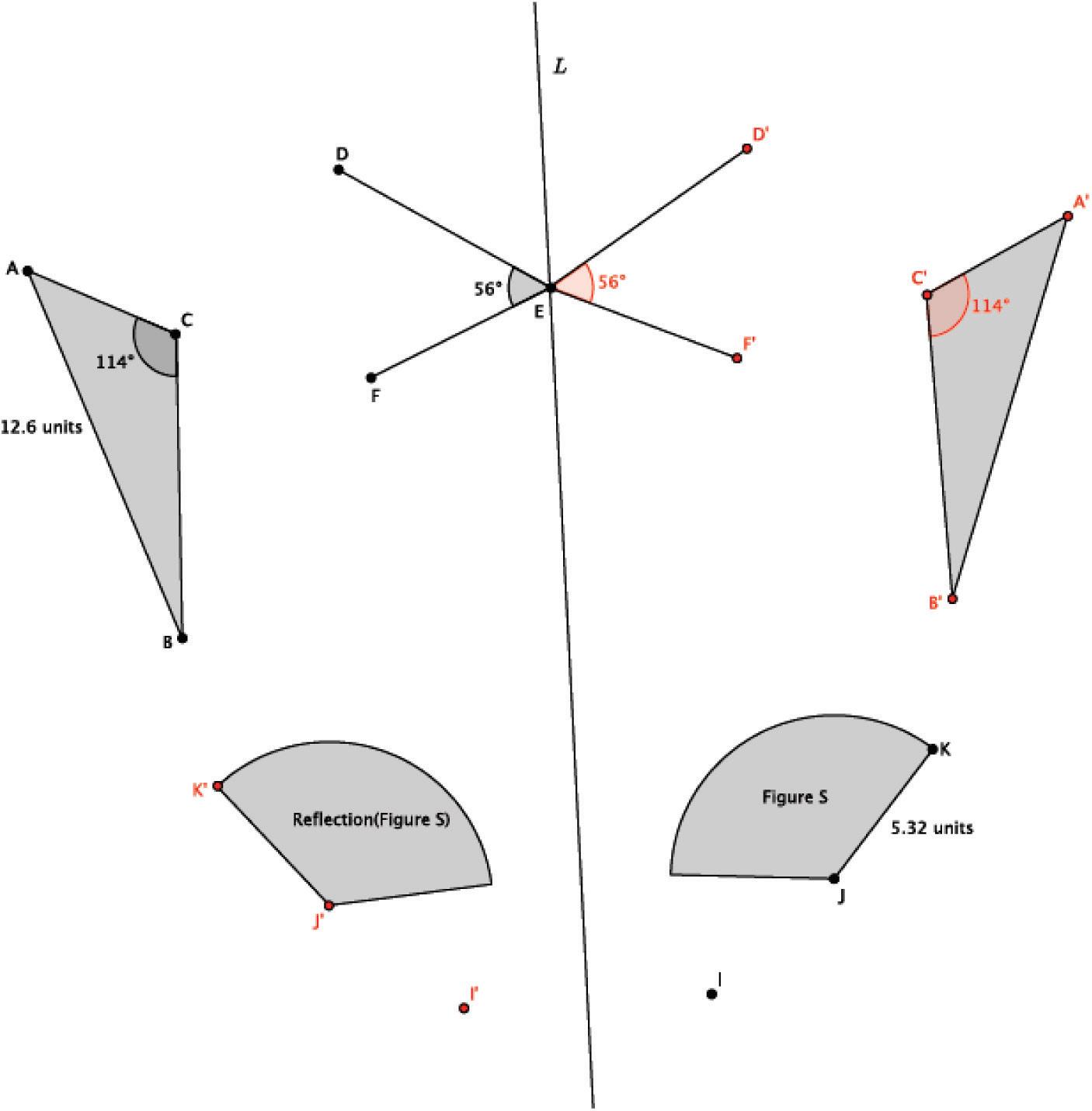
4. Use the diagram from Problem 3 to answer the following questions.
a. What is the measure of Reflection DEF ∠ () ? Explain.
The measure of Reflection DEF ∠ () is 56°. Reflections preserve measures of angles.
b. What is the length of Reflection JK ()? Explain.
The length of Reflection JK () is 532 . units. Reflections preserve lengths of segments.
c. What is the measure of Reflection ACB () ∠ ? Explain.
The measure of Reflection ACB () ∠ is 114° . Reflections preserve measures of angles.
d. What is the length of Reflection AB ()? Explain.
The length of Reflection AB () is 12 6. units. Reflections preserve lengths of segments.
Reflections

⬛ Students learn that the reflection is its own inverse transformation.
⬛ Students understand that a sequence of a reflection followed by a translation is not necessarily equal to a translation followed by a reflection.
Classwork
Discussion (10 minutes)
⬛ When we translate a figure along a vector, we can undo the move by translating along the same vector, but in the opposite direction, creating an inverse transformation.
⬛ Not all transformations are translations, though. To find the inverse of a reflection, we will investigate a sequence of reflections.
⬛ Let there be a reflection across line L. What would undo this action? What is the inverse of this transformation?
A reflection is always its own inverse.
⬛ Consider the picture below of a reflection across a vertical line L.

⬛ Trace this picture of the line L and the points P, A, and Q as shown. Create a reflection across line L followed by another reflection across line L. Is the transformation corresponding to flipping the transparency once across L and then flipping it once more across L? Obviously, the red figure on the transparency would be right back on top of the original black figure. Everything stays the same
Sequencing Reflections and Translations
Let us take this opportunity to reason through the preceding fact without a transparency.
⬛ For a point P not on line L, what would the reflection of the reflection of point P be?
⬛ The picture shows Reflection(P) = P′ is a point to the left of L, and if we reflect the point P′ across L, clearly we get back to P itself. Thus, the reflection of the reflection of point P is P itself. The same holds true for A: the reflection of the reflection of point A is A.
⬛ For point Q on the line L, what would the reflection of the reflection of point Q be?
⬛ The lesson on reflection showed us that a point on the line of reflection is equal to itself, that is, Reflection (Q) = Q. Then, the reflection of the reflection of point Q is Q. No matter how many times a point on the line of reflection is reflected, it will be equal to itself.
⬛ Based on the last two statements, we can say that the reflection of the reflection of P is P for any point P in the plane. Further,
PP I thereflectionoffollowedbythe reflection of , = (4) where I denotes the identity transformation. The identity transformation maps each point P of the plane to P itself. In terms of transparencies, equation (4) says that if we flip the transparency (on which we have traced a given figure in red) across the line of reflection L, then flipping it once more across L brings the red figure to coincide completely with the original figure.
Exercises 1–3 (3 minutes)
Students complete Exercises 1–3 independently.
Exercises 1–3
Use the figure below to answer Exercises 1–3.

Sequencing Reflections and Translations
1. Figure A was translated along vector BA, resulting in Translation(FigureA). Describe a sequence of translations that would map Figure A back onto its original position.
Translate Figure A along vector BA; then, translate the image of Figure A along vector AB
2. Figure A was reflected across line L, resulting in Reflection (FigureA). Describe a sequence of reflections that would map Figure A back onto its original position.
Reflect Figure A across line L; then, reflect the image of Figure A across line L.
3. Can Translation BA of Figure A undo the transformation of Translation DC of Figure A? Why or why not?
No. To undo the transformation, you would need to move the image of Figure A after the translations back to Figure A. The listed translations do not do that
Discussion (10 minutes)
⬛ Does the order in which we sequence rigid motions really matter?
⬛ Consider a reflection followed by a translation. Would a figure be in the same final location if the translation was done first and then followed by the reflection?
⬛ Let there be a reflection across the y-axis, and let T be the translation left 2 units and down 8 units. Let E represent the figure. The following picture shows the reflection followed by the translation of E
Sequencing Reflections and Translations
⬛ Ask students again if they think the image of the figure will be in the same place if we translate first and then reflect. The following picture shows the translation followed by the reflection of E.
Note to Teacher:
In the special case of a translation along a vector with the same direction as the line of reflection, the translation followed by the reflection and the reflection followed by the translation result in the same image.
⬛ It must be clear now that the order in which the rigid motions are performed matters. In the above example, we saw that the reflection followed by the translation of E is not the same as the translation followed by the reflection of E; therefore, a translation followed by a reflection and a reflection followed by a translation are not equal.
Exercises 4–7 (12 minutes)
Students complete Exercises 4–7 independently.
Exercises 4–7
Let S be the black figure.

4. Let there be the translation along vector AB and a reflection across line L.
Use a transparency to perform the following sequence: Translation followed by the reflection of figure S. Label the image S′
The solution is on the diagram above
5. Let there be the translation along vector AB and a reflection across line L
Use a transparency to perform the following sequence: Reflection followed by the translation of figure S. Label the image S″ .
The solution is on the diagram above.
Use this coordinate plane for Exercises 6 and 7.
6. Let there be a translation right 4 units and up 3 units, and a reflection across the x-axis.
a. Perform the following sequence: Translation followed by the reflection of Figure ABCD. Label the image
See the graph above.
b. Identify the coordinates of the vertices of Figure A
7. Let there be a translation right 4 units and up 3 units, and a reflection across the x-axis.
a. Perform the following sequence: Reflection followed by the translation of Figure ABCD. Label the image AèBèCèDè .
See the graph above.
b. Identify the coordinates of the vertices of Figure A
Closing (5 minutes)
Summarize, or have students summarize, the lesson.
⬛ We can sequence rigid motions.
Lesson Summary
⬛ A reflection across a line followed by a reflection across the same line places all figures in the plane back onto their original position.
⬛ A reflection followed by a translation does not necessarily place a figure in the same location in the plane as the translation followed by the reflection. The order in which we perform a sequence of rigid motions matters.
Exit Ticket (5 minutes)
⬛ The sequence of a reflection followed by the same reflection is the identity transformation, and the order in which we sequence rigid motions matters. Sequencing Reflections and
Use this coordinate plane for Problems 1 and 2.
1. Let there be a translation left 3 units and a reflection across the y-axis.
a. Perform the following sequence: Translation followed by the reflection of Parallelogram DEFG. Label the image
D′E′F′G′ .
b. Identify the coordinates of the vertices of Parallelogram D′E′F′G′ .
2. Let there be a translation left 3 units and a reflection across the y-axis.
a. Perform the following sequence: Reflection followed by the translation of Parallelogram DEFG. Label the image D″E″F″G″
b. Identify the coordinates of the vertices of Parallelogram D″E″F″G″
Sequencing Reflections and Translations
Use this coordinate plane for Problems 1 and 2.
1. Let there be a translation left 3 units and a reflection across the y-axis.
a. Perform the following sequence: Translation followed by the reflection of Parallelogram DEFG. Label the image
See the graph above.
b. Identify the coordinates of the vertices of Parallelogram
2. Let there be a translation left 3 units and a reflection across the y-axis.
a. Perform the following sequence: Reflection followed by the translation of Parallelogram DEFG. Label the image
See the graph above.
b. Identify the coordinates of the vertices of Parallelogram
1. Let there be a reflection across line L, and let there be a translation along vector AB, as shown. If S denotes the black figure, compare the translation followed by the reflection of S with the reflection followed by the translation of figure S.

Students should notice that the two sequences place the image of figure S in different locations in the plane
2. Let L1 and L2 be parallel lines, and let Reflection1 and Reflection2 be the reflections across L1 and L2, respectively (in that order). Show that a Reflection2 followed by Reflection1 results in a different image than Reflection1 followed by Reflection2. (Hint: Take a point on L1 and see what each of the sequences does to it.)
Let D be a point on L1, as shown, and let D′ be the transformation given by Reflection2 followed by Reflection1. Notice where D′ is.

Sequencing Reflections and Translations
Let D″ be the transformation given by Reflection1 followed by Reflection2. Notice where the D″ is.

Since D′ ≠ D″, the sequences do not result in the same image.
Use this coordinate plane for Problems 3 and 4.
Sequencing Reflections and Translations
3. Let there be a translation up 4 units and right 8 units, and a reflection across the x-axis.
a. Perform the following sequence: Translation followed by the reflection of Figure ABCDE. Label the image
See the graph above.
b. Identify the coordinates of the vertices of
4. Let there be a translation up 4 units and right 8 units, and a reflection across the x-axis.
a. Perform the following sequence: Reflection followed by the translation of Figure ABCDE. Label the image
See the graph above.
b. Identify the coordinates of the vertices of
Sequencing Reflections and Translations

⬛ Students know how to rotate a figure a given degree around a given center.
⬛ Students know that rotations move lines to lines, rays to rays, segments to segments, and angles to angles. Students know that rotations preserve lengths of segments and measures of angles. Students know that rotations move parallel lines to parallel lines.
In general, students are not required to rotate a certain degree nor identify the degree of rotation. The only exceptions are when the rotations are multiples of 90°. For this reason, it is recommended that the teacher shows students how to use the transparency to rotate in multiples of 90°, that is, turn the transparency one-quarter turn for each 90° rotation. In Topic B, students use the properties of rotations to support their understanding of why vertical angles are congruent.
Discussion (8 minutes)
⬛ What is the simplest transformation that would map one of the following figures to the other?

⬛ Would a translation work? Would a reflection work?
Because there seems to be no known simple transformation that would do the job, we will learn about a new transformation called rotation. Rotation is the transformation needed to map one of the figures onto the other
Let O be a point in the plane, and let d be a number between −360 and 360, or in the usual notation, −360 < d < 360
⬛ Why do you think the numbers −360 and 360 are used in reference to rotation?
Rotating means that we are moving in a circular pattern, and circles have 360°.
The rotation of d degrees with center O is defined by using transparencies. On a piece of paper, fix a point O as the center of rotation, let P be a point in the plane, and let the ray OP be drawn. Let d be a number between −360 and 360
Instructions for performing a rotation. If there is a rotation of d degrees with center O, the image Rotation(P) is the point described as follows. On a piece of transparency, trace O, P, and OP in red. Now, use a pointed object (e.g., the leg-with-spike of a compass) to pin the transparency at the point O. First, suppose d ≥ 0. Then, holding the paper in place, rotate the transparency counterclockwise so that if we denote the final position of the rotated red point (that was P) by P′, then m∠P′OP is d degrees. For example, if d = 30, we have the following picture:
As before, the red rectangle represents the border of the rotated transparency. Then, by definition, Rotation(P) is the point P′
If, however, d < 0, then holding the paper in place, we would now rotate the transparency clockwise so that if we denote the position of the red point (that was P) by P′, then m∠POP′ is d degrees. For example, if d = −30, we have the following picture:
Again, we define Rotation(P) to be P′ in this case. Notice that the rotation moves the center of rotation O to itself, that is, Rotation(O) = O
Exercises 1–4 (4 minutes)
Students complete Exercises 1–4 independently.
Exercises
1. Let there be a rotation of d degrees around center O. Let P be a point other than O. Select d so that d � 0. Find P′ (i.e., the rotation of point P) using a transparency.
Verify that students have rotated around center O in the counterclockwise direction

2. Let there be a rotation of d degrees around center O. Let P be a point other than O. Select d so that d � 0. Find P′ (i.e., the rotation of point P) using a transparency.
Verify that students have rotated around center O in the clockwise direction.

3. Which direction did the point P rotate when d � 0? It rotated counterclockwise about point O
4. Which direction did the point P rotate when d � 0? It rotated clockwise about point O
Discussion (5 minutes)
Observe that, with O as the center of rotation, the points P and Rotation(P) lie on a circle whose center is O and whose radius is OP

⬛ Assume we rotate the plane d degrees around center O. Let P be a point other than O. Where do you think P′ will be located?
The points P and P′ will be equidistant from O; that is, P′ is on the circumference of the circle with center O and radius OP. The point P′ would be clockwise from P if the degree of rotation is negative. The point P′ would be counterclockwise from P if the degree of rotation is positive
⬛ If we rotated P d degrees around center O several times, where would all of the images of P be located?
All images of P will be on the circumference of the circle with radius OP

⬛ Why do you think this happens?
Because, like translations and reflections, rotations preserve lengths of segments. The segments of importance here are the segments that join the center O to the images of P. Each segment is the radius of the circle.
⬛ Consider a rotation of point P, around center O, 180 degrees and −180 degrees. Where do you think the images of P will be located?
Both rotations, although they are in opposite directions, will move the point P to the same location, P′. Further, the points P, O, and P′ will always be collinear (i.e., they will lie on one line, for any point P).

Concept Development (5 minutes)
⬛ Now that we know how a point gets moved under a rotation, let us look at how a geometric figure gets moved under a rotation. Let S be the figure consisting of a segment (not a line) and two points. Let the center of rotation be O, the lower endpoint of the segment, as shown.
⬛ Then, the rotation of 30 degrees with center O moves the point represented by the left black dot to the lower red dot, the point represented by the right black dot to the upper red dot, and the vertical black segment to the red segment to the left at an angle of 30 degrees, as shown.
Discussion (2 minutes)
Revisit the question posed at the beginning of the lesson and ask students:
⬛ What is the simplest transformation that would map one of the following figures to the other?

We now know that the answer is a rotation
Show students how a rotation of approximately 90 degrees around a point O, chosen on the perpendicular bisector (⊥ bisector) of the segment joining the centers of the two circles in the figures, would map the figure on the left to the figure on the right. Similarly, a rotation of −90 degrees would map the figure on the right to the figure on the left.

Students complete Exercises 5 and 6 independently.
Note to Teacher:
Continue to remind students that a positive degree of rotation moves the figure counterclockwise, and a negative degree of rotation moves the figure clockwise.
5. Let L be a line, AB be a ray, CD be a segment, and ∠EFG be an angle, as shown. Let there be a rotation of d degrees around point O. Find the images of all figures when d ≥ 0.

Verify that students have rotated around center O in the counterclockwise direction
6. Let AB be a segment of length 4 units and ∠CDE be an angle of measure 45°. Let there be a rotation by d degrees, where d � 0, about O. Find the images of the given figures. Answer the questions that follow.

Verify that students have rotated around center O in the clockwise direction
a. What is the length of the rotated segment Rotation ( AB )?
The length of the rotated segment is 4 units
b. What is the measure of the rotated angle Rotation (∠CDE)?
The measure of the rotated angle is 45°.
Based on the work completed during the lesson, and especially in Exercises 5 and 6, we can now state that rotations have properties similar to translations with respect to (Translation 1)–(Translation 3) of Lesson 2 and reflections with respect to (Reflection 1)–(Reflection 3) of Lesson 4:
(Rotation 1) A rotation maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
(Rotation 2) A rotation preserves lengths of segments.
(Rotation 3) A rotation preserves measures of angles.
Also, as with translations and reflections, if L1 and L2 are parallel lines and if there is a rotation, then the lines Rotation(L1) and Rotation(L2) are also parallel. If a line L is rotated around a center O not on line L by degreed ≠ 180, and L is a line, L and Rotation(L) are not parallel. (Note to teacher: Exercises 7 and 8 illustrate these two points.) Rotations
Exercises 7–8 (5 minutes)
Students complete Exercises 7 and 8 independently.
7. Let L1 and L2 be parallel lines. Let there be a rotation by d degrees, where -360 � d � 360, about O. Is (L1)′ ‖ (L2)′?

Verify that students have rotated around center O in either direction. Students should respond that (L1)′ ‖ (L2)′
8. Let L be a line and O be the center of rotation. Let there be a rotation by d degrees, where d ≠ 180 about O. Are the lines L and L′ parallel?

Verify that students have rotated around center O in either direction any degree other than 180 Students should respond that L and L′ are not parallel. Rotations
Closing (3 minutes)
Summarize, or have students summarize, what we know of rigid motions at this point:
⬛ We now have definitions for all three rigid motions: translations, reflections, and rotations.
⬛ Rotations map lines to lines, rays to rays, segments to segments, angles to angles, and parallel lines to parallel lines, similar to translations and reflections.
⬛ Rotations preserve lengths of segments and measures of angles similar to translations and reflections.
⬛ Rotations require information about the center and degree of rotation, whereas translations require only a vector, and reflections require only a line of reflection.
Lesson Summary
Rotations require information about the center of rotation and the degree in which to rotate. Positive degrees of rotation move the figure in a counterclockwise direction about the center of rotation. Negative degrees of rotation move the figure in a clockwise direction about the center of rotation.
Basic Properties of Rotations:
⬛ (Rotation 1) A rotation maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
⬛ (Rotation 2) A rotation preserves lengths of segments.
⬛ (Rotation 3) A rotation preserves measures of angles.
Exit Ticket (5 minutes)
1. Given the figure H, let there be a rotation by d degrees, where d ≥ 0, about O. Let Rotation(H) be H′. Find H′

2. Using the drawing above, let Rotation1 be the rotation d degrees with d < 0, about O. Let Rotation1(H) be H″ Find H″ .
1. Given the figure H, let there be a rotation by d degrees, where d � 0, about O. Let Rotation(H) be H′. Find H′

Sample rotation shown above. Verify that the figure H′ has been rotated counterclockwise with center O
2. Using the drawing above, let Rotation1 be the rotation d degrees with d � 0, about O. Let Rotation1(H) be H″ Find H″
Sample rotation shown above. Verify that the figure H″ has been rotated clockwise with center O.
1. Let there be a rotation by -90° around the center O. Find the images of each figure. Rotated figures are shown in red

2. Explain why a rotation of 90 degrees around any point O never maps a line to a parallel line.
I know that a line only maps to a parallel line if there is a rotation about a center O not on line L by a degree of d = 180 or d = -180. So, a rotation of 90 degrees around any point O will not map a line to a parallel line.

3. A segment of length 94 cm has been rotated d degrees around a center O. What is the length of the rotated segment? How do you know?
The rotated segment will be 94 cm in length. Rotations preserve lengths of segments, so the length of the rotated segment will remain the same as the original.
4. An angle of measure 124° has been rotated d degrees around a center O. What is the measure of the rotated angle? How do you know?
The rotated angle will be 124° Rotations preserve the measures of angles, so the rotated angle will have the same measure as the original
Rotations

⬛ Students learn that a rotation of 180 degrees moves a point on the coordinate plane (a, b) to (−a, −b)
⬛ Students learn that a rotation of 180 degrees around a point, not on the line, produces a line parallel to the given line.
Example 1 (5 minutes)
⬛ Let′s look at a 180-degree rotation, Rotation0 around the origin O of a coordinate system. If a point P has coordinates (a, b), it is generally said that Rotation0(P) is the point with coordinates (−a, b)
⬛ Suppose the point P has coordinates (−4, 3); we show that the coordinates of Rotation0(P) are (4, −3)
Example 1
The picture below shows what happens when there is a rotation of 180° around center O, the origin of the coordinate plane.
⬛ Let P′ = Rotation0(P). Let the vertical line (i.e., the line parallel to the y-axis) through P meet the x-axis at a point A. Because the coordinates of P are (−4, 3), the point A has coordinates (−4, 0) by the way coordinates are defined. In particular, A is of distance 4 units from O, and since Rotation0 is length-preserving, the point A′ = Rotation0(A) is also of distance 4 units from O. However, Rotation0 is a 180-degree rotation around O, so A′ also lies on the x-axis but on the opposite side of the x-axis from A. Therefore, the coordinates of A′ are (4, 0). Now, ∠PAO is a right angle and—since Rotation0 maps it to ∠P′A′O and also preserves angle measures—we see that ∠P′A′O is also a right angle. This means that A′ is the point of intersection of the vertical line through P′ and the x-axis. Since we already know that A′ has coordinates of (4, 0), then the x-coordinate of P′ is 4, by definition.
⬛ Similarly, the y-coordinate of P being 3 implies that the y-coordinate of P′ is −3. Altogether, we have proved that the 180-degree rotation of a point of coordinates (−4, 3) is a point with coordinates (4, −3)
The reasoning is perfectly general: The same logic shows that the 180-degree rotation around the origin of a point of coordinates (a, b) is the point with coordinates (−a, −b), as desired.
Students complete Exercises 1–2 independently. Check solutions. Then, let students work in pairs on Exercises 3–4. Students complete Exercises 5–9 independently in preparation for the discussion that follows.
Exercises 1–9
1. Using your transparency, rotate the plane 180 degrees about the origin. Let this rotation be Rotation0. What are the coordinates of Rotation0(2, −4)?
Rotation0(2, −4) = (−2, 4)

Rotations of 180 Degrees
2. Let Rotation0 be the rotation of the plane by 180 degrees about the origin. Without using your transparency, find the coordinates of Rotation0(−3, 5).
Rotation0(−3, 5) = (3, −5)

3. Let Rotation0 be the rotation of 180 degrees around the origin. Let L be the line passing through (−6, 6) parallel to the x-axis. Find Rotation0(L). Use your transparency if needed.

Rotations of 180 Degrees
4. Let Rotation0 be the rotation of 180 degrees around the origin. Let L be the line passing through (7, 0) parallel to the y-axis. Find Rotation0(L). Use your transparency if needed.

5. Let Rotation0 be the rotation of 180 degrees around the origin. Let L be the line passing through (0, 2) parallel to the x-axis. Is L parallel to Rotation0(L)?
Yes, L ‖ Rotation0(L)
Rotations of 180 Degrees
6. Let Rotation0 be the rotation of 180 degrees around the origin. Let line L be the line passing through (−4, 0) parallel to the y-axis. Is L parallel to Rotation0(L)?
Yes, L ‖ Rotation0(L)

7. Let Rotation0 be the rotation of 180 degrees around the origin. Let L be the line passing through (0, −1) parallel to the x-axis. Is L parallel to Rotation0(L)?
Yes, L ‖ Rotation0(L)
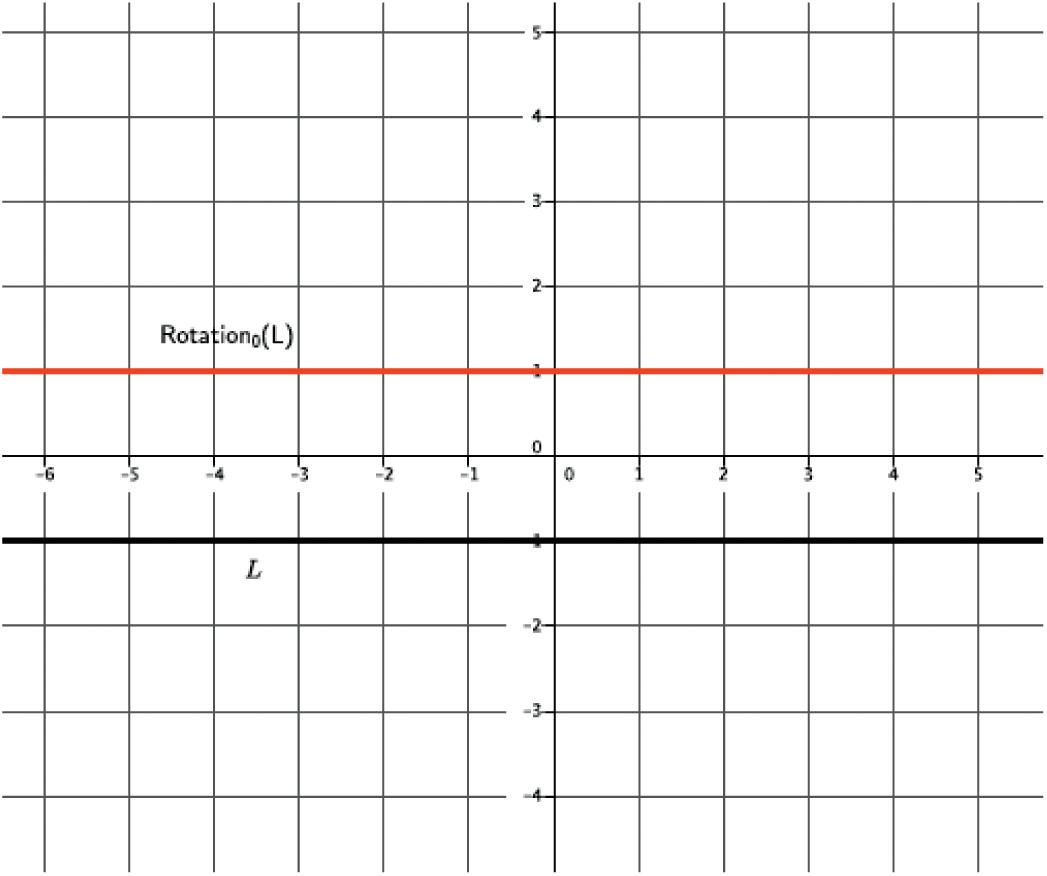
Rotations of 180 Degrees
8. Let Rotation0 be the rotation of 180 degrees around the origin. Is L parallel to Rotation0(L)? Use your transparency if needed.
Yes, L ‖ Rotation0(L).

9. Let Rotation0 be the rotation of 180 degrees around the center O. Is L parallel to Rotation0 (L)? Use your transparency if needed.
Yes, L ‖ Rotation0(L)

Discussion (5 minutes)
⬛ In Exercises 3–9, we found the images of lines after a 180-degree rotation around a point. What did you notice about each line L and its image, Rotation0(L)?
L and Rotation0(L) were always parallel.
⬛ Based on our observations in these problems, we can conclude that if a line L is rotated 180 degrees around a point O not on L, then L and its image are parallel.
⬛ Do you think line L and its image would still be parallel if O were a point on L? Why?
No, if O were a point on L and L were rotated 180 degrees around O, line L and its image would coincide.
Closing (5 minutes)
Summarize, or have students summarize, the lesson.
⬛ Rotations of 180 degrees are special:
A point, P, that is rotated 180 degrees around a center O, produces a point P′ so that P, O, and P′ are collinear.
When we rotate around the origin of a coordinate system, we see that the point with coordinates (a, b) is moved to the point ( a, b).
⬛ We now know that when a line is rotated 180 degrees around a point not on the line, it maps to a line parallel to the given line.
Summary
⬛ A rotation of 180 degrees around O is the rigid motion so that if P is any point in the plane, P, O, and Rotation(P) are collinear (i.e., lie on the same line).
⬛ Given a 180-degree rotation around the origin O of a coordinate system, R0, and a point P with coordinates (a,b), then R0(P) is the point with coordinates ( a, b)
Theorem: Let O be a point not lying on a given line L. Then, the 180-degree rotation around O maps L to a line parallel to L.
Exit Ticket (5 minutes)
Rotations of 180 Degrees
Name Date
Exit Ticket
Let there be a rotation of 180 degrees about the origin. Point A has coordinates ( 2, 4), and point B has coordinates ( 3, 1), as shown below.

1. What are the coordinates of Rotation(A)? Mark that point on the graph so that Rotation(A) = A′. What are the coordinates of Rotation(B)? Mark that point on the graph so that Rotation(B) = B′.
2. What can you say about the points A, A′, and O? What can you say about the points B, B′, and O?
3. Connect point A to point B to make the line LAB. Connect point A′ to point B′ to make the line LA′B′. What is the relationship between LAB and LA′B′?
Rotations of 180 Degrees
Let there be a rotation of 180 degrees about the origin. Point A has coordinates (−2, −4), and point B has coordinates (−3, 1), as shown below.

1. What are the coordinates of Rotation(A)? Mark that point on the graph so that Rotation(A) = A′. What are the coordinates of Rotation(B)? Mark that point on the graph so that Rotation(B) = B′
A′ = (2, 4), B′ = (3, 1)
2. What can you say about the points A, A′, and O? What can you say about the points B, B′, and O?
The points A, A′, and O are collinear. The points B, B′, and O are collinear
3. Connect point A to point B to make the line LAB. Connect point A′ to point B′ to make the line LA′B′. What is the relationship between LAB and LA′B′?
LAB ‖ LA′B′
Rotations of 180 Degrees
Let Rotation0 be the rotation of the plane by 180 degrees about the origin. Use your transparency if needed.
a. Graph Rotation0(ABC ) and find the coordinates of each vertex.
b. Graph Rotation0 (EFGH ) and find the coordinates of each vertex.
c. Graph Rotation0(ABC ) and find the coordinates of each vertex.

8.5, 8.7
Focus Standards: 8.5 The student will use the relationships among pairs of angles that are vertical angles, adjacent angles, supplementary angles, and complementary angles to determine the measure of unknown angles.
8.7 The student will a. given a polygon, apply transformations, to include translations, reflections, and dilations, in the coordinate plane.
Instructional Days: 5
Lesson 8: Sequences of Rigid Motions (P)1
Lesson 9: Congruence by Using Rigid Motions (S)
Lesson 10: Angle Relationships (S)
Lesson 11: Problem Solving with Angle Relationships (P)
Lesson 12: More Problem Solving with Angle Relationships (P)
In Topic B, students extend their understanding of rigid motions and apply them to congruence and angle relationships. In Lesson 8, students perform sequences of translations, rotations, and reflections, which prepares them to define congruence in Lesson 9 in terms of a sequence of the basic rigid motions. In Lesson 10, students use rotation to show why vertical angles are congruent and why corresponding angles are congruent when parallel lines are cut by a transversal. They also explore and apply other angle relationships: adjacent angles, supplementary angles, complementary angles, angles at a point, and angles on a line. Topic B concludes with Lessons 11 and 12, where students solve problems by using all of these angle relationships to write and solve equations for unknown angle measures.
1Lesson Structure Key: P-Problem Set Lesson, M-Modeling Cycle Lesson, E-Exploration Lesson, S-Socratic Lesson



⬛ Students describe a sequence of rigid motions that maps one figure onto another.
Example 1 (8 minutes)
So far, we have seen how to sequence translations and reflections. Now that we know about rotation, we can move geometric figures around the plane by sequencing a combination of translations, reflections, and rotations. Let’s examine the following sequence:
⬛ Let E denote the ellipse in the coordinate plane as shown.

⬛ Let Translation1 be the translation along the vector v from (1,0) to ( 1,1), let Rotation2 be the 90-degree rotation around ( 1,1), and let Reflection3 be the reflection across line L joining ( 3,0) and (0,3). What is the image of E after Translation1 followed by the Rotation2 followed by the Reflection3?
Sequences of Rigid Motions
⬛ Which transformation do we perform first, the translation, the reflection, or the rotation? How do you know? Does it make a difference?
The order in which transformations are performed makes a difference. Therefore, we perform the translation first. So now, we let E1 be Translation1(E).

⬛ Which transformation do we perform next?
The rotation is next. So now, we let E2 be the image of E after the Translation1 followed by the Rotation2

Sequences of Rigid Motions
⬛ Now, the only transformation left is Reflection3. So now, we let E3 be the image of E after the Translation1 followed by the Rotation2 followed by the Reflection3

minutes)
Show video1 that describes how to map one figure onto an identical figure using a sequence of basic rigid motions. http://youtu.be/O2XPy3ZLU7Y
Exercises 1–5 (25 minutes)
Give students one minute or less to work independently on Exercise 1. Then have the discussion with them that follows the likely student response. Repeat this process for Exercises 2 and 3. For Exercise 4, have students work in pairs. One student can work on Scenario 1 and the other on Scenario 2, or each student can do both scenarios and then compare with a partner.
1The video was developed by Larry Francis.
Sequences of Rigid Motions
Exercises
1. In the following picture, triangle ABC can be traced onto a transparency and mapped onto triangle A′B′C′ Which basic rigid motion, or sequence of, would map one triangle onto the other?
Solution provided below with likely student responses.
Reflection
Elicit more information from students by asking the following:
⬛ Reflection requires some information about which line to reflect over; can you provide a clearer answer?
Reflect over line LBC
Expand on their answer. Let there be a reflection across the line LBC . We claim that the reflection maps ABC onto A′B′C′. We can trace ABC onto a transparency and see that when we reflect across LBC, ABC maps onto A'B'C' The reason why ABC maps onto A′B′C′ is because ∠ABC and ∠A′B′C′ are equal in measure and BA on the transparency falls on B′A′ . Similarly, CA on the transparency falls on C′A′ . From the picture, we can see that point A on the transparency falls exactly on point A′ so the reflection of ABC across LBC is exactly A′B′C′
Note to Teacher: A precise explanation of why ABC maps onto A'B'C' does not require using a transparency. Since a reflection does not move any point on LBC , we already know that Reflection(B) = B′ and Reflection(C) = C′ We just need to show that the reflection maps A to A'. The hypothesis says the measure of ∠ABC is equal to the measure of ∠A′B′C′; therefore, BC is the angle bisector of ∠ABA′ The reflection maps BA to B′A′ Similarly, the reflection maps CA onto C'A' . Therefore, the reflection maps the intersection of BA and CA , which is A, to the intersection of B′A′ and C′A′ , which is A. So, Reflection(A) = A′; therefore, Reflection(ABC) = A′B′C′.
2. In the following picture, triangle ABC can be traced onto a transparency and mapped onto triangle A′B′C′ . Which basic rigid motion, or sequence of, would map one triangle onto the other?
Rotation

Sequences of Rigid Motions
Elicit more information from students by asking:
⬛ Rotation requires some information about what point to rotate around (the center) and how many degrees. If we say we need to rotate d degrees, can you provide a clearer answer?
Rotate around point B as the center, d degrees
Expand on their answer. Let there be a (clockwise) rotation of d degrees around point B where d represents the opposite of the measure of ∠CBC'. We claim that the rotation maps ABC onto A′B′C′. We can trace ABC onto a transparency and pin the transparency at B, which is the same point as point B′. When we perform a rotation of d degrees, we see that BC on the transparency maps onto B′C′ ; the two segments are equal in length because we can trace one on the transparency and show it is the same length as the other. Also, A on the transparency and A′ are on the same side, or half-plane, of line LB′C′ . The triangles are in the same position as they were at the end of Exercise 1; therefore, ABC on the transparency and A'B'C' completely coincide.
Note to Teacher: A precise explanation of why ABC maps onto A'B'C' does not require using a transparency. By the definition of rotation, a rotation maps BC onto B′C′ . We know |BC| = |B′C′|, so Rotation(C) = C′. The picture implies that after the rotation, A and Rotation(A) lie on the same side of LB′C′ . If we compare A′B′C′ and Rotation(ABC), the triangles are in the same position as they were at the end of Exercise 1; therefore, Rotation(ABC) = A′B′C′
3. In the following picture, triangle ABC can be traced onto a transparency and mapped onto triangle A′B′C′ . Which basic rigid motion, or sequence of, would map one triangle onto the other?

Rotation and reflection
Elicit more information from students. Prompt students to think back to what was needed in the last two examples.
⬛ What additional information do we need to provide?
Rotate around point B as the center d degrees; then, reflect across line LB'C'
Expand on their answer. We need a sequence this time. Let there be a (clockwise) rotation of d degrees around B where d represents the opposite of the measure of ∠CBC' and let there be the reflection across LB'C' . We claim that the sequence of a rotation followed by a reflection maps ABC onto A'B'C'. We can trace ABC onto a transparency and pin the transparency at B, which is the same point as B′. When we perform a rotation of d degrees, we see that BC on the transparency maps onto B'C' . Now, ABC and A'B'C' are in the exact position they were in at the end of Exercise 2; therefore, the reflection across LB′C′ would map ABC on the transparency onto A'B'C'
Sequences of Rigid Motions
Students may say that they only need to reflect, but point out that we would first have to find the appropriate line of reflection in order to state which line to reflect across. For that reason, it makes more sense to rotate first to bring BC and B'C' together and then reflect across the common side of the two triangles.
Note to Teacher: An explanation of why ABC maps onto A'B'C' does not require a transparency. By the definition of rotation, a rotation maps BC onto B'C' We know |BC| = |B'C'|, so Rotation(C) = C' When comparing A'B'C' and Rotation(ABC), we see that we are back to the situation in Exercise 1; therefore, the reflection maps Rotation(ABC) onto A'B'C' This means that rotation followed by a reflection maps ABC onto A'B'C'
4. In the following picture, we have two pairs of triangles. In each pair, triangle ABC can be traced onto a transparency and mapped onto triangle A′B′C′
Which basic rigid motion, or sequence of, would map one triangle onto the other?
Scenario 1:

Scenario 2:

In Scenario 1, a translation and a rotation; in Scenario 2, a translation, a reflection, and then a rotation
Elicit more information from students by asking the following:
⬛ What additional information is needed for a translation?
We need to translate along a vector.
⬛ Since there is no obvious vector in our picture, which vector should we draw and then use to translate along?
When they do not respond, prompt them to select a vector that would map a point from ABC to the corresponding point in A′B′C′. Students will likely select vectors BB′ , AA′ , or CC′
Sequences of Rigid Motions
Make it clear to students that we can use any of those vectors, but using BB' makes the most sense. By using BB' , we can use the reasoning given in previous exercises. For example, from Exercises 1–3 we know that B = B'
Expand on their answer: Let there be the translation along BB' . In Scenario 1, A'B'C' and Translation(ABC) would be similar to the situation of Exercise 2. In Scenario 2, A'B'C' and Translation(ABC) would be similar to the situation of Exercise 3. Based on the work done in Exercises 2 and 3, we can conclude the following: In Scenario 1, the sequence of a translation along BB' followed by a rotation d degrees around B' would map ABC onto A'B'C'. In Scenario 2, the sequence of a translation along BB' followed by a rotation d degrees around B′ followed by a reflection across LB′C′ would map ABC onto A'B'C'.
Students complete Exercise 5 independently or in pairs.
5. Let two figures ABC and A′B′C′ be given so that the length of arc AC is equal to the length of arc A′C′ , m∠ABC = m∠A′B′C′ = 80°, and |AB| = |A′B′| = 5 units. With clarity and precision, describe a sequence of rigid motions that would map figure ABC onto figure A′B′C′

Closing (5 minutes)
Let there be a translation along vector AA′, let there be a rotation of d degrees around point A′, and let there be a reflection across line LA′B′. Translate so that Translation(A) = A′. Rotate so that Rotation(B) = B′ and Rotation (AB ) coincides with A′B′. Reflect across LA′B′ so that Reflection(C) = C′ and Reflection(CB ) coincides with C′B′ . Since m∠ABC = m∠A′B′C′ = 80° , we know that CB will coincide with C′B′. The length of arc AC is the same as the length of arc A′C′, so the arcs will coincide. Therefore, a sequence of a translation, then a rotation, and then a reflection will map figure ABC onto figure A′B′C′
Summarize, or have students summarize, the lesson and what they know of rigid motions to this point:
⬛ We can now describe, using precise language, how to sequence rigid motions so that one figure maps onto another.
Exit Ticket (5 minutes)
Sequences of Rigid Motions
Name
Exit Ticket
Triangle ABC has been moved according to the following sequence: a translation followed by a rotation followed by a reflection. With precision, describe each rigid motion that would map �ABC onto �A′B′C′. Use your transparency and add to the diagram if needed.

Sequences of Rigid Motions
Triangle ABC has been moved according to the following sequence: a translation followed by a rotation followed by a reflection. With precision, describe each rigid motion that would map �ABC onto �A′B′C′. Use your transparency and add to the diagram if needed.

Let there be the translation along vector AA' so that A is mapped to A′. Let there be the clockwise rotation by d degrees around point A′ so that C is mapped to C′ and AC = A′C′. Let there be the reflection across LA′C′ so that B is mapped to B′ .
Sequences of Rigid Motions
1. Let there be the translation along vector v , let there be the rotation around point A, 90 degrees (clockwise), and let there be the reflection across line L. Let S be the figure as shown below. Show the location of S after performing the following sequence: the translation followed by the rotation followed by the reflection. Solution is shown in red.

2. Would the location of the image of S in the previous problem be the same if the translation was performed last instead of first? In other words, does the translation followed by the rotation followed by the reflection produce the same image as the rotation followed by the reflection followed by the translation? Explain. No, the order of the transformation matters. If the translation was performed last, the location of the image of S, after the sequence, would be in a different location than if the translation was performed first.
Sequences of Rigid Motions
3. Use the same coordinate grid to complete parts (a)–(c).
a. Reflect triangle ABC across the vertical line, parallel to the y-axis, going through point (1,0). Label the transformed points A, B, C as A′ , B′ , C′, respectively.
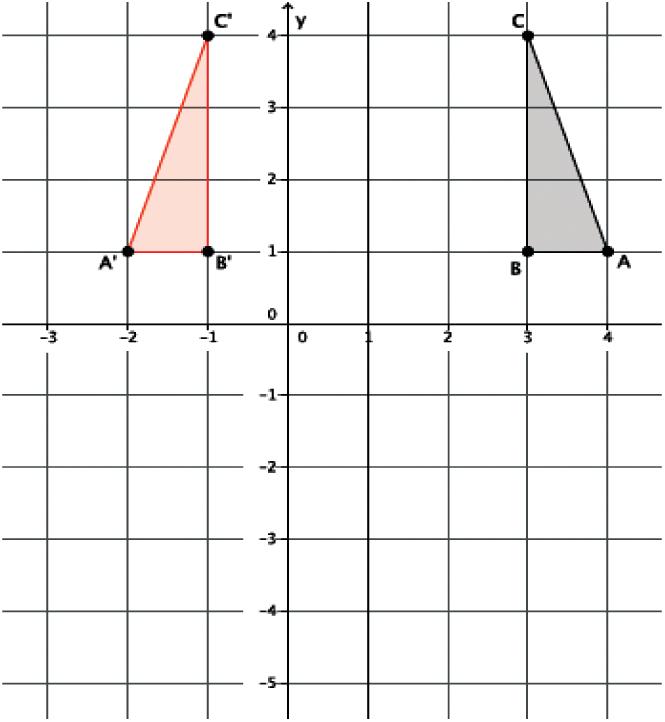
b. Reflect triangle A′B′C′ across the horizontal line, parallel to the x-axis going through point (0, 1). Label the transformed points of A′ , B′ , C′ as A″ , B″ , C″, respectively.

c. Is there a single rigid motion that would map triangle ABC to triangle A″B″C″? Yes, a 180° rotation around center (1, 1) The coordinate (1, 1) happens to be the intersection of the two lines of reflection A STORY OF RATIOS
Sequences of Rigid Motions

⬛ Students know the definition of congruence and related notation, that is, ≅. Students know that to prove two figures are congruent, there must be a sequence of rigid motions that maps one figure onto the other.
⬛ Students know that the basic properties of congruence are similar to the properties for all three rigid motions (translations, rotations, and reflections).
Example 1 (5 minutes)
⬛ In previous grades, we learned that congruent figures have equal side lengths and angle measures.
⬛ Sequencing basic rigid motions has been practiced before this lesson because, in general, the sequence of (a finite number of) basic rigid motions is called a congruence. A geometric figure S is said to be congruent to another geometric figure S′ if there is a sequence of rigid motions that maps S to S′, that is, Congruence(S) = S′ The notation related to congruence is the symbol ≅. When two figures are congruent, like S and S′ , we can write S ≅ S′
⬛ We want to describe the sequence of rigid motions that demonstrates the two triangles shown below are congruent, that is, △ABC ≅ △A′B′C′ .

Note to Teacher:
Demonstrate, or have students demonstrate, the rigid motions as they work through the sequence.
⬛ What rigid motion will bring the two triangles together? That is, which motion would bring together at least one pair of corresponding points (vertices)? Be specific.
Translate △ABC along vector AA′
⬛ What rigid motion would bring together one pair of sides? Be specific.
Rotate d degrees around center A′
⬛ After these two rigid motions, we have shown that △ABC ≅ △A′B′C′ through the sequence of a translation followed by a rotation. Notice that only two rigid motions were needed for this sequence. A sequence to demonstrate congruence can be made up of any combination of the basic rigid motions using all three or even just one.
Congruence by Using Rigid Motions
⬛ The concept of congruence between two geometric figures is one of the cornerstones of geometry. Congruence is now realized as “a sequence of basic rigid motions that maps one figure onto another.”
Note to Teacher:
The preceding definition of congruence is meant to replace the existing “same size and same shape” definition.
⬛ It is said that S is congruent to S′ if there is a congruence so that Congruence (S) = S′. This leaves open the possibility that, although S is congruent to S′, the figure S′ may not be congruent to S.
Ask students:
⬛ If there is a Congruence1 so that Congruence1(S) = S′, do we know that there will also be a Congruence2 so that Congruence2(S′) = S?
Make sure students understand the question.
⬛ Can you say for certain that if they begin by mapping figure 1 onto figure 2, they can also map figure 2 onto figure 1?
Students will likely say yes, but without proof, further work is necessary
⬛ Let Congruence be the transformation that first translates by vector MN followed by a reflection across line L. Let S be the figure on the left below, and let S′ be the figure on the right below. Then, the equation
Congruence(S) = S′ says that if we trace S in red on a transparency, then translate the transparency along MN , and flip it across L, we get the figure to coincide completely with S′

⬛ Now, keeping in mind what we know about how to undo transformations in general, we can find a congruence to map S′ to S. Namely, tracing the figure S′ in red, flipping the transparency across L so the red figure arrives at the figure in the middle, and then translating the figure along vector NM . (Note the change in direction of the vector from MN .) The red figure now coincides completely with S. The sequence of the reflection across L followed by the translation along vector NM achieves the congruence.
Congruence by Using Rigid Motions
⬛ The general argument is that if there is a Congruence1 so that Congruence1(S) = S′, then there will also be a Congruence2 so that Congruence2 (S′) = S is similar. The only additional comment to complete the picture is that, in addition to 1. The sequence required to show that Congruence2 followed by Congruence1 is equal to Congruence1 followed by Congruence2,
2. A reflection is undone by a reflection across the same line.
We also have to draw upon the sequence of rotations that maps a figure onto itself to be certain that each of the three basic rigid motions can be undone by another basic rigid motion.
⬛ In summary, if a figure S is congruent to another figure S′, then S′ is also congruent to S. In symbols S ≅ S′ It does not matter whether S or S′ comes first.
Students work on Exercise 1 in pairs. Students will likely need some guidance with part (a) of Exercise 1. Provide support, and then allow them to work with a partner to complete parts (b) and (c).
a. Describe the sequence of basic rigid motions that shows S1 ≅ S2.
Let there be the translation along vector AB . Let there be a rotation around point B, d1 degrees. Let there be a reflection across the longest side of the figure so that S1 maps onto S2 Then, the Translation(S1) followed by the rotation followed by the reflection is S2. Congruence by Using Rigid Motions

b. Describe the sequence of basic rigid motions that shows S2 ≅ S3.
Let there be a translation along vector BC . Let there be a rotation around point C, d2 degrees so that S2 maps onto S3. Then, the Translation(S2) followed by the rotation is S3.

c. Describe a sequence of basic rigid motions that shows S1 ≅ S3.
Sample student response: Let there be a translation along vector AC . Let there be a rotation around point C, d3 degrees. Let there be the reflection across the longest side of the figure so that S1 maps onto S3. Then, the Translation(S1) followed by the Rotation followed by the Reflection is S3 Congruence by

Discussion and Exercise 2 (10 minutes)
Ask students if they really need to do all of the work they did in part (c) of Exercise 1. Students should say no. The reason they do not need to do all of that work is because they already know that translations, rotations, and reflections preserve angle measures and lengths of segments. For that reason, if they know that S1 ≅ S2 and S2 ≅ S3, then S1 ≅ S3
Ask students to help summarize the basic properties of all three basic rigid motions.
Elicit from students the following three statements:
A basic rigid motion maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle
A basic rigid motion preserves lengths of segments
A basic rigid motion preserves measures of angles
Ask students if they believe these same facts are true for sequences of basic rigid motions.
⬛ Specifically, under a sequence of a translation followed by a rotation: If there is a translation along a vector AB , and there is a rotation of d degrees around a center O, will a figure that is sequenced remain rigid? That is, will lengths of segments and measures of angles be preserved? Will lines remain lines or segments remain segments?
Students should say that yes, sequences of rigid motions also have the same basic properties of rigid motions in general.
⬛ Given that sequences enjoy the same basic properties of basic rigid motions, we can state three basic properties of congruences:
(Congruence 1) A congruence maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
(Congruence 2) A congruence preserves lengths of segments.
(Congruence 3) A congruence preserves measures of angles.
Exercise 2
Perform the sequence of a translation followed by a rotation of Figure XYZ, where T is a translation along a vector AB , and R is a rotation of d degrees (you choose d) around a center O. Label the transformed figure X ′Y ′Z ′ Is XYZ ≅ X′Y′Z′? Congruence by

Closing (5 minutes)
Summarize, or have students summarize, the lesson.
⬛ We now have a definition for congruence, that is, a sequence of basic rigid motions.
⬛ We have notation for congruence, ≅.
⬛ The properties that apply to the individual basic rigid motions also apply to congruences.
Given that sequences enjoy the same basic properties of basic rigid motions, we can state three basic properties of congruences:
(Congruence 1) A congruence maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
(Congruence 2) A congruence preserves lengths of segments.
(Congruence 3) A congruence preserves measures of angles.
The notation used for congruence is ≅.
Exit Ticket (5 minutes)
Name Date
Exit Ticket
1. Is △ABC ≅ △A′B′C′? If so, describe a sequence of rigid motions that proves they are congruent. If not, explain how you know.

2. Is △ABC ≅ △A′B′C′? If so, describe a sequence of rigid motions that proves they are congruent. If not, explain how you know.

1. Is △ABC ≅ A′B′C′? If so, describe a sequence of rigid motions that proves they are congruent. If not, explain how you know.

Sample student response: Yes, △ABC ≅ △A′B′C′
Translate △A′B′C′ along vector A′A.
Rotate △A′B′C ′ around center Ad degrees until side A′C ′ coincides with side AC
Then, reflect across line AC.
2. Is △ABC ≅ △A′B ′C ′? If so, describe a sequence of rigid motions that proves they are congruent. If not, explain how you know.

Sample student response: No, △ABC is not congruent to △A′B′C′. Though I could translate and rotate to get some of the parts from each triangle to coincide, there is no rigid motion that would map segment A′C′ to segment AC or segment A′B′ to segment AB because they are different lengths. Basic rigid motions preserve length, so no sequence would map △A′B′C′ onto △ABC.
Students practice describing sequences of rigid motions that produce a congruence.
1. Given two right triangles with lengths shown below, is there one basic rigid motion that maps one to the other? Explain.

Yes, a rotation of d degrees around some center would map one triangle onto the other. The rotation would map the right angle to the right angle; the sides of length 7 and length 11 would then coincide. Congruence by Using Rigid Motions
2. Are the two right triangles shown below congruent? If so, describe a congruence that would map one triangle onto the other.

Sample student response: Yes, they are congruent. Let there be the translation along vector KL . Let there be the rotation around point L, d degrees. Then, the translation followed by the rotation will map the triangle on the left to the triangle on the right.
3. Given two rays, OA and O′A′ :
a. Describe a congruence that maps OA to O′A′
Sample student response: Let there be the translation along vector OO′. Let there be the rotation around point O′d degrees. Then, the Translation(OA ) followed by the Rotation is O′A′ .

b. Describe a congruence that maps O′A′ to OA .
Sample student response: Let there be the translation along vector O′O. Let there be the rotation around point Od1 degrees. Then, the Translation (O′A′) followed by the Rotation is OA

Congruence by Using Rigid Motions

⬛ Students use rigid motions to verify vertical angles and corresponding angles.
⬛ Students identify the relationships of adjacent angles, complementary angles, supplementary angles, vertical angles, and corresponding angles.
Lesson Notes
This lesson is a review followed by a continuation of the angle relationships that students learned in Grades 6 and 7. Students need a transparency, a dry-erase marker, a straightedge, and a protractor.
Classwork
Opening Exercise (6 minutes)
Have students work with a partner on the Opening Exercise.
Opening Exercise
Use the diagram, which shows point C on line AB, to complete the table.
Angle Relationship
Two angles that share a vertex and a ray. The angles do not overlap.
Two or more adjacent angles with measures that sum to 180°
Two or more adjacent angles with measures that sum to 360° .
Two angles with measures that sum to 90° .
Two angles with measures that sum to 180°
⬛ What are the similarities and differences between supplementary angles and angles on a line?
Both relationships represent angles with measures that sum to 180°.
Angles on a line will always be adjacent to each other. Supplementary angles do not have to be adjacent to one another.
Supplementary angles consist of two angles, but angles on a line can consist of two or more angles.
⬛ How can we draw supplementary angles that are not adjacent angles?
We can draw two separate angles with measures that sum to 180°, but the angles do not share a common ray.
Example 1 (7 minutes)
Work through Example 1 as a class.
Example 1
1. The diagram shows two lines n and m that intersect at point A. Point X lies on n, and point Y
a. Rotate the figure 180° about point A. Label the image appropriately. Answer shown.
b. What do you know about the relationship between ∠ XAY and ∠ X'AY'? Explain. I know that ∠ XAY and ∠ X'AY' are congruent because rotations preserve angle measures.
c. If m∠XAY is 48°, then determine the measures of ∠YAX', ∠X'AY', and ∠Y'AX. Explain. The measure of ∠ YAX' is 132° because ∠ XAY and ∠ YAX' are supplementary angles and 180 - 48 = 132. The measure of ∠ X′AY' is 48° because ∠ X'AY and ∠ X'AY' are supplementary angles and 180 - 132 = 48. The measure of ∠ Y'AX is 132° because ∠ XAY and ∠ Y'AX are supplementary angles and 180 - 48 = 132
d. What do you notice about the angle measures of ∠XAY' and ∠X'AY? I notice the angle measures of ∠ XAY' and ∠ X'AY are equal.
We say that two angles are vertical angles if their sides form two pairs of opposite rays. What angles are vertical angles in the diagram in Example 1 after you rotated the figure 180° about point A?
∠ XAY and ∠ X'AY' are vertical angles. ∠ XAY' and ∠ X'AY are also vertical angles.
⬛ What can we say about the relationship between vertical angles?
Vertical angles are congruent.
Have students work on Exercises 1 and 2 independently.
Exercises
1. In the diagram, m∠ 3 = 27°. Determine the measures of the other unknown angles and identify the relevant angle relationships.
I know that
I
I know
2. In the diagram,
Determine the measures of each of the unknown angles and identify the relevant angle relationships.
Have students use a protractor to determine the measures of all the angles.
Example 2
2. The diagram shows two lines n and m that are cut by a transversal t 1 5 8
Determine the measure of each of the eight angles. Round to the nearest degree.
m∠ 1 = _________ m∠ 2 = _________
m∠ 3 = _________ m∠ 4 = _________
m∠ 5 = m∠ 6 =
m∠ 7 = _________ m∠ 8 = _________
⬛ What do you notice about the figure and the angle measures?
I notice that there are four sets of vertical angles.
I notice that ∠ 1 and ∠ 2 are supplementary angles with measures that sum to 180°, as well as ∠ 2 and ∠ 3; ∠ 3 and ∠ 4; ∠ 4 and ∠ 1; ∠ 5 and ∠ 6; ∠ 6 and ∠ 7; ∠ 7 and ∠ 8; ∠ 8 and ∠ 5
I notice that ∠ 1, ∠ 2, ∠ 3, and ∠ 4 are angles at a point with measures that sum to 360°, as well as ∠ 5, ∠ 6, ∠ 7, and ∠ 8
⬛ We say that ∠ 1 and ∠ 5 are corresponding angles because they are on the same side of the transversal in corresponding positions. In the diagram, ∠ 1 is the top left angle among the four angles created by line n and transversal t, and ∠ 5 is the top left angle among the four angles created by line m and transversal t.
⬛ What other angle pairs are corresponding angles?
∠ 2 and ∠ 6, ∠ 3 and ∠ 7, ∠ 4 and ∠ 8
Have students trace the diagram in Example 3 on their transparencies and label each point and line. Then have students perform the rotation and determine the measures of all the angles.
Example 3
3. The diagram shows two lines t and m that intersect at point A.
a. Rotate the figure by 180° around point C. Label the image of each point. Answer shown.
b. Label the angles with the numbers 1–8 in the same way they are labeled in Example 2. Then determine the measure of each of the eight angles.
⬛ What do you notice about lines m and m'?
Lines m and m' are parallel.
⬛ How do we know that lines m and m' are parallel?
When we rotate a line 180°, the line and its image are parallel.
⬛ What do you notice about the measures of the corresponding angles when lines m and m' are parallel?
I notice that the measures of the corresponding angles are equal.
⬛ Why are corresponding angles congruent when lines m and m' are parallel?
A rotation about point C maps ∠ EAB to ∠ E'A'B' and line m to m'. A rotation of a line 180° around a point creates parallel lines. Because rigid motions are angle-preserving, ∠ EAB is congruent to ∠ E'A'B'. Also, ∠ E'A'B' is congruent to ∠ CAʹDʹ because they are vertical angles, which means ∠ EAB is congruent to ∠ CAʹDʹ
⬛ So, ∠ EAB and ∠ CA'D' are both corresponding and congruent angles because line m and m' are parallel
Exercises 3–4 (5 minutes)
Have students work with a partner on Exercises 3 and 4.
Exercises 3–4
3. In the diagram, lines n and m are parallel and cut by a transversal t. Fill in the blank: ∠ 5 and are corresponding angles.
4. In the diagram, lines n and m are parallel and cut by a transversal t, and m∠ 2 = 108°. Determine the measures of each of the unknown angles and identify the relevant angle relationships.
72
; ∠ 1 and ∠ 2 are supplementary angles
108°; ∠ 4 and ∠ 2 vertical angles
108°; ∠ 6 and ∠ 5 are supplementary angles
108°; ∠ 8 and ∠ 5 are supplementary angles
;
3 and ∠ 2 are supplementary angles
°; ∠ 5 and ∠ 1 are corresponding angles
°; ∠ 7 and ∠ 5 are vertical angles
Closing (2 minutes)
Summarize, or have students summarize, the lesson and what they know about transformation to this point:
⬛ Vertical angles are created by two intersecting lines. We know vertical angles are congruent.
⬛ Corresponding angles are created when two lines are cut by a transversal. Corresponding angles are on the same side of the transversal in corresponding positions. We know corresponding angles are congruent when two parallel lines are cut by a transversal.
Lesson Summary
⬛ Adjacent angles are two angles that share a vertex and a ray. The angles do not overlap.
⬛ Angles on a line are two or more adjacent angles with measures that sum to 180°
⬛ Angles at a point are two or more adjacent angles with measures that sum to 360°
⬛ Complementary angles are two angles with measures that sum to 90° .
⬛ Supplementary angles are two angles with measures that sum to 180° .
⬛ Vertical angles are created by two intersecting lines. Vertical angles are congruent.
⬛ Corresponding angles are created when two lines are cut by a transversal. Corresponding angles are on the same side of the transversal in corresponding positions. Corresponding angles are congruent when two parallel lines are cut by a transversal.
Exit Ticket (5 minutes)
Exit Ticket
Use the diagram to complete parts (a)–(e). In the diagram, lines a and b are parallel.
a. Identify a pair of vertical angles.
b. Identify a pair of complementary angles.
c. Identify a pair of supplementary angles.
d. Identify an angle adjacent to ∠ 4.
e. Identify a pair of corresponding angles.
Use the diagram to complete parts (a)–(e). In the diagram, lines a and b are parallel.
a. Identify a pair of vertical angles.
Sample student response: ∠ 3 and ∠ 6
b. Identify a pair of complementary angles.
Sample student response: ∠ 1 and ∠ 2
c. Identify a pair of supplementary angles.
Sample student response: ∠ 9 and ∠ 10
d. Identify an angle adjacent to ∠ 4.
Sample student response: ∠ 5
e. Identify a pair of corresponding angles.
Sample student response: ∠ 2 and ∠ 9
1. Use the diagram to complete parts (a)–(e).
a. Identify all pairs of adjacent angles.
∠ 1 and ∠ 2, ∠ 2 and ∠ 3, ∠ 3 and ∠ 4, ∠ 4 and ∠ 1
b. Identify all pairs of complementary angles. There are no pairs of complementary angles.
c. Identify all pairs of supplementary angles.
∠ 1 and ∠ 2, ∠ 2 and ∠ 3, ∠ 3 and ∠ 4, ∠ 4 and ∠ 1
d. Identify all pairs of vertical angles.
∠ 1 and ∠ 3, ∠ 2 and ∠ 4
e. If m∠ 1 = 28°, determine the measures of the unknown angles.
m∠ 2 = 152°
m∠ 3 = 28°
m∠ 4 = 152°
2. Use the diagram to complete parts (a)–(c). Lines n and m are parallel and cut by transversal t 1 4 2 3 5 8 6 7 n t m
a. Identify all pairs of vertical angles.
∠ 1 and ∠ 3, ∠ 2 and ∠ 4, ∠ 5 and ∠ 7, ∠ 6 and ∠ 8
b. Identify all pairs of corresponding angles.
∠ 1 and ∠ 5, ∠ 2 and ∠ 6, ∠ 3 and ∠ 7, ∠ 4 and ∠ 8
c. If m∠ 1 = 55°, determine the measures of the unknown angles.
m∠ 2 = 125° m∠ 6 = 125°
m∠ 3 = 55° m∠ 7 = 55°
m∠ 4 = 125° m∠ 8 = 125°
m∠ 5 = 55°
10: Angle
3. In the diagram, m∠ 1 = 110° and m∠ 2 = 70°. Lily says ∠ 1 and ∠ 2 are supplementary angles. Sara says ∠ 1 and ∠ 2 are adjacent angles. Explain why both are correct.
1 2
Because m∠ 1 + m∠ 2 = 180°, then ∠ 1 and ∠ 2 are supplementary angles. They are adjacent angles because the two angles have the same vertex, share a ray, and do not overlap.
4. Dylan says that ∠ 1 and ∠ 2 are vertical angles because they both measure 90° 1 2 4 3
a. Explain Dylan’s mistake. Although ∠ 1 and ∠ 2 both measure 90°, their sides do not form opposite rays, so they are not vertical angles.
b. Identify a pair of vertical angles.
Student sample response: ∠ 1 and ∠ 3

Students use relationships among pairs of angles that are adjacent angles, complementary angles, supplementary angles, vertical angles, and corresponding angles to determine the measure of unknown angles.
Lesson Notes
In Lessons 11 and 12, students apply their knowledge of angle relationships and equations to solve unknown angle problems. They write equations based on angle relationships they learned about in Grade 7 and earlier in this topic. The problems in this lesson are more complex than the problems in Grade 7 because the diagrams combine angle relationships with equations that have variables on both sides.
Opening Exercise (5 minutes)
Have students complete the Opening Exercise on their own and then share their answers with a partner.
Opening Exercise
a. Draw complementary angles ∠ QRS and ∠ SRT, where the measure of ∠ QRS is 32° .
b. Determine the measure of ∠ SRT. 90° - 32° = 58° The measure of ∠ SRT is 58° .
c. Draw supplementary angles ∠ JKL and ∠ LKM, where the measure of ∠ JKL is 32°
11: Problem Solving with
d. Determine the measure of ∠ LKM
180° - 32° = 148° The measure of ∠LKM is 148°
Examples 1–4 (15 minutes)
Have students read Example 1. Then ask the following questions:
⬛ How is Example 1 similar to parts (a) and (b) of the Opening Exercise?
Example 1 is similar to parts (a) and (b) because they all have complementary angles.
⬛ How is Example 1 different from parts (a) and (b) of the Opening Exercise?
We had to draw the diagram in the Opening Exercise.
In Example 1, neither angle measure is given.
⬛ What can we to do to help determine the angle measures in the diagram?
We can write an equation.
Have students write an equation independently and invite a few students to share their equations with the class. Then have the students solve their equations and determine the measure of ∠ PQS. Look for students who stop after determining the value of x. Encourage them to read the question again to see if they can realize their error. Then ask them how they can determine the measure of ∠ PQS by using the value of x that they found.
Examples 1–4
1. The diagram shows rays QP, QS, and QR. Determine the measure of ∠ PQS
The measure of ∠ PQS is 25° .
Work though Examples 2–4 as a class. For each example, first have students study the diagram and then ask them which angle relationship can be used to help them write an equation to determine the value of x or y. Next, have the students write an equation for each example and invite a few students to share their equations. Have students work with a partner to solve the equation and determine the unknown angle measures, and then bring the class back together to confirm answers.
2. In the diagram, line XZ and ray YW intersect at point Y. Determine the measure of ∠ XYW.
+ 13)�
3. In the diagram, lines LN and MO intersect at point P. Determine the measure of ∠ MPN.
The measure of ∠ MPN is 56° .
4. In the diagram, m and n are parallel lines cut by a transversal
determine the value of x.
Exercises 1–4 (16 minutes)
Have students work independently on Exercises 1–4. After each exercise, have students discuss with a partner their equation, work, and answer.
Exercises 1–4
1. The diagram shows rays BA, BC, BD, and BE. Determine the measure of ∠ DBE
2. Use the diagram to determine the values of x, y, and z
3. In the diagram, lines AD, BF, and CG intersect at point H. Adrian thinks that ∠ AHB is a right angle. Is he correct? Show your thinking.
Adrian is not correct. The measure of ∠ AHB is 91°, not 90° .
4. In the diagram, m and n are parallel lines cut by a transversal t. Determine the values of x and y
Closing (4 minutes)
Summarize, or have students summarize, the lesson and what they know about angle relationships to this point:
⬛ When we are given a diagram, we can use angle relationships to write equations about the diagram.
– When two angles are supplementary, we know that their angle measures sum to 180°
– When two angles are complementary, we know that their angle measures sum to 90°
– When two angles are vertical or corresponding, we know that their angle measures are congruent.
Exit Ticket (5 minutes)
Name Date
Exit Ticket
The diagram shows line EC intersecting ray AD at point A. Determine the measures of ∠ DAE and
The diagram shows line EC intersecting ray AD at point A. Determine the measures of ∠ DAE and ∠ DAC.
The measure of ∠ DAE is 48°, and the measure of ∠ DAC is 132°
1. Use the diagram to determine the value of x
2. In the diagram, line AH and ray BC intersect at point B. Determine the measure of ∠ ABC (6
The measure of ∠ ABC is 48°
3. In the diagram, line QS intersects line RT at point U. Determine the measure of ∠ TUS.
The measure of ∠ TUS is 32°
4. In the diagram, n and m are parallel lines cut by a transversal
, determine the measures of ∠ 3 and ∠ 7
The measures of ∠ 3 and ∠ 7 are both 120° .
5. In the diagram, points A, C, and E are on a line, and ∠ ACB is a right angle. Determine the measure of ∠ DCE
The measure of ∠ DCE is 75

Students use relationships among pairs of angles that are adjacent angles, complementary angles, supplementary angles, vertical angles, and corresponding angles to determine the measure of unknown angles.
Lesson Notes
Lesson 12 continues where Lesson 11 ended and incorporates slightly more difficult problems. The lesson focuses on a jigsaw activity in which students describe the angle relationships and then use them to write and solve an equation for unknown angle measures.
Classwork
Opening Exercise (5 minutes)
Have students complete the Opening Exercise on their own and then share their answers with a partner.
Opening Exercise
In the diagram, line CF intersects line AD at point E.
a. Jennifer made an error when determining the measure of ∠ CED. Write a statement describing Jennifer’s error. Jennifer’s work:
The measure of ∠ CED is 36°
Jennifer should have made the sum of (x + 30) and (24 + 2x) equal to 180 because the two angles are supplementary.
12:
b. Determine the correct measure of
Split students into groups of five. Assign a different problem from Jigsaw Activity Exercises 1–5 to each of the five students in each group. Have the students assigned to each exercise meet in a specified area of the classroom. Tell them that these exercisespecific groups are referred to as “expert groups.” Allow students to work together in their expert groups on their assigned exercise for a few minutes. Then have students return to their original groups.
Have group members complete Jigsaw Activity Exercises 1–5, beginning with Exercise 1. Students should solve each exercise independently as the expert guides individual students when necessary, without giving away the answer. The expert can accomplish this by asking the individual students questions. Students should check their solutions. Once group members have finished solving the exercise and checking their solutions, the expert should facilitate a discussion that includes comparing solutions and asking students to share their strategies with each other. Then have all students repeat the process for the remaining exercises.
Circulate as the groups work. If additional support is needed, consider having the expert formulate a question. Only answer the expert’s questions, and rely on them to communicate the answer to the rest of the group.
Support students in organizing and planning for group work. Consider projecting a timer, posting group assignments, and providing written directions for students to reference, such as the following:
Small Group A
Members Your Expert Group
Eve #1
Kabir #2
Maya #3
Liam #4
Nora #5
Jigsaw directions:
1. Move to your expert group.
2. Collaborate to solve the Jigsaw Activity Exercise (8 minutes).
3. Return to your small group.
4. Collaborate to solve Jigsaw Activity Exercises 1–5 (25 minutes).
⬛ Act as the group expert for your assigned exercise.
⬛ Ask questions of other experts to ensure you understand what strategies to apply.
Jigsaw Activity Exercises
1. In the diagram, AC intersects DB at point E.
Scaffolding:
Geometric notation for lines and rays is used in this lesson. It may be useful to review the notation, pointing out that AB represents line AB and EB represents ray EB. Consider creating a visual aid such as an anchor chart for the jigsaw activity. Alternately, you can ensure that each expert group discusses the notation.
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
The measures of ∠ AEB and ∠ CED are equal because they are vertical angles. x x 4 120 30 = =
b. Determine the measures of ∠ DEA, ∠ AEB, and ∠ BEC
2. In the diagram, MP , NQ ,and OR intersect at point S
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
The measures of ∠ NSM, ∠ MSR, and ∠ RSQ sum to 180° because the angles are on a line.
b. Determine the measures of ∠ NSM, ∠ MSR, ∠ RSQ, ∠ OSP, ∠ PSQ, and ∠ OSN.
3. In the diagram, AD, BE , and FC intersect at point F.
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
The measures of ∠ EFD, ∠ DFC, and ∠ CFB sum to 180° because the angles are on a line.
b. Determine the measures of ∠ EFD, ∠ CFB,
4. In the diagram, RM , RN , RO , and RQ intersect at point R
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation. The measures of ∠ MRN, ∠ NRO, ∠ ORQ, and ∠ QRM sum to 360° because they are angles at a point.
b. Determine the measure of
Exit Ticket
In the diagram, PA, PB , PC , and PD intersect at point P
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
b. Determine the measures of ∠ BPC and ∠ APD
In the diagram, PA , PB , PC , and PD intersect at point P
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
The sum of the measures of ∠ DPA, ∠ APB, ∠ BPC, and ∠ CPD is 360° because they are angles at a point.
b. Determine the measures of ∠ BPC and ∠ APD
1. In the diagram, m and n are parallel lines cut by a transversal t. The measure of ∠1 is 125°. Determine the measure of each of the remaining angles.
The measures of ∠ 3, ∠ 5, and ∠ 7 are each 125° The measures of ∠ 2, ∠ 4, ∠ 6, and ∠ 8 are each 55°
2. In the diagram, AB and CD intersect at point P.
P (3x – 6)° (6x + 6)°
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
The measures of ∠ APC and ∠ BPC sum to 180° because they are supplementary angles. xx
() ()
66 180
b. Determine the measures of
3. In the diagram, BC , DE , AF , and AG intersect at point A.
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
The measures of ∠ BAD and ∠ EAC are equal because they are vertical angles.
b. Determine the measure
∠ GAE.
c. Determine the measure of ∠ EAB
4. In the diagram, PA , PB , PC , and PD intersect at point P
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
The sum of the measures of ∠ APB, ∠ BPC, ∠ CPD, and ∠ APD is 360° because they are angles at a point.
b. Determine the measure of ∠ APD
5. In the diagram, AF , PB , PC , PD , and PE intersect at point P. Determine the measure of ∠ BPC.
Name Date
1. Describe the transformation or sequence of transformations that maps Figure A to Figure B.
B
A
2. Use Figure ABCD to complete each part.
a. Graph the image of Figure ABCD after a reflection across the y-axis and then a translation right 3 units. Label the image by using prime notation.
b. Graph the image of Figure ABCD after a translation right 3 units and then a reflection across the y-axis. Label the image by using prime notation.
3. In this diagram, two lines meet at a point. Determine the measures of ∠1, ∠2, and ∠3. Describe the angle relationship used to determine each unknown angle measure.
4. In this diagram, rays ZB, ZC, and ZD have a common vertex, Z, on line AE. Determine the measures of ∠AZB and ∠CZD . Describe the angle relationship used to determine each unknown angle measure.
5. In this diagram, line PR intersects ray QS at point Q.
(4x + 7)° (2x – 13)°
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
b. Determine the measure of ∠PQS .
6. In this diagram, lines EF and GH intersect at point J.
(6x – 7)° (3x + 14)°
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
b. Determine the measure of ∠HJF
c. Determine the measure of ∠EJH .
STEP 1
Assessment
Task Item
1 8.7
Missing or incorrect answer and little evidence of reasoning or application of mathematics to solve the problem.
STEP 2
Missing or incorrect answer but evidence of some reasoning or application of mathematics to solve the problem.
STEP 3
A correct answer with some evidence of reasoning or application of mathematics to solve the problem. OR
An incorrect answer with substantial evidence of solid reasoning or application of mathematics to solve the problem.
STEP 4
A correct answer supported by substantial evidence of solid reasoning or application of mathematics to solve the problem.
2 a–b 8.7
Student does not attempt the problem or gives a completely incorrect answer.
Student does not attempt either part of the problem.
Student correctly identifies one of the transformations.
3 8.5
4 8.5
Student incorrectly determines all angle measures.
Student incorrectly describes all angle relationships.
Student performs both transformations but correctly performs only one of the transformations.
Student does not label the image or labels the image incorrectly.
Student correctly determines one angle measure.
Student correctly describes one angle relationship.
Student correctly identifies the two transformations but incorrectly identifies the number of units in the translation or states that the reflection is across the x-axis.
Student performs two transformations but may have performed them in the wrong order.
Student labels the image correctly.
Student correctly determines two angle measures.
Student correctly describes two angle relationships.
Student correctly identifies the two transformations.
Student does not attempt the problem.
Student incorrectly determines all angle measures. Conceptual errors, such as an equation that does not reflect the angle relationship, lead to incorrect answers. Student incorrectly describes all angle relationships.
Student correctly determines one angle measure. A calculation error, such as an arithmetic error, leads to an incorrect measure of the second angle. Student correctly describes one angle relationship.
Student correctly performs two transformations and labels the images correctly.
Student correctly determines 1 143 m∠= ° , ∠= ° m 237 , and ∠= ° m 3 143
Student correctly describes three angle relationships.
Student correctly determines ∠= ° mAZB 66 and ∠= ° mCZD 25 .
Student correctly describes both angle relationships.
5 a–b
8.5
6 a–c
8.5
Student incorrectly describes the angle relationship.
Student may set up an equation to solve for x, but no further work is shown.
Student incorrectly describes the angle relationship.
Student may set up an equation to solve for x, but no further work is shown.
Student incorrectly describes the angle relationship.
Student sets up an equation but incorrectly determines a value for x and does not determine any angle measure for ∠ PQS
Conceptual errors, such as an equation that does not reflect the angle relationship, leads to an incorrect value for x
Student incorrectly describes the angle relationship.
Student sets up an equation but incorrectly determines a value for x and does not determine any angle measures for ∠ HJF and ∠ EJH. Conceptual errors, such as an equation that does not reflect the angle relationship, lead to incorrect answers.
Student correctly describes the angle relationship.
Student sets up an equation and correctly determines the value of x
A calculation error, such as an arithmetic error, leads to an incorrect angle measure for ∠ PQS
Student correctly describes the angle relationship.
Student sets up an equation and correctly determines the value of x
A calculation error, such as an arithmetic error, leads to incorrect angle measures for ∠ HJF and/or ∠ EJH
Student correctly describes the angle relationship.
Student determines = x 31 and ∠= ° mPQS 131 , showing the correct equation.
Student correctly describes the angle relationship.
Student determines = x 7 , ∠= ° mHJF 35 , and ∠= ° mEJH 145 , showing the correct equation.
1. Describe the transformation or sequence of transformations that maps Figure A to Figure B.
A
Sample student response:
Figure A is translated up 4 units and then reflected across the y-axis.
2. Use Figure ABCD to complete each part.
a. Graph the image of Figure ABCD after a reflection across the y-axis and then a translation right 3 units. Label the image by using prime notation.
See the graph.
b. Graph the image of Figure ABCD after a translation right 3 units and then a reflection across the y-axis. Label the image by using prime notation.
See the graph.
3. In this diagram, two lines meet at a point. Determine the measures of ∠1, ∠2, and ∠3. Describe the angle relationship used to determine each unknown angle measure.
Sample student response:
The measure of ≠1 is 143ç because ≠1 and the given angle of 37ç are supplementary angles.
The measure of ≠2 is 37ç because ≠2 and the given angle of 37ç are vertical angles.
The measure of ≠3 is 143ç because ≠3 and ≠1 are vertical angles.
4. In this diagram, rays ZB, ZC, and ZD have a common vertex, Z, on line AE. Determine the measures of ∠AZB and CZD∠ . Describe the angle relationship used to determine each unknown angle measure.
I know that ≠BZC and ≠CZD are complementary angles.
65ç + m≠CZD = 90ç
m≠CZD = 25ç
I know that ≠AZB, ≠BZC, ≠CZD, and ≠DZE are angles on a line, so the sum of their angle measures is 180ç .
m≠AZB + m≠BZC + m≠CZD + m≠DZE = 180ç
m≠AZB + 65ç + 25ç + 24ç = 180ç
m≠AZB + 114ç = 180ç m≠AZB = 66ç
The measure of ≠AZB is 66ç, and the measure of ≠CZD is 25ç .
5. In this diagram, line PR intersects ray QS at point Q.
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
I know that ≠PQS and ≠SQR are supplementary angles, so the sum of their angle measures is 180ç
(2x - 13) + (4x + 7) = 180 6x - 6 = 180 6x = 186 x = 31
b. Determine the measure of ∠PQS . m≠PQS = (4x + 7)ç = (4(31) + 7)ç = 131ç
The measure of ≠PQS is 131ç .
6. In this diagram, lines EF and GH intersect at point J
(6x – 7)° (3x + 14)°
a. Write an equation to solve for x. Describe the angle relationship used to write the equation. Then solve the equation.
I know that ≠GJE and ≠HJF have the same angle measure because they are vertical angles. 3x + 14 = 6x - 7 3x + 14 - 3x = 6x - 7 - 3x 14 = 3x - 7
21 = 3x 7 = x
b. Determine the measure of ∠HJF m≠HJF = (6x - 7)ç = (6(7) - 7)ç = 35ç
The measure of ≠HJF is 35ç
c. Determine the measure of≠EJH. m≠EJH = 180ç - 35ç = 145ç
The measure of ≠EJH is 145ç .

8.7
Focus Standard: 8.7 The student will a. given a polygon, apply transformations, to include translations, reflections, and dilations, in the coordinate plane; and b. identify practical applications of transformations.
Instructional Days: 7
Lesson 13: What Lies Behind “Same Shape”? (E)1
Lesson 14: Properties of Dilations (P)
Lesson 15: Examples of Dilations (P)
Lesson 16: Fundamental Theorem of Similarity (FTS) (S)
Lesson 17: First Consequences of FTS (P)
Lesson 18: Dilations on the Coordinate Plane (P)
Lesson 19: Identifying Transformations (P)
Topic C begins by demonstrating the need for a precise definition of dilation instead of “same shape, different size” because dilation is applied to geometric shapes that are not polygons. Students begin their work with dilations off the coordinate plane by experimenting with dilations using a compass and straightedge to develop conceptual understanding. It is vital that students have access to these tools in order to develop an intuitive sense of dilation and to prepare for further work in high school Geometry.
In Lesson 13, dilation is defined, and the role of scale factor is demonstrated through the shrinking and magnification of figures. In Lesson 14, properties of dilations are discussed. As with rigid motions, students learn that dilations map lines to lines, segments to segments, and rays to rays. Students learn that dilations are angle-preserving transformations. In Lesson 15, students use a compass to perform dilations of figures with the same center and figures with different centers. In Lesson 15, students begin to look at figures that are dilated followed by congruence.1
In Lessons 16 and 17, students learn and use the fundamental theorem of similarity (FTS): If in △ABC, D is a point on line AB and E is a point on line AC, and r AB AD AC AE || || || || == , then r BC DE || || = , and lines DE and BC are parallel. Students verify this theorem, experimentally, using the lines of notebook paper. In Lesson 18, the
1Lesson Structure Key: P-Problem Set Lesson, M-Modeling Cycle Lesson, E-Exploration Lesson, S-Socratic Lesson


work with dilations is tied to the coordinate plane; students use what they learned in Lessons 16 and 17 to conclude that when the center of dilation is the origin, the coordinates of a dilated point are found by multiplying each coordinate of the ordered pair by the scale factor. Students first practice finding the location of dilated points in isolation; then, students locate the dilated points that comprise two-dimensional figures. In Lesson 19, students analyze preimages and images and then identify and describe the transformations performed.

⬛ Students learn the definition of dilation and why “same shape” is not good enough to say when two figures are similar.
⬛ Students know that dilations magnify and shrink figures.
Lesson Notes
The goal of Topics C and D is to arrive at a precise understanding of the concept of similarity: What does it mean for two geometric figures to have “the same shape but not necessarily the same size?” Note that students explored the concept of congruence in Grade 6 and Topics A and B of Module 4 in Grade 8. Students are now being introduced to the concept of dilation. A similarity transformation (or a similarity) is a composition of a finite number of dilations or basic rigid motions.
The basic references for this module are Teaching Geometry According to the Common Core Standards (http://math.berkeley.edu/~wu/Progressions_Geometry.pdf ) and Pre-Algebra (http://math.berkeley.edu/~wu/PreAlgebra.pdf ), both by Hung-Hsi Wu. The latter is identical to the document cited on page 92 of the Common Core State Standards for Mathematics: Wu, H., “Lecture Notes for the 2009 Pre-Algebra Institute,” September 15, 2009.
Exploratory Challenge (10 minutes)
Have students examine the following pairs of figures and record their thoughts.
Exploratory Challenge
Two geometric figures are said to be similar if they have the same shape but not necessarily the same size. Using that informal definition, are the following pairs of figures similar to one another? Explain.
Pair A:

Yes, these figures appear to be similar. They are the same shape, but one is larger than the other, or one is smaller than the other
Pair B:

No, these figures do not appear to be similar. One looks like a square and the other like a rectangle.
What Lies Behind “Same Shape”?
Pair C:
These figures appear to be exactly the same, which means they are congruent.
Pair D:
Yes, these figures appear to be similar. They are both circles, but they are different sizes.
Pair E:

Yes, these figures appear to be similar. They are the same shape, but they are different in size
Pair F:

Yes, these figures appear to be similar. The faces look the same, but they are just different in size.
Pair G:

They do not look to be similar, but I’m not sure. They are both happy faces, but one is squished compared to the other.
Pair H: No, these two figures do not look to be similar. Each is curved but shaped differently

What Lies Behind “Same Shape”?
Discussion (20 minutes)
⬛ In mathematics, we want to be absolutely sure about what we are saying. Therefore, we need precise definitions for similar figures. For example, you may have thought that the figures in Pair G are similar because they are both happy faces. However, a precise definition of similarity tells you that they are in fact NOT similar because the parts of the face are not in proportion. Think about trying to adjust the size of a digital picture. When you grab from the corner of the photo, everything looks relatively the same (i.e., it looks to be in proportion), but when you grab from the sides, top, or bottom of the photo, the picture does not look quite right (i.e., things are not in proportion).

Note to Teacher:
Choose a picture to demonstrate this in the classroom.
⬛ You probably said that the curved figures in Pair H are not similar. However, a precise definition of similarity tells you that in fact they ARE similar. They are shapes called parabolas that you will learn about in Algebra. For now, just know that one of the curved figures has been dilated according to a specific factor.
⬛ Now we must discuss what is meant by a transformation of the plane known as dilation. In the next few lessons, we will use dilation to develop a precise definition for similar figures.
⬛ Definition: For a positive number r, a dilation with center O and scale factor r is the transformation of the plane that maps O to itself, and maps each remaining point P of the plane to its image P′ on the ray OP so that |OP′ | = r|OP|. That is, it is the transformation that assigns to each point P of the plane a point Dilation(P) so that
1. Dilation(O) = O (i.e., a dilation does not move the center of dilation)
Scaffolding:
Explain to students that the notation |OP| means the length of the segment OP.
2. If P ≠ O, then the point Dilation(P) (to be denoted more simply by P′) is the point on the ray OP so that |OP′ | = r|OP|.

⬛ In other words, a dilation is a rule that moves each point P along the ray emanating from the center O to a new point P′ on that ray such that the distance |OP′| is r times the distance |OP|.
⬛ In previous grades, you did scale drawings of real-world objects. When a figure shrinks in size, the scale factor r will be less than one but greater than zero (i.e., 0 < r < 1). In this case, a dilation where 0 < r < 1, every point in the plane is pulled toward the center O proportionally the same amount.
⬛ You may have also done scale drawings of real-world objects where a very small object was drawn larger than it is in real life. When a figure is magnified (i.e., made larger in size), the scale factor r will be greater than 1 (i.e., r > 1). In this case, a dilation where r > 1, every point in the plane is pushed away from the center O proportionally the same amount.
⬛ If figures shrink in size when the scale factor is 0 < r < 1 and magnify when the scale factor is r > 1, what happens when the scale factor is exactly one (i.e., r = 1)?
When the scale factor is r = 1, the figure does not change in size. It does not shrink or magnify. It remains congruent to the original figure
What Lies Behind “Same Shape”?
⬛ What does proportionally the same amount mean with respect to the change in size that a dilation causes?
Think about this example: If you have a segment, OP, of length 3 cm that is dilated from a center O by a scale factor r = 4, how long is the dilated segment OP′?
The dilated segment OP′ should be 4 times longer than the original (i.e., 4 · 3 cm or 12 cm).
⬛ For dilation, we think about the measures of the segments accordingly:
|OP′| = r|OP| The length of the dilated segment OP′ is equal to the length of the original segment OP multiplied by the scale factor r
⬛ Now think about this example: If you have a segment OQ of length 21 cm, and it is dilated from a center O by a scale factor 1 3 r = , how long is the dilated segment OQ′?
According to the definition of dilation, the length of the dilated segment is 21 1 3 (i.e., 1 3 the original length). Therefore, the dilated segment is 7 cm. This makes sense because the scale factor is less than one, so we expect the length of the side to be shrunk.
⬛ To determine if one object is a dilated version of another, you can measure their individual lengths and check to see that the length of the original figure, multiplied by the scale factor, is equal to the dilated length.
Exercises (8 minutes)
Have students check to see if figures are, in fact, dilations and find measures using scale factor.
Exercises
1. Given |OP| = 5 in.
a. If segment OP is dilated by a scale factor r = 4, what is the length of segment OP′?
|OP′| = 20 in because the scale factor multiplied by the length of the original segment is 20; that is, 4 · 5 = 20
b. If segment OP is dilated by a scale factor r = 1 2 , what is the length of segment OP′?
|OP′| = 2.5 in. because the scale factor multiplied by the length of the original segment is 2.5; that is,
Use the diagram below to answer Exercises 2–6. Let there be a dilation from center O. Then, Dilation(P) = P′ and Dilation(Q) = Q′. In the diagram below, |OP| = 3 cm and |OQ| = 4 cm, as shown.

2. If the scale factor is r = 3, what is the length of segment OP′?
The length of the segment OP′ is 9 cm.
What Lies Behind “Same Shape”?
3. Use the definition of dilation to show that your answer to Exercise 2 is correct. |OP′| = r |OP|; therefore, |OP′| = 3 3 cm = 9 cm.
4. If the scale factor is r = 3, what is the length of segment OQ′?
The length of the segment OQ′ is 12 cm.
5. Use the definition of dilation to show that your answer to Exercise 4 is correct. |OQ′| = r |OQ|; therefore, |OQ′| = 3 4 cm = 12 cm.
6. If you know that |OP| = 3, |OP′| = 9, how could you use that information to determine the scale factor?
Since we know |OP′| = r |OP|, we can solve for r: OP OP || || ′ = r, which is 9 3 = r or 3 = r.
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We need a precise definition for similar that includes the use of dilation.
⬛ A dilation magnifies a figure when the scale factor is greater than one, and a dilation shrinks a figure when the scale factor is greater than zero but less than one.
⬛ If we multiply a segment by the scale factor, we get the length of the dilated segment (i.e., |OP′| = r|OP|).
Lesson Summary
Definition: For a positive number r, a dilation with center O and scale factor r is the transformation of the plane that maps O to itself, and maps each remaining point P of the plane to its image P′ on the ray OP so that |OP′| = r|OP|. That is, it is the transformation that assigns to each point P of the plane a point Dilation(P) so that
1. Dilation(O) = O (i.e., a dilation does not move the center of dilation).

2. If P ≠ O, then the point Dilation(P) (to be denoted more simply by P′) is the point on the ray OP so that |OP′| = r|OP|.
In other words, a dilation is a rule that moves each point P along the ray emanating from the center O to a new point P′ on that ray such that the distance |OP′| is r times the distance |OP|.
What Lies Behind “Same Shape”?
Exit Ticket
1. Why do we need a better definition for similarity than “same shape, not the same size”?
2. Use the diagram below. Let there be a dilation from center O with scale factor r = 3. Then, Dilation(P) = P′. In the diagram below, |OP| = 5 cm. What is |OP′|? Show your work.

3. Use the diagram below. Let there be a dilation from center O. Then, Dilation(P) = P′. In the diagram below, |OP| = 18 cm and |OP′| = 9 cm. What is the scale factor r? Show your work.

What Lies Behind “Same Shape”? Name
1. Why do we need a better definition for similarity than “same shape, not the same size”?
We need a better definition that includes dilation and a scale factor because some figures may look to be similar (e.g., the smiley faces), but we cannot know for sure unless we can check the proportionality. Other figures (e.g., the parabolas) may not look similar but are. We need a definition so that we are not just guessing if they are similar by looking at them
2. Use the diagram below. Let there be a dilation from center O with scale factor r = 3. Then, Dilation(P) = P′. In the diagram below, |OP| = 5 cm. What is |OP′|? Show your work.
Since |OP′| = r |OP|, then
|OP′| = 3 5 cm, |OP′| = 15 cm.

3. Use the diagram below. Let there be a dilation from center O. Then, Dilation(P) = P′. In the diagram below, |OP| = 18 cm and |OP′| = 9 cm. What is the scale factor r? Show your work.
Since |OP′| = r |OP|, then 9 cm = r 18 cm, = r 1 2

Have students practice using the definition of dilation and finding lengths according to a scale factor.
1. Let there be a dilation from center O. Then, Dilation(P) = P′ and Dilation(Q) = Q′. Examine the drawing below. What can you determine about the scale factor of the dilation?

The scale factor must be greater than one, r > 1, because the dilated points are farther from the center than the original points.
What Lies Behind “Same Shape”?
2. Let there be a dilation from center O. Then, Dilation(P) = P′, and Dilation(Q) = Q′. Examine the drawing below. What can you determine about the scale factor of the dilation?

The scale factor must be greater than zero but less than one, 0 < r < 1, because the dilated points are closer to the center than the original points.
3. Let there be a dilation from center O with a scale factor r = 4. Then, Dilation(P) = P′ and Dilation(Q) = Q′ . |OP| = 3.2 cm, and |OQ| = 2.7 cm, as shown. Use the drawing below to answer parts (a) and (b). The drawing is not to scale.

a. Use the definition of dilation to determine |OP′|. |OP′| = r|OP|; therefore, |OP′| = 4 · (3.2 cm) = 12.8 cm.
b. Use the definition of dilation to determine |OQ′|. |OQ′| = r|OQ|; therefore, |OQ′| = 4 · (2.7 cm) = 10.8 cm.
What Lies Behind “Same Shape”?
4. Let there be a dilation from center O with a scale factor r. Then, Dilation(A) = A′, Dilation(B) = B′, and Dilation(C) = C′. |OA| = 3, |OB| = 15, |OC| = 6, and |OB′ | = 5, as shown. Use the drawing below to answer parts (a)–(c).

a. Using the definition of dilation with lengths OB and OB′, determine the scale factor of the dilation.
|OB′| = r|OB|, which means 5 = r 15; therefore, r = 1 3
b. Use the definition of dilation to determine |OA′|. |OA′| = OA 1 3 || ; therefore, |OA′| =⋅ = 1 3 31, and |OA′| = 1.
c. Use the definition of dilation to determine |OC′|. |OC′| = OC 1 3 ||; therefore, |OC′| =⋅ = 1 3 62 , and |OC′| = 2.
Lies Behind “Same Shape”?

Student Outcomes
⬛ Students learn how to use a compass and a ruler to perform dilations.
⬛ Students learn that dilations map lines to lines, segments to segments, and rays to rays. Students know that dilations are angle-preserving.
Lesson Notes
In this lesson, students become familiar with using a straightedge and a compass to perform dilations. Students can follow along on their own papers as the teacher works through Examples 1–3 so that students can begin to develop independence with these tools.
Classwork
Discussion (5 minutes)
Ask students to make a conjecture about how dilations affect lines, segments, and rays.
⬛ Fold a piece of paper into fourths. At the top of each fourth, write one each of line, segment, ray, and angle along with a diagram of each. What do you think happens to each of these after a dilation? Explain.
Have students spend a minute recording their thoughts, share with a partner, and then the whole class. Consider recording the different conjectures on a class chart. Then, explain to students that, in this lesson, they investigate what happens to each of these figures after their dilation; that is, they test their conjectures.
Example 1 (5 minutes)
Examples 1–3 demonstrate that dilations map lines to lines and how to use a compass to dilate.
⬛ This example shows that a dilation maps a line to a line. This means that the image of a line, after undergoing a dilation, is also a line. Given line L, we dilate with a scale factor r = 2 from center O. Before we begin, exactly how many lines can be drawn through two points?
Only one line can be drawn through two points
⬛ To dilate the line, we choose two points on L (points P and Q) to dilate. When we connect the dilated images of P and Q (P′ and Q′ ), we have the dilated image of line L, L′
⬛ First, let’s select a center O off the line L and two points P and Q on line L
Examples 1–2: Dilations Map Lines to Lines

⬛ Second, we draw rays from center O through each of the points P and Q. We want to make sure that the points O, P, and P′ (the dilated P) lie on the same line (i.e., are collinear). That is what keeps the dilated image “in proportion.” Think back to the last lesson where we saw how the size of the picture changed when pulling the corners compared to the sides. Pulling from the corners kept the picture “in proportion.” The way we achieve this in diagrams is by drawing rays and making sure that the center, the point, and the dilated point are all on the same line.

⬛ Next, we use our compass to measure the distance from O to P. Do this by putting the point of the compass on point O, and adjust the radius of the compass to draw an arc through point P. Once you have the compass set, move the point of the compass to P, and make a mark along the ray OP (without changing the radius of the compass) to mark P′. Recall that the dilated point P′ is the distance 2|OP| (i.e., |OP′| = 2|OP|). The compass helps us to find the location of P′ so that it is exactly twice the length of segment OP. Use your ruler to prove this to students.

⬛ Next, we repeat this process to locate Q′ .

Properties of Dilations
⬛ Finally, connect points P′ and Q′ to draw line L′

⬛ Return to your conjecture from before, or look at our class list. Which conjectures were accurate? How do you know?
Answers may vary depending on conjectures made by the class. Students should identify that the conjecture of a line mapping to a line under a dilation is correct
⬛ What do you think would happen if we selected a different location for the center or for the points P and Q?
Points O, P, and Q are arbitrary points. That means that they could have been anywhere on the plane. For that reason, the results would be the same; that is, the dilation would still produce a line, and the line would be parallel to the original
⬛ Look at the drawing again, and imagine using our transparency to translate the segment OP along vector OP to segment PP′ and to translate the segment OQ along vector OQ to segment QQ′. With that information, can you say anything more about lines L and L′?
Since P and Q are arbitrary points on line L, and translations map lines to parallel lines when the vector is not parallel to or part of the original line, we can say that L is parallel to L′ .
⬛ How would the work we did change if the scale factor were r = 3 instead of r = 2?
We would have to find a point P′ so that |OP′| is 3 times the length of segment OP instead of twice the length of segment OP. Same for the point Q′
⬛ Do you think line L would still be a line under a dilation with scale factor r = 3? Would the dilated line, L′, still be parallel to L? (Allow time for students to talk to their partners and make predictions.)
Yes, it is still a line, and it would still be parallel to line L. The scale factor being three instead of two simply means that we would perform the translation of the points P′ and Q′ more than once, but the result would be the same
⬛ Here is what would happen with scale factor r = 3.

Example 3 (2 minutes)
Example 3: Dilations Map Lines to Lines

⬛ What would happen if the center O were on line L? (Allow time for students to talk to their partners and make predictions.)
If the center O were on line L, and if we pick points P and Q on L, then the dilations of points P and Q, P′ and Q′, would also be on L. That means that line L and its dilated image, line L′, would coincide

⬛ What we have shown with these three examples is that a line, after a dilation, is still a line. Mathematicians like to say that dilations map lines to lines.
Properties of Dilations
Example 4 (5 minutes)
Example 4 demonstrates that dilations map rays to rays. It also demonstrates how to use a ruler to dilate with scale factor 1 2 r = . Similar to Example 1, before this example, discuss the conjectures students developed about rays. Also, consider getting students started and then asking them to finish with a partner.
⬛ This example shows that a dilation maps a ray to a ray. Given ray AB , we dilate with a scale factor 1 2 r = from center O
⬛ To dilate the ray, we choose a center O off of the ray. Like before, we draw rays from center O through points A and B.

⬛ Since our scale factor is 1 2 r = , we need to use a ruler to measure the length of segments OA and OB. When you get into high school Geometry, you learn how to use a compass to handle scale factors that are greater than zero but less than one, like our 1 2 r = . For now, we use a ruler.

⬛ Since our scale factor is 1 2 r = , we know that the dilated segment, OA′, must be equal to 1 2 the length of segment OA (i.e., |OA′| 1 2 = |OA|). Then, |OA′| must be 5 1 2 ; therefore, |OA′| = 2 5. What must |OB′| be?
We know that |OB′| 1 2 = |OB|; therefore, |OB′| 84 1 2 =⋅ = , and |OB′| = 4.
⬛ Now that we know the lengths of segments OA′ and OB′, we use a ruler to mark off those points on their respective rays.

⬛ Finally, we connect point A′ through point B′. With your partner, evaluate your conjecture. What happened to our ray after the dilation?
When we connect point A′ through point B′, then we have the ray A′B′ .

14:
Properties of Dilations
⬛ What do you think would have happened if we selected our center O as a point on the ray AB ?
If our center O were on the ray, then the ray AB would coincide with its dilated image A′B′ , which is similar to what we saw when the line L was dilated from a center O on it
In this exercise, students verify experimentally that segments are mapped to segments under a dilation. They also verify experimentally that dilations map angles to angles of the same degree. Before students begin, revisit the conjectures made at the beginning of class, and identify which were true.
Exercise
Given center O and triangle ABC, dilate the triangle from center O with a scale factor r = 3.

a. Note that the triangle ABC is made up of segments AB, BC, and CA. Were the dilated images of these segments still segments?
Yes, when dilated, the segments were still segments
b. Measure the length of the segments AB and A′B′. What do you notice? (Think about the definition of dilation.)
The segment A′B′ was three times the length of segment AB. This fits with the definition of dilation, that is, |A′B′| = r|AB|
c. Verify the claim you made in part (b) by measuring and comparing the lengths of segments BC and B′C′ and segments CA and C′A′. What does this mean in terms of the segments formed between dilated points?
This means that dilations affect segments in the same way they do points. Specifically, the lengths of segments are dilated according to the scale factor.
Properties of Dilations
d. Measure ∠ABC and ∠A′B′C′. What do you notice?
The angles are equal in measure.
e. Verify the claim you made in part (d) by measuring and comparing the following sets of angles: (1) ∠BCA and ∠B′C′A′ and (2) ∠CAB and ∠C′A′B′. What does that mean in terms of dilations with respect to angles and their degrees?
It means that dilations map angles to angles, and the dilation preserves the measures of the angles.
Discussion (4 minutes)
⬛ The exercise you just completed and the examples from earlier in the lesson demonstrate several properties of dilations:
1. Dilations map lines to lines, rays to rays, and segments to segments.
2. Dilations map angles to angles of the same degree.
⬛ In this lesson, we have verified experimentally a theorem about dilations. Theorem: Let a dilation with center O and scale factor r be given. For any two points P and Q in the plane, let P′ = Dilation(P) and Q′ = Dilation(Q) Then:
1. For any P and Q, |P′Q′| = r|PQ|.
2. For any P and Q, the segment joining P to Q is mapped to the segment joining P′ and Q′ (Exercise 1), the ray from P to Q is mapped to the ray from P′ to Q′ (Example 4), and the line joining P to Q is mapped to the line joining P′ to Q′ (Examples 1–3).
3. Any angle is mapped to an angle of the same degree (Exercise 1).
⬛ We have observed that the length of the dilated line segment is the length of the original segment, multiplied by the scale factor. We have also observed that the measure of an angle remains unchanged after a dilation.
Consider using one (or both) of the above explanations about what dilation does to a line segment and an angle.
Closing (3 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We know how to use a compass to dilate when the scale factor r > 1. We know how to use a ruler to dilate when the scale factor 0 < r < 1
⬛ Dilations map lines to lines, rays to rays, and segments to segments.
⬛ Dilations map angles to angles of the same degree.
Lesson Summary
Dilations map lines to lines, rays to rays, and segments to segments. Dilations map angles to angles of the same degree.
Exit Ticket (4 minutes)
Properties of Dilations
Name Date
Exit Ticket
1. Given center O and quadrilateral ABCD, using a compass and ruler, dilate the figure from center O by a scale factor of r = 2. Label the dilated quadrilateral A′B′C′D′

2. Describe what you learned today about what happens to lines, segments, rays, and angles after a dilation.
1. Given center O and quadrilateral ABCD, using a compass and ruler, dilate the figure from center O by a scale factor of r = 2. Label the dilated quadrilateral A′B′C′D′.
Sample student work is shown below. Verify that students have magnified the image ABCD.

2. Describe what you learned today about what happens to lines, segments, rays, and angles after a dilation. We learned that a dilation maps a line to a line, a segment to a segment, a ray to a ray, and an angle to an angle. Further, the length of the dilated line segment is exactly r (the scale factor) times the length of the original segment. Also, the measure of a dilated angle remains unchanged compared to the original angle.
Students practice dilating figures with different scale factors.
1. Use a ruler to dilate the following figure from center O, with scale factor r = 1 2 .
The dilated figure is shown in red below. Verify that students have dilated according to the scale factor r = 1 2
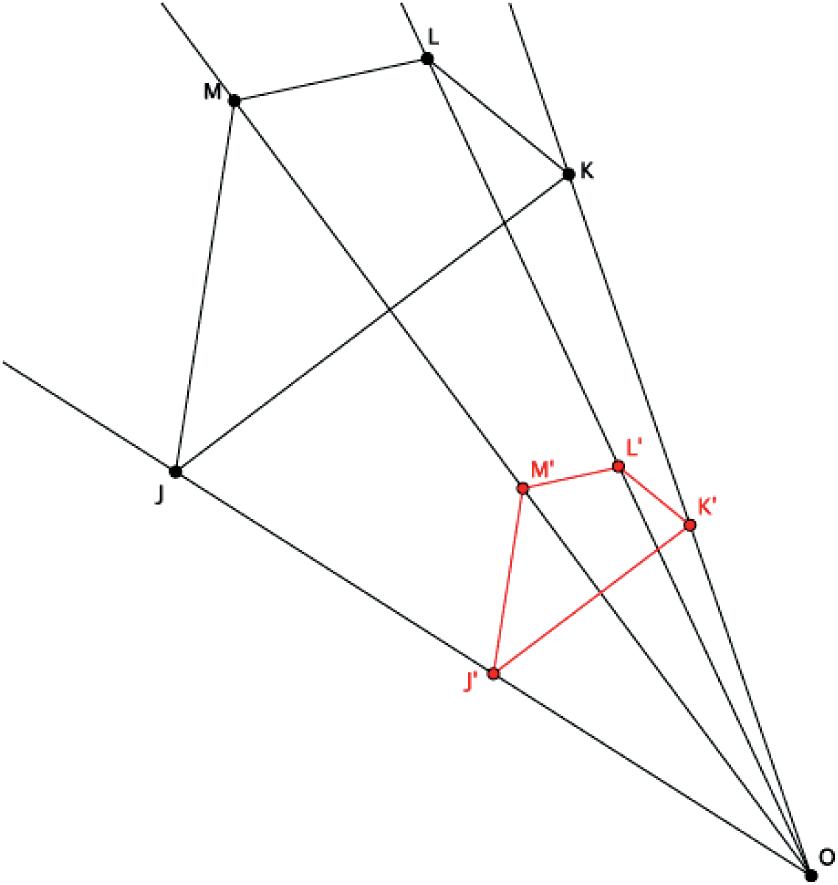
2. Use a compass to dilate the figure ABCDE from center O, with scale factor r = 2.
The figure in red below shows the dilated image of ABCDE.

Properties of Dilations
a. Dilate the same figure, ABCDE, from a new center, O′, with scale factor r = 2. Use double primes (A″B″C″D″E″) to distinguish this image from the original.
The figure in blue below shows the dilated figure A″B″C″D″E″

b. What rigid motion, or sequence of rigid motions, would map A″B″C″D″E″ to A′B′C′D′E′?
A translation along vector A″A′ (or any vector that connects a point of A″B″C″D″E″ and its corresponding point of A′B′C′D′E′) would map the figure A″B″C″D″E″ to A′B′C′D′E′
The image below (with rays removed for clarity) shows the vector A″A′ .

Properties of Dilations
3. Given center O and triangle ABC, dilate the figure from center O by a scale factor of r = 1 4 . Label the dilated triangle A′B′C′

4. A line segment AB undergoes a dilation. Based on today’s lesson, what is the image of the segment?
The segment dilates as a segment.
5. ∠GHI measures 78°. After a dilation, what is the measure of ∠G′H′I′? How do you know?
The measure of ∠G′H′I′ is 78°. Dilations preserve angle measure, so it remains the same size as ∠GHI.

⬛ Students know that dilations map circles to circles and ellipses to ellipses.
⬛ Students know that to shrink or magnify a dilated figure back to its original size from center O with scale factor r the figure must be dilated by a scale factor of 1 r
Example 1 (8 minutes)
Ask students to (1) describe how they would plan to dilate a circle and (2) conjecture about what the result is when they dilate a circle. Consider asking them to collaborate with a partner and to share their plans and conjectures with the class. Then, consider having students attempt to dilate the circle on their own, based on their plans. As necessary, show students how to dilate a curved figure, namely, circle A (i.e., circle with center A).
⬛ We want to find out how many points we need to dilate in order to develop an image of circle A from center of dilation O at the origin of the graph, with scale factor r = 3.
Example 1
Dilate circle A from center O at the origin by scale factor r = 3.

Examples of Dilations
⬛ Are three points enough? Let’s try.
⬛ (Show a picture of three dilated points.) If we connect these three dilated points, what image do we get?
With just three points, the image looks like a triangle

⬛ What if we dilate a fourth point? Is that enough? Let’s try.
⬛ (Show the picture of four dilated points.) If we connect these four dilated points, what image do we get?
With four points, the image looks like a quadrilateral

Examples of Dilations
⬛ What if we dilate five, six, or ten points? What do you think?
The more points that are dilated, the more the image looks like a circle.
⬛ (Show the picture with many dilated points.)

⬛ Notice that the shape of the dilated image is now unmistakably a circle. Dilations map circles to circles, so it is important that when we dilate a circle we choose our points carefully.
⬛ Would we have an image that looked like a circle if all of the points we considered were located on just one part of the circle? For example, what if all of our points were located on just the top half of the circle? Would the dilated points produce an image of the circle?

Examples of Dilations
⬛ Or consider the image when we select points just on the lower half of the circle:

⬛ Consider the image when the points are focused on just the sides of the circle:

⬛ The images are not good enough to truly show that the original figure was a circle.
⬛ How should we select points to dilate when we have a curved figure?
We should select points on all parts of the curve, not just those points focused in one area.
⬛ The number of points to dilate that is enough is as many as are needed to produce a dilated image that looks like the original. For curved figures, like this circle, the more points you dilate the better. The location of the points you choose to dilate is also important. The points selected to dilate should be spread out evenly on the curve.
Examples of Dilations
Exercises 1–2 (10 minutes)
Prior to this exercise, ask students to make a conjecture about what figure results when we dilate an ellipse. Similarly, ask them to develop a plan for how they perform the dilation. Then, have students dilate an ellipse on the coordinate plane.
Exercises 1–2
1. Dilate ellipse E, from center O at the origin of the graph, with scale factor r = 2. Use as many points as necessary to develop the dilated image of ellipse E.
The dilated image of E is shown in red below. Verify that students have dilated enough points evenly placed to get an image that resembles an ellipse

2. What shape was the dilated image?
The dilated image was an ellipse. Dilations map ellipses to ellipses.
Examples of Dilations
Example 2 (4 minutes)
⬛ In the picture below, we have triangle ABC, that has been dilated from center O, by a scale factor of 1 3 r � . It is noted by A′B′C′ .

Ask students what can be done to map this new triangle, triangle A′B′C′, back to the original. Tell them to be as specific as possible. Students should write their conjectures or share with a partner.
⬛ Let’s use the definition of dilation and some side lengths to help us figure out how to map triangle A′B′C′ back onto triangle ABC. How are the lengths |OA′| and |OA| related?
We know by the definition of dilation that |OA′| = r|OA|.
⬛ We know that r = 1 3 . Let’s say that the length of segment OA is 6 units (we can pick any number, but 6 makes it easy for us to compute). What is the length of segment OA′?
Since |OA′| = OA || 1 3 , and we are saying that the length of segment OA is 6, then |OA′| 1 3 = 6= 2 , and |OA′| = 2 units.
⬛ Now, since we want to dilate triangle A′B′C′ to the size of triangle ABC, we need to know what scale factor r is required so that |OA| = r|OA′|. What scale factor should we use, and why?
We need a scale factor r = 3 because we want |OA| = r|OA′| Using the lengths from before, we have 6 = r · 2 Therefore, r = 3
⬛ Now that we know the scale factor, what precise dilation would map triangle A′B′C′ onto triangle ABC?
A dilation from center O with scale factor r = 3
Examples of Dilations
Example 3 (4 minutes)
⬛ In the picture below, we have triangle DEF that has been dilated from center O by a scale factor of r = 4. It is noted by D′E′F′ .

⬛ Based on the example we just did, make a conjecture about how we could map this new triangle D′E′F′ back onto the original triangle.
Let students attempt to prove their conjectures on their own or with a partner. If necessary, use the scaffolding questions that follow.
⬛ What is the difference between this problem and the last?
This time the scale factor is greater than one, so we need to shrink triangle D′E′F′ to the size of triangle DEF.
⬛ We know that r = 4. Let’s say that the length of segment OF is 3 units. What is the length of segment OF′?
Since |OF′| = r|OF| and we are saying that the length of segment OF is 3, then |OF′| = 4 · 3 = 12, and |OF′| = 12 units.
⬛ Now, since we want to dilate triangle D′E′F′ to the size of triangle DEF, we need to know what scale factor r is required so that |OF| = r|OF′|. What scale factor should we use, and why?
We need a scale factor r = 1 4 because we want |OF| = r|OF′|. Using the lengths from before, we have 3 = r · 12 Therefore, r = 1 4
⬛ What precise dilation would make triangle D′E′F′ the same size as triangle DEF?
A dilation from center O with scale factor r = 1 4 would make triangle D′E′F′ the same size as triangle DEF
Examples of Dilations
Discussion (4 minutes)
⬛ In the last two problems, we needed to figure out the scale factor r that would bring a dilated figure back to the size of the original. In one case, the figure was dilated by a scale factor r = 1 3 , and to map the dilated figure back to the original size we needed to magnify it by a scale factor r = 3. In the other case, the figure was dilated by a scale factor r = 4, and to map the dilated figure back to the original size we needed to shrink it by a scale factor r = 1 4 . Is there any relationship between the scale factors in each case?
The scale factors of 3 and 1 3 are reciprocals of one another, and so are 4 and 1 4
⬛ If a figure is dilated from a center O by a scale factor r = 5, what scale factor would shrink it back to its original size?
A scale factor of 1 5
⬛ If a figure is dilated from a center O by a scale factor r = 2 3 , what scale factor would magnify it back to its original size?
A scale factor of 3 2
⬛ Based on these examples and the two triangles we examined, determine a general rule or way of determining how to find the scale factor that maps a dilated figure back to its original size.
Give students time to write and talk with their partners. Lead a discussion that results in the crystallization of the rule below.
⬛ To shrink or magnify a dilated figure from center O with scale factor r back to its original size, you must dilate the figure by a scale factor of r 1 .
Allow students to work in pairs to describe sequences that map one figure onto another.
Exercise 3
3. Triangle ABC has been dilated from center
O by a scale factor of r � 1 4 denoted by triangle A′B′C′. Using a centimeter ruler, verify that it would take a scale factor of r = 4 from center O to map triangle A′B′C′ onto triangle ABC
Sample measurements provided. Note that, due to print variations, the measurements may be slightly different.
Verify that students have measured the lengths of segments from center O to each of the dilated points. Then, verify that students have multiplied each of the lengths by 4 to see that it really is the length of the segments from center O to the original points.

Examples of Dilations
Closing (5 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ To dilate curved figures, we need to use a lot of points spread evenly throughout the figure; therefore, we focused on the curves to produce a good image of the original figure.
⬛ If a figure is dilated by scale factor r, we must dilate it by a scale factor of 1 r to bring the dilated figure back to the original size. For example, if a scale factor is r = 4, then to bring a dilated figure back to the original size, we must dilate it by a scale factor r = 1 4 .
Lesson Summary
Dilations map circles to circles and ellipses to ellipses.
If a figure is dilated by scale factor r, we must dilate it by a scale factor of 1 r to bring the dilated figure back to the original size. For example, if a scale factor is r = 4, then to bring a dilated figure back to the original size, we must dilate it by a scale factor r = 1 4
Exit Ticket (5 minutes)
Examples of Dilations
Name Date
Exit Ticket
1. Dilate circle A from center O by a scale factor r = 1 2 . Make sure to use enough points to make a good image of the original figure.

2. What scale factor would magnify the dilated circle back to the original size of circle A? How do you know?
1. Dilate circle A from center O by a scale factor r � 1 2 . Make sure to use enough points to make a good image of the original figure.
Student work is shown below. Verify that students used enough points to produce an image similar to the original.

2. What scale factor would magnify the dilated circle back to the original size of circle A? How do you know?
A scale factor of r = 2 would bring the dilated circle back to the size of circle A. Since the circle was dilated by a scale factor of r = 1 2 , then to bring it back to its original size, you must dilate by a scale factor that is the reciprocal of 1 2 , which is 2.
Examples of Dilations
Students practice dilating a curved figure and stating the scale factor that would bring a dilated figure back to its original size.
1. Dilate the figure from center O by a scale factor r = 2. Make sure to use enough points to make a good image of the original figure.
Sample student work is shown below. Verify that students used enough points to produce an image similar to the original

2. Describe the process for selecting points when dilating a curved figure.
When dilating a curved figure, you have to make sure to use a lot of points to produce a decent image of the original figure. You also have to make sure that the points you choose are not all concentrated in just one part of the figure
3. A figure was dilated from center O by a scale factor of r = 5. What scale factor would shrink the dilated figure back to the original size?
A scale factor of r = 1 5 would bring the dilated figure back to its original size.
4. A figure has been dilated from center O by a scale factor of r = 7 6 . What scale factor would shrink the dilated figure back to the original size?
A scale factor of r = 6 7 would bring the dilated figure back to its original size.
5. A figure has been dilated from center O by a scale factor of r = 3 10 . What scale factor would magnify the dilated figure back to the original size?
A scale factor of r = 10 3 would bring the dilated figure back to its original size
Examples of Dilations

Student Outcomes
⬛ Students experimentally verify the properties related to the fundamental theorem of similarity (FTS).
Lesson Notes
The goal of this activity is to show students the properties of the fundamental theorem of similarity (FTS) in terms of dilation. FTS states that given a dilation from center O and points P and Q (points O, P, Q are not collinear), the segments formed when P is connected to Q and P′ is connected to Q′ are parallel. More surprising is that |P′Q′| = r|PQ|. That is, the segment PQ, even though it was not dilated as points P and Q were, dilates to segment P′Q′, and the length of segment P′Q′ is the length of segment PQ multiplied by the scale factor. The following picture refers to the activity suggested in the Classwork Discussion below. Also, consider showing the diagram (without the lengths of segments), and ask students to make conjectures about the relationships between the lengths of segments PQ and P′Q′

Classwork
Discussion (30 minutes)
For this Discussion, students need a piece of lined paper, a centimeter ruler, a protractor, and a four-function (or scientific) calculator.
⬛ The last few days, we have focused on dilation. We now want to use what we know about dilation to come to some conclusions about the concept of similarity in general.
Fundamental Theorem of Similarity (FTS)
⬛ A regular piece of notebook paper can be a great tool for discussing similarity. What do you notice about the lines on the notebook paper?
The lines on the notebook paper are parallel; that is, they never intersect.
⬛ Keep that information in mind as we proceed through this activity. On the first line of your paper, mark a point O. This is our center.
⬛ Mark the point P a few lines down from the center O. From point O, draw a ray OP . Now, choose a P′ farther down the ray, also on one of the lines of the notebook paper. For example, you may have placed point P three lines down from the center and point P′ five lines down from the center.
⬛ Use the definition of dilation to describe the lengths along this ray.
By the definition of dilation, |OP′| = r|OP|.
⬛ Recall that we can calculate the scale factor using the following computation: = || || r OP OP . In my example, using the lines on the paper as our unit, the scale factor is r 5 3 = because point P′ is five lines down from the center, and point P is three lines down from the center. On the top of your paper, write the scale factor that you have obtained.
⬛ Now draw another ray, OQ . Use the same scale factor to mark points Q and Q′. In my example, I would place Q three lines down and Q′ five lines down from the center.
⬛ Now connect point P to point Q and point P′ to point Q′. What do you notice about lines PQ and P′Q′?
The lines PQ and P′Q′ fall on the notebook lines, which means that lines PQ and P′Q′ are parallel lines
⬛ Use your protractor to measure ∠OPQ and ∠OP′Q′. What do you notice, and why is it so?
∠OPQ and ∠OP′Q′ are equal in measure. They must be equal in measure because they are corresponding angles of parallel lines (lines PQ and P′Q′ ) cut by a transversal (ray OP )
⬛ (Consider asking students to write their answers to the following question in their notebooks and to justify their answers.) Now, without using your protractor, what can you say about ∠OQP and ∠OQ′P′?
These angles are also equal for the same reason; they are corresponding angles of parallel lines (lines PQ and P′Q′) cut by a transversal (ray OQ )
⬛ Use your centimeter ruler to measure the lengths of segments OP and OP′ . By the definition of dilation, we expect |OP′| = r|OP| (i.e., we expect the length of segment OP′ to be equal to the scale factor times the length of segment OP). Verify that this is true. Do the same for lengths of segments OQ and OQ′
Sample of what student work may look like:

Note to Teacher: Using a centimeter ruler makes it easier for students to come up with a precise measurement. Also, let students know that it is okay if their measurements are off by a tenth of a centimeter, because that difference can be attributed to human error.
⬛ Bear in mind that we have dilated points P and Q from center O along their respective rays. Do you expect the segments PQ and P′Q′ to have the relationship |P′Q′ | = r|PQ|?
(Some students may say yes. If they do, ask for a convincing argument. At this point, they have knowledge of dilating segments, but that is not what we have done here. We have dilated points and then connected them to draw the segments.)
⬛ Measure the segments PQ and P′Q′ to see if they have the relationship |P′Q′ | = r|PQ|.
⬛ It should be somewhat surprising that, in fact, segments PQ and P′Q′ enjoy the same properties as the segments that we actually dilated.
⬛ Now mark a point A on line PQ between points P and Q. Draw a ray from center O through point A, and then mark point A′ on the line P′Q′. Do you think |P′A′| = r|PA|? Measure the segments, and use your calculator to check.
Students should notice that these new segments also have the same properties as the dilated segments.
⬛ Now mark a point B on the line PQ but this time not on the segment PQ (i.e., not between points P and Q). Again, draw the ray from center O through point B, and mark the point B′ on the line P′Q′. Select any of the segments, AB , PB , or QB , and verify that it has the same property as the others.
Sample of what student work may look like:
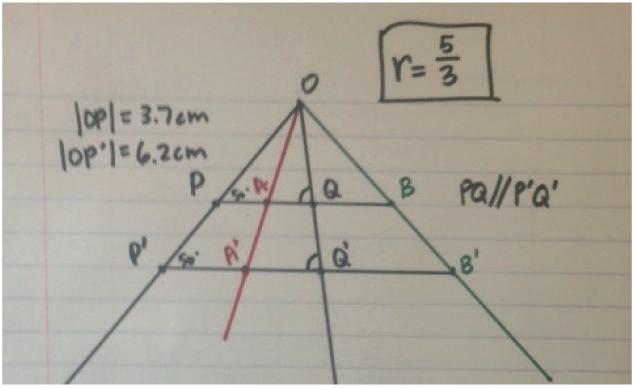
⬛ Does this always happen, no matter the scale factor or placement of points P, Q, A, and B?
Yes, I believe this is true. One main reason is that everyone in class probably picked different points, and I’m sure many of us used different scale factors.
⬛ In your own words, describe the rule or pattern that we have discovered.
Encourage students to write and collaborate with a partner to answer this question. Once students have finished their work, lead a discussion that crystallizes the information in the theorem that follows.
⬛ We have just experimentally verified the properties of the fundamental theorem of similarity (FTS) in terms of dilation, namely, that the parallel line segments connecting dilated points are related by the same scale factor as the segments that are dilated.
Theorem: Given a dilation with center O and scale factor r, then for any two points P and Q in the plane so that O, P, and Q are not collinear, the lines PQ and P′Q′ are parallel, where P′ = Dilation(P) and Q′ = Dilation(Q), and furthermore, |P′Q′ | = r|PQ|.
Ask students to paraphrase the theorem in their own words, or offer them the following version of the theorem: FTS states that given a dilation from center O and points P and Q (points O, P, and Q are not on the same line), the segments formed when you connect P to Q and P′ to Q′ are parallel. More surprising is the fact that the segment PQ, even though it was not dilated as points P and Q were, dilates to segment P′Q′, and the length of segment P′Q′ is the length of segment PQ multiplied by the scale factor.
⬛ Now that we are more familiar with properties of dilations and FTS, we begin using these properties in the next few lessons to do things like verify similarity of figures.
Exercise (5 minutes)
Exercise
In the diagram below, points R and S have been dilated from center O by a scale factor of r = 3.

a. If |OR| = 2.3 cm, what is |OR′|?
|OR′| = 3(2.3 cm) = 6.9 cm
b. If |OS| = 3.5 cm, what is |OS′|?
|OS′| = 3(3.5 cm) = 10.5 cm
c. Connect the point R to the point S and the point R′ to the point S′. What do you know about the lines that contain segments RS and R′S′?
The lines containing the segments RS and R′S′ are parallel
d. What is the relationship between the length of segment RS and the length of segment R′S′?
The length of segment R′S′ is equal to the length of segment RS, times the scale factor of 3 (i.e., |R′S′| = 3|RS|).
e. Identify pairs of angles that are equal in measure. How do you know they are equal?
|∠ORS| = |∠OR′S′| and |∠OSR| = |∠OS′R′| They are equal because they are corresponding angles of parallel lines cut by a transversal.
Closing (5 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We know that the following is true: If |OP′| = r|OP| and |OQ′| = r|OQ|, then |P′Q′| = r|PQ|. In other words, under a dilation from a center with scale factor r, a segment multiplied by the scale factor results in the length of the dilated segment.
⬛ We also know that the lines PQ and P′Q′ are parallel.
⬛ We verified the fundamental theorem of similarity in terms of dilation using an experiment with notebook paper.
Lesson Summary
Theorem: Given a dilation with center O and scale factor r, then for any two points P and Q in the plane so that O, P, and Q are not collinear, the lines PQ and P′Q′are parallel, where P′ = Dilation(P) and Q′ = Dilation(Q), and furthermore, |P′Q′| = r |PQ|
Exit Ticket (5 minutes)
Fundamental Theorem of Similarity (FTS)
Name Date
Exit Ticket
Steven sketched the following diagram on graph paper. He dilated points B and C from point O. Answer the following questions based on his drawing.
1. What is the scale factor r? Show your work.
2. Verify the scale factor with a different set of segments.

3. Which segments are parallel? How do you know?
4. Are ∠OBC and ∠OB′C′ right angles? How do you know?
Steven sketched the following diagram on graph paper. He dilated points B and C from point O. Answer the following questions based on his drawing.
1. What is the scale factor r? Show your work.
2. Verify the scale factor with a different set of segments.

3. Which segments are parallel? How do you know?
Segments BC and B′C′ are parallel since they lie on the grid lines of the paper, which are parallel.
4. Are ∠OBC and ∠OB′C′ right angles? How do you know?
The grid lines on graph paper are perpendicular, and since perpendicular lines form right angles, ∠OBC and ∠OB′C′ are right angles.
Students verify that the fundamental theorem of similarity holds true when the scale factor r is 0 < r < 1.
1. Use a piece of notebook paper to verify the fundamental theorem of similarity for a scale factor r such that 0 < r < 1.
� Mark a point O on the first line of notebook paper.
� Mark the point P on a line several lines down from the center O. Draw a ray, OP . Mark the point P′ on the ray and on a line of the notebook paper closer to O than you placed point P. This ensures that you have a scale factor such that 0 < r < 1. Write your scale factor at the top of the notebook paper.
� Draw another ray, OQ , and mark the points Q and Q′ according to your scale factor.
� Connect points P and Q. Then, connect points P′ and Q′.
� Place a point, A, on the line containing segment PQ between points P and Q. Draw ray OA . Mark point A′ at the intersection of the line containing segment P′Q′ and ray OA
Sample student work is shown in the picture below:

a. Are the lines containing segments PQ and P′Q′ parallel lines? How do you know?
Yes, the lines containing segments PQ and P′Q′ are parallel. The notebook lines are parallel, and these lines fall on the notebook lines.
b. Which, if any, of the following pairs of angles are equal in measure? Explain.
i. ∠OPQ and ∠OP′Q′
ii. ∠OAQ and ∠OA′Q′
iii. ∠OAP and ∠OA′P′
iv. ∠OQP and ∠OQ′P′
All four pairs of angles are equal in measure because each pair of angles are corresponding angles of parallel lines cut by a transversal. In each case, the parallel lines are line PQ and line P′Q′, and the transversal is the respective ray.
c. Which, if any, of the following statements are true? Show your work to verify or dispute each statement.
i. |OP′| = r|OP|
ii. |OQ′| = r|OQ|
iii. |P′A′| = r|PA|
iv. |A′Q′| = r|AQ|
All four of the statements are true. Verify that students have shown that the length of the dilated segment was equal to the scale factor multiplied by the original segment length.
d. Do you believe that the fundamental theorem of similarity (FTS) is true even when the scale factor is 0 < r < 1? Explain.
Yes, because I just experimentally verified the properties of FTS for when the scale factor is 0 < r < 1
2. Caleb sketched the following diagram on graph paper. He dilated points B and C from center O.

a. What is the scale factor r? Show your work. |OB′| = r|
b. Verify the scale factor with a different set of segments.
c. Which segments are parallel? How do you know?
Segment BC and B′C′ are parallel. They lie on the lines of the graph paper, which are parallel.
d. Which angles are equal in measure? How do you know? |∠OB′C′| = |∠OBC|, and |∠OC′B′| = |∠OCB| because they are corresponding angles of parallel lines cut by a transversal.
3. Points B and C were dilated from center O.

a. What is the scale factor r? Show your work.
|OC′| = r|OC| 63 6 3 2 r r r = = =
b. If |OB| = 5, what is |OB′|?
|OB′| = r|OB|
|OB′| = 2.5
|OB′| = 10
c. How does the perimeter of triangle OBC compare to the perimeter of triangle OB′C′? The perimeter of triangle OBC is 12 units, and the perimeter of triangle OB′C′ is 24 units.
d. Did the perimeter of triangle OB′C′ = r × (perimeter of triangle OBC)? Explain. Yes, the perimeter of triangle OB′C′ was twice the perimeter of triangle OBC, which makes sense because the dilation increased the length of each segment by a scale factor of 2 That means that each side of triangle OB′C′ was twice as long as each side of triangle OBC

⬛ Students verify the converse of the fundamental theorem of similarity experimentally.
⬛ Students apply the fundamental theorem of similarity to find the location of dilated points on the plane.
Concept Development (5 minutes)
Begin by having students restate (in their own words) the fundamental theorem of similarity (FTS) that they learned in the last lesson.
⬛ The fundamental theorem of similarity states: Given a dilation with center O and scale factor r, then for any two points P and Q in the plane so that O, P, and Q are not collinear, the lines PQ and P′Q′ are parallel, where P′ = Dilation(P) and Q′ = Dilation(Q), and furthermore, |P′Q′| = r|PQ|.
The paraphrased version from the last lesson was: FTS states that given a dilation from center O, and points P and Q (points O, P, and Q are not on the same line), the segments formed when you connect P to Q and P′ to Q′ are parallel. More surprising is the fact that the segment PQ, even though it was not dilated as points P and Q were, dilates to segment P′Q′, and the length of segment P′Q′ is the length of segment PQ multiplied by the scale factor.
⬛ The converse of this theorem is also true. That is, if lines PQ and P′Q′ are parallel, and |P′Q′| = r|PQ|, then from a center O, P′ = Dilation(P), Q′ = Dilation(Q), and |OP′| = r|OP| and |OQ′ | = r|OQ|.
The converse of a theorem begins with the conclusion and produces the hypothesis. FTS concludes that lines are parallel and the length of segment P′Q′ is the length of segment PQ multiplied by the scale factor. The converse of FTS begins with the statement that the lines are parallel and the length of segment P′Q′ is the length of segment PQ multiplied by the scale factor. It ends with the knowledge that the points P′ and Q′ are dilations of points P and Q by scale factor r, and their respective segments, OP′ and OQ′, have lengths that are the scale factor multiplied by the original lengths of segment OP and segment OQ. Consider providing students with some simple examples of converses, and discuss whether or not the converses are true. For example, “If it is raining, then I have an umbrella,” and its converse, “If I have an umbrella, then it is raining.” In this case, the converse is not necessarily true. An example where the converse is true is “If we turn the faucet on, then water comes out,” and the converse is “If water comes out, then the faucet is on.”
⬛ The converse of the theorem is basically the work we did in the last lesson but backward. In the last lesson, we knew about dilated points and found out that the segments between the points P, Q and their dilations P′ , Q′ were dilated according to the same scale factor, that is, |P′Q′| = r|PQ|. We also discovered that the lines containing those segments were parallel, that is, PQ P′Q′ . The converse states that we are given parallel lines, PQ and P′Q′ , where a segment, PQ , in one line is dilated by scale factor r to a segment, P′Q′, in the other line. With that knowledge, we can say something about the center of dilation and the relationship between segments OP′ and OP, as well as segments OQ′ and OQ
In Exercise 1 below, students are given the information in the converse of FTS, that is, PQ P′Q′ and |P′Q′| = r|PQ|. Students then verify the conclusion of the converse of FTS by measuring lengths of segments and their dilated images to make sure that they have the properties stated, that is, |OP′| = r|OP| and |OQ′| = r|OQ|.
Consider showing the diagram below and asking students to make conjectures about the relationship between segment OP′ and segment OP, as well as segment OQ′ and segment OQ. Record the conjectures and possibly have the class vote on which they believe to be true.
In the diagram below, the lines containing segments PQ and P′Q′ are parallel, and the length of segment P′Q′ is equal to the length of segment PQ multiplied by the scale factor r, dilated from center O

Have students verify experimentally the validity of the converse of the theorem. They can work independently or in pairs. Note that the image is to scale in the student materials.
Exercise 1
In the diagram below, points P and Q have been dilated from center O by scale factor r PQ PQ '' , |PQ| = 5 cm, and |P′Q′| = 10 cm.

If students need help getting started, have them review the activity from Lesson 16. Ask what they should do to find the center O. Students should say to draw lines through PP′ and QQ′; the point of intersection is the center O.
a. Determine the scale factor r.
According to FTS, |P′Q′| = r |PQ|. Therefore, 10 = r · 5, so r = 2.
b. Locate the center O of dilation. Measure the segments to verify that |OP′| = r |OP| and |OQ′| = r|OQ|. Show your work below.
Center O and measurements are shown above.
Example 1 (5 minutes)
⬛ Now that we know FTS and the converse of FTS in terms of dilations, we practice using them to find the coordinates of points and dilated points on a plane. We begin simply.
⬛ In the diagram, we have center O and ray OA . We want to find the coordinates of point A′. We are given that the scale factor of dilation is r = 2

⬛ To find A′, we could use a ruler or compass to measure |OA|, but now that we know about FTS, we can do this another way. First, we should look for parallel lines that help us locate point A′. How can we use the coordinate plane to ensure parallel lines?
We could use the vertical or horizontal lines of the coordinate plane to ensure lines are parallel. The coordinate plane is set up so that the lines never intersect. You could also think of those lines as translations of the x-axis and y-axis. Therefore, we are guaranteed to have parallel lines
First Consequences of FTS
⬛ Let’s use the x-axis as one of our rays. (Show the picture below.) Where should we place a point B on the ray along the x-axis?

Since we are using the lines on the coordinate plane to verify parallelism, we should place point B directly below point A on the x-axis. Point B should be at (5, 0)
⬛ (Show the picture below.) This is beginning to look like the activity we did in Lesson 16. We know that the scale factor is r = 2. Where should we put point B′?

It is clear that |OB| = 5; therefore, |OB′| = 2 · 5, so the point B′ should be placed at (10, 0).
First Consequences of FTS
⬛ (Show the picture below.) Now that we know the location of B′, using FTS, what do we expect to be true about the lines containing segments AB and A′B′ ?
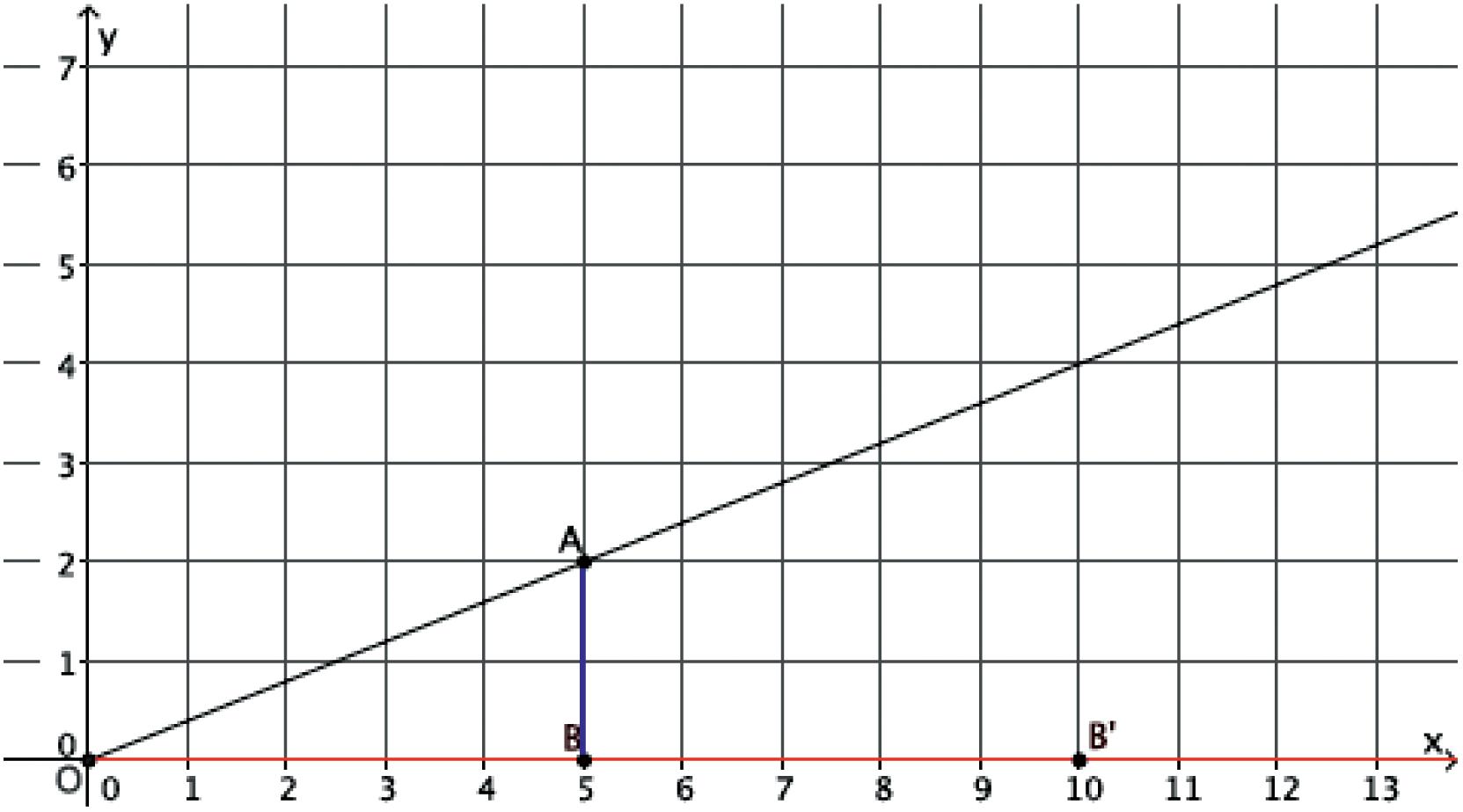
We expect the lines containing segments AB and A′B′ to be parallel
⬛ (Show the picture below.) Then what is the location of point A′?
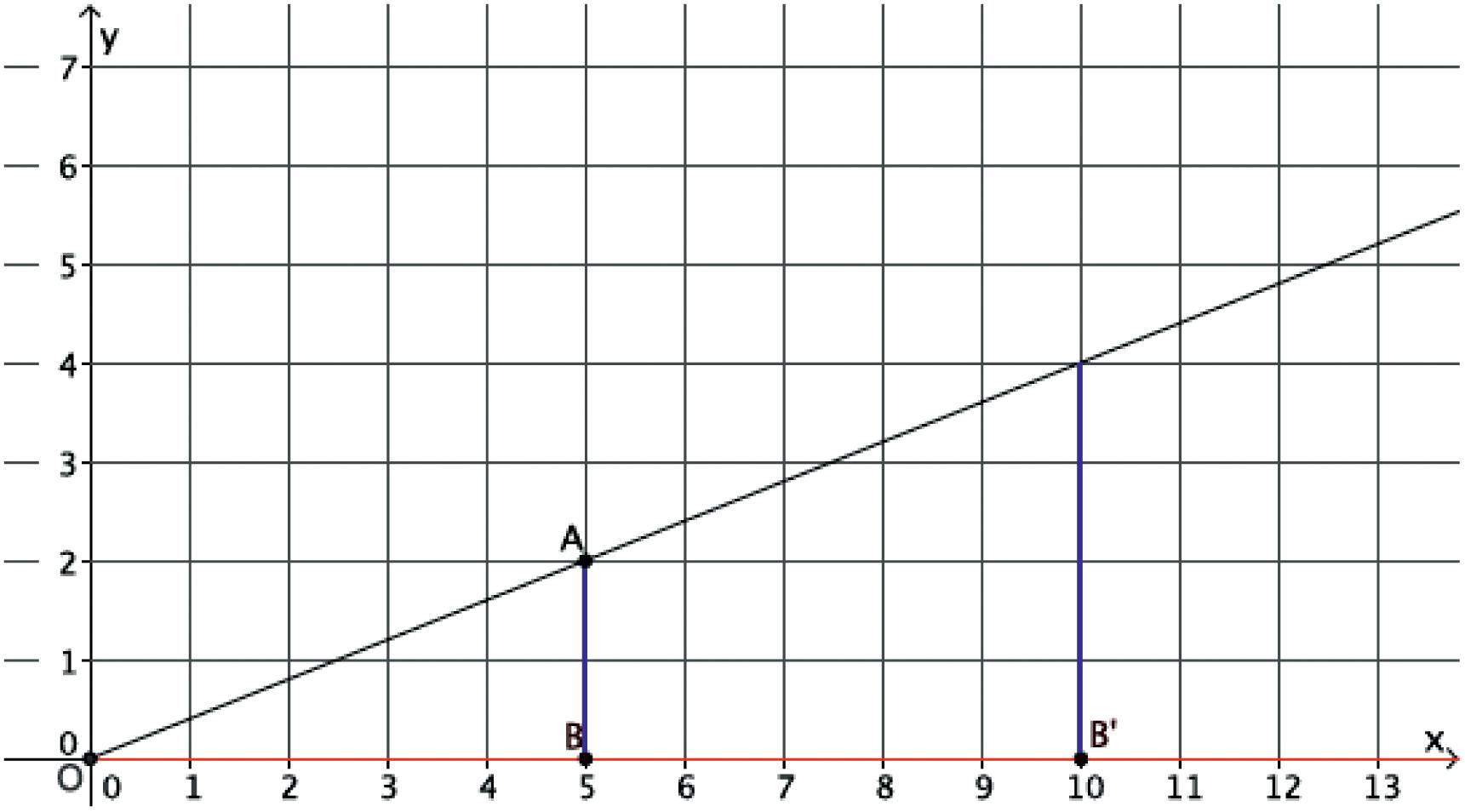
Point A′ is located at (10, 4)
⬛ (Show the picture below.) Could point A′ be located anywhere else? Specifically, could A′ have a different x-coordinate? Why or why not?

No, Point A′ must be at (10, 4). If it had another x-coordinate, then lines AB and A′B′ would have not been dilated by the scale factor r = 2.
⬛ Could point A′ be located at another location that has 10 as its x-coordinate? For example, could A′ be at (10, 5)? Why or why not?
No, Point A′ must be at (10, 4). By the definition of dilation, if point A is dilated from center O, then the dilated point must be on the ray OA , making points O, A, and A′ collinear. If A′ were at (10, 5) or at any coordinate other than (10, 4), then the points O, A, and A′ would not be collinear.
First Consequences of FTS
Exercise 2 (3 minutes)
Students work independently to find the location of point A′ on the coordinate plane.
Exercise 2
In the diagram below, you are given center O and ray OAPoint A is dilated by a scale factor r = 4. Use what you know about FTS to find the location of point A′.

⬛ In the diagram, we have center O and ray OA . We are given that the scale factor of dilation is 11 7 r = . We want to find the precise coordinates of point A′. Based on our previous work, we know exactly how to begin. Draw a ray OB along the x-axis, and mark a point B, directly below point A, on the ray OB . (Show the picture below.) The question now is, how do we locate point B′? Think about our work from Lesson 16.

⬛ In Lesson 16, we counted lines to determine the scale factor. Given the scale factor, we know that point B should be exactly 7 lines from the center O and that the dilated point, B′, should be exactly 11 lines from the center. Therefore, B′ is located at (11, 0).
⬛ Now that we know the location of B′, where do we find A′?
Point A′ is at the intersection of the ray OA and the vertical line through point B′ , which must be parallel to the line containing AB .
First Consequences of FTS
⬛ (Show the picture below.) Now that we know where A′ is, we need to find the precise coordinates of it. The x-coordinate is easy, but how can we find the y-coordinate? (Give students time to talk in pairs or small groups.)
The y-coordinate is the exact length of the segment A′B′ To find that length, we can use what we know about the length of segment AB and the scale factor since |A′B′| = r|AB|.

⬛ The length of segment A′B′ gives us the y-coordinate. Then |A′B′| 6 11 7 66 7 =⋅ = . That means that the location of A′ is �11, 66 7 �
Students work independently or in pairs to find the location of point A′ on the coordinate plane.
Exercise 3
In the diagram below, you are given center O and ray OA . Point A is dilated by a scale factor r = 5 12 . Use what you know about FTS to find the location of point A′.

The x-coordinate of A′ is 5. The y-coordinate is equal to the length of segment A′B′. Since |A′B′| = r |AB|, then |A′B′| 5 12 8 40 12 33 ≈ =⋅ = The location of A′ is (5, 3.3)
First Consequences of FTS
Example 3 (8 minutes)
⬛ In the diagram below, we have center O and rays OA and OB . We are given that the scale factor is 5 8 r = . We want to find the precise coordinates of points A′ and B′

⬛ Based on our previous work, we know exactly how to begin. Describe what we should do.
Draw a ray OC along the x-axis, and mark a point C, directly below point A, on the ray OC .
⬛ (Show the picture below.) Based on our work in Lesson 16 and our knowledge of FTS, we know that points B and B′ along ray OB enjoy the same properties we have been using in the last few problems. Let’s begin by finding the coordinates of A′. What should we do first?
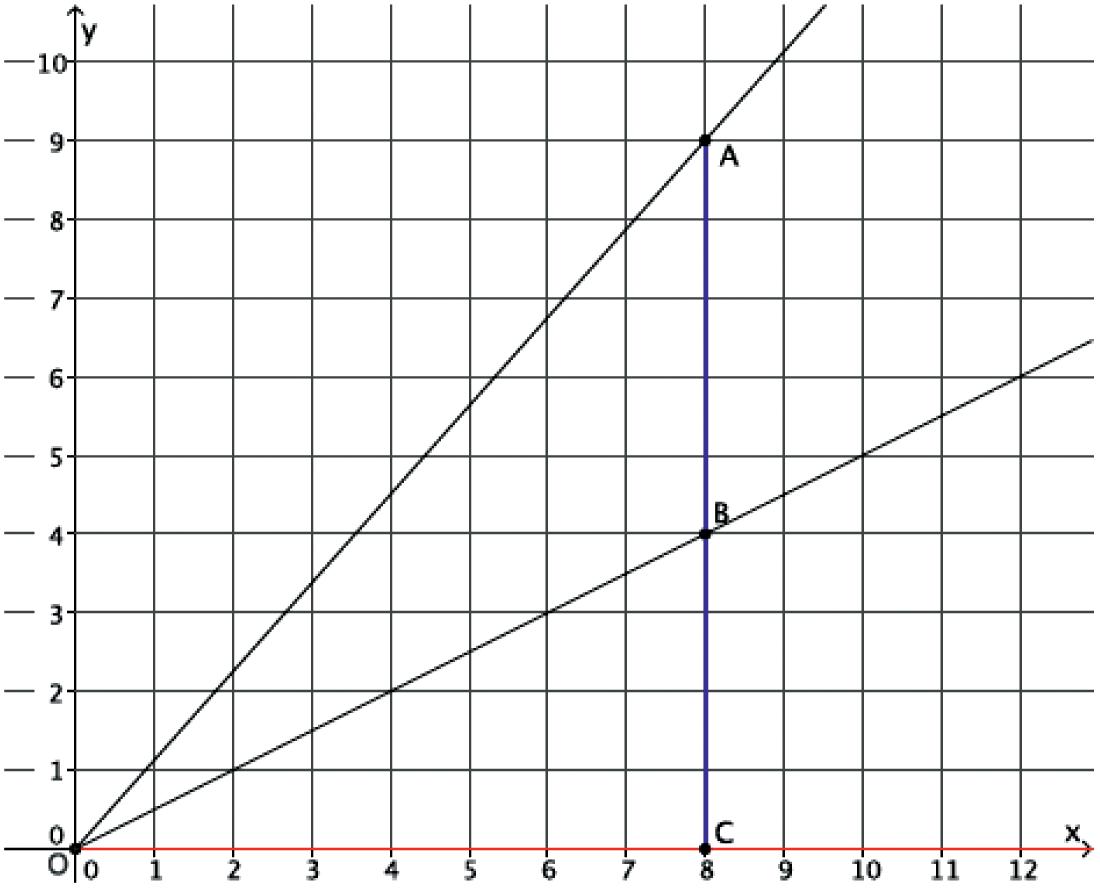
First, we need to place the points A′ , B′ , and C′ on their respective rays by using the scale factor. Since the scale factor 5 8 r = , A′ , B′ , and C′ have an x-coordinate of 5. (Also, they are 5 lines from the center.)
First Consequences of
⬛ (Show the picture below.) Now that we know the x-coordinate, let’s now find the y-coordinate of A′. What do we need to do to find the y-coordinate of A′?

The y-coordinate of A′ is the length of the segment A′C′ . We can calculate that length by using what we know about segment AC and the scale factor.
⬛ The y-coordinate of A′ is |A′C′| rAC|| 95.6 5 8 45 8 == ⋅= ≈ . Then the location of A′ is (5, 5 6)
⬛ Work with a partner to find the y-coordinate of B′ . The y-coordinate of B′ is the length of segment B′C′ Then |B′C′| rBC|| 42.5 5 8 20
== ⋅= = The location of B′ is (5, 2.5).
First Consequences of FTS
Closing (4 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We experimentally verified the converse of FTS. That is, if we are given parallel lines PQ and P′Q′ and know |P′Q′| = r |PQ|, then we know from a center O, P′ = Dilation(P), Q′ = Dilation(Q), |OP′| = r|OP|, and |OQ′| = r|OQ|. In other words, if we are given parallel lines PQ and P′Q′, and we know that the length of segment P′Q′ is equal to the length of segment PQ multiplied by the scale factor, then we also know that the length of segment OP′ is equal to the length of segment OP multiplied by the scale factor and that the length of segment OQ′ is equal to the length of segment OQ multiplied by the scale factor.
⬛ We know how to use FTS to find the coordinates of dilated points, even if the dilated point is not on an intersection of graph lines.
Lesson Summary
Converse of the fundamental theorem of similarity:
If lines PQ and P′Q′ are parallel and |P′Q′| = r|PQ|, then from a center O, P′ = Dilation(P), Q′ = Dilation(Q), |OP′| = r|OP|, and |OQ′| = r|OQ|.
To find the coordinates of a dilated point, we must use what we know about FTS, dilation, and scale factor.
Exit Ticket (5 minutes)
First Consequences of FTS
Exit Ticket
In the diagram below, you are given ray OA . Point A is dilated from the origin by a scale factor 6 4 r = . Use what you know about FTS to find the location of point A′ .

In the diagram below, you are given ray OAPoint A is dilated from the origin by a scale factor r = 6 4 . Use what you know about FTS to find the location of point A′.

The y-coordinate of A′ is 6 The x-coordinate is equal to the length of segment A′B′ Since |A′B′| = r |AB|, then |A′B′| 6 4 3 18 4 45 =⋅ == The location of A′ is (4.5, 6)
Students practice using the first consequences of FTS in terms of dilated points and their locations on the coordinate plane.
1. Dilate point A, located at (3, 3) from center O, by a scale factor r = 5 3 . What is the precise location of point A′?

The y-coordinate of point A′ is the length of segment A′B′. Since |A′B′| = r|AB|, then |A′B′| 5 3 35 =⋅ = . The location of point A′ is (5, 5).
First Consequences of FTS
2. Dilate point A, located at (9, 7) from center O, by a scale factor r = 4 9 . Then, dilate point B, located at (9, 5) from center O, by a scale factor of r = 4 9 . What are the coordinates of points A′ and B′ ? Explain.

The y-coordinate of point A′ is the length of segment A′C′. Since |A′C′| = r|AC|, then |A′C′| 4 9 7 28 9 =⋅ = . The location of point A′ is �4, 28 9 �, or approximately (4, 3.1) The y-coordinate of point B′ is the length of segment B′C′ Since |B′C′| = r|BC|, then |B′C′| 4 9 5 20 9 =⋅ = The location of point B′ is �4, 20 9 �, or approximately (4, 2.2)
3. Explain how you used the fundamental theorem of similarity in Problems 1 and 2. Using what I knew about scale factor, I was able to determine the placement of points A′ and B′, but I did not know the actual coordinates. So, one of the ways that FTS was used was actually in terms of the converse of FTS. I had to make sure I had parallel lines. Since the lines of the coordinate plane guarantee parallel lines, I knew that |A′C′| = r |AC|. Then, since I knew the length of segment AC and the scale factor, I could find the precise location of A′ The precise location of B′ was found in a similar way but using |B′C′| = r |BC|

⬛ Students describe the effect of dilations on two-dimensional figures using coordinates.
Example 1 (7 minutes)
Students learn the multiplicative effect of scale factor on a point. Note that this effect holds when the center of dilation is the origin. In this lesson, the center of any dilation used is always assumed to be (0, 0).
Show the diagram below, and ask students to look at and write or share a claim about the effect that dilation has on the coordinates of dilated points.
⬛ The graph below represents a dilation from center (0, 0) by scale factor r = 2.

Show students the second diagram below so they can check if their claims were correct. Give students time to verify the claims that they made about the above graph with the one below. Then, have them share their claims with the class. Use the discussion that follows to crystallize what students observed.
⬛ The graph below represents a dilation from center (0, 0) by scale factor r = 4.

⬛ In Lesson 17, we found the location of a dilated point by using the knowledge of dilation and scale factor, as well as the lines of the coordinate plane to ensure equal angles, to find the coordinates of the dilated point. For example, we were given the point A(5, 2) and told the scale factor of dilation was r = 2. Remember that the center of this dilation is (0, 0). We created the following picture and determined the location of A′ to be (10, 4)

⬛ We can use this information and the observations we made at the beginning of class to develop a shortcut for finding the coordinates of dilated points when the center of dilation is the origin.
⬛ Notice that the horizontal distance from the y-axis to point A was multiplied by a scale factor of 2. That is, the x-coordinate of point A was multiplied by a scale factor of 2. Similarly, the vertical distance from the x-axis to point A was multiplied by a scale factor of 2
Dilations on the Coordinate Plane
⬛ Here are the coordinates of point A(5, 2) and the dilated point A′(10, 4). Since the scale factor was 2, we can more easily see what happened to the coordinates of A after the dilation if we write the coordinates of A′ as (2 · 5, 2 · 2), that is, the scale factor of 2 multiplied by each of the coordinates of A to get A′
⬛ The reasoning goes back to our understanding of dilation. The length r|OB| = |OB′|, by the definition of dilation, and the length r|AB| = |A′ B′|; therefore, r OB OB AB AB || || || || , == where the length of the segment OB′ is the x-coordinate of the dilated point (i.e., 10), and the length of the segment A′B′ is the y-coordinate of the dilated point (i.e., 4).
In other words, based on what we know about the lengths of dilated segments, when the center of dilation is the origin, we can determine the coordinates of a dilated point by multiplying each of the coordinates in the original point by the scale factor.
Example 2 (3 minutes)
Students learn the multiplicative effect of scale factor on a point.
⬛ Let’s look at another example from Lesson 17. We were given the point A(7, 6) and asked to find the location of the dilated point A′ when 11 7 r = . Our work on this problem led us to coordinates of approximately (11, 9.4) for point A′. Verify that we would get the same result if we multiply each of the coordinates of point A by the scale factor.
and � 69 4 11 7 66 7 ⋅= ≈ 9.4
Therefore, multiplying each coordinate by the scale factor produced the desired result
Example 3 (5 minutes)
⬛ The coordinates in other quadrants of the graph are affected in the same manner as we have just seen. Based on what we have learned so far, given point A( 2, 3), predict the location of A′ when A is dilated from a center at the origin, (0, 0), by scale factor r = 3
Provide students time to predict, justify, and possibly verify, in pairs, that A′(3 · ( 2), 3 · 3) = ( 6, 9). Verify the fact on the coordinate plane, or have students share their verifications with the class.
Dilations on the Coordinate Plane
⬛ As before, mark a point B on the x-axis. Then, |OB′| = 3|OB|. Where is point B′ located? Since the length of |OB| = 2, then |OB′| = 3 · 2 = 6. But we are looking at a distance to the left of zero; therefore, the location of B′ is ( 6, 0).

⬛ Now that we know where B′ is, we can easily find the location of A′. It is on the ray OA , but at what location?
The location of A′( 6, 9), as desired

Exercises 1–5 (5 minutes)
Students complete Exercises 1–5 independently.
Exercises 1–5
1. Point A(7, 9) is dilated from the origin by scale factor r
2.
3. Point C(6,
4. Point D(0, 11) is dilated from the origin by scale factor r = 4. What are the coordinates of point D′? D′(4 · 0, 4 · 11) = D′(0, 44)
5. Point E( 2, 5) is dilated from the origin by scale factor r = 3 2 . What are the coordinates of point E′?
Example 4 (4 minutes)
Students learn the multiplicative effect of scale factor on a two-dimensional figure.
⬛ Now that we know the multiplicative relationship between a point and its dilated location (i.e., if point P(p1, p2) is dilated from the origin by scale factor r, then P′ (rp1, rp2)), we can quickly find the coordinates of any point, including those that comprise a two-dimensional figure, under a dilation of any scale factor.
⬛ For example, triangle ABC has coordinates A(2, 3), B( 3, 4), and C(5, 7). The triangle is being dilated from the origin with scale factor r = 4. What are the coordinates of triangle A′ B′ C′?
⬛ First, find the coordinates of A′
A′(4 · 2, 4 · 3) = A′(8, 12)
⬛ Next, locate the coordinates of B′
B′(4 · ( 3), 4 · 4) = B′( 12, 16)
⬛ Finally, locate the coordinates of C′
C′(4 · 5, 4 · 7) = C′(20, 28)
⬛ Therefore, the vertices of triangle A′B′C′ have coordinates of (8, 12), ( 12, 16), and (20, 28), respectively.
Dilations on the Coordinate Plane
Example 5 (4 minutes)
Students learn the multiplicative effect of scale factor on a two-dimensional figure.
⬛ Parallelogram ABCD has coordinates of ( 2, 4), (4, 4), (2, 1), and ( 4, 1), respectively. Find the coordinates of parallelogram A
after a dilation from the origin with a scale factor
Therefore, the vertices of parallelogram A
respectively.
Exercises 6–8 (9 minutes)
Students complete Exercises 6–8 independently.
Exercises 6–8
coordinates of (
6. The coordinates of triangle ABC are shown on the coordinate plane below. The triangle is dilated from the origin by scale factor r = 12. Identify the coordinates of the dilated triangle A′B′C′
Point A( 2, 2), so A′(12 ( 2), 12 2) = A′( 24, 24).
Point B( 3, 3), so B′(12 ( 3), 12 ( 3)) = B′( 36, 36)
Point C(6, 1), so C′(12 · 6, 12 · 1) = C′(72, 12).
The coordinates of the vertices of triangle A′B′C′ are ( 24, 24), ( 36, 36), and (72, 12), respectively
7. Figure DEFG is shown on the coordinate plane below. The figure is dilated from the origin by scale factor r = 2 3 . Identify the coordinates of the dilated figure D′E′F′G′, and then draw and label figure D′E′F′G′ on the coordinate plane.

8. The triangle ABC has coordinates A(3, 2), B(12, 3), and C(9, 12). Draw and label triangle ABC on the coordinate plane. The triangle is dilated from the origin by scale factor r = 1 3 . Identify the coordinates of the dilated triangle A′B′C′, and then draw and label triangle A′B′C′ on the coordinate plane. Point
Closing (4 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We know that we can calculate the coordinates of a dilated point given the coordinates of the original point and the scale factor.
⬛ To find the coordinates of a dilated point, we must multiply both the x-coordinate and the y-coordinate by the scale factor of dilation.
⬛ If we know how to find the coordinates of a dilated point, we can find the location of a dilated triangle or other two-dimensional figure.
Lesson Summary
Dilation has a multiplicative effect on the coordinates of a point in the plane. Given a point (x,y) in the plane, a dilation from the origin with scale factor r moves the point (x,y) to (rx,ry)
For example, if a point (3, 5) in the plane is dilated from the origin by a scale factor of r = 4, then the coordinates of the dilated point are (4 3, 4 ( 5)) = (12, 20)
Exit Ticket (4 minutes)
1. The point A(7, 4) is dilated from the origin by a scale factor r = 3. What are the coordinates of point A′?
2. The triangle ABC, shown on the coordinate plane below, is dilated from the origin by scale factor
2 r = . What is the location of triangle A′B′C′? Draw and label it on the coordinate plane.
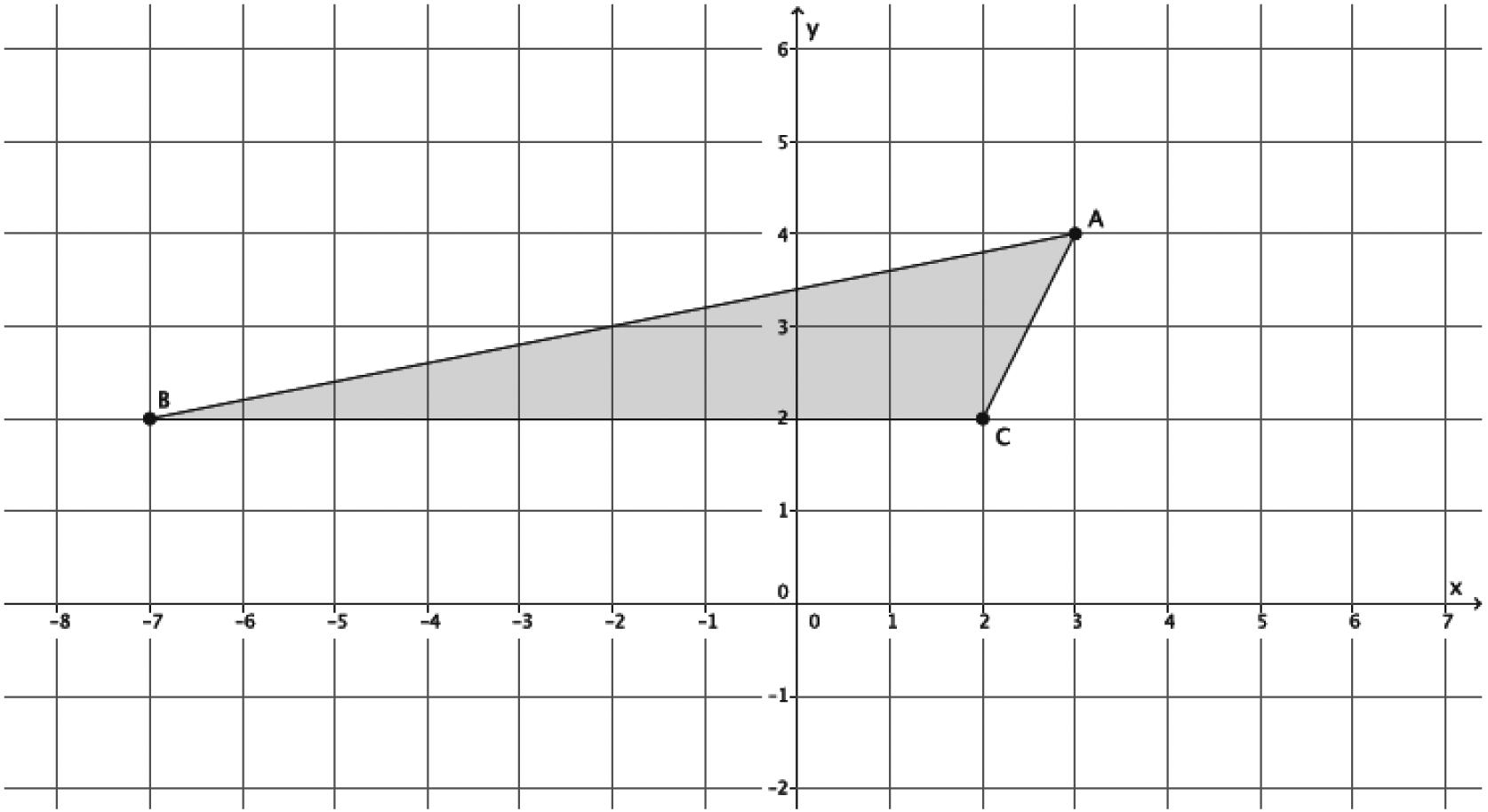
1. The point A(7, 4) is dilated from the origin by a scale factor r = 3. What are the coordinates of point A′?
Since point A(7, 4), then A′(3 7, 3 4) = A′(21, 12)
2. The triangle ABC, shown on the coordinate plane below, is dilated from the origin by scale factor r = 1 2 . What is the location of triangle A′B′C′? Draw and label it on the coordinate plane.

Students practice finding the coordinates of dilated points of two-dimensional figures.
1. Triangle ABC is shown on the coordinate plane below. The triangle is dilated from the origin by scale factor r = 4. Identify the coordinates of the dilated triangle A′B′C′.

Point A( 10, 6), so A′(4 · ( 10), 4 · 6) = A′( 40, 24)
Point B( 11, 2), so B′(4 · ( 11), 4 · 2) = B′( 44, 8).
Point C( 4, 4), so C′(4 ( 4), 4 4) = C′( 16, 16).
The coordinates of the vertices of triangle A′B′C′ are ( 40, 24), ( 44, 8), and ( 16, 16), respectively
18:
Dilations on the Coordinate Plane
2. Triangle ABC is shown on the coordinate plane below. The triangle is dilated from the origin by scale factor r = 5 4 Identify the coordinates of the dilated triangle A′B′C′

Point A(
The coordinates of the vertices of triangle
3. The triangle ABC has coordinates A(6, 1), B(12, 4), and C( 6, 2). The triangle is dilated from the origin by a scale factor r = 1 2 . Identify the coordinates of the dilated triangle A′B′C′
Point A(6, 1), so A′
Point B(12, 4), so B′ ()
= CC 1 2 6 1 2 23 1 ,, ''C′CC 1 23
Point C( 6, 2), so C′ () ()
The coordinates of the vertices of triangle A′B′C′ are �3, 1 2 �, (6, 2), and ( 3, 1), respectively
Dilations on the Coordinate Plane
4. Figure DEFG is shown on the coordinate plane below. The figure is dilated from the origin by scale factor r = 3 2 . Identify the coordinates of the dilated figure D′E′F′G′, and then draw and label figure D′E′F′G′ on the coordinate plane.

The coordinates of the vertices of figure
5. Figure DEFG has coordinates D(1, 1), E(7, 3), F(5, 4), and G( 1, 4). The figure is dilated from the origin by scale factor r = 7. Identify the coordinates of the dilated figure D′E′F′G′
Point D(1, 1), so D′(7 1, 7 1) = D′(7, 7)
Point E(7, 3), so E′(7 · 7, 7 · 3) = E′(49, 21).
Point F(5, 4), so F′(7 5, 7 ( 4)) = F′(35, 28).
Point G( 1, 4), so G′(7 · ( 1), 7 · ( 4)) = G′( 7, 28)
The coordinates of the vertices of figure D′E′F′G′ are (7, 7), (49, 21), (35, 28), and ( 7, 28), respectively.

Students identify a transformation given a preimage and an image.
Students describe a transformation or sequence of transformations that maps a preimage to its image.
Students sketch an image for a given transformation or sequence of transformations.
Lesson Notes
In this lesson, students analyze preimages and images to identify and describe the transformations performed. Before class, copy and cut out the cards provided at the end of this lesson. Prepare one set of Transformation Examples cards and one set of Transformation Descriptions cards per student pair.
Classwork
Discussion (15 minutes)
Have students work in pairs to sort a set of cards showing various transformations. Distribute one set of Transformation Examples cards to each student pair. Have student pairs examine the information on their cards. Have them identify and group the cards that display similar information. Students should be prepared to describe their groups to the class.
Circulate as students work to observe how they are sorting the cards. Accept any initial groups that students make. Possible groups may include the following:
⬛ By transformation: translation (B, H); reflection (A, F); rotation (E, G); dilation (C, D)
⬛ By coordinate plane (B, C, F, G) or no coordinate plane (A, D, E, H)
⬛ By shape: trapezoid (A, C); parallelogram (F, H); pentagon (B, D, E, G)
When all student pairs have finished sorting, allow time for each pair to observe the groups of other student pairs. Have them identify how the other pairs sorted the cards. Then invite student pairs to explain how they sorted their own cards into groups and how their groups are similar to and different from the groups of others. Then facilitate a discussion with students.
⬛ One way to group the cards is by the transformation performed. In this set of examples, there are translations, reflections, rotations, and dilations. Each transformation appears twice.
⬛ How would you determine whether a transformation is a translation? A reflection? A rotation? A dilation?
I know that the transformation is a translation if the preimage and the image are the same size, the image is not turned, and the corresponding vertex labels go in the same direction around the figures.
I know that the transformation is a reflection if the preimage and the image are the same size, but the figures look like mirror images of each other, and the corresponding vertex labels go in opposite directions around the figures.
Identifying Transformations
I know that the transformation is a rotation if the image looks turned, the preimage and the image are the same size, and the vertex labels go in the same direction around the figures.
I know that the transformation is a dilation if the preimage and the image are different sizes and have proportional side lengths.
Have students discuss with their partner how to precisely describe the transformation shown on each card, rather than simply naming it. For example, the transformation on Card B can be described as a translation of Figure ABCDE down 11 units and then right 3 units. Then, for each card, invite one student pair to share their description with the class.
Have students work in pairs. Distribute one set of Transformation Descriptions cards to each student pair. Have each partner choose four cards from the set at random and place them face down in separate piles. For each exercise, have students choose one card from their own pile and, without showing it to their partner, draw the image of the given figure based on the transformation described on their card. Then have them trade their work with their partner, analyze their partner’s work, and describe the transformation that they think was performed by their partner.
Note to Teacher:
If student pairs finish early, have them draw their own figures on a coordinate plane on graph paper. Then, have them shuffle the cards and repeat the activity with their figures.
Circulate as students work. Encourage students to use precise language as they describe the transformations. Once a card has been used, have students place it aside into a separate pile. Have each partner complete four transformations. As time allows, have two student pairs join together. Have each pair analyze and describe the transformations performed by the other pair.
Exercises 1–4
You and your partner will each choose four Transformation Description cards and place them face down in separate piles. For each exercise, you and your partner will each choose one Transformation Description card from your own pile. Do not show the card to your partner. Draw the image of the given figure based on the transformation(s) described on the card. Then trade your work with your partner and describe the transformation(s) performed.
Graphs will vary. Sample student responses shown.
Identifying Transformations
Rotation 180° around the origin
Translation left 5 units and then a reflection across the x-axis
Identifying Transformations
Closing (5 minutes)
Summarize, or have students summarize, the lesson.
We can identify the transformation performed by comparing the preimage of a figure to its image. We compare orientation, size, and location to determine which transformation or sequence of transformations was performed.
We can precisely describe
– translations by identifying direction and units in a coordinate plane or a vector;
– reflections by identifying a line of reflection;
– rotations by identifying a center of rotation, a number of degrees, and the direction of rotation; and
– dilations by identifying a center of dilation and a scale factor.
Exit Ticket (5 minutes)
Identifying Transformations
Exit Ticket
1. Quadrilateral A′B′C′D′ is the image of Quadrilateral ABCD after a transformation.
a. Identify the transformation.
b. Describe the transformation.
Identifying Transformations
2. Parallelogram D′E′F′G′ is the image of Parallelogram DEFG after a transformation.
a. Identify the transformation.
b. Describe the transformation.
Identifying Transformations
1. Quadrilateral A′B′C′D′ is the image of Quadrilateral ABCD after a transformation.
a. Identify the transformation.
Dilation
b. Describe the transformation.
Dilation with center at the origin and scale factor r = 2
Identifying Transformations
2. Parallelogram D′E′F′G′ is the image of Parallelogram DEFG after a transformation.
a. Identify the transformation.
Translation
b. Describe the transformation.
Translation right 10 units and then down 11 units
Identifying Transformations
1. Use the given figures.
a. Which triangle is a translation of ABC?
JKL
b. Which triangle is a reflection of ABC?
DEF
c. Which triangle is a rotation of ABC?
QRS
d. Which triangle is a dilation of ABC?
GHI
Identifying Transformations
2. Quadrilateral A′B′C′D′ is the image of Quadrilateral ABCD after a transformation.
a. Identify the transformation.
Reflection
b. Describe the transformation.
Reflection across the x-axis
3. Figure Q′R′S′T′ is the image of Figure QRST after a transformation.
a. Identify the transformation.
Dilation
b. Describe the transformation.
Identifying Transformations
4. Parallelogram A′B′C′D′ is the image of Parallelogram ABCD after a transformation.
a. Identify the transformation.
Translation
b. Describe the transformation.
Translation right 10 units and then down 2 units
5. Square D′E′F′G′ is the image of Square DEFG after a single transformation. Is the transformation a translation, a reflection, or a rotation? Explain.
Square D′E′F′G′ is the image of Square DEFG after a 180° rotation around the origin. The transformation is not a translation because the corresponding vertices did not stay in the same locations on the square. The transformation is also not a reflection because the vertex D′ is not on the left of the square and the vertex F′ is not on the right of the square.
Identifying Transformations
6. Figure A′B′C′D′E′F′ is the image of Figure ABCDEF.
Three students each described a way to map Figure ABCDEF to Figure A′B′C′D′E′F′.
Henry: A translation left 13 units and up 4 units
Zara: A 180° rotation around the origin
Elle: A reflection across the y-axis and then a reflection across the x-axis
Who is correct? Explain.
Both Zara and Elle are correct. A 180° rotation around the origin or a reflection across the y-axis and then a reflection across the x-axis both result in the given image. The transformation cannot be the translation Henry described because the figures are not facing in the same direction. A translation only changes the location of a figure, not the direction it is facing.
Card A
B
Card C
Card E
G
Transformation Descriptions Cards
Translation up 4 units and then right 3 units
Dilation with center at the origin and scale factor r 1 4 =
Reflection across the x-axis
Rotation 180° around the origin
Dilation with center at the origin and scale factor r 2 =
Translation down 6 units
Reflection across the y-axis
Translation left 5 units and then a reflection across the x-axis

8.7
Focus Standards: 8.7 The student will a. given a polygon, apply transformations, to include translations, reflections, and dilations, in the coordinate plane; and b. identify practical applications of transformations.
Instructional Days: 5
Lesson 20: Similarity (P)1
Lesson 21: Basic Properties of Similarity (E)
Lesson 22: Informal Proof of AA Criterion for Similarity (S)
Lesson 23: More About Similar Triangles (P)
Lesson 24: Modeling by Using Similarity (M)
Topic D begins with the definition of similarity and the properties of similarity. In Lesson 20, students learn that similarities map lines to lines, change the lengths of segments by factor r, and are angle-preserving. In Lesson 21, students investigate additional properties about similarity; first, students learn that congruence implies similarity (e.g., congruent figures are also similar). Next, students learn that similarity is symmetric (e.g., if figure A is similar to figure B, then figure B is similar to figure A) and transitive (e.g., if figure A is similar to figure B, and figure B is similar to figure C, then figure A is similar to figure C). Finally, students learn about similarity with respect to triangles.
Lesson 22 provides students with an informal proof of the angle-angle (AA) criterion for similarity of triangles. Lesson 22 also provides opportunities for students to use the AA criterion to determine if two triangles are similar. In Lesson 23, students use what they know about similar triangles and dilation to find an unknown side length of one triangle. Since students know that similar triangles have side lengths that are equal in ratio (specifically equal to the scale factor), students verify whether or not two triangles are similar by comparing their corresponding side lengths.
1Lesson Structure Key: P-Problem Set Lesson, M-Modeling Cycle Lesson, E-Exploration Lesson, S-Socratic Lesson


In Lesson 24, students apply their knowledge of similar triangles and dilation to real-world situations. For example, students use the height of a person and the height of his shadow to determine the height of a tree. Students may also use their knowledge to determine the distance across a lake, the height of a building, and the height of a flagpole.

⬛ Students know the definition of similarity and why dilation alone is not enough to determine similarity.
⬛ Given two similar figures, students describe the sequence of a dilation and a congruence that would map one figure onto the other.
It should be noted that congruence, together with similarity, is the fundamental concept in planar geometry. It is a concept defined without coordinates. In fact, it is most transparently understood when introduced without the extra conceptual baggage of a coordinate system. This is partly because a coordinate system picks out a preferred point (the origin), which then centers most discussions of rotations, reflections, and translations at or in reference to that point. They are then further restricted to only the “nice” rotations, reflections, and translations that are easy to do in a coordinate plane. Restricting to “nice” transformations is a huge mistake mathematically because it is antithetical to the main point that must be made about congruence: that rotations, translations, and reflections are abundant in the plane; that for every point in the plane, there are an infinite number of rotations up to 360°, that for every line in the plane there is a reflection and that for every directed line segment there is a translation. It is this abundance that helps students realize that every congruence transformation (i.e., the act of “picking up a figure” and moving it to another location) can be accomplished through a sequence of translations, rotations, and reflections, and further, that similarity is a sequence of dilations or congruence transformations.
Concept Development (5 minutes)
⬛ A dilation alone is not enough to state that two figures are similar. Consider the following pair of figures:
⬛ Do these figures look similar?
Yes, they look like the same shape, but they are different in size
⬛ How could you prove that they are similar? What would you need to do?
We would need to show that they could become the same size by dilating one of the figures
⬛ Would we be able to dilate one figure so that it was the same size as the other?
Yes, we could dilate to make them the same size by using the appropriate scale factor.
⬛ We could make them the same size, but would a dilation alone map figure S onto figure S0?
No, a dilation alone would not map figure S onto figure S0.
⬛ What else should we do to map figure S onto figure S0?
We would have to perform a translation and a rotation to map figure S onto figure S0.
⬛ That is precisely why a dilation alone is not enough to define similarity. Two figures in the plane are similar if one can be mapped onto the other using a finite sequence of dilations or basic rigid motions. This mapping is called a similarity transformation (or a similarity). We will use the fact that all similarities can be represented as a dilation followed by a congruence.
1 (4 minutes)
Example 1
In the picture below, we have triangle ABC that has been dilated from center O by a scale factor of = r 1 2 . It is noted by A′B′C ′. We also have triangle A″B″C ″, which is congruent to triangle A

Describe the sequence that would map triangle A″B″C ″ onto triangle ABC
⬛ Based on the definition of similarity, how could we show that triangle A″B″C″ is similar to triangle ABC ?
To show that △A″B″C″∼ △ABC, we need to describe a dilation followed by a congruence
Scaffolding:
Remind students of the work they did in Lesson 15 to bring dilated figures back to their original size.
⬛ We want to describe a sequence that would map triangle A″B″C″ onto triangle ABC. There is no clear way to do this, so let’s begin with something simpler: How can we map triangle A′B′C′ onto triangle ABC ? That is, what is the precise dilation that would make triangle A′B′C′ the same size as triangle ABC ?
A dilation from center O with scale factor r = 2
⬛ Remember, our goal was to describe how to map triangle A″B″C″ onto triangle ABC. What precise dilation would make triangle A″B″C″ the same size as triangle ABC ?
A dilation from center O with scale factor r = 2 would make triangle A″B″C″ the same size as triangle ABC.
⬛ (Show the picture below with the dilated triangle A″B″C″ noted by A‴B‴C‴.) Now that we know how to make triangle A″B″C″ the same size as triangle ABC, what rigid motion(s) should we use to actually map triangle A″B″C″ onto triangle ABC ? Have we done anything like this before?

Problem 2 of the Problem Set from Lesson 14 was like this. That is, we had two figures dilated by the same scale factor in different locations on the plane. To get one to map to the other, we just translated along a vector.
⬛ Now that we have an idea of what needs to be done, let’s describe the translation in terms of coordinates. How many units and in which direction do we need to translate so that triangle A‴B‴C‴ maps to triangle ABC ?
We need to translate triangle A‴B‴C‴ 20 units to the left and 2 units down
⬛ Let’s use precise language to describe how to map triangle A″B″C″ onto triangle ABC. We need information about the dilation and the translation.
The sequence that would map triangle A″B″C″ onto triangle ABC is as follows: Dilate triangle A″B″C″ from center O by scale factor r = 2 Then, translate the dilated triangle 20 units to the left and 2 units down
⬛ Since we were able to map triangle A″B″C″ onto triangle ABC with a dilation followed by a congruence, we can write that triangle A″B″C″ is similar to triangle ABC, in notation, △A″B″C″∼ △ABC.
⬛ In the picture below, we have triangle DEF that has been dilated from center O, by scale factor r = 3. It is noted by D′E′F′. We also have triangle D″E″F″, which is congruent to triangle D′E′F′ (i.e., △D′E′F′ ≅ △D″E″F″).

⬛ We want to describe a sequence that would map triangle D″E″F″ onto triangle DEF. This is similar to what we did in the last example. Can someone summarize the work we did in the last example?
First, we figured out what scale factor r would make the triangles the same size. Then, we used a sequence of translations to map the magnified figure onto the original triangle
⬛ What is the difference between this problem and the last?
This time, the scale factor is greater than one, so we need to shrink triangle D″E″F″ to the size of triangle DEF. Also, it appears as if a translation alone does not map one triangle onto another.
⬛ Now, since we want to dilate triangle D″E″F″ to the size of triangle DEF, we need to know what scale factor r to use. Since triangle D″E″F″ is congruent to D′E′F′, then we can use those triangles to determine the scale factor needed. We need a scale factor so that |OF| = r |OF′|. What scale factor do you think we should use, and why?
We need a scale factor = 1 3 r because we want |OF| = r |OF′|.
⬛ What precise dilation would make triangle D″E″F″ the same size as triangle DEF?
A dilation from center O with scale factor = 1 3 r would make triangle D″E″F″ the same size as triangle DEF
⬛ (Show the picture below with the dilated triangle D″E″F″ noted by D‴E‴F‴.) Now we should use what we know about rigid motions to map the dilated version of triangle D″E″F″ onto triangle DEF. What should we do first?

We should translate triangle D‴E‴F‴ 2 units to the right
⬛ (Show the picture below, the translated triangle noted in red.) What should we do next (refer to the translated triangle as the red triangle)?

Next, we should reflect the red triangle across the x-axis to map the red triangle onto triangle DEF.
⬛ Use precise language to describe how to map triangle D″E″F″ onto triangle DEF
The sequence that would map triangle D″E″F″ onto triangle DEF is as follows: Dilate triangle D″E″F″ from center O by scale factor = 1 3 r . Then, translate the dilated image of triangle D″E″F″ , noted by D‴E‴F‴ , two units to the right. Finally, reflect across the x-axis to map the red triangle onto triangle DEF
⬛ Since we were able to map triangle D″E″F″ onto triangle DEF with a dilation followed by a congruence, we can write that triangle D″E″F″ is similar to triangle DEF. (In notation: △D″E″F″∼ △DEF)
⬛ In the diagram below, △ABC ∼ △A′B′C′. Describe a sequence of a dilation followed by a congruence that would prove these figures to be similar.

⬛ Let’s begin with the scale factor. We know that r |AB| = |A′B′|. What scale factor r makes △ABC the same size as △A′B′C′?
We know that r · 2 = 1; therefore, = 1 2 r makes △ABC the same size as △A′B′C′ .
⬛ If we apply a dilation from the origin of scale factor = 1 2 r , then the triangles are the same size (as shown and noted by triangle A″B″C″). What sequence of rigid motions would map the dilated image of △ABC onto △A′B′C′?

We could translate the dilated image of △ABC, △A″B″C″ , 3 units to the right and 4 units down and then reflect the triangle across line A′B′ .
⬛ The sequence that would map △ABC onto △A′B′C′ to prove the figures similar is a dilation from the origin by scale factor = 1 2 r , followed by the translation of the dilated version of △ABC 3 units to the right and 4 units down, followed by the reflection across line A′B′ .
⬛ In the diagram below, we have two similar figures. Using the notation, we have △ABC ∼ △DEF. We want to describe a sequence of the dilation followed by a congruence that would prove these figures to be similar.

⬛ First, we need to describe the dilation that would make the triangles the same size. What information do we have to help us describe the dilation?
Since we know the length of side AC and side DF , we can determine the scale factor.
⬛ Can we use any two sides to calculate the scale factor? Assume, for instance, that we know that side AC is 18 units in length and side EF is 2 units in length. Could we find the scale factor using those two sides, AC and EF ? Why or why not?
No, we need more information about corresponding sides. Sides AC and DF are the longest sides of each triangle (they are also opposite the obtuse angle in the triangle). Side AC does not correspond to side EF . If we knew the length of side BC , we could use sides BC and EF .
⬛ Now that we know that we can find the scale factor if we have information about corresponding sides, how would we calculate the scale factor if we were mapping △ABC onto △DEF?
|DF| = r |AC|, so 6 = r 18, and = 1 3 r
⬛ If we were mapping △DEF onto △ABC, what would the scale factor be?
|AC| = r |DF|, so 18 = r · 6, and r = 3.
⬛ What is the precise dilation that would map △ABC onto △DEF?
Dilate △ABC from center O, by scale factor = 1 3 r
⬛ (Show the picture below with the dilated triangle noted as △A′B′C′.) Now we have to describe the congruence. Work with a partner to determine the sequence of rigid motions that would map △ABC onto △DEF.
Translate the dilated version of △ABC 5.5 units to the right and 2 units down. Then, rotate d degrees around point E so that segment B′C′ maps onto segment EF. Finally, reflect across line EF.
Note that “d degrees” refers to a rotation by an appropriate number of degrees to exhibit similarity. Students may choose to describe this number of degrees in other ways.
⬛ The sequence of a dilation followed by a congruence that proves △ABC ∼ △DEF is as follows: Dilate △ABC from center O by scale factor = 1 3 r . Translate the dilated version of △ABC 5.5 units to the right and 2 units down. Next, rotate around point E by d degrees so that segment B′C′ maps onto segment EF, and then reflect the triangle across line EF.
⬛ Knowing that a sequence of a dilation followed by a congruence defines similarity also helps determine if two figures are in fact similar. For example, would a dilation map triangle ABC onto triangle DEF (i.e., is △ABC ∼ △DEF )?

No. By FTS, we expect the corresponding side lengths to be in proportion and equal to the scale factor.
When we compare side AC to side DF and BC to EF , we get ≠ 18 6 15 4
Therefore, the triangles are not similar because a dilation does not map one to the other
⬛ Again, knowing that a dilation followed by a congruence defines similarity also helps determine if two figures are in fact similar. For example, would a dilation map Figure A onto Figure A′ (i.e., is Figure A ∼ Figure A′)?

No. Even though we could say that the corresponding sides are in proportion, there exists no single rigid motion or sequence of rigid motions that would map a four-sided figure to a three-sided figure. Therefore, the figures do not fulfill the congruence part of the definition for similarity, and Figure A is not similar to Figure A′ .
Allow students to work in pairs to describe sequences that map one figure onto another.
Exercises
1. Triangle ABC was dilated from center O by scale factor � r 1 2 . The dilated triangle is noted by A′B′C′. Another triangle A″B″C″ is congruent to triangle A
(i.e.,
′C′). Describe a dilation followed by the basic rigid motion that would map triangle A″B″C″ onto triangle ABC

Triangle A″B″C″ needs to be dilated from center O, by scale factor r = 2 to bring it to the same size as triangle ABC. This produces a triangle noted by A‴B‴C‴ Next, triangle A‴B‴C‴ needs to be translated 4 units up and 12 units left. The dilation followed by the translation maps triangle A″B″C″ onto triangle ABC.
2. Describe a sequence that would show △ABC ∼ △A′B′C ′

Since r |AB| = |A′ B′|, then r · 2 = 6, and r = 3 A dilation from the origin by scale factor r = 3 makes △ABC the same size as △A′B′C′ . Then, a translation of the dilated image of △ABC ten units right and five units down, followed by a rotation of 90 degrees around point C′ , maps △ABC onto △A′B′C′ , proving the triangles to be similar
3. Are the two triangles shown below similar? If so, describe a sequence that would prove △ABC ∼ △A′B′C ′. If not, state how you know they are not similar.

Yes, △ABC ∼ △A′B′C ′ . The corresponding sides are in proportion and equal to the scale factor:
To map triangle ABC onto triangle A′B′C ′ , dilate triangle ABC from center O, by scale factor � r 2 3 Then, translate triangle ABC along vector AA′ . Next, rotate triangle ABCd degrees around point A. == == r 10 15 4 6 12 18 2 3
4. Are the two triangles shown below similar? If so, describe a sequence that would prove △ABC ∼ △A′B′C′ If not, state how you know they are not similar.
Yes, triangle △ABC △A′B′C′ The corresponding sides are in proportion and equal to the scale factor: == = 4 3 8 6 4 3 1. 33; = 10. 67 8 1.33375 ; therefore, r = 1.33 which is approximately equal to 4 3
To map triangle ABC onto triangle A′B′C′ , dilate triangle ABC from center O, by scale factor � r 4 3 . Then, translate triangle ABC along vector AA′ . Next, rotate triangle ABC 180 degrees around point A′ .
Closing (4 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We know that a similarity can be represented as a sequence of a dilation followed by a congruence.
⬛ To show that a figure in the plane is similar to another figure of a different size, we must describe the sequence of a dilation followed by a congruence (one or more rigid motions) that maps one figure onto another.
Lesson Summary
A similarity transformation (or a similarity) is a sequence of a finite number of dilations or basic rigid motions. Two figures are similar if there is a similarity transformation taking one figure onto the other figure. Every similarity can be represented as a dilation followed by a congruence.
The notation △ABC △A′B′C′ means that △ABC is similar to △A′B′C′
Exit Ticket (5 minutes)
Exit Ticket
In the picture below, we have triangle DEF that has been dilated from center O by scale factor = 1 2 r . The dilated triangle is noted by D′E′F′. We also have a triangle D″EF, which is congruent to triangle DEF (i.e., △DEF ≅ △D″EF).
Describe the sequence of a dilation followed by a congruence (of one or more rigid motions) that would map triangle D′E′F′ onto triangle D″EF

In the picture below, we have triangle DEF that has been dilated from center O by scale factor 1 2 = r . The dilated triangle is noted by D′E′F′. We also have a triangle D″EF, which is congruent to triangle DEF (i.e., △DEF ≅ △D″EF).
Describe the sequence of a dilation, followed by a congruence (of one or more rigid motions), that would map triangle D′E′F′ onto triangle D″EF.

Triangle D′E′F′ needs to be dilated from center O by scale factor r = 2 to bring it to the same size as triangle DEF. This produces the triangle noted by DEF. Next, triangle DEF needs to be reflected across line EF. The dilation followed by the reflection maps triangle D′E′F′ onto triangle D″EF.
Students practice dilating a curved figure and describing a sequence of a dilation followed by a congruence that maps one figure onto another.
1. In the picture below, we have triangle DEF that has been dilated from center O by scale factor r = 4. It is noted by D′E′F′. We also have triangle D″E″F″, which is congruent to triangle D′E′F′ (i.e.,
D″E″F″). Describe the sequence of a dilation, followed by a congruence (of one or more rigid motions), that would map triangle D″E″F″ onto triangle DEF

First, we must dilate triangle D″E″F″ by scale factor � r 1 4 to shrink it to the size of triangle DEF. Next, we must translate the dilated triangle, noted by D‴E‴F‴ , one unit up and two units to the right. This sequence of the dilation followed by the translation would map triangle D″E″F″ onto triangle DEF.
2. Triangle ABC was dilated from center O by scale factor = r 1 2 . The dilated triangle is noted by A′B′C′. Another triangle A″B″C″ is congruent to triangle A′B′C′ (i.e., △A″B″C″ ≅ △A′B′C′). Describe the dilation followed by the basic rigid motions that would map triangle A″B″C″ onto triangle ABC

Triangle A″B″C″ needs to be dilated from center O by scale factor r = 2 to bring it to the same size as triangle ABC. This produces a triangle noted by A‴B‴C‴ Next, triangle A‴B‴C‴ needs to be translated 18 units to the right and two units down, producing the triangle shown in red. Next, rotate the red triangle d degrees around point B so that one of the segments of the red triangle coincides completely with segment BC. Then, reflect the red triangle across line BC. The dilation, followed by the congruence described, maps triangle A″B″C″ onto triangle ABC
3. Are the two figures shown below similar? If so, describe a sequence that would prove the similarity. If not, state how you know they are not similar.

No, these figures are not similar. There is no single rigid motion, or sequence of rigid motions, that would map Figure A onto Figure B
4. Triangle ABC is similar to triangle A′B′C′ (i.e., △ABC ∼ △A′B′C′). Prove the similarity by describing a sequence that would map triangle A′B′C′ onto triangle ABC.

The scale factor that would magnify triangle A′B′C′ to the size of triangle ABC is r = 3 The sequence that would prove the similarity of the triangles is a dilation from center O by a scale factor of r = 3, followed by a translation along vector A′A , and finally, a reflection across line AC.
5. Are the two figures shown below similar? If so, describe a sequence that would prove △ABC ∼ △A′B′C′. If not, state how you know they are not similar.

Yes, the triangles are similar. The scale factor that triangle ABC has been dilated is � r 1 5 . The sequence that proves the triangles are similar is as follows: dilate triangle A′B′C′ from center O by scale factor r = 5; then, translate triangle A′B′C′ along vector C′C ; next, rotate triangle A′B′C′ d degrees around point C; and finally, reflect triangle A′B′C′ across line AC.
6. Describe a sequence that would show △ABC ∼ △A′B′C′

Since r|AB| = |A′B′|, then r 3 = 1 and � r 1 3 . A dilation from the origin by scale factor � r 1 3 makes △ABC the same size as △A′B′C′ . Then, a translation of the dilated image of △ABC four units down and one unit to the right, followed by a reflection across line A′B′ , maps △ABC onto △A′B′C′ , proving the triangles to be similar

⬛ Students know that similarity is both a symmetric and a transitive relation.
Classwork
Concept Development (4 minutes)
⬛ If we say that one figure, S, is similar to another figure, S′, that is, S ∼ S′, can we also say that S′ ∼ S? That is, is similarity symmetric? Keep in mind that there is a very specific sequence of a dilation followed by a congruence that would map S to S′ .
Expect students to say yes; they would expect similarity to be symmetric.
⬛ If we say that figure S is similar to another figure, T (i.e., S ∼ T), and figure T is similar to yet another figure, U (i.e., T ∼ U), is it true that S ∼ U? That is, is similarity transitive?
Expect students to say yes; they would expect similarity to be transitive
The Exploratory Challenges that follow are for students to get an intuitive sense that, in fact, these two statements are true.
Exploratory Challenge 1 (10 minutes)
Students work in pairs to complete Exploratory Challenge 1.
Exploratory Challenge 1
The goal is to show

a. First, determine whether or not △ABC is in fact similar to △A′B′C′. (If it isn’t, then no further work needs to be done.) Use a protractor to verify that the corresponding angles are congruent and that the ratios of the corresponding sides are equal to some scale factor.
The corresponding angles are congruent: ∠
and
, and ∠C ≅ ∠C′ , therefore
The ratios of the corresponding sides are equal: == = r 4 8 3 6 2 4 .
b. Describe the sequence of dilation followed by a congruence that proves △ABC ∼ △A′B′C′ .

To map △ABC onto △A′B′C′ , dilate △ABC from the origin by scale factor = r 1 2 , noted in the diagram above by the red triangle. Then, translate the red triangle up two units and five units to the right. Next, rotate the red triangle 180 degrees around point A′ until AC coincides with A′C′
Basic Properties of Similarity
c. Describe the sequence of dilation followed by a congruence that proves △A′B′C′ ∼△ABC.
Note that in the diagram below, both axes have been compressed.

To map △A′B′C′ onto △ABC, dilate △A′B′C′ from center O by scale factor r = 2, noted by the blue triangle in the diagram. Then, translate the blue triangle ten units to the left and four units down. Next, rotate the blue triangle 180 degrees around point A until side A′C′ coincides with side AC
d. Is it true that △ABC ∼ △A′B′C′ and △A′B′C′ ∼ △ABC? Why do you think this is so? Yes, it is true that △ABC ∼ △A′B′C′ and △A′B′C′ ∼ △ABC. I think it is true because when we say figures are similar, it means that they are the same figure, just a different size because one has been dilated by a scale factor. For that reason, if one figure, like △ABC, is similar to another, like △A′B′C′ , it must mean that △A′B′C′ ∼ △ABC. However, the sequence you would use to map one of the figures onto the other is different
Ask students to share what they wrote for part (d) of Exploratory Challenge 1.
Expect students to respond in a similar manner to the response for part (d). If they do not, ask questions about what similarity means, what a dilation does, and how figures are mapped onto one another.
⬛ For any two figures S and S′, if S ∼ S′, then S′ ∼ S. This is what the statement that similarity is a symmetric relation means.
Basic Properties of Similarity
Exploratory Challenge 2 (15 minutes)
Students work in pairs to complete Exploratory Challenge 2.
Exploratory Challenge 2
The

a. Describe the similarity that proves △ABC ∼ △A′B′C′ .

To map △ABC onto △A′B′C′ , we need to first determine the scale factor that makes △ABC the same size as
. Dilate △ ABC from center O by scale factor r = 3, shown in red in the diagram. Then, translate the red triangle 5 units up
b. Describe the similarity that proves △A′B′C′

map
, we need to first determine the scale factor that makes △A
the same size as
C′ from center O by scale factor = r 2 3 , shown in blue in the diagram. Then, translate the blue triangle 3.5 units down and 5 units to the right. Next, rotate the blue triangle 90 degrees clockwise around point A″ until the blue triangle coincides with
Basic Properties of Similarity
c. Verify that, in fact, △ABC ∼ △A″B″C″ by checking corresponding angles and corresponding side lengths. Then, describe the sequence that would prove the similarity

The corresponding angles are congruent: ∠ A
, and ∠C ≅ ∠C″; therefore, |∠ A
and
The ratio of the corresponding sides is equal:
Dilate △ABC from center O by scale factor r = 2, shown as the pink triangle in the diagram. Then, translate the pink triangle 5 units to the right. Finally, rotate the pink triangle 90 degrees clockwise around point A″ until the pink triangle coincides with △A″
d. Is it true that if
Yes, it is true that if
and
Why do you think this is so?
Again, because these figures are similar, it means that they have equal angles and are made different sizes based on a specific scale factor. Since dilations map angles to angles of the same degree, it makes sense that all three figures would have the “same shape.” Also, using the idea that similarity is a symmetric relation, the statement that △ABC
implies that
Since we know that
Ask students to share what they wrote for part (d) of Exploratory Challenge 2.
Expect students to respond in a similar manner to the response for part (d). If they do not, ask questions about what similarity means, what a dilation does, and how they might use what they just learned about similarity being a symmetric relation.
⬛ For any three figures S, T, and U, if S ∼ T and T ∼ U, then S
. This is what the statement that similarity is a transitive relation means.
Closing (5 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We know that similarity is a symmetric relation. That means that if one figure is similar to another, S ∼ S′, then we can be sure that S′ ∼ S. The sequence that maps one onto the other is different, but we know that it is true.
⬛ We know that similarity is a transitive relation. That means that if we are given two similar figures, S ∼ T, and another statement about T ∼ U, then we also know that S ∼ U. Again, the sequence and scale factor are different to prove the similarity, but we know it is true.
Lesson Summary
Similarity is a symmetric relation. That means that if one figure is similar to another, S ∼ S′, then we can be sure that S′ ∼ S.
Similarity is a transitive relation. That means that if we are given two similar figures, S ∼ T, and another statement about T ∼ U, then we also know that S ∼ U.
Exit Ticket (5 minutes)
Exit Ticket
Use the diagram below to answer Problems 1 and 2.

1. Which two triangles, if any, have similarity that is symmetric?
2. Which three triangles, if any, have similarity that is transitive?
Use the diagram below to answer Problems 1 and 2.

1. Which two triangles, if any, have similarity that is symmetric?
△S ∼ △R and △R ∼△S △S ∼ △T and △T ∼ △S △T ∼ △R and △R ∼ △T
2. Which three triangles, if any, have similarity that is transitive?
One possible solution: Since △S ∼ △R and △R ∼ △T, then △S ∼ △T.
Note that △U and △V are not similar to each other or any other triangles. Therefore, they should not be in any solution
1. Would a dilation alone be enough to show that similarity is symmetric? That is, would a dilation alone prove that if △ABC ∼ △A′B′C′, then △A′B′C′ ∼ △ABC? Consider the two examples below. a. Given △ABC ∼ △A′B′C′, is a dilation enough to show that △A′B′C′ ∼ △ABC? Explain.

For these two triangles, a dilation alone is enough to show that if △ABC △A′B′C′ , then △A′B′C′ △ABC. The reason that dilation alone is enough is because both of the triangles have been dilated from the same center. Therefore, to map one onto the other, all that would be required is a dilation.
Basic Properties of Similarity
b. Given △ABC ∼ △A′B′C′, is a dilation enough to show that △A′B′C′ ∼ △ABC ? Explain.

For these two triangles, a dilation alone is not enough to show that if △ABC ∼ △A′B′C′ , then △A′B′C′ ∼ △ABC. The reason is that a dilation would just make them the same size. It would not show that you could map one of the triangles onto the other. To do that, you would need a sequence of basic rigid motions to demonstrate the congruence.
c. In general, is dilation enough to prove that similarity is a symmetric relation? Explain.
No, in general, a dilation alone does not prove that similarity is a symmetric relation. In some cases, like part (a), it would be enough, but because we are talking about general cases, we must consider figures that require a sequence of basic rigid motions to map one onto the other. Therefore, in general, to show that there is a symmetric relationship, we must use what we know about similar figures, a dilation followed by a congruence, as opposed to dilation alone.
2. Would a dilation alone be enough to show that similarity is transitive? That is, would a dilation alone prove that if △ABC ∼ △A′
and
B″C″, then △ABC ∼ △A″B″C″? Consider the two examples below.
a. Given △ABC ∼ △A′B′C′ and △A′B′C′ ∼ △A″B″C″, is a dilation enough to show that △ABC ∼ △A″B″C″? Explain.

Yes, in this case, we could dilate by different scale factors to show that all three triangles are similar to each other.
b. Given △ABC ∼ △A′B′C′ and △A′
C″, is a dilation enough to show that △ABC ∼ △A″B″C″? Explain.

In this case, it would take more than just a dilation to show that all three triangles are similar to one another. Specifically, it would take a dilation followed by a congruence to prove the similarity among the three.
c. In general, is dilation enough to prove that similarity is a transitive relation? Explain. In some cases, it might be enough, but the general case requires the use of dilation and a congruence. Therefore, to prove that similarity is a transitive relation, you must use both a dilation and a congruence.
3. In the diagram below, △ABC ∼ △
and
C″. Is △ABC ∼ △A″B″C″? If so, describe the dilation followed by the congruence that demonstrates the similarity.

Yes, △ABC ∼ △A″B″C″ because similarity is transitive. Since r |AB| = |A″B″|, then r 4 = 2, which means = r 1 2 . Then, a dilation from the origin by scale factor = r 1 2 makes △ABC the same size as △A″B″C″ . Translate the dilated image of △ABC 8 1 2 units to the left and then reflect across line A″B″ The sequence of the dilation and the congruence map △ABC onto △A″B″C″ , demonstrating the similarity.
Basic Properties of Similarity

⬛ Students know an informal proof of the angle-angle (AA) criterion for similar triangles.
⬛ Students present informal arguments as to whether or not triangles are similar based on the AA criterion.
Concept Development (5 minutes)
⬛ Recall the exercise we did using lined paper to verify experimentally the properties of the fundamental theorem of similarity (FTS). In that example, it was easy for us to see that that the triangles were similar because one was a dilation of the other by some scale factor. It was also easy for us to compare the size of corresponding angles because we could use what we know about parallel lines cut by a transversal.

Scaffolding:
Consider having students review their work of the activity by talking to a partner about what they did and what they proved with respect to FTS.
⬛ Our goal today is to show that we can say any two triangles with equal angles are similar. It is what we call the AA criterion for similarity. The theorem states: Two triangles with two pairs of equal angles are similar.
⬛ Notice that we only use AA instead of AAA; that is, we only need to show that two of the three angles are equal in measure. Why do you think that is so?
We only have to show two angles are equal because the third angle has no choice but to be equal as well. The reason for that is the triangle sum theorem. If you know that two pairs of corresponding angles are equal, say they are 30° and 90°, then the third pair of corresponding angles have no choice but to be 60° because the sum of all three angles must be 180°
⬛ What other property do similar triangles have besides equal angles?
The lengths of their corresponding sides are equal in ratio (or proportional)
⬛ Do you believe that it is enough to say that two triangles are similar just by comparing two pairs of corresponding angles?
Some students may say yes, and others may say no. Encourage students to justify their claims. Either way, they can verify the validity of the theorem by completing Exercises 1 and 2
Students complete Exercises 1 and 2 independently.
Exercises 1–2
1. Use a protractor to draw a pair of triangles with two pairs of interior angles that are equal in measure. Then, measure the lengths of the sides, and verify that the lengths of their corresponding sides are equal in ratio.
Sample student work is shown below

Scaffolding:
If students hesitate to begin, suggest specific side lengths for them to use.
2. Draw a new pair of triangles with two pairs of interior angles that are equal in measure. Then, measure the lengths of the sides, and verify that the lengths of their corresponding sides are equal in ratio.
Sample student work is shown below.
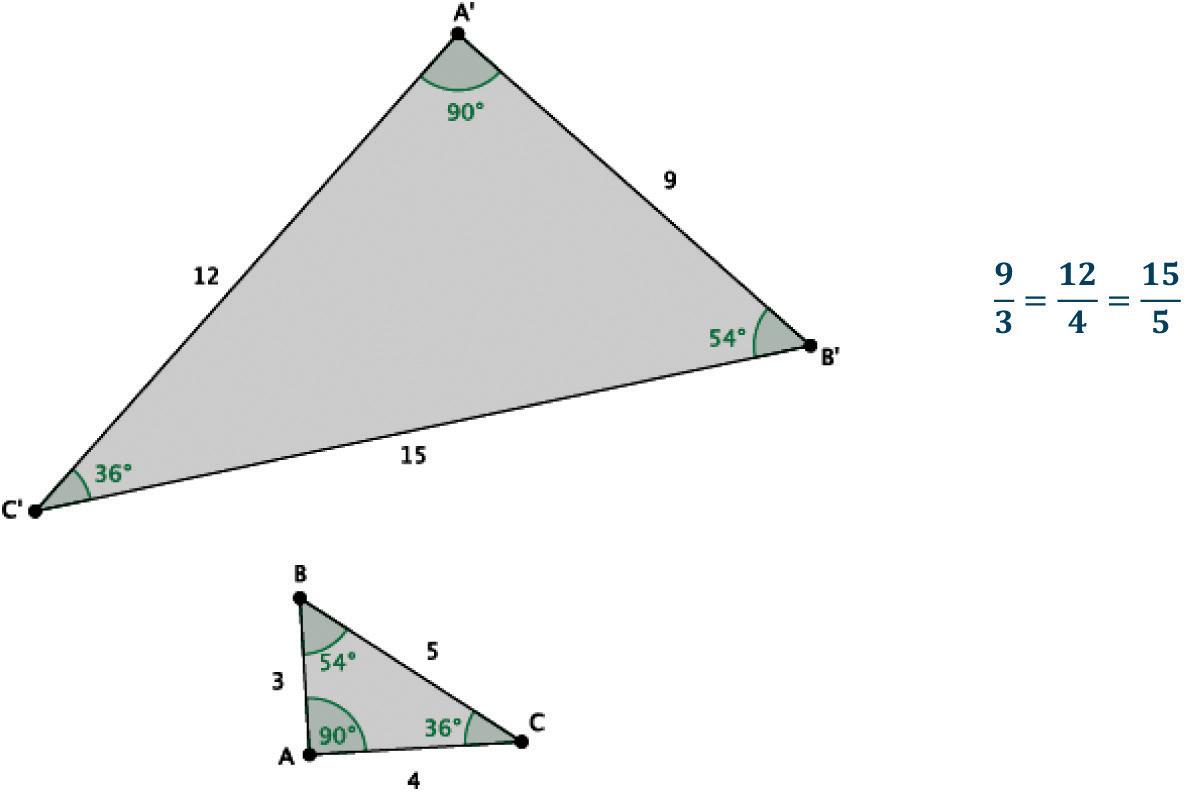
Informal Proof of AA Criterion for Similarity
Discussion (10 minutes)
⬛ Did everyone notice that they had similar triangles in Exercises 1 and 2?
Yes
If students respond no, ask them how close the ratios were with respect to being equal. In some cases, human error either in measuring the angles or side lengths can cause the discrepancy. Another way around this is by selecting ahead of time one student to share her work on a document camera for all to see.
To develop conceptual understanding, students may continue to generate triangles with two pairs of equal angles and then generalize to develop the AA criterion for similarity. A more formal proof follows, which may also be used.
⬛ What we need to do now is informally prove why this is happening, even though we all drew different triangles with different angle measures and different side lengths.
⬛ We begin with a special case. Suppose A = A′, and B′ and C′ lie on the rays AB and AC, respectively.

⬛ In this case, we are given that |∠A′B′C′| = |∠ABC| and |∠B′A′C′|
|∠BAC| (notice that the latter is simply saying that an angle is equal to itself). The fact that |∠ A′B′C′ | = |∠ABC| implies that B′C′BC BC || '' BC because if corresponding angles of two lines cut by a transversal are equal, then the two lines are parallel.
Now, if we let r AB AB = || || ' r AB = || || ' , then the dilation from center A with scale factor r means that |AB′| = r |AB|. We know from our work in Lessons 16 and 17 that the location of C′ is fixed because |AC′| = r |AC|. Therefore, the dilation of △ABC is exactly △A′B′C′ .
Ask students to paraphrase the proof, or offer them this version: We are given that the corresponding angles |∠ A′B′C′| and |∠ABC| are equal in measure. The only way that corresponding angles can be equal in measure is if we have parallel lines. That means that B′C′BC BC || '' . If we say that |AB′| is equal to |AB| multiplied by some scale factor, then we are looking at a dilation from center A. Based on our work in previous lessons with dilated points in the coordinate plane, we know that C′ has no choice as to its location and that |AC′ | must be equal to |AC| multiplied by the same scale factor r. For those reasons, when we dilate △ABC by scale factor r, we get △A′B′C′ .
⬛ This shows that, given two pairs of equal corresponding angles, △ABC ∼ △A′B′C′
⬛ In general, if △A′B′C′ did not share a common point (i.e., A) with △ABC, we would simply perform a sequence of rigid motions (a congruence) so that we would be in the situation just described. | ′| |AB|
Informal Proof of AA Criterion for Similarity
The following are instructions to prepare manipulatives to serve as a physical demonstration of the AA criterion for similarity when the triangles do not share a common angle. Prepare ahead of time cardboard or cardstock versions of triangles A′B′C′ and ABC (including △AB0C0 drawn within △ABC). Demonstrate the congruence
△A′B′C′ ≅ △AB0C0 by moving the cardboard between these two triangles.

Example 1 (2 minutes)
⬛ Are the triangles shown below similar? Present an informal argument as to why they are or why they are not.

Informal Proof of AA Criterion for Similarity
Example 2 (2 minutes)
⬛ Are the triangles shown below similar? Present an informal argument as to why they are or why they are not.

No, △ABC is not similar to △A′B′C′ They are not similar because they do not have two pairs of corresponding angles that are equal, namely, |∠B| ≠ |∠B′|, and |∠C| ≠ |∠C′|.
Example 3 (2 minutes)
⬛ Are the triangles shown below similar? Present an informal argument as to why they are or why they are not.

Yes, △ABC ∼ △A′B′C′ They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠A| = 44° or |∠B′| = 88° Then, you can see that |∠A| = |∠A′| = 44°, |∠B| = |∠B′| = 88°, and |∠C| = |∠C′| = 48°.
Informal Proof of AA Criterion for Similarity
minutes)
Exercises 3–5
3. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Yes, △ABC ∼ △A′B ′C ′ . They are similar because they have two pairs of corresponding angles that are equal, namely, |∠B| = |∠B ′| = 103° , and |∠A| = |∠A′| = 31°
4. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

No, △ABC is not similar to △A′B ′C ′ They are not similar because they do not have two pairs of corresponding angles that are equal, just one, namely, |∠A | = |∠A′|, but |∠B| ≠ |∠B′|
5. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
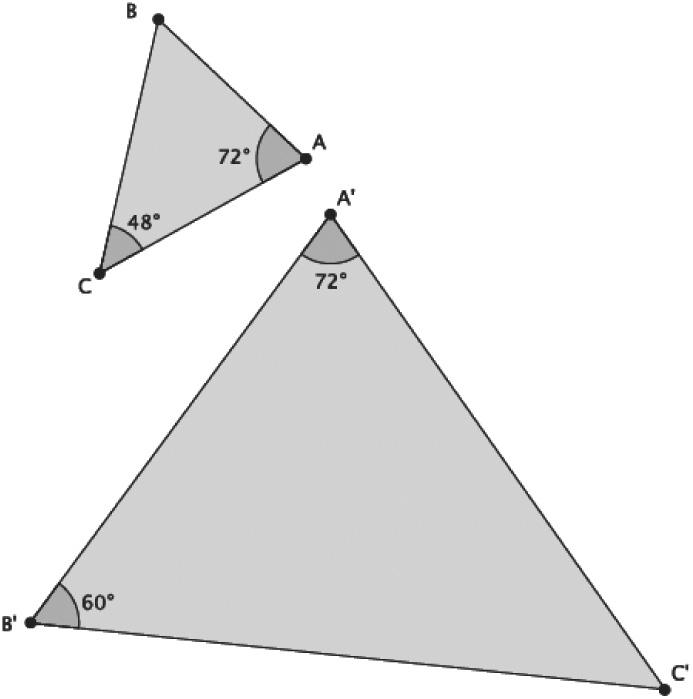
Yes, △ABC △A′B ′C ′ They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B| = 60° or |∠C′| = 48° Then, you can see that | ∠A| = |∠A′| = 72° , |∠B| = |∠B′| = 60° , and |∠C| = |∠C ′| = 48°
Informal Proof of AA Criterion for Similarity
Closing (3 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We understand a proof of why the AA criterion is enough to state that two triangles are similar. The proof depends on our understanding of dilation, angle relationships of parallel lines, and congruence.
⬛ We practiced using the AA criterion to present informal arguments as to whether or not two triangles are similar.
Lesson Summary
Two triangles are said to be similar if they have two pairs of corresponding angles that are equal in measure.
Exit Ticket (5 minutes)
Name Date
Exit Ticket
1. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

2. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
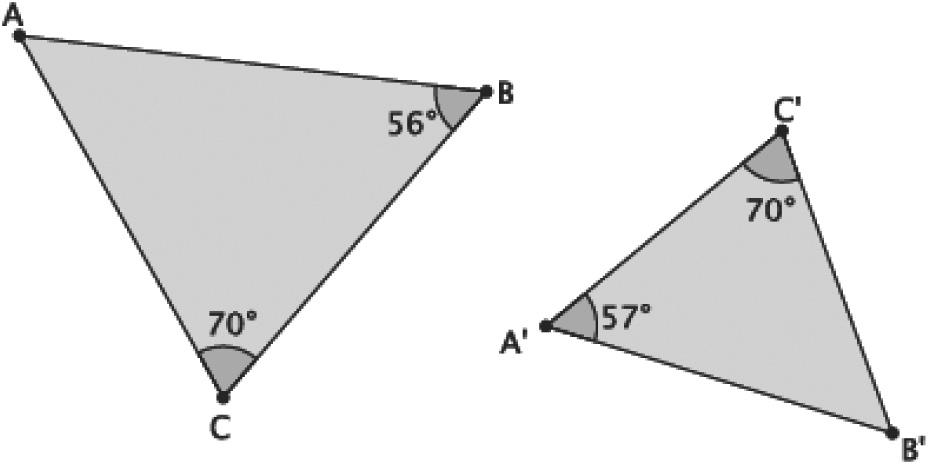
1. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Yes, △ABC ∼ △A′B′C′ . They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B′| = 45° or |∠A| = 45° . Then, you can see that |∠A| = |∠A′| = 45° , |∠B| = |∠B′| = 45° , and |∠C | = |∠C ′| = 90°
2. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
No, △ABC is not similar to △A′B′C′ They are not similar because they do not have two pairs of corresponding angles that are equal, namely, |∠A| ≠ |∠A′|, and |∠B| ≠ |∠B′|
Students practice presenting informal arguments to prove whether or not two triangles are similar.
1. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Yes, △ABC ∼ △A′B′C′ . They are similar because they have two pairs of corresponding angles that are equal, namely, |∠B| = |∠B′| = 103° , and |∠A| = |∠A′| = 31°
2. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Yes, △ABC ∼ △A′B′C′ . They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B′| = 84° or |∠C| = 32° Then, you can see that |∠A| = |∠A′| = 64° , |∠B| = |∠B′| = 84° , and |∠C| = |∠C ′| = 32° .
3. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

We do not know if △ABC is similar to △A′B′C′ . We can use the triangle sum theorem to find out that |∠B| = 44° , but we do not have any information about |∠A′| or |∠C′| To be considered similar, the two triangles must have two pairs of corresponding angles that are equal. In this problem, we only know of one pair of corresponding angles, and that pair does not have equal measure.
4. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Yes, △ABC ∼ △A′B′C′ . They are similar because they have two pairs of corresponding angles that are equal, namely, |∠C| = |∠C′| = 46° , and |∠A| = |∠A′| = 31°
5. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Yes
6. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

7. Are the triangles shown below similar? Present an informal argument as to why they are or are not similar. Yes

pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out

⬛ Students present informal arguments as to whether or not two triangles are similar.
⬛ Students practice finding lengths of corresponding sides of similar triangles.
This lesson synthesizes the knowledge gained thus far in Module 4. Students use what they know about dilation, congruence, the fundamental theorem of similarity (FTS), and the angle-angle (AA) criterion to determine if two triangles are similar. In the first two examples, students use informal arguments to decide if two triangles are similar. To do so, they look for pairs of corresponding angles that are equal (wanting to use the AA criterion). When they realize that information is not given, they compare lengths of corresponding sides to see if the sides could be dilations with the same scale factor. After a dilation and congruence are performed, students see that the two triangles are similar (or not) and then continue to give more proof as to why they must be. For example, by FTS, a specific pair of lines are parallel, and the corresponding angles cut by a transversal must be equal; therefore, the AA criterion can be used to state that two triangles are similar. Once students know how to determine whether two triangles are similar, they apply this knowledge to finding lengths of segments of triangles that are unknown in Examples 3–5.
Classwork
Example 1 (6 minutes)
⬛ Given the information provided, is △ABC ∼ △DEF? (Give students a minute or two to discuss with a partner.)

Students are likely to say that they cannot tell if the triangles are similar because there is only information for one angle provided. In the previous lesson, students could determine if two triangles were similar using the AA criterion
⬛ What if we combined our knowledge of dilation and similarity? That is, we know we can translate △ABC so that the measure of ∠ A is equal in measure to ∠D. Then, our picture would look like this:

⬛ Can we tell if the triangles are similar now?
We still do not have information about the angles, but we can use what we know about dilation and FTS to find out if side EF is parallel to side BC . If they are, then △ABC ∼ △DEF because the corresponding angles of parallel lines are equal
⬛ We do not have the information we need about corresponding angles. So, let’s examine the information we are provided. Compare the given side lengths to see if the ratios of corresponding sides are equal: Is = AE AB AF AC ? That’s the same as asking if = 1 2 3 6 . Since the ratios of corresponding sides are equal, then there exists a dilation from center A with scale factor = 1 2 r that maps △ABC to △DEF. Since the ratios of corresponding sides are equal, then by FTS, we know side EF is parallel to side BC , and the corresponding angles of the parallel lines are also equal in measure.
⬛ This example illustrates another way for us to determine if two triangles are similar. That is, if they have one pair of equal corresponding angles and the ratio of corresponding sides (along each side of the given angle) are equal, then the triangles are similar.
Example 2 (4 minutes)
⬛ Given the information provided, is △ABC ∼ △AB′C′? Explain. (Give students a minute or two to discuss with a partner.)

If students say that the triangles are not similar because segments BC and B′C′ are not parallel, ask them how they know this. If they say, “They don’t look parallel,” tell students that the way they look is not good enough. They must prove mathematically that the lines are not parallel. Therefore, the following response is more legitimate:
We do not have information about two pairs of corresponding angles, so we need to examine the ratios of corresponding side lengths. If the ratios are equal, then the triangles are similar.
⬛ If the ratios of the corresponding sides are equal, it means that the lengths were dilated by the same scale factor. Write the ratios of the corresponding sides.
The ratios of the corresponding sides are |AC′| |AC| = |AB′| |AB|
⬛ Does |AC′| |AC| = |AB′| |AB| ? That is the same as asking if 7.1 2.7 and 8 4.9 are equivalent fractions. One possible way of verifying if the fractions are equal is by multiplying the numerator of each fraction by the denominator of the other. If the products are equal, then we know the fractions are equivalent.
The products are 34.79 and 21.6. Since 34.79 ≠ 21.6, the fractions are not equivalent, and the triangles are not similar
Example 3 (4 minutes)
⬛ Given that △ABC ∼ △AB′C′, could we determine the length of AB′? What does it mean to say that △ABC ∼ △AB′C′? (Give students a minute or two to discuss with a partner.)

It means that the measures of corresponding angles are equal; the ratios of corresponding sides are equal, that is, |AC′| |AC| = |AB′| |AB| = |BC′| |BC| , and the lines containing segments BC and B′C′ are parallel
⬛ How can we use what we know about similar triangles to determine the length of AB′?
The lengths of corresponding sides are supposed to be equal in ratio: |AC′| |AC| = |AB′| |AB| is the same as AB = 15 5 2 ' AB = 15 5 2 ' |AB′| .
⬛ Since we know that for equivalent fractions, when we multiply the numerator of each fraction by the denominator of the other fraction, the products are equal, we can use that fact to find the length of side AB′
Let x represent the length of AB′; then, AB = 15 5 2 ' AB = 15 5 2 ' |AB′| is the same as = 15 52 x . Equivalently, we get 30 = 5x.
The value of x that makes the statement true is x = 6. Therefore, the length of side AB′ is 6.
Example 4 (4 minutes)
⬛ If we suppose XY is parallel to X′Y′ , can we use the information provided to determine if △OXY ∼ △OX′Y′? Explain. (Give students a minute or two to discuss with a partner.)

Since we assume XY XY XY || ''X′Y′ , then we know we have similar triangles because each triangle shares ∠O, and the corresponding angles are congruent: ∠OXY ≅ ∠OX′Y′ , and ∠OYX ≅ ∠OY′X′ By the AA criterion, we can conclude that △OXY ∼ △OX′Y′.
⬛ Now that we know the triangles are similar, can we determine the length of side OX′? Explain.
By the converse of FTS, since we are given parallel lines and the lengths of the corresponding sides XY and X′Y′ , we can write the ratio that represents the scale factor and compute using the fact that cross products must be equal to determine the length of side OX′ .
⬛ Write the ratio for the known side lengths XY and X′Y′ and the ratio that would contain the side length we are looking for. Then, use the cross products to find the length of side OX′ |X′Y ′| |XY| = |OX′| |OX| is the same as |OX′| OX = 6.25 5 4 OX' = 6.25 5 4 ' . Let z represent the length of side OX′ . Then, we have = 6.25 5 4 z , or equivalently, 5z = 25 and z = 5 Therefore, the length of side OX′ is 5
⬛ Now find the length of side OY ′
|X′Y ′| |XY| = |OY ′| |OY| is the same as |OY ′| OY 6.25 56 = ' 6.25 56 = ' Let w represent the length of side OY ′ Then, we have = 6.25 56 w , or equivalently, 5w = 37.5 and w = 7.5. Therefore, the length of side OY ′ is 7.5.
More About Similar Triangles
Example 5 (3 minutes)
⬛ Given the information provided, can you determine if △OPQ ∼ △OP′Q′? Explain. (Give students a minute or two to discuss with a partner.)

No. In order to determine if △OPQ ∼ △OP′Q′ , we need information about two pairs of corresponding angles. As is, we only know that the two triangles have one equal angle, the common angle with vertex O. We would have corresponding angles that were equal if we knew that sides '' || PQ PQ . Our other option is to compare the ratio of the sides that comprise the common angle. However, we do not have information about the lengths of sides OP or OQ For that reason, we cannot determine whether or not △OPQ ∼ △OP′Q′
Exercises (14 minutes)
Students can work independently or in pairs to complete Exercises 1–3.
Exercises
1. In the diagram below, you have △ABC and △AB′C′. Use this information to answer parts (a)–(d).

a. Based on the information given, is △ABC ∼ △AB′C′ ? Explain.
There is not enough information provided to determine if the triangles are similar. We would need information about a pair of corresponding angles or more information about the side lengths of each of the triangles.
b. Assume the line containing BC is parallel to the line containing B′C′ . With this information, can you say that △ABC ∼ △AB′C′? Explain.
If the line containing BC is parallel to the line containing B′C′ , then △ABC ∼ △AB′C′ . Both triangles share ∠A. Another pair of equal angles is ∠AB′C′and ∠ABC. They are equal because they are corresponding angles of parallel lines. By the AA criterion, △ABC ∼ △AB′C′ .
c. Given that △ABC ∼ △AB′C′, determine the length of side AC′ .
Let x represent the length of side AC′ .
x 6 2 8 = x 6 2 8
We are looking for the value of x that makes the fractions equivalent. Therefore, 8x = 12, and x = 1.5. The length of side AC′ is 1.5.
d. Given that △ABC ∼ △AB′C′, determine the length of side AB .
Let y represent the length of side AB
y 27 2 8 . =
We are looking for the value of y that makes the fractions equivalent. Therefore, 2y = 21.6, and y = 10.8. The length of side AB is 10.8.
More About Similar Triangles
2. In the diagram below, you have △ABC and △A′B′C′. Use this information to answer parts (a)–(c).

a. Based on the information given, is △ABC ∼ △A′B′C′? Explain.
Yes, △ABC ∼ △A′B′C′ There are two pairs of corresponding angles that are equal in measure, namely, ∠ A = ∠ A′ = 59°, and ∠B = ∠B′ = 92° By the AA criterion, these triangles are similar.
b. Given that △ABC ∼ △A′B′C′, determine the length of side A′C′
Let x represent the length of side A′C′
x 61 512 32 =
We are looking for the value of x that makes the fractions equivalent. Therefore, 3.2x = 31.232, and x = 9.76. The length of side A′C′ is 9.76
c. Given that △ABC ∼ △A′B′C′, determine the length of side BC
Let y represent the length of side BC y 8965 12 32 =
We are looking for the value of y that makes the fractions equivalent. Therefore, 5.12y = 28.672, and y = 5.6. The length of side BC is 5.6.
3. In the diagram below, you have △ABC and △A′B′C′. Use this information to answer the question below.

Based on the information given, is △ABC ∼ △A′B′C′? Explain.
No, △ABC is not similar to △A′B′C′ . Since there is only information about one pair of corresponding angles, then we must check to see that the corresponding sides have equal ratios. That is, the following must be true:
When we compare products of each numerator with the denominator of the other fraction, we see that 48.668 ≠ 61.798 Since the corresponding sides do not have equal ratios, then the fractions are not equivalent, and the triangles are not similar.
Closing (5 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We know that if we are given just one pair of corresponding angles as equal, we can use the side lengths along the given angle to determine if triangles are in fact similar.
⬛ If we know that we are given similar triangles, then we can use the fact that ratios of corresponding sides are equal to find any missing measurements.
Lesson Summary
Given just one pair of corresponding angles of a triangle as equal in measure, use the side lengths along the given angle to determine if the triangles are in fact similar.
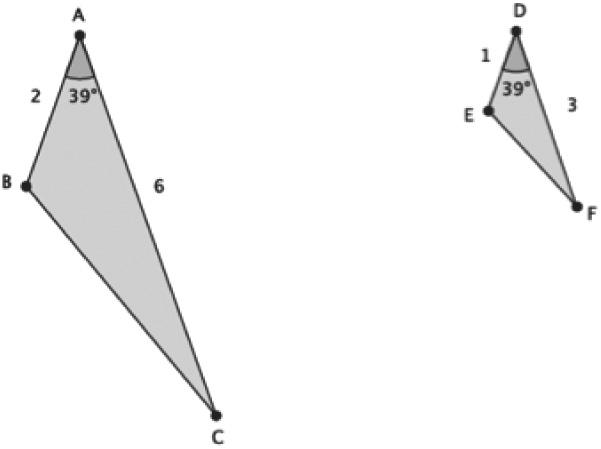
Given similar triangles, use the fact that ratios of corresponding sides are equal to find any missing measurements.
Exit Ticket (5 minutes)
Exit Ticket
1. In the diagram below, you have △ABC and △A′B′C′. Based on the information given, is △ABC ∼ △A′B′C′? Explain.

2. In the diagram below, △ABC ∼ △DEF. Use the information to answer parts (a)–(b).

a. Determine the length of side AB . Show work that leads to your answer.
b. Determine the length of side DF . Show work that leads to your answer.
1. In the diagram below, you have △ABC and △A′B′C′. Based on the information given, is △ABC ∼ △A′B′C′? Explain.

Since there is only information about one pair of corresponding angles, we need to check to see if corresponding sides have equal ratios. That is, does |AB| |A′B′| = |AC| |A′C′| , or does = 35 875 6 21 ? The products are not equal; 73. 5 ≠ 52. 5. Since the corresponding sides do not have equal ratios, the triangles are not similar.
2. In the diagram below, △ABC ∼ △DEF. Use the information to answer parts (a)–(b).

a. Determine the length of side AB . Show work that leads to your answer.
Let x represent the length of side AB .
Then, = x 17 64 63 13 23 . We are looking for the value of x that makes the fractions equivalent. Therefore, 111.132 = 13.23x, and x = 8.4. The length of side AB is 8.4
b. Determine the length of side DF . Show work that leads to your answer.
Let y represent the length of side DF .
Then, y 41 63 13 23 .. = We are looking for the value of y that makes the fractions equivalent. Therefore, 54.243 = 6.3y, and 8.61 = y. The length of side DF is 8.61
Students practice presenting informal arguments as to whether or not two given triangles are similar. Students practice finding measurements of similar triangles.
1. In the diagram below, you have △ABC and △A′B′C′. Use this information to answer parts (a)–(b).

a. Based on the information given, is △ABC ∼ △A′B′C′? Explain.
Yes, △ABC △A′B′C′ . Since there is only information about one pair of corresponding angles being equal, then the corresponding sides must be checked to see if their ratios are equal 10 65 71 9 6 63 9639 = =
Since the cross products are equal, the triangles are similar.
b. Assume the length of side AC is 4.3. What is the length of side A′C′?
Let x represent the length of side A′C′ . x 43 9 6 =
We are looking for the value of x that makes the fractions equivalent. Therefore, 6x = 38.7, and x = 6.45. The length of side A′C′ is 6.45.
2. In the diagram below, you have △ABC and △AB′C′. Use this information to answer parts (a)–(d).

a. Based on the information given, is △ABC △AB′C′? Explain.
There is not enough information provided to determine if the triangles are similar. We would need information about a pair of corresponding angles or more information about the side lengths of each of the triangles.
More About Similar Triangles
b. Assume the line containing BC is parallel to the line containing B′C′. With this information, can you say that △ABC △AB′C′? Explain.
If the line containing BC is parallel to the line containing B′C′ , then △ABC △AB′C′ . Both triangles share ∠A. Another pair of equal angles are ∠AB′C′ and ∠ABC. They are equal because they are corresponding angles of parallel lines. By the AA criterion, △ABC ∼ △AB′C′
c. Given that △ABC ∼ △AB′C′, determine the length of side AC′
Let x represent the length of side AC′ . = x 16 1 16 11 2
We are looking for the value of x that makes the fractions equivalent. Therefore, 11.2x = 25.76, and x = 2.3. The length of side AC′ is 2.3.
d. Given that △ABC △AB′C′, determine the length of side AB′
Let y represent the length of side AB′ y 77 16 11 2 =
We are looking for the value of y that makes the fractions equivalent. Therefore, 11.2y = 12.32, and y = 1.1. The length of side AB′ is 1.1
3. In the diagram below, you have △ABC and △A′B′C′. Use this information to answer parts (a)–(c).

a. Based on the information given, is △ABC ∼ △A′B′C′? Explain.
Yes, △ABC ∼ △A′B′C′ There are two pairs of corresponding angles that are equal in measure, namely, ∠A = ∠A′ = 23°, and ∠C = ∠C′ = 136° By the AA criterion, these triangles are similar.
23:
More About Similar Triangles
b. Given that △ABC ∼ △A′B′C′, determine the length of side B′C′
Let x represent the length of side B′C′ . x 39 875 7 =
We are looking for the value of x that makes the fractions equivalent. Therefore, 7x = 34.125, and x = 4.875. The length of side B′C′ is 4.875.
c. Given that △ABC ∼ △A′B′C′, determine the length of side AC .
Let y represent the length of side AC . y 58 75 7 =
We are looking for the value of y that makes the fractions equivalent. Therefore, 8.75y = 35, and y = 4
The length of side AC is 4.
4. In the diagram below, you have △ABC and △AB′C′. Use this information to answer the question below.

Based on the information given, is △ABC ∼ △AB′C′ ? Explain.
No, △ABC is not similar to △AB′C′ . Since there is only information about one pair of corresponding angles, then we must check to see that the corresponding sides have equal ratios. That is, the following must be true: = 9 3 12 6 41
When we compare products of each numerator with the denominator of the other fraction, we see that 36.9 ≠ 37.8. Since the corresponding sides do not have equal ratios, the fractions are not equivalent, and the triangles are not similar
More About Similar Triangles
5. In the diagram below, you have △ABC and △A′B′C′. Use this information to answer parts (a)–(b).

a. Based on the information given, is △ABC ∼ △A′B′C′? Explain.
Yes, △ABC ∼ △A′B′C′ . Since there is only information about one pair of corresponding angles being equal, then the corresponding sides must be checked to see if their ratios are equal
82 20 5 75 18 75 =
When we compare products of each numerator with the denominator of the other fraction, we see that 153.75 = 153.75 Since the products are equal, the fractions are equivalent, and the triangles are similar
b. Given that △ABC ∼ △A′B′C′, determine the length of side A′B′
Let x represent the length of side A′B′ x 26 75 18 75 =
We are looking for the value of x that makes the fractions equivalent. Therefore, 18.75x = 195, and x = 10.4. The length of side A′B′ is 10.4

⬛ Students use properties of similar triangles to solve real-world problems.
Lesson Notes
This lesson is an opportunity for students to see how the mathematics they have learned in Topics C and D relates to real-world problems. Each example, exercise, and item in the Problem Set is in a real-world context (e.g., the height of a tree, the distance across a lake, and the length needed for a skateboard ramp). Many of the problems begin by asking students if they have enough information to determine if the situation described lends itself to the use of similar triangles. Once that criterion is satisfied, students use what they know about dilation and scale factor to solve the problem and explain the real-world situation.
Classwork
Example (7 minutes)
Consider offering this first task without any scaffolding in order to build students’ persistence and stamina in solving problems. Allow students time to make sense of the situation, offering scaffolding only as necessary.
Example
Not all flagpoles are perfectly upright (i.e., perpendicular to the ground). Some are oblique (i.e., neither parallel nor at a right angle, slanted). Imagine an oblique flagpole in front of an abandoned building. The question is, can we use sunlight and shadows to determine the length of the flagpole?

Assume that we know the following information: The length of the shadow of the flagpole is 15 feet. There is a mark on the flagpole 3 feet from its base. The length of the shadow of this three-foot portion of the flagpole is 1.7 feet.
Students may say that they would like to directly measure the length of the pole. Remind them a direct measurement may not always be possible
⬛ Where would the shadow of the flagpole be?
On the ground, some distance from the base of the flagpole
Modeling by Using Similarity
⬛ In the picture below, OA is the length of the flagpole. OB is the length of the shadow cast by the flagpole. OC represents the segment from the base to the 3-foot mark up the flagpole, and OD is the length of the shadow cast by the length of OC that is 1.7 feet in length. (Note: The picture is not drawn to scale.)
⬛ If we assume that all sunbeams are parallel to each other (i.e., || CD AB ), do we have a pair of similar triangles? Explain.
If || CD AB , then △COD ∼ △AOB, by the AA criterion. Corresponding angles of parallel lines are equal, so we know that ∠CDO = ∠ABO, and ∠COD is equal to itself.
⬛ Now that we know △COD ∼ △AOB, how can we find the length of the flagpole?
Since the triangles are similar, then we know that the ratios of their corresponding sides must be equal. Therefore, if we let x represent the length of the flagpole (i.e., OA), then
⬛ We are looking for the value of x that makes the fractions equivalent.
Therefore, 1.7x = 45, and x ≈ 26.47. The length of the flagpole is approximately 26.47 feet.
Students work in small groups to model the use of similar triangles in real-world problems. Exercise 1 is classified as an ill-defined modeling task because some of the information in the problem is not absolutely clear. The purpose of this is to motivate students to discuss in their groups what is meant by “straight down,” whether or not it is safe to assume that the building is perpendicular to the ground, and whether or not it is safe to assume that the person is standing perpendicular to the ground. These kinds of mathematical discussions should be encouraged as they demonstrate students’ learning of a topic. 3 = 15 1.7 x
Modeling by Using Similarity
Mathematical Modeling Exercises 1–3
1. You want to determine the approximate height of one of the tallest buildings in the city. You are told that if you place a mirror some distance from yourself so that you can see the top of the building in the mirror, then you can indirectly measure the height using similar triangles. Let point O be the location of the mirror so that the person shown can see the top of the building.

a. Explain why △ABO ∼ △STO
The triangles are similar by the AA criterion. The angle that is formed by the figure standing is 90° with the ground. The building also makes a 90° angle with the ground. The measure of the angle formed with the mirror at ∠ AOB is equal to the measure of ∠ SOT. Since there are two pairs of corresponding angles that are equal in measure, then △ABO ∼ △STO
b. Label the diagram with the following information: The distance from eye level straight down to the ground is 5.3 feet. The distance from the person to the mirror is 7.2 feet. The distance from the person to the base of the building is 1,750 feet. The height of the building is represented by x.

c. What is the distance from the mirror to the building?
1750 ft. 7.2 ft. = 1742.8 ft.
Modeling by Using Similarity
d. Do you have enough information to determine the approximate height of the building? If yes, determine the approximate height of the building. If not, what additional information is needed?
Yes, there is enough information about the similar triangles to determine the height of the building. Since x represents the height of the building, then
We are looking for the value of x that makes the fractions equivalent. Then, 7.2x = 9236.84, and x ≈ 1282.9 The height of the building is approximately 1,282.9 feet
2. A geologist wants to determine the distance across the widest part of a nearby lake. The geologist marked off specific points around the lake so that the line containing DE would be parallel to the line containing BC . The segment BC is selected specifically because it is the widest part of the lake. The segment DE is selected specifically because it is a short enough distance to easily measure. The geologist sketched the situation as shown below.

a. Has the geologist done enough work so far to use similar triangles to help measure the widest part of the lake? Explain.
Yes, based on the sketch, the geologist found a center of dilation at point A. The geologist marked points around the lake that, when connected, would make parallel lines. So, the triangles are similar by the AA criterion. Corresponding angles of parallel lines are equal in measure, and the measure of ∠DAE is equal to itself. Since there are two pairs of corresponding angles that are equal, then △DAE ∼ △BAC.
b. The geologist has made the following measurements: |DE| = 5 feet, |AE| = 7 feet, and |EC| = 15 feet. Does she have enough information to complete the task? If so, determine the length across the widest part of the lake. If not, state what additional information is needed.
Yes, there is enough information about the similar triangles to determine the distance across the widest part of the lake.
Let x represent the length of segment BC; then
= x 5 22 7
We are looking for the value of x that makes the fractions equivalent. Therefore, 7x = 110, and x ≈ 15.7 The distance across the widest part of the lake is approximately 15.7 feet
Modeling by Using Similarity
c. Assume the geologist could only measure a maximum distance of 12 feet. Could she still find the distance across the widest part of the lake? What would need to be done differently?
The geologist could still find the distance across the widest part of the lake. However, she would have to select different points D and E at least 3 feet closer to points B and C, respectively. That would decrease the length of EC to, at most, 12 feet. Then DE , in its new position, would still have to be contained within a line that was parallel to the line containing BC in order to calculate the desired distance.
3. A tree is planted in the backyard of a house with the hope that one day it is tall enough to provide shade to cool the house. A sketch of the house, tree, and sun is shown below.

a. What information is needed to determine how tall the tree must be to provide the desired shade?
We need to ensure that we have similar triangles. For that reason, we need to know the height of the house and the length of the shadow that the house casts. We also need to know how far away the tree was planted from that point (i.e., the center). Assuming the tree grows perpendicular to the ground, the height of the tree and the height of the house would be parallel, and by the AA criterion, we would have similar triangles
b. Assume that the sun casts a shadow 32 feet long from a point on top of the house to a point in front of the house. The distance from the end of the house’s shadow to the base of the tree is 53 feet. If the house is 16 feet tall, how tall must the tree get to provide shade for the house?
If we let x represent the height the tree must be, then
= x 16 32 53
We are looking for the value of x that makes the fractions equivalent. Therefore, 32x = 848, and x = 26.5. The tree must grow to a height of 26.5 feet to provide the desired shade for the house.
c. Assume that the tree grows at a rate of 2.5 feet per year. If the tree is now 7 feet tall, about how many years will it take for the tree to reach the desired height?
The tree needs to grow an additional 19.5 feet to reach the desired height. If the tree grows 2.5 feet per year, then it will take the tree 7.8 years or about 8 years to reach a height of 26.5 feet
Closing (5 minutes)
Summarize, or ask students to summarize, the main points from the lesson.
⬛ We can use similar triangles to determine the height or distance of objects in everyday life that we cannot directly measure.
⬛ We have to determine whether or not we actually have enough information to use properties of similar triangles to solve problems.
Exit Ticket (5 minutes)
Modeling by Using Similarity
Name Date
Exit Ticket
Henry thinks he can figure out how high his kite is while flying it in the park. First, he lets out 150 feet of string and ties the string to a rock on the ground. Then, he moves from the rock until the string touches the top of his head. He stands up straight, forming a right angle with the ground. He wants to find out the distance from the ground to his kite. He draws the following diagram to illustrate what he has done.

a. Has Henry done enough work so far to use similar triangles to help measure the height of the kite? Explain.
b. Henry knows he is 5 1 2 feet tall. Henry measures the string from the rock to his head and finds it to be 8 feet. Does he have enough information to determine the height of the kite? If so, find the height of the kite. If not, state what other information would be needed.
Henry thinks he can figure out how high his kite is while flying it in the park. First, he lets out 150 feet of string and ties the string to a rock on the ground. Then, he moves from the rock until the string touches the top of his head. He stands up straight, forming a right angle with the ground. He wants to find out the distance from the ground to his kite. He draws the following diagram to illustrate what he has done.

a. Has Henry done enough work so far to use similar triangles to help measure the height of the kite? Explain.
Yes Based on the sketch, Henry found a center of dilation, point A. Henry has marked points so that, when connected, would make parallel lines. So, the triangles are similar by the AA criterion. Corresponding angles of parallel lines are equal in measure, and the measure of ∠BAC is equal to itself. Since there are two pairs of corresponding angles that are equal, then △BAC ∼ △DAE
b. Henry knows he is 5 1 2 feet tall. Henry measures the string from the rock to his head and finds it to be 8 feet. Does he have enough information to determine the height of the kite? If so, find the height of the kite. If not, state what other information would be needed.
Yes, there is enough information. Let x represent the height DE. Then,
= x 8 150 55 .
We are looking for the value of x that makes the fractions equivalent. Therefore, 8x = 825, and x = 103.125 feet. The height of the kite is approximately 103 feet high in the air
Modeling by Using Similarity
Students practice solving real-world problems using properties of similar triangles.
1. The world’s tallest living tree is a redwood in California. It’s about 370 feet tall. In a local park, there is a very tall tree. You want to find out if the tree in the local park is anywhere near the height of the famous redwood.

a. Describe the triangles in the diagram, and explain how you know they are similar or not. There are two triangles in the diagram, one formed by the tree and the shadow it casts, △ESO, and another formed by the person and his shadow, △DRO. The triangles are similar if the height of the tree is measured at a 90° angle with the ground and if the person standing forms a 90° angle with the ground. We know that ∠DOR is an angle common to both triangles. If ∠ESO = ∠DRO = 90° , then △ESO ∼ △DRO by the AA criterion.
b. Assume △ESO ∼ △DRO. A friend stands in the shadow of the tree. He is exactly 5 5 feet tall and casts a shadow of 12 feet. Is there enough information to determine the height of the tree? If so, determine the height. If not, state what additional information is needed.
No, there is not enough information to determine the height of the tree. I need either the total length of the shadow that the tree casts or the distance between the base of the tree and the friend.
c. Your friend stands exactly 477 feet from the base of the tree. Given this new information, determine about how many feet taller the world’s tallest tree is compared to the one in the local park. Let x represent the height of the tree; then
= x 55 489 12
We are looking for the value of x that makes the fractions equivalent. Therefore, 12x = 2689.5, and x = 224.125. The world’s tallest tree is about 146 feet taller than the tree in the park
Modeling by Using Similarity
d. Assume that your friend stands in the shadow of the world’s tallest redwood, and the length of his shadow is just 8 feet long. How long is the shadow cast by the tree?
Let x represent the length of the shadow cast by the tree; then
We are looking for the value of x that makes the fractions equivalent. Therefore, 5.5x = 2960, and x ≈ 538.2 The shadow cast by the world’s tallest tree is about 538 feet in length.
2. A reasonable skateboard ramp makes a 25° angle with the ground. A two-foot-tall ramp requires about 4.3 feet of wood along the base and about 4.7 feet of wood from the ground to the top of the two-foot height to make the ramp.
a. Sketch a diagram to represent the situation.
A sample student drawing is shown below

b. Your friend is a daredevil and has decided to build a ramp that is 5 feet tall. What length of wood is needed to make the base of the ramp? Explain your answer using properties of similar triangles.
Sample student drawing and work are shown below.
△EDA △CBA by the AA criterion because ∠A is common to both triangles, and ∠EDA = ∠CBA = 90°
If we let x represent the base of the 5-foot ramp, then
We are looking for the value of x that makes the fractions equivalent. Therefore, 2x = 21.5, and x = 10.75. The base of the 5-foot ramp must be 10 75 feet in length
c. What length of wood is required to go from the ground to the top of the 5-foot height to make the ramp?
Explain your answer using properties of similar triangles.
If we let y represent the length of the wood needed to make the ramp, then
We are looking for the value of y that makes the fractions equivalent. Therefore, 2y = 23.5, and y = 11.75. The length of wood needed to make the ramp is 11.75 feet. = x 8 370 55 = x 43 2 5 = y 47 2 5
Modeling by Using Similarity
Name Date
1. Use the diagrams to answer the questions.
a. Figure A′B′C′D′ is the image of Figure ABCD after a transformation. Identify the transformation.
b. A′B′C′ is the image of ABC after a transformation. Identify the transformation.
Module 4: Transformations
c. A′B′C′ is the image of ABC after a transformation. Identify the transformation.
2. Is there a dilation with center O that would map Figure PQRS to Figure P′Q′R′S′? Explain your answer in terms of scale factor, center, and coordinates of corresponding points. Use a ruler and a compass, as needed. –1 1 2 3
Module 4: Transformations
3. Use Figure PQRT to complete each part.
a. Dilate Figure PQRT from center O by a scale factor of r = 1 2 . Label P′ , Q′ , R′, and T′
b. Identify the coordinates of the vertices of Figure P′Q′R′T′
c. Are the angle measures of ∠RQP and ∠R′Q′P′ equal? Explain.
d. If the length of segment RP is 10.3 units, what is the length of segment R′P′? Explain.
Module 4: Transformations
4. In the diagram, ABC ∼
a. Describe a sequence of transformations that maps ABC and A′B′C′ .
b. Describe a sequence of transformations that maps ABC and A″B″C″ Module 4: Transformations
5. Let there be a dilation with center O and a scale factor of r > 0 so that Dilation(P) = P′ and Dilation(Q) = Q′ .
a. Use |OQ| = 10 units and |OQ′| = 15 units to determine the scale factor r of the dilation. Determine the coordinates of P′, and then explain how you used the coordinates of P to find the coordinates of P′
b. If |OQ| = 10 units, |OQ′| = 15 units, and |PQ| = 11.2 units, determine |P′Q′|. Round your answer to the tenths place, if necessary. Module 4: Transformations
STEP 1
Assessment
Task Item
Missing or incorrect answer and little evidence of reasoning or application of mathematics to solve the problem.
STEP 2
Missing or incorrect answer but evidence of some reasoning or application of mathematics to solve the problem.
STEP 3
A correct answer with some evidence of reasoning or application of mathematics to solve the problem. OR
An incorrect answer with substantial evidence of solid reasoning or application of mathematics to solve the problem.
STEP 4
A correct answer supported by substantial evidence of solid reasoning or application of mathematics to solve the problem.
1 a–c 8.7
Student does not attempt the problem.
Student correctly identifies one transformation.
2 8.7 Student does not attempt the problem.
Student correctly identifies two transformations.
Student incorrectly determines the scale factor. Student may attempt to describe the dilation in terms of coordinates of corresponding points.
3 a 8.7
Student does not attempt the problem.
b 8.7
Student does not attempt the problem.
Student draws a rectangle that is not a dilation according to the scale factor, and the points are not labeled.
Student correctly identifies the coordinates of one of the vertices. OR
Student may have transposed the coordinates of some or all of the vertices.
Student correctly determines the scale factor but is not able to clearly describe the dilation in terms of coordinates of corresponding points.
Student draws a rectangle and labels the points P′ , Q′ , R′, and T′, but the rectangle is not a dilation according to the scale factor.
Student correctly identifies the coordinates of two or three of the vertices.
Student correctly identifies the transformations as reflection, dilation, and translation.
Student correctly determines the scale factor as r = 3 and the center.
Student clearly describes the dilation in terms of the coordinates for at least one pair of corresponding points.
Student draws a rectangle according to the scale factor and labels the points P′ , Q′ , R′, and T′
Student correctly identifies the coordinates of the vertices as P′(1, 1), Q′(5.5, 1), R′(5.5, 3,5), and T′(1, 3.5).
c 8.7
d 8.7
Student does not attempt the problem or states that the measures of ∠RQP and ∠R′Q′P′ are not equal.
Student states that ∠RQP and ∠R′Q′P′ are equal in measure.
Student does not attempt an explanation, or the explanation is not mathematically based. For example, student states that the angle measures look the same.
Student states that ∠RQP and ∠R′Q′P′ are equal in measure.
Student attempts an explanation that includes mathematical language, but the explanation is not complete. For example, student states that dilations preserve angle measures without explaining Dilation(∠RQP) = ∠R′Q′P′ .
Student states that ∠RQP and ∠R′Q′P′ are equal in measure. Student explanation includes mathematical language that includes Dilation(∠RQP) = ∠R′Q′P′ because dilations preserve angle measures.
4 a 8.7
Student does not attempt the problem.
Student does not attempt the problem.
Student incorrectly determines the length of segment R′Q′ Student explanation includes significant gaps.
Student correctly determines that the length of segment R′Q′ is 5.15 units.
Student explanation or reasoning is not complete.
Student states that there is a dilation but does not state the center or scale factor.
Student states that there is a reflection but does not state the line of reflection.
Student may attempt an explanation, but the explanation is not mathematically based. For example, the student states that one figure looks about three times bigger than the other figure.
Student states that there is a dilation.
Student states either that the dilation is centered at the origin or has a scale factor of r = 2, but not both.
Student states that there is a reflection but states the incorrect line of reflection.
Student uses some mathematical language in explanation or reasoning.
Student correctly determines that the length of segment R′Q′ is 5.15 units. Student explanation includes mathematical language, references to similar triangles, and that the value of the ratio of corresponding side lengths is equal to the scale factor.
Student correctly states that there is a dilation with the center at the origin and scale factor r = 2. Student states there is a reflection across the y-axis.
Student uses mathematical language in explanation or reasoning.
Student reasoning is thorough and complete.
b 8.7
Student does not attempt the problem.
5 a 8.7
b
8.7
Student does not attempt the problem.
Student states that there is a dilation but does not state the center or scale factor. Student states that there is a rotation but does not state the degree or center of rotation. Alternatively, student states that there is a reflection but does not state the line of reflection.
Student may attempt an explanation or reasoning, but the explanation is not mathematically based. For example, student states that one figure looks about half the size of the other figure.
Student incorrectly determines the scale factor.
Student finds the coordinates of point P′ by using the incorrect scale factor but does not explain how to calculate the coordinates or relate the coordinates to the scale factor and point P
Student does not attempt the problem.
Student incorrectly writes a proportion to determine |P′Q′|. For example, student may have inverted one of the fractions of the equal ratios.
Student incorrectly determines |P′Q′|.
Student states that there is a dilation.
Student states either that the dilation is centered at the origin or has a scale factor of r = 1 2 , but not both.
Student correctly states a rotation of 180° centered at the origin or one of two reflections.
Student uses some mathematical language in the explanation or reasoning.
Student correctly determines the scale factor as r = 1.5 or its equivalent.
Student correctly determines the coordinates of point P′ but does not explain how to calculate the coordinates or relate the coordinates to the scale factor and point P.
Student correctly writes a proportion to determine |P′Q′| but incorrectly determines |P′Q′|
Student does not include units in the answer.
Student correctly states that there is a dilation with the center at the origin and a scale factor of r = 1 2
Student either states that there are two reflections, one across each axis, or a rotation of 180° centered at the origin.
Student uses mathematical language in explanation or reasoning.
Student reasoning is thorough and complete.
Student correctly determines the scale factor as r = 1.5 or its equivalent.
Student explains that the coordinates of point P′ are found by multiplying the coordinates of point P by the scale factor.
Student determines the coordinates of point P′ as (-6, -4.5)
Student correctly writes a proportion to determine |P′Q′| Student correctly determines |P′Q′| is 16.8 units. Student identifies the units.
Name Date
1. Use the diagrams to answer the questions.
a. Figure A′B′C′D′ is the image of Figure ABCD after a transformation. Identify the transformation.
Reflection
b. A′B′C′ is the image of ABC after a transformation. Identify the transformation.
c. A′B′C′ is the image of ABC after a transformation. Identify the transformation.
2. Is there a dilation with center O that would map Figure PQRS to Figure P′Q′R′S′? Explain your answer in terms of scale factor, center, and coordinates of corresponding points. Use a ruler and a compass, as needed.
Yes, there is a dilation with center O and a scale factor of 3 that maps PQRS to P′Q′R′S′. We can determine the coordinates of a dilated point by multiplying each of the coordinates in the original point by the scale factor of 3. Because point P has coordinates (3, -2), then P΄(3 · 3, 3 · (-2)) = P΄(9, -6).
P(3, -2) P΄(9, -6)
Q(3, -1) Q΄(9, -3)
R(4, 1) R΄(12, 3)
S(0, 2) S΄(0, 6)
3. Use Figure PQRT to complete each part.
a. Dilate Figure PQRT from center O by a scale factor of r = 1 2 . Label P′ , Q′ , R′, and T′ . See the graph.
b. Identify the coordinates of the vertices of Figure P′Q′R′T′
P′(1, 1) Q′(5.5, 1) R′(5.5, 3.5) P′(1, 3.5)
c. Are the angle measures of ∠RQP and ∠R′Q′P′ equal? Explain.
Yes. I know that ≠R′Q′P′ is an image of ≠RQP after a dilation. Because dilations preserve angle measures, ≠RQP and ≠R΄Q΄P΄ are equal in measure.
Module 4: Transformations
d. If the length of segment RP is 10.3 units, what is the length of segment R′P′? Explain. Because there was a dilation, we know that Figure PQRT is similar to Figure P′Q′R′T′. By sketching a segment from R to P and from R′ to P′, I create two triangles. I know that RPQ and R′P′Q′ are similar. So the value of the ratio of corresponding side lengths is equal to the scale factor.
The length of segment R′P′ is 5.15 units.
4. In this diagram, ABC ∼
and
a. Describe a sequence of transformations that maps ABC to A′B′C′ .
Sample student response: |B′C′| = r|BC| 2 = r · 1 2 = r
A dilation with the center at the origin and a scale factor of r = 2 followed by a reflection across the y-axis maps ABC to A′B′C′.
b. Describe a sequence of transformations that maps ABC to A″B″C″
Sample student response:
A dilation with the center at the origin and a scale factor of r = 1 2 followed by a reflection across the x-axis and a reflection across the y-axis maps ABC to A″B″C″.
5. Let there be a dilation with center O and a scale factor of r > 0 so that Dilation(P) = P′ and Dilation(Q) = Q′ .
a. Use |OQ| = 10 units and |OQ′| = 15 units to determine the scale factor r of the dilation. Determine the coordinates of P′, and then explain how you used the coordinates of P to find the coordinates of P′ .
The scale factor r is 3 2 .
Because point P has coordinates (-4, -3), the coordinates of the dilated point P′ can be found by multiplying the coordinates of P by 3 2 . Therefore, P′
4) 3) ) (- ,(-= (-6, -4.5 3 2 3 2
b. If |OQ| = 10 units, |OQ′| = 15 units, and |PQ| = 11.2 units, determine |P′Q′|. Round your answer to the tenths place, if necessary.
The length of segment P′Q′ is 16.8 units.
Great Minds® has made every effort to obtain permission for the reprinting of all copyrighted material. If any owner of copyrighted material is not acknowledged herein, please contact Great Minds for proper acknowledgment in all future editions and reprints of this module.
Eureka Math helps students truly understand mathematics and connect it to the real world, preparing them to solve problems they have not encountered. Great Minds teachers and mathematicians believe that it is not enough for students to know the process for solving a problem; they need to understand why that process works.
Eureka Math presents mathematics as a story, one that develops from grades PK through 12. In A Story of Ratios®, our middle school curriculum, this sequencing has been joined with methods of instruction that have been proven to work, in this nation and abroad.
Great Minds is here to make sure you succeed with an ever-growing library of resources, including videos, family resources, pacing guides, materials lists, state crosswalks, case studies, and more at eureka-math.org.
Module 1: Expressions, Equations, and Inequalities in One Variable
Module 2: Rational and Irrational Numbers
Module 3: Geometry
Module 4: Transformations
Module 5: Linear Equations
Module 6: Linear Functions, Data Analysis, and Probability
On the cover Bell, early 5th century B.C.. Eastern Zhou dynasty, Spring and Autumn period. Bronze, H. 15 in. (38.3 cm); W. 9 5/8 in. (24.4 cm). Charlotte C. and John C. Weber Collection, Gift of Charlotte C. and John C. Weber through the Live Oak Foundation, 1988 (1988.20.7).
Location: The Metropolitan Museum of Art, New York, NY, USA
Photo Credit: Image copyright © The Metropolitan Museum of Art. Image source: Art Resource, NY
What does this ancient bell have to do with math?
In an effort to take advantage of every opportunity to build cultural literacy, Great Minds features an important work of art or architecture on the cover of each book we publish. We select images that we know students and teachers will love to look at again and again. These works also relate, in visual terms, to ideas taken up in the book. Around 2700 B.C., Chinese music master Ling Lun created a set of bronze bells at the behest of “Yellow Emperor” Huang Ti. The bells were tuned using a set of pitch pipes whose lengths were determined by a ratio of integers. The pipes, cut according to the formula “subtract and add one-third,” comprise the now familiar 12-tone scale. A similar scale was not created again until Pythagoras did so more than 2000 years later.
VIRGINIA EDITION
Published by Great Minds PBC