

A. Summer 2024


From The Editor
Dr Ed Wilson
In the early days of the Internet, the rate at which information could be transferred was 1,000 bits per second. Over the last 30 years, this has accelerated to 1,000,000,000 bits per second.
Clearly, this increase has the potential for huge gains in efficiency.
But what is lost?
Every year, in the English Department, we teach a handful of Romantic poems to GCSE students. Although the world the Romantics inhabited was radically different to ours in many ways, it too was characterised by the perception that technological advances had accelerated the pace of life to a sometimes terrifying speed, allowing no time to look inwards.
The Romantic response to this was to search for time and space for contemplation. They found this in nature, but also in writing and, in the case of William Blake, art too.
For William Wordsworth, poetry was not about instant communication - the rapid transfer of information from one place to another - but was instead ‘emotion recollected in tranquility’.
Writing and art are not quick to produce, nor are they quick to consume, if we are going to appreciate them properly. As always, we are very proud of the time, care and attention that the students featured in the magazine have taken in order to express themselves, about everything from the assassination of Julius Caesar to recent trends in inflation.
In the spirit of the Romantics, please make time to enjoy their work.
Poppies
Lucy F, Year 7
How would you feel when you’re not in the action?
If your child asks “What did you do in the war?”
Are you just going to say nothing?
You’re not going to be a coward, right?
Come on, lads, you’ll get your own gun! Everyone will look up to you.
Wouldn’t you rather come back with a mark, Than quiver in fear at home?
Yes, it won’t be easy, But yes, it’ll be fun.
It’s not a walk in the park. Your country needs help; She needs you.
All your mates are going; Come on, give us a hand!
We’ll be victorious with you on our team.
Escaping Flames Leila
P, Year 9
Purple leaves stared at the top of my head, the occasional yellow lantern lighting my way. I had to reach the end of the path. It was gritty and felt bumpy underfoot. Moonlight shone on the river, making it look like a pearly light ribbon. I began to walk with a bit more haste, as if time was closing in on me.
Covered in moss, a small, arched bridge appeared. As I ran over the withering bridge, a loud creak escaped into the air. It was as if it was screaming ‘Help!’ Wet grass grew on this side of the path. I carried on, my dark-blonde hair trailing behind me. I had tucked it into a neat ponytail with a red ribbon holding it together. I was aware of my time falling away with every step I took. It felt like watching a sand timer, grains falling, seconds of my life slipping away. Footsteps… behind me. I needed to walk faster… breath in, out, in… out… of… breath.
The sun-like lanterns were guiding me to freedom - my only way out. The only way to leave this messed up world. I turned around. A dark figure stood there. I tried to run, but I couldn’t. I felt like the trees were surrounding me, my feet rooted to the ground.
“Stop.”
The figure stepped out of the darkness with blue, crystal eyes. They seemed delicate, unlike her stare. I felt like I was walking a red carpet, people staring at me. Her hair was long, purple and almost touching the ground. Slowly, she walked towards me; her arm reached out and her hand touched my shoulder.
Darkness.
I woke up in a place that was unrecognisable. A small, grey room, which I think was made of concrete. There was no way out, no windows… no air?
I realised I hadn’t breathed at all since I woke up. Somehow, I had survived on no air. Electricity suddenly flowed through my veins. Is there any way out? All the anger that had built up inside me from being trapped in this unfamiliar world felt uncontrollable. I was trapped again, but it felt much worse… I screamed. The walls crashed down and bundles of oxygen flew into my lungs.
“40682 has escaped. I repeat number 40682 has escaped. Catch them.”
This was when I realised my only option was to run. Men in grey army uniforms appeared behind me, with multiple guns tied to belts wrapped round their waists. All I could hear was muffled, forceful shouting from within the crowd. I ran as fast as my legs would carry me. Above me, concrete fell from what seemed like the sky. Had I destroyed this facility with my escape? The only way out was the one I made for myself, through the falling concrete. I ran up a set of stairs, an army of soldiers following. Gunshots came from every angle. There was hardly anything left of the first floor. I could see the same purple trees I had run past earlier; the same lanterns, the same ethereal river.
The same escape.
I leapt into the river from the building. It was cold and sent a shiver down my spine. I swam to the edge of the river as one of the soldiers followed behind. He cornered me into one of the trees. I couldn’t escape, unless…
He held the gun at me and I looked down at his belt. I ducked and grabbed one of his other guns. I held it at him only to realise it was out of ammunition. I breathed.
“You’ll never take me alive!”
He pulled the trigger.
It flew into the tree bark.
The man tried to reload. The biggest mistake he ever made was not paying close attention to his target before him. I grabbed a chunky lighter from his belt. I brought it towards the tree and watched as it slowly lit up each branch.
Flames…
Now, I found myself standing in a clearing, with blood-curdling screams filling the air around me. A burning red was the only thing visible right now. The lady from earlier emerged from the flames, running towards me…
“What... have you done?!”
I stared at her… breathed…
What had I done?
She spoke again.
“For damaging my homeland, you shall perish!”
Blood… all over me… over the floor...
Burning red.
Burning red trees stared down at my face as I slowly perished.
I smiled at the once yellow lanterns, now crimson and heated.
Like me.


All Hail, Caesar
Amelia R-B, Year 9
Inspired by Julius Caesar, this letter describes the run-up to Caesar’s assassination from the point of view of Amelia, a young woman living in Rome, writing to her sister in Britain.
My dear sister,
What a few weeks!
It has been quite ominous, really, what with the tension between Julius Caesar and his supporters (and enemies). Since I moved here, much has occurred between the common people and the select few; now is the time for me to tell you more about what I have been doing in Rome.
Perhaps drunk on the success of his military victories, Caesar is pompous, hubristic and a fool in his decisions. However, the public simply adore him, and want him as their king. Preposterous! I have good reason to believe that there is a plot afoot to end his reign before it has properly begun. The attack is rumoured to be planned for the 15th of March.
A few days ago Caesar was being hailed by an enormous crowd, his purple robe (only the finest for Caesar, of course) perched upon his shoulders in a royal manner, when a soothsayer stepped out from the crowd. His hair was concealed under his eerie grey cloak, his orange eyes glinting with knowledge.
“Caesar!” he called out.
“Caesar is turned to hear!” Caesar called back. This, I felt, was a rather arrogant thing to say and my fists clenched with discomfort.
“Beware the Ides of March!”
So this was his prediction; Caesar would fall on the 15th of March.
Caesar didn’t listen (which is actually the first sensible thing he has ever done – you know I don’t believe in that nonsense) and continued along on his merry way, so the attack remains planned for that date! Caesar had better be ready, that unsuspecting, idiotic, paranoid old gas bag!
Even more excitingly, rumour has it that Caesar has fallen ill! Maybe that will finish him off before the plotters take action. To be perfectly honest, I don’t quite like the actual idea of assassinating him, but I do want him dead. I want him gone.
How are you? Is Britannia still the same? Write to me soon.
Your sister, Amelia
P.S. Don’t share a word of this with anyone!!!
Christmas Poems
Tara B and Alyssa F, Year 9
The lights glowed bright beneath the soft winter snow, Guiding people exactly where they need to go.
Fair, small snowflakes drift about in the air, Children hop about, without so much as a care.
Rooftops sprinkled with frost and snow, Glistening in the moonlight’s comforting glow. Gifts are about to be exchanged and so,
Spend time with your loved ones, Be warm in your home, Light a comforting fire and remember, You’re not alone.
It’s completely pitch black, lights gone, under snow; No people to guide and nowhere to go.
Chilled and rigid, cold, still air; Limp frozen limbs, does anyone care?
Rooftops like tombstones peep out of the snow, Glaring in the moonlight’s harsh winter glow.
People are stuck and dying, so, Dig up your loved ones, Hide in your home, The fire’s snuffed out and remember, You’re all alone.
The Curious Incident of Bachman and Kolen
Kalea L, Year 9
‘Ah, you crooked fella, Jones!’ Alfred bellowed across Horace Lane.
The figure, silhouetted in the shadows of the house across the street from his, replied with a deep bass voice: ‘Shut it, Alfred! Just chuck it over here, mate!’
Alfred bent over to pick up the pink-laced rag from the muddy puddle, then threw it across the narrow lane. The lane belongs to the town of Angel’s Acre. But the name missed one quite important detail: that the worst of the worst people - those who steal, loiter and scam - are banished here. There is only one law in Angel’s Acre: do not kill. In 1857, one person had broken this law, and the punishment had been compared by many to eternal hell.
Alfred and his wife Evanthe were approaching Alma Boulevard as the crowd was preparing to harass the newcomers, Angus Bachman and Ashley Kolen. Evanthe approached them kindly: ‘Oh, welcome, dear! Welcome to Angel’s Acre! I am Evanthe, one of the board members, along with my husband. Can I help you with anything? What crime did you commit?’
‘Thank you, I am Ashley Kolen and this is my adopted brother… Angus Bachman. To be honest, I stole a loaf of bread from a rich man’s penthouse. I was too poor to feed my family…’.
Evanthe peeked over at Alfred, who was pickpocketing Angus. Alfred stood up, waiting for Evanthe to give the signal to depart. Evanthe gave Ashley no time to react and speak; she continued by hinting, ‘Ashley, dear, don’t go around believing what other people say to you. Just be careful - you never know when people here are lying or not. Have fun, my dear!’ With Evanthe’s unkempt teeth glaring at Ashley’s eyes, she was taken aback. She stood there, bewildered that this place could be called a hellhole by survivors. Then Ashley felt her pocket for her money - empty. She felt her other pocket for her jewellery - missing.
Angus and Ashley strolled along Horace Lane; their house was across from Alfred and Evanthe’s house. Angus took out the key which was given by the only person of authority here, Baroness Justina. Ashley took the key from Angus and pushed open the oak door. The door let out a creak. It hit something, something with the figure of a human. There was a puddle on the floor. Water? No. Mud? No. Blood? Yes. This was not normal. Ashley bent to feel the object blocking their way. Skin, skin, skin, clothing. She gasped ‘Angus, sweetie, turn the lamp on…’
Angus traced his hand along the thin wooden wall to feel the switch. The light was on, the truth was out; Ashley was smeared with blood. Angus shrieked with such horror that even the Pradmoore twins next door, Oliver and Oscar, had to step out of the house. On the door of Angus and Ashley’s house there was writing in blood: GET OUT GET OUT. And on the floor was Jones’ body, his mouth open from shock. The Pradmoore twins reached their door to find Oliver faint and Oscar questioning, ‘Who are you? Where did you come from? WHY DID YOU KILL JONES? WHY? WHY? WHY? WHY?’
Angus turned around the twins, identical, both wearing a canvas straitjacket. The jacket came with a label that read 'This person is wearing this for a reason: do not touch.’ Angus and Ashley stumbled back with fear as the twin dragged his brother back to their house, snickering while shouting, ‘MURDER! MURDER! MURDER ON HORACE LANE!’ Crowds were gathering around their house. Ashley’s hands told people that she had killed Jones. Could this be the end for both Ashley and Angus?
The next day, the board of the Angel’s Acre gathered. The Acre’s Baroness Justina, wearing an all-pink outfit, announced ‘Fellow citizens! As we are all aware, our fellow member of the board, Richard Jones, has been brutally murdered.’ She glared over in Ashley and Angus’ direction, before continuing: ‘Now, clearly, I wasn’t at the scene of the murder. Any accusations from all of you?’
Alfred stood up as he spoke. ‘Baroness, as you are aware, there are two new citizens here. I am not making an accusation, but don’t you think that rather than interrogating the natives, we should ask the newcomers who coincidentally were at the scene of murder?’ All members nodded in unison as the Baroness called Angus and Ashley to defend themselves. They did so accurately, recounting events as they had happened, and pointing out the pickpocketing. The Baroness, however, didn’t believe their story. She shook her head in disbelief. ‘Oh, dear’, she said.
‘No… no… no… NO! I didn’t do it! I just’ Ashley stumbled onto the confession podium, which hadn’t been seen since the last murder in 1864. Her hands were tied, and she was silenced as she was placed on a burning hot podium, which would shortly drop her into boiling oil. Ashley was scared. Angus was next. She had merely 10 seconds to save herself. ‘Please, please, please. I didn’t do it. I promise...’ Goodbye, Bachman and Kolen.
Justina pushed the oak door open. It screeched slightly on its hinges. She pulled out a pink-laced rag as she barged in to say ‘Ministry of the Acre, rent is due!’ A man sat on a chair, smoking a cigarette. He had his prosthetic leg propped on the table.
‘Seriously Justina,’ he said, ‘it has been literally 30 years since you-’
Justina shoved the rag on his mouth and nose, attempting to silence his screams. Then she threw the rag out into the street and stabbed him. As she was pulling the knife out, she heard Alfred’s voice, saying ‘Ah, you crooked fella, Jones!’ The Baroness told the man to ask for it back.
With his dying breath he said ‘Ah, shut it, Alfred! Just chuck it over, mate!’
The Baroness whispered into his ear ‘I took your leg 30 years ago and I am not scared to extinguish the only threat to my safety and position. Enough is enough, you didn’t win after all, huh?’
She stepped over the body and splattered out the note in blood to Bachman and Kolen. Then she elegantly stepped away from the house. She walked over to Alma Boulevard to hand Angus the key to Jones’ house.
‘Perfection…’

Free Will vs Determinism Connor S-S, Year 13
The free will versus determinism debate explores whether humans have free will in the choice of their behaviour or if it is already pre-determined. Free will is based upon the idea that we have complete control over our behaviour and most closely links to a humanistic view of human behaviour – the idea that each person is an active agent and shapes their own experiences. Our criminal justice system is also based upon the idea that people have free will and can make their own decisions.
Determinism is the idea that we do not have conscious control over our behaviour and that instead it is determined by internal or external factors. Hard determinism is the idea that all behaviour is caused by external or internal influences and that we have zero conscious control over this, whereas soft determinism believes that whilst there are internal/external influences that can affect behaviour we still have an element of choice in whether we act upon these influences.
Biological determinism is a form of hard determinism, believing that behaviour and thoughts are due to biological factors such as genetics, hormones, brain structures and anything that is biological. When we take the biological approach to explaining OCD, for example, it is believed that this disorder is caused by a lack of serotonin and can be treated by taking SSRIs (Selective Serotonin Reuptake Inhibitors). Furthermore, the biological approach to explaining gender dysphoria focuses on the idea that gender dysphoric people have a structural difference in the brain, with their BSTc (bed nucleus of the stria terminalis) being of a similar size and chromosome pattern to those of the opposite sex. This suggests that the person doesn’t have control over their gender dysphoric thoughts and behaviour but instead that this is biologically determined by these brain structures and genetics.
Environmental determinism believes that free will is just an illusion. This type of determinism is based upon the idea that our behaviour is determined by the environment around us and past social experiences, such as socialisation, reinforcement and conditioning. It most closely links in with the behaviourist approach. For example, we can explain that phobias are acquired through Mowrer’s
Two Process model: the phobia is first learnt through classical conditioning (usually a frightening event that pairs this neutral stimulus with this frightening event) and is then maintained through negative reinforcement, avoiding the phobic stimulus (operant conditioning). This demonstrates, once again, that we do not have free will in choosing to have these behaviours, but they are instead produced by our environment.
Finally, psychic determinism is the idea that our unconscious thoughts and past experiences will determine our behaviour. These usually come from childhood experiences. We do not have any conscious control over our behaviour because it is determined by these unconscious past experiences. This links closely with the psychodynamic approach and can be used to explain gender development. Through this approach we can explain gender identity being learnt through the Oedipus/Electra complex, where a child gains the same-sex parent’s gender identity through identification and internalisation. This all takes place in the unconscious and it is believed that this will determine future gender behaviours. Once again, this suggests that we have no control over this behaviour and that it is determined.
Let us take a case study as an example. Dancho is a musician whose behaviour can be explained through environmental determinism. It is mentioned that at age 4 he attended a specialist music school. This shows that his musical success could have been because of this environment; from doing concerts, the applause would act as reinforcement which could shape his future success. Furthermore, it is mentioned that his father is also a concert pianist; this could suggest that there may be biological determinism and he may have inherited this behaviour from his father.
A strength to determinism is that it is consistent with the aims of science. We are able to predict behaviour using determinism; this has a lot of real world applications that can benefit people. For example, biological determinism would suggest that there is a genetic component to behaviour, which can allow us to develop drugs and therapies to try and help sufferers from this disorder. Successful therapies have been developed for schizophrenia, for example, because of the biological determinism of the disorder. There are also some mental disorders where sufferers have no control over their behaviour. This is a strength to determinism, as real world disorders have shown that there is an element of determinism to them.
However, a limitation to biological determinism is that it is not a scientific approach and goes against our criminal justice system. The criminal justice system is based upon the idea of free will and therefore we cannot use this approach in a real world context within the justice system. Furthermore, determinism is unfalsifiable. This is a limitation to the approach as it cannot be proven scientifically and lacks empirical evidence to back it up.
Another strength to determinism is that there have been supporting studies that give evidence that biological factors may have influence on behaviour. A study was conducted where participants had to choose whether to pick an object up with their left or right hand. It was found that there was neuron activity within the brain already 10 seconds before the participant recalled consciously making the decision. This is evidence for biological determinism, as this study demonstrates that biological factors do influence our behaviours.

Kingship in “Macbeth” Hannah A, Year 10
In his 17th-century play, Macbeth, Shakespeare explores the dangers of a leader whose Christian virtues are unbalanced with their political values, through three contrasting monarchs in his play. Through his second, tragic tyrant, Shakespeare exposes the devastating consequences when these traits misalign, and he encourages his audiences to reflect and act on what makes a good leader. This was important to Shakespeare after the exposure of the Gunpowder Plot, when questions of good leadership became a priority.
Firstly, Shakespeare shows the downfall of a leader whose Christian traits overpower their political intelligence through King Duncan. In Act One, Scene Four, after it is revealed that the king was betrayed by a former thane, Duncan explains that “he was a gentleman on which I built an absolute trust”. Shakespeare uses dramatic irony in this phrase because the audience may recognise the repeating pattern already – of Duncan displaying loyalty towards men who don't reciprocate it. Additionally, the use of the noun “gentleman” suggests how Duncan still has respect for his betrayer by referring to him in a formal way. Furthermore, the verb “trust” suggests naivety and poor judgement from Duncan as he admits that he was obviously misled by his former thane into thinking there was a mutual bond between them. This suggests that Duncan is a misguided king who is unfit to rule the country. Then, in Act Four, Scene Three, after his murder, Duncan is referred to as a “royal father who was a most sainted king”. The use of the adjective “sainted” has connotations to holiness and divinity and it is amplified using the word “most” to suggest the depth of his goodness. This creates an effect of benevolence around the leadership of Duncan. Shakespeare encourages his modern audience to reflect on what truly makes a good leader: not only goodness and nobleness. Shakespeare also warns leaders through Duncan about the dangers of not exhibiting traits like prudence and scepticism. Shakespeare does this as a reply to Machiavelli’s The Prince of 1532, where he introduces the idea of Christian virtue not being the most important trait for a good leader. He suggests how a good king must rely on his own courage instead of others.
Secondly, Shakespeare warns against disrupting the Great Chain of Being and being a tyrannical leader though his second king, Macbeth. In Act Two, Scene Four, soon after Macbeth had murdered the previous king, it is said that the horses had “turn’d wild” during the night and that nature had “made war with mankind”. Using personification, Shakespeare suggests that nature was rebelling against the people
in an unnatural and absurd way. This creates an effect of instability and danger for the people of Scotland. Similarly, the use of the adjectives “wild” and “war” connote to violence, aggression and danger, amplifying the sense of unease and frenzy in Scotland after the murder was committed. As a Jacobean audience, some may feel anger or disgust towards Macbeth for disrupting the Great Chain of Being and causing Scotland to turn to chaos and possibly would begin to form a dislike for his character. Furthermore, Shakespeare continues the imagery of chaos and disruption when in Act Three, Scene Two, Macbeth exclaims how his “mind is full of scorpions”. The metaphor suggests complete inner turmoil and instability. The noun “scorpions” suggests poison and suffering and the adjective “full” amplifies this. This creates the impression of pain within Macbeth which suggests that disrupting the Great Chain of Being not only causes nature into disorder but also inner anguish. Shakespeare does this to warn leaders away from the idea of disrupting the Great Chain of Being or the Divine Right of Kings to get power. For, despite Macbeth being a completely different personality to Duncan, their outcomes are the same and the consequences of both leaders are devastating for the country. In Jacobean society, some people would have believed in the Divine Right of Kings, in which God was said to have annointed the monarch, as well as the Great Chain of Being, which describes how chaos can happen if you disrupt the order that God set out for the world, like how murdering a king would turn a country to frenzy.
Thirdly, Shakespeare encourages a model of leadership where the leader’s traits are balanced between Christian virtues and political intelligence through the third king Malcolm. In Act Four Scene Three, Malcolm lists an assortment of characteristics he associates with balanced leadership. He mentions “The king-becoming graces, As justice, verity, temp’rance, stableness, bounty, perseverance, mercy, lowliness, devotion, patience, courage, fortitude.” Shakespeare uses this list of nouns to provide an overview of Malcolm’s character and the qualities he aspires to achieve. Using the noun “lowliness”, we can infer Malcolm’s humbleness and ability to restrain his ego and pride which creates an effect of good-naturedness and Christianity around him because humbleness is a respected trait in the religion. The noun “courage” Malcolm mentions has connotations of bravery, valour and strength and we can infer that despite his sincerity, Malcolm also holds the ability to be a powerful and capable leader – which is something neither of the other kings were capable of doing. This paints a picture of Malcolm as the ideal king because his Christian virtues align with his masculine strength so he can be a fair and stable king. The audience may respect and appreciate Malcolm because he holds the ability to restore Scotland to greatness after much badness. Shakespeare provides a response to Machiavelli’s “The Prince” through the three kings.
Kingship in “Macbeth” Phoebe
P, Year 10
In his 1606 play, Macbeth, Shakespeare presents kingship as a thin line to tread between tyranny and naivety. He explores the different models of leadership, whilst exposing the consequences of bad leadership and its effect on the country. He encourages the audience to reflect on what makes a good leader and to be wary of corruption.
Firstly, Shakespeare presents a model of naïve leadership with good Christian virtues through the character of Duncan. Duncan is demonstrated as a good king by his abundance of Christian values, but a weak king by Machiavellian standards. When Duncan is talking about the treasonous thane, he describes him as “a man on whom I built absolute trust”. The word “absolute” suggests that he is a very trusting king and therefore a model of naïve leadership.
Near the start of the play, Shakespeare uses dramatic irony to forewarn the audience of Duncan’s downfall and this, linked with his Christian virtues, could communicate to the audience that too many Christian values in a king would ultimately lead to their downfall. A Jacobean audience may be blinded by Duncan’s Christian values, as Jacobean England was heavily Protestant under the reign of King James I, preceding Elizabeth I’s conversion back to the Church of England, after the reign of her halfsister, Bloody Mary. This use of dramatic irony could possibly allow a more modern audience, that may be less religious, to experience Duncan’s naivety, maybe with a more cynical view on the benefits of Christian leadership to the welfare of the state. Furthermore, even when Macbeth is plotting to kill Duncan, Macbeth still thinks about Duncan’s virtues, which sing out, “angel-like” […] trumpet tongued”. The simile “angel-like’’ further illustrates this Christian model of leadership, but ultimately concretizes the idea that Duncan’s naivety led to his downfall. Shakespeare may intend to do this to demonstrate how the wrong method of leadership (a weak, trusting model) can be the downfall of a king, but subtly communicating to King James I the negative qualities in a leader. Therefore, Shakespeare presents kingship as accommodating many possible virtues, but also communicates the negative aspects of leadership that is too meek and trusting in character.
Secondly, Shakespeare presents the theme of kingship through a different lens, with the use of the tyrannical character of Macbeth. Shakespeare presents Macbeth as a king with a more Machiavellian leadership style; however, the tyranny that Macbeth displays could also be a negative quality in a king. When Lady Macbeth convinces Macbeth to kill Duncan, she says “look like th’ innocent flower but be the serpent under’t”.The Italian philosopher Machiavelli says that leaders should not show the moral corruption they possess, though the fact that Lady Macbeth encourages Macbeth to hide his thoughts suggests that Macbeth struggles to hide his own moral corruption and dissimulate as a likeable man. This quickly dissolves, as Macbeth is later described by Lennox (among others) as a “tyrant”. This suggests that people do not like him, which also contradicts Machiavelli’s ideas. Therefore, contemporary and modern audiences may both dislike Macbeth due to his regicide and infanticide; Shakespeare may use this dislike as a tool to encourage the audience to reflect on a tyrannical model of kingship and the dire consequences that lead to the breakdown of the country. As well as this, Shakespeare displays Macbeth as a person lacking any Christian values, when Malcolm calls him “devilish Macbeth”. The use of the imagery “devilish” implies Macbeth is the opposite of Duncan, and therefore lacks any Christian values and virtues. Therefore, Shakespeare presents Macbeth as a tyrannical king, but explores the influence of Machiavellian ideas of kingship over the play.
On the other hand, Shakespeare uses the character of Malcolm to promote the model of a good leader, through the combination of pragmatism and Christian values. After he has misled Macduff into thinking he would make an awful king, Malcolm says “what I am truly is thine and my poor country’s to command”. Here, the use of the possessive pronoun “thine” implies that Malcolm regards himself not as his own person, but as the object of his country and the people of Scotland. As well as this, the use of the word “my” suggests Malcolm believes he is at the disposal of his country, which together demonstrates the commitment to his country and responsibility Malcolm feels towards Scotland. This also communicates Malcolm’s selflessness towards his country, which contrasts with Macbeth’s selfish view of Scotland, having sought to protect himself by killing Banquo and Macduff’s children. When Macduff first meets Malcolm in England, Malcolm tells Macduff “he hath not touched you yet”. The suspicion with which Malcolm regards Macduff’s approach highlights the qualities in Malcolm that may make him a good king, using a new, prudent model of leadership; distrust, duplicity (when he deceives Malcolm) and prudence. His cynicism is a good example of Machiavellian values, as it demonstrates the lack of naivety in Malcolm, which was ultimately the downfall of his father, Duncan. Another way in which Malcolm demonstrates a Machiavellian way of
leadership is when he tricks Macduff into believing he will make a bad king before apparently revealing the truth when he “unspeak[s] mine own detraction”. The ability to control how Malcolm presents himself juxtaposes with Macbeth’s inability to dissimulate, which indicates to the audience that Malcolm may make a better king than Macbeth. Malcolm also demonstrates good Christian values as well (“scarcely have coveted what was mine own”) and, by doing this, Shakespeare presents an ideal model of leadership to King James I.


Introducing Non-Euclidean Geometry with Beetles Millie T-B, Year 12
“When a blind beetle crawls over the surface of the globe, he doesn’t realise the track he has covered is curved. I was lucky enough to have spotted it.” –Albert Einstein
What links Einstein’s Theory of Relativity and Pringles?
The answer: Non-Euclidean geometry.
For me, this geometry is a truly fascinating and exciting realm, which, when understood, can open up whole new dimensions (sometimes quite literally!). Yet many people find the initial concept overwhelming and off-putting, so never get the chance to enjoy and experience where this sometimes dark and often twisty geometry can lead.
In this essay, I hope to introduce the two main non-Euclidean geometries, the hyperbolic and elliptic planes, and leave you with the confidence – and hopefully desire – to research these further.
Oh, and one more thing: I shall be using beetles throughout in order to prove Einstein wrong (brave, I know) and show that even a blind beetle can understand curved space.
1. In the Beginning
To understand non-Euclidean geometry, we should first grasp where the ‘non’ came from, and go back to around 300 BCE, in Alexandria, Egypt, when a man was born.
Little is known about his life, but his academic contribution was immense: from guiding and impacting philosophy; to defining and “shaping” (pun intended) our understanding of mathematics for thousands of years; and producing one of the most widely read books on record.
His name was Euclid.
The book in question, Elements, effectively laid down the laws of geometry, including 23 definitions, five geometric axioms, five additional axioms called “common notions”, and 465 theorems, which he derived from the above. Though history didn’t care to keep information regarding his personal story, she did take the time to save Elements, the contents of which were originally written on scrolls and passed down through time – much like a cherished family recipe – to become the book we know today. The foundations of his geometry lie with his five axioms, which are illustrated, using beetles as points, and written in modern and simpler terms below:

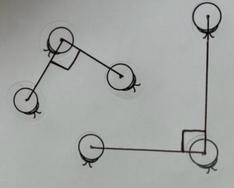
1. Given any two points, a line segment can be drawn with those points as its endpoints.
2. Any line segment can be extended indefinitely in either direction.
3. Given any point, a circle with any radius can be drawn with that point at its centre.
4. All right angles are equal.
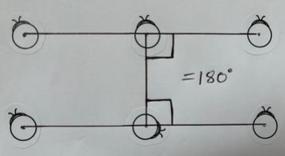
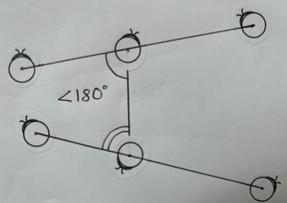
5. Given a line segment that crosses two lines in a way that the sum of the inner angles on the same side is less than 180°, then the two lines will eventually meet.
In other words, given a line and an external point (a point not on that line), there is exactly one other line that passes through the external point and is parallel to the given line.
I hope you would agree that the first four of these axioms feel pretty straightforward and lovely, seemingly intuitive and logical, and phrased relatively sleekly. Yet Euclid’s fifth postulate doesn’t manage to land quite so well. Despite its similarly intuitive nature, it sounds clunky and unnecessarily complicated – an issue which tormented mathematicians, who tried to prove this postulate using the others (thereby making it redundant) for over 2,000 years.
One of these mathematicians was John Wallis, from Ashford, Kent. His approach to this pesky postulate was not to prove it, but to instead replace it with his own version, which could be read as follows:
Given any side of a triangle, the triangle can be blown up or shrunk so that the chosen side has any length you like – but the angles of the triangle are not altered.
Simply put, this is the concept of similar triangles, which relies on the ability to translate lines using linear scale factors, so that they can be “moved” through space such that the distance between any two points on a line is proportional to the distance between them on the “moved” line, and that this proportionality can be written as a scalar constant.
Although Wallis’ work does not replace the fifth axiom, it is incredibly useful to understand, because it exposes a crucial element of non-Euclidean geometry, for it shows that if a space exists in which the parallel postulate does not hold, then no similar triangles exist. This means that when a line is “moved” through non-Euclidean space, it is also distorted.
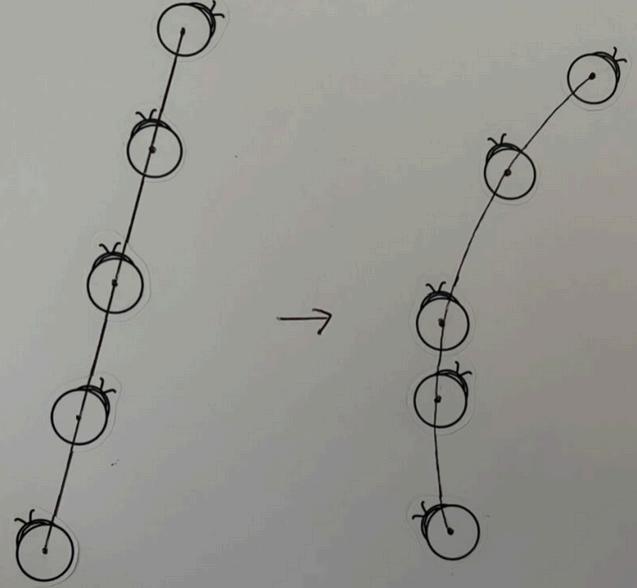
With an understanding of Euclidean geometry, the problem with his fifth parallel postulate, and the implications of Wallis’ alternative, we can head on to hyperbolic space, the first of the space revolutions.
2. Hyperbolic space
Fast forward to April 30, 1777, when Carl Friedrich Gauss was born.
Just as Euclid had formalised geometry for the world, Gauss, along with Wolfgang Bolyai and Nikolay Ivanovich Lobachevsky, would rewrite the rules and create a whole new type of space.
Gauss, like the many mathematicians before him, also had an issue with the parallel postulate, but his ran far deeper. Rather than replacing it or proving it, he imagined a space where it simply wasn’t true. He pictured this by devising a numerical notion of “curvature”:
a flat, Euclidean plane has 0 curvature. a plane such as the surface of a sphere has positive curvature. a plane such as the surface of a Pringle has negative curvature.
It was this last type of plane that Gauss took further, eventually establishing a complete geometric system. In 1824, he wrote that “The assumption that the sum of the three angles [of a triangle] is less than 180° leads to a special geometry, quite different from ours [Euclidean], which is absolutely consistent, and which I have developed quite satisfactorily for myself…”
This hyperbolic space was a new playground for mathematicians and physicists alike. It was discovered almost simultaneously by Gauss, Bolyai and Lobachevsky, but was arguably best described by Henri Poincaré in the 1880s.
Instead of an infinite plane, Poincaré created an infinitely thin disc with a perfectly circular boundary, on which Poincaré’s lines can be drawn. These lines he described as “any arcs of circles that intersect the boundary of the disc at right angles.” Despite the revised definition of a line, the concept of “points” in Poincaré’s universe remains what we would expect, simply dots defining a particular position in space.
Once Poincaré had built this picture, he defined the geometric concepts that existed within it. Ensuring Euclid’s first four postulates held true, and in order to deal with congruence, he defined a system to measure angles and length: he chose to define the angle between two of his lines as the angle between their tangent lines at their point of intersection.
“But what about the second axiom? How can a line be extended indefinitely in a finite region?” I hear you cry. In order to get past this, Poincaré chose to define distance in Poincaré Universe such that space is compressed as you near the boundary, meaning that length becomes infinite as you approach it.
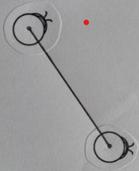
Using an imaginarily perfect circular shell of a beetle, and making it infinitely thin, we can illustrate Poincaré’s space, and parallel lines, as shown on the next page:
This demonstrates how Euclid’s fifth, parallel postulate fails to hold in hyperbolic space, because instead of one, there are an infinite number of lines that can be drawn through a point, which are parallel to another given line, as they will never intersect. Instead, in hyperbolic space, parallel lines continuously diverge.
As Gauss discovered, this leads to triangles where the sum of the angles is always less than 180°, by a number which he called the angular defect. This links back rather nicely to Wallis’ inadvertent discovery that in non-Euclidean space similar triangles cannot exist, for the size of the triangle is inherently linked to its angular defect. Larger triangles are distorted more by the space, causing a greater angular defect, whereas smaller triangles can appear more Euclidean – geometry’s epitome of the phrase “Close, yet oh, so far”.
Assuming unit curvature, this leads to a new formula for the area of a triangle, for in hyperbolic space the area can be calculated with only the angles in the triangle, using:
�������� = �� (�� + �� + ��)
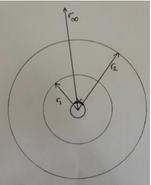
This means that there is a limit to the total area a triangle in hyperbolic space can be: ��. This can again be shown using Poincaré’s model on an infinitely thin beetle:
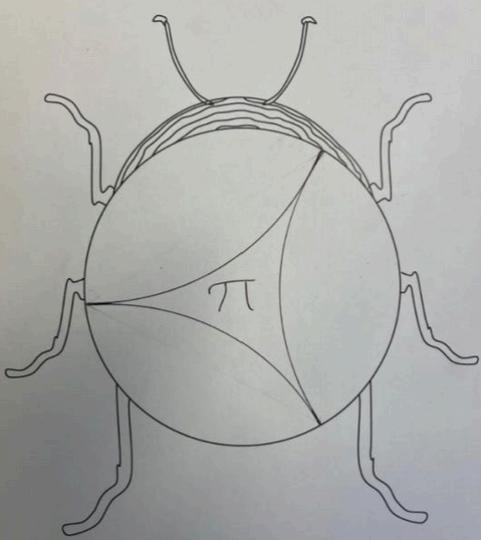
The maximum possible area of a triangle in hyperbolic space is ��, when all of the interior angles are 0°. �� = ��
(0 + 0 + 0)
This occurs when the vertices are “infinite” vertices; they are vertices on the boundary of the plane.
Furthermore, in hyperbolic space, the circumference of a circle is: �� = 2�� sinh(��), where 0 ≤ �� < ∞ and 2 sinh �� ~��
This means that the circumference of the circle is exponential, which highlights how large the space really is. The area of a circle is also exponential, and interestingly, it grows at the same rate as the circumference, in contrast to the area in a Euclidean plane, which grows at the same rate as the square.
This can be seen as the area of a circle in hyperbolic space follows the formula: �� = 2��(cosh(��) − 1)
Hopefully by now, we have a basic understanding of hyperbolic space, the first (and yummiest – in the case of Pringles) of the two non-Euclidean planes I would like to introduce. But it gets even better – because non-Euclidean geometry only becomes more fascinating when we compare hyperbolic space to elliptic space, the hyperbolic plane’s antithetical twin…
3. Elliptic space
In 1854, a man named Georg Riemann was twenty-seven and attempting to secure a lectureship at Göttingen University, Germany. His final task was to deliver a trial lecture, and Gauss, one of the faculty professors, chose to make it Herculean. Against university tradition, Gauss selected Riemann’s third choice topic to be the subject of his lecture, titled, “On the Hypotheses Which Lie at the Foundations of Geometry”. In it, Riemann revealed another non-Euclidean plane: he explained how the sphere could be used to interpret a two-dimensional elliptic space.
Imagine a flat, Euclidean plane, as defined by his axioms. It would resemble an infinite 2D grid, much like Rene Descartes’ familiar cartesian graph. Now, if we use Gauss’ concept of “curvature” to add a positive curvature to the plane, it will form a spherical shell, such as the spherical shell of a beetle: x
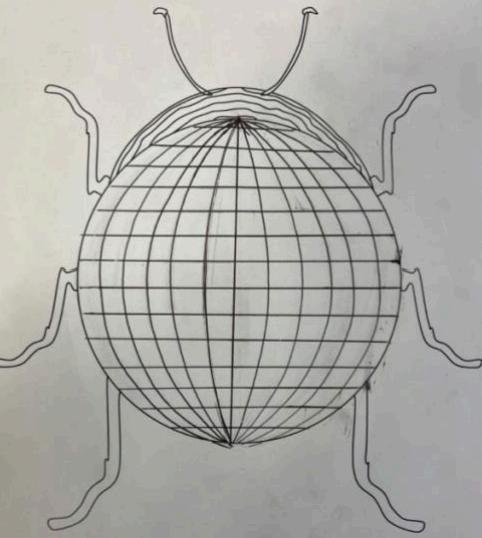
It is important to remember that this is not actually a “beetle-sphere” – both 3D shapes – but is still a plane, with no inside or outside space to be curving into, a concept which was proved by Gauss in his 1827 Theorema Egregium. We are simply picturing this plane in 3D in order to make it more accessible to ourselves as higher dimensional beings.
For lines in elliptic space, Riemann used “great circles”, the circles that can be drawn on a sphere so that they pass directly through two opposite points, and once again, his definition of points remained the same as Euclid’s.
Just like Gauss, it was Euclid’s second axiom which could have caused technical difficulty for Riemann, as it seems wrong to accept the existence of line segments with arbitrarily large length, if all lines are circles – therefore capped to the length of their circumference, 2����. To bypass this, he argued that the function of the second postulate was not to make line segments arbitrarily long, but to instead ensure that lines had no bounds, which is true with great circles.
By defining lines as great circles, Riemann demonstrated that in elliptic space Euclid’s parallel postulate does not hold. For, in contrast to hyperbolic geometry, there are no parallel lines in elliptic space, because all lines will intersect infinitely, as they continuously converge to meet at two opposite points on the plane.
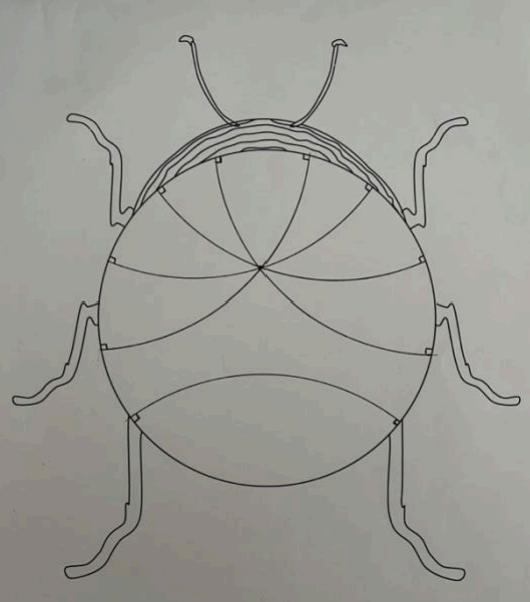
On the beetle-sphere, an example of great circles are lines of longitude paired with their antimeridian, plus the line of latitude equivalent to the “equator” of the beetlesphere. You can see that the longitudinal great circles all intersect at both “poles” on the beetle sphere.
If we zoom in on our beetle-sphere, we can see that a triangle in this plane has angles that sum to greater than 180°. Again, the larger the triangle, the greater the distortion, therefore the greater the angular defect!
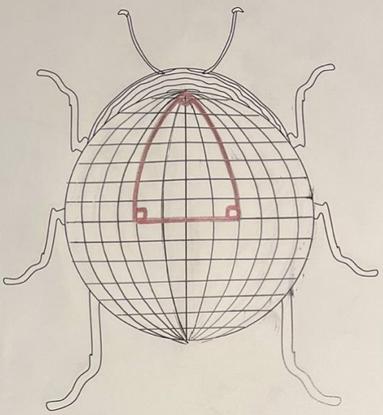
The triangle highlighted is comprised of two longitudinal great circles intersecting the equator. As all lines of longitude are perpendicular to lines of latitude, the bottom two angles in this triangle are both 90°. Assigning the third angle (at the “pole”) a value of ��, where �� ≥ 0, the sum of the interior angles in this triangle is therefore:
Assuming unit curvature, this leads to some nifty new equations once more!
For the area of a triangle in elliptic space, the formula is: �������� = (�� + �� + ��) ��
You may have noticed that this is the opposite formula to the area of a triangle in hyperbolic space, and as a general rule, for most equations this is true, because whilst lines in hyperbolic space always diverge, lines in elliptic space continuously converge.
The circumference of a circle in elliptic space is given as:
= 2�� sin(��)
This can be visualised by imagining any circle on the beetle-sphere, perhaps starting with a unit radius and centre O, effectively the “north pole”. Now increase the radius of this circle to match the radius of the beetle-sphere itself – the circle now has the same circumference as the beetle-sphere. If we were to expand this circle any further across the surface of the beetle-sphere, we would find that the radius would actually shrink as the boundary of the circle neared the point on the surface opposite O, the “south pole”, until it reached this point, when the radius would be 0.
This pattern repeats cyclically, hence the sine function.
The area of a circle follows a similar cyclical pattern, with the formula (you guessed it):
2��(1 cos(��))
4. Einstein and beyond
“So why does this matter? This theoretical maths might be interesting and form pretty patterns, but what does it have to with me?” I hear you ask.
Well, as both Einstein and Mr Pringle discovered, non-Euclidean space is everywhere. In fact, the very universe we live in is probably non-Euclidean, it’s just that the fraction of it that we experience is so small, it feels Euclidean!
I hope this essay has not only introduced you to the non-Euclidean world for the first time (or explained it in a different, and hopefully entertaining way!) but has also encouraged you to go forth and explore beyond this starting point (or should I say beetle)…


A Letter to the Prime Minister Joshua M, Year 9
Dear Mr Sunak,
I am writing to show you that more urgency is needed in moving away from specifically fossil fuels in the UK.
If we continue to use fossil fuels, energy prices will continue to rise, further worsening the cost-of-living crisis. Graphs from our World in Data show that the price of solar energy has decreased 89% in the years from 2009 to 2019. The price of onshore wind energy has also decreased by 70%. Data from the eco exports shows that gas prices increased from £0.03/MWh to £0.24/MWh in just two years (20202022). Relying on fossil fuels also means we will have no oil or gas left in the North Sea by 2027, giving us three years to act.
On the other hand, using renewable energy means that less money will be spent on electricity. Keeping the lights on and providing heating will be much easier for the citizens of the UK. The Russia-Ukraine war has caused oil prices to rocket by around 54%, which presents another reason to adopt more renewable energy.
I sincerely hope that you take my advice and increase renewable energy production and usage in the UK.
Best regards,
Joshua M



Silhouette Salem D, Year 12
I pressed the tip of my index finger into the shard of glass. I was transfixed, staring into my mother’s favourite mirror – I let it shatter. I watched it gliding; smashing; colliding; slashing every other inconvenient – or naïve – fragment that would stand in its way.
I picked it up, placing it on my palm and I pushed it through my flesh.
I watched how it broke the skin and changed my pigment, from peach to red to grey.
A little piece chipped off and made a home; swaddled inside the warmth of a rouge blanket.
The larger piece?
Removed and forgotten; it is a distant thing.
Though I remember the silhouette of the slice; there was a delicacy in its sculpture. Its edges were intricate; dipping and rising.
And I recall the reflection: a rusty point, meeting plumpness. It left a mark, a dent, a scar. So now I am tainted with a sliver of the slice, which is floating, dancing with my blood.
Why People Conform Gaby I-H, Year 12
One psychologist who investigated conformity and social influence was Solomon Asch. He designed an experiment where 123 US male undergraduates took part in a task matching lines of different length and were tested in groups of 6 to 8. Within these groups there was always one naïve participant who was placed in the last or second-to-last seat. All other participants were actors taking part in the experiment and gave scripted answers to the line-matching task.
Asch found that the naïve participant agreed with the actors and gave the incorrect answer 36% of the time, and only 25% of the naïve participants didn’t give the incorrect answer. This suggests that the participants conformed due to Normative Social Influence – the need to be liked by the group.
Even though the correct answer was clear in each question, the naïve participant felt pressured to conform and agree with their fellow participants, perhaps to feel a part of the group. Asch also repeated the experiment, changing the task difficulty by making the lines to be matched more similar in length. This caused conformity to increase. Many have suggested that this is probably due to Information Social Influence (the need to be right) and, as the difficulty has increased, the answer isn’t so obvious, making copying more likely.
Although from this study we can tell a lot about habits surrounding conformity, one limitation of this experiment is the sample bias: all participants were US male undergraduates, and there was no variation of gender, ethnicity or age. Therefore, the results for this category of people cannot be generalised for all people. Additionally, students are known to be more likely to conform due to their day-today environment, increasing the bias further.
Another limitation for this experiment is that the task the participants completed was very artificial. As the task is artificial, we cannot associate it with any norms we may come across in our day-to-day life. This could perhaps suggest that these results cannot be generalised to realistic day-to-day tasks we encounter, but only work for this artificial style task. Participants attempting to guess the purpose of the study, and modifying their answers accordingly, could present a further limitation.
Another psychologist who investigated social influence was Philip Zimbardo. Zimbardo conducted an experiment in which 24 emotionally stable male students were randomly assigned to play the role of a prison guard or a prisoner. Participants were encouraged to conform to social roles through uniforms and the guards were instructed to keep peace. They were urged to identify with the role and were reminded that the guards had complete control over the prisoners.
Within two days, prisoners had begun to rebel by ripping uniforms, and using foul language against the authority of the guards. The guards then retaliated, forcing the prisoners to become more subdued. The prisoners were also said to have become depressed and significantly more anxious – with one even leaving early due to signs of psychological disturbance. Throughout the experiment, the guards’ behaviour became increasingly more brutal, forcing Zimbardo to stop the experiment early.
This experiment shows that, without instruction, we attempt to conform to behaviour which we have seen in the past, often through TV and media. It's suggested that the guards behaved in such a brutal manner because that is often how TV dramas depict prison life, even though the prisoners were not real prisoners. It appears that all participants by the end had internalised their roles and began to believe that they really had this power, or they really were imprisoned. Additionally, it shows how we can group together and form some kind of social identity, causing us to work as a team – in this case, in a brutal manner.
One limitation of this experiment is the ethical implications surrounding it. Although all 24 men were said to be emotionally stable on entry, this certainly wasn’t the case on exit. Perhaps this happened because Zimbardo entered the experiment himself as a prison superintendent and didn’t keep an investigatory distance.
Another limitation of this experiment is the sample bias. All participants were male students. Similarly to Asch’s experiment, there was no variation of gender or age, therefore the results for this category of people cannot be generalised. Additionally, just like Asch’s experiment, students are known to be more likely to conform due to their day-to-day environment which increases the bias further.
A positive of Zimbardo’s experiment is the amount of control and realism within the experiment.
Foxgloves and Dandelions
Elisha H, Year 12
Darlene,
The things I wish that I could express to you Are as many as there are stars in the sky. Although I am much older, I still think on our time together As adolescents.
I think on the time we spent together in the fields, Frolicking among the foxgloves Dancing among the dandelions. When we would hide from our fathers And escape the house to see each other. We would sit together Among the foxgloves and dandelions.
There was not an hour in which I did not think of you. I think on when I looked into your eyes.
I could see a reflective pool, A deep ocean full of dreams and nightmares, Love and hate, Happiness and sadness.
Yet I am starting to forget the sound of your laughter. That time we spent together is still there, Tucked away under a careless pile of foxgloves and dandelions, In the back of my mind,
But our time together is just a memory. For, Darlene, I miss those moments, The time we spent running away, Even the times we were caught and got into trouble. I wish we could relive those moments, And I hope you feel the same. But instead, I am stuck.
Stuck
With Peter Honningbrew. I have nothing against him, My father approves. But he never Frolicked among the foxgloves,
He never Danced among the dandelions, His eyes are not oceans, And I have never heard him laugh. He haunts me with his presence
And I dread the time we must spend together. Because he is not you, Darlene. And when he tells me that we are to spend time together And when he forces me away, I think of us
Frolicking among the foxgloves, Dancing among the dandelions, Wishing that I could run away and dance one more time, A time that would last forever.
But tomorrow is my wedding day; This is my last chance to escape. A chance I shall not be taking,
As you and I cannot be together. They would hang me at noon if they were to find out.
And so, I take no more chances, For society has squandered any hope that I had And I begin to question my faith. But time is nothing if not cruel, And it appears it was not on the cards this lifetime. But our souls will reunite, And as the seasons change through the year Our memories together will die, Just like Foxgloves and dandelions. I have decided that I will not let time win. Time may be cruel, But it shall not take away my memory. So, remember me fondly my darling foxglove As I am whisked away by the breeze
Like a dandelion seed. And when you join me, Look for me
Among the foxgloves and the dandelions. Sincerely, Your dandelion, Elizabeth.
Inflationary Pressures
Milena D, Year 13
There has been an inflationary trend since the beginning of 2021 due to the increase in spending on goods. Russia's invasion of Ukraine has exacerbated this situation, in terms of cost push inflation (when prices rise due to increases in production costs). Due to a significant increase in energy and agricultural price, the ONS (Office for National Statistics) reported that inflation, as measured by the CPI (Consumer Price Index), rose to 9.1% in May 2022. This is the highest inflation rate since 1982, and the increase in interest rates has led to the biggest cost of living crisis for British households in the past 40 years. This essay will analyze the impact on the most affected households based on income, identify causes and suggest suitable policies to minimize the effect.
The cost of living crisis has hit the lowest income households hardest as they spend most of their income on fuel and food, and these households are mostly concentrated in Wales and parts of the northwest. Although the law of demand states that, under the assumption of ceteris paribus (“all things being equal”), the increase in price will lead to the decrease in demand, in real life price elasticity is particularly significant. The British Retail Consortium (BRC) states that food inflation in the UK peaked in May 2022 at 4.3% following April 2012. However, food sales fell by only 1.6%, well below the rate of price inflation. Food priced are inelastic and therefore householders cannot reduce necessity purchases in equal proportion as the price increases, which leads them to spend more money. The lowest income group spends more proportion of income (about 40%) on food, housing and energy than the highest income group (about 30%). The disparity in spending does not seem large at first glance, but the richest 10% spend about 16 times more money on housing and mortgages than the poorest. The pursuit of quality accommodation by the rich proves that the poor actually spend more money on food and energy than expected. Therefore, under the hit of inflation and inelastic pricing, the poor have to use a higher proportion of their income to buy necessities during this period.
In addition, low income households that spend a higher proportion of income on food and energy bear a higher raw expenditure on energy than the rich. Labour analysis shows that the poorest 10% of households in the UK pay an average of £756 per person per year for electricity, gas and other fuel costs – higher than the national
average of £226 – with the addition of inflation leading to a wider gap. The reason for this is that the poor have a "credit crisis", so they can only use the pre-paid meter, which is considerably more expensive than direct debit transactions. An Ofgem policy enacted last April could make future energy prices even more exaggerated, with the energy cap rising from April 1, 2022, for around 22 million customers.
There is no doubt that the government is taking action against such high inflation. It raised interest rates to the highest in a decade. It is trying to reduce borrowing and consumption and increase savings to prevent the inflation rate from remaining high. However, suppressing consumer demand could dampen economic growth. This could exacerbate the risk of recession as the soaring cost of living already threatens a downturn in spending. In the case of retirees, which make up a large proportion of low income households, the Treasury plans to reinstate the “triple lock” system, which could increase pensions by around 10%. But this strategy has a time lag and is not a good solution to the current cost of living crisis. In April 2022, pensions increased by 3.1%, which is the same as last year's CPI, but inflation rates far outstripped the increase in pensions, and the real purchasing power of pensioners continued to be undermined. The UK Treasury also announced that almost all of the 8 million most vulnerable households would receive a government subsidy of at least £1,200, including “heavily hit” pensioners and other low income households.
In conclusion, the main factor behind the sky high inflation is the scarcity of food and energy. Shortage in the market has led to price spikes, then a crisis of living, especially among low income households. Despite the £1,200 funding, low income families may be worse off, stemming from the limitation of the CPI itself. The Centre for Economic and Business Research says that house rents rose by an average of 10.6% in the year to May 2022, and even by15.7% in London. An English housing survey reported that low income savers spending more than 30% of their income at this level supported the limitation. For the time being, there is a need for contractionary monetary policy and no need for an increase in wages, as those would be very helpful in controlling inflation. The government could abolish the £300 fixed charge on energy and give subsidies on prepaid meters to reduce the pressure on the poor. Going further, government can provide more public housing with lower rents for people on low incomes.



A.
Editor: Dr E. Wilson
Editorial and Design Assistance: Olivia C.
With thanks to: Mrs N. Rayner, Mr I. Rayner and Dr J. Hayes
Special thanks to: The Ashford School Marketing Team
