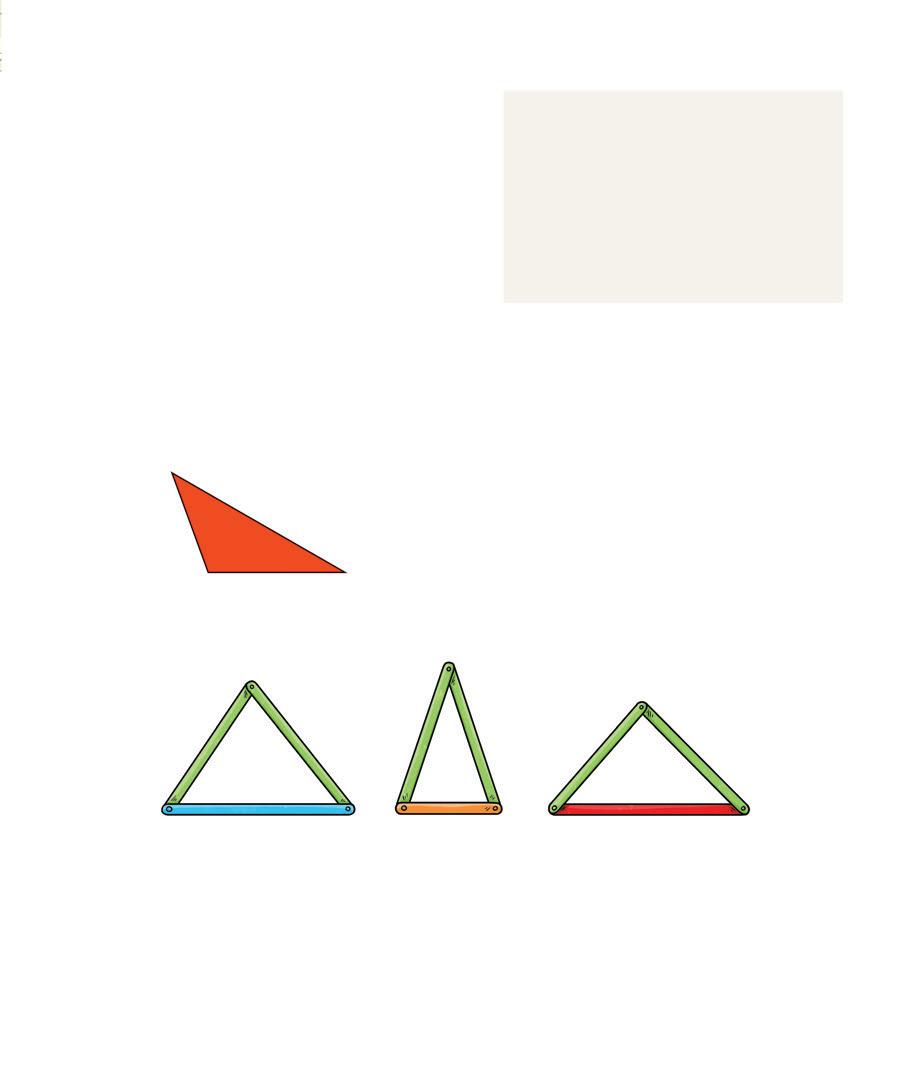La comparaison et l’arrondissement des nombres
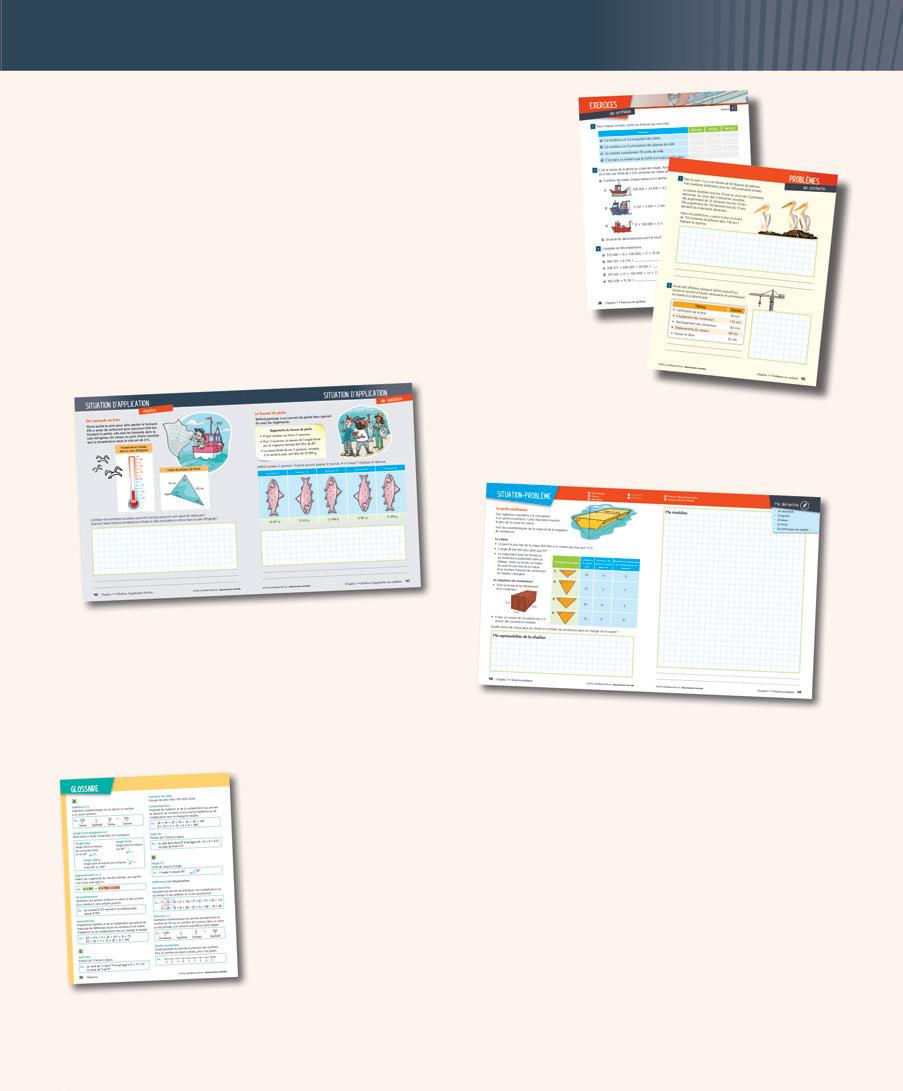
Caroline, l’architecte navale, supervise la construction de 2 paquebots. Elle a prévu le nombre d’heures (h) nécessaires par type d’ouvrier.
1 soudeur 1 000 h 1 mécanicien 100 h 1 peintre 10 h
a Calcule le nombre total d’heures prévues par type d’ouvrier pour construire chaque paquebot.
Construction du paquebot 1
400 soudeurs : h
200 mécaniciens : h
500 peintres : h
Construction du paquebot 2
400 soudeurs : h
100 mécaniciens : h
500 peintres : h
b Compare le nombre d’heures consacrées à la mécanique et à la peinture pour les 2 paquebots. Utilise le symbole ,, ou
Paquebot 1SymbolesPaquebot 2
Heures consacrées à la mécanique
Heures consacrées à la peinture
Caroline estime à 2 000 le nombre total d’ouvriers nécessaires pour construire les 2 paquebots.
c À l’aide des informations en a , calcule le nombre total d’ouvriers nécessaires et écris-le au bon endroit sur la droite numérique.

Estimation de Caroline
d Quelle est la différence entre le résultat exact et l’estimation de Caroline ?
DÉCOUVERTE Unité 14 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.2
1.2
1 000 2 000 3 000
La comparaison et l’ordre
Comparer 2 nombres, c’est dire s’ils sont égaux () ou inégaux () S’ils sont inégaux, l’un des nombres est inférieur (,) et l’autre est supérieur ()
• Un tableau de numération permet de faire rapidement cette comparaison.

On compare d’abord les chiffres qui ont la plus grande valeur dans chaque nombre. Si ces valeurs sont égales, on compare les chiffres à la position inférieure.
est inférieur à 361 934 , 365 934
est supérieur à 365 934 361 934
• La droite numérique permet de comparer des nombres, puis de les classer dans l’ordre croissant ou décroissant.
Le pas de graduation correspond à la mesure du saut entre 2 traits consécutifs. Sur cette droite, le pas de graduation est de 1 000.
Le nombre 361 934 est plus petit que le nombre 365 934, car il est situé plus à gauche sur la droite.
Le nombre 365 934 est plus grand que le nombre 361 934, car il est situé plus à droite sur la droite.
L’estimation et l’arrondissement
L’estimation d’une quantité permet de se faire une idée sur la valeur approximative de cette quantité. Par exemple, on pourrait estimer qu’il y a à peu près 1 000 travailleurs sur un chantier naval.
L’arrondissement permet d’obtenir la valeur la plus proche d’un nombre à une certaine position. Par exemple, le nombre 361 934 arrondi à l’unité de mille près devient 362 000. Pour estimer le résultat d’un calcul, on arrondit les nombres.
Souviens-toi
Pour arrondir :
1. On souligne le chiffre à la position à arrondir.
2. Si le chiffre situé immédiatement à droite du chiffre souligné est égal ou supérieur à 5, on ajoute 1 au chiffre souligné. Sinon, on ne change pas le chiffre souligné.
3. On remplace par un 0 tous les chiffres situés à droite du chiffre souligné.
15 SAVOIRS © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.2
Positions CMDMUMC DU 1er nombre3 6 1 9 3 4 2e nombre3 6 5 9 3 4
361 000 362 000 363 000 364 000 365 000 366 000 361 934 365 934 1 000
1 Place ces nombres par ordre croissant.
2 Place ces nombres par ordre décroissant.
3 Au fil des années, l’équipe de Caroline a construit plusieurs bateaux.
a) Compare le nombre de kilomètres parcourus par ces bateaux au cours de 2 années. Utilise le symbole ou . Dans chaque nombre, souligne le chiffre qui t’a permis de comparer.

b) Le nombre de kilomètres parcourus par les bateaux suivants au cours de l’année 1 est-il inégal () ou égal () ? Écris le bon symbole.
c) Encercle les bateaux dont le nombre de kilomètres parcourus chaque année est inférieur à 100 unités de mille.
16 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.2 EXERCICES
644 464 684 366 641 166 641 146 614 146
722 707 777 227 772 727 777 727 727 722
Année 1Année 2 Année 1Année 2 1) 157 917 167 987 4) 43 107 34 207 2) 243 051 234 151 5) 122 071 122 061 3) 87 835 87 825 6) 243 051 234 051
1) 2)
1) 2) 3)
4 Annie doit transporter ces 2 charges de boîtes de feuilles dans un conteneur. Elle estime qu’il y a à peu près 40 000 feuilles à transporter. Caroline pense qu’il y en a environ 60 000.
a) Utilise la droite numérique pour placer les 2 estimations et le nombre exact de feuilles. Écris à quoi correspond chaque nombre.
b) Qui a fait l’estimation la plus près du nombre exact de feuilles ?
Annie Caroline
5 Un bateau de croisière construit par l’équipe de Caroline commence un long voyage. Cette droite numérique représente les distances entre les escales du bateau.
Réponds aux devinettes.
a) C’est l’escale la plus proche des États-Unis.
b) C’est la distance entre le Brésil et le Pérou.
c) C’est l’escale dont la distance à partir du Canada est à la fois plus grande que 10 000 km et plus petite que 15 000 km.
d) C’est la distance entre les États-Unis et la Russie.

e) C’est l’escale située à moins de 5 000 km du Canada.
f) C’est l’escale située à une distance supérieure à 35 000 km du Canada.
17 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.2
0 20 000 10 000 Canada États-Unis Japon Brésil Bahamas Pérou Russie 20 000 40 000 30 000 40 000 60 000 Distance en kilomètres (km)
6 Un bateau a effectué 5 voyages.
a) Pour chaque voyage, arrondis la distance parcourue aux positions demandées.
Voyages
1 132 350
2 159 725
3 227 414
4 171 866
5 301 479
b) À l’aide des distances arrondies à la centaine de mille près, trouve la distance totale approximative que le bateau a parcourue au cours des 5 voyages.
7 Complète les énoncés.
Ex. : Le nombre 254 887 devient 254 900 lorsqu’on l’arrondit à la centaine près.
a) Le nombre 451 746 devient 452 000 lorsqu’on l’arrondit à près.
b) Le nombre 943 888 devient 900 000 lorsqu’on l’arrondit à près.
c) Le nombre 716 279 devient 720 000 lorsqu’on l’arrondit à près.
d) Le nombre 373 775 devient 373 780 lorsqu’on l’arrondit à près.
8 Sur la droite numérique, place les distances parcourues par 5 bateaux.
520 000
Distance en kilomètres (km)
18 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.2
Distances (km)
À la dizaine prèsÀ l’unité de mille près À la centaine de mille près
200 520 800 522 500 523 900 526 300
525
525
000
9 À quelle position ces nombres ont-ils été arrondis ? Coche toutes les réponses possibles. Nombres
a)
b)
c)
000
10 Annie charge des conteneurs de chandails sur un bateau :
• 1 conteneur contient 10 caisses ;
• 1 caisse contient 10 boîtes ;
• 1 boîte contient 10 emballages ;

• 1 emballage contient 10 chandails.
a) Combien de chandails y a-t-il dans 3 conteneurs ?
b) Un conteneur vide pèse 2 500 kilogrammes (kg) et une caisse de chandails pèse 100 kg. La charge maximale du chariot élévateur d’Annie est de 3 000 kg. Si la masse de la charge est plus grande, Annie doit utiliser une grue au lieu du chariot.

1) Quelle est la masse d’un conteneur rempli de chandails ?
2) Encercle l’appareil que doit utiliser Annie pour charger les conteneurs de chandails.
19 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.2
exacts Nombres
Positions CMDMUMCD Ex. : 427 595 427 600 ✔✔
arrondis
13 882 13 880
48
49
999
000
899
900
998
A B
L’addition et la soustraction de nombres naturels
Un bateau accoste au port avec une grosse cargaison de bidons d’huile d’olive. Norbert doit en superviser le déchargement. Sous ses ordres, les grutiers déchargent 25 800 bidons. Ce nombre correspond à 9 300 bidons de plus que le nombre de bidons qu’il reste à décharger.
a Combien de bidons reste-t-il à décharger ?
b Combien de bidons y avait-il à bord du bateau à son arrivée au port ?
Un autre bateau accoste au port avec des sacs de farine : 28 760 sacs à l’avant, 35 000 sacs au milieu et 15 000 à l’arrière.
c Norbert cherche le nombre total de sacs à décharger. Il hésite entre 3 calculs. Encercle ceux qui lui permettraient de déterminer ce nombre.
d Quel est le nombre total de sacs à décharger ?

Unité 20 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.3
DÉCOUVERTE
1.3
1) 28 760 35 000 15 000 2) 35 000 15 000 28 760 3) 35 000 28 760 15 000
L’addition et la soustraction de nombres naturels
Pour additionner ou soustraire 2 nombres, on peut procéder de la façon suivante.
1 On aligne les chiffres selon leur position dans les nombres.
2 On additionne ou on soustrait les chiffres position par position en débutant par les unités. Au besoin, on fait un échange en laissant des traces.
Pour faire l’approximation d’une addition ou d’une soustraction, on arrondit chacun des termes

Les propriétés de l’addition
Des stratégies de calcul mental
21 SAVOIRS © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.3
Addition : 32 875 10 362 Soustraction : 68 729 23 054 DMUMCDU DMUMCDU 3 1 1 2 0 1 8 3 7 6 5 2 6 2 8 3 6 7 0 2 5 9 4 43237 45675
32 875 10 362 est à peu près égal à () 30 000 10 000 40 000 68 729 23 054 est à peu près égal à () 70 000 20 000 50 000
Descriptions Exemples Commutativité Dans une
ne change
le résultat. 1 200 5 600 5 600 1 200 6 800 Associativité Dans des additions consécutives, modifier l’ordre des additions ne change pas le résultat. (400 300) 95 400 (300 95) 795
Propriétés
addition, modifier l’ordre des termes
pas
Stratégies Exemples Décomposer le second terme. 42 56 42 50 6 92 6 98 87 24 87 20 4 67 4 63 Arrondir le second terme et ajuster le calcul. 35 59 35 60 1 95 1 94 64 28 64 30 2 36 Utiliser la commutativité de l’addition. 600 517 400 600 400 517 1 517 Utiliser l’associativité de l’addition. 57 32 8 57 (32 8) 57 40 97 1 Les parenthèses indiquent les opérations à effectuer en premier.
22 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.3 EXERCICES a) 350 492 e) 46 011 20 500 b) 652 431 f) 29 465 23 814 c) 917 8 400 g) 233 005 139 400 d) 7 052 2 610 h) 589 051 289 040 1 Effectue les opérations.
2 Complète les approximations en arrondissant chaque terme à sa plus grande position.
a) 6 438 2 701
b) 72 830 50 988
c) 325 000 270 100
3 Écris les nombres appropriés.
a) Pour obtenir 33 333, il faut ajouter à 22 222.
b) Pour obtenir 1 000 000, il faut additionner et 1.
c) Pour obtenir 100 000, il faut soustraire de 300 000.
d) Pour obtenir 0, il faut retrancher de 5 703.
4 Cette semaine, Norbert et son équipe ont déchargé tous les conteneurs de 2 bateaux.
a) Combien de conteneurs chaque bateau transportait-il ?

b) Combien de conteneurs Norbert et son équipe ont-ils déchargés cette semaine ?
Ofret : Le Géant :
23 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.3
BateauxJoursNombres de conteneurs déchargés Ofret Lundi 4 212 Mardi 7 186 Le Géant Mercredi 12 963 Jeudi 8 716 Vendredi 6 405
5 Écris les nombres manquants dans chaque calcul.
a) 49 (280 20) 49
b) 111 444 444
c) 17 75 25 75 17
d) 893 (999 1) 893
6 Norbert et son équipe ont chargé 2 762 conteneurs sur un bateau. Ils en ont placé 2 045 devant le poste de pilotage. Combien en ont-ils placé derrière le poste de pilotage ?
7 Des dizaines de milliers de conteneurs de couleurs diverses sont entreposés sur les quais du port. Remplis le tableau à l’aide des informations suivantes.

• Il manque 11 850 conteneurs verts pour avoir autant de conteneurs verts que de conteneurs rouges.
• Il y a 12 050 conteneurs bleus de plus que de conteneurs rouges.
24 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité
1.3
Conteneurs CouleursNombres Vert Bleu Rouge 24 650
8 Un bateau décharge successivement 1 633 conteneurs dans un 1er port, 810 conteneurs dans un 2e port et les 2 100 conteneurs restants dans un 3e port. Combien de conteneurs le bateau transportait-il au départ ?
9 Trouve la régularité de chaque suite et ajoute les termes manquants.
a) 700 000, 600 000, 500 000, , Régularité :
b) , 1 717, 2 534, 3 351 Régularité :
c) 20 400, 23 500, , 29 700, 32 800 Régularité :

10 Un bateau arrive au port pour prendre un chargement de sacs de farine.
À tous les 10 000 sacs, le bateau s’enfonce de 35 cm dans l’eau. Voici les détails du chargement.
De combien de centimètres le bateau se sera-t-il enfoncé à la fin du chargement ?
25 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.3
Moments de la journéeNombres de sacs Avant-midi 9 752 Après-midi 13 402 Soirée 6 846
Les triangles et la mesure des angles
DÉCOUVERTE
Crac ! Le cadran de la grande horloge du port s’est brisé. Participe à sa réparation !
a Trace la partie brisée sur ce cadran.
• Il s’agit d’un polygone à 3 côtés.
• Il relie le centre du cadran à 2 sommets de l’hexagone.
• Il y a 2 de ses côtés qui passent par les nombres 1 et 3.
b Quel polygone as-tu tracé ?
Nom du polygone :
Ses caractéristiques :
c Partage le cadran en 6 parties identiques à la partie brisée.
À quelle fraction de l’hexagone correspond chaque partie ?
Fraction de l’hexagone :
d Imagine qu’il y a une grande aiguille sur le cadran.
1) Si cette aiguille se déplace de 1 à 5, à combien de minutes correspond ce déplacement ?

2) À quelle fraction d’une heure correspond ce déplacement ?
Fraction d’une heure :
Unité 26 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.4 1.4
La classification des triangles
On distingue les triangles selon le nombre de côtés isométriques et le type d’angles
Types d’angles
3 angles aigus
1 angle droit (triangles rectangles)
1 angle obtus
Triangles scalènes (pas de côtés isométriques)
Triangles isocèles (2 côtés isométriques)
Triangle équilatéral (3 côtés isométriques)
Tous les triangles ont 2 angles aigus. Le 3e angle peut être aigu, droit ou obtus.
La mesure des angles
Pour mesurer un angle, on utilise un rapporteur d’angles L’unité de mesure d’un angle est le degré (°).
On peut former un angle par un mouvement circulaire.
• Un quart de tour détermine un angle droit (90°).
• Un demi-tour détermine un angle plat (180°).

• Un tour complet détermine un angle plein (360°).
La description des triangles
Pour décrire un triangle, on utilise des mots ou des symboles.
• Le DABC est isocèle rectangle.
• L’angle B est droit (∠B 90°).
• Les côtés AB et BC sont isométriques (AB BC).
• Les côtés AB et BC sont perpendiculaires (AB ⊥ BC).
• Les angles A et C sont isométriques (∠A ∠C 45°).
27 SAVOIRS © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.4 A B C
Angle droit = 90° 90° , Angle obtus , 180° 0° , Angle aigu , 90° Angle plat Angle plein 90° 60° 60° 60° 90° 90° , 90°
1 Ming a remorqué 3 bateaux dans le port aux heures indiquées par ces horloges.
a) Sous chaque horloge, écris le type d’angle formé par les aiguilles.

b) Sur chaque horloge, prolonge les aiguilles jusqu’au contour du cadran. Relie ensuite ces nouveaux sommets entre eux pour former un triangle.
1) Observe les côtés des triangles. Quelle est leur caractéristique commune ?
2) En se basant sur la mesure de leurs côtés, comment appelle-t-on les triangles formés ?
2 a) Trace les triangles demandés. Le segment donné est un côté perpendiculaire du triangle.
b) Combien de triangles isocèles rectangles différents peut-on tracer dans la case à gauche ?
c) Dans la case à droite, trace 2 autres triangles scalènes rectangles à partir du même segment.
28 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.4 EXERCICES
A B C
Triangle isocèle rectangle Triangle scalène rectangle
3 Compare les côtés des triangles.
a) Quel triangle n’appartient pas à ce groupe ?
Explique ta réponse.
b) Comment s’appelle cet intrus ?
4 Remplis le tableau :
1) estime la mesure des angles du triangle en degrés ;
A B
2) mesure les angles à l’aide d’un rapporteur afin de valider tes estimations.
A B C
Angle A
Angle B
Angle C
EstimationsMesures
a) De quel type de triangles s’agit-il ?
b) Tu dois former un triangle équilatéral en changeant 1 bâtonnet dans le triangle de ton choix.
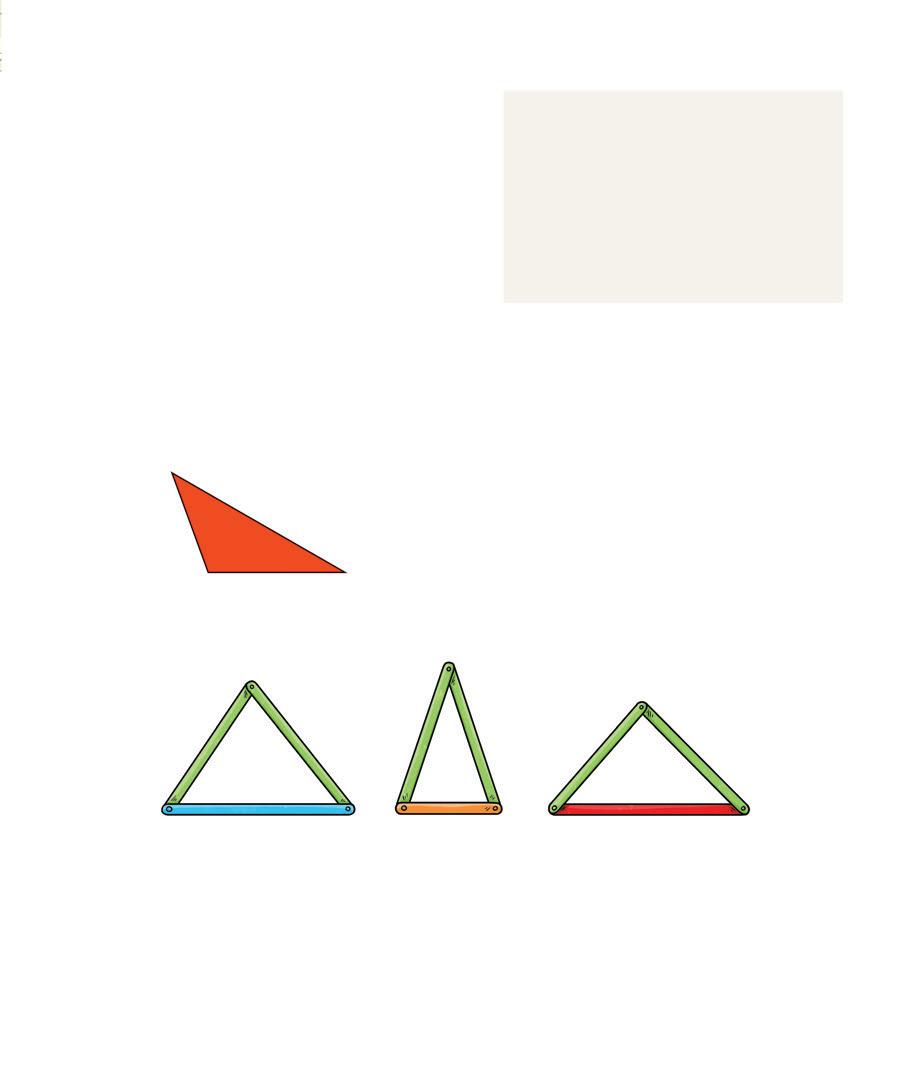
1) De quelle couleur sera le nouveau bâtonnet ?
2) Quelle sera la mesure de l’angle formé par 2 bâtonnets ?
c) Quelle est la propriété commune à tous ces triangles ?
29 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.4
C D
5 Voici 3 triangles formés avec des bâtonnets.
6 Trace les axes de réflexion sur les triangles, s’il y a lieu. Ensuite, remplis le tableau.

Triangles Types de triangles
Nombres d’axes de réflexion
7 Voici la forme de 3 drapeaux observés sur des mâts de bateau.
Souviens-toi
Un axe de réflexion est une droite qui partage une figure en 2 parties qu’on peut superposer par pliage.
a) Remplis le tableau :
1) mesure les angles des triangles à l’aide d’un rapporteur ;
2) additionne les mesures des 3 angles de chaque triangle.
b) Complète les énoncés à l’aide de nombres et de mots.
1) Chacun de ces triangles a au moins angles aigus.
2) Le 3e angle peut être aigu, ou
3) La somme des 3 angles de chaque triangle est de .
30 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.4
A B C 1 A C B 2 A B C 3 Triangles A B C A B C 1 2 3
8 Classe ces triangles en écrivant les lettres correspondantes dans le diagramme de Venn.
Tourne ton cahier pour mieux observer les formes des triangles.
Triangles isocèles
Triangles scalènes
Triangles rectangles
9 Qui suis-je ?
a) Je suis un triangle ayant 1 axe de réflexion et 1 angle droit.
b) Je ne suis pas un triangle symétrique.
10 En réparant l’horloge du port, un ouvrier a fait tomber l’aiguille des heures !
a) Sachant que les 2 aiguilles formaient un angle de 120°, dessine les 2 positions possibles de l’aiguille des heures.
b) Quelle heure est-il si ce n’est pas le matin ? Écris les 2 possibilités.
c) Prolonge les aiguilles jusqu’au contour de l’horloge, puis relie leurs nouvelles extrémités.

d) Combien de triangles y a-t-il en tout maintenant ?
e) Les sommets du grand triangle se trouvent tous sur le contour du cadran. Quel type de triangle est-ce ?
31 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.4
Astuce D E F A B C
Les nombres entiers
Maria et Rodrigo sont ravis ! Ils partent en croisière pour fêter leur anniversaire de mariage. Comme ils n’ont pas tout l’argent nécessaire, ils font un emprunt à la banque.

a Observe le solde des comptes de Maria et de Rodrigo. Que constates-tu ?
b Qui a la meilleure situation financière, Maria ou Rodrigo ? Explique ta réponse.
c Si Rodrigo dépose 500 $ dans son compte de banque, quel montant s’affichera à l’écran ? Explique ta réponse.
d Un mois après la croisière, le compte de banque de Maria affiche 1 100 $. Que s’est-il passé ? Encercle la bonne réponse.
2) Elle a remboursé 300 $.
Unité 32 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.5 1.5
DÉCOUVERTE
1) Elle a emprunté 300 $.
Les nombres entiers
Les nombres entiers sont constitués des nombres entiers positifs et négatifs
• On utilise souvent les nombres entiers positifs pour le dénombrement. Les nombres entiers positifs sont 0, 1, 2, 3, 4, 5…
En croisière, Oscar se procure un porte-clés à chaque escale. Sa collection en compte déjà 125 !
• On utilise souvent les nombres entiers négatifs pour décrire un manque, une dette ou un niveau plus bas que le niveau 0. Ces nombres sont précédés du signe . Les nombres entiers négatifs sont 0, 1, 2, 3, 4, 5…
Jeanne emprunte 1 500 $ à la banque. Le solde indiqué sur son relevé bancaire est 1 500 $
Le placement de nombres entiers sur une droite numérique

Attention !
Le nombre 0 est à la fois positif et négatif. On ne met pas de signe devant le 0.
• La droite numérique permet d’ordonner et de comparer des nombres entiers : plus un nombre est situé à gauche, plus il est petit ; plus un nombre est situé à droite, plus il est grand
De plus en plus grand
Le nombre 25 est situé à gauche du nombre 10. 25 , 10 ou 10 25
Le nombre 50 est situé plus à gauche que le nombre 20. 50 , 20 ou 20 50
Nombres négatifs
Nombres positifs
33 SAVOIRS © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.5
70 60 50 40 30 20 100102030406050 70
1 Compare les nombres à l’aide du symbole , ou
a) Ci-dessous, écris le bon nombre à côté de chaque lettre.
b) Écris un nombre entier situé :

1) entre la lettre E et la lettre G ;
2) entre la lettre B et la lettre H, mais plus proche de B que de H ;
3) entre la lettre A et la lettre D, mais plus proche de A que de D ;
4) entre la lettre H et la lettre F, mais plus proche de H que de F
34 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.5 EXERCICES
. a) 6 4 b) 0 695 c) 1 200 1 300 d) 69 120 e) 1 200 1 300 f) 1 200 1 300 g) 523 485 h) 1 200 1 300 i) 0 3
231 30 117 59 135 14 184 58
2 Chaque lettre placée sur la droite numérique correspond à l’un des nombres suivants.
A B C D E F G H 250 200 150 100 50 0 50 100 A D G E B H F C
a) À quoi sert la touche / de la calculatrice ?
b) À ton tour ! Affiche ces nombres sur ta calculatrice.
4 Durant la croisière, Alice fait ses devoirs. Elle doit placer les nombres 2 et 7 sur cette droite numérique. Malheureusement, la mauvaise qualité de la photocopie ne permet pas de lire toutes les graduations.
a) Comment Alice peut-elle placer correctement les nombres ? Propose une démarche.
b) Place les 2 nombres sur la droite en suivant la démarche que tu as proposée.
5 Réécris ces nombres par ordre croissant.
35 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.5
0 2 7
3 Voici des nombres affichés à l’écran d’une calculatrice.
421 24 685 985 52 5 5 78
8 524 6 985 0 56 611 759 10
6 Réécris ces nombres par ordre décroissant.
7 Écris 2 nombres entiers consécutifs :
a) compris entre 5 et 23 ;
b) plus grands que 13, mais plus petits que 1 ;
c) inférieurs à 35, mais supérieurs à 50 ;
d) situés juste avant 67 sur une droite numérique ;
e) plus grands que 5, mais plus petits que 1.
8 Ce tableau montre le solde du compte de banque de Maria à la fin de chaque mois.
À la fin de quel mois Maria a-t-elle :
a) le plus d’argent ?
b) le moins d’argent ?

36 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.5
43 87 321 123 8 1 729 0 10
MoisSoldes à la fin du mois Janvier 400 $ Février 100 $ Mars 0 $ Avril 600 $ Mai 300 $
9 Pour se rafraîchir, Rodrigo se sert un verre de limonade. La température du verre est de 21 °C et celle des glaçons est de 8 °C. Quel est l’écart entre la température du verre et celle des glaçons ?
10 Un bateau arrive au port pour charger des marchandises. La coque du bateau est peinte de bandes rouges et de bandes noires. Chaque bande a une hauteur de 2 m.
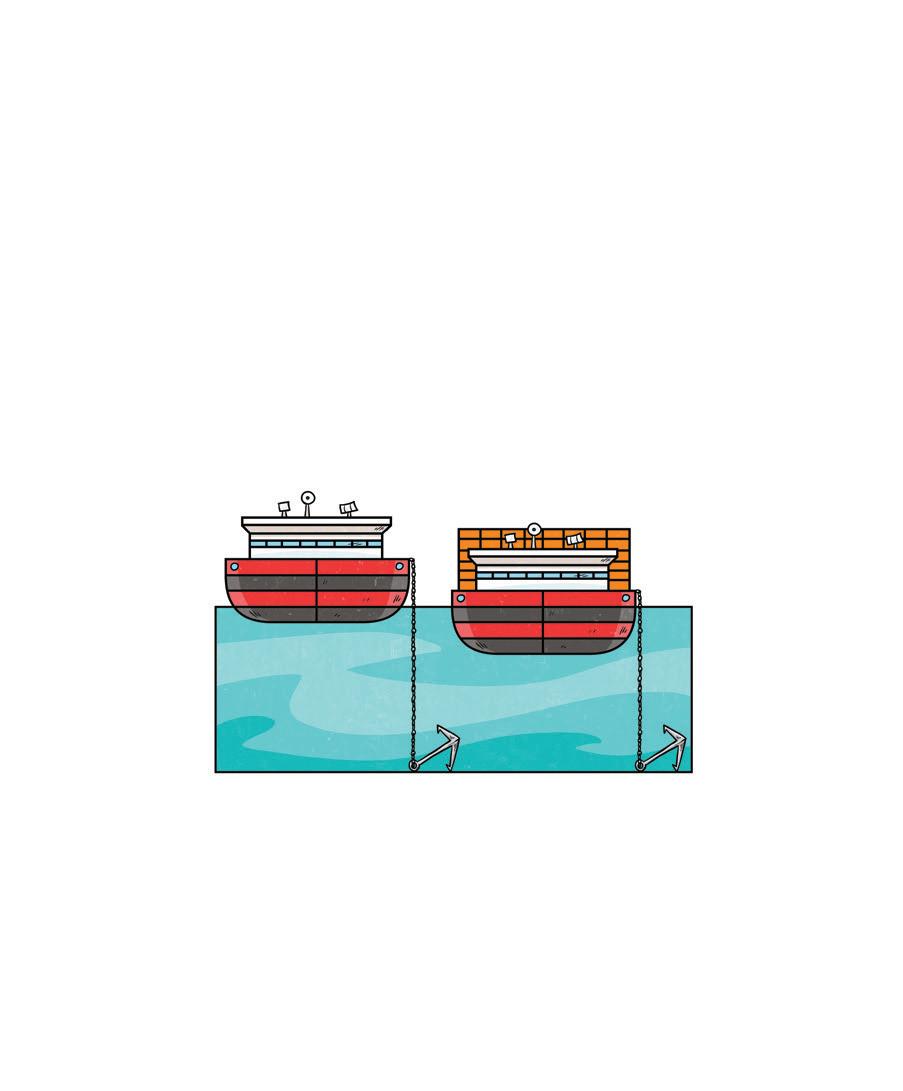
a) À quel niveau se trouve le point le plus bas de la coque du bateau :
1) lorsqu’il est vide ? 2) lorsqu’il est plein ?
b) Quelle longueur de chaîne est nécessaire pour ancrer le bateau :
1) lorsqu’il est vide ? 2) lorsqu’il est plein ?
c) Le point le plus bas de la coque doit toujours être au-dessus de 10 m. Le niveau de l’eau peut baisser d’un maximum de combien de mètres ?
37 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Unité 1.5
Bateau vide 0 m 20 m Bateau plein Niveau de la mer
°C 30 20 10 0 10 20 30 25 15 5 5 15 25
1 Pour chaque nombre, coche les énoncés qui sont vrais.
a) Ce nombre a un 3 à la position des unités.
b) Ce nombre a un 0 à la position des dizaines de mille.
c) Ce nombre a exactement 76 unités de mille.
d) C’est dans ce nombre que le chiffre 6 a la plus petite valeur.
2 C’est le temps de la pêche au crabe des neiges. Pour protéger l’espèce, on a fixé une limite de 2 333 centaines de crabes par bateau.
a) Combien de crabes chaque bateau a-t-il pêchés ?
b) Encercle les décompositions dont le résultat respecte la limite fixée.

38 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Exercices de synthèse EXERCICES de synthèse p. 9 Savoirs
607 42376 023760 233
Énoncés
1) 200 000 43 000 6 000 800 60 3 2) 2 CM 3 DM 3 UM 3 C 3) (2 3 100 000) (3 3 10 000) (3 3 1 000) (3 3 100)
a) 573 648 (5 3 100 000) (7 3 10 000) (3 3 1 000) (6 3 100) (4 3 10) b) 894 783 8 CM 4 UM 7 C 8 D 3 U c) 658 371 600 000 50 000 300 70 1 d) 763 502 (7 3 100 000) ( 6 3 10 000) (3 3 1 000) (2 3 1) e) 902 438 9 CM 4 C 3 D 8 U
3 Complète les décompositions.
4 Voici la distance totale parcourue par 4 animaux marins au cours de leur vie. 912 437 km

478 km
a) Écris ces distances par ordre croissant.
b) Arrondis ces distances à la centaine près.
5 Vrai ou faux ? Coche la bonne réponse.
a) 238 centaines sont plus grandes que 238 000.
b) 102 dizaines sont égales à 1 020.
c) 89 dizaines de mille sont plus petites que 89 000.
d) 48 000 unités sont égales à 48 unités de mille.
6 Compare les nombres à l’aide du symbole , ou . Dans chaque nombre, souligne le chiffre qui t’a permis de comparer.
a) 52 987 55 987
b) 897 377 987 377
d)
030 e)
39 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Exercices de synthèse p. 15 Savoirs
906
754 499
336 419 km
km
Énoncés VraiFaux
330 030 303
994 668 994 669
c) 650 056 650 556 753 987 754
f)
988
7 Écris le nombre manquant dans chaque calcul.
a) 8 514 5 312
b) 324 600 90 222
c) 7 540 8 407
d) 49 855 38 485
8 Un petit bateau peut transporter 12 300 barils de mélasse, un bateau moyen peut en transporter 34 700 et un gros bateau peut en transporter 46 000.
a) Complète les phrases à l’aide des bons nombres.
1) Un petit bateau peut transporter barils de mélasse de moins qu’un gros bateau.
2) Ensemble, un moyen et un gros bateau peuvent transporter barils de mélasse.
b) Vrai ou faux ? Coche la bonne réponse.
1) Un gros bateau peut transporter plus de barils de mélasse que peuvent en transporter un petit et un moyen ensemble.
Vrai Faux
2) Deux bateaux moyens peuvent transporter plus de barils de mélasse que peuvent en transporter un petit et un gros ensemble.
Vrai Faux

40 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Exercices de synthèse p. 21 Savoirs
9 a) Classe ces triangles en écrivant les lettres correspondantes dans le tableau.

Types d’angles
3 angles aigus
1 angle droit (triangle rectangle)
1 angle obtus
b) Complète les phrases.
Triangles scalènes (pas de côtés isométriques)
Triangles isocèles (2 côtés isométriques)
Triangle équilatéral (3 côtés isométriques)
1) Un triangle qui a 3 côtés isométriques est un triangle .
2) Tous les triangles ont au moins 2 angles
3) Un triangle qui n’a pas de côtés isométriques est un triangle
10 Encercle l’intrus dans chaque groupe de triangles. Précise la caractéristique qui distingue l’intrus des 2 autres triangles.
11 Trace les triangles demandés.
41 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Exercices de synthèse p. 27 Savoirs
A B E F C D G
Triangle isocèle rectangle
Triangle isocèle ayant un angle obtus
Triangle scalène rectangle
12 Réécris ces nombres par ordre décroissant.
13 Compare les nombres à l’aide du symbole , ou
14
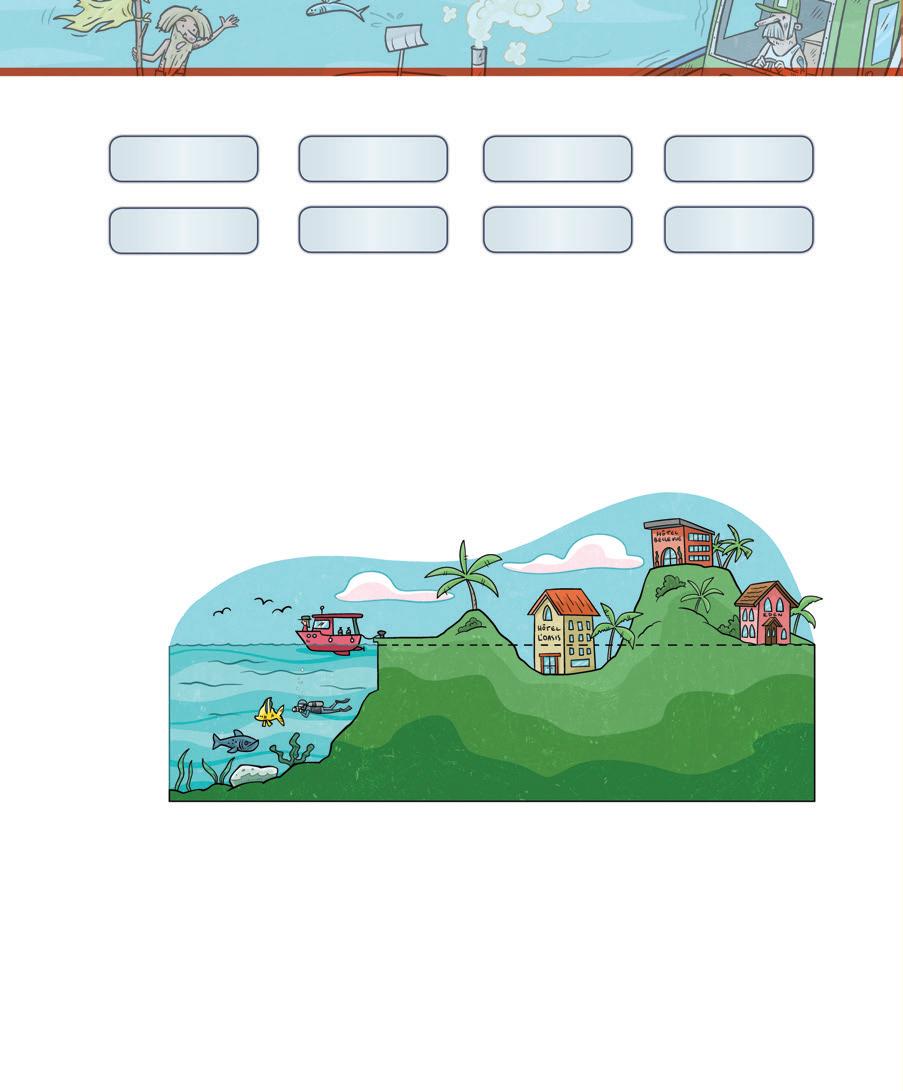
a) Observe l’illustration. À quoi correspond l’altitude 0 m ?
b) Sur l’illustration, encercle l’hôtel où logent Maria et Rodrigo. Explique ton choix.
42 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Exercices de synthèse p. 33 Savoirs
a) 850 1 b) 259 260 c) 625 4 003 d) 259 260 e) 1 652 1 653 f) 96 31
123 8 1 729 87 321 0 43 10
Au cours d’une escale, Maria et Rodrigo logent dans un hôtel situé à une altitude de 2 m.
Niveau de la mer
1 Près du port, il y a une colonie de 50 dizaines de pélicans. Voici quelques prédictions pour les 100 prochaines années.
La colonie doublera tous les 10 ans au cours des 3 premières décennies. Au cours des 3 décennies suivantes, elle augmentera de 23 centaines tous les 10 ans. Elle augmentera de 150 dizaines tous les 10 ans pendant les 4 dernières décennies.
Selon ces prédictions, y aura-t-il plus ou moins de 150 centaines de pélicans dans 100 ans ? Explique ta réponse.
2 Annie doit effecteur plusieurs tâches aujourd’hui. Estime le nombre d’heures nécessaires en arrondissant les durées à la dizaine près.

43 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Problèmes en contexte PROBLÈMES en contexte
Tâches Durées • Vérification de la grue 38 min • Chargement des conteneurs 119 min • Déchargement des conteneurs182 min • Déplacements du camion 48 min • Pauses et dîner 92 min
3 Un bateau pouvant transporter 3 710 conteneurs arrive au port avec 360 conteneurs à son bord. Avec la grue, Annie doit ajouter sur le bateau 2 240 conteneurs de nourriture et 800 conteneurs de vêtements. Y a-t-il assez de places libres sur le bateau ? Explique ta réponse.
4 Un plongeur doit réparer la coque d’un bateau. Il dispose de 2 bonbonnes d’air pleines. Une bonbonne pleine lui permet de plonger pendant 7 200 secondes (s).
Le matin, le plongeur utilise une bonbonne pendant 4 190 s. L’après-midi, il utilise l’autre bonbonne pendant 3 500 s. Au total, combien de secondes de plongée lui reste-t-il ?
5 Il est 10 h 10, et le bateau doit partir à 11 h 30. L’aiguille des minutes avance jusqu’à former un angle de 90° avec sa position initiale. À partir de cette nouvelle position, elle avance jusqu’à former un angle de 150°. Combien de temps reste-t-il avant le départ du bateau ?

44 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Problèmes en contexte
6 Maria et Rodrigo participent à un tirage organisé par le capitaine du bateau. Voici les nombres que la boîte du tirage contient.
Parmi les événements suivants, lequel a le plus de chances de se produire ? Explique ta réponse.
Obtenir un nombre positif inférieur à 3.
Obtenir un nombre négatif supérieur à 3.
Obtenir un nombre positif supérieur à 3.
7 On prévoit que la température extérieure au port variera de façon régulière au cours des prochains jours. Le graphique suivant illustre cette situation.
Quelle température devrait-il faire le 6e jour ?
45 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Problèmes en contexte
5
1 2 3 2 1 8 6 0 A B C 3 2 1 1 2 0 Températures au cours des prochains jours Température (°C) Temps (jours) 12 34 5 4 5 6 7
d’action
Des homards au frais

Florie quitte le port pour aller pêcher le homard. Elle a assez de carburant pour parcourir 630 km. Pendant la pêche, elle met les homards dans la cale réfrigérée. De retour au port, Florie constate que la température dans la cale est de 3 °C.
Combien de kilomètres le bateau pourrait-il encore parcourir sans ajout de carburant ? Quel est l’écart entre la température initiale et celle constatée au retour dans la cale réfrigérée ?

46 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Situation d’application d’action
SITUATION D,APPLICATION
°C 30 20 10 0 10 20 30 25 15 5 5 15 25 Température initiale dans la cale réfrigérée 147 km 215 km Port 70° 70° 40°
Le tournoi de pêche
Wilfrid participe à un tournoi de pêche bien spécial ! En voici les règlements.
Règlements du tournoi de pêche
• Il faut ramener au moins 3 saumons.
• Pour 3 saumons, la mesure de l’angle formé par la nageoire dorsale doit être de 80°.
• La masse totale de ces 3 saumons, arrondie à la centaine près, doit être de 52 800 g.

47 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Situation d’application de validation SITUATION D,APPLICATION de validation
Wilfrid ramène 5 saumons. Il pense pouvoir gagner le tournoi. A-t-il raison ? Explique ta réponse.
16 327 g 12 015 g 21 646 g 8 981 g 31 856 g
Saumon 1 Saumon 2 Saumon 3 Saumon 4 Saumon 5
Le porte-conteneurs
Des ingénieurs travaillent à la conception d’un porte-conteneurs. Cette illustration montre le plan de la coque du navire.
Voici les caractéristiques de la coque et de la cargaison de conteneurs.
La coque
• Le point le plus bas de la coque doit être à un niveau plus bas que 3 m.
• L’angle A doit être plus petit que 55°.
• La coque peut avoir les formes et les dimensions présentées dans ce tableau. Selon sa forme, le niveau du point le plus bas de la coque et le nombre maximal de conteneurs en hauteur changent.
La cargaison de conteneurs
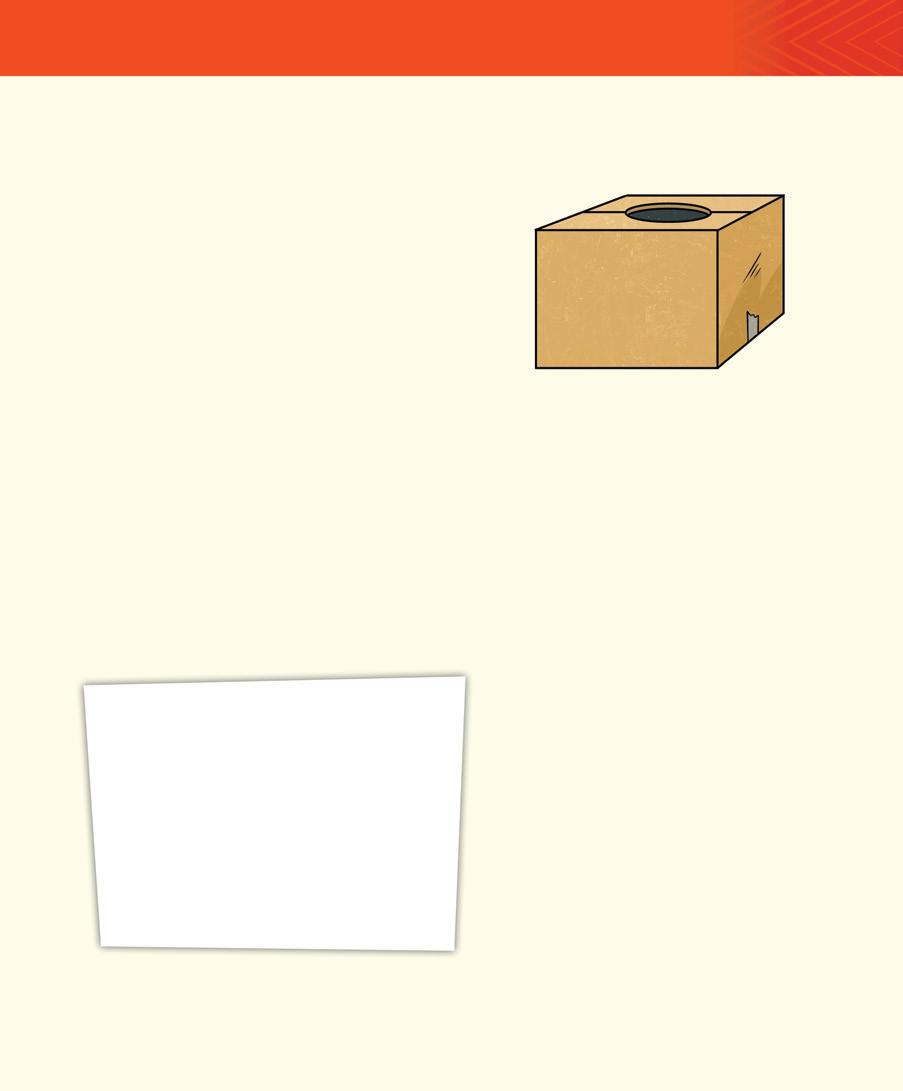
• Voici la forme et les dimensions d’un conteneur.
• Il faut un couloir de circulation de 2 m autour des conteneurs empilés.
Quelle forme de coque peut-on choisir et combien de conteneurs peut-on charger sur le navire ?
Ma représentation de la situation
48 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Situation-problème SITUATION-PROBLÈME ✔ Probabilité ✔ Statistique ✔ Arithmétique ✔ Mesure ✔ Géométrie
2 m 2 m 5 m 50 m 0 m A Largeur du pont
Formes de la coque Largeurs du pont (m) Niveaux du point le plus bas (m) Nombres maximaux de conteneurs en hauteur 1) 22 3 5 2) 13 7 7 3) 20 4 6 4) 15 5 8
Ma résolution
✔ Je comprends
✔ J’organise
✔ Je résous
✔ Je révise
✔ Je communique mes résultats

49 © 2019, Les Éditions CEC inc. • Reproduction interdite Chapitre 1 • Situation-problème
✔ Plusieurs démarches possibles ✔ Plusieurs résultats attendus
Ma démarche

Addition (1)
Opération mathématique où on ajoute un nombre à un autre nombre.
Ex. : 524 1 52 5 576
Terme Symbole Terme Somme
Angle d’un polygone ()
Angle aigu
Angle dont la mesure est comprise entre 0° et 90°.
A
Angle obtus
Angle dont la mesure est 90°.
Angle dont la mesure est comprise entre 90° et 180°.
Approximation ()
A A
Processus qui consiste à trouver une valeur qui s’approche du résultat attendu, qui signifie « est à peu près égal à ».
Ex. : 4 3 867 4 3 900 5 3 600
Arrondissement
Opération qui permet d’obtenir la valeur la plus proche d’un nombre à une certaine position.
Ex. : Le nombre 8 372 arrondi à la centaine près donne 8 400.
Associativité
Propriété de l’addition et de la multiplication qui permet de regrouper de différentes façons les nombres d’une chaîne d’additions ou de multiplications sans en changer le résultat.
Ex. : (25 1 41) 1 9 5 25 1 (41 1 9) 5 75 (10 3 8) 3 3 5 10 3 (8 3 3) 5 240
Carré de Produit de 2 facteurs égaux.
Centaine de mille Groupe de cent mille (100 000) unités.
Commutativité
Propriété de l’addition et de la multiplication qui permet de déplacer les nombres d’une chaîne d’additions ou de multiplications sans en changer le résultat.
Ex. : 38 1 45 1 25 5 45 1 25 1 38 5 108 8 3 10 3 6 5 10 3 6 3 8 5 480
Cube de Produit de 3 facteurs égaux.
Ex. : Le cube de 8 s’écrit 83 et est égal à 8 3 8 3 8 5 512. Le cube de 8 est 512.
Degré (°)
Unité de mesure d’angle.
Ex. : L’angle A mesure 50°. A 50°
Différence Voir Soustraction
Distributivité
Propriété qui permet de distribuer une multiplication sur les termes d’une addition ou d’une soustraction.
Division (4)
Opération mathématique qui permet de déterminer le nombre de fois qu’un nombre est contenu dans un autre ou de partager une certaine quantité en parts égales.
Ex.
: 1
Droite numérique
: 3 2 101234

52 © 2019, Les Éditions CEC inc. • Reproduction interdite Glossaire
GLOSSAIRE A
C
D
7 3 (10 1 6) 5 (7 3 10) 1 (7 3 6) 5 70 1 42 5 112 5 3 (20 3) 5 (5 3 20) (5 3 3) 5 100 15 5 85
Ex. :
Droite graduée qui permet d’ordonner des nombres. Plus un nombre est placé à droite, plus il est grand. 025 4 5 5 205
Dividende Symbole Diviseur Quotient
5
Ex.
Ex. : Le carré de 9 s’écrit 92 et est égal à 9 3 9 5 81. Le carré de 9 est 81.
Écart entre 2 côtés consécutifs d’un polygone.
Angle droit
Égalité (5)
Il y a égalité lorsque 2 expressions ont la même valeur.
Ex. : 200 1 200 5 300 1 100
Équation Égalité avec au moins un terme manquant.
Ex. : 60 1 ? 5 160
Est inférieur à () Est plus petit que.
Ex. : 120 250
Est supérieur à () Est plus grand que.
Ex. : 250 120
Exposant Voir Notation exponentielle.
F
Facteur premier
Nombre premier qui fait partie de la décomposition d’un nombre en facteurs. Ex.
I
Inégalité ()
Il y a inégalité quand 2 expressions n’ont pas la même valeur.
Ex. : 100 1 2 200 1 1
M
Multiplication (3)
Opération mathématique qui consiste à multiplier 2 ou plusieurs nombres appelés « facteurs ».
Ex. : 241 3 12 5 2 892
Facteur Symbole Facteur Produit
N
Nombre composé Nombre qui a plus de 2 diviseurs.
Ex. : Le nombre 10 est un nombre composé, car il a 4 diviseurs : 1, 2, 5 et 10.
Nombre entier
Nombre de la suite … 5, 4, 3, 2, 1, 0,
Nombre négatif Nombre égal à 0 ou plus petit que 0.
Ex. : 238, 7, 62
Nombre positif Nombre égal à 0 ou plus grand que 0.
Ex. : 8, 1 245, 324
Nombre premier
Nombre qui a exactement 2 diviseurs différents : 1 et lui-même.
Ex. : Le nombre 7 est un nombre premier, car il a 2 diviseurs : 1 et 7.
Notation exponentielle Représentation d’un nombre à l’aide d’une base et d’un exposant.
Ex. : Base 53 5 125
Notation exponentielle
Exposant Puissance P
Parenthèses ( )

Signes qui encadrent :
• une expression à évaluer en priorité ;
• les coordonnées d’un point.
Ex.
Ex. : Dans un plan cartésien, ( 2, 4 ) signifie 2 sur l’axe horizontal et 4 sur l’axe vertical.
Pas de graduation
Valeur du saut entre 2 traits de graduation sur une droite numérique ou un axe.
Ex. : Le pas de graduation de cet axe est 4
0481216 20
53 © 2019, Les Éditions CEC inc. • Reproduction interdite Glossaire
E
: Facteurs premiers de 462
5 2 3 3 3 7 3 11
1, 2, 3, 4, 5 …
: ( 4 3 8 ) 1 2 5 32 1 2 5 34
Plan cartésien
Système de repérage formé d’un axe horizontal et d’un axe vertical.
Position Voir Valeur de position
Priorité des opérations
Ordre à respecter pour effectuer les opérations dans une chaîne d’opérations.
1) Les opérations entre parenthèses : 500 25 3 (10 1 4) 1 8 4 4
2) L’exponentiation : 500 – 25 3 14 1 8 4 4

Soustraction ( )
Quadrant
Opération mathématique qui consiste à retrancher un nombre à un autre nombre.
Ex. : 860
47 5 813
Terme Symbole Terme Différence
TTerme
Chacun des nombres : • qui interviennent dans une addition ou une soustraction ; • d’une suite.
Ex. : 102 1 68 5 170
3) La multiplication et la division de gauche à droite : 500 32 3 14 1 8 4 4
4) L’addition et la soustraction de gauche à droite : 500 – 448 1 2
Produit Voir Multiplication
Quotient Voir Division
Rapporteur d’angles
Instrument de mesure qui sert à mesurer des angles en degrés.
Ex. : A
Régularité
60°
Lien qui existe entre les termes d’une suite.
Ex. : Dans la suite 4, 8, 16…, la régularité est 3 2.
Somme Voir Addition
Terme Terme
Triangle Polygone à 3 côtés (ou à 3 angles).
Triangle équilatéral
Triangle dont tous les côtés sont isométriques.
Triangle isocèle
Triangle ayant 2 côtés isométriques.
Ex. : 100, 110, 120, 130 … Termes 90° 90°
Triangle rectangle Triangle qui a un angle droit.
Triangle scalène Triangle dont tous les côtés sont de mesures différentes.
Unité de million
Groupe d’un million (1 000 000) d’unités.
VValeur de position
Valeur d’un chiffre en fonction de sa position dans un nombre.
Ex. : Dans le nombre 751 200, le chiffre 5 occupe la position des dizaines de mille et vaut 50 000.
54 © 2019, Les Éditions CEC inc. • Reproduction interdite Glossaire
Q
R
S
U
Puissance Voir Notation exponentielle 1 1 1 2 3 2 3 1 2 3 23 A (2, 1) Coordonnées (ou couple) 0
Ma représentation de la situation
Les étapes Les actions
4 Je comprends
• Je lis le problème pour le comprendre.
• Je souligne les questions ou les tâches à effectuer.
• Je repère les informations importantes et je les surligne.
• Je me demande quelles sont les connaissances dont j’ai besoin.
• Je me demande si j’ai déjà résolu un problème semblable.
2 3
4 J'organise
Ma résolution
1 4 5
4 Je résous
• Je représente le problème.
• Je choisis les stratégies à utiliser.
• J’estime les résultats.
• J’applique mes stratégies.
• Je laisse des traces de ma démarche.
• Je réponds aux questions ou j’effectue les tâches.
4 Je révise
• Je compare mes résultats avec mes estimations.
• Je vérifie que mes réponses ont un sens.
• Je révise mes calculs.
4 Je communique mes résultats
• Je donne des réponses complètes aux questions.
• S’il y a lieu, j’indique les bonnes unités de mesure.
55 © 2019, Les Éditions CEC inc. • Reproduction interdite Ma démarche
Ma démarche
La collection MathiQ offre une approche simple et graduelle, qui assurera la réussite des élèves.
La collection MathiQ propose :
• des thèmes originaux, ancrés dans la réalité, pour explorer les mathématiques ;
• un visuel accrocheur, qui inclut des ouvertures de chapitre ludiques permettant d’activer les connaissances antérieures ;
• une présentation simple et efficace de la théorie, avec des exemples concrets ;
• un grand nombre et une grande variété d’exercices, de problèmes en contexte et de situations-problèmes respectant une progression graduelle ;
• une proposition clé en main pour l’enseignement, incluant plusieurs types d’évaluations, comme les évaluations de fin d’étape qui préparent à celle du Ministère ;
• une organisation facilitant l’enseignement dans les classes multiniveaux.