Introdução às funções elementares

LUDMILA BOURCHTEIN ANDREI BOURCHTEIN

INTRODUÇÃO ÀS FUNÇÕES ELEMENTARES

INTRODUÇÃO ÀSFUNÇÕESELEMENTARES

LudmilaBourchtein

AndreiBourchtein

Introduçãoàsfunçõeselementares

c ⃝ 2023LudmilaBourchtein,AndreiBourchtein

EditoraEdgardBlücherLtda.

Publisher EdgardBlücher

Editor EduardoBlücher

Coordenaçãoeditorial JonatasEliakim

Produçãoeditorial KedmaMarques

Diagramação Autores

Revisãodetexto LidianeGonçalves

Capa LaércioFlenic

Imagemdacapa Autor

EditoraBlucher

RuaPedrosoAlvarenga,1245,4o andar

CEP04531-934–SãoPaulo–SP–Brasil

Tel.:55113078-5366

contato@blucher.com.br

www.blucher.com.br

SegundooNovoAcordoOrtográfico,conforme6.ed.do VocabulárioOrtográficodaLíngua Portuguesa,AcademiaBrasileiradeLetras,julhode2021.Éproibidaareproduçãototalou parcialporquaisquermeiossemautorizaçãoescritadaeditora.Todososdireitosreservados pelaEditoraEdgardBlücherLtda.

DadosInternacionaisdeCatalogaçãonaPublicação(CIP)

AngélicaIlacquaCRB-8/7057

Bourchtein,Ludmila.

Introduçãoàsfunçõeselementares/LudmilaBourchtein,AndreiBourchtein.—SãoPaulo: Blucher,2023.

455p.

ISBN978-65-5506-778-1(impresso)

ISBN978-65-5506-779-8(eletrônico)

1.Matemática2.Cálculo3.Funções.I.TítuloII.Bourchtein,Andrei 23-0947

Índiceparacatálogosistemático:1.Matemática

CDD510

Capítulo1

Conjuntosnuméricose coordenadascartesianas

AmatériadeFunçõesElementareséumadisciplinapreliminar,preparatóriapara estudodeCálculoque,porsuavez,éaversãosimplificadadeAnáliseReal.Um dosprincipaisobjetivosdeAnáliseéoestudodepropriedadesgeraiseespecíficasdefunçõespartindodasuadefiniçãoanalítica.Seguindoessarelaçãonatural entretrêsdisciplinas,podemosformularoprincipalproblemanoestudodefunçõeselementarescomoainvestigaçãodepropriedadesdefunçõessimplesusando osmétodosanalíticoselementares.Quandofalamosdefunçõessimplesentãotemosemvistafunçõesdeumavariávelreal,cujaformaébastantecompreensível (atéconhecidadaescola),equandoreferimosamétodosanalíticoselementares, entãoentendemosaquelesquenãoenvolvemosconceitoseresultadosmaisfinos relacionadosalimite(econsequentemente,acontinuidade,derivada,etc.)deuma função.

EmAnálise/Cálculo,afunçãousualmenteédadaemsuaformaanalítica(via fórmula)eapartirdissotemosquedescobrirsuaspropriedadesessenciais,incluindosuascaracterísticasgeométricasrefletidasnaformadoseugráfico.Avisualizaçãogeométricadeumafunçãoéumaferramentaimportantedeavaliaçãodo seucomportamento,maselanormalmenteéobtidacomoresultadodeumestudo detalhadodesuaspropriedadesanalíticas.

TendodeterminadooproblemaprincipaldadisciplinadeFunçõesElementares,podemosverque,antesdecomeçaroestudoanalíticodefunçõeserevelar suaspropriedadesgeométricas,precisamosterumconhecimentobásicodealguns conceitospreliminaresusadosnesseestudo.Realmente,entrepropriedadesgeométricasdefunçõesquebuscamosdeterminarsão:apropriedadedográficosubirou descer,deteraformadeumcopooudeumsino,seográficoalcançapontosmáximosemínimos,seeletemalgumtipodesimetria,etc.Parainvestigareprovar amaioriadessaspropriedadesprecisamosaplicarosmétodosanalíticosdeestudo,

trabalhandocomnúmerosreais,localizaçãodepontosnoplanocoordenado,critériosdesimetria,etc.Dessaforma,oprimeiroCapítuloédedicadoaumarevisão concisadessestópicos,osquaissãoestudados,numnívelbásico,noensinomédio, masrequeremumarepresentaçãomaissistemática,formaleprecisaparaestudo analíticodefunçõesnoscapítulosposteriores.

1 Conjuntos

EmAnáliseeCálculo,econsequentementeemFunçõesElementares,oconjunto éconsideradogeralmenteumdosconceitosbásicos,intuitivamenteclaros,que nãosãodefiniveisporviadeoutrosconceitos.Portanto,vamosdarapenasuma descriçãodesseconceito.

1.1 Descriçãodeumconjunto

Conjunto.Um conjunto éumacoleçãodeobjetosunidosporalgumacaracterísticacomum.Emparticular,essacaracterísticapodesersóapropriedade deestarincluídonomesmoconjunto.Osobjetosusadosnaconstruçãodecerto conjuntosãochamadosdeelementosdesseconjunto.

Obviamente,estanãoéumadefiniçãoformal,massimplesmenteéumadescriçãointuitivaquefazreferênciaaosoutrosconceitos,quepodemparecerintuitivamenteclaros,mascujadefiniçãopodeseraindamaiscomplicadadoquea definiçãodopróprioconjunto.Noentanto,essadescriçãoserásuficienteparaestudaramatériadeFunçõesElementares(eatémuitomais,paraestudarCálculo eAnálise).Nessadefiniçãointuitiva,aspalavras“coleção”,“família”e“classe” podemserusadascomosinônimosdeconjunto.

Umconjuntopodeser finito ou infinito,istoé,contendonúmerofinitoou infinitodeelementos,respectivamente.

Adescriçãodeconjuntosvaiserfeita,porenquanto,usandoarepresentação dosseuselementos.Essarepresentaçãopodeserouexaustiva(citandotodosos elementos),oqueépossivelsóparaconjuntosfinitos,oupelacaracterísticaespecíficadosseuselementos,oqueseaplicatantoaconjuntosfinitoscomoainfinitos. Noprimeirocaso,oselementossãocolocadosemalgumaordem(quepodeser modificada),separadosporvirgula,e,nosegundocaso,oselementossãorepresentadosdealgumaformaapropriadacomespecificaçãoposteriordacaracterística doselementos.Emambososcasosseusamparênteses(usualmente,parênteseschave)paracompreenderoselementosdoconjunto.Porexemplo,umconjunto A,contendoosdoiselementos a e b,podeserdenotadonaforma A = {a,b}.

Oconjunto B detodososdiasdeumasemanapodeserdescritonaforma: B = {b : b = diadeumasemana} (osímbolo“:”nessadescriçãosignifica“tal que”).Daquiemdiante,vamosusarletrasmaiúsculasparadenotarconjuntose

letrasminúsculasparaseuselementos.

Relaçãoentreconjuntoeelemento.Umelementopodepertencerounãoa umconjunto.Paradenotarapertinênciaéusadosímbolo ∈ eparanãopertinência ̸∈.Usandoexemplodoconjunto A,podemosafirmarque a ∈ A e b ∈ A,mas c ̸∈ A

Exemplos

1.Conjuntosfinitos:conjuntodosnúmerosnaturaisde 1 até 5: A ={1,2,3,4,5}; conjunto B dasletrasnumalfabeto.Paraestesdoisconjuntos, 2 ∈ A,mas a ̸∈ A; a ∈ B,mas 3 ̸∈ B.

2.Conjuntosinfinitos:conjuntodosnúmerosnaturais(aquelesqueusamos nacontagemdeobjetos): N = {1, 2, 3,...} (maisformalmente,esteconjuntoé definidocomoaquelequecontémprimeiroelemento 1 ecadapróximoelementoé obtidodoanterioracrescentando 1);conjuntodosnúmerosnaturaispares,istoé, A = {n ∈ N : n =2k,k ∈ N}.Paraosdoisúltimosconjuntos, 2 ∈ N,mas 2 ̸∈ N; 2 ∈ A,mas 3 ̸∈ A.(Anotação N étradicionalparaoconjuntodosnaturais.)

Conjuntosespeciais.Osdoisconjuntosespeciaissãoo conjuntovazio,que nãocontémnenhumelemento,eo conjuntouniversal,quecontémtodososobjetos danaturezaemconsideração.Oprimeiroédenotadopor ∅ eosegundomuitas vezesédenotadopor U.Oprimeirosempreéomesmo,masosegundopode mudar,dependendodosobjetivosdoestudo.Porexemplo,seonossointeresseé restritoaosnúmerospares,entãoessepodeseroconjuntouniversal,masseampliamosnossaconsideraçãoparaosnúmerosnaturais,então N podeseroconjunto universal.

Nesseestudo,vamosusarváriasrelaçõeseoperaçõeselementaresentreconjuntosquesãoestudadasaindanaescola.Mas,paramanterotextocompleto e,também,parafixaraterminologiaenotação,reproduzimosessasdefiniçõese propriedadesaseguir.

1.2 Operaçõeselementarescomconjuntos

Relaçõesentreconjuntos.Umconjunto A podeserpartedeoutro B (se diz,também,que A estácontidoem B),istoé,qualquerelementode A pertencea

B.Nessecaso, A échamadode subconjunto de B eseusaaseguintenotação: A ⊂

B.Emparticular,oconjunto B éseuprópriosubconjunto,qualquerconjuntoé subconjuntodoconjuntouniversale,porconvênio,oconjuntovazioésubconjunto dequalquerconjunto.

Se A ésubconjuntode B e B ésubconjuntode A,entãoosdoisconjuntossão iguais (coincidem)eusamosanotação A = B.Emoutraspalavras,doisconjuntos sãoiguaisse,esomentese,elestêmosmesmoselementos.Casoosdoisconjuntos nãosãoiguais,escrevemos A = B.Podeacontecer,também,quenenhumdosdois

conjuntosestácontidonooutro,mesmoquandoháelementosemcomumentreos dois.

Exemplos

Se A = {1, 2, 3, 4, 5} e B = {2, 3, 4},então B ⊂ A (B estácontidoem A) ou A ⊃ B (A contém B).Se A = {a,b,c,d} e B éconjuntodetodasasletras doalfabetolatino,então A ⊂ B.Se A éconjuntodetodasasletrasdoalfabeto cirílicoe B éconjuntodetodasasletrasdoalfabetolatino,entãonenhumdosdois conjuntosésubconjuntodooutro.

Operaçõesentreconjuntos

1. Uniãodeconjuntos.A uniãodedoisconjuntos A e B éoconjunto C quecontémtodososelementosde A ede B (lembramosqueoselementosque pertencemtantoa A comoa B sãotomadosumavezsóem C).Anotaçãopadrão é C = A ∪ B.Essadefiniçãoéfacilmenteextendidaauniãodequalquernúmero deconjuntos: C = ∪ i Ai separaqualquer x ∈ C existetalconjunto Ai,entreos consideradosnaunião,que x ∈ Ai

2. Interseçãodeconjuntos.A interseçãodedoisconjuntos A e B éo conjunto C quecontémtodososelementosquepertencemtantoa A comoa B

Anotaçãousadaé C = A ∩ B.Extendendoadefiniçãoaqualquernúmerode conjuntos,temos C = ∩ i Ai sequalquerelemento x ∈ C pertenceatodosos conjuntosdainterseção: x ∈ Ai, ∀i.

3. Diferençadeconjuntos.A diferençadedoisconjuntos A e B (nessa ordemespecífica)éoconjunto C,denotado C = A\B,quecontémtodosaqueles elementosde A quenãopertencema B.

4. Produtocartesiano.O produtocartesiano dedoisconjuntos A e B (nessa ordemespecífica)éoconjunto C cujoselementossãotodososparesordenados c =(a,b) taisque a ∈ A,b ∈ B.Anotaçãousualé C = A × B

2.Se A = {2, 3, 4, 5} e B = {1, 2, 3},então A ∩ B = {2, 3}.Se A = {a,b,c,d} e B = {d,e},então A ∩ B = {d}.Se A = {a,b,c,d} e B = {g,h},então A ∩ B = ∅ Se A = {2, 3, 4, 5} e B = N,então A ∩ B = A.

3.Se A = {2, 3, 4, 5} e B = {1, 2, 3},então A\B = {4, 5} e B\A = {1}.Se A = {a,b,c,d} e B = {d,e},então A\B = {a,b,c} e B\A = {e}.Se A = {a,b,c,d} e B = {g,h},então A\B = {a,b,c,d} e B\A = {g,h}.Se A = {2, 3, 4, 5} e B = N, então A\B = ∅ e B\A = {1, 6, 7,...}

1.3 Propriedadeselementaresdeconjuntos

1.

2.

3.

B) ∩ (A ∪ C), A ∩ (B ∪ C)= (A ∩ B) ∪ (A ∩ C).

4. Relaçõescomconjuntovazio: ∅ ⊂ A, A∪∅ = A, A∩∅ = ∅, A\∅ = A, A × ∅ = ∅.Notamosqueessasrelaçõessãoválidasparaqualquerconjunto A

5. Relaçõescomconjuntouniversal U: A ⊂ U, A ∪ U = U, A ∩ U = A, A\U = ∅.Notamosqueessasrelaçõessãoválidasparaqualquerconjunto A.

6. Númerodeelementosdeconjuntosfinitos:se A e B sãoconjuntos finitoscom m e n elementos,respectivamente,e A ∩ B tem k elementos,então, A ∪ B tem m + n k elementos, A\B tem m k elementos, B\A tem n k elementos,e A × B tem mn elementos(assimcomo B × A).

Asdemonstraçõesdessaspropriedadessãobastantesimples,feitascomemprego dasdefiniçõesacimaelógicaelementar.Emboraissofujadoescopodestetexto, vamosdaralgunsexemplosdetaisdemonstraçõesparaosleitoresinteressados.

Demonstraçãodacomutatividadeparaunião: A ∪ B = B ∪ A.Qualquer elemento x ∈ A ∪ B,peladefinição,tempropriedadedeque x ∈ A ou x ∈ B,o queéomesmoquedizerque x ∈ B ou x ∈ A,istoé, x ∈ B ∪ A.Domesmojeito, qualquer y ∈ B ∪ A tambéméelementode A ∪ B.Assim,oselementosde A ∪ B e B ∪ A coincidem,istoé,osdoisconjuntossãoiguais.

Demonstraçãodaassociatividadeparainterseção: (A ∩ B) ∩ C = A ∩ (B ∩ C).

Qualquerelemento x ∈ (A ∩ B) ∩ C,peladefinição,tempropriedadedeque x ∈ A ∩ B e,aomesmotempo, x ∈ C.Especificandoaindaaprimeirainclusão, concluímosque x pertencesimultaneamenteaostrêsconjuntos– A, B e C.Por outrolado,qualquer y ∈ A∩(B ∩ C),peladefinição,tempropriedadedeque y ∈ A e,aomesmotempo, y ∈ B ∩ C.Ou,abrindoaúltimarelação,concluímosque y pertencesimultaneamenteaostrêsconjuntos– A, B e C.Assim,oselementosde (A ∩ B) ∩ C e A ∩ (B ∩ C) têmasmesmaspropriedadese,portanto,essesdois conjuntossãocompostospelosmesmoselementos,istoé,sãoiguais.

Demonstraçãodaprimeiraleidistributiva: A ∪ (B ∩ C)=(A ∪ B) ∩ (A ∪ C). Vamoscomeçardapartedireita.Qualquerelemento x doconjunto (A ∪ B) ∩ (A ∪ C) pertenceaomesmotempoa A ∪ B e A ∪ C.Comoessesdoisconjuntos têmaparteidênticaqueéoconjunto A,entãoasuainterseçãopodeserdividida

Capítulo2

Funçõesesuaspropriedades analíticas

Nestecapítulointroduzimosoconceitomaisimportantedaáreadeanálise,eprovavelmentedetodamatemática,queéafunção.Vamosconhecerosmodosdiferentes dadefiniçãodeumafunçãoe,oqueémaisimportanteparaanálise,asformasdiferentesdedefiniçãodeumafunçãoviafórmula.Vamosconsiderar,numaforma geral,propriedadesessenciaisdefunçõesquepodemsertratadasusandotécnicas rudimentaresdoensinomédio(técnicaspertinentesaPré-Cálculo,disponíveisantesdeestudodelimites).Essaspropriedadesserãodefinidaseinvestigadascom todoorigormatemáticotantonaformageralcomonosexemplosilustrativos.Algumaspropriedadescomplementares,comotendênciasdeumafunção,cujoestudo exatoexigeousodeconceitosmaisavançadosdeCálculo(limitesecontinuidade), vãotertratamentoaproximadoacessívelparaníveldePré-Cálculo.

OestudodequalquerfunçãoemAnálise,econsequentemente,emCálculo, começapeladefiniçãoanalíticadessafunçãoeconsistenainvestigaçãodesuas propriedadesprincipaisusandométodosanalíticos,oque,nofinal,levaàpossibilidadedevisualizaraformageométricadamesmafunção(construiroseugráfico). Nessetextovamosseguiresseesquemacomumnoestudodefunçõeselementares, usandoastécnicasmatemáticasmaissimplesdePré-Calculo(pré-limites).

1 Função:definição,domínioeimagem

Definiçãodefunção.Uma função éumarelaçãoentredoisconjuntos X e Y talqueacadaelementodoconjunto X correspondeumesomenteumelemento doconjunto Y .Oconjunto X échamadode domínio dafunçãoeoconjunto Y é chamadode contradomínio

Aprópriafunção,chamadatambémdefunçãode X em Y ,podeserdenotada

daseguintemaneira: f : X → Y ,ou f (x): X → Y ,ou X f −→ Y ,ou y = f (x),x ∈ X semespecificaçãode Y ,ouainda y = f (x) semespecificaçãode X ede Y .Asprimeirastrêsnotaçõesdestacamostrêselementosdadefinição dafunção–domínio X,contradomínio Y earegra f darelaçãoentreosdois primeiros.Asduasúltimasmostramqueaindicaçãodoconjuntocontradomínioé desnecessária,umavezquenaqualidadedesseconjuntosemprepodemostomaro conjuntouniversal R.Oselementos x sãochamadosde variávelindependente ou argumento dafunçãoeoselementos y de variáveldependente ou valor dafunção. Osúltimossãousualmentedenotadoscomo y = f (x),damesmamaneiracomo umadasnotaçõesdeumafunção,semespecificaçãododomínioecontradomínio. Emboraessanotaçãosejaambígua,poisaprópriaregra f eoresultadodasua ação f (x) sãocoisasdiferentes,écomumeconvenienteusaranotação y = f (x) ou f (x) tantoparaosvaloresdafunçãocomoparaaprópriafunção.Osignificado específicodessesímboloficausualmenteclaronocontexto.Nessetextovamos considerarsomenteasfunçõescujodomínioecodomíniosãosubconjuntosde R. Comojáfoinotado,oconjuntocontradomíniotempouca(setiveralguma) relevâncianadefiniçãodefunçõesnadisciplinadeFunçõesElementares,porqueo tipogeraldefunçõesépre-determinado:sãoestudadasfunçõesquelevamalguns númerosreais(istoé,odomínio X ⊂ R)emoutrosnúmerosreais(istoé,o contradomínio Y ⊂ R).Poressarazão,naqualidadedocontradomíniosempre podemostomaroconjunto R,oquenãoespecificanadaemrelaçãoàfunção.A próximadefiniçãocorrigeessadeficiênciadocontradomínio.

Definiçãodaimagemdeumafunção.A imagem (conjuntoimagem)de função y = f (x) étalpartedoseucontradomínioemqualcadaelemento y tem pelomenosumvalorcorrespondente x dodomínioqueafunçãotransformaem y. Grossomodo,aimageméomenorcontradomíniodetodos.

Muitasvezes,oconjuntocontradomínionãovainosinteressar(jáqueelenão traznenhumainformaçãosobrefunção,semprepodendoser R)esenósconseguirmosdeterminaraimagemdafunção(oquepodeserumproblemanãosimples), entãovamosusaranotação Y paraoconjuntoimagem.Issonãovaigerarconfusão,porqueousodosímbolo Y (comocontradomínioouimagem)vaificarclaro docontextoespecífico.Casoocontradomínioeaimagemsejamconsideradosao mesmotempo,vamosmanteranotação Y paracontradomínioeusar ˜ Y ou f (X) paraimagem.

Àsvezeséimportanteconsideraraspropriedadesdeumafunçãonumaparte doseudomínio,digamosnumsubconjunto S de X.Emparticular,podeser necessáriodeterminara imagemdoconjunto S,queentãovamosdenotarde f (S) Naturalmente, f (S) étalconjuntoquecadaumdosseuselementos y tempelo menosumvalorcorrespondentede S queafunçãotransformaem y.

Exemplos:Relaçõesentreconjuntos

1.Dadosconjuntos X = {1} e Y = {1, 2},arelação f : X → Y queleva oelemento 1 ∈ X em 1 ∈ Y eessemesmo 1 ∈ X em 2 ∈ Y nãoéumafunção, porqueaomesmoelementode X correspondemdoiselementosde Y (vejaFig.2.1).

2.Dadosconjuntos X = {1, 2} e Y = {3},arelação f : X → Y quesomente associaaoelemento 1 ∈ X oelemento 3 ∈ Y nãoéumafunção,umavezquetem elementosde X (número 2)nãoassociadosaelementoalgumde Y (vejaFig.2.2).

3.Dadosconjuntos X = {1, 2} e Y = {3, 4},arelação f : X → Y queassocia aoelemento 1 ∈ X oelemento 3 ∈ Y eaoelemento 2 ∈ X –oelemento 4 ∈ Y é umafunção,conformeadefinição.Oconjunto X éseudomínioe Y éaimagem (vejaFig.2.3).

4.Dadosconjuntos X = {1, 2} e Y = {3, 4},arelação f : X → Y queassocia aoelemento 1 ∈ X oelemento 3 ∈ Y eaoelemento 2 ∈ X –omesmoelemento 3 ∈ Y éumafunção,conformeadefinição.Oconjunto X éseudomínio, Y é contradomínioe Y = {3}⊂ Y éaimagem(vejaFig.2.4).

Observação. Notamosque,peladefiniçãodafunção,ospapeisdodomínio X edocontradomínio Y são,emgeral,diferentes.Primeiro,afunçãoéuma relaçãode X em Y enãoocontrário.Segundo,paracadaelementode X a regradecorrespondênciacomalgumelementode Y deveserdefinida(issofaltou noExemplo2).Terceiro,acadaelementode X podeserassociadosomenteum

Figura2.1 Relaçãoentreconjuntos X = {1} e Y = {1, 2}

Figura2.2 Relaçãoentreconjuntos X = {1, 2} e Y = {3}

elementode Y (issonãofoicumpridonoExemplo1).Cadaumadasduasúltimas regrasdodomínionãoéválidapara Y :umelementode Y podeserassociado adiferenteselementosde X (comonoExemplo4)epodehaverelementosde Y nãorelacionadosanenhumelementode X (denovooExemplo4).Aúltima possibilidadeéeliminadasenaqualidadedocontradomínioéusadaaimagem.

2 Modosdedefiniçãodeumafunção

Hádiferentesmaneirasdedefiniraformadeumafunção.Normalmentesãousadas omodoanalítico,geométrico,numéricoedescritivo,oualgumacombinaçãodesses tipos.EmAnálise/Cálculoe,consequentemente,emFunçõesElementaresomodo primáriodadefiniçãoéanalítico,e,portanto,vamosnosfocaraseguir,emprimeiro lugar,nessetipodadefinição.

2.1 Modoanalítico(algébrico)

Na definiçãoanalítica,afunçãoestádefinidaviafórmula,emqueodomínio X é dado(naformaexplícitaouimplícita), Y podesersempreconsiderado R eaforma dacorrespondência f entre X e Y édadapelafórmulaqueligaelementosdosdois conjuntos.Caso X sejaespecificadoexplicitamentenadefiniçãodafunção,temos queusaresseconjuntocomodomínio.Caso X nãosejaindicadoexplicitamente

Figura2.3 Relaçãoentreconjuntos X = {1, 2} e Y = {3, 4}.

Figura2.4 Relaçãoentreconjuntos X = {1, 2} e Y = {3, 4}

(dadoimplicitamente),peloconvênio,naqualidadede X éconsideradoomaior subconjuntode R paraoqualafórmuladadatemsignificado.

Exemplos

1. f (x)= x +2 (ou y = x +2).

Nessecaso,odomínionãoestádefinidoporexplícito,masafórmula x +2 tem sentidoparaqualquer x ∈ R e,então, X = R.Ocontradomíniopodeser Y = R, eregraquefazcorresponderacada x ∈ R umúnicovalor y ∈ R éafórmula y = x +2

Nesseexemplo,aimagemdafunçãoé Y = R,porquequalquer y ∈ R temum valordodomínio(queseencontrapelafórmula x = y 2,bastaresolverafórmula emrelaçãoa x)queafunçãolevaem y.

2. f (x)= x +2, X =[0, +∞).

Nessecaso,odomínioestádefinidoporexplícito,portantotemosquetomar X =[0, +∞),mesmoqueafórmula x +2 tenhasentidoparaqualquer x ∈ R.O contradomíniopodeser Y = R,earegraquefazcorresponderacada x ∈ [0, +∞) umúnicovalor y ∈ R éafórmula y = f (x)= x +2

Obviamente,nesseexemplo,aimagemnãoé R,umavezquetemnúmeros reais,porexemplo, y =0,paraosquaisnãotemnenhumnúmerocorrespondente x ∈ [0, +∞),porque y = x +2 ≥ 2 paraqualquer x ≥ 0.Masaúltimaobservação jápermitedeterminaraimagemnaforma Y =[2, +∞).Realmente,paraqualquer y ∈ [2, +∞) existevalorcorrespondente x ∈ [0, +∞) (encontradopelafórmula x = y 2)queafunçãotransformanesse y

3. f (x)= 1 x

Odomínionãoestádefinidoporexplícito,entãotemosqueencontrartodos x reaisparaosquaisafórmula 1 x podeserexecutada.Obviamente,aúnicarestrição quetemoséoanulamentododenominador,queocorrequando x =0.Então,a fórmulatemsentidoparaqualquer x =0,istoé, X = R\{0}.Ocontradomínio, comosempre,podeser Y = R.Aregraquefazcorresponderacada x ∈ X um únicovalor y ∈ R éafórmula y = 1 x

Nessecaso,encontraraimagemésimples:bastanotarqueafórmula y = 1 x podeserresolvidaem x naforma x = 1 y ,oquequerdizerqueparaqualquer y =0 existeumelemento x dodomínio(queseencontrapelafórmula x = 1 y )quea funçãolevaem y.Logo, Y = R\{0}

4. f (x)= √x Comoodomínionãoestádefinidoporexplícito,temosqueencontrartodos x reaisparaosquaisafórmula √x temsignificado.Lembramosqueraizquadrada (real)estádefinidasomenteparaosnúmerosnãonegativos,oquequerdizerque X =[0, +∞).Ocontradomínio,comosempre,podeser Y = R.Aregraquefaz corresponderacada x ∈ X umúnicovalor y ∈ R éafórmula y = √x

Capítulo3

Funçõesalgébricas:polinomiais, racionaiseirracionais

Tudooquevimosatéagorafoiumapreparaçãoparapoderrealizarumestudo bastantecompletodeváriasfunçõesespecíficaseconstruirseusgráficos.Apartir deagoracomeçaremosaestudarmaisprofundamenteasfunçõeselementarese suaspropriedades.

Nestecapítuloconsideremosoprimeirogrupodefunções,asalgébricas,começandodemaissimples,polinomiais,passandopararacionaisefinalizandocom asmaiscomplicadasnessegrupo,asirracionais.Oesquemadeestudosegueo padrãodeCálculoeAnálise,emboranumaformasimplificada,jáapresentadana resoluçãodeexercíciosdoCapítulo2(vejaaúltimapartedaseçãodeExercícios).

Dadaaformaanalítica(fórmula)deumafunção,oestudodassuaspropriedades consisteemseguintespassos:

1)identificarodomínioeaimagem;

2)determinarseafunçãoélimitadaounão;

3)verificaraspropriedadesdesimetria(paridadeeperiodicidade);

4)encontrarpontosdeinterseçãocomoseixosdecoordenadaseregiõesondea funçãomantémomesmosinal;

5)investigarmonotoniaeextremos;

6)investigarconcavidadeepontosdeinflexão;

7)analisarpropriedadescomplementares,taiscomotendênciasinfinitasenoinfinito,assíntotashorizontaiseverticais;

8)desenharográficocombasenaspropriedadesreveladas.

Valeapenalembrarquenemtodosessespassossãoobrigatórioseexecutáveispara todasasfunçõeselementares:paraalgumasfunçõessimplesosresultadospodem seróbvios,paraoutras,análisedealgumaspropriedadespodeserligadacomelevadosproblemastécnicos,especialmentequandopodemosusarsomentetécnicas rudimentaresdePré-Cálculo,comonestetexto.Mesmoquandotodos(ouvários)

passospodemserexecutados,asuaordemnãoérígidae,dependendodotipo dafunção,podesermaisvantajosotrocarasequênciadepropriedadesestudadas, porquealgumaspropriedadesmaisavançadaspodemprovidenciarresultadossobre propriedadesanteriores,maissimplesparaformulação.

DeacordocomoindicadonoCapítulo2,noestudodeconcavidade,sistematicamente,usamosoconceitomaissimplesdeconcavidadedopontomédio,sem mencionarmaisisso.

1 Funçõespolinomiais

Adefiniçãodeumafunçãopolinomialéaseguinte.

Definiçãodeumafunçãopolinomial.Uma funçãopolinomial (um polinômio)temaforma y = Pn(x)=

,onde ai,i =0,...,n sãoconstantesreaise an =0.Ocoeficiente an échamadode coeficienteprincipal.

Nestaseçãovamosconsideraralgunscasosparticularesdefunçõespolinomiais, começandodocasomaissimplesdeumafunçãolinear(n =1),passandopara aquadrática(n =2)edepoisconsiderandoalgumasformasmaisgerais,como monômios y = xn , n ∈ N

1.1 Funçãolinear

Definiçãodeumafunçãolinear.Umafunçãonaforma y = ax + b,onde a e b sãoduasconstantesreaiséchamadade linear.Ocoeficiente a échamadode coeficientedeinclinação oude coeficienteangular Comovamosdescobriremseguida,essaterminologiavemdaformageométrica (gráficos)dessasfunçõesquerepresentamlinhasretas,cujainclinaçãoemrelação aoeixo Ox édeterminadapelocoeficiente a Vamoscomeçarestudodessasfunçõescomosdoiscasosparticulares: y = b (a =0) e y = x (a =1,b =0)

Estudode y = b (a =0)

Essafunçãoéchamadade constante

1.Domínioeimagem.Odomínioé X = R (afórmulaédefinidapara ∀x ∈ R) eaimagemé Y = {b} umavezqueparaqualquer x afunçãoassumeomesmo valor b

2.Limitação.Afunçãoélimitada,asuacotasuperioreinferioréaprópria constante b

3.Paridade. f ( x)= b = f (x), ∀x ∈ X,oquemostraqueafunçãoépar.

4.Periodicidade. f (x + T )= b = f (x), ∀x ∈ X, ∀T> 0,istoé,afunção

éperiódica,masnãoháumperíodomínimo,umavezquequalquer T =0 éo períododessafunção.

5.Monotoniaeextremos.Comoparaqualquerpar x1 <x2 temos f (x1)= b = f (x2),essafunçãoécrescente(eaomesmotempodecrescente)nãoestritamente emtodooseudomínio.Nãotemmonotonianosentidoestrito.Paraqualquer x0 temos f (x0) ≥ f (x) para ∀x ∈ X etambém f (x0) ≤ f (x) para ∀x ∈ X,oque significaquequalquerpontododomínioéomáximoeaomesmotempoomínimo localeglobalnãoestritos.Nãoháextremosestritos.

6.Concavidadeeinflexão.Assimcomoamonotonia,aconcavidade(dedois tipos)temsónosentidonãoestrito.Porisso,nãohápontosdeinflexão.

7.Interseçãoesinal.Paratodosospontosdodomínioafunçãomantémo mesmosinalse b =0 (ouéiguala 0 caso b =0).Portanto,elanãoteminterseções comoeixo Ox se b =0 (oucoincidecomesseeixocaso b =0).Opontode interseçãocomoeixo Oy é (0,b)

8.Inversa.Afunção f (x)= b : X = R → Y = {b} ésobrejetora,mas nãoinjetora,poisatodososvaloresde x correspondeomesmovalor y = b. Consequentemente,afunçãonãoébijetorae,portanto,nãoadmiteinversa.

Paratornarafunçãoinjetora,éprecisorestringirodomínioaumponto,oque tornafunçãomuitosingularesimples,seminteresseparaestudo.

9.Ográficodafunçãoéaretaparalelaaoeixo Ox comadistânciade b unidadesatéesseeixo,mostradanaFig.3.1.

Figura3.1 Gráficodafunção y = b.

Estudode y = x (a =1,b =0)

Essafunçãoéchamadade identidade

1.Domínioeimagem.Odomínioé X = R (afórmulaédefinidapara ∀x ∈ R) eaimagemé Y = R umavezqueparaqualquer y ∈ R existe(umúnico)valor x = y dodomíniotalque f (x)= f (y)= y

2.Limitação.Deacordocomaimagemdeterminada,afunçãoéilimitada tantoinferiormentecomosuperiormente.

3.Paridade. f ( x)= x = f (x), ∀x ∈ X,oquemostraqueafunçãoé ímpar.

4.Periodicidade.Acondição f (x + T )= x + T = x = f (x), ∀x ∈ X,levaa conclusãodequeissoépossívelsomentequando T =0,oquecontradizadefinição daperiodicidade.Assim,afunçãonãoéperiódica.

5.Monotoniaeextremos.Comoparaqualquerdupla x1 <x2 temos f (x1)= x1 <x2 = f (x2),essafunçãoécrescenteestritamenteemtodooseudomínio. Dissoseguequeelanãotemextremoslocaisnemglobais,estritosounão.Isso segueimediatamentedarelaçãogeralentreextremosemonotonia(seção6.1do Capítulo2).Amesmaafirmaçãopodesermostradadiretopara f (x)= x:qualquer queforponto x0,emqualquervizinhançadessepontoexistempontosdodominio ondefunçãotemvaloresmenoresque f (x0) etambémaquelesondeelatemvalores maiores: ∀x1 <x0 → f (x1)= x1 <x0 = f (x0) e ∀x2 >x0 → f (x2)= x2 >x0 = f (x0).

6.Concavidadeeinflexão.Aconcavidade(dedoistipos)ocorresónosentido nãoestrito.Logo,nãohápontosdeinflexão.

7.Interseçãoesinal.Ainterseçãocomoeixo Oy ocorrenaorigemeomesmo éválidoparainterseçãocom Ox.Resolvendoasdesigualdades f (x)= x< 0 e f (x)= x> 0,especificamosqueafunçãotemosinalnegativopara x< 0 e positivopara x> 0.

8.Inversa.Afunção f (x)= x : X = R → Y = R ésobrejetoraeinjetora. Consequentemente,afunçãoébijetorae,portanto,temainversaqueéapropria função: f 1(x)= x : R → R.

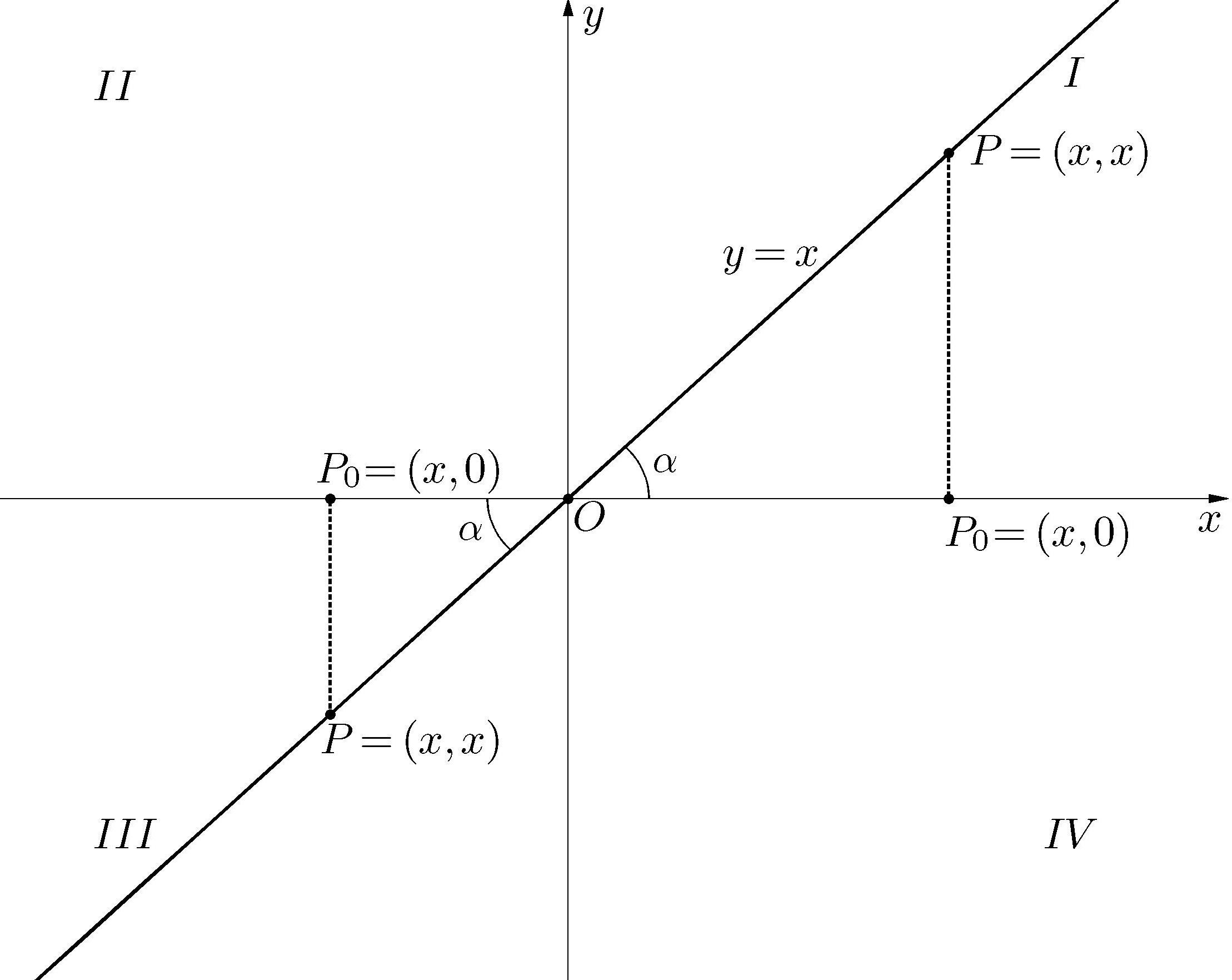
9.Ográficodafunçãoéaretaquepassapelaorigemeteminclinaçãode 45o comoeixo Ox,istoé,representaabissetrizdo I e III quadrantes.Realmente, qualquerponto P =(x,x) dográficotemmesmaabscissaeordenadae,portanto, otriânguloretângulo PP0O,onde P0 =(x, 0) éaprojeçãode P sobre Ox,éum triânguloisóscelescom |PP0| = |OP0| = |x|,oquesignificaqueoângulo POP0 tem 45o (vejaFig.3.2).Notamosqueocoeficiente a =1 éigualarazãoentre oscomprimentosdosdoiscatêtosdotriângulo PP0O queexpressaatangentedo ângulo POP0: a = |PP0| |OP0| =tan POP0 =tan α =1.

Voltamosaocasogeraldafunçãolinear y = ax + b com a =0

Estudode y = ax + b, a =0

1.Domínioeimagem.Odomínioé X = R (afórmulaédefinidapara ∀x ∈ R)

eaimagemé Y = R umavezqueparaqualquer y ∈ R existe(único)valor x = y b a dodomíniotalque f (x)= f ( y b a )= a y b a + b = y

2.Limitação.Deacordocomadeterminaçãodaimagem,afunçãoéilimitada tantoinferiormentecomosuperiormente.

3.Paridade.Se b =0,entãoafunçãoéimpar,umavezque f ( x)= ax = f (x), ∀x ∈ X.Se b =0,entãonãoháparidade: f ( x)= ax+b = ax+b = f (x) e f ( x)= ax + b = ax b = f (x), ∀x ∈ X.Porexemplo, f ( 1)= a + b =

a + b = f (1) e f ( 1)= a + b = a b = f (1).

4.Periodicidade.Acondição f (x + T )= a(x + T )+ b = ax + b + aT = ax + b = f (x), ∀x ∈ X,levaaconclusãoqueissoépossívelsomentequando T =0,oque contradizadefiniçãodaperiodicidade.Assim,afunçãonãoéperiódica.

5.Monotoniaextremos.Paraqualquerdupla x1 <x2 temos f (x2) f (x1)= a(x2 x1).Como x2 x1 > 0,entãoemtodooseudomínioafunçãoéestritamentecrescentese a> 0 eestritamentedecrescentese a< 0.Comoafunçãoé estritamentemonótonaem R,elanãotemextremoslocaisnemglobais,estritosou não.Issosegueimediatamentedarelaçãogeralentreextremosemonotonia(seção 6.1doCapítulo2).

6.Concavidadeeinflexão.Aconcavidade(dedoistipos)ocorresónosentido nãoestrito.Logo,nãohápontosdeinflexão.

Figura3.2 Gráficodafunção y = x.

Capítulo4

Funçõestranscendentais: exponenciais,logarítmicas, trigonométricas

Nessecapítulovamosinvestigarasfunçõestranscendentais,divididasemdoisgrupos:primeiro,funçõesexponenciaiselogarítmicas,esegundo,funçõestrigonométricas.

OesquemadeestudosegueopadrãodoCapítulo3:dadaaformaanalítica (fórmula)deumafunção,primeiro,identificamososeudomínioeaimagem,logo determinamosseelaélimitadaounão,depoispassamosaspropriedadesdesimetria(paridadeeperiodicidade),emseguida,investigamosmonotoniaeextremose, também,concavidadeeinflexão,logoencontramospontosdeinterseçãocomeixos decoordenadoseavaliamososinaldafunção,depoisanalisamosaspropriedades deinjeçãoesobrejeção,efinalizamosrealizandoconstruçãodográficocombase naspropriedadesinvestigadas.

Relembrequenemtodosessespassossãoobrigatórioseexecutáveisparaqualquerfunçãoelementar.Mesmoquandotodos(ouvários)passospodemserexecutados,asuaordemnãoérígidae,dependendodotipodafunção,podeser maisvantajosotrocarasequênciadepropriedadesestudadas,porquealgumas propriedadesmaisavançadaspodemprovidenciarresultadossobrepropriedades anteriores,maissimplesparaformulação.

1 Funçõesexponenciaiselogarítmicas

1.1 Conceitospreliminares.Expoentereal esuaspropriedades

Expoentenatural

Caso a ∈ R e n ∈ N,a expoente an (chamada n-ésima potência de a)édefinida pelafórmula an = a· ... ·a (a multiplicadoporelemesmo n vezes).Nessaoperação, a échamadode base e n de expoente.

Expoenteinteira

Caso a =0 e n ∈ N,aexpoente a n édefinidapelafórmula a n = 1 an ;para qualquer a =0, a0 =1 (aexpressão 00 éindeterminada).

Hádoistiposdepropriedadesdepotências:aspropriedadesdeigualdadeeas decomparação.

Aspropriedadesprincipaisdeigualdadedepotênciasinteirassãoasseguintes: paraquaisquerdoisnúmerosreais a =0 e b =0,equaisquer n e m inteiros,temos

1) (ab)n = anbn;

2) ( a b )n = an bn ;

3) anam = an+m;

4) an am = an m;

5) (an)m = anm .

Asdemonstraçõesseguemdiretodadefiniçãodepotênciainteiraesãoelementares.

Aspropriedadesprincipaisdecomparaçãosãoasseguintes:paraquaisquerdois númerosinteiros n e m temos

1)se a> 1,entãode n>m segue an >am;emparticular, an > 1 para n> 0,e an < 1 para n< 0;

2)se 0 <a< 1,entãode n>m segue an <am;emparticular, an < 1 para n> 0, e am > 1 para m< 0.

Asdemonstraçõessãosimpleseseguemdadefiniçãodepotênciainteira.

Raiz n √a –expoente 1 n , n ∈ N

Paraqualquer a ∈ R e n =2k 1,k ∈ N,a n-ésimaraiz (ou raizdeordem n) n √a étalnúmero b que bn = a.Paraqualquer a ≥ 0 e n =2k,k ∈ N,a n-ésima raiz n √a étalnúmero b ≥ 0 que bn = a (noteque,nessecaso,onúmeronegativo b tambémtemapropriedadeque ( b)n = a).Para a< 0 e n =2k,k ∈ N a operaçãonãoestádefinida(nãoexisteumnúmerorealcujapotênciaparvaidaro númeronegativo).Assim,paraasraízesdeordempartemduasrestrições:elassão definidassomenteparaosnúmerosnãonegativoseoresultadodaoperaçãotambém deveserumnúmeronãonegativo.Araizquadradatemanotaçãosimplificada √a.Senãotiverambiguidade,a n-ésimaraizpodeserchamadasimplesmentede

raiz.

Conformeadefinição, ( n √a)n = a emtodososcasosquandoaraizestádefinida.Portanto,amesmaoperaçãoédenotada,naturalmente,pelapotênciacom expoente 1 n , n ∈ N: n √a ≡ a 1 n .Entãoapropriedadedadefiniçãoassumeaforma (a 1 n )n = a noscasosdescritosnadefinição,asaber:se n éímpar,então a 1 n étal númeroque (a 1 n )n = a paraqualquer a real;se n épar,então a 1 n étalnúmeronão negativoque (a 1 n )n = a paraqualquer a ≥ 0.Apotência a 1 n nãoestádefinidano caso n pare a< 0

Notamosque,naordeminvertidadeexpoentes 1 n e n,apropriedadeanálogaé válidanosmesmoscasos.Realmente,se n éímpar,então (an) 1 n = a paraqualquer a ∈ R,porque an éabaseda n-ésimaraiz.Se n épare a ≥ 0,entãotemos amesmaigualdade (an) 1 n = a pelasmesmasrazões.Noentanto,se n épare a< 0,então,diferentementede (a 1 n )n quenãotemsentidonessecaso,aoperação (an) 1 n estádefinida(umavezque an > 0),masoresultadonãovaiser a esim a. Realmente,raizdeordempardeveserumnúmeronãonegativoe,porisso,não podeser a,mas a éoresultadocorreto,porque a> 0 e ( a)n = an para n par.Juntandoosresultadospara n par,temos (an) 1 n = |a| paraqualquer a ∈ R

Emparticular, √a2 = |a| paraqualquer a ∈ R.

Devidoàsrestriçõesdoargumentodaraizdeordempar(nãoexisteraizde umnúmeronegativo)edoseuresultado(deveserumnúmeronãonegativo), aspropriedadesdeexpoentesinteirasnãosãotransmitidasdiretamenteparaas expoentesfracionárias 1 n , n ∈ N.Realmente,osresultadosdiferentesquepodem surgirpara (a 1 n )n e (an) 1 n quando n épar(comoacabamosdemostrar)jásugerem queparaasraízesasituaçãoémaiscomplicada.Exemplificandoessadiferença, podemostomar a = 1, n =2 etemosqueonúmero ((

não existe,enquanto (( 1)2)1 2 =1.Issoinvalidaousodaspropriedadesdeexpoentes inteirasnocasoderaízes.Paraaprimeirapropriedade,podemoschegaraoseguinte resultadoabsurdo:

,ondeaexpressãodo ladodireitonãoexiste.Usandoaterceirapropriedade,tambémpodemoscairnum resultadosemelhante:

Noentanto,aspropriedadesdeexpoentesinteiraspodemserextendidasàs raízes,seconsideramossomentebasespositivas a> 0.Nestecaso,asseguintes trêspropriedadessãomantidas:

3) m n √a = mn√a.

Asduaspropriedadesrestantesenvolvemasoperaçõesaindanãointroduzidaspara raízeseserãoadicionadasquandovamosconsiderarexpoentesracionais.

Expoenteracional ap,p ∈ Q

Paraquaisquer a ∈ R e p = m n ,m ∈ Z,n ∈ N,apotência ap édeifinidapela

fórmula ap = n √am =( n √a)m emtodososcasosquandoasoperaçõesenvolvidas estãodefinidaseasduasexpressõesrepresentamomesmoresultado.

Ascondiçõesdadefiniçãoestãosatisfeitas,emparticular,quando a éumnúmerorealqualquere n éimpar,ouquando a> 0 e p éracionalqualquer.

Arestriçãodebaseparavalidadedascincopropriedadesdepotênciaséherdada docasodasraízes.Se a> 0,b> 0,entãoparaquaisquer p,q ∈ Q sãoválidasas seguintespropriedades:

1) (ab)p = apbp;

2) ( a b )p = ap bp ;

3) apaq = ap+q;

4) ap aq = ap q;

5) (ap)q = apq .

Paraexpoentesracionaissãoválidas,também,asseguintespropriedadesde comparação:

1)se a> 1,entãode p>q segue ap >aq,evice-versa;

2)se 0 <a< 1,entãode p>q segue ap <aq,evice-versa.

Expoentereal

Passandoparaexpoentesreais,desdeiníciosupomosqueabase a épositiva. Comoaspotênciascomexpoentesracionaisjáforamdefinidas,vamosnosconcentrarnocasoquandoaexpoente x éumnúmeroirracional.Ésuficientedefinir ax quando x épositivo,porque,peladefinição, a x = 1 ax . Consideremos,primeiro,asituaçãoquando a> 1.Tomamosqualquernúmero positivoirracional x = x0,x1 ...xn econsideramosváriasaproximaçõesracionaisde x,superioreseinferiores.Podemoscomeçarcom x0 <x<x0 +1,depois passamosparaoprimeirodígitodecimal x0 ≤ x0,x1 <x<x0,x1+0, 1 ≤ x0+1,depoisparaosegundo x0 ≤ x0,x1 ≤ x0,x1x2 <x<x0,x1x2 +0, 01 ≤ x0,x1 +0, 1 ≤ x0 +1,etc.Cadapróximaaproximaçãoficamaispertode x queaanterior, tantonaaproximaçãosuperiorcomonainferior.Comisso,a n-ésimaaproximaçãoinferior pn = x0,x1x2 ...xn satisfazadesigualdade pn 1 ≤ pn <x,enquantoa n-ésimaaproximaçãosuperior qn = x0,x1x2 ...xn +10 n satisfaza desigualdade x<qn ≤ qn 1.Deacordocomessasaproximaçõesracionaisde x,temosasaproximaçõescorrespondentesde ax asquais,conformeaprimeira propriedadedecompraçãodepotênciasracionais,satisfazemasdesigualdades ap0 ≤ ... ≤ apn 1 ≤ apn ≤ ... ≤ aqn ≤ aqn 1 ≤ ... ≤ aq0.Comoadiferença entre pn e qn éiguala 10 n ediminuicomaumentode n,énaturaldeesperar

queessasaproximaçõesdepotênciasficamcadavezmaispróximasdeumúnico númeroqueéchamadode ax.Emboraintuitivamenteaexistênciaeunicidade dessenúmeropossamparecerevidentes,acomprovaçãoexatadessefatoébaseada nosconceitoseresultadosqueficammuitoalémdoescopodestetexto.

Quando 0 <a< 1,seguimosomesmoesquemadeaproximações,comaúnica diferençaqueasdesigualdadesparapotênciasvãotersinalinvertido(deacordo comasegundapropriedadedecomparaçãodepotênciasracionais).

Aspropriedadesdeigualdadedepotênciasreaissãoasmesmasdocasode potênciasracionais,asaber,se a> 0,b> 0,entãoparaquaisquer x,y ∈ R são válidasasseguintespropriedades:

1) (ab)x = axbx;

2) ( a b )x = ax bx ;

3) axay = ax+y;

4) ax ay = ax y;

5) (ax)y = axy

Aspropriedadesdecomparaçãotambémsãomantidas.Paraquaisquer x e y reais,temososseguintesresultados:

1)se a> 1,entãode x>y segue ax >ay,evice-versa;

2)se 0 <a< 1,entãode x>y segue ax <ay,evice-versa.

Acomprovaçãodessaspropriedadesexigeconhecimentodeconceitoseresultadosmaisavançadosquevãomuitoalémdoescopodestetexto.

1.2 Funçãoexponencial

Definiçãodeumafunçãoexponencial.Umafunçãoexponencial y = f (x)= ax,ondeaconstante a> 0 échamadadebaseeavariável x deexpoente,éumafunçãocomdomínio R queacada x realfazcorresponderoúnico número y = ax .

Antesdecomeçarainvestigaçãogeral,descartamosocasoquando a =1, porqueentãotemosasituaçãosingularetrivialdeumafunçãoconstante y =1x = 1, ∀x ∈ R,quejáfoivistanoCapítulo3.Apartirdessemomentoconsideramos que a =1

Estudode y = ax

1.Domínioeimagem.Peladefinição,odomínioé X = R (umavezquea operaçãodeelevaçãodeumnúmeropositivonumapotênciaestádefinidapara qualquerpotênciareal).Comoqualquernúmero ax , a> 0 épositivo(peladefiniçãodapotência),aimagemdafunçãoestácontidaem (0, +∞).Alémdisso,é pressuposto(semdemonstração)que ax podeassumirqualquervalorpositivo,o quesignificaque Y =(0, +∞).

2.Limitação.Aimagemdafunçãodeterminaqueafunçãoélimitadainferiormente(porexemplo,pelaconstante m =0)enãoélimitadasuperiormente.

Este livro considera métodos analíticos de investigação de funções elementares relativos ao nível de Pré-Cálculo, o que corresponde a disciplinas introdutórias de matemática na universidade e cursos avançados de Álgebra no ensino médio. O texto é direcionado para os ingressantes nos cursos universitários de matemática e afins, e para os alunos do ensino médio interessados em aprofundar seu conhecimento.

As abordagens desenvolvidas mostram como as propriedades importantes de funções elementares podem ser deduzidas seguindo o caminho lógico rigoroso, sem necessidade de suposições adicionais e memorização mecânica. Isso deve preparar estudantes para o uso de raciocínio analítico nas disciplinas matemáticas mais avançadas e criar uma base sólida para cursar as disciplinas de Cálculo e Análise.