Mecânica by Editora Blucher

IVAN

MECÂNICA DE OLIVEIRA

Mecânica IvandeOliveira

Mecânica

EditoraEdgardBlücherLtda.

Publisher EdgardBlücher

Editores EduardoBlüchereJonatasEliakim

Coordenaçãoeditorial AndressaLira

Produçãoeditorial LidianePedrosoGonçalves

Revisãodetexto MaurícioKatayama

Capa LaércioFlenic

Imagemdacapa iStockphoto

EditoraBlucher

RuaPedrosoAlvarenga,1245,4º andar CEP04531-934–SãoPaulo–SP–Brasil

Tel.:55113078-5366

contato@blucher.com.br www.blucher.com.br

SegundooNovoAcordoOrtográﬁco,conforme6.ed.do VocabulárioOrtográﬁcodaLíngua Portuguesa,AcademiaBrasileiradeLetras,julhode2021.Éproibidaareproduçãototalou parcialporquaisquermeiossemautorizaçãoescritadaeditora.Todososdireitosreservados pelaEditoraEdgardBlücherLtda.

DadosInternacionaisdeCatalogaçãonaPublicação(CIP)

AngélicaIlacquaCRB-8/7057

Oliveira,Ivande

Mecânica/IvandeOliveira.—SãoPaulo:Blucher,2023. 370p.

Bibliograﬁa

ISBN978-65-5506-761-3

1.Mecânica2.Física3.MatemáticaI.Título 23-1333

Índiceparacatálogosistemático:1.Mecânica

CDD531

Conteúdo 1Conceitospreliminares1 1.1Referenciais.............................. 1 1.2Vetorposiçãoetrajetória....................... 1 1.3Velocidade................................ 3 1.4Aceleração............................... 8 1.4.1Aceleraçãotangencialenormal................ 14 1.5Velocidadeeaceleraçãoemcoordenadaspolares........... 18 1.6Velocidadeeaceleraçãorelativa................... 25 Problemas................................... 32 2LeisdeNewton44 2.1Força................................... 45 2.1.1Forçaresultante........................ 46 2.1.2Tiposdeforças......................... 51 2.1.2.1Forçagravitacional................. 51 2.1.2.2Forçaelástica..................... 52 2.1.2.3Forçadetração................... 55 2.1.2.4Forçadeatrito................... 58 2.2ValidadedasleisdeNewton...................... 64 Problemas................................... 65 3LeisdeNewtonI–Estática75 3.1Estática................................. 75 3.2Centrodemassa............................ 75 3.2.1Cálculodecentrodemassa.................. 76 3.2.1.1Centrodemassaparaumsistemadepartículas.. 76 3.2.1.2Centrodemassaparaumadistribuiçãolineare uniformedemassa.................. 78 3.2.1.3Centrodemassaparaﬁgurasplanas........ 83 3.2.1.4Centrodemassadeumsólidoderevolução.... 88 3.2.2Exercícios............................ 90 3.2.3Equilíbriodeumpontomaterial............... 96 3.2.4Exercícios............................ 100 3.2.5Momentodeumaforça.................... 102 i

ii Mecânica 3.2.5.1Momentodeumsistemadeforças......... 109 3.2.5.2Momentoemrelaçãoaumeixo........... 110 3.2.5.3Sistemaequivalentedeforças............ 112 3.2.5.4Momentodeumbinário............... 114 3.2.6Exercícios............................ 117 3.2.7Equilíbriodeumcorporígido................ 122 3.2.8Exercícios............................ 126 3.2.9Cargadistribuída........................ 130 3.2.10Exercícios............................ 135 Problemas................................... 137 4LeisdeNewtonII–Dinâmica145 4.1Movimentocomvelocidadeconstante................. 145 4.2Movimentocomaceleraçãoconstante................. 146 4.2.1Exercícios............................ 152 4.3Análisegráﬁcadomovimento..................... 158 4.3.1Exercícios............................ 164 4.4MovimentopróximoàsuperfíciedaTerra.............. 167 4.4.1Exercícios............................ 177 4.5Movimentososcilatórios........................ 180 4.5.1Exercícios............................ 190 Problemas................................... 193 5Leisdeconservação207 5.1Trabalhodeumaforça........................ 207 5.1.1Exercícios............................ 217 5.2Potência................................. 219 5.2.1Exercícios............................ 221 5.3Energiacinética............................ 223 5.3.1Trabalhoeenergiacinética.................. 223 5.4Energiapotencial........................... 226 5.4.1Energiapotencialgravitacional................ 226 5.4.2Energiapotencialelástica................... 228 5.4.3Exercícios............................ 231 5.4.4Forçaapartirdaenergiapotencial.............. 236 5.4.5Exercícios............................ 238 5.5Sistemasconservativos......................... 239 5.5.1Conservaçãodaenergiamecânica............... 239 5.5.2Exercícios............................ 243 5.5.3Gráﬁcodaenergiapotencial................. 246 5.5.4Exercícios............................ 247 5.6Conservaçãodaenergia........................ 249

Conteúdo iii 5.7Momentolineareimpulsodeumaforça............... 250 5.7.1Exercícios............................ 259 5.7.2Conservaçãodomomentolinear................ 262 5.7.2.1Colisões........................ 262 5.7.3Exercícios............................ 268 5.8Momentoangular........................... 272 5.8.1Movimentoderotaçãodeumcorporígidonoplano..... 276 5.8.2Cálculodomomentodeinércia................ 282 5.8.3Exercícios............................ 291 5.8.4Energiacinéticaderotação.................. 302 5.9Conservaçãodomomentoangular.................. 305 5.9.1Exercícios............................ 307 Problemas................................... 309 Apêndices316 ApêndiceAConceitosdeMatemática316 A.1Regrasdepotenciação......................... 316 A.2Propriedadedoslogaritmos...................... 316 A.3Relaçõestrigonométricas........................ 316 A.4Númeroscomplexos.......................... 317 A.5Geometria................................ 318 A.6Derivadas................................ 319 A.6.1Regrasdederivação...................... 319 A.6.2Algumasderivadas....................... 320 A.6.3Interpretaçãográficadaderivada............... 320 A.6.4Pontosdemáximo,mínimoeinflexão............ 321 A.7Integrais................................. 323 A.7.1Regrasdeintegração...................... 323 A.7.2Algumasintegraisindefinidas................. 323 A.8Equaçõesdiferenciais.......................... 325 A.9TeoremadeStokes........................... 327 A.10Séries.................................. 327 ApêndiceBVetores328 B.1Representaçãodegrandezasvetoriais................. 328 B.2Operaçõescomvetores......................... 328 B.2.1Somaesubtraçãodevetoresgeometricamente........ 328 B.2.2Vetoresunitários........................ 329 B.2.3Componentescartesianasdeumvetor............ 330 B.2.4Somaesubtraçãodevetoresalgebricamente......... 331 B.2.5Produtoentrevetores..................... 331

iv Mecânica B.2.5.1Produtoescalar................... 332 B.2.5.2Produtovetorial................... 332 B.3Algumasidentidadesvetoriais..................... 334 Respostas335 Referências357 Índiceremissivo359

Conceitospreliminares

Algunsconceitoscomoposição,velocidadeeaceleraçãosãofundamentaisparao entendimentoeparaadescriçãodomovimento,sejadeumpontomaterialou deumcorporígido.Dessaforma,nasseçõesqueseguemiremosdescreveresses conceitos.

1.1 Referenciais

Adescriçãodomovimentodeumapartículaoudeumcorporígidotemcomo princípiofundamentalalocalizaçãosejadapartículaoudaspartículasquecompõemocorporígidonoespaço.Entretanto,essalocalizaçãodeveserfeitacom basenoquechamamosdereferencial.

Umreferencialéumsistemadecoordenadasqueserveparaindicaraposição daspartículasnoespaço.Umrelógiotambémdeveserconectadoaessesistema decoordenadasparaindicarotempo,assimpodemosdescreveromovimento,ou seja,amudançadaposiçãocomtempoecomrelaçãoaumdadoreferencial.

Umreferencialquesemovimentacomvelocidadeconstanteéchamadode referencialinercial.Nessereferencialoscorpossemovimentamlivresdeforças externas.

Aimportânciadedeﬁnirmosreferencialsetraduz,porexemplo,nadeﬁnição doconceitoderepouso.Quandoavelocidademedidaporumobservadoremum sistemadereferênciainercialfornula,dizemosqueoobjetoestáemrepouso.

1.2 Vetorposiçãoetrajetória

Ovetorposiçãoéumvetorquelocalizaopontomaterialnoespaçoemrelação aumdadoreferencial.NaFig.1.1temososvetores r1 e r2 localizandooponto materialemrelaçãoàorigemdosistemadecoordenadas.Oconjuntodepontos ocupadosnoespaçopelopontomaterialaolongodotempodeﬁnimoscomosendo atrajetória C desseponto.

1 Capítulo

Utilizandoascoordenadascartesianas,osvetores r1 e r2,emrelaçãoàorigemdo sistemadecoordenadas,sãodadospor,

sãoosvetoresunitáriosaolongodoseixos x, y e z,respectivamente.

Consideremosagoraqueopontomateriallocalizadopelovetor r1 mudede posição,sendoagoralocalizadopelovetor r2.Deﬁnimoscomosendoovetor deslocamentoovetor ∆r ,queémostradonaFig.1.2,equerepresentaamudança daposiçãoaolongodatrajetória.

2 Mecânica x y r1 r2 t1 t2 z O C

Figura1.1:Vetoresposição r1 e r2 aolongodatrajetória C

r1 = x1 ˆ i + y1 ˆ j + z1 ˆ k (1.1) r2 = x2 ˆ i + y2 ˆ j + z2 ˆ k (1.2) onde ˆ i, ˆ j e ˆ k

x y r1 r2 t1 t2 z O C ∆r

ÉfácilperceberpelaFig.1.2que r2 = ∆r + r1 (1.3) e,dessaforma,ovetor ∆r ﬁcadadopor ∆r = r2 r1 (1.4)

Figura1.2:Vetordeslocamento ∆r.

UtilizandoasEqs.(1.1)e(1.2),podemosaindaescreverque

respectivamente.

1.3 Velocidade

Oconceitodevelocidadeéamplo,podendoseraplicadoadiferentessituações eemdiferentesáreasdoconhecimento.Usamosoconceitodevelocidade,por exemplo,naquímica(velocidadedereação),nabiologia(taxadecrescimentos deseresvivos)naeconomia(taxadecrescimentooudereduçãodoPIB),entre outras.Dessaforma,intuitivamentepodemosperceberqueavelocidadeestá associadaàrapidezcomquealgumfenômenovariacomotempo.Comoestaremos interessadosnadescriçãodomovimentodeumobjeto,avelocidadenosdaráa informaçãodarapidezcomquevariaaposiçãodesseobjetonotempo.Dessa

ÉimportantenotarmosqueoladodireitodaEq.(1.12)éadefiniçãodaderivada deumafunção.Sendoassimavelocidadeficasendodefinidacomoataxade variaçãodaposiçãocomrelaçãoaotempo,ouseja,

Conceitospreliminares 3

∆r =(x2 x1)ˆ i +(y2 y1) ˆ j +(z2 z1) ˆ k (1.5) ∆r = ∆x ˆ i + ∆y ˆ j + ∆z ˆ k (1.6) onde

∆r aolongodasdireções x , y e z,

∆x, ∆y e ∆z sãoascomponentesdovetor

v = lim ∆t→0 ∆r ∆t (1.7) Consideremosqueosvetores r1 e r2,mostradosnaFig.1.1,sejamosvetores posiçãodonossoobjetoaolongodatrajetórianosinstantesdetempos t1 = t e t2 = t + ∆t,ouseja, r1 = r(t) (1.8) r2 = r(t + ∆t) (1.9) Dessaformaovetordeslocamentopodeserescritocomosendo ∆r = r2 r1 (1.10) ∆r = r(t + ∆t) r(t) (1.11) que,substituindonaEq.(1.7),resultaem v = lim ∆t→0 r(t + ∆t) r(t) ∆t (1.12)

forma,temos

v = dr dt (1.13)

onde vx, vy e vz sãoascomponentescartesianasdovetorvelocidade.

AEq.(1.7)nosdizqueadireçãoeosentidodovetorvelocidadeﬁcamdeterminadospelovetordeslocamento ∆r.Paraentendermosumpoucomaissobreo vetorvelocidadevamosanalisaraFig.1.3,emquealinhatracejadarepresenta ovetordeslocamentoparadiferentesinstantesdetempo.PelaFig.1.3podemos perceberque,àmedidaqueointervalodetempo, ∆t,diminuiovetorvelocidade vaiseaproximandodeumaretatangenteaoponto P.Issoquerdizerque,quando ∆t → 0,ovetorvelocidadepassaasertangenteàtrajetória.

Essasobservaçõespodemsergeneralizadasparaqualquertipodetrajetória, ouseja,podemosaﬁrmarqueovetorvelocidadeésempretangenteàtrajetória percorridapeloobjetoemquestão.

Exemplo1.3.1

Omovimentodepartículanoespaçoédescritopelovetorposição r como funçãodotempodaseguinteforma:

a)Encontreovetorvelocidadecomofunçãodotempo.

b)Descrevaatrajetóriadescritapelapartícula.

4 Mecânica

r = x ˆ i + y ˆ j + z ˆ k,daseguintemaneira: v = dx dt ˆ i + dy dt ˆ j + dz dt ˆ k (1.14) v = vx ˆ i + vy ˆ j + vz ˆ k (1.15)

equepodeserescrita,considerandoque

C v1 v2 v3 v r(t) r(t + ∆t) P P1 P2 P3 O z y

Figura1.3:Vetorvelocidadetangenteàtrajetória C.

r(t)= ˆ i + 2t 2 ˆ j t ˆ k

LeisdeNewton

Umdosgrandesdesaﬁosdohomemsemprefoiodeentenderedescreverosfenômenosdanatureza.Atarefa,namaioriadasvezes,dedescreveressesfenômenos foidadaaoscientistas.Umdosmaiorescientistasquesededicouaexecutaressa tarefafoi SirIsaacNewton.AsideiasdeNewtonacercadeváriosfenômenos danaturezasãoválidasatéosdiasdehoje.Newtoncontribuicomaevolução dopensamentocientíﬁcoemdiferentesáreasdoconhecimento.Muitosdosfenômenosdanaturezapodemserdescritosporumconjuntodetrêsleisconhecidas comoasleisdeNewton,quesão:

Primeiralei :“Todocorpotendeapermaneceremrepousoouasemovimentar emumalinharetacomvelocidadeconstanteamenosqueumaforçaseja aplicadosobreele.”

Segundalei :“Aforçaresultantequeatuaemumcorpoéigualataxadevariação domomentolinear”,ouseja,

onde p = mv éomomentolinear,com v sendoavelocidadee m amassa.

Terceiralei :“Atodaaçãocorrespondeumareaçãodemesmaintensidadee mesmadireção,porémdesentidocontrário.”

Exemplo2.0.1

Emumapartículademassa m = 1 kgatuaumaforçaconstante F que modiﬁcaavelocidadedapartículade v1 = 2 ˆ i 3 ˆ j + 2 ˆ k m/spara v2 = 6 ˆ i + 4 ˆ j 5 ˆ k m/sem2segundos.Qualomódulodessaforça?

SOLUÇÃO: Aforça F nointervalodetempo ∆t podeserdeterminadapor

2 Capítulo

R = d p dt (2.1)

F = ∆ p ∆t 44

2.1 Força

AsleisdeNewtonestãofortementerelacionadasaoconceitodeforça.Aprimeira leiaﬁrmaquenaausênciadequalquerforça(ação)ocorpomantémseuestado, ouderepousooudemovimentoemlinharetacomvelocidadeconstante.Jáa segundaleireferequeaaçãoéoagenteprovocadordamudançadomomento linear p.Aterceiraleinosdizque,quandoaaçãoocorresobreumcorpo,ele reageaessainteraçãoprovocandoumaaçãoigual,opostaenamesmadireção. Aessaaçãochamamosdeforça,ouseja,forçaéumaaçãoquepodemodiﬁcaro estadodeumcorpoe/oudeformá-lo.

LeisdeNewton 45 onde

∆ p = mv2 mv1 ∆ p = 1(6 ˆ i + 4 ˆ j 5 ˆ k) 1(2 ˆ i 3 ˆ j + 2 ˆ k) ∆ p = 4 ˆ i + 7 ˆ j 7 ˆ kkgm/s Comissoaforça F ﬁcasendoiguala F = ∆ p ∆t F = 4 ˆ i + 7 ˆ j 7 ˆ k 2 F = 2 ˆ i + 3, 5 ˆ j 3, 5 ˆ kN eseumóduloédadopor F = F 2 x + F 2 y + F 2 z = 22 + 3, 52 +( 3, 5)2 F = 5, 34 N

∆ p = mv2 mv1.Utilizandoosdadosfornecidostemosque

2.1.1 Forçaresultante

Aforçaresultante(FR)éasomavetorialdetodasasforçasqueatuamnocorpo. Matematicamenterepresentamospor

onde Fi,com i = 1 ··· n,sãoasforçasqueatuamnocorpo.Asforçasdevem sersomadasseguindoasregrasdaálgebravetorial.Paraocasodeduasforças, F1 e F2,quesãoaplicadasnomesmoponto,comomostradonaFig.2.1,aforça resultantepodeserfacilmentedeterminada.

ConsiderandoaFig.2.1éfácilperceberque

OmódulodaforçaresultanteparaasforçasmostradasFig.2.1édadopor

Expandindooladodireitodarelaçãoacimaerearranjandoostermos,temosque omódulodaforçaresultanteﬁcaentãodeterminadopor

VamosvoltaràdeﬁniçãodeforçaresultantedadapelaEq.(2.2)eescrevero ladoesquerdodaseguinteforma:

46 Mecânica

FR = F1 + F2 + F3 + + Fn (2.2) FR = n ∑ i=1 Fi (2.3)

θ F1 F2 FR

Figura2.1: Somadeforçasutilizandoaregradoparalelogramo.

FR = F1 + F2 (2.4)

F 2 R =(F1 + F2) · (F1 + F2) (2.5)

F 2 R = F 2 1 + F 2 2 + 2F1F2 cos θ (2.6)

e F2

onde θ éoânguloentreosvetores

FR = FRx ˆ i + FRy ˆ j + FRz ˆ k (2.7)

onde FRx, FRy e FRz sãoascomponentescartesianasdaforçaresultante.Dessa maneiraascomponentesdaforçaresultante,Eq.(2.2),podemserdeterminadas por

OladodireitodasEqs.(2.8)-(2.10)indicaquepodemosdecomporcadaumadas forças, F1, F2, F3, ··· Fn,nasrespectivasdireções x, y e z paraencontrarmosas componentes FRx, FRy e FRz e,consequentemente,determinarmosomóduloda forçaresultanteapartirde

Consideremosagoraqueumadeterminadaforçademódulo F sejaaplicadaao longodasualinhadeaçãodeﬁnidapelaretaquepassapelosponto A(x1, y1, z1) e B(x2, y2, z2) comoindicadosnaFig.2.2etendoosentidodoponto A paraoponto B.Conhecendoomódulodaforçaeospontosquepertencemàlinhadeaçãoda força,podemosentãodeterminarovetor F daseguintemaneira:

(2.12) onde ˆ λ éumvetorunitárioaolongodalinhadeaçãodaforça.

LeisdeNewton 47

FRx = F1x + F2x + F3x + ··· + Fnx (2.8) FRy = F1y + F2y + F3y + ··· + Fny (2.9) FRz = F1z + F2z + F3z + ··· + Fnz (2.10)

FR = F 2 Rx + F 2 Ry + F 2 Rz (2.11)

F ˆ λ

F ˆ λ A(x1,y1,z1) B(x2,y2,z2) x y z O

Figura2.2: Representaçãodeumforçanoespaço.

LeisdeNewtonI–Estática

AsleisdeNewtonpossuemumvastocampodeaplicações,porémonossointeresse aquiestáemutilizaressasleisnadescriçãodoequilíbriodepontosmateriaisassim comodecorposrígidos,ouseja,discutiremososconceitosdaestática.

3.1 Estática

Aestáticatemcomofundamentoascondiçõesdeequilíbrio.Analisandoasleis deNewton,pode-seperceberqueacondiçãodeequilíbrioestáticoocorrequando FR = 0,eainda v = 0,ouseja,quealémdaforçaresultantenulaocorpodeveestar emrepousoemrelaçãoaumdeterminadoreferencial.Entretantoessacondição sógarantequenãohaverámovimentodetranslação,porémocorpopodeainda terummovimentoderotação.Dessaforma,paraqueocorpoestejaemequilíbrio estático,tantoomovimentodetranslaçãoquantooderotaçãonãopodemexistir. Paragarantirmosquenãoocorraomovimentoderotaçãodocorpo,devemos imporacondiçãodequeomomentodaforçaresultante(outorqueresultante) sejatambémnulo.

Nasseçõesqueseguemiremosprimeiramentedefiniroconceitodecentrode massae,comoconsequência,oconceitodepontomaterial.Alémdisso,descreveremoscomodeterminarocentrodemassaparaumadistribuiçãodiscretae paraumadistribuiçãocontínuademassa.Umavezdefinidooconceitodeponto material,descreveremosascondiçõesdeequilíbrioparaospontosmateriais.Em seguidaestudaremosoequilíbriodoscorposrígidose,paraisso,definiremoso conceitode momentodeumaforça ousimplesmente torque

3.2 Centrodemassa

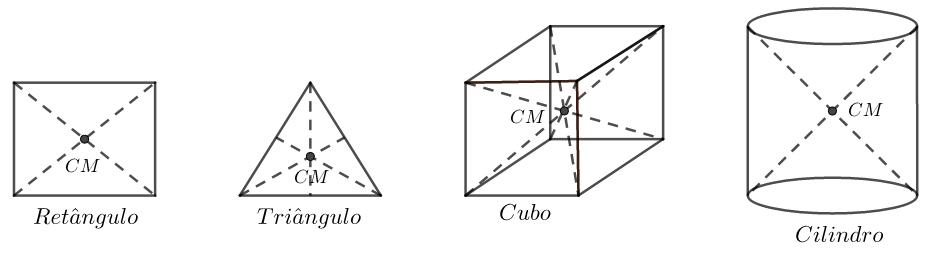
Ocentrodemassadeumcorpoédefinidocomosendoopontodocorpoonde podemosconsiderarquetodaamassadessecorpoestálocalizada.Ocentrode massatempapelimportantenadescriçãodomovimentoetambémemsituações deequilíbrio.Paraummelhorentendimentodadefiniçãodecentrodemassa, consideramosaFig.3.1,ondemostramosalgumasfigurassimétricaseuniformes.

3 Capítulo

Ficaclaroqueocentrodemassadeﬁguras(comdistribuiçãouniformede massa)quepossuemumeixodesimetriaestálocalizadoaolongodesseeixo. Entretanto,paracorposcujasimetrianãosejatãoevidente,ascoordenadasdo centrodemassapodemserdeterminadasutilizandoocálculodiferencialeintegral. Nasseçõesqueseguemdescrevemoscomodeterminarascoordenadasdocentrode massaparadiferentessistemas.Umcorpodemassauniformepodeserequilibrado apoiando-onocentrodemassa.

3.2.1 Cálculodecentrodemassa

Nestaseçãodescreveremoscomodeterminarocentrodemassaparadiferentessistemas,taiscomo:conjuntodepartículasdiscretas,distribuiçãolineareuniforme demassa,ﬁgurasplanasedesólidosderevolução.

3.2.1.1 Centrodemassaparaumsistemadepartículas

ConsidereadistribuiçãodemassamostradanaFig.3.2,onde mi representaa massadecadapartículae (xi, yi) aposiçãodamassaemrelaçãoaoseixos x e y

76 Mecânica

Figura3.1: Centrosdemassa(CM)deﬁgurassimétricasecomumadistribuiçãodemassa uniforme.

m1 m2 m3 mi m4 x1 x2 x3 xi x4 y1 y2 y3 y4 yi x y O

Figura3.2: Sistemadiscretodepartículasdemassa m1, m2, m3, m4 ··· mi

Ascoordenadas, (xcm, ycm),docentrodemassaparaosistemadepartículas mostradonaFig.3.2sãodeﬁnidascomosendo

Exemplo3.2.1

Considerequeaspartículasdemassas m1=10kg, m2=25kge m3=15kg estãolocalizadasaolongodoeixo x nospontos x1=2m, x2=4me x3=12 m,respectivamente.Determineascoordenadasdocentrodemassapara essesistemadepartículas.

SOLUÇÃO: Comoaspartículasestãolocalizadasaolongodoeixo x ﬁcafácil perceberque ycm=0e zcm=0.Agoraacoordenada xcm édadapor

NaFig.3.3mostramosalocalizaçãodocentrodemassaparaosistemadepartículasdemassas m1=10kg, m2=25kge m3=15kg.

LeisdeNewtonI–Estática 77

xcm = m1x1 + m2x2 + m3x3 + m4x4 + + mnxn m1 + m2 + m3 + + mn (3.1) ycm = m1y1 + m2y2 + m3y3 + m4y4 + ··· + mnyn m1 + m2 + m3 + ··· + mn (3.2) quepodemserescritascomo xcm = n ∑ i=1 ximi n ∑ i=1 mi e ycm = n ∑ i=1 yimi n ∑ i=1 mi (3.3) onde n ∑ i=1 mi éamassatotaldosistema.Éevidentequeparaumsistemadepartículaslocalizadasnoespaço(trêsdimensões)ocentrodemassaé CM(xcm, ycm, zcm), com zcm sendodadapor zcm = n ∑ i=1 zimi n ∑ i=1 mi (3.4)

xcm = m1x1 + m2x2 + m3x3 m1 + m2 + m3 xcm = 10 × 2 + 25 × 4 + 15 × 12 10 + 25 + 15 = 6 m

Umpontoimportanteaquiquedevemosnotarpeloresultadodoexemplo3.2.1 équeocentrodemassaestarálocalizadoemumpontopróximoàregiãodemaior concentraçãodemassa.ConsideremosaFig.3.4,ondeapartículademassa m2 é muitomaiorque

2 >> m1.

UtilizandoaEq.(3.1)paraocentrodemassaaolongodoeixo x,temos

ouseja,ocentrodemassasempreestarámaispróximoderegiõesondepossuia maiorconcentraçãodemassa.

3.2.1.2 Centrodemassaparaumadistribuiçãolineareuniformedemassa

Paradeterminarmosocentrodemassadeumadistribuiçãolineardemassa,utilizaremosadeﬁniçãodecentrodemassaparaumsistemadepartículasdescritona seçãoanterior.ConsideremosadistribuiçãolineardemassamostradanaFig.3.5.

Amassa m dalinhaestádistribuídauniformementeaolongodocomprimento total L.

78 Mecânica 2 4 12 x(m) y O CM(6,0) 6 m1 m2 m3

Figura3.3: Exemplo3.2.1.

m1. x2 x y O m1 m2 x1

Figura3.4: Localizaçãodocentrodemassadeduaspartículasdemassasm1 em2 quandom

xcm = m1x1 + m2x2 m1 + m2 = m2( m1 m2 x1 + x2) m2( m1 m2 + 1) = m1 m2 x1 + x2 m1 m2 + 1 (3.5) Levando-seemcontaque m2 >> m1,conseguimosque xcm x2 (3.6)

LeisdeNewtonII–Dinâmica

AsleisdeNewtonpodemserutilizadasparaadescriçãodadinâmica(movimento) deumpontomateriale/oudeumcorporígido.Adescriçãodomovimentoque seráfeitanestecapítuloéaquelaquechamamosdedescriçãoclássica,ouseja, quandoosefeitosrelativísticosequânticosnãosãoconsiderados.

4.1 Movimentocomvelocidadeconstante

Consideremosqueumpontomaterialsemovimentaemumatrajetóriaretilínea aolongodeumadadadireção,porexemplo,adireção x.Levemosemconsideraçãoaindaqueaforçaresultantesobreopontomaterialénula,ouseja, FR = 0. AplicandoagoraasegundaleiEq.(2.1)paraessecasotemos

Éimportantenotarque,comoconsequênciadaforçaresultantenula,omovimento sedácomvelocidadeconstantee,nessecaso,aposiçãodopontomaterialpode serdeterminadaaolongodotempopor

onde x0 éaposiçãonoinstantedetempo t = 0 medidaemrelaçãodoponto O, origemdosistemadereferência.Aposiçãoemfunçãodotempoparaumponto materialemmovimentocomvelocidadeconstanteémostradonaFig.4.1.Aﬁgura v > 0 indicaqueomovimentosedánamesmaorientaçãodatrajetória,já v < 0 indicamovimentonosentidocontrárioàorientaçãodatrajetória.

4 Capítulo

FR = m dv dt (4.1) 0 = m dv dt ⇒ v = cte (4.2)

x = x0 + vt (4.3)

145

4.2 Movimentocomaceleraçãoconstante

Naseçãoanteriormostramosque,quandoomovimentoocorrenacondiçãode forçaresultantenula,omesmosedácomvelocidadeconstante.Agoravamoslevar emconsideraçãoqueaforçaresultantenãovaria,ouseja,queelaéconstante.

SendoassimaEq.(2.1)podeserescritacomo

ComoFR éconstante,éfácilperceberqueoladoesquerdodaEq.(4.5)também seráumaconstante,pois m éamassa.Dessamaneirapodemosdizerqueataxade variaçãodavelocidadecomotempo,ouseja,aaceleração,éconstante.Issoquer dizeraindaqueomovimentosedácomaceleraçãoconstante.Nessascondições aevoluçãotemporaldavelocidadeﬁcasendodeterminadadaseguintemaneira:

146 Mecânica x O t v> 0 x t O v< 0 x0 x0

Figura4.1: Posiçãoemfunçãodotempoparaomovimentocomvelocidadeconstante.

FR = m dv dt (4.4) FR m = dv dt (4.5)

a = dv dt (4.6) dv = adt ⇒ v = at + C (4.7) Considerandoquenoinstante t = 0 temos v = v0,encontramos C = v0 e,comisso, temosque v = v0 + at (4.8)

Graﬁcamenteavelocidadeemfunçãodotempoparaomovimentocomaceleração constanteestárepresentadanaFig.4.2paraoscasos a > 0 e a < 0.

Umavezqueconhecemosavelocidade,Eq.(4.8),podemosencontraraposição emfunçãodotempodaseguinteforma:

Assimcomofoifeitoparaavelocidade,podemosrepresentargraficamenteaposiçãoemfunçãodotempo.NaFig.4.3temosaevoluçãotemporaldaposição, Eq.(4.12),quando a > 0 e a < 0.Umpontoimportanteaquiéqueográficodo movimentofoiobtidoatravésdaEq.(4.12),porémpodemosobterinformações acercadomovimentofazendoumaanálisesomentedosgráficos v × t ou x × t sem oconhecimentodaleiqueescreveomovimento.Maisadiantemostraremoscomo essaanálisepodeserfeita.

LeisdeNewtonII–Dinâmica 147

v v0 t O a> 0 v v0 a< 0 t O

Figura4.2: Velocidadeemfunçãodotempoparaomovimentocomaceleraçãoconstante.

v = dx dt (4.9) dx = vdt (4.10) SubstituindoaEq.(4.8)naEq.(4.10),temos dx = (v0 + at)dt ⇒ x = v0t + 1 2 at 2 + C (4.11) Considerandoque,noinstante t = 0, x = x0,determinamosque C = x0 e,comisso, conseguimos x = x0 + v0t + 1 2 at 2 (4.12)

AsEqs.(4.8)e(4.12)sãoasevoluçõestemporaistantodavelocidadequando daposição,ouseja,sãoequaçõesqueenvolvemagrandezatemponadescriçãodo movimento.Entretantoemalgunscasosnãotemosoconhecimentodagrandeza tempoparaadescriçãodomovimento.Nessecasoéinteressantetermosuma equaçãoquenãoenvolvaotempo.ParaissovamosconsiderarqueaEq.(2.1) possaserescritadaseguinteforma:

Considerandoaindaqueaforçaresultantenãovariaeque FR/m determinaa aceleração,temos

Sabendo-seque v0 éavelocidadenaposição x0,encontramosovalordaconstante C e,comisso,conseguimos

com ∆x = x x0 sendoodeslocamento.Éimportantenotarqueagoraavelocidade ﬁcarelacionadaàposição,enãoàgrandezatempo.

148 Mecânica x O t a> 0 x t O a< 0

Figura4.3: Posiçãoemfunçãodotempoparaomovimentocomaceleraçãoconstante.

FR = mv dv dx (4.13) umavezque dv dt = v dv dx (4.14)

a = v dv dx (4.15) ouainda adx = vdv ⇒ ax = v2 2 + C (4.16)

v 2 = v 2 0 + 2a∆x (4.17)

Leisdeconservação

MuitosdosproblemasquesãoresolvidosutilizandoasegundaleideNewton, Eq.(2.1),pressupõemoconhecimentodaforça,sejaelacomofunçãodotempo F (t) oudaposição F (x, y, z).Entretanto,nocasodeproblemasemquenãoseconhece aforça,aindaépossívelresolvê-los.Aresoluçãodessetipodeproblemaépossível conhecendoalgumaspropriedadesdaforçaqueatuanosistema.Osconceitosde trabalhoeenergiasãoferramentasquepermitemconhecertaiscaracterísticase dessaformaaresoluçãodessesproblemas.

5.1 Trabalhodeumaforça

ConsidereaFig.5.1,ondeumaforça F éaplicadaaumpontomaterial.Consideremosaindaque,devidoàaçãodaforça,opontomaterialdesloca-sedoponto a aoponto b aolongodatrajetória C.

Figura5.1: Forçaaplicadaaolongodeumatrajetória C sobreumapontomaterial.

Deﬁnimosotrabalhodeumaforçaaolongodeumatrajetória C comosendo

(5.1)

onde F éaforçaaplicadae dr odeslocamentoaolongodatrajetória.Nosistemainternacionaldeunidades(SI)aunidadeparaagrandezatrabalhoéoNm (Newton×metro),quetemcomoequivalênciaoJoule(J),ouseja,1Nm=1J.O

5 Capítulo

F dr θ a b C

= b a F · dr

207

trabalhodeumaforçaéumagrandezaescalare,porisso,podeserpositivo, negativoounulo.Para 0 ≤ θ < 90o,otrabalhodaforçaserápositivo,porém, quando 90o < θ ≤ 180o,otrabalhoseránegativo.Jáparaforçasperpendiculares (θ =90o)àtrajetóriaotrabalhoseránulo.Otrabalhorealizadopelaforçapode serinterpretadocomosendoamedidadavariaçãodaenergiadopontomaterial, ouseja,quando W > 0 aforçaprovocouumaumentonaenergiadopontomaterial;quando W < 0 aforçafoiresponsávelpeladiminuiçãodaenergiadoponto material;jáquando W = 0 aforçanãoprovocavariaçãodaenergiadoponto material.Sendoassimotrabalhodeterminaatransferênciadeenergia.

AEq.(5.1)determinaotrabalhodeumaúnicaforça,entretantoparaum sistemadeforçasotrabalhodaforçaresultanteﬁcasendo

Levando-seemconsideraçãoqueaforçaresultante FR podeserescritacomoa Eq.(2.2),ouseja,

ÉimportantenotarquecadaumdostermosdoladodireitodaEq.(5.4)representa otrabalhodecadaumadasforçasqueatuamindividualmentenosistemae,dessa forma,otrabalhodaforçaresultadaﬁcadeterminadopor

medidasemmetros,determineotrabalhorealizadopelaforça

208 Mecânica

WR = b a FR dr (5.2)

FR = F1 + F2 + F3 + + Fn onde Fi,com i = 1, 2, 3, ··· , n sãoasforçasqueatuamnosistema,otrabalhoda forçaresultanteﬁca WR = b a (F1 + F2 + F3 + ··· + Fn) · dr (5.3) WR = b a F1 dr + b a F2 dr + b a F3 dr + + b a Fn dr (5.4)

WR = W1 + W2 + W3 + + Wn (5.5) WR = n ∑ i=1 Wi (5.6) onde Wi,com i = 1, 2, 3, ··· , n,sãoostrabalhosrealizadosporcadaumadasforças. Exemplo5.1.1 Umaforça F =(20 ˆ i 30 ˆ j + 15 ˆ k) Natuaemumapartículadeslocando-ada posição r1 = 2 ˆ i + 6 ˆ j 4 ˆ k paraaposição r2 = 7 ˆ i 2 ˆ j 8 ˆ k.Sendoasposições

F aolongo

dodeslocamento.

SOLUÇÃO: Comoaforçaqueatuasobreapartículaéconstante,otrabalhopode serdeterminadopor

Exemplo5.1.2

Considereaforça F = ky

i,com k sendoumaconstantepositiva,edetermine otrabalhorealizadoporessaforçaparairdoponto O paraoponto A ao longodoscaminhos C1 e C2 mostradosnaFig.5.2.

SOLUÇÃO: Otrabalhorealizadopelaforçaaolongodeumcaminho C édeterminadopor

Leisdeconservação 209

W = F ∆r comovetordeslocamento ∆r sendo ∆r = r2 r1 ∆r =(7 ˆ i 2 ˆ j 8 ˆ k) (2 ˆ i + 6 ˆ j 4 ˆ k) ∆r = 5 ˆ i 8 ˆ j 4 ˆ k e,comisso,temosqueotrabalhorealizadopelaforça F éiguala W = F · ∆r W =(20 ˆ i 30 ˆ j + 15 ˆ k) · (5 ˆ i 8 ˆ j 4 ˆ k) W = 280 J

W = C F · dr Caminho C1 W = C1 F · dr W = C1 ky ˆ i (dx ˆ i + dy ˆ j)= C1 kydx

Comoocaminho C1 éumareta,temosque

C1 éiguala

Otrabalhoaolongocaminho C2 éiguala

Aolongodotrecho Oa aforçaézero,entãoaprimeiraintegralénula.Jápara otrecho aA,comoaforçaéperpendicularaodeslocamento,aintegraltambémé

210 Mecânica O a A b y C1 C2 x Figura5.2:

Exemplo5.1.2.

C1 : y = b a x que,substituindonaequaçãoanterior,resultaem W = C1 kydx W = k a 0 b a xdx

F ao

W = k ab 2 Caminho

e,resolvendoaintegral,encontramosqueotrabalhorealizadopelaforça

longodocaminho

W = C2 F · dr = Oa F · dr + aA F · dr W = Oa F · dr + aA F · dr

ConceitosdeMatemática A.1

A.2 Propriedadedoslogaritmos

ln(M.N)= ln M + ln N

ln M N = ln M ln N

A.3 Relaçõestrigonométricas

sin2 a + cos2 a = 1

sin2a = sin a cos a

cos2a = cos2 a sin2 a

tan2 a + 1 = sec2 a

sin(a ± b)= sin a cos b ± cos a sin b

cos(a ± b)= cos a cos b ∓ sin a sin b

tan(a ± b)= tan a ± tan b 1 ∓ tan a tan b

sin a + sin b = 2sin a + b 2 cos a b 2

sin a sin b = 2cos a + b 2 sin a b

ln(M)q = p ln M logb M = loga M loga b

A Apêndice

Regrasdepotenciação a 0 =

a 0 am an = am+n am an = am n 1 am = a m n √a = a 1/n n √am = am/n (am)n = am n (a

bm n a b = n √a n √b

)m =

2 316

cos a + cos b = 2cos a + b 2 cos a b 2

sin a sin b = 2sin a + b 2 sin a b 2

A.4 Númeroscomplexos

Somaesubtração

(a + ib) ± (c + id)=(a ± c)+(b ± d)ii = √ 1

Multiplicação

(a + ib)(c + id)=(ac bd)+(ad + bc)ii = √ 1

Divisão

a + ib

c + id = a + ib c + id c id c id = ac + bd c2 + d2 + bc ad c2 + d2 ii = √ 1

Formapolardeumnúmerocomplexo

x = r cos θ y = r sin θ

x + iy = r(cos θ + i sin θ )

xéaparterealey,aparteimaginária donúmero (x + iy)

r = x2 + y2

RelaçãodeEuler

ApêndiceA:ConceitosdeMatemática 317

θ r O x y ℑ ℜ

cos θ + i

θ x + iy = re iθ sin θ = eiθ e iθ 2i

e i

sin

cos θ = eiθ + e iθ 2

Complexoconjugado

(i)∗ = i (∗)complexoconjugado

(x + iy)∗ =(x iy)= re iθ

A.5 Geometria

318 Mecânica

r C

θ r A B O Área

θ emradianos

θ emradianos Funçõestrigonométricasnotriânguloretângulo A B C a b c α β sin α = BC AB = b c cos α = AC AB = a c tan α = BC AC = b a sin β = AC AB = a c cos β = BC AB = b c tan β = AC AC = a b a 2 + b2 = c 2 TeoremadePitágoras

Círculoderaio r

Área A = π r2 Comprimento C = 2π r Setorcircularderaio r

A = θ r2/2 com

Comprimentodoarco AB = θ r com

ApêndiceA:ConceitosdeMatemática 319 Leidossenos A B C α β γ AB AC BC sin α BC = sin β AB = sin γ AC Leidoscossenos A B C α β γ a b c a 2 = b2 + c 2 2bc cos β c 2 = a 2 + b2 2ab cos α b2 = a 2 + c 2 2ac cos γ A.6 Derivadas A.6.1 Regrasdederivação d(cx) dx = c (A.1) d(cxn) dx = cnxn 1 (A.2) d(u ± v) dx = du dx ± dv dx u = u(x) e v = v(x) (A.3) d(uv) dx = u dv dx + v du dx (A.4) d dx u v = u(dv/dx) v(du/dx) v2 (A.5) w = u(x)n dw dx = dw du du dx = nun 1 du dx , regradacadeia (A.6)

B s

v ou v –Grandezavetorial

A –Origemdovetor

B –Extremidadedovetor

Direçãodovetor –odareta s

B.1 Representaçãodegrandezasvetoriais v A

Sentidodovetor –deAparaB

Módulodovetor –igualàdistânciaentreospontos A e B

B.2 Operaçõescomvetores

B.2.1 Somaesubtraçãodevetoresgeometricamente

B Apêndice Vetores

a b c S a b c S = a + b + c SUBTRAÇÃO a b b a d d = a +( b) b ⇒ Vetoroposto 328

SOMA

ApêndiceB:Vetores 329

Vetoresunitários Vetoresquetêmmódulosiguaisa

eapontamparaumadeterminadadireção. Coordenadascartesianas ˆ i ˆ j ˆ k x y z |ˆ i| = | ˆ j| = | ˆ k| = 1 ˆ i ⊥ ˆ j ⊥ ˆ k Coordenadaspolares ˆ r ˆ θ θ r y x | ˆ r| = | ˆ θ | = 1 ˆ r ⊥ ˆ θ r = r ˆ r r = x ˆ i + y ˆ j r = r cos θ ˆ i + r sin θ ˆ j ˆ θ = sin θ ˆ i + cos θ ˆ j Coordenadascilíndricas θ ρ P P = P(ρ,θ,z) x y z ˆ k ˆ ρ ˆ θ θ x y z

B.2.2

ρ , θ

cujoslimitessão 0 ≤ ρ < ∞ 0 ≤ θ ≤ 2π ∞ < z < ∞

FiguraB.1:

Coordenadascilíndricas. Umponto P emcoordenadascilíndricasédeﬁnidopelascoordenadas(

)

Oponto P podeserlocalizadonoespaçopelovetor

ρ sendoovetorunitárioaolongodoraioedadopor

B.2.3

Acomponentedeumvetor A éaprojeçãodessevetoraolongodeumadada direção.NaFig.B.2ovetor A noespaçotemcomocomponentescartesianas

Componentesdeumvetor.

NaFig.B.3ovetor A noplano xy temadireçãodeﬁnidapeloângulo θ esuas componentes x e y são

sendo θ adireçãodovetor A emrelaçãodoeixo x.

330 Mecânica

r = ρ ˆ ρ + z ˆ k com ˆ

ˆ ρ = cos θ ˆ i + sin θ ˆ j

Componentescartesianasdeumvetor

Ax, Ay e Az. z y x A Az ˆ k Ay ˆ j Ax ˆ i O

FiguraB.2:

Ax = A cos θ Ay = A sin θ

Oprodutoentrevetorespodeserfeitodeduasformasdistintas,quesãochamadas deprodutoescalareprodutovetorial.Adiferençafundamentalentreeleséque oprodutoescalartemcomoresultadoumescalarquepodeserpositivo,negativo ounulo,jáoprodutovetorialtemcomoresultadoumvetor.

ApêndiceB:Vetores 331 x y A Ax ˆ i Ay ˆ j O θ FiguraB.3: Componentesdeumvetornoplano

. Omódulodovetor A édadopor A = A2 x + A2 y eadireçãodovetor A édadapor tan θ = Ay Ax B.2.4 Somaesubtraçãodevetoresalgebricamente Dadososvetores A = Ax ˆ i + Ay ˆ j + Az ˆ k B = Bx ˆ i + By ˆ j + Bz ˆ k emcoordenadascartesianas,asomaeasubtraçãoentresosvetores A e B são determinadaspor A + B =(Ax + Bx)ˆ i +(Ay + By) ˆ j +(Az + Bz) ˆ k A B =(Ax Bx)ˆ i +(Ay By) ˆ j +(Az Bz) ˆ k B.2.5 Produtoentrevetores

Mecânica é um livro que apresenta os conceitos descritos pelas leis de Newton. Os assuntos relacionados à mecânica Newtoniana são tratados de forma continuada diferentemente das obras tradicionais em que os assuntos são abordados de forma seccionada. Isso permite ao estudante/leitor perceber ao longo do livro as conexões entre os diferentes assuntos desenvolvidos.

O livro contém exercícios resolvidos e exercícios para cada assunto desenvolvido. Além disso, há um conjunto de problemas no final de cada capítulo com diferentes níveis de aprofundamento. Para os exercícios propostos, assim como para os problemas do final de cada capítulo, são apresentadas as respostas.

Por fim, utiliza-se o formalismo matemático adequado e de forma objetiva ao tratar o conteúdo da obra. Com o objetivo de auxiliar o estudante/leitor, um conjunto de apêndices com a descrição de conceitos fundamentais de matemática elementar, vetores e de cálculo diferencial e integral é apresentado no final do livro.

Ivan de Oliveira

www.blucher.com.br