Vetores e Geometria Analítica

VETORES E GEOMETRIA ANALÍTICA

Do seu jeito

VETORESEGEOMETRIAANALÍTICA

Doseujeito

Vetoresegeometriaanalítica:doseujeito

©2022TuannyMaciel

EditoraEdgardBlucherLtda.

Publisher EdgardBlücher

Editor EduardoBlücher

Coordenaçãoeditorial JonatasEliakim

Produçãoeditorial ArianaCorrêa

Revisãodetexto MaurícioKatayama Capa LeandroCunha

Imagemdacapa iStockphoto

Blucher

RuaPedrosoAlvarenga,1245,4ºandar 04531-934SãoPauloSPBrasil Tel55113078-5366 contato@blucher.com.br www.blucher.com.br

SegundoNovoAcordoOrtográfico,conforme 6.ed.do VocabulárioOrtográficodaLíngua Portuguesa,AcademiaBrasileiradeLetras, 21dejulhode2021.

Éproibidaareproduçãototalouparcialpor quaisquermeios,semautorizaçãoescritada Editora. TodososdireitosreservadospelaEditora EdgardBlücherLtda.

DadosInternacionaisdeCatalogaçãona

Publicação(CIP)AngélicaIlacquaCRB-8/7057

Maciel,Tuanny

Vetoresegeometriaanalítica:doseujeito/ TuannyMaciel.–SãoPaulo:Blucher,2022. 128p.:il. Bibliografia ISBN978-65-5506-400-1(impresso)

1.Geometriaanalítica2.Cálculovetorial I.Título. 22-5490 CDD516

Índiceparacatálogosistemático: 1.Geometriaanalítica

Capítulo1

Vetores

Nestecapítuloapresentaremosumelementodefundamentalimportânciaparaonosso estudo: ovetor.Estaremosinteressadosemdefiniroqueentenderemosporumvetor, bemcomoapresentarpropriedadeseoperaçõesentrevetores,sejadeformageométrica oualgébrica.

1.1Vetores

1.1.1Definição

Valeapenainiciarnossadiscussãoapartirdoconceitodegrandezafísica,quepode serentendidacomoalgumapropriedadequesepodemediremumfenômenofísico. Porexemplo,seestamosestudandoomovimentoemdeterminadosistema,podemos medirpropriedadescomootempo,comprimentoouamassa.Estasúltimaspropriedades podemsermedidasquantitativamenteecadaumadessaspropriedadesmensuráveisé chamadadegrandezafísica.

Porsuavez,algumasdessaspropriedadespodemserdefinidascompletamentea partirdeumnúmeroedeumaunidadedemedida:aessastaischamamos grandezas

escalares.Adefiniçãocompletadeoutrasgrandezasdependedaapresentaçãodonúmero, daunidadedemedidaedeumaorientaçãoparaagrandeza;aessastaisnóschamamos grandezasvetoriais.

Otempo,aárea,ovolumeeatemperaturasãoalgunsexemplosdegrandezas escalares.Poroutrolado,velocidade,aceleraçãoeforçasãoexemplosdegrandezas vetoriais.Estaremosinteressadosnoestudodevetores,quesãograndezasvetoriais. Antesdedefiniroqueentenderemosporumvetor,apresentaremosalgumasdefinições.

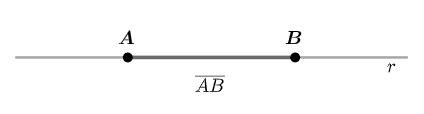
Definição1. Sejamdoispontos �� e �� arbitrários,quedeterminamumareta ��.Chamamos desegmento,edenotamospor ����,aoconjuntodepontosdareta �� compreendidosentre ospontos �� e ��

Figura1.1:Segmentodereta

Observação: Ossegmentos ���� e ���� sãoiguais;jáque,pordefinição,representamo mesmoconjuntodepontos.

Estabeleceremosaquiadefiniçãodeum segmentoorientado. Definição2. Sejamdoispontos �� e �� arbitrários,quedeterminamumareta ��.Definimos umsegmentoderetaorientado,ouapenassegmentoorientado, −−→ ����,comosendoo segmentoquetemcomopontoinicialoponto �� ecomopontofinaloponto ��.Noteque estamosestabelecendoospontosondecomeçaeterminaosegmento.Comisto,estamos dandoumaorientaçãoaosegmento.

Observação: Notequeossegmentosorientados −−→ ���� ≠ −−→ ����.

Agorajáconseguimosidentificarsegmentosquetêmmesmadireçãoetambém compararaorientaçãodesegmentosorientados,istoé,compararosentidodossegmentos.

Capítulo2

Produtoentrevetores

Estamosinteressadosemestudarosprodutosentrevetores,asaber: oprodutointerno ou produtoescalar,oprodutovetorial e oprodutomisto.Paracadaprodutoteremosuma interpretaçãogeométrica,quenosajudanocálculodedimensõesdecomprimento,área evolumes,adependerdoprodutoutilizado.

P.3 ��(�� · ��) = (����)· �� = �� ·(����);

P.4 �� · �� = |��|2,ouainda, |��| = √�� · ��.

Adefiniçãopresenteem(2.1)representaoprodutoescalarentreosvetores �� e �� emsuaformaalgébrica.Outrapossibilidadeétrabalharcomumadefiniçãodecaráter geométricoparaoprodutoescalar,representadapor: �� · �� = |��||��| cos ��, (2.2) onde �� éoânguloentre �� e ��,talque 0◦ ≤ �� ≤ 180◦ .

Podemosobteraexpressão(2.2),ouseja,ovalordoprodutoescalarentredois vetores,apartirdousodaleidoscossenosedapropriedade ��.4.Assim,apartirdalei doscossenostemos: |�� − ��|2 = |��|2 +|��|2 2|��||��| cos ��, (2.3) edapropriedadeP.4, |�� − ��|2 = (�� − ��)·(�� − ��) = |��|2 +|��|2 2�� · ��. (2.4)

Assim,considerandoasequações(2.3)e(2.4),eascomparando,obtemos(2.2). Observação: Utilizandoaspropriedadesdoprodutointerno,sãoválidasasrelações |�� + ��|2 = (�� + ��)·(�� + ��) = |��|2 +|��|2 2�� · �� e |�� − ��|2 = (�� − ��)·(�� − ��) = |��|2 +|��|2 2�� · ��.

Capítulo3

Areta

Asnoçõesprimitivasdeponto,retaeplanosãoaceitassemumadefiniçãoformal, levandoemconsideraçãoaintuiçãogeométricadecadaum.Valeressaltarqueanoçãode retaédeextremaimportânciaparaosurgimentodageometriaeuclidiana,asaber,pelos postuladosdeEuclides.Ageometriaeuclidiana,porsuavez,podeserrepresentada deformaalgébrica,atravésdosrecursosdageometriaanalítica,facilitandoinúmeros processosecriandonovastécnicas.

Nageometriaanalítica,umdostópicosabordadoséo estudodareta.Abordando conceitos,propriedades,representaçãoalgébricaegeométricaerelacionandotantocom oplano R2 quantocomoespaço R3

3.1Asequaçõesdareta

Parainiciarmosnossoestudo,vamossuporumpontonoespaço R3,digamos ��(��0,��0,��0),eumvetor �� = (��,��,��).Observeaimagemabaixo:

Figura3.1

Oquedeveriaacontecerparaqueumponto ��(��,��,��) pertençaaumareta,digamos ��,quecontenhaoponto �� equetenhasidoconstruídanadireçãodovetor �� ? Observeafiguraabaixo:

Figura3.2:Reta �� nadireçãodovetor ��

Dosconceitosjáestabelecidosanteriormentecomoestudodevetores,um ponto �� ∈ R3 pertenceráàreta �� se,esomentese,ovetor �� forparaleloaovetor construído −−→ ����.Emsímbolos,

Capítulo4

Oplano

Nestecapítuloestaremosinteressadosemdefiniroqueentenderemospor plano. Podemoslembrardadefiniçãoquenosfoidadanosprimeirosanosdeescola,quando, namaioriadoscasos,eleeradefinidocomosendooconjuntoderetas.Sendoassim, podemosimaginaroesboçogeométricodeumplanocomosendoo“pedaço”deuma folhadepapel(sedesprezássemosaespessuradafolha),comooquadrodasalaoucomo umaparededasuacasa.Éinteressantequetenhamosumreferencial,poisfacilitarána interpretaçãonoestudodeplanos.Emborasaibamosqueessarepresentaçãosejainfinita, podemosesboçargeometricamentecomo:

4.1Asequaçõesdoplano

Assimcomofoifeitonocapítuloanteriorparaoestudodareta,apresentaremos asformasderepresentaçãodaequaçãodeumplano.Asaber,épossíveldeterminar algebricamenteatravésde:umpontoeumvetor,umpontoedoisvetoresouaindapor trêspontosnãocolineares.

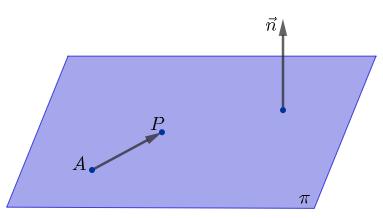
Paracomeçarmos,suponhamosumponto ��(��0,��0,��0)∈ R3 pertencenteaumplano ��,comonafiguraabaixo,eumvetornormal(ortogonal)aoplano,digamos, �� = (��,��,��).

Figura4.2

Oquequeremosencontraréumacondiçãoparaqueumponto ��(��,��,��) pertençaao plano. Istoé,oqueénecessáriopara �� ∈ �� ? Noteque,comoospontos �� e �� pertencemaoplano ��,entãoovetorformadopor eles,digamos, −−→ ����,tambémpertencerá.Assim,se �� ⊥ ��,então �� ⊥ −−→ ����. Porém,dizerque �� ⊥ −−→ ���� éomesmoquedizerqueoprodutointernoentreelesénulo. Emsímbolos, �� · −−→ ���� = 0 (4.1) Logo,como −−→

temos: (��,��,��)·(�� ��0,�� ��0,�� ��0) = 0 ⇔ ��(�� ��0)+ ��(�� ��0)+ ��(�� ��0) = 0.

Capítulo5

Cônicas

Inúmerasatividadespresentesnonossocotidianopodemserexemplosdouso, mesmoqueinconsciente,dascônicas.Sejanaanálisedeumsimpleslançamentode umabolaemumjogodefutebol,naobservaçãodeantenasquetransmitemsinaisde televisão,telefoneouinternet,queseriamrepresentaçõesdetrajetóriasparabólicas,ou atémesmoemsituaçõesumpoucomaisrebuscadas,comoestudosmaisespecíficos naastronomia,observandoatrajetóriadosasteroidesecometas,quepodemdescrever trajetóriashiperbólicasouelípticas.

Circunferência,elipse,hipérboleeparábolaserãoas cônicas queestudaremosneste capítulo.Podemosvisualizaressasquatrocônicaspormeiode“cortes”feitosporum planoqueintersectaasuperfíciedeumconeduploderevolução,conformemostradona figuraaseguir.

Figura5.1:Superfíciecônica

Notequeoplanopodeintersectaroconeduploderevolução(oqualtambém chamaremosdesuperfíciecônica)deformasdistintas,e,adependerdoângulode inclinação,doplanocomageratrizdoconeduploderevolução,teremosdiferentes cônicas.Quedefinimoscomosendoolugargeométricodoplanoquesurgiuapósfeitaa interseção.

Nestecapítuloabordaremosasequaçõesquecaracterizamdiferentescônicas, discutindosuascaracterísticas,bemcomoaapresentaçãodesuasequaçõesgerale reduzidaearepresentaçãogeométricadecadauma.

cônica édefinidapelaequação

Ouseja,umacônicaéolugargeométricoformadopeloconjuntodosparesordenados

Capítulo6

Quádricas

Nocapítuloanteriorabordamosascônicas,eaquiestamosinteressadosemestudar oqueacontececomumacônicaemcasoderotaçãoemtornodeumdeterminadoeixo. Comissoteremossuperfícies,asquaisdenominaremosde quádricas.Todaquádrica será,algebricamente,representadaporumaequaçãodosegundograunasvariáveis ��, �� e ��,e,alémdisso,asquádricasserãocaracterizadascomosuperfíciesderevolução, cilíndricas,esféricas,parabólicas,hiperbólicasoucomocone,adependerdaequação queapresentar.

6.1Aequação

Umaquádrica,ousuperfíciequádrica,éumasuperfícieformadapeloconjuntode pontos ��(��,��,��)∈ R3 quesatisfazaequaçãodosegundograu,nasvariáveis ��, �� e ��, dadapor: ����2 + ����2 + ����2 + ������ + ������ + ������ + ���� + ���� + ���� + �� = 0 (6.1) Observequepelomenosumdostermos(coeficientes) ��,��,��,��,�� ou �� deveráser nãonulo.

Nossoobjetivoéestudareclassificarasquádricasapartirdeinterseçõescom planos1,emespecialcomosplanoscoordenados.Dessaformaesperamosreconhecer oselementosdecadaquádricaevisualizá-lasnoespaço.Paraisso,apresentamosalguns exemplos.

Exemplo28. Aequação ��2 + ��2 + ��2 + 6�� 4�� 12 = 0 representaumaesferadecentro ��(−3, 2, 0).

Solução: Defato,utilizandoocompletamentodequadradosparacadavariável ��, �� e ��,temos (�� + 3)2 9 +(�� 2)2 4 + �� 2 12 = 0. Implicando (�� + 3)2 +(�� 2)2 + �� 2 = 25.

Assim,faremosinterseçõescomosplanoscoordenados ��1 : �� = 0, ��1 : �� = 0 e ��3 : �� = 0,buscandoreconhecercônicasapartirdaequaçãoencontrada.Emoutras palavras,busca-seidentificareclassificaraquádricaapartirdarotaçãodecônicas. Logo,apartirdainterseçãocomoplano ��1 : �� = 0,tem-se (�� 2)2 + �� 2 = 25,

querepresentaumacircunferência,noplano ����,decentro (2, 0) eraio 5,dadapela equaçãoacima.Demodoanálogo,fazendoainterseçãocomoplano ��2 : �� = 0 ,teremos aequaçãodeumacircunferêncianoplano ����,centradaem (−3, 0) eraio 5,dadapela equação (�� + 3)2 + �� 2 = 25. E,porfim,tomandoainterseçãocomoplanocoordenado ��3 : �� = 0,também

1Valeressaltarquepoderemosterounãointerseções,então,emborautilizemosapalavrainterseção, estaremosanalisandoaprojeçãodacurvanoplanoescolhido.

Esta obra foi pensada, em especial, para os alunos que cursam a disciplina de Geometria Analítica. Aborda os conteúdos de vetores e operações, produtos interno, vetorial e produto misto, retas e planos, além de temas sobre cônicas e algumas quádricas especiais. Em todos os temas, busca-se trazer ao leitor tanto uma interpretação geométrica como uma interpretação algébrica.

Além dos assuntos já conhecidos por tantos livros e materiais de geometria analítica, este livro trata os conteúdos de forma didática. A ideia, aqui, vai além de apresentar os conteúdos de maneira formal e com rigor matemático, em geral, apresentado em outras bibliografias, oferecendo aos leitores uma espécie de manual para consultas rápidas, por meio de perguntas e respostas estabelecidas ao longo do texto, favorecendo o entendimento do leitor e contribuindo para que ele consiga resolver outras questões sobre os conteúdos abordados, sempre utilizando de uma linguagem simples e mais próxima da linguagem do aluno.