CLAVES DEL PROYECTO
Situaciones de aprendizaje
Ofrecemos contextos actuales, vitales y emocionales conocidos por el alumnado, que plantean un reto o un problema cuya resolución creativa implica realizar distintas tareas y actividades que vehiculan las competencias específicas, los criterios de evaluación y los saberes básicos propios del área. Las programaciones didácticas de las situaciones de aprendizaje se ajustan a la plantilla modelo de la Junta de Andalucía (Instrucción 1/2022, de 23 de junio).
Objetivos de Desarrollo Sostenible
Sensibilizamos al alumnado en relación con los Objetivos de Desarrollo Sostenible por medio de las situaciones de aprendizaje, para que emprendan acciones responsables y que contribuyan a la creación de sociedades participativas comprometidas, sostenibles e igualitarias.
2 ZZ ESO MATEMÁTICAS
03 04 05 06 08 10 11 12 14 17 18 19 20 21 22
Cultura andaluza
Presentamos la cultura andaluza para que sea conocida, valorada y respetada como patrimonio propio y en el marco de la cultura española: el flamenco, mitos y leyendas, autores, la modalidad lingüística andaluza…
Evaluación competencial
Damos respuesta a la evaluación de las competencias específicas del área y de las competencias clave del perfil de salida del alumnado a lo largo de la situación de aprendizaje planteada, conectando los indicadores de desempeño de la asignatura con los criterios de evaluación del currículum.
El alumno, agente de su propio aprendizaje
Profesor en casa
Incorporamos ejercicios resueltos y tutoriales para consolidar los contenidos de la materia.
Solucionario extendido
La propuesta didáctica incluye el solucionario extendido con el desarrollo de todas las actividades.
Abierto al trabajo colaborativo
Empoderamos al alumnado con sentido de la iniciativa, fomentamos la creatividad y promovemos una relación activa con las matemáticas.



Prepárate
Para activar conocimientos previos a partir de una dinámica de gamificación.

Facilitamos un aprendizaje continuo y formativo a partir del itinerario Prepárate-Mejora-Ponte a prueba basado en la neurociencia, que vertebra cada situación de aprendizaje.

Mejora
Para reforzar o ampliar los saberes básicos y las competencias específicas del área.

Ponte a prueba Para autoevaluarse.











Quien tiene el código tiene la llave













ZZ ESO MATEMÁTICAS
,










Matemáticas 1
Libro del alumnado
ISBN papel: 978-84-218-8181-1
ISBN digital: 978-84-218-8083-8 ¡NOVEDAD!
Matemáticas 2
Libro del alumnado
ISBN papel: 978-84-218-8182-8
ISBN digital: 978-84-218-8084-5 ¡NOVEDAD!
Matemáticas 3
Libro del alumnado
ISBN papel: 978-84-218-8183-5
ISBN digital: 978-84-218-8085-2 ¡NOVEDAD!
Matemáticas 4A
Libro del alumnado
ISBN papel: 978-84-218-8184-2
ISBN digital: 978-84-218-8086-9
PRÓXIMAMENTE
Matemáticas 4B
Libro del alumnado
ISBN papel: 978-84-218-8014-2
ISBN digital: 978-84-218-8087-6
PRÓXIMAMENTE
4 ESO MATEMÁTICAS MATERIAL DEL ALUMNADO
El proyecto de Matemáticas incluye más de 100 recursos multimedia con finalidades distintas:
• Vídeos «Profesor/a en casa»: vídeos tutoriales en los que se ofrecen explicaciones sobre aspectos teóricos y se resuelven ejercicios, a modo de clase particular.


• Recursos interactivos prácticos para crear o consolidar conocimientos.


• Fotografías e ilustraciones técnicas descargables.


• Documentación para realizar actividades.


• Itinerario Prepárate, Mejora y Ponte a prueba para facilitar un aprendizaje continuo y formativo.
Prepárate
Para activar conocimientos previos.

Mejora
Para reforzar o ampliar conocimientos.
Ponte a prueba
Para comprobar el nivel de logros alcanzado.
Consulta los recursos digitales más relevantes que completan el proyecto educativo.
5 ESO MATEMÁTICAS RECURSOS DEL ALUMNADO
1. Presentación de la situación de aprendizaje y del reto
Contexto (personal, escolar, social, científico y humanístico) en el que se van a experimentar las matemáticas, con la finalidad de interpretar, modelizar y resolver problemas tanto de la vida cotidiana como propios de las matemáticas.
Contexto de la unidad
Reto propuesto al finalizar la situación de aprendizaje
«Prepárate»: vídeo para activar conocimientos previos
4. Actividades


Preguntas que vehiculan la situación de aprendizaje

Saberes básicos de los diferentes sentidos matemáticos que se desarrollan en la situación de aprendizaje
Existen dos tipologías de actividades para asegurar la adquisición de las distintas competencias matemáticas: actividades de ejercitación y actividades en contexto. Para atender la diversidad del aula, se dispone del banco digital de actividades autocorregibles Mejora, con propuestas de refuerzo y de ampliación.
Actividades de ejercitación
Banco digital de actividades autocorregibles



Problemas contextualizados que indican la gradación de los procesos matemáticos (PISA) y las habilidades de la competencia matemática
5. Organizo los conceptos
Los saberes básicos se interrelacionan durante todo el curso hasta completar todos los conocimientos, destrezas y actitudes que exige el currículum. De esta manera, los alumnos llegarán a emplear los saberes de una manera funcional y dispondrán de la flexibilidad necesaria para establecerconexiones entre los diferentes sentidosmatemáticos
Resumen de los saberes básicos y sus diferentes sentidos matemáticos



6 ESO MATEMÁTICAS
EL LIBRO DEL ALUMNADO. PASO A PASO
2. Construcción del conocimiento
En cada situación de aprendizaje se plantean dos o tres situaciones reales y de interés para el alumnado, a partir de las cuales se irán construyendo distintos conocimientos matemáticos.
Retos o problemas que el alumnado podrá resolver mediante actividades dirigidas y orientadas



Nuevo conocimiento matemático adquirido para afrontar retos futuros
3. Saberes básicos
Se desarrollan los saberes básicos que integran cada situación de aprendizaje mediante ejemplos resueltos, ilustraciones y recursos multimedia
Conceptos teóricos básicos para el desarrollo del contenido de cada situación



Vídeos «Profesor/a en casa», en los que se resuelven ejercicios y se explican conceptos básicos
6. Activa tus habilidades y competencias
Actividades de evaluación por competencias específicas y criterios de evaluación, conectadas con los descriptores del perfil de salida del alumnado


3 propuestas de pensamiento computacional

Producto final de la situación de aprendizaje
3 proyectos por curso
7 ESO MATEMÁTICAS EL LIBRO DEL ALUMNADO. PASO A PASO
+
Matemáticas 3
SITUACIONES DE APRENDIZAJE
1 Campamento de verano
1 Diversión a raudales
2 Actividades al aire libre
3 MasterMate
2 Naturaleza matemática
1 Números grandes y pequeños
2 Irracionales y naturales
3 Patrones
4 ¿Jardines matemáticos?
3 En movimiento
1 Ecuaciones viajeras
2 Movimientos para todo
3 De viaje
Socioafectivo
• Fases y tareas de un estudio estadístico
• Métodos de selección de una muestra estadística
SENTIDOS MATEMÁTICOS
Numérico
• Representación de números en la recta real. Intervalos
• Transformación de fracciones en decimales y viceversa
• Números exactos y periódicos. Fracción generatriz
• Operaciones con fracciones y decimales. Cálculo aproximado y redondeo. Cifras
• Jerarquía de las operaciones
• Investigación de regularidades, relaciones y propiedades que aparecen en conjuntos de números
• Patrones
4 Historias matemáticas
1 ¿Qué es una raíz?
2 Figuras perfectas
3 Laplace y la equiprobabilidad
5 Tiempo libre y ocio
1 ¡A montar en las atracciones!
2 Don Quijote de las matemáticas
3 Juegos y tiempo libre
6 El mundo de la publicidad
1 Negocios
2 Artes gráficas
3 El precio de la publicidad
• Utilización de las funciones cuadráticas para representar situaciones de la vida cotidiana
• Potencias de números racionales con exponente entero. Significado y uso
• Potencias de base 10. Aplicación para la expresión de números muy pequeños
• Operaciones con números expresados en notación científica
• Operaciones con fracciones y decimales. Cálculo aproximado y redondeo
• Raíces cuadradas
• Raíces no exactas. Expresión decimal
• Representación de números en la recta real
• Expresiones radicales: transformación y operaciones
• Jerarquía de operaciones
• Cálculo aproximado y redondeo. Cifras significativas. Error absoluto y relativo
Pensamiento computacional
• Experiencias aleatorias simples y compuestas en casos sencillos
• Utilización de la probabilidad para tomar decisiones fundamentadas en diferentes contextos
• Utilización de la probabilidad para tomar decisiones fundamentadas en diferentes contextos
• La calculadora
• Polígonos. Circunferencia y círculo. Perímetro y área
• Escalas
• Áreas y volúmenes de cuerpos geométricos
• Análisis de una situación a partir del estudio de las características locales y globales de la gráfica
• Interpretación conjunta de la media y la desviación típica
• Operaciones con fracciones y decimales
• Raíces cuadradas
• Raíces no exactas. Expresión decimal
• Escalas
Pensamiento
8 ESO MATEMÁTICAS EL LIBRO DEL ALUMNADO. CONTENIDO
Medida
ODS 15 ODS 13
computacional • Excel
SENTIDOS MATEMÁTICOS
Espacial Algebraico Estocástico
• Análisis y descripción cualitativa de gráficas que representan fenómenos del entorno cotidiano y de otras materias
• Análisis de una situación a partir del estudio de las características locales y globales de la gráfica correspondiente
• Análisis y comparación de situaciones de dependencia funcional dadas mediante tablas y enunciados
• Utilización de modelos lineales para estudiar situaciones de los diferentes ámbitos de conocimiento y de la vida cotidiana, mediante la confección de tablas, la representación gráfica y la obtención de expresiones algebraicas
• Fases y tareas de un estudio estadístico
• Población, muestra
• Variables estadísticas: cualitativas, discretas y continuas
• Métodos de selección de una muestra estadística
• Representatividad de una muestra
• Frecuencias absolutas, relativas y acumuladas
• Parámetros de posición. Cálculo, interpretación y propiedades
• Polígonos Circunferencia y círculo. Perímetro y área
• Poliedros, poliedros regulares. Vértices, aristas y caras
• Cilindro, cono, tronco de cono. La esfera
• Traslaciones, giros y simetrías en el plano
• Frisos y mosaicos
• Investigación de regularidades, relaciones y propiedades que aparecen en conjuntos de números
• Expresión usando lenguaje algebraico
• Sucesiones numéricas. Sucesiones recurrentes. Progresiones aritméticas y geométricas
• Ecuaciones de primer grado con una incógnita. Resolución por el método algebraico
• Sistemas de ecuaciones. Resolución por el método de sustitución, de igualación y de reducción
• Resolución de problemas mediante la utilización de ecuaciones de primer grado y de sistemas de ecuaciones
• Funciones cuadráticas. Representación gráfica
• Utilización de las funciones cuadráticas para representar situaciones de la vida cotidiana
• Reconocimiento de las funciones de proporcionalidad inversa: aplicaciones a contextos y situaciones reales
• Asíntotas
• Poliedros, poliedros regulares. Vértices, aristas y caras. Teorema de Euler
• Planos de simetría en los poliedros
Pensamiento computacional • La calculadora
• Polinomios. Transformación de expresiones algebraicas
• Operaciones elementales con polinomios
• Igualdades notables
• Resolución de ecuaciones sencillas de grado superior a 2
• Teorema de Tales
• Aplicación a la resolución de problemas
• Uso de las nuevas tecnologías para estudiar formas, configuraciones y relaciones geométricas
• Ecuaciones de segundo grado con una incógnita. Resolución de ecuaciones de segundo grado por el método algebraico
• Resolución de problemas con ecuaciones de segundo grado
• Progresiones aritméticas y geométricas
• Resolución de ecuaciones sencillas de grado superior a 2
• Análisis y descripción cualitativa de gráficas que representan fenómenos del entorno cotidiano y de otras materias
• Análisis de una situación a partir del estudio de las características locales y globales de la gráfica
• Análisis y comparación de situaciones de dependencia funcional dadas mediante tablas y enunciados
• Utilización de modelos lineales para estudiar situaciones provenientes de los diferentes ámbitos de conocimiento y de la vida cotidiana
• Expresiones de la ecuación de la recta
• Funciones cuadráticas. Representación gráfica
• Utilización para representar situaciones de la vida cotidiana
• Función de proporcionalidad inversa. Asíntotas
• Uso de las nuevas tecnologías para estudiar formas, configuraciones y relaciones geométricas
Pensamiento computacional • Excel
• Experiencias aleatorias simples y compuestas en casos sencillos
• Sucesos y espacio muestral
• Cálculo de probabilidades mediante la regla de Laplace
• Diagramas de árbol sencillos
• Permutaciones. Factorial de un número
• Utilización de la probabilidad para tomar decisiones fundamentadas en diferentes contextos
• Cálculo de probabilidades mediante la regla de Laplace
• Diagramas de árbol sencillos
• Permutaciones. Factorial de un número
• Utilización de la probabilidad para tomar decisiones fundamentadas en diferentes contextos
• Frecuencias. Agrupación de datos en intervalos
• Análisis y comparación de situaciones de dependencia funcional dadas mediante tablas y enunciados
• Gráficas estadísticas
• Parámetros de posición y de dispersión. Diagrama de caja y bigotes
• Interpretación conjunta de la media y la desviación típica
Conoce las situaciones de aprendizaje del proyecto.
9 ESO MATEMÁTICAS EL LIBRO DEL ALUMNADO. CONTENIDO
SITUACIONES DE APRENDIZAJE
7 Los números te cuidan
1 La dosis exacta
2 Lati2 del corazón
8 Arquitectura matemática
1 ¡Construyendo catedrales!
2 De las pirámides a la actualidad
3 Arquitectura icónica en el mundo
SENTIDOS MATEMÁTICOS Socioafectivo Numérico
• Análisis y descripción cualitativa de gráficas que representan fenómenos del entorno cotidiano y de otros ámbitos
• Análisis de una situación a partir del estudio de las características locales y globales de la gráfica correspondiente
• Uso de modelos para estudiar situaciones de los diferentes ámbitos de conocimiento y de la vida cotidiana, mediante la confección de tablas, la representación gráfica y la obtención de la expresión algebraica
• Gráficas estadísticas: interpretación y propiedades
• Potencias de números racionales con exponente entero. Significado y uso
• Potencias de base 10. Aplicación para la expresión de números muy pequeños
• Operaciones con números expresados en notación científica
• Decimales y fracciones. Fracción generatriz
• Proporcionalidad compuesta
• Porcentajes encadenados
9 Comer con cabeza
1 Nutrientes
2 Dietas
3 Ni tan gordo ni tan delgado
• Fases y tareas de un estudio estadístico
• Experiencias aleatorias simples y compuestas en casos sencillos
• Expresiones radicales: transformación y operaciones. Jerarquía de operaciones
• Polinomios. Transformación de expresiones algebraicas. Operaciones elementales con polinomios
• Igualdades notables
• Operaciones con fracciones y decimales
• Cálculo aproximado y redondeo. Cifras significativas
• Error absoluto y error relativo
• Cálculo de porcentajes
Pensamiento computacional • Symbolab
Proyecto 1 · La guapura está en las mates
Proyecto 2 · ¿Cómo éramos y cómo seremos?
Proyecto 3 · Este mundo es una función
• Teorema de Tales. Aplicación a la resolución de problemas
10 ESO MATEMÁTICAS EL LIBRO DEL ALUMNADO. CONTENIDO
Medida
ODS 3 ODS 3 ODS 9
SENTIDOS MATEMÁTICOS
Espacial Algebraico
• Ecuaciones de primer y segundo grado con una incógnita.
• Análisis y descripción cualitativa de gráficas que representan fenómenos del entorno cotidiano y de otros ámbitos
• Análisis de una situación a partir del estudio de las características locales y globales de la gráfica correspondiente
• Análisis y comparación de situaciones de dependencia funcional dadas mediante tablas y enunciados
• Uso de modelos para estudiar situaciones de los diferentes ámbitos de conocimiento y de la vida cotidiana, mediante la confección de tablas, la representación gráfica y la obtención de la expresión algebraica
• Función de proporcionalidad inversa. Asíntotas
• Geometría del plano
• Teorema de Tales. Aplicación a la resolución de problemas. División de un segmento en partes proporcionales
• Traslaciones, giros y simetrías en el plano
• Lugar geométrico: cónicas
• La esfera. El globo terráqueo. Coordenadas geográficas y husos horarios. Longitud y latitud de un punto
• Sucesiones numéricas. Sucesiones recurrentes.Progresiones aritméticas y geométricas
• Polinomios. Transformación de expresiones algebraicas
• Funciones cuadráticas. Representación gráfica
• Función de proporcionalidad inversa. Representación gráfica
Estocástico
• Sucesiones numéricas. Sucesiones recurrentes. Progresiones aritméticas y geométricas
• Polinomios. Transformación de expresiones algebraicas
• Operaciones elementales con polinomios
• Ecuaciones de primer y segundo grado con una incógnita. Resolución por el método algebraico y gráfico de ecuaciones de primer grado. Resolución de problemas mediante el uso de ecuaciones de primer grado y de sistemas de ecuaciones
Pensamiento computacional • Symbolab
Proyecto 1 · La guapura está en las mates
Proyecto 2 · ¿Cómo éramos y cómo seremos?
Proyecto 3 · Este mundo es una función
Fases y tareas de un estudio estadístico. Población, muestra
• Métodos de selección de una muestra estadística. Representatividad de una muestra
• Frecuencias absolutas, relativas y acumuladas
• Experiencias aleatorias simples y compuestas en casos sencillos
• Cálculo de probabilidades mediante la regla de Laplace
• Diagramas de árbol sencillos
• Probabilidad condicionada
Conoce las situaciones de aprendizaje del proyecto.
11 ESO MATEMÁTICAS EL LIBRO DEL ALUMNADO. CONTENIDO










Matemáticas 1
Propuesta didáctica
ISBN papel: 978-84-218-7522-3
ISBN digital: 978-84-218-8083-8 ¡NOVEDAD!
Matemáticas 2
Propuesta didáctica
ISBN papel: 978-84-218-7526-1
ISBN digital: 978-84-218-8084-5
PRÓXIMAMENTE
Matemáticas 3
Propuesta didáctica
ISBN papel: 978-84-218-7524-7
ISBN digital: 978-84-218-8085-2 ¡NOVEDAD!
Matemáticas 4A
Propuesta didáctica
ISBN papel: 978-84-218-7528-5
ISBN digital: 978-84-218-8086-9
PRÓXIMAMENTE
Matemáticas 4B
Propuesta didáctica
ISBN papel: 978-84-218-7809-5
ISBN digital: 978-84-218-8087-6
PRÓXIMAMENTE
ADAPTACIÓN CURRICULAR
Aprende lo básico, material de adaptación curricular.
• Cuaderno para el docente en formato fotocopiable, para que los alumnos con necesidades educativas especiales puedan trabajar los mismos contenidos del libro del alumnado pero en un nivel básico.
• Planifica y ajusta los contenidos siguiendo la metodología del libro del alumnado.
• Incluye solucionario










12 ESO MATEMÁTICAS MATERIAL DEL DOCENTE
LOS RECURSOS DIDÁCTICOS
• Plantilla con el diseño de las situaciones de aprendizaje


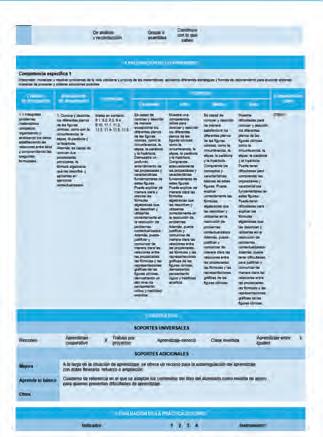



Plantilla adaptada que responde a la Instrucción conjunta 1/2022, de 23 de junio, de la Junta de Andalucía, por la que se establecen aspectos de organización y funcionamiento para los centros que impartan Educación Secundaria Obligatoria para el curso 2022/2023.
• Propuestas de exámenes trimestrales y de unidad por competencias específicas y criterios de evaluación, conectadas con los descriptores del perfil de salida del alumnado.
• Rúbricas de seguimiento.
• Rúbricas de evaluación de las competencias específicas y los descriptores del perfil de salida del alumnado.

• Descripción y finalidad de los recursos digitales
• Gestión de aula en el entorno digital eCasals.
13 ESO MATEMÁTICAS RECURSOS DEL DOCENTE
1. El material de referencia
Para facilitar la evaluación, el docente tiene acceso a material creado para cada asignatura.

La rúbrica proporciona una evaluación cualitativa para que el alumno sea consciente de su aprendizaje y pueda progresar.
4.


La prueba escrita



Indicadores de desempeño asociados a cada criterio de evaluación.
Al finalizar la situación de aprendizaje, se ofrece una prueba escrita como un instrumento de evaluación más. Las activiades que la componen se asocian a un criterio de evaluación y a un descriptor del perfil de salida, que se evalúan con una rúbrica.








5. La evaluación trimestral
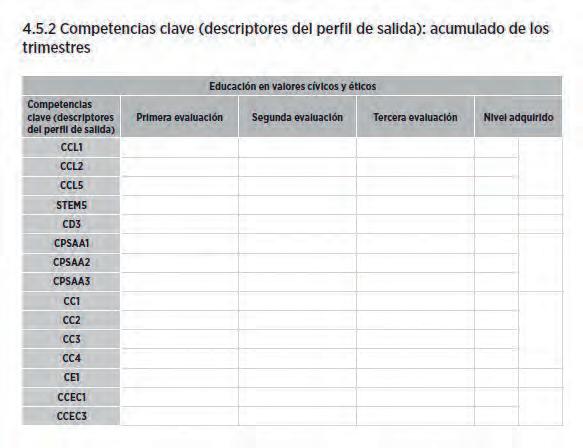
En cada trimestre, el docente dispone de dos pruebas escritas y de las rúbricas para llevar a cabo la evaluación de competencias específicas y de los descriptores del perfil de salida. Se ofrecen dos documentos para registrar la evaluación de las situaciones de aprendizaje abordadas y de la prueba escrita trimestral.

Evaluación de competencias específicas con una propuesta de distribución de porcentajes que permite una nota cuantitativa.
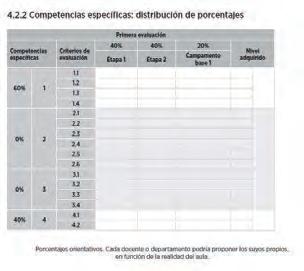

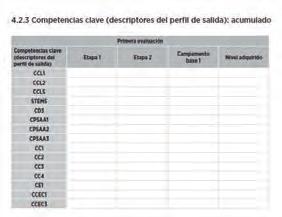


Evaluación de competencias clave.
14 ESO MATEMÁTICAS EVALUACIÓN COMPETENCIAL. PASO A PASO
2. Doble evaluación: de competencias específicas y de competencias clave
A partir del material de referencia, el docente evalúa con las evidencias (actividades) que ofrece la editorial. No obstante, puede incorporar sus propias actividades a la evaluación.
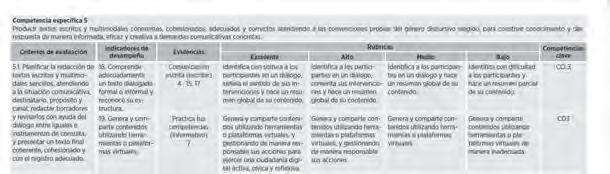


3. Evaluación de la situación de aprendizaje
En la programación de la situación de aprendizaje se especifican las competencias específicas y los descriptores del perfil de salida que se evalúan.

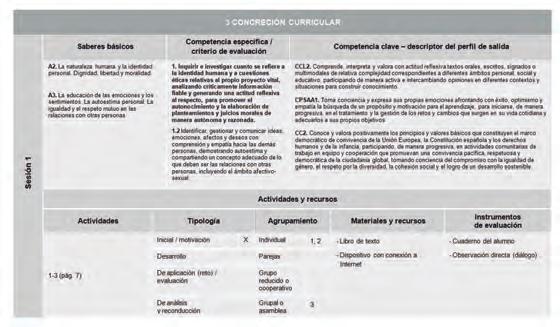


Cada sesión lleva asociados los criterios de evaluación y los descriptores del perfil de salida.
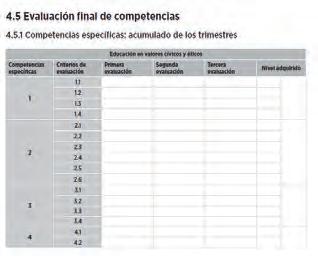
6. Evaluación final de competencias

Cuadro sinóptico para las actividades de creación propia que conecta los descriptores operativos del perfil de salida y las competencias específicas del área.



Competencias

específicas: rúbricas (evaluación cualitativa)
Una vez evaluado cada trimestre, se registra el acumulado de la evaluación en dos documentos.




15 ESO MATEMÁTICAS
, nuestro entorno virtual de aprendizaje
eCasals es el espacio personal del docente donde se ubican todos los recursos, contenidos y herramientas digitales del proyecto Código Abierto LOMLOE.
La plataforma está diseñada específicamente para facilitar la enseñanza y el aprendizaje en el entorno virtual.
Generador de tareas Crea tareas a partir de las actividades disponibles en el libro del alumnado y en la propuesta didáctica. Atiende a la diversidad de tu aula asignando tareas de forma individual. También puedes crear actividades propias con el editor.
Programación propia de Andalucía
Actividades y recursos de la unidad
Todas las actividades del libro resolubles en formato digital (autoevaluables y de respuesta abierta) y los recursos multimedia organizados por unidad.
Recursos del alumnado siempre en abierto.
En el entorno virtual eCasals encontrarás los recursos para ESO y Bachillerato. ¡Nos integramos!
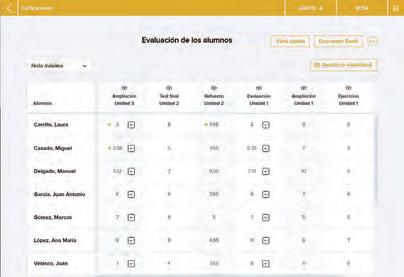
Calificaciones
Puedes visualizar, evaluar y comentar los resultados del alumnado. También puedes exportar todos los resultados en Excel.
Ayuda y contacto
Manuales y tutoriales con los temas de ayuda más frecuentes, contacto con el servicio de soporte técnico y asesoría digital.
• Integración compatible con las principales plataformas EVA. Admite el protocolo Marsupial y LTI.
• Permite compartir el contenido en GoogleClassroom y MicrosoftTeams
• El libro y los recursos están disponibles para la plataforma Blinklearning de acuerdo con sus funcionalidades.


App eCasals off-line




Accede a tu libro digital a través del ordenador o de cualquier otro dispositivo móvil sin necesidad de estar conectado. Disponible para los sistemas Android, iOS, Windows y Chromebook.






ESO MATEMÁTICASECASALS
Evaluación competencial
Selecciona las competencias específicas que quieras evaluar, los criterios de evaluación y los descriptores del perfil de salida asociados. Asigna las actividades correspondientes a tu alumnado y genera informes con sus resultados y el nivel de competencia que han adquirido.
Situaciones de aprendizaje basadas en centros de interés.

Muro, grupo y alumnos
Trabaja con tu alumnado a través de la plataforma creando todos los grupos que necesites. Gestiona a los usuarios y sus contraseñas, y consulta el registro de actividad de cada uno de ellos.
Digiteca
Accede al buscador de recursos digitales vinculados a la materia. Filtra por palabras, libro o tema, y descubre todos los contenidos multimedia.
Carpeta del profesorado
Espacio que te permite incorporar y compartir recursos propios. Añade tus materiales en cualquier formato y consúltalos cuando los necesites.







• Servicio personalizado de asesoramiento y soporte técnico de nuestros materiales y recursos.
• Formación personalizada del entorno digital.
• Webinars formativos a cargo de nuestros asesores digitales.
• Estamos a tu disposición en docencia@editorialcasals.com
17 MATEMÁTICAS
¡Te acompañamos
en todo tu proceso digital!
@
CLAVES DEL PROYECTO
Nuevo proyecto global de Bachillerato
Los autores de la ESO ponen en marcha este innovador proyecto orientado a las pruebas de acceso a la universidad de todas las comunidadesautónomas.
Aprendizaje a través de contextos
Aprendizajes basados en contextos de la vida real y acompañados de una propuesta de actividades y una evaluación creada a partir de las directrices de la LOMLOE.
Actividades con GeoGebra Ejercicios programados con GeoGebra para consolidar los conocimientos. El alumnado podrá investigar, interpretar, analizar y resolver problemas.
Solucionario extendido
La propuesta didáctica incluye el solucionario extendido con el desarrollo de todas las actividades.
Estrategia de resolución de problemas
Banco de actividades y ejercicios resueltos paso a paso para afianzar conceptos y para que el alumnado sea autónomo en su proceso de aprendizaje.
Evaluación competencial
Damos respuesta a la evaluación de las competencias específicas del área y de las competencias clave del perfil de salida del alumnado, conectando los indicadores de desempeño de la asignatura con los criterios de evaluación del currículum.































































19 ZZ BA MATEMÁTICAS
MATERIAL DEL ALIUMNNADO







RECURSOS DEL ALUMNADO

1 BA
Matemáticas
Libro del alumnado
ISBN papel: 978-84-218-7458-5
ISBN digital: 978-84-218-7761-6
1 BA
Matemáticas aplicadas a las ciencias sociales
Libro del alumnado
ISBN papel: 978-84-218-7460-8
ISBN digital: 978-84-218-7763-0
2 BA
Matemáticas
Libro del alumnado
ISBN papel: 978-84-218-7462-2
ISBN digital: 978-84-218-7765-4
2 BA
Matemáticas aplicadas a las ciencias sociales
Libro del alumnado
ISBN papel: 978-84-218-7464-6
ISBN digital: 978-84-218-7767-8
Accede a una muestra digital




El proyecto de Matemáticas incluye más de 100 recursos multimedia con finalidades distintas:
• Vídeos «Profesor/a en casa»: vídeos tutoriales en los que se ofrecen explicaciones de aspectos teóricos y se resuelven ejercicios paso a paso, a modo de clase particular.
• Vídeos «Profesor/a en casa-Paso a paso»: vídeos tutoriales que ofrecen estrategias de resolución de problemas.
• Investigaciones matemáticas: casos de estudio reales donde se aplican los conocimientos adquiridos a lo largo de la unidad.
• «Repasa la unidad»: infografía con los contenidos más importantes de la unidad.
• «Ponte a prueba»: test de autoevaluación para que el alumnado pueda comprobar si ha adquirido los conocimientos de la unidad.
• Itinerario Prepárate, Mejora y Ponte a prueba para facilitar un aprendizaje continuo y formativo.
Prepárate
Para activar conocimientos previos.
Ponte a prueba
Para comprobar el nivel de logros alcanzado. Mejora Actividades autoevaluables con GeoGebra para practicar los contenidos.
20 BA MATEMÁTICAS MATERIAL Y RECURSOS DEL ALUMNADO
MATERIAL DEL DOCENTE MATERIAL Y RECURSOS DEL DOCENTE








RECURSOS DEL DOCENTE
El docente dispone de los siguientes documentos didácticos:
Programación de curso.
Desarrollo de las unidades didácticas:
• Orientaciones didácticas
• Programación de aula
• Solucionario
Propuestas de exámenes trimestrales y de unidad por competencias específicas y criterios de evaluación, que conectan con los descriptores del perfil de salida del alumnado.
1 BA
Matemáticas
Propuesta didáctica
ISBN papel: 978-84-218-7621-3
1 BA
Matemáticas aplicadas a las ciencias sociales
Propuesta didáctica
ISBN papel: 978-84-218-7623-7
2 BA
Matemáticas
Propuesta didáctica
ISBN papel: 978-84-218-7625-1
2 BA
Matemáticas aplicadas a las ciencias sociales
Propuesta didáctica
ISBN papel: 978-84-218-7627-5
Gestión de aula en el entorno digital eCasals.

Descripción y finalidad de los recursos digitales. Tabla de calificaciones del alumnado
Consulta el itinerario de la evaluación competencial en las páginas 12-13 del catálogo.
21 BA MATEMÁTICAS
1. Contextos reales
Aplicación de los saberes básicos que se trabajan en la unidad en diferentes contextos y ámbitos de conocimiento

«Prepárate». Vídeo que introduce la unidad







4. Estrategias de resolución de problemas
Explicación paso a paso de la resolución de problemas asociados a los conceptos y conocimientos de la unidad.
Estrategias de resolución de problemas
Ejemplos resueltos en vídeo
5. Actividades





Ejercicios y problemas para poner en práctica los conocimientos adquiridos a lo largo de toda la unidad.




«Investigación matemática». Casos reales donde se aplican los conocimientos adquiridos en la unidad





22 BA MATEMÁTICAS EL LIBRO DEL ALUMNADO. PASO A PASO 4 A B C D Sistemas de ecuaciones Educativo ¿Qué aspecto tienen los extraterrestres? Aunque Asorraf es un planeta en el que se puede vivir, está completamente deshabitado. Por eso, los habitantes de los planetas Divad, Ogeid, Olbap Leafar, pertenecientes otro sistema solar cuya estrella se apaga, han decidido colonizar Asorraf y repartírselo. este modo, Asorraf quedará poblado por una gran diversidad de criaturas, ya que los seres de esos planetas presentan distintas morfologías: Los habitantes de Divad tienen una cabeza, dos manos tres pies. Los habitantes de Ogeid tienen una cabeza, dos manos y cuatro pies. Los habitantes de Olbap tienen dos cabezas, cuatro manos seis pies. Los habitantes de Leafar tienen dos cabezas, tres manos cinco pies. Dividirán la superficie de Asorraf en cuatro regiones y se las repartirán así: Zona A será ocupada por los pobladores de Divad, Ogeid y Olbap. Zona B en ella vivirán los habitantes de Divad, Ogeid y Leafar. la ocuparán seres procedentes de Divad, Leafar Olbap. la poblarán los habitantes de Ogeid, Olbap y Leafar. Resolución de problemas. Sabemos que la zona han llegado 100 seres, que suman entre todos 145 cabezas 290 pies. ¿Cuántos habitantes de cada planeta se encuentran en esta zona? En la ciencia ficción CONTENIDOS 1 Resolución de problemas mediante sistemas Preparación de un sistema para su resolución 4 Interpretación geométrica de un sistema de 5 Discusión de sistemas de ecuaciones 6 Sistemas de ecuaciones no lineales 7 Sistemas de tres ecuaciones lineales con tres incógnitas 8 El método de Gauss 9 Discusión de sistemas por el método de Gauss OBJETIVOS Aplicar la resolución de sistemas de ecuaciones contextos reales. HABILIDADES solución de problemas. Aplicar estrategias para resolver problemas en situaciones reales. Analizar las suposiciones no explícitas que se hacen en textos reales. Estudiar las soluciones de los problemas en su contexto. Pensamiento creativo. Identificar situaciones en las que es posible aplicar los conocimientos adquiridos. l Toma de decisiones. Analizar las diversas opciones que se plantean la hora de resolver un problema elegir la más conveniente. Prepárate Sistemas de ecuaciones Métodos de resolución 4 actividades Practica Representa gráficamente los siguientes sistemas de ecuaciones e indica qué tipo de solución van tener: b y 2 4 12 6 8 10 y d 2 5 10 10 25 50 ⎧ ⎨ ⎩ 3 4 ⎧ ⎨ ⎩ Sistemas de ecuaciones no lineales Resuelve estos sistemas: a y xy 6 b y 34 y 1 d xy 4 12 e 2 5 + y 10 ⎧ ⎨ ⎩ 10 ⎧ ⎨ ⎩ g 1) 3 y ⎧ ⎨ ⎪ ⎩ h xy y 5 ⎧ ⎨ ⎪ ⎩ ⎪ 25 Resuelve estos sistemas: 6 y 15 y b 3 2 d y 8 5 y y 4x 1 ⎧ ⎨ ⎪ ⎩ ⎪ y 4 ⎧ ⎨ ⎪ ⎩ ⎪ g 3 2 Sistemas de tres ecuaciones con tres incógnitas Resuelve los siguientes sistemas utilizando el método de 6 y 2 5 0 1 2 ⎧ ⎨ ⎪ ⎩ ⎪ 2 y + 2z 3 4 2 y d y 4y z 2 6 2 6 e y 2 2 5 y g 6 y 3x 4y + 8z h x + 2 2 y ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ y 2 3 2 5 ⎧ ⎨ ⎪ ⎩ ⎪ 3 2 2 4 ⎧ ⎨ ⎪ ⎩ ⎪ 10 ⎧ ⎨ ⎪ ⎩ ⎪ x + + 2 4 2 3 0 y ⎧ ⎨ ⎪ ⎩ ⎪ 27 Personal ¿Cuántos pasajeros transportó el autobús? Un autobús transporta a 60 pasajeros. Cierto número de ellos ha abonado 1,2 € por cada billete sencillo; otro grupo ha pagado el 80 % del billete sencillo (ya que ha adquirido el billete para grupos numerosos) y un tercer grupo, formado por personas mayores de 65 años, ha abonado el 50 % del billete sencillo. La recaudación del autobús fue de 46,56 €. Calcula el número de viajeros de cada clase sabiendo que la cantidad de viajeros que se benefició del mayor descuento es el doble que la cantidad del resto de viajeros. 28 universidad El precio de tres lápices, un rotulador dos carpetas es de 15 €, mientras que el de dos lápices, cuatro rotuladores una carpeta es de 20 €. Sabiendo que un lápiz y siete rotuladores cuestan 25 €, ¿podemos deducir el precio de cada uno de los artículos? Razona tu respuesta. Si por el precio de una carpeta se pueden pagar diez lápices, ¿cuánto cuesta cada uno de los artículos? 4 investigaciones matemáticas C A D B Social Caso de estudio Triangular para localizar ¿Por qué existen tantas antenas de telecomunicaciones? ¿Cómo funciona la red de satélites GPS? EL CONTEXTO ¿Qué hacen los agentes de policía cuando reciben el aviso de que una persona ha desaparecido? Pueden comenzar a buscarla localizando el lugar de procedencia de la última señal de su teléfono móvil, si disponía de él. Aunque el teléfono tenga desactivada la función de rastreo mediante GPS, este sistema está en contacto con la red de antenas de telecomunicaciones que están repartidas por todo el territorio, siempre cuando el móvil disponga de batería. Las antenas pueden localizar los teléfonos móviles mediante una técnica parecida la que usan los murciélagos para moverse en la oscuridad. El sentido de la vista de estos animales está bastante limitado; aun así, pueden desplazarse por la noche. Como quizá sepas, envían ultrasonidos que producen ecos, los cuales, cuando retornan, llegan a sus oídos. Mediante el análisis inconsciente de esos ecos, construyen un mapa mental de la distancia a la que se encuentran los objetos que hay a su alrededor; de este modo, consiguen orientarse. De forma parecida, para localizar un teléfono móvil, las antenas de telefonía emiten periódicamente señales electromagnéticas que los móviles reciben estos, su vez, devuelven otras señales. Entonces, si se sabe cuánto tiempo ha transcurrido entre la emisión de una señal su eco, teniendo en cuenta que las señales electromagnéticas viajan la velocidad de la luz, es posible calcular la distancia entre el teléfono cada una de las antenas. Por tanto, es posible trazar, con centro en cada una de las antenas, las circunferencias que determinan los puntos desde los que se podría haber enviado la señal. Observa que se necesitan tres antenas para conocer una ubicación concreta (en este caso, el punto D), ya que con dos conoceríamos solo dos posibles ubicaciones. Cada par de circunferencias se corta en dos puntos. Del cálculo de la posición del móvil se encarga un programa informático que resuelve un sistema de tres ecuaciones. En ese sistema, cada ecuación representa una circunferencia: –() y –() –() – b () –() –() En las ecuaciones b es la ubicación del centro de las circunferencias (la antena) y es el radio (la distancia al teléfono). Este método de cálculo de la posición de un objeto se llama triangulación. Es la técnica que se usa en la red de satélites GPS y en la red de sismógrafos para hallar los epicentros de los terre4 18 estrategias de resolución de problemas Actividad resuelta Discusión de un sistema de tres ecuaciones con tres incógnitas y un parámetro 6Discute el sistema según sean los valores que tome el parámetro x + y () ⎧ ⎨ ⎪ ⎩ ⎪ Se trata de un sistema de tres ecuaciones con tres incógnitas que podemos resolver usando el método de Gauss. Observamos que la primera ecuación tiene dos incógnitas, pues no está presente la incógnita Asimismo, nos damos cuenta de que no hay que hacer nada con la segunda ecuación, ya que presenta la forma que necesitamos (en este caso, sin la incógnita Restamos la tercera ecuación la primera para eliminar colocamos el resultado en el lugar de la tercera ecuación: y my + z () ⎧ ⎨ ⎪ ⎩ ⎪ my + ⎧ ⎨ ⎪ ⎩ ⎪ Seguidamente, restamos a la tercera ecuación la segunda, con lo que eliminamos la incógnita my my mz m ⎧ ⎨ ⎪ ⎩ ⎪ my 1 () ⎧ ⎨ ⎪ ⎩ ⎪ Para discutir el sistema nos fijamos en la tercera ecuación: () la última ecuación tiene la forma es decir, podemos despejar Esto indica que se trata de un sistema compatible determinado. Veamos qué sucede si 1, la última ecuación queda así: () Cualquier valor de hace que se cumpla la ecuación, luego es un sistema compatible indeterminado. ¡Ten cuidado! Observa que si damos el valor 0 0), el sistema queda: 1 my () 1 0z 0 ⎧ ⎨ ⎪ ⎩ ⎪ Vuelve a ser un sistema compatible indeterminado, a pesar de que habíamos visto que, para el sistema era compatible determinado. A veces, el método de Gauss falla, por lo que hemos de tener cuidado al utilizarlo. Aplícalo Discute este sistema según los valores que tome m my mz 0 2 ⎧ ⎨ ⎪ ⎩ ⎪ Considera el parámetro como más discute el sistema. Ten en cuenta que no siempre todos los métodos sirven para todos los sistemas. 3 En el siguiente curso aprenderás otro métodopara discutir cualquier tipo de sistema. Estrategia y en la segunda ecuación depende del parámetro. Profesor en casa tres incógnitas y un parámetro A A ? A 10 Ω Social Educativo Los sistemas de ecuaciones en la historia s sistemas de ecuaciones lineales se usan desde la Antigüedad. Los babilónicos sabían resolver estos sistemas de ecuaciones; en ellos empleaban palabras longitud anchura área volumen para designar nuestras actuales incógnitas. Eran, incluso, capaces de solucionar sistemas con alguna ecuación cuadrática. También los antiguos griegos sabían resolver sistemas de ecuaciones utilizando métodos geométricos. Thymaridas (400 a. C.) fue capaz de hallar una fórmula que permitía dar con la solución de un determinado sistema de incógnitas. Asimismo, aparecen sistemas de ecuaciones en documentos indios, los cuales muestran que se conocía el modo de resolver algunos tipos especiales de sistemas, aunque sin llegar obtener un método de resolución general. de autor chino desconocido (siglo a. C.), contiene algunos problemas que se solucionan mediante sistemas de ecuaciones. En este libro se halla un esbozo de un método matricial para resolver sistemas de ecuaciones lineales. 1 Resuelve este sistema de ecuaciones. Se trata de un problema extraído de una tablilla babilónica corresponde al primer sistema de ecuaciones del que se tiene constancia. 1/4 anchura + longitud 7 manos longitud + anchura 10 manos 2 Pensamiento creativo. ¿Puedes plantear un sistema de ecuaciones semejante al babilónico que tenga solución? En la historia Profesional ¿Cómo se representan los sistemas eléctricos? En los circuitos eléctricos electrónicos, es habitual encontrar problemas en los que dos o más variables se relacionan mediante ecuaciones de primer grado. Son frecuentes los problemas en los que se desea hallar los valores de las corrientes eléctricas o los voltajes de circuitos con resistencias. 1 Se conecta una batería en serie con una resistencia desconocida y otra de 4 W Un amperímetro nos muestra la lectura de 2,5 A. Se repite la experiencia sustituyendo la resistencia conocida por otra de 10 W En este caso, la lectura del amperímetro es de A. ¿Cuál es el voltaje de la fuente? ¿Cuál es Recuerda la ley de Ohm y la primera ley de Kirchhoff. Ley de Ohm diferencia de potencial entre dos puntos de un circuito es igual al producto de la resistencia entre esos dos puntos la corriente que fluye. imera ley de Kirchhoff La suma de los voltajes de un circuito cerrado es igual a 0. En la electrónica 4 actividades Practica 29 PSA Profesional Sillas, mecedoras y sofás Una empresa de fabricación de muebles tiene tres productos en su catálogo: sillas, mecedoras sofás. Para fabricar cada producto necesita las unidades de madera, plástico aluminio que se reflejan en la tabla siguiente: MaderaPlásticoAluminio Mecedora unidad1 unidad3 unidades La empresa tenía unas existencias de 400 unidades de madera, 600 unidades de plástico 1500 unidades de aluminio. Si las utilizó todas, ¿cuántas sillas, mecedoras y sofás fabricó? 30 Un estudiante pidió en una cafetería tres bocadillos, dos refrescos y dos bolsas de patatas, pagó un total de 19 €. Al mirar el tique de compra, se dio cuenta de que le habían cobrado un bocadillo y una bolsa de patatas de más. Reclamó le devolvieron 4 €. Para compensar el error, el vendedor, además, le ofreció un bocadillo y un refresco por solo 3 €, lo que suponía un descuento del 40 % respecto a sus precios originales. ¿Cuáles eran los respectivos precios, sin descuento, de un bocadillo, un refresco una bolsa de patatas? La AFA (Asociación de Familias de Alumnos) del Instituto El Cisne subvenciona los 120 estudiantes de Bachillerato una excursión con destino Andalucía, Cataluña y Galicia, con 14 700 €. Se asignan 100 € a los alumnos alumnas cuyo destino es Andalucía, 120 € a los que van Cataluña y 150 € a los que viajan a Galicia. Además, el total de estudiantes que van las dos primeras comunidades excede en 50 los que tienen como destino Galicia. Calcula el número de estudiantes que visitan cada comunidad autónoma. Profesional ¿Cuántos clientes tuvo el hotel? El precio genérico de la estancia diaria en un hotel es de 50 € por persona. No obstante, el establecimiento ofrece descuentos a los niños a los jubilados. Los niños pagan el 50 % del precio diario y los jubilados han de abonar solo el 60 %. Cierto día, en el hotel se alojaron 200 personas, de tal modo que los jubilados suponían el 25 % del número total de niños alojados. La recaudación del hotel ascendió a 5 680 €. Determina el número de niños, jubilados personas que no eran niños ni jubilados que alojaron en el hotel ese día. 33 universidad PSA Profesional Obras en la comunidad de vecinos El administrador de una comunidad de vecinos quiere saber el precio por hora de trabajo de un electricista, un fontanero un albañil. Para ello, revisa las facturas de trabajos que han realizado en tres domicilios del inmueble. En el piso 4.º B el electricista estuvo una hora y el albañil dos horas, cobraron 78 €. En el 3.º A pagaron 85 € por dos horas de trabajo del fontanero y una hora de trabajo del albañil. En el 1.º A, por una hora del fontanero, una hora del electricista y tres horas del albañil se pagaron 133 €. ¿Cuánto cuesta la mano de obra por hora de trabajo de cada profesional? Discusión de sistemas aplicando el método de Gauss 34 Discute estos sistemas usando el método de Gauss: 2 2 y b my 3 0 5 2 0 x + y + 2 y d 1 x y + 0 y x + 2y mz 0 ⎧ ⎨ ⎪ ⎩ ⎪ g 4 4 h 2 0 ⎧ ⎨ ⎪ ⎩ ⎪ z 1 y () ⎧ ⎨ ⎪ ⎩ ⎪ 3 y 3 2 ⎧ ⎨ ⎪ ⎩ ⎪ 0 1) 1) 0 0 () Mejora Ecuaciones de segundo grado Polinómicas Algebraicas Irracionales Logarítmicas Exponenciales Investigaciones matemáticas
.
2. Contenidos y ejemplos
Desarrollo de los saberes básicos de la unidad alternando conocimientos teóricos con ejemplos, ilustraciones y recursos digitales de apoyo.


«Profesor en casa».
Vídeos tutoriales donde se resuelven ejercicios y se aplican los conceptos


«Mejora». Propuesta de actividades autoevaluables con GeoGebra para practicar los contenidos


3. Pensamiento computacional
Resolución de problemas asociados a los conceptos desarrollados durante la unidad mediante el uso de herramientas tecnológicas (calculadora científica, GeoGebra, vídeos…).








6. Activa tus habilidades y competencias
Actividades de evaluación en contexto donde se aplican los conocimientos adquiridos a lo largo de la unidad.




«Ponte a prueba». Test de autoevaluación







Accede al índice de contenidos de tu comunidad autónoma.





«Repasa la unidad». Infografía con los contenidos destacados de la unidad
23 BA MATEMÁTICAS EL LIBRO DEL ALUMNADO. PASO A PASO 2 22 Activa tus habilidades y competencias Profesional ¿Le importa si le doy el cambio en monedas? Con frecuencia, uno de los problemas con los que se encuentran los dependientes de los comercios es el de la vuelta o el cambio, es decir, la cantidad de dinero que superior la que cuesta el producto que adquieren el El problema reside en determinar la cantidad exacta que ha de devolverse, pero también en el modo más adecuado de hacerlo, que suele ser dando al cliente el menor número posible de monedas y billetes. Para determinar el cambio, basta con hacer una simple resta entre el dinero entregado el precio de la compra, de lo cual se encargan las máquinas registradoras de forma adecuado, ya que no siempre se dispone de las monedas o posible de estos. En muchas ocasiones, el dependiente estrictamente necesarios. Así, es habitual que se excuse doy el cambio en monedas?». El cliente de un establecimiento hace una compra por valor de 65,50 € y entrega dos billetes de 50 €. ¿Qué cantidad tiene que devolverle el dependiente? Indica qué cantidad de billetes y monedas (así como su cuantía) tiene que entregar el dependiente de tal modo que ofrezca el mínimo número posible de billetes y monedas. Cuando el dependiente se dispone dar la vuelta al cliente, repara en que no queda ningún billete en la máquina registradora. Indica, en este caso, el menor número posible de monedas que puede devolverle y 4 Si solo le quedan en la caja 10 monedas de 2 €, 10 monedas de 1 € 10 monedas de 50 céntimos, ¿puede hacer la devolución? 5 Justifica si se podría hacer la devolución usando los tres tipos de monedas del ejercicio anterior en las siguientes condiciones: El dependiente tiene que usar exactamente un total de 30 Debe devolver el mismo número de monedas de 1 € que de céntimos y monedas de 2 € juntas. 6 El cliente ofrece al dependiente una moneda de 50 céntimos con la intención de redondear la vuelta y disminuir el número de monedas. ¿Cuánto le tiene que devolver ahora el Justifica si es posible no seguir haciendo la devolución con las condiciones que se han descrito en el ejercicio 5. Profesional ¿Cómo se resuelven problemas con porcentajes? Son frecuentes las confusiones al trabajar con porcentajes. Así, hay quien cree que, si se aumenta un 30 % una cantidad para reducirla seguidamente otro 30 %, se dad que al principio, lo tres ejemplos con sistemas de ecuaciones en los que se trabajan porcentajes. ¿Eres capaz Por un rotulador, un cuaderno una carpeta se pagan 3,56 €. Se sabe que el precio del cuaderno es el 50 % del precio del rotulador y que el precio de la carpeta es igual al precio del cuaderno más el 20 % del precio del rotulador. Calcula los precios de cada producto sabiendo que se les ha aplicado un 10 % de descuento. para tres amigos. Hemos pagado 117 € por los tres regalos tras la aplicación de un descuento del 10 % sobre el precio total. Además, sabemos que el precio del regalo es el doble que el del regalo que el regalo cuesta 20 € más que el regalo ¿Cuánto dinero hemos gastado en cada regalo? universidad Julia, Clara Miguel reparten hojas total. Miguel reparte 100 hojas más que Julia. Entre reparte cada uno? Calcula el dinero que ha recibido por hoja repartida. 4 Sistemas de ecuaciones 2 x 2 Clasificación de sistemas Discusión de sistemas Método de Gauss Discusión de sistemas por el método de Gauss Sistemas no lineales Preparación de un sistema para su resolución Resolución de problemas mediante sistemas b b ⇒ a b c axbyc by axbyc by by by by d by d by d ++ by by ++ Se interpreta el enunciado se identifican las incógnitas. 3 Se resuelve el sistema de ecuaciones se 4 Se interpreta el resultado se responde explícitamente a las preguntas del enunciado. Se deben seguir estos pasos: 1 Se eliminan los denominadores multiplicando por el m. c. m. de estos. Se eliminan los paréntesis y se reagrupan los Según el número de soluciones, un sistema puede ser: Compatible: Indeterminado: tiene infinitas soluciones. Incompatible: no tiene solución. En estos sistemas, alguna de las ecuaciones no es lineal, sino polinómica de grado mayor 1, racional, radical, exponencial logarítmica, Si se tiene entonces Compatible Compatible indeterminado Se basa en reducir el sistema de tal manera que en cada ecuación haya una incógnita menos que en la ecuación precedente. Así, se obtiene un sistema escalonado Sistemas de tres ecuaciones con tres incógnitas C'' ≠0 ≠0 =0 D'' Compatible Determinado Compatible Incompatible x-y=1 Rectas paralelas 2 23 () () b 25 30 Resuelve los siguientes sistemas: 3 2 2 3 b 2 3 3 2 3 3 unidades de medida de longitud la toesa el pie. En un pasaje: «Las dimensiones del mural eran toesas pies de en la actualidad, se ha medido con la máxima precisión datos, ¿sabes cuánto miden, en metros, una toesa un pie? Un grupo de estudiantes financia su viaje de fin de curso con la venta de participaciones de lotería cuyos importes son 1 €, 2 € 5 €. Se han recaudado 620 € se ha vendido el doble de participaciones de 1 € que de 5 €. Si se han vendido 280 participaciones en total, ¿cuántas se han vendido de cada importe? 5 Discute el siguiente sistema según el valor que tome () Evalúa Educativo ¿Cómo se coloniza un planeta? Al inicio de la unidad se planteó la colonización de Asorraf por parte de los habitantes de los planetas Divad, Ogeid, Olbap y Leafar. Se ha recabado información precisa quedado dividido el planeta C D), que se registra en Seres 100 110 110 Manos 290 253 311 327 enunciado del problema en la primera página de la unidad con la tabla, plantea el sistema de ecuaciones que permite determinar el número de seres de cada planeta que pueblan ¿Qué observas? ¿Qué tipo de sistema presenta cada región? ¿Has encontrado alguna solución? ¿Necesitas más datos para responder las preguntas? Nos ha llegado la información adicional de que el número de pies de la primera zona es 469. Intenta plantear y resolver un recuento en la zona de tal modo que el número de manos es 235 en lugar de 253. Plantea resuelve el nuevo sistema con el dato correcto. ¿Qué sucede? ¿De qué tipo de sistema llegar información sobre el número de pies que hay en la incorporando este nuevo dato. Desde el puesto de control nos informan de que en la zona C han desembarcado tantos seres como en la zona Con esta nueva información, plantea y resuelve el sistema para conocer el número de seres de cada planeta que hay en el Plantea resuelve el sistema correspondiente al sector sabiendo que hay 180 cabezas. Tras resolver todos los sistemas, ¿puedes determinar el número total de seres que habitan el planeta Asorraf? ¿Habría sido necesario resolver todos los sistemas para dar la respuesta la pregunta anterior? Justifica razonadamente tu respuesta. Repasa la unidad Sistemas Ponte a prueba Sistemas de ecuaciones 4 pensamiento computacional RESOLUCIÓN DE SISTEMAS APLICANDO EL MÉTODO GRÁFICO CON GEOGEBRA El método gráfico para resolver sistemas de ecuaciones es útil cuando las soluciones son enteras y disponemos de papel cuadriculado que nos permita determinar el punto de corte exacto entre las diferen-males, este método no resulta tan eficaz. GeoGebra permite representar las rectas que corresponden a las ecuaciones lineales de un sistema y, así, determinar el punto de intersección o, lo que es lo mismo, la solución del sistema. Basta con escribir en la barra de entrada las ecuaciones del sistema (sin necesidad de despejar la incógnita y el programa facilitará las gráficas de las rectas correspondientes. Por ejemplo, considera este sistema: y 6x 5y 2 Si escribimos las ecuaciones en la barra de entrada, obtenemos la representación que se observa en la figura de arriba. Para obtener la solución hay que determinar el pun-nando Intersección w del desplegable de la opción Punto (Point). Ya solo falta pinchar en las dos rectas para obtener el punto que buscamos. El punto A es la solución del sistema: 1,75 y 2,5 Resuelve los siguientes sistemas de ecuaciones lineales: a x + y 3 4 0 b 2 2 1 y y d 3 10 4 Ahora tú DISCUSIÓN DE SISTEMAS APLICANDO EL MÉTODO GRÁFICO CON GEOGEBRA GeoGebra también permite discutir sistemas. Para hacerlo, basta con representar las rectas correspondientes y analizar cómo son estas: 2 7 2 ⎧ ⎨ ⎩ 3x 2 6 4 6 0 x + 2 4 2 4 8 ⎧ ⎨ ⎩ sistema compatible determinado. Las rectas son paralelas: sistema incompatible. coincidentes: sistema compatible indeterminado. Discute los siguientes sistemas, sin llegar resolverlos: 2 3 y b () y ⎧ ⎨ ⎪ ⎩ ⎪ y Ahora tú 4 10 contenidos y ejemplos 7 Sistemas de tres ecuaciones lineales con tres incógnitas Una ecuación lineal con tres incógnitas es una ecuación de la forma ax + by + cz d donde son coeficientes (es decir, números reales) y son las incógnitas. Desde el punto de vista geométrico, este tipo de ecuaciones corresponde a la expresión algebraica de un plano del espacio. Las soluciones de estas ecuaciones son ternas de númeLos sistemas de tres ecuaciones lineales con tres incógnitas se pueden escribir así: + b y + c d b y d b d ⎧ ⎨ ⎪ ⎩ ⎪ Para resolver estos sistemas, se pueden usar los métodos que se aplican en los sistemas de dos ecuaciones con dos incógnitas –sustitución, igualación y reducción–, pero la resolución resulta larga y, en ocasiones, complicada. En su lugar se emplea el método de las reducciones sucesivas método de Gauss 8 El método de Gauss Este método se basa en reducir el sistema de tal manera que en cada ecuación haya una incógnita menos que en la ecuación precedente. Así, se obtiene un la forma: y 5Resuelve este sistema por el método de Gauss: y 2x 3 + 5 3 2 ⎧ ⎨ ⎪ ⎩ ⎪ 1.º Ordenamos las ecuaciones de tal manera que la primera de ellas sea la que tenga el coeficiente en más pequeño. En este caso, ya están ordenadas. Aplicamos el método de reducción a las ecuaciones primera segunda para elimide la segunda ecuación: 2 7 y 2 4 6 14 2 4 14 13 Seguidamente, sustituimos la segunda ecuación por el resultado de la reducción. Tenemos la siguiente equivalencia: 2 3 7 y 3 2 4 3 y 3 4 ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ De este modo, obtenemos un nuevo sistema equivalente al primero tal que la segunda ecuación tiene dos incógnitas, una menos que la primera ecuación. Actividad resuelta Pensamiento crítico ¿En qué circunstancias el método de Gauss puede que no resulte completamente útil? Fig. 1. (1777-1855), matemático astrónomo Profesor en casa Resolución de un sistema aplicando el método de Gauss 4 11 b y d b y + c z d d contenidos y ejemplos Practica cógnitas aplicando el método de Gauss: y 3x y + 2z b y 2x + 3 + 4 11 3 3 x + 3 6 7 ⎧ ⎨ ⎪ ⎩ ⎪ d 2 0 3 y + 0 ⎧ ⎨ ⎪ ⎩ ⎪ universidad En una residencia de estudiantes se compran semanalmente 110 helados de distintos sabores: vainilla, chocolate y nata. El presupuesto destinado a esta compra asciende a 540 €. Un helado de vainilla cuesta 4 €; uno de chocolate, 5 € y 6 € uno de nata. Como se conocen los gustos de los estudiantes, se sabe que, entre helados de chocolate y nata, se ha de comprar el 20 % más que de helados de vainilla. Plantea el sistema de ecuaciones y resuélvelo a través del método de Gauss. Mejora 3.º Aplicamos el método de reducción a las ecuaciones primera y tercera para eliminar 2 ⎫ ⎬ ⎪ ⎭ 3 6 9 21 ⎫ ⎬ ⎪ ⎭ 3 6 21 y 11 17 Obtenemos, por tanto, la siguiente equivalencia: 13 y 13 y ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ 4.º Aplicamos el método de reducción a las ecuaciones segunda y tercera para elimiy 5 11 17 ⎫ ⎬ ⎪ ⎭ ⎪ y 5y 11z 17 y 5 11 17 Y resulta la siguiente equivalen11a entre sistemas: 2 3 y 11 17 ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ 3 7 y 6 48 ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ 5.º Una vez que tenemos el sistema escalonado (apunte 5), reparamos en que la tercera ecuación es una ecuación lineal con una incógnita, que se puede despejar directamente en esa ecuación: 48 Una vez hemos obtenido el valor de es posible calcular el valor de la incógnita continuación, el valor de Así: Si consideramos ahora la segunda ecuación, tenemos: 8) y y Tomando la primera ecuación, obtenemos el valor de 21) 8) Apunte 5 Observa que el sistema que hemos obtenido es triangular: Profesor en casa Resolución de sistemas por el método de Gauss
ecuacio
El nuevo proyecto educativo de Editorial Casals
Quien tiene el código tiene la llave
Accede a ecasals.net/demo y prueba una demo.





Contacta con tu delegado comercial para solicitar muestras.
Atención al cliente Tel. 902 107 007 Tel. 954 359 562 casals@editorialcasals.com ecasals.net
Síguenos en: @EditorialCasals
24 ZZ ESO MATEMÁTICAS
SME2303





















































































































































































































































