C LAUS d EL P r O j EC t E
Metodologia per contextos quotidians
Cada unitat desenvolupa un context proper al dia a dia de l’alumnat i interrelaciona els sabers bàsics dels diversos sentits matemàtics que es plantegen en el currículum.
El professor a casa Incorporem exercicis resolts i vídeos turorials (Professor a casa) per consolidar els continguts de la matèria.
Aprenentatge significatiu
Les unitats estan estructurades en situacions d’aprenentatge que afavoreixen un ensenyament competencial.
Solucionari desenvolupat

La proposta didàctica inclou el solucionari amb el desenvolupament de totes les activitats.
Obert al treball col·laboratiu
Empoderem l’alumnat amb el sentit de la iniciativa, fomentem la creativitat i promovem una relació activa amb les matemàtiques.
Avaluació competencial
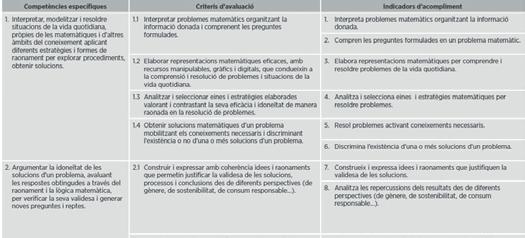
Donem resposta a l’avaluació de les competències específiques de l’àrea i de les competències clau del perfil de sortida de l’alumnat, connectant els indicadors d’acompliment de l’assignatura amb els criteris d’avaluació del currículum.
ESO M At EM àt IQUES 6
rECUrSOS dE L’ALUMNAt
El projecte de Matemàtiques disposa de més de 1000 recursos multimèdia amb diferents finalitats:
• Vídeos «Professor/a a casa»: vídeos tutorials en què s’ofereixen explicacions i es resolen exercicis pas a pas, a manera de classe particular.

rECUrSOS dEL dOCENt
El docent disposa d’aquests documents didàctics: Programació de curs. Desenvolupament de les unitats didàctiques
• Orientacions didàctiques, que incorporen: – Estratègies de neuroeducació
– Itineraris de personalització de l’aprenentatge
– Objectius de desenvolupament sostenible de l’Agenda 2030.
• Programació d’aula.
• Solucionari.
Propostes d’exàmens trimestrals i d’unitat per competències específiques i criteris d’avaluació, connectant amb els descriptors del perfil de sortida de l’alumnat.
• Recursos interactius pràctics per crear o consolidar coneixements.
• Fotografies i il·lustracions tècniques descarregables.
• documentació per fer activitats.
• Itinerari Prepara’t, Millora i Posa’t a prova per facilitar un aprenentatge continu i formatiu.
rúbriques d’avaluació. Descripció i finalitat dels recursos digitals
Treball per projectes:
• Bases metodològiques del treball per projectes de Casals.
• Presentació del projecte del llibre de l’alumnat.
• Sessions de treball i tasques assignades.
Rúbriques: avaluació de disseny del projecte, avaluació del projecte i autoavaluació de l’alumnat.
Gestió d’aula en l’entorn digital eCasals.
Avaluació competencial
Consulta l’itinerari de l’avaluació competencial a les pàgines 20-21 del catàleg.
rECU r SOS d E L’ALUMNAt i d EL d OCEN t ESO M At EM àt IQUES 7
Prepara’t Per activar coneixements previs. Millora Per reforçar i ampliar coneixements.
Posa’t a prova Per comprovar el nivell d’èxits aconseguits.
Consulta una mostra dels recursos digitals que complementen el projecte educatiu.
.
1. Contextos
Cada unitat didàctica desenvolupa un context d’un àmbit específic proper a l’alumnat (personal, laboral, social o educatiu) i interrelaciona els sabers bàsics dels diferents sentits matemàtics.
4. Activitats
activitats
5. Organitzo els conceptes


8 6 12 9 Millora
10 b d 14 30. 24 14 21 b 15 d 42 31. Troba una fracció equivalent a les següents que compleixi la condició que s’indica en cada cas a 3 4 amb denominador 16 b 8 6 amb denominador 3 c 9 amb denominador 10 32. Calcula simplifica a 8 6 d 7 g ++ 5 3 6 b 7 2 9 3 h 15 3 4 8 6
Mates en context Laboral Usain Bolt, l’home més ràpid del món Usain Bolt va néixer a Jamaica el 21 d’agost de 1986. Quan tenia 14 anys, Bolt va començar a guanyar curses en els campionats atlètics regionals i, quan en tenia 15, ja va guanyar la seva primera medalla d’or dues de plata en el Mundial Juvenil d’Atletisme, a Kingston (Jamaica). El rècord dels 100 m és actualment de 9,58 s, el va aconseguir Bolt en els Campionats del Món de Berlín, el 2009. La seva darrera participació en un campionat mundial va ser a Londres, el 2017, la seva última cursa va ser la de 100 m. Els participants els temps que van fer cadascun són aquests: Atletes Temps (s) Jimmy Vicaut França 10,08 Usain Bolt (Jamaica) 9,95 Bingtian Su Xina 10,27 Justin Gatlin 9,92 Yohan Blake (Jamaica) 9,99 Akani Simbine Sud-àfrica 10,01 Christian Coleman Reece Prescod
Problemes Escriu el nom dels corredors segons l’ordre d’arribada a la meta. En quin lloc va arribar Usain Bolt? 2 Quina és la diferència entre el temps de l’últim classificat el del primer? entre el temps del segon el del primer? 3 Si haguessin corregut d’un a un, quants segons hauria durat la cursa? Com és el temps del primer classificat respecte del que va aconseguir Bolt l’any 2009?
Argumenta: 3,
Matematitza: 1, 2
bustible d’un vehicle.
Problemes Escriu les fraccions que representen les línies més gruixudes. En quina fracció comença la línia d’alerta (vermella)?
2 53
6 4 5
Social Trufes per berenar La Sara, la Carme el Xavier visiten una amiga que està malalta. Passen per davant d’una pastisseria hi compren una dot-
Mentre parlaven, la Sara la Carme s’han menjat una trufa cadascuna el Xavier se n’ha menjat tres. Problemes Escriu les fraccions que expressen les trufes que s’ha menjat cadascú respecte del total que havien comprat. Quina fracció representa el nombre de trufes que s’han menjat entre tots tres?
3 Quina fracció n’ha quedat per a la seva amiga?
7
Matematitza: 1, 2 Argumenta: 3
L’aigua del cos humà
Problemes Troba fraccions equivalents a les del gràfic de manera que totes tinguin denominador 100.
La quantitat d’aigua del cos és més de la meitat
part entera una altra d’inferior a la unitat, separada de la primera per una coma. Es classifiquen en aquests tipus: Exactes Tenen una quantitat limitada (finita) de xifres decimals diferents de zero. Periòdics Tenen la part decimal formada per un dígit o un grup de dígits que es repeteixen indefinidament. N’hi ha dos subtipus: –Purs El dígit o el grup de dígits que es repeteix comença després de la coma.
–Mixtos El dígit el grup de dígits que es repeteix no comença després de la coma.
No periòdics Tenen una quantitat il·limitada de xifres decimals no repetides.
Comparació de nombres decimals
Per comparar dos nombres amb decimals, primer se’n compara la part entera. Si és igual, es comparen també les xifres decimals d’una a una fins a trobar la primera que sigui diferent. Operacions amb decimals Se sumen o es resten els dígits que ocupen la mateixa posició. Multiplicació Primer es multipliquen sense tenir en compte els decimals després es col·loca la coma tenint en compte que el nombre de decimals del producte és la suma dels decimals dels factors.
Fraccions és un nombre que expressa les porcions que s’agafen d’un tot que s’ha dividit en parts iguals.
Les fraccions equivalents són fraccions que representen la mateixa quantitat. Dues fraccions són equivalents si els seus productes encreuats són iguals.
Per obtenir una fracció equivalent una altra, es multipliquen o es divideixen els seus termes per un mateix nombre. Comparació de fraccions És més petita la de numerador més petit. Amb el mateix numerador És més petita la de denominador més gran.




Altres casos Se substitueixen les fraccions per altres d’equivalents que tinguin el mateix denominador s’hi aplica el primer criteri
Per sumar restar fraccions, totes han de tenir el mateix denominador. Si no el tenen, cal transformar-les en altres d’equivalents que sí que el tinguin igual. El resultat és una fracció amb el mateix denominador que té com numerador la suma la resta dels numeradors.
Relació entre fraccions decimals Una fracció també és el quocient indicat de dues quantitats enteres. En dividir el numerador pel denominador s’obté un valor decimal.

SENTIT ALGEBRAIC I PENSAMENT COMPUTACIONAL
Expressions algebraiques
Una expressió algebraica és una combinació de lletres (anomenades variables incògnites nombres relacionats per operacions matemàtiques.
Les lletres acostumen a representar quantitats desconegudes; no tenen un valor fix. El valor numèric d’una expressió algebraica és el resultat que s’obté de substituir les variables (incògnites) per nombres determinats fer les operacions indicades.
Equacions
Una equació és una igualtat entre dues expressions, anomenades membres en què hi ha elements coneguts, les dades elements desconeguts, les incògnites relacionats mitjançant operacions matemàtiques.
La incògnita representada generalment per una lletra, representa els valors que es busquen. S’anomena primer membre l’expressió que hi ha l’esquerra del signe igual s’anomena segon membre l’expressió de la dreta. Solucions d’una equació La solució de l’equació és el nombre que, quan substitueix la incògnita, fa que la igualtat plantejada sigui correcta.
Equacions equivalents Dues més equacions són equivalents si tenen la mateixa solució (o solucions). Qualsevol equació es transforma en una altra d’equivalent quan s’executen operacions elementals iguals en tots dos membres; per exemple:
organitzo els conceptes
2 67
Si als dos membres d’una equació se’ls suma o se’ls resta una mateixa quantitat. Si els dos membres d’una equació es multipliquen o es divideixen per una mateixa quantitat no nul·la. Resoldre equacions una equació consisteix a trobar la solució (o les solucions) de l’equació.
Per resoldre-la, s’ha de transformar l’equació inicial per intentar deixar la incògnita en un membre la resta de les dades en l’altre.
SENTIT NUMÉRIC





Raó proporció és la relació o comparació entre dues magnituds S’expressa com una fracció:

Una proporció és la igualtat de dues raons.
Relació de proporcionalitat
Dues magnituds són directament proporcionals quan, en multiplicar o dividir la primera per un nombre, la segona queda multiplicada o dividida per aquell mateix
Percentatges percentatge representa una quantitat determinada de 100 unitats. El seu símbol és %.
Per
ESO Mate M àtiques 8 E L LL i B r E d E L’ALUMNAt. PAS A PAS
Hi ha dues tipologies d’activitats per assegurar l’adquisició de les diferents competències matemàtiques
Els sabers bàsics s’interralacionen durant tot el curs fins
completar
ses i actituds que exigeix
currículum.
2 La llista d’anar a comprar Activa les teves habilitats i competències Prepara’t Matemàtiques pe fer la compra DECIMALS O FRACCIONS? COMPRAR AMB FRACCIONS? Situació d’aprenentatge 2 Avui toca anar a comprar SENTIT NUMÉRIC • Nombres decimals Fraccions • Relació entre fraccions decimals COM ES TRANSPORTEN LES MERCADERIES? QUINES MESURES TENEN? Situació d’aprenentatge 1 La passejada dels menjars SENTIT DE LA MESURA NUMÉRIC • Magnituds unitats El sistema mètric decimal Unitats de mesura de longitud, massa capacitat • Unitats de mesura de superfície Unitats de mesura de volum enciam 2 kg de tomàquets 1 kg de pomes 1/2 kg de pebrots 1/4 kg de formatge 250 g de carn picada 2,5 kg de carbassons 500 de lluç 0,5 kg de porros 4 kg de patates 200 de pernil dolç 8 1,5iogurts kg de taronges 750 g de sardines 2500 g de cebes Quart meitat de pernil 500 d’espinacs 3/4 kg de filets de pit de pollastre 02_MATES1ESO_2022.indd 40 La llista d’anar a comprar Activa les teves habilitats i competències de problemes EM SÉ ORGANITZAR? APROFITO LA MILLOR OFERTA? Situació d’aprenentatge 3 Viatge de final de curs SENTIT NUMÉRIC • Raó proporció Relació de proporcionalitat Percentatge Situació d’aprenentatge 4 Comprar per internet SENTIT ALGEBRAIC PENSAMENT COMPUTACIONAL Expressions algebraiques Equacions • Resoldre equacions Plantejar problemes QUANTS DINERS HE DE PAGAR? QUANTES COSES PUC COMPRAR? enciam 2 kg de tomàquets kg de pomes 1/2 kg de pebrots 1/4 kg de formatge 250 g de carn picada 2,5 kg de carbassons 500 de lluç 0,5 kg de porros 4 kg de patates 200 de pernil dolç 8 1,5iogurts kg de taronges 750 g de sardines 2500 g de cebes Quart meitat de pernil 500 d’espinacs 3/4 kg de filets de pit de pollastre SENTIT SOCIOEMOCIONAL Introducció al llenguatge algebraic • Plantejar problemes 02_MATES1ESO_2022.indd 41 Context de la unitat Preguntes inicials per a cada situació d’aprenentatge Sabers bàsics dels diferents sentits matemàtics que es desenvolupen a la unitat «Prepara’t». Vídeos d’activació de coneixements previs 2 52 activitats Entrena’t 20. ndica la posició que ocupa el 3 en els nombres següents 4,231 0,8031 b 91,347 d 18,4593 21. Escriu com es llegeixen aquests decimals 2,543: _____________ mil·lèsimes b 31,2: ______________ dècimes 32,75: ______________ ____________. d 8,014: _____________ ___________. 22. Compara els decimals següents escrivint el símbol < o >, segons calgui 5,48 3,02 16,301 16,31 b 7,12 7,23 d 9,217 9,215 23. Ordena del més gran al més petit els nombres de cada sèrie 3,18; 3,015; 3,14 3,147 12,036; 12,03; 12,034 12,0369 7,21; 7,25; 7,217 7,205 24. Resol les operacions següents amb nombres decimals 318,42 820,35 d 3908,67 2839,152 b 2743,215 + 7352,69 845,36 2,4 c 589,53 − 43,82 308,72 3,05 25. Resol aquestes operacions combinades 450,1 + 32,19 235,84 b 572,47 98,34 + 412,091 8437,32 − 1438,503 − 745,018 d 4 573,12 3,9 + 1240,37 2,36 (3,2 8,15) 896,405 + 4,8 7,29 26. Escriu la fracció que representa la zona acolorida c b d 27. Compara les fraccions següents escrivint els símbols o > 5 b 10 10 9 28. Recorda que que 8 9 72 6 12 = 72, són fraccions equivalents Comprova si els següents parells de fraccions són equivalents a 6 18 15 c 35 30 14 12 b 1 d 16 29 20 25 29. Troba tres fraccions equivalents cada una de les següents per amplificació una per simplificació 12
a
tots els coneixements, destre-
el
D’aquesta manera, l’alumnat arribarà a fer servir els sabers de manera funcional, proporcionant la flexibilitat necessària per establir connexions entre els diferents sentits matemàtics.
de la massa corporal? 3 Quina és més gran, la fracció de l’aigua de la sang o la fracció de l’aigua del cervell? 4 On hi ha menys aigua? 5 Les 5 parts de la massa corporal d’un nadó són aigua. En té més o menys que una persona adulta? Matematitza: Argumenta: 2 Matematitza: Argumenta: 2, 3, 4, 5 QUANTA AIGUA TENIM? massa corporal són aigua de la sang 18 25 3 4 4 83 100 Competències matemàtiques: 2, (act. 4); (act. 5, 6); 2, 6 (act. 7). Activitats d’exercitació Exemples resolts Banc digital d’activitats autocorregibles Problemes contextualitzats que indiquen la gradació dels processos matemàtics (PiSA) i les habilitats de la competència matemàtica 2 66 organitzo els conceptes SENTIT DE LA MESURA Magnituds unitats Una magnitud és qualsevol qualitat d’un objecte que es pot mesurar. Per mesurar una magnitud, es compara amb una altra quantitat fixa que s’anomena unitat de mesura El sistema mètric decimal (SMD) és un sistema d’unitats en què els múltiples els submúltiples de la unitat estan relacionats entre si per múltiples submúltiples de 10. Mesures de longitud, massa capacitat La unitat fonamental del SMD per mesurar la longitud és el ( ). La unitat fonamental del SMD per mesurar la és el ). per mesurar la capacitat es fa servir el litre L). Els seus múltiples submúltiples s’anomenen amb els mateixos prefixos que els del metre tenen la mateixa relació Mesures de superfície La unitat fonamental del SMD és el metre quadrat m ). Mesures de volum ( ). La relació entre les mesures de capacitat de volum és la següent: m = kL 1 dm = 1 L 1 cm = mL km hm dam dm 1000 1000 1000 1000 1000 1000
Nombres decimals Un nombre decimal és aquell que és format per una
SENTIT NUMÉRIC
calcular el percentatge d’una quantitat, es multiplica aquesta quantitat pel decimal que representa el percentatge. Un percentatge es pot expressar mitjançant un decimal o una fracció. També estableix una relació de proporcionalitat directa. Variacions percentuals La variació percentual és l’expressió, mitjançant un percentatge, de l’augment o la disminució d’una quantitat. Per tant, hi pot haver disminucions percentuals augments percentuals d ü ⎧ ⎨ ⎪ ⎩ ⎪ b d d és proporcionalitat
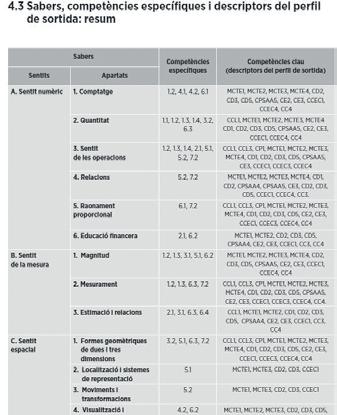
sabers
resum dels
bàsics i els seus diferents sentits matemàtics
Matemàtiques 1 BA
Llibre de l’alumnat
ISBN paper: 978-84-218-7457-8 ISBN digital: 978-84-218-7760-9
Matemàtiques aplicades a les Ciències Socials 1 BA


Llibre de l’alumnat
ISBN paper: 978-84-218-7459-2 ISBN digital: 978-84-218-7762-3
Matemàtiques 2 BA
Llibre de l’alumnat
ISBN paper: 978-84-218-7461-5

ISBN digital: 978-84-218-7764-7
Matemàtiques aplicades a les Ciències Socials 2 BA
Llibre de l’alumnat

ISBN paper: 978-84-218-7463-9 ISBN digital: 978-84-218-7766-1
Accedeix a una mostra digital
BA M At EM àt IQUES 10 M At E ri AL d E L’ALUMNAt
descarrega l’App eCasals Ar per accedir directament als recursos. tots els recursos de l’alumnat disponibles a on-line i off-line.
Matemàtiques 1 BA

Proposta didàctica ISBN paper: 978-84-218-7620-6




Matemàtiques aplicades a les Ciències Socials 1 BA Proposta didàctica ISBN paper: 978-84-218-7622-0
Matemàtiques 2 BA
Proposta didàctica ISBN paper: : 978-84-218-7624-4
Matemàtiques aplicades a les Ciències Socials 2 BA Proposta didàctica ISBN paper: 978-84-218-7626-8
BA M At EM àt IQUES 11 M At E ri AL d EL d OCEN t
C LAUS d EL P r O j EC t E
Nou projecte global de Batxillerat

Els autors d’ESO posen en funcionament aquest innovador projecte orientat a les proves d’accés a la universitat
Aprenentatge a través de contextos
Aprenentatges basats en contextos de la vida real acompanyats d’una proposta d’activitats i d’una avaluació creada partir de les directrius de la LOMLOE.
Exercicis amb GeoGebra
Exercicis programats amb GeoGebra per consolidar els coneixements. L’alumnat podrà investigar, interpretar, analitzar i resoldre problemes.
Solucionari desenvolupat
La proposta didàctica inclou el solucionari amb el desenvolupament de totes les activitats.
Estratègia de resolució de problemes
Banc d’activitats i exercicis resolts pas a pas per consolidar conceptes i perquè l’alumnat sigui autònom amb el procés d’aprenentatge.
Avaluació competencial
Donem resposta a l’avaluació de les competències específiques de l’àrea i de les competències clau del perfil de sortida de l’alumnat, connectant els indicadors d’acompliment de l’assignatura amb els criteris d’avaluació del currículum.
BA M At EM àt IQUES 12
El projecte de Matemàtiques disposa de més de 1000 recursos multimèdia amb diferents finalitats:
• Vídeos «Professor/a a casa»: vídeos tutorials en què s’ofereixen explicacions d’aspectes teòrics i es resolen exercicis pas a pas, com si es tractés d’una classe particular.

• «Repassa la unitat»: infografia amb els continguts més importants de la unitat.
• «Posa’t a prova»: test d’autoavaluació perquè l’alumnat pugui comprovar si ha adquirit els coneixements de la unitat.
• Vídeos «Professor/a a casa-Pas a pas»: vídeos tutorials que ofereixen estratègies de resolució de problemes.
• «Investigacions matemàtiques»: casos d’estudi reals on s’apliquen els coneixements adquirits al llarg de la unitat.

• Itinerari Prepara’t, Millora i Posa’t a prova per facilitar un aprenentatge continu i formatiu.
Prepara’t Per activar coneixements previs.
Millora Activitats autoavaluables amb GeoGebra per practicar i aplicar els coneixements de la unitat.
Posa’t a prova Per comprovar el nivell d’èxits aconseguits.
Consulta una mostra dels recursos digitals que complementen el projecte educatiu.
rECU r SOS d E L’ALUMNAt BA M At EM àt IQUES 13
El professorat disposa dels següents documents didàctics:
Programació de curs.
Desenvolupament de les unitats didàctiques:

• Orientacions didàctiques que incorporen itineraris de personalització de l’aprenentatge.
• Programació d’aula.
• Solucionari.
Propostes d’exàmens trimestrals i d’unitat per competències específiques i criteris d’avaluació, connectant amb els descriptors del perfil de sortida de l’alumnat. Descripció i finalitat dels recursos digitals
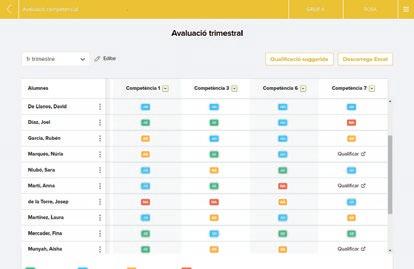
Gestió d’aula en l’entorn digital eCasals.
Avaluació competencial
Consulta l’itinerari de l’avaluació competencial a les pàgines 20-21 del catàleg.
BA M At EM àt IQUES 14 r ECU r SOS d EL d OCEN t




codi QR podràs accedir a la nostra web, on trobaràs tutorials
avaluació competencial
Estem convençuts que la nostra proposta t’ajudarà en la teva tasca com a docent! AVALUACIÓ COMPETENCIAL Llengua catalana i Literatura Música Matemàtiques Tecnologia i Digitalització Lengua por tareas Biologia i Geologia Religió Catòlica Cultura clàssica i Llatí Educació en valors cívics i ètics Lengua castellana y Literatura Física i Química Plàstica, Visual i Audiovisual ESO Lengua castellana y Literatura Història del món contemporani Religió Catòlica Llengua catalana i Literatura Física i Química Filosofia Història de
Història de l’art Matemàtiques Economia Llatí Dibuix tècnic BAtxiLLErAt ESO | BA M At EM àt IQUES 15
Coneix els avantatges d’avaluar per competències amb el projecte educatiu Codi Obert de l’editorial Casals. Et facilitem les eines i els recursos necessaris per fer l’avaluació competencial del teu alumnat i t’acompanyem en aquest procés d’avaluació al llarg del curs. Amb aquest
sobre l’
i, si ho necessites, podràs sol·licitar una sessió formativa personalitzada.
la Filosofia
1. Contextos reals
Aplicació dels sabers bàsics que es treballen a la unitat a diferents contextos i àmbits de coneixement
4.
Estratègies de resolució
de problemes
Explicació pas a pas de la resolució de problemes associats als conceptes i coneixements de la unitat.
5. Activitats
estratègies de resolució de problemes Activitat resolta Discussió d’un sistema de tres equacion amb tres incògnites un paràmetre Discuteix el sistema segons els valors que pren el paràmetre x y ⎧ ⎨ ⎪ ⎩ ⎪
Es tracta d’un sistema de tres equacions amb tres incògnites que podem resoldre usant el mètode de Gauss. Observem que la primera equació té dues incògnites, ja que no hi figura la incògnita A més, ens adonem que no s’ha de fer res amb la segona equació, ja que presenta la forma que necessitem (en aquest cas, sense la incògnita ). Restem la primera equació de la tercera per eliminar col·loquem el resultat en el lloc de la tercera equació: y my z ⎧ ⎨ ⎪ ⎩ ⎪ my ⎧ ⎨ ⎪ ⎩ ⎪
Seguidament, restem la segona equació de la tercera, d’aquesta manera eliminem la incògnita m m m

⎧ ⎨ ⎪ ⎩ ⎪ 1
⎧ ⎨ ⎪ ⎩ ⎪
Per discutir el sistema, ens fixem en la tercera equació: la darrera equació té la forma és dir, podem aïllar indica que es tracta d’un sistema compatible determinat.
Vegem què passa si 1, la darrera equació queda així: fa que es compleixi l’equació; per tant, és un sistema compatible indeterminat.
Ves amb compte! Observa que si donem a el valor 0 0), el sistema queda així: x y 1 1 x y ⎧ ⎨ ⎪ ⎩ ⎪
Torna ser un sistema compatible indeterminat, malgrat que havíem vist que, per a m el sistema era compatible determinat.
A vegades, el mètode de Gauss falla, per això hem d’anar amb compte l’hora d’utilitzar-lo.
Aplica-ho Discuteix aquest sistema segons els valors que pren m 0 2 2
4 18
Exercicis i problemes proposats a l’alumnat per posar en pràctica els coneixements adquirits al llarg de tota la unitat.
x y 2 3 4 2 ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ d y x 4y 3z 2 6 2 6




























⎧ ⎨ ⎪ ⎩ ⎪ 2 2 y
⎪ ⎩ ⎪ d 4 2 ⎧ ⎨ ⎪ ⎩ ⎪
e 5 y 0 0 g 3 y h y y 25 Resol aquests sistemes: x 3y y

⎧ ⎨ ⎪ ⎩ b 3 y
⎧ ⎨ ⎪ ⎩ ⎪ 1 2
⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ d y 8 5
y y 4x 4 g 3 2 2
⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪
Sistemes de tres equacions amb tres incògnites 26 Resol els sistemes següents utilitzant el mètode de Gauss: 2 5 0


⎧ ⎨ ⎪ ⎩ ⎪ 2
33 universitat PSA Professional Obres a la comunitat de veïns L’administrador d’una comunitat de veïns vol saber el preu per hora de feina d’un electricista, un lampista un paleta. Per esbrinar-ho, revisa les factures de feines que han dut a terme en tres domicilis de l’immoble. Al 4t B l’electricista hi va estar una hora el paleta, dues, van cobrar 78 €. Al 3r
⎧ ⎨ ⎪ ⎩ ⎪
⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ y ⎧ ⎨ ⎪ ⎩ ⎪ g 3 6 3 y 3x 4y + 8z 4
h 2 2 y x y 3z 5 5 3 y 10 y 2 4 2 0 y 27 Personal Q transportar l’autobús Un autobús transporta 60 passatgers. Un cert nombre d’ells ha abonat 1,2 € per cada bitllet senzill; un altre grup ha abonat el 80 % del bitllet senzill (ja que ha adquirit el bitllet per grups nombrosos) un tercer grup, format per persones més grans de 65 anys, ha abonat el 50 % del bitllet senzill. La recaptació de l’autobús va ser de 46,56 €. Calcula el nombre de viatgers de cada classe sabent que la quantitat de viatgers que s’ha beneficiat del descompte més important és el doble que la quantitat de la resta de viatgers.

Un cert dia l’hotel es van allotjar 200 persones, de manera que els jubilats suposaven el 25 % del nombre total d’infants allotjats. La recaptació de l’hotel va pujar a 5680 €. Determina el nombre d’infants, jubilats persones que no pertanyien a cap d’aquests dos grups que es van allotjar a l’hotel aquell dia.

28 universitat El preu de tres llapis, un retolador dues carpetes és de 15 €, mentre que el de dos llapis, quatre retoladors una carpeta és de 20 . Sabent que un llapis set retoladors costen 25 €, podem deduir el preu de cada un dels articles? Raona la resposta. Si pel preu d’una carpeta es poden pagar deu llapis, quant costa cadascun dels articles?
de bateria. Les antenes poden localitzar els telèfons mòbils mitjançant una tècnica semblant a la que fan servir els ratpenats per moure’s en


El sentit de la vista d’aquests animals està bastant limitat; així tot, poden desplaçar-se la nit. Com potser saps, envien ultrasons que produeixen ecos, els quals, quan retornen, són captats per la seva oïda. Mitjançant l’anàlisi inconscient d’aquests ecos, construeixen un mapa mental de la distància a la qual es troben els objectes que hi ha al seu voltant; d’aquesta manera, aconsegueixen orientar-se. De manera semblant, per localitzar un telèfon mòbil, les antenes de telefonia emeten periòdicament senyals electromagnètics que els mòbils reben aquests, alhora, retornen altres senyals. Llavors, si se sap quant de temps ha transcorregut entre l’emissió d’un senyal el seu eco, tenint en compte que els senyals electromagnètics viatgen a la velocitat de la llum, és possible Per tant, és possible traçar, amb el centre en cadascuna de les antenes, les circumferències que determinen els punts des dels quals es podria haver enviat el senyal.
Observa que es necessiten tres antenes per conèixer una ubicació concreta (en aquest cas, el punt ), ja que amb dues coneixeríem només dues possibles ubicacions. Cada parell de circumferències es talla en dos punts.
Del càlcul de la posició del mòbil s’encarrega un programa informàtic que resol un sistema de tres equacions. En aquest sistema, cada equació representa una circumferència: – – b – y –– – b En les equacions a, b és la ubicació del centre de les circumferències (l’antena) és el radi (la distància al telèfon). Aquest mètode de càlcul de la posició d’un objecte es diu trian-
4 A B C D Sistemes d’equacions Educatiu Quin aspecte tenen els extraterrestres? Tot que Asorraf és un planeta on es pot viure, està completament deshabitat. Per això, els habitants dels planetes Divad, Ogeid, Olbap Leafar, que pertanyen un altre sistema solar l’estel del qual s’apaga, han decidit colonitzar Asorraf repartir-se’l D’aquesta manera, Asorraf quedarà poblat per una gran diversitat de criatures, ja que els éssers d’aquests planetes presenten diverses morfologies Els habitants de Divad tenen un cap, dues mans tres peus Els habitants d’Ogeid tenen un cap, dues mans quatre peus Els habitants d’Olbap tenen dos caps, quatre mans sis peus Els habitants de Leafar tenen dos caps, tres mans cinc peus Dividiran la superfície d’Asorraf en quatre regions se les repartiran així Zona A serà ocupada pels pobladors de Divad, Ogeid Olbap Zona B hi viuran els habitants de Divad, Ogeid Leafar Zona C l’ocuparan éssers procedents de Divad, Leafar Olbap la poblaran els habitants d’Ogeid, Olbap Leafar Resolució de problemes. Sabem que a la zona A han arribat 100 éssers, que sumen entre tots 145 caps 290 peus. Quants habitants de cada planeta es troben en aquesta zona En la ciència-ficció CONTINGUTS 1 Resolució de problemes mitjançant sistemes Preparació d’un sistema per a la seva resolució Classificació dels sistemes d’equacions 4 Interpretació geomètrica d’un sistema d’equa5 Discussió de sistemes d’equacions 6 Sistemes d’equacions no lineals 7 Sistemes de tres equacions lineals amb tres incògnites 8 El mètode de Gauss 9 Discussió de sistemes pel mètode de Gauss OBJECTIUS Resoldre sistemes d’equacions Aplicar la resolució de sistemes d’equacions a contextos reals. HABILITATS solució de problemes. Aplicar estratègies per resoldre problemes en situacions reals. Analitzar les suposicions no explícites que es fan en textos reals. Estudiar les solucions dels problemes en el seu context. Pensament creatiu. Identificar situacions en les quals és possible aplicar els coneixements adquirits. Presa de decisions. Analitzar les diverses opcions que es plantegen a l’hora de resoldre un problema triar la més convenient. Prepara’t Sistemes d’equacions Mètodes de resolució 4 activitats Practica Representa gràficament aquests sistemes d’equacions indica quin tipus de solució tindran: 2 9 2 ⎧ ⎨ ⎩ b y 2 4 2 ⎧ ⎨ ⎩ 6 8 0 y ⎧ ⎨ ⎩ d 0 0 2 0 y Sistemes d’equacions no lineals Resol aquests sistemes: y x y 6 ⎧ ⎨ ⎩ b y 34 ⎧ ⎨ ⎩ y ⎧ ⎨
Considera el paràmetre com si discuteix el sistema. 2 Tingues en compte que no sempre tots els mètodes serveixen per a tots els sistemes. 3 En el curs vinent aprendràs un altre mètode per discutir qualsevol tipus de sistema. Estratègia Aquesta situació es dona quan en la segona equació depèn del paràmetre Professor a casa Discussió d’un sistema de tres equacions amb tres incògnites amb un paràmetre A A ? A 10 Ω Social Educatiu Els sistemes d’inequacions en la història Els sistemes d’inequacions lineals s’usen des de l’antiguitat. Els babilonis sabien resoldre aquests sistemes d’equacions; hi empraven paraules com longitud amplada àrea volum per designar les nostres incògnites actuals. Fins tot eren capaços de solucionar sistemes amb alguna equació quadràtica. També els antics grecs sabien resoldre sistemes d’equacions utilitzant mètodes geomètrics. Timàrides (400 aC) va trobar una fórmula que permetia arribar la solució d’un determinat sistema de equacions amb incògnites. A més, apareixen sistemes d’equacions en documents indis, els quals mostren que es coneixia la manera de resoldre alguns tipus especials de sistemes, encara que sense arribar obtenir un mètode de resolució general. El llibre L’art matem tic d’autor xinès desconegut (segle iii aC), conté alguns problemes que se solucionen mitjançant sistemes d’equacions. En aquest llibre trobem l’esbós d’un mètode matricial per resoldre sistemes d’equacions lineals Resol aquest sistema d’equacions. Es tracta d’un problema extret d’una tauleta babilònica correspon al primer sistema d’equacions del qual es té constància 1/4 amplada longitud = mans longitud amplada 10 mans Sabries plantejar un sistema d’equacions semblant al babilònic que tingui solució? En la història Profesional Com es representen els sistemes elèctrics? En els circuits elèctrics electrònics,
A. Es repeteix l’experiència substituint la resistència coneguda per una altra de 10 W En aquest cas, la lectura de l’amperímetre és d’1 A. Quin és el voltatge de la font? Quin és el valor de la resistència desconeguda Recorda la llei d’Ohm la primera llei de Kirchhoff La diferència de potencial entre dos punts d’un circuit
4 activitats Practica 29 PSA Professional Cadires, balancins sofàs Una empresa de fabricació de mobles té tres productes en el catàleg: cadires, balancins sofàs. Per fabricar cada producte necessita les unitats de fusta, plàstic alumini que es reflecteixen la taula següent: Fusta Plàstic Alumini Cadira unitat unitat unitats Balancí Sofà unitat 2 unitats unitats L’empresa tenia unes existències de 400 unitats de fusta, 600 unitats de plàstic 1500 unitats d’alumini. Si les va utilitzar totes, quantes cadires, balancins sofàs va fabricar? 30 Un estudiant va demanar en una cafeteria tres entrepans, dos refrescos dues bosses de patates, va pagar un total de 19 €. En mirar el tiquet de compra, es va adonar que havien cobrat un entrepà una bossa de patates de més. Va reclamar van retornar 4 €. Per compensar l’error, el venedor, més, va oferir un entrepà un refresc per només 3 €,
visiten cada comunitat autònoma. rofessional Quants clients va tenir l’hotel? El preu genèric de l’estada diària en un hotel és de 50 € per persona. No obstant això, l’hotel ofereix descomptes als infants les persones jubilades. Els infants paguen el 50 % del preu diari els jubilats n’han d’abonar només el 60 %.
és habitual trobar problemes en els quals dues més variables es relacionen mitjançant equacions de primer grau. Són freqüents els problemes en els quals es pretenen trobar els valors dels corrents elèctrics o els voltatges de circuits amb resistències 1 Es connecta una bateria en sèrie amb una resistència desconeguda una altra de 4 W Un amperímetre ens mostra la lectura de 2,5
és igual al producte de la resistència entre aquests dos punts el corrent que flueix Primera llei de Kirchhoff La suma dels voltatges d’un circuit tancat és igual 0 En l’electrònica
la qual cosa suposava un descompte del 40 % respecte als preus originals. Quins eren els preus respectius, sense descompte, d’un entrepà, un refresc una bossa de patates? L’AFA de l’Institut El Cigne subvenciona als 120 estudiants de Batxillerat una excursió amb destinació a les comunitats d’Andalusia, Catalunya Galícia, amb un total de 14 700 €. S’assignen 100 € als alumnes alumnes que tenen com a destinació Andalusia, 120 € als que van a Catalunya 150 € als que es dirigeixen cap a Galícia. A més, el total d’alumnes que van a les dues primeres comunitats supera en 50 els que tenen com a destinació Galícia. Calcula el nombre d’estudiants que
A van pagar 85 € per dues hores de feina del lampista una hora de feina del paleta. Al 1r A, per una hora del lampista, una hora de l’electricista tres hores del paleta es van pagar 133 €. Quant costa la mà d’obra per hora de feina de cada professional? D scussió de sistemes aplicant el mètode de Gauss 34 nt el mètode de Gaus 2 y 5 ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ b 3 0 3 0 ⎧ ⎨ ⎪ ⎩ ⎪ 2 y ⎧ ⎨ ⎪ ⎩ ⎪ d m ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ 0 ⎧ ⎨ ⎪ ⎩ ⎪ 2 0 ⎧ ⎨ ⎪ ⎩ ⎪ 4 h y 2 y m 0 0 Mejora Equacions de segon grau Polinòmiques Algebraiques Irracionals Logarítmiques Exponencials Investigacions matemàtiques 4 investigacions matemàtiques
D
Social Cas d’estudi Triangular per localitzar Per què hi ha tantes antenes de telecomunicacions? Com funciona la xarxa de satèl·lits GPS? EL
Què fan els agents de policia quan reben
Poden començar a buscar-la localitzant el lloc de procedència de l’últim senyal del seu telèfon mòbil, si en disEncara que el telèfon tingui desactivada la funció de rastreig mitjançant GPS, aquest sistema està en contacte amb la xarxa d’antenes de telecomunicacions que estan repartides per tot el territori, sempre que el mòbil disposi
C
B
CONTEXT
l’avís que una persona ha desaparegut?
gulació. És la tècnica que es fa servir en la xarxa de satèl·lits GPS en la xarxa de sismògrafs per trobar els epicentres dels terratrèmols.
.
E L LL i B r E d E L’ALUMNAt. PAS A PAS BA M At EM àt IQUES 16 Estratègies de resolució de problemes «Prepara’t».
introdueix la unitat Exemples resolts en vídeo «Investigació matemàtica». Casos reals on s’apliquen els coneixements explicats a la unitat
Vídeo que
2. Continguts i exemples


Desenvolupament dels sabers bàsics de la unitat alternant coneixements teòrics amb exemples, il·lustracions i recursos digitals de suport.
«Professor/a a casa». Vídeos tutorials on es resolen exercicis i s’apliquen els conceptes
de
lineals amb
Una
Els sistemes de tres equacions lineals amb tres incògnites es poden escriure així: b y c d b y d b d
⎧ ⎨ ⎪ ⎩ ⎪
3r Apliquem el mètode de reducció a les equacions primera tercera per eliminar el de la tercera equació: 2 ⎫ ⎬ ⎪ ⎭
3 6 y 1 Obtenim, per tant, l’equivalència següent: 3 y 3 y
⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ 4t Apliquem el mètode de reducció a les equacions segona tercera per eliminar el y de la tercera equació: 5 7 ⎫ ⎬ ⎪ ⎭ ⎪ y 5y z 17
y 5 7 n’obtenim aquesta equivalència entre sistemes: 2 3 y 1
3. Pensament computacional


⎧ ⎨ ⎪ Apunte 5 Observa que el sistema que hem obtingut és un sistema triangular: Professor a casa Resolució de sistemes per el mètode de Gauss

3 7 y 6 48 ⎪ ⎩ ⎪ ⎪ 5è Tan bon punt tenim el sistema esglaonat (apunt 5), ens adonem que la tercera equació és una equació lineal amb una incògnita, z, que es pot aïllar directament en aquesta equació: 48 Quan hem obtingut el valor de és possible calcular el valor de la incògnita a continuació, el valor de Així: Si considerem ara la segona equació, tenim: y y Agafant la primera equació, obtenim el valor de
⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪
aplicant el mètode de Gauss: y 3x y + 2z b y 2x + 3 + 4 3 3 x + 3 6 7 ⎧ ⎨ ⎪ ⎩ ⎪ d 2 0 3 y + 0 ⎧ ⎨ ⎪ ⎩ ⎪



de la forma: y 5 Resol aquest sistema pel mètode de Gauss: y 2x 3 + 5 3 2 ⎧ ⎨ ⎪ ⎩ ⎪ 1r Ordenem les equacions de tal manera que la primera sigui la que tingui el coeficient més petit. En aquest cas, ja estan ordenades. Apliquem el mètode de reducció a les equacions primera segona per eliminar el de la segona equació: 2 7 y 2 4 6 4 2 4 Seguidament, substituïm la primera equació pel resultat de la reducció. Tenim l’equivalència següent: 2 3 7 y 3 2 4 3 y 3 4 ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ D’aquesta manera, obtenim un nou sistema equivalent al primer tal que la segona equació té dues incògnites, una menys que la primera equació. Activitat resolta Pensament crític En quines circumstàncies el mètode de Gauss pot ser que no resulti completament útil? Fig. 1. (1777-1855), matemàtic astrònom Professor a casa Resolució d’un sistema aplicant 4 11 b y d b y + c z d d continguts exemples Practica Resol aquests sistemes de tres equacions amb tres inc gnites

«Millora». Proposta d’activitats autoavaluables amb Geogebra per practicar els continguts
Resolució de problemes associats als conceptes desenvolupats durant la unitat mitjançant l’ús d’eines tecnològiques (calculadora científica, Geogebres, vídeos…).
Ara, tu
4 pensament computacional RESOLUCIÓ DE SISTEMES APLICANT EL MÈTODE GRÀFIC
GEOGEBRA El mètode gràfic per resoldre sistemes d’equacions és útil quan les solucions són senceres disposem de paper quadriculat que ens permet determinar el punt de tall exacte entre les diferents rectes. Si les solucions contenen nombres decimals, aquest mètode no resulta tan eficaç. GeoGebra permet representar les rectes que corresponen a les equacions lineals d’un sistema així, determinar el punt d’intersecció o, el que és el mateix, la solució del sistema. N’hi ha prou d’escriure la barra d’entrada les equacions del sistema (sense necessitat d’aïllar la incògnita perquè el programa faciliti les gràfiques de les rectes corresponents. Per exemple, considera aquest sistema: y 6x 5y 2 Si escrivim les equacions a la barra d’entrada, obtenim la representació que s’observa a la figura. Per obtenir la solució, cal determinar el punt de tall de les dues rectes. Per fer-ho, seleccionem del desplegable de l’opció Punt. Ara només cal clicar a les dues rectes per obtenir el punt que busquem. El punt5 7 4 5 5 2



3
6. Activa les teves habilitats i competències
Activitats d’avaluació en context en què s’apliquen els coneixements adquirits al llarg de la unitat.
Accedeix a l’índex de continguts de la teva comunitat autònoma.
Per un retolador, un quadern una carpeta es paguen 3,56 €. Se sap que el preu del quadern és el
E L LL i B r E d E L’ALUMNAt. PAS A PAS BA M At EM àt IQUES 17

2 22
Professional Sovint, un dels problemes amb què es troben els dependents dels comerços és el del canvi, és dir, la quantitat de diners que han de retornar als clients que que adquireixen o el servei que contracten. El problema rau a determinar la quantitat exacta que s’ha de retornar, però també en la manera més adequada de ferho, que acostuma ser donant al client el menor nombre possible de monedes bitllets. Per calcular el canvi, simplement cal restar el preu de la compra dels diners entregats. D’això se n’encarreguen les màquines enregistradores de manera automàtica. adequada, ja que no sempre es disposa de las monedes o possible. Moltes vegades, el dependent es veu obligat a necessaris. Així doncs, és habitual que s’excusi davant del en monedes?». El client d’un establiment fa una compra per valor de 65,50 € entrega dos bitllets de 50 €. Quina quantitat ha de retornar-li el dependent? Indica quina quantitat de bitllets monedes (així com el valor) ha d’entregar el dependent de manera que doni el mínim nombre possible de bitllets monedes. Quan el dependent es disposa a donar el canvi al client, s’adona que no queda cap bitllet a la màquina enregistradora. Indica, en aquest cas, el menor nombre possible de monedes que pot retornar la quantitat d’aquestes. Si només li queden a la caixa 10 monedes de 2 €, 10 monedes d’1 € 10 monedes de 50 cèntims, pot fer la devolució? 5 Justifica es podria fer la devolució usant els tres tipus de monedes de l’exercici anterior en les condicions següents: El dependent ha d’usar exactament un total de 30 monedes. Ha de retornar el mateix nombre de monedes d’1 € que de cèntims monedes de 2 € juntes. El client ofereix al dependent una moneda de 50 cèntims amb la intenció d’arrodonir el canvi disminuir el nombre de condicions que s’han descrit en l’exercici 5. Professional Com es resolen problemes amb percentatges? Són freqüents les confuamb percentatges. Així, hi ha qui creu que, si s’augmenta un 20 % una quantitat tot seguit, es redueix un altre 20 %, s’obté la mateixa quantitat que al principi, la qual Per això, et proposem tres exemples amb sistemes d’equacions en els quals es treballen percentatges. Sabries
Activa les teves habilitats i competències
50 % del preu del retolador que el preu de la carpeta és igual al preu del quadern més el 20 % del preu del retolador. Calcula els preus de cada producte sabent que se’ls ha aplicat un 10 % de descompte. tres amics. Hem pagat 117 € pels tres regals després d’haver aplicat un descompte del 10 % sobre el preu total. A més, sabem que el preu del regal doble que el del regal que el regal més que el regal Quants diners hem gastat en cada regal? universitat La Júlia, la Clara el Miquel reparteixen del total. El Miquel reparteix 100 fulls més que la Quants fulls reparteix cada un? Calcula els diners cèntim per full repartit. 4 repassa la unitat Sistemes d’equacions 2 x 2 Classificació de sistemes Discussió de sistemes Mètode de Gauss Discussió de sistemes pel mètode de Gauss Sistemes no lineals Preparació d’un sistema per a la seva resolució Resolució de problemes mitjançant sistemes b b ⇒ a b c by by by by by by by d by d by d ++ by by ++ ’interpreta l’enunciat s’identifiquen les incògnites. 2 3 E resol el sistema d’equacions se’n comprova la solució. ’interpreta el resultat es respon explícitament les preguntes de l’enunciat. Cal seguir aquests passos: 1 S’eliminen els denominadors multiplicant pel m. c. m. d’aquests. S’eliminen els parèntesis es reagrupen els Segons el nombre de solucions, un sistema pot ser: Compatible: Indeterminat: té infinites solucions. Incompatible: no té solució. En aquests sistemes, alguna de les equacions no és lineal, sinó polinòmica de grau més gran que 1, racional, radical, exponencial logarítmica. Si tenim aleshores C d Es basa reduir el sistema de tal manera que en cada equació hi hagi una incògnita menys que en l’equació anterior. Així, s’obté un sistema esglaonat: Sistemes de tres equacions amb tres incògnites Després d’haver aplicat el mètode de Gauss, el sistema queda d’aquesta manera: C'' ≠0 ≠0 =0 D Compatible Compatible Incompatible x-y=1 Rectas paralelas 2 23 Resol aquests sistemes no lineals: b 2 0 Resol els sistemes següents: 3 2 2 3 b 2 3 3 2 3 3 mesura de longitud la toesa el peu. En un document del del mural eren toeses peus de llarg, 3 toeses pes mesurat amb la màxima precisió possible: té 4,82 m de llarg en metres, una toesa un peu? Un grup d’estudiants finança el seu viatge de de curs amb la venda de participacions de loteria d’imports d’1 €, 2 € 5 €. S’han recaptat 620 € s’han venut el doble de participacions d’1 € que de 5 €. Si s’han venut 280 participacions en total, quantes participacions s’han venut de cada import? 5 Discuteix el sistema següent segons el valor que pren Avalua Educatiu Com es colonitza un planeta? A l’inici de la unitat s’ha plantejat la colonització d’Asorraf per part dels habitants dels planetes Divad, Ogeid, Olbap Leafar. S’ha recopilat informació precisa sobre els dividit el planeta D), que figura en la taula adjunta. Éssers 100 110 110 Caps Mans 290 253 311 327 l’enunciat del problema en la primera pàgina de la unitat permet determinar el nombre d’éssers de cada planeta que 2 Pensament crític. Què observes? Quin tipus de sistema presenta cada regió? Has trobat alguna solució? Necessites més dades per respondre a les preguntes? 3 Ens ha arribat la informació addicional que el nombre de peus de la primera zona és 469. Intenta plantejar resoldre un sistema amb aquesta nova dada. Horror! Acabem de saber que hi ha hagut un error de recompte la zona B de manera que el nombre de mans és 235 en lloc de 253. Planteja resol el nou sistema amb la dada correcta. Què passa? De quin tipus de sistema es tracta? d’arribar informació sobre el nombre de peus que hi ha la regió que puja a 431. Planteja resol el sistema incorporant desembarcat tants éssers com la zona A Amb aquesta nova informació, planteja resol el sistema per conèixer el Planteja resol el sistema corresponent al sector sabent que hi ha 180 caps. 8 Després d’haver resolt tots els sistemes, pots determinar el nombre total d’éssers que habiten el planeta Asorraf? sistemes per donar la resposta a la pregunta anterior? Justifica raonadament la teva resposta. Repassa l’unitat Sistemes Posa’t a prova Sistemes d’equacions
AMB
DISCUSSIÓ DE SISTEMES APLICANT EL MÈTODE GRÀFIC AMB GEOGEBRA GeoGebra també permet discutir sistemes. Per fer-ho, n’hi ha prou de representar les rectes corresponents analitzar com són aquestes: 2 7 2 ⎧ ⎨ ⎩ 3x 2 6 4 6 0 x 2 4 2 4 8 ⎧ ⎨ ⎩ rectes es tallen: sistema compatible determinat. Le rectes són paral·leles: patible. ón coincidents: sistema compatible indeterminat. Discuteix els sistemes següents, sense arribar a resoldre’ls 2
y
⎨ ⎪ ⎩ ⎪ y Ara, tu
10
Resol aquests sistemes d’equacions lineals a x y 3 4 0 b 2 2 1 y y d 3 0 4 exemples
b y ⎧
4
continguts
7 Sistema
tres equacions
tres incògnites
ecuación lineal con tres incógnitas es una ecuación de la forma x by c d en què són coeficients (és dir, nombres reals) són les incògnites. Des del punt de vista geomètric, aquest tipus d’equacions correspon a l’expressió algebraica d’un pla de l’espai. Les solucions d’aquestes equacions són ternes de nombres.
Per resoldre aquests sistemes, es poden usar els mètodes que s’apliquen en els sistemes de dues equacions amb dues incògnites –substitució, igualació reducció–, però la resolució resulta llarga i, de vegades, complicada. Per això s’empra el ètode de les reduccions successives o mètode de Gauss 8 El mètode de Gauss Aquest mètode es basa a reduir el sistema de tal manera que en cada equació hi hagi una incògnita menys que en l’equació anterior. Així s’obté un sistema esglaonat
universitat En una residència d’estudiants es compren cada setmana 110 gelats de sabors diferents: vainilla, xocolata nata. El pressupost destinat a aquesta compra puja a 540 €. Un gelat de vainilla costa 4 €; un de xocolata, 5 €, un de nata, 6 €. Com que es coneixen les preferències dels estudiants, se sap que, entre gelats de xocolata nata, se n’han de comprar el 20 % més que de gelats de vainilla. Planteja el sistema d’equacions resol-lo mitjançant el mètode de Gauss. Millora
3 6 9 21 ⎫ ⎬ ⎪ ⎭
«Repassa la unitat». Infografia amb els continguts destacats de la unitat «Posa’t a prova». test d’autoavaluació
,
el nostre entorn virtual d’aprenentatge
eCasals és l’espai personal del docent on se situen tots els recursos, continguts i eines digitals del projecte Codi Obert LOMLOE. La plataforma està dissenyada per tal de facilitar l’ensenyament i l’aprenentatge a l’entorn virtual.
Generador de tasques
Crea tasques a partir de les activitats disponibles al llibre de l’alumnat i a la proposta didàctica. Atén la diversitat de la teva aula assignant tasques de forma individual. també pots crear activitats pròpies amb l’editor.
Activitats i recursos de la unitat
totes les activitats del llibre resolubles en format digital (autoavaluables i de resposta oberta) i els recursos multimèdia organitzats per unitat. descobreix-ne les funcionalitats!
Qualificacions
Pots visualitzar, avaluar i comentar els resultats de l’alumnat. també pots exportar-ne els resultats amb Excel.
Ajuda i contacte Manuals i tutorials amb els temes d’ajuda més freqüents, contacte amb el servei de suport tècnic i assessoria digital.
En l'entorn virtual eCasals hi trobaràs els recursos per a ESO i Batxillerat.
Ens integrem!
•
•
• Els llibres i els recursos estan disponibles per a la plataforma Blinklearning amb les seves pròpies funcionalitats.
App eCasals
Accedeix al teu llibre digital per mitjà de l’ordinador o de qualsevol dispositiu mòbil sense la necessitat de disposar de connexió. Disponible per als sistemes Android, iOS, Windows i Chromebook.

eCasals
E BACASALS H IS t ORIA DEL M UNDO C ON t EMPOR á NEO · H IS t ORIA DE E SPA ñ A CASALS
Integració compatible amb les principals plataformes EVA. Admet el protocol Marsupial i Lti.
Permet compartir el contingut a Google Classroom i Microsoft teams
Avaluació competencial
Selecciona les competències específiques que vulguis avaluar, els criteris d’avaluació associats i els descriptors del perfil de sortida. Assigna les activitats corresponents al teu alumnat i genera informes amb els seus resultats i el nivell de competència que han adquirit.
NOVETAT LOMLOE!
Mur del grup Espai de comunicació entre el professorat i l’alumnat, on també pots publicar contingut digital.
Grup i alumnes treballa amb el teu alumnat a través de la plataforma creant tots els grups que necessitis. Gestiona’n els usuaris i contrasenyes i consulta el registre d’activitat de cadascun d’ells.
digiteca
Accedeix al cercador de recursos vinculats a la matèria. Filtra per paraules, llibre o tema i descobreix tots els continguts multimèdia.
Carpeta del professorat
Espai que et permet incorporar i compartir recursos propis. Afegeix els teus materials en qualsevol format i consulta’ls quan els necessitis.
Prova una demo!
Et convidem a provar totes les funcionalitats del portal. Accedeix a ecasals.net/demo i escull el teu llibre.
• Servei personalitzat d’assessorament i suport tècnic dels nostres materials i recursos.

• Formació personalitzada de l’entorn digital.
• Webinars formatius a càrrec dels nostres assessors digitals
• Estem a la teva disposició a docencia@editorialcasals.com
eCasals
19 ORIA DEL M UNDO C ON t EMPOR á NEO · H IS t ORIA DE E SPA ñ A
t’acompanyem en el teu procés digital!
1. El material de referència
Per tal de facilitar l’avaluació, el docent té accés a material creat per a cada assignatura i comunitat autònoma.
rúbrica dels descriptors del perfil de sortida Criteris d’avaluació Sabers bàsics indicadors d’acompliment
4. La prova escrita

La proposta didàctica conté una prova escrita per a cada trimestre amb el material necessari perquè sigui avaluada per competències.
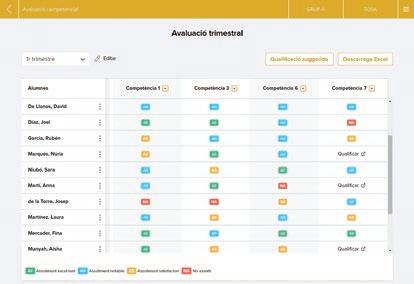
5. L’avaluació trimestral
A cada trimestre el docent registra l’avaluació de les unitats didàctiques i de la prova escrita en dos documents.
Avaluació per competències específiques amb una proposta de distribució de percentatges.
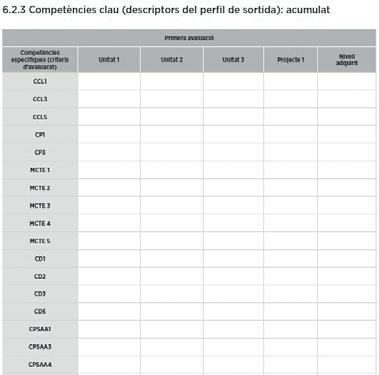
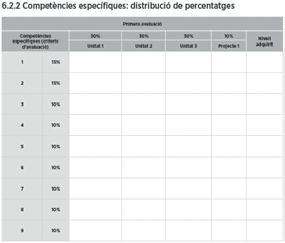

La rúbrica proporciona una avaluació qualitativa perquè l’alumnat pugui progressar.
Avaluació per competències clau.
eso | BA Mate M àtiques 20 AVALUACIÓ COMPETENCIAL . PA s A PA s
2. Doble avaluació: de competències específiques i de competències clau
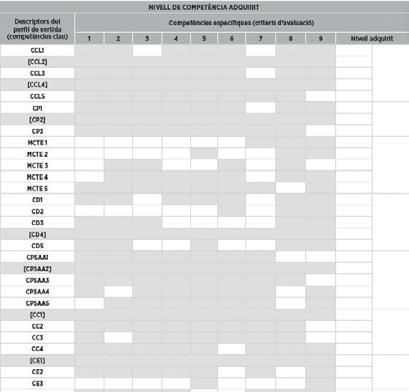
A partir del material de referència, el docent avalua amb les evidències (activitats) que ofereix l’editorial.
Quadre sinòptic per a les activitats de creació pròpia que connecta els descriptors operatius i les competències específiques.
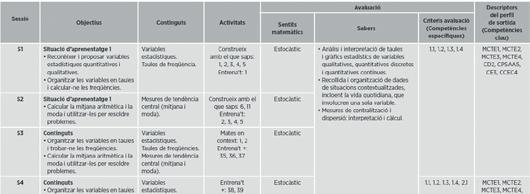
3. Avaluació unitat per unitat
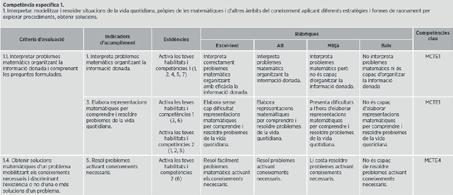
Per a cada unitat didàctica oferim: 1. la programació d’aula amb les competències específiques de cada sessió; 2. les rúbriques de les competències específiques associades a les evidències (activitats) de cada unitat, connectades amb els descriptors del perfil de sortida.
Programació d’aula
Els indicadors d’acompliment connecten les competències específiques i els descriptors del perfil de sortida.
Competències específiques: rúbriques (avaluació qualitativa)
6. Avaluació final de competències
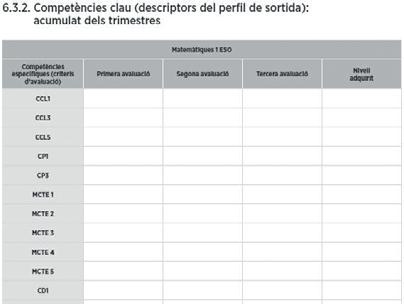
Quan ja s’ha avaluat cada trimestre, es registra l’acumulat de l’avaluació en dos documents.
Accedeix a l’avaluació competencial de la teva comunitat autònoma.
eso | BA Mate M àtiques 21 AVALUACIÓ COMPETENCIAL . PA s A PA s
MAtEPrACtiC
ESO i 1r de Batxillerat
Autors: Àngel Alsina i Fernando García
Matepractic és un mètode pràctic i didàctic que ajuda l’alumnat a adquirir les destreses matemàtiques per fer front als reptes de la vida real.

• Proposa tasques centrades en contextos reals.
• S’adapta a les possibilitats de cada alumne/a.
• Es basa en les pautes d’avaluació de les proves internacionals tIMSS i PISA.
• Es fonamenta en els plantejaments del NCtM dels Estats Units i d’altres països, com ara Singapur, que centren l’ensenyament i l’aprenentatge de les matemàtiques en fets visuals i concrets.

Matepractic està disponible en dos formats
Quaderns
Quaderns de treball impresos + prova de
Quaderns Matepractic, pas a pas
diAGNOStiCA
Prova de diagnòstic
MiLLOrA
Quaderns amb 15 nivells des de 1r de l’ESO i 1r de Batxillerat.
AVALUA
Solucionari i avaluació.
Activitats, prova de diagnòstic i avaluació 100% digitals al portal matepractic.cat mitjançant l’adquisició d’una llicència anual.

informació a
Más información en matepractic.es

22 ESO | BA M At EM àt IQUES MAt E ri AL COMPLEMEN tA ri
1
Nombres naturals. Nombres enters. Divisibilitat. Fraccions i decimals. Percentatges. Sistemes de numeració.




2
Llenguatge algebraic. Magnituds directament i inversament proporcionals. Percentatges. Funció lineal. Gràfiques.






3
Rectes i angles. Perímetres i àrees. El teorema de Pitàgores. Freqüència absoluta i relativa. Diagrama de sectors. Gràfic de barres. Regla de Laplace.
4
6
Lògica. Figures geomètriques. àrees i perímetres. Semblança. Escala. Punts i rectes notables del triangle. Sòlids platònics.

7
Potenciació i radicació. Notació científica. Aproximació i errors. Successions. Progressions aritmètiques i geomètriques.
8
Percentatges. Proporcionalitat inversa. Funció parabòlica. Sistemes d’equacions. Angles i semblança. Vectors. Simetries, girs i translacions.
9
11
Visió espacial. Perímetres, àrees i volums en poliedres i en superfícies de revolució.
12
Probabilitat condicionada. taules i gràfics. Distribucions bidimensionals. Recta de regressió i interpolació.
13
Nombres reals. Equacions i sistemes. Inequacions. Estudi de funcions. Límits. Continuïtat. Derivades. (1 BA)
14
Operacions
amb nombres naturals, enters i decimals. Divisibilitat. Unitats de pes i de volum. Gràfiques i paràmetres estadístics. Llei dels grans nombres.

5

Funcions. Expressió algebraica i gràfica d’una funció. Equacions de primer i segon grau. Interpretació de gràfiques.
Paràmetres de centralització i desviació. Diagrames d’arbre. Variacions i combinacions. Probabilitat condicionada.
10
Codis i divisibilitat. Potenciació i radicació. Interès compost. Funció exponencial i logarítmica.

Rectes i distàncies. Angles. Radiants. trigonometria. Resolució de triangles. Nombres complexos. Còniques. (1 BA)
15
Operacions amb successos. Probabilitat total. teorema de Bayes. Correlació i regressió. Distribució binomial i normal. (1 BA)

23 ESO | BA M At EM àt IQUES MAt E ri AL COMPLEMEN tA ri
PrOGrAMACiÓ dE SECUNdÀriA


SMC2301 El nou projecte educatiu d’Editorial Casals Atenció al client tel. 902 107 007 tel. 932 449 550 casals@editorialcasals.com ecasals.cat Contacta amb el teu delegat comercial per sol·licitar mostres. Qui té el codi té la clau Accedeix a ecasals.cat/demo i prova una demo. segueix-nos a: @EditorialCasals































































































