Introduction to Chaos, Fractals and Dynamical Systems Phil Laplante Visit to download the full and correct content document: https://ebookmass.com/product/introduction-to-chaos-fractals-and-dynamical-systems -phil-laplante/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
A Modern Introduction to Dynamical Systems Richard Brown
https://ebookmass.com/product/a-modern-introduction-to-dynamicalsystems-richard-brown/
Qualitative Theory of ODEs: An Introduction to Dynamical Systems Theory 1st Edition Henryk Zoladek
https://ebookmass.com/product/qualitative-theory-of-odes-anintroduction-to-dynamical-systems-theory-1st-edition-henrykzoladek/
The Dynamical Ionosphere: A Systems Approach to Ionospheric Irregularity 1st Edition Massimo Materassi (Editor)
https://ebookmass.com/product/the-dynamical-ionosphere-a-systemsapproach-to-ionospheric-irregularity-1st-edition-massimomaterassi-editor/
Introduction to Modern Dynamics: Chaos, Networks, Space, and Time 2nd Edition David D. Nolte
https://ebookmass.com/product/introduction-to-modern-dynamicschaos-networks-space-and-time-2nd-edition-david-d-nolte-2/
Introduction to Modern Dynamics: Chaos, Networks, Space, and Time 2nd Edition David D. Nolte
https://ebookmass.com/product/introduction-to-modern-dynamicschaos-networks-space-and-time-2nd-edition-david-d-nolte/
Computational Methods for Nonlinear Dynamical Systems: Theory and Applications in Aerospace Engineering Xuechuan Wang
https://ebookmass.com/product/computational-methods-fornonlinear-dynamical-systems-theory-and-applications-in-aerospaceengineering-xuechuan-wang/
Introduction to linear control systems Bavafa-Toosi
https://ebookmass.com/product/introduction-to-linear-controlsystems-bavafa-toosi/
Introduction to Food Science and Food Systems 2nd Edition Rick Parker
https://ebookmass.com/product/introduction-to-food-science-andfood-systems-2nd-edition-rick-parker/
Introduction to the Theory of Complex Systems Stefan Thurner
https://ebookmass.com/product/introduction-to-the-theory-ofcomplex-systems-stefan-thurner-2/
Problem Solving in Mathematics and Beyond Print ISSN: 2591-7234
Online ISSN: 2591-7242
Series Editor: Dr. Alfred S. Posamentier
Distinguished Lecturer
New York City College of Technology - City University of New York
There are countless applications that would be considered problem solving in mathematics and beyond. One could even argue that most of mathematics in one way or another involves solving problems. However, this series is intended to be of interest to the general audience with the sole purpose of demonstrating the power and beauty of mathematics through clever problem-solving experiences.
Each of the books will be aimed at the general audience, which implies that the writing level will be such that it will not engulfed in technical language — rather the language will be simple everyday language so that the focus can remain on the content and not be distracted by unnecessarily sophiscated language. Again, the primary purpose of this series is to approach the topic of mathematics problemsolving in a most appealing and attractive way in order to win more of the general public to appreciate his most important subject rather than to fear it. At the same time we expect that professionals in the scientific community will also find these books attractive, as they will provide many entertaining surprises for the unsuspecting reader.
Published
Vol. 29 Introduction to Chaos, Fractals and Dynamical Systems by Phil Laplante and Chris Laplante
Vol. 28 Seduced by Mathematics: The Enduring Fascination of Mathematics by James D Stein
Vol. 27 Mathematics: Its Historical Aspects, Wonders and Beyond by Alfred S Posamentier and Arthur D Kramer
Vol. 26 Creative Secondary School Mathematics: 125 Enrichment Units for Grades 7 to 12 by Alfred S Posamentier
For the complete list of volumes in this series, please visit www.worldscientific.com/series/psmb
Published by
World Scientific Publishing Co. Pte. Ltd.
5 Toh Tuck Link, Singapore 596224
USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601
UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE
Library of Congress Cataloging-in-Publication Data
Names: Laplante, Phillip A., author. | Laplante, Chris, author.
Title: Introduction to chaos, fractals and dynamical systems / Phil Laplante (Penn State University, USA), Chris Laplante (Agilent Technologies, USA).
Description: New Jersey : World Scientific, [2024] | Series: Problem solving in mathematics and beyond, 2591-7234 ; vol. 29 | Includes bibliographical references and index.
Identifiers: LCCN 2023015059 | ISBN 9789811273247 (hardcover) | ISBN 9789811273902 (paperback) | ISBN 9789811273254 (ebook for institutions) | ISBN 9789811273261 (ebook for individuals)
Subjects: LCSH: Fractals. | Dynamics. | Chaotic behavior in systems.
Classification: LCC QA614.86 .L368 2024 | DDC 006.601/514742--dc23/eng20230711
LC record available at https://lccn.loc.gov/2023015059
British Library Cataloguing-in-Publication Data
A catalogue record for this book is available from the British Library.
Copyright © 2024 by World Scientific Publishing Co. Pte. Ltd.
All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher.
For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher.
For any available supplementary material, please visit https://www.worldscientific.com/worldscibooks/10.1142/13331#t=suppl
Desk Editors: Sanjay Varadharajan/Ana Ovey
Typeset by Stallion Press
Email: enquiries@stallionpress.com
Printed in Singapore
ForKaitlin This page intentionally left blank
AbouttheAuthors PhillipA.Laplante startedplayingwithcomputersinthe1970s.Byhissenioryearincollege, hewaswritingsoftwarefortheSpaceShuttleand otheravionicsapplications.Later,heworkedon computer-aideddesignsoftwareformicrowaveand electronicssystemsandthenonadvancedtesting tools.Whileworkingontheseprojects,hecompletedhisMaster’sdegreeinelectricalengineering andhisPhDincomputerscience.Heiscurrently ProfessorofSoftwareandSystemsatPennStatewherehisteachingand researchinterestshaveincludedimageprocessing,real-timesystems,softwaretesting,artificialintelligence,criticalinfrastructureandtheInternet ofThings.Youcanfindoutmoreabouthisotherbooksandpublicationsat https://phil.laplante.io.
ChristopherP.Laplante wasintroducedtothe BASICprogramminglanguageataveryyoungage byhisfather,Phil.Hequicklybecamefascinated byprogrammingandcomputersingeneral.Heis currentlyasoftwareengineeratAgilentTechnologieswhereheworksonembeddedLinuxsystems forgaschromatographsandautomatedliquidsamplers.Youcanlearnmoreabouthissideprojectsat https://blog.laplante.io.
This page intentionally left blank
Acknowledgments Wewouldliketothankthefollowingindividuals:
• ouracquisitioneditor,RochelleKronzek,forcommissioningthisproject andsupportandencouragementalongtheway;
• Dr.AlfredS.Posamentierforincludingourbookinhiswonderful ProblemSolvinginMathematicsandBeyond bookseries.
We’dalsoliketoacknowledgethefollowingfriendsforreviewingportions ofthetextatvariousstagesofdraft:
• Dr.JoannaDeFranco,PennState
• Dr.MohamadKassab,PennState
• LenTaddei,AgilentTechnologies
• SteveKirk,AgilentTechnologies
Ofcourse,anyremainingerrorsorinconsistenciesareourown.
Wehopeyouenjoythisexplorationofchaos,fractalsanddynamical systems.Ifyouthinkyouhavefoundanerrorinthebookandwouldliketo reportit,pleasecontactusviaemailat:
PhillipA.Laplante, plaplante@psu.edu
ChristopherP.Laplante, chris@laplante.io
This page intentionally left blank
1.11BriefHistoryofChaos,Fractalsand DynamicalSystems.....................34 1.12ExercisesandThingstoDo................35
2.FoundationsofChaosandFractalTheory39 2.1ComplexNumbersandFunctions.............39
2.1.1PlottingComplexNumbers.
2.1.2ArithmeticwithComplexNumbers...
2.2FunctionsofComplexVariables..............44
2.3.4TheMandelbrotSet.................61
2.3.5ANoteontheImages................64
2.3.6TheInverseIterationandBoundary ScanningMethods.
3.5.1Trees,LeavesandFlowers.
3.5.2Clouds.
3.5.3RocksandBoulders.................92
3.5.6Coastlines
3.6FractalsintheHumanBody................99
3.6.1BronchialGrowth..................100
3.6.2NeuronGrowth...................100
3.6.3PhysiologicalProcesses... ............102
3.6.4ChaosoftheMind?.................103
3.7ExercisesandThingstoDo................103
4.ChaosandFractalsinHuman-MadePhenomena107
4.1TurbulentFlow.......................107
4.2Structures..........................108
4.3ComputerSceneAnalysis.................111
4.4ImageCompression .....................111
4.4.1ProblemswithFractalCompression.. ......113 4.5EconomicSystems .....................115
4.6CellularAutomata.....................118
4.6.1One-DimensionalCellularAutomata........119
4.6.2Two-DimensionalCellularAutomata........124
4.7ExercisesandThingstoDo................127
5.DynamicalSystemsandSystemsTheory129
5.1BasicSystemTheory....................130
5.1.1ModelingThingsasSystems............131
5.1.2LinearGrowth....................133
5.1.3ResponseTime.. .................136
5.1.4ControlSystems...................136
5.1.5DeterministicSystems...............139
5.1.6Time-VariantandTime-InvariantSystems.....140
5.1.7LinearSystems...................140
5.1.8NonlinearSystems.................143
5.1.9SummaryofSystemTypes.............144
5.2SystemsThinking......................144
5.2.1EmergentBehavior.................145
5.2.2Second-OrderEffects ................147
xiv IntroductiontoChaos,FractalsandDynamicalSystems
5.3Uncertainty.........................148
5.3.1StateUncertainty..................148
5.3.2HeisenbergUncertainty...............149
5.3.3UncertaintyandChaos...............150
5.3.4DealingwithUncertainty..............150
5.4SwarmBehavior......................155
5.4.1SimulatingaSwarm.................157
5.4.2ApplicationsofSimulatedSwarms.........158
5.4.3SwarmComputing.................159
5.5BriefHistoryofDynamicalSystemsand SystemsTheory.......................160
5.5.1DynamicalSystems.................160
5.5.2SystemsEngineering................161
5.5.3OriginsofSystemsThinking............161
5.6ExercisesandThingstoDo................161
ListofFigures 1.1Twosectionsoftheinfiniterollercoaster.(a)Stableequilibrium; (b)Unstableequilibrium.... .................2
1.2Increasinglynearerviewsofasectionofcoastline. ......4
1.3TheMandelbrotset........................4
1.4Bifurcationdiagramfor f ( x ) = x 2 + c with x = 0and c swept from 2.0to1.0.........................10
1.5RuleforcreationofaSierpinskitriangle. ............13
1.6ASierpinskitriangle. ......................14
1.7Sierpinskitriangle-mappingprocedure. ............15
1.8VerticesforSierpinskitriangle-mappingprocedure. ......16
1.9Startertriangle... .......................18
1.10Theoriginaltriangle(dashed)scaledto50%scale. ......19
1.11Translationsofscaledtriangle. .................19
1.12FirstiterationofSierpinskitriangle... ............20
1.13Sierpinskicarpet.........................24
1.14Affinetransformationsforconstructingfirstiterationof Sierpinskicarpet.Originalsquare(dashed)isscaledto 33%scale.Thenitisclonedandtranslatedineight differentdirections........................25
1.15ConstructionoftheCantorset..................28
2.1Thecomplexplaneandsomepointsonit............41
2.2TheplottingwindowforJuliaandMandelbrotprograms....49
2.3Juliasetfor f ( z ) = cos ( z )....................50
2.4Douady’srabbit.........................51
2.5Infernocolorscheme.......................52
2.6Douady’srabbitcreatedusing10iterations...........53
2.7Infernocolorschemeutilization(dashedbox)forDouady’srabbitwith10iterations.Notehowthedarkercolorsontheleftare notusedbecausetheescapeiterationcountstartsat3. .....53
2.8Douady’srabbitcreatedusing50iterations...........54
2.9Infernocolorschemeutilization(dashedbox)forDouady’srabbitwith50iterations.......................54
2.10Douady’srabbitcreatedusing200iterations..........55
2.11Douady’srabbitcreatedusing800iterations..........56
2.12Douady’srabbitcreatedusing800iterationswithhistogramcoloring...............................57
2.13ASiegeldisk...........................58
2.14Adragon.
2.18TheMandelbrotsetusingthehistogramcoloring algorithm. ............................65
2.19BasinofattractionusedinBSM.................66 2.20Mexicanhatfunctionmotherwavelet..............69
2.21SomedaughterwaveletsoftheMexicanhatfunction. .....70
2.22SimulatedelectrocardiogramimageproducedbyMexicanhat wavelets.............................70
3.1Populationdynamicsofcaribou–wolfsystemwith K = 0.000006... .......................76
3.2Populationdynamicsofcaribou–wolfsystemwith K = 0.000010... .......................76
3.3Populationdynamicsofcaribou–wolfsystemwith K = 0.000014... .......................77
3.4Seals...............................78
3.5Anamoeba-likeimagegeneratedfromthefilledJuliasetof f ( z ) = Z 2 + 0 3 4i ......................80
3.6Afernleaf............................81
3.7AfernleafgeneratedviaIFS...................82
3.8IFSrepresentationofatree... .................84
3.9Aforestofrandomlygeneratedfractaltrees. ..........85
3.10Aredwoodforest.........................88
3.11Greenseaweed..........................89
3.12Four-petaledflowerfromtheJuliasetof f ( z ) = z 2 + 0.384. .......................90
3.13Anotherfour-petaledflowerfromtheJuliasetof f ( z ) = z 2 + 0.2541. ......................91
3.14Afractalstormcloud. ......................91
3.15“Three-dimensional”fractalclouds... ............93
3.16FractalrocksusingsameIFScodesastheclouds.. ......94
3.17Snowflakesgeneratedbymandel_julia.rs............95
3.18Asnowfallgeneratedbyfall.rs.................97
3.19Crossfractalusedtogeneratesnowflakes............98
3.20Arandomlygeneratedviewofspace.. ............99
3.21Thebronchialtreestructureinourlungsresembles afractal..............................100
3.22Dendritestructuregeneratedby f ( z ) = z 2 + i .........101
3.23AnEKGoutputsimulatedusingaJuliaset...........102
4.3“Winterreflections”bywaferboardismarkedwith CCBY2.0.Toviewtheterms,visithttps://creativecommons. org/licenses/by/2.0/?ref=openverse.Originallyincolor.....113
4.4Computer-generatedequivalentofswampypondshownin “winterreflections.”.......................114
4.5Self-similarityofcottonpricesovercenturies,years, andmonths............................116
4.6Bifurcationdiagramformodeleconomicsystem.. ......117
4.7Sierpinskitriangleoutputofprogram1d_life.rs... ......121
4.8Sampleoutputfrom1d_life.rsusing Rule2..........123
4.9GameofLife...........................125
xviii IntroductiontoChaos,FractalsandDynamicalSystems
4.10GameofLifeaftermanyiterationsconsistingofjuststableand bi-stableformationsofcells...................126
5.1Ageneralsystemwithinputsandoutputs. ...........130
5.2Asystemwithoneinputandoneoutput. ............131
5.3Controlsystemblockdiagram..................137
5.4Arealsysteminteractswiththeenvironmentinobvious andsubtleways..........................145
5.5HoneybeeswarmnearWilmington,Delaware,courtesyof SmallWonderHoney,https:// www.face book.com/smallwonde rhoney..............................156
5.6ScreencaptureofanartificialswarmusingWolfram’sBoids Simulatorathttps://demonstrations.wolfram.com/BoidsSimul atedFlockingBehavior.©WolframResearch.... ......158
ListofTables 1.1IFStransformationruleforSierpinskitriangle... ......20
1.2IFStransformationruleforSierpinskicarpet..........23
3.1IFStransformationruleforseals. ................79
3.2IFStransformationruleforfern.................83
3.3IFStransformationrulefortree.................83
3.4IFStransformationruleforseaweed...............90
3.5IFScodesforthree-dimensionalfractalclouds... ......93
3.6IFScodesforcrossfractal....................98
4.1IFScodesforcastle.......................109
4.2IFScodesformaze. .......................111
4.3IFScodesforoneclumpinaswamp...............115
5.1Principalandinterestfortwoyearsinasavingsaccount....134
5.2Simplifiedinterestgrowthmodel................134
This page intentionally left blank
Introduction 1.BackgroundandObjectives Thankyouforchoosingthisbook.Ourgoalistoprovideafunandenriching introductiontochaostheory,fractalsanddynamicalsystems.Anemphasis ismadeonnaturalandhuman-madephenomenonthatcanbemodeledas fractalsandontheapplicationsoffractalstocomputer-generatedgraphics andimagecompression.
Tokeepthemathematicsrelativelysimple,werelyonintuitivedescriptions,computer-generatedgraphicsandphotographsofnaturalscenesto makeourpoints.Buttherearesufficientmathematicaldefinitions,representations,discussionsandexercisessothatthisbookcanbeusedasprimaryor secondarysourceinhomeschoolingenvironments.Wealsopresentabrief historyoftheevolutionofchaostheory,fractalsanddynamicalsystems. Again,justenoughinformationisgiventointriguethereaderandgetthem startedonotherscientificjourneys.
Toindulgecuriousminds(bothoursandthereaders’),we’veincluded numerousfactoids,biographiesandshortdiscussionsinfootnotes.Wedon’t intendtheseasdistractions,butrathertoencouragefurtherinquiry.Insome cases,thesefootnoteitemsreappearattheendofthechapterasexercises andthingstodo.Wealsotriedtokeepthecitationstoamanageablelevel. Wedidn’tintendthistobereferencedasascholarlypaper.Rather,wegive justenoughcitationsforthoseinterestedinconductingfurtherresearch.
2.MathematicalBackground Thebookisaccessibletothosewithabasicknowledgeofalgebraand geometry.Inparticular,thereadershouldbefamiliarwithsimplefunctions ofrealnumbersanditwouldalsobehelpfulifthereaderwerefamiliar withalittletrigonometry,suchassinesandcosines.However,muchof theneededmathematicalbackgroundisdevelopedalongtheway.Inafew places,weexpandsomewhatintohighermathematics,includingtheuseof alittlecalculus.Inthesecases,however,themathematicscanbeignoredor usedasthestaringpointforfurtherexploration.
Themathematicsisintroducedinaveryinformal(thatis,notrigorous) way.Werealizethatinsomecases(e.g.thedefinitionofarealnumber,linear system,fractal)wehavetakenliberties.Buttodootherwisewouldrequire ahigherlevelofsophisticationonthepartofthereaderandmightdeter themfromfurtherstudy.We’drathergivethemoreinformaldefinitions, lettingthereader(orteacherorprofessor)introducefurtherrigortothe leveldesired.
3.RustandOpenGL Whilethebookcanbeenjoyedwithoutacomputer,wehopethatthereader willexperimentwiththecodesamplesprovided—theseareavailableat https://code.laplante.iofordownload.Wechosetoimplementthevarious fractalsandotherprogramsintheRustprogramminglanguage.Ourreasons fordoingsoaredetailedinthefollowingsection.Pleasekeepinmindthat thisbookisnotintendedtobeanintroductionortutorialonRust,nor programmingingeneral.Thatbeingsaid,wehavetriedourbesttoexplain thecodethatappearsinthisbook.
3.1 TheRustProgramLanguage RustisaprogramminglanguagewithsyntaxsimilartoC/C++butincorporatingfeaturesmorecommonlyfoundintheML-familyoflanguages,
suchasalgebraicdatatypesandpatternmatching.Forprofessionalsoftwaredevelopers,Rust’smostimportantfeatureiscompile-timesafety.The Rustcompile-timecheckerlooksfornullpointers,danglingreferences,data racesandotherkindsofundefinedandunsafebehaviorusingavarietyof techniquesincludinga“borrowchecker,”whichanalyzesthelifetimesof objectsandreferenceslookingforanomalies.Sincetheborrowcheckerruns atcompiletime,thegeneratedassemblycodeperformssimilartothecode writteninCandC++(Langlands etal.,2021).
WeprimarilychoseRustforthisbookbecauseitprovidesanexcellent developerexperience.Itissimpletoinstallwithrustup(https://rustup.rs/) andrunsonWindows,LinuxandmacOS.Thebuilt-inpackagemanager andbuildsystem,cargo,makesiteasytobuildsoftware.It’salsovery reliable,asmentionedpreviously.Rusthasgreatdocumentationandavery user-friendlycompiler—theerrormessagesarenotcrypticunlikemany otherprogramminglanguageimplementations.Formoreinformationon Rust,checkouthttps://www.rust-lang.org.Thereisanexcellentonline freeRustbookhere:https://doc.rust-lang.org/book.
A1993predecessortothisbookcontainedcodewritteninPascal,which wasapopularteachinglanguageatthetime.Codeforalloftheprogramsin thebookwasalsomadeavailableinC.Thelegacyversionsofthecodein Ccanbedownloadedfromhttps://github.com/introtochaosbook/c-fractalcode.Thesewillneedtobemodifiedtoruninyourparticularprogramming computingenvironmentifyouwishtorunthecode.
3.2 OpenGLandHardware-AcceleratedGraphics Forthemostpart,theRustcodeismerelyawrapperaroundoneormore OpenGLprograms.TheOpenGLprogramsareresponsiblefordeterminingwhatwillbedrawntothescreen.OpenGL(“OpenGraphicsLibrary”) isastandardizedAPIformanipulatinggraphicshardware.OpenGLprogramsarecalled shaders andarewritteninaC-likelanguage calledGLSL.1
1 OpenGLShadingLanguage.
xxiv IntroductiontoChaos,FractalsandDynamicalSystems
ShadersarecompiledintoinstructionsthatrundirectlyonGPUsandother graphicshardware(Kessenich etal.,2017).
ItmayseemlikeoverkilltousebothRustandOpenGL,butwehave goodreasonsfordoingso.Whilewecertainlycouldhavewrittenprograms entirelyinRustthatdrawfractalsonthescreen,theresultingcodewould beextremelyslowandinefficient.2 Thisisbecausesuchprogramswould needtoiterateovereverypixel3 onthescreenandperformacalculation— adauntingtaskfortoday’sdensest4Kor8Kmonitors.ByusingOpenGL, weoffloadprocessingfromtheCPU(whichisnotparticularlyoptimized foranyonetask)totheGPU(whichwaspurpose-builtfordrawingtothe screen).
AnotherbenefitofusingOpenGListhatsincethe“meat”ofthecode iswritteninGLSL,you caneasilyportthefractalstootherprogramming languagesbysimplyrewritingtheRustwrappercode.OpenGLbindingsare availableformostpopularprogramminglanguagesandplatforms.Tutorials andprojecttemplatesarealsoreadilysearchableonline.
ForreadersthatarenotfamiliarwithOpenGL,werecommendthefree website,https://learnopengl.com.ThecodesamplesareinC++,butthe conceptsarethesame.Thefollowingsectionscoverthebareminimum OpenGLknowledgerequiredtounderstandtheexampleprograms.
3.3 OpenGLCoordinateSystem TheOpenGLcoordinatesystemisrathersimple.Regardlessofscreenwidth andheight, x -and y -coordinatesrangefrom 1.0to1.0.Seethefollowing figureforanillustrationoftheOpenGLcoordinatesystem:
2 Forthesakeofsimplicity,this is theapproachwetookforsomefractals,specificallythe iteratedfunctionsystem(IFS)classoffractals.
3 Thispixel-by-pixelapproachishowthefractalsintheaforementioned1993predecessor tothisbookwereimplemented.Forsomehistoricalcontext,OpenGLwasfirstreleasedin 1994,butthefirstcommerciallyavailableGPU(theNVIDIAGeForce256)wasn’twidely availableuntil1999.
( 1.0, 0)
(0, 1.0)
(1.0, 0) x y
(0, 1.0)
3.4 Vertices,ShadersandtheOpenGLRenderPipeline
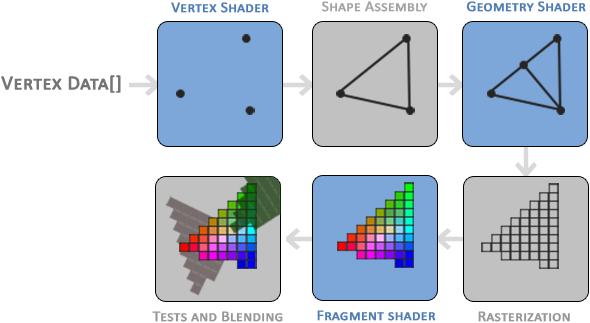
OpenGLspecifiesahandfulofdifferentshadertypes.Wewillbeusing three:vertex,geometry,andfragmentshaders.4 Theshadersarecomposed togethertoformarenderpipelinewhichcontrolshowOpenGLrendersa scene.TheOpenGLrenderpipelineisdepictedinthefollowingfigure: 4 Forthefulllist,seehttps://www.khronos.org/opengl/wiki/Shader.
IntroductiontoChaos,FractalsandDynamicalSystems
Source:ImagecopyrightJoeydeVries,https://twitter.com/JoeyDeVriez,licensedunder CCBY4.0(https://creativecommons.org/licenses/by/4.0/).Fromarticlehttps://learn opengl.com/Getting-started/Hello-Triangle.Retrievedfromhttps://learnopengl.com/ img/getting-started/pipeline.png.
Therenderingprocessbeginswithusfeedingalistofvertices(points in3Dspace)totheGPU.Foreachvertex,the vertexshader isrun.Vertexshadersmanipulatethe3Dcoordinatesofeachvertex,oneatatime. Onecommonusageforvertexshadersistoimplementcameratransforms. Ourprogramswon’tactuallyneedtoperformanyvertexprocessing,but OpenGLstillrequiresavertexshader.Wewillsimplyuseapass-through vertexshaderthatreturnseachinputvertexunchanged:
#version140 in vec2 position; //(x,y) void main(){
//output(x,y,z,depth)withz=0.0,depth=1.0 gl_Position = vec4(position, 0.0, 1.0); }
Verticesarethenassembledintoprimitiveshapes.Assemblyrequires thatwetellOpenGLhowtointerpretthevertices.Mostofourexample programsusetriangles,inwhichcaseOpenGLconsumestheverticesthree atatimeandinterpretsthemastheendpointsofatriangle.Nearlyall theexampleprogramsusetwotriangles(sixverticesintotal)thatwhen
combinedformasquarethatcoversthewholescreen.Incodeform,the verticeslooklikethis:
[1.0, 1.0].into(), [1.0, -1.0].into(), [-1.0, 1.0].into(), let vertices:[Vertex; 6] = [ ];
//firsttriangle
[1.0, -1.0].into(), [-1.0, 1.0].into(), [-1.0, -1.0].into(), //secondtriangle
Refertotheearlierfigure,showinganillustrationofthe OpenGLcoordinatesystem,toconvinceyourselfthatthesetwotrianglescoverthewhole screen.
Assembledshapesarethensenttothe geometryshader ifpresent.Geometryshadershavetheabilitytoemitnewvertices.Theonlytimewewill needgeometryshadersisforthefirstexampleprogram.
Afterthegeometryshader,thefinalsetofprimitivesismappedinto thesetofpixelsthatwillbedisplayedonthescreen(i.e.rasterized).The fragmentshader runsoneachofthesepixels.Fragmentshadersarewhere mostoftheinterestingworkisdoneinourprograms.Theyareresponsible fordeterminingthefinalcolorofeachpixel.
Finally,OpenGLperformsper-sampleoperationsthatcanincludecertaintestsandblendingoperations.Thesewillbeignoredforourpurposes.5
4.RunningthePrograms Ifyou’dliketorunanyofthefractalsforyourself,youwillneedtodownload (clone)thesourcecodefromourGitHubpage:https://code.laplante.io.You willalsoneedtoinstallRustandafewotherpackagesdependingonyour operatingsystem.Wewillkeepupdatedinstructionsforsetuponthatpage.
5 Iftheseinterestyou,seehttps://www.khronos.org/opengl/wiki/Per-Sample_ Processing.
xxviii IntroductiontoChaos,FractalsandDynamicalSystems
Throughoutthebook,youwillseeboxesthatlooklikethis:
Commandline
cargorun--binmandelbrot_simple
Theseboxesgivetheparticularcommandthatyoushouldtypeinyour terminaltorunthefractalyouseeonthepage.
5.Organization Thisbookissuitableforhomeschoolingasafocusedcourseonthesubject matterorasaclassroomsupplementforavarietyofcoursesatthelatejunior highorearlyhigh-schoollevel.Forexample,inadditiontoastandalone courseonChaos,FractalsandDynamicalSystems(orsimilartitle),this bookcouldbeusedwiththefollowingcourses:
• Precalculus
• Geometry
• Computerprogramming(e.g.Rust,C,C++,Python,Java,Pascal)
• Computergraphics
Thetextcanbeusedinconjunctionwithmathematicscoursesforundergraduateswhoarenotsciencemajors.Thebookcanalsobeusedforinformal familystudyanddiscussion.
Foreachchapter,we’veincludedexercisesandthingstodothatrange fromsimplecomputationaltaskstomoreelaboratecomputerprojects, relatedactivities,biographicalresearchandwritingassignments.We encouragetheuseofWolframAlphaforconfirmingtheanswerstothecomputationalexercisesandforfurtherexperimentation.WolframResearch’s Website,www.wolfram.com,providesmanyopportunitiesforplayful experimentation.
6.AbouttheImages Sincethebookisprintedingrayscale,wecouldnotincludecolorimages— andyouarereallymissingoutonsomeofthebeautyofthefractalsand variousfractal-likepictures.However,colorfilesforallimagesinthebook canbefoundatourwebsiteathttps://fractals.laplante.io.Foryourconvenience,wehaveaddedQRcodesnexttoeachimagethatwilltakeyouto thefull-colorversions.
Theylooklikethis: Full-colorimage:
Exceptwhereotherwisenoted,thecopyrightstoallimages,drawings, figuresandcodeusedinthebookareheldbyChristopherLaplanteandused withpermissioninthisbook.Useofanyoftheseimages,drawings,figures andcodeisprohibitedunlessexplicitpermissionisobtained.
7.OurWish Wehopeyoufindthestudyofchaos,fractalsanddynamicalsystemsto beinformative,entertainingandtimely.Afterall,inthecomplexworldin whichwelive,thesephenomenaarefoundeverywhere,andwehopeto enablereaderstorecognizetheseinstancestoenjoyandunderstandthem.