IntroductiontoAerosolModelling
FromTheorytoCode
Editedby
DavidTopping UniversityofManchester Manchester,UK
MichaelBane
ManchesterMetropolitanUniversity& HighEndComputeLtd Manchester,UK
Thiseditionfirstpublished2022 © 2022JohnWiley&SonsLtd
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedinaretrievalsystem,or transmitted,inanyformorbyanymeans,electronic,mechanical,photocopying,recordingorotherwise, exceptaspermittedbylaw.Adviceonhowtoobtainpermissiontoreusematerialfromthistitleisavailableat https://www.wiley.com/go/permissions.
TherightofDavidToppingandMichaelBanetobeidentifiedastheauthorsoftheeditorialmaterialinthis workhasbeenassertedinaccordancewithlaw.
RegisteredOffices
JohnWiley&Sons,Inc.,111RiverStreet,Hoboken,NJ07030,USA
JohnWiley&SonsLtd,TheAtrium,SouthernGate,Chichester,WestSussex,PO198SQ,UK
EditorialOffice 9600GarsingtonRoad,Oxford,OX42DQ,UK
Fordetailsofourglobaleditorialoffices,customerservices,andmoreinformationaboutWileyproductsvisit usatwww.wiley.com.
Wileyalsopublishesitsbooksinavarietyofelectronicformatsandbyprint-on-demand.Somecontentthat appearsinstandardprintversionsofthisbookmaynotbeavailableinotherformats.
LimitofLiability/DisclaimerofWarranty
Thecontentsofthisworkareintendedtofurthergeneralscientificresearch,understanding,anddiscussion onlyandarenotintendedandshouldnotberelieduponasrecommendingorpromotingscientificmethod, diagnosis,ortreatmentbyphysiciansforanyparticularpatient.Inviewofongoingresearch,equipment modifications,changesingovernmentalregulations,andtheconstantflowofinformationrelatingtotheuse ofmedicines,equipment,anddevices,thereaderisurgedtoreviewandevaluatetheinformationprovidedin thepackageinsertorinstructionsforeachmedicine,equipment,ordevicefor,amongotherthings,any changesintheinstructionsorindicationofusageandforaddedwarningsandprecautions.Whilethe publisherandauthorshaveusedtheirbesteffortsinpreparingthiswork,theymakenorepresentationsor warrantieswithrespecttotheaccuracyorcompletenessofthecontentsofthisworkandspecificallydisclaim allwarranties,includingwithoutlimitationanyimpliedwarrantiesofmerchantabilityorfitnessfora particularpurpose.Nowarrantymaybecreatedorextendedbysalesrepresentatives,writtensalesmaterials orpromotionalstatementsforthiswork.Thefactthatanorganization,website,orproductisreferredtoin thisworkasacitationand/orpotentialsourceoffurtherinformationdoesnotmeanthatthepublisherand authorsendorsetheinformationorservicestheorganization,website,orproductmayprovideor recommendationsitmaymake.Thisworkissoldwiththeunderstandingthatthepublisherisnotengaged inrenderingprofessionalservices.Theadviceandstrategiescontainedhereinmaynotbesuitableforyour situation.Youshouldconsultwithaspecialistwhereappropriate.Further,readersshouldbeawarethat websiteslistedinthisworkmayhavechangedordisappearedbetweenwhenthisworkwaswrittenand whenitisread.Neitherthepublishernorauthorsshallbeliableforanylossofprofitoranyother commercialdamages,includingbutnotlimitedtospecial,incidental,consequential,orotherdamages.
AcataloguerecordforthisbookisavailablefromtheLibraryofCongress
PaperbackISBN:9781119625650;ePubISBN:9781119625711;ePDFISBN:9781119625667
Coverimage:CoverillustrationkindlyprovidedbyHarriKokkola,FinnishMeteorologicalInstitute. Photograph ©TuukkaKokkola CoverdesignbyWiley
Setin9.5/12.5ptSTIXTwoTextbyIntegraSoftwareServicesPvt.Ltd,Pondicherry,India
Contents
Contributors ix
Preface xi
Acknowledgments xii
AbouttheCompanionWebsite xiii
1 IntroductionandthePurposeofthisBook 1
1.1AerosolScienceandChapterSynopses 4
1.2ComputersandProgrammingLanguages 10
1.3RepresentingAerosolParticlesasModelFrameworks 15
1.3.1SizeDistributions 18
1.3.2TheSectionalDistribution 22
1.3.3TheModalDistribution 25
1.4CodeAvailability 28
Bibliography 28
2 Gas-to-particlePartitioning 32
2.1Adsorption 33
2.2EquilibriumAbsorptivePartitioning 37
2.3KnudsenRegimesandtheKelvinEffect 43
2.4KineticAbsorptivePartitioning:TheDropletGrowthEquation 46
2.4.1SolvingtheDropletGrowthEquation:ASectionalApproach 49
2.5CloudCondensationNucleiActivation 65
2.5.1KöhlerTheory 65
2.5.2HygroscopicGrowthFactorsandKappaKöhlerTheory 71 Bibliography 75
3 Thermodynamics,NonidealMixing,andPhaseSeparation 78
3.1ThermodynamicsandNonidealMixing 78
3.1.1ChemicalThermodynamics 78
3.2ActivityCoefficientModel 83
3.3BATModelImplementation 85
3.3.1Example1:CalculationofBinaryMixtureActivitiesUsingthe BATModel 89
3.4PhaseSeparation 96
3.4.1Example2:DetectionandComputationofLLPSinaBinarySystem 97
3.5MulticomponentAerosolThermodynamicsModels 117
3.6ActivityandLLEComputationswiththeAIOMFACModel 118
3.6.1CustomizingandRunningAIOMFAC-LLE 121 Bibliography 129
4 ChemicalMechanismsandPureComponentProperties 133
4.1ChemicalMechanisms 134
4.1.1GasPhaseOnlyModel 134
4.1.2CouplingtheGaseousandCondensedPhaseUsingaFullyMoving SectionalApproach 153
4.1.3AnExampleUsingtheSectionalModelGeneratorJlBox 158
4.1.4ModalModelforCondensationalGrowth 163
4.2ChemicalIdentifiersandParsingStructures 169
4.3CodingPropertyPredictionTechniques 172
4.3.1GroupContributionMethods 175
4.3.2VaporPressurePredictionMethods 176
4.3.3Example:AddingtheSIMPOLMethodtoUManSysProp 176
4.4SubcooledLiquidDensity 181 Bibliography 183
5 Coagulation 187
5.1CoagulationProbabilitiesandRates 187
5.2StochasticCoagulationwithDiscreteParticleMasses 189
5.2.1Gillespie’sBasicAlgorithmforDiscreteNumberConcentrations 189
5.2.2FirstSpeedup:BinningParticles 192
5.2.3SecondSpeedup:DiscretizeTimeandUseTau-leaping 194
5.2.4ThirdSpeedup:Large-number-limitUsingContinuousNumber Concentration 197
5.3CoagulationwithContinuousParticleMasses 202
5.3.1Particle-resolvedApproachforCoagulation 202
5.3.2SectionalApproachforCoagulation 206
5.3.3ModalApproachforCoagulation 208
5.4AdvancedCoagulationTopics 213
5.4.1CoagulationforaMulti-dimensionalCompositionSpace 213
5.4.2OtherConsiderations 215
5.5IntroductiontoParticle-resolvedMonteCarlo(PartMC) 217
5.5.1PartMCInput(.dat)FilesPreparation 218
5.5.2SpecFilePreparation 219
5.5.3PartMCExecutionandPostprocessing 220 Bibliography 220
6 Nucleation:FormationofNewParticlesfromGasesby MolecularClustering 223
6.1ModellingParticleFormation:FromAtomstoMolecular ClusterPopulations 224
6.1.1TheDiscreteGeneralDynamicEquation 227
6.1.2TheDiscreteClusterGDEvs.theContinuousAerosolGDE 229
6.1.3RateConstantsoftheClusterDynamicsProcesses 229
6.1.4ClusterFormationinDifferentAtmosphericEnvironments 232
6.2CodingtheDiscreteGDE:TheStraight-forwardCaseofaOne-component System 233
6.3Multi-componentSystems:NeedforanEquationGenerator 239
6.4BriefIntroductiontoAtmosphericClusterDynamicsCode 241
6.4.1ACDCInput 242
6.4.2RunninganACDCSimulation 246
6.4.3CodeFeaturesUsefulforStudyingClusteringMechanisms 248
6.4.4ACDCApplications 250
6.5FromClusteringtoParticleGrowth:ImplementationofInitialParticle FormationinAerosolDynamicsModels 252
6.5.1TheDefaultApproach:ParticleFormationRateasanInputParameter 252
6.5.2TheDynamicApproach:CombinationofMolecularClusterandAerosol GDEs 255 Bibliography 256
7 BoxModels 259
7.1 box_model.py260
7.2RemappingSizeDistributionWhenUsingtheSectionalMethod 264
7.2.1Quasi-StationarySectionalMethod 265
7.2.2MovingCenterMethod 269
7.2.3HybridBinMethod 270
7.3SimulatingAbsorptiveUptakeandNewParticle FormationSimultaneously 279
7.4CloudParcelModels 280
7.4.1SectionalCloudParcelModel 281
7.5SALSA 284 Bibliography 286
8 SoftwareOptimization 288
8.1Portability 288
8.2Performance 289
8.2.1CompilerOptimization 289
8.2.2Profiling 290
8.2.3CaseStudy:Speeding-upBoxModel 291
8.2.4Vectors 297
8.2.5HandHoldingtheCompiler 298
8.2.6CaseStudy:PartMC 298
8.2.7InterprettedLanguages 302
8.2.8CaseStudy:DropletGrowthEquation 303
8.3Parallelization 305
8.3.1MakingtheMostofaSingleNode 307
8.3.2MakingUseofMultipleNodes 308
8.3.3OtherTechnologies 309
8.4CollaborativeSoftwareEngineering 310
8.4.1CodingStylesheets 311
8.4.2ModularityandRe-use 311
8.4.3VersionControl 312
8.4.4SoftwareDevelopmentLifeCycle 312
8.4.5ContinuousIntegrationandUnitTests 312
8.5InConclusion 313 Bibliography 314
A AppendixA 316
A.1Exercises 316
A.2PhysicalConstants 329
A.3ConversionFactor 330
A.4VariableDefinitions 330 Bibliography 345
Index 347
Contributors
MichaelBane hasspentseveraldecadesinoptimizingcodesandhelpingothers understandhowtheycanoptimizecodes.HeiscurrentlyaLectureratManchesterMetropolitanUniversity,UK,andDirectorofHighEndComputeLTD.Michael wroteChapter8andgavesupportiveinputtootherchapters,particularlyChapter1.
JeffreyCurtis, PostdoctoralResearchAssociateintheDepartmentofAtmosphericSciencesattheUniversityofIllinoisatUrbana-Champaign.JeffreycontributedtoChapter5.
HarriKokkola, GroupleaderoftheAtmosphericModelingGroupattheAtmosphericResearchCentreofEasternFinland.Hehasdevelopedandappliedmodels simulatingatmosphericaerosol,clouds,andclimatefromprocessscaletoglobal scale.HarriwroteChapter7.
BenjaminMurphy, PhysicalScientistintheUnitedStatesEnvironmentalProtectionAgencyOfficeofResearchandDevelopmentatResearchTrianglePark,North Carolina.BenjamincontributedtoChapters1,4,and5.
TinjaOlenius, researchscientistintheAirQualityUnitatSwedishMeteorological andHydrologicalInstitute(SMHI).Tinja’sresearchinterestsincludedevelopingthe chainofmodelingtoolsfromquantummechanicstolarge-scalemodelsforimprovingtherepresentationofsecondaryparticleformationfromvapors.Tinjawrote Chapter6.
OlliPakarinen, universitylecturerattheInstituteforAtmosphericandEarth SystemResearch(INAR),UniversityofHelsinki,Finland.Ollicontributedto Chapter6.
NicoleRiemer, ProfessorintheDepartmentofAtmosphericSciencesattheUniversityofIllinoisatUrbana-Champaign,IL,USA.Nicole’sresearchinterestsinclude thedevelopmentofaerosolmodels,fromtheprocessleveltotheglobalscale.Nicole wroteChapter5.
PetrocShelley, PhDstudentintheDepartmentofEarthandEnvironmentalScienceattheUniversityofManchester,UK.Hiscurrentspecialismisinthe measurementandpredictionofpurecomponentproperties.Petroccontributedto Chapter4.
DavidTopping, ProfessorintheDepartmentofEarthandEnvironmentalScience attheUniversityofManchester,UK.SincehisPhD,Davidhasdevelopedandapplied
x Contributors
modelsofaerosolparticlesacrossarangeofscales.Davidconvenedthewritingteam behindthisbookandwroteChapters1,2,and4.
MatthewWest, AssociateProfessorintheDepartmentofMechanicalScience andEngineeringattheUniversityofIllinoisatUrbana-Champaign,IL,USA.His researchinterestsincludestochastictimeintegrationmethodsandscientificcomputing.MattwroteChapter5.
ZhonghuaZheng, PhDinEnvironmentalEngineeringinCivilEngineeringwith aconcentrationinComputationalScienceandEngineeringattheUniversityof IllinoisatUrbana-Champaign,IL,USA.ZhonghuacontributedtoChapter5.
AndreasZuend, ProfessorintheDepartmentofAtmosphericandOceanicSciencesatMcGillUniversity,Montreal,Quebec,Canada.Hisresearchinterestsinclude thedevelopmentofpredictivethermodynamicaerosolmodelsforgas–particlepartitioning,aswellasreduced-complexitymethodsformixturepropertiesofaerosols andclouddroplets.AndreaswroteChapter3.
Preface
Aerosolscienceisonethatstraddlesmanydisciplines.Thereisanaturaltendency fortheaerosolscientisttothereforeworkattheinterfaceofthetraditionalacademic subjectsofphysics,chemistry,biology,mathematics,andcomputing.Theimpacts thataerosolparticleshaveontheclimate,air-quality,andthushumanhealthare linkedtotheirevolvingchemicalandphysicalcharacteristics.Likewise,thechemical andphysicalcharacteristicofaerosolparticlesreflecttheirsourcesandsubsequent processestheyhavebeensubjectto.Computationalmodelsarenotonlyessentialfor constructingevidence-basedunderstandingofimportantaerosolprocesses,butalso topredictchangeandpotentialimpact.Seminalpublicationsprovideanextensive overviewonthehistoryandbasisofcoretheoreticalframeworksthataerosolmodels arebasedon.Howeverthereislittleonhowwecantranslatesuchtheoryintocode. Whilewefocusonatmosphericaerosolinthisbook,thetheoryandtoolsdeveloped arebasedoncoreaerosolphysicsthattranslateacrossmultipledisciplines.Likewise, demonstratingaprogrammingsolutiontocommonnumericaloperationsisvaluable toalargenumberofscientificdisciplines.Youmaybereadingthisbookasan undergraduate,postgraduate,seasonedresearcherintheprivate/publicsectororas someonewhowishestobetterunderstandthepathwaystoaerosolmodeldevelopment. Whereveryoupositionyourself,itishopedthatthetoolsyouwilllearnthroughthis bookwillprovideyouwiththebasistodevelopyourownplatformsandtoensurethe nextgenerationofaerosolmodelersareequippedwithfoundationalskillstoaddress futurechallengesinaerosolscience.
Manchester
ProfessorDavidTopping July2022
Acknowledgments
TheidentifiedneedforthisbookwasinspiredbytheAerosolandDropletScienceCentreforDoctoralTraining[CDT],fundedbytheUKEngineeringandPhysicalSciences ResearchCouncil(EPSRC)(grantno.EP/S023593/1)(https://www.aerosol-cdt.ac.uk/).
TheauthorswouldalsoliketothankHannaVehkamäki,AnaCristinaCarvalho, ManuThomasandCeciliaBennetforusefuldiscussionsandcomments.TheSwedish ResearchCouncilVR(grantno.2019-04853)andtheSwedishResearchCouncilforSustainableDevelopmentFORMAS(grantno.2019-01433)areacknowledgedforfinancial supportforChapter6.
Allofthecodesnippetsandexamplesprovidedwiththebookcanalsobedownloaded fromtheprojectGithubrepository:
https://github.com/aerosol-modelling/Book-Code.git
IntroductionandthePurposeofthisBook
Anaerosolparticleisdefinedasolidorliquidparticlesuspendedinacarriergas. Theterm“aerosol”technicallyincludesboththeparticleandcarriergas,thoughit iscommontooftenhearthisusedwhenreferringtojusttheparticle.Inthisbook, wewillretaintheuseoftheterm“aerosolparticle”.Whilstweoftentreatscientific challengesinasiloedway,aerosolparticlesareofinterestacrossmanydisciplines.For example,atmosphericaerosolparticlesarekeydeterminantsofairquality[1–3]and climatechange[4–6].Improvingourunderstandingofsources,processesandsinksis importantaswedevelopstrategiestolessontheimpactswehaveonhumanhealthand environmentalsystems.Knowledgeofaerosolphysicsandgenerationmechanismsis keytoallfactorsoffueldelivery[7]anddrugdeliverytothelungs[8].Likewise,various manufacturingprocessesrequireoptimalgeneration,deliveryandremovalofaerosol particlesinarangeofconditions[9].
Thepurposeofthisbookistoprovideyou,thereader,withthetoolstotranslate theoryonwhichnumericalaerosolmodelsarebasedintoworkingcode.Infollowing thecontentprovidedinthisbook,youwillbeabletoreproducemodelsofkeyprocesses thatcaneitherbeusedinisolationorbroughttogethertoconstructademonstrator0D box-modelofacoupledgaseous-particulatesystem.
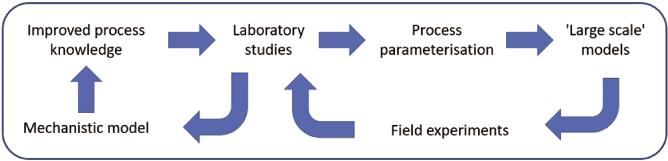
Youmaybereadingthisbookasanundergraduate,postgraduate,seasoned researcherintheprivate/publicsectororassomeonewhowishestobetterunderstand thepathwaystoaerosolmodeldevelopment.Whereveryoupositionyourself,thecouplingbetweenexperimentalandmodelinginfrastructureisimportantinanydiscipline. Whilstthedrivingfactorsthatinfluencebothcanvary,Figure1.1presentsanidealized workflowofmodeldevelopmentandmodelscalesbothinresponsetoandasadriving forcebehindaerosolexperiments.Particularemphasisisgiventoatmosphericaerosol particlesinthisworkflowwhere,aswemovefromlefttoright,wemovefromaerosol modelsatthemolecularandsingleparticlescaletoaerosolmodelsactingasanimport componentinregionalandglobalscalemodels.Thepurposeofthisfigureistorepresentaworkflowthatmigratesourunderstandingofaerosolprocessestoaframework thatmaybeusedtopredictimpacts.Inaperhapscontroversialapproach,wecanimagineascaleatthebottomofthefigurethatassumesaswemovefromlefttorightwe reducethephysicalandchemicalcomplexityofouraerosolmodels.Thissetsthescene forunderstandingtheresearchlandscapeofmuchofthedevelopmentsyouwillfind inthisbook.
Ifwestartattheleft-handsideofthefigure,weusethetermmechanisticmodel.In aerosolmodelingparlance,amechanisticmodelisonethatisbuiltaroundanumericalrepresentationofanunderlyingphysicaltheory.Forexample,thismightinclude asetofcoupleddifferentialequationsthatdescribethemovementofmassbetween agaseousandcondensedphase,orbetweendifferentcompartmentsofacondensed phase.Parametersinthesemechanisticmodelsmaydescribechemicalandphysical propertiesthatareincludedinthesedifferentialequationsandhavebeenderivedfrom aseriesofexperimentsorprovidedthroughseparatemodels.Inamechanisticmodel, ourmathematicalframeworkprovidesaclearnumericalnarrativeandseparationof theprocesseswewishtoinclude.Wecanthenchooseanappropriatenumericalmethod toprovide,forexample,atime-varyingsolutiontoasetofinitialconditionsorpredictapointofequilibrium.Oncewehaveconstructedourmechanisticmodel,we canconsideruncertaintiesassociatedwiththemodelarchitectureitselfand/orerrors associatedwiththeparametersweuseinoursimulation.Indeed,thenextphasein ourworkflowinFigure1.1istocomparewithtargetedlaboratoryexperimentsthat servetoquantifytheaccuracyofourmodeloridentifyuncertaintiesthatneedfurtherreduction.Youmayfindmechanisticframeworksusedatthesingleparticlelevel, orindeedinmodelsthataredesignedtocapturetheevolutionofapopulationof particles.Wheremechanisticmodelscannotreplicateobservedbehaviorwithinaspecificlevelofaccuracy,orsimplydonothaveanappropriatetheoreticalbasistobuild on,parameterizationscanbedeveloped.Thiscanbeusedincombinationwith,or asanalternativeto,themechanisticmodel.Weoftenstatethataparameterization hasahighercomputationalefficiencythananequivalentmechanisticmodel.Specifically,thetimetosolutionisreduced.AswemovefurtherrightinFigure1.1,and typicallystarttoconsiderpopulationsofparticlesandmultipleprocesses,wemight refertohybridmodelsthatcombinebothmechanisticandparameterizations.Wemay alsostarttoconsiderthecomputationalresourceavailabletoconductmorecomplex simulations.Attheglobalscale,anaerosolmodelisoneofmanycomponentsina frameworkthatattemptstocapturethedynamicsofmultiplecomponentsoftheearth system(e.g.,ocean,biosphere,land-airinteractionsetc.).Thelevelofphysicaland chemicalcomplexityretainedinouraerosolmodelisdictatedbyanumberoffactors. Theseincludethecomputationalresourceavailable,theassociateddetailcarriedin componentsthatdriveandrespondtoaerosolprocesses(e.g.,howmanyemissions thatleadtoaerosolformationarecaptured)andongoingeffortstoresolvehowmuch detailisneededtoresolvepotentialimpactson,forexample,humanhealth.Ofcourse, thisnarrativeisanidealonebutatleastprovidesaninsightintofactorsthatdictatethemethodsweusetoconstructouraerosolmodels.Inthismanner,westartto appreciatetheecosystemofaerosolsmodelsandwhytheyexist.Theaerosolscientist maycomeacrossarangeof“simple”and“complex”modelsthathavebeendesigned toprovidebenchmarksimulationsinisolation.Youwillfindadescriptionofthese benchmarkmodelsinthechaptersofthisbook.Oncewebegintocaptureprocesses acrossmultiplescales,anaerosolmodeldeveloperstartstoconsideranyapproximationsthatmaybeneededaccordingtothenumericalmethodsandcomputeresource available.
Whilstwefocusonatmosphericaerosoltodefineourcompositionspaceinthis book,thetheoryandtoolsdevelopedarebasedoncoreaerosolphysicsthattranslate
Figure1.1 Idealworkflowofaerosolmodeldevelopmentinenvironmentalscience. acrossmultipledisciplines.Likewise,demonstratingaprogrammingsolutiontocommonnumericaloperationsisvaluabletoalargenumberofscientificdisciplines.
Researchdevelopmentsoftenmoveatarapidpaceand,astheglobalaerosolcommunitydevelopnewobservationalandmodelingplatforms,wecontinuallyhypothesize andverifynewspeciesand/orprocessesdeemedimportanttoimproveourunderstanding.Wedonotprovideacomprehensivecouplingofallknownandemergingchemical andprocesscomplexityinthisbook.Indeed,thereareremainingchallengesonhow weactuallydothatfromaprogrammingandreal-worldvalidationperspective.The landscapeofcomputinghardwareandsoftwarealsomovesatarapidpace.Thechoice ofprogramminglanguagetosolveaparticularproblem,orprovideaparticularservice, isinfluencedbyanumberoffactorsrangingfromrequiredtime-to-solutionandability toshareacrossmultipleplatforms.Aswithnumericalrepresentationsofaerosolprocesses,wedonotprovideacomprehensivemultilanguagedemonstrationinthisbook. Itisanticipatedthatreadersofthisbookwillhaveawiderangeofprogrammingexperience;fromthosewhohavenopriorexperiencetothosewhoregularlydeveloptheir ownapplications.Weexpectthereforethatyouwilltakeawaydifferentlessonsfrom workingthroughthematerialprovided,whetheritbethesolutiontoasetofcommon operationsorlearninghowtodevelopyourfirstnumericalmodelinyourfirstprogramminglanguage.Youwillfindthereareoftenmultiplewaystowriteapieceofcodethat performsaparticulartask.Youwillalsofindthatasweoftenhaveourownstylein writing,sotoocanwedevelopourownstyleofdevelopingcode.Inthisbook,weprovidecompletedemonstrationsofhowtodevelopworkingcodearoundkeyconcepts (highlightedinfigure1.2),butwedonotforceaparticularstylebeyondrequirements ofthelanguagesyntax.Wealsohoweverprovideexamplesofhowwecanoptimizethe codewedevelop.Bylookingatarangeofexamples,thiswillhelpyoustarttomore broadlyconsiderhowefficientyourcodeisandperhapsembedtheseconsiderations asyoustarttodevelopmodeapplications.Wealsodiscussbestpracticeinsharingany codeinthepublicdomainandensuringreproducibility.
Seminalpublications[e.g.,[2,19]]provideanextensiveoverviewonthehistoryand basisofcoretheoreticalframeworksthataerosolmodelsarebasedon.Wedonotrepeat thatcontentinthisbook;ratherwepresentthetheoreticalbasisusedinconstructing amodelandthenfocusonhowwemapthistocodedevelopment.
Thetoolsyouwilllearnthroughthisbookarefoundational.Astheresearchcommunityexplorenewhardwareplatformsandprogramminglanguagesinanattempt totacklegrowingcomplexity,thesefoundationalskillswillprovideyouwiththebasis todevelopyourownplatforms.Willanyonetackletheentiretyofaerosolmodeling complexity?Maybeitwillbeyou.
1.1 AerosolScienceandChapterSynopses
Aerosolscienceismultidisciplinarybynature.Thisisreflectedinthehugebodyofliteraturethatnowexistsinpeer-reviewedjournals.Thereisanaturaltendencyforthe aerosolscientisttothereforeworkattheinterfaceofthetraditionalacademicsubjects ofphysics,chemistry,biology,mathematics,andcomputing.Ofcourse,anaerosolscientistworkingineithermedicineorclimatechangewillfindthemselvesfocusingon distinctareasandthelevelofunderstandingineachwillbedependentontheresearch challenge.However,chancesarethatbothwill,atsomepoint,requiretraininginkey conceptsofaerosolsciencethatapplytobothdomains.Indeed,onebenefitofbecoming anaerosolscientististhatunderstanding,refinementandapplicationofcoreconcepts istransferablebetweendisciplines.
In2018,theAerosolSocietyoftheUnitedKingdompublishedtheoutcomesof anindustrialengagementworkshop[12],definingapipelineofresearch,innovation
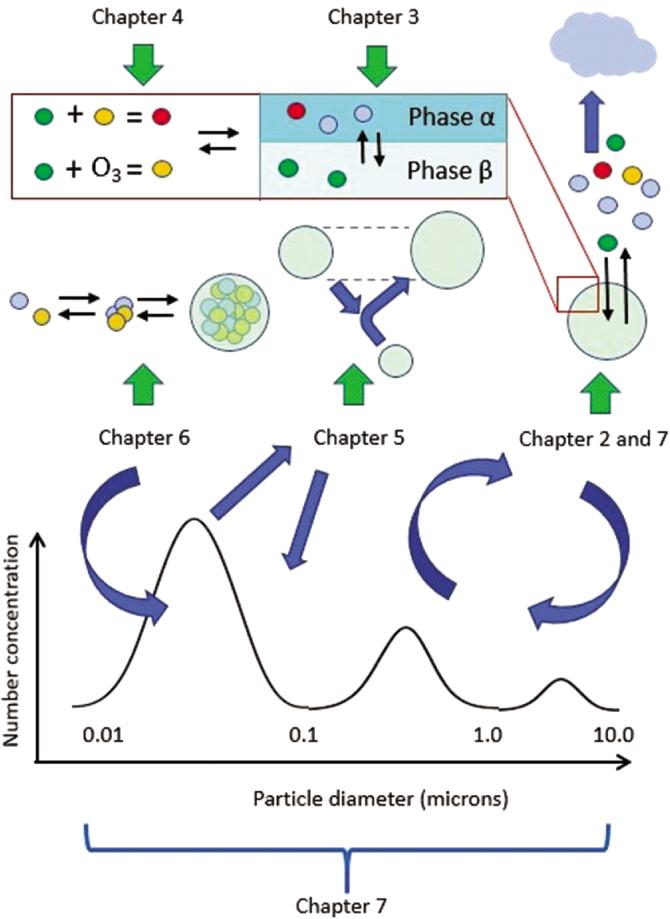
Figure1.2 Thetopicscoveredineachchapter,summarizedinthemainbodyoftextinthis chapter,asavisualschematicthatconnectsprocessesacrosstheaerosolsizespectrum.Inthis hypotheticalexample,theaerosolsizedistributionhasthreepeaksrepresentedasmultiple log-normalcontributions.Westarttodiscusslog-normaldistributionsinSections1.3.2and 1.3.3.
1.1AerosolScienceandChapterSynopses 5 andtechnologydevelopmentforaerosolscience.Inthistheynotethatestimatesof theglobalaerosolmarketsizesuggestitwillreach$84billionperyearby2024with productsinthepersonalcare,household,automotive,food,paints,andmedicalsectors.However,theyalsonotethatdespitethegrowinginterestintothemacro-effects andindustrialexploitationofaerosols,aerosolscienceisarelativelyyoungdiscipline encompassingresearchtopicswhichcanconcomitantlybeunderstoodasbiological, chemical,engineering,environmental,material,medical,pharmaceutical,orphysical science.
Wefocusonatmosphericaerosolparticlesfortheremainingportionsofthisbook. Theimpactsthataerosolparticleshaveontheclimate,air-qualityandthushuman health,arelinkedtotheirevolvingchemicalandphysicalcharacteristics[3,5].Likewise,thechemicalandphysicalcharacteristicofaerosolparticlesreflecttheirsources andsubsequentprocessestheyhavebeensubjectto[2,14].Atmosphericaerosolparticlescanrangeinsizefromafewnanometerstohundredsofmicrons.Theycanbeof primaryorsecondaryorigin.Primaryparticlesaredirectlyemittedintotheatmosphere, whilstsecondaryparticlesareproducedfromgas-to-particleconversionprocesses.An aerosolparticlemaycompriseinorganicand/ororganiccomponentswhichcanbe associatedwithbothprimaryandsecondaryparticles.Whilsttheinorganicfraction maybecomprisedbyarelativelysmallnumberofcomponents[2],theorganicfractionmaycomprisemanythousandsofcompoundsfrommultiplesources[15,16].As anaerosolparticleresidesintheatmosphere,weknowthatmanyprocessestaking placein/onatmosphericaerosolparticlesareaccompaniedbychangesintheparticles’morphology(sizeandshape)[17].Theseprocessesalsochangethechemical compositionofaerosolparticlesaccordingtotheavailabilityof,forexample,keygas phaseoxidantsandambientconditions[16].Likewise,particlesofprimaryoriginal (e.g.desertdust,volcanicash,soot,pollen)canhavewidelyvaryingmorphological features[19–21].Mechanismsareimportantinunderstandinglifetimesandpotential impacts[22].
Letusbeginwithanidealizedsphericalrepresentationofaerosolparticles.Theirsize andcompositionwillvary,butwewishtosimulatehowtheirconcentrationchanges overtime.Whilstcontrolledexperimentsmaybeabletoisolatesinglelevitatedparticles [23],underatmosphericconditionsweexpectarangeofparticlesizesandnumber densities.Letustakeanisolatedparticlewithdiameter ���� anddensity �� withunits in m and kg m−3,respectively.Asingleparticlehasamass �� in kg calculatedusing Equation(1.1):
Ifweobserve���� particlespercubiccentimeter,wecanuseEquation(1.2)tocalculate thetotalconcentrationofparticleswithsize ����, ��������,usingthecommonairquality metricof µgm−3
(1.2) wherethefactor 1015 isaproductofconverting cm−3 to m−3 (106)and kg to µg (109). Thisformulahasnoinformationontheparticlecompositionormorphology.Indeed, ouridealizedsphericalrepresentationmaybewrongundercertainconditionsand/or
forcertainaerosoltypes.Nonetheless,wecanuseourparticlerepresentation,which hasavolume �� (m)givenbyEquation(1.3),asacommonparticlereference.
Ifwenowspecifythattheconcentration(numberdensity)ofparticleswiththisspecificvolume,ataspecifictime ��,canberepresentedbyavariable ����,��,wecanstartto formulateanexpressionthatcapturestheevolutionofparticleswithvariablevolumes intoanalgebraicform.
Forexample,inFigure1.3ontheleft-handsidewehaveapopulationofparticleswith aspecificvolumeatagivenpointintime.Thetotalconcentrationoftheseparticlesis ����,��.Ontheright-handside,thispopulationhasevolvedafteratimeincrement∆�� and wehaveparticlesatsmallerandlargervolumes,representedbyadiscretechange ∆��. Specifically, ����,��+∆
and
representtheconcentrationofparticles thathavetheoriginalvolume,theconcentrationofparticleswithasmallervolumeand theconcentrationofparticleswithalargervolumeatanewtime ��+∆��,respectively. Inrealitytheseparticleswillhavebeencreatedthroughprimaryand/orsecondary mechanisms.
Equation(1.4)isthecontinuousgeneraldynamicequation[24].Thisordinarydifferentialequation(ODE)describestherateofchangeof ����,�� resultingfromkeyprocesses whichareidentifiedasnucleation,coagulationandcondensation.Wealsoincludea generictermthatrepresentsemissionandremovalmechanisms.
Equation(1.4)isthefirstalgebraicformulationofaerosolevolutioninthisbook. Eachcontributiontothisequationhasitsowntheoreticalbasisandthusalgebraic
Figure1.3 Aninitialpopulationofparticleswithvolume �� ontheleft-handsideofthis figureevolvetoapopulationwithmultiplevolumesafteratimeincrement ∆
1.1AerosolScienceandChapterSynopses 7 formulation.Thesearepresentedanddiscussedinspecificchapters,andalsohighlightedinfigure1.2anddiscussedshortly.Wealsoneedtotranslateouralgebraic formulationsintocode.Youwillfindarangeofapproachesarepresentedtoperform thistranslationthatprovideyouwithagroundingincommonapproachesusedacross aerosolscience.Figure1.5providesaschematicthatmapsprocessesonourbookstructurebyhighlightingtherelevantchaptersthatfocusoneachinturn.Whilstweisolate processesincludingnucleationandcoagulationindistinctchapters,wealsocover propertiesandbridgingtechnologiesthatarenotexplicitlyhighlightedinEquation (1.4)butarenonethelessimportanttoprovidingasolutiontoit.Theseincludedevelopingmodelsthatcapturecondensedphasethermodynamicsandsimulatediffusion withinaparticle,simulatingareactivegasphaseandpresentingthestructurerequired tobuildasimplemodelofaerosoltoclouddropletactivation.Asynopsisofeachchapter isprovidedbelow.Atthebeginningofeachchapteryouwillfindanoverviewofthelanguagechosenanduseofanyfunctionsprovidedwithinthatenvironment.Youwillalso findthat,insomechapters,wecombineabreakdownoftranslatingtheorytocodewith instructionsonhowtorunexistingcommunitymodelswhichhavebeenwrittenina varietyofprogramminglanguages.
● Chapter1:Followingonfromanintroductiontoaerosolscience,herewediscuss generalconceptsaroundrepresentingaerosolparticlesasanumericalmodel.This encouragesyoutoconsiderwhatinformationanaerosolmodelmayneedtocarryand howwethenmapthatintoanumericalmodelthroughtheprogramminglanguage constructs.Forexample,atthesingleparticlelevelwemaywishtoconstructamodel thatsimulatesthepartitioningofmassbetweenagaseousphaseandhomogeneous droplet.Ifwehave�� compoundsinthegasphaseandoneparticle,thenitisreasonabletodesignamodelbuiltaroundaonedimensionalarrayofsize��+1.Ofcourse, onceweconsiderpopulationsofparticleswithvaryingsizesand,perhaps,interparticlemorphology,thenourchoicebecomesmorecomplex.Inthischapter,wetherefore presentsomegeneralconsiderationsaroundtheseissueswhichhelpcontextualize thedesignchoicesyouwillcomeacrossintheproceedingchapters.Wefollowthis byintroducingourfirsttheorytocodedemonstrationswhereweimplementtwodifferentapproachestorepresentapopulationofparticlesinPython.Knownasthe modalandsectionalmethods,thisprovidesabasisforsubsequentchapters.
● Chapter2:Inthischapter,wepresentandimplementtheoriesthatallowustosimulatemovementofmassbetweenagasandcondensedphase.Wefirstintroduce equationsthatprovidethebasisforpredictingthecompositionofboththegasand condensedphaseatequilibrium.Thisissplitbetweentheprocessesofadsorption andabsorptionandconsidersboththeparticulateandgaseousphasetobenonreactive.Uptothispointweassumeourparticulatephasetohavenosize,considering atotalmassthatcompoundsinthegasphasecanadsorborabsorbto.Followingon fromthiswethenmovetosimulatingdynamicabsorptivepartitioningbyintroducing andsolvingthedropletgrowthequation.Whilstbothourgasandparticulatephase remainsnonreactive,weusePythontosimulatethegrowthofbothmono-andpolydispersepopulationsasafunctionoftime.Thesizeandcompositionofthesimulated aerosolparticlesinfluencethepartitioningprocessthroughachangeinequilibrium pressureabovethecondensedphase,butthecondensedphasecomponentsdonot interactwitheachother.Weuseboththemodalandsectionaldistributionscovered
inChapter1,wherewecomparePythonandJuliamodelsforthesectionalapproach. Ineachcase,whendesigningourmodelstructure,wealsoneedtobeawareofhow weutilizeanyspecificsolverroutines.Inthiscase,weuseexistingordinarydifferentialequation(ODE)solverswithinpopularPythonandJuliapackages.Attention isthengiventopredictingaerosolwateruptakethroughequilibriumframeworks,at thesingleparticlelevel,belowandabove100% relativehumidity.
● Chapter3:Inthischapter,weintroducetheoreticalframeworksthatunderpinthermodynamicsandnonidealmixing.WhilstinChapter2weassumedouraerosol particleswereconstructedofahomogeneousidealmixture,hereweaccountfor nonidealmixing.Wespecificallymovetotreatingnonidealinteractionsthatdictate thepredictedequilibriumstateand,insomecases,leadtophaseseparationinthe particulatephase.YouwillseetheuseofPythonagaininconstructingsimulations ofsimplemixturesandtherequiredstructureofourcode.Youwillalsofindinformationofhowtouseanexistingcommunitymodeltosimulatephaseseparationin complexmixtures,writteninFortran.Onceagain,translatingtherelevanttheoryinto codehererequiressomeconsiderationofanappropriatemodelstructure.InChapter 2wediscussseparationofaerosolparticlesizeaswedesignthearraysthatwilltrack informationonaerosolcompositionthroughthesimulation;likewisehereweneed toconsiderhowwetrackthecompositionofourparticle.
● Chapter4:Inallpreviouschapters,wehaveusedanonreactive“static”gasphase.As aerosolparticlesresideinagaseousmedium,theyaresubjecttoprocessesthatare drivenbytheavailabilityofcompoundsinsaidmedium.Likewise,theavailabilityof gaseouscompoundsisdrivenbythecomplexchemistrythatunfoldsascompounds reactwitheachandarangeofoxidants.Inthischapter,webeginwithanexample ofhowtosimulate,andthustrack,thevariableconcentrationofcompoundsinagas phase.Wediscusstheconceptofachemicalmechanisminthecontextofafilethat holdsinformationabouttheinteractionofcompoundsinthegasphase.Wethenuse toolsinPythontoextractinformationinthesefilesandcreateacodestructurethat allowsustosimulatetheconcentrationofeachcompoundasafunctionoftime.Once againweconsideranappropriatestructurethatisdrivenbytheinformationwewish totrackandourchosenODEsolvers.Withanevolvinggasphase,wecanalsoconsiderthepropertiesofindividualcompoundsthatdictategas-to-particlepartitioning. Predictingthosepropertiesrequiresustomapanalgebraicformofapredictivetechniquetoachemicalstructure.YouwillthereforefindtheuseofPythonandexisting informaticspackagestoextractandautomatethepredictionofpropertiesformany thousandsofcompounds.Withallofthepreviousworkonrequiredcodestructures andsolversforsimulatingcondensationalgrowthandareactivegasphase,wealso provideademonstrationofhowtouseexistingcommunity-drivenmodelsthathave beendesignedtoautomatetheprocessfromreadingachemicalmechanismfileand thencreatingamodelthatwillsimulatetheevolutionofacoupledparticulateand gasphase,writteninbothPythonandJulia.
● Chapter5:Ifthepopulationofourparticleshavedifferentvelocities,thereisachance theywillcollide.Twoparticlescollidingtoproducealargerparticlereducethetotal numberconcentrationovertime.Thisprocessiscalledcoagulationandisinfluenced byanumberoffactorsincludingambientconditions,theconcentrationsofaerosol particlesandtheirphasestate.Inthischapter,wedevelopstochasticanddeterministicrepresentationsofthecoagulationprocessinPython.Inallotherchapters,
wehavebuiltdeterministicmodels.Aspartofthischapter’sdevelopmentofthe stochasticanddeterministicrepresentations,wediscusstheimpactofdesignchoices oncomputationalefficiency,includingacomparisonbetweenamodalandsectional approach.Followingonfromthiswestarttoconsidermorecomplexcoagulation scenariosincluding,forexample,thetreatmentofnonsphericalparticles.
● Chapter6:WhilstChapter2focusesongas-to-particlepartitioningtoanexisting condensedphase,inthischapterwepresentunderlyingtheoriesthatareusedto predictnewparticleformation.Thisisreferredtoasaerosolnucleation.AsChapter 5treatstheinteractionbetweenaerosolparticles,herewemoveourfocustothe molecularlevel.Wecontextualizethisworkintermsofaerosolsizerangeswehave metinallotherchaptersandnowconsiderclustersofmoleculesasdiscreteunits. Theboundarybetweenamoleculeandanaerosolparticlebecomesblurred,butthe challengetodesignanappropriatenumericalmodelremains.WebuildaMatlab solutiontoadiscreteformofthe“birth-death”equationformolecularclusters.You willfindadiscussiononhowmodelswedevelophaveaplaceanddependencyin awiderecosystemofnumericalmodels.Inthisinstance,thatspecificallyincludes thoseconductingmoleculardynamicsandquantumchemistrysimulations.Moving beyondtheMatlabbasedexampleswebuildhere,youwillalsofindanintroduction andtutorialonusingtheAtmosphericClusterDynamicsCode(ACDC)whichhas componentswritteninthelanguagesPerl,MatlabandFortran.
● Chapter7:Chapters1–6canbelookedatinisolationandthecodeexamplesallow youthereadertofurtherdevelopthemorintegratethemintoothersoftware.Of course,weknowfromthegeneraldynamicequationthatwewishtoconnectthese processdescriptionssuchthatwecansimulatethelife-cycleofanaerosolparticle,or populationofparticles.Inthischapterwethereforeintroducetheconceptofaboxmodelandpresentanumericalandcodedesignstrategytointegratingnucleation, coagulationandcondensationalgrowth.Focusingonasectionalapproach,youwill findthatthemechanismfortrackingparticlesizepresentedinChapter2haslimitationswhenwewishtoincludenucleationandcoagulation.Wepresentmethods forrestructuringournumericalarraysinPython.Wefinishthischapterbyassumingouraerosoldistributioniswithinarisingparcelofairwhichleadstoincreasing relativehumidityabovesaturationandleadstoformationofclouddroplets.Inthis manneryouwilllearnhowtocreateacloudparcelmodelandlaythefoundation foranotherlargeareaofresearchincapturingandpredictingcloudmicro-physics fromapopulationofaerosolparticles.Intheendofthechapter,wewillpresenta boxaerosol-cloudmodelSALSAwhichcomprisesatmosphericallyrelevantmicrophysicalprocesseswhichinteractwithaerosolparticles,clouddroplets,precipitation dropletsandicenuclei.
Translatingtheoryintocoderequiresustoconsiderhowwecanrepresentinformationonthepropertiesoftheaerosolsystemweareinterestedin.Thisisinfluenced bychoiceofprogramminglanguage,whichinturnmaybedrivenbytheavailability ofnumericalmethodsoryourrelianceonexistinglegacycodethatmayhavebeen developedinyourcommunity.Thisalsofundamentallyrequiresconsiderationofhow werepresentaerosolparticlesinnumericalmodels.Whilsteachchapterprovidesyou withagroundingincommonapproachestosolvingtherelevantprocess,withthisin mind,inSection1.2weprovideyouwithabriefoverviewofcomputerprogramming
languagesusedinthisbook,shouldthisbeneeded.Followingthis,inSection1.3we thenpresentageneralconsiderationofhowwerepresentaerosolparticlesandtheir physicalandchemicalcharacteristicswithinnumericalconstructsinoursoftware.This isdesignedtoprovideextracontexttothecontentyouwillfindineachchapter.
1.2 ComputersandProgrammingLanguages
Acomputationalmodelisbuiltaroundasetofrules;asingleofsetofalgorithms.The interfacebetweentheaerosolscientist,whohasdrawnuptheserules,andthecomputerisprovidedbyaprogramminglanguage.Therearemanyprogramminglanguages available,eachwithitsownsetofadvantagesanddisadvantagesdependingonwhatthe problemisyouwishtosolve.Therearegeneral“rulesofthumb”thatcanbefollowedin ordertoselectthemostappropriatelanguage,andthemoretimeyouspendcodingand exploringthemultitudeofapplicationsavailable,theclearerthischoicewillbecome. Oneshouldavoidthepitfallsofsnobberythatmaysurroundsoftwaredevelopment, especiallyifyouarestartingyourjourneyonbecominganaerosolmodeldeveloper. Ifyouselectrelativelysimpleexamplestostartpracticingtranslatingtheoryintocode thenyouarefreetopickarangeoflanguages.Truethatsomearefaster,andothershave amuchbroaderecosystem(e.g.forvisualization,connectingnumericalsimulationsto machinelearninglibrariesetc).However,itisimportanttoenjoyandexploretheworld ofprogrammingasbestyoucan.Whenyoustarttorequirethatelementofspeed,or specificdependencies,thenyoucanrevisitwhichlanguageyouwishtodevelopin.In thisbookyouwillindeedcomeacrossarangeoflanguages.Pythonisusedthroughoutthebook,butwealsopresentexamplesinFortran,JuliaandMatlab.Theseare influencedinpartbytheexistinglanguageinwhichaerosolcommunitymodelsare currentlybased,butitalsoprovidesuswithanopportunityforyoutoexplorethese varyinglanguages.
Inordertoappreciatethedifferencesincomputerlanguages,weneedtounderstand alittleaboutthehardwarewewishtorunouraerosolmodelson.
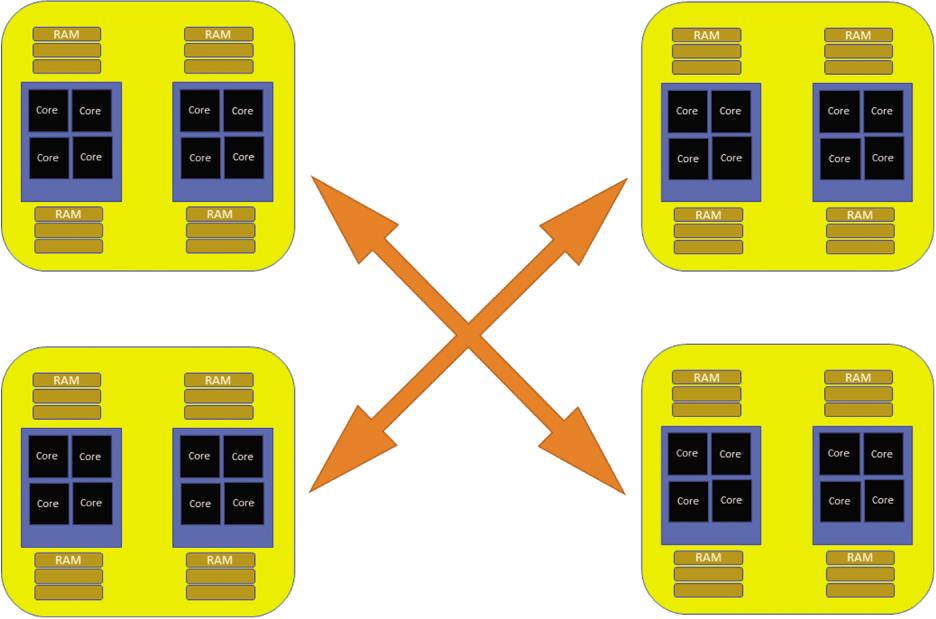
Letusstartfromthetop.Imaginewehavereceivedablueprintofahighperformance computing(HPC)centerwithplansforacluster,nodesandindividualprocessors.As illustratedinFigure1.4,a cluster willhaveseveralnodes(representedbyeachyellow box);a node canbethoughtofasamotherboardwithoneofmoresockets;a socket containsaCPUprocessor(representedbyeachbluebox);anda CPUprocessor may haveoneormore cores asrepresentedbyeachblackboxinthediagram.Muchcloser tohome,youmayhavealaptopordesktopcomputeratyourdisposalthatlikewise containsamotherboardwith(probably)onesocket;the socket containsaCPUprocessor;andthe CPUprocessor mayhaveoneormore cores.Yourdesktopwilllikely havefewercoresthantheCPUprocessorintheHPCcenter.TheCPUandothercomponentswillhavebeenmanufacturedbyasetofpopularvendorsthatincludeIntel, AMD,ARMandIBM.AsSection8.3.2discusses,inaclusterthenodesareconnected bysomeformof interconnect asillustratedinorangeinthefigure.
Wealsoneedtoconsiderhowahigh-levelprogramminglanguagethathumanscan readandunderstandendsupgettingrunonacomputer.
Traditionalcomputers(asopposedtothelikesofquantumcomputingdiscussedin Section8.3.3)haveaverylimitedsetofinstructionstheyrecognize.Thisisknown
Figure1.4 IllustrationofhardwarecomponentsofanHPCcluster.
formallyastheInstructionSetArchitecture(ISA)anditisnecessarytotranslatethe high-levelprogramminglanguageinto machinecode thatadherestoagivenCPU processor(sincewemaypresumeallcoresonagivenCPUprocessorhavethesame ISA).
Therearetwoapproachestotranslatingfromthechosenprogramminglanguageto machinecode.Compiledlanguagesdothistranslationinaseparatesteppriortorunninganyofthecode.Havingcompiledthesourcecodestoan executable (shorthand for“executablefile”)foragivenCPUprocessor,theexecutablecanberunagainand againonthatCPUprocessorarchitecture,withfurthercompilationonlyrequiredwhen youmakechangestothesourcecodes.Thisisincontrastto interpretedlanguages whichtranslateeachlineofcodeasitisrequiredduringtheactualrunningofthesource code.Manypopularlanguagesare“interpreted,”whichcanbethoughtofasabasic “compileeachlineofcodeaswewanttorunit.”Fromafunctionalviewpointthereis nothingwrongwiththis.Manyinterpretedlanguagesarehighlypopular,duetotheir easeoflearning,includingPython.
Table1.1illustratesandcomparesthesetwoapproaches.
ThemaincompiledlanguagesareC,C++,FortranandpopularinterpretedlanguagesthatincludePythonandJulia.Youmaybewonderingwhythereisachoice andperhapswhichyoushoulduse.Intermsofwhichcanbeusedtoimplementthe algorithmsdiscussedinthisbook,itdoesn’tmatter—youcancodeeachalgorithmin anyoralloftheselanguages.Buttheeaseofdoingso,andtheresultingperformance, mayvary.Therearesomeprosandconsrelatingtocompiledversusinterpretedlanguages,aslistedinTable1.1.Programminglanguagesthemselvesarebasedondifferent approaches,andmostevolveovertime.Forexample,Javawasdesignedwiththe“object oriented”(OO)styleinmind,wherethefocusofprogrammingistheconsiderationof thehierarchicalclassesofobjectsandthevarious“methods”operatinguponthem.
Table1.1 Comparisonofcompiledandinterpretedlanguages.
Comparisonofapproaches
Interpretedlanguages
–
Translatedlinebylineatruntime
Compiledlanguages
Requiresacompiler
Allofcodeiscompiledinseparatestage beforerunning
Alinemaybetranslatedmanytimes –
Noopportunitytoseebiggerpicture
Generallyfelttobeeasiertolearn
Compilercananalyzefullcodetomake deepoptimizations
Generallyfelttogivebetterperformance CanusesamesourceondifferentplatformsNeedtocompileforeachISA
OtherlanguagessuchasC++,Julia,andPython(andtosomeextentmodernFortran) alsonowsupportOOprogramming.
Mostprogramminglanguagesscientistsencounterare imperativelanguages, wherethecontrolisimplementedbyaseriesofstatementsthatmanipulatethedata ofthesimulation.Fortran,C,C++,Julia,Python,andMATLABareallimperativeprogramminglanguages.Thealternativeiswhereitistheflowofdatathatisdescribed bytheprogrammer,leavingtheimplementationofhowthisisachievedtoacompiler. TheseareknownasfunctionallanguagesandincludeHaskell,Lisp,Erlang,andClojure.Dataflowiskeytoprogrammingconcurrentlyandthereisgrowinginterestin useoffunctionalprogrammingforFPGAs(seeSection8.3.3inChapter8)andhighly concurrentsystems.
Letustakeaquicklookatthelanguagesusedinthisbookintermsoftheirprovenanceanduse.Wereiteratethatthebestwaytolearnandbecomemorefamiliarwith eachistosolveaparticularproblem,whichyoucandoacrossthechaptersinthisbook.
● Python[Officialdocumentation:https://www.python.org/]:Firstreleasedin1991, Pythonisauniversallypopularlanguagefindinguseacrossnotjustscientific domains,butfromdatabasedesigntowebdevelopment.Atofthetimeofwriting, Pythonisreleasedasversion3.8withsupportforpackagesbuiltinversion2discontinued.Pythonisaninterpretedlanguageandisoftenregardedasthebestchoice tostartprogramming.Thisisinpartrelatedtothereadabilityofthecode,butalso thehugeecosystemoftoolsandfacilitiesthatyoucannowintegratewithyourown personaldevelopments.Forexample,theabilitytointegratewithchemicalinformaticstools[25],machinelearning[26],orpowerfulvisualizations[27]isanattractive prospectforthemultidisciplinaryscientistwithanumberofexamplesusedacross aerosolscience.Whilstspeedhasbeenaconcernwhendevelopingrelativelylarge numericalmodelsusingPythonalone,Pythoncanalsoactasthe“glue”toconnectlibrariesbuiltinotherlanguageswhilsttheNumba“HighPerformancePython Compiler”[28]translatesPythonfunctionstooptimizedmachinecodeatruntime withminimaleffort.Evenifaresearcherdoesnotworkdirectlywithanyformof numericalmodels,PythonmodulessuchasPandasoffertremendousflexibilityin
ingestingandmanipulatingdata.Similarly,Pythonprovidesaninterfacetoarangeof popularmachine-learningmodulessuchasScikit-learn[26]andKeras[29].Perhaps themostcommonroutetoinstallingPythononapersonalmachineistousetheAnacondadistribution(https://www.anaconda.com/products/individual),whichcomes withaflexiblepackagemanagercalled Conda.TheCondapackagemanagercanbe veryhelpfulforthosewhowishtobuildanenvironmentwithanumberofmodules thatneedtobeinstalledseparatelyorarenotincludedinthedefaultAnacondadistribution.ThisisbecauseCondamanagestherequireddependenciesandwillinstall additionalmoduleswhererequired.AlongsideCondathereisalsothe pip packageinstallerwhichcanbeusefulwherethereisnoCondachannelforaparticular module.TherearemultiplewaysyoucaninteractwithandusePythonforyourown projects,buttheyallrequireustowritesomecode!Foragraphicaluserinterface (GUI)experience,theSpyderInteractiveDevelopmentEnvironment(IDE)combines atexteditorwithinteractiveconsoleandvariableexplorer(https://www.spyderide.org/).JupyternotebooksarehugelypopularenvironmentforteachingPython. AJupyterNotebookisanopen-sourcewebapplicationthatallowsyoutocreateand sharedocumentsthatcontainlivecode,equations,visualizationsandnarrativetext (https://jupyter.org/)andisnotlimitedtoPython.Throughoutthisbookwewill provideyouwithPythonexampleswrittenasindividualtextfilesthathavea .py extension.Imaginewehavecreatedafilecalledtest.py.Onceyouhaveadistribution ofPythoninstalled,wewouldopenupaterminalwindow,orAnacondaprompt,and askthePythonInterpretertorunourfileasfollows:
python test.py
● Fortran[Officialdocumentation:https://fortran-lang.org/]:TheFortranlanguage hasarichhistoryof,todate,morethansixdecadesasahigh-levellanguage,with specialemphasisonbeingastructured,compiledlanguageofferinggoodoptimizationpotentialforperformance-criticalnumericalprogramsandlibraries(e.g.26). Inparticular,theFORTRAN77language(nameatthosetimeswrittenincapital letters)andthesubstantiallyrevisedandimprovedFortran90standard(released intheyear1991;perhapstheoriginof“modern”Fortran)havefoundwide-spread applicationsinmanyfieldsofscienceandengineeringandhavebeenapopular choicefordecadesinthosedisciplines.TheFortranlanguagealsokeepsevolving, withanewstandardtypicallybeingreleasedeveryfivetotenyears.Themorerecent versionsofFortran,describedbytheFortran2003,2008,and2018standards,have addedimprovedsupportofdynamicdatatypes,object-orientedprogramming,new intrinsicarrayfunctions,nativeparallelprogramming,standardizedinteroperabilitywiththeClanguage,andclarified/revisedlanguagedefinitions(seehttps://wg5fortran.orgforofficiallanguagestandardpublicationsanddescriptionsofaddedfeatures).ThestandardizedinteroperabilitywiththeClanguagealsosupportsimproved interoperabilityofFortranmoduleswithPython(e.g.,viathe“f2py”methodwithin Python’sNumPylibrary).
OnevaluablefeatureoftheFortranlanguagedevelopmentandrevisionprocessis thatitremainsbackward-compatiblewitholderstandardsandprograms(solongas theywerestandard-conformingattheirtime).Inthegeosciencedisciplines,Fortran programshavebeenatthecoreofnumerousapplications;manyofthecomputationallyexpensive,highlyparallelizedprogramsforoperationalweatherforecasting,
atmosphericchemistryandtransportmodeling,andEarthsystemorclimatesimulationshavebeenwritteninFortran.
AsFortranisacompiledlanguageweneedacompiler.Thechoiceofcompilermay dependontheoperatingsystemandyourpersonalpreference.Forexample,Fortran codepresentedinthisbookhasbeendevelopedonboththeMicrosoftWindowsand theLinuxplatforms.UnderWindowswehavechosentousetheIntel® Fortrancompiler,knownas“ifort”,viaintegrationintoMicrosoftVisualStudioCommunity2019 (whichprovidesanedit-compile-runIDE(seebelow)).Forstudents,theIntel® FortrancompilerisavailableforfreeaspartoftheIntel® oneAPIHPCToolkit.Wealso compileandexecuteexampleprogramsusingthefreeGNU“gfortran”compileron aLinuxenvironment.1 Inthiscasewecreateatextfile,say test.f90.Ifwewere tousethegfortrancompiler,thenwithinaterminalorcommandpromptwewould createanexecutablefile example.out byenteringthefollowingcommand: gfortran-oexample.out test.f90
Uponsuccessfulcompilation,wecanrunthisexecutablewithintheLinuxterminal byenteringthecommand ./example.out.Inthisverysimpleexamplewehave omittedanumberofadditionalcompileroptionsthatcantellthecompilerwhatlevel ofoptimizationisrequired,whichwecoverinmoredetailinSection8.2.1. ● Julia[Officialdocumentation:https://julialang.org/]:Atthetimeofwriting,Juliais arelativelynewprogramminglanguagepositionedatversion1.6.Thereisgrowing interestinJuliaasitwascreatedwiththeunderstandingthat Scientificcomputing hastraditionallyrequiredthehighestperformance,yetdomainexpertshavelargely movedtoslowerdynamiclanguagesfordailywork (https://julia-doc.readthedocs. io/en/latest/manual/introduction/).Indeed,onceyoustartcreatingcodeinJulia, youmayfindanumberofsimilaritiestothePythonsyntaxthoughthespeedof thecode,thustime-to-solution,canapproachthatofFortran[31].Juliaachieves thisusingjust-in-time(JIT)compilation,wherethecodewewriteiscompiledto machinecodeduringexecutionofaprogramratherthanbeforeexecution.There areanumberofveryusefulfeaturesprovidedinJulia,includingtheabilitytoimplementautomaticdifferentiationofthecodeyouwrite.Likewise,whilsttheecosystem oftoolsinJuliamaynotmatchthatofPython,fornumericalcomputingthereare overonehundreddifferentialequationssolversavailable.LikePython,Juliaalso hasapackagemanagertohelpintegratearangeofmodulesintoyourworkflow. YoucaninstallJuliafollowingtheinstructionsontheofficialJuliawebpage.Once installed,youcanopenaJuliaconsoleandtype ] toenterPackagemanagement state,alsoknownas Pkg.Pleaserefertothedocumentationforinstallingpackages(https://docs.julialang.org/en/v1/stdlib/Pkg/).Again,wecancreateatextfile thatcontainsJuliacodewhichwethenwishtorun.Imaginewecreateafilecalled test.jl.OnceJuliaisinstalledonyourmachine,openupaterminal[Max/Linux] orcommandpromptandwecanrunourfilesasfollows:
julia test.jl
1NotethatonsomeLinuxdistributions,“f95”isasynonymfor“gfortran”.
● Matlab[officialwebsite:https://uk.mathworks.com/products/matlab.html]:Matlab isaproprietarysoftwareproductthatprovidesauserwithaninteractivedevelopment environment,throughaGUI.DevelopedbyMathworks,Matlabhasbeenusedacross academiaandengineeringwidelyforanumberofdecadesandisparticularlyuseful whenprototypingnewideas.WhenworkingwithintheMatlabGUIyouwillhave accesstoarangeoftoolspackagedintoaseriesof toolboxes,dependingonwhich licenseyouhaveaccessto.Forexample,accordingtotheofficialdocumentation, the PartialDifferentialEquationToolbox���� providesfunctionsforsolvingstructural mechanics,heattransfer,andgeneralpartialdifferentialequations(PDEs)usingfinite elementanalysis. WecanwriteMatlabcodeinatextfilethathasthe .m extension. Inthemostrecentversions,theusercanexecuteMatlabcodefromanumberoflanguages,includingC/C++,Fortran,Java,andPython.Likewise,Matlabcodecancall functionsdevelopedinotherlanguages.WhilstyoucanrunMatlabcodefromthe commandline,itismorecommontoruncodefromwithintheMatlabGUIusing themenuoptionsprovided(clickingontheruniconprovided).
Eachlanguagehasitsownuniquesyntax.Asyoumovebetweendifferentlanguages, youwillfindsomearesimilarinstyleandthiscanmakeiteasiertotranslatethesame theoryintomultiplelanguagesorconvertanexistingcodebaseintoanotherlanguage. ProductssuchasMatlabcomewiththeirownintegrateddevelopmentenvironment (IDE),providingauserwithacodeeditorthatisabletohighlightthevariablesyntaxyouusetoconstructacodefile.Alternatively,youmaybeusingtheSpyderIDE todevelopPythonorMicrosoftVisualStudiotodevelopFortrancodethatlikewise providesyntaxhighlighting.However,thereareanumberofalternativetexteditors thatcanbeusedinisolation. Syntaxhighlighting referstothekeywordsofthegiven programminglanguagebeinghighlightedinbold,orasanothercolor,oftenwithautorepeatandhintsonusage.UsinganIDEasyoucodeupthemanycodesnippets providedinthisbook,youwillnoticethatsomeofthetextcommandsandwordsused arecoloredinaparticularway.Thisallowsustomoreeasilyidentifydifferentstructural componentstoourcode.Intermsofavailabletexteditors,Atom(https://atom.io/)isa cross-platform,freetousetexteditorthatalsointegrateswithGitandGitHubdirectly (seeSection8.4.3).ForWindowsusers,Notepad++likewiseprovidesaflexiblesyntaxhighlightingenvironment(https://notepad-plus-plus.org/downloads/).Tryafew differenttexteditors;oftenthechoicecanbesomewhatpersonaldependingonthe machineandhowyourprojectevolves.
1.3 RepresentingAerosolParticlesasModelFrameworks
Intheprevioussection,weprovideabriefoverviewonthephysicalandchemicalcharacteristicsofatmosphericaerosolparticlesandthesubsequentprocessescoveredin thisbook.Asyoureadeachchapter,youwillfindaspecificmethodfortranslatingthe theorythatunderlinetheseprocessesintocode.
Therearemultipleapproachestorepresentanaerosolparticle,andpopulationof particles,withinanumericalmodel.Theinformationthatwerepresentandthereforetrackthroughoutasimulationbringstogetherlayersofchemicalcomplexityand metricsthatrepresentthephysicalstateofthecondensedphase.Likewise,wehaveto
makeadecisiononhowthegaseousandcondensedphaseareconnected.Thisneeds aconsiderationof,forexample,whatinformationisimportantforaparticularimpact wemightbeinterestedin;whatdataisavailable;whatcomputingresourceisavailable; andsoon.Therecanalsobeatrade-offbetweencomputationalefficiencyandchemical and/orprocesscomplexitytoberepresented.
Weknowthatparticlescanrangeinsizefromafewnanometerstohundreds ofmicrons.Likewise,weknowthataerosolparticlescanexistinmultiplephysical statesfromasolidtoanamorphousandnonviscousliquid.Theremayalsobeinhomogeneousmixinginsideeachparticlewhichmaycoincidewithphaseseparated regions.
Withthisinmind,wecanstarttoconsiderhowwemightrepresentthechemical andphysicalstateofindividualparticlesandpopulationsofparticles.Dowebeginata molecularscale,ahomogeneoussingleparticlescaleorperhapsbydiscretizingregions withineachparticle?Throughoutthisbookyouwillfindwecantakeeitherapproach dependingonourneed.
Letusstartwithageneralnarrative.Itiscommontovisualizeandanalyzeaerosol populationsintermsofnumberdistributionsormassdistributionsasafunctionof particlesize[2].Foratmosphericaerosolparticles,weknowsizeisimportantwhen understandingimpactsonhealthandtheclimate.Wealsoknowthatthecomposition isimportantwhenconsideringdifferentialtoxicity[2,32,33],forexample,andthe potentialtoformclouddroplets[4,15,34].Likewise,forcharacterizinganaerosol, sizedistributionsarelimitingsincethesamesizedistributioncancorrespondtomany differentmixingstates.Weusetheterm“mixingstate”asreferencetothewaysthe aerosolchemicalspeciesaredistributedamongsttheparticlesinthepopulation.
Wecanstarttomapthisnarrativetobothalgebraicformulaandvisualreferences. Wecanstatethatanaerosolparticlecontainsmass���� ≥0ofspecies��,for��=1,…,��, sothattheparticlecompositionisdescribedbythe ��-dimensionalcompositionvector ⃗ �� ∈ ℝ��.Thesymbol ∈ denotesasetmembershipandthuscanbereadas“belongs to,”whilst ℝ meansasetofrealnumbers,and ℝ�� thusan“A”dimensionalsetofreal numbers.Forexample,ifwehaveasingleparticlecomprisingtwocomponents“1”and “2,”wecouldwriteourcompositionvectoras ⃗ ��=(��1,��2) whereboth ��1 and ��2 representasetofconcentrationaxes.Eachaerosolparticlerepresentsthereforeapointin the ��-dimensional compositionspace.Figure1.5illustratesthisconceptforanaerosol populationthathasanumberdistributionasshowninFigure1.5(a),andconsistsof twospecies(��=2)withmassdistributionasshowninFigure1.5(b).Figure1.5(c)–(e) showshowparticlesamplesfromthreepossiblepopulationspopulatethecompositionspace.Thecompositionspaceisinthiscasetwo-dimensional,soeachparticleis againrepresentedbyavector ⃗ ��=(��1,��2).Thebrokengreylinesarelinesofconstant diameter(assumingsphericalparticles).Thesepopulationsareallconsistentwiththe numberandmassdistributionabove,buttheydifferintheirmixingstate.Figure1.5(c)–(e)alsoshowscorrespondingpictorialrepresentationsofeachpopulation.Atthispoint weareonlyconcernedwiththechemicalcomposition,sothefactthattheparticlescan havedifferentshapesandstructuresisnotrepresented,andtheparticlesareshownas genericpie-chartswiththesizeandcolorsrepresentingparticlesizeandcomposition respectively,ratherthananyparticularmorphology.
Figure1.5(c)depictstheclassic“externalmixture,”whereeachparticleonlycontains oneofthetwospecies.Inthecompositionspacegraph,theparticlesarearrangedonly
Figure1.5 Theconceptofaerosolcompositionspaceforapopulationconsistingoftwo chemicalspecies.(a)Exampleofanumbersizedistribution,(b)correspondingmasssize distribution,(c),(d),and(e)arecompositionspacedepictionsofexampleparticlesfrom populationsthatareconsistentwiththedistributionsshownin(a)and(b).
alongthetwoaxes,andoneofthetwocomponentsoftheircompositionvectoriszero, asrepresentedbypointsalongeitheraxis.Incontrast,Figure1.5(d)showstheclassic “fullyinternalmixture,”whereeachparticlecontainsthesamemixtureofspecies1 and2.Theseparticlesarethereforearrangedalongalinethroughtheorigininthe compositionspacegraph,withslope3/2,sincethemassratioofthetwospeciesis3:2 ineachparticle.Figure1.5(e)showsastateinbetween,neitherfullyinternallynor externallymixed.Suchapopulationismoreakintoambientaerosolpopulationsthan theextremecasesmentionedabove.
Wehavealreadynotedthataerosolparticlesexperiencecontinuoustransformations duringtheirlifetimeintheatmosphere.Asthesizeandcompositionoftheparticles change,theymoveincompositionspaceduetoaerosolprocessesactingonthem.For example,ifspecies2inFigure1.5wassemivolatile,wewouldobservetheparticlesmovingparalleltothe��2-axisasspecies2condensesontheparticlesorevaporatesfromthe particles.Hence,condensationandevaporation(Chapter2)canbeseenasanadvectionprocessincompositionspace.Incontrast,coagulation(Chapter5)isastochastic, discontinuousjumpprocessthatproducesaparticlethatwillbeplacedaccordingtothe sumofthevectorcomponentsofitsparentparticles.Likewise,nucleation(Chapter6) producesparticlesatthesmallestendofthesizespectrumwhosecompositionvectors areformedinitiallythroughdiscretesummationsofparentmolecules.