CalibrationinAnalyticalScience
MethodsandProcedures
PawełKo ́ scielniak
Author
ProfessorDr.PawełKo ´ scielniak JagiellonianUniversity DepartmentofAnalyticalChemistry GronostajowaSt.2 30-387Krakow Poland
CoverDesignandImage: Wiley
Allbookspublishedby WILEY-VCH arecarefully produced.Nevertheless,authors,editors,and publisherdonotwarranttheinformation containedinthesebooks,includingthisbook, tobefreeoferrors.Readersareadvisedtokeep inmindthatstatements,data,illustrations, proceduraldetailsorotheritemsmay inadvertentlybeinaccurate.
LibraryofCongressCardNo.: appliedfor BritishLibraryCataloguing-in-PublicationData Acataloguerecordforthisbookisavailable fromtheBritishLibrary.
Bibliographicinformationpublishedby theDeutscheNationalbibliothek TheDeutscheNationalbibliotheklists thispublicationintheDeutsche Nationalbibliografie;detailedbibliographic dataareavailableontheInternetat <http://dnb.d-nb.de>
©2023WILEY-VCHGmbH,Boschstr.12, 69469Weinheim,Germany
Allrightsreserved(includingthoseof translationintootherlanguages).Nopartof thisbookmaybereproducedinanyform–by photoprinting,microfilm,oranyother means–nortransmittedortranslatedintoa machinelanguagewithoutwrittenpermission fromthepublishers.Registerednames, trademarks,etc.usedinthisbook,evenwhen notspecificallymarkedassuch,arenottobe consideredunprotectedbylaw.
PrintISBN: 978-3-527-34846-6
ePDFISBN: 978-3-527-83110-4
ePubISBN: 978-3-527-83112-8
oBookISBN: 978-3-527-83111-1
Typesetting Straive,Chennai,India
Contents
Preface ix
1CalibrationFundamentals 1
1.1AnalyticalContext 1
1.2PrinciplesofAnalyticalCalibration 2
1.3CalibrationStandardsandModels 5
1.4CalibrationProceduresandMethods 7
1.5CalibrationintheContextofMeasurementErrors 8
1.5.1UncontrolledAnalyticalEffects 9
1.5.2EliminationandCompensationofUncontrolledEffects 11
1.6CalibrationinQualitativeAnalysis 14
1.7CalibrationinQuantitativeAnalysis 18
1.8GeneralRulesforCorrectCalibration 22 References 24
2“Calibration-Free”Analysis 25
2.1NovelApproach 25
2.2EmpiricalCalibration 26
2.3TheoreticalCalibration 30
2.3.1FixedModels 30
2.3.2FlexibleModels 36 References 45
3CalibrationMethodsinQualitativeAnalysis 47
3.1Classification 47
3.2ExternalCalibrationMethods 49
3.2.1ExternalStandardMethod 49
3.2.2ReferenceSampleMethod 59
3.3InternalCalibrationMethods 71
3.3.1InternalStandardMethod 71
3.3.2IndirectMethod 75
3.4StandardAdditionMethod 80 References 83
4IntroductiontoEmpiricalCalibrationinQuantitative Analysis 85
4.1Classification 85
4.2FormulationofModelFunctions 86
4.3ExaminationofInterferenceEffect 93
4.4MathematicalModelingofRealFunction 98 References 100
5ComparativeCalibrationMethods 103
5.1ExternalCalibrationMethods 103
5.1.1ExternalStandardMethod 103
5.1.1.1ModifiedProcedures 110
5.1.2DilutionMethod 115
5.2InternalCalibrationMethods 125
5.2.1InternalStandardMethod 125
5.2.2IndirectMethod 133 References 141
6AdditiveCalibrationMethods 143
6.1BasicAspects 143
6.2StandardAdditionMethod 144
6.2.1ExtrapolativeVariant 144
6.2.1.1ModifiedProcedures 155
6.2.2InterpolativeVariants 162
6.2.3IndicativeVariant 167
6.3Titration 172
6.4IsotopeDilutionMethod 180
6.4.1RadiometricIsotopeDilution 182
6.4.2IsotopeDilutionMassSpectrometry 189
6.4.2.1ModifiedProcedures 197 References 199
7CalibrationinNonequilibriumConditions 203
7.1FlowInjectionAnalysis 203
7.1.1ManipulationTechniques 205
7.1.2GradientTechnique 212
7.2KineticAnalysis 220 References 231
8ComplexCalibrationApproaches 233
8.1ExtrapolativeMethods 233
8.1.1ExtrapolativeIndirectMethod 234
8.1.2ExtrapolativeInternalStandardMethod 239
8.1.3ExtrapolativeDilutionMethod 244
8.2MixedMethods 252
8.3CombinedMethods 256
8.3.1IntegratedCalibrationMethods 256
8.3.1.1SimpleIntegratedMethod 256
8.3.1.2ComplementaryDilutionMethod 261
8.3.2GeneralizedCalibrationStrategy 270
8.3.2.1VersatileFlowInjectionCalibrationModule 276
8.3.3StandardDilutionAnalysis 280 References 286
9CalibrationApproachesforDetectionandExaminationof InterferenceEffects 289
9.1Introduction 289
9.2SimpleProceduresforDetectionandExaminationofInterference Effects 290
9.3DetectionandCompensationofAdditiveInterferenceEffect 295
9.3.1InterpolativeProcedure 297
9.3.2ExtrapolativeProcedure 301
9.3.3IntegratedProcedure 308 References 311
10Calibration-BasedProceduresforCorrectionofPreparative Effects 313
10.1Introduction 313
10.2SpecificProcedures 314
10.3SurrogateRecoveryMethod 316
10.3.1ReliabilityoftheMethod 318
10.3.2InterpretationsoftheMethod 321
10.3.3Recoveryvs.InterferenceEffect 324
10.3.4Recoveryvs.SpeciationEffect 329 References 333
11Calibration-RelatedApplicationsofExperimentalPlans 335
11.1Introduction 335
11.2ExaminationofInterferenceEffects 337
11.3ModelingofRealFunctions 342
11.4MulticomponentAnalysis 347 References 356
12FinalRemarks 359 References 365 Index 367
Preface
Analyticalchemistryisanexceptionallybeautifulscientificarea.Behindsuch adescriptionstandsnotonlytheauthor’sundoubtedlysubjectiveviewbutalso completelyobjectiveobservations.Inprobablynootherchemicaldisciplineis thepurposeoftheoreticalandexperimentalworksoclearlyandunambiguously definedasinanalyticalchemistry.Thisaimissimplytolookdeepintothematter andtodeterminethetypeoramountofcomponentscontainedinit.Takinginto accountthattheguidingprincipleofallscientificresearchisthepursuitoftruth, itcanbesaidthateverychemicalanalysis(andtherearemanythousandsofsuch analysescarriedouteverydayintheworld)isinfactthefulfillmentofthisprinciple, andeveryanalyticalchemistcanhavethefeelingofgettingasclosetothe“truth”as possibleduringhiswork,ifonlyhedoesitcorrectlyandcarefully.Thisiscertainly amotivatingandrewardingaspect.
Thespecificityofanalyticalchemistryalsoliesinthefactthatthescientific principles,rules,andmethodsdevelopedovertheyearscanbeusedinpractice extremelydirectly,rapidly,andusefully,whichontheotherhandpromotesthe developmentofnewtheoreticalandinstrumentalconcepts.Thiscouplingisthe reasonwhy,especiallyinrecentdecades,analyticalchemistryhasdevelopedrapidly andbecomeincreasinglyimportantinallareasofbusinessandsociety.Through theapplicationofnewanalyticalmethodsandtechniques,innovativechemical andbiochemicalmaterials,aswellasspecialized,high-techapparatus,analysts areabletopenetratedeeperanddeeperintomatter,detectinganddeterminingthe componentscontainedinitineversmallerquantitiesandinavarietyofchemical forms.
Inthecurrentofthisprogress,however,itiseasytosuccumbtothefascinationof itstechnicalandinstrumentalaspects,graduallyforgettingthatthemerecreationof newanalyticalmethodsandinventions–thatis,thesearchforpathsto“truth”–is insufficient,evenifthesepathsarethemostingeniousandinnovative.Itisequally importantthattheanalyticalresultsobtainedbytheseroutesshould,asfaraspossible,havethecharacteristicsofthe“true,”which,inanalyticallanguage,means abovealltheirmaximallyhighaccuracyandprecision.
Nooneneedstobeconvincedoftheimportanceofhigh-qualitychemicalanalysis. Severalyearsago,itwascalculatedthatrepetitionsofanalysesperformedinindustriallaboratoriesintheUSA,whicharenecessaryduetoincorrectanalyticalresults,
x Preface
generatelossesofseveralbilliondollarsayear.Butevenmoreimportantisthefact thatonlyonthebasisofreliableresultsofvarioustypesofanalysis,inparticular clinical,pharmaceutical,environmentalorforensicanalysis,itispossibletomakea reliablediagnosis,whichconsequentlydeterminesourhealthandlivingconditions todayandinthefuture.
Whatisthemeaningandroleofanalyticalcalibrationinthiscontext?Theanswer tothisquestioncanbegiveninoneword–enormous.Oneneedonlyrealizethat acalibrationprocessmustaccompanyalmosteveryanalyticalproceedingregardlessofwhethertheanalysisisqualitativeorquantitativeinnature.Inotherwords, withoutthisprocess,achievingtheanalyticalgoal–or,ifyouprefer,gettingcloser totheanalyticaltruth–issimplyimpossible.Moreover,theproperchoiceofthe calibrationpathanditscorrectadaptationtothedifferentstagesoftheanalytical procedurecancontributesignificantlytothemaximumapproximationofthetrue result.Againstthisbackground,itseemsobviousthat,amongthevariousanalytical issues,thesubjectofcalibrationrequiresspecialattentionandinterest.
Unfortunately,therealitycontradictsthisthesis–interestincalibrationissues amonganalystsisrelativelylowbothscientificallyandpractically.Firstofall,there arenobookpositionsentirelydevotedtothistopic,exceptperhapsformultivariatecalibration,which,however,isnotwidelyusedinanalyticallaboratories.In analyticalchemistrytextbooks,littleisusuallysaidaboutcalibrationmethods,usuallylimitingthemselvestobasic,customaryapproachesandsolutions.Ontheother hand,overtheyearsmanyarticleshaveappearedinwhichnewcalibrationsolutions canbefound,testifyingtoprogressinthisanalyticalfieldaswell.Mostly,however, thesereportsareusuallytreatedaspurelyacademicandaregenerallynotapplicable inlaboratorypractice.
Itmustalsobesaidthatinthefieldofcalibrationthereisanextremelylarge nomenclaturalchaos,concerningnotonlythenomenclatureandclassificationof calibrationmethodsbutalsotheconceptoftheanalyticalcalibrationprocessassuch. Thisstateofaffairsobviouslyhasnegativeconsequences.Aboveall,itisnotconducivetoteachingpurposes,sinceitisdifficulttoreliablyconveyspecificanalytical knowledgeusingalanguagethatisnotstandardizedandgenerallyaccepted.The lackofacommongroundforcommunicationinthisareacanalsobecomeasource ofmisunderstandingsandambiguitiesleadingtoerroneousandincorrectanalyticalprocedures.Andyet,noonebutananalystshouldbeparticularlysensitiveto “order”and“purity”inhiswork.
Themainpurposeofthisbookistofill,atleasttosomeextent,thesegapsand backlogs.Itcollectsanddescribesavarietyofcalibrationmethodsandprocedures fordeterminingthenatureandquantityofsamplecomponentsindifferentways. Theseapproachesaretailoredtothespecificchemicalandinstrumentalconditions ofthequalitativeandquantitativeanalysesperformed,aswellastothespecific objectivestheanalystwishestoachieveinadditiontotheoverarchinggoal.Based onthecalibrationpropertiesofthesemethods,theirnomenclatureandclassification areproposed.Itisalsoshownhowcalibrationapproachescanbecombinedandintegratedmainlytodiagnose,evaluate,andeliminateanalyticalerrorsandthusachieve resultswithincreasedprecisionandaccuracy.
Thecontentsofthisbookarelargelybasedontheauthor’smanyyearsofexperience.Thisistosomeextenttheresultofboththelayoutofthebookandthedetailed selectionoftheissuescovered,whichcertainlydoesnotexhausttheentirecalibrationsubjectmatter.Forthesamereason,onecanfindhereoriginal,authorial approachestothissubject,which–althoughpreviouslypublishedinscientificarticlesandthusverified–maybefurtherdebatable.Therefore,Iapologizeinadvanceto thosewhohaveslightlydifferentviewsontheissuesraisedinthebook.Iunderstand thisandatthesametimeinviteopponentstosuchadiscussion.Ibelieve,however, thatdespiteallpossiblereservationsanddoubts,thebookwillbeausefulsourceof informationonanalyticalcalibrationand,formany,avaluableadditiontoanalytical knowledgeandahelpfultoolinscientificandlaboratorywork.
Asmentioned,thecalibrationprocessisinextricablylinkedtotheanalyticalprocess.Wanderingthroughthevariousavenuesofperformingcalibrationsisthusalso anopportunitytolearnorrecallvariousanalyticalmethodsandgeneralproblems relatedtoanalyticalchemistryandchemicalanalysis.Withthisinmind,theauthor alsoseesthisbookasasupplementtogeneralanalyticalknowledgedeliveredin aslightlydifferentwayandfromadifferentanglethantypicalanalyticalscience textbooks.
Finally,IwouldliketoexpressmywarmgratitudetoProfessorAndrzejParczewski for“infecting”memanyyearsagowiththesubjectofcalibration.Iwouldalsolike tothankmycolleaguesfromtheDepartmentofAnalyticalChemistryoftheJagiellonianUniversityinKrakowforaccompanyingmeonexcitinganalyticaladventure andforprovidingmewithmanyoftheirresearchresultsforit.
ButIammostgratefultomybelovedWife–formotivation,wordsofsupport,and timewhich,attheexpenseofbeingwithher,Icoulddevotetothiswork.Without you,Ania,thisbookwouldnothavebeenwritten.
Kraków,March2022
PawełKo ´ scielniak
CalibrationFundamentals
Thegeneralunderstandingoftheterm“calibration”isfarfromwhatappliesto theconceptinananalyticalsense.Leavingasidecolloquialconnotations,such ascalibratingaweapon,thetermisgenerallyassociatedwiththeadjustmentof specificparametersofanobjecttofixedordesiredquantities,andinparticularwith theadjustmentofaspecificinstrumenttoperformacorrectfunction.Itis,therefore, understoodmoreasaprocessofinstrumentalstandardizationoradjustment.This isreinforcedbypubliclyavailablenomenclaturalsources.Forexample,inthe CambridgeAdvancedLearner’sDictionary[1]calibrationisdefinedas“ theprocessofcheckingameasuringinstrumenttoseeifitisaccurate,”andinthe http://Vocabulary.comonlinedictionaryas“theactofcheckingoradjusting(by comparisonwithastandard)theaccuracyofameasuringinstrument”[2].Evenin amoderntextbookinthefieldofinstrumentalanalysis,youcanread:“Inanalytical chemistry,calibrationisdefinedastheprocessofassessmentandrefinementof theaccuracyandprecisionofamethod,andparticularlytheassociatedmeasuring equipment ”[3].
Theambiguityoftheterm“calibration”makesitdifficulttounderstanditproperly inapurelyanalyticalsense.Tounderstandtheterminthisway,onemustofcourse takeintoaccountthespecificityofchemicalanalysis.
1.1AnalyticalContext
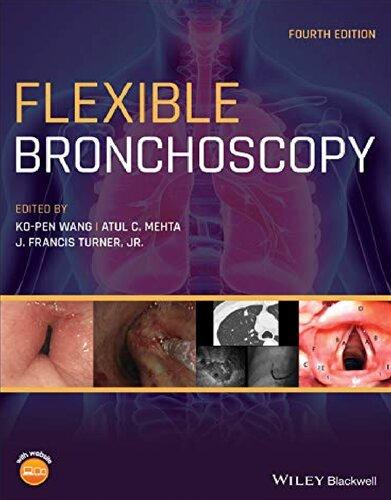
Theanalystaimstoreceive theanalyticalresult,i.e.toidentify thetype (inqualitativeanalysis)ortodeterminethe quantity (inquantitativeanalysis)ofaselected component(analyte)inthematerial(sample)assayed.Toachievethisgoal,he mustundertakeaseriesofoperationsthatmakeup theanalyticalprocedure,the generalschemeofwhichisshowninFigure1.1.
Whenstartingananalysis,thesamplemustfirstbepreparedformeasurementin suchawaythatitsphysicalandchemicalpropertiesaremostsuitableformeasuringthetypeoramountofanalyteinquestion.Thisstepconsistsofsuchprocesses as,e.g.takingthesamplefromitsnaturalenvironmentandthenchangingitsaggregatestate,dilutingit,pre-concentratingit,separatingthecomponents,changingthe temperature,orcausingachemicalreaction.
CalibrationinAnalyticalScience:MethodsandProcedures,FirstEdition.PawełKoscielniak. ©2023WILEY-VCHGmbH.Published2023byWILEY-VCHGmbH.
Sample preparation
Sample measurement
Analytical signal
Sample preparation
Sample measurement
Analytical signal
Analytical result
Figure1.1 Analyticalprocedurealone(a)andsupplementedbyanalyticalcalibration(b).
Themeasurementisgenerallyperformedbythechosenusinganinstrument thatoperatesontheprincipleofaselected measurementmethod (e.g.atomic absorptionspectrometry,potentiometry,etc.).Theinstrumentshouldrespondto thepresenceoftheanalytestudiedintheformof measurementsignals.Froma calibrationpointofview,themostrelevantsignalistheso-called analyticalsignal, i.e.thesignalcorrespondingtothepresenceofanalyteinthesample.
Ananalyticalprocedurecarriedoutinadefinedmannerbyaspecificmeasurementmethodformsan analyticalmethod
Thebasicanalyticalproblemisthat theanalyticalsignalisnotadirect measureofthetypeandamountofanalyteinthesample,butonlyinformationindicatingthatacertaincomponentinacertainamountispresentinthe sample.Toperformacompleteanalysis,itisnecessarytobeable totransformthe analyticalsignalintotheanalyticalresult andtoperformthistransformation. Thisistheroleofanalyticalcalibration.AsseeninFigure1.3,theanalytical calibrationprocessisanintegralpartoftheanalyticalprocedureandwithout analyticalcalibration,qualitativeandquantitativeanalysiscannotbeperformed. Realizingthisaspectallowsonetolookatthesubjectofcalibrationasa fundamentalanalyticalissue.
1.2PrinciplesofAnalyticalCalibration
However,thereisstillthequestionofwhattheprocessoftransformingananalytical signaltoananalyticalresultconsistsof,i.e.howanalyticalcalibrationshouldbe defined.Inthisregard,thereisalsonounifiedapproach,soitisbesttorelyonofficial recommendations.
Theprocessofanalyticalcalibrationislargelyconcernedwiththemakingof measurementsandtheinterpretationofmeasurementdataandthereforefalls withinthescopeofmetrology.IntheJointCommitteeforGuidesinMetrology (JCGM)documentonbasicandgeneraltermsinmetrology,calibrationisdefinedas “ operationthat,underspecifiedconditions,inafirststep,establishesarelation betweenthequantityvalueswithmeasurementuncertaintiesprovidedbymeasurementstandardsandcorrespondingindicationswithassociatedmeasurement uncertaintiesand,inasecondstep,usesthisinformationtoestablisharelation forobtainingameasurementresultfromanindication”[4].Atthesame,the documentmakesitclearthat“calibrationshouldnotbeconfusedwithadjustment ofameasuringsystem ”.
Themetrologicalterm,althoughitallowsforadeeperunderstandingofthe conceptofcalibration,isstillrathergeneralbecauseitisinherentlyapplicableto differentmeasurementsystemsanddifferenttypesofresultsobtained.Theconcept ofcalibrationintheanalyticalsenseismorecloselyapproximatedbypublications issuedbytheInternationalUnionofPureandAppliedChemistry(IUPAC).In thepaper[5],theIUPACdefinitionisalignedwiththeJCGMdefinitioninthat itdefinesanalyticalcalibrationas“...thesetofoperationswhichestablish,under specifiedconditions,therelationshipbetweenvalueindicatedbytheanalytical instrumentandthecorrespondingknownvaluesofananalyte,”andinasubsequent IUPACpublication[6]wefindanexpressreferenceofanalyticalcalibrationtoboth quantitativeandqualitativecalibration: “Calibrationinanalyticalchemistry istheoperationthatdeterminesthefunctionalrelationshipbetweenmeasuredvalues(signalintensitiesatcertainsignalpositions)andanalytical quantitiescharacterizingtypesofanalytesandtheiramount(content, concentration).”
Suchapurelytheoreticalapproachistoogeneral,evenabstract,andunrelated toanalyticalpractice.Inparticular,itdoesnotprovideguidanceonhowthefunctionalrelationship(calibrationmodel)shouldbeformulatedindifferentanalytical situationsandhowitrelatestothedifferenttypesofmethodsusedinqualitative andquantitativeanalysis.Nordoesitsayanythingabouttherelativenatureofthe calibrationprocessthattheterm“measurementstandard”givestotheconceptin metrologicalterms.
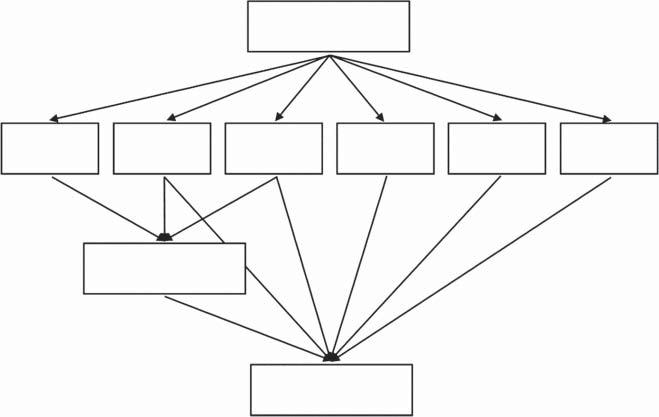
Toextendthedefinitionofanalyticalcalibration,theauthorproposestointroduce theconceptofthreefunctionsthatrelatethesignaltotheanalyticalresult:thetrue function,therealfunction,andthemodelfunction[7].Thisapproachisillustrated inFigure1.2.
Ifasamplethatananalysttakesforqualitativeorquantitativeanalysiscontainsa component(analyte)ofinterest,thenbeforeanyactionistakenwiththesample,the typeofanalyteanditsquantityinthesamplecanbereferredtoasthe truevalue (typeorquantity), x true ,oftheanalyte.Ifitwerepossibletomeasuretheanalytical signalforthatanalyteatthatmoment,thentherelationshipbetweentheresulting signalanditstruetypeorquantity, Y true = T (x true )couldbecalledthe truefunction. However,thedeterminationofthetruefunctionandthetruevalueoftheanalyteisnotpossibleinpracticebecauseitrequirestheanalyst’sinterventioninthe
function, Y = T(x)
True analyte value, Xtrue Real analyte value, X0 Real function, Y = F(x)
of model function Model function, Y = G(x)
result, Xx
Figure1.2 Conceptofanalyticalcalibrationbasedonthetermsoftrue, Y = T (x ),real, Y = F (x ),andmodel, Y = G (x ),functions(virtualanalyticalstepsandtermsaredenotedby dottedlines;fordetailsseetext).
formofpreparingthesampleformeasurementandperformingthemeasurement. Theinitiationofeventhesimplestandshortestanalyticalstepsresultsinachange ofthetrueanalyteconcentrationinthesamplethatcontinuesuntiltheanalytical signalismeasured.Thus,theconceptsoftruefunctionandtrueanalytevalueare essentiallyunrealisticandimpossibletoverifyexperimentallyormathematically.
Whenthesampleispreparedforanalysis,thetypeoramountofanalyteinthe sampletobeanalyzedtakesona realvalue, x 0 .Therelationshipbetweentheanalyticalsignalandthetypeoramountofanalyteisdescribedatthispointbythe real function, Y = F (x ),whichtakesthevalue Y 0 forthevalue x 0 :
0 = F (x0 ) (1.1)
Althoughthevalueof Y 0 ismeasurable,theexactformoftherealfunctionis unknownbecauseitdependsonanumberofeffectsandprocessesthatledtothe currentstateofthisrelationshipduringthepreparationofthesampleformeasurement.Consequently,thedeterminationoftherealresult x 0 bymeansofthereal functionisimpossible.
Thissituationforcestheformulationofanadditionalauxiliary modelfunction, Y = G(x ).Theroleofthisfunctionistoreplacetherealfunctioninthesearchfor thetruevalue, x 0 .Itshouldthereforemeettwobasicconditions:tobeknown andwell-definedandtobethemostaccurateapproximationoftherealfunction (G(x ) ↔ F (x )).Tofulfilltheseconditions,a calibrationstandard (oneormore) shouldbeused,whichshouldbesimilartothesampleandproperlypreparedfor measurement.
Assumingthattheapproximationoftherealfunctionbythemodelfunction, Y = G(x ),isaccurate,thentheinverseformofthemodelfunction, x = G 1 (Y ),has
True
Y
1.3CalibrationStandardsandModels 5 tobecreated,whichiscalledtheevaluationfunction[6].Theoretically,itallowsthe valueof Y 0 tobetransformedintotherealresult, x 0 :
0 = G 1 (Y0 )
Inpractice,theapproximationoftherealfunctionbythemodelfunctionisnever accuratebecausetherealfunctionisessentiallyunknown.Therefore,transformation(1.2)leadstoacertainvalue x x :
= G 1 (Y0 )
whichisanapproximatemeasureoftherealresult, x 0 .Thisresultcanalsobeconsideredasthefinal analyticalresult.
Theprocessesofcreatingamodelfunctionanditsapproximationandtransformationarefundamental,integral,andnecessaryelementsofanalyticalcalibration. Thus,itcanbesaidthat analyticalcalibrationconsistsofapproximatingthe realrelationshipbetweenthesignal, Y ,andthetype, b,oramount, c,ofan analyteinasamplebymeansofamodelfunction,andthenapplyingthis functiontotransformthesignalobtainedfortheanalyteinthesampleto theanalyticalresult.
Notethenaturallogicoftheabovedescriptionofanalyticalcalibration.Suchquantitiesas“sample”(consideredasacollectionofunknownchemicalconstituents), “realfunction”and“realtypeoramountofanalyte”havetheircounterpartsinthe termsof“standard”,“modelfunction”and“obtainedtypeoramountofanalyte”, whichareassociatedwithanalyticalcalibration.Theformerarelargelyhypothetical, unknowninfacttotheanalyst,whilethelatterareknownandareapproximations oftheformer.Justasthecompositionandpropertiesofasamplecanneverbefaithfullyreproducedinastandard,theformoftherealfunctioncannotbeaccurately approximatedbyamodelfunction,andtherealtypeoramountofanalyteinthe sampleatthetimetheanalyticalsignalismeasuredcanonlybeapproximatedby theanalyticalresultobtained.
1.3CalibrationStandardsandModels
Dependingonthetypeofunivariatemodelfunctionused,analyticalcalibrationcan bebroadlydividedinto empiricalcalibration and theoreticalcalibration [7]. Insomecases,thecalibrationisalsoofacomplexnaturetovaryingdegrees (empirical–theoreticalortheoretical–empirical)when,tobetterrepresentthe realfunction,empiricalinformationissupportedbytheoreticalinformationor viceversa.
Anessentialpartofanycalibrationprocessistheuseofcalibrationstandards, whichcanbeofdifferentnature: chemical,biological,physical,ormathematical [7].Acommonfeatureofcalibrationstandardsisthattheydirectlyorindirectly enabletheassignmentofameasurementsignaltoaknown,well-definedtype oramountofanalyte.Thesestandardsarethereforeusedtoformulateamodel function.Accordingtotheprincipleofanalyticalcalibration,astandardshouldbe abletoformulateamodelfunctionthatapproximatesthetruefunctionasclosely aspossible.
Inempiricalcalibration,themodelfunctionisformulatedonthebasisoftheperformedexperiment,sensoryperception,orobservation.Thesourcesofinformation neededtocreatethistypeof empiricalmodelfunction, Y = G(x ),aremeasurementsofanalyticalsignalsobtaineddirectlyorindirectlyforchemical,biological,or physicalstandards.Inthiscase,theanalystdoesnotgointothetheoreticalaspectsof thedependenceoftheanalyticalsignalonthetypeoramountofanalyte(althoughin somecasesthelawsandrulesunderlyingthisdependence,e.g.Nernst’sorLambert Beer’slaw,maybehelpful).
Awidelyrecognizedandusedmethodofanalyticalcalibrationistheempirical calibrationperformedwitha chemicalstandard.Thisisasyntheticor(lesscommonly)naturalmaterial,singleormulticomponent,containingananalyteofknown typeoramount.Inspecialcases,achemicalstandardcontainsaknowntypeor amountofasubstancethatreactswiththeanalyteoraknowntypeoramountof anisotopeoftheelementbeingdetermined.Calibrationwithchemicalstandardsis auniversalprocedureinthesensethatitdoesnotdependonthechosenmeasurementmethod.Themodelfunctionformulatedismathematicallyusuallysimpleand itsgraphicalformiscalledacalibrationgraph.
Intheoreticalcalibration,themodelfunctionisformulatedonthebasisofa mathematicaldescriptionofphysicochemicalphenomenaandprocessesoccurring duringtheanalysisusingagivenanalyticalandmeasurementmethod.Sucha descriptionincludesphenomenologicalquantitiesbasedonphysicalorchemical measurements(electrochemicalpotentials,diffusioncoefficients,etc.),universal quantities(molarmass,atomicnumber,stoichiometricfactors),and/orfundamentalphysicalconstants(Faradayconstant,Avogadroconstant,etc.).Theindividual elementsofthemathematicaldescriptionactas mathematicalstandards,and thefunctioncreatedwiththem, Y = G(x ),isa theoreticalmodelfunction.
Inanalyticalchemistry,therearerelativelyfewcasesofwell-definedtheoretical modelsofrelativelysimplemathematicalform.However,intheliterature,onecan findmanynewproposalsofsuchfunctionsformulatedforvariousmeasurement methods.Asarule,theyhaveaverycomplexmathematicalstructure,whichresults fromthedesiretoapproximatetherealfunctionasaccuratelyaspossible.Astrong motivationforthesescientificeffortsisthatthetheoreticalmodelallowsthecalculationoftheanalyticalresultwithouttheneedtopreparechemicalstandardsand performmeasurementsfortheanalyteinthesestandards.
Asmentioned,othertypesofcalibrationstandardscanbefoundinchemical analysis,aswellasmodelfunctionsofadifferentnatureformulatedwiththem, asdiscussedinChapter2ofthischapter.Itcanbehypothesizedthat analytical calibrationisinherentlyconnectedwiththeuseofstandardsandthe creationofmodelfunctionswiththeirhelp.
Theimplicationsofthisapproachtoanalyticalcalibrationareinteresting.Qualitativeorquantitativeanalysisperformedonthebasisofatheoreticalmodelfunction isoftenreferredtointheliteratureascalibration-freeanalysisorabsoluteanalysis. Fromthepointofviewoftheaccepteddefinitionofanalyticalcalibration,thisterm ismisleading,becausetheformulationofthetheoreticalmodelfunction,likethe empiricalmodel,ispartofthefullcalibrationprocedure.Thus,thequestionsarise:
canchemicalanalysisbeperformedinpracticewithoutanalyticalcalibrationand whatconditionsmustananalyticalmethodmeettobecalleda“absolutemethod”? ThediscussionofthisissuewillbethesubjectofChapter2ofthisbook.
1.4CalibrationProceduresandMethods
Theconceptofanalyticalcalibrationpresentedaboveperhapsdonotyetgiveaclear pictureofthisprocess.How,then,doesthefullempiricalandtheoreticalcalibration procedurelookingeneral?
Asalreadystated,thecalibrationprocessisessentialtotheperformanceofchemicalanalysis–bothqualitativeandquantitative–andisanintegral,inseparablepart ofanyanalyticalmethod.Whatthecalibrationprocesscontributestotheanalyticalprocedureisthehandlingofthecalibrationstandardnecessarytoformulatethe modelfunctionanduseittotransformthemeasurementsignaltotheanalytical result.Thus,thecalibrationprocedureconsistsofthreesteps:preparative,measurement,andtransformation.
The preparativestep consistsinpreparingthesampleandthestandardinsuch asuitablewaythatthetruefunction, Y = F (x ),andthemodelfunction, Y = G(x ), aresimilartoeachotherasmuchaspossible.Inthecaseofempirical z-calibration, therearetwomainroutestothisgoal:
● thesampleandstandardarepreparedseparately,takingcarethatthechemicalcompositionofthestandardissimilartothatofthesampleandthatthepreparationofthesampleandstandardformeasurementissimilar,
● thestandardisaddedtothesample priortomeasurement(lessfrequentlyprior tosampleprocessing).
Inthecaseoftheoreticalcalibration,separatetreatmentofthesampleandthe standardisobviousandnatural.Appropriatepreparationofthestandardinrelation tothesampleconsistsinintroducingsuchmathematicalstandardstothetheoreticalmodelthatmostadequatelydescribethestateofthesampleandthephenomena andprocessesthatthesampleundergoesundertheconditionsofthespecificmeasurementmethod.
Inthemeasurementstage,signalmeasurementsaremadeusingaselectedmeasurementmethod.Ifthecalibrationisempirical,measurementsarerelatedtothe sampleandstandardoronthesampleandsamplewiththeadditionofthestandard (dependingontheirpreparationatthepreparativestage).Ineithercase,themeasurementsinvolvingthestandardareusedtoformulateanempiricalmodelfunction. Inthecaseofatheoreticalcalibration,measurementsaremadeonlyforthesample andtheformulatedtheoreticalmodelisconsideredasthemodelfunction.
Inthe transformationstep,thevalueofthesignalobtainedforthesampleis enteredintoanempiricalortheoreticalmodelfunctionandthusthefinalanalytical result(typeoramountofanalyteinthesample)isdetermined.
Referringtotheformulatedextendeddefinitionofanalyticalcalibration,itcanbe noticedthatthepreparativeandmeasurementstagesareusedtoapproximatethe
Empirical calibration
Standard
sample + standard preparation or Standard
sample + standard measurement or
Empirical model function Analytical result
Theoretical calibration
preparation
measurement
Formulation theoretical model function of Analytical result
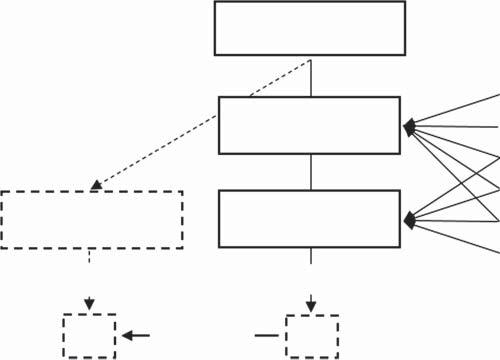
Figure1.3 Generalschemeofempiricalandtheoreticalcalibration.
modelfunctiontotherealfunction,andthekey,transformationalcalibrationprocesstakesplaceatthelaststage.Aschematicdiagramoftheproceduresofempirical andtheoreticalcalibrationisshowninFigure1.3.
Calibrationprocedureswithspecificpreparationofsampleandstandardfor measurementform calibrationmethods.Ingeneral,therefore,twogroups ofmethodscanbedistinguishedinanalyticalcalibration,whichcanbecalled comparativemethods (whenthesampleandstandardaretreatedseparately)and additivemethods (whenthestandardisaddedtothesample).Withineachof thesetwogroups,itispossibletodistinguishmethodsthatdiffermorespecifically onthepreparativeside(e.g.externalstandardmethod,internalstandardmethod, standardadditionmethod,etc.).Thesenamesaremostlycustomaryanddonot alwayscorrespondtothespecificsoftheindividualmethods.Therefore,another, moreessentialcriterionforthedivisionofthecalibrationmethodsintermsof themathematicalwayoftransformingthemeasurementsignalintotheanalytical resultwillalsobeproposed.
1.5CalibrationintheContextofMeasurementErrors
Theroleofanalyticalcalibrationisnotonlytomakeitpossibletoidentifyor determineananalyteinasample,butalsotodosowithasmuch accuracyand precision aspossible.Themeasureofaccuracyisthestatisticallysignificant differencebetweentheanalyticalresultobtained, x x ,andthetruetypeoramount ofanalyte, x true ,inthesamplebeforeitwassubjectedtoanyanalyticalprocess. Themeasureofprecisionistherandomdifferenceinanalyticalresultsobtainedin
so-calledparallelanalyses,thatis,performedinthesamewayandunderthesame experimentalconditions.Theaccuracyandprecisionofananalyticalresultarethus determinedbyanysystematicandrandomchangesinthetruefunctionbeforeit becomes,atthetimeofmeasurement,thetruefunction,andthenbythesystematic andrandomdifferencebetweenthetruefunctionanditsrepresentation,themodel function.
Changesintheanalyticalsignalthatoccurbothduringsamplepreparationfor measurementandduringmeasurement,resultinginthetransformationofthetrue functiontothemodelfunction,canbecalledanalyticaleffects[7].Theycanbe controllableanduncontrollable.Controlledanalyticaleffectsinclude,forexample, changescausedbyatargetedactionbytheanalysttodecreaseorincreasetheconcentrationofananalyteinasamplebydilutionorconcentration,respectively.Effects ofthistypecanusuallybecalculatedandcorrectedatthestageofanalyticalresult calculation.
Duringqualitativeandquantitativeanalysis,however,therearealsosuchchanges intheanalyticalsignalthatarepartiallyorcompletelyoutoftheanalyst’scontrol. These uncontrolledanalyticaleffects canbebothrandomandsystematic. Althoughtheanalystisusuallyawareoftheriskoftheiroccurrenceandusually triestopreventthemaccordingly,heorshemayoverlookorevenneglectthem whileperformingtheanalysis.Asaresult,controlovertheentireanalyticalprocess islostinasense.Uncontrolledeffectsmanifestthemselvesbychangingtheposition andintensityoftheanalyticalsignal,i.e.theyareimportantinbothqualitativeand quantitativeanalysis.
1.5.1UncontrolledAnalyticalEffects
Uncontrolledeffectscanbecausedbymanyfactorsmanifestingthemselvesatdifferentstagesoftheanalyticalprocess.Theclassificationoftheseeffectscoveringall possiblefactorsis,ofcourse,amatterofconvention.Thedivisionpresentedbelow istheauthor’sproposal[7].
Uncontrolledeffectsareprimarilycausedbytheanalysthimself(theso-called humanfactor)asaresultofincorrectorcarelessbehavioratvariousstagesof theanalyticalprocess.Themagnitudeofthesechangesdependsprimarilyonthe analyst’sknowledgeandskills,thatis,onhisorherprofessionalabilitiesand qualifications.Personalfactorssuchastiredness,nervousness,andhurryplaya largerole.Theminimizationofthehumanfactorisalsonotfavoredbyaroutine, “automatic”approachtoindividualanalyticalactivities,resulting,forexample, fromperforminganalysesaccordingtoasingle,unchanginganalyticalmethodover alongperiodoftime.
Thebasiceffectsinclude preparativeeffect.Underthisterm,weunderstand signalchangescausedbysuchsampleprocessingthatresultsinuncontrolled change(loss,lessoftengain)ofanalyteamountinthesample.Theanalytecan bepartiallyloste.g.whenchangingtheaggregatestateofthesample(tomakeit suitableforthegivenmeasurementmethod)orwhenseparatingitscomponents. Theprocessofchangingtheamount(orrarelythetype)ofsamplecanalsotake
placeoutsidethepurposive,controlledactionoftheanalystasaresultofe.g.an inducedchemicalreaction.Apreparativeeffectisalsoinvolvedwhenthechangein signalresultsdirectlyfromphysicalchangesinthesampleorstandard(e.g.solution viscosity),orfromchangesinenvironmentalconditionsunderwhichthesample andstandardareprocessed(e.g.temperature,humidity,illumination,etc.).
The instrumentaleffect iscausedbytheactionofvariousinstrumentalcomponentsusedintheanalyticalprocesstoprocessthesamplepriortomeasurement. Inthiscase,thesourceofrandomchangesintheanalyticalsignalisallnatural imperfectionsinthedesignandoperationoftheseinstruments,includingthemeasurementsystemsthatcharacterizethemeasurementmethod.However,asaresult ofinstrumentmalfunction,signalchangescanalsobesystematic.
Theinstrumentalmeasurementsystemisthesourceofseparatespecificmeasurementchangesoccurringinthedetectionsystem.Thisphenomenoncantherefore becalleda detectioneffect.Thesechangesaremanifested,forexample,bythe limitedabilityofthesystemtorespondproportionallytotheanalyteconcentration,whichisnaturalforeachdetector.Anotherphenomenonistheso-called measurementtrend,whichconsistsofasuccessiveincreaseordecreaseinsignal intensityovertime.Inspectrometricmethods,thereissometimestheproblemof baseline,whichvariesmoreorlessrandomlybetweenspectra.Thedetectioneffect canalsoberelatedtonaturalphenomenaunderlyingthemeasurementmethod (atypicalexampleisthephenomenonofself-absorptionofradiationemittedinthe emissionspectrometrymethod,causingachangeinanalyticalsignalintensityout ofproportiontotheamountofanalyteinthesample).
Thesignalmeasuredforaspecifictypeoramountofanalytecanalsobeaffectedby othercomponentsbothnaturallypresentinthesample(native)andintroducedduringsamplepreparationformeasurement.Thesecomponentsthentakeontherole ofinterferents,andthesignalchangecausedbythemistheso-called interference effect.Iftheeffectcomesexclusivelyfromthenativecomponentsofthesample, thenitiscalleda matrixeffect,whileiftheinterferentsarecomponentsaddedto thesampleduringsampleprocessing,thentheinducedchangesarecalleda blank effect.Theinterferenceeffectcanoriginateatthestageofsamplepreparationfor measurement(e.g.duetoaddedreagents),butcanalsobeinducedduringmeasurementoftheanalyticalsignalasaresultofphenomenaandprocessesoccurringat thisstage.
Finally,aspecificeffectisthe speciationeffect.Itoccurswhenananalytecontainedinasampleunexpectedlyfortheanalystchangesitschemicalformandatthe sametimechangesitsmeasurementsensitivity.Aswiththeinterferenceeffect,this changecanoccurbeforemeasurement(e.g.asaresultofachemicalreaction)orat thetimeofmeasurement,whenitinvolvesachangeinthatformthatisresponsible forcausingtheanalyticalsignalinthedetectionsystem(e.g.achangefromatoms toanalyteionsinatomicabsorptionspectrometry).
Uncontrolledeffectsarerevealedbyachangeintheanalyticalsignaleither directlyorindirectlybychangingthetypeoramountofanalyte,asillustratedin Figure1.4.
1.5CalibrationintheContextofMeasurementErrors 11
Uncontrolled effect
SpeciesHumanPreparativeInstrumentalDetectionInterference
Change of form or amount of analyte
Change of analytical signal
Figure1.4 Pathwaysofthevariousuncontrolledeffects.Source:Ko ´ scielniak[7]/ Elsevier/CCBY4.0.
1.5.2EliminationandCompensationofUncontrolledEffects
Thenaturalwaytoavoiduncontrolledeffectsrevealedduringsamplehandlingisto employvariousmeansof eliminating them.Effectivenessoftheseactionslargely dependsonproperidentificationofthetypeoftheseeffectsandtheirsources,which aredifferentlysituatedontheanalyticalprocedureplan.ThisisshowninFigure1.5.
Sample measurement
Sample with unknown, true analyte value
Sample preparation
Sample measurement
Instrumental Preparative
Human Interference
Species Detection
Figure1.5 Impactofuncontrolledeffectsonananalyteinthesampleduringits preparationandmeasurement;duetoeliminationofeffectstherealanalytevalue approachesthetruevalue(x 0 ≈ x true ).Source:Ko ´ scielniak[7]/Elsevier/CCBY4.0.
Theprerequisiteforreducingtheinfluenceofthehumanfactoristhatanalyses shouldbeperformedonlybyqualifiedstaff,withahighlevelofknowledgeandskills, maintainingcareandcautionduringthework.Instrumentalanddetectioneffects maynotbeamajorproblemiftheinstrumentsusedareofhighquality,provenreliability,andlowmaintenance.Inspecialcaseswherethereare,forexample,strong timetrendsorbaselineshifts,specialcorrectionproceduresareused[8].
Incontrasttoinstrumentalanddetectioneffects,speciationeffectscanbedifficult toeliminateiftheanalyticalprocedureisrelativelycomplexandinvolvestheuseof differenttypesofchemicalreactions.Thepreparativeeffectcanalsobedifficultto eliminateeffectively.Thisisbecausenosampleprocessingisinpracticefreefrom partiallossofanalyte.Thedegreeofthisphenomenonshouldineachcasebewell recognizedbypreliminaryexperimentsandthenreducedasmuchaspossible.The amountofanalytelostcanalsobequantified(e.g.bytherecoverymethod,which isdiscussedlaterinChapter10)andthefinalanalyticalresultcanbecorrectedon thisbasis.
Theinterferenceeffectcanbeeliminatedinbasicallytwoways.Theuniversal wayistoremovetheinterferentsfromthesampleortoisolatetheanalytefromthe samplematrixbyappropriatelyselectedlaboratorytechniques(e.g.byextraction, crystallization,gaseousdiffusion,etc.).Anotherapproachistoaddanappropriately selectedreagenttothesampletoeliminateinterferentsbychemicalmeans.
Progressiveeliminationofuncontrolledeffectscausesthetwoanalytevalues,true, x true ,andreal, x 0 ,tobecomeincreasinglysimilar,ascanbeseeninFigure1.5. When theeffectsarecompletelyeliminated,thetrueanalytevaluebecomesan accurate(withinrandomerror)measureofthetrueanalytevalueinthe sample,i.e x 0 ≈ x true .
Whenproceedingwithananalyticalcalibration,theanalystisforcedtouseastandard.Importantly,however,thisconstraintsimultaneouslyprovidesanopportunity tomakethestandardsimilartothesample.Ifthesampleandstandardaresimilar,thenalluncontrolledeffectsoccurringduringtheanalyticalprocedureshould, intheory,manifestthemselvesinthesamewayandwithappropriatestrengthwith respecttoboththesampleandthestandard.Asaresult, compensation forthese effectsoccurs.Notethateffectcompensationdiffersfromtheprocessofelimination inthatitdoesnoteliminatetheuncontrolledeffects,butmerelyinvolvesequalizing theminthesampleandstandard.
Inanempiricalcalibrationperformedusingachemicalstandard,itiseasiestto compensateforinstrumentaleffectsbecauseitissufficienttomaintaininstrumentalconditionsatthesameoptimumlevelduringsampleandstandardpreparation formeasurement.Thedetectioneffectiscompensatedforjustaseasilybyusingthe sameinstrumentforbothsampleandstandardmeasurementsandkeepingtheconditionsofthemeasurementsthesame.
Compensatingforpreparativeeffectsismoredifficult,althoughitcanbeachieved tosomeextentbysubjectingthestandardtothesamepreparativetreatmentsto whichthesamplewassubjected.However,itmustbetakenintoaccountthatthe analyteinthestandardmaybesubjecttothiseffecttoadifferentdegreethanthe nativeanalyteduetothedifferentchemicalenvironmentandpotentiallydifferent
1.5CalibrationintheContextofMeasurementErrors 13 chemicalform.Forspeciationeffects,itisveryimportantthatthechemicalformof theanalyteremainsthesameinthesampleandinthestandardduringthecalibrationprocedure.Iftheanalyteispresentinseveralchemicalformsinthesample,the analyteinthestandardneednottakealloftheseformsbutshouldbeintheformin whichtheanalyteistobedeterminedinthesample.
Themostdifficulteffecttocompensateforeffectivelyistheinterferenceeffect. Itisonlyrelativelysimpletocompensatefortheblankeffectbyaddingthereagents usedinsamplepreparationtothestandards.Theeffectfromnativesamplecomponentsrequiresthatthecompositionofthesampleinthestandardisaccurately reproduced(whichisverydifficultorevenimpossibleinpractice)andthatthisconditionbemaintaineduntilmeasurementsaremade.However,therearevariousways tomakethesampleandthestandardatleastpartiallysimilarinchemicalcompositionortocompensatefortheeffectbyusinganappropriatecalibrationmethod. ThesesolutionswillbeshownanddiscussedinChapter6.
Thecompensationofeffectsisofferedbythecalibrationprocess andis thereforecloselyrelatedtotherepresentationoftherealfunctionbythemodelfunction.Themoreaccuratetheapproximationofthetwofunctionsis,themorecompletethecompensationprocessis.Progressivecompensationofeffectspromotesa progressiveapproximationoftheanalyticalresult, x x ,totherealresult, x 0 ,aswell astherealresult, x 0 ,tothetrueresult, x true .Thus, aftercompletecompensation, theanalyticalresultbecomesanaccurate(withinrandomerror)estimate ofthetruevalueoftheanalyteinthesample,i.e. x x ≈ x true . Thisisillustrated schematicallyinFigure1.6.
Intheoreticalcalibration,compensatingforuncontrolledeffectsinvolvesdescribingthemadequatelybymeansofamathematicalstandard,i.e.includinginthis descriptiontheeffectsofvariousfactorsonthesignalmeasuredfortheanalytein thesample.However,whileachemicalstandardcanbemadesimilartoasample duetoitssimilarnature,makingamathematicalstandardsimilartoasample isextremelydifficult.Thus,whendecidingtouseatheoreticalcalibration,itis
Standard preparation Standard measurement
Figure1.6 Impactofuncontrolledeffectsonananalyteinboththesampleandstandard duringitspreparationandmeasurement;duetocompensationforeffectstheanalytical resultvalueapproachesthetruevalue(x x ≈ x true ).Source:Ko ´ scielniak[7]/CCBY4.0.
importanttoeliminate,asmuchaspossible,uncontrolledeffectsaffectingthe analyteinthesample.
Analyticalcalibrationthusleadstoanaccurateanalyticalresulteitherbycomplete eliminationofuncontrolledeffectsorbytheircompletecompensation.Elimination ofaneffectthusdoesnotrequireitscompensation(e.g.onceaninterferenceeffect hasbeeneliminatedwithaspecialreagent,thereisnoneedtoreconstructthecompositionofinterferentsinthestandard),althoughifitisknownthattheelimination ofaneffectmaybeincomplete,itshouldbecompensated.Similarly,compensation foreffects(e.g.instrumentaleffects)doesnotrequiretheirelimination,althoughany smallreductionincreasesthechanceoftheircompletecompensation.Theprocesses ofeliminationandcompensationofuncontrolledeffectsarethuscomplementary activitiesinthesensethat,takentogether,theyprovidethebestchanceofachievinganaccurateassessmentofthetruevalueoftheanalyteinthesamplefromthe analyticalresultobtained.
Sohowshouldtheanalyticalcalibrationprocessbeevaluatedinthecontextof errorsmadeduringtheanalyticalprocedure?Certainly,calibrationisapotential sourceofitsownrandomandsystematicanalyticalerrors.Thisisprimarilydue totheneedtouseastandard.Theempiricalstandard,likethesample,issubject touncontrolledeffectsthatmaybeofadifferenttypethanthosefoundinthe sampleandthereforenotcompensable.Furthermore,thesampleisalwaysmore orlessdifferentfromthestandardeitherbecauseofpropertiesandcomposition (inempiricalcalibration)orbecauseofmathematicalapproximationsandcorrections(intheoreticalcalibration).Fromtheimperfectionofthecalibrationstandard comestheimperfectionofthemodelfunctionandtheaddeddifficultyofaccurately approximatingthetruefunction.
Ontheotherhand,itshouldbenotedthatifitwerepossibletodeterminethe truevalueofananalyteinasamplewithoutthecontributionofanystandard,the analyticalprocedureusedwouldhavetobecompletelyfreeofuncontrolledeffects, ortheseeffectswouldhavetobecompletelyeliminated,andbothareimpossible inpractice.Theparticipationofacalibrationstandard,i.e.theperformanceofan analyticalcalibration,isthereforenotonlyanecessaryconditionforobtainingan analyticalresult,butalsooffersanadditionalopportunitytoimprovethequalityof thisresultbycompensatingforuncontrolledeffects.
1.6CalibrationinQualitativeAnalysis
Analyticalcalibrationappliesequallytoqualitativeandquantitativeanalysis[6]. However,inbothcasestheformoftherealfunctionisdifferent,thebasisfortheformulationofthemodelfunctionisdifferent,andtheaccuracyoftheresultsofanalyte identificationanddeterminationisalsoevaluateddifferently.Itisthereforeworth takingacloserlookatthesecalibrationaspectsinbothtypesofchemicalanalysis. Whenproceedingwithaqualitativeanalysis,theanalystgenerallywantsto identifytheanalyte,thatis,tofindoutwhatcomponentispresentinthesample beinganalyzedorwhatchemicalcomponentsthesampleiscomposedof.Insome
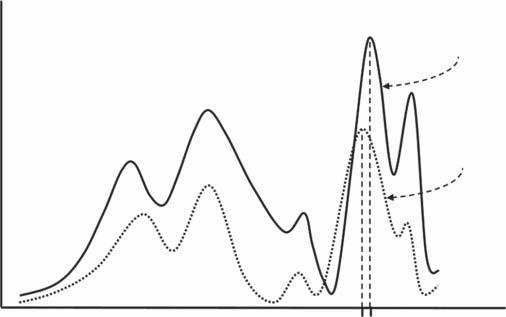
Figure1.7 Measurementimagesofthesampleandstandardusedinqualitativeanalysis: theanalyteisidentifiedfromthepositionofthe Y 0 and Y x signalsobtainedforthe unknownanalyteinthesampleandtheknownanalyteinthestandard,respectively.
cases,heaskswhetheraspecificcomponentorseveralcomponentsarepresent inthesample.Inothersituations,hemayalsobeinterestedinquestionssuchas: whatisthekindofthewholesample,whetherthesampleunderstudyissimilarto anothersample,orwhetherthesampleunderstudybelongstoaparticulargroup ofsamples.
Therelationshipbetweenmeasurementsignalandanalytetypecanbeillustrated bythemeasurementimagesshowninFigure1.7.Theyarecreatedbysubjectinga multicomponentsampleandastandardofsimilarchemicalcompositiontothesampletomeasurementsunderidenticalconditionswithaspecificinstrumentinsuch awaythatachangeinsignalintensityisrecordedasthespecificquantitycharacteristicofthemeasurementmethodused(e.g.wavelength,time,etc.)changes.These signals,whensignificantlylargerthanthemeasurementnoise,correspondtothe presenceofunknowncomponentsinthesampleandatleastoneknowncomponent, bx ,presentinthestandard(solidline). Thetypeofcomponentisindirectlyindicatedbythesignalposition ontheabscissaaxis,thatis,thevalueofthespecific quantitycorrespondingtothemaximumintensityofitssignal.
Empiricalcalibrationinqualitativeanalysisusuallyinvolvescomparingthesignalpositionvalue Y 0 obtainedforthesamplewithasimilarvalue Y x obtainedfor thestandard(seeFigure1.4).1 Sincethevalueof Y x obtainedforthestandardcorrespondstotheknowncomponent bx ,itcanbesaidthatbothvaluesformamodel function, Y = G(b),atapointwithcoordinates[Y x , bx ].Becauseofthesimilarityof thevaluesof Y x and Y 0 ,therealfunction, Y = F (b),canalsobeconsideredaswell approximatedbythemodelfunctionatthispoint.Insuchasituation,thevalueof Y 0 isassignedacomponent bx usingtheevaluationfunction: bx = G 1 (Y 0 ),anditis
1Thiscalibrationapproachreferstoaspecificcomparativecalibrationmethod,mostcommonly usedinquantitativeanalysis.
position, Y
Figure1.8 Analytical calibrationinqualitative analysis:analyte b0 inasample (emptypoints)isidentifiedas analyte bx inastandard(full points)onthebasisofmutual signalpositions, Y 0 and Y x
claimedthatthecomponent b0 presentinthesampleisprobablythecomponent bx presentinthemodel.ThisprocedureisillustratedinFigure1.8.
Theoreticalcalibrationinvolvesthemathematicalformulationofamodelfunction, Y = G(b).Itshouldbestapproximatetherealfunction, Y = F (b),atleastinone pointwithcoordinates[Y x , bx ].Whenthesignalobtainedforthesample, Y 0 ,issubstitutedintotheformulaoftheinversefunctionoftheformulatedmodelfunction, thesignalpositionvalue, bx ,isobtained,indicatingthetruetype, b0 ,oftheanalyte sought.
Mathematically,therealfunctionandthemodelfunctionarediscretefunctions inqualitativeanalysis,asshowninFigure1.5.Whentherealfunctionismapped sufficientlyaccuratelywiththemodelfunction,anysignalofaparticularposition obtainedforknowncomponentsofthestandardistheoreticalevidenceforthepresenceorabsenceofthosecomponentsinthesample.Somecomponentsmaybeidentifiedbytwoormoresignals,2 whichareanalyticalsignalsforthem.Inmanycases, amodelfunctioncanbeusedtoidentifymultiplecomponentsofasample,thatis, toperformamulticomponentanalysis.
Whenapplyingthechosenanalyticalmethodandrecordingthesignalunder appropriatelyestablishedoptimumconditions,theanalystshouldhaveathis disposalatleastonesignalcorrespondingtoaspecifictypeofanalyte.Itismost advantageousifhehasameasurementimageofthetypeshowninFigure1.7,which coversawiderangeofmagnitudecharacterizingthetypeofconstituent.Suchan image,obtainedunderspecificexperimentalconditions,reflectsthechemical compositionoftheentiresampleandischaracteristicofit.Thepresenceofthe desiredanalyteinthesamplecanthenbeindicatednotonlybythecorresponding positionsoftheanalyticalsignals,butadditionallybyotherparameters,suchasthe numberofthesesignals,theirabsoluteandrelativeheights,andeventheshape oftheentiresignalrecordedinagivenmeasurementrange(somemeasurement
2Nevertheless,therelationships Y = F (b)and Y = G(b)canbecalledfunctionsbecause,dueto thenaturalrandomerrorsoftheobtainedmeasuredandcalculatedvalues,differentsignalscannot representperfectlythesamemeasureofaparticularsamplecomponent.