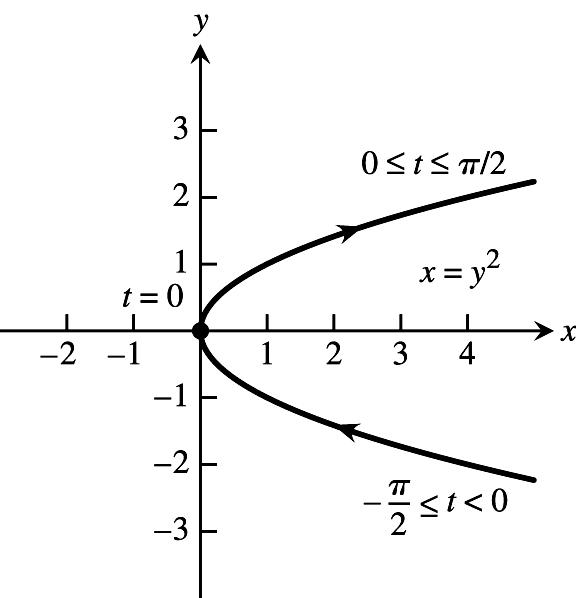
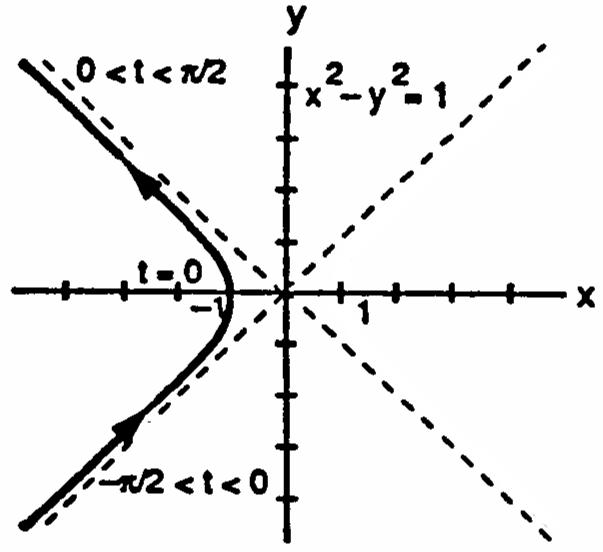
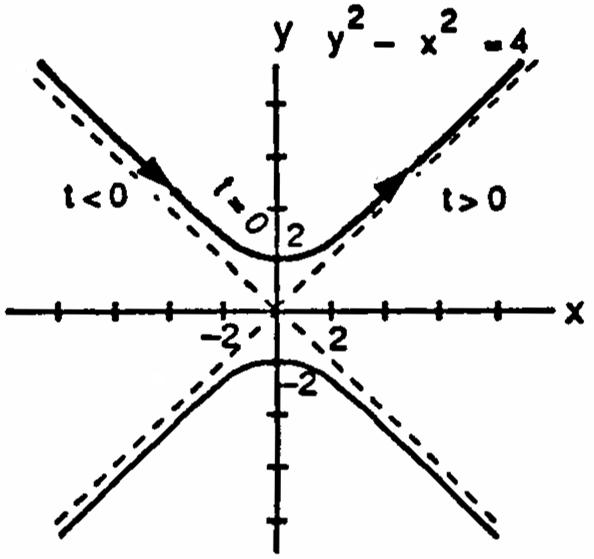
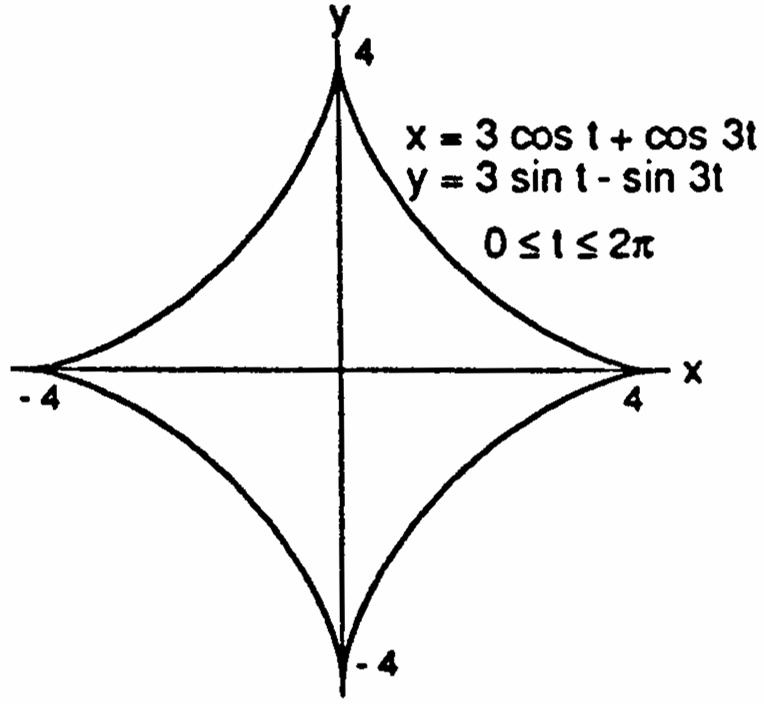
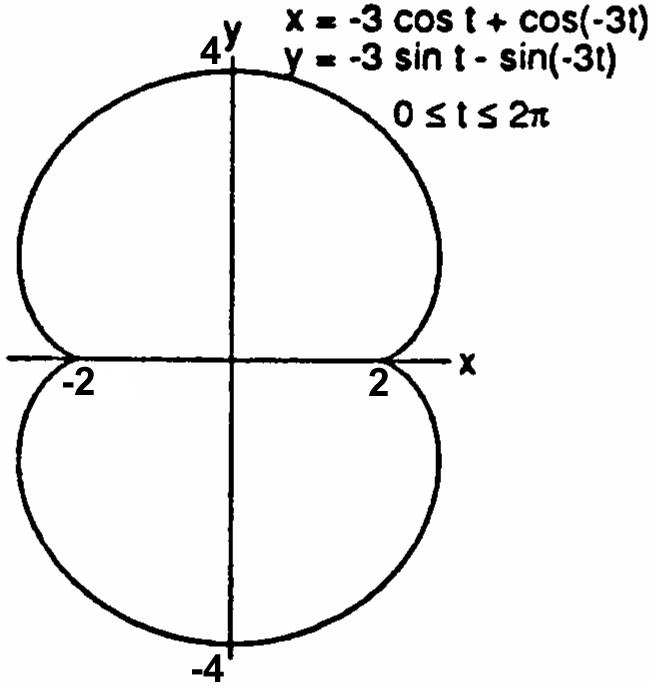
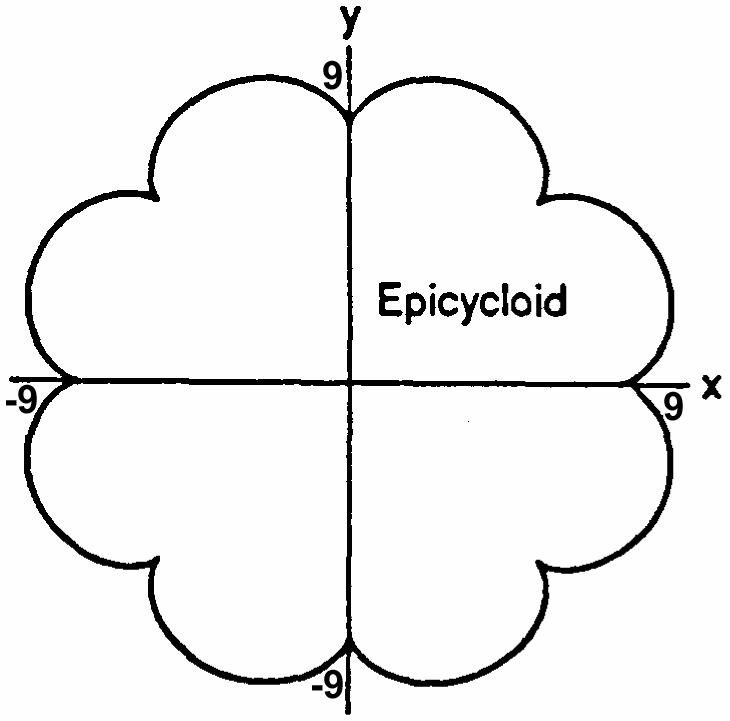
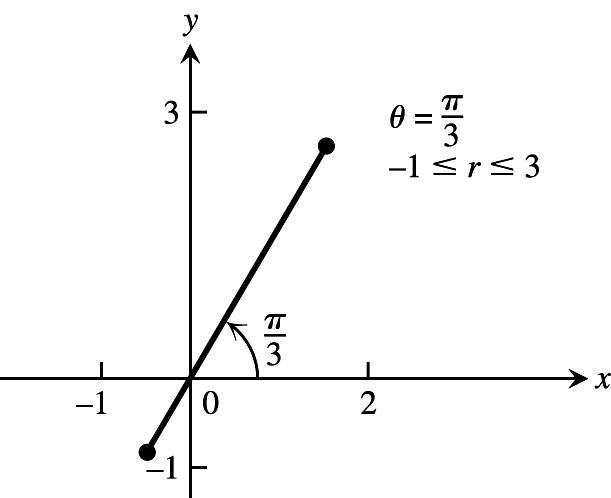
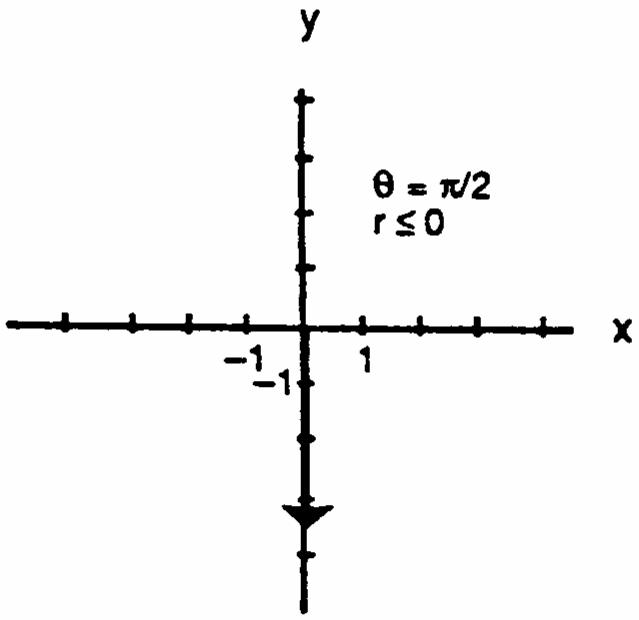
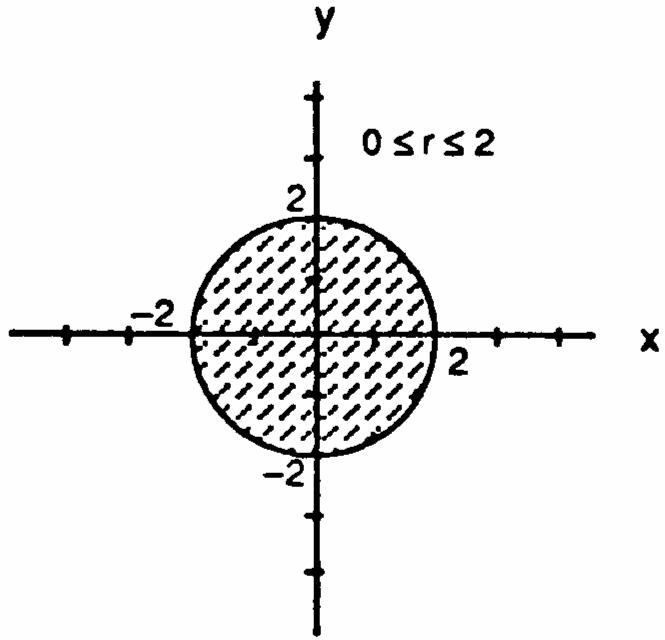
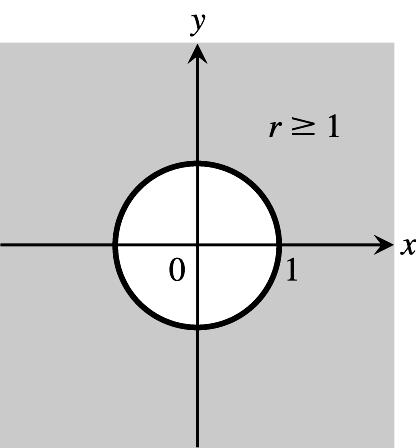
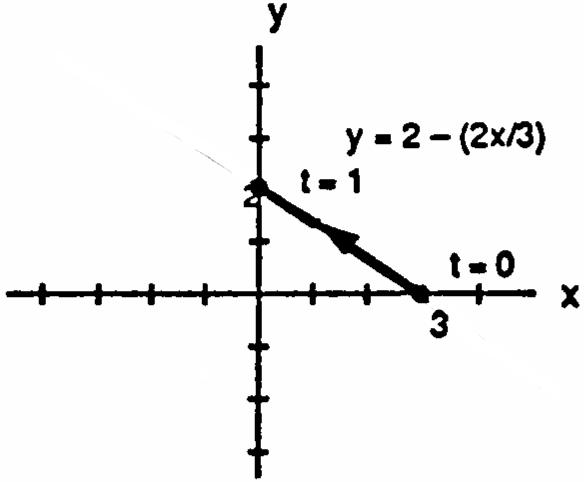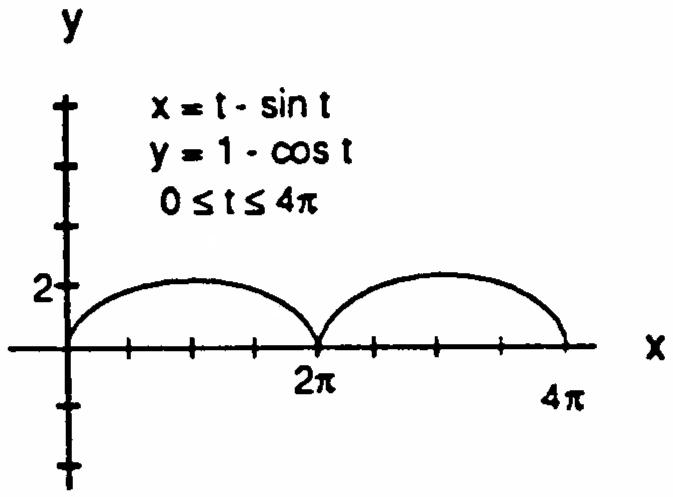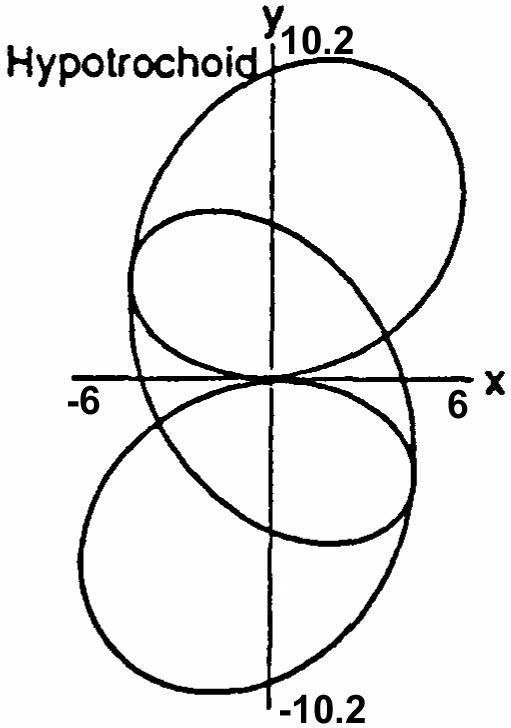CHAPTER 11 PARAMETRIC EQUATIONS AND POLAR COORDINATES
11.1 PARAMETRIZATIONS OF PLANE CURVES
1.x3t,y9t,tyx2.xt,yt,t0xy œœ _ _Êœœ œ Êœ ## È È oryx,x0 œŸ #
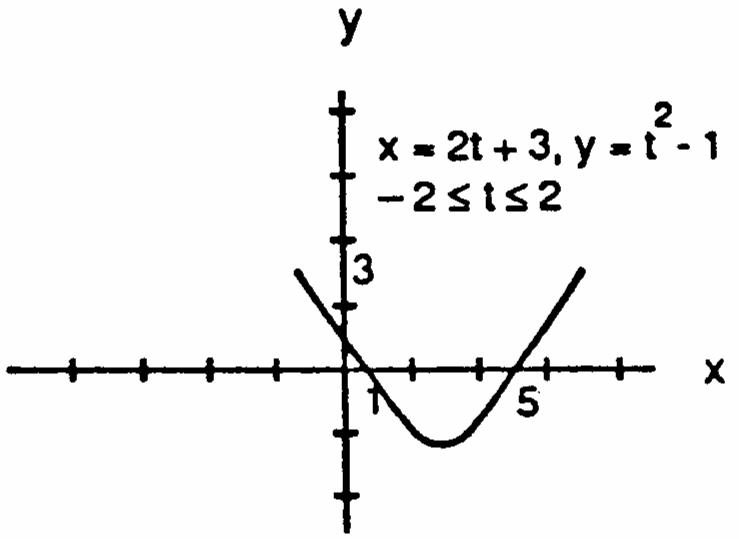
3.x2t5,y4t7,t4.x33t,y2t,0t1t œ œ _ _œ œŸŸÊœ y # x52t2(x5)4tx332x63y Ê œÊ œÊœ Êœ ˆ‰ y # y2(x5)7y2x3y2x,xÊœ Êœ Êœ !ŸŸ$ 2 3
5.xcos2t,ysin2t,0t6.xcos(t),ysin(t),0t œœŸŸœ œ ŸŸ 1111 cos2tsin2t1xy1cos(t)sin(t)1 Ê œÊ œÊ œ ######11 xy1,y Ê œ ! ##
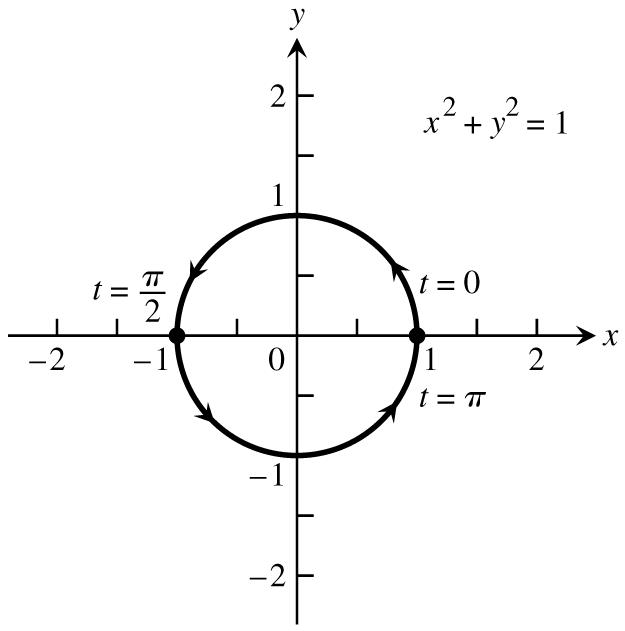
648Chapter11ParametricEquationsandPolarCoordinates
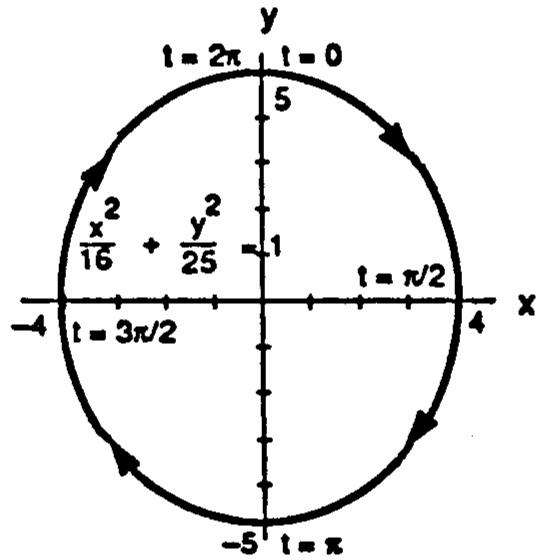
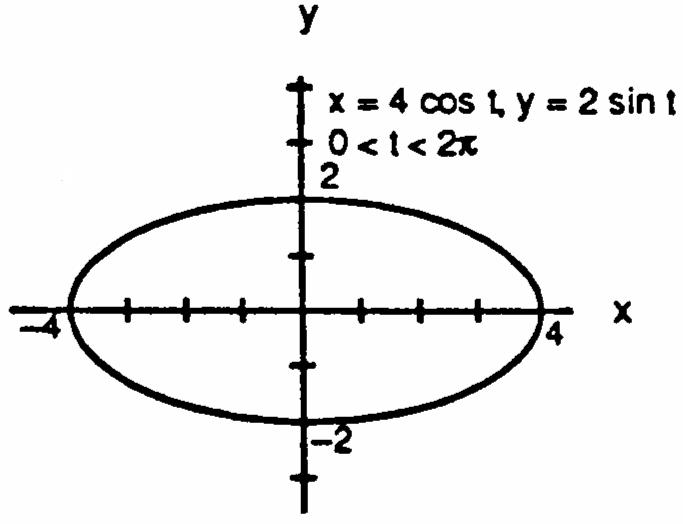
7.x4cost,y2sint,0t28.x4sint,y5cost,0t2 œœŸŸœœŸŸ 11 1111 Ê œÊ œÊ œÊ œ 16cost4sintx16sint25costx 1641641625165 yy ###### # # #
9.xsint,ycos2t,t10.x1sint,ycost2,0t œœ ŸŸœ œ ŸŸ 11 22 1 ycos2t12sinty12xsintcost1x1y21Êœœ Êœ Ê œÊ œ ##### 2 abab
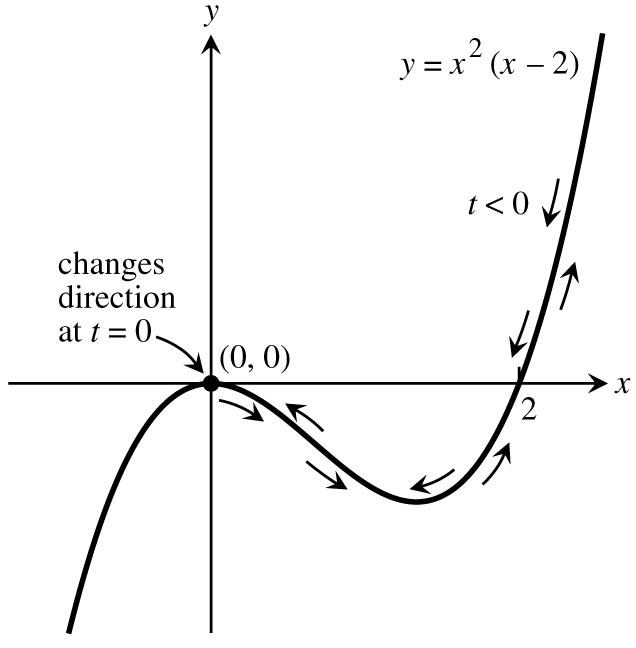
11.xt,yt2t,t12.x,y,1t1 œœ _ _œœ 264tt2 t1t1 yt2tyx2xtyÊœ Êœ ʜʜ abab2232 32x2x x12x1
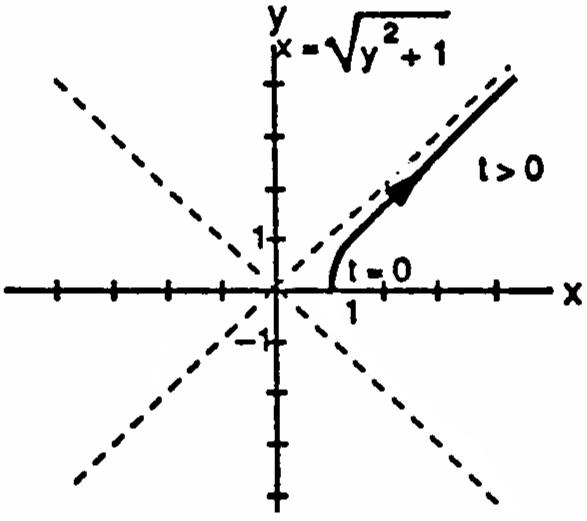
13.xt,y1t,1t014.xt1,yt,t0 œœ ŸŸœ œ È È È # y1xytxy1,y0Êœ ʜʜ È È ## #
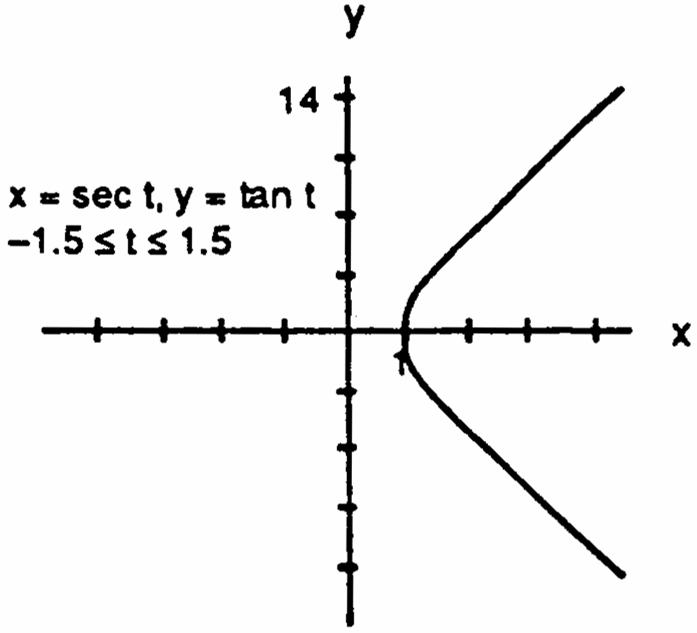
15.xsect1,ytant,t16.xsect,ytant,t œ œ œ œ # #### 1111 sect1tantxysecttant1xy1 Ê œÊœÊ œÊ œ #######
17.xcosht,ysinht,118.x2sinht,y2cosht,t œ œ _ _œœ _ _ coshtsinht1xy14cosht4sinht4yx4 Ê
19.(a)xacost,yasint,0t220.(a)xasint,ybcost,t œœ ŸŸœœŸŸ 1 11 ## 5 (b)xacost,yasint,0t2(b)xacost,ybsint,0t2 œœŸŸœœŸŸ 11 (c)xacost,yasint,0t4(c)xasint,ybcost,t œœ ŸŸœœŸŸ 1 11 ## 9 (d)xacost,yasint,0t4(d)xacost,ybsint,0t4 œœŸŸœœŸŸ 11
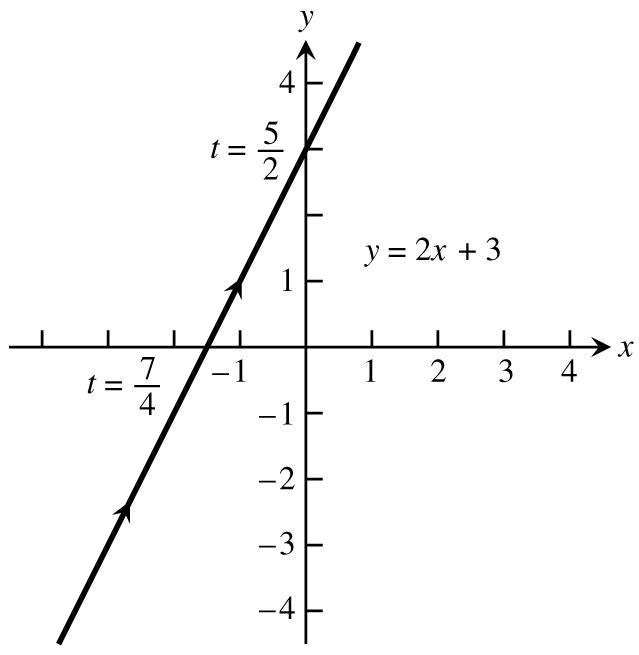
21.Usingwecreatetheparametricequationsxatandybt,representingalinewhichgoes ab "ß $œ " œ $ throughatt.Wedetermineaandbsothatthelinegoesthroughwhent. abab "ß $œ!%ß"œ" Sinceaa.Sincebb.Therefore,onepossibleparameterizationisxt, %œ " Êœ&"œ $ Êœ%œ " & yt,0t. œ $ %ŸŸ"
22.Usingwecreatetheparametricequationsxatandybt,representingalinewhichgoesthrough ab"ß$œ " œ$ att.Wedetermineaandbsothatthelinegoesthroughwhent.Sinceaa.abab "ß$œ!$ß #œ"$œ " Êœ% Sincebb.Therefore,onepossibleparameterizationisxt,yt,0t. #œ$ Êœ &œ " %œ$ &ŸŸ"
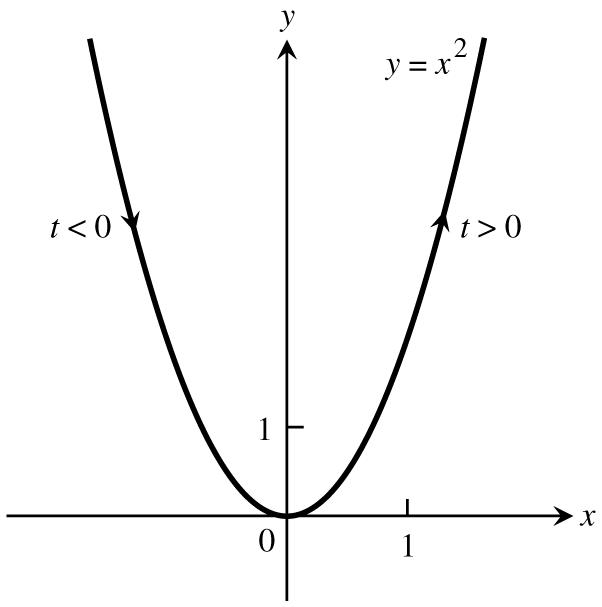
23.Thelowerhalfoftheparabolaisgivenbyxyfory.Substitutingtfory,weobtainonepossible œ "Ÿ! # parameterizationxt,yt,t0 œ "œŸÞ #
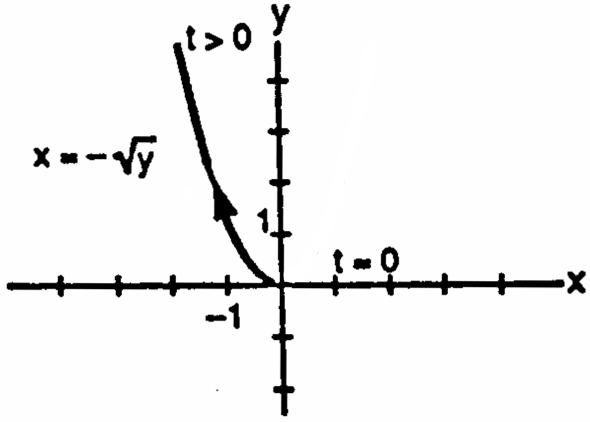
24.Thevertexoftheparabolaisat,sothelefthalfoftheparabolaisgivenbyyxxforx.Substituting ab "ß "œ #Ÿ " # tforx,weobtainonepossibleparametrization:xt,ytt,t. œœ #Ÿ " #
25.Forsimplicity,weassumethatxandyarelinearfunctionsoftandthatthepointx,ystartsatfortandpasses abab#ß$œ! throughatt.Thenxft,wherefandf. abababab "ß "œ"œ!œ#"œ " Sinceslope,xfttt.Also,ygt,wheregandg. œœœ $œœ $ #œ# $œ!œ$"œ " ? ? x t " # " ! abababab Sinceslope4.ygttt. œœœ œœ % $œ$ % ? ? y t 3 " " ! ab Onepossibleparameterizationis:xt,yt,t. œ# $œ$ % !
Copyright © 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
26.Forsimplicity,weassumethatxandyarelinearfunctionsoftandthatthepointx,ystartsatfortand abab"ß#œ! passesthroughatt.Thenxft,wherefandf. abababab !ß!œ"œ!œ ""œ!
Sinceslope,xfttt.Also,ygt,wheregandg. œœœ"œœ" "œ " œ!œ#"œ! ? ? x t !" " ! ab ababababab Sinceslope.ygttt. œœœ #œœ # #œ# # ? ? y t !# " ! ab Onepossibleparameterizationis:xt,yt,t. œ " œ# # !
27.Sinceweonlywantthetophalfofacircle,y0,soletx2cost,y2sint,0t4 œœllŸŸ 1
28.Sincewewantxtostaybetween3and3,letx3sint,theny3sint9sint,thusx3sint,y9sint, œœœœœ ab2 ## 0t Ÿ _
29.xya2x2y0;letttxyt.Substitutionyields ###œÊ œÊœ œÊ œÊœ dydydy dxdxydxy xx ytyayandx,t ####œÊœœ _ _ aat 1t1t
30.Intermsof,parametricequationsforthecirclearexacos,yasin,02.Since,thearc ))))1) œœŸ œ s a lengthparametrizationsare:xacos,yasin,and020s2aistheintervalfors. œœŸ ÊŸŸ sss aaa 11
31.Dropaverticallinefromthepointx,ytothex-axis,thenisanangleinarighttriangle,andfromtrigonometrywe ab ) knowthattanyxtan.Theequationofthelinethrough0,2and4,0isgivenbyyx2.Thus )) œÊœœ y x2 1 abab xtanx2xandywhere0. )) œ ÊœœŸ144tan 22tan12tan12 )) )1
32.Dropaverticallinefromthepointx,ytothex-axis,thenisanangleinarighttriangle,andfromtrigonometrywe ab ) knowthattanyxtan.Sinceyxyxxtanxxcotycotwhere ))))) œÊœœÊœÊœÊœÊœ y x 22 2 È ab 0. Ÿ ) 1 2
33.Theequationofthecircleisgivenbyx2y1.Dropaverticallinefromthepointx,yonthecircletothe abab œ 22 x-axis,thenisanangleinarighttriangle.Sothatwecanstartat1,0androtateinaclockwisedirection,let ) ab x2cos,ysin,02. œ œŸŸ )))1
34.Dropaverticallinefromthepointx,ytothex-axis,thenisanangleinarighttriangle,whoseheightisyandwhos ab ) e baseisx2.Bytrigonometrywehavetanyx2tan.Theequationofthecircleisgivenby œÊœ )) y x2 ab xy1xx2tan1xsec4xtan4tan10.Solvingforxweobtain 2222222 2 œÊ œÊ œ ab ab ))))
x2sincoscos3sin œœœ „ „„4tan4tan4sec4tan1 2sec2sec 4tan213tan222 2222 2 22 22 )))) )) )) Éabab È )))) È 22coscos4cos3andy22coscos4cos32tan œ „ œ „ 2222 )))))))
2sincossin4cos3.Sinceweonlyneedtogofrom1,0to0,1,letœ„)))) È abab 2 x22coscos4cos3,y2sincossin4cos3,0tan. œ œ ŸŸ 21 221 2 )))))))) ÈÈ ˆ‰
Toobtaintheupperlimitfor,notethatx0andy1,usingyx2tan12tantan. )))) œœœ ʜʜ ab ˆ‰11 2
35.ExtendtheverticallinethroughAtothex-axisandletCbethepointofintersection.ThenOCAQx œœ andtantx2cott;sintOA;and(AB)(OA)(AQ)ABx œœÊœœœÊœœÊœ 222222 OCxtantOAsintsint ## ˆ‰ ABAB.Nexty2ABsinty2sint ʜʜœ Êœ œ ˆ‰ˆ‰ˆ‰ 222sint2sint sinttanttanttant # # # 222cost2sint.Thereforeletx2cottandy2sint,0t. œ œœœ 2sint tant # # ### 1
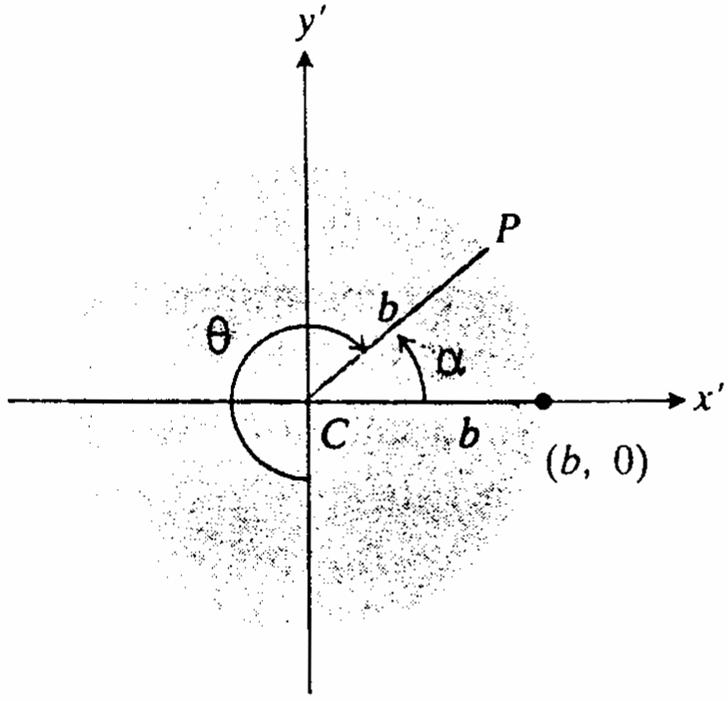
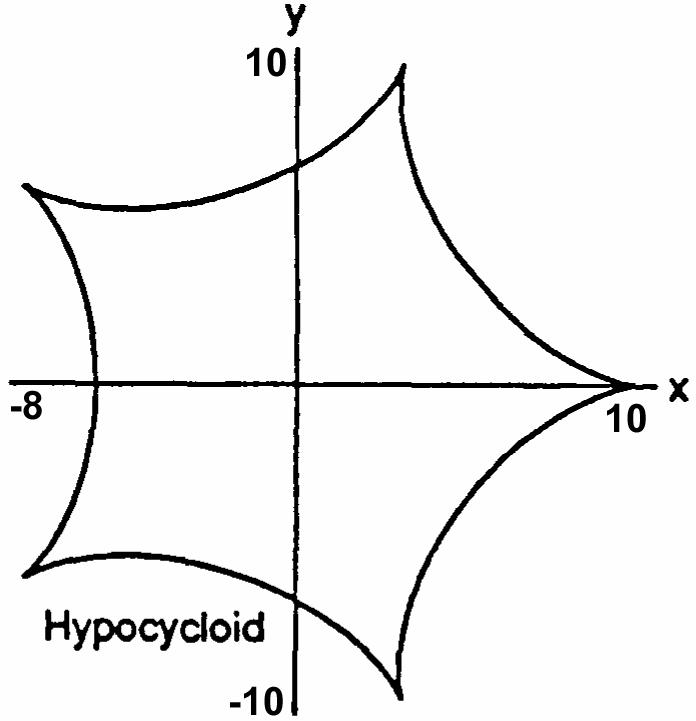
36.ArcPFArcAFsinceeachisthedistancerolledand œ ArcFCPArcPFb(FCP); PFArcAF ba œnÊœnœ )
ArcAFaab(FCP)FCP; ʜʜnÊnœ ))) a b
OCG;OCGOCPPCEnœ nœn n 1 # )
OCP.NowOCPFCPœn nœ n ˆ‰ 1 # !1
.ThusOCG œ nœ Ê 1)1)!) aa bb 11 ## œ Êœ œ 1)!!1))1) aaab bbb 1 # ˆ‰
ThenxOGBGOGPE(ab)cosbcos(ab)cosbcos œ œ œ œ )!)1) ˆ‰ ab b (ab)cosbcos.AlsoyEGCGCE(ab)sinbsin œ œœ œ )))! ˆ‰ ab b (ab)sinbsin(ab)sinbsin.Therefore œ œ )1))) ˆ‰ˆ‰ abab bb x(ab)cosbcosandy(ab)sinbsin. œ œ )))) ˆ‰ˆ‰ abab bb
Ifb,thenxacoscos œœaaa 444 a ˆ‰ Š‹)) ˆ‰ ˆ‰ a 4 a 4 coscos3cos(coscos2sinsin2) œ œ 3aa3aa 4444))))))) cos(cos)cossin(sin)(2sincos) œ 3aa 44))))))) ab ab ## coscoscossinsincos œ 3aaa2a 4444)))))) $## coscos(cos)1cosacos; œ œ 3aa3a 444))))) $#$ ab
yasinsinsinsin3sin(sincos2cossin2) œ œ œ ˆ‰ Š‹ aa3aa3aa 444444 a ))))))))) ˆ‰ ˆ‰ a 4 a 4 sin(sin)cossin(cos)(2sincos) œ 3aa 44))))))) ab ab ## sinsincossincossin œ 3aaa2a 4444)))))) #$# sinsincossin œ 3a3aa 444)))) #$ sin(sin)1sinsinasin. œ œ 3a3aa 444))))) ab#$$
37.DrawlineAMinthefigureandnotethatAMOisaright n anglesinceitisaninscribedanglewhichspansthediameter ofacircle.ThenANMNAM.Now,OAa, ### œ œ tant,andsint.NextMNOPANAM aa œœœ OPANAMatantasintÊœ œ ####### OPatantasintÊœ È #### (asint)sect1.IntriangleBPO, œ œ È # asint cost # xOPsintasinttantand œœœ asint cost $ # yOPcostasintxasinttantandyasint. œœÊœœ###
38.Letthex-axisbethelinethewheelrollsalongwiththey-axisthroughalowpointofthetrochoid (seetheaccompanyingfigure).
Letdenotetheanglethroughwhichthewheelturns.Thenhaandka.Nextintroducexy-axes ))œœ ww paralleltothexy-axesandhavingtheiroriginatthecenterCofthewheel.Thenxbcosand w œ ! ybsin,where.Itfollowsthatxbcosbsinandybsin www ### œœ œ œ œ !!)))) 333 111
bcosxhxabsinandykyabcosareparametricequationsofthetrochoid. œ Êœ œ œ œ )))) ww
39.D(x2)yD(x2)y(t2)tDt4t œ Êœ œ Êœ É ˆ‰ˆ‰ˆ‰ #""" ### ########% 17 4
4t40t1.Thesecondderivativeisalwayspositivefort0t1givesalocal Êœ œÊœÁÊœ dD dt ab # $ minimumforD(andhenceD)whichisanabsoluteminimumsinceitistheonlyextremumtheclosest # Ê pointontheparabolais(11). ß
40.D2cost(sint0)D2costsint œ Êœ Ê Éˆ‰ˆ‰ 33 44dt dD ##### ab # 22cost(2sint)2sintcost(2sint)3cost02sint0or3cost0 œ œ œÊ œ œ ˆ‰ˆ‰333 4 ## t0,ort,.Now6cost3cost6sintsothat(0)3relative Êœœœ œ Ê 1 11 33dtdt 5dDdD ## ## # # abab ## maximum,()9relativemaximum,relativeminimum,and dDdD dtdt32 9 #### # # abab 1 œ ÊœÊ ˆ‰ 1 dDrelativeminimum.Thereforebothtandtgivepointsontheellipseclosestto dt333 595 ## # ab ˆ‰111 œÊœœ # thepoint1and1arethedesiredpoints. ˆ‰ Š‹Š‹ 3 4 33ß!ÊßßÈÈ ##
41.(a)(b)(c)
42.(a)(b)(c)
47.(a)(b)(c)
48.(a)(b) (c)(d)
11.2 CALCULUS WITH PARAMETRIC CURVES
1.tx2cos2,y2sin2;2sint,2costcott œÊœœœœœ œÊœœœ 111 444dtdtdxdx/dt2sint dx2cost dydydy/dt ÈÈ cot1;tangentlineisy21x2oryx22;csct Êœ œ œ œ œ ¹Š‹ÈÈÈ dydy dx4dt tœ 1 4 1 w # 2 Êœœœ Êœdydy/dtdy dxdx/dt2sint2sintdx csct #w# #$# # " ¹ È t 1 4
2.txsin2sin,ycos2cos;2cos2t, œ Êœ œ œ œ œ œœ"""" ## 66363dt 3dxˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰ˆ‰ 1111 11 È 2sin2ttan2ttan2tan3;dydydy dtdx2cos2tdx63 2sin2t œ Êœœ Êœ œ œ 1111 " 11 1 11 ¹ ˆ‰ˆ‰ ˆ‰ È tœ 1 6 tangentlineisy3xory3x2;2sec2t œ œ œ Êœ " ## # ÈÈ ’“ Š‹ È 3dydy dtdx2cos2t 2sec2t w# # # 11 11 11 8 œ Êœ " cos2tdx dy $# # 1 ¹ tœ 1 6 Copyright © 2010 Pearson Education,
Section11.2CalculusWithParametricCurves655
3.tx4sin22,y2cos2;4cost,2sint œÊœœœœœœ Êœœ 111 444dtdtdxdx/dt4cost dx2sint dydydy/dt ÈÈ
tanttan;tangentlineisy2x22oryx22; œ Êœ œ œ œ """"" ##### ¹Š‹ÈÈÈ dy dx4 tœ 1 4 1
sect dydydy/dtdy2 dtdxdx/dt4cost8costdx4
sect w#w# #$# " # # œ Êœœœ Êœ "" # # ¹ tœ 1 4 È
4.txcos,y3cos;sint,3sint3 œÊœœ œœ œ œ Êœœ 222dx 333dtdtdxsint 33sint dydy 111 " ##ÈÈÈ ÈÈ
3;tangentlineisy3xory3x;00 Êœ œ œœÊœœ¹Š‹ÈÈÈ ˆ‰‘ dydydy dxdtdxsint 30 t23 1 È ## " w# # 0 Êœ ¹ dy dx # # t23 1
5.tx,y;1,1;tangentlineis œÊœœœœÊœœÊœœ 11dx1 44dtdtdxdx/dtdx dydydy/dtdy t2t """ ### ÈÈ É ¹ tœ 1 4 " 4 y1xoryx;tt2 œ œ œ Êœœ Êœ """"" # $Î#$Î# † ˆ‰ ¹ 44dt4dxdx/dt4dx dydydy/dtdy w#w# ## tœ 1 4
6.txsec11,ytan1;2secttant,sect œ Êœ œœ œ œœ 111 444dtdt dxdy ### ˆ‰ˆ‰ cottcot;tangentlineisÊœœœÊœ œ dydy dx2secttant2tantdx4 sect # # """" ### ¹ ˆ‰ tœ 1 4 1 y(1)(x1)oryx;csctcott œ œ œ Êœœ """"" #### #$dydy dtdx2secttant4 csct w# ## " # # Êœ ¹ dy dx4 # # tœ 1 4 "
7.txsec,ytan;secttant,sect œÊœœœœœœÊœ 111 666dtdtdxdx/dt 2dx 33 dydydy/dt ÈÈ "# csctcsc2;tangentlineisy2xory2x3;œœÊœœ œ œ sect2 secttantdx6 dy 33 # ¹Š‹ È tœ 1 6 1 " ÈÈ
csctcottcott33dydydy/dtdy dtdxdx/dtsecttantdx
csctcott w#w# ## œ Êœœœ Êœ $ ¹ È tœ 1 6
8.t3x312,y3(3)3;(t1),(3t) œÊœ œ œœœ œÊœ È È dx3 dtdtdx dydy(3t) (t1) " ## "Î#"Î# ˆ‰ ˆ‰ 3 # "Î# " # "Î# 2;tangentlineisy32[x(2)]ory2x1; œ œœœ œ œ 3t1331 3t dy dx3(3) ÈÈ ÈÈ ¹ t3 œ dydy dt3tdx 3t(t1)3t1(3t)33 2t3tt1t3t w # ## "Î# "Î# # œœÊœœ È ‘ ‘ È ÈÈ È Š‹ Š‹ 333 2t3tt1 1 2t1 È È È
Êœ ¹ dy dx3 # # t3 œ "
9.t1x5,y1;4t,4tt(1)1;tangentlineis œ ÊœœœœÊœœœÊœ œ dx4t dtdtdxdx/dt4tdx dydydy/dtdy$## $ ¹ t1 œ y11(x5)oryx4;2t œ œ œÊœœœÊœ dydydy/dtdy dtdxdx/dt4tdx 2t w#w# ## "" ## ¹ t1 œ
10.t1x1,y2;,t1;tangentlineis œÊœœ œ œÊœœ Êœ dx dttdttdxdx dydydy"" # " " # ˆ‰ Š‹ t t ¹ t1 œ y(2)1(x1)oryx1;1t1 œ œ œ ÊœœÊœdydydy dtdxdx 1 w## ## " # # Š‹ t ¹ t1 œ
11.txsin,y1cos1;1cost,sint œÊœ œ œ œ œœ œÊœ 11111 33333dtdtdxdx/dt 3dxdydydy/dt È ### "" 3;tangentlineisy3x œÊœœœ œ sint 1costdx3 dysin 1cos 3 ## " ¹Š‹ ÈÈ t 1 3 ˆ‰ ˆ‰ Š‹ ˆ‰ È 1 1 3 3 3 È # " # 1
y3x2;Êœ œœÊœœ È 1 È ˆ‰ 3 3dt(1cost)1costdxdx/dt1cost
dy(1cost)(cost)(sint)(sint)dydy/dt 1 w #w ## 1 1cost 4 œÊœ 1 (1cost)dx dy ## # ¹ tœ 1 3
12.txcos0,y1sin2;sint,costcott œÊœœœ œœ œÊœœ 111 222dtdtdxsint dxcost dydy cot0;tangentlineisy2;csctcsct1 Êœ œœœÊœœ Êœ ¹ ¹ dydydydy dxdtdxsintdx csct tt œ œ 1 1 22 1 # #$ w## ## #
13.t2x,y2;,9; œÊœœœœœœÊœÊœœ 112dx11 21321dtdtdxdxt1t1t121 dydydyt121 abababab abab 2222 22 ¹ t2 tangentlineisy9x1;108 œ œ ʜʜœdydydy dtdxdx 4t14t1421 t1t121 w## ## ababab ababab 333 33 ¹ t2 œ
14.t0x0e1,y1e0;1e,e; œÊœ œœ œœ œ ʜʜœ 00ttdxee1 dtdtdx1edx1e2 dydydyt0 t0 ¹ t0 œ tangentlineisyx; œ œÊœÊœœ 11eee1 22dtdxdx8 dydydy 1e1e1e w## ## tt0 tt 233 0 abab ab ¹ t0 œ
15.x2t93x4t03x4t; 322dxdxdx4t dtdtdt3x œÊ œÊœ Êœ # 2 2y3t46y6t0;thus;t2 $## œÊ œÊœœœœœœœdydydydy/dtt(3x) dtdt6yydxdx/dty(4t)4y 6tt3x #### # Š‹ Š‹ t y 4t 3x2 22 x2(2)9x89x1x1;t22y3(2)4 Ê œÊ œÊœÊœœÊ œ 333#$# 2y16y8y2;therefore ʜʜʜœœ $$" # ¹ dy dx16 3 4 3 t2 œ ab ab 2 #
16.x5t5tt;y(t1)ty(t1)t œ Êœ œ œÊ œ É ÈÈÈ ˆ‰ˆ‰ dx dtdt 4t5t dy """" ### "Î#"Î#"Î# ÈÈ É t1y;thus Ê œ Êœœœœœ† ab dydydy dtdtt1dx ttt2t yyt " ## "# ÈÈÈ ab È " ## " # " ÈÈÈ È ÈÈ É ttt2t yt 4t5t dy dt dx dt " # # " " yt tt 4t5t È È ab ÈÈ É ;t4x543;t4y34yœœÊœ œœÊ†œÊœ #" #& " ˆ‰ÈÈ É ytt t É ÈÈ È 2 3 therefore, ¹ dy dx9 103 t4 œœ 2244 4 Š‹abÈÈ É " & " 2 3 È
17.x2xtt3x2t113x2t1;yt12ty4 œ Ê œ Ê œ Êœ œ $Î##"Î#"Î#dxdxdxdx2t1 dtdtdtdt13x ˆ‰ È È "Î# t1y(t1)2y2ty0t12y0 Ê œÊ œ dydydyydy dtdtdtydt 2t1 t ÈȈ‰ˆ‰ÈÈ Š‹ "" ## "Î#"Î# ÈÈ t12y;thus Ê œ Êœœ Š‹ È È t ydtdt dyydy 2t1ÈÈ Š‹ È Š‹ È È È È È y 2t1 t y È È 2y t1 yy4yt1 2y(t1)2tt1 dydy/dt;t0x2x0x12x0x0;t0 dxdx/dtœœœÊ œÊ œÊœœ Œ Š‹ "Î# yy4yt1 2y(t1)2tt1 2t1 13x È È È È $Î#"Î#ˆ‰ y012(0)y4y4;therefore6 Ê œÊœœœ È È ¹ dy dxt0 œ Œ Œ "Î# 444(4)01 24(01)2(0)01 2(0)1 13(0) È È È È
18.xsint2xtsintxcost21(sint2)1xcost; œÊ œÊ œ Êœ dxdxdxdx1xcost dtdtdtdtsint2 tsint2tysinttcost2;thus;txsin2x œÊ œœœÊ œ dydy dtdx sinttcost2 ˆ‰ 1xcost sint2 111 x;therefore4 Êœœœœ 11111 1 # ¹ dy dx2 sincos248 tœ1 –— 1cos sin2 # Š‹ 1 1 1
Copyright © 2010 Pearson Education, Inc. Publishing
19.xtt,y2t2xt3t1,6t22t23t12t6t2t2 œ œ Êœ œ Êœ œ 3322222 dxdx dtdtdtdt dydy ab 1 ʜʜœ dydy dx3t1dx 2t2212 31122 ¹ t1 ab ab
20.tlnxt,yte11xt1xt1,tee; œ œÊœ Ê œ Êœ œ ab ˆ‰ ttt 1dxdxdx xtdtdtdtdt dy ;t00lnx0x1ÊœœÊœ ʜʜœdydy dxxt1dx1012 tee1 tt0ee00 ab ¹ t0 œ ab
21.Aydxa1costa1costdta1costdta12costcostdt œœ œ œ '''' 0000 2222 222 2 1111 abababab a12costdta2costcos2tdtat2sintsin2t œ œ œ 222 22 1cos2t3131 22224 2 '' 00
11
a30003a œ œ 22 ab11
22.Axdyttedtuttdu12tdt;dvedtve œœ œ Êœ œ Êœ '' 00 11 2t2tt abababab”• ette12tdtu12tdu2dt;dvedtve œ œ Êœ œÊœ t2ttt 11 ababº”• 0 0' ette12t2edtette12t2e œ œ t2ttt2tt 111 1 ababababº”º•”•º 000 0' e0e12ee0e12e13e1 œ œ œ abab abababab 11100013 e
23.A2ydx2bsintasintdt2absintdt2abdtab1cos2tdt œœ œœœ ''''' 11 111 00 000 21cos2t 2 ababab abtsin2tab0ab œ œ !œ ’“ ab ab 1 20 1 11
24.(a)xt,yt,0t1Aydxt2tdt2tdtt0 œœŸŸÊœœœœœ œ 26678 111 111 444 0 1 ''' 000 ab ’“
(b)xt,yt,0t1Aydxt3tdt3tdtt0 œœŸŸÊœœœœœ œ 39921112 111 111 444 0 1 ''' 000 ab ’“
ʈ‰ Š‹ Éabab È ####
25.sintand1costsint1cost22cost dxdx dtdtdtdt dydy œ œ Ê œ œ
Length22costdt2(1cost)dt2dtÊœ œ œ ''' 000 1costsint 1cost1cost 111 È ÈÈ Éˆ‰ É # 2dt(sincesint0on[0]);[u1costdusintdt;t0u0, œ ßœ ÊœœÊœ È '0 sint 1cost 1 È 1 tu2]2udu22u4 œÊœÄœœ 1 ÈÈ ‘ '0 2 "Î#"Î# # !
26.3tand3t3t(3t)9t9t3tt1sincet0on03 dxdx dtdtdtdt dydyœœÊ œ œ œ ß #####%## # ʈ‰ Š‹Š‹ Éab È È ’“ È
Length3tt1dt;ut1du3tdt;t0u1,t3u4Êœ œ ÊœœÊœœÊœ '0 3 È È ’“ È ## # 3 uduu(81)7Äœœ œ '1 4 3 # "Î#$Î# % " ‘
27.tand(2t1)t2t1t1t1t1since0t4 dxdx dtdtdtdt dydyœœ Ê œ œ œ œ ŸŸ "Î##### ʈ‰ Š‹ È ababkk É
Lengtht1dtt8412Êœ œ œ œ '0 4 t 2 abab ’“ # % ! Copyright © 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
28.2t3and1t2t31tt4t4t2t2 dxdx dtdtdtdt dydy œ œ Ê œ œ œ œ abababkk ʈ‰ Š‹ É È "Î##### since0t3Length(t2)dt2t ŸŸÊœ œ œ '0 3 t21 2 3 ’“ # !#
29.8tcostand8tsint8tcost8tsint64tcost64tsint dxdx dtdtdtdt dydyœœÊ œ œ ʈ‰ Š‹ Éabab È ######## 8t8tsince0tLength8tdt4t œœŸŸÊœœœ kkcd 1 1 1 # Î## Î# ! '0 2 1
30.secttantsectcostsectcostandsint dxdx dtsecttantdtdtdt dydy œ œ œ Ê ˆ‰ˆ‰ ab Ê Š‹ "### sectcostsintsect1tanttanttantsince0t œ œ œœœŸŸÉababkk ÈÈ #### 1 3 Lengthtantdtdtlncostlnln1ln2 Êœœœ œ œ '' 00 33 sint cost 11 1 ÎÎÎ$ ! " # cd kk
31.sintandcostsintcost1Area2yds dxdx dtdtdtdt dydy œ œÊ œ œÊœ ʈ‰ Š‹ Éabab #### ' 1 22sint1dt22tcost2[4101]8 œ œ œ œ '0 21 1 11111 ababcdabab # ! #
32.tandtttArea2xds dxdxt1 dtdtdtdtt dydyœœÊ œ œÊœ "Î#"Î###" ʈ‰ Š‹ È É # ' 1 2tdttt1dt;ut1du2tdt;t0u1,œœ œ ÊœœÊœ '' 00 33 ÈÈ 1 ˆ‰É È c 2t4 3t3 $Î## "# # 1 t3u4uduu ’“ È È ‘ œÊœÄœœ '1 4 2428 399 111 $Î# % "
Note:2tdtisanimproperintegralbutlimftexistsandisequalto0,where '0 3 È 1 ˆ‰É ab 2t1 3t $Î# # t Ä!
ft2t.Thusthediscontinuityisremovable:defineFtftfort0andF00 abababab ˆ‰É œœ œ 1 2t 3t $Î#" #
Ftdt.Êœ '0 3 È ab 28 9 1
33.1andt21t2t22t3Area2xds dxdx dtdtdtdt dydyœœ Ê œ œ Êœ ÈÈÈ ÊÊ ˆ‰ Š‹Š‹ É' ##### 1 2t2t22t3dt;ut22t3du2t22dt;t2u1, œ œ Êœ œ Êœ ' È È 2 2 1 Š‹’Š‹ ÈÈÈÈÈ É ## t2u9uduu271 ’“ È È ‘ ab œÊœÄœœ œ '1 9 2252 33311 $Î# * " 11
34.FromExercise30,tantArea2yds2costtantdt2sintdt ʈ‰ Š‹ dx dtdt dy 00 33 ##ÎÎ œÊœœœ''' 111 11
2cost2(1) œ œ œ 111 cd ‘ 1 Î$ ! " #
35.2and1215Area2yds2t15dt dxdx dtdtdtdt dydy1œœÊ œ œÊœœ ʈ‰ Š‹ È ÈÈ ab #### ''11 0
25t35.Check:slantheightis5Areais12535. œ œÊ œ 1111 ÈÈÈÈÈ ’“ ab t 2 # " !
36.handrhrArea2yds2rthrdt dxdx dtdtdtdt dydy1œœÊ œ Êœœ
2rhrtdt2rhrrhr.Check:slantheightishrAreais
1 È ##
37.Letthedensitybe1.Thenxcosttsinttcost,andysinttcosttsint $ œœ Êœœ Êœ dx dtdt dy dm1dsdt(tcost)(tsint)tdttdtsince0t.Thecurve'smassisÊœœ œ œœŸŸ † ʈ‰ Š‹ È kk dx dtdt dy #### # 1
Mdmtdt.AlsoMydmsinttcosttdttsintdttcostdt œœœœœ œ µ '''''' 0000 2222 8 1111 1 ÎÎÎÎ# # x ab
sinttcosttsint2sint2tcost3,whereweintegratedbyparts.Therefore, œ
œœœ
costtsinttcost2cost2tsint3,againintegratingbyparts.Hence œ œ cdcd 1 1 1 Î# ! #Î# !# 3 x.Thereforexy2. œœœ ßœ ß M M y31224122424 ˆ‰
38.Letthedensitybe1.Thenxecostecostesint,andyesintesintecost $ œœÊœ œÊœ tttttt dx dtdt dy dm1dsdtecostesintesintecostdt2edt2edt.Êœœ œ œœ ʈ‰ Š‹ Éabab È È dx dtdt dytttt2tt ####
Thecurve'smassisMdm2edt2e2.AlsoMydmesint2edt œœœ œœ µ '''' 00 tt 11 ÈÈÈÈabŠ‹ t x 1
2esintdt2(2sintcost)2y.œœ œ Êœœœ '0 eee 555M5e1 M2 2e2 1 1 ÈÈÈ’“Š‹ 2t2t22 e2 55 ! "" 11 1 1 1 x ÈŠ‹ ÈÈ ab "
NextMxdmecost2edt2ecostdt22costsint2 y 2t œœœœ œ µ ''' 00 tte2e2 555 11 1 ababŠ‹’“Š‹ ÈÈÈÈ2t2 ! 1 x.Thereforexy.Êœœœ ßœ ß M M5e15e15e1 2 2e2 y2e22e2e1 ÈŠ‹ ÈÈ ababab 2e2 2 55222 1 1 111 111 ab Š‹
39.Letthedensitybe1.Thenxcostsint,andytsint1cost $ œœÊœ œ Êœ dx dtdt dy dm1dsdtsint1costdt22costdt.Thecurve'smassÊœœ œ œ ʈ‰ Š‹ Éabab È dx dtdt dy #### isMdm22costdt21costdt22cosdt2cosdt œœ œ œœ ''''' 0000 tt 1111 ÈÈÈÈ É ˆ‰¸¸ ˆ‰ # ## 2cosdtsince0t022sin4.AlsoMydm œŸŸÊŸŸœœœ µ '' 0 ttt 2 1 1 1 ˆ‰ˆ‰ ˆ‰‘ ###! 1 x tsint2cosdt2tcosdt2sintcosdt œ œ ''' 000 ttt 111 abˆ‰ˆ‰ˆ‰ ### 24cos2tsin2costcost4y. œ œ Êœœœ ‘ ˆ‰ˆ‰ˆ‰ˆ‰‘ tt3164 233M43 M4 ###!! "" 1 1 1 11 x ˆ‰ 16 3
NextMxdmcost2cosdtcostcosdt2sin2 y œœœœ œ µ ''' 00 ttt2 233 sint 11 1 abˆ‰ˆ‰ˆ‰’“ ##! ˆ‰ 3 # x.Thereforexy.œÊœœœßœß 44 3M4333 My ˆ‰ 4 3 "" ab ˆ‰ 1
40.Letthedensitybe1.Thenxt3t,andy3tdm1ds $ œœÊœœÊœÊœ $# # dx3t dtdt dy #
ʈ‰ Š‹ ÉabkkÈÈ È dx dtdt dy ###### # isMdm3tt1dtt17.AlsoMydm3tt1dt œœ œ œœœ µ '''' 00 33 x È È ÈÈ’“Š‹ ab ## #$Î# !# È 3 3t# tt1dt17.4(bycomputer)y2.49.NextMxdm œ œœÊœœ¸œ µ 98717.4 5M7 M # $# '' 0 3 y È È x
dt3t(3t)dt3tt1dt3tt1dtsince0t3.Thecurve'smass œ œ œ œ ŸŸ
t3tt1dt3tt1dt16.4849(bycomputer)x2.35.œ† œ ¸Êœœ¸ '' 00 33 ÈÈ $%##Èab È M M7 y16.4849
Therefore,xy2.352.49. abab ߸ß
41.(a)2sin2tand2cos2t2sin2t2cos2t2 dxdx dtdtdtdt dydy œ œÊ œ œ
Length2dt2t Êœœœ '0 2 1 1 ÎÎ# ! cd 1
(b)costandsintcostsint dxdx dtdtdtdt dydyœœ Ê œ œ 111111111 ʈ‰ Š‹ Éabab ####
Lengthdtt Êœœœ ' Î Î"Î# "Î# 12 12 111 cd
42.(a)xgyhastheparametrizationxgyandyyforcydgyand1;then œœœŸŸÊœœ ababab dx dydy dy w
Lengthdy1dy1[gy]dy œ œ œ ''' ccc ddd dy dydydy dxdxÊÊ Š‹Š‹Š‹ È ab ### w#
(b)xy,0yyL1ydy1ydy1y œŸŸÊœÊœ œ œ† 32124dx339429 3dy224934 00 43431232 0 43 ÎÎÎÎ
41 œ œ 8856 272727 3232ababÎÎ (c)xy,0y1yL1ydy1dydy œŸŸÊœÊœ œ œ 3dx1 2dy 2313
43.x12sincos,y12sinsin2cossin12sin,2cossincos12sin œ œ Êœ œ abababab ))))))))))) dx dd 2dy )) Êœœœ dy dx2cossin12sin2cos2sinsin2cos2sin 2cossincos12sin4cossincos2sin2cos )))) )))))))) ))))) ab ab 222
(a)x12sin0cos01,y12sin0sin00; œ œœ œœœœ abababab abab º dy dx2cos20sin0202 0 2sin20cos0011 ) œ abab ab abab ab
(b)x12sincos0,y12sinsin3;0 œ œœ œœœœ ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰ˆ‰ º 1111 )1 #### œ dy dx21 /2 2sin2cos 2cos2sin 00 ˆ‰ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ 11 11 ## ##
(c)x12sincos,y12sinsin; œ œœ œœ
œ 44 33 44 33 11 11 433 œœœ È È È 3 1 231 32 1 2 3 2 È
ˆ‰ˆ‰ º 4444 332332dx 3133dy 4/3 2sin2cos 2cos2sin 1111 )1 ÈÈ ˆ‰ˆ‰
44.xt,y1cost,0t21,sintsintcostcost.The œœ ŸŸÊœœÊœœÊœÊœœ 1 dxsintdcost dtdtdx1dtdxdx1 dydydydy Š‹ 2 2 maximumandminimumslopewilloccuratpointsthatmaximize/minimize,inotherwords,pointswhere0 dydy dxdx 2 2 œ cost0tort 232 ʜʜœÊœ
11 22dx 3dy 2 2 11
(a)themaximumslopeissin1,whichoccursatx,y1cos1 dy dx222 t2º ˆ‰ˆ‰ œÎ 1
(a)theminimumslopeissin1,whichoccursatx,y1cos1 dy dx222 t32 333 º
45.costand2cos2t;then00 dx2cos2t dtdtdxdx/dtcostcostdxcost dydydy/dtdy22cost122cost1 œœÊœœœœÊœ abab ## 2cost10costt,,,.Inthe1stquadrant:txsinand Ê œÊœ„ÊœœÊœœ#" # È È 2444444 3572 111111 ysin211isthepointwherethetangentlineishorizontal.Attheorigin:x0andy0 œœÊßœœ ˆ‰ Š‹ 1 4 2 È #
sint0t0ortandsin2t0t0,,,;thust0andtgivethetangentlinesat ʜʜœœÊœœœ 111 11 ## 3 theorigin.Tangentsatorigin:2y2xand2y2x
¹¹
dydy dxdx t0t œÊœœ Êœ 1
46.2cos2tand3cos3tdx3cos3t dtdtdxdx/dt2cos2t22cost1
dydydy/dt3(cos2tcostsin2tsint)œœÊœœœ ab # œœœ 32cost1(cost)2sintcostsint 22cost122cost122cost (3cost)2cost12sint(3cost)4cost3 cd ab ababab abab # ### ### 1;then dy003cost0or4cost30:3cost0t,and dx22cost1 (3cost)4cost33œÊœÊœ œœÊœ ab ab # # ## # 11 4cost30costt,,,.Inthe1stquadrant:txsin2 # ## œÊœ„ÊœœÊœœ È È 33 666666 5711 111111ˆ‰ andysin311isthepointwherethegraphhasahorizontaltangent.Attheorigin:x0 œœÊßœ ˆ‰ Š‹ 1 6 3 È # andy0sin2t0andsin3t0t0,,,andt0,,,,,t0andtgive œÊœœÊœœÊœœ 111111 ##111 3245 3333 thetangentlinesattheorigin.Tangentsattheorigin:yx,and ¹¹ dydy dx2cos0dx 3cos033 t0t œœÊœ## 1 yx œœ Êœ 3cos(3) 2cos(2) 33 1 1 ##
47.(a)xatsint,ya1cost,0t2a1cost,asintLength œ œ ŸŸÊœ œÊ ababab 1 dx dtdt dy a1costasintdta2acostacostasintdt œ œ '' 00 22 11 Éabab ab È ######## a21costdta22sindt2asindt4acos œ œœœÈÈ È É ˆ‰ˆ‰ˆ‰ ’“ ''' 000 222 2ttt 2220 2 111 1 4acos4acos08a œ œ 1 ab (b)a1xtsint,y1cost,0t21cost,sintSurfacearea œÊœ œ ŸŸÊœ œÊœ 1 dx dtdt dy 21cost1costsintdt21cost12costcostsintdt œ œ '' 00 22 11 11 abababab É È #### 21cost22costdt221costdt221cos2dt œ œ œ † 111 ''' 000 22232t 2 32 111 abab È ÈÈ
ÎÎ 222sindt8sindt œœ È ˆ‰ˆ‰ ˆ‰ 11 '' 00 22 23 tt 22 32 11 Î
ududtdt2du;t0u0,t2u ’“ œÊœÊœœÊœœÊœ t1 22 11 16sinudu16sinusinudu161cosusinudu16sinudu16cosusinudu œœœ œ 11111 ''''' 00000 3222 11111 ab 16cosucosu1616 œ œ œ ’“
11116161664 3333 3 0 1111 1
48.xtsint,y1cost,0t2;Volumeydx1cost1costdt œ œ ŸŸœœ111 '' 00 222211 abab
13cost3costcostdt13cost3costcostdt œ œ 11 '' 00 22 232 1cos2t 2 11 ab
3costcos2t1sintcostdt4costcos2tsintcostdt œ œ 11 '' 00 22 5353 2222 22 11 ˆ‰ˆ‰ ab t4sintsin2tsint500005 œ œ œ 1111 ’“ ab 531 243 32 0 21
47-50.ExampleCAScommands: :Maple with(plots); with(student); x:=t->t^3/3; y:=t->t^2/2; a:=0; b:=1; N:=[2,4,8]; forninNdo
tt:=[seq(a+i*(b-a)/n,i=0..n)];
pts:=[seq([x(t),y(t)],t=tt)];
L:=simplify(add(student[distance](pts[i+1],pts[i]),i=1..n));#(b) T:=sprintf("#47(a)(Section11.2)\nn=%3dL=%8.5f\n",n,L); P[n]:=plot([[x(t),y(t),t=a..b],pts],title=T):#(a) enddo:
display([seq(P[n],n=N)],insequence=true);
ds:=t->sqrt(simplify(D(x)(t)^2+D(y)(t)^2)):#(c) L:=Int(ds(t),t=a..b): L=evalf(L);
11.3 POLAR COORDINATES
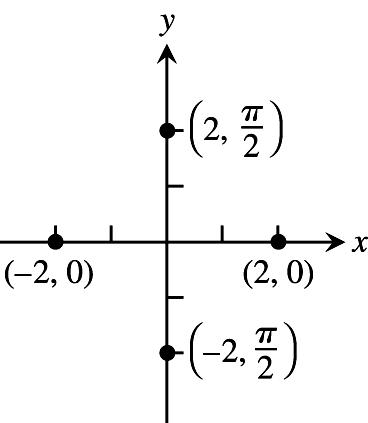
1.a,e;b,g;c,h;d,f2.a,f;b,h;c,g;d,e
3.(a)22nand2(2n1),naninteger ˆ‰ˆ‰ ß ß 11 ##11 (b)(2n)and((2n1)),naninteger #ß #ß 11 (c)22nand2(2n1),naninteger ˆ‰ˆ‰ ß ß 33 11 ##11 (d)((2n1))and(2n),naninteger #ß #ß 11
4.(a)32nand32n,naninteger ˆ‰ˆ‰ ß ß 11 44 5 11
(b)32nand32n,naninteger ˆ‰ˆ‰ ß ß 11 44 5 11
(c)32nand32n,naninteger ˆ‰ˆ‰ ß ß 11 44 3 11
(d)32nand32n,naninteger ˆ‰ˆ‰ ß ß 11 44 3 11
5.(a)xrcos3cos03,yrsin3sin00Cartesiancoordinatesare(0) œœœœœœÊ$ß ))
(b)xrcos3cos03,yrsin3sin00Cartesiancoordinatesare(0) œœ œ œœ œÊ $ß ))
(c)xrcos2cos1,yrsin2sin3Cartesiancoordinatesare13 œœœ œœœÊ ß ))22 33 11
(d)xrcos2cos1,yrsin2sin3Cartesiancoordinatesare13 œœœœœœÊß ))77 33 11 ÈÈŠ‹
(e)xrcos3cos3,yrsin3sin0Cartesiancoordinatesare(30) œœ œœœ œÊß )1)1
(f)xrcos2cos1,yrsin2sin3Cartesiancoordinatesare13 œœœœœœÊß ))11 33
(g)xrcos3cos23,yrsin3sin20Cartesiancoordinatesare(30) œœ œ œœ œÊ ß )1)1
(h)xrcos2cos1,yrsin2sin3Cartesiancoordinatesare13 œœ œ œœ œÊ ß ))ˆ‰ˆ‰ ÈÈŠ‹ 11 33
6.(a)x2cos1,y2sin1Cartesiancoordinatesare(11) œœœœÊß ÈÈ11 44
(b)x1cos01,y1sin00Cartesiancoordinatesare(10) œœœœÊß
(c)x0cos0,y0sin0Cartesiancoordinatesare(0) œœœœÊ!ß 11 ##
(d)x2cos1,y2sin1Cartesiancoordinatesare(11) œ œ œ œ Ê ß ÈȈ‰ˆ‰ 11 44
(e)x3cos,y3sinCartesiancoordinatesare œ œœ œ Êß 5533 626 333311 È È ###Š‹
(f)x5costan3,y5sintan4Cartesiancoordinatesare(4) œœœœÊ$ß ˆ‰ˆ‰ "" 44 33
Copyright © 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
Section11.3PolarCoordinates663
(g)x1cos71,y1sin70Cartesiancoordinatesare(10) œ œœ œÊß 11
(h)x23cos3,y23sin3Cartesiancoordinatesare33 œœ œœÊ ß ÈÈÈÈŠ‹ 22 33 11
7.(a)1,1r112,sinandcosPolarcoordinatesare2, ab È ÈÈŠ‹ Êœ œœœÊœÊ2211 2244))) ÈÈ 11
(b)3,0r303,sin0andcos1Polarcoordinatesare3, ababab É Êœ œœœ ÊœÊ 22 )))11
(c)3,1r312,sinandcosPolarcoordinatesare2, Š‹ÊŠ‹ ÈÈ ab ˆ‰ Êœ œœ œÊœÊ 2211111 2266 3 ))) È 11
(d)3,4r345,sinandcosarctanPolarcoordinatesare abab É ˆ‰ Êœ œœœ Êœ Ê 22434 553)))1
5,arctan ˆ‰ ˆ‰ 1 4 3
8.(a)2,2r2222,sinandcosPolarcoordinatesare ababab É È Êœ œœ œ Êœ Ê 22113 224))) ÈÈ 1
22, Š‹ È 3 4 1
(b)0,3r033,sin1andcos0Polarcoordinatesare3, ab È ˆ‰ Êœ œœœÊœÊ 22 22 ))) 11
(c)3,1r312,sinandcosPolarcoordinatesare2, Š‹ÊŠ‹ ÈÈ
Êœ œœœ ÊœÊ 2 2155 2266 3 ))) È 11
(d)5,12r51213,sinandcosarctanPolarcoordinatesare abab É ˆ‰ Êœ œœ œÊœ Ê 2212512 13125))) 13,arctan ˆ‰ ˆ‰ 12 5
9.(a)3,3r3332,sinandcosPolarcoordinatesare ab È È Êœ œ œ œ ÊœÊ22115 224))) ÈÈ 1 32, Š‹ È 5 4 1
(b)1,0r101,sin0andcos10Polarcoordinatesare1,0 ababab É Êœ œ œœÊœÊ 22 )))
(c)1,3r132,sinandcosPolarcoordinatesare Š‹ÊŠ‹ ÈÈ ab Êœ œ œ œÊœÊ 223 223 15))) È 1 2, ˆ‰ 5 3 1
(d)4,3r435,sinandcosarctanPolarcoordinatesare abab É ˆ‰ Êœ œ œœ Êœ Ê 22343 554)))1 5,arctan ˆ‰ ˆ‰ 1 4 3
10.(a)2,0r202,sin0andcos10Polarcoordinatesare2,0 ababab É Êœ œ œœÊœÊ 22 )))
(b)1,0r101,sin0andcos1orPolarcoordinatesare1,or ab ab È Êœ œ œœ Êœœ Ê 22 )))1)11 1, ab 1
(c)0,3r033,sin1andcos0Polarcoordinatesare3, abab É ˆ‰ Êœ œ œœÊœÊ 22 22 ))) 11
(d),r1,sinandcosorPolarcoordinates Š‹ÊŠ‹ ˆ‰ ÈÈÈ 333 22222266 11175 22 Êœ œ œ œ Êœœ Ê ))))11 are1,or1,ˆ‰ˆ‰ 75 66 11
27.rcos2x2,verticallinethrough(0)28.rsin1y1,horizontallinethrough(01) )) œÊœ#ßœ Êœ ß
29.rsin0y0,thex-axis30.rcos0x0,they-axis )) œÊœœÊœ
31.r4cscrrsin4y4,ahorizontallinethrough(04) œÊœÊœÊœß )) 4 sin )
32.r3secrrcos3x3,averticallinethrough(30) œ ʜʜ Êœ ß )) 3 cos )
33.rcosrsin1xy1,linewithslopem1andinterceptb1 )) œÊ œœ œ
34.rsinrcosyx,linewithslopem1andinterceptb0 ))œÊœœœ
35.r1xy1,circlewithcenterC(0)andradius1 ### œÊ œœ!ß
36.r4rsinxy4yxy4y44x(y2)4,circlewithcenterC(02)andradius2 ####### œÊ œÊ œÊ œœß )
37.rrsin2rcos5y2x5,linewithslopem2andinterceptb5 œÊ œÊ œœœ 5 sin2cos)) ))
38.rsin222rsincos2(rsin)(rcos)1xy1,hyperbolawithfocalaxisyx ##))))) œÊœÊœÊœœ
39.rcotcscrsincosrsinrcosyx,parabolawithvertex(00) œœÊœÊœÊœß )))))) ˆ‰ˆ‰ cos sinsin ) )) "#### whichopenstotheright
40.r4tansecr4rcos4sinrcos4rsinx4y,parabolawith œÊœÊœÊœÊœ )))))) ˆ‰ sin cos ) ) # #### vertex(0)whichopensupward œ!ß
41.r(csc)ersineye,graphofthenaturalexponentialfunction œÊœÊœ ))rcosrcosx ))
42.rsinlnrlncosln(rcos)ylnx,graphofthenaturallogarithmfunction ))) œ œÊœ
43.r2rcossin1xy2xy1x2xyy1(xy)1xy1,twoparallel ####### œÊ œÊ œÊ œÊ œ„ )) straightlinesofslope1andy-interceptsb1 œ„
44.cossinrcosrsinxyxyxy,twoperpendicular ######## )))) œÊœÊœÊœÊ„œ kkkk linesthroughtheoriginwithslopes1and1,respectively.
45.r4rcosxy4xx4xy0x4x4y4(x2)y4,acirclewith ######### œ Ê œ Ê œÊ œÊ œ ) centerC(20)andradius2 ß