Pre-Course Material
Chapter Y: Review of Characteristics of Functions
Many events that occur in everyday life involve two related quantities. For example, to operate a vending machine, you insert money and make a selection. The machine gives you the selected item and any change due. Once your selection is made, the amount of change you received depends on the amount of money you put into the machine.
Money is the INPUT
Change is the OUTPUT
The vending machine is an example of a function where there is a rule that determines the OUTPUT (change) depending on the INPUT (money inserted). This chapter will review the characteristics of several important functions that you will be using throughout this course. These functions include:
polynomial
exponential
logarithmic
rational
periodic
1
Y.1 Characteristics of Polynomial Functions
Which of the following functions are examples of polynomials? Explain.
a)
b)
c)
d) For each polynomial, identify the degree, leading coefficient and constant.
Polynomial Degree Leading Coefficient Constant
Is it possible to determine the y-intercept of the above polynomials? If so, how?
2
Definition: A polynomial function has the form
where:
n is a whole number
x is a variable
the coefficients an to a0 are real numbers
the degree of the polynomial function is n, the exponent of the greatest power of x
the leading coefficient is an, the coefficient of the greatest power of x the constant term is a0
Polynomial Graphs – A Summary
If the graph of a polynomial has two raising arms, then the degree of the polynomial is and the leading coefficient is . This means the left end behaviour is and the right end behaviour is .
If the graph of a polynomial has two drooping arms, then the degree of the polynomial is and the leading coefficient is . This means the end behaviour is
If the graph of a polynomial has a right arm up and a left arm down, then the degree of the polynomial is and the leading coefficient is . This means the end behaviour is .
If the graph of a polynomial has the left arm up and the right arm down, then the degree of the polynomial is and the leading coefficient is . This means the end behaviour is
3
Example 1: Sketching a Polynomial Function
a) Sketch the polynomial
b) Does the function have a minimum or maximum value?
c) Explain your choice.
How to Do It
a)
b) The function has no global maximum or minimum values, but it does have a local maximum of (0.816, 6.177) and a local minimum at ( 0.816, 1.823) – determined graphically.
c) Since the domain and range of the function are all real numbers, there is no global (absolute) maximum or minimum.
What to Think About
What do the degree and leading coefficient tell you about the shape of the graph?
What does the constant term tell you about the graph?
4
Your Turn
a) Sketch the polynomial
b) Does the function have an overall (global or absolute) minimum or maximum value?
c) Explain your choice.
5
Example 2: Determine the Equation of a Polynomial Function
What is the equation of the polynomial, P(x), that has 3 identical x-intercepts at x = 2 (multiplicity of 3), 1 at x = 1 (multiplicity of 1) and a y-intercept at 16?
How to Do It
Each x-intercept corresponds to a zero and therefore a factor of the function.
What to Think About
What is the minimum degree of the polynomial function?
How does the degree of the polynomial relate to the shape of the graph?
Therefore, the equation of the polynomial function is
What is the x-value when the yintercept is 16?
6
Your Turn
Determine the equation of the polynomial function shown below.
Practice
7
Example 3: Write an absolute value equation as a piecewise function
What is the piecewise equation of the absolute function ?
How to Do It
Draw the graph of in red and in blue. We can see the xintercept is shared by both equations. To write the function as piecewise we must determine the equation of each piece of the line to the left and right of the x-intercept.
Your Turn
What to Think About
What is the equation of the line to the right of x = 2?
What is the equation of the line to the left of x = 2?
Why are the two functions opposite signs?
What is the piecewise equation of the absolute function ?
8
Practice
1. For each polynomial function, state the degree. If the function is not a polynomial, explain why.
2. State whether the polynomial function is odd or even degree. Then, state whether the function has a global maximum value, a global minimum value, or neither. a. b. c.
9
a. b. c. d.
d.
3. State the number of real x-intercepts, domain, and range for each polynomial function.
a.
10
b.
c.
4. Determine the equation for each polynomial function in question 3
a)
b)
c)
11
5. State the possible number of x-intercepts and the value of the y-intercept for each polynomial function.
a.
b.
c.
d.
6. Identify the following characteristics for each polynomial function:
• the type of function and whether it is of even or odd degree
• the end behaviour of the graph of the function
• the number of possible x-intercepts
• whether the function will have a maximum or minimum value
• the y-intercept
a.
b.
12
7. Given the polynomial , determine the following without graphing.
a. Describe the end behaviour of the graph of the function.
b. Determine the possible number of x-intercepts of the function.
c. Determine the y-intercept of the function.
d. Now, use graphing technology to create a sketch of the graph.
13
8. Write the following functions in piecewise notation and graph the absolute value function.
a.
b.
9. For
a. Algebraically determine the vertex of
b. Algebraically determine the x and y-intercepts of
c. Identify the domain and range of
d. Write in piecewise notation.
14
Y.2 Characteristics of Exponential and Logarithmic Functions
On the same grid graph and its inverse. (Reminder: To graph an inverse function switch the x- and y-values.)
Complete the table below:
Domain Range
x-intercept
y-intercept
Equation of any Asymptotes
15
A logarithmic function is the inverse of an exponential function.
value of the logarithm
argument of the logarithm
base of the logarithm
The inside of the logarithm, in this case x, is called the argument of the logarithm.
The argument can never be negative.
The base, b > 0
When the base is e (Euler’s Number 2.71828…), then it is called the natural logarithm and is denoted as
When the base is 10, then it called a common logarithm and is denoted by .
Did You Know
Euler’s number is also know as Napier’s constant because John Napier, a Scottish mathematian, published a book 113 years before Euler used the symbol e in his manuscript Meditatio en experimenta explosione tormentorum nuper instituta. Napier described the approximate description of the motion of someone covering a distance d whose speed at each instant is equal to the remaining distance to be covered (in appropriate units). He divided the time into short intervals of length λ, and assumed that the speed was constant within each short interval. He tabulated the corresponding values of distance and time obtained in this way. He coined a name for their relationship out of the Greek words logos (ratio) and arithmos (number). He used a latinized version of his word: logarithm.
16
Example 1: Convert between and exponential and logarithmic forms
How to Do It
Exponential Form Logarithmic Form
a.
b.
c.
d.
e.
f.
What to Think About
What is the base of the logarithm?
The base of the exponential expression.
What is the argument of the logarithm?
What the exponential expression is equal to.
What does the logarithm represent?
It represents the exponent in the exponential expression.
What does the result in question e suggest?
That the natural logarithm and base e exponential functions are inverses.
Your Turn
What is the logarithmic equivalent of
Base is e, argument is y, and exponent is x + 2
Therefore the equivalent expression is
17
Laws of Logarithms
Name Law
Product
Quotient
Power
Description
The logarithm of a product of numbers is the sum of the logarithms of the numbers.
The logarithm of a quotient of numbers is the difference of the logarithms of the numbers.
The logarithm of a power of a number is the exponent times the logarithm of the number.
Example 2: Rewrite the expression using a single logarithm. State the restrictions on the variable.
How to Do It
What to Think About
Which logarithm rules can you use?
Power and division
Or
How can you prove the two answers are equivalent?
Use the power rule to show that each answer can be re-written as the other. Why is there a restriction?
The logarithm of a negative number does not exist.
Your Turn
Rewrite the expression using a single logarithm. State the restrictions on the variable.
18
How to Do It
Using exponent laws
Using log laws
What to Think About
What must happen before exponential rules can be used? The base must be the same
Why can you equate the exponents?
Since the bases are the same and the expressions are equal the exponents must be the same.
Why was applied to the function?
Because the equation can be expressed in terms of base 3.
Could a different base have been used?
Yes, but you would then have to use a calculator to solve the equation.
Your Turn
Solve each equation algebraically to the nearest hundredth.
a)
b)
19
Example 3: Solve the following equation using two methods
Practice
1. Use the definition of a logarithm to evaluate each expression.
a)
b)
c)
d)
2. Express in logarithmic form. a) b)
c)
d)
3. Determine the value of x. a)
b)
c)
d)
4. Write each expression in terms of the individual logarithms of x, y, and z
a)
b)
5. Use the laws of logarithms to simplify and evaluate each expression.
a)
b)
20
6. Evaluate each of the following.
a) If , determine the value of
8. If , write an algebraic expression in terms of k for each of the following.
a)
b)
b) Determine the value of if and
7. Simplify.
a)
9. Write each expression as a single logarithm in simplest form. State any restrictions on the variable.
a)
b)
b)
21
Y.3 Characteristics of Rational Functions
Warm-Up:
a) Graph
b) Use the graph of f(x) to graph , the reciprocal function.
c) Summarize the characteristics of the function using a table.
Characteristic
Non-permissible Value
Behaviour near non-permissible value.
As from the left and as from the right
End behaviour As
Domain Range
Equation of Vertical Asymptote
Equation of Horizontal Asymptote.
What equations could you use to graph using transformations?
22
Example 1: Sketch a rational function
For : a) identify the characteristics; and, b) sketch the graph of the function.
How to Do It
a) Summarize the characteristics of using a table.
Characteristic
Nonpermissible Value
Behaviour near non-permissible value. As from either side
What to Think About
What is the parent function that you should start with and what does this look like?
x-intercept
y-intercept
Domain Range
Equation of Vertical Asymptote
Equation of Horizontal Asymptote.
How is the non-permissible value related to the domain and equation of the vertical asymptote?
The NPV is the domain restriction and the equation of the vertical asymptote
How is the end behavior related to the range and horizontal asymptote?
The y-value of the end behavior is the range restriction and the equation of the horizontal asymptote
23
b) Sketch the graph:
Your Turn
What values should be labelled on the sketch?
Vertical and asymptote, xintercept and y-intercept.
Identify the characteristics of and use them to sketch a graph of the function.
Rewrite in standard form (use synthetic division)
Non-permissible Value
Behaviour near non-permissible value.
As from either side
x-intercept
24
y-intercept
Domain Range
Equation of Vertical Asymptote
Equation of Horizontal Asymptote.
25
Example 2: Identify types of discontinuities
For each function identify the indicated characteristics and use this information to determine the type of discontinuity.
a)
How to Do It
Simplified Expression
Nonpermissible value(s)
Equation of Vertical Asymptote NA
b)
What to Think About
Does the rational function simplify?
They both simplify
Should the non-permissible values be included in the simplified expression?
Yes, if they aren’t included as domain restrictions then the simplified expression no longer accurately represents the original equation.
What do the graphs look like?
26
of Discontinuity Point at x = 2 Point at x = 2 and Infinite at x = 1
Type
Coordinates of the Point of Discontinuity
Your Turn
a) Sketch the graph of the function
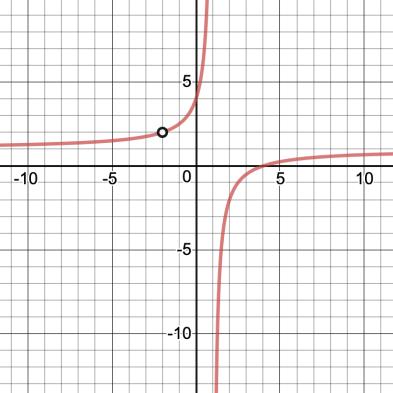
b) Identify the type(s) of discontinuity and where it occurs. point discontinuity at
27
Practice
1. Sketch and graph each function. Identify the domain and range, intercepts, and asymptotes.
a)
b)
c)
28
2. Analyse the function . Then, complete the table.
Characteristic
Non-permissible value
Behaviour near non-permissible value
End behaviour
Domain Range
Equation of vertical asymptote
Equation of horizontal asymptote
3. Explain the behaviour at each non-permissible value in the graph of the rational function .
4. Explain how the equation of the rational function can be analysed to determine whether the graph of the function has an asymptote or a point of discontinuity.
29
5. Complete the table for the given rational function.
Characteristic
Non-permissible value(s)
Feature exhibited at each non-permissible value
Behaviour near each non-permissible value
Domain
Range
6. Analyse each function and predict the location of any vertical asymptotes, points of discontinuity, and intercepts. Then, graph the function to verify your predictions. a) b)
30
Y.4 Characteristics of Periodic Function
Warm Up
The point P(12, 9) is on the terminal arm of an angle in standard position.
a) Sketch a diagram to represent the angle in standard position.
b) Determine the length of the terminal arm, r
c) Determine the exact value of the primary trigonometric ratios and their inverses.
d) Which trigonometric function would we have to use to calculate the measure of the reference angle? Why?
cosine as the x-coordinate is positive for angles in quadrants I and IV
e) Calculate the measure of R, in radians.
f) Use your reference angle to calculate the measure of
31
Example 1: Graph the cosine function
How to Do It
a) Complete the table of values for the function
What to Think About
What special triangle is being used?
30 , 60 , 90 or
b) Use the values above to graph the function
c) Complete the following characteristics.
Will the graph look different if the angle is in degrees rather than radians?
No, the scale is different, but the shape is the same.
Can the amplitude be greater than 1?
Not for but multiplying the function by a value greater than 1 or less than 1 changes the amplitude by a factor of |a|
How many x-intercepts are there?
Infinitely many
32
x 0 2 y 1 0 1 0 1
Maximum Value 1 Minimum Value 1 Amplitude 1 Period 2 y-intercept 1 x-intercept(s) Domain Range
Your Turn
Graph the sine function
a) Complete the table of values for the function
b) Use the values above to graph the function
c) Complete the following characteristics.
33
x 0 2 y 0 1 0 1 0
Maximum Value 1 Minimum Value 1 Amplitude 1 Period 2 y-intercept 0 x-intercept(s) Domain Range
Example 2: Graph the tangent function
How to Do It
a) Complete the table of values for the function
What to Think About
What special triangle is being used?
45,45,90 or
b) Use the values above to graph the function
c) Complete the following characteristics.
Maximum Value DNE
Value DNE
Will the graph look different if the angle is in degrees rather than radians?
No, the scale is different, but the shape is the same.
Can the amplitude be greater than 1?
Yes, the amplitude is infinite.
How many x-intercepts are there?
Infinitely many
How many vertical asymptotes are there?
Infinitely many
Domain Range
34
x 0 y -¥ 1 0 1 ¥ 1 0 1 ¥
-intercept
Minimum
Amplitude Period y
0 x-intercept(s)
Your Turn
Complete the characteristic chart for , then sketch the graph over Max/Min Value
35
DNE
x-intercept(s)
Amplitude Period y-intercept 0
0, 2 Asymptote(s)
amplitude = 2
period = 6
36
Practice
1. Graph each pair of functions on the same grid. For each, clearly plot the key points.
a) and
b) and
c) and
d) and
37
2. For each function, determine the phase shift and vertical displacement with respect to .
a)
b)
3. Determine the period and range for each function.
a)
b)
38
4. Given the following characteristics, write the equation of the sine function for each in the form .
a) phase shift of , period of , vertical displacement of 5, and amplitude of 3
b) period of and vertical displacement of 2
5.Graph for then:
a) State the coordinates of the x-intercepts.
b) State the equations of the asymptotes.
39
Y.5 Chapter Review
1. Complete the chart for each polynomial function. Polynomial Function Degree Type Leading Coefficient Constant Term
a)
b)
c)
2. For each of the following,
determine whether the graph represents on odd-degree or an even-degree polynomial function
determine whether the leading coeffi cient of the corresponding function is positive or negative
state the number of x-intercepts
state the domain and range
a)
b)
40
3. For each exponential function, state the domain, range, y-intercept, horizontal asymptote, and whether a graph of the function would be increasing or decreasing. Verify your answers by using technology to graph the functions.
a) b) c)
4. Solve each of the following equations algebraically. Use graphing technology to checkyour answer.
a)
b) c)
5. Write each expression in logarithmic form.
a)
b) c)
6. Use the laws of logarithms to evaluate each of the following.
a)
b) c)
41
7. Sketch a graph of each function. Label the important parts of the graph.
a)
b)
8. Solve each rational equation algebraically.
a)
b)
42
9. Graph at least two cycles of
. What are the amplitude and period in radians?
10.Graph at least two cycles of
. What are the amplitude and period in radians?
43
y 0 θ
y 0 θ
11.Without graphing, determine the amplitude and period, in radians, of each function.
a)
b)
c)
d)
44
12.Determine the amplitude, period, phase shift, and vertical displacement with respect to or for each function.
a)
b)
13.Graph at least two cycles of
45
14.Graph over the domain
15.Solve graphically over the domain .
46