mathimatika by Εφημερίδα των Συντακτών

ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ’ ΓΕΛ

12:45

ΗΜΕΡΟΜΗΝΙΑ ΕΞΕΤΑΣΗΣ: 4/6/2024

ΕΞΕΤΑΖΟΜΕΝΟ

Σελίδα 2 από 11 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ΄ ΤΑΞΗΣ ΗΜΕΡΗΣΙΩΝ – ΕΣΠΕΡΙΝΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ

ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ’ ΓΕΛ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ

Θεωρία, σχολικό βιβλίο σελ. 76 Α.2. Ορισμός, σχολικό βιβλίο σελ. 155

Θεωρία, σχολικό βιβλίο σελ. 216

α) Σ β) Σ γ) Λ δ) Λ ε) Σ ΘΕΜΑ Β Β.1.   :1, g  με τύπο   1 gxx x    :1, h  με τύπο   1 hxx x    1, g D  και   1, hD        1,1,1, ghgh DDD   Για την συνάρτηση g f h    2 111 0000101 xx hxxxx xxx            :01,:11, fggh h DDxDhxxx             2 2 111 1 1 ,1 11 1 1 1 xx x gxxx x xxx fxx x hxx xx x x xx x     

ΘΕΜΑ

Α.1.

Α.3.

Α.4.

Σελίδα 3 από 11 Για την συνάρτηση rgh          1,1, rghgh DDxDx           2 2 1111 ,1rxgxhxxxxxx x xxx     Β.2. Έχουμε   1 1 x fx x   με   1, fD  Η f είναι συνεχής στο   1, fD  ως ρητή με                222 1111 112 0 111 xxxx xx fx xxx     Άρα η f είναι γνησίως φθίνουσα στο   1, fD  άρα f 1-1 άρα αντιστρέφεται Έχουμε λοιπόν           1 1 11 1 1111 1 111 11 110 111 11 Αάρα1 112 00101 11 xfy yyx f x fxyyxyxyyxxyxyy x xfyfxyyx xx yyx xx xx xx xx xx                Άρα     1 1, f f  Β’ τρόπος για σύνολο τιμών Αφού f είναι συνεχής και γνησίως φθίνουσα στο   1, fD  ισχύει:         1 lim,lim f x x fDfxfx       1 limlimlim1 1 xxx xx fx xx         111 11 limlimlim12 11xxx x fxx xx    Διότι 1 lim10101 x xx ά      άρα 1 1 lim 1 x x   

Σελίδα 4 από 11 Τελικά   1 1 1 x fx x   με     1 1, f f DfD Άρα 1 ff  Β.3. Έχουμε     1 1, r rxxD x  Κατακόρυφες ασύμπτωτες δεν έχει διότι είναι συνεχής στο   1, r D  Πλάγια ασύμπτωτη της r C καθώς x    2 1 1 limlimlim1101 xxx x rx x xxx        11 lim1limlim0 xxx rxxxx xx       Άρα η πλάγια ασύμπτωτη της συνάρτησης r στο  είναι η ευθεία με εξίσωση 10 yxyx  Β’ τρόπος         11 1 lim0lim0 xx rxxrxx xx rxx x      Άρα από ορισμό η ευθεία yx  πλάγια ασύμπτωτη της συνάρτησης r στο  . Β.4.     1 ffxx  για κάθε   1, f x  άρα η εξίσωση γίνεται           2 1 14 ffxrx                0 2 12232 3222 144 1414144 440440410 x ffxrxxxxxxxxx xxx xxxxxxxx       Άρα    2 2 404 410 ή 101 ή1 xx xx xxx    Η λύση 4 x  είναι δεκτή ενώ οι λύσεις 1 x  και 1 x  απορρίπτονται αφού   1, x 

Σελίδα 5 από 11 ΘΕΜΑ Γ   2 24,02 , 43,2 xex fx xxx          Γ.1. Η συνάρτηση f είναι συνεχής στο  0,2 ως πολυωνυμική Η συνάρτηση f είναι συνεχής στο   2,  ως πολυωνυμική Αφού η f είναι συνεχής στο   0,  θα είναι συνεχής και στο 0 2 x  άρα θα ισχύει:                 22 22 22 22 limlim2 limlim2422444 limlim43242348312 110 xx xx xx fxfxf fxxeeee fxxxf ee                     Θεωρούμε τη συνάρτηση   1, x gxexx             "11 0 0 0 11,0, 01010 01010 01010 x x x xx e xxx e xxx e xxx gxexex gxeeeex gxeeeex gxeeeex          1 2   0 001110ge Άρα ισχύει   0 gx  για κάθε     ,00, x  Άρα η εξίσωση   0 gx  έχει ακριβώς μία ρίζα την 0 x  . Άρα 0  . Γ.2. Έχουμε       2 2 2 241,02 24,02 43,2 43,2 25,02 43,2 xx xex fxfx xxx xxx xx fx xxx                02 x   η f είναι συνεχής με   20 fx   άρα η f είναι γνησίως φθίνουσα στο  0,2 2 x   η f είναι συνεχής με   240fxx   άρα η f είναι γνησίως φθίνουσα στο   2, 

Σελίδα 6 από 11 Για   1 0,2  η f είναι συνεχής και γνησίως φθίνουσα άρα          1 2 lim,01,5 x ffxf      διότι   22 limlim25225451 xx fxx     02055 f  Για   2 2,  η f είναι συνεχής και γνησίως φθίνουσα άρα          2 lim,2,1 x ffxf     διότι         22limlim43lim xxx fxxxx     2 224234831 f  Επομένως             12 1,5,1,5 f fDff Η f είναι συνεχής και γνησίως φθίνουσα στο   0, fD  επομένως δεν παρουσίαζει ακρότατο στο 0 2 x  Άρα η f παρουσιάζει ολικό μέγιστο στο 0 0 x  το   05 f  Γ.3. i)   2 241,02 43,2 xx fx xxx     ή   2 25,02 43,2 xx fx xxx     Η f είναι συνεχής στο  0,3 αφού η f είναι συνεχής στο 0 2 x  Η f είναι παραγωγίσιμη στο    0,22,3  ως πολυωνυμική. Εξετάζουμε στο 0 2 x              2222 2 22 22222 2 251242 limlimlim2lim2 2222 22 43144 limlimlimlimlim20 2222 xxxx xxxxx fxf xxx xxxx fxfx xxxx x xxxx        Αφού         22 22 limlim 22xx fxffxf xx   , η f δεν είναι παραγωγίσιμη στο 0 2 x  Άρα η συνάρτηση δεν ικανοποιεί τις προϋποθέσεις του Θ.Μ.Τ στο διάστημα  0,3 ii) Αναζητούμε  0,3  τέτοιο ώστε      30 912355 3033 ff f    

Σελίδα 7 από 11 και   2,02 24,2 x fx xx      Για 02 x  έχουμε: 5 2 3  αδύνατη Για 2 x  έχουμε: 551717 24242 3336 xxxx  δεκτή αφού   17 2,3 6  . Γ.4. Για 0tt  το σημείο Μ κινούμενο κατακόρυφα προς τα πάνω θα συναντήσει την f C στην κορυφή της παραβολής  2,1  οπότε       00 , xtyt  γίνεται  2,1  άρα   0 2 xt  και   0 1 yt        22 yt y άt                        2 2 1111 222 tyttyttytt t      Για 0tt              222221455   0 2 5 t     Για 0tt            2 2 00000 112221 0,5 sec 22555 5 rad tyttytyt     

Σελίδα 8 από 11 ΘΕΜΑ Δ Δ.1.             2 2 2 0 2 0 2 ln ,0, 1ln ,0, 1ln 001ln0ln10 1ln 001ln0ln1 x x x fxx x x fxx x x fxxxxe x x fxxxxe x           Οι ρίζες και το πρόσημο της  fx  καθώς και τα διαστήματα μονοτονίας και τα ακρότατα της f φαίνονται στον παρακάτω πίνακα.   1 fe e    000 ln1 limlimlimln xxx x fxx xx        γιατί 0 1 lim x x    και 0 limln x x          ln ln1 limlimlimlim xxxx x x fx xx x               γιατί 1 lim0 x x   ● Στο διάστημα   1 0,e  η f είναι συνεχής και 1 Άρα        1 0 1 lim,, x ffxfe e            ● Στο διάστημα   2 ,e  η f είναι συνεχής και 2 Άρα        2 1 lim,, x ffxfe e                  12 1 0,,fff e      Άρα 11 11 ee   , άρα   ln ,0 xx fxx x  

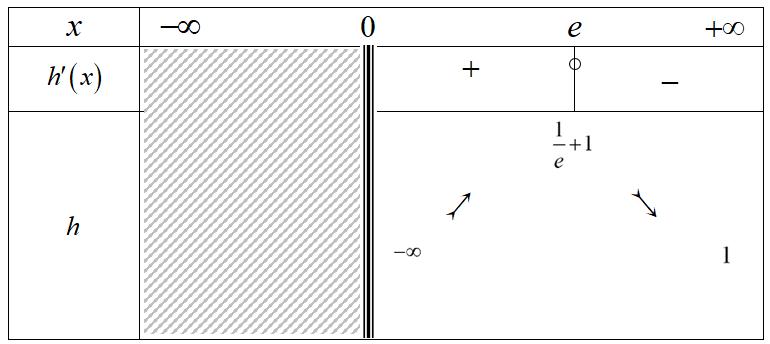
Σελίδα 9 από 11 Δ.2. Έχουμε     1 0,,1fe e          00,fe  άρα υπάρχει   0 0, xe  τέτοιο ώστε   0 0 fx  Επειδή η f γνησίως αύξουσα στο   0,e το 0x είναι μοναδικό Ακόμα lnln2111 1 222 ln41ln4ln0 11 2 22 fe        110 f  Έτσι   1 10 2 ff     άρα από θεώρημα Bolzano υπάρχει 0 1 ,1 2 x    τέτοιο ώστε   0 0 fx  .     1 ,1,1fe e          0, fe  άρα η f δεν έχει ρίζα στο   ,e  Άρα η εξίσωση   0 fx  έχει μοναδική ρίζα 0x , η οποία ανήκει στο διάστημα 1 ,1 2   

Θεωρούμε τη συνάρτηση h με         4,0,hxfxfx και   40 h     hxfx   άρα η  hx έχει την ίδια μονοτονία με την f         2ln212ln21 ln21ln41 2240 244 hff    Στο διάστημα   0,e η  hx είναι γνησίως αύξουσα και   20 h  άρα το 1 2 x  είναι η μοναδική της ρίζα.

Δ.3. i)

Σελίδα 10 από 11 Στο διάστημα   ,e  η  hx είναι γνησίως φθίνουσα και   40 h  άρα το 2 4 x  είναι η μοναδική της ρίζα. ii) Με 0 x  έχουμε:     ln 22 ln2ln 2ln2lnln22ln 2 lnln2 112 2 x xx x xxxx x x fxf x   1 Όμως    24ff     2 fxf  και f γνησίως αύξουσα στο   0,e άρα 2 x     4 fxf  και f γνησίως φθίνουσα στο   ,e  άρα 4 x  Αν       0, 022 fe xefxf   1 Αν       , 44 fe xefxf    2 Άρα τελικά 24 x  Δ.4.       000 ln2ln2ln2 11 xx xx xx gxdxfedxfedx ee   Γιατί ln20 x  άρα 10 x  και 0 x e  Θέτω ln x uexu  άρα 1 dxdu u  Αλλαγή άκρων: ln2 ln2 11 ln2 2 xue e  και 0 01xue Άρα                 0 0 111 111 2 222 1 1 2 1ln11ln x x uu fudufudufufudu uuu fufudufufudu      Όπου 0x η ρίζα της εξίσωσης   0 fx  Αν       στο0, 00 1 010 2 fe xxefxfx  1 Αν     0010 f xxfxfx 1

2ln211 4ln24ln211 2ln22ln21. 22

Σελίδα 11 από 11 Άρα                                 0 0 0 0 1 1 22 1 1 2 2 2 * 22222 00 2 2 2 0 11 = 22 1 1 111111 2 1 2222222

*0,11 x x x x

f fxfffxf fxf                  Με 11 ln 1 22 2ln21 1 2 2 f     

fufudufufudufufu