Chapter Review

FIGURE 2.21 Improving on the estimate of the value of the area under a curve by “squeezing” DQ.

As noted, A and TC(Q) can differ only by the value of some arbitrary constant c,which in this case is TFC.

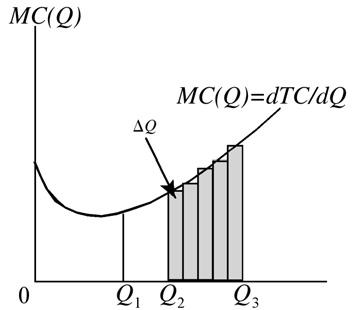
Consider,now,the area under the marginal cost curve from Q1 to Q3. The total cost of production over that interval is

(2.102)

Problem 2.10. Suppose that a firm’s the marginal cost function is MC(x) = 50x + 600. a.Find the total cost function if total fixed cost is $4,000. b.What is the firm’s total cost of producing 5 units of output? c.What is the firm’s total cost of producing from 2 to 5 units of output?

TC MCQdQ TVCQ TFC Q = ( ) = ( ) + QÚ 1 3

Solution

a. ÚMC(x)dx =Ú(50x + 600)dx = ( ) + TVCQ TFC = + + = ()x x TCx25 600 4000 2 , b. TC(x) = 25(5)2 + 600(5) + 4,000 = 625 + 3,000 + 4,000 = $7,624 c. TC5 2 =Ú5 2 (50x + 600)dx = Ú2 5 ,() + () + [ ] 255 6005 4000 2 = () + () + [ ] - () + () + [ ] 255 6005 4000 252 6002 4000 2 2 , , = + +( ) - + +( ) 625 3000 4000 100 1200 4000 , , , , = - +7625 5300 2325 $, $, $,

CHAPTER REVIEW

Economic and business relationships may be represented in a variety of ways,including tables,charts,graphs,and algebraic expressions.These rela-

tionships are very often expressed as functions.In mathematics,a functional relationships of the form y = f(x) is read “y is a function of x.”This relationship indicates that the value of y depends in a systematic way on the value of x.The expression says that there is a unique value for y for each value of x.The y variable is referred to as the dependent variable.The x variable is referred to as the independent variable.

Functional relationships may be linear and nonlinear.The distinguishing characteristic of a linear function is its constant slope;that is,the ratio of the change in the value of the dependent variable given a change in the value of the independent variable is constant.The graphs of linear functions are straight lines.With nonlinear functions the slope is variable.The graphs of nonlinear functions are “curved.” Polynomial functions constitute a class of functions that contain an independent variable that is raised to some nonnegative power greater than unity.

Two of the most common polynomial functions encountered in economics and business are the quadratic function and the cubic function.

Many economic and business models use a special set of functional relations called total,average,and marginal functions.These relations are especially useful in the theories of consumption,production,cost,and market structure.In general,whenever a function’s marginal value is greater than its corresponding average value,the average value will be rising.Whenever the function’s marginal value is less than its corresponding average value, the average value will be falling.Whenever the marginal value is equal to the average value,the average value is neither rising nor falling.

Many problems in economics involve the determination of “optimal” solutions.For example,a decision maker might wish to determine the level of output that would result in maximum profit.In essence,economic optimization involves maximizing or minimizing some objective function,which may or may not be subject to one or more constraints.Finding optimal solutions to these problems involves differentiating an objective function,setting the result equal to zero,and solving for the values of the decision variables. For a function to be differentiable,it must be well defined;that is,it must be continuous or “smooth.”Evaluating optimal solutions requires an evaluation of the appropriate first- and second-order conditions.There are generally two methods of solving constrained optimization problems:the substitution and Lagrange multiplier methods.

Integration is the reverse of differentiation.Integration involves recovering an original function,such as a total cost equation,from its first derivative,such as a marginal cost equation.The resulting function is called an indefinite integral because the value of the constant term in the original equation,such as total fixed cost,cannot be found by integrating the first derivative.Thus,the integral of the marginal cost equation is the equation for total variable cost.Integration is particularly useful in economics when trying to determine the area beneath a curve.