Nel cuore dei saperi - Matematica 4

saperi

Didattica laboratoriale Logica

Problematicamente

Ra-giocando Storie matematiche

ELi Oltre l’insegnamento Educ Ability

Alfia Lucia Fazzino • Paola Hippoliti

I NUMERI NATURALI

2 IL NOSTRO SISTEMA DI NUMERAZIONE

4 I numeri con le migliaia

6 Numeri a confronto

8 Numeri approssimati

10 Scritture diverse dei numeri

11 PROBLEMATICAMENTE

Storie matematiche

12 Pitagora: mito e leggenda

14 Numeri in forma

OPERARE CON I NUMERI NATURALI

16 L’ADDIZIONE

17 Le proprietà dell’addizione

18 LA SOTTRAZIONE

19 La proprietà della sottrazione

20 Addizione e sottrazione: che relazione c’è?

21 CALCOLO RAGIONATO

22 Esercizi

23 LA MOLTIPLICAZIONE

24 Le proprietà della moltiplicazione

27 Moltiplicazioni a graticola

28 Moltiplicazioni in colonna

29 Moltiplicare con le bacchette

30 LA DIVISIONE

31 Le proprietà della divisione

33 CALCOLO RAGIONATO

34 Esercizi

35 Esercizi

36 Divisioni in colonna

38 Moltiplicazione e divisione: che relazione c’è?

40 MULTIPLI E DIVISORI

42 Moltiplicare e dividere per 10, 100, 1000

43 La divisione canadese

44 Esercizi

45 PROBLEMATICAMENTE

LE FRAZIONI

46 Unità frazionaria

48 Frazionare quantità

49 Oltre l’unità frazionaria

50 Frazioni complementari e uguali a 1

51 Frazioni minori di 1

52 Frazioni maggiori di 1

53 Esercizi

54

56 Frazioni a confronto

58 La frazione di un numero

59 Dalla frazione all’intero

60 Esercizi

61 PROBLEMATICAMENTE

Storie matematiche

62 L’occhio di Horus

I NUMERI DECIMALI

64 Le frazioni decimali

65 I numeri decimali

66 I centesimi

67 I millesimi

68 Numeri decimali ed euro

69 Addizioni e sottrazioni con i decimali

70 Moltiplicazioni con i decimali

71 Moltiplicazioni per 10, 100 e 1000

72 Divisioni decimali

73 Divisioni per 10, 100 e 1000

74 Costo unitario, costo totale

75 Esercizi

76

100

PI GRECO DAY • 14 marzo

102 LA SIMMETRIA

104 LA TRASLAZIONE

105 LA ROTAZIONE

PERIMETRO E SUPERFICIE

106 LE FIGURE PIANE

108 Poligoni speciali

109 IL PERIMETRO

111 LA SUPERFICIE

113 Misurare la superficie

114 Misure isoperimetriche e figure equivalenti

116 Figure equicomposte

118 IL TRIANGOLO

120 Classificare i triangoli

121 L’altezza nei triangoli

122 I QUADRILATERI

124 I TRAPEZI

125 IL PARALLELOGRAMMA

126 IL RETTANGOLO

127 IL ROMBO

128 IL QUADRATO

130 L’AREA DELLE FIGURE

132 PROBLEMATICAMENTE

133 Esercizi

DATI E PREVISIONI

134 L’INDAGINE STATISTICA

135 La raccolta dei dati

136 Rappresentare i dati

137 LA MEDIA

138

LA MODA

139 EVENTI CERTI, POSSIBILI E IMPOSSIBILI

140 La probabilità di un evento

141 Esercizi

142 LA GIORNATA DEI CALZINI SPAIATI • 5 febbraio

144

147

COMPITO DI REALTÀ Ritratti fruttuosi

TAPPA COMPETENZE

Verso l’Invalsi

156 PROVE INVALSI

159

QUADERNO OPERATIVO

I NUMERI NATURALI

IL NOSTRO SISTEMA DI NUMERAZIONE

Nell’immagine vedi un abaco costruito con delle scatole trasparenti e con dentro delle cannucce.

Serve per rappresentare i numeri.

• Completa scrivendo il numero rappresentato.

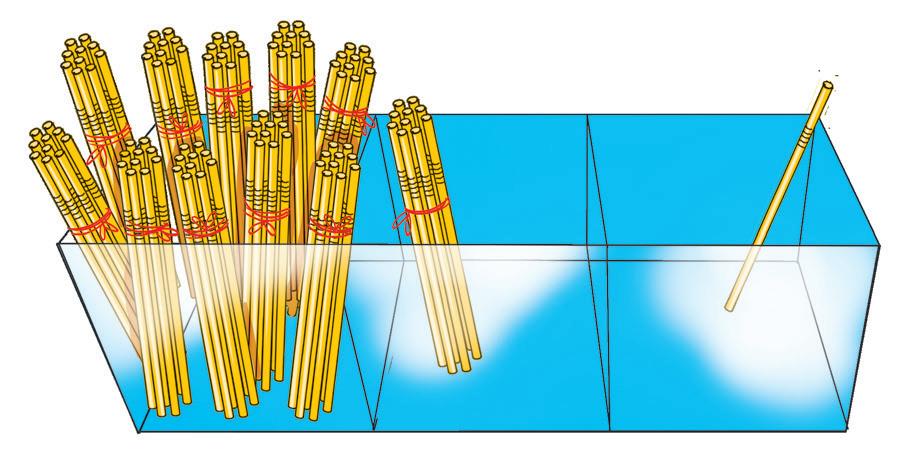
• Rappresenta lo stesso numero sull’abaco ad aste e scrivi il valore di ciascuna pallina. h ............... ............... ...............

u da

Quante volte hai usato la cifra 1 per scrivere il numero 111?

Ha sempre lo stesso valore?

Infatti la cifra 1 scritta al posto delle unità indica il numero , scritta al posto delle decine indica il numero e scritta al posto delle centinaia indica il numero

Perché? Il valore di una cifra cambia a seconda

Come già hai scoperto, nel nostro modo di scrivere i numeri, le quantità si raggruppano ogni volta che si arriva a

Per scrivere questo numero hai usato dei simboli e delle regole.

L’insieme di questi simboli e di queste regole si chiama Sistema di numerazione.

Nel corso della sua evoluzione l’essere umano ha cercato di inventare un modo semplice e pratico per scrivere i numeri e così, nel tempo, sono nati diversi Sistemi di numerazione.

Il nostro Sistema di numerazione è di origine araba ed è arrivato in Europa intorno al 1200 d.C. grazie al matematico Leonardo Fibonacci. Viaggiando lungo le coste del Mar Mediterraneo, lo imparò dagli Arabi.

Il sistema per scrivere i numeri e per contare in uso presso gli Arabi era molto più comodo di quello romano e così, al suo ritorno, lo spiegò scrivendo un libro intitolato Liber abaci

Ricordi le caratteristiche del nostro sistema di numerazione?

• I simboli: per scrivere i numeri utilizziamo questi simboli: 0 • 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9

Si chiamano cifre. Quante sono in tutto?

• Le regole: il nostro sistema di numerazione è:

– decimale, perché raggruppiamo ogni volta per 10 (10 u = 1 da; 10 da = 1 h…);

– posizionale, perché il valore di una cifra dipende dal posto che occupa nel numero;

– ordinato, perché ogni numero è maggiore del suo precedente e minore del suo successivo.

PROVO IO

1. Nei salvadanai ci sono solo banconote da € 10 , € 100 e monete da € 1 . Disegna i soldi dentro ai salvadanai.

65 euro

251 euro

2. Scrivi tutti i numeri a tre cifre che si possono formare con i seguenti numeri senza ripetere le cifre due volte.

2 • 5 • 7

6 • 1 • 9

4 • 8 • 3

3. Usa sempre tutte le cifre di ciascuna riga per formare i numeri richiesti.

2

6

4

4. Completa le relazioni scrivendo dei numeri adatti.

785 < < 120 > >

201 < < 2634 < < 3124

3564 < < 3567

5362 > > 5358

I NUMERI CON LE MIGLIAIA

• Osserva i due numeri.

• Che cosa hanno in comune?

• In che cosa si differenziano?

• Li leggi nello stesso modo? Sì No

• Perché?

Per scrivere i numeri con le migliaia è necessario separare le cifre in gruppi da tre cominciando da destra. Ogni gruppo di tre cifre forma una classe e ogni classe è suddivisa in unità (u), decine (da) e centinaia (h).

● Osserva il numero 510 634.

classe delle MIGLIAIA classe delle UNITÀ semplici

centinaia di migliaia decine di migliaia unità di migliaia centinaia decine unità

510 classe delle migliaia

Per leggere più facilmente un numero con le migliaia, si separano le due classi.

Per pronunciare i numeri con le migliaia.

634 classe delle unità semplici

Se li scrivi a mano, lascia un piccolo spazio vuoto: 510634; Anche nella carta stampata e nella digitazione al computer si lascia uno spazio vuoto tra le cifre: 510634.

Si fa seguire il suffisso -MILA alle cifre delle migliaia:

510 MILA 634

cinquecentodieciMILAseicentotrentaquattro.

Si pronuncia MILLE se il numero è formato solo da una unità di migliaia (uk):

1224 MILLE 224 MILLEduecentoventiquattro.

1. Disegna sul quaderno una tabella come quella sotto e inserisci i numeri come nell’esempio, partendo sempre dalle unità, poi leggili.

17526 • 40869 • 246853 • 605214 • 253481 • 5784

2. Circonda i numeri che hanno la corretta suddivisione delle classi e riscrivi in modo corretto quelli con la suddivisione sbagliata.

15 236 • 5 68 • 25 36 • 95 781 • 475 9 • 36 478 • 2 0145 • 3 600 • 9 84

3. Leggi i seguenti numeri e completa, come nell’esempio.

3584 25143 30 694 1039 270950 658214 89 204

3mila

4. Riscrivi i numeri lasciando uno spazio vuoto per individuare ciascuna classe. Poi scrivili in lettere, come nell’esempio.

3964 = 3964 = treMILAnovecentosessantaquattro

12795 = 7012 = 640231 =

5. Per ciascun numero, indica con una X la scrittura NON corretta.

2657: duemilaseicentocinquantasette duemilasettecentocinquantasette

6405: seimilaquattrocentocinquanta seimilaquattrocentocinque

4312: quattrocentododici quattromilatrecentododici

7098: settemilanovantotto settemilanovecentootto

ottomilaquattro: 8040 8004

diciottomilaseicento: 18600 18060

venticinquemilaquattrocentotrentuno: 25431 25413

NUMERI A CONFRONTO

• Osserva i numeri scritti da questi alunni e queste alunne.

4 002

• Quali cifre hanno usato i bambini per scrivere i numeri?

• Quanti numeri diversi hanno scritto? ................................

Tra due numeri messi a confronto esiste una relazione, infatti si può sempre stabilire se un numero

è maggiore o minore di un altro.

Si tratta di una relazione reciproca, cioè si può leggere da sinistra a destra o da destra a sinistra

Si legge: 4002 è maggiore di 402 è maggiore di

4 002 > 402 è minore di Si legge: 402 è minore di 4002.

PROVO IO

1. Indica con una X se le relazioni sono vere (V) o false (F).

3025 > 3205 V F 1025 > 125 V F

203 < 2003 V F 6009 < 6090 V F

2. Inserisci il simbolo che esprime la relazione tra i due numeri.

2400

420

4020

402

4200

• Per facilitare il confronto, esegui uno dei seguenti procedimenti.

• Osserva da quante cifre è formato ciascun numero: il numero che ha meno cifre è quello minore.

• Se i due numeri sono formati dalla stessa quantità di cifre, allora osserva le migliaia

• Se i due numeri hanno le stesse cifre nell’ordine delle migliaia, allora osserva le centinaia, le decine e le unità.

1.

2.

3.

402 3 cifre 4002 4 cifre

402 < 4002

4002 > 402

4002 4 cifre 2400 4 cifre

4 migliaia > 2 migliaia

4002 > 2400 2400 < 4002

4002 4 cifre 4200 4 cifre

4 migliaia = 4 migliaia

0 centinaia < 2 centinaia

4002 < 4200

4200 > 4002

le coppie di numeri scrivendo il simbolo per stabilire la loro relazione d’ordine.

NUMERI APPROSSIMATI

• Osserva.

FINALE DI CAMPIONATO

Biglietti venduti

poltrone riservate: 65 settori ospiti: 754 settori casa: 3 027

TOTALE BIGLIETTI: 3 846

Il 6 giugno tantissimi appassionati di basket e tutti i media nazionali saranno a Siena per assistere alla grande finale di campionato. Sono stati venduti 4 000 biglietti per un evento di importanza nazionale. Il palazzetto è pieno.

• Quanti biglietti sono stati venduti in tutto alla biglietteria del palazzetto?

• L’articolo giornalistico a destra dice che sono stati venduti ............................... biglietti.

HO CAPITO CHE...

Non sempre è necessario riportare un numero in modo esatto. In questo caso è sufficiente riportare il numero approssimato per far capire, più o meno, quanti sono gli spettatori alla partita.

Approssimare significa sostituire un numero con un altro a lui vicino; un numero meno preciso, ma più facile da ricordare. Di solito si approssimano i grandi numeri.

• Approssima alle decine i numeri 62 e 87 aiutandoti con la linea dei numeri.

Il numero 62 è più vicino a 60 o a 70?

Allora si approssima a 60. Poiché abbiamo tolto qualcosa al numero di partenza, si dice che abbiamo approssimato per difetto

Il numero 87 è più vicino a 90 che a 80?

Allora si approssima a 90. Poiché abbiamo aggiunto qualcosa al numero di partenza, si dice che abbiamo approssimato per eccesso

• Aiutati con la linea dei numeri per approssimare il numero 412 alle centinaia. Poi rispondi.

• 412 è più vicino a 400 o a 500? , quindi approssimi per

HO CAPITO CHE...

412 I numeri si possono approssimare a unità, decine e centinaia semplici o a unità, decine e centinaia di migliaia. Ogni volta decido quale arrotondamento è più conveniente: se arrotondo al numero superiore, approssimo per eccesso; se arrotondo al numero inferiore, approssimo per difetto.

• Che cosa devi fare per approssimare un numero? Osserva.

1. Consideriamo questi due numeri: 147 e 256

2. Scegliamo di approssimarli alle centinaia: 147 e 256

3. Osserviamo la prima cifra a destra delle centinaia: 147 e 256:

se la cifra è 0, 1, 2, 3 oppure 4, si approssima per difetto.

In 147 è 4, quindi, fra 100 e 200, si considera 100.

se la cifra è 5, 6, 7, 8 oppure 9, si approssima per eccesso.

In 256 è 5, quindi, fra 200 e 300, si considera 300.

1. Approssima i seguenti numeri alle decine.

3. Approssima i seguenti numeri in maniera opportuna, per eccesso o per difetto.

2. Approssima i seguenti numeri alle centinaia.

SCRITTURE DIVERSE DEI NUMERI

Uno stesso numero può essere scritto con differenti modalità:

• in lettere;

• in base al valore posizionale delle cifre;

• in cifre;

• con una qualsiasi operazione.

Lisa e Marco dal fornaio hanno comprato la merenda da fare insieme ai cugini.

€ 3 ciascuna

• Quanto ha speso Lisa?

• Quanto ha speso Marco?

• Marco ha comprato

• Puoi sapere con esattezza che cosa ha comprato Lisa? Sì No

PROVO IO

1. Collega ogni numero con i modi in cui puoi scriverlo.

Io ho speso 10 euro per le paste

+ 3 euro per la pizza.

Io ho speso 12 euro.

€ 1,50 ciascuna

€ 0,50 ciascuno

HO

Un numero si può scrivere in tanti modi. La scrittura in cifre è quella più semplice, ma non dà informazioni su come si è formato il numero.

2. Sul quaderno, trova modi diversi per scrivere il numero 42. Segui lo schema.

€ 2 ciascuno

PROBLEMATICAMENTE

Carlo ha fatto confusione e ha incollato in disordine le varie parti del testo. Aiutalo a riordinare le parti numerandole nella giusta successione.

In tutto le pagine sono 103

Aiuta Gianna a scoprire quante volte ha scritto ciascuna cifra.

Ha numerato tutte le pagine.

In un quaderno Gianna ha scritto i ricordi più belli delle sue vacanze.

Per numerare le prime 15 pagine ha scritto, in tutto, 21 cifre.

Rifletti sul testo per risolvere il problema

Sottolinea le risposte che ritieni giuste.

1 Che cosa devi scoprire in questo problema?

a. Quante sono le pagine in tutto.

b. Che cosa ha scritto Gianna nel suo diario.

c. Quali cifre ha usato per scrivere i numeri.

d. Quante volte ha scritto ciascuna cifra per scrivere tutti i numeri.

2 Quali informazioni ti servono per aiutare Gianna?

a. Sapere che è un diario dei ricordi delle vacanze.

b. Sapere che le pagine in tutto sono 103

c. Sapere che il diario l’ha scritto una bambina.

d. Sapere quali sono le cifre usate per scrivere i numeri.

Nel quaderno scrivi che cosa devi scoprire e le informazioni che hai a disposizione.

3 Ecco le azioni che devi compiere per trovare la risposta. Riordinale.

Scrivi una sotto l’altra tutte le cifre.

Conta quante volte è stata ripetuta la cifra nei numeri che hai scritto accanto.

Accanto a ogni cifra, scrivi i numeri da 1 a 103 che contengono quella cifra.

4 Rappresenta il problema sul quaderno e risolvilo seguendo le azioni che hai rimesso in ordine. Poi, scrivi la risposta.

Storie matematiche

PITAGORA:

MITO E LEGGENDA

Avete mai sentito parlare di Pitagora?

Si, quello della tavola Pitagorica! Se non lo conoscete, leggete con attenzione.

Non sappiamo di preciso il giorno e l’anno della sua nascita, ma deve essere nato fra il 570 e il 580 a.C a Samo, isoletta greca poco distante dall’attuale Turchia.

Alla vostra età non andava a scuola, perché la scuola non esisteva, ma studiò con dei maestri che gli insegnarono a leggere, a scrivere sulla sabbia o sulle tavolette di cera e a rappresentare i numeri usando le lettere dell’alfabeto.

Era curioso e desideroso di conoscere il mondo. Si dedicò allo studio della musica e a quello dei pianeti.

Era convinto che i pianeti muovendosi nel cielo producessero un suono celestiale, così studiò le matematiche che regolano la composizione musicale. Costruì uno strumento musicale formato da una sola corda e con un ponticello movibile.

A seconda della posizione nella quale si metteva il ponticello, la corda veniva suddivisa in modi differenti ottenendo suoni diversi. Nacque così la scala musicale pitagorica.

Ritornato a Samo, fondò una scuola nella quale insegnò tutto quello che aveva imparato. Le idee di fraternità, di giustizia e di armonia che diffondeva Pitagora nella sua scuola non piacevano affatto a Policrate, il tiranno di Samo. Per sfuggire alla tirannia di Policrate, Pitagora emigrò a Crotone, colonia greca nel sud dell’Italia, dove fondò una scuola Pitagorica nella quale erano ben accolte anche le donne.

Il motto di Pitagora era “TUTTO È NUMERO”.

Secondo lui, non solo l’Universo ma anche ogni altro aspetto della vita poteva essere misurato e descritto con i numeri naturali: il numero era l’elemento che formava tutto

Per studiare il mondo, quindi, dobbiamo studiare i numeri.

Pitagora immaginava i numeri come un insieme di palline disposte in modo da formare delle figure geometriche.

Per Pitagora il numero 10 era considerato perfetto.

Come mai? Osserva le palline disposte qui accanto e somma le palline di ogni riga:

1 + 2 + =

È la somma di primi quattro numeri naturali! Questo numero si chiama TETRAKTYS, una figura sacra sulla quale ogni discepolo giurava per essere ammesso alla scuola.

Osserva la Tetraktys: quale figura geometrica ti ricorda?

Ma quali altre forme geometriche possono avere i numeri? Scopriamolo insieme, girando la pagina.

LA FORMA DEI NUMERI

• Osserva i disegni: ciascun corrisponde a 1.

+ 2 + figura c

+

figura a figura b figura d

• Disegna tu come sarà la figura d.

• Quale numero è rappresentato da ciascuna figura? a: b: c: d:

• Che forma hanno questi numeri?

I numeri che si possono rappresentare a forma di triangolo si dicono numeri triangolari

• Il primo numero triangolare è 1.

• Il secondo numero triangolare è 1 + 2 =

• Il terzo numero triangolare è + + =

• Il quarto numero triangolare è ................. + ................. + ................. + ................. = .................

• Quale sarà il settimo numero triangolare?

• Disegnalo.

• Come hai ottenuto il settimo numero triangolare?

• E se volessi ottenere il ventesimo numero triangolare?

• E il centesimo?

• Quindi, in generale, hai capito che

E se metti insieme due numeri triangolari consecutivi?

• Disegna tu come sarà la figura d.

• Quale numero è rappresentato da ciascuna figura? a: b: c: d:

• Che forma hanno questi numeri?

Posso ottenere il numero quadrato sommando anche i primi due, i primi tre, i primi quattro… numeri dispari

• Il primo numero quadrato è 1

• Il secondo numero quadrato è = 1 + 3 = ottenuto sommando i primi due numeri dispari.

• Il terzo numero quadrato è = + + = ottenuto sommando i tre due numeri dispari.

HO CAPITO CHE...

Se unisco due numeri triangolari consecutivi, ottengo un numero quadrato

E se metti insieme due numeri triangolari uguali?

• Che forma hanno questi numeri?

HO CAPITO CHE...

Se unisco due numeri triangolari uguali, ottengo un numero rettangolare

figura b figura c

figura d figura a

OPERARE CON I NUMERI NATURALI

L'ADDIZIONE

• Leggi e completa.

Anna ha 4 anni e suo fratello Nico ha 7 anni più di lei.

Quanti anni ha Nico?

Anna Nico 4 + = anni

Marta ha ......... euro e sua sorella Lucia euro.

Quanti euro hanno insieme?

Marta

Lucia

Il cuoco Mario fa una torta e mette prima 6 uova e poi ne aggiunge altre 2. Quante uova ha usato?

+ = € + = uova

Per rispondere hai usato , l’operazione che serve per aumentare la quantità, unire o aggiungere diverse quantità.

RIPASSA i termini dell'addizione

uk h da u

5 1 3 + 3 8 +

4 7 2 =

1 0 2 3

addendi somma

• Esegui, osserva i risultati e completa.

Quando esegui l’addizione è necessario incolonnare i termini rispettando il valore posizionale.

8 + 0 = 0 + 12 =

Se aggiungo zero a un numero

il risultato è

5 + 1 = 1 + 8 =

Se aggiungo uno a un numero

il risultato è il successivo.

HO CAPITO CHE...

Lo zero è l’elemento neutro dell’addizione perché se aggiungo zero a un numero, il risultato è lo stesso numero. 7 + 0 = 7 e 0 + 7 = 7

Se aggiungo 1 a un numero, ottengo il numero successivo. 7 + 1 = 8

LE PROPRIETÀ DELL' ADDIZIONE

Proprietà commutativa

Alice gioca “al tiro ai barattoli”: osserva i tiri che ha fatto e calcola i punti.

• Quanti punti ha fatto nella prima partita?

5 9

HO CAPITO CHE...

• E nella seconda?

• Osserva gli addendi 9 + 5 e 5 + 9.

• È cambiato l’ordine degli , ma il risultato non è

Nell’addizione, se cambio l’ordine degli addendi, la somma non cambia.

Proprietà associativa

Alice continua a giocare: osserva i tiri che ha fatto e calcola i punti.

• Quanti punti ha ottenuto in ogni partita ?

• Sostituendo a due addendi la loro somma il risultato: non è cambiato. è cambiato.

PROVO IO

HO CAPITO CHE...

Nell’addizione, se sostituisco due addendi con la loro somma, il risultato non cambia

1. Per il calcolo veloce, sul quaderno, metti vicine le coppie del 100, come nell’esempio.

10 + 50 + 90 + 50 = (90 + 10) + (50 + 50) = 100 + 100 = 200

50 + 20 + 50 + 80 = 40 + 30 + 60 + 70 = 20 + 10 + 90 + 80 = 30 + 20 + 70 = 10 + 90 + 40 =

LA SOTTRAZIONE

• Leggi e completa.

Davide ha portato a scuola 8 quaderni mentre Sara ne ha portati 6. Quanti quaderni ha in meno Sara?

8 – = quaderni

Sara ha quaderni in meno.

Gaia vuole comprare un astuccio che costa 9 euro.

Se ha solo 5 euro, quanti euro le mancano?

€ 9

• Colora i soldi che possiede.

€ 9 – € = €

A Gaia mancano euro.

Francesco ha 20 figurine da attaccare nel suo album.

Ne ha attaccate 11, le altre sono doppioni. Quanti sono i doppioni?

• Colora le figurine attaccate.

– = I doppioni sono

Per rispondere hai eseguito una ......................................................., l’operazione che ti permette di calcolare la differenza, trovare quanto manca e quanto rimane.

RIPASSA i termini della sottrazione h da u

7 6 3 –4 2 5 =

3 3 8

HO CAPITO CHE...

Per eseguire la sottrazione è necessario incolonnare i termini rispettando il valore posizionale. sottraendo

minuendo resto o differenza

Con i numeri naturali, la sottrazione è possibile solo se il minuendo è maggiore o uguale al sottraendo.

9 – 4 = 5 Si può fare. 7 – 7 = 0 Si può fare. 5 – 8 Non si può fare.

Se il minuendo è uguale al sottraendo, il resto è zero. 12 – 12 = 0

Se il sottraendo è zero, il resto è uguale al minuendo. 15 – 0 = 15

LA PROPRIETÀ DELLA SOTTRAZIONE

Proprietà invariantiva

Laura e il fratellino Gianni costruiscono delle torri con i cubetti.

• Osserva le torri costruite da Laura e Gianni e rispondi.

Laura Gianni

• Da quanti cubetti è formata la torre di Laura?

• E quella di Gianni?

• La torre di Laura ha cubetti in più della torre di Gianni. In linguaggio matematico scrivi: 6 – 4 = 2

Laura e Gianni hanno aggiunto ciascuno 3 cubetti alla propria torre.

• Quanti cubetti ha adesso la torre di Laura?

• E quella di Gianni?

• La torre di Laura ha cubetti in più della torre di Gianni.

Laura Gianni

Laura e Gianni decidono infine di togliere 5 cubetti dalle proprie torri.

Laura Gianni

• Qual è adesso la differenza fra le torri dei due fratelli?

In linguaggio matematico scrivi: (9 – 5) – (7 – 5) = 4 – 2 = 2

In linguaggio matematico scrivi: (6 + 3) – (4 + 3) = 9 – 7 = 2

In tutti e tre i casi, la differenza di cubetti è sempre ........................................

PROVO IO

1. Esegui i calcoli sul quaderno applicando la proprietà invariantiva.

a. 56 – 14 = (56 – 4) – (14 – ) = 56 – 14 = (56 + 4) – (14 + ) =

b. 72 – 25 = (72 – ) – (25 – ) = 72 – 25 = (72 + ) – (25 + ) =

c. 89 – 36 = (89 – 6) – ( – ) = 89 – 36 = (89 + 1) – ( + ) =

d. 67 – 43 = (67 – 3) – ( – ) = 67 – 43 = (67 + 3) – ( + ) =

HO CAPITO CHE...

Nella sottrazione, se aggiungo o tolgo lo stesso numero sia al minuendo sia al sottraendo, il risultato non cambia.

ADDIZIONE E SOTTRAZIONE: CHE RELAZIONE C ' È?

• Leggi, osserva e disegna i salti.

La rana blu saltella sulle foglie dello stagno. Dopo i primi salti la rana incontra un fiore rosso.

• Quanti salti ha fatto?

Prosegue a saltellare fino al fiore giallo.

• Quanti salti ha fatto dal fiore rosso al fiore giallo?

• Quanti salti ha fatto da quando è partita?

• Scrivi in linguaggio matematico tutto il percorso fatto dalla rana.

0 + 3 + =

La rana decide di ritornare dal fiore giallo al punto di partenza seguendo il percorso dell’andata passando dal fiore rosso.

• Scrivi in linguaggio matematico il percorso del ritorno.

9 – ............ – ............ =

• Ora completa.

I due percorsi hanno gli stessi ma le operazioni sono ..................................................................................

HO

2 20 + 18 – 18 PROVO IO Operare

CALCOLO RAGIONATO

Per semplificare i calcoli da eseguire a mente, oltre alle proprietà delle operazioni, puoi utilizzare anche le possibili diverse scritture dei numeri.

Puoi scrivere 9 anche come 10 – 1, quindi se devi fare…

+ 9 aggiungi 10 poi sottrai 1 – 9 sottrai 10 poi aggiungi 1

28 + 9 = 28 + 10 – 1 = 38 – 1 = 37

23 – 9 = 23 – 10 + 1 = 13 + 1 = 14

Puoi scrivere 11, 22… anche 10 + 1, 20 + 2, quindi se devi fare…

+ 11 aggiungi 10 poi aggiungi 1 – 11 sottrai 10 poi sottrai 1

34 + 11 = 34 + 10 + 1 = 44 + 1 = 45

27 – 11 = 27 – 10 – 1 = 17 – 1 = 16

Puoi scrivere 99 anche come 100 – 1, quindi se devi fare…

+ 99 aggiungi 100 poi sottrai 1 – 99 sottrai 100 poi aggiungi 1

38 + 99 = 38 + 100 – 1 = 138 – 1 = 137 256 – 99 = 256 – 100 + 1 = 156 + 1 = 157

PROVO IO

2. Spezza i numeri, come negli esempi.

a. 87 + 36 = (80 + 7) + (30 + 6) = (80 + 30) + (7 + 6) = 110 + 13 = 123

16 + 37 = (10 + 6) + (30 + ) = (10 + ) + (6 + 7) =

47 + 55 = (40 + ...........) + (50 + ...........) = (........... + 50) + (7 + ...........) = ............................................................................................................

b. 73 – 17 = (73 – 10) – 7 = (63 – 3) – 4 = 60 – 4 = 56

139 – 25 = (139 – 20) – 5 = – 5 =

146 – 38 = (146 – ) – 8 =

1.

1 Indica con una X le risposte corrette.

L’addizione gode delle proprietà: La sottrazione gode delle proprietà:

Sì No

commutativa associativa invariantiva distributiva

2 Quali proprietà sono state applicate? Collega.

14 + 15 = 15 + 14

16 + 14 + 7 = (16 + 14) + 7

23 + 5 + 5 = 23 + (5 + 5)

23 + 81 + 15 = 81 + 23 + 15

98 – 63 = (98 – 3) – (63 – 3)

4 + 9 + 5 + 6 + 1 = (4 + 6) + (9 + 1) + 5

Sì No

commutativa associativa invariantiva distributiva

Proprietà commutativa

Proprietà associativa

Proprietà invariantiva

3 Nell’eseguire le operazioni, in ciascun passaggio è stata applicata una proprietà. Scrivi quale proprietà è stata applicata e calcola.

42 + 15 + 28 =

42 + 28 + 15 = Proprietà

70 + 15 = Proprietà

39 + 27 + 11 + 22 =

39 + 11 + 27 + 22 = Proprietà

50 + 49 = Proprietà

58 – 37 =

(58 – 7) – (37 – 7) = Proprietà

51 – 30 =

67 – 58 = (67 + 2) – (58 + 2) = Proprietà

69 – 60 =

4 Usa le proprietà per semplificare il calcolo e calcola a mente.

98 – 74 = 13 + 37 + 45 =

32 + 26 + 28 = 231 + 49 + 13 + 37 =

LA MOLTIPLICAZIONE

• Leggi e completa.

blu arancione verde rosa

Mario prepara 4 sacchetti di caramelle da regalare ai suoi amici.

In ogni sacchetto mette 7 caramelle. Quante caramelle in tutto? x =

La cartoleria “Tuttoscuola” ha 2 modelli di zaino e di ciascun modello ci sono 4 colori diversi. Fra quanti zaini puoi scegliere? x =

Per rispondere hai usato una , l’operazione che ti permette di aggiungere più volte la stessa quantità o di calcolare le combinazioni.

RIPASSA i termini della moltiplicazione

h da u

3 2 6 x 1 8 =

2 6 0 8 +

3 2 6 0 =

5 8 6 8

HO CAPITO CHE...

fattori prodotto

• Esegui, osserva e completa.

MOLTIPLICA PER 1

10 x 1 = 25 x 1 = 1 x 30 =

Se uno dei fattori è 1, il prodotto è ..................................................... all’altro fattore.

MOLTIPLICA PER 0

15 x 0 = 0 x 8 = 8 x 0 =

Se uno dei fattori è 0, il prodotto è sempre

Nella moltiplicazione lo zero è l’elemento nullo perché annulla l’operazione. 16 x 0 = 0

Il numero uno è l’elemento neutro perché se uno dei fattori è 1, il prodotto è l’altro fattore. 26 x 1 = 26 1 x 34 = 34

Operare con i numeri naturali

LE PROPRIETÀ DELLA MOLTIPLICAZIONE

Proprietà commutativa

• Osserva e completa.

Ci sono scatole.

In ogni scatola ci sono ovetti.

HO CAPITO CHE...

• Calcola quanti ovetti ci sono nelle scatole.

Puoi procedere in due modi.

a. Conta gli ovetti in una scatola e poi moltiplicali per tutte le scatole: 4 x =

b. Conta quante scatole e poi moltiplicale per gli ovetti che ci sono in una scatola: 3 x =

Nella moltiplicazione posso invertire l’ordine dei fattori e il risultato non cambia 4 x 3 = 3 x 4

Proprietà associativa

• Leggi, osserva e completa.

Federica ha comprato 2 scatole con dentro 6 bustine di figurine.

Ogni bustina contiene 4 figurine. Quante figurine ha comprato?

Le scatole sono

Le bustine di figurine in ogni scatola sono

Le figurine in ogni bustina sono ................

Per calcolare quante figurine ha comprato Federica puoi procedere in due modi:

a. (4 figurine x bustine) x 2 scatole =

b. figurine x (6 bustine x 2 scatole) =

In linguaggio matematico:

(4 x 6) x 2 = 24 x 2 = oppure 4 x (6 x 2) = x =

HO CAPITO CHE...

Nella moltiplicazione il prodotto non cambia se sostituisco a uno o più fattori il loro prodotto.

Proprietà distributiva della moltiplicazione

Marta ha rappresentato una moltiplicazione: quale moltiplicazione ha disegnato?

• Osserva e rispondi.

• Che forma ha?

È un È formato da righe e colonne.

• Colora una colonna e una riga, poi completa.

Le colonne sono , le righe sono quindi la moltiplicazione rappresentata è x

Per calcolare procedi così: ripassa la linea tratteggiata.

Hai “tagliato” il rettangolo e hai ottenuto due rettangoli più piccoli: colorali con due colori diversi.

• Osserva e scrivi da quante colonne e da quante righe sono formati.

colonne x 6 righe colonne x righe

Se sommi i prodotti dei due rettangoli trovi quanto è grande il rettangolo intero.

• Riporta quello che hai fatto in questa tabella.

x 6

• Aiutati con il disegno per calcolare 17 x 4.

Operare con i numeri naturali

• Ripassa le linee tratteggiate del rettangolo disegnato. Colora in modo diverso i rettangoli ottenuti e scrivi le moltiplicazioni che rappresentano.

colonne x righe

colonne x righe

colonne x righe

colonne x righe

Scrivi in riga le operazioni: (10 x ) + (10 x ) + (6 x ) + (6 x )

• Scrivi come hai proceduto per calcolare.

• Ho scomposto 12 in .................... e 16 in ....................

• Ho moltiplicato

• Infine ho sommato

• Riporta quello che hai fatto in questa tabella.

E se voglio moltiplicare 12 x 16?

• Ora disegna su un foglio un rettangolo e divertiti a rappresentare una moltiplicazione a tua scelta, poi completa la tabella.

PROVO IO

1. Applica la proprietà distributiva per eseguire le seguenti moltiplicazioni. Aiutati disegnando e “tagliando” i rettangoli.

25 x 14

18 x 23

13 x 12

21 x 16

MOLTIPLICAZIONI A GRATICOLA

Nel XVI secolo, per eseguire la moltiplicazione, nei Paesi arabi si usava uno schema a reticolo o a graticola.

• Segui le indicazioni per eseguire 125 x 26 con questo metodo.

a. Disegna una tabella che abbia tante colonne quante sono le cifre del moltiplicando e tante righe quante sono le cifre del moltiplicatore, poi dividi ogni casella in due parti.

b. Scomponi i due fattori della moltiplicazione:

125 x 26 (1 h + 2 da + 5 u) x (2 da + 6 u)

1

1 2 5

c. Moltiplica 125 per le 2 da e scrivi i numeri sopra e sotto la diagonale (se hai solo unità aggiungi uno zero sopra).

d. Moltiplica 125 x 6 u e procedi come per le decine.

e. Ora somma in diagonale cominciando dalle unità, considerando gli eventuali riporti.

Il prodotto di 125 x 26 è 3250.

PROVO IO

1. Esegui sul quaderno le moltiplicazioni con il metodo a graticola.

2. La moltiplicazione a graticola si può eseguire anche con la tabella inclinata. Prova!

41 x 36 =

MOLTIPLICAZIONI IN COLONNA

Oggi, la moltiplicazione in colonna si esegue in un modo simile alla moltiplicazione a graticola.

• Calcola 23 x 35.

a. Applica la proprietà distributiva della moltiplicazione: 23 x 35 = 23 x (5 + 30)

b. Moltiplica 23 per le 5 u e per le 3 da.

• Calcoliamo 235 x 52.

Prima moltiplichiamo 235 per le 2 u, poi per le 5 da…

PROVO IO

MOLTIPLICARE CON LE BACCHETTE

Si possono fare le moltiplicazioni anche senza conoscere le tabelline? Sì, vediamo come.

I Cinesi per fare la moltiplicazione usano le bacchette.

Le incrociano e contano i nodi che si formano.

• Esegui 3 x 4.

Disponi 4 bacchette in verticale e 3 in orizzontale.

Poi conta i nodi (gli incroci) che si sono formati.

Moltiplicazione con un fattore di due cifre:

15 x 3

da

Moltiplicazione con entrambi i fattori di due cifre: 24 x 12.

2 da

2 nodi da 100 unità

8 nodi da 10 unità

4 bacchette

3 bacchette

12 nodi da 1 unità quindi 3 x 4 = 12

Disponi come in figura, poi conta.

1 da 5 u

3 u

3 nodi + 1 nodo 1 5 nodi da 1 unità da da

10 unità 10 unità

40 5

40 + 5 = 45 quindi 15 x 3 = 45

PROVO IO

1. Usa gli spaghetti per eseguire le seguenti moltiplicazioni con il metodo cinese.

1 da

4 u 2 u

8 nodi da 1 unità

200 + 80 + 8 = 288 quindi 24 x 12 = 288

6 x 5 = 8 x 10 =

18 x 4 = 8 x 4 =

27 x 5 = 23 x 7 =

9 x 5 = 7 x 4 =

6 x 9 = 42 x 6 =

33 x 25 = 21 x 24 =

36 x 7 = 3 x 82 =

6 x 54 = 48 x 3 =

1

5 u 3 u

LA DIVISIONE

• Leggi e completa.

Giulia ha disposto la sua collezione di 16 gattini in gruppi da 4. Quanti gruppi ha formato?

Marco, in occasione del suo compleanno, ha comprato 10 pasticcini che divide in parti uguali su 2 vassoi. Quanti pasticcini ha messo in ogni vassoio?

: = : =

Per rispondere hai usato una , l’operazione che ti permette di distribuire o di raggruppare una quantità in parti uguali.

RIPASSA i termini della divisione

h da u

6 4 8 9

divisore quoziente dividendo

6 3 7 2

– 1 8 1 8 – –

HO CAPITO CHE...

• Esegui, osserva e completa.

12 : 1 = 245 : 1 = 160 : 1 =

Se il divisore è 1 il quoziente è uguale al .............................................

0 : 8 = 0 0 : 12 = 0 : 342 =

Se il dividendo è 0, il quoziente è

15 : 0 è impossibile, quindi non è possibile dividere un numero per

PROVO IO

Nella divisione, se il divisore è 1, il quoziente è uguale al dividendo. 9 : 1 = 9

Se il dividendo è 0, il quoziente è sempre zero. 0 : 7 = 0

È impossibile dividere un numero per zero.

8 : 0 impossibile

1. Esegui le divisioni; scrivi impossibile (IMP) quando non puoi eseguirle.

0 : 4 = 63 : 9 =

40 : 8 = 0 : 321 =

875 : 0 = 456 : 2 =

LE PROPRIETÀ DELLA DIVISIONE

Proprietà invariantiva

Lillo, il gatto di Youssef, consuma 20 scatolette di cibo per gatti in 10 giorni.

Quante scatolette al giorno mangia Lillo?

In linguaggio matematico si scrive 20 : 10 = ........... scatolette al giorno.

Youssef decide di comprare il doppio delle scatolette, così dureranno il doppio dei giorni. Lillo avrà a disposizione sempre 2 scatolette al giorno?

• Scrivi: il doppio delle scatolette il doppio dei giorni :

In linguaggio matematico: (20 x 2) : (10 x 2) = : =

Se invece Youssef compra la metà delle scatolette dureranno la metà dei giorni. Il gatto mangerà ancora due volte al giorno?

• Scrivi: la metà delle scatolette la metà dei giorni :

In linguaggio matematico: (20 : 2) : (10 : 2) = : =

HO CAPITO CHE...

Se moltiplico o divido entrambi i termini della divisione per uno stesso numero diverso da zero, il risultato non cambia.

PROVO IO

1. Inserisci i numeri mancanti per rendere vere le uguaglianze.

20 : = 5 : 9 = 0 12 : = 1 : 6 = 9 : 15 = 1

2. Calcola applicando proprietà invariantiva, come nell’esempio.

450 : 15 = (450 : 5) : (15 : 5) = 90 : 3 = 30

200 : 40 =

108 : 9 =

3 200 : 20 =

144 : 36 =

La proprietà distributiva della divisione

Per eseguire la divisione 96 : 3 Cecilia e Mario hanno semplificato il calcolo.

Cecilia ha fatto così:

96 : 3 = (90 + 6) : 3 = ha riscritto il numero 96 come somma: ............ + ............ (90 : 3) + (6 : 3) = ha diviso ogni addendo per 30 + 2 = 32 ha i quozienti ottenuti

• Osserva.

Cecilia ha scelto di scrivere 96 con una somma (90 + 6) perché sia 90 che 6 sono multipli del divisore, cioè di 3.

Mario invece ha fatto così:

96 : 3 = (102 – 6) : 3 = ha riscritto il numero 96 come differenza: –(102 : 3) – (6 : 3) = ha diviso minuendo e sottraendo per 34 – 2 = 32 ha i quozienti ottenuti

• Osserva.

Mario ha scritto 96 con una differenza (102 – 6). Puoi dire che entrambi sono multipli del divisore, cioè di 3?

Per semplificare i calcoli Cecilia e Mario hanno usato la proprietà distributiva della divisione. Puoi usarla anche tu, ma fai attenzione: per applicare questa proprietà, i numeri nei quali scomponi il dividendo devono essere entrambi multipli del divisore.

PROVO IO

Rifletti

Se Cecilia volesse scomporre 96 in 91 + 5, potrebbe applicare la proprietà distributiva? Sì No Perché?

1. Scomponi il dividendo per applicare la proprietà distributiva.

96 : 8 = (80 + 16) : 8 = (80 : 8) + (16 : ) = + =

92 : 4 = (100 – 8) : 4 = ( : 4) – (8 : 4) = – =

45 : 5 = (............... – 5) : 5 = ...................................................................................................................................................................................................................................................

54 : 3 = (30 + ) : 3 =

86 : 2 = ( + 6) : 2 =

CALCOLO RAGIONATO

Moltiplicazione

• Scomponi un fattore e applica la proprietà distributiva.

Se devi fare 10 x 11 puoi fare 10 x (10 + 1) = 10 x 10 + 10 x 1 = 100 + 10 = 110

12 x 11 = 12 x (10 + 1) = (12 x 10) + (12 x 1) = 120 + 12 = 132

15 x 11 =

Se devi fare 13 x 12 puoi fare 13 x (10 + 2) = (13 x 10) + (13 x 2) = 130 + 26 = 156

• Ora continua tu.

15 x 12 = 15 x (10 + ) = ( x 10) + (15 x ) = + =

20 x 15 = 20 x (10 + ) = ( x 10) + ( x 5) = + =

12 x 14 =

• Scomponi un fattore per eseguire moltiplicazioni più semplici.

Se devi fare 14 x 6 puoi fare 14 x 2 x 3 = 28 x 3 = 84

12 x 8 =

15 x 4 =

Divisione

• Scomponi il divisore per ottenere divisioni più semplici.

Se devi fare 100 : 4 puoi fare (100 : 2) : 2 = 50 : 2 = 25

120 : 15 = (120 : 3) : 5 = : 5 =

108 : 12 = (108 : ) : =

126 : 18 =

112 : 14 =

• Scomponi il dividendo e applica la proprietà distributiva, come nell’esempio.

68 : 4 = (60 + 8) : 4 = (60 : 4) + (8 : 4) = 15 + 2 = 17

126 : 3 = (90 + 36) : 3 = ( ) + ( ) = + =

182 : 7 = (............ + 42) : 7 = + = + =

144 : 9 =

196 : 4 =

ESERCIZI

1 Indica con una X le risposte corrette.

La moltiplicazione gode delle proprietà: La divisione gode delle proprietà:

Sì No

commutativa associativa invariantiva distributiva

2 Quali proprietà sono state applicate? Collega.

8 x 2 x 5 = 8 x 10

340 : 5 = 680 : 10

12 x 16 = 16 x 12

9 x 50 x 2 = 9 x 100

12 x 16 = 12 x (10 + 6)

2400 : 300 = 24 : 3

3200 : 20 = 320 : 2

3 Esegui sul quaderno applicando la proprietà associativa in modi diversi, come negli esempi.

6 x 10 x 7 =

(6 x 10) x 7 = 60 x 7 = 420

6 x (10 x 7) = 6 x 70 = 420

(6 x 7) x 10 = 42 x 10 = 420

6 x 20 x 3 =

3 x 14 x 5 =

30 x 40 x 6 =

5 x 10 x 3

4 Applica la proprietà invariantiva, come nell’esempio.

150 : 15 = (150 : 5) : (15 : 5) = 30 : 3 = 10

48 : 16 = (48 : ) : (16 : 8) = =

81 : 27 = (81 : ) : (27 : 9) = =

350 : 50 = (350 : 10) : (50 : ) = =

Sì No

commutativa associativa invariantiva distributiva

Proprietà commutativa

Proprietà associativa

Proprietà distributiva

Proprietà invariantiva

5 Applica la proprietà associativa e calcola a mente.

3 x 8 x 3 =

4 x 9 x 5 =

3 x 10 x 5 =

4 x 13 x 5 =

2 x 11 x 4 =

2 x 14 x 5 =

6 Scopri le cifre e i numeri mancanti.

96 : 3 = 2 : 2 = 423

804 : = 201

.................... : 2 = 75

ESERCIZI

1 Per ciascuna operazione, indica con una X quale proprietà è stata applicata.

Operazione

53 – 18 = (53 – 3) – (18 – 3) =

50 – 15 = 35

5 x 3 x 8 = (5 x 3) x 8 =

15 x 8 = 120

13 + 52 = 52 + 13 = 65

24 x 7 = (20 + 4) x 7 =

(20 x 7) + (4 x 7) =

140 + 28 = 168

112 : 4 = (100 + 12) : 4 = (100 : 4) + (12 : 4) = 25 + 3 = 28

13 + 27 + 40 = (13 + 27) + 40 =

40 + 40 = 80

25 : 5 = (25 x 2) : (5 x 2) = 50 : 10 = 5

Proprietà commutativa Proprietà associativa Proprietà distributiva Proprietà invariantiva

2 Nello schema, scrivi in parola ciascuna definizione.

1. È la somma di 13 e 8.

2. È la differenza fra 18 e 5.

3. È il quoziente tra 6 e 3.

4. Il triplo della metà di 8.

5. È il prodotto di 8 e 4.

6. È il segno che esprime l’azione di aggiungere.

7. È la metà del doppio di 6.

8. È la differenza fra 13 e la somma di 5 e 3.

9. È la metà del prodotto di 4 e 5.

10. È il doppio della somma di 7 e 13.

11. È il quadruplo della differenza fra 11 e 7.

DIVISIONI IN COLONNA

Marta vuole fare dei braccialetti per le sue compagne. Ha comprato un barattolino con dentro 42 perline. Marta si chiede: “Quanti braccialetti riesco a fare se metto

6 perline in ogni braccialetto?”.

Per rispondere alla domanda devi fare una

Esistono diversi modi per eseguire una divisione e tutti sono validi. Un modo è quello della divisione a danda lunga. Osserva.

Per eseguire la divisione calcola a mente o scrivi a fianco della divisione, quante volte il 6 è contenuto nel 42

Per calcolarlo, raggruppa per 6 fino ad arrivare a 42 o al numero minore più vicino a 42

togli il 6 per 7 volte

42 : 6 = braccialetti. Restano perline.

Se Marta comprasse un barattolo con 76 perline, e volesse mettere 15 perline in ogni braccialetto, quanti braccialetti riuscirebbe a fare?

Prova a eseguire la divisione. Calcola a mente o scrivi a fianco quante volte puoi ripetere il divisore fino ad arrivare a 76 o al numero minore più vicino.

In questo caso vedi che la divisione ha un resto diverso da 0

togli il 15 per 5 volte

76 : 15 = collane. Resta perlina.

Nella realtà, puoi avere divisioni con resto uguale a 0 e con il resto diverso da 0

Un altro modo di eseguire la divisione è quello di fare una stima, cioè fare un’ipotesi su quante volte si pensa che il divisore sia contenuto nel dividendo.

Questo modo di calcolare aiuta soprattutto a eseguire le divisioni con i grandi numeri.

Osserva 285 : 12

h da u

Con 2 h non puoi formare gruppi da 12, quindi considera 28 da.

2 2

8 4 4

5 12

2 –

h da u

Stima: 28 da puoi dividerle in 2 gruppi da 12?

Verifica: 2 x 12 = 24. Considera che 24 < 28, quindi li puoi formare.

Scrivi 2 nel quoziente.

A 28 sottrai 24 e trovi che restano 4 da.

Accanto alle 4 da rimaste scrivi le 5 u e ottieni il numero 45

2 2 –

8 4 4 3

5 5 6 9

12 23 –

Stima: Quanti gruppi da 12 puoi formare con 45?

Potrebbero essere 3 gruppi?

Verifica: 3 x 12 = 36, 36 < 45, quindi potrebbero essere 3

Stima: Potrebbero essere 4 gruppi?

Verifica: 4 x 12 = 48, 48 > 45, quindi NON possono essere 4

Allora dividi 45 in 3 gruppi.

Scrivi 3 nel quoziente accanto al 2.

A 45 sottrai 36 e trovi che restano 9 u.

PROVO IO

1. Risolvi e completa. h da u 4 8 7 1 5

––

• Considera 48 da.

• Stima in quanti gruppi da 15 puoi dividere 48. Puoi dividerlo in 2 gruppi? Verifica: 2 x 15 = In 3 gruppi? Verifica: 3 x 15 =

• Scrivi al posto del quoziente quanti gruppi hai formato.

• Sottrai per trovare il resto. Il resto è da.

• Riscrivi le unità accanto alle da. Ora hai il numero ............

• Stima: in quanti gruppi da 15 puoi dividere ? gruppi?

Verifica:

• Scrivi nel quoziente quanti gruppi hai formato.

• Sottrai per trovare il resto.

Operare con i numeri naturali

MOLTIPLICAZIONE E DIVISIONE: CHE RELAZIONE C’È?

Luca sta attaccando degli adesivi di animali su 3 pagine del suo album. In ogni pagina mette 4 adesivi. Quanti adesivi ha attaccato alla fine?

• Completa disegnando gli adesivi attaccati da Luca.

• Scrivi in linguaggio matematico l’operazione da fare per trovare quanti adesivi ha attaccato.

3 pagine 4 adesivi = adesivi in tutto

• Rappresenta l’operazione con uno schema.

4 adesivi in ogni pagina pagine adesivi

Luca riceve dal suo amico Alberto altri 12 adesivi che attacca mettendone 4 in ogni pagina, come prima. Quante pagine riempie?

• Rappresenta la situazione disegnando le pagine con gli adesivi incollati da Luca.

• Scrivi in linguaggio matematico l’operazione da fare per trovare le pagine completate.

12 adesivi 4 adesivi per pagina = pagine

• Rappresenta l’operazione con uno schema.

4 adesivi in ogni pagina adesivi pagine

• Confronta le due situazioni.

1a situazione pagine

adesivi per ogni pagina

adesivi in tutto

• Osserva le informazioni che hai scritto: che cosa noti?

2a situazione adesivi in tutto adesivi per ogni pagina pagine

• Hai usato sempre le stesse informazioni, ma hai eseguito operazioni differenti: perché?

• Completa gli schemi che rappresentano le operazioni eseguite.

1a situazione

operazione eseguita: 3 x =

1 a pagina

2a pagina

3 a pagina

Dal numero delle pagine hai trovato il numero di tutti gli adesivi attaccati.

HO CAPITO CHE...

2a situazione operazione eseguita: : 4 =

Dal numero di tutti gli adesivi attaccati hai trovato il numero delle pagine.

La divisione e la moltiplicazione sono operazioni inverse.

x 4 adesivi in ogni pagina : 4 adesivi in ogni pagina

3 pagine 12 adesivi in tutto

Operare con i numeri naturali

MULTIPLI E DIVISORI

Alice gioca a saltelli. Parte dalla casella START e salta sulla casella 2, poi sulla 4, poi sulla 6… e così via per tutta la griglia.

• Colora tutte le caselle sulle quali salta Alice, poi rispondi.

• Dopo 5 salti, in quale casella si trova Alice?

• E dopo 8 salti?

• Metterà i piedi nella casella 19? Sì No

• Scrivi i primi dieci numeri delle caselle su cui salta Alice.

• Riscrivi gli stessi numeri come moltiplicazioni.

2 = 2 x 1 4 = 2 x 2 6 =

I numeri ottenuti sono i multipli di 2, perché li hai ottenuti moltiplicando per 2 i numeri naturali: 1, 2, 3…

• Quanti multipli di 2 hai ottenuto?

• Potresti proseguire ancora? Sì No

Puoi dire quindi che i multipli sono

PROVO IO

3. Scrivi i primi sette multipli dei numeri indicati. Poi rispondi.

Multipli di 5: ..............................................................................................................................................

Multipli di 10:

• Ci sono multipli che appartengono a entrambi i numeri?

Sì No

• Quali? ..............................................................................................................................................................

HO CAPITO CHE...

Il prodotto di un numero per un qualsiasi numero naturale si chiama multiplo.

Ma un numero può avere più multipli?

1. Trova i primi cinque multipli di 6.

2. Circonda solo i multipli di 4.

Ho scoperto che 20 è multiplo di 5 e 10. Ma 20 posso dividerlo per questi due numeri?

• Aiuta Marta a trovare la risposta eseguendo le divisioni. 20 : 5 = e resta 20 : 10 = e resta

HO CAPITO CHE...

I divisori di un numero sono numeri che lo dividono in modo esatto, cioè con resto zero. Se un numero è multiplo di un altro, allora questo numero è un suo divisore.

Entrambe le divisioni hanno resto : vuol dire che 5 e 10 dividono in modo esatto il 20. In questo caso si dice che sono i suoi divisori. PROVO

1. Trova tutti i divisori.

Ogni divisore divide il numero in modo esatto.

Per trovarli, esegui prima le divisioni e circonda quelli che non hanno resto. Inizia come nell’esempio.

16 : 1 = 16 (resto 0)

: 2 = 8 (resto 0)

: 3 = 5 (resto 1)

: 4 = 4 (resto 0) …

2. Circonda i divisori di ciascun numero.

MOLTIPLICARE E DIVIDERE PER 10, 100, 1000

Per la festa di fine anno le classi IV devono realizzare dei festoni per decorare la scuola.

La maestra stima che serviranno circa 650 fogli di carta. In cartoleria ci sono confezioni da 10, 100 e 1000 fogli. Quali confezioni converrà comprare?

• La maestra compra 6 confezioni. Completa.

Confezioni da 10 fogli:

6 x 10 = fogli

• Inserisci i numeri ottenuti nella tabella, poi osserva.

Quali confezioni converrà comprare?

Confezioni da 100 fogli:

6 x 100 = fogli

Confezioni da 1000 fogli:

6 x 1000 = fogli

Ogni volta che moltiplichi per 10, 100 o 1000 il numero aumenta il suo valore di 10 volte, 100 volte, 1000 volte.

In un grande magazzino devono sistemare 3 000 perline in confezioni da 10, da 100 oppure da 1000. Quante confezioni di ciascun tipo potranno fare?

• Calcola quante volte il 10 o il 100 o il 1000 sono contenuti nelle 3000 perline.

Se preparo confezioni da 10, 3000 : 10 = confezioni

• Inserisci i numeri ottenuti nella tabella, poi osserva.

Se preparo confezioni da 100, 3000 : 100 = confezioni

Se preparo confezioni da 1000, 3000 : 1000 = confezioni

Ogni volta che dividi per 10, 100 o 1000, il numero diminuisce il suo valore di 10 volte, 100 volte, 1000 volte.

LA DIVISIONE CANADESE

Questo tipo di divisione si esegue facendo sottrazioni ripetute.

Io so bene le tabelline, quindi so fare molto bene le divisioni.

Marta ha 50 perline e deve dividerle mettendone 8 in ogni collana, quindi si deve fare 50 : 8

• Forma gruppi da 8 perline.

E se Marta avesse 76 perline e ne mettesse 15 in ogni collana?

• Si deve fare 76 : 15, formando ogni volta gruppi da 15.

• Scrivi che cosa hai fatto nel disegno.

50 8

– 8 1 hai tolto 1 volta 8

– 8 1 hai tolto 2 volte 8

– 8 1 hai tolto volte 8

– 8 1 hai tolto ............. volte .............

– 8 1 hai tolto volte

– 8 1 hai tolto ............. volte ............. resto

• Ora rispondi e completa.

• Quante volte hai tolto l’8?

• Quante perline sono rimaste?

Con 50 perline hai fatto collane da 8 perline e ti sono rimaste perline.

50 : 8 = collane e restano perline.

• Scrivi che cosa hai fatto nel disegno.

76 15

– 15 1 hai tolto 1 volta 15

– 15 1 hai tolto 2 volta 15

– 15 hai tolto volte 15

– 15 hai tolto volte

– 15 hai tolto volte resto

• Ora rispondi e completa.

• Quante volte hai tolto il 15?

• Quante perline sono rimaste?

Con 76 perline hai fatto collane da 15 perline ed è rimasta perlina.

76 : 15 = ............. collane e resta ............. perlina.

1 Il cinema di Borgonuovo ha 480 posti; 296 posti sono in platea e gli altri in galleria. Quanti sono i posti in galleria?

2 La nonna Mariolina ha preparato 377 caramelle al miele. Vuole preparare dei sacchettini da 5 caramelle ciascuno. Quanti sacchettini riuscirà a preparare? Le avanzano delle caramelle?

3 Omar ha 60 matite colorate. Vuole sistemarle in astucci che ne possono contenere 8. Qual è il numero massimo di astucci necessari per conservare tutte le matite? Quanti astucci riuscirà a riempire?

4 Marco ha 68 figurine e, di queste, 5 sono doppioni. Deve sistemarle nel suo album formato da 10 pagine.

Se ognuna può contenere solo 8 figurine, quante pagine riesce a completare Marco? Quante figurine gli mancano per completare tutto l’album?

5 Per la festa del paese il fornaio Fernando ha preparato dei dolcetti di diversi gusti. I dolcetti al cioccolato sono 46, quelli alla crema sono il doppio di quelli al cioccolato e quelli alla marmellata sono la metà di quelli al cioccolato.

Quanti dolcetti ha preparato in tutto?

Alla fine della giornata Fernando si accorge che gli sono rimasti solo 28 dolcetti, quanti ne ha venduti?

6 Questa è la famiglia Allegri. Quanti anni ha ciascun componente della famiglia?

Quando

è nato Gianni avevo 31 anni. Io ho 8 anni. Io ho 3 anni meno di Gianni.

Ho 38 anni più di Marco.

7 Al pasticciere Alberto hanno ordinato 170 biscotti per la festa della scuola. Per disporre i biscotti Alberto possiede tre tipi di vassoi:

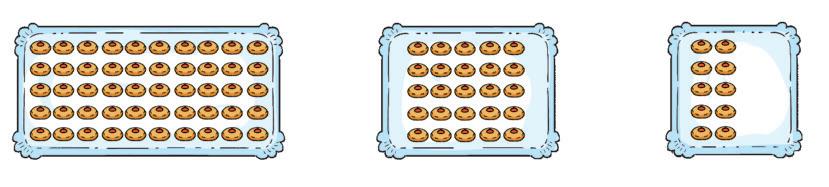
Quali vassoi può prendere il pasticciere per disporre i biscotti in modo ordinato?

Quanti vassoi di ciascun tipo?

Gianni Marco

PROBLEMATICAMENTE

Tutti i 24 alunni e alunne della classe IV B hanno aderito alla settimana bianca organizzata dalla scuola. Per accontentare le richieste degli alunni e delle alunne, gli/le insegnanti decidono di lasciarli liberi di scegliere come distribuirsi nelle camere per dormire.

Nella struttura che li ospiterà possono avere a disposizione 3 camere da 6 posti letto, 3 camere da 4 posti e 3 camere da 3 posti. Ogni camera dovrà essere occupata completamente. Come potranno disporsi gli alunni e le alunne nelle camere?

Rifletti sul testo per risolvere il problema

1 Che cosa ti viene chiesto di trovare in questo problema?

2 Cerca nel testo le informazioni che ti servono per trovare la risposta. Elimina le informazioni che non ti servono tracciando una linea sopra le parole del problema.

3 Ora scrivi le informazioni che hai trovato.

• Alunni e alunne

• Camere a disposizione

• Ogni camera ............................................................................................................................................................................................................................................................................

4 Qui sotto puoi vedere due rappresentazioni del problema. Scegli la rappresentazione che ritieni utile per aiutarti a riflettere e trovare la risposta.

1 camera 1 camera 1 camera

Camera da 6 posti letto

Camera da 4 posti letto

Camera da 3 posti letto

5 Esiste un solo modo per disporre gli alunni nelle camere? Sì No Mostra tutte le possibili combinazioni sul quaderno.

LE FRAZIONI

UNITÀ FRAZIONARIA

Gli alunni e le alunne della 4a C vogliono decorare i vetri rettangolari delle finestre della loro aula, ricoprendoli con forme geometriche fatte di pellicola trasparente colorata. Divisi in gruppi, disegnano dei rettangoli per rappresentare i vetri e progettano come decorarli.

• Osserva i progetti disegnati su fogli a quadretti, completa e rispondi.

In questo progetto il vetro è stato diviso in ............. rettangoli.

Ogni rettangolo è formato da quadratini.

Ogni parte ha:

la stessa forma. la stessa superficie. diversa forma. diversa superficie.

In questo progetto il vetro è stato diviso in 4

Ogni è formato da quadretti.

Ogni parte ha:

la stessa forma. la stessa superficie. diversa forma. diversa superficie.

• In ciascuno dei due progetti il vetro è stato diviso in 4 parti uguali? Sì No

• Osserva la parte gialla del primo progetto: è 1 parte su 4 di tutto il rettangolo.

• Osserva la parte blu del secondo progetto: è ............. parte su ............., come la parte gialla.

• Puoi dire allora che ogni pezzo è parte su , cioè 1 4 del rettangolo intero.

In linguaggio matematico si scrive 1 4 e si chiama unità frazionaria.

HO CAPITO CHE...

Frazionare significa dividere un intero in parti uguali.

Ma anche in questo progetto la finestra è stata divisa in quarti?

• Osserva e completa.

Il vetro è stato diviso in 4 parti: 2 sono e 2 sono .

Ogni rettangolo è formato da ............. quadratini. Ogni triangolo è formato da quadratini.

Quindi il vetro è stato diviso in parti che hanno forme diverse, ma hanno superficie.

Anche in questo caso il vetro è stato diviso in 4 parti uguali e ciascuna parte è 1 4 dell’intero rettangolo.

PROVO IO

1. Osserva e rispondi.

Rappresenta una frazione?

HO CAPITO CHE...

Frazionare significa dividere un intero in parti di uguale superficie. Le parti possono avere anche forme diverse

Sì No

2. Scrivi la frazione corrispondente alla parte colorata di ciascun intero.

Sì No

Sì No

3. Collega ciascuna frazione alla parte corrispondente.

Le frazioni

FRAZIONARE QUANTITÀ

Che cosa succede se frazioniamo una quantità?

Marco deve dividere le caramelle di questo sacchetto con le sue due sorelle.

• Osserva e rispondi.

• Quante caramelle contiene il sacchetto?

• In quante parti uguali deve dividere le caramelle?

Marco divide le caramelle e le mette dentro a delle scatoline.

• Aggiungi le scatoline che mancano e disegna le caramelle. Poi rispondi.

• Quante scatoline ha usato Marco per metterci le caramelle?

La prima rappresenta 1 scatolina su 3, cioè 1 3

• Quante caramelle contiene la prima scatolina? sono 1 parte su 3 di tutte le caramelle.

La seconda scatolina rappresenta la scatolina su , cioè e anche questa contiene caramelle.

• E la terza scatolina che parte è? È .............................................., quindi le caramelle che contiene sono di Puoi dire allora che 1 3 corrisponde a caramelle.

• Potresti dividerle in un modo differente? Sì No Spiega a voce perché.

HO CAPITO

Quando fraziono una quantità di oggetti, ogni parte dell’intero frazionato contiene la stessa quantità di oggetti.

OLTRE L’UNITÀ FRAZIONARIA

Per decorare l’aula, gli alunni di una classe IV hanno realizzato questo festone.

• Osserva il disegno e completa.

Il festone intero è formato da pezzi. Ogni pezzo colorato è di tutto il festone.

Se ogni pezzo giallo è 1 12 del festone, allora 1 12 + + + + +

sono tutti i pezzi gialli, quindi i 6 12 del festone.

Per i pezzi in giallo, hai considerato un numero di parti maggiori di 1 (l’intero)? Sì No

Hai considerato solo parti dell’intero, che è diviso in 12 parti uguali, cioè è stato frazionato.

La parte celeste del festone rappresenta i 12 del festone.

La parte blu rappresenta i del festone.

HO CAPITO CHE...

6 12

In linguaggio matematico

6 12 , 4 12 , 2 12 si chiamano frazioni.

significa che l’intero è stato diviso in 12 parti uguali e ne sono state considerate 6.

6 12

numeratore: indica quante parti consideri linea di frazione: indica che è stata effettuata una divisione denominatore: indica in quante parti hai diviso l’intero

1. Osserva, rispondi e completa.

• Da quanti pezzi è formata la costruzione? .............

• Il mattoncino rosso è di tutta la costruzione.

• Che parte sono i mattoncini verdi rispetto a tutta la costruzione? 7

• Che parte sono i mattoncini gialli rispetto a tutta la costruzione?

Le frazioni

FRAZIONI COMPLEMENTARI E UGUALI A 1

Quanti pezzi mancano ad Anna per completare la bandiera?

• Colora di arancione i 5 8 ricoperti da Anna.

• Hai colorato tutta la bandiera? Sì No

• Quante parti non sono colorate? ..........

La frazione 3 8 indica le parti che servono per completare la bandiera e si chiama frazione complementare.

Anna completa la bandiera ricoprendo con il cartoncino blu i 3 8 che mancano.

• Colora di blu i 3 8 della bandiera.

Puoi dire adesso di averla colorata tutta? Sì No

Rifletti

In quante parti è stata frazionata?

Quante sono le parti colorate?

Hai colorato parti su , cioè la bandiera intera.

In linguaggio matematico si scrive: 8 8 = 1

Una frazione è uguale a 1 quando dividi l’intero in parti uguali e consideri tutte le parti 3 3 = un intero = 1

PROVO IO

1. Circonda le frazioni minori di 1 e ricopiale sul quaderno; poi, per ciascuna, scrivi la frazione complementare.

2. Sul quaderno scrivi le frazioni rimaste. Che frazioni sono?

FRAZIONI MINORI DI 1

Anna, Sara e Marco per partecipare alla festa della scuola devono realizzare delle bandiere a colori.

Hanno disegnato le loro proposte.

Anna Sara Marco

Per ricoprirle Anna ha 5 pezzi di cartoncino arancione, Sara 7 pezzi di cartoncino verde e Marco 6 pezzi di cartoncino blu.

• Rispondi.

Colora sulle rispettive bandierine i pezzi di Anna, di Sara e di Marco.

Sono riusciti a costruire le bandiere? Sì No Perché?

Quindi nessuno dei tre bambini/e ha completato una bandiera intera.

• Scrivi quale parte di bandiera è riuscito a realizzare ciascuna bambino/a, poi completa.

Anna = 5

Sara = Marco = 8

In ogni frazione che hai scritto il numeratore è del denominatore e indica che le parti considerate sono maggiori minori di un intero.

Una frazione è minore di 1 quando le parti considerate sono meno delle parti in cui è stato diviso l’intero.

Se 1 = 7 7 allora 3 7 < 1

1.

FRAZIONI MAGGIORI DI 1

• Piega un foglio di forma quadrata lungo le diagonali e riaprilo.

Disegna le pieghe che hai ottenuto.

• Osserva: il quadrato è stato diviso in ............. parti uguali.

• Scrivi la frazione che rappresenta il quadrato intero:

• Adesso colora una parte e completa.

• Hai colorato 1 parte su .............

In linguaggio matematico si scrive che indica l’unità frazionaria.

• Ora ricalca e ritaglia l’unità frazionaria che hai colorato e sovrapponila alla figura che vedi a lato. Scrivi quante volte hai ripetuto l’unità frazionaria.

1 4 + + =

• Disegna nel quaderno altre figure che rappresentino la frazione 5 4 .

• Le figure disegnate sono maggiori del quadrato di partenza? Sì No

Nella frazione 5 4 il numeratore è maggiore del denominatore e indica che le parti considerate sono maggiori dell’intero di partenza.

In linguaggio matematico si scrive: 5 4 > 1

Siccome il quadrato intero è rappresentato dalla frazione 4 4 , la frazione 5 4 rappresenta l’intero quadrato più un quarto.

In linguaggio matematico si scrive: 5 4 = 4 4 + 1 4

PROVO IO

HO CAPITO CHE...

Una frazione è maggiore di 1 quando le parti considerate sono più delle parti in cui è stato diviso l’intero.

7 5 > 1

1. Usa l’unità frazionaria ritagliata per disegnare sul quaderno figure che rappresentino le seguenti frazioni.

7 4 3 4 6 4 10 4 2 4 4 4

2. Circonda le frazioni maggiori di 1.

1 Colora le frazioni indicate e circonda solo le frazioni che sono minori di 1.

2 Circonda le frazioni minori di 1. Poi, per ciascuna, scrivi la frazione complementare.

Che frazioni sono quelle rimaste?

3 Lisa ha usato l’unità frazionaria colorata di verde per fare queste figure:

Colora le figure disegnate da Lisa. Poi conta le unità frazionarie necessarie per disegnarle e scrivi sotto a ciascuna quale frazione rappresenta. Quale figura rappresenta la frazione maggiore di 1?

4 Circonda le frazioni maggiori di 1.

Che frazioni sono quelle rimaste?

Le frazioni

FRAZIONI EQUIVALENTI

Said, Lina e Ambra si allenano in pista correndo ciascuno nella propria corsia.

Said Lina

Ambra

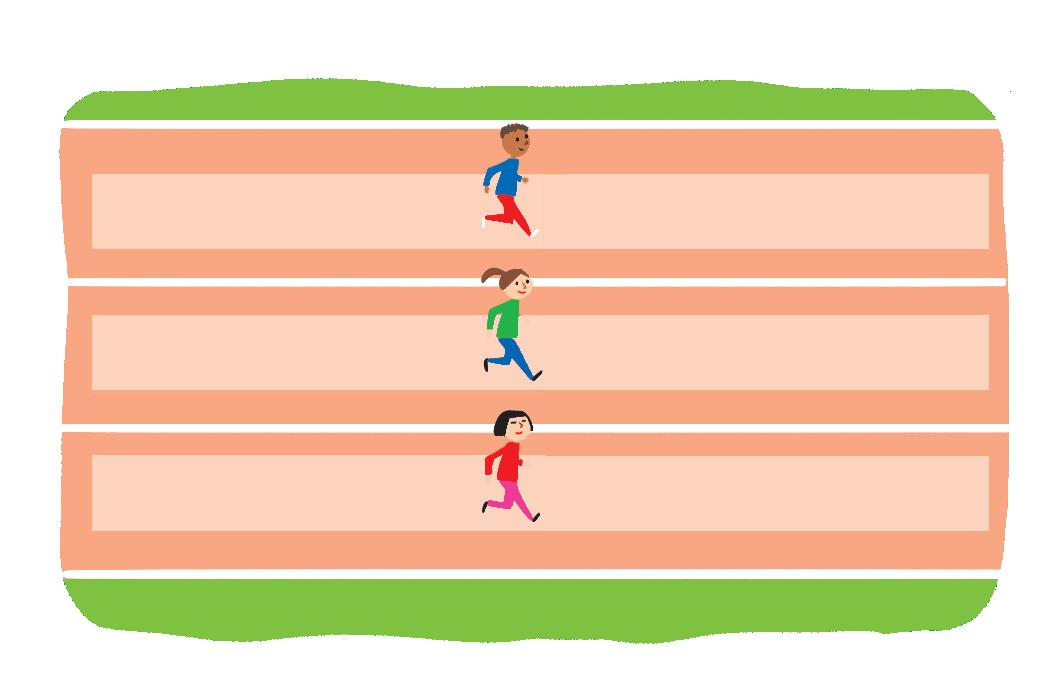
• Osserva, rispondi e completa.

Qualcuno dei tre amici ha corso più degli altri?

Sì No

Le frazioni che esprimono le parti percorse dai

bambini sono uguali diverse ma indicano tutte la parte di corsia, infatti i tre bambini

sono arrivati tutti nello stesso punto.

1.

Said ha corso per della sua corsia.

Lina ha corso per i della sua corsia.

Ambra ha corso per i della sua corsia.

Posso frazionare un intero in modi diversi. Le frazioni che indicano la stessa quantità si dicono equivalenti.

1 2 = 3 6 = 6

parti

2. Sotto a ciascun rettangolo, scrivi le frazioni che indicano la parte colorata e rispondi.

Le frazioni sono equivalenti?

• Osserva e completa.

Scrivi in frazione la parte colorata.

• Adesso moltiplica il numeratore e il denominatore per 2.

Hai ottenuto la frazione

Colorala nella corsia qui sotto.

Confronta le due corsie: come sono le quantità colorate? Uguali. Diverse.

Scrivi in frazione le parti colorate nelle due corsie.

Le frazioni indicano la stessa parte dell’intero? Sì No

Puoi dire allora che le due frazioni sono equivalenti

In linguaggio matematico si scrive: 6 = 8

• Adesso dividi per 2 il numeratore e il denominatore.

Hai ottenuto la frazione

Colorala nella corsia qui sotto.

Confronta le frazioni colorate nelle tre corsie.

Le tre frazioni indicano la stessa parte dell’intero? Sì No

In linguaggio matematico si scrive: 6 = 8 = 3

HO CAPITO CHE...

Per trovare una frazione equivalente applico la proprietà invariantiva, cioè divido o moltiplico il numeratore e il denominatore per uno stesso numero.

PROVO IO

1. Scrivi tre frazioni equivalenti per ciascuna delle frazioni date. 24 40 = = = 7 8 = = =

Le frazioni

FRAZIONI A CONFRONTO

Anna e Lea fanno una gita in bici lungo il fiume. Dopo un po’ si fermano perché sono stanche. Quanta parte del percorso hanno fatto le due amiche?

• Osserva, rispondi e completa.

Anna partenza stop Lea

• Anna ha percorso i 4 11 del tragitto. E Lea?

• Quale delle due bambine ha fatto più strada?

• Oltre che dal disegno, puoi capirlo confrontando le due frazioni: 4 11 e 7 11 .

Osserva i denominatori: sono , perché il percorso è stato diviso nello stesso numero di parti.

• E i numeratori? Sono Perché?

• Quindi la frazione 7 11 è maggiore della frazione 4 11 . Si scrive: 7 11 > 4 11 .

HO CAPITO CHE...

Se due frazioni hanno lo stesso denominatore, la frazione più grande è quella con il numeratore maggiore

PROVO IO

1. Scrivi le frazioni corrispondenti e stabilisci qual è la frazione minore.

Colora le frazioni e stabilisci qual è la frazione maggiore.

3 8 5 8

2.

E se le frazioni avessero lo stesso numeratore?

Gianni e Matteo hanno colorato delle strisce di carta, come vedi nel disegno.

• Osserva, rispondi e completa.

Gianni

Matteo

• Scrivi la frazione che indica la parte di striscia colorata da Gianni: ..........

• Matteo, invece, quanta ne ha colorata?

• Chi ha colorato più striscia?

Oltre che dal disegno, puoi capirlo confrontando le due frazioni: e

• Come sono i numeratori delle due frazioni? ...................................................... Perché? ...................................................................................................................

• E i denominatori?

Perché?

Entrambi i bambini hanno colorato 2 pezzetti di striscia, ma i pezzi sono diversi fra loro perché Matteo ha diviso la sua striscia in un numero maggiore di parti.

La parte blu allora è maggiore minore di quella rossa.

Quindi, la frazione è maggiore della frazione

Si scrive: 2 3 > 2 6

HO CAPITO CHE...

Se due frazioni hanno lo stesso numeratore, la frazione maggiore è quella con il denominatore più piccolo.

1. Confronta le coppie di frazioni e stabilisci qual è la frazione maggiore.

LA FRAZIONE DI UN NUMERO

Zoe ha 12 mele: di queste, 3 4 sono rosse e le rimanenti sono verdi.

• Colora le mele rosse e le mele verdi seguendo le istruzioni. Osserva, rispondi e completa.

Dividi le mele in 4 parti uguali, come avviato nel disegno.

• Quante mele ci sono in ogni parte?

Colora di rosso i 3 4 delle mele. Hai colorato mele.

• Quante mele sono rimaste?

Indicala con la frazione

In linguaggio matematico hai:

• diviso le 12 mele in parti uguali. 12 : 4 = 3 mele per ogni parte;

• trovato l’unità frazionaria 1 4 , cioè una parte di tutto l’intero;

• colorato di rosso i 3 4 , cioè 1 4 + + 3 + + = 9 mele.

Le mele verdi sono quelle rimaste, cioè 1 parte su 4, quindi sono

PROVO IO

1. Questo nastro è lungo 15 cm. Quanto misurano i 3 5 ?

Comincia così: il denominatore della frazione 3 5 indica che l'intero nastro è stato diviso in parti uguali, in linguaggio matematico scrivi: 15 : 3 = cm.

Hai trovato quanto misura l’unità frazionaria, cioè 1 5

Il numeratore indica le parti che devi considerare, cioè ............... parti su ................

Quindi scrivi: 1 5 + + 3 + + = cm

DALLA FRAZIONE ALL’INTERO

Valentino vuole raggiungere il Rifugio Stambecco. Guarda sulla cartina e vede di essere arrivato al Rifugio Marmotta, che si trova a 1 di tutto il sentiero.

RIFUGIO STAMBECCO

RIFUGIO MARMOTTA

2km

• Aiuta Valentino a capire quanto è lungo il sentiero per arrivare al rifugio Stambecco.

• Per rappresentarlo, prendi una striscia di carta di forma rettangolare, lunga quanto vuoi perché non sai quant’è lungo il sentiero.

• Valentino ha già percorso 1 3 del sentiero.

1 3 è la parte già percorsa sono le parti in cui è stato diviso

• Dividi allora la striscia in ............... parti uguali e scrivi che frazione rappresenta ogni parte.

• Colora la parte già percorsa da Valentino, cioè 1 3 . Quanto è lungo tutto il sentiero in frazione?

1 3 + + =

• Sai che 1 3 corrisponde a km. Scrivilo sopra la striscia.

Ora puoi scoprire quant’è lungo tutto il sentiero in km: 2 + = km

Io un quarto della tavoletta di cioccolato.

Liam

• Se ciascun bambino aveva la stessa tavoletta di cioccolato, chi ha mangiato più cioccolata? ..................................

• Chi, invece, ne ha mangiata di meno?

2 Colora gli elementi indicati dalla frazione, poi completa.

5 7 di 14 14 : 7 = x =

3 Risolvi sul quaderno.

a. Sullo scaffale di scienze della libreria della scuola ci sono 20 libri. I libri sugli animali sono 2 5 , il resto sono libri sui fiori. Quanti sono i libri sui fiori?

b. Aurora ha mangiato 9 cioccolatini che corrispondono ai 3 5 dei cioccolatini che c’erano nella scatola. Quanti cioccolattini c’erano nella scatola?

c. Gianni ha comprato delle focaccine per fare merenda con il suo amico. Ne hanno mangiato 2 5 e ne sono avanzate 6

Quante focaccine aveva comprato Gianni?

d. Alla verifica di Matematica Matteo ha fatto 20 punti, cioè i 4 5 del punteggio massimo.

Qual era il punteggio massimo?

e. Nel frigo di zia Maria ci sono 8 vasetti di yogurt. 3 4 sono alla fragola. Quanti sono i vasetti di yogurt alla fragola?

f. Antonio ha percorso 4 6 di una pista. Ha percorso più della metà o meno della metà? Quanto di più o di meno? Se ha già percorso 16 km, quanto è lunga tutta la pista?

g. Il maestro vuole far preparare la macedonia alla sua classe, ma non sa quanta frutta comprare.

Per facilitare il calcolo, divide i 24 alunni/e della sua classe in 4 gruppi. Stima che per la macedonia di un/a bambino/a serviranno i seguenti ingredienti: 1 cucchiaio di zucchero, mezzo limone strizzato, 1 4 di mela, 1 2 di kiwi, 1 3 di banana, 4 fragole e 2 noci. Quanta frutta servirà per ciascun gruppo? Quanta frutta dovrà comprare il maestro per fare la macedonia a tutta la classe?

Luca

Alissa

PROBLEMATICAMENTE

Sofia deve riordinare le parti del suo problema. Aiutala tu, come nell'esempio.

Lucia, invece, sta leggendo il libro “Peter Pan” e ha letto 5 9 delle 180 pagine del libro.

Quale dei due bambini ha letto meno pagine?

Mirko sta leggendo “Le avventure di Pinocchio” e ha letto

i 2 5 delle 200 pagine del libro.

A quale dei due bambini mancano meno pagine per vincere la gara?

Mirko e Lucia fanno una gara di lettura: vince chi finisce prima il proprio libro.

Rifletti sul testo per risolvere il problema

Sottolinea le risposte che ritieni giuste.

1 Che cosa devi scoprire in questo problema?

• Quale libro leggono i due bambini.

• A quale bambino mancano meno pagine per vincere la gara di lettura.

• Quale bambino ha letto meno pagine.

• A quale bambino è piaciuto di più il libro che sta leggendo.

2 Quali informazioni ti servono? Puoi sottolineare più di una risposta.

a. Le pagine del libro di Pinocchio sono 200, quelle della Sirenetta sono 180

b. I bambini sono 2.

c. Lucia ha letto 5 9 del suo libro.

d. Come si chiamano i due bambini.

e. Mirko ha letto 2 5 delle pagine del suo libro.

3 Ora ordina nella giusta successione le azioni necessarie per trovare la risposta.

Calcolare il numero delle pagine lette da Lucia.

Confrontare il numero di pagine lette dai due bambini e stabilire chi ne ha lette meno.

Calcolare i numero delle pagine lette da Mirko.

4 Risolvi il problema sul quaderno seguendo le azioni individuate.

Storie matematiche

L’OCCHIO DI HORUS

Horus è il più antico dio degli Egizi.

Veniva rappresentato come un falco oppure come uomo con la testa di falco, talvolta anche come un bambino nudo, senza capelli ma con la treccia reale che scendeva da una parte del capo. Poteva vedere tutto, aveva il potere della chiaroveggenza e dominava gli elementi naturali mantenendoli in equilibrio.

Era figlio della dea Iside e del dio Osiride (benefattore dell’umanità). Quando Osiride venne ucciso da Seth, suo fratello minore, il piccolo Horus venne educato alla missione di sconfiggere il perfido Seth e vendicare la morte del padre. La battaglia tra Seth e Horus durò otto anni fino a quando, nel corso di un ennesimo scontro, Seth riuscì a strappare l’occhio sinistro di Horus riducendolo a pezzi.

I vari pezzi furono ritrovati da Ator, dea della gioia, che lo guarì con il latte di gazzella. L’occhio fu poi aggiustato dal dio Thot, che riuscì a ricomporlo.

Gli antichi Egizi usavano le parti dell’occhio di Horus per indicare le frazioni.

Osserva l’occhio qui a fianco e le parti in cui è stato diviso. È possibile ottenere altre frazioni combinando queste parti.

Per esempio puoi ottenere 3 4 ? SÌ NO

E 1 3 ? SÌ NO

Quindi puoi ottenere solo alcune frazioni. L’occhio intero rappresentava l’unità, ma... Hai notato qualcosa di strano?

Prova a sommare tutti i pezzi, 1 2 + 1 4 + 1 8 + 1 16 + 1 32 + 1 64 = 63 64

Ottieni .............. .............. Manca .............. ..............

Ma perché manca 1 64 ?

Immagina che questo quadrato accanto sia l’occhio di Horus.

• Ora ricalcalo e piegalo lungo la diagonale. Ottieni due triangoli .......................................... , ciascuno dei quali è 1 2 del quadrato.

Continuando a piegare sempre lungo le diagonali ottieni dei triangoli rettangoli più piccoli dei precedenti.

Ecco i triangoli ottenuti dalla suddivisione del quadrato disegnato sopra. Scrivi sotto ogni triangolo a che frazione corrisponde rispetto al quadrato di partenza.

Adesso ricalca i vari triangoli, ritagliali e incollali cercando di ricomporre il quadrato bianco in alto.

• È stato possibile? SÌ NO

• Che cosa noti?

Se tu continuassi a suddividere, otterresti altri triangolini, ma non riusciresti lo stesso a ricoprire l’intero quadrato: ne mancherà sempre un pezzettino.

LA LEGGENDA CONTINUA...

Gli Egizi si sono dati una spiegazione: infatti, la leggenda diceva che “il pezzettino mancante sarebbe comparso grazie a una magia di Thot” sotto forma di piccola lacrima. La leggenda ci fa capire che quando esegui una divisione non è necessario avere il risultato esatto, ma basta anche solo la sua approssimazione.

I NUMERI DECIMALI

LE FRAZIONI DECIMALI

Paolo e Luca si divertono con il Gioco del pagliaccio. Questa è la regola del gioco: a turno, si pesca una delle carte del mazzo e si colora sul vestito la parte indicata dalla frazione. Vince chi dei due riesce a completare per primo i pantaloni.

• Ricopia e ritaglia le carte.

I due bambini hanno iniziato a giocare e hanno registrato nelle tabelle le carte pescate finora.

• Completa e rispondi.

• A questo punto del gioco, chi dei due amici è in vantaggio?

Paolo Luca

Paolo Luca

I NUMERI DECIMALI

I pantaloni sono formati da 10 toppe.

Ogni toppa è dei pantaloni.

Ogni frazione decimale si può scrivere anche come numero. Il numero che ottieni dividendo l’intero, cioè 1, in 10 parti uguali si chiama numero decimale.

In linguaggio matematico si scrive 1 : 10 = 0,1 e si legge: “un decimo” o “0 u e 1 decimo”.

Studiando le frazioni hai capito che oltre ai numeri naturali esistono anche i numeri decimali, che sono minori di 1

• Aiuta Alice. Completa il disegno e scrivi in rosso dove si trova 0,4.

HO CAPITO CHE...

La frazione 1 10 si chiama frazione decimale.

Le frazioni che hanno al denominatore 10 si chiamano frazioni decimali.

Le frazioni 1 10 • 2 10 • 3 10 … si possono scrivere come numero decimale: 0,1 • 0,2 • 0,3... La virgola serve a separare la parte intera del numero dalla parte decimale

Dove scriverò 0,4?

Il numero 0,4 è maggiore di 0 e ......................................................... di 1.

E il numero 0,8 dove andrà?

E 0,2? E 0,7?

• Scrivi dove si trovano.

1. Colora nello stesso modo le scritture che indicano le stesse quantità.

Questo disegno rappresenta una toppa dei pantaloni del pagliaccio.

è stata divisa in 10 strisce uguali.

• Osserva e rispondi.

• Che parte è ogni striscia rispetto a tutta la toppa?

• Se dividi tutte le 10 toppe dei pantaloni in 10 strisce uguali, in quante strisce hai diviso i pantaloni? 10 x 10 =

• Allora che parte è una striscia rispetto ai pantaloni interi? ..........

La frazione 1 100 si chiama frazione decimale. La puoi scrivere come numero decimale dividendo 1 per 100.

Si scrive 1 : 100 = 0,01 e si legge: “un centesimo” oppure “0 u e 1 centesimo”. In questo caso, la cifra 0 indica l’unità e i decimi.

• Per farti vedere i centesimi abbiamo ingrandito il decimo e diviso in 10 parti uguali. Aiutati con i numeri già scritti per capire dove Alice deve scrivere 0,04.

Dove scriverò 0,04? PROVO

1. Scrivi sulla linea i decimi che mancano, poi colloca i seguenti

Vestito

Toppa Striscia

Questo disegno rappresenta una delle 10 strisce in cui abbiamo diviso ogni toppa dei pantaloni del pagliaccio.

• Osserva e rispondi.

Che frazione è ogni quadratino rispetto alla striscia?

Se dividi tutte le strisce di una toppa in 10 quadratini, in quanti quadratini verrà divisa una toppa? 10 quadratini x strisce = quadratini.

Se dividi in 10 quadratini le 10 strisce di tutte le 10 toppe, da quanti quadratini saranno formati i pantaloni del pagliaccio?

x x =

Allora ogni quadratino rispetto ai pantaloni è 1 1 000 .

La frazione 1 1 000 è una frazione decimale, che puoi scrivere come numero decimale.

In linguaggio matematico si scrive

1 : 1 000 = 0,001 e si legge: “un millesimo” oppure “0 u e 1 millesimo”.

• Dove scriveremo sulla linea 0,004? Prova tu.

Quaderno

Le frazioni che hanno per denominatore 10, 100 e 1 000 sono frazioni decimali.

Le posso scrivere anche come numeri decimali.

1. Scrivi in numero decimale e aggiungi, se servono, gli 0 segnaposto, come nell’esempio.

NUMERI DECIMALI ED EURO

• Osserva i due scontrini e rispondi.

Che cosa rappresentano i numeri che vedi?

Per acquistare un oggetto spendi dei soldi.

Pizzeria “Mangiobene ”

I soldi che spendi esprimono il valore che è stato attribuito all’oggetto che acquisti.

Il valore di ciò che compri è, quindi, una grandezza misurabile e in alcuni Paesi dell’Unione Europea, come l’Italia, questo valore si misura con l’euro.

• Collega ciascun oggetto con il valore che ritieni sia quello giusto. 1,90

Dietro l’angolo”

• Ora riporta nella tabella qui sotto il prezzo di ciascun oggetto.

,

Osserva la tabella. Nella scrittura dei numeri in euro passi direttamente dall’euro (unità) ai centesimi. Questo significa che quando scrivi un valore in euro è necessario scrivere tutte le cifre fino ai centesimi.

Per esempio:

2,5 euro NO 2,50 euro SÌ

ADDIZIONI E SOTTRAZIONI CON I DECIMALI

15,30 euro

Quanto spende?

3,20 euro

2,40 euro

Per scoprirlo puoi calcolare in due modi.

A MENTE

Riscrivi i numeri separando gli euro interi dalla parte decimale.

(3 + 0,20) + (2 + ) + ( + 0,30) = (3 + 2 + ) + (0,20 + + 0,30) =

+ = euro

IN COLONNA

da u d c 3 , 2

0 +

Anche in questo caso puoi calcolare in due modi diversi.

A MENTE

Riscrivi il numero 20,90 separando gli euro interi dalla parte decimale.

50 – 20 – = (50 – 20) – 0,90 =

IN COLONNA

da u d c 5 0 , 0 0 –2 0 , 9 0 = ,

1.

Scrivi quanto manca per arrivare all’intero. 0,8 + = 1 • 0,18 + = 1 • 1,4 + = 2 • 0,756 + = 1 PROVO IO I numeri decimali 69

E più semplice?

MOLTIPLICAZIONI CON I DECIMALI

La società di pallavolo compra 14 magliette per la squadra, pagandole 12,90 euro l’una. Quanto spende?

Per rispondere alla domanda devi fare una

Come puoi eseguire l’operazione con i numeri decimali?

12,90 euro

1. Scrivi i fattori senza incolonnarli, per rispettare il valore posizionale delle cifre.

2. Esegui la moltiplicazione come se i numeri fossero interi.

3. Ora conta le cifre decimali dei due fattori.

4. Metti la virgola nel prodotto in modo da avere a destra tante cifre decimali quante sono quelle dei fattori.

Moltiplicare significa sempre aumentare?

Al termine dell’allenamento, 4 amici e amiche si fermano a mangiare la pizza. Se ciascuno di loro mangia mezza pizza, quante pizze mangiano?

Ricorda che la metà di 1 si scrive 1 2 oppure 0,5.

Allora l’operazione che devi eseguire è 0,5 x =

Risposta: mangiano in tutto pizze.

Che strano! Il prodotto è di uno dei due fattori.

PROVO IO

1. Metti la virgola al posto giusto nei prodotti di queste operazioni.

23

5,6 x 15 = 840 8,62 x

12,3 x 0,2 = 246

Se uno dei fattori è minore di 1, allora il prodotto è minore dell’altro fattore.

2. Esegui le operazioni sul quaderno.

HO CAPITO CHE...

MOLTIPLICAZIONI PER 10, 100 E 1000

Se moltiplichi un numero intero per 10, 100 e 1000, ciascuna cifra aumenta il suo valore di 10, 100, 1000 volte. Con i numeri decimali succede la stessa cosa, ma c’è sempre la virgola che separa la parte intera dalla parte decimale.

• Osserva la tabella.

PROVO

1. Completa la tabella e le operazioni.

2. Esegui in riga le moltiplicazioni.

3. Completa scrivendo il fattore mancante.

DIVISIONI CON I DECIMALI

Nadia, Pietro, John e Elena decidono di dividere la spesa della merenda in parti uguali. Se hanno speso 11,40 euro, quanto deve pagare ciascuno di loro?

Per rispondere alla domanda devi fare una

Come puoi eseguire l’operazione con i numeri decimali?

Se il dividendo è un numero decimale: esegui la divisione normalmente; scrivi la virgola nel quoziente nel momento in cui la incontri, cioè quando dividi la cifra dei decimi.

Dividere significa sempre diminuire?

Se il divisore è un numero decimale: prima applica la proprietà invariantiva in modo che diventi un numero intero; poi esegui la divisione.

La maestra ha portato in classe 12 tavolette di cioccolato e vuole dare mezza tavoletta a tutti i suoi alunni e a tutte le sue alunne.

Per quanti bambini e bambine sarà sufficiente la cioccolata?

Per rispondere alla domanda devi eseguire la divisione : 0,5 = Che strano! Il quoziente è del Se il divisore è minore di 1, il quoziente è maggiore del dividendo

HO CAPITO CHE...

1. Esegui le operazioni sul quaderno.

a. 76,4 : 16 = 768 : 1,2 =

230,4 : 18 = 456 : 2,5 =

b.

: 2,1 =

DIVISIONI PER 10, 100 E 1000

Se dividi un numero intero per 10, 100 e 1000, ciascuna cifra diminuisce il suo valore di 10, 100, 1000 volte.

Con i numeri decimali succede la stessa cosa.

• Osserva le tabelle e completa le operazioni.

724,3

PROVO IO

1. Completa le tabelle e le operazioni.

2. Esegui le divisioni.

3. Completa scrivendo il divisore mancante.

COSTO UNITARIO, COSTO TOTALE

Franco e Lia stanno guardando in Internet il costo dei palloncini da comprare per la festa della scuola. Questi sono i prezzi che hanno trovato.

• Calcola la spesa per ciascun tipo di palloncino: leggi, rispondi e completa.

1. 50 cent 30 euro

2. 65 cent 30 euro

3. 1,20 euro

30 euro

Conosci il costo di ogni palloncino e sai che te ne servono 30.

• Quale operazione dovrai eseguire?

La

• Calcola per ciascun tipo di palloncino:

1. x =

2. x =

3. ........................... x ........................... = ...........................

Continuano a cercare e trovano delle confezioni di palloncini.

Quanto gli costerà 1 palloncino se prendono una confezione per ciascun tipo?

• Calcola la spesa di 1 palloncino per ciascuna confezione: leggi, rispondi e completa.

1.

2.

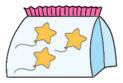
euro

3.

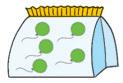
euro

Nella prima confezione ci sono palloncini. La confezione costa ................ euro.

• Quale operazione dovrai eseguire?

La ............................................................................................

• Calcola per ciascuna confezione:

1. : =

2. : =

3. : =

1 Esegui e rispondi.

Colora di verde i 3 10 del rettangolo.

Colora di rosa altri 5 10 .

Hai colorato tutto il rettangolo? Sì No

Quale parte di rettangolo rimane

NON colorata?

3 Circonda solo le frazioni decimali.

4 Trasforma i numeri decimali in frazioni, come nell’esempio.

0,04 = 4 100 0,005 = 0,34 =

0,765 = 12,05 = 203,4 =

6

7 Esegui le operazioni sul quaderno.

2 Completa la tabella, come nell’esempio.

In lettere In frazione In numero nove decimi

0,005 quattro unità e sei centesimi 12,08

5 Dividi un nastro lungo 145,5 cm in 15 parti uguali. Quanto è lungo un pezzo?

1 Risolvi sul quaderno.

a. Osserva la confezione. Quanto costa un gelato? Quanto pesa un gelato?

€ 4,20

b. La nonna ha mandato Alessio a comprare alcune cose dal panettiere.

€ 2,50

€ 1,80

€ 1,20

Dopo gli acquisti a Alessio sono rimasti 4,50 euro. Quanti soldi le aveva dato la nonna?

c. Federica va al centro commerciale con 50 euro. Le piacerebbe acquistare una maglietta da 18,20 euro; un paio di pantaloni da 25,80 euro e un braccialetto da 65 cent. Potrà acquistare quello che desidera? Se sì, le restano dei soldi? Quanti?

d. Sara e Franco hanno comprato queste confezioni di lecca lecca:

€ 12,60

€ 6,90

Franco sostiene che lui ha pagato ogni lecca lecca meno di Sara, ma lei non è d’accordo. Chi ha ragione? Motiva la tua risposta.

e. Alberto ha comprato una bottiglia da 2 litri di olio extravergine d’oliva al prezzo di 13 euro. Quanto costerà un bottiglione da 5 litri dello stesso olio?

f. Silvio vuole comprare i biscotti preferiti del suo gatto Baffo. Al supermercato trova queste due confezioni.

€ 22,50

12 Kg 2,5 Kg

€ 4,50

Quale confezione gli conviene comprare?

Perché?

g. Nella palestra “Tuttinforma” un ingresso singolo costa 5,70 euro, mentre l’abbonamento mensile costa 50 euro. Xelenia ha calcolato che nel prossimo mese potrà andare in palestra 9 volte. Le conviene comprare i singoli ingressi oppure l’abbonamento? Perché?

h. Andrea ha 6 euro a disposizione per fare un braccialetto. Dalla grandezza del polso ha calcolato che gli serviranno circa 10 perline, oltre al filo e al fermaglio per chiuderlo. Nel negozio trova il necessario a questi prezzi:

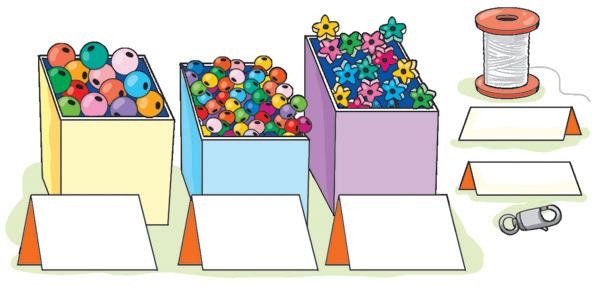
€ 0,80 cadauno € 0,50 cadauno

€ 0,30 cadauno

Potrà realizzare il suo braccialetto? Come?

€ 1,20

€ 0,50

PROBLEMATICAMENTE

Mattia ha concordato con i suoi genitori che riceverà un pacchetto di figurine per ogni volta che aiuterà a fare qualche lavoretto in casa, così segna su un foglio i lavori che ha compiuto.

Alla fine della settimana i suoi genitori gli danno 10 euro e lui va a comprare le figurine.

I pacchetti di figurine costano 80 cent ciascuno, ma il giornalaio gli dice che ci sono anche le figurine della stessa serie con il bordo brillante, che costano 90 cent a pacchetto. Mattia è indeciso…

Aiuta Mattia a capire quali pacchetti può comprare.

Rifletti sul testo per risolvere il problema

1 Per capire quali pacchetti Mattia può comprare è necessario rispondere prima a due domande. Indica con una X le domande necessarie.

In quali giorni della settimana Mattia ha eseguito le faccende?

Quanto può spendere al massimo se compra i pacchetti di figurine che costano 80 cent?

Quale faccenda preferisce fare Mattia?

Quanto può spendere al massimo se compra i pacchetti di figurine che costano 90 cent?

2 Riscrivi sul quaderno le due domande che hai scelto.

3 Scrivi le informazioni che ti servono per rispondere alla prima domanda che hai inserito e poi quelle per rispondere alla seconda.

4 Confronta la spesa per l’acquisto dei pacchetti di figurine da 80 cent con quella dei pacchetti che costano 90 cent.

5 Ora puoi rispondere: quali figurine comprerà Mattia? Perché?

CHE COSA VUOL DIRE MISURARE?

Alla fine di una festa di classe, l’insegnante raccoglie le bottiglie di acqua avanzate e le sistema sulla cattedra.

Il giorno seguente chiede agli alunni e alle alunne: – Quanta acqua è avanzata?

• Aiuta i bambini e le bambine a trovare la risposta.

• Che cosa devono fare per scoprire quanta acqua è avanzata?

• Che cosa devono misurare?

• I bambini e le bambine in classe hanno a loro disposizione questi oggetti. Indica con una X l’oggetto che possono usare per misurare.

• Ora che hai scelto l’oggetto necessario a compiere la misura, che cosa devono fare i bambini e le bambine con quell’oggetto?

Rifletti

Per misurare l’acqua avanzata hai:

1. considerato la grandezza che volevi misurare, in questo caso la capacità;

2. scelto una unità di misura, cioè una grandezza simile a quella da misurare, con la quale confrontare ciò che stai misurando; in questo caso ;

3. espresso con un numero quante volte hai ripetuto o diviso l’unità di misura.

HO CAPITO CHE...

“Misurare” significa confrontare una grandezza con la sua unità di misura e vedere quante volte l’unità di misura è contenuta nella grandezza. Il numero che esprime “quante volte” l’unità è contenuta è la misura della grandezza.

TUTTO PUÒ ESSERE MISURATO?

Gianna va dalla dottoressa per la visita di controllo che fa tutti gli anni.

• Che cosa può misurare la dottoressa di Gianna?

Sei pronta Gianna? Adesso ti misuro!

Può misurare la simpatia di Gianna? Sì No E quanto è alta? Sì No

E quanto è intonata? Sì No E quanto pesa? Sì No

Quindi la dottoressa può misurare e di Gianna.

• Osserva queste unità di misura e rispondi.

chilogrammo • litro • secondo • metro • grado

• Quale di queste unità deve usare la dottoressa per misurare l’altezza di Gianna?

• E per misurare per il suo peso? .........................................................

deve usare la dottoressa per misurare l’altezza di Gianna? E per il peso? gli strumenti necessari.

La dottoressa ha utilizzato lo stesso strumento per entrambe le misurazioni? Sì No Perché?

Le qualità di una persona o di un oggetto non possono essere misurate.

Tutto ciò che si può misurare di una persona o di un oggetto si chiama grandezza.

Ogni grandezza ha una sua unità di misura.

MISURE DI LUNGHEZZA

Tutti i giorni, senza nemmeno accorgertene, effettui misurazioni: misuri la distanza per andare a scuola, la velocità della macchina, la temperatura dell’aria… Misurare è stata, insieme al contare, una delle attività più antiche dell’essere umano.

Le misure di lunghezza sono fra le prime misure usate, poiché c’era bisogno di calcolare la lunghezza dei confini dei campi, dei muri delle case e delle stoffe per gli abiti. Per lungo tempo, però, ogni popolazione ha utilizzato unità di misura proprie.

•

• Che cosa veniva usato per misurare?

• Sono campioni uguali? Sì No

• Perché?

• Osserva la tabella e scopri quale unità di misura usavano…

… i Sumeri e gli Egizi.

… gli antichi Greci e i Romani.

Vorrei 6 “piedi” di stoffa.

MMMM… Qui però la vendiamo a “braccia”.

Usare unità di misura differenti rendeva complicati gli scambi commerciali, così, nel 1791, alcuni scienziati francesi proposero di utilizzare in tutti i Paesi la stessa unità di misura.

Per le misure di lunghezza fu scelta una lunghezza a cui è stato dato il nome di metro, parola di origine greca, metron, che significa “misurare”.

• Ma quant’è lungo 1 metro? Più o meno di un tuo braccio o di una gamba?

Confronta alcuni oggetti intorno a te e completa.

Oggetti lunghi circa 1 metro:

Oggetti più lunghi di 1 metro:

Oggetti meno lunghi di 1 metro:

E per misurare lunghezze maggiori di 1 metro come si può fare? E quelle minori?

Siccome il nostro Sistema di numerazione è decimale, cioè si conta sempre per 10, anche il metro si moltiplica o si divide ogni volta per 10

• Osserva la prima tabella (sui numeri) e completa la seconda tabella (sul metro).

MISURE DI MASSA

Marco e Valentina fanno merenda con una fetta di crostata. Marco stima che la sua fetta è più grossa di quella di Valentina, che invece è sicura del contrario. Marco e Valentina non trovano un accordo.

Marco può essere sicuro che la sua fetta sia più pesante di quella di Valentina? Sì No

• Osserva il disegno e rifletti.

I due bambini decidono di usare la bilancia a lato e scoprono che la fetta di Valentina è di quella di

Per sapere quanta crostata in più mangia Valentina, si devono usare le misure di massa

L’unità fondamentale delle misure di massa è il chilogrammo. Il suo simbolo è kg.

Le misure di massa permettono di misurare la quantità di materia che forma le cose. HO CAPITO CHE...

Per misurare la massa di oggetti molto leggeri si usano i sottomultipli del grammo

PROVO IO

1. In ciascuna misura, circonda la cifra riferita all’unità di misura indicata. Poi scomponi, come nell’esempio.

15,24 g = 1 dag, 5 g, 2 dg, 4 cg

12,6 g =

351 g = ......................................................................................................................

2. Scrivi il valore della cifra evidenziata.

13,58 dag =

378,9 g =

a. 450 g 5 b. 6,54 dg 4 c. 688 dg 6 6,52 kg 6 ................... 52300 hg 5 ................... 3 108 mg 1 ...................

3. Esegui le equivalenze, come nell’esempio.

dag g dg

5, 3 dag g dg

5 3

• Leggi e completa.

5,3 dag = 53 g

8 kg = Mg 645 mg = dg

6,23 g = mg 0,04 kg = dag

0,41 g = dag 0,005 Mg = kg

300 g = kg 0,349 hg = cg

Il papà di Paola deve andare a Parigi con l’aereo. Può portare solo una valigia da 10 kg. La sua valigia vuota pesa 1,8 kg.

Quale deve essere al massimo il peso delle cose che il papà di Paola può mettere in valigia?

Il peso della valigia con gli oggetti è il peso lordo

PROVO IO

1. Rispondi.

In linguaggio matematico scrivi – =

Che cosa indica questo numero?

Il peso degli oggetti è il peso netto

Il peso della valigia vuota è la tara

Per fare una torta a Carla serve 1 2 kg di fragole. Al mercato compra un cestino come quello che vedi.

Sarà sufficiente? Sì No Perché?

MISURE DI CAPACITÀ

Per festeggiare il suo compleanno Giulio ha invitato tre amici al mare, nello stabilimento balneare dove va tutti gli anni. Per divertirsi ha preparato delle sfide.

1a SFIDA Quale brocca contiene più succo?

A La misura 84

B

Gianni dice che la brocca B è quella con più succo, per Marco invece è la brocca A, mentre Luca sostiene che contengono tutte la stessa quantità.

• Secondo te, che cosa devono fare per capire chi ha ragione?

2a SFIDA Vince chi riesce a trasportare più sabbia dall’ombrellone alla riva usando uno fra questi contenitori, a scelta.

Marco vuole vincere la sfida.

Per conoscere quanto succo o quanta sabbia contengono i recipienti i tre bambini devono usare le misure di capacità.

L’unità fondamentale delle misure di capacità è il litro. Il suo simbolo è <l.

Le misure di capacità permettono di misurare la capienza di un recipiente.

1 Completa la tabella.

m<l d<l <l c<l

Tubetto di colla 200

Boccetta di profumo 0,25

Shampoo 3

Aranciata 150

2 Evidenzia la cifra a cui si riferisce la marca.

38,2 m 4,82 hm 3,84 km 28 cm 14,3 m

345 mm 682 m 23,1 m 2,51 hm 70,6 km

3 Esegui le equivalenze con le misure di massa.

5 kg = Mg 12 g = hg 1,9 dag = g 129 Mg = dag

4 Collega ciascun contenitore alla misura corrispondente.

5 Indica con una X i contenitori che hanno la capacità di 1 litro. Poi rispondi.

Quale contenitore ha la capacità di mezzo litro? E di un quarto di litro? a. b. c. d.

6 Scomponi e indica il valore di ciascuna cifra, come nell’esempio.

14,2 da<l = 1 h<l , 4 da<l , 2 <l

85,2 <l =

2105 g =

8,42 dam =

0,52 d<l =

MISURE DI TEMPO

In classe l’insegnante propone il gioco dei suoni. Il gioco consiste nel seguire con il dito il suono rappresentato dalla linea dicendo a voce alta la lettera A, mentre un compagno o una compagna mette delle palline in un contenitore e si ferma quando finisce il suono.

L’insegnante chiede a Marta e Marco di giocare e, così, mentre Marta segue con il dito la linea 1 emettendo la A a voce alta, Marco mette le palline nel primo contenitore.

AAA AAAAAAA

Facciamo un gioco.

Successivamente, Marta segue con il dito il suono rappresentato dalla linea 2 e Marco mette le palline in un secondo contenitore.

AAA AAAAAAAAA

• Rispondi.

• Che cosa misura Marco mettendo le palline nei contenitori?

• Può sapere Marco quale dei due suoni è durato di più? Sì No Come?

• Quale suono, secondo te, è durato più a lungo?

contenitore 2

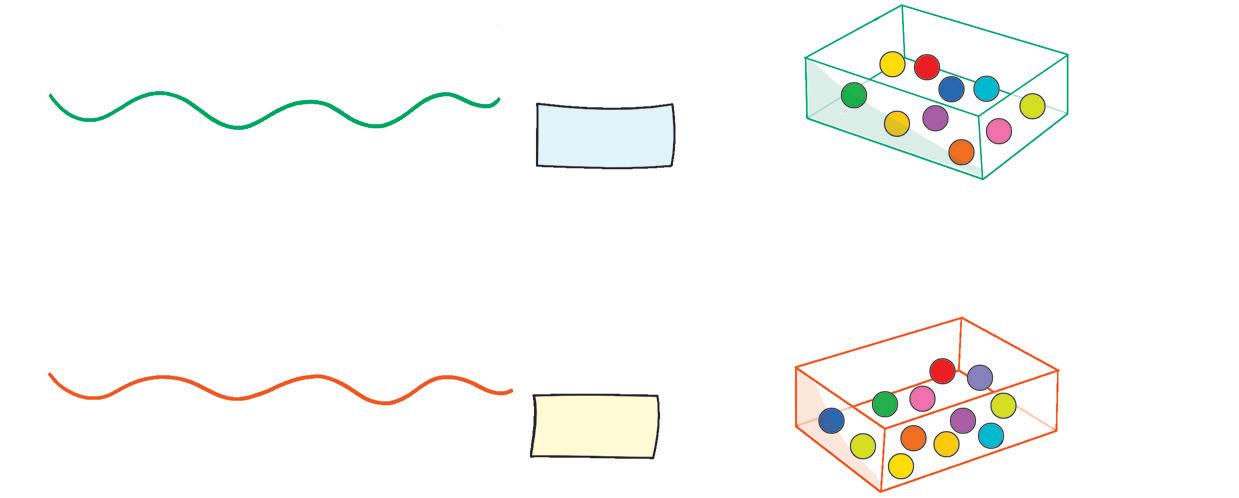
contenitore 1 linea 1 linea 2

Marco e Marta ripetono il gioco ma questa volta l’insegnante chiede a Marta di leggere un nuovo suono, mentre Marco metterà le palline nel suo contenitore; poi ripetono il gioco invertendo i ruoli. Queste sono le palline messe dai due bambini nelle scatole:

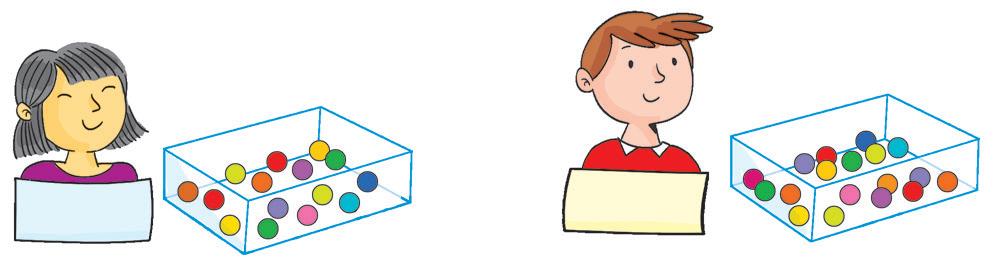Marta

Marco

• Rispondi.

• Quanto dura il suono secondo Marta? E secondo Marco?

• Come mai le palline di Marco sono più numerose? .....................

• Puoi sapere con certezza quale dei due bambini ha sbagliato a misurare? Sì No

• Quale strumento puoi usare per avere una misura oggettiva della lunghezza del suono, cioè una misura uguale per entrambi i bambini?

HO CAPITO CHE...

Il tempo è una grandezza e, quindi, è misurabile.

La grandezza che misuro è la durata, cioè l’intervallo di tempo.

Gli strumenti che si usano per misurare la durata sono l’orologio o il cronometro.

L’unità di misura fondamentale del tempo è il secondo. Il suo simbolo è s

MULTIPLI UNITÀ ora h minuto min secondo s

1 min x 60 = .................. min = 1 h 1 s x 60 = .................. s = 1 min 1

• Completa e rispondi.

2 min sono 2 x s = s 5 min sono 5 x s = s

3 h sono 3 x min = min 10 h sono min = min

• Le misure di tempo seguono il sistema decimale? Sì No , perché per completare hai sempre moltiplicato per

Quando gli intervalli di tempo sono molto più lunghi conviene misurare in giorni, mesi oppure in anni.

HO CAPITO CHE...

La misura di tempo ti permette di misurare gli intervalli di tempo trascorsi fra la fine e l’inizio di un evento. L’unità di misura del tempo è il secondo (s).

Per misurare intervalli di tempo lunghi si usano i giorni, i mesi o gli anni

PROBLEMATICAMENTE

I bambini e le bambine del campo estivo “W lo sport!” stanno disputando una gara e al termine della giornata verrà stabilita la squadra vincitrice. Quale sarà?

I bambini e le bambine sono stati divisi in tre squadre: gialli, verdi e rossi. Ogni squadra ha partecipato alle gare del giorno e ha segnato nel tabellone i risultati ottenuti da ciascun/a componente.

Il punteggio viene attribuito nel seguente modo:

• al primo classificato 5 punti;

• al secondo 4 punti;

• al terzo 3 punti;

• al quarto 2 punti;

• al quinto 1 punto;

• agli altri nessun punto.

Rifletti sul testo per risolvere il problema

1 Osserva i tabelloni delle squadre e completa.

Gara di salto in alto

GIALLI Lisa Gianni Mattia Ludovica

VERDI Emily Genni Marco Edoardo

ROSSI Francy Eva Luca Michele

• Scrivi la classifica del salto in alto.

• Scrivi il punteggio ottenuto dalle squadre per il salto in alto.

Gialli: Verdi: Rossi:

Gara di salto in lungo

GIALLI Lisa 424 cm

VERDI Emily 420 cm

ROSSI Francy 4,08 m

• Scrivi la classifica del salto in lungo.

487 cm

5,03 m Ludovica 3,12 m

4,77 m Edoardo 489 cm

• Scrivi il punteggio ottenuto dalle squadre per il salto in lungo.

Gialli: Verdi: Rossi:

I bambini e le bambine stanno disputando l’ultima gara: devono correre per 1,5 km.

Al traguardo sono già arrivati alcuni partecipanti con i seguenti tempi:

Lisa 16’ 20’’ (cioè 16 minuti e 20 secondi)

Marco 16’ 15’’ Gianni 16’ 18’’

Genni 15’ 50’’ Francy 16’ 50’’

Eva 16’ 09’’ Michele 16’ 52’’

Luca 15’ 45’’

Quattro stanno ancora correndo.

2 Osserva a che punto del percorso sono e completa.

NOME METRI GIÀ PERCORSI METRI CHE MANCANO ALL’ARRIVO

Edoardo m 900 m

Mattia 1400 m m

Ludovica 900 m m

Emily m 400 m

3 Ora rispondi.

• A chi mancano meno metri per arrivare al traguardo?

• Se l’ordine resta questo fino alla fine, chi arriverà per ultimo/a?

4 Osserva i tempi dei bambini e delle bambine che sono già arrivati/e e scrivi i primi cinque. 1° 2° 3° 4° 5°

• Scrivi il punteggio ottenuto dalle squadre per la corsa:

Gialli: Verdi: Rossi:

5 A questo punto puoi stabilire la graduatoria finale. In ciascuna tabella scrivi i punteggi ottenuti nella gara, poi completa.

Punteggio GIALLI

Gara salto in alto: ....................

Gara salto in lungo:

Corsa:

Punteggio finale:

• La squadra vincitrice della giornata è

Punteggio VERDI

Gara salto in alto: ....................

Gara salto in lungo:

Corsa:

Punteggio finale:

Punteggio ROSSI

Gara salto in alto: ....................

Gara salto in lungo:

Corsa:

Punteggio finale:

LINEE E ANGOLI

LA GEOMETRIA

Quando l’essere umano scoprì che poteva coltivare la terra e allevare gli animali iniziò a costruire abitazioni e confini per delimitare i campi da coltivare.

Quale forma conviene dare alla mia casa?

Quanto grande devo fare il recinto per le mie pecore?

Gli uomini e le donne studiavano le forme e prendevano le misure per rispondere a queste domande. Nacque così la Geometria, quella parte della Matematica che osserva le forme, studia le loro caratteristiche e le semplifica costruendo dei modelli. I modelli che trovi nel mondo che ti circonda sono tre:

hanno 3 dimensioni

• Osserva e completa.

hanno 2 dimensioni

hanno 1 dimensione

FORMA NELLA REALTÀ RAPPRESENTAZIONE GEOMETRICA QUANTE DIMENSIONI? FIGURA

piramide di Cheope piramide

solida

piana

solida

piana

lineare

lineare disegno rettangolo

mare linea retta

solida

piana lineare

FIGURE SOLIDE

FIGURE PIANE

FIGURE LINEARI

RETTE, SEMIRETTE E SEGMENTI

• Ripassa con la matita la linea tratteggiata.

Il segno lasciato sul foglio dalla matita è la rappresentazione di una linea.

Esistono diversi tipi di linee: linea curva

• Indica con una X.

• Se metti un punto P sulla retta, hai diviso la retta in: 2 parti. 3 parti.

linea spezzata

linea retta

La semiretta è ciascuna delle due parti in cui è divisa una retta; il punto (P) è l’origine delle semirette.

• Se metti un altro punto Q sulla retta, la parte di retta tra P e Q è il segmento.

semiretta P semiretta P Q " "

Il segmento è una parte di retta compresa tra due punti.

Si indica con le lettere maiuscole dei suoi estremi (PQ).

A seconda della posizione due rette possono essere:

perpendicolari, se sono incidenti e dividono il piano in quattro parti uguali

incidenti, se si incontrano in un punto parallele, se non hanno punti in comune e restano sempre alla stessa distanza

• Rifletti.

Puoi misurare una retta? Sì No Puoi misurare un segmento? Sì No

• Collega ciascun disegno al suo nome. segmento

rette perpendicolari rette incidenti rette parallele

• Ora disegna e completa.

• Quante rette passano per il punto P?

Disegnale.

• Se invece hai due punti, quante rette possono passare attraverso entrambi? • P

Per un punto passano: infinite rette. due rette.

PROVO IO

Per due punti passa retta.

1. Osserva l’immagine e stabilisci come sono le rette tra loro.

a e b sono

b e c sono

c e a sono ......................................................

a e d sono

d e b sono

Verifica la tua risposta prolungando le due rette.

P • Q a c

b d

L’ANGOLO NEL LINGUAGGIO QUOTIDIANO

Nella lingua italiana alla parola “angolo” vengono dati significati diversi.

Quando parliamo di “angolo cottura” intendiamo quella parte dell’appartamento dove ...................................

Quando parliamo di “angolo di mondo” intendiamo una parte di un paesaggio spesso particolarmente bella e affascinante.

Quando parliamo di “calcio d’angolo” intendiamo quella parte del dove viene messa la palla per

In Geometria, però, la parola “angolo” ha un significato differente da quello usato nella lingua italiana.

• Scrivi che cos’è per te un “angolo” in Geometria e poi confronta la tua idea con quella dei tuoi compagni e delle tue compagne.

• Avete tutti/e la stessa idea di angolo? Sì No

L’ANGOLO IN GEOMETRIA

• Osserva il ventaglio che ha costruito Angela.

È formato da:

• 2 bastoncini;

• la superficie compresa tra i 2

La superficie compresa fra i due bastoncini è un angolo

Angela apre il ventaglio come nella figura qui a fianco.

• Colora l’angolo che ha formato e rispondi.

• Per ottenere questo angolo Angela ha mosso un bastoncino.

Quale movimento ha fatto fare al bastoncino?

PROVO IO

1. Angela si diverte a giocare con il ventaglio e ogni volta ottiene posizioni diverse. Osserva, rispondi e completa.

• Che cosa ha formato?

• Per ottenere questi angoli Angela ha un bastoncino rispetto all’altro. La freccia disegnata accanto a ogni angolo indica il verso di rotazione del bastoncino.

• Nella figura A ha ruotato in senso: orario. antiorario.

• Nelle figure B e C ha ruotato in senso ...................................................................

UN ALTRO MODO PER FORMARE ANGOLI

Prendi un foglio e disegna sulla sua superficie un punto.

Dal punto fai partire due semirette e continua a disegnarle fino alla fine del foglio, come nel modello accanto.

Ora taglia il foglio lungo le semirette che hai disegnato: hai diviso la superficie del foglio in due parti. Colora una superficie di azzurro e una di arancione.

Hai ottenuto due angoli

HO CAPITO CHE...

L’angolo è ciascuna delle due parti in una superficie viene divisa da due semirette che hanno l’origine in comune. Il punto di origine dell’angolo si chiama vertice

Poiché le semirette che formano i lati dell’angolo sono infinite, anche l’angolo è infinito

angolo

lato

• Osserva il disegno. Le due parti colorate sono angoli. La misura di un angolo si chiama ampiezza. Rifletti e rispondi.

• Quale angolo è meno ampio?

• Quale angolo è più ampio?

Le semirette tratteggiate sono i prolungamenti dei lati dell’angolo. I prolungamenti dei lati attraversano l’angolo più grande.

L’angolo che viene attraversato dai prolungamenti dei lati si chiama angolo concavo

L’angolo che non viene attraversato dai prolungamenti dei lati si chiama angolo convesso.

lato

vertice

Linee e angoli

CLASSIFICARE GLI ANGOLI

Angela con il suo ventaglio si diverte a formare angoli.

• Scegli due colori diversi e usali per ripassare i lati di ciascun angolo.

Questo è il primo angolo che forma (Fig. 1).

Sai dire perché, secondo te, lo hanno chiamato angolo GIRO?

Come vedi, i due lati dell’angolo si sovrappongono.

Fig. 1

Angela chiude e riapre di nuovo il ventaglio per formare un angolo PIATTO (Fig. 2).

L’angolo piatto rispetto all’angolo giro è: la metà. il doppio.

I due lati dell’angolo questa volta hanno la stessa direzione ma verso opposto.

Fig. 2

Angela continua a giocare e forma un angolo RETTO (Fig. 3).

L’angolo retto rispetto a quello piatto è: la metà. il doppio. Rispetto all’angolo giro è

I due lati dell’angolo sono: perpendicolari. paralleli.

Fig. 3

Ora forma un angolo ACUTO (Fig. 4).

L’angolo acuto è meno ampio dell’angolo retto.

I due lati dell’angolo sono: incidenti. perpendicolari.

Fig. 5

Fig. 4

Prova ancora e forma un angolo OTTUSO (Fig. 5).

L’angolo ottuso è dell’angolo retto.

I due lati dell’angolo sono: incidenti. perpendicolari.

Se Angela lascia chiuso il ventaglio non forma angoli: ottiene l’angolo nullo.

CONFRONTARE GLI ANGOLI

Carlo e Luisa hanno disegnato e ritagliato due angoli.

Angolo di Carlo Angolo di Luisa

Carlo e Luisa confrontano gli angoli e riflettono: Luisa dice che il suo è più ampio di quello di Carlo, ma lui non è convinto. Aiutali a scoprirlo confrontando i due angoli.

Procedi così per confrontarli:

• ricalca su un foglio di carta i due angoli, poi ritagliali;

• sovrapponi i vertici dei due angoli ritagliati, poi sovrapponi un lato di un angolo con un lato dell’altro angolo;

• osserva gli altri due lati: se si sovrappongono significa che sono due angoli uguali; se non si sovrappongono significa che sono due angoli

• Ora puoi rispondere.

Ha ragione Luisa? Sì No

PROVO IO

1. Confronta gli angoli ricalcandoli con carta trasparente e sovrapponendoli. Poi tra angolo e angolo traccia la freccia che indica questa relazione:

è meno ampio di

MISURARE GLI ANGOLI

Carlo e Luisa adesso sanno quale fra i due angoli

è più ampio.

• Ma sanno di quanto è più ampio? Sì No

• Secondo te, che cosa devono fare per scoprirlo?

• Colora un angolo grado.

90°

360°,0° 180° 270°

PROVO IO

1. Osserva come ha fatto Carlo a misurare il suo angolo.

Per misurare gli angoli è stata scelta come unità di misura un altro angolo, ottenuto dividendo l’angolo giro in 360 angoli uguali.

Ogni angolo è 1 360 dell’angolo giro e si chiama “angolo grado” o semplicemente grado Lo strumento usato per misurare un angolo si chiama goniometro e rappresenta l’angolo giro diviso in 360 angoli grado.

• È stato facile colorarlo? Sì No

• Ha sovrapposto il vertice del suo angolo con il centro del goniometro; un lato dell’angolo coincide con il primo segmento della scala del goniometro, cioè quello che indica 0° (a sinistra);

• ha guardato quale segmento del goniometro coincide con l’altro lato; in questo caso è il segmento che indica 60°

1 Colora gli angoli, dove ci sono.

2 Sovrapponi a ciascun angolo disegnato un angolo meno ampio.

3 Le semirette disegnate sono i lati di un angolo. Completa disegnando per ciascuna semiretta l’angolo dell’ampiezza indicata, come nell’esempio.

4 Sul quaderno, disegna i seguenti angoli.

5 Stima quale delle misure indicate può essere quella corretta, indicandola con una X.

6 Verifica se hai stimato in modo corretto, misurando ciascun angolo con il goniometro.

Il 14 marzo di ogni anno si festeggia il Pi Greco day. Perché proprio in questo giorno?

Perché in Inghilterra la data si scrive anteponendo il mese al giorno quindi 03/14 come le prime tre cifre del Pi Greco.

La festa è nata nel 1988 negli Stati Uniti e dal 2020 coincide con la Giornata Internazionale della Matematica: un’ottima occasione per giocare con la Matematica.

Costruiamo insieme la barchetta di carta

Piega a metà un foglio di forma quadrata sovrapponendo due vertici opposti e poi riapri.

La piega che hai ottenuto è la diagonale del quadrato. Taglia il foglio lungo la diagonale e otterrai due triangoli congruenti, cioè di uguale forma e dimensione.

Osserva i lati e gli angoli dei triangoli: che triangoli sono rispetto ai lati? E rispetto agli angoli?

Prendi ora uno dei triangoli: piegalo a metà e poi riapri. La piega che ottieni è l’altezza del triangolo rispetto al lato più lungo, chiamato ipotenusa.

Ora porta il vertice dell’angolo retto sul piede dell’altezza, ottieni un trapezio formato da tre triangoli.

Porta il lato del triangolo a sinistra sull’altezza e così anche l’altro.

Hai ottenuto un quadrato.

Porta il vertice chiuso del quadrato al centro del quadrato.

Ribalta il foglio: ecco la tua barca a vela. Ti piace?

Quali pieghe sono nascoste dentro alla barchetta?

Riapri tutta la barca e ripassa con la matita le pieghe che si sono formate. Osservale.

Le linee delle pieghe formano poligoni diversi: quali vedi?

Adesso aguzza la vista e, come un/una detective, vai a cercare solo i triangoli. Quanti ne riesci a vedere? E di trapezi?

E di parallelogrammi?

• Colora i poligoni evidenziati in figura: quali poligoni sono?

• Confrontali fra di loro: quale frazione è il triangolo viola rispetto al triangolo di partenza?

E rispetto al foglio quadrato che avevi all’inizio?

• Considera adesso il triangolino rosso. Ricalcalo, ritaglialo e sovrapponilo al trapezio verde per vedere quanti triangoli rossi ti servono a ricoprirlo.

Quale frazione è rispetto al trapezio?

• Procedi come prima per scoprire quanti triangoli rossi servono per fare il triangolo viola.

Quale frazione è il triangolo rosso rispetto a quello viola?

A questo punto puoi dire quanti triangoli rossi servono per il triangolo di partenza: sono

Quale frazione è allora il triangolo rosso rispetto al triangolo di partenza?

• Richiudi la tua barchetta e colora le vele a piacere.

Puoi usarla per fare un quadro: incollala e disegna l’ambiente che le sta intorno.

Ma se pieghi più barchette, puoi fare delle belle composizioni: con due? E con tre? E con quattro? Dai spazio alla tua fantasia e prova a comporre dei puzzle come questo.

LA SIMMETRIA

Quando un paesaggio si specchia in un lago, si vede l’immagine del paesaggio riflessa nell’acqua.

Se Loretta si specchia, vede la sua immagine riflessa nello specchio.

L’immagine riflessa si dice simmetrica rispetto a quella originale.

• Leggi, osserva e completa.

Loretta si diverte a dipingere con le tempere. Sulla parte destra del foglio disegna tre frecce usando colori diversi.

Loretta ha dipinto una freccia rossa, una freccia e una freccia

Numera le frecce che ha dipinto nella parte destra del foglio, partendo dall’alto.

Poi piega il foglio, lo riapre e ripassa con una matita la piega. Ha ottenuto una linea retta che divide il foglio in parti.

• Scrivi tu “destra” e “sinistra” sui puntini nelle rispettive parti del foglio piegato e completa. Piegando e riaprendo il foglio, hai ottenuto le “impronte” delle frecce: per ogni freccia dipinta a c’è la sua corrispondente impronta a

Questa linea si chiama asse di simmetria

Ogni freccia-impronta (a sinistra) ha la stessa forma e le stesse dimensioni della freccia di partenza, ma ha il verso

sinistra destra

• Scrivi accanto a ciascuna impronta a sinistra il numero della freccia corrispondente nella parte destra del foglio. Poi rispondi.

• Con un righello Loretta ha unito la punta di ciascuna freccia con la sua impronta. Come sono le linee ottenute rispetto alla piega del foglio?

Misura le distanze dall’asse di simmetria fino alla punta di ogni freccia (a destra) e le distanze dall’asse di simmetria fino alla punta delle frecce-impronte (a sinistra).

• Che cosa osservi?

PROVO IO

HO CAPITO CHE...

Se ribalto una figura rispetto a un asse ottengo la sua impronta; l’immagine ottenuta è la figura simmetrica rispetto a quella di partenza.

La figura simmetrica mantiene la stessa forma e la stessa dimensione della figura di partenza, ma è orientata nel verso opposto

I segmenti che uniscono i vertici corrispondenti delle due figure sono perpendicolari rispetto all’asse di simmetria Ogni punto della figura di partenza e della sua figura simmetrica ha la stessa distanza dall’asse di simmetria.

1. Colora nello stesso modo i punti simmetrici a quelli dati e disegna quelli che mancano.

Linee e angoli

LA TRASLAZIONE

Pietro disegna sul quaderno una cornicetta con dei topolini.

• Colora il primo topo che Pietro ha disegnato a sinistra.

Pietro continua a disegnare: traccia un altro asse di simmetria a destra del secondo topo e inizia a disegnare il terzo.

• Completa il disegno.

• Rifletti e rispondi.

• Ripassa i due assi di simmetria: come sono fra loro?

Il secondo topo rispetto al primo è simmetrico.

• Com’è il terzo topo rispetto al secondo?

Ora osserva il primo e il terzo topo: ricalca con un foglio di carta trasparente il primo e poi fallo scivolare verso destra seguendo la freccia rossa.

• Riesci a sovrapporlo al secondo? Sì No E al terzo? Sì No

Hai visto che il primo e il terzo topo sono

Hai spostato il primo topo verso destra di tanti lati di quadretto quanti ne indica la freccia rossa, che si chiama vettore

HO CAPITO CHE...

Lo spostamento che hai fatto dal primo al terzo pesce è una traslazione

Se effettuo una doppia simmetria con assi paralleli ottengo una traslazione.

La figura ottenuta ha stessa forma, stesse dimensioni e anche stesso verso. Il vettore indica la direzione, il verso (destra, sinistra, alto, basso) e la misura dello spostamento (la lunghezza).

LA ROTAZIONE

Che cosa succede se gli assi di simmetria non sono paralleli?

Pietro disegna due assi non paralleli e ottiene il disegno a destra.

• Leggi, osserva e rispondi.

Ricalca su un foglio di carta trasparente la barca della Fig. 1. Fissa con la punta della matita il foglio sul punto d’incontro degli assi (P) e muovi il foglio verso destra fino a fare coincidere la barca con una delle altre due disegnate.

• Con quale barca coincide?

I due disegni sono uguali.

Hai spostato la Fig. 1 sulla Fig. 3 con un movimento che si chiama rotazione. La rotazione avviene intorno al punto P, detto centro di rotazione.

Per sapere di quanto hai ruotato la figura osserva l’angolo formato dalle frecce.

È un angolo quindi hai fatto una rotazione di

HO CAPITO CHE...

Se effettuo una doppia simmetria con assi incidenti e perpendicolari ottengo una rotazione. La figura ottenuta ha stessa forma, stessa lunghezza dei lati (stesse dimensioni) e anche stesso verso. La rotazione avviene intorno a un punto chiamato centro di rotazione Avviene in un senso (orario o antiorario).

PROVO IO

1. Disegna le figure simmetriche rispetto agli assi e colora di blu le figure ruotate.

Fig. 1

Fig. 2

Fig. 3

PERIMETRO E SUPERFICIE

LE FIGURE PIANE

NON SONO POLIGONI

Forme racchiuse da una linea curva, chiusa e semplice oppure da una linea mista, chiusa e semplice.

• Osserva, rispondi e completa.

• In quale cesta andrà la forma che vedi in basso?

Le forme nella cesta arancione si chiamano poligoni perché sono formate da una linea

Tutte le forme nella cesta verde, quindi,

• Disegna nella prima cesta una forma che NON sia poligono e nella seconda una forma che sia un poligono.

SONO POLIGONI

Forme racchiuse da una linea spezzata, chiusa e semplice.

PROVO IO

1. Colora di blu le forme che NON sono poligoni e di rosso le forme che sono poligoni.

Daniel disegna questi due poligoni e traccia il prolungamento dei lati delle figure.

Gli angoli sono convessi e i prolungamenti dei lati

sono esterni al poligono

In questo poligono c’è un angolo concavo e i prolungamenti di questo angolo attraversano il poligono

POLIGONO CONVESSO POLIGONO CONCAVO

HO CAPITO CHE...

La parte di piano delimitata da una linea spezzata chiusa si chiama poligono

Un poligono può essere concavo o convesso

LE PARTI DI UN POLIGONO

• Osserva, colora gli angoli e completa.

Conta: i lati sono ; i vertici sono

Puoi dire che il numero dei lati è sempre uguale al .................................................. che è uguale al numero degli angoli.

• Completa.

TRIANGOLO

n. lati

n. angoli

n. vertici

ESAGONO

n. lati

n. angoli

n. vertici

HO CAPITO CHE...

linea di contorno

angolo

QUADRILATERO

n. lati

n. angoli

n. vertici

OTTAGONO

n. lati

n. angoli

n. vertici

B A

C D E

lato

vertice

PENTAGONO

n. lati

n. angoli

n. vertici

DECAGONO

n. lati

n. angoli

n. vertici

In ogni poligono il numero dei lati è sempre uguale al numero degli angoli

I vertici del poligono si nominano con lettere scritte in stampato maiuscolo: A, B, C…

Il nome del poligono dipende dal numero degli angoli e, quindi, dal numero dei lati

Quaderno

POLIGONI SPECIALI

• Osserva i poligoni, rispondi e completa.

Misura la lunghezza dei lati del poligono. I lati sono uguali fra loro? Sì No

Un poligono che ha tutti i lati di lunghezza

è equilatero.

PROVO IO

Osserva gli angoli interni del poligono. Sono uguali fra loro? Sì No

Un poligono che ha tutti gli angoli di ampiezza

è equiangolo.

A A

Osserva i lati e gli angoli del poligono. Sono uguali fra loro? Sì No

Un poligono che ha tutti i lati e gli angoli

è regolare.

1. Finisci di nominare i vertici e ripassa di arancione il lato AB di ciascun poligono. A

2. Completa il disegno per formare i poligoni richiesti. pentagono quadrilatero triangolo esagono

3. Classifica i poligoni in base alle caratteristiche indicate.

Poligoni equilateri: Poligoni equiangoli: Poligoni regolari:

IL PERIMETRO

Nel cassetto della scrivania, Elia e Carla hanno trovato queste cordicelle colorate.

Le hanno usate per formare queste figure.

A B C D

• Scopri quale cordicella hanno usato per formare ciascuna figura e colora il contorno dello stesso colore della cordicella usata.

Per scoprirlo, procedi così:

• prendi una cordicella, sovrapponila a quella blu e tagliala in modo che sia della stessa lunghezza;

• colora un pezzettino della cordicella di blu;

• sovrapponi la cordicella blu alla linea di contorno di ciascuna figura e scopri quale di queste ha la stessa lunghezza;

• colora la linea di contorno della figura di blu.

Ripeti la stessa cosa per la cordicella marrone e per quella viola

• Confronta la lunghezza dei contorni delle figure disegnando la freccia che indica la relazione:

è maggiore di

Posso confrontare i contorni delle figure con lo spago e scoprire quale relazione esiste tra loro.

IL PERIMETRO

Elia gioca con alcuni ritagli di carta. Mette vicini i ritagli e ottiene questa figura.

• Ripassa il contorno del poligono formato da Elia. Rispondi.

• Da quanti vertici è formato? ..................... E da quanti lati? .....................

Elia decide di incollare un filo dorato lungo il contorno del suo poligono. Aiutalo a misurare quanto filo gli occorre.

• Scegli come unità di misura il lato di un quadretto e stabilisci la misura la lunghezza di ciascun lato del poligono.

AB = 10 lati di quadretto = =

BC = = =

CD = =

• Ora che conosci la misura di ciascun lato, calcola la lunghezza del contorno.

............ + ............ + ............ + ............ + ............ + ............ + ............ + ............ = ............

Per fare il contorno Elia dovrà prendere un filo lungo lati di quadretto.

La lunghezza del filo rappresenta il perimetro del poligono.

In un poligono la misura del suo contorno si chiama perimetro della misura della lunghezza dei lati.

LA SUPERFICIE

Riccardo sta cercando un pezzetto di cartoncino per ricoprire la superficie di questo quadrato.

Nel cassetto ha trovato questi ritagli.

• Secondo te, ci sarà almeno un ritaglio che gli permetterà di ricoprire il quadrato?

Per trovare la risposta, procedi in questo modo.

• Ricalca la Fig. A e ritagliala. Sovrapponila al quadrato. Che cosa noti?

Perché?

• Ricalca ora la Fig. B, ritagliala e sovrapponila al quadrato. Che cosa noti?

Perché?

• Ricalca ora la Fig. C, ritagliala e sovrapponila al quadrato.

Che cosa noti?

Perché?

• Ritaglia il pezzo che avanza e con quello riempi la superficie del quadrato che è rimasta bianca. Riesci a ricoprirlo completamente? Sì No

Procedi nello stesso modo con la Fig D.

Ora sai che i ritagli che può usare Riccardo sono

HO CAPITO CHE...

È sufficiente confrontare due superfici tra loro per stabilire se sono uguali o diverse.

Perimetro e superficie

LA SUPERFICIE

Luisa ha usato tante tessere uguali di forma triangolare per comporre queste figure.

Poligono 1 Poligono 2

• Ripassa il contorno di ciascuna figura e colora la sua superficie interna.

Poi misura la superficie usando un triangolo come unità di misura e completa.

Per formare il poligono 1 Luisa ha usato triangoli mentre, per formare il poligono 2, ha usato triangoli.

• Quale dei due poligoni ha la superficie maggiore?

Poligono 1 Poligono 2

Adesso puoi dire che il ha l’area maggiore.

• Osserva queste figure e rispondi.

Il numero di triangoli usati esprime la misura della superficie che occupa ciascun poligono e si chiama area.

• Quale unità di misura è stata scelta per disegnare queste figure?

• Ripassa il contorno di ciascuna figura e calcola il perimetro e l’area, poi completa.

Le figure 1 e 3 hanno perimetro e forma ma l’area

Le figure 1 e 4 hanno perimetro, forma e area quindi sono congruenti.

HO CAPITO CHE...

In una figura piana il contorno racchiude una superficie; la misura della superficie si chiama area

Figure con uguale forma, uguale perimetro e uguale area si dicono congruenti

FIG. 1 FIG. 2 FIG. 3 FIG. 4

PERIMETRO AREA

Fig. 1

Fig. 2

Fig. 3

Fig. 4

MISURARE LA SUPERFICIE

Per misurare una superficie bisogna scegliere un’unità di misura adatta e contare quante volte è contenuta nella figura stessa.

• Colora l’unità di misura usata per ciascuna figura. 1 dm

L’unità di misura per le superfici è il metro quadrato (m2), cioè un quadrato che ha il lato lungo 1 m. Come tutte le misure, il metro quadrato ha multipli e sottomultipli.

• Osserva il disegno del decimetro quadrato.

1 dm

Legenda

= mm2 = 1 cm2

Conta i quadratini per individuare i sottomultipli.

1 dm2 = cm2

1 cm2 = .......................... mm2

1 m2 = dm2

Ogni misura è 100 volte più piccola di quella che precede e 100 volte più grande di quella che segue.

• Quanti mm2 ci sono in un dm2?

Perimetro e superficie

FIGURE ISOPERIMETRICHE E FIGURE EQUIVALENTI

Delia ha disegnato queste due figure su una striscia di carta.

• Rispondi e completa.

• Le figure hanno uguale forma? Sì No

Ripassa il contorno delle figure e calcola il perimetro usando il lato di un triangolo come unità di misura.

Perimetro Fig. 1: ...................................................

Perimetro Fig. 2: ...................................................

• Le due figure hanno stesso perimetro? Sì No

Due poligoni che hanno uguale perimetro sono isoperimetrici.

Delia disegna poi altre due figure su un’altra striscia di carta.

PROVO IO

1. Disegna una figura isoperimetrica accanto alla Fig. 2.

• Rispondi e completa.

Le figure hanno uguale forma? Sì No

Colora le superfici dei due poligoni e misurale usando un triangolo come unità di misura:

Area Fig. 3: ...................................................

Area Fig. 4: ...................................................

• Le due figure hanno uguale superficie? Sì No

Due poligoni che hanno uguale superficie sono equivalenti o equiestesi

PROVO IO

1. Disegna una figura equivalente accanto alla Fig. 4.

Fig. 1 Fig. 2

Fig. 4

Fig. 3

• Rispondi e completa.

Se due poligoni hanno uguale area, hanno anche uguale perimetro?

• Tra i poligoni disegnati ci sono poligoni con lo stessa area? Sì No Quali? ........................................

• Ci sono poligoni con lo stesso perimetro? Sì No Quali?

I poligoni A e C sono equivalenti e isoperimetrici.

I poligoni B e D hanno la stessa area ma hanno lo stesso

I poligoni B e D sono equivalenti, ma non sono isoperimetrici: puoi dire che due poligoni equivalenti non sempre sono isoperimetrici.

HO CAPITO CHE...

Due poligoni che hanno uguale perimetro sono isoperimetrici

Due poligoni che hanno uguale superficie sono equivalenti o equiestesi

I poligoni equiestesi non sempre sono isoperimetrici

PROVO IO

1. Disegna 2 poligoni equivalenti ma non isoperimetrici e 2 poligoni isoperimetrici ma non equivalenti.

FIGURE EQUICOMPOSTE

Benjamin ha tagliato un rettangolo lungo la linea tratteggiata dividendo a metà uno dei due lati lunghi.

• Rispondi e completa.

• Quanti pezzi ha ottenuto?

Fig. A

Fig. B

La Fig. A è un poligono con vertici, lati, angoli: è un

La Fig. B è un poligono con vertici, lati, angoli: è un

Benjamin ha poi composto nuovi poligoni muovendo i due pezzi ottenuti e facendo coincidere i lati della stessa lunghezza. Eccone rappresentati alcuni.

• Colora i pezzi che compongono ciascuna figura come nel rettangolo. Poi rispondi e completa.

• Che cosa hanno di diverso?

L’area del rettangolo di partenza è uguale diversa all’area dei poligoni costruiti perché

Benjamin per costruirli ha usato

HO CAPITO CHE...

Due o più figure composte dagli stessi poligoni si dicono equicomposte e sono equivalenti.

PROVO IO

1. Ricalca e ritaglia il rettangolo di partenza. Riesci a formare figure diverse da quelle di Benjamin? Disegnale sul quaderno.

Le figure equicomposte hanno lo stesso

• Aiuta Alina a trovare la risposta. Alina ha colorato di rosso e di blu i segmenti che formano il contorno delle figure.

• Il perimetro della Fig. B si ottiene sommando: 2 segmenti rossi e 1 segmento blu.

In linguaggio matematico:

P (Fig. B) = 2 rossi + 1 blu

• Il perimetro della Fig. A si ottiene sommando:

4 segmenti + 1 segmento

In linguaggio matematico:

P (Fig. A) = .................................. + ..................................

• Adesso ripassa i lati dei seguenti poligoni usando gli stessi colori di Alina, rispettando la regola: lati uguali hanno colori uguali.

• Completa.

Perimetro Fig. C: segmenti rossi + segmenti blu

In linguaggio matematico: P = ............................................................................................

Perimetro Fig. D: segmenti rossi

In linguaggio matematico: P =

Perimetro Fig. E: segmenti rossi + segmenti blu

In linguaggio matematico: P = ............................................................................................

• Ci sono poligoni isoperimetrici? Sì No Quali?

• Puoi dire che le figure equicomposte sono tutte isoperimetriche? Sì No

Fig. A

Fig. B

Fig. C

Fig. E

Fig. D

Le figure equicomposte non sempre sono anche isoperimetriche HO

perimetro?

IL TRIANGOLO

Eleonora ritaglia 4 strisce di cartoncino colorato e le unisce con dei fermacampioni.

• Osserva: che poligono ha costruito?

Premendo leggermente su un vertice il quadrilatero cambia

Puoi dire che il quadrilatero è una figura deformabile perché ..........................................................................................................................................

vertice Perimetro e superficie

HO CAPITO CHE...

• Aiuta Eleonora a trovare la risposta. Prendi 3 strisce di cartoncino e fermacampioni e costruisci un triangolo. Premi su un vertice del triangolo: il triangolo cambia

• Puoi dire che il triangolo è una figura deformabile? Sì No Il triangolo è una rigida.

Un quadrilatero è una figura deformabile. Il triangolo è una figura rigida.

Questa è la proprietà che ha reso il triangolo indispensabile nelle costruzioni reali (perché “sostiene”).

5 cm

Non si forma.

10 cm

2 cm

10 cm > 5 cm + 2 cm

Il lato più lungo è

della somma degli altri due lati.

HO CAPITO CHE...

• Aiuta Gianni a trovare la risposta. Prendi tre strisce di cartoncino di lunghezza e colore uguale a quelli che Gianni ha disegnato qui sotto. Puoi sempre fare un triangolo? Rifletti e completa.

6 cm 4 cm

10 cm

Si forma? Sì No

10 cm = 6 cm + 4 cm

Il lato più lungo è alla

degli altri due lati.

Il triangolo si può costruire solo se il lato più lungo è minore o uguale della somma degli altri due lati.

Quanto misura la somma degli angoli interni di un triangolo?

• Aiuta Anna a trovare la risposta.

Disegna un triangolo e colora in modo diverso i suoi angoli (Fig. 1).

Poi ritaglia gli angoli e disponili uno accanto all’altro facendo combaciare un lato (Fig. 2). Che cosa ottieni?

Si forma? Sì No

12 cm

Il lato più lungo è

della

• Riesci a costruire un poligono con due lati?

Sì No

Puoi dire quindi che il triangolo è il poligono con il minor di lati.

HO CAPITO CHE...

La somma degli angoli interni di un triangolo è 180°, cioè un angolo piatto

Fig. 1

Fig. 2

Posso

CLASSIFICARE I TRIANGOLI

Manuel ha disegnato delle linee spezzate per fare dei triangoli.

• Osserva, rispondi e completa.

• Prolungando i lati con un righello ottieni sempre dei triangoli? Sì No

• Con quali linee spezzate puoi ottenere dei triangoli? E con quali no?

• Perché?

Puoi dire che: un triangolo non può avere due angoli retti; non può avere un angolo e uno retto; non può avere due angoli

Un triangolo, rispetto ai lati, può essere:

scaleno

se ha tutti i lati diversi

Un triangolo, rispetto agli angoli, può essere:

isoscele se ha 2 lati uguali (congruenti)

equilatero se ha tutti i lati uguali (congruenti)

rettangolo se ha un angolo retto

acutangolo se ha tutti gli angoli acuti

ottusangolo se ha un angolo ottuso

L’ALTEZZA NEI TRIANGOLI

Liam ha disegnato il triangolo che vedi a destra e, osservandolo, si chiede come fare a disegnare l’altezza.

• Aiuta Liam a disegnare l’altezza.

Fai scorrere il vertice A sul lato AB fino a che la piega del foglio non passa sul vertice C, quindi piega bene.

Poi aprilo e ripassa la piega (la linea tratteggiata in figura) con il pennarello. Indica con H il punto in cui la piega incontra il segmento AB.

Hai ottenuto il CH. Questo segmento cade perpendicolare su AB e ti indica la distanza tra un vertice e il lato opposto e si chiama altezza

Ripeti le pieghe per ogni lato del triangolo e ottieni altezze.

Il triangolo ha tre , una per ogni

• Osserva.

Ricalca il triangolo e ritaglialo. A

L’altezza h, rispetto al lato blu, cade esternamente al triangolo.

HO CAPITO CHE...

L’altezza di un triangolo è il segmento perpendicolare che congiunge un vertice con il lato opposto.

Può essere interna al triangolo, coincidere con un lato o essere esterna.

Ogni triangolo ha tre altezze.

PROVO IO

Nel triangolo rettangolo una delle altezze coincide con un lato (in questo caso CA).

1. In quali triangoli l’altezza è stata disegnata correttamente? Ripassala di rosso.

I QUADRILATERI

Giulio gioca con delle strisce di cartoncino di diversa lunghezza. Prende 4 strisce a caso: riuscirà a costruire un quadrilatero?

• Osserva e completa.

Non lo costruisce.

13 cm > 5 cm + 4 cm + 3 cm

Il lato più lungo è della somma degli altri

Lo costruisce? Sì No

12 cm 8 cm + 9 cm + 4 cm

Il lato più lungo è della somma degli

Lo costruisce? Sì No

14 cm 7 cm + 3 cm + 4 cm

Il lato

Un quadrilatero si può costruire se il lato più lungo è uguale o minore della somma degli altri tre lati.

Giulio aggiunge una striscia di colore diverso al quadrilatero che ha costruito, congiungendo due vertici opposti.

• Osserva, completa e rispondi.

Il quadrilatero è diviso in due

Il segmento aggiunto da Giulio si chiama diagonale

La diagonale è il segmento che unisce vertici non consecutivi.

• Puoi disegnare altre diagonali? Sì No

• Quante? Disegnala.

Un quadrilatero ha due che si in un punto.

HO CAPITO CHE...

Un quadrilatero ha due diagonali

La diagonale è il segmento che unisce due vertici non consecutivi

A

C D

B

• Aiuta Sofia a rispondere.

C

C

B

B

D A

A

Fig. 1

Disegna un quadrilatero e colora in modo diverso i suoi angoli (Fig. 1).

Poi ritaglia gli angoli e disponili uno accanto all’altro, facendo combaciare un lato e il vertice. Che cosa ottieni?

Quanto misura la somma degli angoli interni di un quadrilatero?

HO

La somma degli angoli interni di un quadrilatero è 360°, cioè un angolo giro.

PROVO IO

2. Osserva, esegui e rispondi.

B

A

3. Trova la misura dell’angolo mancante.

Traccia le diagonali nei due quadrilateri.

• In quale quadrilatero le diagonali sono entrambe interne?

• In quale sono una interna e una esterna?

4. Indica con una X con quale gruppo di segmenti puoi costruire un quadrilatero.

Fig. 2

1. Colora solo le figure che sono quadrilateri.

I TRAPEZI

Leo ha trovato un vecchio modellino di quadrilatero formato da tre lati fissi (neri) e un lato mobile di cartoncino rosso. Si chiede quali quadrilateri si formano muovendo il lato mobile sempre nello stesso verso.

• Rispondi.

• Quanti quadrilateri si possono formare?

Tanti. Quattro.

Tutti i quadrilateri che vedi hanno due lati paralleli.

Un quadrilatero con due lati paralleli si chiama trapezio

La distanza tra i due lati paralleli si chiama altezza

HO CAPITO CHE...

Il trapezio è un quadrilatero con due lati paralleli.

Osservando i lati non paralleli possiamo classificare i trapezi.

trapezio isoscele quando i lati sono di uguale lunghezza

trapezio rettangolo quando uno dei due lati è perpendicolare ai due lati paralleli

trapezio scaleno quando i lati sono di diversa lunghezza

IL PARALLELOGRAMMA

Leo ha disegnato la figura a fianco con il modellino dei quadrilateri e si chiede quale quadrilatero sarà.

• Aiuta Leo a rispondere: leggi e completa.

Il quadrilatero è un trapezio, perché ha due lati paralleli, ma anche gli altri due lati sono tra loro.

Il trapezio con i lati e a due a due è un parallelogramma.

lato lato

HO CAPITO CHE...

Il parallelogramma è un quadrilatero con i lati uguali e paralleli a due a due.

• Osserva, rispondi e completa.

Come sono gli angoli del parallelogramma qui accanto? a due a due. Disegna le diagonali nel parallelogramma, poi misurale. Non sono uguali, ma si dividono

HO CAPITO CHE...

Nel parallelogramma le diagonali si incontrano in un punto e si dividono a metà.

Quindi, i trapezi fanno parte dei quadrilateri e i parallelogrammi fanno parte dei trapezi.

Se usi gli insiemi puoi rappresentarli così

1. Chiudi le spezzate aperte. Poi indica con una X in quali casi ottieni un trapezio.

2. Classifica i seguenti trapezi.

a. c.

b. d. c.

b. d.

IL RETTANGOLO

• Aiuta Camilla a rispondere.

Ritaglia da un cartoncino quattro strisce uguali a due a due e collegale con dei fermacampioni.

Come vedi, ottieni sicuramente un parallelogramma.

Se premi leggermente su un lato si formano tanti parallelogrammi. Durante il movimento cambia l’ampiezza degli , ma la lunghezza dei lati rimane .............................., quindi i parallelogrammi che si formano hanno tutti lo stesso

HO CAPITO CHE...

Con quattro strisce uguali a due a due, che quadrilatero posso ottenere?

Tra i parallelogrammi, quello che ha tutti gli angoli della stessa , cioè sono tutti di gradi, è il rettangolo

Il rettangolo è un parallelogramma con tutti gli angoli uguali.

• Disegna le diagonali nel rettangolo e misurale. Poi rispondi.

• Come sono? Le diagonali sono .................................... e si dividono a ....................................

HO CAPITO CHE...

Le diagonali del rettangolo sono uguali e si dividono a metà.

Quindi i rettangoli fanno parte dei parallelogrammi.

• Scrivi nel grafico dei quadrilateri dove si trovano i rettangoli.

QUADRILATERI TRAPEZI PARALLELOGRAMMI

PROVO IO

1. Chiudi le linee spezzate e rispondi.

a b c d

• In quali casi il quadrilatero ottenuto è un rettangolo?

• Perché sei sicuro/a che siano rettangoli?

IL ROMBO

• Fai come Lucy e aiutala a rispondere.

Prendi quattro strisce di cartoncino di uguale lunghezza e uniscile con i fermacampioni. Hai ottenuto sicuramente un parallelogramma perché i lati opposti sono

Questo parallelogramma ha una caratteristica particolare: ha tutti i lati

HO CAPITO CHE...

Il rombo è un parallelogramma con tutti i lati uguali

• Disegna le diagonali nel rombo e misurale. Poi completa. Le diagonali non sono e formano 4 angoli di 90°, quindi sono

Osserva gli angoli opposti: puoi dire che sono

HO CAPITO CHE...

Il rombo ha le diagonali perpendicolari e gli angoli opposti uguali

Quindi anche i rombi fanno parte dei parallelogrammi.

• Osserva il grafico.

Il grande contenitore-quadrilateri si suddivide via via in altri contenitori contenenti quadrilateri sempre più particolari, cioè quadrilateri che hanno più proprietà.

E se costruisco un parallelogramma

Il parallelogramma con tutti i lati uguali è un rombo

QUADRILATERI

TRAPEZI

PARALLELOGRAMMI

RETTANGOLI ROMBI

IL QUADRATO

Se si preme su un vertice del rombo, che cosa si ottiene?

• Aiuta Manfredi a rispondere.

Costruisci un rombo e premi leggermente su un vertice. Vedi tanti rombi nei quali cambia l’ampiezza degli angoli.

I lati, invece, restano sempre tutti

Il quadrato è un rombo con i lati tutti e gli angoli tutti

HO CAPITO CHE...

Il quadrato è un rombo con tutti gli angoli uguali

• Disegna le diagonali nel quadrato accanto e misurale. Poi completa. Le diagonali sono e si incontrano formando 4 angoli

, quindi sono tra di loro

HO CAPITO CHE...

Nel quadrato le diagonali sono uguali e perpendicolari tra loro

• Osserva i quadrilateri e completa.

Il quadrato ha tutte le proprietà del rombo e, in più, ha tutti gli angoli

Il quadrato ha gli angoli e le diagonali come il rettangolo. Quindi, il quadrato è un e anche un ...................................................

HO CAPITO CHE...

Il quadrato è un rombo con gli angoli uguali e le diagonali uguali. Il quadrato è anche un rettangolo con i lati uguali e le diagonali perpendicolari

• Aiuta Federico e Miriam a rispondere. Completa la tabella indicando con X.

trapezio

parallelogramma

rettangolo rombo quadrato

Il quadrato starà con i rettangoli o con i rombi?

Il quadrato ha tutte le proprietà degli altri quadrilateri.

QUADRILATERI

TRAPEZI

PARALLELOGRAMMI

RETTANGOLI ROMBI

QUADRATI

A questo punto, in base a tutte le informazioni studiate finora, è possibile completare il grafico dei quadrilateri.

• Osserva e completa.

Il trapezio è un

Il parallelogramma è

Il rettangolo e il rombo sono , quindi anche .............................................................

Il quadrato è un rettangolo e anche un , quindi è un e anche un

Questo grafico si chiama diagramma di Eulero-Venn, e venne introdotto nel 1700 dal matematico Eulero e ripreso dal collega Venn nel 1800.

In questo caso mostra che i quadrilateri stanno uno dentro l’altro. Perciò, i quadrilateri che stanno all’interno hanno proprietà rispetto a quelli che stanno più all’esterno.

HA TUTTI I LATI UGUALI

Perimetro e superficie

L’AREA DELLE FIGURE

Matteo si chiede quanto misura la superficie del suo rettangolo.

• Leggi, osserva e completa.

Il rettangolo è formato da tanti che hanno il lato di 1 cm, e per questo sono 1 cm2. Matteo allora decide di usare come unità di misura un

I quadretti nel rettangolo sono disposti lungo delle righe.

• Quante sono le righe? Quanti cm2 ci sono in ogni riga? Calcola il numero totale dei cm2 contenuti nel rettangolo così: moltiplica il numero dei cm2 di ogni riga per il delle righe.

In linguaggio matematico: cm2 × 3 = cm2

• Puoi dire che: il lato maggiore del rettangolo misura lati di quadretto cioè cm, e il lato minore misura ....................... lati di quadretto cioè ....................... cm, quindi puoi trovare l’area del rettangolo così: moltiplica la misura del lato per la misura del minore.

In linguaggio matematico: × 3 = cm2

HO CAPITO CHE...

L’area del rettangolo si calcola moltiplicando la misura delle due dimensioni. A = l1 × l2

• Aiuta Matteo a rispondere.

Sai che il quadrato è un rettangolo con tutti i lati

Per trovare la sua area potrai allora procedere come nel rettangolo? Sì No

Quindi l’area è: misura del lato ×

In linguaggio matematico: A = l × l

Come si calcola l’area del quadrato?

HO CAPITO CHE...

L’area del quadrato si calcola moltiplicando la misura di un lato per se stesso. A = l × l

• Aiuta Marianna a rispondere. Disegna un rettangolo e una sua diagonale.

… e l’area del triangolo?

La diagonale divide il rettangolo in triangoli uguali.

Colorane uno. Ogni triangolo rettangolo ha due lati ai lati del rettangolo:

la base del rettangolo è uguale alla del triangolo; del rettangolo è uguale all’altezza del Puoi dire, quindi, che l’area di ciascun triangolo è la metà dell’area del Se l’area del rettangolo si calcola: A = × per il triangolo diventa: A = ( × ) : 2

• Aiuta ancora Marianna e completa.

Osserva il triangolo ABC.

… e di un triangolo qualsiasi?

L’altezza CH divide il triangolo in due rettangoli. Ricalca e ritaglia il triangolo giallo e costruisci un rettangolo facendo combaciare i lati più lunghi.

Ripeti la stessa cosa con il triangolo verde.

Hai ottenuto un formato da due triangoli gialli e da due triangoli

L’area del triangolo è la dell’area del rettangolo costruito.

Quindi l’area del triangolo sarà: A = ( x ) : 2

HO CAPITO CHE...

L’area del triangolo si calcola moltiplicando la misura della base per la misura dell’altezza e dividendo il prodotto per due:

A = (b × h) : 2

PROBLEMATICAMENTE

Il maestro ha distribuito a ciascun alunno e ciascuna alunna un cartoncino e ha chiesto di ritagliare dei triangoli rettangoli con un lato lungo 4 cm e un altro lungo la metà. Se il cartoncino da ritagliare ha la forma rettangolare, con i lati di 13 cm e 8 cm, quanti triangoli rettangoli potrà ritagliare al massimo ogni bambino/a dal proprio cartoncino?

Rifletti sul testo per risolvere il problema

1 Sottolinea le parole del testo dove ti viene richiesto che cosa devi scoprire.

2 Riscrivi le parole del testo dove ci sono le informazioni che ti servono per cercare la risposta.

3 Osserva e cancella il cartoncino che non rappresenta quello dato dal maestro. = 1 cm

4 Ora colora la forma che corrisponde alla figura da ritagliare. Poi risolvi il problema.

5 Indica con una X le azioni corrette fra le due proposte.

Osservo che il triangolo è la metà di un rettangolo con i lati di 2 cm e di 4 cm. Disegno sul foglio i rettangoli in modo che combacino per un lato e poi li divido a metà per formare i triangoli. Conto quanti triangoli ho disegnato.

Rappresento sul foglio la figura scelta e la riproduco fino quando è possibile lasciando 1 cm tra una figura e un’altra. Conto quanti triangoli ho disegnato.

1 Il disegno a lato rappresenta la stanza di Anita e dei i suoi fratelli.

Scrivi il nome di ciascun bambino dentro alla propria stanza sapendo che:

• la stanza di Anita ha la stessa superficie di quella di Rosa, ma non lo stesso perimetro;

• la stanza di Pietro, invece, ha lo stesso perimetro di quella di Anita, ma non la stessa superficie.

Ogni quadretto corrisponde a 1 m2.

Scrivi l’area di ogni stanza.

2 Emma ha costruito questa stella mettendo insieme tanti triangolini.

Quanti ne ha usati?

3 Martina ha un foglio quadrato con il perimetro di 24 cm. Lo piega a metà e poi ancora a metà, lo riapre e ottiene il foglio diviso in quattro quadrati più piccoli. Quanto misura il perimetro di un quadrato piccolo?

4 Questi due triangoli hanno lo stesso perimetro. Quanto misurano i lati del triangolo equilatero?

5 Calcola il perimetro di un trapezio isoscele che ha il lato non parallelo di 23 cm e le basi di 14 cm e 21 cm.

6 Calcola l’area delle seguenti figure:

7 Trova il perimetro del quadrato grande, sapendo che il quadrato arancione ha il perimetro di 20 cm.

DATI E PREVISIONI

L'INDAGINE STATISTICA

Nella scuola di Caterina l’ultimo giorno di scuola viene offerto il gelato agli alunni e alle alunne.

La responsabile della mensa può scegliere fra 4 gusti diversi: cioccolato, panna, fragola o pistacchio.

È, però, indecisa perché non conosce i gusti preferiti dai bambini e dalle bambine.

• Rispondi.

• Che cosa potrebbe fare, secondo te?

La responsabile chiede aiuto agli insegnanti perché lo domandino direttamente ai bambini e alle bambine. Così ogni insegnante fa un’indagine nella propria classe.

• Quale domanda dovrà fare?

• A chi dovrà rivolgere la domanda?

• Che cosa dovrà fare l’insegnante per ricordarsi tutte le risposte?

La maestra di Caterina scrive le risposte di tutti i suoi alunni e di tutte le sue alunne su un bloc-notes.

Si rende conto, però, che in questo modo non si capiscono subito a colpo d’occhio i gusti preferiti e così disegna una tabella.

• Completala inserendo i dati che mancano, poi rispondi.

GUSTO NUMERO PREFERENZE cioccolato 8

panna fragola pistacchio

• C’è un gusto preferito? Sì No Perché?

• Quanti preferiscono la fragola?

Quanti il pistacchio?

• Quanti sono gli alunni e le alunne della classe? ..................

LA RACCOLTA DEI DATI

La tabella fatta dalla maestra di Caterina si chiama tabella di frequenza

I numeri indicano la frequenza con la quale un dato si ripete, cioè quante volte si presenta.

Il gruppo di bambini e bambine ai quali è stata rivolta l’indagine si chiama campione.

Alla responsabile della mensa arrivano, infine, le risposte di tutte le classi della scuola;

le riporta quindi in una tabella di frequenza.

• Osserva la tabella, poi rispondi.

CLASSE CIOCCOLATO PANNA FRAGOLA PISTACCHIO

• Puoi capire con certezza qual è il gusto di gelato preferito? Sì No

• Che cosa devi fare per saperlo con certezza?

Totale

• Calcola le preferenze di ciascun gruppo e rispondi.

• Qual è il gusto di gelato preferito?

• Qual è il gusto di gelato scelto di meno?

• Quanti sono i bambini e le bambine intervistati/e?

• Grazie a questa indagine, secondo te, i responsabili della mensa possono sapere adesso quali gusti comprare? Sì No

HO CAPITO CHE...

Un’indagine nasce dal bisogno di trovare una risposta certa a una situazione di incertezza

In un’indagine si raccolgono, si organizzano e si analizzano informazioni riguardanti un particolare fenomeno.

Per svolgere un’indagine devo:

1. formulare una domanda;

2. scegliere un campione, cioè il gruppo di persone o di cose che voglio studiare;

3. registrare le risposte;

4. rappresentarle con tabelle;

5. leggere i dati per ricavarne le informazioni che mi permettono di trovare una risposta.

RAPPRESENTARE I DATI

• Osserva la tabella, poi completa e rispondi.

Questa è una tabella di

REGIONE NUMERO CANI DOMESTICI

Sicilia 571581

Puglia 445103

Toscana 636316

Liguria 199564

Piemonte 848850

Sardegna 457845

• Qual è l’oggetto dell’indagine?

• Dove è stata svolta l’indagine?

Ordina le regioni da quella che ha meno cani a quella che ha più cani:

I dati raccolti si rappresentano con dei grafici, perché in un disegno si vedono meglio ed è più facile riuscire a confrontarli e ricavare informazioni. Ne esistono diversi tipi.

Il diagramma a barre serve quando devi confrontare dei dati.

I dati sono rappresentati da colonne e l’altezza di ogni colonna indica il valore del dato che rappresenta.

Per disegnare un diagramma a barre devi:

0

Legenda: = 100000 cani domestici

Anche l’ideogramma serve quando devi confrontare dei dati fra loro. I dati sono rappresentati da un’immagine che si ripete e che corrisponde a una certa quantità

Per disegnare un ideogramma devi:

1. scegliere l’immagine che ti dà subito l’idea dell’argomento dell’indagine;

2. decidere a quale numero corrisponde;

3. approssimare i dati quando necessario, come in questo caso.

1. scegliere l’unità di misura;

2. approssimare i dati quando necessario, come in questo caso.

Sicilia

Puglia

Toscana

Liguria

Piemonte

Sardegna

Legenda: = 100000 cani domestici

Sicilia Puglia Toscana Liguria Piemonte Sardegna

LA MEDIA

Per fare merenda Elena distribuisce delle ciliegie alle sue amiche.

Elena Fatima Alice Emma

• Inserisci nella tabella le informazioni che mancano.

BAMBINA NUMERO CILIEGIE

Elena Fatima

Alice

Emma

• Rispondi.

• Ora rappresenta i dati della tabella con un diagramma a barre.

Elena Fatima Alice Emma

• Puoi dire che tutte le bambine hanno mangiato la stessa quantità di ciliegie? Sì No

• Come avrebbero dovuto fare, secondo te, per avere tutte lo stesso numero di ciliegie?

Al ritorno dal lavoro, la mamma di Elena chiede quante ciliegie, all’incirca, hanno mangiato a testa.

• Leggi e completa.

Elena calcola così: considera tutte le ciliegie e le divide per il numero delle bambine. In linguaggio matematico si scrive: (11 + 6 + + ) : 4 =

numero ciliegie

ciliegie per bambina bambine

Elena riferisce alla mamma che ogni bambina ha mangiato in media ciliegie. Quando si fa una media, si esprime un numero indicativo.

HO CAPITO CHE...

La media è un valore che semplifica i risultati di un’indagine.

Si calcola sommando il valore di tutti i dati e dividendo la somma per il numero dei dati.

LA MODA

Alberto e Annika devono comprare la frutta per preparare una macedonia con i loro compagni e le loro compagne, ma non sanno quale tipo di frutta prendere. Decidono quindi di fare un’indagine chiedendo a ciascuno di esprimere due preferenze. Queste sono le risposte che hanno registrato.

FRUTTA PREFERENZE

banana 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8

mela 8 8 8

kiwi 8 8 8 8 8 8

fragola 8 8 8 8 8 8 8 8 8 8 8

ciliegia 8 8 8 8 8 8 8 8 8 8 8 8 8

• Completa prima la tabella di frequenza, poi il testo.

FRUTTA NUMERO PREFERENZE

Ordina i frutti da quello che è stato scelto da meno bambini/e a quello che è stato scelto da più bambini/e:

• Qual è il frutto che compare con maggiore frequenza?

Il dato che compare con maggiore frequenza si chiama moda. In questo caso la moda è ....................................................................................

Anche Lisa ha fatto la stessa indagine nella sua classe.

Queste sono le risposte.

• Osserva, rispondi e completa.

• C’è un frutto che compare con maggiore frequenza? Sì No In questo caso non c'è una sola moda, perché ci sono più dati che hanno la stessa frequenza, cioè la , la e la

HO CAPITO CHE...

FRUTTA PREFERENZE

banana 8 8 8 8 8 8 8 8 8 8 8

mela 8 8 8 8 8 8 8 8

kiwi 8 8 8 8 8 8 8 8 8

fragola 8 8 8 8 8 8 8 8 8 8 8

ciliegia 8 8 8 8 8 8 8 8 8 8 8

La moda è il dato che si presenta con maggiore frequenza

Se ci sono più dati con la stessa frequenza, la moda non è una sola

EVENTI CERTI, POSSIBILI, IMPOSSIBILI

Omar ha risolto per primo il rebus della maestra e ha vinto la possibilità di scegliere un premio dalla Scatola delle meraviglie. Omar pesca a caso il premio, senza guardare dentro la scatola.

• Osserva e rispondi.

• Puoi sapere con certezza quale sarà l’oggetto che pescherà Omar? Sì No

In linguaggio matematico l’estrazione a caso si chiama evento casuale, cioè un evento che è “dovuto al caso”, perché è impossibile prevedere che cosa succederà.

• Estrarre un oggetto dalla scatola è un evento possibile. certo. impossibile.

Perché?

• Estrarre una gomma multicolor è un evento possibile. certo. impossibile.

Perché?

• Estrarre una matita nera è un evento possibile. certo. impossibile.

Perché?

• Quale oggetto è più probabile che venga estratto da Omar?

Perché?

Un evento è certo se si verifica sicuramente, è impossibile se non ha alcuna probabilità di verificarsi, è possibile se può verificarsi, ma non si può prevedere esattamente.

Dati e

LA PROBABILITÀ DI UN EVENTO

La probabilità di estrarre un oggetto si può esprimere con una frazione.

• Osserva e completa.

Posso conoscere quale probabilità ho di estrarre un pupazzo?

La scatola contiene oggetti. Tutti gli oggetti della scatola in frazione sono 8 8

I 5 animaletti in frazione sono della scatola, quindi la probabilità di pescare un animaletto è di 5 su 8.

Le 2 gomme in frazione sono , quindi la probabilità di pescare una gomma è di su

La bottiglietta di profumo è 1 su 8, in frazione degli oggetti della scatola, pertanto la probabilità di pescarla è di su

Le frazioni 5 8 , 2 8 e 1 8 sono tutte frazioni minori di

Il denominatore delle frazioni indica i casi possibili, in questo caso , tanti quanti sono gli oggetti della scatola. Di questi casi possibili sono i casi favorevoli a prendere un animaletto; sono i casi favorevoli a prendere una gomma; ................... è il caso favorevole a estrarre la bottiglietta di profumo.

HO CAPITO CHE...

La probabilità che accada un evento si indica con una frazione: casi favorevoli casi possibili

PROVO IO

1. Completa scrivendo se ciascuno degli eventi è certo, possibile o impossibile.

Lanciare un dado e far uscire un numero tra 1 e 6

La mia squadra del cuore vincerà il campionato.

Lanciare un dado e far uscire il numero 8.

1 Ordina i dati nella tabella di frequenza.

Peso bambini/e della classe: 32 kg, 30 kg, 31 kg, 30 kg, 33 kg, 29 kg, 30 kg, 35 kg, 33 kg, 33 kg, 31 kg, 33 kg, 30 kg, 33 kg, 31 kg, 33 kg

PESO NUMERO BAMBINI/E

29 kg

30 kg

2 Completa il diagramma a barre inserendo i dati della tabella di frequenza dell’esercizio 1.

3 Leggi, osserva e completa.

Al campo sportivo è stato organizzato un torneo di calcio tra le classi quarte. L’allenatore ha registrato in questo grafico i gol segnati dai giocatori e dalle giocatrici.

Calcola la media dei gol segnati nel torneo.

Chi ha segnato un numero di gol superiore alla media?

Chi ha segnato un numero inferiore?

Chi è nella media dei gol segnati?

4 Su dei foglietti uguali sono state scritte le lettere della parola MAGICAMENTE.

I foglietti sono stati poi piegati, mescolati e messi in un sacchetto.

Qual è la probabilità che, pescando a caso dal sacchetto, esca:

a. la lettera M b. una vocale c. una consonante d. una lettera qualsiasi

LA GIORNATA DEI CALZINI

C’era una volta un vento allegro che amava i calzini colorati sugli stendini. Quando vedeva tutti quei calzini pieni di colori impazziva di gioia e, soffiando, li faceva svolazzare spaiandoli e creando un allegro arcobaleno.

Quando succedeva questo, i calzini guardavano i nuovi compagni con diffidenza: quando mai un calzino a pallini poteva fare amicizia con uno a righe? Stando vicini, però, si accorsero quanta allegria creava questa differenza e come fosse bello avere vicino qualcuno così diverso da sé. Intanto il vento guardava da lontano e se la rideva.

Questa che hai letto è la “Storia dei calzini spaiati”, inventata da una classe di alunni e alunne per riflettere sul valore della diversità. Nella realtà, ti capita di perdere un calzino e di trovarti con alcuni calzini spaiati che non metti? Se ci pensi bene, anche se diversi per forma o per colore, possono sempre proteggere i tuoi piedi. Perché non indossare calzini differenti? Possono aggiungere un tocco di allegria e fantasia. Festeggiamo questa giornata giocando con i calzini.

• Colora tutte le coppie di calzini spaiati che puoi formare.

Calzini stesi al filo

Vicino al muro che fa da confine al giardino di Elio, c’è un filo teso tra due pali. Sul filo Elio ha steso le sue tre paia di calzini preferiti: un paio di colore blu a righe, un paio di colore giallo a pallini e un paio tutto di colore rosso.

• Osserva il disegno e colora i calzini di Elio.

Il vento soffia tra i calzini, ne strappa due diversi e li fa volare oltre il muro. Quando Elio tornerà nel suo giardino, cosa potrà trovare appeso al filo?

• Disegna le possibili situazioni; eventualmente, colora sul quaderno.

Calzini nel cassetto

1 Oggi è la giornata dei calzini spaiati: Elio decide di indossare i calzini prendendoli a caso, senza guardare nel cassetto.

• Per ciascuna situazione, scrivi se è possibile, impossibile o certo che Elio peschi due calzini uguali.

• Se pesca una sola volta:

• Se pesca due volte:

• Se pesca quattro volte:

2 Scrivi con quale probabilità Elio, senza guardare nel cassetto, può prendere:

• 1 calzino rosso:

• 1 calzino di qualunque colore:

• 1 calzino che non sia rosso:

• 1 calzino nero:

Ritratti fruttuosi

L’Expo è una mostra che viene organizzata ogni 5 anni e coinvolge Nazioni da tutto il mondo. Ogni volta viene scelto un tema d’interesse generale per tutti i popoli. Per l’Expo avvenuta a Milano nel 2015 il tema scelto fu “Nutrire il pianeta, energia per la vita” e venne realizzata una mascotte fatta di frutta chiamata “Foody”. Il suo autore si ispirò a un pittore del 1500, Giuseppe Arcimboldo, che dipinse di numerosi ritratti fatti tutti con frutta, verdura e altri oggetti. Come Arcimboldo, realizza un ritratto utilizzando la frutta fresca.

Fase 1 • Il pittore

Lavoro individuale e in piccoli gruppi

• Documentati sul pittore Arcimboldo e sulle sue opere più famose. Porta le tue informazioni e le immagini dei ritratti che ti hanno colpito in classe e condividile con i compagni e le compagne.

• Scrivi sul quaderno le informazioni condivise e incolla anche alcune immagine dei quadri.

• Lavora in piccoli gruppi e analizza insieme ai/alle componenti del tuo gruppo questo quadro.

• Che cosa ha usato per rappresentare il naso?

E per la bocca? E per le guance?

• Fai l’elenco di tutta la frutta utilizzata.

• Ha usato frutta di una sola stagione?

Fase 2 • La frutta

Lavoro individuale

• Documentati sulla frutta di stagione e in quale zona viene prodotta.

• Condividi le informazioni che hai trovato con i compagni e le compagne e registra i dati in una tabella come questa.

• Individua la frutta di stagione preferita dalla classe facendo un’indagine.

FRUTTA ZONA DI PRODUZIONE

• Scrivi la domanda adatta.

• Registra le risposte in una tabella come questa e riporta i dati in un diagramma a barre.

FRUTTA NUMERO DELLE PREFERENZE

pesche

• Puoi capire qual è la frutta preferita? Sì No

• Nel quaderno metti in ordine la frutta da quella che ha avuto più preferenze a quella che ha avuto meno preferenze.

Fase 3 • Il progetto

Lavoro in piccoli gruppi

• Disegna con il tuo gruppo il progetto del ritratto che volete realizzare scegliendo la frutta che vi servirà fra quella individuata precedentemente.

• Fate l’elenco della quantità di frutta che vi può servire a realizzare il ritratto.

• Condividete la stima con quella degli altri gruppi e, insieme, stimate la quantità di frutta necessaria per tutti i ritratti.

Fragole € 3,50 al kg conf. da 250 g

Pesche gialle € 1,96 al kg

Melone giallo sfuso € 0,80 al kg

Ciliegie € 3,90 al kg

Fase 4 • La spesa

Lavoro in piccoli gruppi

• Procuratevi dei volantini di alcuni supermercati e portateli in classe: ogni gruppo prenderà un volantino di un supermercato differente per calcolare la spesa totale.

• Insieme ai membri del tuo gruppo ritaglia le immagini della frutta che volete acquistare e incollatele sul quaderno con i relativi prezzi, come nell’esempio.

• Leggete con attenzione i prezzi: in alcuni prodotti il prezzo si riferisce a una confezione, in altri si riferisce a una quantità espressa con una misura (g, kg, ecc.).

• In quale caso il prezzo si riferisce alla confezione?

• In quali casi il costo si riferisce a una quantità?

• Con il tuo gruppo calcola la spesa totale della frutta.

Confrontate le spese dei vari gruppi: avranno tutti lo stesso costo?

Sì No Perché?

• Scegliete quella che, per tutti, ha il costo più conveniente e calcolate il costo per ogni bambino/a.

Fase 5 • Il quadro

Lavoro in piccoli gruppi

• Dopo aver lavato e tagliato a pezzi la frutta, mettetela in delle ciotole a disposizione di tutti e tutte.

• Prendete uno dei piatti scelti per la base e realizzate il vostro quadro. Alla fine del lavoro l’insegnante fotograferà i quadri per realizzare un cartellone da attaccare in classe.

E ora, via: si festeggia mangiando “il ritratto”!

il mio PERCORSO

• Che cosa pensi del lavoro che hai fatto? Mi è piaciuto. Non mi è piaciuto. Non so.

• Pensi sia stato importante lavorare in gruppo? Sì No

• Scrivi tre cose che hai imparato dall’attività che hai appena svolto e che potranno esserti utili per un lavoro successivo.

1.

2.

3.

• In che modo?

• Hai contribuito attivamente al lavoro del gruppo?

• Quali vantaggi o svantaggi hai incontrato?

• Scegli tre aggettivi che, secondo te, descrivono meglio l’attività che hai svolto e sottolineali: divertente, impegnativa, noiosa, semplice, complessa, istruttiva, coinvolgente, inutile, utile, improduttiva.

1 Indica con una X.

Nel numero 9668:

a. i due 6 hanno lo stesso valore posizionale.

b. un 6 rappresenta le centinaia e un 6 rappresenta le unità.

c. il 6 a sinistra indica il numero con valore posizionale minore del 6 a destra.

d. il 6 a sinistra indica il numero con valore posizionale maggiore del 6 a destra.

2 Osserva il numero 30747. Quale delle seguenti affermazioni è esatta?

a. La cifra che indica il numero con maggiore valore posizionale è 7

b. La cifra che indica il numero con minor valore posizionale è 0.

c. La cifra che indica il numero con maggior valore posizionale è 3.

d. Le due cifre uguali indicano numeri con lo stesso valore posizionale.

3 Quale numero corrisponde a 300 + 80000 + 60 + 300000 + 7000?

a. 38637 b. 387361 c. 83736 d. 387360

4 Che numero è quello formato da 4 u + 13 h + 6 da + 7 uk?

a. 8364 b. 71364 c. 74364 d. 7139

5 Che numero è quello formato da 25 h + 12 da + 3 u?

a. 25312 b. 2623 c. 25123 d. 2515

6 Quale equivalenza NON è corretta?

a. 24 da = 240 u

b. 5 uk = 500 da

c. 130 da = 13 h

d. 35 da = 3500 u

7 Quale scrittura del numero 50 NON è corretta?

a. (5 x 2) x 5

b. (5 x 5) x 2

c. 100 : 2

d. 20 + 20 + 5

TAPPA COMPETENZE

1 Colora il numero che manca per completare ciascuna operazione e trascrivilo.

a. ................ + 24 = 50 b. ................ x 7 = 63 c. 68 – ................ = 45 d. ................ : 8 = 6

2 Indica con una X se ciascuna uguaglianza è vera (V ) o falsa (F).

56 : 1 = 56 V F

43 x 1 = 1 V F

27 – 0 = 0 – 27 V F 15 + 1 = 1 + 15 V F

13 = 1 x 13 V F

24 x 0 = 24 V F

18 : 0 = 18 V F

72 – 0 = 72 V F

3 Completa le operazioni scrivendo i numeri che mancano.

a. 24 x = 240

............... x 100 = 800

1000 x 6 =

b. 27 x = 2700

............... x 1000 = 34000 x 12 = 120

c. 340 : 10 = ............... : 10 = 63 : 1000 = 5

4 Inserisci i numeri che mancano per rendere vere le uguaglianze.

d. 2400 : = 240

............... : 100 = 41

6300 : = 63

1 Quale figura non è stata frazionata? Colora la lettera corrispondente.

a. c.

b. d.

2 In quali figure sono stati colorati correttamente i 2 5 ? Colora le lettere corrispondenti.

3 In quale caso sono stati colorati correttamente 3 6 ? Colora la lettera corrispondente.

4 Queste caramelle al limone sono 1 5 delle caramelle che ci sono nel sacchetto. Indica con una X quante caramelle ci sono in tutto nel sacchetto.

a. 10 b. 15 c. 18 d. 5

5 Luca ha letto i 4 6 di un libro. Quanto gli manca, in frazione, per terminarlo? Indica con una X.

a. 5 6 c. 2 6

b. 1 6 d. 3 6

1 Quale pesce è più lungo? Aiutati a stabilirlo con il righello disegnato sotto.

2 Indica quanti euro ci sono nel salvadanaio.

3 Che cosa puoi comprare con i soldi dell’esercizio 2?

a. Un pezzo di pizza da 3,80 euro e 1 lattina di aranciata da 2,50 euro.

a. 5,9

b. 6,30

c. 6,03

d. 6,01

b. Un album di figurine da 4,70 euro e 1 pacchetto di figurine da 1,50 euro.

c. Due gelati da 2,70 e 1 bottiglietta d’acqua da 1 euro.

d. Una crêpe da 3 euro e un gelato da 2,80 euro.

4 Carlo, Liam e Anna hanno trascorso una giornata in piscina. Hanno speso 48 euro per l’entrata e 12 euro per le bibite. Vogliono dividere la spesa in parti uguali. Quanto paga ciascuno?

a. 15 b. 20 c. 21 d. 30

Competenze L’alunno/L’alunna è in grado di utilizzare numeri decimali, frazioni e percentuali per descrivere situazioni quotidiane.

TAPPA COMPETENZE

1 Risolvi.

Nicola prepara un dolce seguendo questa ricetta.

• 2,8 hg farina

• 1,8 hg zucchero

• 150 g di burro fuso

• 1 hg cioccolato fondente

• 2 uova

• 1 pizzico vanillina

V erso l’Invalsi

Siccome non ha la bilancia per pesare gli alimenti, cerca in Internet quanto peso può contenere 1 cucchiaio da minestra e trova queste informazioni:

1 cucchiaio da minestra corrisponde a:

• 50 g di burro fuso

• 15 g zucchero

• 20 g farina

• 20 g cioccolato fondente

Aiuta Nicola a riscrivere i primi 4 ingredienti della ricetta in cucchiai. .............. cucchiai di farina .............. cucchiai di burro cucchiai di zucchero cucchiai di cioccolato fondente

2 Per ciascun intervallo di tempo, colora il rettangolo che contiene la scrittura dello stesso intervallo.

1 4 di h 150 min 15 min 15 h

1 h e 3 4 105 min 134 min 90 sec

2 4 di h 80 min 1 h 30 min

1 min e 1

2 60 s 90 s 75 s

1 60 di h 60 min 1 s 1 min

4 Completa le successioni.

3 Indica con una X quale delle seguenti equivalenze è stata eseguita correttamente.

a. 7 m = 0,007 km

b. 87 hm = 8,7 dam

c. 0,4 km = 40 hm

d. 12,3 dam = 123 dm

e. 8 m = 800 cm

f. 0,4 hm = 0,004 km

g. 300 cm = 3 m

h. 44 dam = 4,4 km

8 <l d<l c<l m<l

2 h<l ..................... da<l ..................... <l ..................... d<l

5 m<l c<l d<l <l

1 d<l <l da<l h<l

1 Disegna quanto richiesto usando lo strumento che ritieni opportuno.

• una retta parallela alla retta a

• una retta perpendicolare alla retta c

• una retta incidente alla retta b

a

b d

• una retta incidente e perpendicolare alla retta d c

2 Osserva le immagini e rispondi.

Osserva gli angoli colorati: come si chiamano?

In quale caso la stella si trova:

• nell’angolo?

• sul lato dell’angolo?

• sul vertice dell’angolo?

• C’è un caso in cui la stella è fuori dall’angolo? Sì No

3 Indica con una X se le affermazioni sono vere (V ) o false (F). Sul quaderno, correggi quelle false.

a. L’angolo piatto è il doppio dell’angolo retto. V F

b. L’angolo ottuso è minore dell’angolo piatto. V F

c. L’angolo retto è la metà dell’angolo giro. V F

d. L’angolo retto è il doppio dell’angolo acuto. V F

e. L’angolo giro è il doppio dell’angolo ottuso. V F

f. L’angolo acuto è maggiore dell’angolo ottuso. V F

4 Laura voleva disegnare solo angoli da 65°. Ci sarà riuscita? Verifica e correggi gli eventuali errori.

A B C D A B C D

1 Giulio ha piegato dei fogli, ha ritagliato delle figure e poi li ha riaperti. Collega ciascuna figura con il foglio dal quale è stata tagliata.

C D TAPPA COMPETENZE

2 Filippo ha scelto la combinazione della sua cassaforte: al posto dei numeri ha scritto di quanti gradi va ruotata ogni volta la freccia in senso antiorario.

Leggi i gradi, disegna la rotazione della freccia e scrivi il numero.

La combinazione della cassaforte di Filippo è: –

Competenze L’alunno/L’alunna è in grado di riconoscere figure ruotate, traslate e riflesse.

A B V erso l’Invalsi 153

Le figure traslate sono:

a. A e B

b. A e C

c. B e C

d. D e B

TAPPA COMPETENZE V erso l’Invalsi

1 Quanti triangoli mancano per completare la figura?

a. 18

b. 15

c. 20

d. 30

2 Indica con una X quale pentagono è diviso in modo da ottenere tre triangoli isosceli.

a. b. c. d.

3 Giulia ha ricevuto in regalo il tangram e si diverte a fare delle costruzioni con i pezzi. Indica con una X che cosa ha usato per costruire queste figure.

a. Tutti i pezzi.

b. Solo alcuni pezzi.

c. Solo i triangoli.

d. Tutti i pezzi.

e. Solo alcuni pezzi.

f. Solo i triangoli.

g. Tutti i pezzi.

h. Solo alcuni pezzi.

i. Solo i triangoli.

1 Alessandro per la festa del suo compleanno ha

invitato i compagni e le compagne di classe. Per merenda decide di offrire il gelato, ma è indeciso sui gusti da comprare, così chiede a ciascun compagno e ciascuna compagna qual è il suo gusto preferito. Queste sono le risposte.

Crema X X

Fragola X X

Cioccolato X X X

Limone X

Panna X X X

Indica con una X il grafico che rappresenta le risposte ottenute.

a.

b.

Legenda:

X = 2 bambini/e

2 Indica con una X.

1. L’oggetto dell’indagine è:

a. i gusti di gelato preferiti da Alessandro.

b. i gusti di gelato più venduti.

c. i gusti di gelato preferiti dai compagni di Alessandro.

2. Quanti sono i bambini intervistati?

a. 13

b. 22

c. 15

Panna

Crema

Fragola

Cioccolato

Limone

01234567

3. Quale gusto ha ricevuto il doppio delle preferenze rispetto al limone?

a. Panna. b. Fragola. c. Crema.

4. Alessandro decide di comprare solo due gusti: quali gusti gli conviene comprare per fare contenti i suoi compagni?

a. Cioccolato e panna.

b. Fragola e cioccolato.

c. Fragola e panna.

a. È più probabile che esca una pallina verde di una gialla.

b. È impossibile che esca una pallina rossa.

c. È meno probabile che esca una pallina blu di una verde.

d. C’è il doppio della possibilità che esca una pallina blu di una gialla.

VERO FALSO

3 Indica con una X se le affermazioni sono vere (V ) o false (F).

NUMERI

A1. Scrivi i numeri al posto giusto.

1784 31460 6542 98521

a. Numero cha ha la cifra 6 al posto delle migliaia:

b. Numero che ha la cifra 8 al posto delle decine:

c. Numero che ha la cifra 1 al posto delle unità:

d. Numero che ha la cifra 4 al posto delle centinaia:

A2. A quale numero si avvicina di più il numero 1564?

a. 1500 b. 1570 c. 1580 d. 1560

A3. Quale espressione esprime la frase: “È la somma di 8 con il triplo di 9”?

a. 8 + 9

b. 8 + 3 x 3

c. 8 x 9 x 3

d. 8 + 3 x 9

A4. In quali bandiere il rettangolo colorato rappresenta 1 4 di tutta la bandiera?

A B C D

a. Nelle bandiere B e C.

b. Nelle bandiere B, C e D.

c. Nelle bandiere A e B.

d. Nelle bandiere A, B e D.

MISURA

B1. Lisa ha mangiato 3 palline di gelato, suo fratello Marco invece ne ha mangiate il doppio. Quanti grammi di gelato ha mangiato ciascun bambino?

Lisa:

Marco:

B2. Michela vuole comprare la bottiglia piccola di aranciata, ma sulla confezione non si legge il prezzo. Accanto c’è la bottiglia da 1,5 litri con il prezzo. Come può Michela capire quanto costerà la bottiglia più piccola?

1,5 <l

Spiega come hai trovato la risposta:

B3. Caterina torna da scuola e guarda l’orologio. Impiega 15 minuti per fare merenda, poi si siede sul divano e guarda una puntata del suo documentario preferito, che dura 20 minuti. Finita la puntata, parte per andare all’allenamento di pattinaggio. A che ora parte da casa?

STATISTICA

C1. Giulia è più vecchia di Asia e Martina è più giovane di Giulia. Quale delle seguenti frasi è sicuramente vera?

a. Asia è la più giovane.

b. Giulia è più vecchia di tutte.

c. Martina è più giovane di Asia.

d. Martina è più vecchia di Asia.

C2. L’allenatore di pallanuoto ha diviso i nuotatori della squadra in due gruppi. Ogni componente del gruppo tirerà a turno in porta. I tiri saranno ripetuti tre volte e ogni giro viene segnata la somma dei gol. Vincerà la squadra che riuscirà a fare una media di 3 gol. Osserva i punteggi.

1° gruppo

1° giro 2° giro 3° giro

5 2

2° gruppo

1° giro 2° giro 3° giro 3 4

Che punteggio dovrà fare ciascuno dei due gruppi al terzo tiro per riuscire ad avere la media di 3 punti?

a. 3

b. 1

c. 2

C3. Carla e Paolo giocano a pari e dispari. Carla sceglie pari e Paolo dispari. Buttano giù in contemporanea una mano ciascuno e, senza usare lo zero, contano le dita. Uno dei due bambini ha maggiore probabilità di vincere? Sì No

Motiva la tua risposta:

Le indicano gli esercizi graduati su livelli

I NUMERI NATURALI

160 Valore posizionale

162 Valore posizionale

164 Composizione e scomposizione dei numeri /

166 Confronto fra numeri /

168 Numeri approssimati /

170 Altri modi per scrivere i numeri /

172 Problemi con i numeri naturali /

OPERARE CON I NUMERI NATURALI

174 Addizione: proprietà e calcolo /

176 Sottrazione: proprietà e calcolo /

178 Addizione e sottrazione operazioni inverse /

180 Moltiplicazione: proprietà e calcolo /

182 Divisione: proprietà e calcolo /

184 Moltiplicazione e divisione operazioni inverse /

186 Multipli e divisori /

188 Moltiplicare e dividere per 10, 100 e 1 000 /

190 Problemi /

LE FRAZIONI

192 Unità frazionaria

194 Unità frazionaria

196 Oltre l’unità frazionaria /

198 Frazioni maggiori, uguali o minori di 1 /

199 Frazioni complementari /

200 Confronto tra frazioni /

202 Frazioni equivalenti /

204 La frazione di un numero /

208 Esercizi con le frazioni /

206 Dalla frazione all’intero /

I NUMERI DECIMALI

210 Dalla frazione ai numeri /

211 Modi diversi di scrivere i numeri /

212 Linea dei numeri /

214 Oltre l’unità /

216 Diversa scrittura, ma stesso valore /

217 Operazioni con i numeri decimali /

218 Decimali ed euro /

219 Costo unitario/Costo totale /

LA MISURA

220 Tutto può essere misurato? /

222 Le misure di lunghezza /

223 Il metro e i suoi sottomultipli /

224 Il metro e i suoi multipli /

225 Problemi /

226 Misure di massa

228 Misure di massa

230 Le bilance /

231 Peso netto, peso lordo e tara /

232 Misure di capacità /

234 Misure di tempo /

236 Problemi /

238 Gioca con la logica – Ra-Giocando

240 Gioca con la logica – Problemi

LINEE E ANGOLI

242 Rette, semirette e segmenti /

244 L’angolo in Geometria

246 L’angolo in Geometria

248 Classificare gli angoli /

250 Confrontare gli angoli /

252 Misurare gli angoli /

254 La simmetria

256 La simmetria

258 La traslazione /

260 La rotazione /

PERIMETRO E SUPERFICIE

262 Le figure piane /

264 Perimetro / 266 Superficie /

268 Figure isoperimetriche ed equivalenti /

270 Figure equicomposte /

272 Triangoli /

274 Triangoli /

276 Quadrilateri

278 Quadrilateri

DATI E PREVISIONI

280 L’indagine /

282 I grafici /

284 La media /

285 La moda /

286 La probabilità /

COME COSTRUIRE UN VENTAGLIO

288 Istruzioni per costruire il ventaglio

Valore posizionale

Riscrivi i numeri separando le cifre che appartengono alla classe delle migliaia dalle cifre che appartengono alla classe delle unità semplici. Poi scrivi i numeri in lettere.

5364

734

604237

4120

918

200436

36945

Riscrivi i numeri in cifre e separa con uno spazio la classe delle migliaia da quella delle unità semplici. tredicimilaseicentodieci

diecimilaseicentotrenta trecentodiecimilaquattrocentonove novantaquattromilatrecentodieci tremilatrecentotrentatré

trentamilatrecento

In ciascuna terna di numeri, indica con una X i due nei quali la cifra delle dak è la stessa di

Per ciascun numero, indica con una X la scrittura corretta.

6

In ciascun numero ci sono tre cifre uguali: circonda di blu quella con minor valore posizionale e di giallo quella con maggior valore posizionale.

13303

909 912

Per ciascun gruppo di cifre, forma il numero maggiore e il numero minore possibile.

7

Inserisci i numeri nella tabella sotto. Poi scrivi ciascun numero formato.

a. 9 dak + 2 uk + 1 h + 6 da + 4 u

b. 2 hk + 4 uk + 7 h + 1 da + 6 u

c. 79 u + 4 da + 3 uk + 2 dak + 6 h

dak decine di migliaia

a.

b.

c.

d.

e.

f.

d. 2 h + 3 u + 6 uk + 2 da + 6 hk

e. 5 da + 1 uk + 3 hk + 2 h + 6 dak

f. 6 uk + 2 da + 5 u + 7 dak

uk unità di migliaia ......................... ......................... ......................... ......................... ......................... .........................

h centinaia da decine u unità ..............................................

Scrivi in unità il valore delle cifre scritte in blu, come nell’esempio.

Obiettivo di apprendimento Riconoscere il valore posizionale delle cifre. Comporre e scomporre un numero, comprendendo il valore posizionale delle cifre.

Valore posizionale

Dato il numero 2876, scrivi il numero che ottieni di volta in volta se…

• inverti la cifra delle unità con quella delle centinaia

• inverti la cifra delle migliaia con quella delle decine

• inverti la cifra delle unità con quella delle migliaia

Riscrivi in ordine crescente i tre numeri che hai ottenuto nell’esercizio precedente.

Usa tutte le cifre per scrivere il numero pari più piccolo e il numero pari più grande.

Numero pari più piccolo

Numero pari più grande

Usa sempre tutte le cifre per formare sei numeri dispari. 2

Cambia di posto alla cifra 3 per formare numeri maggiori di quello dato, come negli esempi.

2130 2301; 2310; 3210

12123

42231

214350

123071

Cambia di posto alla cifra 6 per formare i numeri minori di quello dato, come negli esempi.

4652 4562; 4526

765

5674

76318

21796

7 8

Completa le frasi.

a. Il numero più grande con quattro cifre uguali è ...................................................

b. Il numero più piccolo con quattro cifre uguali è

c. Il numero più piccolo con quattro cifre diverse è

d. Il numero più grande con quattro cifre diverse è

Qual è il biglietto vincente della lotteria “Amici pelosi a quattro zampe”?

9 10

Segui le istruzioni, completa e circonda il biglietto vincente.

a. Il numero del biglietto è formato da cinque cifre, quindi può essere quello col numero:

b.

c. Si tratta di un numero pari:

d.

e. La cifra 5 occupa il posto delle uk:

f.

g. La cifra delle dak è 8:

h.

Completa le uguaglianze.

Composizione e scomposizione dei numeri

Completa le tabelle, come nell’esempio. 1

3 uk 4 h 7 da 6 u

3 x 1000 4 x 100

3000 tremila

Completa la scomposizione dei numeri. 2

3476

3 uk + 4 h + 7 da + 6 u

(3 x 1000) + (4 x 100) + 3000 + tremila

Inserisci ciascun addendo nella tabella. Poi esegui la somma.

3 u + 8 uk + 6 h + 4 dak + 2 da =

Classe delle migliaia k

Classe delle unità u

hk dak uk h da u

3 Prima trasforma tutti i numeri in unità, poi esegui le addizioni, come nell’esempio.

6 hk + 3 da + 4 h + 8 u + 2 dak + 1 uk =

Classe delle migliaia k

Classe delle unità u

hk dak uk h da u

4

5 u + 2 dak + 1 h + 3 da + 6 uk = 5 + 20000 + 100 + 30 + 6000 = 26 135

2 h + 5 dak + 3 u + 6 da + 7 uk = ................................................................................................................................................

35 u + 4 h + 3 da + 8 uk =

9 da + 3 uk + 1 u + 7 dak =

12 da + 8 u + 8 h + 2 uk =

7 uk + 3 da + 8 h + 4 dak + 2 hk = ..............................................................................................................................................

6 u + 24 h + 8 da + 3 uk =

Quale scomposizione corrisponde al numero 364069? Indicala con una X, poi esegui i calcoli.

(3 x 100000) + (6 x 10000) + (4 x 1000) + (6 x 100) + (9 x 1)

(3 x 10000) + (6 x 10000) + (4 x 1000) + (6 x 10) + (9 x 1)

(3 x 100000) + (6 x 10000) + (4 x 1000) + (6 x 10) + (9 x 1)

(3 x 100000) + (6 x 1000) + (4 x 100) + (6 x 10) + (9 x 1

Obiettivo di apprendimento Riconoscere il valore posizionale delle cifre. Comporre e scomporre un numero, comprendendo il valore posizionale delle cifre.

Confronto fra numeri

Completa con i numeri che mancano.

Confronta ciascuna coppia di numeri inserendo il simbolo giusto, come nell’esempio.

Utilizza ogni volta tutte e quattro le cifre per scrivere i numeri possibili. Poi circonda di giallo il numero maggiore e di azzurro il numero minore.

Riscrivi in ordine crescente (dal minore maggiore) i numeri ottenuti nell’esercizio precedente.

Ordina i seguenti valori dal maggiore al minore, come nell’esempio.

9 u 2 da 6 dak 3 h 6 dak > 3 h > 2 da > 9 u

6 hk 9 u 7 uk 4 h > > >

5 da 38 h 64 dak 2 uk > > >

9 u 25 da 31 uk 12 h > > >

34 h 35 u 2 da 2 uk ......................... > ......................... > ......................... > .........................

Scrivi un numero che renda vere le relazioni.

<

La tabella riporta i dati dei visitatori del “Parco avventure nel bosco”.

Indica con una X se ciascuna affermazione è vera ( V ) o falsa (

2019

2021

2022

2023

Affermazione V F

Il numero dei visitatori adulti è sempre aumentato di anno in anno.

Il numero di bambini e bambine è sempre aumentato di anno in anno.

Il 2018 è l’anno in cui ci sono stati meno visitatori fra i bambini.

Il 2017 è l’anno in cui ci sono stati più visitatori fra gli adulti.

Ogni anno ci sono stati più visitatori adulti che bambini.

ciascun numero sulla retta, poi riscrivilo approssimato alle decine più vicine, come nell’esempio.

Approssima alle centinaia i numeri che indicano le altezze di alcuni monti italiani, poi indica con una X se hai approssimato per eccesso o per difetto.

Approssimazione

Monte Altezza Numero approssimato per difetto per eccesso

Monte Bianco 4806 m

Monte Rosa 4634 m

Monte Cevedale 3769 m

Marmolada 3343 m

Monte Corvo 2623 m

Etna 3357 m

Esegui le operazioni, poi approssima il numero ottenuto come richiesto. Se necessario, aiutati con la calcolatrice. Se non puoi eseguire una approssimazione, lascia vuoti gli spazi della tabella.

Operazione Numero ottenuto

3100 – 759

1694 : 2

45 x 63

3650 + 521

12897 – 849

86945 : 5

526 x 87

Approssima alle centinaia Approssima alle decine

Approssima alle unità di migliaia

Altri modi per scrivere i numeri

Colora nello stesso modo i riquadri che contengono lo stesso numero.

4 x 5

– 25 6 x 6 25 – 10

Indica con una X se le seguenti uguaglianze sono vere ( V ) o false (F).

77 : 11 = 17 – 10 V F

25 x 2 = 50 : 2 V F

60 – 20 = 5 x 8 V F

7 x 3 = 41 – 10 V F

Completa le uguaglianze.

50 – 15 = 32 +

x 2 = 50 : 2 V F

– 40 = 48 : 8 V F

– 25 = 5 x 10 V F

+ 23 = 70 – 14 V F

Scegli tre numeri e due operazioni differenti per formare ciascun numero, come nell’esempio.

60 : 3 + 8

28 =

= 50 – 30 + 8 120 =

7

Collega ciascuna frase alla sua scrittura in linguaggio matematico.

la somma di 15 e 9 15 – 9 + 2

il prodotto di 9 e 2 15 – 9

a 15 sottraggo 9 15 + 9 – 2

aggiungo 2 alla differenza fra 15 e 9 9 x 2

sottraggo 2 alla somma di 15 e 9 15 + 9

Scrivi a parole le frasi matematiche.

63 – 12

10 + 4 – 3

5 x 2 + 6

3 x 6 + 2 x 4

7 + 18 : 2

Luigi è riuscito a formare il numero 66 usando cinque volte la cifra 2 e la moltiplicazione e l’addizione come operazioni. Ha fatto così: 2 x 22 + 22 = 66. Prova anche tu come Luigi.

a. Forma il numero 2 usando sei volte la cifra 3 e la somma e la divisione come operazioni.

33 +

b. Forma il 20 usando cinque volte la cifra 4, la moltiplicazione e la sottrazione.

8

c. Forma il 40 usando cinque volte la cifra 2, la moltiplicazione e la sottrazione.

d. Forma il 10 usando quattro volte la cifra 3, la sottrazione e la divisione.

Devi mettere 5 litri di acqua in un recipiente, ma hai solo un secchio da 7 litri e uno da 3 litri. Spiega come puoi fare. C’è solo un modo?

9

Aggiungi o togli pesi da ciascuna bilancia perché torni in equilibrio, cioè abbia lo stesso peso su entrambi i piatti.

10 kg

20 kg

30 kg

Problemi con i numeri naturali

Risolvi sul quaderno.

a. Il papà di Luca deve comprare un’auto nuova e sfogliando una rivista di auto ha visto questi modelli:

Sport

€ 19050

Elettrica new

€ 14350

Utilitaria

€ 14650

Monovolume

€ 14290

Berlina

€ 11390

Fuori strada

€ 18600

Se il padre di Luca ha a disposizione per l’acquisto 14500 euro, potrà comprare una delle auto?

Fra quali modelli potrà scegliere?

Spiega come hai trovato la risposta.

b. Andrea è andato a trovare José. Arrivato a casa dell’amico, prende la catena col lucchetto per legare la bici, ma non ricorda la combinazione del lucchetto.

Ricorda solo che:

• è un numero di tre cifre;

• la prima cifra è 9;

• le altre sono due cifre dispari tra 0 e 5 (compresi).

Quanti tentativi potrà fare al massimo Andrea prima di trovare la combinazione giusta?

Spiega come hai trovato la risposta.

c. Silvana vorrebbe usare il computer della sorella

Lina, ma non ricorda la password.

Ricorda solo che:

• inizia con le consonanti del nome della sorella scritte in stampato maiuscolo;

• poi segue un numero di tre cifre;

• il numero è formato dalle cifre 3, 5, 7;

• non ci sono cifre ripetute.

Quale potrebbe essere la password del computer?

Ce n’è solo una?

Silvana riuscirà a usare il computer?

d. Il pasticciere ha preparato 4 torte di compleanno. Deve mettere le candeline per indicare il numero degli anni che compiono i festeggiati. Cerca nel cassetto e trova le candeline che gli servono.

Quali candeline metterà sopra a ciascuna torta sapendo che:

• per ogni torta servono due candeline;

• dovrà formare numeri compresi tra 64 e 85;

• non ci sono torte con numeri consecutivi;

• potrà usare ogni candelina una sola volta.

Puoi sapere con sicurezza quali candeline metterà il pasticciere sopra a ciascuna torta? Perché?

e. Clara ha vinto la gara di tiro alle freccette totalizzando 39 punti con quattro lanci. Qui sotto è disegnato il bersaglio: quali settori del bersaglio può aver colpito Clara?

f. Nella partita di basket, Manuel ha totalizzato 12 punti. I canestri possono valere 1, 2 o 3 punti. Con quali canestri Manuel è riuscito a fare 12 punti? Trova il maggior numero di soluzioni possibili.

g. Gaia sta sistemando in due scatole grandi e tre piccole i 30 vestiti da bambola che possiede. Nelle due scatole grandi ha messo lo stesso numero di vestiti e vuole fare la stessa cosa anche con le tre scatole piccole. In quali modi può sistemare i vestiti? Li può sistemare in un solo modo?

h. Karim ha tre album di figurine: l’album degli animali acquatici, quello degli animali terrestri e quello dei volatili. È curioso di sapere quante figurine possiede e decide di contarle.

Ogni album è formato da 10 pagine e in ogni pagina ci sono 10 figurine da attaccare.

Karim ha completato tutto l’album dei volatili, ha completato 6 pagine dell’album degli animali terrestri, 3 pagine di quello degli animali acquatici e gli sono rimasti 15 doppioni.

Quante figurine ha in tutto Karim, considerando sia i doppioni che quelle attaccate?

Spiega come hai trovato la risposta.

Addizione: proprietà e calcolo

Esegui le addizioni sul quaderno spiegando le azioni eseguite in ciascun passaggio, come nell’esempio.

63 + 45 =

Scomponi i numeri 60 + 30 + 40 + 5 =

Cambia l’ordine degli addendi 60 + 40 + 03 + 5 =

Calcola associando agli addendi 100 + 8 = 108

Quali proprietà hai applicato?

a. 25 + 34 =

18 + 69 =

43 + 72 =

57 + 34 =

b. 62 + 74 =

64 + 39 =

43 + 56 =

63 + 52 =

Sul quaderno, semplifica i calcoli cercando le coppie del 10 o del 100 dove è possibile, come negli esempi.

2 + 6 + 8 + 4 + 3 = 24 + 27 + 73 + 82 =

(2 + 8) + (6 + 4) + 3 = 10 + 10 + 3 = 23 (24 + 82) + (27 + 73) = 106 + 100 = 206

8 + 5 + 3 + 5 + 7 = 30 + 40 + 60 + 70 = 81 + 53 + 19 + 52 =

1 + 6 + 4 + 9 + 4 = 20 + 90 + 10 + 80 = 75 + 67 + 34 + 18 + 33 =

4 + 0 + 9 + 5 + 1 = 60 + 50 + 10 + 90 + 40 = 62 + 44 + 38 + 11 + 56 =

Quali proprietà hai applicato?

Riscrivi uno dei due addendi, per arrivare alla decina successiva, poi calcola, come negli esempi.

6 + 8 =

4 + 2 + 8 = 4 + 10 = 14

+ 24 =

+ 3 + 21 = 50 + 21 = 71

a. 9 + 8 = b. 34 + 12 = c. 14 + 28 = d. 66 + 19 =

+ 35 =

+ 29 =

+ 16 =

Sul quaderno, scomponi i numeri 11, 22, 33 e 44 per semplificare i calcoli, come negli esempi.

23 + 11 = 23 + 10 + 1 = 33 + 1 = 34

23 + 22 = 23 + 20 + 2 = 43 + 2 = 45

a. 65 + 11 = b. 36 + 22 = c. 19 + 33 = d. 24 + 44 =

47 + 11 = 57 + 22 = 64 + 33 = 18 + 44 =

Sul quaderno, scomponi tutti gli addendi per semplificare i calcoli, come nell’esempio.

36 + 18 + 5 = (30 + 6) + (10 + 8) + 5 = (30 + 10) + (6 + 8 + 5) = 40 + 19 = 59

a. 29 + 37 + 2 + 15 =

b. 125 + 36 + 230 =

c. 2324 + 4251 + 35 =

37 + 9 + 63 + 41 = 305 + 365 + 24 = 5104 + 654 + 3 284 =

Quali simboli puoi mettere nell’altro piatto perché la bilancia sia in equilibrio?

a.

b.

6 Individua il valore numerico di ciascuna lettera e scrivi il procedimento per trovarlo.

= 600 = 300 = 150 = 20 = 10 = 5

c.

..........................

d.

7

L + L + L = 18 L =

M + M + L = 22 H =

L + M + H = 16 M =

H + H + A = 14 A =

8

Applica la strategia per facilitare i calcoli e spiegala, come negli esempi.

234 + 19 = (234 + 20) – 1 = 254 – 1 = 253

403 + 19 =

78 + 29 =

114 + 99 =

86 + 99 = ................................................................................................

325 + 99 =

9

142 + 299 = (142 + 300) – 1 = 442 – 1 = 441

156 + 299 =

304 + 299 =

412 + 399 =

206 + 399 = ................................................................................................

1450 + 499 =

Nei riquadri ci sono addizioni con quattro numeri consecutivi. Osserva e rispondi.

• In ciascun riquadro somma il 1° addendo con il 4° addendo e il 2° addendo con il 3°

• Che cosa noti?

• Verifica se questa proprietà accade anche per altre somme da te inventate.

• Puoi dire che vale sempre? Sì No

Trova due numeri consecutivi che, sommati, formino i numeri assegnati, come nell’esempio.

Obiettivo di apprendimento Eseguire addizioni con i numeri naturali usando strategie di calcolo. Comporre numeri naturali.

Sottrazione: proprietà e calcolo

Sostituisci ai simboli i numeri corrispondenti, poi esegui le sottrazioni, come nell’esempio.

= 600 = 200 = 50 = 20 = 10 = 5

a. – = c. – = – = – =

600 (50 + 10) 540

b. – = d. – = – = – =

Semplifica le sottrazioni applicando la proprietà invariantiva.

a. Usa l’addizione affinché il sottraendo arrivi alla decina superiore, come nell’esempio.

81 – 36 = (81 + 4) – (36 + 4) = 85 – 40 = 45

72 – 34 = .................................................................................................................

65 – 48 =

93 – 67 = .................................................................................................................

81 – 52 =

292 – 56 = 373 – 229 =

b. Usa la sottrazione affinché il sottraendo arrivi alla decina precedente, come nell’esempio.

74 – 26 = (74 – 6) – (26 – 6) = 68 – 20 = 48

64 – 12 = 57 – 35 =

168 – 47 = 285 – 163 =

268 – 59 = 329 – 115 =

c. Usa una volta la sottrazione e una volta l’addizione, come nell’esempio.

54 – 37 = (54 – 7) – (37 – 7) = 47 – 30 = 17; (54 + 3) – (37 + 3) = 57 – 40 = 17

38 – 23 = ;

71 – 46 = .................................................................................................................; .........................................................................................................................................................

295 – 59 = ;

254 – 41 = ;

Quale numero ti conviene utilizzare per semplificare ciascuna sottrazione applicando la proprietà invariantiva? Colora la casella. –

43 – 15

76 – 34

95 – 37

66 – 32

81 – 36

53 – 25

91 – 58

49 – 36

Ciascun calcolo è stato semplificato applicando la proprietà invariantiva. Scrivi il numero che manca ed esegui l’operazione.

56 – 23 = (56 – ) – (23 – ) = 53 – 20 =

72 – 28 = (72 + ) – (28 + ) = 74 – 30 =

94 – 56 = (94 – ) – (56 – ) = 88 – 50 =

83 – 65 = (83 + ) – (65 + ) = 88 – 70 =

Usa una sola volta le cifre di ciascun gruppo per inventare quattro sottrazioni, come nell’esempio. Scrivile ed esegui i calcoli in colonna o a mente.

Sottrazioni possibili: 382 – 57; 823 – 75; 782 – 35; 532 – 87

Completa le sottrazioni inserendo le cifre che mancano.

Addizione e sottrazione operazioni inverse

Per ciascuna tabella, scrivi in linguaggio matematico il percorso indicato dalle frecce, sia per l’andata sia per il ritorno, come nell’esempio.

In ciascuna tabella, inventa un percorso con le frecce (vedi esercizio 1), poi scrivi in linguaggio matematico i passi fatti.

Tabella

Ritorno:

Tabella B

Andata:

Ritorno:

Tabella C

Andata:

Ritorno: .........................................................................................................................................................................................................................................................................................................

In ciascuna nuvola, scrivi il numero mancante, poi indica quale operazione hai eseguito per scoprirlo.

Le operazioni non sono complete: inserisci i numeri che mancano.

Operare con i numeri naturali

Moltiplicazione: proprietà e calcolo

Completa le tabelle scrivendo le coppie di numeri il cui prodotto è il numero indicato, come nell’esempio.

Sul quaderno, esegui le moltiplicazioni associando due numeri a tua scelta, come nell’esempio. 2

Sul quaderno, scomponi i fattori applicando la proprietà distributiva, inserisci i numeri in una tabella, poi calcola, come nell’esempio.

Proprietà distributiva 14 x 35 = (10 + 4) x (30 + 5)

Procedimento per il calcolo 10 x

In ciascuna moltiplicazione, circonda i due fattori che ti conviene associare per velocizzare i calcoli ed eseguili, come nell’esempio.

5

6 7 8

Completa le richieste usando, anche più volte, i numeri della tabella. Come operatore usa solo la moltiplicazione.

5 50 20 4

10 0 2 18

1 25 13 10

Operare con i numeri naturali

a. Le coppie che come prodotto formano il numero 50 sono: e ; e ; e

b. Le coppie che formano come prodotto il numero 100 sono: e ; e ; e .; e

c. Colora i numeri che hai utilizzato per completare le richieste a. e b.

d. Quali numeri non hai utilizzato?

Individua due numeri la cui somma è 9 e il cui prodotto è 18, poi spiega come hai trovato la risposta.

+ = 9 x = 18

Individua due numeri il cui prodotto è 35 e la cui somma è 12, poi spiega come hai trovato la risposta.

x = 35 + = 12

Completa gli schemi rispettando questa regola: il numero che sta nel cerchio in alto è il prodotto dei numeri che stanno nei cerchi in basso.

Sul quaderno, esegui le moltiplicazioni in

Divisione: proprietà e calcolo

Completa le tabelle.

Confronta ciascuna coppia di operazioni inserendo il simbolo giusto, come nell’esempio.

a. 14 : 7 < 8 : 2

: 9 48 : 2

16 : 8 24 : 6

25 : 5 9 : 3 28 : 4 100 : 25 54 : 6 72 : 9

56 : 8 35 : 5

27 : 3 24 : 12

: 15

: 2

: 5 36 : 6

: 6

: 7

Semplifica le divisioni applicando la proprietà invariantiva, come nell’esempio. Risolvi sul quaderno.

480 : 40 = (480 : 10) : (40 : 10) = 48 : 4 = 12

630 : 30 = 9000 : 300 = 240000 : 2 000 =

6400 : 800 = 7200 : 900 = 54000 : 60 =

Calcola la metà della metà, come nell’esempio. Risolvi sul quaderno.

64 : 8 = Calcolo la metà (64 : 2) : (8 : 2) = 32 : 4 e poi ancora la metà (32 : 2) : (4 : 2) = 16 : 2 = 8

80 : 16 =

600 : 20 = 420 : 60 =

48 : 8 = 800 : 160 = 360 : 12 =

Calcola sul quaderno usando la danda lunga con la tabellina scritta accanto.

Prima scomponi il dividendo della divisione (proprietà distributiva), poi calcola, come nell’esempio.

39 : 3 = (30 + 9) : 3 = (30 : 3) + (9 : 3) = 10 + 3 = .................

a. 46 : 2 =

b. 48 : 4 =

c. 63 : 3 =

In ciascuna uguaglianza, disegna il simbolo che la rende vera.

= 600 = 200 = 60 = 20 = 10 = 3

Sul quaderno, esegui le seguenti divisioni in colonna.

a. 156 : 12 = b. 375 : 15 = c. 289 : 5 = d. 205 : 25 = 504 : 21 = 672 : 28 = 754 : 16 = 654 : 12 = 845 : 13 = 742 : 14 = 657 : 24 = 351 :

Operare

Moltiplicazione e divisione operazioni inverse

Trova il risultato della divisione aiutandoti con la tabella della moltiplicazione, come nell’esempio.

24

32

28 : 4 = infatti

45 : 9 = infatti

30 : 10 = infatti

Aiutati con la tabella della moltiplicazione per scrivere due divisioni per ciascun numero, come nell’esempio.

14 : 7 = 2 infatti 2 x

: 2 = 7 infatti 7 x 2 = 14

5

Scopri e scrivi il numero di partenza, seguendo gli operatori.

x 4 : 2 x 10 = 160 : 5 : 4 x 20 = 40

: 10 x 5 x 2 = 90

x 3 : 6 x 2 = 60

Scopri e scrivi il numero di partenza, seguendo gli operatori.

x 7 x 2 : 4 = 21

x 9 : 10 x 5 = 135

a. b. c.

5

moltiplica per 3

fai la metà

moltiplica per 4

dividi per 3

raddoppia 20

triplica

dividi per 4

moltiplica per 8

fai la metà

fai la metà 12

Sul quaderno, inventa tu una catena come quelle dell’esercizio 5.

triplica

dividi per 4

raddoppia

moltiplica per 3

fai la metà 36

Multipli e divisori

Colora la casella che rende esatta ciascuna affermazione.

Per ciascun numero, scrivi quattro multipli e tutti i divisori possibili.

Indica con una X i divisori di ciascun numero, come nell’esempio.

Operare con i numeri naturali

Trova…

5 Colora di giallo i numeri divisibili per 2 e 7.

• un multiplo di 4 compreso fra 53 e 59 .....................

• un multiplo di 5 compreso fra 61 e 69

• un multiplo di 6 compreso fra 85 e 92

• un multiplo sia di 7 sia di 6

• un multiplo sia di 4 sia di 2, minore di 20 .....................

• un multiplo sia di 3 sia di 4, maggiore di 12

• un divisore a due cifre di 45

• un divisore pari di 30

• un divisore dispari di 72 .....................

Colora il divisore comune a ciascuna terna di numeri.

Indica con una X se ciascuna affermazione è vera ( V ) o falsa (F).

• Il numero 7 ha come unici divisori il numero 1 e se stesso. V F

• Tutti i numeri che terminano con 0 o 5 sono multipli di 5 V F

• I multipli di 3 sono tutti numeri dispari. V F

• I multipli di 2 sono tutti numeri pari. V F

• I divisori di 40 sono tutti numeri pari. V F

Scrivi almeno quattro divisori per ciascun numero.

Moltiplicare e dividere per 10, 100 e 1000

Completa la tabella scrivendo il costo totale degli oggetti.

8

17 euro In

moltiplicazione, scrivi il fattore mancante.

Completa le tabelle: barra le caselle che non puoi completare.

Completa la tabella scomponendo il moltiplicatore, come nell’esempio. x

39

130

241

Completa la tabella scomponendo il divisore, come nell’esempio.

88000

Osserva la confezione di biscotti, calcola e rispondi.

a. Quanti pacchetti di biscotti ci sono:

• in una confezione?

• in 4 confezioni?

• in 60 confezioni?

b. Quanto pesa un pacchetto di biscotti?

c. Se in ogni pacchetto ci sono 10 biscotti, quanto pesa un biscotto? 10 pacchetti 400 gr.

Problemi

1

Risolvi.

a. Sabato sera, il ristorante “Mangiotanto” era quasi al completo. Erano occupati i 5 tavoli da 4 persone, i 4 tavoli da 6 persone, gli 8 tavoli da 2 persone, mentre erano rimasti vuoti i due tavoli da 10 persone. Quanti tavoli ha in tutto il ristorante? Quante persone hanno mangiato al ristorante sabato sera? Quante persone può accogliere il ristorante in tutto?

b. Lorenzo ha quattro anni in più di Francesco. Se Lorenzo ha 15 anni, quanti anni ha Francesco? Quanti anni di differenza avranno fra 7 anni? E quale sarà l’età di Francesco quando Lorenzo avrà 50 anni?

d. I genitori di Marco stabiliscono che riceverà una paghetta ogni volta che la aiuterà a fare qualche lavoretto in casa. Marco si impegna: martedì, mercoledì e giovedì riesce a guadagnare 7 euro al giorno, mentre lunedì solo 5 euro. Con i soldi ricevuti Marco il sabato va a mangiare una pizza e spende 15 euro. Quanti soldi restano a Marco della paghetta guadagnata?

c. Anna e Giervin, durante la ricreazione, piegano dei fogli di carta per fare dei gattini. Vogliono creare un quadro composto da 42 gattini. Anna ne ha già fatti 8 e Giervin ne ha fatti 13. Al termine della ricreazione, ciascuno dei due bambini è riuscito a fare altri 7 gattini. Quanti gattini ha fatto in più Gier vin rispetto ad Anna? Sono riusciti a fare tutti i gattini necessari per creare il quadro?

e. Nei primi due tempi della partita di basket, Elisa ha realizzato 31 punti e Luca ne ha realizzati 24. Nei secondi due tempi hanno realizzato entrambi ancora 16 punti. Qual è la differenza di punti fra Elisa e Matteo alla fine della partita?

f. Lo scuolabus sul quale salgono Martina e Giacomo arriva a scuola alle 8:25. Martina sale alle 8:00, mentre Giacomo sale alle 7:50

Quanto tempo impiega ciascun bambino per arrivare a scuola? Quanto tempo impiega in più Giacomo rispetto a Martina? Questa mattina, dopo aver fatto salire Martina, lo scuolabus ha trovato traffico ed è arrivato a scuola alle 8:33. Quanto tempo ha impiegato in più Giacomo rispetto a Martina?

g. Francesca ha già letto 35 pagine di un libro di avventure.

Domenica decide di leggere 5 pagine e poi, per finirlo più alla svelta, decide di leggere ogni giorno due pagine in più rispetto al giorno precedente.

Dopo 10 giorni ha terminato il libro.

Quante pagine ha letto Francesca in 10 giorni?

Quante pagine ha il libro?

h. Irene prepara dei sacchettini da regalare alle sue 4 amiche.

In ogni sacchettino metterà 6 caramelle, 1 lecca-lecca e 3 gomme da masticare.

Quando comincia a preparare i sacchetti, però, Irene si accorge che suo fratello le ha mangiato 8 caramelle e 4 gomme da masticare e si trova costretta a mettere meno dolci in ogni sacchetto. Quanti dolci potrà mettere in ogni sacchetto?

i. Nel suo portafoglio Maria ha 34 euro in banconote da 10 euro e monete da 2 euro.

Quante banconote da 10 e quante monete da 2 euro può avere nel portafoglio?

Disegna le possibili soluzioni.

l. Mattia ha una tavoletta di cioccolato formata da 30 quadretti. Vuole fondere ogni quadretto per farci dei cioccolatini usando uno stampino a forma di cuore.

Fondendo un quadretto, Mattia riesce a fare un cioccolatino e gli avanza ancora della cioccolata. Quanti cioccolatini a forma di cuore riesce sicuramente a ottenere Mattia fondendo tutti i quadretti di cioccolata?

Mattia riesce a fare ancora un cioccolatino a forma di cuore con 5 avanzi di cioccolata.

Quanti cioccolatini a forma di cuore riesce a fare Mattia con tutti i 30 quadretti di cioccolata?

Unità frazionaria

1

Colora solo le figure che sono state frazionate in modo corretto.

2

Fraziona le figure a tuo piacere, poi scrivi l’unità frazionaria.

3

Scrivi il valore frazionario di ciascuna parte colorata.

4

In ciascun segmento, colora l’unità frazionaria e poi scrivila in frazione.

5

Per ciascun bicchiere, scrivi la frazione corrispondente all’intero. Colora l’unità frazionaria indicata.

6

Calcola l’unità frazionaria, poi completa.

7

Considero UN vaso di fiori su vasi, in frazione si scrive .

I fiori in un vaso sono su fiori in tutto. Quindi è formato da ......... fiori.

Considero UN vassoio di pasticcini su vassoi, in frazione si scrive ..........

I pasticcini in un vassoio sono su pasticcini in tutto.

Quindi è formato da pasticcini.

Circonda 1 5 del denaro contenuto in ciascun salvadanaio.

Unità frazionaria

Osserva con attenzione le figure e, dove è possibile, colora 1 5 . 1

2

Colora 1 6 di ciascuna figura.

3

Indica con una frazione ciascuna parte colorata.

Per ciascuna unità frazionaria, disegna una figura e colora la frazione indicata.

4

Osserva il disegno e completa.

Un foglio quadrato è stato piegato lungo le due diagonali e poi lungo le due linee mediane, che nel disegno sono tratteggiate. Nel foglio si sono formati triangoli grandi, medi e piccoli.

I triangoli grandi sono 1 2 del quadrato.

• Quanti triangoli grandi vedi? ..............

• Quanti triangoli piccoli vedi?

• Scrivi il valore frazionario di un triangolo piccolo:

5 Colora e scrivi l’unità frazionaria di ciascuna figura.

• Ci sono triangoli medi, formati da 2 triangoli piccoli. Quanti sono?

• Scrivi il valore frazionario di un triangolo medio:

6

1

Oltre l’unità frazionaria

In quali figure la parte colorata corrisponde a 3 7 ? Circondale.

2

3

Carlo voleva colorare i 2 5 di ciascuna figura, ma in alcuni casi ha fatto degli errori.

Circonda le figure che ha colorato in modo sbagliato.

Quali bambini hanno 3 4 di caramelle colorate? Indicali con una X.

Ingrid

Samuel

Cecilia

Ivan

Scrivi la frazione che corrisponde alle parti colorate.

4 parti colorate parti colorate parti colorate

5

Scrivi in frazione la parte di percorso che Silvia, Luca e Andrea hanno già fatto per tornare a casa da scuola.

ANDREA

SILVIA

SCUOLA

6

Osserva gli animali e rispondi con una frazione.

LUCA

• Quale parte di animali ha le pinne?

• Quale parte striscia?

• Quale parte ha 2 zampe?

• Quale parte ha il becco?

Obiettivo di apprendimento Riconoscere e usare rappresentazioni diverse di oggetti matematici. Calcolare la frazione di una quantità.

SILVIA

LUCA

ANDREA

Frazioni maggiori, uguali o minori di 1

Queste frazioni sono formate da uno o più interi e da una parte frazionaria.

Scrivi le frazioni in modo da vedere qual è l’intero e quale la parte frazionaria, come nell’esempio.

cioè 1 intero + 3

= 1 + 3

=

a. =

b. = 5 2

4 3 = 3 3 +

cioè intero + +

cioè interi + + +

Disegna sul quaderno le frazioni indicate, poi stabilisci quali frazioni sono maggiori, minori o uguali a 1, come nell’esempio.

In ciascuna frazione, scrivi il numeratore per ottenere una frazione che corrisponde alle indicazioni date.

In ciascuna frazione, scrivi il denominatore per ottenere una frazione che corrisponde alle indicazioni date.

Frazioni complementari

Scrivi la frazione che corrisponde alle parti colorate e la frazione complementare, cioè quella che indica le parti non colorate. 1

Parti colorate 6 16

Parti non colorate

2

Parti colorate

Parti non colorate

Collega le figure che rappresentano frazioni tra loro complementari, come nell’esempio. Poi completa.

Completa scrivendo la frazione complementare.

In ciascun gruppo di uguaglianze, indica con una X quella esatta.

3

Confronto tra frazioni

Confronta le coppie di frazioni e inserisci il segno minore, maggiore o uguale.

2

Riscrivi ciascun gruppo di frazioni mettendole in ordine crescente.

Riscrivi ciascun gruppo di frazioni mettendole in ordine decrescente.

C’è un messaggio per te: per scoprirlo, riscrivi le frazioni in ordine crescente e sotto a ciascuna scrivi la lettera corrispondente.

Confronta ciascuna coppia di frazioni inserendo il simbolo giusto.

Completa con frazioni opportune.

< 5 9 < < 2 9 <

1 8 < < < < 4 7

< 7 2 < < 4 <

8

9

Rispondi e completa.

1 3 è una frazione maggiore di 1? Sì No

5 4 è una frazione maggiore di 1? Sì No

Concludi che 1 3 è di 5 4

Confronta le coppie di frazioni, operando come hai fatto nell’esercizio 7.

a. 7 3 e 2 5 7 3 è

5 2 e 3 4

b. 6 9 e 7 7

1 8 e 8 3

c. 16 8 e 7 9

9 15 e 15 12

d. 3 5 e 9 2

2 7 e 10 8

Completa in modo opportuno.

a. 3 7 > 2 2 15 < 15

b. 1 4 > 1 ..........

Obiettivo

7 8 < 8

7 c. 2 3 > 5 7 12 < 11

d. 19 10 > 6 9 13 < 16

2

Frazioni equivalenti

In ciascun disegno, colora la frazione indicata, poi completa.

La frazione 3 4 e la frazione sono equivalenti.

La frazione e la frazione sono equivalenti.

Di ciascuna figura, scrivi la frazione corrispondente alle parti colorate. Poi collega le frazioni equivalenti a quelle date, come nell’esempio.

Colora la parte di frazione indicata, poi circonda con lo stesso colore le frazioni equivalenti.

Continua frazionando ciascuna striscia, poi colora la parte indicata dalla frazione.

3

a.

b.

c.

5

Rispondi all’indovinello di Emma.

a. Per verificare se la tua risposta è esatta scrivi, per ciascuna frazione della tabella sotto, la rispettiva lettera.

b. Riscrivi le frazioni che sono fra loro equivalenti.

6

In ciascuna nuvoletta, colora tutte le frazioni equivalenti a quella indicata.

la città?

ciascuna frazione alla sua equivalente e lo scoprirai.

La frazione di un numero

Colora la quantità che corrisponde al valore numerico della frazione e poi scrivi in linguaggio matematico come hai operato.

a. 2 7 di 14

Dividi i 14 fiori in ............ parti uguali: 14 : ............ = ............ questa è l’unità frazionaria.

Ripeti l’unità frazionaria per volte, poi colora i 2 7 dei 14 fiori.

In linguaggio matematico: 14 7 = 2 2 =

b. 3 4 di 12

Scrivi in linguaggio matematico come hai operato: 3 4 di 12 12

c. 7 9 di 18

Scrivi in linguaggio matematico come hai operato: 7 9 di 18 18

d. 5 6 di 24

Scrivi in linguaggio matematico come hai operato: 5 6 di 24 24

Calcola il valore numerico di ciascuna frazione.

3 5 di 45 =

7 8 di 80 =

di 150 =

3

Colora la parte indicata dalla frazione e scrivi quali calcoli hai eseguito.

5 7

5 7 di = infatti

7 8

7 8 di = infatti

5

5 6 di ............ = ............ infatti .........................................................................................................................................

Dalla frazione all’intero

Osserva il disegno e completa.

I palloncini disegnati rappresentano 1 3 dei palloncini rimasti dopo la festa di compleanno di Marco.

Quanti palloncini aveva preparato per la sua festa?

La frazione 1 3 è l’unità frazionaria e rappresenta una parte di tutti i ...................................................

Tutti i palloncini sono stati divisi in ......... parti uguali, quindi Marco aveva preparato + = di palloncini.

Ma 1 3 è formato da ......... palloncini, quindi Marco aveva preparato ......... + ......... + ......... = ......... palloncini.

Osserva il disegno e completa.

Le mele disegnate rappresentano quelle rimaste dopo che Sophie ha preparto una torta.

Queste mele sono i 2 5 di tutte le mele che aveva. Quante mele aveva Sophie?

Se 2 5 sono le mele rimaste, significa che mancano i delle mele.

2 5 è formato da 1 5 + .......... . Se 2 5 sono mele, quante mele sono 1 5 ?

1 5 è formato da mele, quindi Sophie aveva + + + + = mele.

In linguaggio matematico: 4 : = è il valore dell’unità frazionaria; x 5 = è l’intero.

Risolvi sul quaderno.

a. Nella bottiglia che vedi è avanzato del succo di arancia, che rappresenta i 3 5 dell’intero succo. Quanti d<l di succo c’erano nell’intera bottiglia?

3 5 = 9 d<l

b. Nel salvadanaio di Mirko sono rimasti 6 euro, cioè i 3 8 dei soldi che aveva. Quanti soldi aveva Mirko? Quanti soldi ha speso Mirko?

c. La nonna aveva preparato la crostata per i suoi nipotini. Dopo la merenda ne sono rimasti 120 g, che sono i 3 9 della crostata iniziale. Quanti grammi pesava la crostata preparata dalla nonna? Quanta crostata è stata mangiata dai nipoti?

d. La mamma aveva messo dei vasi di gerani sul terrazzo. La gatta Fusa, rincorrendo un uccellino, ne ha rotti alcuni facendoli cadere. Sono rimasti interi solo 6 vasi, che rappresentano i 3 5 dei vasi che c’erano.

Quanti vasi aveva messo la mamma sul terrazzo? Quanti vasi ha rotto Fusa?

e. I bambini e le bambine che vedi sono i 4 12 degli alunni e delle alunne della 4a C. Quanti sono tutti i componenti della classe?

f. Le pizzette che vedi sono quelle avanzate dopo la festa di fine anno e sono i 5 18 di quelle preparate. Quante pizzette erano state preparate per la festa?

1

Esercizi con le frazioni

I 2 3 degli orsacchiotti sono di colore marrone, il resto sono grigi.

Quanti sono gli orsacchiotti marroni? E quelli grigi? Colorali.

2

3

Paolo ha una collezione di 10 robot. I 3 5 sono gialli, il resto sono rossi.

Quanti sono i robot gialli? E quelli rossi? Colora.

4

Tra i giocattoli di Loris, ci sono 15 macchinine. I 2 5 sono rosse, 1 5 sono blu, il resto sono verdi. Quante sono le macchinine verdi? Colora.

5

Annik ha una collezione di 12 gattini di peluche. Di questi, 2 6 sono bianchi, 3 6 sono neri, il resto sono marroni. Quanti sono i gattini bianchi? E quelli neri? E quelli marroni? Colorali.

Sul terrazzo della casa di Linda, ci sono 30 piantine di fiori: 1 5 sono vasi con garofani rossi, 2 5 sono vasi con garofani gialli, gli altri sono vasi con garofani rosa. Colora.

6

7

Per fare una torta al cioccolato la zia deve preparare un impasto di 700 grammi. Osserva la tabella che indica in frazione la quantità di ingredienti che devono essere mescolati.

Farina Zucchero Burro Cioccolato 5 14 2 7 1 7 3 14 grammi grammi grammi grammi

Scrivi il peso di ogni singolo ingrediente che la zia deve preparare per fare l’impasto per la torta.

Alla gara “Bici in città” si sono iscritte 200 persone. Degli iscritti solo 7 20 hanno completato il percorso.

Quante sono le persone che hanno completato la gara?

Quante persone non sono arrivate al traguardo?

8

9

In una classe 4a di 24 alunni e alunne, i 5 8 giocano a calcio e i rimanenti praticano altri sport.

Quanti sono i bambini e le bambine che giocano a calcio? Quanti sono i bambini e le bambine che praticano altri sport?

10

Per la festa del paese, 45 persone si sono iscritte alla caccia al tesoro; di queste i 3 5 sono femmine.

Quanti sono i maschi che partecipano alla caccia al tesoro?

Cecilia ha comprato delle ciambelline per la merenda con gli amici. Ne hanno mangiate i 5 8 e ne sono rimaste 9. Quante ciambelline aveva comprato Cecilia?

1

Dalla frazione ai numeri

Osserva, rispondi e completa.

• In quante parti è stato diviso ciascun quadrato? Scrivi l’unità frazionaria:

• Scrivi i numeri rappresentati in ciascun quadrato.

2

Osserva, rispondi e completa.

• Qual è il numero maggiore? .................

• Qual è il numero minore?

• In quante parti è stato diviso ciascun quadrato? Scrivi l’unità frazionaria: .......... ..........

• Osserva il quadrato A: che cosa rappresentano 10 parti di tutto il quadrato?

10 però sono anche la stessa cosa di 1

• Scrivi, prima in centesimi e poi in decimi, i numeri rappresentati in ciascun quadrato.

Modi diversi di scrivere i numeri

Completa le tabelle, come nell’esempio. 1

In lettere

quattro millesimi

sei centesimi

Indica con una X se ciascuna uguaglianza

Completa per arrivare all’unità.

Linea dei numeri

1

Scrivi sulla linea in frazione e in numero decimale i numeri indicati sulla linea.

2

Esegui quanto richiesto.

a. Con una freccia, inserisci sulla linea i numeri indicati.

b. Riscrivi in numero decimale le frazioni decimali che hai inserito sulla linea.

c. Osserva i numeri che hai inserito sulla linea, rispondi e completa.

• Qual è il numero maggiore? E quello minore?

• I numeri minori di 0,6 sono:

• E quelli maggiori di 0,3 e minori di 0,8:

• Metti in ordine crescente i numeri inseriti:

Ordina dal più piccolo al più grande.

Esegui quanto richiesto.

a. Con una freccia, inserisci sulla linea i numeri indicati.

Riscrivi in numero decimale le frazioni decimali che hai inserito sulla linea.

Osserva i numeri che hai inserito sulla linea e completa.

• Qual è il numero maggiore? E quello minore?

• I numeri minori di 0,3 sono:

• E quelli maggiori di 0,1 e minori di 0,4:

• Metti in ordine crescente i numeri inseriti:

b. Con una freccia, inserisci sulla linea i numeri indicati.

Riscrivi in numero decimale le frazioni decimali che hai inserito sulla linea.

Osserva i numeri che hai inserito sulla linea, rispondi e completa.

• Qual è il numero maggiore? E quello minore?

• I numeri minori di 0,009 sono: ......................................................................................................................................................................................

• E quelli maggiori di 0,009 e minori di 0,02:

• Metti in ordine crescente i numeri inseriti:

Oltre l’unità

Indica con una X la coppia che rappresenta 18 10 .

Colora i pacchetti di caramelle come indicato dai numeri.

Completa le collane disegnando fili e perle necessari a rappresentare in modo corretto i numeri.

3

5

Scrivi i numeri indicati dalla freccia in forma di numero decimale e di frazione, poi rispondi.

a.

6

b.

• Quali numeri sono maggiori di 1?

• Quale minore di 1?

• Quale maggiore di 2?

• Quali minori di 2 e maggiori di 1?

• Quali numeri sono maggiori di 3,5?

• Quali minori di 3,5?

• Quali minori di 3,7 e maggiori di 3,2?

Inserisci nella tabella i numeri e poi scrivili in forma di numero decimale. Circonda di rosso la parte intera del numero e di verde la parte decimale.

In lettere

3 decimi e 4 centesimi

3 unità e 2 decimi

8 centesimi e 2 millesimi

1 unità e 7 centesimi

5 unità e 16 centesimi

4 da e 3 u e 6 millesimi

12 u e 35 millesimi

27 decimi e 4 centesimi

230 centesimi

Numero decimale 0,34

I numeri decimali

Diversa scrittura, ma stesso valore

Rispondi.

• Quanti decimi servono per formare 1 u? .............. d • 4 u? .............. d • 10 u ? .............. d

• Quanti centesimi servono per formare 1 u? c • 7 u? c • 10 u ? c

• Quanti centesimi servono per formare 1 decimo? c • 5 d? c • 9 d? c

• Quanti millesimi per formare 1 u? m

• Quanti millesimi servono per formare 3 u ? .............. m • 9 u? .............. m • 10 u? .............. m

• Quanti millesimi per formare 1 centesimo? m • 20 c? m • 10 c ? m

• Quanti millesimi per formare 1 decimo? m • 5 d ? • 10 d ? m

In ciascuna tabella, scrivi in modi diversi il numero scritto di blu.

1

Operazioni con i numeri decimali

Esegui in riga: colora la parte intera di ogni numero e aggiungi, se necessario, lo zero, come nell’esempio.

a. 30,60 + 18,23 =

42,72 + 6,1 =

90,5 + 20,26 =

2,77 + 15,2 =

2

Esegui in riga.

a. 3,2 x 10 =

3,2 x 100 =

3,2 x 1000 =

0,732 x 10 =

0,732 x 100 =

0,732 x 1000 =

b. 7 : 10 =

7 : 100 =

70 : 1000 =

877,2 : 10 = .....................

877,2 : 100 =

877,2 : 1000 =

3

Esegui sul quaderno.

a. 735,9 + 47,8 =

412,96 + 135,2 =

88,76 + 239,171 =

90,26 + 3,758 =

4

Esegui sul quaderno.

a. 1,1 x 5 = 3,12 x 20 =

1,1 x 50 = 4,2 x 30 =

3,12 x 2 = 4,2 x 3 =

31,2 x 2 = 4,2 x 2 =

b. 45,3 – 10,1 =

89,7 – 13,4 =

96,83 – 11,7 =

275,9 – 0,82 =

c. 8,4 x 10 =

8,4 x 100 =

8,4 x 1000 = 3,29 x 10 = 3,29 x 100 = 3,29 x 1000 =

d. 72,36 : 10 =

72,36 : 100 =

72,36 : 1000 =

8 : 10 = .....................

8 : 100 =

8 : 1000 =

b. 826,7 – 35,2 = 473,84 – 470,9 =

727,45 – 38,6 =

272 – 38,47 =

b. 9,6 : 3 = 50,5 : 2 = 96,6 : 3 = 5,05 : 2 =

: 3 = 4,08 : 2 =

: 4 = 40,8 : 2 =

Decimali ed euro

1

Scrivi la quantità di denaro contenuta in ciascun salvadanaio.

2

Circonda le monete che servono per comporre il numero indicato.

3

Confronta i prezzi di ciascuna coppia di oggetti inserendo il simbolo giusto.

4

Indica con una X la scrittura corretta in euro delle monete raffigurate.

Costo unitario/Costo totale

1

Risolvi sul quaderno.

a. Per comprare 18 pennarelli Andrea ha speso € 39,60. Quanto è costato un singolo pennarello?

b. Una risma di carta per fotocopie costa € 5,60. Quanto costano 6 risme?

c. Sofia ha speso € 14 per comprare delle penne. Se ciascuna è costata € 3,50 quante penne ha comprato Sofia?

2

Nelle tabelle sono riportati i consumi giornalieri della famiglia di Lisa e di quella di Leonardo, che acquistano gli stessi prodotti ma di marche differenti. Completa le tabelle e rispondi.

Consumi della famiglia di Lisa

spesa

pane € 2,80

acqua € 1,20

latte € 1,25

pasta € 0,65

Consumi della famiglia di Leonardo

spesa

pane € 73,50

acqua € 11,00

latte € 9,10

pasta € 1,30

• Quale famiglia spende di più per comprare l’acqua?

• Quale famiglia spende di meno per comprare il pane?

• Per quale alimento le due famiglie spendono gli stessi soldi?

1

Tutto può essere misurato?

Indica con una X ciò che puoi misurare di ciascun elemento della tabella, poi rispondi e completa.

Elemento Altezza Bellezza Allegria Peso Fatica Profumo persona

gatto

auto

tavolo

• Hai segnato tutto? Sì No

• Scrivi ciò che hai potuto misurare:

• Scrivi ciò che non hai potuto misurare:

2

Che cosa puoi o non puoi misurare di questi oggetti? Completa, come nell’esempio.

Oggetto Posso misurare Non posso misurare

succo di frutta quantità di liquido bottiglietta con profumo

libro

biscotto

quadro

3

Di ciascun elemento della tabella, indica con una X le grandezze che puoi misurare.

Elemento Peso Lunghezza Capacità Durata Calore Superficie bambola

canzone

mattonella

succo alla pera

cartone animato gelato

4

Leggi la richiesta della maestra, osserva che cosa ha disegnato ciascun alunno e rispondi.

5

• Qual è l’unità di misura che i bambini dovevano usare per disegnare la linea?

• Chi non ha disegnato correttamente la linea richiesta della maestra?

• Perché?

Calcola la lunghezza delle tre linee senza usare il righello, poi completa.

Linea A: Linea B: Linea C:

• Quali unità di misura hai usato per misurare le linee?

• Ordina le linee dalla più lunga alla meno lunga: ................ – ................ – ................

Completa lo schema inserendo la freccia:

Disegna una linea spezzata chiusa lunga 12 lati di quadretto. è meno lunga di

Ricalca e ritaglia le strisce colorate. Usale per misurare i riquadri bianchi, cercando di usare meno strisce colorate possibile. Puoi utilizzare anche più volte le stesse strisce colorate.

Quali riquadri hai usato come unità di misura per misurare i nastri bianchi?

A: B: C:

Misure di lunghezza

Scegli l’unità più adatta per misurare ciascun oggetto. Poi effettua le misurazioni e scrivile.

MULTIPLI

UNITÀ SOTTOMULTIPLI

tesa braccio cubito spanna palmo dito

1 tesa = 2 braccia

1 braccio = 2 cubiti

Oggetto

Lunghezza di una stringa delle scarpe.

Larghezza di una gomma per cancellare.

La tua altezza.

Larghezza della porta dell’aula.

Lunghezza della tua matita.

Il lato lungo del tuo banco.

Esegui le trasformazioni.

2 spanne = 1 cubito

3 palmi = 1 spanna

4 dita = 1 palmo

Unità di misura scelta Misura

1 braccio = cubiti 1 cubito = spanne 1 tesa = braccia = cubiti

Il metro e i suoi sottomultipli

1 Sul quaderno, disegna segmenti delle lunghezze indicate.

4

Stima la lunghezza delle parti del tuo corpo, poi misurale con il metro e l’aiuto di un compagno o una compagna.

Parti del corpo Stima Misura un braccio un piede un passo

cm 5 mm 93 mm 1 dm 1,3 dm

Lunghezza Numero espresso con le parole Numero espresso in m

18 dm 1 metro e 8 decimetri 1,8

530 cm

71 dm

1890 mm

e

.....................

dm cm mm 2

L’unità

5 Completa le tabelle e trasforma.

dm cm mm 2

7,2 mm m 0,007 5 34 .................... .................... 0,063 2 179 350

Prima trasforma ciascun addendo in una stessa unità di misura, a piacere, poi esegui le addizioni sul quaderno.

3 dm + 14 mm + 12 dm + 23 cm =

2 m + 278 cm + 43 dm =

9 mm + 57 cm + 35 mm + 7 dm =

205 mm + 40 cm + 51 dm + 8 dm =

3 m + 78 cm + 15 m + 24 dm =

1

Il metro e i suoi multipli

Indica con una X l’unità di misura che ritieni adatta per misurare ciò che è indicato in tabella.

Lunghezza di un fiume. km m cm

Altezza di un bicchiere per l’acqua. m cm mm

Lunghezza di una corsia della piscina. dam m cm

Distanza fra due città. km hm dam

Lunghezza della punta della tua matita. dm cm mm

2

Indica con una X se ciascuna uguaglianza è vera ( V ) o falsa (F).

1 km = 1000 volte l’unità di misura, cioè 1000 m

1 dm = 10 volte l’unità di misura, cioè 10 m

1 hm = 100 volte l’unità di misura, cioè 100 m

1 cm = 1 100 dell’unità di misura, cioè 0,01 m

1 dam = 1 10 dell’unità di misura, cioè 0,1 m

1 mm = 1000 volte l’unità di misura, cioè 1000 m

V F

V F

V F

V F

V F

V F

Trascrivi le lunghezze collocando ciascuna cifra sotto l’unità di misura corrispondente.

Poi esprimi ciascuna lunghezza con tutte le unità di misura della tabella, come nell’esempio.

Lunghezza km hm dam m Scritture diverse

10 m 1 0 10 m = 1 dam = 0,1 hm = 0,01 km

75 hm

862 dam

95 hm

7093 hm

307 dam

Problemi

1

Risolvi.

a. Giulio e la sua famiglia vivono a Parma. Oggi vanno a Faenza per trovare gli zii e Giulio guarda la cartina per controllare il percorso da fare. Aiuta Giulio a calcolare quanti km deve percorrere per arrivare a Faenza.

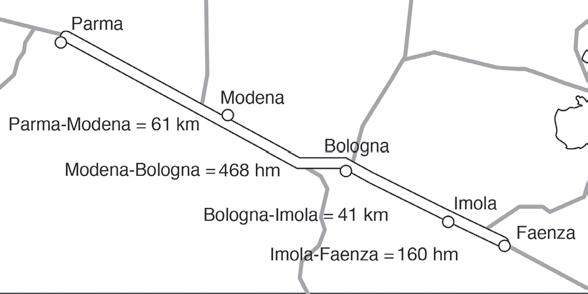
b. Laura corre tutti i giorni per 5,3 km. Dopo una settimana quanti km avrà percorso? E dopo 15 giorni?

c. Biancaneve era alta 1,68 m.

La porta della casetta dei 7 nani era più piccola di 35 cm dell’altezza di Biancaneve. Quanto era alta la porta della casetta dei sette nani?

d. Qual è l’animale più lungo?

Ricorda: per confrontare la lunghezza degli animali è necessario che questa sia espressa con la stessa unità di misura. Scegli con quale unità di misura ti conviene esprimere la lunghezza di ciascun animale ed esegui le trasformazioni.

• Squalo balena 2 dam =

• Squalo bianco 70 dm =

• Pitone reticolato 100 cm =

• Balenottera azzurra 0,25 hm =

• Calamaro gigante 1,5 dam =

• Balenottera comune 0,21 hm =

Ora scrivi le lunghezze degli animali in ordine crescente:

e. Il papà di Arturo vuole dipingere la facciata della casa alta 10 m.

Ha una scala di 8 m con 40 scalini e un’altra scala di 36 scalini distanti fra loro 25 cm.

Quale scala conviene prendere al papà per dipingere la parete?

f. Per recintare il suo giardino il nonno di Lorenzo deve comprare 15 rotoli di rete metallica da 4,5 dam l’uno.

Quanti metri di rete sono?

Se paga € 4,70 al metro, quanto spenderà il nonno di Lorenzo?

g. Per l’allenamento del lunedì Giorgio e Luca devono correre lungo la pista di atletica per 5 km. Iniziano a correre e dopo un po’ di tempo Luca chiede a Giorgio: – Abbiamo fatto già 9 giri, quanti ce ne mancano per completare l’allenamento?

400 m

Misure di massa

Indica con una X l’unità di misura più adatta per esprimere il peso di ciascun elemento.

arancia g hg dg

automobile kg Mg hg

Stima il peso di questi oggetti, poi verifica pesandoli e registrando i risultati in tabella.

Oggetto

scarpa quaderno

gomma per cancellare un bicchiere vuoto

...................................... ......................................

Collega i prodotti che hanno la stessa massa.

1 250 g 0,5 kg

quaderno g dg cg 21,5 dag 2,05 hg

penna dg g mg 0,25 kg 0,205 kg 215 g 500 g

...................................................................................................................................

5

Trascrivi in ordine crescente le seguenti misure.

0,074 kg • 72 dg • 39 g • 0,37 hg • 12 g • 1,2 kg

Trascrivi i pesi collocando ciascuna cifra sotto l’unità di misura corrispondente.

Poi esprimi ciascun valore con tutte le unità di misura in tabella, come nell’esempio.

Massa kg hg dag g

140 g 1 4 0

342 dag

52 hg

30 g

5,4 kg

173 dag

0,74 hg

105 g

6

Scrivi ciascun valore con le unità di misura indicate.

Scritture diverse

140 g = 14 dag = 1,4 hg = 0,14 kg

325 g

hg dag dg

7

Scomponi, come nell’esempio.

340 g 3 hg + 4 dag + 0 g

0,4 kg

hg g dag

74,45 cg

310 mg 5,12 hg

864 dag

452 dg

8007,4 kg

65,9 hg

Obiettivo di apprendimento Associare a grandezze unità di misura appropriate. Stimare misure. Operare trasformazioni tra grandezze omogenee.

dag g dg kg

56 hg

Completa le tabelle.

Misure di massa

2

In ciascuna equivalenza, scrivi la marca giusta.

800 g = 8

25,3 hg = 2530

8,7 g = 0,087

3

kg = 2,3

mg = 0,35

hg = 2,1

kg = 870

g = 40

Prima trasforma gli addendi in una stessa unità di misura, a piacere, poi esegui le addizioni.

56 g + 0,73 hg + 21 dg + 7 dag = 56 g + + + = g

7,345 dg + 0,59 g + 0,041 dag + 0,02 cg = + + + =

3,54 kg + 52 hg + 1,6 dag + 10 dg = + + + =

86 dg + 1,36 dag + 6,7 g + 5 cg = + + + =

Collega i riquadri con i valori equivalenti, poi esprimili in dag.

5

6

Scegli l’unità di misura adatta a esprimere il peso di ciascun uccello: kg, hg, g, cg, mg. Esegui le trasformazioni.

Colibrì ape

2000 mg Chiurlo americano

2900 dg

36 dag

3800 cg

Piccione selvatico

1200 dg

Passero

Gabbiano

Ora confronta le misure che hai trovato e scrivi i nomi degli uccelli in ordine crescente di peso. ..................................................................................................................................................................................................................................................................................................................................

Completa gli schemi con i valori mancanti.

7 hg + hg dag + 35 dag

Obiettivo di apprendimento Associare a grandezze unità di misura appropriate. Confrontare grandezze. Operare trasformazioni tra grandezze omogenee.

Le bilance

1

Osserva la bilancia a sinistra e completa. Poi disegna i cilindri mancanti in quella a destra.

Un pesa quanto

2

Leggi, osserva e rispondi.

a. Sai che = 50 g

b. Sai che = 2 kg

Quanto pesa una ?

3

Osserva e calcola il peso dei tre pacchi di cereali a sinistra.

Quanto pesa un ?

Quanto pesa una ?

300g50g

Osserva e calcola il peso di 5 dolcetti.

1

Peso netto, peso lordo e tara

Osserva le immagini. Inserisci i pesi negli schemi e completa.

a.

320 g

1,5 hg

Peso netto Tara Peso lordo

Peso lordo

570 g

490 g

Peso lordo 3,7 kg

120 dag

b.

Peso netto Tara Peso lordo

Peso netto Tara Peso lordo

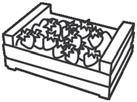
Risolvi sul quaderno.

a. Il contadino Alfonso vuole sistemare 36 kg di pesche in 9 casse. Se il peso di ciascuna cassa vuota è 850 g, quale sarà il peso lordo di una cassa?

b. Al supermercato "Risparmio" sono in vendita due confezioni di biscotti. Una ha il peso netto di 450 g, l’altra il peso lordo di 5,3 hg e tara di 40 g. Se hanno lo stesso prezzo, quale conviene comprare? Perché?

1

Misure di capacità

Colora la capacità adatta per ciascun oggetto.

2

3

Leggi le misure e scrivi a quanti litri corrispondono.

4

Completa gli schemi con le capacità mancanti.

7

Completa le successioni aggiungendo anche gli operatori.

a. 4 h<l da<l <l

Prima trasforma gli addendi in una stessa unità di misura a piacere, poi esegui le addizioni.

4

42 <l + 278 c<l + 39 d<l =

95

205

6

Obiettivo di apprendimento Associare a grandezze unità di misura appropriate. Operare trasformazioni fra grandezze omogenee.

1

Misure di tempo

Indica con una X la casella che indica l’unità di misura adatta a misurare il tempo che…

s min h d anni secoli

… trascorri a scuola.

… è passato dalla tua nascita.

… è passato dalla costruzione della piramide di Cheope.

… impieghi per fare un giro di corsa della palestra della scuola.

… impieghi per andare da casa a scuola.

… impieghi per allacciarti le scarpe.

2

Circonda quale strumento puoi usare per misurare il tempo che impieghi a fare i compiti a casa.

3

Completa le uguaglianze.

1 h = min = s

1 d = h = min

4

h = min = s

h = min

1 M = d oppure d oppure d 3 d = h = min

1 A = d oppure d oppure M

A = M

Scrivi le ore indicate negli orologi con le lancette, come negli esempi.

6

Roma New York Giacarta San Francisco Sidney Dubai h

Scrivi la parola che corrisponde a ciascuna definizione. Poi cancellala nello schema.

I minuti che formano 1 ora:

Da quanti anni è formato un lustro:

I minuti che formano 1 4 di ora:

I giorni di quattro settimane:

È formata da 60 min:

I mesi di un trimestre:

È 1

60 di minuto: ..................................................................................................

Il sesto mese dell’anno:

È formato da 100 anni:

Ci vogliono 24 ore per formarne un:

52 settimane lo compongono:

Dura trenta minuti:

Il quinto mese dell’anno:

Trova il valore temporale di ciascun simbolo e scrivi il numero che manca.

min

min

30 min 30 min

Osserva la differenza di ore fra alcune città del mondo. Disegna l’ora di ciascuna città.

Problemi

Risolvi.

a. Il papà di Pietro vuole preparare una bibita alla menta. Per fare un’ottima bibita serve 1 d<l di sciroppo ogni 100 c<l di acqua. In casa ha 2,5 d<l di sciroppo, quanti litri di acqua dovrà usare?

b. Lidia la mattina fa colazione con cereali e latte. La scatola con i cereali pesa 390 g, mentre solo la scatola pesa 15 g. Lidia consuma una scatola di cerali in 15 giorni e mangia ogni giorno la stessa quantità.

Quanti grammi di cereali mangia Lidia in un giorno?

c. Il nonno di Eleonora cammina ogni giorno nel parco. Se il parco è lungo 3,5 km e il nonno lo percorre tutto due volte al giorno, quanti km percorrerà in una settimana?

d. Azzurra ha 5 audiolibri. In ogni audiolibro ci sono 8 storie e ogni storia dura in media 5 minuti e 25 secondi.

Quanto tempo occorre per ascoltare tutto un audiolibro? E per ascoltarli tutti e cinque?

e. Lucio e la sua gemella Nina hanno finito di svolgere i compiti. Nina ha iniziato alle 15:30 e ha finito alle 17:00. Suo fratello ha impiegato un’ora e tre quarti. Chi è stato il più veloce?

f. La nonna di Matilde deve prendere delle pasticche pari a 3 mg al giorno. Ogni pasticca pesa 0,6 mg. Quante pasticche deve prendere la nonna ogni giorno?

g. Cesare è bravo a preparare il tè, usa sempre una bustina per 3 d<l di acqua. Oggi aspetta due suoi amici e prepara una teiera da un litro e mezzo. Quante bustine userà?

Cesare e i suoi amici bevono ciascuno 2 tazze da 2 d<l di tè e mangiano dei biscottini.

Quanto tè hanno bevuto? Quanto tè rimane nella teiera?

h. Il contadino Sandro raccoglie le pere nella sua azienda agricola e il figlio Paolo lo aiuta. Sandro, che è molto veloce a raccogliere le pere, riesce a riempire 8 cassette in un’ora; Paolo, più lento, riempie invece 4 cassette l’ora. Quando il lavoro è finito sono riusciti a raccogliere 48 cassette di pere.

Se hanno mantenuto sempre lo stesso ritmo, per quante ore hanno lavorato?

E quante cassette ha riempito ciascuno?

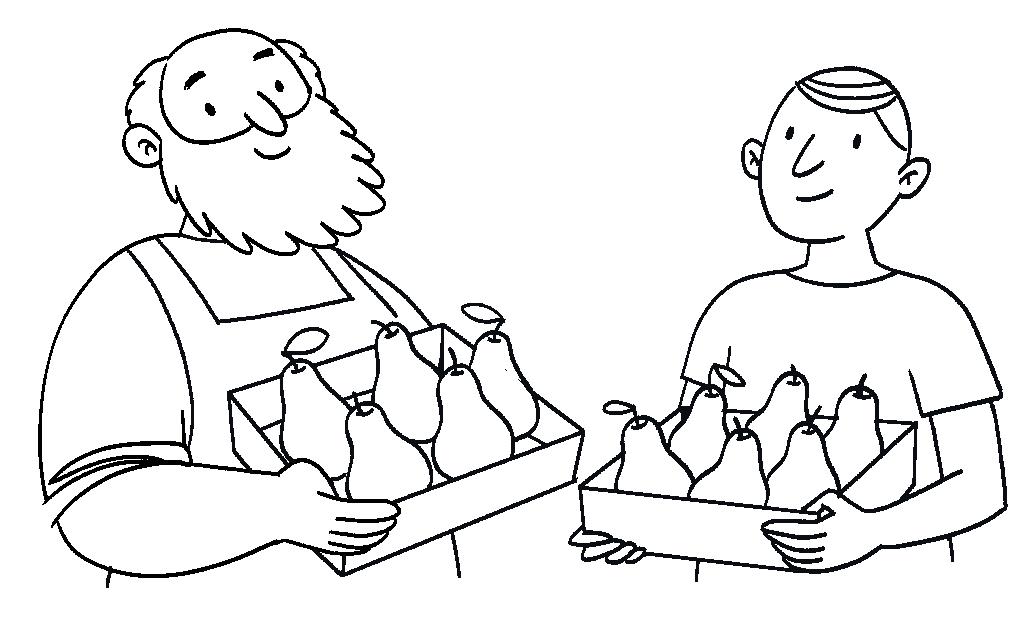
i. Danilo si allena per partecipare alla “Biciclettata di primavera” organizzata nella sua città. Lunedì, che è il primo giorno di allenamento, riesce a fare 5 km; il giorno dopo percorre 4 km in più e il terzo giorno 6 km in più del martedì. Giovedì, per migliorarsi, vuole percorrere per forza 19 km. Quanti chilometri in più deve fare rispetto al giorno precedente?

l. In una gara di corsa campestre iniziata alle 14:15, un gruppo di amici e amiche si confronta sulle prestazioni come riportato nel riquadro.

• Greta è arrivata seconda;

• Mimì ha vinto la gara ed è arrivata 20 minuti prima rispetto all’ultimo arrivato e 5 minuti prima del secondo;

• Gianni ha tagliato il traguardo alle ore 16:00, 15 minuti dopo Greta;

• Omar è arrivato 10 minuti prima di Gianni;

• Luisa è arrivata 5 minuti prima di Gianni, ma 5 minuti dopo Omar.

Scrivi nella tabella a destra l’ordine di arrivo, i nomi e gli orari.

Quanto tempo ha impiegato il 1° arrivato. E il secondo? Quanto tempo è durata tutta la gara?

Ordine d’arrivo Nome Ora di arrivo

5° arrivato Gianni

m. Per le vacanze estive Marco va al paese di Marebello con la famiglia. Per raggiungere il paese la famiglia deve percorrere 15 km per arrivare all’autostrada, 280 km di autostrada e 27,6 km di strada provinciale che porta al mare. Il papà di Marco decide di fermarsi, per una sosta, dopo 175 km. A questo punto, hanno percorso più o meno della metà dell’intero tragitto? Quanto di più o di meno?

Quanti km devono ancore fare per raggiungere Marebello?

Ra-Giocando

Osserva e risolvi. Confronta la tua soluzione con quella dei compagni e delle compagne. Avete trovato la stessa soluzione? Perché?

a. + = 12

2

Completa le tabelle, come nell’esempio.

3

Inserisci nelle caselle vuote le lettere associate alle risposte esatte di ciascuna operazione. Leggerai il nome di un fiore.

Sostituisci i numeri al posto delle carte in modo che la somma delle righe, delle colonne e della diagonale sia 15.

5

Quante palline servono per pesare una bottiglia e un bicchiere? Disegnale.

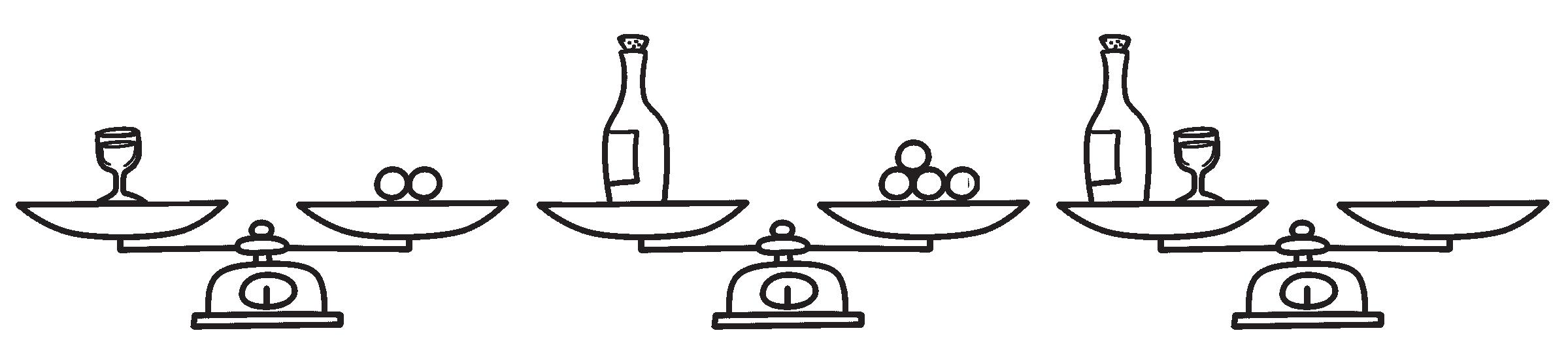
6

Quante stelle servono per pesare una pallina? Disegnale.

7

Qual è la massa della mela e dell’albicocca?

8

Scrivi i numeri da 1 a 6 nei cerchi di questo triangolo in modo che la somma di ciascun lato sia sempre 11.

9

Scopri il numero misterioso.

• È multiplo di 2.

• È maggiore di 40 e minore di 60.

• La somma delle sue cifre è 11.

Qual è il numero?

Problemi

Risolvi.

a. La maestra Elisa ha una età compresa tra i 20 e i 30 anni. Se dividi il numero dei suoi anni per 4 o per 5 avanza sempre 3. Sai dirmi quanti anni ha la maestra Elisa? Spiega il tuo ragionamento.

b. Nel paese di Pontebello ci sono 100 nuove case a cui si vogliono mettere ai portoni i numeri civici belli e colorati. Viene chiamato Tobia, l’anziano artigiano del paese, per svolgere il lavoro. Tobia, che ama la matematica, appena inizia a lavorare si chiede “scriverò più volte la cifra 5 o la cifra 0?”

Aiuta Tobia e spiega il tuo ragionamento.

d. L’anno scorso Leo era alto 1 m e 51 cm e suo cugino Teo 1 m e 48 cm. Nell’ultimo anno però entrambi sono cresciuti di 3 cm.

Quale sarà adesso la differenza di altezza tra Leo e Teo?

Spiega il tuo ragionamento.

c. In pizzeria Anna, Bice, Piero, Francesco e Luisa devono sedersi a questo tavolo rotondo. Però: Bice non vuole accanto né Francesco né Anna. Anna vuole Francesco alla sua sinistra. Piero vuole stare accanto a Bice ma non accanto a Luisa.

Come possono disporsi a tavola i 5 amici?

e. Giovanni ha dimenticato il PIN del suo cellulare. Ricorda solo che:

• è un numero di 4 cifre;

• la prima cifra è 9;

• la seconda cifra è 2 o 3;

• la terza cifra è minore di 6;

• l’ultima cifra è 7.

Riesci ad aiutare Giovanni a trovare il suo Pin?

Perché?

f. Tonio, la guardia forestale della riserva naturale “pianabella”, registra tutti i giorni in un quaderno il numero dei mammiferi e degli uccelli che vede dalla sua postazione che usa come osservatorio. Oggi aveva fretta e nel suo quaderno ha registrato solo “14 zampe”. La sera nel rileggere gli appunti non riesce a ricordare quanti erano gli uccelli e quanti invece i mammiferi. Aiutalo tu e spiega il tuo ragionamento.

Rispondi.

1. Qual è la spesa minima e qual è la spesa massima che può fare una persona per un pasto completo in rosticceria?

Primo € 8,50

Secondi di carne € 7

Secondi di pesce € 8

Contorno € 1,50

Dessert € 2,30

Aranciata o Cola € 2

Acqua € 1

2. Elenca tutte le possibili combinazioni di menù e scrivi per ciascuna il prezzo. ...........................................................................................................................................

2

1

Rette, semirette e segmenti

Disegna una coppia di rette incidenti, una coppia di rette parallele e una coppia di rette perpendicolari.

2

Disegna tutti i segmenti che ottieni unendo i punti in tutti i modi possibili. Poi rispondi.

A

D

3

• B C

• Quanti segmenti hai ottenuto?

4

Unisci il punto A con il punto B, il punto C con il punto D, poi completa.

C

B A

• Questi segmenti si incontrano in

• I segmenti che si incontrano in un punto si dicono .........................................................................................................................................

Unisci i punti con due segmenti, poi completa.

• A C

• B

• Questi segmenti hanno un ...................................... in comune.

• I segmenti che hanno un vertice in comune si dicono

5

Ripassa di rosa le rette incidenti, di verde quelle perpendicolari e di arancione quelle parallele.

6

In ciascun riquadro, disegna con il righello ciò che viene chiesto.

È una linea che non cambia direzione:

ha un inizio, ma non ha una fine.

È una parte di linea che non cambia direzione.

È misurabile, ha un inizio e una fine.

È una linea che non cambia direzione.

7

Osserva il disegno e completa.

Le rette a e b sono

c d

Le rette a e d sono

Le rette c e d sono

Le rette c e b sono

8 r q

Ripassa di rosso i segmenti che vedi in figura e di verde le semirette.

p a b

Le rette c e a sono

Le rette b e d sono

L’angolo in Geometria

Colora la decorazione che contiene angoli. Poi rispondi. 1

• Perché l’altra decorazione non contiene angoli?

Scopri gli angoli nascosti dentro a ciascuna lettera del nome e colorali. Poi rispondi.

• Quale lettera contiene più angoli?

• Perché?

Indica se le semirette sono lati di un angolo.

Quale lettera non contiene nessun angolo?

Sì No Sì No

2

4

Completa la figura inserendo i nomi corretti nei cartellini.

6

Scrivi se gli angoli disegnati sono concavi o convessi.

5

Colora in due modi diversi gli angoli di ciascuna coppia di semirette.

Completa i disegni di ciascun riquadro in modo da formare angoli, poi colora di giallo l’angolo concavo e di arancione l’angolo convesso. 7

1

L’angolo in Geometria

Completa la “Carta di identità” dell’angolo.

Un angolo è

Il punto in comune alle semirette si chiama

Le semirette sono i

L’ampiezza dell’angolo si misura in

Rispetto all’ampiezza un angolo può

essere: giro, , , ,

2

Indica con una X se le affermazioni sono vere ( V ) o false (F).

• Se disegni due semirette che partono da un punto formi sempre due angoli.

• Le semirette che formano un angolo sono infinite, quindi anche l’angolo è infinito.

• Il vertice di un angolo è il punto di origine delle due semirette che lo formano.

• I lati dell’angolo non hanno mai l’origine in comune.

• L’angolo concavo non è attraversato dai prolungamenti dei lati.

3

Colora l’angolo di maggiore ampiezza e completa.

V F

V F

V F

V F

V F

4

Colora l’angolo di minore ampiezza e completa.

È un angolo

È un angolo

5

Clelia è seduta al tavolo della sua scrivania e guarda fuori dalla finestra. Che cosa vede? Osserva e completa.

6

In ciascun riquadro, evidenzia con un colore l’angolo indicato, poi completa.

Clelia vede

Punti che appartengono all’angolo convesso:

Punti che non appartengono all’angolo convesso:

Tutte queste cose sono: all’interno dell’angolo. all’esterno dell’angolo.

Punti che appartengono all’angolo concavo:

Punti che non appartengono all’angolo concavo:

1

Classificare gli angoli

Confronta gli angoli sovrapponendoli a un modello di angolo retto e classificali completando la tabella.

Angoli acuti Angoli retti Angoli ottusi

2

Colora di giallo gli angoli acuti e di arancione quelli ottusi, poi rispondi.

Ci sono angoli retti? Sì No E angoli piatti? Sì No

Disegna tre angoli acuti minori di quello disegnato. 3

4

Disegna tre angoli ottusi maggiori di quello disegnato.

Classifica gli angoli completando la tabella.

Disegno angolo Nome

angolo giro

angolo

angolo

Posizione dei lati fra di loro

Caratteristiche

I lati sono ....................................... È il dell’angolo piatto; è il dell’angolo retto.

I lati hanno la stessa direzione, ma verso opposto

È la dell’angolo giro; è dell’angolo retto.

I lati sono È la ............................................................. dell’angolo piatto; è dell’angolo giro.

angolo

I lati sono È minore dell’angolo retto. angolo ottuso

I lati sono È dell’angolo retto, di quello piatto e di quello giro.

I lati sono

angolo

Non è stata effettuata nessuna rotazione dei lati.

Colora gli angoli che riesci a individuare in un campo da basket, poi scrivi quanti sono.

Angoli acuti

Angoli ottusi .....................................................................

Angoli retti

Angoli piatti

Angoli giro

5

6

1

Confrontare gli angoli

Completa la tabella. Procedi in questo modo:

• confronta gli angoli celesti con l’angolo grigio facendo una stima;

• per verificare la tua stima, ricalca su un foglio l’angolo grigio, ritaglialo e usalo per confrontarlo con gli angoli celesti.

2

Stima Verifica angoli minori dell’angolo nero angoli uguali all’angolo nero angoli maggiori dell’angolo nero

Confronta gli angoli aiutandoti con un modello. Poi completa scrivendo le relazioni, come nell’esempio.

B < A B C

C A C D

D A B D

Traccia le frecce che esprimono la relazione indicata e ordina gli angoli dell’esercizio precedente dal meno ampio al più ampio.

è meno ampio di …

4

Aiutati con un modello di angolo retto e un righello per disegnare sul quaderno:

• 3 angoli retti;

• 3 angoli minori di quello retto;

• tre angoli maggiori di quello retto.

Osserva intorno a te e cerca alcuni oggetti sulla cui superficie vedi angoli retti. Scrivi il loro nome. 5

6

Confronta gli angoli creandoti un modello adatto e riscrivili in ordine decrescente.

7

8

A B C D E F

Ordine decrescente:

Ricalca gli angoli che vedi qui sotto e colorali come nel disegno.

Ora ritagliali e incollali sul quaderno, mettendoli uno accanto all’altro e facendo coincidere un lato e il loro vertice. Poi completa. Hai ottenuto un angolo ampio. L’ampiezza di questo angolo è dato dalla ......................................... delle ampiezze degli angoli di partenza. Hai ottenuto “l’ somma”.

Ricalca gli angoli che vedi a destra e colorali come nel disegno.

Ora ritagliali e confrontali.

L’angolo è maggiore dell’angolo

Sovrapponi i due angoli facendo coincidere il loro vertice e un lato e incollali sul quaderno. Poi completa.

Hai ottenuto tre angoli: l’angolo celeste, che ha un’ampiezza dell’angolo grigio; l’angolo grigio che ha un’ampiezza dell’angolo celeste e un terzo angolo formato dall’avanzo dell’angolo Questo terzo angolo si chiama “angolo differenza” perché è l’angolo che ottieni dalla dei due angoli di partenza.

9 A C

Scopri qual è il vertice di ciascun angolo. Cercalo nel riquadro a destra, ricalcalo con la carta lucida e incollalo sull’angolo.

B D

Obiettivo

1

Misurare gli angoli

Osserva l’esempio e scrivi quanto misurano gli angoli indicati.

3

Il vigile sulla strada dà indicazioni muovendo le braccia. Misura e scrivi qui sotto gli angoli formati dalle braccia del vigile.

a. b. c. d.

2 Disegna sul quaderno angoli con le seguenti ampiezze.

Misura gli angoli e riscrivili in ordine crescente.

Usa il goniometro per individuare gli angoli di uguale ampiezza e colorali nello stesso modo.

6

Osserva il disegno e completa. Caterina ha infilato un paletto nella sabbia e osserva l’ombra del sole che si sposta. Di quanti gradi si è spostato il sole?

Disegna l’ombra del sole quando si sarà spostato ancora di 70° in senso orario.

7

Segui le istruzioni per costruire un piccolo origami e completa.

1. Prendi un foglio di carta quadrato e piegalo lungo una diagonale. Poi sovrapponi i due estremi della diagonale e individua il punto (A) che divide a metà quel lato. Che angolo hai formato?

Quanto misura?

A

2. Partendo dal punto A, piega verso l’alto il lato di destra come nel disegno. Che angolo hai formato?

Quanto misura?

Osserva anche l’altro angolo che hai formato. Che angolo è? Quanto misura? A

3. Esegui la stessa piega con il lato di sinistra. Sei riuscito a formare un angolo uguale? Sì No

Osserva l’angolo * compreso fra i due angoli che hai

formato con le pieghe: che angolo è?

*

Quanto misura? A

4. Prendi il vertice in alto e piegalo a piacere verso il basso.

5. Ribalta il foglio e poi disegna il musetto di un gattino.

a. Osserva solo le orecchie del gattino: colora gli angoli che vedi. Usa un colore diverso per ogni angolo

Quanti sono? ..................... Classificali: ................. ottusi; ................. acuti; ................. retti; 0 piatto; 0 giro.

Scrivi quanto misurano:

b. Ora osserva la faccia del gattino: colora tutti gli angoli che vedi.

Quanti sono? Classificali: ottusi; acuti; retti; piatti; giro.

Scrivi quanto misurano:

La simmetria

1

Le figure sono state ribaltate nelle pagine dei libri?

2

3

Disegna l’asse di simmetria in ciascuna coppia di figure. Poi segna nelle figure riflesse i vertici indicati nelle figure di partenza.

Nomina i punti riflessi con le stesse lettere di quelli di partenza, come nell’esempio.

4

Controlla se le figure sono state disegnate in modo simmetrico e, se serve, correggi gli errori.

Sono simmetriche? Sì No

Sono simmetriche? Sì No

Sono simmetriche? Sì No

5

Verifica se sono state disegnate correttamente le simmetrie. Correggi se ci sono errori.

6

Sì No

Sì No

Sì No

Sì No

Le linee tratteggiate che vedi sono le impronte che indicano dove è stato appoggiato uno specchio. Disegna come si vedono i numeri.

7

Quali di questi cartelli stradali hanno almeno un asse di simmetria? Indicali con una X e disegna gli assi.

8

Pinguino gioca a saltare sui blocchi di ghiaccio. Salta solo su quelli che hanno almeno 2 assi di simmetria. Colora i blocchi sui quali salta.

Obiettivo di apprendimento Riconoscere ed effattuare movimenti nel piano di punti e figure.

La simmetria

1

Disegna l’asse di simmetria. Scopri quale lettera è nascosta.

2

Individua e disegna l’asse di simmetria.

3

Nomina i punti simmetrici rispetto all’asse di simmetria.

4

Disegna i punti che mancano.

5

Disegna i segmenti simmetrici.

6

Le cornicette sono simmetriche rispetto all’asse orizzontale.

Disegna le linee che mancano e continua il disegno.

7

Quali parole sono nascoste? Completa le lettere che sono simmetriche rispetto all’asse di simmetria e scoprile.

Parola:

Parola:

Parola:

Parola:

1

La traslazione

Disegna le figure simmetriche rispetto agli assi di simmetria tratteggiati. Poi colora di rosso e di verde, in modo alternato. Infine rispondi.

2

3

• Che movimento hanno fatto i triangoli rossi?

• Che movimento hanno fatto i triangoli verdi?

Quale tra i disegni a destra è stato usato per disegnare la decorazione? Coloralo.

4

Disegna figure simmetriche a quella al centro, rispetto agli assi di simmetria tratteggiati. Come sono fra di loro gli assi di simmetria? Colora solo le figure traslate rispetto a quella già disegnata.

Colora solo le figure traslate rispetto a quella colorata. Poi indica con una freccia lo spostamento di ciascuna figura traslata rispetto alla precedente.

A B A B

fig. 4 fig. 3 fig. 2 fig. 1 A1 A3 A B

A3 A2 A1 A B1 B

fig. 1 fig. 2 fig. 3 fig. 4 B1 A2

Scrivi di quanti lati di quadretto è stata traslata ogni volta la figura.

Fig. 1: Fig. 3: Fig. 2: Fig. 4: Fig. 1: Fig. 3: Fig. 2: Fig. 4:

Colora la coppia di figure che è stata traslata in modo corretto rispetto alle indicazioni date dal vettore. 6

Completa gli spostamenti indicati dalle frecce disegnando le figure traslate, poi completa. 5 A B1

Obiettivo

di apprendimento Riconoscere e disegnare movimenti nel piano di figure. Riconoscere traslazioni.

misurazioni dello spostamento sul piano.

1

La rotazione

Disegna le figure simmetriche rispetto agli assi tratteggiati, poi colora solo la figura ruotata rispetto alla figura di partenza e rispondi.

a.

La figura ruotata rispetto alla figura di partenza:

• ha forma diversa? Sì No

• ha dimensione diversa? Sì No

• ha posizione diversa sul piano del foglio? Sì No

b.

La figura ruotata rispetto alla figura di partenza:

• ha forma diversa? Sì No

• ha dimensione diversa? Sì No

• ha posizione diversa sul piano del foglio? Sì No

La girandola ruota facendo un giro completo in senso antiorario. Scrivi la giusta successione che rappresenta la sua rotazione.

Successione:

2

3

Completa l’ultima forma di ciascuna sequenza.

a.

b.

c.

d.

6

Completa la rotazione di ciascuna coppia di figure disegnando il quadratino celeste che manca.

5

4 Partendo da questa figura, inventa un mandala.

Disegna gli oggetti nella posizione raggiunta dopo averli ruotati intorno al centro del cerchio di quanto indicato dalle frecce.

Obiettivo di apprendimento Riconoscere movimenti nel piano di figure. Operare trasformazioni geometriche.

1

Le figure piane

Luca sceglie dei ritagli da incollare su un foglio per creare un piccolo quadro. Osserva le figure che rappresentano i ritagli e completa.

2

3

Le figure sono tutte dei perché il loro contorno è formato da una linea ....................................................., ....................................................., e .....................................................

Unisci con un segmento le coppie di punti evidenziati in ciascun poligono e indica quali di essi sono concavi e quali convessi.

concavo convesso concavo convesso concavo convesso concavo convesso

Scrivi se il poligono possiede o meno la proprietà indicata, come nell’esempio.

Poligono

Equilatero (ha tutti i lati uguali)

Equiangolo (ha tutti gli angoli uguali)

Regolare (ha lati e angoli uguali) no .................................. ..................................

4

Colora solo le figure che sono poligoni, poi completa.

2

3

Sono poligoni le figure n. perché

Non sono poligoni le figure n. perché

5

In ciascun piano, unisci i punti a piacere per formare un poligono concavo. Poi completa.

Il poligono formato ha: vertici

lati

angoli convessi angoli concavi

Il poligono formato ha: vertici lati

angoli convessi angoli concavi

Il poligono formato ha: vertici lati

angoli convessi angoli concavi

Colora i poligoni regolari che formano i fiori. Per ciascuno, scrivi quali poligoni sono stati usati. 6

Obiettivo

Fig. 1 Fig.

Fig.

Fig 4 Fig. 5

1

Unisci i vertici per formare i poligoni ACEF e BEDG.

Perimetro

Completa nominando i vertici di ciascun poligono, poi ripassa di arancione il lato BC e di verde il lato DE, quando ci sono.

F E A

C D

3

Quale figura ha fatto ciascun bambino?

Per fare la mia figura ho usato 12 stuzzicadenti.

A A

Ripassa il contorno dei poligoni che hanno il perimetro lungo 10 lati di quadretto. 4

A B C D E

5

6

Disegna un quadrato di perimetro 24 lati di quadretto. Poi rispondi.

• Puoi disegnare un quadrato più grande, ma con lo stesso perimetro? Sì No

• Perché?

7

a. Disegna sul quaderno poligoni di forma differente, ma che abbiano tutti il perimetro di 8 lati di quadretto. Quanti ne hai trovati?

b. Disegna poligoni di forme differenti, ma che abbiano tutti il perimetro di 8 lati di triangolo. Poi rispondi e completa.

• Quanti sei riuscito a farne?

• Rispetto ai poligoni disegnati su carta a quadretti sono: di più. di meno.

Disegna il contorno del poligono ABCDEF, poi rispondi.

• Quanto misura il lato più lungo?

• E il lato più corto?

• Ci sono due lati di uguale lunghezza? Quali sono? ............................................

• Quanto misurano?

• Quanto misura il perimetro?

• La linea MN divide il disegno in due poligoni.

• Confronta i loro perimetri: sono uguali? Sì No

1

Superficie

Usa ogni volta un’unità di misura differente per misurare la superficie della lettera H. Poi completa e rispondi.

Misura dell’area rispetto all’unità di misura scelta A B C D

• Spiega come hai calcolato l’area: .....................................................................................................................................................................................................

• Confronta il valore numerico ottenuto misurando la superficie con ciascuna unità di misura: è sempre uguale? Sì No

• Con quale unità di misura hai ottenuto il numero maggiore?

• E con quale il numero minore?

• È cambiata la superficie? Sì No È cambiata la misura dell’area? Sì No

• Perché?

2

Usa un quadretto per misurare la superficie di ciascuna figura.

Area: Area: Area: Area:

3

Disegna poligoni con area di 8, 10 e 13 triangoli.

4

Sul quaderno, disegna poligoni con area di 3 quadretti. Quanti sei riuscito/a a disegnarne? ........................

Confronta le tue soluzioni con quelle dei compagni e delle compagne.

Perimetro e superficie

5 A B C

Per ciascun poligono, scegli una delle tre unità di misura e usala per stabilire la sua area. Non puoi usare due volte la stessa unità di misura. Poi completa.

Fig. 1: unità di misura scelta

Area:

Fig. 2: unità di misura scelta

Area:

Fig. 3: unità di misura scelta

Area:

6

Misura l’area dei seguenti poligoni: usa come unità di misura il quadretto. Poi completa e rispondi.

Area A:

Area B:

Area C:

7 Nome Pezzi avanzati

Area D:

Area E:

Ci sono polignoni con la stessa area? Sì No Quali?

Leo ha ritagliato il suo nome da un cartoncino di forma rettangolare e sono avanzati due pezzi. Ricomponi il cartoncino, poi calcola la sua area.

Fig. 1 Fig. 2 Fig. 3

Perimetro e superficie

Figure isoperimetriche ed equivalenti

1

Colora nello stesso modo solo le coppie di poligoni isoperimetrici.

2

Quale poligono non è isoperimetrico rispetto agli altri? Coloralo.

3

Indica quali poligoni non sono equiestesi rispetto a quello colorato.

4

Per ciascuno dei seguenti poligoni, disegna sul quaderno un poligono equiesteso.

5

Per ciascuna coppia di poligoni, scrivi se sono isoperimetrici, equiestesi, entrambe le cose o nessuna delle due.

Fig. 1

Fig. 2

Fig. 3

Fig. 4

6

Leggi e completa.

a. Al quadrato sono stati tolti due quadretti.

Il poligono ottenuto è: isoperimetrico. equiesteso.

sia isoperimetrico sia equiesteso.

b. Adesso prova tu a fare un poligono isoperimetrico rispetto al quadrato di partenza togliendo 2 quadretti, diversi da quelli precedenti.

c. Adesso togli 2 quadretti per formare un poligono con il perimetro maggiore rispetto a quello di partenza.

7

Disegna una figura a tuo piacere che abbia la stessa area del fungo. Poi rispondi.

8

• Puoi dire che le due figure sono equiestese?

• E isoperimetriche?

Sul quaderno disegna tre poligoni di forme differenti che abbiano tutti il perimetro di 12 lati di quadretto. Poi confronta le superfici dei tre poligoni che hai disegnato e rispondi.

• Come sono fra loro?

• Puoi dire che i tre poligoni sono isoperimetrici ed equiestesi?

Perimetro e superficie

Figure equicomposte

1

2

Stefano ha fatto due tovagliette con dei ritagli e per ognuna gli è avanzato solo un pezzo. Disegna i pezzi in ciascuna tovaglietta e circonda quello che non ha usato.

Tovagliette Pezzi ritagliati

3

Inserisci i pezzi necessari per ricomporre il rettangolo, scegliendo fra quelli a disposizione. Utilizza i pezzi scelti per formare tre figure differenti e disegnale sul quaderno. Poi rispondi.

• Puoi dire che tutte le figure sono fra di loro equicomposte?

• Perché?

Osserva da quali poligoni è formata la lettera C. Quali altre lettere sono state formate usando gli stessi poligoni? Indica con una X.

4

5

Inserisci i pezzi necessari per completare il muro. Puoi anche ruotare i pezzi. Colora poi nello stesso modo i pezzi congruenti a quelli già inseriti.

Per ottenere la Fig. 2 sono stati tolti dei pezzi dalla Fig. 1. Colora i pezzi tolti scegliendoli fra quelli che sono disegnati accanto.

6

Ricalca e poi ritaglia i seguenti poligoni in modo da avere un quadrato e due triangoli equilateri.

Quante figure differenti potrai ottenere unendo i tre poligoni in modo che combacino per un lato?

Disegna sul quaderno le figure che hai trovato.

Confrontati con i compagni e le compagne: hanno trovato le stesse figure?

Fig. 1 Fig. 2

Perimetro e superficie

Triangoli

1

Completa.

Se costruisci un poligono con tre strisce di carta e un fermacampione ai vertici, ottieni una figura: rigida. articolabile.

Colora solo i poligoni che sono figure rigide.

3

Colora solo i lati con i quali puoi costruire un triangolo.

2 Verifica se hai colorato i lati giusti nell’esercizio precedente.

4

5

Fig. 1 Lato lungo cm; somma dei lati più corti + = quindi, il lato lungo > < = somma dei lati corti.

Fig. 2 Lato lungo cm; somma dei lati più corti + = quindi, il lato lungo > < = somma dei lati corti.

Fig. 3 Lato lungo cm; somma dei lati più corti + = quindi, il lato lungo > < = somma dei lati corti.

In questo caso il triangolo che si forma è un caso limite e si chiama triangolo degenere.

Completa.

Un triangolo si può costruire solo se il lato più lungo è della degli altri due lati. Posso costruire un triangolo con i lati delle seguenti misure: cm; cm; cm.

Fig. 1

Fig. 2

Fig. 3

Perimetro e superficie

6

Classifica i triangoli rispetto ai lati.

7

Il triangolo equilatero ha lati

Il triangolo isoscele ha lati Il triangolo scaleno ha ................. i lati

Classifica i triangoli rispetto agli angoli, scrivi la misura dell’ampiezza di ciascun angolo e completa.

Il triangolo acutangolo ha gli angoli

Il triangolo ottusangolo ha un angolo e angoli

Il triangolo rettangolo ha un angolo e angoli

8

Osserva i triangoli e colora le affermazioni giuste. Poi completa.

Rettangoli

Un triangolo rettangolo può essere non può essere isoscele.

Un triangolo rettangolo può essere non può essere scaleno.

Un triangolo rettangolo può essere non può essere equilatero.

Ottusangoli

Acutangoli

Un triangolo ottusangolo può essere non può essere isoscele.

Un triangolo ottusangolo può essere non può essere scaleno.

Un triangolo ottusangolo può essere non può essere equilatero.

Un triangolo acutangolo può essere non può essere isoscele.

Un triangolo acutangolo può essere non può essere scaleno.

Un triangolo acutangolo può essere non può essere equilatero.

Un triangolo equilatero può essere solo

Obiettivo di apprendimento Classificare triangoli.

Perimetro e superficie

Triangoli

1

In ciascun tringolo sono stati tracciati due segmenti rispetto al lato colorato di celeste, ma uno solo è l’altezza. Ripassala di rosso l’altezza.

2

Indica con una X le misure dei segmenti con i quali puoi formare un triangolo.

Ricorda: per formare un triangolo la lunghezza del lato maggiore deve essere minore della somma della lunghezza degli altri due lati.

5 cm, 10 cm, 4 cm

2 cm, 6 cm, 8 cm

3

12 cm, 10 cm, 10 cm

14 cm, 6 cm, 5 cm

Indica con una X le terne di angoli che potrebbero appartenere a un triangolo.

80°, 100°, 30°

50°, 80°, 50°

4 A C

B

90°

45°

70°, 80°, 30°

60°, 45°, 90°

Calcola l’ampiezza dell’angolo che manca. A C

Calcola l’angolo BĈA

CÂB + AB ˆ C = 45°+ 90° =

180° – =

L’angolo BĈA misura

B

B 90° 45°

90°

30° 110°

B

90° 45° A C

Calcola l’angolo BĈA + = – =

45° A C

L’angolo BĈA misura

5

Perimetro e superficie

Cerca tutti i triangoli che ci sono in figura. Aiutati colorando un triangolo diverso in ciascuna riproduzione della figura di partenza e scrivi che tipo di triangolo è.

6

Triangolo scaleno e Acutangolo

Scrivi in tabella quanti triangoli di ciascun tipo hai colorato.

Calcola il perimetro dei seguenti triangoli. 7

Triangolo Isoscele Scaleno Equilatero

Rettangolo

Ottusangolo

Acutangolo

Perimetro = 10,8 cm

lato AB =

Perimetro = 20 cm

lato AB =

lato AC =

Perimetro = 21,6 cm

lato AC =

lato AB = .......................

lato BC =

Perimetro e superficie

Quadrilateri

1

3

In ciascun quadrilatero, ripassa con lo stesso colore le coppie di lati che sono fra loro paralleli. Poi completa la tabella e rispondi.

B F G

Quadrilateri A

N. di coppie di lati paralleli

B

C D E F G

• Come si chiamano i quadrilateri con almeno due lati paralleli?

Colora di giallo i trapezi e di verde i parallelogrammi dell’esercizio precedente. Poi rispondi e completa.

• Alcuni quadrilateri li hai colorati sia di giallo sia di verde: perché?

• Scrivi i quadrilateri che sono solo trapezi:

• Scrivi i quadrilateri che sono trapezi e anche parallelogrammi:

• Scrivi il quadrilatero che è un rombo e un rettangolo:

Disegna le diagonali di ciascun quadrilatero, poi rispondi.

Ricorda: la diagonale è il segmento che unisce due vertici non consecutivi.

A

B C D E F

• In quali quadrilateri le diagonali hanno la stessa lunghezza? ...................................................................

• In quale quadrilatero le diagonali sono fra loro perpendicolari?

• In quali quadrilateri le diagonali si dividono reciprocamente a metà?

• In quale quadrilatero le diagonali coincidono con gli assi di simmetria?

Perimetro e superficie

4

I quadrilateri si presentano. Indica con una X quello che dice una bugia.

Rettangolo: ho almeno una coppia di lati paralleli, per cui posso dire che sono un trapezio.

Quadrato: ho tutti gli angoli retti, per cui posso dire che sono un rettangolo.

Rombo: ho i lati opposti paralleli e congruenti, per cui posso dire che sono un parallelogramma.

Trapezio: ho due coppie di lati paralleli, per cui posso dire che sono un parallelogramma.

5

Scopri le proprietà che hanno in comune ciascuna coppia di quadrilateri.

a.

Tutti e due hanno i lati opposti

Quindi tutti e due sono dei

b. Tutti e due hanno i lati opposti e tutti gli angoli

Quindi tutti e due sono dei

c. Tutti e due hanno i lati opposti

Quindi tutti e due sono dei

d. Tutti e due hanno una coppia

Quindi tutti e due sono dei

6

Nella figura sono disegnate le diagonali di 6 quadrilateri.

Disegna i quadrilateri e scrivi il loro nome.

Perimetro e superficie

Quadrilateri

1

Disegna due quadrilateri, uno cancavo e uno convesso, aventi i lati congruenti di 3 cm, 4 cm, 6 cm, 7 cm.

2 3 A 87°

Indica con una X le quaterne di angoli che potrebbero appartenere a un quadrilatero.

60°, 100°, 30°, 70° 70°, 80°, 100°, 50°

100°, 80°, 50°, 130° 120°, 85°, 90°, 65°

Calcola l’angolo che manca nei seguenti quadrilateri.

4

5

Disegna un rettangolo e traccia le sue diagonali. In quanti triangoli il rettangolo resta diviso? Come sono tra loro questi triangoli? Che triangoli sono?

Con quattro segmenti di cui tre sono lunghi 5 cm, 12 cm e 3 cm, vogliamo costruire un quadrilatero Quanti centimetri, al massimo, potrà essere lungo il quarto segmento? Perché?

Perimetro e superficie

6

Disegna su un foglio di carta colorata tre triangoli equilateri con il lato di 4 cm.

Ritaglia e incolla i triangoli i su un foglio del quaderno in modo da formare un trapezio. Poi rispondi.

• Che trapezio ottieni?

• Quanto misurano gli angoli interni del trapezio ottenuto?

• Quanto misurano i lati del trapezio?

• Calcola la misura del perimetro del trapezio.

7

Disegna su un foglio di carta colorata 8 triangoli rettangoli isosceli congruenti.

Ritaglia i triangoli e incollane quattro in modo da formare un trapezio. Poi rispondi.

• Che trapezio ottieni?

• Incolla anche gli altri 4 triangoli in modo da formare un parallelogramma.

• I due quadrilateri hanno la stessa area?

• Hanno anche lo stesso perimetro?

• Spiega il tuo ragionamento.

Calcola. 8

È un ..................................................................................................................

Perimetro = 52 cm

Lato = È un

Perimetro = 17 cm

Lato = 3 cm

L’altro lato =

9

Un quadrato con il perimetro di 20 cm può avere un lato lungo 8 cm?

Perché?

10

Un rettangolo ha un lato lungo 6 cm e l’altro lato lungo il doppio. Rispondi.

• Quanto misura il lato corto?

• E il lato lungo?

• Quanto misura il perimetro?

11

In un rettangolo un lato misura 4,5 cm ed è la metà dell’altro lato. Rispondi.

• Quanto misura il lato corto?

• E quello lungo?

• E il perimetro? ......................................................

1

2

L’indagine

Per quali azioni può essere utile svolgere un’indagine prima di essere eseguite?

Indica con una X.

• Attaccare le figurine nell’album. Sì No

• Comprare dei cioccolatini per tutti i bambini della classe. Sì No

• Scegliere dove andare in gita con i compagni. Sì No

• Andare agli allenamenti di pallanuoto. Sì No

Joy sta facendo un’indagine per capire come trascorrono il tempo libero i bambini e le bambine delle classi più grandi. Sottolinea la domanda che dovrà fare per ottenere le informazioni che desidera.

• Che cosa fai quando esci da scuola?

• Quanto tempo dedichi al gioco?

• Quante volte alla settimana ti alleni?

• Che cosa fai nel tuo tempo libero?

3

Indica con una X il campione al quale ti devi rivolgere per indagare sui temi proposti.

Tema su cui indagare Campione

Mezzi di trasporto più usati per andare a scuola.

Il bambino della squadra che ha totalizzato più punti nella partita di basket.

Genitori dei compagni e delle compagne di classe. Bambini e bambine della scuola.

Insegnanti della scuola.

Autisti dello scuolabus.

Chi arbitra.

Spettatori e spettatrici.

Compagni e compagne di squadra.

Custode del palazzetto.

Bambini e bambine della scuola.

La meta preferita per la vostra gita di classe.

Genitori.

Custodi.

Compagni e compagne di classe.

4

Scrivi la domanda che devi porre se fai un’indagine nella tua classe per sapere…

… quale sport è più praticato: .......................................................................................................................................................................................................................

… qual è la colazione più consumata a casa prima di andare a scuola:

… quali animali domestici sono più diffusi:

… i mesi dell’anno in cui sono nati più bambini e bambine: ................................................................................................................................

… quanti alunni e alunne frequentano una scuola di danza:

5

Scrivi a quali persone ti devi rivolgere se vuoi effettuare le seguenti indagini.

• Quali sono le aule che restano più pulite alla fine di tutte le lezioni della giornata:

• Il numero dei fratelli e delle sorelle nella tua classe:

• Quale materia insegna più volentieri: .............................................................................................................................................................................................

• Quale alimento è stato consumato maggiormente nell’ultima settimana a casa:

• Quanti alunni e alunne frequentano la tua scuola:

Scrivi che cosa devi osservare se vuoi sapere…

… se sono di più le macchine con le targhe pari o quelle con le targhe dispari nel parcheggio della scuola:

… quanti giorni di pioggia ci sono stati nell’ultimo mese: ......................................................................................................................................

… quale specie di albero è più presente ai giardini:

… qual è il colore più diffuso delle bici al parco:

… quante ore di matematica fanno nella classe 4a B in una settimana:

7

Svolgi un’indagine su un tema a piacere e completa con tutte le informazioni che ti servono.

TEMA SCELTO:

CAMPIONE A CUI RIVOLGERSI:

DOMANDA:

6

2

Osserva la tabella a sinistra, poi completa quella a destra, come nell’esempio.

N. cugini/e per bambino/a Bambini/e

N. cugini/e per bambino/a Bambini/e

1 X X X X X X

Per ciascun grafico, scrivi di che tipo è e che fenomeno osserva.

DOLCI VENDUTI IN UN GIORNO

1.

3

cioccolata

caramelle lecca lecca

biscotti

I bambini e le bambine della classe 4ª hanno venduto delle spille con alcuni origami. Osserva il grafico delle vendite e rispondi.

• Che tipo di grafico hanno disegnato i bambini e le bambine? ................................................................................................

• Che cosa rappresenta l’immagine indicata nella legenda?

• Quante spille hanno venduto in tutto?

• Quali spille sono piaciute di meno?

• Da che cosa lo hai capito?

Scuole di Colle N. degli alunni/e

Infanzia

Primaria

Secondaria 1°

Secondaria 2°

Legenda: = 100 alunni/e = 10 alunni/e

Forma della spilla Spille vendure

coccinella

farfalla

cane fiore

Legenda: = 5 spille

Approssima i dati e indica con una X quale dei tre grafici li rappresenta in modo corretto.

Film più visti cartoni animati commedia thriller avventura fantasy

Legenda: = 10 bambini/e

Film più visti

cartoni animati

commedia

thriller

avventura

fantasy

Legenda: X = 5 bambini/e

Film più visti

cartoni animati X X X X X X X X

commedia X X X X

thriller X X X X X X X X

avventura X X

fantasy X X X X X X X X X

La media

1

Leggi e completa.

a. Nella tabella sono registrate le caramelle che Giulia ha dato ai suoi compagni e alle sue compagne. Osserva e rispondi.

N. caramelle ricevute Bambini/e

1 8

2 4 3 8

• Quanti bambini e bambine hanno 3 caramelle?

• Quanti una sola? .................

• Ci sono bambinie bambine che hanno 4 caramelle?

Sì No

• Quanti bambini e bambine ci sono in tutto?

b. Aiutati con questa tabella per capire quante caramelle sono in tutto:

N. caramelle ricevute Bambini/e Caramelle in totale

1 8

2 4

3 8

c. Ora calcola la media.

In tutto le caramelle sono: + + =

2

Se tutti i bambini e le bambine avessero ricevuto lo stesso numero di caramelle, quante ne avrebbe ricevute ciascuno?

Per capirlo dividi tutte le caramelle per il numero dei bambini e delle bambine. In linguaggio matematico:

: = La media è di per ogni bambino o bambina.

Calcola la media. Poi rispondi.

7

6

5

4

3

0 2

lenticchie fagioli cecipiselli

• Quale tuffo ha ottenuto la media più alta?

Osserva e rispondi. 1

La moda

pastasciutta

tortellini

risotto

lasagne

minestra in brodo

minestra di verdura

• Su quale fenomeno hanno indagato?

• Qual è il valore indicato dalla moda?

N. fratelli e sorelle = 1 bambino/a Bambini/e

1 2 3 4 nessuno

• Su quale fenomeno hanno indagato?

• Qual è il valore indicato dalla moda?

• Il valore 1 indica che la maggior parte dei

bambini e delle bambine ha

In questi grafici è già stato inserito il valore che indica la moda: completa inserendo gli altri valori.

Età componenti campo estivo Bambini/e

Legenda: = 6 bambini/e

Confronta le tue risposte con quelle dei compagni e delle compagne: avete inserito gli stessi dati? Sì No

Perché?

La probabilità

Se hai queste carte coperte sul tavolo e ne devi pescare una, quale probabilità hai di pescare le carte indicate nella tabella? Completala e rispondi.

Quantità

Carte

Totale carte

Misura della probabilità espressa in frazione

re di picche

tre di quadri

carta con figura

.......... un fante

carta di cuori

• Quale tipo di carta pescherai con certezza?

• Quale carta non potrai pescare?

• Hai più probabilità di pescare il re di picche o la regina di cuori?

Adele mangia i biscotti pescandoli dal sacchetto senza guardare. Colorali in base alla probabilità indicata. Poi rispondi.

• Quale tipo di biscotto è più probabile che peschi Adele?

Lancia un dado a sei facce e completa la tabella indicando con una X la probabilità dell’evento.

Uscirà

Uscirà

Obiettivo di apprendimento Valutare la probabilità di verificarsi di un evento.

Istruzioni per costruire il ventaglio

Materiale occorrente

2 fogli A4 di due colori diversi, 2 bastoncini di legno (bacchette cinesi o da spiedino), un filo resistente, colla, un elastico

Come fare

1. Incolla i due fogli di carta sovrapponendo i lati più corti.

2-3

2. Fai una piega di circa 1 cm sul lato corto del foglio, ribaltalo e fai una nuova piega dello stesso spessore.

3. Procedi così fino a quando non avrai esaurito la carta del foglio, piegandolo a fisarmonica.

4. Ora piegalo a metà facendo in modo che le due estremità superiori si congiungano, e incollale.

5. Fora e inserisci un pezzo di filo robusto al centro del ventaglio, quindi annodalo in modo da legare tutte le pieghe insieme.

6. Incolla i due bastoncini sui lati rimasti liberi del foglio. Poi chiudi il ventaglio: un elastico ti aiuterà a tenerlo ben fermo.

1

Responsabile editoriale: Mafalda Brancaccio

Coordinamento redazionale: Valentina Dell’Aprovitola

Consulenza didattica: Chiara Tannoia

Redazione: Cecilia Barletta, Giulia De Giorgi

Responsabile di produzione: Francesco Capitano

Progetto grafico: Ilaria Raboni

Impaginazione: Bluedit - Torino

Illustrazioni: Francesca Galmozzi

Copertina: A come Ape di Alessia Zucchi

Illustrazione di copertina: Silvia Colombo

Ricerca iconografica: Paola Rainaldi

Referenze iconografiche: Shutterstock

Stampa: Tecnostampa – Pigini Group Printing Division Loreto – Trevi 24.84.063.0

Per esigenze didattiche i testi sono stati quasi tutti ridotti e/o adattati. L’editore è a disposizione degli aventi diritto tutelati dalla legge per eventuali e non volute omissioni o errori di attribuzione.

È assolutamente vietata la riproduzione totale o parziale di questa pubblicazione, così come la trasmissione sotto qualsiasi forma o con qualunque mezzo, senza l’autorizzazione della Casa Editrice.

Produrre un testo scolastico comporta diversi e ripetuti controlli a ogni livello, soprattutto relativamente alla correttezza dei contenuti. Ciononostante, a pubblicazione avvenuta, è possibile che errori, refusi, imprecisioni permangano. Ce ne scusiamo fin da ora e vi saremo grati se vorrete segnalarceli al seguente indirizzo: redazione@elionline.com

Tutti i diritti riservati

© 2024 Cetem, Gruppo Editoriale ELi info@gruppoeli.it

EquiLibri • Progetto Parità è un percorso intrapreso dal Gruppo Editoriale ELi, in collaborazione con l’Università di Macerata, per promuovere una cultura delle pari opportunità rispettosa delle differenze di genere, della multiculturalità e dell’inclusione.

Si tratta di un progetto complesso e in continuo divenire, per questo ringraziamo anticipatamente il corpo docente e coloro che vorranno contribuire con i loro suggerimenti al fine di rendere i nostri testi liberi da pregiudizi e sempre più adeguati alla realtà.

Matematica saperi

classe 4

AMBITO ANTROPOLOGICO

• Sussidiario Storia con Quaderno operativo 4

• Sussidiario Geografia con Quaderno operativo 4

• Atlante multidisciplinare 4-5

ISBN per l’adozione: 9788847307414

AMBITO SCIENTIFICO

• Sussidiario Matematica con Quaderno operativo 4

• Sussidiario Scienze e Tecnologia con Quaderno operativo 4

ISBN per l’adozione: 9788847307421

#altuofianco

• KIT DOCENTE comprensivo di guida alla programmazione, risorse didattiche e tutto il necessario per il corso.

• LIBRO DIGITALE (scaricalo subito seguendo le istruzioni all’interno della copertina) con LIBRO LIQUIDO ACCESSIBILE: volumi sfogliabili, esercizi interattivi, VIDEO, carte storiche e geografiche digitali, audiolibri, percorsi semplificati stampabili

AMBITO ANTROPOLOGICOEAMBITO SCIENTIFICO

ISBN per l’adozione: 9788847307452

Ambiente di apprendimento interattivo per la verifica delle competenze disciplinari.

IL GIOCO

DELLO SVILUPPO SOSTENIBILE

equilibri Sistema Digitale

Accessibile

Gamification MISSION 2030