

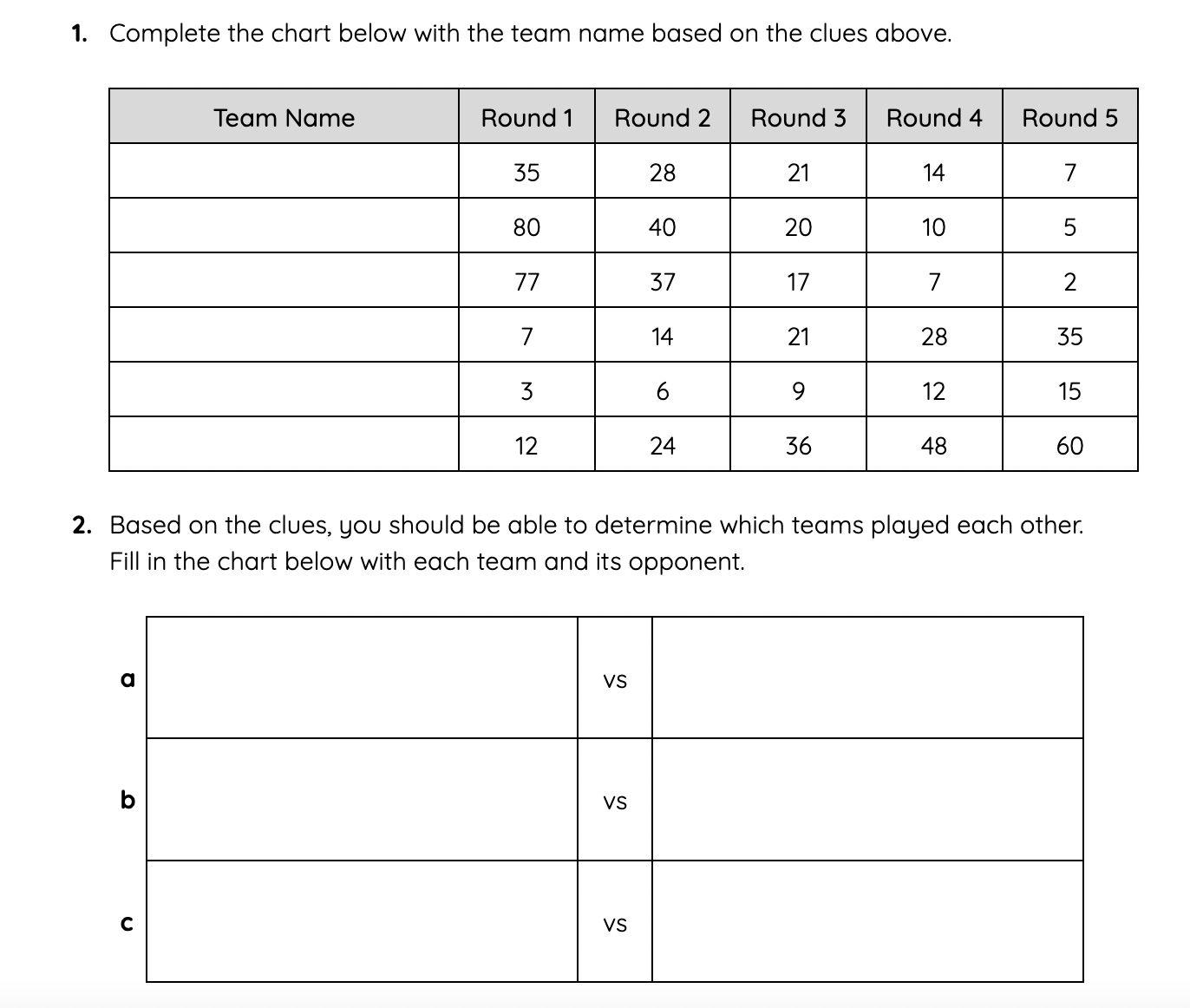
Grade 5 Math Morning
Heather Zetterberg
Math Specialist, Grades K-9




Algebraic Reasoning
In the Lower School




Historical Approach to Algebra Instruction
● Arithmetic instruction then algebra
● Primary practice prior to 1990
● Educators recognized the abrupt cognitive transition from computational work to abstract concepts of High School Algebra
● National shift around 2000 when algebraic reasoning appeared in K-8 instruction
● Shift prompted ideological debates




The Center of the Debate

● What is “algebra”?
● What does it mean to “do” algebra?
● What does “algebraic” reasoning look like in the elementary grades?



Researchers Have Discovered
● Students can begin to reason algebraically much younger than initially thought
● Students can reason in ways that ameliorate difficulties encountered in high school algebra
● Early algebra is not “algebra early”
Source: The Compendium for Research in Mathematics Education, NCTM, 2017: Algebraic Thinking in the Elementary and Middle Grades. Ana C. Stephens University of Wisconsin–Madison, United States Amy B. Ellis University of Georgia, United States Maria Blanton TERC, United States Bárbara M. Brizuela Tufts University, United States. Research supported by NSF.





“Algebraic reasoning is a process in which students generalize
mathematical ideas
from a
set of particular instances, establish those generalizations through the discourse of argumentation, and express them in increasingly formal and age-appropriate ways.”
Kaput, J., & Blanton, M. (2005). Algebrafying the elementary mathematics experience in a teacher-centered, systemic way. In T. Romberg & T. Carpenter (Eds.), Understanding mathematics and science matters (pp. 99–125). Mahwah, NJ: Lawrence Erlbaum Associates.



“Algebraic thinking or reasoning involves forming generalizations from experiences with number and computation, formalizing these ideas with the use of a meaningful symbol system, and exploring the concepts of pattern and functions.”

Van de Walle, J. A., Karp, K., & Bay-Williams, J. (2011). Elementary and middle school mathematics: Teaching developmentally. Boston, MA: Allyn & Bacon.



Algebraic Reasoning as Generalizing Arithmetics
● Exploring properties and relationships

● Exploring equality as a relationship between quantities
● Using symbols, including letters, as variables



Big Ideas of Algebraic Reasoning
1. Representation
2. Proportional Reasoning
3. Balance
4. Variable
5. Function

6. Inductive and Deductive Reasoning



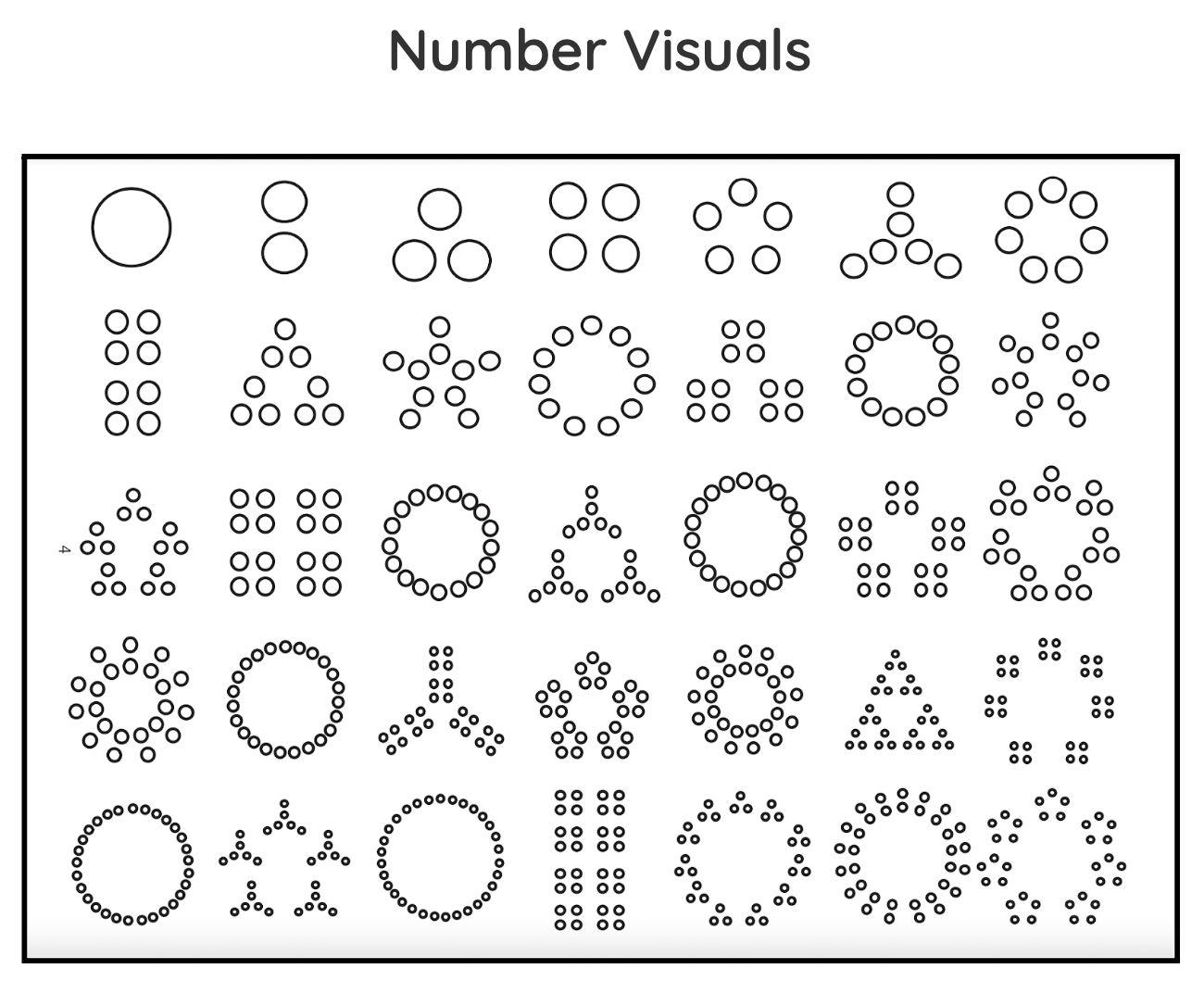
Representation
● Display mathematical relationships in diagrams, drawings, graphs, tables, time lines, and symbols
● Create or match different representations of the same relationships
○ Equations with graphs,
○ Equations with function tables, etc…
● Recognize how a change to one aspect of a representation impacts the representations of others




Making Connections Through Representations
● Concrete or Pictorial Representations

● Graphical Representations
● Unordered and Ordered Tables of Values
● Word Problems and Stories
● Symbolic Representation















Proportional Reasoning
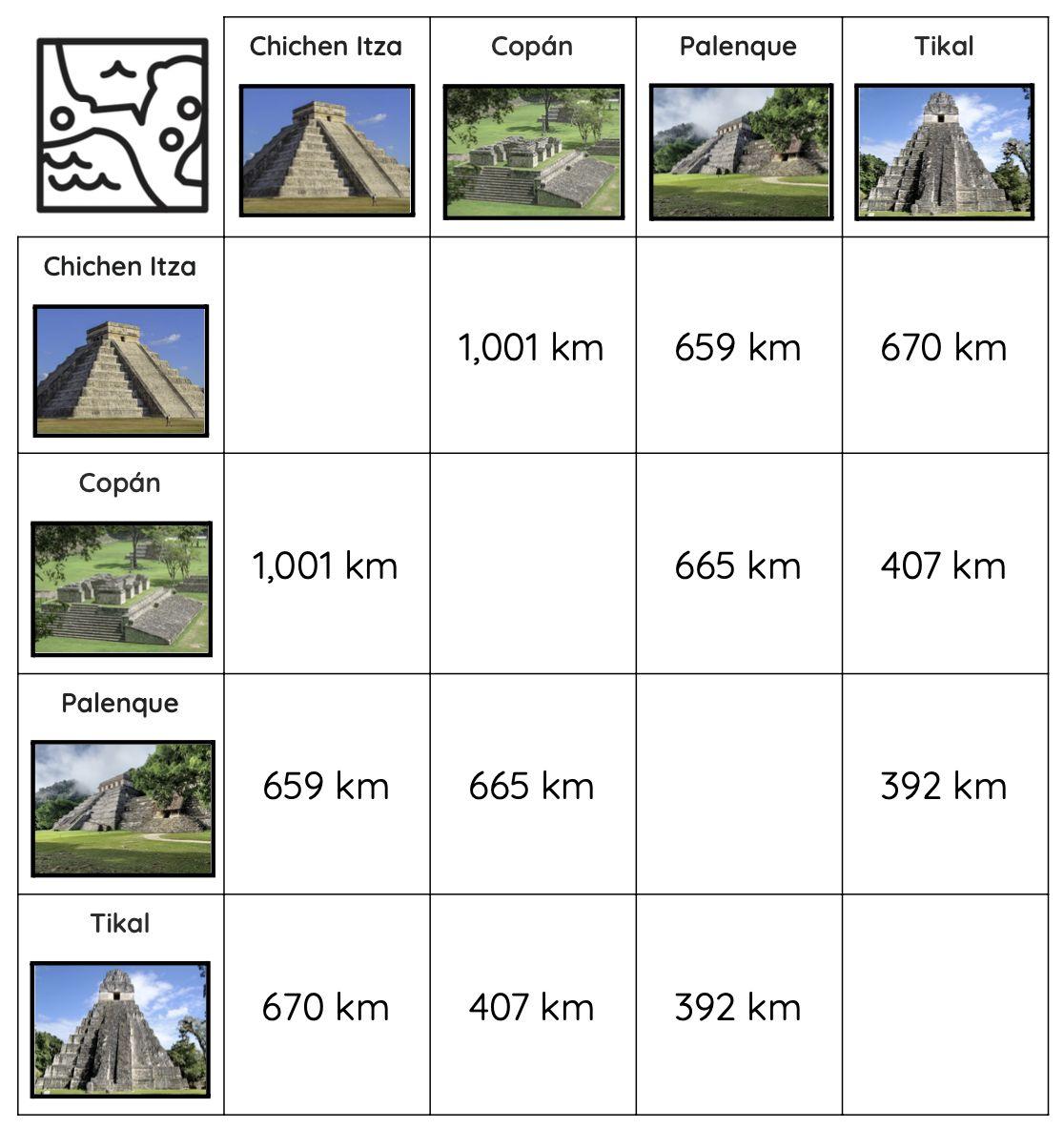
● Determine how objects or quantities vary in relation to one another
● Interpret maps and scale drawings
● Determine dimensions of enlargements and reductions
● Compute unit costs, generating equivalent ratios, identifying percentages











Balance
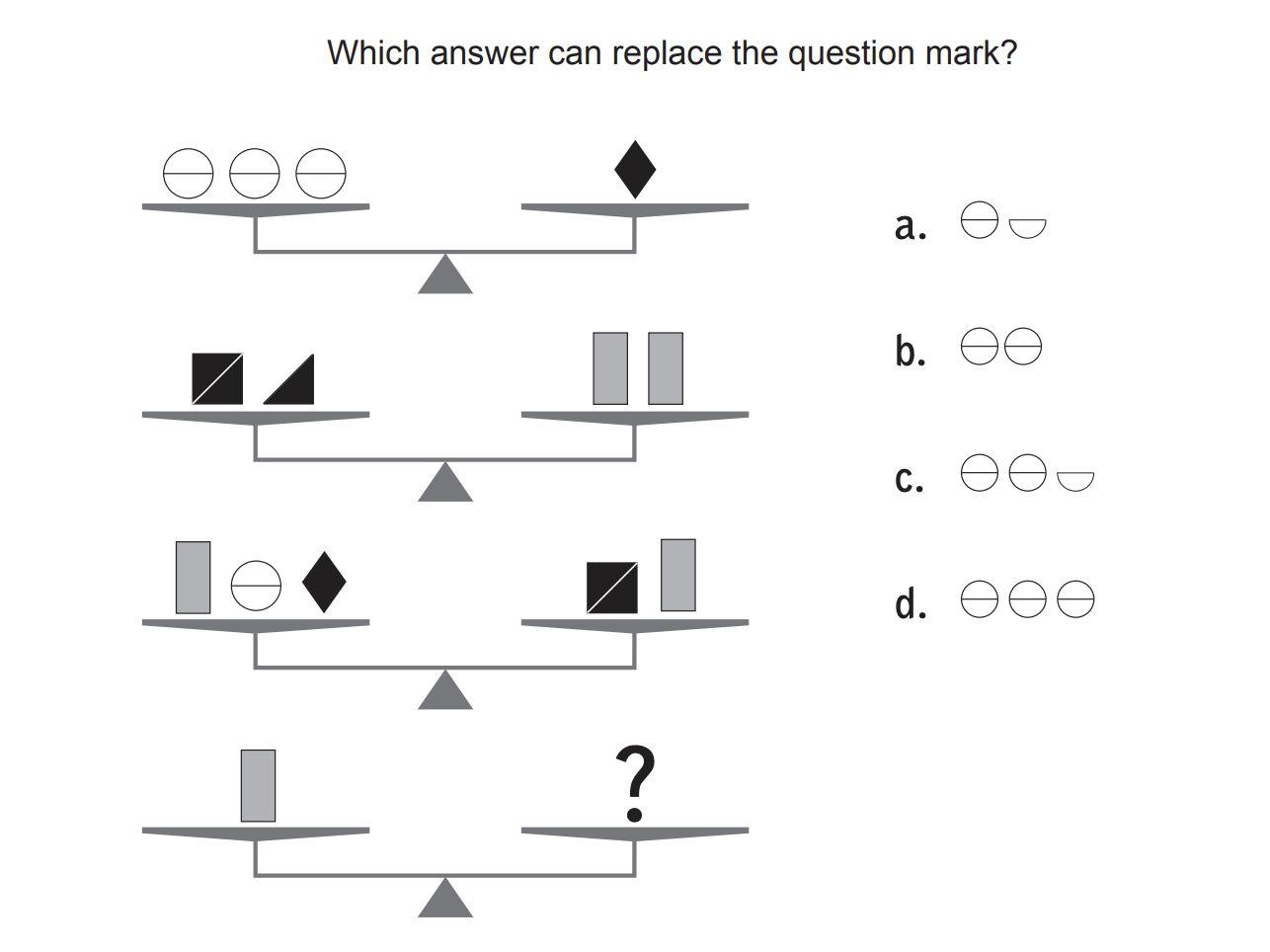
● Modify inequalities to achieve balance or equality
● Solve equations and inequalities
● Understanding the meaning of the equal sign
● Understanding the meaning of inequality signs: <, ≤, >, ≥





Variable
● Generalize relationships
● Represent quantities in formulas, functions, equations and expressions









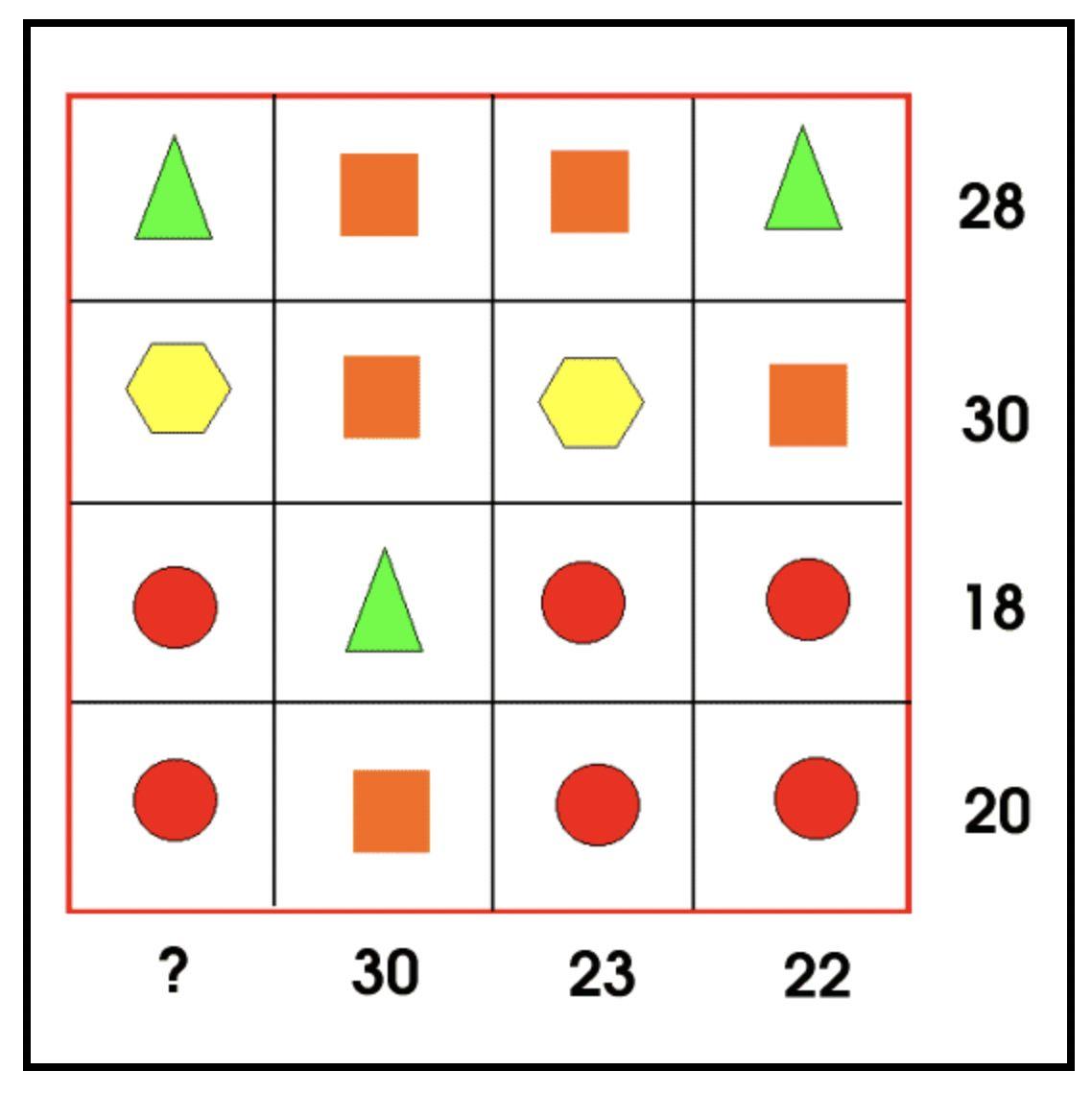




Function
● Generalize patterns
● Identify relationships of two sets that are linked by a rule
● Describe in words or symbols rules for relating inputs and outputs
● Use inverse operations - to undo what other operations did





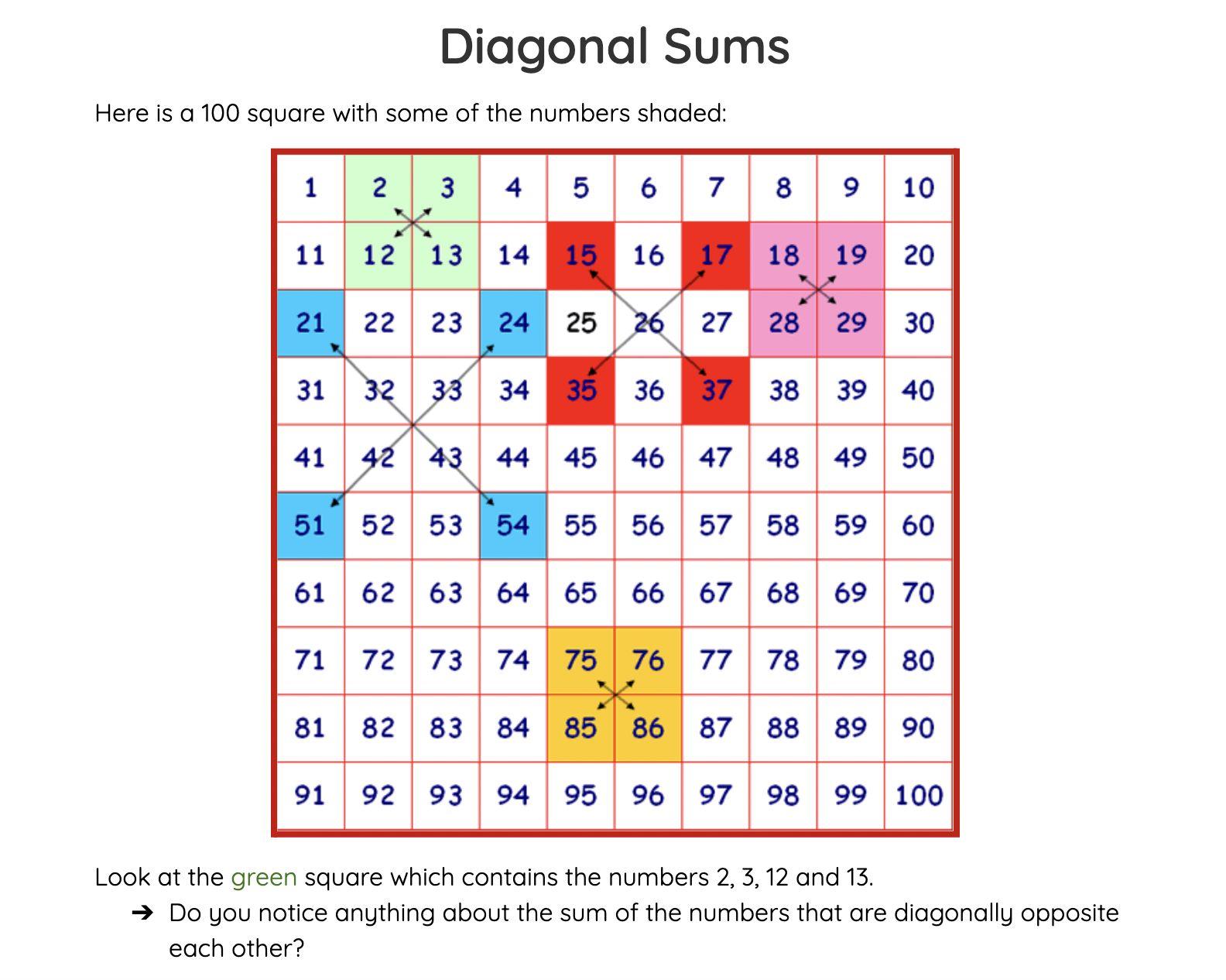


Inductive and Deductive Reasoning
● Inductive Reasoning
○ Examine particular cases, identify patterns and relationships among those cases, and extend the patterns and relationships
○ Recognize, extend, and generalize patterns
● Deductive Reasoning
○ Infer a new relationship gleaned from two or more stated or displayed relationships




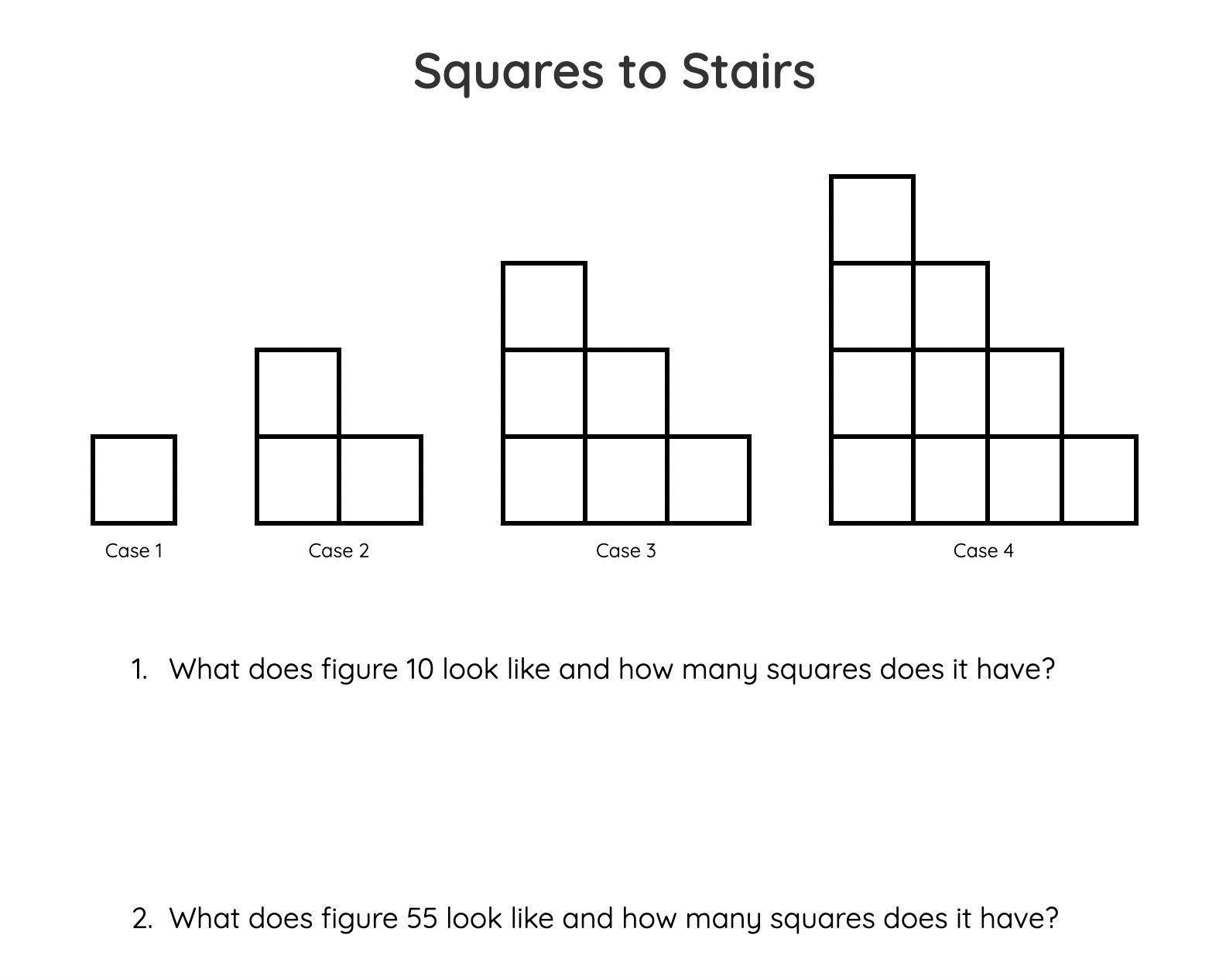

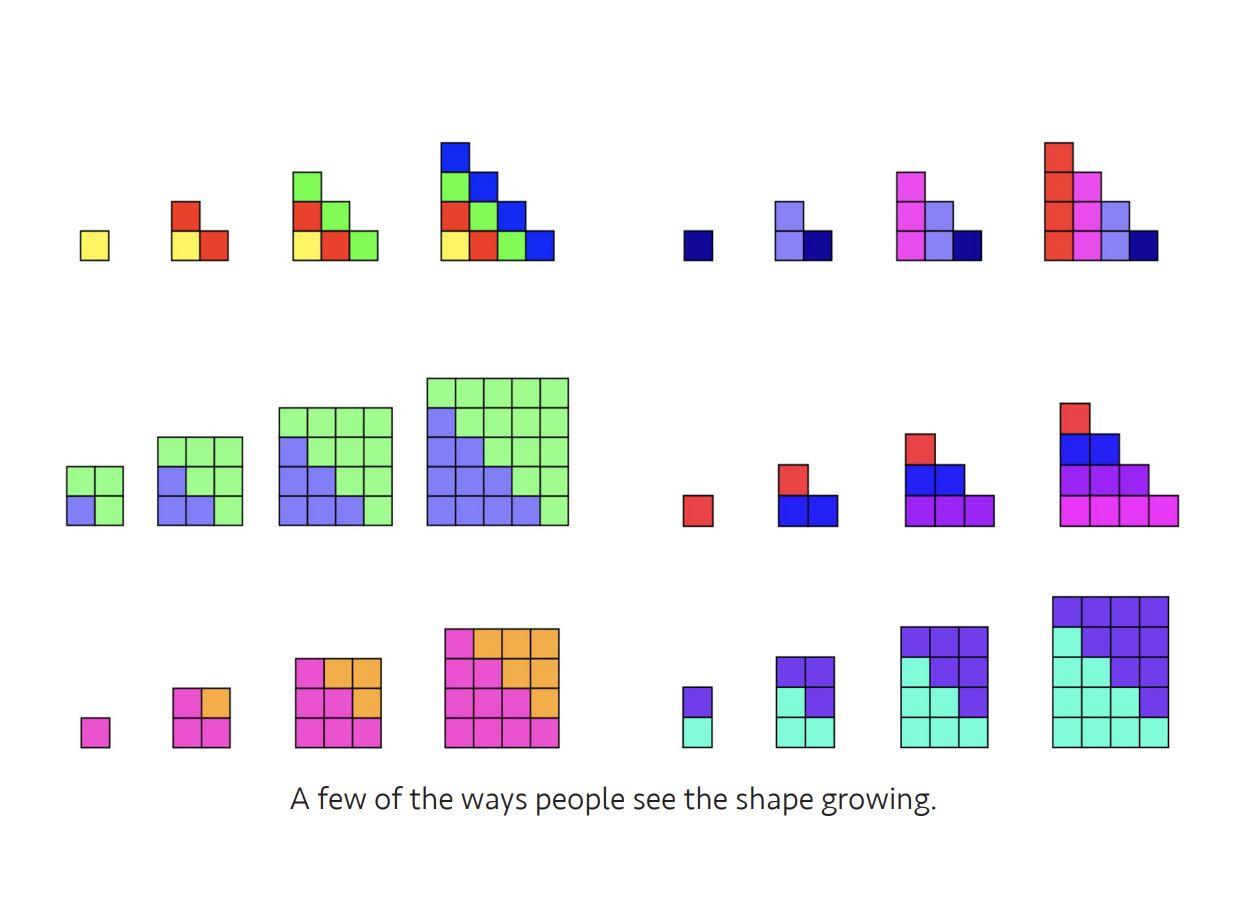






Actions that Develop Algebraic Reasoning
● Generating and testing conjectures - A conjecture is a guess or prediction based on limited evidence.

● Justifying and proving
● Predicting



How Do We Promote Algebraic Reasoning?
● Ask questions
○ To allow students the opportunity to analyze information, build mathematical arguments, and explain their reasoning

● Provide students with many opportunities to construct their own understanding



Constructing Understanding









Foote Values
● Mathematical Reasoning
● Making Sense of Problems
● Perseverance in Solving Problems
● Engaging in Mathematical Discourse
● Constructing Viable Arguments
● Critiquing the Reasoning of Others
● Opportunity for Practice
● Joyful Engagement



Final Thoughts





Connecting Algebraic Reasoning to Algebra Skills

1. Identify Function Rules
2. Write Expressions
3. Write Equations
4. Evaluate Expressions
5. Solve Equations
6. Solve Systems of Equations


