Global Thinkers: Mathematics 4. Secondary (sample)

SECONDARY EDUCATION

Basic knowledge in the course

Practice solving problems

1. Draw a diagram, graph or table to help you organise the information

2. Make drawings for the geometry problems

3. Experiment, use trial and error, give examples... estimate and check...

4. Investigate

Problems

Arithmetic problems

CHALLENGES THAT LEAVE AN IMPRINT

Algebra and geometry

1 Real numbers

1. Irrational numbers

2. Real numbers: the real number line

3. Sections of the real number line: intervals and half-lines

4. Roots and radicals

5. Approximate numbers. Errors

6. Numbers in scientific notation. Error control

7. Logarithms

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

2 Polynomials and algebraic fractions

1. Polynomials. Operation

2. Ruffini’s rule

3. Root of a polynomial. Finding roots

4. Factorising polynomials

5. Divisibility of polynomials

6. Algebraic fractions

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

3 Equations, inequations and systems

1. Equations

2. Systems of equations

3. Inequations with one unknown

4. Linear equations with two unknowns

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

Sequences that approximate interesting numbers

CHALLENGES THAT LEAVE AN IMPRINT

Geometry

4 Similarity. Applications

1. Similarity

2. Homothety

3. Rectangles with interesting dimensions

4. Similarity between triangles

5. Similarity between right-angled triangles

6. Similarity of right-angled triangles in three-dimensional shapes

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

5 Trigonometry

1. Trigonometric ratios of an acute angle

2. Basic trigonometric identities

3. Using a calculator in trigonometry

4. Trigonometric ratios of 0° to 360°

5. Angles of any measurement. Trigonometric ratios

6. Solving right-angled triangles

7. Solving non-right-angled triangles

8. Some interesting theorems

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

6 Analytic geometry

1. Vectors in the plane

2. Calculations using vectors

3. Vectors which represent points

4. Midpoint of a segment

5. Aligned points

6. Equations of a straight line

7. Straight lines. Parallelism and perpendicularity

8. Straight lines parallel to the coordinate axes

9. Relative positions of two straight lines

10. Distance between two points

11. Equation of a circumference

12. Studying some types of motion

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

Science around Barcelona

CHALLENGES THAT LEAVE AN IMPRINT Functions

7 Functions I

1. Basic concepts

2. How functions are presented

3. Domain of definition

4. Axis intercepts. Sign of a function

5. Continuous functions. Discontinuities

6. Variations of a function

7. Tendency and periodicity

8. Linear functions

9. Quadratic functions

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

8 Functions II

1. Piecewise linear functions

2. Radical functions

3. Inversely proportional functions

4. Exponential functions

5. Logarithmic functions

6. Trigonometric functions. The radian Exercises and problems

Maths workshop

Self-assessment

Botanical research

CHALLENGES THAT LEAVE AN IMPRINT Statistics and probability

9 Statistics

1. Statistics and statistical methods

2. Frequency tables

3. Statistical parameters: x and q

4. Dispersion parameters for isolated data

5. Position parameters for grouped data

6. Box-and-whisker plots

7. Statistical inference

8. Statistics in the media

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

10 Bivariate distributions

1. Bivariate distributions

2. Correlation value

3. Using the line of best fit to make estimations

4. Let’s think: does correlation imply cause and effect?

5. Bivariate distributions with a calculator

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

11 Combinatorics

1. Strategies based on the product

2. Variations and permutations (the order matters)

3. When the order does not matter. Combinatronics

4. An interesting number triangle

5. Newton’s Formula

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

12 Calculating probability

1. Random events

2. Probability of events. Properties

3. Probability in simple experiments

4. Probability in compound experiments

5. Creating independent experiments

6. The structure of dependent experiments

7. Contingency table

Exercises and problems solved

Exercises and problems

Maths workshop

Self-assessment

Lottery games inspired by the classics

REAL NUMBERS 1

Since ancient times, natural numbers have been used by all civilisations. The idea of zero and negative numbers took longer to understand. Integers emerged in the late 7th century in India. From this, 9th century Arabic mathematics merged with the decimal-positional numeral system.

Fractions were not used in the way they are today until around the 14th century.

Irrational numbers were discovered by the Pythagoreans around the 5th century BCE. However, for almost 2 000 years they were treated as geometric magnitudes.

The concept of real number has emerged over time through the study of functions. A German mathematician, Cantor, changed the way we thought about rational and irrational numbers in 1871. It was then that we started to think of these numbers as forming a single set, with their own characteristics.

Georg Cantor (1845-1918).

Use what you have learned to solve problems

The number π in ancient times

The number π is an irrational number. However, over the centuries it has been given many different rational values. Some of these include:

Ancient Egypt (approx. 20th century BCE)

Ancient Babylon (approx. 20th century BCE)

Archimedes (3rd century BCE)

Ptolemy (2nd century)

Liu Hiu (5th century)

The organisation of different types of numbers

3,16

25/8

22/7

377/120

355/113

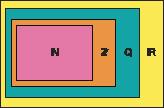
The sets of numbers that we know and have a clear structure are:

• Natural numbers, N

• If we include their opposites (negatives), we get the set of integers, Z

• If we include fractional numbers as well, we get the rational numbers, Q

• If we also include the irrational numbers, do we get a clearly structured set?

❚ Solve

1

a) Write three natural numbers and three integers that are not natural numbers.

b) Write three rational numbers that are not integers and three irrational numbers.

c)In your notebook, organise the numbers from your previous answers in a diagram like the one at the beginning of this exercise.

2 Given that the value of π is 3.14159265359… give the margin of error in each of the approximations from the previous page.

For example: 377 120 = 1 3,141666… 3,141592… The margin of error is less than 1 ten thousandth: error < 0.0001

IRRATIONAL NUMBERS 1

Rational numbers are numbers that can be expressed as the quotient of two integers. Their decimal expression is terminating or recurring.

Irrational numbers are non-rational numbers, in other words, they cannot be expressed as the quotient of two integers. Their decimal expression is infinite and non-recurring. For example, π = 3.14159265359…

There are infinite irrational numbers. Let’s take a look at some interesting examples.

The diagonal of a square: the number √2

The Pythagorean theorem gives us the value of the diagonal of a square with sides measuring 1:

d = 11 2 22+=

We are going to demonstrate that 2 is irrational, in other words, that it cannot be expressed as the quotient of two integers. We will do this through reduction to absurdity (supposing it is rational and then showing it reaches an absurdity).

— Suppose that 2 is rational.

Remember

When we break down a perfect square into prime factors, each prime number appears an even number of times. For example:

N = 22 · 3 · 53

N 2 = (22 · 3 · 53)2 = 24 · 32 · 56

All the exponents are even.

— As such, it could be expressed as the quotient of two integers: b a 2=

— We square the two sides: 2 = b a 2 2 8 a 2 = 2b 2

Since b 2 is a perfect square, it contains the factor 2 an even number of times. Therefore, 2b 2 has factor 2 an odd number of times, which is impossible since 2b 2  = a 2 is another perfect square.

In this way, our reasoning is as follows: ‘If we presume that 2 is rational, we reach an absurdity’. Therefore, we have shown, through reduction to absurdity, that 2 is not rational.

Other irrational numbers expressed through radicals

For the same reason as 2 , if p is not a perfect square, p is irrational.

If p is not an exact nth power, p n is an irrational number.

For example, 8 , 9 3 and 10 5 are irrational numbers.

The result of performing an operation using a rational number and an irrational one is irrational (except in the case of multiplying by zero).

For example, the following are irrational numbers: 2 + 3, 4 – 10 5 , 9 3 : 7.

Let’s show that 4 – 10 5 is irrational based on the fact that 10 5 is.

anayaeducacion.es

Recognising irrational numbers.

Think and practise

— We will call N = 4 – 10 5 8 10 5 = 4 – N

— If N were rational, 4 – N would also be rational. In other words, 10 5 would be rational, which is not true.

1 Demonstrate that the following numbers are irrational: a) 3 b) 4 3 c) 5 + 4 3

Pentagram

The golden ratio: F = √5 + 1

This shape is formed by the five diagonals of a regular pentagon. It was the symbol of the Pythagoreans.

anayaeducacion.es

Interesting facts about π and other irrational numbers.

Remember

Unlike 2 , 5 , F, and other irrational numbers, π and e cannot be represented exactly on the real number line.

Think and practise

The diagonal of a pentagon with a side length of 1 unit is ( 5 + 1) : 2 which is obviously irrational. Furthermore, historically, it is the first irrational number to be discovered.

Greek artists believed that proportions based on the number F were especially harmonious, which is why they decided to call F the golden number.

The name, F (phi, the letter ‘F’ in Greek), comes from Phidias, a Greek sculptor from the 5th century BCE who often used this ratio.

The number π

As you know, π is the relationship between the length of the circumference of a circle and its diameter. You have known and used this number for many years now.

It is an irrational number and, therefore, has infinite non-recurring decimal digits.

π is the Greek letter corresponding to ‘p’. Why is it called Pi? The Greek word perifereia means ‘circumference’ (the periphery of the circle).

The number e

The number e is another fundamental irrational number in mathematics. It is named after Leonhard Euler, one of the most important mathematicians in history.

Its approximate value is 2.7182... and you will come across it in many different situations:

— When describing the growth of an animal or plant population, we use an exponential function which contains the number e.

— It is also used to describe the change in radioactivity of a radioactive substance over time.

— If we hang a chain, a cable, a rope, etc. with each end at the same height, the curve it forms (a catenary) is also described using the number e

2 Explain why these constructions contain a segment that measures the same as F 2 5 2 1 2 51 = + =+

3 Demonstrate that the golden number, F, is irrational. This rectangle has the peculiarity that if we cut a square out of it, the rectangle that is left is similar to the initial one. Demonstrate that its longest side is x = F.

REAL NUMBERS: THE REAL NUMBER LINE 2

Interesting fact

You may study other sets of numbers in later years, but Û fills the whole number line and leaves no gaps, as we will see below.

Notation

When any number, x, is natural, it is expressed as x ∈ N, if it is an integer as x ∈ Z, if it is rational as x ∈ Q, and if it is real as x ∈

The set formed by rational and irrational numbers is called the set of real numbers and is represented by the letter Á

In other words, both rational and irrational numbers are real numbers. They form all the real numbers there are. With the Á set, we can complete the table of sets of numbers:

Observe

The product of two negative integers is not a negative integer. For example: (–2) · (–3) = 6

And the result of adding two fractional numbers is not necessarily a fraction. For example:

With real numbers, we can perform the same operations as with rational numbers: addition, subtraction, multiplication and division (except for zero), and the same properties are maintained.

We can also extract roots of any index (except roots with even indices of negative numbers) and the result is still a real number. This does not happen with rational numbers.

We can see that the N, Z, Q and, now, Á sets are closed when working with addition and multiplication; in other words, both the sum and product of two elements of one of these sets are also part of that set. However, this is not the case for negative integers, fractions and irrational numbers: the sum of two irrational numbers can be rational (for example: (1 + 2 ) + (3 – 2 ) = 4) and the product of two irrational numbers can also be rational (for example: · 28 = 4).

The real number line

Rational numbers, as you know, are grouped densely on the number line, in other words, each section, no matter how small, contains an infinite number of rational numbers. However, as strange as it may seem, there are also an infinite number of gaps between them. These gaps are filled with the irrational numbers. Together, they fill the line.

Remember

The real number line is complete, in other words, there is a real number for each point on the line and a point on the line for each real number.

If we place an initial point (0, zero) on a line and mark the length of one unit, each point on the line will correspond to a rational or irrational number. In other words, each point on the line corresponds to a real number. This is why we call this number line the real number line.

Once all the real numbers have been put in place, we can be sure that between any two numbers, no matter how close together they are, there are infinite rational and irrational numbers.

Example

Representation of 6 5 :

Representing numbers on the real number line using thales’ theorem to represent fractional numbers

Have a look at how we use Thales’ theorem to place the number 5 14 on the real number line:

Focus

on English

procedure: an accepted way of doing something.

anayaeducacion.es GeoGebra. Representing numbers on the real number line.

Think and practise

14 = 2 + 5 4

5

using the pythagorean theorem to represent radicals

The following procedure* allows us to calculate n for any n é N: For example:

32 1 2 2 =+ ` j

10 =+3122

However, most real numbers cannot be represented exactly using this type of procedure. For example, how would you represent 842 5 ? We normally use an approximate representation.

approximate representation of real numbers

We can represent a real number given as a decimal with as close an approximation as we like. For example: 842 5 = 3.8464…:

Notice how each expansion involves splitting the previous subinterval into ten parts and then taking one of those parts. We can get as close to the number we want as we like.

Depending on their type, real numbers can be represented on the real number line either exactly or with as close an approximation as we like.

1 a) Demonstrate that the point represented is 21 .

2 What number is the arrow in the following diagram pointing at?

b) Represent 27 (27 = 36 – 9) and 40 (40 = 36 + 4).

Represent 2.716 in the same way.

SECTIONS OF THE REAL NUMBER LINE: INTERVALS AND HALF-LINES 3

In the world of science, we often need to determine the scope of a certain variable. For example, ‘the period of time between 3 s and 11 s’. Therefore, we need to learn the right names for certain sections of the real number line.

Open interval

The open interval (a, b) is the set of all the numbers between a and b, but not including a or b : { x ∈ Á / a < x < b }.

It is represented as follows: a b

For example, the interval (–2, 1) is formed by the real numbers between –2 and 1, but not including –2 or 1: { x ∈ Á / –2 < x < 1}.

Another example: to make a box using a sheet of card measuring 15 cm × 10 cm, you need to cut four squares out at its corners and then fold it. The sides of the squares, in this case, have to be less than 5 cm 8 (0, 5).

Closed interval

The closed interval [a, b] is the set of all the numbers between a and b, including both of them: { x ∈ Á / a ≤ x ≤ b }.

It is represented as follows: a b

For example, the interval [–2, 1] is formed by the real numbers between –2 and 1, including –2 and 1: {x ∈ Á / –2 ≤ x ≤ 1}.

Another example: the parcels we deliver must weigh 2 kg or above, but no more than 5 kg 8 [2, 5].

Half-open interval

• The interval (a, b] is the set of all the numbers between a and b, including b but not a: {x ∈ Á / a < x ≤ b }.

It is represented as follows: a b

• The interval [a, b) is the set of all the numbers between a and b, including a but not b : {x ∈ Á / a ≤ x < b }.

Think

• Which numbers are in the interval

• Which inequality would express the integers included in the interval [–2, 0)?

It is represented as follows: a b

For example, the interval (3, 4] is formed by all the real numbers between 3 and 4, including 4 but not 3: {x ∈ Á / 3 < x ≤ 4}.

Another example: a nursery school admits children that have turned 1 but are not yet 4 years old 8 [1, 4).

Half-lines

x < a}

Half-lines and the real number line

(– ∞, a) are the numbers less than a: { x ∈ Á / x < a}.

(– ∞, a] are the numbers less than a and including a: { x ∈ Á / x ≤ a}.

(a, +∞) are the numbers greater than a: { x ∈ Á / x > a}.

[a, +∞) are the numbers greater than a and including a: { x ∈ Á / x ≥ a}.

• (–∞, 2) is the set { x ∈ Á / x < 2} 8 2

• [2, +∞) is the set { x ∈ Á / x ≥ 2} 8 2

The union of two intervals or halflines is represented by á: (–∞, 2) á (0, 5] = (–∞, 5]

The intersection of two intervals or half-lines is represented by Ü:

(–∞, 2) Ü (0, 5] = (0, 2)

Problems solved

1 Write the following in interval form and draw them:

a) 2 < x ≤ 3 b) x ≤ 1

c) x > 0

2 Write the following as inequalities and draw them:

a) [–2, 0] b) [–1, +∞)

c) (0, 1)

3 For which values of x is the following expression true?

(x 2) () x3 – +

• In order to be able to vote, you need to be 18 8 [18, +∞). Of course, in this context, +∞ has to be put into perspective, because nobody lives forever.

The real number line itself is represented as an interval like this:

Á = (–∞, +∞).

a) Half-open interval (2, 3] 2 3

b) Half-line (– ∞, 1] 1

c) Half-line (0, +∞) 0

a) {x / –2 ≤ x ≤ 0} –2 0

b) {x / x ≥ –1} –1

c) {x / 0 < x < 1} 0 1

The square root can be calculated when the radicand is zero or positive, and this happens when one of the factors is zero, both are negative or both are positive. In other words, if x ≤ –2 or if x ≥ 3.

(–∞, –2] ∪ [3, +∞) –3 –2 –1 0 1 2 3 4

Think and practise

1 Write the following sets in interval form and represent the numbers that meet the conditions on the number line in each case:

a) Numbers between 5 and 6, both included.

b) Greater than 7.

c) Less than or equal to –5.

anayaeducacion.es GeoGebra. Intervals on the real number line.

2 Write the following in interval form and draw them:

a) { x ∈ Á / 3 ≤ x < 5} b) { x ∈ Á / x ≥ 0}

c) { x ∈ Á / –3 < x < 1} d) { x ∈ Á / x < 8}

3 Write as inequalities and draw them.

a) (–1, 4] b) [0, 6] c) (–∞, – 4) d) [9, +∞)

ROOTS AND RADICALS 4

Mental arithmetic

1. Indicate the value of k in each case: a) k 3 = 2 b) 243 3 k =

c) k 3 2 4 = d) 1 024 2 k =

2. Calculate the following roots: a) 8 –3 b) 32 5 c) –32 5 d) 0 8

81 4 f ) 125 3

The nth root of a number, a, (written a n ) is the name given to a number, b, that meets the following condition:

a n = b if b n = a

a n is called a radical; a, radicand; and n, the index of the root.

When working on expressions like this one, you will sometimes need to calculate the numerical value. To do so, you need to bear in mind the definition, like in the exercises in the margin of this page, or use a calculator. However, in other cases, you will need to keep the radical, simplify it, perform operations with other radicals, etc.

Some peculiarities of roots

• If a ≥ 0, a n exists no matter what the value of n is.

• If a < 0, only its roots of odd indices exist.

• Although 4 has two square roots, when we write 4 we are referring to the positive root: 4 = 2.

In general, a positive number, a, has two square roots: a and – a .

Radicals in exponential form

Radicals can be expressed as powers:

anayaeducacion.es GeoGebra. Activities for reviewing the properties of powers.

1 Express each of the following roots in exponential form:

2 Calculate.

41/2

3 Express the following in radical form:

7/9

6251/4

Operations with radicals

Radicals have a series of properties that you need to know and be able to use easily. You will find them listed in the margin of this page and the next one. All of them are the direct consequences of known properties of powers. We will pay special attention to the operations that they can be used for.

simplification of radicals

When expressing radicals as powers, we sometimes notice that they can be simplified. For example:

93 33 3 // 4 2 4 24 12 = ===

We have applied property 1 (see margin).

reduction of radicals to a common index

It is not always easy to compare two radicals with different indices. If we express them with the same index, it is much easier. This actually just means reducing them to a common denominator.

For example, to compare 586 3 to 70 ,

We have applied property 1 again (see margin).

taking out factors from roots

In order to simplify some radicals, and to add and subtract them, sometimes we need to take out factors from a root. Let’s look at some examples:

We have applied property 2 (see margin).

product and quotient of radicals with the same index

For example: · 15 20 15 20 300 · == (property 2, see margin)

product and quotient of radicals with a different index

To multiply or divide radicals with a different index, we reduce them to a common index:

We have applied properties 1, 2 and 3 (see margin).

Only identical radicals can be added together.

For example:

We have applied property 4 (see margin).

For

We have applied property 5 (see margin).

We cannot add two different radicals together unless we find their approximate decimal expressions. We can only add identical radicals. For example:

We can only solve them approximately, or leave them in this form.

We can, however, simplify the following expression: 75 11

Sometimes, the possibility of simplifying an addition of radicals is hidden. First, we need to take out any factors that we can from the roots or simplify them. For

Activities to consolidate your knowledge of radicals.

7

8

9

Observe

2 = 1.4142…

It is more difficult to calculate:

1.00000000 1.4142 0100600 0.7071… 016060 01918 than to calculate: 1.4142… 2 014 0.7071… 02 0

and we get the same result.

Rationalising the denominator

In antiquity, when instruments used for calculation did not exist, people had to try and find methods to make operations easier. For example, calculating 2 1 by hand can be done directly (calculating a few figures of 2 and then dividing the result by 1). However, we can simplify the calculations much more if we remember that:

Remember

Rationalising is making something rational that was not rational to begin with.

Focus on English vary: change.

If you perform the operation both ways, you will see that it is much easier if you remove the radical from the denominator (see margin).

Although nowadays we do not need to do so, thanks to the powerful calculation tools available, the final results of problems are still usually given with numerical expressions that do not have radicals in the denominator.

The process we use to remove the radicals from the denominator is called the rationalisation of the denominator.

In each case, we should ask ourselves this question: Which expression do I need to multiply the denominator by for the product not to have radicals? Once we have found the expression, we will also multiply the numerator by it so that the final result does not vary*.

Remember

• (a + b ) · (a – b ) = a 2 – b 2

• We call the expression ab – the conjugate of ab + And, the other way round, ab + is the conjugate of ab –

Think and practise anayaeducacion.es Consolidate your knowledge with some new rationalisation exercises.

10 Rationalise the following denominators:

APPROXIMATE NUMBERS. ERRORS 5

Observe

a) 34 m has 2 significant figures.

b) 0.0863 hm3 has 3 significant figures.

c) It is possible that 53 000 L only has 2 significant figures if the zeros are just used to designate the number. In this case, it would be better to say 53 thousands of litres.

Observe

Measurement: 34 m

a)

Absolute error< 05 m

b) :.

Measurement0 0863 hm

Absolute error< 0 00005 hm In other words, bs.error< 50 m a

Approximations and errors

For practical applications, we generally work with approximate numbers. Let’s review some of the concepts and procedures for using them.

We call the figures used to express an approximate number significant figures. We only need to use those we are sure of, and in such a way that they are relevant for the information we want to transmit.

For example, if the capacity of a swimming pool is 718 900 L, it might be more sensible to say it was 719 m3, using only three significant figures. However, if the measurement was not very accurate, or we did not want to give such an exact measurement, it might be better to say 720 m3, or even 72 tens of m3

The absolute error of an approximate measurement is the difference between the real value and the approximate value.

Absolute error = |Real value – Approximate value|

Measurement: thousand Ae error

c) L L 53 500 bsolut <

Observe

The relative errors of the previous measurements are:

a) R.e. < . 34 05 < 0.015 = 1.5 %

b) R.e. < 0.0863 0 00005 < 0.0006 = 0.06 %

c) R.e. < 53 000 500 < 0.0095 < 0.01 = 1 %

Problems solved

1 Use a reasonable number of significant figures to express the following quantities:

a) Visitors to an art gallery in one year: 183 594.

b) People attending a demonstration: 234 590.

c) Number of bacteria in 1 dm3 of a preparation: 302 593 847.

The real value is generally unknown. Therefore, the absolute error is also unknown. The most important thing is to be able to put limits on it: the absolute error is less than… We get the limit of the absolute error from the last significant figure used.

In the previous example (capacity of the swimming pool: 719 m3), the last significant figure (9) gives units of m3. The absolute error is less than half a cubic metre (error < 0.5 m3).

The relative error is the quotient of the absolute error and the real value. It is therefore lower the more significant figures we use. The relative error is usually also expressed as a percentage (%).

In the example, the relative error is less than: 719 05 < 0.0007 = 0.07 %.

a) It is quite possible that this number is accurate, as the visitors to a museum pay for a ticket, which is recorded and counted. Let’s suppose that this number, 183 594, is the number of tickets sold.

Nevertheless, the figure can be simplified: ‘almost two hundred thousand’ or ‘more than one hundred eighty thousand’ are valid estimations.

b) It would be impossible to count the demonstrators this accurately. Even if this figure has not been ‘inflated’ or ‘played down’ for political reasons, it is impossible to get so close to the actual figure. For example, it would be reasonable to say ‘more than two hundred thousand’, or even ‘between 200 000 and 250 000’.

c) One, or at most two, figures is the most accurate approximation possible with this type of quantity: 3 hundred millions of bacteria, or 30 ten millions of bacteria.

2 Give a limit of absolute error and of relative error for each of the estimations of the amounts in the previous exercise.

a) If we say the number of visitors is 180 thousand (or, even better, 18 ten thousands), we have an absolute error of 183 594 – 180 000 = 3 594 people. We can be this accurate because we know the exact amount. However, whoever we give this information to (18 ten thousands) will need to understand that there may be an error of up to 5 units from the first unused figure: 5 000 people. To summarise:

Estimation: 180 thousand

Absolute error < 5 000

Relative error < 180 000 5 000 < 0.028 < 0.03 8 R.e. < 0.03 = 3 %

b) Estimation: 200000

Absolute error < 50000

Relative error < 200 000 50 000 = 0.25 = 25 %

c) Estimation: 3 hundred millions = 300 million

Absolute error < 0.5 ten millions = 5 million

Relative error < 300 5 < 0.017 < 0.02 8 R.e. < 0.02 = 2 %

Think and practise anayaeducacion.es Practise calculating errors.

1 True or false? Explain your answers.

a) Saying that a swimming pool holds 147 253 892 thousand drops of water is correct if the measurements are very accurate.

b) Saying that a swimming pool holds 147 253 892 thousand drops of water is not reasonable, as it is impossible to measure it this accurately. It would be much more sensible to say that the swimming pool holds 15 ten thousands of millions of drops.

c) If we correctly estimate that the number of drops of water that a swimming pool holds is 15 ten thousands of millions, the absolute error is less than half of ten thousand million drops; in other words, absolute error < 5 000 000 000 drops.

d) If the relative error for a certain measurement is less than 0.019, we can say that it is less than 19 %.

e) If the relative error for a certain measurement is less than 0.019, we can say that it is less than 2 %.

f ) The calculator tells us that π = 3.14159265. If we take π = 3.14, we can say that the absolute error is less than 0.00159266, but it is more reasonable to say that the absolute error < 0.0016 or even that the absolute error < 0.002.

2 Explain why it is not reasonable to say that there are 11 892 583 grains of rice in a sack.

3 Express it in a suitable way and give a limit of absolute error and relative error for the expression.

4 Give a limit of absolute error and relative error for when you approximate π as 3.1416.

NUMBERS IN SCIENTIFIC NOTATION. ERROR CONTROL 6

Test yourself

Express the following numbers in scientific notation: a)

The numbers 3.845 · 1015 and 9.8 · 10–11 are written in scientific notation because:

— They are made up of two factors: a decimal number and a power of 10.

— The decimal number is greater than or equal to 1 and less than 10.

— The power of 10 has an integer exponent. The first, 3.845 · 1015 = 3 845 000 000 000 000, is a ‘large’ number. The second, 9.8 · 10–11 = 0.000000000098, is a ‘small’ number.

advantageS of thiS notation

As its name suggests, this form of notation is intended to be used in contexts that require precision, not in everyday language. Can you imagine saying something like this?

— How many children do you have? 8 5 · 100

— How many students are there in your school? 8 6.74 · 102

— Do you have any pins with a width of 2.5 · 10–4 m?

Obviously not. Clearly, this form of notation is not for use in everyday life. However, this form of expression is very useful for handling very large or very small approximate quantities, since:

• You can see the ‘size’ of the number at a glance. It can be seen in the second factor and it is given by the exponent of 10.

• We can see how accurate the quantity is. The more significant figures given in the first factor, the more accurate the number is.

Interesting fact

You might come across an explanation like this:

If an integer ends in one or more zeros, you can easily determine the number of significant figures it has by expressing it in scientific notation. However, another way to indicate that these zeros are significant figures is to put a decimal point at the end of the number. Like this:

3 200 would have 2 significant figures.

3 200. would have 4 significant figures. This rule is not approved by the scientific community (and we will not use it in this book), but if the teacher thinks it might help to clarify things, why not use it?

For example, we can see that 7.6 · 108 and 7.603 · 108 are approximately equal (‘very similar sizes’). However, the second one is more accurate, as it has four significant figures, whereas the first one has only two.

Operations with numbers given in scientific notation

We can easily do operations in scientific notation with a calculator. Remember that to write a number in scientific notation you use the key. For example, 7.6 ·

if we wanted to do this ‘by hand’, we would have to take great care.

product and quotient

We do the operations involving the decimal components separately from the powers of 10. Then, we adjust the result so that it is expressed correctly using scientific notation. For example:

Note that in the quotient 3.25 : 4.6 we have used four significant figures. If the context of the problem does not suggest the right number of significant figures to use, we have to make the decision subjectively.

anayaeducacion.es

Operations with numbers in scientific notation.

addition and subtraction

We have to prepare the addends so that they have the same power of base 10. That way we can use it as a common factor. Then, once the addition has been performed, the result is readjusted. For example:

Attention

The information given by the following numbers is different: 2.5 · 102; 2.50 · 102; 2.500 · 102

The zeros added to the end of the decimal number are used to indicate the number of figures that are accurate.

Problem solved

We are told that 1 400 million people live in China.

a) Express this quantity in scientific notation.

b) Is it an exact or approximate amount?

c) Give a limit of absolute error based on how the figure was given.

d) Give a limit of relative error.

Controlling error in a number in scientific notation

If we are told that ‘there are 2 500 bags of flour in this warehouse’, this could be an approximate quantity. If so, the statement might only mean that there are approximately 25 hundreds of bags, with an error of less than 50 bags. Or it might mean there are 250 tens, with an error of less than 5 bags.

If we use scientific notation, the expression is unambiguous: 2.5 · 102 means that there are only two significant figures. If there are three, we write 2.50 · 102.

a) 1 400 million = 1.4 · 109 inhabitants

b) Obviously, this is an approximate number, as it is impossible to calculalte such a large, dispersed and changeable amount accurately.

c) and d) When we are told ‘1 400 million people’, we expect the first two figures to be accurate. However, it is possible that one of the zeros that comes after them is also accurate.

If only the two first figures in the measurement are accurate:

Measurement: 14 hundred millions of people.

Absolute error < 0.5 hundred millions = 50 000 000

Relative error < 0.5/14 < 0.036 = 3.6 %

If the first zero in the measurement is accurate:

Measurement: 140 ten millions of people. In this case, we can express it using scientific notification as follows: 1.40 · 109. Notice how the fact that the zero comes after the decimal point means that it is an accurate digit.

Absolute error < 0.5 ten millions = 5 000 000

Relative error < 0.5/140 < 0.0036 = 0.36 %

Think and practise

1 Calculate and check your answers with a calculator:

a) (6.4 · 105) · (5.2 · 10– 6)

b) (2.52 · 104) : (4 · 10– 6)

c) 7.92 · 106 + 3.58 · 107

2 The distance from the Earth to the Sun is 149 000 000 km.

a) Express it using scientific notation.

b) Express it in centimetres to two significant figures.

c) Express it in centimetres to four significant figures.

d) Give a limit of the absolute and relative errors for the three cases mentioned above.

The equality 23 = 8 can also be written: log2 8 = 3.

log2 8 is read ‘base-2 logarithm of 8’. Similarly, we can say:

log5 125 = 3 because 53 = 125

log5 5 2 1 = because 51/2 = 5

log10 1 000 000 = 6 because 106 = 1 000 000

log10 0.0001 = – 4 because 10– 4 = 1/104 = 0.0001

The exponent to which base a must be raised to get P (a > 0 y a ≠ 1)) is called base a logarithm of a number P > 0 and written as log a P.

Properties of logarithms

1. Two simple logarithms

The logarithm of the base is 1. The logarithm of 1 is 0 in any base.

2. Product and quotient

The logarithm of a product is the sum of the logarithms of the factors. The logarithm of a quotient is the difference of the logarithms of the dividend and the divisor.

3.

The logarithm of a power (P k or PP / n n 1 = ) is equal to the exponent multiplied by the logarithm of the base of the power.

4. Base change

If we know how to calculate base-a logarithms, we can use the formula above to calculate logarithms with any base, b.

Interesting fact

At this level: log means decimal logarithm (base 10) and ln means Napierian logarithm (base e). However, in more advanced mathematics books log is used to refer to Napierian logarithms, since at these levels this type of logarithm is used almost exclusively.

Decimal logarithms

Base-10 logarithms are called decimal logarithms. For a long time, they were the most widely used logarithms. This is why we just write log, without the base. For example, log 10 = 1, log 100 = 2, log 1 000 = 3, log 0.001 = – 4.

And log 587 = 2. ... since 587 is greater than 100 but less than 1 000. There is a specific button for these logarithms on calculators. But in modern calculators, you have to press the SHIFT button to access this function:

log 200 8 s 200 = 2.301029996

Napierian logarithms

Remember the number e? Its value is 2.71828… and at the beginning of this unit we explained that it is used to describe growth in plant or animal populations, radioactive decay, and catenaries.

Logarithms with base e are called Napierian logarithms and they are written ln (in other words, loge x = ln x). On calculators there is a button, , for accessing these logarithms.

Problems solved

1 Give the value of these logarithms, putting the numbers in the form of powers:

a) log6 1 296

b) log2 0.125

2 With the calculator, find log 5, log 50, log 500 and log 5 000.

All of them have the same decimal part. Why?

a) 1 296 = 64. Therefore, log6 1 296 = 4.

b) 0.125 = 1 000 125 8 1 2 1 3 == = 2–3

Therefore, log2 0.125 = –3.

log 5 = 0.69897… log 50 = 1.69897…

log 500 = 2.69897… log 5 000 = 3.69897…

T hey have the same decimal part because all of them are the following type: log10 (5 · 10n) = log10 5 + n log10 10 = n + log10 5 log10 5 is the decimal part of all of them, with an integer, n, added in each case.

Think and practise anayaeducacion.es Practise calculating logarithms.

1 Use the definition above to find these logarithms:

a) log5 125 b) log5 0.04

d) log2 0.0625

c) log2 128

e) log a 1 f ) log10 0.0001

g) log2 / 12` j h) log3 (1/3)

log3 9 5

2 Work out the base of the following logarithms:

a) log a 10 000 = 2 b) log b 216 = 3

c) log c 125 = 3 d) log d 3 = 2 1

3 Use the calculator to find log 7 and log 70. Explain why both have the same decimal part.

The importance of decimal logarithms

Look at these two numbers:

= 6 748 B = 67.48 = A/100

log B = log (A/100) = log A – log 100 = = log A – 2

This means that both logarithms have the same decimal part. In logarithm tables we would look for the decimal part of the logarithm of 6 748 and then add the integer part as appropriate, depending on whether it was 6 748; 67.48 or 67 480 000.

A bit of history

Several centuries before the emergence of calculators, logarithms were invented to cope with the enormous operations that had to be done by hand. This was done by converting products and quotients into additions and subtractions (which are operations that are much easier to work with than the others). To do this, people had to use enormous tables (in very thick books), which contained the exact or approximate values of the decimal logarithms of the factors. And what about Napierian logarithms? What role did they play? The number e arose naturally in the laborious process used to obtain the decimal logarithms for many numbers by hand, and therefore, so did Napierian logarithms. In other words, Napierian logarithms were the instrument used to obtain the values of decimal logarithms, which were the ones needed in practice. They were called natural logarithms, while decimal logarithms were known as common logarithms. Now that we have calculators, why do we need logarithms? Well, it is mostly a question of culture, but also because we find them in algebraic simplifications (for example, for solving some types of equations) and functional expressions in the world of science and technology.

Logarithms on a calculator

As you already know, the calculators we use today have three keys for calculating logarithms: , j and . The first two are easy to find. The third (decimal logarithm), however, is more complicated. It is the second function of the button, so to use it, we have to press s .

To find a logarithm with a base other than 10 and e, newer calculators also include the j button. However, sometimes it may be preferable to use property 4, base change (introduced in page 50), rather than this button. To do this, it is better to use the ln key, since that way you do not need to use the shift button. Let’s look at an example of the two ways of doing it:

Problem solved

Use a calculator to find the following logarithms both ways: using the j key and by changing the base.

Think and practise

4 Use the j and keys of your calculator to calculate these logarithms using both methods described above:

AND PROBLEMS SOLVED

1 Intervals

Write in interval form the numbers that verify the following inequalities:

a) ≤ x 5 b) x 24 < +

c) How would you write the inequality opposite to the one in a)?

Your turn

Express with intervals.

a) ≤ x 31 – b) x 23 > +

2 Radicals

Prove

3 Logarithms

Find the value of x in each case:

a) 3 = 5 + log x

b) logx 36 = 2

c) log x + 2log 5 = 2

a)

b)

c)

We apply the definition of a logarithm in each case:

a) 3 – 5 = log x 8 x = 10–2

b) x 2 = 36 8 x = 6 (x = – 6 does not work)

c) We apply the properties of logarithms:

4 Interest, errors and logarithms

An investor places 2 · 10 6 at 3.6 % annual interest. When he withdraws it it has become €2.43 · 10 6  approximately.

a) Give a limit of absolute and relative error for this approximation.

b) How long was it in the bank?

It was in the bank for 5 and a half years.

(*) We take logarithms from both sides to clear n.

Your turn If I deposit €5 000  in a bank at 3.53% a year, how long would it take for it to double?

EXERCISES AND PROBLEMS

DO YOU KNOW THE BASICS?

Number sets

1 Look at the following numbers. // ,, 23 3567 17 18 26 16 18 ;; ;; ;; !

a) Which are integers?

b) Are there any natural numbers?

c) Are there any irrational numbers?

Powers, roots and radicals

9 Calculate the value of these expressions:

25 / 52 b)

/ 43 c) 81 ,

10 Express in exponential form.

2

a) Classify into rational and irrational numbers.

;, ;; ;; ;π e 2 3 08 74 3 7 2 1 2 3 !

b) Put them in order from smallest to biggest.

c) Which are real numbers?

3 Find an integer, a non-integer rational number and an irrational number between 29 – and 8 –

4 Indicate which of the sets (N, Z, Q or Á) these numbers belong to:

π , 7 4 6 13 52 152 2 13 –; ;; ;; ; + !

Intervals and half-lines

5 Represent each of the following intervals and halflines on the real number line:

A = [–2, 4] B = (1, 6) C = [–7, –3)

D = (0, 5] E = (– ∞, 1] F = (–1, +∞)

6 Write the following sets of numbers in interval or half-line form:

a) Greater than 2 and less than 7.

b) Between –1 and 3, both included.

c) Greater than or equal to 5.

d) Less than 10.

7 Represent each of the following intervals and halflines as the real number line:

a) –3 ≤ x ≤ 2 b) 5 < x c) x ≥ –2

d) –2 ≤ x < 3/2 e) 4 < x < 4.1 f ) –3 ≤ x

8 Express each of the following sets of numbers as an interval or half-line and as an inequality. a) –1 0 3 b) 1 5 c)

11 Write as roots.

a) 51/2 b) (–3)2/3 c)

d) (a 3)1/4 e) (a 1/2)1/3 f ) (a –1)3/5

12 Express each of these numbers as a power with the base 2 and then find their product: a) 16 / 32 3 –`j b) 4

13 Express the following radicals as powers with fractional exponents and simplify:

14 Simplify.

Approximate numbers. Scientific notation

15 Find the absolute and relative errors in these approximations:

a) 3 41 to two decimal places

b) 72 to one decimal place

c) 17 123 to one hundredth

16 Give a limit of absolute error and of relative error for these approximations of the number of votes in an election:

a) 348 thousand votes b) 5 632 000

c) 890 000 d) 78945

e) 9 million f ) 134 thousand

17 Calculate mentally.

a) (1.5 · 107) · (2 · 105) b) (3 · 106) : (2 · 1011)

c) (4 · 10–7) : (2 · 10–12) d) · 410 8

18 Use scientific notations to perform these calculations and give a limit of absolute error.

a) (3.5 · 107) · (4 · 108) b) (5 · 10–8) · (2.5 · 105)

c) (1.2 · 107) : (5 · 10–6) d) (6 · 10–7)2

Logarithms

19 Apply the definition of logarithm and calculate.

25 Express each of the sets of numbers below as a union of intervals, using the symbol ∪:

20 Calculate the base of the following logarithms:

a) logb 64 = 3 b) logb 100 = 2

c) logb 243 = 5 d) logb 625 = 4

21 Use a calculator to find: a) log4 23.4 b) log3 543 c) log

20.8

PRACTICE MAKES PERFECT

22 Place the following numbers on a diagram like this one:

1; , 723 # ; 1 – 2 ;

3.5; 9 11 ; 4 1 ;

6 ; π 4 ; –104

23

a) Which irrational numbers are represented by points A, B, C and D ?

27 Express as powers and calculate x in each case, equalling the exponents of the two sides:

b) Represent 8 and 11 .

24

a) Indicate which of the following numbers are included in A = [–3, 7) or in B = (5, +∞): –3; 10; 0,5; 7; – 4; 5 ; , 63 ! ; π; 5 27 ; 48 ; 1 – 2

b) Which of these intervals represents the numbers included in A and in B ?

(–3, 5) [2, 7) [5, 7] (5, 7)

c) Express A ∪ B and A ∩ B as intervals and as inequalities.

Take out all possible factors

30 Reduce to a common index and express the results with a single radical.

EXERCISES AND PROBLEMS

36 Rationalise and simplify if possible. a)

43 Express each of the following intervals as neighbourhoods of the type E(M, r):

a) (–3, 3) b) (2, 4) c) (0, 6) d) (–1, 4)

e) (–3, 2) f) (0; 7.5) g) (–5; –2.2) h) (1.2; 4.7)

37 State which of these blood test results are outside the reference ranges:

44 Express M without logarithms in each case. (Remember that if log M = log k, then M = k).

a) () loglog log Mx x 32 –=+

b) () loglog loglog Mx y 13 – =+ +

c) () ln ln ln ln Mx yx22 3 – =+ +

45 An cuboid measures 81827 ## in cm. Calculate:

38 Calculate by applying the definition of logarithm. log4 163 + log4 2 + log 0.0001 + log

39 If log x = 1.3 and log y = 0.8, calculate:

a) The total area. Use radicals to express the exact result.

b) The length of the diagonal. Use radicals to express this measurement and approximate to one decimal place.

c) Calculate the absolute error and relative error of the above approximation.

40 Transform the expression A

logarithms and applying their properties, like in the example:

46 In an isosceles triangle the uneven side measures 53 cm and the height referred to that side is one quarter of it. Calculate the perimeter of the triangle. Use radicals to express the result.

ADVANCED PROBLEM SOLVING

47 The diameter of the Milky Way is 105 700 light years, and a light year is 1.461 · 1012 km.

a) What is the diameter of our galaxy in kilometres?

Do the same for the following expressions:

SOLVE SIMPLE PROBLEMS

41 Find out for which values of x can the following roots be calculated:

42 The open interval whose midpoint is M and whose endpoints are M - r and M + r is called a neighbourhood with midpoint M and radius r, and it is represented by N(M, r).

For example: E(0, 2) = (–2, 2) and E(2, 3) = (–1, 5) Express the following neighbourhoods as intervals:

a) E(0, 1) b) E(0, 3) c) E(3, 5) d) E(–2; 1.5)

e) E(–3; 0.3) f) E(2.1; 3) g) E(–0.2; 5.3)

b) How many millenia would it take for a spacecraft to cross it if travelling at 2 000 km/s?

c) Given that the diameter of an electron is 4 · 10–15 m, how many electrons would it take to form a line all the way around the Milky Way? (Assume it is a circumference).

48 Calculate the height of a regular tetrahedron with 8 cm edges. Use radicals to express the results.

49 Calculate the volume of a regular octahedron with edges measuring 6 cm. Use radicals to express the results.

50 Prove that the ratio between the areas of these two hexagons is 4/3. (Bear in mind that each hexagon can be divided into 6 equilateral triangles).

51 Write in interval form the numbers that verify the following inequalities:

a) | x | < 3 b) | x  – 1| ≤ 5 c) | x + 3| < 4 How would you express the numbers that verify the inequalities opposite to the previous ones? | x | ≥ 3 | x  – 1| > 5 | x + 3| ≥ 4

UNDERSTAND

52 Calculate as a fraction. 1 1 1 2 1 1 1 + + +

a) Substitute 2 with 1 + 1/2 and re-calculate. Repeat this process again.

b) Check that the numerators and denominators of the results are terms in the Fibonacci sequence.

c) What is the approximate value of the quotients obtained?

53 a) Express the terms of the following sequence as a power:

aa a 13 13 13 13 13 13 12;; 3 == ==

b) Check that the exponents are the sum of the terms of a geometric progression with ratio 1/2.

c) What is the approximate value of this sequence?

54 If I deposit a sum of money in a bank at 3% annual interest, how many years will it take for it to triple?

YOU CAN ALSO TRY THIS

55 Check that it is not possible to use a calculator to obtain 5129 · 463 because the number is too large. Use the properties of powers to express it in scientific notation.

56 Calculate the value of x in these expressions:

a) loglog x 2237 =+ b) · 75 63 x =+

57 We have taken a 2 cm square and constructed a rectangle, ABFE.

Is it a golden triangle?

Check that the quotient between the sides is the golden number Φ

58 The equation for the golden number is:

Φ2  – Φ – 1 = 0

Use it to check the following equalities:

a) Φ2  = Φ + 1 b) Φ – 1 =  1 U

c) Φ3 = 2Φ + 1 d) Φ4 = 3Φ + 2

REMEMBER THE THEORY REFLECT

59 True or false? Explain your answer and give examples.

a) Some irrational numbers are not real.

b) There are an infinite number of irrational numbers between two rational numbers.

c) The inverse of a recurring decimal number can be a terminating decimal.

d) The number 0.83 · 109 is not expressed in scientific notation.

60 If ≥ loglogab 2 –33 , what is the relationship between a and b?

61 Look at this way of representing m on the real number line. Explain it.

62 If x is a number of the interval [–1, 3) and y is a number of the interval (0, 4], explain in which interval you might find x + y And x – y ?

63 Are these equalities true or false? Why? a)

MATHS WORKSHOP

READ AND LEARN

Golden rectangles

A rectangle is called a golden rectangle when the ratio between its sides coincides with the golden number. In other words, if we take the shorter side as one unit, the longer side will measure the golden number, F = 2 1 5+ = 1.618…

These rectangles have a curious property: if you put a square on the long side, you get another golden rectangle. Try it:

• If you keep adding ever-bigger squares, you will get a series of golden rectangles that you can use to construct a pretty spiral made up of arcs.

This spiral is very well known and widely studied in mathematics (the equiangular or logarithmic spiral). But the most surprising thing about it is that it appears naturally in many species of plants and animals (flowers, fruit, mollusc shells, etc.).

• Now construct the series of successive radii of the spiral, which are the same length as the sides of the squares that fit together to make it:

R1 = F

R2 = F + 1

R3 = 2F + 1

R4 = 3F + 2

R5 = 5F + 3

…

Can you find a relationship between this and the Fibonacci sequence?

Leonardo of Pisa (1170-1250)

Also called Fibonacci (which means ‘son of a good man’). His father was a merchant and consul of Pisa in the city of Béjaïa, in present-day Algeria.

This allowed him to learn Arabic mathematics, especially the decimal numeral system, which he helped to introduce to Europe.

He was the first to describe the famous sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

in which each term is obtained by adding the previous two. This Fibonacci sequence is closely tied to the golden number, F.

Nautilus shell.

SELF-ASSESSMENT

1 a) Classify the following numbers into natural numbers, integers, rational numbers and real numbers:

3 4 6 – ; 2π; . log 05 2 ; . 347 # ; 2.03333…; 81 ; 4 3 ; 3 5 ; – 9 13 ; – 8

b) Which are irrational?

c) Put them in order from smallest to largest.

2 Which numbers represent A, B, C and D.

anayaeducacion.es Solutions to these problems.

7 Operate and simplify.

a) () 3 32 3 2 +

c) 50 5 2 2 –

b) 54 26 150 –+

d) 23 10 2 –

8 Apply the definition of logarithm, or use a calculator, to operate:

a) log3 9 1 3 b) log2 32 1 2 4 cm

9 Find the value of x in each case:

a) logx 73 – 2 = b) log 20 2 x = c) loglog x 51 +=

3 This table shows the population and annual GDP in millions of euros in some EU countries.

10 Calculate the area of the annulus between the inscribed and circumscribed circumferences in a 6 m2 square. Give the exact value.

a) Express them in scientific notation and calculate the GDP per capita for each country. Give a limit of absolute and relative error in each case.

b) What is the percentage of GDP in Estonia compared to Spain, Finland and France?

4 a) Write the following number sets in interval form and represent them on a number line:

i) ≤ x –<27 ii) x –1 > iii) | x | < 4

b) Write the following intervals as inequalities: A = [–3, 4) B = (–∞ , 3 )

c) Express A ∪ B y A ∩ B as intervals and as inequalities.

5 Express in exponential form:

a) 5 6 3 b) 7 2 4 c) 6 d) a 1 4 – e) () –3 5 3

6 Take out all the possible factors from the radical.

11 We cut a right-angled isosceles triangle from each corner of a square with 10 cm sides to obtain a regular octagon.

a) Find the exact measurement of the side of the octagon.

b) Calculate its area. c) Calculate its radius.

Look back at the content you have worked on and plan solutions to the problems that you may find. To do this, download the assessment from anayaeducacion.es, think individually and share in groups.

TEST YOUR SKILLS

Now you can do the skills self-evaluation included in anayaeducacion.es.

POLYNOMIALS AND ALGEBRAIC FRACTIONS 2

Today’s algebraic language is simple and easy to use. However, it took a long time to reach this point. We can divide its history into three main phases.

• rhetorical algebra It was written in everyday language. It was used in Babylon, Egypt and Greece. It was then used by Arabic mathematics in the 9th century.

• syncopated algebra Diophantus (3rd c.) pioneered this type of algebra. He made the processes easier by using abbreviations. During the Renaissance (15th and 16th centuries), it was improved through the incorporation of new symbols: operations, coefficients, powers, etc.

• symbolic algebra This is the predecessor of the algebraic language we know today and consists of a full set of symbols. It was created by Viète in the 16th century. It was then perfected by Descartes in the 17th century.

The lack of a functional form of algebra meant that mathematicians had to come up with ingenious ways to find or demonstrate algebraic relationships. In many cultures they used geometric shapes, giving rise to geometric algebra.

François Viète (1540-1603). French mathematician who published In Artem Analyticam Isagoge (1591). In the book, he introduced the use of letters in mathematical formulas as common practice.

Use what you have learned to solve problems

Diophantus’ intriguing system of notation

Let’s look at an example of how Diophantus described polynomials

notation → ss7

2

5 M

4 u6 s means ‘squared’ (therefore, ss means ‘fourth power’); c, ‘cubed’; x, ‘the unknown’; u, ‘number’. M means ‘minus’ and precedes all monomials with negative coefficients. Looks odd, doesn’t it?

Using geometric algebra

With our modern form of algebraic notation, it is very easy to prove that:

But rhetorical algebra had no way of performing this operation, so mathematicians had to find another way to prove the expression.

Look how Pythagoras did it:

If a and b are segments, ab is the area of a rectangle.

1 Use modern algebraic notation to express the following polynomial, given using Diophantus’ notation:

2 Express the following polynomial using Diophantus’ notation:

3 Use Pythagoras’ reasoning to demonstrate the expression above, taking

POLYNOMIALS. OPERATIONS 1

The order of monomials

The monomials that make up a polynomial can appear in any order. However, they are most commonly ordered by degree, from largest to smallest.

Subtracting polynomials

Subtracting is a special type of addition; therefore, the result of subtracting two polynomials is another polynomial.

P – Q = P + (–Q )

The polynomial –Q is obtained by changing the sign for all the Q monomials.

Focus

on English

smoothly: without problems or difficulties.

anayaeducacion.es

Comparing polynomials to integers.

Problem solved

1 Given the polynomials:

Basic terminology

As you already know, the following expression is a polynomial:

It is made up of four monomials: 2x 5; 3/7x 3; – 3 x 2 and 2.7, the degrees of which are 5, 3, 2 and 0, respectively (2.7 has a degree of 0, since 2.7 = 2.7 · x0).

The degree of the polynomial is 5 (that of the monomial with the highest degree).

The variable, x, is also called the indeterminate.

The numbers 2, 3/7, – 3 and 2.7 are the coefficients. As there is no thirddegree monomial, we can say that its coefficient is 0.

In a polynomial, the coefficients are any real numbers.

Operations with polynomials. Sum and product

The result of adding or multiplying two polynomials is another polynomial. These operations have certain properties that allow us to perform operations easily and smoothly*. Let’s take a look:

product could have been found by placing one polynomial underneath the other and placing each term of each product underneath the similar term:

Practise adding, subtracting and multiplying polynomials.

Division of polynomials

The result of adding, subtracting or multiplying two polynomials is another polynomial. However, this is not true for division: in general, the quotient of two polynomials is not a polynomial.

Let’s take a look:

Remember how to divide two polynomials, and how we interpret the result. Let’s divide

Remember

Degree of the dividend, m

Degree of the divisor, n m ≥ n

Degree of the quotient: m – n

Degree of the remainder < n Integer division in Z 89 = 5 · 17 + 4, or 5 89 17 5 4 =+

The result of the division is not an integer.

The result can be written in one of the following two ways:

This way of dividing polynomials, where as well as the quotient there is a remainder other than zero, is called integer division.

When the remainder is zero, we say that it is an exact division.

For example, let’s divide the

anayaeducacion.es

Practise dividing polynomials.

Breaking down into factors

P (x) = x 4 + x 3 – 10x 2 – 4x + 24 has been broken down into a product of two factors: P (x) = (x 2 – 4)(x 2 + x – 6). And each of these factors can also be broken down:

x 2 – 4 = (x – 2)(x + 2)

x 2 + x – 6 = (x – 2)(x + 3)

Therefore:

P (x) = (x – 2)(x + 2)(x – 2)(x + 3) = = (x – 2)2 (x + 2)(x + 3)

We need to try and break down all polynomials using this method.

As it is an exact division, the dividend can be given as the product of two factors:

Polynomials, like integers, can be broken down into products of factors. When we try doing this, we face the following problem:

Given a polynomial P (x), how can we work out which other polynomial to divide it by for the division to be exact?

When working with integers, we used the divisibility criteria to answer this question. However, for polynomials,we will use something distantly related.

To find the divisor we need, we will have to perform many divisions, mostly using expressions of the type x – a. The next section will teach us to do this.

RUFFINI’S RULE 2

Division of a polynomial by x – a

Let’s use some examples to review how to divide a polynomial by x – a using Ruffini’s rule. •

‘Ruffini’s’ rule?

Paolo Ruffini was an Italian mathematician who lived in the 18th and 19th centuries. This rule bears his name because he used it to prove an important mathematical property. However, the same rule had already appeared in a book about algebra written by Pietro Paoli 25 years before.

anayaeducacion.es

Activities for consolidating the application of Ruffini’s rule.

Dividing P ( x ) by ( mx + n )

mx + n = m x m n + bl

Therefore:

Do the division P(x) : (x + n/m) (Ruffini’s rule, where a = –n/m).

Quotient: C(x); Remainder: R.

So the result of the division P(x) : (mx + n) is:

Quotient: m 1 C(x); : R

• We can use Ruffini’s rule to divide by 2x + 8. Let’s see how: Since 2x + 8 = 2(x + 4), we divide by x + 4 and ‘work it out’. For example, we divide x 3 + 2

Think and practise

1 Calculate the quotient and the remainder when you divide x 4 + 3x 3 – 3x 2 + 3x – 4 by:

a) x – 1 b) x + 1 c) x – 2

d) x – 4 e) x + 4 f ) x – 3

For each of them, say whether the division is an integer or exact division.

2 Divide P (x) = 4x 3 + 12x 2 + 5x – 6 by each of the following polynomials and express the result as follows: divisor dividend = quotient + divisor remainder . a) x

anayaeducacion.es

Applications of Ruffini’s rule with SpreadSheetS.

Value of a polynomial for x = a

The numeric value of a polynomial, P (x), for x = a, is the number we get when we replace x with a and perform the operations. This number is called P (a).

For example, if P (x) = 5x 3 – 3x 2 + 12x – 8, for x = 2 we get:

P (2) = 5 · 23 – 3 · 22 + 12 · 2 – 8 = 44

This value, P (2) = 44, coincides with the remainder when we divide P (x) by x – 2. This is not just by chance, it is a general rule.

Polynomial remainder theorem

The value given to a polynomial, P (x), when we perform x = a, coincides with the remainder of the division P (x) : (x – a). That is, P (a) = r.

In other words:

— If in P (x) we replace x with a and perform the operations, we get a number which we call P (a) (value of the polynomial for x = a).

— If we divide P (x) by x – a, the remainder is a number r.

Therefore, the theorem proves that P (a) = r

According to this result, we can use Ruffini’s rule to calculate P (a).

did you know? If we apply Ruffini’s rule leaving the operations written in full, the remainder takes the form of P (a).

The remainder is the result of replacing the x in the polynomial with 2.

It is evident that the remainder is the result of substituting the x by 2 in the polynomial.

The polynomial remainder theorem.

If when we divide P (x) by x – a the quotient is C (x) and the remainder is the number r, we get the following relationship: P (x) = (x – a) · C (x) + r

If we make x = a, we get:

Think and practise anayaeducacion.es Practise dividing using Ruffini’s rule.

3 Use Ruffini's rule to find P (a) in the following cases:

a) P (x) = 4x 4 – 5x 2 + 2x – 24, a = 2, a = –5, a = 10

b) P (x) = 3x 3 – 8x 2 + 3x, a = –3, a = 1, a = 8

c) P (x) = x 5 –x 2 – x + 3, a = 1, a = –1, a = 7

d) P (x) = –x 6 – 2x 5 + 4x + 7, a = –2, a = –1, a = 9

4 Calculate the value of A in each case:

a) The division of the polynomial x 4 – 2x 3 + ax – 15 by (x – 3) is exact.

b) The remainder of the division (3x 3 + 4x 2 – 3x + a) : (x + 2) is 4.

c) The numeric value of the polynomial x 5 – 8x 2 + ax – a for x = 2 is –3.

Key point

In order for the division to be exact, the independent term, 15, has to be a multiple of 3 8 15 = 3 · 5

Remember

This criterion is very useful for limiting the search for the divisors of a polynomial. It is only valid for polynomials with integer coefficients. And it can only be used to locate the integer values of a.

Problems solved

1 Find a divisor x – a (where a is an integer) of the polynomial: P (x) = x 3 + x 2 – 7x + 20

A number, a, is called a root of a P(x) polynomial if P(a) = 0. The roots of a polynomial are the solutions of the equation P(x) = 0. Therefore, if a is the root of P(x), then P(x) = (x – a) Q(x).

For example, 5 is the root of x 3 – 8x 2 + 17x – 10 because:

53 – 8 · 52 + 17 · 5 – 10 = 0

We can check it using Ruffini’s rule (see margin).

Ruffini’s rule helps us break down a polynomial into factors. However, to do this we need to learn how to find its roots. The following criterion helps us with this search.

Criterion for finding the roots of a polynomial

The division (3x 3 – 7x 2 – 11x + 15) : (x – 3) is exact. For this to be so, in the division process using Ruffini’s rule, the last product 3 · (–5) has to be the same as the independent term, 15, but with the sign changed. In other words, the independent term must be a multiple of 3.

By using this reasoning, we obtain the following rule, which is very useful for locating the integer roots of a polynomial.

If a polynomial has integer coefficients, in order for it to be divisible by x – a, its independent term needs to be a multiple of a (integer a).

Therefore, to find expressions x – a that are divisors of a polynomial, we try out integer values of a (positive and negative) that are divisors of the independent term.

In order for P (x) to be divisible by x – a, a needs to be a divisor of 20. We try giving a the values ±1, ±2, ±4, ±5, ±10.

We do not get a remainder of 0 with the numbers 1, –1, 2 and –2.

We now try with a = 4. The remainder is not 0. Therefore, P (x) is not divisible by x – 4 either.

However, with a = –4 the division is exact, since the remainder is 0.

P (x) divided by (x + 4) is x 2 – 3x + 5.

careful! It is possible that P (x) was not divisible by x – a for any divisor a of the independent term. In other words, for any integer a.

2 Say whether x = 5 could be a root of these polynomials:

P1(x) = x 5 – 11x 3 + 17x + 18

P2(x) = 2x 4 – 10x 3 – 2x 2 + + 12x – 10

P3(x) = 2x3 – 17x2 + 23x + 40

If so, check that it really is.

• P1(x) is not divisible by x – 5 because its independent term, 18, is not a multiple of 5.

• P2(x) could be divisible by x – 5 because its independent term, –10, is a multiple of 5. Let’s see if it is:

2 –10 –2 12 –10

5 10 0 –10 10

2 0 –2 2 0

P2(x) is divisible by x – 5:

P2(x) = (x – 5)(2x 3 – 2x + 2)

• P3(x) could be divisible by x – 5 because its independent term, 40, is a multiple of 5. Let’s see if it really is:

2 –17 23 40

5 10 –35 – 60

2 –7 –12 –20

3 Invent a 3rd-degree polynomial that has roots of 0, 1 and 2.

4 Invent a 2nd-degree polynomial that has no roots.

5 Invent a 4th-degree polynomial that has no roots.

6 Invent a 3rd-degree polynomial that has no roots.

The division is not exact. Therefore, P3(x) is not a multiple of x – 5.

Therefore, x = 5 is only the root of P2(x).

This is true for P (x) = x (x – 1)(x – 2). In general, it is true of any polynomial of the type:

Kx (x – 1)(x – 2), where K ≠ 0

Any second-degree expression without real roots. For example: P (x) = x 2 + 5x + 10

We find two second-degree polynomials without roots and multiply them. For example: P (x) = (x 2 + 1)2 = x 4 + 2x 2 + 1

Impossible! An odd-degree polynomial, P(x), is bound to have at least one root. This is not easy to demonstrate, so we will just have to accept that it is true.

Think and practise anayaeducacion.es Practise finding the roots of a polynomial.

1 Without performing the operations, say whether x = –3 could be a root of each of these polynomials:

a) P (x) = x 2 – x – 12

b) P (x) = x 4 + 2x 2 – x + 8

c) P (x) = x 3 + 3x 2 – 5x – 27

d) P (x) = x 3 + 3x 2 + x + 3

If you think it could be, prove whether it is a root or not.

2 Indicate the possible integer roots of each of the polynomials in the previous exercise. Work out which of them are actual roots.

3 The polynomial x 4 + 3x 3 – 2x 2 – 10x – 12 is divisible by x – a for two integer values of a. Find them and give the quotient in both cases.

4 Check that the polynomial x 4 + x 3 + 7x 2 + 2x + 10 is not divisible by x – a for any integer value of a.

5 Invent a third-degree polynomial that has roots of 3, –2 and –1.

6 Invent a fourth-degree polynomial that has no roots. It must be different from the one in problem solved 5.

7 Invent a fourth-degree polynomial that has only two roots: x = 2 and x = –3.

8 Invent a second-degree polynomial that has x = –3 as a double root.

9 Is there any first-degree polynomial that has no roots? Explain your answer and give an example.

FACTORISING POLYNOMIALS 4

Observe Ruffini’s rule allows us to find integer roots. However, we are very unlikely to be able to factorise a polynomial with a degree greater than two that does not have integer roots. For example, the roots of the polynomial 12x 3 + 4x 2 – 3x – 1 are 1/2, –1/2 and –1/3, but finding them is not easy. 9

To factorise a polynomial means to break it down into the product of polynomials (factors) of the lowest possible degree.

Factorising polynomials is, therefore, a similar process to breaking down an integer into prime factors. The ‘polynomials of the lowest possible degree’ that we will use this year and that play the same role as prime numbers are:

— First-degree expressions of the type x, x – a, x + a.

— Second-degree expressions without real roots.

Procedure for factorising a polynomial

If possible, we start by taking out a common factor. In some cases, we will be able to identify notable products. We use Ruffini’s rule to look for integer roots of the polynomial. We can also find roots of second-degree polynomials by solving the equations. Let’s look at some examples:

Example 1

We factorise P (x) = 9x 4 + 18x 3 – 28x 2 – 2x + 3:

In order to locate the roots of P (x), we try with the divisors of 3 (both positive and negative). Let’s begin with –1 (*) and 1 (**) (see margin).

Given that 1 is a root, we can write P (x) = (x – 1)(9x 3 + 27x 2 – x – 3).

Now, we find the roots of P1(x) = 9x 3 + 27x 2 – x – 3:

We have discarded the value –1. We try again with 1 but it is not a root of P1(x) (in other words, 1 is a simple root). Next, we try with –3 (***), and we see that this time it is a root of P1(x) and, therefore, of P (x).

P1(x) = (x + 3)(9x 2 – 1)

We see that 9x 2 – 1 = (3x + 1)(3x – 1). Therefore, the final result is:

P (x) = (x – 1)(x + 3)(3x + 1)(3x – 1) = 9(x – 1)(x + 3)(x + 1/3)(x – 1/3)

Example 2

We factorise Q (x) = x 5 + 5x 4 – 14x 3 .

We start by taking out x 3 as a common factor: Q (x) = x 3 (x 2 + 5x – 14)

Now, we solve the equation x 2 + 5x – 14 = 0, which gives x1 = 2 and x2 = – 7. Therefore, Q (x) = x 3(x – 2)(x + 7). important

Geogebra. Create a factored polynomial.

• If we reach a second-degree polynomial without roots, that polynomial remains as a single factor (it cannot be broken down into two factors).

For example:

anayaeducacion.es Factorising polynomials using Ruffini’s rule.

• If a polynomial has more than two non-integer roots, although it can be factorised, we are unlikely to be able to do it.

For example: 18x 3 + 9x 2

2

1 = 18(x – 1/3)(x + 1/3)(x + 1/2)

Problems solved

1 Factorise and identify the roots.

P (x) = 12x 5 – 36x 4 + 27x 3

All the addends have the factor x3. The coefficients 12, –36 and 27 are multiples of 3. Therefore, we can extract 3x3 as the common factor.

P (x) = 3x 3 (4x 2 – 12x + 9)

We see that 4x2 – 12x + 9 is equal to (2x – 3)2.

P (x) = 3x 3 (2x – 3)2

We obtain the roots by making each factor equal to 0. The roots of P(x) are 0 (triple root) and 3/2 (double root).

2

We look for the roots by making it equal to 0 and solving:

or rather:

Use Ruffini’s rule to find a root among the divisors of 6:

–2 is a root of R (x).

We find roots of x 2 – 2x + 3:

2 – 2x + 3 = 0 has no solution.

We have reached a second-degree polynomial that has no roots. So:

We find the integer roots among the divisors of 4:

As we cannot find any more integer roots, we try to solve the equation:

Think and practise anayaeducacion.es Factorising polynomials.

1 Factorise the following polynomials:

DIVISIBILITY OF POLYNOMIALS 5

We have already looked at the divisibility of polynomials in earlier parts of this unit: exact division, breaking them down into factors, etc. Now we are going to systematise this information and compare it to the divisibility of integers.

Multiples and divisors

A polynomial, D(x), is a divisor of another, P(x), if the division P(x) : D(x) is exact. In this case, P(x) is a multiple of D(x), since P(x) = D(x) · C(x).

For example, x 2 + x is a divisor of x 3 – x because (x 3 – x) : (x 2 + x) = x – 1 is exact. Therefore, x 3 – x is a multiple of x 2 + x, since x 3 – x = (x 2 + x) · (x – 1).

Even though 6x + 3 = 3(2x + 1), 6x + 3 is not really considered to be a multiple of 2x + 1, because the factor 3 is a number and not a polynomial with a degree greater than or equal to 1.

Irreducible polynomials

A polynomial is said to be irreducible if it has no divisors with a degree lower than its own.

For example, x, x – 3, x 2 + 1 and x 2 – 3x + 3 are irreducible polynomials

Relatively prime polynomials

Two polynomials are relatively prime when there is no polynomial divisor of both. For example:

• 2x 2 – 2 and 6x – 4 are relatively prime, even though they can both be divided by 2.

• x 2 – 1 and x2 – x are not relatively prime because they can both be divided by x – 1.

6x + 3 is also irreducible, even though it is divisible by 3.

x 2 + 8x + 15 is not irreducible because it is equal to (x + 3)(x + 5).

Irreducible polynomials can only be first- or second-degree. Even if we are unable to factorise a fourth-degree polynomial without roots, we know that it is the product of two second-degree polynomials.

Irreducible polynomials play the same role as prime numbers in numerical divisibility.

Breaking down into factors (factorising)

Factorising polynomials as a product of irreducible polynomials is similar to breaking down an integer into prime factors. When finding roots, we can write out the results in the same way as with numbers. For example:

It has no roots. Therefore, it is irreducible.

Greatest common divisor and lowest common multiple

GCD (18, 30) = 6, because 6 is a divisor of 18 and 30, and there is no other number higher than 6 that is a divisor of both.

Reminder: GCD (1 320, 2 100):

1 320 = 23 · 3 · 5 · 11

2 100 = 22 · 3 · 52 · 7

GCD (1 320, 2 100) = = 22 · 3 · 5 = 60

LCM (18, 30) = 90, because 90 is a multiple of 18 and 30, and there is no other number lower than 90 that is a multiple of both.

We say that D(x) is the greatest common divisor of two polynomials, P(x) and Q(x):

if it is a divisor of both and there is no other polynomial common divisor with a greater degree.

To find it in practice, we do the same as with numbers: we start by breaking down the polynomials into factors, and we take the common factors with the smallest exponent with which they appear. For example:

We say that M(x) is the lowest common multiple of two polynomials, P(x) and Q(x):

if it is a multiple of both and there is no other polynomial common multiple with a smaller degree.

Reminder: LCM (1 320, 2 100):

1 320 = 23 · 3 · 5 · 11

2 100 = 22 · 3 · 52 · 7

LCM (1 320, 2 100) = = 23 · 3 · 52 · 7 · 11 = 46 200

To find it in practice, we do the same as with numbers: we start by breaking down the polynomials into factors, and we take the common and non-common factors with the largest exponent with which they appear. For example:

Think and practise anayaeducacion.es Consolidation of the GCD and LCM of polynomials.

1 Is there any divisibility relationship between the following pairs of polynomials? Explain your answer.

a) P (x) = x 3 – 7x 2 and Q (x) = x 3 – 7x

b) P (x) = x 3 – 7x 2 and Q (x) = x 2 – 7x

c) P (x) = x 4 – 3x – 10 and Q (x) = x – 2

2 Find two third-degree polynomials that are divisible by x – 5 and x. Calculate their GCD and LCM.

3 Say which of the following polynomials are irreducible and factorise those that are not.

a) x 2 – 3x + 2 b) x 2 – 5x + 6

c) 3x 2 + 5x d) 3x 2 – 5x – 2

e) 3x 2 – 5x + 3 f) 3x 3 – 5x 2 + 3x

4 Mentally calculate the GCD and the LCM of the following pairs of polynomials:

a) x 2 – 1 and (x + 1)2 b) x 2 + x and x 2 – x

c) x 3 – x and x 2 – 1 d) x 2 + 1 and x 2

5 Find the GCD and LCM of P and Q in each case:

a) P (x) = x 2 – 9, Q (x) = x 2 – 6x + 9

b) P (x) = x 3 – 7x 2 + 12x, Q (x) = x 4 – 3x 3 – 4x 2

c) P (x) = x (x – 3)2(x + 5), Q (x) = x 3(x – 3)(x 2 + x + 2)

6 P (x) = (x – 2)2 x 2. Find a third-degree polynomial, Q (x), for which the following is true:

a) GCD [P (x), Q (x)] = x 2 – 2x

b) LCM [P (x), Q (x)] = (x – 2)2 x 2 (x + 5)

ALGEBRAIC FRACTIONS 6

Polynomial fractions also behave in a similar way to numerical fractions. Note their similarity in the following definitions and procedures.

Remember

A polynomial can be considered as an algebraic fraction with a denominator of 1. Observe

An algebraic fraction is irreducible if its numerator and denominator are relatively prime.

Mental arithmetic

1. Simplify these fractions:

We call the quotient of two polynomials an algebraic fraction:

For example, the following are algebraic fractions:

Simplification

If the numerator and the denominator of an algebraic fraction can be divided by the same polynomial (of a degree greater than or equal to 1), doing so will simplify the fraction.

If we divide the numerator and the denominator of an algebraic fraction by their GCD, we get an irreducible fraction.

Equivalent fractions

Two algebraic fractions are equivalent if:

• One of them is obtained by simplifying the other.

2. Say whether the fractions in each pair are equivalent or not:

• Both result in the same fraction when simplified.

For example, the following fractions are equivalent because both result in the same fraction when simplified:

Think and practise anayaeducacion.es Simplify algebraic fractions.

1 Simplify the following fractions:

2 Are the fractions in each pair equivalent? Check.

Mental arithmetic

1. Reduce the following to a common denominator.

Reduction to a common denominator

When we multiply the numerator and the denominator of an algebraic fraction by the same polynomial, we get an equivalent fraction.

Therefore, if we have several algebraic fractions, we can obtain others that, being respectively equivalent to the first ones, have the same denominator. When we do this, we say that we have reduced them to a common denominator.

x 1 3 1 2 and –2 +

2. Calculate. a) x x x 31 3 –2 +

Operations: addition, subtraction, multiplication and division

To add algebraic fractions, we reduce them to a common denominator and add the numerators together. Subtraction is a special type of addition.

The product of two algebraic fractions is equal to the product of their numerators divided by the product of their denominators.

b) x x 1 3 1 2 –2 + + c) · x x x x 2 24 –2 + d) : x x x x 25 5 –– 2 2 3 Perform the operations and simplify the result.

Inverse fractions. The inverse of x xx 31 5 ––2 is xx x 5 31 ––2 , as their product is a fraction equivalent to 1.

The quotient of two algebraic fractions is equal to the first multiplied by the inverse of the second.

anayaeducacion.es Operations with algebraic fractions. Breaking down algebraic fractions into simpler fractions

When multiplying and dividing algebraic fractions, sometimes it is easier to simplify them first. We do this by factorising the numerator and denominator. For example:

x(x

+

EXERCISES AND PROBLEMS SOLVED

1 Dividing P (x) by (mx + n)

Use Ruffini's rule to find the quotient C(x) and R in the following division:

(3x 3 + 6x 2 – 4x – 1) : (3x – 2)

To apply Ruffini's rule we must express the divisor as (x − a). We extract the common factor 3 in the divisor: (3x – 2) = 3(x – 2/3).

() x C =+ () () () x x x P dd R → () x C =+ () (/ )( /) x x P x R 23 23 3– 3–

We multiply both sides of the equality by 3: () x C3 =+ () // x x P x R 23 23

If we divide the polynomial by (x – 2/3), the quotient will be 3C (x), and so we need to divide it by 3 to obtain C (x). The remainder stays the same. Now we apply Ruffini's rule:

Your turn Use Ruffini's rule to find the quotient and remainder in the division.

(2x 3 – 9x 2 + 4x + 15) : (2x – 1)

2 Factorising

Factorise these expressions:

a) 3x(x – 3) – (x + 1)(x – 3)

b) ax 2 – ay + bx 2 – by

c) x 3 – a 3

We obtain the quotient x x8 3 3 4 2 ++ .

The quotient of the division is therefore x x 3 8 9 4 2 ++

The remainder is the same, –1/9.

a) We take out the common factor (x – 3):

3x (x – 3) – (x + 1) (x – 3) = (

b) In the first two addends, a is the common factor; in the third and the fourth addends the common factor is b

factor is (

), therefore:

c) We find a root of the polynomial among the divisors of a 3. Let’s try with a:

Your turn Factorise.

a) x 2m + x 2n – ym – yn

b) x 3 + a 3

3 Operations with algebraic fractions

a) Simplify these fractions:

b) Calculate and simplify:

Your turn Calculate and simplify:

a) We break down the denominators into factors and we simplify:

EXERCISES AND PROBLEMS

DO YOU KNOW THE BASICS?

Polynomials. Operations

1 Calculate and simplify:

a) 3x(2x – 1) – (x – 3)(x + 3) + (x – 2)2

b) (2x – 1)2 + (x – 1)(3 – x) – 3(x + 5)2

c) 3 4 (x – 3)2 – 3 1 (3x – 1)(3x + 1) – 3 1 (4x 3 + 35)

2 Perform the operations with these polynomials:

8 Copy and complete in your notebook with the right coefficient:

a) () () xx xx xx 73 44 1 32 32 32 ++ += 44 4

b) () () xx xx xx 52 59 11 22 2 ++ =+ 44 4

c) ()() xx xx xx xx 35 51110 32 43 2 += + 44 4

Dividing polynomials

9 Find the quotient and the remainder of each of these divisions:

a) (7x 2 – 5x + 3) : (x 2 – 2x + 1)

x x x Ax xB xx

(( ) () ) , ,

Cx x 53 21 5 05 –

3 3

22 2 == + =+

a) A (x) + C (x) b) A (x) – B (x) c) A (x) · C (x)

3 Express as the square of a binomial.

a) 16x 2 + 1 – 8x b) 36x 2 + 25y 2 + 60xy

c) 9x 4 + y 2 + 6x 2y d) y 4 – 2y 2 + 1

4 Express the following as a product of two binomials.

a) 49x 2 – 16 b) 9x 4 – y 2 c) 81x 4 – 64x 2

d) 25x 2 – 3 e) 2x 2 – 100 f) 5x 2 – 2

5 Copy and complete these expressions in your notebook so they are the square of a binomial:

a) 16x 2 + (…) – 8xy b) (…) + 25y 2 + 60xy

c) 6 19 x 2 + 4y 2 + (…) d) (…) +  y xy 93 4 –2 2

6 Take out the common factor and identify the notable products like in the example.

• 2x 4 + 12x 3 + 18x 2 = 2x 2(x 2 + 6x + 9) = 2x 2(x + 3)2

a) 20x 3 – 60x 2 + 45x b) 27x 3 – 3xy 2

c) 3x 3 + 6x 2y + 3y 2x d) 4x 4 – 81x 2y 2

7 Multiply each expression by the LCM of the denominators and simplify:

a) () ()xx x 4 2 6 1 ––2 +

b) () () () () xx xx x 5 35 4 21 2 44 ––2 ++ + +

c) () () () () () xx xx x 10 81 2

b) (2x 3 – 7x 2 + 5x – 3) : (x 2 – 2x)

c) (x 3 – 5x 2 + 2x + 4) : (x 2  – x + 1)

10 Express the following in the form: Dividend = divisor × quotient + remainder

a) (6x 3 + 5x 2 – 9x) : (3x – 2)

b) (x 4 – 4x 2 + 12x – 9) : (x 2 – 2x + 3)

c) (4x 4 + 2x 3 – 2x 2 + 9x + 5) : (– 2x 3 + x – 5)

Ruffini's rule. Applications

11 Apply Ruffini’s rule to find the quotient and remainder of the following divisions:

a) (5x 3 – 3x 2 + x – 2) : (x – 2)

b) (x 4 – 5x 3 + 7x + 3) : (x + 1)

c) (–x 3 + 4x) : (x – 3)

d) (x 4 – 3x 3 + 5) : (x + 2)

12 Use Ruffini’s rule to calculate P (3), P (–5) and P (7) in the following cases:

a) P (x) = 2x 3 – 5x 2 + 7x + 3 b) P (x) = x 4 – 3x 2 + 7

c) P (x) = x 5 – 2x + 1

13 Work out which of the numbers 1, –1, 2, –2, 3, –3 are roots of the following polynomials:

a) P (x) = x 3 – 2x 2 – 5x + 6

b) Q (x) = x 3 – 3x 2 + x – 3

c) R (x) = x 5 + 3x 4 – 5x 3 – 15x 2 + 4x + 12

14 Without actual division, find out if the following polynomial is divisible by (x + 1):

P (x) = x 10 – 3x 5 + 8x + 4

Factorising polynomials

15 Take out the common factor and use notable identities to factorise the following polynomials:

a) 3x 3 – 12x

c) 45x 2 – 5x 4

e) x 6 – 16x 2

b) 4x 3 – 24x 2 + 36x

d) x 4 + x 2 + 2x 3

f) 16x 4 – 9

EXERCISES AND PROBLEMS

16 Break these polynomials down into factors:

a) x 2 + 4x – 5 b) x 2 + 8x + 15

c) 7x 2 – 21x – 280 d) 3x 2 + 9x – 210

e) 2x 2 – 9x – 5 f ) 3x 2 – 2x – 5

g) 4x 2 + 17x + 15 h) –x 2 + 17x – 72

17 Factorise the following polynomials and give their roots:

a) x 3 + 2x 2  – x – 2 b) 3x 3 – 15x 2 + 12x c) x 3 – 9x 2 + 15x – 7 d) x 4 – 13x 2 + 36

Algebraic fractions

18 Simplify these algebraic fractions

PRACTICE MAKES PERFECT

25 Divide and express these divisions like this: divisor dividend = quotient + divisor remainder

a) (3x5 – 2x 3 + 4x – 1) : (x 3 – 2x + 1)

b) (x 4 – 5x 3 + 3x – 2) : (x 2 + 1)

c) (4x5 + 3x 3 – 2x) : (x 2  – x + 1)

d) (x 3 – 5x 2 + 3x + 1) : (x 2 – 5x + 1)

26 Perform the following divisions:

a) (2x 3  – x 2 + 3x – 1) : (2x 2 + 2x)

b) (6x 4  – x 3 – 3x + 1) : (2x 2 – 1)

c) (x 5 – 3x 2 – 2x – 5) : (x 3 + 4x – 1)

19 Check that these pairs of fractions are equivalent: a) x x 312 4 3 1 ––y b) x xx x 22 y 2 + c) xy xy xy 1 –y – 22 + d) xx x x 22 2 –y – 2

20 Write an equivalent fraction in each case: a) x 1 –3 + b) x 5 21 + c) x x 2 1 –+

21 Find P (x) so that the fractions are equivalent

22 Break down into factors and simplify.

() x x 3 9 –2 2 + b) x x 4 2 –2 +

x xx 25 25 10 ––2 2 + d) xxyy xxy 2 –

–22 2 +

e) xx x 6 2 ––2 + f ) xy xy xy 2 3 –2 22

23 Reduce to a common denominator and calculate.

a) x x x 2 1 4 11 –+ b) x xx 1 3 11 –2 +

c) x x 2 3 1 – + d) x x x 2 3 1 –2 +

e) x x x 3 3 –– f ) x x x x 1 3 3 ––+ +

24 Calculate and simplify where possible:

a) x xx 4 3 2 –· 2 b) xx 8 21 6 : –

c) xx x x 3 9 2 · ––22 d) : x x x x 1 1 1 3 –2 + +

27 Apply Ruffini’s rule to find the quotient and remainder of the following divisions:

a) (4x 2 – 8x + 3) : (4x – 2)

b) (2x 3 – 4x 2 + 3x – 2) : (2x – 3)

c) (3x 3 – 2x – 1) : (3x + 1)

28 Break down the following polynomials into factors:

a) (x 2 – 25)(x 2 – 6x + 9)

b) (x 2 – 7x)(x 2 – 13x + 40)

29 Factorise the following polynomials and give their roots:

a) x 3 – 2x 2 – 2x – 3 b) 2x 3 – 7x 2 – 19x + 60

c) x 3  – x – 6 d) 4x 4 + 4x 3 – 3x 2 – 4x – 1

e) 6x 3 + 13x 2 – 4 f ) 4x 3 + 12x 2 – 25x – 75

30 Break down the following polynomials into factors and give their roots:

a) x 4 – 2x 2 + 1 b) x 3 – 2x 2 – 9x + 18

c) x 4 – x 3 – 7x 2 + x + 6 d) 8x 3 + 6x 2 – 11x – 3

e) 3x 3 + 8x 2 + 3x – 2 f ) x 3 – 2x 2 + 2x – 4

31 Find the value of m that makes each of the following divisions exact.

a) () x xm x 15 1 –:)( 2 ++

b) () ): ( xx x mx 2 2 –2 3 ++ +

c) ) xxmx mx62 2 – () :( 2 3 +

32 Find m so that () ( Px xx mx m 52 ) =+32 ++ is divisible by x – 1.

33 Break down the dividend and the divisor into factors, then simplify.

40 Replace the dots with expressions that make the fractions equivalent.

c) xx x 4 21 12 1 –––2 cm d) : x y y x 11++c c m m

SOLVE SIMPLE PROBLEMS

UNDERSTAND AND APPLY IN THE CHALLENGE

39 Calculate a, b and c to verify the

41 Express the following polynomials in the form

ax 3 + bx 2 + cx + d:

a) () ) x xx22 25 – )( ( 2 3 ++ +

b) () ) )( ( xx x 3 32 3 –32

c) )) x x 14 13 2 – (( 3 +

42 Write a third-degree polynomial that has the given roots in each case:

a) 0, 1 and 2 b) –1 and 3 c) 0 and 5

43 For each of the following, write a polynomial that meets the given condition:

a) Fourth-degree without roots.

b) Has two double roots, 2 and –2.

c) Third-degree with a single root.

d) Fourth-degree and with three roots.

44 Calculate the value of the dividend in each of the following cases:

a) Divisor: (x 2 – 2). Quotient: (x + 3). Remainder: 7

b) Divisor: (x 2 + 2x). Quotient: (x 2 +  x – 2). Remainder: (–3x + 4)

c) Divisor: (x 2 + 1). Quotient: (x – 2). Remainder: (2x + 10)

45 Calculate the value of m that makes the polynomial mx 3 – 3x 2 + 5x + 9m divisible by x + 2.

46 Calculate the value of m and n that makes the polynomial P (x) =  x 3  –  m x 2 +  n x + 4 divisible by x – 2 and x + 2. What are the roots of P (x)?

47 Calculate the values a and b that make the polynomial P (x) = x 4 – 2x 3 + ax 2 + bx + 15 divisible by (x + 3) and by (x – 5).

48 Calculate the value of m that gives the following divisions the remainder indicated:

a) (x 3 – 2x 2  – x + m) : (x + 1) Remainder = –1

b) (2x 3 – 12x + 2m) : (x – 3) Remainder = –5

49 The remainder of this division is – 8: (2x 4 + kx 3 – 7x + 6) : (x – 2) What is the value of k?

EXERCISES AND PROBLEMS

50 Find the values that a and b must have so that when we divide P (x) =  x5 +  ax 4 +  x 2 +  bx + 8 by (x + 1) the remainder is 9, and when we divide it by (x – 2) the remainder is 6.

51 Find the lowest common multiple and the greatest common divisor for each of the following polynomials:

a) x 2 ; x 2  – x; x 2 – 1 b) x – 3; x 2 – 9; x 2 – 6x + 9

c) 2x; 2x + 1; 4x 2 – 1 d) x + 2; 3x + 6; x 2 + x – 2

52 Calculate the GCD and LCM of the following polynomials from exercise 30:

a) Sections a and c. b) Sections b and c.

53 Check whether there is any divisibility relationship between these pairs of polynomials:

a) P (x) = x 4 – 4x 2 y Q (x) = x 2 – 2x

b) P (x) = x 2 – 10x + 25 y Q (x) = x 2 – 5x

c) P (x) = x 3 + x 2 – 12x y Q (x) = x – 3

54 Factorise the following expressions:

ADVANCED PROBLEM SOLVING

59 Inside rectangle ABCD with sides AB  = 3 cm and BC  = 5 cm, we have inscribed the quadrilateral '' ABCD'' where '' '' AA BB CC DD == =  = x. Write the area of '' ABCD'' as a function of x

55 Simplify the following algebraic fractions:

60 In the triangle below, BC  = 10 cm, AH  = 4 cm. We draw a point D on the line so that AD  =  x and we draw a line MN through D, parallel to BC Starting at points M and N we draw lines that are perpendicular to BC

a) Express MN as a function of x. (Use the similarity of triangles AMN and ABC).

b) Write a polynomial expressing the area of rectangle MNPQ as a function of x.

61 We have a rectangle with a perimeter of 20 cm. If the base is reduced by 2 cm and the height by 3 cm, by how much is the area of the rectangle reduced? Express it as a function of the base.

62 A triangle has a base of 20 cm and a height of 15 cm. If the height is increased by x % and the base by (x + 2) %, express the new area of the triangle as a function of x.

56 A tap takes 4 hours to fill a tank. Another tap takes 6 hours to fill the same tank. If both taps are open and the plug is taken out, it takes 12 hours to fill the tank. Express, as a function of x, how long it takes to empty the tank if both taps are closed.

57 Express the total surface area of this truncated pyramid as a function of x: x + 1 is the height of a lateral face.

58 M is any point along segment AB which is 6 cm. Express the blue shaded area as a function of xAM = .

63 A shop owner sold two bicycles. He made a 20% profit on one of the bicycles, and a loss of 10% on the other one. In total, he made a profit of 15%. Use algebra to express this statement.

64 We cut a piece of wire that is 1 m long into two unequal parts. With one of these parts, we form an equilateral triangle, and with the other, a square. Write the sum of the areas of both figures.

65 Using a rectangular piece of card that measures 30 cm and 20 cm, we make a box without a lid by cutting a square with sides of length each corner. Write the volume of the box as a function of x.

YOU CAN ALSO TRY THIS

66 a) Check that ) nn nn 1 1 1 1 1

( + = +

b) What will the value of A be in the following expression?

·· · · A 12 1 23 1 34 1 910 1 = +++ +

And if the last summand were · 99 100 1 ?

67 Prove that when a second-degree polynomial is divided Px ax bx c () 2 =+ + by Qx x 1 – () = , the remainder of the division is equal to the sum of the P coefficients (x).

Would this be true for ()Px ax bx cx d 32 =+ ++ ?

UNDERSTAND AND APPLY IN THE CHALLENGE

68 How many squares do stairs with 5 steps have? Write a formula to show how many squares there are in stairs with n steps.

69 If we increase the length of the base of a rectangle by x % and its height by 2x %, the area increases by 31 %. Write this in algebraic language.

70 Find a third-degree polynomial that we know is divisible by (2x 2 – 3), the remainder of dividing it by (x + 1) is 15 and whose highest degree coefficient is 6.

REMEMBER THE THEORY REFLECT

71 What do the values of a and b have to be for the polynomials P (x) and Q (x) to be equal?

P (x) = x 3 – (4 + a)x + (1 + b ) Q (x) = (a + 3)x 3 + (a + 2)x 2 – 2x + 5

72 The roots of P (x) are 0, 2 and –3.

a) Write three first-degree divisors of P (x).

b) Write one second-degree divisor of P (x).

73 a) If the division P(x) : (x – 2) P (x) : (x – 2) is exact, what can you say about the value P (2)?

b) If –5 is a root of the polynomial P (x), what can you say about the division P (x) : (x + 5)?

c) What result did you use to answer these two questions?

74 True or false? Explain your answer and give examples.

a) If a polynomial has a degree of 3, and another polynomial has a degree of 2, their product will have a degree of 6.

b) If P (0) = 1, then P (x) is divisible by (x – 1).

c) If we add two third-degree polynomials together, we always get a third-degree polynomial.

d) If P (3) ≠ 0, the polynomial P (x) is not divisible by x – 3.

e) If P (–2) = 0, then x + 2 is a factor of P (x).

f ) If P (x) =  ax 2 +  bx + 2 y P (±2) ≠ 0, then P (x) cannot have integer roots.

g) It is not possible to write a fourth-degree polynomial that only has a triple root.

h) A polynomial that is zero for the numbers 0, 1, 2, 3, 4 cannot be a fourth-degree polynomial.

75 Invent two second-degree polynomials that meet the condition given in each case:

a) LCM [P (x), Q (x)] = x 2(x – 3)(x + 2)

b) GCD [P (x), Q (x)] = 2x + 1

76 Given the polynomial P (x) = (x – 1)2(x + 3) find a second-degree polynomial, Q(x), Q (x), that meets the following conditions:

a) GCD [P (x), Q (x)] = x – 1

b) LCM [P (x), Q (x)] = (x – 1)2(x 2 – 9)

77 By which fraction do we need to multiply x x 1 5 ––to get xx xx 34 5 ––2 2 + ?

78 Prove that the polynomial x2 + (a +  b)x +  ab is divisible by x + a and by x + b or any value of a and

b. What would they look like broken down into factors?

79 If a polynomial A has a degree of 4 and another polynomial B has a degree of 3, state the degree of the following polynomials:

a) Sum of A and B. b) Subtraction of A and B.

c) Product of A and B.

80 True or false?

d) Quotient of A and B

a) When three polynomials with different degrees are added together, the resulting polynomial has the same degree as the highest of them.

b) The result of adding three third-degree polynomials is a sixth-degree polynomial.

c) The result of adding two fifth-degree polynomials is another polynomial with a degree of 5 or higher.

EXERCISES AND PROBLEMS

FINDING PATTERNS AND GENERALISING

Observe, check and compare:

Can you add another row to this number triangle? (It is called Pascal’s triangle).

READ AND LEARN

Cutting up

Cutting this trapezium into two or three equal pieces is very simple, but cutting it into four is much harder. Try it.

THINK AND EXPRESS YOURSELF

How interesting!

Think of any three digits that are not all the same

Can you expand the polynomial for (a + b )5 without multiplying the binomial (a + b ) by itself five times?

• Check that the difference is always a multiple of 9 and 11.

• Using algebraic language, show that the observation above is true for any three digits, x, y, z, as long as at least two of them are different.

Tip:

For example, 5, 8 and 3.

SELF-ASSESSMENT

1 Break down the following polynomials into factors using notable products.

a) xx21 –42 + b) yxyx 9124 –22 +

c) x 16 –4 d) y 81 –4

2 Calculate the values a, b and c to verify the following equality.

() ( ax xb cx x 32 415 – –) 2 += +

3 Multiply each expression by the LCM of the denominators and simplify.

() () () () () xx xx x 3 21 8 31 12 23 23 ––2 + + +

4 Find the quotient and the remainder of this division: (3x 4 – 5x 3 + 4x 2 – 1) : (x 2 + 2)

5 Calculate the value of m that makes the polynomial P (x) = 7x 3  –  mx 2 + 3x – 2 divisible by x + 1.

6 Break these polynomials down into factors:

a) x 4 – 12x 3 + 36x 2 b) 2x 3 + 5x 2 – 4x – 3

7 Take out the common factor in each expression:

a) (x – 2)(2x + 3) – (5 – x)(x – 2)

b) (x + 5)(2x – 1) + (x – 5)(2x – 1)

8 Calculate and simplify where possible. a)

9 Given the polynomial P (x) = (x – 1)2(x – 3):

a) Invent a second-degree polynomial Q (x) such that P (x) and Q (x) are relatively prime.

b) Find a polynomial R (x) for which this is true:

GCD [P (x), R (x)] = (x – 1)(x – 3)

LCM [P (x), R (x)] = (x – 1)2(x – 3)2(x + 2)

10 Find the value of a and b so that when we divide x 3 + ax 2 + bx – 4 by x + 1 the remainder is –10, and when we divide it by x – 2 the remainder is 2.

anayaeducacion.es Solutions to these problems.

11 We inscribe a rhombus inside this rectangle with sides x and y Write the perimeter of the rhombus as a function of the sides of the rectangle.

12 We mix x kg of a paint that costs €5 /kg with y kg of another paint that costs €3 /kg. What would 1 kg of the mixture cost? Express it as a function of x and y Express it as a function of x and y

13 One leg of a right-angled triangle measures 14 cm. Write the perimeter and area of the triangle as a function of the hypotenuse x.

14 Two towns, A and B, are 60 km apart. A car leaves A for B at a velocity of v. At the same time, another car leaves B for A at a velocity of v + 3. Express the time they take to meet as a function of v.

15 Use algebraic language to express the area of the coloured part of this shape using x and y.

16 True or false?

If P (x) = (x 2 – 5) · (x + 7) 2 then:

a) The roots of P (x) are 5 y –7.

b) P (x) has a double root.

c) P (x) has two irrational roots

LEARNING SITUATION

THINK

Look back at the content you have worked on and plan solutions to the problems that you may find. To do this, download the assessment from anayaeducacion.es, think individually and share in groups.

TEST YOUR SKILLS

Now you can do the skills self-evaluation included in anayaeducacion.es.

© GRUPO ANAYA, S.A., 2023 - C/ Valentín Beato, 21 - 28037 Madrid.