AndalusiaSECONDARY EDUCATION
José Colera J.
M.ª José Oliveira G. IgnacioGazteluA.
Ramón Colera C. Rosario García P. Ana Aicardo B.

4
O BAL THINKERS Mathematics
sample
What are we going to learn?



• Draw a diagram, graph or table to help you organise your data
• For geometric problems, draw a picture!
• Irrational numbers
• Real numbers: the real number line
• Sections of the real number line: intervals and half-lines
• Polynomial
• Ruffini's rule
•



•
•
•
• Vectors in the
•
using vectors
• Vectors which represent points
• Midpoint of a segment


•
• How functions are
•
•
•




•
•
•
•
•
and σ
• Using the line of best fit to make estimations
• Strategies based on the
• Variations and permutations (the order matters)
• When the order doesn't matter. Combinatorics
•
•
•
Train yourself by solving problems 8
1 Real numbers 32 Solar sails and real numbers Industry, innovation and infrastructure
2 Polynomials and algebraic fractions 60 Are integers and polynomials similar? Quality education
operations
3 Equations, inequations and systems 84 Equations in the market! Responsible consumption and production
Equations
Systems of equations MORE THAN MATHS 4 Similarity. Applications 118 Similarity at the museum! Life on land
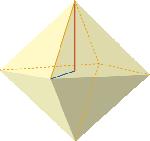
Similarity • Homothety 5 Trigonometry 142
calculate the height of a monument! Sustainable cities and communities
•
•
We
Trigonometric ratios
of an acute angle
trigonometric identities
Basic
Using a calculator
trigonometry 6 Analitic geometry 168 Geometry in a city? Sustainable cities and communities
in
plane
Calculations
THAN MATHS 7 Functions I 200 An amazing freefall! Industry, innovation and infrastructure
MORE
concepts
Basic
presented
8 Functions II 228 How is gravity measured? Industry, innovation and infrastructure
Domain of definition
functions
Piecewise-defined
Radical functions
THAN MATHS 9 Statistics 256 What do questionnaires and statistics have in common? Partnership for the goals
MORE
Statistics and statistical methods
Frequency
tables
Statistical parameters: X
10 Bivariate distributions 286 Travelling around the world Good health and well-being
Bivariate distributions
Correlation value
11 Combinatorics 306 Algorithms in our life? Quality education
product
12 Calculating probability 330 Which door are you choosing? Quality education
Random events
Probability of events. Properties
Probability in simple experiments MORE THAN MATHS + GLOSSARY LEARNING EXPERIENCE · SDG BASIC KNOWLEDGE PAGE
I Arithmetic and algebra
II Geometry
III Functions BLOCK IV Statistics and probability
BLOCK
BLOCK
BLOCK
• Experiment, try out, give examples, conjecture and check...
• Roots and radicals
• Approximate numbers. Errors
• Root of a polynomial. Finding roots
• Factorising polynonials
• Equations with one unknown
• Linear inequations with two unknowns
• Investigate
• Numbers in scientific notation. Error control
• Logarithms
• Divisibility of polynomials
• Algebraic fractions
Do the maths and compare the data to make it easier to understand.
Similarities between integers and polynomials.
How to solve diophantine equations.
• Rectangles with interesting dimensions
• Similarity between triangles
• Trigonometric rations from 0° to 360°
• Angles of any measurement. Trigonometric ratios
• Aligned points
• Equations of a straight line
• Straight lines. Parallellelism and perpendicularity
• Straight lines parallel to the coordinate axes
• X- and Y-intercepts. Sign of a function
• Continuous functions. Discontinuities
• Variations in a function
• Inversely proportional functions
• Dispersion parameters for isolated data
• Position parameters for grouped data
• Box-and-whisker plots
• Does correlation imply cause and effect?
• Bivariate distributions with a calculator
• An interesting number triangle
• Newton's binomial
• Probability in compound experiments
• Creating individual experiments
• Similarity between right-angled triangles
• Similarity of right-angled triangles in three-dimensional shapes
• Solving right-angles triangles
• Solving non-right-angled triangles
• Interesting theorems
• Relative positions of two straight lines
• Distance between two points
• Equation of a circumference
• Studying motion
• Tendency and periodicity
• Linear functions
• Quadratic functions
• Exponential functions
• Logarithmic functions
• Trigonometric functions. The radian
• Statistical inference
• Statistics in the media
Why did the Dimetrodon have a huge spinal sail? What other strange curiosities does similarity in nature have for us?
Measure heights and distances between inaccesible points.
Use analytical geometry to locate and describe places in the city of Rome.
From parabolas to straight lines, breaking the fall.
How gravity varies with changing altitude or changing planets.
• The structure of dependent experiments
• Contingency tables
Let's make a survey about sustainability!
Correlation to interpret our world.
How to expand the steps to find solutions to some NP problems.
Keys and doors.
PORTFOLIO


Solar sails are based on complex physical principles: the distances are inconceivable, the speeds are enormous and the width of the sails is very small. To make the dimensions and results easier to understand, you will work on this data and compare it to other data more familiar to you. After that, you will write your own scientific article about solar sails.

1. The star system Alpha Centauri is 4.37 light years away. The speed of light is 300 000 km/s. How many kilometres is Alpha Centauri from the Sun?
You should use scientific notation to make the operations easier and give the solution to 3 significant figures.
2. Have you ever heard of the Blackbird? It is one of the fastest aeroplanes in the world. It can reach 3 540 km/h. How long would it take to arrive at Alpha Centauri in this plane? DO

32
Industry, innovation and infrastructure
9.
NUMBERS 1
RNING EXPERIENCE
REVIEW WHAT
KNOW
THE QUIZ! REAL
TAKE ACTION? What can youdo to LEA
BEFORE STARTING…
YOU
WATCH THE VIDEO
Solar sails and real numbers.
What are yougoing to learn to
TAKE ACTION?
IRRATIONAL NUMBERS


APPROXIMATE NUMBERS. ERRORS

NUMBERS IN SCIENTIFIC NOTATION. ERROR CONTROL ROOTS AND RADICALS
Learning by doing videos 1-minute explanations videos
REAL NUMBERS: THE REAL NUMBER LINE

SECTIONS OF THE REAL NUMBER LINE: INTERVALS AND HALF-LINES

• Radicals in exponential form
• Simplification and reduction to a common index
• Product and quotient with the same index. Taking out factors from roots

• Operations with numbers in scientific notation
MY MATHS DICTIONARY
• Product and quotient with a different index
• Power and root of a radical
• Addition and subtraction of radicals
• Rationalising the denominator

LOGARITHMS
• Properties of logarithms
Key language
Φ (phi)
Non-recurring Margin of error
∈ (is an element of/belongs to/is a member of)
In context
This construction contains a segment that measures the same as Φ (phi).
π is an irrational number; it is infinite and non-recurring. The margin of error is less than 0.0001.
x ∈ Á: x is an element of the set of real numbers.
33
1 Irrational numbers
Rational numbers can be expressed as the quotient of two integers. Their decimal expression is terminating or recurring.
Irrational numbers are non-rational numbers. They cannot be expressed as the quotient of two integers. Their decimal expression is infinite and non-recurring. For example: π = 3.14159265359… . There are infinite irrational numbers.
The diagonal of a square: the number 2
The Pythagorean theorem gives us the value of the diagonal of a square with sides measuring 1:
d = 11 2 22+=
2 is irrational because it cannot be expressed as the quotient of two integers. We can demonstrate this by reduction to absurdity:
– Suppose 2 is rational.
– It could be expressed as the quotient of two integers: b a 2=
– We square the two sides: 2 = b a 2 2 → a2 = 2b2
2b2 has factor 2 an odd number of times, which is impossible since 2b2 = a2 is another perfect square.
If we presume that 2 is rational, we reach an absurdity.
Other irrational numbers expressed through radicals
For the same reason as 2 , if p is not a perfect square, p is irrational.
If p is not an exact nth power, p n is an irrational number.
For example, 8 , 9 3 and 10 5 are irrational numbers.
Keep in mind
When decomposing a perfect square into prime factors, each prime number appears an even number of times.
N = 22 · 3 · 53
N 2 = (22 · 3 · 53)2 = 24 · 32 · 56
All the exponents are even.
We have shown, by reduction to absurdity, that 2 is not rational.
The results of doing an operation with a rational number and an irrational one is irrational (except when we multiply by zero).
For example, the following are irrational numbers: 2 + 3, 4 – 10 5 , 9 3 : 7.
Let’s show that 4 – 10 5 is irrational based on the fact that 10 5 is irrational.
– We will call N = 4 – 10 5 → 10 5 = 4 – N
– If N were rational, 4 – N would also be rational. In other words, 10 5 would be rational, which is not true.
Let’s practise!
1 Demonstrate that the following numbers are irrational: a) 3 b) 4 3 c) 5 + 4 3
34
1 1 2
The golden ratio: U = 5 + 1 2
The diagonal of a pentagon with a side length of 1 unit is ( 5 + 1) : 1. It is an irrational number. It was the first irrational number mathematicians discovered in history. d
d = Φ
Greek artists called Φ golden number because they believed that the proportions based on it were especially harmonious.
The name, Φ (phi, the letter ‘f’ in Greek) comes from Phidias. He was a Greek sculptor from the 5th century BC. He often used this ratio.
The number r
As we already know, the number r is the relationship between the length of the circumference of a circle and its diameter. It is an irrational number and has infinite non-recurring decimal digits.
π corresponds to the letter ‘p’ in Greek. This number got the name from the Greek word perifereia (‘circumference’ the periphery of the circle).
The number e
The number e is another fundamental irrational number in mathematics. It is named after Leonhard Euler, one of the most important mathematicians in history.
The approximate value of the number e is 2.7182… and we can find it in many different situations:
– We apply the exponential function with the number e to the growth of animal and plant populations.
– To describe the change in radioactivity of a radioactive substance over time.
– We use the number e to describe the curve (a catenary) formed by a cable or rope, etc. between two fixed points at the same height.
2 Explain why these constructions contain a segment that measures the same as Φ
It is formed by the five diagonals of a regular pentagon. It was the symbol of the Pythagoreans.
Keep in mind
π and e cannot be represented exactly on the real number line.
3 Demonstrate that the golden number, Φ, is irrational.
4
1 When we cut a square out of this particular rectangle, the remaining rectangle is similar to the initial one. Demonstrate that its longest side is
35
l
Pentagram
2 51 2 5 2 1 = + =+ 1 1/2 1 2 1 2 √ 5 2 Φ Φ 1
x
x = Φ.
2
L π
L
r
r
2 =
y
xx –= + Catenary
ee 2
2 Real numbers: the real number line
Set of real numbers (Á) is the set of rational and irrational numbers.
Rational and irrational numbers are real numbers. They form all the real numbers there are. With the Á set, we can complete the table of sets of numbers:
Notation
When any number, x, is natural, it is expressed as x ∈ N; if it is an integer, as x ∈ Z; if it is rational, as x ∈ Q, and if it is real, as x ∈ Á.
With real numbers we can do additions, subtractions, multiplications and divisions (except for zero), as we can do with rational numbers. They maintain the same properties.
We can also extract the root of any index (except for roots with an even index of negative numbers) and the result is still a real number. This does not happen with rational numbers.
The N, Z, Q and now Á sets are closed under addition and multiplication: the sum and product of two elements of one of these sets are also part of that set.
However, for negative integers, fractional numbers and irrational numbers, the sum of two irrational numbers can be rational (for example: (1 + 2 ) + (3 – 2 ) = 4) and the product of two irrational numbers can also be rational (for example: 28 · = 4).
The real number line
Rational numbers are grouped densely on the number line. Each section contains an infinite number of rational numbers. However, there are also infinite number of gaps between them. These gaps are filled with the irrational numbers. Together, they fill the line.
1 0
If we place an initial point (0, zero) on a line and mark the length of one unit, each point on the line corresponds to a real number, rational or irrational. This is why we call this number line the real number line.
Once all the real numbers are in place, there are infinite rational and irrational numbers between any two numbers.
Observe
The result of adding two fractional numbers is not always a fraction:
3 1 3 5 3 6
2 += =
The product of two negative integers is not a negative integer:
(–2) · (–3) = 6
Remember
The real number line is complete: there is a real number for each point on the line and a point on the line for each real number.
36
rational Q integers Z natural N → 0, 4, 6 24 , 121 real Á negative integers → –11, – 3 27 , 8 –3 fractional → 5.84; 2 1 ; . 583 # ; – 10
irrational → 2 , 3 , Φ, π, – 5 + 2 , 5 23 +
3
Representing numbers on the real number line
Using Thales’ theorem to represent fractional numbers
Look at how we use Thales’ theorem to place the number
on the number line:
Using the Pythagorean theorem to represent radicals
We can use the procedure below to represent n for any
We cannot represent most real numbers exactly with this type of procedure. For example, we can use an approximate representation to represent 842 5 .
Approximate representation of real numbers
We can represent a real number in the form of a decimal with as close an approximation as we want. For example: 842 5 = 3.8464…:
Notice how each expansion involves dividing the previous subinterval into ten parts and then taking one of those parts. We can get as close to the chosen number as we want.
We can represent real numbers on the real number line either exactly or with as close an approximation as we like.
Let’s practise!
1 a) Demonstrate that the point represented is 21 .

2 What number is the arrow in this diagram pointing at? 0 1 2
b) Represent 27 (27 = 36 – 9) and 40 (40 = 36 + 4).
Represent 2.716 in the same way.
37
5 14
5 14 = 2 + 5 4 0 4 2 + 5 1 2 3
n ∈
For example: 32 1 2 2 =+ `j 3 0 1 1 2 10 5 3 2 10 =+3122
N:
0 1 2 3 3.8 4 3.9 3.8 3.84 3.85 3.9 3.84 3.85 3.846 3.847
Representation of 6 5 : 1 1 2 3 4 5 6 0 5 6 Example
√21 0
1
3 Sections of the real number line: intervals and half-lines
We often need to determine the scope of a certain variable, so we need to learn the right names for certain sections of the real number line.
Open interval
The open interval (a, b) a b
the set of values of all the numbers between a and b, but not including a or b: { x ∈ Á / a < x < b }
The interval (–2, 1) contains the real numbers between –2 and 1, but not –2 or 1: { x ∈ Á / –2 < x < 1}.
For example, to make a 15 cm × 10 cm box with a piece of card, we cut out four squares at the corners and then fold it. The sides of the squares must be less than 5 cm → (0, 5).
Closed interval
The closed interval (a, b) a b
10 cm
15 cm
Remember
(a, b) = {x ∈ Á / a < x < b}
a b
We read the above expression: set of numbers x that are greater than a but less than b { x ∈ Á / a < x < b }
the set of all the numbers between a and b, including both of them:
{ x ∈ Á / a ≤ x ≤ b }
The interval [–2, 1] contains the real numbers between –2 and 1, including –2 and 1: {x ∈ Á / –2 ≤ x ≤ 1}.
For example, the bags can weigh 2 kg or above, but no more than 5 kg → [2, 5].
Half-open interval
• The interval (a, b] a b
• The interval [a, b) a b
the set of all the numbers between a and b, including b but not a:
{x ∈ Á / a < x ≤ b }
the set of all the numbers between a and b, including a but not b:
{x ∈ Á / a ≤ x < b }
The interval (3, 4] contains all the real numbers between 3 and 4, including 4 but not 3: {x ∈ Á / 3 < x ≤ 4}.
For example, children can attend a particular nursery school after the age of 1, but before the age of 4 → [1, 4).
Closed interval
[a, b] = {x ∈ Á / a ≤ x ≤ b}
a b
Half-open interval
(a, b] = {x ∈ Á / a < x ≤ b}
a b
[a, b) = {x ∈ Á / a ≤ x < b}
a b
• Which inequality expresses the integers in the interval [–2, 0)? Think
• Which numbers are in the interval {x ∈ Z / –2 < x ≤ 4}?
38
Half-lines and the real number line
(– ∞, a) are the numbers less than a: { x ∈ Á / x < a}.
(– ∞, a] are the numbers less than a, including a: { x ∈ Á / x ≤ a}.
(a, +∞) are the numbers greater than a: { x ∈ Á / x > a}.
[a, +∞) are the numbers greater than a, including a: { x ∈ Á / x ≥ a}.
• (– ∞, 2) is the set { x ∈ Á / x < 2} → 2
• [2, +∞) is the set { x ∈ Á / x ≥ 2} → 2
• To vote, you need to be 18 years old → [18, +∞). Of course, in this context, +∞ has to be put into perspective, because nobody lives forever.
The real number line’s representation as an interval is: Á = (– ∞, +∞).
When there is no number that satisfies a specific condition, it is represented by the empty set, whose symbol is ∅. For example, the values of x for which x 2 < 0 correspond to the empty set: {x ∈ Á / x 2 < 0} = ∅
Problem solved
1 Write the following in interval form and draw them:
a) 2 < x ≤ 3 b) x ≤ 1 c) x > 0
2 Write the following as inequalities and draw them:
a) [–2, 0] b) [–1, +∞) c) (0, 1)
3 For which values of x is the following expression true?
(2)( –3) xx +
Let’s practise!
Half-lines
(–∞ , a) = {x ∈ Á / x < a} a
(– ∞ , a] = {x ∈ Á / x ≤ a} a
(a, +∞) = {x ∈ Á / x > a} a
[a, +∞) = {x ∈ Á / x ≥ a} a
Observe
The union of two intervals or half-lines is represented by ∪: (–∞, 2) ∪ (0, 5] = (–∞, 5] The intersection of two intervals or half-lines is represented by ∩: (–∞, 2) ∩ (0, 5] = (0, 2)
a) Half-open interval (2, 3] 2 3
b) Half-line (– ∞, 1] 1
c) Half-line (0, +∞) 0
a) { x ∈ Á / –2 ≤ x ≤ 0} –2 0
b) { x ∈ Á / x ≥ –1} –1
c) { x ∈ Á / 0 < x < 1} 0 1
You can calculate the square root when the radicand is zero or positive. This happens when one of the factors is zero, both are negative or both are positive. In other words, if x ≤ –2 or if x ≥ 3.
(–∞, –2] ∪ [3, +∞) –3 –2 –1 0 1 2 3 4
1 Write the following sets in interval form and represent the numbers that meet the conditions on the number line in each case:
a) Numbers between 5 and 6, both included.
b) Greater than 7.
c) Less than or equal to –5.
2 Write the following in interval form and draw them.
a) { x ∈ Á / 3 ≤ x < 5} b) { x ∈ Á / x ≥ 0}
c) { x ∈ Á / –3 < x < 1} d) { x ∈ Á / x < 8}
3 Write the following as inequalities and draw them.
a) (–1, 4] b) [0, 6] c) (–∞, – 4) d) [9, +∞)
39
4 Roots and radicals
The nth root of a number, a, (written a n ) is the name given to a number, b, that meets the following condition:
a n = b if bn = a
a n is a radical; a is a radicand; n, the index of the root
To work with this type of expression, you will sometimes need to calculate their numerical value. To do so, remember the definition or use a calculator. However, in other cases, you will need to keep the radical, simplify it, perform operations with other radicals, etc.
Some peculiarities of roots
• If a ≥ 0 a n exists irrespective of the value of n.
• If a < 0 only the roots with an odd index exist.
• When we write 4 we refer to the positive root: 4 = 2.
In general, a positive number, a, has two square root a – a
Radicals in exponential form
We can express radicals as powers:
For example:
64 2 3 6 3 = = 26/3 = 22 = 4
Let’s practise!
1 Express each of the following roots in exponential form:
a) x 5 b) x 2 3 5`j
c) a 6 15 d) a a 6 13
e) x x 2 3 6 f )
Mental arithmetic
1 Indicate the value of k in each case:
2 Calculate the
2 Calculate.
a) 41/2 b) 1251/3 c) 6251/4
d) 82/3 e) 645/6 f ) 363/2
3 Express in radical form.
a) x 7/9
c) a 1/2 · b 1/3
e) [(x 1/2)5]1/3
b) (m 5 · n 5)1/3
d) [(x 2)1/3]1/5
f ) (y 3 · z 2)2/3
40
a) k 3 = 2 b) 243 3 k = c) k 3 2 4 = d) 1 024 2 k =
roots: a) 8 –3 b) 32 5 c) –32 5 d) 0 8 e) 81 4 f ) 125 3
following
a n n
a1
a a
a n m , since a m n = (am) n 1 = a m · n 1 = a n m
a n = a n 1 , since (a n 1 )n =
=
=
m n =
6 2 =
27 3 6 2 3
` ` j j = (33/6)2 = 36/6 = 3
a n = a n 1 a m n = a n m
Watch out
2
x x 4 5
4 eo >H
Operations with radicals
Radicals have a series of properties that you need to know and be able to use easily. You can see them on the right, on this page and the next. They are the direct consequences of known properties of powers. Pay special attention to the operations you can use them for.
Simplification of radicals
We can simplify radicals when we express them as powers.
Reduction of radicals to a common index
It is not always easy to compare two radicals with different indices. It gets easier when we express them with the same index. This means reducing them to a common denominator.
Taking out factors from roots
To simplify some radicals, and to add and subtract them, we sometimes need to take out factors from a root.
To
41
93 33 3 // 4 2 4 24 12 = === property 1 aa p np n = , since: aa aa// p np pnpn n 1 == = Property 1 ab ab n n n = , since: () ab ab / n n 1 == ab · //nn11 == ab · n n = Property 2 b a b a n n n = , since: b a b a b a b a / / / n n n n n n 1 1 1 == = bl
Property 3
To compare 586 3 to 70 : 586 586 586 586 343 396 70 70 70 70 343 000 // // 3 13 26 2 6 6 12 36 3 6 6 == == == == 4 → 586 70 > 3 property 1
·· 18 32 32 32 22 == = ·· ·· ·· 720 23 52 35 23 5125 42 42 2 == == property 2 Product and quotient of radicals with the same index For example: 15 20 15 20 300 == property 2 20 15 20 15 4 3 == property 3 Product and quotient of radicals with a different index
multiply or divide radicals
a different
to a common index: ·· · 32 32 32 108 3 3 6 2 6 32 6 6 == = () 32 16 32 16 2 2 2 2 22 6 3 6 2 6 5 42 6 5 8 6 3 6 == == = property 3
with
index, we reduce them
4 Roots and radicals
Power of a radical
For example:
22 3 4 12 = ` j = 212/2 = 26 = 64
22 8 5 3 3 5 5 == ` j property 4
Root of a radical
For example:
3 4 12 = property 5
22 3 6 = 55
Addition and subtraction of radicals
We cannot add two different radicals together unless we find their approximate expressions. For example:
32 77 –3 + 4
We can only solve them approximately, or leave them in this form.
We can, however, simplify the following expression:
75 11 55 17 5 –+=
Sometimes, it is difficult to see how to simplify an addition of radicals. First, we need to take out any factors we can from the roots or simplify them. For example: 32
4 Simplify.
5 Which of the two is greater in each case?
7
6 Reduce.
()aa aa// n p np pn p n 1 == = ` j
Property 5
Property 4 aa n m mn = , since:
()aa aa // /( ) n m nm mn mn 11 1· == =
We can only add identical radicals together. Remember aa n p p n = ` j , since:
42
a) x 9 12 b) x 8 12 c) y 10 5 d) 8 6 e) 64 9 f ) 81 8
a) 31 4 and 13 3 b) 51 3 and 132 650 9
a) 22 3 5 b) 63 3 6 c) ab46 10
Take out all possible factors from the radicals. a) x32 4 3 b) ab c 81 35 3 c) 64 5 8 Simplify. a) 3 9 3 b) 2 16 5 c) ab c ab c 33 35 4 d) a 2 3 6`j e) · xx 3 3 ` ` j j f ) 2 8ak 9 Calculate. a) 18 50 28 + b) 75 22748 – +
18 50 23 25 2 55–· –· 52 2 += += 42 25 22 15 14 – =+ = 84 22 22 23 2 4 32 4
+= += +=
Rationalising the denominator
Before calculation tools, people had to find methods to make operations easier.
For example, to calculate 2 1 by hand directly, we can calculate a few digits of 2 and then divide the result by 1.
But, to simplify the calculations more
When we do the operation both ways, it is easier if we remove the radical from the denominator.
With calculation tools, the final results of problems usually appear in numerical expressions without radicals in the denominator.
The rationalisation of the denominator is the process we use to remove the radicals from the denominator.
In each case, we should ask ourselves: which expression do I need to multiply the denominator by to get a product without radicals? Once we find the expression, we will also multiply the numerator by it so that the result does not vary.
1st case: square roots
2nd case: other roots
3rd case: addition and subtraction of roots
Some operations are easier to solve after we
them:
10 Rationalise the denominators.
2 = 1.4142…
It is more difficult to calculate:
1.00000000 1.4142
0100600 0.7071…
016060
01918
than to calculate:
1.4142… 2
014 0.7071… 02 0 and we get the same result.
Rationalising is making rational something that was not rational before. Remember
Keep in mind
• (a + b ) · (a – b
• We call the expression ab – the conjugate of ab +
And, the other way round, ab + is the conjugate of ab –.
43
a) 2 5 b) 7 5 c) 2 1 3 d) 3 2 2 5 e) 32 4 + f ) 23 3 –
· · 2 1 2 12 2 2 2 ==
rationalise
32 2 2 1 3 2 1 23 22 2 2 3 23 –+= + += 6 12 3122 6 32 6 43 6 83 15 2 – = + += +
Observe
2 – b 2
) = a
( ·( ( )· () ) )( ) 5 1 5 15 5 5 2 5 33 53 3 3 33 –22 == = + + ++ ( ·( ( )· () ) ) 32 2 32 23 2 32 62 2 92 62 2 7 62 2 32 –––––22 + = + == =
· · 3 2 3 23 3 23 3 ==
7 1 77 17 7 7 7 7 · · 2 5 2 5 3 5 3 5 5 5 3 5 3 5 == =
5 Approximate numbers. Errors
Approximation and errors
For practical applications, we generally work with approximate numbers.
Significant figures are the figures we use to express an approximate number. We should only use those we are sure of and in a way that is logical or relevant to the information we want to transmit.
For example, when a swimming pool has a 718 900 L capacity, it is more reasonable to say it is 719 m3, with three significant figures. But, if the measurement is not very accurate or we do not need the exact capacity, it is better to say 720 m3
The absolute error of an approximate measurement is the difference between the real value and the approximate value.
Absolute error = |Real value – Approximate value|
The real value is generally unknown, so the absolute error is also unknown. But it is important to put limits on it: the absolute error is less than… We get the limit of the absolute error from the last significant figure used.
In the example above, the last significant figure (9) gives units of m3. The absolute error is less than half a cubic metre (error < 0.5 m3).
The relative error is the quotient of the absolute error and the real value. The more significant figures we use, the lower the relative error is. It is usually expressed as a percentage (%).
In the example, the relative error is less than: 719 05 < 0.0007 = 0.07 %.
Observe
a) 34 m has 2 significant figures.
b) 0.0863 hm3 has 3 significant figures.
c) It is possible that 53 000 L only has 2 significant figures if the zeros are just used to designate the number. In this case, it would be better to say 53 thousand litres.
a) Measurement: 34 m
Absolute error< 05 m *
b)
Problem solved
1 Use a reasonable number of significant figures to express the following quantities:
a) Visitors to an art gallery in one year: 183 594.
b) People attending a demonstration: 234 590.
c) Number of bacteria in 1 dm3 of a preparation: 302 593 847.
:. . Measurement0 0863 hm
In otherwords,abs.error< 50 m 3 3 3 Z [ \ ] ] ] ]
Absolute error< 0 00005 hm
Absolute error< *
Measurement: thousand
c) L L 53 500
The relative errors of the previous measurements are:
a) R.e. < 34 05 < 0.015 = 1.5 %
b) R.e. < 0.0863 0 00005 < 0.0006 = 0.06 %
c) R.e. < 53 000 500 < 0.0095 < 0.01 = 1 %
a) It is quite possible that this number is accurate, as there is a record of visitors to a museum because they pay for a ticket. Let’s suppose 183 594 is the number of tickets sold. But we can also simplify it by saying ‘almost two hundred thousand’ or ‘more than one hundred and eighty thousand’. Those are valid estimations.
b) It is not possible to count the demonstrators this accurately. Sometimes these figures are inflated or reduced for political reasons. It is not possible to know the exact figure. It would be reasonable to say ‘more than two hundred thousand’, or even ‘between 200 000 and 250 000’.
c) Two figures is the most accurate approximation possible with this type of quantity: 3 hundred million bacteria.
44
Problem solved
2 Give a limit of absolute error and of relative error for each of the estimations of the amounts in the previous problem solved.
a) If we say the number of visitors is 180 thousand we have an absolute error of 183 594 – 180 000 = 3 594 people. We can be this accurate because we know the exact amount. However, when we use this information it should be clear that there may be an error of up to 5 units from the first unused figure: 5 000 people.
To summarise:
Estimation: 180 thousand
Absolute error < 5 000
Relative error < 180 000 5 000 < 0.028 < 0.03 → R.e. < 0.03 = 3 %
b) Estimation: 200000
Absolute error < 50000
Relative error < 200 000 50 000 = 0.25 = 25 %
c) Estimation: 3 tens of millions = 300 million
Absolute error < 0.5 tens of millions = 5 million
Relative error < 300 5 < 0.017 < 0.02 → R.e. < 0.02 = 2 %
Let’s practise!
1 True or false? Explain your answers.

a) Saying that a swimming pool holds 147 253 892 thousand drops of water is correct if the measurements are very accurate.
b) Saying that a swimming pool holds 147 253 892 thousand drops of water is not reasonable. It is not possible to measure it this accurately. It is more sensible to say that the swimming pool holds 15 tens of thousands of millions of drops.
c) If we correctly estimate that the number of drops of water that a swimming pool holds is 15 tens of thousands of millions, the absolute error is less than half of ten thousand million drops; in other words, absolute error < 5 000 000 000 drops.
d) If the relative error for a certain measurement is less than 0.019, we can say that it is less than 19 %.
e) If the relative error for a certain measurement is less than 0.019, we can say that it is less than 2 %
f) The calculator tells us that π = 3.14159265. If we use π = 3.14, we can say that the absolute error is less than 0.00159266. But it is more reasonable to say that the absolute error is < 0.0016 or even that the absolute error < 0.002.
2 Explain why it is not reasonable to say that there are 11 892 583 grains of rice in a sack.
Think of a more reasonable way to express it. Give a limit of absolute error and relative error for the expression.

3 Give a limit of absolute error and relative error for when you round π to 3.1416.
45
6 Numbers in scientific notation. Error control
The numbers 3.845 · 1015 and 9.8 · 10–11 are in scientific notation:
• They are made up of two factors: a decimal number and a power of 10.
• The decimal number is greater than or equal to 1 and less than 10.
• The power of 10 has an integer exponent.
3.845 · 1015 = 3 845 000 000 000 000 ‘large’ number
9.8 · 10–11 = 0.000000000098 ‘small’ number
Advantages of this notation
We use this notation in contexts that need precision. We do not say things like:
– How many children do you have? → 5 · 100
– Do you have any pins with a width of 2.5 · 10–4 m?
This form of expression is useful for very large or very small approximate quantities, because:
• We can see the ‘size’ of the number immediately in the second factor, with the exponent of 10.
• We can see how accurate the quantity is. The more significant figures there are in the first factor, the more accurate the number is.
For example, 7.6 · 108 and 7.603 · 108 are approximately equal (‘very similar sizes’), but the second one is more accurate because it has four significant figures.
Operations with numbers in scientific notation
We can do operations in scientific notation with a calculator. To write a number in scientific notation, we use the � key.
For example, 7.6 · 108 → 7.6 � 8; 2.5 · 10–4 → 2.5 �f 4. But if we want to do this without a calculator, we need to be really careful.
Product and quotient
We do the operations involving the decimal components separately from the powers of 10. Then, we adjust the result to express it correctly using scientific notation:
(3.25 · 105) · (4.6 · 1011) = (3.25 · 4.6) · (105 · 1011) = 14.95 · 1016 = 1.495 · 1017 (3.25 · 105) : (4.6 · 1011) = (3.25 : 4.6) · (105 : 1011) = 0.7065 · 10–6 = 7.065 · 10–7
In the quotient 3.25 : 4.6 we have used four significant figures. When the context of the problem does not suggest the right number of significant figures to use, we must make the decision subjectively.
Test yourself
Express the following numbers in scientific notation:
a) 340 000 b) 0.00000319
c) 25 · 106 d) 0.04 · 109
e) 480 · 10– 8 f ) 0.05 · 10– 8

Interesting fact
You might find an explanation like this:
If an integer ends in one or more zeros, you can easily determine the number of significant figures it has by expressing it in scientific notation. However, another way to indicate that these zeros are significant figures is to put a decimal point at the end of the number. Like this:
3 200 would have 2 significant figures.
3 200. would have 4 significant figures.
This rule is not approved by the scientific community, so it will not appear in this book. But some teachers might use it because it can help to clarify things.
46
Addition and subtraction
We must prepare the addends so that they have the same power of base 10. That way we can use it as a common factor. Then, when we have done the addition, we adjust the result.
3.7 · 1011 + 5.83 · 108 – 4 · 109 = 3 700 · 108 + 5.83 · 108 – 40 · 108 = = (3 700 + 5.83 – 40) · 108 = 3 665.83 · 108 = 3.66583 · 1011
Or alternatively:
3.7 · 1011 + 5.83 · 108 – 4 · 109 = 3.7 · 1011 + 0.00583 · 1011 – 0.04 · 1011 = = (3.7 + 0.00583 – 0.04) · 1011 = 3.66583 · 1011
Controlling error in a number in scientific notation
If we hear that ‘there are 2 500 bags of flour’, this could be an approximate quantity. It could mean that there are approximately 25 hundreds of bags, with an error of less than 50 bags, or that there are 250 tens, with an error of less than 5 bags.
If we use scientific notation, the expression is unambiguous: 2.5 · 102 means there are only two significant figures. If there are three, we write 2.50 · 102.
Problem solved
We read that 1 400 million people live in China.
a) Express this quantity in scientific notation.
b) Is it an exact or approximate amount?
c) Give a limit of absolute error based on the figure.
d) Give a limit of relative error.
a) 1 400 million = 1.4 · 109 inhabitants
Attention
The information in these numbers is different:
2.5 · 102; 2.50 · 102; 2.500 · 102
The zeroes at the end of the decimal number indicate the number of figures that are accurate.
b) Obviously, this is an approximate number, as it is impossible to calculate such a large, dispersed and changeable amount accurately.
c) and d) When we read ‘1 400 million people’, we expect the first two figures to be accurate. However, it is possible that one of the zeroes that comes after them is also accurate.
If only the two first figures in the measurement are accurate:
Measurement: 14 hundred million people.
Absolute error < 0.5 hundred million = 50 000 000
Relative error < 0.5/14 < 0.036 = 3.6 %
If the first zero in the measurement is accurate:
Measurement: 140 tens of millions of people. In this case, we can express it using scientific notification like this: 1.40 · 109. Notice how the fact that the zero comes after the decimal point means that it is an accurate digit.
Absolute error < 0.5 ten millions = 5 000 000
Relative error < 0.5/140 < 0.0036 = 0.36 %
Let’s practise!
1 Calculate and check your answers with a calculator.
a) (6.4 · 105) · (5.2 · 10– 6)
b) (2.52 · 104) : (4 · 10– 6)
c) 7.92 · 106 + 3.58 · 107
d) 6.43 · 1010 + 8.113 · 1012 – 8 · 1011
2 The distance from the Earth to the Sun is 149 000 000 km.
a) Express this in scientific notation.
b) Express this in centimetres to two significant figures.
c) Express this in centimetres to four significant figures.
d) Give a limit of the absolute and relative errors in a), b) and c) above.
47
7 Logarithms
We can also write the equality 23 = 8 as: log2 8 = 3. We read log2 8 as the logarithm of 8 with base 2. Similarly: log5 125 = 3 because 53 = 125
log5 5 2 1 = because 51/2 = 5
log10 1 000 000 = 6 because 106 = 1 000 000
log10 0.0001 = – 4 because 10– 4 = 1/104 = 0.0001
The exponent to which base a must be raised to get P (a > 0 and a ≠ 1) is called base a logarithm of a number P > 0. We write it as log a P.
log a P = x ⇔ a x = P
Properties of logarithms
1. Two simple logarithms
log a a = 1 log a 1 = 0
The logarithm of the base is 1. The logarithm of 1 is 0.
2. Product and quotient
log a (P · Q ) = log a P + log a Q log a Q P = log a P – log a Q
The logarithm of a product is the sum of the logarithms of the factors. The logarithm of a quotient is the difference between the logarithms of the dividend and the divisor. For
3. Power and root
log a P k = k log a
The logarithm of a power (P k or PP / n n 1 = ) is equal to the exponent multiplied by the logarithm of the base of the power.
4. Base change

If we know how to calculate base-a logarithms, we can use the formula above to calculate logarithms with any base, b.
Let’s check
48
log2 loglog log 2 84 84 2 –3 22 3 2 =+
example:
P log
log P n
1 n a =
a
P
For example: log5 () loglog log 125 125 2 1 125 2 1 5 2 1 3 2 3 / 5 12 55 3 == == =
log
b
a
b P = log log
P
a
2 84 2 22 · / / 3 12 32 3 == 22 // / 32 31 2196 –== + loglog loglog loglog 82 3 42 3 2 22 2 1 / / 22 3 2 3 2 23 22 12 == == == _ ` a b b b b b b → → 3 3 2 2 1 6 19 –+=
Logarithms are used to measure an earthquake’s intensity.
Decimal logarithms
Decimal logarithms are base-10 logarithms. For a long time, they were the most common logarithms. Therefore, we just write log, without the base.
For example, log 10 = 1, log 100 = 2, log 1 000 = 3, log 0.0001 = – 4.
And log 587 = 2. ... since 587 is greater than 100 but less than 1 000.
There is a specific button for these logarithms on calculators. But on modern calculators, you have to press the SHIFT button to access this function:
log 200 → s 200 = 2.301029996
Napierian logarithms
Remember the number e with its value: 2.71828… It is used to describe growth in plant or animal population, radioactive decay and catenaries.
Logarithms with base e are Napierian logarithms. They are written ln (in other words, loge x = ln x).
On calculators there is a button, , for accessing these logarithms.
At this level: log means decimal logarithm (base 10) and ln means Napierian logarithm (base e).
However, in more advanced mathematics books log is used to refer to Napierian logarithms, since at these levels this type of logarithm is used almost exclusively.
Problem solved
1 Give the value of these logarithms, putting the numbers in the form of powers:
a) log6 1 296
b) log2 0.125
2 Using a calculator, find log 5, log 50, log 500 and log 5 000. All of them have the same decimal part. Why?
Let’s practise!
a) 1 296 = 64. Therefore, log6 1 296 = 4.
b) 0.125 = 1 000 125 8 1 2 1 3 == = 2–3
Therefore, log2 0.125 = –3.
log 5 = 0.69897… log 50 = 1.69897…
log 500 = 2.69897… log 5 000 = 3.69897…
T hey have the same decimal part because all of them are the following type: log10 (5 · 10n) = log10 5 + n log10 10 = n + log10 5 log10 5 is the decimal part of all of them, with an integer, n, added in each case.
1 Use the definition above to find these logarithms:
a) log5 125 b) log5 0.04 c) log2 128
d) log2 0.0625 e) log a 1 f ) log10 0.0001
g) log2 / 12 `j h) log3 (1/3) i) log3 9 5
2 Work out the base of the following logarithms:
a) log a 10 000 = 2 b) log b 216 = 3
c) log c 125 = 3 d) log d 3 = 2 1
3 Use your calculator to find log 7 and log 70. Explain why both have the same decimal part.
49
7 Logarithms
A bit of history
Before calculators appeared, logarithms were invented to simplify difficult operations people did by hand.
People converted products and quotients into additions and subtractions because they are easy to work with. They used enormous tables inside thick books with the exact or approximate values of the decimal logarithms of the factors.
Napierian logarithms were the instrument used to obtain the values of decimal logarithms, the ones needed in practice. They were called:
decimal logarithms
natural logarithms
common logarithms
Napierian logarithms
Nowadays, we have logarithms for cultural reasons and because we find them in algebraic simplifications (for example, for solving some types of equations) and functional expressions in the world of science and technology.
Logarithms on a calculator
The calculators we use today have three keys for calculating logarithms: , j and . The first are easy to find, but the third is more complicated. It is the second function of the button, so to use it, we have to press s
To find a logarithm with a base other than 10 or e, newer calculators also include the j button. However, sometimes it may be preferable to use property 4, base change (introduced on page 48), rather than this button. To do this, it is better to use the ln key, since that way you do not need to use the shift button. Let’s look at an example of the two ways of doing it:
• log 5 2 → jí 2 ”” 5 = 4.64385619
• log 5 2 = ln ln 2 5 → l 5 ) /lí 2 = 4.64385619
Problem solved
Use a calculator to find the following logarithms both ways: using the j key and by changing the base.
log2 1 024
log5 300
The importance of decimal logarithms
Look at these two numbers:
A = 6 748 B = 67.48 = A/100 log B = log (A/100) = = log A – log 100 = = log A – 2
This means that both logarithms have the same decimal part.
In logarithm tables we used to look for the decimal part of the logarithm of 6 748 and then add the integer part as appropriate, depending on whether it was 6 748; 67.48 or 67 480 000.

4 Use the j and keys of your calculator to calculate these logarithms using both methods above:
50
a) log
b) log3 100 c) log5 0.533 d) log8 0.004 e) log 3 350
2 740
a)
b)
a) log2 1 024 → j 2 ” 1 024 = 10 log2 1 024 = ln ln 2 1 024 → l 1 024 ) /l 2 = 10 b) log5 300 → j 5 ” 300 = 3.543959311 log5 300 = ln ln 5 300 → l 300 ) /l 5 = 3.543959311
My visual summary
Irrational numbers
Rational number:
It can be expressed as the quotient of two integers. Its decimal expression is terminating or recurring.
The
Irrational number:
It cannot be expressed as a quotient of two integers. Its decimal expression is infinite and non-recurring.
Some irrational numbers
The number π
p n is irrational if p is not an exact nth power. e = 2.7182…
Intervals
The number e
Real numbers
Representing fractional numbers
integers fractional irrational
Representing radicals rational Q integers Z
Approximate representation of real numbers
51
golden number
π = 3.1415… 2 51 2 5 2 1 U = + =+ = 1.6180…
natural
Á negative
N real
3 0 1 1 2 10 5 3 2 32 1 2 2 =+ `j 10 =+3122 5 14 = 2 + 5 4 0 4 2 + 5 1 2 3 0 1 2 3 3.8 4 3.9 3.8 3.84 3.85 3.9 3.84 3.85 3.846 3.847 842 5 = 3.8464…
Half-open interval Closed interval (a, b) = {x / a < x < b} a b [a, b] = {x / a ≤ x ≤ b} a b (a, b] = {x / a < x ≤ b} a b [a, b) = {x / a ≤ x < b} a b (– ∞ , a) = {x / x < a} a (– ∞ , a] = {x / x ≤ a} a (a, +∞) = {x / x > a} a [a, +∞) = {x / x ≥ a} a
Half-lines Open interval
Roots and radicals
Exponential form
Operations with radicals
Rationalising the denominator
1
2
Approximations and errors
= Real value
Scientific notation
Integer part (a single figure, not zero)
Decimal part Properties
Logarithms
52
a. b c d... . 10n
of base 10
Power
(with integer exponent)
aa p np n = ab ab · n n n = b a b a n n n = aa n p p n = ` j aa n m mn · = a n = a n 1 a m n = a n m a = bn a= b n Radicand Index 1 2 3 4 5
Square
roots
3 Addition and subtraction of roots 3 2 3 23 3 23 3 == 7 1 77 17 7 7 7 7 · 2 5 2 5 3 5 3 5 5 5 3 5 3 5 == = ( ·( ( )· () ) )( ) 5 1 5 15 5 5 2 5 33 53 3 3 33 –22 == = + + ++ ( ·( ( )· () ) ) 32 2 32 23 2 32 62 2 92 62 2 7 62 2 32 –––––22 + = + == = (3.25 · 105) · (4.6 · 1011) = (3.25 · 4.6) · 1016 (3.25 · 105) : (4.6 · 1011) = (3.25 : 4.6) · 10–6 ×÷ 3.7 · 1011 + 5.83 · 108 – 4 · 109 = = 3 700 · 108 + 5.83 · 108 – 40 · 108 = 3 665.83 · 108 = 3.66583 · 1011 +log a 1 = 0 log a a = 1 log a (P · Q ) = log a P + log a Q log a Q P = log a P – log a Q log a P k = k log a P log a log P n P 1 n a = log b P = log log b P a a log a P = x a x = P
Other roots
Absolute error = |Real value – Approximate value|
Absolute error
Relative error
Exercises and problems solved
1. Intervals
Write in interval form the numbers that verify the following inequalities:
a) ≤ x 5 ;; b) x 24 < ;; +
c) How would you write the opposite inequality of the one in a)?
Your turn Express as intervals:
a) ≤ x 31 –;; b) x 23 > ;; +
2. Radicals
Prove that the number – 12 211 –122 11 + is an integer.
Your turn Simplify. 23 3 36 22 + +
3. Logarithms
Find the value of x in each case:
a) 3 = 5 + log x
b) logx 36 = 2
c) log x + 2log 5 = 2
a) If x 5 ;; = → x 5 = or x –5 = Then: ≤ x 5 ;; → ≤ x –≤55 → [, ] x –55 !
b) If x 24;;+= → x +=24 or x 24 – += → x 2 = or x –6 =
Therefore: x 24 < ;; + → x –<62 < → () , x –62 !
c) The inverse inequality of a) is x 5 > ;; . It is expressed as a union of intervals.
x 5 > ;; → x x 5 5 – < > ) → → (–∞, –5) (5, +∞) → x ∈ (–∞, –5) ∪ (5, +∞)
We write A =
211122 11 + and we square both sides.
== = → Therefore, if A2 = 4, then A = ±2
–
Since 12 211122 11 – > + , we rule out the negative solution → A = 2
We apply the definition of a logarithm in each case:
a) 3 – 5 = log x → x = 10–2
b) x 2 = 36 → x = 6 (x = – 6 does not work)
c) We apply the properties of logarithms:
x
log 52 = 2 → log (x · 52) = 2 → 25x
Your turn Calculate x in each case:
a)
4. Interest, errors and logarithms
A woman invests 2 · 106 at 3.6 % annual interest. When she withdraws it, it is approximately €2.43 · 106.
a) Give a limit of absolute and relative error for this approximation.
b) How long was it in the bank?
It was in the bank for 5 and a half years.
(*) We take logarithms from both sides to clear n.
Your turn I deposit €5 000
bank at 3.53
a year. In how long will I have double the amount?
53
102
x = 4
log
+
=
→
= 2 1 b) 2log x – log 4 = –2
log3 x
a) A.e. € 0 005 10 510 .· < 63 = Re.. :. .. 5102 43 10 0 0021 021 · ·% < 36 == b) We know that CC r 1 100 n FINAL =+bl → . . 243102 10 1 100 ·· 36 n 66=+dn → → .( .) 2432 1 036 n = → . 1.215 1 036 n = → (*) → (*) ln 1.215 = n ln 1.036 → n = ln 1.215 : ln 1.036 = 5.5
in a
%
A 12 211122 11 12 211122 11 22 2 2 =+ =+ + `` ` jj j 2122 11 12 211122 11 12 2112 12 411 – · · 2 += ++ `j = 24 2 100 24 20
12
4
–
Exercises and problems
DO YOU KNOW THE BASICS?
Number sets
1 Look at the following numbers.
23// 3567 17 18 26 16 18 ;; ;; ;; !
a) Which are integers?
b) Are there any natural numbers?
c) Are there any irrational numbers?
2 a) Classify as rational or irrational numbers.
;; ;; ;; . π e 2 3 08 74 3 7 2 1 2 3 !
b) Put them in order from smallest to biggest.
c) Which are real numbers?
3 Find an integer, a non-integer rational number and an irrational number between 29 – and 8 –
4 Indicate which of the sets (N, Z, Q or Á) these numbers belong to:
. π 7 4 6 13 52 152 2 13 –; ;; ;; ; + !
Intervals and half-lines
5 Represent each of the following intervals and halflines on the real number line.
A = [–2, 4] B = (1, 6) C = [–7, –3)
D = (0, 5] E = (– ∞, 1] F = (–1, +∞)
6 Write the following sets of numbers in interval or half-line form.
a) Greater than 2 and less than 7.
b) Between –1 and 3, both included.
c) Greater than or equal to 5.
d) Less than 10.
7 Show each of the following as an interval or halfline on the real number line.
a) –3 ≤ x ≤ 2 b) 5 < x c) x ≥ –2
d) –2 ≤ x < 3/2 e) 4 < x < 4.1 f ) –3 ≤ x
8 Express each of the following sets of numbers as an interval or half-line and as an inequality:
a) –1 0 3 b) 1 5
c) –2 0 d) 0 4
Powers, roots and radicals
9 Calculate the value of these expressions.
a) 25 / 52 b) () –343 / 43 c) 81 –025 d) 8 6 8
10 Express in exponential form.
a) x 2 5 b) 2 c) 10 6 3 d) 20 2 4
e) () –3 3 5 f ) a 4 g) x 2 5 3 – ` j h) a 5 15
11 Write as roots.
a) 51/2 b) (–3)2/3 c) 3 4 / 13cm
d) (a 3)1/4 e) (a 1/2)1/3 f ) (a –1)3/5
12 Express each of these numbers as a power with the base 2 and then find their product.
a) 16 / 32 3 –`j b) 4 6 c) 2 1 –3eo
13 Express the following radicals as powers with fractional exponents and simplify.
a) · aa 2 5 b) x x 2 3 c) a 1 3 4
14 Simplify.
a) 3 2 4 b) a 8 12 c) a 15 5
d) ab24 8 e) a 8 4 3 f ) ab69 3
Approximate numbers. Scientific notation
15 Find the absolute and relative errors in these approximations.
a) 3 41 to two decimal places
b) 72 to one decimal place
c) 17 123 to the hundredths
16 Give a limit of absolute error and of relative error for these approximations of the number of votes in an election:
a) 348 thousand votes b) 5 632 000
c) 890 000 d) 78 945
e) 9 million f ) 134 thousand
17 Calculate mentally.
a) (1.5 · 107) · (2 · 105) b) (3 · 106) : (2 · 1011)
c) (4 · 10–7) : (2 · 10–12) d) 410 8
54
18 Use scientific notations to do these calculations and give a limit of the absolute error.
a) (3.5 · 107) · (4 · 108) b) (5 · 10–8) · (2.5 · 105)
c) (1.2 · 107) : (5 · 10–6) d) (6 · 10–7)2
Logarithms
19 Apply the definition of logarithm and calculate.
a) log2 64 b) log2 16 c) log2 4 1
d) log2 2 e) log3 243 f ) log3 27 1
g) log3 9 3 h) log 0.001 i) log5 0.2
20 Calculate the base of the following logarithms.
a) logb 64 = 3 b) logb 100 = 2
c) logb 243 = 5 d) logb 625 = 4
21 Use a calculator.
a) log4 23.4 b) log3 543 c) log5 0.06
d) log6 20.8 e) log5 123 f ) log2 0.872
TRAINING AND PRACTICE
22 Place the following numbers on a diagram like this one:
1; . 723 # ; 1 – 2 ; 3.5; 9 11 ; 4 1 ; 6 ; π 4 ; –104
23
a) Which irrational numbers correspond to points A, B, C and D ?
1 2
b) Represent 8 and 11
24
a) Indicate which of the following numbers are included in A = [–3, 7) or in B = (5, +∞):
–3; 10; 0.5; 7; – 4; 5 ; . 63 ! ; π; 5 27 ; 48 ; 1 – 2
b) Which of these intervals represents the numbers included in A and in B ?
(–3, 5) [2, 7) [5, 7] (5, 7)
c) Express A ∪ B and A ∩ B as intervals and as inequalities.
25 Express each of the sets of numbers below as a union of intervals, using the symbol ∪.
–4 0 b) 0 3
3 6 d) –1 0
26 Simplify.
a 15 5 b) a 9 3 c) ab 6 42 d) a 3 4 8
27 Express as powers and calculate x in each case, equalling the exponents of the two sides:
a) 3 27 1 x 1 = + b) () 81 3 1 x–= c) 4 22 2 x 3 =
28 Multiply and simplify.
29 Take out all possible factors from the radical.
30 Reduce to a common index and express the results with a single radical.
a) · 42 3 b) : 20 10 4 6 c) 23·: 23 3 3 ``jj
31 Introduce inside the root and simplify.
32 Solve.
33 Solve.
52 35 23 –+ ``jj b) 25 3 –2 ` j
32 43 24 2 + ` j d) 32 58 2 + ` j
34 Simplify.
35 Rationalise and simplify if possible.
55
3 0 1 D C B A
a)
c)
a)
a)
aa a
236 b) aa a 4 3 4 c)
13 3 5 6
a)
a
d) a
a16 3 3 b) ab81 53 4 c)
8 5
24 4 3 e) 75 162 f ) 32 9 5
a) 5 5 3 b) 2 4 7 3 c) 2 12 5 4 d) 3 2 4 9 3
a)
63 b) / 96 32 3
+ c) 2 81 375 3 72 –3 3 3 3 + d) 64 7 4 7 7 4 ++
3287
55
a)
c)
a)
5
4
18 281 4 3 b) () a aa 2 84
4 2 2 3 c) a aa
22 3 4 2 3
a)
d) 5
26
3 3 b) 2 23 3 c) 10 22 +
2 3 e)
3 2 3 f ) 2 81 5
Exercises and problems
36 Rationalise and simplify if possible.
a) 13 3 + b) 12 12 –+ c)
3 + e)
37 State which of these blood test results are outside the reference ranges: Results Reference ranges Units
White
Red blood cells 5.87 (4.3-5.9)
Platelets 1.9 (1.50-4.50) × 105 µL
Creatinine 0.68 (0.7-1.3) × 105 mg/dL
38 Calculate by applying the definition of logarithm. log4 163 + log4 2 + log 0.0001 + log 100 10 3
39 If log x = 1.3 and log y = 0.8, calculate:
a) log (x · y) b) log () xy c) log x y 2 d) log y x
40 Transform the expression A z xy 3 42 –= by taking logarithms and applying their properties, like in the example:
43 Express each of the following intervals as neighbourhoods of the type N(M, r).
a) (–3, 3) b) (2, 4) c) (0, 6) d) (–1, 4)
e) (–3, 2) f) (0; 7.5) g) (–5; –2.2) h) (1.2; 4.7)
44 Express M without logarithms in each case.
(Remember that if log M = log k, then M = k).
a) () loglog log Mx x 32 –=+
b) () loglog loglog Mx y 13 – =+ +
c) () ln ln ln ln Mx yx22 3 – =+ +
45 A cuboid measures 81827 ## in centimetres. Calculate.
a) The total area. Use radicals to express the exact result.
b) The length of the diagonal. Express this measurement using radicals and rounding to one decimal.
c) Calculate the absolute error and relative error in b) above.
46 In an isosceles triangle the unequal side measures 53 cm and the height corresponding to that side is one quarter of it. Calculate the perimeter of the triangle. Use radicals to express the result.
THINK A LITTLE MORE
47 Take Action. The diameter of the Milky Way is 105 700 light years, and a light year is 9.461 · 1012 km.
Do the same for the following expressions:
a) xy M 10 3 2 = b) N xy z 23 = c) P y x 2 3 =
SOLVE SIMPLE PROBLEMS
41 Which values of x can you use to calculate these roots?
a) x 7 – b) x 5– c) x– d) x 1 2 +
42 The open interval with midpoint is M and endpoints M – r and M + r is called a neighbourhood with midpoint M and radius r, and it is represented by N(M, r).
For example: N(0, 2) = (–2, 2) and N(2, 3) = (–1, 5) Express the following neighbourhoods as intervals:
a) N(0, 1) b) N(0, 3) c) N(3, 5) d) N(–2; 1.5)
e) N(–3; 0.3) f) N(2.1; 3) g) E(–0.2; 5.3)
a) What is the diameter of our galaxy in kilometres?
b) How many millenia would it take for a spacecraft to cross it travelling at 2 000 km/s?
c) The diameter of an electron is 4 · 10–15 m. How many electrons would it take to form a line all the way around the Milky Way? (Assume it is a circumference).
48 Calculate the height of a regular tetrahedron with 8 cm edges. Use radicals to express the results. h h/3 2h/3

49 Calculate the volume of a regular octahedron with edges measuring 6 cm. Use radicals to express the results. h 6 6 2 2
56
a 2 4 32 4
5 5
–+
a a 1 + d) 22 11
ab
f )
3 3
blood cells 3.16 (3.5-11) × 103 µL
× 106 µL
A z xy 3 42
= → ln ln A z xy 3 42 –= = ln ln ln xy z –42 3 –+
=
•
–
=
ln ln ln xy z 42 3 1
50 Prove that the ratio between the areas of these two hexagons is 4/3. (Remember, you can divide each hexagon into 6 equilateral triangles).
51 Write in interval form the numbers that verify the following inequalities:
a) | x | < 3 b) | x – 1| ≤ 5 c) | x + 3| < 4
How would you express the numbers that verify the inequalities opposite to the previous ones?
| x | ≥ 3 | x – 1| > 5 | x + 3| ≥ 4
52 Calculate as a fraction.
1 1 1 2 1 1 1 + + +
a) Substitute 2 for 1 + 1/2 and re-calculate. Repeat this process again.
b) Check that the numerators and denominators of the results are terms in the Fibonacci sequence.
c) What is the approximate value of the quotients obtained?
53 a) Express the terms of the following sequence as a power.
aa
a 13 13 13 13 13 13 12;; 3 == =
b) Check that the exponents are the sum of the terms of a geometric progression with the ratio 1/2.
c) What is the approximate value of this sequence?
54 I deposit a sum of money in a bank at 3 % annual interest rate. In how many years will I have triple the amount?
YOU CAN ALSO DO THIS
55 Check that it is not possible to use a calculator to obtain 5129 · 463 because the number is too large. Use the properties of powers to express it in scientific notation.
56 Calculate the value of x in these expressions.
a) loglog x 2237 =+ b) 75 63 x =+
57 We have taken a 2 cm square and constructed a rectangle, ABFE. Is it a golden rectangle? Check that the quotient between the sides is the golden number Φ
58 The equation for the golden number is:
Φ2 – Φ – 1 = 0 Use it to check the following equalities:
a) Φ2 = Φ + 1
c) Φ3 = 2Φ + 1
b) Φ – 1 = 1 U
d) Φ4 = 3Φ + 2
DO YOU UNDERSTAND IT? THINK
59 True or false? Explain your answers and give examples.
a) Some irrational numbers are not real.
b) There are an infinite number of irrational numbers between two rational numbers.
c) The inverse of a recurring decimal number can be a terminating decimal.
d) The number 0.83 · 109 is not expressed in scientific notation.
60 If ≥ loglogab 2 –33 , what is the relationship between a and b?
61 Look at this way of representing m on the real number line. Explain it. m
m m 0 1
62 If x is a number of the interval [–1, 3) and y is a number of the interval (0, 4], explain in which interval you might find x + y. And x – y ?
63 Are these equalities true or false? Why?
a) log (a · b) = log a · log b
b) log b a bl = log a – log b
c) loglogaa 3 1 3 =
d) log (a 2 · b ) = 2(log a + log b )
57
A B E F D C 2 cm

1 a) Classify the following numbers into natural numbers, integers, rational numbers and real numbers:
3 4 6 – ; 2π; log 05 2 ; 347 # ; 2.03333…; 81 ; 4 3 ; 3 5 ; – 9 13 ; – 8
b) Which are irrational?
c) Put them in order from smallest to largest.
2 Which numbers correspond to A, B, C and D?
2
3 This table shows the population and annual GDP in millions of Euros of four EU countries.
Spain
Estonia
Finland
France 67 842 582
a) Express them in scientific notation and calculate the GDP per capita for each country. Give a limit of absolute and relative error in each case.
b) What is the percentage of GDP in Estonia compared to Spain, Finland and France?
4 a) Write the following number sets in interval form and represent them on a number line:
i) ≤ x –<27 ii) x –1 > iii) | x | < 4
b) Write the following intervals as inequalities:
A = [–3, 4) B = (–∞ , 3 )
c) Express A ∪ B and A ∩ B as intervals and as inequalities.
5 Express in exponential form:
a) 5 6 3 b) 7 2 4 c) 6 d) a 1 4 – e) () –3 5 3
6 Take out all the possible factors from the radical. z ab 16 81 4 25 3

7 Calculate and simplify.
8 Apply the definition of logarithm, or use a calculator, to calculate.
9 Find the value of x in each case.
a) logx 73 – 2 =
b) log 20 2 x =
c) loglog x 51 +=
10 Calculate the area of the annulus between the inscribed and circumscribed circumferences in a 6 m2 square. Give the exact value.
11 We cut a right-angled isosceles triangle from each corner of a square with 10 cm sides to obtain a regular octagon.
a) Find the exact measurement of the side of the octagon.
b) Calculate its area.
c) Calculate its radius.
12 Take Action. LightSail2 was a satellite with a small solar sail. It went into orbit in 2019 and successfully demonstrated its mission of sailing on sunlight alone. In one month of navigation, it reached a speed of 549 km/h.
a) How many kilometres would it travel in one year at that speed?
b) How many years would it take to travel one light year?
c) In the future, this speed could increase to 6 ∙ 104 km/s. How long will it take to travel one light year, then? Express the results in scientific notation. x x l l
Answer key.
THE ESCAPE ROOM
TEST YOURSELF! 58
Self-assessment anayaeducacion.es
GO TO
AND
1 0
1 2 A D B C 3
Countries Populations Annual GDP
1
M
47 432 805
206 842
1
331 796 31 445 M
5
548 241 251 367 M
2
500 870 M
a) () 3 32 3 2 + b) 54 26 150 –+ c) 50 5 2 2 – d) 23 10 2 –
1 3 b) log
32 1 2 4
a) log3 9
2
cm
Do the maths and compare the data to make it easier to understand
To write a scientific article, we need to look up information, collect data, check it, look for reliable references to compare them and do calculations.
Find some data and do some calculations:
• We say that Alpha Centauri is 4.37 light years from the Sun. Give a value for the absolute error, in kilometres, of this measurement and another value for the relative error.
• The distance from the Earth to the Sun is 1.5 · 108 km. Is there any difference between the distance from Alpha Centauri to the Sun or to the Earth considering the absolute error calculated above?
• Solar sails have reached accelerations of 1 mm/s2. With this acceleration, how much does the speed (in km/h) increase over one day? Write the solution to one significant figure.
• The fastest probe, powered by engines, reached 22.88 km/s. How many days does the solar sail above need to reach this speed?
• One of the solar sails was 7.5 microns thick. An average human hair is 0.07 mm thick. Compare the size of the two. (1 micron = 0.001 mm)
• The space-time equation for uniformly accelerated motion, if the initial velocity is 0, is as follows:
s = a 2 . t2
How many years would it take the spacecraft to travel the distance to Alpha Centauri with a constant acceleration of 1 mm/s2? Is it enough to get there in 20 years? The distance is 4.37 light years.
• What constant acceleration would it need to reach Alpha Centauri in 20 years?
• What mistake are we making when we say that the speed of light is 300 000 km/s if it is in fact 299 792 458 m/s?
Now, it's your turn...
• Look up information about past, present and future solar sail projects. Which ones have been successful? Are there any new ones that you would like to see in the future?
• Look up information about how origami is used to fold and unfold the solar sails.


• Using all this data and any other facts that you discover in your research, write an article to share the importance of the results you obtained.
59
LEA RNING EXPERIENCE I TAKE ACTION
Maths in context Apply languageyourskills www.anayaeducacion.es
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior permission of the publishers.
© GRUPO ANAYA, S.A., 2024 - C/ Valentín Beato, 21 - 28037 Madrid.




















