DAUKA Munduahelburu
hiruhilekoa
LEHEN HEZKUNTZA 6 12HILEKO LIZENTZIA PROIEKTU DIGITALA
Lehen
Matematika

1 5 9
2 6 10
3 7 11
4 8 12
Zenbakiak eta eragiketak Zaindu bizia
Multiploak eta zatitzaileak
Besarkatu bakea
Berreketak Konektatuta
Zenbaki dezimaldunak eta eragiketak Kontsumitu arduraz
DIZIPLINARTEKOA
IKASKUNTZA-EGOERA HELBURUA AURRERA GJH
Zergatik da beharrezkoa zuhaitzak zaintzea?
Egin biziaren zuhaitz bat, natura zaintzearen aldeko mezu eta guzti.
Lehorreko bizitza
Zatikiak eta eragiketak Elkarrekin hobeto
Sistema metriko hamartarra Zientzialari izan nahi?
Ehunekoa eta proportzionaltasuna Antolatu zure aisialdia
Angeluak eta angeluen neurria Marraztu, zaintzeko
Poligonoak Aldeen garrantzia
Irudi zirkularrak Ni, zu, gu... Denok berritzaile
Gorputz geometrikoak Itsasoa zaintzeak saria du
Zoria eta probabilitatea Etorkizuna iragartzea
Zergatik da garrantzitsua bakea lortzearen alde jardutea?
Eraiki bakea besarkadekin: diseinatu kanpaina bat, 8 segundoko besarkadak sustatzeko.
Zergatik da garrantzitsua denok izatea eskura Internet?
Diseinatu kamiseta bat, informazioa izateko eskubidea denok izan behar dugula aldarrikatzeko.
Zer esan diezaiekegu ikaskideei arduraz kontsumitzea gomendatzeko?
Eztabaidatu dezagun ea paga eman behar den edo ez eta zer egin behar den paga arduraz erabiltzeko.
1. HIRUHILEKOAREN BERRIKUSPENA STEAM: Sophie Germain










Nola egin dezakegu bat gure artean, elkartuta aritzeko?
Sortu ELKARTU!, jendeak helburu berberen alde bat eginda jarduteko gunea.
Nola eman dezakegu jakitera denok ez ditugula ikasteko aukera berberak? Egin dezagun literatura-lehiaketa bat, izenburu hau duena: Zientzialari izan nahi dut
Zer gertatuko da zure adineko jendeak aisialdi guztia gailu teknologikoak erabiltzen ematen badu? Prestatu teknologiarekin zerikusirik ez duen aisialdi-plan alternatibo bat zure adineko neska-mutilentzat.
Nola kontzientziatu dezakegu jendea ura zaindu beharraz?
Marraztu logo bat, ura zaintzea sustatzeko.


2. HIRUHILEKOAREN BERRIKUSPENA STEAM: Grace Hooper
Zer beste emakumek egin dituzte ekarpen garrantzitsuak matematikaren esparruan?
Adierazi denbora-lerro batean emakume matematikarien datu pertsonalak eta ekarpenak.
Nola treba dezakegu sormena gaur egungo arazoei erantzun berritzaileak emateko?
Neurtu zure sormena!
Zer egin dezakegu gure itsasoak zaintzeko?
Egin trofeo bat irudi geometrikoekin, itsasoa zaintzearekin lotutako jardunbide onak saritzeko.
Zer egin dezakegu klima-aldaketa geldiarazteko?
Egin infografia bat, klima-aldaketa geldiarazteko zenbait gomendio emateko.
3. HIRUHILEKOAREN BERRIKUSPENA STEAM: Clara Grima
Bakea, justizia eta erakunde sendoak
Industria, berrikuntza eta azpiegitura
Ekoizpen eta kontsumo arduratsua
Itunak, helburuak garatzeko
Kalitate oneko hezkuntza
Osasuna eta ongizatea
Edateko ura eta saneamendua
Generoberdintasuna
Industria, berrikuntza eta azpiegitura
Uretako bizitza
Klima babesteko ekintza
8 80 152 24 100 168 42 116 184 56 132 202 OR. Zer ikasiko dugu?
OINARRIZKO JAKINTZAK EBATZI BAIETZ!
• Zenbaki-sistema hamartarra. Zenbatzeko teknikak.
• Oinarrizko eragiketak zenbaki arruntekin. Propietateak.
• Eragiketa konbinatuak.
• Zenbaki baten multiploak. Multiplo komun txikiena.
• Zenbaki baten zatitzaileak. Zatitzaile komun handiena.
• Zenbaki arrunt baten berreketa.
• Karratuak eta kuboak.
• Erro karratua.
• Hamarrenak, ehunenak eta milarenak. Zenbaki dezimaldunak: irakurtzea, idaztea eta posizio-balioa. Prezioak.
• Zenbaki dezimaldunak konparatzea eta ordenatzea.
• Zenbaki positiboak eta zenbaki negatiboak.
• Konparatzea eta ordenatzea.
• Koordenatu kartesiarrak.
• Problema aritmetikoak: aldaketa-, berdinketaeta konparazio-problemak.
• Zatigarritasun-irizpideak.
• Zenbaki lehenak eta zenbaki konposatuak.
• 10 oinarriko berreketak.
• Deskonposizio polinomikoa.
• Zenbaki dezimaldunak biribiltzea. Zenbaki dezimaldunen arteko batuketak, kenketak, biderketak eta zatiketak.
• Problema aritmetikoak: konparazio-, banaketa- eta multzokatze-problemak, eta multzo berdinak
• Estrategia heuristikoa: Deszifratu kodeak.
• Buruzko kalkulua: 4z biderkatzea.
• Pentsamendu konputazionala: Deskonposizioa.
• Estrategia heuristikoa: Bilatu erantzun posible guztiak.
• Buruzko kalkulua: 20z biderkatzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Bilatu erregulartasunak.
• Buruzko kalkulua: 50ez biderkatzea.
• Pentsamendu konputazionala: Kodetzea.
• Estrategia heuristikoa: Kalkulatu soluzioa iritzira.
• Buruzko kalkulua: 4z zatitzea.
• Pentsamendu konputazionala: Deskonposizioa.
DIZIPLINARTEKO PROIEKTUA · Kutxa magikoa eta haren zaintza: Kutxa logikoa
• Zatikiak. Zatikia eta unitatea. Zatiki propioak eta inpropioak.
• Kopuru baten zatikia.
• Zatiki baliokideak. Zatiki laburtezina.
• Zatikiak konparatzea.
• Luzera, edukiera, masa, azalera eta bolumena adierazteko neurri-unitateak.
• Unitate-aldaketak.
• Magnitude proportzionalak.
• Unitatera laburtzea. Hiruko erregela.
• Ehunekoak. Kopuru baten ehunekoa.
• Angeluen sailkapena, zabaleraren eta kokapenaren arabera.
• Angeluak neurtzea: graduak, minutuak eta segundoak.
• Zatikien arteko batuketak, kenketak, biderketak eta zatiketak.
• Problema aritmetikoak: konbinazio-, aldaketaeta multzokatze-problemak, biderketazko konparaziokoak eta multzo berdinak egitekoak.
• Adierazpen sinpleak eta adierazpen konplexuak.
• Problema aritmetikoak: konbinazio-, aldaketaeta multzokatze-problemak.
Igoerak eta beherapenak.
• Eskala: grafikoa eta zenbakizkoa.
• Estrategia heuristikoa: Egin tarteko galderak.
• Buruzko kalkulua: 20z zatitzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Bilatu erregulartasunak.
• Buruzko kalkulua: Zatiki batez biderkatzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Egin eskema bat.
• Buruzko kalkulua: Kopuru baten 1 4
• Pentsamendu konputazionala: Funtzioak.
• Estrategia heuristikoa: Egin marrazki bat.
• Angeluen arteko batuketak eta kenketak.
• Problema aritmetikoak: berdinketa-problemak.
• Buruzko kalkulua: Kopuru baten % 10.
• Pentsamendu konputazionala: Algoritmoa.
DIZIPLINARTEKO PROIEKTUA · Orain edo inoiz ez: Zer aztarna uzten duzu?
• Poligonoak: elementuak eta sailkapena.
• Poligono ahurrak eta poligono ganbilak.
• Poligonoen perimetroa.
• Zirkunferentzia. Zirkulua eta irudi zirkularrak.
• Puntuen, zuzenen eta zirkunferentzien posizio erlatiboa.
• Poliedroak eta gorputz biribilak.
• Poliedro erregularrak. Biraketa-gorputzak.
• Zorizko esperimentuak. Gertaera ziurra, posiblea eta ezinezkoa.
• Paralelogramoen eta triangeluen azalera.
• Poligono erregularren azalera.
• Irudi konposatuen azalera.
• π zenbakia. Zirkunferentziaren luzera.
• Zirkuluaren azalera.
• Prismen azalera eta bolumena.
• Piramideen azalera eta bolumena. Irudi konposatuen azalera eta bolumena.
• Gertaera baten probabilitatea. Laplaceren erregela.
• Zenbatzeko teknikak.
• Estrategia heuristikoa: Hasi egoera errazagoetatik.
• Buruzko kalkulua: Kopuru baten % 50.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Egin marrazki bat.
• Buruzko kalkulua: Kopuru baten % 20.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Baztertu erantzun ezinezkoak.
• Buruzko kalkulua: 0,1ez biderkatzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Aztertu datu-lagin bat.
• Buruzko kalkulua: 0,5ez biderkatzea.
• Pentsamendu konputazionala: Datuak.
DIZIPLINARTEKO PROIEKTUA · Birika berdea: Iraul ditzagun datuak
Zertarako balio du nik ikasitakoak?


Unitate bakoitzean ikaskuntza-egoera bat eta unitatearen amaierarako helburu bat proposatzen dira.

Jarraitu hariari!



Lantzen ditugun gaitasunak
Jarduera motibagarriak egiten ikasteko...
Ebatz i baietz! Graduak, minutuak eta segundoak 3 Angeluen arteko
5 Angeluen arteko batuketak 4 Honelakoa da zure liburua
kenketak
lantzekoKonpetentziakariketak
Gogoan hartu
Eta hiruhileko bakoitzean...
Hiruhilekoaren berrikuspena, ariketa ludikoen eta STEAM txokoaren bidez.



Informazioa ondo zabaldu behar dugu, ikastetxearen aztarna ekologikoa zein
proiektua, ezagutza-arlo desberdinak helburu komun batekin barneratzeko.

Z er ikasi dut?
zure etxeak? Zalantzak argitzeko, ikertu!
1 Neurtu angelu hauek garraiagailuarekin, eta sailkatu zabaleraren arabera:

Ikertu ea zer parametrok duten eragina aztarna ekologikoan. Horri buruzko informazio aurkituko duzu. Aukeratu zuri baliagarri gertatuko zaizuna aztarna ekologikoari buruz egin behar duzuen gidarako datuak biltzeko, kalkulatzeko eta lantzeko. Aztarna ekologikoaren kalkulagailuak ere aurkituko dituzu; erabili, laguntza gisa. Karbono-aztarna ere aipatzen da. Zer lotura du aztarna ekologikoarekin?
Egin aztarna ekologikoa zer den eta horretan zer parametrok eragiten duten jendeari jakinarazteko gida. Informazio guztia taldeen artean banatzen baduzue, eraginkorragoak izango zarete. Garrantzitsua da ikastetxeko gainerako ikasleek informazioa ulertzea, eta beste sektoreek ulertzea ere bai. Beraz, berrikusi ondo zirriborroa, eta, informazioarekin batera, Zertan lagundu dit matematikak?
6 Adierazi segundotan, eta ordenatu txikienetik handienera.
Ebatzi baietz!

7 Adierazi gradu, minutu eta segundotan.
a) 21 889'' b) 10 862''





2 Marraztu angelu hauek:
= 50°
3 Garraiagailua erabili gabe, kalkulatu eta idatzi zer neurri duten B eta
4 Ikusi arretaz eta erantzun.
a) Nolakoak dira kokapena kontuan hartuta?
2 1
horietako batek 180





9 Pentsatu eta ebatzi.
?
8 Zer neurri du hirugarren angeluak? 40° 68°
















a) Danel eta Eguzki pizza jaten ari dira. Danelen zatiak 86° 45' ditu, eta Eguzkirenak, 89° 10'. Zer neurri du platerean utzitako zatiak?

Geure buruari galdezka
Kolorea, ikurra, irudia (KII) estrategia erabiliz, hausnartu dezagun taldeka ura zaintzearen garrantziaz. Aukeratu hiru ideia, eta irudikatu ideia bakoitza kolore, ikur eta irudi baten bidez.
b) Haize-errota baten hegalek 160° 58'-ko bira egin dute. Zenbat gehiago biratu behar dira oraindik bira-erdia egiteko?
c) Joar eta Pello Baionan elkartzekoak dira. Joa-
Gero, sortu zuen hausnarketa laburbilduko duen logo bat, kontuan izanda jende guztia ura zaintzera animatzea dela helburua. Logoa sortzeko, erabili angeluak.
144 U8 EBATZI BAIETZ! Egin marrazki bat Pellok badaki triangelu baten bi angeluk 40 eta 60 dituztela eta bi angelu horiek partekatzen duten aldea 6 cm luze dela. Zer luzera dute beste bi aldeek? Aldeek zer luzera duten jakiteko, triangelua marraztuko dugu. B 60° Erregelarekin, marraztu 6 cm-ko zuzenki bat. Erpintzat A puntua hartuta, marraztu 40°-ko angelu bat. 130 140 160 40 60 140 150 A 130 140 50 60 40 120 140 6 cm A cm 60˚ 40˚ angelu bat. Bi angeluen aldeek elkar ebakitzen duten puntua triangeluaren hirugarren erpina da. Orain, soluzioa jakiteko, urrats bakarra falta zaizu: erregelarekin, neurtu triangeluaren aldeak. Beste bi aldeen luzerak 5,3 cm eta 3,9 cm dira. Soluzioak badu zentzurik? Egiaztatu edozein bi alderen luzeren batura beti handiagoa dela beste aldearen luzera baino. Triangelu isoszele baten oinarriak cm ditu, eta alde hori partekatzen duten angeluak 50°-koak dira. Zer luzera dute beste bi aldeek? Zer neurri du beste angeluak? 2 Lidek badaki triangelu baten bi aldek 6 cm eta 4 cm dituztela. Gainera, badaki bi alde horiek eratzen duten angeluak 55° dituela. Zer neurri du hirugarren aldeak? Eta beste bi angeluek? Problemak arin-arinka Esan osagarriak diren bi angelu eta betegarriak diren beste bi. Bi angelu auzokideak badira, izan ditzake horietako batek 180 2 1 Bi angelu osagarriak eta berdinak badira, zer neurri du bakoitzak? Bi angelu betegarriak badira, baina biak berdinak badira, izan daitezke biak zorrotzak? Eta biak kamutsak? Nolakoak dira? 4 3 Urratsez urrats Frogatu, paper zatitxoak erabiliz, esaldi hauek egia direla. Gero, idatzi nola egin behar den urratsez urrats. Deskargatu txantiloia, webgunean: anayaharitza.es Erpinez aurkakoak diren bi angeluk neurri bera dute. Triangeluen angeluen batura beti 180° da. Buruzko kalkulua Kalkulatu 40ren % 10. Orain, zuk zeuk: 30en % 10 50en % 10 70en % 10 80ren % 10 120ren % 10 130en % 10 140ren % 10 150en % 10 Ikusi nola egiten den, hemen: anayaharitza.es Sistema hirurogeitarrean angeluak neurtzen ditugu. Eta zer gehiago? Zenbat minutu dira gradu bat? Eta zenbat segundo? 5 40˚ 60˚ 5 cm 90 180° 1° Luzera? Masa? Denbora? 4444444444 % 100 :10 Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: ? ? ? Ikusi nola egin triangeluak, webgunean: anayaharitza.es Begira nola pentsatzen dudan 2. HIRUHILEKOA 150 151 Denon artean, hitz egin dezagun: Ezagunak zaizkizu aztarna ekologiko hitzak? Zer-nolako eragina du gure bizimoduak ingurunean? Irudikatzen duzuna baino handiagoa dela iruditzen zaizu? Badakizu nola neurtzen den? Animatzen zara kalkulatzen zer aztarna ekologiko duen gure ikastetxeak?
den sektore guztiek jakin dezaten, denek parte hartzeko. Horretarako, adibidez, ikastetxeko webguneaz baliatuta, zuen idatzia prentsaurreko batean aurkeztu dezakezue, eta bertara hezkuntza-komunitateko sektore guztietako ordezkariak gonbidatu. Tokiko ikus-entzunezko hedabideak aliatu bikainak izan daitezke zuen ideiak bultzatzeko; oihartzun mediatiko handia lortu dezakezue. Zorte on! Gu ziur gaude: datuak emanez, denok kontzientziatuko gara, ikastetxearen jasangarritasuna hobetzeko. Nolako aztarna utzi nahi duzu planetan? Kontzientziatu zaitez! Informatu dezagun jendea gure ikastetxearen aztarna ekologikoaz. ZER AZTARNA UZTEN DUZU? Orain edo inoiz ez EZAGUTU DIZIPLINARTEKO PROIEKTUA ITZALAPROIEKTUAK UZTENDUTEN 1 Th nk P ENTSATU D s g 2 DISEINAT U 3 M ke EGIN 4 PRESENTA S ge s EGIAZTATU 5 U8 146 HELBURUA AURRERA Zer ikasi dut? PORTFOLIOA Neurtu angelu hauek garraiagailuarekin, eta sailkatu zabaleraren arabera: C D ^ E 2 Marraztu angelu hauek: a) A = 50° b) B = 135° 3 Garraiagailua erabili gabe, kalkulatu eta idatzi zer neurri duten B eta C angeluek. 4 Ikusi arretaz eta erantzun. a) Nolakoak dira kokapena kontuan hartuta? A eta B ^ E eta B D eta E A eta D E eta A C eta D b) Zertan dira antzekoak eta zertan desberdinak A eta B ? Eta D eta E? Neurtu garraiagailuarekin eta adierazi angelu hauen zabalerak minututan: Â 6 Adierazi segundotan, eta ordenatu txikienetik handienera. 62° 31' 40'' 18° 15' 21'' 3 040' 52'' Adierazi gradu, minutu eta segundotan. a) 21 889'' b) 10 862'' Zer neurri du hirugarren angeluak? 40° 68° ? Pentsatu eta ebatzi. a) Danel eta Eguzki pizza jaten ari dira. Danelen zatiak 86° 45' ditu, eta Eguzkirenak, 89° 10'. Zer neurri du platerean utzitako zatiak? b) Haize-errota baten hegalek 160° 58'-ko bira egin dute. Zenbat gehiago biratu behar dira oraindik bira-erdia egiteko? c) elkartzekoak dira. Joarrek 2 17 min 48 behar ditu autoz iristeko, eta Pellok, 3 h, autobusez. Ordu berean abiatzen badira, zenbat lehenago iritsiko da Joar? Semaforoa. Margotu koadernoan, ariketa bakoitzaren ondoan, honela: Erantzuna badakizu Laguntza behar izan baduzu Erantzuna jakin ez baduzu A 25° C D E 148 149 BERRIKUSPENA HIRUHILEKOA 2 2 Kopiatu, egin batuketak eta osatu. Zaku bat irinek 5 kg gehiago Kalkulatu angelu guztien neurria. Baina adi! Ez erabili garraiagailua! 8 Pentsatu azkar eta erantzun. a) Bi angelu zuzen batzen baditugu, nolako angelua lortuko dugu? b) Eta angelu zuzen bat eta angelu zorrotz bat batzen baditugu? c) Bi angelu zorrotz, izan daitezke betegarriak? Arrazoitu zure erantzuna. d) Zer neurri du angelu batek bere angelu betegarriaren laurdena bada? e) Zer neurri du angelu batek bere angelu osagarriaren bikoitza bada? Eˆ 50° B = 120° Â Cˆ = ? Jˆ 90° = = Gˆ = ? Jakin nor den zientzialari misteriotsua sTEAM Matematikari misteriotsu honengatik ez balitz, beharbada ez genuke izango bideojokorik, ez Internet, ez telefono adimendunik. 1906an jaio zen, New Yorken. Hark erabili zuen lehenbiziko aldiz bug hitza (zomorroa) errore informatiko bat izendatzeko, baita debug hitza ere. Hark sortu zuen ordenagailuko lehen programa-lengoaia konplexua: COBOL programa (enpresa-aplikazioetara zuzendutako lengoaia orokorra). Eta azken pista bat: hark programatu zuen edukiera handiko lehen ordenagailua, Mark I, Harvard Unibertsitatean. Aldi berean egin zituen Estatu Batuetako Marinan karrera militarra eta zientzialari-ibilbidea. Pistak Eskaneatu, eta jakin nor den zientzialari misteriotsua ? HELBURUA AURRERA
PORTFOLIOA
A B ^ C ^ D ^ E
a) ^ A
b) ^ B = 135°
A eta B ^ E eta B D eta E ^ A eta ^ D ^ E eta ^ A ^ C eta ^ D
62° 31' 40'' 18° 15' 21'' 3 040' 52''
A = 25° ^ C = ? ^ D = 140° Kolorea ^ A ^ B ^ C ^ D ^ E 144 145 U8 EBATZI BAIETZ! Egin marrazki bat Pellok badaki triangelu baten bi angeluk 40 eta 60 dituztela eta bi angelu horiek partekatzen duten aldea 6 cm luze dela. Zer luzera dute beste bi aldeek? Aldeek zer luzera duten jakiteko, triangelua marraztuko dugu. B 40° 60° 1. Erregelarekin, marraztu 6 cm-ko zuzenki bat. 2. Erpintzat A puntua hartuta, marraztu 40°-ko angelu bat. 100 110 120 130 140 150 160 170 80 70 50 30 20 60 30 20 100 120 140 150 160 A 100 110 120 130 140 150 160 170 80 70 50 30 60 30 100 120 140 160 6 cm 60˚ B A 40˚ 40° 6 cm 3. Erpintzat B puntua hartuta, marraztu 60°-ko angelu bat. 4. Bi angeluen aldeek elkar ebakitzen duten puntua triangeluaren hirugarren erpina da. Orain, soluzioa jakiteko, urrats bakarra falta zaizu: erregelarekin, neurtu triangeluaren aldeak. Beste bi aldeen luzerak 5,3 cm eta 3,9 cm dira. Soluzioak badu zentzurik? Egiaztatu edozein bi alderen luzeren batura beti handiagoa dela beste aldearen luzera baino. Triangelu isoszele baten oinarriak 5 cm ditu, eta alde hori partekatzen duten angeluak 50°-koak dira. Zer luzera dute beste bi aldeek? Zer neurri du beste angeluak? 2 Lidek badaki triangelu baten bi aldek 6 cm eta 4 cm dituztela. Gainera, badaki bi alde horiek eratzen duten angeluak 55° dituela. Zer neurri du hirugarren aldeak? Eta beste bi angeluek? Problemak
Esan
arin-arinka
osagarriak diren bi angelu eta betegarriak diren beste bi. Bi angelu auzokideak badira, izan ditzake
?
osagarriak eta berdinak badira, zer neurri du bakoitzak? Bi angelu betegarriak badira, baina biak berdinak badira, izan daitezke biak zorrotzak? Eta biak kamutsak? Nolakoak dira? 4 3 Urratsez urrats Frogatu, paper zatitxoak erabiliz, esaldi hauek egia direla. Gero, idatzi nola egin behar den urratsez urrats. Deskargatu txantiloia, webgunean: anayaharitza.es Erpinez aurkakoak diren bi angeluk neurri bera dute. Triangeluen angeluen batura beti 180° da. • Laukien angeluen batura beti 360° da. Buruzko kalkulua Kalkulatu 40ren % 10. Orain, zuk zeuk: 30en % 10 50en % 10 70en % 10 80ren % 10 90en % 10 120ren % 10 130en % 10 140ren % 10 150en % 10 200en % 10 Ikusi nola egiten den, hemen: anayaharitza.es Sistema hirurogeitarrean angeluak neurtzen ditugu. Eta zer gehiago? Zenbat minutu dira gradu bat? Eta zenbat segundo? 6 5 40˚ 60˚ 50˚ 50˚ 5 cm 90 ° 180 1° Luzera? Masa? Denbora? 4444444444 % 100 % 10 40 4 :10 Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es 6 cm ? ? ? ? Ikusi nola egin triangeluak, webgunean: anayaharitza.es Begira nola pentsatzen dudan Lankidetzako ikaskuntza Hezkuntza emozionala Gamifikazioa IKTak GJH Pentsamenduaren garapena Audioa Ebaluazioa Ikonoak
Bi angelu
Diziplinarteko
Portfolioa Helb u r u a a u r r e ra
Honelakoa da zure proiektu digitala



Proiektu honek ikasturteko eduki guztiak eskaintzen dizkizu, bai liburu digitalaren bidez, bai era askotako baliabideen bidez.



Ikasteko beste modu bat ezagutuko duzu, erraza, intuitiboa eta edozein plataforma eta gailurekin bateragarria.
Nola sartu?



Zure liburuko lehenbiziko orrialdearekin batera aurkituko dituzu proiektu digitalean sartzeko behar dituzun argibide guztiak.

140 4 Zer gertatzen da angeluen arteko batuketan ordena aldatzen baduzu? Egiaztatu. 5 Ikusi zer neurri duen alboko angeluak. a) Angelu hauetatik zein da alboko horren osagarria? A 43° 43' 27'' B 134° 43' 27'' C 44° 43' 27'' b) Eta betegarria? A 134° 44' 27'' B 134° 43' 27'' C 44° 43' 27'' 6 Pentsatu eta ebatzi. a) Mirentxu 4 min 12 s-an dutxatzen da, eta Kattin ahizpak, berriz, Mirentxuk baino 2 min 40 s gehiago behar izaten ditu. Zenbat denboran dutxatzen dira bi ahizpak? b) Lolok Donostiatik El Prat de Llobregat hirira joan nahi du. Aurrena trena hartu du Bartzelonaraino; bidaiak 5 h 27 min iraun du. Gero, Bartzelonan autobusez jarraitu du, beste 34 minutuan. Zenbat denboran iritsi da helmugara? 5 h 27 min ? 34 min 1 Kopiatu eta egin batuketak. a) 13° 1 1' 1 7'' + 6° 29' 42'' c) 27° 9' 52'' 53° 18' 26'' b) 8° 41' 30'' 3° 6' 50'' d) 20° 1 3' 38'' 49° 55' 4'' 2 Kalkatu angeluak, eta batu biak grafikoki. A = 42' 37'' B = 13' 21'' 3 Egin batuketak. B = 10° 5' C = 8° 26' D = 81° 34' A = 36° 34' a) A B b) A + C c) C + D Angelu txikiagoak elkartuta, handiagoak marraztu ditzakegu, eta horien neurriak kalkulatu. Angeluen arteko batuketak 4 Angeluen arteko batuketak egiteko, egin urrats hauek: Nola neur dezakegu alboko angelu honen zabalera garraiagailua erabiliz? 1. Luzatu angeluaren bi aldeetako bat. 2 angelu eratzen dira: B eta C bat laua da. C 55° 2. Neurtu angelu laua ez bestea. B C 140 150 160 140 B C Binaka jarrita, marraztu 180° baino gehiago dituen angelu eta kalkulatu zer neurri duen, urrats horiek eginez. Angelu laua baino handiagoak neurtzen 1. Egin datuen arteko batuketa 2. Aldatu datuak. 3. Adierazi emaitza. Angeluen arteko batuketa egindakoan segundoak 60 edo gehiago badira, bihurtu minutu; minutuak 60 edo gehiago badira, bihurtu gradu. 54° 1 6' 49'' + 32° 27' 1 3'' 86° 43' 62'' 86° 43' 62'' 86° 44' 2'' 60 + 2 54° 1 6' 49'' 32° 27' 1 3'' 86° 44' 2'' 54° 16' 49' + 32° 27' 13'' 86° 44' 2'' Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es Gogoratu 60'' = 1' 60' = 1° Batuketa grafikoki ere kalkula dezakegu. Ohartu honetaz 10° 5' 36° 34' 10° 05' 36° 34' + 10° 5' ✗ ✓ + = A A B B
Zer eskaintzen dizu?
Era askotako baliabideak ditu; paperezko liburuaren erreprodukzioa baino askoz gehiago da.
Honakoak egiteko aukera izango duzu:
Ariketak egin
ariketa elkarreragileak
Aztertu
laburpen elkarreragileak, eskemak...

Ikasi
audioak, bideoak, Game Room-ak...
Ebaluatu
autoebaluazioa, portfolioa...
Nolakoa da?
Erantzun globala era askotako hezkuntza-ingurune baterako.
Intuitiboa
Zuk erraz erabiltzeko modukoa.
Gailu anitzekoa
Edozein gailu motatan (ordenagailuan, tabletan, smartphonean…) egokitzen eta ikusten da, pantailaren edozein tamaina eta bereizmenetan.

Deskargagarria

Aukera ematen du Interneteko konexiorik gabe lan egiteko eta gailu batean baino gehiagotan deskargatzeko.

Sinkronizagarria
Erabiltzaileak egiten dituen aldaketak berez sinkronizatzen dira, lan egiteko erabilitako edozein gailu konektatzean.
Unibertsala
Bateragarria da ikastetxeetan gehien erabiltzen diren sistema eragileekin, ikaskuntzako inguru birtualekin (IIB) eta hezkuntza-plataformekin (LMS).
141 U8 aldatzen 27'' 27'' ahizpak, izaten du. min beste garraiagailua 3. Kalkulatu zer neurri duen hasierako angeluak. angelu bat, Gogoratu Denbora-datuen arteko batuketak angeluen artekoak bezalaxe egiten dira. 45° 16' 33'' A Ebatzi urratsez urrats, hemen: anayaharitza.es A = B + C A 180° + 55° = 235° Hortxe duzu soluzioa!
1 Zaindu bizia
Gaur egun dugun erronka handienetako bat planeta zaintzearen garrantziaz jabetzea eta planeta zaintzen laguntzea da. Zergatik da garrantzitsua flora babestea, zehazki zuhaitzak, ingurumena zaintzea lortzeko? Zuhaitzek espezie-aniztasuna babesten dute, oxigenoa sortzen dute, klima-aldaketari aurre egiten laguntzen dute eta animaliek nahiz gizakiok jateko behar ditugun fruituak ematen dituzte. Onura horiek eta beste asko ditugu zuhaitzei esker.


Zuhaitzak gure lagunak eta kideak dira. Zaindu zuk ere gure planetako bizia! Babestu zuhaitzak!
Unitate honetarako...
Helburua aurrera
Zergatik da beharrezkoa zuhaitzak zaintzea?
Egin biziaren zuhaitz bat, natura zaintzearen aldeko mezu eta guzti.
hariari!
Zenbakiak eta eragiketak
Oinarrizko
Jarraitu
Zenbaki-sistema hamartarra
eragiketak
Eragiketa
konbinatuak
Zenbaki positiboak eta negatiboak
Koordenatu kartesiarrak

Zenbaki-sistema hamartarra
Gure zenbaki-sisteman, zifren balioa zenbakian duten posizioaren araberakoa da.
Nola batuko zenituzke 1etik 100era arteko zenbakiak?
Esan 10 000tik
1 000 000ra bitarteko zenbaki arrunt batzuk.
Nola zenbatuko duzu zenbat dauden?
ZENBAKI ARRUNTAK
Imajinatu zenbakirik ez dagoela.
Berridatzi albiste hau.
Deskargatu albistea hemen: anayaharitza.es
Jarri adibide batzuk.
BIKOITIAK BAKOITIAK
1 Kopiatu taula, eta idatzi bi zenbakiak han. Adierazi zenbat balio duen 5 zifrak zenbaki bakoitzean.
EMM HMM MM EM HM M E H U ? ? ? ? ? ? ? ? ?


a) Zazpi milioi hirurehun eta zortzi mila bostehun eta hamaika.
b) Ehun eta berrogei milioi ehun eta hamabost mila eta seiehun.
2 Irakurri eta idatzi zenbaki hau ezkerretik eskuinera eta eskuinetik ezkerrera:
Ehun milioi!
Ezagutzen duzu milioika dagoen zerbait?
MM milioikoak
HMM hamar milioikoak
EMM ehun milioikoak
Zer gertatzen da? Nolakoa da zenbakia? Idatzi beste adibide batzuk.
10 1
7 EMM 6 HM 1 HMM 3 E 3 MM 1 H 7 U
EMM HMM MM EM HM M E H U
3 Ikusi arretaz adibidea, eta deskonposatu zenbakiak.
87 604 021



8 0 000 000 + 7 000 000 + 6 00 000 + 4 000 + 2 0 + 1
8 × 10 000 000 + 7 × 1 000 000 + 6 × 100 000 + 4 × 1 000 + 2 × 10 + 1



a) 125 386 090
b) 9 999 999
c) 31 402 578
4 Bilioi bat, guretzat, milioi bat milioi da. Baina Ingalaterran eta beste herrialde batzuetan, mila milioi da. Idatzi, zifraz, zenbat den bilioi bat bi modu hauetan:
BILIOI BAT ONE BILLION

5 Irakurri pistak, eta jakin hiru nortasun-agirietatik zein den Kauldirena.
1. PISTA: Zenbakiak 8 zifra ditu, baina hamar milioikoen zifrak ez du baliorik.
2. PISTA: Milakoen zifra eta ehun milakoen zifra berdinak dira.
6 Unitatearen hasieran irakurri dugun bezala, «1990etik gaur arte, gure planetak 178 milioi hektareako baso-azalera galdu du». Zenbat ehun milioiko dira, gutxi gorabehera?
Zenbakiak nola hurbiltzen diren oroitzen ez bazara, «Berehala kontatuko dizut», webgunean: anayaharitza.es
Nola zenbatuko duzu zenbat dauden?
Ikusi irudia, eta azaldu nola zenbatuko duzun zenbat dauden. Hori zenbatzeko modu asko daude, eta modu bikainak dira denak!
Eta…
… elementu bakoitzak 1 H balio badu?
… elementu bakoitzak 1 E balio badu?
… elementu bakoitzak 1 M balio badu?
Berdin zenbatuko zenuke? Azaldu zure arrazoiak.
Gogoan hartu!
Zenbaki handiak erabiliz, Lurrean urtean zenbat zuhaitz galtzen edo lortzen diren zenbatu dezakezu.
11 U1
1 ha = 1 hm2 1 1 hm 1 hm 1 hm
Hektarea bat hektometro karratu bat da.
Oinarrizko eragiketak
Batuketa, kenketa, biderketa eta zatiketa dira oinarrizko eragiketak, eta eguneroko bizitzako egoera matematiko errazak ebazteko erabiltzen ditugu.


1 Lapitzak erdira Irakurri, kalkulatu eta erantzun.
a) Zenbat puntu dituzte talde gorriak eta talde urdinak biek batera?
b) Talde berdeak baino zenbat puntu gehiago ditu gorriak?
c) Talde horiak talde urdinak baino 5 aldiz puntu gehiago baditu, zenbat puntu ditu?
d) Zer taldek irabazi du? Berdinketarik izan da?
2 Nortasun-agiriak 8 zifrako zenbaki bat eta letra bat ditu.




a) Binaka jarrita, bilatu informazioa, jakiteko zer urrats egin behar diren NANeko letra kalkulatzeko.
b) Jolastu edozein NANeko letra zein den asmatzera, webgunean: anayaharitza.es
3 Pentsatu eta erantzun.
Zein da hondarraren propietatea?
4 Eskema Egin koadernoan eskema bat kontzeptu hauekin, eta idatzi adibide bat kasu bakoitzean.
GAIAK PROPIETATEAK

5 Naturagunetan espezializatuta dagoen argazkilari batek baso hostoerorkorren 125 320 argazki eta baso hostoiraunkorren 93 008 argazki ditu. Zenbat argazki ditu, gutxi gorabehera? Lehenbizi, biribildu datu bakoitza milakoetara.



Oroitzen ez bazara, «Berehala kontatuko dizut»: anayaharitza.es
Informazioa behar baduzu, deskargatu hemen: anayaharitza.es
Ebatzi urratsez urrats, hemen: anayaharitza.es


12
2
750
?
1
225 125630 628150
? 125 320
93 008 anayaharitza.es
6 Baso batean 2 585 zuhaitz landatu dituzte. Orain guztira 24 310 zuhaitz badaude, zenbat zeuden hasieran?
2 585 ? 24 310
7 Málaga hiriak 571 026 biztanle zituen 2018an. Sevilla hiriak 117 685 biztanle gutxiago balitu, bi hiriek biztanle kopuru bera izango zuten. Zenbat biztanle zituen Sevillak?
571 026 117 685 ?
Zuhaitzak landatu badituzte, hasieran orain baino gutxiago zeuden.
2018ko datuak dira.
Ebatzi urratsez urrats, hemen: anayaharitza.es
8 Urteko liburu-azoka handienean, Parisen, 2 139 705 nobela saldu dira. Guztira saldu diren haurrentzako ipuinak baino 1 850 329 liburu gehiago dira. Zenbat ipuin saldu dituzte? ?

2 139 705
1 850 329
9 Emmak furgoneta bat erosi du. Sarrerako kuota 6 000 � ordaindu du, eta gainerakoa 40 kuota berdinetan ordainduko du. Furgonetak 40 000 � balio badu, zenbat falta zaio ordaintzeko? Zenbat izango da kuota bakoitza?
Eragiketak egiteko, deskonposatzea
Ebatzi urratsez urrats, hemen: anayaharitza.es
40 kuota ordaintzeak esan nahi du 40 aldiz ordaintzea.
Eragiketak egiteko beste modu batzuk ere badaude; adibidez, gaiak deskonposatzea. Praktikatu, modu errazena edo azkarrena zein iruditzen zaizun jakiteko.
BATUKETA edo KENKETA: 16 489
1 6 4 8 9 = 10 000 + 6 000 + 400 + 80 + 9
5 2 2 6 = − 5 000 − 200 − 20 − 6 10 000 + 1 000 + 200 + 60 + 3 = 11 263




BIDERKETA:

«Berehala kontatuko dizut», webgunean: anayaharitza.es
• Kalkulatu, gaiak deskonposatuz. Kenketan, prestatu ondo bururakoa.
a) 25 730 + 500
b) 8 423 − 2 980


c) 125 × 15

13 U1
Málaga Sevilla
5 226
25 257 x 200 50 7 20 4 000 1 000 140 5 1 000 250 35
6 425 + 1 250 + 175
257 × 25
5 000
=
Málaga Cádiz
Sevilla
Kordoba Jaén Granada Almería
Huelva
Eragiketa konbinatuak
Batzuetan oso lagungarria da zenbait eragiketa
adierazpen bakarrean idaztea, baina garrantzitsua da eragiketak zer ordenatan egin behar diren jakitea.
Zenbait eragiketako adierazpenak ebazteko, kalkuluak ordena honetan egin behar ditugu:
1. Parentesi barruko eragiketak.
2




2. Biderketak eta zatiketak, ezkerretik eskuinera.
a) 5 + 4 × 3



b) 10 − 2 × (3 + 1) + 5
c) 4 × 7 − 24 : 2

d) 5 × (3 + 18) − (20 − 4)


Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
3 Idatzi esaldiak zenbakizko adierazpen moduan, eta kalkulatu emaitzak.
a) Biderkatu 3z 8 gehi 4ren emaitza.
b) 3ren bikoitzari batu 5 bider 8ren emaitza.
c) Biderkatu 6z 4 gehi 3ren emaitza, eta horri kendu 9.
d) Batu 20ri 10 ken 6ren emaitzaren eta 4ren biderkadura.
4 1–2–4 Kopiatu eta idatzi parentesiak, edo ez, kasu bakoitzean emaitza handiena eta txikiena lortzeko.
90 + 10 × 5
90 – 10 × 5
5 Idatzi batuketa bat eta biderketa bat dituen adierazpen bat, parentesiekin, kontuan izanda emaitzak 100 izan behar duela. 100
3. Batuketak eta kenketak, ezkerretik eskuinera.
Zerbait gaizki egin baduzu, ez du axola. Ikastea eta huts egitea elkarrekin doaz!
Parentesiak idazten ez badituzu, kenketaren ikurrak biderketaren emaitzari eragiten dio.
14
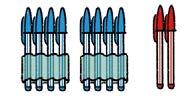
1 Ikusi arretaz, eta esan zer letra dagokion zenbaki bakoitzari.
B Lau bolaluma urdin eta bi bolaluma gorri dituzten bi pakete.
× (4 + 2)
A Lau bolaluma urdin dituzten bi pakete, eta bi bola luma gorri.
2 × 4 + 2
1.
2.
2 Kalkulatu koadernoan.
3
6 Kopiatu eragiketak, eta idatzi parentesiak behar diren tokian, adierazitako emaitzak lortzeko.
a) 5 × 3 + 2 × 4
Emaitza posibleak: 68 55 23 100
b) 2 × 5 + 100 : 5
Emaitza posibleak: 42 30 22 50
c) 10 + 2 × 5 5 : 5
Emaitza posibleak: 19 18 3 59
7 Beñatek zenbait gauza erosi ditu: 2 bonboi-kaxa, bakoitza 28 � -an; arraina, 32 � -an, eta 4 laranja-zorro, bakoitza 4 � -an. Baina... erositakoa ordaintzeko 4 � falta zaizkio!
a) Zenbat balio du Beñatek erositakoak? Idatzi adierazpen bakarrean.
b) Zenbat diru du Beñatek?
c) Lagun batek 20 � uzten badizkio, zenbat geratuko zaio?
Parentesiak eta parentesi karratuak
Binaka lan egiteak batak bestearen ikuspuntua ezagutzeko aukera ematen digu.
• Adierazpen matematikoek batzuetan parentesiak eta parentesi karratuak dituzte. Nola ebazten dira?
250 + (100 + 50) × [10 − (3 + 2)] [ ] parentesi karratuak ( ) parentesiak
• Oso erraza da! Urrats hauek egin, eta kito:

1. Kalkulatu parentesi karratuen barruko eragiketa.
250 + (100 + 50) × [10 − (3 + 2)] = 250 + (100 + 50) × [10 − 5] = 250 + (100 + 50) × 5 Aplikatu eragiketen hierarkia.

2. Kalkulatu parentesien barruko eragiketak.
250 + (100 + 50) × 5 = 250 + 150 × 5
3. Kalkulatu gainerako eragiketak, eragiketen hierarkia aplikatuta.
250 + 150 × 5 = 250 + 750 = 1000
• Orain, ebatzi koadernoan adierazpen hauek:
a) (2 + 3) × [100 : (1 + 4)]
b) [100 : (7 + 3)] × [150 − (20 + 30)]
15 U1
Zenbaki positiboak eta negatiboak
Horrelako zenbakiak erabiltzen ditugu tenperaturak esateko, eraikin bateko solairuak adierazteko eta altxor bat itsasoan zer sakoneran dagoen adierazteko, adibidez.
• +1, +2, +3, +4… zenbaki positiboak dira.
• −1, −2, −3, −4… zenbaki negatiboak dira.


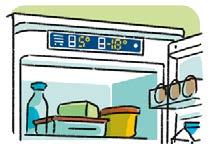




Hozkailua

1 Zer zenbaki mota erabiliko zenituzke gertaera hauek adierazteko, positiboak ala negatiboak? Sailkatu taula batean.
a) Igo – Jaitsi c) Zorretan izan – Jaso



b) I rabazi – Galdu d) Zero azpitik – Zero gainetik
2 Egiaztatu Kopiatu esaldiak, eta idatzi zer zenbaki positibo edo negatibo den bakoitza.
a) c)
Negatiboak Positiboak ? ?
3 solairu beherago noa. 10 puntu galdu ditut.
b) d)
20 � ditut.
−3

Itsas mailatik gora 1 200 m-ra dago.
Zenbaki osoen multzoa zenbaki negatiboek, 0 zenbakiak eta zenbaki positiboek osatzen dute. ? ? ?
16
4
–2 solairura noa.
–18 °C-an dago.
Altxorra itsaspean 75 m-ra dago.
3 Zer tenperatura adierazten du termometro bakoitzak?
Zenbaki batek zeinurik ez badu, positiboa da. 5 = + 5



4 Marraztu adierazitakoa, eta markatu zenbakiak.
a) Eraikin bat, 6 solairu eta lurpeko 3 dituena.
b) Urpeko ontzi bat itsas mailatik behera 150 m-ra.
c) Hegazkin bat 2 100 m-ko altueran hegan.
5 Anek hirugarren solairuan igogailua hartu du. 5 solairu behera jaitsi da, zaborra botatzera, eta 1 gora igo da, bizikleta hartzera.
a) Zer solairutan dago hondakinen gela?
b) Eta bizikleten gela?
Nola adierazi zenbaki osoak zenbakizko zuzenean
• Tenperatura hauetatik zein da maximoa? Eta minimoa?

• Zenbakiak konparatzeko, zenbakizko zuzenean jar ditzakegu.
Zenbaki negatiboak 0tik ezkerrera jartzen dira.
Edozein zenbaki txikiagoa da zenbakizko zuzenean haren eskuinean dauden zenbakiak baino.
Zenbaki positiboak 0tik eskuinera jartzen dira.
Edozein zenbaki handiagoa da zenbakizko zuzenean haren ezkerrean dauden zenbakiak baino.
Gogoan hartu!



• Termometro batek −4 ° C-tik +5 ° C-ra arteko tenperaturak adierazten ditu. Zer tenperatura adierazten ditu tarte horretan? Idatzi ordenan.

Laguntza behar baduzu, «Berehala kontatuko dizut», hemen: anayaharitza.es
Lurrean zuhaitzak galtzen edo lortzen ari garen adierazteko, erabili zenbaki positiboak eta negatiboak.
17 U1
−2 °C +4 °C −5 °C
–1 0 123 4 5678910 –2 –3 –4 –5 –6 –7 –10–8–9
Koordenatu kartesiarrak
Planoan puntuak adierazteko, koordenatu kartesiarrak erabiltzen ditugu.
Ardatz kartesiarrak bi zuzen dira, eta ezaugarri hauek dituzte:
• Ardatzak elkarzutak dira.
• Zenbakizko zuzenean bezala zenbakitzen dira.
• Elkar ebakitzen duten lekua 0 puntua da.
• Lauki-sarea lau zatitan banatuta uzten dute, eta zati horiei koadrante esaten zaie.
Plano bateko puntu bat adierazteko, bi koordenatu erabiltzen dira.
• Lehen koordenatua ardatz horizontalean irakurtzen da.

• Bigarren koordenatua ardatz bertikalean irakurtzen da.
1 Ikusi arretaz irudia, eta erantzun.
a) Idatzi koadernoan zer koordenatu dituzten adierazitako puntuek.
b) Puntuetako bat ardatz bertikalean bertan dago. Zein da puntu horren lehen koordenatua?
c) Beste puntu bat ardatz horizontalean bertan dago. Zein da puntu horren bigarren koordenatua?
2 Kokatu puntu hauek koordenatu-ardatz batean. Marraztu koadernoan.
A = (+3, −1) B = (0, 0) C = (−5, +2)

18
5 –1 123456 1 –1 –2 –3 –4 –5 –6 2 3 4 5 –2 –3 –4–5–6 –7
–1 123456 1 –1 –2 –3 –4 –5 –6 2 3 4 5 –2 –3 –4–5–6 –7 –1 123456 1 –1 –2 –3 –4 –5 –6 2 3 4 5 –2 –3 –4–5–6 –7 (+3, +1) (−2, +4) (−3, −4) (+3, −3)
1. koadrantea
4. koadrantea
2. koadrantea
3. koadrantea
Biderik laburrena
Tomas basoko eremu batean zuhaitzak landatzen ari da; (+4, +4) puntua da. Begiratu behar du ea beste bi eremutan ere beharrezkoa den zuhaitzak landatzea: (−3, −2) eta (−7, +4) puntuetan.
Tomas lehenbizi eremu gertuenera joaten bada, nora joango da?
1. Datuak koordenatu-ardatz batean kokatuko ditugu.
– Tomas (+4, +4) puntuan dago.
– Bi puntu hauetara joan behar du: (−3, −2) eta (−7, +4).

2. Tomas dagoen puntua beste bi puntuekin lotuko dugu.
3. Erregela erabiliz, bi zuzenkiak neurtuko ditugu, eta, gero, luzerak konparatuko ditugu.
Luzera laburrena zein zuzenkik duen, puntu horixe dago Tomasengandik gertuen.
a) Binaka jarrita, aukeratu Tomasentzat beste kokapen bat eta beste bi puntu. Kalkulatu zer puntu dagoen gertuen.
b) Maddi, hain zuzen, (−3, −2) puntuan dago. Zer koadrantetan dago Tomas? Eta Maddi?
• Aukeratu bigarren koadranteko puntu bat, kontuan izanda gertuago egon behar duela Tomasengandik Maddirengandik baino.
Gogoratu: bi punturen arteko distantzia laburrena lerro zuzena da.
• Aukeratu laugarren koadranteko puntu bat, kontuan izanda gertuago egon behar duela Maddirengandik Tomasengandik baino.
19 U1
–1 123456 1 –1 –2 2 3 4 –2 –3 –4
–1 123456 1 –1 –2 2 3 4 –2 –3 –4
–1 1234 1 –1 –2 –3 2 3 4 –2 –3 –4–5–6 –7 –1 1234 1 –1 –2 –3 2 3 4 –2 –3 –4–5–6 –7 Tomas Tomas Tomas Tomas Maddi Maddi
EBATZI BAIETZ!
Deszifratu kodeak
Olaiak badaki antzinako erromatarrek beste zenbaki-sistema bat erabiltzen zutela, ez gurea bezalakoa. Ikusi izan ditu zenbaki erromatarrak bere herriko eraikin batzuetan. Olaia bizi den etxea 1953an eraiki bazen, nola idatziko zen zenbaki erromatarretan?
Antzinako erromatarrek 7 letra larri erabiltzen zituzten zenbakiak adierazteko. Letra bakoitzak balio bat zuen.
I V X L C D M
1 5 10 50 100 500 1 000
1. Deskonposatu zenbakia unitatetan, eta idatzi, zenbakien ordez, balio horiek dituzten letrak.
2. I, X, C eta M letrak gehienez hiru aldiz jarraian idatz daitezke.

3. I, X eta C letrak balio handiagoko baten ezkerrean baldin badaude, eskuinekoaren balioari ezkerrekoarena kendu behar zaio.
Hori jakinda, 1 953 idatziko dugu zenbaki erromatarretan:
1. Deskonposatu zenbakia unitatetan.
1 953 = 1 000 + 900 + 50 + 3
2. Idatzi zenbakien ordez letrak, lehen esandako arauak kontuan hartuta.
1 000 + 900 + 50 + 3
M CM L III
C-k balio txikiagoa du M-k baino. Beraz:
CM = 1 000 − 100 = 900
I letra hiru aldiz jarraian dago. Beraz: 1 + 1 + 1 = 3
Olaiaren etxea zer urtetan eraiki zen, honela idazten da: MCMLIII.
Soluzioak badu zentzurik?
Batu letra guztien balioak, eta egiaztatu emaitza 1 953 dela.
MCMLIII → 1 000 + (1 000 − 100) + 50 + 1 + 1 + 1 = 1 953



1 Idatzi zuretzat garrantzitsuak diren zenbaki batzuk zenbaki-sistema erromatarrean.
Oso garrantzitsua da zenbakia unitatetan deskonposatzea.
Landu zenbaki-sistema erromatarra, webgunean: anayaharitza.es
2 Asmatu zenbaki-sistema bat, eta idatzi zenbaki batzuk sistema horretan.
20
ZENBAKI ERROMATARRETAN IDAZTEKO ARAUAK
1953
Problemak arin-arinka

2 1

Zein da 9 zifrako zenbakirik handiena? Eta txikiena?
Zenbat milako ditu zenbaki honek? 1 000 000
Buruzko kalkulua
Kalkulatu 12 × 4.
3 5
Kopuru bat 25 zatitan banatzen badugu, gerta daiteke sobera 25 unitate geratzea? Azaldu zergatik.
Termometroak −1 °C adierazten zuen, baina orain hotz handiagoa dago.
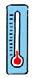
Zer tenperatura izan dezakegu orain?
Begira nola pentsatzen dudan
Kontatu istorio bat, adierazpen honetan oinarrituta:
10 : 5 – 2
4 6
Esan koadrante bakoitzeko puntu baten koordenatuak.
Zatitu eta zeu garaile
Imajinatu egoera hau: hiztegian hitz baten esanahia bilatu nahi duzu, eta, hiztegia irekitakoan, hitzak desordenatuta daude. A zer saltsa!
Ordenatzea garrantzitsua da. Informazioa errazago ulertzen dugu.
Quicksort izeneko metodoak multzo bateko elementuak azkar ordenatzeko balio du. Honela egiten da:
1. Aukeratu zenbaki bat, edozein; zenbaki horri pibot esango diogu.
2 Konparatu beste elementuak pibotarekin banan-banan.
– Elementua pibota baino txikiagoa bada, idatzi ezkerrean.
– Elementua pibota baino handiagoa bada, idatzi eskuinean.
Praktikatu quicksort metodoa, hemen: anayaharitza.es
4 = 2 × 2 24 12
× 2 × 2 48
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:
6 × 4
8 × 4
9 × 4
7 × 4
14 × 4
15 × 4 35 × 4 45 × 4 21 × 4 13 × 4




21 U1
1 Zer zenbaki da deskonposizio bakoitza?
a) 3 MM + 2 EM + 6 M + 7 H + 2 U
b) 2 000 000 + 100 000 + 20 000 + 3
2 Zenbat balio du 4 zifrak zenbaki hauetan?
a) 649 d) 240 012
b) 4 e) 4 830 000
c) 4 913 f ) 24 120 978
3 Zenbat urte ditu Anek? Hori jakiteko, jarraitu urratsei.
6 Marraztu orri batean koordenatu-ardatz bat.
a) Kokatu puntu hauek:
A = (+3, +5) C = (−3, −5)
B = (+3, −5) D = (−3, +5)
b) Lotu puntuak. Zer irudi marraztu duzu?
7 Marraztu lauki bat, kontuan hartuta lau erpinek koordenatu-ardatzetan bertan egon behar dutela. Idatzi erpin bakoitzaren koordenatuak.
8 Baserri ekologiko batean 57 000 arrautza zituzten. 3 542 dozena saldu badituzte, zenbat arrautza geratu zaizkie?

1 . Ikusi zer zifra dagoen hamar milakoetan zenbaki honetan: 527 341.
2. Kalkulatu zifra horren hirukoitza.
2. Horren emaitzari, batu hamarrekoen zifra.
4. Kopuru horixe da Aneren adina! 4 Kalkulatu.
9 Anbulatorio batean 5 250 txerto zituzten. Lehenbiziko astean 2 296 txerto jarri zituzten, eta bigarrenean, 1 985. Itxaron-zerrendan 1 200 pertsona badaude, badituzte nahikoa txerto?
10 Eski-estazio batean termometroan 3 ° C jartzen zuen goizeko 8etan. Eguerdian tenperatura 8 °C igo zen, eta 20:00etan, berriz, eguerdiko tenperaturatik 4 ° C jaitsi. Zer tenperatura zegoen 20:00etan?

5 Idatzi esaldi bakoitza zenbakizko adierazpen moduan. Gero, kalkulatu adierazpen bakoitzaren emaitza.
a) 25 gehi 75 egin, eta batura 2z biderkatu dut.
b) 8z biderkatu dut 25en eta 5en arteko kendura.
c) 16 zati 4 egin dut, eta zatidurari batu diot 9ren eta 5en arteko kendura 3z biderkatuta lortu dudan emaitza.
Semaforoa. Margotu koadernoan, ariketa bakoitzaren ondoan, honela:
Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu

22 PORTFOLIOA
8 + 5 × (7 − 2) 22 − 3 × 5 − 4 3 × (2 + 6) − (7 −5) × 2 106 + 2 × (22 −
: 3
10)
Z
er ikasi dut?
HELBURUA AURRERA
Irakurri arretaz taulako datuak: lau lurraldetan gutxi gorabehera zenbat milioi hektarea baso galdu edo lortu den ikusiko duzu. 1990etik 2000ra 2000tik 2010era 2010etik 2020ra
a) Kopiatu taula, eta adierazi lurralde bakoitzak hamarkada bakoitzean zenbat milioi hektarea galdu edo lortu dituen, zenbaki positiboak edo negatiboak erabiliz.
b) Zenbat galdu edo lortu zuen lurralde bakoitzak guztira hiru hamarkadetan?
c) Zenbat galdu edo lortu zen guztira lau lurraldeetan hiru hamarkadetan? Adierazi kopuru hori unitatetan.
d) Zer lurraldek lortu zuen gehien? Eta gehien galdu?
Geure buruari galdezka


Ondorioak eta emaitzak estrategia erabiliz, aztertuko dugu zergatik den beharrezkoa zuhaitzak zaintzea.

a) Kopiatu eta osatu antolatzailea.
b) Ikertu zer den biziaren zuhaitzaren irudia eta zer irudikatzen duen.
c) Talde-lanean, egin ikastetxerako biziaren zuhaitz erraldoi bat, eta zintzilikatu zuhaitzean natura zaintzearen aldeko mezuak. Gonbidatu eskola guztia parte hartzera.
N o la ikasi dut?
Osatu koadernoan.
Zer gertatuko da zuhaitzak desagertzen badira?
Epe luzean Zer gerta daiteke? Zer ondorio izango ditu?
Epe laburrean Zer gerta daiteke? Zer ondorio izango ditu?
Identifikatu matematika arloan lan egiteko zuk dituzun hiru indargune.

Identifikatu matematikan zuk hobeto lan egiteko hobetu ditzakezun hiru gauza.
Zer egin dezakezu horiek hobetzeko?
U1 23
Afrika 3 milioi galdu. 3 milioi galdu. 4 milioi galdu. Hego Amerika 5 milioi galdu. 6 milioi galdu. 3 milioi galdu. Europa Milioi 1 lortu. 2 milioi lortu. Milioi 1 lortu. Ozeania Milioi 1 galdu. Milioi 1 galdu. Milioi 1 lortu.
Egin biziaren zuhaitz bat.
Multiploak eta zatitzaileak
2 Besarkatu bakea
Gizakiok beste pertsona batzuekin bizi gara. Elkarrekin bizitzeak aberastu egiten gaitu eta ondo sentiarazten digu, baina bizikidetza horretan, batzuetan, egoera zailak sortzen dira, eta haserretu edo tristatu egiten gara. Bizikidetza hobetzea denon kontua da.
Gure gorputzeko substantzia kimiko batzuek gogo-aldartean eragina izan dezakete. Bazenekien, adibidez, norbait benetan sentituta eta luze besarkatzen dugunean gorputzak oxitozina izeneko hormona sortzen duela eta horrek lasaitzen eta seguru sentitzen laguntzen digula?
Besarkadak maitasun-keinu handienetako bat dira gure kulturan, eta ondo sentitzen laguntzen digute.
Unitate honetarako...
Helburua aurrera

Zergatik da garrantzitsua bakea lortzearen alde jardutea?
Eraiki bakea besarkadekin: diseinatu kanpaina bat, 8 segundoko besarkadak sustatzeko.

Jarraitu hariari!
Zenbaki
baten multiploak Multiplo komun txikiena
Zenbaki baten

zatitzaileak Zatitzaile komun handiena
Zatigarritasunirizpideak
Zenbaki lehenak eta konposatuak

Zenbaki baten multiploak
baten multiploak kalkulatzeak zenbait multzo berdinetan guztira zenbat dauden jakiteko balio digu.
Zenbaki
Ikastetxeko jolastokian zenbait esku zuri margotu dituzte, bakearen ikur gisa. Erabaki dute hatz bakoitzean ikastetxe horretan dabilen ikasle baten izena idaztea.
• Eskurik margotuta ez badago, ez dago izenak idazteko lekurik.
0 × 5 = 0
• Esku bakoitzean izenak idazteko 5 leku daude.
1 × 5 = 5
Zenbat leku daude eskuak bat, bi, hiru, lau… badira?
2 × 5 = 5 + 5 = 10
3 × 5 = 5 + 5 + 5 = 15
4 × 5 = 5 + 5 + 5 + 5 = 20
1 Irakurri adibidea, eta osatu koadernoan.
20 zenbakia 5en multiploa da; izan ere, 4 × 5 = 20.
a) 24 zenbakia 8ren multiploa da; izan ere, ? × ? = ?


b) 30 zenbakia 2ren multiploa da; izan ere, ? × ? = ?
c) 100 zenbakia 10en multiploa da; izan ere, ? × ? = ?

2 Bilatu zenbaki hauek 100eko taulan.

26 1
Zenbaki bat bider 0, 1, 2, 3, 4, 5, 6… egiten dugunean,
kalkulatzen ari gara. 0 × 5 1 × 5 2 × 5 3 × 5 4 × 5 5 × 5 6 × 5 × 5 5en multiploak 0 5 10 15 20 25 30 …
zenbaki baten multiploak
5en multiploak.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 100eko taula
10en multiploak.
Zenbaki bikoitiak 2naka multzokatu daitezke!
3 Pentsatu, eta erantzun koadernoan.
a) Idatzi 2 zenbakiaren lehenbiziko hamar multiploak.
b) Aurkitu 100 baino handiagoa den 2ren multiplo bat.
? × 2 = 100 baino handiagoa!


c) Nolako zenbakiak dira 2ren multiploak?
d) 2ren multiploak al dira zenbaki hauek? Azaldu zergatik.
14 50 21 158 3 726

e) Idatzi 2ren multiploak diren beste zenbaki batzuk.
f) Idatz al daitezke 2ren multiplo guztiak? Zergatik?
4 Paulek dendan 4 jogurteko paketeak saltzen ditu. Irakurri, eta erantzun, arrazoiak emanez.
a) Zenbat jogurt daude 3 paketetan?
b) Eros al daitezke zehazki 15 jogurt?
c) Zenbat pakete erosiko zenituzke 15 jogurt behar badituzu?
5 Zer dela eta diozu hori? Pentsatu, eta azaldu zergatik diren esaldi hauek zuzenak:
0 edozein zenbakiren multiploa da.
Zenbaki oro bere buruaren multiploa da.
Zenbaki baten multiplo guztiak idaztea ezinezkoa da.
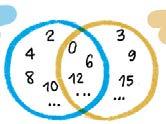
Multiplo komunak
Zer zenbaki dira 2ren multiploak? Eta 3renak? Multiplo komunik badute?
2ren multiploak
3ren multiploak
a) Marraztu koadernoan diagramak, hauekin:








– 2ren eta 5en multiploak. – 5en eta 10en multiploak.
2ren multiploak

5en multiploak 5en multiploak
b) Zer ikusten duzu azken diagraman? Azaldu, zure hitzak erabiliz.
Zenbaki bikoitiek azken zifra 0, 2, 4, 6 edo 8 dute.
Zenbaki bakoitiek azken zifra 1, 3, 5, 7 edo 9 dute.
Honela adierazten ditut 2ren eta 3ren multiploak diagrama bidez.
10en multiploak

Gogoan hartu!
Denbora-tarte batean zenbat besarkada eman ditzakezun aztertzeko, erabili multiploak.
27 U2
Multiplo komun txikiena
den jakiteko balio digu multiplo komun txikiena kalkulatzeak.
Multiplo berdin guztietatik txikiena zein
Bi zenbakiren multiplo komun txikiena kalkulatzeko, hau egin behar dugu: 4ren eta 6ren multiplo komun txikiena.
1. Kalkulatu zenbaki bakoitzaren lehenbiziko multiploak.
4ren multiploak: 0, 4, 8, 12, 16, 20...

6ren multiploak: 0, 6, 12, 18, 24, 30...
2. Bilatu multiplo komunak, eta aukeratu txikiena, 0 kontuan hartu gabe.
4ren multiploak: 0, 4, 8, 12 , 16, 20, 24
6ren multiploak: 0, 6, 12 , 18, 24 , 30...

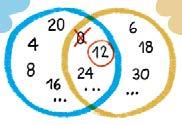
1 Kalkulatu zenbaki hauen multiplo komun txikiena. Adierazi hori diagrama baten bidez, adibidean bezala.
a) 4 eta 10 b) 3 eta 7 c) 8 eta 6 d) 4 eta 5
2 Danel 14 egunean behin joaten da zinemara, eta Maria, 21 egunean behin. Biek urriaren 1ean egin zuten topo zineman. Beraz, noiz egingo dute berriro topo? Egin urrats hauek:

1. urratsa: Kalkulatu 14ren eta 21en multiplo batzuk, biek duten lehenbiziko multiplo komuna aurkitu arte.
× 1 × 2 × 3 × 4 14 ? ? ? ? 21 ? ? ? ?



2. urratsa: Adierazi egoera eskema baten bidez, eta bilatu eguna egutegian. 14 14 14 21 21
URR. 1

3 A autobusa Lukenen etxe aurreko geralekura 3 minutuan behin etortzen da, eta B autobusa, 5 minutuan behin. Goizeko 8etan biak etortzen dira. Beraz…
a) Noiz egiten dute hurrena topo geraleku horretan?
b) Goizeko 8etatik 9etara, noiz egiten dute topo?
Multiplo komun guztietan txikiena 12 da. m.k.t. (4, 6) = 12
multiploak 6ren multiploak
28 2
▼
A 3 min B 5 min
✗ 12
✗
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
4ren
URRIA al. ar. az. og. ol. lr. ig. al. ar. az. og. ol. lr. ig.
AZAROA
4 5 minutuko geraldia Goizean, Nikoren iratzargailuak 15 minutuan behin jotzen du; Ganixenak, 5 minutuan behin, eta Julerenak, 10 minutuan behin. Hiru iratzargailuek lehenbiziko aldiz 07:30ean jotzen dute.


a) Zer ordutan jotzen dute hiru iratzargailuek aldi berean berriro?
b) Iratzargailuek aldi berean bigarren aldiz jotzen dutenean jaikitzen dira Niko, Ganix eta Jule, eta ordu erdi ematen dute gosaltzen eta hortzak-eta garbitzen. Zer ordutan amaitzen dute?
c) Gosaritako ontziak jaso eta ohea egiten 10 minutu ematen dute. Orduan, eskolara abiatu, eta 15 minutuan iristen dira. Eskolak 9etan hasten badira, garaiz iristen dira?
Erlazio bereziak: zein da bi zenbakiren m.k.t., bat bestearen multiploa bada?
Zein da 5en eta 100en multiplo komun txikiena? Nanosegundo bakarrean jakin dezakezu hori!


Zenbaki bat beste baten multiploa bada, bi zenbaki horietatik handiena da bien multiplo komun txikiena.
m.k.t. (5, 100) = 100



100 zenbakia 5en multiploa da.
• Kalkulatu multzo bakoitzeko bi zenbakien multiplo komun txikiena.
Nanosegundoa segundo baten mila milioirena da; alegia, 0,000000001 segundo.
Zure emaitza erregeletekin eta lauki-sare batekin egiaztatu nahi baduzu, deskargatzeko aukera duzu hemen: anayaharitza.es

29 U2
N iko G anix J ule
15 min. 5 min. 10 min.
2 eta 4 2 eta 10 2 eta 6 2 eta 8 3 eta 6 3 eta 9 4 eta 8 5 eta 10
5 10
Zenbaki baten zatitzaileak
Zenbaki baten zatitzaileak kalkulatzeak beste zenbaki bat zehazki zenbat aldiz sartzen den jakiteko balio digu.
Zenbat modutan multzokatu daitezke 10 pertsona multzo berdinetan, inor kanpoan geratu gabe?
Pertsona 1eko, 2ko, 5eko edo 10eko multzoak egin daitezke.
10 zenbakiaren zatitzaileak 1, 2, 5 eta 10 dira.
Zenbaki bat beste zenbaki baten zatitzailea da, zatiketa eginda hondarra 0 bada.
zatikizuna zatitzailea 0 zatidura
Zenbaki baten zatitzaileak zenbaki hori baino txikiagoak edo berdinak dira.
a) 8 zenbakia 24ren zatitzailea da; izan ere, ? : ? = ? (hondarra 0).



b) 2 zenbakia 30en zatitzailea da; izan ere, ? : ? = ? (hondarra 0).
c) 10 zenbakia 100en zatitzailea da; izan ere, ? : ? = ? (hondarra 0).
30
1 Kalkulatu zenbaki hauek zatitzaileak: 5
7 6 8 9
2 Irakurri adibidea, eta osatu koadernoan.
5 zenbakia 20ren zatitzailea da; izan ere, 20 : 5 = 4 (hondarra 0).
3
1 0 1 0 10 1 0 6 4 1 1 0 2 0 5 1 0 7 3 1 1 0 3 1 3 1 0 8 2 1 1 0 4 2 2 1 0 9 1 1 1 0 5 0 2 1 0 10 0 1 5 10 10 1 2
3 Kalkulatu 18ren zatitzaileak, honela:
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
4 Aldaerak Zenbat modutan jar daitezke 12 aulki ilara berdinetan?
5 Eiderrek 24 m soka ditu. Neurri bereko zatitan ebaki nahi du, sokasaltoan ibiltzeko zenbait soka prestatzeko. Zenbat modutan ebaki dezake? Zein aukeratuko du, zure ustez? Azaldu zergatik.
Zatitzaile komunak
Zer zenbaki dira 12ren zatitzaileak? Eta 18renak? Zatitzaile komunik badute?
12ren zatitzaileak 18ren zatitzaileak
a) Marraztu koadernoan diagramak, hauekin:




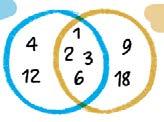


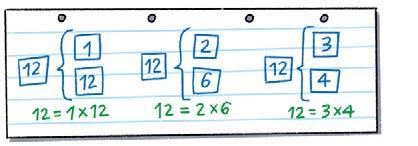
– 2ren eta 15en zatitzaileak






– 5en eta 10en zatitzaileak.
b) Zer ikusten duzu azken diagraman? Azaldu, zure hitzak erabiliz.
Honela adierazten ditut 12ren eta 18ren zatitzaileak diagrama bidez.

Gogoan hartu!
Zenbat besarkada eman ditzakezun kalkulatzeko, erabili zenbaki baten zatitzailearen kontzeptua.
31 U2
2ren zatitzaileak 15en zatitzaileak 5en zatitzaileak 10en zatitzaileak
Zatitzaile komun handiena
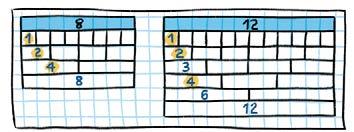
Zatitzaile berdin guztietatik handiena zein den jakiteko balio digu zatitzaile komun handiena kalkulatzeak.
Bi zenbakiren zatitzaile komun handiena kalkulatzeko, hau egin behar dugu:
12ren eta 18ren zatitzaile komun handiena.
1. Kalkulatu zenbaki bakoitzaren zatitzaileak.
12ren zatitzaileak: 1, 2, 3, 4, 6, 12
18ren zatitzaileak: 1, 2, 3, 6, 9, 18
Zatitzaile komun guztietan handiena 6 da.
z.k.h. (12, 18) = 6


2. Bilatu zatitzaile komunak, eta aukeratu handiena.
12ren zatitzaileak: 1 , 2 , 3 , 4, 6 , 12
18ren zatitzaileak: 1 , 2 , 3 , 6 , 9, 18
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Kalkulatu zenbaki hauen zatitzaile komun handiena. Adierazi hori diagrama baten bidez, adibidean bezala.
a) 8 eta 10 b) 15 eta 18 c) 24 eta 36 d) 9 eta 21


2 Pentsatu eta binaka jarrita komentatu Olaiak soka urdin bat du, 12 m-koa, eta soka hori bat, 8 m-koa. Bi sokak neurri bereko zatitan ebaki nahi ditu, puskarik sobera geratu gabe.
a) Zenbat modutan ebaki ditzake sokak?
b) Zer luzera izango du gehienez zati bakoitzak?
Laguntzatxoa: egin honelako eskema bat, eta ikusi zein diren zatitzaile komunak eta zein den handiena.
12ren zatitzaileak
18ren zatitzaileak
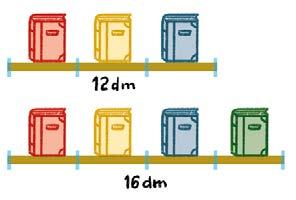
3 Liburu-denda batean nobedadeak bi apaletan jartzen dituzte, liburuak elkarrengandik distantzia berera.
a) Apal bat 12 dm luze da, eta bestea, 16 dm luze. Zenbat dezimetrotik zenbat dezimetrora jar ditzakete liburuak?
Idatzi aukera posible guztiak.
b) Aukera guztiak gauzatu ditzakete egiaz, zure ustez? Azaldu zergatik.
c) Liburuen artean ahalik eta tarte handiena uztea erabakitzen badute, zenbat dezimetroan behin jarriko dituzte liburuak?
12 dm

16 dm

32
4
6
4 6A gelan 20 ikasle dira, eta 6B gelan, berriz, 16. Datorren astean Opera Jaialdira joatekoak dira.
a) Talde berdinak egiten badituzte, baina bi geletako ikasleak nahasi gabe, zenbat ikaslekoak izan daitezke taldeak? 20 16

b) Jaialdira joateko taldeak ahalik eta ikasle gehienez osatuak izatea nahi badute, zenbat ikaslekoak izango dira?
c) Zenbat talde egingo dituzte 6A gelan? Eta 6B gelan?
d) Jaialdira 6 irakasle ere joango dira. 16 plazako mikrobus bat eta 26ko beste bat kontratatu dituzte. Nola banatu daitezke, talde bereko ikasleak bereizi ezin badira eta irakasleak bi autobusetan egon behar badira?
Erlazio bereziak: zein da bi zenbakiren z.k.h., bat bestearen zatitzailea bada?
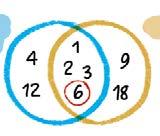
Zein da 5en eta 100en zatitzaile komun handiena? Unetxo bat eta… badakizu!



Zenbaki bat beste baten zatitzailea bada, bi zenbaki horietatik txikiena da bien zatitzaile komun handiena.
z.k.h. (5, 100) = 5


5 zenbakia 100en zatitzailea da.
Kalkulatu multzo bakoitzeko bi zenbakien zatitzaile komun handiena.
Laguntzatxoa: bilatu 20ren eta 16ren zatitzaileak, eta ikusi zein diren komunak.
Zure emaitza erregeletekin eta lauki-sare batekin egiaztatu nahi baduzu, deskargatzeko aukera duzu hemen: anayaharitza.es
33 U2
2 eta 4 2 eta 10 2 eta 6 3 eta 6 4 eta 8 5 eta 10 5 eta 15 2 eta 8 3 eta 9
5 10 5 5 2 1 1 10 6A
6B
Zatigarritasun-irizpideak
Zenbaki baten zatitzaileetako batzuk zein diren jakiteko, zatigarritasun-irizpideak erabil ditzakegu.
1 Aurkitu 100eko taulan zer zenbaki diren zatigarriak 2z, 4z, 3z, 9z, 5ez eta 10ez. Egiaztatu ondo egin duzula, zatigarritasunirizpideak erabiliz.
2z zatigarriak
4z
Zenbaki bat 2z zatigarria da, azken zifra 0 edo bikoitia badu.
3z zatigarriak
Zenbaki bat 4z zatigarria da, azken bi zifrek osatzen duten zenbakia 4ren multiploa edo 00 bada.
9z zatigarriak
Zenbaki bat 3z zatigarria da, zifren batura 3ren multiploa bada.
5ez
Zenbaki bat 9z zatigarria da, zifren batura 9ren multiploa bada.
10ez
Zenbaki bat 5ez zatigarria da, azken zifra 0 edo 5 bada.
Zenbaki bat 10ez zatigarria da, azken zifra 0 bada.
Deskargatu 100eko taularen txantiloia, webgunean: anayaharitza.es
14 zenbakia


2z zatigarria da; izan ere, 14 : 2 eginda, hondarra 0 da.

34
5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
zatigarriak 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
zatigarriak
zatigarriak
3 Begiratu aurreko ariketako emaitzei, eta erantzun.
a) 2z zatigarriak diren zenbaki guztiak 4z ere badira?
4z zatigarriak diren zenbaki guztiak 2z ere badira?
b) 3z zatigarriak diren zenbaki guztiak 9z ere badira?
9z zatigarriak diren zenbaki guztiak 3z ere badira?
c) 5ez zatigarriak diren zenbaki guztiak 10ez ere badira?
10ez zatigarriak diren zenbaki guztiak 5ez ere badira?
4 Isabelen eskolan Lehen Hezkuntzako 6. mailan 116 ikasle dira. Ikasbidaiarako zozketa-txartelak saltzeko, 2, 3 edo 4 ikasleko taldeak egin nahi dituzte. Antolatu daitezke horrela?
5 Entzulearen eskaria Ikertu kalkulagailuarekin. Zer gertatu behar du zenbaki bat 6z zatigarria izan dadin?
Aho-korapiloa?

Aho-korapiloak ematen dute, baina ez: enuntziatu baliokideak dira, hau da, gauza bera esan nahi duten enuntziatuak. Adibidez:
2 10en ZATITZAILEA da
Kontuan izan: 6 = 2 × 3

10 2z ZATIGARRIA da

10 2ren MULTIPLOA da
• Egin zuk gauza bera zenbaki hauekin. Ondo pentsatuta, oso erraza da!
a) 3 eta 60 b) 9 eta 45 c) 50 eta 200 d) 10 eta 1 000

Gogoan hartu!
Zatigarritasun-irizpideak erabiliz, oso erraz kalkula dezakezu zehazki zenbat besarkada eman ditzakezun.
35 U2
200 16 124 20 40 14 2z zatigarriak ? 4z zatigarriak ? 3 3z zatigarriak ? 9z zatigarriak ? 9 30 120 90 180 50 25 75 100 5ez zatigarriak ? 10ez zatigarriak ? 5 10
2 Kopiatu taulak, eta osatu, adierazitako zenbakiak idatzita.
Zenbaki lehenak eta konposatuak
Zenbaki lehenak eta konposatuak bereizten ditugu, 2 zatitzaile edo gehiago dituzten jakiteko.
Orri laukidun batean 2tik 10era arteko zenbakiak eta horien zatitzaileak marrazten badituzu… Zer ikusten duzu?

Hori da!
• Zenbaki batzuek bi zatitzaile bakarrik dituzte: 1 eta zenbakia bera.

Horiek zenbaki lehenak dira. Adibidez: 2, 3, 5 eta 7.

• Beste batzuek bi zatitzaile baino gehiago dituzte: 1, zenbakia bera eta beste batzuk.
Horiek zenbaki konposatuak dira. Adibidez: 4, 6, 8, 9 eta 10.

Zenbaki bat lehena da, bi zatitzaile soilik baditu: 1 eta zenbakia bera.
Zenbaki bat konposatua da, bi zatitzaile baino gehiago baditu.
1 Sailkatu zenbaki hauek bitan: lehenak eta konposatuak.
Behar baduzu, erabili kalkulagailua.
Zatitzaile batzuk aurkitzeko, zatigarritasun-irizpideak erabil ditzakezu.
2 Frogatu zenbaki hauek ez direla zenbaki lehenak.
36
6
2 3 4 5 6 7 10 9 8
12 23 15 31 17 38 20 42
3 000 1 285 303 2 002 801 216 6 060 1234
3 Zer zenbaki lehen daude 1etik 100era? Egin urrats hauek 100eko taularekin:
1. urratsa: Zirrimarratu 1 zenbakia; ez da lehentzat hartzen.
2. urratsa: Zirrimarratu 2ren multiploak (2z zatigarriak dira).
3. urratsa: Ikusi zer zenbaki dagoen hurrena zirrimarratu gabe (3), eta zirrimarratu zenbaki horren multiploak.
4. urratsa: Jarraitu horrela, amaierara iritsi arte.
Webgunean ere egin dezakezu: anayaharitza.es.
4 A zer problema! Museoan bisita gidatua egiteko 31 pertsona daude zain, baina zenbait taldetan joan behar dute eta talde guztiek pertsona kopuru berekoak izan behar dute. Egin ditzakete taldeak? Eta bisita egitera beste 2 pertsona joaten badira?
5 Kattinek gelako 23 mahaiak ilaratan jarri behar ditu, eta ilara guztiek mahai kopuru bera izatea nahi du.
a) Jar ditzake horrela? Azaldu zergatik.
b) 24 mahai balira, ahalko luke? Idatzi modu posible guztiak.
Biderkagai lehenetan deskonposatzea
Edozein zenbaki deskonposa daiteke biderkagai lehenetan. Horretarako, egin urrats hauek:
Deskonposatu 280
1. Bilatu 280ren bi biderkagai, edozein.
280 = 28 × 10
2. Bilatu biderkagai horietako bakoitzaren bi biderkagai.
28 = 4 × 7 10 = 2 × 5

3. Jarraitu horrela, biderkagai guztiak zenbaki lehenak izan arte.
4 = 2 × 2
4. Lortu duzu! Adierazi hasierako zenbakia biderkagai lehen guztien biderketa moduan.


280 = 2 × 2 × 7 × 2 × 5 = = 2 x 2 x 2 x 5 x 7
4 2 7 5
Soluzioa dotore emateko, ordenatu biderkagaiak.

37 U2
zer
honela.
Begira
polita! Egin
280 28
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
= 2 × 2 × 2 × 5 × 7
Metodo hau Eratostenesen bahea da. 280
10 2 2
Bilatu erantzun posible guztiak
Lehen Hezkuntzako 6. mailan 100 ikasle baino gutxiago dira. Gaur goizean kopuru bereko taldetan banatu behar dira, bakeari buruzko horma-irudi bat egiteko. Kalkuluak eginez, ohartu dira 7ko edo 3ko taldetan banatu daitezkeela, baina ez binaka, ikasle guztiek parte hartuko badute behintzat. Zenbat ikasle dira Lehen Hezkuntzako 6. mailan?


Hori kalkulatzeko, erantzun posible guztiak bilatuko ditugu, 100eko taula erabiliz.
2. Aukeratutako zenbaki horietatik, aukeratu 3ren multiploak diren zenbakiak.
Lehen Hezkuntzako 6. mailan 21 edo 63 ikasle dira.
Soluzioak badu zentzurik?
Egiaztatu emaitzek baldintzak betetzen dituztela.
- 100 baino txikiagoak dira.
- 7ren eta 3ren multiploak dira.
- Ez dira 2ren multiploak.
1 Ginkana batean parte hartu dutenen kopurua 40-70 bitartekoa izan da. Ginkanako probak egiteko, 2 edo 9 kideko taldetan jarri dira, inor kanpoan geratu gabe. Zenbat pertsonak hartu dute parte ginkanan?
2 Karlosek 100 karta baino gutxiagoko sorta bat du. Ohartu denez, 3, 4 edo 7 jokalari direnean, jokalari guztiek karta kopuru bera jasotzen dute eta ez da kartarik geratzen sobera. Zenbat karta dira?


38 EBATZI BAIETZ!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
1. Aukeratu 100etik behera dauden 7ren multiplo guztiak.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 ✗ ✗
3. Zirrimarratu 2ren multiploak diren zenbakiak.
Problemak arin-arinka
Buruzko kalkulua
Idatz al ditzakezu 5 zenbakiaren multiplo guztiak? Azaldu erantzuna.
Gutxienez zenbat zatitzaile ditu edozein zenbakik?
1 3 5

Bizkor! Esan bost zenbaki lehen.
Esan 10 zenbakiaren zatitzaile guztiak.
Kalkulatu 14 × 20.
20 = 2 × 10
× 2 × 10
28 14
280
Nola esaten zaio 2z zatigarriak diren zenbaki arrunten multzoari?
2 4 6
123 456 789 zenbakia lehena da? Azaldu zergatik.
Kodeak deszifratzen
Idatzi gustukoa duzun zerbaiti buruzko poema bat. Erabili Sophie Germainen poemak duen patroi bera:
- Ahapaldi bakoitzak 4 lerro.
- Lerro bakoitzak 7 edo 8 silaba, gehienetan behintzat.
Askatasuna, berdintasuna, senidetasuna!
Gizon-emakumeen eskubideak errespetatu behar dira!
Oihu haiek leihotik entzuten zituen Sophiek. Artean txikitxoa zen, eta iraultzaile zetorren.
Aske izan nahi zuen, eta beste haurren berdina, baina laster ohartu zen neska zela, eta ez mutila.
Ezin zen eskolara joan. Ez zioten uzten ikasten, ez etxean bertan zeuden liburuak irakurtzen.
Baina Sophiek ez zuen onartzen pentsatzeko era hura. Ikasten aritzen zen gauetan, ezkutuan.
Handitan, sinatzeko, bai lanak eta bai gutunak, gizona zela jartzen zuen, har zezaten kontuan.
Nahiz eta borrokan jardun, beti oztopoz oztopo, bide ederra egin zuen Sophiek, bikaintasunez lepo.
Poema deskargatzeko, jo webgunera: anayaharitza.es
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:




8 × 20
12 × 20
15 × 20
24 × 20
25 × 20
Poemek abestiak ematen dute, egitura ordenatua dutelako.
7 × 20
11 × 20
13 × 20
21 × 20
41 × 20
Gauza askoren artean, zenbaki lehenak zituen aztertu: zenbaki bitxiak dira horiek, besteek ezin dituzte zatitu.
Eta halaxe hasi zuen Sophiek bere iraultza sutsua, haren kalkuluei esker, hobea baita mundua.
39 U2
Begira nola pentsatzen dudan
Z er ikasi dut?
1 Irakurri, eta idatzi koadernoan.
a) Hiru zenbaki hauen lehenbiziko bost multiploak: 6 12 100
b) Hiru zenbaki hauen zatitzaile guztiak: 10 20 50
2 Pentsatu eta erantzun, eragiketarik egin gabe.
a) Zenbaki hauek zergatik ez dira 10en multiploak? 7 3 4 9
b) Zenbaki hauek zergatik ez dira 10en zatitzaileak? 33 15 20 100
3 Kalkulatu multzo bakoitzeko bi zenbakien multiplo komun txikiena.
4 eta 7 6 eta 9
4 Kalkulatu multzo bakoitzeko bi zenbakien zatitzaile komun handiena. 10 eta 15 8 eta 16
5 Kalkulurik egin gabe! Pentsatu eta erantzun.
a) m.k.t. (5, 10) eta z.k.h. (5, 10)
b) m.k.t. (2, 12) eta z.k.h. (2, 12)

6 Zatigarritasun-irizpideak erabiliz, erabaki zenbaki hauek zatigarriak diren 2z, 3z, 4z, 5ez, 9z edo 10ez.
12
900 150 123 40
7 Kopiatu zenbaki hauek eta osatu unitateen zifra, 3z zatigarriak izan daitezen. 2_ 13_ 28_ 104_
8 Idatzi zenbaki hauetatik zein diren lehenak eta zein diren konposatuak. Azaldu zergatik. 3 12 31 35 17 20
9 Minutu bakarrean! 100eko taula erabiliz, seinalatu ikusten dituzun zenbaki lehenak.
Deskargatu taula, hemen: anayaharitza.es
10 Sarak 80 € ditu, 2 € -ko txanponetan.
a) Egin ditzake txanpon kopuru bereko 2 pakete?
b) Eta 3 pakete? Eta 4?
c) Egin ditzake 5 edo 10 pakete?
d) Erantzuna baiezkoa denean, esan zenbat txanpon izango dituen pakete bakoitzak.
11 Ane lasterka egitera joaten da 2 egunean behin, eta Naroa, berriz, 5 egunean behin. Astelehen honetan topo egin badute, asteko zer egunetan egingo dute topo berriro?
12 Laukizuzen formako bizkotxo bat 24 cm luze da, eta forma bereko beste bat, 30 cm luze. Pellok zati berdinetan ebaki nahi ditu. Zenbat modutan ebaki ditzake? Zer modu aukeratuko zenuke zuk?
Semaforoa. Margotu koadernoan, ariketa
bakoitzaren ondoan, honela:
Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu
40
PORTFOLIOA
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
HELBURUA AURRERA
Diseinatu kanpaina bat, besarkadak sustatzeko.
Gaur goizean proba egin nahi izan dugu, ea alderik badagoen 3 segundoko besarkada baten eta 8 segundoko baten artean. Oso dibertigarria izan da, bene-benetan besarkatu baitugu elkar!

a) Ikaskideak besarkatzen bata bestearen jarraian etenik gabe 15 segundoan egon banaiz…
– Zenbat besarkada eman ditut, 3 segundokoak baziren?
– Posible da 8 segundoko besarkadak izatea? Zergatik?
– Posible da besarkada batzuk 8 segundokoak eta beste batzuk 3 segundokoak izatea? Bakoitzeko zenbat?
b) Erantzun berriro galdera horiei, pentsatuta ikaskideak besarkatzen 24 segundoan egon naizela.
c) Gure gelan 20 ikasle bagara, zenbat denbora behar dut, gutxienez, ikaskide guztiei 3 segundoko besarkada bana emateko? Eta 8 segundokoa emateko? Arrazoitu erantzuna.
Geure buruari galdezka
Puntu kardinalak estrategia erabiliz, aztertuko dugu zergatik den garrantzitsua bakea lortzearen alde jardutea.
Ez hartu kontuan besarkada batetik hurrengora dagoen tartea.
Zer informazio behar duzu bakea eraikitzea garrantzitsua zergatik den erantzuteko?
Izandako I H
Zer oztopo ikusten dituzu bakea eraikitzeko bidean?

a) Kopiatu eta osatu antolatzailea koadernoan.
b) Talde-lanean, diseinatu kanpaina bat, 8 segundoko besarkadak sustatzeko. Jarri martxan
8 segundoko besarkaden ohitura eskolan bertan, lagunekin, familiartekoak elkartzen zaretenean…
N o la ikasi dut?
Osatu koadernoan.
,
beharrak Hartutako jarrerak M E I M E H
, gogo



Zerk sortzen dizu emozioa ideia horretatik? Bakea eraiki egiten da?
Idatzi matematikako ariketak egiten ari zarenean sentitzen dituzun hiru emozio positibo.
Idatzi arlo hau lantzen ari zarenean pizten zaizkizun hiru emozio negatibo. Zer egin dezakezu emozio horiek aldatzeko?
U2 41
Emozioa
bizia Oztopoa
Zer iritzi duzu zuk gai horri buruz? Zer iradokizun egingo zenituzke bakea eraikitzeko? kezka
3 Konektatuta
Teknologia behar-beharrezkoa da zenbait zerbitzuren kalitatea hobe tzeko: osasun-arreta, hezkuntza, merkataritza, nekazaritza… Gainera, ezinbestekoa da hainbat arlotan formakuntza jasotzeko eta ikasteko.
Baina teknologia erabiltzea ez dago jende guztiaren esku; izan ere, munduko eskualde eta herri batzuetan, adibidez, Internetera nahiz oinarrizko beste zerbitzu batzuetara sartzeko aukera oso mugatua da.

Teknologia erabiltzeko aukera berak ez baditugu, batzuek garatzeko mugak izango dituzte, eta herrialdeen artean nahiz herrialde bereko eskualdeen artean gero eta alde handiagoak izango dira.
Zer deritzozu?
Ezagutzen duzu Internetera sartzeko arazoak dituen eskualde edo herririk?

Zure ustez, zergatik ditu arazo horiek? Eta zergatik handitu da hainbeste Interneten erabilera munduko leku guztietan?
Helburua aurrera
Zergatik da garrantzitsua denok izatea eskura Internet?
Diseinatu kamiseta bat, informazioa izateko eskubidea denok izan behar dugula aldarrikatzeko.
zituen Internetek: munduko
Kaixo! Zermoduz? Zurefaltasentitzendut.
Jarraitu hariari!
Ezagutu berreketak
Karratuak eta kuboak
42
Unitate honetarako...
Berreketak
Igandea





43 9 Ebatzi baietz! 10 berrekizuneko berreketak Erro karratuak
Ezagutu berreketak
Berreketak erabiltzen ditugu zenbaki bat bere buruaz
zenbat aldiz biderkatu behar dugun adierazteko.
Berreketa zera da: biderkagai berdinen arteko biderketa modu laburtuan adierazteko modu bat.
Berretzailea: biderkagaia zenbat aldiz errepikatzen den.
Berrekizuna: errepikatzen den biderkagaia.
Berreketak honela irakurtzen dira: 2 4 bi ber lau 1 4 bat ber lau
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Ikusi arretaz adibidea, eta adierazi biderketak berreketa moduan. Adierazi zein diren berrekizuna eta berretzailea.
8 × 8 × 8 = 8 3 Berrekizuna: 8 Berretzailea: 3



2 Irakurri, eta adierazi zifraz.
a) Bi ber sei. c) Zortzi ber bost.


b) Sei ber bi. d) Bost ber zortzi.
3 Idatzi zenbaki hauekin eratu daitezkeen berreketa guztiak eta, alboan, nola irakurtzen diren. 4 7 10
4 Lapitzak erdira Zein da berretzailea berreketa hauetan? Osatu koadernoan.
24 berreketa bat da.
5 Adierazpen hauetatik zeini dagokio hiru ber bost berreketa?
47 honela irakurtzen da: lau ber zazpi.
44
a) 3 × 3 × 3 × 3 d) 9 × 9 × 9 × 9 × 9 b) 7 × 7 × 7 e) 6 × 6 × 6 × 6 × 6 × 6 c) 10 × 10 f ) 1 × 1 × 1 × 1 × 1 × 1 × 1 × 1
a) 8 ? = 8 × 8 × 8 × 8 c) 11 ? = 11 × 11 × 11 b) 5 ? = 5 × 5 × 5 × 5 × 5 d) 14 ? = 14
A 3 + 3 + 3 + 3 + 3 C 3 × 3 × 3 × 3 × 3 B 5 + 5 + 5 D 5 × 5 × 5 1
2 × 2 × 2 × 2 = 2
4
6 Egin adibidean bezala, eta kalkulatu berreketa hauen balioa. Egiaztatu emaitzak kalkulagailuarekin.
Honela kalkula dezakezu:
a) 92 b) 10 6 c) 73 d) 5 4 e) 35 f) 12 1
7 Ikusi arretaz adibidea. Gero, berreketak erabiliz, adierazi beheko zenbakiak biderkagai lehenen arteko biderketa gisa.
a) 18 b) 20 c) 24 d) 36 e) 40



8 Osatu segida koadernoan. Zenbat da 1 berrekizuneko berreketa bat? 1
? 1 4 = ? 1 5 = ?
9 Zer dela eta diozu hori? Eragiketarik egin gabe, pentsatu zer berreketa den handiagoa. Azaldu zure erantzuna. 27 23
10 Irakurri galderak, eta aukeratu problema bakoitza ebazteko egin daitezkeen eragiketak. Gero, idatzi soluzioa.
a) Zenbat puntu lortu ditu Felixek dadoak botatakoan?
A 4 × 2
B 2 + 2 + 2 + 2
C 2 2
b) Zenbat marrubi jarri ditu Itziarrek guztira?
A 3 + 3 + 3
B 3 3
C 9 × 3

c) Lehen Hezkuntzako 6. mailako ikasleak 5eko taldetan banatu dira. Guztira 5 gela badira eta gela bakoitzean 5 talde badaude, zenbat ikasle dira 6. mailan guztira?

Gogoan hartu!
Internetek munduan zenbat erabiltzaile dituen adierazteko, erabili berreketak.

45 U3
2 5 = 2 × 2 × 2 × 2 × 2 = 4 × 4 × 2 = 16 × 2 = 32
12 = 2 × 2 × 3 = 2 2 × 3
1 2 = ? 1 3 =
1 = ?
3 × 5 B 53 C 5 + 5 + 5
A
Karratuak eta kuboak
2 eta 3 berretzaileak dituzten berreketak adierazteko, karratu eta kubo ere esaten da, hurrenez hurren, geometrikoki nola ebazten diren kontuan hartuta.
2 berretzailea duten berreketak adierazteko, karratu (edo koadro) ere esaten da.
3 berretzailea duten berreketak adierazteko, kubo ere esaten da.
irakurtzen
16 karratu perfektua da, 2 berretzailea duen berreketa moduan adieraz daitekeelako.
64 kubo perfektua da, 3 berretzailea duen berreketa moduan adieraz daitekeelako.

Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Idatzi nola irakurtzen diren berreketa hauek:
a) 2 2 c) 6 2 e) 12 2 g) 1 2 i) 102


b) 3 3 d) 93 f ) 53 h) 73 j) 8 3
2 Adierazi zenbat karratutxoz osatuta dagoen irudi bakoitza, biderketa banaren bidez.
A irudiak
2 × 2 karratutxo ditu; alegia, 2 2
a) Zeinetan adieraz dezakezu zenbat karratutxo dituen berreketa baten bidez?
b) Nolako forma dute irudi horiek?
3 Adierazi zenbat kubotxoz osatuta dagoen irudi bakoitza, biderketa banaren bidez.
a) Zeinetan adieraz dezakezu zenbat kubotxo dituen berreketa baten bidez?
b) Nolako forma dute irudi horiek?
46 2
4 2 = 4 × 4 = 16 4 3 = 4 × 4 × 4 = 64
4
4 4 4 4
2 4 4 4 2 3 2 2 3 3 2 3 4 3 3 A B C D E G F
4 2 honela ere
da: lauren karratua. 4 3 honela ere irakurtzen da: lauren kuboa.
4 Osatu segida, lehenbiziko hamar zenbaki arrunten karratuak adierazi arte.
1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16




Erreparatu ondoz ondo dauden bi karratuez osatutako pare guztiei. Zer alde dago pare bakoitzeko bi karratuen artean? Zer ikusten duzu emaitzetan?
5 Osatu segida, lehenbiziko hamar zenbaki arrunten kuboak adierazi arte. Laguntza gisa, erabili kalkulagailua.

1 3= 1 2 3= 8 3 3= 27 4 3= 64

6 Eraikuntzak egiteko bideojoko batean gela karratu bateko zorua blokez estali behar da. Alde bat jada osatu dute, 9 bloke jarriz. Zenbat bloke behar dira guztira?
7 Galdera Mattinek kubo handi bat egin du, musuzapien kaxa kubikoak erabiliz. Alde bakoitzean 12 jarri baditu, zenbat kaxa erabili ditu guztira?
Zenbaki karratuak eta zenbaki triangeluarrak
• Zenbaki batzuei zenbaki karratu esaten diegu, objektu kopuru hori karratu forman jar dezakegulako.
• Baina, bazenekien zenbaki triangeluarrak ere badaudela? Zenbaki bat triangeluarra baldin bada, objektu kopuru hori triangelu forman jar dezakegu, honela:
Bazenekien hau? Ondoz ondoko bi zenbaki triangeluar batzen badituzu, emaitza beti zenbaki karratu bat da. Egiaztatu hala den!

47 U3
Erro karratuak
Objektu kopuru bat karratu moduan jar dezakegun jakiteko, erro karratua erabil dezakegu.
Zenbaki baten erro karratua kalkulatzea zera da: objektu kopuru horrekin egin daitekeen karratu handienak zenbateko aldea duen kalkulatzea.
16ren erro karratua 4 da; izan ere, 4 2 = 16.
Honela idazten da: √16 = 4.



Zenbaki baten erro karratua beste zenbaki hau da: ber bi eginda emaitza zenbaki hura duena.
2 Zer zenbaki falta dira? Idatzi koadernoan.
a) √ ? = 5 b) √ ? = 10 c) √ ? = 8 d) √ ? = 9


3 Kalkulatu. Laguntza gisa, erabili kalkulagailua.
a) √121 b) √400 c) √225 d) √169

4 Zer baieztapen da zuzena? Erantzun eragiketarik egin gabe.
A 289ren erro karratua 17 da.
B 17ren erro karratua 289 da.
4 4 2 = 16
48
√ 1 = ? √4 = ? √9 = ? √16 = ? √25 = ? √36 = ?
√
√100 =
1 Osatu koadernoan.
√49 = ? √64 = ?
81 = ?
?
3
4
√121 kalkulagailuarekin egiteko, sakatu tekla hauek:
5 Hartu 10 polikubo edo objektu txiki, eta egin ahal duzun karratu handiena.
a) Zenbat polikubo jarri dituzu alde bakoitzean?
b) Zenbat polikubo ez dituzu erabili?
c) Zenbat da 10en erro karratua, gutxi gorabehera?
6 Ikusi arretaz adibidea, eta kalkulatu beheko zenbakien gutxi gorabeherako erro karratuak.
√16 < √20 < √25 4 < √20 < 5 √20 , gutxi gorabehera, 4 da.



a) √19 c) √85 e) √54
b) √40 d) √98 f ) √102

7 Uxuek bere katuaren 36 marrazki egin ditu txartel karratutan, eta txartelak karratu bat eratzeko moduan jarri nahi ditu kartoi mehe batean. Zenbat jarriko ditu alde bakoitzean?
8 Informatika-gelan 27 mahai karratu daude, eta karratu bat eratzeko moduan jarri nahi ditu Karlosek. Zenbat mahai jar ditzake? Geratuko da mahairik sobera?
9 Asmatu problema bat irudi honetan oinarrituta:
Zaila
Zenbat da zenbaki hauen erro kuboa?
Erro karratua zehatza ez denean, behetik hurbilen dagoen zenbakia hartu behar dugu.
49 U3
dirudi, baina ez da
3
2 2 2 3 3 3 4 4 4 5 5 5 27 64 125
Ikusi arretaz kubo hau: 2
= 8 bada, orduan 8ren erro kuboa 2 da.
10 berrekizuneko
Lurretik
berreketak
1 Adierazi berreketa hauek biderketa moduan, eta kalkulatu emaitzak:
a) 102 b) 10 4 c) 107 d) 10 9 e) 101

2 Kopiatu eta idatzi berreketa hauetako berretzaileak:
a) 10 ? = 1 000 c) 10 ? = 1 000 000
b) 10 ? = 100 000 d) 10 ? = 100 000 000
3 Idatzi zenbaki hauek 10 berrekizuneko berreketa moduan:
10 berrekizuneko berreketak
10 berrekizuneko berreketa bat zenbaki hau da: bataren atzetik berretzaileak adierazi adina zero dituen zenbakia.
3 zero
10 3 = 10 × 10 × 10 = 1 000
4 Ikusi arretaz adibidea, eta idatzi zenbaki hauek 10 berrekizuneko berreketa moduan: 36 000 = 36 × 1 000 = 36 × 103
a) 120 c) 20 000 e) 410 000
b) 8 700 d) 75 000 f ) 9 000 000
5 Kopiatu esaldiak, baina idatzi zenbakiak 10 berrekizuneko berreketa moduan:
a) Eguzkitik Lurrerainoko distantzia 150 000 000 km da. 150 000 000 km

Ohartu honetaz
Oso zenbaki handiak modu laburtuan adierazteko erabiltzen ditugu 10 berrekizuneko berreketak.
107 000 000 = 107 × 10 6


Bazenekien Google googol hitzetik datorrela?
Bada, googol edo gugol bat zenbaki hau da:
1 eta ondoren 100 zero!
b) Argiaren abiadura 300 000 000 m/s da.
c) Gorputzean 38 000 000 000 000 zelula inguru ditugu.
d) Munduan, guztira, 8 000 000 000 biztanle gara.
50
1 000 10 000 1 00 100 000 1 000 000
Ilargirainoko distantzia edo ordenagailu baten edukiera adierazteko, 10 berrekizuneko berreketak erabiltzen ditugu.
4
6 Ikusi arretaz adibidea, eta idatzi zenbaki hauen deskonposizio polinomikoa:
45 632 4 0 000 + 5 000 + 6 00 + 3 0 + 2 =

Deskonposizio polinomikoa
Edozein zenbaki deskonposa daiteke zifren posizio-balioaren arabera 10 berrekizuneko berreketak erabiliz.
Horri deskonposizio polinomiko esaten zaio.
7 Zer zenbaki dira adierazpen hauek?
a) 2 × 10 4 + 6 × 103 + 3 × 102 + 1
b) 5 × 10 6 + 9 × 103 + 8 × 102 + 7
c) 3 × 10 5 + 4 × 10 4 + 1 × 103 + 7 × 102
8 Batu Badakizu zer den notazio zientifikoa eta zertarako erabiltzen den? Ikertu, eta idatzi adibide batzuk.
Informazio-unitateak
• Noiz edo noiz galdetuko zenion zeure buruari zer esan nahi duen ordenagailu baten disko gogorrak 256 gigabyteko (GB) edukiera izateak.
Informatikan, gailu batean zenbat informazio sartzen den adierazteko, informazio-unitateak erabiltzen dira.
Informazio-unitate txikienari bit esaten zaio.
INFORMAZIO-UNITATEAK
1 byte = 2 3 bit
1 kilobyte = 103 byte

1 megabyte = 10 6 byte
1 gigabyte = 10 9 byte
1 terabyte = 1012 byte
a) Ikusi zer edukiera duen zure ordenagailu, tableta edo mugikorrak. Zenbat gigabyte bete dituzu? Zenbat geratzen zaizkizu libre?
b) Ordenagailu baten edukiera terabyte 1 bada, eta beste batena 256 GB, zein aukeratuko zenuke?
terabyte 1
256 byte
Gogoan hartu!
10 berrekizuneko berreketen bidez, Interneten erabiltzaile kopurua adieraziko dugu.

51 U3
= 4 × 10 4
5 ×
6 × 102 + 3 × 10 + 2 702 9 670 3 245 12 380 671 048 929 392
+
103 +
256 GB?
Bilatu erregulartasunak
Badakigu 10en karratua 100 dela. Hortaz, nola kalkula dezakegu zenbat den 11ren karratua biderketarik egin gabe?
Horretarako, karratu perfektuak marraztuko ditugu, eta ondoz ondokoen artean zer erlazio dagoen aztertuko dugu.
Gehitu puntuak, 2 puntuko aldea duen karratu bat egiteko.
Gehitu puntuak, 3 puntuko aldea duen karratu bat egiteko.
Gogoratu: zenbaki bat karratu perfektua bada, objektu kopuru hori karratu forman jar dezakezu.

Beraz: 10 2 + 10 + 11 = 11 2
100 + 10 + 11 = 121

11ren karratua 121 da.
Soluzioak badu zentzurik?
Egiaztatu kalkulagailuarekin 11 2 = 121 dela.

1 Kalkulatu 12tik 20ra bitarteko zenbakien karratuak biderketarik egin gabe eta kalkulagailua erabili gabe.
2 Gogoratuko duzunez, zenbaki bat triangeluarra bada, objektu kopuru hori triangelu forman jar daiteke. Hori kontuan izanda, bilatu erregulartasunak, eta aurkitu zein den hamargarren zenbaki triangeluarra.

52
EBATZI BAIETZ!
PISTA BAT! 1 1 + 2 = 3 1 + 2 + 3 = 6 1 + 2 + 3 + 4 = 10 3 2 + 3 + 4 = 4 2 4 2 + 4 + 5 = 52 52 + 5 + 6 = 6 2
Problemak arin-arinka
1
Zer da handiagoa, 3ren karratua ala 5en karratua?
Buruzko kalkulua
Adierazi berreketa moduan zenbat kubotxo dituen Rubiken kuboak.
Zer kopuru da handiagoa, 5en karratua ala 5en kuboa?
4 3 5
Adierazi 10 berrekizuneko berreketa moduan.
10 100 1000
Begira nola pentsatzen dudan
2 6
Kalkulatu 12 × 4.
Zer zenbakiren artean dago 20ren erro karratua?
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:



6 × 4

8 × 4
9 × 4
× 4
Zer unitate erabiliko zenuke agiri batek ordenagailuan zenbat leku hartzen duen adierazteko?
KB MB GB
Kodeak deszifratzen
7 × 4
× 4
Ordenagailuek kodeak erabiltzen dituzte informazioak memorian leku gutxiago hartu dezan. Adibidez, errepikatuta dauden 2 letra edo gehiago multzokatzen dituzte eta gauza bakartzat hartzen dituzte.
Kopiatu olerkia, eta inguratu errepikatzen diren letra multzoak kolore berberaz.
Hara Londres, Ingalaterra, hemeretzigarren mendea, batzuk dantz an , jolase an , Ada irakurtzen ari da.
Lord Byron du ai ta , idazle eta poe ta

Anna Isabella Noel, ama, emakume apar ta
Adak ondo du ikasia galdetzen gauzen zergatia. Arazorik sortzen bazaio, jakin-minez aurre egingo dio.
Charles Babbage lagunarekin hau argitu nahian dabil: makinarik egin liteke, bere kabuz aritu dadin?

Deskargatu olerkia, hemen: anayaharitza.es
Charlesek asmatu zuen lehena eta eraikitzen saiatu zen. Adak buruan darabil: zertarako balio dezake?
Orduan, buru-belarri, programa bat sortu zuen, makinari azaltzeko zer kalkulatu behar duen.
Makina hark azkenean ez zuen funtzionatu, baina lehen ordenagailua handik zuten sortu!
53 U3
25
35
45
4 21
4 13
4
14
× 4
×
×
×
4 = 2 × 2
24 12 × 2
2
×
MATEMAT IKA , KALAMATR IKA ? 48
Z er ikasi dut?
1 Irakurri, eta aukeratu erantzun zuzenak.
a) Zer adierazten dugu modu laburtuan berreketen bidez?
A Biderkagai berdinen arteko biderketak.
B Batugai berdinen arteko batuketak.
b) Zer da berreketa bateko berrekizuna?
A Errepikatzen den batugaia.
B Errepikatzen den biderkagaia.
c) Zer adierazten du berreketa bateko berretzaileak? Zenbat aldiz errepikatzen den…
A berreketa.
B berrekizuna.
2 Kopiatu eta osatu koadernoan.
Biderketa Berreketa Berrekizuna Berretzailea
×
3 Aurkitu multzo honetan lekuz kanpo dagoen hitza, eta azaldu zergatik.
6 Kalkulatu erro karratu hauen emaitzak:
a) √25 c) √49 e) √36
b) √100 d) √81 f ) √64
7 Idatzi berreketa hauen emaitzak:
a) 10 3 b) 10 5 c) 10 8 d) 10 10
8 Idatzi zenbaki hauen deskonposizio polinomikoak:
a) 4 505 b) 84 019 c) 700 253
9 Ikastetxera 12 kaxa iritsi dira. Kaxa bakoitzean 12 ordenagailu eramangarri daude. Zenbat ordenagailu iritsi dira guztira?
10 Eraikin batek 3 solairu ditu. Solairu bakoitzean 3 apartamentu daude, eta apartamentu bakoitzean 3 pertsona bizi dira. Zenbat pertsona bizi dira eraikinean?

berreketa berrekizuna
berretzailea
karratua kuboa triangelua
4 Adierazpen hauetatik zein da zenbaki baten karratua?
A 3 + 3 B 3 × 3 C 3 × 3 × 3
5 Adierazpen hauetatik zein da zenbaki baten kuboa?
11 Saioak lauza karratuak jarri nahi ditu bainugelako zoruan. Guztira 88 lauza baldin baditu, zenbat jarriko ditu alde bakoitzean? Zenbat geratuko zaizkio sobera?
Semaforoa. Margotu koadernoan, ariketa bakoitzaren ondoan, honela:
Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu
54
PORTFOLIOA
?
6
6 × 6 ? ? ? ? ? 8 10 ? 35 ? ?
? 4 7
A 3 × 7 B 7 + 7 + 7 C 7 × 7 × 7
HELBURUA AURRERA
Diseinatu kamiseta aldarrikatzaile bat.

Alboko taulan, Internet mundu guztian gutxi gorabehera zenbat jendek erabiltzen duten adierazi da, milioi pertsonatan.
a) Idatzi urte bakoitzeko milioi erabiltzaileen kopurua 2 berrekizuneko berreketa moduan.
b) Erregulartasunik ikusi duzu? Zein?
c) Idatzi erabiltzaileen kopuruak 10 berrekizuneko berreketak erabiliz.
d) 2002an 580 milioi erabiltzaile ziren. Aztertu ea bat datorren urtez urteko erabiltzaile-hazkundeari buruz aurkitu duzun erregulartasunarekin.
Geure buruari galdezka
Alderdi guztiak aztertu estrategia erabiliz, aztertuko dugu zergatik den garrantzitsua denok izatea eskura Internet.
a) Kopiatu eta osatu antolatzailea koadernoan.
6. arrazoia

5. arrazoia
1. arrazoia
Zergatik da garrantzitsua
Internet izatea?


2. arrazoia
3. arrazoia
4. arrazoia
b) Ikertu hemengo zer eskualdetan dituzten zailtasun handiak Internet erabiltzeko.
c) Taldeka, diseinatu kamiseta bat, informazioa izateko eskubidea denok izan behar dugula aldarrikatzeko.
N o la ikasi dut?
Osatu koadernoan.
Pentsatu unitate honetan egindako zer ariketatan sentitu zaren zeure buruaz harro. Idatzi hiru ariketa, eta azaldu zergatik sentitu zaren horrela.
Pentsatu unitate honetan egindako zer ariketatan sentitu duzun hobeto egin zenezakeela, eta idatzi hiru ariketa. Zer egin dezakezu hurrengo batean hori hobetzeko?
U3 55
Urtea Zenbat milioi erabiltzaile 1 995 1 996 1 997 1 998 16 32 64 128




Ulertu eta ezagutu zenbaki dezimaldunak
Neurri batzuk eta produktuen prezioak adierazteko eta ulertzeko, zenbaki dezimaldunak erabiltzen ditugu.
Unitatea (U) 10, 100, 1 000... zati berdinetan banatzen badugu, zati bakoitza hamarren bat (h), ehunen bat (e), milaren bat (m)... da. unitatea


unitate 1 = 10 hamarren = 100 ehunen = 1 000 milaren

Zenbaki dezimaldunek bi zati dituzte, koma batez bereizita.
zati osoa zati dezimala
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Zer zenbaki dezimaldun da margotutako zatia?
Aurren-aurrena, ohartu zenbat zati berdinetan dagoen banatuta unitatea.
2 Adierazi zatiki bakoitza zenbaki dezimaldun moduan.
3 Kopiatu eta osatu, falta diren zenbakiak idatzita.
58
1
1 h = 1 10 = 0,1 U 1 m = 1 1 000 = 0,001 U 1 e = 1 100 = 0,01 U H U h e m 1 6 3 9 5 ,
36 100 = ? : ? = ? ? ehunen dira. 580 1 000 = ? : ? = ? milaren dira. 4 10 = 4 : 10 = ? ? hamarren dira.
a) 16 10 b) 175 1 00 c) 8 1 000 d) 29 1 000 e) 703 1 000
a) ? 10 = 2,4 b) 69 ? = 0,69 c) ? 1 000 = 0,093
4 Osatu koadernoan.
a) 3 U = ? h = ? e = ? m c) ? U = 4 h = ? e = ? m
b) 12 U = ? h = ? e = ? m d) ? U = ? h = 280 e = ? m


5 Kopiatu eta osatu taula.
Zenbakia Zati osoa Zati dezimala Nola irakurtzen da?
4,625 ? ? ? ? 38 501 ? ? ? ? 90 unitate eta 6 hamarren


7,009 ? ? ?
6 Deskonposatu zenbakiak adibidean bezala.
7 H + 1 U + 5 h + 3 e + 2 m 71,532 70 + 1 + 0,5 + 0,03 + 0,002
7 Zenbat diru dago kasu bakoitzean? Adierazi zenbaki dezimaldun baten bidez.
Nola irakurri zenbaki dezimaldunak
Zenbaki dezimaldunak irakurtzeko bi modu daude:
• Bereiz irakurri zati osoa eta zati dezimala.
• Lehenbizi zati osoa irakurri eta gero dezimala, tartean koma esanda.
Gogoratu
Prezioak adierazteko, bi zifra dezimal idazten dira.
36,50 €
36 € eta 50 zm.


8 Egiaztatu Zenbat balio dezakete produktu hauek? Adierazi bakoitzaren prezioa zenbaki dezimaldun baten bidez.


9 Junek bigarren eskuko jertse bat erosi du. Irakurri pistak, eta jakin zenbat ordaindu duen.
– Prezioa 9,7 eta 9,8 zenbakien artean dago.
– Zati dezimaleko zifren batura 12 da.
Lagunek zenbat diru zor dizuten adierazteko, erabili zenbaki dezimaldunak.
59 U4
162,7 5,908 26,04 9,031
Gogoan hartu!
a) b) c) d) ?
Konparatu zenbaki dezimaldunak
Jakin nahi dugunean zer ontzitan sartzen den gehiago edo gutxiago, edo nor den altuagoa edo txikiagoa, zenbaki dezimaldunak konparatzen ditugu.
1 Kopiatu eta idatzi ikur egokia: > edo <.
a) 6,419 ? 11,2 c)
b) 786,6 ? 78,6

?
2 Adierazi multzo bakoitzeko zer zenbaki diren handiena eta txikiena.
Nola konparatu zenbaki dezimaldunak
Konparatu zenbakien zati osoak.
• Desberdinak badira, zati oso txikiena duen zenbakia da txikiena.
H U h e m
6 8 5


4 2 3 , , 6,85 < 42,3
3 Kopiatu zenbakizko zuzena.
a) Adierazi zuzenean beheko zenbakiak.
• Berdinak badira, konparatu zati dezimaletako zifrak ezkerretik eskuinera, bi zifra desberdin aurkitu arte.
H U h e m
1 5 7 9 2
b) Zer zenbaki da handiena? Eta txikiena?
4 Zer zenbaki da letra bakoitza? Zein da handiena? Eta txikiena?
1 5 7 3 4 , , 15,792 > 15,734

Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
5 Idatzi hiru zenbaki:
a) 17,5 eta 17,6 artekoak.
b) 8,43 eta 8,44 artekoak.
c) 40 eta 40,1 artekoak.
d) 28,10 eta 28,15 artekoak.
6 Zenbat zenbaki aurkitu ditzakezu 5,1 eta 5,10 artean? Arrazoitu zure erantzuna.
7 Egiaztatu Idatzi multzo bakoitzeko zifrekin egin daitezkeen zenbaki dezimaldun handiena eta txikiena. Ez ahaztu koma!
a) b)
Zuzenean eskuinean dagoen zenbakia ezkerrekoa baino handiagoa da beti.
60 2
3,28 e) 8,46 ? 8,5
3,25 ?
d) 47,9
47,36 f ) 0,2 ? 0,61
7,8 72,001 27,456 8,15 6,54 25,99 25,009 25,09 25,9 2,555 1,5 5,1 5,001 11,5 1,55
5 6 7 6,5 5,5 5,7 6,2 5,1 5,9 6,8
9,2 AB C D E 9,5 9,4 9,3
6 3 8 1 7 8 1
8 Ikusi arretaz eta erantzun.
a) Ordenatu prezioak, txikienetik handienera.
Ez erosi gauzak modu inpultsiboan. Erosi benetan behar duzuna bakarrik.
b) Demagun 15,50 € dituzula aurreztuta. Produktu horietatik zein eros ditzakezu? Behar dituzu?

9 Dantza-txapelketa batean finalistek puntu hauek lortu dituzte:

a) Nork lortu du puntu gehien?
b) Nor geratu da hirugarren?
10 Irakurri pistak, eta jakin zer altuera eta masa dituen haur bakoitzak.
• Paulo Galder baino altuagoa da, baina Iñigo baino txikiagoa.
• Iñigok 40 kg eta 50 kg bitarteko masa du.
• Paulok du masa txikiena.
Ordenatu prezioak
Ebaki 3 etiketa, eta idatzi produktu baten izena eta prezioa. Nahiago baduzu, marraztu produktua.
1. Aztertu denok denon etiketak. Prezioak zentzuzkoak diren aztertu behar duzue.
2. Ikastetxeko korridorean edo gelako leku zabal batean, antolatu ibilbide bat, etiketak prezio txikienekotik handienekora jarrita. Neurtu zenbat denbora behar izan duzuen ibilbidea prestatzeko.

3. Egin berriro ariketa. Denbora gehiago edo gutxiago behar izan duzue?


61 U4
Ainhoa Julen Ismael Eli Izarbe 8,753 9,067 8,342 9,412 8,706
1,58 m 49,33 kg 1,42 m 50,65 kg 1,56 m 39,8 kg
Biribildu zenbaki dezimaldunak
Batzuetan zenbaki dezimaldun baten ordez gutxi gorabehera
balio bera duen beste bat erabiltzen dugu, errazago gogoratzeko.
Zenbaki dezimaldun bat unitateetara biribiltzeko:
1. Adierazi zer unitateren artean dagoen, eta markatu erdiko puntua.
2. Idatzi zenbakia zuzenean, eta inguratu hurbilen dagoen unitatea.
Zenbaki dezimaldun bat hamarrenetara biribiltzeko:
1. Adierazi zer hamarrenen artean dagoen, eta markatu erdiko puntua.
2. Idatzi zenbakia zuzenean, eta inguratu hurbilen dagoen hamarrena.
Zenbaki dezimaldun bat ehunenetara biribiltzeko:
1. Adierazi zer ehunenen artean dagoen, eta markatu erdiko puntua.
2. Idatzi zenbakia zuzenean, eta inguratu hurbilen dagoen ehunena.
1 Kopiatu zuzen hau, idatzi bertan zenbakiak eta biribildu unitateetara:
3
a) 2,2 c) 1,6 e) 2,8
3,7 d) 0,4 f) 3,5
2 Idatzi zenbaki hauek zuzenean, eta biribildu hamarrenetara: 15,6 15,7 15,8
a) 15,68 c) 15,61 e) 15,79

b) 15,73 d) 15,65 f) 15,70
3 Idatzi zenbaki hauek zuzenean, eta biribildu ehunenetara: 9,71 9,72 9,73
a) 9,721 c) 9,712 e) 9,724
b) 9,726 d) 9,718 f) 9,715
62
3
0 1 2
4
b)
7,62 hamarrenetara biribilduta 7,6 da. 7,628 ehunenetara biribilduta 7,63 da. Biribildu nahi dugun zenbakia erdiko puntua bada, hautatu zenbaki handiena. 6 6,5 7 6,5 7 7,5 8 7,6 7,6 7,6 7,65 7,7 7,62 7,62 7,628 7,62 7,625 7,63 7,628 7,6 unitateetara biribilduta 8 da.
4 Ikusi arretaz adibidea. Gero, marraztu zer unitateren, hamarrenen eta ehunenen artean dauden beheko zenbaki dezimaldunak, eta markatu erdiko puntua.
Zer unitate-maila eskatu dizuten, hartu horrainoko zifrak. Hortxe duzu tartearen hasiera!
a) 2,176 c) 5,238 e) 30,82 g) 59,73


b) 12,902 d) 3,951 f ) 47,14 h) 7,69
5 Biribildu 8,147 zenbakia adierazitako unitate-mailetara.
a) Unitateetara. U h e m
8 1 4 7 ,
b) Hamarrenetara. U h e m

8 1 4 7 ,
c) Ehunenetara. U h e m
8 1 4 7 ,
6 Kopiatu eta osatu taula koadernoan.
Unitateetara biribilduta Hamarrenetara biribilduta Ehunenetara biribilduta
5,821 ? ? ?
7,572 ? ? ? 1,083 ? ? ?
7 Biribildu produktu hauen prezioak. Zer mailatara biribildu dituzu? Zergatik?
Nola biribildu edozein unitate-mailatara
1,578 hamarrenetara biribiltzeko, egin hau:



1. Adierazi zer zenbakiren artean dagoen 1,578, kontuan izanda zer mailatara hurbildu behar duzun, eta markatu erdiko puntua. 1,5 1,55
2. Idatzi zenbakia zuzenean, eta aukeratu hurbilen dagoen hamarrena.
63 U4
4 4,3 4,37 5 4,4 4,38 4,5 4,35 4,375 4,372 unitateak 4,372
4,372
hamarrenak
ehunenak
1,6
1,5 1,55 1,6
1,578
4,38 � 16,74 � 1,75� 15,18�
Batu eta kendu zenbaki dezimaldunak
Zenbat diru gastatu dugun eta zenbat geratzen zaigun kalkulatzen badugu, batuketak eta kenketak eginez, errazagoa da arduraz kontsumitzea.
1 Kopiatu eta kalkulatu.
2 Jarri zenbakiak bata bestearen azpian, eta kalkulatu.
a) 92,6 + 6,302
c)
+ 13,4 + 38,75
3 Kopiatu eta idatzi falta diren zifrak.
4 Kalkulatu falta diren gaiak koadernoan. a) 8,32 + ? = 11,2
= 68,19
5 115,63ri zer batu behar zaio 346,85 izateko?
6 Kalkulatu. a) 2,85 − 1,3 + 3,04

b) 7,002 − (1,8 + 5,12)

13,1 + 1,04 − 10,25
7 Kalkulagailua erabiliz, jakin zer zenbaki diren kasu bakoitzean.
Nola egin batuketak edo kenketak zenbaki dezimaldunen artean
Zenbaki dezimaldunen arteko batuketak edo kenketak egiteko, egin urrats hauek:
1. Idatzi zenbakiak bata bestearen azpian, komak pare-parean geratzeko moduan.
Zifra dezimalak falta badira, idatzi zeroak.
2. Egin eragiketa, eta idatzi koma emaitzan, zati osoa eta zati dezimala bereizteko.
Gogoratu
Batuketak eta kenketak dituzten adierazpenak ebazteko:
1. Kalkulatu parentesien barruan dauden eragiketak.
2. Kalkulatu batuketak eta kenketak, ezkerretik eskuinera.
a) Zenbaki horietako biren batura 47,25 da.
b) Zenbaki horietako hiruren batura 21,687 da.
c) Handienari zenbaki horietako bat kentzen badiogu, emaitza 24,76 da.
Kalkulagailuan koma dezimala idazteko, sakatu tekla hau:
64
7 0 , 1 2 2 + 8 , 3 9 4 2 , 1 5 7 1 5 9 , 4 1 + 6 , 7 9 9 2 , 3 8 1 8 , 1
d) 51,43 −
8,2
e) 421,5 − 4,81
b) 80,36 + 15,2
f ) 5,3 − 0,006
5,102
2
3
4 7 , ? 1 ? , 3 ? 1 ,
7 ? , 4
4 , ? 1 + ? 2 , 1 3 ? 7 1 , 7 ?
5
d) 17,23
e) ? − 0,2 = 0,05
f ) 3,6 − ? = 1,5
− ? = 9,66 b) ? + 54,21
c) 196,4 + ? = 869,1
c) 9 − (3,4 − 2,65)
d)
43,04
0,007 18,28
3,4 28,97
4
5 2 , 7 0 1 3 , 4 8 1 2 , 7 1 + 4 2 , 0 9
1 2 , 7 1 + 4 2 , 0 9 5 4 , 8 0 5 2 , 7 0 1 3 , 4 8 3 9 , 2 2
8 Mikelek asteko paga gordeta dauka, lagunekin zinemara joateko. Zenbat ordainduko ditu zinemako sarrera, krispetazorro bat eta ur-botila bat?
Zinemara joaten zarenean, erosi egiaz jan eta edango duzuna bakarrik. Eta krispetak partekatzen badituzu?

10,50 € 3,15 € 0,85 €

9 Irenek 370,5 g fruitu lehor erosi ditu, eta Pellok, Irenek baino 80,75 g gutxiago.
a) Zenbat gramo erosi ditu Pellok? ? 80,75
370,5





Ebatzi urratsez urrats, hemen: anayaharitza.es
b) Zenbat gramo erosi dituzte bien artean?
10 Maddik eta Esterrek beren sokak elkartu dituzte, 6,54 m-koa bata eta 8,3 m-koa bestea, korapiloa eginda. Zer luzera du orain sokak, korapiloa egiten 0,7 m galdu badira? 6,54 ? ?

8,3 0,7
11 Anddek 30 € zituen etxetik atera denean. Fruta-dendan

18,20 € gastatu ditu, eta okindegian, 5,75 € . Zenbat diru geratzen zaio? 30 ? ?
18,20 5,75
Gogoan hartu!


Janari-dendako erosketa zenbat ordaindu duzun kalkulatzeko, erabili zenbaki dezimaldunak.

65 U4
Biderketa zenbaki dezimaldunen artean
Erosketa guztira zenbat izango den edo astebetean zenbat kilometro egin ditugun kalkulatzeko, zenbaki dezimaldunak biderkatu behar ditugu.
Nola egin biderketak zenbaki dezimaldunen artean
Zenbaki dezimaldunen arteko biderketak egiteko:
1. Egin biderketa, komarik ez balego bezala.
5 , 1 8 × 3 , 4
2 0 7 2 + 1 5 5 4
1 7 6 1 2
2. Biderkaduran, bereizi koma batez, eskuinetik hasita, bi biderkagaiek dituzten dezimal adina zifra.
5 , 1 8 × 3 , 4
2 0 7 2 + 1 5 5 4
1 7 , 6 1 2
eta kalkulatu. 4,12 × 200 = 4,12 × 2 × 100 = 8,24 × 100 = 824 ▲
a) 6,2 × 20 c) 5,1 × 500 e) 13,5 × 8 000
b) 4,6 × 30 d) 7,22 × 400 f ) 20,5 × 6 000


6 Lapitzak erdira Ebatzi adierazpen hauek, eta egiaztatu emaitzak kalkulagailuarekin:
a) (8,6 − 2,8) × 1,2 c) 23,5 − 9,6 x 2,4
b) 3,5 x 0,4 + 12,6 d) 0,08 × 5,5 + (9,2 − 1,1)
Gogoratu
zifra dezimal 1
2 zifra dezimal 3 zifra dezimal
Zenbait eragiketa dituzten adierazpenak ebazteko, kalkulatu ordena honetan:
1. Parentesien barruko eragiketak.
2. Biderketak.
3. Batuketak eta kenketak, ezkerretik eskuinera.

66 1 Eragiketarik egin gabe, lotu biderketak eta biderkadurak. Adi! Zenbaki arruntek 0 zifra dezimal dituzte. 6,37 × 1,8 10,81 4,7 × 2,3 7,6 1,9 × 4 11,466 2 Kalkulatu koadernoan. 5 1 , 9 × 6 5 , 6 2 × 1 , 8 3 4 3 1 , 8 × 0 , 4 0 , 0 1 6 × 1 , 2 3 Kalkulatu bertikalean, eta hurbildu emaitzak hamarrenetara. a) 7,13 × 4 b) 45,03 × 2,2 c) 15,8 × 5,6 4 Gogoratu eta kalkulatu. 2,56 × 10 = 25,6 2,56 × 100 = 256 2,56 × 1 000 = 2 560 ▲ ▲ ▲ a) 8,3 × 10 d) 9,2 × 100 g) 4,4 × 1 000 b) 6,45 × 10 e) 0,38 × 100 h) 1,87 × 1 000 c) 0,79 × 10 f ) 8,103 × 100 i) 5,032 × 1 000 5 Ikusi arretaz adibidea,
5
12,40 × 0,5 × 0,25 × 0,1 × 0,01 × 0,5 × 0,25 × 0,1 × 0,01




? ? ? ?
? ? ? ?

8 Superheroien mozorro bat egiteko, Anttonek 3,25 m oihal behar ditu.

3,25 3,25 3,25 3,25 3,25 ?
3,25 3,25 3,25 3,25 3,25 3,25 3,25 3,25 3,25 3,25
?
Ebatzi urratsez urrats, hemen: anayaharitza.es

9 Mariari astero 7,50 € -ko paga ematen diote, eta Eduri, berriz, hilean behin 30,20 € . Nori eman zioten diru gehiago joan den hilean? Zenbat gehiago?
7,50
4 30,20
0,75
100

11 Manex asteartero eta ostegunero entrenatzera joaten da 0,525 km-ko zirkuitu batera. Saio bakoitzean 10 bira egiten ditu. Zenbat kilometro egiten ditu astean?
Lehenbizi, kalkulatu zenbat litro olio erosi dituzten.

Gogoan hartu!
Zenbait produkturen guztizko prezioa kalkulatzeko, biderkatu zenbaki dezimaldunak.
67 U4
8,8 1,5
7 Pentsatu eta binaka jarrita komentatu Binaka jarrita, osatu segida hauek, eta aztertu emaitzak:
213
a) Zenbat metro behar ditu horrelako 5 mozorro egiteko?
b) Eta 10 mozorro egiteko?
10 Ikastetxe bateko jantokian 0,75 L-ko 100 botila olio erosi dituzte. Litro bat oliok 4,70 € balio badu, zenbat ordaindu dute erositako olio guztia? 4,70
? ?
Zer gertatzen da zenbaki bat bider 0,5 egiten badut?
? ?
Zatiketa: zenbaki dezimaldun bat zati zenbaki arrunt bat
Produktu bat zenbaiten artean erosi eta bakoitzak zenbat jarri
behar duen jakiteko, zenbaki arrunt batez zatitu behar da.
28,5 m-ko soka bat 5 zati berdinetan banatzen badugu, zenbat metro izango ditu zati bakoitzak?
Hori jakiteko, zatiketa hau egin behar da: 28,5 : 5.
1. Banatu zati osoa.
H U h
2 8 , 5 5 3 5
Zati bakoitzak 5,7 m izango ditu.
1 Kalkulatu zatiketa hauen zatidurak:

28,5 m
2. Hamarrenen zifra behera jaitsitakoan, idatzi koma zatiduran, eta jarraitu zatiketa egiten.
H U h

2 8 , 5 5
3 5 5 , 7 0
Ohartu honetaz
a) 89,5 : 5 b) 75,08 : 8 c) 7,776 : 24 d) 353,4 : 38
2 Gogoratu eta ebatzi.
3,2 : 10 = 0,32 3,2 : 100 = 0,032 3,2 :

000 = 0,0032
a) 75,8 : 10 b) 13 : 100 c) 34,7 : 100 d) 4,9 : 1 000



3 Egiaztatu zatiketa hauek ondo eginda dauden, zatiketaren proba aplikatuz:
zatikizuna = zatitzailea × zatidura + hondarra 7
4 Banatu.
a) 7,58 kg fruta 2 poltsatan. b) 10,5 L ur 6 pitxerretan.
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
Ohartu honetaz
0,1
7,58 kg
10,5 L ?
?
Ebatzi urratsez urrats, hemen: anayaharitza.es
68
▲ ▲ ▲
1
1 5 , 5 9 8 5 7 9 , 5 4 5 0 6 , 8 2 5 1 8 1 , 3 6 3 2 2 9 8 , 7 8 2 1 6 7 1 , 2 3
6
U
e 3
h
, 6 8 4 3 6 0 , 9 2 0 8 0
U h 5 , 3 2 1 3 2
6
,
1 hondarra:
Zatiketa: zenbaki arrunt bat zati zenbaki dezimaldun bat
Litro eta erdiko zenbat ontzi bete daitezkeen jakin nahi badugu, zenbaki dezimaldun batez zatitu behar da.
1,5 L-ko zenbat botila bete daitezke bidoi horretako olioarekin?

Hori jakiteko, zatiketa hau egin behar da: 39 : 1,5.
1. Ikusi zenbat zifra dezimal dituen zatitzaileak, eta bataren atzetik zifra kopuru hori adina zero dituen zenbakiaz biderkatu zatikizuna eta zatitzailea.
2. Egin zatiketa aurreko urratsean lortutako zenbakien artean.
3 9 0 1 5
9 0 2 6 0
26 botila bete daitezke.
1 Biderkatu zatikizuna eta zatitzailea 10ez, eta kalkulatu.
a) 18 : 1,2 b) 27 : 0,5 c) 72 : 4,5
2 Biderkatu zatikizuna eta zatitzailea 100ez, eta kalkulatu.
a) 74 : 0,02 b) 42 : 0,35 c) 555 : 1,25
3 Kalkulatu falta diren gaiak.
a) 2,4 × ? = 672 b) 7,2 × ? = 1 512 c) 6,38 × ? = 638







4 Lotu adierazpen bakoitza dagokion emaitzarekin.
:
5 Pentsatu eta binaka jarrita komentatu Irakurri eta ebatzi.
a) 2,50 € -ko zenbat marmelada-poto eros ditzaket 15 € baldin baditut?
15
Gogoratu
Zenbait eragiketa dituzten adierazpenak ebazteko, kalkulatu ordena honetan:
1. Parentesien barruko eragiketak.
2. Biderketak eta zatiketak, ezkerretik eskuinera.
3. Batuketak eta kenketak, ezkerretik eskuinera.
2,5
b) 0,5 kg-ko zenbat poltsa prestatu ditzaket 5 kg fruitu lehor baditut? 0,5

5
5 kg
Ebatzi urratsez urrats, hemen: anayaharitza.es
69 U4
7
75 4,06 32,14 18,14
63
4,5 10,06 − 15 : 2,5 (7,68
10,32)
0,24
+
+
:
3 90 1 5 1 , 5 × 10 × 10 39
Zatiketa zenbaki dezimaldunen artean
Zenbaki dezimaldunen arteko zatiketak egiten jakinda, errazago
kalkula dezakegu gure fruta gogokoenaren kiloa zenbatean dagoen.
0,15 m-ko zenbat begizta egin ditzakegu biribilki honetako zintarekin?
Hori jakiteko, zatiketa hau egin behar dugu: 2,7 : 0,15.
1. Ikusi zenbat zifra dezimal dituen zatitzaileak, eta bataren atzetik zifra kopuru hori adina zero dituen zenbakiaz biderkatu zatikizuna eta zatitzailea.
0 , 1 5 × 100 × 100


15
18 begizta egin ditzakegu.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Egin zatiketa hauek, hondarra zero izan arte:
a) 3,63 : 0,03 c) 6,8 : 2,5 e) 9,6 : 1,2
b) 1,42 : 0,25 d) 1,4 : 0,7 f ) 0,78 : 0,12
2 Kalkulatu, zatiduran bi zifra dezimal izan arte.
a) 5,65 : 3,5 b) 3,3 : 0,4 c) 7,18 : 4,3

3 Zatiketak egin gabe, erantzun: zeinek du zatidura handiena, zure ustez? A
4 Irakurri eta ebatzi.
a) Zenbat balio du kilo bat mandarinak?
b) Bolaluma batek 1,28 € balio badu, zenbat bolaluma eros ditzakegu 5,40 € -rekin? Zenbat diru geratuko zaigu?

Ikertu kalkulagailuarekin
Egin zatiketa hauek kalkulagailuarekin:
Nolakoak dira zatidurak? Taldeka, ikertu nola esaten zaien horrelakoei eta zer patroiri jarraitzen dioten.
Gogoan hartu!
Geratzen zaizun diruarekin zenbat ur-botila eros ditzakezun jakiteko, egin zenbaki dezimaldunen arteko zatiketa.
70
8
5 6 2 , 3 B 1 8 , 5 6 2
3 C 1 8 , 5 6 3 , 2
,
,
8
2,7
270
2
1 5 1
2,7
2. Egin zatiketa aurreko urratsean lortutako zenbakien artean.
7 0
2 0 1 8 0
m
0,1
0,4
1,1 1,3
0,6
: 0,3
:
:
Zatiketak zatidura dezimaldunekin
Banaketa bat egindakoan zatidura dezimalduna bada, bakoitzari zehatz-mehatz zenbat dagokion jakin dezakegu.
Zatiketa hau egingo dugu: 59 : 7.
Zatiduran zifra dezimalik
zatidura: 8
zatidura: 8,4
zatidura: 8,42
Nola banatu ditzaket 59 € 7 pertsonaren artean?
3


0,2

hondarra: 0,06
1 Egin zatiketak, zatiduran adierazitako zifra dezimalen kopurua izan arte. Gero, idatzi bakoitzaren zatidura eta hondarra.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
2 Zer dela eta diozu hori? Zer madalena-zorro erosiko zenuke? Zergatik?
3 Marenek 2 € ordaindu ditu 20 fotokopia.
a) Zenbat kostatu zaio fotokopia bakoitza?
b) 36 fotokopia egiten baditu, zenbat kobratuko diote?
Asmatu problemak

Moztu orri bat erditik. Zati bakoitzean, idatzi eta irudiztatu problema dibertigarri bat, kontuan izanda zenbaki dezimaldunak izan behar dituela.
Gorde problema hori ikaskideek asmatu dituzten beste problemekin batera. Problema-bilduma bat egin duzue!
Erabili bilduma hori berrikusketa moduan.

71 U4 9
Zifra dezimal 1 39 : 6 97 : 4 2 zifra dezimal 64 : 7 201 : 92 3 zifra dezimal 451 : 8 125 : 42
hondarra:
hondarra:
ez Zatiduran zifra dezimal bat Zatiduran bi zifra dezimal H U h e 5 9 7 3 8 H U h e 5 9 7 3 0 8 , 4 2 H U h e 5 9 7 3 0 8 , 4 2 2 0 6
EBATZI BAIETZ!

Kalkulatu soluzioa iritzira

Aritzek zapatilak oparitu nahi dizkie hiru ilobei.
Maddi txikiari, lokarririk gabeak eta euritakoak, eta Aner eta Oier bikiei, oihalezkoak eta baxuak. Beretzat ere erosiko ditu: altuak eta larruzkoak. Zenbat ordainduko du guztira, gutxi gorabehera?
Oihala Larrua Euritakoak
12,95 € 15,50 € 22,45 €
Lokarririk gabe
Baxuak Altuak
14,50 € 18,20 € 26,95 €
18 € 23,70 € 29,85 €

Gutxi gorabeherako prezioa kalkulatzeko:
1. Bilatu taulan zapatilen prezioa.
Lokarririk gabe eta euritakoak 22,45 €
Baxuak eta oihalezkoak 14,50 €
Altuak eta larruzkoak 23,70 €


2. Biribildu prezioak.
22,45 € 22 € 14,50 € 15 € 23,70 € 24 €
3. Kalkulatu zenbat ordainduko duen gutxi gorabehera.
22 + 15 × 2 + 24 = 22 + 30 + 24 = 76
Guztira 76 € ordainduko du, gutxi gorabehera.
Soluzioak badu zentzurik?
Kalkulatu zenbat ordainduko duen benetan, eta egiaztatu soluzio hori eta kopuruak biribilduta lortu duzuna antzekoak direla.
22,45 + 14,50 × 2 + 23,70 = 75,15 €
1 Aritz iritziz aldatu da, eta erabaki du Oierri gehiago gustatuko zaizkiola euritakoak diren zapatila altuak.
a) Kalkulatu iritzira zenbat ordainduko duen orain.
b) 5,95 € -ko deskontua egiten badiote, baina bidaltzeagatik 2,50 € kobratzen badiote, zenbat ordaindu beharko du, gutxi gorabehera?

2 Aukeratu lagunei oparituko zenizkiekeen zapatila pare batzuk, eta kalkulatu iritzira zenbat ordaindu beharko zenukeen.
Soluzioa egiaztatzeko, kalkulagailua erabil dezakezu, nahi baduzu.
72
Problemak arin-arinka
2 1
Zein da zifra hauekin eratu daitekeen zenbaki dezimaldun handiena? Eta txikiena?
9 5 1

Asmatu istorio bat eragiketa honetan oinarrituta:
Buruzko kalkulua
Kalkulatu 48 : 4.
4 3
Zenbaki bat bider 0,5 egitea zer da, 2z zatitzea ala 4z zatitzea?
× 0,5
5
Zer esan nahi du zatiketa honen
Patroi bila
Zenbaki bat bider 0,25 egitea zer da, 2z zatitzea ala 4z zatitzea?
× 0,25
6
Asmatu zatiketa bat, kontuan izanda zatidurak zenbaki hau izan behar duela:
15,698
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:





40 : 4
44 : 4
60 : 4
64 : 4
Ordenatu laukiko objektuak prezioaren arabera, quicksort metodoa erabiliz.

Deskargatu informazioa anayaharitza.es webgunean, eta ordenatu txartelak.
1. Aukeratu objektu bat, edozein; horri pibot esango diogu.
2. Konparatu beste objektuen prezioak banan-banan.
– Prezioa pibotarena baino txikiagoa bada, jarri haren ezkerrean.
– Prezioa pibotarena baino handiagoa bada, jarri haren eskuinean.
3. Aukeratu alde bakoitzean beste pibot bat, eta egin berriro urrats berberak, txartel guztiak prezioaren arabera ordenatuta izan arte.



73 U4
8 , 2 5 2 0 2 4 , 1 2 0 5 1
hondarrak?
80 : 4
4
: 4 200 : 4 240 : 4
84 : 4 88 :
100
4 = 2 × 2 24 48 : 2 : 2 12
21 € 2,99 € 34 € 15 zm. 17,05 € 28 € 75 zm. 95 zm. 8,01 € 75 zm. 39,95 zm. 18,15 zm. 38,25 € 1,99 € 50–23,99 Begira nola pentsatzen dudan
Z er ikasi dut?
1 Deskonposatu zenbaki hauek:
a) Hamabost unitate eta bederatzi hamarren.
b) Zazpi unitate eta hogeita hiru ehunen.
c) Laurogeita hemeretzi ehunen.
d) Ehun eta zortzi unitate eta sei ehunen.
2 Adierazi lau zenbaki hauek zenbakizko zuzen berean: 3,29 3,25 3,21 3,27
3 Biribildu. Unitateetara Hamarrenetara 2,36 € ? ? 17,58 € ? ? 5,14 € ? ? 81,89 € ? ?
4 Ordenatu eragiketa hauen emaitzak, txikienetik handienera:
a) 18,06 + 273,5 + 0,04
b) 307,6 − 16,54
c) 62,1 × 0,5
d) 5 × 6,3
5 Ebatzi.
a) (4,2 + 15,63) × 0,5
b) 13,26 + 4,38 : 2
c) 831,5 : 100 − 4,7 × 0,1
6 Kalkulatu buruz.
a) 6,4 × 10 d) 7,59 : 10
b) 83,5 × 100 e) 93,7 : 100
c) 0,07 × 1 000 f ) 451,4 : 1 000
7 Kopiatu eta osatu taula.
8 Paulok eskolako materiala erosi du: koaderno bat, 1,23 € -an; errotuladoreak, 3,85 € -an, eta arkatz bat, 0,82 € -an. Dendariari 10 € -ko billete bat eman badio, zenbat itzuli dio hark?
9 Sorta hauetatik zeinetan ateratzen da merkeago esne-brika?
10 Banatu.
a) 24,6 km, hiru etapa berdinetan. Zenbat kilometro egin behar dira etapa bakoitzean?
b) 1,5 L-ko 8 botila freskagarri, 0,25 L-ko edalontzitan. Zenbat edalontzi bete daitezke?
c) Padel-pista alokatzea 27,40 € -an, lau lagunen artean. Zenbat ordaindu behar du bakoitzak?
d) Noraren etxetik eskolara dauden 300 m-ak, 0,5 m-ko urratsetan. Zenbat urrats egin behar ditu Norak eskolara iristeko?
Semaforoa. Margotu koadernoan, ariketa
bakoitzaren ondoan, honela: Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu
74
PORTFOLIOA
zk ? 54,42 30,79 33,9 zt 3 6 25 1,4 zd 26,8
1,23 ? h
?
0,2 0 ? 0,06
HELBURUA AURRERA
Eztabaidatu dezagun pagari buruz eta paga arduraz erabiltzeaz.
Gaur parkean emango dugu arratsaldea. Hara joan baino lehen, janari-dendara joan gara, eta hau erosi dugu:
a) Zenbat ordaindu dugu guztira?
b) Nik ordaindu dut, eta gero kontuak egin ditugu. Ura Julek, Danelek, Liamek eta Thiagok nahi zuten; pipitak, Mattinek, Liamek eta nik; eta gominolak guztiontzat ziren. Zenbat diru eman behar dit bakoitzak?
c) Niri 1,50 € geratzen zaizkit. Zenbat ur-botila eros ditzaket?

Geure buruari galdezka
Arrazoitu, oztopatu, erantzun, laburbildu estrategia erabiliz, aztertuko dugu nerabeei paga emateak zer alde on eta txar dituen. Erabaki zuk zer iritzi duzun (aldekoa edo kontrakoa), eta bilatu zure iritzi berekoa den bikotekide bat.
a) Kopiatu eta osatu antolatzailea.
b) Denon artean eztabaidatu ondoren, aldeko eta kontrako arrazoiak emanez, jaso idatziz ondorioak eta dirua arduraz erabiltzeko aholkuak. Gero, azaldu hori guztia gelan.
N o la ikasi dut?
Osatu koadernoan.
Laburbildu
Atera ondorioak, familiei emateko aholku moduan: bai pagari buruz, bai arduraz kontsumitzeari buruz.
Arrazoitu
Zergatik uste duzu BAI eman behar dela edo EZ dela eman behar?
Eragozpenak jarri Zure ustez, zer arrazoi dituzte kontrako iritzia dutenek?
Pentsatu unitate honetan zer akats egin dituzun behin bakarrik eta, gero, zuzendu. Identifikatu hiru.

Identifikatu unitate honetan edo beste batzuetan behin baino gehiagotan egin dituzun hiru akats. Zergatik egin dituzu berriro? Zer egin dezakezu berriro ez egiteko?



U4 75
1,69 � 0,60 � 0,60 �
EZ? Erantzun
horiei erantzuteko arrazoiak. 1,69 � 0,22 � 0,22 0,22 � 0,22 � 0,60 �
PAGA BAI ALA
Prestatu




76 BERRIKUSPENA 1
2
Osatu segida koadernoan.
Kopiatu, eta idatzi zenbakiak dagokien lekuan.
8 8 + 2 × 5 25 − 4 × (3 + 2) + 5 ? ? 6 × 6 − 40 : 2 ? 3 × (8 + 2) − (20 − 10) ? 3 3 − 4 2 + 3 ? 92 − 10 × 7 + 1 ? 11 × 6 : 2 − 3 × 3 ? 6 2 − √49 × 2 + √16 ? √64 × 4 − 2 × 5 ? √81 + √25 − √100 + 2 2 ? 10 12 14 16 18 20 22 24 26 ? A
Zein da ondoz ondo dauden zenbaki pare bakoitzaren multiplo komun txikiena?
Ismaelek egunkaria idazten du. Oraintxe 5. orrialdearen erdian badago, zenbat orrialde idatzi ditu?







A 4,5 orrialde.
B 5,5 orrialde.
C Ia 6 orrialde.

Zeroak garrantzitsuak dira, baina… beti dira beharrezkoak?
Jakin nor den zientzialari misteriotsua

Gure zientzialari misteriotsuak zerikusi handia du zenbaki hauekin. Pistei jarraituta, nor den jakingo duzu:
Pistak

Parisen jaio zen, 1776an.

Bere lanak ezizen batekin sinatu zituen.
Zenbaki hauek
zenbaki lehenak dira, baina bereziak, baldintza bat betetzen baitute: 2z biderkatu eta unitate bat batuz gero, emaitza ere beste zenbaki lehen bat da.

Matematika bere kabuz ikasi zuen.
Pariseko Zientzien Akademiak Matematikako Aparteko Saria eman zion.
Eskaneatu, eta jakin nor den zientzialari misteriotsua

HIRUHILEKOA
7
sTEAM
5 6
1 000 36,70 00,5 9 120 0,200 4076 0,85 0,301 0438
Kopiatu zenbakiak, eta ezabatu behar ez diren zeroak.
77
EZAGUTU DIZIPLINARTEKO PROIEKTUA
KUTXA LOGIKOA
Sortu ditzagun joko logiko-matematikoak, garuna lantzeko.
Zer joko matematikok laguntzen digute buru-jarduna osasuntsu mantentzen? Sortu ditzagun geure jokoak!
Denon artean, saiatu gaitezen galdera hauei erantzuten:
Zer dakigu gorputz-osasunaz?
1 T hink P ENTSATU D esign 2 DISEINA T U

Eta buruko osasunaz? Zertan dira desberdinak eta zertan antzekoak?

Ezagutzen duzu joko matematikorik?
Zer joko logiko-matematikok dute eragin positiboa garunean?
Animatzen zara estimulazio kognitiboa lortzeko joko batzuk sortzen?
Bazenekien arreta, arrazoiketa eta beste hainbat gaitasun mental landu daitezkeela estimulazio kognitiboaren bidez?
Logikaren eta matematikaren erabileran oinarritutako jokoak sortu nahi ditugu, gure garuna estimulatzen laguntzeko.
Taldeka, ikertu mota horretako jokoei buruz. Harritu egingo zara, ikusiko duzu! Izan ere, orain arte horietako askotan ibiliko zinen, baina zertarako ziren jakin gabe!
Aukeratu gehien gustatzen zaizkizuenak eta egiteko errazak iruditzen zaizkizuenak.
Ondo aztertu zuen proposamenak benetan egiteko modukoak diren!
Komentatu denon artean talde bakoitzak aukeratutakoak. Joko guztietan ibiltzeko gogo itzela sortuko zaizue, seguru!
Kutxa magikoa eta haren zaintza 78
ITZALAPROIEKTUAK UZTENDUTEN
Garrantzitsua da denon artean erabakitzea talde bakoitzak zein aukeratuko duen. Hartara, ez da jokorik errepikatuko, eta kutxa matematikoa egongo den gure txokoan era askotako joko ederrak izango ditugu. Joko bakoitzerako zenbait zailtasunmaila pentsa ditzakezue. Jokoak edozein adinetarako egokiak izatea nahi dugu!


Garuna beti zaindu behar da, adin guzti-guztietan! Ekin lanari! Zer material behar duzue? Jokoaren arauak idaztea ere garrantzitsua izango da.
Iritsi da une gogokoena: Taldean sortu dugun jokoa besteei erakutsiko diegu!

Garrantzitsua izango da jokoari izen bat jartzea, arauak idatzita edukitzea eta ulertzen errazak izatea, gure jokoak egongo diren txokoa apaintzea eta, batez ere, jolasten hastea!
Eta gure familiakoak gonbidatzen baditugu joko logiko-matematikoen txokoa ikustera?
Zer sentitzen dut talde-lanean aritzen garenean?
1. HIRUHILEKOA 79 3 M
EGIN 4 PRESENTA
EGIAZTAT
aker
S tage AURKEZTU T est
U 5

1 5 9
2 6 10

3 7 11
4 8 12
Zenbakiak eta eragiketak Zaindu bizia
Multiploak eta zatitzaileak
Besarkatu bakea
Berreketak Konektatuta
Zenbaki dezimaldunak eta eragiketak Kontsumitu arduraz
Zergatik da beharrezkoa zuhaitzak zaintzea?
Egin biziaren zuhaitz bat, natura zaintzearen aldeko mezu eta guzti.
Lehorreko bizitza
Zatikiak eta eragiketak Elkarrekin hobeto
Sistema metriko hamartarra Zientzialari izan nahi?
Ehunekoa eta proportzionaltasuna Antolatu zure aisialdia
Angeluak eta angeluen neurria Marraztu, zaintzeko
Poligonoak Aldeen garrantzia


Irudi zirkularrak Ni, zu, gu... Denok berritzaile
Gorputz geometrikoak Itsasoa zaintzeak saria du
Zoria eta probabilitatea Etorkizuna iragartzea
Zergatik da garrantzitsua bakea lortzearen alde jardutea?
Eraiki bakea besarkadekin: diseinatu kanpaina bat, 8 segundoko besarkadak sustatzeko.
Zergatik da garrantzitsua denok izatea eskura Internet?




Diseinatu kamiseta bat, informazioa izateko eskubidea denok izan behar dugula aldarrikatzeko.
Zer esan diezaiekegu ikaskideei arduraz kontsumitzea gomendatzeko?
Eztabaidatu dezagun ea paga eman behar den edo ez eta zer egin behar den paga arduraz erabiltzeko.
Bakea, justizia eta erakunde sendoak
Industria, berrikuntza eta azpiegitura
Ekoizpen eta kontsumo arduratsua
Nola egin dezakegu bat gure artean, elkartuta aritzeko? Sortu ELKARTU!, jendeak helburu berberen alde bat eginda jarduteko gunea.
Nola eman dezakegu jakitera denok ez ditugula ikasteko aukera berberak? Egin dezagun literatura-lehiaketa bat, izenburu hau duena: Zientzialari izan nahi dut
Zer gertatuko da zure adineko jendeak aisialdi guztia gailu teknologikoak erabiltzen ematen badu? Prestatu teknologiarekin zerikusirik ez duen aisialdi-plan alternatibo bat zure adineko neska-mutilentzat.
Nola kontzientziatu dezakegu jendea ura zaindu beharraz?
Marraztu logo bat, ura zaintzea sustatzeko.





Zer beste emakumek egin dituzte ekarpen garrantzitsuak matematikaren esparruan?
Adierazi denbora-lerro batean emakume matematikarien datu pertsonalak eta ekarpenak.
Nola treba dezakegu sormena gaur egungo arazoei erantzun berritzaileak emateko?
Neurtu zure sormena!
Zer egin dezakegu gure itsasoak zaintzeko?
Egin trofeo bat irudi geometrikoekin, itsasoa zaintzearekin lotutako jardunbide onak saritzeko.
Zer egin dezakegu klima-aldaketa geldiarazteko?
Egin infografia bat, klima-aldaketa geldiarazteko zenbait gomendio emateko.
Itunak, helburuak garatzeko
Kalitate oneko hezkuntza
Osasuna eta ongizatea
Edateko ura eta saneamendua
Generoberdintasuna
Industria, berrikuntza eta azpiegitura
Uretako bizitza
Klima babesteko ekintza
OR. Zer ikasiko dugu?
IKASKUNTZA-EGOERA HELBURUA AURRERA GJH DIZIPLINARTEKOA
8 80 152 24 100 168 42 116 184 56 132 202
3. HIRUHILEKOAREN BERRIKUSPENA STEAM: Clara Grima
1. HIRUHILEKOAREN BERRIKUSPENA STEAM: Sophie Germain
2. HIRUHILEKOAREN BERRIKUSPENA STEAM: Grace Hooper
OINARRIZKO JAKINTZAK EBATZI BAIETZ!
• Zenbaki-sistema hamartarra. Zenbatzeko teknikak.
• Oinarrizko eragiketak zenbaki arruntekin. Propietateak.
• Eragiketa konbinatuak.
• Zenbaki baten multiploak. Multiplo komun txikiena.
• Zenbaki baten zatitzaileak. Zatitzaile komun handiena.
• Zenbaki arrunt baten berreketa.
• Karratuak eta kuboak.
• Erro karratua.
• Hamarrenak, ehunenak eta milarenak. Zenbaki dezimaldunak: irakurtzea, idaztea eta posizio-balioa. Prezioak.
• Zenbaki dezimaldunak konparatzea eta ordenatzea.
• Zenbaki positiboak eta zenbaki negatiboak.
• Konparatzea eta ordenatzea.
• Koordenatu kartesiarrak.
• Problema aritmetikoak: aldaketa-, berdinketaeta konparazio-problemak.
• Zatigarritasun-irizpideak.
• Zenbaki lehenak eta zenbaki konposatuak.
• 10 oinarriko berreketak.
• Deskonposizio polinomikoa.
• Zenbaki dezimaldunak biribiltzea. Zenbaki dezimaldunen arteko batuketak, kenketak, biderketak eta zatiketak.
• Problema aritmetikoak: konparazio-, banaketa- eta multzokatze-problemak, eta multzo berdinak
• Estrategia heuristikoa: Deszifratu kodeak.
• Buruzko kalkulua: 4z biderkatzea.
• Pentsamendu konputazionala: Deskonposizioa.
• Estrategia heuristikoa: Bilatu erantzun posible guztiak.
• Buruzko kalkulua: 20z biderkatzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Bilatu erregulartasunak.
• Buruzko kalkulua: 50ez biderkatzea.
• Pentsamendu konputazionala: Kodetzea.
• Estrategia heuristikoa: Kalkulatu soluzioa iritzira.
• Buruzko kalkulua: 4z zatitzea.
• Pentsamendu konputazionala: Deskonposizioa.
DIZIPLINARTEKO PROIEKTUA · Kutxa magikoa eta haren zaintza: Kutxa logikoa
• Zatikiak. Zatikia eta unitatea. Zatiki propioak eta inpropioak.
• Kopuru baten zatikia.
• Zatiki baliokideak. Zatiki laburtezina.
• Zatikiak konparatzea.
• Luzera, edukiera, masa, azalera eta bolumena adierazteko neurri-unitateak.
• Unitate-aldaketak.
• Magnitude proportzionalak.
• Unitatera laburtzea. Hiruko erregela.
• Ehunekoak. Kopuru baten ehunekoa.
• Angeluen sailkapena, zabaleraren eta kokapenaren arabera.
• Angeluak neurtzea: graduak, minutuak eta segundoak.
• Zatikien arteko batuketak, kenketak, biderketak eta zatiketak.
• Problema aritmetikoak: konbinazio-, aldaketaeta multzokatze-problemak, biderketazko konparaziokoak eta multzo berdinak egitekoak.
• Adierazpen sinpleak eta adierazpen konplexuak.
• Problema aritmetikoak: konbinazio-, aldaketaeta multzokatze-problemak.
Igoerak eta beherapenak.
• Eskala: grafikoa eta zenbakizkoa.
• Estrategia heuristikoa: Egin tarteko galderak.
• Buruzko kalkulua: 20z zatitzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Bilatu erregulartasunak.
• Buruzko kalkulua: Zatiki batez biderkatzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Egin eskema bat.
• Buruzko kalkulua: Kopuru baten 1 4
• Pentsamendu konputazionala: Funtzioak.
• Estrategia heuristikoa: Egin marrazki bat.
• Angeluen arteko batuketak eta kenketak.
• Problema aritmetikoak: berdinketa-problemak.
• Buruzko kalkulua: Kopuru baten % 10.
• Pentsamendu konputazionala: Algoritmoa.
DIZIPLINARTEKO PROIEKTUA · Orain edo inoiz ez: Zer aztarna uzten duzu?
• Poligonoak: elementuak eta sailkapena.
• Poligono ahurrak eta poligono ganbilak.
• Poligonoen perimetroa.
• Zirkunferentzia. Zirkulua eta irudi zirkularrak.
• Puntuen, zuzenen eta zirkunferentzien posizio erlatiboa.
• Poliedroak eta gorputz biribilak.
• Poliedro erregularrak. Biraketa-gorputzak.
• Zorizko esperimentuak. Gertaera ziurra, posiblea eta ezinezkoa.
• Paralelogramoen eta triangeluen azalera.
• Poligono erregularren azalera.
• Irudi konposatuen azalera.
• π zenbakia. Zirkunferentziaren luzera.
• Zirkuluaren azalera.
• Prismen azalera eta bolumena.
• Piramideen azalera eta bolumena. Irudi konposatuen azalera eta bolumena.
• Gertaera baten probabilitatea. Laplaceren erregela.
• Zenbatzeko teknikak.
• Estrategia heuristikoa: Hasi egoera errazagoetatik.
• Buruzko kalkulua: Kopuru baten % 50.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Egin marrazki bat.
• Buruzko kalkulua: Kopuru baten % 20.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Baztertu erantzun ezinezkoak.
• Buruzko kalkulua: 0,1ez biderkatzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Aztertu datu-lagin bat.
• Buruzko kalkulua: 0,5ez biderkatzea.
• Pentsamendu konputazionala: Datuak.
DIZIPLINARTEKO PROIEKTUA · Birika berdea: Iraul ditzagun datuak




Zatikiak
Zatikiak unitate baten zati berdinak adierazteko erabiltzen ditugu.
Zatikiak zenbakiak dira, eta zenbait zati berdinetan banatuta dagoen unitate batetik zenbat zati hartu diren adierazten dute.
3 4
Zenbakitzailea: zenbat zati hartu diren.
Izendatzailea: unitatea zenbat zati berdinetan dagoen banatuta.
4



Zatikiak propioak, inpropioak edo unitate zatikiak izan daitezke.

1 Zer zatikik adierazten du margotuta dagoen zatia?
a) b) c)
2 Marraztu eta idatzi zifraz zatiki hauek:
a) Lau bosten. c) Hamaika hamarren.

b) Hamabi hamabiren. d) Zortzi laurden.
3 Idatzi zatiki hauen balio dezimala:
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es Balio dezimala
Zatiki baten balio dezimala kalkulatzeko, zenbakitzailea zati izendatzailea egin behar da.
82
1
= 1 : 2 = 0,5 1 2 L 1 2 kg 1 4 m 3 4
< 1 3 4
Zenbakitzailea txikiagoa da izendatzailea baino. = 1 4 4 Unitate zatikia Berdinak dira zenbakitzailea eta izendatzailea. > 1 5 4
Zenbakitzailea handiagoa da izendatzailea baino.
Zatiki propioa
Zatiki inpropioa
3
zenbakia zatiki bat da. Honela irakurtzen da: hiru laurden.
4 Ikusi arretaz alboko irudia. Unitatetzat barra laranja hartzen badugu, zer zatiki adierazten dute gainerako barrek? Idatzi bakoitzaren balio dezimala.
5 Kopiatu eta osatu zenbakizko zuzen hau:
6 Egiaztatu Aztertu arretaz zatiki hauek: 3 2 9 4 6 3 7 2 8 5 11 5

a) Adierazi zatikiak zenbaki misto moduan. Laguntza gisa, egin marrazki bat.
b) Kalkulatu lehengo zatiki horien balio dezimala bi modutan. Zer modu iruditzen zaizu errazena?
7 Irakurri eta ebatzi.
a) Beak pentagrama batean 7 musika-notetatik 3 idatzi ditu. Musika-noten zer zatiki dira idatzitakoak?



Zenbaki mistoa
Zatiki inpropioak zenbaki misto moduan ere adieraz daitezke. = 1
Honela irakurtzen da: unitate bat eta laurden.
b) Karlosek baloia 9 aldiz jaurti, eta 4 saskiratze egin ditu. Egindako jaurtiketen zer zatiki dira huts egindakoak?
c) Anderrek 2 ordu eta erdian egin du maratoi-erdia. Zatikitan, zenbat ordu dira? Adierazi zenbaki misto moduan.
Denbora-pasa geometrikoak

Poligono bakoitzaren zer zatiki dago margotuta? Kalkulatu binaka jarrita.
Gogoan hartu!

Hainbat intsektuko multzo batean zenbat diren inurriak eta zenbat diren armiarmak adierazteko, erabili zatikiak.
Beste denbora-pasa batzuk, hemen: anayaharitza.es
83 U5
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 0 1 10 4 10 7 10 ? ? ? ? ? ? 1
5
1
5 4 = 5 : 4 = 1,25
4 = 1
4 = 1 + 0,25= 1,25
1 0 2 1 1
1 4 5 4
4
1
Kopuru baten zatikia
Kopuru baten zatikia jakinda, multzo bateko zati batean

zenbat elementu dauden kalkula dezakegu.
10en 3 5 zenbat den kalkulatzeko, egin urrats hauek:


10 : 5 = 2
Ohartu honetaz: 10en 3 5 = (10 : 5) × 3 = 6




2 × 3 = 6
Kopuru baten zatikia kalkulatzeko, honela egin behar dugu: kopuru hori zati izendatzailea, eta emaitza bider zenbakitzailea.
84
a) 18ren 2 3 b) 24ren 3 8 c) 100en 9 10
20 � -ren 1 2 50 � -ren 1 5 20 � -ren 1 4 50 � -ren 1 10
1 Kalkulatu.
2 Kalkulatu buruz.
30en 1 5 30en 2 5 30en 3 5 30en 4 5
3 Zer dela eta diozu hori? Kalkulatu kopuru berberaren zatiki hauek, eta azaldu zertaz ohartu zaren.
2
1. Banatu elementuak izendatzaileak adierazten duen adina multzo berdinetan.
2. Hartu zenbakitzaileak adierazten duen adina multzo.
4 Aztertu arretaz taula, eta, zatiketarik edo biderketarik egin gabe, osatu koadernoan.
a) 60ren 1 2 = ? d) 60ren 1 5 = ? g) 60ren 2 5 = ?
b) 60ren 1 3 = ? e) 60ren 1 6 = ? h) 60ren 3 4 = ?




c) 60ren 1 4 = ? f ) 60ren 4 6 = ? i) 60ren 2 3 = ?

5 Aner jostuna da, eta oihal-biribilki honen 3 4 erabili ditu eskolako eztabaida-taldeko kideen jantziak egiteko. Zenbat metro erabili ditu?
Zer gertatzen da kopurua izendatzaileaz zatitutakoan zatiketa zehatza ez bada? «Berehala kontatuko dizut», hemen: anayaharitza.es
6 Udal batek herria hobetzeko zer egingo luketen galdetu die herritarrei, eta 30 proposamen jaso ditu: 2 5 parkeen zaintzari buruzkoak dira; 1 3 , kaleen garbiketari buruzkoak, eta gainerakoak, herritarren elkartasunari buruzkoak. Mota bakoitzeko zenbat proposamen jaso ditu udalak?
7 Irakurri, pentsatu eta ebatzi.
a) Uxuek pitxerkada bat esneren laurdena erabili du. Uxuek 2,5 dL erabili baditu, zer edukiera du pitxerrak?
b) Xubanek dokumental baten bi heren ikusi ditu. Amaitzeko 15 minutu falta badira, zer iraupen du guztira dokumentalak?
50 m ?
Ebatzi urratsez urrats, hemen: anayaharitza.es
2,5 dL
Gogoan hartu!
Kilometro karratu batean zenbat inurri dauden jakiteko, kalkulatu kopuru baten zatikia.
85 U5
60 12 12 12 12 12 10 10 10 10 10 10 15 15 15 15 20 20 20 30 30
15 2 3
Zatiki baliokideak
Zatiki baliokideek unitatearen zati bera modu desberdinetan adierazteko aukera ematen digute.
Zatiki baliokideek unitatearen zati bera adierazten dute.
3 4 eta 6 8 zatiki baliokideak dira.
3 4 6 8
• Bi zatiki baliokideak diren jakiteko, zatikien gaiak gurutzean biderkatu behar ditugu. Bi biderketen emaitzak berdinak badira, zatikiak baliokideak dira.
3 4 6 8



3 × 8 = 24
4 × 6 = 24
3 4 eta 6 8 baliokideak dira.
• Zatiki baliokideak lortzeko bi modu daude: anplifikazioa eta sinplifikazioa.
Anplifikazioz: biderkatu zenbakitzailea eta izendatzailea zenbaki berberaz.
Sinplifikazioz: zatitu zenbakitzailea eta izendatzailea zenbaki berberaz.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Kopiatu eta margotu, zatikiak baliokideak izan daitezen.
2 Aztertu pare bakoitzeko zatikiak baliokideak diren.
86
a) 1 4 = ? 12 b) 3 8 = ? ? c) ? ? = ? ?
a) 1 5
3 15 b) 7 9
2 3 c) 5 15 eta 2 6 d) 9 11 eta 4 5
eta
eta
3
3 4
6 8
× 2 × 5 × 2 × 5 30 40
=
=
= = 6 8 : 2 : 5 : 2 : 5 30 40 3 4
Lagungarri bazaizu, egin marrazki bat.
3 Eragiketarik egin gabe, azaldu zatiki hauek zergatik ez diren baliokideak:
3 5 eta 6 5 4 5 eta 4 10
4 Kalkulatu zatiki baliokideak. Gero, egiaztatu emaitzak, ikaskideenekin konparatuta. Zertaz ohartzen zara?
Anplifikazioz Sinplifikazioz
a) 1 2 b) 3 4 c) 7 8 a) 8 10 b) 9 12 c) 10 20
5 Kopiatu esaldiak, baina zatiki hauen ordez bakoitzaren zatiki laburtezina idatzita:
a) Laburpenak orrialdearen 5 10 betetzen du.
b) Dagoeneko 6 8 ordu igaro dira.
c) Pitxerreko uraren 8 12 erabili dut.
6 Julek aurreztuta 60 � zituen eta 20 � gastatu ditu. Bere aurrezkien zer zatiki gastatu du Julek? Adierazi kopurua ahalik eta modu sinpleenean.



Zatiki laburtezina urrats bakarrean
Joni kalkumagoa deitzen diote, oso zatiki zailen zatiki laburtezinak azkar-azkar kalkulatzen dakielako. Nola egiten du?
Truko bat du.
1. Kalkulatu zenbakitzailearen eta izendatzailearen zatitzaile komun handiena.
2. Zatitu zenbaki horretaz zenbakitzailea eta izendatzailea, eta… voilà! Hortxe duzu zatiki laburtezina urrats bakarrean.
12
z.k.h. (36, 60) = 12 36 60 = 3 5
12
• Jonen trukoa erabiliz, kalkulatu zatiki hauen zatiki laburtezinak. Balio du?
Zatiki laburtezina
Zatiki bat laburtezina da, gehiago sinplifikatu ezin bada.
4
: 2 : 2
6 = 2 3
zatiki laburtezina
Informazioa modu sinpleagoan emateko, zatiki laburtezinak erabiltzen ditugu.

36
60 zatikiaren zatiki laburtezina da…

87 U5
:
:
a)
c)
d)
18 60 b) 12 30
44 66
20 80
Konparatu zatikiak
Unitatearen zati bat beste bat baino handiagoa den jakiteko, zatikiak konparatzen ditugu.
• Bi zatikik izendatzaile bera badute, zenbakitzaile handiena duena da zatiki handiena.

• Bi zatikik zenbakitzaile bera badute, izendatzaile txikiena duena da zatiki handiena.
• Bi zatikik zenbakitzaile eta izendatzaile desberdinak badituzte, zatiki baliokideak kalkulatu behar ditugu, zatiki bakoitzeko gaiak bestearen izendatzaileaz biderkatuta.
Matematikan horri biderketa gurutzatuen metodoa esaten zaio.

88
1 Idatzi zatikiak, eta ordenatu handienetik txikienera.
4
2 Idatzi zatikiak, eta ordenatu txikienetik handienera.
4 5 3 5 2 5 4 7 2 5 3 10 4 5 > 2 5 4 5 handiagoa da 2 5 baino. 3 5 > 3 10 3 5 handiagoa da 3 10 baino. 2 5 = 14 35 × 7 × 7 4 7 = 20 35 × 5 × 5 14 35 < 20 35 da; beraz, 2 5 < 4 7
3 Zatikien zerrendak erabiliz, konparatu.
a) 2 5 eta 2 7 b) 5 12 eta 5 10 c) 6 8 eta 6 7 d) 4 5 eta 4 9
4 Konparatu zatikiak koadernoan, ikur hauekin: >, < edo =. Erabili biderketa gurutzatuen metodoa.
a) 3 8 ? 2 5 b) 4 7 ? 7 10 c) 1 4 ? 2 6
5 Ordenatu zatikiak txikienetik handienera. Nola egin duzu? 1 2 , 4 5 eta 2 5 5 8 , 3 5 eta 3 4 2 10 , 6 5 eta 1 4
6 Irakurri eta erantzun.
a) Izarbe albaitaria da. Gaur kontsultara ekarri dizkioten animalien 5 6 txakurrak ziren, eta 4 5 , katuak. Zer izan dira gehiago gaur, txakurrak ala katuak?
b) Xantik tarta baten 1 6 mugurdiz apaindu du, eta 2 8 , masustaz. Tartaren zer zati da handiagoa, mugurdiz apaindutakoa ala masustaz apaindutakoa?
Izendatzaile berberaz adieraztea
Badago modu bat zenbakitzaile eta izendatzaile desberdinak dituzten zatikiak azkar-azkar konparatzeko. Ikasi nahi?
1. Kalkulatu izendatzaileen multiplo komun txikiena.
4ren multiploak 0, 4, 8, 12, 16, 20 , 24… 5en multiploak 0, 5, 10, 15, 20 , 25…


m.k.t. (4 eta 5) = 20

2. Ikusi zer zatiki baliokidek dituzten izendatzailetzat bi zatikietako izendatzaileen multiplo komun txikiena.
12 20

5 20 < 12 20 da; beraz, 1 4 < 3 5
Bikaina benetan!
• Orain, egin zeuk. Konparatu, izendatzaile berberaz adierazita.
a) 5 6 eta 3 4 b) 7 15 eta 9 10
9 16 eta 2 12
3 4 > 3 8
Zatikiak konparatzeko beste modu bat zatidurak konparatzea da.
1 2 = 0,5 3 4 = 0,75
1 2 < 3 4
1 4 zatikia 3 5 baino handiagoa ala txikiagoa da?
Gogoan hartu!
Intsektu-populazio batean ugariagoak inurriak edo armiarmak diren jakiteko, konparatu zatikiak.
89 U5
1
× 5 ×
3
=
× 4 × 4
4 = 5 20
5
5
c)
Ohartu honetaz
Batuketa eta kenketa zatikien artean
Zatikien arteko batuketak eta kenketak eginez, unitateen zatiekin egin ditzakegu eragiketak.
• Izendatzaile bera duten zatikien arteko batuketak edo kenketak egiteko, zenbakitzaileen arteko batuketa edo kenketa egin behar dugu, eta izendatzaile bera utzi.

• Izendatzaile desberdinak dituzten zatikien arteko batuketak edo kenketak egiteko, urrats hauek egin behar ditugu:

90
5
1 Kalkulatu, batuketa eginez, irudien zer zatiki dagoen margotuta.
a) b) c)
2 Kalkulatu, kenketa eginez, irudien zer zatiki dagoen margotuta.
a) b) c)
3 Jolastu koloretako polikuboekin, eta asmatu izendatzaile bera duten zatikien arteko batuketa eta kenketa batzuk.
m.k.t. (6
= 24 5 13 + 2 13 = 7 13 6 13 2 13 = 4 13 3 8 + 2 6 3 8 = 9 24 × 3 × 3 2 6 = 8 24 × 4 × 4
1. Adierazi zatikiak izendatzaile berberaz.
eta 8)
3 8 + 2 6 = 9 24 + 8 24 = 17 24 3 8 + 4 8 = 7 8 1 7 8 = 8 8 7 8 = 1 8
2. Egin batuketa zatiki baliokide berrien artean.
4 Kalkulatu eragiketak.
a) 1 2 + 2 3 b) 8 15 + 2 5 c) 5 7 2 5 d) 7 12 2 6






5 Ikusi arretaz adibidea, eta kalkulatu eragiketak.
2 + 1 5 = 10 5 + 1 5 = 11 5
2 zenbakia zatidura gisa adieraziko dugu: izendatzailea 5 duen zatikiaren zatidura gisa.
a) 2 + 3 6 b) 1 4 + 5 c) 4 1 6 d) 10 4 2
6 Egiaztatu Ebatzi zatikiak dituzten adierazpen hauek:
a) 2 5 + 3 4 1 4 b) 2 3 ( 5 6 1 2 ) c) 2 ( 1 3 + 3 4 )
7 Irakurri eta ebatzi.
a) Atzo Kattinek liburu bateko kapituluen bi bosten irakurri zituen eta gaur laurdenak irakurri ditu. Liburuak dituen kapituluen zer zatiki ditu irakurriak?
Ebatzi urratsez urrats, hemen: anayaharitza.es
b) Beñatek deposituko uraren 1 3 erabili badu, deposituaren zer zatiki dago oraindik urez betea?
3 8 10 ?
c) Zinema batean ikusgai dauden filmen 3 4 animaziokoak dira; 1 6 , erromantikoak, eta gainerakoak, beldurrezkoak. Filmen zer zatiki dira beldurrezkoak ?
Erabili biderketa gurutzatuen metodoa edo multiplo komun txikienarena.
Gogoratu Aurren-aurrena parentesien barruan dagoen eragiketa egin behar da. ?

8 10
Ebatzi urratsez urrats, hemen: anayaharitza.es
Gogoan hartu!
Inurriak eta armiarmak guztira zer zatiki diren jakiteko, egin zatikien arteko batuketa.

91 U5
1
1 4 2 5
Biderketa zatikien artean
Zatikien arteko biderketak eginez, bi multzoren ebakidurak zer balio duen
kalkula dezakegu.
Ikusi arretaz nazioarteko ikastetxe bateko ikasleen zer zatikik egiten duen ingelesez eta zer zatikik egiten duen alemanez.
«I like math». «Ich mag Mathe».





Ikasleen zer zatikik egiten du ingelesez eta alemanez?
Hori jakiteko, zatikien arteko biderketa egin behar dugu.
Ohartu honetaz:



3 20 ek egiten dute ingelesez eta alemanez.
Bi zatikiren edo gehiagoren biderkadura ere zatiki bat da: zenbakitzaileen biderkadura du zenbakitzailea, eta izendatzaileen biderkadura du izendatzailea.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
Zatiki bat sinplifikatzea zatiki laburtezina bilatzea da.
92
2 4 3 5 × 2 3 1 3 × 2 3 2 4 ×
1 Lotu koadernoan marrazkiak eta eragiketak.
= : 2 1 10 2 5 1 4 × = 2 20 : 2 a) 2 5 3 4 × b) 5 8 2 3 × c) 3 10 4 6 2 3 × ×
2 Egin biderketa, eta sinplifikatu emaitza.
6
Ikasleen
3 5 1 4 3 5 1 4 1 4 3 5 eta × = = 3 × 1 5 × 4 3 20
3 Kalkulatu eta sinplifikatu emaitza.
a) 5 × 2 7 b) 1 9 × 8 c) 2 9 × 6 × 1 2 d) 4 × 2 12 × 6 8




4 Irakurri eta ebatzi.
a) Nire lagunen erdiek txakurra dute eta bi bostenek arrainak dituzte. Nire lagunen zer zatikik dituzte txakurra eta arrainak?
b) Gure familiako kideen seirena ilegorria da eta herenek ile kizkurra dute. Kideen zer zatikik du ile gorri kizkurra?
c) Mireiak 4 poto tomate erabili ditu saltsa egiteko. Zenbat tomate erabili du guztira? ?

Ez dira gauza bera 1 4 × 1 2 eta




Nola biderkatu zenbaki bat zatiki batez
Zenbaki bat zatiki batez biderkatzeko, hau egin behar dugu: zenbakia bider zenbakitzailea egin, eta izendatzaile bera utzi.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
Ebatzi urratsez urrats, hemen: anayaharitza.es
Nire lagunen zer zatikik ditu gogoko marrubizko eta mendazko izozkiak? Irakurri eta ohartu.
Nire lagunen 1 4 i marrubizko izozkia gustatzen
zaie, eta 1 2 i, berriz, mendazkoa.
Nire lagunen 1 4 i marrubizko izozkia gustatzen
zaie, eta horien 1 2 i, mendazkoa ere bai.
1 8 i gustatzen zaizkie bi zaporeak.
Ohartu honetaz: bi kasuetan soluzioa berdina da, baina egoera ez da bera.
• Asmatu problema bat irudi bakoitzarentzat.
93 U5
kg 1 4 kg 1 4 kg 1 4 kg 1 4 kg 1 4 kg 1 4 kg 1 4 kg 1 4
1 2 . 1 4 1 2 1 8 × =
1 4 en
4 4 2 3 2 3 2 3 8 3 8 3 2 3 2 3 2 3 × × = = = + + + 1 4 1 2 1 4 1 4 en 1 2
Zatiketa zatikien artean
arteko zatiketak eginez, zatiki bat beste zatiki handiago baten barruan zenbat aldiz sartzen den jakin dezakegu.
Zatikien

Olaiak izar formako intsigniak egin nahi ditu bere taldeko kideentzat. Izar bakoitza egiteko, 1 6 metro oihal behar du. Zenbat izar egin ditzake?
Kalkula dezagun grafikoki 2 3 en barruan zenbat aldiz sartzen den Olaiak 4 izar egin ditzake.

Praktikan, zatikien arteko zatiketak egiteko, gaiak gurutzean biderkatu behar dira.
Bi zatikiren zatidura ere zatiki bat da, eta zatikien gaiak gurutzean biderkatuz lortzen da.
Deskargatu zatikien zerrendak, webgunean: anayaharitza.es

94
: 2 3 1 6 = 4 a) 1 2 1 4 : b) 3 6 1 12 : c) 2 3 1 10 : d) 4 8 1 6 :
1 Ikusi arretaz adibidea eta zatikien zerrendak, eta egin beheko zatiketak grafikoki.
a) 5 2 1 4 : b) 9 10 4 5 : c) 6 11 5 10 : d) 8 12 2 6 :
2 Egin zatiketak, eta sinplifikatu emaitzak.
a) 4 : 1 2 b) 5 : 1 3 c) 2 : 1 4 d) 3 : 1 5
3 Ikusi adibidea, eta egin zatiketak, marrazki bat erabiliz.
7
4
= = = 4 2 × 6 3 × 1 12 3 2 3 1 6 : 1 1 1 1 2 1 2 1 2 1 2 1 2 1 2 3 : 1 2 = 6
4 Ikusi arretaz eta kalkulatu.
5 Nola egin daitezke zatikien arteko zatiketak biderketa erabiliz?
Gauza bera dira zatiki batez zatitzea eta zatiki horren alderantzizkoaz biderkatzea.
Kalkulatu, zatiketa bakoitza biderketa bihurtuta.
6 Ebatzi eragiketa konbinatu hauek:



7 Irakurri eta ebatzi.
a) Anerrek 3 L esne banatu ditu 1 5 litroko edalontzi batzuetan. Zenbat bete ditu? L 1 5
Alderantzizko zatikia
Zatiki bat beste baten alderantzizkoa da bi zatikien biderkadura unitatea bada.
2 3 × 3 2 = 6 6 = 1
Gogoratu

Zenbait eragiketako adierazpenak ebazteko, ordena honetan kalkulatu behar dira:
1. Parentesi barruan dauden eragiketak.
2. Biderketak eta zatiketak, ezkerretik eskuinera.
3. Batuketak eta kenketak, ezkerretik eskuinera.
Adierazi zenbaki mistoa zatiki inpropio moduan.
b) Koldok gazta hau 1 4 kiloko zatitan banatu du. Zenbat zati egin ditu? kg 1 4
2 kilo eta erdi
2 kilo eta erdi
Ebatzi urratsez urrats, hemen: anayaharitza.es

95 U5
4 : 2 3 = 4 1 : 2 3 = 4 × 3 2 × 1 = 12 2 = 6
2 b) 1 4 : 2 c) 4 : 1 3 d) 3 4 : 6
a) 5 : 1
3 2 : 4 5 = 3 × 5 2 × 4 = 15 8 3 2 : 4 5 = 3 2 × 5 4 = 3 × 5 2 × 4 = 15 8
7 5
2 3 b)
3
7 c) 15 4 : 2 3 d) 12 8 : 3 4
a)
:
11
: 1
3 4 × 1 2 4 b) 1 5 : ( 4 6 3 5 ) c) 2 × 1 7 : 1 3
a)
3 L
EBATZI BAIETZ!
Egin tarteko galderak

Eiderrek 30 m-ko zinta-biribilki bat du. Zintaren 1 3 opari batzuk apaintzeko erabili du, eta gainerakoa metro-erdiko zati berdinetan banatu nahi du.
Zenbat zati egin ditzake?
Hori jakiteko, lehenbizi hau jakin behar dugu:
Zenbat metro zinta geratzen zaizkio opariak apaindu eta gero?
Opariak apaintzen zinta guztiaren 1 3 erabili duenez, oraindik 2 3 ditu.
Kalkula dezagun zenbat metro diren.
30 m-ren 2 3 = (30 m : 3) × 2 = 10 m × 2 = 20 m
20 m zinta geratzen zaizkio. 10 m erabili ditu.
30 m
40 zati egin ditzake.

20 m
Datu hori jakinda, jada ebatz dezakegu problema. m 1 2
20 : 1 2 = 40
Soluzioak badu zentzurik?
Egiaztatu metro-erdiko 40 zati eta opariak apaintzen erabilitako 10 m-ak guztira 30 m direla.
40 × 1 2 + 10 = 20 + 10 = 30
1

Lastozko zenbat kapela dituzte dendan?
2 Tomasek bizikletaz 160 km egin ditu hiru etapatan. Lehenbiziko etapan bide guztiaren 3 8 egin zituen, eta bigarrenean, 1 4 . Zenbat kilometro egin ditu hirugarrenean?

96
Denda batean 60 kapela dituzte. 2 5 beltzak dira; 1 4 , loredunak, eta gainerakoak, lastozkoak.
Problemak arin-arinka
2 1
Zer zenbaki dezimaldun da…? Botila batean 2 10 ur geratzen da. Pellok ezetz dio, 1 5 bakarrik geratzen dela. Oker dabil?
1 2 eta 1 4 , zenbat laurden dira? 4 3
Urtebetetzeko tartaren 3 4 jan ditugu. Geratzen den zatia jan duguna baino handiagoa ala txikiagoa da?
6 5
Orri baten erdia -



ren 1 4 , orriaren zer zatiki da?
Patroi bila
1 2 en barruan zenbat aldiz sartzen da 1 4 ?
1 2 1 4 :
Buruzko kalkulua
Kalkulatu 180 : 20.
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:
1 1 60 : 20

1 80 : 20
100 : 20
120 : 20
240 : 20
300 : 20
420 : 20
480 : 20
840 : 20
900 : 20
Zati dezimalean 142 857 errepikatzen da!
142 857 zenbakiak eta 1 7 zatikiak oso erlazio berezia dute.
1 7 = 1 : 7 = 0,142857142857142857…
Eta begira hau, are harrigarriagoa da eta: izendatzailea 7 duten zatiki propio guztiek zati dezimalean zifra horiexek dituzte! Ikusi arretaz, eta osatu koadernoan.
Egiaztatu zure emaitzak kalkulagailuarekin!
= 0,142857…
= 0,285714…
= 0,428571…
97 U5
7
4 7 = ? 2 7
5 7 = ?
7
6 7 = ?
2
90 180 : 2
10 9
1
3
20 =
× 10
:
1 7 4 7 2 7 5 7 3 7 6 7 1
1 2
1
1
4
×
10
2 1 4 Begira nola pentsatzen dudan
Z er ikasi dut?
1 Idatzi zer zatikik adierazten duten irudietan margotuta dauden zatiak.
a)
b) c)
2 Adierazi zatiki hauek:
a) 1 000 g-ren 1 4 c) 50 � -ren 4 5
b) 25 m-ren 1 2 d) 750 mL-ren 2 3
3 Kalkulatu zatiki laburtezinak.
a) 12 16 b) 24 36 c) 50 100 d) 15 60
4 Konparatu zatikiak.
a) 4 7 eta 2 7 b) 7 4 eta 7 2 c) 1 2 eta 4 5
5 Esaldi hauetatik zein dira okerrak? Aurkitu, eta idatzi zuzen.
A Zatiki baten zenbakitzaileak zera adierazten du: unitatea zenbat zatitan dagoen banatuta.
B Zatiki baliokideek unitatearen zati bera adierazten dute.
C Bi zatikik zenbakitzaile bera badute, izendatzaile handiena duen zatikia da handiena.
6 Kalkulatu.
a) 3 8 + 1 8 c) 3 10 + 1 3
7 Ebatzi eta sinplifikatu.
8 Iñigok aurreztuta zuen diruaren 3 10 gastatu du. Zenbat diru geratzen zaio?





9 Problema bat ebazteko, gela bateko ikasleak bi taldetan banatu dira. A taldean gelako ikasleen 3 8 daude, eta B taldean, berriz, ikasleen 3 5 .
a) Zer taldetan dago ikasle gehien?
b) Ikasle guztiek hartu dute parte problema ebazten? Zergatik?
10 Felixek atzo sobera geratutako tortillaren 2 3 jan ditu . Tortillaren zer zatiki jan du? Zer zatiki geratu da?

11 Naroak 1 5 kilogramo azenario behar ditu tarta bat egiteko. Kilo-erdiko sorta bat erosi badu, zenbat tarta egin ditzake? Geratuko zaio azenariorik sobera?
Semaforoa. Margotu koadernoan, ariketa bakoitzaren ondoan, honela:
Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu
98
PORTFOLIOA
e) 2 + 3 5 b) 9 12 5 12 d) 8 12 3 6 f ) 3 1 4
1 8
4 5 c) 2 7 × 3 6 e) 4 × 5 9
5 8 : 1 10 d) 3 4 : 1 6 f ) 3 : 2 9
a)
×
b)
HELBURUA AURRERA
Sortu jendeak bat eginda jarduteko gune bat.
Gure planetan dauden izaki bizidun guztien 14 25 intsektuak dira. Horietatik, 20tik 3 inurriak dira eta 1 5 armiarmak dira
a) Izaki bizidunen zer zatiki ez dira intsektuak? Harritu egin zaitu horrek?
b) Zer zatiki dira inurriak?
c) Zer daude gehiago, inurriak ala armiarmak?
d) Intsektuen zer zatiki dira inurriak eta armiarmak batera?
e) Intsektuen zer zatiki ez dira ez armiarmak eta ez inurriak?
f) Egindako kalkuluen arabera, kilometro karratu bakoitzean 40 000 intsektu inguru daude. Zenbat dira inurriak?

Geure buruari galdezka
Nire lehengo eta oraingo iritzia estrategia erabiliz, aztertuko dugu zergatik den garrantzitsua jendeak helburu berberen alde bat egitea.
a) Kopiatu eta osatu antolatzailea koadernoan.
Gaia: Bat egitea ? ? ?



Lehen pentsatzen nuen... Orain pentsatzen dut... Zergatiak
b) Sortu dezagun ELKARTU!, ikastetxean helburu berberen alde beste batzuekin bat egiteko gunea.
Antolatu ikastetxean ageriko leku batean edo ingurune digital batean horrelako gune bat, jendeak bere proposamenak jar ditzan, helburu berberak dituzten beste batzuekin elkartzeko. Ekimenen bat abiatu nahi baduzu, idatzi han eta ez ahaztu izena jartzea!
N o la ikasi dut?
Osatu koadernoan.
Aipatu talde-lanean aritzeko zuk dituzun hiru indargune.
Aipatu talde-lanean aritzean zailak egiten zaizkizun hiru gauza. Zer egin dezakezu horiek gainditzeko?
Bizikidetza hobetzeko proposamenak egiteko norbaitekin elkartu nahi dut.
Jolastokia garbi edukitzea lortzeko norbaitekin elkartu nahi dut.
U5 99
Ander Uranga
Gema Gonzalez




Neurtu luzerak, edukierak eta masak
Inguruko objektuei buruzko informazio gehiago emateko eta lortzeko, neurri-unitateak oso lagungarriak dira.
Luzera-, edukiera- eta masa-unitateak sistema metriko hamartarrekoak dira (SMH).
Unitate nagusiak metroa (m), litroa (L) eta kilogramoa (kg) dira.
Masa adierazteko neurri-unitate erabiliena gramoa da.
kilometroa km hektometroa hm dekametroa dam metroa m dezimetroa dm zentimetroa cm milimetroa mm kilolitroa kL hektolitroa hL dekalitroa daL litroa L dezilitroa dL zentilitroa cL mililitroa mL kilogramoa kg hektogramoa hg dekagramoa dag gramoa g dezigramoa dg zentigramoa cg miligramoa mg

1 Zer dela eta diozu hori? Zer neurri-unitate erabiliko zenuke luzera, edukiera eta masa hauek adierazteko?
a) Zenbat bide dagoen zuen gelatik hurbilen dagoenera.
b) Zenbat urdaiazpiko dagoen zure ogitartekoan.
c) Zenbat ur edaten duzun egunero.
d) Zer distantzia dagoen zure etxetik Parisera.
e) Zenbat zuku dagoen edalontzi batean.
f) Zenbat fruta dagoen erosketa-organ.
2 Zeure buruaren zer neurri dakizkizu? Galdetu familiakoei
ea zer neurri zenituen jaiotakoan, eta idatzi koadernoan oraingo neurriekin batera.
Jaiotakoan Orain

Gorputz-masa ? ?
Altuera ? ?

Buruaren perimetroa ? ?
Beste batzuk ? ?



102
1
200 m 1 L 200 g
3 Osatu koadernoan, unitate egokiena idatzita.
kg g mg

650 ? 500 ? 10 ?
4 Neurtu zure mahaia eta matematikako liburua, erregela edo neurketa-zinta erabiliz.
a) Konparatu zure neurriak eta ikaskideenak. Berdinak dira?
b) Mahaiaren eta liburuaren beste neurriren bat ere hartzea bazeneukaten? Zein?
5 Badakizu zenbat hazbete dituen zure telebistak? Etxean, neurtu pantailaren diagonala zentimetrotan, eta egin zati 2,54. Lortzen duzun emaitza, hazbete horiek ditu telebistak!
6 Nola jakin dezakezu gutxi gorabehera zer edukiera duen zure ur-botilak ontzi-aldaketak eginez? Deskribatu.
7 25 cL-ko ur-botila bat betetzen baduzu, eta gero ur hori 1 L-eko pitxer batera bota, zenbat ur dago pitxerrean?
A 1 L B 25 cL C litro-erdi



Oinetakoetan, zer zenbaki erabiltzen duzu?
Badakizu zer esan nahi duen oinetakoetan erabiltzen duzun zenbakiak? Hori jakiteko, egin urrats hauek:
1. Oinutsik zaudela, jarri oin bat orri baten gainean, eta markatu hasiera eta bukaera, eskeman bezala.
2. Erregelarekin, neurtu bi marken arteko tartea, zentimetrotan. Neurri horri gehitu 0,5 cm; oinetakoak oina ez estutzeko behar da.

3. Egin gauza bera beste oinarekin. Berdinak dira?
4. Begiratu taulan: oinetakoaren luzeraren eta oin-neurriaren arteko baliokidetasunak dira. Zure kasuan, hala da?
Ikertu zertarako balio duen baskula digitaleko tekla bakoitzak.
25
Hau bai bitxia!
xviii. mendearen hasieran, oinetakoak egiten zituzten artisauentzat, neurri-uni- tate bat finkatu zen, nahiz eta ez zuen neurri bera es- kualde guztietan: puntua. Europan Paris puntua era- biltzea hedatu zen: gutxi gorabehera 0,65 cm zen. Oinetakoetan 37 erabiltzen baduzu, zure oina 24 cm inguru da.
37 x 0,65 = 24,05 cm
Gogoan hartu!
Neurri-unitateen bidez, esperimentua egiteko osagai bakoitzetik zenbat behar duzun adieraz dezakezu.
103 U6
oinetako-neurriak europa 35 36 37 38 39 40 41 42 43 zentimetroak 22,8 23,5 24,1 24,8 25,4 26 26,7 27,3 27,9 1 L ? ?
cL GATZA
Aldatu neurri-unitateak
Neurri-unitateen artean eragiketak eta konparaketak egin ahal izateko, batzuetan unitate-aldaketak egin behar dira.
1 Idatzi neurri hauek adierazitako unitateetan: metroak litroak gramoak
4,7 km 186 cL 274 hg
dm 0,27 daL 85 dg
hm 5 675 mL 0,95 kg
2 Egin unitate-aldaketak.
a) 8 hm = ? dm d) 9 daL = ? kL g) 6 cg = ? mg
b) 15 m = ? km e) 64 hL = ? L h) 0,07 g = ? cg
c) 350 mm = ? cm f ) 0,7 cL = ? mL i) 80 kg = ? hg
3 Kopiatu eta osatu.
33 cL ? L = ? dL = 33 cL = ? mL ? kL = ? hL = ? daL = 790 L

790 L
4 Kalkulatu zer masa duen fruitu bakoitzak.
Nola aldatu unitatea
Luzera-, edukiera- edo masaunitateak aldatzeko, egin bider edo zati 10, 100, 1000…
5 Ordenatu neurri hauek, txikienetik handienera:
1,2 km 18,36 m 1 836 dm 185 cm
6 Kopiatu eta kalkulatu.
a) 6,3 daL + 5,7 L = ? L c) 78,02 g + 358 cg = ? dg
b) 0,81 kL − 240 L = ? daL d) 93 dag − 7,5 hg = ? g



× 10 × 10 × 10 × 10 × 10 × 10
Luzera km hm dam m dm cm mm


: 10 : 10 : 10 : 10 : 10 : 10
Edukiera
× 10 × 10 × 10 × 10 × 10 × 10
kL hL daL L dL cL mL
: 10 : 10 : 10 : 10 : 10 : 10
× 10
× 10 × 10 × 10 × 10 × 10
Masa kg hg dag g dg cg mg
: 10 : 10 : 10 : 10 : 10 : 10
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
Eragiketak egiteko edo alderatzeko, adierazi neurri guztiak unitate berean.
104
25
4,1
225g 210g
415g
2
7 Adierazi animalia hauen masak tonatan:
Tona eta kintala

Kilogramoa baino masa handiagoak adierazteko, tona (t) eta kintala (q) erabiltzen ditugu. 1 t = 1 000 kg


1 q = 100 kg

8 5 minutuko geraldia Irakurri, pentsatu eta ebatzi.
a) Arkakuso batek 33 cm egiten ditu aurrera jauzi bakarrean. Zenbat jauzi egin behar ditu 6,6 m-ko bidea egiteko? 33 cm
6,6 m

b) Bizkotxo bat egiteko, 265 g irin behar ditugu. Zenbat bizkotxo egin ditzakegu 1 kg irinekin?
c) Laranjaz beteta doan kamioi batek 12 t-ko masa du. Hutsik zegoenean kamioiaren masa 7 180 kg bazen, zenbat kilo laranja daramatza?

12 t
7 180 kg ?
d) Elenek okindegian 2 kintal eta erdi irin zituen, eta ogia egiten 186 kg erabili ditu. Zenbat kilo irin geratzen zaizkio?
?
186 kg 2,5 q

e) Auto baten erregai-tangak 45 L-ko edukiera du. Bidaia batean 170 dL gastatzen baditu, zenbat litro geratuko zaizkio?

f ) Litro bat urek, ur garbia bada, kilo bateko masa du. Hortaz, zenbat gramoko masa du litro eta erdi urek?
Ebatzi urratsez urrats, hemen: anayaharitza.es
Problemak ebazten ikasten baduzu, zure helburuak errazago lortuko dituzu.
Gogoan hartu!


Esperimentuko osagai bakoitzetik zenbat behar den zehaztasunez adierazteko, idatzi neurriak unitate egokienean.

105 U6
18 000 kg 200 kg
500 kg
6
Adierazpen sinpleak eta konplexuak
Neurriak adierazteko, unitate bakarra edo batzuk erabil ditzakegu, baina neurria berbera izango da.
Luzera, edukiera nahiz masa zenbait modutan adieraz daitezke.
Adierazpen konplexua: neurri-unitate bat baino gehiago.
2 dL 5 cL 25 cL
Adierazpen sinplea: neurri-unitate bakarra.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Idatzi neurri hauek adierazitako unitateetan. Laguntza gisa, erabili unitate-taula.
6 km 25 dam
km hm dam m dm cm mm
dm-tan 6 2 5 0 0 62 500 dm
m-tan 6 2 5 0 6 250 m
dam-tan 6 2 5, 0 625 dam
hm-tan 6 2, 5 0 62,5 hm
km-tan 6, 2 5 0 6,25 km
a) 1 dam 237 cm = ? m c) 63 m 52 cm = cm e) 9 hm 35 dm 6 cm = ? dm



b) 5 m 481 mm = ? mm d) 2 km 18 dam = ? hm f ) 27 hm 5 dam 1 m = ? km



2 Nor bizi da eskolatik hurbilago?
Goizetan bizikletaz 5 hm 74 m egiten ditut eskolaraino.
Eskolaraino amonak laguntzen dit. Oinez egiten dugu 2 hm 80 m-ko bidea, berriketan.
3 Zenbat falta da…
a) metro batekoa izateko? b) … litro bat zuku egiteko?

106
A 13 cm B 0,13 cm C 1,3 cm A 0,9 L B 9 dL C 90 mL 8 dm 7 cm 9 dL 10 mL
3
Behar duzun guztietan, erabili unitate-taula.
4 Kopiatu eta osatu.
a) 5,62 m = ? m ? cm d) 2 894 m = ? dam ? dm
b) 97,4 dL = ? L ? dL ? cL e) 35 hL = ? kL ? L
c) 346 dag = ? hg ? g f ) 8,408 kg = ? hg ? g
5 Ebatzi eragiketak.
a) 18 km 45 dam 4 m + 32 hm 860 dm
b) 64 L 37 dL 42 mL − 489 cL 2 mL





c) 7 dag 5 g 90 cg × 3


d) 90 hm 4 dam 50 dm : 5


Eragiketak egin aurretik, adierazi neurri guztiak unitate berean.
6 Garbigailua jarri aurretik, Katixak arropa zikina sailkatu du: 5 kg 464 g arropa zuria da, eta 8 kg 91 g arropa, koloretakoa. Zenbat kilo arropa garbituko du guztira? ?
5 kg 464 g
8 kg 91 g
Ebatzi urratsez urrats, hemen: anayaharitza.es
7 30 cL-ko zenbat edalontzi bete daitezke pitxer horretan dagoen esnearekin? 30 cL

1 L 80 cL
1 L 80 cL
Ebatzi urratsez urrats, hemen: anayaharitza.es
8 Pentsatu eta binaka jarrita komentatu Norak litro-erdi zuku prestatu du, hauek nahasita: mahats beltzarekin egindako 3 dL 5 mL zuku, 14,5 cL ur eta limoi-zuku zurrustatxo bat. Zenbat mililitro limoi-zuku erabili du?

107 U6
0,5 L ? ? 3 dL 5 mL 14,5
cL
Neurtu azalerak
batek edo gure etxeak zer neurri duten adierazteko, oso lagungarria da azalera-unitateak ezagutzea.
Futbol-zelai


Bi gainazal horiek forma bera dute, baina azalera desberdina.
Azalera adierazteko neurri-unitate nagusia metro karratua (m2) da; metro koadro ere esaten zaio.
• Azalera txikiak adierazteko, metro karratua baino unitate txikiagoak erabiltzen ditugu. •
• Azalera handiak adierazteko, metro karratua baino unitate handiagoak erabiltzen ditugu.
1 Zer dela eta diozu hori? Zer unitate erabili zenuke gainazal hauen azalerak adierazteko?
Partxis-taula bat Zure herria Museo bat

108
4
Azalera-unitateak 100naka handitzen
txikitzen dira. dezimetro karratua dm 2 metro karratua m 2 zentimetro karratua cm 2 milimetro karratua mm 2 dekametro karratua dam 2 metro karratua m2 hektometro karratua hm 2 kilometro karratua km 2
eta
1 m 2 = 100 dm 2 1 dm 2 = 100 cm 2 1 cm2 = 100 mm2 1 dam 2 = 100 m 2 1 hm 2 = 100 dam 2 1 km2 = 100 hm2 km2 hm2 dam2 m2 dm2 cm2 mm2 × 100 × 100 × 100 × 100 × 100 × 100 : 100 : 100 : 100 : 100 : 100 : 100 «Berehala
1 m 1 dm 1 m 1 dm 1 cm 1 cm 1 m2 1 dm2 1 cm2 1 mm 1 mm 1 mm2 1 m 1 dam 1 m 1 dam 1 hm 1 hm 1 m2 1 dam2 1 hm2 1 km 1 km2 1 km Gainazala lerro itxi baten barruan dagoen espazioa da. Azalera gainazal baten neurria da.
kontatuko dizut», webgunean: anayaharitza.es
2 Zer neurri du karratu bakoitzaren aldeak? 25 cm2 16 cm2 4 cm2
3 Osatu baliokidetasunak.
a) 6 km 2 = ? hm 2 = ? dam 2 c) 5 000 cm2 = ? dm2 = ? m2
b) 9 m 2 = ? dm 2 = ? cm 2 d) 700 dam2 = ? hm2 = ? km2

4 Lapitzak erdira Ikusi arretaz adibidea, eta adierazi neurriak metro karratutan. Laguntza gisa, erabili unitate-taula.
91 m 2 5 dm 2
km2 hm2 dam2 m2 dm2 cm2 mm2 91, 05 91,05 m2
a) 6 m 2 17 dm 2 c) 24 dm 2 6 mm 2


b) 3 hm 2 52 dam 2 d) 1 m
5 Ikusi arretaz adibidea, idatzi neurriak adierazpen konplexu moduan. 75,381 m 2 = 75 m
a) 46,9231 m 2 b) 820,259 m 2 c) 0,5143 m 2
Nekazaritzako azalera-unitateak
9,8 dam 2
475 m 2
6 Ikastetxe batek 9,8 dam2-ko azalera du. Eraikinak 475 m2-ko azalera badu, zenbat metro karratu hartzen dituzte jolastokiak eta kirol-pistek? ?
Ebatzi urratsez urrats, hemen: anayaharitza.es .
7 Koldok 5 ha 64 a 30 ca-ko lursail bat du. Erdia erein du. Zenbat metro karratu utzi ditu erein gabe?
8 Libek 2,70 ha-ko lursail bat erosi du, 31 860 € -an. Zenbat ordaindu du metro karratua?
Lursailen neurria adierazteko, hiru neurri-unitate hauek ere erabiltzen dira: zentiarea (ca), area (a) eta hektarea (ha).
1 ca = 1 m 2
1 a = 1 dam 2

1 ha = 1 hm 2 ha a ca
× 100 × 100 : 100 : 100
109 U6
2 9 dm 2 3 mm 2
2
2
2 38 dm
10 cm
Kontuz! Idatzi bi zifra lauki bakoitzean.
Neurtu bolumenak
Zure gauzak gordetzeko lekuek, adibidez, zenbat espazio duten adierazteko, bolumen-unitateak erabili behar dira.
Irudi baten bolumena kalkulatzeko, unitatetzat kuboa hartzen da.
9 unitate kubo unitate kuboa
Bi irudi horiek forma desberdina dute, baina bolumen bera.
Bolumena adierazteko neurri-unitate nagusia metro kuboa da.
9 unitate kubo
• Objektuen bolumena adierazteko, bolumen-unitateak erabiltzen ditugu.

metro kuboa (m 3)
dezimetro kuboa (dm 3)
zentimetro kuboa (cm 3)
Metro kuboa: 1 m-eko ertza duen kubo baten bolumena.
Dezimetro kuboa: 1 dm-eko ertza duen kubo baten bolumena.
Zentimetro kuboa: 1 cm-eko ertza duen kubo baten bolumena.
• Bolumen-unitateak 1 000naka handitzen eta txikitzen dira.
1 Hartu unitatetzat kuboa, eta kalkulatu irudi hauen bolumena:
Gorputz baten bolumena gorputz horrek betetzen duen espazioa da. unitatea
110
5
1 m 3 = 1 000 dm 3 1 dm 3 = 1 000 cm 3 m3 dm3 cm3 × 1 000 : 1 000 : 1 000 × 1 000 1 m 1 m 1 m 1 dm 1 dm 1 dm 1 cm 1 cm 1 cm
2 Egin zenbait irudi polikuboekin. Gero, bikotekideak hau egin beharko du: unitatetzat polikuboa hartuta irudiaren bolumena kalkulatu, eta nola egin duen zuri kontatu.
3 Bi irudi hauek espazio berdina betetzen dute. Orduan, zergatik idatzi ditu Manuelak bi bolumen-neurri desberdin?
2 unitate kubo
16 unitate kubo
4 Pentsatu eta binaka jarrita komentatu Zer unitatetan adieraziko zenituzke objektu hauen bolumenak: m 3-tan, dm 3-tan ala cm 3-tan?

5 Kopiatu eta osatu.
a) 4 m 3 = ? dm 3 = ? cm 3 c) 5 100 cm3 = ? dm3 = ? m3

b) 2,7 m 3 = ? dm 3 = ? cm 3 d) 64 500 cm3 = ? dm3 = ? m3

6 Zenbat litro ur behar ditut ontzi hauek betetzeko?
Bolumena eta edukiera
Objektu baten bolumena da zenbat espazio hartzen duen, eta edukiera, berriz, zenbat espazio duen barruan. Bolumena eta edukiera unitate baliokideak dira.
Baliokidetasunak
Bolumena m3 dm3 cm3
3 dm3 0,12 m3
7 Hegazkin baten tangak 200 m 3-ko bolumena du. Bidaia hasi duenean, tanga beteta zegoen. Helmugara iritsi denean, 125 kL geratzen zaizkio. Zenbat litro erregai gastatu ditu? ?
125 kL 200 m 2
8 Josuk 1,2 m 3-ko igerileku bat bete nahi du. Dagoeneko laurdena bete badu, beste zenbat litro bota behar ditu?
Edukiera kL L mL



1 dm 3-eko ontzi bat betetzeko, 1 L ur behar duzu.
Esperimentuetan, kantitate txikiak adierazteko, erabili bolumen-unitate egokienak.
111 U6
Gogoan hartu!
Bilatu erregulartasunak
Anek dorre hau egin du, hainbat kubo berdin erabiliz. Zenbat kubo beharko ditu 20 pisuko dorre bat egiteko?
• Lehenbizi, egin irudia urratsez urrats, eta zenbatu kuboak.
• Antolatu datuak taula batean.
Zenbat pisu 1 2 3 4 5

Zenbat kubo 1 22 32 42 52
Ikusi duzu zer erlazio dagoen kubo kopuruaren eta pisu kopuruaren artean?
Eureka! Irudiak dituen kuboen kopurua da pisu kopurua ber bi.
Beraz, 20 pisuko dorre bat egiteko, kubo kopuru hau beharko du: 202 = 400 kubo

Anek 400 kubo beharko ditu.
Soluzioak badu zentzurik?
Ohartu beste modu batean ere kalkula dezakezula kubo kopurua: lehenbiziko 20 zenbaki bakoitiak batuta.
1 Ikusi arretaz Eduk egin duen irudi hau. Zenbat kubo beharko ditu dorreak 10 pisu izatea nahi badu?
112
EBATZI BAIETZ!
Pisu 1 2 pisu 3 pisu 4 pisu 5 pisu 1 + 3 = 4 = 22 1 + 3 + 5 = 9 = 32 1 + 3 + 5 + 7 = 16 = 42 1 + 3 + 5 + 7 + 9 = 25 = 52 1
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
21
23
25 + + 27 + 29 + 31 + 33 + 35 + 37 + 39
400
+
+
+
=
Batuketa kalkulatzeko, erabili kalkulagailua.
Problemak arin-arinka
2 1
Esan luzerak, edukierak eta masak adierazteko normalean erabiltzen dituzun unitate batzuk.
Zer unitate erabiliko zenuke zure etxearen azalera adierazteko? m2 km2 cm2 ?
3 4
Hektarea bat, zenbat metro karratu dira? 1 ha = 1 hm 2 1 hm = 100 m
Zenbat litro sartzen dira metro kubo batean?
Buruzko kalkulua
Kalkulatu 5 × 2 3 .
Ikusi nola egiten den, hemen: anayaharitza.es .
Orain, zuk zeuk:


Begira nola pentsatzen dudan
Patroi bila
Kopiatu irudi hauek, eta margotu, kontuan izanda lerro batez bereizitako eremuek ez dutela kolore bera izan behar. Erabili ahalik eta kolore gutxien!
2 kolore bakarrik. 3 kolore bakarrik. Ahal da 2 kolorerekin?
4 kolore bakarrik. Ahal da 2 edo 3 kolorerekin?
Eta mapa politiko bat margotu behar baduzu? Zenbat kolore behar dituzu gutxienez?
MU NDU GUZTIA MARGOTZEKO, 4 KOLORE ASKI DIRA!
Ez duzu sinesten? Egiaztatu zuk zeuk!
Hau bai aurkikuntza! Matematikako teorema garrantzitsu bat da hau: 4 koloreen teorema
– Erabili 4 kolore bakarrik. Zuk nahi dituzunak, baina 4 bakarrik!
– Espainiako mapa politiko batean, margotu probintzia bakoitza kolore batez, kontuan izanda mugakide diren bi probintziak ezin dutela kolore bera izan.
113 U6
hm2 1 hm =
1
100 m
1 L = 1 dm 3 1 m 1 m3 1m 1 m
3 × 3 4 4 × 6 9 7 × 3 5 5 × 4 7 2 × 5 4 6 × 4 5 3 × 6 7 4 × 2 3 2 × 4 6 5 × 3 7
5 × 2
2 3 = 10 3 ×
3 = 5 ×
Z er ikasi dut?
1 Kopiatu eta osatu taula.
Luzera ? ? ? m ? ? ?
Edukiera ? hL ? ? ? cL ?
Masa kg ? ? ? ? ? mg
2 Idatzi datu hauek adierazitako unitateetan:
a) 234 m = ? hm d) 4 600 cg = ? dag
b) 651 km = ? m e) 1,9 mL = ? dL
c) 0,47 kg = ? g f ) 78 dL = ? L
3 Kopiatu eta osatu.
a) 25 dam 18 dm = ? m
b) 73 hL 6 daL 45 L = ? L
c) 10 kg 5 dag 35 cg = ? g

4 Ordenatu edukierak, handienetik txikienera.
2 578 L 260 daL 25 hL 7 daL
5 Ebatzi.
a) 4 m 5 dm 8 cm + 69 dm 30 cm = ? cm
b) 8 kL 27 daL 9 dL – 14 daL 29 dL = ? L
c) 0,43 hg 12 g × 5 = ? g
d) 18 ha : 6 = ? m 2
6 Zer unitatetan adieraziko zenituzke gainazal hauen azalerak?
km 2 m 2 cm 2
Nafarroa 10 391 ?
Sortako karta bat 60 ?
Futbol-zelai bat 9 000 ?
7 Zenbat metro karratu dira?
6 400 dm 2
0,21 ha 78 a
8 Laguntza gisa unitate-taula erabiliz, idatzi neurri hauek adierazitako unitateetan:
a) 9,35 km 2 16 dam 2 = ? hm 2
b) 30,9 dm 2 4 cm 2 50 mm 2 = ? cm 2
9 Pentsatu eta ebatzi.
a) Eiderren etxetik eskolaraino 300 m daude Urrats handiak eginez joaten bada, 0,60 m-koak, zenbat urrats egin behar ditu?
b) Disko hori batek 530 dag-ko masa du, eta disko gogor batek, 37 hg-koa. Hortaz, zenbat kilo ditu altxatuta Xantik?
c) Anttonen autoak minutuko 20 hm egiten ditu. Zenbat kilometro egiten ditu ordu-erdian?
d) Zenbat kilo patata behar dira 20 t-ko edukiontzi bat betetzeko?
e) Zenbat zentilitro ur erabili ditugu izotzontzi hau betetzeko, kontuan izanda izotz-koskor bakoitzak 8 cm 3-ko bolumena duela?
Semaforoa. Margotu koadernoan, ariketa bakoitzaren ondoan, honela:
Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu
114
PORTFOLIOA
530 dag 37 hg
8 cm3
HELBURUA AURRERA
Egin dezagun literatura-lehiaketa bat.
Gaur zientzialariak gara! Esperimentu bat egin nahi dugu, baina laborategiko gure ikaskideari ahaztu egin zaio neurri-unitatea idaztea. Idatziko duzu zuk?
• 600 ? edo koilarakada txiki bat piperbeltz (hautsa).

• 0,250 ? edo basokada bat ur.
• 2 tanta detergente.


Esperimentua egin aurretik, aldatu kantitateak, kasu bakoitzean unitate egokiena izateko.
• Piperbeltz-hautsa ? -tan adieraziko dugu.

• Ura ? -tan adieraziko dugu.
Esperimentua egiteko urratsak
Geure buruari galdezka
1. urratsa Bota ura plater sakon batera.
2. urratsa Hautseztatu piperbeltza.
3. urratsa Bota bi tanta detergente.
Zer gertatu zaio piperbeltz-hautsari?
Istorio-laukia estrategia erabiliz, istorio bat idatziko dugu, jakitera emateko zergatik ez ditugun denok ikasteko aukera berberak. Hauxe izango da izenburua: Zientzialari izan nahi dut!
Pentsatu non kokatuko duzun istorioa eta zein izango pertsonaiakdiren
N o la ikasi dut?
Osatu koadernoan.
Non gertatu zen? Noiz?
Zer gertatu NorZergatik?zen? zeuden Zer gertatu azkenean?zen
Pentsatu noiz gozatu izan duzun izugarri matematika ikasten, eta aipatu hiru egoera. Nola sentitu zinen une horietan eta zergatik?
Pentsatu noiz ez zaizun atsegina gertatu matematika lantzen aritzea, eta aipatu hiru egoera. Zergatik ez zen izan atsegina?
Zer egin dezakezu zuri atseginagoa gertatzeko?

U6
115
Egin literatura-lehiaketa bat idatzi dituzuen istorio guztiekin.




Bi
Elene eskolako futbol-entrenatzailea da. Baloiak eskatu zituen, eta gaur iritsi dira. Baloi bakoitzak 8 € balio du. Zenbat balio dute 3 baloik?

• Baloi kopurua eta baloien prezioa erlazionatuko dituen baliotaula bat egingo dugu.
Baloien kopurua bikoizten badut, prezioa bikoizten da. Baloien kopurua hirukoizten badut, prezioa hirukoizten da.
1 1 × 8 = 8 8
× 2 × 2 × 3 × 3
2 2 × 8 = 16 16
3 3 × 8 = 24 24
Horregatik, baloien kopurua eta prezioa proportzionalak dira.
Bi magnitude proportzionalak dira, baldin eta magnitudeetako bat biderkatuz edo zatituz aldatutakoan beste magnitudea berdin aldatzen bada.
• Balio-taula horizontalean ere egin daiteke.



Taula horrela jarrita, datu gehiago idatz ditzakezu leku txikiagoan.
Proportzionaltasun-taula bi magnitude erlazionatzen dituen balio-taula bat da, eta magnitude horien balioak zenbaki berberaz biderkatuz edo zatituz lortzen da.
1 Proportzionalak dira?
A Liburu baten orrialde kopurua eta hitz kopurua.
Pentsatu: orrialde batek 100 hitz baditu, bi orrialdek 200 hitz izango dituzte?
2 Puntu bakoitzeko, 2 fitxa irabazten dira.
B Zinemako sarreren kopurua eta prezioa.
Pentsatu: sarrera batek 5 € balio badu, hiru aldiz sarrera gehiagok hiru aldiz gehiago balio dute?
a) Zenbat fitxa irabaziko dira 4 puntukoa ateratzen bada?
b) Bi aldiz puntu gehiago ateratzen badira, bi aldiz fitxa gehiago irabazten dira? Azaldu nola jakin duzun.
c) Norbaitek 10 fitxa irabazi baditu, zer zenbaki atera zaio?
118
1
magnitude proportzionalek zer jokaera duten ikasteak problemak ebazten lagunduko digu.
Magnitude proportzionalak
Baloi kopurua Prezioa (€)
Baloi kopurua 1 2 3 4 5 6 Prezioa (€) 8 16 24 32 40 48 × 8 : 8 × 2 × 2 × 3 × 3
3 Adierazi zer magnitude diren proportzionalak.






4 Kopiatu eta osatu proportzionaltasun-taula hau. Zer bi magnituderi buruzkoa izan daiteke? 1 2 ? ? 9 ? ? ? 40 70 ? 100 × 10 : 10
5 Fabrika batean tomatea orduero modu proportzionalean ontziratzen dute. 3 orduan behin 1 000 poto egiten dituzte.

a) Zenbat denbora behar dute 3 000 tomate-poto egiteko?


b) Zenbat tomate-poto egiten dituzte 12 orduan?
Luzera eta azalera… Magnitude
Luzera bikoizten baduzu, zer gertatzen zaio gainazal karratu horien azalerari?
Bikoiztu egiten da?
Hortaz, magnitude proportzionalak dira luzera eta azalera? Azaldu zure erantzuna.
? 12





2 Bikoiztu egin da azalera?
5 10 52 = 25 102 = 100

119 U7
Pentsatu 1etik 10era bitarteko luzera-tarteak dituzula.
1 4 9 16 25 36 49 64 81 100 1 2 2 2 3 2 4 2 52 6 2 72 8 2 92 102
Gero, luzera horietan oinarrituta, egin gainazal karratuak.
proportzionalak?
Adina (urteak) 1 2 5 8 Masa (kilogramoak) 6 10 19 26 Edukiera (litroak) 1 2 4 5 Prezioa (€) 2,50 5 10 12,50 Denbora (orduak) 1 2 6 10 Distantzia (kilometroak) 16 32 96 160
1 000
3
3 000 ?
Arrazoitu adibide batekin:
×
1 2 3 4 5 6 7 8 9 10
Kopuruak konparatzen ditu, baina magnitudeak dira (edo ez) proportzionalak.
Unitatera laburtzea
Magnitude proportzionalen datuak oso agerikoak ez direnean, lagungarria izaten da unitatera laburtzea.
Ikastetxeko zuzendariak 1 472 € ordaindu ditu 4 tableta. Orain 5 ikasle berri etorri direnez, zenbat ordainduko ditu haientzako 5 tabletak?
1. Kalkulatu zer prezio duen tableta batek. 1 472 € : 4 = 368 €
Bost tabletak 1 840 € ordainduko ditu.



= 1 840 €
Batzuetan, benetan jakin nahi dugun datua kalkulatzeko, oso baliagarria da unitate bati zenbat dagokion kalkulatzea.
1 Irakurri eta kalkulatu.
a) Karlosek 5 jogurt-pakete erosi ditu. Guztira 20 jogurt dira. Zenbat jogurt daude 6 paketetan?
Paketeak 5 1 6
Jogurtak 20 ? ?
b) 4 pertsonarentzako errezeta bat egiteko, 32 arbendol behar dira. Zenbatentzat da errezeta 24 arbendol behar badira?
Pertsonak 4 1 ?
Arbendolak 32 ? 24

c) Hiru tomate-potok 4,50 € balio dute. Zenbat poto erosi ditut 15 € ordaindu badut?
Potoak 3 1 ?
Prezioa 4,50 ? 15
Hori jakiteko, lehenbizi kalkulatu zenbat jogurt dauden pakete batean.
120
2
2. Kalkulatu zer prezio izango duten bost tabletak. 368 € × 5
FAKTURA GUZTIRA1472Є
Kalkulatu zenbat bira egiten dituen minutu batean. Pentsatu zenbat minutu dituen ordu-erdik.
2 Gurpil batek 7 minutuan 840 bira egiten ditu. Zenbat bira egiten ditu ordu-erdian?
3 Denda batean, hartz itxurako 3 eranskailu erosten badituzu, bihotz itxurako 6 oparitzen dizkizute. Hartz itxurako 4 erosiz gero, berriz, bihotz itxurako 8 ematen dituzte.
a) Zenbat bihotz ematen dituzte hartz bat erosita?
b) Zenbat oparitzen dituzte 5 hartz erosita?
c) 20 bihotz eman badizkizute, zenbat hartz erosi dituzu?
4 Iturri batean, 3 minutuan 12 L ur ateratzen dira. Zenbat litro ateratzen dira ordu eta laurdenean?

Hiruko erregela
Proportzionaltasunarekin zerikusia duen problema bat dugunean eta lau datuetatik hiru dakizkigunean, hiruko erregela erabil dezakegu.
Hiru ogi erosi, eta 3,60 € ordaindu dut.
Hiruko erregela
Ogi kop. Prezioa 3 3,60 € 5 ?
5 ogi 6 € ordainduko ditut.
Zenbat ordainduko ditut 5 ogi? ? = 3,60 × 5 3 = 18 3 = 6

Ebatzi 1. ariketako problemak hiruko erregela erabiliz. Egiaztatu emaitza berberak lortu dituzula.
Biderkatu zenbakiak diagonalean, eta zatitu beste zenbakiaz.
Gogoan hartu!



Hiruko erregela erabiliz, kalkulatu gelako zenbatek izango duten mugikorra.

121 U7
Urik alferrik ez galtzeko, itxi txorrota.
Ehunekoak
Ehunekoek zati bat multzo guztiaren zenbat den ulertzen laguntzen digute.
Eskola batean, ikasleen % 25 etxera joaten da bazkaltzera.
• Horrek esan nahi du 100 ikasletik 25ek etxean bazkaltzen duela.
• % 25 adierazpena ehuneko bat da. Honela irakurtzen da: ehuneko 25
Ez gara 25 pertsona etxean jaten. 100eko multzo bakoitzetik 25 gara.
% 100
% 25

% 75
Ehunekoa Irakurri Esanahia Zatiki dezimala
Etxean bazkaldu % 25 ehuneko 25 100eko multzo bakoitzetik 25 25 100 = 0,25

100etik 25
Ehunekoa % 25
Zatikia 25 100
Forma dezimala 0,25
Ehunekoak 100 zati berdinetan banatutako guztizko baten parte bat adierazten du. Ehunekoa adierazteko, lehenbizi % ikurra idazten da, eta, gero, zenbakia. Multzo guztia % 100 da, eta honela irakurtzen da: ehuneko ehun
1 Kopiatu eta osatu taula koadernoan.
Ehunekoa Irakurri Esanahia Zatiki dezimala
% 15 ? ? 15 100 = 0,15
? ehuneko 50 ? ? ? ?
100eko multzo bakoitzetik 75 ?
2 Pentsatu eta ebatzi.
a) Eskolako ikasleen % 62 futbolean ibiltzen da. Zer ehuneko ez da ibiltzen futbolean?
b) Herri ba teko biztanleen % 59k 172 cm-ko altuera baino handiagoa du. Zer ehunekok du 172 cm edo gutxiago?
c) Parke batean 350 zuhaitz daude. Horietatik % 42 magnoliak dira. Zuhaitzen zer ehuneko ez dira magnoliak?
Guztizkoa % 100 da. % 62 + ? = % 100
122
3
3 Kopiatu eta osatu, ehuneko bakoitzari dagokion zatiki laburtezina idatzita.
% 25 = 25 100 = 1 4 % 50 = 50 100 = ? ? % 75 = 75 100 = ? ?


4 Ordenagailu eramangarriari bateriaren % 25 geratzen zaio.
a) Azaldu, zure hitzak erabiliz, zer esan nahi duen horrek.
b) Zenbat bateria gastatu da?
c) Zer iruditzen zaizu: bateria kargatutakoan % 80 handitu daiteke? Azaldu zergatik.
Kopuru baten ehunekoa
Eskola batean, ikasleen % 25 etxera joaten da bazkaltzera. Eskolan guztira 300 ikasle badira, zenbatek bazkaltzen dute etxean?
• Grafikoki ebatz dezakegu. Gogoratu % 25 horrek hau esan nahi duela: 25 100 = 1 4
Etxean 75 ikaslek bazkaltzen dute.
Kopuru baten ehunekoa zenbat den oso erraz kalkula daiteke hiruko erregela erabiliz.
• 300en % 25 kalkulatzeko beste modu bat hiruko erregela da.
Eskolan Etxean 100 25 300 ?
?
Etxean 17 ikaslek bazkaltzen dute.
Kalkulatu kopuru hauek:
% 25 a)
50 b)
1 950 % 20
Gogoan hartu!

123 U7
25 25 25 300 100 100 100 25
3
×
= 75
Ehunekoak erabiliz, konparatu mugikorra duten haurren kopuruak urtez urte. %
= 300 × 25 100 = 75 1 000
1 000ren % 25 630
630en % 50
c) 1 950en % 20
Igoerak eta beherapenak
datuari batzen edo kentzen zaizkio, amaierako datua kalkulatzeko.
Igoerak eta beherapenak hasierako
Joko batean, enigma bat akatsik egin gabe argitzea lortzen baduzu, puntuazioa % 15 igotzen dizute. Aldiz, bidean akatsen bat egiten baduzu, % 10 jaisten dizute.
Zenbat puntu lortu dituzte egoera hauetako bakoitzean?
HASIERAKO PUNTUAK: 60 PUNTU%15eko IGOERA
Hasierako datua: 60 puntu
Zenbateko igoera:
60ren % 15 = 60 × 15 100 = 9
Amaierako datua: Batu hasierako datuari igoera: 60 + 9 = 69 puntu
Guztira 69 puntu lortu dituzte.
HASIERAKO PUNTUAK: 60 PUNTU %10eko BEHERAPENA
Hasierako datua: 60 puntu

Zenbateko beherapena: 60ren % 10 = 60 × 10 100 = 6






Amaierako datua: Kendu hasierako datuari beherapena: 60 − 6 = 54 puntu
Guztira 54 puntu lortu dituzte.
1 Auzoko paper-dendan merkealdia da. Ikusi datuak arretaz, eta kalkulatu produktu bakoitzaren amaierako prezioa.
% 5
42 € 34 €

% 10
% 50
86,50 €
Laguntza gisa, egin honelako taula bat:
Hasierako prezioa Beherapena Amaierako prezioa
Bizkar-zorroa ? ? ?
Bozgorailua ? ? ?
Margoen kutxa ? ? ?
Prezioa merkatzea beherapena egitea da.
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
124
4
BEZ hitzak hau esan nahi du: Balio Erantsiaren gaineko Zerga.
3 Produktu guztietan, hasierako balioari BEZa gehitzen diote (diru kopuru bat), amaierako prezioa kalkulatzeko. Zenbat da produktu hauen amaierako prezioa?

Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
Laguntza gisa, egin honelako taula bat:
Hasierako p. Igoera Amaierako p.
Betaurrekoak ? ? ?
Ogia ? ? ?




Ordenagailua ? ? ?

4 Kauldik marrazteko tableta grafiko bat erosi du, 435 € -koa. Epeka ordaindu nahi duenez, % 10eko interesa kobratuko diote. Zenbat ordainduko du guztira tableta?
Hasierako p. Interesa (igoera) Amaierako p. ? ? ?



5 Gela batean irakurketa-plana egin dutela-eta, ikasleek liburuak irakurtzen denbora gehiago eman dezakete. Lehen, astean 10 ordu inguru zituzten irakurtzeko; orain, denbora hori % 15 igo da. Zenbat denbora ematen dute orain irakurtzen?
% 15 10 h ?
Ebatzi urratsez urrats, hemen: anayaharitza.es
Aisialdian, gozatu irakurtzen. Gutxitu gailu digitalekin pasatzen dituzun orduak.

125 U7
% 10 BEHERAPENA! % 40 BEHERAPENA! 130€ 180€
2 Zer dela eta diozu hori? Zein aukeratuko zenuke? Azaldu zergatik.
135 € BEZ a : % 10 1 € BEZ a : % 4 830 € BEZ a : % 21
Eskala
Krokis edo mapa bateko distantziak benetan zenbat diren jakiteko, eskala erabiltzen dugu.
Plano hau 1 : 50 eskalan eginda dago.
1 : 50 eskalak esan nahi du planoko 1 cm benetan 50 cm direla. Hortaz, zer neurri du benetan egongelak?
1. Ikusi zer luzera eta zabalera dituen egongelak planoan.
Zabalera planoan 6 cm
Luzera planoan 9 cm
2. Kalkulatu zer zabalera duen benetan egongelak, jakinda eskala 1 : 50 dela.
Planoan Benetan 1 cm 6 cm 50cm ?
}
Bainugela Sukaldea Terraza Logela Egongela 9 cm 6 cm
Eskala 1 : 50
3. Kalkulatu zer luzera duen benetan egongelak, jakinda eskala 1 : 50 dela.
Planoan Benetan
1 cm 9 cm 50cm ?
}
? = 50 × 9 1 = 450 cm = 4,5 m

Egongelak benetan 3 m-ko zabalera eta 4,5 m-ko luzera ditu.
1 Zer esan nahi dute eskala hauek?
1 : 100 1 : 50 000 1 : 3 000
2 Zenbat metroko perimetroa du benetan irudiko haur-parke honek?
6 cm
cm
Gogoratu
126 5
Eskala 1 : 1 000 3,2
Eskalak adierazten du zer erlazio dagoen plano edo krokis bateko luzeren eta benetako luzeren artean.
? = 50 × 6 1 = 300 cm = 3 m
Irudi baten perimetroa alde guztien luzeren batura da.
3 Irakurri alboko laukiko testua, eta erantzun.
a) Azaldu zer esan nahi duten eskala hauek:
A 0 5 10 15
kilometroak
B 0 20 40 60
kilometroak
C 0 10 20 30
kilometroak
b) Erlazionatu lehengo eskala grafiko horiek zenbakizko eskala hauekin:
1 : 5 000 000 1 : 20 000 000 1 : 1 000 000
4 Ikusi zein den eskala, neurtu distantziak krokisean, eta kalkulatu koadernoan.
Aterpetxea
Aintzira Mendia
a) Idatzi zenbat kilometro dauden puntu batetik beste batera.
b) Eskala beheko hau balitz, zenbat kilometrokoak izango lirateke lehengo distantzia horiek?
0 5 10 15
kilometroak
5 Ikusi arretaz mapa eta eskala.
a) Zer esan nahi du mapako eskala grafikoak?
Eskala
0 200 400 600

kilometroak
b) Zer distantzia dago Madrildik Lisboara? Eta Madrildik Sevillara?
c) Egiaztatu Aukeratu munduko leku bat, zuk nahi duzuna. Marraztu koadernoan distantziak irudikatzeko mapa bat, eta sortu eskala grafikoa, zure maparen tamainaren arabera.
Eskala grafikoa
0 1 2 3
kilometroak
barrak 1 cm du.
Mapako 1 cm benetan 1 km da; hau da, 100 000 cm.
Zenbakizko eskala hau da:
E = 1 : 100 000
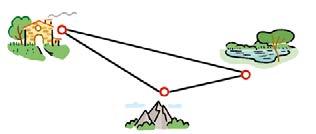
127 U7
0 200400600 kilometroak Zaragoza Valentzia Madril Sevilla Lisboa Bartzelona Bilbo Coruña Alacant PORTUGAL FRANTZIA Kantauri itsasoa M e d i t e r r a n e o it s a s o a OZEANO ATLANTIKOA
0 1 2 3 kilometroak
EBATZI BAIETZ!
Egin eskema bat
Gelan inkesta bat egin dugu, jakiteko zenbat ikaslek erabiltzen duten ordenagailua edo tableta, ikasteko. Ikasleen % 56k ordenagailua erabiltzen du, eta % 20k, tableta. Gainera, ikasteko gailuren bat erabiltzen duten ikasleen % 7k biak erabiltzen ditu.
Ikasleen zer ehunekok ez du erabiltzen ez ordenagailurik ez tabletarik?





Hori jakiteko, datuak eskema moduan adieraziko ditugu.
1. Kalkulatu ikasleen zer ehunekok erabiltzen duen ordenagailua bakarrik.
% 56 − % 7 = % 49
2. Kalkulatu ikasleen zer ehunekok erabiltzen duen tableta bakarrik.
% 20 − % 7 = % 13
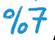
3. Azkenik, kalkulatu ikasleen zer ehunekok ez duen erabiltzen ez ordenagailurik ez tabletarik.
% 100 – (% 49 + % 13 + % 7) = % 100 – % 69 = % 31

Ikasleen % 31k ez du erabiltzen ez ordenagailurik ez tabletarik.

Soluzioak badu zentzurik?
Egiaztatu ehuneko guztien batura % 100 dela.
% 49 + % 13 + % 7 + % 31 = % 100
1 Herrialde bateko biztanleen % 40k frantsesez egiten du, eta % 16k, alemanez. Horietatik, % 5 elebiduna da; hau da, bi hizkuntzak dakizki: frantsesa eta alemana. Biztanleen zer ehunekok ez du egiten ez frantsesez ez alemanez?
Ikasle guztien kopurua % 100 da.
128
Problemak arin-arinka
2 1
Adina eta altuera, magnitude proportzionalak dira?
Azaldu, zure hitzak erabiliz.
4 arkatzek 2 € balio badute, zenbat balio dute 5 arkatzek?
Zer zatiki dezimal da ehuneko hauen baliokidea?
%25 %50 %75
4 3 5
Mapa baten eskala 1 : 100 bada, benetako zenbat zentimetro dira mapako 2 cm?
Nola dabil?
Badakizu nola? Egin urrats hauek:
1. Ikusi arretaz taulako datuak.
Beroki bat % 50 merkatuta dago. Amaierako prezioa 24 € du. Zenbat balio zuen hasieran?
2. Marraztu koordenatu-ardatz bat.
0 1 2 3 kilometroak
3. Adierazi taulako datuak grafikoan, koordenatu-puntuak balira bezala (bolaluma kopurua, prezioa).
4. Erregela erabiliz, lotu markatu dituzun puntuak.
5. Puntuek lerro zuzena eratzen badute, magnitude proportzionalak dira!
÷ 2 12 6 3 ÷ 2 3 3 3 3 } 12 Bolaluma kop. 3 5 7 8 Prezioa (€) 4,50 7,50 10,50 12 12 11 10 9 8 7 6 5 4 3 2 1





Bilatu unitate honetan magnitude proportzionalen datu batzuk, eta adierazi grafikoki. Lerro zuzena atera da?
Praktikatu tresna digital batekin, webgunean: anayaharitza.es
Buruzko 28ren 1 4 32ren 1 4 36ren 1 4 40ren 1 4 44ren 1 4
Ikusi nola egiten den, hemen: anayaharitza.es
6 kalkulua Kalkulatu 12ren 1 4 . Orain, zuk zeuk: 4ren 1 4 8ren 1 4 16ren 1 4 20ren 1 4 24ren 1 4

ahaztu
puntuak lotzeko erregela erabiltzea.
129 U7
Benetako zenbat kilometro adierazten ditu eskalako barratxo beltz honek?
Batzuetan, marrazki bat egitea aski da bi magnitude proportzionalak diren jakiteko.
Prezioa (€) Bolaluma kop.
12345678
Ez
Ondo egina!
Begira nola pentsatzen dudan
Z er ikasi dut?
1 Magnitude hauek proportzionalak dira?
Esne-litroen kopurua eta irabiakien kopurua.
Pentsatu:
3 aldiz irabiaki gehiago egin nahi badut, 3 aldiz esne gehiago behar dut?
Ikasten emandako ordu kopurua eta azterketan aterako dudan nota.
Pentsatu:
2 aldiz ordu gehiagoz ikasita, 2 aldiz nota handiagoa lortuko dut?
2 Kopiatu eta osatu proportzionaltasun-taula hau:
6 Kalkulatu buruz.
a) 300en % 8 c) 100en % 14
b) 200en % 30 d) 500en % 10


7 Zer zatiki dagozkie ehuneko hauei? Idatzi bakoitzaren zatiki dezimala eta zatiki laburtezina.
% 25 % 50 % 75
8 Kopiatu eta margotu koadernoan. Irudi guztiaren zer ehuneko geratu da margotu gabe?
1 2 5 9 12 ? ? ?
3 Zinemara joateko lau sarrerak 26 € balio dute. Zenbat balio dute bost sarrerak? Ebatzi unitatera laburtuz.
Sarrerak 4 1 5
Prezioa (€) 26 ? ?

4 850 g-ko gazta zati batek 8,50 € balio du. Zenbat balioko du 625 g-ko zati batek? Ebatzi hiruko erregela erabiliz.
9 Tapaki batek 92 € -ko balioa du, eta % 21eko BEZa gehitu diote. Zein da tapakiaren amaierako prezioa?
10 465 € balio zuen garbigailu bati % 25eko beherapena egin diote. Zer prezio du orain?

LEHEN 465 Є
ORAIN % 25eko BEHERAPENA!
11 Kalkulatu benetan zer distantzia dagoen bi herriren artean, jakinda 1 : 50 000 eskalan eginda dagoen mapa batean distantzia 8 cm dela.
Semaforoa. Margotu koadernoan, ariketa
bakoitzaren ondoan, honela:

Erantzuna badakizu
5 Hiri bateko biztanleen % 58 alokairuko etxeetan bizi da. Biztanleen zer ehuneko ez da bizi alokairuan?
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu
130
PORTFOLIOA
0,10 % 15 % 25 20 100
HELBURUA AURRERA
Prestatu teknologiarekin zerikusirik ez duen aisialdi-plan bat.
Irakurri arretaz datu hauek, eta erantzun galderei:
2022an, 13 urteko 10 haurretik 9k bere mugikorra zuen.
2013an, 13 urteko 4 haurretik 3k bere mugikorra zuen.
a) 13 urteko haurren zer ehunekok zuen bere mugikorra 2022an? Zure gelako zenbat ikasle lirateke? Hori kalkulatzeko, erabili hiruko erregela.
b) Haurren zer ehunekok zuen mugikorra 2013an?



c) Zer urtetan da handiagoa ehunekoa?

d) Egin zuen ikastaldeari buruzko azterketa estatistiko bat, jakiteko nork duzuen mugikorra eta zenbat denbora ematen duzuen mugikorrean ibiltzen. Bat dator hasierako datuetan emandako ehunekoarekin?
Geure buruari galdezka
Ondorioak eta emaitzak estrategia erabiliz, aztertuko dugu zer gatik den garrantzitsua aisialdian teknologiarekin ematen den denbora mugatzea.
a) Kopiatu eta osatu antolatzailea. Behar baduzu, bilatu informazioa.
Zer
gertatuko
da zure
adineko jendeak aisialdi guztia gailu teknologikoak erabiltzen ematen badu?
Epe luzean Zer gerta daiteke?
Zer ondorio izango lituzke?
Zer ondorio izango ditu?
Epe laburrean Zer gerta daiteke?
Zer ondorio izango lituzke?
Zer ondorio izango ditu?
Zuretzat ? Zuretzat ? Gainerakoentzat ?
Gainerakoentzat ?
b) Taldeka, partekatu zuen gogoetak, eta prestatu teknologiarekin zerikusirik ez duen aisialdi-plan alternatibo bat.
N o la ikasi dut?
Osatu koadernoan.
Aipatu zure bizitzarako baliagarriak izan zaizkizun matematikako hiru eduki. Nola sentitu zara horiek erabiltzean?
Aipatu baliagarriak iruditzen ez zaizkizun hiru eduki. Nola bilatu dezakezu benetako bizitzan duten erabilera?
U7 131
aurrera
Nola kontzientziatu dezakegu jendea ura zaindu beharraz?

Marraztu logo bat, ura zaintzea sustatzeko.
Jarraitu hariari!
1 2



Sailkatu angeluak zabaleraren arabera
Sailkatu angeluak kokapenaren arabera
132






133
minutuak eta segundoak 3
arteko kenketak
arteko batuketak
Ebatzi baietz! Graduak,
Angeluen
5 Angeluen
4
Sailkatu angeluak zabaleraren arabera
Angeluak sailkatzea oso baliagarria da zer propietate dituzten eta nolakoak diren jakiteko.
Angelu baten zabalera edo zabaltasunaren neurria adierazteko erabiltzen dugun unitatea gradu hirurogeitarra da.
Angeluak neurtzeko, angelu-garraiagailua erabiltzen da.
• Zabaleraren arabera, honela sailkatzen dira angeluak:

zuzena zorrotza laua osoa kamutsa
• Zabaleren baturaren arabera, bi angelu honelakoak izan daitezke:

1 Kopiatu esaldiak, eta osatu, hitz hauek idatzita:
zuzenerdi zabalera neurria
erpina puntua angeluak aldeak
a) Bi zuzen ebakitzailek lau eremu eratzen dituzte: ? dira.
b) Angeluek elementu hauek dituzte: ? , ? eta ?
c) Erpina aldeak elkartzen diren ? da.
d) Zabalera aldeen zabaltasunaren ? da, eta aldeak bi ? dira.
2 Zer dela eta diozu hori? Garraiagailua erabiltzeko modu hauetatik zein da zuzena angelu bat neurtzeko? Azaldu zergatik.
Angeluen elementuak
Angeluek hiru elementu dituzte:
Erpina

Aldeak
Zabalera
Angeluak garraiagailuarekin nola neurtu ikusi nahi baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
134
90 100 110 120 130 140 150 160 170 180 80 70 60 50 40 30 20 10 0 90 80 70 60 50 40 30 20 10 0 100 110 120 130 140 150 160 170 180 90 100 110 120 130 140 150 160 170 180 80 70 60 50 40 30 20 10 0 90 80 70 60 50 40 30 20 10 0 100 110 120 130 140 150 160 170 180 90 100 110 120 130 140 150 160 170 180 80 70 60 50 40 30 20 10 0 90 80 70 60 50 40 30 20 10 0 100 110 120 130 140 150 160 170 180 A
B C
1
osagarriak betegarriak
60° + 30° = 90° 140° + 40° = 180° 90 100 110 120 130 140 150 160 170 180 80 70 60 50 40 30 20 10 0 90 80 70 60 50 40 30 20 10 0 100 110 120 130 140 150 160 170 180 45° 360° 180° > 90° < 90° 90° 60° 30° 140° 40°
Batuta 90° dira. Batuta 180° dira.
3 Marraztu angelu zorrotz bat, eta adierazi zein diren elementuak. Zer neurri du? Erabili garraiagailua.
4 Neurtu eta sailkatu angelu hauek:
5 Ikusi arretaz adibidea, eta marraztu adierazitako angeluak.
Nola neurtu angeluak
Eskuinerantz zabaltzen diren angeluak neurtzeko, kanpoko zenbaki ilara erabili behar dugu.
a) ^ A = 45° b) ^ B = 110° c) ^ C = 60° d) ^ D = 180°
6 Esan pare bakoitzeko bi angeluak osagarriak edo betegarriak diren.
a) 50° eta 40° c) 90° eta 90° e) 70° eta 20°
b) 60° eta 120° d) 165° eta 15° f ) 45° eta 45°
7 Kalkatu eta neurtu A ^ eta B ^ angeluak. Gero, marraztu angelu bakoitzaren osagarria.
Ezkerrerantz zabaltzen direnak neurtzeko, barruko zenbaki ilara.
8 Lapitzak erdira Zer neurri dute angelu hauek? Pentsatu eta ebatzi.
a) ^ A eta ^ B osagarriak dira. ^ A -k 35° baditu, zer neurri du ^ B -k?




b) ^ C eta ^ D betegarriak dira. ^ C -k 115° baditu, zer neurri du ^ D -k?

c) ^ E eta ^ F osagarriak dira. Berdinak badira, zer neurri dute?
d) ^ G eta ^ F betegarriak dira. Berdinak badira, zer neurri dute?
Marrazki bat eginda, problemak errazago ebazten dira askotan.
Gogoan hartu!
Publizitateko logoetan ikusitako angeluak zer motatakoak diren identifikatzeko, erabili angeluen sailkapena.
135 U8
 B C D E
1. Marraztu zuzenki bat, eta markatu angeluaren erpina.
2. Jarri gainean garraiagailua; markatu zabalera, eta marraztu angeluaren beste aldea.
 B
90 100 110 120 130 140 150 160 170 180 80 70 60 50 40 30 20 10 0 90 80 70 60 50 40 30 20 10 0 100 110 120 130 140 150 160 170 180 30° 50°
90 100 110 120 130 140 150 160 170 180 80 70 60 50 40 30 20 10 0 90 80 70 60 50 40 30 20 10 100 110 120 130 140 150 160 170 180 70°
Sailkatu angeluak kokapenaren arabera
Angeluen kokapenak esaten digu angelu batzuk non eta nola dauden jarrita beste angelu batzuekiko.
1 Kopiatu eta osatu, hitz hauek idatzita. Marraztu adibide bana.
auzokide ondoz ondoko zorrotzak
erpinez aurkako
zuzenak
a) ? angeluek erpin bera dute, eta alde bat ere bai.
b) Angelu ? guztiak ondoz ondokoak dira.
c) ? angeluak berdinak dira.
d) Bi angelu auzokide berdinak badira, biak ? dira.
e) Bi angelu auzokide ezin dira ? izan.
2 Idatzi nolakoak diren angelu hauek kokapenaren arabera:
a) b) c)
3 Irudi-diktaketa! Marraztu pertsonaia bakoitzak esandakoa.
Angeluak kokapenaren arabera
Ondoz ondokoak
Erpin bera dute, eta aldeetako bat ere bai.
Ondoz ondoko bi angeluk batuta 180o badituzte, auzokideak dira.
Erpinez aurkakoak
Erpin bera dute, eta bataren aldeak bestearen aldeen luzapenak dira.
Bi angelu, ondoz ondokoak, baina ez auzokideak.
a) b)
Bi angelu, 90°-koak eta auzokideak.
4 Irakurri, kalkulatu eta marraztu angeluak.
a) ^ A eta ^ B auzokideak dira. ^ A -k 60° baditu, zer neurri du ^ B -k?


b) ^ C eta ^ D erpinez aurkakoak dira. ^ C -k 30 ° baditu, zer neurri du ^ D -k?
5 Idatzi zer neurri duten angeluek, garraiagailua erabili gabe.

136
2
^ A ^ B ^ C ^ D = 135° F ^ = 25° ^ E G ^ I ^ L ^ = 140° H ^ = 70° J ^ K ^
6 Egiaztatu Ikusi arretaz aurreko ariketako angeluak, eta sailkatu pare hauek kokapenaren arabera:
7 Beheko planoa Madrilgo metroaren zati bat da. Binaka jarrita, aztertu arretaz planoa, bilatu angelu batzuk, eta sailkatu zabaleraren eta kokapenaren arabera.
Egin gauza bera zuen herriko kaleen plano batekin.
Erdikariak marrazten
Angelu baten erdikaria da angeluaren erpinetik igaro eta bi zati berdinetan banatzen duen zuzenerdia. Angelu baten erdikaria marrazteko, egin urrats hauek:
1. Jarri konpasaren punta angeluaren erpinean, eta egin arku bat.
2. Arkuak angeluaren aldeak ebakiko zituen. Puntu horietatik, eta konpasaren zabalera aldatu gabe, egin beste bi arku.
3. Erregelarekin, marraztu arkuak elkartzen diren puntutik eta erpinetik igarotzen den zuzenerdia. Hori da erdikaria!
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
• Irakurri, eta erantzun binaka.
a) 100°-ko angelu baten erdikaria marrazten baduzu, zer neurri dute eratzen diren bi angeluek?
b) Nolakoak dira bi angelu berri horiek kokapenaren arabera?

c) Beheko kasu hauetatik zeinetan marraztu da erdikaria?
Gogoan hartu! A B C D


Bilatu angelu auzokideak, ondoz ondokoak eta erpinez aurkakoak publizitateko logoetan.

137 U8
^ A eta ^ B ^ B eta ^ D ^ D eta ^ A ^ E eta ^ F ^ G eta H ^ ^ I eta K ^ L ^ eta ^ J L ^ eta K ^
A B A B A B erdikaria
Graduak, minutuak eta segundoak
Angelu batek zehatz-mehatz zer neurri duen adierazteko, graduak,
minutuak eta segundoak erabiltzen ditugu.
• Angeluen neurria adierazteko unitateak gradua (°), minutua (') eta segundoa ('') dira. gradu 1 = 60 minutu
1° = 60' minutu 1 = 60 segundo
1' = 60''
• Orduak minutu eta segundo bihurtzeko, edo alderantziz, hau egin behar da:
Graduak, minutuak eta segundoak 60naka handitzen eta txikitzen dira. Unitate horiek sistema hirurogeitarrekoak dira.
• Angeluen neurriak zenbait modutan adieraz daitezke.
Adierazpen konplexua: neurri-unitate bat baino gehiago.
^ A = 15° 10' 30''
1 Idatzi angeluen neurri hauek zifraz:
a) Hirurogeita hamar gradu, hamabi minutu eta lau segundo.
b) Ehun eta hamalau gradu eta berrogeita zortzi segundo.
c) Berrogeita bederatzi minutu eta hemeretzi segundo.
2 Idatzi angelu hauek adierazitako unitateetan. Zer eragiketa egin duzu aldaketa bakoitzean?
a) 2° = ? ' b) 10 ' = ? '' c) 5° = ? '' b) 420 ' = ? °
3 Buru pentsalariak Zer eragiketa egin behar duzu graduak segundotan adierazteko? Eta segundoak gradu bihurtzeko?
4 Neurtu angelu hauek garraiagailuarekin, eta idatzi zer zabalera duten minututan:
Adierazpen sinplea: neurri-unitate bakarra.
^ A = 54 630 ''



138
3
x 60 : 60 x 60 : 60 GRADUAK MINUTUAK SEGUNDOAK Â B Â GRADUAK MINUTUAK SEGUNDOAK
5 Zenbat segundo dituzte angelu hauek? Ikusi arretaz adibidea, eta kalkulatu. Nahi baduzu, erabili kalkulagailua.
^ A = 1° 18' 26''
^ A = 1° × 3 600 + 18' × 60 + 26'' = 3 600'' + 1 080'' + 26'' = 4 706"

^ B = 2° 45' 9'' ^ C = 3° 37' ^ D = 14' 50''
6 Erreparatu adibideari, eta adierazi beheko kopuruak modu konplexuan: gradu, minutu eta segundotan.
8 3 7 5'' 60
2 3 7 1 3 9' 6 0
5 7 5 1 9' 2° 3 5''
8 375'' zati 60 dira: 139' eta sobera 35''. 139' zati 60 dira: 2° eta sobera 19'.
8 375'' = 2° 19' 35''
a) 90 560'' b) 43 540'' c) 5 620'
7 Ordenatu angeluak zabalera handienekotik txikienekora.
^ A = 1° 25' 93'' ^ B = 5 100'' ^ C = 87' 3''
8 Angelu hauetatik zein da angelu zuzena? Nolakoak dira besteak zabalera kontuan hartuz?
A 87° 243' 12'' B 87° 178' 120'' C 5 329' 74''
9 Zenbat segundo dira? Zertaz ohartzen zara?
a) 1° 27' 34'' c) 2° 48' 3''
b) 1 h 27 min 34 s d) 2 h 48 min 3 s

10 Iturriko ura hartzeko, 12 ° 30'-ko inklinazioa duen arrapala bat egin behar da. Ondo egin dute?
Gogoratu:
1° = 3 600''
1' = 60''
Gogoratu
Denbora neurtzeko ere sistema hirurogeitarra erabiltzen dugu.
x 60 x 60 : 60 : 60
Gogoan hartu!
Publizitateko logoetan angelu berdinak aurkitzeko, neurtu angeluak.
139 U8
ORDUAK MINUTUAK SEGUNDOAK 750 '
Angeluen arteko batuketak
Angelu txikiagoak elkartuta, handiagoak marraztu ditzakegu, eta
horien neurriak kalkulatu.
Angeluen arteko batuketak egiteko, egin urrats hauek:
1. Egin datuen arteko batuketa
49'' + 32° 27' 1 3''
2. Aldatu datuak.
3. Adierazi emaitza.


Batuketa grafikoki ere kalkula dezakegu.
Angeluen arteko batuketa egindakoan segundoak 60 edo gehiago badira, bihurtu minutu; minutuak 60 edo gehiago badira, bihurtu gradu.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Kopiatu eta egin batuketak.
a) 13° 1 1' 1 7'' + 6° 29' 42''
b) 8° 41' 30'' + 3° 6' 50''
c) 27° 9' 52'' + 53° 18' 26''
d) 20° 1 3' 38'' + 49° 55' 4''

2 Kalkatu angeluak, eta batu biak grafikoki.
^ A = 42' 37'' ^ B = 13' 21''

3 Egin batuketak. ^

140
B
5' ^ C = 8° 26' ^ D = 81° 34' ^ A = 36° 34'
^ A + ^ B b) ^ A + ^ C c) ^ C + ^ D
= 10°
a)
4
54° 1 6'
86° 43' 62'' 86° 43' 62'' 86° 44' 2'' 60 + 2 54° 1 6'
32°
86° 44' 2'' 54° 16' 49' + = 32° 27' 13'' 86° 44' 2''
49'' +
27' 1 3''
Gogoratu 60'' = 1' 60' = 1°
Ohartu honetaz 36° 34' + 10° 5' 36° 34' + 10° 0 5' 36° 34' + 10° 5' ✗ ✓ + = ^ A ^ A ^ B ^ B
4 Zer gertatzen da angeluen arteko batuketan ordena aldatzen baduzu? Egiaztatu.
5 Ikusi zer neurri duen alboko angeluak.
a) Angelu hauetatik zein da alboko horren osagarria?
A 43° 43' 27'' B 134° 43' 27'' C 44° 43' 27''
b) Eta betegarria?
A 134° 44' 27'' B 134° 43' 27'' C 44° 43' 27''

6 Pentsatu eta ebatzi.
a) Mirentxu 4 min 12 s-an dutxatzen da, eta Kattin ahizpak, berriz, Mirentxuk baino 2 min 40 s gehiago behar izaten ditu. Zenbat denboran dutxatzen dira bi ahizpak?
b) Lolok Donostiatik El Prat de Llobregat hirira joan nahi du. Aurrena trena hartu du Bartzelonaraino; bidaiak 5 h 27 min iraun du. Gero, Bartzelonan autobusez jarraitu du, beste 34 minu tuan. Zenbat denboran iritsi da helmugara?


5 h 27 min ?
34 min
Angelu laua baino handiagoak neurtzen
Nola neur dezakegu alboko angelu honen zabalera garraiagailua erabiliz?
1. Luzatu angeluaren bi aldeetako bat.
2 angelu eratzen dira:
^ B eta ^ C ; bat laua da.
^ C = 55°
• Binaka jarrita, marraztu 180° baino gehiago dituen angelu bat, eta kalkulatu zer neurri duen, urrats horiek eginez.
45° 16' 33''
Ebatzi urratsez urrats, hemen: anayaharitza.es. ^
^
= 180° + 55° = 235°
Hortxe duzu soluzioa!
141 U8
donostia bartzelona el prat de llobregat
2. Neurtu angelu laua ez bestea.
B ˆ C 90 100 110 120 130 140 150 160 170 180 80 70 60 50 40 30 20 10 0 90 80 70 60 50 40 30 20 10 0 100 110 120 130 140 150 160 170 180 B C
3. Kalkulatu zer neurri duen hasierako angeluak.
Gogoratu Denbora-datuen arteko batuketak angeluen artekoak bezalaxe egiten dira.
A
ˆ
A
B
C
= ^
+ ^
A
Angeluen arteko kenketak
Angeluen arteko kenketa eginda, jakin dezakegu, adibidez, zenbat falta zaigun norian bira osoa egiteko.
Angeluen arteko kenketak egiteko, egin urrats hauek:
1. Jarri datuak bertikalean
110° 25' 1 5'' 40° 35' 1 0''
2. Aldatu datuak.

1 +60
110° 25' 1 5'' 40° 35' 1 0''
Egin kenketa.
109° 85' 1 5''
40° 35' 1 0''
69° 50' 1 5''
Kenketa grafikoki ere kalkula dezakegu.
110° 25' 15'' = 40° 35' 10'' 69° 50' 1 5''
Angeluen arteko kenketak egiteko, prestatu kenketa: kenkizuneko datuek handiagoak izan behar dute kentzailekoak baino.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Kopiatu eta egin kenketak. a)
2 Kalkulatu angeluen arteko kenketa hauek grafikoki:
a) 75° − 46° b) 95° − 38° c) 118° − 53°
3 Zer angelu falta da eragiketa bakoitzean?
a) 92° 5' 44'' − 19° 7' 15'' = ?


b) 110° 24' 13'' + ? = 125° 2' 52''

c) ? − 35° 17' 30'' = 90°
4 Pentsatu eta binaka jarrita komentatu Binaka jarrita, pentsatu eta kalkulatu zer neurri duen angelu ezezagun bakoitzak, garraiagailua erabili gabe.
^ E = ?
^
Gogoratu: 1° bihurtu dezakezu 60 ' eta 1 ' bihurtu dezakezu 60“.

A = 160° 12' 9''

^ D = 123° 25'
^ B = ?
^ C = ?
142
5
89°
23° 20' 1 5'' c) 116° 7' 43'' 70° 10' 3 1'' b) 48° 31' 8'' 6° 27' 42'' d) 90° 13' 1 8'' 50° 15' 20''
56' 1 7''
3.
=
–
5 Kalkulatu.
a) 45° 12'-ko angeluaren osagarria.
b) 117° 3' 11''-ko angeluaren betegarria.

6 Triangelu isoszeleak bi angelu berdin ditu. Angelu horietako bakoitzak 36° 25' ditu. Zer neurri du hirugarren angeluak?
7 Naroak txorimalo bat jarri nahi du baratzeko angelu zabalenean. Zer neurri du angelu horrek?
Gogoratu
Triangelu guztietan, barruko angeluen zabaleren batura 180° da.
Lauki guztietan, barruko angeluen zabaleren batura 360° da.
62° 7' 44''
8 Putzu batetik ura ateratzeko, noria bat erabiltzen dute. Jada 246° 47' 52''-ko bira egin du. Zenbat falta zaio bira osatzeko? 246° 47' 52'' ?
360°

Ebatzi urratsez urrats, hemen: anayaharitza.es
9 June 18 min 26 s berandu iritsi da entrenamendura. Juneren taldea ordu eta erdi entrenatzen bada, zenbat denbora entrenatuko da gaur June?
10 Mikelek 58 min 27 s eman ditu bizkotxo bat egiten. Osagaiak prestatzen-eta 14 min 52 s egon bada, zenbat denbora egon da bizkotxoa labean?
Angelu laua baino handiagoak marrazten
Nola marraztu dezakegu 220 ° -ko angelu bat garraiagailua erabiliz?
Gogoratu
Denbora-datuen arteko kenketak angeluen artekoak bezalaxe egiten dira.
220° − 180° = 40°
• Praktikatzeko, marraztu 255 ° -ko angelu bat.
143 U8
1. Marraztu angelu lau bat. 2. Erpina aldatu gabe, marraztu ondoz ondoko angelu bat, 220°-ra iristeko falta zaigun neurrikoa.
36˚ 25' 36˚ 25' Hortxe duzu! 40° 220°
180°
EBATZI BAIETZ!
Egin marrazki bat
Pellok badaki triangelu baten bi angeluk 40 ° eta 60 ° dituztela eta bi angelu horiek partekatzen duten aldea 6 cm luze dela. Zer luzera dute beste bi aldeek?
Aldeek zer luzera duten jakiteko, triangelua marraztuko dugu.
1. Erregelarekin, marraztu 6 cm-ko zuzenki bat.
3. Erpintzat B puntua hartuta, marraztu 60°-ko angelu bat.
6 cm
2. Erpintzat A puntua hartuta, marraztu 40°-ko angelu bat.
4. Bi angeluen aldeek elkar ebakitzen duten puntua triangeluaren hirugarren erpina da.
Orain, soluzioa jakiteko, urrats bakarra falta zaizu: erregelarekin, neurtu triangeluaren aldeak.

Beste bi aldeen luzerak 5,3 cm eta 3,9 cm dira.
Soluzioak badu zentzurik?
Egiaztatu edozein bi alderen luzeren batura beti handiagoa dela beste aldearen luzera baino.
1 Triangelu isoszele baten oinarriak 5 cm ditu, eta alde hori partekatzen duten angeluak 50°-koak dira. Zer luzera dute beste bi aldeek? Zer neurri du beste angeluak?

2 Lidek badaki triangelu baten bi aldek 6 cm eta 4 cm dituztela. Gainera, badaki bi alde horiek eratzen duten angeluak 55° dituela. Zer neurri du hirugarren aldeak? Eta beste bi angeluek?
? ? ? ?
Ikusi nola egin triangeluak, webgunean: anayaharitza.es
50˚ 5 cm

144
B 40° 60°
90 100 110 120 130 140 150 160 170 180 80 70 60 50 40 30 20 10 0 90 80 70 60 50 40 30 20 10 0 100 110 120 130 140 150 160 170 180 A 90 100 110 120 130 140 150 160 170 180 80 70 60 50 40 30 20 10 0 90 80 70 60 50 40 30 20 10 0 100 110 120 130 140 150 160 170 180 6 cm A B 6 cm 60˚ B C A 40˚ 40° 6 cm
40˚ 60˚ 50˚
Problemak arin-arinka

2 1
Esan osagarriak diren bi angelu eta betegarriak diren beste bi.
Bi angelu auzokideak badira, izan ditzake horietako batek 180 ° ?
Buruzko kalkulua
Kalkulatu 40ren % 10.
4 3
Bi angelu osagarriak eta berdinak badira, zer neurri du bakoitzak?
Bi angelu betegarriak badira, baina biak berdinak badira, izan daitezke biak zorrotzak? Eta biak kamutsak? Nolakoak dira?
6 5

Sistema hirurogeitarrean angeluak neurtzen ditugu. Eta zer gehiago?
90 ° 180 ° 1° Luzera? Masa? Denbora?
Zenbat minutu dira gradu bat? Eta zenbat segundo?
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:


30en % 10
50en % 10
70en % 10
80ren % 10
90en % 10
120ren % 10
130en % 10
140ren % 10
150en % 10
200en % 10
Begira nola pentsatzen dudan
Urratsez urrats
Frogatu, paper zatitxoak erabiliz, esaldi hauek egia direla. Gero, idatzi nola egin behar den urratsez urrats.
Deskargatu txantiloia, webgunean: anayaharitza.es
• Erpinez aurkakoak diren bi angeluk neurri bera dute.
• Triangeluen angeluen batura beti 180° da.
• Laukien angeluen batura beti 360° da.



Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es

145 U8
4 4 4 4 4 4 4 4 4 4 % 100 % 10 40 4 :10
• ERPINEZ AURKAKOAK DIREN BI ANGELUK NEURRI BERA DUTE. • TRIANGELUEN ANGELUEN BATURA BETI 180º DA. • LAUKIEN ANGELUEN BATURA BETI 360º DA. 1. URRATSA: 2. URRATSA: 3. URRATSA: 4. URRATSA: 1. URRATSA: 2. URRATSA: 3. URRATSA: 4. URRATSA: 1. URRATSA: 2. URRATSA: 3. URRATSA: 4. URRATSA:
Z er ikasi dut?
6 Adierazi segundotan, eta ordenatu txikienetik handienera.
3 040' 52''
^ C
^ D
1 Neurtu angelu hauek garraiagailuarekin, eta sailkatu zabaleraren arabera: ^ A ^ B
2 Marraztu angelu hauek:
a) ^ A = 50° b) ^ B = 135°
3 Garraiagailua erabili gabe, kalkulatu eta idatzi zer neurri duten ^ B eta ^ C angeluek.
^ B = ?
^ C = ?
^ A = 25°
4 Ikusi arretaz eta erantzun.
^ D = 140°
62° 31' 40''
18° 15' 21''
7 Adierazi gradu, minutu eta segundotan.
a) 21 889'' b) 10 862''
8 Zer neurri du hirugarren angeluak?
?
40° 68°
9 Pentsatu eta ebatzi.
a) Danel eta Eguzki pizza jaten ari dira. Danelen zatiak 86° 45' ditu, eta Eguzkirenak, 89° 10'. Zer neurri du platerean utzitako zatiak?

^ A
^ B ^ C
^ D ^ E
a) Nolakoak dira kokapena kontuan hartuta?
^ A eta ^ B ^ E eta ^ B ^ D eta ^ E
^ A eta ^ D ^ E eta ^ A ^ C eta ^ D
b) Zertan dira antzekoak eta zertan desberdinak
^ A eta ^ B ? Eta ^ D eta ^ E ?
5 Neurtu garraiagailuarekin eta adierazi angelu hauen zabalerak minututan:
b) Haize-errota baten hegalek 160° 58'-ko bira egin dute. Zenbat gehiago biratu behar dira oraindik bira-erdia egiteko?
c) Joar eta Pello Baionan elkartzekoak dira. Joarrek 2 h 17 min 48 s behar ditu autoz iristeko, eta Pellok, 3 h, autobusez. Ordu berean abiatzen badira, zenbat lehenago iritsiko da Joar?
Semaforoa. Margotu koadernoan, ariketa
bakoitzaren ondoan, honela:
Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu
146
PORTFOLIOA
E
^
 B
HELBURUA AURRERA
Geure buruari galdezka

Kolorea, ikurra, irudia (KII) estrategia erabiliz, hausnartu dezagun taldeka ura zaintzearen garrantziaz.
Aukeratu hiru ideia, eta irudikatu ideia bakoitza kolore, ikur eta irudi baten bidez.

Gero, sortu zuen hausnarketa laburbilduko duen logo bat, kontuan izanda jende guztia ura zaintzera animatzea dela helburua. Logoa sortzeko, erabili angeluak.

N o la ikasi dut?
Osatu koadernoan.
Pentsatu ikasturtean zehar noiz izan zaren saiatua lanean.
Identifikatu hiru egoera. Nola sentitu zara?
Pentsatu noiz ez zaren saiatua izan. Identifikatu egoera bat, eta esan zer ondorio izan dituen. Nola sentitu zara?
Zer egin dezakezu saiatuagoa izateko?

U8 147
Kolorea Ikurra Gaia Irudia



148 BERRIKUSPENA 1 2
?
Kopiatu, egin batuketak eta osatu. Zaku bat irinek 5 kg gehiago
Kalkulatu angelu guztien neurria. Baina adi! Ez erabili garraiagailua!
Pentsatu azkar eta erantzun.
a) Bi angelu zuzen batzen baditugu, nolako angelua lortuko dugu?
b) Eta angelu zuzen bat eta angelu zorrotz bat batzen baditugu?
c) Bi angelu zorrotz, izan daitezke betegarriak? Arrazoitu zure erantzuna.
d) Zer neurri du angelu batek bere angelu betegarriaren laurdena bada?
e) Zer neurri du angelu batek bere angelu osagarriaren bikoitza bada?
Jakin nor den zientzialari misteriotsua

Matematikari misteriotsu honengatik ez balitz, beharbada ez genuke izango bideojokorik, ez Internet, ez telefono adimendunik.

Pistak
Aldi berean egin zituen Estatu Batuetako Marinan karrera militarra eta zientzialari-ibilbidea.
Hark sortu zuen ordenagailuko lehen programa-lengoaia konplexua: COBOL programa (enpresa-aplikazioetara zuzendutako lengoaia orokorra).

Hark erabili zuen lehenbiziko aldiz bug hitza (zomorroa) errore informatiko bat izendatzeko, baita debug hitza ere.
1906an jaio zen, New Yorken.


Eta azken pista bat: hark programatu zuen edukiera handiko lehen ordenagailua, Mark I, Harvard Unibertsitatean.
Eskaneatu, eta jakin nor den zientzialari misteriotsua
149 HIRUHILEKOA 2
7 8
Eˆ = 50° B ˆ =
 = ? D ˆ = ? Cˆ = ? Jˆ = 90° Fˆ = 25° Hˆ = ? Iˆ = ? Gˆ = ?
120°
sTEAM
? ?
ITZALAPROIEKTUAK UZTENDUTEN
EZAGUTU DIZIPLINARTEKO PROIEKTUA
Orain edo inoiz ez
ZER AZTARNA UZTEN DUZU?
Informatu dezagun jendea gure ikastetxearen aztarna ekologikoaz.

Nolako aztarna utzi nahi duzu planetan? Kontzientziatu zaitez!
Denon artean, hitz egin dezagun: Ezagunak zaizkizu aztarna ekologiko hitzak?
Zer-nolako eragina du gure bizimoduak ingurunean? Irudikatzen duzuna baino handiagoa dela iruditzen zaizu?
Badakizu nola neurtzen den?
Animatzen zara kalkulatzen zer aztarna ekologiko duen gure ikastetxeak?

Eta zure etxeak?
Zalantzak argitzeko, ikertu!
Ikertu ea zer parametrok duten eragina aztarna ekologikoan.
Horri buruzko informazio asko aurkituko duzu.
Aukeratu zuri baliagarri gertatuko zaizuna aztarna ekologikoari buruz egin behar duzuen gidarako datuak biltzeko, kalkulatzeko eta lantzeko.
Aztarna ekologikoaren kalkulagailuak ere aurkituko dituzu; erabili, laguntza gisa.
Karbono-aztarna ere aipatzen da.
Zer lotura du aztarna ekologikoarekin?
150
1 T hink P ENTSATU D esign 2 DISEINA T U
M aker

Egin aztarna ekologikoa zer den eta horretan zer parametrok eragiten duten jendeari jakinarazteko gida.

Informazio guztia taldeen artean banatzen baduzue, eraginkorragoak izango zarete.
Garrantzitsua da ikastetxeko gainerako ikasleek informazioa ulertzea, eta beste sektoreek ulertzea ere bai.

Beraz, berrikusi ondo zirriborroa, eta, informazioarekin batera,
Informazioa ondo zabaldu behar dugu, ikastetxearen aztarna ekologikoa zein den sektore guztiek jakin dezaten, denek parte hartzeko.
Horretarako, adibidez, ikastetxeko webguneaz baliatuta, zuen idatzia prentsaurreko batean aurkeztu dezakezue, eta bertara hezkuntza-komunitateko sektore guztietako ordezkariak gonbidatu.
Tokiko ikus-entzunezko hedabideak aliatu bikainak izan daitezke zuen ideiak bultzatzeko; oihartzun mediatiko handia lortu dezakezue.
Zorte on! Gu ziur gaude: datuak emanez, denok kontzientziatuko gara, ikastetxearen jasangarritasuna hobetzeko.
Zertan lagundu dit matematikak?

2. HIRUHILEKOA 151
3
EGIN 4
T est
PRESENTA S tage AURKEZTU
EGIAZTAT U 5
Begira nola pentsatzen dudan
Ezagutu Scratch-eko oinarrizko algoritmoak
Scratch tresna erabiliz, istorioak, animazioak eta jokoak sortu ditzakegu, besteak beste. Horretarako, lehenbizi, oinarrizko algoritmo batzuk berrikusiko ditugu, eta, gero, praktika honetan landuko ditugun erdi-mailako algoritmoei helduko diegu.
anayaharitza.es webgunean Scratch-en sartzeko eta tresna horrekin programatzen ikasteko informazio guztia duzu. Gainera, orain arte pentsamendu konputazionalari buruz ikasitakoa gogora ekarri beharko duzu.
Urratsez urrats

1. Erabiliko ditugun elementuak eta pertsonaiak aukeratu, eta gure esze naren gainean jarri.
a) Aukeratu gure abenturarentzat atzealde bat; adibidez, espazioa.
b) Aukeratu gure pertsonaia izango den objektu bat (adibidez, robota) eta bestelako batzuk (esaterako, espazio-ontzia eta izarrak; pertsonaiaren mugimenduetarako erreferentzia gisa balioko digute).
c) Scratch-ek diseinu batzuk eskaintzen ditu, baina bestelako botoiak ere sortu ditzakegu guk, PowerPoint erabiliz, adibidez. Gero, irudi gisa gorde behar ditugu, eta Scratch-era igo. Tuneatu nahi badituzu, «Tankerak» izeneko fitxa erabil dezakezu.
d) Jarri mugimenduko botoiak pantailaren eskuinaldeko izkinan, eta gehitu botoi horiei mezuak, gure pertsonaiari aginduak emateko. Botoi bakoitza programatu eta gero, gure pertsonaiaren gainean sakatutakoan, egin ditzakeen ekintza guztiak ikusi ahal izango ditugu.

2. Robota programatu, zenbait mugimendu exekuta ditzan. Adibidez:

a) Robotak gora, behera, eskuinera edo ezkerrera joateko mugimenduak exekutatuko ditu, koordenatu-ardatzei jarraituz. Beraz, gure pertsonaia balio jakin bat mugitzea nahi badugu, programatu egin behar dugu.
b) Robota etxera joateko (banderara, alegia), «Home jasotzean» algoritmoa erabili behar dugu, eta adierazi behar diogu irristatu dadila hara denbora jakin batean.
c) Agindu konposatuak ere eman ditzakegu; adibidez, oparia jasotzea, espazio-ontzira eramatea, eta, gero, etxera itzultzea. Horretarako, «PickBox jasotzean» algoritmoa erabiliko dugu. Kasu horretan, hurrenez hurren zenbait blokeri deituko die, guk aukeratutako ordenan. Adibidez, aurrena adieraziko diogu opari-kaxaraino irristatzeko. Gero, kaxa hartzeko eskatu ezin diogunez, esango diogu tankera aldatu eta robot2-rena hartzeko; pertsonaia hori lehenago sortuko genuen «Tankerak» fitxan, eta robota eskuetan kaxa daramala ageriko da. Ondoren, esango diogu espazio-ontzira irristatzeko (Rocketship); han kaxa utziko du. Etxera itzuli aurretik, berriro tankera aldatzeko esango diogu, kaxarik gabe agertzeko.
d) Gure pertsonaia 7 izarretan barrena bidaian bidaltzeko, hau egin behar dugu, aurrena izarrak eszenan jarri eta robotari etxean amaitzeko eskatu eta gero: «Patrol jasotzean» aukeratu, eta banan-banan izar batetik bestera irristatu dadila eskatu. Azkenik, etxera itzul dadin programatuko dugu (bandera berdera, alegia).
Ezagutu Scratch-eko oinarrizko algoritmoak
3. Robota programatu, algoritmo konplexuagoak erabiliz. Prest zaude?

Lortu nahi duguna da orain arte ikusi ditugun eragiketak modu antolatuagoan exekutatzea edo modu konpletoagoan exekutatzea. Hori lortzeko, kontzeptu berri batzuk landuko ditugu: baldintza, begizta, egiaztatzea eta aldagaia, besteak beste.
LEHEN URRATSA. Bi ekintza berri gehituko ditugu: robota piztea eta itzaltzea. Horrela, gure pertsonaiak piztuta dagoenean bakarrik bete ahalko ditu aginduak.
a) Robotak aginduak betetzeko piztuta egon behar izatea nahi badugu, aldagai bat sortu behar dugu; kasu honetan, On eta Off.
c) Kode hori sortzeko, urrats hauek egin behar ditugu: Pertsonaia honetan klik egitean, galdetuko digu ea On_Off alda gaia = 0 den. Alegia: robota itzalita dago? Aldagai hori 0 bada, esan nahi du robota itzalita dagoela.
Robota pizteko, aukera hau gehitu behar dugu: On_off aldagaiari 1 balioa ematea (robotari pizteko aginduko diogu, alegia).
Pizten denerako, botoiaren tankera aldatuko dugu, gorriaren ordez berdea izateko; piztuta edo itzalita dagoen adieraziko du horrek. Botoi hori «Tankerak» fitxan sortu dezakegu, eta itxura hutsa da; ez du zerikusirik pertsonaiaren programazioarekin.
d) Zer gertatzen da robota itzalita ez badago?
Orduan, galdetuko diogu ea piztuta dagoen; hots, ea On_off = 1 den. Eta, gero, 0 balioa emango diogu, itzaltzeko. Azkenik, botoiaren tankera aldatu dezakegu, berdearen ordez gorria izateko.

Zer gertatzen da robotak pizteko agindua jasotzen duenean? Agindu hori jasotakoan robota espazio-ontzitik kaxarik gabe (kaxarik gabeko tankerarekin) atera dadin programatuko dugu. Robota ateratzea diogunean, esan nahi dugu eszenan agertzea; bestela, izan ere, espazio-ontzian ezkutuan egongo da. Gero, Home paketea exekutatu dezala eskatuko diogu (banderara joatea).
Zer gertatzen da robotak itzaltzeko agindua jasotzen duenean? Gure pertsonaia espazio-ontzira joan eta ezkutatu egingo da. Robotari horixe agintzeko programatuta dago botoi hori: edonon egonda ere, egiten ari dena egiteari utzi eta itzaltzeko agindua betetzeko. Horretarako, «gelditu pertsonaiaren beste script batzuk» erabiliko dugu. Gero, segundo batean Rocketshipera irristatzeko aukera gehituko dugu; alegia, espazio-ontzira joan eta ezkutatzeko eskatuko diogu.
Begira nola pentsatzen dudan
b) Gero, botoi berri bat sortuko dugu («OFF» botoia), eta pantailan ageri den kodea esleituko diogu.
BIGARREN URRATSA. Hasieran sortu genituen posizioak aldatuko ditugu (Up, Down, Rigth eta Left), eta beste aldagai bat gehituko dugu («Gas» aldagaia), robotaren gasolina kontrolatzeko eta badugun edo ez aztertzeko.


a) Orain arte, y edo x posizioari balio bat batzen edo kentzen genion (adibidez, 1), eta robota jauzitxoka mugitzen zen.
b) Oraingo programazioarekin, mugitzeko modu hori hobetuko dugu, jauzitxoak egin ez ditzan. Horretarako, hauek aukeratuko ditugu: «errepikatu 10 aldiz» eta «aldatu x 1 unitate». Horrela, robotak 1 gehituko du hamar aldiz, eta naturalago mugituko da, jauzirik gabe.
c) «Gas» aldagaia sartuko dugu, eta, gainera, lortu nahi dugu gasolina baduen edo ez robota mugitzen den lauki bakoitzean aztertzea. Horretarako, hauxe programatuko diogu: aurrera egiten duen lauki bakoitzeko, gasolinatan 1 gastatzea; hau da, balioa -1 unitate aldatzea. Beraz, mugimendu bakoitzean, 10 aldiz errepikatzea aukeratu dugunez, robotak gasolinatan 10 gastatuko du.
HIRUGARREN URRATSA. Orain, robota bandera berdera joaten den aldiro erregaiz bete dadin programatuko dugu. Horretarako, hasierako kodea aldatu behar dugu, hau gehituta: robota piztuta dagoenean bakarrik mugituko dela eta banderara joaten den bakoitzean gasolinatan 100 jasoko duela.
LAUGARREN URRATSA. Kaxa jasotzeko modua ere hobetuko dugu: alde batetik, robota piztuta dagoenean bakarrik mugituko dela gehituko dugu, berriro ere; bestetik, «PickBox» aldagaiaren balioa "1 unitate" aldatzea aginduko diogu (espazio-ontzian kaxa bat uzten duen bakoitzean 1 aldatzea, alegia); eta, gainera, kaxa bat uzten duen bakoitzean erregaia gastatuko duela gehituko dugu.
Nola aztertuko dugu robotak zenbat erregai duen? Horretarako, baldintza konposatu hau erabiliko dugu: «Gas» aldagaia < 0 bada, edo «Gas» = 0 bada, orduan robota etxera bidaliko dugu.

1 5 9
2 6 10

3 7 11
4 8 12
Zenbakiak eta eragiketak Zaindu bizia
Multiploak eta zatitzaileak
Besarkatu bakea
Berreketak Konektatuta
Zenbaki dezimaldunak eta eragiketak Kontsumitu arduraz
Zergatik da beharrezkoa zuhaitzak zaintzea?
Egin biziaren zuhaitz bat, natura zaintzearen aldeko mezu eta guzti.
Lehorreko bizitza
Zatikiak eta eragiketak Elkarrekin hobeto
Sistema metriko hamartarra Zientzialari izan nahi?
Ehunekoa eta proportzionaltasuna Antolatu zure aisialdia
Angeluak eta angeluen neurria Marraztu, zaintzeko
Poligonoak Aldeen garrantzia


Irudi zirkularrak Ni, zu, gu... Denok berritzaile
Gorputz geometrikoak Itsasoa zaintzeak saria du
Zoria eta probabilitatea Etorkizuna iragartzea
Zergatik da garrantzitsua bakea lortzearen alde jardutea?
Eraiki bakea besarkadekin: diseinatu kanpaina bat, 8 segundoko besarkadak sustatzeko.
Zergatik da garrantzitsua denok izatea eskura Internet?




Diseinatu kamiseta bat, informazioa izateko eskubidea denok izan behar dugula aldarrikatzeko.
Zer esan diezaiekegu ikaskideei arduraz kontsumitzea gomendatzeko?
Eztabaidatu dezagun ea paga eman behar den edo ez eta zer egin behar den paga arduraz erabiltzeko.
Bakea, justizia eta erakunde sendoak
Industria, berrikuntza eta azpiegitura
Ekoizpen eta kontsumo arduratsua
Nola egin dezakegu bat gure artean, elkartuta aritzeko? Sortu ELKARTU!, jendeak helburu berberen alde bat eginda jarduteko gunea.
Nola eman dezakegu jakitera denok ez ditugula ikasteko aukera berberak? Egin dezagun literatura-lehiaketa bat, izenburu hau duena: Zientzialari izan nahi dut
Zer gertatuko da zure adineko jendeak aisialdi guztia gailu teknologikoak erabiltzen ematen badu? Prestatu teknologiarekin zerikusirik ez duen aisialdi-plan alternatibo bat zure adineko neska-mutilentzat.
Nola kontzientziatu dezakegu jendea ura zaindu beharraz?
Marraztu logo bat, ura zaintzea sustatzeko.





Zer beste emakumek egin dituzte ekarpen garrantzitsuak matematikaren esparruan?
Adierazi denbora-lerro batean emakume matematikarien datu pertsonalak eta ekarpenak.
Nola treba dezakegu sormena gaur egungo arazoei erantzun berritzaileak emateko?
Neurtu zure sormena!
Zer egin dezakegu gure itsasoak zaintzeko?
Egin trofeo bat irudi geometrikoekin, itsasoa zaintzearekin lotutako jardunbide onak saritzeko.
Zer egin dezakegu klima-aldaketa geldiarazteko?
Egin infografia bat, klima-aldaketa geldiarazteko zenbait gomendio emateko.
Itunak, helburuak garatzeko
Kalitate oneko hezkuntza
Osasuna eta ongizatea
Edateko ura eta saneamendua
Generoberdintasuna
Industria, berrikuntza eta azpiegitura
Uretako bizitza
Klima babesteko ekintza
OR. Zer ikasiko dugu?
IKASKUNTZA-EGOERA HELBURUA AURRERA GJH DIZIPLINARTEKOA
8 80 152 24 100 168 42 116 184 56 132 202
3. HIRUHILEKOAREN BERRIKUSPENA STEAM: Clara Grima
1. HIRUHILEKOAREN BERRIKUSPENA STEAM: Sophie Germain
2. HIRUHILEKOAREN BERRIKUSPENA STEAM: Grace Hooper
OINARRIZKO JAKINTZAK EBATZI BAIETZ!
• Zenbaki-sistema hamartarra. Zenbatzeko teknikak.
• Oinarrizko eragiketak zenbaki arruntekin. Propietateak.
• Eragiketa konbinatuak.
• Zenbaki baten multiploak. Multiplo komun txikiena.
• Zenbaki baten zatitzaileak. Zatitzaile komun handiena.
• Zenbaki arrunt baten berreketa.
• Karratuak eta kuboak.
• Erro karratua.
• Hamarrenak, ehunenak eta milarenak. Zenbaki dezimaldunak: irakurtzea, idaztea eta posizio-balioa. Prezioak.
• Zenbaki dezimaldunak konparatzea eta ordenatzea.
• Zenbaki positiboak eta zenbaki negatiboak.
• Konparatzea eta ordenatzea.
• Koordenatu kartesiarrak.
• Problema aritmetikoak: aldaketa-, berdinketaeta konparazio-problemak.
• Zatigarritasun-irizpideak.
• Zenbaki lehenak eta zenbaki konposatuak.
• 10 oinarriko berreketak.
• Deskonposizio polinomikoa.
• Zenbaki dezimaldunak biribiltzea. Zenbaki dezimaldunen arteko batuketak, kenketak, biderketak eta zatiketak.
• Problema aritmetikoak: konparazio-, banaketa- eta multzokatze-problemak, eta multzo berdinak
• Estrategia heuristikoa: Deszifratu kodeak.
• Buruzko kalkulua: 4z biderkatzea.
• Pentsamendu konputazionala: Deskonposizioa.
• Estrategia heuristikoa: Bilatu erantzun posible guztiak.
• Buruzko kalkulua: 20z biderkatzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Bilatu erregulartasunak.
• Buruzko kalkulua: 50ez biderkatzea.
• Pentsamendu konputazionala: Kodetzea.
• Estrategia heuristikoa: Kalkulatu soluzioa iritzira.
• Buruzko kalkulua: 4z zatitzea.
• Pentsamendu konputazionala: Deskonposizioa.
DIZIPLINARTEKO PROIEKTUA · Kutxa magikoa eta haren zaintza: Kutxa logikoa
• Zatikiak. Zatikia eta unitatea. Zatiki propioak eta inpropioak.
• Kopuru baten zatikia.
• Zatiki baliokideak. Zatiki laburtezina.
• Zatikiak konparatzea.
• Luzera, edukiera, masa, azalera eta bolumena adierazteko neurri-unitateak.
• Unitate-aldaketak.
• Magnitude proportzionalak.
• Unitatera laburtzea. Hiruko erregela.
• Ehunekoak. Kopuru baten ehunekoa.
• Angeluen sailkapena, zabaleraren eta kokapenaren arabera.
• Angeluak neurtzea: graduak, minutuak eta segundoak.
• Zatikien arteko batuketak, kenketak, biderketak eta zatiketak.
• Problema aritmetikoak: konbinazio-, aldaketaeta multzokatze-problemak, biderketazko konparaziokoak eta multzo berdinak egitekoak.
• Adierazpen sinpleak eta adierazpen konplexuak.
• Problema aritmetikoak: konbinazio-, aldaketaeta multzokatze-problemak.
Igoerak eta beherapenak.
• Eskala: grafikoa eta zenbakizkoa.
• Estrategia heuristikoa: Egin tarteko galderak.
• Buruzko kalkulua: 20z zatitzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Bilatu erregulartasunak.
• Buruzko kalkulua: Zatiki batez biderkatzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Egin eskema bat.
• Buruzko kalkulua: Kopuru baten 1 4
• Pentsamendu konputazionala: Funtzioak.
• Estrategia heuristikoa: Egin marrazki bat.
• Angeluen arteko batuketak eta kenketak.
• Problema aritmetikoak: berdinketa-problemak.
• Buruzko kalkulua: Kopuru baten % 10.
• Pentsamendu konputazionala: Algoritmoa.
DIZIPLINARTEKO PROIEKTUA · Orain edo inoiz ez: Zer aztarna uzten duzu?
• Poligonoak: elementuak eta sailkapena.
• Poligono ahurrak eta poligono ganbilak.
• Poligonoen perimetroa.
• Zirkunferentzia. Zirkulua eta irudi zirkularrak.
• Puntuen, zuzenen eta zirkunferentzien posizio erlatiboa.
• Poliedroak eta gorputz biribilak.
• Poliedro erregularrak. Biraketa-gorputzak.
• Zorizko esperimentuak. Gertaera ziurra, posiblea eta ezinezkoa.
• Paralelogramoen eta triangeluen azalera.
• Poligono erregularren azalera.
• Irudi konposatuen azalera.
• π zenbakia. Zirkunferentziaren luzera.
• Zirkuluaren azalera.
• Prismen azalera eta bolumena.
• Piramideen azalera eta bolumena. Irudi konposatuen azalera eta bolumena.
• Gertaera baten probabilitatea. Laplaceren erregela.
• Zenbatzeko teknikak.
• Estrategia heuristikoa: Hasi egoera errazagoetatik.
• Buruzko kalkulua: Kopuru baten % 50.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Egin marrazki bat.
• Buruzko kalkulua: Kopuru baten % 20.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Baztertu erantzun ezinezkoak.
• Buruzko kalkulua: 0,1ez biderkatzea.
• Pentsamendu konputazionala: Orokortzea.
• Estrategia heuristikoa: Aztertu datu-lagin bat.
• Buruzko kalkulua: 0,5ez biderkatzea.
• Pentsamendu konputazionala: Datuak.
DIZIPLINARTEKO PROIEKTUA · Birika berdea: Iraul ditzagun datuak



Irudi lauak. Poligonoak
Poligonoek zer propietate dituzten jakinda, errazago ulertuko dugu irudi lau horiek nolakoak diren.
Poligonoa lerro poligonal itxi batek mugatutako irudi laua da.
• Poligono guztiek elementu hauek dituzte: aldeak, erpinak, angeluak eta diagonalak.
diagonala
• Poligono baten perimetroa alde guztien luzeren batura da.
Aldeen arabera:
Triangelua: 3 alde
Laukia: 4 alde
Pentagonoa: 5 alde
Hexagonoa: 6 alde

Heptagonoa: 7 alde
Angeluen arabera:
Oktogonoa: 8 alde
Poligono ganbila: angelu guztiak 180° baino txikiagoak ditu.
Aldeen eta angeluen arabera:
Poligono erregularra: alde
guztiak eta angelu guztiak berdinak ditu.
Eneagonoa: 9 alde
Dekagonoa: 10 alde
Poligono ahurra: angeluren bat 180° baino handiagoa du.
Poligono irregularra: erregularra izateko baldintzetako bat, gutxienez, ez du betetzen.
154 1
aldea
erpina
3
3
3
angelua
cm
cm 3 cm
cm 3 cm + 3 cm + 3 cm + 3 cm = 12 cm
NOLA SAILKATU POLIGONOAK?
1 Marraztu 4 alde baino gehiago dituen poligono bat, eta egin diagonal guztiak. Ez nahasteko, marraztu diagonalak ordenan.
2 Pentsatu eta binaka jarrita komentatu Ikusi arretaz eta ebatzi. 5cm 5,1cm 4 cm 6,8cm 7cm 5 cm
a) Kalkulatu poligono bakoitzaren perimetroa.
b) Zenbat modutan kalkula dezakezu poligono erregular baten perimetroa?
3 Sailkatu A, B eta C poligonoak bitan: ganbilak eta ahurrak.
4 Marraztu koadernoan.
a) Lauki erregular ganbil bat. c) Hexagono ganbil bat.
b) Lauki ahur bat. d) Oktogono ahur bat.



5 Jolastu bloke geometrikoekin, eta eratu hauek:

a) Poligono erregularrak. c) Poligono ahurrak.
b) Poligono irregularrak. d) Poligono ganbilak.
Beste definizio batzuk aurkitzen
Nahi baduzu, deskargatu txantiloia, webgunean: anayaharitza.es
A B C

a) Imajinatu igerileku hauen ertzetik oinez zoazela. Zer igerilekutan biratu zara zure eskuinerantz eta baita zure ezkerrerantz ere: ganbilean ala ahurrean? Zeinetan egin duzu beti bira mota bera?
b) Imajinatu soka bat jarri duzula, guztiz tenkatuta, igerilekuan ondoz ondo ez dauden bi erpinen artean, diagonal bat balitz bezala. Zer igerilekutan igarotzen da soka beti uretatik? Zeinetan igarotzen da noizbait behintzat igerilekuaren kanpotik?
Zer dela eta diozu hori? Idatzi poligono ganbilen eta ahurren beste definizio batzuk, poligonoen diagonalen edo biraren kontzeptuak erabiliz.
POLIGONOA
AHURRA
DIAGONALAK
Gogoan hartu!
Identifikatu planoa estaltzen duten teseletako poligonoak.
155 U9
BIRA DIAGONALAK
GANBILA BIRA
Paralelogramoen azalera
Paralelogramoen azalera kalkulatzen jakinda, paralelogramo formako gainazalak neur ditzakegu; adibidez, lauzak.


Zer azalera dute paralelogramoek?
LAUKIA

KARRATUA
8 cm
cm
8 × 3 = 24 Azalera = 24 cm 2
Erronboideak betetzen duen espazioa oinarri eta altuera bereko lauki baten berdina da.
ERRONBOIDEA
× 4 = 24 Azalera = 24 cm

A = oinarria × altuera
1 Ikusi arretaz eta ebatzi.
4

cm
A = aldea × aldea
Erronboak betetzen duen espazioa oinarri bera eta altuera erdia dituen lauki baten berdina da.
ERRONBOA
A = (diagonal handia × diagonal txikia) : 2
Irudiak deskribatzeko, erabili lexiko egokia.
a) Idatzi zer izen duten paralelogramo horiek. Adierazi nolakoak diren bakoitzaren aldeak eta angeluak.
b) Kalkulatu irudi bakoitzaren perimetroa eta azalera. Ez ahaztu datu guztiak unitate berean jartzea.
156
2
1
85
6 cm 2,5
4
4
3
dm
mm
cm
cm
cm
m
6 cm 4 cm 4 cm 6 cm 8 cm 4 cm 8 cm 4 cm 6
2 (8
× 4) : 2 = 32 : 2 = 16 Azalera = 16 cm 2
A = oinarria × altuera 3
4
4 × 4 = 16 Azalera = 16 cm 2
cm
Abiapuntua, beti, laukiaren azalera da!
2 Julek zurezko tangram bat du, baina erronboide formako pieza galdu zaio. Aitonak egingo dio pieza, baina neurriak jakin behar ditu horretarako. Lagunduko diozu?

a) Idatzi zer oinarri eta altuera dituen erronboide formako piezak.
b) Zer azalera du piezak?

c) Zer azalera du tangramak guztira?
3 Buru pentsalariak Karlosek alboko lauza bezalako 100 erabili ditu bainugelako zorua estaltzeko. Lauzak erronbo forma du. Zer azalera du lauzaz estalitako gainazalak?
4 Laukizuzen formako gela batean, zoruan bi alfonbra karratu daude: batak 75 cm-ko aldea du, eta besteak, 1,5 m-koa. Zoruaren zer azalera ez dago alfonbraz estalita?
Gainazal desberdinak, baina azalera bera

Granadako Alhambran, gainazal ugari era askotako marrazkiz estalita daude, hutsunerik utzi gabe. Irudi ospetsuenetako bat hezur nazaria da, karratutik abiatuta egiten dena.
a) Karratua eta hezur nazaria gainazal desberdinak dira, forma desberdina dutelako. Baina, azalera bera ote dute? Zer uste duzu?
b) Egin hezur nazari bat, eta margotu zuk nahi duzun bezala. Gero, ikaskideek egindako hezurrekin elkartuta, sortu mosaiko bat.
Ariketa hau egiteko, txantiloia deskargatu dezakezu, edo geometria dinamikoko programa bat erabili, webgunean: anayaharitza.es


Aurkitu paralelogramoak teseletan, eta erabili beste batzuk sortzeko.

157 U9
6 m 2,75 m 75 cm
6 cm 10 cm
Gogoan hartu!
1,5
Eragiketak egiteko, adierazi unitate berean.
m
Triangeluen azalera
Irudi horien azalera kalkulatzen baldin badakigu, triangelu formako gainazalak neur ditzakegu; adibidez, bide-seinaleak.
Aldeen arabera Angeluen arabera
aldeberdina isoszelea zorrotza eskalenoa zuzena kamutsa
Zein dira oinarria eta altuera?
Zein da triangelu baten azalera?
altuera
oinarria

Oinarria edozein alde da.
Altuera oinarritzat aukeratu dugun aldearekiko (edo aldearen luzapenarekiko) zut aurkako erpinera doan zuzenkia da.
1 Ikusi arretaz eta ebatzi.
(8 × 4) : 2 = 32 : 2 = 16 Azalera = 16 cm 2

A = (oinarria × altuera) : 2
Triangeluak betetzen duen espazioa oinarri eta altuera bereko laukiaren erdia da.
a) Sailkatu triangeluak aldeen eta angeluen arabera.
b) Kalkulatu irudi bakoitzaren perimetroa eta azalera.
158
3
CLASIFICACIÓN Sailkapena 4 cm 8 cm 8 cm 4 cm 6 cm 4 cm 8 cm 5 cm 5 cm 6 cm 7,07 cm 5,6 cm 7,07 cm 5,2 cm 5,65 cm 5,6 cm 4 cm 13 cm 5 cm 12 cm
2 Kalkatu alboko triangeluak, eta erantzun.
a) Sailkatu triangeluak angeluen arabera.

b) Marraztu altuera; kontuan izan zer alde aukeratu duzun oinarritzat.
c) Zer ikusten duzu altueretan?

Lerro elkarzutak nola marrazten diren gogoratzen ez baduzu, «Berehala kontatuko dizut», hemen: anayaharitza.es
3 Egiaztatu Zer triangelu mota da?
a) Altueretako bat triangelutik kanpo dago.
b) Hiru altuerak triangeluaren barruan daude.

c) Altueretako bat triangeluaren aldeetako bat da.
4 Zer azalera du alboko bide-seinaleak?
5 Zer azalera du zelaiak? Eta parkeak guztira?
Gainazal desberdinak, baina azalera bera
Granadako Alhambran dagoen beste irudietako bat begizta edo pajarita nazaria da. Irudi horrek ere erabat estaltzen ditu gainazalak, hutsunerik utzi gabe.

Izar moduko bat da, eta triangelutik abiatuta egiten da.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
a) Triangelua eta pajarita nazaria gainazal desberdinak dira, forma desberdina dutelako. Baina azalera bera ote dute?
b) Egin pajarita nazari bat, eta margotu zuk nahi duzun bezala. Gero, ikaskideek egindakoekin elkartuta, sortu mosaiko bat .
Ariketa hau egiteko, txantiloia deskargatu dezakezu, edo geometria dinamikoko programa bat erabili, webgunean: anayaharitza.es .


Identifikatu triangeluak planoa estaltzen duten teseletan.

159 U9
Gogoan hartu!
3m 3m 3m 70 cm 60,62 cm oinarria oinarria oinarria
Poligono erregularren azalera



Irudi horien azalera kalkulatzen baldin badakigu, alde
Poligono erregular horren azalera kalkulatzeko, egin urrats hauek:
160
6 cm 4,1 cm 7,2 cm 6 cm 4,15 cm 4 cm
1 Kalkulatu poligono erregular bakoitzaren perimetroa eta azalera.
2 Deskargatu anayaharitza.es webgunean poligono erregularren txantiloia, eta marraztu apotema bat poligono bakoitzean.
ditzakegu.
eta angelu berdinak dituzten gainazalak neur
4
1. Zatitu poligonoa triangelu berdinetan.
2. Kalkulatu triangeluetako baten azalera.
5 cm 4,3 cm Triangeluaren azalera = oinarria × altuera 2 (5 × 4,3) : 2 = 10,75 cm 2 10,75 cm2 × 6 = 64,5 cm2
azalera × triangelu kop. Poligono erregularraren azalera = oinarria × altuera 2 × triangelu kop. = perimetroa × apotema 2 Poligono erregularren apotema zentrotik aldeetako baten erdiko puntura dagoen distantzia da. 1 4 2 3 5 6 5 cm 4,3 cm Apotema Aldea
3. Biderkatu triangeluaren azalera poligonoak duen triangelu kopuruaz.
Triangeluaren
3 Zenbat metro karratu behar dira oihal hau egiteko?
4 Eduren sukaldeko hormetako bat 100 lauzaz estali dute. Lauzak hexagono erregularrak dira, eta 12 cm-ko aldea eta 10,4 cm-ko apotema dituzte. Zer azalera du hormak?
Poligono erregularrei buruzko bitxikeriak ikasten
Poligono erregularren azalera kalkulatzeko beste modu bat poligonoa triangelu berdinetan deskonposatzea da.
1. Zatitu poligonoa triangelu berdinetan.
Moztu triangeluak, eta egin paralelogramo bat.
3. Ohartu honetaz: poligono erregularraren azalera eta paralelogramoarena berdinak dira.
cm

erregularraren azalera = Erronboidearen azalera =
perimetroa × apotema 2 =
oinarria × altuera =
3 × 0,87 = 2,61 cm 2 = 6 × 0,87 2 = 3 × 0,87 = 2,61 cm 2
• Egin gauza bera oktogono erregular honekin:
Nahi baduzu, deskargatu poligono erregularren txantiloiak anayaharitza.es webgunean, eta kalkulatu poligonoen azalerak, triangelutan zatitu eta beste irudi batzuk konposatuz.

161 U9
1 cm 0,87 cm 1 cm 3 cm 0,87 cm 1
2.
Hexagono
=
3
0,87
5 m 9,18 m 6 cm 7,2 cm =
=
cm
cm
Irudi konposatuen azalera
Irudi horien azalera kalkulatzeko, azalera ezaguneko iruditan deskonposa ditzakegu.
Zatitu

a) Erabili tangrameko triangelu txikiena eredu gisa, eta zatitu gainerako piezak triangelu berdinetan.
b) Hartu tangrama unitatetzat. Tangramaren zer zatiki da pieza bakoitza?
c) Erreparatu marrazkiko datuei. Zer azalera du pieza bakoitzak? Aztertu ikaskideak eta biok nola ebatzi duzuen.
Deskargatu tangramaren txantiloia: anayaharitza.es


162 5
24 m 4 m 4 m 5 m 7 m 10 m 6,08 cm 50 cm 30 cm 5 cm 3 cm 6 cm 60 cm 80 cm 16 m
1 Kalkulatu irudi bakoitzaren perimetroa eta azalera.
5 mm 10 mm
2 Ikusi arretaz eta ebatzi.
irudiak azalera ezaguneko beste batzuetan.
3 Ideiabiltzarra Ikusi arretaz irudia, eta erantzun.
C D



3,5m  B

4 m
a) Zer neurri du ^ A angeluak?
Kontuan izan triangelu aldeberdina erregularra dela.
c) Zer neurri du ^ C angeluak?
Hexagono erregularra triangelu aldeberdinez osatuta dago.
b) Zer neurri du ^ B angeluak?



Ohartu karratu baten angelua dela.
d) Zer neurri du ^ D angeluak?
Pentsatu zer angelu osatzen duten ^ A , ^ B , ^ C eta ^ D angeluek batera.
e) Zer azalera du irudi bakoitzak? Kalkulatu zer neurri duen gainazal guztiak.
Zer neurri dute karratuaren aldeek?
Zer neurri dituzte hexagonoaren aldeak eta apotemak?
4 Pentsatu eta kalkulatu zer neurri duen zerrenda bakoitzaren gainazalak. Idatzi datuak adierazitako unitateetan.
Kontuan izan pieza guztiak triangelu berdinetan deskonposa daitezkeela.
163 U9
mm 2 tan cm 2 tan 8 cm 64 mm 8 cm 8 cm 128 mm
Hasi egoera errazagoetatik
Triangeluek 3 alde eta 0 diagonal dituzte. Karratuek 4 alde eta 2 diagonal dituzte. Hortaz, zenbat diagonal dituzte 12 alde dituzten poligonoek? Kalkulatu!

1. Marraztu poligono errazenak eta bakoitzaren diagonalak, erregulartasunak bilatzeko.
3 alde

0 diagonal
4

2
2. Ohartu honetaz: alde bat gehitzen dugun aldiro, diagonalen kopurua
2, 3, 4, 5… handitzen da.
3. Antolatu datu horiek taula batean. Alde
164
EBATZI BAIETZ!
kop. 3 4 5 6
9
kop. 0 2 5 9 14 20 27 35 44 54
7 8
10 11 12 Diagonal
+2 +3 +4 +5 +6 +7 +8 +9 +10 12 aldeko poligonoek 54 diagonal dituzte.
alde
diagonal
alde
diagonal
alde
diagonal
alde
1 Amaiak alboko mosaikoa egin du bere bloke geometrikoekin. Mosaikoak 10 karratu izatea nahi badu, zenbat hexagono beharko ditu? diagonal
5
5
6
9
7
14
Erabili geometria dinamikoko programa bat, edozein poligonoren diagonal kopurua kalkulatzeko, webgunean: anayaharitza.es
Problemak arin-arinka
Buruzko kalkulua
Poligono ganbilek ba al dute 180° baino handiagoa den angelurik?
Zer formularekin kalkulatzen da triangeluaren azalera?
1 3 5
Hexagono erregularra sei triangeluz osatuta dago. Zer triangelu mota dira?
Begira nola pentsatzen dudan
Patroi bila
2 4 6
Kalkulatu 28ren % 50.
Zer formularekin kalkulatzen da laukizuzenaren azalera? Eta erronboidearena?
28 14 :2 % 50
14 14 % 100
Triangelu baten altuera triangelutik kanpo badago, zer triangelu mota da? Triangeluaren oinarria eta altuera elkarrekiko paraleloak ala zutak dira?
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:



4ren % 50
8ren % 50
12ren % 50
16ren % 50
18ren % 50
Zertarako balio du karratu batek? Bada, esaterako, hau bezalako batuketa oso interesgarrien emaitzak jakiteko: 1
Ez duzu sinesten? Ikusi nola adieraz daitekeen batuketa hori karratu baten bidez, eta azaldu ikusitakoa, zure hitzak erabiliz.
24ren % 50

26ren % 50
50en % 50
100en % 50 200en % 50
Noski! Karratua unitatea da! Bai polita!

165 U9
2
+ 1 4 + 1 8 + 1 16 + … = 1
1 2 1 4 1 8 1 16
Z er ikasi dut?
1 Idatzi zer izen duten poligono hauek. Adierazi zein diren ahurrak eta zein diren ganbilak.
4 Deskribatu nolakoak diren triangelu hauek, eta kalkulatu bakoitzaren azalera. Gero, erantzun.
a) Triangelu horiek, gainazal berdinak dira?
b) Azalera bera dute?
5 Anek neurri hauek dituen ispilu bat egin nahi du:
2 Zergatik ezin da triangelu ahurrik marraztu? Arrazoitu zure erantzuna, arrazoi matematikoak emanez.

Pentsatu edozein triangeluren angeluen batura 180° dela.

Edo zer bira egin behar dituzun triangelu baten ertzetatik ibiltzeko.
a) Zer azalera du kristalaren zatiak?
b) Kalkulatu markoaren perimetroa.
6 Estal daiteke igerileku hau 15 dam 2-ko olana batekin?
Semaforoa. Margotu koadernoan, ariketa bakoitzaren ondoan, honela:
Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu

166
PORTFOLIOA
3 Zer azalera dute lauza hauek?
3 cm 5 cm
40 m 40 m a) c) b) d) 5 cm 6 cm a) c) b) d) 4 cm 3 cm 7 cm 4 cm 4 cm 5 cm 5 cm 3 cm 3 cm 4 dm 28 cm
HELBURUA AURRERA
Adierazi denbora-lerro batean emakume matematikarien ekarpenak.
Badakizu zer den plano bat teselatzea? Bada, planoa erabat estaltzea, hutsunerik utzi gabe, patroi bati jarraitzen dioten irudi geometrikoekin; hau da, irudi geometrikoek erregulartasun bat betetzen dute.





Ikusi arretaz irudi hauek, eta erantzun galderei, irudi bakoitzarekiko:
a) Zenbat poligono errepikatzen dira? Zein dira?
b) Aukeratu erpin bat ausaz. Zenbat aldek egiten dute bat erpin horretan? Aukeratu beste erpin bat. Zenbatek egiten dute bat orain? Beti gertatzen da?
c) Zenbat irudik egiten dute bat erpin batean? Zer erpin aukeratzen duzun, emaitza desberdina izango da.
d) Ausartzen zara teselekin mosaiko bat diseinatzen? Egin zeuk bat.
Geure buruari galdezka
Denbora-lerroa estrategia erabiliz, jaso dezagun ordenan emakume matematikariek historian zehar egin dituzten ekarpenak.
a) Ikertu emakume matematikariei buruz.
b) Taldeka, egin denbora-lerro bat; formatuak alboko antolatzailearen antzekoa izan behar du.
Emakume matematikariei buruzko informazioa kontsultatzeko, webgunera jo dezakezu: anayaharitza.es
N o la ikasi dut?
Osatu koadernoan.
Esan zergatik den garrantzitsua hizkuntza matematiko zehatza erabiltzea; aipatu hiru arrazoi. Adibideak aurkitzeko, pentsatu noiz gertatu izan zaizun zuk behar bezala ez erabiltzea. Nola sentitu zinen zuzendu zenutenean?
Pentsatu noiz gertatu izan zaizun objektuen edo eragiketen izenak behar bezala ez erabiltzea; aurkitu adibide bat. Zer egin dezakezu hizkuntza matematikoa zure ohiko lexikoan sartzeko?
U9 167
Informazioa 1. gertaera… Informazioa 3. gertaera… Informazioa 5. gertaera… Informazioa 7. gertaera… Informazioa 2. gertaera… Informazioa 4. gertaera… Informazioa 6. gertaera… Informazioa 8. gertaera…




Zirkunferentzia

elementu asko hobeto ulertuko ditugu.
Mariari marraztea asko gustatzen zaio, eta konpasarekin zirkunferentziak egiten ikasi duenetik oso margolan originalak egiten ditu.
Badakizu nola marraztu zirkunferentziak konpasarekin?
Egin urrats hauek:




1. Zabaldu konpasa erradioak dituen adina zentimetro.
Zirkunferentzia lerro kurbatu itxi eta lau bat da, eta lerroko puntu guztiak zentrotik distantzia berera ditu.
1 Egin gurutzegrama, zirkunferentziaren elementuak idatzita.
Horizontalak

1. Zirkunferentziako edozein bi puntu lotzen dituen zuzenkia.
3. Zirkunferentziaren erditik igarotzen den korda.
6. Zirkunferentziaren erdia den arkua.
Bertikalak
2. Zirkunferentziako edozein puntutatik distantzia berera dagoen puntua.
4. Zirkunferentziako edozein puntu eta zentroa lotzen dituen zuzenkia.
5. Zirkunferentziako edozein bi punturen artean dagoen zirkunferentzia zatia.
2 Zer dela eta diozu hori? Ikusi arretaz, neurtu, eta azaldu irudi hauek zergatik ez diren zirkunferentziak:

170
Zirkunferentzia zer den eta zer propietate dituen jakinda, inguruko
1
2. Jarri konpasaren orratza orrian, nahi duzun lekuan.
3. Mugitu konpasa orratza mugitu gabe, eta egin zirkunferentzia.
Deskargatu gurutzegrama,
4 6 zirkunferentzia
zentroa erradioa diametroa korda arkua
webgunean: anayaharitza.es
zirkunferentzierdia
3 Kopiatu eta osatu koadernoan.
a) O puntua ? da.
b) CF zuzenkia ? bat da.
c) OF zuzenkia ? bat da.





d) B-tik C-ra bitarteko lerro kurbatua ? bat da.
e) F-tik C-ra bitarteko lerro kurbatua ? bat da.
f) AF zuzenkia ? bat da.
4 Irudi-diktaketa! Marraztu pertsonaia bakoitzak esandakoa.
Zirkunferentzia bat; zentroa O puntua du, eta 5 cm-ko erradioa du.

Zirkunferentzia bat, eta diametroa ez den korda bat.
Zirkunferentzia bateko hiru puntu, eta puntu horien erradioak.
Zirkunferentzia baten diametroa, eta eratzen diren bi arkuak. Zer izen dute arku horiek?
5 Zer dela eta diozu hori? Pentsatu eta erantzun, arrazoiak emanez.
a) Edozein korda diametro bat da?
b) Diametro bat beti erradioaren bikoitza da?

c) Zirkunferentzia batean marraztu daitekeen korda luzeena, zein da?
d) Zirkunferentzia baten arku bat beti zirkunferentzierdi bat da? Eta zirkunferentzierdi bat beti arku bat da?
e) Edozein diametro zirkunferentziaren korda bat da?
Sortu zeure diseinu bat!
Diseinu artistiko askok oinarrian zirkulu edo zirkunferentzia bat dute.
Alboko zirkunferentziak zenbait puntu distantziakide ditu, eta horietatik beste puntuetaraino kordak ateratzen dira. Nahiko zenituzke zure diseinuak sortu?
Txantiloiak erabiliz, marraztu zirkunferentzia bakoitzean adierazita dauden puntuetatik beste puntuetarainoko korda posible guztiak. Zenbat korda marraztu dituzu zirkunferentzia bakoitzean?
Deskargatu txantiloiak anayaharitza.es webgunean, eta idatzi emaitzak taula batean.
Identifikatu zirkunferentzien elementuak uraren indarraz dabilen noria batean.
171 U10
Gogoan
F O E D C B A
hartu!
3 3 4 ? 5 ? 6 ?
Puntu kop. Korda kop.
Zirkulua eta irudi zirkularrak
Zirkulua eta irudi zirkularrak zer diren eta zer propietate dituzten jakinda, inguruko elementu asko hobeto ulertuko ditugu.
Zirkulua zirkunferentziak mugatzen duen plano zatia da.
Zirkuluaren atal batzuek izen berezia dute. Atal horiek irudi zirkularrak dira.
ZIRKULUA ZIRKULUERDIA ZIRKULUSEKTOREA ZIRKULUSEGMENTUA KOROA ZIRKULARRA


1 Lotu definizio bakoitza bere izenarekin.

zirkulua zirkuluerdia zirkulu-segmentua
zirkulu-sektorea koroa zirkularra
a) Bi erradiok eta haien arkuak mugatutako zirkulu zatia.
b) Diametro batek eta haren arkuak mugatutako zirkulu-erdia.
c) Korda batek eta haren arkuak mugatutako zirkulu zatia.
d) Zirkunferentzia batek mugatutako plano zatia.
e) Zentro bera duten bi zirkunferentziaren artean dagoen zirkulu zatia.
2 Zer forma dute objektu hauek?
3 Koadernoan, itsatsi zirkunferentzia, zirkulu edo beste edozein irudi zirkularren forma duten objektuen argazki batzuk.
172
2
zirkunferentzia zirkulua
4 Buru pentsalariak Zertan dira desberdinak? Azaldu, arrazoituta.
a) Zirkulua eta zirkunferentzia. b) Zirkulu-sektorea eta zirkulu-segmentua.
5 Irakurri, marraztu eta erantzun.
Zirkunferentzia bat, 6 cm-ko diametrokoa. Marraztu bi erradio, baina ez dezatela eratu diametro bat.
a) Zer irudi zirkular margotu ditzakezu?
b) Azalera bera dute?


Zirkunferentzia bat, 6 cm-ko erradiokoa. Marraztu diametro bat.


a) Margotu irudi zirkularrak.
b) Margotu duzu zirkulu-segmenturik, zirkulu-sektorerik edo zirkuluerdirik? Arrazoitu zure erantzuna.

6 Irudi-diktaketa! Marraztu pertsonaia bakoitzak esandakoa.
Zirkulu bateko korda luzeena. Zer izen du?
Diametro bat, eta eratzen diren bi zirkuluerdiak.
Ikusi-makusi, zer ikusi?
Korda bat, eta eratzen dituen bi arkuak.
Bi erradiok eta arku batek mugatzen duten zirkulu-sektorea.
Binaka jarrita, aztertu arretaz marrazkiak, eta azaldu zer ikusten duzuen. Pentsatu honelako gauzak:
• Bi diametro elkarzutek, zer angelu eratzen dituzte? Zirkuluaren zer zatiki da zirkulu-sektore bakoitza?
• Diametro batek eratzen duen angeluak, zenbat gradu ditu?
Zirkuluaren zer zatiki da zirkuluerdi bakoitza?
• Erradio batek bira osoa egindakoan eratzen duen angeluak, zer neurri du? Edozein zirkulutan gertatzen da hori?


Aurkitu zirkuluen atalak forma zirkularra duen noria batean.

173 U10
Gogoan hartu!
Puntuen, zuzenen eta zirkunferentzien posizio erlatiboa
Irudi geometriko batzuek zer posizio erlatibo duten dakigunean, irudi horien datu batzuk igarri ditzakegu.
• Puntu bat, zirkunferentzia batekiko, izan daiteke:
Kanpokoa Zirkunferentziakoa
Zirkunferentziatik kanpo dago.
Barrukoa
Zirkunferentziaren barruan dago.
• Zuzen bat, zirkunferentzia batekiko, izan daiteke:


Kanpokoa
Ez dute puntu komunik.
Ukitzailea
Puntu komun bat dute.
• Bi zirkunferentzia, elkarrekiko, izan daitezke:
Kanpokoak edo barrukoak
Kanpotik edo barrutik ukitzaileak
Zirkunferentzian bertan dago.
Ebakitzailea
Bi puntu komun dituzte.
Ebakitzaileak
Ez dute puntu komunik.
Puntu komun bat dute.
Bi puntu komun dituzte.
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es ? ?
1 Luken, Willy eta Maia lorategiak eratzen duen zirkunferentziarekiko hiru puntu desberdinetan daude: Luken kanpoan dago; Willy, zirkunferentzian bertan, eta Maia, barruan. Kopiatu marrazkia, eta idatzi hiru lagunen izenak.
174
3
?
2 Ikusi arretaz alboko irudia. Gero, osatu esaldiak koadernoan, hitz hauek idatzita:
baino handiagoa baino txikiagoa adinakoa

a) Zirkunferentziako puntua: zirkunferentziaren zentroraino duen distantzia erradioa ? da.

b) Zirkunferentziaren barruko puntua: zirkunferentziaren zentroraino duen distantzia erradioa ? da.

c) Zirkunferentziatik kanpoko puntua: zirkunferentziaren zentroraino duen distantzia erradioa ? da.
3 Lapitzak erdira Ikusi arretaz alboko irudia, eta erantzun.
a) Nolakoak dira zuzenak zirkunferentziarekiko?
b) Zer angelu eratzen du OA erradioak zirkunferentziarekiko ukitzailea den zuzenarekin?
c) Irudian izendatuta dauden puntuetatik zein daude O zentrotik distantzia berera?
d) Adierazi zuzenen bateko punturen bat, kontuan izanda O-tik A, B edo C puntuak baino distantzia txikiagora egon behar duela.
4 Jonek alanbrezko zirkunferentziekin belarritakoak egiten ditu.
a) Nolakoak dira uztai txikiak elkarrekiko?
b) Nolakoa da uztai handia bi uztai txikietako batekiko?
c) Zer neurri du uztai handiaren erradioak? Eta uztai txikien erradioak?
Ulertzen badut, marraztuko dut
Ikusi arretaz eta kopiatu koadernoan beheko marrazkiak. Kontuan izan zirkunferentzia urdinaren erradioa 6 cm dela, eta gorriarena, 4 cm.
Identifikatu zer posizio erlatibo duten zirkunferentziek, puntuek eta zuzenek benetako objektuetan.
175 U10
Binaka jarrita, azaldu nola egin duzuen.
4 cm
Gogoan hartu!
A B C D O E 4 cm
Erabili erregela eta konpasa!
Zirkunferentziaren luzera
Zirkunferentzia baten luzera kalkulatzeko, aski dugu zer erradio edo diametro duen jakitea.
Zenbaki berezi bat
Egin esperimentua, eta partekatu zure emaitzak.
Material hau behar duzu:







Objektu zirkular batzuk:
Egin urrats hauek:


1. Inguratu objektu bakoitzaren ertza soka batez. Gero, moztu soka.
2. Neurtu soka zati bakoitzaren luzera, eta idatzi emaitzak.
3. Jarri beste soka bat objektu bakoitzaren diametroaren gainean, eta moztu.
4. Neurtu soka zati bakoitzaren luzera, eta idatzi emaitzak.
5. Konparatu objektu bakoitzeko bi sokak. Zenbat aldiz sartzen da laburrena luzeenean, gutxi gorabehera?
6. Kalkulagailuarekin, egin zatiketa: luzera luzeena zati laburrena. Zertaz ohartzen zara?
Egiaztatu edozein zirkunferentziarekin gertatzen dela hori, geometria dinamikoko programa baten bidez, webgunean: anayaharitza.es
Edozein zirkunferentziaren luzera (L) zati diametroa (d) egiten badugu, beti zenbaki bera lortzen dugu: gutxi gorabehera, 3,14. Zenbaki horri pi esaten zaio, eta letra greko batekin adierazten da: π
176
4
L : d = π L = d × π
Erregela
sokak Kalkulagailua
Guraizeak
Koloretako
1 Zer luzera dute zirkunferentzia hauek? Erreparatu marrazkietako datuei.
2 Irakurri eta kalkulatu.
a) Zer erradio du iturri zirkular batek, luzera 25,12 dm bada?
L = 25,12 dm




L = 7,85 m
b) Zer diametro du baratze zirkular honek, 7,85 m-ko luzera badu? ? ?
3 Zer luzera du alboko arkuak? Azaldu nola kalkulatu duzun.
4 Ibonek 24 cm-ko diametroa duen bizkotxo bat egin du. Bizkotxoa apaintzeko, ertzean esne-gain harrotuzko hari bat jarri dio. Zer luzera du apaingarri horrek?
5 Pentsatu eta binaka jarrita komentatu Auzoko bizikleta-dendara oso bizikleta bitxia ekarri dute. Antzinako modelo bat da: atzeko gurpilak 20 cm-ko erradioa du, eta aurrekoak, 40 cm-koa.
a) Zer bide egiten du aurreko gurpilak bira oso bat ematen duen aldiro?
b) Eta atzeko gurpilak?
c) Aurreko gurpilak bira oso bat egiten duen bakoitzean, zenbat bira egiten ditu atzeko gurpilak?
Oso data berezia
Euskaraz, Ingalaterran eta beste herrialde batzuetan bezala, data adierazi behar dugunean, aurrena hila esaten dugu, eta, gero, eguna.
Martxoaren 14a oso egun berezia da. Pi Eguna da (pi zenbakiaren eguna), zeren eta, begira!
hila 3.14 eguna
Sartu www.piday.org webgunean, eta gozatu.

177 U10
luzera Luzera = diametroa × π = = 2 × erradioa × π = 2 × π × r diametroaerradioa d = 7 cm d = 8 cm r = 2 cm r = 2,5 cm
zer luzera duen noria
zirkunferentziak. Gogoan hartu!
Zirkunferentziaren
Kalkulatu
zirkular baten
1,5 dm
Zirkuluaren azalera
Zirkulu baten azalera kalkulatzeko, aski dugu zer erradio edo diametro duen jakitea.
Ikusi arretaz alboko irudiak. Poligono erregularrek zenbat eta alde gehiago izan, orduan eta zirkulu itxura handiagoa dute.
Gogoratu nola kalkulatzen den poligono erregularren azalera:
Poligono erregularren azalera = perimetroa × apotema 2
Beraz, nola kalkulatuko da zirkuluaren azalera?
Zirkuluaren perimetroa zirkunferentziaren luzera da. Apotema erradioa da.
Zirkuluaren azalera = zirkunferentziaren luzera × erradioa
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
1 Zer azalera dute zirkulu hauek? Erreparatu marrazkietako datuei. d
2 Irakurri eta kalkulatu.
a) Zer erradio du plater honek, azalera 314 cm 2 bada?
A = 314 cm2
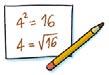
b) Zer diametro du alfonbra honek, 50,24 m2-ko azalera badu?
= 50,24 m2



Zirkuluaren azalera
Zirkuluaren azalera = π × r 2
Gogoratu
Zenbaki baten karratua kalkulatzearen alderantzizkoa erro karratua kal kulatzea da.
178 5
d = 8
r = 2,5 cm r =
= 7 cm
cm
2 cm
n = 8 A5 A6 A7 A8 A9 A10 n = 9 n = 10 n = 5 n = 6 n = 7
2 = 2 × π × r × r 2 = π × r 2
diametroaerradioa
3 Egiaztatu Kalkulatu zer azalera duten objektu hauek:
a) Pizza hau, 22 cm-ko diametrokoa:



c) G alleta hau, 4 cm-ko erradiokoa:
b) Mahai honen ohol zirkularra:
d) Ispilu zirkular hau: 75 cm 20cm
eta diozu hori? Erreparatu loreak dituen lorategi zatiari. Zer azalera du zirkulu-sektore horrek? Azaldu nola kalkulatu duzun.
Zer




Beste irudi batzuen azalera
Zer azalera dituzte margotuta dauden zatiek? Azaldu nola kalkulatu duzun.
Zer ederra den arrazoitzea!
Gogoan hartu!
Noria estaltzeko zenbat olana behar den jakiteko, kalkulatu zirkuluaren azalera.

179 U10
4
dela
5 cm
2 cm 2 cm 1 cm 1 cm 2 cm 4 cm 3 cm 1 cm 5 cm 10 cm 7 cm
EBATZI BAIETZ!

Egin marrazki bat

Orube triangeluar batean haurrentzako parke bat egin nahi du udalak. Parkea zirkularra izatea nahi dute, eta ahalik handiena izatea. Nola egin dezakete?
• Hori jakiteko, aurrena galdera hau egingo dugu: triangelu baten barruan, zer zirkuluk du azalera handiena?
• Baina nola marraztuko dugu zirkunferentzia hori?
1. Bilatu zirkunferentziaren zentroa, triangeluko hiru angeluen erdikariak marraztuta.
2. Marraztu zirkunferentzia, zentrotzat puntu hori hartuta. Zirkunferentzia triangeluaren aldeekiko ukitzailea da.
Puntu hori inzentroa da.
Angeluen erdikariak nola marrazten diren gogoratzen ez baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es .
Parkea egiteko, triangeluaren aldeekiko ukitzailea den zirkunferentzia marraztu behar dute.
Soluzioak badu zentzurik?
Konpasa erabiliz, egiaztatu triangeluaren barruan marraztu daitekeen zirkunferentzia handiena dela hori.
1 Eta orubeak triangelu aldeberdinaren forma balu? Kalkatu triangelua, eta marraztu triangelu horren aldeekiko ukitzailea den zirkunferentzia.
2 Eta orubeak karratu forma balu? Azaldu eta marraztu nola egingo zenukeen.
180
Problemak arin-arinka
2 1
10 cm-ko diametroa duen zirkunferentzia bat marrazteko, zenbat ireki behar da konpasa?
Zirkunferentzia edo zirkulu batean, zein da kordarik
Buruzko kalkulua
Kalkulatu 60ren % 20.
Nolakoak dira koroa zirkular bat eratzen duten zirkunfe rentziak?
Zer formularekin kalkulatzen da zirkunferentzien luzera?
Patroi bila
Zenbat zatitan mozten duzu pizza? Zergatik mozten dugu ia beti modu berean?

Ikertu zer beste modu dauden zirkulu bat 2, 3 edo 4 zuzen eginez mozteko. Zenbat zati lortu ditzakezu?
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:


20ren % 20
40ren % 20
50en % 20
80ren % 20
90en % 20
120ren % 20
160ren % 20
180ren % 20
200en % 20
240ren % 20
181 U10
Partekatu marrazkiak ikaskidearekin.
= % 10 × 2
2 zuzen eginez 3 zati 4 zati 4 zati 6 zati 3 zuzen eginez 4 zuzen eginez 7 zati 9 zati Gora sormena! ✎
60 6 12 :10 % 20
× 2
Begira nola pentsatzen dudan
Z er ikasi dut?
1 Kopiatu eta osatu koadernoan.
a) O puntua ? da.
b) OA zuzenkia ? bat da, eta BG zuzenkia, berriz, ? bat.
c) EF zuzena zirkunferentziarekiko ? da.
d) DC zuzenkia ? bat da.
e) B-tik A-ra bitarteko zirkunferentzia zatiari ? esaten zaio.
f) Zirkunferentzia H puntuan ukitzen ari den zuzena zirkunferentziarekiko ? da.
2 Nahikoa da bi zirkunferentzia barrukoak izatea koroa zirkular bat eratzeko? Azaldu zure erantzuna.
3 Neurtu, eta osatu taula koadernoan.
Zirkunferentziaren luzera (L) Diametroa (d) L : d ? ? ? ? ? ?


4 Kalkulatu zer perimetro duen margotutako zatiak, kontuan izanda zirkuluaren diametroa 12 cm dela.
Pentsatu:
a) Zer erradio du zirkunferentziak?
b) Nola kalkulatzen da zer luzera duen margotutako zatiaren arkuak?
5 Kalkulatu margotutako zati bakoitzaren azalera. 10 cm 14 cm R1 = 15 m R2 = 8 m
d = 20 cm
6 Kalkulatu zer azalera duen margotuta dagoen zirkulu-segmentuak. R2 = 3,5 cm
Gogoratu nola kalkulatzen den triangeluen azalera.
7 Bizikleta baten gurpilek 25 cm-ko erradioa dute. Gurpilek 100 bira egin badituzte, zer distantzia egin du bizikletak?
8 32 m-ko erradioa duen patinaje-pista zirkular baten inguruan babesteko zinta jarri nahi dute.
a) Zenbat metro zinta behar dituzte?
b) Metro bat zintak 25 € balio badu, zenbat kostako zaie zinta guztia?
Semaforoa. Margotu koadernoan, ariketa bakoitzaren ondoan, honela:
Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu

182
PORTFOLIOA
E F G H A O D C B
a) c) b) d)
HELBURUA AURRERA
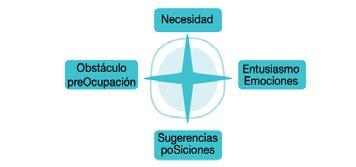
Neurtu zure sormena.
Gaur egun noria aisialdirako erabiltzen dugu, baina ez da beti hala izan. Bazenekien ura lortzeko lehenbiziko makina izan zela noria?
Ikusi arretaz alboko noria.
a) Identifikatu noria horretan zirkunferentzien elementuak.
b) Identifikatu zer zuzen dauden eta zer posizio duten zuzen horiek zirkunferentziarekiko.
c) Erradioa 20 m bada, zer luzera du?
d) Noria olana batekin estali nahi badugu, zer azalera izan behar du olanak gutxienez, noria guztia estali ahal izateko?


Geure buruari galdezka Iparrorratza estrategia erabiliz, azter dezagun nola egiten diogun aurre sortzeko dugun ahalmenari.
a) Kopiatu antolatzailea, eta osatu galderak.
b) Neurtu zure sormena! Orri zuri batean, marraztu 20 zirkulu. Bost minutuan, osatu ahalik eta zirkulu gehien, zirkuluetan marrazkiak eginez: objektuak, pertsonak, ideiak…
N o la ikasi dut?
sormena hobetzeko?
Zure ustez, zer behar duzu sormen handiagoz aritzeko?
Zerk sortzen dizu zirrara sormenetik?
Iritziz aldatzen zara ingurukoek bestelako iritzia izate hutsagatik?

Ariketa bat egitea lortzen ez duzunean, erraz onartzen duzu beste proposamen batzuen bidetik jotzea edo plana aldatzea? Aipatu hori gertatu den bi egoera.

Pentsatu noiz gertatu izan zaizun zu iritziz ez aldatzea eta ariketa egiten ez asmatzea edo egiteko modua okerra izatea. Identifikatu horrelako egoera bat. Nola sentitu zinen orduan?
Zer egin dezakezu malguagoa izateko eta planak aldatzea zuri errazagoa gertatzeko?
sormena hobetzeaz?
U10 183




Poliedroak eta gorputz biribilak
Gorputz geometrikoek zer propietate dituzten jakinda, errazago identifika ditzakegu.

GORPUTZ GEOMETRIKOAK

POLIEDROAK


Aurpegi guztiak poligonoak dira.
GORPUTZ BIRIBILAK
Aurpegietako bat kurbatua da.
PRISMAK PIRAMIDEAK BESTE BATZUK ZILINDROA KONOA ESFERA BESTE BATZUK


1 Irakurri arretaz esaldiak, eta osatu koadernoan, hitz hauek idatzita:
ESFERA ZILINDROA KONOA PRISMA PIRAMIDEA
a) ? poliedro bat da, eta bi oinarri berdin paralelo (poligonoak) eta zenbait alboko aurpegi (paralelogramoak) ditu.

b) ? poliedro bat da, eta oinarri bat (poligonoa) eta zenbait alboko aurpegi (triangeluak) ditu; oinarriak eta alboko aurpegiek bat egiten duten erpinari goi-erpin ere esaten zaio.
c) ? gorputz biribil bat da, eta gainazal kurbatu bakar batez osatuta dago.
d) ? gorputz biribil bat da, eta oinarri bat (zirkulua) eta alboko gainazal kurbatu bat ditu.
e) ? gorputz biribil bat da, eta bi oinarri berdin paralelo (zirkuluak) eta alboko gainazal kurbatu bat ditu.
2 Adierazi zer forma duten objektu hauek:
Gorputz geometrikoak nolakoak diren ikusi nahi baduzu, kontsultatu Gorputzak mugimenduan baliabidea, hemen: anayaharitza.es
186
1
3 Zer dela eta diozu hori? Irudi batek alboko aztarna utzi du plastilinan.


a) Izan daiteke poliedro bat? Azaldu, arrazoiak emanez.
b) Izan daiteke gorputz biribil bat? Arrazoitu zure erantzuna.
c) Idatzi zer gorputz geometrikok utzi ahal izan duten aztarna hori.
4 Bai bitxia! Aspaldi, prisma formako angurriak hazteko modua aurkitu zuten Japonian; zehazki, kubo formakoak. Zure ustez, zergatik nahi izan zuten hori asmatu? Ikertu zer abantaila dituen esfera formako angurrien ordez kubo formakoak hazteak.
5 Polikuboekin jolastuz, sortu zenbait gorputz geometriko mota.





a) Zer gorputz geometriko egin dituzu? Idatzi bakoitzaren izena eta propietateak.
Prismak polikuboekin
b) Zer gorputz geometriko ezin izan dituzu egin? Azaldu zergatik. Egin eraikuntzak polikuboekin.
a) 4 polikubo erabiliz, eraiki ahal dituzun poliedro guztiak. Zenbatek dute prisma forma?
b) Egin gauza bera 5 polikuborekin. Zenbatek dute prisma forma?
c) Hautatu aukera egokia, eta arrazoitu zure erantzuna. Zenbat polikubo behar dira prisma bat baino gehiago egiteko?
A Polikubo kopuru bikoiti bat.
B Polikubo kopuru bakoiti bat.
Gogoan hartu!
Gorputz geometrikoak ezagututa, errazago egingo duzu horiekin trofeo bat.

187 U11
Poliedro erregularrak
Poliedro erregularrek zer propietate dituzten jakinda, errazago identifika ditzakegu.
Poliedro erregularretan aurpegi guztiak poligono erregular berdinak dira, eta erpin guztietan aurpegi kopuru bera elkartzen da.
5 poliedro erregular bakarrik daude:




TETRAEDROA

HEXAEDROA EDO KUBOA
OKTAEDROA
4 aurpegiak triangelu aldeberdinak dira.
DODEKAEDROA
12 aurpegiak pentagono erregularrak dira.
6 aurpegiak karratuak dira.
8 aurpegiak triangelu aldeberdinak dira.
IKOSAEDROA
20 aurpegiak triangelu aldeberdinak dira.
Egin poliedro erregularrak, webgunean dauden txantiloiak erabiliz: anayaharitza.es
1 Zer forma dute objektu hauek?
2 Taldeka interpretatu Poliedro erregularrei solido platoniko ere esaten zaie. Ikertu eta bilatu informazioa bost poliedro berezi horiei buruz.
Ohartu honetaz
Poliedro erregularren aurrizkien esanahia:
Tetra– 4 Dodeka– 12
Hexa– 6 Ikosa– 20



Okta– 8



188
2
a) d) e) b) c)
3 Ikusi arretaz alboko irudia, eta azaldu zergatik ez den poliedro erregularra.
4 Dado batean, aurrez aurre dauden aurpegien batura 7 da. Zer garapen da dado honena? Erreparatu puntuei eta koloreei.
5 Entzulearen eskaria Sailkatu bost poliedro erregularrak, motatan: prismak, piramideak eta beste poliedro batzuk.
prismak piramideak beste batzuk
Zenbat zotz eta bolatxo?


Plastilinazko bolatxoak eta zotzak erabiliz, egin poliedro erregularrak, eta osatu taula koadernoan.
Aurpegi kopurua Erpin kopurua Ertz Aurpegiak + Erpinak – Ertzak

Tetraedroa ? ? ? ?


Kuboa edo hexaedroa ? ? ? ?
Oktaedroa ? ? ? ?

Dodekaedroa ? ? ? ?
Ikosaedroa ? ? ? ?
Egiaztatu zure emaitzak eta ikaskideenak berdinak direla.
Nola egiten den ikus dezakezu webgunean: anayaharitza.es
Gogoan hartu!
Poliedro erregularrak marrazteko nahiz kartoi mehez egiteko, erabili haien propietateak.
189 U11
Biraketa-gorputzak

Biraketa-gorputzek zer propietate dituzten jakinda, errazago identifika ditzakegu.
Zilindroa, konoa eta esfera biraketa-gorputzak dira; hau da, irudi lau bat ardatz baten inguruan biratzean sortzen dira.
ZILINDROA


Oinarria
Alboko gainazala
KONOA Erpina Alboko gainazala
ESFERA



Oinarria
Laukizuzen bat aldeetako baten inguruan biratzen bada, zilindroa sortzen da.
Oinarria
Triangelu zuzen bat angelu zuzenaren aldeetako baten inguruan biratzen bada, konoa sortzen da.
Zirkuluerdi bat alde zuzenaren inguruan biratzen bada, esfera sortzen da.
Irudi horiek nola eratzen diren ikusi nahi baduzu, «Berehala kontatuko dizut», hemen: anayaharitza.es
1 Irakurri esaldiak, eta osatu koadernoan.
a) ? bi oinarri zirkular berdin paralelo eta alboko gainazal kurbatu bat ditu. ? bat ? baten inguruan biraraziz sortzen da.
b) ? oinarri zirkular bat eta alboko gainazal kurbatu bat ditu. ? bat ? baten inguruan biraraziz sortzen da.
c) G ainazal laurik ez duen biraketa-gorputzak ? izena du. ? bat ? baten inguruan biraraziz sortzen da.
2 Ideiabiltzarra Pentsatu eta erantzun, arrazoiak emanda.
a) Zilindro bera sortzen al da laukizuzen bat alde handiaren inguruan birarazita eta alde txikiaren inguruan birarazita?
b) Kono bera sortzen al da triangelu zuzen isoszele bat berdinak diren aldeen inguruan birarazita?
c) Eta triangelu zuzen eskaleno bat angelu zuzenaren aldeen inguruan birarazita?
190
3
Erradioa
Zentroa
3 Pentsatu eta binaka jarrita komentatu Alboko bi gorputz geometrikoak ere biraketa-gorputzak dira, irudi lau bat ardatz baten inguruan biratzean sortzen baitira.
a) Adierazi eta marraztu zer irudi lauk sortzen duen gorputz geometriko horietako bakoitza.

b) Konparatu zure marrazkiak eta ikaskidearenak. Biok irudi lau mota bera pentsatu duzue?
4 Marraztu koadernoan zer objektu sortuko diren alboko lau irudiak birarazten baditugu adierazitako ardatzen inguruan.
5 Identifikatu garapen lau hauetatik zein den zilindroarena eta zein den konoarena. Muntatu bi gorputz geometrikoak, bakoitzaren garapen lautik abiatuta.
Deskargatu garapen lauak webgunean: anayaharitza.es

6 Irakurri eta gozatu olerkia.
Hona hemen Arkimedes, Sirakusakoa bera, asmakariak egitez aspertzen ez zena.
"Gauzak ondo egiteko, probak egin behar dira. Behin kale eginda ere, segi tira ahala tira."
Matematika maite zuen, maite zuen geometria. Zilindroan, sartzen da esfera? Bai, horixe! Ez da fantasia!


Problema bat otuz gero, ez zuen ahanzten sekula. Erantzuna topatutakoan esango zuen, Eureka!
Itsasontziak altxatzeko, atzapar bat asmatu zuen, eta garabi hartaz gain, biraderadun torloju bat, aizue!
Planetarioa, katapultak, itsasontzi bat erraldoia, barruan zer jarriko eta lorategi eta gimnasioa.
Hori guztia egin zuelako, miresgarritzat daukagu: ingeniari aparta, oso jakintsu, eta zientziazale porrokatu.
Gogoan hartu!


Zilindroa, konoa eta esfera marrazteko nahiz kartoi mehez egiteko, erabili haien propietateak.

191 U11
A B
Ohartu honetaz Esferak ez du garapen laurik.
a) b)
Prismen azalera eta bolumena
Prismen azalera eta bolumena kalkulatzen badakigu, problema geometrikoetan erabakiak errazago hartuko ditugu.
Prismaren azalera prismaren garapen lauak duen gainazalaren neurria da.
Unitate karratutan adierazten da; adibidez, zentimetro karratutan (cm 2).
PRISMA
PRISMAREN AZALERA
Prismaren azalera = alboko aurpegien azalera + 2 × oinarriaren azalera
A PRISMA= A ALBOKOA + 2 × AOINARRIA
Laguntza behar baduzu, «Berehala kontatuko dizut», hemen: anayaharitza.es
1 Zer azalera dute beheko prismek? Ikusi arretaz adibide ebatzia.
1. Kalkulatu alboko aurpegien azalera; 5 laukizuzen berdin dira.
A ALBOKO AURPEGIA = oinarria × altuera = 6 cm × 12 cm = 72 cm 2
A ALBOKOA = 5 × 72 cm 2 = 360 cm 2
2. Kalkulatu oinarrietako baten azalera; pentagono erregular bat da. perimetroa = 5 × 6 cm = 30 cm apotema = 4 cm
AOINARRIA = (perimetroa × apotema) : 2 = (30 cm × 4 cm) : 2 = 60 cm 2

3. Kalkulatu guztizko azalera.
a) b)
cm

cm 15
cm 30 cm
12 cm 6 cm 4 cm 5 cm 15 cm

192
4
4,33
5
A PRISMA= A ALBOKOA + 2 × AOINARRIA = 360 cm 2 + 2 × 60 cm 2 = = 360 cm 2 + 120 cm 2 = 480 cm 2 10 cm
Kontuan izan zer formularekin kalkulatzen den oinarri bakoitzaren azalera.
Oinarria
Oinarria Alboko aurpegia
Prismaren bolumena prismak duen edukieraren neurria da.

Unitate kubotan adierazten da; adibidez, zentimetro kubotan (cm 3).
PRISMAREN BOLUMENA
Altuera (h)
Pentsa oinarri bera behin eta berriro jartzen dugula, prismaren altuera osatu arte. Bada, horrelako zerbait da!
Prismaren bolumena = oinarriaren azalera × prismaren altuera
V PRISMA= AOINARRIA × h
2 Zer bolumen dute 1. ariketako prismek? Ikusi arretaz adibide ebatzia.
1. Identifikatu prismaren oinarriak eta altuera. Oinarria Oinarria
Altuera (h)
2. Kalkulatu oinarri baten azalera; karratu bat da.
AOINARRIA = aldea × aldea = 15 mm × 15 mm = 225 mm 2
15 mm
mm
15 mm
3. Kalkulatu bolumena. Kontuan izan zer neurri-unitatetan dauden oinarriaren azalera eta altuera.
V PRISMA = AOINARRIA × h = 225 mm 2 × 30 mm = 6750 mm 3 = 6,75 cm 3

3 Egiaztatu Sarak eraikuntza hau margotu du:
6 dm
6,6 dm 15 dm

5,4 dm
a) Zenbat metro karratu margotu ditu?
b) 3 m 2-ko gainazala margotzeko 1 L pintura behar bada, zenbat litro erabili ditu?
c) Zer bolumen du eraikuntzak?
Kontuz ibili alboko azalera kalkulatzean. Aurpegi guztiak ez dira berdinak!
193 U11
30
Piramideen azalera eta bolumena
Piramideen azalera eta bolumena kalkulatzen badakigu, problema geometrikoetan erabakiak errazago hartuko ditugu.
Piramidearen azalera piramidearen garapen lauak duen gainazalaren neurria da. Unitate karratutan adierazten da; adibidez, metro karratutan (m 2).
Piramidearen bolumena piramideak duen edukieraren neurria da. Unitate kubotan adierazten da; adibidez, metro kubotan (m 3).
Alboko aurpegia
PIRAMIDEA PIRAMIDEAREN AZALERA PIRAMIDEAREN BOLUMENA h
A PIRAMIDEA= A ALBOKOA + AOINARRIA V PIRAMIDEA = 1 3 × AOINARRIA × h
Laguntza behar baduzu, «Berehala kontatuko dizut», hemen: anayaharitza.es
1 Zer azalera dute beheko piramideek? Ikusi arretaz adibide ebatzia.
1. Kalkulatu alboko aurpegien azalera; 6 triangelu berdin dira.
A ALBOKO AURPEGIA = (oinarria × altuera) : 2 = (6 cm × 12 cm) : 2 = 36 cm 2
A ALBOKOA = 6 × 36 cm 2 = 216 cm 2
2. Kalkulatu oinarriaren azalera; hexagono erregular bat da.
perimetroa = 6 × 6 cm = 36 cm apotema = 5,2 cm

AOINARRIA = (perimetroa × apotema) : 2 = (36 cm × 5,2 cm) : 2 = 93,6 cm2
3. Kalkulatu guztizko azalera.
A PIRAMIDEA = A ALBOKOA + AOINARRIA = 216 cm 2 + 93,6 cm 2 = 309,6 cm 2
12 cm
Kontuan izan zer formularekin kalkulatzen den oinarri bakoitzaren azalera.
cm


194
5
6
4 cm 6 cm 4,33 cm 5cm 5 cm
5,2 cm
Oinarria a) b)
2 Zer bolumen dute 1. ariketako piramideek? Ikusi arretaz adibide ebatzia.
1. Identifikatu piramidearen oinarria eta altuera.

2. Kalkulatu oinarriaren azalera; pentagono bat da.

AOINARRIA = (perimetroa × apotema) : 2 = (50 m × 6,9 m) : 2 = 172,5 m 2

3. Kalkulatu bolumena. Kontuan izan zer neurri-unitatetan dauden oinarriaren azalera eta altuera
V PIRAMIDEA = 1 3 × AOINARRIA × h = 1 3



3 Egiaztatu Kalkulatu zer bolumen duten prisma batek eta piramide batek, kontuan izanda 10 cm-ko altuera dutela, eta 5 cm-ko aldea duen oinarri karratua. Egiaztatu piramidearen bolumena prismaren bolumenaren herena dela.

Ikusi
Prisma baten bolumena 3 aldiz handiagoa da oinarri eta altuera bereko piramide batena baino.
Prismaren bol. = oinarriaren azalera × altuera Piramidearen bol. = oinarriaren azalera × altuera 3
• Hori hala dela egiaztatzeko, egin esperimentu erraz hau:
Prisma baten eta piramide baten garapen lauak, biak oinarri eta altuera berekoak.
Muntatu irudiak, garapen lauetatik.
Bota piramideko arroza prismara.
Errepikatu 2. eta 3. urratsak, prisma arrozez bete arte.
a) Zenbat aldiz bota duzu piramideko arroza prismara?
b) Badu zentzurik zure emaitzak, bi irudien bolumena kalkulatzeko formula erabiliz lortzen den emaitzaren aldean?
Deskargatu esperimentu honetarako garapen lauak webgunean: anayaharitza.es .
195 U11
× 172,5 m 2 × 16 m = 920 m 3 10 m 16 m 6,9 m
1. urratsa
2. urratsa Bete piramidea arrozez.
3. urratsa
4. urratsa
eta ikasi Guraizeak Kola Arroza
Irudi konposatuen azalera eta bolumena
Irudien azalera eta bolumena errazago kalkulatzeko modu bat irudi ezagunetan deskonposatzea da.
1 Zer azalera du eskuineko eraikuntza honek? Pentsatu zenbat aurpegi dituen eta nolako aurpegiak diren.
1. Kalkulatu karratu forma duten aurpegi guztien azalera.
A = aldea × aldea
2. Kalkulatu triangelu forma duten aurpegi guztien azalera.
A = (oinarria × altuera) : 2


3. Bestelako formaren bat duen aurpegirik badago, zure ustez?
4. Batu aurpegi guztien azalerak.
2 Kalkulatu gorputz geometriko honen azalera:
Alboko aurpegi guztiak berdinak dira, eta trapezio forma dute.
3 Kalkulatu eskuineko eraikuntzaren azalera.
a) Kopiatu taula. Gero, marraztu pieza bakoitzaren irudia eta idatzi neurriak dagokien laukian.
Pieza

urdina Pieza gorria Pieza horia
Triangeluak ? ? ?
Laukiak ? ? ?
b) Adierazi zenbat irudi dauden kasu bakoitzean.
c) Kalkulatu irudi bakoitzaren azalera, eta, gero, eraikuntzaren azalera.
Ikusi irudia ikuspuntu guztietatik, hemen: anayaharitza.es
4 Zenbat zentimetro karratu paper behar dira eskuineko irudi hau paperez estaltzeko?
196
10 cm 6 cm 14 cm 10 cm 6 cm 14 cm
6
7,5 cm 5 cm 6 m 6m 5 m 4 m 10 cm 6,9 cm 6 cm
5 Zer bolumen du eraikuntza honek? Pentsatu zenbat aurpegi dituen eta nolako aurpegiak diren.
1. Kalkulatu prismaren bolumena.
V PRISMA = AOINARRIA × h
2. Kalkulatu piramidearen bolumena.

V PIRAMIDEA = 1 3 × AOINARRIA × h


3. Batu gorputz geometrikoen bolumenak.
6 Zer dela eta diozu hori? Ikusi arretaz eta erantzun.
a) Zer bolumen dute eraikuntza horiek?
b) Zer ikusten duzu emaitzetan? Azaldu zergatik diren emaitzak horrelakoak, zure ustez.
7 Ruthek diamante formako artelan bat marraztu du. Museoan muntatzen dutenean, diamante barrura 3 litro ur bota behar ditu. Sartuko da hainbeste ur?
Trofeoa egiteko zenbat kartoi mehe behar duzun jakiteko, kalkulatu irudien azalerak.
197 U11
10 cm 20 cm
6 m 6 m 6 m 18 m 6m 6 m 1 dm 15 cm 8,7cm
1 L = 1 dm 3
Ohartu honetaz
Gogoan
1 dm 1 dm 1dm 20 cm 20 cm 10 cm 10 cm
hartu!
EBATZI BAIETZ!
Baztertu erantzun ezinezkoak
Manu herriko plazan dagoen eskulturaren aurrean jarri da. Argazki hauetatik zein egin du, zure ustez?
Hori jakiteko, erantzunak baztertuz joango gara, zenbait irizpideren arabera ezinezkoak direnak kenduta.

1. Erreparatu eskulturaren erdian dagoen kuboari, eta baztertu eskuinaldean karraturik ez duen argazkia.
2. Erreparatu atzealdeko piezak duen formari, eta baztertu horrelako forma ez duen argazkia.
3. Erreparatu eskulturaren oinarriari, eta baztertu elkarren ondoan karratu bat eta laukizuzen bat ez dituzten argazkiak.





Manuk laugarren argazkia egin du.
Soluzioak badu zentzurik?
Egiaztatu laugarren argazkia Manuk ikusten duena dela.
1 Imajinatu Manu alboko marrazkian ikusten den lekuan jarri dela eta beste argazki bat egin duela. Zer argazki da?


198
Kontuan izan Manuk kuboa karratu bezala ikusten duela.
Problemak arin-arinka
Buruzko kalkulua
Zer poliedro erregular falta da?
tetraedroa
oktaedroa ikosaedroa dodekaedroa
3
Zertan dira berdinak prisma eta piramidea? Eta desberdinak?

1 5
Zer bolumen du prismak? Eta piramideak?
Begira nola pentsatzen dudan
Patroi bila
Zer gorputz biribilek ditu bi oinarri berdin?
4
Laukizuzen bat alde baten inguruan biratzean, zer biraketa-gorputz sortzen da?
2 6
Oinarri eta altuera bereko prisma bat eta piramide bat ditugu. Zeinek du bolumen handiena?
Kalkulatu 70 × 0,1.
Carrollen diagrama taula mota bat da, eta ezaugarri desberdineko datuak antolatzeko balio du. Zer testu falta dira taula honetan?
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:



40 × 0,1
80 × 0,1
100 × 0,1
120 × 0,1
160 × 0,1
× 0,1
× 0,1
Praktikatu beste diagrama batzuekin, webgunean: anayaharitza.es
199 U11
240
260
280
420
200
× 0,1
× 0,1
× 0,1
0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 1 70 7 : 10 ? ? ? ? IRUDI LAUA GORPUTZ GEOMETRIKOA URDINA EZ URDINA
Z er ikasi dut?
Tetraedroa ? ? ?
Hexaedroa ? ? ?
Oktaedroa ? ? ?
Dodekaedroa ? ? ?
Ikosaedroa ? ? ?

Gogoratu
Semaforoa. Margotu koadernoan,
bakoitzaren ondoan, honela:

Erantzuna badakizu
Laukizuzena •
Triangelu zuzena •
Zirkuluerdia •
• Esfera
• Konoa
• Zilindroa
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu

200
PORTFOLIOA
A B C D
1 Sailkatu gorputz hauek poliedrotan eta gorputz biribiletan. Idatzi bakoitzaren izena.
2 Osatu taula koadernoan. Aurpegiak Erpinak Ertzak
3 Esan zer irudi den kono baten garapen laua eta zein ez, eta azaldu zergatik.
4 Kopiatu koadernoan eta lotu irudi bakoitza dagokion biraketa-gorputzarekin.
5 Kalkulatu opari-kaxa hauen azalerak:
6 Ikusi arretaz datuak, eta kalkulatu bolumena.
7 1 L = 1 dm 3 da. Hortaz, zenbat litro ur sartzen dira 6. ariketako arrainontzian?
neurri-unitateak aldatu behar dituzula.
ariketa
20cm 0,80m 1,5 m 80 cm 5 dm 6 m 2 m 5,2m 2,5 cm 5 cm 50 cm 13 cm 10 cm 12 cm
HELBURUA AURRERA
Egin trofeo bat irudi geometrikoekin.

Itsasoa zaintzeko jardunbide onak sarituko ditugu. Saria trofeo bat izango da, geuk talde-lanean egina, prismekin, piramideekin, konoekin, zilindroekin edo esferekin.
a) Ikertu eta bilatu trofeoen adibide batzuk.
b) Diseinatu trofeoa, eta pentsatu zer neurri izango dituen irudi bakoitzak.
c) Kalkulatu zenbat kartoi mehe beharko duzuen trofeoa egiteko.
d) Egin trofeoa, aukeratu dituzuen gorputz geometrikoen garapen lauetatik abiatuta. Irudietan esloganak ere jar ditzakezue.
Irudi batzuen garapen lauak deskarga ditzakezu webgunean: anayaharitza.es


Geure buruari galdezka

Talde-lanean, galdetegi bat prestatuko dugu, ikastetxeko ikasleek itsasoa zaintzearekin lotutako zer jardunbide on dituzten identifikatzeko.

Zer dela eta diozu hori? estrategia erabiliz, jardunbide onenak zein diren aztertuko dugu.
a) Aplikatu antolatzailea galdetegiaren bidez bildutako jardunbide on bakoitza aztertzeko.
b) Eman trofeoa zuen ustez jardunbide onengatik ikastetxean nabarmentzekoa den pertsonari edo taldeari.
N o la ikasi dut?
Osatu koadernoan.
Problema bat ebazteko ideia originalak edo besteenez bestelakoak izan dituzunean, nola sentitu izan zara?
Pentsatu noiz gertatu izan zaizun ariketa bat ebazteko modurik ez zitzaizula bururatzen. Identifikatu egoera bat. Nola sentitu zinen orduan? Zer egin dezakezu problemak ebazteko ideiak sortzeko?
Honen deskribapena edo interpretazioa: … Justifikazioa eta ebidentziak
Zer dela eta diozu hori?
U11 201


202


203
Zorizko esperimentuak
Erruleta bat biraraztea eta harri-orri-ar jolasean ibiltzea,


adibidez, zorizko esperimentuak dira.
Euria egingo du gaur?

Zorizko esperimentuetan, badakigu zer emaitza atera daitezkeen, baina ez dakigu horietatik zein gertatuko den.
1 Esperimentu hauetatik zein dira zorizkoak?
Opari-kaxa baten barruan zer dagoen jakitea.
Puzzle baten pieza guztiak muntatzea.




Baloia saskira jaurti eta sartzea.

Botila batean zenbat ur sartzen den neurtzea.
Ez utzi zoriaren esku. Egin lan klima-aldaketaren efektuaren kontra!
Tenis-partida batek zer iraupen duen jakitea.


Gauean zer tenperatura izango dugun jakitea.
2 Zer dela eta diozu hori? Pentsatu zure eguneroko bizitzan gertatzen diren egoeretan, eta idatzi zorizkoak diren bi eta zorizkoak ez diren beste bi. Azaldu zergatik diren edo ez diren zorizkoak.
204
1
a) Txanpon bat airera botatzen badugu, zer emaitza lortu ditzakegu? Zorizko esperimentua da?
b) Bikoiti edo bakoiti asmatzera jolasten bagara, zer emaitza lortu ditzakegu? Zorizko esperimentua da?
c) Partxis-jokoan, berdeak fitxa mugitu eta gero, zer kolorek botako du dadoa? Zorizko esperimentua da?
4 Ezagutzen duzu hein batean edo erabat zoriaren esku dagoen jokorik? Aipatu batzuk.
5 Zer dela eta diozu hori? Maddi eta Paul bola-jokoan aritu dira, eta puntuazio bera lortu dute. Irabazlea nor den erabakitzeko zer modu da bidezkoena? Aukeratu, eta arrazoitu zure erantzuna.
A Txanpon bat airera bota, eta aurkia hartu duena aukeratzea.
B Irabazlea bi jokalarietatik zaharrena izendatzea.
C Berdinketa hausteko, beste txanda bat jokatzea.
D Maddiren eta Paulen lagunek erabakitzea. Badakizu nola den harri-orri-ar jolasa? Ez badakizu, ikertu, eta ibili lagun batekin.
Harri-orri-ar



a) Zein dira emaitza posibleak?





b) Zer iruditzen zaizu: harria aukeratzen baduzu, irabazi egingo duzu? Eta orria aukeratuta? Eta artaziak aukeratuta? Azaldu zure erantzuna.
c) Esaten dute, beti irabazteko, lehiakidea nahasi behar dela: jokaldia irabaziz gero, ez errepikatu; eta galduz gero, ez aldatu. Probatu estrategia hori lagun batekin. Balio du?
d) Poto honetatik errotuladore bat hartzen badugu, zer kolore lortu dezakegu? Zorizko esperimentua da? Pentsatu
205 U12
3 Lapitzak erdira Irakurri eta erantzun.
Gogoan hartu!
+
=
bakoiti !
eguraldian eragina duen faktoreetako bat zoria dela.
2
3
5
Gertaera ziurra, posiblea eta ezinezkoa
Zertan dira desberdinak zerbait posiblea izatea eta ezinezkoa izatea? Zerbait posiblea denean, ziurra ere bada?
Zorizko esperimentuetako emaitzak gertaerak dira.
• Gertaera bat ziurra da, beti gertatzen bada.

• Gertaera bat posiblea da, batzuetan gertatzen bada.
• Gertaera bat ezinezkoa da, inoiz gertatzen ez bada.
6 aurpegiko dado bat botatzea.
Poltsatik bola bat ateratzea.
Zuzena/okerra erako galdera bati erantzutea.
Birla horiek botatzeko, bola jaurtitzea.
Txanpon bat botatzean, emaitza posibleak bi dira: aurkia eta ifrentzua.
Ateratzea… Ziurra, posiblea edo ezinezkoa da?



urdina ?
horia ?








laranja ?
edozein koloretakoa ?
gorria edo arrosa ?
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es
206
1 Egiaztatu Irakurri, eta idatzi emaitza posibleak.
2 Imajinatu: uztaiak igerilekura bota dituzu, eta bat atera behar duzu urpetik, begiak ireki gabe. Kopiatu eta osatu taula.
2
Hara, ekaitza! Euria egingo du, ziur.
Ez dago hodeirik. Oraintxe ezinezkoa da euria egitea.
Hodei batzuk daude. Posible da euria egitea.
3 Erruleta birarazi duzu. Pentsatu zer emaitza den ezinezkoa, eta azaldu zergatik. Emaitza posiblea bada, jarri adibide bat.

a) 5en multiplo bat ateratzea.





b) Horia eta 2ren multiploa ateratzea.
c) Berdea eta bikoitia ateratzea.
d) Beltza eta bakoitia ateratzea.
e) Beltza edo gorria ateratzea.
Ohartu honetaz
A eta B: esan nahi du bi gauzak batera gertatzen direla.
A edo B: esan nahi du gauza bat edo bestea gertatzen dela.
ZIURRA POSIBLEA EZINEZKOA
5 Irakurri eta ebatzi.
a) Goiatzi gehien gustatzen zaion jogurta kokozkoa da. Pakete hauetako bat erosi nahi badu, zein aukeratu behar du? Azaldu zergatik. A B C
b) Elik tratu hau proposatu dio nebari: bion logela berak txukunduko duela, baldin eta sei aurpegiko dadoa botata batura 13 bada. Anek txukunduko du logela? Zergatik?
c) Anerrek kaxa hauetatik txanpon bat hartu behar du, begiratu gabe. Zein hartu duen aukeratzen badu, beretzat izango da. Zer kaxa aukeratuko zenuke zuk? Zergatik?
A B C

Gogoan hartu!
Euria egingo duen iragartzeko, erabili gertakari ziurraren, posiblearen eta ezinezkoaren definizioa.
207 U12
4 Marraztu eta margotu koadernoan, «bola urdina edo berdea ateratzea» gertaera ziurra, posiblea edo ezinezkoa izan dadin.
Gertaera baten probabilitatea



Poltsetako batetik, begiratu gabe, bola gorri bat atera behar baduzu, zein aukeratuko zenuke?
Bola gorri bat ateratzeko aukera asko dago.
Aukera bera dago bola gorri bat ateratzeko edo urdin bat ateratzeko.
Bola gorri bat ateratzeko aukera gutxi dago.
Gertaera baten probabilitateak adierazten du zenbateko aukera dagoen gertatzeko.
1 Osatu esaldiak, hitz hauek idatzita:
aukera gehiago aukera bera aukera gutxiago
a) ? dago berdea ateratzeko edo horia ateratzeko.
b) ? dago horia ateratzeko urdina ateratzeko baino.
c) ? dago urdina ateratzeko berdea ateratzeko baino.
2 Marraztu poltsa batean 5 bola, eta margotu, baldintza hauek bete ahal izateko:
• Bola gorriak, urdinak eta berdeak daude.
• Aukera bera dago bola gorri bat edo urdin bat ateratzeko.
• Aukera gutxiago dago bola urdin bat ateratzeko berdea ateratzeko baino.
3 Zer probabilitate dago bolaluma gorri bat hartzeko, begiratu gabe? Hori kalkulatzeko, egin urrats hauek:
1. Zenbatu aldeko kasuen kopurua. bolaluma gorrien kop. ?
2. Zenbatu kasu posibleen kopurua. kaxako bolalumen kop. ?
3. Probabilitatea = aldeko kasuen kop. kasu posibleen kop. = ?


Laplaceren erregela
Pierre-Simon Laplace matematikariak gertaera baten probabilitatea kalkulatzeko erregela erraz hau idatzi zuen:

P = aldeko kasuen kop. kasu posibleen kop.
Ondo ulertzeko, «Berehala kontatuko dizut», webgunean: anayaharitza.es
208
3
Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es .
Zerbait gertatzea errazagoa denean, esaten dugu aukera gehiago dauzkala edo probabilitate handiagoa duela.
4 Irakurri, pentsatu eta kalkulatu.
a) Zer probabilitate dago dado bat bota eta 5 ateratzeko?
b) Eta zenbaki bikoitia ateratzeko?
c) Eta 7 baino zenbaki txikiago bat ateratzeko?
d) Eta 6 baino zenbaki handiago bat ateratzeko?
e) Dadoa botatakoan, zerk dauka aukera gehiago, zenbaki bakoiti bat lortzeak edo 4 baino zenbaki txikiago bat lortzeak?
5 Ikusi txartel hauek: 1 3 5 7 2 4 6 8



a) Asmatu gertaera bat, % 50eko probabilitatea duena.
b) Asmatu gertaera bat, probabilitatea 1 duena. Nolakoa da gertaera hori? Ziurra, posiblea ala ezinezkoa?
c) Asmatu gertaera bat, probabilitatea 0 duena. Nolakoa da gertaera hori? Ziurra, posiblea ala ezinezkoa?
6 Pentsatu eta binaka jarrita komentatu Jonek eta Anek zotz egingo dute, azken sagarra nork jango duen erabakitzeko. Karta bat hartuko dute sortatik, zoriz. Batekoa bada, Jonek; urrea bada, Anek.
a) Nork du irabazteko probabilitate handiena?
b) Idatzi bidezkoagoa den zotz egiteko beste modu bat.
Probabilitatearekin esperimentatzen
Idatzi zein diren aldeko kasuak eta kasu posibleak.
Gertaera baten probabilitatea




Gertaera baten probabilitatea 0tik 1era arteko zenbaki bat da.
Hiru modutan adieraz daiteke: zatiki moduan, zenbaki dezimaldun gisa edo ehuneko moduan.
1
2 = 0,5 = % 50
Txanpon bat airera botatzen dugunean, zer probabilitate dago aurkia ateratzeko?
Eta ifrentzua ateratzeko? Hori hala dela egiaztatu nahi?
Taldeka, bota txanpon bat 30 aldiz edo gehiagotan; zenbat eta gehiagotan, hobeto. Idatzi emaitzak.
Emaitza Zenbaketa Maiztasun absolutua Maiztasun erlatiboa aurkia ? ? ?
ifrentzua ? ? ?

GUZTIRA ? ? ?
a) Begiratu taulan. Zer maiztasun erlatibo du aurkia ateratzeak? Eta ifrentzuak?
b) Konparatu zuen taula eta beste talde batzuena. Antzekoak dira emaitzak?
c) Ondoriozta dezakezue gutxi gorabehera kasuen erdietan aurkia ateratzen dela eta beste erdietan ifrentzua?
Txanpona botatzeko simulazioa egin dezakezu webgunean: anayaharitza.es
Gogoan hartu!
Laplaceren erregela erabiliz, euria egiteko zer probabilitate dagoen kalkula dezakezu.
209 U12
Zenbatzeko teknikak
eta zuhaitz-diagramak erabiliz, errazago zenbatu dezakegu zorizko esperimentuetan kasu posibleak zenbat diren.
Taulak


1 Nork du irabazteko probabilitate handiagoa? Hori jakiteko, egin urrats hauek:




Puntuen batura 6 baino handiagoa bada, ni irabazle.
Puntuen batura zenbaki bikoitia bada, ni irabazle.
2. Zenbatu zenbat kasutan izan daitekeen irabazle bakoitza.
RAUL ?



ISABEL ?
3. Kalkulatu irabazteko zer probabilitate duten Raulek eta Isabelek. Kontuan izan zenbat emaitza posible dauden.
4. Nork du irabazteko probabilitate handiena?

2 Bi txanpon botako ditugu airera. Zer emaitza aukeratuko zenuke, irabazteko probabilitate handiena izateko? Zergatik?
Gogoratu
Probabilitateak kalkulatzeko, aplikatu Laplaceren erregela.
P = aldeko kasuen kop. kasu posibleen kop. Kontuan izan bi txanponak berdinak direla.
210 4
1. Kopiatu taula, eta osatu, puntuen batura idatzita, emaitza posibleak zein diren jakiteko.
AA AI IA II
3 Kaxa bakoitzetik bola bat atera behar duzu, begiratu gabe. Zer probabilitate dago bi bolak kolore berekoak izateko? Hori kalkulatzeko, egin urrats hauek: A
1. Osatu zuhaitz-diagrama koadernoan, emaitza posibleak zein diren jakiteko.
A KAXA B KAXA
2. Zenbatu zenbat kasutan gerta daitekeen kaxetatik ateratako bi bolak kolore berekoak izatea.
3. Kalkulatu probabilitatea, eta idatzi soluzioa.
4 1-2-4 Uxue eta Galder harri-orri-ar jolasean ari dira. Osatu zuhaitz-diagrama, falta diren aukerak idatzita.
Probabilitatea kalkulatzeko, erabili kalkulagailua.
harria harria harria, harria harria, orria harria, artaziak orria artaziak



a) Zenbait emaitza posible atera daitezke?


b) Zer probabilitate dago Uxuek eta Galderrek berdintzeko?
c) Zer probabilitate dago Uxuek irabazteko? Eta Galderrek irabazteko?
d) Kalkulatu dituzun probabilitateak batzen badituzu, zer lortzen duzu? Azaldu ea baduen zentzurik, zure hitzetan.
Problema ebazteko, antolatu datuak zuhaitzdiagrama batean.
211 U12
Aztertu datu-lagin bat
Danel jakin-minez dago: bere ikastetxean dabiltzan ikasleek elikadura osasungarria duten jakin nahi luke. Baina guztira 2 000 ikasle dira! Nola jakin dezake?
Danelek ikasle guztiei galdetu ezin dienez, 20 ikasle aukeratzea erabaki du. Baina nola aukeratuko ditu?
A Lehen Hezkuntzako 6. mailako ikasleak.

B Zenbait mailatako ikasleak.


C Neskak bakarrik.
3 aukera horietatik, B hautatu du, aukera horretan egongo baitira ondoen adierazita ikastetxe guztiko ikasleak. Taula honetan jaso ditu erantzunak:
Ondorioak ateratzeko, oso garrantzitsua da osotasuna ondo adieraziko duen multzo bat aukeratzea.
Erantzunak aztertuta, Danelek ondorioztatu du bere ikastetxeko ikasle guztiek elikadura osasungarria eta askotarikoa dutela.
1 Gaur akzioko film bat estreinatu behar dute. Ikusleei gustatu zaien edo ez jakiteko, zein aukera hautatuko zenuke? Arrazoitu zure erantzuna.
A Saio guztietako ikusle guztiei galdetzea.
B Saio guztietako ikusle batzuei galdetzea.
C Saio guztietako haur guztiei galdetzea.

2 Egin ikerketatxo bat, 12 urteko neska-mutilei zer musika mota gustatzen zaien jakiteko. Zer ondorio atera
Aukeratzean, gogoan izan multzo horrek ondo adierazi behar dituela adin horretako neska-mutilak.
212
EBATZI BAIETZ!
dituzu?
Gosaritan zereal azukredunak jaten dituzu? 3 17 Gosaritan ogia oliba-olioarekin edo gurinarekin jaten duzu? 15 5 Gosaritan indioilarra, urdaiazpikoa edo arrautzak jaten dituzu? 12 8 Egunean zehar esnea edo jogurta edaten edo jaten duzu? 19 1 Entsalada edo barazkiak egunero jaten dituzu? 17 3 Arraina gutxienez astean hirutan jaten duzu? 18 2 Egunean fruta ale bat baino gehiago jaten duzu? 14 6 Egunean zehar nahikoa ur edaten duzu? 20 0
BAI EZ
Problemak arin-arinka

Buruzko kalkulua
Erruleta bateko gezia biraraztea, zorizko esperimentua da?
3
Gertaera baten probabilitatea 0 bada, nolakoa da: ziurra, posiblea ala ezinezkoa?
1 5
Gertaera baten probabilitatea 1 bada, nolakoa da: ziurra, posiblea ala ezinezkoa?
Begira nola pentsatzen dudan
Patroi bila
Bola gorria hartzea posible izatea baina aukera gutxi egotea nahi dugu. Zer koloretakoak izan daitezke?
4
Asmatu gertaera bat, gertatzeko probabilitatea 0 duena.
2 6
P = 0
Asmatu gertaera bat, gertatzeko probabilitatea 1 duena.
P = 1
Imajinatu egoera hau: ontzi hauetako baten azpian bolatxo bat dago; ontzi bat altxatzen baduzu eta bolatxoa hor badago… Aupa! Irabazi duzu!
1. Aukeratu ontzi bat, baina ez altxatu.
2. Bolatxoa non dagoen badakien norbaitek beste bi ontzietako bat altxatuko du, bolatxoa haren azpian ez dagoela erakusteko.
3. Orain, galdera egiten dizu: zer egingo zenuke, iritzia aldatu eta altxatu ez duen beste ontzia aukeratu?
Kalkulatu 28 × 0,5.
0,5 0,5
: 2 } 1
Ikusi nola egiten den, hemen: anayaharitza.es
Orain, zuk zeuk:

1 1 4 × 0,5
1 8 × 0,5
12 × 0,5
14 × 0,5
16 × 0,5
22 × 0,5 24 × 0,5 26 × 0,5 40 × 0,5 42 × 0,5




Ikus dezagun zer aukera dauden eta irabazteko zer probabilitate dagoen ontzia aldatuta edo ez aldatuta.
Aukeratu duzu: ontzi urdina.
Altxatu du: ontzi horia edo gorria.
Aukeratu duzu: ontzi urdina.
Altxatu du: ontzi gorria.
Aukeratu duzu: ontzi urdina.
Aldatuz gero, zuk galdu.
1 3
Aldatuz gero, zuk irabazi.
1 3
Aldatuz gero, zuk irabazi.
Altxatu du: ontzi gorria. 1 3
Irabazteko probabilitatea…








ontzia aldatzen baduzu: 1 3 + 1 3 = 2 3

ontzia aldatzen ez baduzu: 1 3
Jolastu ikaskidearekin eta ikusi zer gertatzen den.
Eta orain… aldatuko zenuke ontzia?
213 U12
14 28
Z er ikasi dut?
1 Adierazi esperimentu hauetatik zein diren zorizkoak.
a) Bost urte barru zer altuera izango dudan jakitea.
b) Lasterketa baten ondoren minutuko zenbat taupada ditudan jakitea.
c) Txorrota ireki, eta urik ateratzen den ikustea.
d) Nire herrian gaur zenbat haur jaioko diren jakitea.
e) Ikusiko dudan filmak zer iraupen duen jakitea.
2 Ikusi arretaz frutaontzi honetako sagarrak, eta idatzi:

5 Karta espainoletan, sortak 40 karta ditu. Begiratu gabe karta bat hartzen badugu, zer probabilitate dago hauek ateratzeko? Kalkulatu.
a) 5eko bat.

b) Bastoia ez den karta bat.
c) Zaldun bat.
d) 5 baino zenbaki txikiagoa den karta bat.
6 20 pertsonako talde batean, 8k txakurra dute; 5ek, katua, eta gainerakoek ez dute maskotarik.
a) Zer probabilitate dago taldeko pertsona bat zoriz aukeratu eta txakurra duenetako bat izateko?
b) Eta maskota duenetako bat izateko?
7 Tonbola batean, peluxe hauek dira sariak:
a) Gertaera ziur bat.
b) Gertaera posible bat.
c) Ezinezko gertaera bat.
3 Kopiatu eta margotu, kontuan izanda erruleta birarazitakoan urdina ateratzeko aukera gutxi egon behar duela.
a) Zer probabilitate dago hartz bat egokitzeko?
b) Eta peluxe urdin bat egokitzeko?
8 Urtebetetze-festarako, Juliok sandwichak egin ditu: ogi zuriarekin eta ogi integralarekin, urdaiazpikoarekin edo indioilarrarekin, gaztarekin edo gaztarik gabe.
a) Zenbat sandwich mota egin ditu?

4 Zer zakutan dago aukera gutxi bola horia ateratzeko? Eta zeinetan dago aukera asko bola berdea ateratzeko?
b) Mota bakoitzeko sandwich kopuru bera baldin badago, zer probabilitate dago urdaiazpikoa eta gazta dituen sandwich integral bat hartzeko?
Semaforoa. Margotu koadernoan, ariketa bakoitzaren ondoan, honela:
Erantzuna badakizu
Laguntza behar izan baduzu
Erantzuna jakin ez baduzu
214
PORTFOLIOA
A
B C
HELBURUA AURRERA
Egin infografia bat.


Klima ausazko fenomeno bat da; izan ere, baldintza berberak izanda ere, emaitza ezin da iragarri erabateko ziurtasunez.
a) Begiratu leihotik kanpora. Euria egitea zer da, gertaera ziurra, posiblea ala ezinezkoa? Arrazoitu zure erantzuna.
b) Bihar den egunean azken hamar urteotan zure herrian euririk egin ez badu, bihar euria egitea zer da, ziurra, posiblea edo ezinezkoa?
c) Irakurri eta aztertu Munduko Meteorologia Erakundeak egin duen baieztapen hau. Zer esan nahi du? Zure ustez, nola kalkulatu ahal izan dute hori? Berridatzi albistea, zure hitzak erabiliz.

«2016 inoiz erregistratu den urterik beroena izan zen. % 93ko probabilitatea dago 2022tik 2026ra bitarteko gutxienez urteetako batek hori gainditzeko».
Geure buruari galdezka
Pentsatu, gogoko izan, ikertu estrategia erabiliz, klima-aldaketa aztertuko dugu.
a) Osatu antolatzailea koadernoan. Behar baduzu, bilatu informazioa.
Pentsatu Gogoko izan Ikertu ? ? ?
b) Taldeka jarrita, partekatu zuen gogoetak, eta egin infografia bat, klima-aldaketa geldiarazteko zenbait gomendio emateko.
N o la ikasi dut?
Osatu koadernoan.
Pentsatu zure bizitzan noiz erabili izan duzun pentsamendu matematikoa egoeraren bat ebazteko. Identifikatu horrelako hiru egoera. Nola sentitu zinen pentsamendu matematikoaz baliatu zinenean?
Pentsatu zer egoeratan gertatu izan zaizun pentsamendu matematikoa erabili izan bazenu hobeto ebatziko zenukeela. Identifikatu egoera bat. Zure bizitzako zer egoeratan erabil dezakezu gehiago pentsamendu matematikoa?

U12 215
Zenbat triangelu hori sartzen dira urdin batean?

Bi irudi hauek perimetro bera eta azalera bera dituzte. Kalkulatu aldeen neurria.
Zer azalera dute irudi hauek? Osatu koadernoan.
216 BERRIKUSPENA 4 1 2 3
Zenbat irudi ikusten dituzu?
? ? ? 1 2 3 4 5 6 7 8 93,6 cm 2 21 cm 2 30 cm 2 35 cm 2 36 cm 2 78,5 cm 2 ? ? ? ? ? 9 cm 4 cm ? 7 cm 6 cm 8 cm 6 cm 5 cm 10 cm triangelu karratu pentagono 12 cm 5 cm 6 cm 5,2 cm ? ? ?
Zenbat diametro marraztu daitezke zirkunferentzia batean?
Ilara bakoitzean, aukeratu garapen zuzena. Zer irudiren garapenak dira?
Egongela garbitzen hasi baino lehen, Maiak eta Pellok bi dado bota dituzte.
Batura bakoitia bada, Maiak garbituko du; bikoitia bada, Pellok. Bidezkoa da?
Azaldu zure erantzuna.
Jakin nor den zientzialari misteriotsua sTEAM
Asmatu zein den forma misteriotsu hau… eta nork aurkitu zuen.

Gorputz geometrikoa da.
Ez da prisma.
Ez da piramidea.

Pistak

1. Duela gutxi arte, irudi hau ez ge nuen ezagutzen.
2. Intsektuen tora xeko eskutelo izeneko zatiak forma bera due lako jarri zioten irudiari izen hori.

1971n jaio nintzen, Sevillan. Ikertzailea eta irakaslea naiz
Matematika dibulgatzeko lan handia egiten dut blogen bidez, liburuetan eta irratiko nahiz telebistako programen bidez.
Unibertsitatean.Sevillako
Eskaneatu, eta jakin nor den zientzialari misteriotsua
3. Zure milioikagorputzeko zelulak ere forma hori bera dute!
4. Gorputz geome triko bitxi hori aztertzen parte hartu zuen gu re misteriotsuak.matematikari



217 HIRUHILEKOA 3 5 7 6
A B C A B C A B C
ITZALAPROIEKTUAK UZTENDUTEN
EZAGUTU DIZIPLINARTEKO PROIEKTUA
Birika berdea
IRAUL DITZAGUN DATUAK
Grabatu dezagun telebista-saio bat, Espainian gertatutako baso-suteei buruzko datu kezkagarrienen ingurukoa.
Zer esaten digute Espainian gertatutako baso-suteei buruzko datuek? Mobiliza gaitezen datu horiek apaltzeko!

Denon artean, hitz egin dezagun: Ezagutzen dugu gure herritik hurbil gertatu den baso-suterik?
Zure ustez, baso-sute asko ala gutxi gertatzen dira? Suteak gertatzeko arrisku handiena zer hilabetetan izaten dela iruditzen zaizu?

Azken urteotan, zer-nolako bilakaera izan du baso-suteen kopuruak, zure iritziz?
Nola neurtzen da zenbateko gainazala erre duten suteek?
Zenbat ur eraman dezake suteen kontrako helikoptero batek?
Badakizu zer den 30-30-30 erregela?
Idatzi ideia-jasa honetan atera diren ideiak.
Espainian 1961etik gaur arte izan diren baso-sute guztiei buruzko informazioa jasota dago datu-base batean.
Ikertu baso-suteen gaian izan den bilakaera, eta bilatu gure autonomia-erkidegoarekin edo probintziarekin lotutako datuak.
Taldeka, banatu ideia-jasan sortu diren gaiak, alderdi jakin bati buruz ikertzen hasteko.
Garrantzitsua da datuak ondo antolatzea tauletan, grafikoetan… Bilatu kokatzen lagunduko diguten mapak; suteek erretako hektareak grafikoki adierazteko, erabili irudiak…
Informazioak ekoarduratsuagoak izaten lagunduko digu!

218
1 T hink P ENTSATU D esign 2 DISEINA T U
M aker
Aukeratutako informazioa laburbildu egin behar dugu, eta txukun idatzi, gure ikusleek erraz ulertu ahal izan dezaten; hori bai, ez ahaztu zorroztasun zientifikoa zaintzea.


Ikasgelan, banatu ardurak: nor arduratuko den grabatzeaz, argiaz, soinuaz, nor izango diren aurkezleak, gidoigileak, zer irudi erabiliko dituzuen, Interneten aurkitutako bideorik erabiliko duzuen…
Telebista-saio bat egitearen helburua zein zen? Bada, ikasi duguna jendarteratzea, besteak ere ingurumen-arazo larri honetaz kontzientziatu daitezen.
Erabaki noiz emango duzuen zuen telebista-saioa. Ikasgelan proiekta dezakezue, edota ikastetxeko areto nagusian; beste aukera bat udalari edukiera handiagoko areto bat erabiltzeko baimena eskatzea da, edota ikastetxeko webgunera igotzea, tokiko telebista batean ematea…

Telebista-saio ikusiena bihurtuko da!
Zerk harritu nau gehien?
3. HIRUHILEKOA 219
3
EGIN
4 PRESENTA S tage AURKEZTU T est EGIAZTAT U 5