Operació Món: Matemàtiques 4 A Comunitat Valenciana (mostra)

4 ESO MATEMÀTIQUES A

José Colera J., M.ª José Oliveira G., Ignacio Gaztelu A., Ramón Colera C., Ana Aicardo B.

Índex Els sabers bàsics del curs

Entrena’t resolent problemes

• Fes un esquema, un gràfic o una taula que t’ajude a organitzar les dades

• En els problemes geomètrics, fes un dibuix!

• Experimenta, tempteja, posa exemples... conjectura i comprova...

• Investiga Problemes

Repassa i aprofundix en els problemes aritmètics

1. Monomis i polinomis. Valor numèric

2. Operacions amb polinomis

3. Divisió d’un polinomi per (x a)

4. Arrels d’un polinomi

5. Factorització de polinomis

6. Preparació per a equacions

1. Nombres naturals

2. Nombres enters

3. Fraccions

4. Operacions amb fraccions

5. Problemes amb fraccions

6. Potències

3

1. Importància del sistema de numeració decimal

2. Tipus de nombres decimals

3. Pas de decimal a fracció

4. Quantitats aproximades. Errors

5. La notació científica Exercicis i problemes

1. Equació. Solució d’una equació

2. Equacions de primer grau

3. Equacions de segon grau

4. Altres tipus d’equacions

reals

1. Nombres irracionals

2. Nombres reals: la recta real

3. Trams de la recta real: intervals i semirectes

4. Arrels i radicals Exercicis i problemes

1. Sistemes d’equacions lineals

2. Resolució de sistemes d’equacions

3. Sistemes d’equacions lineals més complexos

4. Sistemes no lineals

5. Resolució de problemes mitjançant sistemes

6. Inequacions amb una incògnita Exercicis i problemes

7

1.

2.

3.

4.

5.

6.

1. Conceptes bàsics

2. Taules de freqüències

3. Paràmetres estadístics: x i σ

4. Paràmetres de posició

5. Diagrames de caixa

6. Estadística inferencial

7. Estadística en els mitjans de comunicació

1.

2.

3.

4.

5.

1. Distribucions bidimensionals

2. El valor de la correlació

3. La recta de regressió per a fer estimacions

4. Reflexionem: La correlació significa causa-efecte?

5. Distribucions bidimensionals amb calculadora Exercicis i problemes

1.

2.

3.

4.

5.

1. Obtenció de probabilitats: experimentació o càlcul matemàtic?

2. Esdeveniments aleatoris

3. Probabilitat d’un esdeveniment

4. Obtenció de la probabilitat d’un esdeveniment

5. Experiències compostes. Probabilitat

6. Taules de contingència

i problemes

Així és el teu llibre

UNITAT INICIAL: ENTRENA’T RESOLENT PROBLEMES

Estratègies de resolució de problemes, a través de les quals podràs trobar-ne, de forma més senzilla, la solució.

Pensa i intenta resoldre. Problemes per a practicar les estratègies treballades al llarg d’aquesta unitat.

Entrena’t resolent problemes

Adquirir una destresa raonable en la resolució de problemes no és tasca d’un dia, no hi ha un mètode concret que, una vegada aprés, assegure l’èxit en la tasca. No obstant això, és ben sabut que la capacitat de resolució millora amb l’experiència (resolent-ne molts), que hi ha unes certes pautes generals que servixen d’ajuda en moltes ocasions. Te’n recordarem algunes que, segurament, ja coneixes d’anys anteriors.

RECOMANACIONS PER A RESOLDRE PROBLEMES No comences a cegues. Assabenta’t bé del problema Has de comprendre’l fins a ser capaç d’explicar-lo amb les teues pròpies paraules a un company o companya.

2 Experimenta Comença pel més fàcil.

5 Pensa si coneixes algun problema similar ja resolt Recorre la memòria, al quadern, al llibre…

A partir del text inicial, aprendràs a diferenciar entre exercici i problema, i establiràs els passos bàsics per resoldre un autèntic problema.

OBERTURA D’UNITAT

SITUACIÓ D’APRENENTATGE

7 Sigues conscient del que has fet No et limites a donar la solució. Descriu tot el pro cés que has seguit de manera que puga entendre’l un company o companya qui li ve de noves. 8 si vols aprendre més… Busca altres solucions. Inventa nous problemes. En les pàgines següents desenvoluparem algunes d’aques tes recomanacions amb exemples i, després, et proposa rem problemes per entrenar-te practicar. BLOC

ARITMÈTICA

TRES NÚMEROS CARISMÁTICOS

Hi ha tres nombres molt coneguts importants en el món de les matemàtiques:

És la relació entre el perímetre d’una circumferència el seu diàmetre servix per a calcular longituds, àrees perímetres de figures «redones».

Regix la proporció àuria, que tan important paper juga en l’art en infinitat de configuracions de la naturalesa: flors, caragols, galàxies… El més important nombre matemàtic, present en els processos de creixement en l’equació de les catenàries.

Doncs bé, no és sorprenent trobar-nos-els en realitzar aquestes estranyes operacions que tenen

1. Nombres naturals, enters fraccionaris 2. Nombres decimals 3. Nombres reals

L’ordre la regularitat de les seues estructures, la potència precisió dels seus mecanismes fan que, en tota excursió pel camp numèric, trobem bellesa eficàcia.

L’aritmètica, amb els seus eficients procediments, permet afrontar resoldre multitud de problemes en tots els àmbits. El bon maneig de la calculadora els programes informàtics ajuden, no sols a culminar processos aritmètics complexos, sinó també, de forma molt significativa, a indagar contrastar noves relacions noves propietats. La recerca la investigació sobre propietats curiositats numèriques abasten un amplíssim camp plagat de sorpreses de bells resultats.

32

un nombre infinit de sumands? 4 4 3 + 4 5 4 7 + …     1 + 1! + 2! + 1 3! + π Φ e + 1 + 1 + FAMÍLIES DISTINGIDES DE NOMBRES Nombres primers: 2, 3, 5, 7, 11, 13, 17, 19, 23, … Recordes el sedàs d’Eratòstenes? Sabries esbrinar si un nombre que estiga més enllà d’aquesta llista és o no primer?? Nombres de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … Els nombres d’aquesta successió tenen interessants propietats. Quadrats perfectes: 1, 4, 9, 16, 25, 36, … Cubs perfectes: 1, 8, 27, 64, 1125, 216, …

EL DESAFIAMENT

Aquest treball va de nombres. Et proposarem: Que recordes, indagues, trobes demostres propietats numèriques ja conegudes o noves.

Que obtingues per camins sorprenents alguns nombres que ja coneixes.

Que t’endinses en noves curiosíssimes famílies de nombres per a conéixer-les, comprendre-les i, potser, detectar-hi algunes noves propietats.

Que indagues pel teu compte (per Internet o altres llocs) per aprofundir en les famílies de nombres que ací veuràs o en unes altres que valguen la pena.

33

U 8

1 Funcions lineals Funcions lineals en la vida quotidiana La naturalesa, la ciència, la tècnica, l’economia… estan plenes de funcions en les quals les variacions de les causes influïxen proporcionalment en les variacions dels efectes Totes aquestes funcions s’anomenen lineals es representen amb rectes.

8

Funcions

Durant els segles xix xx es van produir discussions apassionants sobre quins requisits eren imprescindibles per a definir una

allargament una molla 1 kg 2 kg 3 kg 4 kg 10

funció quins no. Al llarg d’aquest procés, nombrosos matemàtics, entre els quals destaquen Dirichlet, Riemann Weierstrass, van anar perfilant el concepte, tractant de donar una definició precisa de funció. Fins que, el 1923, es va arribar a la definició següent, molt semblant a la que s’usa actualment: Es diu que y és una funció de x si a cada valor de x li correspon un valor de y Aquesta correspondència s’indica mitjançant l’equació y = f (x).

Però en aquesta recerca de la precisió, es van generar una sèrie de funcions estrafolàries que van contrariar Poincaré, incòmode amb la deriva que estava portant la definició de funció, la qual cosa el va dur, el 1899, a afirmar el següent:

«Durant mig segle hem vist una massa de funcions estranyes construïdes de manera que s’assemblen el menys possible a les funcions honestes que servixen a algun propòsit. Abans, quan s’inventava alguna funció, era amb alguna meta pràctica. Hui s’inventen amb la finalitat de mostrar que el raonament dels nostres antecessors va ser erroni».

En aquesta unitat ens dedicarem a aquestes funcions honestes que propugnava el gran Poincaré, aquestes funcions que servixen per a alguna cosa més que per a construir o desmuntar conceptes.

Henri Poincaré (1854-1912).

°F 100 212 0 32 150

Vegem-ne alguns exemples relació entre la temperatura en c i en °F (Fahrenheit)

150

Un europeu als EUA fa l'experiència següent: mesura distintes temperatures amb dos termòmetres, un en graus centígrads (°C) i un altre en graus Fahrenheit (°F). Aquests són alguns dels resultats: 0 °C → 32 °F, 10 °C → 50 °F, 60 °C → 140 °F, 100 °C → 212 °F

Situació d’aprenentatge, una per a cada bloc, que t’exigirà posar en acció els coneixements, destreses i actituds que hi treballaràs, i que contribuirà a l’adquisició i al desenvolupament de les teues competències.

Quina longitud assolirà la molla de l’exemple = 32 + 1,8

Anomenant:  = temperatura en °C  = temperatura en °F els resultats anteriors responen la relació y = 32 + 1,8x (Comprova-ho). Per exemple:

La temperatura normal d’una persona sana és de 36,5 °C. Quina és en °F? 200 (100, 212) (60, 140) (10, 50) (0, 32) 50 100 °C

clínic abasta temperatures des de 35 °C 50

Quina és la gamma en 100

(cm) (kg) PENSA PRACTICA 1 Copia completa, en el teu quadern, les igualtats se0

y 30 + 15 anterior si hi pengem un pes de 4,6 kg? b) ¿Qué peso hay que colgar del muelle para que alcance una longitud de 1 m?

151

Recursos relacionats amb LES CLAUS del projecte

Cada unitat comença amb una breu introducció històrica sobre els continguts que estudiaràs.

S’hi proposen una sèrie d’activitats motivadores amb la finalitat de posar en funcionament els coneixements que ja posseïxes.

Compromís ODS Pla lingüístic Desenvolupament del pensament Aprenentatge cooperatiu

SABERS BÀSICS I ADQUISICIÓ DE COMPETÈNCIES

2 Equacions de primer grau

Una equació de primer grau és aquella en la qual només apareixen expressions algebraiques de grau u. Després de simplificar-la, arribarem a una igualtat del tipus b = 0. Recordem, amb un exemple, els passos que convé donar per resoldre una equació de primer grau que tinga una fisonomia complicada. () () 4 31 22 3 51 –

() 4 37 1 2 4 38 26 24 –2 · 7 –  () 3 57 1 14 3 56 ––  = 14 – 10 = 4

solucions.

Exercicis i problemes resolts. Es mostren estratègies, suggeriments, pistes i maneres de pensar.

Comprén i aplica en el desafiament. Activitats que et prepararan per enfrontar-te al desafiament del bloc.

a) 3  + 11 + 2

b) 6x – 15 + 3

– 6

b) Expressa en radiants els angles següents tenint en compte que són múltiples dels anteriors: 150°;

135°; 240°; 300° 270°.

c) Troba, amb la calculadora, les raons dels angles de l’apartat anterior expressats en radiants.

26 a) Expressa en graus els angles següents: ;;;;

3 2 2 3 4 5 6 7 95 r r r r rr

b) Digues quin és el signe de les seues raons trigonomètriques.

27 El gràfic d’una funció exponencial y ka passa pels punts (2; 0,75) (−1; 6). a) És creixent o decreixent?

b) Calcula k representa’n la funció.

28 El gràfic d’una funció radical ax b + passa pels punts (1, 1) (4, 4).

a) Determina els valors de a b

b) Quin és el domini de definició d’aquesta funció?

c) Representa’n la funció.

29 Andrea ha comprat per 100 € un regal d’aniversari per a Carles. La resta dels amics del grup decidixen pagar el regal entre tots.

Construïx una funció que ens done els diners que ha de posar cada un depenent del nombre de persones que hi haja dibuixa-la. Té sentit unir els punts? Raona-ho.

30 El sou inicial d’Anna és de 24 000 € anuals. En el seu contracte figura que pujarà un 8 % anual.

a) Quant guanyarà d’ací 10 anys? b) Escriu la funció que relaciona sou temps. c) Per a quins valors de la variable està definida?

COMPRÉN APLICA EN EL DESAFIAMENT

31 Meta 11.3. Un estudi demogràfic indica que el creixement de població d’una ciutat es pot predir amb la funció PP0 00 P0 és la població inicial t el temps en anys. Si la població actual és de 5 000 habitants, quants anys tardarà arribar a 75 000?

TANCAMENT D’UNITAT

Exercicis i problemes

PER A PENSAR UN POC MÉS

35 Àlvar s’ha de situar a 3 m d’un toll per veure la copa d’un arbre reflectida en aquest. Si la distància del toll a l’arbre és de 10,5 m els ulls d’Àlvar estan a 1,72 m, quina altura té l’arbre?

TAMBÉ POTS FER AIXÒ 39 Tallant els quatre cantons d’una planxa quadrada de fusta, d’un metre de costat, es vol obtindre un tauler d’una taula amb forma d’octàgon regular.

32 La intensitat del so que ens arriba procedent d’un focus sonor és inversament proporcional al quadrat de la distància que ens separa d’aquest. Per exemple: I  d 25 2 d distància en metres intensitat del so Representa el gràfic, prenent, en l’eix X 1 quadrat = 1 m, i en l’eix Y 1 quadrat = 5 u. A quina distància s’ha de posar una persona amb problemes auditius que només senta sons superiors a 100 u?

33 Posem un glaçó de 4 cm en un got d’aigua cada minut el 10 % del seu volum es dissol en l’aigua. Quant de gel quedarà després de 5 minuts? En quant de temps es reduïx a la meitat?

34 El preu d’un automòbil és de 15 000 € Sabem que es deprecia a un ritme d’un 12 % anual. a) Escriu la funció que dona el valor del cotxe al cap de anys. b) Calcula els anys que han de passar perquè el seu preu siga la meitat del preu de compra.

35 Una planta es reproduïx per bipartició cada dos dies. Aquest ritme es manté durant un mes. a) Quantes plantes hi haurà d’ací a 10 dies? b) Quina funció s’ajusta aquest creixement?

PER A PENSAR UN POC MÉS

36 a) Representa gràficament la funció exponencial 2 5 dn fent ús d’una taula de valors.

b) Quina és la funció inversa o recíproca de 2 5 dn Representa-la en els mateixos eixos. Recorda que si (a, b) pertany al gràfic, (b, a) pertany al de la inversa.

37 Una persona deposita un capital de 10 000 € en un banc que li oferix un interés del 3,4 % anual.

a) Quin en serà el capital d’ací 4 anys? b) Escriu la funció que indica el capital que tindrà en funció del temps. c) En quants anys tindrà més de 15 000 € d) Respon les mateixes preguntes si el pagament d’interessos fora trimestral.

La unitat es dividix en epígrafs, i aquests en subepígrafs, dins dels quals es distribuïxen els sabers bàsics.

Exemples i exercicis resolts. Per a practicar els procediments més importants.

Pensa i practica. Són exercicis d’aplicació directa.

38 En un centre escolar s’organitza una excursió a un parc natural. Cada estudiant ha de pagar 5 € per l’entrada al parc, més el viatge amb autobús. El lloguer de l’autobús de 60 places costa 420 € La visita se suspén si s’hi apunten menys de 15 estudiants.

a) Si x és el nombre d’estudiants que van al parc, quina és la funció que dona el preu que ha de pagar cada un? b) Quin n’és el domini de definició? el recorregut?

c) Representa-la gràficament.

39 La concentració d’un fàrmac en sang disminuïx un 20 % cada hora. A un pacient li injecten 150 mg d’aquest fàrmac. a) Escriu la funció que ens indica la quantitat de fàrmac en sang segons les hores transcorregudes.

b) Quan el fàrmac arriba a 1/3 de la quantitat inicial cal tornar a injectar-lo. Quan ocorrerà això?

40 Expressa les funcions següents de la forma y  xa k – + b representa-les:

a) 1 31 –– b) y 1 2 c) x 1 1–Indica quin n’és el domini de definició les asímptotes.

41 Estudia el domini de definició de les funcions següents, fes una taula de valors i representa-les: a) () lo yx 2 – b) () log yx 3–

42 El gràfic d’una funció () log yx1– passa per (−1, 1) (1, 2). a) Calcula a b b) Indica’n el domini de definició. c) Representa-la.

TAMBÉ POTS FER AIXÒ

43 Calcula el valor del paràmetre k perquè la funció següent siga contínua:

] ] ]

45 A partir dels gràfics de les funcions y sin y representa les funcions següents en l’interval [0, 2 ]: a) y b)  = |sin x c) y = 1 + sin x 46 Representa la funció sin 2 Per a això, usa la calculadora en manera radiant com a unitat d’angles completa la taula següent en el quadern: 0 π/4 π/2 3π/4 π 5π/4 3π/2 7π/4 2π y 0 1 0 HO HAS ENTÉS? REFLEXIONA 47 L’expressió analítica d’aquesta funció és del tipus: ya xb 1 –Observa el gràfic calcula el valor de a b

–4 –6 –2 –4 –6 –8 –10 –2

Exercicis i problemes. Contemplen l’aplicació de tots els sabers bàsics de la unitat.

AUTOAVALUACIÓ 1 En un mapa, dues ciutats estan separades 2,5 cm. Si en la realitat estan a 37,5 km: a) Quina és l’escala del mapa? b) A quina distància real estaran unes altres dues ciutats que se separen 4 cm en el mapa?

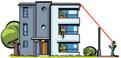
➜ anayaeducacion.es Resolucions d’aquests exercicis. 5 Quina altura té l’edifici que mira Marc?

2 [ \

≤ xk 52 2 1 42 i–si –

44 Representa el gràfic de les funcions següents: a)  = | 2 – 1| – 2 b)  = 1 + | c)  = 1 – | 2 – 6  + 5| d)  = | | – |4 –

48 Quina d’aquestes expressions correspon al gràfic d’aquesta funció? a) x y 21 – =+ b) x y 12 – =+ c) x y 21 – =+ 49 Totes les funcions exponencials de la forma y passen per un mateix punt. Indica quin punt és i justifica-ho. Per a quins valors de a la funció és decreixent? 50 Vertader o fals? a) Les funcions y – formen una paràbola tombada en representar-les en els mateixos eixos. b) La funció és decreixent. c) Les funcions y = 4 y 4 són simètriques respecte a l’eix Y d) Les funcions  = 4 4 1 cm són simètriques respecte a l’eix Y e) La funció log té dues asímptotes, una vertical una altra d’horitzontal. Les funcions y  log x  = 10 són simètriques respecte a la recta y

Les icones incloses en algunes activitats suggerixen la clau del projecte que es pot aplicar.

36 En la taula de billar, a quina distància de A ha de donar en la banda la bola blanca, perquè en rebotar xoque amb la negra? A B

30 cm 20 cm 70 cm

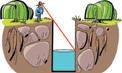
37 El pou per reg d’un hort té una profunditat de set metres i un diàmetre de tres metres. El llaurador comprova que hui, per arribar a veure l’aigua, s’ha de col·locar a menys de metre mig de la vora.

Quins són hui les reserves d’aigua del pou, sabent que el llaurador mira des d’una altura d’1,80 m?

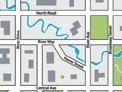
38 Aquest és el plànol d’una part d’una certa ciutat, a escala 1:20 000:

A B

1 m a) Quines dimensions han de tindre els cantons? b) Calcula l’àrea de l’octàgon.

Observa que els dos triangles acolorits són semblants analitza el sistema d’equacions.

1 x xy 2 1 21 ` a

b b b b

40 El rècord d’altura aconseguida per un globus aerostàtic el va establir Felix Baumgartner el 2012 quan va pujar un poc més de 39 km d’altura. a) Troba la distància a la qual es trobava del punt més allunyat que podia veure en l’horitzó terrestre. b) Quina proporció de la Terra veia des d’aquesta altura?

41 A una empresa de daus li costa 2 cèntims fabricar cada dau de parxís: 1 cèntim per la fusta i 1 cèntim per la pintura. a) Quant gasta en la fabricació d’un dau amb el triple d’aresta que el de parxís? un amb l’aresta 10 vegades major que el de parxís? b) Com serà l’aresta d’un dau nou en relació amb la d’un dau de parxís si val 36 € fabricar-lo?

C

Estima quant es tarda a anar passejant, per l’itinerari més curt, des de A fins a C passant per B suposant que es camina a 3 km/h.

c) Repetix l’apartat a) suposant que el cost de fabricació del dau de parxís és de 3 cèntims: 1 per la fusta 2 per la pintura. Amb aquest cost, com seria l’aresta d’un dau nou comparada amb el del parxís si costa 12 € fer-lo? Potser has de resoldre algunes preguntes temptejant.

c) Quina serà la distància en aquest mapa entre dues ciutats la distància real de les quals és de 360 km?

2 En el plànol d’un pis l’escala del qual és 1:200, el saló ocupa una superfície de 7 cm Quina és la superfície real del saló?

3 En la següent figura BD és paral·lel a AE a) Són els triangles ACE BCD semblants? b) Quina és la raó de semblança entre aquests? c) Calcula CD d) Troba E CBD BDC

A

37°

SITUACIÓ D’APRENENTATGE

15 cm

3,5 m 1,5 m 25 m

E

80° 11cm 6,4 cm

B C

4 Una torre està coronada per una teulada en forma de con de 12 m d’altura 10 m de diàmetre de la base. Quant costarà renovar la coberta a 85 €/m L’àrea lateral d’un con de radi de la base generatriu és A = πrg.

REFLEXIONA Revisa els aspectes treballats planteja solucions als problemes que es detecten. Per a això, descarrega d’anayaeducacion.es la rúbrica corresponent, reflexiona de manera individual compartix en grup.

A PROVA LES TEUES COMPETÈNCIES Fes l’autoavaluació competencial inclosa en anayaeducacion.es.

CURIOSITATS MATEMÀTIQUES Proporció cordovesa i nombre cordovés Aquest triangle isòsceles amb un angle de 45° s’anomena triangle cordovés. Per què? Perquè la relació entre els costats, a/b és la mateixa que hi ha entre els dos costats de la planta rectangular de la Mesquita de Còrdova. El rectangle els costats del qual seguixen aquesta proporció s’anomena rectangle cordovés. Aquesta relació s’anomena proporció cordovesa el quocient, a/b nombre cordovés. Quant val el nombre cordovés? 11 306562964… b a 2 2

45

b Aquesta proporció va ser introduïda el 1973 per l’arquitecte Rafael de la Hoz, establit a Còrdova, on la va estudiar en edificis, tessel·les, rosetons multitud de construccions geomètriques.

Interessant La relació, r/l entre el radi el costat d’un decàgon regular és el nombre d’or. La relació, r/l entre el radi el costat d’un octàgon regular és el nombre

En anayaeducacion.es disposes d’una autoavaluació competencial per a comprovar si has adquirit, al llarg de la unitat, les destreses necessàries per enfrontar-te al desafiament.

Educació emocional TIC Orientació acadèmica i professional Avaluació

Així és el teu projecte digital

Un projecte que t’oferix tots els continguts del curs a través del llibre digital, juntament amb una gran diversitat de recursos.

Descobrix una altra forma d’aprendre senzilla, intuïtiva i compatible amb qualsevol plataforma i dispositiu.

estudiants nota en nota V b d g h j

6 8 3 6 4 10 2 5

10 nre. cistelles distància (m)

4 9 2 1 6 7 6 4 5 10 6

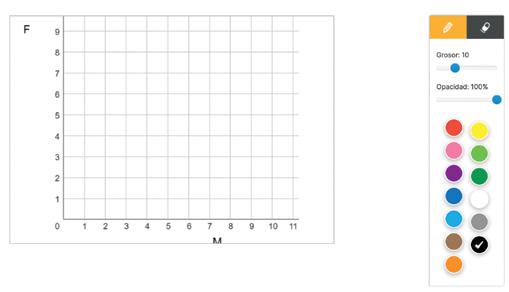
Com hi accedixes? U10 La correlació pot ser més o menys forta Vegemunaaltradistribucióbidimensional:lesnotesdelsmateixosdeuestudiants a …) enMatemàtiques,M,ienl’assignaturadeValencià,V.Icomparem el núvol de punts d’aquesta distribució bidimensional MV amb la que hem vist enlapàginaanterior,M-F F M

5 5 10

distància (en m) nre cistelles 1 2 4 5 6 7 8

10 ÉsevidentquelacorrelacióentreM FésmésfortaquelacorrelacióentreMiV, jaqueenlaprimera,elspuntsestanmésestretsalvoltantdelarectaderegressió queenlasegona La correlació entre dues variables pot ser més o menys forta segons que els puntsdelnúvolestiguenmésomenyspròximsalarectaderegressió La correlació admet signe Unajugadoradebàsquetfa10llançamentsacistella des d’una distància d’1 m, uns altres 10 des de 2 m, així successivament fins 8 m. En cada cas ha pres nota del nombre d’encistellades. Si observem, en el marge, el núvol de punts, veiem que la correlació és forta però negativa, ja que a més distància, menys cistelles

10 6 4 2 0 1 Una correlació és positivaquanenaugmentarunavariable, x, tendix augmentar l’altra variable y Una correlació és negativa quan en augmentar x, tendix a disminuir y correlació negativa correlació positiva El signe de la correlació coincidix amb el signe del pendent de la recta de regressió

Tens totes les indicacions necessàries per a accedir-hi al costat de la primera pàgina del teu llibre. 271

Funcions. Característiques

El concepte de funció ha anat evolucionant perfilant-se al llarg del temps. Quins requisits s’ha anat exigint a aquest concepte? — Una funció relaciona dues variables. — Les funcions descriuen fenòmens naturals. Les relacions funcionals es poden descriure mitjançant fórmules (relacions algebraiques). Les funcions es poden representar gràficament. Les següents són algunes de les contribucions més importants per a perfilar el paper de les funcions la seua definició formal: Nicolau Oresme (segle ) va ser el primer a descriure les lleis de la naturalesa com a relacions de dependència entre dues variables. Galileu (segle ) va usar per primera vegada l’experimentació (va dissenyar, va experimentar, va mirar, va anotar) per a establir numèricament aquestes relacions.

134

Descartes (segle xvii), amb l’algebrització de la geometria, va propiciar que les funcions es pogueren representar gràficament. Leibniz (segle ), el 1673, va usar per primera vegada la paraula funció per a designar aquest tipus de relacions. Euler (segle xviii va anar perfilant el concepte, al qual va donar precisió generalitat. En va presentar una definició general molt rigorosa, que no dista molt de la que usem actualment. En va aportar la nomenclatura f ( ). Dirichlet (segle va ampliar el concepte de funció admetent, finalment, que una relació entre dues variables pot ser funció encara que no hi haja una expressió analítica que la descriga.

Una funció lliga dues y x és la variable La relació entre les variables un únic valor de Per visualitzar el com portament d’una funció, recorrem a la seua repre sentació gràfica. Es diu domini de definició junt de valors de per Es diu recorregut de conjunt de valors de EXERCICI RESOLT Explicar per què és funció la relació següent: Carrega el teu mòbil al 100 % i apunta cada 15 min el percentatge de càrrega que té, fins que s’esgote Es lliguen dues variables: el temps, La primera és la variable independent. En cada instant, el mòbil té un hi ha un únic valor de p Per tant, p és una funció que

Y totalment.

367 producció plàstic (tm)

X

Recorregut de Domini de PENSA I PRACTICA Aquest gràfic descriu l’evolució de la producció mundial de plàstics (en milions de tones anuals). a) Quines en són les dues variables? b) Explica per què és una funció. c) Quins en són el domini de definició el recorregut?

400 300 100 19501960197019801990200020102020 2 18 41 62 108

187

2 3

Què t’oferix?

Coordenades del punt definició d’una funció, es designa per Dom el conper als quals existix la funció. f el conjunt de valors que pren la funció. És a dir, el per als quals hi ha una tal que ) = y temps, t, mesurat en minuts, i el percentatge, p de bateria. independent. La segona és la variable dependent. percentatge de càrrega. És a dir, per cada valor de depén de p t). Indica el domini el recorregut d’aquestes funcions: a) b) c) Y 10 1 X

U 7

Com és?

Una resposta global per a un entorn educatiu divers.

Intuïtiu

Fàcil d’utilitzar per a tu.

Multidispositiu

S’adapta i es visualitza en qualsevol tipus de dispositiu (ordinador, tauleta, smartphone...) a qualsevol grandària i resolució de pantalla.

Descarregable

Et permet treballar sense connexió a Internet i descarregar-ho en més d’un dispositiu.

Sincronitzable

Els canvis que faces se sincronitzen automàticament en connectar qualsevol dels dispositius en els quals estigues utilitzant-ho.

que tinga

Ordenada del punt 5] recorregut {1}.

[0,

135

Exercitar activitats interactives

Estudiar resums interactius, esquemes...

Aprendre àudios, vídeos, gameroom...

Avaluar autoavaluació, Dossier d’aprenentatge...

Universal Compatible amb tots els sistemes operatius, els entorns virtuals d’aprenentatge (EVA) i les plataformes educatives (LMS) més utilitzades en els centres escolars.

Abans de començar

Coneix els teus desafiaments

SITUACIÓ D’APRENENTATGE

COM SÓN?

Són quatre propostes de situacions d’aprenentatge, una per a cada bloc:

• Pensades per a mobilitzar coneixements, actituds i destreses i fomentar l’intercanvi de sabers i el desenvolupament de les teues competències.

• Compromeses amb els Objectius de Desenvolupament Sostenible 2030.

• Pròximes i respectuoses amb el teu món real i amb les teues experiències.

• Amb una estructura clara i senzilla de les tasques i activitats que hauràs de dur a terme.

COM HI TREBALLARÀS?

SITUACIÓ D’APRENENTATGE

BLOC ARITMÈTICA

1. Nombres naturals, enters fraccionaris Nombres decimals 3. Nombres reals

L’ordre la regularitat de les seues estructures, la potència precisió dels seus mecanismes fan que, en tota excursió pel camp numèric, L’aritmètica, amb els seus eficients procediments, permet afrontar resoldre multitud de problemes en tots els àmbits. El bon maneig de la calculadora els programes informàtics ajuden, no sols a culminar processos aritmètics complexos, sinó també, de forma molt significativa, indagar contrastar noves relacions noves propieLa recerca la investigació sobre propietats curiositats numèriques abasten un amplíssim camp plagat de sorpreses de bells resultats.

32

TRES NÚMEROS CARISMÁTICOS

Hi ha tres nombres molt coneguts importants en el món de les matemàtiques: És la relació entre el perímetre d’una circumferència el seu diàmetre servix per a calcular longituds, àrees perímetres de figures «redones». Regix la proporció àuria, que tan important paper juga en l’art en infinitat de configuracions de la naturalesa: flors, caragols, galàxies… El més important nombre matemàtic, present en els processos de creixement en l’equació de les catenàries. Doncs bé, no és sorprenent trobar-nos-els en realitzar aquestes estranyes operacions que tenen un nombre infinit de sumands? 4 4 + 4 4 + …     1 + + +

π Φ e + +

EL DESAFIAMENT Aquest treball va de nombres. Et proposarem: Que recordes, indagues, trobes demostres propietats numèriques ja conegudes o noves. Que obtingues per camins sorprenents alguns nombres que ja coneixes. Que t’endinses en noves curiosíssimes famílies de nombres per a conéixer-les, comprendre-les i, potser, detectar-hi algunes noves propietats. Que indagues pel teu compte (per Internet o altres llocs) per aprofundir en les famílies de nombres que ací veuràs o en unes altres que valguen la pena.

33

• Un text motivador que et descobrirà un marc de desafiaments relacionats amb les unitats del bloc.

• La proposta d’una situació d’aprenentatge.

• La seqüència d’aprenentatge de la situació proposada.

ENTRENA’T PRACTICA 14 Resol gràficament aquests sistemes: a) y 35 1 * b) y 4

Exercicis i problemes RESOL PROBLEMES SENZILLS 28 La diferència de dos nombres és 24. Si li sumem cada un, s’obtenen altres dos tals que el major és triple que el menor. De quins nombres es tracta? El preu d’un museu és 7 l’entrada adulta 3 la infantil. El dimarts van visitar el museu 235 persones es van recaptar 1 485 € Quantes entrades adultes quantes infantils s’hi van vendre? 30 El pressupost d’una biblioteca és de 100 € llibres discos. Si compren 3 llibres discos, en sobren € si compren 4 llibres 4 discos, hi falten 10 € Troba el preu d’un llibre el d’un disc. 31 Un test consta de 48 preguntes. Per cada encert s’hi sumen 0,75 punts per cada error se’n resten 0,25. La meua puntuació va ser de 18 punts. Quants encerts errors hi vaig tindre, si vaig contestar a totes les preguntes? Troba una fracció tal que si se li suma una unitat al numerador es deixa el mateix denominador, la fracció és igual 1/2. si es manté el numerador inicial se sumen 3 unitats al denominador, la fracció és igual a 1/3.

] ] d) y 4 311 1 6 23 2 21 4 –

] ] ] ] Resol comprova les solucions. a) 11 3 ––22 * b) () () 32 0 24 c) y y23 74 23 – * d) xy xy 35 7 2113 ––19 Resol: a) 2 73 1 – b) ≥ 3 4 3 10 c) – 2(3 5) < d) 2 –

Z [ \

33 Traduïx a llenguatge algebraic: a) El quadrat d’un nombre és menor que el doble d’aquest nombre més 15. b) Si cresquera 15 cm, superaria l’alçada que es requerix per a entrar en l’equip de bàsquet, que és 1,80 m. c) El perímetre d’un quadrat és menor que 15 m. 34 El triple d’un nombre natural menys 5 és menor que la seua meitat més 15. Quin pot ser aquest nombre? 35 La suma de dos nombres consecutius és menor que 27. Quins poden ser aquests nombres si sabem que són de dues xifres? 36 En una pescateria, un client s’emporta un llucet de quilo mig tres quarts de quilo d’aladrocs. Després d’ell, una senyora demana mig llucet que pesa 600 grams un quilo d’aladrocs. El primer paga 21 € per la compra, la senyora, 12,60 € per la seua. A com està el quilo de llucet? el d’aladrocs?

37 En un aparcament cobren un fix per entrar un tant a l’hora. Hui, per hora mitja, hi he pagat 2,60 € ahir hi vaig pagar 3,40 € per dues hores deu minuts. Quin és el fix quin és el cost per hora? Andreu té dos comptes en el banc. Si passara 600 € del primer al segon, aquest quedaria amb saldo doble. Però si la transferència fora de 300 € sentit contrari, seria el primer el que tindria el doble. Quant hi ha en cada un? Si té euros en el primer compte en el segon, amb la transferència de 600 tindrà – 600 en el primer 600 en el segon. 39 Una empresa rep l’encàrrec de fabricar cossiols per una data determinada. En planificar la producció, la gerent advertix que si se’n fabricaren 250 diaris, en faltarien 150 en concloure el termini. Però que si se’n fabricaren 260 diaris, en sobrarien 80. Quants dies de termini tenien quants cossiols els van encarregar? Anomenem el nombre de dies el nombre de cossiols encarregats. Si n’hi fabriquen 250 per dia, en tindran 250 x, que són – 150 dels encarregats. 40 La setmana passada, Sara va comprar una camisa un jersei per 76 € Ara, Rosa pagaria 65,80 € pels mateixos articles, perquè la camisa té un 15 % de rebaixa, el jersei, un 12 %. Quant costava cada article abans de la rebaixa? Si el preu de la camisa x abans de les rebaixes, una vegada rebaixat serà 0,85x. 41 Fa tres anys, l’edat de Rubén era el doble que la de Marta. D’ací a 7 anys, serà de 4/3 de la que tinga Marta aleshores. Calcula’n les edats. Si x és l’edat de Rubén hui, fa 3 anys era 3, d’ací anys serà + 7. Anomena l’edat de Marta hui fes el mateix raonament. 42 L’any que ve, l’edat de Raquel serà el triple que la del seu fill Ivan, però d’ací 12 anys només serà el doble. Quants anys té cada un? 43 La diferència de dos nombres és 6, la dels quadrats, 144. Troba els nombres. Calcula dos nombres la suma dels quals siga 24, el seu producte, 135. 45 Troba dos nombres la suma dels quals siga 20, la dels seus quadrats, 232.

FAMÍLIES DISTINGIDES DE NOMBRES Nombres primers: 2, 3, 5, 7, 11, 13, 17, 19, 23, … Recordes el sedàs d’Eratòstenes? Sabries esbrinar si un nombre que estiga més enllà d’aquesta llista és o no primer?? Nombres de Fibonacci: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … Els nombres d’aquesta successió tenen interessants propietats. Quadrats perfectes: Cubs perfectes: 1, 8, 27, 64, 1125, 216, … 127 126

• Activitats que t’ajudaran a comprendre i aplicar els sabers bàsics necessaris per enfrontarte al desafiament del bloc.

A L’INTERIOR DE LES UNITATS DEL BLOC TROBARÀS:

A L’INICI DE CADA BLOC TROBARÀS:

QUINS SÓN?

•  Tres nombres carismàtics, per al primer bloc.

• Mercat ambulant ecològic i sostenible, per al segon bloc.

• Investigacions biològiques, per al tercer bloc.

• Loteries i altres jocs d’atzar, per al quart bloc.

EN LES PÀGINES FINALS DE CADA UNITAT TROBARÀS:

Exercicis i problemes PER A PENSAR UN POC MÉS 35 Àlvar s’ha de situar a 3 m d’un toll per veure la copa d’un arbre reflectida en aquest. Si la distància del toll l’arbre és de 10,5 m els ulls d’Àlvar estan

1,72 m, quina altura té l’arbre?

36 En la taula de billar, a quina distància de A ha de donar en la banda la bola blanca, perquè en rebotar xoque amb la negra? 30 cm

37 El pou per a reg d’un hort té una profunditat de set metres un diàmetre de tres metres. El llaurador comprova que hui, per arribar a veure l’aigua, s’ha de col·locar menys de metre mig de la vora.

TAMBÉ POTS FER AIXÒ 39 Tallant els quatre cantons d’una planxa quadrada de fusta, d’un metre de costat, es vol obtindre un tauler d’una taula amb forma d’octàgon regular.

m

a) Quines dimensions han de tindre els cantons? b) Calcula l’àrea de l’octàgon.

Observa que els dos triangles acolorits són semblants analitza el sistema d’equacions. y y xy

Quins són hui les reserves d’aigua del pou, sabent que el llaurador mira des d’una altura d’1,80 m?

Aquest és el plànol d’una part d’una certa ciutat, escala 1:20 000:

C Estima quant es tarda anar passejant, per l’itinerari més curt, des de A fins a C passant per B suposant que es camina 3 km/h.

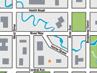
AUTOAVALUACIÓ En un mapa, dues ciutats estan separades 2,5 cm. Si en la realitat estan a 37,5 km: a) Quina és l’escala del mapa?

b) A quina distància real estaran unes altres dues ciutats que se separen 4 cm en el mapa? c) Quina serà la distància en aquest mapa entre dues ciutats la distància real de les quals és de 360 km? 2 En el plànol d’un pis l’escala del qual és 1:200, el saló ocupa una superfície de 7 cm Quina és la superfície real del saló?

anayaeducacion.es Resolucions d’aquests exercicis. Quina altura té l’edifici que mira Marc?

3,5 m 1,5 m 25 m

EN FINALITZAR EL BLOC TROBARÀS:

INFLUÈNCIA DE L’ALTURA EN LA QUANTITAT DE PLANTES PER HECTÀREA SITUACIÓ

joves investigadors estudien una espècie vegetal freqüent en una comarca. Analitzen parcel·les a diferents altures estimen com a vàlids aquests

1 21 ` a

b b b b El rècord d’altura aconseguida per un globus aerostàtic el va establir Felix Baumgartner el 2012 quan va pujar a un poc més de 39 km d’altura. a) Troba la distància a la qual es trobava del punt més allunyat que podia veure en l’horitzó terrestre.

b) Quina proporció de la Terra veia des d’aquesta altura?

41 A una empresa de daus li costa 2 cèntims fabricar cada dau de parxís: 1 cèntim per la fusta 1 cèntim per la pintura.

a) Quant gasta en la fabricació d’un dau amb el triple d’aresta que el de parxís? I un amb l’aresta 10 vegades major que el de parxís?

b) Com serà l’aresta d’un dau nou en relació amb la d’un dau de parxís si val 36 fabricar-lo? c) Repetix l’apartat a) suposant que el cost de fabricació del dau de parxís és de 3 cèntims: 1 per la fusta 2 per la pintura. Amb aquest cost, com seria l’aresta d’un dau nou comparada amb el del parxís si costa 12 € fer-lo? Potser has de resoldre algunes preguntes temptejant.

3 En la següent figura BD és paral·lel a a) Són els triangles BCD semblants? b) Quina és la raó de semblança entre aquests? c) Calcula CD d) Troba E CBD BDC

15 cm

37° 11cm 6,4 cm

C

4 Una torre està coronada per una teulada en forma de con de 12 m d’altura 10 m de diàmetre de la base. Quant costarà renovar la coberta 85 L’àrea lateral d’un con de radi de la base generatriu és = πrg.

E

REFLEXIONA Revisa els aspectes treballats planteja solucions als problemes que es detecten. Per a això, descarrega d’anayaeducacion.es la rúbrica corresponent, reflexiona de manera individual compartix en grup.

POSA A PROVA LES TEUES COMPETÈNCIES Fes l’autoavaluació competencial inclosa en anayaeducacion.es.

CURIOSITATS MATEMÀTIQUES Proporció cordovesa nombre cordovés Aquest triangle isòsceles amb un angle de 45° s’anomena triangle cordovés. Per què? Perquè la relació entre els costats, és la mateixa que hi ha entre els dos costats de la planta rectangular de la Mesquita de Còrdova. El rectangle els costats del qual seguixen aquesta proporció s’anomena rectangle cordovés. Aquesta relació s’anomena proporció cordovesa el quocient, a/b nombre cordovés. Quant val el nombre cordovés? 11 306562964… 2

45 Aquesta proporció va ser introduïda el 1973 per l’arquitecte Rafael de la Hoz, establit a Còrdova, on la va estudiar en edificis, tessel·les, rosetons multitud de construccions geomètriques. La relació, r/l entre el radi el costat d’un decàgon regular és el nombre d’or. La relació, r/l entre el radi el costat d’un octàgon regular és el nombre cordovés.

• Una proposta d’avaluació de les teues competències que podràs descarregar-te d’anayaeducacion.es

D’APRENENTATGE (centenars de m) 100 300 10 15 + 100 0 10 9 semilogarítmic

LA VELA DEL DIMETRODONT El guia del museu els va dir que l’enorme aleta dorsal del dimetrodont jugava un paper termoregulador, per rebre calor o per a refrescar-se quan el necessitaven.

Però, per què només la tenien els animals enormes? S’informen, reflexionen arriben la conclusió següent: La irradiació es realitza a través de la pell és, per tant, proporcional a la seua superfície, és dir, al quadrat de la seua longitud, mentre que la calor que es necessita es repartix en tot el volum del cos és, per tant, proporcional al cub de la seua longitud. Quan l’animal es fa més més gran, la seua superfície no és suficient per a atendre tant de volum necessita d’un increment en forma d’aleta dorsal (augment considerable de superfície sense incrementar quasi el volum), com el dimetrodont. Les enormes orelles dels elefants per mitjà de les quals es refresquen complixen una Vegem algunes preguntes per emfatitzar en la relació superfície-volum Per què els mamífers xicotets mengen més (en proporció amb el seu pes) que els grans? Busca dades relatives a, per exemple, un ratolí un lleó. El Sol irradia més calor que una persona, tant! De fet, el Sol emet en cada segon 9,46 10 cal, una persona 3 10 cal. – Compara la quantitat de calor que emeten per unitat de superfície (1 dm ), en cada segon, el Sol una persona. Dades: radi del Sol: 696 340 km, superfície d’una persona: 2 m2 aproximadament. ara compara la quantitat de calor que emeten, per unitat de volum, el Sol una persona amb un volum de 80 litres. sorprén-te amb el resultat. Els viatges de Gulliver els lil·liputencs mesuraven uns 15 cm Gulliver, 180 cm. Si el rei de Lil·liput es menjara una poma, quantes hauria d’oferir a Gulliver perquè menjara la mateixa quantitat en proporció a la seua grandària? Imagina, ara, que el rei portara una capa que va costar dobló d’or volguera obsequiar a Gulliver amb una altra proporcional la seua grandària. Quant costaria?

Ara fes-ho tu Indaga com usaríem el paper semilogarítmic per a representar exponencials decreixents (amb base menor que 1). En el paper semilogarítmic de la pàgina anterior dividix tots els valors de l’eix Y per 10 000, amb la qual cosa dalt queda l’1. Pots representar sobre aquest el gràfic (pàg. 165) de la desintegració radioactiva, M = (1/2) Busca altres casos similars als de la ficció de Gulliver en els quals les diferències de mesures porten a situacions sorprenents. Investiga sobre els límits de la grandària dels grans animals. Estudia, també, per què els animals de major grandària habiten en la mar.

pregunta-li al professor o professora. Recorda que disposes, en el teu banc de recursos: de diversos tallers per gestionar les teues emocions d’una diana per avaluar-les.

Descarrega d’anayaeducacion.es una rúbrica per revisar les teues competències corresponents aquest desafiament. Autoavalua la teua planificació del projecte descarregant la diana sobre planificació de tasques. Com ha anat el treball en equip? Usa la diana de coavaluació d’anayaeducacion.es per valorar-ho.

• Altres propostes de desafiaments que et poden interessar.

• Propostes d’instruments de diagnòstic, descarregables d’anayaeducacion.es.

• Una rúbrica del perfil d’eixida, descarregable d’anayaeducacion.es, per a autoavaluar l’adquisició de competències aconseguida.

BLOC ARITMÈTICA

1. Nombres naturals, enters i fraccionaris

2. Nombres decimals

3. Nombres reals

L’ordre i la regularitat de les seues estructures, la potència i precisió dels seus mecanismes fan que, en tota excursió pel camp numèric, trobem bellesa i eficàcia.

L’aritmètica, amb els seus eficients procediments, permet afrontar i resoldre multitud de problemes en tots els àmbits. El bon maneig de la calculadora i els programes informàtics ajuden, no sols a culminar processos aritmètics complexos, sinó també, i de forma molt significativa, a indagar i contrastar noves relacions i noves propietats.

La recerca i la investigació sobre propietats i curiositats numèriques abasten un amplíssim camp plagat de sorpreses i de bells resultats.

TRES NOMBRES CARISMÀTICS

Hi ha tres nombres molt coneguts i importants en el món de les matemàtiques: És la relació entre el perímetre d’una circumferència i el seu diàmetre i servix per a calcular longituds, àrees i perímetres de figures «redones».

Regix la proporció àuria, que juga un paper tan important en l’art i en infinitat de configuracions de la naturalesa: flors, caragols, galàxies…

El nombre matemàtic més important, present en els processos de creixement i en l’equació de les catenàries.

Doncs bé, no és sorprenent trobar-nos-els en realitzar aquestes operacions estranyes que tenen un nombre infinit de sumands?

FAMÍLIES DISTINGIDES DE NOMBRES

Nombres primers: 2, 3, 5, 7, 11, 13, 17, 19, 23, … Recordes el sedàs d’Eratòstenes? Sabries esbrinar si un nombre que estiga més enllà d’aquesta llista és o no primer?

Nombres de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … Els nombres d’aquesta successió tenen propietats interessants.

Quadrats perfectes: 1, 4, 9, 16, 25, 36, …

Cubs perfectes: 1, 8, 27, 64, 1125, 216, …

EL DESAFIAMENT

Aquest treball va de nombres. Et proposarem:

• Que recordes, indagues, trobes i demostres propietats numèriques ja conegudes o noves.

• Que obtingues per camins sorprenents alguns nombres que ja coneixes.

• Que t’endinses en noves i curiosíssimes famílies de nombres per a conéixer-les, comprendre-les i, potser, detectar-hi algunes noves propietats.

• Que indagues pel teu compte (per Internet o altres llocs) per aprofundir en les famílies de nombres que ací veuràs o en unes altres que valguen la pena.

Nombres naturals, enters i fraccionaris

L’origen dels nombres enters

Els nombres naturals han sigut usats per totes les civilitzacions des de l’antiguitat més remota. Egipcis, babilonis, grecs, romans, xinesos, indis, àrabs, maies… han manejat sistemes molt diversos amb similituds i diferències.

L’assoliment d’un sistema de tipus posicional, amb el qual les operacions es feren amb agilitat, va costar molts segles de recerca. El paper dels negatius, i sobretot del zero, va resultar més difícil de concebre.

Per això, els nombres enters no van acabar de prendre forma fins a finals del segle vii , a l’Índia. D’allí ens van arribar per mitjà dels àrabs en el segle  ix , juntament amb el sistema de numeració decimal-posicional.

Les fraccions

Les fraccions es van començar a usar des de molt antic. A Babilònia es feien servir fraccions sexagesimals (els denominadors eren potències de 60) i encara actualment fem servir aquesta nomenclatura en les mesures angulars i en les de temps.

Els egipcis només manejaven fraccions unitàries (amb numerador u: 1 2 , 1 3 , 1 4 , 1 5 , … eo . Per sorprenent que resulte, per a posar 2 5 no posaven 1 5 + 1 5 sinó  1 3  +  1 15 ,

ja que cada fracció només es posava una vegada. Més sorprenent és que aquesta nomenclatura es prolongara durant molts segles. L’ús de les fraccions a l’estil actual no es va acabar de consolidar fins al segle xvii

RECORDA

Els cardinals servixen per a comptar i els ordinals, per a ordenar. Per exemple, en l’afirmació: «Dels 8 finalistes de la carrera, Màrius ha arribat tercer», el 8 és cardinal i el 3 és ordinal.

Nombres naturals 1

Comptem els estudiants d’una classe, el nombre de llosetes que hi ha en un sòl o el nombre de maneres d’ordenar els asos d’una baralla de pòquer. Amb els nombres naturals comptem. Com saps, són 0, 1, 2, 3, …, 10, 11, 12, … 99, 100, 101, … N’hi ha d’infinits. El conjunt de tots es denomina N. En estar ordenats podem representar-los sobre una recta:

EXEMPLE

En repartir 100 elements entre 7 individus, obtenim de quocient 14 (a cada individu li corresponen 14 elements) i de residu 2 (queden 2 elements sense repartir).

Els naturals també servixen per a numerar. Per exemple, diem que Olívia Gomis és la tretzena de la llista de classe.

Suma i multiplicació

Els nombres naturals es poden sumar i multiplicar; el resultat d’aquestes operacions és, també, un nombre natural.

Recorda que en les expressions a ∙ b + c i a + b ∙ c la multiplicació s’efectua abans de la suma. Quan volem donar prioritat a la suma, ho hem d’indicar amb parèntesis: a ∙ (b + c), (a + b) ∙ c

Divisió

La idea de divisió de nombres naturals és la de repartiment. La divisió 100 : 5 = 20 s’interpreta com un repartiment de 100 elements (dividend) entre 5 parells (divisor), de manera que a cada part li corresponen 20 elements (quocient). Quan amb el repartiment posem fi a tots els elements disponibles, com és aquest cas, la divisió es diu exacta. Quan n’hi sobren alguns elements, la divisió es diu entera. En aquesta, a més d’un quocient, s’obté un residu.

Potències i arrels

Com saps, una potència de nombres naturals és, en definitiva, una multiplicació reiterada. Per exemple: 74 = 7 ∙ 7 ∙ 7 ∙ 7. Amb només aquesta referència s’obtenen les propietats de les potències.

La radicació és l’operació inversa de la potenciació. Si 74 = 2 401, aleshores

En N només tenen sentit les arrels exactes.

PENSA I PRACTICA

2 Hui és dilluns. Demà serà… D’ací a dos dies serà… D’ací a 25 dies serà…

a) Quin dia de la setmana serà d’ací a 357 dies?

b) Quin dia de la setmana serà passats 7a + 3 dies, on a és nombre natural qualsevol?

c) Com expressaries, en general, el nombre de dies que han de transcórrer perquè siga dissabte?

Nombres enters 2

A vegades, és necessari usar quantitats negatives. Vegem-ne uns exemples:

• Estar a –5 °C vol dir que fa 5 °C davall zero.

• Un saldo en el banc de –108 € significa que es deuen 108 €…

Ja saps que els enters negatius juntament amb els naturals formen el conjunt dels nombres enters, que s’expressa com a Z. Amb aquests podem sumar i multiplicar, i obtindre un nombre enter. A més, al contrari del que passa amb els naturals, també en restar dos nombres enters, obtenim un altre enter.

Els nombres enters es representen en la recta d’aquesta manera:

Aquesta representació en la recta suposa el següent criteri d’ordenació:

• Els naturals (el zero i els enters positius) ja estaven ordenats.

• Tots els nombres naturals són majors que els enters negatius.

• Si a i b són nombres naturals i a < b aleshores, –a > –b.

Valor absolut d’un nombre enter

El valor absolut d’un nombre és la magnitud del mateix si prescindim del seu signe. S’escriu així: | x |, i es definix de la manera següent:

• El valor absolut d’un nombre natural és el mateix: | 5 | = 5, | 0 | = 0

• El valor absolut d’un nombre negatiu és el seu oposat: | –27 | = 27

• Gràficament, el valor absolut d’un nombre és la seua distància al 0:

Regles per a operar amb nombres enters

• Per sumar nombres positius i negatius, agrupem els uns i els altres, restem els resultats i hi posem el signe del que tinga major valor absolut.

• Si un parèntesi va precedit del signe menys, es pot suprimir canviant el signe de tots els sumands que hi haja dins.

• Per multiplicar nombres enters, recordem la «regla dels signes»:

1 Ordena de menor a major: –4, 19, 7, 0, –6

2 Calcula. a)

3 Calcula.

a) (1 – 4) – (5 – 3) – (–6)

b) –3(4 – 2) – 4(3 – 8)

c) (–2)3 + (–3)4 – 52

d) 15 – 4(3 – 6) – 2[4 – 5(2 – 3)]

RECORDA

Els enters es poden expressar en forma de fracció:

4 1 4 2 8 3 12 === =

CÀLCUL MENTAL

1. Simplifica les fraccions:

a) 15 10 b) 8 6 c) 2 4 d) 21 14 e) 18 12 f ) 100 75

g) 44 33 h) 17 34 i) 26 52

2. Les nou fraccions anteriors són equivalents 3-3. Classifica-les.

3. Escriu sis fraccions equivalents a 500 300 .

Quina és la corresponent fracció irreductible?

Fraccions 3

Nombres fraccionaris per a expressar mesures

Per a mesurar, sol ser necessari fraccionar la unitat. D’ací sorgix la idea de nombre fraccionari: la meitat, la cinquena part, la mil·lèsima part… de la unitat.

Les fraccions són les expressions numèriques dels nombres fraccionaris.

Són nombres fraccionaris: ,,,, , 2 1 5 1 5 3 7 4 100 1 1 000 145

En totes aquestes fraccions, el numerador és menor que el denominador i, per tant, són parts de la unitat. Es diuen fraccions pròpies.

També són fraccionaris nombres com 2 3 , 3 7 – i 4 19 , que es poden expressar com la suma d’un enter i una fracció pròpia (nombres mixtos):

Els nombres fraccionaris es poden representar en la recta al costat dels enters:

Els nombres fraccionaris, juntament amb els enters, formen el conjunt dels nombres racionals, que es designa amb la lletra Q.

Els elements de Q es caracteritzen perquè es poden posar en forma de fracció.

Simplificació de fraccions. Fraccions equivalents

Recorda que simplificar una fracció és dividir-ne el numerador i el denominador per un mateix nombre enter.

Per exemple: 24 28

= 6

==

=

Una fracció que no es pot simplificar direm que és irreductible. Dues fraccions són equivalents si en simplificar-les donen lloc a la mateixa fracció irreductible.

Per exemple, 35 –10 i 28 8 –són equivalents:

PENSA I PRACTICA

1 Expressa com a suma d’un enter i una fracció.

a) 9 40 b) 5 86 c) 10 127 d) 12 127 e) 8 43 –

2 Obtín la fracció irreductible.

a) 21 18 b) 35 14 c) 36 42 d) 56 14 e) 200 75

➜ anayaeducacion.es Practica el càlcul de la fracció irreductible.

3 Copia la recta en el quadern i representa, aproximadament, les fraccions.

–2

CÀLCUL MENTAL

a) 3 2 6 1 + b) 3 2 6 1 –

c) 3 2 4 3 d) 3 9 4

e) 1 :  3 1 f ) : 7 3 4

g) 3 1 de 600 h) 3 2 de 600

i) 3 2 de 4 3 j) 3 2 4 3 · de 600

k) 2 1 d’ 5 1 l) 2 1 de 5 3 de 800

Operacions amb fraccions 4

Suma de fraccions

Sumar fraccions amb el mateix denominador és una tasca summament fàcil: se’n sumen els numeradors i es manté el denominador.

Per sumar (i restar) fraccions amb diferent denominador, haurem de transformar-les en unes altres equivalents amb el mateix denominador.

Producte de fraccions

La tercera part de la quarta part d’alguna cosa és la dotzena part: · 11 3

Raonant de manera anàloga, podem veure que: 2 4 5 34 25 12 10 5 36 · · == =

El producte de dues fraccions és una altra fracció amb el denominador producte dels seus denominadors, i el numerador producte dels seus numeradors: · · b a d c bd ac ·=

La fracció d’una quantitat és un cas particular del producte de fraccions, perquè, com ja saps, un nombre enter es pot expressar com una fracció amb denominador la unitat i el numerador de la qual és aquest nombre.

Per exemple: Àlvar ha gastat 3 2 dels 1 260 € que tenia estalviats per pagar el viatge de fi de curs. Per tant, el viatge ha costat:

Fracció inversa d’una altra. Quocient de fraccions

L’invers del nombre 4 és 4 1 . I viceversa, l’invers de 4 1 és 4.

La inversa de la fracció 5 3 és 3 5 . I viceversa.

Tota fracció, b a , excepte el 0, té una inversa, a b , tal que a ba b · = 1.

El quocient de dues fraccions és el producte de la primera per la inversa de la segona:

b a d

b a b a c d c d ==

Per exemple:

Problemes amb fraccions 5

➜ anayaeducacion.es Practica la resolució de problemes amb fraccions.

TIN EN COMPTE

Per a calcular el total coneguda la fracció i la part, es dividix la part entre el numerador i es multiplica pel denominador.

3 de T = 48

5

? 150 Venudes Per vendre

TIN EN COMPTE

La suma de les fraccions que representen les parts d’un tot és igual a la unitat (el tot).

b a d c f e 1 ++ = b a d c f e 1– +=

Xics Xiques

❚ problema 1

Una ciutat tenia 120 000 habitants l’any 2000. En un decenni en va augmentar 4/15. En el decenni següent en va augmentar 9/16. Quants habitants tenia el 2020?

Augment en el primer decenni:

4 de 120 000 = (120 000 : 15) · 4 = 32 000

15

En 2010 hi havia 120 000 + 32 000 = 152 000 habitants.

Augment en el segon decenni:

9 de 152 000 = (152 000 : 16) · 9 = 85 500

16

En 2020 hi havia 152 000 + 85 500 = 237 500 habitants.

❚ problema 2

Una ONG organitza una carrera solidària i, per recaptar fons, posa a la venda un lot de samarretes commemoratives de l’esdeveniment. Al cap d’una setmana en porta venudes 600 unitats, fet que suposa els 4/7 del total. Quantes samarretes componien el lot?

Anomenant T el total de samarretes del lot:

7 4 de T = 600 → 7 1 de T = 600 : 4 = 150 → 7 7 de T = 150 · 7 = 1 050

En resum: T = (600 : 4) · 7 = 1 050

El lot contenia 1 050 samarretes.

❚ problema 3

Un executiu té la tercera part del seu capital en un fons de pensions, tres cinquenes parts, invertides en accions, i els 3 836 euros restants, en el compte corrent. A quant ascendix el seu capital?

Fracció de capital invertit: Fracció en el compte corrent:

Quantia del capital: 3 836 · 15 = 57 540 €

❚ problema 4

En una classe de 36 alumnes, 2/3 són xics. Les 3/4 parts de les xiques fan música. Quina fracció del total són les xiques de música? Quantes en són?

3 2 són xics → 3 1 són xiques

Fracció de xiques que fan música:

del total de la classe

Xiques que fan classe de música: 4 1 de 36 = 36 : 4 = 9

TIN EN COMPTE

La fracció d’una quantitat equival al producte de la fracció per la quantitat.

b a de · d c b a d c =

Tres amics es repartixen un premi, de manera que el primer s’emporta 2/5 del total; el segon, 5/9 del que queda, i el tercer, 92 €. A quant ascendia el premi?

El primer s’emporta 5 2 del premi; en queden 5 3 .

El segon s’emporta 9 5 de 5 3  =  9 5  ·  3 5  =  9 3  =  3 1 del premi.

Entre el primer i el segon s’emporten 5 2 3 1 15 65 15 11 += + = del premi.

El tercer s’emporta 15 15 15 11 15 4 –= del premi.

PENSA I PRACTICA

4 del premi són 92 €; 15 1 són 92 : 4 = 23 €; 15 15 són 23 · 15 = 345 €

15

Per tant, el premi ascendia a (92 : 4) · 15 = 345 €.

1 Un terreny es dividix en tres parts. Dues parts són 2/5 i 1/3 del total. Quina és la més gran?

2 En el problema anterior, si el terreny mesura 240 m2, quina superfície ocupa cada una de les parts?

3 Els 2/5 dels xics d’una classe porten ulleres. En la llista d’aquesta classe hi ha 36 persones, de les quals 7/12 són xiques. Quants xics porten ulleres?

4 Jordi s’ha gastat 2/7 de la paga en música i 1/5 en llibres. Quina fracció de la paga s’ha gastat? Quina fracció li queda?

5 En una fruiteria es venen, al matí, 3/5 de la fruita que hi havia i, a la vesprada, la meitat de la que quedava

a) Quina fracció en queda per vendre?

b) Si en començar el dia n’hi havia 750 kg, quants quilos se’n van vendre?

6 D’un sou de 1 500 €, es gasta en menjar la sisena part, i en el pagament de la hipoteca, 350 € més que en menjar. Quina fracció del sou queda per a altres despeses?

7 En tancar la parada del mercat, el meloner pensa: «Hui he venut prou melons. Només me n’han quedat onze, que són la desena part dels venuts».

Quants melons tenia quan va obrir la parada?

8 El pressupost anual d’una oficina és de 297 000 €. Les despeses fixes en suposen la cinquena part i els 2/11 de la resta s’invertixen en equipament. Quant queda per a altres despeses?

9 Un club disposa de 1 200 entrades per a un partit. Assigna 3/5 parts a la seua afició i 5/8 de la resta a la visitant. Quantes entrades queden per a venda lliure?

10 Un dentista dedica 1 h i 3/4 a la consulta. Si rep 15 pacients, quina fracció d’hora pot dedicar a cada un? Quants minuts són?

11 Repartiment entre quatre: A i B s’emporten, respectivament, 2/7 i 13/21 del total. C rep 7/10 de la resta. I D, finalment, 390 €. Quants diners es van repartir?

12 Un corredor ciclista abandona la carrera quan en porta coberts els 2/3 del recorregut. Si haguera aguantat 10 quilòmetres més, hi hauria cobert les tres quartes parts. Quants quilòmetres van fer els que van arribar a la meta?

13 Sis amics compren solidàriament un regal per al seté membre de la colla. A l’hora de pagar, un no té diners i, així, cada un dels altres hi ha de posar 1,50 euros més. Quant costava el regal?

ENCARA MÉS SENZILL

Calcula mentalment:

a) 22 b) (–2)2 c) 23

d) (–2)3 e) 52 f) (–10)3

g) 17 h) (–1)7 i) 104

j) (–10)4 k) (–5)4 l) (–3)3

Potències 6

Base entera i exponent enter positiu

EXERCICIS RESOLTS

1 Calcular aquestes potències:

3 2, –3 2, (–3) 2, –(–3) 2

2 3, –2 3, (–2) 3, –(–2) 3

1 28, –1 28, (–1) 105, –(–1) 105

2 Simplificar.

a) 3 5 · 2 3 · 2 2

b) (5 2) 3  ·  2 2 2 8

3 Realitzar.

(–3 + 1) 3 + (5 – 8) 4 · (–1) 9 –– (–5) 2 · (–1) 4

PENSA I PRACTICA

1 Calcula les potències següents:

Recorda: aa aa a ·· ·…· vs egade

n n

= 12 3 a és la base; n, l’exponent.

Per exemple: 24 = 2 · 2 · 2 · 2 = 16 (–2)4 = (–2) · (–2) · (–2) · (–2) = 16 25 = 2 · 2 · 2 · 2 · 2 = 32 (–2)5 = (–2) · (–2) · (–2) · (–2) · (–2) = –32

• Si a és positiu, an és positiu qualsevol que siga n.

• Si a és negatiu: n n( parell → an positiu. Per exemple, (–2)4 = 16. imparell → an negatiu. Per exemple, (–2)5 = –32.

❚ propietats de les potències

(–2)3 · (–2)5 = (–2)3 + 5 = (–2)8

64 = (2 · 3)4 = 24 · 34

(–2)5 = (–1 · 2)5 = (–1)5 · 25 = –25

(53)4 = 53 · 4 = 512

32 = 9 –32 = –9 (–3)2 = 9 –(–3)2 = –9

23 = 8 –23 = –8 (–2)3 = –8 –(–2)3 = –(–8) = 8

128 = 1 –128 = –1 (–1)105 = –1 –(–1)105 = –(–1) = 1

a) 35 · 23 · 22 = 35 · (23 · 22) = 35 · 25 = (3 · 2)5 = 65

b) (52)3 ·  2 2 2 8  = 52 · 3 · 28 – 2 = 56 · 26 = (5 · 2)6 = 106

(–3 + 1)3 + (5 – 8)4 · (–1)9 – (–5)2 · (–1)4 = (–2)3 + (–3)4 · (–1) – 52 · 1 =   = –8 – 81 – 25 = 114

a) –105 b) (–10)5 c) (–10)6 d) –(–10)5

e) (–1)100 f) –106 g) –16 h) –(–1)101

2 Simplifica: 5 · [( )] () () 3 33 ––33 58 4

3 Efectua les operacions següents:

a) [(1 – 7) – (8 – 3) – (–2)5] · [15 + (–11)]2

b) (7 – 3) · [4 – (–3)] + (5 – 1)2 · [6 – (–3)4]

c) (–3)2 – (–33) + 52 · (–5)2 – [2 – (–3)4 · (–2)]

d) 17 – (–4)(–3 + 6) – 2[4 – 5(2 – 3)7]2

PENSA

5 Calcula el valor d’aquestes potències:

Base racional i exponent enter

En la pàgina anterior hem repassat les potències d’exponent enter positiu. Vegem ara com són les potències quan l’exponent és zero o un nombre enter negatiu.

1 Calcular el valor de les potències següents:

= 3–5 + 4 = 3–1

Exercicis i problemes

DOMINES ALLÒ BÀSIC?

Nombres enters

1 Calcula com es fa en l’exemple.

• 6 – 2 – 8 + 4 – 7 + 3 = (6 + 4 + 3) – (2 + 8 + 7) = = 13 – 17 = –4

a) 7 + 2 + 5 – 9 – 1 – 6

b) 8 – 4 + 3 – 7 + 8 – 5 + 2

c) –6 + 4 – 10 – 2 + 9 – 7 + 1

d) 13 – 5 – 11 + 6 – 15 + 6

e) 11 – 7 – 8 – 2 + 5 – 4 + 8

2 Lleva parèntesis i calcula.

a) (+5) + (–4)

b) (+3) – (–7)

c) (–2) + (–9) – (–3)

d) (–5) – (+3) – (–10)

e) –(+6) – (– 4) + (–7)

f) –(–3) – (–1) – (–5)

3 Calcula.

a) 5 + (–3) – (–2) + (4 – 6) – [3 – (6 – 4)]

b) (3 + 6 – 11) · (4 – 2 – 9) · (–1)

c) 5 · [8 – (2 + 3)] – (–4) · [6 – (2 + 7)]

d) (–7) · [4 · (3 – 8) – 5 · (8 – 5)]

Fraccions. Operacions

4 Expressa com la suma d’un enter i una fracció.

a) 3 5 b) 3 8 c) 6 17 d) 5

e) –

5 Obtín la fracció irreductible en cada cas.

a) 27 12 b) 14 4 c) 6 –2 d) 30 18 e) –30 40 f)

6 Calcula mentalment.

a) La meitat de 8 7 .

b) La tercera part de 5 9 .

c) La meitat de la cinquena part de –4.

d) El triple de la meitat de 3 2

7 Calcula mentalment.

a) 3 4 de 21 b) 2 5 de 10

c) 10 3 d’1 milió d) 20 7 de cent mil

8 Calcula mentalment.

a) Els dos cinquens de 400.

b) El nombre els dos cinquens del qual són 160.

c) Els tres setens de 140.

d) El nombre els cinc sisens del qual són 25.

9 Expressa en forma de fracció d’hora.

a) 15 minuts b) 20 minuts

c) 10 minuts d) 1 minut

e) 120 segons f) 1 segon

10 Troba el total en cada cas.

a) 5 3 del pressupost són 351 €

b) 7 6 del centre són 492 estudiants.

c) 8 5 del palau ocupen 2 850 m2.

Potències

11 Elimina parèntesis i simplifica.

ENTRENA’T I PRACTICA

14 Calcula.

a) 16 – 3 · [8 – 2 · (5 – 6)]

b) 2 + 8 : [14 – 5 · (6 – 4)]

c) 30 : [12 · (4 – 6) – 6 · (4 – 7)]

d) 4 · [5 – (2 – 6)] – 3 · [8 – (4 – 7)]

e) 3 · (6 – 9) – 7 · [10 + 3 · 5 – 3 · (5 + 4)]

f) 2 · (5 – 9 · [7 + 3 · (5 – 7)]) + 6

15 Calcula.

a) |(2 – 3) – (1 – 7) – 5| · [–(11 + (–4))]

b) (1 – 4) · 3 + (7 – 5) · |5 + 2 · (–3)|

c) (–2) + 3 · (–2) + |4 · (–6) – [1 – 3 · (–2)]|

d) 5 – |(–2) · |– 4 + 5|| – 2[4 – |–2| · |2 – 3|]

e) |–2 – |(–2) · (–4)| · (–5 + 4)| – |–1 + 3| · (–2)

16 Calcula.

a) 1/3 dels 2/5 dels 30 estudiants.

b) 4/7 de la meitat dels 42 vehicles.

c) 7/13 d’un quart de les setmanes d’un any.

d) 3/5 d’un terç dels dies d’abril.

17 Troba la fracció que queda en llevar al total:

a) 8 3 d’ 1 2 b) 7 1 de 5 2 c) 10 1 de 3 2 d) 8 5 de 4 3

18 Troba el total en cada cas:

a) 3/5 del pressupost són 351 €

b) 6/7 del centre són 492 estudiants.

c) 5/8 del palau ocupen 2 850 m2.

19 Reduïx a una sola fracció. a) 5 3 4 1 2 4 3 5 2 1

20 Representa en la recta numèrica.

22 Calcula. a) (–2)4 b) –24 c) (–2)3

d) –23 e) 2–3 f) (–2)–3

g) (–1)16

Exercicis i problemes

RESOL PROBLEMES SENZILLS

27 La temperatura d’un congelador baixa 2°C cada 3 minuts fins a arribar a –18 °C. Quant tardarà a arribar a –12 °C si quan l’encenem està a 16 °C?

28 Aristòtil va morir l’any 322 aC i va viure 62 anys. En quin any va nàixer?

29 Amb un barril que conté 510 litres de vi, quantes botelles de 3/4 de litre es poden omplir? Quantes de litre i mig?

30 Amb una garrafa de 5/2 de litre s’omplin 25 gots. Quina fracció de litre entra en un got?

31 D’una botella de 3/4 de litre s’ha consumit la cinquena part. Quina fracció de litre hi queda?

32 a) Si Rafa es gasta 2/3 dels diners en roba i 1/4 del total en menjar, quina és la fracció gastada?

b) Quina fracció li queda per gastar?

c) Si va eixir amb 180 €, quina quantitat no s’ha gastat?

33 En una parcel·la es cultiven 4/5 parts de blat i la resta, 100 m2, de dacsa. Quina és la superfície de la parcel·la?

34 Una pilota cau a terra i s’eleva cada vegada als 2/3 de l’altura anterior. Després de botar tres vegades, s’ha elevat a 2 m. Des de quina altura va caure?

35 Una operària rega en un dia 2/5 parts del jardí. Quants dies tardarà a regar tot el jardí? Quant guanyarà si cobra 50 € per dia?

36 En una parada de fruites i verdures, els 5/6 de l’import de les vendes d’un dia corresponen a fruites. Del que s’ha recaptat per fruita, els 3/8 corresponen a les taronges. Si la venda de taronges ascendix a 89 €, quina caixa ha fet l’establiment?

37 A Pau li descompten al mes, del sou brut, la huitena part d’IRPF i la desena part per a la Seguretat Social. Si el sou net és 1 302 €, quin és el sou brut mensual?

38 D’una classe, 3/7 del total dels estudiants han anat al museu de ciències i 2/5 a un concert.

a) On han anat més estudiants?

b) Si 6 estudiants no han anat a cap activitat, quants estudiants hi ha en la classe?

39 En un dipòsit, el dilluns hi havia 3 000 litres d’aigua i estava ple. El dimarts se’n va gastar 1/6 del depòsit. El dimecres se’n van traure 1 250 litres. Quina fracció n’hi queda?

PER A PENSAR UN POC MÉS

40 D’un solar, es venen els 2/3 de la superfície i després els 2/3 del que quedava. L’ajuntament n’expropia els 3 200 m2 restants per a un parc públic. Quina era la superfície del solar?

41 Una obrera ha tardat 1 hora i tres quarts a polir 3/5 parts d’un pis. Si va començar a les 10 a.m., a quina hora acabarà de polir el pis sencer?

42 Un tren tarda 3 hores i quart a recórrer 5/9 d’un trajecte de 918 km.

a) Calcula el temps que tarda a realitzar el trajecte si continua a la mateixa velocitat.

b) Quina n’ha sigut la velocitat mitjana?

TAMBÉ POTS FER AIXÒ

43 Una gallina va pondre durant huit setmanes una mitjana de 3 ous cada 4 dies i, durant les següents dotze setmanes, 5 ous cada 6 dies. Quina va ser la posta mitjana diària al final d’aquest període?

44 Una tela per a entapissar encull, en llavar-la, 3/20 al llarg i 7/25 a l’ample. Quants metres s’han de comprar d’una peça de 125 cm d’ample per cobrir una superfície de 39,9 m2?

45 Un venedor ambulant porta una cistella de taronges. En la primera casa que visita, ven la meitat de les taronges més mitja. En la segona casa ven la meitat de les que li quedaven més mitja. En la tercera i en la quarta casa, repetix la mateixa operació, amb la qual cosa se li acaba la mercaderia. Quantes taronges portava?

nota: En cap moment partix taronges.

COMPRÉN I APLICA EN EL DESAFIAMENT

46 Els divisors propis d’un nombre són tots els divisors diferents d’aquest (comptant l’1). Un nombre es diu perfecte si coincidix amb la suma de tots els divisors propis.

Esbrina quins d’aquests nombres són perfectes: 4, 6, 60, 100

AUTOAVALUACIÓ

1 Resol.

a) |4 – |–7|| b) 1 – |3 + |–4|| c) 8 – |–11|

2 Fes aquestes operacions:

a) 20 – 4 · (6 – 2 · 2 – 5)

b) 12 + (–3) · [16 – 4 · 9 – 6 · 5]

c) 2 · [–1 + (1 – 3)] – 2 · [5 – (2 – 5)]

3 Separa la part entera com en

➜ anayaeducacion.es Resolucions d’aquests exercicis.

6 Una pilota perd en cada bot 2/5 de l’altura a la qual ha arribat en el bot anterior. Quina fracció de l’altura inicial, des de la qual ha caigut, aconseguirà quatre bots després?

7 De les persones que assistixen a un congrés, 1/6 són d’Europa; 1/3, d’Àsia; 2/5, d’Amèrica, i la resta, d’Àfrica. Sabent que n’hi ha 60 d’Europa, quantes n’hi ha d’Àfrica?

8 Un vehicle cobrix 3/8 del recorregut al matí i 2/3 de la resta a la vesprada. Sabent que li falten 130 km:

a) Quants quilòmetres mesura el recorregut?

b) Quant de temps (hores i minuts) tardarà a recórrer-lo de tornada a 120 km/h?

REFLEXIONA

Revisa els aspectes treballats i planteja solucions als problemes que es detecten.

Per a això, descarrega d’anayaeducacion.es la rúbrica corresponent, reflexiona de manera individual i compartix en grup.

POSA A PROVA LES TEUES COMPETÈNCIES

Fes l’autoavaluació competencial inclosa en anayaeducacion.es

CURIOSITATS MATEMÀTIQUES

Leonardo de Pisa (1179-1250)

També anomenat Fibonacci (fill d’home bo). El pare va ser comerciant i cònsol de Pisa a la ciutat de Bugia, en l’actual Algèria. Això li va permetre aprendre les matemàtiques dels àrabs, especialment el sistema de numeració decimal, que va contribuir a introduir a Europa.

Va ser qui va descriure per primera vegada la famosa successió: 1, 1, 2, 3, 5, 8, 13, … en la qual cada terme s’obté de la suma dels dos anteriors.

Relaciona

Reproduïx aquesta espiral en un paper quadriculat i anima’t a ferla un poc més gran.

Sabries explicar la seua relació amb la successió de Fibonacci?

COMPRÉN I APLICA EN EL DESAFIAMENT

Nombres perfectes

Hem vist (exercici 46) que un nombre perfecte és el que coincidix amb la suma dels seus divisors propis. Només es coneixen 48 nombres perfectes i cap és imparell. Es creu que n’existixen d’infinits, però encara no s’ha pogut demostrar.

SITUACIÓ D’APRENENTATGE

© GRUPO ANAYA, S.A., 2023 - C/ Valentín Beato, nº 21 - 28037 Madrid.

Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.