Operación mundo: Matemáticas 5º (demo)

Matemáticas

¿Qué

vamos a aprender?

1 5 9

2 6 10

3 7 11

4 8 12

Los números. La suma y la resta ¿Pueblo o ciudad?

La multiplicación. Potencias Multiplica la vida

La división Repartir y compartir

Las fracciones Cultiva vida

SITUACIÓN DE APRENDIZAJE OBJETIVO EN ACCIÓN ODS PÁG.

¿Cómo podemos hacer poblaciones más inclusivas y seguras? Elabora un listado de los servicios esenciales que debe tener una población para conseguirlo.

¿Por qué debemos reciclar materiales? Construye un objeto con materiales reciclados.

¿Cómo podrías concienciar a las personas para colaborar en el reparto de comida?

Elabora un cartel publicitario para animar a todo el mundo a participar en la recogida de alimentos.

¿Cómo podemos contribuir en el cuidado del medio ambiente? Elabora una presentación con tus propuestas.

REPASO TRIMESTRE 1 STEAM: Hypatia de Alejandría

Ciudades y comunidades sostenibles

Producción y consumo responsables Hambre

Los números decimales Vida minúscula

Operaciones con números decimales Ahorra décimas de energía

Longitud, capacidad, masa y superficie Kilos de salud

Organización de la información Bajo el mar

Medida del tiempo Más rápido, más alto, más fuerte

Rectas y ángulos Historias de geometría

Figuras planas Geometría de la paz

Área de figuras planas Innovar para mejorar

¿Cómo podemos conocer mejor a los animales? Elabora cartas informativas e inventa un juego para jugar con ellas.

Vida de ecosistemas terrestres

¿Qué podemos hacer para ahorrar energía? Elabora un plan de ahorro energético con consejos para tu familia.

Energía asequible y no contaminante

¿Por qué es importante cuidar la salud y el bienestar? Elabora una receta saludable para cocinar con tu familia.

Salud y bienestar

¿Qué podemos hacer para cuidar los océanos? Elabora un eslogan publicitario para promover el cuidado de las playas.

REPASO TRIMESTRE 2 STEAM: Florence Nightingale

¿Cómo podemos fomentar que cualquier deporte sea para hombres y mujeres?

Conviértete en periodista y escribe una noticia sobre una deportista olímpica.

¿Cómo podemos divertirnos aprendiendo?

Inventa una historia en la que los personajes sean elementos matemáticos que vas a estudiar en esta unidad.

¿Cómo construimos la paz?

Inventa un símbolo de la paz con figuras geométricas para promover entre las personas la importancia de vivir en paz.

¿Cómo puede la innovación ayudar a construir un mundo más sostenible? Elabora un decálogo con ideas innovadoras para cuidar los libros de texto.

REPASO TRIMESTRE 3 STEAM: Hypatia

Vida submarina

Igualdad de género

Educación de calidad

Paz, justicia e instituciones sólidas

Industria, innovación e infraestructura

cero

Acción por el clima

SABERES BÁSICOS

• Números de hasta siete cifras: conteo, lectura, composición, descomposición, valor de posición, comparación y ordenación.

• Aproximación por redondeo.

• Propiedades de la suma y relación con la resta.

• Propiedades de la multiplicación: conmutativa, asociativa y distributiva.

• Multiplicación por decenas, centenas y millares.

• Multiplicación por varias cifras.

• La división con divisores de dos y tres cifras.

• División exacta e inexacta.

• Propiedad fundamental de división.

• División entre decenas, centenas y millares.

• Operaciones combinadas.

Fracciones. Medios, tercios y cuartos.

• Fracción y unidad. Fracciones propias e impropias. Fracciones equivalentes. Comparación de fracciones.

• Comprobación del resultado en problemas matemáticos mediante la prueba de la resta y coherencia entre el resultado y el contexto.

• Problemas aritméticos: de comparación.

Operaciones combinadas.

• Potencias, cuadrados y cubos.

• Fases de resolución de un problema.

• Problemas aritméticos: de grupos iguales.

• Comprobación del resultado en problemas matemáticos mediante la prueba de la división y coherencia entre el resultado y el contexto.

• Problemas aritméticos: de reparto, de agrupación.

Suma y resta de fracciones de igual denominador.

• Fracción de una cantidad. Problemas aritméticos: de combinación.

LO RESUELVO SIN PROBLEMA

• Estrategia heurística: Busco regularidades

• Cálculo mental: Sumar una cifra con llevadas

• Pensamiento computacional: Algoritmo

• Estrategia heurística: Estimo la solución

• Cálculo mental: Restar una cifra con llevadas

• Pensamiento computacional: Funciones

• Estrategia heurística: Planteo preguntas intermedias

• Cálculo mental: Sumar con llevadas en las unidades

• Pensamiento computacional: Generalización

• Estrategia heurística: Hago un dibujo

• Cálculo mental: Restar con llevadas en las unidades

• Pensamiento computacional: Generalización

PROYECTO INTERDISCIPLINAR · Nuestra cumbre por el clima: Todo controlado

• Décimas, centésimas y milésimas.

• Números decimales: lectura, escritura y valor de posición. Precios.

• Suma y resta de números decimales.

• Multiplicación de un decimal por natural.

• Multiplicación de dos números decimales.

• Multiplicación por decenas, centenas y millares.

• División de naturales con cociente decimal.

• Unidades de medida de longitud, capacidad, masa y superficie.

• Transformación de unidades.

• Tablas de frecuencias absolutas y relativas. Datos cualitativos y cuantitativos.

• Moda, media y rango.

• Comparación de números decimales.

• Aproximación de un decimal a un natural.

• División de decimal entre natural.

• División entre decenas, centenas y millares.

• Fases de resolución de un problema.

• Problemas aritméticos: de combinación, de grupos iguales, de reparto.

• Expresiones complejas e incomplejas. Problemas artiméticos: de comparación, de igualación, de grupos iguales.

• Gráficos de barras y de líneas.

• Histogramas.

• Gráficos de sectores.

• Estrategia heurística: Elimino posibles respuestas

• Cálculo mental: Restar décimas a números naturales

• Pensamiento computacional: Generalización

• Estrategia heurística: Empiezo por el final

• Cálculo mental: Sumar una fracción a la unidad

• Pensamiento computacional: Algoritmo

• Estrategia heurística: Tanteo la solución

• Cálculo mental: Sumar una fracción a un número natural

• Pensamiento computacional: Simulación

• Estrategia heurística: Organizo los datos en una tabla

• Cálculo mental: Restar una fracción a la unidad

• Pensamiento computacional: Generalización

PROYECTO INTERDISCIPLINAR · Hacemos camino : Antes del primer paso

• Unidades menores y mayores que el año.

• Horas, minutos y segundos.

• Expresiones complejas e incomplejas.

• Recta, semirrecta y segmento. Clasificación de ángulos según su amplitud y su posición.

• Polígonos: elementos y clasificación.

• Polígonos regulares.

• Perímetro.

• Triángulos: elementos y clasificación.

• Medida de superficies.

• Área del cuadrado y del rectángulo.

• Suma y resta de datos de tiempo. Problemas aritméticos: de agrupación, de comparación multiplicativa.

• Medida de ángulos. Clasificación de ángulos según la suma de sus amplitudes.

Cuadriláteros: elementos y clasificación.

• Circunferencia y círculo: elementos.

• Simetría, traslación y giro.

• Área del triángulo.

• Área del romboide y del rombo.

• Estrategia heurística: Busco todos los casos posibles

• Cálculo mental: Restar una fracción a un número natural

• Pensamiento computacional: Simulación

• Estrategia heurística: Empiezo por casos más sencillos

• Cálculo mental: Restar centésimas a la unidad

• Pensamiento computacional: Generalización

• Estrategia heurística: Busco regularidades

• Cálculo mental: Sumas de números utilizando el redondeo

• Pensamiento computacional: Algoritmo

• Estrategia heurística: Estimo la solución

• Cálculo mental: Multiplicar por descomposición

• Pensamiento computacional: Generalización

PROYECTO INTERDISCIPLINAR · El lugar de mi recreo: El patio de nuestros sueños

Los números. La suma y la resta

1 ¿Pueblo o ciudad?

Este verano he estado en el pueblo de mi padre. Lo he pasado genial con mis primas y primos, y la gente del pueblo. Cuando estamos allí entro y salgo de casa cuando quiero, no hay horarios, la comida está riquísima y me dejan hacer un montón de cosas solo.

Me gustaría vivir allí, ¡me encantaría! Sin embargo, mi prima mayor me recuerda que el pueblo no tiene algunas ventajas que sí hay en la ciudad como cines, pabellones de baloncesto o centros comerciales… Incluso algunos pueblos no tienen conexión a Internet. ¡Vaya dilema!

¿Cómo lo ves?

¿Qué piensas sobre el dilema que tiene este chico?

¿Cómo crees que influye la población de una localidad en la oferta de servicios esenciales (médicos, colegios…) y ocio (cines, centros comerciales…)?

Para esta unidad...

Objetivo en acción

¿Cómo podemos hacer poblaciones más inclusivas y seguras?

Elaborad un listado de los servicios esenciales que debe tener una población para conseguirlo.

El dato

En España una población es una ciudad si tiene más de 10 000 habitantes.

¡Sigue el hilo!

1 2

¿Para qué sirven los números?

Los números de hasta siete cifras

¿Para qué sirven los números?

Estoy en el piso 21.°.

1 Di cómo se leen los números que ves en la imagen anterior.

2 Escribe en tu cuaderno estos números con cifras.

a) diez mil d) seiscientos mil

b) veintitrés mil cien e) cien mil cuatro

c) dieciocho mil quinientos tres f) doscientos mil cincuenta

3 Escribe cómo se leen estos números.

a) 2 025 d) 1 948

b) 54 310 e) 30 503

c) 300 303 f) 800 605

4 Cuenta en voz alta.

• De 1 000 en 1 000, desde el número 1 000.

• De 100 en 100, desde el número 1 300.

• De 10 en 10, desde el número 1 540.

• Los números ordinales, hasta el 30.°.

El número 1 000 se escribe con una sola palabra: mil

El resto de millares, decenas de millar y centenas de millar se escriben con dos palabras:

2 000 Dos mil

20 000 Veinte mil

200 000 Doscientos mil

Cuenta hasta donde quieras o sepas.

Con los números puedes contar cuántos sois en clase, identificar los habitantes de una población o medir tu altura.

El número mil

¿Cuál es el número siguiente al 999?

¿Cuál es el número siguiente al 9 999?

¿Cuál es el número siguiente al 99 999?

Antes de hablar, ya sabía contar. ¡Gauss era un niño espectacular! Hacía cuentas con la mente, y a los tres años, con estos cálculos, ya impresionaba mucho a la gente.

En el colegio, el profesor dijo:

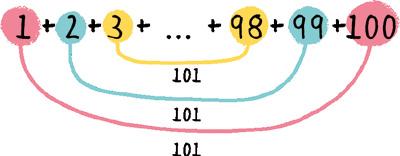
«Sumad los números del uno al cien». En un minuto, Gauss fue y lo hizo. ¡Y lo mejor es que lo hizo bien!

Siempre puedes sumar 1 a un número y obtienes otro mayor. ¡Los números no terminan nunca!

A él le encantaba descubrir formas y que tuvieran lados iguales. Con un compás y con una regla las dibujaba, ¡y eran geniales!

También fue un genio de los idiomas: hablaba ruso, francés, latín, inglés, danés, alemán y griego... le faltó el chino mandarín.

¿Cómo lo hace? ¿Tiene un secreto? Gauss contestaba siempre que sí. «No tengo miedo de equivocarme. Sé que en la vida se aprende así».

Todos los números le interesaban, pequeño o grande, impar o par. «Esto es igual que con las personas. Nunca se debe discriminar».

En parejas, investigad cómo resolvió Gauss la suma de los números del 1 al 100 tan rápidamente. ¡Qué gran idea!

¡Toma nota!

Con los números indicamos cuántas personas viven en una localidad.

5 Lee y responde en tu cuaderno.

6 Lee y disfruta este poema.

1

Los números de hasta siete cifras

Hay dos millones cuatrocientos treinta y cinco mil setecientos noventa y tres habitantes.

El valor de las cifras de un número depende del lugar que ocupan.

Para comprenderlo mejor, «Te lo cuento en un momento» en anayaeducacion.es

? ? ? ? ? ? ?

a) Tres millones quinientos cincuenta y tres mil setecientos cuarenta y ocho.

b) Un millón trescientos sesenta y tres mil ochocientos setenta y tres.

c) Seis millones trescientos cuarenta y dos.

Copia la tabla y escribe estos números en ella. Indica el valor del 3 en cada caso.

UMM CM DM UM C D U

A veces necesitamos utilizar números grandes para indicar los habitantes del lugar donde vives o comparar datos distintos.

2 Escribe con cifras y con letras el número que contiene cada recuadro.

2 CM 3 C 6 UM 7 UMM 5 DM 6 CM 3 D 1 UM 4 UMM 4 DM 8 U

3 Descompón los números como en el ejemplo.

2 570 324 = 2 UMM + 5 CM + 7 DM + 3 C + 2 D + 4 U = = 2 000 000 + 500 000 + 70 000 + 300 + 20 + 4

a) 7 405 308 b) 1 800 625 c) 6 554 310

4 Copia y completa la tabla en tu cuaderno.

Anterior Número Posterior ? 1 724 305 ? ? 2 777 779 ? ? 999 999 ? ? 1 000 000 ?

5 Ordena estos números de menor a mayor.

3 427 132   3 427 032   4 327 132

6 ¿Cuántos habitantes hay en la localidad de Berta?

• El número de habitantes tiene cinco cifras.

• La cifra de las decenas de millar es la mayor cifra par.

• La cifra de las unidades de millar y de las decenas es 5.

• La cifra de las centenas es el doble que la de las unidades, y entre las dos cifras suman 6.

Jugamos con las cifras

Comparar

• Si tienen distinta cantidad de cifras, es menor el que tiene menos cifras.

0 3 1 5 976 251 < 2 160 315

• Si tienen la misma cantidad de cifras, comparamos de izquierda a derecha hasta que encontremos cifras distintas. UMM CM DM UM C D U 6 7 1 3 0 4 9

números 4 > 1

7 1 3 0 1 9 6 713 049 > 6 713 019

Para comprenderlo mejor, «Te lo cuento en un momento» en anayaeducacion.es

Escribe estas cifras en trozos de papel. Colócalas sobre la mesa formando estos números:

a) El número mayor.

b) El número menor.

c) Un número par mayor que 500 000.

d) Un número capicúa. ¡Se lee igual de izquierda a derecha que de derecha a izquierda!

Con los números comparamos la población de una localidad para saber si es pueblo o ciudad.

Aproximo números

1 ¿Cuánto cuestan? Aproxima los precios a las unidades de millar.

Redondear a las unidades de millar

Buscamos la unidad de millar más cercana a 4 238.

• Marca entre qué unidades de millar está el 4 238.

4 000 5 000

• Señala el punto medio.

2 Copia la recta numérica en tu cuaderno y aproxima cada número a las decenas de millar.

10 000 20 000 30 000 40 000

a) 14 069   b) 36 000   c) 21 487   d) 26 572

3 Redondea estos números al orden que se indica.

a) 48 a las decenas.

b) 432 a las centenas.

c) 1 975 a las unidades de millar.

d) 25 880 a las decenas de millar.

e) 690 500 a las centenas de millar.

f) 1 075 980 a las unidades de millón.

4 ¿Qué te hace decir eso? ¿Cómo redondeas un número que está a la misma distancia de los dos extremos a los que se aproxima?

4 000 5 000 4 500

• Coloca el número en la recta.

4 000

4 238 5 000 4 500

• Como 4 238 < 4 500, elegimos la unidad de millar menor.

4 000

4 238 5 000 4 500

La unidad de millar más cercana a 4 238 es 4 000.

En estos casos siempre se elige el extremo mayor.

5 En la avenida que va de casa de María a su colegio, se han plantado 75 árboles. ¿Cuál es la oración correcta, A o B?

A Se han plantado 70 árboles, aproximadamente.

B Se han plantado 80 árboles, aproximadamente.

1 235 €

2 795 € 1 059 €

Vacaciones

En algunas ocasiones nos interesa sustituir un número por otro que tenga un valor aproximado, para que sea más fácil de recordar.

6 Redondea el número 1 627 418 a todos los órdenes de unidades. Sigue las pistas.

6 2 7 4 1 8

• A las UMM: 1 627 418 está entre 1 000 000 y 2 000 000

• A las CM: 1 627 418 está entre 1 600 000 y 1 700 000

• A las DM: 1 627 418 está entre 1 620 000 y 1 630 000

• A las UM: 1 627 418 está entre 1 627 000 y 1 628 000

• A las C: 1 627 418 está entre 1 627 400 y 1 627 500

• A las D: 1 627 418 está entre 1 627 410 y 1 627 420

7 Copia y completa la tabla, redondeando estos números a las unidades de millar.

¿Entre qué unidades de millar se encuentra? Redondeo a las unidades de millar

2 718 Entre 2 000 y 3 000 3 000

20 834 ? ?

135 655 ? ?

8 Petición del oyente ¿Verdadero o falso? Copia las oraciones verdaderas y corrige las falsas.

a) El número 372 redondeado a las decenas es 380.

b) 3 127 128 redondeado a las decenas de millar es 3 100 000.

c) Si redondeas un número que está a la misma distancia de los dos extremos a los que se aproxima, se elige el extremo mayor.

9 Redondea el mayor número de cuatro cifras a las unidades de millar. Explica a la clase cómo lo has hecho.

Redondear a cualquier orden

Para redondear 4 238 a las centenas, hacemos lo siguiente:

• Marca entre qué números está el 4 238, teniendo en cuenta el orden al que aproximas. 4 200

• Señala el punto medio.

4 200 4 300 4 250

• Coloca el número en la recta.

4200

4 238 4 300 4 250

• Como 4 238 < 4 250, elegimos la centena menor.

4 238 4 300 4 250 4 238 redondeado a las centenas es 4 200.

4200

Si las matemáticas sabes utilizar, pocas veces te podrán engañar.

Observa estos mensajes publicitarios y explica por qué son engañosos.

Practico la suma y la resta

Las operaciones nos ayudan a realizar cálculos y poder comprender mejor lo que ocurre: ¿Cuánto hay en total? ¿Cuánto falta? ¿Cuánto sobra?

1 Calcula estas operaciones e indica sus términos.

a) 425 603 + 718 021 c) 17 089   5 302

b) 1 090 300 + 25 700 d) 125 400   23 100

2 Recuerda la prueba de la resta y aplícala en cada caso.

Términos de la suma y de la resta

5 1 2 8

+ 2 7 9

5 4 0 7

2 5 8 3

7 9 0

1 7 9 3

sumandos suma minuendo sustraendo diferencia

a) 493   219 b) 5 619   1 077 c) 15 746   2 933

3 Calcula los términos que faltan. Explica a los demás cómo lo has hecho. minuendo 254 820 ? 1 750 sustraendo 84 015 760 ? diferencia ? 13 167 550

4 Copia y completa los números que faltan. ¿Qué propiedad has aplicado?

a) 95 +  ?  = 15 + 95 =  ?

b) 120 +  ?  =  ?  + 120 = 166

c) 25 + 75 + 100 =  ?  + 175 =  ?

d) 10 + 60 + 20 = 70 +  ?  =  ?

5 Calcula el total de esta compra. Pregunta a los demás en qué orden han sumado los precios. ¿Os da el mismo resultado?

Propiedades de la suma

Conmutativa

En una suma, si cambiamos el orden de los sumandos, el resultado es el mismo.

4 + 5 = 9

5 + 4 = 9

Asociativa

En una suma, si cambiamos el orden en el que agrupamos los sumandos, el resultado es el mismo.

5 + 4 + 1 = 9 + 1 = 10

5 + 4 + 1 = 5 + 5 = 10

6 Escribe dos sumas y dos restas utilizando solamente estos tres números.

7 ¿Cuántos habitantes hay en el pueblo, aproximadamente?

Para estimar una suma, redondeamos primero los sumandos.

8 Comprobamos Piensa y escribe en tu cuaderno.

a) Una suma de dos números cuyo resultado sea 400 aproximadamente.

b) Una resta cuya diferencia se estime en 400.

9 En la ciudad de Sole hay 312 345 habitantes. En la de Raúl hay 2 508 habitantes más que en la de Sole. ¿Cuántos habitantes hay en la ciudad de Raúl?

312 345 2 508 ?

Resuelve paso a paso en anayaeducacion.es Resuelve paso a paso en anayaeducacion.es

124 320

10 Una casa cuesta 124 320 € y un coche cuesta 105 000 € menos que la casa. ¿Cuánto cuesta el coche? ? 105 000

Recuerda cuando utilices la resta para resolver un problema, puedes aplicar la prueba para comprobar tu solución.

¿Sabías que hay muchas maneras de sumar y restar? Observa el ejemplo.

71 243 + 7 532

Ahora tú. Realiza estas sumas y restas descomponiendo los números.

41 255

Con las operaciones obtenemos información sobre municipios.

¡Suma y resta de otra forma!

Busco regularidades

Carla ha construido esta figura con policubos de colores. ¿Cuántos policubos necesitará para construir otra con 10 filas?

Construimos la figura paso a paso y contamos el número de policubos.

Para construir una figura de 4 filas, ha utilizado 1 + 2 + 3 + 4 policubos.

Por tanto, para construir una figura de 10 filas, necesitará esta cantidad de policubos:

Para sumar más rápido, buscamos regularidades. ¡Formamos parejas que sumen lo mismo!

Necesitará 55 policubos.

¿La solución tiene sentido?

Comprueba tu resultado con la calculadora.

1 Observa la figura que ha formado Javier con fichas de parchís. ¿Cuántas fichas necesitará añadir para que la figura tenga 10 filas?

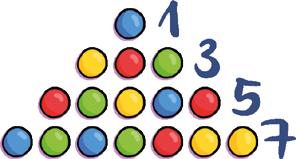
pista Observa que el número de fichas que forman las filas siempre es impar: 1, 3, 5, 7…

1 fila 1

2 filas

1 + 2 = 3

3 filas

1 + 2 + 3 = 6

4 filas

1 + 2 + 3 + 4 = 10

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

¡Qué gran idea!

Problemas exprés

2 1

¿Cuál es el mayor número de 7 cifras? ¿Y el menor?

Di un número capicúa mayor que 305 503 y otro menor.

Cálculo mental

Resuelve

6

3 5

En un pueblo hay menos habitantes que en una ciudad. Inventa cuántos puede haber en cada lugar.

4 6

El coche de Olga tiene 149 630 km. ¿Cuántos son aproximadamente? Aproxima a la decena de millar.

En una ciudad hay 2 940 311 habitantes. ¿Cuántos son aproximadamente? Aproxima a la unidad de millón. Hay 300 000 personas inscritas en la maratón, pero solo 200 000 dorsales. ¿Cuántos dorsales faltan?

Mira cómo pienso

Paso a paso

Ordena los pasos para calcular 1 250 000 + 3 500 con tu calculadora.

Enciendo la calculadora.

Presiono la tecla

Presiono la tecla

Presiono la tecla

Presiono la tecla

Presiono la tecla dos veces seguidas.

Presiono la tecla cuatro veces seguidas.

Presiono la tecla

Presiono la tecla ¡Ya lo tengo!

En anayaeducacion.es puedes ver cómo se hace.

Puedes repetir algún paso si lo necesitas.

¿Q ué he aprendido?

1 Copia y completa las oraciones en tu cuaderno.

a) El valor de las cifras de un número depende ?

b) En una suma, si cambiamos el orden de los sumandos ?

c) En una suma, si cambiamos el orden en el que agrupamos los sumandos ?

2 Completa las oraciones con las palabras del recuadro.

suma  diferencia  sumandos minuendo  sustraendo

a) Los términos de la suma son ?

b) Los términos de la resta son ?

3 ¿Cuál es el valor de las cifras de este número?

6 Descubre el código secreto. ? ? ?

1.° La cifra de las unidades es 3 unidades menor que las unidades de millar.

2.° La cifra de las decenas de millar es igual a la cifra de las decenas.

3.° La cifra de las centenas es el número posterior a la cifra de las centenas de millar.

7 En una cooperativa agrícola tienen alubias, lentejas y garbanzos.

4 Escribe las siguientes cantidades utilizando todas las cifras del 1 al 7 una sola vez.

a) El número menor.

b) El número mayor.

c) Un número par menor que 2 millones.

d) Un número impar mayor que 7 millones.

5 Completa la tabla en tu cuaderno.

Anterior Número Posterior ? 125 799 ?

2 079 999 ? ?

? ? 111 111

357 231 kg 9 342 513 kg 2 432 270 kg

a) Ordena la producción de menor a mayor.

b) ¿De qué tipo de legumbre se han recogido más de tres millones de kilos? ¿Y menos de dos millones?

c) Calcula cuántos kilos se han recogido aproximadamente.

8 Hace 47 años que Paco vive en el edificio más alto de la cuidad. María lleva 13 años más que Paco viviendo allí también. ¿Cuántos años lleva María viviendo allí?

47 13 ?

9 Los primeros Juegos Olímpicos se celebraron en 1896, y 64 años más tarde se celebraron los primeros Juegos Paralímpicos oficiales. ¿Qué año fue?

El semáforo. Junto a cada actividad, colorea así en tu cuaderno:

si has sabido la respuesta

si has necesitado ayuda

si no has sabido responder

OBJETIVO EN ACCIÓN

Elabora un listado

En España hay 8 131 municipios, de los cuales 5 372 tienen menos de 10 000 habitantes.

a) ¿Cuántos municipios tienen más de 10 000 habitantes?

b) Escribe de nuevo esta afirmación aproximando las cantidades: «En España hay 13 096 centros de salud que corresponden a un total de 27,8 por cada 100 000 habitantes».

c) Investiga la población del lugar donde vives. ¿Es ciudad o pueblo? ¿Qué servicios esenciales tiene tu localidad?

Nos planteamos

Utilizamos la estrategia El espejo para comparar la vida en las ciudades y en los pueblos.

a) Copia el organizador en tu cuaderno y completa la información.

El pueblo La ciudad Rasgos diferenciadores Similitudes Rasgos diferenciadores ? ? ?

b) Elaborad en grupo un listado de los servicios imprescindibles para vivir en una población y conseguir que:

1. Sea más inclusiva.

2. Sea más segura. Que se preocupe de nuestra salud o la seguridad ciudadana. Que tenga ofertas para todos.

¿C ómo he aprendido?

¿Cómo te sientes cuando trabajas en equipo?

Escribe tres cosas que te hagan sentir bien cuando trabajas en equipo.

Escribe tres cosas que no te dejan disfrutar del trabajo en equipo.

¿Qué puedes hacer para mejorar tu trabajo en grupo?

Figuras planas

11 Geometría de la paz

Muchas personas hablan de cambiar el mundo, de conseguir que todos vivamos en paz. ¡No debe ser fácil esto de cambiar el mundo!

Cuando hay conflictos entre nosotros, no siempre los resolvemos de manera dialogada y tranquila, como nos dicen los profes. A veces, nos decimos cosas feas o nos peleamos. Pero lo mejor es cuando nos reconciliamos, siempre nos hace sentir bien.

Deberíamos evitar llegar a ese punto, y saber resolver las cosas respetando siempre a los demás.

¿Cómo lo ves?

¿Qué símbolos de la paz conoces?

¿Cómo podemos ayudar a construir la paz?

El dato

El logo de la paz fue creado por Gerald Holtom, un diseñador inglés, en 1958.

Para esta unidad...

Objetivo en acción

¿Cómo construimos la paz?

Inventad un símbolo de la paz con figuras geométricas para promover entre las personas la importancia de vivir en paz.

¡Sigue el hilo!

Los polígonos

Los triángulos

Los polígonos

Conocer las propiedades de los polígonos nos ayuda a entender cómo son estas figuras planas.

1 Comprobamos Observa estas figuras. Copia y completa las oraciones con estas palabras.

lados  diagonales  ángulos  curva  vértices

a) La figura azul no es un polígono porque está limitada por una línea ? y otra línea poligonal

b) Un polígono tiene el mismo número de ? , ?  y ?

c) El cuadrado tiene dos ?

2 Escribe cuántos lados tienen estos polígonos.

triángulo cuadrilátero pentágono hexágono

heptágono octógono eneágono decágono

3 Traza las diagonales de un hexágono con un geoplano o dibújalas en tu cuaderno. Sigue estos pasos.

Paso 1: Elige un vértice y traza las diagonales desde él.

Paso 2: Elige otro vértice y vuelve a trazar las diagonales.

Elementos de un polígono

Un polígono es una figura plana limitada por una línea poligonal cerrada.

Sus elementos son: lados, vértices, ángulos y diagonales. lado diagonal vértice ángulo

Diagonales de un polígono

Las diagonales de un polígono son segmentos que unen dos vértices no consecutivos.

Vértices no consecutivos: hay uno o más vértices entre ellos.

Es importante dibujar las diagonales siguiendo un orden.

Paso 3: Elige el siguiente vértice y traza las diagonales sin repetir las que están trazadas.

Paso 4: Elige otro vértice y traza la diagonal que falta. ¡Ya no hay más diagonales!

4 Nombra estos polígonos e indica cuál es regular.

a) c) b) d)

5 Lee y elige la respuesta correcta.

a) ¿Es el rombo un polígono regular?

A Sí, porque sus lados y sus ángulos son iguales.

B No, porque sus lados no son iguales.

C No, porque sus ángulos no son iguales.

b) ¿Es el rectángulo un polígono regular?

A Sí, porque sus lados y sus ángulos son iguales.

B No, porque sus lados no son iguales.

C No, porque sus ángulos no son iguales.

6 Observa y completa.

a) Calcula el perímetro de estas figuras.

Polígonos regulares

Un polígono regular tiene todos sus lados y todos sus ángulos iguales entre sí.

El perímetro de un polígono es la suma de las longitudes de sus lados.

b) ¿Qué operación has utilizado para calcular el perímetro del hexágono?

A Suma B Multiplicación

c) ¿Qué operación has utilizado para calcular el perímetro del pentágono?

A Suma B Multiplicación

d) ¿Podrías calcular el perímetro del pentágono con la otra operación? Explica por qué.

Identifica figuras en símbolos de la

Los triángulos

1 Observa y contesta. Puedes utilizar los bloques geométricos para representar la figura.

a) ¿Qué figuras ves en la imagen? ¿Son regulares?

b) ¿Cuántos triángulos se han utilizado para construir este hexágono regular?

c) ¿Qué tipo de triángulos son?

2 ¿Con qué tipo de triángulos está formado este cuadrado?

¿Y este pentágono regular?

3 En una hoja cuadriculada, comprueba que puedes dibujar los triángulos y que no puedes dibujar los triángulos

Acutángulo Rectángulo Obtusángulo

Según sus lados

Escaleno: 3 lados desiguales

Isósceles: 2 lados iguales

Equilátero: 3 lados iguales Según sus ángulos

Acutángulo: 3 ángulos agudos

Rectángulo: 1 ángulo recto

Obtusángulo: 1 ángulo obtuso

Equilátero

Isósceles

Escaleno

4 ¿Cuál es el perímetro de estos triángulos?

5 Un parque tiene forma de triángulo isósceles y está rodeado de una valla de 80 m. Si el lado desigual mide 20 m, ¿cuánto miden los otros dos lados?

Clasificar triángulos nos ayuda a obtener información sobre figuras.

6

¿Cuál es la base y la altura de un triángulo? altura

base

base base

La base de un triángulo es cualquiera de sus lados.

La altura de un triángulo es el segmento perpendicular a la base que elijamos o a su prolongación, trazado desde el vértice opuesto a la base.

Para comprenderlo mejor, «Te lo cuento en un momento» en anayaeducacion.es

C C C B

El lado AB de un polígono es el segmento cuyos extremos son el punto A y el punto B.

a) Repasa el lado AB en cada triángulo.

b) En cada triángulo, traza la altura que va desde el punto C al lado AB o a su prolongación.

Si no recuerdas cómo se trazan líneas perpendiculares, «Te lo cuento en un momento» en anayaeducacion.es

7 Piensa y comparte en pareja Observa el dibujo y contesta.

a) ¿Cómo están dibujadas las bases del triángulo, con líneas continuas o con discontinuas?

b) ¿Cómo están dibujadas las alturas del triángulo?

c) Si eliges el lado azul como base del triángulo, ¿cuál es la altura?

d) ¿Y si eliges el lado rojo? ¿Y el naranja?

e) Observa que cualquier altura de este triángulo lo divide en otros dos triángulos iguales. ¿Crees que esto ocurre en todos los triángulos? Explícalo con un ejemplo.

Utiliza las propiedades de los triángulos para inventar símbolos de la paz.

Calca estos triángulos en tu cuaderno.

Los cuadriláteros

Clasificar cuadriláteros nos ayuda a obtener información sobre figuras.

Los cuadriláteros pueden tener sus lados opuestos paralelos o no.

Paralelogramos: sus lados opuestos son paralelos.

No paralelogramos: no todos sus lados opuestos son paralelos.

1 Piensa y comparte en pareja Describe las figuras anteriores. Piensa:

¿Cómo son sus lados opuestos: paralelos o no paralelos?

¿Cómo son las longitudes de sus lados?

¿Cómo son las amplitudes de sus ángulos?

2 Forma un cuadrado y un rectángulo con tiras de mecano.

a) Transforma el cuadrado en un rombo. ¿En qué se parecen?

¿En qué se diferencian?

b) Transforma el rectángulo en un romboide. ¿En qué se parecen? ¿En qué se diferencian?

Si quieres ver cómo se transforman las figuras, «Te lo cuento en un momento» en anayaeducacion.es

3 Juega con los bloques geométricos a formar hexágonos regulares con diferentes figuras.

Describe las figuras utilizando vocabulario adecuado.

¿Cuál es la base y la altura de un paralelogramo?

altura base

altura base

La base de un paralelogramo es cualquiera de sus lados.

altura base

altura base

La altura de un paralelogramo es el segmento perpendicular a la base que elijamos o a su prolongación, trazado desde uno de los vértices opuestos a la base.

4 Calca estos paralelogramos en tu cuaderno.

a) Repasa el lado AB en cada paralelogramo.

b) Traza la altura de cada figura desde un vértice opuesto al lado AB o a su prolongación.

5 La altura de un cuadrado es de 5 cm. ¿Cuál es su perímetro? Haz un dibujo si te ayuda.

6 En el Día de la Paz se celebró un gran concierto al aire libre en una explanada rectangular de 1,5 km de perímetro.

a) ¿Cuántos metros mide el perímetro?

b) Los lados más largos miden medio kilómetro cada uno. ¿Cuántos metros son?

c) ¿Cuánto miden los lados más cortos?

7 Piensa y comparte en pareja Un cuadrado y un rectángulo tienen la misma altura. ¿Pueden tener el mismo perímetro?

Utiliza las propiedades de los cuadriláteros para inventar símbolos de la paz.

La circunferencia y el círculo

Los elementos de la circunferencia y el círculo son:

La circunferencia es una línea curva cerrada. Todos sus puntos están a la misma distancia del centro.

El círculo es la figura plana delimitada por la circunferencia.

1 Completa las oraciones con estas palabras. radio   cuerda   semicircunferencias   centro

a) Los puntos de una circunferencia están todos a la misma distancia de un punto que se llama ?

b) El diámetro de un círculo mide el doble que el ?

c) El diámetro es una ? que pasa por el ? de la circunferencia.

d) Los arcos que delimita un diámetro son dos ?

2 Aprende a dibujar una circunferencia paso a paso.

1.° Abre el compás tantos centímetros como mida el radio.

2.° Pincha la aguja del compás en la hoja.

3 Traza circunferencias sin compás en la arena.

Si quieres saber cómo se hace, «Te lo cuento en un momento» en anayaeducacion.es

3.° Mueve el compás sin mover la aguja y traza la circunferencia.

Conocer las propiedades de la circunferencia y el círculo nos ayuda a entender cómo son.

Aprendo curiosidades sobre el círculo

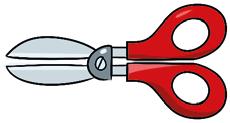
¿Qué relación existe entre la longitud de la circunferencia y el diámetro del círculo? Haz este experimento y descubre lo que ocurre. ¿Qué material necesitas?

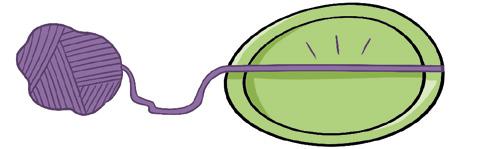
1.° Rodea el borde del plato con la lana y corta la lana.

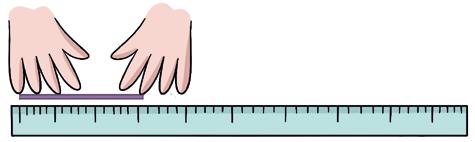
2.° Mide la lana con la regla o la cinta métrica, y apunta el resultado.

Primero, piensa qué unidad de medida eliges para medir la longitud de la lana.

3.° Estira otro trozo de cuerda sobre el diámetro del plato.

El diámetro divide al círculo en dos semicírculos iguales.

4.° Mide la lana con la regla o la cinta métrica, y apunta el resultado.

Divide la longitud del borde del plato entre la longitud de su diámetro con la calculadora. ¿Qué número obtienes?

Piensa y comparte en pareja Compartid vuestros resultados y repetid el experimento con otro objeto circular de diferente tamaño. ¿Qué observáis?

Encuentra elementos de una circunferencia en símbolos de la paz para poder comprender cómo son.

El borde del plato es la longitud de la circunferencia.

Plato circular Tijeras Regla o cinta métrica Lana o cuerda

Simetría

Reconocer simetrías en las figuras nos ayuda a conocer mejor cómo son.

Una figura es simétrica si puedes doblarla y que las dos partes coincidan.

La recta por la que se dobla la figura es el eje de simetría.

Dos figuras son simétricas respecto a un eje si las figuras son iguales pero tienen distinta orientación.

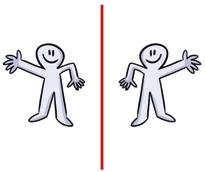
Los puntos correspondientes de las figuras están a la misma distancia del eje de simetría.

Para comprenderlo mejor, «Te lo cuento en un momento» en anayaeducacion.es

1 Indica cuáles de estos dibujos son simétricos y cuáles no.

2 Juega con un libro de espejos y encuentra los ejes de simetría de estas figuras.

a) b) c)

3 Indica cuáles de estas figuras son simétricas y cuáles no.

4 Copia este dibujo en tu cuaderno y dibuja la figura simétrica respecto al eje.

Figura simétrica

Figuras simétricas

5 Observa este alicatado y busca ejes de simetría. Comparte lo que has visto con los demás.

Busca simetrías en otras imágenes de la Alhmabra de Granada. Puedes visitar su página web.

Aprendo curiosidades de polígonos regulares

¿Cuántos ejes de simetría tienen los polígonos regulares ? Puedes descargar dibujos de polígonos regulares en anayaeducacion.es

1.° Recorta un polígono regular, por ejemplo, un triángulo equilátero.

2.° Dibuja o marca los ejes de simetría del triángulo equilátero. Puedes doblar la figura para encontrar los ejes.

3.° Haz lo mismo con otros polígonos regulares.

4.° Copia y escribe en tu cuaderno cuántos ejes de simetría tiene cada polígono regular.

• Triángulo equilátero (3 lados) tiene ? ejes de simetría.

• Cuadrado (4 lados) tiene ? ejes de simetría.

• Pentágono regular (5 lados) tiene ? ejes de simetría.

• Hexágono regular (6 lados) tiene ? ejes de simetría.

Comprobamos ¿Qué relación ves entre el número de lados de los polígonos regulares y el número de ejes de simetría?

Puedes comprobarlo con un programa de geometría dinámica en anayaeducacion.es

Traslaciones y giros

Reconocer cuándo una figura se traslada o gira, nos ayuda a comprender cómo se mueve en el plano.

1 Observa y contesta.

a) Dibuja una figura como esta en tu cuaderno y trasládala 5 cuadraditos a la derecha.

b) Ahora, parte de la figura de la derecha y trasládala 5 cuadraditos a la izquierda. ¿Qué observas?

c) Si trasladas una figura y después haces el movimiento en sentido contrario, obtienes…

A una figura distinta.

B la misma figura en el lugar de partida.

C la misma figura en otro lugar diferente a los anteriores.

2 La flecha azul indica la dirección en la que se ha trasladado el cuadrado.

Trasladar figuras

Trasladar una figura en el plano es moverla en una dirección.

7

La figura se ha movido 7 cuadraditos a la derecha.

Para comprenderlo mejor, «Te lo cuento en un momento» en anayaeducacion.es

Girar figuras

Copia estos dibujos y dibuja la flecha correspondiente a su movimiento de traslación.

3 Indica cómo se han girado estas figuras. Utiliza las expresiones:

la derecha hacia la izquierda

Girar una figura es moverla fijando un punto que se llama centro. Se puede girar en dos sentidos: hacia la derecha o hacia la izquierda.

La figura se ha girado 90° hacia la derecha.

Para comprenderlo mejor, «Te lo cuento en un momento» en anayaeducacion.es

Otras curiosidades de polígonos regulares

Si giras los polígonos regulares hasta dar una vuelta completa, ¿cuántas veces coincide cada polígono con su silueta?

1.° Recorta polígonos regulares en cartulina. Puedes descargar los dibujos en anayaeducacion.es

3.°

una chincheta en el centro de las figuras y colócalas en un corcho. Pinta la silueta de cada figura con un rotulador.

4.° Gira despacio las figuras hasta que el punto vuelva a estar en el lugar de partida, es decir, hasta que las figuras giren una vuelta completa.

¿Cuántas veces coincide la forma del polígono regular con su silueta? Escribe los resultados en tu cuaderno:

• Triángulo (3 lados) coincide ? veces.

• Cuadrado (4 lados) coincide ? veces.

• Pentágono (5 lados) coincide ? veces.

• Hexágono (6 lados) coincide ? veces.

Comprobamos ¿Qué relación ves entre el número de lados de los polígonos regulares y las veces que coincide la forma del polígono con su silueta al girarlo?

Puedes comprobarlo con un programa de geometría dinámica en anayaeducacion.es

2.° Dibuja un punto en una esquina de cada figura.

Pincha

Busco regularidades

Darío sabe que la suma de la amplitud de los ángulos interiores de un triángulo es 180°. Y se pregunta, ¿cuánto sumarán los ángulos interiores de un polígono de 20 lados?

Dibujamos polígonos más sencillos y los dividimos en triángulos para buscar regularidades.

Un polígono de 4 lados se puede dividir en 2 triángulos.

45°

60° + 45° + 75° = 180°

Un polígono de 5 lados se puede dividir en 3 triángulos.

La suma de los ángulos interiores es:

180° × 2  = 360°

4   2

Un polígono de 6 lados se puede dividir en 4 triángulos.

La suma de los ángulos interiores es:

180° × 3  = 540°

5   2

Un polígono de 7 lados se puede dividir en 5 triángulos.

La suma de los ángulos interiores es:

180° × 4  = 720°

6   2

La suma de los ángulos interiores es:

180° × 5  = 900°

7   2

Observamos que, para calcular la suma de los ángulos interiores, multiplicamos 180° por el número de lados del polígono menos 2.

Entonces, en un polígono de 20 lados:

180° ×  (20   2) = 180° ×  18 = 3 240°

La suma de los ángulos de un polígono de 20 lados es 3 240°.

1 ¿Cuántos ejes de simetría tiene un dodecágono regular? Dibuja polígonos regulares más sencillos y busca regularidades.

Un dodecágono es un polígono de 12 lados.

Problemas exprés

Cálculo mental

¿En qué se parecen un cuadrado y un rectángulo?

3

Si la altura de un triángulo coincide con uno de sus lados, ¿cómo es el triángulo?

1 5

¿Es un rectángulo un polígono regular? Explica por qué.

Mira cómo pienso

Paso a paso

¿En qué se parecen un rombo y un romboide?

4

Si para trazar una circunferencia abres 5 cm un compás, ¿cuánto medirá el radio de la circunferencia?

2 6

¿Cuántos ejes de simetría tiene un hexágono regular?

¿Sabes que puedes demostrar con trocitos de papel cuánto suman los ángulos interiores de cualquier triángulo o de cualquier cuadrilátero?

La suma de los ángulos interiores de un triángulo es 180°.

Resuelve

La suma de los ángulos interiores de un cuadrilátero es 360°.

Si necesitas ayuda, «Te lo cuento en un momento» en anayaeducacion.es

¿Q ué he aprendido?

1 ¿Cuántos cuadrados encuentras en esta figura? Una pista: Hay cuadrados de 3 tamaños.

4 Copia el dibujo en tu cuaderno e indica cómo se llaman los elementos del círculo.

2 Observa este esquema de los paralelogramos y contesta.

5 Explica si ves simetrías, traslaciones o giros en estas imágenes.

a) Si el rombo tiene 4 lados iguales y ángulos iguales 2 a 2, ¿es el cuadrado un tipo de rombo?

b) Si el rectángulo tiene 4 ángulos iguales y lados iguales 2 a 2, ¿es el cuadrado un tipo de rectángulo?

c) Si el romboide tiene lados paralelos 2 a 2 y ángulos iguales 2 a 2, ¿es el rombo un tipo de romboide? ¿Y el rectángulo?

3 Mide el radio y el diámetro de estas circunferencias, y completa en tu cuaderno.

–  El diámetro de una circunferencia o de un círculo mide ? que el radio.

–  El radio de una circunferencia o de un círculo mide ? que el diámetro.

El semáforo. Junto a cada actividad, colorea así en tu cuaderno: si has sabido la respuesta si has necesitado ayuda

si no has sabido responder

OBJETIVO EN ACCIÓN

Inventa un símbolo de la paz

a) Estas figuras simbolizan la paz. Identifica los elementos geométricos que las forman.

b) ¿Crees que las líneas cortas de la primera figura son radios de la circunferencia? ¿Por qué?

Nos planteamos

a) ¿Por qué es importante vivir en paz? Utilizamos la estrategia Considera todos los factores para argumentar tu respuesta. Copia el organizador y completa en tu cuaderno.

Razón 1

Razón 6

Es importante vivir

Razón 2

Razón 5

Razón 4

Razón 3

b) En equipo inventad un símbolo de la paz con figuras geométricas. Explicad su significado a otras clases y promoved la importancia que tiene vivir en paz.

¿C ómo he aprendido?

Completa en tu cuaderno. ¿Colaboras todo lo que debes en el trabajo en grupo?

Escribe tres cualidades que aportes en el trabajo en grupo.

Escribe tres situaciones en las que no hayas colaborado cuanto debías en el trabajo en grupo.

¿Qué puedes hacer para participar de modo más activo en tu equipo?

Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.

© GRUPO ANAYA, S.A., 2023 - C/ Valentín Beato, 21 - 28037 Madrid.