Operació món: Matemàtiques 6º. Illes Balears (demo)

IllesBalears

Matemàtiques

LLICÈNCIA 12 MESOS

1 5 9

2 6 10

3 7 11

4 8 12

Nombres i operacions Suma’t a l’objectiu de cuidar la vida

Múltiples i divisors Abraça la pau

Potències Connectats

Nombres decimals i operacions Uneix-te al consum responsable

Com podem fer per cuidar els arbres? Cream junts un arbre de la vida amb missatges per cuidar la naturalesa.

Vida d’ecosistemes terrestres

Per què és necessari treballar per aconseguir la pau? Construïm la pau amb abraçades: dissenya una campanya per fomentar les abraçades de 8 segons.

Per què és important que tots tenguem accés a Internet? Dissenya una camiseta per reivindicar el dret de tots i totes a l’accés a la informació.

Com podem aconsellar a les companyes i companys perquè duguin a terme un consum responsable? Debatem sobre si s’ha de donar paga o no i com emprar-la de manera responsable.

REPÀS TRIMESTRE 1 STEAM

Com podem establir aliances entre nosaltres? Crea ALIA’T!, un espai per generar aliances entre persones.

Sistema mètric decimal Vols ser científic o científica?

Percentatge i proporcionalitat Organitza el teu temps lliure

Els angles i la seva mesura

Dibuixar per cuidar

Polígons Diferències que sumen

Figures circulars Innov, innoves, innovam

Cossos geomètrics

Premi per cuidar la mar

Atzar i probabilitat

Predir el futur

Què podem fer per donar a conèixer que no tots tenim les mateixes oportunitats d’aprendre? Fem un concurs literari amb el títol: «Vull ser científic o científica».

Com pot afectar l’ús dels dispositius electrònics el benestar dels adolescents?

Elabora un pla d’oci alternatiu a la tecnologia per a al·lotes i al·lots de la teva edat.

Com podem conscienciar tothom de la necessitat de cuidar l’aigua? Dibuixam un logo per fomentar la necessitat de cuidar l’aigua.

REPÀS TRIMESTRE 2 STEAM

Quines altres dones han contribuït en el camp de les matemàtiques? Elabora una línia del temps indicant-ne dades personals i les seves aportacions.

Com podem entrenar la creativitat per donar respostes innovadores als problemes actuals?

Mesura la teva creativitat!

Què podem fer per cuidar les nostres mars? Elabora un trofeu amb figures geomètriques per premiar les bones pràctiques que cuiden la mar.

Què podem fer per frenar el canvi climàtic? Elabora una infografia amb recomanacions d’accions per frenar el canvi climàtic.

REPÀS TRIMESTRE 3 STEAM

Pau, justícia i institucions sòlides

Indústria, innovació i infraestructura

Producció i consum responsables

Aliances per aconseguir objectius

Educació de qualitat

Salut i benestar

Aigua neta i sanejament

Igualtat de gènere

Indústria, innovació i infraestructura

Vida submarina

Acció pel clima

SABERS BÀSICS

• El sistema de numeració decimal. Tècniques de recompte.

• Operacions bàsiques amb nombres naturals. Propietats.

• Operacions combinades.

• Nombres positius i negatius.

• Comparació i ordenació.

• Coordenades cartesianes.

• Problemes aritmètics: de canvi, d’igualació, de comparació.

HO RESOLC SENSE PROBLEMA

• Estratègia heurística: Desxifr codis

• Càlcul mental: Multiplicar per 4

• Pensament computacional: Descomposició

• Estratègia heurística: Cerc totes les respostes possibles

Múltiples d’un nombre. Mínim comú múltiple.

• Divisors d’un nombre. Màxim comú divisor. Criteris de divisibilitat.

• Nombres primers i compostos.

• Càlcul mental: Multiplicar per 20

• Pensament computacional: Generalització

• Potència d’un nombre natural.

• Quadrats i cubs.

• Arrel quadrada.

• Dècimes, centèsimes i mil·lèsimes. Nombres lectura, escriptura i valor de posició. Preus.

• Comparació i ordenació de nombres decimals.

• Potències de base 10.

• Descomposició polinòmica.

• Arrodoniment de nombres decimals. Suma, resta, multiplicació i divisió de nombres.

• Problemes aritmètics: de comparació, de grups iguals, de repartiment, d’agrupació.

• Estratègia heurística: Cerc regularitats

• Càlcul mental: Multiplicar per 50

• Pensament computacional: Codificació

• Estratègia heurística: Estim la solució

• Càlcul mental: Dividir entre 4

• Pensament computacional: Descomposició

PROJECTE INTERDISCIPLINARI · La caixa màgica i com cuidar-la: Misteris de la caixa màgica

• Fracció. Fracció i unitat. Fraccions pròpies i impròpies.

• Fracció d’una quantitat.

• Fraccions equivalents. Fracció irreductible.

• Comparació de fraccions.

• Unitats de mesura de longitud, capacitat, massa, superfície i volum.

• Transformació d’unitats.

• Magnituds proporcionals.

• Reducció a la unitat. La regla de tres.

• Percentatges. Percentatge d’una quantitat.

• Classificació d’angles segons l’amplitud i la posició.

• Mesura d’angles: graus, minuts i segons.

• Suma, resta, multiplicació i divisió de fraccions.

• Problemes aritmètics: de combinació, de comparació multiplicadora, de canvi, de grups iguals, d’agrupació.

• Expressions complexes i incomplexes.

• Problemes aritmètics: de combinació, de canvi, d’agrupació.

• Augments i descomptes. L’escala: gràfica i numèrica.

• Suma i resta d’angles.

• Problemes aritmètics: d’igualació.

• Estratègia heurística: Planteig preguntes intermèdies

• Càlcul mental: Dividir entre 20

• Pensament computacional: Generalització

• Estratègia heurística: Començ per casos més senzills

• Càlcul mental: Multiplicar per una fracció

• Pensament computacional: Generalització

• Estratègia heurística: Faig un esquema

• Càlcul mental: 1 4 d’una quantitat

• Pensament computacional: Funcions

• Estratègia heurística: Faig un dibuix

• Càlcul mental: 10 % d’una quantitat

• Pensament computacional: Algoritme

PROJECTE INTERDISCIPLINARI · Ara o mai: Salut planetària

• Polígons: elements i classificació.

• Polígons còncaus i convexos.

• Perímetre de polígons.

• La circumferència. El cercle i les figures circulars.

• Posició de punts, rectes i circumferències.

• Poliedres i cossos rodons.

• Poliedres regulars.

• Cossos de revolució.

• Experiències d’atzar.

• Esdeveniment segur, possible i impossible.

• Àrea de paral·lelograms i triangles.

• Àrea de polígons regulars.

• Àrea de figures compostes.

• El nombre π. Longitud de la circumferència.

• Àrea del cercle.

• Àrea i volum de prismes.

• Àrea i volum de piràmides.

• Àrea i volum de figures compostes.

• Probabilitat d’un esdeveniment. Regla de Laplace. Tècniques de recompte.

• Estratègia heurística: Començ per casos més senzills

• Càlcul mental: 50 % d’una quantitat

• Pensament computacional: Generalització

• Estratègia heurística: Faig un dibuix

• Càlcul mental: 20 % d’una quantitat

• Pensament computacional: Generalització

• Estratègia heurística: Elimin possibles respostes

• Càlcul mental: Multiplicar per 0,1

• Pensament computacional: Generalització

• Estratègia heurística: Analitz una mostra de dades

• Càlcul mental: Multiplicar per 0,5

• Pensament computacional: Dades

PROJECTE INTERDISCIPLINARI · Pulmó verd: Per extingir

El sistema de numeració decimal

En el nostre sistema de numeració, la posició de les xifres en determina el valor.

Com sumaries els nombres de l’1 al 100?

Com comptes quants n’hi ha?

Digues nombres entre 10 000 i 1 000 000.

Imagina que no existissin els nombres.

Reescriu aquesta notícia.

Descarrega la notícia a anayaeducacion.es

Indica'n diversos exemples.

PARELLS IMPARELLS

1 Copia la taula i escriu-hi aquests nombres. Indica el valor de la xifra 5 en cada cas.

CMM DMM UMM CM DM UM C D U

? ? ? ? ? ? ? ? ?

a) Set milions tres-cents vuit mil cinc-cents vint-i-u.

b) Cent quaranta milions cent trenta-cinc mil sis-cents.

2 Llegeix i escriu aquest nombre d’esquerra a dreta i de dreta a esquerra.

Què observes? Quin tipus de nombre és? Escriu-ne altres exemples.

Cent milions!

Coneixes alguna cosa que es pugui comptar per milions?

UMM unitats de milió

DMM desenes de milió

CMM centenes de milió

3 Observa l’exemple i descompon aquests nombres.

87 604 021

8 0 000 000 +  7  000 000 +  6 00 000 +  4  000 +  2 0 +  1

8 × 10 000 000 +  7 × 1 000 000 +  6 × 100 000 +  4 × 1 000 +  2 × 10 +  1

a) 125 386 090 b) 9 999 999 c) 31 402 578

4 Un bilió és un milió de milions. Però en altres països, com Anglaterra, significa mil milions. Escriu un bilió de les dues formes possibles.

UN BILIÓ ONE BILLION

5 Segueix les pistes i descobreix quin és el document nacional d’identitat, o DNI, d’en Jordi.

PISTA 1: És un nombre de 8 xifres, però la xifra de les desenes de milió no té valor.

PISTA 2: La xifra de les unitats de miler és igual que la xifra de les centenes de miler.

Una hectàrea és un hectòmetre quadrat.

6 Tal com hem llegit al començament de la unitat: «El món ha perdut una superfície de 178 milions d’hectàrees de bosc des del 1990». Quantes centenes de milió són aproximadament?

Si no recordes com s’aproximen nombres, «T’ho explic en un moment» a anayaeducacion.es

Com comptes quants n’hi ha?

Observa la imatge i explica com comptes quants n’hi ha.

Hi ha moltes maneres de fer-ho i totes fantàstiques!

I si…

… cada element val 1 D?

… cada element val 1 C?

… cada element val 1 UM?

Comptaries de la mateixa manera?

Explica les teves raons.

Amb nombres grans pots comptar la quantitat d’arbres que es perden o es guanyen anualment a la Terra.

Operacions bàsiques

La suma, la resta, la multiplicació i la divisió són les operacions bàsiques que utilitzam per resoldre situacions matemàtiques senzilles.

1 Llapis al centre Llegeix i resol-ho.

a) Quants de punts tenen entre l’equip vermell i el blau?

b) Quants en té l’equip vermell més que el verd?

c) Si els punts de l’equip groc són 5 vegades els del blau, quants de punts són?

d) Quin és l’equip guanyador? Hi ha cap empat?

2 El document nacional d’identitat està format per un nombre de 8 xifres i una lletra.

a) En parelles, cercau informació sobre els passos que s’han de seguir per al càlcul de la lletra del DNI.

b) Juga a descobrir la lletra de qualsevol DNI a anayaeducacion.es

3 Pensa i contesta.

Quina és la propietat del residu?

4 Esquema Fes un esquema al quadern amb aquests conceptes i afegeix-ne un exemple en cada cas.

TERMES PROPIETATS

5 Un fotògraf d’espais naturals té 125 320 fotografies de boscs de fulla caduca i 93 008 de boscs de fulla perenne. Quantes fotografies té aproximadament? Primer arrodoneix cada dada a les unitats de miler.

1

628150 ?

125630

Si no ho recordes, «T’ho explic en un moment» a anayaeducacion.es

Si ho necessites, pots descarregar la informació a anayaeducacion.es

125 320

?

93 008

Resol-ho pas a pas a anayaeducacion.es

6 En un bosc han plantat 2 585 arbres. Si ara hi ha 24 310 arbres, quants n’hi havia al principi?

2 585 ? 24 310

7 A la ciutat de Màlaga vivien 571 026 habitants l’any 2018. Si la ciutat de Sevilla hagués tengut 117 685 habitants menys, les dues ciutats haurien tengut la mateixa població. Quants d’habitants tenia Sevilla?

571 026 117 685 ?

Si planten arbres, aleshores al principi n’hi havia menys que ara.

Són dades de l’any 2018.

Resol-ho pas a pas a anayaeducacion.es

2 139 705

8 A la fira del llibre més important de l’any, s’han venut 2 139 705 novel·les. Són 1 850 329 més que els contes infantils que s’han venut. Quants de contes són? ?

1 850 329

9 N’Emma canvia el seu vehicle per una furgoneta més sostenible. Ha pagat 6 000 � d’entrada i la resta ho pagarà en 40 quotes iguals. Si la furgoneta costa 40 000 � , quants de doblers li queden per pagar? Quant haurà de pagar a cada quota?

Descompondre per operar

Resol-ho pas a pas a anayaeducacion.es

Pagar 40 quotes significa pagar 40 vegades.

Hi ha altres maneres de resoldre operacions, com la descomposició dels termes. Practica per trobar la manera que et resulti més ràpida o senzilla.

SUMA o RESTA: 16 489 5 226

MULTIPLICACIÓ: 257 × 25

1 6 4 8 9 =  10 000 + 6 000 + 400 + 80 + 9

5 2 2 6 = − 5 000 − 200 − 20 − 6

10 000 +  1  000  + 200 + 60 + 3 = 11 263

«T’ho explic en un moment» a anayaeducacion.es

• Calcula descomponent els termes. Prepara bé la resta duent-ne.

a) 25 730 + 500

b) 8 423 − 2 980

c) 125 × 15

Màlaga Sevilla

Màlaga Cadis

Sevilla

Còrdova Jaén Granada Almeria

Huelva

Operacions combinades

1 Observa i relaciona cada nombre amb la lletra corresponent.

Per resoldre expressions amb diverses operacions, calculam:

1r Operacions entre parèntesis.

A Dos paquets de quatre bolis blaus, i dos bolis vermells.

2 × 4 + 2

2 Resol-ho al quadern.

a) 5 + 4 × 3

b) 10 − 2 × (3 + 1) + 5

B Dos paquets de: quatre bolis blaus i dos bolis vermells.

2 × (4 + 2)

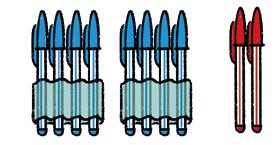
c) 4 × 7 − 24 : 2

d) 5 × (3 + 18) − (20 − 4)

Si necessites ajuda, «T’ho explic en un moment» a anayaeducacion.es

3 Converteix aquestes oracions en expressions numèriques i calcula’n els resultats.

a) Multiplica per 3 la suma de 8 i 4.

b) Al doble de 3 suma el producte de 5 i 8.

c) Multiplica per 6 la suma de 4 i 3, i resta-n’hi 9.

d) Suma a 20 el producte de 4 per la diferència de 10 menys 6.

4 1–2–4 Copia i posa parèntesis, o no, per obtenir el major i el menor resultat en cada cas.

90 + 10 × 5 90 – 10 × 5

5 Escriu una expressió amb parèntesis que contengui una suma i una multiplicació i que doni com a resultat 100.

100

2n Multiplicacions i divisions d’esquerra a dreta.

3r Sumes i restes d’esquerra a dreta.

No passa res si t’equivoques. L’error és part de l’aprenentatge!

Si no poses parèntesis, el signe de la resta afecta el resultat de la multiplicació.

1.

2.

De vegades és útil escriure diverses operacions en una sola expressió, però és important saber l’ordre en què es resol.

6 Copia i posa parèntesis on ho necessitis per aconseguir les solucions que s’indiquen.

a) 5 × 3 + 2 × 4

Possibles solucions: 68 55 23 100

b) 2 × 5 + 100 : 5

Possibles solucions: 42 30 22 50

c) 10 + 2 × 5 5 : 5

Possibles solucions: 19 18 3 59

7 A la cistella de la compra d’en Bruno hi ha 2 caixes de bombons de 28 � cada una, peix per valor de 32 � i 4 malles de taronges de 4 � cada una. Però... li falten 4 � per pagar la compra!

a) Quant costa la compra? Escriu-ho amb una expressió.

b) Quants de doblers tenia en Bruno?

c) Si una amiga li presta 20 � , quants de doblers li sobren?

Parèntesis i claudàtors

Feim feina en parelles per compartir punts de vista diferents.

• Hi ha expressions matemàtiques amb parèntesis i claudàtors. Com es resolen?

250 + (100 + 50) × [10 − (3 + 2)] [ ] claudàtors ( ) parèntesis

• Molt fàcil! Només has de seguir aquests passos:

1r Resol l’expressió entre claudàtors.

250 + (100 + 50) × [10 − (3 + 2)] = 250 + (100 + 50) × [10 − 5] = 250 + (100 + 50) × 5 Aplica-hi la jerarquia d’operacions.

2n Resol els parèntesis.

250 + (100 + 50) × 5 = 250 + 150 × 5

3r Resol la resta de les operacions aplicant-hi la jerarquia d’operacions.

250 + 150 × 5 = 250 + 750 = 1000

• Ara, resol al quadern aquestes expressions.

a) (2 + 3) × [100 : (1 + 4)]

b) [100 : (7 + 3)] × [150 − (20 + 30)]

Nombres positius i negatius

Amb aquests nombres podem mesurar temperatures, situar-nos en les plantes d’un edifici o conèixer la profunditat a la qual es troba un tresor a la mar.

• Els nombres +1, +2, +3, +4… són nombres positius.

• Els nombres −1, −2, −3, −4… són nombres negatius.

El conjunt de nombres enters està format pels nombres negatius, el nombre 0 i els nombres positius.

1 Amb quins nombres representes aquestes expressions: positius o negatius? Classifica-ho en una taula.

a) Pujar – Baixar c) Deure – Rebre

b) Guanyar – Perdre d) Davall zero – Damunt zero

2 Ho comprovam Copia les oracions i escriu el nombre positiu o negatiu que correspon en cada cas.

Negatius Positius ? ?

a) c)

Baix 3 plantes.

−3

He perdut 10 punts.

b) d)

Tenc 20 �

Està a 1 200 m damunt del nivell de la mar.

Vaig a la planta –2.

El congelador està a –18 °C.

El tresor es troba a 75 m davall de la mar.

3 Quina temperatura marca cada termòmetre?

Quan un nombre no duu signe, és positiu. 5 = + 5

4 Dibuixa i marca els nombres que corresponen.

a) Un edifici amb 6 plantes i 3 soterranis.

b) Un submarí a 150 m davall del nivell de la mar.

c) Un avió volant a 2 100 m d’altura.

5 N’Anna agafa l’ascensor al tercer pis. Baixa 5 plantes per tirar els fems i puja una planta per agafar la bicicleta.

a) En quina planta es troben els fems?

b) I les bicicletes?

Representar nombres enters a la recta numèrica

• Quina d’aquestes temperatures és la màxima? I la mínima?

• Per comparar els nombres, els situam a la recta numèrica.

Els nombres negatius se situen a l’esquerra del 0.

Qualsevol nombre és menor que els que estan situats a la seva dreta a la recta numèrica.

Els nombres positius se situen a la dreta del 0.

Qualsevol nombre és major que els que estan situats a la seva esquerra a la recta numèrica.

Pren nota!

• Un termòmetre marca −4 °C i arriba fins als +5 °C. Quina temperatura marca el termòmetre en aquest recorregut? Indica-ho de manera ordenada.

Usa els nombres positius i negatius per expressar si es guanyen o es perden arbres a la Terra. Si necessites ajuda, «T’ho explic en un moment» a anayaeducacion.es

Coordenades cartesianes

Per representar punts en el pla, empram les coordenades cartesianes.

Els eixos cartesians són dues rectes amb aquestes característiques.

• Són dos eixos perpendiculars.

• Es numeren de la mateixa manera que a la recta numèrica.

• Es tallen en el punt 0 dels dos eixos.

• Divideixen la quadrícula en quatre parts que es diuen quadrants.

Un punt es representa en un pla mitjançant dues coordenades.

• La primera coordenada es llegeix a l’ eix horitzontal.

• La segona coordenada es llegeix a l’ eix vertical.

1 Observa la imatge i contesta les preguntes.

a) Indica al quadern quines són les coordenades dels punts senyalats.

b) Quina és la primera coordenada del punt que està sobre l’eix vertical?

c) Quina és la segona coordenada del punt que està sobre l’eix horitzontal?

2 Situa aquests punts en un eix de coordenades. Dibuixa-ho al quadern.

A = (+3, −1) B = (0, 0) C = (−5, +2)

El camí més curt

En Tomàs està repoblant una zona d’un bosc en el punt (+4, +4). Necessita comprovar si en unes altres dues zones, (−3, −2) i (−7, +4) és necessària la repoblació.

Si en Tomàs va primer a la zona més pròxima, quina zona serà?

1r Situam les dades en un eix de coordenades.

– En Tomàs està en el punt (+4, +4).

– Ha d’anar a les zones (−3, −2) i (−7, +4).

2n Unim el punt on està en Tomàs amb els altres dos punts.

3r Mesuram els segments amb un regle i comparam les longituds. La longitud més curta ens indica quina és la zona més pròxima a en Tomàs.

a) En parelles, triau una altra posició per a en Tomàs i uns altres dos punts. Cercau quin és el punt més pròxim.

b) Na Marta està justament en el punt (−3, −2). En quin quadrant està en Tomàs? I na Marta?

• Tria un punt del segon quadrant que estigui més a prop d’en Tomàs que de na Marta.

• Tria un punt del quart quadrant que estigui més a prop de na Marta que d’en Tomàs.

Desxifr codis

N’Olívia sap que els antics romans usaven un sistema de numeració diferent del nostre. Ha vist xifres romanes en alguns edificis de la seva ciutat. Si el seu edifici es va construir el 1953, com s’escriuria l’any en què es va construir sa casa en xifres romanes?

Els antics romans usaven 7 lletres majúscules per representar els nombres. Cada lletra tenia un valor diferent.

I V X L C D M

1 5 10 50 100 500 1 000

REGLES PER ESCRIURE XIFRES ROMANES

1a Descomponem el nombre en unitats i substituïm els nombres per les lletres del seu valor.

2a Les lletres I, X, C i M es poden repetir fins a tres vegades seguides.

3a Si col·locam les lletres I, X o C a l’esquerra d’una altra de major valor, se’n resten els valors.

Amb aquesta informació, escrivim en romà el nombre 1 953:

1r Descomponem el nombre en unitats.

1 953 = 1 000 + 900 + 50 + 3

2n Substituïm els nombres per lletres, aplicant-hi les regles anteriors.

1 000 + 900 + 50 + 3

M CM L III

Com que el valor de C és menor que el de M:

CM = 1 000 − 100 = 900

L’any de construcció s’escriu MCMLIII.

La solució té sentit?

La lletra I repetida tres vegades és:

1 + 1 + 1 = 3

1953

És molt important descompondre el nombre en unitats.

Sumam els valors de les lletres i comprovam que el resultat és 1 953.

MCMLIII → 1 000 + (1 000 − 100) + 50 + 1 + 1 + 1 = 1 953

1 Escriu alguns nombres importants per a tu en el sistema de numeració romà.

Treballa amb el sistema de numeració romà a anayaeducacion.es

2 Inventa el teu propi sistema de numeració i escriu-hi alguns nombres.

Problemes exprés

2 1

Quin és el major nombre de 9 xifres? I el menor?

Quantes unitats de miler té 1 000 000?

Càlcul mental

Resol 12 × 4.

3 5

Si repartim una quantitat entre 25, poden sobrar 25 unitats? Explica per què.

El termòmetre marcava −1 °C, però ara fa més fred. Quina temperatura pot fer ara?

Mira com pens

Conta una història a partir de l’expressió:

10 : 5 – 2

4 6

Digues les coordenades d’un punt de cada quadrant.

Divideix i venceràs

A anayaeducacion.es pots veure com es fa.

Ara, fes-ho tu.

6 ×  4

8 ×  4

9 ×  4

7 ×  4

14 ×  4

×  4

×  4

×  4

×  4

Imagina que vols cercar el significat d’una paraula al diccionari i, en obrirlo, les paraules estan desordenades. Quin embolic!

Ordenar és important. Ajuda a comprendre la informació fàcilment.

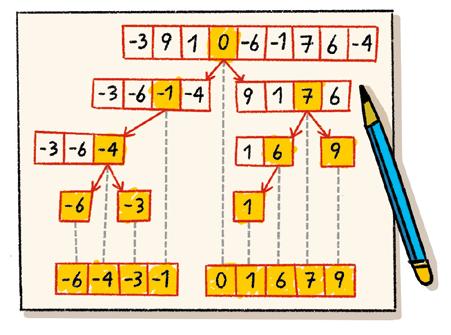
Hi ha un mètode per ordenar ràpidament els elements d’un conjunt anomenat quicksort . Observa com es fa:

1r Triam un nombre qualsevol que anomenem pivot.

2n Comparam un a un la resta dels elements amb el pivot.

– Si l’element és menor que el pivot, l’escrivim a l’esquerra.

– Si l’element és major que el pivot, l’escrivim a la dreta.

Practica el mètode quicksort a anayaeducacion.es

Q uè he après?

1 Quin nombre correspon a cada descomposició?

a) 3 UMM + 2 CM + 6 UM + 7 D + 2 U

b) 2 000 000 + 100 000 + 20 000 + 3

2  Indica el valor de la xifra 4 en aquests nombres.

a) 649 d) 240 012

b) 4 e) 4 830 000

c) 4 913 f) 24 120 948

3  Quants anys té na Lara? Segueix els passos.

6  Dibuixa un eix de coordenades en un full de paper.

a) Situa-hi aquests punts.

A = (+3, +5) C = (−3, −5)

B = (+3, −5) D = (−3, +5)

b) Uneix els punts. Quina figura has dibuixat?

7  Dibuixa un quadrilàter que tengui els quatre vèrtexs sobre els eixos de coordenades. Escriu les coordenades de cada vèrtex.

8  En una granja ecològica hi ha 57 000 ous. Si se’n venen 3 542 dotzenes, quants d’ous queden?

1r Fixa’t en la xifra de les desenes de miler del nombre 527 341.

2n Calcula el triple d’aquesta xifra.

3r Suma-li la xifra de les desenes.

4t El resultat és l’edat de na Lara!

9  Un centre mèdic té 5 250 vacunes. La primera setmana s’han posat 2 296 vacunes, i la segona, 1 985. Si hi ha 1 200 persones en llista d’espera, hi haurà vacunes a bastament?

10  En una estació d’esquí el termòmetre marcava 3 °C a les 8 del dematí. Al migdia la temperatura va pujar 8 °C i a les 20:00 va baixar 4 °C respecte al migdia. Quina era la temperatura a les 20:00?

5 Escriu l’expressió numèrica que correspon a aquests textos. Després, calcula’n els resultats.

a) A 25 n’hi sum 75 i el resultat el multiplic per 2.

b) Multiplic 8 per la diferència de 25 i 5.

c) Al quocient de dividir 16 entre 4 sum el resultat de restar 5 de 9 i multiplicar-lo per 3.

El semàfor. Al costat de cada activitat, acolorix així en el quadern:

al quadern:

si has sabut la resposta

si has necessitat ajuda

si no has sabut respondre-la

pinta-ho

OBJECTIU EN ACCIÓ

Crea un arbre de la vida

Observa les següents dades aproximades sobre la pèrdua de milions d’hectàrees de boscs en els diferents continents.

Entre 1990 i 2000 Entre 2000 i 2010 Entre 2010 i 2020

Àfrica Se’n varen perdre 3 milions. Se’n varen perdre 3 milions. Se’n varen perdre 4 milions.

Amèrica del Sud Se’n varen perdre 5 milions. Se’n varen perdre 6 milions. Se’n varen perdre 3 milions.

Europa

Se’n varen guanyar 1 milió. Se’n varen guanyar 2 milions. Se’n varen guanyar 1 milió.

Oceania Se’n varen perdre 1 milió. Se’n varen perdre 1 milió. Se’n varen guanyar 1 milió.

a) Copia la taula i expressa el guany o pèrdua a l’any de cada continent mitjançant nombres positius o negatius.

b) Quants de milions d’hectàrees va guanyar o va perdre cada continent al final de les tres dècades?

c) Quants de milions d’hectàrees varen guanyar o varen perdre en total entre els quatre continents en les tres dècades? Expressa aquesta quantitat en unitats.

d) Quin continent en va guanyar més? Quin continent en va perdre més?

Ens ho plantejam

Usam l’estratègia Conseqüències i resultats per analitzar per què és bo treballar en equip.

a) Copia i completa l’organitzador.

b) Investiga quina és la imatge de l’arbre de la vida i què representa.

c) En equip, cream un arbre de la vida gegant per a la nostra escola i hi penjam missatges per defensar la naturalesa. Convidam tota l’escola a participar-hi.

C om ho he après?

Completa-ho al quadern.

Què

ocorrerà

si desapareixen els arbres?

A llarg termini Què pot passar? Quines conseqüències produirà? Quins resultats tendrà?

A curt termini Què pot passar? Quines conseqüències produirà? Quins resultats tendrà?

Identifica tres fortaleses que tenguis per treballar a l’àrea de Matemàtiques.

Identifica tres aspectes que puguis millorar en el treball de matemàtiques..

Què pots fer per millorar-los?

Múltiples d’un nombre

Calculam els múltiples d’un nombre per saber quants n’hi ha en total en diversos grups iguals.

Al pati de l’escola han pintat mans blanques com a símbol de la pau. Entre tots i totes han decidit que a cada dit escriuran el nom d’un al·lot o al·lota de l’escola.

•  Si no hi ha mans pintades, no hi ha espais per escriure noms.

5  × 0 = 0

•  En una mà hi ha 5 espais per escriure noms.

5  × 1 = 5 Quants n’hi haurà en dos, tres, quatre… mans?

5  × 2  = 5 + 5 = 10

5  × 3 = 5 + 5 + 5 = 15

5  × 4 = 5 + 5 + 5 + 5 = 20

1 Llegeix l’exemple i completa-ho al quadern.

20 és múltiple de 5 perquè 5 × 4 = 20.

a) 24 és múltiple de 8 perquè ?  ×  ? =   ?

b) 30 és múltiple de 2 perquè ?  ×  ? =   ?

c) 100 és múltiple de 10 perquè ?  ×  ? =   ?

2 Cerca aquests nombres a la taula 100.

Múltiples de 5. Múltiples de 10.

Els parells es poden agrupar de 2 en 2!

3 Pensa i contesta les qüestions al quadern.

a) Escriu els deu primers múltiples de 2.

b) Troba un múltiple de 2 que sigui major que 100.

2 ×  ?  = major que 100!

c) Quin tipus de nombres són els múltiples de 2?

d) Són aquests nombres múltiples de 2? Explica per què.

14 50 21 158 3 726

e) Escriu altres nombres que siguin múltiples de 2.

f) És possible escriure tots els múltiples de 2? Per què?

4 A la botiga d’en Pau venen packs de 4 iogurts. Llegeix i contesta les preguntes raonadament.

a) Quants de iogurts hi ha en 3 packs ?

b) És possible comprar 15 iogurts exactament?

c) Quants de packs compraries si necessites 15 iogurts?

5 Què et fa dir això? Pensa i explica per què aquestes oracions són vertaderes.

El 0 és múltiple de qualsevol nombre.

Tot nombre és múltiple de si mateix.

No és possible escriure tots els múltiples d'un nombre.

Múltiples comuns

Quins són els múltiples de 2? I de 3? En tenen cap en comú?

Els nombres parells acaben en 0, 2, 4, 6 u 8.

Els nombres imparells acaben en 1, 3, 5, 7 o 9.

Així represent els múltiples de 2 i de 3 en el diagrama. Múltiples de 2 Múltiples de 3

a) Dibuixa al quadern els diagrames amb:

– Múltiples de 2 i de 5.

Múltiples de 2 Múltiples de 5

– Múltiples de 5 i de 10.

Múltiples de 5 Múltiples de 10

b) Què observes en el darrer diagrama? Explica-ho amb les teves paraules.

Pren

en un temps fixat.

Usa els múltiples per analitzar quantes abraçades pots donar

nota!

Mínim comú múltiple

Per calcular el mínim comú múltiple de dos nombres, feim el següent:

Mínim comú múltiple de 4 i de 6.

1r Calculam els primers múltiples de cada nombre.

Múltiples de 4: 0, 4, 8, 12, 16, 20...

Múltiples de 6: 0, 6, 12, 18, 24, 30...

2n Cercam els múltiples comuns i triam el menor, sense tenir en compte el 0.

Múltiples de 4: 0, 4, 8, 12 , 16, 20, 24

Múltiples de 6: 0, 6, 12 , 18, 24 , 30...

Si necessites ajuda, «T’ho explic en un moment» a anayaeducacion.es

1 Calcula el mínim comú múltiple d’aquests nombres. Expressa-ho amb un diagrama com el de l’exemple.

a) 4 i 10

b) 3 i 7 c) 8 i 6 d) 4 i 5

2 En Dídac va al cine del barri cada 14 dies i na Maria va al mateix cinema cada 21. Si han coincidit en el cine l’1 d’octubre, quin dia tornaran a coincidir-hi? Segueix aquests passos.

Pas 1: Calcula diversos múltiples de 14 i de 21, fins que trobis el primer que sigui comú. × 1 × 2 × 3 × 4 14 ? ? ? ? 21 ? ? ? ?

Pas 2: Fes un esquema que representi la situació i cerca la data en un calendari. 14 14 14 21 21

3 L’autobús A passa per la parada al costat de la casa de Lluc cada 3 minuts i l’autobús B hi passa cada 5 minuts. Si els dos hi passen a les 8 del matí…

a) Quan tornen a coincidir-hi?

b) De 8 a 9 del dematí, a quines hores coincideixen a la parada?

Dels múltiples comuns, el menor és el 12. m.c.m. (4, 6) = 12

Múltiples de 4 Múltiples de 6

Calculam el mínim comú múltiple per saber quin és el menor dels múltiples iguals.

4 Aturada de 5 minuts Al dematí, el despertador d’en Nico sona cada 15 minuts; el d’en Biel, cada 5 minuts i el de na Martina, cada 10 minuts. Els tres despertadors sonen per primera vegada a les 07:30.

a) Quan tornaran a sonar els tres despertadors alhora?

N ico B iel M artina

Cada 15 min. Cada 5 min. Cada 10 min.

b) S’aixequen la segona vegada que sonen els despertadors alhora, i tarden mitja hora a berenar i arreglar-se. A quina hora acaben?

c) Recullen el berenar i fan el llit en 10 minuts. Llavors, surten cap a l’escola i tarden 15 minuts a arribar-hi caminant. Arribaran puntuals si entren a les 9 en punt?

Relacions especials: Quin és el m.c.m. de dos nombres, un múltiple d’un altre?

Quin és el mínim comú múltiple de 5 i 100? En un nanosegon ho pots saber!

Quan un nombre és múltiple d’un altre, el mínim comú múltiple d’aquests nombres és el major dels dos.

m.c.m. (5, 100) = 100

100 és múltiple de 5.

• Troba el mínim comú múltiple d’aquests parells de nombres.

Un nanosegon és una mil milionèsima part d’un segon, és a dir, 0,000000001 segons.

Pots comprovar el teu resultat amb reglets i una quadrícula que pots descarregar a anayaeducacion.es

Divisors d’un nombre

Calculam els divisors d’un nombre per saber quantes vegades hi cap un altre nombre de manera exacta.

De quantes formes es poden agrupar 10 persones en grups iguals sense que en sobri cap?

Poden fer grups d’1, de 2, de 5 i de 10 persones.

Els divisors del nombre 10 són 1, 2, 5 i 10.

Un nombre és divisor d’un altre si en fer la divisió el residu és 0.

Dividend divisor 0 quocient

Els divisors d’un nombre són menors o iguals que aquest nombre.

1 Calcula els divisors d’aquests nombres.

5 7 6 8 9

2 Llegeix l’exemple i completa-ho al quadern.

5 és divisor de 20 perquè 20 : 5 = 4 (residu 0).

a) 8 és divisor de 24 perquè ? : ? = ? (residu 0).

b) 2 és divisor de 30 perquè ? : ? = ? (residu 0).

c) 10 és divisor de 100 perquè ? : ? = ? (residu 0).

3 Calcula d’aquesta manera els divisors de 18.

4 Les variacions De quantes formes es poden col·locar 12 cadires en diverses files iguals?

Si necessites ajuda, «T’ho explic en un moment» a anayaeducacion.es

5 Na Cèlia té 24 m de corda. La vol tallar en trossos per fer diverses cordes de la mateixa grandària. De quantes formes ho pot fer? Quina deu haver triat? Explica per què.

Divisors comuns

uins són els divisors de 12? I de 18? En tenen cap en comú?

Divisors de 12

Divisors de 18

a) Dibuixa al quadern els diagrames amb: – Divisors de 2 i 15.

Divisors de 2

Divisors de 15

– Divisors de 5 i 10.

Divisors de 5

Així represent els divisors de 12 i 18 en el diagrama.

Divisors de 10

b) Què observes en el darrer diagrama? Explica-ho amb les teves paraules.

Usa el concepte de divisor d’un nombre per calcular el nombre d’abraçades que pots donar.

Màxim comú divisor

Per calcular el màxim comú divisor de dos nombres, feim el següent:

Màxim comú divisor de 12 i de 18.

1r Calculam els divisors de cada nombre.

Divisors de 12: 1, 2, 3, 4, 6, 12 Divisors de 18: 1, 2, 3, 6, 9, 18

Dels divisors comuns, el major és el 6. m.c.d. (12, 18) = 6

2r Cercam els divisors comuns i triam el major.

Divisors de 12: 1 , 2 , 3 , 4, 6 , 12

Divisors de 18: 1 , 2 , 3 , 6 , 9, 18 6

Si necessites ajuda, «T’ho explic en un moment» a anayaeducacion.es

1 Calcula el màxim comú divisor d’aquests nombres. Expressa-ho amb un diagrama com el de l’exemple.

a) 8 i 10 b) 15 i 18 c) 24 i 36 d) 9 i 21

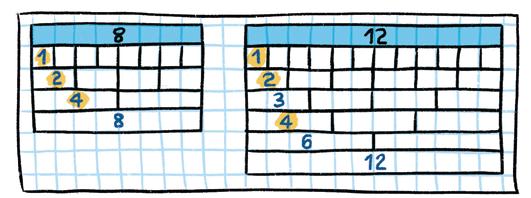
2 Pensa i comparteix en parella N’Olívia té una corda blava de 12 m i una corda groga de 8 m. Talla les dues cordes en trossos de la mateixa grandària sense que sobre corda.

a) De quantes formes pot tallar les cordes?

b) Quina serà la longitud màxima de cada tros?

Una ajuda: Fes un esquema com aquest. Observa els divisors comuns i quin és el major.

Divisors de 12 Divisors de 18

3 En una llibreria exposen les novetats en dues prestatgeries, a la mateixa distància uns llibres d’uns altres.

a) Si les estanteries fan 12 dm i 16 dm, respectivament, cada quants decímetres poden col·locar els llibres? Indica’n tots els casos possibles.

b) Creus que totes les opcions es poden dur a terme? Explica per què.

c) Si col·loquen els llibres respectant el major espai possible entre aquests, cada quants de decímetres ho faran?

12 dm

16 dm

Calculam el màxim comú divisor per saber quin és el major dels divisors iguals.

4 A 6è A hi ha 20 estudiants i a 6è B, 16. La setmana vinent aniran d’excursió al Palau de les arts.

Una ajuda: cerca els divisors de 20 i de 16, i troba’n els comuns.

a) Si formen equips iguals sense mesclar estudiants de les dues classes, de quantes persones poden ser els equips? 20 16

6è A 6èB

b) Si volen anar a l’excursió amb el màxim nombre de persones en cada equip, quantes persones el formaran?

c) Quants equips es formen a 6è A? I a 6è B?

d) A l’excursió van també 6 professors i professores. Contracten un microbús de 16 places i un altre de 26. Com es poden distribuir si els estudiants d’un mateix equip no es poden separar i ha d’anar professorat a cada autobús?

Relacions especials. Quin és el m.c.d. de dos nombres, l'un divisor d’un altre?

Quin és el màxim comú divisor de 5 i de 100? Un instant i… el tens!

Quan un nombre és divisor d’un altre, el màxim comú divisor d’aquests nombres és el menor dels dos.

m.c.d. (5, 100) = 5

5 és divisor de 100.

Troba el màxim comú divisor d’aquests parells de nombres.

Pots comprovar el teu resultat amb reglets i una quadrícula que pots descarregar a anayaeducacion.es .

Criteris de divisibilitat

Usam els criteris de divisibilitat per saber quins són alguns dels divisors d’un nombre.

1 Troba en la taula 100 els nombres que són divisibles per 2, 4, 3, 9, 5 i 10. Comprova que ho has fet bé amb els criteris de divisibilitat.

Divisibles per 2

Divisibles per 4

14 és divisible per 2 perquè en dividir 14 : 2 el residu és 0.

Un nombre és divisible per 2 si acaba en 0 o en xifra parella.

Divisibles per 3

Un nombre és divisible per 4 si el nombre que formen les dues darreres xifres és múltiple de 4 o acaba en 0.

Divisibles per 9

Un nombre és divisible per 3 si la suma de les xifres és un múltiple de 3.

Divisibles per 5

Un nombre és divisible per 9 si la suma de les xifres és un múltiple de 9.

Divisibles per 10

Un nombre és divisible per 5 si acaba en 0 o en 5.

Un nombre és divisible per 10 si acaba en 0.

Pots descarregar la plantilla de la taula 100 a anayaeducacion.es

2 Copia i completa les taules amb els nombres que s’hi indiquen.

3 Observa els resultats de l’activitat anterior i contesta.

a) Tots els nombres divisibles per 2 ho són per 4?

Tots els nombres divisibles per 4 ho són per 2?

b) Tots els nombres divisibles per 3 ho són per 9?

Tots els nombres divisibles per 9 ho són per 3?

c) Tots els nombres divisibles per 5 ho són per 10?

Tots els nombres divisibles per 10 ho són per 5?

4 A l’escola de na Isabel hi ha 116 estudiants de 6è de Primària. Es volen organitzar en grups de 2, de 3 o de 4 per vendre paperetes del viatge de fi de curs. Ho poden fer?

5 Petició de l'oïdor Investiga-ho amb la calculadora. Què ha d’ocórrer perquè un nombre sigui divisible per 6?

Embarbussament?

Semblen embarbussaments però són, simplement, enunciats equivalents. És a dir, enunciats diferents que signifiquen el mateix. Per exemple:

10 és DIVISIBLE per 2

2 és DIVISOR de 10

10 és Múltiple de 2

• Fes el mateix amb aquests parells de nombres. És senzill si ho penses bé!

a) 3 i 60 b) 9 i 45

c) 50 i 200 d) 10 i 1 000

Pensa que: 6 = 2  × 3

Amb els criteris de divisibilitat podràs calcular el nombre exacte d’abraçades que pots donar.

Nombres primers i composts

Distingim nombres primers i composts per saber si tenen 2 o més divisors.

Si en un full quadriculat dibuixes els nombres del 2 al 10 i els seus divisors… Què observes?

Efectivament!

• Hi ha nombres que només tenen dos divisors: l’1 i ell mateix. Són nombres primers. Per exemple: 2, 3, 5 i 7.

• Altres nombres tenen més de dos divisors: l’1, ell mateix i altres divisors. Són nombres composts. Per exemple: 4, 6, 8, 9 i 10.

Un nombre és primer si només té dos divisors: l’1 i ell mateix. Un nombre és compost si té més de dos divisors.

Usa la calculadora si ho necessites.

Per descobrir alguns divisors, pots usar els criteris de divisibilitat.

1 Classifica aquests nombres en primers i composts.

2 Demostra que aquests nombres no són primers.

3 Quins nombres primers hi ha de l’1 al 100? Segueix aquests passos amb la taula 100.

Pas 1: Retxa el nombre 1, no es considera primer.

Pas 2: Retxa els múltiples de 2 (són divisibles per 2).

Pas 3: Retxa els múltiples del nombre següent que no apareix retxat (3)..

Pas 4: Segueix així fins que acabis la taula.

També ho pots fer a anayaeducacion.es.

4 Quin problema! Hi ha 31 persones per a la visita guiada al museu, però han d’anar en diversos grups del mateix nombre de persones. Ho poden fer? I si s’uneixen 2 persones més a la visita?

5 Na Katia vol col·locar les 23 taules de l’aula en diverses files amb el mateix nombre de taules.

a) Creus que ho pot fer? Explica per què.

b) Podria si fossin 24 taules? Descriu-ne totes les formes possibles.

Descompondre en factors primers

Pots descompondre qualsevol nombre en factors primers. Per fer-ho, segueix aquests passos:

Descompon 280

1r Cerca dos factors qualssevol de 280.

280 = 28 × 10

2n Cerca dos factors d’aquests factors. 28 = 4 × 7 10 = 2 × 5

3r Fes el mateix fins que tots els factors siguin nombres primers. 4 = 2 × 2

4t Ja ho tens! Expressa el nombre amb tots els seus factors primers.

Ordena els factors per donar-ne una solució més elegant.

Cerc totes les respostes possibles

A 6è de Primària hi ha menys de 100 estudiants. Aquesta setmana han de formar grups iguals per participar en la realització d’un gran mural sobre la pau. Han comprovat que, perquè tots hi participin, es poden col·locar en grups de 7 o de 3, però no per parelles. Quants estudiants hi ha a 6è de Primària?

Per esbrinar-ho, cercam totes les respostes possibles amb ajuda de la taula 100.

1r Triam els múltiples de 7 menors que 100.

A 6è de Primària hi pot haver 21 o 63 estudiants.

La solució té sentit?

Comprovam que els resultats compleixen les condicions.

- Són nombres menors que 100.

- Són múltiples de 7 i de 3.

- No són múltiples de 2.

1 En una gimcana han participat entre 40 i 70 persones. Per realitzar les diferents proves, s’han col·locat en grups de 2 o de 9 sense que en sobràs cap. Quantes persones han participat a la gimcana?

2 En Carles té una baralla amb menys de 100 cartes. S’ha adonat que si són 3, 4 o 7 jugadors, cada un rep el mateix nombre de cartes i no en sobra cap. Quantes cartes té la baralla?

Problemes exprés

Càlcul mental

Podries escriure tots els múltiples del nombre 5? Explica la resposta.

Com a mínim, quants de divisors té qualsevol nombre?

1 3 5

De pressa! Digues cinc nombres primers.

Mira com pense

Desxifrant codis

Digues tots els divisors del nombre 10.

Com es diu el conjunt de nombres naturals que no són divisibles per 2?

2 4 6

És 123 456 789 un nombre primer? Explica per què.

Escriu un poema sobre alguna cosa que t’agradi. Segueix el mateix patró que té el poema de Sophie Germain:

- Estrofes de 4 versos.

- Versos de 8 síl·labes, en la majoria dels casos.

Llibertat, Igualtat, Fraternitat! Respectam els drets de tota la Humanitat!

Sophie escoltava aquells crits amb una atenció extraordinària. Encara era molt petita, però era revolucionària.

Ella volia ser lliure, igual que ho eren els nens, però aviat va descobrir que ser nena era diferent.

No podia anar a l’escola. no deixaven que estudiés, ni tan sols que llegís res, ni els llibres que tenia a la vora.

Però la Sophie no acceptava aquella forma de pensar. D’amagat, a les nits, es dedicava a estudiar.

De gran, sempre signava les cartes i els treballs com si ella fos un home per tal que li fessin cas.

Encara que havia lluitat amb tantes dificultats, Sophie va fer una carrera plena de genialitats.

Pots descarregar el poema a anayaeducacion.es.

Els poemes semblen cançons perquè seguixen una estructura ordenada.

Va estudiar, entre d’altres coses, els nombres primers, per fi! Els que no es deixen dividir ni tan sols pels seus veïns.

I així Sophie posà en marxa la seva revolució, ja que els seus càlculs canviaren el món per a millor.

Q uè he après?

1 Llegeix i escriu al quadern:

a) Els cinc primers múltiples dels nombres següents. 6 12 100

b) Tots els divisors d’aquests nombres. 10 20 50

2 Pensa i contesta les preguntes sense fer operacions.

a) Per què aquests nombres no són múltiples de 10? 7 3 4 9

b) Per què aquests nombres no són divisors de 10? 33 15 20 100

3 Calcula el mínim comú múltiple d’aquests parells de nombres. 4 i 7 6 i 9

4 Calcula el màxim comú divisor d’aquests parells de nombres. 10 i 15 8 i 16

5 Sense fer càlculs! Pensa i contesta:

a) m.c.m. (5, 10) i m.c.d. (5, 10)

b) m.c.m. (2, 12) i m.c.d. (2, 12)

6 Usa els criteris de divisibilitat per a esbrinar si aquests nombres són divisibles per 2, 3, 4, 5, 9 o 10.

12

900 150 123 40

7 Copia i completa la xifra de les unitats d’aquests nombres perquè siguin divisibles per 3. 2_ 13_ 28_ 104_

8 Indica quins d’aquests nombres són primers i quins són composts. Explica per què. 3 12 31 35 17 20

9 En 1 minut! Amb ajuda de la taula 100, senyala els nombres primers que veus.

Descarrega la taula a anayaeducacion.es.

10 Na Sol té 80 € en monedes de 2 € .

a) Podrà fer 2 paquets amb la mateixa quantitat de monedes?

b) Podrà fer-ne 3 paquets? I 4?

c) Podrà fer-ne 5 o 10 paquets?

d) En els casos que sí que pugui, indica quantes monedes tendrà cada paquet.

11 N’Aina surt a córrer cada 2 dies i na Berta surt cada 5 dies. Si coincideixen aquest dilluns, quin dia de la setmana tornaran a coincidir?

12 Una coca rectangular fa 24 cm de llarg i una altra amb la mateixa forma fa 30 cm. Si en Pere les vol tallar en porcions iguals, de quantes formes ho pot fer? Quina triaries tu?

El semàfor. Al costat de cada activitat, pinta-ho així al quadern:

si has sabut la resposta

si has necessitat ajuda

si no has sabut respondre-la

OBJECTIU EN ACCIÓ

Dissenya una campanya per fomentar les abraçades

Avui dematí hem provat si hi havia diferència entre una abraçada de 3 segons i una altra de 8 segons. Ha estat molt divertit perquè ens hem abraçat realment!

a) Si he estat fent abraçades ininterrompudament durant 15 segons…

– Quantes abraçades he fet si eren de 3 segons?

– Podria haver fet només abraçades de 8 segons? Per què?

– Podria haver fet abraçades de 8 segons i de 3 segons?

Quantes de cada classe?

b) Respon les mateixes preguntes si hagués fet abraçades durant 24 segons.

c) Si a la meva classe hi ha 20 persones, quant de temps com a mínim necessit per poder abraçar tothom amb abraçades de 3 segons? I de 8? Justifica la teva resposta.

Ens ho plantejam

Empram l’estratègia Punts cardinals per analitzar per què és necessari construir la pau.

Quina informació necessitaries per respondre a la pregunta de per què és necessari construir la pau?

Necessitat

No tenguis en compte el temps que tardes entre abraçada i abraçada.

Quins obstacles veus en la construcció de la pau?

a) Copia i completa l’organitzador al quadern.

b) En equips, dissenyau una campanya per fomentar les abraçades de 8 segons. Poseu-la en marxa a l’escola, en el vostre entorn, en les reunions familiars…

C om ho he après?

Completa-ho al quadern.

Obstacle Preocupació

Entusiasme Emocions

Suggeriments

Posicions

Quina és la teva opinió personal sobre el tema? Quins suggeriments faries per a la construcció de la pau?

Què t’entusiasma d’aquesta idea?

Creus que la pau es construeix?

Escriu tres emocions positives que sentis quan estàs fent les activitats de matemàtiques.

Escriu tres emocions negatives que sorgeixin quan treballes aquesta àrea. Què podries fer per canviar-les?

© GRUPO ANAYA, S.A., 2022 - C/ Valentín Beato, 21 - 28037 Madrid.

Reservats tots els drets. El contingut d’aquesta obra està protegit per la llei, que estableix penes de presó, multes o ambdues ensems, ultra les indemnitzacions corresponents per danys i perjuís, per a aquells qui reproduïren, plagiaren, distribuïren o comunicaren públicament, en tot o en part, una obra literària, artística o científica, o la seua transformació, interpretació o execució artística fixada en qualsevol tipus de suport o comunicada per qualsevol mitjà sense autorització prèvia.