Mundua helburu: Matematika 6º (demoa)

1 5 9

2 6 10

3 7 11

4 8 12

Zenbakiak eta eragiketak Zaindu bizia

eta zatitzaileak Besarkatu

Berreketak Konektatuta

Zenbaki dezimaldunak eta eragiketak Kontsumitu arduraz

eta

Sistema metriko hamartarra Zientzialari izan nahi?

Ehunekoa eta proportzionaltasuna Antolatu zure aisialdia

Angeluak eta angeluen neurria Marraztu, zaintzeko

Poligonoak Aldeen garrantzia

Irudi zirkularrak Ni, zu, gu... Denok berritzaile

Gorputz geometrikoak Itsasoa zaintzeak saria du

Zoria eta probabilitatea Etorkizuna iragartzea

DIZIPLINARTEKOA

IKASKUNTZA-EGOERA HELBURUA AURRERA GJH

Zer egin dezakegu zuhaitzak zaintzeko?

Egin dezakegun elkarrekin biziaren zuhaitz bat, natura zaintzearen aldeko mezu eta guzti.

Zergatik da garrantzitsua bakea lortzearen alde jardutea?

Sortu dezagun bakea besarkadekin: diseinatu kanpaina bat, 8 segundoko besarkadak sustatzeko.

Zergatik da garrantzitsua denok izatea eskura Internet?

Diseinatu kamiseta bat, informazioa eskuratzeko eskubidea denok izan behar dugula aldarrikatzeko.

Zer esan diezaiekegu ikaskideei arduraz kontsumi dezatela gomendatzeko?

Eztabaidatu dezagun ea paga eman behar den edo ez eta zer egin behar den paga arduraz erabiltzeko.

1. HIRUHILEKOAREN BERRIKUSPENA STEAM: Grace Hooper

Nola egin ditzakegu gure artean itunak, elkartuta aritzeko? Sortu ELKARTU!, jendea helburu berberen alde jarduteko gunea.

Nola eman dezakegu jakitera denok ez ditugula ikasteko aukera berberak?

Egin dezagun literatura-lehiaketa bat, izenburu hau duena: Zientzialari izan nahi dut

Zer-nolako eragina izan dezake nerabeen ongizatean gailu elektronikoen erabilerak?

Prestatu teknologiarekin zerikusirik ez duen aisialdi-plan alternatibo bat zure adineko neska-mutilentzat.

Nola kontzientziatu dezakegu jendea ura zaindu beharraz?

Marraztu dezagun logo bat, ura zaintzea sustatzeko.

2. HIRUHILEKOAREN BERRIKUSPENA STEAM: Sophie Germain

Zer beste emakumek egin dituzte ekarpen garrantzitsuak matematikaren esparruan?

Denbora-lerro batean, adierazi haien datu pertsonalak eta ekarpenak.

Nola treba dezakegu sormena gaur egungo arazoei erantzun berritzaileak emateko?

Neurtu zure sormena!

Zer egin dezakegu gure itsasoak zaintzeko?

Egin trofeo bat irudi geometrikoekin, itsasoa zaintzearekin lotutako jardunbide zuzenak saritzeko.

Lehorreko bizitza

Bakea, justizia eta erakunde sendoak

Industria, berrikuntza eta azpiegitura

Ekoizpen eta kontsumo arduratsua

Itunak, helburuak garatzeko

Kalitate oneko hezkuntza

Osasuna eta ongizatea

Edateko ura eta saneamendua

Generoberdintasuna

Industria, berrikuntza eta azpiegitura

Uretako bizitza

Zer egin dezakegu klima-aldaketa geldiarazteko?

Egin infografia bat, klima-aldaketa geldiarazteko zenbait gomendio emateko.

3. HIRUHILEKOAREN BERRIKUSPENA STEAM: Clara Grima

Klima babesteko ekintza

OINARRIZKO JAKINTZAK EBATZI BAIETZ!

• Zenbaki positiboak eta zenbaki negatiboak.

• Zenbaki-sistema hamartarra. Zenbatzeko teknikak.

• Oinarrizko eragiketak zenbaki arruntekin. Propietateak.

• Eragiketa konbinatuak.

• Zenbaki baten multiploak. Multiplo komun txikiena. Zenbaki baten zatitzaileak. Zatitzaile komun handiena.

• Zenbaki arrunt baten berreketa.

• Karratuak eta kuboak.

• Erro karratua.

• Hamarrenak, ehunenak eta milarenak.

• Zenbaki dezimaldunak: irakurtzea, idaztea eta posizio-balioa. Prezioak.

• Zenbaki dezimaldunak konparatzea eta ordenatzea.

• Konparatzea eta ordenatzea.

• Koordenatu kartesiarrak.

• Problema aritmetikoak: aldaketa-, berdinketaeta konparazio-problemak.

Zatigarritasun-irizpideak.

• Zenbaki lehenak eta zenbaki konposatuak.

• 10 oinarriko berreketak.

• Deskonposizio polinomikoa.

• Zenbaki dezimaldunak biribiltzea.

• Zenbakien arteko batuketak, kenketak, biderketak eta zatiketak.

• Problema aritmetikoak: konparazio-, banaketa- eta multzokatze-problemak, eta multzo berdinak

• Estrategia heuristikoa: Deszifratu kodeak.

• Buruzko kalkulua: 4z biderkatzea.

• Pentsamendu konputazionala: Deskonposizioa.

• Estrategia heuristikoa: Bilatu erantzun posible guztiak.

• Buruzko kalkulua: 20z biderkatzea.

• Pentsamendu konputazionala: Orokortzea.

• Estrategia heuristikoa: Bilatu erregulartasunak.

• Buruzko kalkulua: 50ez biderkatzea.

• Pentsamendu konputazionala: Kodetzea.

• Estrategia heuristikoa: Kalkulatu soluzioa iritzira.

• Buruzko kalkulua: 4z zatitzea.

• Pentsamendu konputazionala: Deskonposizioa.

DIZIPLINARTEKO PROIEKTUA · Kutxa magikoa eta haren zaintza: Kutxa logikoa

• Zatikiak. Zatikia eta unitatea. Zatiki propioak eta inpropioak.

• Kopuru baten zatikia.

• Zatiki baliokideak. Zatiki laburtezina.

• Zatikiak konparatzea.

• Luzera, edukiera, masa, azalera eta bolumena adierazteko neurri-unitateak.

• Unitate-aldaketak.

• Magnitude proportzionalak.

• Unitatera sinplifikatzea. Hiruko erregela.

• Ehunekoak. Kopuru baten ehunekoa.

• Angeluen sailkapena, zabaleraren eta posizioaren arabera.

• Angeluak neurtzea: graduak, minutuak eta segundoak.

• Zatikien arteko batuketak, kenketak, biderketak eta zatiketak.

• Problema aritmetikoak: konbinazio-, aldaketaeta multzokatze-problemak, biderketazko konparaziokoak eta multzo berdinak egitekoak.

• Adierazpen konplexuak eta adierazpen sinpleak.

• Problema aritmetikoak: konbinazio-, aldaketaeta multzokatze-problemak.

• Igoerak eta beherapenak. Eskala: grafikoa eta zenbakizkoa.

• Estrategia heuristikoa: Egin tarteko galderak.

• Buruzko kalkulua: 20z zatitzea.

• Pentsamendu konputazionala: Orokortzea.

• Estrategia heuristikoa: Hasi egoera errazagoetatik.

• Buruzko kalkulua: Zatiki batez biderkatzea.

• Pentsamendu konputazionala: Orokortzea.

• Estrategia heuristikoa: Egin eskema bat.

• Buruzko kalkulua: Kopuru baten 1 4

• Pentsamendu konputazionala: Funtzioak.

• Estrategia heuristikoa: Egin marrazki bat.

• Angeluen arteko batuketak eta kenketak.

• Problema aritmetikoak: berdinketa-problemak.

• Buruzko kalkulua: Kopuru baten % 10.

• Pentsamendu konputazionala: Algoritmoa.

DIZIPLINARTEKO PROIEKTUA · Orain edo inoiz ez: Zer aztarna uzten duzu?

• Poligonoak: elementuak eta sailkapena.

• Poligono ahurrak eta poligono ganbilak.

• Poligonoen perimetroa.

• Zirkunferentzia. Zirkulua eta irudi zirkularrak.

• Puntuen, zuzenen eta zirkunferentzien posizioa.

• Poliedroak eta gorputz biribilak.

• Poliedro erregularrak.

• Biraketa-gorputzak.

• Zorizko esperimentuak.

• Gertaera ziurra, posiblea eta ezinezkoa.

• Paralelogramoen eta triangeluen azalera.

• Poligono erregularren azalera.

• Irudi konposatuen azalera.

• π zenbakia. Zirkunferentziaren luzera.

• Zirkuluaren azalera.

• Prismen azalera eta bolumena.

• Piramideen azalera eta bolumena.

• Irudi konposatuen azalera eta bolumena.

• Gertaera baten probabilitatea. Laplaceren erregela. Zenbatzeko teknikak.

• Estrategia heuristikoa: Hasi egoera errazagoetatik.

• Buruzko kalkulua: Kopuru baten % 50.

• Pentsamendu konputazionala: Orokortzea.

• Estrategia heuristikoa: Egin marrazki bat.

• Buruzko kalkulua: Kopuru baten % 20.

• Pentsamendu konputazionala: Orokortzea.

• Estrategia heuristikoa: Baztertu erantzun ezinezkoak.

• Buruzko kalkulua: 0,1ez biderkatzea.

• Pentsamendu konputazionala: Orokortzea.

• Estrategia heuristikoa: Aztertu datu-lagin bat.

• Buruzko kalkulua: 0,5ez biderkatzea.

• Pentsamendu konputazionala: Datuak.

DIZIPLINARTEKO PROIEKTUA · Birika berdea: Iraul ditzagun datuak

1 Zaindu bizia

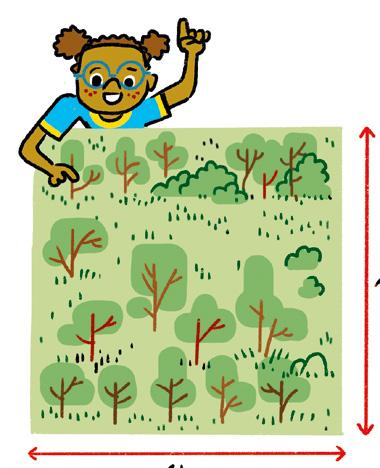
Gaur egun dugun erronka handienetako bat planeta zaintzearen garrantziaz jabetzea eta planeta zaintzen laguntzea da. Zergatik da garrantzitsua flora babestea, zehazki zuhaitzak, ingurumena zaintzea lortzeko? Zuhaitzek espezie-aniztasuna babesten dute, oxigenoa sortzen dute, klima-aldaketari aurre egiten laguntzen dute eta animaliek nahiz gizakiok jateko behar ditugun fruituak ematen dituzte. Onura horiek eta beste asko ditugu zuhaitzei esker.

Zuhaitzak gure lagunak eta kideak dira. Zaindu zuk ere gure planetako bizia! Babestu zuhaitzak!

Unitate honetarako...

Helburua aurrera

Zergatik da beharrezkoa zuhaitzak zaintzea?

Egin biziaren zuhaitz bat, natura zaintzearen aldeko mezu eta guzti.

hariari!

Eragiketa

konbinatuak

Zenbaki positiboak eta negatiboak

Koordenatu kartesiarrak

Zenbaki-sistema hamartarra

Gure zenbaki-sisteman, zifren balioa zenbakian duten posizioaren araberakoa da.

Nola batuko zenituzke 1etik 100era arteko zenbakiak?

Nola zenbatuko duzu zenbat dauden?

ZENBAKI ARRUNTAK

Imajinatu zenbakirik ez dagoela.

Berridatzi albiste hau.

Deskargatu albistea hemen: anayaharitza.es

Jarri adibide batzuk.

BIKOITIAK BAKOITIAK

1 Kopiatu taula, eta idatzi bi zenbakiak han. Adierazi zenbat balio duen 5 zifrak zenbaki bakoitzean.

EMM HMM MM EM HM M E H U ? ? ? ? ? ? ? ? ?

a) Zazpi milioi hirurehun eta zortzi mila bostehun eta hamaika.

b) Ehun eta berrogei milioi ehun eta hamabost mila eta seiehun.

2 Irakurri eta idatzi zenbaki hau ezkerretik eskuinera eta eskuinetik ezkerrera:

Zer gertatzen da? Nolakoa da zenbakia? Idatzi beste adibide batzuk.

Esan 10 000tik

1 000 000ra bitarteko zenbaki arrunt batzuk.

Ehun milioi!

Ezagutzen duzu milioika dagoen zerbait?

MM milioikoak

HMM hamar milioikoak

EMM ehun milioikoak

EMMHMM MM EM HM M E H U

3 Ikusi arretaz adibidea, eta deskonposatu zenbakiak.

87 604 021

8 0 000 000 +  7  000 000 +  6 00 000 +  4  000 +  2 0 +  1

8 × 10 000 000 +  7 × 1 000 000 +  6 × 100 000 +  4 × 1 000 +  2 × 10 +  1

a) 125 386 090

b) 9 999 999

c) 31 402 578

4 Bilioi bat, guretzat, milioi bat milioi da. Baina Ingalaterran eta beste herrialde batzuetan, mila milioi da. Idatzi, zifraz, zenbat den bilioi bat bi modu hauetan:

BILIOI BAT ONE BILLION

5 Irakurri pistak, eta jakin hiru nortasun-agirietatik zein den Kauldirena.

1. PISTA: Zenbakiak 8 zifra ditu, baina hamar milioikoen zifrak ez du baliorik.

2. PISTA: Milakoen zifra eta ehun milakoen zifra berdinak dira.

6 Unitatearen hasieran irakurri dugun bezala, «1990etik gaur arte, gure planetak 178 milioi hektareako baso-azalera galdu du». Zenbat ehun milioiko dira, gutxi gorabehera?

Zenbakiak nola hurbiltzen diren oroitzen ez bazara, «Berehala kontatuko dizut», webgunean: anayaharitza.es

Nola zenbatuko duzu zenbat dauden?

Ikusi irudia, eta azaldu nola zenbatuko duzun zenbat dauden. Hori zenbatzeko modu asko daude, eta modu bikainak dira denak!

Eta…

… elementu bakoitzak 1 H balio badu?

… elementu bakoitzak 1 E balio badu?

… elementu bakoitzak 1 M balio badu?

Berdin zenbatuko zenuke? Azaldu zure arrazoiak.

Gogoan hartu!

Zenbaki handiak erabiliz, Lurrean urtean zenbat zuhaitz galtzen edo lortzen diren zenbatu dezakezu.

Hektarea bat hektometro karratu bat da.

Oinarrizko eragiketak

1 Lapitzak erdira Irakurri, kalkulatu eta erantzun.

a) Zenbat puntu dituzte talde gorriak eta talde urdinak biek batera?

Batuketa, kenketa, biderketa eta zatiketa dira oinarrizko eragiketak, eta eguneroko bizitzako egoera matematiko errazak ebazteko erabiltzen ditugu. 1

b) Talde berdeak baino zenbat puntu gehiago ditu gorriak?

c) Talde horiak talde urdinak baino 5 aldiz puntu gehiago baditu, zenbat puntu ditu?

d) Zer taldek irabazi du? Berdinketarik izan da?

2 Nortasun-agiriak 8 zifrako zenbaki bat eta letra bat ditu.

a) Binaka jarrita, bilatu informazioa, jakiteko zer urrats egin behar diren NANeko letra kalkulatzeko.

b) Jolastu edozein NANeko letra zein den asmatzera, webgunean: anayaharitza.es

3 Pentsatu eta erantzun.

Zein da hondarraren propietatea?

4 Eskema Egin koadernoan eskema bat kontzeptu hauekin, eta idatzi adibide bat kasu bakoitzean.

GAIAK PROPIETATEAK

5 Naturagunetan espezializatuta dagoen argazkilari batek baso hostoerorkorren 125 320 argazki eta baso hostoiraunkorren 93 008 argazki ditu. Zenbat argazki ditu, gutxi gorabehera? Lehenbizi, biribildu datu bakoitza milakoetara.

anayaharitza.es

Oroitzen ez bazara, «Berehala kontatuko dizut»: anayaharitza.es

Informazioa behar baduzu, deskargatu hemen: anayaharitza.es

125 320

?

93 008

Ebatzi urratsez urrats, hemen: anayaharitza.es

6 Baso batean 2 585 zuhaitz landatu dituzte. Orain guztira 24 310 zuhaitz badaude, zenbat zeuden hasieran?

2 585 ? 24 310

7 Málaga hiriak 571 026 biztanle zituen 2018an. Sevilla hiriak 117 685 biztanle gutxiago balitu, bi hiriek biztanle kopuru bera izango zuten. Zenbat biztanle zituen Sevillak?

571 026 117 685 ?

Zuhaitzak landatu badituzte, hasieran orain baino gutxiago zeuden.

2018ko datuak dira.

Ebatzi urratsez urrats, hemen: anayaharitza.es

8 Urteko liburu-azoka handienean, Parisen, 2 139 705 nobela saldu dira. Guztira saldu diren haurrentzako ipuinak baino 1 850 329 liburu gehiago dira. Zenbat ipuin saldu dituzte? ?

2 139 705

1 850 329

9 Emmak furgoneta bat erosi du. Sarrerako kuota 6 000 � ordaindu du, eta gainerakoa 40 kuota berdinetan ordainduko du. Furgonetak 40 000 � balio badu, zenbat falta zaio ordaintzeko? Zenbat izango da kuota bakoitza?

Eragiketak egiteko, deskonposatzea

Ebatzi urratsez urrats, hemen: anayaharitza.es

40 kuota ordaintzeak esan nahi du 40 aldiz ordaintzea.

Eragiketak egiteko beste modu batzuk ere badaude; adibidez, gaiak deskonposatzea. Praktikatu, modu errazena edo azkarrena zein iruditzen zaizun jakiteko.

BATUKETA edo KENKETA: 16 489

1 6 4 8 9 =  10 000 + 6 000 + 400 + 80 + 9

5 2 2 6 = − 5 000 − 200 − 20 − 6  10 000 +  1  000  + 200 + 60 + 3 = 11 263

«Berehala kontatuko dizut», webgunean: anayaharitza.es

BIDERKETA:

• Kalkulatu, gaiak deskonposatuz. Kenketan, prestatu ondo bururakoa.

a) 25 730 + 500

b) 8 423 − 2 980

c) 125 × 15

Málaga Sevilla

Málaga Cádiz

Sevilla

Kordoba Jaén Granada Almería

Huelva

Eragiketa konbinatuak

Batzuetan oso lagungarria da zenbait eragiketa

adierazpen bakarrean idaztea, baina garrantzitsua da eragiketak zer ordenatan egin behar diren jakitea.

Zenbait eragiketako adierazpenak ebazteko, kalkuluak ordena honetan egin behar ditugu:

1. Parentesi barruko eragiketak.

2. Biderketak eta zatiketak, ezkerretik eskuinera.

a) 5 + 4 × 3

b) 10 − 2 × (3 + 1) + 5

2

c) 4 × 7 − 24 : 2

d) 5 × (3 + 18) − (20 − 4)

Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es

3 Idatzi esaldiak zenbakizko adierazpen moduan, eta kalkulatu emaitzak.

a) Biderkatu 3z 8 gehi 4ren emaitza.

b) 3ren bikoitzari batu 5 bider 8ren emaitza.

c) Biderkatu 6z 4 gehi 3ren emaitza, eta horri kendu 9.

d) Batu 20ri 10 ken 6ren emaitzaren eta 4ren biderkadura.

4 1–2–4 Kopiatu eta idatzi parentesiak, edo ez, kasu bakoitzean emaitza handiena eta txikiena lortzeko.

90 + 10 × 5

90 – 10 × 5

5 Idatzi batuketa bat eta biderketa bat dituen adierazpen bat, parentesiekin, kontuan izanda emaitzak 100 izan behar duela. 100

3. Batuketak eta kenketak, ezkerretik eskuinera.

Zerbait gaizki egin baduzu, ez du axola. Ikastea eta huts egitea elkarrekin doaz!

Parentesiak idazten ez badituzu, kenketaren ikurrak biderketaren emaitzari eragiten dio.

1 Ikusi arretaz, eta esan zer letra dagokion zenbaki bakoitzari.

B Lau bolaluma urdin eta bi bolaluma gorri dituzten bi pakete.

× (4 + 2)

A Lau bolaluma urdin dituzten bi pakete, eta bi bola luma gorri.

2 × 4 + 2

1.

2.

2 Kalkulatu koadernoan.

6 Kopiatu eragiketak, eta idatzi parentesiak behar diren tokian, adierazitako emaitzak lortzeko.

a) 5 × 3 + 2 × 4

Emaitza posibleak: 68 55 23 100

b) 2 × 5 + 100 : 5

Emaitza posibleak: 42 30 22 50

c) 10 + 2 × 5 5 : 5

Emaitza posibleak: 19 18 3 59

7 Beñatek zenbait gauza erosi ditu: 2 bonboi-kaxa, bakoitza 28 � -koa; arraina, 32 � -koa, eta 4 laranja-zorro, bakoitza 4 � -koa. Baina... erositakoa ordaintzeko 4 � falta zaizkio!

a) Zenbat balio du Beñatek erositakoak? Idatzi adierazpen bakarrean.

b) Zenbat diru du Beñatek?

c) Lagun batek 20 � uzten badizkio, zenbat geratuko zaio?

Parentesiak eta parentesi karratuak

Binaka lan egiteak batak bestearen ikuspuntua ezagutzeko aukera ematen digu.

• Adierazpen matematikoek batzuetan parentesiak eta parentesi karratuak dituzte. Nola ebazten dira?

250 + (100 + 50) × [10 − (3 + 2)] [ ] parentesi karratuak ( ) parentesiak

• Oso erraza da! Urrats hauek egin, eta kito:

1. Kalkulatu parentesi karratuen barruko eragiketa.

250 + (100 + 50) × [10 − (3 + 2)] = 250 + (100 + 50) × [10 − 5] = 250 + (100 + 50) × 5

Aplikatu eragiketen hierarkia.

2. Kalkulatu parentesien barruko eragiketak.

250 + (100 + 50) × 5 = 250 + 150 × 5

3. Kalkulatu gainerako eragiketak, eragiketen hierarkia aplikatuta.

250 + 150 × 5 = 250 + 750 = 1000

• Orain, ebatzi koadernoan adierazpen hauek:

a) (2 + 3) × [100 : (1 + 4)]

b) [100 : (7 + 3)] × [150 − (20 + 30)]

Zenbaki positiboak eta negatiboak

Horrelako zenbakiak erabiltzen ditugu tenperaturak esateko, eraikin bateko solairuak adierazteko eta altxor bat itsasoan zer sakoneran dagoen adierazteko, adibidez.

• +1, +2, +3, +4… zenbaki positiboak dira.

• −1, −2, −3, −4… zenbaki negatiboak dira.

Hozkailua

1 Zer zenbaki mota erabiliko zenituzke gertaera hauek adierazteko, positiboak ala negatiboak? Sailkatu taula batean.

a) Igo – Jaitsi c) Zorretan izan – Jaso

b) Irabazi – Galdu d) Zero azpitik – Zero gainetik

2 Egiaztatu Kopiatu esaldiak, eta idatzi zer zenbaki positibo edo negatibo den bakoitza.

a) c)

Negatiboak Positiboak ? ?

3 solairu beherago noa.

−3

10 puntu galdu ditut.

b) d)

20 � ditut.

Itsas mailatik gora 1 200 m-ra dago.

Zenbaki osoen multzoa zenbaki negatiboek, 0 zenbakiak eta zenbaki positiboek osatzen dute. ? ? ?

–2 solairura noa.

–18 °C-an dago.

Altxorra itsaspean 75 m-ra dago.

3 Zer tenperatura adierazten du termometro bakoitzak?

Zenbaki batek zeinurik ez badu, positiboa da. 5 = + 5

4 Marraztu adierazitakoa, eta markatu zenbakiak.

a) Eraikin bat, 6 solairu eta lurpeko 3 dituena.

b) Urpeko ontzi bat itsas mailatik behera 150 m-ra.

c) Hegazkin bat 2 100 m-ko altueran hegan.

5 Anek hirugarren solairuan igogailua hartu du. 5 solairu behera jaitsi da, zaborra botatzera, eta 1 gora igo da, bizikleta hartzera.

a) Zer solairutan dago hondakinen gela?

b) Eta bizikleten gela?

Nola adierazi zenbaki osoak zenbakizko zuzenean

• Bi tenperatura hauetatik zein da maximoa? Eta minimoa?

• Zenbakiak konparatzeko, zenbakizko zuzenean jar ditzakegu.

Zenbaki negatiboak 0tik ezkerrera jartzen dira.

Edozein zenbaki txikiagoa da zenbakizko zuzenean haren eskuinean dauden zenbakiak baino.

Zenbaki positiboak 0tik eskuinera jartzen dira.

Edozein zenbaki handiagoa da zenbakizko zuzenean haren ezkerrean dauden zenbakiak baino.

Gogoan hartu!

• Termometro batek −4  ° C-tik +5  ° C-ra arteko tenperaturak adierazten ditu. Zer tenperatura adierazten ditu tarte horretan? Idatzi ordenan.

Laguntza behar baduzu, «Berehala kontatuko dizut»: anayaharitza.es

Lurrean zuhaitzak galtzen edo lortzen ari garen adierazteko, erabili zenbaki positiboak eta negatiboak.

Koordenatu kartesiarrak

Planoan puntuak adierazteko, koordenatu kartesiarrak erabiltzen ditugu.

Ardatz kartesiarrak bi zuzen dira, eta ezaugarri hauek dituzte:

• Ardatzak elkarzutak dira.

• Zenbakizko zuzenean bezala zenbakitzen dira.

• Elkar ebakitzen duten lekua 0 puntua da.

• Lauki-sarea lau zatitan banatuta uzten dute, eta zati horiei koadrante esaten zaie.

Plano bateko puntu bat adierazteko, bi koordenatu erabiltzen dira.

• Lehen koordenatua ardatz horizontalean irakurtzen da.

• Bigarren koordenatua ardatz bertikalean irakurtzen da.

1 Ikusi arretaz irudia, eta erantzun.

a) Idatzi koadernoan zer koordenatu dituzten adierazitako puntuek.

b) Puntuetako bat ardatz bertikalean bertan dago. Zein da puntu horren lehen koordenatua?

c) Beste puntu bat ardatz horizontalean bertan dago. Zein da puntu horren bigarren koordenatua?

2 Kokatu puntu hauek koordenatu-ardatz batean. Marraztu koadernoan.

A = (+3, −1) B = (0, 0) C = (−5, +2)

1. koadrantea

4. koadrantea

2. koadrantea

3. koadrantea

Biderik laburrena

Tomas basoko eremu batean zuhaitzak landatzen ari da; (+4, +4) puntua da. Begiratu behar du ea beste bi eremutan ere beharrezkoa den zuhaitzak landatzea: (−3, −2) eta (−7, +4) puntuetan.

Tomas lehenbizi eremu gertuenera joaten bada, nora joango da?

1. Datuak koordenatu-ardatz batean kokatuko ditugu.

– Tomas (+4, +4) puntuan dago.

– Bi puntu hauetara joan behar du: (−3, −2) eta (−7, +4).

2. Tomas dagoen puntua beste bi puntuekin lotuko dugu.

3. Erregela erabiliz, bi zuzenkiak neurtuko ditugu, eta, gero, luzerak konparatuko ditugu.

Luzera laburrena zein zuzenkik duen, puntu horixe dago Tomasengandik gertuen.

a) Binaka jarrita, aukeratu Tomasentzat beste kokapen bat eta beste bi puntu. Kalkulatu zer puntu dagoen gertuen.

b) Maddi, hain zuzen, (−3, −2) puntuan dago. Zer koadrantetan dago Tomas? Eta Maddi?

• Aukeratu bigarren koadranteko puntu bat, kontuan izanda gertuago egon behar duela Tomasengandik Maddirengandik baino.

Gogoratu: bi punturen arteko distantzia laburrena lerro zuzen bat da.

• Aukeratu laugarren koadranteko puntu bat, kontuan izanda gertuago egon behar duela Maddirengandik Tomasengandik baino.

EBATZI BAIETZ!

Deszifratu kodeak

Olaiak badaki antzinako erromatarrek beste zenbaki-sistema bat erabiltzen zutela, ez gurea bezalakoa. Ikusi izan ditu zenbaki erromatarrak bere herriko eraikin batzuetan. Olaia bizi den etxea 1953an eraiki bazen, nola idatziko zen zenbaki erromatarretan?

Antzinako erromatarrek 7 letra larri erabiltzen zituzten zenbakiak adierazteko. Letra bakoitzak balio bat zuen.

I V X L C D M

1 5 10 50 100 500 1 000

1. Deskonposatu zenbakia unitatetan, eta idatzi, zenbakien ordez, balio horiek dituzten letrak.

2. I, X, C eta M letrak gehienez hiru aldiz jarraian idatz daitezke.

3. I, X eta C letrak balio handiagoko baten ezkerrean baldin badaude, eskuinekoaren balioari ezkerrekoarena kendu behar zaio.

Hori jakinda, 1 953 idatziko dugu zenbaki erromatarretan:

1. Deskonposatu zenbakia unitatetan.

1 953 = 1 000 + 900 + 50 + 3

2. Idatzi zenbakien ordez letrak, lehen esandako arauak kontuan hartuta.

1 000 + 900 + 50 + 3

M CM L III

C-k balio txikiagoa du M-k baino. Beraz:

CM = 1 000 − 100 = 900

I letra hiru aldiz jarraian dago. Beraz: 1 + 1 + 1 = 3

Olaiaren etxea zer urtetan eraiki zen, honela idazten da: MCMLIII.

Soluzioak badu zentzurik?

Batu letra guztien balioak, eta egiaztatu emaitza 1 953 dela.

MCMLIII → 1 000 + (1 000 − 100) + 50 + 1 + 1 + 1 = 1 953

1 Idatzi zuretzat garrantzitsuak diren zenbaki batzuk zenbaki-sistema erromatarrean.

Oso garrantzitsua da zenbakia unitatetan deskonposatzea.

Landu zenbaki-sistema erromatarra, webgunean: anayaharitza.es

2 Asmatu zenbaki-sistema bat, eta idatzi zenbaki batzuk sistema horretan.

Problemak arin-arinka

2 1

Zein da 9 zifrako zenbakirik handiena? Eta txikiena?

Zenbat milako ditu zenbaki honek? 1 000 000

Buruzko kalkulua

Kalkulatu 12 × 4.

3 5

Kopuru bat 25 zatitan banatzen badugu, gerta daiteke sobera 25 unitate geratzea? Azaldu zergatik.

Termometroak −1 °C adierazten zuen, baina orain hotz handiagoa dago.

Zer tenperatura izan dezakegu orain?

Begira nola pentsatzen dudan

Kontatu istorio bat, adierazpen honetan oinarrituta:

10 : 5 – 2

4 6

Esan koadrante bakoitzeko puntu baten koordenatuak.

Zatitu eta zeu garaile

Imajinatu egoera hau: hiztegian hitz baten esanahia bilatu nahi duzu, eta, hiztegia irekitakoan, hitzak desordenatuta daude. A zer saltsa!

Ordenatzea garrantzitsua da. Informazioa errazago ulertzen dugu.

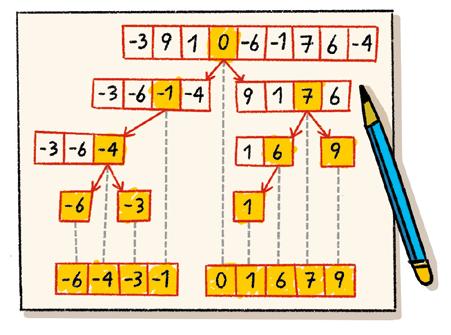
Quicksort izeneko metodoak multzo bateko elementuak azkar ordenatzeko balio du. Honela egiten da:

1. Aukeratu zenbaki bat, edozein; zenbaki horri pibot esango diogu.

2 Konparatu beste elementuak pibotarekin banan-banan.

– Elementua pibota baino txikiagoa bada, idatzi ezkerrean.

– Elementua pibota baino handiagoa bada, idatzi eskuinean.

Praktikatu quicksort metodoa, hemen: anayaharitza.es

4 = 2 × 2 24 12

× 2 × 2 48

Ikusi nola egiten den, hemen: anayaharitza.es

Orain, zuk zeuk:

6 ×  4

8 ×  4

9 ×  4

7 ×  4

14 ×  4

15 ×  4  35 ×  4  45 ×  4    21 ×  4    13 ×  4

1 Zer zenbaki da deskonposizio bakoitza?

a) 3 MM + 2 EM + 6 M + 7 H + 2 U

b) 2 000 000 + 100 000 + 20 000 + 3

2 Zenbat balio du 4 zifrak zenbaki hauetan?

a) 649 d) 240 012

b) 4 e) 4 830 000

c) 4 913 f) 24 120 948

3 Zenbat urte ditu Anek? Hori jakiteko, jarraitu urratsei.

6 Marraztu orri batean koordenatu-ardatz bat.

a) Kokatu puntu hauek:

A = (+3, +5) C = (−3, −5)

B = (+3, −5) D = (−3, +5)

b) Lotu puntuak. Zer irudi marraztu duzu?

7 Marraztu lauki bat, kontuan hartuta lau erpinek koordenatu-ardatzetan bertan egon behar dutela. Idatzi erpin bakoitzaren koordenatuak.

8 Baserri ekologiko batean 57 000 arrautza zituzten. 3 542 dozena saldu badituzte, zenbat arrautza geratu zaizkie?

1 . Ikusi zer zifra dagoen hamar milakoetan zenbaki honetan: 527 341.

2. Kalkulatu zifra horren hirukoitza.

2. Horren emaitzari, batu hamarrekoen zifra.

4. Kopuru horixe da Aneren adina!

9 Anbulatorio batean 5 250 txerto zituzten. Lehenbiziko astean 2 296 txerto jarri zituzten, eta bigarrenean, 1 985. Itxaron-zerrendan 1 200 pertsona badaude, badituzte nahikoa txerto?

10 Eski-estazio batean termometroan 3  ° C jartzen zuen goizeko 8etan. Eguerdian tenperatura 8 °C igo zen, eta 20:00etan, berriz, eguerdiko tenperaturatik 4  ° C jaitsi. Zer tenperatura zegoen 20:00etan?

5 Idatzi esaldi bakoitza zenbakizko adierazpen moduan. Gero, kalkulatu adierazpen bakoitzaren emaitza.

a) 25 gehi 75 egin, eta batura 2z biderkatu dut.

b) 8z biderkatu dut 25en eta 5en arteko kendura.

c) 16 zati 4 egin dut, eta zatidurari batu diot 9ren eta 5en arteko kendura 3z biderkatuta lortu dudan emaitza.

Semaforoa. Margotu koadernoan, ariketa

bakoitzaren ondoan, honela:

Erantzuna badakizu

Laguntza behar izan baduzu

Erantzuna jakin ez baduzu

HELBURUA AURRERA

Irakurri arretaz taulako datuak: lau lurraldetan gutxi gorabehera zenbat milioi hektarea baso galdu edo lortu den ikusiko duzu. 1990etik 2000ra 2000tik 2010era 2010etik 2020ra

a) Kopiatu taula, eta adierazi lurralde bakoitzak hamarkada bakoitzean zenbat milioi hektarea galdu edo lortu dituen, zenbaki positiboak edo negatiboak erabiliz.

b) Zenbat galdu edo lortu zuen lurralde bakoitzak guztira hiru hamarkadetan?

c) Zenbat galdu edo lortu zen guztira lau lurraldeetan hiru hamarkadetan? Adierazi kopuru hori unitatetan.

d) Zer lurraldek lortu zuen gehien? Eta gehien galdu?

Geure buruari galdezka

Ondorioak eta emaitzak estrategia erabiliz, aztertuko dugu zergatik den beharrezkoa zuhaitzak zaintzea.

a) Kopiatu eta osatu antolatzailea.

b) Ikertu zer den biziaren zuhaitzaren irudia eta zer irudikatzen duen.

c) Talde-lanean, egin ikastetxerako biziaren zuhaitz erraldoi bat, eta zintzilikatu zuhaitzean natura zaintzearen aldeko mezuak. Gonbidatu eskola guztia parte hartzera.

N o la ikasi dut?

Osatu koadernoan.

Zer gertatuko da zuhaitzak desagertzen badira?

Epe luzean Zer gerta daiteke? Zer ondorio izango ditu?

Epe laburrean Zer gerta daiteke? Zer ondorio izango ditu?

Identifikatu matematika arloan lan egiteko zuk dituzun hiru indargune.

Identifikatu matematikan zuk hobeto lan egiteko hobetu ditzakezun hiru gauza.

Zer egin dezakezu horiek hobetzeko?

Egin biziaren zuhaitz bat.

Multiploak eta zatitzaileak

2 Besarkatu bakea

Gizakiok beste pertsona batzuekin bizi gara. Elkarrekin bizitzeak aberastu egiten gaitu eta ondo sentiarazten digu, baina bizikidetza horretan, batzuetan, egoera zailak sortzen dira, eta haserretu edo tristatu egiten gara. Bizikidetza hobetzea denon kontua da.

Gure gorputzeko substantzia kimiko batzuek gogo-aldartean eragina izan dezakete. Bazenekien, adibidez, norbait benetan sentituta eta luze besarkatzen dugunean gorputzak oxitozina izeneko hormona sortzen duela eta horrek lasaitzen eta seguru sentitzen laguntzen digula?

Besarkadak maitasun-keinu handienetako bat dira gure kulturan, eta ondo sentitzen laguntzen digute.

Unitate honetarako...

Helburua aurrera

Zergatik da garrantzitsua bakea lortzearen alde jardutea?

Eraiki bakea besarkadekin: diseinatu kanpaina bat, 8 segundoko besarkadak sustatzeko.

Jarraitu hariari!

Zenbaki

Zenbaki baten

zatitzaileak Zatitzaile komun handiena

Zatigarritasunirizpideak

Zenbaki lehenak eta konposatuak

Zenbaki baten multiploak

baten multiploak kalkulatzeak zenbait multzo berdinetan guztira zenbat dauden jakiteko balio digu.

Zenbaki

Ikastetxeko jolastokian zenbait esku zuri margotu dituzte, bakearen ikur gisa. Erabaki dute hatz bakoitzean ikastetxe horretan dabilen ikasle baten izena idaztea.

• Eskurik margotuta ez badago, ez dago izenak idazteko lekurik.

0  × 5 = 0

• Esku bakoitzean izenak idazteko 5 leku daude.

1  × 5 = 5

Zenbat leku daude eskuak bat, bi, hiru, lau… badira?

2  × 5  = 5 + 5 = 10

3  × 5 = 5 + 5 + 5 = 15

4  × 5 = 5 + 5 + 5 + 5 = 20

1 Irakurri adibidea, eta osatu koadernoan.

20 zenbakia 5en multiploa da; izan ere, 4 × 5 = 20.

a) 24 zenbakia 8ren multiploa da; izan ere, ?  ×  ? =   ?

b) 30 zenbakia 2ren multiploa da; izan ere, ?  ×  ? =   ?

c) 100 zenbakia 10en multiploa da; izan ere, ?  ×  ? =   ?

2 Bilatu zenbaki hauek 100eko taulan.

Zenbaki bikoitiak 2naka multzokatu daitezke!

3 Pentsatu, eta erantzun koadernoan.

a) Idatzi 2 zenbakiaren lehenbiziko hamar multiploak.

b) Aurkitu 100 baino handiagoa den 2ren multiplo bat. ?  × 2 = 100 baino handiagoa!

c) Nolako zenbakiak dira 2ren multiploak?

d) 2ren multiploak al dira zenbaki hauek? Azaldu zergatik.

14 50 21 158 3 726

e) Idatzi 2ren multiploak diren beste zenbaki batzuk.

f) Idatz al daitezke 2ren multiplo guztiak? Zergatik?

4 Paulek dendan 4 jogurteko paketeak saltzen ditu. Irakurri, eta erantzun, arrazoiak emanez.

a) Zenbat jogurt daude 3 paketetan?

b) Eros al daitezke zehazki 15 jogurt?

c) Zenbat pakete erosiko zenituzke 15 jogurt behar badituzu?

5 Zer dela eta diozu hori? Pentsatu, eta azaldu zergatik diren esaldi hauek zuzenak:

0 edozein zenbakiren multiploa da.

Zenbaki oro bere buruaren multiploa da.

Zenbaki baten multiplo guztiak idaztea ezinezkoa da.

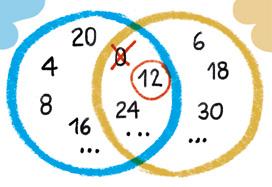
Multiplo komunak

Zer zenbaki dira 2ren multiploak? Eta 3renak? Multiplo komunik badute? 2ren multiploak

Zenbaki bikoitiek azken zifra 0, 2, 4, 6 edo 8 dute.

Zenbaki bakoitiek azken zifra 1, 3, 5, 7 edo 9 dute.

a) Marraztu koadernoan diagramak, hauekin:

– 2ren eta 5en multiploak. – 5en eta 10en multiploak.

Honela adierazten ditut 2ren eta 3ren multiploak diagrama bidez.

Gogoan hartu!

b) Zer ikusten duzu azken diagraman? Azaldu, zure hitzak erabiliz.

Denbora-tarte batean zenbat besarkada eman ditzakezun aztertzeko, erabili multiploak.

Multiplo komun txikiena

Multiplo berdin guztietatik txikiena zein den jakiteko

balio digu multiplo komun txikiena kalkulatzeak.

Bi zenbakiren multiplo komun txikiena kalkulatzeko, hau egin behar dugu: 4ren eta 6ren multiplo komun txikiena.

1. Kalkulatu zenbaki bakoitzaren lehenbiziko multiploak.

4ren multiploak: 0, 4, 8, 12, 16, 20...

6ren multiploak: 0, 6, 12, 18, 24, 30...

2. Bilatu multiplo komunak, eta aukeratu txikiena, 0 kontuan hartu gabe.

4ren multiploak: 0, 4, 8, 12 , 16, 20, 24

6ren multiploak: 0, 6, 12 , 18, 24 , 30... ✗

1 Kalkulatu zenbaki hauen multiplo komun txikiena. Adierazi hori diagrama baten bidez, adibidean bezala.

a) 4 eta 10 b) 3 eta 7 c) 8 eta 6 d) 4 eta 5

2 Danel 14 egunean behin joaten da zinemara, eta Maria, 21 egunean behin. Biek urriaren 1ean egin zuten topo zineman.

Beraz, noiz egingo dute berriro topo? Egin urrats hauek:

1. urratsa: Kalkulatu 14ren eta 21en multiplo batzuk, biek duten lehenbiziko multiplo komuna aurkitu arte.

× 1 × 2 × 3 × 4 14 ? ? ? ? 21 ? ? ? ?

2. urratsa: Adierazi egoera eskema baten bidez, eta bilatu eguna egutegian. 14 14 14 21 21

URR. 1

3 A autobusa Lukenen etxe aurreko geralekura 3 minutuan behin etortzen da, eta B autobusa, 5 minutuan behin. Goizeko 8etan biak etortzen dira. Beraz…

a) Noiz egiten dute hurrena topo geraleku horretan?

b) Goizeko 8etatik 9etara, noiz egiten dute topo?

Multiplo komun guztietan txikiena 12 da. m.k.t. (4, 6) = 12

multiploak 6ren multiploak

Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es

4ren

URRIA al. ar. az. og. ol. lr. ig. al. ar. az. og. ol. lr. ig.

AZAROA

4 5 minutuko geraldia Goizean, Nikoren iratzargailuak 15 minutuan behin jotzen du; Ganixenak, 5 minutuan behin, eta Julerenak, 10 minutuan behin. Hiru iratzargailuek lehenbiziko aldiz 07:30ean jotzen dute.

a) Zer ordutan jotzen dute hiru iratzargailuek aldi berean berriro?

b) Iratzargailuek aldi berean bigarren aldiz jotzen dutenean jaikitzen dira Niko, Ganix eta Jule, eta ordu erdi ematen dute gosaltzen eta hortzak-eta garbitzen. Zer ordutan amaitzen dute?

c) Gosaritako ontziak jaso eta ohea egiten 10 minutu ematen dute. Orduan, eskolara abiatu, eta 15 minutuan iristen dira. Eskolak 9etan hasten badira, garaiz iristen dira?

Erlazio bereziak: zein da bi zenbakiren m.k.t., bat bestearen multiploa bada?

Zein da 5en eta 100en multiplo komun txikiena? Nanosegundo bakarrean jakin dezakezu hori!

Zenbaki bat beste baten multiploa bada, bi zenbaki horietatik handiena da bien multiplo komun txikiena.

m.k.t. (5, 100) = 100

100 zenbakia 5en multiploa da.

• Kalkulatu multzo bakoitzeko bi zenbakien multiplo komun txikiena.

Nanosegundoa segundo baten mila milioirena da; alegia, 0,000000001 segundo.

Zure emaitza erregeletekin eta lauki-sare batekin egiaztatu nahi baduzu, deskargatzeko aukera duzu hemen: anayaharitza.es

Zenbaki baten zatitzaileak

Zenbaki baten zatitzaileak kalkulatzeak beste zenbaki bat zehazki zenbat aldiz sartzen den jakiteko balio digu.

Zenbat modutan multzokatu daitezke 10 pertsona multzo berdinetan, inor kanpoan geratu gabe?

Pertsona 1eko, 2ko, 5eko edo 10eko multzoak egin daitezke.

10 zenbakiaren zatitzaileak 1, 2, 5 eta 10 dira.

Zenbaki bat beste zenbaki baten zatitzailea da, zatiketa eginda hondarra 0 bada.

zatikizuna zatitzailea 0 zatidura

Zenbaki baten zatitzaileak zenbaki hori baino txikiagoak edo berdinak dira.

a) 8 zenbakia 24ren zatitzailea da; izan ere, ? : ? = ? (hondarra 0).

b) 2 zenbakia 30en zatitzailea da; izan ere, ? : ? = ? (hondarra 0).

c) 10 zenbakia 100en zatitzailea da; izan ere, ? : ? = ? (hondarra 0).

1 Kalkulatu zenbaki hauek zatitzaileak: 5

2 Irakurri adibidea, eta osatu koadernoan.

5 zenbakia 20ren zatitzailea da; izan ere, 20 : 5 = 4 (hondarra 0).

3 Kalkulatu 18ren zatitzaileak, honela:

Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es

4 Aldaerak Zenbat modutan jar daitezke 12 aulki ilara berdinetan?

5 Eiderrek 24 m soka ditu. Neurri bereko zatitan ebaki nahi du, sokasaltoan ibiltzeko zenbait soka prestatzeko. Zenbat modutan ebaki dezake? Zein aukeratuko du, zure ustez? Azaldu zergatik.

Zatitzaile komunak

Zer zenbaki dira 12ren zatitzaileak? Eta 18renak? Zatitzaile komunik badute?

12ren zatitzaileak 18ren zatitzaileak

a) Marraztu koadernoan diagramak, hauekin:

– 2ren eta 15en zatitzaileak

– 5en eta 10en zatitzaileak.

b) Zer ikusten duzu azken diagraman? Azaldu, zure hitzak erabiliz.

Honela adierazten ditut 12ren eta 18ren zatitzaileak diagrama bidez.

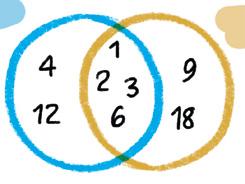
Gogoan hartu!

Zenbat besarkada eman ditzakezun kalkulatzeko, erabili zenbaki baten zatitzailearen kontzeptua.

Zatitzaile komun handiena

Zatitzaile berdin guztietatik handiena zein den jakiteko balio digu zatitzaile komun handiena kalkulatzeak.

Bi zenbakiren zatitzaile komun handiena kalkulatzeko, hau egin behar dugu:

12ren eta 18ren zatitzaile komun handiena.

1. Kalkulatu zenbaki bakoitzaren zatitzaileak.

12ren zatitzaileak: 1, 2, 3, 4, 6, 12

18ren zatitzaileak: 1, 2, 3, 6, 9, 18

Zatitzaile komun guztietan handiena 6 da.

z.k.h. (12, 18) = 6

2. Bilatu zatitzaile komunak, eta aukeratu handiena.

12ren zatitzaileak: 1 , 2 , 3 , 4, 6 , 12

18ren zatitzaileak: 1 , 2 , 3 , 6 , 9, 18

Laguntza behar baduzu, «Berehala kontatuko dizut», webgunean: anayaharitza.es

1 Kalkulatu zenbaki hauen zatitzaile komun handiena. Adierazi hori diagrama baten bidez, adibidean bezala.

a) 8 eta 10 b) 15 eta 18 c) 24 eta 36 d) 9 eta 21

2 Pentsatu eta binaka jarrita komentatu Olaiak soka urdin bat du, 12 m-koa, eta soka hori bat, 8 m-koa. Bi sokak neurri bereko zatitan ebaki nahi ditu, puskarik sobera geratu gabe.

a) Zenbat modutan ebaki ditzake sokak?

b) Zer luzera izango du gehienez zati bakoitzak?

Laguntzatxoa: egin honelako eskema bat, eta ikusi zein diren zatitzaile komunak eta zein den handiena.

12ren zatitzaileak

18ren zatitzaileak

3 Liburu-denda batean nobedadeak bi apaletan jartzen dituzte, liburuak elkarrengandik distantzia berera.

a) Apal bat 12 dm luze da, eta bestea, 16 dm luze. Zenbat dezimetrotik zenbat dezimetrora jar ditzakete liburuak?

Idatzi aukera posible guztiak.

b) Aukera guztiak gauzatu ditzakete egiaz, zure ustez? Azaldu zergatik.

c) Liburuen artean ahalik eta tarte handiena uztea erabakitzen badute, zenbat dezimetroan behin jarriko dituzte liburuak?

12 dm

16 dm

4 6A gelan 20 ikasle dira, eta 6B gelan, berriz, 16. Datorren astean Opera Jaialdira joatekoak dira.

a) Talde berdinak egiten badituzte, baina bi geletako ikasleak nahasi gabe, zenbat ikaslekoak izan daitezke taldeak? 20 16

b) Jaialdira joateko taldeak ahalik eta ikasle gehienez osatuak izatea nahi badute, zenbat ikaslekoak izango dira?

c) Zenbat talde egingo dituzte 6A gelan? Eta 6B gelan?

d) Jaialdira 6 irakasle ere joango dira. 16 plazako mikrobus bat eta 26ko beste bat kontratatu dituzte. Nola banatu daitezke, talde bereko ikasleak bereizi ezin badira eta irakasleak bi autobusetan egon behar badira?

Erlazio bereziak: zein da bi zenbakiren z.k.h., bat bestearen zatitzailea bada?

Zein da 5en eta 100en zatitzaile komun handiena? Unetxo bat eta… badakizu!

Zenbaki bat beste baten zatitzailea bada, bi zenbaki horietatik txikiena da bien zatitzaile komun handiena.

z.k.h. (5, 100) = 5

5 zenbakia 100en zatitzailea da.

Kalkulatu multzo bakoitzeko bi zenbakien zatitzaile komun handiena.

Laguntzatxoa: bilatu 20ren eta 16ren zatitzaileak, eta ikusi zein diren komunak.

Zure emaitza erregeletekin eta lauki-sare batekin egiaztatu nahi baduzu, deskargatzeko aukera duzu hemen: anayaharitza.es

Zatigarritasun-irizpideak

Zenbaki baten zatitzaileetako batzuk zein diren jakiteko, zatigarritasun-irizpideak erabil ditzakegu.

1 Aurkitu 100eko taulan zer zenbaki diren zatigarriak 2z, 4z, 3z, 9z, 5ez eta 10ez. Egiaztatu ondo egin duzula, zatigarritasunirizpideak erabiliz.

2z zatigarriak

4z

Zenbaki bat 2z zatigarria da, azken zifra 0 edo bikoitia badu.

3z

zatigarriak

Zenbaki bat 3z zatigarria da, zifren batura 3ren multiploa bada.

5ez zatigarriak

Zenbaki bat 4z zatigarria da, azken bi zifrek osatzen duten zenbakia 4ren multiploa edo 00 bada.

9z zatigarriak

Zenbaki bat 9z zatigarria da, zifren batura 9ren multiploa bada.

10ez zatigarriak

14 2z zatigarria da; izan ere, 14 : 2 eginda, hondarra 0 da.

Zenbaki bat 5ez zatigarria da, azken zifra 0 edo 5 bada.

Zenbaki bat 10ez zatigarria da, azken zifra 0 bada.

Deskargatu 100eko taularen txantiloia, webgunean: anayaharitza.es

3 Begiratu aurreko ariketako emaitzei, eta erantzun.

a) 2z zatigarriak diren zenbaki guztiak 4z ere badira?

4z zatigarriak diren zenbaki guztiak 2z ere badira?

b) 3z zatigarriak diren zenbaki guztiak 9z ere badira?

9z zatigarriak diren zenbaki guztiak 3z ere badira?

c) 5ez zatigarriak diren zenbaki guztiak 10ez ere badira?

10ez zatigarriak diren zenbaki guztiak 5ez ere badira?

4 Isabelen eskolan Lehen Hezkuntzako 6. mailan 116 ikasle dira. Ikasbidaiarako zozketa-txartelak saltzeko, 2, 3 edo 4 ikasleko taldeak egin nahi dituzte. Antolatu daitezke horrela?

5 Entzulearen eskaria Ikertu kalkulagailuarekin. Zer gertatu behar du zenbaki bat 6z zatigarria izan dadin?

Aho-korapiloa?

Aho-korapiloak ematen dute, baina ez: enuntziatu baliokideak dira, hau da, gauza bera esan nahi duten enuntziatuak. Adibidez:

10 2z ZATIGARRIA da

2 10en ZATITZAILEA da

10 2ren MULTIPLOA da

• Egin zuk gauza bera zenbaki hauekin. Ondo pentsatuta, oso erraza da!

a) 3 eta 60 b) 9 eta 45 c) 50 eta 200 d) 10 eta 1 000

Kontuan izan: 6 = 2  × 3

Gogoan hartu!

Zatigarritasun-irizpideak erabiliz, oso erraz kalkula dezakezu zehazki zenbat besarkada eman ditzakezun.

2 Kopiatu taulak, eta osatu, adierazitako zenbakiak idatzita.

Zenbaki lehenak eta konposatuak

Zenbaki lehenak eta konposatuak bereizten ditugu, 2 zatitzaile edo gehiago dituzten jakiteko.

Orri laukidun batean 2tik 10era arteko zenbakiak eta horien zatitzaileak marrazten badituzu… Zer ikusten duzu?

Hori da!

• Zenbaki batzuek bi zatitzaile bakarrik dituzte: 1 eta zenbakia bera.

Horiek zenbaki lehenak dira. Adibidez: 2, 3, 5 eta 7.

• Beste batzuek bi zatitzaile baino gehiago dituzte: 1, zenbakia bera eta beste batzuk.

Horiek zenbaki konposatuak dira. Adibidez: 4, 6, 8, 9 eta 10.

Zenbaki bat lehena da, bi zatitzaile soilik baditu: 1 eta zenbakia bera.

Zenbaki bat konposatua da, bi zatitzaile baino gehiago baditu.

1 Sailkatu zenbaki hauek bitan: lehenak eta konposatuak.

Behar baduzu, erabili kalkulagailua.

Zatitzaile batzuk aurkitzeko, zatigarritasun-irizpideak erabil ditzakezu.

2 Frogatu zenbaki hauek ez direla zenbaki lehenak.

3 Zer zenbaki lehen daude 1etik 100era? Egin urrats hauek 100eko taularekin:

1. urratsa: Zirrimarratu 1 zenbakia; ez da lehentzat hartzen.

2. urratsa: Zirrimarratu 2ren multiploak (2z zatigarriak dira).

3. urratsa: Ikusi zer zenbaki dagoen hurrena zirrimarratu gabe (3), eta zirrimarratu zenbaki horren multiploak.

4. urratsa: Jarraitu horrela, amaierara iritsi arte.

Webgunean ere egin dezakezu: anayaharitza.es.

4 A zer problema! Museoan bisita gidatua egiteko 31 pertsona daude zain, baina zenbait taldetan joan behar dute eta talde guztiek pertsona kopuru berekoak izan behar dute. Egin ditzakete taldeak? Eta bisita egitera beste 2 pertsona joaten badira?

5 Kattinek gelako 23 mahaiak ilaratan jarri behar ditu, eta ilara guztiek mahai kopuru bera izatea nahi du.

a) Jar ditzake horrela? Azaldu zergatik.

b) 24 mahai balira, ahalko luke? Idatzi modu posible guztiak.

Biderkagai lehenetan deskonposatzea

Edozein zenbaki deskonposa daiteke biderkagai lehenetan. Horretarako, egin urrats hauek:

Deskonposatu 280

1. Bilatu 280ren bi biderkagai, edozein.

280 = 28 × 10

2. Bilatu biderkagai horietako bakoitzaren bi biderkagai.

28 = 4 × 7 10 = 2 × 5

3. Jarraitu horrela, biderkagai guztiak zenbaki lehenak izan arte.

4 = 2 × 2

4. Lortu duzu! Adierazi hasierako zenbakia biderkagai lehen guztien biderketa moduan.

280 = 2 × 2 × 7 × 2 × 5 = = 2 x 2 x 2 x 5 x 7

Soluzioa dotore emateko, ordenatu biderkagaiak.

4 2 7 5

Bilatu erantzun posible guztiak

Lehen Hezkuntzako 6. mailan 100 ikasle baino gutxiago dira. Gaur goizean kopuru bereko taldetan banatu behar dira, bakeari buruzko horma-irudi bat egiteko. Kalkuluak eginez, ohartu dira 7ko edo 3ko taldetan banatu daitezkeela, baina ez binaka, ikasle guztiek parte hartuko badute behintzat. Zenbat ikasle dira Lehen Hezkuntzako 6. mailan?

Hori kalkulatzeko, erantzun posible guztiak bilatuko ditugu, 100eko taula erabiliz.

2. Aukeratutako zenbaki horietatik, aukeratu 3ren multiploak diren zenbakiak.

Lehen Hezkuntzako 6. mailan 21 edo 63 ikasle dira.

Soluzioak badu zentzurik?

Egiaztatu emaitzek baldintzak betetzen dituztela.

- 100 baino txikiagoak dira.

- 7ren eta 3ren multiploak dira.

- Ez dira 2ren multiploak.

1 Ginkana batean parte hartu dutenen kopurua 40-70 bitartekoa izan da. Ginkanako probak egiteko, 2 edo 9 kideko taldetan jarri dira, inor kanpoan geratu gabe. Zenbat pertsonak hartu dute parte ginkanan?

2 Karlosek 100 karta baino gutxiagoko sorta bat du. Ohartu denez, 3, 4 edo 7 jokalari direnean, jokalari guztiek karta kopuru bera jasotzen dute eta ez da kartarik geratzen sobera. Zenbat karta dira?

1. Aukeratu 100etik behera dauden 7ren multiplo guztiak.

3. Zirrimarratu 2ren multiploak diren zenbakiak.

Problemak arin-arinka

Buruzko kalkulua

Idatz al ditzakezu 5 zenbakiaren multiplo guztiak? Azaldu erantzuna.

Gutxienez zenbat zatitzaile ditu edozein zenbakik?

1 3 5

Bizkor! Esan bost zenbaki lehen.

Esan 10 zenbakiaren zatitzaile guztiak.

Nola esaten zaio 2z zatigarriak diren zenbaki arrunten multzoari?

2 4 6

123 456 789 zenbakia lehena da? Azaldu zergatik.

Kodeak deszifratzen

Idatzi gustukoa duzun zerbaiti buruzko poema bat. Erabili Sophie Germainen poemak duen patroi bera:

- Ahapaldi bakoitzak 4 lerro.

- Lerro bakoitzak 7 edo 8 silaba, gehienetan behintzat.

Askatasuna, berdintasuna, senidetasuna!

Gizon-emakumeen eskubideak errespetatu behar dira!

Oihu haiek leihotik entzuten zituen Sophiek. Artean txikitxoa zen, eta iraultzaile zetorren.

Aske izan nahi zuen, eta beste haurren berdina, baina laster ohartu zen neska zela, eta ez mutila.

Ezin zen eskolara joan. Ez zioten uzten ikasten, ez etxean bertan zeuden liburuak irakurtzen.

Baina Sophiek ez zuen onartzen pentsatzeko era hura. Ikasten aritzen zen gauetan, ezkutuan.

Handitan, sinatzeko, bai lanak eta bai gutunak, gizona zela jartzen zuen, har zezaten kontuan.

Nahiz eta borrokan jardun, beti oztopoz oztopo, bide ederra egin zuen Sophiek, bikaintasunez lepo.

Poema deskargatzeko, jo webgunera: anayaharitza.es

Kalkulatu 14 × 20.

20 = 2 × 10

× 2 × 10

28 14

280

Ikusi nola egiten den, hemen: anayaharitza.es

Orain, zuk zeuk:

8 ×  20

12 ×  20

15 ×  20

24 ×  20

25 ×  20

Poemek abestiak ematen dute, egitura ordenatua dutelako.

7 ×  20

11 ×  20

13 ×  20

21 ×  20

41 ×  20

Gauza askoren artean, zenbaki lehenak zituen aztertu: zenbaki bitxiak dira horiek, besteek ezin dituzte zatitu.

Eta halaxe hasi zuen Sophiek bere iraultza sutsua, haren kalkuluei esker, hobea baita mundua.

Begira nola pentsatzen dudan

Z er ikasi dut?

1 Irakurri, eta idatzi koadernoan.

a) Hiru zenbaki hauen lehenbiziko bost multiploak: 6 12 100

b) Hiru zenbaki hauen zatitzaile guztiak: 10 20 50

2 Pentsatu eta erantzun, eragiketarik egin gabe.

a) Zenbaki hauek zergatik ez dira 10en multiploak? 7 3 4 9

b) Zenbaki hauek zergatik ez dira 10en zatitzaileak? 33 15 20 100

3 Kalkulatu multzo bakoitzeko bi zenbakien multiplo komun txikiena.

4 eta 7 6 eta 9

4 Kalkulatu multzo bakoitzeko bi zenbakien zatitzaile komun handiena. 10 eta 15 8 eta 16

5 Kalkulurik egin gabe! Pentsatu eta erantzun.

a) m.k.t. (5, 10) eta z.k.h. (5, 10)

b) m.k.t. (2, 12) eta z.k.h. (2, 12)

6 Zatigarritasun-irizpideak erabiliz, erabaki zenbaki hauek zatigarriak diren 2z, 3z, 4z, 5ez, 9z edo 10ez.

12

900 150 123 40

7 Kopiatu zenbaki hauek eta osatu unitateen zifra, 3z zatigarriak izan daitezen. 2_ 13_ 28_ 104_

8 Idatzi zenbaki hauetatik zein diren lehenak eta zein diren konposatuak. Azaldu zergatik. 3 12 31 35 17 20

9 Minutu bakarrean! 100eko taula erabiliz, seinalatu ikusten dituzun zenbaki lehenak.

Deskargatu taula, hemen: anayaharitza.es

10 Sarak 80 € ditu, 2 € -ko txanponetan.

a) Egin ditzake txanpon kopuru bereko 2 pakete?

b) Eta 3 pakete? Eta 4?

c) Egin ditzake 5 edo 10 pakete?

d) Erantzuna baiezkoa denean, esan zenbat txanpon izango dituen pakete bakoitzak.

11 Ane lasterka egitera joaten da 2 egunean behin, eta Naroa, berriz, 5 egunean behin. Astelehen honetan topo egin badute, asteko zer egunetan egingo dute topo berriro?

12 Laukizuzen formako bizkotxo bat 24 cm luze da, eta forma bereko beste bat, 30 cm luze. Pellok zati berdinetan ebaki nahi ditu. Zenbat modutan ebaki ditzake? Zer modu aukeratuko zenuke zuk?

Semaforoa. Margotu koadernoan, ariketa

bakoitzaren ondoan, honela:

Erantzuna badakizu

Laguntza behar izan baduzu

Erantzuna jakin ez baduzu

HELBURUA AURRERA

Diseinatu kanpaina bat, besarkadak sustatzeko.

Gaur goizean proba egin nahi izan dugu, ea alderik badagoen 3 segundoko besarkada baten eta 8 segundoko baten artean. Oso dibertigarria izan da, bene-benetan besarkatu baitugu elkar!

a) Ikaskideak besarkatzen bata bestearen jarraian etenik gabe

15 segundoan egon banaiz…

– Zenbat besarkada eman ditut, 3 segundokoak baziren?

– Posible da 8 segundoko besarkadak izatea? Zergatik?

– Posible da besarkada batzuk 8 segundokoak eta beste batzuk 3 segundokoak izatea? Bakoitzeko zenbat?

b) Erantzun berriro galdera horiei, pentsatuta ikaskideak besarkatzen 24 segundoan egon naizela.

c) Gure gelan 20 ikasle bagara, zenbat denbora behar dut, gutxienez, ikaskide guztiei 3 segundoko besarkada bana emateko? Eta 8 segundokoa emateko? Arrazoitu erantzuna.

Geure buruari galdezka

Puntu kardinalak estrategia erabiliz, aztertuko dugu zergatik den garrantzitsua bakea lortzearen alde jardutea.

Zer oztopo ikusten dituzu bakea eraikitzeko bidean?

a) Kopiatu eta osatu antolatzailea koadernoan.

b) Talde-lanean, diseinatu kanpaina bat, 8 segundoko besarkadak sustatzeko. Jarri martxan

8 segundoko besarkaden ohitura eskolan bertan, lagunekin, familiartekoak elkartzen zaretenean…

N o la ikasi dut?

Osatu koadernoan.

Ez hartu kontuan besarkada batetik hurrengora dagoen tartea.

Zer informazio behar duzu bakea eraikitzea garrantzitsua zergatik den erantzuteko?

Zerk sortzen dizu emozioa ideia horretatik? Bakea eraiki egiten da?

Zer iritzi duzu zuk gai horri buruz? Zer iradokizun egingo zenituzke bakea eraikitzeko?

Idatzi matematikako ariketak egiten ari zarenean sentitzen dituzun hiru emozio positibo.

Idatzi arlo hau lantzen ari zarenean pizten zaizkizun hiru emozio negatibo. Zer egin dezakezu emozio horiek aldatzeko?

© GRUPO ANAYA, S.A., 2022 - C/ Valentín Beato, 21 - 28037 Madrid.

Eskubide guztiak gordeta. Legeak lan honen edukia babestu eta espetxe-zigorrak edota isunak eta kalte-galeren ondoriozko kalte-ordainak ezartzen ditu honako hauentzat: edozein literatura-lan, artelan zein zientzia-lan, edo horren eraldaketa, interpretazioa edo gauzapena (edozein euskarritan finkatuta edo edozein eratan komunikatuta), oso-osorik edo zati batean, baimenik gabe erreproduzitu, plagiatu, banatu edo komunikatzen dutenentzat.